Impact de la structure de treillis dans le domaine de fouille de données et la représentation des connaissances.

i

Table des matières

1 I 2	Introduction Cadre conceptuel et théorique Généralités sur la théorie des treillis 2.1 Origine de la théorie des treillis 2.2 Treillis ordinale et treillis algébrique 2.2.1 Définitions algébrique et ordinale d'un treillis 2.2.2 Irréductibles et générateurs minimaux d'un treillis 2.3 Treillis de fermés et système de fermeture 2.3.1 Treillis de fermés 2.3.2 Système de fermeture 2.4 Treillis des concepts et treillis de Galois 7		1 5 6 6 7 10 15 16 16 16
		2.4.1 Treillis des concepts	17
		2.4.2 Treillis de Galois	18
3	Aspects algorithmiques des treillis		19
	3.1	Algorithme de construction du graphe de couverture d'un treillis . . .	20
	3.2	Algorithme de construction de treillis de concepts	26
		3.2.1 Définitions	26
		3.2.2 Algorithme Genall	29
		3.2.3 Etude de la compléxité	35
	3.3	Algorithme de génération de treillis quelconques	35
		3.3.1 Algorithme de L.Nourine	36
		3.3.2 Etude de la compléxité	37
II	Application de la méthode		39
4	Fouille de données et navigation dans un treillis		40
	4.1	Bref aperçu sur les fouilles de données	40
		4.1.1 La fouille d'images	41
		4.1.2 La fouille de textes	41
		4.1.3 La fouille du web	42
	4.2	Chaîne d'extraction des connaissances	42
	4.3	L'Analyse Formelle des Concepts	44
		4.3.1 L'extraction de motifs fréquents	44
		4.3.2 Algorithme d'extraction des motifs fréquents	46
		4.3.3 Extraction de règles d'associations	48

ii

5	4.3.4 Règles d'association 4.3.5 Algorithme de génération de règles d'associations valides . . Application des treillis en représentation des connaissances et extraction d'informations			49 50 53
	5.1	Web sémantique et représentation des connaissances		53
		5.1.1	Web sémantique	53
		5.1.2	Représentation des connaissances	54
	5.2	Extraction d'informations		58
		5.2.1	Recherche d'informations	59
		5.2.2	Traitement automatique de la langue	60
	5.3	Application des règles d'associations aux textes		63
		5.3.1	Description du problème	63
		5.3.2	Expérimentations	65
		5.3.3	Extraction de connaissances par règles d'association	69
		5.3.4	Interprétation des résultats	73
6	Conclusion et perspectives			78

iii

Table des figures

2.1	Exemple de treillis	10
2.2	Exemple de treillis distributif et treillis booléen	11
2.3	Autre exemple de treillis	12
2.4	Treillis de la figure 2.3 où sont precisés, pour chaque noeud de x, les
	ensembles Jx et Mx 13
2.5	Treillis des concepts du contexte de la table 2.3	18
3.1	Arbre lexicographique de la famille F	24
3.2	le graphe de couverture G = (F, ?)	26
3.3	Arbre lexicographique associé au dictionnaire	28
3.4	Matrice decrivant la relation R du contexte K = (X, Y, R)	29
3.5	Treillis des concepts formels, extrait du contexte K, décoré par quelques
	générateurs minimaux	34
3.6	Un ordre qui ne représente pas un treillis 37
4.1	Chaîne d'extraction de connaissances	42
4.2	Exemple de treillis des parties ordonnées par inclusion	49
5.1	Exemple d'ontologie dans le domaine zoologique	54
5.2	Représentation graphique d'un ensemble classique et d'un ensemble
	flou	57
5.3	Schéma général de la recherche d'information	59
5.4	Représentation syntaxiques d'une phrase	62
5.5	Exemple d'un document du corpus	65
5.6	Treillis des concepts généré à partir du logiciel Concept Explorer 1.3	76

iv

Liste des tableaux

2.1	Générateurs minimaux des éléments du treillis de la figure 2.3 . . . .	13
2.2	Table du treillis de la figure 2.3	15
2.3	Exemple de contexte	17
3.1	Notation utilisée dans l'algorithme GENALL	31
3.2	Le contexte d'extraction K	33
4.1	Exemple de base de données formelle	45
5.1	Illustration de l'appartenance à A, selon la théorie choisie	58
5.2	Contexte d'extraction associé à la base de données textuelle (Livres
	éléctroniques et mots clés)	68
5.3	Mots clés candidats à l'analyse et leurs supports respectifs	70
5.4	Dépendance des règles d'association	74
5.5	Intérêt des règles d'association	75

v

Avant propos

Avant de soumettre ce travail aux critiques de ceux qui sont épris du goût de la connaissance, nous tenons à remercier tous ceux qui, par leurs connaissances, nous ont apporté soutien, assistance et consolation durant notre parcours universitaire et nous ont prêté main forte pour la réalisation du présent travail.

Nos remerciements s'adressent à l'Eternel notre Dieu pour la grâce, la paix, la force nous accordées dès nos premiers pas sur le chemin de l'éducation jusqu'au jour où nous rédigeons ce travail. Que l'honneur, la magnificence et la gloire Lui appartiennent aux siècles des siècles, Amen!

Nos sentiments de profonde gratitude s'adressent au Professeur Kaninda Mu-sumbu pour nous avoir fait l'honneur de diriger ce travail.

Notre reconnaissance s'adresse à tous les professeurs, chefs des travaux et assistants de la faculté des sciences et en particulier à ceux du département des mathématiques et informatique, à savoir : Professeur Saint Jean Djungu, Professeur Bavueza Munsana Daniel, Professeur Ramadhani Issa, Professeur Mabela Matendo Rostin, Professeur Bukweli Kyemba Joseph Désiré, Professeur Ntumba Pele, Professeur Kalala Mutombo Franck, Professeur Yumba Nkasa, Professeur Lubala Toto Ruanaza, CT Lunda Mwakono, CT Balowayi Bondo Bernard, CT Omari Baba, CT Nkomba Tshola Norbert, Chargé des cours Kumakinga Mobimba Patrice, Chargé des cours KATOTO, CT Kumwimba Didier, CT Charles Kitenge, Ass Mathina di Mathina, Ass Bukasa Serge, Ass Mulumba Bidwaya, Ass Bula Axel, Ass Mayuke Jean-Paul, Ass Tshidingi Matthieu, Ass Tailoshi Mateso Brigitte, Chargé des cours Marc Songolo pour nous avoir donné la formation et la connaissance nécessaires.

Nos remerciements s'adressent également à nos amis et connaissances, neveux et nièces, cousins et cousines à savoir : Kishiko Cedrick, Kabuya Arsène, Faila Annie, Wasingya Héritier, Banza Ilunga Shoudelle, Nzaji Gabriel, Mukatshung Elvis, Mwenge Kestia, Mwilambwe Joyce,...Pour leurs affection, conseils et leurs soutien nous témoignés. Les amis nous sécurisent et nous réequilibrent. Les ennemis et les obstacles nous traumatisent, mais nous poussent à remettre constamment notre vie et notre univers en question et nous font comprendre que « La vie n'est jamais un acquis. »

Enfin, que toute personne dont le nom ne figure pas dans ce travail, trouve ici l'expression de notre sincère reconnaissance.

Plaise à la divine bonté de vous accorder ses belles et solides récompenses que recevront les justes dans l'au-delà.

SUNGU NGOY Pascal

1

Chapitre 1

Introduction

L

E 4 mai 1980, alors que le pays s'appelait encore Zaïre, le Pape Jean-Paul II, alors aux affaires au Vatican, s'adressait aux intellectuels de la République Démocratique du Congo et encourageait les universitaires à poursuivre les objectifs de science et de conscience qui sont l'apanage de toute formation universitaire.

Nous voilà 35 ans plus tard, en train d'accomplir ce devoir noble que nous ont légué nos parents.

Une des caractéristiques du travail universitaire et du monde intellectuel est que, plus qu'ailleurs peut-être, chacun se trouve constamment renvoyé à sa propre responsabilité dans l'orientation qu'il donne à son travail. Le nôtre, vous présente deux facettes : la première est tournée vers les mathématiques et la seconde vers l'intelligence artificielle. Ces facettes sont complémentaires et constituent les deux ailes dont nous avons besoin pour voler vers la connaissance.

1.1 Choix et intérêt du sujet

Il est un fait que les mathématiques sont de plus en plus présentes en science et interviennent dans beaucoup de domaines. Si la forte composante mathématique dans plusieurs domaines n'est un secret pour personne, nombre de gens découvrent avec effroi qu'ils devraient « faire les maths » dans le cadre de leurs études. Au-delà de ces possibles déceptions, le caractère abstrait des mathématiques les rend hostiles à beaucoup de personnes, opposant ainsi une résistance hermétique à la moindre équation. Alors, pourquoi servir les mathématiques à toutes les sauces jusque dans les domaines où on ne les attendaient pas a priori? Est-ce un phénomène de mode ou une réelle nécessité? En toute honnêteté, on ne peut pas exclure le phénomène de mode.

En effet, le caractère réputé difficile des mathématiques évoqué ci-dessus fait que celles-ci impressionnent et par là inspirent une certaine forme de respect : elles rendent tout de suite une étude plus sérieuse ou un chercheur plus savant. Ainsi il arrive que les mathématiques soient effectivement utilisées sans aucune nécessité particulière, simplement pour donner au discours une apparence plus scientifique. Au-delà de ce phénomène de mode, le but de ce travail est toutefois de convaincre que si les mathématiques sont de plus en plus utilisées, c'est aussi et surtout parce qu'elles sont réellement utiles à la démarche scientifique en général, et dans le domaine de fouille de données et la représentation des connaissances en particulier.

L'exploration des données pour en extraire des connaissances est une préoccupa-

2

tion constante de l'être humain car elle est une condition essentielle de son évolution. L'homme a toujours mémorisé sur des supports différents des informations qui lui ont permis d'inférer des lois. En effet, le développement des capacités de stockage et les vitesses de transmission des réseaux ont conduit ce dernier à accumuler de plus en plus de données. Certains experts estiment même que le volume des données double tous les ans. Ainsi, il a fallu une méthode pouvant traiter ces données et bien les structurer afin d'en extraire les connaissances indispensables. Le data mining en tant que méthode mais aussi en tant qu'art d'extraire les connaissances à partir d'une base de données utilise des outils et la structure de treillis s'est avérée être un outil adéquat en vue de permettre au data mining d'arriver à ses fins.

Quant à l'intérêt porté sur ce thème, trois aspects essentiels sont à relever :

1. Intérêt scientifique;

2. Intérêt personnel;

3. Intérêt social.

Sur le plan scientique, cette étude nous permet d'appréhender la notion de fouille de données textuelles en se servant des outils mathématiques qu'est la structure de treillis.

Sur le plan personnel, le thème sous étude nous permet de fouiller dans le profondeur de la science, les quelques notions sur les structures de treillis pouvant nous permettre, dans l'avenir, de représenter les connaissances qu'on aura extraites de nos bases de données géologiques.

Sur le plan social, notre travail constituera un outil pour des nombreux chercheurs qui effectueront des investigations analogues au notre pour leurs recherches à comprendre l'extraction de connaissances à partir des bases de données.

1.2 Problématique

La problématique est considérée comme une question maîtresse à laquelle nous allons répondre tout au long du travail.

Cependant, la seule question qu'il importe de ne pas se poser c'est : « pourquoi... ? ». Nous pouvons plutôt nous demander « comment une science aussi exacte et rigoureuse comme les mathématiques peut être utilisée pour comprendre l'extraction des connaissances à partir des bases de données textuelles ? » Le présent travail éclairera votre lanterne.

1.3 Hypothèse

L'hypothèse est l'ensemble de réponses provisoires posées sur un sujet d'étude lesquelles attendent une vérification.

En effet, l'Analyse Formelle des Concepts en tant que branche de la théorie des treillis permettant la génération des règles d'association à partir des concepts formels, s'est avéré être un cadre théorique intéressant pour la fouille de données. Introduite par Wille en 1980, elle est appliquée à l'acquisition automatique de connaissances, elle a donc pour objectif d'étudier le problème de l'extraction et de la représentation des connaissances sous l'angle de la théorie mathématique des treillis.

3

1.4 Etat de l'Art

Rien n'étant nouveau sous le soleil, pas même le sujet que nous traitons à ce jour, il est important de mentionner les travaux qui ont été réalisés avant nous. Cependant, nous évoquerons les travaux réalisés par:

1. Karell Bertet portant sur La structure de treillis ainsi que ses contributions algorithmiques. Ses travaux portent sur la structure de treillis avec des contributions qui se situent à la fois sur un plan fondamental, avec des aspects structurels et algorithmiques des treillis, et sur un plan applicatif, avec l'étude de quelques usages de treillis pour de données images.[1]

2. Yannick Toussaint lui, nous a présenté Les méthodes symboliques pour la construction d'ontologies et l'annotation sémantique guidée par les connaissances appliquées à la fouille de textes. Dans cette thèse, il construit une ontologie à partir d'une base de données textuelles, en nous montrant que la construction de cette ontologie depend à la fois du domaine et de la tâche à laquelle cette ontologie est déstinée.[11]

Pour ce qui nous concerne, nous avons étudié l'impact de la structure de treillis dans le domaine de data mining en considérant une base de données constituées des documents éléctroniques et nous avons extrait mais aussi représenté ces connaissances à l'aide de cette théorie mathématique de treillis.

1.5 Méthodes et techniques de recherche

Pour bien effectuer notre recherche, nous avons utlisé l'Analyse Formelle des Concepts qui est une branche de la théorie de treillis nous permettant d'extraire les connaissances de manière automatique à partir d'une base de donnée avec un outil appelé règles d'association.

1.6 Délimitation du sujet

Dans ce sujet, il sera question de montrer l'utilisation des outils mathématiques, les treillis, en extraction et représentation des connaissances en utilisant les règles d'associations. Par la suite, nous allons générer un treillis associé aux connaissances extraites de la base de données et nous allons éventuellement interpréter ces résultats en se basant sur quelques indices stastiques associés aux règles d'association : le support, la confiance,...

En revanche, nous ne vous présenterons pas un logiciel approprié capable d'ex-traire et de représenter ces connaissances. Cela fera l'objet de nos travaux ultérieurs.

4

1.7 Division du travail

Notre travail est subdivisé de la manière suivante :

Le premier chapitre est consacré à l'introduction afin de présenter le travail de manière sommaire. Le deuxieme chapitre traite de la structure de treillis qui constitue même la théorie mathématique sur laquelle portera notre étude. Dans le souci de rendre cette étude plus sérieuse, afin, non seulement de réveiller la curiosité, mais aussi d'attirer l'attention des « non boréliens » ou « non matheux », nous présenterons, en plus, un aspect algorithmique des treillis. Tel est l'objet du troisième chapitre.

Les structures mathématiques, y compris les treillis, étant, cependant, des notions non concrètes, il sera important de les utiliser dans un domaine concret afin de les rendre plus « palpables». C'est ainsi que nous consacrerons tout un chapitre qui sera intitulé Fouille de données et navigation dans un treillis.

Le data mining est cet art d'extraire des connaissances à partir de données, lesquelles données auront besoin d'être traitées mais aussi représentées à des fins soit de prédiction, soit de description. En effet, pour manipuler ces connaissances, les notions sur les modèles de représentation des connaissances reposant essentiellement sur des théories issues de la logique sont nécessaires. C'est dans ce cadre que, dans notre cinquième chapitre, nous appliquerons les structures vues au deuxième chapitre dans la représentation de ces connaissances et la recherche d'information. Par la suite, nous vous présenterons, une conclusion générale de ce qu'aura été notre travail ainsi que nos perspectives dans ce domaine.

Première partie

5

Cadre conceptuel et théorique

6

Chapitre 2

Généralités sur la théorie des treillis

C

E chapitre a pour but d'introduire les éléments de base de la théorie des treillis, et s'organise de la manière suivante : La section 2.1 présente un bref historique de la théorie de treillis. La section 2.2 pose les définitions algébrique et ordinale d'un treillis qui introduisent toutes deux la notion de borne superieure et borne inferieure (section 2.2.1). La théorie des treillis repose en partie sur l'existence d'éléments particuliers d'un treillis que sont ses éléments irréductibles qui décrivent la structure même du treillis, et servent à en définir ses générateurs minimaux (section 2.2.2). C'est sur la base des éléments irréductibles que se définissent des représentations d'un treillis qui contiennent l'information nécessaire à sa reconstruction. Il sera introduit également, dans cette section, la table d'un treillis ainsi que son graphe de dépendance (section 2.2.3)

La section 2.3 introduit la représentation d'un treillis sous forme ensembliste par une famille de parties d'un ensemble S, stable par intersection et contenant S lui-même. Cette représentation permet ainsi de manipuler de façon équivalente un treillis sous sa forme algébrique, ordinale ou ensembliste, car tout treillis est représentable par un treillis de fermés (section 2.3.1). Un treillis de fermés est classiquement associé à un système de fermeture, ensemble muni d'un opérateur de fermeture, et l'apport principal de cette représentation ensembliste reside dans le lien unissant treillis et système de fermeture (section 2.3.2). En effet, tout treillis étant représentable par un treillis de fermés, il l'est également par un système de fermeture.

Le système de fermeture étant un ensemble muni d'un opérateur de fermeture est utilisé, non seulement dans le treillis des concepts (section 2.4.1) mais aussi dans le treillis de Galois (section 2.4.2) qui est présenté comme une généralisation du treillis des concepts à des données plus complexes pour lesquelles il existe une connexion de Galois. Ce deux notions réunit feront l'objet de la section 2.4.

2.1 Origine de la théorie des treillis

La notion de treillis définie comme une structure algébrique munie de deux opérateurs appelés borne inférieur et borne supérieur a été introduit par Dedekind et Ernest Schöder, puis oubliée. Elle a été redécouverte et développée au 20^e siècle sous diverses formes et terminologies entre 1928 et 1936 dans les travaux de Merger, Klein, Stone, Garrett Birkhoff, Oystein Öre ou encore Von Newman. L'introduction d'un treillis sous forme ordinale, structure ordonnée définie par l'existence d'élé-

7

ments particuliers appelés bornes superieures et inferieures, trouve son origine dans les axiomatiques des treillis booléens dues à Pierce en 1880 ou à Huntington. Le terme de treillis a, quant à lui, été proposé par Birkhoff lors du premier symposium sur la structure de treillis en 1938, pour être finalement repris dans son ouvrage de référence « G. Birkhoff. Lattice theory. American Mathematical society, 1^st edition, 1967 ». De nombreux ouvrages sur la théorie de treillis portent sur la définition ordinale, en particulier celui de Davey et Priestley ou encore de Grätzer.[2]

Un resultat fondamental de la théorie des treillis se constitue, selon Karell Ber-tet[1], autour d'un résultat principal qui établit que tout treillis fini est isomorphe au treillis de Galois ou treillis de concepts de sa table. Barbut et Monjardet introduisent ainsi le terme de treillis de Galois, alors que le terme de correspondance de Galois a quant à lui été introduit par Öre en 1944. Plusieurs travaux font apparaître la notion d'éléments irréductibles d'un treillis qui permettent par exemple de caractériser certaines classes de treillis, ou encore d'en concevoir des représentations compactes du treillis.

Le treillis des concepts a été introduit dans les années 1980 par Wille dans le cadre de l'Analyse Formelle des Concepts( AFC) avec un ouvrage de référence dantant de 1999, « Formal Concept Analysis, Mathematical foundations. Spriger Verlag, Berlin, 1999 ». L'AFC est une approche à la représentation des connaissances en pleine emérgence dans les années 90 qui définit le treillis des concepts à partir de données binaires de types Objet x attributs. L'émergence du treillis des concepts ces dernieres années s'explique à la fois par la part grandissante de l'informatique dans la plupart des champs disciplinaires, ce qui conduit à la production de données en quantité de plus en plus importante ; mais également par la recente montée en puissance des ordinateurs qui, bien que la taille du treillis puisse être exponentielle en fonction des données dans le pire des cas, rend possible le développement d'un grand nombre d'applications le concernant.[1]

2.2 Treillis ordinale et treillis algébrique 2.2.1 Définitions algébrique et ordinale d'un treillis

On appelle treillis ou lattis ou encore ensemble réticulé, un ensemble partiellement ordonné dans lequel, pour toute paire d'éléments, existent une borne inférieure et une borne supérieure[4]. On trouve, également, dans la littérature deux autres définitions d'un treillis : Une définition algébrique et une définition ordinale. Ces définitions introduisent toutes deux la notion de borne supérieure (ou supremum) et de borne inferieure (ou infimum) alors qu'il s'agit d'opérateurs binaires dans la définition algébrique, ce sont des éléments particuliers dans la définition ordinale.[1]

Définition 1 (Définition algébrique)

Un treillis ou encore une algèbre de treillis est un triplet L = (S, V, ?) ou V et ? sont deux opérateurs binaires sur l'ensemble S qui vérifient les propriétés suivantes :

- Associativité : Pour tout x, y, z E S, (x V y) V z = x V (y V z) et (x ? y) ? z = x ? (y ? z).

- Commutativité : Pour tout x, y E S, x V y = y V x et x ? y = y ? x

- Idempotence : Pour tout x E S, x V x = x = x ? x

8

- Loi d'absorption : Pour tout x, y E S, x V (x ? y) = x = x ? (x V y)[1] Définition 2 (Définition ordinale)

Un treillis est une paire L = (S,<) où < est une relation d'ordre sur l'ensemble S, c'est à dire une relation binaire qui vérifie les proprietés suivantes :

- Réflexivité : Pour tout x E S, on a xRx.

- Antisymetrie : Pour tout x, y E S, xRy et yRx impliquent x = y.

- Transitivité : Pour tout x, y, z E S, xRy et yRz impliquent xRz.[1][3]

Un ensemble sur lequel est défini une relation d'ordre (partiel ou total) est dit (partiellement ou totalement) ordonné.

Considérons un ensemble S partiellement ordonné par la relation < (être inférieur ou égal à) et une partie X de cet ensemble[4] ;

Définition 3 Minorant (Majorant) :

Un élément m(M) de S qui est inférieur (supérieur) ou égal à tout élément x de X est un minorant (majorant) de X.

Définition 4 Elément maximal (minimal) :

Un élément noté T(1) de X, tel qu'il n'existe pas d'éléments de X supérieur (inférieur) à T(1) est un élément maximal (minimal) de X.

Définition 5 Plus grand (petit) élément :

Le plus grand (petit) élément E(e) ou encore le maximum (minimum) de X est l'élément de X tel que pour tout x E X, E > x(e < x).

Définition 6 Borne supérieure (inférieure) :

La borne supérieure (inférieure) de X Ç S notée VX (?X) ou le supremum (infimum) de X noté sup(X) (inf(X) ) est le plus petit (grand) élément de l'ensemble des majorants (minorants) de X. Les bornes inférieure et supérieure entre x et y notée respectivement par x ? y et x V y se définissent de la même manière que pour une partie X Ç S

Définition 7 Elément universel (nul) :

L'élément universel (nul) de S est le plus grand (petit) élément de S. Exemple 1

Soit S = {1, 2, 3, 5, 10, 20, 30} un ensemble partiellement ordonné par la relation x||y (x divise y).

N.B : x||y peut s'interpréter comme x < y et x|y comme x < y.

1. Prenons X = {2, 3,5, 10}

Il existe un majorant de X qui vaut 30 et un minorant qui vaut 1, un élément maximal : 10, trois élément minimaux : 2, 3, 5 ni plus grand élément, ni plus petit élément de X. La borne supérieure de X est 30 et la borne inférieure vaut 1. S

9

n'admet pas d'élément universel, mais un élément nul : 1.

2. Prenons maintenant X = {2, 5,10}

X compte 3 majorants : 10, 20, 30, un minorant : 1, un élément maximal : 10, deux éléments minimaux : 2 et 5, un plus grand élément : 10, pas de plus petit élément. La borne supérieure de X est 10 et la borne inférieure est 1.

Pour une partie réduite à deux éléments {x, y}, d'un ensemble ordonné, il peut exister une borne inférieure, une borne supérieure. Lorsque seule l'existence de la borne inférieure est vérifiée, on parle d'inf-demi-treillis. Un sup-demi-treillis est défini dans le cas dual où seule l'existence d'une borne supérieure est vérifiée. Un treilis est donc à la fois un inf-demi-treillis et un sup-demi-treillis[1].

Définition 8 (Relation d'ordre strict) :

Une relation d'ordre strict notée < est une relation vérifiant les propriétés suivantes :

- Irréflexive : Pour tout x E S, (x, x) E6 R.

- Asymétrique : Pour tout x, y E S, (x, y) E R implique (y, x) E6 R.

- Transitive : Pour tout x, y, z E S, (x, y) E R et (y, z) E R = (x, z) E R.[5]

Définition 9 (Relation de couverture) :

On dit qu'un couple (x, y) E X x X avec X C_ S est une couverture ou que y couvre x (y est successeur immédiat de x) ou encore x est couvert par y (x est prédécesseur immédiat de y), s'il n'existe pas z tel que x < z < y lorsque x < y. Elle est notée par "-<" et elle se déduit de la relation d'ordre en supprimant les relations de réflexivité et de transitivité[6].

Définition 10 (Diagramme de Hasse) :

La représentation graphique d'un treillis s'exprime à l'aide d'un diagramme, appelé diagramme de Hasse, dans lequel les noeuds correspondent aux éléments de l'ensemble et les arcs aux relations de couverture (successeurs et prédécesseurs immédiats) entre ces noeuds.

Le plus souvent, Relation binaire et Graphe orienté simple (C'est-à-dire un graphe sans arcs multiples) s'identifient où chaque élément est représenté par un sommet du graphe, et où la relation entre deux éléments x et y est représentée par un arc du graphe entre le sommet x et le sommet y. Le diagramme de Hasse, tel que décrit ci-haut, est une représentation proche de la représentation habituelle d'un graphe ; les orientations des arcs ne sont pas toujours représentées parce qu'elles peuvent se déduire du positionement des noeuds. Ainsi il permet de ne pas surcharger le dessin pour faciliter une meilleure lisibilité[1].

Exemple 2

Considérons, à titre d'exemple, les diviseurs de 30 : {1, 2, 3, 5, 6,10,15, 30} ordonnés par la relation x divise y[4]. Ces éléments forment un treillis dont le diagramme de Hasse est donné par la figure Figure 2.1.

On peut vérifier que toute paire d'éléments admet une borne inférieure(p.g.c.d) et une borne supérieure(p.p.c.m). Ainsi :

- 5 V 6 = 5 x 6 = 30; 5 ? 6 = 1; 6 V 15 = 5 x 3 x 2 = 30; 6 ? 5 = 3; etc. L'élément

10

FIGURE 2.1 - Exemple de treillis universel de ce treillis est 30 et l'élément nul est 1.

Définition 11 (Treillis distributif) :

Un treillis est distributif si V et ? verifient la proprieté de distributivité : Pout tout x, y, z E S, x V (y ? z) = (x V y) ? (x V z).[5]

Définition 12 (Treillis complémenté) :

Un treillis est complémenté si tout élément x E S admet au moins un complément, c'est-à-dire un élément x' E S tel que x V x' = T (élément maximal) et x ? x' = 1 (élément minimal)[1].

Définition 13 (Treillis V-Complémenté) :

Un treillis est V-Complémenté si pour tout élément x E S, il existe un V-complément (c'est-à-dire un élément x' E S tel que x V x' = T). Un treillis ?-complémenté est défini dans le cas dual[1].

Définition 14 (Treillis booléen) :

Un treillis est booléen s'il est à la fois distributif et compléménté[1]. Exemple 3

Un exemple classique d'un treillis distributif est fourni à la figure 2.2(a). La relation d'ordre est la relation « ... divise... ». L'ensemble P(S) des parties d'un ensemble S muni de la relation d'inclusion est quant à lui un exemple classique de treillis booleen (figure 2.2(b))[1]

2.2.2 Irréductibles et générateurs minimaux d'un treillis

Soient x ? y et x V y les bornes inférieur et supérieur respectivement. Un élément d'un treillis est dit réductible s'il est résultat de x ? y ou x V y. Dans le cas contraire, il sera dit irréductible.

11

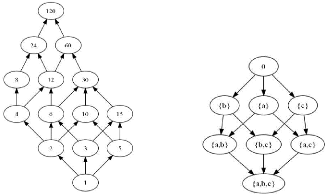
FIGURE 2.2 - Exemple de treillis distributif et treillis booléen.

Définition 15 (Elements irréductibles)

Soit L = (S, ) un treillis.

- Un élément j E S est appelé sup-réductible s'il existe dans S des éléments x1 et x2 tel que j = x1 V x2 avec x1 < x et x2 < x. Un élément x de S ne possédant pas de décomposition de cette forme est dit sup-irréductible.

- Dualement, un élément in E S est appelé inf-réductible s'il existe dans S des éléments x1 et x2 tel que j = x1 ? x2 avec x1 > x et x2 > x. Un élément x de S ne possédant pas de décomposition de cette forme est dit inf-irréductible. L'ensemble des sup-irréductible et celui des inf-irréductible du treillis L est noté respectivement par JL et ML[3].

Proposition 1

Soit L = (S, ) un treillis.

- Un élément j E S est un sup-irréductible, si et seulement si j couvre un seul élément dans le diagramme de Hasse.

- Un élément in E S est un inf-irréductible, si et seulement si in est couvert par un seul élément dans le diagramme de Hasse.

Définition 16 (Treillis atomistique) :

Un treillis est dit atomistique lorsque tous les sup-irréductibles sont des atomes (un atome est un élément qui couvre l'élément minimal I).[3]

Définition 17 (Treillis co-atomistique) :

Un treillis est dit co-atomistique lorsque tous les inf-irréductibles sont des co-atomes (un co-atome est un élément qui est couvert par l'élément maximal T). Tout élément x E S d'un treillis L = (S, ) est la borne supérieure de l'ensemble de ses prédécesseurs, ainsi que la borne inférieure de l'ensemble de ses successeurs. La

12

FIGURE 2.3 - Autre exemple de treillis

définition latticielle permet d'établir qu'il est possible de réduire ces ensembles aux seuls prédécesseurs sup-irréductibles, et un successeurs inf-irréductibles[3] :

x = ?J_x = ?{y sup-irréductible tel que y = x} (2.1)

x = ?M_x = ?{y inf-irréductible tel que y = x} (2.2)

Par conséquent, les ensembles d'éléments irréductibles peuvent nous permettre de reconstruire le treillis dans sa globalité par reconstruction successives de bornes supérieures ou de bornes inférieures en utilisant respectivement les sup-irréductibles et les inf-irréductibles.[1]

Exemple 3

Considérons la figure 2.3. Nous constatons que seul six éléments possèdent un seul arc entrant, et forment ainsi l'ensemble des sup-irréductibles alors que les inf-irrédutibles, caractérisés, quant à eux, par un seul arc sortant sont au nombre de huit:

J = {b, f, e, a, c, d} (2.3)

M = {b,l,m,n,d,k,i,c} (2.4)

Quatre sup-irréductibles {b, f, e, a} sont des atomes et que trois inf-irréductibles {l, i, c} sont des co-atomes. Ces éléments irréductibles sont utilisés dans le treillis de la figure 2.4 où dans le noeud de chaque élément x sont precisés l'ensemble J_x des sup-irréductibles inférieurs ou égaux à x ainsi que l'ensemble M_x des inf-irréductibles supérieurs ou égaux à x. Les générateurs minimaux de chaque élément sont, quant à eux, donnés par la table 2.1. On peut ainsi observer que chaque sup-irréductible est son propre générateur minimal, mais aussi que tous les éléments, excepté l'élément maximal T, ont pour unique générateur minimal l'ensemble de leurs prédécesseurs sup-irréductibles.[1]

TABLE 2.1 - Générateurs minimaux des éléments du treillis de la figure 2.3

13

FIGURE 2.4 - Treillis de la figure 2.3 où sont precisés, pour chaque noeud de x, les ensembles J_x et M_x

14

Définition 18 (Générateur minimal)

Soit L = (S,=) un treillis et x ? S un élément du treillis. Un générateur minimal de x est un sous ensemble B de J_x tel que x = ?B et qui soit minimal au sens de l'inclusion, c'est-à-dire pour tout A ? B, on a x < ?A. La famille â_x des générateurs minimaux de x se définit par :[6]

â_x = {B ? J_x : x = ?B et x < ?A pour tout A ? B} (2.5)

Définition 19 (Table et graphe de dépendance d'un treillis)

La notion d'éléments irréductibles d'un treillis permet de concevoir des représentations compactes du treillis entre autre la représentation par une table composée en colonne par des sup-irréductibles et en ligne par des inf-irréductibles. Il existe, cependant, une différence entre une table binaire d'un treillis et une table complète.[1]

La table (complète) d'un treillis se définit à partir des relations flèches qui parti-tionnent les différents liens possibles entre un sup-irréductible et un inf-irréductible à l'aide de relations binaires définies sur JL ×ML. Nous avons entre autre, la relation de comparabilité = qui permet d'établir une première partition de JL × ML en deux parties notées P= et _P6= définit par :

P= = {(j,m) ? JL × ML : j = m} (2.6)

P6= = {(j,m) ? JL × ML : j =6 m} (2.7)
Définition 20 (Relations flèches)

Soit L = (S,=) un treillis, j ? JL et m ? ML. Une relation flèche est définit comme suit[1] :

- j ? m si j =6 m et j < m⁺(unique successeur, dans le diagramme de Hasse, pour tout m ? ML).

- j ? m si j =6 m et j^- < m avec j^- unique prédécesseur pour tout j ? LL. Notons que les relations flèches (j ? m et j ? m ) affinent les cas où j et m ne sont pas comparables. C'est-à-dire, de cette relation d'incomparabilité, il en résulte quatre autres combinaisons possibles qui permet de partitionner l'ensemble de paires (j, m) ? P6= en quatre parties notées P?, P?, Pl, P_? définit par :

P? = {(j,m) ? JL × ML : j ? m et j ?6m} (2.8)

P? = {(j,m) ? JL × ML : j ?6m et j ? m} (2.9)

Pl = {(j, m) ? JL × ML : j ? m et j ? m} (2.10)

P_? = {(j,m) ? JL × ML : j ?6m et j ?6m} (2.11)

La table d'un treillis se définit comme étant une représentation tabulaire de ce partionnement.

meture se sont avérées fondamentales pour plusieurs domaines de l'informatique : Base de données, Analyses formelles de concepts.

15

TABLE 2.2 - Table du treillis de la figure 2.3 Définition 21 (Table d'un treillis) :

La table T d'un treillis L = (S, <) est composée des sup-irréductibles qui apparaissent en colonne et des inf-irréductibles qui apparaissent en ligne. Ainsi pour m E ML et j E JL, la table T[m, j] contient x, t, 1,, $ ou o selon que (m, j) appartienne à P<, Pt, P~, P$ ou P_o(cf table 2.2).

Il vient que la table binaire se définit juste à partir d'une seule partition composée de deux parties P< et Pg où T[m, j] contient x si (m, j) E P< et rien dans le cas contraire, c'est-à-dire le cas où (m, j) E Pg

Notons que lorsque la table (complète) possède exactement une double flèche sur chacune de ses lignes et colonnes, alors on parle d'un treillis distributif. Un treillis atomistique se caractérise quant lui par l'absence de flèche t dans sa table, alors qu'un treillis co-atomistique se caractérise par l'absence de flèche 1,. Il en découle que la table d'un treillis booléen, qui en revanche est à la fois distributif, atomistique et co-atomistique se carastérise par une unique double flèche $ sur chacune de ses lignes et colonnes, ainsi que par l'absence de flèches simples t et 1,.[1]

Définition 22 (Graphe de dépendance) :

Le graphe de dépendance se définit pour les sup-irréductibles sur la base de la relation de dépendance. Soit L = (S, <) un treillis, le graphe de dépendance du treillis L est un graphe valué G = (JL, 8, w) tel que :

- 8 relation de dépendance définie sur JL par j8j'. Alors 8 est une relation de dépendance s'il existe un élément de l'ensemble S qui ne majore pas j et j' éléménts de JL, c'est-à-dire s'il existe x E S tel que j <6 x, j' <6 x et j < j' V x ;

- w une valuation des arcs définie pour chaque relation j8j' de tel sorte que l'arc (j, j') peut être valué par les générateur minimaux de x, c'est-à-dire les parties de l'ensemble J_x défini pour x :[5]

J_x = {j < x tel que j E JL}

2.3 Treillis de fermés et système de fermeture

Comme la notion de treillis, les familles de Moore, dites aussi systèmes de fer-

16

Soit S un ensemble stable. Une famille de Moore est une famille de parties fermées de l'ensemble S stable par intersection et contenant l'ensemble lui-même. Elle est aussi définie comme étant une partie de l'ensemble de parties de S vérifiant certaines propriétés(cf définition 8)[1].

2.3.1 Treillis de fermés

Toute famille F E P(S) munie de la relation d'inclusion est ordonnée, l'inclusion étant transitive, réflexive et antisymétrique. Il s'en suit que (F, Ç) est un treillis. On parle alors de treillis de fermés.

Définition 23 (Treillis de fermés) :

Un treillis de fermés sur un ensemble S est une paire (F, Ç) où F est une famille sur S possèdant les propriétés d'une famille de Moore, encore appelée famille de fermés[3] :

- F contient S ;

- F est stable par intersection : Pour tout F, F' E F, on a F n F' E F

Exemple 4 :

Soit S = {a, b, c, d, e}. Alors F = {ø, a, b, d, de, bcd, abcde} est une famille de Moore sur l'ensemble S. Les ensembles finis, ici, sont notés comme des mots. Par exemple »de» designe la paire {d, e}

2.3.2 Système de fermeture

La propriété principale des treillis de fermés reside dans le lien qui les unissent au système de fermeture.

Définition 24 (Système de fermeture) :

Un système de fermeture est une paire C = (S, ?) où S est un ensemble et ? un opérateur de fermeture, c'est-à-dire une application définie sur P(S) à la fois isotone, extensive et idempotente[3] :

- isotonie : Pour tout X, Y Ç S, X Ç Y = ?(X) Ç ?(Y ).

- extensivité : Pour tout X Ç S, X Ç ?(X).

- idempotence : Pour tout X Ç S, ?(?(X)) = ?(X).

Pour une partie X Ç S quelconque, ?(X) est appelée fermeture de X ou encore un fermé de C. L'ensemble de fermé forme une famille de Moore F :[1]

F = {?(X) : X Ç S} (2.12)

2.4 Treillis des concepts et treillis de Galois

Une structure mathématique permettant de représenter les classes non disjointes sous jacentes à un ensemble d'objets (exemples, instances, tuples ou observations) décrits à partir d'un ensemble d'attributs (propriétés, descripteurs ou items), les treillis de concepts formels (ou treillis de Galois) permet d'organiser l'information concernant des classes d'objets possédant des propriétés communes. Ces classes non

17

TABLE 2.3 - Exemple de contexte

disjointes sont aussi appelées concepts formels, hyper-rectangles ou ensembles fer-més[1].

2.4.1 Treillis des concepts

En analyse de données, l'analyse formelle des concepts pose le treillis des concepts comme espace de recherche sous-jacent à des données qui s'organisent sous forme d'un table binaire objets × attributs encore appélé contexte. Le treillis de concepts et un treillis dont les noeuds, appelés concepts sont composés à la fois d'un ensemble d'objets et un ensemble d'attributs.[11]

Définition 25 (Treillis des concepts)

Le treillis des concepts se définit pour une relation binaire R entre un ensemble O d'objets et un ensemble I d'attributs, encore appelés contexte[1]. Le treillis des concepts d'un contexte (O, I, R) est une paire (C, ) où :

- C est un ensemble de concepts définit sur P(O) × P(I) par :

(A,B) ? C ? A ? O,B ? I,B = á(A) et A = â(B)

avec

á(A) = {b ? I, aRb pour touta ? A}

â(B) = {a ? O, aRb pour toutb ? B}

- est une relation binaire définie sur l'ensemble des concepts C par, pour (A1,B1) et (A2,B2) ? C :

(A1, B1)(A2, B2) ? B1 ? B2 ? A1 ? A2 (2.13)

Lorsque le contexte est représenté sous forme d'une table, un concept correspond à un rectangle maximal, ou encore à une sous matrice première. Un contexte pourra être noté par (O, I, R) ou encore par (O, I, (á, â)) selon que l'on considère la relation binaire R entre O et I, ou, de façon équivalente, les deux applications á et â, l'une de O vers I, l'autre dans le sens contraire.[1][5]

18

FIGURE 2.5 - Treillis des concepts du contexte de la table 2.3 Exemple 5 :

Considérons comme exemple le contexte décrit par la table 2.3 définie par un ensemble d'objets {1, 2, 3, 4, 5, 6, 7, 8, 9} et un ensemble d'attributs {a, b, c, d, e, f, g, h}, ainsi que son treillis des concepts donné par la figure 2.6.[1] On constate que :

- L'objet numéro 9 possède tous les attributs, et par conséquent il apparaît dans tous les concepts;

- L'attibut g est partagé par tous les objets, il apparaît, ipso facto, dans tous les concepts;

- L'attribut h, quant à lui, est partagé par seulement 3, 4, 5 et 9, c'est-à-dire par les objets possédant à la fois l'attribut e et f. Par conséquent l'attribut h n'apparaît que dans les concepts contenant à la fois l'attribut e et f.

2.4.2 Treillis de Galois

Le treillis de Galois se définit à partir d'une correspondance de Galois entre deux ensembles qui elle-même définit deux opérateurs de fermetures sur chacun de deux ensembles.

Définition 26 (Treillis de Galois)

Un treillis de Galois se définit à partir d'une correspondance de Galois (á, 8) entre deux ensemble S et U où :[7]

- á est une application isotone de P(S) vers P(U) : X C_ Y = á(X) C_ á(Y ) ;

- 8 est une application antitone de P(U) vers P(S) : X C_ Y = 8(X) D 8(Y ) ;

- (8 o á) est une application extensive sur P(U) : X C_ U = X C_ (8 o á)(X) ;

- (á o 8) est une application extensive sur P(S) : X C_ S = X C_ (á o 8)(X). Les termes (8 o á) et (á o 8) sont les deux opérateurs de fermeture, l'un définit sur U et l'autre sur S.

19

Chapitre 3

Aspects algorithmiques des treillis

P

Rocédure de calcul bien définie qui prend en entrée une valeur ou un ensemble de valeurs, et qui donne en sortie une valeur ou un ensemble de valeurs. Un algorithme est donc une sequence d'étapes de calcul qui transforment l'entrée en sortie. La notion d'algorithme est intimement liée à la notion de complexité. En informatique, le mot compléxité recouvre en faite deux réalités :

· La compléxité des algorithmes :

C'est l'étude de l'efficacité comparéé des algorithmes. On mesure ainsi le temps et aussi l'espace nécessaire à un algorithme pour resoudre un problème.

· La compléxité des problèmes :

La compléxité des algorithmes a abouti à une classification des problèmes en fonction des performances des meilleurs algorithmes connus qui les resolvent. Ils en existent de trois sortes :

* La classe P se compose des problèmes qui sont résolubles en temps polynomial. Plus précisement, il existe des problèmes qui peuvent être résolus en temps O(n') pour une certaine constante k(n est la taille des données en entrée).

* La classe NP se compose des problèmes qui sont vérifiables en temps polynomial. Cela signifie : si l'on nous donne d'une façon ou d'une autre une solution certifiée, nous pouvons vérifier que cette solution est correcte en un temps qui est polynomial par rapport à la taille de l'entrée.

* La classe NPC encore appelée Classe NP- Complet. Un problème est dans la classe NPC s'il appartient à NP et s'il est aussi difficile que n'importe quel autre problème de NP.[8][10]

Les calculs à effectuer pour évaluer les temps d'exécution d'un algorithme peuvent parfois être longs et pénibles. Ainsi on aura recours à une approximation de ce temps de calcul, représentée par la notation O(·).

Soient f et g deux fonctions positives d'une même variable entière n. Avec n, la taille des données à traiter.

la fonction f est dite avoir un ordre de grandeur au plus égal à celui de la fonction g s'il existe un entier strictement positif k et un entier N tels que,

- Pour tout n = N, on ait |f(n)| = k|g(n)| c'est-à-dire que f(·) est toujours dominée par la fonction g(·), à une constante multiplicative fixée près;

- On écrira f = O(g) (notation de Landau).[9]

20

Dans ce chapitre, nous vous présenterons les quelques aspects algorithmiques qu'ils soient. En effet, il existe deux familles d'algorithmes de génération ou de contruction des treillis.

* Algorithmes incrémentaux Ce sont des algorithmes qui contruisent le treillis au fur et à mesure qu'on a connaissances des objets.

* Algorithmes non incrémentaux ce sont des algorithmes qui contruisent le treillis une fois que tous les objets sont connus.

3.1 Algorithme de construction du graphe de couverture d'un treillis

Nourine et Raynaud sont les concepteurs de cet algorithme non incrémental. Il a été conçu pour la construction et le calcul du graphe de couverture d'un treillis; il utilise une approche en deux étapes :[1]

* Génére la famille F représentée dans un arbre lexicographique.

* Calcule les relation de couverture des éléments de F

Première étape : L'algorithme calcule l'arbre lexicographique représenté par la famille F générée par la base B.

Soit X un ensemble, P un ordre total sur X et B une base composée par l'ensemble des parties de X. Désignons par F la famille générée par l'union des éléments de la

base B, avec;

_U

F = {b, b E I/I ? B}

on dit aussi que B est un générateur de la famille F. Chaque élément de F est représenté par un couple (f, ã(f)) où;

ã(f) = {b E B/b ? f}

Il faut voir chaque constituant comme un mot de l'alphabet X ordonné dans l'ordre croissant.

Montrons maintenant comment construire cet arbre lexicographique à partir d'une base;

B = {b1,b2,...,b_m}

* La racine correspond à F⁰ qui est un ensemble vide;

* A l'etape j c'est le calcul de la famille F fermée par l'union. Ce calcul se fait à partir de F ^-1 en utilisant la formule suivante :

F = F ^-1 u {f u b /f E F ^-1}; avec B = {b1,b2,...,b }

Ainsi l'algorithme de construction du graphe de couverture d'un treillis et le sui-

vant :[5]

Algorithme 1 Graphe de couverture d'un treillis;

Donnée : La base B

Résultat : Arbre lexicographique TF de F

Début F = {ø}; {La racine de TF}; ã(F) = {ø}

Pour chaque b E B faire

Pour f E F faire

f' = f u b

f» = f ? {b/b ? 0(f», f)} = f'

21

Si f^' ?6 F alors

F = F ? {f^'}

ã(f^') = ã(f) ? b

ã(F) = ã(F) ? ã(f^')

Fin si

Fin pour

Fin pour

Fin

Théorème 3.1 L'algorithme 1 calcule l'arbre lexicographique de la famille F générée

par la base B en O((|X| + |B|) * |B| * |F|) étapes.

Preuve La première instruction dans la deuxième boucle Pour ainsi que la deuxième

instruction dans Si...alors sont faites en O(|X|+|B|) étapes; l'instruction Si...alors

vérifie si f^' est dans l'arbre ; sinon elle l'insère( première instruction du test). Elle

est donc implémentée en O(|F|). Ainsi la compléxité de la deuxième boucle Pour

vaut O((|X| + |B|) * |F|).

Il s'en suit que la première boucle Pour se répète |B| fois.D'où le résultat obtenu.

Deuxième étape Cette étape consiste à calculer le graphe de couverture G = (F, ?)

à partir de l'arbre lexicographique de la famille F générée par la base B ; et cela en

utilisant le théorème de couverture suivant :

Théorème 3.2 On définit ;

0(f^', f) = ã(f^')\ã(f);

et on note par ? la relation de couverture. Soient f et f^' ? F tels que f ? f^' alors :

f ? f^' ? ?(b1, b2) ? 0(f^', f), b1\f^' = b2\f. Preuve Soient f et f^' ? F tels que f ? f^' alors f^' peut s'ecrire :

f' = f ? {b/b ? 0(f^',f)}

(1) Supposons que f soit couvert par f^', montrons que pour tous les (b1, b2) ? 0(f^', f) ; nous avons :

b1\f^' = b2\f.

Supposons que b1\f^' ?6 b2\f ; il vient que : f ? b1 = f» ? f^' = f ? {b/b ? 0(f^', f)} . Par conséquent :

f ? f» ? f'.

ce qui est en contradiction avec l'hypothèse selon laquelle f est couvert par f^' ainsi :

b1\f^' ? b2\f

De même b1\f^' ? b2\f en utilisant le même raisonnement.

(2) Inversement, supposons que pour tout (b1, b2) ? 0(f^', f) on a : b1\f^' = b2\f. Soit f» ? F tel que f ? f» ? f' ce qui implique que ;

ã(f) ? ã(f») ? ã(f')

ainsi donc ;

22

ce qui implique que :

ã(f»)\ã(f) ? ã(f')\ã(f) = Ä(f', f)

Le corollaire suivant est une conséquence du théorème précédent : Corollaire 3.1 Soient f et f' ? F tels que ;

f ? f';

alors :

f ? f' ? ?f' = f ? b pour tout Ä(f', f);

Decrivons maintenant comment calculer le graphe de couverture G = (F, ?). Consi-derons la famille F généré par la base B utilisée dans l'algorithme 1. La strategie de cet algorithme consiste à calculer l'ensemble des éléments de couverture noté par Imsucc(f) pour chaque élément de la famille F. En clair f' ? F est candidat si f ? f' et f' peut être calculé par f' = f ? b pour certains b ? B\ã(f).

Posons ;

S(f) = {f ? b/b ? B\ã(f)}

Cet ensemble de candidats S(f) pour la couverture f, peut avoir des éléments redon-

dants, l'algorithme explore cet ensemble et décide que f' ? S est une couverture de

f si f' est trouvé |Ä(f', f)| fois dans S(f). Pour ce faire, nous calculons l'ensemble

S(f) en maintenant le nombre d'occurences de chaque élément f' dans le compteur

count(f'), ensuite pour chaque élément f' ? S, on vérifie si |Ä(f', f)| = count(f')

alors f' couvre f.

L'algorithme suivant construira le graphe de couverture de G = (F, ?), étant donné

l'arbre lexicographique TF de la famille F générée par la base B.[5]

Algorithme 2 Graphe de couverture de G = (F, ?)

Donnée Arbre lexicographique de F et de ã(F)

Résultat Listes d'adjacence des Imsucc du graphe de couverture du treillis (F, ?).

Début

Initialiser count(f) à 0 pour tout f ? F

Pour f ? F faire

S(f) = {f ? b/b ? B\ã(f)}

Pour b ? B\ã(f) faire

f' = f ? b

count(f') = count(f) + 1

Si |ã(f')| = count(f') + |ã(f)| faire

Imsucc(f) = Imsucc(f) ? {f'}

Fin si

Fin pour

réinitialiser count(f^')

Fin pour

Fin

Théorème 3.3 L'algorithme 2 calcule les listes d'adjancence des Imsucc du graphe

de couverture pour le treillis (F, ?) en O((|X| + |B|)|B| * |F|) étapes.

Preuve L'algorithme 2 calcule le graphe de couverture du treillis (F, ?) par corol-

laire 3.1

Le calcul de |ã(f)| et |ã(f')| (l'instruction Si...alors) se fait en O(|X| + |B|) en

utilisant la recherche dans l'arbre lexicographique ; d'où la compléxité de la boucle

23

interne Pour est de O((|X| + |B|) * |B|).

Reinitialiser count pour tous les éléments calculés par la première et la deuxième instruction de la boucle interne Pour qui se fait en O(|F|). Il s'en suit que la compléxité de l'algorithme 2 est de O((|X| + |B|)|B| * |F|).[13]

Exemple 1

Soit X = {1, 2, 3, 4, 5} un ensemble et B une base composée par quelques parties

de X.

On désigne par F la famille générée par l'union des éléments de la base B, tel que

F = {UbEB /I C B}. Par abus d'écriture, on pose {1, ..., 5} = {12345}. On définit

B={x=245,y=1234,z=15}.

Appliquons l'algorithme 1 afin de générée la famille F représentée dans un arbre

lexicographique.

On pose ã(f) = {b ? B/b ? f}

1.F = {0} ; (la racine de l'arbre TF ) ; ã(F) = {0} ;

(a) Pour b = {245} et f = 0 ;

f'=fUb=0U{245}={245} ?6F ;

F = F U {f'} = {0} U {{245}} = {0,{245}};

ã(f') = ã(f) U b = {245} = x;

ã(F) = {0, {x}} ;

2.F = {0, {245}}, ã(F) = {0, {x}};

(a) Pour b = {1234} et f = 0 ; f' = f U b = {1234} ?6F ; F = {0, {245}, {1234}} ; ã(f') = ã(f) U b = {1234} = y ; ã(F) = {0, {x}, {y}} ;

(b) Pour b = {1234} et f = {245} ;

f' = f U b = {12345} ?6F ;

F = {0, {245}, {1234}, {12345}} ;

ã(f') = ã(f) U b = {12345} = xyz ;

ã(F) = {0, {x}, {y}, {xyz}} ;

3.F = {0, {245},{1234},{12345}},ã(F) = {0, {x}, {y}, {xyz}};

(a) Pour b = {15} et f = 0 ;

f' = f U b = {15} ?6F ;

F = {0, {245}, {1234}, {12345}, {15}} ;

ã(f') = ã(f) U b = {15} = z ;

ã(F) = {0, {x}, {y}, {xyz}, {z}} ;

(b) Pour b = {15} et f = {245} ;

f' = f U b = {1245} ?6F ;

F = {0, {245}, {1234}, {12345}, {15}, {1245}} ;

ã(f') = ã(f) U b = {1245} = xz ;

ã(F) = {0, {x}, {y}, {xyz}, {z}, {xz}} ;

(c) Pour b = {15} et f = {1234} ; f' = f U b = {12345} ? F ;

(d) Pour b = {15} et f = {12345} ;

f' = f U b = {12345} ? F ;

Finalement à partir de la base B = {x = 245, y = 1234, z = 15}, on obtient :

F = {0, {245}, {1234}, {12345}, {15}, {1245}}

24

FIGURE 3.1 - Arbre lexicographique de la famille F
`y(F) = {0, {x}, {y}, {xyz}, {z}, {xz}};

Ainsi nous obtenons l'arbre lexicographique de F présenté à la figure 3.1. Appliquons maintenant l'algorithme 2 qui consiste à calculer le graphe de couverture à partir de l'arbre lexicographique des familles ;

F = {0, {245}, {1234}, {12345}, {15}, {1245}}

et

`y(F) = {0, {x}, {y}, {xyz}, {z}, {xz}};

générée par la base ;

B={x=245,y=1234,z=15}.

Cet algorithme donne les listes d'adjacence des successeurs immédiats du graphe de couverture du treillis (F, Ç). Ainsi on démarre l'algorithme 2 par ;

count(f) = 0 ; pour tout f E F, on calcule ;

8(f) = {f U b/b E B\`y(f)};

1. f = 0; 8(f) = 8(0) = {0 U {245}, 0 U {1234}, 0 U {15}} = {{245}, {1234}, {15}} ; calcule de count(f') pour f' E 8(f)

(a) Pour f' = {245}, count(f') = count({245}) = 1;

A(f',f) = `y(f') \ `y(f) = {x} \ 0 = {x};

|A(f',f)| = 1 = |A(f',f)| = count(f') = 1;

(f, f') = (0, {245}) est une couverture ;

Imsucc(f) = Imsucc(0) = {{245}} ;

(b) Pour f' = {1234}, count(f') = count({1234}) = 1 ;

A(f', f) = `y(f') \ `y(f) = {y} \ 0 = {y} ;

|A(f', f)| = 1 = |A(f', f)| = count(f') = 1;

(f, f') = (0, {1234}) est une couverture ;

Imsucc(f) = Imsucc(0) = {{245}, {1234}} ;

(c) Pour f' = {15}, count(f') = count({15}) = 1; A(f', f) = `y(f') \ `y(f) = {z} \ 0 = {z} ;

|A(f',f)| = 1 = |A(f',f)| = count(f') = 1;

25

(f, f') = (0, {15}) est une couverture; Imsucc(f) = {{245}, {1234}, {15}} ; count(f') = 0;

2. f = {245}; S(f) = S({245}) = {{245} U {1234}, {245} U {15}} = {{12345},{1245}}; calcule de count(f') pour f' E S(f)

(a) Pour f' = {12345}, count(f') = count({12345}) = 1 + 1 = 2;

Ä(f', f) = -y(f') \ -y(f) = {xyz} \ {x} = {yz} ; |Ä(f', f)| = 2 = |Ä(f', f)| = count(f') ;

(f, f') = ({245}, {12345}) est une couverture;

(b) Pour f' = {1245}, count(f') = count({1245}) = 2 ;

Ä(f', f) = -y(f') \ -y(f) = {xz} \ {x} = {z} ; |Ä(f', f)| = 1 = |Ä(f', f)| =6 count(f') ;

(f, f') = ({245}, {1245}) n'est pas une couverture;

Imsucc(f) = Imsucc({245}) = {{1245}} ; count(f') = 0;

3. f = {1234}; S(f) = {{1234} U {245}, {1234} U {15}} = {12345} ;

calcule de count(f') pour f' E S(f)

(a) Pour f' = {12345}, count(f') = count({12345}) = 2 ;

Ä(f', f) = -y(f') \ -y(f) = {xyz} \ {y} = {xz} ;

|Ä(f',f)| = 2 = |Ä(f',f)| = count(f') = 2;

(f, f') = ({1234}, {12345}) est une couverture;

Imsucc(f) = Imsucc({1234}) = {{12345}} ;

count(f') = 0;

4. f = {12345}; S(f) = S({12345}) = 0; count(f') = 0

5. f = {15}; S(f) = S({15}) = {{15} U {245}, {15} U {1234}} = {{1245}, {12345}} ; calcule de count(f') pour f' E S(f)

(a) Pour f' = {1245}, count(f') = count({1245}) = 2 ;

Ä(f', f) = -y(f') \ -y(f) = {xz} \ {z} = {x} ; |Ä(f', f)| = 1 = |Ä(f', f)| = count(f') = 1;

(f, f') = ({15}, {1245}) n'est pas une couverture;

(b) Pour f' = {12345}, count(f') = count({12345}) = 2 ;

Ä(f', f) = -y(f') \ -y(f) = {xyz} \ {z} = {xy} ; |Ä(f', f)| = 2 = |Ä(f', f)| = count(f') ; (f, f') = ({15}, {12345}) est une couverture; Imsucc(f) = Imsucc({15}) = {{12345}} ;

count(f') = 0;

6. f = {1245}; S(f) = S({1245}) = {{1245} U {1234}} = {{12345}} ;

calcule de count(f') pour f' E S(f)

(a) Pour f' = {12345}, count(f') = count({12345}) = 2 + 1 = 3;

Ä(f', f) = -y(f') \ -y(f) = {xyz} \ {xz} = {y} ;

|Ä(f', f)| = 1 = |Ä(f', f)| = count(f') = 1;

(f, f') = ({1245}, {12345}) n'est pas une couverture;

On va récupèrer toutes les informations necessaires pour pouvoir déssiner le graphe

de couverture G = (F,=) du treillis.

Les couvertures (f, f') ou successeurs immédiats sont les suivants :

1.(0, {245}) est une couverture; Imsucc(0) = {{245}};

2.(0, {1234}) est une couverture; Imsucc(0) = {{245}, {1234}};

3.(0, {15}) est une couverture; Imsucc(0) = {{245}, {1234}, {15}};

26

FIGURE 3.2 - le graphe de couverture G = (F, Ç)

4. ({245}, {12345}) est une couverture; Imsucc({245}) = {{12345}};

5. ({1234}, {1245}) est une couverture; Imsucc({1234}) = {{1245}};

6. ({15}, {1245}) est une couverture; Imsucc({15}) = {{12345}};

7. ({12345}, {1245}) est une couverture; Imsucc({1245}) = {{12345}}; On récupère aussi F et ã(F) tels que :

F = {ø, {245}, {1234}, {12345}, {15}, {1245}}

et

ã(F) = {ø, {x}, {y}, {xyz}, {z}, {xz}};

Ainsi nous obtenons le graphe de couverture G = (F, Ç) presenté à la figure 3.2.

3.2 Algorithme de construction de treillis de concepts

Un concept étant un regroupement maximal d'objets possédant des caractéristiques communes, l'algorithme de construction de treillis de concepts construit un treillis dans lequel chaque concepts formel est décoré par l'ensemble de générateurs minimaux qui lui est associé. Les « input »sont représentés sous forme de contexte formel. Un contexte est représenté sous forme d'un tableau dont les objets X sont en lignes et les attributs Y en colonnes.[5]

3.2.1 Définitions

Définition 1 (Contexte d'extraction ou contexte formel)

Un contexte d'extraction ou formel est un triplet K = (X, Y, R) où X et Y sont respectivement l'ensemble d'objets et celui d'attributs et R Ç X X Y une relation binaire telle que ?(x, y) E R, y est un attribut de l'objet x.

Définition 2 (Contexte binaire)

Un contexte K = (X, Y, R) est dit binaire si les éléments de Y ont uniquement deux valeurs (0 ou 1) qui indique l'absence ou la présence de l'attribut concerné respectivement.

27

Définition 3 (Fermeture des ensembles)

Soient deux fonctions g et h qui nous serviront à calculer la fermeture des sous ensembles d'objets O et d'attributs A. Ainsi, les ensembles fermés sont définis comme suit :

O» = h(g(O))

A» = g(h(A))

Alors, un ensemble est dit fermé s'il est égal à sa fermeture.[4]

Définition 4 (Concept formel)

Un concept formel est une paire Ck = (O, A) avec O C X et A C Y tel que :

O = {x E X/Va E A, (x, a) E R} où O = h(A)

est l'extension ou objets couverts, elle est notée Ext(Ck).

A = {y E Y/Vo E O,(o,y) E R} où A = g(O)

est l'intention ou attributs partagés, elle est notée Int(Ck).[11] Définition 5 (Ordre sur les concepts)

Soient C1 = (O1, A1) et C2 = (O2, A2) deux concepts, une relation d'ordre notée « < »peut être définie sur ces deux concepts de la manière suivante :

(O1, A1) < (O2, A2) = O1 C O2 et A1 D A2

C1 < C2 = (O1, A1) est un sous-concept de (O2, A2) et
(O2, A2)est un sur-concept de(O1, A1).

Définition 6 (Ordre lexicographique)

La plupart des méthodes proposées dans les fouilles des données définissent un ordre total sur les itemsets ou sous ensemble d'attributs. Cet ordre total pouvant s'étendre en un ordre lexicographique, permet à la fois d'éviter des redondances des calculs en parcourant chaque itemset au plus une seule fois, mais également de stocker efficacement les itemsets dans des structures de données appropriées. Ainsi, on étend l'ordre total sur X en un ordre lexicographique comme suit :

Soient A, B deux sous-ensembles distincts d'un ensemble X totalement ordonné. On dit que A est inférieur lexicographiquement à B si le plus petit élément qui distingue A et B appartient à A. On note « A _-<lex B »et on lit « A est inférieur lexicographiquement à B. »[5]

Définition 7 (Arbre lexicographique)

Soit une liste de mots ordonnée. Si l'ordre sur les mots est obtenu comme un ordre lexicographique à partir des composants des mots, alors on peut représenter un ensemble de mots en utilisant la structure d'arbre de recherche lexicographique.

Soit le dictionnaire constitué des mots suivants : AI, AIL, AILE, AINE, ALE, BAT, BAS ; où à chaque mot du dictionnaire on adjoindra un chemin de la racine à un noeud comme representé dans l'arbre lexicographique de la Figure 3.3 :[5]

28

FIGURE 3.3 - Arbre lexicographique associé au dictionnaire Définition 8 (Treillis de Galois)

La notion de treillis de Galois ou treillis de concepts est definie sur l'ensemble des concepts L

L = {(o, a) E P(X) x P(Y )/O = h(A), A = g(O)} muni de la relation d'ordre <. On le note T = (L, <).[1][11]

Définition 9 (Face)

Soit Ck = (O, A) un concept formel et soit predi(Ck) le ième prédécesseur immédiat de Ck. La ième face du concept formel Ck correspond à la différence entre son intention et l'intention de son ième prédécesseur. Soit p le nombre de prédécesseurs immédiats du concept formel Ck et _FCk la famille des faces. La famille des faces du concept formel Ck est exprimée par la relation suivante[5] :

FCk = {A - Intent(predi(Ck))}, i E {1, ..., p}. Définition 10 (Bloqueur)

Soit G = {G1, ..., G_n} une famille de n ensembles, un bloqueur B de la famille de G est un ensemble où son intersection avec tout ensemble Gi E G est non vide.[12]

Définition 11 (Bloqueur minimal)

Un bloqueur B est dit minimal s'il n'existe pas B1 C B et VGi E G, B1f1Gi =6 0.[5] Définition 12 (Générateur minimal)

Soit Ck un concept formel et _FCk sa famille de faces. L'ensemble G des générateurs minimaux associés à l'intention A du concept formel Ck, correspond aux bloqueurs minimaux associés à la famille de ses faces FCk.

D'une manière équivalente, soit Y un ensemble d'attribut, un itemset a C_ Y est appelé générateur minimal d'un concept formel Ck = (O, A), si et seulement si h(a) = A et , a1 C a tels que h(a1) = A.[5][12]

29

FIGURE 3.4 - Matrice decrivant la relation R du contexte K = (X, Y, R) Exemple 2

Soit une application permettant de calculer une correspondance de galois, un

concept et les opérateurs de fermeture à partir d'une matrice binaire (Figure 3.4)

générée par un contexte K = (X, Y, R)

X = {1,2,3,4,5,6,7} et Y = {a,b,c,d,e,f,g,h};

g({1,2,3,4}) = {a,b,c,d} et h({a,b,c,d}) = {1,2,3,4}

On constate que ({1, 2, 3, 4}, {a, b, c, d}) est un concept; alors que ({1, 2}, {e, f})

ne l'est pas parce que :

g({1, 2}) = {a, b, c, d, e, f} et h({e, f}) = {1, 2}

Si X = {2, 4, 5} alors g(X) = {a, b, d}

X» = {1, 2, 3,4, 5} = h(g(X))

Si X = {1,5} alors g(X) = {a,b,d,e,g}; X» = {1,3,5}

Si Y = {a}, alors h(Y ) = {1, 2, 3, 4, 5, 6, 7}; Y » = {a}

Si Y = {a,c}, alors h(Y ) = {1, 2, 3, 4, 6, 7}; Y » = {a,c}

Seuls les ensembles {a} et {a, c} sont fermés.

3.2.2 Algorithme Genall

L'algorithme « Genall »élaboré par Ben Tekaya et al. construit le treillis dans lequel chaque concept formel est décoré par l'ensemble de générateurs minimaux qui lui est associé. Les données d'entrées sont sous forme de contexte d'extraction et en sortie nous aurons l'arbre lexicographique de la famille F des concepts formels Ck, la liste ImmSucc des successeurs immédiats du concept Ck ainsi que la liste des générateurs minimaux du concept.[12]

1. Algorithme Genall

Entrée Le contexte d'extraction K = (X, Y, R)

Sortie Arbre lexicographique de F, ImmSucc, Liste - gen

Début

// Initialiser la famille des concepts à l'ensemble des attributs

2. F = (ø,Y )

3. Pour chaque tuple t ? K Faire

// Initialiser la liste de l'ensemble des concepts trouvés dans une itération

4. L = ø

30

5. Pour chaque concept Ck E F Faire

6. C.intent = Ck.intent f1 t.items

7. Si C.intent E6 F Alors // Nouveau concept

8. F=FUC

9. C.extent = Ck.extent U t.TID

10. C.ImmSucc = {t} U {Ck} \ {C}

11. L=LUC

12. Sinon

// Concept existant

13. C.extent = C.extent U Ck.extent U t.TID

14. Si C E6L Alors

15. L=LUC

16. Fin Si

17. C.LP = {t} U {Ck} \ {C} // Mise à jour de C.ImmmSucc

18. Pour chaque Pk E C.LP Faire

19. Pour chaque Succ E C.ImmSucc Faire

20. Compare - Concept(Succ, Pk)

21. Fin Pour

22. Fin Pour

23. Fin Si

24. Fin Pour

// déterminer l'ensemble des successeurs immédiats et les générateurs minimaux

25. Pour chaque concept Ck E L Faire

26. Ck.ImmSucc = Find - Succ(Ck, L)

27. Pour chaque Succ E Ck.ImmSucc Faire // Calcul de la face du successeur immédiat

28. face = Succ \ Ck

29. Pour chaque facek E Succ.liste - face Faire

30. Succ.liste - face = Compare - Face(face, facek)

31. Fin Pour

32. Fin Pour

33. Fin Pour

34. Fin Pour Fin

Sont presentés dans la table 3.1, les notations utilisées dans l'algorithme GE-NALL Cet algorithme est scindé deux partie : D'une part il génère les concepts formels et de l'autre, il raffine la liste des successeurs immédiats et détermine les générateurs minimaux.[5]

31

TABLE 3.1 - Notation utilisée dans l'algorithme GENALL Génération des concepts formels

Cette génération est montrée à partir de la ligne 4 jusqu'à la ligne 22. Dans cette étape, nous commençons par initialiser la liste L avec l'ensemble vide (ligne 4). Cette liste sera utile pour la mise à jour de l'ensemble des successeurs immédiats de chaque concept formel trouvé dans une itération.

Pour calculer l'ensemble des concepts formels, nous effectuons une intersection entre l'intension de chaque concept formel de la famille F et chaque transaction de la base de données. Il en résulte deux cas:

1. L'intention n'existe pas dans la famille F : Dans ce cas, un nouveau concept formel est trouvé et doit être ajouté à la famille F. Ensuite l'exten-sion du concept est calculée (ligne 9). Les successeurs immédiats potentiels de ce nouveau concept formel sont alors initialisés avec les concepts formels utilisés(ligne 10). En effet, pour déterminer le successeur immédiat potentiel d'un concept formel, nous devrions distinguer deux cas particuliers :

- Si le concept formel produit est égal à la transaction, alors seul le concept formel utilisé dans cette intersection peut être un successeur immédiat. En effet un concept formel ne peut pas être égal à son successeur immédiat;

- Sinon la transaction et le concept formel sont considérés comme successeurs immédiats potentiels du concept formel.

Ensuite, ce nouveau concept formel est ajouté à la liste L(ligne 11).

2. L'intention existe déjà dans la famille F : Dans ce cas l'extension du concept formel (ligne 13) doit être mise à jour, et nous vérifions si le concept existe déjà dans la liste L (14-15). Le but étant de mettre à jour la liste des successeurs immédiats ImmSucc du concept formel, et étant donné que nous maintenons, pour chaque concept formel, une liste ImmSucc, nous allons construire une liste LP devant contenir les concepts formels utilisés. Cette liste est nécessaire pour pouvoir faire les comparaisons et mettre à jour la liste des ImmSucc. En effet pour chaque élément dans LP et pour chaque élément dans la liste des ImmSucc, nous examinons l'inclusion de ces concepts formels en utilisant la fonction Compare-concept(ligne 20). Cette fonction est appliquée

32

pour mettre à jour la liste ImmSucc des concepts formels considérés. Ainsi cette liste ne peut subir des modifications que dans les deux cas suivants :

(a) L'élément de LP est plus petit (en terme d'inclusion) par rapport à un élément de ImmSucc. Dans ce cas, l'ancien successeur sera remplacé par le nouveau successeur.

(b) les deux concepts sont incomparables : un nouveau successeur sera alors ajouté à la liste ImmSucc du concept formel en considération.

Raffinement de la liste des successeurs immédiats et la détermination des généateurs minimaux

Les concepts formels trouvés dans une itération, représentent une branche du treillis, cela veut dire que pour chaque concept formel (excepté le plus grand), nous trouvons un autre concept formel calculé dans cette même itération, qui le couvre. Pour cela, nous parcourons la liste L des concepts formels trouvés dans l'itération et pour chacun des concepts de la liste L, nous faisons appel à la fonction Find - Succ (ligne 26). Cette fonction est basée sur le fait qu'un concept formel de cardinalité n(c'est-à-dire la longueur de son intention est égal à n) soit au moins couvert par un concept de cardinalité (n + 1) ou plus. Pour cela, étant donné que la liste L est triée selon l'ordre croissant de la cadinalité de l'intention, nous cherchons pour chaque concept formel de cardinalité n, un concept formel qui le couvre dans la liste de cardinalité (n + 1). En cas de défaut, nous passons à la cardinalité (n + 2), et ainsi de suite jusqu'à ce que nous trouvons un concept qui le couvre. Par la suite, nous allons comparer ces différents concepts formels pour une mise à jour de la liste de ImmSucc.

Une fois que la liste des successeurs immédiats du concept formel courant est établie, nous parcourons cette liste et pour chaque successeur immédiat nous devons calculer l'ensemble de ses générateurs minimaux.Comment obtenir ce résultat?

Pour y arriver, nous allons d'abord calculer les faces associées aux successeurs immédiats (ligne 28) et ensuite nous les comparons à la liste des faces correspondante en faisant appel à la fonction Compare - face (ligne 30). L'ensemble de faces Liste - face(successeur immédiat) d'un concept formel ne peut être modifié que dans les deux cas suivants :

1. face est plus petit (en terme d'inclusion) que l'élément Liste - face : Dans ce cas nous calculons Compare - face, et nous remplaçons l'ancienne face par la nouvelle. Si Compare - face n'existe pas dans une des faces du concept formel, alors nous supprimons chaque générateur contenant cette différence. Cette suppression est fondée étant donné qu'un attribut qui n'existe pas dans les faces ne peut exister les générateurs.

2. face est incomparable avec toutes les faces Liste - face : Dans ce cas, nous ajoutons cette face à la liste - face.[12]

Exemple 3 Soit le contexte d'extraction illustré à la table 3.2 avec l'ensemble d'attri-buts I = {a, b, c, d, e, f, g, h, i} et lensemble de transactions du contexte d'extraction, dénotées de 1 à 8.

Considerons la transaction 4 = {acghi}, la famille F, après traitement des trois premières itérations est comme suit :

F = {(abcdefghi, Ø), (abg, 123), (abgh, 23), (abcgh, 3)}.

L'ensemble des successeurs immédiats de chaque concept est comme suit :

33

TABLE 3.2 - Le contexte d'extraction K

{abg}.ImmSucc = {{abgh}};

{abgh}.ImmSucc = {{abcgh}};

{abcgh}.ImmSucc = {{abcdefghi}}.

Première étape : Génération des concepts formels

Chaque concept formel de F est manipulé individuellement. Par conséquent, pour

le premier concept formel C1, nous aurons C1.intent = {abcdefghi} l'application de

l'opérateur d'intersection avec la quatrième transaction donne un nouveau concept

formel avec une intention égale à {acghi}. L'extension de ce nouveau concept formel

sera calculée dans les lignes qui suivent. Ainsi, la famille F est mise à jour en lui

ajoutant cette nouvelle intention C5 qu'on vient de calculer:

F = {(abcdefghi, 0), (abg, 123), (abgh, 23), (abcgh, 3), (acghi, 4)}.

L'ensemble des successeurs immédiats de C5 est initialisé avec C1 et l'extension

de C5 est initialisé avec l'union de C1.extent et l'identificateur de la transaction

considéré. Par conséquent, C5.extent = {4} et C5.ImmSucc = {abcdefghi} et la

liste L et initialisé avec {acghi}

Le processus mentionné ci-dessus est répété pour tous les concepts formels existants

dans la famille F.

A la fin de cette première étape, nous obtenons la famille des concepts formels mises

à jour:

F = {(abcdefghi, 0), (abg, 123), (abgh, 23), (abcgh, 3), (acghi, 4), (ag, 1234), (agh, 234), (acgh, 34)}

Ainsi la liste des successeurs immédiats de chaque concept formel est la suivante :

{ag}.ImmSucc = {{abg}, {acghi}}

{agh}.ImmSucc = {{abgh}, {acghi}}

{acgh}.ImmSucc = {{abcgh}, {acghi}}

{acghi}.ImmSucc = {{abcdefghi}}

La liste L contient toutes les intentions des concept formels découverts dans l'itéra-

tion courante :

L = {{ag}, {agh}, {acgh}, {acghi}}

Raffinnement de la liste des successeurs immédiats et détermination des

générateurs minimaux

Pour le premier concept de la liste L, nous avons {ag}.ImmSucc = {{abg}, {acghi}}.

L'intention du concept formel {agh} couvre {ag} et nous avons {agh} Ç {acghi}.

Nous allons donc remplacer {acghi} par {agh} dans {ag}.ImmSucc. Ainsi, l'an-

cien arc liant {ag} à {acghi} est un lien transitif. Par conséquent {ag}.ImmSucc =

34

FIGURE 3.5 - Treillis des concepts formels, extrait du contexte K, décoré par quelques générateurs minimaux

{{abg}, {agh}}

Pour chaque successeur immédiat de {ag}, nous devons calculer liste - face et liste - gen qui devra contenir la liste des générateurs minimaux, en utilisant la fonction Compare - face. Il vient donc que :

1. {abg}.liste - face = {b} et {abg}.liste - gen = {b}

2. {agh}.liste - face = {h} et {agh}.liste - gen = {h}

Après le traitement de {ag}.ImmSucc, nous devons manipuler la liste de succes-

seurs du concept formel dont l'intention est égal à {agh} c'est-à-dire {agh}.ImmSucc.

Ainsi nous avons {agh}.ImmSucc = {{abgh}, {acghi}}. Commençons par raffiner

la liste des successeurs immédiats {agh}.ImmSucc. Nous constatons que {acgh} Ç

{acghi}. Alors nous devons remplacer {acghi} par {acgh} dans {agh}.ImmSucc.

Ainsi les successeurs immédiats de {agh} sont {agh}.ImmSucc = {{abgh}, {acgh}}.

Après le calcul de liste - face de {abgh} nous obtenons :

{abgh}.liste - face = {h} U {b}. Etant donné que {h} n {b} = Ø, alors {b}

ne peut pas être un bloqueur pour l'ensemble des faces {{h}, {b}}. Raison pour

laquelle nous remplacerons la liste des générateurs minimaux par {bh} c'est-à-dire

{abgh}.liste - gen = {bh}

Le processus de raffinnement tels que decrit ci-dessus est appliqué sur {acghi}.ImmSucc

Ainsi:

{acghi}.ImmSucc = {{abcdefghi}};

{abcdefghi}.liste - face = {defi} U {bdef};

{abcdefghi}.liste - gen = {defbi}

Le processus de génération et de raffinement sont repetés pour toute les transactions

restantes. La figure 3.4 décrit le treillis des concepts formels associé au contexte d'ex-

traction K presenté dans la table 3.2. Notons que certains générateurs minimaux

sont indiqués par des flèches, décorant les noeuds des concepts formels.[6]

35

3.2.3 Etude de la compléxité

Dans cette section, nous allons étudier la compléxité, dans le pire des cas, de

l'algorithme GENALL. Soit O l'ensemble de transaction d'une base, Y l'ensemble

d'attributs de la base et F l'ensemble des concepts trouvés. L'étude de la boucle :

Pour(ligne 5) donne:

- L'instruction 6 s'effectue en O(|Y |) étant donné que dans le pire des cas, nous

allons effectuer une intersection avec tous les attributs de la base.

- L'instruction 7 s'effectue en O(|Y |) puisqu'on ne peut avoir au maximum que

|Y | branches.

- L'instruction 13 peut se faire dans le pire des cas en O(|O|).

- La recherche dans la liste L (ligne 14) est réalisé en O(|F |

2 ) dans le pire de cas.

En effet, une iteration peut donner autant de nouveau concept qu'il y a dans

|F |.

- La boucle Pour(ligne 18) peut se repeter au maximum deux fois.

- Celle de la ligne 19 se répète |ImmSucc| fois.

- La fonction Compare - concept se fait O(|Y |)

De ce fait la complexité des instructions 5 - 23 est O(|F | + 2|Y | + |O| + |F |

2 +

2|Y |.|ImmSucc|). L'instruction 25 s'effectue en O(|ImmSucc|), alors que la

complexité de l'instruction 28 vaut O(|Y | + |liste - gen|). Par conséquent la

complexité du bloc des instructions (25 - 34) vaut :

O(|F |

2 * |ImmSucc|².(|Y | + |liste - gen|)).

Etant donné que notre algorithme se répète |K| fois (la première boucle Pour

de la ligne 3 ). Il vient alors que la compléxité totale de l'algorithme est :

O(|K|.|F |[1 2 * |ImmSucc|².(|Y | + |liste - gen|) + |K| + |F |

2 ]).[13]

3.3 Algorithme de génération de treillis quelconques

Dans cette section, nous présenterons un algorithme permettant de vérifier si un graphe orienté sans circuit represente un treillis. Mais avant cela, nous vous présentons quelques définitions qui seront utilisées par la suite.

Soit X un ensemble fini et = une relation d'ordre définie sur X ; (i.e refléxive, antisymétrique et transitive). On note par P = (X, =P) un ensemble sur lequel on a défini un ordre. Alors:

- Deux éléments x et y de X sont dits comparables si x =P y ou y =P x, sinon ils sont dits incomparables.

- Un ordre total ou chaîne est un ensemble d' éléments deux à deux comparables.

- Q = (X, =Q) est une extension de P = (X, =P) si x =P y = x =Q y pour tout x,y ? X.

- Un ordre total L = (X, =L) est une extension lineaire de P = (X, =P) si L est une extension de P.

- Un ensemble A muni de deux lois + et * est appelé anneau si :

1. (A, +) est un groupe Abélien;

2. La loi * est associative;

36

3. La loi * est distributive par rapport à la loi +

Si de plus, la loi interne * est commutative alors l'anneau sera dit commutatif.

- Soit A un anneau commutatif. un sous ensemble S c A est un idéal si :

1. a + a' E S pour tout a, a' E S ;

2. r.a E S pour tout a E S et r E A

En d'autres termes, un "Idéal" est un sous ensemble fermé pour l'addition et stable pour la multiplication par un élément quelconque de A

- Un Idéal I d'un ordre P, est une Partie héréditaire supérieure ou filtre ; c'est-à-dire I C X tel que si y E I et x E X vérifient x <P y alors x E I[50]

Propriété 1 Soit T = (X, <) un treillis et x E X. Si a < b alors a V x < b V x. Preuve Soientz,tEX,z<zVtett<tVz.Puisquea<bonaaVb=bet (xVa)Vb=xVbparconséquent:xVa<xVb.

Soit ô = x1, x2, ...x_n une extension linéaire de G. Pour tout k E [1, n] il vient que Yk-1 = xk-1, ..., x_n est un filtre. Ainsi l'algorithme devra vérifier si _Yk-1 est un sup-demi-treillis pour k variant de n à 2 ; il se base sur le lemme suivant :

Lemme 1 Soit G = (X, U) un graphe orienté sans circuit et Yk-1 = xk-1, ..., x_n tel que tout couple d'éléments de _Yk-1 admet une borne supérieure.

Alors pour tout z E _Yk-1, xk V z existe, si et seulement si y V z tel que y E ImmSucc(xk) admet un élément minimal w = y V z.

Preuve Si pour z E _Yk-1, xk V z existe, alors pour tout y E ImmSucc(xk) on a : xk V y > xk V z.

Puisque xk V z > xk, alors il existe t0 < xk. De ce qui précède, on en déduit que xk V z > z et donc xk V z > t0 V z.

Si pour z E _Yk-1 il existe t0 E ImmSucc(xk) tel que w = t0 V z, soit un élément minimal de y V z tel que y E ImmSucc(xk) alors w > z et w > xk

Soit v E X tel que v > z et v > xk. Alors v E _Yk-1 et il existe t0 E ImmSucc(xk) tel que v > t0 et puisque v > t0 V z > w > xk V z, il vient alors que w = xk V z.[6]

3.3.1 Algorithme de L.Nourine

L'algorithme de Lhouari Nourine reconnait si un graphe G = (X, U) est le graphe

de couverture d'un treillis.[5]

Algorithme Reconnaissance d'un treillis.

Donnée : La reduction transitive d'un graphe sans circuits G = (X, U), donnée par

sa liste d'adjacence de prédécesseurs.

Résultat : G est-il le graphe de couverture d'un treillis ?

Début

// Calculer une extension linéaire ô = x1, x2, ...x_n de G

Y = (x_n) est un sup-demi-treillis.

Pour i = n - 1,2 faire

le calcul des bornes supérieurs entre xi et ses successeurs.

Pour y E]xi, x_n] faire

xi V y = y ;

marquer y.

Fin pour

// Calcul des bornes supérieures entre xi et les elements qui lui sont incomparables.

Pour j = n, i + 1 faire

37

FIGURE 3.6 - Un ordre qui ne représente pas un treillis

Si x est non marqué alors

x est incomparable à xi

Si w = min(xi ? z) tel que z ? ImmSucc(xi) existe alors

xi ? x = w.

Sinon

G n'est pas la graphe de couverture d'un treillis.

Fin si

Fin si

Fin pour

Fin pour

Fin

3.3.2 Etude de la compléxité

Le bloc 1 de l'algorithme calcule la borne supérieur entre xi et ses successeurs. Pour tout successeur z de xi on a : xi ? z = z.. Ainsi la compléxité de ce bloc vaut O(|U|)

Le bloc 2 de l'algorithme calcule la borne supérieur entre xi et les éléments qui lui sont incomparables. L'algorithme calcule l'ensemble W des bornes supérieures entre les successeurs immédiats de xi et l'élément z qui lui est incomparable. Ensuite, l'algorithme teste si cet ensemble possède un élément minimum. Ainsi le calcul de W coûte O(|ImmSucc(xi)|) et la vérification qu'il possède un élément minimum revient à vérifier si l'élément le plus petit de W est un élément minimum.

Le test de comparabilité se fait en O(1) en utilisant les bornes supérieurs déjà calculées, la compléxité totale est alors de l'ordre de O(|X|.|ImmSucc(xi)|) soit O(|X|.|U|).[5]

Exemple 4 Soit le diagramme figure(3.6) ci-dessus, essayons d'appliquer l'algo-rithme à cet exemple pour bien comprendre les différentes étapes et instructions utilisées dans celui-ci. On pose :

Succ(xi) : L'ensemble de tous les successeurs de xi dans G.

Inc(xi) : L'ensemble de tous les successeurs de xi dans r qui lui sont incomparables

38

dans G.

ImmSucc(xi) : L'ensemble des successeurs immédiats de xi.

B(a) = {a V y tel que y E ImmSucc(xi)} avec a = Inc(xi)

Soit r = a, b, c, d, e, f, g une extension lineaire. L'algorithme demarre à partir de f

avant dernier élément de l'extension linéaire.

Pour f :

Succ(f) = {g};

Inc(f) = Ø;

Pour e :

Succ(e) = {g};

Inc(e) = {f};

ImmSucc(e) = {g};

B(f) = f V g = {g};

minB(f) = g ;

Pourd :

Succ(d) = {g};

Inc(d) = {e, f};

ImmSucc(d) = {g};

B(e) = e V g = {g};

minB(e) = g ;

B(f) = f V g = {g};

minB(f) = g ;

Pourc :

Succ(c) = {d,e,g};

Inc(c) = {f};

ImmSucc(c) = {d, e};

B(f) = f V d,f V e = {g};

minB(f) = g ;

Pourb :

Succ(b) = {d,e,f,g};

Inc(b) = {c};

ImmSucc(b) = {d, e, f};

B(c) = {c V d,c V e,c V f} = {d,e,g};

minB(c) n'existe pas, car d et e sont incomparables. D'où G n'est pas le graphe

de couverture d'un treillis.

Deuxième partie

39

Application de la méthode

40

Chapitre 4

Fouille de données et navigation dans

un treillis

L

'Exploration de données, connue aussi sous l'expression de fouille de données, forage de données, prospection de données ou encore data mining a pour objectif d'extraire un savoir ou une connaissance à partir de grandes quantités de données par des méthodes appropriées.

4.1 Bref aperçu sur les fouilles de données

Le data mining, dans sa forme et comprehension actuelle, à la fois comme champ scientifique et industriel, est apparu au debut des années 90. Cette émergence n'est pas le fruit du hasard mais le résultat de la combinaison de nombreux facteur à la fois technologique mais aussi économiques. Cette discipline se présente comme une nécessité imposée par le besoin des entreprises de valoriser les données qu'elles accumulent dans leurs bases de données.

En effet, le développement des capacités de stockage et les vitesses de transmission des données ont conduit les utilisateurs à accumuler d'enormes quantités d'informations dans leurs bases de données. Alors, une question reste, cependant, poseé : Que doit-on faire avec des données coûteuses à collecter et à conserver? Dès lors est né l'analyse de données ainsi que ses différentes méthodes que l'on retrouve dans différents domaines sous des formulations différentes et ayant une caractéristique commune à la fois d'analyser des données qui s'organisent sous forme tabulaire (Objets × attributs).[14]

Une confusion subsiste encore entre Data mining qui signifie en anglais « fouille de données » et Knowledge discovery in data bases (KDD) que nous appelons en français « Extraction des connaissances à partir des données(ECD) ». Le data mining est l'un des maillons de la chaîne de traitement pour la découverte des connaissances à partir des données. Sous forme imagée, nous pourrions dire que l'ECD est un véhicule dont le data mining est le moteur.

Le data mining est l'art d'extraire des connaissances à partir des données. Elles peuvent aussi être stockées dans des entrepôts de données[1]. En effet, un entrepot de données ou Data warehouse est une collection de données provenant des sources differentes et groupées en un seul endroit afin de rendre ses informations facilement accessible par l'utilisateur[15]. Le data mining ne se limite pas seulement au traitement des données mais vers les années 2010, ses spécialisations techniques telles que

41

la fouille d'images ou image mining (section 4.1.1), la fouille de textes ou text mining (section 4.1.2), la fouille du web ou web data mining (section 4.1.3),... attirèrent l'attention de plusieurs chercheurs.

4.1.1 La fouille d'images

Les données sous forme d'images peuvent être traitées par les techniques de data mining en vue d'extraire des connaissances. Celles-ci permettraient d'identifier, de reconnaître ou de classer automatiquement des bases volumineuses d'images.

Pour être exploitées par des méthodes de data mining, les images doivent subir une serie de pré-traitement en vue d'obtenir des tabeaux numériques. Les principales étapes du pré-traitement sont les suivantes :

1. Transformation, filtrage et mise en forme Les usagers sont souvent conduits à modifier les images initiales pour faire ressortir certaines caractéristiques qu'ils considèrent comme importantes. Par exemple, accentuer le contraste sur l'ensemble des images.

2. Extraction de caractéristiques Pour être traitées par des techniques de data mining, les images doivent être representées sous forme tabulaire : Chaque ligne étant une image et chaque colonne une caractéristique sur l'image.

3. Mise en oeuvre des méthodes de data mining A l'issue de l'étape précédente, le corpus d'image est transformé en un tableau de données numériques sur lesquelles les méthodes d'explorations de données peuvent être appliquées.[1][14]

4.1.2 La fouille de textes

Les données textuelles disponibles sur support infomatique représentent près de 70 pourcent des données numériques et se retrouvent sous forme de rapport, de courriers, de publications, de manuels, etc.

La fouille de données textuelles est un ensemble de traitements informatiques consistant à extraire des connaissances selon un critère de similarité. On y distingue deux niveau de traitement :

1. Le premier niveau porte sur la recherche d'information dans les bases de données textuelles. Par exemple rechercher les textes qui contiennent les mots X et Y ou Z. Grâce au developpement des technologies du traitement de la langue naturelle, on peut également formuler des requêtes plus ou moins complexes contenant des expressions ou même des textes.

2. Le segond niveau porte sur l'extraction de connaissences à partir d'une base de données textuelles. En effet, certaines recherches peuvent paraître extrêmement difficiles pour l'utilisateur car il ne saura toujours pas comment formuler la bonne requête en vue d'avoir des réponses pertinentes pour sa recherche. Par exemple comment rechercher dans un document les textes qui incitent à la violence dans les stades. Des tels réponses sont difficiles à trouver étant donné que ces textes peuvent ne contenir aucun des mots « violence » ou « stade ». C'est là qu'interviennent les méthodes de data mining qui peuvent aider l'usager à déterminer certaines règles qui permettent de reconnaître ces textes.[14][11][15]

42

FIGURE 4.1 - Chaîne d'extraction de connaissances

4.1.3 La fouille du web

Les réseaux électroniques, de l'intranet à internet, constitue une formidable source d'informations de par son large volume de données. Les interêts de fouiller dans ces données sont multiples et variés mais se heurtent à deux problématiques majeurs; l'une concernant « l'internaute » et l'autre concernant « le diffuseur » des informations.

- La problématique de l'internaute peut se résumer à celle de la recherche et de l'analyse d'informations pertinentes;

- La problématique du diffuseur ou propriétaire de sites web consiste à déterminer les différents profils d'internautes en fonction de leur parcours sur le site afin de pouvoir cibler ses offres, orienter son discours et donc proposer rapidement les informations rechérchées par des clients potentiels.

- les propriétaires de sites internet sont quant à eux intéresser par des visiteurs. A chaque passage sur les pages web, un internaute laisse ses traces. Outre la date et l'heure de la visite, le site hôte enregistre le numéro de la machine, le navigateur utilisé, l'ensemble de pages visitées, etc. En s'appuyant sur ces données, les techniques de data mining, text mining et d'image mining peuvent offrir des solutions intéressantes.[14][16]

4.2 Chaîne d'extraction des connaissances

L'extraction des connaissances a pour principal objectif d'extraire dans des grands volumes de données « des éléments de connaissances non triviaux et nouveaux pouvant avoir un sens et un intérêt pour être réutilisés ». Elle est composée de plusieurs étapes (figure 4.1) dont la principale est la fouille de données.[1][17][20]

1. Phase de consolidation de données

La consolidation de données est une étape de l'extraction de connaissance qui consiste à collecter les données. Ces données n'ont pas toujours le même format et la même structure. On peut avoir des textes, des pages web, des images, etc. La phase de consolidation cible ainsi l'espace de données qui va être exploré.

43

Le specialiste du data mining agit un peu à l'image du géologue qui définit aussi des zones de prospection étant persuadé que certaines régions seront probablement vite abandonnées car elles ne recèlent ou ne contiennent aucun ou peu de minerais. Ainsi cette étape met en oeuvre des requêtes ad hoc ou appropriée afin de recueillir des données potentiellement utiles selon le point de vue du spécialiste.

A l'issue de la phase de consolidation, l'analyste est en possession d'un stock de données contenant potentiellement l'information ou la connaissance recher-chée.F1]F14]F11]

2. La phase de pré-traitement de données

Les données issues des entrepôts ne sont pas nécessairement toutes exploitables par des techniques de fouille de données parce que la plupart des techniques utilisées ne traitent que des tableaux de données numériques. Ces tableaux associent à un objet(en ligne) un ensemble de valeurs d'attributs(en colonne). Des vocabulaires peuvent se différencier selon les domaines : Un objet peut également être appelé enregistrement, individu, observation,... alors qu'un attribut peut se dénommer caracteristique, champ, descripteur, etc.

Le pré-traitement permet de présenter les données de manière adaptée à la méthode de fouille de données qu'on devra utiliser. Elle regroupe différentes étapes :

- Integration de données Cette étape consiste à regrouper et à uniformiser les données provenant de plusieurs sources.

- Le nettoyage : Cette étape s'occupe de la gestion des doublons ainsi que des erreurs de saisie.

- Le traitement des valeurs maquantes ou aberrantes

Certaines données peuvent être absentes ou encore absurdes et peuvent ainsi gêner l'analyse. Cette étape permet donc de définir certaines régles ou principes afin de gérer ou même remplacer ces données maquantes ou illogiques.

- L'enrichissement des données : Dépassé l'étape de traitement des valeurs maquantes, il peut s'averer que certains attributs ne figurent toujours pas parmi les informations recherchées. Ainsi vient l'étape d'enrichessement qui consiste à ajouter des nouveaux attributs par combinaison d'attributs existants. Notons cependant que le processus d'extraction des connaissances n'est pas linéaire car il arrive aussi que l'on revienne, après analyse, rechercher des nouvelles données.

- Traitement de données complexes : Toutes les étapes ou méthodes de pré-traitement citées ci-haut, opèrent sur des tableaux de données lignes/colonnes. Or il peut arriver que les données sous études ne soient pas structurées de cette manière là. Par exemple, en fouille de texte, nous pouvons disposer d'un ensemble de textes de longueurs variées que nous devons ramener sous forme tabulaire. L'une des techniques consiste à recenser l'ensemble des mots de tout le corpus et d'en calculer la fréquence de chacun d'eux. On obtiendra ainsi un tableau codé. Mais le codage des textes fait généralement appel à des procedures plus élaborées s'appuyant sur la linguistique ou l'ontologie du domaine.F14]F11]

3. Phase de fouille de données

La fouille de données concerne le data mining dans son sens restreint et se situe au coeur même de l'extraction des connaissances. Elle est définie comme étant

44

un processus qui utilise une variété de méthodes d'analyse de données afin d'extraire des informations intéressantes et appropriées à partir de données. La classification des méthodes de fouille de données dépend d'une part, du but poursuivi dans l'analyse et d'autre part, de la nature et de la quantité de données considérées. En conséquence, elles sont groupées en deux classes principales :

- Méthodes prédictives : Ces méthodes ont pour objectif de rechercher à partir de données disponibles un modèle explicatif ou prédictif entre, d'une part, un attribut particulier à prédire et de l'autre, des attributs prédictifs. Il s'agira donc de prédire de nouvelles informations à partir de données, ou plus précisément de prédire les valeurs d'un attribut en fonction des autres attributs.

- Méthodes descriptives : L'objectif de ces méthodes est de permettre à l'ana-lyste d'avoir une compréhension synthétique de l'ensemble de ses données. Il s'agira de : décrire au mieux les données dans le but de les réduire ou de les résumer pour une meilleure manipulation; mettre en valeur des informations présentes mais cachées; décrire les associations entre attributs sous forme de règles; rassembler tous les objets similaires.[1][14][11]

La phase d'interprétation et d'evaluation des résultats fait appel aux techniques de visualisation permettant d'afficher les résultats d'une manière compréhensible par l'être humain.

En effet, on remarque un intérêt grandissant pour les méthodes de découverte de connaissances à partir des données généralement formalisées sous forme de règles d'associations. Ces méthodes issues, pour la plupart, de l'Analyse Formelle de Concepts et proposées en fouille de données, sont développées dans un objectif de prédic-tion(méthodes prédictives) ou de description(méthodes descriptives) et exploitent la structure du treillis de concepts, ou bien les règles d'associations qui les décrivent, et qui ont pour caractéristique commune de s'appliquer sur des données binaires. Par conséquent, la section suivante sera consacrée à l'Analyse Formelle de Concepts qui est une approche à la représentation des connaissances et qui définit le treillis de concepts(section 2.4.1) à partir des données binaires du types Objets× attri-buts.[14][11]

4.3 L'Analyse Formelle des Concepts

L'analyse formelle des concepts est une branche de la théorie des treillis qui permet la génération de concepts, de treillis de concepts et à partir de là, des règles d'associations. A cet effet, elle s'est avéré être un cadre théorique intéressant pour la fouille de données. Elle a été introduite par Wille en 1980 et appliquée à « l'acquisi-tion automatique de connaissances », elle a donc pour objectif d'étudier le problème de l'extraction et de la représentation des connaissances sous l'angle de la théorie mathématique des treillis.[19][11][1]

4.3.1 L'extraction de motifs fréquents

L'extraction de motifs fréquents est une technique très utilisée en fouille de données son objectif est de trouver les motifs que apparaissent fréquemment dans une

45

TABLE 4.1 - Exemple de base de données formelle

base de données formelle dont les valeurs sont des booleens indiquant la présence ou l'absence d'une proprieté.[11][14][16]

Définition 1(base de données formelle)

Une base de données formelle est la donnée d'un triplet O, P, R où :

1. O est un ensemble fini d'objets;

2. P est un ensemble fini de proprietés;

3. R est une relation sur OxP qui permet d'indiquer si un objet x a une proprieté P

Considérons la base de données formelle telle que montrée à la table 4.1 : Où

- O = {x1, x2, x3, x4, x5, x6};

- P = {a, b, c, d, e};

- xRp si et seulement si la ligne de x et la colonne de p se croisent sur un 1.[11]

Définition 2 (motif)

Un motif d'une base de données formelle (O, P, R) est un sous ensemble de P.On dit qu'un objet contient un motif si l'objet contient chacun des attributs du motif. La longueur d'un motif est le nombre d'attributs de ce motif. L'image d'un motif est des objets possédant ce motif. Ainsi l'ensemble de tous les motifs d'une base noté 2|P| est donc l'ensemble de partie de P.[11][19]

Un objet x ? O possède un motif in si ?p ? P, xRp. Pour la base de donnée montrée à la table 4.1 :

1. 1 motif de taille 0 : 0.

2. 5 motif de taille 1 : {a}, {b}, {c}, {d}et{e} ou pour simplifier l'écriture, on notera a, b, c, d, e.

3. 10 motif de taille 2 : ab, ac, ad, ae, bc, bd, be, cd, ce, ed.

4. 10 motif de taille 3 : abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.

5. 5 motif de taille 4 : abcd, abce, abde, acde, bcde

6. 1 motif de taille 5 : abcde

Ainsi on peut dire que x1 possède les motifs 0, a, c, d, ac, ad, cd, acd

On cherchera ensuite parmi l'ensemble de 2|^P| motifs ceux qui apparaissent fréquemment. Pour cela on va introduire les notions de connexion de Galois et de support d'un motif

46

Définition 3 (connexion de Galois)

Soient f et g deux fonctions définies par :[22][1]

f : 2^P -? 2O

in 7-? f(in) = {x ? O | x possède in}

g : 2^O -? 2P

X 7-? g(X) = {p ? P | ?x ? X,xRp}

f représente l'ensemble de tous les attributs communs à un groupe d'objets O (on parle d'intension) et g l'ensemble des objets qui possèdent tous les attributs de P (extension). Le couple (f, g) définit la connexion de Galois entre P et O associée à une base de donnée formelle (O, P, R). Les opérateurs de la fermeture de Galois sont définis par : h = f ? g et h^' = g ? f.

Le terme de connexion est motivé par le fait que la relation binaire R de la base de donnée formelle connecte chaque attribut à chaque objet et vice-verca.[6][11][1]

Définition 4 (support d'un motif)

Soit in ? 2|^P|, un motif. Le support de in est la proportion d'objets dans O qui possèdent le motif:

support: 2^P -? [0; 1]

in 7-? support(in) = |f(m)|

|O|

Exemple : soit la base de données (cfr table 4.1)

support(a) = 3 ₆, support(b) = 5 ₆, support(ab) = 2 ₆, support(P) = 1

Proprieté 1

Si in est un sous motif de in⁰ (in ? in⁰) alors support(in) = support(in⁰).

Le support mesure la fréquence d'un motif, plus il est élevé, plus le motif est fréquent. Ainsi le seuil d'un motif u₅ marque la différence entre ceux qui sont fréquents de ceux qui ne le sont pas.

Motif fréquent

Une observation o ? O supporte un motif in si tous les attributs de in apparaissent dans l'observation o. Un motif m est fréquent relativement à un support minimal minsup si support(m) = u₅. Avec u₅ le seuil( ou support minimal) qui est une valeur à partir de laquelle un motif sera fréquent ou non selon qu'il est supérieur ou non au seuil. [25][27]

4.3.2 Algorithme d'extraction des motifs fréquents

L'algorithme d'extraction des motifs fréquents, baptisé A-priori, est un algorithme d'exploration de données concu en 1994 par Rakesh Agrawal et Ramakrish-nan Sikrant. Il sert à parcourir l'ensemble 2|^P| de tous les motifs(ou items), à calculer leurs supports et à ne garder que les plus fréquents.

L1 = {a, b, c, e}

47

L'approche que nous allons décrire effectue une extraction par niveau selon le principe suivant : Tout d'abord, on commence par déterminer les motifs fréquents de taille 1; on note cet ensemble L1. Ensuite, on construit l'ensemble C2 des motifs fréquents candidats de taille 2 (ce sont tous les couples construits à partir des motifs fréquents de taille 1). On obtient ainsi la liste des motifs fréquents de taille 2 qu'on note par L2. On ne conservera, bien sûr, que les éléments de C2 dont le support est supérieur au seuil. On construit encore l'ensemble C3 des motifs fréquents candidats de taille 3 et on ne retient que ceux dont le support est supérieur au seuil, ce qui produit L3. On continue le processus jusqu'à ce que l'ensemble Li n'ait plus d'éléments.[16]

Cette approche s'appuie sur deux principes fondamentaux suivants(Principe de la décroissance du support)[51] :

1. Tout sous motif d'un motif fréquent est fréquent. (Si m' C_ m et support(m)> u_s, alors support(m')> u_s).

2. Tout sur-motif d'un motif non fréquent est non fréquent. (Si m' D m et sup-port(m)< u_s, alors support(m')< u_s).

Plus clairement on a l'algorithme suivant[17] :

Algorithme : Algorithme A-priori

Entrée :(O, P, 7Z) : Une base de donnée formelle ; u_s E [0; 1]

Sortie : L'ensemble des motifs fréquents de la base relativement au seuil u_s

Début

L1 -- liste des motifs dont le support est > u_s

i-1

répéter

i + +

à partir de _Li-1, déterminer l'ensemble Ci des motifs fréquents

candidats comprenant i motifs.

Li --

O

Pour tout motif m E Ci faire

si support(m) > u_s alors

ajouter m à Li

fin si

fin pour

jusque Li = O

Retourner _ui=1 Li

Fin

Nous allons simulé le déroulement de l'algorithme en considérant la base de donnée

formelle donnée à la table 4.1 pour un seuil u_s = ²₆.[51]

Génération de candidats de taille 1 :

C1 = {a,b,c,d,e}

dont le support respectif est :	3	5	5	1 6 et	5
D'où	6;	6;	6;		6

48

Génération de candidats de taille 2 : Combiner 2 à 2 les candidats de taille 1 de L1

C2 = {ab, ac, ae, bc, be, ce}

dont le support respectif est :

4

6

2324 5

₆' ₆' ₆' 6, ₆ et

Ainsi L2 = C2 parce que tous les motifs de C2 sont fréquents.

Génération de candidats de taille 3 : Combiner 2 à 2 les candidats de taille 2 de L2

N.B: Nous ne considérons que les motifs dont la taille vaut 3.

C3 = {abc, abe, ace, bce}

le support respectif est :

2

2

2

4

_{6' 6' 6'} 6

Tous les motifs sont fréquents, d'où L3 = C3 Génération de candidats de taille 4 :

2

6

C4 = {abce} le support vaut

On a : L4 = C4 pour la même raison que précédemment. Génération de candidats de taille 5 :

C5 = O d'où L5 = O

L'algorithme retourne ainsi l'ensemble des motifs fréquents :

L = L1 ? L2 ? L3 ? L4 ? L5

Remarque 1

Le déroulement de cet algorithme est similaire au parcours du treillis des parties de P ordonnées pour l'inclusion. Supposons que P = {a, b, c}. Le treillis des parties de P, comme illustré à la figure 4.2, est parcouru par niveau croissant à partir du niveau j = 1. Quand un motif n'est pas fréquent, tous ses super-motifs sont non fréquents. Exemple du motif c qui n'est pas fréquent(il a été barré), et par conséquent, aucun de ses super-motifs n'est considéré. Cela nous permet d'optimiser l'accès à la base de donnée [51].

Notons que la valeur du seuil _u,9 est fixé par l'analyste. Celui-ci peut suivre une approche itérative en fixant un seuil au départ, et en fonction du résutat mais aussi de l'objectif poursuivi, changera la valeur du seuil.

4.3.3 Extraction de règles d'associations

Dans cette section nous vous présenterons le concept de règles d'associations dont la contribution à l'émergence du data mining, en tant que domaine scientifique à part entier, est non négligeable.

49

FIGURE 4.2 - Exemple de treillis des parties ordonnées par inclusion

4.3.4 Règles d'association

Un gérant d'un super marché a observé que les clients qui achètent les couchent culottes achètent également un pack de bières alors il s'est dit qu'il serait judicieux de disposer ces deux articles côte à côte afin de permettre au client de trouver vite les produits qu'il cherche. Ainsi, si vous visitez le site de vente de livres en ligne amazone.com et que vous recherchez des livres sur le data mining, vous pouvez voir ressortir des livres de statistique mais pas de livres de topologie par exemple. Ce résultat peut être issu du fait que l'étude des transactions des anciens clients a montrée qu'un nombre significatif de ceux qui ont acheté un ou plusieurs livres de data mining ont également acheté un ou plusieurs livres de statistique et non de topologie. [23]

Les règles d'associations interviennent dans plusieurs applications comme l'ana-lyse du panier de la menagère où elles servent à trouver les association entre les produits achetés par un consomateur particulier ou encore sur internet dans le but d'associer les différentes pages visitées par les internautes, comme illustré dans le paragraphe précédent.[11][15]

Définition 5(règle d'association)

Une règle d'association R est la donnée de deux motifs A et B où A est appelé prémisse de la règle et B la conséquence. Elle est notée par:

R = A -+ B

L'extraction de règles d'associations nous donne une information générale des relations existant entre motifs d'une base de donnée. Elle a pour objectif de déterminer si l'occurence du motif A est associé à l'occurence du motif B. Ainsi la qualité d'une règle sera évaluée en fonction de son support et de sa confiance.[25]

Définition 6(support d'une règle d'association)

Le support d'une règle d'association est défini comme étant le nombre d'oc-currences dans lesquelles les associations entre motifs sont observées divisé par le nombre total d'événements : [25]

Nombre de cas favorables

support{A -+ B} = support(A B) = (4.1)

Nombre de cas possible

50

On peut rapprocher la notion de support d'une règle à celle de probabilité des évé-nements[23]. En effet le support(A -+ B) est la probabilité que x possède le motif

A et que x possède le motif B (en supposant que x soit une variable aléatoire sur O avec une distribution uniforme)

Définition 7(confiance d'une règle d'association)

La confiance est défini comme étant la proportion de cas dans lequel les associations entre motifs sont réalisées sur le nombre de cas contenant la prémisse. Elle st notée par :[25]

support(A U B)

confiance(A -+ B) = (4.2)

support(A)

En effet, confiance(A -+ B) est la probabilité que la variable x possède la motif

B sachant qu'elle possède déjà la motif A. Ainsi :

- confiance(A -+ B) = 1 signifie que tous les objets possédant le motif A possèdent le motif B ;

- confiance(A -+ B) = 0 signifie qu'aucun n'objet possédant le motif A ne possède le motif B ;

Définition 8(Règle valide)

Une règle d'association R est valide si elle vérifie :

· support(R) > ó_s ;

· confiance(R) > ó_c ;

où ó_s, ó_c E [0; 1] sont des valeurs seuils prédéfinies.

N.B : Dans l'extraction de règles d'associations, seuls les règles valides intéressent l'analyste parce qu'elles renferment un maximum d'informations nécessaires pour celui-ci. Cependant L'extraction des règles d'association consiste à extraire toutes les règles solides ayant un support et une confiance suffisants par rapport à des seuils fixés à priori, à savoir le support et la confiance minima. [51]

Définition 8(Règle exacte, règle approximative)

Une règle d'association est exacte si sa confiance vaut 1. Dans le cas contraire, elle est dite approximative.

Si R = A -+ B est exacte, alors support(A U B) = support(A). En se basant sur la base de données formelle (table 4.1) on a :

3

support(a) = support(ac) = 6

Donc a -+ b est une règle exacte. Sa confiance vaut 1.[24]

4.3.5 Algorithme de génération de règles d'associations valides

Soit la règle d'association définit par R = p1 -+ p2 \p1 avec p1 Ç p2(Notons que E \ F = {x|x E E et x E6 F}). Le principe de l'algirithme est le suivant : On s'in-téresse aux règles valides c'est-à-dire dont support(R) = support(p2) > ó_s. Etant donné que p1 Ç p2, par le principe de la décroissance du support, support(p1) > ós

51

1. On considère les règles de la forme p1 -? p2 \ p1 où la conclusion est de longueur 1;

2. On supprime les règles non valides ;

3. On combine les conclusions des règles valides ;

4. Puis on passe à des conclusions de longueur 2, on supprime les règles non valides et on combine les conclusions des règles valides ;

5. On passe à des conclusions de longueur 3 et ainsi de suite

Comme exemple, considérons toujours la base de donnée de la table 4.1. On fixe le seuils ó_s = 26 et ó_c = ²₅. [51]

Motifs fréquents de longueur 1 : a, b, c, e. A ce niveau il est difficile d'appliquer l'algorithme parce qu'il n'y a pas de règles d'association à partir de ces motifs. Il faut un motif de longueur 2 au moins.

Motifs fréquents de longueur 2 : ab, ac, ae, bc, be, ce. Pour chacun de ces motifs fréquents m on regarde les règles p1 -? p2 \ p1 avec p2 = m.

- Pour m = p2 = ab, deux règles peuvent être engendrées : a -? b (pour p1 = a) et b -? a (pour p1 = b). Le support de ces deux règles est le même :

= 23 = ó_c

2

6

support(p2) = 2 ₆, et la confiance donne : confiance(a -? b) = 3

6

et confiance(b -? a) =

2 6 5 6

=

25 = óc. On obtient donc deux règles valides :

a -? b et b -? a.

- Pour m = p2 = ac, on a deux règles a -? c et c -? a dont le support est le même et vaut ³₆. La confiance de a -? c vaut 33 = 1(règle exacte) et celle de c -? a vaut ⁵³

- Pour m = p2 = ae dont le support est ²₆, on a les règles a -? e de confiance ²³ et e -? a de confiance ²₅.

- Pour m = p2 = bc dont le support est ⁴₆, on a les règles b -? c de confiance ⁴⁵ et c -? b de confiance ⁴₅.

- Pour m = p2 = be dont le support est ⁵₆, on a les règles b -? e de confiance 5 5 = 1 et e -? b de confiance 55 = 1.

- Pour m = p2 = ce dont le support est ⁴₆, on a les règles c -? e de confiance ⁴⁵ et e -? c de confiance ⁴₅.

Motifs fréquents de longueur 3 : abc, abe, ace, bce. Pour chacun de ces motifs fréquents m de longueur 3 on regarde les règles p1 -? p2 \ p1 avec p2 = m.

- Pour m = p2 = abc dont le support est ²₆, on a les règles :

1. A conclusion de longueur 1 : ab -? c (de confiance 22 = 1), ac -? b (de confiance ²₃), bc -? a (de confiance 24 = â )

2. A conclusion de longueur 2 (obtenue par union de conclusion de longueur 1) : a -? bc (de confiance ²₃), b -? ac (de confiance ²₅), c -? ab (de confiance ²₅)

- Pour m = p2 = abe dont le support est ²₆, on a les règles :

1. A conclusion de longueur 1 : ab -? e (de confiance 22 = 1), ae -? b (de confiance 22 = 1), be -? a (de confiance ²₅)

2. A conclusion de longueur 2 (obtenue par union de conclusion de longueur 1) : a -? be (de confiance ²₃), b -? ae (de confiance ²₅), e -? ab (de confiance ² 5)

- Pour m = p2 = ace dont le support est ²₆, on a les règles :

52

1. A conclusion de longueur 1 : ac -+ e (de confiance ²₃), ae -+ c (de confiance 22 = 1), ce -+ a (de confiance 24 = ¹₂)

2. A conclusion de longueur 2 (obtenue par union de conclusion de longueur 1) : a -+ ce (de confiance ²₃), c -+ ae (de confiance ²₅), e -+ ab (de confiance ²₅)

- Pour m = p2 = bce dont le support est 46 = ²₃, on a les règles :

1. A conclusion de longueur 1 : bc -+ e (de confiance 22 = 1), be -+ c (de confiance ⁴₅), ce -+ b (de confiance 22 = 1)

2. A conclusion de longueur 2 (obtenue par union de conclusion de longueur 1) : b -+ ce (de confiance ⁴₅), c -+ ae (de confiance ⁴₅), e -+ ab (de confiance ⁴₅)

Motifs fréquents de longueur 4 : abce

Pour chacun de ces motifs fréquents m de longueur 4 on regarde les règles p1 -+ p2 \ p1 avec p2 = m. Son support vaut ²₆. On a les règles suivantes :

1. A conclusion de longueur 1 : abc -+ e (de confiance 22 = 1), abe -+ c (de confiance 22 = 1), ace -+ b (de confiance 22 = 1), bce -+ a (de confiance

=

1)

₂ .

2

4

2. A conclusion de longueur 2 (obtenue par union de conclusion de longueur 1) : ce -+ ab (de confiance 24 = ¹₂), be -+ ac (de confiance ²₅), bc -+ ae (de confiance 24 = ¹₂), ae -+ bc (de confiance 22 = 1,), ac -+ be (de confiance ²₃), ab -+ ce (de confiance 22 = 1).

3. A conclusion de longueur 3 (obtenue par union de conclusion de longueur 2) : e -+ abc (de confiance ²₅), c -+ abe (de confiance ²₅), b -+ ace (de confiance ²₅), a -+ bce (de confiance ²₃).

Remarque 2

Pour un motif donné, si on a une règle R = p1 -+ p2 \ p1 valide et p'₁ tel que p1 g p'₁ g p2 (support(p1) > support(p'₁)) alors R' = p'₁ -+ p2 \ p'₁. Ainsi

support(R) = support(R') = support(p2)

Et

support(p2) confiance(R) = < support(p)1

support(p2) support(p'1)

= confiance(R')

Donc si R est valide, R' l'est aussi. Par exemple, la règle e -+ abc est valide. On peut en déduire que les règles suivantes sont également valides [51] :

ea -+ bc, eb -+ ac, ec -+ ab, abe -+ c, ebc -+ a, ace -+ b.

53

Chapitre 5

Application des treillis en

représentation des connaissances et

extraction d'informations

S

I agent veut agir de façon intelligente dans un environnement donné, il est important que cet agent ait des connaissances relatives à cet environnement. Pour concevoir un agent doué d'une intelligence artificielle, deux problèmes majeurs se posent à nous : comment, d'une part représenter les connaissances de l'agent, et comment d'autre part raisonner à partir de ces connaissances? Ces deux problématiques sont interconnectées car la façon dont on représente les connaissances a un impact sur les types de raisonnements qui peuvent être effectués ainsi que sur la compléxité du raisonnement.[33]

5.1 Web sémantique et représentation des connaissances

Les technologies de l'internet, principalement le Web initié au debut des années 90, ont permis de mettre de nombreuses informations à la disposition d'un nombre toujours croissant de personnes. Le Web permet la recheche d'informations sur in-ternet. De ce fait, il est aujourd'hui considéré comme une source incortounable de connaissance. Alors, comment aider les utilisateurs du Web dans leurs tâches de recherche d'information, de construction et de combinaison des resultats.

C'est à partir de cette question qu'est née la notion du Web sémantique, attribuée à Tim Berners-Lee. Le Web sémantique est une extension du Web dont le but est de donner du sens aux informations contenues sur la toile, afin de faciliter l'obtention des résultats pertinents aux requêtes.

5.1.1 Web sémantique

Pour comprendre l'expression Web sémantique, il est important de définir d'abord ce que c'est la sémantique.

En effet, la sémantique est définit comme une étude scientifique du sens des unités linguistique et de leurs combinaisons.[29] Pour l'intelligence artificielle, la sémantique porte sur la capacité d'un réseau à représenter de la manière la plus humaine possible des relations entre des objets, des idées ou des situations.

54

FIGURE 5.1 - Exemple d'ontologie dans le domaine zoologique

Ainsi, le Web sémantique est un Web intelligent dans lequel les informations, auxquelles on donne une signification bien définie, sont reliées entre elles de façon à ce qu'elles soient comprises par les ordinateurs, dans le but de trouver rapidement les informations recherchées.[30]

La quantité des informations stockées sur le Web étant importante, cela a été indispensable d'envisager une classification cohérentes et partagée de celles ci. Ainsi est née la notion d'ontologie.

Ontologie

Une ontologie décrit un domaine par un ensemble de concepts de ce domaine et les liens existant entre eux. Parmis ces liens, les plus fréquemment utilisés est le lien de généralité entre concepts, qui indiquent qu'un concepts A est plus général qu'un concept B, ce qui veut dire que tous les individus dénotés par A les sont par B. Les concepts sont alors organisés en hierarchie comme le montre la figure 5.1.[51]

5.1.2 Représentation des connaissances

La première question qui nous vient à l'esprit quant on nous parle de la représentation de connaissance est celle de savoir : « Qu'est-ce qu'une connaissance ou plus encore pourquoi représenter ces connaissances? ».

Le point de vue d'un ingenieur, informaticien de surcroît, sur la connaissance est étroitement lié à l'histoire de ce qu'on appelle les Techniques de l'Intelligence Artificielle (TIA) qui se sont imposées dès le début des années 70 comme une solution alternative à la conception des logiciels d'Enseignement Assisté par Ordinateur en sigle EAO (en anglais : Computer Aided Instruction ou CAI).

Les techniques de l'intelligence artificielle (IA) sont des méthodes numériques qui exploitent la connaissance. Les principales techniques de l'intelligence artificielle sont la représentation des connaissances, la recherche d'une solution ou le raisonnement et l'apprentissage.[31][32][33]

Ainsi la connaissance est cette faculté de connaître propre à un être vivant. Et la représentation des connaissances, comme son nom le suggère, désigne un ensemble d'outils et de technologies destinés d'une part à représenter, d'autre part à organiser le savoir humain pour l'utiliser et le partager. Elle a pour but l'étude des formalismes qui permettent la représentation de toutes formes de connaissances afin de percer le mystère de l'humanité.[35][36]

Les modèdes de représentation des connaissances reposent essentiellement sur des théories issues de la logique. En effet, pour manipuler des connaissances explicites, un système doit utiliser un langage formel de représentation. Toute expression de ce langage s'établit à l'aide de symboles dont les associations sont régies par des

55

règles qui forment la syntaxe de la représentation. Si à toute expression syntaxique-ment correcte de la représentation on fait correspondre une situation de l'univers de référence, on adjoint alors une sémantique à ce formalisme de représentation. Cette sémantique s'exprime souvent en terme bouléens : La situation est vrai (dans l'univers considéré) ou elle ne l'est pas. [32]

Ainsi, la logique mathématique se veut une modélisation des raisonnements mathématiques, et il s'agit principalement d'un formalisme qui permet d'effectuer des raisonnements pour trouver de nouvelles connaissances à partir de celles qui existent déjà. Elle fournit ainsi un cadre adéquat pour représenter des connaissances. Un rappel sur les bases de la logique propositionnelle, la logique du premier ordre ainsi que les quelques autres logiques (logiques de description, logiques temporelles, logiques floues,...) se revèle donc inéluctable. [31]

Logique propositionnelle

La logique propositionnelle est une logique qui se trouve à la base de presque toutes les autres logiques. Les éléments de bases sont des propositions (ou variables propositionnelles) qui représentent des énoncés qui peuvent être vrais ou faux dans une situation donnée.[35]

Une proposition est une affirmation qui a un sens. Cela signifie que l'on peut dire sans ambiguïté si cette affirmation est vraie ou fausse. C'est ce qu'on appelle le « principe du tiers exclu ». Elle ne peut donc être jamais à la fois vraie et fausse,« principe de non-contradiction »[37]

Nous pouvons citer à titre d'exemple une proposition P qui représente « Pascal Sungu est un ingénieur »ou une proposition Q qui représente l'énoncé « L'ingénierie des connaissances est un domaine de l'informatique ». D'autres formules peuvent être construites à partir de ces propositions en utilisant des connecteurs logiques : ? (« et »), ? (« ou »), et #172; (« négation »). Par exemple nous pourrions avoir les formules P ? Q « Pascal Sungu est un ingénieur et l'ingénierie des connaissances est un domaine de l'informatique », P ? Q « Pascal Sungu est un ingénieur ou l'ingénierie des connaissances est un domaine de l'informatique », et #172;q « L'ingénierie des connaissances n'est pas un domaine de l'informatique ».[35]

Il existe d'autres types de connecteurs logiques tels que :

- Le connecteur d'implication(=)

Soient P et Q deux propriétés sur l'ensemble E, P = Q est une propriété sur E définie par :

1. P = Q est fausse si P est vraie et Q et fausse;

2. P = Q est vraie sinon.

- Le connecteur d'équivalence(?)

Soient P et Q deux propriétés sur l'ensemble E, P ? Q est une propriété sur E définie par :

P ? Q si [(P = Q) ? (Q = P)]

Logique du premier ordre

La logique du premier ordre, aussi appelée calcul des predicats est la logique des formules mathématiques telles que :[38]

?å > 0, ?8 > 0(|x - x0| < 8 = |f(x) - f(x0)| < å)

56

En logique des propositions, les expressions ( formules ou phrases) sont construites à partir de symboles propositionnels pouvant prendre des valeurs vrai ou faux. Ces énoncés élémentaires sont non structurés. Parfois, on peut être amené à décomposer ces propositions élémentaires en faisant une opération qui ressemble à une paramé-trisation. Par exemple, au lieu d'avoir un symbole propositionnel pour représenter « SunguEstAmiDePascal », on peut considerer que « EstAmi »est une relation qui porte sur deux arguments (c'est donc une relation d'arité 2) : dans le cas présent sur deux entités identifiées « Sungu »et « Pascal », et plus généralement sur deux arguments quelconques x et y ce que l'on notera par ami(x, y). Dans un tel énoncé « EstAmi »s'appelle un prédicat et x et y sont des variables. Dans l'énoncé EstAmi(Sungu, Pascal), Sungu et Pascal désignent des entités précises, ce sont des constantes. Les constantes et les variables ont pour valeurs des éléments d'un certains ensemble appelé le « domaine »de l'interprétation.

La logique du premier ordre introduit deux quatificateurs qui portent sur des variables : ?, le quantificateur universel(« pour tout ») et ? le quantificateur existentiel (« il existe »). En voici quelques exemples illustratifs :[41]

· ?x(18 = 3x) signifie « 18 est multiple de 3 »

· ?x(x * 1 = x) signifie « 1 est neutre pour * » Et la négation d'une formule quantifiée est donnée par:

· #172;(?x : A(x)) ? ?x(#172;A(x))

· #172;(?x : A(x)) ? ?x(#172;A(x))

A étant un énoncé quelconque.[42]

La logique propositionnelle et la logique du premier ordre sont de loin les deux logiques les plus étudiées, mais on constate un intérêt grandissant pour d'autres logiques qui sont parfois plus adaptés pour représenter certains types de connaissances. En voici quelques unes :

Logique de description

La logique de description [41] est une logique qui se trouve à mi-chemin entre la logique propositionnelle et la logique du premier ordre.

Effet, cette logique possède deux types de formules : des axiomes qui décrivent des relations entre des concepts et des assertions qui expriment les caractéristiques des individus ainsi que des relations qui existent entre eux.

Citons à titre d'exemple : Oiseau v Animal ce qui se traduit par « Chaque oiseau est un animal » et Oiseau v ? enfant.Oiseau qui se traduit par « les enfants des oiseaux sont aussi des oiseaux » et des assertions Oiseau(Pigeon) « Pigeon est un oiseau » et enfant(Pigeonneau, Pigeon) qui se traduit par « Pigeonneau est un enfant de Pigeon ». Nous pourrions alors inférer que Pigeon est un oiseau et que Pigeonneau et Pigeon sont tous deux des oiseaux.

Logiques temporelles

La logique temporelle est une extension de la logique [41] Informatique 18 juin 2004 propositionnelle, elle intègre des nouveaux opérateurs qui expriment la notion du temps, exemple « maintenant », « dorénavant », « toujours »qui permettent de

57

FIGURE 5.2 - Représentation graphique d'un ensemble classique et d'un ensemble flou

parler des propriétés qui sont vraies à différents moments dans le temps. On pourrait par exemple exprimer dans une telle logique le fait « Pascal sungu est un étudiant mais un jour il ne le sera plus »ou « deux est toujours un nombre pair ».

En effet, il n'est pas possible d'exprimer dans la logique classique une assertion liée au comportement d'un programme telle que « après exécution d'une instruction j, le système se bloque ». Dans cette assertion, les actions s'exécutent suivant un axe de temps : à l'instant t, exécution de l'instruction j, et à t + 1 blocage du système. Il faut donc une logique appropriée à même de modéliser les expressions du passé et du futur.[43]

Logique floue

Nous vivons dans un monde où très peu de notions sont binaire. Nous côtoyons l'imprécision au quotidien. Par exemple, quand nous disons « Pascal a la vingtaine », la connaissance que nous adoptons est imprécise. Le besoin de modéliser ce type de connaissances se fait sentir. C'est ainsi que dans la seconde moitié du XX^e siècle le professeur Lotfi Zadeh introduisit une logique permettant de formuler de tels énoncés.[44]

La logique floue[45] est une extension de la logique booléenne. Elle se base sur la théorie des ensembles flous(figure 5.2), qui est une généralisation de la théorie des ensembles classiques. En introduisant la notion de degré dans la vérification d'une condition, elle permet à une condition d'être dans un autre état que vrai ou faux. La logique floue confère ainsi une fléxibilité très appréciable aux raisonnements qui l'utilisent, ce qui rend possible la prise en compte des imprécisions et des incertitudes. Prenons par exemple : comment déterminer si une personne est âgée ou non? Ce problème est difficile à cerner, une personne qui a 60 ans est-elle âgée? Et qu'en est-il d'une personne qui a 70 ou 80 ans? En logique classique on va être obliger de définir une frontière qui va déterminer l'ensemble de personnes âgées, disons qu'une personne est dite âgée si elle a 80 ans ou plus. Si par exemple Ilunga a 80 ans et sa femme 70, on dira que Ilunga est âgé mais sa femme ne l'est pas.

Si on utilise un raisonnement flou, on a un jugement plus nuancé :

- Ilunga est « certainement »âgé.

- Sa femme est « quasiment »âgée.

- Leur petit enfant ne l'est « pas du tout ».

Définissons A l'ensemble des personnes âgées, on voit que cet ensemble diffère entre logique classique et logique floue tel que présenté par la table 5.1[44]

58

TABLE 5.1 - Illustration de l'appartenance à A, selon la théorie choisie Logique de connaissances et/ou croyances

L'une des caractéristiques du raisonnement humain est sa faculté de raisonner sur ses propres connaissances ou sur celles des autres. Un certain nombre de logiques ont été proposées pour formaliser ce type de raisonnement. Dans ces logiques, nous pouvons exprimer les informations de type « je sais que Shoudelle a un enfant, et je crois que c'est une fille mais je suis pas sûr »ou « je crois qu'il croit que je sais qui a volé le diamant, mais je ne le sais pas. »Le raisonnemet sur les connaissances devient un sujet de plus en plus populaire grâce à son utilité dans de nombreux domaines tels que l'Intelligence artificielle, la linguistique.[52]

Logique non monotone

La logique non monotone est une logique formelle dont la relation de conséquence n'est pas monotone. De nombreuses logiques formelles sont monotones, ce qui signifie qu'ajouter un fait à un ensemble de règles n'enleve pas de deductions à cet ensemble. Or cette propriété ne semble pas toujours vérifiée dans le raisonnements humains. Pour prendre un exemple classique, donnons un nom à un oiseau par exemple « Tweety », il est tout a fait évident qu'il vole, du fait que c'est un oiseau. Admettons maintenant que Tweety est un Pingouin et si on vous demandait de dire s'il vole, vous repondrais par la négation parce qu'un pingouin ne vole pas. C'est un raisonnement non-monotone parce que le fait d'ajouter une hypothèse (Tweety est un pingouin) fait perdre l'une des conséquences (Tweety vole). Ce type de raisonnement ne satisfait pas les lois de la logique classique mais il est rationnel tout de même car il nous permet de raisonner en l'absence d'informations complètes. Les logiques non-monotones essaient de formaliser ce type de raisonnement.[46]

5.2 Extraction d'informations

L'extraction d'information est une technique qui consiste à extraire des connaissances à partir de différents documents en utilisant entre autres des techniques lin-guistiques.[52]

La Recherche d'Informations(RI) et le Traitement Automatique de la Langue(TAL) sont deux techniques incontournables dès lors qu'il s'agit d'extraire des elements de sens à partir des textes. Une question reste alors pendante : pourquoi seulement les textes?

En effet, la province du Katanga est une province qui dispose d'un potentiel important de ressources minières. les gîtes des substances minières sont localisés dans presque tout le Katanga. Jusqu'à ce jour, certains gisements demeurent encore

59

FIGURE 5.3 - Schéma général de la recherche d'information

inéxploités. Le Katanga et par delà la RDC est devenu un immense chantier. Alors pourquoi ne pas appliquer nos méthodes dans le domaine minière afin de rendre notre étude plus intéressantes?

L'exploration minière est l'un des domaines où la géophysique est très souvent appliquée comme outil de détection directe. Une bonne connaissance dans ce domaine ainsi que les différentes phases d'un projet minier(Prospection, construction de routes d'accès, préparation et déblaiement du site,...) est requise afin d'y appliquer par la suite nos connaissances mathématiques. Le temps nous faisant défaut, cela fera l'objet de nos travaux ultérieurs.[47]

En effet, les données textuelles contiennent des informations et des connaissances utiles et parfois critiques pour la gestion et la prise de décision dans les entreprises. Une bonne étude des techniques de fouilles de ces données se revèle donc primordiale afin de fournir un outil important au décideur.

Ainsi, nous vous présenterons dans la suite de ce paragraphe les fondements de la recherche d'information(section 5.2.1) et le traitement automatique de la langue(section 5.2.2) qui constituent les deux ailes dont requièrent les données textuelles pour nous emmener vers l'extraction d'informations qu'elles renferment.[11]

5.2.1 Recherche d'informations

La recherche d'information (RI) se définit par un ensemble de méthodes et d'ou-tils qui permettent à un utilisateur de formuler une requête et qui selectionnent dans un fond documentaire les documents répondant à ces critères. Les documents sont au préalable indéxés : chaque mot de chaque document est répertorié dans une table inverse, avec ou sans consérvation des positions des mots dans le texte d'ori-gine. L'appariement entre la requête et l'index va déterminer les documents qui sont considérés comme repondant le mieux au besoin informationnel initial.[11]

Une extension de ce schéma permet d'effectuer de la recherche d'information interlangue : le sujet de recherche est formulé dans une langue (par exemple français) différente de celle des documents (par exemple anglais). Dans ce cas le système de RI inclut une étape de traduction du sujet en une requête dans la langue cible. Les documents trouvés peuvent en retour être également traduits dans la langue source.

La recherche d'information passe par plusieurs étapes dont voici les principales [11] :

60

Simplification de documents

La simplification de documents consiste à rendre plus pertinent et plus efficace le processus d'appariement entre requête et index. Elle s'effectue selon les étapes suivantes :

- Suppressions des « mots stop » ou des mots fréquents;

- Racination : Elle consiste à reduire les mots de la même famille morphologique à une racine commune;

- Transformation du texte en un sac ou ensemble de mots.

Indexations

L'indexation peut se faire sur des mots simples ou sur des syntagmes. Dans ce dernier cas, des groupes de mots constituent des index du document. Ces syntagmes peuvent être obtenus par des techniques symboliques (par étiquetage,...), ou encore des techniques statistiques (en étudiant les mots cooccurents dans des documents).

Traitement et appariement des requêtes

Le traitement et l'appariement des requêtes se base sur deux principes :

- En raison de leurs tailles : Les requêtes sont analysées par procedures plus lentes et plus complexes;

- En raison de leurs syntaxes : Elles sont analysées par des procedures symboliques aux contraintes syntaxiques lâches.

Une fois traitées, les requêtes sont appariées avec l'index des documents. Il s'en suit alors trois types d'approches :

1. Le modèle booléen : Ce modèle suit une approche du type base de données : les documents sont recherchés sur la base d'une formule logique sur les descripteurs, et les réponses sont de la forme Oui/Non. C'est le modèle classique en recherche bibliographique où l'on interroge sur le contenu des champs :Auteur, Titre, etc;

2. Le modèle vectoriel : Ce modèle se base sur le principe suivant; plus un document partage des descripteur avec la requête, meilleur il est. Les reponses sont qualifiées par un pourcentage exprimant leur pertinence;

3. Le modèle probabiliste : Il complète le modèle vectoriel en calculant la pertinence de chaque index pour un document en fonction des documents répondant à des requêtes sur une base documentaire comparable. Un pourcentage qualifie la pertinence des réponses.[11]

5.2.2 Traitement automatique de la langue

Les Traitements Automatique des Langues(TAL) est une discipline qui associe étroitement linguistes et informaticiens. Il repose sur la linguistique, les forma-lismes(représentation de l'information et des connaissances dans des formats interprétables par la machine) et l'informatique. Le TAL a pour objectif de développer des logiciels ou des programmes informatiques capables de traiter de façon automatique des données linguistiques. [48]

61

Ainsi le traitement automatique de la langue peut se définir comme étant l'en-semble des méthodes et des programmes qui permettent un traitement par ordinateur du materiau linguistique : analyse de textes, génération de textes, traduction automatique, correction orthographique et grammaticale,...

Nous présentons ici les grands domaines du TAL, en s'appuyant sur un découpage méthodologique classique dans le domaine de la linguistique tel que présenté dans. Les différents domaines qui seront présentés ici sont [49] :

La morphologie

D'un point de vue informatique, un texte est une chaîne de caractère. La première étape de l'analyse d'un texte est la reconnaissance, dans cette chaîne de caractères, d'unités linguistique de base, les mots, ainsi que des informations associées puisées dans un lexique.

Pour commencer, la chaîne de caractères d'entrée doit utiliser un encodage dé-terminer(pour le français, l'encodage ISO-latin-1), les caractères de contrôle(fin de ligne,...) étant eux aussi normalisés. On élimine généralement les caractères non répectoriés.

Ensuite il s'agira de segmenter la chaîne d'entrée en unité élémentaires. Différents choix peuvent être effectués à ce stade, selon les séparateurs choisis : tous les caractères non alphabétiques(espaces, apostrophes, tirets...) ou les espaces seulement; et selon que l'on prend en considération les « mots composés »« pomme de terre » en le considérant comme « une » unité.

La lexique quant à lui est définie comme étant une liste des mots de la langue, et associé à chaque mot les informations linguistiques corréspondantes : catégorie syntaxique, traits morphosyntaxiques(genre, nombre, etc), etc. Il faut cependant bien préciser la définition du lexique compte tenue de plusieurs phénomènes qui surgissent.

- Un mot peut avoir plusieurs sens( polysème ) : « avocat », « coup », « livre »en sont des exemples.

- Plusieurs mots peuvent se trouver partager une forme commune( homographes ) : « montre »est une forme du nom « montre »aussi bien que du verbe « montrer ». « pu »est un autre exemple d'homographes qui est en même temps le participe passé du verbe « pouvoir »mais aussi de « paître ».

- Un mot peu être construit à partir d'un autre : par dérivation (« penser » -+ « pensable » -+ « impensable ») ou par composition (« compter » + « gouttes » -+ « compte-gouttes »; « un » + « jambe » -+ « unijambiste »; « sclérose » + « artère » -+ « artériosclérose » )

Syntaxe

Pour repérer quels mots fonctionnent ensemble dans une phrase, un premier niveau de modélisation consiste à constituer des classes de mots(catégories syntaxiques, parties du discours) possédant un fonctionnement similaire : Nom(N), Verbe(V), Adjectif(A), etc

Les relations syntaxiques entre les mots d'une phrase peuvent se représenter de plusieurs façons. Le modèle en constituants considère des groupes de mots, ou syntagmes, généralement centrés sur un mot de tête(Nom, Verbe, Pronom etc), et les modélises par des catégories spécifiques(Syntagme nominal ou SN, Syntagme

62

FIGURE 5.4 - Représentation syntaxiques d'une phrase

verbal ou SV, Syntagme adjectival ou SA, etc). Ces syntagmes peuvent eux-même être éléments d'autres syntagmes, et la structure d'une phrase est alors un arbre de constituants(figure 5.4(a)). Le modèle en dépendance considère directement les mots de tête(recteurs ou régissants), et leur attache les mots qui en dépendent. La structure d'une phrase est alors un arbre de dépendance(figure 5.4(b)). Une phrase peut donner lieu à plusieurs structures syntaxiques(ambiguïté structurelle). En voici un exemple: « je vois un homme avec un téléscope », dans laquel « avec un téléscope » peut designer la manière dont je vois l'homme (attachement au verbe « vois » qui est un complément circonstanciel de manière) ou au contraire une caractéristique de l'homme (attachement au nom « homme », complément du nom.)

Sémantique

La sémantique, à la manière de la syntaxe, comprend un premier niveau de modélisation qui consiste à former des classes des mots(catégories sémantiques). Ces classes regroupent des mots dont le sens est proche, ou au minimum des mots qui possèdent certaines propriétés sémantiques proches.

Un mot, même syntaxiquement non ambigu, peut posséder plusieurs sens. Par exemple, on pourra distinguer l'« artère » qui veut dire vaisseau sanguin de l'« artère » avenue, même si le second est étymologiquement un sens figuré du premier. Le contexte permet en général de déterminer quel sens est à l'oeuvre dans un énoncé.

Les mots d'une langue entretiennent un réseau riche de relations sémantiques : hyperonymie/hyponymie(« vaisseau »/« artère »), métonymie(partie d'un tout: « vaisseau »/« système cardiovasculaire »), antonymie(« benin »/« malin »),etc

Pragmatique

L'interprétation d'un énoncé depend de son contexte. Dès que l'on veut traiter plusieurs phrases (et même pour une seule phrase), cette dimension intervient.

Le co-texte désigne le texte qui précède(et suit) la phrase courante. Deux facteurs concourent à faire qu'une phrase s'insère bien dans un texte.

- La cohésion régit la continuité du texte. Elle est assuré par l'emploi d'ana-phore(figure de rhétorique qui consiste à répéter le même mot au commencement de plusieurs phrases), l'homogéneité du thème, un emploi judicieux d'el-lipses(figure par laquelle on retranche un ou plusieurs mot dans une phrase), etc

63

- La cohérence détermine l'intelligibilité du texte. Elle s'appuie sur des structures de discours(direct ou indirect).[49]

5.3 Application des règles d'associations aux textes

Les règles d'associations ont été appliquées dans plusieurs domaines particuliè-rements dans ceux traitant des données textuelles. Cette section s'inscrit dans cette même démarche.

En effet la fouille des textes, comme nous l'avons souligné à la section 4.1.2, est un ensemble de processus permettant, à partir d'un ensemble de ressources textuelles, de construire des connaissances pouvant être représentées dans un langage formel de représentation des connaissances et exploitées pour raisonner sur le contenu des textes. Ainsi elle donne une vue synthétique du contenu d'une collection d'un ou plu-sieur milliers de textes, exhibe des relations entre les differentes notions impliquées dans un texte ou des relations entre les textes.[11][29]

L'objectif de cette fouille est de retrouver, à travers la collection des textes, des relations connues dans le domaine, de pouvoir les localiser rapidement dans les documents, d'observer des familles de documents contruites à partir d'une ou plusieurs de ces relations. Elle permet également de découvrir des relations non encore connues.

C'est ainsi que, nous recherchons l'expression de ces relations par le biais des règles d'associations extraites à partir des textes.

5.3.1 Description du problème

Le processus de fouille de textes est fondé sur l'utilisation de méthodes symboliques. Elles sont basée sur l'extraction de règles d'association ainsi que l'Analyse Formelle de Concepts et se subdivise en 2 étapes :[11]

1. L'extraction de règles d'association;

2. Le classement des règles suivant des indices statistiques;

L'extraction de règles d'association se fait à l'aide de l'Analyse Formelle de Concepts par la construction des motifs fréquents générés par l'algorithme A-priori(section 4.3.2). Les motifs ainsi obtenus permettent le calcul des règles d'association. Les indices statistiques sont, quant à eux, des mesures de pondération affectés aux règles. Ces indices donnent un poids à chaque règle et permettent alors de les classer.

3.1.1 Règle d'association

Les règles d'associations sont utilisées en fouille de données afin de trouver des correlations dans des bases de données relationnelles.Elles ont été appliquées, par la suite, à la fouille de textes.

Définition 1 (Règle d'association)

Une règle d'association est du type [29] :

R : t1 ? t2 = t3 ? t4 ? t5 où t1,t2,...,t_n sont des termes (5.1)

64

Elle est constituée d'une conjoction de termes en partie gauche(qu'on nomme B) impliquant une conjoction de termes en partie droite(nommée H). La règle sera donc notée par :

R : B = H

L'interprétation de la règle donnée en (5.1) est que : si les documents possèdent les termes {t1, t2} alors ils possèdent également les termes {t3, t4, t5}. Deux indices ont été ainsi associés aux règles d'association à savoir : Le support et la confiance de la règle.

Définition 2 (Support)

Le support d'une règle d'association représente le nombre de documents qui sont décrits par les termes présents en partie gauche et droite de la règle [29].

sup[B = H] = nombre de documents verifiant {t1, t2, t3, t4, t5} (5.2)

C'est la probabilité d'apparition de l'ensemble des documents correspondant à B?H soit :

support[B = H]

P(B, H) = E [0, 1] (5.3)
nombre total de documents du corpus

Définition 3 (Confiance)

La confiance d'une règle est donnée par :

nombre de documents verifiant {t1, t2, t3, t4, t5}

conf[B = H] = (5.4)
nombre de documents verifiant {t1, t2}

En termes probabilistes la confiance mesure la probabilité conditionnelle de H sachant B [1] :

sup[B = H]

P(H|B) = (5.5)
nombre de documents verifiant {t1, t2}

3.1.2 Indices statistiques associés aux règles d'association

Le support et la confiance ne sont pas les seuls indices permettant d'indiquer la qualité d'une règle. D'autres indices statistiques apportent des informations supplémentaires et permettent ainsi différents classements des règles. A savoir : La dépendance, l'intérêt, la conviction, l'étonnement.

L'indice de dépendance est utilisée en probabilité, il permet de calculer l'apport du prémisse B dans la règle.

Définition 4 (Dépendance)

L'indice de dépendance renforce une règle en mesurant la fait que B et H soient dépendants ou pas:

dep[B = H] = |P(H|B) - P(H)| (5.6)

Les termes très fréquent dans un corpus n'apportent pas d'information particulière puisque tout terme du corpus devra impliquer un terme fréquent. Alors que les termes rares, qui peuvent porter de l'information, apparaissent dans des règles à faible support et sont par conséquent peu intéressants. C'est ainsi que l'indice suivant a été défini au vue de cette différence d'apparition des termes dans un corpus.

65

FIGURE 5.5 - Exemple d'un document du corpus Définition 5 (Intérêt)

L'intérêt mesure la dépendance entre B et H. Cet indice privilégie les termes rares aux dépens des termes trop répandus dans le corpus.

P (B, H)

int[B = H] = (5.7)
P (B) x P (H)

L'intérêt a un comportement symetrique pour B et pour H, c'est-à-dire que : int[B = H] est égal à int[H = B]. [28]

5.3.2 Expérimentations

Considérons un corpus constitué de 43 documents d'environs 200 000 mots dont l'extrait d'un des documents est montré à la figure 5.5. Un document est constitué d'un identifiant unique (c'est-à-dire un numéro), d'un titre, d'un (ou des) auteur(s), du résumé sous forme textuelle et d'une liste de termes caractérisant ce resumé.

Soit une base de donnée comprénant des livres, thèses, cours ainsi que des articles en format numérique :

1. La proie

2. Adéquation d'indices statistiques à l'interprétation de règles d'association

3. Analyse comparative de corpus cas de l'ingénierie des connaissances

4. Analyse en ligne de l'information: une approche permettant l'extraction d'in-formations

5. Analyse statistique implicative

66

6. Annotation documentaire et peuplement d'ontologie à partir d'extractions linguistiques

7. Apprentissage statistisque pour l'extraction des concepts à partir des textes.

8. Application aux filtrage des textes

9. Approche linguistique pour l'analyse syntaxique

10. Balades aléatoires dans les Petits Mondes lexicaux

11. Construction de ressources terminologiques ou ontologiques à partir de textes

12. Construction d'ontologie à partir des textes

13. Programmation Java

14. Créez votre application web avec java Entreprise Edition

15. Dévellopement Java avec Jquery

16. Développons en Java

17. Documents électroniques et constitution de ressources terminologiques ou ontologiques

18. Engagement sémantique et engagement ontologique conception et réalisation d'ontologies en ingénierie des connaissances

19. Enrichissement automatique d'une base de connaissances biologiques a l'aide des outils du Web semantique

20. Etude et realisation d'un systeme d'extraction de connaissances à partir des textes

21. Evaluation de la qualité de la représentation en fouille des donnée

22. Extraction automatique des motifs syntaxiques

23. Extraction de connaissances dans les bases de donnees comportant des valeurs manquantes

24. Extraction et impact des connaissances sur les performances des systemes de recherche d'information

25. Fouille de textes hiérarchisée, appliquée à la détection des fautes

26. Fouille de données séquentielles pour l'extraction de l'information dans le texte

27. Hierarchisation des regles d'association en fouille de textes

28. Ontologie de domaine pour la modélisation des contextes en recherche d'infor-mation

29. Ingénierie des connaissances entre science de l'information et science de gestion

30. La Programmation Orientée Objet

31. Optimisation des réseaux intelligents et des réseaux hétérogènes

32. Modelisation du domaine par une methode fondee sur l'analyse du corpus

33. Modelisation XML

34. Ontologies pour l'aide à l'exploration d'une collection des documents

35. Plate forme d'analyse morpho-syntaxique pour l'indexation automatique et la recherche d'information

36. Précis de recherche opérationnelle

67

37. Résumé automatique par filtrage semantique d'informations dans des textes

38. Système d'exploration contextuelle

39. Tout sur les Réseaux sans fil

40. Un systeme de visualisation pour l'extraction, l'evaluation, et l'exploration interactives des regles d'association

41. Une étude comparative de quelques travaux sur l'acquisition de connaissances

42. Vers le traitement de la masse de donnée disponible

43. Vers une acquisition automatique de connaissances

Soit un groupe de mots (simples ou composés) que nous devons chercher dans cette base de donnée :

1. règles d'associations

2. fouille de textes

3. ontologie

4. corpus

5. analyse syntaxique

6. extraction d'information

7. traitement du langage naturel

8. intelligence artificielle

9. treillis de galois

10. connaissances

11. recherche d'information

12. linguistique

13. représentation des connaissances

14. traitement automatique des langues

15. ingénierie des connaissances

16. contexte formel

17. connexion de galois

18. web sémantique

19. base de connaissances

20. base de données

Nous contruirons un contexte d'extraction K = (X, Y, R) où X est l'ensemble de livres de notre base de donnée, Y l'ensemble de termes ou mots clés de notre corpus et la relation R désignera la presence d'un mot dans un document et sera simbolisé par × dans la case correspondante au croisement de la ligne du nom d'un livre et la colonne du nom d'un motif tel que montré par la figure ci-dessous.

Les documents seront symbolisés par la variable x
·(j allant de 1 à 43) et les termes (ou mots clés) par les lettres de l'alphabet français (a = 1... t = 20).

TABLE 5.2 -- Contexte d'extraction associé à la base de données textuelle (Livres éléctroniques et mots clés)

68

'R.

a

h

c:

ci

cT

I

g

h

i

j

k

l

in

u

ca

p

c1

r

s

t

3: I

X

X

3:2

X

X

X

X

X

X

X

3:4.!

X

X

X

X

X

X

X

X

X

X

:4'i

X

X

X

X

X

X

X

X

X

;1::,

X

X

X

X

X

X

X

:!.'i;

X

X

X

X

X

X

X

X

X

r7

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

3:8

X

X

X

X

X

X

X

X

3:1i

X

X

X

X

X

X

X

11]

X

X

X

X

X

X

X

X

X

X

X

xii

X

X

X

X

X

X

X

X

X12

X

X

X

ZIA

X

X

X

X

ZIA

X

XII")

X

X

X

2Iy

X

X

X

X

T X

X

X

X

X

x.17

X

X

X

X

X

X

X

X

3:1#]

X

X

X

X

X

X

X

X

X

X

X

X

X

3:19

X

X

X

X

X

X

X

X

X

X

X

X

3:21]

X

X

X

X

3:21

X

X

X

X

3:22

X

X

X

X

X

X

X

X

X

3:23

X

X

X

X

X

X

X

:#:2 ·1

X

X

X

X

X

X

X

X

X

x25

X

X

X

X

X

X

:L`.){;

X

X

X

X

X

X

;i:27

X

X

X

X

X

X

X

z2A

X

^3:29

X

X

X

X

X

3:34]

X

X

X

X

X

^37-411

^27;12

X

X

X

X

X

X

X

X

1:33

X

X

X

X

X

X

X

^1.'34

X

X

X

X

X

X

X

X

X

X

X

X

X

X

;1.3r,

X

X

X

X

X

X

:a':cents,.

X

X

X

X

X

X

X

X

X

X

X

X

X

;a':g ;

X

X

X

X

X

X

X

3.';

X

X

X

3.';s1]~

X

X

X

X

X

X

X

X

l'..1 I)

X

X

X

X

1:4 L

X

X

X

X

:!',12

X

X

X

X

X

+1: ·1;s

X

X

X

X

X

69

5.3.3 Extraction de connaissances par règles d'association

L'extraction des connaissances est une technique qui consiste à trouver des éléments de sens à partir d'une base de données. Dans cette section, nous utiliserons la notion de règles d'association pour arriver à extraire ces connaissances.

En effet, les règles d'associations sont basées sur des motifs qui apparaissent fréquemment dans la base de donnée. Ainsi nous commencons par trouver des motifs et ne retenir que ceux qui sont fréquents.

3.3.1 Extraction de motifs fréquents

Pour extraire les motifs fréquents, nous nous baserons sur l'algorithme A-priori vu à la section 4.3.2 pour un seuil ó,9 = 15 ₄₃.Pour cela, on commence par déterminer les motifs fréquents de taille 1; on note cet ensemble L1. Ensuite, on construit l'ensemble C2 des motifs fréquents candidats de taille 2 (ce sont tous les couples construits à partir des motifs fréquents de taille 1). On obtient ainsi la liste des motifs fréquents de taille 2 qu'on note par L2. On ne conservera, bien sûr, que les éléments de C2 dont le support est supérieur au seuil. On construit encore l'ensemble C3 des motifs fréquents candidats de taille 3 et on ne retient que ceux dont le support est supérieur au seuil, ce qui produit L3. On continue le processus jusqu'à ce que l'ensemble Li n'ait plus d'éléments.

Génération de candidats de taille 1

La génération de motif candidat de taille 1 est présenté par le tableau suivant avec leurs motifs respectifs. Seuls les motis fréquents(support = 15

₄₃₎ seront retenus

(valeurs en gras). Ainsi la liste L1 nous donne les motifs fréquents de taille 1.

L1 = {c, d, e, h, j, l, n, o, s, t}

Génération de candidats de taille 2 : Obtenus par combinaison 2 à 2 des candidats de taille 1 de L1. La liste L2 donne les motifs fréquents de taille 2.

L2 = {cd, cj, cl, dh, dj, dl, hj, hl,jl,jn,jo,js,jt}

Génération de candidats de taille 3 : Obtenus par combinaison 2 à 2 des candidats de taille 2 de L2. Nous ne considererons que les motifs dont la taille vaut

3. La liste L3 nous donne la liste des motifs fréquents de taille 3.

L3 = {cdj, cdl, cjl, djl, hjl}

Génération de candidats de taille 4 : Obtenus par combinaison 2 à 2 des candidats de taille 3 de L3. Nous ne considererons que les motifs dont la taille vaut

4. La liste L4 nous donne la liste des motifs fréquents de taille 4.

L4 = {cdjl}

Nous constatons qu'il ne sera pas possible de générer les candidats de taille 5. D'où L5 = Ø. Ainsi l'ensemble L de motifs fréquents est :

L = {L1,L2,L3,L4} (5.8)

Le tableau de tous les motifs candidats est montré à la table 5.3.

70

TABLE 5.3 - Mots clés candidats à l'analyse et leurs supports respectifs

71

3.3.2 Extraction de règles d'associations

Dans cette section nous allons extraire les règles d'associations en se basant sur les motifs fréquents. La probabilité ainsi que la confiance pour qu'une règle soit valide est de a_s = 15

42 = a_c. Les règles d'associations étant de la forme A -? B, nous ne commencerons que par les motifs de longueur 2 afin que l'algorithme s'y applique sans anicroche.

Motifs fréquents de longueur 2 :cd, cj, cl, dh, dj, dl, hj, hl, jl, jn, jo, js, jt

Ainsi pour chacun des motifs fréquents m, on regarde les règles p1 -? p2 \ p1 avec p2 égal au motif.

- Pour m = p2 = cd, deux règles peuvent être engendrées : c -? d (pour p1 = c)

et d -? c (pour p1 = d). Le support de ces deux règles vaut :

19

support(c -? d) = support(d -? c) = 43

et la confiance donne :

19 19

confiance(c -? d) = 24 et confiance(d -? c) = 27 On obtient donc deux règles valides : c -? d et d -? c.

- Pour m = p2 = cj, on a deux règles c -? j et j -? c dont le support est le même et vaut :

24

support(c -? j) = support(j -? c) = 43

et la confiance donne :

24

confiance(c -? j) = 1 et confiance(j -? c) = 40

On obtient qu'une seule règle valide : c -? j

- Pour m = p2 = cl dont le support est ¹⁹

_43, on a les règles c -? l de confiance

19

₂₄ et l -? c de confiance ^2s

Ainsi c -? l et l -? c sont valides

- Pour m = p2 = dh dont le support est ¹⁵

_43, on a les règles d -? h de confiance

₂₇ et h -? d de confiance ¹⁵

15 19.

Ainsi d -? h et h -? d sont valides

- Pour m = p2 = dj dont le support est ²⁴

24

27 = 1 et j -? d de confiance ²⁴

40 = 1.

_43, on a les règles d -? j de confiance

Seul la règle d -? j est valide

- Pour m = p2 = dl dont le support est _2423, on a les règles d -? l de confiance

22

₂₇ et l -? d de confiance ²²

26.

Les deux règles sont valides.

-

17

₁₉ et j -? h de confiance ¹⁷

40.

Ainsi h -? j et j -? h sont valides

Pour m = p2 = hj dont le support est _4137, on a les règles h -? j de confiance

- Pour m = p2 = hl dont le support est _4163, on a les règles h -? l de confiance

16

₁₉ et l -? h de confiance ¹⁶

26.

Ainsi h -? l et l -? h sont valides

72

- Pour m = p2 = jl dont le support est ²⁵

_43, on a les règles j -? l de confiance

₄₀ et l -? j de confiance ²⁵

25 26.

Ainsi j -? l et l -? j sont valides

- Pour m = p2 = jn dont le support est ¹⁵

_43, on a les règles j -? n de confiance

₄₀ et n -? j de confiance 1.

15

Ainsi j -? n et n -? j sont valides

- Pour m = p2 = jo dont le support est ¹⁶

_43, on a les règles j -? o de confiance

₄₀ et o -? j de confiance 1.

16

Ainsi j -? o et o -? j sont valides

- Pour m = p2 = js dont le support est ¹⁹

_43, on a les règles j -? s de confiance

₄₀ et s -? j de confiance 1.

19

Ainsi j -? s et s -? j sont valides

- Pour m = p2 = jt dont le support est ²¹

_43, on a les règles j -? t de confiance

₄₀ et t -? j de confiance 1.

21

Ainsi j -? t et t -? j sont valides

Motifs fréquents de longueur 3 :cdj, cdl, cjl, djl, hjl. Pour chacun de ces motifs fréquents m, on considère les règles p1 -? p2 \ p1 avec p2 = m.

- Pour m = p2 = cdj dont le support est ¹⁹

_43, on a les règles :

1. A conclusion de longueur 1 : cd -? j (de confiance égale 1), cj -? d

(de confiance ₂¹⁹₄), dj -? c (de confiance ¹⁹

24)

2. A conclusion de longueur 2 (obtenue par union de conclusion de longueur

1) : c -? dj (de confiance ¹⁹₂₄), d -? jc (de confiance ¹⁹

_27), j -? dc (de

confiance ¹⁹

40)

- Pour m = p2 = cdl dont le support est ¹⁶

_43, on a les règles :

1. A conclusion de longueur 1 : cd -? l (de confiance égale ¹⁶ _19), cl -? d

(de confiance ¹⁶

_19), dl -? c (de confiance ¹⁶

22)

2. A conclusion de longueur 2 (obtenue par union de conclusion de longueur

1) : c -? dl (de confiance ¹⁶₂₄), d -? lc (de confiance ¹⁶

_27), l -? dc (de

confiance ¹⁶

26)

- Pour m = p2 = cjl dont le support est ¹⁹

_43, on a les règles :

1. A conclusion de longueur 1 : cj -? l (de confiance égale ¹⁹ _24), cl -? j

(de confiance 1), jl -? c (de confiance ¹⁹

25)

2. A conclusion de longueur 2 (obtenue par union de conclusion de longueur

1) : c -? jl (de confiance ¹⁹₂₄), j -? lc (de confiance ¹⁹

_40), l -? jc (de

confiance ¹⁹

26)

- Pour m = p2 = djl dont le support est ²¹

_43, on a les règles :

1. A conclusion de longueur 1 : dj -? l (de confiance égale ²¹ _24), dl -? j

(de confiance 1), jl -? d (de confiance ²¹

25)

2. A conclusion de longueur 2 (obtenue par union de conclusion de longueur

1) : d -? jl (de confiance ²¹₂₇), j -? ld (de confiance ²¹

_40), l -? jd (de

confiance ²¹

26)

- Pour m = p2 = hjl dont le support est _4153, on a les règles :

1. A conclusion de longueur 1 : hj -? l (de confiance égale 15

_17), hl -? j

(de confiance ¹⁵

_16), jl -? h (de confiance ¹⁵

25)

73

2. A conclusion de longueur 2 (obtenue par union de conclusion de longueur 1) : h -? jl (de confiance 1519), j -? lh (de confiance 4150), l -? jh (de

confiance ¹⁵

26)

Motifs fréquents de longueur 4 : cdjl

Pour ce motif fréquent m de longueur 4 on ne considère que les règles dont

p1 -? p2 \ p1 avec p2 = m. Son support vaut ¹⁶

_43. On a les règles suivantes :

1. A conclusion de longueur 1 : cdj -? l (de confiance ¹⁶

_19), cdl -? j (de confiance

1), cjl -? d (de confiance ¹⁶₁₉), djl -? c (de confiance ¹⁶

21).

2. A conclusion de longueur 2 (obtenue par union de conclusion de longueur 1) :

cd -? lj (de confiance ¹⁶

_19), cj -? ld (de confiance ¹⁶

_24), dj -? lc (de confiance

₂¹₄⁶),

₄) cl -? jd (de confiance 19), dl -? jc (de confiance ¹⁶

_22), jl -? dc (de

confiance ¹⁶

25).

3. A conclusion de longueur 3 (obtenue par union de conclusion de longueur 2) :

j -? ldc (de confiance ¹⁶

_40), c -? ldj (de confiance ¹⁶

_24), d -? lcj (de confiance

16

_27), l -? jdc (de confiance _26).

3.3.3 Indices statistiques associés aux règles d'association

Comme présenté dans la section 3.1.2, le support ainsi que la confiance ne sont pas les seuls indices capables de nous fournir des amples informations sur la qualité d'une règle. C'est ainsi que nous vous présentons, sous forme tabulaire, d'autres indices statistiques à même de nous apporter des informations supplémentaires.

Dépendance

Nous allons calculer la dépendance des motifs et nous ne considérerons que les motifs ayant engendrés des règles valides. Notons cependant qu'un motif B dépend fortement d'un motif A si le pourcentage de la règle A -? B est supérieur ou égal à 50%. La dépendance des règles d'association est montrée à la table 5.4.

Intérêt

Nous allons calculer l'interêt des motifs. Seuls ceux ayant engendrés des règles valides seront considérés. Notons cependant que plus la règle A -? B admet une valeur faible, intéressant est le motif B par rapport au motif A.L'intérêt des règles d'association est montrée à la table 5.5.

Le treillis ainsi obtenu à partir du contexte formel K = (X, Y, R) avec X l'en-semble de livres, Y l'ensemble de mots et R la relation montrant la correspondance entre mot et livre est montré à la figure 5.6.

En effet, le logiciel concept Explorer a été conçu par l'entreprise Serhiy Yevtu-shenko et associés en 2006. Il permet d'éditer un contexte formel et génère, les règles d'associations ainsi que le treillis associé à ce contexte en considerant un seuil égal au support minimum.

5.3.4 Interprétation des résultats

Nous avons au total 296 motifs qui ont engendrés 66 règles valides par rapport au seuil que nous nous sommes fixé. Nous nous baserons sur ces règles pour interpréter les résultats. Notons cependant qu'il est important, pour nous, de repérer quelles

74

TABLE 5.4 - Dépendance des règles d'association

75

TABLE 5.5 - Intérêt des règles d'association

76

FIGURE 5.6 - Treillis des concepts généré à partir du logiciel Concept Explorer 1.3

règles sont à nos yeux interprétables en se basant, non seulement, sur le support et la confiance mais aussi sur la dépendance et l'interêt d'une règle d'association. Ce qui nous amène à définir l'interprétabilité d'une règle.

Définition 8 (Règle inteprétable)

Une règle B = H est dite interprétable si l'on peut arriver à relier tous les termes de B et F afin que ceux ci nous emmène vers la connaissance recherchée. Il sera donc question d'expliquer pourquoi il est normal que tel terme apparaisse avec tel autre. Cet explication va souvent refléter ce qui est exprimé par des liens sémantiques(section 5.1.1) dans le domaine considéré.

3.3.1 Les meilleures règles interprétées

Nous vous présentons dans cette section quelques règles qui peuvent facilement nous permettre de trouver la connaissance recherchée.

Règle : 'ontologie' 'linguistique' 'connaissance' = 'corpus' support : "16"; Intérêt: "1.34"; Dépendance : "22%"

Cette règle indique les 16 documents cités présentent des notions sur la linguistique des connaissances mais aussi celles traitant de l'ontologie des connaissances qui est une branche de l'intelligence artificielle qui consiste à représenter les connaissances relatives à un domaine bien spécifique associant ainsi les concepts de base de ce domaine et ses relations afin qu'ils soient compréhensible par les machines. Elle admet un intérêt de 1.34 ce qui signifie que le motif corpus est moyennement intéressant

77

par rapport au motif 'ontologie' 'linguistique' 'connaissance' mais aussi admet une dépendance moyenne par rapport à celui-ci.

Règle : 'ontologie' 'connaissance' = 'corpus' 'linguistique' support : "16"; Intérêt: "1.51"; Dépendance : "28%"

Cette règle d'association admet le même support que pour la règle présentée précédemment en revanche elle a un indice de dépendance de 28% et un intérêt de 1.51. Ce qui signifie que la nouvelle conclusion devient intéressant par rapport à l'ancienne et admet une dépendance d'au moins 4% de plus que celui de son prédécesseur.

Il sied de noter qu'il existe plusieurs techniques qui peuvent nous permettre d'aboutir à des conclusions encore plus satisfaisantes en essayant de reduire par exemple le bruit lié à la synonymie ou encore à la polysémie. Pour aboutir à de tels résultats, les notions du Web sémantique mais aussi de l'ontologie relative au domaine sous études seront d'une grande importance. Il ne faut cependant pas sous estimer l'apport d'autres indices statistiques tels que la conviction et l'étonnement qui sont des outils des méthodes symboliques.

78

Chapitre 6

Conclusion et perspectives

Des travaux de recherche relativement récents dans le domaine de la prospection de données, plus particulièrement dans le processus de fouille de données textuelles, ont démontré l'intérêt des règles d'association. La découverte des règles d'associa-tions se fait en deux étapes : (i) la détermination de l'ensemble des motifs fréquents (c'est-à-dire ceux dont le support dépasse un seuil déterminé) à partir d'un contexte formel sur lequel une connexion de Galois est définie, puis (ii) la génération des règles d'association à partir de ces motifs. Cependant, l'interprétation de ces règles et l'évaluation de leur qualité par des indices statistiques restent difficiles à maîtriser. Le nombre de règles extrait ne permet pas une vue globale, précise et une exploitation efficace des régularités et d'éventuelles connaissances qui émergent d'un grand corpus de textes. Notons cependant que face à cette éventualité, il a été important de recourir encore aux « maths » avec une théorie inéluctable pour une étude qui se veut sérieuse dans le domaine de fouille de données et la représentation des connaissances. Les treillis de concepts formels sont une structure mathématique permettant de représenter et d'organiser l'information concernant des classes d'objets possédant des propriétés communes; ainsi ces concepts sont construits à partir de l'Analyse Formelle de Concepts. Etant une approche à la représentation des connaissances, l'AFC est une méthode qui répose sur la structure de treillis et est utilisée dans la structuration des connaissances.

Pour arriver à nos fins, nous avons eu à diviser notre travail de la manière que voici:

Le premier chapitre a été consacré à l'introduction afin de présenter le travail de manière sommaire. Le deuxieme chapitre a traité de la structure de treillis qui constitue même la théorie mathématique sur laquelle a porté notre étude. Le souci de rendre cette étude plus sérieuse nous ayant animé, afin d'attirer aussi les « non boréliens » ou les « non matheux », nous avons jugé utile de présenter un aspect algorithmique des treillis. Tel a été l'objet du troisième chapitre.

Les structures mathématiques, y compris les treillis, étant, cependant, des notions non concrètes, il s'est averé important de les utiliser dans un domaine concret afin de les rendre plus « palpables ». C'est ainsi que, l'exploration des données connue aussi sous le nom de fouille de données ou data mining a fait parti de notre domaine d'étude et nous y avons consacré tout un chapitre que nous avons intitulé Fouille de données et navigation dans un treillis.

Le data mining est cet art d'extraire des connaissances à partir de données, lesquelles connaissances auront besoin d'être traitées mais aussi représentées à des fins soit de prédiction, soit de description. En effet, pour manipuler ces connaissances, les notions sur les modèles de représentation des connaissances reposant essentiellement

79

sur des théories issues de la logique sont nécessaires. C'est dans ce cadre que, dans notre cinquième chapitre, nous avons eu à appliquer les structures vues au deuxième chapitre dans la représentation de ces connaissances et la recherche d'information.

Cependant, notre objectif étant d'étudier l'impact de ces structures dans le domaine de fouille de données afin de représenter les connaissances qui en seront extraites, nous avons jugé utile de les appliquer dans le domaine de fouille de données textuelles. Nous avons élaboré un corpus de 43 livres sous format électronique dont la plupart développe un thème axé sur l'intelligence artificielle et nous avons constitué un contexte d'extraction formé en colonne des livres et en ligne des mots clés qui en sont issus. Nous avons fixé un seuil minimum et à partir de cela nous avons extrait des motifs ainsi que des règles valides. A partir de ces règles nous avons tiré nos conclusions en nous basant sur l'intérêt et la dépendance qui sont des indices qui nous ont permis de tirer des règles interprétables.

Notre objectif en abordant ce sujet, n'était pas seulement de nous limiter à une application montrant l'importance de la structure de treillis dans le domaine de fouille de données et la représentation des connaissances, mais aussi de concevoir un outil pouvant nous aider à extraire et à représenter ces connaissances d'une manière automatique.

Etant dans une province qui regorge d'énormes gisements miniers, nous souhaiterions, comme perspective, poursuivre cette étude en thèse et appliquer les structures de treillis dans ce domaine afin de répondre aux objectifs d'une science qui se veut pratique.

80

Bibliographie

[1] Karell Bertet; Structure de treillis : Contributions structurelles et algorith-miques.Quelques usages pour des données images; Université de La Rochelle; 2011

[2] J. B. Nation; Notes on lattice theory; University of Hawaii

[3] Daniel Rajaonasy Feno; Mesures de qualité des règles d'association : normalisation et caractérisation des bases; Université de La Réunion; 2007

[4] Robert Faure; Précis de recherche opérationnel : Méthode et exercices d'ap-plication; Dunod; 1974

[5] Mr Belhadj Abdelaziz; Génération de treillis et propriétés algébrique; Mou-loud Mammeri; 2011

[6] Ganaël Jatteau; Approximation du treillis de concept pour la fouille de données; Université du quebec; 2005

[7] Robert Godin, Guy Mineau, Rokia Missaoui, Hafedh Mili; Méthodes de classification conceptuelle basées sur les treillis de Galois et applications; Intelligence Artificielle; 1995

[8] Sébastien Rohaut; Algorithmique : Techniques fondamentales de programmation (exemples en PHP); eni edition; 2009

[9] Saint Jean Djungu; Algorithmique et structure des données; Note de cours; 2012-2013

[10] Thomas Cormen, Charles Leiserson, Ronald Rivest, Clifford Stein; Introduction à l'algorithmique : Cours et algorithmique; Dunod; 2009

[11] Yannick Toussain; Fouille de textes : des méthodes symboliques pour la construction d'ontologies et l'annotation sémantique guidée par les connaissances; Ecole doctorale IAEM Lorraine; 2012

[12] Sondess Ben Tekaya, Sadok Yahia, Yahya Slimani; GenAll Algorithm: Decorating Galois lattice with minimal generators; Vaclav Snasel; 2005

[13] Lhouari Nourine, Olivier Raynaud; A fast algorithm for building lattices; Université Montpellier; 1999

[14] Djamel Abdelkader Zighed, Ricco Rakotomalala; Extraction des Connaissances à partir des Données (ECD); Techniques de l'Ingénieur; 2002

[15] Rob Mattison; Artech Computer Science Library; Data Warehousing and Data mining for Telecommunications; Artech House; 1997

[16] I. Tellier; Introduction à la fouille de textes; Notes de cours

[17] Philippe Preux; Fouille de données; Notes de cours

[18] Ronald J. Brachman, Tej Anand; The Process of Knowledge Discovery in Databases A First Sketch; Technical Report WS-94-03; 1994

[19] Gaël Le Mahec; Utilisation des arbres de radicaux pour les algorithmes de Data-Mining sur grille de calcul.; Université de Picardie Jules Verne; 2004

[20] M. H. Rouane, M. Dao, M. Huchard, P. Valtchev; Analyse formelle de données relationnelles pour la réingénierie des modèles UML; LMO; 2007

81

[21] M. JAY NORTON; Knowledge Discovery in Databases; The Board of Trustees; 1999

[22] Usama Fayyad, Gregory Piatetsky Shapiro, Padhraic Smyth; From Data Mining to Knowledge Discovery in Databases; Artificial Intelligence; 1996

[23] François Rioult; Extraction de connaissances dans les bases de donnùees comportant des valeurs manquantes ou un grand nombre d'attributs; Université de Caen Basse-Normandie; 2005

[24] PAOLO Giudici, SILVIA Figini; Applied Data Mining for Business and Industry; John Wiley Sons Ltd; 2009

[25] Pascal Poncelet, Maguelonne Teisseire, Florent Masseglia; Data Mining Patterns : New Methods and Applications; IGI Global; 2008

[26] Andrea Ahlemeyer Stubbe, Shirley Coleman; A Practical Guide to Data Mining for Business and Industry; John Wiley Sons, Ltd; 2014

[27] Mehdi Kaytoue, Sébastien Duplessis, Amedeo Napoli; L'Analyse Formelle de Concepts pour l'Extraction de Connaissances dans les Données d'Expression de Gènes; Intelligence artificielle; 2009

[28] Karima Mouhoubi, Lucas Létocart, Céline Rouveirol; Extraction de motifs ensemblistes dans des contextes bruités; LIPN; 2011

[29] Hacène Cherfi, Yannick Toussaint; Adéquation d'indices statistiques à l'in-terprétation de règles d'association; Journées internationales d'Analyse statistique des Données Textuelles; 2002

[30] Dictionnaire Larousse 2010

[31] Saint Jean, A.O, Djungu; Outils et langages du web n.0; Mediaspaul; 2013

[32] Brown, J., S, Burton, R. R.; Diagnostic models for procedural bugs in basis mathematical skills. Cognitive Science; learntec; 1978

[33] Dillenbourg P., Martin-Michiellot S.; le rôle de techniques d'IA dans les logiciels de formation; CBT; 1992

[34] Wenger E. ;Artificial intelligence and Tutoring systèms : Computational and cognitive approches to the communication of knoledge; Los Altos : Morgan Kauff-mann Publishers; 1987

[35] Pierre Dillenbourg, Silvère Martin-Michiellot; Le rôle des techniques d'in-telligence artificielle dans les logiciels de formation; Université de Genève; 1991

[36] Philippe Fournier-Viger; Un modèle de représentation des connaissances à trois niveaux de sémantique pour les systèmes tutoriels intelligents; Notes de cours

[37] Meghyn Bienvenu; Introduction à l'Intelligence Artificielle; Notes de cours

[38] Stuart Russell; Peter Norvig; Artificial Intelligence : A Modern Approach; Livre

[39] Vincent Isoz; Elements de mathématiques appliqués; sciences.ch; 2005

[40] Patrick Dehornoy; Logique du premier ordre; Notes de cours version 2006-07

[41] ML Mugnier; Bases de la logique du premier ordre; Notes de cours

[42] Musumbu, Kaninda; Logique propositionnelle; Notes de cours

[43] M'SAKNI Charfeddine; La logique Temporelle; Travail d'étude Licence Informatique; 18 juin 2004

[44] PAGANI Clara, SADAOUI Akim, CHABOT Simon; Introduction à la logique floue; Automne; 2011

[45] Franck Dernoncourt; Introduction à la logique floue; Paris; 2011

[46] G. Brewka, J. Dix, K. Konolige; Nonmonotonic Reasoning- An Overview; CSLI publications, Stanford; 1997

82

[47] Pierre Andrieux; La place de la géophysique dans l'exploiration minière; Cours

[48] Marcel Cori ; Qu'est-ce que le traitement automatique des langues; Notes de Cours

[49] Christian Jacquemin; Traitement automatique des langues pour l'accès au contenu des documents; LIMSI-CNRS; 2003

[50] Daniel FREDON; Myriam MAUMY-BERTRAND, Frédéric BERTRAND; Mathématiques Algèbre et géométrie en 30 fiches; Dunod,2009

[51] Jean Lieber, Fouille de données, Notes de Cours

[52] Paul LOTIN, Représentation de connaissances complexes: Un formalisme à base de rôles sémantiques, Université Blaise Pascal,1995,Novembre