
i
EPIGRAPHIE
« Déployant la force de son bras; Il disperse
les superbes.
Il renverse les puissants de leurs trônes,
Et il
élève les humbles »
Luc 1,51-52
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE

ii
DEDICACE
A mes parents, PAPA RICHARD DEBATALA et
MAMAN LUCIE NIANGA ; nous dédions ce travail.
DEBATALA Archange Michel
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

iii
REMERCIEMENTS
Etant donné que tout n'était pas facile pour
nous au courant ce cycle, mais avec l'aide de tous les miens nous y sommes
arrivé. C'est pourquoi nous voulons exprimer par ces quelques lignes
notre profonde gratitude à toutes les personnes qui nous ont, d'une
manière ou d'une autre, aidé à l'élaboration du
présent travail.
Premièrement nous rendons grâce et remercions
l'éternel Dieu tout puissant père de notre seigneur et sauveur
Jésus-Christ ; lui la source intarissable de notre intelligence et de
notre sagesse.
Nous remercions ensuite le professeur KAMPEMPE BUSILI
JUSTIN DUPAR pour sa disponibilité en dépit de ses
multiples occupations, pour son attention et ses conseils et remarques envie
que nous fassions bien ce travail ; nous lui sommes très reconnaissant
;
Nos remerciements à tous les professeurs, chef de
travaux et assistants qui nous ont encadré depuis le début de ce
cycle jusqu'à ce jour.
Nous serons ingrats si nous ne remercions pas tous les membres
de notre famille principalement Mon père Richard DEBATALA, Ma
mère Lucie NIANGA, pour leur amour, leur affection, leurs conseils et
surtout pour les moyens financiers mis à notre disposition malgré
les difficultés et la conjoncture du pays ; puis Judith DEBATALA, Zozo
DEBATALA, et Taty MUSILUKULA ;
Neveux et nièces : Lablonde et Hervé AKO,
Jovanie KILAPI, Djovanie MUTEKI et Lysa LUKULA ;
Suivant le même ordre d'idée nous remercions
particulièrement CHANCELINE SIMER pour tout son amour, son soutien moral
et physique ;
A tous les compagnons de lutte : Lionnel NGOMA, Henry GWANA,
Pacific KINKELA, et Jeef KALENGAY, Alain TSHILEMBI, Kas KASONGO, celeste
NZIENGI, Sr PHOLA Véronique.
Nous pensons aussi à nos frères et soeurs : Sr
Mireille TSHITSHI, Faida MUSUMADI, Alex MUTUMBULA, Verlaine LUILA, Nicole
MUZEMBO, Emery KINVUKA, Didier KIMOLO, Fiston KASWA, Tonton KIBALA, Souza
KUB'S.
Et à tous ceux, de près ou de loin ont
participé à la réalisation
de cette oeuvre nous disons grand merci.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

1
INTRODUCTION
La présente étude porte sur « vers la
gestion scientifique des stocks. » Le stock étant un ensemble
des produits ou des bien qu'une personne ou une entreprise peut posséder
en vue d'une utilisation future. Il doit de ce fait, faire objet d'une bonne
gestion avec des techniques approuvé.
Les stocks peuvent constituer de 20 à 60% des actifs
d'une entreprise. Ils représentent donc une immobilisation de la
trésorerie qui pourrait être consacrée au
développement d'autres activités d'une entreprise. A cet
égard le poids du stock peut contribuer à fragiliser la situation
financière d'une entreprise.
Mais, jadis beaucoup des personnes voir même des
entreprises détenant des stocks utilisaient des méthodes empires
pour stocker leurs stocks. Ces méthodes empiriques ne le permettaient
pas à atteindre tous leurs objectifs et à maximiser les
intérêts dans leurs commerces. Parce que ces méthodes
empirique utilisés étaient limiter et ne les aidaient pas
à éviter certains inconvénients sur les stocks tels que :
la pourriture, l'obsolescence, des livraisons tardives, la pénurie,
etc.
Dans ce travail, nous proposons quelques méthodes
scientifiques de gestion des stocks qui apporte des éclairages dans la
recherche de l'amélioration de leurs systèmes de gestion des
stocks ; afin de lutter contre tous ces inconvénients, en minimisant le
coût de détention des stocks ; Tout en sachant : à quel
moment commander ? Puis quelle quantité s'approvisionner ?
Avec les méthodes scientifique que nous proposons les
détenteurs du stock doivent comprendre que :
? ils devront se réapprovisionner quand la
quantité en stock démunie sensiblement mais pas au point de
tomber en pénurie, avant la réception des nouvelles marchandises
;
? ils devront réapprovisionner une quantité
relative à la
quantité totale des provisions qu'ils ont toujours et
au temps c.-à-d. ils devront commander la quantité
nécessaire afin de ne pas tomber en disette ou ne pas aussi avoir
beaucoup dans les ensilages.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE

2
Cette étude est subdivisé notre travail en trois
chapitres à la réserve de l'introduction et de la conclusion:
i' Le premier chapitre qui porte sur les
généralités. Il s'agit des notions fondamentales de la
gestion des stocks ;
i' Le second : Modèles de gestion stocks est axé
sur certains modèles de gestion des approvisionnements ;
i' Et enfin le dernier se focalise sur l'étude des cas
de gestion des stocks.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

3
CHAPITRE I : GENERALITES SUR LA GESTION DES
STOCKS
Pour rédiger ce chapitre, nous avons consulté
les documents ci-après : [1], [3], [4], [5], [6];
Toute entreprise, quel que soit son activité doit
veiller à assurer une bonne gestion des stocks pour éviter le
sur-stockage ou le sous-stockage; ainsi qu'une activité dans la rotation
des stocks et la gestion des approvisionnements pour être performante.
En effet, quel gaspillage énorme une mauvaise gestion
des stocks n'entraine-t-elle pas ? Ce pourquoi, il faut éviter de
dilapider ses biens en utilisant une bonne gestion des stocks.
1) QUELQUES DEFINITIONS
Plusieurs notions doivent être définies, avant de
parler de la gestion des stocks afin de favoriser la compréhension
surtout des locutions clés de cette notion dans les lignes qui suivent.
Ainsi, commençons par définir :
a) Le stock :
? le stock est toute réserve des biens tangibles ou
intangibles en vue de satisfaire à des demandes éventuelles ;
? Ensemble des produits finis et des produits au cours de
production possédé par une entreprise à une
date précise ;
? Une réserve constituée en vue de satisfaire un
besoin ultérieur.
Le stock peut être vu, en effet, comme l'accumulation
des produits qui peuvent être utilisés pour satisfaire une demande
future. Physiquement, un stock se présente comme un ensemble d'objets en
attente d'utilisation, à un moment donné, dans un endroit
précis. C'est ainsi que dans une entreprise on trouvera des stocks
à différents stades du processus de production tels que :
i' Matière première ;
i' Produits semi-finis ;
i' Produits finis pour la consommation ou la vente ; i'
Matériel et pièces des rechanges ;
i' Des biens fabriqués ; ou en cours de fabrication,
destinée
à la vente ; défectueux, destinés à
être réparés ;
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l
b)

4
Le stockage : est le déplacement
intelligent des stocks afin de pouvoir retrouver facilement un ou des produits
précis.
Le stockage aussi appelé entreposage répond
à certaines règles afin de garantir le maintien de la marchandise
en bon état; d'optimiser l'espace et d'assurer la sécurité
des salariés.
Un bon stockage permet de connaitre à tout moment la
quantité de marchandise disponible et mise en vente.
c)La gestion :
? Action de gérer, d'administrer ;
? organisation et contrôle administratif d'une entreprise
privée ou public.
2) LA GESTION DES STOCKS
Une des missions principales de tout logisticien est de savoir
gérer son stock avec efficacité. Les enjeux de cette gestion sont
de servir au mieux les clients pour une satisfaction optimale tout en
maintenant les coûts de stockage les plus bas possibles. Pour
réussir cet exercice d'équilibriste, le gestionnaire s'appuie sur
des techniques éprouvées.
Il existe des méthodes permettant d'évaluer les
quantités optimales des stocks en fonction de plusieurs
paramètres comme le nombre des commandes, le délai
d'approvisionnement etc. C'est la gestion économique des stocks.
Avant de voir comment les stocks peuvent être
gérés donc parler de la gestion de stock, il semble
nécessaire de comprendre les raisons d'existantes des stocks.
a) LA FONCTION DES STOCKS
Les fonctions des stocks sont des différentes raisons
justifiant la détention ou l'existence des stocks.
En effet, dans une entreprise, une activité doit
disposer des produits dont elle a besoin d'une manière
instantanée. Par contre l'entreprise acquiert ces produits auprès
de ses fournisseurs dans le délai qui peuvent être beaucoup plus
long. La constitution des stocks permet de garantir la continuité des
activités et permet à l'entreprise de produire à un rythme
stable.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

5

6
La présence des stocks intermédiaire (ou stocks
de transite) dans une chaine de production réduit le risque
d'arrêt de la production en cas de panne de l'une de machine. De l'autre
côté, un niveau de stocks faible augmente le risque de rupture et
peut provoquer l'arrêt de production. Il est clair que s'il y a
arrêt de production, la demande des clients sera insatisfaite.
Alors, la non satisfaction de la demande du client peut avoir
de répercussion négative dans l'entreprise tel que perte de la
confiance du client en plus du manque à gagner de l'entreprise.
Lorsque le nombre de commande est réduit, on remarque
l'existence d'un coût entrainant le lancement d'une commande et qui ne
dépend pas de la quantité commandée. Le fait de commander
des quantités plus importantes (qui seront stockées) permettent
de réduire le nombre de commande et induit naturellement, la baisse des
charges dues à la passation de commandes.
De plus, en achetant de quantité plus importante,
l'entreprise peut bénéficier d'escompte sur la quantité ;
les remises peuvent être intéressantes et importante par rapport
au coût de stockage.
Si l'on peut prévoir les hausses (ou baisses) des prix,
l'entreprise a tout intérêt à constituer des stocks. Ainsi,
elle peut éviter d'acheter plus tard à un prix plus
élevé. Les produits stockés peuvent aussi être vendu
plus tard à des prix supérieur. Dans certaine situation, les
stocks peuvent être utilisés pour influencer les prix des produits
sur le marché.
Le stock peut servir aussi, pour parer aux fluctuations de la
demande du client (elle peut être plus importante que prévue) et
pour palier au long délai de livraison (car de retard peuvent se
produire), le stock agit donc contre l'effort de l'incertitude.
b) INCONVENIENT DE STOCK
Le produit mit de côté à plusieurs
écueils dont nous citerons quelques-uns :
? immobilisation du capital : étant donné que
l'entreprise a une concupiscence de ressource financière pour
développer son activité, les stocks peuvent représenter
une grande partie du capital de l'entreprise ; or cette partie du capital est
immobilisée et régénère aucun
bénéfice.
? potentiel de risques : les marchandises stockés
deviennent potentielle de risque au cas où il y aura vol ou incendie ou
encore obsolescence. L'entreprise aura à tout perdre sans rien
généré.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l
? Avoir les stocks devient embarrassant parce qu'il
nécessite des espaces des stockages, du personnel pour la gestion, le
frais de maintien (assurance, location des espaces de stockages, etc.) c'est ce
qu'on appelle le coût de maintien.
c) UTILITE DE LA GESTION DES STOCKS
Elle est indispensable pour répondre au mieux aux
demandes des clients. Un stock doit contenir les articles demandés en
quantité adaptée. Les responsables de stock doivent donc
connaitre les tendances du marché avant de sustenter les autres
entreprises.
d) LES ELEMENTS DE LA GESTION DES STOCKS
Maintenant que nous avons vus quelques notions ayant trais
avec la gestion des stocks, alors définissons la :
i. La gestion des stocks est l'ensemble des procédures
appliqué par une entreprise pour déterminer quand
s'approvisionner, les quantités à acheter, etc.
Elle consiste à planifier et à mettre en oeuvre
une méthode pour maximiser la rentabilité.
ii. Gérer un stock : c'est définir des
règles des approvisionnements tels qu'on ne manque pas trop souvent des
marchandises, des produits en stock et que le coût de gestion soit
minimal.
Les entreprises constituent des stocks pour plusieurs raisons;
ici, nous énumérons quelques-unes:
1. Raison technique : on parle de raison technique
lorsque le
débit des productions et d'utilisation présente des
profits différents ;
2. Raison économique : lorsque les
coûts fixes ou de rendement
croissant apparaissent dans le processus
de production et d'approvisionnement ;
3. Raison financière : si l'entreprise
intervient sur le marché en
amont ou en avale aux cours des
fluctuants ;
4. Raison de sécurité : chaque fois
que l'incertitude caractérise la
demande et les conditions
d'approvisionnement.

7
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l
Une question nous vient à l'esprit afin de stimuler la
suite de notre travail : « comment peut-on maintenir le stock à un
niveau suffisamment élevé ?»
Sachant que le but de la gestion des stocks est justement de
déterminer par des méthodes de gestion des stocks les moments et
les quantités optimales des commandes afin de satisfaire la demande des
clients en minimisant les couts ; Le critère usuel d'optimisation est
celui de l'espérance des couts éventuellement sous contraintes de
niveau de services.
Pour le moment examinons d'abord les différents
éléments constituant ces modèles tout en sachant que les
modèles proprement dites feront l'objet du chapitre suivant de notre
travail.
? Structures de stockage : ce sont des endroits
réservés pour garder des stocks. Une structure de stockage est
à un seul niveau si le même magasin reçoit le produit du
fournisseur et le délivre aux utilisateurs.
A l'opposé, dans une structure multi-échelons,
un magasin souvent appeler magasin central (dépôt) reçoit
les produits du fournisseur et les transferts vers d'autre magasin, qui eux
à leurs tours serviront d'autre et ce, jusqu'aux magasins appelés
détaillants ; qui, eux fournissent directement aux utilisateurs.
? Articles à stocker : la gestion des stocks n'est pas
l'apanage d'un produit seulement ; car on peut stocker un ou plusieurs produit
différents. Et de fois, il y a des interactions entre eux ; car,
certains produits sont fait pour être stocker sous des conditions
contrôlées (humidité, température....) d'autres sont
périssables, d'autres encore non périssables ; etc. Donc il est
naturel qu'ils doivent être gérés différemment.
Dans ce cas, le modèle est appelé mono ou
multi-articles.
? Dans le cas des modèles mono articles : on prend en
compte un seul article a géré indépendamment.
? En outre, y a des modèles multi produits : ou
plusieurs produits doivent être gérés
simultanément.
? La politique de contrôle : cette politique de
contrôle peut être continue ou périodique :
o Le système a revue continue : dans cette politique,
toute les transactions congrues (demandes, commandes, réceptions des
commandes, ...) sont enregistrées de sortes que le
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

8
gestionnaire a la main mise au système et connait
l'état du système a tout moment.
o Le système a revues périodiques : dans ce
système, le gestionnaire examine seulement a un certain temps. Son
avantage est de pouvoir rassembler les commandes de plusieurs produits en une
seule commande, tout en choisissant une période donnée pour tous
les produits. Mais Il nécessite un niveau de sécurité
assez élevé.
· . La demande : diverses hypothèses peuvent
également être posées concernant les
caractéristiques de la demande. La demande d'articles qui peut
être constante ou variables, déterminée (connue avec
exactitude) ou aléatoire (probabiliste), stationnaire ou dynamique,
discrète ou continue. La plus simple des hypothèses est de
considérer la demande comme connue (déterministe) et constante
dans le temps. C'est l'hypothèse du modèle EOQ que nous allons
développer plus tard ; cette hypothèse est cependant peu
réaliste.
Dans une période donnée, le processus de la
demande est composé de deux éléments distincts tout en
sachant que ces deux éléments peuvent être
aléatoires :
· Le nombre des clients qui arrivent dans une
période;
· Le nombre d'articles demandés par clients.
Lorsque l'arrivée des clients suit par exemple la loi de
poisson c'est-à-dire
????
P(× = ê) = ??-?? ??!
La distribution obtenue par le nombre total des articles
demandés est appelé poisson composée.
· . Délai de livraison : qui peut être nul,
fixe ou déterminé, aléatoire ou dépendant du volume
de la commande de réapprovisionnement. C'est l'espace-temps entre le
lancement d'une commande et le moment de sa réception.
· . Réaction aux ruptures : ceci est possible
lorsque le niveau du stock n'est pas suffisant pour satisfaire, une demande qui
arrive suite à une perte de marchandise ou à un report de
livraison. Devant ce dommage, le client dans le besoin, peut choisir entre:
soit
i' Attendre le prochain réapprovisionnement ; i' Annuler
sa demande.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

9
? Capacité de stockage : dans un certain cas pratique,
la quantité des produits que peut acquérir le gestionnaire suite
à une commande est limitée ou aléatoire. La commande est
limitée suite à la capacité de stockage mais aussi
à d'autres considérations telles que la capacité du
fournisseur etc.
? Les différents niveaux de stocks : soit le niveau
maximal, niveau instantanée, niveau minimal, niveau d'alerte ou niveau
de réapprovisionnement ;
? Le cout de possession du stock ou cout de stockage(Cs) : les
couts de stockage comprennent l'ensemble de cout lié au système
de stockage et affectés par les décisions concernant le stock
actif, le stock de sécurité, le stock de complétements, et
le stock de réapprovisionnement. Il s'agit plus
précisément de :
? Couts d'approvisionnement ;
? Cout de détention ;
? Cout de surplus ;
? Cout de rupture de stock ou cout de de pénurie ;
? Cout de dépassement ;
a) Cout d'approvisionnement
correspond à l'acte de reconstitution des stocks.
Lorsqu'il est d'origine externe, l'acte de réapprovisionnement comporte
un cout de commande composé essentiellement de frais administratifs et
un cout d'acquisition composé du prix d'achat et des frais de transports
des produits. Lorsque le stock est d'origine interne, l'approvisionnement
suscite un cout de lancement des séries de fabrication un cout de
fabrication des produits.
Partant du premier aspect « lorsque le stock est
d'origine externe » nous remarquerons que le cout de commande et de
lancement sont généralement fixe par rapport au volume de la
commande ou du lot de fabrication. Sur une période de temps donné
; ces couts sont donc proportionnels au nombre des commandes ou des lancements.
Le cout unitaire d'acquisition et le cout unitaire de fabrication sont
très souvent dégressifs par rapport au volume commandé
(rabais obtenu des fournisseurs) ou par rapport au volume fabriqué
(économie d'échelle)
b) Le coût de détention :
on parle du cout de détention lorsqu'il y a une
détention des produits en stocks. Il est fonction de la quantité
en stock c'est-à-dire il augmente proportionnellement avec
l'augmentation des stocks.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

10
Il comporte beaucoup des composantes dont nous citerons
quelques-unes :
· Cout d'entreposage : Une composante
indépendante du volume de stock c'est-à-dire les charges
liées à la capacité d'entreprendre : loyer ou
amortissement des entrepôts, dépenses de gardiennage etc.
· Une composante liée au niveau du stock total et
comprenant les charges d'assurance, d'entretien et de manutention des produits
stockés ;
· Une composante constituée de charges
financières suscitées par l'immobilisation de capitaux dans le
stock. Il est proportionnel au stock moyen.
c) Le coût de surplus qui
apparait lorsque l'entreprise ne parvient pas à écouler la
totalité de son stock. Ce cout est nul lorsque l'excèdent d'une
période de stockage peut être écoulé sans perte au
cours de la période suivante. Mais s'il s'agit de produits
périssables ou des denrées obsolescentes, tout excès de
stockage par rapport à la demande comporte un cout. Si la perte est
totale, le cout de surplus équivaut au cout d'acquisition du produit.
Par ailleurs, il implique la différence entre cout d'acquisition et le
prix de récupération.
d) Le coût de rupture de stock
: intervenant lorsqu'il y a scission de stock
c'est-à-dire la demande d'une période n'est pas satisfaisante.
Dans le cas d'une demande interne, la rupture du stock risque
de provoqué le chômage technique des ateliers situés en
aval. Le cout de rupture peut être fixe et correspondant au cout de
réorganisation de l'entreprise pendant le temps supposé de
scission du stock.
Dans le cas d'une demande externe s'exhalant de la
clientèle, il peut comporter :
· Le manque à gagner à l'entreprise, si
les clients n'acceptaient pas d'atermoyer sa demande;
· Les indemnités dues aux clients en cas de
manque aux engagements de l'entreprise ;
· Un élément difficilement chiffrable
imputable à la dégradation de l'image de marque de l'entreprise,
a la lassitude du client. Un élément du cout correspond à
l'hypothèse d'achat répété à l'accroissement
de l'espérance du manque à gagner futur imputable à la
rupture du stock.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l
e)

11
Le coût de dépassement
: ce cout intervient lorsque le stock dépasse les
capacités d'entreposage.
Dans ce cas précis, l'entreprise ou le gestionnaire
cherche de trouver nécessairement et, ou momentanément des
capacités de stockage supplémentaire et éventuellement,
aux dommages subit par les produits.
Lorsque les couts sont identifiés et
évalués, ils sont intégrés à une relation
exprimant le cout total de stockage en fonction du volume de produits
stockés.
Les techniques analytiques d'optimisation ou encore la
simulation permettant ensuite de préciser pour chaque catégories
de stocks un volume optimal, c'est-à-dire un volume rendant minimal le
cout total de stockage.
f) Coût de maintien : ce sont
le résultat direct du maintien d'une quantité donnée
d'articles en stock et incluent : taxes, assurance, couts d'immobilisation du
capital, cout d'obsolescence, couts de fonctionnement (éclairage,
chauffage...) etc.
Certains des couts énumérés ci-haut tel
que le cout de maintien, le cout de rupture et le cout de commande sont
difficile à estimer (en particulier celui de pénurie). Pour cette
raison, le risque de rupture est fréquemment modélisé
à travers une contrainte de maintien d'un niveau de service
prédéterminé.
En pratique, on rencontre plusieurs situations
différentes et chacune nécessite une analyse sur mesure.
Les trois mesures de services suivantes sont les plus
utilisées :
? P1 mesure de non rupture = nombres de
cycles sans ruptures
nombre total cycles
La proportion de cycles dans lesquels aucune rupture n'est
enregistrée ;
Un cycle est l'intervalle de temps entre la réception
de deux commandes consécutives.
? P2 mesure de taux de remplissage =
nombres d'articles servis du stock
nombre articles demandés
La proportion de demandes satisfaites directement du stock en
main ;
? P3 mesure de non rupture =temps
/stock>0
temps
La proportion de temps ou le niveau du stock est positif.

12
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l
Lorsque les couts sont identifiés et
évalués, ils sont intégrés à une relation
exprimant le cout total de stockage en fonction du volume des denrées
stockées. Les techniques analytiques d'optimisation permettent ensuite
de préciser pour chaque catégories des stocks un volume optimal,
c'est-à-dire rendant minimale le cout total de stockage.
Dans le cas où les couts de pénuries peuvent
être déterminés, on peut utiliser l'approche cout. Dans
cette approche, on essaye de trouver la règle de contrôle optimal
par minimisation de la moyenne du cout total (somme de couts).
Si par contre, les couts de pénuries ne peuvent pas
être déterminés, ce qui est souvent le cas, on essaye de
trouver la règle de contrôle optimale en minimisant les couts de
commande et de possession sous contrainte de niveau de service. C'est ce qu'on
appelle l'approche niveau de service.
Comme nous l'avons bien dit dans les lignes
précédentes, la quantité du stock peut varier d'un moment
à un autre suite aux réapprovisionnements des clients; La
présentation graphique d'une variation du stock en fonction du temps
entre deux réapprovisionnements successifs sera présentée
comme suite :

F(t) est le niveau du stock à l'instant t. le cout de
stockage entre l'instant t et ?? + ???? peut s'écrire si (???? ? 0):
???? ??(??)????.
Entre 0 et T le cout de stockage est donc égal à
:
? ??????(??)???? = ???? ? ??(??)????.
?? ??
0 0
Ce réfèrent du schéma
précédent, ? ??(??)????
?? équivaut à la surface S
0
donc la partie hachurée. Dans ce cas, le cout de
stockage peut donc s'écrire :
????* ??.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

13
D'une manière analogue, nous pouvons transposer le
raisonnement appliqué au cout de stockage pour celui de cout de
pénurie qui sera donc égale à?? ?? * ??'. Avec ??
?? le cout de pénurie ;
Soit ? ??????(??)???? = ?? ?? ? ??(??)????.
?? ??
0 0
Qui sera écrit au final comme :
???? * ??'
Dans la plus part des problèmes de stock, on
étudie l'évolution d'une quantité Q qui est la
quantité des produits en stocks, qui diminue des quantités ? ????
à des dates ? ????
?? ?? . C'est le cas des
??=1 ??=1
marchandises commandées par des clients donc nous avons
la courbe en escaler du figure suivant :

Il est rare, mais cela se présente aussi que
l'évolution du stock n'affecte pas la forme d'une courbe en escalier.
Dans cet autre cas l'évolution du stock aura la forme de l'eau d'un
barrage dont des quantités variables sont turbinées pour fournir
de l'énergie électrique. Dans ce deux cas, on définit
d'abord une consommation
moyenne ?? = ??0 ?? , représentant la pente de la
droite de consommation, pris en valeur absolue.
En claire, assurer une bonne gestion des stocks revient
à éviter la rupture de stocks, les sur-stockages ou les
sous-stockages et en minimisant les couts liés au stockage.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

14

15
CHAP II : MODELES DE GESTION DES STOCKS
Pour rédiger ce chapitre, nous avons
consulté les documents ci-après :[2], [3], [4], [6]
Comme nous l'avons dit précédemment tout
logisticien à une mission principale celui de savoir gérer son
stock avec efficacité. Les enjeux de cette gestion sont de servir au
mieux les clients pour une satisfaction optimale tout en maintenant les couts
de stockage les plus bas possibles. Pour réussir cet exercice
d'équilibriste, le gestionnaire s'appuie sur des techniques
éprouvées ; dans ce chapitre nous allons voir certaines de ces
techniques qu'on appelle modèle de gestion des stocks.
Il existe des méthodes qui permettent d'évaluer
les quantités optimales à stocker en fonction des plusieurs
paramètre comme le nombre de commandes, le délai
d'approvisionnement etc. c'est la gestion économique des stocks.
Par ailleurs, les méthodes de gestion sont des
premières méthodes de gestions scientifiques des
approvisionnements des produits.
Remontant de la première guerre mondiale, elles ont
pour origine les travaux de l'ingénieur de la société
Westinghouse F. HARRIS (1915) qui ont conduit au modèle connu
universellement sous le nom de modèle de WILSON ou encore de
modèle « EOQ » de l'anglais qui veut dire « Economic
Order Quantity-modele.»
Mais bien avant, la méthode aurait pu être
négligé et oublié si la crise qui éclata aux USA en
1929 n'était pas venu rappeler l'importance de gérer les stocks
disponibles en moindre coût.
Par la méthode de gestion des stocks on entend une
méthode consistant à reconstituer systématiquement un
stock après consommation, soit dès que celui-ci passe en dessus
d'un certain seuil, soit fréquence déterminée.
Ce sont des méthodes qui ressortent d'une logique de
gestion sur la consommation c'est-à-dire que l'évènement
déclencheur d'un réapprovisionnement est une consommation. Cette
logique conduit à une reconstitution systématique du stock.
Il existe plusieurs modèles de gestion scientifique des
stocks ; les plus connus peuvent être regroupés en deux
catégories que nous allons détailler dans les lignes qui suivent
:
? Les méthodes à avenir certains et
? Les méthodes à avenir aléatoire ou
incertain.
Etant donné que la gestion sur le stock est une
méthode particulière de gestion économique des
approvisionnements, nous
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l
supposons qu'il n'y a pas une méthode archétype
mais chaque méthode présente ses propres avantages et
inconvénients à ses domaines d'application
privilégiés.
Il importe en premier temps au gestionnaire d'effectuer une
analyse des consommations et une classification des articles afin d'identifier
la méthode de gestion la plus appropriée.
Toutes fois, il est important de signaler que les seules
données de consommations sont insuffisante pour classer de
manière pertinente les produits disponibles. Sachant que chaque produits
à son cycle de vie propre, la demande des certains produits est parfois
saisonnier, d'autres ont un caractère continu ou discret ; tous ces
caractères sont également des données
prépondérantes à prendre en compte avant de choisir une
méthode de gestion de données.
Ainsi, comme détailler dans le chapitre
précèdent l'existence de stocks au sein d'une entreprise
amène le gestionnaire à se poser la question du niveau optimal de
stock tout en évitant le sur-stockage et le sous-stockage.
C`est dans ce même optique que vont les
différentes modèles de gestion des stocks. Elles ont pour
objectif de minimiser le cout de gestion dans ce système des contraintes
déterminants la fréquence de réapprovisionnement et la
quantité associée.
Définir une politique d'approvisionnement consiste
essentiellement à répondre donc à ces deux questions :
? Quand approvisionner ?
? Combien commander ?
La réponse à ces deux questions dépend
alors de la politique de la gestion adoptée.
En effet, il est possible de commander soit à date
fixe, soit à date variable. De même que la quantité a
commandée peut être fixe ou variable.
S'appuyant sur ces deux contraintes, quatre combinaisons sont
envisageables. Elles correspondent à autant des méthodes de
gestions de stocks possibles :
1) La méthode de réapprovisionnement :
elle est également appeler « méthode calendaire »
et consiste à commander à date fixe une quantité fixe ;
voisine de la quantité économique de commande ; c'est la formule
de WILSON.
2) La méthode de gestion a point de commande :
elle adopte un
système de commande à date variable mais a
quantité fixe dans la mesure où c'est atteindre d'un niveau
donné de stock appelé « point de commande » qui
déclenche la commande de réapprovisionnement.
3) La méthode de re complètement : il
s'agit ici de commander à date fixe, une quantité variable
puisque le niveau de stock a
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

16
complètements varié en fonction du volume de vente
alors que la date reste la même.
4) La méthode de réapprovisionnement
à la commande : elle consiste à passer la commande d'une
quantité variable, a date variable en fonction de la demande.
SECTION I : METHODE DE GESTION A AVENIR CERTAIN
Les modèles des gestions des stocks peuvent se
différer par rapport aux aspects suivants : le nombre de locations et
échelons, le nombre de produits, les processus de la demande, les
structure des couts, les exigences et mesures des services, les possibles
moments des commande, les traitements des ruptures, les délais de
livraison des marchandises, etc.
Il existe plusieurs modèles d'optimisation de gestion
des stocks notamment :
1. La méthode de WILSON
2. La méthode statistique ;
3. La méthode 20/ 80 . Etc.
Parmi tous ces modèles, nous allons nous atteler sur la
méthode dit de WILSON qui est le plus connu et le plus utilisée
mais pas forcément le plus réaliste.
II.1 MODELE DE WILSON
Le modèle de Wilson ou le modèle de la
quantité économique de commande (EOQ) est le premier
modèle de gestion de stock permettant de déterminer la
fréquence et la quantité optimale de réapprovisionnement.
Elle a été introduite en 1913 par F. HARRIS comme nous l'avons
souligné précédemment.
C'est un modèle déterministe c'est à dire
ces données sont connus avec exactitude car la date et quantité
à réapprovisionner sont fixe. Il a pour but de la
stratégie qu'il faut adopter pour que le total périodique des
commandes ou des fabrications des pièces minimise le cout total de cout
d'acquisition et de possession de stocks pour l'entreprise.
Etant donné que le gestionnaire doit veiller ou niveau
optimal de son stock pour éviter le sous stockage et le sur stockage ;
les différents modèles de gestion a pour objectif de minimiser le
cout de gestion.
En admettant, en effet que la consommation soit constante et
le réapprovisionnement instantané on peut définir pour une
période données de gestion, la fréquence optimal de
réapprovisionnement.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

17
a) Hypothèses et notations
Supposons les hypothèses suivantes :
( la demande est connue et constante ;
( le réapprovisionnement est instantané
c.-à-d. le délai
de réapprovisionnement est nul
( la rupture de stock est interdite.
Et les notations utilisées sont:
· Consommation par unité de temps : C
· Cout d'entretien du stock : C??
· Cout de réapprovisionnement ou cout de
Lancement : C1
· Quantité commandé : Q
· Période optimale de gestion : 0
· La période de durée a: n
· Quantité a géré pendant n
période : q
Dans ce modèle, l'objectif est de déterminer les
moments de commande et les quantités à commander de
manière de manière à minimiser le cout total lancement et
du stockage.
b) Analyse du problème
Le processus est la suivante : le stock atteint une
quantité donnée Q au moment du réapprovisionnement puis
diminue progressivement et de façon constante suivant la demande C.
Quand, il atteint le niveau nul, on lance une nouvelle
(réapprovisionnement) commande qui entre en stock aussitôt afin
d'éviter des ruptures de stocks.

Fig. II.1
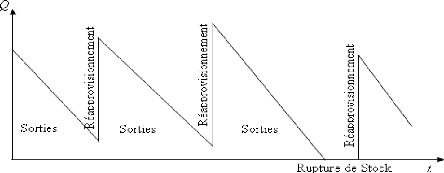
En simplifiant la représentation nous obtenons un
graphique dit « en dent de scie »
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

18
Fig. II.2
En effet, dans ce modèle, les variables
contrôlables sont Q et la quantité d'un réapprovisionnement
mais la demande C et les couts éventuels c.-à-d. ???? et ????
sont non contrôlables.
c) Modèle et solution
Fig. II. 3

?? ?? ??
Dans le graphique ci-haut nous avons n périodes
de durée ??,
donc n.?? = n nous avons une quantité
q qui
devra être géré.
Pendant chaque période ?? le stock moyen est ?? 2.
Le coût d'entretien du stock pendant chaque ??
période est : ???? * ?? 2 * ?? étant donné qu'il y a n
période, le cout total d'entretien
s'élèvera à :
??
?? * 2 * ???? * ??
Et le coût total de réapprovisionnement sera : ??.
???? puis qu'il y
a n
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

19
Donc le Coût global a géré pendant la
période È sera :
???? ??+ ?? ???? (1)
???? = ?? ??
2
Sachant que ?? * È ? ?? = È ?? étant
donné qu'il y a n période ??
pendant È.
Normalement, la somme de la quantité de stock
utilisée pendant la durée de réapprovisionnement ?? doit
être égale à la quantité de stock disponible pendant
toute la période È de gestion.
Ce qui implique : ?? = È*??
??
En replaçant ?? * ?? par È et n par
È*?? dans (1), on aura :
??
????(??) = È * ?? 2 * ???? + È*??
?? * ???? (2)
L'équation (2) ci-haut est la quantité que l'on
veut minimiser, en la dérivant par rapport à q, les
éléments de cette relation sont représentés sur la
figure ci-après.
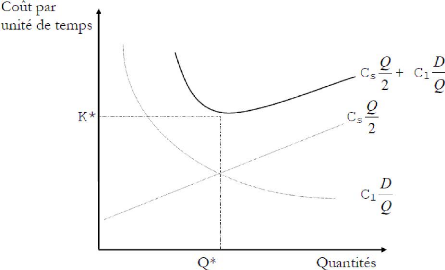
Fig.II.4
On remarque dans la fonction ci-haut que nous n'avons plus qu'une
variable : q.
Lorsque la quantité commandée augmente, le
coût d'approvisionnement (Lancement) diminue alors qu'au même
moment le coût de stockage (la détention du stock) augmente.
D'où, il faut trouver la quantité qui optimise la
fonction de coût.
Ainsi, on peut alors dérivé aisément et on a
:
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

20
?????? È
=
???? 2
Èc
????+??2 ???? ; (3)
|
????
Si
????
|
= 0
|
|
Alors È
2
|
????+ ÈC
q2 ????= 0
|
È???? 2
|
Èc È.?? È.????
+ ??2 ???? ??2 ???? =
2
|
|
??2 * È * ????= 2 * È * ??* ????
Èc 2 * ??* ????
??2 = -2 * * ???? =
È. ????
????
Donc ??2 = 2 * ?? * ????
????
Et on peut tirer la quantité économique à
commander
(4)
??* = v2 * ??* ????
È ????
Il faudra s'assurer qu'on a bien à faire un minimum :
la dérivée seconde doit nécessairement être
positive
??2????
????2
= 2 ?? ???? (5)
??3
L'équation (5) est toujours positive
c'est-à-dire ????et C sont positive et q l'est
toujours.
L'équation (4) est appelé « série
économique » et la valeur optimale de È est appelé
« période économique » correspondant à la valeur
de q est :
|
È=??* ??
|
Avec la
|
??=v2*?? È *??????? ?
|
(6)
|
On a : ??* = v2 * ????
??*?? ??
En remplaçant ??* dans (1) On a:
|
v2*?? È* ????
????
????* = ??*
2
|
????* ??+ ??* ???? (7)
|
Après une série de manipulation on trouve que :
????* = È v2 * ??* ????* ????= v2 * ??* È * ????*
???? (8)
On a donc interpréter ces résultat de cette
manière : en revenant l'expression (2) en fonction de
q, on constate que CT est la somme d'une fonction linaire de
q donc le graphe représentatif passe
par l'origine et d'une fonction de la forme ??/?? ,
représentée par un arc
d'hyperbole (voir figure à haut). La courbe
représentative de CT est donc asymptote à l'hyperbole
pour les petites valeurs de q et asymptotes à la droite pour
toutes grandes valeurs de q.
On constate que le minimum est atteint lorsque
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

21
È
|
*
2
??* =
??C'est-à-dire
|
????*
|
??=
|
È ??
|
|
????
|
|
v2??
|
* ????????
|
Et on a aussi ??* = È.??
??*
Connaissant ??* on peut alors avoir ??* = È.??
= È.v?? .????
2????
v2 ??*????????
Et on remarque que ??* > 1 si ???????? < È2.??
2 c.-à-d. que si???? < ???? * È2.??
2
On a donc intérêt à appliquer la formule
dès que le cout total de stockage de la quantité È * ??
pendant È dépasse le cout de lancement, ce qui est
vérifié dans la pratique.
Dans un contexte déterministe, Harris a donné
une réponse à la question « combien approvisionner ? ».
Il s'agit du concept de quantité économique ou EOQ. Harris a
démontré (formule dite de Wilson) que la quantité optimale
d'approvisionnement était égale à
??* = v2 * ??È * ????
????
Avec :
> Q : la quantité commandé ;
> È : la période de gestion ; > ???? : cout
d'entretien ; > ???? : cout de lancement.
II.2 CRITIQUE DE MODELE
Le modèle développé ci-dessus n'est pas
modèle parfait car il s'éloigne de la vie pratique. Etant
donné que ce modèle suppose la consommation constante et le
réapprovisionnement régulier et surtout n'envisage même pas
le cas de la rupture du stock, alors que c'est ce qui se vit au quotidien.
Or, dans la vie pratique jamais la consommation n'est
constante et le gestionnaire craint toujours la rupture de stock qui peut
intervenir à tout moment.
Nous devons dépasser le point de vue
déterministe en tenant compte des phénomènes
aléatoires. Les grandeurs aléatoires qu'on rencontre plus souvent
dans les problèmes de stock sont : la demande et le délai de
réapprovisionnement.
Il arrive que la demande, si elle est faible suit la loi de
poisson et si elle forte suit une loi normale ; sans oublier qu'elle peut aussi
être d'un autre type Eulérienne, bi normale négative
etc.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

22
Et le délai de réapprovisionnement suit souvent
une loi Binomiale et quelque fois aussi une loi de poisson.
Toute fois si les lois auxquelles on aboutit ont une
expression analytique nous avons les possibilités suivantes :
1. Soit de mettre le problème sous forme
d'équation ; de manière à
nous permettre de déterminer les couts qui interviennent
;
notamment :
> le cout d'entretien du stock ;
> le cout de manipulation ;
> le cout de lancement ;
> le cout de rupture ;
2. Soit utiliser les méthodes de simulation lorsque la
complexité des équations ne permet pas de résoudre
aisément le problème.
Il sied de signaler que mes méthodes de simulation ne
fonds pas partie de notre travail donc nous n'en parlerons pas.
L'un des couts le plus difficiles à déterminer
est le cout de rupture. La détermination de ce cout fait intervenir des
éléments difficile à chiffrer, tel que
l'infidélité des clients, la désaffections de la
clientèle etc. toute en sachant qu'il n'est pas facile de traduire en
nombre le contre publicité qu'on fait en tolérant une certaine
proportion de demandes non satisfaites.
Ce modèle peut être corrigé en prenant un
de ces paramètres comme aléatoire. Donc ce modèle est
corrigé avec soit avec la méthode de re complètement, soit
par la méthode à point de commande.
SECTION II : METHODE DE GESTION TENANT COMPTE DES
ALEAS
II.3 MODELE PAS A PAS
Dans ce modèle, nous avons deux systèmes :
> Le modèle a période fixe et
> Le modèle à période variable ;
Le modèle a période fixe fait
référence à la méthode de re
completement car la date de réapprovisionnement est
déjà fixé à
l'avance le gestionnaire ne travaille que sur la
quantité à
réapprovisionner.
Et dans le modèle a période variable ; nous
faisons allusion à la méthode de réapprovisionnement
à la demande car la période de réapprovisionnement est
variable et la quantité à réapprovisionner est aussi
variable.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

23
1) Système a période fixe
La règle de réapprovisionnement dans ce
modèle est particulièrement simple puis que les dates de
réapprovisionnement sont connues avec exactitude du fait que
fixées à l'avance ; on a plus de problème qu'à
définir la quantité réapprovisionné.
La quantité à réapprovisionner ici est :
soit instantané, soit en délai variable.
a) Si c'est instantané, partant de chaque
début de la période, il y a trois cas qui se présentent
:
i.

Q
Pendant la période T, la consommation est
égale au stock maximal (cas idéal); pas de vente perdue, la
quantité à commander reste la même ;
ii. Pendant la période T, la consommation est
inférieure au stock maximal, pas de vente perdu mais il reste une
quantité des produits en stock ; la quantité à commander
est la quantité initial moins la quantité restante ;
iii. Pendant la période T, la demande est
supérieure au stock maximal, il y a des ventes perdues, la
quantité à commander reste la même.

QM
QM
3emeCas
QR
QM - QR
Q
1erCas
2emeCas
t t-T

T T T
Fig.II.5
Dans ce système c'est la fixation de stock maximal
QM et la période T qui sont des paramètres et qui
dépendent de la demande qui est aléatoire.
Avec ces paramètres et d'autre encore tel que la
capacité de stockage et le cout d'entretien, de pénurie ou de
lancement qu'on peut établir une étude analytique.
Bien qu'on puisse agir avec des analytiques, la
possibilité de tomber à une pénurie et
l'éventualité d'un dépassement du stock ne sont pas
écartées.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

24
s
s
??/
2
r
??/
2
lerCas
?? - ??
2
??,
Q
?? - ??/2
2emeCas
r
t
T T
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l
0

??)
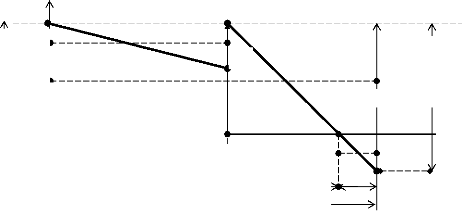
Fig.II.6
Analytiquement le modèle peut se peut se
représenter de manière suivante :
a) Hypothèse, notation et solution Nous
avons des hypothèses suivantes :
v Gestion à période fixe ou variable ;
v La demande discrète ou continue ;
v Le cout de stockage et de pénurie proportionnelle ou
non par rapport au temps ;
Et ces notations :
> S : stock à déterminer ou quantité en
stock en début de
la période ;
> X : la demande enregistré pendant une période
T ;
> PT (r) : La probabilité d'une demande r
pendant une
période T ;
> Cs : Coût d'entretien du stock ;
> Cl : Coût de lancement ;
> Cp : Coût de pénurie ;
Suivant l'importance de la demande en rapport avec le niveau
du stock de début de période, avec un réapprovisionnement
instantané on distingue deux cas (résumer dans la figure II.
Suivante):
i. On arrive enfin de période avec un stock ;
ii. On arrive enfin de période avec un manquant ;
i.

25
Dans une période telle qu'on arrive à la fin
avec un stock ; Le
stock moyen est ?? - ??2 et si le cout d'entretien du
stock est
???? par unité de temps et par unité de
consommation, le cout par période sera :
????= (??- ??2) * ???? * ??
ii. Dans une période telle qu'on arrive enfin de
période avec un
manquant ; le stock moyen sera ??2 pendant
un temps ??1 égale a
??- ??2 ; ???? ???? ?? ??-??= ?? D??où
??2 = ??????* ?? et
??2
?? - ??
??1 = ??
??
* ??= ??*
??
??
D'où le coût d'entretien par période sera
:
?? ??
2
* * ?? * ???? ??
Comme le cout de pénurie ???? par unité de
consommation et par unité
de temps ; avec une pénurie moyenne de ??-??
2 pendant ??2 ; on atteint le
coût de pénurie par période qui est :
??- ?? ??- ??
* * ??* ????
2
??
Le coût d'entretien du stock par unité de
consommation et par unité de temps ; le cout d'entretien par
période et le cout de pénurie par période sont des
coûts affectés par la probabilité de la demande
????(??).
Le coût d'entretien du stock ne se présente que si
?? = ??
Et le coût d'entretien par période et le cout de
pénurie ne sont présent que quand ?? > ??.
En ajoutant le coût de lancement ?? * ???? on a donc
pour n période T on a :
2
= ??? (??- ??
8 2) * ????* ?? * ????(??) + ?? ? ??2
8 8
2??* ????* ?? * ????(??) + ??? (??-??
2??) * ????* ?? *
??=0 ??=??+1 ??=??+1
????(??) + ??* ????
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

26
Soit en groupant des termes on a :
(??, ??) = 0 [???? * ? (s - r 2) ????(r) + ???? *
? ????(r) + ???? * ? (r - s)2 ????(r) +
??=?? ??=??+1 r= s+ 1
?? 00 00
2r ????? ? ]
Avec 0 = n * ?? et sachant toujours que 0 est
la durée total de gestion.
Par contre, il peut se faire aussi que le
réapprovisionnement soit atermoyé a un certain délai et si
ce délai est fixe. On a des cas suivants :
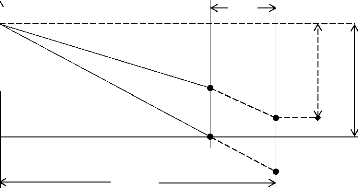
a. A l'instant T-d, on extrapole la droite de consommation et
elle vient couper la verticale de T en un certain point. Si ce point, tel que
A', est au-dessus de T, on commande a T-d la quantité
QA, dont on imagine, si la consommation se poursuit,
postérieurement à T-d au même rythme, qu'elle re
complètera exactement le stock maximale à T, ??A'
étant le stock résiduel.
.Q
Si B', le point d'intersection est au-dessous de T, on
commande, T-d, la quantité QM; on suppose, en effet,
qu'on sera en pénurie, à partir d'une certaine date en T-d en T,
donc que le stock résiduel sera 0 à T.
Q
d
QM
A
QA
QB= QM
A'
B
0
T-d
T t
B'
T
Fig.II.7
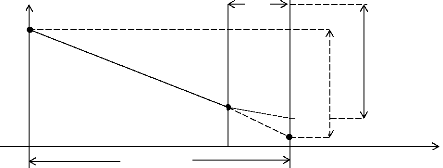
b. en fait, quelle que soit la position du point
d'intersection a T-d, si la consommation diminue suffisamment à partir
de T-d, on risque à T d'obtenir un
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

27
réapprovisionnement excédant, compte tenu du stock
résiduel, le stock maximal.
t
T
Q
QM
d
Qa
Qa
Stock résiduel
a
a'
Fig.II.8
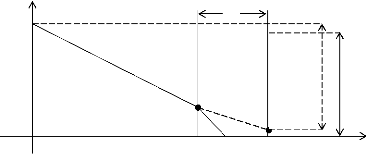
c. Si, par contre, la consommation augmente suffisamment, on
risque une pénurie inattendue ou une pénurie plus forte que celle
qu'on avait prévue, et, si l'on avait attendu un stock résiduel
à T, d'obtenir finalement un réapprovisionnement insuffisant.
a
Fig.II.9
t
Qa
a
Qa
a'
Q
QM
0
Cependant, il peut arriver que le délai de
réapprovisionnement soit aléatoire ; dans ce cas précis
nous pouvons ne prendre en compte que la figure (II.6) du point b
précèdent pour ne pas inventorier toutes les situations qui se
présenterai.
A ?? - ??, extrapolant la droite de consommation, on
a estimé la commande de recomplètement Q. en supposant que la
consommation continuerais à suivre le même rythme , si le
délai
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

28
de réapprovisionnement s'est écourté et
s'est trouvé être d' < d à
l'arrivée du réapprovisionnement le stock maximal sera
dépassé, si alors le délai s'est trouvé
alléché à d?> d, le stock
QM n'est atteint lors du réapprovisionnement ;
Et si la droite de consommation s'est incliner suffisamment,
on a pu enregistrer une pénurie ; même si le délai d'est
raccourci, si elle est élevée extrêmement, on enregistrera
un dépassement du stock maximal même si le délai s'est
allongé.

Q
QM
d
Q
Qa
a
d»
T-d
Fig.II.10
d'
Toute fois La détermination de la commande
résulte dans ce modèle de l'extrapolation de la droite de
consommation, à l'époque T - d, d etant le délai
moyen de réapprovisionnement.
2) Système à période
variable
Ce système demande trop d'effort et de la vigilance car
ayant un stock de départ dit « stock initial »
QM, on doit veiller sur la pente de la droite de la
consommation ; et à chaque instant calculer dans quel délai la
quantité en stock va s'épuiser et voir aussi si la consommation
demeure comparable à sa moyenne depuis le début de la
période.
Admettons alors qu'on passe notre commande de
réapprovisionnement égale à QM' au
moment où la quantité en stock couvre exactement la consommation
correspondante au délai de réapprovisionnement d ; ainsi on a une
gestion a période variable.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

29

Q
QM

t
d2

t1 t2
d1
d3 = d
Fig.II.11
Sachant que le délai de réapprovisionnement d
est variable et la consommation peut augmenter ou diminuer après
passation de l'ordre ; nous remarquons que la méthode de gestion du
système a période variable ne garantit pas non plus comme les
autres méthodes contre la pénurie avant l'arrivée d'un
autre réapprovisionnement ; il y a aussi des excédant, avec un
stock résiduel.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

30
CHAP III : STOCKS ET ETUDES DES CAS
Pour rédiger ce chapitre nous avons consulté
les références : [3], [4], [6] III.1 STOCK
D'ALERTE
Le stock d'alerte aussi appelé « stock critique
» est le niveau de stock pour lequel on déclenche une commande au
risque de connaitre une rupture.
Ce stock est une des méthodes des gestions à
point de commande. Etant donné que l'importance du cout de
pénurie pousse le gestionnaire à éviter une trop grande
partie des ventes perdues, la gestion a période variable s'accommode le
plus avec l'introduction d'un niveau de stock appelé « stock
d'alerte ». Ce stock permet au gestionnaire de déterminer
facilement le point de commande afin d'éviter une pénurie
grave.
Nous tenons à signaler que le point de commande veut
dire le stock atteint un niveau où il est nécessaire de commander
tenant compte des délais pour ne pas tomber en rupture de stock.
Nous ne devons pas perdre de vue que la consommation et le
délai de réapprovisionnement sont aléatoire dans ce
modèle.
Etant donné que le stock d'alerte est une des
méthodes de gestion a point de commande, nous pouvons dire qu'il
requiert un précis et fréquent de niveau de stock. Il permet une
certaine variabilité de la demande en déclenchant les demandes
d'approvisionnement plus tôt ou plus tard en cas de hausse ou de baisse
de ces prix.
Considérons que nous avons une quantité maximal
QM en stock, à livrer petit à petit pendant un temps
T, avec un stock d'alerte initial Q0, pendant le délai de
réapprovisionnement de d jours.

d
d
QM
QA
Q0
QM
Fig.III.1
Supposons alors qe ous vulons baisser les risques de
?? T-d T
pénuries, il nous faudra forcement relever le stock
d'alerte et le porter
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

31
à un quelconque niveau QA (cfr
figure ci-haut) ; des lors nous pouvons déclencher une commande à
u n point a < T - d ; alors la droite de consommation franchi
QA à l'instant a donc le nouveau point de
commande.
Reste à savoir quelle quantité Commander
à cette date sachant que, si on commande QM, le
risque est grand d'avoir un excèdent à a + d ; si la
consommation reste constante et si le délai de la d ne s'allonge pas.
Nous pouvons envisager une des multiples solutions qui peuvent
être imaginé qui est de commander une quantité juste
suffisante, selon le besoin du moment pour re compléter le stock
à a + d ; nous aurons alors
QM+ (QA- Q0) = QM+
Q0 - QA
Dans ce cas précis, le gestionnaire devrait surveiller
la droite de consommation pour voir à quelle date elle rencontrera
l'horizontal QA pour faire enfin un nouvel
réapprovisionnement.
Il nous semble trivial de constater que cette méthode
autant comme les précédents n'apporte aucune justesse quant
à l'absence de pénurie, ni quant à la présence d'un
résidu au moment de l'arrivé du réapprovisionnement.
III.2 STOCK DE SECURITE
Tout d'abord, il est important de comprendre
l'intérêt des stocks de sécurité et leurs raisons
d'être.
Comme leur nom l'indique, ce stock sécurise
l'entreprise quant au besoin non prévus ; c'est-à-dire
répondre aux aléas les plus fréquents lies à la
consommation et la livraison.
L'objectif premier de stock de sécurité est de
prévenir les pénuries causées par la demande et le
délai d'approvisionnement qui ne sont pas toujours constants.
Toutes fois, les motifs pour lesquels les gestionnaires y ont
recours sont diverses mais nous pouvons citez quelques-uns :
> Demandes inattendus des clients ;
> Livraisons des fournisseurs en retard ; > Arrêt des
machines ;
> Panne d'électricité ; etc.
Pour se prémunir contre ces incertitudes, il est
possible de faire usage de quelques stratégies de gestion. La plus
connus et la plus populaire demeure le stock de sécurité mais on
retrouve également d'autre stratégies telles que la
capacité supplémentaire, les délais de
sécurité ou encore la période gelées et les hausses
des besoins bruts que nous avons cités juste pour raison d'informer.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

32
Il importe cependant de rappeler que la majorité des
modèles de gestions des stocks de sécurité se concentre
sur la variabilité de la demande puisse qu'elle est la source
d'incertitude la plus difficilement maitrisable.
Ce modèle consiste à définir
principalement deux niveaux de
stock :
> Q?? (niveau de commande), qui détermine le point
de commande, par l'instant ou la droite de consommation la franchit ;
> Q?? (niveau de sécurité) qui entraine des
modifications de la politique de livraison, dès qu'il est atteint.

>
Q
QM
Q??
Q??
t
Fig.III.2
On peut par illustration montrer qu'à partir d'un
certain seuil ne livrer que des quantités inférieures aux
commandes reçues ou ne livrer que les clients prioritaires etc. ; cela
pour ne pas tomber en pénurie.
Nous pouvons établir ce modèle en prenant en
compte deux cas :
a) Quand on dispose d'une évaluation du cout de
pénurie ;
b) Quand on ne peut pas raisonnablement estimer le cout de
pénurie.
a. Quand on dispose d'une évaluation du cout de
pénurie
On a des notations suivantes :
> D : la demande enregistré pendant une période
T ;
> C?? : Coût d'entretien du stock ;
> Ci, : Coût de pénurie ;
> Q* : quantité commandée en une fois
;
> X : demande pendant le délai de livraison ;
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

33

34
> ??(??) : distribution de la demande pendant le
délai de livraison.
> ?? : demande moyenne pendant le délai
égale a ??(??) Avec des hypothèses analogues à la
méthode précédente
|
Le stock de sécurité équivaut à
(S-??
|
) ;
|
Le cout attaché au stock de sécurité par
unité de temps partant de la fonction économique sera donc :
8
????= ???? * ?(?? - ??) * ??(??)??(??) ?? ??* + ???? * (S -
??)
??
En annulant la dérivée première, on obtient
:
|
????
???? =-?? ??+
|
8
?? ??* ?(??)??(??) +
|
????= 0
|
|
D'ou
|
|
??
|
|
???? ??*
??(??*) = 1 - * ??
????
b) Quand on ne peut pas raisonnablement estimer le cout
de pénurie
Ici on se fixe une probabilité de pénurie
admise. On procède comme suit :
Si l'on admet la probabilité par unité de temps
?? de tomber en rupture de stock quel que soit la quantité qu'on a en
stock ; on calcule ; en première approximation que la probabilité
admise par le
réapprovisionnement est ?? * ??*??.
On peut alors exprimer la relation devra exister pour la
probabilité maximum permise.
??*
?? = ?? * ??
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l
Avec p la demande durant le délai de
dépassement du stock disponible
8
I ??(??)????= ?? * ??*
??
s
|
1 ??(??)
-
|
=
|
??
|
*
|
??*
|
|
|
|
|
|
??
|
|
??(??) 1
=
|
-
|
??
|
*
|
??*
|
|
|
|
|
|
??
|
En comparant les deux cas pour la détermination du
point de commande, on constate que les deux expressions qui donnent le point de
commande sont identiques si on pose
Cs
?? = C??
Ces méthodes permettent d'atteindre plus
aisément le réapprovisionnement en cours et limite les effets
tragiques d'une longue pénurie.
III.3 ETUDE DE CAS
Un revendeur d'huiles industrielles se réapprovisionne
chaque mois et reçoit son réapprovisionnement dans un
délai d'un mois. Sa capacité de stockage s et connait les
coûts de stockage par tonne par mois C1, le
coût de pénurie par tonne par mois C2 et le
coût supplémentaire de stockage par tonne, lorsque la
capacité s est dépassée C3.
1. Q est quantité égale au montant de la
commande majoré de la quantité existant en stock, au moment de la
passation de la commande ;
Si P(x) est la densité de probabilité de la
demande mensuelle ; Calculer le coût total CT(q), et en déduisant
la formule permettant de calculer la valeur de q correspondant au coût
minimal.
2. On a les valeurs des coûts suivantes : C1
= 100$ ; C2 = 1000$; C3 = 500$ ;
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

35
Calculer les valeurs optimales de q pour E ??i
5 ??=1 ; en supposant
que p(??) =
??????-??x
????(??+1)
Et en sachant que la variance et la moyenne valent 2.
?? ??+1
RESOLUTION DU PROBLEME
Soient x et y sont des demandes de la clientèle pour 2
mois consécutifs.
Nous observons 3 cas dans ce problème : nous aurons a
calculez les stocks et les pénuries moyens dans chacune des cas :
1) q - y > s : dans ce cas il y aura un
excèdent en stock. La quantité excédentaire ?? - ?? -
?? subit le coût ??3 par tonne au début
du second mois, on aura un stock s.

q-y
x
a) ??= ??
s
Stock moyen Stock fin

Stock moyen
Stock fin
1 2
t
Coût : CT = c1 * (??-
x2) + c3 * (??- ??- ??)
b) ??> ??
2
??2
t
1
??1
q-y
s
x
Penurie moyenne
|
On a ??
??1
|
= ?? ; t1 = ?? ; t2 = 1- ?? avec
un stock moyen pendant
x x
|
t1 = Z et une pénurie moyenne pendant
t2 = xZ ?? ; et le coût
x-?? * x-??
*
+ c3 * (??- ??- ??)
2 x 2 x
total ???? = c1 * ?? * ?? c2
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

36
2) 0 = ?? - ?? = ?? : au début du second mois la
quantité ?? - ?? sera en stock.
a) ??= ??- ??
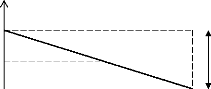
Le stock moyen pendant la période ??- ??- ??2
q-y
x
Stock moyen
Stock fin
1 ?? 2 t
???? = ??1 * (??- ??- 2)

s
a) ??> ??- ??
q-y
Stock moyen
1
x
??1
??2
2
On a donc ??-??
??1
= ??; ??1 = ??-??
?? ??2 Penurie??
??-??
moyenne
;
Stock moyen pendant ??2 = ??-??+??
2
?? - ?? ?? - ??+ ??2 * (?? - ?? + ??
2 ) * (?? - ?? + ??
????= ??1 * 2 * ?? )
??
3) ?? - ?? < 0 : au début du second mois on sera en
pénurie ;
1
2 t
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

37
La pénurie moyenne pendant la période est : ??2 -
?? + ??
????= ??2 * (??2 + ??- ??)
Sur n'importe quel période on aura :
??
????(??) = ? - ??? ??(??)??(??)(??1 * (?? -
2) + ??3 * (?? - ?? - ??)) ??(??)??(??)
??=0 ??=0

??=0 ??=??
+ ?
??-??
= ? ? ??(??)??(??) ??1 * (?? - ?? - ??
??
2)
??=??-??
??=0
???? ????

?? 8 ??(??)??(??)??1 * ((??- ??)2
??=??-?? ??=??-??
+ ? ?
+ ? ? ??(??)??(??) ??2 * (??
8 8
2 + ??- ??)???? ????
??=?? ??=0
Sachant que si É(??) = ? ??(??, ??)????:
??
??
??É = ? ????
?? ???? + ??(??, ??) ????
???? - ??(??, ??) ????
????
???? ????
??
Ce qui peut s'écrire, lorsqu'il s'agit
d'intégration doubles :
?? ?? ??
?? = ? ??(??) (? ??(??)?? (??, ??, ??)???? ) ???? = ?
??(??)[??(??, ??, ??) - ??(??, ??, ??)]????
?? ?? ??
??
=
?Ö(??, ??)???? ??
???? = ? ??Ö
Donc ?? ???? + Ö(??, ??) ????
?? ???? ? Ö(??, ??) ????
????
???? ????
Afin de restreindre les calculs, on constate que si l'on
intervertit l'ordre des intégrations, seules les 3???????? et
4???????? intégrales de CT(q) ont des limites en x par rapport à
q et qu'alors :
??-?? ? ??(??)??(??)(??1 * ??2
8 (?? - ??)2
2?? + ??3 2?? + ??2(?? - ?? - ??)????????
2?? + ??2 * (?? - ?? + ??)2
2?? ) ???? ????
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

38
Ö(??, ??) ????
???? ? Ö(??, ??) ????
????
= ? ??(??) ??1 * (?? - ?? - ?? - ??
?? 2 )????- ? ??(??) ??1 * (?? - ??)2
??
????= 0
2(?? - ??)
??-?? ??-??
Et dans ces conditions on aura :
??-??
?????? = (??2 + ??3) ? ??(??)???? -
??2
????
0
8 + (??1 + ??2) ?
??(??)(?0??-??
??(??)???? + (?? - ??) ???
??(??) ????)????
??-?? ??-??
On doit déterminer q tel que ??????
???? = 0. Or ?? (??) = ????-??, dont ?? = 2 ???? ?????? = 2
Ainsi, on obtient la valeur de q tel que :
??-??
(??2 + ??3) ? ????-?????? - ??2
+ (??1
0
?? ??-?? ?? 8
+ ??2) (? ????-?? ? ????-?? ???? ???? + ? ????-??(??
- ??) ? ??-?????? ???? ) = 0
??-?? 0 ??-?? ??-??
Sachant que :
? ????-?????? = -??-??(1 + ??) + ??, ? ??-?????? =
-??-?? + ?? Où ??,?? sont
constante d'intégration.
On aura :
??3???? = ?? [???? (??3 - ??1)
+ (??1 + ??2)(1 + ??)] + ????(1 -
??)(??3 - ??1) + (??1 + ??2)
A partir de la formule ci-haut nous pouvons maintenant trouver
:
??3 - ??1 = 400; ??1 +
??2 = 1100; ??3 = 500; (???? ???????????? ??????????????
?????? 100),
On a : ??3 - ??1 = 4; ??1 +
??2 = 11; ??3 = 5
Avec ?? = 2,72; ??2 = 7,39; ??3 = 20,09 ;
??4 = 54,60; ??5 = 148,41 Calculons alors les valeurs
optimales de q :
2
?? = 1; 5???? = ??[2,72 (4) + (11)(1 + 1)] + 2,72 (1 - 1)(4) +
(11)(1 - 2 )
5???? = 32,88 ?? + 5,50
2
?? = 2; 5???? = ??[7,39 (4) + (11)(1 + 2)] + 7,39 (1 - 2)(4) +
(11)(1 - 2 )
5???? = 62,56 ?? - 40,56
2
?? = 3; 5???? = ??[20,09 (4) + (11)(1 + 3] + 20,09(1 - 3)(4) +
(11)(1 - 2 )
5???? = 124,36 ?? - 199,22
2
?? = 4; 5???? = ??[54,60(4) + (11)(1 + 4] + 54,60 (1 - 4)(4) +
(11)(1 - 2 )
5???? = 273,4 ?? - 732,2
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

39

52
2
5???? = 659,64 ?? - 2501,56
Une méthode de résolution graphique est
utilisée. Comme chaque droite a deux intersections avec l'exponentielle,
il importe de noter que CT n'a pas de minimum pour q<s, entre q et s. Pour
le voir, reprendre la valeur de CT(q) lorsque q<s, c'est-à-dire que
:
? ? ??(??) ??(??) ??1 (??- ??- ??
?? ??-?? (?? - ??)2 (??- ??+ ??)2
?? 8
2)???? ????+ ? ? (??1 2?? + ??2 2?? )
????????
0 0 0 ??-??
+ ? ? ??(??)??(??)??2 (??
88
2 + ?? - ??)????????
?? 0
1 2 3 4 5 q
Le minimum est atteint pour la deuxième valeur de q
(q>s) :
??1 = 3,10; ??2 = 3,60; ??3 =
4,20; ??4 = 4,70; ??5 = 5,30
??
????
??
-
-
= 5; 5
=
[148,41(4) + (11)(1 + 5] + 148,41(1
5)(4) + (11) 1
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

40
CONCLUSION
Au terme de ce travail porté sur : « vers la
gestion scientifique des stocks.» nous avons répondu à
notre problématique qui était :
? Quand doit-on approvisionner ? ? Combien doit-on commander ?
Au regard de cette problématique nous avons
formulée les hypothèses comme suit : On devra se
réapprovisionner lorsque le stock atteint le niveau appelé point
de commande qui correspond à la quantité permettant de satisfaire
la demande jusqu'à la nouvelle livraison. Et La quantité à
réapprovisionner dépend du modelé choisit : Une
quantité fixe à chaque réapprovisionnement ; Une
quantité variable qui permet de retrouver un niveau de stock fixé
(niveau de complétement) ; Une quantité variable selon la demande
prévue.
Voilà pourquoi nous affirmons que dans chaque
méthode des stocks, on sait voir l'évolution de la
quantité Q des marchandises qui est fonction de la demande durant un
temps donné c.-à-d. le stock qui diminue avec l'achat donc
l'entrepreneur doit veiller à cette évolution pour arriver
à ses fins, afin de ne pas tomber en rupture de stock et ne pas avoir un
sur-stockage ; tout en sachant que la demande n'est toujours pas constante
c'est qui veut dire que le nombre des clients qui arrivent pour
s'approvisionner et le nombres d'articles demander par chaque est
aléatoire.
Vu les méthodes développer dans ce travail nous
dirons qu'il n y a pas un modèle idéal car chacun de
méthodes détailler précédemment à ses
imperfections et aucun ne garantit contre une pénurie avant
l'arrivée d'un nouvel réapprovisionnement, tout en évitant
aussi des excédents et des stocks résiduels.
C'est pourquoi, chaque entrepreneur doit choisir la
méthode qui lui convient le mieux suivant les objectifs qu'il a à
atteindre.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

41
BIBLIOGRAPHIE
[1] : Boualem RABTA, « gestion scientifique des stocks
», université de Bejaia, (Algérie), 2007 ;
[2] : Fevrier J. « la gestion scientifique des stocks
», Paris, Dunod; 1962 ;
[3] : Fortet R., ABADIEN J. BERNARDAT J. , et autres, «
mathématique des programmation économique », Paris, Dunod
;1976 ;
[4] : J.P CAMPAGNE, « méthodes de gestion de
stock », INSA de Lyon, 2006
[5] : M. Robert FAURE, « vers une gestion scientifique
des stocks, méthodes et exercices d'application », Faculté
des sciences de Rabbat (Libye), DUNOD, 1968 ;
[6] : Marc GIAGA, « les principaux outils de gestion des
stocks », CARNEGE, 2003
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

42
Table de matière
EPIGRAPHIE i
DEDICACE ii
REMERCIEMENTS iii
INTRODUCTION 1
CHAPITRE I : GENERALITES SUR LA GESTION DES STOCKS 3
1) QUELQUES DEFINITIONS 3
a) Le stock : 3
b) Le stockage : est le déplacement intelligent des
stocks afin de pouvoir retrouver facilement
un ou des produits précis. 4
c) La gestion : 4
2) LA GESTION DES STOCKS 4
a) LA FONCTION DES STOCKS 4
b) INCONVENIENT DE STOCK 5
c) UTILITE DE LA GESTION DES STOCKS 6
d) LES ELEMENTS DE LA GESTION DES STOCKS 6
CHAP II : MODELES DE GESTION DES STOCKS 14
SECTION I : METHODE DE GESTION A AVENIR CERTAIN 16
II.1 MODELE DE WILSON 16
a) Hypothèses et notations 17
b) Analyse du problème 17
c) Modèle et solution 18
II.2 CRITIQUE DE MODELE 21
SECTION II : METHODE DE GESTION TENANT COMPTE DES ALEAS 22
II.3 MODELE PAS A PAS 22
1) Système a période fixe 23
a) Hypothèse, notation et solution 24
2) Système à période variable 28
CHAP III : STOCKS ET ETUDES DES CAS 30
III.1 STOCK D'ALERTE 30
III.2 STOCK DE SECURITE 31
a. Quand on dispose d'une évaluation du cout de
pénurie 32
b) Quand on ne peut pas raisonnablement estimer le cout de
pénurie 33
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

43
III.3 ETUDE DE CAS 34
RESOLUTION DU PROBLEME 35
CONCLUSION 40
BIBLIOGRAPHIE 41
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l



