CHAPITRE 3
LOCALISATION A BASE D'EMPREINTE RADIO
3.1 Introduction
La technique de fingerprinting ou de pattern matching a
déjà été explorée dans le cadre de la
localisation par réseau GSM. Depuis quelques années, on peut
utiliser des outils de prédiction de couverture radio permettant
d'optimiser les réseaux lors de leur mise en place. Ces outils
prédisent le niveau de champ radioélectrique en tenant compte des
différents phénomènes de propagation auxquels sont
soumises les ondes radio. Ils déterminent le niveau de champ à
chaque position de la zone de couverture.
L'opération de localisation consiste à
rechercher dans la base de données, constituée à l'aide
des outils de prédiction de couverture radio, le n-uplet de puissance le
plus proche du n-uplet des puissances mesurées par le terminal mobile.
Une fois ce n-uplet de la base de données identifiée, la position
du mobile correspond à celle de la mesure
référencée dans la base de données. [17]
Ainsi, la localisation à base d'empreinte radio
exploite les réseaux existantes (réseau cellulaire, le WLAN...)
tout en utilisant les mesures génériques qui sont disponibles
à partir des interfaces radios. Elle permet une localisation plus
précise que Cell-ID. La méthode ne demande pas une grande
consommation d'énergie.
3.2 Description d'un système de LFP
Le système de LFP est divisé en deux phases :
? La phase d'apprentissage (training phase)
? La phase de localisation (localization phase)
3.2.1 Phase d'apprentissage
Une « phase d'apprentissage » ou « training
phase », ou une « phase hors ligne », est constituée par
la création d'une base de données avec les
caractéristiques mesurées par chaque récepteur du
réseau à un ensemble d'emplacements représentatifs pour
les positions possibles de l'objet mobile. Un maillage de la zone
d'intérêt est réalisé. Pour chaque noeud, les
caractéristiques mesurées par chaque récepteur du
réseau sont enregistrées.
46
3.2.2 Phase de localisation
Une fois que la base de données est construite, les
mobiles peuvent entrer dans la « phase de
localisation » ou « localization phase » ou
« phase en ligne ».
Le mobile effectue des mesures de test, et sera
localisé en associant ces mesures aux éléments qui
sont déjà enregistrés dans la base.
Plus précisément, la phase consiste à
trouver, à partir des caractéristiques mesurées de
l'objet
mobile, un correspondant dans la base de données
à l'aide d'un algorithme de positionnement.
Ces algorithmes sont classés en deux catégories
qui sont :
? Déterministes
? Probabilistes
3.2.2.1 Déterministes :
a. VPP
Le VPP ou Voisin le Plus Proche dans la base de données
des puissances (ou plus rarement la TOA) du signal est enregistré durant
la phase hors ligne.
La méthode évalue la distance euclidienne entre
les caractéristiques mesurées dans la phase en ligne et celles
stockées dans la base des données. Le point pour lequel la
distance euclidienne est minimale est considéré comme
représentant la position de l'objet mobile.
b. Moyenne des k voisins les plus proches dans l'espace
puissance du signal reçu
Cette méthode constitue une extension de la
précédente méthode en permettant d'améliorer les
résultats.
Les coordonnées spatiales des k voisins les
plus proches en termes de puissance du signal reçu sont moyennées
pour donner une estimation de la position de l'objet d'intérêt.
[15]
c. Plus petit polygone
Cette méthode consiste à choisir un nombre de
voisins rapprochés et à construire des polygones à partir
de leurs coordonnées spatiales connues. La position de l'objet mobile
est donnée par le centre du polygone d'aire minimale dans l'ensemble de
polygones. [15]
3.2.2.2 Probabilistes:
Ces techniques emploient les distributions de la puissance du
signal reçu au niveau de chaque récepteur du réseau.
Elles essayent d'améliorer les performances des
méthodes déterministes affectées par les problèmes
de stationnarité de l'environnement de mesures. [15]
La figure 3.01 présente une vue d'ensemble
schématique d'un système LFP avec les méthodes
associées.

Phase de localisation
(Classification ,
prédiction)
Mesure effectué par le
mobile.
Phase d'apprentissage
(Construction de la
BD,
étude
supervisé/non
supervisé
Position estimée
Estimation
Position estimée
Classification
Traitement
Traitement (compression de
la BD par PCA, KCCA, etc)
BD initiale
Méthode de
régression
(SVM, ANN)
Méthode de
classification
(KNN, SVM, ANN)
47
Figure 3.01 : Architecture d'un système
LFP
48
3.3 Terminologie et modélisations
mathématiques
Dans cette section, nous allons essayer d'expliquer les
terminologies et les modélisations utilisées dans la
méthode LFP, particulièrement aux systèmes LFP
basés sur les mesures RSS.
3.3.1 Base de données radio et
enregistrement
Une "base de données radio" est un ensemble
"d'enregistrements". Dans ce contexte, chaque enregistrement est
constitué de deux parties: la partie de position (location part), et la
partie radio (radio part). La partie de position décrit la position d'un
point spécifique et la partie radio montre la mesure radio
exécutée à cette position spécifique.
3.3.2 Mesure radio
La mesure radio comprend de nombreux types de
paramètres, disponibles à partir des interfaces radios (par
exemple RSS, Timing Advance ou TA, etc...).
Elle est représentée par un vecteur s E
R???? comprenant ???? éléments
réels.
La partie position est également représentée
par un vecteur x E R????.
De ce fait, un enregistrement est donné par r =
(x, s) E R??, et on a :
?? = ???? + ???? (3.01)
3.3.3
Modèle de propagation radio
Un modèle de propagation radio est nécessaire
pour modéliser les mesures RSS. Le modèle OSLN ou One Slop
Log-Normal model est un modèle classique, qui décrit la perte
radio (pathloss) comme suit:
??????(d) = -k + 10 oc?? log(d) +
????h (3.02)
avec :
? Pla : perte moyenne (en dB),
? k : constant,
? d : distance,
? oc?? : paramètre de propagation
exponentielle (propagation exponent)
? ????h : variable aléatoire log-Normal
qui représente l'effet de shadowing.
Pour l'effet de shadowing, ce modèle ne considère
aucune corrélation géographique.
49
3.4 Méthodes de compression de base de
données radio
L'enrichissement de la base de données n'entraine pas
toujours l'amélioration de la qualité de la localisation. La
taille de la base est un facteur important (surtout dans les approches
mobile-based) parce qu'elle influence la charge de calcule, la charge de
transmission ainsi que l'autonomie énergétique du terminal.
Il y a plusieurs méthodes qui visent à
compresser la base de données radio. La plupart d'entre eux tente de
réduire la dimension de la base, en utilisant des contraintes de
covariance.
Nous allons présenter les 03 méthodes les plus
reconnues :
· La technique de clustering,
· Le PCA ou Principal Component Analysis,
· Le KCCA ou Kernel Canonical Correlation Analysis.
3.4.1 Technique de clustering
Clustering ou regroupement permet de faire une collection
d'objets :
· Similaires au sein d'un même groupe ou,
· Dissimilaires quand ils appartiennent à des
groupes différents.
Ainsi, la technique de clustering réduit le nombre des
enregistrements. Chaque enregistrement est représenté par : ?? =
(??, ??) ? R??
Les positions inclues dans la base sont données par
l'ensemble X tels que : ?? = {??1, ... , ????, ... , ????}
La base radio est données par : ?? = {????}??=1...??
La base de données finale R pourrait être obtenue
en traitant les éléments d'une base de données
« initiale » notée ????; qui est une base radio
constituée selon les mesures terrains brutes.
Un enregistrement de ???? est donné par : ??0
= (??0, ??0)
Les techniques clustering sont très efficaces pour
compresser la base de données initiale ??0 =
{????0}??=1...?? afin d'obtenir une base de données plus
compacte ?? = {????}??=1...??(??<??).
3.4.1.1 Algorithme de clustering
Supposons une base comprenant ?? data-points ??0 =
{????0}dans une espace de
??=1...??
dimension ?? (????0 ? R??). Une
technique de clustering tente de diviser ??0 en ??(?? < ??)
sous-ensemble ou clusters, telle que les points dans chaque cluster soient
similaires dans certain sens.
Pour un système LFP, on considère deux types de
méthode pour réaliser l'étape de clustering :
· L'algorithme de k-means
· La technique hiérarchique agglomérative
a. Algorithme de k-means
Cet algorithme est basé sur le critère de
minimum de la variance intra-cluster (minimum intra-cluster variance). Dans
cette technique, l'algorithme de clustering essaie de chercher une partition
des données qui minimise la somme des variances intra-cluster. Pour
l'ensemble de R° donné, une partition pourrait
être représentée par une matrice ?? x ??, U =
[umn], qui satisfait les critères suivants [16] :
umn ? {0,1}, (3.03)
??
? umn = 1; pour 1 < ??< ??, m=1
|
(3.04)
|
|
??
? umn
|
> 0; pour 1 < ?? < ??,
|
(3.05)
|
|
n=1
Etant donnée la définition ci-dessus,
l'algorithme de k-means essaie de minimiser la fonction d'objective suivante
:
?? ??
j2(U, R) = ? ?umn????(??) 2(rn°
(3.06)
, rm)
50
n=1
avec :
R = {rm}m=1...?? : Ensemble de M vecteur
représentant les centroides des clusters.
????(??) : Distance Euclidien pondérée,
qui a été adopté pour calculer les variances. b.
Technique hiérarchique agglomérative
Cette technique consiste à minimiser la même
fonction d'objective que celle de k-means. Mais, l'optimisation se fait
hiérarchiquement. En supposant que chaque vecteur dans
R°constitue un cluster, on fusionne les deux clusters
qui minimise la variation dans j2 à chaque
étape de la procédure.
51
3.4.1.2 Méthode BWC
La méthode de Bloc-based Weighted Clustering ou BWC
consiste en un algorithme pondéré, adapté à la
structure de la base de données radio. Avant de développer cette
méthode, on formalise le concept de feature type.
a. Principe
Supposons une base de données ?? = {????}??=1...??. On
remarque que tous les éléments dans un
enregistrement ???? n'appartiennent pas à la
même nature. On définit un feature type comme l'ensemble de tous
les paramètres qui appartiennent à la même nature. Dans le
cas le plus simple, il faut au moins deux feature types dans la base : le
feature type « position », et le feature type « RSS ». On
peut envisager des cas plus compliqués, où il existe des feature
types variés (RSS 2G et 3G, TA, etc.). Un enregistrement peut être
représenté aussi comme suit :
?? = ??1, ... , ??h, ...,?????? (3.07)
avec :
???? : Le nombre total des features types
??h : Le sous-vecteur correspondant à
l'hème feature type.
3.4.2 PCA
Un PCA (analyse en composantes principale) permet :
· De représenter des individus
· De représenter des variables
· De compresser des données et d'éliminer du
bruit
Elle peut être appliquée à la compression
d'image. Ainsi, elle est parmi les méthodes permettant de compresser la
base de données radio.
Pour faire une PCA, il faut :
· Réduire et centrer les données
· Calculer la matrice des corrélations
· En extraire les valeurs et les vecteurs propres
· Reconstruire les nouvelles variables
· Choisir k le nombre de facteurs significatifs
3.4.2.1 Valeurs propres :
Soit M une matrice carrée symétrique
définie positive (M = XTX) de dimension p. Il existe
:
· p réels positifs Al, i = 1, p
et
· p vecteurs de RP, vl, i = 1, p tels que :
Mvl = illvl (3.08)
b. Propriétés des valeurs et des vecteurs
propres
· Par convention, on ordonne les valeurs propres Al
<_ .1l_1,i = 2, p
· Par convention, les vecteurs propres sont normés
vlT vl = 1
· Les vecteurs propres sont orthogonaux entre eux :
vlT v' = 0, i * j
· La matrice des vecteurs propres V forme une base
de RP
· La décomposition spectrale : M =
Ep1 yllvlvi
· Le programme([V, D] = eig(M)) permet de calculer
les valeurs et les vecteurs propres.
3.4.2.2 Reconstruction de la matrice
La meilleure représentation linéaire du nuage de
points est donnée par le couple de vecteurs u E Rn et v E
RP permettant au mieux de reconstruire la matrice X. Le couple de
vecteur résout le problème de minimisation suivant :
minJ(u, v) (3.09)
u,v
avec :
n P
J(u, v) = I I(xl' - ulv')2
(3.10)
52
l '
3.4.2.3 Meilleure approximation
Soit X une matrice :
La meilleure approximation de rang k de X, la
matrice Ak minimisant le critère suivant :
minIIX - Ak IIF avec rang(Ak) = k (3.11)
Ak
53
ceci s'obtient à l'aide des ?? vecteurs propres ????, ?? =
1, ?? associées aux ?? plus grandes valeurs propres de la matrice
XTX de la manière suivante :
??k = UkVkT (3.12)
où Vk est la matrice des vecteurs
propres ????; ?? = 1, ??
et Ukest la matrice des vecteurs ???? = X????, ?? = 1, ?? et donc
:
??k = XUkVkT (3.13)
L'erreur
d'approximation est donnée par la somme des valeurs propres restantes
:
|
??
?X - ??k???2 = ? ????
??=k+1
|
(3.14)
|
??k = ?X - UkVkT??? 2 (3.15)
avec : ?? = 1,?? 3.4.3 KCCA
La KCCA présente deux caractéristiques
avantageuses. C'est une analyse qui permet l'intégration de
différents types de données et de faire un apprentissage par
rapport à un jeu de données standard pour lequel les relations
entre objets sont connues. De plus, elle agrée l'inférence de
liens entre tous les objets utilisés.
La KCCA est basée sur l'analyse de corrélation
canonique ou CCA.
Soient deux groupes de variables Y1 et
Y2 décrivant un même objet x. L'analyse de
corrélation canonique consiste à trouver des repères qui
se correspondent pour représenter l'objet dans chacun de ces
repères. Ces derniers sont obtenus en recherchant des combinaisons
linéaires des variables (canoniques) de chaque groupe. [18]
(??))
Le but de la KCCA est de détecter des corrélations
entre deux jeux de données x1 = (x1 (1), ... ,
x1
et x2 = (x2(1), ...
,x2(??)) où ?? est le nombre d'objets et chaque
jeu de données appartient à X1/X2 pour ?? = 1, ... , ??. [18]
3.5 Méthode de classification
3.5.1 KNN
Pendant la phase de localisation, le mobile fait une mesure s'
à la position x'. Afin de localiser le terminal, on utilise
la méthode de classification de KNN ou K Nearest Neighbours.
54
Deux types de métrique sont considérés
pour implémenter la classification KNN : la distance Euclidien, et le
coefficient de corrélation. [16]
Une fois que le mobile est localisé, l'erreur de la
localisation est donnée par :
E(x') = 11x' - x^11 (3.16)
où ^?? est la position estimée pour le terminal.
3.5.1.2 Classification supervisée
En quelques mots, la classification supervisée, dite
aussi discrimination est la tâche qui consiste à spécifier
des données, de façon supervisée (avec l'aide
préalable d'un expert), un ensemble d'objets ou plus largement de
données, de telle manière que les objets d'un même groupe
(appelé classes) sont plus proches (au sens d'un critère de
similarité choisi) les unes aux autres que celles des autres groupes.
Généralement, on passe par une première
étape dite d'apprentissage où il s'agit d'apprendre une
règle de classification à partir de données
annotées (étiquetées) par l'expert et pour lesquelles les
classes sont connues, pour prédire les classes de nouvelles
données, pour lesquelles les données sont inconnues.
La prédiction est une tâche principale
utilisée dans de nombreux domaines, y compris l'apprentissage
automatique, la reconnaissance de formes, le traitement de signal et d'images,
la recherche d'information, etc. [19]
3.5.1.3 Données
Les données traitées en classification peuvent
être des images, signaux, textes, autres types de mesures, etc.
3.5.1.4 Classes
Une classe (ou groupe) est un ensemble de données
formée par des données homogènes qui se ressemblent au
sens d'un critère de similarité (distance, densité de
probabilité, etc). Le nombre de groupes (noté K) en
prédiction est supposé fixe.
3.5.1.5 Algorithme des K-ppv
C'est une approche très simple et directe. Elle ne
nécessite pas d'apprentissage mais simplement le stockage des
données d'apprentissage. En principe, une donnée de classe
inconnue est comparée à
55
toutes les données stockées. On choisit pour la
nouvelle donnée la classe majoritaire parmi ses K plus proches voisins
(Elle peut donc être lourde pour des grandes bases de données) au
sens d'une distance choisie. [19]
Afin de trouver les K plus proches d'une donnée
à classer, on peut choisir la distance euclidienne. Soient deux
données représentées par deux vecteurs x?? et
x??, la distance entre ces deux données est donnée par la
formule suivante :
|
??(x??,x??) =
|
v?? ?(x??k - x??k)2 k=1
|
(3.17)
|
3.5.2 SVM
Les SVM ou Support Vector Machines souvent traduit par
l'appellation de Séparateur à Vaste Marge ou SVM sont une classe
d'algorithmes d'apprentissage initialement définis pour la
discrimination c'est-à-dire la prévision d'une variable
qualitative binaire. Ils ont été ensuite
généralisés à la prévision d'une variable
quantitative. Ils sont basés sur la recherche de l'hyperplan de marge
optimale qui, lorsque c'est possible, classe ou sépare correctement les
données tout en étant le plus éloigné possible de
toutes les observations.
Le principe de base des SVM consiste de ramener le
problème de la discrimination à celui, linéaire, de la
recherche d'un hyperplan optimal.
3.5.2.1 Remarque
Il est parfois utile d'associer des probabilités aux
SVM. Ces derniers peuvent également être mis en oeuvre en
situation de régression.
3.5.3 ANN
3.5.3.1 Définition
Artificial Neural Networks ou Réseaux de Neurones
Artificiels ou RNA sont des réseaux fortement connectés de
processeurs élémentaires fonctionnant en parallèle. Chaque
processeur élémentaire calcule une sortie unique sur la base des
informations qu'il reçoit. Toute structure hiérarchique de
réseaux est évidemment un réseau. [20]
56
Les réseaux de neurones artificiels ont été
développés avec pour objectifs principaux d'une part la
modélisation et compréhension du fonctionnement du cerveau et
d'autre part pour réaliser des architectures ou des algorithmes
d'intelligence artificielle. [21]
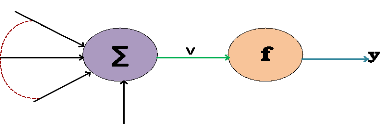
3.5.3.2 Principe de fonctionnement
Le principe de fonctionnement d'un neurone artificiel est
montré par le schéma suivant :
Xn
W1
Wi
1
W0
X1
Figure 3.02 : Schéma d'un neurone
artificiel
Wn
Un neurone artificiel est une unité de traitement qui
dispose de ?? entrées {X??}??=1,..,?? qui sont
directement les entrées du système ou peuvent provenir des autres
neurones.
Pour le biais, l'entrée est toujours à 1, ce qui
permet d'ajouter de la flexibilité au réseau en permettant de
varier le seuil de déclenchement du neurone par l'ajustement du poids du
biais lors de l'apprentissage.
La sortie y correspond à la transformation par
une fonction d'une somme pondérée des entrées : y=
f(??) avec ??= w0 + ? w??????
?? (3.18)
??=1
Les quantités {w??}??=0,...,?? sont les poids du
neurone. Ce sont des facteurs multiplicateurs qui affectent l'influence de
chaque entrée sur la sortie du neurone.
La fonction f est appelée fonction d'activation
ou fonction de transfert du neurone. Les fonctions les plus communément
utilisées sont la fonction échelon unité ou Heaviside, la
fonction signe, la fonction linéaire ou semi-linéaire, la
fonction tangente hyperbolique, ou la fonction sigmoïde. [21] La fonction
sigmoïde est définie par :
|
f(??) =
|
1
|
(3.19)
|
|
1 + e-??
|
|
La figure ci-dessous nous présente l'allure d'une fonction
sigmoïde :

57
Figure 3.03 : Sigmoïde
b. Remarque
Dans un neurone artificiel, on appelle « noyau » tous
ce qui intègre toutes les entrées et le biais et calcule la
sortie du neurone selon une fonction d'activation qui est souvent
non-linéaire pour donner une plus grande flexibilité
d'apprentissage.
3.5.3.3 Classification à l'aide d'un neurone
Considérons des événements
caractérisés par un ensemble de ?? mesures (nombres et
types de particules, impulsions, énergies, etc.) que nous notons
{??1}1=1,..,??. Nous souhaitons classer ces événements
entre deux classes.
Supposons que nous avons un échantillon d'apprentissage
de n événements dont nous connaissons la classe d'appartenance
ainsi que les mesures. Pour chaque événement d'apprentissage nous
notons x l'ensemble de ses mesures et c sa classe (0 ou
1).
Le principe de l'apprentissage peut être décrit par
l'algorithme suivant :
1. Choix aléatoire des poids
2. Présentation d'un événement
d'apprentissage en entrée et calcul de la sortie y(x)
3.
(3.20)
Modification des poids :
w'1 = w1 + [c - ??(x)]x1 w'0 = w0 +
[c - ??(x)]
4. Retour à l'étape 2
58
3.6 Traitement des données manquantes dans les
systèmes LFP
Dans les systèmes LFP, la problématique des
données manquantes est très importante.
Pour le cas des systèmes basés sur les mesures de
RSS; ces mesures sont normalement obtenues par
une procédure nommée scanning process qui est
indispensable dans les réseaux radios mobiles, où
chaque terminal mesure le niveau de RSS des cellules en
voisinage.
Cependant, certaines stations de base ne peuvent pas être
détectées au cours de cette procédure, à
cause de différentes raisons :
? Le signal reçu pourrait être plus faible que le
seuil de la sensibilité du terminal,
? Le signal reçu pourrait être perdu dans la forte
interférence,
? Le nombre des stations de base mesurable pourrait être
limité au niveau du terminal,
? Certaines stations de base pourraient être
éteintes.
Tous les signaux non mesurés sont considéré
comme des données manquantes.
Les méthodes statistiques pour le traitement des
données manquantes ont considérablement évolué
depuis les dernières années. [16]
Prenons comme exemple les mesures RSS effectuées par le
terminal mobile, sur une région A où se
trouve B la station de base.
Une mesure complète à la position ?? peut
être représentée par le vecteur s = (s1,
..., s??, ..., s?? ) ?
R??.
La modélisation du mécanisme d'effacement
s'effectue à l'aide de deux paramètres : l'un, X qui
représente le seuil de sensibilité du terminal, et l'autre
notée B?????? qui est le nombre maximum des stations de base
mesurable au niveau du terminal (B?????? = B). Ensuite, pour
formaliser le concept d'effacement, on définit le vecteur indicateur
j ?? {0,1}??correspondant à chaque mesure
s, comme suit :
Supposons que a = ( a(1), a(2), ..., a(B)) est une
permutation d'indices des stations de base, tel
que s??(1) = s??(2) = ? = s??(??) ; le vecteur j
correspondant à s est alors défini comme :
???, 1 = ?? = B, j?? = {1 sj ?? ? {a(1), a(2), ...,
a(B??????)}, et s?? = A, (3.21)
0 ??utre??ent
On définit l'ensemble ø comme l'ensemble de tous
les paramètres qui modélisent le mécanisme d'effacement
(ø = {A, B??????}).
Finalement, pour une position donnée ??, B
(??) = {??: j?? = 1} représente l'ensemble des stations de base
observées à la position ??.
59
Dans les systèmes de LFP, les données manquantes
pourront arriver pendant les deux phases d'apprentissage et localisation.
Dans ce travail, nous traitons le problème en deux
étapes :
· Etape 1 :
On suppose que le mécanisme d'effacement est
présent exclusivement pendant la phase de localisation ; autrement dit,
on suppose que l'on a une base de données complète, mais les
mesures du terminal incomplètes. [16]
· Etape 2 :
Pendant la deuxième étape, on enlève
l'hypothèse d'une base de données complète ; le
mécanisme d'effacement est censé être présent
pendant les deux phases d'apprentissage et localisation. [16]
3.6.2 Algorithme de localisation basé sur le
maximum de vraisemblance
Les algorithmes de localisation basés sur le maximum de
vraisemblance (Maximum Likelihood ou ML) sont déjà
proposés dans le contexte des systèmes de LFP. La méthode
de ML que nous proposons dans ce travail est différente dans le sens
qu'elle prend en compte l'effet d'effacement et les données manquantes.
[16]
La mesure du terminal durant la phase de localisation ??' peut
être décomposée en une partie observée ??'(??????)
et une partie manquante ??'(??????), ayant pour résultat un vecteur
indicateur d'effacement ??'. [16]
Notre algorithme de ML estime la position du terminal comme
suit :
??^ = ????^, ??^ = ?????????????? ?? (??'(??????), ??'|??, ????,
??) (3.22)
avec :
??^ : La position estimée du terminal
???? : Ensemble qui modélise la distribution des mesures
RSS complètes sur les clusters Etant donné le mécanisme
d'effacement, on obtient :
|
??(??'(??????), ??'|??, ????, ??) = ? ??(??'(??????),
??'(??????) |??, ????)????'(??????)
??
|
(3.23)
|
où ?? est un évènement définit par
:
?? = {??': ??? ? ?? (??'), ??'?? = ??'(??')} (3.24)
avec:
(3.25)
??'(??')} = { ?? ????|??(??')| < ??????????????{??'(??????)}
????|??(??')| = ????????
60
Supposant une distribution Gaussienne pour les mesures autours
des centroids. On peut écrire:
p(S'|m, 8L)"'N(Sm, rm) (3.26)
avec :
8L = [(Sm, rm)}??=1,...,?? (3.27)
Sm et r,.,,, : ce sont respectivement le
centroid et la covariance matrice du m-ème cluster.
En prenant une hypothèse d'indépendance parmi les
signaux des différentes stations de base, on obtient:
|
p(S'(obs),iF|m,8L,ip) = pb(S'b |m,8L)
Fb(
Y'bEB(x')
beB(x')
|
(3.28)
??'(??')|??, 8L)
|
où Fb (. |m, 8L) représente
le CDF ou Cumulative Distribution Functions de la distribution Gaussien,
correspondant au b-ème composant radio.
3.6.3 Algorithme de Multiple
Imputation
Ce niveau du problème suppose la présence du
mécanisme d'effacement pendant toutes les deux phases d'apprentissage et
localisation. Afin de traiter les données manquantes au niveau de la
phase d'apprentissage, on propose une méthode de "Multiple Imputation"
ou MI, qui essaie de remplir les valeurs manquantes dans la base. Une fois que
la base radio est complémentée, le traitement des données
manquantes pendant la phase de localisation revient à la même
problématique étudiée dans l'étape
précédente. [16]
La figure 3.04 ci-dessous illustre la méthodologie
proposée.
Phase d'apprentissage Phase de localisation
Imputation
Clustering

Base de
données
initiale

Base de données
complémentées
Classification
Mesure effectué par le
mobile.
Figure 3.04 : Architecture proposée
comprenant l'étape d'imputation
3.6.3.2 Le modèle des données complètes
Le modèle des données complètes, à
cette étape, modélise la base de données radio
complète ??0. Prenant un modèle classique log-Normal,
chaque mesures de RSS pourrait être modélisée comme suivant
:
??(???? 0|????)~??([????,1, ... , ????,??], ?)
(3.29)
oÙ ???? inclut les paramètres du modèle
log-Normal, qui permettent de calculer ????,1, ... , ????,?? et ?. Prenant une
hypothèse d'indépendance parmi les différentes stations de
base, on obtiendra:
|
??
??(???? 0|????) = ? ????(
|
???? 0|????)
|
(3.30)
|
61
??=1
oÙ ????(.|????) est la densité marginale du b
ème composant, pour 1 = ?? = ??.
3.7 Positionnement utilisant la méthode de
fingerprinting basé sur OTD
OTD ou Observed Time Differences est un procédé
de positionnement couramment utilisé parce qu'il a la capacité de
recueillir l'héritage des terminaux. Cette méthode est
spécifique aux réseaux UMTS et nécessite la
réception au niveau de l'objet mobile des signaux provenant d'au moins
trois stations de base. La position de l'objet mobile est donnée par
l'intersection d'au moins deux hyperboles résultant de la
différence des retards des signaux, encodés dans les trames UMTS,
provenant des stations de base prises par deux. [15]
La méthode des différences de temps
d'arrivées observées ou OTDOA est basée sur les mesures
des différences des temps d'arrivée des signaux de liaison
descendante reçus par le mobile. Dans cette méthode, c'est le
mobile qui s'engage à prendre les mesures nécessaires.
L'équipement utilisateur calcule les temps d'arrivée des signaux
reçus simultanément des Node Bs voisins. Le signal mesuré
est le CPICH ou Common Pilot Channel. Le terminal calcule le temps de
propagation du signal à partir de la corrélation entre le signal
reçu et le signal pilot du Node B considéré. Le pic
résultant de la corrélation représente le temps de
propagation du signal observé.
L'estimation des différences des temps d'arrivée
peut s'effectuer soit sur les signaux de la liaison montante soit sur ceux de
la liaison descendante. [22]
On peut calculer les TDOAs par deux méthodes
différentes :
? Soit directement par
l'inter-corrélation des signaux reçus de deux BTSs
62
? Soit indirectement par la soustraction des temps
d'arrivées de deux BTSs, ce qui requiert le calcul des TOAs.
3.7.1 Estimation des TDOAs pour un réseau
3G
L'estimation des TDOAs est obtenue à partir de
plusieurs estimations robustes du profile du canal de transmission. Le canal
CPICH est composé d'une séquence prédéfinie de bits
dits pilotes, qui sont transmis en permanence sur la cellule. Il peut
être considéré comme un canal balise dont les terminaux
mobiles se servent pour faire des mesures de puissance et pour estimer la
réponse impulsionnelle du canal de propagation. [22]
Considérons le cas où un mobile reçoit
trois canaux CPICH issus de trois Node B (station de base) différents,
à partir de la sortie du corrélateur on peut accéder
facilement aux TDOAS comme suit :
1. On réalise des corrélations avec les CPICH
de chaque Node B sur une fenêtre de durée maximale égale au
temps nécessaire de transit du signal à partir du Node B le plus
éloigné.
2. On localise le premier pic de chaque CPICH qui correspond,
soit au trajet direct Node B mobile, soit au plus court trajet indirect,
c'est-à-dire celui produisant le moins d'erreurs.
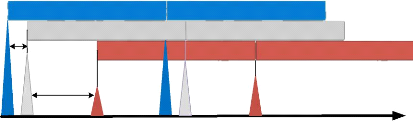
3. Les TDOAs sont égales à la différence
temporelle entre les premiers pics relatifs aux différents Node Bs comme
nous montre la figure 3.05.
A l'émission:

NodeB_1
NodeB_2
NodeB_3
CPICH
CPICH
CPICH
CPICH
CPICH
CPICH
A la réception:
T3 -
T1

T2 -
T1
ô2 ô3
T3 -T2
CPICH
CPICH
CPICH
CPICH
CPICH
Sortie du corrélateur
CPICH
Figure 3.05 : Calcul des TDOAs
3.7.2 Structure de l'algorithme
Quand un utilisateur passe en mode active, il doit rester
connecter et les rapports de mesures par l'UE vers le réseau doit
être effectué sans interruption. De ce fait, le réseau doit
aider l'UE.
Les rapports de mesures contiennent les informations concernant
la cellule active et la cellule serveuse avec les spécifications
données ci-dessous. [23] [24]
3.7.2.1 Chargement à l'entrée
Les informations concernant le Node B et le MRMs ou Mesurement
Report Messages (figure 3.06) sont des données d'entrée
nécessaires pour calculer, dans une marge d'erreur tolérable,
l'estimation de la position physique de l'UE. On distingue :
a. Données de MRMs
Les données de MRMs sont :
· Rapport d'évènement
réalisé
· Cell IDs de l'Active Set
· Primary Scrambling Codes ou PSCs de l'Active and
Monitored sets Pour chaque liaison radio :
· Ec/N0 en dB
· RSCP en dBm
· Paramètres de synchronisation frame offset (OFF)
et chip offset (Tm)
OFF [1] Tm [1]
PSC [1] Ec/No [1] RSCP [1]
OFF [3] Tm [3]
PSC [3] Ec/No [3] RSCP [3]
OFF [4] Tm [4]
PSC [4] Ec/No [4] RSCP [4]
OFF [2] Tm [2]
PSC [2] Ec/No [2] RSCP [2]
63
Figure 3.06 : Données MRMs sur chaque
liaison radio
???? = 10
|
P?? - 69.55 - 26.16 log10 f + 13.82 log10
hB + ??????
|
(3.32)
|
|
|
|
64
b. Données du Node B
Les données du Node B sont :
· Nom de la cellule
· Cell IDs
· PSCs
· Primary CPICH power measurements
· Coordonnées géographique
· Hauteur de l'antenne
3.7.2.2 Calcul initial
a. Identification de la cellule
Pour la cellule de la station mobile, l'identification à
l'aide d'un PSC n'est pas suffisante. Ainsi, la valeur de l'Ec/N0 de la cellule
active est utilisée comme référence.
b. Elimination de mesures redondantes et identification du
site
Les mesures des cellules localisées dans un même
site génèrent une redondance de données. Les valeurs du
RSCP est un critère de décision.
c. Première estimation de la position
L'algorithme de position utilisé a besoin d'une estimation
initiale, l'exactitude est important pour la convergence. La méthode
consiste à utiliser les trois meilleures cellules :
Calcul de la pathloss
La perte radio est donnée par la formule suivante
où Tx est la puissance de transmission et RSCP le niveau de la puissance
reçue:
P??[??B] = ????[??B??] - ??????P[??B??] (3.31)
Calcul de la distance ????
La distance ???? entre une cellule i et un UE est obtenue par
:
65
où f est fréquence de transmission, hB
est la hauteur de l'antenne et CLc est un paramètre du
modèle spécifique pour une zone urbaine.
A l'aide des coordonnées des 03 meilleures cellules
(x, Y)A,B,c et les distances calculées dA,B,C, les
coordonnées de la première estimation de la position du mobile
(x, Y)UE est obtenue en utilisant la trilatération
géométrique suivante :
{
(xUE - xA)2 + (YUE -
YA)2 - d = 0 (3.33)
(xUE -
xB)2 + (YUE - YB)2 -
dB2 = 0 (xUE - xC)2 + (YUE - YC)2 -
dC = 0 Les coordonnées sont obtenues après avoir
résolu ce système d'équation en appliquant la
méthode
de Cramer.
d. Calcul de l'OTD
L'OTD sur le k-ième MRM, entre l'UE et la cellule i est
donnée par :
OTDK(i) = 38400 X OFF(i) + Tm(i)
(3.34)
(Calculé pour chaque liaison radio non redondante)
avec :
OFF(i) : Frame offset Tm(i) : Chip offset
Remarque :
Le paramètre OFF peut prendre une valeur de 0 à 255
tandis que celle du Tm varie de 0 à 38399. 3.7.2.3 Cycle de
positionnement
a. Estimation du retard de propagation :
Sur le k-ième MRM, le retard de propagation T entre l'UE
et la cellule i est donnée par :
|
Tk(i) =
|
1 2 (3.35)
C X (xc(i) - xue)2 + (Yc(i) - Yue)
|
avec :
C : Vitesse de la lumière
(x, Y)UE : Position du mobile
(X, y)?? : coordonnées du cell i
b. Calcul de la RTD ou Relative Time Differences Le
modèle de RTD entre 02 cells/sites i et j peut être obtenu par:
????(??, ??) (3.36)
????????(??, ??) = (????????(??, ??) - 0.26 ×
10-6)??????(256 × 38400)
L'échantillon calculé est sauvegardé dans
une matrice tridimensionnelle, de position (i,j,end). La valeur utilisée
est une valeur absurde de la médiane atténuée du tableau
(i,j) de la matrice, RTD'(i,j).
c. Méthode RLS ou Recursive Least Squares non
linéaire
Il s'agit d'une multilatération utilisant la
méthode de moindre carrée récursive non linéaire.
Le système d'équation est généré par :
f??(X,y) =
[
f??,1,2(X, y)
f??,1,3(X, y)
?
f??,1,??(X,
y)
(3.37)
A chaque itération, une correction de la valeur est
appliquée, afin de réduire la somme des résidus au
carré :
|
min
??,??
|
IIf (X, y)II2 2 = min
??,??
|
(f1(X,y)2 + f2 (X,y)2
+ ? + f??(X,y)2) (3.38)
|
66
Chaque équation utilise des mesures provenant de k MRM
d'une paire de cell/site (i,j) :
f??,??,?? (X, y) = ????,??,?? - ????,??,?? (X, y)
(3.39)
où
????,??,?? = C × 78 × (??????(??) - ??????(??) -
??????'??(??, ??))
et
????,??,??(X,y) = (X??(??) - X????)2 + (y??(?) -
y????)2 - (X??(??) - X????)2 + (y??(??) -
y????)2
3.7.2.4 Critère de validité
L'estimation de la position n'est pas valide si :
? Le nombre du cycle d'itération k est atteint.
? La méthode a échoué : flag de sortie RLS
négative.
·
67
Un ou plusieurs échantillons est excessivement
dévié de la valeur absurde de la médiane
atténuée.
· Les valeurs des MRMs peuvent être
contaminées d'erreur.
La vérification de la validité finale est
déterminée par le nombre de k-ième échantillon de
MRM RTD divergent des valeurs de RTD'.
La différence
8RTD est
donnée par :
8RTD = |RTDk(i,
j) - RTD'k(i, j)| (3.40)
La position d'UE donnée par cette MRM est
considérée invalide si l'inégalité suivante est
vraie, pour la valeur tolérée d'erreur maximum
prédéfini ORTD tel que :
8RTD ~ ORTD
(3.41)
3.7.2.5 Génération de sortie
La génération de sortie est la phase finale de
l'algorithme. Les sorties générées sont :
· Le text logs de chaque opération
effectuée,
· Les données brutes des MRMs, contenant toutes
les valeurs et structures utilisées pour l'estimation de positions,
· Un fichier tableur CSV ou Comma Separated Values dans
lequel chaque ligne correspond à une mesure et contient les
coordonnées (latitude et longitude) de la position de l'UE, la taille de
l'Active Set, et les mesures RSCP et Ec/N0.
· 02 Fichiers Google Earth KML ou Keyhole Markup
Language (taille de l'active Set et valeurs de l'Ec/N0), pour visualiser les
données contenant tous les points obtenus par l'algorithme.
3.8 Positionnement utilisant le paramètre
TA
Le paramètre Timing Advance ou TA représente le
temps de propagation aller et retour des ondes radioélectriques entre le
mobile et la station de base avec laquelle il est en communication. Ce
paramètre est codé sur six bits et prend des valeurs
entières allant de 0 à 63. Une unité de TA correspond
à la durée d'un bit, soit 3,7 us. Les valeurs de TA correspondent
donc à des valeurs de temps de propagation comprises entre 0 et 233 us.
[25]
68
Un TA de valeur 1 correspond à une distance
aller/retour de deux fois 550 m. Le TA est transmis dans les messages de
signalisation du protocole GSM associé au canal dédié. Sa
valeur est rafraîchie toutes les 480 ms. Le paramètre TA
évolue si le mobile s'éloigne ou se rapproche de la cellule
courante ou si en cours de communication, il y a un changement de station de
base. [25]
On peut calculer les coordonnées du mobile à
partir du paramètre TA, comme nous montre la figure 3.07 ci-après
où il s'agit d'un exemple de calcul des points d'intersection de deux
cercles :

Figure 3.07 : Intersection de deux cercles
D'après la figure ci-dessus :
· XZ, YZ et X2,
Y2 sont respectivement les coordonnées géographiques
connues des stations de base BTSZ et BTS2.
· Latdecl et Londecl représentent respectivement
la latitude et la longitude en valeurs décimales de ces stations de base
(i =1,2)
· rZ et r2 sont les rayons des cercles centrés
sur les stations BTSZ et BTS2.
69
? ??12 est l'angle que fait l'axe horizontal du
repère trigonométrique avec les stations ??????1 et
??????2.
? âest l'angle que fait un des points communs des
deux cercles avec les stations ??????1 et ??????2. ?
P1 et P2 sont les points
d'intersections recherchés de coordonnées respectives
????1, Y??1 et ????2,
Y??2
Il convient de convertir au préalable les valeurs de
longitude et de latitude en valeurs métriques, ce qui donne les
relations suivantes:
??1 = 60 X 1180 X ??????d????1 ??2 = 60 X 1180 X ??????d????2
(3.42)
Y1 = 60 X 1852 X ??????d????1 Y2
= 60 X 1852 X ??????d????2 (3.43)
La valeur de ?????? reçue de la station i
(i=1,2) est convertie en distance r; correspondant au rayon du cercle qui
s'exprime alors sous la forme :
???? = (3,69 X ?????? X 300)/2 (3.44)
L'angle
â est donné par la relation suivante :
??22 - ??12 -
d2 (3.45)
/3 = arccos (-2??1d )
L'angle ??12 est calculé en prenant en compte les
quatre cas de figures rencontrés correspondant aux 4 cadrans du
repère trigonométrique.
Enfin, les coordonnées des points d'intersection sont
données par les relations :
|
????1 = ??1 + ??1 cos(??12 + /3)
|
????2
|
= ??1 + ??1 cos(??12 -
|
/3)
|
(3.46)
|
|
Y??1 = Y1 + ??1sin(
??12 + /3)
|
Y??2
|
= Y1 + ??1 sin( ??12 -
|
/3)
|
(3.47)
|
3.9 Conclusion
Le développement de la localisation à base
d'empreinte radio nous a permis de présenter des modèles
mathématiques et des algorithmes associés. Ainsi, il existe
plusieurs méthodes de compression de base de données radio et de
classification. Et, afin de réaliser notre application de traitement de
traces et localisation d'abonnés, nous avons étudié la
méthode basée sur l'OTD pour le 3G et, le TA pour le 2G, qui sont
des procédés dérivés du système LFP.
70
| 


