4.2.3.2 MODELISATION MATHEMATIQUE DE LA TOPOLOGIE A
POTENTIEL DISTRIBUEE
Cette méthodologie donne le modèle de la Partie
Opérative Discontinue modélisant le hacheur Boost à
potentiel distribué à 3 niveaux suivant :
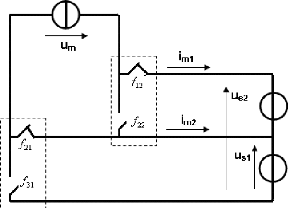
Fig. 6.6 Modèle du hacheur à 3 niveaux à
potentiel distribué associé à ses fonctions de
connexion.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
74
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Le hacheur à trois niveaux de la figure comme
étant une matrice d'interrupteurs (fonctions de connexion) reliant une
source de tension( inductance L) avec deux sources de courant (condensateur
C),
Les deux fonctions de connexions f12
et f31 dépendent directement de commande envoyés
aux transistors :
f12 = T1 f31 = T2 (6.1)
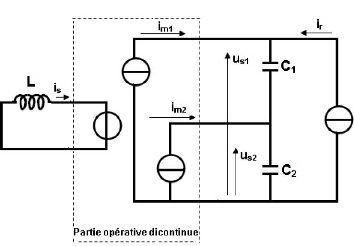
Fig. 6.7. Modèle du hacheur à 3 niveaux à
potentiel distribué avec sa Partie Opérative Discontinu.
La fonction de cette topologie est de générer des
grandeurs modulées (um ; im) associées
à des grandeurs équivalents.
Elle obéit à deux conditions :
· à tout instant les interrupteurs de chaque cellule
doivent être dans des états complémentaires ;
· les sources connectées de chaque de cette
topologie doivent être de nature différente.
Dans le schéma de la figure, on définit une
fonction de connexion fjk qui représente l'état de
l'interrupteur Kjk se trouvant à l'intersection de la ligne j
et de colonne k.
Il vient que :
i m(t) = f(t).i s (t) et um(t)
= (1 - f(t)).u s (t) (6.2)
Cependant nous obtenons les relations matricielles de conversion
suivantes :
[Im] = [F][I s ] (6.3)
75
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
On appelle [F] la matrice fonctionnelle (tous ses
éléments sont des fonctions) Regroupant toutes les fonctions de
connexion du convertisseur considéré.
[M] est la matrice de conversion du convertisseur et mi
représente une fonction de conversion.
On rappelle qu'en modèle moyen, on définit les
fonctions génératrices de connexion sur une période de
commutation Te telle que :
(k+1)Te
1
< f (t) lim[
>= ? ô ô
f ( )d. ] et
lc lc
T e 0
?Te kTe
(6.4)
|
(k+1)Te
1
< m (t) lim[
>= ? ô ô
m ( )d. ]
lc lc
T e 0
? Te kTe
|
|
Les valeurs limites de la fonction de connexion et celle de
commutation sont :
0 = f lc = 1
- 1= m lc = 1
Les relations qui lient les fonctions de connexion à
celles de conversion dans ce convertisseur s'expriment par :
m1 = f31 m2 = f21 -
f22 = f12 - f31 (6.5)
Avec : 0=m1=1 et -1=m2=1
De cette façon les expressions de courant du
convertisseurs sont telles que :
im1 =
m1.is (6.6)
i i m2 =m2.i s (6.7)
im1, im2 désignent les courants modulés.
is désigne le courant commuté issus de
la source de courant (l'inductance L)
Les tensions élémentaires modulées sont
produites par conversion d'une source de tension :
[Um] = [M][U s ] (6.8)
76
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
um1 = m1.us1 (6.9)
um2 = m2.u s2 (6.10)
La tension modulée en multiniveau est la somme de deux
niveaux de tension élémentaires telle que:
um = um1+um2 =m1.u s1+m2.u s2 (6.11)
um1 ; um2 désignent les tensions
modulées. Avec :
u s1 = u c1 + u c2 (6.12)
u s2 =u c2 (6.13)
uc1 et uc2 désignent les tensions
commutées issues des sources de tensions (condensateurs C1 et C2)
im et um sont les grandeurs
modulées, pour lesquelles l'indice « m » rappelle qu'elles
sont modulées.
is et us les grandeurs commutées
pour lesquelles « s » rappelle qu'elles sont issues des sources.
Le fonctionnement de ce convertisseur peut être alors
assimilé à un ensemble de deux générateurs
équivalents de courants modulés et un générateur
équivalent de tension modulée.
| 


