
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
1
RÉSUMÉ 7
1 INTRODUCTION 8
2 CHAIPITRE : GENERALITE SUR LES SYSTEMES EOLIEN ET
SOLAIRE 10
2.1 CHOIX DE L'ARCHITECTURE 10
2.1.2 TOPOLOGIE AVEC BUS CONTINU INTERMEDIAIRE
11
2.2 ARCHITECTURE RETENUE POUR L'ETUDE 13
2.3 DESCRIPTION DU SYSTEME A ETUDIER 13
2.4 DESCRIPTION DES DIFFERENTES PARTIES DU SYSTEME
14
2.4.1 LES SOURCES D'ENERGIE DU SYSTEME 14
2.4.1.1 LES AEROGENERATEURS 14
2.4.1.2 LES CELLULES PHOTOVOLTAÏQUES 16
2.4.2 LES CONVERTISSEURS STATIQUES DU SYSTEME
18
2.4.2.1 ALIMENTATION DU BUS CONTINU 18
2.4.2.1.1 LE CONVERTISSEUR AC-DC (Redresseur)
18
2.4.2.1.2 LE CONVERTISSEUR DC-DC (Hacheur) 20
2.4.2.2 ALIMENTATION DU RESEAU ELECTRIQUE 21
2.4.2.2.1 LE CONVERTISSEUR DC- AC 21
2.4.3.1 LE BUS CONTINU 24
3 CHAPITRE : SYNTHESE DE LA PROBLEMATIQUE ET PROPOSITION
DE
SOLUTIONS 25
3.1 SYNTHESE DE LA PROBLEMATIQUE 25
3.2 PROPOSITION DE SOLUTIONS 27
4 CHAPITRE : ETUDE DU HACHEUR 30
4.1 HACHEUR SURVOLTEUR 30
4.1.1 STRUCTURE DU HACHEUR SURVOLTEUR 30
4.1.1.1 COMMANDE DES INTERRUPTEURS ET FORMES D'ONDE
31
4.1.1.2 EXPRESSION DE LA TENSION DE SORTIE UBUS
32
4.1.1.2.1 EXPRESSION DE Is
PAR RAPPORT à IL 36
4.1.1.3 DETERMINATION DES COMPOSANTS REACTIFS
36
4.1.1.3.1 L'INDUCTANCE L 36
4.1.1.3.2 LE CONDENSATEUR C 38
4.1.1.4 LIMITATION DE COURANT ET TENSION DANS
LES
SEMICONDUCTEURS 39
4.1.1.5 DIMENSIONNEMENT DES COMPOSANTS 40
4.1.1.5.1 DIMENSIONNEMENT DES ELEMENTS REACTIFS L ET C
DU
HACHEUR 40
4.1.1.5.1.1 VALEUR DE L'INDUCTANCE L 41
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
2
4.1.1.5.1.2 VALEUR DU CONDENSATEUR C 42
4.1.1.5.2 CHOIX DES SEMI-CONDUCTEURS 42
4.1.2 MODELISATION DU HACHEUR SURVOLTEUR 42
4.1.2.1 MODELISATION SOUS FORME DE SCHEMA BLOC
42
4.1.2.1.1 PRINCIPE DE REGULATION LINEAIRE EN CASCADE
44
4.1.2.1.2 EQUATION BILAN ENERGETIQUE DU SYSTEME
45
4.1.2.1.3 FONCTION DE TRANSFERT DU SYSTEME 46
4.1.2.1.4 CHOIX DU REGULATEUR DU SYSTEME 47
4.1.2.1.5 LIMITEUR DE LA TENSION ET DU COURANT
48
4.1.2.1.6 CHAINE DE COMMANDE 50
4.1.2.1.6.1 MISE EN PLACE DE LA BOUCLE DE COURANT
50
4.1.2.1.6.2 MISE EN PLACE DE LA BOUCLE DE TENSION
51
4.1.2.1.7 DETERMINATION DES PARAMETRES DU REGULATEUR
52
4.1.2.1.7.1 REGULATEUR DE COURANT 52
4.1.2.1.7.2 REGULATEUR DE TENSION 54
4.1.2.1.7.3 CALCUL DES COMPOSANTS DU REGULATEUR
55
4.1.3 MODELISATION GRAPHIQUE DU HACHEUR 58
4.1.3.1 LA REPRESENTATION MACROSCOPIQUE ENERGETIQUE
58
4.1.3.1.1 OBJECTIFS 58
4.1.3.1.2 REGLES DE BASE 58
4.1.3.1.3 ELEMENTS CONSTITUTIFS 58
4.1.3.1.3.1 LES ELEMENTS SOURCES 58
4.1.3.1.3.2 LES ELEMENTS D'ACCUMULATION 59
4.1.3.1.3.3 LES ELEMENTS DE CONVERSION 59
4.1.3.1.4 STRUCTURE GENERIQUE ELEMENTAIRE 60
4.1.3.1.5 REGLES D'ASSOCIATION 60
4.1.3.1.5.1 ASSOCIATIONS DIRECTES 60
4.1.3.1.5.2 REGLE DE CONCATENATION 61
4.1.3.1.5.3 REGLE DE PERMUTATION 61
4.1.3.1.6 COUPLAGE ELECTRIQUE 61
4.1.3.1.7 STRUCTURE DE COMMANDE MAXIMALE DEDUITE DE LA
REM 61
4.1.3.1.8 APPLICATION DE LA REM A LA MODELISATION DU
HACHEUR
SURVOLTEUR 62
4.1.3.1.8.1 REM DES ELEMENTS SOURCES DU HACHEUR
SURVOLTEUR
CLASSIQUE 62
4.1.3.1.8.2 REM DES ELEMENTS D'ACCUMULATION DU
HACHEUR
SURVOLTEUR 63
3
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.1.3.1.8.3 REM DE L'ELEMENT DE CONVERSION DU
HACHEUR
SURVOLTEUR 65
4.1.3.1.8.4 REM DU HACHEUR SURVOLTEUR CLASSIQUE
65
4.1.3.1.9 STRUCTURE MAXIMALE DE COMMANDE (SMC) DU
PROCESSUS
DEDUITE DE LA REM 67
4.1.3.1.9.1 SMC POUR L'ELEMENT DE CONVERSION (HACHEUR)
EN
MODELE MOYEN ET PAR INVERSION DIRECTE 68
4.1.3.1.9.2 SMC POUR LES ELEMENTS D'ACCUMULATION ET
PAR
INVERSION INDIRECTE PAR ASSERVISSEMENT 68
4.1.3.1.10 REM ET SMC DU HACHEUR SURVOLTEUR CLASSIQUE
69
4.2 ETUDE DU HACHEUR MULTINIVEAU 70
4.2.1 CONTEXTE 70
4.2.2 STRUCTURE ET FONCTIONNEMENT 71
4.2.2.1 TOPOLOGIE A POTENTIEL DISTRIBUE 71
4.2.2.2 TOPOLOGIE A CELLULES IMBRIQUEES 72
4.2.3 MODELISATION DU HACHEUR SURVOLTEUR MULTINIVEAU
72
4.2.3.1 RELATIONS DE CONVERSION DU HACHEUR A 3
NIVEAUX
(TOPOLOGIE BOOST) 72
4.2.3.2 MODELISATION MATHEMATIQUE
DE LA TOPOLOGIE A
POTENTIEL DISTRIBUEE 74
4.2.3.3 RESUME DES RELATIONS
DES GRANDEURS ECHANGEES ET
FORMES D'ONDE 77
4.2.3.4 MODELISATION ELECTRIQUE DE LA
TOPOLOGIE A CELLULES IMBRIQUEES 78
4.2.3.5 MODELISATION REM ET STRUCTURE DE COMMANDE
DU
HACHEUR A TROIS NIVEAUX (MONTAGE BOOST) 80
4.2.3.5.1 REM DES SOURCES D'ENERGIE : 81
4.2.3.5.2 REM DES ACCUMULATEURS D'ENERGIE 82
4.2.3.5.3 REM DU CONVERTISSEUR D'ENERGIE 83
4.2.3.5.4 REM DU HACHEUR SURVOLTEUR MULTINIVEAU
83
4.2.3.5.5 STRUCTURE MAXIMALE DE COMMANDE (SMC) DU
HACHEUR
SURVOLTEUR MULTINIVEAU 84
5 CHAPITRE : SIMULATION ET INTERPRETATION DES RESULTATS
85
5.1 TRANSPOSITION DU MODELE REM DU HACHEUR CLASSIQUE
ET
DUHACHEUR MULTINIVEAU SOUS LE LOGICIEL MATLAB SIMULINK
85
5.2 RESULTATS DE SIMULATION 87
5.2.1 ALLURES OBTENUES POUR SIMULATION DU HACHEUR
SURVOLTEUR
CLASSIQUE ET DU HACHEUR SURVOLTEUR MULTINIVEAU
87
5.2.1.1 POUR LE HACHEUR CLASSIQUE 87
5.2.1.2 POUR LE HACHEUR MULTINIVEAU 90
5.2.1.3 INTERPRETATION 91
6 CONCLUSION 92
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
SUJET DE MEMOIRE D'INGENIEUR EN ELECTRONIQUE ET
INFORMATIQUE
INDUSTRIELLES
Domaine : Électronique de
puissance
STRATEGIE DE COMMANDE ET DE REGLAGE DE BUS CONTINU DEDIE
AUX
SYSTEMES DE PRODUCTION D'ENERGIE EOLIENNE ET SOLAIRE
Thème :
Le bus continu est le moyen de regrouper le
générateur éolien (centrale éolienne) et/ou le
module solaire (centrale solaire) pour avoir de puissance
élevée.
Le problème consiste à déterminer le
moyen de réglage et de commande de ce bus continu le plus adapté
pour avoir de bon rendement à l'ensemble de système au
réseau.
Travail demandé :
· Recherche bibliographique
· Modéliser les différentes parties du
système
· Modéliser le flux d'énergie
· Proposer la stratégie de commande et de
réglage pour servir le système
· Application : simulation avec MATLAB SIMULINK
Encadreurs :
· Mr Prof. RAZAFIMAHENINA Jean Marie
· 5
Mr RANDRIAMIARINARIVO Jean Marie
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
REMERCIMENT
A mon défunt père Mr ABDOULHALIM Hassani
Soilihi (hélas, il aurait bien aimé être là pour
savourer les premiers fruits de ma maturité), à ma mère
Mme ZAINA Mohamed Halidi et à mes frères et soeurs de leurs sens
du sacrifice et soutien sans faille.
A mes enseignants de l'Ecole Supérieure Polytechnique
d'Antsiranana, en particulier mes directeurs de mémoire à savoir
; Mr le Professeur RAZAFIMAHENINA Jean Marie et Mr RANDRIAMIARINARIVO Jean
Marie sans qui cette érudition ne serait pas réussite.
Je rends grâce à ces piliers et
à tous ceux qui m'ont éduqué, assisté et
résisté.
6
ZAIDOU Abdoulhalim Hassani
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
RÉSUMÉ
L'objectif dans ce mémoire consiste à proposer un
procédé technique qui permet de régler et commander le
circuit intermédiaire appelé bus continu situé entre un
premier convertisseur statique MLI (généralement un redresseur ou
un hacheur) qui raccorde un module éolien ou solaire et un second
convertisseur MLI (généralement un onduleur de tension) qui
alimente un réseau triphasé de tension alternative 220V /50Hz.
La problématique est de trouver par quel moyen pallier
aux défaillances de tension au niveau de bus continu afin de satisfaire
à une demande de tension continue de valeur moyenne 750V qui alimente
l'onduleur.
La solution proposée pour répondre à cette
initiative est basée sur le principe de compensation de la tension
d'alimentation de cet onduleur (tension de bus continu) par le biais d'un
système régulateur connecté en amont du bus continu,
composé d'une batterie de 48V et d'un hacheur survolteur classique en
cascade. Par pousser plus loin encore, une extension de l'étude sur le
système de régulation est élaborée avec cette
fois-ci un hacheur survolteur multiniveau, afin d'obtenir la stratégie
la mieux adaptée.
Les modélisations REM de deux processus
étudiés ont permis de mettre en évidence les
échanges énergétiques de ceux-ci avec le bus continu qui
leur est connectés.
Cependant une conclusion sur les avantages et
inconvénients de chaque processus (régulateur avec un hacheur
classique et régulateur avec un hacheur multiniveau) peut être
établie grâce aux résultats de simulation sous le logiciel
MATLAB SIMULINK..
7
Mots clés : bus continu / éolien
et solaire/ hacheur survolteur classique/ hacheur multiniveau/ modèle
REM/ modèle MATLAB SIMULINK.
1 INTRODUCTION
Le besoin mondial en énergie électrique ne
cesse d'augmenter en rencontre de préoccupations des écologistes
liées aux problèmes environnementaux engendrés par les
sources d'énergie traditionnelle (nucléaire). Ce défi
entraîne de plus en plus la mise en place des sites industriels qui
transforment des sources d'énergie naturelle en
électricité.
De nos jours des centrales éoliennes et solaires sont
mises en service chaque année au profit de l'écologie pour
produire plus 2% de l'électricité mondiale. Ainsi des nombreux
consommateurs, particuliers ou industriels relativement lointains couvrent
leurs besoins en énergie électrique grâce au vent et au
soleil regroupés sous le vocable sources d'énergie
renouvelable.
Bien que la technologie de ces dernières ait nettement
évolué, la nécessité d'apporter des solutions
innovatrices d'électronique de puissance et de commande et
réglage se fait encore sentir lorsque l'on veut optimiser
l'énergie extraite de ces sources.
Les convertisseurs de puissance occupent une place de plus en
plus importante dans le processus industriel et en particulier parmi les
éléments de la chaîne de conversion d'énergie dans
ce type de système. Leur intérêt est sollicité tant
pour l'amélioration de l'électricité produite que pour
combiner différentes sources d'énergie et gérer le
contrôle du système.
Leur interconnexion dans le système fait émerger
une notion de noeud électrique intermédiaire,
désigné par bus continu dont la gestion, du point de vue
réglage et commande, pose problème.
Dans toutes les structures envisageables, ce bus à
tension continue constitue une colonne vertébrale
énergétique habituelle. Il représente un noeud de
confluence des puissances électriques de la source productrice
d'énergie (générateur éolien ou solaire) et du
consommateur. C'est donc une jonction équipotentielle de puissances dont
le réglage se réalise grâce au degré de
liberté offert par un appoint énergétique extérieur
dont un système de régulation (généralement un
dispositif de stockage inertiel associé à un convertisseur
statique DC-DC).
De part en part, l'utilisation d'un onduleur de tension
à MLI relié au réseau demande un gradient de tension
élevée et sans variation, délivrée par le bus
continu.
En pareille occurrence, l'électricité produite
à partir des aérogénérateurs ou des cellules
photovoltaïques peut être transférée au réseau
dans son intégralité, en partie ou pas du tout ; sa mise en norme
au réseau électrique et son optimalité doivent faire
l'objet d'un réglage des puissances reparties en amont et en aval du bus
continu et par extension d'une commande bien adaptée à ce
processus.
D'où notre thème : « Stratégie de
commande et de réglage de bus continu dédié au
système de production d'énergie éolienne et solaire
».
L'objet dans ce mémoire est de proposer, dans les
systèmes de conversion d'énergie éolienne et solaire, une
solution constructive appliquée au bus continu pour contrôler et
régler sa tension, en vue de satisfaire à une demande de
puissance de l'onduleur connecté au réseau ; ce qui permettrait
en conséquence l'optimisation du rendement énergétique du
système.
La problématique d'un tel sujet soulève
néanmoins ces questions :
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
8
· Quelle architecture pour interconnecter les
différents éléments du système ?
· Quelles solutions mettre en oeuvre pour adapter les
niveaux de tension de bus continu afin d'obtenir un réseau
d'énergie 220Veff / 50Hz ?
· En quoi ces solutions sont intéressantes ? Quelles
sont leurs limites ?
· Comment élaborer la commande du bus continu pour
que le système fournisse sa puissance optimale?
Ce sujet demande en préalable, une aperçue
générale sur les différents éléments du
système dont il faut comprendre l'importance dans une chaîne de
conversion d'énergie électrique au moyen de sources
naturelles.
Ensuite, nous présenterons une synthèse de
problématique posée par le bus continu au sein de ce type de
système (une ou trois générateurs éoliens ou
solaires connectés à un réseau moyenne tension par
l'intermédiaire d'un système à double convertisseur ayant
en commun à un bus continu à condensateur).
Enfin, nous proposerons la stratégie de réglage
et de commande de bus continu en rapprochement de deux solutions technologiques
distinctes :
· l'une utilisant un hacheur classique ;
· l'autre utilisant un hacheur multiniveau.
En vue de satisfaire à ces initiatives, nous allons
développer une méthodologie de modélisation assez
générale qu'est le formalisme graphique REM
(Représentation Energétique Macroscopique). Il nous permettra
d'élaborer des modèles simples et lisibles par la description
externe des échanges énergétiques du processus avec son
environnement.
La structure de commande sera déduite par principe
d'inversion du modèle développé.
En adoptant cette approche systémique, nous pouvons
également bâtir des modèles du processus à partir
d'une bibliothèque de composants sous l'environnement MATLAB
SIMULINK.
Pour évaluer les résultats de l'étude et
montrer sa validité aux dépens de la stratégie
proposée (par rapport aux solutions apportées) nous allons
procéder à des simulations des modèles MATLAB SIMULINK
établis.
Nous terminerons ce rapport par une conclusion sur l'approche
comparative entre les deux procédés techniques utilisés
pour pallier ces problèmes.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
9
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
2 CHAIPITRE : GENERALITE SUR LES SYSTEMES EOLIEN ET
SOLAIRE
2.1 CHOIX DE L'ARCHITECTURE
De nombreuses architectures peuvent être
utilisées pour réaliser la conversion de l'énergie
éolienne ou photovoltaïque en électricité. Le
principe consiste à connecter la source principale d'énergie au
réseau électrique par l'intermédiaire d'un ou plusieurs
convertisseurs statiques d'interface.
Pour cela, nous pouvons distinguer deux types des structures
:
· -l'architecture sans bus continu intermédiaire,
· -l'architecture avec un bus continu
intermédiaire.
Les figures suivantes illustrent ces deux familles de
système de production d'énergie électrique à partir
de module éolien ou solaire :
2.1.1 TOPOLOGIE SANS BUS CONTINU INTERMEDIAIRE

2.1.1.1 Fig.1.1 Architecture sans bus continu
intermédiaire
Dans cette architecture, la source d'énergie est
directement raccordée au réseau électrique via un onduleur
de tension. La gestion de l'énergie ne se fait pas par la commande de
bus continu (Il n'y a pas de contrôle et de réglage de la tension
de bus continu). Cette architecture est donc peut intéressante pour
notre étude.
2.1.1.2 Exemple de topologie pour laquelle le bus
continu intermédiaire n'est pas utilisé

Fig.1.2 Système d'énergie photovoltaïque
sans bus continu intermédiaire.
10
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
2.1.2 TOPOLOGIE AVEC BUS CONTINU INTERMEDIAIRE
Une centrale d'énergie éolienne ou solaire
utilisant le bus comme circuit intermédiaire peut être
architecturée comme suit :

Fig. 1.3 Architecture avec bus continu
intermédiaire
Dans cette topologie, le convertisseur de courant coté
source (redresseur lorsque la source principale est un module éolien ;
hacheur dans le cas d'un module solaire) délivre une tension continue U
à l'entrée de l'onduleur de tension. Ce dernier est normalement
un onduleur triphasé qui est raccordé à un réseau
alternatif moyenne tension (220V/50Hz).
A l'intermédiaire du convertisseur de courant et de
l'onduleur de tension se trouve le bus à tension continue ; puisqu'il
faut imposer une tension continue constante à l'entrée de
l'onduleur.
Le condensateur C est le principal élément
constitutif de ce circuit intermédiaire (bus continu). Il sert de
condensateur-tampon à l'entrée de l'onduleur pour prendre en
charge les variations rapides du courant d'entrée de l'onduleur. Ce
condensateur a aussi la tâche de lisser la tension continue
redressée.
Ainsi modéliser le bus continu passe par la
connaissance de la tension aux bornes de ce condensateur.
2.1.2.1 Exemples de topologies pour lesquelles la
liaison bus continu est utilisée Une installation
alimentant un réseau électrique peut être
architecturée comme suit :

Fig.1.4 Centrale à un générateur
éolien couplé au réseau électrique avec un bus
continu intermédiaire.
11
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Nous pouvons également percevoir l'architecture du genre
:

Fig.2.5 Centrale à une cellule photovoltaïque
couplée au réseau avec un bus continu
intermédiaire.
Avec cette architecture, nous pouvons également connecter
plusieurs sources d'énergie (grâce aux convertisseurs statiques de
liaison côté source) afin d'obtenir une tension de bus continu,
suffisante pour l'utilisation d'un onduleur :
Pour une installation éolienne :

Fig.2.6 Centrale à trois générateurs
éoliens couplés au réseau avec un bus continu
intermédiaire.
Pour une installation solaire :

Fig.2.7. Centrale à trois cellules
photovoltaïques couplées au réseau avec un bus continu
intermédiaire.
12
2.2 ARCHITECTURE RETENUE POUR L'ETUDE
L'architecture générique que l'on rencontre le
plus souvent dans des nombreux systèmes de conversion d'énergie
éolienne et solaire, actuels, peut être comparée au
synoptique suivant :

Fig. 2.8. Source d'énergie couplée au
réseau avec un bus continu intermédiaire
Cette configuration réunit tous les problèmes
posés par le bus continu dans une chaîne de conversion
d'énergie éolienne et solaire.
Nous allons dorénavant restreindre notre étude au
cas d'un système (fig.) de production d'énergie éolienne
ou solaire avec un bus continu intermédiaire.
2.3 DESCRIPTION DU SYSTEME A ETUDIER
Le système sur lequel porte notre étude est
rappelé par le schéma fonctionnel suivant :

Fig.2.9 Architecture générique de conversion
d'énergie éolienne ou solaire
La chaîne de conversion proposée est
composée de 4 blocs essentiels formant un ensemble ordonné de
fonctions :
· La source principale englobe les
générateurs solaires et éoliens associés à
une conversion statique d'énergie. Elle est raccordée au
réseau alternatif au moyen d'un système de deux convertisseurs
à Modulation de Largeur d'Impulsions (MLI) liés entre eux par un
noeud électrique appelé Bus Continu.
· Le premier convertisseur (côté source)
est sensé transférer continue et sans variation la tension
extraite de la source vers le bus continu.
· le bus continu est le circuit intermédiaire sur
lequel la gestion et le contrôle de flux d'énergie du
système doivent se faire.
· Le second convertisseur (uniquement onduleur) connecte le
bus continu au réseau alternatif et permet de contrôler les
échanges de puissance active et réactive avec le
réseau.
Le contrôle de la tension du bus continu sera
particulièrement étudié en relation avec le transit de
puissance entre la source et le réseau.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
13
2.4 DESCRIPTION DES DIFFERENTES PARTIES DU SYSTEME
2.4.1 LES SOURCES D'ENERGIE DU SYSTEME
Les sources d'énergie sont les principaux
générateurs d'électricité. Elles doivent
délivrer une puissance de valeur égale à celle de la
puissance moyenne nécessaire pour accomplir la (les) mission(s)
typique(s) du système.
Parmi les sources d'énergie, nous
pouvons citer :
· les aérogénérateurs
associés à l'énergie éolienne,
· les cellules photovoltaïques
associées à l'énergie solaire.
2.4.1.1 LES AEROGENERATEURS
Les aérogénérateurs
(éoliennes par abus de langage) sont les sources
énergétiques des systèmes éoliens. Ils capturent
l'énergie cinétique des vents de surface et la convertissent
en électricité.
Pour ce faire, elles ont besoin de trois composants
de base : des pales, un arbre et une génératrice. Lorsque le vent
se déplace sur les pales de l'éolienne, il provoque une
sustentation qui fait tourner les pales qui mettent en mouvement un arbre
déplaçant des aimants de la génératrice, qui
crée à son tour de l'électricité. Cette
électricité peut être utilisée sur place en flux
continu mais elle peut être stockée et pompée vers un
réseau électrique grâce à des véhicules
électriques (convertisseurs statiques, stockage...).

14
Stratégie de commande et réglage du bus
continu dédiée aux systèmes de production d'énergie
éolienne et solaire
Fig. 2.10. Eoliennes à axe horizontal Fig.2.11.
Eoliennes à axe vertical
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
2.4.1.1.1 Formule pour calculer l'énergie
produite par un aérogénérateur
Nous pouvons déterminer aisément
l'énergie électrique produite par un
aérogénérateur
connaissant sa surface et le vent qui le traverse.
Pour ce faire, considérons une éolienne dont
les pales ont un rayon r [m] ; traversée par une
masse d'air m [kg], de vitesse v [m/s] et de densitéd
[kg/m3].
m = ð * r * e * d , avec d=1,225 kg/m3
(densité de l'air) et e distance parcourue.
2
L'énergie cinétique Ec (en joule) du
vent est la demi-masse fois la vitesse au carré :
E = 1 mv2 = 1 *ð *r2
*e*d*v2
c 2 2 (2.1)
La puissance p (en watt) est la quantité d'énergie
par seconde, or, e par seconde = v.
Ainsi p=2*ð* r2*v*e*d*v2 (2.2)
La puissance absolue pa par l'éolienne est
:
pa =1.924 * r * v
2 3 (2.3)
Toutefois, toute l'énergie ne peut être
captée. La vitesse du vent n'est pas nulle après son passage dans
l'éolienne !
Tenant compte de l'aérodynamique, la puissance
maximale pMAX d'une éolienne est donnée 16
par la formule de Betz ( MAX
p = p ) : pa = 1.14 * r * v
2 3 (2.4)
a
27
Soit p ? 0.363 * v 3 (2.5)
MAX/m2
La puissance pratique pprat d'une éolienne
est inférieure àpMAX . Ceci est dû au fait que,
du vent à la distribution sur le réseau, il y a plusieurs
étapes de conversion d'énergie, chacune avec son propre rendement
:
Hélice (85%), multiplicateur (95%),
générateur (98%), transformateur (98%) - redresseur (98%),
stockage, distribution.
Bref, le rendement optimal est de 70 à 60%. Cependant,
en pratique, tous les organes ne sont pas à leur rendement maximum en
même temps, ce qui réduit encore le rendement global. On
considère celui entre 55 - 50% pour une éolienne «
industrielle » et 40 - 25 % pour une éolienne « artisanale
» :
· éolienne industrielle : =
pprat 0.627 * r * v
2 3 (2.6)
· éolienne artisanale : =
pprat 0.456 * r * v
2 3 (2.7)
15
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
2.4.1.2 LES CELLULES PHOTOVOLTAÏQUES
Les systèmes solaires ont pour source d'énergie
un module solaire composé des cellules photovoltaïques
(abréviation PV). Ce module emmagasine les rayonnements lumineux du
soleil et les transforme directement en un courant électrique par ces
cellules à base de silicium ou un autre matériau ayant des
propriétés de conversion
lumière/électricité. Chaque cellule délivrant une
faible tension, ainsi on les assemble en panneau.
Le plus de lumière ils reçoivent, le plus ils
produisent de l'électricité. Pour régulariser, stocker,
conditionner et verser l'électricité au réseau, on
connecte dans le système de composantes telles que régulateurs de
charge, batteries et convertisseurs statiques.

Fig. 2.12 Module solaire formé de cellules
photovoltaïques
Les cellules photovoltaïques en silicium monocristallin ont
un rendement (15%) élevé par rapport aux cellules en silicium
polycristallin produites à partir des déchets du silicium
monocristallin (rendement de 12%). Les cellules en silicium amorphe (couche
mince) sont obtenues par la projection du gaz de transformation du silicium
naturel en silicium pur sur une feuille de verre ont un rendement (6 à
8%) plus faible.
2.4.1.2.1 Formule pour calculer
l'électricité produite par une photovoltaïque
À partir des paramètres donnés du
générateur photovoltaïque, on peut obtenir l'énergie
électrique qu'il produit.
Le modèle électrique le plus proche du
générateur photovoltaïque est un modèle à deux
diodes avec des facteurs de forme différents et des lois de
comportement, par rapport à la température, différentes
:

Fig. 2.13 Modèle électrique d'une cellule
photovoltaïque.
16
Pour une température et un éclairement
donnés (normalement 25°C et 1.000 W.m-2). Nous obtenons
les équations suivantes :
? ?+ ? ?
e.(V R .I
S
I I exp ? - ?
1
D1 S1
= ? ? (2.8)
? ? ? ç1.k.T ? ? ?
? -
IS1 = K1 .T3.expE g ?
k.T
?
(2.9)
?
?
?
·
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
e : charge de l'électron
· k : constant de Boltzmann : constant dépendant du
matériau semi-conducteur [sans dimension]
· T : température [K]
· Is : courant inverse de saturation de la
diode, il est dépendant de la température selon une loi
différente pour chaque matériau [A]
· K1 : constant thermique du fabricant
· Eg : Energie de gap [J]
· V : tension [V]
· I : courant [A].
· K2 : constant thermique du fabricant
Ainsi, l'équation globale la plus complexe pour
modéliser une cellule réelle est la suivante :
?- ? ? ? + ?
3 g S
I I .
std [
G E
= e.(V R .I
. äI .(T - 298)+1 - K .T .exp
] . exp 1
CC T 1 ? ? ? ? ? ? ? ?
ç ? ? -
1000 k.T 1.k.T
5 ? - ? ? ? + ? ? +
E g e.(V R .I V I.R
2 s S
-K .T .exp . exp
2 ? ? - ? ? -
1
? ? ? ? ? ? ? ? ç
k.T 2.k.T Rsh
|
(2.10)
|
|
· ICCstd : courant de court-circuit de la cellule
photovoltaïque dans les conditions
· standards et optimales: G =1.000 W/m2 et T
=25°C=298K.
· G : éclairement [W/m2] T :
température [K]
· IT : variation de courant de court-circuit par
rapport à la température [K-1]
Dans cette équation, le courant est fonction de la
température, de la tension aux bornes de la cellule, de
l'éclairement et de lui-même.
17
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
2.4.2 LES CONVERTISSEURS STATIQUES DU SYSTEME
Les convertisseurs de puissance doivent permettre d'associer
deux sources de tension, en l'occurrence la source principale d'énergie
et l'organe de stockage.
Leur rôle principal sera donc de gérer les
grandeurs électriques échangées entre ces deux
éléments.
Accessoirement il pourra également avoir à charge
de réaliser l'adaptation entre les niveaux nominaux de tension des
différents éléments constitutifs du système.
A ce rôle le convertisseur statique peuvent être
considéré comme des alimentations en tension et/ou courant
alternatif ou continu.
2.4.2.1 ALIMENTATION DU BUS CONTINU
Pour alimenter directement en tension continue le bus DC
à condensateur, l'on se sert généralement de deux types de
convertisseur statique :
· un convertisseur AC-DC (redresseur) lorsque la source
principale d'énergie est un aérogénérateur,
· un convertisseur DC-DC (hacheur) lorsque la source
principale d'énergie est une cellule photovoltaïque
·
·
2.4.2.1.1 LE CONVERTISSEUR AC-DC
(Redresseur)
Le convertisseur alternatif-continu utilisé dans le
système pour connecter l'aérogénérateur sur le bus
continu est une classique structure de redresseur caractérisé par
un montage en pont triphasé mixte (à diodes et thyristors)
présenté par la figure suivante :

Fig. 2.14. Montage redresseur en pont triphasé mixte
alimentant un bus continu.
18
Un redresseur est un convertisseur AC-DC qui fournie une
tension continue lorsqu'il est alimenté par une tension alternative.
Symbole :

Fig. 2.15 Symbole d'un redresseur.
De nombreux types de ce montage (type parallèle avec
source montée en étoile : P2 P3 P6 ; type série avec
source montée en triangle : S3 S6 ...) redresseur formé à
partir des diodes et/ou des thyristors sont rependus dans le milieu
industriel.
Dans le montage présenté figure, la
régulation de la tension du bus continu Ubus consiste
à contrôler le système triphasé sinusoïdal de
tension (u1, u2, u3 ) afin de générer une grandeur de
référence de la tension de bus continu.
La relation entre les tensions alternatives alimentant le pont
découle de conditions posées aux tensions.
Tension redressée :
La valeur moyenne de la tension redressée donnée
par le groupe de commutateur plus positif formé par des thyristors est
:
q ð
v - v = V sin .cos á M 0 ð M q
|
(2.11)
|
|
Celle de la tension délivrée par le commutateur
plus négatif formé par des diodes est :
q
v - v = - V sin
N 0 ð M
|
ð q
|
(2.12)
|
|
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
La valeur moyenne est donnée par :
Ud=(vM-v0)moy-(vN-v0) (2.13)
q ð
U = ( V sin ).(1 + cos á ) d ð M q
|
(2.14)
|
|
q ð
Or d0
U = 2 V sin (2.15)
ð M q
1 + cosá
D'où d
U=U (2.16)
d0 2
19
Le nombre de tensions alternatives à redresser est
noté q=3. á correspond à l'angle d'allumage des
semi-conducteurs.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
2.4.2.1.2 LE CONVERTISSEUR DC-DC (Hacheur)
La conversion d'énergie côté source du
système est assurée par un hacheur lorsque la source
d'énergie connectée sur le bus continu est un module solaire.
Le hacheur est un convertisseur statique doté d'un ou
plusieurs interrupteurs commandés, utilisés pour varier de
façon périodique la valeur de la tension d'une source de tension
continue constante. Il est généralement utilisé comme
variateur de courant ou tension continue dans les applications industrielles en
permettant en ce sens d'élever et/ou d'abaisser une tension
d'alimentation continue fixe, donnée.
A cet effet on parlera de :
· hacheur élévateur, lorsque la tension
délivrée est supérieure à la tension
appliquée à l'entrée ;
· hacheur abaisseur dans le cas contraire ;
· hacheur inductif lorsqu'il réalise de
manière successive ces deux opérations.
Les convertisseurs DC-DC utilisés dans notre
système de conversion sont considérés comme étant
des sources de tension ou courant de régulation : ce sont donc des
régulateurs.
Symbole :

Fig. 2.16. Symbole d'un hacheur
Parmi les variantes de hacheurs utilisables dans notre
système de conversion pour connecter la source principale ; nous
citerons le hacheur élévateur classique :
Hacheur élévateur (parallèle) classique
:

Fig.2.17. Modèle électrique du hacheur
élévateur
Les caractéristiques du hacheur élévateur
sont définies par :
> la tension d'alimentation Ue de valeur moyenne
constante, > la tension de sortie us d'expression,
> la puissance utile nominalep= u s .i s
20
> la fréquence de découpage :
f déc
1
= avec T déc = t e + t d
T déc
Td éc est la période de
découpage du hacheur
te et td représentent
respectivement le temps d'enclenchement et le temps de
déclenchement
du semi-conducteur commandé.
· L'ondulation du courant d'entrée iL
(pour des raisons de volume, les énergies maximal stockées dans
les inductances sont limitées) et l'ondulation de la tension de
sortie.
2.4.2.2 ALIMENTATION DU RESEAU ELECTRIQUE
Pour verser l'électricité dans le réseau
alternatif, on utilise des convertisseurs DC-AC
2.4.2.2.1 LE CONVERTISSEUR DC- AC
La conversion continu-alternatif dans notre système
est assurée par un onduleur triphasé. On dispose dans le
schéma représenté figure, d'une tension continue
délivrée par un bus continu à condensateur, et si l'on
relie les deux bornes de ce condensateur à l'entrée de
l'onduleur, grâce à ses semi-conducteurs il fournit aux
équipements du réseau une tension sinusoïdale
triphasée 220V/50Hz :

Fig. 2.18 Modèle électrique d'un onduleur
triphasé en pont
On appelle onduleur triphasé à MLI, un onduleur
alimenté par une source de tension continue (la tension u n'est pas
affectée par les variations du courant i qui la traverse) et
délivrant une tension alternative (sinusoïdale) triphasée.
Cet onduleur utilise une Modulation à Largeurs d'impulsions qui lui
permet d'approximer sa tension de sortie sinusoïdale en formant chacune
des alternances de celle-ci d'une succession de créneaux de largeurs
convenables.
Lorsqu'on relie le point neutre N au point 0, on obtient
également à partir de la figure 2.4.2.3.1, une structure
d'onduleur triphasé en demi- pont à six interrupteurs : ceci
équivaut à
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
21
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
associer trois demi-ponts monophasés en utilisant un
diviseur capacitif commun comme l'indique la figure 2.19 :

Fig. 2.19. Modèle électrique d'un onduleur
triphasé en demi-pont.
Un onduleur est donc un convertisseur statique qui
réalise une conversion DC-AC.
Il possède des caractéristiques variées
(générateur ou récepteur de tension ou de courant) qui
dépendent de la nature des commutations à effectuer en
particulier des semiconducteurs à employer.
Ainsi, nous pouvons distinguer deux types d'onduleurs :
· les onduleurs de tension
· les onduleurs de courant
Les premiers sont alimentés par une source de tension
continue, les seconds par une source de courant continu.
La tension ou le courant de sortie d'un onduleur de tension ou
de courant peut être formé non pas d'un seul mais de plusieurs
créneaux par alternance. Dans ce dernier cas on parle des onduleurs
à Modulation de Largeur d'Impulsions (MLI).
On symbolise un onduleur par le schéma suivant :

2.4.3 Fig. 2.20. Symbole d'un onduleur
Dans le schéma représenté figure,
l'onduleur triphasé est constitué d'une cellule de commutation
polyphasée qui permet de régler les échanges
d'énergie entre 3 sources de tension et une source de courant : chaque
interrupteur est connecté, d'une part, à une source de tension
et, d'autre part, à la source de courant.
les trois cellules de commutation ( K1 et K1' ; K2
et K2' ; K3 et K3' ) de deux interrupteurs chacune sont
commandés de façon complémentaire comme suit :
22
Stratégie de commande et réglage du bus
continu dédiée aux systèmes de production d'énergie
éolienne et solaire
On ferme,
K1 pour ùt = 0 K1' pour ùt =
rr
K2 pour ùt = 2rr /3 K2' pour
ùt = rr+2rr /3
K3 pour ùt = 4rr /3 K3' pour
ùt = rr+4rr /3
Les grandeurs électriques échangées :
· si les courants iA ; iB
;ic sont sinusoïdaux et forment un système
triphasé équilibré :
iA =I 2 sin(ùt- ?), (2.17)
2 ð
i =I 2sin(ùt-? - ), (2.18)
B 3
4 ð
i = I2 sin(ùt - ? - ), (2.19)
c 3
leur somme instantanée est nulle.
Composition du système de tension triphasé Les
tensions fournies par les demi ponts sont :
v - v
A 0
v - v
B 0
v - v
C 0
|
u
= , quand K1 est fermé ;
2
= u , Quand K1' est fermé ; 2
u
= v, quand K2 est fermé,... 2
|
|
De ces tensions on en déduit les tensions
composées entre les bornes de sortie : uAC = (vA -
v0) - (vB - v0)
uCB = (vB - v0) - (vC -
v0 ) uBA = (vC - v0) - (vA -
v0 )
si la charge est déséquilibrée et
couplée en étoile, on détermine les tensions aux bornes de
trois phases à l'aide des relations suivantes :
23
2 1 1
u = (v - v ) - (v - v ) - (v - v ) (2.20)
AC A 0 B 0 C 0
3 3 3
1 2 1
u = - (v - v ) + (v - v ) - (v - v ) (2.21)
CB A 0 B 0 C 0
3 3 3
1 1 2
u = - (v - v ) - (v - v ) + (v - v ) (2.22)
AC A 0 B 0 C 0
3 3 3
2.4.3.1 LE BUS CONTINU
Le bus continu est un noeud électrique qui se situe
entre deux alimentations (ici convertisseurs statiques) fournissant de la
tension ou du courant continu.
Mini d'un réservoir d'énergie, le bus continu
devient le point de rencontre de puissance de la chaîne de conversion
où tous les éléments peuvent être
dimensionnés afin d'être adaptés précisément
aux conditions existant et ainsi des performances maximales peuvent être
obtenues.

Un des principaux avantages d'une structure à bus DC
relève du fait qu'elle peut profiter de l'utilisation directe d'une
source continue telle qu'un module photovoltaïque et un
aérogénérateur en produisant peu de pertes et en utilisant
peu de matériel, permettant une configuration simple comportant peu de
pièces.
Dans toutes les architectures utilisant le bus DC, l'on se
sert uniquement des onduleurs pour fournir la tension alternative.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
24
3 CHAPITRE : SYNTHESE DE LA PROBLEMATIQUE ET
PROPOSITION DE SOLUTIONS
3.1 SYNTHESE DE LA PROBLEMATIQUE
L'objectif principale de cette étude est de mettre au
point un moyen de réglage et de commande appliqué au bus continu
dédié au système de production d'énergie
électrique à partir des sources éoliennes ou solaires afin
d'avoir un bon rendement de l'ensemble de système et réseau.
Atteindre cet objectif exige de prendre en compte les
contraintes en tension et les lois de commande au niveau du bus continu.
Pour synthétiser la problématique appuyons-nous
sur le modèle générique des systèmes rappelé
ci-dessous :

Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Fig.3.1 Architecture générique d'une centrale
éolienne ou solaire
Les systèmes de production d'énergie
électrique à partir de sources naturelles
(générateur photovoltaïque,
aérogénérateur...) connecté à un bus continu
utilisent un onduleur de tension pour mettre l'énergie extraite de la
source au norme du réseau électrique.
En considérant les architectures de models
utilisés précédemment, l'on constate aisément que
la tension d'alimentation de l'onduleur est imposée par le noeud (bus
continu).
Pour mieux étayer la position du problème,
limitons-nous sur le cas d'une installation éolienne rappelée par
le synoptique suivant :

Fig. 3.2. Topologie d'une centrale éolienne avec un bus
continu intermédiaire.
Le système étudié est composé
d'une source éolienne, d'un redresseur triphasé, d'un onduleur
triphasé de tension et d'un bus continu intermédiaire.
Ce dernier est dans la réalité un condensateur
qui sert d'élément de stockage pour envoyer l'énergie vers
un réseau alternatif, via l'onduleur. L'onduleur de tension a un
caractère dévolteur ; c'est-à-dire, il abaisse la tension
qui lui est délivrée à l'entrée par le bus continu
: ce qui entraîne une demande de tension de bus élevée.
25
Le problème fondamental consiste à
élaborer un processus permettant d'alimenter en tension suffisante et
continue le circuit intermédiaire appelé bus continu lorsque la
source principale (ici l'éolienne) est basse tension.
En effet la tension ubus en sortie du condensateur
est appelée à remplir certaines exigences afin d'obtenir un
réseau normalisé 220V/50Hz.
La tension de bus continu est variable en fonction de celle
générée par les principales sources d'énergie ; ce
qui peut entraîner un surdimensionnement de l'onduleur.
Par ailleurs un raisonnement développé dans l'acte
du colloque présenté par B. Robyns et M. Nasser sur la
«Modélisation et simulation d'une éolienne à vitesse
variable basée sur une génératrice asynchrone à
cage« (C.f. Bibliographie) a montré que « la tension fournie
par le convertisseur côté source (hacheur ou redresseur) est
généralement supposée faible du fait que les sources
délivrent de l'énergie électrique sous forme d'un bus
continu basse tension ».
Or, pour pouvoir utiliser un onduleur de tension raccordé
à un réseau triphasé dont les tensions simples atteignent
240V, nous avons besoin d'une tension de bus continu élevée,
obéissant à la relation suivante :
ub u s = 240 2 3 + äV = 588 + äV ;
Avec äV: chutes de tension dans les semi-conducteurs de
l'onduleur, estimés à äV = 20V ».
Ainsi nous souhaitons avoir une tension de bus continu
supérieure à 600V, soit donc ubus = 750V pour pouvoir fonctionner
dans toutes les conditions.
En particulier, si l'on admet que la tension en valeur moyenne
délivrée par une source d'énergie naturelle est de 48 V,
dans ce cas, il faudrait mettre en association plus de 15 sources
(éoliennes ou photovoltaïques) pour obtenir une tension de bus
continu suffisante (750V) ; ce qui entraîne de dépenses
matérielles énormes.
Le flux d'énergie au niveau du bus continu peut
être modélisé dans le schéma de la figure 3.3.comme
suit:

Fig.3.3. Modélisation de flux de puissance du
système non régulé
L'enjeu consiste donc à proposer une solution
technologique qui offre une bonne gestion de flux d'énergie qui transite
au niveau de bus continu afin d'obtenir un réseau normalisé
220V/50Hz.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
26
3.2 PROPOSITION DE SOLUTIONS
La première solution que nous proposons, met en oeuvre
un système extérieur de régulation de bus continu
constitué d'un convertisseur DC-DC classique et d'une batterie en
cascade.
Nous introduisons ce processus dans le système de
conversion de la manière représentée par la figure
suivante :

Fig. 4.1. Modèle développé du
système de conversion retenu Le système considéré
porte les caractéristiques suivantes :
· Un redresseur triphasé délivrant une
tension continue dépendant de sa tension d'alimentation issue de la
source éolienne
· Un système de régulation de bus continu
composé d'une batterie associée à un convertisseur
à transfert d'énergie direct (hacheur)
· Un onduleur triphasé de tension alimentant un
réseau alternatif triphasé 230V/50Hz
L'onduleur est raccordé sur un redresseur par
l'intermédiaire d'un bus continu sur lequel se connecte également
un hacheur ayant pour fonction principale d'assurer l'adaptation des niveaux de
tension entre une batterie et ce bus continu.
Le système de régulation permet le contrôle
du bus continu dans cette installation. Ce dispositif est un régulateur
muni d'un convertisseur DC-DC qui interconnecte deux sources de tension :
· la batterie dont le niveau de tension est supposée
constant de 48V.
· le bus continu dont le niveau de tension (normalement
750V) doit permettre d'alimenter un onduleur triphasé de tension.
Au cas où une défaillance énergique
apparaît au niveau du bus continu, c'est donc ce système de
régulation qui est prévu de le palier sinon l'onduleur ne fournit
pas la puissance demandée au réseau.
Le rôle principal de ce convertisseur sera donc de
réaliser la compensation de tension entre le producteur éolien et
le consommateur réseau (utilisateur).
Parmi les convertisseurs DC-DC possibles, et eu égard de
la fonction compensatrice par élévation de tension, nous opterons
pour un hacheur survolteur (élévateur de tension).
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
27
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Cette conversion est destinée à remédier aux
imperfections liées au bus continu et a en charge de subvenir aux
besoins transitoires de puissance en fournissant la puissance moyenne et
assurant l'autonomie énergétique du système.
Dans ce mémoire, les convertisseurs statiques à
MLI en amont (redresseur) et en aval (onduleur) du bus continu sont
modérément exposés précédemment. Cependant
l'étude est essentiellement consacrée sur le convertisseur
DC-DC.
Le schéma électronique équivalent de la
chaîne de conversion pour un système éolien :

Fig. 4.2. Modèle électronique du système
En termes de puissance, nous pouvons traduire
également cette stratégie par la configuration suivante :

Fig. 4.3. Flux de puissance du système
régulé.
Le système considéré doit donc
répartir la puissance transitée au bus continu entre le
producteur (source éolienne raccordée à un redresseur) et
le consommateur (réseau électrique raccordé à un
onduleur) ; comme le montre la figure selon une stratégie de gestion
énergétique.
Les puissances à prendre en considération dans le
système sont :
· Pe : la puissance délivrée par
la source principale.
· Ps : la puissance consommée par le
réseau via un onduleur de tension à MLI.
· Pc : la puissance compensatrice,
générée par le système de régulation pour
équilibrer la puissance délivrée et la puissance
demandée.
28
Les puissances du producteur (Pe) et du consommateur (Ps)
dans ce système sont gérées par le bus continu.
Ce processus régulateur (batterie + hacheur
survolteur) est très utile pour compenser les creux de puissance(ou
tension) : il introduit un degré de liberté
énergétique permettant de découpler les fonctionnements
énergétiques du consommateur Ps et du producteur Pe en
fournissant la différence de puissance Pe - Ps.
A cet égard, le réglage et la commande du bus
continu dépendront directement du hacheur survolteur qui le compose ; ce
qui exige la mise en oeuvre d'un dimensionnement adéquat de ces
composants visant à optimiser le rendement du système.
Il n'est pas ainsi nécessaire de mettre en association
plusieurs sources pour atteindre la tension de bus continu dans le cas
où le hacheur est survolteur.
Nous sommes ainsi conduits à élaborer notre
étude à partir du processus schématisé par la
figure suivante :

Fig. 4.4. Système de régulation utilisé
pour régler et commander le bus continu.
Il s'agit donc de synthétiser un hacheur survolteur
destiné à répondre au cahier des performances suivant :
· fournir une tension de bus continu 750V à
partir d'une tension d'alimentation 48V issue d'une batterie.
Le hacheur réalisé étant destiné
à alimenter un onduleur qui supporte peu de variation de tension ; il
faut ensuite :
· définir et mettre en place une boucle
analogique de tension à erreur statique nulle visant à
réguler la tension de sortie Ubus (tension de bus continu) en
plus de l'inévitable boucle analogique de courant à erreur
statique nulle assurant une limitation de courant iL.
En ce qui suit, nous déterminerons les
caractéristiques (fonctionnement, dimensionnement, modélisation
et simulation) du hacheur survolteur pour répondre à ces
exigences.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
29
4 CHAPITRE : ETUDE DU HACHEUR
4.1 HACHEUR SURVOLTEUR
Le hacheur survolteur est un convertisseur assurant le transfert
d'énergie d'une source de courant vers une source de tension, dont la
tension de sortie Us est supérieure à la tension
d'entrée Ue.
D'où l'appellation de convertisseur
élévateur ou encore survolteur (STEPUP converter).
On l'appelle également hacheur « parallèle
» (BOOST converter) du fait que le semiconducteur commandé est
délivré aux bornes du générateur.
4.1.1 STRUCTURE DU HACHEUR SURVOLTEUR
Le hacheur survolteur est essentiellement utilisé pour la
conversion DC/DC.
Son schéma de principe est donné par la figure
suivante:

Fig. 5.1. Schéma de principe du hacheur survolteur
Le hacheur élévateur est constitué d'un
semi-conducteur alimenté sous la tension Ue
délivrée par la source, qui se comporte en interrupteur
commandé à l'amorçage (transistor bipolaire, MOS, IGBT...)
et une diode (amorçage et blocage spontanés) de manière
périodique, avec un angle de commande á compté à
partir de 0, et compris entre ð/2 et á ( á en rad).
· L'inductance L permet de lisser le courant
appelé sur la source. Elle stocke de l'énergie électrique
puis la restitue pour créer la surtension.
· Le condensateur C permet de limiter l'ondulation de
tension de sortie.
· Les composants semi-conducteurs utilisés dans
le hacheur survolteur seront considérés comme parfaits (chute de
tension nulle à l'état passant et courant nul à
l'état bloqué).
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
30
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Le schéma électrique correspond à la figure
:

Fig.5.2 Modèle électrique du hacheur
survolteur
4.1.1.1 COMMANDE DES INTERRUPTEURS ET FORMES
D'ONDE
L'élévation de la tension de sortie du hacheur
BOOST est obtenue grâce à une commande en MLI (Modulation à
Largeur d'Impulsions). Celle-ci est liée à un principe de
fonctionnement du hacheur élévateur.
Les semi-conducteurs de ce convertisseur forment une cellule
de commutation élémentaire. Celle-ci permet de connecter une
source de courant (l'inductance L) à une source de tension (condensateur
C).Ces semi-conducteurs sont considérés comme deux interrupteurs
statiques fonctionnant de façon complémentaire et
commandés suivant la séquence suivante (figure) :
Fig. 5.3. Commande des semi-conducteurs
· entre 0 et áT , seul le transistor K est
commandé à la fermeture
· entre áT et T , seul la diode D est
commandé à la fermeture
· durant l'intervalle de temps t tel que : 0< t
< áT ; le transistor K est passant et la diode D est
bloquée. L'inductance L stocke de l'énergie.
· durant l'intervalle de temps t tel que : áT
< t < T ; le transistor K est bloqué et la
diode D est passante. Cette énergie stockée est restituée
à la charge.
31
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
á est le rapport cyclique du hacheur, et T la
période de fonctionnement.
Les formes d'ondes sont de la forme suivante (en supposant la
tension et le courant de Sortie continus).

Fig. 5.4 Formes d'ondes des grandeurs électriques du
hacheur survolteur.
4.1.1.2 EXPRESSION DE LA TENSION DE SORTIE UBUS
Le model mathématique du hacheur
élévateur se détermine par l'analyse de deux
séquences de fonctionnement liées aux états des
contacteurs statiques (on adopte la notation K pour le transistor) :
· à l'enclenchement ; 0 < t < áT K
fermé et D devient bloquée :

Fig 5.6 Modèle électrique du hacheur survolteur
à l'enclenchement
32
l
d i
d t
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Nous obtenons le système d'équation
différentielle suivante :
???
u =ri +L
e L
0=C
d u
+is (5.1) ?? d t
· au déclenchement; aT < t < T K ouvert et D
devient fermée :

Fig. 5.7 Modèle électrique du hacheur Boost au
déclenchement
Le système d'équation différentielle qui en
résulte s'écrit :
???
d i l
u =ri +L +u
e L s
d t
s
(5.2)
(5.3)
??iL=Cdd ts+i
???
??
En valeur instantanée :
d i l
u =ri +L +(1-a )u
e L s
d t
s
d u s
i (1-a )=C +i
L d t
En valeur moyenne :
?
??
?
T
d i 1
U r I L ( )
L
= + +
e L m o y ? u d t
aT
s
d t T
1 i d t C (d u )
T U
s s
? = + (5.4)
33
L m o y
? T d t RaT
Stratégie de commande et réglage du bus
continu dédiée aux systèmes de production d'énergie
éolienne et solaire
En régime cyclique : L
di du
( ) ( )
moy et s sont nulles.
m oy
dt dt
Ainsi :
IL l
|
U =rI +(1-á)U
e L s
I (1 ? á ) =
L R
U s (5.5)
|
|
Alors, on tire :
IL
U s
(5.6)
(5.7)
(5.8)
US
R(1-á)
D'où :
U (1-á)
e
2
r
R+(1- á)
Si l'on néglige la résistance interne r de
l'inductance L, nous obtenons :
Ue
I =
L
R(1 )2
? á
Par conséquent, l'expression de la tension de sortie du
hacheur survolteur s'écrit :
Us =
Ue
(5.9)
34
(1 ?á )
Remarque :
á est appelé rapport cyclique ; il est
défini comme étant le rapport entre l'intervalle de temps
où le transistor est passant et la période de découpage T
.
t e
Soit : á = T , avec T = t e + t d =
|
1 f
|
|
Or ; 0<te<T alors 0< á <1
Par conséquent : Ue <U s < 8
La tension de sortie du hacheur survolteur varie de sa tension
d'alimentation à l'infini.
te et td sont respectivement la
durée de l'enclenchement et la durée de déclenchement du
semi-conducteur.
f est la fréquence de découpage( hachage) du
hacheur.
Expression de U s en fonction de te et
td La tension de sortie U s est telle que :

Ue
Us
= e
U
(1?á)
(1 ? á + á) (1?á)
t e
á
= Ue (1 + ) T
= U (1 + )
e
1 - á te
1
-
te
= U (1 + )
e
T-t
e
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
T
Or : Tdéc - te=td
t e
Alors : U = U (1 +
s e t d
|
) (5.10)
|
|
Expression deá en fonction de r et R :
U (1 ? á )
e
En dérivant l'expression U =
s ;
r (1 ) 2
R
35
+ ? á
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Nous avons :
r
U U [(1 ) ]
' ?á ?
2
s = e R
Us ? 0 , alors :
'
á = ?
max 1 R (5.10)
r
4.1.1.2.1 EXPRESSION DE Is
PAR RAPPORT à IL
En considérant le hacheur parfait avec un rendement de
100% ; il vient alors que :
Pentrée = Psortie
Alors : UeIL = UsI s (5.11)
Soit : e L
U I
I = = I (1 )
- á
s L
Us
Is =IL(1- á) (5.12)
4.1.1.3 DETERMINATION DES COMPOSANTS REACTIFS
4.1.1.3.1 L'INDUCTANCE L
Le hacheur possède une inductance qui lui permet de
fonctionner à courant d'induit de valeur moyenne I constante.
On se place en régime permanent et le schéma
équivalent du hacheur survolteur, où L est l'inductance de
l'induit, est le suivant.

Fig.5.8 Modèle moyen du hacheur déterminant L
36
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Le taux d'ondulation de courant dans l'inductance L permet de
déterminer L.

Fig. 5.9. Ondulation de courant
À l'instant t = 0, le courant d'induit i prend sa
valeur minimale Imin ; à l'instant t = áT, il
prend sa valeur maximale Imax.
La loi d'Ohm en valeurs instantanées aux bornes de
l'inductance L s'écrit :
di U
L e
-pour 0 < t < áT : L = U i = t + I (5.13)
e L m
dt L
di U - U
L s e
-pour áT < t < T : L = U - U i = t + I (5.14)
e s L M
dt L
Nous en déduisons l'expression littérale de
l'ondulation de courant, notée ÄiL = IM
-Im
Nous obtenons :
U
Ä = á
e
i T (5.15)
L L
Le maximum d'ondulation est obtenu pour un rapport
cycliqueá =0.5 et s'écrit :
Ue
Ä i = T (5.16)
Lmax 2L
Alors ;
U U
e e
L = á T = t
Ä i Ä i
L L
|
(5.17)
e
|
|
Soit :
áUe
L = (5.18)
Ä i f
L
37
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.1.1.3.2 LE CONDENSATEUR C
Considérons le cas où le transistor T n'est pas
commandé, et étudions l'évolution de la tension aux bornes
du condensateur C.
Le modèle équivalent est le suivant (figure...)
:

Fig. 5.10. Modèle moyen du hacheur déterminant
C
Le taux d'ondulation de tension dans le condensateur permet de
déterminer C

Fig. 5.11 Ondulation de tension
À l'instant t = 0, la tension aux bornes de C prend sa
valeur minimale Um ; à l'instant t = áT, elle prend sa
valeur maximale UM.
L'expression de uc (t) entre 0 et áT, puis
entre áT et T s'écrit :
s -pour 0<t< áT :
du s - I t
C = - et
i s
s U = + U (5.19)
s m
38
dt C
-pour aT < t < T
iL=Cdus+i s et
Us=-Ist+IL+Um (5.20)
dt C C
L'accroissement de uc(t) sur une période
s'exprime par : Aus = UM - Um
Alors
(5.21)
(5.22)
(5.23)
Au = a Ue Tdéc = Is te
1-aRC C
Le maximum d'ondulation est obtenu pour un rapport cyclique
=0.5 et s'écrit :
e U
Ausmax = T
Soit :
C
a
RC
=
A
Is u sf
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.1.1.4 LIMITATION DE COURANT ET TENSION DANS LES
SEMICONDUCTEURS
La tension maximale qui traverse le transistor T est :
UKmax = Ue (5.24)
Celle qui traverse la diode D:
U = U
Dmax smax
|
A u
+ smax
2
|
(5.25)
|
|
L'expression de la tension de sortie en considérant la
résistance interne r de l'inductance L s'écrit :
U s =
U (1-a)
e
2
39
r
R+(1- a)
r
Avec ; a = 1 -
max R

Pour le courant :
I Kmax Dmax L
= I = I
+ ÄiL2 ax (5.27)
U á T
e
= et Ä i = max déc
U
Lmax e
r (1 ) 2 L
+ ? á
R
I L
(5.28)
(5.29)
Alors :
1 ámax
I Kmax Dmax
=I = U ( + T )
e 2 déc
r+R(1 ? á max ) L
Ainsi ; U =
smax
2r R
Alors ;
R r 3te
U = U (+ (5.26)
Dmax e 2r R 32LC
RU r
e
r 1 r Tdéc
á = 1? et I = (5.30)
max Kmax Dmax
= I U ( + (1- ) )
e
R r R L
4.1.1.5 DIMENSIONNEMENT DES COMPOSANTS
4.1.1.5.1 DIMENSIONNEMENT DES ELEMENTS REACTIFS L ET C
DU HACHEUR
Considérons le schéma suivant
Fig. 5.13. Schéma équivalent du hacheur
élévateur
Stratégie de commande et réglage du bus
continu dédiée aux systèmes de production d'énergie
éolienne et solaire
40
Or,
Soit :
Les valeurs des éléments réactifs L et C
de ce convertisseur, seront déterminées en fonction des exigences
imposées par le cahier des charges en terme d'ondulation de courant dans
l'inductance d'entrée et de l'ondulation de tension aux bornes du
condensateur de sortie.
Supposons que le hacheur est parfait. Les
caractéristiques du hacheur élévateur servant à
l'alimentation du bus continu sont définies par le cahier de
performances suivant :
· tension d'alimentation Ue= 48V
· tension de sortie Us= 750V
U e
· rapport cyclique : á = 0.93 ( á = 1 - )
U s
· fréquence de découpage f = 50 KH
· ondulation de courant d'entrée : 15%
· ondulation de tension de sortie : 10 %
On choisit une résistance de charge R=1000 pour une
puissance de 7.5KW.
· courant d'entrée IL = 108 A
· courant de sortie Is= 7 A
Classiquement on se fixe l'ondulation maximum de courant et de
tension par un pourcentage çL(typiquement de 10 %)du courant moyen
maximum et de la tension moyenne.
On souhaite déterminer les valeurs de L et C
conformément à ce cahier des charges.
4.1.1.5.1.1 VALEUR DE L'INDUCTANCE L
L'expression qui détermine la valeur de l'inductance L
s'écrit :

U
á
i f
L
=
Ä
L
e
AN :
3
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
L 0.93 * 48
0.1*108 * 50 *10
41
L= 83 pH
4.1.1.5.1.2 VALEUR DU CONDENSATEUR C La
formule qui calcule C s'exprime par :
C=
A
u f
s déc
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
0.93 * 10
AN : C=
0.10 * 750 * 50 *10 3
C=2pF
4.1.1.5.2 CHOIX DES SEMI-CONDUCTEURS
La fréquence de modulation étant de 50 KHz
(Tdéc=20ps, te=19ps td=1ps), on choisit un
transistor MOS dont la fréquence d'utilisation peut atteindre 100KHz ou
plus judicieusement un transistor IGBT ayant en plus une simplicité de
commande avec la tension utilisée.
4.1.2 MODELISATION DU HACHEUR SURVOLTEUR
4.1.2.1 MODELISATION SOUS FORME DE SCHEMA BLOC
Etant donné la structure du hacheur survolteur ainsi que
ses grandeurs électriques qui les caractérisent :

Fig. 5.14 Schéma de principe du hacheur survolteur
Le modélisation mathématique du hacheur
survolteur décrit par le schéma ci-dessus passe par l'analyse des
différentes séquences de fonctionnement que l'on supposera de
durées fixées par la commande.
42
Ce qui permet en outre de représenter les
équations caractéristiques du modèle moyen du
convertisseur.
En valeur instantanée :
d i l
u =ri +L +(1-á )u
e l d t
il(1-á )=C dd ts +i
???
??
s
s
(5.31)
En valeur moyenne
? ??
1
T
Ue=rIl+L (dtt)m o y+ T ?
usd t
T

á
? T d t R
1 ? idt=C ( d us
áT T
l m o y
) +U s (5.32)
Soit alors :
(1)
(2)
Ue=L dil dt+(1- á)us
Et
du s
i (1-á)=C + I
l s
dt
Cependant le schéma équivalent en modèle
moyen du convertisseur est donné par la figure :

Fig. 5.15. Modèle schéma bloc du hacheur
survolteur
Le réglage de hacheur survolteur met en oeuvre
généralement une régulation de type cascade dont la
connaissance de son principe serait un atout pour bien comprendre le processus
décrit.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
43
4.1.2.1.1 PRINCIPE DE REGULATION LINEAIRE EN CASCADE
(à boucles multiples)
De nos jours, trois concepts de systèmes
d'asservissement dont la régulation en boucles convergentes, la
régulation à boucles parallèles et la régulation en
cascade sont en usage. Ils permettent en principe de contrôler la
variable principale et de limiter les variables secondaires.
Dans cette étude nous adopterons un système de
régulation en cascade au regard des exigences nécessaires pour
une contrôlabilité adéquate du convertisseur.
On définit ainsi :
· un boucle de contrôle de la tension de bus continu
(variable principale) afin qu'elle corresponde à une
référence.
· un boucle de contrôle du courant dans l'inductance
L(variable d'état intermédiaire ou secondaire).
En effet, le système de régulation en cascade
comporte un régulateur individuel pour chacune des variables
contrôlées :

Fig. 5.16. Régulation en cascade du hacheur survolteur
La variable asservie principale (tension de bus continu) est
réglée par la boucle extérieure.
La sortie du régulateur de la tension du bus continu
sert d'entrée, c'est-à-dire de signal de référence
au régulateur de la boucle intérieure (boucle de courant dans
l'inductance).
En limitant la sortie du régulateur externe de la
tension dans le condensateur (tension de bus continu), on limite donc la
référence du régulateur de courant dans l'inductance et on
obtient très simplement la caractéristique de limitation
désirée.
Ce type de système agit par des « saturations »
:
Une saturation constante de la sortie du régulateur de
la tension du bus continu donne une limitation de courant de valeur constante,
indépendante de toute grandeur.
On peut rendre la tension de sortie du régulateur de
tension de bus continu dépendante de la tension dans l'inductance L : on
obtient alors une limitation variable.
La mise en service d'une régulation en cascade est
facile et rationnelle, puisque les caractéristiques statiques et
dynamiques des différents boucles sont indépendantes les unes des
autres.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
44
4.1.2.1.2 EQUATION BILAN ENERGETIQUE DU
SYSTEME
Les équations caractéristiques du modèle
moyen du hacheur dans la phase (1-á)de la durée de pulsation sont
:
il(1-á)=C dt + Is (1)
et
Ue =L dt +(1? á)us
(2)L'équation (1) nous donne :
(1- á) = i 1(C duU
s dt + R
1 )
|
(5.34)
|
|
La suppression de (1-á) dans l'équation (2)
conduit à :
di 1 du u
l s s
U =L + (C + )u
e s
dt i dt R
l
Nous obtenons ainsi l'équation bilan
énergétique du système :
U2 2
Ueil = s + 1 C dus +
Lil
dil
R 2 dt dt
|
(5.35)
(5.36)
|
|
U2
s
R
|
: l'énergie dissipée par la charge R
|
|
: l'énergie emmagasinée par le condensateur C
1 Cd u
2 dt
2 s
l
di
Li
l
dt
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
: l'énergie emmagasinée par l'inductance L Ueil :
l'énergie fournie par la source (batterie)
Or par rapport aux autres énergies on peut
pratiquement négliger celle emmagasinée par l'inductance.
Par conséquent :
2 2
i
s
Ue
= U
+ 1 C dus R 2 dt
(5.37)
45
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.1.2.1.3 FONCTION DE TRANSFERT DU SYSTEME
On détermine au moyen de l'expression
précédente la fonction de transfert G(s) du système.
La fonction de transfert (transmittance) est le rapport de la
fonction de sortie sur la fonction d'entrée.
Pour ce faire, on introduit les grandeurs relatives.
Soit Un = Ue
On tire aisément
:
I n =
Ue R
Et on note :
2
I
s
x = et l
U y =

U2 I
n n
Ainsi, nous avons :
R U
U 2 dt U
I 1 d U
l RC (
2 e 2 U2
n n n
= )+
2 U 2
s s
Ou bien :

I 1 d U U
2 2
l s s
= RC ( ) +
I 2 dt U U
2 2
n n n
Ce qui donne l'équation :
1 d U 2
y RC ( ) x
s
= +

2 dt U 2 n
Posons :
Y(s) = L[y(t)] et X(s) = L[x(t)]
46
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Avec « L » Laplacien et « s
»variable de Laplace,
Finalement :
1
Y(s) = ( RC.s + 1)X(s)
2
La fonction de transfert s'écrit donc :
X(s) 1
G(s) = =
Y(s) 1 1 RC.s
+
2
|
(5.38)
|
|
1
C'est un système de 1erordre avec une
constante de temps dominante Ta = RC
2
En considérant les petites constantes de temps dans
l'équation :
1
-retard de l'organe de commande estimé à p
1 T avec T p =
2 f p
Tp : la période de pulsation du
signal de commande à MLI de l'interrupteur K. Nous pouvons écrire
:
1
G(s) = 1
(1+ sT )(1 + sT )
a p
2
|
(5.39)
|
|
4.1.2.1.4 CHOIX DU REGULATEUR DU SYSTEME
Le système possède une constante de temps
dominante Ta et une petite constante de temps
de retard statique moyen équivalent à p
1 T .
2
A l'égard de ses caractéristiques, on choisit un
régulateur PI (Proportionnel et Intégrateur) dont la fonction de
transfert est telle que :
Ce correcteur, de type Proportionnel et Intégral,
réalise la relation suivante:
K
U (t) = Ke(t) ( ) e(t)dt
s + ?
T i 0
t
(5.41)
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
K et Ti sont des coefficients positifs, caractéristiques
du correcteur. La constante de temps dominante Ta est à
compenser par Tn :
Ta = T n =RC
4.1.2.1.5 LIMITEUR DE LA TENSION ET DU
COURANT
En principe la surtension aux bornes du condensateur C du
hacheur survolteur est crée par le courant ou que l'inductance restitue
à l'instant (1-á) de la durée de pulsation (ouverture de
K) :
du s
i (1 ? á ) = C + I
l s
dt
|
(4.42)
|
|
Dans tous les cas (régulation de courant et
régulation de tension), pour contrôler ces grandeurs
électriques, l'on se sert d'un limiteur d'amplitude dont la
caractéristique est la suivante :

48
Fig. 5.17. Caractéristique du limiteur d'amplitude de
courant
On le modélise en schéma bloc par la
représentation suivante :

Fig. 5.18 Limitation de courant de consigne
Non seulement cette limitation contrôle la valeur maximale
du courant dans l'inductance L, mais aussi elle a pour effet de limiter la
tension en sortie du hacheur (tension de bus continu), puisque ces grandeurs
sont interdépendantes en fonctionnement moyen.
Preuve :
Soit en fonctionnement moyen l'expression liant le courant dans
l'inductance l et la tension aux bornes du condensateur C :
du s
(5.43)
i (1 - á ) = C + I
l s
dt
Avec
I s
=
Us
R
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Le saut de tension de bus continu vers une valeur maximale (
Usmax) s'obtient en fonction de la valeur maximale du courant ( Il
max) dans l'inductance L :
Puisque d us 0
= (en conduction continue) et en supposant maximale, le courant
dans
dt
l'inductance ; alors :
Us
I (1 ? á ) =
R
lmax
Or encore,
e
U
(1-á)= U s
Ainsi :
Ilmax
|
U U e = s
U R
s
|
(5.44)
|
49
|
|
Soit :
U s = U e RI lmax 2
D'où l'expression de la tension maximale
(Usmax ) en sortie du hacheur survolteur :
Usmax = UeRIlmax (5.44)
4.1.2.1.6 CHAINE DE COMMANDE
Régler la tension de sortie (tension de bus continu)
revient au préalable à contrôler le courant dans
l'inductance (grandeur électrique qui est à l'origine de
surtension).
Ayant opté pour une régulation cascade, nous
définirons un mode rapide correspondant au courant dans l'inductance
(boucle interne) et un mode lent correspondant à la tension aux bornes
du condensateur (boucle externe).
4.1.2.1.6.1 MISE EN PLACE DE LA BOUCLE DE
COURANT
Nous réalisons les compensations pour linéariser
le système (Figure). Nous trouvons donc comme fonction de transfert en
boucle ouverte :
I (s) 1
l
T (s)= (5.45)
1 1 ? á (s) Ls
Le schéma correspondant à la boucle de courant est
donné par la figure :

Fig. 5.19 Boucle de courant du hacheur.
En plus de la boucle de régulation de courant, le
hacheur élévateur nécessite une boucle de
régulation de tension.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
50
4.1.2.1.6.2 MISE EN PLACE DE LA BOUCLE DE
TENSION
Pour la définition du régulateur de tension, nous
supposons que la boucle de courant est parfaite, soit, au sens des valeurs
moyennes, sur une période de découpage :
iK1 = (1 - á )i l-réf (5.46)
Si on néglige la chute de tension aux bornes de
l'inductance, la tension aux bornes de l'interrupteur K1 à l'état
bloqué vaut Ue . Par ailleurs, nous savons qu'en valeur
moyenne :
UK 1 =(1- á)U s (5.47)
Dans le cadre de cette approche, nous modélisons le
convertisseur par un générateur de courant équivalent de
valeur :
U e
I = i
éq U -
l réf
s
Conformément à la figure.
|
(5.48)
|
|

Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Fig. 5.20. Synthèse de la boucle de tension.
Ce qui conduit à l'équation différentielle
:
U dU
e s
I = C + I
l - réf s
U dt
s
La chaîne de commande de tension devient donc :
|
(5.49)
|
|

Fig. 5.21 Boucle de tension du hacheur.
51
4.1.2.1.7 DETERMINATION DES PARAMETRES DU
REGULATEUR
On démontre qu'on peut également obtenir
d'autres expressions de la fonction de transfert du régulateur PI qui
sont en adéquation avec les paramètres que nous avons
utilisés.
Soit :
GR(s) = 1+ sTn = 1 + Tn (5.50)
sTi sTi T
On pose ;
Alors :
|
T Kn = Ti
|
: composante proportionnelle.
|
|
1
(5.51)
G (s) = + K
R sT i
Si on considère valable l'égalité suivante
:
Tn = ôi
=
K
Ainsi :
ô i T i
ô
Soit : Ti K
=
i
Alors,
K
G R(s)
1 + sT 1 + s ô
n i
=
sTi s
(5.52)
i
ô
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.1.2.1.7.1 REGULATEUR DE COURANT
En valeurs moyennes, on peut modéliser le hacheur
contrôlé en courant par la synoptique ci-dessous :

Fig. 5.22. Hacheur moyen contrôlé en courant
52
La transmittance résultant est donnée par :
I (s) 1
l
T (s)= (5.53)
1 1 ? á (s) Ls
Si on suppose que la compensation Ue et la
linéarisation 1/Us sont exactes, on peut utiliser
la transmittance T1(s) pour le calcul du
régulateur G R1 (s).
La fonction de transfert pour un régulateur de type PI
correspond à :
? + ô ?
1 s
i
G (s) K
= ? ? (5.54)
R 1 ?ô ?
i s
Il faut s'assurer que la bande passante soit inférieure
d'un rapport minimum de 4 par rapport
à la pulsation de découpage.
Nous prendrons un rapport 20 et par conséquent une bande
passante de fréquence
fBP=1KHz.
La fonction de transfert correspondant à la boucle
ouverte corrigée est de la forme:
GsBO(s) = GR1(s)*T1(s)
? + ô ?
1 s 1
i
Soit G (s) K
= ? ?
sBO ? ô ?
i s Ls
|
(5.55)
|
|
Un raisonnement fondé sur une analyse en
fréquence [FLUMIAN] nous permet de calculer les coefficients du
correcteur pour une marge de phase de 60° offrant ainsi une bonne
robustesse au système en boucle fermée.
D'où :
ô =
i
|
tan(m ö )
|
(5.56)
|
et
|
ù
|
BP
|
|

K
L.
ô ù 2 i BP
2
(5.57)
1 +
[ ]
ô ù
i BP
.
Application numérique :
L= 83pH WBP = 2u.fBP=2u.103 (rd/s) mi= 60°
tan(60)
ô = = 275 ps
i 2 .10 3
ð
K
|
83.10 * 275.10 * (2 10 )
- 6 - 6 3 2
ð
|
= 0.442
|
|
|
2
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
1 275 * 10 * 2 .10
+ ? - 6 ð
3
53
? ?
4.1.2.1.7.2 REGULATEUR DE TENSION
Le modèle de hacheur contrôlé en tension
correspondant en valeurs moyennes :

Fig.5.23 Modèle de hacheur contrôlé en
tension La transmittance résultant est donnée par :
1
T (s) = (5.58)
2 Cs
Si on suppose que la compensation Is et la
linéarisation Us/Ue sont exactes, on peut utiliser la
transmittance T2(s) pour le calcul du régulateur
GR1(s).
La fonction de transfert pour un régulateur de type PI
correspond à :
[1+ ô.s1 ô?
is (5.59)
G (s)=K
R2
La fonction de transfert correspondant à la boucle
ouverte corrigée est de la forme: GsBO(s) = GR2(s)*T2(s)
?Soit GsBO(s)= K 1+ ôis 1 1
ôi
Cs
s~ LI
(5.60)
Le même raisonnement que précédemment
conduit en définitive à :
ô =
i
|
tan(m ö )
|
(5.61)
|
|
|
BP
|
|
Application numérique : C=2pF
ôi= 28 ms
K 2.10-6 * 28.10-3 * (2ð103 )2
2
= 0.001
(5.62)
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
1+[28 *10-3 * 2ð.103] 2
54
4.1.2.1.7.3 CALCUL DES COMPOSANTS DU REGULATEUR
La structure d'un régulateur PI correspond à :

Fig. 5.24 Schéma d'un régulateur Proportionnel
Intégral (PI)
G (s)
R
(5.63)
La fonction de transfert du régulateur PI est de la forme
: 1+ sTn
sT i
Nous en déduisons les valeurs suivantes :
275.10-6
Tn = 275 ms et T = = 7 s : pour le régulateur
de courant
i 0.0442
28.10 - 3
Tn = 28 ms et T = = 28 s : pour le régulateur
de tension.
i 0.001
En fonction des éléments passifs du schéma
de la figure, elle correspond à :
1+sR1C1
sR C U
1 1 sn
G (s)
R
Ucn
(5.64)
On obtient : T n = R1C1 : Dosage de la
corrélation intégrale
U U
sn sn
T = R C = R C
i c 1 r 1
U U
cn rn
|
: Constante de temps d'intégration
|
|
Supposons que R1=1000 ; alors C1=2.75 pF en
considérant l'expression du dosage de corrélation Tn
.
Considérons l'expression ci-dessous pour calculer les
éléments du régulateur :
1+sR1C1
sR C U
1 1 sn
G (s)
R
Ucn
(5.65)
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
1 1 1 1 1+sR1C1
Nous avons : = + et R = R + =
c 1
R R R sC sC
55
0 c r 1 1
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
En introduisant les grandeurs nominales, la fonction de transfert
du régulateur devient :
(5.66)
1+sR1C1 Ucn
(x-x )
y=
s sR C U
1 1 sn
c r
Elle s'exprime également par :
1+sT
ur(s) = sTi n
[uc(s)-um(s)] (5.67)
Ou bien :
|
1 + sT n
i(s) = [ u(s) - v(s) ]
sT i
|
(5.68)
|
|
xc
Uc
=
U cn
Us
et y = (5.69)
s
Usn
Grandeurs nominales :
On veut que Uc soit égale à 75V pour
Us=750V :
Pour une tension de sortie réelle U qui varie de 0
à 750 V ; on suppose que :
Or xc = Uc
Ucn
C'est-à-dire : Un ? Ue et U ?
Us
D'une part on doit avoir xc = u :
|
U U2
c =
U U 2
cn n
|
|
Alors :
|
U = U
cn c
|
[Un 1 U~
|
2
|
|
D'autre part toutes les grandeurs de l'organe de commande et
de réglage du courant doivent être multipliés par
rn
= Rin (coefficient multiplicateur) pour avoir une tension.
U
I n
Supposons que Rin= 0.1
Et que e
U = Us ; on prendra : In= 15.6 A A.N :
Is Il
Uc=75 V Un= 48 V U=750 V
In=15.6 A Rin=0.7 Ucn= 554mV et Urn= 1.56 V
56
·
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Tn= 28.10-3 s
· R1= 1000
· C1= 2750.10-9 F
· Ti=7s
· Ucn= 554mV
· Urn= 1.56 V
R c
|
U T = cn i :
U C
rn 1
|
|
· Rc= 52940 soit Rc= 5 k0
Le hacheur survolteur avec son dispositif de commande peut
être modélisé sous forme schéma bloc selon la figure
suivante :

57
Fig. 5.25. Modèle du hacheur survolteur associé
à son dispositif de commande
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.1.3 MODELISATION GRAPHIQUE DU HACHEUR
4.1.3.1 LA REPRESENTATION MACROSCOPIQUE ENERGETIQUE
(REM)
4.1.3.1.1 OBJECTIFS
La Représentation Energétique Macroscopique
(REM) est un formalisme graphique qui présente une description
homogène des composantes d'un système énergétique
en vue de le modéliser, en mettant en évidence leurs
interactions, leurs échanges énergétiques et les
contraintes de leurs associations.
La modélisation ainsi élaborée à
partir de cette représentation synthétique permet de proposer une
structure maximale de commande (SMC) et d'aider à la structuration de la
simulation du système.
4.1.3.1.2 REGLES DE BASE
La REM respecte la causalité et le principe de l'action
et la réaction.
A une variable imposée par un élément sur
un autre (action) correspond une réaction due à cette
sollicitation. Le produit entre la variable d'action et celle de
réaction donne la puissance instantanée échangée
par les deux éléments.
4.1.3.1.3 ELEMENTS CONSTITUTIFS
la REM s'attache cependant à décrire trois
types de composantes de puissances dans une chaîne de conversion
énergétique.
4.1.3.1.3.1 LES ELEMENTS SOURCES
Les éléments sources, qui induisent des
variables d'état et qui sont en bout de la chaîne de conversion
(représentation : ovales de couleur vert pâle au contour vert
foncé). Une source énergétique est ainsi munie de deux
vecteurs. Elle produit une sortie qui ne peut physiquement subir de
discontinuité et possède également une entrée de
réaction qui agit comme perturbation.
Une source peut donc être réceptrice ou
génératrice d'énergie. :

Fig. 5.26 REM d'une source génératrice
d'énergie
58

Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Fig. 5.27 REM d'une source réceptrice
d'énergie
4.1.3.1.3.2 LES ELEMENTS D'ACCUMULATION
Les éléments d'accumulation, qui induisent une
accumulation d'énergie (une variable d'état) entre deux sources
(représentation : rectangle orange au contour rouge avec une barre
oblique). Ils permettent de connecter d'autres
éléments (sources, élément
de
conversion)grâce à un stockage inertiel. Ils sont munis
d'une entrée d'action et sortie de réaction en amont et en
aval.

Fig. 5.28. REM d'un élément d'accumulation
4.1.3.1.3.3 LES ELEMENTS DE CONVERSION
Les éléments de conversion, qui assurent une
conversion énergétique entre deux sources sans accumulation ni
perte (représentations : un carré pour une conversion
électrique, un cercle pour une conversion
électromécanique, un triangle pour une conversion
mécanique, tous oranges au contour rouge).
Ils convertissent de l'énergie réglable par une
entrée de réglage. Ils sont munis de deux vecteurs en amont une
entrée d'action et sortie de réaction ainsi qu'en aval.
Un troisième vecteur vertical définit une grandeur
de réglage ou de commande

Fig. 5.29 REM d'un élément de conversion
59
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.1.3.1.4 STRUCTURE GENERIQUE ELEMENTAIRE
Une structure générique décrit de
façon homogène un système énergétique
élémentaire avec les éléments constitutifs de REM
présentés précédemment. Elle est donc
constituée d'une source en amont, d'une source en aval, d'un
élément de conversion qui va gérer le transfert
d'énergie, et de deux éléments d'accumulation assurant une
adaptation énergétique entre les sources et
l'élément de conversion.
La figure qui suit représente un exemple de structure
générique élémentaire. :

Fig. 5.30 Structure générique
élémentaire
Les flèches caractérisent les échanges
d'énergie dans le système selon le principe d'action et de
réaction. Ces échanges définissent le mode de transfert
d'énergie et par conséquent le sens du flux d'énergie.
En admettant que ce système est réversible, on
peut distinguer deux chaînes qui dépendent du sens de transfert
:
· la chaîne d'action définie par la suite des
vecteurs « x1-- x2 - x3 - x4 » dans le sens de la source S1 vers la
source S2.
· la chaîne de réaction définie par la
suite des vecteurs « y4 - y3 - y2 - y1 » dans le sens de la source S2
vers la source S1.
La chaîne de réglage correspond à la
suite de vecteurs reliant l'entrée de réglage à la sortie
que l'on veut imposer sur l'une des sources (par exemple z23). Elle
est indépendante du sens de transfert énergétique.
4.1.3.1.5 REGLES D'ASSOCIATION
4.1.3.1.5.1 ASSOCIATIONS DIRECTES
Deux éléments peuvent être connectés
directement si :
60
leurs variables d'échange sont de même domaine et de
même nature, la sortie du premier correspond à l'entrée du
second, l'entrée du premier correspond à la sortie du second, les
variables ont la même valeur à l'instant de connexion.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.1.3.1.5.2 REGLE DE CONCATENATION
En REM, deux éléments d'accumulation ayant la
même sortie peuvent être associés par concaténation
pour obtenir un élément d'accumulation fictif équivalent
qui produirait le même effet, et dont les paramètres sont issus
d'une combinaison des paramètres des deux éléments
initiaux.
4.1.3.1.5.3 REGLE DE PERMUTATION
Deux éléments de conversion ou d'accumulation
dont les variables d'échange ont des évolutions continues,
peuvent être permutés.
4.1.3.1.6 COUPLAGE ELECTRIQUE
Pour modéliser un élément de conversion
multicellulaire par REM, nous pouvons combiner les représentations de
ses éléments constitutifs couplés par leurs symboles
imbriqués.
La représentation qui suit, illustre le couplage
électrique qui correspond à la mise en commun de ressources
électriques entre plusieurs convertisseurs électriques.

Fig. 5.31 REM d'un couplage électrique.
4.1.3.1.7 STRUCTURE DE COMMANDE MAXIMALE DEDUITE DE LA
REM
Le principe d'inversion est appliqué aux deux types
d'élément qui assurent la modification de l'énergie :
inversion directe pour les éléments de
conversion,
inversion indirecte par un asservissement pour les
éléments d'accumulation,
Tous les blocs sont représentés par deux
losanges bleus car ils ne manipulent tous que de l'information.
61
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
La structure de commande déduite est ainsi
appelée Structure Maximale de Commande (SMC) car elle demande un maximum
de capteurs et un maximum d'opérations. Une structure de commande
pratique peut en être déduite par simplification et estimation des
grandeurs mesurables.
Remarque :
En modélisation REM, on peut s'en passer des couleurs
; elles ne sont pas primordiales, elles sont juste utilisées pour plus
de lisibilité.
4.1.3.1.8 APPLICATION DE LA REM A LA MODELISATION DU
HACHEUR SURVOLTEUR
On reprend la structure survoltrice du hacheur (montage BOOST)
suivant :

Fig.5.32. schéma électrique du hacheur BOOST
4.1.3.1.8.1 REM DES ELEMENTS SOURCES DU HACHEUR
SURVOLTEUR CLASSIQUE
Une batterie est une source de tension, de sortie la tension
ue, et d'entrée le courant iL qui peut perturber la tension
(impédance interne, limitation et sécurité - fusible...).
C'est une source génératrice d'énergie.

62
Fig. 5.33 Modèle moyen de la batterie alimentant le
hacheur Boost
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
La modélisation macroscopique correspondante :

Fig. 5.34 REM de la batterie du hacheur Boost
Une charge R reçoit de l'énergie grâce au
condensateur avec lequel ils sont montés en parallèle. Elle peut
être considérée comme une source (de courant) de sortie le
courant is et d'entrée la tension vs : C'est une
source réceptrice d'énergie.

Fig.5.35. Modèle moyen de la charge du hacheur Boost
Le modèle REM résultant :

Fig. 5.36. REM de la charge du hacheur
4.1.3.1.8.2 REM DES ELEMENTS D'ACCUMULATION DU HACHEUR
SURVOLTEUR
Les éléments réactifs (L et C) sont des
réservoirs d'énergie entre les deux sources. Ce sont donc des
éléments d'accumulation.
Pour l'inductance le courant iL variable d'état,
correspond à la sortie en amont et à la sortie en aval.
.
63


Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Fig. 5.37. Modèle moyen de l'inductance du hacheur
Boost
La modélisation macroscopique résultante :

Fig. 5.38 REM de l'inductance du hacheur Boost
Quant au condensateur C, la tension uC variable
d'état, correspond à la sortie en amont et à la sortie en
aval.
Fig. 5.39. Modèle moyen du condensateur du hacheur
Boost
La modélisation macroscopique équivalente :

Fig. 5.40 REM du condensateur du hacheur Boost
64
4.1.3.1.8.3 REM DE L'ELEMENT DE CONVERSION DU HACHEUR
SURVOLTEUR
Le hacheur est constitué d'une cellule de commutation
à 2 interrupteurs statiques. Cette cellule élémentaire de
commutation est donc considéré comme étant un
élément de conversion.
Son vecteur de réglage correspond aux ordres de
commutation des interrupteurs (fonctions de connexion m ).
Les pertes par conduction et par commutations sont
inhérentes à cet élément.
Le modèle correspondant en valeurs moyennes est
représenté ci-dessous (figure).

Fig. 5.41. Modèle moyen des semi-conducteurs du hacheur
Boost
Ce qui correspond à la REM suivante :

Fig. 5.42 REM des semi-conducteurs du hacheur Boost
Le vecteur de réglage m représente les ordres de
commutation des interrupteurs.
4.1.3.1.8.4 REM DU HACHEUR SURVOLTEUR
CLASSIQUE
En somme, en modèle moyen il en résulte une
structure de hacheur survolteur à quatre quadrants avec en tête
l'inductance L qui alimente un bus continu à condensateur C et
crée la surtension.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
65

Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Fig. 5.43 Modèle moyen du hacheur Boost
Tenant compte des règles d'association des
éléments en REM, on en déduit : u C = ubus = u
s
Par conséquent la REM du système correspond
à la structure suivante :

Fig. 5.44 REM du hacheur élévateur classique
Remarque
La tension ue qui alimente l'inductance L est issue
d'une batterie. Celle-ci délivre une tension continue de valeur moyenne
45V.
Le courant ie est supposé ne pas perturber la
valeur de cette tension. Le hacheur est composé de deux
éléments d'accumulation d'énergie :
En entrée, l'inductance L assure une conversion
électrique d'énergie par accumulation inductive, dont la variable
d'état iL est issue de la tension d'alimentation UL et de la tension du
hacheur Uhach :
di L
L = u - u
e hach
66
dt
En sortie le condensateur C assure une mise en forme de
transfert d'énergie par accumulation capacitive, dont la variable
d'état uC est issue du courant du hacheur ihach et
du courant de charge is :
du C
C = i hach s
- i
dt
Le convertisseur est représenté par la cellule
élémentaire de commutation qui relie la source de courant et la
source de tension. Pour une modélisation aux valeurs moyennes (pas de
prise en compte de la modulation) au travers du coefficient mhach on
peut le décrire par les équations suivantes :
?
? ?
|
u = m .u
hach hach C
i = m .i
hach hach L
|
|
mhach est la fonction de modulation. Elle correspond au
rapport cyclique. uhach et ihach sont la tension et le
courant produit par le hacheur.
iL et is sont le courant
imposé par l'inductance L et le courant de charge.
4.1.3.1.9 STRUCTURE MAXIMALE DE COMMANDE (SMC) DU
PROCESSUS DEDUITE DE LA REM
La structure de commande doit permettre de maintenir
constante la tension du bus continu à une valeur moyenne de 750V. Pour
ce faire, considérons alors le modèle REM du hacheur survolteur
rappelé dans la figure.
Ce modèle est constitué de deux
éléments d'accumulation (une inductance et un condensateur) et un
élément de conversion (une cellule élémentaire de
commutation).
Pour élaborer une structure maximale de commande
déduite de cette REM, on procède de la façon suivante :
on applique le principe d'inversion aux
éléments qui assurent la modification de l'énergie dans le
système.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
67
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.1.3.1.9.1 SMC POUR L'ELEMENT DE CONVERSION (HACHEUR) EN
MODELE MOYEN ET PAR INVERSION DIRECTE

Fig. 5.45 SMC du hacheur « moyen ».
4.1.3.1.9.2 SMC POUR LES ELEMENTS D'ACCUMULATION ET PAR
INVERSION INDIRECTE PAR ASSERVISSEMENT
Pour l'inductance L :

Fig. 5.46. SMC de l'inductance.
Pour le condensateur C :

68
Fig. 5.47. SMC du condensateur.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.1.3.1.10 REM ET SMC DU HACHEUR SURVOLTEUR
CLASSIQUE
En conséquence en associant les SMC des
éléments constitutifs du hacheur survolteur, on obtient la
structure suivante :

Fig. 5.48 REM et Structure Maximale de Commande du hacheur
survolteur Remarques
Nous pouvons ainsi distinguer deux boucles dont une boucle de
courant et une boucle de tension obtenues par inversion indirecte par
asservissement. A partir de la mesure de la tension du bus continu, le
convertisseur est commandé de
manière à imposer des références aux
tensions simples.
Ainsi Les relations de commande se déterminent par les
relations :
> pour l'asservissement de courant dans l'inductance L :
iL-réf = K(Uhach-réf - Ue-mes) + ie-mes
> pour l'asservissement de tension dans le condensateur C
: Ubus - réf = K(is - réf - is-mes) + Ubus-mes
> pour l'inversion directe du hacheur « moyen »
:
Avec K la fonction correcteur du système.
Ces grandeurs de référence sont
régulées à l'aide d'un correcteur PI (fig. 5.24)
69
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.2 ETUDE DU HACHEUR MULTINIVEAU
4.2.1 CONTEXTE
Bien que la structure du hacheur classique paraisse simple,
son utilisation dans ce système de conversion d'énergie
électrique ne se fait pas sans problème : elle présente
des inconvénients non négligeables tenant compte des contraintes
des composants semiconducteurs dont la limitation en tension et en courant.
En effet, le hacheur survolteur classique doit combiner une
tension élevée de bus continu au-delà de la
capacité que peut supporter une cellule élémentaire de
commutation.
Ainsi l'idée de pallier ce genre de problème a
donné naissance à une nouvelle structure de hacheur qui contourne
cette limitation en tension de blocage des principaux semiconducteurs de
puissance en mettant en oeuvre des associations de composants, voire de
convertisseurs élémentaires.
Il s'agit précisément du hacheur à
niveau multiple ou hacheur multiniveau. L'utilisation de la topologie
multiniveau devient actuellement une application de grand intérêt
pour alimenter des systèmes en moyenne et haute tension à
fréquence de pulsation élevée.
Elle présente d'énormes avantages :
· D'une part, elle permet de limiter les contraintes en
tension ou en courant subies par les interrupteurs de puissance (une
augmentation de la puissance contrôlable grâce à une
augmentation du calibre global en tension ou en courant) : chaque composant,
lorsqu'il est à l'état bloqué, supporte une fraction
d'autant plus faible de la pleine tension de bus continu que le nombre de
niveaux est élevé (réduction de la tension à
commuter en des valeurs plus petites et directement commutables par les semi-
conducteurs actuels),
· D'autre part, la tension de sortie délivrée
par ce convertisseur multiniveau présente d'intéressantes
qualités spectrales : le fait de multiplier le nombre de niveaux
intermédiaires permet de réduire l'amplitude de chaque front
montant ou descendant de la tension de sortie. L'amplitude des raies
harmoniques est par conséquent d'autant moins élevée.
Notre objectif étant de trouver la stratégie le
mieux adaptée pour le réglage et la commande de bus continu afin
d'optimiser le rendement du système, il s'avère cependant
indispensable d'étendre notre étude sur une seconde technologie
qui repose sur l'utilisation du hacheur à 3 niveaux en vue de comparer
l'utilisation de celui-ci en remplacement du hacheur classique.

Fig.6.1 Centrale à tension de bus continu
contrôlée par un hacheur multiniveau
70
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Ainsi la solution compensatrice de déséquilibre de
puissances au niveau du bus continu a été réalisée
grâce à une batterie en association d'un hacheur multiniveau.
Cette alternative permet de résoudre les problèmes
de tension vis à vis du réseau tout en augmentant la « plage
» de puissance fournie à l'onduleur de tension.
4.2.2 STRUCTURE ET FONCTIONNEMENT
Un hacheur est dit multiniveau ou à niveau multiple,
lorsqu'il délivre une tension découpée de sortie
composée d'au moins trois niveaux.
De nombreuses variantes de hacheurs peuvent être mises en
oeuvre pour générer une tension multiniveau.
Parmi les topologies Boost multiniveau résultant d'un
moyen de mise en série, citons :
· Le hacheur multiniveau à potentiel
distribué, obtenu à partir de l'association en série de
cellules de commutation.
· Le hacheur multiniveau à cellules
imbriquées, obtenu par l'imbrication de cellules de commutation.
Les schémas qui suivent représentent les deux
familles de hacheur à 3 niveaux Boost.
4.2.2.1 TOPOLOGIE A POTENTIEL DISTRIBUE

Fig.6.2. Hacheur multiniveau Boost à potentiel
distribué
Cette structure comprend deux cellules de commutation ( T1 D1 et
T2 D2)à transistor et diode
.
Chaque cellule est un hacheur élémentaire qui peut
fonctionner de façon indépendante. La tension d'alimentation est
de 48V fixe. Celle de sortie est continue de 750 V,
La topologie à potentiel distribué permet de
réduire le taux de distorsion harmonique, limitant ainsi la taille des
éventuels filtres. Plus le nombre de niveaux de la tension
générée est
71
élevé, plus faible est la tension bloquée
par les interrupteurs. Ils commutent à faible fréquence,
réduisant ainsi les pertes par commutation.
Cette topologie requiert malheureusement un nombre
élevé de semiconducteurs de puissance, ce qui réduit
considérablement sa fiabilité.
4.2.2.2 TOPOLOGIE A CELLULES IMBRIQUEES

Fig. 6.3 Hacheur multiniveau Boost à cellules
imbriquées.
Cette structure représentée sur la figure
permet de générer également une tension de sortie sur
trois niveaux.
Elle possède deux cellules de commutation : chaque
cellule est formée d'un couple d'interrupteurs (T2 D1 et T1 D2) qui sont
donc commandés de façon complémentaire.
La topologie basée sur des cellules imbriquées
permet aussi la réduction du taux de distorsion harmonique ; en plus
grâce à l'existence d'états redondants, on peut
contrôler la charge et la décharge des condensateurs. Le nombre
élevé de condensateurs requis rend cette topologie lourde et
encombrante. Le contrôle de l'état de charge des condensateurs
nécessite une méthode de commande relativement complexe, ce qui
pourrait augmenter la fréquence de commutation des interrupteurs, donc
leurs pertes par commutation.
4.2.3 MODELISATION DU HACHEUR SURVOLTEUR MULTINIVEAU
4.2.3.1 RELATIONS DE CONVERSION DU HACHEUR A 3 NIVEAUX
(TOPOLOGIE BOOST)
Le hacheur à 3 niveaux du système (figure)
comme tout autre convertisseur statique convertit de l'énergie
électrique sous différentes formes par connexion et
déconnexion de circuits électriques comportant des
générateurs et des récepteurs.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
72
La fonction « interrupteur » des semi-conducteurs
d'un côté et la nature continue ou discontinue des grandeurs
échangées de l'autre, donnent naissance à une
modélisation mathématique caractérisée par deux
parties :
· une « Partie Commande » qui met en
évidence les conditions d'ouverture et des fermetures des
semi-conducteurs,
· une « Partie Opérative » qui se
décompose elle-même en une Partie Opérative Discontinue qui
décrit l'effet des connexions sur la conversion des grandeurs
électriques (grandeurs modulées) par des modèles
matriciels. Ensuite, une Partie Opérative Continue établit
à partir des équations différentielles l'évolution
temporelle des grandeurs électriques continues qui ont été
converties.
Nous modélisons ces deux parties par la figure ci-dessous
:

Fig. 6.4. Structure de modélisation mathématique
d'un convertisseur statique
A cet égard, pour modéliser le hacheur
multiniveau nous nous appuyons sur cette méthodologie.
Cependant, rappelons le schéma de la figure
précédente représentant un hacheur à 3 niveaux
(topologie Boost à potentiel distribué) :

Fig.6.5. Hacheur Boost à 3 niveaux à potentiel
distribué
Ce convertisseur est alimenté par une batterie de tension
supposée constante de Ug = 48 V.
Il est composé d'une cellule de commutation
élémentaire sur chaque phase qui permet la distribution du
potentiel commun du diviseur capacitif.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
73
Remarque :
Une cellule de commutation élémentaire permet
de connecter une source de tension (ici un condensateur) à une source de
courant (ici une inductance) et comporte deux interrupteurs (transistor et
diode) fonctionnant de manière complémentaire.
En adoptant l'approche matricielle développée
au L2EP de Lille ([Fra96A] [Fra96B]), et étayée
précédemment, nous allons donc prendre essentiellement en compte
la Partie Opérative Discontinue de ce hacheur pour sa
modélisation.
A cet effet, on considère ses semi-conducteurs
à des interrupteurs idéaux constituant les paramètres
d'une « fonction de connexion ». Cette fonction permet de lier les
grandeurs électriques propres à l'interrupteur (u, i) entre elles
et avec les grandeurs converties (us, is),
déterminées par l'environnement de cet interrupteur.
Ainsi à partir de cette approche ; on admet que :
· un interrupteur K, dans son fonctionnement idéal
est un dipôle énergétiquement neutre (sans perte
d'énergie) qui établit une connexion binaire (f = 0 si K ouvert ;
f=1 si K fermé).
· la chute de tension aux bornes d'un interrupteur
fermé est nulle et le courant s'annule quand l'interrupteur est ouvert,
et que les commutations sont instantanées (durées nulles).
Cependant on fait correspondre, à chaque interrupteur une
« fonction de connexion », notée
f.
4.2.3.2 MODELISATION MATHEMATIQUE DE LA TOPOLOGIE A
POTENTIEL DISTRIBUEE
Cette méthodologie donne le modèle de la Partie
Opérative Discontinue modélisant le hacheur Boost à
potentiel distribué à 3 niveaux suivant :
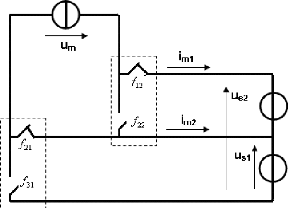
Fig. 6.6 Modèle du hacheur à 3 niveaux à
potentiel distribué associé à ses fonctions de
connexion.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
74
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Le hacheur à trois niveaux de la figure comme
étant une matrice d'interrupteurs (fonctions de connexion) reliant une
source de tension( inductance L) avec deux sources de courant (condensateur
C),
Les deux fonctions de connexions f12
et f31 dépendent directement de commande envoyés
aux transistors :
f12 = T1 f31 = T2 (6.1)
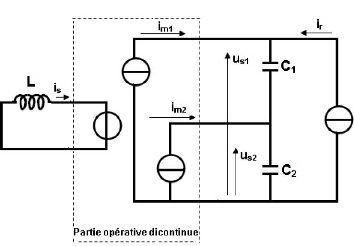
Fig. 6.7. Modèle du hacheur à 3 niveaux à
potentiel distribué avec sa Partie Opérative Discontinu.
La fonction de cette topologie est de générer des
grandeurs modulées (um ; im) associées
à des grandeurs équivalents.
Elle obéit à deux conditions :
· à tout instant les interrupteurs de chaque cellule
doivent être dans des états complémentaires ;
· les sources connectées de chaque de cette
topologie doivent être de nature différente.
Dans le schéma de la figure, on définit une
fonction de connexion fjk qui représente l'état de
l'interrupteur Kjk se trouvant à l'intersection de la ligne j
et de colonne k.
Il vient que :
i m(t) = f(t).i s (t) et um(t)
= (1 - f(t)).u s (t) (6.2)
Cependant nous obtenons les relations matricielles de conversion
suivantes :
[Im] = [F][I s ] (6.3)
75
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
On appelle [F] la matrice fonctionnelle (tous ses
éléments sont des fonctions) Regroupant toutes les fonctions de
connexion du convertisseur considéré.
[M] est la matrice de conversion du convertisseur et mi
représente une fonction de conversion.
On rappelle qu'en modèle moyen, on définit les
fonctions génératrices de connexion sur une période de
commutation Te telle que :
(k+1)Te
1
< f (t) lim[
>= ? ô ô
f ( )d. ] et
lc lc
T e 0
?Te kTe
(6.4)
|
(k+1)Te
1
< m (t) lim[
>= ? ô ô
m ( )d. ]
lc lc
T e 0
? Te kTe
|
|
Les valeurs limites de la fonction de connexion et celle de
commutation sont :
0 = f lc = 1
- 1= m lc = 1
Les relations qui lient les fonctions de connexion à
celles de conversion dans ce convertisseur s'expriment par :
m1 = f31 m2 = f21 -
f22 = f12 - f31 (6.5)
Avec : 0=m1=1 et -1=m2=1
De cette façon les expressions de courant du
convertisseurs sont telles que :
im1 =
m1.is (6.6)
i i m2 =m2.i s (6.7)
im1, im2 désignent les courants modulés.
is désigne le courant commuté issus de
la source de courant (l'inductance L)
Les tensions élémentaires modulées sont
produites par conversion d'une source de tension :
[Um] = [M][U s ] (6.8)
76
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
um1 = m1.us1 (6.9)
um2 = m2.u s2 (6.10)
La tension modulée en multiniveau est la somme de deux
niveaux de tension élémentaires telle que:
um = um1+um2 =m1.u s1+m2.u s2 (6.11)
um1 ; um2 désignent les tensions
modulées. Avec :
u s1 = u c1 + u c2 (6.12)
u s2 =u c2 (6.13)
uc1 et uc2 désignent les tensions
commutées issues des sources de tensions (condensateurs C1 et C2)
im et um sont les grandeurs
modulées, pour lesquelles l'indice « m » rappelle qu'elles
sont modulées.
is et us les grandeurs commutées
pour lesquelles « s » rappelle qu'elles sont issues des sources.
Le fonctionnement de ce convertisseur peut être alors
assimilé à un ensemble de deux générateurs
équivalents de courants modulés et un générateur
équivalent de tension modulée.
4.2.3.3 RESUME DES RELATIONS DES GRANDEURS ECHANGEES
ET FORMES D'ONDE
La conversion de grandeurs ainsi effectuée par
l'application des relations précédentes peut être
résumée dans le tableau suivant :

Tableau. 1. Tensions modulées par un hacheur à 3
niveaux
Un décalage temporel des ordres de commande de ces
deux cellules permet de générer les trois niveaux de tension :
uc1 uc2 us
77
Lors d'un fonctionnement dans des conditions normales, la
tension aux bornes de chaque condensateur s'équilibre naturellement
autour d'une certaine fraction de la tension de bus continu
On démontre qu' à l'équilibre la tension
aux bornes du condensateur C2 a une valeur constante et égale à
la moitié de la tension imposée :
us2 = uc2 = us1/2 (6.14)
On obtient ainsi une modulation multiniveau symétrique
et les niveaux de la tension modulée se réduisent à
trois.
La tension modulée par un hacheur à 3 niveaux
Boost a la forme d'onde suivante :

Fig. 6.8 .Évolution temporelle d'une tension
multiniveau (3 niveaux) symétrique.
Cette tension est donc constituée d'un ensemble de 3
valeurs distinctes, appelées niveaux.
Nous allons en ce qui suit étudier le hacheur à 3
niveaux à cellules imbriquées afin de mettre en évidences
les éventuelles analogies existant entre ces deux topologies.
4.2.3.4 MODELISATION ELECTRIQUE DE LA TOPOLOGIE A
CELLULES IMBRIQUEES
Nous conserverons les notations des grandeurs
précédentes de manière à retrouver des
similitudes.
Pour cela, on rappelle le schéma électrique du
hacheur à 3 niveaux à cellules imbriquées suivant :
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
78

Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Fig. 6.9. Hacheur à 3 niveaux à cellules
imbriquées
Le hacheur à 3 niveaux à cellules
imbriquées est alimenté également par une batterie de
tension constante Ug =48 V.
Composé de deux cellules de commutation, celles-ci
permettent de mettre en série ou en opposition la tension aux bornes de
deux condensateurs C1 et C2.
Les grandeurs à contrôler sont:
· le courant commuté is issu de
l'inductance L débité sur la charge R influencé par la
tension multiniveau modulée um
-la tension aux bornes du condensateur (C1) qui est
influencée par le courant im2.
Le transistor et la diode d'une même cellule sont
supposés être dans des états complémentaires.
En adoptant l'approche matricielle comme
précédemment, la Partie Opérative Discontinue de ce
convertisseur se schématise par :

Fig. 6.10. Structure de fonctions de connexion du hacheur
à 3 niveaux à cellules imbriquées
79

Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Fig.6.11. Partie Opérative Discontinue Hacheur à
3 niveaux à cellules imbriquées du hacheur à 3 niveaux
à cellules imbriquées
On remarque que la Partie Opérative Discontinue de ce
convertisseur ne correspond pas à une topologie matricielle
d'interrupteurs idéaux (fig. )
Toutefois une approche purement électrique
basée sur la mise en équation des grandeurs électriques de
ce convertisseur débouche à un modèle mathématique
identique à celui du hacheur à 3 niveaux à potentiel
distribué, résumé dans tableau.
Remarque
En règle générale pour obtenir une tension
de n Niveaux, n -1 capacités sont nécessaires.
Ainsi la tension modulée sur 3 niveaux nécessite
donc 2 sources de tension.
Ces tensions aux bornes des condensateurs sont toutes
égales à us /2 ; us est la tension totale
du bus continu.
Une onde à 3 niveaux est donc obtenue par une
sommation de 2 fonctions de conversion qui est pondérée par les 2
sources de tension.
Lorsque les sources de tension ont la même amplitude
(uc1= uc2 ), la tension multiniveau obtenue est dite symétrique. Nous
entendons par hacheur multiniveau symétrique, un hacheur à niveau
multiple constitué de cellules partielles dont les tensions continues
sont toutes égales.
Les valeurs prises par chaque fonction de conversion
dépendent de la topologie du convertisseur et des ordres de commande des
transistors.
4.2.3.5 MODELISATION REM ET STRUCTURE DE COMMANDE DU
HACHEUR A TROIS NIVEAUX (MONTAGE BOOST)
Pour obtenir la modélisation REM de ce convertisseur,
on s'intéresse cependant à son modèle équivalent en
fonctionnement moyen.
80
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Les caractéristiques du convertisseur
considéré sont :
· deux éléments sources dont une batterie
(source génératrice) en entrée et une charge R (source
réceptrice) en sortie du circuit ;
· eux éléments d'accumulations dont une
inductance L et deux condensateurs alimentés parallèlement.
· Un élément de conversion dont un ensemble
formé par les cellules de commutation.
La représentation des éléments constitutifs
du hacheur à trois niveau hérite la même configuration que
celle du hacheur classique sauf que nous adoptons une nouvelle notation des
grandeurs énergétiques échangées.
Nous obtenons alors en modèle moyen un ensemble
d'équations caractéristiques des fonctions
génératrices de conversion suivante :
um = um1 + um2 (6.15)
Remarque :
La valeur moyenne de la tension multiniveau est la somme des
valeurs moyennes de deux
tensions élémentaires modulées
um1 et um2 obtenues par action sur les valeurs
moyennes des deux fonctions de modulation m1 et
m2

um1 = m1 .u s 1 et
um2 = m2 .u s 2 ;
(6.16)
um = m1 .u s1 + m2 u
s2 ; (6.17)
i m1 = m1 .i s et im2 =
m2 .i s ; (6.18)
Cependant, cet ensemble d'équations
élaborées à partir des grandeurs échangées
dans le système (hacheur à 3 niveaux) donne sous forme d'une REM
les représentations suivantes :
4.2.3.5.1 REM DES SOURCES D'ENERGIE :
· Pour la batterie :

Fig. 6.12 REM de la batterie
81
· Pour la charge :

Fig. 6.13 REM de la charge
4.2.3.5.2 REM DES ACCUMULATEURS D'ENERGIE
· L'inductance L :

Fig. 6.14 REM de l'inductance L
· Les condensateurs C1 et C2 :

Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Fig. 6.15 REM du condensateur C1

82
Fig. 6.16. REM du condensateur C2
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.2.3.5.3 REM DU CONVERTISSEUR D'ENERGIE

Fig.6.17. REM du couplage électrique de 2 cellules de
commutation.
4.2.3.5.4 REM DU HACHEUR SURVOLTEUR
MULTINIVEAU
En somme, nous pouvons modélisé le hacheur
à 3 niveaux par la représentation de la figure :

83
Fig. 6.18. REM du hacheur à 3 niveaux Boost.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
4.2.3.5.5 STRUCTURE MAXIMALE DE COMMANDE (SMC) DU HACHEUR
SURVOLTEUR MULTINIVEAU
En adoptant la même modélisation des
éléments constitutifs du système que celle utilisée
pour le hacheur classique, on obtient la SMC suivante :

84
Fig. 6.19. REM et SMC d'un hacheur multiniveau
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
5 CHAPITRE : SIMULATION ET INTERPRETATION DES
RESULTATS
5.1 TRANSPOSITION DU MODELE REM DU HACHEUR CLASSIQUE
ET DUHACHEUR MULTINIVEAU SOUS LE LOGICIEL MATLAB SIMULINK
.

85
Fig. 7.1. Modèle MATLAB SIMULINK du hacheur classique

86
.
Fig.7.2. Modèle MATLAB SIMULINK du hacheur
multiniveau
|
|
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
5.2 RESULTATS DE SIMULATION
La commande et le réglage du bus continu dans le
système considéré ont été
réalisés en réglant la tension (ou le courant) ainsi que
la puissance transitant à ce niveau ( bus continu) grâce à
deux procédés techniques de régulation ; l'une utilisant
un hacheur classique élévateur de tension et l'autre un hacheur
multiniveau (topologie Boost), munis d'un contrôle de puissance,
basé sur la structure maximale de commande (SMC) déduite de la
modélisation REM de ces deux structures.
Ce système régulateur doit compenser la puissance
active issue de la source principale délivrée en sortie d'un
convertisseur de puissance côté source.
Ce système est constitué :
· d'une boucle d'asservissement de courant dans
l'inductance L et d'une boucle d'asservissement de tension dans le(s)
condensateur(s) C obtenues par principes d'inversion indirecte avec un
correcteur Proportionnel -Intégral dont les éléments ont
été calculés de manière à avoir une tension
du bus continu constante de 750V.
Les figures suivantes montrent les résultats de
simulation obtenus sous MATLABSIMULINK
Pour les caractéristiques des hacheurs suivantes:
· Hacheur survolteur classique : L=80 pH, R=1200, Ue=48,
C=4,8pF ;
· Hacheur survolteur multiniveau : L=80 pH , R=1200 ,
C1==4,8 pF, Ug=48 V.
5.2.1 ALLURES OBTENUES POUR SIMULATION DU HACHEUR
SURVOLTEUR CLASSIQUE ET DU HACHEUR SURVOLTEUR MULTINIVEAU
5.2.1.1 POUR LE HACHEUR CLASSIQUE
Allure de la tension du bus continu

L4\1
-100
400
800
700
600
500
300
200
100
0
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
t[s]
87
Fig. 7.3. Allure de la tension de bus continu en sortie du
hacheur classique
Allure de courant du bus continu

i[A]
-1
4
7
6
5
3
2
0
1
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
t[s]
Fig. 7.4. Allure de courant de bus continu en sortie du
hacheur classique
allure de puissance de bus continu

Ps[VV]
4500
4000
5000
3500
3000
2500
2000
1500
1000
500
0
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
t[s]
Fig. 7.5. Allure de la puissance de bus continu en sortie du
hacheur classique
88
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Allure de tension dans la diode classique

Ud[A]
-100
-200
-300
400
700
600
500
300
200
100
0
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
t[s]
Fig.7.9. Allure de la tension dans la diode du hacheur
classique
Allure de puissance dans le transistor classique

Pt[W]
4500
4000
3500
3000
2500
2000
1500
1000
-500
500
0
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
t[s]
Fig.7.10. Allure de puissance dans le transistor du hacheur
classique
89
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
5.2.1.2 POUR LE HACHEUR MULTINIVEAU
allure de tension du bus continu multinivo

U[V]
-100
400
800
700
600
500
300
200
100
0
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
t[s]
Fig.7.12. Allure de la tension de bus continu en sortie du
hacheur multiniveau
allure de puissance de bus c multinivo

Ps[w]
4500
4000
5000
3500
3000
2500
2000
1500
1000
500
0
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
t[s]
90
Fig.7.14. Allure de puissance de bus continu du hacheur
multiniveau
allure de tension de transistor multinivo

Ut[V]
-20
-40
-60
-80
40
20
0
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
t[s]
Fig.7.15. Allure de la tension dans le transistor du hacheur
multiniveau
5.2.1.3 INTERPRETATION
Les résultats pratiques déduits de la simulation
reflètent une analogie avec la théorie :
On constate en effet une bonne régulation de la tension
de bus continu dans les deux procédés, maintenue constante de
valeur moyenne 750V.
La puissance de bus continu est également constante
voisine de 5KW conformément à la théorie.
Cette observation confirme la robustesse du système de
contrôle considéré pour réguler et commander la
tension ainsi que la puissance de bus continu.
Le niveau de puissance que supportent les semi-conducteurs d'un
hacheur survolteur
classique est très élevé par rapport
à celui supporté par un hacheur survolteur multiniveau.
En particulier la puissance qui transite dans le transistor du
hacheur classique est deux fois plus élevée que celle transitant
sur l'un de transistor multiniveau.
91
Ceci confirme un léger avantage d'utilisation du hacheur
en remplacement du hacheur classique.
6 CONCLUSION
L'objectif dans ce mémoire, en guise de rappel,
était d'élaborer un procédé technique
d'électronique industrielle (électronique de puissance, de
commande et réglage) pour palier aux problèmes posés par
l'utilisation de bus continu dans les système de production
d'énergie éolienne et solaire.
Cependant, ce but a été atteint et même
dépassé.
Nous avons premièrement proposé d'utiliser un
système de régulation de bus continu avec un hacheur survolteur
classique. Ce procédé technique a l'avantage d'être simple,
utilise peu de composant électronique. Il est en effet sans beaucoup de
dépenses matérielles malgré l'inconvénient de
contraintes en tension et courant limités pour les composants
semiconducteurs d'une cellule élémentaire de commutation.
Nous avons ensuite essayé d'aller plus loin afin de
mettre en oeuvre la stratégie la mieux adaptée pour
répondre à cette initiative; ainsi nous avons étendu
l'étude au cas d'un
système de régulation de bus continu utilisant un
hacheur survolteur multiniveau. Les résultats de simulation obtenus pour
ce procédé technique présentent des nets avantages
notamment sur l'augmentation de la puissance transitée au niveau de bus
continu et de la capacité double des semi-conducteurs à supporter
la puissance transitée dans la cellule de commutation multiniveau ; mais
également il présente l'inconvénient d'être
compliqué (deux fois plus de boucles d'asservissement dus au nombre
double des grandeurs électriques à contrôler que pour la
structure classique). Ce qui occasionne impérativement des
dépenses matérielles doubles.
Dans tous les cas, on constate un bon maintien de la tension de
bus continu ainsi que la puissance de bus continu à un niveau constant,
ce qui confirme une bonne régulation de part et d'autre de deux
procédés techniques utilisés.
D'où une bonne gestion de flux de l'énergie
transitée au niveau de bus continu et par conséquent une
optimalité de la puissance extraite de la source principale
d'énergie éolienne ou solaire.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
92
Stratégie de commande et réglage du bus
continu dédiée aux systèmes de production d'énergie
éolienne et solaire
BIBLIOGRAPHIE
A. Belot , Electronique de puissance, E.S.E, n2312, 1973.
A. Cossié, le hacheur en traction électrique
à courant continu, revue générale des chemins de fer,
Janvier 1973.
F. Lucas, les régulateurs en traction
électrique du type hacheur et leur application en traction
électrique, publication scientifique et techniques des arts et
métier, 1973.
J. Bonifas, généralité sur les
convertisseurs E.S.E interne 198.
H. BULHER, électronique industrielle1 :
électronique de puissance, traité d'électricité de
l'Ecole Polytechnique fédérale de Lausanne, Georgi, 1978.
H. BULHER, électronique de puissance,
Traité Electricité Vol XV, 4è édition, PPR.
Lausanne, 1987.
G.SEGUIER, convertisseur continu-continu, convertisseur de
l'électronique de puissance, technique et documentation, Lavoisier,
Paris 1992
R. CHAUPRADE, Evolution des circuits de commande des
convertisseurs de puissance à thyristors R.G.E, t. 79,
juillet-août 1970.
R.CHAUPRADE, commande des moteurs à courant
continu, ELECTRONIQUE DE PUISSANCE. 3 éditions, 1981.
B.Robyns, M.Nasser, «Modélisation et simulation
d'une éolienne à vitesse variable
basée sur une génératrice asynchrone
à cage«, Actes du colloque Electrotechnique du Futur,
EPF'01, Nancy, novembre 2001, pp.77-82.
P. Bartholomeus, P. Lemoigne, C. Rombaut, «Etude des
limitations en puissance des convertisseurs et apport des techniques
multiniveaux«, Actes du colloque Electronique
de puissance du Futur, EPF'96, Grenoble, 1996, pp.
121-126
J.M RAZAFIMAHENINA, cours d'électronique de
réglage et commande, Ecole Supérieure Polytechnique,
Antsiranana, 2004.
J.N RAZAFINJAKA, cours d'automatique I et II, Ecole
Supérieure Polytechnique, Antsiranana, 2004, 2005.
93
C.B ANDRIANIRINA, cours d'Electronique de puissance I et
II, Ecole Supérieure Polytechnique, Antsiranana, 2004, 2005.
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
GLOSSAIRE
Ec : Energie cinétique [J]
r : Rayon [m] ;
m : Masse [kg]
v : vitesse [m/s]
d : Densité [kg/m3]
p : Puissance [W]
pa : Puissance absolue [W] pMAX
Puissance maximale [W] pprat La puissance pratique [W]
· e : charge de l'électron en [C]
· k : constant de Boltzmann [sans dimension]
· T : température [K]
· Is : courant inverse de saturation de
la diode [A]
· K1 : constant thermique du fabricant
[sans dimension
· Eg : Energie de gap [J]
· V : tension [V]
· I : courant [A].
· K2 : constant thermique du fabricant
[sans dimension
ICCstd : courant de court-circuit [A]
· G : éclairement [W/m2]
· ?T : température [K]
· IT : variation de courant de
court-circuit par rapport à la température [K-1] U : tension de
bus continu [V]
94
I : courant de bus continu [A] Ps : puissance de
sortie [W] Ue : tension d'entrée [V]
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Ut : tension de transistor [V]
Ud : tension de diode [V]
UC : courant en sortie du condensateur [V]
Uhach : tension du hacheur [V]
Ihach : courant du hacheur [A]
IL : courant de l'inductance [A]
Is : courant de sortie [A]
Ie : courant d'entrée [A]
UL tension de l'inductance[V]
Pe : puissance d'entrée [W]
Pc : puissance compensée [W]
Um : tension de modulation en [V]
Im : courant de modulation en [A]
F : fréquence de découpage en [Hz]
T : période de découpage [s]
á : rapport cyclique [sans dimension]
95
Ir: courant en sortie du hacheur multiniveau[A]
Stratégie de commande et réglage du bus
continu dédiée aux systèmes de production d'énergie
éolienne et solaire
ANNEXE
LISTING DE PROGRAMMATION
HACHEUR CLASSIQUE.
Pour afficher l'allure de la tension de bus continu du
hacheur classique
clear all; Rch = 120;
L = 80e-6;
C = 4.8e-6;
K1 = 1.0008;
K2 = 1/K1;
Ue = 48;
sim('hacheur1',[0 0.02]);
plot(t,uc,'r');grid;
title('Allure de la tension du bus continu');
ylabel('U[V]');
xlabel('t[s]');
Pour afficher l'allure de courant du bus continu du
hacheur classique
clear all;
Rch = 120;
L = 80e-6;
C = 4.8e-6;
K1 = 1.0008;
96
K2 = 1/K1; Ue = 48;
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
sim('hacheur2',[0 0.02]);
plot(t,is,'r');grid;
title('Allure de courant du bus continu');
ylabel('i[A]'); xlabel('t[s]');
Pour afficher l'allure de puissance de bus continu du
hacheur classique
clear all;
Rch = 120; L = 80e-6; C = 4.8e-6;
K1 = 1.0008;
K2 = 1/K1;
Ue = 48;
sim('hacheur3',[0 0.02]);
Ps = uc.*is;
plot(t,Ps,'r');grid;
title('allure de puissance de bus continu');
ylabel('Ps[W]');
xlabel('t[s]');
Pour afficher l'allure de tension dans le transistor du
hacheur classique
97
clear all; Rch = 120; L = 80e-6; C = 4.8e-6;
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
K1 = 1.0008;
K2 = 1/K1;
Ue = 48;
sim('hacheur4',[0 0.02]);
plot(t,Uhach,'r');grid;
title('Allure de tension dans le transistor classique');
ylabel('Ut[A]');
xlabel('t[s]');
Pour afficher l'allure de tension dans la diode du
hacheur classique
clear all;
Rch = 120; L = 80e-6; C = 4.8e-6;
K1 = 1.0008;
K2 = 1/K1;
Ue = 48;
sim('hacheur5',[0 0.02]);
Ud=uc-Uhach;
plot(t,Ud,'r');grid;
title('Allure de tension dans la diode classique');
ylabel('Ud[A]');
98
xlabel('t[s]');
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
HACHEUR MULTINIVEAU
Pour afficher l'allure de tension dans le condensateur C1
du hacheur multiniveau
clear all; Rch = 120;
L = 80e-6;
C1 = 4.8e-6;
= 4.8e-6;
K1 = 1.42;
K2 = 1/K1;
Ug = 48;
sim('multinivo1',[0 0.02]);
plot(t,uc1,'r'); grid;
title('allure de tension dans C1 multinivo');
ylabel('U[V]');
xlabel('t[s]');
Pour afficher l'allure de tension du bus continu du
hacheur multiniveau
clear all; Rch = 120; L = 80e-6;
C1 = 4.8e-6;
= 4.8e-6;
K1 = 1.42;
99
K2 = 1/K1; Ug = 48;
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
sim('multinivo2',[0 0.02]);
us=uc1+uc2
plot(t,us,'r'); grid;
title('allure de tension du bus continu multinivo');
ylabel('U[V]');
xlabel('t[s]');
Pour afficher l'allure de courant de bus continu du
hacheur multiniveau
clear all; Rch = 120; L = 80e-6;
C1 = 4.8e-6;
= 4.8e-6;
K1 = 1.42;
K2 = 1/K1;
Ug = 48;
sim('multinivo3',[0 0.02]);
plot(t,ir,'r'); grid;
title('allure de courant de bus continu multinivo');
ylabel('i[A]');
xlabel('t[s]');
Pour afficher l'allure allure de puissance de bus continu
du hacheur multiniveau
100
clear all;
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
Rch = 120;
L = 80e-6;
C1 = 4.8e-6;
= 4.8e-6;
K1 = 1.42;
K2 = 1/K1;
Ug = 48;
sim('multinivo4',[0 0.02]);
Us = uc1+uc2;
Irs=2*ir;
Ps = Us.*Irs;
plot(t,Ps,'r'); grid;
title('allure de puissance de bus c multinivo');
ylabel('Ps[w]');
xlabel('t[s]');
Pour afficher l'allure de tension de transistor du
hacheur multiniveau
clear all; Rch = 120; L = 80e-6;
C1 = 4.8e-6;
= 4.8e-6;
K1 = 1.42;
101
K2 = 1/K1; Ug = 48; sim('multinivo5',[0 0.02]); plot(t,Um1,'r');
grid;
Stratégie de commande et réglage du bus continu
dédiée aux systèmes de production d'énergie
éolienne et solaire
title('allure de tension de transistor multinivo');
ylabel('Ut[V]');
xlabel('t[s]');
Pour afficher l'allure de tension des diodes du hacheur
multiniveau
clear al
Rch = 120; L = 80e-6;
C1 = 4.8e-6;
= 4.8e-6;
K1 = 1.42;
K2 = 1/K1;
Ug = 48;
sim('multinivo6',[0 0.02]);
Ud=uc1-Um1
plot(t,Ud,'r'); grid;
title('allure de tension de diodes multinivo');
ylabel('Ud[V]');
102
xlabel('t[s]');



