4.3.1.1.
Propriétés statistiques des variables utilisées
Avant de faire les estimations, nous allons procéder
à une analyse exploratoire de nos données. Dans cette
étape, il s'agit d'étudier l'évolution et le comportement
de nos variables dans le temps. Ceci nous permet d'éviter de faire des
estimations qui n'ont aucune signification économétrique
«spuriousregressions ou régressions fallacieuses» au cas
où les données ne sont pas stationnaires. Il convient d'en
étudier les caractéristiques stochastiques (espérance et
variance). Si elles se trouvent modifiées dans le temps, la série
est considérée comme non stationnaire; dans le cas d'un processus
stochastique invariant, la série est alors stationnaire. Nous allons
effectuer un test de stationnarité pour déterminer la nature des
variables. Cette étape est nécessaire car elle permet de trouver
la meilleure méthode d'estimation à utiliser pour l'analyse. Elle
est par ailleurs importante parce que l'application au hasard d'une
méthode d'estimation peut conduire à des résultats
fallacieux et aussi dans la mesure où l'hypothèse de
l'indépendance entre la variable explicative et l'erreur n'est pas
respectée.
4.3.1.2. Les différents tests statistiques
à appliquer et méthode d'estimation
Pour déterminer la méthode d'estimation
adéquate pour l'estimation de notre modèle, nous devons tester la
stationnarité des variables, l'autocorrélation des résidus
ainsi que l'hétéroscedasticité.
L'hétéroscedasticité qualifie les
données qui n'ont pas une variance constante. Elle ne biaise pas
l'estimation des coefficients, mais l'inférence habituelle n'est plus
valide puisque les écarts types trouvés ne sont plus les bons. Le
test de BREUSCH PAGAN et WHITE permet de la détecter. L'idée de
base est de vérifier si les carrés des résidus sont
expliqués par les variables du modèle ; auquel cas il y a
hétéroscédasticité. C'est un test statistique qui
utilise la statistique F (Fisher). L'interprétation consiste à
comparer les valeurs critiques aux valeurs obtenues de la statistique
concernée. Si la valeur de la statistique F obtenue est supérieur
à la valeur critique, on rejette l'hypothèse nulle. On note aussi
que les résultats statistiques sont souvent donnés sous la forme
de « P-value » dans stata, un nombre compris entre 0 et 1
qui indique la probabilité sous Ho d'obtenir la valeur trouvée.
Ainsi, si la P-value est inférieure à la
valeurdésirée de   (5% par exemple), on rejette l'hypothèse nulle. Cette
hypothèse nulle suppose ici que tous les coefficients de la
régression des résidus au carré sont nuls. Autrement dit,
les variables du modèle n'expliquent pas la variance observée
donc il yahomoscédasticité. L'hypothèse alternative est
celle de l'hétéroscédasticitéet signifie que
l'hypothèse nulle est rejetée
(«P-value »<alpha). (5% par exemple), on rejette l'hypothèse nulle. Cette
hypothèse nulle suppose ici que tous les coefficients de la
régression des résidus au carré sont nuls. Autrement dit,
les variables du modèle n'expliquent pas la variance observée
donc il yahomoscédasticité. L'hypothèse alternative est
celle de l'hétéroscédasticitéet signifie que
l'hypothèse nulle est rejetée
(«P-value »<alpha).
L'étude de la stationnarité s'effectue
essentiellement à partir de l'analyse des fonctions
d'autocorrélation ou de leur représentation graphique
appelée corrélogramme. Dans le cadre de ce travail de recherche,
nous vérifions la stationnarité des variables à l'aide du
test de Dickey-Fuller Augmenté qui tient compte de
l'autocorrélation des erreurs dans le temps. Il est celui qui est le
plus utilisé pour le cas des séries temporelles à cause de
sa maniabilité. L'application de ce test nous a permis de constater que
nos variables son stationnaires à niveau : ce qui nous
emmène à utiliser la méthode des moindres carrés
ordinaires (MCO) pour l'estimation des paramètres de notre
modèle.
Pour tester la significativité des paramètres et
celle du modèle, nous allons effectuer respectivement le test individuel
t de Student et le test global de Fischer.
a) Le test t de
Student
Il est applicable lorsque la taille de l'échantillon
est inférieure à 30. Au cas contraire, la valeur lue dans la
table sera celle correspondant à la valeur infinie ou celle de la table
de la loi normale (Bourbonnais, 2002). Il se déroule ainsi :
après avoir défini un seuil de significativité (on choisit
généralement 5%, mais parfois on retient 1 ou 10%), on
détermine le degré de liberté qui est égal à
n-k-1 (n est la taille de l'échantillon, k est le nombre de variables
exogènes) et on pose les hypothèses à tester.
Ø l'hypothèse nulle (H0) :  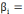 0 0
Ø l'hypothèse alternative (H1) :
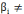 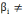 0 0
Pour la valeur estimée d'un paramètre, la valeur
calculée de la statistique s'obtient à partir de la formule
suivante :
 valeur estimée du paramètre = (valeur
estimée - valeur réelle)/ écart-type de la valeur
estimée du paramètre. valeur estimée du paramètre = (valeur
estimée - valeur réelle)/ écart-type de la valeur
estimée du paramètre.
Le calcul de cette valeur nous permet de la comparer à
la valeur lue dans la table qui est : 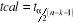 pour une valeur de pour une valeur de 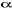 choisie. Si choisie. Si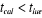 , alors, on accepte l'hypothèse nulle et on conclut que le
paramètre n'est pas significatif. , alors, on accepte l'hypothèse nulle et on conclut que le
paramètre n'est pas significatif.
b) Significativité globale du
modèle : le test de Fisher
Ce test permet de s'assurer de la qualité du
modèle à représenter convenablement le
phénomène étudié. Il s'effectue sur la base de la
valeur du coefficient de détermination R2 (Chauvat, 2003).
Comme le test précédent, on choisit d'abord un seuil de
signification, puis, on cherche la valeur calculée de la statistique sur
la base de la formule : . Cette valeur est comparée à celle lue dans la table de
Fischer à (k-1, n-k-1) degré de liberté. Les
hypothèses sur lesquelles repose ce test sont les suivantes : . Cette valeur est comparée à celle lue dans la table de
Fischer à (k-1, n-k-1) degré de liberté. Les
hypothèses sur lesquelles repose ce test sont les suivantes :
Ø l'hypothèse nulle (H0) : tous
les paramètres du modèle sont nuls ;
Ø l'hypothèse alternative (H1) :
au moins un paramètre est différent de zéro.
La règle de décision est la suivante :
si , on accepte l'hypothèse nulle. , on accepte l'hypothèse nulle.
Demeke et al (2003), pensent que l'analyse de
l'élasticité croissance emploi a une signification si on tente
d'observer corrélativement l'évolution de la productivité
du travail. Il se peut en effet, qu'une élasticité
élevée, couplée à une productivité du
travail faible traduise une création hautement élevée
d'emplois appauvrissant. L'analyse de la corrélation entre l'emploi et
sa productivité peut se faire suivant l'interprétation de
l'élasticité emploi.
| 


