Etude et évaluation des performances des systèmes de gestion de batteries lithium- ion

Cycle de formation des ingénieurs en Télécommunications

Option :
Architecture des systèmes de télécommunications

Rapport de Projet de fin d'études

Thème :

Etude et évaluation des performances des

systèmes de gestion de batteries

Lithium- Ion

Réalisé par :

Zied JELASSI

Encadrants :

M. Dominique DALLET
M. Chiheb REBAI

Travail proposé et réalisé en collaboration avec

Année universitaire : 2009/2010

Dédicace

Dédicace

À ma mère «Aïcha» et mon père «Hammadi»
en témoignage de leur affection, leurs sacrifices

et de leurs précieux conseils qui m'ont conduit à la réussite
dans mes études ;

À mes frères Mohamed et Bacem,
à ma soeur Khawla et à ma tente Naziha

en leur souhaitant la réussite dans leurs études et dans leurs
vies,

À tous ceux qui m'ont aidé afin de réaliser ce travail,
Et à tous ceux que j'aime et qui m'aiment.
Je dédie ce travail

Zied ...

Résumé

Résumé

L'époque actuelle est caractérisée par une explosion de la demande des solutions mobiles. Suite à cette croissance, les appareils sont devenus de plus en plus gourmands en énergie. Pour assurer une autonomie importante, plusieurs industriels emploient des batteries à haute densité d'énergie.

Dans ce cadre, les fabricants de batteries et en particulier Saft ont déjà commencé à produire des batteries Lithium-Ion dont leur densité d'énergie dépasse la 350 Wh/l.

Comme toutes les batteries Li-Ion, ces batteries nécessitent encore un BMS, ou encore un système de gestion de batterie, pour assurer son exploitation optimale et pour garantir une durée de vie maximale.

Au cours de ce projet, nous avons étudié la structure multiplexée de deux BMS (MAX11068 et LTC6802). Cette étude s'intéresse aux problèmes liés à cette architecture, notamment par rapport à la diaphonie et à l'injection de charge.

Mots clés : Li-Ion, BMS, diaphonie, injection de charge, CAN ?-?, CAN-SAR, LC-ADC

Abstract

The present era is characterized by an explosion in mobile solutions demand. As consequence, electronic devices have become increasingly energy depending and consuming. In order to ensure a substantial autonomy, many industrialists employ very high energy density batteries.

In this context, battery manufacturers and Saft, for instance, have already begun to produce Li-Ion batteries whose energy density is exceeding 350 Wh / l.

These batteries, like all Li-Ion ones, still require a BMS (Battery Management System) to ensure an optimum use and a maximum life time.

During this project, we have studied the structure of two multiplexed BMSs (MAX11068 and LTC6802). This study has examined the problems referring to this architecture and has particularly focused on the crosstalk and charge injection limitations.

Keywords: Li-Ion, BMS, crosstalk, charge injection, Ó-Ä ADC, SAR-ADC, LC-ADC

Avant propos

Avant propos

Ce travail a été effectué dans le cadre de mon projet de fin d'études pour l'obtention du diplôme d'Ingénieur en télécommunications de l'Ecole Supérieure des Communications de Tunis (SUP'COM). Il a été réalisé au sein du laboratoire d'Intégration de Matériau au Système (IMS) de Bordeaux, dans l'équipe `Circuits et Systèmes Numériques' du groupe `Conception' du département COFI.

Au terme de ce projet, Je tiens à remercier et à exprimer ma profonde gratitude à mes encadrants Mr. Dominique DALLET et Mr. Chiheb REBAI pour leur aide précieuse, leurs conseils et leurs suggestions avisées qui m'ont aidé à mener à bien ce travail.

De même, je tiens à remercier l'ensemble des personnes travaillant au laboratoire IMS, les post-doctorants, les ingénieurs, les étudiants en Maîtrise ainsi que les autres stagiaires qui ont contribué à créer une ambiance de travail agréable.

Je remercie aussi tous les enseignants de l'Ecole Supérieure des Communications qui n'ont épargné aucun effort pour me fournir une formation efficace et robuste.

J'étais enchanté de travailler sur ce projet et j'espère que le présent rapport reflète cet enthousiasme. Je tiens enfin à remercier les membres du jury qui me feront l'honneur d'évaluer la contribution de ce travail.

Table de matières

DEDICACE I

RESUME II

AVANT PROPOS III

LISTE DES FIGURE VI

LISTE DE TABLEAUX IX

LISTE DES ABRÉVIATIONS X

INTRODUCTION GENERALE 1

LE CHAPITRE 1: LES BATTERIES: PRINCIPES ET SYSTEME DE GESTION 3

1.1. INTRODUCTION 4

1.2. PRINCIPE DE FONCTIONNEMENT D'UNE BATTERIE 4

1.2.1. Terminologies de Batterie 5

1.2.2. Les types de Batteries 13

1.3. BATTERY MANAGEMENT SYSTEM (BMS) 19

1.3.1. Acquisition de données 20

1.3.2. Détermination de l'état de la batterie 20

1.3.3. Gestion électrique 21

1.3.4. Gestion de la sécurité 21

1.3.5. Gestion thermique 22

1.3.6. Communication 22

1.4. CONCLUSION 23

CHAPITRE 2: MODELISATION DES BATTERIES LITHIUM ION 24

2.1. INTRODUCTION 25

2.2. LA BATTERIE LITHIUM-ION 26

2.3. LA BATTERIE VL34480 26

2.3.1. Le système électrochimique de la VL34480 27

2.3.2. La composition de la VL34480 28

2.4. LA MODELISATION DES BATTERIES LITHIUM-ION 28

2.4.1. Modèle d'Olivier Tremblay et Louis-A. Dessaint 29

2.4.2. Le modèle de MathWorks 34

2.4.3. Modèle de L. Gao 39

2.4.4. Discussion 45

2.5. CONCLUSION 47

CHAPITRE 3: ANALYSE DES PERFORMANCES DES SYSTEMES DE MESURES DE
TENSION MULTIPLEXEES 48

3.1. INTRODUCTION 49

3.2. SYSTEMES D'ACQUISITION DE DONNEES MULTIPLEXES 50

3.2.1. Le convertisseur analogique-numérique ?? 51

3.2.2. Le convertisseur analogique-numérique SAR 53

3.2.3. Etude comparative entre le MAX11068 et LTC6802 54

3.3. MESURES ET RESULTATS 56

3.3.1. Introduction d'une perturbation à l'entrée du BMS 57

3.3.2. Analyse de mesures 58

3.4. CONCLUSION 69

CONCLUSION GENERALE 70

ANNEXE 1: LA DATASHEET DE LA BATTERIE VL34480 71

ANNEXE 2: LE CONVERTISSEUR A/N A TRAVERSEE DE NIVEAU 73

BIBLIOGRAPHIE 80

Liste des figure

Figure 1.1: Cellule voltaïque composée de deux demi-cellules reliées par un électrolyte. 5

Figure 1.2 : Cycle de vie d'une batterie Li-ion à différents taux de déchargement 6

Figure 1.3 : Représentation de Nyquist d'une résistance interne d'une batterie Plomb-acide. 9

Figure 1.4 : L'effet de la température sur la résistance effective totale [38]. 9

Figure 1.5 : Diminution de Qd en fonction du nombre de cycle Cn 13

Figure 1.6 : Représentation schématique d'une batterie Li-ion 16

Figure 1.7 : Statistique de la demande des batteries rechargeables. 17

Figure 1.8 : Schéma du BMS 20

Figure 1.9: Flux d'état de la batterie. 21

Figure 2.1: Classification des batteries suivant leurs densités énergétiques 26

Figure 2.2 : La batterie VL34480 [annexe1] 27

Figure 2.3 : Modèle de batterie Lithium-Ion présenté dans [24] 29

Figure 2.4 : Le circuit électrique de base formé par tension en circuit ouvert en série avec une

résistance et un circuit RC en parallèle. 30

Figure 2.5 : Caractéristique de décharge de la batterie VL34480 pour C/5(0.9A) 32

Figure 2.6 : Comparaison directe entre la caractéristique de décharge (0.9A, 0.2C) et la

caractéristique générée par le modèle. 34

Figure 2.7 : Le modèle de MathWorks 35

Figure 2.8 : Modèle MathWorks 36

Figure 2.9 : Fenêtre de configuration du modèle 37

Figure 2.10 : la fenêtre View Discharge Characteristics 38

Figure 2.11 : Courbes de décharge fournies par le deuxième modèle pour différents courants de décharge 38

Figure 2.12 : La comparaison des résultats du modèle de MathWorks et les caractéristiques fournies par Saft. (a) la caractéristique de décharge de la VL34480 extraite de la datasheet. (b) la sortie du modèle de MathWorks. 39

Figure 2.13 : Les sources de données du modèle de L. Gao. (a) Les caractéristiques de décharge de la VL34480 à 20°C pour différents courant de décharge. (b) Les caractéristiques de décharge de

la VL34480 à 0.9A-0.2C pour différentes température. 40

Figure 2.14 : Schéma électrique du modèle de L.GAO [25] 40

Figure 2.15: Détermination du facteur á [i(t)] pour un courent de décharge de 8.8A par rapport à un courent de référence de 0.9A 42

Figure 2.16: Rate factor á pour la batterie Li-Ion VL34480 calculé pour un courant de référence de

0.9A 43
Figure 2.17: Détermination du facteur de température et du potentiel de correction de la dépendance

en température 43
Figure 2.18: Facteur de température (a) et potentiel de correction de la dépendance de la température

(b) pour la batterie VL34480 pour une température de référence de 20°C 44
Figure 2.19: Comparaison directe entre la caractéristique de décharge (4.4A, 1C) à 20°C et la

caractéristique générée par le modèle. 45

Figure 3.1: Principe du système d'acquisition de données multiplexé 50

Figure 3.2 : Schéma bloc d'un CAN ?? 52

Figure 3.3 : Architecture du convertisseur à approximation successive 53

Figure 3.4 : Dispositif de mesure du MAX11068 56

Figure 3.5 : Dispositif de mesure du LTC6802 57

Figure 3.6 : Présentation de l'arrangement des signaux d'entrée pour le MAX11068 et le LTC680258

Figure 3.7 : Bruit impulsif à la fréquence 1/10Hz 59

Figure 3.8 : Bruit impulsif à la fréquence 1/6Hz 59

Figure 3.9 : Représentation temporelle de la sortie de la troisième cellule sur la carte MAX11068 à

0°C et avec un bruit de 62,5Hz 60

Figure 3.10 : Evolution du paramètre << b >> à 0°C pour la MAX11068 61

Figure 3.11 : Représentation du paramètre << a >> pour les cinq premières cellules à 0°C pour la

MAX11068 62
Figure 3.12 : Représentation du paramètre << a >> pour les cinq premières cellules à 20°C pour la

MAX11068 63
Figure 3.13 : Représentation du paramètre << a >> pour les cinq premières cellules à 40°C pour la

MAX11068 63

Figure 3.14: Densité spectrale du bruit à 20°C et une fréquence de 125Hz 65

Figure 3.15 : Densité spectrale du bruit à 20°C et une fréquence de 1 KHz 65

Figure 3.16 : Densité spectrale du bruit à 0°C et à la fréquence 2 KHz 66

Figure 3.17 : Densité spectrale du bruit à 20°C et à la fréquence 2 KHz 66

Figure 3.18 : Densité spectrale du bruit à 40°C et à la fréquence 2 KHz 67

Figure 3.19 : Densité spectrale du bruit de la cellule 3 à 0°C et à la fréquence bruit 4KHz 67

Figure 3.20 : Densité spectrale du bruit de la cellule 2 à 0°C et à la fréquence bruit 4KHz 68

Figure 3.21 : Erreur maximal absolue de la cellule deux, le bleu correspond à la valeur de l'erreur de la LTC6802, le noir correspond à la valeur de l'erreur de la MAX11068 68

Figure II.1 : Processus d'échantillonnage à traversée de niveau 74

Figure II.2 : Erreur du temps de quantification du LC-ADC 77

Liste des tableaux

liste de tableaux

Tableau 1.1: Caractéristiques des batteries rechargeables actuellement utilisées 19

Tableau 2.1 : Composition de la batterie VL34480 28

Tableau 3.1 : Tableau de comparaison entre le MAX11068 et le LTC6802 [9, 10] 55

Tableau II.1: Caractéristiques du LC-ADC face aux ADC classiques 78

Tableau II.2: LC-ADC comparé à une sélection d'architecture de conversion A/N opérationnelles 79

Liste des abréviations

AC: Alternative Current

ADC: Analog to Digital Convertor

AGP: Amplificateur à Gain Programmable

Ah : Ampères-heures

BEV: Battery Electric Vehicle BMS: Battery Management System CAN: Controller Area Network

CAN: Convertisseur Analogique-Numérique

CMOS: Complementary Metal Oxide Semiconductor

DC : Direct Curent

ENOB: Effective Number of Bits FEM: Force Electromotrice

FIR: Finite Impulse Response HEV: Hybrid Electric Vehicle HT: High Temperature

LC-ADC: Level Crossing ADC

LCSS: Level Crossing Sampling Schema

LSB: Least Significant Bit LT: Low Temperature

MSB: Most Significant Bit OV: Overvoltage

PHEV: Plug-in Hybrid Electric Vehicle

SAR: Successive Approximation Register

SNR: Signal to Noise Ratio SoC: State of Charge

SOD: State of Discharge

SoH: State of Health

UPS: Uninterruptible Power Supply UV: Undervoltage

VE: Electric Vehicle

Introduction générale

La découverte de Rachid Yazami en 1980, au Centre National de Recherche Scientifique et à l'institut de technologie de Grenoble, a marqué une nouvelle piste dans le domaine des batteries. Ce chercheur a pu intercaler le lithium dans le graphite. Cette découverte a permis de rendre les batteries au lithium rechargeable. Cet apport fut atteint dix ans après la proposition de la première batterie au lithium.

Les premières batteries au lithium contiennent cette substance chimique sous forme métallique, ce qui engendre des problèmes de stabilité et de sécurité. Pour remédier à ces limitations, la solution fut de l'utiliser sous la forme ionique.

1991 a marqué une nouvelle étape pour ce type de batterie. Sony a lancé la production de cette technologie. A partir de cette date, les batteries Li-Ion n'ont cessé d'évoluer en termes de composition chimique, de densité énergétique, etc.

Du fait de la tendance actuelle vers les applications mobile, tels que la téléphonie portable, les tablettes numériques, les ordinateurs portables, les véhicules électriques, les satellites, etc., les fabricants ont adopté cette technologie. Ce choix est justifié par le faible poids, la petite taille, la haute densité énergétique, etc., de cette batterie.

Les batteries Li-Ion ont nécessairement recours à un système de gestion, le BMS (Battery Management System). Ce dispositif assure l'utilisation optimale de l'énergie emmagasinée au sein de la batterie et une durée de vie maximale.

Sur le marché, plusieurs fabricants proposent différents systèmes de gestion de batteries. En majorité, ces systèmes se basent sur une architecture multiplexée qui fait appel à un seul convertisseur analogique numérique. Cette solution permet de réduire la taille du système et essentiellement son coût.

Ce travail entre dans le cadre de l'étude des différents problèmes liés à cette solution. L'objectif principal de ce projet est de comparer de façon relative deux différentes

technologies d'acquisition de données, à savoir la MAX11068 de Maxim Semiconductors et la LTC6802 de Linear Technology, en termes de diaphonie et d'injection de charge.

Ce document se compose de trois chapitres : le premier chapitre présente le cadre générale de ce projet. En effet, il définit les différentes terminologies liées à la batterie Li-Ion. En plus, il présente le système de gestion de ce type de batterie ainsi que les différentes fonctionnalités qu'il assure.

Pour mieux comprendre cette technologie, le deuxième chapitre traite d'avantage son comportement électrochimique. Ce chapitre commence par présenter la batterie VL34480, la batterie sur laquelle les tests ont été réalisés. Ensuite, l'étude et la mise en oeuvre de trois différents modèles de batterie Li-Ion sont proposées.

Le dernier chapitre est réservé pour présenter le système de mesure multiplexé. Il s'intéresse en particulier aux deux systèmes étudiés. Puis, il présente le test effectué pour évaluer les problèmes reliés à cette architecture, ainsi que les résultats de ce test et le résultat de comparaison entre les deux BMS étudiés.

Le chapitre 1: Les batteries: Principes

et Système de Gestion

1.1. Introduction

Du fait du progrès technologique et de l'évolution rapide des systèmes mobiles, de nombreuses habitudes changent. L'individu demande de plus en plus d'applications portables. Cette nouvelle tendance crée une forte demande en source d'alimentation qui doit être la plus efficace possible, que ce soit en termes de fiabilité, de temps de charge ou de décharge et surtout de surface occupée. Par rapport à tous ces points, la batterie lithium-ion figure apparaît comme la solution la plus adaptée.

Après le mauvais démarrage des batteries en lithium métallique au début des années quatre-vingt-dix, les batteries lithium-ion, connues comme les batteries les plus sûres, ont rapidement récupéré le retard. De nos jours, cette technologie est concurrentielle vis à vis des domaines à haute exigence tel que les applications militaires et spatiales.

Ce chapitre s'intéresse en premier lieu, à définir le principe de fonctionnement des batteries ; ses terminologies ainsi qu'une classification de différents types de batteries. Ensuite nous porterons une attention particulière sur le système de gestion de batterie Lithium-Ion(BMS), son utilité et ses fonctionnalités.

1.2. Principe de fonctionnement d'une batterie

Une batterie est un dispositif qui convertit l'énergie chimique directement en énergie électrique [1]. Il se compose d'une ou plusieurs cellules voltaïques [2]. Chaque cellule voltaïque se compose de deux demi-cellules connectées en série par un électrolyte conducteur contenant des anions (ions négatifs) et des cations (ions positifs). Une demi-cellule contient l'électrolyte et une électrode utilisée pour la migration des anions, c'est l'anode ou l'électrode négative. L'autre demi-cellule comprend l'électrolyte et l'électrode utilisée pour la migration des cations, c'est la cathode ou l'électrode positive. Le principe d'une cellule voltaïque est représenté à travers la figure 1.1.

Figure 1.1: Cellule voltaïque composée de deux demi-cellules reliées par un électrolyte.

La réaction redox, définie comme l'abréviation du processus d'oxydoréduction, fait fonctionner la batterie. La réduction (ajout d'électrons) se produit aux cations au niveau de la cathode, tandis que l'oxydation (enlèvement d'électrons) se produit aux anions au niveau de l'anode. Les électrodes ne se touchent pas les unes aux autres, mais elles sont électriquement reliées par l'électrolyte, qui peut être solide ou liquide. De nombreuses cellules utilisent deux demi-cellules avec des différents électrolytes. Dans ce cas, chaque demi-cellule est enfermée dans un conteneur, et un séparateur qui est perméable aux ions, mais la majorité des électrolytes n'empêche pas le mélange.

1.2.1. Terminologies de Batterie

Dans cette section quelques terminologies communes aux batteries, et employées dans un BMS (Battery Management System) sont brièvement décrites.

1.2.1.1. C-Rate (REGIME de chargement et de décharge)

Le chargement et le déchargement d'une batterie est mesurée en C-Rate. Les batteries portables sont évaluées à 1C [1, 3-5]. Cela signifie que la batterie à 1000 mAh devra fournir 1000mA pendant une heure si elle se décharge à un régime 1C. Théoriquement, si la même batterie se déchargerait à 0.5C, elle devra fournir 500mA pendant deux heures. 1C est souvent désigné comme une décharge à une heure et 0.5C serait une décharge à deux heures. Lors du déchargement d'une batterie à différents C-Rate, une plus grande capacité de lecture est observée si la batterie est déchargée à un bas C-Rate et vice versa [4].

Bien que les batteries rechargeables offrent dans l'ensemble de bonnes capacités de chargement, le nombre de cycles (directement lié à la durée de vie de la batterie) est plus élevé si le courant de décharge est maintenu modéré. La figure 1.2 montre les pertes de capacité permanentes en utilisant des taux de décharge de 1C, 1.3C et 2C. Le test a été effectué sur une batterie lithium-ion.

Figure 1.2 : Cycle de vie d'une batterie Li-ion à différents taux de déchargement.¹ 1.2.1.2. Capacité de stockage de la Batterie

L'énergie emmagasinée dans une batterie correspond à sa capacité de stockage. Généralement, il se mesure en Ah (ampères-heures). Plus il y a de matériel d'électrolyte et d'électrodes dans la cellule, plus la capacité de stockage de la cellule est importante, et vice versa [1, 5, 8]. Ainsi, pour une technologie chimique donnée, une petite cellule a moins de capacité de stockage qu'une cellule plus grande, même si elles développent la même tension en circuit ouvert [3].

La capacité de stockage de la batterie, que les fabricants fournissent avec les spécifications de la batterie, est le produit d'heures multiplié par la valeur maximale du courant constant que cette batterie peut fournir à 20 O C, jusqu'à une tension prédéterminée par cellule [3, 4]. Pour cette raison, une capacité nominale de la batterie est toujours liée à la durée prévue de décharge.

1 Cette figure est extraie de l'adresse suivante : http://www.batteryuniversity.com/images/parttwo-31-1.jpg

t = (1.1)

I

Où, Q est la capacité de stockage de la batterie, en mAh ou en Ah. I est le courant débité en mA ou en A. t est le temps en heure que la batterie met pour une décharge complète.

En raison des réactions chimiques à l'intérieur de la batterie, la capacité de la batterie dépend des facteurs suivants [1, 3-5].

· L'amplitude du courant.

· La tension admissible aux bornes de la batterie.

· La température et d'autres facteurs.

La capacité disponible de la batterie est aussi fonction de son régime de décharge [3, 20]. Si une batterie est déchargée à un taux relativement plus élevé, la capacité disponible sera plus faible que prévu. Une explication mathématique de la raison de ce phénomène a été tout d'abord donnée par W. Peukert en 1897. Ce phénomène suit donc une loi pouvant être exprimée comme suit.

C = I^k . t (1.2)

Ici, C est la capacité de stockage de la batterie en Ah. I est le courant de décharge en A. t est le temps de décharge en heure et k est la constante de Peukert pour une technologie de batterie donnée. Suivant l'équation 1.2, Peukert a démontré que le temps de décharge d'une batterie pouvait être calculé en utilisant l'équation 1.3.

R

C (1.3)

C

t = _k .

? ?

I

? C ?

?? ??

R

Où, R est le battery hour rating mesuré en h. Pour une batterie idéale, k est égal à un et dans ce cas, la capacité devient indépendante du courant de décharge.

1.2.1.3. Résistance Interne

La résistance interne d'une batterie est définie comme l'opposition à la circulation du courant dans une batterie. Il y a deux composantes essentielles pour cette résistance: La résistance électronique et la résistance ionique. Leur effet combiné est dénommée la résistance effective totale.

La résistance électronique englobe la résistivité des matériaux utilisés tels que le métal de couverture et les composants internes. Elle dépend aussi de la façon dont les matériaux sont en contact les uns avec les autres. L'effet de cette résistance est très rapide et peut être détecté dans les millisecondes premières après qu'une batterie est placée sous charge [5, 8].

La résistance ionique est l'opposition au passage du courant dans la batterie due à des facteurs électrochimique divers tels que la conductivité de l'électrolyte, la mobilité des ions et la surface de l'électrode. Cet effet se produit plus lentement que la résistance électronique [5, 8, 9].

Un certain nombre de techniques sont disponibles pour mesurer la résistance interne de la batterie comme la méthode DC (courant continu) ou la méthode AC (courant alternatif) [8, 21]. Pendant la réalisation du test AC, il peut être remarqué que la résistance interne d'une batterie dépend de la fréquence [8, 9], qui entraine une expression complexe de la résistance de la batterie ou plus précisément de son impédance. Cette dernière peut être présentée à l'aide d'une représentation de type Nyquist (partie imaginaire vs partie réelle). Une forme générale d'une représentation de Nyquist de l'impédance électrochimique complexe d'une batterie plomb-acide à haute capacité est donnée par la figure 1.3 [8].

Figure 1.3 : Représentation de Nyquist d'une résistance interne d'une batterie Plomb-acide.

En générale, la résistance interne de la batterie augmente quand la température ambiante diminue. Ce résultat peut s'expliquer par le fait qu'à basse température les réactions électrochimiques qui ont lieu au sein de la batterie ralentissent. En conséquence, la mobilité des ions dans la batterie diminue. L'effet de la température sur la résistance effective totale d'une batterie en alcaline neuve, E91 AA, est représentée dans la figure 1.4.

Figure 1.4 : L'effet de la température sur la résistance effective totale [38]. 1.2.1.4. State of Heath (SoH)

Le SoH reflète un état général de la batterie (état de santé de la batterie) et sa capacité à fournir les performances spécifiées par rapport à une batterie neuve. Elle dépend de

plusieurs paramètres tels que l'acceptation de charge, la résistance interne, la tension, l'autodécharge, etc.

Pendant la durée de vie d'une batterie, sa santé (ses performances) tend à se détériorer progressivement à cause des changements physiques et chimiques irréversibles qui ont lieu lors de l'usage et du vieillissement, jusqu'à ce que finalement la batterie ne soit plus utilisable. Le SoH donne donc une indication sur la position de la batterie par rapport à son cycle de vie des batteries.

Le but du SoH est de fournir une indication sur le temps consommé de la durée de vie utile de la batterie ou le temps restant avant son remplacement. Par exemple, la connaissance du SoH aidera l'ingénieur à anticiper les problèmes, à faire le diagnostic des pannes ou à planifier le remplacement des batteries. Il s'agit essentiellement d'une fonction de suivi de l'évolution à long terme de la batterie.

Tout paramètre qui change considérablement avec l'âge, telle que l'impédance de cellule, peut être utilisée comme une base pour fournir une indication du SoH de la batterie. Comme l'indication du SoH est relative à la condition d'une nouvelle batterie, le système de mesure doit tenir un registre des conditions initiales ou au moins un ensemble de conditions standards. Ainsi, si l'impédance de la cellule est le paramètre surveillé, le système doit garder en mémoire comme une référence, la valeur initiale de l'impédance interne de la batterie avant sa première utilisation.

En pratique, certains fabricants des équipements de test estiment le SoH à partir des mesures d'un seul paramètre comme l'impédance de la cellule. Dans le but d'améliorer la pertinence de cette estimation, d'autres industriels mesurent plusieurs paramètres qui varient en fonction de l'âge de la batterie et font une estimation du SoH à travers une combinaison de ces facteurs. Parmi ces facteurs, on compte la capacité, la résistance interne, l'autodécharge, l'acceptation de charge, les capacités de décharge, la mobilité des électrolytes, le nombre de cycles, etc. Pour améliorer la qualité de cette estimation et surtout l'interprétation de la valeur du SoH, une pondération est appliquée à ces différents paramètres. Cette pondération des facteurs individuels est effectuée sur les bases de l'expérience, la chimie de la cellulaire et de l'application dans laquelle la batterie est utilisée.

Projet fin d'étude Page Zied Jelassi

De ce fait, on peut considérer que le SoH est une mesure subjective puisque différents fabricants modifient sa définition et ses facteurs à partir d'une variété de paramètres mesurables. De cet ensemble de mesures, ils les traduisent en SoH en fonction de leur propre ensemble de règles.

1.2.1.5. State of charge (SOC)

Le SoC (état de charge) est le pourcentage de la charge actuelle par rapport à la charge maximale prévue dans une batterie [5]. Le SoC est l'équivalent d'une jauge de carburant pour le pack de batterie dans un BEV (Battery Electric Vehicle), un HEV (Véhicule Electrique Hybride) ou un PHEV (Plug-in Hybrid Electric Vehicle).

L'indication du SoC n'est pas aussi simple que cela pourrait paraître et elle implique des mesures et une modélisation de la batterie [10]. Pour s'en convaincre, il suffit de considérer un exemple simple où la tension de la batterie V est mesurée, indexant ici une mémoire gérée par un microcontrôleur et dans laquelle serait stockée la relation V-SoC [11, 12]. La taille et la précision des systèmes d'indication de SoC dépendent du nombre de données stockées dans la relation V-SoC. Un autre problème concerne la tension de la batterie qui est fonction de différents paramètres comme la température, les taux de décharge et le vieillissement. Faire la table de correspondance entre la température et le taux décharge permet de résoudre les deux premières dépendances [13]. Par contre, le vieillissement de la batterie est un processus complexe qui implique de nombreux paramètres de la batterie. Le processus est trop complexe pour être abordé avec l'implémentation d'une simple table de recherche [13].

1.2.1.6. La durée de vie résiduelle de fonctionnement

Le SoC est habituellement affiché à l'utilisateur avec une représentation graphique en barre ou en pourcentage. Dans ce dernier cas 100% indique l'état plein de la batterie et 0% l'état vide. Pour un utilisateur, il est important de savoir combien de temps la batterie de son appareil portable (mobile, lecteur de musique ou vidéo, ...) sera en mesure de fournir une énergie suffisante pour assurer sa fonctionnalité. Malheureusement, une simple indication du SoC ne fournit pas suffisamment d'informations sur cet aspect. L'indication du temps restant d'utilisation sera la solution la plus attrayante pour l'utilisateur d'appareil portable et c'est ainsi qu'est apparue la durée de vie résiduelle pouvant être définie comme suit [10] :

Projet fin d'étude Page Zied Jelassi

« La durée de vie résiduelle est le temps estimé pour que la batterie puisse fournir du courant d'alimentation à un appareil portatif dans des conditions de décharge valable avant qu'il ne s'arrête de fonctionner. »

La durée de vie résiduelle peut être déduite de la capacité restante de deux façons, en fonction du type de charge. Premièrement, dans le cas d'un courant de charge, la capacité restante en mAh, donc exprimé en charge, est divisé par le courant absorbé en mA. Deuxièmement, dans le cas d'une puissance de charge, la capacité restante en mWh, donc exprimée en énergie, est divisée par la puissance absorbée en mW [10].

1.2.1.7. La durée de vie de la batterie

Pendant la durée de vie d'une batterie, sa santé (ses performances) tend à se détériorer progressivement à cause des changements physiques et chimiques irréversibles qui ont lieu en raison de l'usage et de l'âge, jusqu'à ce que finalement la batterie ne soit plus utilisable ou morte. Le SoH donne une indication sur le point qui a été atteint dans le cycle de vie des batteries et mesure sa condition par rapport à celle d'une batterie neuve.

Le vieillissement de la batterie est un processus complexe qui implique de nombreux paramètres de la batterie (par exemple l'impédance, la capacité, etc.), la plus importante étant la capacité. Pour illustrer ce phénomène, la figure 1.5 montre la capacité de décharge (Qd) d'une batterie Li-ion en fonction du nombre de cycle (C_n) [5]. La courbe de dégradation fait apparaître clairement un point de rupture ou de transfert à partir duquel le taux de dégradation de la batterie s'accroit. La position exacte du point de transfert varie selon le type de batterie et les conditions d'exploitation [14, 15].

Projet fin d'étude Page Zied Jelassi

Figure 1.5 : Diminution de Qd en fonction du nombre de cycle C_n.

1.2.2. Les types de Batteries

Après avoir exposé le principe de fonctionnement et les différents paramètres de performances d'une batterie, nous allons présenter les différents types de batteries en fonction de la technologie utilisée. Les batteries sont essentiellement classées en deux catégories :

· Les batteries primaires qui transforment de manière irréversible l'énergie chimique en énergie électrique. Quand l'offre initiale de réactifs est épuisée, l'énergie ne peut être facilement restaurée à la batterie par des moyens électriques. Des batteries comme les batteries zinc-carbone et alcalines font partie de cette catégorie.

· Les batteries secondaires qui peuvent être rechargées. Autrement dit, elles peuvent avoir leurs réactions chimiques inversées en fournissant de l'énergie électrique à la cellule, permettant ainsi le rétablissement de leur composition originale. Des batteries comme les batteries NiCd, NiMH, Li-Ion font partie de cette catégorie.

Les deux types de piles ont leurs avantages et leurs inconvénients. Une description détaillée de cette question peut être trouvée dans [16].

En raison de leur fonction de réutilisabilité et avec les avancés technologiques, les batteries secondaires sont de plus en plus utilisées pour un bon nombre d'applications portables comme les téléphones portables, les appareils photo portables, les ordinateurs

Projet fin d'étude Page Zied Jelassi

d'automobile, l'avionique, les missions spatiales, etc. C'est l'une des raisons pour laquelle nous allons décrire plus précisément ce type de batterie.

1.2.2.1. Les Batteries Secondaires

Les batteries secondaires sont essentiellement divisées en deux catégories : batterie à cellule humide et batterie à cellule sèche. Un exemple de cellule humide est la batterie plombacide. Ce type de batterie est fréquemment employé dans l'approvisionnement de grande puissance pour la téléphonie et les centres de calcul, le démarrage des véhicules à moteur, l'éclairage, etc. Comme exemple de batteries sèches, on peut citer les batteries NiCd (Nickel Cadmium), NiMH (Nickel Hydrure Métallique) et Li-Ion (Lithium Ion). Ces batteries sont couramment employées dans les appareils portables tels que les téléphones portables, appareils photo, ordinateurs portables, etc.

Les batteries NiCd sont composées d'une électrode positive Ni(OH)2/NiOOH et d'une électrode négative de Cadmium, Cd. L'électrolyte est une solution aqueuse d'hydroxyde de potassium (KOH). Le grand avantage des batteries NiCd est leur chargement rapide et leur performance à la décharge : il est possible de recharger une batterie en 10 minutes et de délivrer un grand courant lors de la décharge [1, 5, 10]. Les batteries NiCd ont une tension de fonctionnement moyenne de 1,2 V et elles peuvent être utilisées dans de nombreux appareils portables. Ils sont particulièrement utilisés dans les téléphones portables, les rasoirs, les caméscopes, les produits audio portables et les ordinateurs portables.

Les inconvénients des batteries NiCd sont leur densité d'énergie relativement faible et leur possible effet mémoire. Cet effet mémoire fait que la batterie ne pourra délivrer que la capacité utilisée pendant les cycles précédents de charge/décharge. En raison de cette incidence, de préférence, toute la capacité des batteries NiCd doit être utilisée pour chaque cycle de décharge afin d'éviter une diminution du SoC [10]. Un autre inconvénient est la présence de cadmium, qui représente un danger pour l'environnement. Cela peut conduire à une interdiction complète de batteries NiCd dans l'avenir.

La principale différence entre les batteries NiCd et NiMH est que dans une batterie NiMH un alliage d'hydrure métallique est utilisé pour l'électrode négative, au lieu de cadmium. De cette manière, une plus grande densité d'énergie est obtenue et de plus, l'effet de mémoire et l'impact sur l'environnement sont réduits. Les batteries NiMH peuvent d'ailleurs

Projet fin d'étude Page Zied Jelassi

remplacer les batteries NiCd sans modification du système dans lequel elles sont insérées car
elles ont la même tension moyenne d'exploitation par cellule, soit 1,2 V. Les applications ^oüse trouvent ce type de batterie sont les téléphones sans fil et mobiles, les rasoirs, les

caméscopes, les produits audio portables, les ordinateurs portables et les véhicules électriques hybrides (VEH).

Les inconvénients des batteries NiMH sont leur taux d'autodécharge relativement élevé et leur faible robustesse par rapport au sur-chargement, dernier point qui est aggravé par le fait qu'il est difficile de détecter l'état plein de la batterie pendant le processus de charge [5, 10].

Pour pallier aux inconvénients des deux autres batteries, une nouvelle technologie basée sur le Lithium Ion est proposée. Une représentation schématique générale d'une batterie Li-ion est donnée dans la figure 1.6 [17]. La cellule se compose de cinq régions (de la gauche vers la droite dans la figure 1.6) :

· un collecteur d'électrode négative actuelle faite de cuivre,

· une électrode composite poreuse à insertion négative,

· un séparateur poreux,

· une électrode composite poreuse à insertion positive,

· et un collecteur d'électrode positive fait d'aluminium.

Les électrodes composites sont réalisées à partir de particules de matière active maintenues ensemble par un liant et un matériau de remplissage approprié tel que le carbone noir. Lorsque la décharge est sur le point de commencer l'électrode négative est entièrement lithié et l'électrode positive est prête à accepter les ions lithium. Pendant la décharge, les ions lithium quittent les particules de l'électrode négative et entrent dans la phase de solution, alors que dans la région de l'électrode positive, les ions lithium, dans la phase de solution s'intercalent dans les particules LiCoO2. Il en résulte un gradient de concentration, qui pousse les ions de lithium de l'électrode négative vers l'électrode positive. La tension de la cellule baisse pendant la décharge. La cellule est considérée comme ayant atteint la fin de la décharge lorsque sa tension chute d'environ 3,0 V [17].

Projet fin d'étude Page Zied Jelassi

Figure 1.6 : Représentation schématique d'une batterie Li-ion.

L'électrode positive est faite d'oxydes de lithium (par exemple LiCoO2, LiNiO2 or LiMn2O4) pour le stockage des ions de lithium. L'électrode négative en carbone est constituée de graphite ou du coke de pétrole. L'électrolyte est généralement un sel dissous dans un solvant organique. Mais, les batteries avec d'autres solvants tels que le carbonate de propylène existent également. Un exemple de sel utilisé est le LiPF6.

La tension de fonctionnement des batteries Li-ion est critique et la surcharge/décharge provoque un vieillissement rapide de la batterie, pouvant jusqu'à provoquer l'incendie ou l'explosion de la batterie. Ainsi, un circuit de protection électronique est nécessaire pour gérer correctement la charge et décharge de la batterie. Les applications utilisant ce type de batteries sont les téléphones portables, les rasoirs, les caméscopes, les produits audio portables, les ordinateurs portables, etc.

Plusieurs types de systèmes de batteries rechargeables ont été abordés plus haut. Leurs principales caractéristiques sont résumés dans le Tableau 1.1 [10, 18].

Parmi les batteries de type secondaire, la batterie Li-Ion est la plus utilisée, comme le montre la figure suivante, associée à la part de marché de chaque sèche rechargeable [19].

Projet fin d'étude Page Zied Jelassi

Figure 1.7 : Statistique de la demande des batteries rechargeables.

1.2.2.2. Quelle est la meileure batterie

Pour faire une évaluation objective des performances de chacune de ces batteries, nous allons utiliser quelques unes des principales caractéristiques que sont :

· La haute densité énergétique.

· La charge rapide et sure de la batterie.

· La décharge sure et efficace de la batterie.

· La haute FEM (Force Electromotrice).

· La haute efficacité de courant.

· La haute efficacité électrostatique.

· La longue vie avec conservation des performances.

· La faible autodécharge.

· Le faible entretien exigé.

· Le faible impact écologique.

Pris séparément, chacune des caractéristiques décrites ci-dessus pourra être effectivement obtenue, mais il sera impossible de toutes les réunir sur une seule et même batterie [1, 5, 10, 18]. En effet, certaines batteries peuvent être conçues pour une petite taille et une longue utilisation, mais elles ont un cycle de vie limité. Une autre peut être conçut pour augmenter sa durée de vie, mais cela se fera au détriment de sa taille qui pourra être

Projet fin d'étude Page Zied Jelassi

encombrante. Un tiers peut avoir une densité énergétique élevée et une longue durée de vie, au détriment du coût qui sera élevé et qui réduit le nombre d'application cible.

De même, une batterie au lithium peut être conçue pour une densité d'énergie maximale, mais sa sécurité pourrait être compromise. Le Tableau 1.1 [10, 18] résume les points forts et les limites des systèmes de batteries populaires actuellement utilisés.

Système de Batterie	NiCd	NiMH		Li-ion	Tension moyenne de fonctionnement (V)
1.2	1.2	3.6		Energie Spécifique (Wh/Kg)
30-60	50-90	90-115		Autodécharge/mois @ 20 oC
10-20	20-30	1-10		Cycle de vie
300-700	300-600	500-1000		Plage de Température (^oC)
-20-50	-20-50	-20-50		Exigence de Maintenance (jours)
30-60	60-90	Théoriquement pas d'exigence de maintenance		Sécurité
Thermiquement Stable	Thermiquement Stable	Circuit de Protection Obligatoire		Commercialisation depuis
1950	1990	1991		Temps de chargement (h)
1	2-4	1.5-3		Tolérance de Surcharge
Moyenne	faible	Non Toléré

Projet fin d'étude Page Zied Jelassi

Toxicité

élevée

Moyenne

faible

Tableau 1.1: Caractéristiques des batteries rechargeables actuellement utilisées.

1.3. Battery Management System (BMS)

Le système de gestion d'une batterie (BMS) est habituellement employé dans les batteries secondaires. Il s'agit d'un dispositif électronique qui gère une batterie rechargeable. La tâche fondamentale d'un BMS est de veiller à ce qu'une utilisation optimale de l'énergie soit faite à l'intérieur de la batterie équipant le produit portable et que le risque de dommages de la batterie soit empêché [5]. L'utilisation d'un BMS conduira à une durée de vie plus importante et à une exploitation plus sûre de batterie [6].

Un BMS peut effectuer plusieurs opérations comme la détermination de l'état de la batterie, la gestion électrique, la gestion de la sécurité, etc. En résumé, les caractéristiques d'un BMS sont dépendantes de l'application [7]. En général, les fonctionnalités du BMS peuvent être découpées en tâches suivantes [6, 7] :

· Acquisition de données.

· Détermination de l'état de la batterie.

· Gestion électrique.

· Gestion de la sécurité.

· Gestion thermique.

· Communication

Projet fin d'étude Page Zied Jelassi

Figure 1.8 : Schéma du BMS.

La figure 1.8 donne une vision synoptique d'un BMS dont on donne brièvement les fonctionnalités de chaque bloc.

1.3.1. Acquisition de données

Tous les algorithmes de BMS utilisent des données mesurées sur la batterie comme information d'entrée. Par conséquent, la précision du système d'acquisition, qui est fonction des paramètres système tels que le taux d'échantillonnage, la résolution du convertisseur, la réponse du filtre de front end, etc. est très importante. Un choix approprié de ces paramètres dépend de l'application ciblée. Par exemple, les taux d'échantillonnage dans les applications de VE (Véhicules Electriques) ou de HEV (Véhicules Electriques Hybrides) sont plus rapides que 1 échantillon par seconde, alors que dans le cas d'UPS (alimentation en puissance sans interruption) sont en dessous de 0,2 échantillons par seconde [5 -8, 10].

1.3.2. Détermination de l'état de la batterie

L'état de la batterie est utilisé par le BMS comme paramètre d'entrée et de plus, c'est un paramètre important pour l'utilisateur. Cet indicateur peut être utilisé pour estimer l'autonomie d'un véhicule électrique ou la durée de vie de la batterie.

L'état de la batterie peut être décrit par les deux paramètres SoC et SoH [5-8]. Ces deux paramètres influencent les paramètres internes de la batterie comme le montre la figure

Projet fin d'étude Page Zied Jelassi

1.9. Inversement, le SoC et le SoH sont fonction des paramètres internes et externes de la batterie (température, caractéristiques des charges, etc.). C'est pourquoi la connaissance de ces paramètres peut être employée pour estimer le SoC et SoH de batterie à un instant donné [5- 8].

Figure 1.9: Flux d'état de la batterie.

1.3.3. Gestion électrique

La gestion électrique contrôle le processus de charge et de décharge de la batterie. Les tâches suivantes doivent être remplies.

· Le contrôle du processus de chargement.

· Le contrôle du processus de décharge.

· Equilibrage de cellule.

Le processus de contrôle de charge et la limitation de la décharge dépendent fortement de la technologie de batterie employée [5-8, 10].

1.3.4. Gestion de la sécuritéLa gestion de la sécurité protège la batterie contre les conditions d'exploitation

critiques. Par exemple, dans le cas d'un véhicule électrique, les tâches du système de gestion de la sécurité sont les suivantes:

· La protection contre la décharge profonde.

· La protection des cellules individuelles contre la surcharge/décharge Projet fin d'étude Page Zied Jelassi

· La protection contre la température (emballement thermique).

· La batterie s'éteint en cas d'accident.

1.3.5. Gestion thermique

Un système de gestion thermique est nécessaire pour les applications à puissance élevée et pour les batteries à haute température. Il doit assurer les tâches suivantes:

· Egalisation de la température entre les cellules.

· Refroidissement/chauffage de la batterie [6, 7].

Par conséquent, des systèmes avec du liquide ou de l'air (ventilateur) sont utilisés. Le problème majeur est le transfert de chaleur de l'intérieur des cellules de la batterie vers l'extérieur, car la résistance thermique de l'électrolyte et du boîtier de cellules en plastique est assez élevée.

1.3.6. Communication

La communication entre le BMS et d'autres dispositifs est une autre tâche importante du BMS. Selon l'application, différents systèmes d'interface peuvent être utilisés pour l'échange de données. Voici quelques exemples possibles :

· Signaux analogiques.

· signaux modulés par la modulation de largeur d'impulsion.

· Le bus CAN (Controller Area Network) ou le bus I²C (Inter-Integrated Circuit).

Selon l'application, le BMS doit contenir plusieurs caractéristiques. L'optimisation de ces caractéristiques est en fonction de la technologie de batteries et l'application ciblée [6, 7].

Projet fin d'étude Page Zied Jelassi

1.4. Conclusion

Ce présent chapitre représente le cadre générale de ce rapport. On a défini au cours les terminologies qui ont relation avec les batteries Li-Ion, tels que le SOC, le C-rate, etc. En plus, on s'est intéressé au système de gestion de batteries qui représente une entité indispensable pour la technologie étudiée. On a présenté ses principales fonctionnalités.

Afin de mieux comprendre les batteries Li-ion, le chapitre suivant présentera leurs comportements électriques et électrochimiques via l'étude de trois modèles simulant la décharge.

Projet fin d'étude Page Zied Jelassi

Chapitre 2: Modélisation des batteries

Lithium Ion

Projet fin d'étude Page Zied Jelassi

2.1. Introduction

Ces dernières années, la préservation de l'environnement et le développement durable sont devenus deux thèmes majeurs de notre société. De plus, on voit apparaître une multiplication des applications qui fonctionnent avec batterie telles que les voitures électriques (EV), les voitures hybrides (HEV), les applications portables comme la téléphonie mobile et sans fil, les caméscopes, les produits audio portables, etc. Ce point va à l'encontre du développement durable et de la préservation de l'environnement, et la seule façon de faire converger ces deux points serait de minimiser la consommation d'énergie de ces appareils et de rendre les batteries plus efficaces énergétiquement.

Différentes technologies ont été étudiées pour mener à bien cette action, et de part leur densité énergétique élevée et leur durée de vie importante, les batteries Lithium-Ion semblent les plus adaptées. D'ailleurs, c'est la raison pour laquelle elles sont de plus en plus employées dans tout type d'application portable. Afin d'étudier et de simuler leurs comportements, il est nécessaire de développer des modèles tenant compte des caractéristiques technologiques.

La modélisation des batteries n'est pas nouvelle en soi, mais avec la tendance actuelle, elle est devenue primordiale pour le développement d'applications efficaces et plus écologiques. En particulier, elle permet d'analyser les phénomènes électrochimiques qui auront lieu au sein de la batterie et de prévoir son comportement. En fonction de la granularité du modèle, elle simule sa réponse tout en négligeant certains facteurs (variation de la température, C-rate...). Le modèle de batterie peut être :

· un modèle expérimental,

· un modèle électrochimique,

· ou un modèle basé sur un circuit électrique.

Pour mieux comprendre le comportement électrique et électrochimique de la batterie Lithium-Ion et pour présenter les travaux de modélisation de ce type de batterie, ce chapitre commencera par présenter sa composition chimique et métallique. Ensuite, on s'intéressera à l'étude de trois différents types de modèles, dont on fera une comparaison en termes de performances, notamment par rapport à sa capacité à reproduire les phénomènes réels.

Projet fin d'étude Page Zied Jelassi

2.2. La batterie Lithium-Ion

Commercialisée pour la première fois par Sony Energitech en 1991, la batterie lithium-ion occupe aujourd'hui une place prédominante sur le marché de l'électronique portable. Ses principaux avantages sont une densité d'énergie élevée (densité massique deux à cinq fois plus que le Ni-MH par exemple) ainsi que l'absence d'effet mémoire. Enfin, l'autodécharge est relativement faible par rapport à d'autres batteries. Cependant le coût reste important et cantonne le lithium aux systèmes de petite taille [26].

Ce type de batterie est entièrement solide, ce qui annule le risque d'explosion. En plus, elle ne présente pas de polluant majeur dans sa composition, sauf si l'oxyde de vanadium (V2O5) est utilisé. Son inconvénient principal est que le fonctionnement optimal est obtenu pour une température élevée.

Capeeinxrinale (rneh)

6000

4500

4000

5500

5000

3500

3000

2500

2000

1500

1000

500

0

0 25 50 75 100 125 150 175

Gammes d'autres marques Masse ( g )

MP 144350

VL34480

Saft

MP 174865 / VL34570

MP 176065

Figure 2.1: Classification des batteries suivant leurs densités énergétiques²

La figure précédente représente une classification des batteries (Li-Ion ou non) disponibles sur le marché suivant leurs densités énergétiques.

2.3. La batterie VL34480

La batterie que nous allons étudier et modéliser fait partie de la série VL, conçu pour une autonomie et une durée de vie étendue. Elle est dédiée au système mobile et elle est opérationnelle sur un large intervalle de température [-50°C, 60°C]. Elle est connue par sa haute densité énergétique qui est de l'ordre de 380 Wh/l ou encore 160 Wh/Kg. Elle délivre

2 Figure extraite d'une présentation de Saft.

Projet fin d'étude Page Zied Jelassi

une tension de 3.7V et possède une capacité typique de 4.4Ah pour un courant de décharge égal à 0.9A, une température de 20°C et une tension de coupure de 2.5V.

Figure 2.2 : La batterie VL34480 [annexe1]

2.3.1. Le système électrochimique de la VL34480

Dans ce paragraphe, la nature de différentes parties de la batterie étudiée sera spécifiée. L'électrode positive est fabriquée à partir d'oxyde mixte de cobalt et de lithium ou encore appelé oxyde de cobalt lithié (LiCoO2) [22]. Cette structure solide est lamellaire, pouvant être représentée comme des couches d'octaèdres CoO6 d'atomes de cobalt et d'oxygène entre lesquels s'insèrent des atomes de lithium.

C'est la structure lamellaire du LiCoO2 qui lui permet de jouer efficacement le rôle de cathode dans les batteries au lithium :

· En charge, la cathode LiCoO2 est reliée à la borne positive d'un générateur, permettant de libérer des cations Li+ dans l'électrolyte en direction de l'anode en carbone, elle-même reliée à la borne négative du générateur : l'anode << s'épaissit >> d'un dépôt de lithium venu de la cathode à travers l'électrolyte, tandis que la cathode se << vide >> de son lithium entre les couches d'octaèdres CoO6.

· En décharge, la cathode se << reconstitue >> en fixant des cations Li+ de l'électrolyte qui viennent s'insérer entre les couches d'octaèdres CoO6 en absorbant un électron tandis que des cations Li+ passent en solution dans l'électrolyte du côté de l'anode en libérant un électron : ces réactions sont à l'origine de la force électromotrice de ce type de batterie.

Projet fin d'étude Page Zied Jelassi

L'électrolyte est une solution d'hexafluorophosphate de Lithium (LiPF6) dans un mélange de solvants organiques, à savoir : Etylène Carbonate (EC) + DiMéthyl Carbonate (DMC) + DiEythyl Carbonate (DEC) + Ethyl Acétate (EA) [22].

2.3.2. La composition de la VL34480

Le tableau suivant résume la composition de la batterie désignée, en termes de métaux, polymère et autres.

Métaux	%	Plastiques	%	Autres		%	Cuivre, acier, aluminium
31	Polypropylène	10	- Lithium cobaltite	29
			- Carbone	16
			- Solvants organiques	13
			- Sels	1
			- Lithium métal	0

Tableau 2.1 : Composition de la batterie VL34480

2.4. La modélisation des batteries Lithium-Ion

Trois modèles vont être présentés dans cette partie, où les deux premiers s'inspirent des travaux de Shepherd, qui a développé une équation qui décrit le comportement électrochimique de la batterie en fonction de la tension aux bornes de la batterie, la tension en circuit ouvert, la résistance interne, le courant de décharge et l'état de charge. Cette équation décrit à la fois la charge et la décharge des batteries du premier et du second type. Ce modèle est intéressent, mais il souffre du problème de boucle algébrique. C'est la raison pour laquelle beaucoup de chercheurs travaillent au développement de modèles à une seule variable, en particulier le SOC. Ce sont des modèles plus simples mais qui ne présentent pas de problème de boucle algébrique. L'équation suivante est l'équation de base développée dans les travaux de C. M. Shepherd [23]. Les termes de cette équation seront étudiés de prés lors de la présentation des différents modèles.

Projet fin d'étude Page Zied Jelassi

A ( BQ it ) Cit

-1

+ exp - - (2.1)

? Q it

E E _s K

= -

? Q ?

? ? i

- ?

Ni

Le troisième modèle est un modèle plus complexe. Il se base sur un circuit électrique encore plus proche de la réalité et une série d'équations électrochimiques. Il prend en considération la dépendance à la température et au taux de décharge.

2.4.1. Modèle d'Olivier Tremblay et Louis-A. Dessaint

2.4.1.1. Présentation du modèle

Ce modèle est basé sur les travaux d'Olivier Tremblay, Louis-A. Dessaint et AbdelIllah Dekkiche de l'école de Technologie Supérieure de l'Université du Québec, Montréal [24]. Ce modèle de batterie est facile à reprendre sur un logiciel de simulation dynamique. Dans notre cas nous avons utilisé Matlab. Ce modèle utilise uniquement l'état de charge de la batterie (SOC) comme une variable d'état afin d'éviter le problème de boucle algébrique. Il est démontré que ce modèle, composé d'une source de tension commandée en série avec une résistance, peut représenter avec précision quatre types de batteries (la batterie Lithium Ion, la batterie Nickel Cadmium(NiCd), la batterie Nickel Hydrure métallique (NiMH) et la batterie plomb acide). Les paramètres du modèle peuvent être facilement extraits à partir des courbes de décharge fournis par le constructeur. Une méthode d'extraction de ces paramètres sera décrite par la suite. Le modèle et l'extraction de paramètres seront validés par une superposition des résultats de simulation avec les courbes de décharge réelles données dans les spécifications constructeurs de la batterie.

Figure 2.3 : Modèle de batterie Lithium-Ion présenté dans [24]

Projet fin d'étude Page Zied Jelassi

Comme déjà annoncé au début de ce paragraphe, il existe trois grandes catégories de modèle de batterie :

· Modèle expérimental

· Modèle électrochimique

· Modèle basé sur un circuit électrique.

Les deux premiers modèles ne sont pas adaptés pour représenter un modèle dynamique basé sur l'estimation du SOC de la batterie [24]. Par contre, la troisième catégorie peut représenter ses caractéristiques électriques. La plupart des modèles appartenant à cette dernière catégorie se base sur un circuit fait d'une source de tension idéale en série avec une résistance interne, mais ils ne prennent pas en considération le SOC de la batterie. D'autres se basent sur la tension en circuit ouvert en série avec une résistance et un circuit RC en parallèle, la figure suivante illustre ce type de modèle (ce dernier cas sera vu de prés avec le modèle dynamique de Lijun Gao, Shengyi Liu et Roger A. Douger).

Figure 02.4 : Le circuit électrique de base formé par tension en circuit ouvert en série avec une
résistance et un circuit RC en parallèle.

Le modèle que nous allons étudier se base sur la figure 2.3. Il s'articule sur une résistance constante avec une source de tension contrôlée en série. Cette dernière est décrite par l'équation 2 non linéaire.

? Q ?

E E K

= 0 - ? ? + A ( B it

exp ) (2.1)

- ·

? Q it

- ?

Projet fin d'étude Page Zied Jelassi

où E est la tension sans charge (V), E0 est la tension constante de la batterie (V), K est la tension de polarisation (V), Q est la capacité de la batterie (Ah), it est la charge actuelle de la batterie (Ah), A est l'amplitude de la zone exponentielle (V), et B est l'inverse de la constante de temps de la zone exponentielle (Ah)^-1.

En se basant sur le circuit du modèle, la tension de batterie sera donc :

Vbatt = E - R · i (2.2)

Où _Vbatt est la tension de la batterie en (V), R est sa résistance interne en (?) et i est son courant en (A).

? Q ?

Le deuxième terme de l'équation 1, à savoir K ? - , décrit le comportement réel

? i ? Q it ?

de la batterie ; si elle est complètement déchargée, alors i sera égale à zéro et _Vbatt tendra vers E0. C'est le même comportement d'une batterie réelle, mais ça génère la non stabilité de la simulation.

Ce modèle présente un terme dépendant uniquement de la charge actuelle de la batterie. Ce qui signifie qu'en cas de décharge complète de la batterie, sa tension sera prés de zéro. Mais, ce modèle donne des résultats précis et représente également le comportement de la batterie. Ce modèle se base sur une série d'hypothèses et de limitations. Commençons par les hypothèses :

· La résistance interne est supposée constante durant les cycles de charge/décharge et ne dépend pas de l'amplitude du courant.

· Les paramètres du modèle sont déduits des courbes de décharge et sont supposés être les mêmes pour la charge.

· On ne considère pas l'effet de Peukert (la capacité de la batterie ne varie pas en fonction de l'amplitude du courant).

· La température ne perturbe pas le comportement du modèle.

· On ne considère pas l'autodécharge et l'effet mémoire.

Projet fin d'étude Page Zied Jelassi

Les limites du modèle sont :

· Le minimum de E est 0 V et le maximum de Vbatt est non limité.

· Le minimum de Q est 0 Ah et de même son maximum n'est pas limité. Par conséquent, le maximum du SOC peut être supérieur à 100% si la batterie est surchargée.

2.4.1.2. Extraction des paramètres du modèle

L'extraction des paramètres du modèle utilise l'exploitation de la caractéristique de décharge de la batterie qui figure dans sa datasheet (annexe 1). La figure suivante présente la caractéristique de décharge à un régime de 0.2C et à 0.9A comme courant de décharge.

Figure 2.5 : Caractéristique de décharge de la batterie VL34480 pour C/5(0.9A)

Sur cette figure, il apparaît clairement trois zones. La première partie correspond à la mise en service de la batterie et montre une chute de tension exponentielle de courte durée à partir d'une batterie complètement chargée. Selon le type de batterie, cette zone est plus ou moins large. La deuxième partie, représentée par une courbe plus ou moins affine, correspond à la charge qui peut être extraite de la batterie jusqu'à ce que la tension tombe en dessous de la tension nominale de la batterie. Enfin, la troisième représente la décharge totale de la batterie, lorsque la tension chute rapidement. L'objectif est maintenant d'extraire les paramètres du modèle à partir de cette courbe de décharge et de certains éléments donnés dans la description technique de la batterie :

Projet fin d'étude Page Zied Jelassi

· La résistance interne : les techniques de mesure de ce paramètre ont déjà été présentées dans le premier chapitre. Mais comme sa valeur est généralement précisée par les fabricants, il est possible de l'obtenir directement à partir des datasheets. Toutefois, si elle n'est pas donnée, il existe une relation permettant de l'obtenir, à savoir

1 ç (2.3)

-

R V

= nom Q

·

0 .2 · nom

Où R est la résistance interne (?), _Vnom est la tension à la fin de la zone nominale (V), _Qnom est la capacité à la fin de la zone nominale (Ah) et ç est l'efficacité de la batterie.

Pour la détermination des autres paramètres, trois points particuliers apparaissant sur la figure 2.5 sont utilisés. La tension de charge complète _(Vfull) située à l'intersection de la caractéristique de décharge et l'axe de tension, la fin de la zone exponentielle (la tension Vexp et la capacité _Qexp) et la fin de la zone nominale (la tension _Vnom et la capacité Q nom).

En utilisant les deux premiers points, on arrive a déterminé la partie exponentielle dont la forme mathématique est la suivante ( A exp(-B· it) ) :

· A représente la chute de tension durant la partie exponentielle (V), donc

A = Vfull - Vexp (2.4)

· B est la capacité mesurée à la fin de la zone exponentielle (Ah)^-1,

3

B = (2.5)

Qexp

· La tension de polarisation K peut être déduite à partir de l'équation 2, le premier et le dernier point de la figure 3, alors

V l V A

- + (exp( - · ) - 1)) · ( - )

B Q Q Q

ful nom nom nom

K = (2.6)

Qnom

· La tension constante E0 est déduite ainsi

E 0 = Vfull + K + Ri - A (2.8)

Projet fin d'étude Page Zied Jelassi

Cette approche est très générale et elle peut être appliquée à n'importe quel type de batterie.

2.4.1.3. La validation du modèle

Une fois les paramètres extraits, il est important de valider le modèle, pour cela on donne sur la même figure la caractéristique de décharge fournie par Saft et le résultat de ce modèle. On voit bien que la courbe du modèle suit la courbe de la datasheet. Le fait de voir que la courbe du modèle descend à zéro volt pour atteindre la valeur de cinq heures de décharge est déjà expliqué au niveau de la numération des limitations du modèle. A la décharge totale de la batterie _Vbatt tend vers E0 mais pour ce modèle _Vbatt sera au voisinage de zéro.

Figure 2.6 : Comparaison directe entre la caractéristique de décharge (0.9A, 0.2C) et la caractéristique
générée par le modèle.

2.4.2. Le modèle de MathWorks

2.4.2.1. Présentation du modèle

Le deuxième modèle est le modèle proposé par l'environnement MATLAB/SIMULINK et développé par la société << The MathWorks ». Il s'agit d'un modèle proposé dans une démonstration appelée << power_battery ». Dans cette étude, seul le modèle basé sur les travaux présentés dans [23] et [24], a été utilisé. La figure suivante donne le modèle SIMULINK de la batterie avec son environnement de travail.

Projet fin d'étude Page Zied Jelassi

La partie qui nous intéresse

Figure 2.7 : Le modèle de MathWorks

Contrairement au premier modèle, celui-ci attribue une équation différente à chaque type de batterie, et en plus il considère deux équations : l'une associée à la charge et l'autre à la décharge. On donne ici les différentes équations à la charge et à la décharge en fonction des différents types de batteries :

· Modèle de batterie plomb-acide

o équation liée à la décharge (i* > 0)

f₁

- 1[Sel(ss)) 0 Exp ?

(2.9)

( it , i * , i , Exp) = E₀ -K · Q · 1 * - K· · it + Laplace

Q it

.

Q- itQ-

o équation liée à la charge (i* < 0)

f ₂ ( it , i * , i , Exp) = E₀ -K · Q · i* K Q · it + Laplace-1[Exp(s) 1)

it + 0. 1

Sel(s ) s

·

(2.11)

QQ-

it

· Modèle de batterie Lithium-Ion

o équation liée à la décharge (i* > 0)

f_lot , i * , 0= E 0-K· Q i * -K· ^Q· it + A · exp( - B· it) (2.11)

it

Q- itQ-

o équation liée à la charge (i* < 0)

Projet fin d'étude Page Zied Jelassi

Q Q

f it i i E K

2 ( , * , ) 0

= - · · - ·

i K

* · it + A · exp( - B · it)

it + 0. 1 · Q Q - it

(02.12)

· Modèle de batterie Nickel-Cadmium et Nickel-Hydrure Métallique o équation liée à la décharge (i* > 0)

Exp s

( ) ?

1 ? ·

- ? 0 ?

? Sel s

( ) ?

f₁

Q Q

( , * , , )

it i i Exp E K

= - · · - ·

i K

* · +

it Laplace

⁰ Q it

- (2.13)

^{Q it}

^-

^{o équation liée à la charge (i*< 0)}

^f ₂ ^{( it , i * , i , Exp ) = E} ₀ ^{-K · Q · i* K Q ·it + Laplace-1? Exp(s) 1}

0 . 1 Q Q it

it + ·

-

^(2.14)

? Sel s s ( ) ?

oùAEB_attu est la tension non linéaire (V), E0 est la tension constante (V), Exp(s) estla a dynamique de la zone exponentielle (V), Sel(s) est représente le mode de la batterie (Sel(s) = 0 quand la batterie se décharge et Sel(s) = 1 quand elle se charge), K est la constante de polarisation (Ah^-1) ou larésistancee de polarisation (Ohms), i* est la dynamique du courantà a basse fréquence (A), i est le courant de la batterie (A), it est la capacité instantanée (Ah), Qest t la capacité maximale de la batterie(Ah), A est la tension exponentielle (V) et B est la capacité exponentielle (Ah^-1). La figure suivante donne la structure interne dumodèlee :

Figure 2.8 : Modèle MathWorks

Projet fin d'étudee Page Zied Jelassi

2.4.2.2. Détermination des paramètres du modèle

La configuration du modèle se fait à partir de l'environnement SIMULINK où un nombre limité de paramètres est accessible. La figure suivante donne l'interface graphique associée au modèle d'une batterie Ni-MH.

Figure 2.9 : Fenêtre de configuration du modèle

La détermination des paramètres de ce modèle se fait de la même manière que pour le modèle précédant. On se base sur les même trois points : le point de chargement total, la fin de la zone exponentielle et la fin de la zone nominale. Une fois la configuration de ce modèle terminée, il est possible de faire apparaître la courbe de décharge de la batterie ainsi modélisée en ouvrant une fenêtre spécifique « View Discharge Characteristecs » comme montre la figure 2.10.

Projet fin d'étude Page Zied Jelassi

Figure 02.10 : la fenêtre View Discharge Characteristics

Dans cette fenêtre, il faut donner les différents courants de décharge. Dès la sélection de la commande de dessin activée, deux figures apparaissent : la première donne les différentes zones dans la caractéristique de décharge à 0.2C (0.9A) (voir la figure 2.5) et la deuxième présente les différentes courbes de décharge à différentes courants de décharge (Voir la figure suivante).

Figure 2.11 : Courbes de décharge fournies par le deuxième modèle pour différents courants de
décharge

2.4.2.3. Validation du modèle « MathWorks »

Pour la validation du modèle, nous proposons une comparaison entre les courbes de décharge issues du modèle et les courbes de décharges fournies par le constructeur.

Projet fin d'étude Page Zied Jelassi

Malheureusement, il n'est pas possible de superposer ces deux résultats et nous avons donc fait une comparaison des deux figures.

(a) (b)

Figure 2.12 : La comparaison des résultats du modèle de MathWorks et les caractéristiques fournies par
Saft. (a) la caractéristique de décharge de la VL34480 extraite de la datasheet. (b) la sortie du modèle de
MathWorks.

2.4.3. Modèle de L. Gao

2.4.3.1. Présentation du modèle

Ce modèle est basé sur les travaux présentés dans [25]. Il propose un modèle dynamique d'une batterie lithium ion qui tient en compte du potentiel d'équilibre non linéaire, de la dépendance en taux de décharge et en température, des effets thermiques et de la réponse à la demande de puissance transitoire. Le modèle est basé sur des données accessibles aux publics tels que les fiches de données (datasheet) fournies par les fabricants. L'objectif de ce modèle est de reproduire les propriétés électriques et thermiques de la batterie. A ce niveau, on rapproche tous les processus électrochimiques et électrothermiques de la batterie de façon uniforme tout en ignorant les variations spatiales des concentrations, les distributions de phase et de potentiel. Ces hypothèses permettent la modélisation de la batterie en utilisant les paramètres extraits à partir des données expérimentales. La méthode d'extraction des paramètres sera discutée ci-dessous.

Ce modèle s'appui sur les courbes de décharge à courant constant et à température constante. La figure 2.13 représente ces courbes extraites de la datasheet de la batterie.

Projet fin d'étude Page Zied Jelassi

(a) (b)

Figure 2.13 : Les sources de données du modèle de L. Gao. (a) Les caractéristiques de décharge de la
VL34480 à 20°C pour différents courant de décharge. (b) Les caractéristiques de décharge de la
VL34480 à 0.9A-0.2C pour différentes température.

De plus, ce modèle se réfère à un circuit électrique caractérisé par trois paramètres qui

sont:

· Un potentiel d'équilibre E

· Une résistance interne Rint, divisé en deux composantes R1 et R2

· Une capacité effective qui caractérise la réponse transitoire de la batterie. Le schéma électrique mettant en oeuvre ces composants est illustré par la figure 2.14.

Figure 2.14 : Schéma électrique du modèle de L.GAO [25]

Projet fin d'étude Page Zied Jelassi

2.4.3.2. Extraction des paramètres du modèle

Le potentiel d'équilibre E, appelé aussi tension à circuit ouvert, dépend de la température et de la quantité de matière active disponible dans les électrodes, qui peut être spécifié par l'état de décharge (SOD). La capacité de décharge dépend encore du régime de décharge et de la température. Alors, on admet une expression générique de ce potentiel : E (i, T, t).

Les équations suivantes décrivent l'état de décharge, la tension de la batterie et son potentiel d'équilibre :

SOD

1 t

[ i t T t t

( ), ( ), = ? 0 á

] [ i t ] [ T t ] i t dt

( ) · â ( ) ( )

· (2.7)

Q

r

n

k v i t T t t [ ( ) , ( ), ] = ? c SOD i t T t t · [ ( ), ( ) , ] ( ) + Ä E T k

(2.8)

k = 0

E i t T t t

[ ( ), ( ), ] [ ( ), ( ), ]

= v i t T t t R _int i t

- ( ) (2.9)

où ck est le ^kième coefficient du polynôme de la caractéristique de référence (la courbe de décharge à C/5 rate (0.9A) et à 20°C), Q_r est la capacité de la batterie à la tension de coupure (2.5V) sur la caractéristique de référence, á [i(t)J est le facteur qui décrit la variation du taux de charge/décharge, â [Ti(t)J est le facteur qui décrit la variation de la température et ÄE(T) est potentiel de correction de la dépendance en température.

Comme présente l'équation 2.15, le SOD dépend de á [i(t)J, â [Ti(t)J, ÄE(T) et Q_r. Ce dernier peut être identifié directement sur la datasheet dans le champ typical capacity. Les techniques de détermination des autres termes seront décrites dans les paragraphes suivants.

2.4.3.2.1. Détermination du facteur á [i(t)J

La méthode du calcul du facteur á [i(t)J pour les courbes de décharge s'articule principalement sur les caractéristiques de décharge à 20°C. Ce facteur se déduit de façon relatif ; par rapport à la courbe de référence. La figure suivante illustre la méthodologie permettant la détermination de ce facteur pour un courant de décharge de 8.8A.

Projet fin d'étude Page Zied Jelassi

0,4)F,

a b
ba

Figure 2.15: Détermination du facteur á [i(t)] pour un courent de décharge de 8.8A par rapport à un
courent de référence de 0.9A

La détermination du rate factor utilise la forme polynomiale de la courbe de référence et la courbe de décharge. La différence à l'origine de l'axe des abscisses entre ces deux représentations est égale à (i_r-i) _Rint, où, i_r, i et _Rint représentent respectivement le courant de référence (0.9A), le courant de décharge pour lequel on calcule le rate factor et la résistance interne. Le terme b représente la capacité maximale pour la décharge de référence. Le terme a représente l'intersection entre la forme polynomiale de la courbe de référence atténuée par la quantité (i_r-i) _Rint et la droite de la tension de coupure y=2.5V. La valeur du rate factor est définit par l'expression suivante :

a

á( i ) = (2.10)

b

Projet fin d'étude Page Zied Jelassi

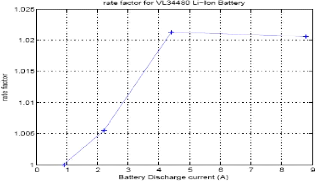
Figure 2.016: Rate factor á pour la batterie Li-Ion VL34480 calculé pour un courant de référence de
0.9A

La figure précédente représente la courbe á(i) calculé pour un courant de référence de 0.9A, ce qui correspond à 0.2C rate et à 20°C.

2.4.3.2.2. Détermination du facteur â [T(t)] et de ÄE(T)

La technique de détermination du facteur de température et du potentiel de correction de la dépendance en température s'appuie sur les courbes de décharge à courent constant (0.9A) et à différents températures. La figure illustre cette méthode appliquée à la détermination du â(-30) et ÄE(-30).

azo

d c

Figure 2.17: Détermination du facteur de température et du potentiel de correction de la dépendance en
température

Projet fin d'étude Page Zied Jelassi

De la même façon, cette technique utilise encore les formes polynomiales des caractéristiques de décharge.

Le terme ÄE(T) représente la différence entre la forme polynomiale de la courbe de référence et celle de la courbe de décharge mesurée à une température T. Après la détermination de cette valeur, on l'utilise dans le but de déterminer le facteur de température. Le terme d est la valeur de capacité pour laquelle le polynôme de la courbe de décharge vaut 2.5V. Le terme c représente la valeur de la capacité pour laquelle le polynôme de la courbe de référence affaibli par ÄE(T) vaut 2.5V.

La valeur du facteur de température est définit par l'expression suivante :

c

â( T ) = (2.11)

d

Les figures suivantes présentent les résultats d'extraction du facteur de température et du potentiel de correction de la dépendance en température.

(a) (b)

Figure 2.18: Facteur de température (a) et potentiel de correction de la dépendance de la température
(b) pour la batterie VL34480 pour une température de référence de 20°C

Après la détermination de ces paramètres, on arrive à exploiter les équations 15-17 pour représenter les caractéristiques de décharge à n'importe quelle température et pour n'importe quel taux de décharge (ou encore pour n'importe quel courant de décharge).

Projet fin d'étude Page Zied Jelassi

2.4.3.3. Validation du modèle

Pour la validation de ce modèle, on a utilisé la superposition des résultats expérimentaux et de simulation. La figure 2.19 représente la superposition de la caractéristique de décharge pour 1C-rate et à 20°C fournie par Saft et celle du modèle.

Figure 2.19: Comparaison directe entre la caractéristique de décharge (4.4A, 1C) à 20°C et la
caractéristique générée par le modèle.

2.4.4. Discussion

Les trois modèles présentés se basent à la fois sur une équation décrivant le comportement électrochimique de la batterie et un circuit électrique simulant son comportement électrique. En plus, ils sont tous dynamiques dans le sens où on peut prévoir la caractéristique de décharge de la batterie Li-Ion à différent C-rate. De plus, ils s'appuient sur les données des fabricants, à savoir les caractéristiques de décharge à courant constant et/ou à température constante.

Les trois modèles sont présentés dans l'ordre de complexité ; du plus simple au plus compliqué. Comme il a déjà été précisé, les deux premiers modèles sont inspirés des travaux de C. M. Shepherd. On remarque bien la ressemblance entre leurs équations électrochimiques et celle de ce dernier. La différence entre eux a eu lieu pour détourner les problèmes de boucle algébrique.

Projet fin d'étude Page Zied Jelassi

Le premier modèle est un modèle assez simple. Il met en évidence une seule équation pour décrire le chargement et le déchargement de différents types de batteries et en particulier les batteries Lithium-Ion. Suivant le signe du courant, on choisie entre la charge et la décharge.

Le deuxième modèle utilise une série de paire d'équations suivant le type de batterie, une pour la charge et l'autre pour la décharge. Par contre, ce modèle ne peut traiter qu'un nombre limité de type de batteries, qui sont les batteries Li-Ion, plomb-acide, NiCd et NiMH. La précision de ces deux modèles est directement liée à la précision avec laquelle on estime la position des trois points : le point de chargement total, le point qui marque la fin de la zone exponentielle et celui qui désigne la fin de la zone nominale et le commencement de la décharge rapide. Pour la détermination de ces points, on a utilisé les courbes de décharge publiées par Saft sur la datasheet de la batterie VL34480. Pour les convertir sous forme de tableur, on a eut recours à un logiciel de reconnaissance de courbes « CurveUnscan ». Comme les données du composant Saft sont grossières et que le logiciel de reconnaissance de courbe est entaché d'une certaine non-précision, on considère que notre source de données est moyennement précise.

Le troisième modèle utilise une régression polynomiale de la caractéristique de référence pour l'extraction des paramètres. Il emploie la SOD comme variable de ce polynôme. Pour la détermination de cette variable, on fait appel à deux facteurs, le facteur de température et celui du taux de charge. L'idée de ce modèle est de simuler le comportement de la batterie considérée à une température et un courant de décharge bien précis, au contraire des deux autres modèles. La précision de ce modèle dépend de la précision de détermination des facteurs á(i), â(T) et ÄE(T) qui dépend à leur tour de la précision des données du fabricant.

Les modèles déjà présentés ont été validés pour des batteries autres que la batterie Li-Ion et à faible densité énergique. Ces batteries possèdent des caractéristiques de décharge « classique » qui semble à la caractéristique de décharge à 0.9A-C/5 rate et à 20°C. Comme les caractéristiques de la batterie VL34480 sont compliquées, on a éprouvé des difficultés à adapter ces modèles à ce type de batterie à haute densité énergétique.

Projet fin d'étude Page Zied Jelassi

Pour la validation de ces modèles, on a préféré comparer directement les résultats de simulations aux données disponibles sur la datasheet de la batterie VL. On a superposé ces résultats pour mieux voir leurs ressemblances et leurs différences. Les figures 2.6, 2.12 et 2.19 représentent ces résultats.

Pour la validation du modèle d'O. Tremblay et L.A. Dessaint, on remarque que la sortie de simulation suit celle fournie par le fabricant. En ce qui concerne le modèle de MathWorks, la sortie est presque identique à la figure prise de la datasheet. Le modèle de L. Gao est le modèle le plus compliqué. Sa sortie ressemble en forme à la caractéristique expérimentale. Mais, elle est un peu au dessus d'elle.

Pour simuler le comportement de ses batteries, Saft dispose de plusieurs modèle Simulink. La différence entre les modèles présentés et les modèles de Saft réside dans la précision.

2.5. Conclusion

La modélisation des batteries est un outil essentiel dans cette industrie qui présente de plus en plus de concurrence. Cette technique permet la prédiction et le suivi du comportement de ces produits. Encore, elle intervient au processus de leur développement. En addition, les modèles de batteries sont devenus eux même des produits commerciaux entre les fournisseurs de batteries et ses clients. Ils permettent à ces derniers de connaître l'état de leurs batteries.

Après un premier chapitre présentant le cadre général de ce projet, ce chapitre était dédié à l'étude du comportement électrique et électrochimique de la batterie sous-test. On a implémenté des modèles dynamiques dépendants de différents paramètres. Et, on les a validés par rapport à la batterie à haute efficacité énergétique de Saft. Le chapitre suivant sera dédié à l'analyser de l'effet d'une perturbation sur deux systèmes d'acquisition de données ou encore deux BMS, a savoir MAX11068 de MAXIM et LTC6802 de LINEAR TECHNOLOGY. Cette perturbation simule le courant de charge /décharge d'une cellule.

Projet fin d'étude Page Zied Jelassi

Chapitre 3: Analyse des performances

des systèmes de mesures de tension

multiplexées

Projet fin d'étude Page Zied Jelassi

3.1. Introduction

La croissance rapide des systèmes mobiles crée une forte demande sur les batteries rechargeables, dont le Li-Ion est la plus nouvelle technologie [19]. L'emploi d'un BMS est essentiel avec ce type de batterie. Il assure l'utilisation optimale de son énergie, l'autonomie du périphérique portable et la minimisation du risque d'endommagement de la batterie. L'utilisation d'un BMS mène à une amélioration de l'autonomie du système. En outre, il rend la durée de vie de la batterie plus longue et son utilisation plus sûre [27].

Le CAN sert d'interface entre les paramètres du monde réel et les circuits numériques. Il est une composante élémentaire du BMS. Habituellement, une batterie est composée de plusieurs cellules. Pour assurer les fonctionnalités du système comme la sécurité, l'équilibrage de cellules, etc., mesurer chaque sortie de cellule est nécessaire [27, 28]. On pourrait utiliser autant de CAN qu'il y a de cellules à contrôler, mais cela entrainerai un surcoût important (surface et puissance consommée). En pratique, le BMS est réalisé à partir d'un seul CAN précédé d'un multiplexeur [29, 30], permettant ainsi de balayer de nombreux canaux [31]. Ainsi, on obtient une solution optimale en réduisant la surface du système d'acquisition de données et sa consommation d'énergie. Cependant, cette solution réduit la vitesse à laquelle les données peuvent être acquises à partir d'un canal individuel, parce que de multiples canaux sont analysés de façon séquentielle. En outre, elle peut aussi entraîner des imprécisions comme la diaphonie, l'injection de charge, etc. [29].

En raison de leur haute résolution et leur fréquence appropriée les CAN ÓÄ et les CAN SAR sont les plus adaptés aux applications de mesures multiplexées [29-31]. Ils sont particulièrement bien adaptés pour un BMS, puisque le signal d'entrée reste à basse fréquence [28].

Ce chapitre présente en premier le concept du système de mesures multiplexées. Il s'intéresse en particulier à deux BMS : le MAX11068 et le LTC6802, basés sur deux différents types de convertisseur analogique-numérique. En second lieu, nous présenterons une étude sur l'effet de l'introduction d'une perturbation simulant le courant de charge/décharge sur l'une des entrées du système d'acquisition de données. Cette étude compare de façon relative la tenue de ces deux BMS face à la diaphonie et l'injection de charge.

Projet fin d'étude Page Zied Jelassi

3.2. Systèmes d'acquisition de données multiplexés

Le système d'acquisition de données multiplexées est basé sur la figure suivante. Les différents étages seront détaillés par la suite.

Figure 3.1: Principe du système d'acquisition de données multiplexé

La figure 3.1 montre le multiplexeur qui reçoit en entrée des canaux analogiques. Ce multiplexeur est un réseau des commutateurs qui dirige les différents signaux d'entrée analogique sur l'entrée du CAN pour la numérisation. Ces commutateurs peuvent être mis en oeuvre via des relais ou des commutateurs à semi-conducteur. Les relais fonctionnent à des fréquences relativement faibles, dans la gamme de quelques kHz, alors que les commutateurs à semi-conducteur peuvent fonctionner dans une bande de plusieurs MHz [29, 30]. Cependant, les relais peuvent faire face à des tensions plus élevées et fournissent une isolation de canal supérieure à celle des commutateurs à semi-conducteur [30].

Les spécifications clés du multiplexeur sont le temps de commutation, la résistance et l'isolement du canal. Un système à multiplexage permet l'utilisation d'un seul CAN, mais cela se fait au détriment de la réduction de la vitesse à laquelle les données peuvent être acquises sur un canal individuel. Ceci est lié au fait que chaque canal est analysé de façon séquentielle. En outre, le multiplexage peut introduire des problèmes. Une source à haute impédance peut se combiner avec la capacité parasite du multiplexeur et entraîner des problèmes de diaphonie entre les canaux. En outre, l'impédance du multiplexeur peut également conduire à une dégradation du signal [29, 30].

L'AGP (amplificateur à gain programmable) permet une amplification différente pour chaque canal. Le gain de l'AGP peut être réglé par canal en fonction du niveau du signal. Cela garantit que tous les canaux utilisent la dynamique complète du CAN. L'AGP prévoit

Projet fin d'étude Page Zied Jelassi

également l'isolement entre la charge et le multiplexeur. Ainsi, il permet de réduire la distorsion du signal qui se produit en raison de la résistance du multiplexeur [29, 30].

Dans une application multiplexée, le CAN doit avoir un cycle de latence nul et un faible temps d'établissement. La latence est liée au nombre de cycles de données nécessaires entre le début de la conversion du signal et la disponibilité des données de sortie correspondantes. La latence est nulle si une conversion entière est atteinte avant le début du prochain cycle.

Le temps d'établissement est la durée entre le début d'acquisition du signal et le moment où les données sont disponibles pour être lu à partir du convertisseur. Contrairement à la latence du cycle, le temps d'établissement ne peut jamais être égale à zéro [29, 30].

La diaphonie et l'injection de la charge sont parmi les principaux paramètres à prendre en compte pour l'étude des performances d'un système d'acquisition multiplexé. La diaphonie se produit lorsqu'une perturbation appliquée à un canal affecte la précision de la mesure d'un autre canal. C'est un phénomène dépendant de la fréquence [29, 30].

L'injection de charge a lieu lors de la commutation, ce qui peut provoquer un changement de tension importante à l'entrée du commutateur. Ce changement rapide de la tension injecte une charge à la sortie du commutateur à cause de la capacité de commutation [29, 30].

Durant cette étude, on mettra l'accent sur les phénomènes de diaphonie et d'injection de charge pour comparer relativement les deux BMS, mais avant tout on rappelle brièvement le principe de fonctionnement des deux CAN utilisés dans les BMS considérés.

3.2.1. Le convertisseur analogique-numérique ??

Le CAN ?? s'appuie sur le sur-échantillonnage et la mise en forme du bruit de quantification dans le but d'obtenir une résolution élevée à partir d'une structure électronique simple. Il est constitué d'un modulateur ?? et d'un filtre décimateur numérique.

Projet fin d'étude Page Zied Jelassi

Figure 3.2 : Schéma bloc d'un CAN ??

Le modulateur ?? permet d'échantillonner l'entrée analogique à haute fréquence et il génère un flux binaire correspondant au codage de l'information. Pour nos applications, ce flux est formé sur un seul bit, mais il arrive que ce flux puisse être codé sur un nombre de bit supérieur. Le bloc numérique assure le filtrage numérique de la sortie du modulateur, et sa fonction principale est de réduire la cadence d'échantillonnage de sortie tout en augmentant la résolution. Cette action est appelé décimation et elle doit être précédée d'un filtrage pour éviter le repliement du spectre sur l'information utile.

Ce type de convertisseur analogique-numérique est reconnu par sa haute résolution, sa linéarité intrinsèque, sa basse consommation de puissance et son faible coût. Par contre, il est à faible bande passante et il peut avoir une latence de cycle non nulle [29, 31]. Grâce à ses caractéristiques, ce CAN est adapté pour les applications de mesure précise et à faible bande passante [31].

Un autre avantage de cette technologie est la simplicité du filtre d'anti-repliement analogique. Donc, c'est encore bénéfique pour les applications multiplexées. La technique de sur-échantillonnage diminue les contraintes sur ce filtre. Généralement, un filtre de premier ordre suffit. On peut noter que pour des structures à temps continu la fonction de filtrage est intrinsèque : le filtre de boucle intègre le signal sur la période bloquée par l'échantillonneur/bloqueur du quantificateur. Plus l'ordre du modulateur augmente, plus la rejection de repliement est forte. Cela simplifie la partie analogique pour une résolution élevée et un bruit faible.

L'emploie d'un filtre numérique est essentiel. Ce filtre ajoute un certain temps d'établissement. Ce qui limite les performances du système [29]. Pour augmenter la précision des systèmes de mesure multiplexée, il faut le prendre en considération.

Projet fin d'étude Page Zied Jelassi

3.2.2. Le convertisseur analogique-numérique SAR

Le convertisseur à approximation successive (SAR) est l'une des architectures les plus populaires pour la conversion analogique numérique. En fait, elle prévoit un temps de conversion de l'ordre du kHz jusqu'au MHz avec une complexité des circuits assez modérée. L'architecture de base d'un CAN SAR est illustrée par la figure suivante.

Figure 3.3 : Architecture du convertisseur à approximation successive

Le SAR emploie un E/B (échantillonneur/bloqueur) en entrée pour que celle-ci reste constant pendant la durée de conversion, basée sur une méthode de dichotomie et nécessitant plusieurs cycles d'horloge. Le principe est le suivant : Il commence par comparer l'entrée analogique à un mot numérique correspondant à la moitié de la pleine échelle (tous les bits à 0 sauf le MSB (Most significant Bit) qui est égal à 1) converti en analogique par le biais d'un convertisseur numérique analogique. Cette séquence est de longueur N (résolution du CAN) et elle est donc équivalente à _VREF/2. Suivant le résultat de la comparaison, supérieure ou inferieure, on introduit un 1 ou un 0 dans le SAR. Ce résultat sera introduit dans une version décalée à droite de la séquence de comparaison déjà utilisée. On répète ce traitement N fois afin d'obtenir la sortie numérique. Le nombre d'itération définit le nombre de décalage à droite de la séquence d'origine et l'emplacement du bit du résultat de la comparaison en cours. Pour la première itération, ce dernier occupe le MSB et pour la dernière itération, il occupe le LSB (Least Significant Bit).

Contrairement au CAN ??, le CAN SAR nécessite un filtre analogique d'antirepliement à l'entrée de chaque canal [33, 34]. En effet, l'impédance totale du système ainsi que le temps d'établissement augmentent. En conséquence, la bande passante du système diminue et la probabilité d'apparition de la diaphonie augmente [29].

Projet fin d'étude Page Zied Jelassi

L'architecture du SAR est capable d'avoir une latence de cycle nulle [29-31]. En plus, en comparaison avec le CAN ??, elle peut fonctionner à une fréquence d'échantillonnage plus haute [32]. Ce sont les critères de base qui font des convertisseurs à approximations successives les plus populaire pour les applications de mesure.

3.2.3. Etude comparative entre le MAX11068 et LTC6802

Le MAX11068 et le LTC6802 sont les deux systèmes de gestion de batteries que nous devions évaluer. Le tableau suivant permet une comparaison de leurs caractéristiques, faisant ainsi apparaître leurs similitudes et leurs différences.

LTC6802		MAX11068	Intervalle de température fonctionnel [-40; 85]°C
Intervalle de température fonctionnel [-40; 105]°C		Mesure · mesure 4-12 cellules par IC · 2 thermistances d'entrée + 1 capteur de température sur-carte
Mesure · mesure 2-12 cellules par IC · 2 thermistances d'entrée · 1 moniteur de température sur-carte		Surveillance · Alarmes OV and UV (Programmable) · Alarmes HT and LT · Détection du circuit ouvert
Surveillance · Alarmes OV and UV (Programmable) · Alarmes HT and LT · Détection du circuit ouvert		Communication · 1MHz SPI (Serial Peripheral Interface) · Architecture empilable jusqu'à 10 cartes via une interface en chaîne (120 cellules)
Communication · 400kHz I2C (Inter Integrated Circuit) · Architecture empilable jusqu'à 31 cartes via une interface en chaîne (372 cellules)

Projet fin d'étude Page Zied Jelassi

Efficacité de puissance

modes veille, surveillance et mesure + mode arrêt thermique

Efficacité de puissance

modes arrêt, veille et mesure + mode arrêt thermique

Mesure des tensions des cellules

· 12 canaux Multiplexés

· CAN ?? de deuxième ordre

· Fréquence d'échantillonnage égale à 512kHz

· Time slot pour chaque canal est de 0.5ms

· Résolution de 12 bits

· L'amplitude du CAN est de 6.14V

· Quantum égale à 1.5mV

· Filtrage de la tension de la cellule

· Pas de filtre analogique est employé

· Un filtre FIR Sinc2 est employé pour la décimation numérique

Mesure des tensions des cellules

· 12 canaux Multiplexés

· CAN SAR

· Fréquence d'échantillonnage égale à

· Time slot pour chaque canal est de 6.6ìs

· Résolution de 12 bits

· L'amplitude du CAN est de 5V

· Quantum égale à 1.22mV

· Filtrage de la tension de la cellule

· Un filtre RC passe bas est utilisé

150kHz

Tableau 3.1 : Tableau de comparaison entre le MAX11068 et le LTC6802 [33, 34]

Après cette brève description, il apparaît clairement que ces deux systèmes d'acquisition de données sont assez similaires. Mais, comme ils emploient différentes architectures de conversion analogique-numérique, le débit d'information sera différent sur une durée fixe. C'est le MAX11068 qui fournit le plus d'information sur une durée d'utilisation constante (débit plus élevé). Cet avantage est très apprécié par les utilisateurs (les fabricants de batteries LI-Ion tel que Saft) car il permet de mieux suivre l'évolution de la batterie. Dans la section suivante, nous allons présenter des résultats de mesures à partir d'une introduction de perturbation sur l'une des entrées des BMS. On comparera de façon relative leurs comportements face aux phénomènes de diaphonie et injection de charge.

Projet fin d'étude Page Zied Jelassi

3.3. Mesures et résultats

Comme déjà vu, il est clair que les CAN ÓÄ et SAR sont adaptés pour les applications de mesures multiplexées. Particulièrement, ils sont indiqués pour les applications à faible bande passante, et leur choix est très pertinent dans une application telle que le BMS. Suivant cette piste, les systèmes d'acquisition de données multicanaux basés sur les CAN ÓÄ et SAR ont été développés par différents constructeurs de système électroniques pour des applications de gestion de batterie Lithium-Ion [31-35].

Au cours de cette étude le MAX11068 et le LTC6802 sont pris en considération. Ils sont développés respectivement par Maxim Semiconductors et Linear Technology. Ces deux systèmes sont conçus pour surveiller et mesurer les signaux des batteries Li-Ion. Ils utilisent un convertisseur analogique-numérique de résolution 12 bits. Ils permettent de mesurer la tension d'au moins 12 cellules montées en série. Le signal de chaque canal varie entre zéro et cinq volts.

Le dispositif de mesure de la MAX11068 est illustré par la figure 3.4. On emploie un MAX11068 EV KIT+ pour convertir les tensions de batterie du domaine analogique au domaine numérique [34]. En plus, on fait appel à un MINIQUSB jouant le rôle d'un adaptateur USB/I²C. Il représente l'interface entre l'ordinateur et la MAX11068 EV KIT+ [36].

Figure 3.4 : Dispositif de mesure du MAX11068

Le dispositif de mesure de la LTC6802 est présenté par la figure 3.5. On utilise le DC1331 pour transformer les tensions de batterie du domaine analogique au domaine

Projet fin d'étude Page Zied Jelassi

numérique [33]. Le DC590B représente l'interface entre l'ordinateur et le DC1331 [37]. En fait, c'est un adaptateur USB/SPI.

Figure 3.5 : Dispositif de mesure du LTC6802

L'objectif était d'étudier la robustesse de ces deux systèmes face à l'injection de charge et la diaphonie. Dans ce contexte, on a envisagé un test d'injection de perturbation à l'entrée du BMS. Le processus sera expliqué dans ce qui suit.

3.3.1. Introduction d'une perturbation à l'entrée du BMS

Pour étudier les performances des systèmes considérés, une source de bruit est superposée sur une des entrées. Ce type de perturbation représente un cas particulier de bruit couramment rencontré dans les systèmes alimentés par des batteries; bruit lié à l'électronique

et à l'environnement. L'ordre de grandeur du bruit est de quelques dizaines de millivolts. ^Iiest généré par le courant de charge/décharge de la batterie. Ce dispositif est valable pour les deux systèmes considérés.

Projet fin d'étude Page Zied Jelassi

Figure 3.6 : Présentation de l'arrangement des signaux d'entrée pour le MAX11068 et le LTC6802

Comme montre la figure 3.6, les six premiers canaux sont reliés à cinq cellules délivrant chacune 3.7V. Le reste des canaux (C6-C12) sont court-circuités. Un courant est appliqué à la troisième cellule. Une description détaillée des caractéristiques du courant est donnée dans les paragraphes suivants.

Pour générer un bruit de l'ordre de plusieurs dizaines de millivolts, on a pris en considération la résistance interne de la batterie Li-Ion et un courant approprié fut employé. Avec les mesures, il est constaté que la résistance interne est de 30 m?. D'après la loi d'Ohm, donnée par l'équation 3.1, un courant de 3A crête à crête sera donc employé. Donc, on génère une perturbation équivalente à 90 mV crête à crête.

(3.1)

Comme déjà vu dans le premier chapitre, la résistance interne des batteries Li-Ion dépend de la température. Les mesures sont faites à trois températures différentes, à savoir 0°C, 20°C et 40°C. En plus, comme la diaphonie varie en fonction de la fréquence, la perturbation appliquée fera apparaître différentes fréquences. De plus, nous avons utilisé trois différentes formes de signal perturbateur : un courant sinusoïdal, un courant impulsif et un courant en dent de scie. La variation de la forme du signal est adoptée pour mieux suivre les perturbations entre les différentes cellules.

3.3.2. Analyse de mesures

La perturbation fut appliquée sur la cellule trois. Théoriquement, son impacte doit être visible sur les cellules voisines directes, à savoir la cellule deux et la cellule quatre. Dans le

Projet fin d'étude Page Zied Jelassi

but de suivre de façon rigoureuse cette perturbation, on a choisie d'étendre l'étude sur les deux autres cellules, la cellule un et la cellule cinq.

Pour les perturbations sous formes sinusoïdale ou en dent de scie, les mesures sont enregistrées pour les fréquences suivantes : 62,5Hz, 125Hz, 250Hz, 500Hz, 1KHz, 2KHz et 4KHz. Pour la perturbation impulsive, on a les deux signaux représentés par les deux figures suivantes.

Figure 3.7 : Bruit impulsif à la fréquence 1/10Hz

Figure 3.8 : Bruit impulsif à la fréquence 1/6Hz

L'analyse de ces mesures s'est effectuée dans le domaine temporel et fréquentiel. Cette étude est une étude relative qui s'intéresse à l'électronique de ces deux BMS (MAX11068 et LTC6802). Donc, on considère ces derniers comme une boite noire. En outre, on ne suit pas les phénomènes de diaphonie et d'injection de charge entre pistes ou entre composants. Car, on ne dispose que des mesures.

Les mesures faites sur les deux systèmes d'acquisition de données sont enregistrées durant la même fenêtre de lecture (durée identique). Le fait d'utiliser un CAN avec un débit plus important pour le MAX11068 fait qu'il y a plus de données à analyser, malgré tout il était important que la durée soit rigoureusement identique car la perturbation peut entraîner des phénomènes de charge et décharge dépendant de la durée d'application de la perturbation.

Par rapport à la ressemblance des résultats des deux BMS, on a préféré représenter l'analyse des mesures suivant le domaine de variation (domaine temporel ou domaine

Projet fin d'étude Page Zied Jelassi

fréquentiel) pour mettre en évidence l'existence des phénomènes de diaphonie et la résistance à l'injection du charge.

3.3.2.1. Analyse temporelle

L'analyse temporelle s'appui sur la forme temporelle de mesures ou encore la variation dans le temps des valeurs enregistrées.

Lors du tracé de l'évolution temporelle des tensions de sorties de différentes cellules, on a constaté qu'elles ne varient pas autour d'une valeur moyenne fixe pour chacune des cellules. Par contre, ces tracés évoluent linéairement comme le montre la figure suivante.

Figure 3.9 : Représentation temporelle de la sortie de la troisième cellule sur la carte MAX11068 à
0°C et avec un bruit de 62,5Hz

Dans le but de minimiser l'erreur de mesure, on a utilisé la régression linéaire pour supprimer cette variation. Cette technique consiste à représenter le signal non bruité sous la forme :

(3.2)

Où << a >> représente la valeur du gain et << b >> la valeur d'offset. Pour la détermination de leurs valeurs les deux équations suivantes l'assurent.

(3.4)

Projet fin d'étude Page Zied Jelassi

(3.5)

Le signe de << a >> reflète l'état de cellules. En effet, si << a >> est positif alors, la cellule étudiée est dans une phase de charge. Par contre, s'il est négatif, cette dernière se décharge. De plus, la valeur de ce paramètre permet d'interpréter qualitativement la valeur de la résistance à l'injection de charge. En outre, si << a >> est importante en valeur alors, la cellule se charge rapidement. Donc la résistance à l'injection de charge est faible et vise versa. De plus, ce paramètre permet de suivre la diaphonie en détectant la similitude du comportement de ce facteur à travers les différentes cellules utilisées.

Le paramètre << b >> qui signifie la valeur à l'origine est mit en valeur pour connaitre l'état de charge de chaque cellule. En effet, ce paramètre permet de déterminer la tension au début du test de chaque cellule.

Figure 3.10 : Evolution du paramètre << b >> à 0°C pour la MAX11068

La figure précédente illustre que les batteries sont utilisées à différents niveau de charge. Ensuite, la variation de ce paramètre est due au chargement de ces cellules causé par la perturbation introduite. On remarque que les valeurs du paramètre << b >> décroit pour les températures de 20°C et 40°C car les cellules sont passées en mode décharge. Les figures du paramètre << a >> illustrent ce changement.

Projet fin d'étude Page Zied Jelassi

Figure 3.11 : Représentation du paramètre << a >> pour les cinq premières cellules à 0°C pour la
MAX11068

La figure précédente représente la variation du paramètre << a >> en fonction de la fréquence de perturbation. Cette variation est représentée pour les cellules testées.

Le fait d'ajouter une source de courant devrait permettre la charge de la batterie. Or plus la fréquence du bruit augmente, plus la valeur de << a >> diminue. Comme le chargement est limité par la résistance de charge, il semble que l'influence de cette dernière soit plus importante lorsque la fréquence augmente.

On examine le comportement des cellules voisines par rapport à la perturbation appliquée sur la troisième cellule. On voit apparaitre une similitude d'évolution. Le paramètre << a >> calculé pour chaque cellule varie sensiblement de la même façon que celui de la cellule 3.

Les figures suivantes décrivent l'évolution du gain à 20°C et à 40°C. On remarque bien que la variation de ce facteur diminue lorsque la température augmente. La variation devient moins importante. Elle tend vers décrire le comportement normale des batteries ; la batterie délivre de l'énergie au cours du temps donc elle se décharge.

Projet fin d'étude Page Zied Jelassi

Figure 3.12 : Représentation du paramètre << a >> pour les cinq premières cellules à 20°C pour la
MAX11068

Figure 3.13 : Représentation du paramètre << a >> pour les cinq premières cellules à 40°C pour la
MAX11068

A ces deux températures, on remarque que la perturbation appliquée sur la cellule trois ne permet pas de la charger. Le domaine de variation du terme << a >> est très faible. Il est intéressent de constater que cette perturbation qui n'applique pas une charge de la troisième cellule implique une décharge des autres cellules. Ceci semble être un fonctionnement normal car sans une source de chargement, les cellules fournissent une tension et donc elles se déchargent.

Comme le montrent les figures précédentes, plus la température augmente plus le fonctionnement des batteries devient normal. Ce résultat est conforme avec le fonctionnement en température des batteries Li-Ion déjà présenté dans le chapitre précédent : les batteries Projet fin d'étude Page Zied Jelassi

Li-Ion atteignent leur fonctionnement optimal pour des températures élevées. En plus, la résistance interne des batteries Li-Ion est inversement proportionnelle à la température. Donc si la température augmente, la résistance interne diminue et donc, l'amplitude de la perturbation diminue.

Ce résultat peut encore évoquer la diaphonie comme étant reliée à la structure en série des cellules : si la cellule trois ne charge pas, les autres se déchargent. Si la cellule centrale se charge, les autres, dans une moindre mesure, se chargent. L'analyse fréquentielle traitera de près le phénomène de diaphonie.

3.3.2.2. Analyse fréquentielle

L'analyse fréquentielle s'appuie sur la comparaison des densités spectrales des signaux issus des différentes cellules. Au cours de cette analyse, on retire la composante continue à partir de l'algorithme de régression linéaire appliquée précédemment et seul l'analyse spectrale du bruit est réalisée.

Afin de mieux mettre en évidence les résultats et les perturbations, les mesures du système BMS MAX11068 avec une perturbation sinusoïdale seront utilisées. Ceci est lié au fait que le système BMS LTC6806 est beaucoup moins sensible à la diaphonie et que par conséquent, rien de significatif apparaît sur l'analyse spectrale des signaux issus de chaque cellule à partir de ce système. En plus, la transformée de Fourier d'un signal sinusoïdal est représentée par deux Dirac en #177; Fsig. ^Où, _Fsig est la fréquence du signal.

L'idée de cette analyse est de suivre les pics, qui apparaissent dans la densité spectrale de puissance de la cellule trois, et celles qui lui sont voisines. Cette étude comparative a permis de conclure qu'il n'y avait aucune transmission du bruit moyen, ou alors en très faible proportion, et que seuls des pics de fréquence étaient transmis, traduisant ainsi de l'importance plus ou moins grande de la diaphonie.

Par définition, la diaphonie est directement proportionnelle à la fréquence. Au cours de cette analyse, on a constaté que la détection de ce phénomène demeure plus simple à haute fréquence. En fait, plus la fréquence augmente, plus l'apparition des pics devient claire. Cela est valable à toutes températures. Les deux figures suivantes illustrent cette interprétation.

Projet fin d'étude Page Zied Jelassi

Figure 3.14: Densité spectrale du bruit à 20°C et une fréquence de 125Hz

Figure 3.15 : Densité spectrale du bruit à 20°C et une fréquence de 1 KHz

L'apparition de plusieurs pics peut être expliquée par l'effet de l'électronique présent dans les deux cartes et les outils de communication avec l'ordinateur. Comme l'émission conduite dépend des structures présentes, qui résonnent à différentes fréquences et comme les tensions des différentes cellules suivent le même parcours de composants électronique, on peut juger que les différents pics doivent apparaitre sur chaque sortie mais à des différences prés de puissance. Cette différence est explicable par l'architecture du test. Donc, la présence de n'importe quels pics ne peut être expliquée que par le phénomène de diaphonie car les batteries fournissent des tensions continues. La comparaison doive être effectuée par carte car elles n'utilisent pas les mêmes composants. Les figures 16-18 illustrent cette théorie.

Cette analyse est faite pour des mesures réalisées à température et à fréquence constantes. On a constaté pour les deux cartes que plus la température augmente, plus elles

Projet fin d'étude Page Zied Jelassi

montrent une résistance à la transmission de perturbation. En addition, les cellules les plus sensibles à ce phénomène sont les cellules directement voisines à la cellule perturbée, à savoir la cellule deux et quatre.

Figure 3.16 : Densité spectrale du bruit à 0°C et à la fréquence 500 Hz

Figure 3.17 : Densité spectrale du bruit à 20°C et à la fréquence 500 Hz

Projet fin d'étude Page Zied Jelassi

Figure 3.18 : Densité spectrale du bruit à 40°C et à la fréquence 500 Hz

Les figures suivantes mettent en évidence l'existence de la diaphonie.

Figure 3.19 : Densité spectrale du bruit de la cellule 3 à 0°C et à la fréquence bruit 4KHz

Projet fin d'étude Page Zied Jelassi

Figure 3.20 : Densité spectrale du bruit de la cellule 2 à 0°C et à la fréquence bruit 4KHz

Ces deux dernières figures illustrent la transmission de moins quatre pics ou encore quatre perturbations. Cette étude confirme la théorie qui considère que les cellules deux et quatre sont les plus sensibles à la perturbation.

Pour la comparaison des deux systèmes d'acquisition de données, on s'est appui sur les mesures en absence du bruit. On a calculé l'erreur maximale défini par la différence entre les mesures bruitées et les mesures non bruitées. Comme montre la figure suivante la carte MAX11068 est plus vulnérable à la diaphonie et à l'injection de charge que la LTC6802.

Figure 3.21 : Erreur maximal absolue de la cellule deux, le bleu correspond à la valeur de l'erreur de la
LTC6802, le noir correspond à la valeur de l'erreur de la MAX11068

La figure précédente montre les erreurs maximales absolues pour les mesures de la MAX11068 et de la LTC6802. Ces résultats sont calculés pour le deuxième canal Projet fin d'étude Page Zied Jelassi

correspondant à une fréquence de bruit allant de 62.5 Hz à 500 Hz tout en utilisant une forme sinusoïdale de perturbation. Il est clair que pour les deux cas, l'erreur augmente avec l'augmentation de la fréquence du bruit. Ce résultat est en accord avec les idées déjà présentées. Tout en regardant dans son ensemble, les erreurs obtenues pour la LTC6802 sont inférieurs à ceux obtenus avec la MAX11068. Il s'ensuit que, pour le cas étudié le BMS LTC6802 montre plus de résistance contre les phénomènes de diaphonie et d'injection de charge que le BMS MAX11068.

3.4. Conclusion

Au cours de ce chapitre, on a effectué une étude et une évaluation de performances de deux systèmes de mesures de tensions multiplexées appliqués aux batteries Li-Ion. La technique de multiplexage représente une solution plus rentable pour les systèmes de mesure. Tout en fournissant des avantages intéressants, le multiplexage peut également introduire des temps de latence dans le système d'acquisition.

Le convertisseur analogique numérique ?? et le convertisseur à approximation successive sont des bons candidats pour les applications multiplexées. Les deux BMS étudiés représentent l'état d'art de ces systèmes de mesure de tension. Une étude de leurs comportements face aux phénomènes de diaphonie et d'injection de charge a été effectuée. Les résultats montrent que la LTC6802 est plus performante que la MAX11068.

Il est connu que le CAN SAR peut obtenir de meilleurs taux d'échantillonnage par rapport au CAN ÓÄ. Cependant, l'emploi du filtre analogique, qui parait nécessaire pour la reconstruction du signal, peut augmenter le temps d'établissement. Cet impact peut dégrader les performances de l'application multiplexée.

Aujourd'hui, les batteries passent de plus en plus du temps en stock avant qu'elles soient liquidées. Cette situation est générée par la concurrence. D'où la nécessité d'un BMS non gourmant en énergie. Les solutions envisagées sont les systèmes qui ne fonctionnent qu'aux certaines conditions, tels que le dépassement de la température maximale ou minimale, etc. Une autre solution envisage assurer l'efficacité énergétique du BMS. En particulier, l'emploi de la technologie de conversion à traversée de niveau ou encore le level crossing analog to digital conversion connu par son efficacité énergétique, sa structure simple, etc., peut être la nouvelle solution adoptée (voir annexe 2).

Projet fin d'étude Page Zied Jelassi

Conclusion générale

Conclusion générale

Dans ce document, nous avons étudié deux systèmes de mesure de tension multiplexés basés sur deux technologies différentes. Nous nous sommes intéressés à l'impact d'une perturbation appliquée à l'entrée des systèmes testés. Nous avons analysé ses effets en termes de diaphonie et d'injection de charge.

En effet, une étude préalable de la batterie lithium-ion, ses terminologies et son BMS, nous a permis de se familiariser avec cette technologie qui représente une partie indispensable des applications de télécommunication et souvent oubliée.

Ensuite, une étude du comportement électrochimique des Li-Ion à travers une étude de modélisation, nous a permis d'approfondir nos connaissances dans ce domaine.

Enfin, une étude relative de deux BMS testés en termes de diaphonie et d'injection de charge a été menée pour évaluer l'effet d'un courant de charge/décharge. Nous avons encore analysé la robustesse de chaque BMS à ces phénomènes et nous avons terminé notre étude par une comparaison dans le domaine temporel et dans le domaine fréquentiel entre eux. Le résultat confirme ceux d'une première étude où il fut montré que le BMS LTC6802 était plus robuste que le BMS MAX11068.

Suite à l'étude des architectures de deux BMS et à partir des nouvelles exigences des fabricants de batteries comme la minimisation de la consommation d'énergie du BMS, nous avons proposé une autre architecture de convertisseur analogique numérique. Celle-ci correspond au CAN à traversée de niveau. Cette étude sera développée dans le cadre d'un projet de mastère.

A travers ces travaux effectués lors de mon projet de fin d'étude, j'ai eu l'occasion de découvrir de nouvelles notions que je n'ai pas eu l'occasion d'étudier tout au long de mon cursus scolaire tel que le module d'alimentation et son gestionnaire. Il m'a permis aussi de renforcer mes connaissances dans le domaine d'architecture des systèmes de télécommunication, grâce à l'étude de différentes architectures multiplexées et de différents CAN.

Projet fin d'étude Page Zied Jelassi

Annexe 1: la datasheet de la batterie

VL34480

Projet fin d'étude Page Zied Jelassi

Annexe 2: Le convertisseur A/N à

traversée de niveau

Introduction

Les applications mobiles tels que les réseaux de capteurs distribués, la téléphonie portable, les systèmes de gestion de batteries, les appareils implémentés pour contrôler les corps humain, etc., sont à ressources et consommation d'énergie limitées et de taille réduite. Dans ce contexte, le LCSS (Level Crossing sampling schema) est proposé comme une solution efficace. Dans cette annexe, on s'intéressera en premier lieu au processus d'échantillonnage. Puis, on présentera le LCSS. Et on terminera par le LC-ADC.

I. Processus d'échantiionnage

Le processus d'échantillonnage est le fait de convertir un signal analogique en une représentation discrète. Dans le domaine temporel, il s'assure en multipliant le signal x(t) par la fonction d'échantillonnage donnée par l'équation suivante :

(II.1)

Où est une fonction de Dirac et {t_n} est la séquence d'instants d'échantillonnage.

Ainsi, le signal échantillonné est donné par l'équation suivante :

(II.2)

Dans le domaine fréquentiel, le processus d'échantillonnage est un produit de convolution entre le spectre du signal analogique et la fonction d'échantillonnage. Si SF(f) est la transformée de Fourier de sF(t), le résultat est décrit par l'expression suivante :

(II.3)

D'où, la transformée de Fourier du signal échantillonné est définie par l'équation suivante :

Projet fin d'étude Page Zied Jelassi

(II.4)

Où X(f) est le spectre du signal analogique d'entrée.

III. L'échantillonnage à traversée de niveau (LC-ADC)

Le concept de l'échantillonnage à traversée de niveau est connu dés les années cinquante. Il est connu aussi comme étant l'échantillonnage par événement. Le principe de prélèvement des échantillons est décrit par la figure suivante. On ne capte un échantillon que lorsque de signal analogique d'entrée traverse un seuil des seuils prédéfinis. Les échantillons ne sont pas équidistants par rapport à l'échelle temporelle. Cette caractéristique dépend de la variation du signal d'entrée.

Figure II.1 : Processus d'échantillonnage à traversée de niveau

Le choix de la distribution des niveaux est relié à la variation du signal X(t). La figure précédente représente une distribution équidistante, où le quantum q est l'espacement entre deux seuils successifs. Encore, la distribution peut être logarithmique ou une autre distribution.

Pour ce type d'échantillonnage, chaque échantillon est un couple (x_n, t_n). Où x_n est l'amplitude et t_n l'instant d'échantillonnage. Voir la quantification du temps, x_n doit être égal à un seuil et t_n peut être calculé en utilisant l'expression suivante :

(II.5)

Projet fin d'étude Page Zied Jelassi

Où, t_n est l'instant de l'échantillon courant, _tn-1 la date de l'échantillon précédant et dt_n est l'intervalle séparant les instants de l'échantillon courant et précédant. Pour initialiser le processus, on propose que t1 et dt1 soient nuls.

L'échantillonnage classique ne s'intéresse pas à la variation temporelle du signal analogique d'entrée. En effet, il échantillonne à une période fixe, choisie pour respecter le critère de Shannon. Donc, il prélève une quantité d'information non utile, en particulier, pour les signaux à faible variation sporadique tels que l'électrocardiogramme, le phono cardiogramme, le signal sismique, etc. Cela peut engendrer une augmentation de l'espace mémoire utilisé, de la band passante de transmission, de la consommation d'énergie, etc.

Si on adapte de processus d'échantillonnage à la variation temporelle du signal, on assure l'efficacité des ressources employées.

IV. Le CAN à traversée de niveau

Par nature, la majorité des signaux réels varie dans le temps. Les CAN classiques sont basés sur l'architecture de Nyquist. Ils ne s'intéressent pas à la variation de signal. Ils échantillonnent le signal à une cadence constante sans pour autant considérer la nature du signal. Par conséquence, si on exploite les signaux à faible variation tel que la décharge d'une batterie Li-Ion, un grand nombre d'échantillons ne rapporte pas de l'information utile. Par contre, cela provoque une activation du système et une consommation d'énergie en plus.

Durant la conversion analogique numérique, les instants d'échantillonnage sont connus. Par contre, l'amplitude est quantifiée à la résolution du CAN. L'erreur est caractérisée par le SNR. Le SNR théorique est donné par l'expression suivante :

(II.6)

Où, N est la résolution du CAN.

Durant la conversion analogique numérique adaptant le LCSS, les amplitudes des échantillons sont connues. Par contre, les instants d'échantillonnage sont quantifiés à la résolution d'une horloge.

En pratique, une horloge est utilisée pour enregistrer les instants d'échantillonnage. Le temps de quantification se produit faute de la résolution finie de l'horloge. Si _Ttimer est la

Projet fin d'étude Page Zied Jelassi

période de l'horloge, le temps de quantification ät peut avoir une valeur entre zéro et cette période.

Le temps de quantification ät engendre une erreur d'amplitude äv en respectant la relation suivante :

(II.7)

Le temps de quantification montre qu'il introduit une erreur à l'amplitude de l'échantillon. Comme l'erreur ät est non corrélée au signal, on peut le modéliser par un bruit blanc. Soit (x_n, t_n) le couple amplitude-temps représentant le nième échantillon. Si ät_n est le temps de quantification produit pour t_n. Alors, la version quantifiée du t_n peut être exprimée ainsi :

(II.8)

La différence entre t_n et tq_n engendre une erreur d'amplitude de l'échantillon. Si äv_n est l'erreur d'amplitude correspondante alors, l'amplitude de l'échantillon est exprimée ainsi :

(II.9)

Projet fin d'étude Page Zied Jelassi

Figure II.2 : Erreur du temps de quantification du LC-ADC

Respectant l'équation A2.7, soient dx(t)/dt et ät deux variables aléatoires indépendantes, alors la puissance du bruit de quantification peut être calculée ainsi :

(II.10)

Considérant dx(t)/dt à moyenne nulle et ät uniformément distribué dans l'intervalle [0, Ttimer], le résultat est donné par l'expression suivante :

(II.11)

D'où

(II.12)

Comme le SNR est égal au ratio puissance signal par puissance bruit, on peut écrire ainsi le SNR :

(II.13)

Où, P_x est la puissance de x(t) et _Px' est celle de dx(t)/dt. Si on réduit _Ttimer par deux, le SNR augmente de six dB, ce qui correspond à un bit de plus pour la résolution effective.

Si x(t) est un signal sinusoïdal, alors le SNR sera ainsi :

(II.14)

Projet fin d'étude Page Zied Jelassi

V. Comparaison entre le LC-ADC et les structures d'ADC actuels

Le tableau suivant représente les différences de principe entre le convertisseur analogique numérique à traversée de niveau et les CAN utilisant la technique d'échantillonnage classique.

Caractéristiques	CAN classique	LC-ADC
Déclencheur de Conversion	Horloge	Traversée de niveau
Amplitude	Quantifiée	Valeur exacte
Temps	Valeur exacte	Quantifié
Dépendance du SNR	Nombre de bit	La période du Timer
Sortie du CAN	Amplitude	Couple Amplitude-temps

Tableau II.1: Caractéristiques du LC-ADC face aux ADC classiques

Le tableau suivant est développé par Kirill Kozmin, Jonny Johansson et Jerker Delsing. Ce tableau représente la différence entre différentes technologies de conversion A/N en termes de surface, de consommation d'énergie, etc.

Nbit	Taux de conversion (Ms/s)	Consommation de puissance (mW)	Surface (mm^2)	SNR (dB)	ENOB	Technologie CMOS	Architecture
14	40	72.8	1.15	64	10.35	0.18 ìm	Pipeline
14	125	1850	70	72	11.7	0.35 ìm	Pipeline
10	20	19.5	1.3	56	9	0.35 ìm	Pipeline
10	50	18	1.43	56	9	0.18 ìm	Pipeline
10	205	111	1	55	8.86	90 nm	Pipeline

Projet fin d'étude Page Zied Jelassi

11	70	49	1.2	60	9.7	0.18 ìm	Pipeline
4	NA	175	1.8	75	12.2	0.35 ìm	LC

Tableau II.2: LC-ADC comparé à une sélection d'architecture de conversion A/N opérationnelles

VI. Conclusion

Les applications mobiles deviennent de plus en plus complexes. On vise toujours un coût raisonnable, une taille minimale et une autonomie maximale. Dans ce contexte, l'architecture LC-ADC est sélectionnée par plusieurs chercheurs pour créer une évolution dans l'évolution courante. Cette technologie ne correspond pas à la conversion A/N classique. Dans le projet prochain, on s'intéressera d'avantage à cette technologie, à la reconstruction du signal converti avec un LC-ADC, etc.

Projet fin d'étude Page Zied Jelassi

Bibliographie

[1]. J.O. Besenhard, «Hand Book of Battery Materials», Wiley-VCH, Nov 2008.

[2]. I. Buchmann, «Batteries in a Portable World», Battery University, (2001).

[3]. I. Buchmann, «Discharge Methods», Battery University, Retrieved 14 August 2008.

[4]. Soo Seok Choi and Hong S. Lim, «Factors that affect cycle-life and possible degradation mechanisms of a Li-ion cell based on LiCoO2», Journal of Power Sources, Volume 111, Issue 1, pp. 130-136, September 2002.

[5]. Valer Pop et al., «Battery Management Systems: Accurate State-of-Charge Indication for Battery Powered Applications», Springer, Volume 9, 2008.

[6]. A. Jossen et al., «Reliable Battery Operation ___ A Challenge for a Battery Management System», Journal of Power Sources, Volume 84, pp. 283-286, June 1999.

[7]. J. Garche and A. Jossen, «Battery Management System (BMS) for Increasing Battery Life», TELESCON 2000, pp. 81-88, 2000.

[8]. A. Jossen, «Fundamentals of Battery Dynamics», Journal of Power Sources, Volume 154, pp. 530-538, 2006.

[9]. F. Huet, «A review of impedance measurements for determination of the state-of-charge or state-of-health of secondary batteries», Journal of Power Sources, Volume 70, pp. 59-69, 1998.

[10] H.J. Bergveld et al., «Battery Management Systems, Design by Modeling», Kluwer Academic Publishers, 2002.

[11] P.A. Boter, «Rechargeable electrochemical cell», US Patent 4,004,943, filed 20 August (1975).

[12] P.H.L. Notten et al., «Nickel-Metal Hydride batteries: from concept to characteristics», Chem. Ind., Volume 54, pp. 102-115, 2000.

Projet fin d'étude Page Zied Jelassi

[13] N. Furukawa et al. «NiMH batteries outperform Li-ion», Nikkei Electronics Asia, pp. 80- 83, 1996.

[14] M. Broussely et al., «Aging Mechanism in Li-ion Cells and Calendar Life Predictions», Journal of Power Sources, Volume 98, pp. 13-21, 2001.

[15] R. Spotnitz, «Simulation of Capacity Fade in Lithium-ion Batteries», Journal of Power Sources, Volume 113, pp. 72-80, 2003.

[16]. I. Buchmann, «Will Secondary Batteries Replace Primaries», Battery University, Retrieved 2005.

[17] P.M. Gomadam et al., «Mathematical Modeling of Lithium-ion and Nickel Battery Systems», Journal of Power Sources, Volume 110, pp. 267-284, 2002.

[18]. I. Buchmann, «What is the Best Battery», Battery University, Retrieved 26 August 2008.

[19]. I. Buchmann, «Battery Statistics», Battery University, Retrieved 11 August 2008.

[20]. P. Caumont et al., «Energy Gauge for Lead-Acid Batteries in Electric Vehicles», IEEE Transactions on Energy Conversion, Volume 15, pp. 354-360, 2000.

[21]. «Battery Internal Resistance», Technical Bulletin, Energizer Holdings, 2005.

[22]. SPECIALTY BATTERY GROUP, Lithium Battery Division, << Fiche de données de sécurité de batteries », Edition 2 Date 11/2003

[23]. C. M. Shepherd, "Design of Primary and Secondary Cells - Part 2. An equation describing battery discharge," Journal of Electrochemical Society, Volume 112, Jul. 1965, pp. 657-664

[24]. Tremblay, O.; Dessaint, L.-A.; Dekkiche, A.-I., "A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles," Vehicle Power and Propulsion Conference, 2007. VPPC 2007. IEEE 9-12 Sept. 2007, pp. 284-289

[25]. Lijun Gao, Shengyi Liu and Roger A.Dougal, << Dynamic Lithium-ion Battery Model for System Simulation», IEEE transaction on components and packaging technologies, vol.25, No.3, September 2002.

Projet fin d'étude Page Zied Jelassi

[26]. W & B van Schalkwijk & Scrosati,» Advances in Lithium-Ion Batteries», Kluwer Academic Publishers, 2002 (ISBN 0306475081)

[27]. A. Jossen et al., «Reliable Battery Operation ___ A Challenge for a Battery Management System», Journal of Power Sources, Volume 84, pp. 283-286, June 1999.

[28]. Valer Pop et al., «Battery Management Systems: Accurate State-of-Charge Indication for Battery Powered Applications», Springer, Volume 9, 2008.

[29]. W. Kester, «Data Conversion Handbook», Newns, 2005.

[30]. S. Lekas, P. Holland et al. "Signal Conditioning and PC-Based Data Acquisition Handbook» IOtech, 1998.

[31]. B. Baker, «The ABC's of A-D Converter Latency» Technical Note, Texas Instruments, 2008.

[32]. D.A. Johns and K. Martin, «Analog Integrated Circuit Design», John Wiley & Sons, Canada, 1997.

[33]. «LTC-6802-1 Multicell Battery Stack Monitor», Linear Technology Corporation, 2009.

[34]. «MAX-11068 12-Channel High Voltage Sensor Smart Data Acquisition Interface», Maxim Semiconductors, 2009.

[35]. «Li-Ion Battery Monitoring System», Analog Devices, 2008.

[36]. «MAXIM MINIQUSB User Guide», Maxim Semiconductors, 2008.

[37]. «Quick Start Guide for Demonstration Circuit 590B», Linear Technology Corporation, 2008.

[38]. Energizer, «Technical Bulletin, Battery internal Resistance», version 1.1.0, December 2005.

Projet fin d'étude Page Zied Jelassi

Résumé

L'époque actuelle est caractérisée par une explosion de la demande des solutions mobiles. Suite à cette croissance, les appareils sont devenus de plus en plus gourmands en énergie. Pour assurer une autonomie importante, plusieurs industriels emploient des batteries à haute densité d'énergie.

Dans ce cadre, les fabricants de batteries et en particulier Saft ont déjà commencé à produire des batteries Lithium-Ion dont leur densité d'énergie dépasse la 350 Wh/l.

Comme toutes les batteries Li-Ion, ces batteries nécessitent encore un BMS, ou encore un système de gestion de batterie, pour assurer son exploitation optimale et pour garantir une durée de vie maximale.

Au cours de ce projet, nous avons étudié la structure multiplexée de deux BMS (MAX11068 et LTC6802). Cette étude s'intéresse aux problèmes liés à cette architecture, notamment par rapport à la diaphonie et à l'injection de charge.

Mots clés : Li-Ion, BMS, diaphonie, injection de charge, CAN ?-?, CAN-SAR, LC-ADC

Abstract

The present era is characterized by an explosion in mobile solutions demand. As consequence, electronic devices have become increasingly energy depending and consuming. In order to ensure a substantial autonomy, many industrialists employ very high energy density batteries.

In this context, battery manufacturers and Saft, for instance, have already begun to produce Li-Ion batteries whose energy density is exceeding 350 Wh / l.

These batteries, like all Li-Ion ones, still require a BMS (Battery Management System) to ensure an optimum use and a maximum life time.

During this project, we have studied the structure of two multiplexed BMSs (MAX11068 and LTC6802). This study has examined the problems referring to this architecture and has particularly focused on the crosstalk and charge injection limitations.

Keywords: Li-Ion, BMS, crosstalk, charge injection, Ó-Ä ADC, SAR-ADC, LC-ADC