Etude d'un glissement de terrain par différente méthodes

DIdieaees

Rien n'est aussi beau à offrir que le fruit d'un labeur qu'on dédie du fond du coeur à ceux Qu'on aime et qu'on remercie en exprimant la gratitude et la reconnaissance durant toute Notre existence.

A ceux que j'aime jusqu'à la frontière de l'imagination : Mon père MILOUD et ma mère KHEIRA.

A ceux que j'adore et respecte : Mes frères et mes soeurs .

Mes tantes et mes oncles . Toute la famille BENOUIS.

A tous Mes Amis

A ceux qui se sont sacrifiés et qui se sont donnés pour les études et dont je rends un vibrant hommage.

DJAMEL EDDINE.

Titre Remerciement	Page 01
dédicaces	02
Sommaire	04
Liste des figures	07
Liste des tableaux	09
Introduction générale.
Introduction	10
But du projet	10
Organisation de la thèse	10
Chapitre I :introduction générale sur les glissements de terrain.
I.I Introduction	10
I.2. Description des glissements de terrain	13
I.2.1 Vitesse et durée des mouvements	14
I.2.1.1. Les écroulements et les éboulements	14
I.2.1.2. les glissements	17
I.2.1.3. Solifluxion, coulées boueuses et glissements coulées	20
I.2.1.4. Le fluage	22
I.2.2. Forme de la surface de rupture	23
I.3. Causes de glissements	23
I.3.1. L'eau et les risques de glissements de terrain	24
I.3.2. La présence des fractions fines	26
I.4. Identification de danger de glissement	27
I.4.1. Documents de base	28
I.4.2. Documentation des événements	28
I.4.3. Carte des phénomènes	28
I.4.4. Les effets dommageables possibles	28
I.4.4.1 .Glissements de terrain	28
I.4.4.2. Processus d'éboulement	29
I.5. Conclusion	32
Chapitre II : Etude Pathologiques de la stabilité des talus.
II. 1 - Introduction.	32
II.1. Quelques cas pathologiques observés	32
II .2.1. En Algérie	32
II.2.2. En Europe	35
II .2.3. En Asie	37
II.2.4.EN Amérique	39
II .3. Conclusion	40
Chapitre III : Reconnaissance du sol
III. 1.Introduction.	41
III .2. Reconnaissance géologique			41
III .3. Reconnaissance géophysique			41
III .4. Reconnaissance géotechnique			42
III. 4. 1. Essais "in situ"			42
III .4 .2. Essais de laboratoire			43
III .4.2.1. Teneur en eau naturelle			43
III .4.2.2. Analyse granulométrique			44
III .4.2.3. Les limites d'Atterberg			44
III .4.2.4. Les essais de cisaillement			44
III .4.2.5. Les essais de compactage			45
III.4.2.6.L'essai oedométrique			46
III. 5. Hydrogéologie			46
III .6. Caractéristiques de sole à prendre en compte dans l'analyse des talus			47
Chapitre IV : Les méthodes de calcul.
IV-1-Introduction.			48
IV. 2. Le principe d'équilibre limite			48
IV.3. Choix de la valeur du coefficient de sécurité dans le calcul de stabilité			49
IV.4. Calculer le coefficient de sécurité			50
IV.5. Facteurs influençant la stabilité des talus			52
V. 6. Les méthodes classiques pour l'analyse de la stabilité			53
V. 6.1. Cas glissement plan			54
IV .6.2. Méthodes de l'équilibre des moments			56
IV .6.2.1. La méthode générale des tranches pour une surface de rupture circulaire			56
IV .6 .2 .2. La méthode de Fellenius			59
IV .6.2.3. Méthode de Bishop (1955)			61
IV .6.2.4. La méthode de Bishop simplifiée			64
IV .6 .3 . Méthodes de l'équilibre des forces			66
IV. 6.3.1. La méthode de Coin			66
IV.6.4. Méthodes de l'équilibre des moments et des forces			67
IV .6.4.1. La méthode de Janbu simplifiée			67
IV.6.4.2. La méthode de Janbu généralisée			68
IV. 6. 4 3. La méthode de Spencer			69
IV .6.4.4. La méthode de Morgenstern et Price			72
IV. 6.4.5. La méthode de Sarma			73
IV .7 . Récapitulation des hypothèses, des équations d'équilibres et des inconnus			74
IV .8.Étude comparative des méthodes de calcul à la rupture			76
IV.9. Analyse des talus par la méthode des éléments finis			79
IV.9.1. Type d'élément finis			79
IV.9.2. Développement de la fonction d'interpolation			79
IV.9.3. Développent de déformation et contrainte			82
IV.9.4. Résolution Eléments Finis		84
IV.9.5. Modélisation des matériaux en SAS-FEM		84
IV.9.6.Coefficient de sécurité Factor (FOS)		85
IV.9.7. La rupture de pente		86
Chapitre V: présentation des logiciels utilisés
V .1. Les logiciels utilisés pour l'analyse de la stabilité		87
V .1.1. Logiciel SLOPE/W		87
V.1. 2. Logiciel LARIX-4S		87
V .1.3. Logiciel CLARA		88
V .2.Définition des paramètres géométriques de surface de rupture		88
V .2. Présentation du logiciel Geoslope Geostudio 2002 V5.03		89
V .2.1 . Le programme SLOPE/W		90
V .2. 2. L'interface du logiciel SLOPE/W		90
V .3. Logiciel SAS-FEM 2008		93
V.3.1.Présentation		93
V .3.2. L'interface du logiciel SLOPE/W		94
Chapitre VI : Etude de cas_ Talus de Riadh.
VI.1. Introduction		99				VI.2. Présentation générale du projet
99
VI.3.Les essaies au laboratoire (L.T.P.O)		104
VI.4. détermination des densités et de la teneur en eau		104
VI .4.1. Principe de la méthode		104
VI .4.2.Méthode d'analyse		104
VI.4.3. Résultats		107
VI.5. L'essai de cisaillement rectiligne direct à la boite		107
VI .5.1. Définitions		107
VI .5.2. Principe de la méthode		108
VI.5.3. Méthode d'analyse		108
VI.5.4. Réalisation de l'essai		109
VI .5.5.Résultats		113
VI.6.Récapitulation		114
VI.7. Calculs et résultats		114
VI.7.1. caractéristique du talus		114
VI.7.2. Méthode de calcul manuelle		115
VI .7.2.2. Description du processus et outils utilisés		115
VI .7. 3. Les résultats obtenus à l'aide du logiciel SLOPE/W		119
VI .7.4. Les résultats obtenus à l'aide du logiciel SAS- FEM		122
VI .8.Récapitulation et comparaison des résultats obtenus		125
Conclusions générales.		126
Références Bibliographiques.		127

LISTE DES FIGURES

N° (I.1)	TITRE Bloc diagramme d'un glissement de terrain			Page 13
(I.2)	Chutes de pierres et de blocs.			14
(I.3)	Un Eboulement.			15
(I.4)	Liaison entre les éboulements et les chutes de blocs			16
(I.5)	Un écroulement			16
(I.6)	Un glissement.			17
(I.7)	les deux types de glissement (plan (a) et rotationnel (b))			18
(I.8)	Une coulée boueuse.			20
(I.9)	le phénomène de fluage.			22
(II.1)	Fissures longitudinales dans la routé affecté par le glissement			33
(II.2)	Cinématique du glissement			33
(II.3)	Construction de l'ouvrage par couches			34
(II.4)	Affaissement de plus de 50cm du glissement en bas du talus (Les Abattoirs Ténès)			35
(II.5)	les modifications géomorphologiques de la surface du glissement de la Clapiers			36
(II.6)	L'éboulement des Ruines de Séchilienne			37
(II.7)	Une coulée de boue a frappé le nord de l'Indonésie			38
(II.8)	Le village de Guinsuagon enseveli sous la boue			38
(II-9)	Glissements de La Leona près de San Vicente(a) et de Las Collinas (b).			39
(II-10)	Morphologie de la zone de glissement de Villatina Medellin en Colombie.			40
(III-1)	différents types de pénétromètre			42
(III-2)	La boîte de Casagrande			45
(III-3)	appareil d'essai oedométrique			46
(IV.1)	Contrainte normale au plan de rupture.			51
(IV-2)	facteurs influençant la stabilité du talus.			53
(IV-3)	pente infinie de surface de rupture plane			54
(IV-4)	La masse du talus découper en tranches			57
(IV-5)	Les forces agissant sur une tranche			60
(IV-6)	Représentation des forces inter-tranches sur une tranche.			62
(IV.7)	La représentation des forces sur une tranche dans la méthode de Bishop			64
(IV.8)	Représentation des forces sur une tranche.			68
(IV.9)	La représentation des forces sur une tranche			69
(IV.10)	Résultante des forces parallèles			70
(IV.11)	représentation de toutes les forces inconnues sur une tranche dans la méthode de Spencer.			70
(IV.12)	les coordonnées pour une surface de rupture non circulaire utilisée dans la			71
		méthode de Spencer.
(IV.13)		représentation graphique des forces sur une tranche	72
(IV.14)		le facteur de sécurité partir des moments d'équilibre	77
(V.1)		Une Illustration d'une surface de rupture circulaire	89
(V.2)		Les menus disponibles sur logiciel SLOPE/W	90
(V.3)		détermination de la surface de rupture par la méthode ((Grid and Radius»	92
(V.4)		détermination de la surface de rupture par la méthode ((Entry and Exit	93
(V.5)		L'interface de logiciel SAS-FEM2008	94
(V.6)		Les menus disponibles sur logiciel SAS-FEM2008	94
(VI.1)		Prise à 421m d'altitude	100
(VI.2)		Prise à 421m d'altitude	101
(VI.3)		début et fin de talus.	102
(VI.4)		maillage des coordonnés	103
(VI.5)		Dispositif de l'essai de cisaillement.	108
(VI.6)		Courbe intrinsèque (remblai & argile)	113
(VI.7)		Les dimension de talus El_Riadh	115
(VI.8)		détails du talus étudié	116
(VI.9)		Résultat obtenu par Méthode de BISHOP	119
(VI.10)		Résultat obtenu par Méthode de MORGENSTEM-PRICE	120
(VI.11)		Résultat obtenu par Méthode de JANBU	120
(VI.12)		Résultat obtenu par Méthode de SPENCER	121
(VI.13)		Résultat obtenu par Méthode G.L.E	121
(VI.14)		Résultat obtenu par Méthode de FELLENIUS	122
(VI.15)		la déformée.	123
(VI.16)		Les Vecteurs de Déformation	123
(VI.17)		La sufrace de rupture	124
(VI.18)		Graphe des Coefficients Sécurité /Nombre des itérations	124

LISTE DES TABLEAUX

N° (I.1)	TITRE Classification selon la taille des composants, les volumes et les vitesses.	Page 17
(I.2)	Classification selon l'activité en fonction de l'évaluation de la vitesse moyenne de glissement à long terme.	19
(I.3)	Classification selon la profondeur de la surface de glissement (En m sous la surface du sol).	20
(IV.1)	Classification FS en fonction de l'importance de l'ouvrage	49
(IV.2)	Les hypothèses, les équations et les inconnus dans les méthodes d'analyses	74
(VI.1)	les coordonnés du projet.	99
(VI.2)	RESULTATS OBTENUS POUR LE REMBLAI	111
(VI.3)	RESULTATS OBTENUS POUR L'argile verte .	111
(VI.4)	Résultats obtenues.	114
(VI.5)	Résultats de calcul par méthode manuelle	117
(VI.6)	Résultats de réévaluation des coefficients de sécurité	118
(VI.7)	Résultats de calcul par Géostudio 2002	122
(VI.8)	Résultats de calcul	125

Introduction

Le phénomène de glissement de terrain est considéré comme dangers naturel permanents rencontrés dans tous les pays du monde car l'importance des effets de glissement pouvant engendrer des dégâts humains et matériels pouvant se chiffrer en plusieurs millions de Dollars dont les gouvernements doivent prêter beaucoup d'attention.

Pour cela, il faut compte tenu de ces phénomènes et de leurs dangers, et de prendre les précautions convenable pour détecter les zones instables afin de trouver les meilleurs solutions de protections ou de traitements.

But du projet

Le projet de fin d'étude qui nous a été confié par la direction des travaux public DTP de Saida est basé sur l'étude de la stabilité d'un versant naturel situé dans la commune de Saida (Riyadh). L'étude s'intéresse à la vérification de la stabilité de ce talus par le calcul de son coefficient de sécurité par plusieurs méthodes afin de les comparer.

Organisation de la thèse

Pour bien présenter les informations sur la stabilité des talus et éclairé les axes de notre étude, la thèse a été articulée suivant les points suivants:

· Chapitre I : Introduction général sur le glissement de terrain: dans ce chapitre On a essayé de donné une aidé sur le phénomène de glissement de terrain, ses types et ses causes.

· Chapitre II: Etude pathologiques : on a représenté dans ce chapitre quelques cas pathologiques dus aux glissements des terrains en plusieurs pays dans le monde pour but de savoir l'importance de l'étude de stabilité des talus.

· Chapitre III: reconnaissances des sols : une présentation générale sur les tests de reconnaissances de sol.

· Chapitre IV: Les méthodes d'analyse de la stabilité des pentes : dans ce chapitre on a présenté les différentes méthodes de calculs qui peuvent être utilisées dans l'analyse

de la stabilité des talus en détail (principes et théories de calcul), et l'évaluation de coefficient de sécurité.

· Chapitre V : présentation des logiciels utiisés : On a donné les caractéristiques générales des logiciels utilisés pour les calculs des talus, avec une démarche simple pour définir un problème de talus dans différent logiciel. Ce chapitre peut être considéré comme un manuel simple pour analysé les talus utilisant des logiciels informatiques.

· Chapitre VI: Etude de cas «Talus Ryiadh » : dans ce chapitre une application directe des différentes méthodes pour calculer le coefficient de sécurité d'un talus existe à la Wilaya de Saida après une présentation géométrique et géotechnique de ce talus. Finalement une comparaison entre toutes les méthodes utilisées a été présentée et discutée.

· Conclusions générales : une conclusion générale sur notre étude.

I.1. Introduction :

Les profondeurs des surfaces de glissement varient ainsi de quelques mètres à plusieurs dizaines de mètres de profondeur. On parle de glissements superficiels dont les signes visibles en surface sont souvent spectaculaires (fissures dans les murs des habitations, bourrelets dans les champs, poteaux penchés...) et de glissements profonds qui présentent moins d'indices observables et qui sont donc plus difficilement détectables.

La nature géologique des terrains est un des principaux facteurs d'apparition de ces phénomènes tout comme l'eau et la pente. Les matériaux affectés sont très variés (roches marneuses ou schisteuses, formations tertiaires altérées, colluvions fines, moraines argileuses, etc.) mais globalement la présence d'argile en forte proportion est toujours un élément défavorable compte tenu de ses mauvaises caractéristiques mécaniques. La saturation des terrains en eau (présences de sources, fortes précipitations, fonte des neiges brutales) joue aussi un rôle moteur dans le déclenchement de ces phénomènes.

L'objectif de ce chapitre est de définir en premier lieu les différents types de glissements de terrain selon leur vitesse (les écoulements, les coulées, le fluage et les glissements) et selon la morphologie de leur surface de rupture et d'envisager en second lieu les principaux causes qui peuvent mobiliser ces glissements et de citer en dernier lieu les différentes informations nécessaires pour identifier le type de glissement de terrain probable et son degré de danger vis-à-vis à son intensité.

La détermination du type de glissement de terrain (glissement plan, circulaire ou quelconque) selon les informations disponibles tel que la géométrie, les caractéristiques mécanique et élastique, et surtout la présence des eaux souterraines et des nappes phréatiques, permet de proposer des analyses et méthodes de calculs pour les différentes modes de rupture.

Qu'il s'agisse de glissements de terrain, d'éboulements ou encore de coulées boueuses, on est cependant toujours en présence du déplacement gravitaire d'un volume de roche ou de sols déstabilisées sous l'effet de sollicitations naturelles (forte pluie, cycle gel/dégel, séisme, fonte des neiges...) ou anthropiques (terrassement, déboisement...).

Chapitre

I : Introduction général sur les glissements

de terrain

s d'accélération parfo

is brutale à

C es différents phéno mènes évoluent irréguli d'évolution lentes à des phase ou moi ns graves.

èrement dans le temps, passant de phases l'origine de catastrophes plus

La vitesse de déplac ement des différents phénomènes permet de distinguer deux grands ensembles de mouve ments de terrain: les mouvements lents et co ntinus pour lesquels la déformation est progressive, parfois accompagnée de rupture mais e n principe d'aucune accélération brutal e. Il s'agit des phéno mènes de fluage et des glissements. Les mo uvements rapides et discontinus, eux-mêmes divis és en deux groupes, selon le mode de propagation des matériaux : en ma s se lorsqu'i l s'agit de matériaux rigides (roche), ou à l'é tat remanié quand il s'agit d e matériaux meuble (argile). Ce s ont les chutes de pierres et de blocs, les éboulements, les coulées boueus e s.

I.2. D e

I

critères

de la surface de rupture, cau s

cinématique du mouvement et la

celles b

asées sur la

scriptio n

l existe de
(nature de

:

nombreus es classifications des g lissements de terrain basées sur différents terrain, cinématique du mouvement, vitess e du mouv ement, morphologie

e de la rupture...). Nous ne déc rirons dans ce paragraphe que

morpholo gie de la surface de rupture.

des gliss

ements d

e terrain

Nous rapp elons dans la figure (I. terrain avec sa terminologie détaillée.

1) le schéma en bloc diagramme

d'un glissement de

Fig. (I.1):

Bloc diagramme d'un

glissement

de terrain

I.2.1 Vitesse et durée des mouvements :

L'évolution dans le temps d'un glissement de terrain peut conduire à distinguer 4 familles qui se différencient par la brutalité du phénomène :

- les écroulements ;

- les glissements ;

- les fluages ;

- les coulées

I.2.1.1. Les écroulements et les éboulements :

Les éboulements au sens large (phénomènes de chute) sont des mouvements rapides de masses. Le matériel éboulé, qui s'est détaché du massif rocheux selon des surfaces de discontinuité (pendage, schistosité, fissures ou fractures), parcourt la plus grande partie de son déplacement dans l'air.

Ces phénomènes peuvent être classés en trois catégories: chutes de pierres et de blocs, éboulements (au sens strict) et écroulements. En général, on peut les subdiviser en trois domaines: la zone d'arrachement, la zone de transit et la zone de dépôt.

o Chutes de pierres et de blocs : Les chutes de pierres et de blocs sont caractérisées par

la chute sporadique de blocs plus ou moins isolés (pierre: Ø < 50cm; bloc: Ø > 50cm).

Ce processus, répété ou soumis à des pointes saisonnières, caractérise la désagrégation continuelle d'une falaise rocheuse, déterminée par ses conditions géologiques, son exposition et son altération. L'estimation du volume des matériaux rocheux qui présente un danger potentiel de chute n'est possible qu'au moyen d'études détaillées de la roche.

Fig. (I.2): Chutes de pierres et de blocs.

Page 14

Chapitre

I : Introduction général sur les glissements

de terrain

Les vitess e mouve ments d'un e de roul ement.

s de chute pierre ou d

vont gén é 'un bloc, i l

ralement de 5 à 30 m/s. Dans la description des convient de distinguer entre les phases de rebond et

que l'é nergie cinétique de la plupart des arbres.

Dans les pentes dont l 'inclinaison est inférie ure à 30° environ, les

en mouvement tendent en général à s'arrêter. La forêt joue un

pierres et les blocs
rôle très important, par le fait
blocs est fortement ré duite par le urs chocs c ontre les

Le mode de rupture au sein du ma ssif a en général peu d'influenc e sur le déroulement de l'év énement. En comparai s on avec le phénomène d'écroule ment, les interactions entre les

éléments de roche formant l'éboulement et l'énergi e mise en oe uvre sont relativement limitées.

Les vite sses de tran sport se situent princip alement e ntre 10 et 4 0m/s.

o Ebouleme nt : Lors d' un éboule ment (au sen s strict), un volume de roche important, se

volume Dans de

fragme ntant plus ou moins intensément, se détache en bloc du massif roc heux et s'éboule. Le de matériaux concernés est en g énéral compris entre 1 00 et 10000 0m³ par événement. s cas exce ptionnels, des volumes sensiblement plus grands peuvent s'ébouler.

Fig. (I.3): Un Ebou

lement.

Dans la pratique, l'estimation d' un volume de roche qui présente un danger p d'éboulement exi ge des études détail lées du massif rocheux, comp renant une approfondie de l'o rientation spatiale des surfaces de discontinuité.

otentiel analyse

Fig. (I.4): Liaison entre les éboulements et les chutes de blocs

o Ecroulement : Lors d'un écroulement, un grand volume du massif rocheux (un à

plusieurs millions de m³) se détache soudainement, sans que le mode de rupture correspondant ne soit déterminant. Le mécanisme initial peut par exemple s'expliquer par le développement d'une surface de glissement inclinée. Le mécanisme de mouvement de l'écroulement est déterminé par la topographie, de même que par l'interaction marquée entre les composants de la masse écroulée et par leur fragmentation intense.

Les caractéristiques particulières de ce phénomène sont des vitesses de chute élevées (de plus de 40m/s) et de très grandes distances de transport (pouvant souvent atteindre plusieurs kilomètres). Compte tenu des grands volumes concernés, les écroulements peuvent modifier le paysage de façon durable. Les énormes masses écroulées forment souvent des barrages naturels dans les vallées de montagne, obstruant les cours d'eau et créant des retenues; en cas de rupture catastrophique du barrage, elles entraînent un danger d'inondation pour les régions en aval.

Fig. (I.5): Un écroulement

Le tableau ci-dessous résume les principales caractéristiques qui nous permettent de différencier entre ces phénomènes.

Tableau (I.1): Classification selon la taille des composants, les volumes et les vitesses.

Chute de pierres		ø < 50cm	Chute de blocs
ø > 50cm		Eboulement Volume Vitesse
100 -100000m^3 10 - 40m/s		Ecroulement Volume Vitesse
> 1 mio.m^3 > 40m/s

I.2.1.2. les glissements :

Les glissements de terrain sont des mouvements de masses compactes et/ou de terrain meuble glissant vers l'aval. Ils résultent d'une rupture par cisaillement et se produisent en général sur des talus ou des versants de pente modérée à raide. Les instabilités naturelles de ce genre sont extrêmement courantes et apparaissent sous de nombreuses formes, étonnamment diversifiées.

Fig.(1.6): Un glissement.

La plupart du temps, l'eau joue un rôle important dans les glissements de terrain, par l'action des pressions interstitielles, des écoulements souterrains ou par les pressions dues au

Chapitre

I : Introduction général sur les glissements

de terrain

gonflement des minéraux arg ileux. En simplifiant b eaucoup, o n peut distinguer deux types de glisse ments:

o Les glisse ments de type rotationnel : Sont en gé néral de volume limité. Ils se

produis ent princip alement dans des terrains meubl es homogè nes surtout argileux et silteux. Dans une coupe verticale, la surface de glisse ment est circulaire et plonge presque vertical ement dan s la niche d 'arrachement. En règl e générale, le mécanisme du gliss ement ne provoque qu'un faible remani ement interne du matériel glissé.

Des dépres sions ave c crevasses ouvertes et des fissures de traction sont souvent visibles dans la moitié supéri eure du glis sement, alors que la masse glissé e tend à s'étaler et à se désagréger au front du glis sement, où peuvent se former des écouleme nts de boue (coulées de terre ) en cas de saturation en eau de la masse.

o L

terrain

es glisse ments tran slationnels: Lors de glissements translation n els, les couches de ou les ens embles de couches str atifiées gli ssent sur u ne zone de faiblesse existante (souve nt pendage stratigraphi que, disco ntinuité stra tigraphique , schistosit é , plan de fissure ou de rupt ure). En p lan, la taill e de tels g lissements est très va riable et p e ut compre ndre des surface s allant de quelques m ètres carrés à plusieurs kilomètres carrés.

L'épaisseu r des mass es en mou vement att eint fréque mment pl usieurs diz aines de

mètres. Les zones de flysch, l e s schistes marno-calc aires ou les schistes métamorphi ques sont

les for mations les plus sujette s à ce genr e de glisse ment.

La figu re ci-desso us schémati s e les deux types de gl issement.

Fig. (I .

(a) 7): les deu x

(b) types de g lissement (plan (a) et

rotationnel (b))

· Vitesse moyenne de mouvement des glissements: La vitesse moyenne de mouvement des glissements atteint le plus souvent quelques millimètres par an pour un glissement substabilisé, très lent, et quelques centimètres à quelques décimètres par an pour un glissement actif.

Il existe quelques cas exceptionnels où le glissement peut être bien plus rapide et où la masse en mouvement, sans perdre sa compacité, peut atteindre plusieurs décimètres par jour. Exceptionnellement, des mouvements très rapides peuvent se produire.

Tableau (I.2) : Classification selon l'activité en fonction de l'évaluation de la

vitesse moyenne de glissement à long terme.

Glissement		Vitesse de glissement	substabilisé, très lent
0 - 2 cm /an		peu actif, lent
2 - 10 cm /an		actif (ou lent avec phases rapides)
> 10 cm /an

· Classification : Les glissements peuvent être classés selon la profondeur estimé de la surface de glissement et selon la vitesse moyenne à long terme des mouvements (comme mesure de leur activité). Lors de l'évaluation du danger potentiel que représente un glissement, on ne doit pas seulement considérer le volume ou la vitesse du glissement.

Il faut aussi tenir compte des mouvements différentiels qui se manifestent et qui peuvent conduire au basculement des bâtiments ou à la formation de fissures. Les glissements peuvent aussi se transformer en glissements coulée (coulées de terre) et atteindre des zones très étendues. Il faut enfin prendre garde aux interactions entre glissements de terrain et cours d'eau, par lesquelles de grandes masses de matériaux alluvionnaires peuvent être mobilisées.

Ce phénomène peut conduire à la formation d'une retenue sur un cours d'eau, puis entraîner des débâcles (laves torrentielles) qui mettent en danger les zones situées en aval.

Tableau (I-3): Classification selon la profondeur de la surface de glissement (En m sous la
surface du sol).

Glissement		Surface de glissement	superficiel
0 - 2m		semi profond
2 - 10m		profond
>10m

I.2.1.3. Solifluxion, coulées boueuses et glissements coulées :

D'une manière générale, la solifluxion et les coulées de boue désignent tous les mouvements de sols ou formations superficielles, en relation directe avec le franchissement des limites de liquidité.

Les coulées ont lieu dans des formations argileuses, ou a granulométrie très fine, (argilite normalement consolidée à surconsolidée, marnes, schiste argileux, flysch argileux...) fissurées et saturées à plasticité moyenne.

Fig. (1.8): Une coulée boueuse.

Etant donné le caractère très particulier des formations argileuses (présence d'argiles gonflantes, forte sensibilité des caractéristiques mécaniques aux conditions hydriques, ...), les processus d'altération mécanique et chimique prennent une importance considérable dans les

processus de déclenchement des coulées boueuses. Les conditions climatiques, les apports d'eau superficiels et les nappes souterraines jouent un rôle important.

Sur le terrain, et d'un point de vue morphologique, les mouvements de solifluxion, ou d'anciennes coulées encore actives peuvent se repérer de plusieurs manières : traces de mouvements, présence de bourrelets, présence de petites marches d'escaliers, mais aussi grâce à la courbure des troncs des arbres présents.

Une coulée active présente, comme un glissement, une morphologie particulière qui peut se décomposer en trois grandes parties :

- une zone source : zone en forme de cuvette ;

- une zone de transition : chenal, limité par des levées latérales, assez long ou lobé, et alimenté par la zone source où transite les matériaux mobilisés ;

- une zone d'accumulation ou lobe : zone de faible pente ou les matériaux ont tendance à s'accumuler.

Dans certains cas, des glissements antérieurs peuvent déterminer la position d'une nouvelle coulée en raison des modifications occasionnées sur les écoulements souterrains.

Cette situation est, parfois, encore plus marquée, puisque les matériaux du glissement, en cours de progression, deviennent à l'aval des matériaux sources pour la génération d'une coulée de boue. Pour ce type d'événement, on parle de glissement coulée.

Les glissements du type "coulées boueuses" sont en général des événements rapides et de forte intensité, avec une « fluidisation » des matériaux glissés au niveau de la coulée. Ces matériaux présentent une faible cohésion initiale, et évoluent rapidement en une masse sans cohésion.

Une coulée, après son déclenchement, peut aussi continuer à évoluer lentement, par fluage ou par des phénomènes de solifluxion localisés, suivant les apports d'eau qu'elle reçoit, soit par infiltration directe, soit par le versant.

Les coulées boueuses se comportent donc, d'un point de vue rhéologique, comme un fluide à seuil, c'est-à-dire un fluide qui a besoin d'une sollicitation en cisaillement minimum pour s'écouler.

Chapitre

I : Introduction général sur les glissements

de terrain

I.2.1.4. Le fluage :

L est caractérisé par des mouvements lents et continus, mais à des vitesses

e fluage

faibles. Dans le ca s de fluage , il est diffi cile de mettre en évidence une surface de rupture. Le
mouve ment se produit généralement sans modification des efforts appliqués (contrairement
sements) : en fait le matériau est sollicité à un état proche de la rupture. Ce

aux glis

type de

oit se stabiliser, soit évoluer vers une rupture

.

mouve ment peut : s

mène de fl uage.

5) montre l e mécanisme du phéno

La figure ci-après (figure III -

Fig. (I.9): le phénomèn

e de fluage.

On distingue deux grandes catégories de déformation de fluage :

- la déformation volumique ;

- la déformation de cisaillement.

Le fluage e n déformation volumi que est causé par un état de contrainte isotropique.

cisaillement, quant à

lui, est provoqué par la partie

Il dépend de l'écoulement de l'eau libre interstitielle et de la variation relative du volume du squelette inter granulaire. L e fluage au

déviato rique du te nseur de co ntraintes.

ssion interstitielle est

seul. La déformation

cisaillement homogène, ou de la

nulle alor

s le squel ette inter-granulaire

de fluage au cisaillement est

boîte de

T ment la pre

héorique

supporte les contraintes appl i quées tout

étudiée à l'aide de l'appareil

a boîte de

triaxial, de l

cisaillement plan.

I.2.2. Forme de la surface de rupture :

La forme des surfaces de rupture dépend beaucoup des caractéristiques du matériau. Dans les terrains plutôt rocheux, les surfaces de glissement seront liées aux surfaces de discontinuité, dans des terrains plus meubles et homogènes, les surfaces de rupture seront grossièrement des cercles en deux dimensions ou des ellipsoïdes en trois dimensions. Dans des terrains hétérogènes, les surfaces de rupture pourront être une combinaison de surfaces circulaires et planaires, mais cela pourra être une forme quelconque. La surface de rupture, d'une manière générale, passera par les zones de terrain dont les caractéristiques sont les plus faibles.

I.3. Causes de glissements :

Les mouvements de terrain sont des déplacements (avec ou sans rupture) vers l'aval de masses rocheuses compactes ou désagrégées et/ou de terrain meuble (sols y compris) et d'eau, sous l'effet de la gravité.

Ils peuvent se produire sous forme de processus brutaux (chute de pierres et de blocs, éboulement et écroulement, glissement soudain, coulée boueuse, effondrement) ou lents et progressifs (fluage, glissement lent permanent).

Les processus à l'origine des mouvements de terrain sont très complexes et dépendent rarement d'une seule cause. La géologie, le relief et l'exposition sont des paramètres fondamentaux, plus ou moins constants sur de longues périodes; ils déterminent la prédisposition générale du terrain aux phénomènes d'instabilité. Le processus qui mène à une telle instabilité commence en fait dès la formation de la roche, c'est à dire lorsque les propriétés chimiques et physiques de celle-ci sont bien établies. Ces propriétés déterminent notamment son comportement face à l'altération et à l'érosion.

Les mouvements de terrain résultent d'un changement de l'équilibre des forces dans le versant (rapport entre forces résistantes et forces motrices), à la suite de processus physiques et / ou chimiques qui, à leur tour, dépendent de différents facteurs. Ainsi, les processus d'altération agissant à long terme (conduisant à une diminution des forces résistantes), de même que les fluctuations de la nappe phréatique, influencent la stabilité d'un versant de manière continue. Par ailleurs, une pente peut aussi être déstabilisée rapidement, soit à la suite

de l'érosion par une rivière au pied du versant, soit, mais plus rarement, suite à un tremblement de terre.

En général, l'eau joue un rôle déterminant pour les mouvements de terrain, elle produit des pressions hydrostatiques dans les pores (pressions interstitielles), les fissures et les failles, de même que des forces de percolation.

A l'état de glace, elle a en plus la capacité d'induire des mécanismes de rupture notables. Par ailleurs, elle peut provoquer le gonflement des minéraux argileux (pression de gonflement). La stabilité des pentes en équilibre critique peut être sensiblement réduite par ces divers effets.

Le déclenchement d'un processus dangereux survient lorsque la valeur limite d'un des facteurs déterminants est atteinte ou dépassée. Les cycles de gel / dégel, les précipitations éventuelles, de forte intensité ou de longue durée - éventuellement combinées à la fonte des neiges -, conduisent souvent à des mouvements de terrain spontanés.

Il n'est pas rare que les mouvements de terrain soient favorisés par des influences anthropiques. Ainsi, la surcharge d'une pente par des bâtiments et des remblais, les excavations sans dispositifs de protection dans un versant lors de travaux de construction, la surélévation du niveau de l'eau souterraine, le dynamitage, l'exploitation inappropriée de matières premières ou l'affectation inadéquate du sol peuvent accroître le danger de mouvements de terrain. Les effets anthropiques peuvent aussi contribuer à une déstabilisation à long terme du versant, en relation avec d'autres activités comme le déboisement, l'entretien insuffisant des forêts, le surpâturage, l'exploitation intensive et la dénudation du sol.

Dans la majorité des cas, les glissements de terrain dépendent de deux causes principales : l'eau et la présence des fractions fines.

I.3.1. L'eau et les risques de glissements de terrain:

Les eaux souterraines et de surface jouent un rôle déstabilisant sur les sols et les massifs rocheux avec des manifestations qui peuvent être extrêmes comme les glissements de terrain ou les éboulements de roches.

Pour prévenir ces risques, la modélisation hydro-mécanique et hydro-géologique doit aller de pair avec des opérations de drainage des eaux et une surveillance.

Les nappes souterraines, et plus exactement leurs fluctuations liées aux conditions météorologiques ou parfois aux actions humaines, sont très souvent à l'origine de déclenchements des mouvements de versants: glissements, éboulements, coulées ou laves torrentielles.

Sur les pentes, l'action déstabilisatrice de l'eau infiltrée dans le sol est triple :

· Accroissement du poids volumique des sols par augmentation de la teneur en eau: cet effet est le plus souvent mineur;

· Changement de comportement rhéologique: le sol passe de l'état solide à l'état de fluide visqueux; certaines coulées de boue ou laves torrentielles sont ainsi engendrées par l'imbibition d'une masse de sol. On peut aussi évoquer, lors d'un séisme, la liquéfaction des sables sous nappe qui est à l'origine de nombreux glissements sur très faible pente. Par ailleurs, des circulations d'eau souterraine peuvent engendrer sur le long terme une altération progressive des terrains encaissants, avec dégradation de leurs caractéristiques mécaniques ;

· Action mécanique défavorable des pressions d'eau souterraine.

La lutte contre l'eau est une des actions les plus efficaces pour prévenir, stabiliser ou ralentir un glissement de terrain. La connaissance du mode d'alimentation de la nappe est indispensable pour intervenir efficacement.

Cela démontre toute l'importance de l'étude hydrogéologique pour la compréhension de l'évolution des glissements de terrain, mais aussi pour la maîtrise du risque correspondant.

Reposant sur les observations de terrain ou la pose de piézomètres, cette étude doit être menée sur une durée suffisante pour apprécier les fluctuations saisonnières ou annuelles des nappes.

L'introduction d'un modèle hydrogéologique dans l'étude de stabilité permet d'évaluer l'influence des eaux souterraines sur la stabilité et de tester l'efficacité d'un traitement par drainage. Il apparaît cependant que le couplage hydraulique/mécanique est parfois complexe. Pour de grands versants rocheux, la compréhension du rôle de l'eau dans la déformation et le mouvement est donc encore très imparfaite.

I.3.2. La présence des fractions fines:

Deux remarques relatives aux conditions du sol s'imposent. Les problèmes les plus critiques de stabilité des pentes se présentent d'ordinaire, en premier lieu, sur les sols à grains fins et particulièrement sur les argiles. Ceci résulte en partie de ce qu'il est difficile de les drainer et de ce que, sur ce genre de sol, les processus d'érosion par ruissellement et vagues amènent de nombreuses pentes au point de rupture.

Le second point concerne le comportement des sols à grain fin impliqués dans un déplacement des terres. En acquérant par moulage une autre forme, ils peuvent perdre une fraction notable de leur résistance. On désigne l'importance de cette perte sous le nom de sensibilité. Les hautes sensibilités correspondent aux grandes pertes de résistance. Il se peut, que les débris d'un glissement de terrain sur sols à haute sensibilité ne séjournent pas au pied de la pente, mais se dispersent et s'en éloignent. Il ressort de ce qui précède que les sols à grain fin sensibles au changement de forme exigent une attention spéciale sous le rapport de la stabilité des pentes.

I.4. Identification de danger de glissement :

L'identification des dangers dus aux mouvements de terrain repose sur une documentation objective de diverses observations et mesures impliquant un danger donné. Il faut s'assurer de prendre en compte les différentes observations sur le site ainsi que les relevés inclinométriques en essayant de bien les interpréter.

I.4.1. Documents de base :

· a)- Cartes topographiques : La carte topographique est le document de base

pour toute analyse de stabilité. Elle contient nombre d'informations pertinentes pour l'identification des dangers sous forme de symboles, de signes et d'autres éléments graphiques. Ainsi, par exemple, la morphologie des zones en glissement est souvent visible par le bombement des courbes de niveau; des symboles de blocs éboulés au pied d'une falaise peuvent laisser présager une production notable d'éboulis.

Le levé topographique se fait à l'échelle locale directement sur la zone concernée par le glissement, nous permet de bien tracer le profil en travers du site et de bien décrire les différentes couches des sols ainsi que leurs caractéristiques physico - mécaniques pris en compte pour l'évaluation de la stabilité du site.

· Cartes géologiques : La carte géologique donne des renseignements utiles sur la lithologie, sur l'agencement structural (orientation et pendage des couches et des discontinuités) et sur la couverture quaternaire (moraine, éboulis ou glissement de terrain, par exemple).

Elle donne encore des indications sur les circulations d'eau souterraine en milieu poreux et fissuré. Sur la base de ces données cartographiques, on peut reconstituer la structure tridimensionnelle des unités géologiques et évaluer le contexte de formation de possibles mouvements de terrain.

Les différents phénomènes d'instabilité de pente, comme les glissements ou les éboulements généralisés sont représentés en général sur une carte géologique au 1:25000 par leur périmètre. Il n'est pas fait mention de l'intensité ou de la fréquence de ces divers phénomènes.

Ces informations permettent toutefois de localiser les zones sensibles aux mouvements de terrain, qui devront faire l'objet d'études plus poussées (voire chapitre V).

I.4.2. Documentation des événements :

La documentation des événements correspond à une liste d'événements observés. Cette documentation comprend des données descriptives sur les processus déterminants, les dommages constatés, la zone affectée, les facteurs déclenchant (en particulier les conditions météorologiques), de même que d'autres données concernant le déroulement de l'événement.

La description d'un événement peut être faite avec plus ou moins de détails selon son importance et selon les dommages causés. Dans chaque cas, la documentation des événements donne au moins une réponse à la question «Que s'est-il passé, quand, où et avec quelle ampleur?».

La documentation détaillée des événements doit en outre répondre aux questions: «Comment l'événement en cause s'est-il déroulé?» et «Pourquoi y a-t-il eu des dégâts?». Elle joue un grand rôle lors de phénomènes ayant des effets considérables et devrait être bien étayée.

I.4.3. Carte des phénomènes :

La carte des phénomènes et le texte qui l'accompagne recensent les signes et indicateurs observés sur le terrain et procède à leur interprétation objective. Elle représente les phénomènes liés à des processus dangereux et décrit les secteurs exposés indépendamment du degré de danger.

L'analyse de terrain contribue à l'établissement de la carte des phénomènes; elle est un complément important de la documentation de l'événement et sert à la reconnaissance et à l'estimation des types de danger possibles (configuration, mécanisme de déclenchement, genre d'effets). Le relevé de terrain s'appuie d'une part sur l'observation et l'interprétation des formes du terrain (p.ex. les endroits critiques), sur les propriétés structurales et géo- mécaniques des surfaces de discontinuité dans la zone de départ des processus d'éboulement, et d'autre part sur des informations relevés sur place , (p.ex. blocs éboulés) résultant des événements dangereux antérieurs et actuels.

Elle permet aussi de tirer au clair les causes, les probabilités d'occurrence et d'autres facteurs importants ou symptômes concomitants relatifs aux événements qui se sont produits.

Afin de cartographier les dangers de manière précise , il est essentiel de connaître à fond l'état passé et actuel du terrain et d'évaluer quelle peut être son évolution possible. Dans le cas des phénomènes de falaise (éboulement et écroulement), la simple représentation des dépôts récents observés au pied des parois rocheuses ne suffit pas.

L'évaluation des aléas (dangers potentiels) et des mécanismes de déclenchement possibles dans la zone de provenance est alors indispensable. Cette étude comprend la détermination de l'agencement structural des couches et des principales discontinuités, du degré d'altération de la falaise, ainsi que du volume probable des compartiments instables et de la taille des blocs. Ces caractéristiques peuvent être synthétisées dans une «carte des aléas».

I.4.4. Les effets dommageables possibles :

I.4.4.1 .Glissements de terrain :

o Intensité forte : Les modifications importantes affectant le terrain conduisent à des

mouvements différentiels notables du sous-sol et portent un sérieux préjudice à la stabilité des

bâtiments. Suite aux fissures qui se développent dans les éléments de structure du bâtiment, aux tassements qu'ils subissent et à leur basculement, une destruction partielle ou totale des bâtiments est possible.

Les portes et les fenêtres ne peuvent plus être utilisées. Les hommes et les animaux sont mis en danger dans les bâtiments. En cas d'écroulement, il y a danger de mort. Des réparations ne peuvent être réalisées qu'à grands frais. La plupart du temps, toutefois, les dommages structurels sont si graves qu'une évacuation et la destruction du bâtiment sont inévitables. Les infrastructures sont fortement affectées (p.ex. routes coupées). Il se produit des ruptures de conduites.

o Intensité moyenne : Les mouvements de terrain causent des fissures dans les murs,

mais cependant pas aux éléments de la structure qui garantissent la stabilité du bâtiment.

L'étanchéité des joints et les liaisons entre les différentes parties du bâtiment sont endommagées. Les portes et les fenêtres coincent. Les hommes et les animaux ne sont pas immédiatement mis en danger dans les bâtiments. Les dommages concernent cependant la qualité de l'habitat. En général, des réparations sont réalisables avec des moyens raisonnables.

Les infrastructures subissent des dommages (p.ex. déformations des routes et des conduites superficielles et souterraines). Les drainages peuvent se boucher.

o Intensité faible : De petits mouvements de terrain conduisent à des dommages légers

(petites fissures, dégâts aux crépis). La stabilité du bâtiment n'est en aucune manière affectée. Les bâtiments rigides de grande taille ne sont en général pas touchés. Les hommes et les animaux ne sont pas mis en danger. Les routes peuvent présenter des dommages insignifiants.

I.4.4.2. Processus d'éboulement :

o Intensité forte : L'impact de pierres et de blocs conduit à de graves dommages. De

grosses fissures dans les murs porteurs de l'immeuble et des trous dans les parois ou le toit peuvent conduire à une destruction partielle ou totale. Les hommes et les animaux sont fortement menacés, même à l'intérieur des bâtiments. En cas d'écroulement de la maison, il y a danger de mort. Des réparations ne peuvent être réalisées qu'à grands frais. Souvent les

dommages structurels sont si graves qu'une évacuation et la destruction du bâtiment sont inévitables.

L'accumulation des matériaux éboulés peut former un barrage de retenue d'un cours d'eau (risque de rupture de ce barrage). Les infrastructures superficielles peuvent être fortement endommagées et coupées (p.ex. routes, lignes de transmission).

o Intensité moyenne : L'impact des pierres cause des dommages plus ou moins grands

aux parois selon les caractéristiques de la construction, mais ne met pas en cause la stabilité du bâtiment (à condition que l'immeuble ait été adéquatement conçu et testé en conséquence). Les portes sont fortement endommagées ou détruites. Les hommes et les animaux sont mis en danger dans les bâtiments.

Les dommages affectent la qualité de l'habitat. En général, des réparations sont réalisables avec des moyens raisonnables. L'accumulation des matériaux éboulés peut former un barrage de retenue sur de petits ruisseaux.

Les routes et les conduites superficielles peuvent être endommagées et momentanément coupées.

o Intensité faible : En cas de chutes de blocs, les parois peuvent être perforées. Les

hommes et les animaux ne sont en général pratiquement pas mis en danger dans les bâtiments (une note de calcul justificative est nécessaire).

c- Coulées de terre :

o Intensité forte : L'impact de grandes masses de graviers, de boue et de bois, mêlés à

de l'eau, sur les structures porteuses des bâtiments, peut conduire à de graves dommages structurels ou à une destruction soudaine. Les hommes et les animaux sont fortement menacés suite aux dangers d'irruption de la coulée et d'inondation.

Les réparations impliquent souvent de grands frais. Les modifications substantielles du terrain avec de grandes zones d'érosion, des dépôts de graviers et des inondations conduisent à l'interruption, l'endommagement ou la destruction des infrastructures (p.ex. routes, conduites).

o Intensité moyenne : Malgré leur faible épaisseur, les coulées de terre sont

dangereuses à cause des blocs et graviers transportés.

L'impact des pierres et des blocs et l'irruption de l'eau peuvent causer des dommages à l'enveloppe du bâtiment et à l'intérieur, sans toutefois mettre en cause la stabilité du bâtiment. Les hommes et les animaux sont mis en danger à l'extérieur. La qualité de l'habitat peut être sérieusement affectée.

Des réparations sont en général réalisables à des coûts raisonnables. Le dépôt de graviers, de boue et de bois peut endommager et interrompre les infrastructures superficielles (p.ex. routes). Les écoulements, les conduites et les drainages peuvent être bouchés.

o Intensité faible : Ne s'applique pratiquement, dans le périmètre d'écoulement des

coulées de terre, que dans le cas de masses de matériaux d'épaisseur réduite ou dont le mouvement a été freiné, ou encore dans le cas d'une irruption d'eau. Dommages modestes à l'enveloppe du bâtiment ou à l'intérieur. La stabilité du bâtiment n'est affectée en aucune manière. Les personnes et les animaux sont peu menacés à l'extérieur.

Toutes ces informations ne présentes qu'un outil d'alerte pour sélectionner les zones qui porte un risque probable de glissement, mais ne sont jamais suffisantes pour identifier le danger d'une manière fiable. Pour cela elles doivent être complétées par d'autres informations (essai in situ et au laboratoire) approfondies permets d'identifier le danger plus précisément (voire chapitre V).

I.5. Conclusion :

Dans ce chapitre nous avons montré les différents types de glissements qui existent dans la nature.

Le traitement et l'étude de ces différents cas, nécessite quelques documentations à savoir les cartes: topographiques, géologiques, hydrogéologique, en vue de procéder à une étude détaillée du site instable.

Dans le chapitre IV, nous allons décrire les différentes méthodes de calculs qui peuvent être utilisées dans l'analyse de la stabilité des talus.

II.1. Introduction :

Les glissements de terrain sont des déplacements lents (quelques millimètres par an à quelques mètres par jour) d'une masse de terrain cohérente le long d'une surface de rupture généralement courbe ou plane. L'extension des glissements de terrain est variable, allant du simple glissement de talus très localisé au mouvement de grande pouvant concerner l'ensemble d'un versant.

Nous allons représenter dans ce chapitre quelques cas pathologiques dus aux glissements des terrains, et qui représentent plusieurs cas de glissement de terrain soit en Algérie, en Europe ,en Asie ou en Amérique.

II.2. Quelques cas pathologiques observés

II .2.1. En Algérie :

On peut citer plusieurs cas de glissement de terrain survenus en Algérie, plus particulièrement celui de Bedjaia et des Abattoirs à Ténès (Chlef).

+ Cas de Bedjaia

Comme le montre la figure II-1, le terrain concerné par le glissement de terrain présente une forte pente supérieure à 60° et qui est sujette à un glissement certain, compte tenu de la forte pluviométrie affectant la région de Bedjaia.

Il a concerné une route avec un profil mixte déblai-remblai dans une zone montagneuse. La zone s'étend sur une longueur de 80m. Les investigations géotechniques ont mis en évidence depuis la surface, des éboulis gréseux, des bancs gréseux et des alternances de marnes schisteuses et de grés.

Fig. (II.1): Fissures

longitudin

ales dans la

routé affecté par le glissement

La figure (II.2) prése nte un schéma global du glisse ment survenu à Bedjai a où des infiltrations d'eau du coté amont et l'absence totale de drainage ont fav orisé l'évolution du glisse ment. Les couches supé rieures ont glissés sur la couche de marne d'épaisseur limitée et la couc he de grés altérés.

Fig. (II.2): Cinématique du glissem ent

Plusieurs propositions techniques de traite ment du glissement et de la reconstruction de la c haussée o nt été prés entées. La solution retenue est celle d'un massif ren forcé par géotextiles avec un parement à face enve loppée en couche végétale (Voir fig II-3).

Fig. (II.3): Construction de l'ouvrage par couches

Les géosynthétiques de renforcement et de drainage ont été utilisés avec succès pour traiter le glissement et reconstruire la chaussée.

+ Cas de Routes des Abattoirs Ténès (Chlef) :

Le glissement des abattoirs Ténès, se trouvant sur un talus de 10m environ de hauteur (D'après des informations recueillies par la DTP de Chlef agissant comme maître de l'ouvrage). Ce glissement a été provoqué dans les années 80 sous l'effet des infiltrations souterraines ayant fait déplacer la masse de remblai composée d'alluvions récentes.

L'étude à été réalisée par le laboratoire des travaux publics du centre (Antenne de Chlef), où une solution à été dégagée consistant à recharger le pieds du talus tout en proposant des murs de soutènement reposant sur des pieux ancrées à plus de 25 m de profondeur.

Cette solution a été en quelques sortes très onéreuse pour le maître de l'ouvrage à l'époque et le projet n'a pas été entamé pour sa réalisation.

Dans ce but depuis 1982 à 2006 de graves préjudices ont été observés sur le terrain (voir fig II-4), dont la partie se trouvant en haut du talus a été complètement déplacée et touchant même les fondations des bâtiments se trouvant à côté de l'emprise.

De ce fait, compte tenu des dégâts observés sur les lieux, les parties concernées ont pris au sérieux ce problèmes pathologiques et ont refait une deuxième fois l'études par le

laboratoire citée ci-dessus et ce pour aboutir aux solutions du mur de soutènement et dont les travaux ont repris incessamment.

Fig. (II.4): Affaissement de plus de 50cm du glissement en bas du talus
(Les Abattoirs Ténès)

II.2.2. En Europe :

+ Cas de La Clapiere (France)

On cite le glissement de terrain survenu au Sud de la France dans une région dénommée la Clapiers en rive gauche de la vallée de la Tinée, au coeur du massif cristallin du Mercantour et à seulement 50 kilomètres de Nice. Dont la constitution géologique du terrain est composé de gneiss plus ou moins altéré.

La comparaison des photographies prises entre 1952 et 2002 permet de suivre les modifications géomorphologiques de la surface du glissement (Voir fig II-5).dont nous montrons ci-dessous des photos prises de 1976 à 2002.

La figure II-5 présent une série photographique des années (1976), (1984), (1987), (1992), (1997) et (2002) ci-dessous, montrent l'évolution des différentes instabilités du site de la région concernée.

Fig(II .5): les modifications géomorphologiques de la surface du glissement de la

Clapiers

+ Cas de Ruines de Séchilienne en Isère (France) :

Ce cas concerne un glissement de terrain survenu à l'Ouest de la France, plus exactement dans une région appelée Ruines de Séchilienne comme le montre la figure II-6 ci-après.

Le risque d'éboulement des Ruines de Séchilienne, dans l'Isère, est connu de longue date et suivi avec une attention particulière de l'Etat depuis 1985. Il affecte le versant sud du Mont Sec, en rive droite de la Romanche à une quinzaine de kilomètres en amont de Grenoble.

L'éboulement est susceptible de couper la Route Nationale 91, située en fond de vallée, et surtout de barrer la vallée sur une hauteur importante.

Fig. (II .6): L'éboulement des Ruines de Séchilienne

II .2.3. En Asie :

+ Cas de l'Indonésie :

La figure II-7 ci-dessous montre un cas pathologique très concret de catastrophes survenues lors d'un glissement de terrain en Indonésie (île de Java).

Au moins 30 personnes sont mortes dans un glissement de terrain provoqué par de fortes pluies. Quelques maisons ont été recouvertes par une coulée de boue, alors que des résidants se trouvaient à l'intérieur. Les glissements de terrain sont fréquents en Indonésie à ce temps-ci de l'année (Hiver). Plus de 150 Indonésiens sont décédés, début janvier, dans des glissements de terrain sur l'île de Java.

Fig. (II.7): Une coulée de boue a frappé le nord de l'Indonésie

+ Cas de Philippines :

Comme le montre la figure II-8 ci-dessous, le glissement de terrain a eu lieu dans une région très peuplée et dont la catastrophe a été causée par une forte pluviométrie dépassant une dizaine de jour et provoquant des coulées boueuses.

Le glissement de terrain a touché le village de Guinsaugon, dans le sud de l'île de Leyte. Selon la Société nationale philippine de la Croix-Rouge il y a 200 morts et 1 500 personnes disparues. Sur les 300 maisons du village, il n'en reste plus que 3 qui sont encore debout. L'école primaire a aussi disparu sous la boue.

Fig.(II .8): Le village de Guinsuagon enseveli sous la boue

II.2.4.EN Amérique :

+ Cas de Salvador :

A la suite d'un tremblement de terre de magnitude 7.6 à l'échelle Richter survenu en 2001 au large des cotes du Salvador, deux glissements de terrain se sont produits : le glissement de La Leona près de San Vicente et le glissement de Las Collinas.

Fig. (II.9): Glissements de La Leona près de San Vicente(a) et de Las Collinas (b).

+ Cas de Colombie:

Le glissement a eu lieu en 1987 au quartier de Villatina Medellin qui est localisé sur le flanc oriental de l'aval du Rio Medellin. Il est l'une des grandes catastrophes naturelles qui ont eu lieu en Colombie dans une zone urbaine. Le nombre des victimes a été entre 450 et 500, avec plus de 120 maisons détruites.

Le glissement est parti de la zone de dunites (roches argileuses fracturées) qui a une pente supérieure à 20%, il est descendu en suivant la ligne de plus forte pente (Figure II-10).

Fig. (II.10): Morphologie de la zone de glissement de Villatina Medellin en Colombie.

II .3. Conclusion:

Ces cas pathologiques cités précédemment montrent l'importance des effets de glissement pouvant engendrer des dégâts humains et matériels pouvant se chiffrer en plusieurs millions de Dinars dont les gouvernements doivent prêter beaucoup d'attention.

Les photos visualisées ci-dessus montrent les dangers permanents rencontrés dans tous les pays du monde dues aux glissements de terrain.

Pour cela, il faut compte tenu de ces phénomènes et de leurs dangers, et de prendre les précautions convenable pour détecter les zones instables afin de trouver les meilleurs solutions de protections ou de traitements.

III .1. Introduction:

La reconnaissance des sols permet d'appréhender les problèmes qui peuvent se poser lors de l'étude d'un projet de construction ou lors de l'expertise de sinistres. La reconnaissance des propriétés d'un terrain constitue le lien entre la cause d'un sinistre et les remèdes que l'on se propose de mettre en place.

Il y a sommairement, deux catégories de moyens de reconnaissances qui complètent les investigations géologiques de surface :

-Les méthodes d'observation du terrain, soit en place, soit à l'aide d'échantillons (prolongement en profondeur de la géologie de surface) : puits, tranchées, sondages...

-Les méthodes de mesure "in situ" basées sur la mesure d'une propriété physique du terrain, dont font parti les essais géophysiques.

III .2. Reconnaissance géologique :

C'est l'identification du sol par observation visuelle des différentes couches, confirmée par l'examen des cartes géologiques. On observe donc pour cela des puits, galeries ou tranchées qui donnent une coupe généralement "fraîche" de sol. Il est aussi possible d'utiliser des cavités existantes. L'examen des carrières ou des tranchées, situées à proximité de la zone considérée, donne des précisions immédiates sur les sous-couches. La reconnaissance peut s'effectuer à l'aide de sondages dont certains exemples sont décrits au paragraphe de la reconnaissance géotechnique. Il sera possible d'établir des coupes prévisionnelles ou même un bloc diagramme qui pourra être confirmé par les sondages.

III .3. Reconnaissance géophysique :

Les méthodes de reconnaissance géophysiques permettent de déterminer la nature des couches profondes en utilisant par exemple leurs caractéristiques:

- magnétiques

- Prospection électrique - Prospection sismique

- Prospection gravimétrique

III .4.	Reconnaissance g			éotechnique :
III. 4. 1		. Essais "in	situ" :

° L e pénétro mètre dyna mique : Il permet la détermination de la résistance mécanique

d'un so l. Une pointe métallique portée par un train de tiges pénètre dans le sol par battage success if. On mesure ensuite à intervalle s d'enfonce ment régul ier, l'énergi e nécessaire corresp ondante.

° L e pénétro mètre statique : Il permet d'enfo ncer, à vites s e lente et c onstante (0 ,5 à 2

cm par s econde) des tiges munies d'une pointe à leur extrémité. Il est conç u pour mesurer le frottement latéral s ur les tubes extérieurs qui entourent la tige c entrale et le s efforts sous la

pointe.

Pour prévenir tout risque de tassement di fférentiel, l e pénétromètre statique est utilisé pour le

contrôl e du compactage de couches de re mblais.

Fig. ( III.1) : différents types

de pénétromètre

° Les sondages destructifs

Ils sont destinés à l'acquisition de données. Les paramètres sont enregistrés soit sur cassettes soit sur diagrammes directement exploitables sur le chantier. Liste des paramètres non exhaustive:

-la vitesse instantanée d'avancement V.I.A.

-la pression sur l'outil P.O.

-le couple de rotation C.R.

-la pression de frappe P.F.

-le temps

L'appareil permet après étalonnage sur un sondage carotté ou à la tarière et interprétation des enregistrements, de retrouver et situer avec précision les différentes couches traversées, de détecter les hétérogénéités à l'intérieur d'une même couche, de localiser les cavités ou les blocs.

° Les essais à la plaqueLes essais à la plaque consistent à déterminer le déplacement vertical moyen de la surface du sol située sous une plaque rigide circulaire chargée. Les essais à la plaque ont essentiellement pour buts :

-soit de mesurer la déformabilité des plateformes de terrassement constituées par des matériaux dont les plus gros éléments ne dépassent pas 200mm. On utilise généralement dans ce cas les mesures faites au cours de 2 cycles de chargement successifs (modules de déformation Ev1 et Ev2)

-soit de contrôler les fonds de fouille de fondations ou d'apporter des éléments complémentaires sur le comportement d'une fondation.

III .4 .2. Essais de laboratoire

III .4.2.1. Teneur en eau naturelle

Elle définit le rapport en % du poids d'eau Ww que le sol contient au poids Wd de ses éléments secs. L'obtention des éléments secs s'obtient par dessiccation du sol pendant 24

heures à l'étuve à 105°C.

III .4.2.2. Analyse granulométrique

Elle permet de déterminer la distribution dimensionnelle en poids des éléments d'un matériau. Elle comprend deux opérations:

-tamisage pour les éléments de dimensions supérieures ou égales à 80 mm.

-sédimentométrie pour les éléments de dimensions inférieures à 80 mm.

III .4.2.3. Les limites d'Atterberg

les limites d'Atterberg définissent à la fois un indicateur qualifiant la plasticité d'un sol, mais aussi l'essai qui permet de définir ces indicateurs. Cet essai a été établi par l'agronome suédois Atterberg.

La teneur en eau d'un sol peut en effet beaucoup varier au cours des opérations de terrassements.

Pour la fraction fine (graviers exclus), la cohésion tient à la présence d'eau : parfaitement sec, le matériau serait pulvérulent. Au-dessus d'une certaine teneur (limite de plasticité), on peut le pétrir en forme de boudin, de boulette ou de fil. Pour une teneur plus forte (limite de liquidité), il forme un liquide, visqueux, qui ne conserve pas la forme qu'on lui a donnée. La détermination, soigneusement normalisée, de ces deux teneurs caractéristiques appelées limites d'Atterberg, est un élément important d'identification, et permet déjà de prévoir certaines propriétés.

III .4.2.4. Les essais de cisaillement

La boîte de Casagrande est constituée de deux demi-coquilles sur lesquelles on exerce perpendiculairement au plan de jonction des deux demi-coquilles, une pression. L'échantillon, comprimé subit une compaction, c'est à dire qu'il perd une certaine proportion d'eau. L'une des deux coquilles étant fixe, on exerce alors une pression latérale, tendant à faire glisser

l'autre parallèleme nt à leur séparation. En augmentant progressivement cett e contraint e , on constat e que la rés istance de l' échantillon croît, passe par un m aximum, pu is décroît j us qu'au momen t où se pro duit la rupt ure. L'usage de cet essai est notam ment appro p rié pour l' ét ude

des glis

sements de

terrain.

Fig. ( III.2) : La bo				îte de Casagrande
III	.4.2.5. Les	essais de compactage

oids principe

Les rés ultats se pré sentent sous la forme d'une courbe dont en ab scisse : la teneur en eau et en

ordonn ée : le poids volumiqu e sec. Cette courbe a un maximum dit "Optimum Proctor "

normal ou modifié selon la nature de l'ess ai. Ce maximum définit la teneur en eau et le poids

volumi que max.

Ils ont pour but d'é tudier l'influence de la teneur en eau d'un éc hantillon de sol sur le p volumi que sec de cet échantil lon soumis à une énergie de compactage déte rminée. Le consiste à compacter avec une énergie définie un échantillon de sol remani é dans un moule normal isé et à mes urer le poi ds volumique sec obtenu. L'essai e st recommencé pour

différe ntes teneurs en eau. Il existe deux types d'ess ai d'usage courant : l'es sai Proctor Normal et l'ess ai Proctor Modifié

III.4.2.6.L'essai oedom

étrique :

dans une b

son drain a

me consta r n

dice des vi d

t en foncti o

on permet d'
un temps d é

ion de la c on
thme du te m

Un échantillon de sol est placé
deux pi erres poreu ses assurant

oîte cylindrique rigide

de sectio n appliquer

terminé. o n

trainte) e t

ps).

circulaire entre sur l'échantillon

peut étab lir des

de consolidation

une contrainte verticale unifo

de compressibilité (in

courbe s

(variation relative de tassemen

ge. Un pist te pendant

es en fonc t
n du logar i

Fig. (III.3 ) : appare		il d'essai oedométrique
III. 5.	Hydrogéologie

les puits, l es

uivi de ces

s instabilité s de pente s, l'étude

de connaître la répartition des pre ssions s et, en prévision de l a réalisation d'un

ens des éc oulements,

repérage des niveaux d'eau dan s

météorolo giques. Le s

alimentation...). Les

disposer d 'une image

Étant donné le rôle primordial que joue l ' eau dans l e hydrog éologique e st très imp ortante. Ell e a pour but interstitielles dans le sol, leur évolution dans le temp drainage, le foncti onnement des nappes ( s techniques utilisée s sont la pi ézométrie, l e mesures de débits de sources, le recueil des données paramè tres doit se faire pendant une année au minimum, afin de représentative des conditions hydrogéolo giques du site.

III .6. Caractéristiques de sole à prendre en compte dans l'analyse des talus:

Dans les calculs de stabilité, le choix des caractéristiques mécaniques est fonction du problème lui-même. Mais d'une manière générale on constate que lorsqu'il s'agit de sols argileux, le calcul à court terme conduit au coefficient de sécurité le plus faible. L'expérience montre que c'est souvent juste après la construction que se produisent les glissements dans les sols argileux. On utilisera donc les caractéristiques mécaniques non drainées (C_u, ö _u). Par

contre dans les sols sableux, le calcul à court terme n'a pas de sens car on atteint très rapidement le long terme. On utilisera donc les caractéristiques mécaniques (CCD, ö _CD) .

Dans le chapitre IV, nous allons décrire les différentes méthodes de calculs qui peuvent être utilisées dans l'analyse de la stabilité des talus.

n :

ance au c i

priétés d u

s pour s' a

er une pen

te à l'échec

IV.1.i ntroducti o

Une fois la rési st pente e t d'autres p ro doivent être effect ué force te nd à provo qu

saillement, la pression d'eau dans les pores, la géométrie de la sol et la p ente sont établis, les calculs de la stabilité des talus ssurer que les forces sont suffisamment résistant supéri eure à la .

ite :

te et on utilisera un coefficient nt de la rupture le long de la ilibre limite forme une bande é de l'ense mble est donc liée à

massif (force H,

IV. 2. Le princ ipe d'équ ilibre lim De manière classi que, on définira les conditions d'é quilibre limi de sécurité. On suppose que l'équilibre limite existe au mom e ligne d e glisseme nt. L'expérience montre que la zone en équ assez é troite de part et d'autre de la zone de rupture. La stabilit celle de la bande c onsidérée.

lle le coeffi cient de

à déterminer le facteur de sécurité

sistance de la surface de gli ssement pour que l a

la limite de l'équilibre. Ce facteur peut être écrit de

Les méthodes de calcul consistent à rec hercher la surface le long de laque sécurit é F est le plus faible.

FS par masse

la façon

Le prin cipe de cal cul de stabilité des talus consiste lequel il faut diviser la ré potenti ellement stable soit à suivante :

Q: cette valeur définit la solli c force V, moment M).

Qmax: valeur maximale de Q.

itation vectorielle ou tensorielle appliquée au

être calcul é, pour un paramètre s électionné,

valeur cal culée sous les conditions de projet

le ratio

de ce paramètre.

en prenant

Le facteur de sécurité pourrait de la v aleur à la rupture, par l a On peut citer plusi eurs exemples :

de l'eau initial (ou de projet) liqué

Fw = niveau de l'eau à la rupture / niveau
FL = chargement ultime / chargement app

FS(Q) = a max (rupture) / a max (Q) ; Q : le chargement sismique d'accélération maximale a max

On distingue deux démarches pour le calcul de facteur de sécurité :

1. Dans la première, le glissement a déjà eu lieu, il s'agit d'une valeur de FS inférieure ou égale à 1, donc :

- soit, on connaît la surface exacte et on cherche à déterminer, pour FS=1, les caractéristiques correspondantes.

- soit, on a les caractéristiques et on cherche à déterminer la surface de glissement.

2. La deuxième, la plus fréquente, consiste à déterminer la marge de sécurité disponible et adopter les solutions adéquates pour améliorer la sécurité de l'ouvrage en répondant à des exigences en fonction de l'emploi des talus.

IV.3. Choix de la valeur du coefficient de sécurité dans le calcul de stabilité :

Le facteur de sécurité minimal FS adopté est assez rarement inférieur à 1.5. Il peut quelquefois être égal à 2, voire à 2.5 pour des ouvrages dont la stabilité doit être garantie à tout prix (grand risque pour les personnes, site exceptionnel), ou pour des méthodes dont l'incertitude est grande (analyse en contrainte totale avec risque d'erreur sur la valeur de la cohésion drainé Cu).

Le ci-dessous, nous donnent les valeurs de FS en fonction de l'importance de l'ouvrage et des conditions particulières qui l'entoure

Tableau (IV-1): Classification FS en fonction de l'importance de l'ouvrage

FS	Etat de l'ouvrage
<1	danger
1.0-1.25	sécurité contestable
	sécurité satisfaisante pour les ouvrages peu importants
1.25-1.4	sécurité contestable pour les barrages, ou bien quand la rupture serait catastrophique
	satisfaisante pour
>1.4	les barrages

La définition des seuils des facteurs de sécurité dépend de l'approche adoptée, des fréquences de sollicitations de l'ouvrage en question et du risque créé par la rupture. En condition normale, Fellenius propose un seuil égale à 1.25, alors que FS = 1.5 pour Bishop (l'approche de Fellenius est plus conservatoire que celui de Bishop)

IV.4. Calculer le coefficient de sécurité :

Considérons un élément carré d'unité (dx = dy = 1) exposé aux contraintes normales a1 et a3 appliquées aux côtés de l'élément. Comme l'élément est assez petit, il est donc logique d'accepter que le plan de rupture soit une ligne droite. L'inclinaison du plan de rupture est définie par l'angle q. La rupture du milieu est normalement due aux contraintes de cisaillement développées à la surface de rupture. A partir des équations d'équilibre, la contrainte mobilisée de cisaillement tf et la contrainte normale mobilisée af au plan de rupture peuvent être déterminées en fonction de a1 et a3.

FIG. (IV-1) : Contrainte normale au plan de rupture.

Contrainte tangentielle au plan de rupture:

On définit le facteur de sécurité FS comme le rapport de la résistance au cisaillement disponible à la résistance au cisaillement mobilisée, ce qui traduit la réserve de sécurité dispose le terrain sous cette sollicitation (ó1, ó3) et en fonction du critère de rupture (c, ö)

FS = Ré

sistance au

cisaillement disponibl

e / Résistance au cisaillement mobilisée

Donc, on peut écrire:

En remp

laçant les é

quations (1

) et (2) dan

s l'équation

(3), on trouve:

En méc anique et selon le critère de Mohr-Coulomb, nous pouv ons prouver que l'angl e du plan de rupture est égal à 45+ö /2 par rapport à la dire ction principale ó3. I l est uniquement

fonction de l'angl e de frottement. nous p ouvons donc calculer l a valeur du facteur de sécurité

par rapport au plan potentiel de rupture. En remplaç ant la valeur de q par 4 5+ö/2 dans la

relation (4), nous trouvons:

IV.5. F

acteurs i

nfluença

nt la stab

ilité des t

alus :

Quelque s facteurs influençant la stabilité

du talus (voir Fig (IV- 2)) :

à l'approche adoptée pour calculer ce coefficient;

à l'état de contraintes dans le milieu (Mé thode adoptée) aux pro priétés du milieu

à l'hyp othèse de l a forme de l a surface de rupture

FIG. (IV.2) : facteurs influençant la stabilité du talus.

V. 6. Les méthodes classiques pour l'analyse de la stabilité :

Il existe plusieurs dizaines de méthodes de calcul de stabilité ayant toutes des avantages et des inconvénients. Aucune n'est parfaite, car aucune ne tient compte de la déformabilité du sol.

Nous étudierons ci-après plusieurs méthodes de calcul traditionnelles mais la confiance que l'on peut leur accorder sera essentiellement fonction de l'expérience que l'on peut en avoir.

Ces méthodes peuvent être classées selon plusieurs critères, dans le présent chapitre ces méthodes seront classées selon la nature des forces considérant dans la vérification de l'équilibre qu'ils soient des forces, des moments ou des forces et des moments en même temps.

V. 6.1. Cas glissement plan :

Pendant longtemps on a préféré croire (par simplicité des calculs) que les surfaces de glissement étaient planes. Or la simple observation sur le terrain prouve que les surfaces sont courbes. Cependant dans des cas particuliers, on peut admettre des rayons de courbure infinis, ce qui nous amène à des glissements plans. D'autre part, cette méthode est une bonne introduction aux méthodes plus élaborées que nous verrons dans la suite de ce chapitre.

Si on considère une pente infinie, la pente est supposée s'étendre infiniment dans toutes les directions et le glissement est supposé se produire le long d'un plan parallèle à la face de la pente. Car la pente est infinie, les contraintes sont les mêmes sur tous les deux plans qui sont perpendiculaires à la pente, comme les plans A-A' et B-B' dans la figure (IV-3).

T

Fig. (IV.3): pente infinie de surface de rupture plane.

Les équations d'équilibre sont calculées en considérant un bloc rectangulaire comme celui de la Figure (IV-3). Pour une pente infinie, les forces sur les deux extrémités du bloc seront identiques en amplitude, en sens opposé, et colinéaires. Ainsi, les forces sur les extrémités du bloc équilibre exactement les uns aux autres et peuvent être ignorés dans l'équilibre des équations. Résumant les forces dans des directions perpendiculaires et parallèles au plan de glissement donne les expressions suivantes pour la force de cisaillement, T, et la force normale, N, sur le plan:

T = W sinâ et N = W cos â (IV-1)

Où â est l'angle d'inclinaison de la pente et du plan de glissement, mesuré par rapport

à l'horizontale, et W est le poids du bloc. Pour un bloc de l'unité d'épaisseur dans la direction perpendiculaire au plan de la section transversale dans la Figure (IV-3), le poids est exprimé en :

W = ã . l . z . cos â (IV-2)

Où ã est l'unité de mesure du poids total du sol, l la distance entre les deux extrémités

du bloc, mesurée parallèlement à la pente, et Z la profondeur verticale au plan de cisaillement. En substituant (IV-2) dans (IV-1) donne :

T = ã . l . z . cos â . sin â (IV-3)

Et :

N = . l . z . cos (IV-4)

ã ² â

Les contraintes normales et de cisaillement sur le plan de cisaillement sont constantes pour une pente de longueur infinie et sont obtenues en divisant les équations (IV-3) et (IV-4) par la surface du plan (l .1), pour obtenir:

ô = ã.z. cos â.sin â (IV-5)

Et :

ó ã

= .z. cos (IV-6)

² â

En substituant ces expressions dans l'équation globale pour obtenir la formule du coefficient de sécurité, on trouve :

â ö

Fs +

c z

ã . . cos ² . tan

= (IV-7)

ã â â

. . cos . sin z

En terme des contraintes effectives :

+ ( ã . . cos ²

z â - u )

ã â â

. . cos . sin

Fs =

c '

z

tan ö'

(IV-8)

Pour un sol purement pulvérulent (c, c'=0), le coefficient de sécurité se réduit à :

tan ö

Fs = (IV-9)

tan á

L'équilibre limite est atteint pour F_min = 1 ; soit: á = ö. Ceci exprime bien que l'angle de talus naturel d'un sol pulvérulent est égal à l'angle de frottement interne.

IV .6.2. Méthodes de l'équilibre des moments :

Les méthodes qui supposent une surface de rupture circulaire envisagent l'équilibre des moments sur le centre du cercle pour l'ensemble de la masse libre composé de toutes les tranches.

IV .6.2.1. La méthode générale des tranches pour une surface de rupture circulaire:

Le principe de la méthode consiste à découper le massif situé au dessus de la ligne de rupture en tranches. L'expérience montre qu'il n'est pas nécessaire de prévoir des tranches très minces pour obtenir une précision suffisante.

Ces méthodes considèrent une surface de rupture circulaire et sont basées sur l'équilibre des moments sur le centre du cercle.

Se référant à la pente et la surface circulaire de rupture illustré dan la figure (IV-3), le moment moteur peut être exprimée comme :

M = ? W _i . a i (IV-10)

Ti

Fig. (IV.4) : La masse du talus découper en tranches

Où W_i est le poids de la ème

i tranche et a_i est la distance horizontale entre le centre du

cercle et le centre de la tranche. Les distances vers la crête de la pente, à la droite du centre montre la figure (IV-4), sont positives; les distances vers le pied de la pente, à la gauche du centre, sont négatives. Bien que théoriquement, le bras de levier est mesuré à partir du centre du cercle au centre de gravité de la tranche, un nombre suffisant de tranches permet de considérer les différences entre le centre et le centre de gravité de la tranche sont Négligeables.

Le bras de levier a_i dans l'équation (IV-10) peut être exprimé en termes de rayon du

cercle et de l'inclinaison de bas de la tranche respectifs. Bien que la base de la tranche est courbé, la base peut être considérée comme une ligne droite, comme l'a suggéré dans la figure (IV-4), avec une perte négligeable de la précision. L'inclinaison de la base du morceau est représentée par l'angle á_i mesuré entre la base de la tranche et de l'horizontale. L'angle entre

une ligne prolongée à partir du centre du cercle au centre de la base de la tranche et une ligne verticale est aussi égal à l'angle á_i (IV-4). Ainsi, le bras de levier est exprimée par :

a i = r. siná_i (IV-11)

Et le moment moteur exprimé dans la relation (V-10) devient :

M = r ? W_i . sin á i (IV-12)

Le rayon dans l'équation (TV-13), a été transféré en dehors de la somme, car le rayon est constant pour un cercle.

Le moment résistant est fourni par la contrainte de cisaillement ô sur la base de chaque tranche; la contrainte normale ó sur la base de chaque tranche agir à travers le centre du cercle, et donc ne produire aucun moment. Le moment résistant de toutes les tranches est :

M r = ? r.T i = r ? T i (TV-13)

Où T_i est la force de cisaillement à la base de la ème

i tranche et la sommation est effectuée pour toutes les tranches. La force de cisaillement est le produit de la contrainte de cisaillement ô_i et la surface de la base de la tranche de l'unité d'épaisseur Äl . Ainsi :

M r = r ? ô _i . Äl i (TV-14)

La contrainte de cisaillement peut être exprimée en termes de la force de cisaillement et le facteur de sécurité à donner

M r i ? Ä T l . i = ^r F

(TV-15)

Assimiler le moment résistant [Eq. (TV-15)] et le moment moteur [Eq. (TV-13)] et les réorganiser, l'équation suivante peut être écrite pour le coefficient de sécurité:

=

? Ä

T l

i . i

Fs

(TV-16)

á i

. sin

W i

?

Pour une contrainte totale, la résistance au cisaillement est exprimée par :

T_i = c+ ó tanö (TV-17)

(Rn)t = C i.AB+N_n.tanöi (IV-2 0)

La somme des mo ments pour toutes les tranches est :

On remplaçant ce-ci dans l'équation (V-16), on trouve :

F_s = (IV-18)

? +

( c ó ö

? W . sin á

tan ) . Ä l

L'équation (IV-18) représente l'équation d'équilibre statique pour les moments du centre d'un cercle. Si ö est égale à zéro, l'équation (IV-18) devient

? Ä

c l

.

F_s = (IV-19)

? W . siná

Si l'angle de frottement n'est pas égal à zéro, l'équation présentée ci-dessus pour le coefficient de sécurité [Eq. (IV-18)] exige que la contrainte normale sur la base de chaque tranche soit connue. Le problème de la détermination de la contrainte normale est indéterminé. La méthode Ordinaire des tranches et de bishop faire deux séries d'hypothèses distinctes pour obtenir la contrainte normale sur la base des tranches et, par la suite, le facteur de sécurité.

IV .6 .2 .2. La méthode de Fellenius:

c'est la méthode la plus simple pour l'analyse de stabilité des talus. Fellenius suppose que le volume de glissement délimité par la surface de glissement et la topographie du talus est subdivisé en n tranches. Chaque tranche est considérée comme un solide indéformable, en équilibre sur la ligne de glissement. Considérons un talus recoupant un certain nombre de couches de sols de caractéristiques différentes Ci, _?öi , ãi. La stabilité est étudiée en considérant le problème 2D, c'est-à-dire en analysant l'équilibre d'une masse de sol d'épaisseur unité dans le sens perpendiculaire à la figure.

Soit un cercle quelconque de centre O et de rayon R pour lequel on vérifie la sécurité vis-à-vis du risque de glissement. La méthode consiste à découper le volume de sol concerné (compris dans l'arc EMF) en un certain nombre de tranches limitées par des plans verticaux. Etudions l'équilibre de l'une de ces tranches, par exemple la tranche "ABCD". Les forces agissant sur cette tranche sont les suivantes:

Fig. (IV.5) : Les forces agissant sur une tranche

-son poids W;

-la réaction du milieu sous-jacent sur l'arc AB;

-les réactions sur les faces verticales BC et AD décomposées en réactions horizontales H et en réactions verticales V. Il s'agit de forces internes au massif étudié.

-les pressions hydrauliques.

Définissons par rapport au centre O :

-le moment moteur, comme celui du poids des terres W (et des surcharges éventuelles), qui tend à provoquer le glissement ;

-les moments résistants, comme ceux des réactions s'opposant globalement au glissement de la tranche.

La surface de rupture étant limitée par les points E et F, le coefficient de sécurité global FS est défini par le quotient:

FS = SEF(des moments résistants maximaux) /SEF(des moments moteurs)

Considérons la somme des moments pour l'arc EF, sachant que la somme des moments des

forces est nulle. Fellenius a fait une hypothèse qui simplifie considérablement les calculs, à
savoir que la seule force agissant sur l'arc AB est le poids W, à l'exception des forces internes.
Dans ces conditions, le moment résistant maximal est fourni par la valeur maximale que peut

prendre la composante tangentielle de Rn : (Rn)t D'après la loi de Coulomb, elle s'écrit

			(IV-21)
urs, le moment moteur	est dû à Tn

m: nombre total de tranc hes, R : rayon du cercle ci & öi : caractéristiques mécaniques de la couche dan tranche AB . Par aille

de glisse ment.

s laquelle est situé l'arc de la et égal à TnxR, d'où:

Dans la mé thode de B ishop l'expression du coefficient de sécurité est obtenue en

écrivant les deux équations d'équilibre statique :

- L'équilibre des forces vertical es qui sont appliquées à chaque tranche.

- L'équilibre global des moments.

		(V-22)
IV .6.2.3. Méthode de Bishop	(1955) :

Soit la tranche représentée dans la figure (IV-6) ci-après.

Vi

T

Vi+1

Fig. (IV.6): Représentation des forces inter-tranches sur une tranche.

Le coefficient de sécurité est déterminé comme suit : - l'équilibre vertical :

Wi + ( Vi - Vi + 1) = N icosai+ T isinai (IV-23)

C i b i tg ? i

W + ( Vi - Vi + 1 ) = N cos

i á + ·

i sin N

á i + ·

i sin (IV - 24)

á i

Fs

Fscos

ai

D'ou la valeur de Ni :

bi

-

ái

i- Vi + 1

)

+ (V

C i

F_s

tg

Ni

i

( IV - 25 )

tg?

ái + siná i

cos

W (V

i +

i - V i+1

) - C i^bitgái

F_s

( IV - 26)

m_á

Ni

F_s

Ou bien sous une forme compacte, en désignant la quantité :

cos

tg tg

á ?

i i

á i +

( 1 ) m

= á

F s

Pour une ligne de glissement circulaire :

n ? b i ?

N tg ?

?? C i + i i

? cos á ??

=

FS i 1 i

= ( V 27 )

I -

n

? i 1 =

W sin i á

i

b i

W (V V ) - C

i + + +

i i 1 i tg á i

1 C bi

i F

On porte dans l'expression de F_s la valeur de Ni précédemment calculée :

FS = [ (

? + tg [

?

? i ] ) ] (IV - 28)

w sin

i á i cosá i m_á

Le deuxième membre contient F_s explicitement et par l'intermédiaire de má mais la formule se prête très bien à une résolution par approximations successives.

L'équilibre horizontal de la tranche s'écrit :

- 29)

tg ? i C b

i i

(E - E ) N (

i i 1

+ + i cos - sin )

á i á +

i = 0 (IV

F s F s

D'ou la valeur de Ni :

i
+ E - E i +

1

(

)

- C i b i

N i

F

s

tg

?

i

= (IV-30)

cos á i

sin á i -

F

L'élimination de Ni entre les deux expressions issue des équilibres horizontaux et verticaux et donne une relation entre les composantes horizontales et verticales des efforts inter-tranches :

i

tg ?

i

cos

á

i

-

F

sin á

?

? -

?? ?

?? cos á i + sin á ? F

tg

? i

i

? C b

i i

F

(IV-31)

sin á

i

tg ?

? - cos á

i

i

?

? ?

F C b

i i

(E - E ) (V - V )

i i 1

+ + i i 1

+ ? ? = W -

i tg á i

i

tg ? F

cos á sin á i

i

?? + ??

? F ?

Puisque les efforts inter-tranches sont des intérieurs au talus leurs sommes sont nulles :

Ó (Ei - Ei+1) = 0 et Ó (Vi - Vi+1) = 0

En sommant la relation précédente sur les efforts inter-tranches verticaux :

tg ? i ? ? tg ? i ?

sin -

á i cos á i sin -

á cos á

n i i

? ? ⁿ C b ? ?

?

i 1

F i i F C b

i i

(IV - 3 2)

(V - V )

i i 1

F

F i ??

+ ? ? ? ⁽W t ) ? ?

tg ? i

= cos á i sin i

?? + á ??

? F ?

IV .6.2.4. La méthode de Bishop simplifiée:

Dans la méthode simplifiée de Bishop, les forces sur les côtés de la tranche sont supposés être horizontale (c'est-à-dire, il n'y a pas de cisaillement entre les tranches). Les forces sont résumées dans le sens vertical pour satisfaire l'équilibre dans cette direction et d'obtenir une expression de la contrainte normale sur la base de chaque tranche. Se référant à la tranche illustrée dans la figure (IV-6) et on détermine les forces verticales, l'équation de l'équilibre suivante peut être écrite pour les forces dans le sens vertical:

N . cos á + T sin á - W = 0 (IV-33)

T

Fig. (IV.7): La représentation des forces sur une tranche dans la méthode de Bishop

Les Forces sont considérées comme positifs lorsqu'ils agissent vers le haut. La force de cisaillement dans l'équation (IV-33) est liée au contrainte de cisaillement par :

T = ô. Äl (IV-34)

Pour les forces de cisaillements exprimés en termes de contraintes effectives avec l'équation de force de Mohr-Coulomb, nous pouvons écrire :

1 c l N u l ö

T = [ ' ( . ) tan ']

Ä + - Ä (IV-35)

F

Combinant les équations (V-33) et (V-35) et pour résoudre la force normale, N, nous obtenons :

? 1 ?

?? ?? (

F

á

W

sin

c l u l

' Ä - Ä

.tan ö ' )

=

N

?
??

+

cos

á

(IV-36)

(sin . tan ' á ö ) ? F??

La contrainte effective normale à la base de la tranche peut être exprimée par la relation :

ó ' = N -u (IV-37)

Äl

Combinant les équations (V-33) et (V-35) et on les introduire dans l'équation d'équilibre (V-18), on peut écrire -après réarrangement des termes- :

? ?

? c l

' cos

Ä á + ( W u l

- Ä cos á ö

) tan ' ?

? ? ?

?

( sin . tan '

á ö ) ??? ?

F ? (IV-38)

W sin á

De l'équation (V-38) ; l'expression finale du coefficient de sécurité de la méthode de bishop simplifiée s'écrie comme suite :

? +

c b W ub

' ( - )tan '

ö ?

? ? ?

m

? á ?

F = (IV-39)

? Wsiná

Avec :

tan tan '

á ö ?

m cos 1

= ? +

á á ?? ??

F

Pour non-drainé l'analyse de la procédure est similaire et le facteur de sécurité devient :

	n ?	( c x + W ) Ä tan ö ui i i ui	? 1 ?^?M ( ) è i	? ??
F =	i=1				. (IV-40).
		n

? W i sin è i

i=1

Avec :

tan ui

M ( ) = [ 1 + è ö

è cos è tan ]

i i ⁱ F

n=nombre de tranches.

IV .6 .3 . Méthodes de l'équilibre des forces :

IV. 6.3.1. La méthode de Coin :

Cette méthode est utilisée quand la surface de rupture peut être approchée de manier satisfaisante par de 2 ou 3 ligne droites.

Il semble qu'actuellement la méthode des tranches paraisse offrir la meilleure approché pour obtenir une solution précise pour n'importe quelle surface de rupture, ainsi que pour des sols stratifies ou zones.

IV.6.4. Méthodes de l'équilibre des moments et des forces :

Jusqu'à présent, toutes les méthodes qui ont été présentées sont basées sur des formes relativement simples à la surface de rupture: un plan ou une cercle.

Mais dans la plupart des temps la surface de rupture est plus complexe, souvent à la suite des zones ou des couches de sol relativement faible. Dans de tels cas, il est nécessaire de calculer la stabilité en utilisant des formes plus complexes de la surface de glissement.

Plusieurs procédures ont été mises au point pour les analyses des surfaces de rupture plus complexes.

IV .6.4.1. La méthode de Janbu simplifiée:

La méthode simplifiée de Janbu est un indice composite basé sur des surfaces de cisaillement (c'est-à-dire non circulaire) et le coefficient de sécurité est déterminé par l'équilibre des forces horizontales. Comme dans la méthode de Bishop, la méthode considère les forces inter-tranches normales, mais néglige les forces de cisaillement (T) (voir figure IV-6). La base de la force normale (N) est déterminé de la même manière que dans la méthode de Bishop et le coefficient de sécurité est calculé par:

Ä E

? Wtaná+ ?

Où :

? ( ( ) )

c l N ul

' + - tan ö '

sec á

F

(IV-41)

Sec	á	=	1
cos				á

Fig. (IV.8) : Représentation des forces sur une tranche.

? ÄE = E₁ - E₂ (Zéro s'il n'y a pas de force horizontale).

Janbu introduit un facteur de correction ( f₀ ), dans le coefficient de sécurité F₀ , pour

tenir compte des effets des forces inter-tranches de cisaillement. Avec cette modification, la méthode de Janbu corrigé donne un coefficient de sécurité supérieur, comme:

F f = f_oF_o (IV-42)

Où :

? + - b c p u ( ( ) ) ' tan ö ' ? ? ?? n ?? á F = Et 0 ? pb tan á

= ? + cos^2 1 tan ö tan ' ? n á á ?? á ?? F

C'est un facteur de correction qui varie en fonction de la profondeur à la longueur de la masse de la terre glissante et du type de sol.

P=W/b=contrainte totale verticale ;

b= largeur d'une tranche.

IV.6.4.2. La méthode de Janbu généralisée :

La méthode généralisées de Janbu (Janbu 1973) considère les deux forces intertranches et suppose une ligne de poussée afin de déterminer une relation des forces intertranches. Par conséquent, le coefficient de sécurité devient une fonction complexe à la fois avec les forces inter-tranches :

Fig. (IV.9) : La représentation des forces sur une tranche

? ( { } ) ? ( )

W T T

- - 1 tan á + E E

-

2 2 1

? ( ( ) )

F

c l N ul

' + - tan ö '

sec á

(IV-43)

De même, la force totale normale à la base (N) devient une fonction de la force inter tranche de cisaillement (T) comme:

1

N = ??? - - -

1 W T T

( ) ( '

c l ul

- tan ' ) sin

ö á ??? (IV-44)

2 1

m F

á

IV. 6. 4 3. La méthode de Spencer :

La méthode de Spencer est initialement présentée pour les surfaces de rupture circulaire, mais la procédure peut être facilement étendu aux surfaces de rupture non circulaires.

( )

á è ö

- tan ' ?

F ??

sin

( F v

+

- F á - F á -

v sin h cos

( )

cos á - F á + Ä

u l

h sin

Q

c l

' Ä

F

(IV-46)

)

tan

ö'

)(

F

?
??

+

cos( )

á è
-

Spencer (1967) a mis au point deux équations de coefficient de sécurité, l'un à l'égard de l'équilibre des forces horizontales et un autre à l'égard de l'équilibre de moment. Il a adopté un rapport constant entre les forces inter- tranches de cisaillement et normal.

Fig. (IV.10) : Résultante des forces parallèles

L'équation de l'équilibre des forces: Et :

? Qi

0

Q_i = Z i - Z i + 1

Parce que les forces inter tranche sont supposées être parallèles, Q_i , Z_i , et Z_i+1 ont la même direction et Q_i est tout simplement est la différence scalaire entre les forces inter- tranches de gauche et de droite de la tranche (Voir figure IV-10).

Fig. (IV.11) : représentation de toutes les forces inconnues sur une tranche dans la méthode
de Spencer.

L'équation d'équilibre des moments est exprimée par la relation :

? Q(x _b sin è - y_Q cosè)= 0 (IV-45)

Fig. (IV.12) : les coordonnées pour une surface de rupture non circulaire utilisée dans la

méthode de Spencer.

Après une série de calcul Spencer a trouvé une expression réduite pour le coefficient de sécurité comme suite :

IV .6.4.4. La méthode de Morgenstern et Price :

La méthode de Morgenstern et Price aussi satisfaire à la fois les forces et les moments et suppose une fonction des forces inter-tranches. Selon Morgenstern - Price (1965), l'inclinaison des forces inter-tranches peut varier par une fonction arbitraire (f (x)) comme:

T=f(x)ëE

(IV-47)

Les forces considérées sont indiquées dans la figure (IV-13) :

Fig. (IV.13) : représentation graphique des forces sur une tranche

Où :

f(x) : Fonction des forces inter-tranches qui varie continuellement le long de la

surface de rupture,

ë : Facteur d'échelle de la fonction supposée.

La méthode propose tout type assumant la fonction de la force, par exemple un demisinus, trapézoïdal ou autre. Les relations de la force normale à la base (N) et les forces inter-

tranches (E, T) sont les mêmes que dans la méthode générale de Janbu. Pour une fonction de
force, les forces inter-tranches sont calculées par la procédure d'itération jusqu'à ce que, F_f est

égal à F_m dans les équations (IV-48) et (IV-49).

? [ { ( ) } ]

c l N u l

' + - tan ' sec

ö á

Ff = (V-48)

? { ( ) } ? ( )

W T T

- - 1 tan á + E E

-

2 2 1

et

? + -

( ( ) )

c l N u l

' tan ö '

F_m = (V-49)

? W sin á

En générale cette méthode :

· Considère les deux forces inter tranches,

· suppose une fonction des forces inter-tranches f (x),

· Permet la sélection de la fonction des forces inter tranches,

· Le coefficient de sécurité est calculé à la fois par les équations d'équilibres des forces et des moments.

IV. 6.4.5. La méthode de Sarma :

Sarma (1973) a développé une méthode pour une tranche verticale ou non pour les blocs. Cette méthode satisfait les deux conditions d'équilibre. En outre, la relation entre les forces inter-tranche est assumée comme un processus linéaire de Mohr-Coulomb expression:

T = c. h + E.tanö (IV-50)

h : hauteur de la tranche,

Les forces inter-tranches sont ajustées jusqu'à ce que le coefficient de sécurité pour l'équilibre des forces et des moments est satisfait.

En générale, la méthode de Sarma :

· Tien compte à la fois de la force et des forces inter-tranches de cisaillement,

· Satisfaire à la fois l'équilibre des forces et des moments.

IV .7 . Récapitulation des hypothèses, des équations d'équilibres et des inconnus dans les méthodes d'équilibre limite:

Comme il est noté au début de ce chapitre, toutes les méthodes d'équilibre limite utilisent les équations d'équilibre statique pour calculer le coefficient de sécurité.

Les hypothèses sont nécessaires pour rendre le problème déterminé statiquement et d'obtenir un équilibre entre le nombre d'équations et le nombre d'inconnues pour qu'ils soient résolus.

Le tableau (IV-2) énumère quelques méthodes examinées dans le présent chapitre ainsi que les hypothèses qui sont faites, les équations d'équilibre qui sont satisfaites, et les inconnus.

Tableau (IV.2): Les hypothèses, les équations et les inconnus dans les méthodes d'analyses

La méthode	Les hypothèses	Les équations d'équilibres		Les inconnus recherchés	Une pente infinie
· Étendue infinie ; · La surface de rupture est parallèle à la surface de la base de la pente.	? Forces perpendiculaires à la pente. ? Forces parallèles à la pente.	· Le coefficient de sécurité. · La force normale (N) à la base.

					Fellenius
· La surface de rupture est circulaire; · Les forces sur les côtés des tranches sont négligées.	? moments par rapport au centre du cercle de glissement.	· Le coefficient de sécurité.		Bishop simplifiée
· La surface de rupture est circulaire; · Les forces sur les côtés des tranches sont horizontaux (pas de cisaillement entre les tranches).	? moments par rapport au centre du cercle de glissement. ? des forces dans le sens vertical.	· Le coefficient de sécurité. · La force normale (N) à la base de la surface de rupture.		Spencer
· Les forces inter- tranches sont parallèles, (c'est-à-dire, toutes ont la même inclinaison). · La force normale (N) agit au centre de la base de la tranche.	? Moments de n'importe qu'elle point sélectionné. ? des forces dans le sens vertical. ? des forces dans le sens horizontal.	· Le coefficient de sécurité. · La force normale (N) à la base. · L'inclinaison des forces inter-tranches (è ). · Résultante des forces inter-tranches (Z). · Emplacement des forces latérales (ligne de poussée).
· Les forces inter tranche de cisaillement sont liée au forces normale par :	? Moments de n'importe qu'elle point sélectionné.	· Le coefficient de sécurité. · La force normale

Morgenstern et Price	T = ë f( x ) E . · La force normale (N) agit au centre de la base de la tranche.	? des forces dans le sens vertical. ? des forces dans le sens horizontal.		(N) à la base. · Le coefficient (ë ). · Les forces inter tranche horizontales. · Emplacement des forces latérales (ligne de poussée).	Sarma
· Les forces inter tranche de cisaillement dépend aux caractéristiques de cisaillement, la pression interstitielle de l'eau Et la composante horizontale de la force inter tranche. · La force normale (N) agit au centre de la base de la tranche.	? Moments de n'importe qu'elle point sélectionné. ? des forces dans le sens vertical. ? des forces dans le sens horizontal.	· Le coefficient de sismicité (k). · La force normale (N) à la base. · Le coefficient (ë). · Les forces inter tranche horizontales. · Emplacement des forces latérales (ligne de poussée).

IV .8.Étude comparative des méthodes de calcul à la rupture :

En 1977, Fredlund et Krahn ont entrepris une étude de comparaison en déterminant le facteur de sécurité pour différentes méthodes de calcul. L'exemple d'un talus simple a été traité avec plusieurs combinaisons de la géométrie, des propriétés du sol et des conditions piézométriques. Mis à part la méthode ordinaire (méthode de Fellenius), les écarts du calcul du facteur de sécurité, avec un même jeu de données, n'excèdent pas de plus de 4% pour l'ensemble des méthodes utilisées (Bishop simplifiée, Spencer, Janbu simplifiée, Janbu

rigoureuse, Morgenstern et Price). La se nsibilité du facteur de s écurité aux hypothèses faites sur les forces inter tranches et pour lesqu elles les conditions d' équilibre so nt satisfaite s , a été examinée. Les facteurs de séc urité dont l 'un est lié à l'équilibre des forces horizontale s Fm et l'autre aux moments d'équilibre Ff ont é té déterminés en utilis ant une fonction des forces inter-tranches f(x) constante et sont reportés en fonction du facteur d'échel le ë sur le

graphi que ci-après . Le facteur d'échelle se définit par la relation :

X : co mposante verticale de l a réaction inter-tranche ;

E : composante ho rizontale d e la réaction inter-tranche ;

f(x) : fonction définissant la forme de la ligne d'action dans la zone de rupture potentie lle, x étant la coordonné e horizontale.

ë : paramètre détermine la po s ition de la l igne d'action des force s inter-tranches.

Deux c as ont été étudiés : une surface circulaire et une surface non circulaire. Cette figure montre que le fact eur de sécurité du moment Fm déterminé à p artir des moments d'équilibre est relativement insensible aux hypothèses faites sur les forces de cisaille ment inter-tranches.

Fig. (IV.14) :

le facteur

de ^sécurité

partir des m

oments d'équilibre

Dans ces cas là, la différence entre le facteur de sécurité obtenu par la méthode de Bishop simplifiée et celui obtenu par les méthodes de Spencer et Morgenstern-Price (avec ë choisi pour satisfaire les forces et les moments d'équilibre), ne dépasse pas 0.4%. A l'inverse, le facteur de sécurité de la force Ff déterminé en satisfaisant l'équilibre des forces est très sensible à ë. Par conséquent les méthodes ne satisfaisant que l'équilibre des forces (exemple Janbu simplifiée sans correction, Lowe et Karafiath, etc.) sont moins précises que la méthode de Bishop qui satisfait les moments d'équilibre. Fredlund et Krahn ont aussi démontré que le choix de la fonction f(x) dans la méthode de Morgenstern et Price a une faible influence sur la Valeur du facteur de sécurité de cette étude comparative des méthodes d'analyse, on en déduit lespointssuivants:

- Les méthodes qui satisfont toutes les conditions d'équilibre (forces et moments) telles que
celle de Janbu rigoureuse, Spencer, Morgenstern et Price donnent des résultats précis.

- La méthode de Bishop simplifiée qui satisfait uniquement l'équilibre des moments donne des résultats aussi précis que celles citées précédemment sauf dans le cas où la surface de glissement est fortement inclinée au pied du talus.

-Quand la surface de glissement est fortement inclinée au pied du talus, le choix de la méthode doit se faire de telle sorte qu'elle donne une distribution correcte des forces inter tranches.

-Les autres méthodes qui ne satisfont pas toutes les conditions d'équilibre peuvent (méthode ordinaire de tranches) être très imprécises.

- Le facteur de sécurité FS, déterminé à partir de l'équilibre des forces est plus sensible aux hypothèses faites sur les forces de cisaillement inter-tranches que le facteur de sécurité Fm déterminé par les moments d'équilibre. Pour cette raison, il est préférable d'utiliser une méthode d'analyse où le moment d'équilibre est satisfait (celle de Bishop par exemple).

- Toutes les méthodes sont imprécises dans le cas où un remblai est sur une fondation

fortement compressible, car dans cette situation la rupture du remblai ne se fait pas par cisaillement, mais par traction et fissuration.

IV.9. Analyse des talus par la méthode des éléments finis :

Dans les références bibliographiques on peut trouver très large type d'éléments et des méthodes de résoudre des problèmes par la méthode des éléments finis. On a concentré dans cette description sur la formulation utilisé dans le logiciel SAS-FEM.

IV.9.1. Type d'élément finis :

L'élément linéaire triangulaire a été le premier type de l'élément 2D développé pour l'analyse des structures planes. La formulation est également plus simple par rapport les éléments finis en 2D. Il a été trouvé que l'élément linéaire triangulaire est moins précis par rapport aux éléments linéaires quadrilatère. Cependant, la réalité est que l'élément triangulaire est encore très utile à cause de sa manière adaptative à la géométrie complexe.

Les éléments triangulaires sont normalement utilisés lorsque l'on veut mailler un model 2D comprenant une géométrie complexes avec des angles aigus. En outre, la simple configuration topologique de triangulaire, permet de développer des programmes générateurs de maillage automatiquement et facilement. Le logiciel SAS-FEM comporte un générateur facile et relativement puissant qui peut générer un maillage pour n'importe quelle structure complexe

IV.9.2. Développement de la fonction d'interpolation : Considérant un élément triangle plane à 3 noeuds :

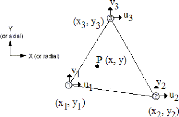
] u

[ (

- x y x y y y x x x y

- ) ( ) ( )

- - + -

1 3 3 1 3 1 3 1

+

+

u x y N x y u N x y u N x y u ( , ) ( , ).

= ( , ) .

1 1 + 2 2 + ₃ ( , ) . 3

Page 81

Chapitre IV : Les méthodes de calcul.

On va écrire u(x,y) et v(x,y) a chaque point P dans l'élément en fonction de : u1, u2, u3, v1, v2, v3. La plus simple forme est d'assumé que u(x,y) et v(x,y) sont des polynômes linaire. Noté que ces équations sont des équations approximés. Aussi u(x,y) et v(x,y) sont indépendant.

u ( x , y ) = a₁ +a₂x +a ₃y (1)

v ( x , y ) = b₁ +b₂x +b₃y (2)

Il faut trouver les constants de chaque équation (1) et (2) après appliquer les condition aux limites par exemple la fonction u(x,y) on a :

? ?

? ?

? ?

? ?

?

?

y 1

y

y 2

y x y x y

u₁

a₁

x₂

x₂

x₃

x₃

-

3

1

1

?

?

y

y y

u₂

a₂

y₂

-

2

A

?

?
? ? ?

?

?

?

?

?

?

?

u₃

a₃

x₃

- - y y

2 3 3 1 1

- x x x

- x x

-

2 1 3 2 1

- -

1 3 1 2

1

?

?

?

a₁

u₁

y 1

x 1

u₁

y 1

= +

a a x a

+

1 2 1 3

1

?

a₂

u₂

y 2

x 2

y 2

?

?

u a a x a

= + +

2 2 2 2 3

a₃

u₃

?

1

y 3

?

?

?

?

?

?

?

?

?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

u a a x a

= + +

3 1 2 3 3

x y

3 3

Donc :

[ ( x y x y y y x x x y u

- ) ( ) ( )

- - + - ]

2 3 3 2 3 2 3 2

u x y

( , )

1

2

A

[ (

- x y x y y y x x x y u

- ) ( ) ( )

- - + - 1 ] 3

1 2 2 1 2 1 2

1

2

A

2

A

1

2

1

(6)

(7-a)

(3)

(5)

Avec la même procédure on aura pour le variable v(x,y) :

v x y N x y v N x y v N x y v ( , ) ( , ) . = + + 1 1 2 ( , ) . 2 3 ( , ) . 3

(7-b)

Où : N1, N2, N3 sont les fonctions d'interpolation de l'élément triangle, ses variation est présenté comme suite :

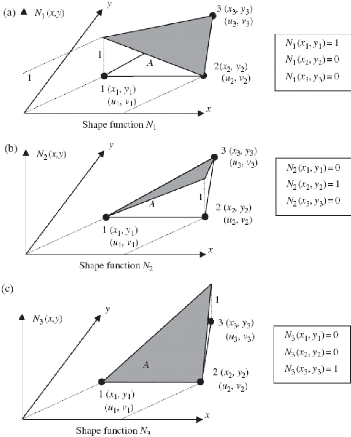
> Donc dans chaque élément on peut écrire:

? ? ? ?

??

u 1 ?

?

v 1 ?

.

?
??

? 0 0 N 0

??? =

??? u x y

( , ) N N

1 2 3

v x y

( , ) ?? 0 N 1 0 N 2 0 N₃

u 2 ? (8)

?
?

??

?

?

v₂
u₃

? u₃

IV.9.3. Développent de déformation et contrainte :

En deux dimensions il y a trois composantes majeur de contrainte ó T = { ó _x ó ó . La

xy }

y

déformation correspondante est å T = { å _x å y åxy}. La déformation peut être exprimé :

?

u

?x

?v

?y

? ? u ? v ?

? + ?

? ? y ? x ?

_å

å

å

x

=

y

=

xy

(2.9)

De l'équation (2.6) et (2.7) the déformation sont donné par:

+

?N₃

?N₁

+

u₁

u₂

u 3

?x

?x

? ? N ? N ?

2 2

+ ? u + v ?

2 2

? ? y ? x ?

?? N ? N ?

3 3

+ ? u + v ?

3 3

? ? y ? x ?

x

=

?y

å

? ?

?

?N₁

?N₁

+

?

?

?

u₁

v₁

?y

?x

En écriture matricielle

?N₂

?x

?N₁

v₁ + ^?N2 v2

?y

? N 2

0 0

? N 2

? y

? N 2

?N₃

?y ?x ?y

? N 3

?y

? N 3

?x

? ? ? ? ? ? ? ? ?

u 1

v 1

u 2

v 2

u 3

v 3

??

?
?

??

?

?

? N 3

0 0

?x

??å

xy

å_x

å_y

?N₁

?x

0

?N₁

?y

0

?N₁

?y

?N₁

?x

.

?

?

?

??

?

??

? N 2

? x

+

v 3

å

å

y

=

xy

?N₃

?y

(2.10)

(2.11)

Ou bien:

{å } = [ B .]{ U} (2.12)

où: [ B] est la matrice déformations-déplacements égale à:

Page 83

1

[ B]

?

?

?

??

A

2

y 2 - ?

0 x - x 0 x - x 0 x - x (2.13)

3

x1- -

Y3

0

Y3

Y1

0

Y1 Y2

0

2

1

2 1

3

x 3 - x ₂ y 2 - y 3

- x ₃ y 3 - y 1

x 2 - x 1

. Y

1 - y2

Pour le développement des contraintes en deux dimensions. La relation déformationcontrainte peut être considérée soit contrainte-plane, soit déformation plane dépond de la structure étudiée.

Généralement l'analyse des talus en deux dimensions sont considérés comme problème déformation plane, oil la relation est donné par:

ó x E?- í) ? ( 1 + 0( 1 - 2í) ?óxy ? 0 Ou bien :

?? ? ( 1-^íí ) ^00?^?åe^xy^? (1-2v)^?1 1 0 låx), I 2 ?` '

(2.14)

{ó } = [ D .]{å} (2.15)

Avec: [ D] matrice de comportement (caractéristiques de matériau). A partir de l'équation (2.12) et (2.15) on peut écrire:

{ó } = [ D ][.B.]{ U} (2.16)

IV.9.4. Résolution Eléments Finis :

Après assemblage des matrices élémentaires dans la matrice de rigidité globale, la forme finale est comme suite :

[ K .]{ U} ={ P}

oil :

{ U} : Vecteur de déplacements

[ K] : matrice de rigidité globale égale à:

[ K ] = ? [B] ^T [ D] [ B] dV = [B] ^T [ D] [ B]? dV = Ah. [B] ^T [ D] [ B] (2.17)

V V

{ P} : le vecteur global des forces composé de

Forces de corps { Pb } = ?	[ N ] ^T [ b] dV (2.18)
Forces de tractions { Pt } = ?		[ N ] ^T [ t] dA (2.19)

Et forces nodales{ Pn} .

IV.9.5. Modélisation des matériaux en SAS-FEM :

L'analyse élastique-plastique en deux dimensions de déformation-plane est utilisée, oil le comportement du matériau de sol est modélisé par le critère de Mohr-Coulomb. Ce dernier, est considéré comme le critère le plus utilisée dans la pratique géotechnique. Le critère de Mohr-Coulomb peut être exprimé comme :

F =I 3 1

sin

ö + ? - 1 ? J cos è sin sin è ö c . cos 2 ?? ?? - 3

ö (2.20)

oil

ö : est l'angle de frottement interne,

c : est la cohésion

1 ? 3 J ?

- 1

è = sin ? ( ) ?

3 3 (2.21)

3 / 2

3 ? 2 J 2 ?

I₁ = (ó _x + ó_y + ó _z) = 3ó_m (2.22)

1 2

[ ( 2 ² ) ( ó ó ó ó ó ó ô ô ô

2 2

J ó ó ó ) ] 2

+ + + (2.23)

² 3

= + + - + +

x y z x y y z z x xy yz zx

2 2 2

J s s s = 2 . . s

3 x y z + ô ô ô - ô - ô - ô

s s (2.24)

xy yz zx x yz y zx z xy

s_x = óx-óm ;;s_yy= ó -ó_m ; s_{z x}= ó-ó_m (2.25))

y'

Le modèle de matériau décrit ci-dessus se compose de six paramètres

· Angle de frottement(ö))

· Cohésionn (c )

· Dilation(ø/ )

· Module de Young (E)

· Module de Poisson (í )

· Poids volumique de sole (ã )

IV.9.6.Coefficient de sécurité Factor (FOS) :

SAS-FEM utilise la technique de réduction de Résistance au cisaillement pour prédire le coefficient de sécurité (FOS), où, dans cette technique la résistance du sol est réduite progressivement par le facteur de réduction de la résistance (SRF) afin de provoquer effondrement, donc, la rupture de pente dans EF se produit naturellement à travers les zones où la résistance au cisaillement du sol est insuffisante pour résister à la contrainte de cisaillement. Au début de rupture la valeur des déplacements nodaux maximale a un grand saut qui provoque la non-réalisation de la convergence de la solution dans un nombre spécifié de l'itération.

Le coefficient de sécurité est simplement calculé

FOS ô

ô f

(2.26)

où

ô : est la résistance au cisaillement de la matière de talus, qui est calculé par le critère de Mohr-Coulomb comme:

ô = c + ó _n tan ö (2.27)

ô_f : est la contrainte de cisaillement sur les surfaces de glissement étant donné que:

ô f = c _f + ó _n tanö_f (2.28)

La résistance au cisaillement pondérée des paramètres c_f et ö_f sont obtenue comme suite :

c

c f = (2.29)

? ?

?? SRF ??

tan ö-

SRF

ö = tan ¹ (2.30)

f

Ainsi, le facteur de cisaillement en cours de réduction est utilisé pour calculer le facteur de sécurité du talus analysés

IV.9.7. La rupture de pente :

La non-convergence dans un nombre d'itération spécifié par l'utilisateur dans le programme dans éléments finis est considérée comme un indicateur valable de rupture du talus. Cela signifie que les pas de la répartition des contraintes peuvent être réalisés pour satisfaire à la fois le critère de Mohr-Coulomb et de l'équilibre global. La rupture de pente et de non-convergence numérique aura lieu en même temps avec une augmentation des déplacements. Habituellement, la valeur du déplacement maximum nodal juste après la rupture de pente a une grande valeur par rapport à celui avant la rupture.

V .1. Les logiciels utilisés pour l'analyse de la stabilité :

L'analyse de la stabilité des talus aujourd'hui peut être effectuée en utilisant divers logiciels de géotechnique sur ordinateur. Les logiciels informatiques utilisant les formulations d'équilibre limite ont été utilisés pendant de nombreuses années. De même, les logiciels qui utilisent la méthode des éléments finis sont basé sur les lois constitutives des sols et des modèles appropriés, a attiré de plus en plus intérêt à la fois des chercheurs et des professionnels. Aujourd'hui, les deux types de logiciels basés sur les éléments finis et la limite d'équilibre (EF et EL) sont couramment utilisés dans les calculs géotechniques.

V .1.1. Logiciel SLOPE/W:

SLOPE/W, développé par GEO-SLOPE International Canada, est utilisé pour l'analyse de la stabilité des talus.

Ce logiciel est basé sur les théories et les principes des méthodes d'équilibre limite discutés dans les sections précédentes, et il peut même utiliser la méthode des éléments finis mais à l'aide de la modélisation obtenu de logiciel SIGMA/W.

Le logiciel calcule le coefficient de sécurité pour différentes surfaces de cisaillement, par exemple circulaire, ou non circulaire. Cependant, seules les surfaces de cisaillement circulaire est automatiquement recherchées.

Plusieurs méthodes de calcul sont disponibles dans SLOPE/W, il permet de calculer le coefficient de sécurité on utilisant la méthode Ordinaire, Bishop, Janbu généralisée, Spencer, Morgenstern -Price, Sarma, Lowe Karafiath, et d'autres.

V.1. 2. Logiciel LARIX-4S :

LARIX-4S est un programme pour le calcul de la sécurité de la stabilité des pentes,

digues, enceintes de fouilles et murs de soutènement selon la méthode des lamelles. La sécurité de la stabilité est déterminée par l'étude de l'équilibre global des efforts agissant sur une tranche verticale de sol en tenant compte des couches de sol, de la pression d'eau interstitielle, des surcharges, de la résistance des ouvrages, des ancrages et des sollicitations sismiques. Les méthodes reconnues de Krey et Janbu sont disponibles.

La sécurité peut être calculée pour des cercles de glissement, avec ou sans tangentes, ou pour des lignes de glissement polygonales. Le programme permet aussi bien de travailler avec le concept des coefficients de sécurité partiels selon les nouvelles normes qu'avec celui des coefficients de sécurité globaux.

V .1.3. Logiciel CLARA :

Le code de calcul CLARA est un programme d'analyse de la stabilité des pentes qui permet de calculer un facteur de sécurité en visualisant les résultats graphiques du volume instable correspondant, développé par «O.Hungr Geotechnical Research Inc.». Les méthodes de calcul du facteur de sécurité intégrées dans CLARA sont: la méthode de Bishop simplifiée (2D et 3D), Janbu simplifiée (2D et 3D), Spencer (2D) et Morgenstern-Price (2D). Elles permettent de calculer un coefficient de sécurité vis à vis d'un type de rupture bien défini. Le modèle géométrique est subdivisé en un nombre fini de colonnes parallélépipédiques (en 3D) ou en tranches verticales (en 2D). Il exécute plusieurs méthodes de recherches automatiques du centre de rotation de la surface de glissement potentiel jusqu'à atteindre le plus faible coefficient de sécurité.

Chaque méthode choisie par l'utilisateur, est limitée en nombre d'opérations par une valeur limite des paramètres géométriques de la surface de glissement analysée.

V .2.Définition des paramètres géométriques de surface de rupture:

Dans ces calculs, il est supposé que: -le volume instable est subdivisé en un nombre fini de colonnes actives.

-la surface de rupture est un loup de glissement dont la base est assimilée à un arc de cercle (en 2D) ou une partie d'ellipsoïde (en 3D);

-tous les points situés sur la surface de glissement ont la même coefficient de sécurité; le matériau du talus analysé obéit au critère de plasticité de Mohr-Coulomb.

Voici une illustration d'une surface de rupture circulaire. C'est l'hypothèse la plus simple et le mode typique le plus courant de rupture dans un sol.

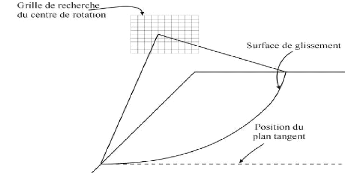
Fig. (V-1) : Une Illustration d'une surface de rupture circulaire

Présentation des logiciel à utilisés

V .2. Présentation du logiciel Geoslope Geostudio 2002 V5.03:

Geostudio 2002 est un logiciel de calcul géotechnique permet de traiter les différents problèmes du sol comme le glissement des terrains, le tassement, la consolidation, les infiltrations des eaux dans le corps de la digue d'un barrage et d'autres problèmes liés à la géotechnique.

Plusieurs programmes sont intégrés dans la fenêtre générale du logiciel:

· SLOPE/W: Permet de calculer le coefficient de sécurité d'un talus naturel ou artificiel par les méthodes d'analyses classiques..

· SEEP/W: Permet de calculer les infiltrations des eaux (Par la méthode des éléments finis).

· SIGMA/W: Permet d'analyser les problèmes de la relation contraintes / déformations (Par la méthode des éléments finis).

· QUAKE/W: Permet de définir le comportement d'un terrain sous l'effet d'un séisme (Par la méthode des éléments finis).

· TEMP/W: Permet d'analyser les problèmes Géothermique du sol (Par la méthode des éléments finis)... et autres logiciels.

Ce que nous s'intéressons parmi ces programmes est SLOPE/W.

V .2.1 . Le programme SLOPE/W:

SLOPE/W est l'un des programmes intégrés dans la fenêtre du Geostudio 2002 et qui est basée sur la théorie de l'équilibre limite dans les calculs du coefficient de sécurité des pentes.

L'élaboration de ce programme permet d'analyser facilement à la fois des problèmes simple et complexe de stabilité de pente en utilisant une variété de méthodes pour calculer le coefficient de sécurité.

Ce programme est de type graphique et compatible avec les versions de Microsoft Windows XP.

V .2. 2. L'interface du logiciel SLOPE/W:

Les menus disponibles et la fonction de chacun sont les suivants:

Fig. (V.2): Les menus disponibles sur logiciel SLOPE/W

· File: Ouvre et enregistre les fichiers, les importations des photos et imprime le dessin.

· Edit: permet de copier le dessin dans la Presse-papiers du windows.

· Set: définir les paramètres de la grille, le zoom, les axes et de la page.

· View (aperçu): Options d'affichage des contrôles, des informations des sols et des points, et d'affiche les forces inter-tranche sur un schéma corporel de chaque tranche et le polygone force.

· Keyin (menu): Permet d'introduire automatiquement à l'aide des tableaux les paramètres géométriques de la pente (coordonnées et couches), les caractéristiques mécaniques des déférentes couches constituant le talus, des conditions complémentaires nécessaires pour le calcul, le niveau de la nappe, de sélectionner les déférentes méthodes de calcul, les surcharges, l'effort sismique et les confortements.

· Draw (dessin): permet d'introduire manuellement les paramètres géométriques de la pente (coordonnées et couches), des conditions complémentaires nécessaires pour le calcul, le niveau de la nappe, les surcharges et les confortements.

· Sketch (croquis): Définit les objets graphiques d'étiqueter, d'améliorer et de clarifier les résultats du problème

· Modify (modifier): Permet de déplacés, modifier ou supprimés les objets graphiques, les textes et les photos.

Les calculs ont été faits en utilisant à la fois la méthode de Fellenius (Méthode ordinaire), de Bishop, de Janbu et la méthode généralisée d'équilibre limite «GLE».

s (Felleni
st lissée a

us, Bishop et Janb

u choix d e

ncer, la m éthode gén

l'utilisateu éralisée d'é

Dans le p

GLE», Sarm a ou autres

, les troi

sélecti o
méthod

limite «

rogramm e nnées par défaut, la e peut être de Morg e

s méthod e quatrième méthode e nstern - P r ice, de sp e méthode s .

u) sont

r. Cette
quilibre

e et spence

méthod

La méthod e GLE env e
es (Morge n stern - Pri c

loppe tout

es les cond r).

itions et les

efforts do nnés par le

s autres

Après la sélection des méthodes

complé mentaires pour exécu ter les calc

du prog ramme.

Nombreuse s informa t ions comp

uites dans

de calcul, l e uls, ces info

lémentaires

program m rmations s

sont prop

e demand

ont introd

osées par

e des infor mations

le menu

le programme, on

site là tr ois inform a tions prin c ipales:

· Grille et rayons (G

rid and Ra

dius):

grille la s u

e grille qui

ster plusie urs cercles d

ère grille d éfinie par l'

e test tout es les cercl e

ide d'une

si une autr

inclus l'

Cet t axe du cer c

rayon du

des poin ts définie p

ermet de

ment et de

définir à l' a

définir au s

s le progra mme va te

point du

rayon e st compris

e option p le de gliss e cercle, alo r entre l'un d ar l'optio n

es points d Radius (Le

e la premi

programm

rface prob able qui inclus le de uxième e glissem e nt où le option Grid , et l'un s possible s ).

Fig. (V.3): détermination de la surfa

ce de rupture par la méthode «Grid

and Radius»

· Entrée

et sortie (E

ntry and Ex

it):

te, car il s u

d'arc du c

ffit de séle

est plus si mple que la précéden

ctionner

e autre

les arcs

Cet te méthod e

une pa

partie o possible

trouve le p remier poi

nt probable

(le progr a

).

ercle et un

tie

ntre ces de

rc du cercl e

de la pent e

mme va te

ster touts

r point d'a

ux parties

r de la p ente oü se ü se trou ve le derni e s compris e

Fig. (V.

4): détermin

ation de la s

urface de rupture par la

méthode «Entry and Exit»

· Localisation automatique (A uto- locate ):

probable ( une infinité de cercles

s une série

Avec ce

program rupture

tte méth o
me fait a u

de, aucun e tomatique m

informatio

ent toute

n n'est de

par défaut

mandée (s

de calcul e

).

auf un cen

t test des c

tre des ce r
entaines c e

cles), le
rcles de

V .3. Logiciel SA S-FEM 20 08 :

V.3.1.P résentatio n SAS-FEM e

dévelop

:

st un logi

lcul spécia

hdar Khalil

l pour l'analyse de en 2008. S ont princip

stabilité d e de calcul

es talus
est base

ciel de ca

pé par not re encadreu r Mr Belak

Dans notre étude on			a utilisé la p		remière m	éthode.
V .3.2. L	'interface d	u logiciel S		LOPE/W:

sur la m éthode de

cisaille m

s éléments

rédire le fa

finis. Il util

ise la techn

curité (FOS

ique de la ).

Réduction

de la Résistance au

ent pour p

cteur de sé

Fig. (V.5): L'interface de logiciel SAS-FEM2008

Fig. (V.6): L		es menus disponibles sur logiciel SA					S-FEM2008
· FILE (fichier) importations			: Nouveau, O	uvre et enr	egistre les fichiers, les

· · Geometric (Géométrique) : Permet d'introduir e les param ètres géom étriques d e la

pe

nte (coordo

nnées

et couches

).

Vie w (aperçu) po ints

: Options

d'affichage

des contrô

les, des info

rmations d

es sols et d es

Page 96

lisés.

V : présentation des l

Chapitre

ogiciels uti

: P

l)

: P

constituan

ermet d'i n

t le talus

troduire le

s caractéristiques

· So

m é

il properties(Les prop riétés du so

caniques d

es déféren

tes couches

· Wa

d' e

ter table (Niveau Hydrostatique)

ermet d'int

roduire le niveau de l

a nappe

au.

· Lo

: Perm

rcharges

uire les su

et d'introd

ading (Chargement)

su

· Meshing (Maillage)

ivant la de nsité de ma

s)

éléments triangulaire

maillage e

n 2D

r automatiq

uement un

: Perme t

illage donn é

de génér e

par l'utili s

ateur. (par

: Permet définir l

es options

d'analyse p

our analyse r le

Page 98

lisés.

V : présentation des l

Chapitre

ogiciels uti

les résulta

: Permet de d'afficher

· Poste processing (Poste de transformation)

rbes)

rme des gr

aphes (cou

ent sous fo

graphiquem

ou contours

: Pe

logiciel.

nnaitre la

version de

rmet seule

ment de co

· Help (Aide)

VI.1. Introduction:

L'analyse de la stabilité; objet de ce chapitre; à pour but de déterminer les cercles de glissements les plus probables pour déférentes sections du talus.

La géométrie du talus est décrite dans un repère cartésien (OXY). L'axe (OX) étant orienté horizontalement et dans la direction de l'aval et l'axe (OY) étant dirigé verticalement; orienté vers le haut.

L'analyse a été faite suivant trois manières de calcul à raison de comparaison des résultats:

· Analyse Manuel: Utilisant la méthode BISHOP simplifiée

· Analyse selon plusieurs méthodes classiques utilisant logiciel (Geostudio 2002 V5.03) pour tester plusieurs surfaces de ruptures probables des glissements observés correspondant à des coefficients de sécurité minimums.

· Analyse selon la méthode des éléments finis utilisant le logiciel SAS-FEM (Stability Analysis of Slopes using Finite Element Method) 2008 V2.00.

VI.2. Présentation générale du projet :

Le projet proprement dit s'intéresse à l'étude de la stabilité d'un talus de 20 m d'hauteur environ et dont les coordonnés sont donnés dans le tableau ci-dessous

Tableau (VI.1): les coordonnés du projet.

Début du projet		Fin du projet	X=0°09'45.12»E
X=0°09'45.68»E		Y=34.50'52.36» N
Y=34°50'52.57N

Avec L'aide D'une GPS (Global Positioning System ou bien Géo-Positionnement par Satellite) et avec l'utilisation de Google Earth en a obtenu ces photos (1, 2, 3,4) qui localisent notre site étudié:

Fig. (VI.1) : Prise à 421m d'altitude

Fig. (VI.2) : Prise à 421m d'altitude

Fig. (I.3) : début et fin de talus.

Fig. (I.4) : maillage des coordonnés

VI.3.Les essaies au laboratoire (L.T.P.O)

Dans toutes les méthodes de définition de coefficient de sécurité on a besoin de connaitre trois principales caractéristiques propres au sol qui sont :

Le poids volumique ã h (t/ m3).

L'Angle de frottement ö ( ° ).

La cohésion C (bar).

Pour cela on a effectuer les essaies au L.T. P. O .

VI.4. détermination des densités et de la teneur en eau :

VI .4.1. Principe de la méthode :

Cette méthode permet ; avec d'autres paramètres ; d'apprécier l'état dans lequel se trouve le sol.

Elle consiste en la mesure de la perte d'eau d'un échantillon de matériau provoquée par étuvage.

Les masses de l'échantillon et de l'eau évaporée sont mesurées par pesage.

VI .4.2.Méthode d'analyse :

On prélève un volume naturel en plan dans le sol, qui est immédiatement plonge dans un bain de paraffine fondue et ramené au laboratoire. En moyenne on a prélève 1.1 dm3 de sol par horizon, sous la forme d'une demi-douzaine d'echantillons.cependant échantillonnes que les horizons profonds (2.0 dm3 contre 0.4 dm3 prélèves en moyenne).

Au laboratoire le volume de l'échantillon enrobé est mesuré par déplacement d'eau. On sépare ensuite la paraffine de la terre. En deux étapes. D'abord grossièrement, manuellement puis en faisant fondre la paraffine.la paraffine est pesée, et son volume calculé (densité constante de 0.89) .la terre est tamisée (2 mm), séchée (105°c, 48h) et pesée. Le volume des éléments grossiers et des racines est mesuré immédiatement par déplacement d' eau.la masse volumique de l'échantillon est le rapport de la masse de terre tamisée sèche au volume initial enrobé. Moins le volume de la paraffine, des cailloux et des éléments grossiers.

Les résultats obtenus sont :

· pour l'argile verte

	I		II			III		N° TARE
35	42	19	70		20	12	POIDS HIMIDE+TARE
19,30	19,10	19	18,8		18,7	20,2	POIDS SEC+TARE
16,70	16,40	16,4	16,3		15,9	17,2	POIDS DE LA TARE
3,90	3,70	3,9	3,7		3,7	4,2	POIDS D'EAU
2,60	2,70	2,60	2,50		2,80	3,00	POIDS DU SOL SEC
12,80	12,70	12,50	12,60		12,20	13,00	TENEUR EN EAU
20%	21%	21%	20%		23%	23%	POIDS DU SOL HUMIDE+PARAFFINE
1130,60	1015,90		1156,70			POIDS DU SOL HUMIDE
1116,20	1000,00		1145,90			POIDS DE LA PARAFFINE
14,40	15,90		10,80			POIDS DU SOL PARAFFINE DANS L'EAU
567,50	472,00		566,40			VOLUME BRUT
563,10	543,90		590,30			VOLUME DE LA PARAFFINE
16,00	17,67		12,00			VOLUME NET
547,10	526,23		578,30			POIDS volumique HUMIDE ãH
2,04	1,90		1,98			TENEUR EN EAU MOYENNE ù
21%	20%		23%			POIDS volumique SECHE ãd
1,69	1,58		1,61

POIDS volumique HUMIDE MOYENNE ãH :		1,97 T/m3	TENEUR EN EAU NATURELLE ù :
21 %		POIDS volumique SECHE ãd :
1,63 T/m3		TENEUR EN EAU DE SATURATION ùsat :
24,45 %		DEGRE DE SATURATION SR :
87 %

AVEC :

POIDS D'EAU = (POIDS HIMIDE+TARE)-(POIDS SEC+TARE).

POIDS DU SOL SEC= (POIDS SEC+TARE) - (POIDS DE LA TARE).

TENEUR EN EAU= (POIDS D'EAU) / (POIDS DU SOL SEC).

POIDS DE LA PARAFFINE = (POIDS DU SOL HUMIDE+PARAFFINE) - (POIDS DU SOL HUMIDE).

VOLUME BRUT = (POIDS DU SOL HUMIDE+PARAFFINE) - (POIDS DU SOL PARA DANS L'EAU). VOLUME DE LA PARAFFINE = (POIDS DE LA PARAFFINE) / 0.89.

VOLUME NET = (VOLUME BRUT) - (VOLUME DE LA PARAFFINE).

POIDS volumique HUMIDE = (POIDS DU SOL HUMIDE) / (VOLUME NET).

POIDS volumique SECHE = (POIDS volumique HUMIDE) / (1+ TENEUR EN EAU MOYENNE).

TENEUR EN EAU DE SATURATION {(1/ POIDS volumique SECHE)-(1/2.7)} * 100.

DEGRE DE SATURATION = (TENEUR EN EAU / TENEUR EN EAU DE SATURATION)*100.

· pour le remblai :

	I		II			III		N° TARE
91	42	19	70		20	12	POIDS HIMIDE+TARE
20,10	20,00	21,4	21,4		21,2	21,3	POIDS SEC+TARE
17,50	17,50	18,5	18,4		18,4	18,6	POIDS DE LA TARE
3,70	3,60	3,6	3,6		3,8	3,9	POIDS D'EAU
2,60	2,50	2,90	3,00		2,80	2,70	POIDS DU SOL SEC
13,80	13,90	14,90	14,80		14,60	14,70	TENEUR EN EAU
19%	18%	19%	20%		19%	18%	POIDS DU SOL HUMIDE+PARAFFINE
693,20	692,20		646,60			POIDS DU SOL HUMIDE
682,20	680,50		635,50			POIDS DE LA PARAFFINE
11,00	11,70		11,10			PODS DU SOL PARAFFINE DANS L'EAU
352,80	355,50		229,20			VOLUME BRUT
340,40	336,70		417,40			VOLUME DE LA PARAFFINE
12,22	13,00		12,33			VOLUME NET
328,18	323,70		405,07			POIDS volumique HUMIDE ãH
2,08	2,10		1,57			TENEUR EN EAU MOYENNE
18%	20%		19%			POIDS volumique SECHE ãd
1,76	1,75		1,32

Poids volumique HUMIDE MOYENNE ãH : 1,92 T/m3

TENEUR EN EAU NATURELLE : 19 %

POIDS volumique SECHE ãd : 1,61 T/m3

TENEUR EN EAU DE SATURATION : 25,07 %

76 %

DEGRE DE SATURATION SR :

VI.4.3. Résultats :

-Remblai :

Poids volumique HUMIDE MOYENNE ãH : 1.92 t/m³

-Argile verte :

Poids volumique HUMIDE MOYENNE ãH : 1.97 t/m³

VI.5. L'essai de cisaillement rectiligne direct à la boite :

VI .5.1. Définitions :

La résistance au cisaillement d'un sol est définie comme étant la contrainte de cisaillement dans le plan de la rupture au moment de celle-ci.

En effet, lorsqu'un système de forces est appliqué à un volume déterminé d'un sol, il se développe des contraintes de cisaillement. Ces contraintes entraînent des déformations du sol qui peuvent être importantes le long de certaines surfaces appelées surfaces de glissement ou de rupture.

Le but de l'essai de cisaillement est de déterminer les valeurs de la cohésion C et de l'angle de frottementö .

Fig . (VI.5) : D

ispositif de

l'essai de

cisaillement.

VI .5.2. P

rincipe de

la méthod e :

L'essai s'effe ctue sur une éprouvette de sol de diamètre plus grand que la hauteur,

placée d ans une boit e de cisaill ement cons tituée de deux demi b oites indép endantes. L e plan de séparation des deux demi boites constitue un plan de glissement correspondant au plan de

cisaillement de l'épr ouvette.

l'éprouvette un effort

normal N maintenu

cisaillement de

tirant la demi boite

l'éprouv ette selon l e inférieur e, imposant

effort, o n produit un

s deux de mi boites en

L'essai c onsiste à appliquer sur la face supérieure de constant, puis, après consolidation sous ce même plan horizontal de gli ssement de

ainsi un déplacement relatif et à vitesse con stante.

L 'éprouvett e ne subit aucune consolidation ni aucun drainage préalables, sous la

contraint e normale ó de l'ess ai. C'est un essai rap ide, et sauf cas parti culier, la droite de

Coulom b dans le diagramme ô = f (ó) est horizontale pour un s ol cohérent saturé. La rapidité

de l'ess ai doit êtr e telle qu'e lle ne permette aucun drainage de l'éch antillon, on obtient l'équatio n : ô = C u .

VI.5.3. M

éthode d'a nalyse :

VI.5.4. Réalisation de l'essai :

Pour valider l'essai, il faut au moins cisailler trois éprouvettes d'un même échantillon, de mêmes dimensions et préparées dans les mêmes conditions. Ces éprouvettes sont cisaillées à la même vitesse mais soumises à des efforts N différents.

La contrainte verticale maximale, appliquée à la série, d'éprouvettes doit être supérieure à la contrainte effective verticale induite dans le sol après la réalisation de l'ouvrage. On choisit généralement 100, 200 et 300 KPa.

Remblai : La contrainte verticale maximale = 01 bar

									Consolidation
Cisaillement						Jour
Heure		"	Tas	L	LA	LA	LA
				0,25	70	370
				0,50	135	365
				0,75	185	350
				1,00	220	340
				1,25	255	320
				1,50	288	310
				1,75	320	305
				2,00	347	303
				2,25	361
				2,50	370
				2,75	373
				3,00	379
				3,25	380
				3,50	378
				3,75	371
				4,00	371

La contrainte verticale maximale = 02 bar.

Consolidation						Cisaillement			Jour
Heure		"	Tas		LA	LA
				0,25	75	620
				0,50	150	630
				0,75	205	635
				1,00	220	640
				1,25	260	630
				1,50	290	624
				1,75	360	600
				2,00	410	550
				2,25	460	530
				2,50	500	510
				2,75	525	500
				3,00	540	490
				3,25	560	470
				3,50	575	445
				3,75	586
				4,00	605

La contrainte verticale maximale = 03 bar.

Caractéristiques phisiques									Consolidation
Cisaillement						Jour
Heure		"	Tas	L	LA	LA	LA
			et Gel	0,25	100	700	840
				0,50	200	728	820
				0,75	240	755	808
				1,00	285	780	790
				1,25	325	810	775

				1,50	365	823		760
			1,75	400	827
			2,00	420	830
			2,25	500	833
			2,50	525	835
			2,75	550	850
			3,00	570	855
			3,25	590	866
			3,50	615	860
			3,75	640	855
			4,00	670	853

Tableau VI-2 : RESULTATS OBTENUS POUR LE REMBLAI

Contrainte verticale en bars	1	2		3	Lecture à l'anneau
380	640	866		Déformation longitudinale
3,25	5,00	7,25		Force nette
29,64	49,92	67,55		Section nette
26,35	25,30	23,95		Contrainte tangentielle
1,125	1,973	2,820

Avec :

Force nette = Lecture à l'anneau*0.078 ; (0.078= Coefficient de l'anneau). Section nette = 28.3 - (Déformation longitudinale*0.6) ; (28.3 Section de l'appareil). Contrainte tangentielle = Force nette / Section nette.

De même pour l'argile :

Tableau VI.3: RESULTATS OBTENUS POUR L'argile verte .

Contrainte verticale en bars	1	2		3	Lecture à l'anneau
960	1330	1390

Déformation longitudinale	9,50	9,75		10,25	Force nette
74,88	103,74	108,42		Section nette
22,60	22,45	22,15		Contrainte tangentielle
3,313	4,621	4,895

Les valeurs de la résistance au cisaillement ainsi définies obtenues lors de l'essai sont portées sur une courbe, en fonction de la contrainte normale ó s'appliquant sur le plan de rupture.

La courbe obtenue est approximativement une droite appelée droite intrinsèque d'équationô =C +ó tanö, elle exprime la loi de Coulomb. L'angle formé entre cette droite et

l'axe des abscisses est l'angle de frottement ? et l'ordonnée à l'origine est la cohésion C.

2.50

2.00

1.50

Série1

Contrainte tengencielle

argile verte

ó(n) Contrainte verticale en bars

0 0.5 1 1.5 2 2.5 3 3.5

6.00

5.50

5.00

4.50

4.00

3.50

3.00

2.50

2.00

1.50

1.00

4.00

3.50

3.00

1.00

0.50

0.00

0 0.5 1 1.5 2 2.5 3 3.5

remblai

Fig. (VI.6) : Courbe intrinsèque (remblai & argile)

VI .5.5. Résultats :

· couche de Remblai dont les caractéristiques mécaniques sont: ö = 4 1 °; et c = 0. 1 5 bar.

· La couche d'argile verte dont les caractéristiques mécaniques sont :

ö = 3 7 °; et c =2. 5 bar.

VI.6.Récapitulation:

Tableau VI.4: Résultats obtenues.

ã (t/m3)

C (bar)

ö(° )

Remblai	1.92	0.15		41	Argile verte
1.97	2.5	37

VI.7. Calculs et résultats :

VI.7.1. caractéristique du talus:

La couche de Remblai dont les caractéristiques mécaniques sont:

ö = 4 1 °; ã_h =1 9.2 KN/m³ et c =0. 1 5 bar;

La couche d'argile dont les caractéristiques mécaniques sont :

ö = 3 7 °; ã_h =1 9. 7 KN/m³ et c =2. 5 bar;

La géométrie de talus est présentée schématiquement comme suite :

Fig. (VI.7) : Les dimension de talus El_Riadh

VI.7.2. Méthode de calcul manuelle :

VI .7.2.2. Description du processus et outils utilisés :

Pour la détermination du coefficient de sécurité Fs, l'utilisation de La méthode de Bishop simplifiée a été préconisée.

· Formule de BISHOP simplifiée :

F =		n ? i=1		? ( c x + W ) 1 ? Ä tan ö ui i i ui ?? M ( ) ?? è i
				Avec
n ? W sin è i i i=1	(VI-1)

tan ui

M ( ) = [ 1 + è ö

è cos è tan ]

i i ⁱ F

· Outils utilisés :

· On avait recours au logiciel AUTOCAD pour réaliser les taches suivantes : - Modéliser le remblai en question.

- Tracer les divers cercles de rupture.

- Élaborer une subdivision en tranches, propre a chaque cercle de rupture .

- Calcul des surfaces des tranches, et l'angle è.

· Le tableur Excel a été aussi utilise pour faciliter les calculs (produits, sommes, itérations ...)

Après avoir effectue les calculs sur plusieurs cercles, on a trouve un cercle qui affiche un Facteur de sécurité minimum.

Fig. (VI.8): détails du talus étudié

Nombres de tranches : 12 Exemple de calculs tranche 8

Äxi = 1.0 m.

èi = 47°.

Wi = A ã = 9.145 × 19.7= 180.15 kN/m

Wi sin èi = 180.15 x sin (47) = 131.75 kN/m

ciÄxi = 22 x 1= 22 kN/m

T*=ciÄxi + (Wi * tan ö ) = 22 + (180.15) tan 41^o = 178.603 kN/m

Supposons maintenant un facteur de sécurité, par exemple F = 2

Mi = cos èi (1 + tan èi tan öi /F) = cos(47)×(1+tan(47)×tan(41)/3) = 0.999

le tableau suivant résume les résultats obtenus ainsi que les coefficients de sécurité calculés :

Tableau (VI.5): Résultats de calcul par méthode manuelle

n			è (^ï)			è (rad)		Äx (m)			A (m^2)		W (kN/m)		Wsinè (kN/m)		cÄx (kN/m)		T* = cÄx + W *tan ö (kN/m)		M		T*/M
	1			16		0.2793			1		0.754		14.858		4.095		22		34.916		1.0811		32.297
	2			20		0.3491			1		2.226		43.858		15.000		22		60.125		1.0883		55.244
	3			24		0.4189			1		3.623		71.379		29.032		22		84.049		1.0903		77.086
4		28			0.4887		1			4.939		97.288		45.674		22		106.572		1.0870		98.042
5		32			0.5585		1			6.164		121.431		64.349		22		127.558		1.0784		118.288
6		36			0.6283		1			7.286		143.526		84.363		22		146.766		1.0645		137.874
7		41			0.7156		1			8.288		163.276		107.118		22		163.933		1.0399		157.649
8		47			0.8203		1			9.145		180.151		131.754		22		178.603		0.9999		178.625
9		51			0.8901		1			9.814		193.330		150.246		22		190.059		0.9671		196.524
10		57			0.9948		1			10.095		198.868		166.784		22		194.873		0.9092		214.344
11		65			1.1345		1			8.577		168.963		153.132		22		168.877		0.8165		206.821
12		76			1.3265		1			5.461		107.590		104.394		22		115.526		0.6637		174.076

.

T

M

Wsinè

*

1 . 5 6

FS

En doit faire une mise à jour du FS donné jusqu'à ce que la solution (FS trouvé) converge.

Tableau (VI.6): Résultats de réévaluation des coefficients de sécurité

FS donné			FS trouvé
2			1.56
1.56			1.424
1.424			1.373
1.373			1.352
1.352			1.344
Chapitre VI: Etude de cas_ Talus de Riadh
	1.344	1.34
	1.34	1.399
	1.399	1.388
	1.388	1.388

DONC FS = 1.388

VI .7. 3. Les résultats obtenus à l'aide du logiciel SLOPE/W

Fig. (VI.9): Résultat obtenu par Méthode de BISHOP

Fig. (VI.10): Résultat obtenu par Méthode de MORGENSTEM-PRICE

Figure (VI.11): Résultat obtenu par Méthode de JANBU

Figure (VI.12): Résultat obtenu par Méthode de SPENCER

Figure (VI.13): Résultat obtenu par Méthode G.L.E

Page

Figure (VI.14): Résultat obtenu par Méthode de FELLENIUS

Les résultats obtenus à l'aide du logiciel Géostudio 2002 sont :

Tableau (VI.7): Résultats de calcul par Géostudio 2002

Methode	BISHOP	MORGENSTEM- PRICE	JUMBU	SPENCER	GLE	Fellenius (ordinary)
Coeff de sécurité	1.377	1.302	1.289	1.302	1.297	1.348

VI .7.4. Les résultats obtenus à l'aide du logiciel SAS-FEM :

Figure (VI.15): la déformée.

Page

Figure (VI.16): Les Vecteurs de Déformation

Figu

re (VI.17):

La sufrace

de rupture

Fig. (VI.1

8): Graphe

des Coeffi

cients Sécurité /Nombre des itérations

Page

Le Coefficient de Sécurité obtenu a l'aide du logiciel SAS-FEM =1.3 VI .8.Récapitulation et comparaison des résultats obtenus: Tableau (VI.8): Résultats de calcul

Méthode	BISHOP	M-P	JUMBU	SPENCER	GLE	Fellenius	Manuel	E-F
						(ordinary)	B.Simp
FS	1.377	1.302	1.289	1.302	1.297	1.348	1.388	1.3

Le résultat obtenu par calcul manuel suivant la méthode de BISHOP simplifiée est presque identique aux celles obtenus à l'aide du logiciel geostudio 2002, avec un intervalle d'erreur très localisé. Cette marge d'erreur est due à la précision qui dépend du nombre de tranches choisies (12 pour le calcul manuel et 30 pour logiciel).

Pour le SAS-FEM malgré que le résultat est très identique aux celles du geostudio 2002, la technique de la réduction de résistance au cisaillement n'a été adopté que par très peu d'ingénieurs géotechniques dans le cas de l'évaluation de la stabilité des pentes. Ceci peut probablement être mis sur le compte d'une expérience très limitée des ingénieurs avec la méthode des éléments finis d'analyse de stabilité de pente, et le peu d'information publiée sur la qualité ou l'exactitude de leurs résultats.

CONCLUSIONS GENERALES

Cette première étude permet de déterminer les caractéristiques mécaniques d'un sol, et a partir des quelle, on peut entamer un calcul de coefficient de sécurité.

L'étude présentée dans ce mémoire avait pour finalité d'analyser la stabilité au glissement des terrains en pente sous seulement son poids propre (effet statique).

Cette étude a permis dans une première étape d'exposer les différentes méthodes de calcul actuellement disponibles (calcul en équilibre limite, calcul en éléments finis) .

Elle a permis d'établir un calcule manuel basé sur la méthode de bishop simplifiée.

Elle a permis de mettre en oeuvre deux outils numériques performants dédiés à ce type d'études : le logiciel Géostudio pour l'analyse de la stabilité des talus en ruptures circulaires et non circulaires par un calcul en équilibre limite avec la méthode des tranches (méthodes de Fellenius, de Bishop, de junbu,de spencer ,et de Morgenstern et Price.) et le logiciel SAS-FEM de calcul en éléments finis

La présente étude a permis aussi de comparer sur un modèle géométrique exemplaire (talus d'el Riyad) les résultats de calcul du coefficient de sécurité par différentes méthodes.

Pour finir, On espère que ce projet sera une base et un point de départ pour notre vie professionnelle ainsi que le prolongement des futurs étudiants travaillant dans ce domaine.

REFERENCES BIBLIOGRAPHIQUES.

Springer Berlin / Heidelberg. Stability analysis of slopes using the finite element method and limiting equilibrium approach.488 pages.

Daniel Cordary . Mécanique des sols octobre 1994. 380 pages. Glissement de Terrain Peguillan Bertrand. janvier 2002.257 pages.

Seve :Stabilisation des glissements de terrain - guide technique janvier 1998 138 pages. Génie géotechnique Applications de la mécanique des sols et des roches 1997 Nombre de pages : 222

Les Glissements de talus routiers : étude de désordres observés entre 1963-1967 (Broché) de Groupe d'étude des talus Laboratoire central des ponts et chaussées (Auteur) 26 pages.

Étude des glissements des talus argileux : Par M. Florentin (Reliure inconnue) de J. Florentin (Auteur)

AIT-IKENE M. (2001). Etude du glissement du talus de la gare Aomar (wilaya de Bouira), P.F.E. sous la direction de M. KHEMISSA.

BOLT B. (1978). Les tremblements de terre. Editions pour la Science.

DAT VU KHOA HUYNH (2005). Modélisation des glissements comme un problème de bifurcation. Thèse de Doctorat de l'institut national polytechnique de Grenoble, 244 Pages.

DURVILLE J.L., SEVE G. (1996). Stabilité des pentes : Glissements en terrain meubles. Techniques de l'ingénieur, 54.

HUANG S. L., YAMASKI K. (1993). Slope stability analysis using local minimum factorof-safety approach. Journal of ASCE, vol.119 (12), 99.1974-1987.

KHEMISSA M., AYADAT T., RAHMOUNI Z. (2002). Méthodologie d'étude et techniques de confortement des versants instables. Rapport de recherche CNEPRU.

MAGNAN J.P., MESTAT Ph (1997). Lois de comportement et modélisation des sols. Techniques de l'ingénieur. 18. 24 pages.

PECKER A. (1984). Dynamique des sols. Presses de l'Ecole Nationale des Ponts et Chaussées, Paris.

PILOT G. (1974). Stabilité des pentes. Techniques de l'ingénieur, 54

RAULIN P., ROUQUES G, TOUBOL A. (1974). Calcul de la stabilité des pentes en rupture non circulaire. Rapport de recherche LPC n°38, 106 pages.

Sites Internet :

http://www.geo-slope.com

www.enpc.fr

http://www.techniques-ingenieur.fr www.lcpc.fr

http://earth.google.fr

http:\\eost.u-strasbg.fr

http://repositorium.sdum.uminho.pt.

Fin.