|
congovirtuel.com:Bibliothèque
virtuelle de la RDC
|
REPUBLIQUE DEMOCRATIQUE DU CONGO
MINISTERE DE
LENSEIGNEMENT SUPERIEUR ET UNIVERSITAIRE
INSTITUT SUPERIEUR DE TECHNIQUES
APPLIQUEES
ISTA/KIN

B.P 6593 KIN 31
APPLICATION DE LA METHODE PEEC POUR LA MODELISATION
ET
LAPREDICTION DES EMISSIONS RAYONNEES PAR LE SYSTEME DES
CABLAGES
ELECTRONIQUES EMBARQUES
Par :
Professeur BASSESUKA SANDOKA NZAO Anthony
bass_sandoka@yahoo.fr
RESUME
La gestion de câblage embarqué au sein d'un
véhicule automobile ne dépend pas que des caractéristiques
des câbles. Les puissances véhiculées par ces câbles
doivent également être prises en compte. L'environnement joue un
rôle prépondérant. À cette problématique, on
doit ajouter que les sources de perturbations embarquées sont souvent
très différentes ainsi que le spectre des puissances
associées. Les solutions préventives à préconiser
dépendent ainsi d'une multitude de facteurs. La prédiction des
perturbations EM1 est donc une étape primordiale dans
l'objectif par exemple de respect des normes en vigueur.
Exemple traité dans le cadre de cet article associe un
système de câblage électronique embarqué à
une source de perturbations EM qui est un convertisseur électronique de
puissance DC-DC (Hacheur).
Cet article s'intéresse à la propagation des
perturbations EM de la source vers le câblage en prenant en compte le
filtre de convertisseur. Une évaluation des émissions
rayonnées est effectuée en régime fréquentiel et
une comparaison avec des mesures en champ proche est réalisée.
Pour terminer, nous effectuons à l'aide la méthode PEEC une
prédiction des perturbations dans le domaine temporel en s'appuyant sur
l'analyse fréquentielle.
Mots clés : Méthode PEEC,
modélisation, prédiction des émissions rayonnées,
système des câblages électroniques embarqué.
1 EM : Electromagnétique
I. INTRODUCTION
La part de l'électronique dans les systèmes
embarqués (automobile, aéronautique, spatial...) ne cesse de
croitre. Soutenue par sa forte intégration, cette électronique
apporte davantage de performances et permet d'offrir des solutions à
l'exigence, entre autres, de sécurité et de confort. Mais, une
telle évolution rapide nécessite une prise en compte de tout
phénomène marginal pouvant nuire au bon fonctionnement des
systèmes électroniques. Au même titre que la gestion de la
thermique ou la gestion des contraintes mécaniques,
l'interférence électromagnétique est devenue un
phénomène à risque de très grande importance pour
tout système de l'électronique de signal ou de puissance. On
parle alors d'un souci de compatibilité électromagnétique
(CEM) auquel les industriels se trouvent confrontés.
La CEM telle que définie dans les normes
européennes [1] [2] est « l'aptitude d'un appareil ou d'un
système à fonctionner dans son environnement
électromagnétique de façon satisfaisante et sans produire
lui-même des perturbations électromagnétiques
intolérables pour les équipements situés dans cet
environnement ». Ainsi, la CEM se doit de participer à la
conception et l'intégration de l'électronique. Une étude
CEM valable doit traiter et résoudre ces deux principaux aspects qui
sont :
- L'Émission : les systèmes ne doivent pas
émettre des perturbations électromagnétiques
gênantes pour leur environnement.
- L'Immunité : les systèmes doivent être
capables de fonctionner dans leur environnement EM.
Nous notons qu'en automobile, les termes usuels pour
désigner ces deux aspects de la CEM sont respectivement le mutisme (pour
l'émission) et la susceptibilité (pour l'immunité).
Afin de limiter le risque d'interférence EM avec
d'autres appareils et en particulier avec ceux de contrôle, il est
nécessaire de prédire, en premier, les émissions EM
générées et ensuite limiter les perturbations nuisibles au
fonctionnement et à la sureté du système global. Donc, il
est nécessaire de prédire les émissions conduites et
rayonnées des câbles qui sont, par leurs grandes tailles, un
risque EM potentiel pour les systèmes électroniques autour.
Dans ce contexte, plusieurs préconisations CEM peuvent
être prises en compte. Une préconisation inévitable
nécessite de séparer les câbles de puissance de ceux de
commande. Même, si on peut considérer diminuer le risque CEM sur
les câbles de transmissions de données, le risque CEM surtout pour
les systèmes radioélectriques demeure élevé puisque
les perturbations rayonnées atteignent même les systèmes se
trouvant à quelques dizaines de mètres avec des niveaux de
puissance menaçants. Ces niveaux de puissance dépendant des
fréquences et de la distance par rapport au système de
câblage sont définis par les normes CEM en vigueur.
Une autre solution, intéressante et très
répandue dans l'industrie des systèmes électroniques
embarqués, est le filtrage CEM. En effet, un filtre CEM permet
d'empêcher la propagation des perturbations vers les câbles. Les
filtres CEM sont conçus à base de composants passifs pour
éviter toute perturbation additionnelle. Notons à-propos le
coût non négligeable d'une telle solution et la difficulté
de la conception des filtres de large bande puisque les composants
dépendent beaucoup de la fréquence.
Certes, les filtres CEM permettent de limiter la propagation
des perturbations vers les câbles. Mais, cela est restreint à une
bande de fréquences plus ou moins large. Tout de même, les
perturbations risquent toujours de se propager vers les câbles. C'est
pourquoi, nous aurons besoin d'autres solutions limitant le rayonnement EM des
câbles. On parle alors de la gestion de câblage.
Une partie de la précaution CEM se passe au niveau de
la fabrication des câbles mais il reste encore le gros travail qui est
lié à la gestion des systèmes de câblage. En effet,
trouver le parcours de câblage le plus adéquat permet de limiter
le rayonnement EM et ainsi diminuer les risques CEM.
La gestion de câblage est loin de dépendre des
seules caractéristiques des câbles qui sont obtenues dès la
fabrication. Elle dépend aussi et en en majorité de
l'environnement et surtout des puissances que ce câblage véhicule.
Les sources de perturbations ne sont jamais les mêmes, leurs spectres de
puissance ne sont pas les mêmes ainsi que leurs rayonnements. Pour cela,
les solutions préventives à préconiser
dépendent fortement du type de perturbateur EM et nous
sommes obligés, pour toute source, de définir une solution
particulière.
D'une façon générale, les aspects de la
CEM, que sont l'immunité et les émissions, doivent être
maitrisés dès la phase de conception. Dans cette optique, la
présente recherche répond à ces préoccupations et
s'appuie sur la modélisation et simulation CEM ayant pour objectif de
répondre à une problématique commune des industriels dans
les applications embarquées, de favoriser l'émergence de
meilleures pratiques entre différents secteurs industriels (automobile,
aéronautique, spatial, ...) en relation avec les centres de recherches
et de développer l'excellence des individus au travers de formations et
du partage d'expérience.
Notre travail de recherche, se situant dans le contexte de la
simulation de l'émission d'un équipement avec ses interfaces,
s'intéresse surtout au rayonnement EM.
Le but final est de pouvoir prédire les
émissions rayonnées d'un système complet qui associe
à la fois l'électronique et le câblage. Les perturbations
EM générées par l'électronique sont
véhiculées via les câbles en mode conduit pour les basses
fréquences. Mais, lorsqu'on dépasse une certaine
fréquence, typiquement 30MHz, les émissions rayonnées
deviennent prépondérantes et l'analyse CEM devient de plus en
plus complexe puisque nous sommes tenus de rendre compte de tous les modes de
couplage.
D'une façon générale, les perturbations
EM rayonnées proviennent majoritairement des câbles surtout que le
rayonnement dépend énormément des dimensions des sources.
Et, puisque les câbles sont les structures les plus longues, elles sont
les meilleures antennes dans les systèmes électroniques
embarqués d'autant plus que les dimensions des circuits
électroniques sont négligeables devant celles des
câbles.
Nous sommes donc tenus de comprendre la façon dont
l'énergie se propage de la source, en l'occurrence les câbles,
vers la victime présentée par tout système de
contrôle ou systèmes travaillant avec des
télécommunications radiofréquences (RF) et à
prédire les émissions rayonnées par ces câbles.
Pour atteindre cet objectif, notre choix s'est orienté
vers une méthode de modélisation ayant la facilité de
traiter des surfaces planes ainsi que des câbles. Le choix de
l'utilisation de la méthode PEEC (PARTIAL ELEMENT EQUIVALENT CIRCUIT)
[3], se conformait aux grandes lignes tracées par le laboratoire
l'IRSEEM.
En effet, la méthode PEEC fut introduite par F.DUVAL
par le biais de ses travaux de thèse [3]. Au début, pour des
modèles BF, une modélisation sans l'effet de la propagation
était suffisante. À cause de la forte exigence d'une
montée en fréquence, la thèse d'I. Yahi fut lancée
[4] [5]. Dans ce dernier travail, l'effet capacitif représentatif de la
propagation dans les câbles a été introduit. Il a permis
une montée significative en fréquence (autour de 1 GHz). Avec
cette montée en fréquence, il apparut logique d'intégrer
le rayonnement électromagnétique.
Dans cet article, nous allons nous intéresser, dans un
premier temps, à la modélisation du rayonnement d'un prototype de
câblage reflétant les phénomènes EM entourant le
câblage automobile. Ensuite, nous allons associer notre câblage
à un convertisseur DC-DC. Cette configuration est une application de
systèmes électroniques embarqués dans lequel la
distribution de l'énergie à différents niveaux se fait
à travers des DC-DC à partir d'une batterie. Le découpage
dans le convertisseur de puissance génère des perturbations HF
qui se propagent vers une charge via le câble. Le rôle du
câble dans une telle configuration n'est pas anodin. En effet, il modifie
le spectre de perturbations et est le principal acteur du le rayonnement du
système complet.
II. DEVELOPPEMENT II.1. Modélisation
PEEC
Sans exception, les méthodes numériques de
modélisation se trouvent confrontées à des
difficultés semblables telles que la montée en fréquence,
la précision de la résolution, les couplages multi-physiques, la
complexité et la grande taille des systèmes etc.
Les diverses méthodes permettent, d'une façon ou
d'une autre, la résolution des équations de Maxwell. Ce qui
diffère entre elles est la manière dont on pose le
problème électromagnétique. On peut distinguer deux
principales catégories : les méthodes basées sur les
équations différentielles et les méthodes basées
sur les équations intégrales.
Bien que les méthodes aux équations
différentielles soient les plus développées, à
l'image de la méthode des éléments Finis (MEF), et
qu'elles traitent les systèmes les plus complexes, elles ne sont pas
adaptées aux systèmes de grandes tailles tels que les
systèmes de câblage. En effet, ces derniers systèmes
nécessitent une discrétisation très fine.
Dans le contexte du câblage, notre choix s'oriente vers
une méthode aux équations intégrales qui est la
méthode PEEC. Par sa formulation intégrale et par sa
possibilité de décrire les phénomènes EM sous forme
de circuit équivalent, la méthode PEEC semble la mieux
placée pour l'étude de câblage dans son environnement
électrique. En effet, elle a été introduite dans plusieurs
applications d'électronique de puissance dans lesquelles on associait le
modèle des circuits imprimés (PCB, Printed Circuit Board)[6][7],
du bus bar [8][9], des plans de masse ou des interconnexions [10] obtenus par
PEEC aux modèles des circuits électroniques actifs (transistors
de commutation) ou passifs (RLC). Aussi, elle a été
utilisée pour la modélisation des antennes [11]. Cependant,
l'effet capacitif comme décrit dans la méthode PEEC
conventionnelle rend la modélisation très exigeante en temps de
calcul. Dans ce chapitre, nous présentons dans un premier temps la
méthode PEEC conventionnelle [12], puis la nouvelle considération
de l'effet capacitif introduite dans [4] et [5].
II.1.1. Méthode PEEC
La méthode a été développée
par RUHELI en 1974 dans le but de calculer le couplage inductif dans les
circuits intégrés de type VLSI [16]. Ensuite, afin d'assurer la
nécessité de la montée en fréquence, l'effet
capacitif [13] a été rajouté au calcul des inductances
pour une méthode de modélisation à part entière
[12]. En 1992 un modèle PEEC prenant en compte les régions
diélectriques a été présenté [14]. Par la
suite, des travaux sur la méthode PEEC ont amélioré
différents aspects tels que l'effet de peau et de proximité [15]
et la stabilité liée à la résolution des
systèmes linéaires [16]. Jusqu'en 1999, dans tous les travaux sur
la méthode PEEC, on a utilisé une discrétisation
orthogonale. Date à laquelle, la discrétisation non orthogonale
des conducteurs a été introduite [17]. Ce type de
discrétisation a été développé et
amélioré dans [18]. Dans [19], la méthode PEEC a
été adaptée aux structures de section circulaire. La
méthode, développée au début pour l'analyse du
comportement électromagnétique des VLSI, est devenue une
méthode incontournable dans l'étude et la modélisation des
pistes de circuit imprimé (PCB) des systèmes électroniques
embarqués (interconnexions), de l'électronique de puissance, des
lignes de transmission, des antennes et aussi dans l'étude des
systèmes de câblage (câbles, plan de masse, bus barre etc.)
[20].
a. Formulation mathématique de la méthode
PEEC
Les méthodes de modélisation EM reposent sur les
quatre équations de Maxwell décrites ci-dessous.
Formulation différentielle Formulation
intégrale

et ñ est la charge volumique.
Dans les équations de Maxwell, Q est la charge
électrique, B? est l'induction magnétique,
D? est l'induction électrique, E? est le champ
électrique, H? est le champ magnétique, j est la
densité de courant, t est le temps
Ces équations de Maxwell ne suffisent pas à
résoudre un problème électromagnétique et ne
permettent
|
pas de déterminer les inconnues E?
|
(r ,t) , H?
|
(r , t), B?
|
(r , t), et D?
|
(r , t) dans la mesure où chacune de ces
|
variables est un vecteur de 3 composantes. Donc, on obtient
plus d'inconnues que d'équations. Pour surmonter cette
difficulté, des hypothèses supplémentaires reliant les
différentes inconnues sont nécessaires : celles-ci sont les
relations de constitution ((1), (2) et (3)). Elles prennent en compte la
permittivité, la perméabilité et la conductivité du
milieu continu considéré. Dans notre travail, le milieu entre
conducteurs est l'air dont la permittivité et la
perméabilité sont données respectivement par å0 et
ì0. De plus, nous utiliserons le cuivre comme conducteur dont la
conductivité est donnée par ó = 59,6 * 106m.
S-1 .
?
|
J = ó * E
? ?
B = ì0 * H
? ?
D = å0 * E
|
(1)
(2)
(3)
|
La formulation mathématique de la méthode PEEC a
été principalement développée dans [16], [17] et
[13]. Selon l'équation intégrale du champ électrique,
à un instant t et à un point r , le champ électrique total
E? T est la somme du champ incident E? i et du champ auto-induit E? .
E? T(r , t) = E? i(r , t) + E?
(r ,t) (4)
Lorsque le point r appartient à un conducteur, le champ
électrique total est donné par la relation suivante :
E? T(r , t) = J (r? ,t) (5)
ó
Où j est la densité du courant dans le conducteur
dont la conductivité électrique est ó . Dans la
relation
précédente, le champ incident E? i ne
dépend que des sources externes au système. Il est donc
indépendant des courants et des charges présents au point r de la
structure contrairement au champ induit qui est un résultat de ceux-ci.
En effet, le champ électrique induit s'écrit :
E? (r ,t) = -äA?? (r? ,t)
ät - ?ö(r ,t) (6)
?
|
Où A
|
est le potentiel vecteur et ö est le potentiel scalaire.
|
A? (r , t) = ì0 ? G?
(r , r '). J (r ', td). dv' (7)
v'
(8)
ö(r ,t) = 1 ? G? (r ,r ') .
óS (r ',td).dS å0 S'
'
Dans la relation (8), óS est la densité
surfacique des charges électriques qui sont physiquement
présentes sur la surface des conducteurs et td est le temps de retard
entre la source et le point d'observation ?r . Ce temps est
donné par : td = t - |r - r '|/c, avec c la
célérité du vide.
Dans les équations (7) et (8), G est appelée
fonction de Green et est donnée par :
G? (r ,r ') = 1 1
4 |
(9)
ð r -r '|
En utilisant les relations (5) et (6), le champ incident
devient:
|
E? i(r ,t) = J (r? ,t)
ó
|
+ äA? (r? ,t) + ?ö(r , t)
(10)
ät
|
Afin de transformer la relation (10) en une équation
intégrale du champ électrique (EFIE), la définition
?
des potentiels électromagnétiques A et ö peut
être utilisée. Cela permet d'avoir la relation suivante :
äJ (r ',td)
E? i(r ,t) = J (r? ,t)
ó +ì0 ? G?
(r ,r '). ät .dv' +å0 ? ? G?
(r ,r ').óS(r ',td).dS' (11)
v' S'
La présentation de l'équation (11) dans un
repère cartésien, permet d'avoir 3 équations scalaires
dont chacune correspond à un axe. En l'absence d'un champ
électrique incident, ces équations se résument dans la
relation (12) dans laquelle ã = x, y ou z.
|
E? i
|
ã(r , t) + ì0
?G? (r ,r ').
v'
|
äJ (r ',td).dv' + 1 ?ã (?
G? (r ,r '). óS (r ', td)
? .dS') = 0 (12)
ät å0 S'
|
Une discrétisation de la structure en Nv
cellules volumiques et Ns surfaces permet d'obtenir la
densité de charge et la densité de courant sous forme d'une
combinaison linéaire définissant ce qu'on appelle l'approche de
Petrov-Galerkin. Les densités s'écrivent comme dans les deux
relations suivantes :
J (r ,t) = ? j m(tdm)fm
Ns (r ) (13)
m=1ó(r ,t) = ?
ón(tdn)gn
Ns (r ) (14)
n=1
Avec fm(r ) = 1 lorsque le point r appartient au
volume vm et fm(r ) = 0 ailleurs. De même,
gn(r ) = 1 lorsque r appartient à la surface sn et
gn(r ) = 0 ailleurs. Les volumes et les cellules
élémentaires sont assez petits. Ce qui assure que le courant et
la charge y soient constants.
tdm = t - |r - ?? ??|/c et tdn = t - |r - ?? ??|/c
représentent respectivement les temps de retard entre la cellule
volumique ???? et la surface ???? par rapport au point ?r .
Au niveau de chaque cellule volumique, la densité du
courant est donnée par le rapport entre le courant ?????? et la section
de la cellule ????.
??????(tdm)
??????(tdm) = (15)
????
Aussi, la densité de charge définie au niveau de
chaque surface élémentaire s'écrit en fonction de la
quantité de charges surfaciques:
??????(??????) = ???? ??(??????) (16)
????
L'association des équations (15) et (16) avec
l'équation (13) et (14) permet d'avoir les densités respectives
de courant et de charge en fonction des courants et des quantités de
charges:
|
J (r , t) = ? ??????(tdm)
Ns
m=1 ????
|
???? (r ) (17)
|
????(r , t) = ? ????
Ns ??(??????)
???? gn (r ) (18)
n=1
A partir de la discrétisation ((13) à (18)), il
devient possible de présenter l'équation EFIE, définie par
relation (12), sous forme d'une équation interprétable en circuit
équivalent RLC. En effet, en substituant les relations (17) et (18) dans
l'équation (12), nous obtenons :
??? ã(r , t) + ? ì0
Ns ????????(tdm) ???? ??(??????)
???? ? G? (r , r ' ??) ???? (? G?
(r , ??? ??).
???? d???? + ? 1
Ns ?? ???? ????) = 0 (19)
m=1 Vm' n=1 ??????0 ????
Cette relation est valable pour tout point ?? , qu'il
appartienne à la structure ou non. Nous choisissons ?? = ?? ?? un point
appartenant au volume de discrétisation ???? de la structure.
La relation demeure valable. En intégrant chacun des
membres de l'équation par l'opérateur défini par la
relation (20) et en appliquant le théorème fondamental du calcul
intégral (21) au 3ième terme de l'équation, nous obtenons
la relation (22) dans laquelle ?????+? et ?????-? sont deux surfaces mettant en
évidence l'aspect capacitif.
1
1
? ?????? = ?????? ? ?????????? (20)
?????? ???? ????
? ?? ???? ??(??) ???? = ? ??(??+) ??????+ - ? ??(??-)
??????- (21)
?? ????+ ????+
1 + ? ì0
Ns m=1 ????.?????? ? ? G? (r , r '
??)
?????? ???? Vm'
????????(tdmi)
d????. ??????
????
+
|
? Ns1 ((? ? G? (r , ??? ????) ????
??(??????). ????. ??????) - 1
??????0?????? (? ? G? (r , ??? ??) ????
??(????????). ????))
n=1 ??????0?????? ???? ????+ ???? ????-
|
(22)
|
C'est sur cette équation (22) que la méthode
PEEC se base. Elle permet la déduction des différents
éléments partiels. Cependant, une discrétisation
adéquate est nécessaire pour arriver au circuit équivalent
global.
b. Implémentation de la méthode PEEC
b1. Discrétisation et circuit
élémentaire PEEC [9] [18][19] [20] [21] [23] [24][25] [26] et
[27].
Le passage de l'équation intégrale du champ
électrique (EFIE) à la méthode PEEC se fait en
discrétisant les conducteurs en des volumes et des surfaces exploitables
pour l'obtention du circuit équivalent RLC. Le choix des dimensions des
cellules de discrétisation qu'elles soient volumiques ou surfaciques est
directement lié à la fréquence maximale de travail,
à la précision de calcul souhaitée et par
conséquent au temps de calcul.
II.2. Émissions conduites
II.2.1 De la méthode PEEC conventionnelle
à la méthode PEEC Hybride
Nous appelons la méthode PEEC conventionnelle la
méthode PEEC telle que décrite par RUHELI et communément
utilisée dans la littérature. Cette appellation permet de
distinguer la méthode PEEC d'origine des différentes
utilisations. En effet, la difficulté de rendre compte des effets
capacitifs par la méthode PEEC a poussé plusieurs chercheurs
à utiliser un couplage avec d'autres méthodes de
modélisation EM [28]. À titre d'exemple, nous notons le couplage
de la méthode PEEC avec la méthode des moments [29] [30][31], ou
avec la méthode des éléments finis [20]. Que ce soit pour
l'un ou l'autre, l'objectif est d'avoir à la fin une meilleure
efficacité surtout avec la présence de milieu non homogène
entre conducteurs. Dans ce milieu intermédiaire entre conducteurs, nous
trouvons de l'air, du diélectrique et des matériaux
ferromagnétiques.
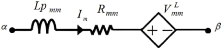
Figure I : Circuit équivalent d'une cellule de
discrétisation
Dans d'autres cas, le couplage de la méthode PEEC avec
d'autres méthodes était dans un souci de complexité et de
temps de calcul. Dans ce contexte, on note le couplage avec la méthode
de ligne de transmission. On parle alors de méthode hybride PEEC/MTL
[32].
Dans notre travail, nous utiliserons les travaux de I.Yahi qui
se basaient sur une méthode PEEC/Analytique [5] [6]. Cette approche se
base sur le fait qu'en BF le circuit équivalent d'une structure
quelconque peut être présenté par les seules
résistances et inductances. Ainsi, le circuit PEEC équivalent
à une cellule de discrétisation pourrait d'être
présenté sous la forme d'un circuit RL (Figure I). Ensuite et
afin de suivre l'évolution du comportement EM du câblage pour des
hautes fréquences (HF), l'effet capacitif sous forme analytique est pris
en compte. Dans ce travail, nous allons plus loin en estimant le
temps de calcul nécessaire pour chaque approche, en
l'occurrence PEEC conventionnelle et PEEC/Analytique.
II.3. Émissions Électromagnétiques
rayonnées
Dans cet article, nous nous intéressons à la
modélisation des émissions EM rayonnées par un
système de câblage. Dans le but de modéliser ces
émissions, nous partons des courants dans la structure, obtenus par la
méthode PEEC. Ensuite, nous calculons la contribution en
émissions rayonnées de chaque cellule de
discrétisation.
Dans un premier temps, une cellule de discrétisation
est considérée équivalente à un dipôle.
Alors, dans ce cas, une seule dimension, qui est la longueur, est
considérée. Dans la littérature, deux principales
approches sont utilisées pour un tel calcul : l'approximation
régime quasi-stationnaire et l'approximation de dipôle infiniment
petit. Des erreurs de calcul, plus ou moins importantes, relatives à ces
deux approximations sont généralement observées.
Dans le but d'améliorer la précision de calcul
des émissions rayonnées, on introduit généralement
un calcul basé sur l'expansion en série de Maclaurin.
II.3.1 Modélisation des émissions
rayonnées
La détermination des émissions rayonnées
d'un système de câblage passe par deux principales étapes :
par le calcul des émissions conduites et par la déduction des
émissions rayonnées. La première consiste à
déterminer pour chaque cellule de discrétisation le courant qui
la traverse. Ensuite, connaissant, à la fois, la géométrie
et la valeur de courant à chaque fréquence, nous utilisons
l'approche de calcul analytique pour définir la contribution de chacune
des cellules de discrétisation. Le champ EM en un quelconque point de
l'espace est la contribution de chacune des cellules et il est obtenu en
sommant les différentes composantes des champs magnétique et
électrique.
II.3.1.1 Équations d'ondes en milieu
homogène
Ces équations d'ondes sont obtenues à partir des
équations de Maxwell décrites dans le premier chapitre. Pour les
champs électrique et magnétique auxquels nous nous
intéressons, les équations d'ondes, en un point ?? et à
l'instant t, sont données respectivement par :
? ?
? × ?
|
? × ??
|
(?? , ??)+ ??0??0????2 ??? (?? , ??) = -??0
??2 ?????? (?? , ??)
?? (23)
|
|
? ?
? × ?
|
? × ??
|
(?? ,??) + ??0??0 ????2 ??? (?? , ??) = ??0??? (?? , ??)
??2 (24)
|
|
Où ??? est le champ
électrique, ??? est le champ magnétique et ??0 et ??0 sont
respectivement la perméabilité magnétique et la
permittivité électrique de l'air (vide).
En utilisant les relations de constitution (1), (2) et (3)
qui sont décrites précédemment, les équations
d'onde (23) et (24) s'écrivent :
?
???
(?? , ??) -??0??0 ????2 ??? (?? , ??) = 1
??2 ??0 ??? (?? , ??) + ??0 ?????? (?? , ??)
?? (25)
|
? ?
? × ?
|
? × ??
|
(?? , ??) + ??0??0 ????2 ??? (?? , ??) = ? × ?? (?? ,
??)
??2 (26)
|
??? (?? , ??) = 1
??0
?? × ?? (?? , ??) (27)
|
On sait que les champs ???
|
(?? , ??) et ???
|
(?? , ??) peuvent être écrits en fonction du
potentiel vecteur ?? et du
|
potentiel scalaire ??. La notion de potentiels a
été utilisée dans le but de simplifier la
résolution des équations de Maxwell.
II.3.1.2. CHAMP MAGNETIQUE ET CHAMP ELECTRIQUE
D'une manière générale, le champ
magnétique (27) est donné en fonction du potentiel vecteur ??
tandis que le champ électrique (28) dépend, en plus, du potentiel
scalaire ??.
??? (?? , ??) = - ???? (?? ,??)
???? - ?? (??(?? , ??)) (28)
II.3.1.3. CHAMPS ELECTROMAGNETIQUES PROCHE ET
LOINTAIN
Dans la littérature, lorsqu'il s'agit de définir
les champs EM proche et lointain, on fait appel aux dipôles
élémentaires : électrique dit de Hertz (Figure II.a) et
magnétique sous forme de boucle (Figure II.b). Pour une fréquence
donnée, suivant la distance d'observation, les champs électrique
et magnétique que ce type de dipôle génère sont
interdépendants ou pas. Ainsi, on définit 3 zones (Figure III)
qui sont : la zone champ proche, zone de transition et champ lointain.
La première région (zone 1) appelée
région de champ proche réactif a pour limite une distance r
inférieure à 0,62v??3/?? où D est la plus
grande dimension de l'antenne et X est la longueur d'onde.
La seconde région (zone 2) appelée région
de champ proche rayonnant est aussi nommée zone de Fresnel en
référence à la terminologie optique car les expressions
des champs dans cette région se réduisent aux
intégrales de Fresnel. Cette région s'étend
entre ?? = 0,62v??3/?? et une distance r inférieure à
D2/X.
La troisième région (zone 3) nommée
région de champ lointain ou zone de Fraunhofer correspond à une
zone où la distribution angulaire du champ est essentiellement
indépendante de la distance r par rapport à l'antenne.
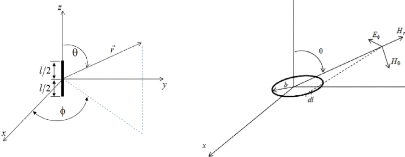
Figure II : Dipôle électrique (a) et dipôle
magnétique (b)

Les notions de champ proche et de champ lointain sont souvent
mises en évidence en considérant l'impédance d'onde ???? .
Elle n'est que le rapport entre le champ électrique transverse
(transverse par
Figure III - Régions : du champ proche au champ lointain
[64]
rapport au vecteur entre le point d'observation et le centre du
dipôle) ??? ?? et le champ magnétique
?
transverse ?? ?? :
???? = |??? ??| (29)
|???? ??|
Cette impédance dépend de la fréquence du
travail, de la distance par rapport à la source et de la
géométrie de la source. Cela est autant vrai qu'on est proche de
la source. Mais, lorsque les conditions d'espace libre et de champ lointain
sont remplies, le champ électrique et le champ magnétique sont
couplés par le rapport invariant ??0 (30). Dans ces conditions, le champ
électromagnétique est une onde plane.
Dans l'équation (30), ??0 est l'impédance
caractéristique du vide qui est donnée par ??0 =120?? = 377??h??
.
|??? ??(???8)| (30)
|???
??0 = ??(???8)|
Lorsque la source est de dimensions comparable ou bien
supérieure à la longueur d'onde, le calcul basé sur le
dipôle d'Hertz devient erroné. Il devient donc nécessaire
de discrétiser la source en des petites
La Figure IV montre la variation de l'impédance d'onde des
dipôles électrique et magnétique en fonction de la distance
par rapport aux dipôles.

Figure IV - Impédance d'onde des dipôles
électrique et magnétique
Dans la Figure IV, ZH est l'impédance d'onde du
dipôle magnétique et ZE est l'impédance d'onde du
dipôle électrique.
Dans la zone très proche du dipôle,
l'impédance d'onde relative au dipôle électrique tend vers
des valeurs supérieures à ??0 contrairement au cas
magnétique où l'impédance y est inférieure. Dans le
cas du dipôle électrique, nous parlons de champ à haute
impédance. Dans le cas du dipôle magnétique, nous parlons
d'un champ à basse impédance. Dans les deux cas,
l'impédance tend vers ??0 quand la distance d'observation est assez
lointaine de la source. Cela n'est vrai que si la source est de faible
dimension vis-à-vis de la longueur d'onde. Une première condition
sur la définition du champ proche s'applique sur les dimensions du
système rayonnant qui doivent être très petites devant la
longueur d'onde. Cette condition ne peut pas être respectée pour
les systèmes de câblage et surtout pour des HF.
En effet, dans les normes CEM, le rayonnement EM est pris en
compte dès la fréquence 30MHz. La longueur d'onde à cette
fréquence est égale à 10 m. Ainsi, pour pouvoir utiliser
la définition des zones champ proche, il ne faut pas que les dimensions
des systèmes étudiés dépassent 1m.
cellules dont chacune représente un dipôle
infiniment petit. Les courants formant ces dipôles sont
déterminés à partir d'une méthode numérique,
dans notre cas de la méthode PEEC.
III. Application au rayonnement de
câblages
La gestion de câblage embarqué au sein d'un
véhicule automobile ne dépend pas que des caractéristiques
des câbles. Les puissances véhiculées par ces câbles
doivent également être prises en compte. L'environnement joue un
rôle prépondérant. À cette problématique, on
doit ajouter que les sources de perturbations embarquées sont souvent
très différentes ainsi que le spectre des puissances
associées. Les solutions préventives à préconiser
dépendent ainsi d'une multitude de facteurs. La prédiction des
perturbations EM est donc une étape primordiale dans l'objectif par
exemple de respect des normes en vigueur.
Nous étudions dans ce paragraphe l'association d'un
système de câblage à une source de perturbations qui est un
convertisseur DC-DC. Nous nous intéressons à la propagation des
perturbations de la source vers le câblage. Une évaluation des
émissions rayonnées est effectuée en régime
fréquentiel et une comparaison avec des mesures en champ proche est
réalisée. Pour terminer, nous effectuons à l'aide du
modèle précédent une prédiction des perturbations
dans le domaine temporel en s'appuyant sur l'analyse fréquentielle.
III.1 Association d'un système de câblage
à un convertisseur DC-DC
L'opération de découpage est la base de la
majorité des systèmes de distribution d'énergie dans les
systèmes électroniques embarqués. Allant de
l'aéronautique à l'automobile, le besoin est le même :
distribuer l'énergie nécessaire vers les appareils
électroniques qui fonctionnent à différents niveaux de
tensions. Notre choix s'est orienté vers l'étude d'un
convertisseur DC-DC de type série (Buck).

Figure V : Topologie du convertisseur étudié
Dans cette partie, nous nous intéressons à une
association entre un système de câblage et ce convertisseur DC-DC.
Dans cette association nous projetons d'étudier les deux types
d'émissions EM: conduites et rayonnées. La Figure VI montre la
procédure adoptée pour aboutir à ces émissions
EM.

Figure V - Association DC-DC et système de
câblage
La topologie du hacheur série étudié est
composé d'un filtre L-C qui assure évidemment le filtrage du
signal découpé. Ce filtrage est de type passe bas qui moyenne le
signal découpé de façon à avoir une tension
continue et fixe à la sortie. Cette tension de sortie est la tension aux
bornes du condensateur C et est donnée par la relation (32).
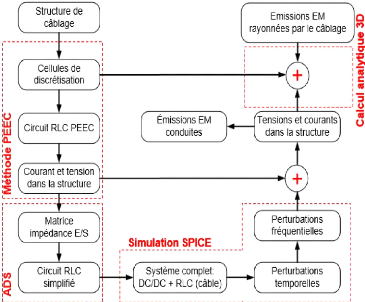
Figure VI - Modélisation des émissions EM
conduites et rayonnées du câblage associé
au
convertisseur DC/DC
Dans la relation (32), E est la tension d'entrée du
convertisseur. Elle est une source de tension fournie par une batterie 12V.
Comme toute alimentation à découpage, les
perturbations EM sont produites lors de la commutation dans le convertisseur de
puissance. Elles traversent le filtre pour atteindre le système de
câblage. La méthode PEEC est utilisée pour l'obtention du
circuit équivalent à partir duquel nous déterminons
l'impédance d'entrée nécessaire à la
modélisation des émissions EM conduites mais aussi la
détermination des courants dans toute la structure de câblage. La
détermination des émissions EM à partir de ces courants
est faite à l'aide du calcul analytique 3-D basé sur la
série de Maclaurin développé et validé dans le
second chapitre. Dans ce type d'alimentation à découpage et comme
toute alimentation à découpage, les transistors de commutation
fonctionnent en mode saturé ou bloqué. Lorsque le transistor est
saturé, la tension est presque nulle (tension due à la
résistance RDSon) et le courant est non nul. Lorsqu'il est
bloqué, la tension est non nulle et le courant (courant de fuite) est
presque nul surtout qu'on est à basse tension.
Sur une période T, le transistor NMOS s'ouvre pendant
???? ?? et se ferme pendant (1-??)T où ?? est le rapport cyclique qui
est défini par (31).
??????
?? = (31)
??
?? ?? = ???? (32)
Une ondulation est observée au niveau de la tension de
sortie. Cette ondulation ????? est une fonction de la fréquence de
découpage, du rapport cyclique, de l'inductance, de la capacité
et de la tension d'entrée. Elle s'écrit sous la forme de
l'équation (33). Elle permet d'estimer la valeur d'ondulation qu'on
souhaite
généralement faible. Ceci permet le dimensionnement
correct du filtre de sortie du convertisseur DC-DC. Elle est donnée par
:
????? = (1-??).E (33)
8.??????????0???2 ???

Figure VII : Illustration des formes d'onde : (a) la tension de
commande (b) la tension aux bornes de la
diode, (c) le courant dans la
bobine, et des ondulations : (d) du courant et (e) de tension de sortie
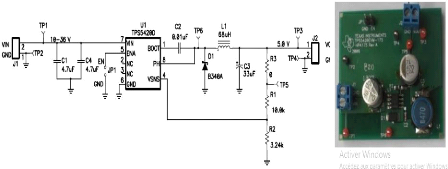
Figure VIII - Convertisseur de puissance DC/DC
(TPS5420EVM-175)
Le convertisseur DC/DC utilisé, dans ce suit, est le
TPS5420EVM-175. Ce convertisseur fournit pour toute charge une tension
"constante" égale à 5V pour toute tension d'entrée variant
entre 5V et 32V. Afin d'assurer l'obtention de la tension 5V en sortie, Ce
convertisseur utilise un régulateur (TPS5420).
Ce dernier circuit permet la modulation de largeur d'impulsions
(MLI) nécessaire pour la fixation de tension à 5V quelle que soit
la tension d'entrée.
III.2. Source de perturbations
D'une manière générale, pour les mesures des
perturbations conduites, on utilise un RSIL (réseau stabilisateur
d'impédance de lignes) implémenté dans le logiciel de
simulation Matlab. Dans cet article, pour la mesure de la tension aux bornes de
la diode de roue libre, nous utilisons un oscilloscope
numérique virtuel intégré dans le
simulateur pouvant aller jusqu'à 1GHz. Dans notre cas, nous ne
dépassons pas la fréquence 300MHz parce que le circuit ne
perturbe pas au-delà de cette fréquence. Le type d'oscilloscope
virtuel utilisé admet deux configurations d'impédance propre :
50? et 1M?. Pour s'assurer que le fonctionnement du circuit n'est pas
modifié, nous utilisons le simulateur de mesure en haute
impédance. Nous obtenons ainsi la tension réelle aux bornes de la
diode (Figure VII). En observant de plus près cette forme d'onde, nous
déterminons, à travers la Figure VIII, les temps de montée
et de descente.
Figure IX - Hacheur série

Figure X - Mesure de la tension aux bornes de la diode
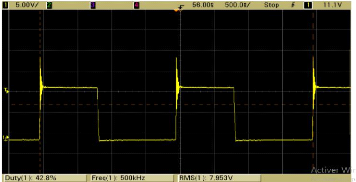
Figure XI :Mesure de la tension aux bornes de la diode
Lors d'une commutation rapide, des oscillations sont
observées au niveau du transistor de découpage (ou de la diode).
Dans notre cas, nous distinguons des oscillations qui sont loin d'être
négligeables. Elles sont générées lors de la
fermeture du MOS. Physiquement, cette ondulation est due aux capacités
intrinsèques du MOS et surtout aux inductances en série. Pour
réduire ces oscillations, la solution est de minimiser ces
inductances.
L'objectif de ce qui suit est de déterminer la fonction
de transfert qui relie un signal de référence (Figure VIII) et la
tension du transistor avec ondulations. Dans ce cas, nous considérons le
signal de référence un signal trapézoïdal qui permet
de prendre en compte a priori le temps de montée et le temps de descente
du signal à obtenir (Figure VIII). Cela facilite l'obtention de la
fonction de transfert souhaitée puisqu'en soustrayant le signal
trapézoïdal du signal global de perturbation nous obtenons un
signal tel que décrit l'équation suivante :
??(??) =
????.??-????.??????(w??).??(??) (34)
Où ???? est une tension caractérisant
la variation exponentielle des points maximum de la tension d'ondulation, w
est la pseudo-pulsation. L'identification des différentes
constantes dans l'équation (35) se fait à partir des mesures. De
cette façon, nous déterminerons la fonction de transfert de la
tension de perturbations qui s'écrit sous la forme de l'équation
suivante :
?????????????????????%o??????
3,967*1017
??(??) = = (35)
??????????è????
??2+9,92*1017??+3,967*1017
Avec ?? = ??w (36)
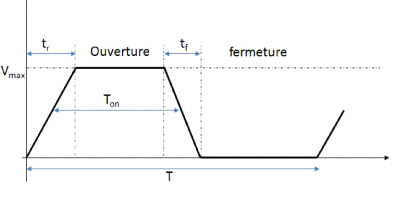
Figure XII : Signal trapézoïdal de
référence
Vtrapèze Est la transformée de Laplace
du signal trapézoïdal (Figure XII) définie à l'aide
du temps de montée, du temps de descente, de la tension maximale, de la
période et des temps d'ouverture et de fermeture.
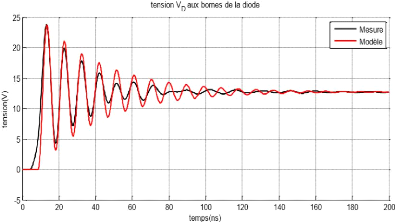
Figure XIII : Comparaison entre perturbations mesurées
et simulées
Le temps de montée est assez petit afin d'assurer la
génération des ondulations mesurées. Le temps de descente
permet de générer le temps descente mesuré avec des
ondulations négligeables. À partir d'un signal
trapézoïdal périodique, il devient facile de
générer les perturbations au niveau de la diode et cela pendant
le temps nécessaire pour dépasser la période transitoire
et nous situer en régime permanent lors de la simulation.
La Figure XIII montre une très bonne concordance entre
notre modèle et la perturbation réelle définie par la
tension aux bornes de la diode.
III.3 Modèle ADS (Advanced Design System)
Pour l'association du modèle PEEC du système de
câblage avec le modèle du convertisseur DCDC, nous aurons besoin
d'un modèle circuit. Mais, le modèle circuit obtenu par la
méthode PEEC, même avec la nouvelle considération
capacitive, demeure pénalisant en mémoire et en temps de calcul.
La solution en temporel demande un temps important de calcul surtout pour
arriver au régime permanant. Alors, nous avons cherché un
modèle simplifié qui reflète le comportement du
câblage. Nous nous sommes basés sur ADS (Advanced Design System)
pour identifier les différents éléments du circuit,
décrit dans la Figure XIV.
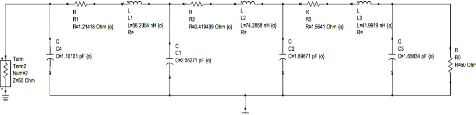
Figure XIV : Circuit équivalent simplifié
Pour un système de câblage tel que le
nôtre, en se référant à la théorie de ligne
de transmission, nous pouvons représenter le circuit équivalent
comme étant une cascade de circuit RLC. Ce circuit de base se termine
par une résistance 50? qui représente la charge mise à
l'autre extrémité du système de câblage.
L'impédance d'entrée simulée, mesurée par analyseur
de réseaux, et obtenue par circuit équivalent simplifié,
est illustrée par la Figure XV. Une bonne concordance entre les trois
résultats est observée.
IV. Simulation sous l'environnement Matlab des
émissions rayonnées IV.1. Domaine fréquentiel
En se basant sur la méthode PEEC, nous calculons, en un
point donné, les émissions rayonnées
générées par le système de câblage lorsque
l'on applique un courant unitaire en entrée. Le champ EM obtenu
représente, en quelque sorte, une fonction de transfert reliant le
courant d'entrée et le champ EM rayonné.
Pour le champ magnétique ou champ électrique le
maximum d'émissions se trouve au-dessus du câble. La composante Hy
du champ magnétique est la plus importante tandis que la composante
???? est la plus importante pour le champ électrique.
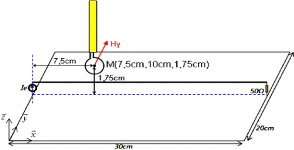
Figure XV : Simulation du champ Hy
Le point M (7,5cm, 10 Cm, 1,75Cm ) situé au-dessus du
câble est ainsi choisi. Les composantes Hy et Ez y sont
évaluées. Elles représentent en quelque sorte la relation
-la fonction de transfert- entre le champ EM et le courant d'excitation. Leurs
variations respectives sur l'intervalle de fréquences [30MHz,
500MHz].
Connaissant le spectre courant IS qui excite le système
de câblage, il est donc possible de déduire, à partir des
fonctions de transfert, le spectre des champs rayonnés. En effet, le
champ EM à une fréquence est donné par le simple produit
du courant et du champ obtenu par une excitation de 1A de courant.
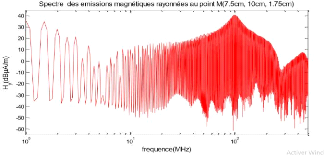
Figure XVI : Spectre des émissions magnétiques
rayonnées par le système de câblage
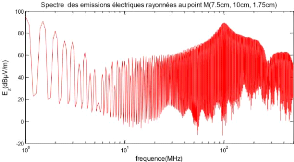
Figure XVII Spectre des émissions électriques
rayonnées par le système de câblage
Les deux figures montrent que la dynamique de l'évolution
des émissions électrique et magnétique est fonction de la
fréquence de commutation de hacheur DC/DC.
Le rayonnement EM peut être déduit du spectre de
courant Is pénétrant dans le câble. En effet, connaissant
le module et la phase de ce courant pour chaque fréquence nf0, nous
pouvons déduire les champs magnétique et électrique
à tout point.
IV.2. Modèle temporel des perturbations EM
La simulation temporelle des perturbations EM permet la
détection et l'analyse des phénomènes transitoires. Ces
phénomènes transitoires réunissent à la fois le
module et la phase de la présentation fréquentielle du champ
rayonné. Alors, ces phénomènes échappent aux normes
CEM en vigueur puisque ces dernières s'intéressent souvent
à l'amplitude des émissions.
En plus, les résultats en régime temporel
contiennent autant d'informations que ceux en régime fréquentiel
et leurs mesures sont plus rapides.
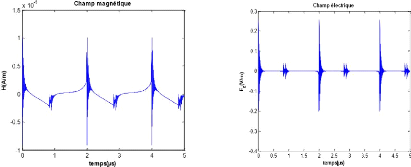
Figure XIX : Composantes (a) Hy du champ magnétique et
(b) Ez du champ électrique
Dans ce qui suit, nous allons déduire, à partir
du spectre de courant IS simulé et de la réponse
fréquentielle de champ EM, les formes d'onde du champ magnétique
et du champ électrique. La reconstruction de ces signaux temporels
à partir de ces spectres du champ EM se fait en utilisant la
transformée de Fourier inverse. Pour le champ magnétique, et de
la même façon pour le champ électrique, la formule
s'écrit :
1-1(t) = E
1-1(??????)e-??27c?????? (37)
??=0
IV.3. Interprétation des résultats
Dans cette simulation, nous nous sommes
intéressés, dans un premier temps, à la
modélisation du rayonnement d'un prototype de câblage
reflétant les phénomènes EM dus au câblage
automobile.
Nous avons pu associer notre câblage à un
convertisseur DC-DC. Cette configuration reflète une application de
systèmes électroniques embarqués dans laquelle la
distribution de l'énergie à différents niveaux se fait
à travers des DCDC à partir d'une batterie.
Le découpage dans le convertisseur de puissance
génère des perturbations HF qui se propagent vers une charge via
le câble. Le rôle du câble dans une telle configuration n'est
pas anodin. En effet, il modifie le spectre de perturbations et participe
énormément au rayonnement du système complet.
Une simulation des formes d'onde du champ magnétique et
champ électrique s'est avérée possible. Ainsi, nous avons
pu présenter en temporel le champ EM même si nous n'avons pas pu
le valider par des mesures essentiellement à cause de la
difficulté de la réalisation de sondes temporelles de mesure.
V. Conclusion
De nos jours, la modélisation des émissions EM
rayonnées des systèmes électroniques embarqués
constitue un grand challenge d'autant plus que ces émissions
représentent un risque énorme pour le bon fonctionnement des
systèmes et aussi pour l'homologation CEM.
La difficulté de rendre compte de ce
phénomène lié à ces systèmes est une
évidence et elle est accentuée par la forte intégration
électronique. En effet, la modélisation EM, elle-même,
nécessite une association de plusieurs méthodes
numériques. Cela dépend des dimensions et surtout de la
géométrie. Alors, le choix d'une méthode de
modélisation EM adéquate pour chaque sous structure ou
l'association de plusieurs méthodes est une solution possible mais
demeure très délicate. De plus, pour intégrer ce
phénomène EM au modèle de l'électronique
embarquée, nous avons besoin d'un modèle électrique du
comportement EM des structures qui rayonnent le plus telles que les bus bars,
les câbles et les plans de masse.
Dans cet article, nous avons porté notre choix
à la méthode PEEC. Par sa formulation intégrale et par sa
possibilité de décrire les phénomènes EM sous forme
de circuit équivalent, la méthode PEEC correspond au besoin de
modéliser le câblage dans son environnement électrique
d'autant plus que la discrétisation est restreinte aux seuls
conducteurs.
Nous avons pu associer notre câblage à un
convertisseur DC-DC. Cette configuration reflète une application de
systèmes électroniques embarqués dans lesquels la
distribution de l'énergie à différents niveaux se fait
à travers des convertisseurs DC-DC à partir d'une batterie.
Le découpage dans le convertisseur de puissance
génère des perturbations HF qui se propagent vers une charge via
le câble. Le rôle du câble dans une telle configuration n'est
pas anodin. En effet, il modifie le spectre de perturbations et participe
énormément dans le rayonnement du système complet.
Une simulation des formes d'onde du champ magnétique
et champ électrique s'est avérée possible. Ainsi, nous
avons pu présenter en temporel le champ EM.
Les simulations en régime temporel dans le domaine de
la CEM est une nécessité. Elles permettent, contrairement
à des simulations fréquentielles, de prédire les
transitoires de champ EM.
VI. BIBLIOGRAPHIQUE
[1] Directive Européenne 2004/108/CE, du parlement
européen et du conseil, 15 Décembre 2004.
[2] Directive Européenne 89/336/CEE, du parlement
européen et du conseil, 03 Mai 1989.
[3] F. DUVAL, "Gestion du câblage des masses
électriques dans un véhicule automobile : Application CEM",
Thèse de Doctorat, Université de Paris Sud XI, 2007.
[4] I. Yahi ,"Modélisation des sources de rayonnement
au sein d'un véhicule automobile avec prise en compte de la
présence du plan de masse" Thèse de Doctorat, Université
de Rouen, 2009
[5] I. Yahi, F. Duval, A. Louis, "A New Capacitive Coupling
Consideration in PEEC Method" 2emc Symposium on embedded EMC, October 2007
[6] M. Besacier, "Adaptation de la méthode PEEC à
la représentation électrique des structures d'électronique
de puissance", Thèse de Doctorat, Institut National Polytechnique de
Grenoble, 2001.
[7] Cyril Buttay, "Contribution à la conception par la
simulation en électronique de puissance : application à
l'onduleur basse tension" thèse Doctorat Institut National des Sciences
Appliquées de Lyon, 30 Novembre 2004.
[8] E. Clavel, "Vers un outil de conception de câblage
: le logiciel INCA", Thèse de Doctorat, Institut National Polytechnique
de Grenoble, 1996.
[10] Jean-Paul Gonnet, "Optimisation des canalisations
électriques et des armoires de distribution", Thèse de doctorat
de l'université Joseph Fourier, 2005.
[9] Sergey V. Kochetov, "Time- and frequency-domain modeling of
passive interconnection structures in field and circuit analysis", rapport de
habilitation, 2008.
[10] Ekman Jonas, Lundgren Urban, "Analysis of printed antenna
structures using the partial element equivalent circuit (PEEC) method",
Conference proceedings: electromagnetic computations - methods and
applications. - Uppsala, Sweden 2001.
[11] A. Ruehli, "Equivalent circuit models for three dimensional
multiconductor systems", IEEE Transactions on Microwave Theory and Techniques,
vol. 22, no. 3, pp. 216-221, mars 1974.
[12] A. E. Ruehli, P. A. Brennan, "Efficient Capacitance
Calculations for Three-Dimensional Multiconductor Systems", IEEE Transactions
on Microwave Theory and Techniques, vol. 21, no. 2, p. 76-82. , February
1973.
[13] A. Ruehli and H. Heeb, "Circuit models for
three-dimensional geometries including dielectrics", IEEE Trans. Microwave
Theory Tech., vol.40, p. 1507-1516, July 1992
[14] K. M Coperich, A. E. Ruehli, and A. Cangellaris, "Enhanced
Skin Effect for Partial Element Equivalent Circuit (PEEC) Models". IEEE
Transactions Microwave Theory and Technique, 48, 1435- 1442, 2000.
[15] J. Garrett, A. E. Ruehli, and C. R. Paul, "Accuracy and
Stability Improvements of Integral Equation Models using the Partial Element
Equivalent Circuit (PEEC) Approach", IEEE Trans. Antennas Propagat., vol. 46,
no. 12, pp. 1824-1831, December 1998.
[16] A. E. Ruehli, G. Antonini, and A. Orlandi, "Extension of
the Partial Element Equivalent Circuit Method to Non Rectangular Geometries",
in: Proceeding. of the Int. Symposium on EMC, pages 728733, Seattle,
Washington, USA, August 1999.
[17] G. Antonini, A. E. Ruehli, J. Esch, J. Ekman, A. Mayo and
A. Orlandi, "Nonorthogonal PEEC Formulation for Time- and Frequency-Domain EM
and Circuit Modeling", IEEE Transactions on Electromagnetic Compatibility, vol.
45, no. 2, pp. 167-176, May 2003.
[18] A. Müsing, J. Ekman and J.W. Kolar, "Efficient
Calculation of Non-Orthogonal Partial Elements for the PEEC Method ", IEEE
Transactions on Magnetics, vol. 45, issue3, p 11401143, March 2009.
[19] Martin Ludwig Zitzmann, "Fast and Efficient Methods for
Circuit-based Automotive EMC Simulation" Thèse de doctorat de
l'université de Nürnberg, Allemagne 2007.
[20] Kenneth L. Kaiser, "Electromagnetic Compatibility Handbook:
Circuits, Signals and Systems" ,Chapter 3, CRC Press, 2004.
[21] E.Vialardi, "Une technique de réduction d'ordre
couplée à des modèles PEEC: application sur des
équipements aéronautiques", Thèse de doctorat de
Politechnico de torino, 2003.
[22] F. Duval "Gestion du câblage des masses
électriques dans un véhicule automobile : Application CEM",
Thèse de Doctorat, Université de Paris Sud XI, 2007.
[23] G. Antonini, J. Ekman, and A. Orlandi, "3D PEEC capacitance
calculations", Proceedings of the IEEE International Symposium on EMC, Boston,
USA, pp. 630-635, August 2003.
[24] J. Ekman, "Electromagnetic Modeling using the Partial
Element Equivalent Circuit Method", PhD Dissertation, EISLAB: Embedded Internet
System Laboratory, Computer Science and Electrical Engineering, Lulea
University of Technology, 2003.
[25] J. Ekman, "Electromagnetic Simulations Using The Partial
Element Equivalent Circuit (PEEC) Approach", in Proceeding of Progress in
Electromagnetics Research Symposium, Honolulu, HI, USA, 13-16 October 2003.
[26] SPICE, from EECS Department of the University of California
at Berkeley,
http://bwrc.eecs.berkeley.edu/Classes/IcBook/SPICE
[27] SPICEWIN, version 3.5f de SPICE de Berkeley, compile pour
les systèmes d'exploitation Microsoft,
http://embedded.eecs.berkeley.edu/pubs/downloads/spice/index.htm
[28] Mathias Enohnyaket "PEEC Modeling and Verification for
Broadband Analysis of AirCore Reactors", dissertation of PhD from University of
Technology lulea, Sweden 2007.
[29] V. Ardon, O. Chadebec, J-M. Guichon, E. Vialardi,
"Extraction des capacités parasites de structures d'électronique
de puissance", Numelec08, 2008.
[30] V. Ardon, J. Aimé, O. Chadebec, E. Clavel, Y. Le
Floch, "Evaluation du modèle capacitif d'une structure
d'électronique de puissance", CEM08 14ème colloque international
et exposition sur la compatibilité électromagntique-JS08
journée scientifique URSI-France, 2008.
[31] Vincent Ardon, Jérémie Aimé, Olivier
Chadebec, Edith Clavel, Enrico Vialardi, "MoM and PEEC Method to Reach a
Complete Equivalent Circuit of a Static Converter" Proceeding EMC Zurich
2009.
[32] J. Ekman and S. Niska, "Combining 2D Transmission Line
Models with 3D PEEC Models", in Proceeding. of EMB04, Gothenburg, Sweden,
2004.



