II.2.1) Extraction des courbes de dispersion
Sur la base du contenu énergétique du champ
d'onde des ondes de surface enregistré, une ou plusieurs courbes de
dispersion peuvent être extraites des spectres de vitesse de phase. Les
caractéristiques de dispersion du mode fondamental sont
généralement les plus intéressantes car les
méthodes d'inversion les plus courantes n'utilisent que la courbe de
dispersion en mode fondamental. L'extraction de la courbe de dispersion est
donc basée uniquement sur le mode fondamental. Cependant, en raison des
avantages rapportés de l'inversion multimodale, l'extraction de courbes
de dispersion multimodales est à noter (Xia, Miller & Park,
2000b).
La figure 22 montre une image de dispersion tridimensionnelle
où le maximum du panneau de dispersion, correspondant à chaque
composante de fréquence dans la gamme de 10 Hz à 39 Hz, a
été extrait. Les valeurs de crête extraites, correspondant
aux fréquences 12,5 Hz et 33,3 Hz, sont spécialement
indiquées par des marqueurs verts agrandis. La courbe de dispersion,
obtenue à partir de l'image de dispersion, qui est fonction de la
vitesse de phase et de la longueur d'onde, est présentée à
la figure 23.
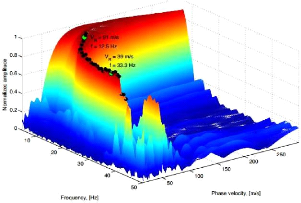
Figure 22 : Caractéristiques de dispersion du
mode fondamental
La figure 22 montre la courbe de dispersion du mode
fondamental obtenue par la méthode de déphasage. Les maximums,
correspondant aux fréquences dans la gamme de 10 Hz à 39 Hz, sont
indiqués par des points noirs. Les maximums, correspondant aux
fréquences 12,5 Hz et 33,3 Hz, sont indiqués par des points
verts.

Figure 23 : Courbe de dispersion en mode fondamental
obtenue à partir de l'image de
dispersion illustré à la
figure 22.
II.2.2) Inversion de la courbe de dispersion
L'inversion de la courbe de dispersion des ondes de surface
permet d'aboutir à l'estimation des propriétés
mécaniques du sous-sol. Le résultat est souvent
présenté sous la forme d'un profil vertical de vitesses des ondes
de cisaillement, VS, comme illustré sur la figure 24.

50
Figure 24 : Profil vertical de la vitesse des ondes de
cisaillement, Vs
51
L'inversion a longuement été
étudiée en géophysique particulièrement dans les
méthodes sismiques (Tarantola, 1987, 2005 ; Snieder, 1998 ; Sambridge,
1999). Elle vise à déterminer une image du milieu et à
attribuer, en chaque point, une valeur représentative. Il s'agit, dans
notre cas, de déduire le profil de vitesse des ondes de cisaillement
d'un site en fonction de la profondeur.
Les méthodes d'ondes de surface possèdent de
nombreux avantages, cependant elles présentent aussi des limites.
L'incertitude liée à l'inversion en est la raison principale.
Elle est liée tant au type du milieu ausculté (sols
hétérogènes, piégeage de l'énergie dans des
zones de faibles caractéristiques mécaniques, absence
d'informations géologiques) qu'au mode d'acquisition (la profondeur de
résolution dépend de la taille du dispositif, de la taille de la
zone de contraste par rapport à l'espacement entre les capteurs, les
bruits gênants, l'offset proche et l'offset lointain). Ne pas tenir
compte de ces limites pourrait induire une interprétation erratique du
profil sismique vertical pour le milieu ausculté et avoir une approche
trop simplifiée de la méthode (Bodet et al., 2005).
52
| 


