Détermination de parametres géotechniques par la méthode sismique

I

I G	:t^1
Institut Supérieur d'Application Des Gécsciences	Logging Instrumentation Measurement

l'IrLkSTER EN GEOSCIENCES
OPTION : GEOPHYSIQUE APPLIQUEE

ilL?ERMIHITI0N1D_Ë METIRES;

iOIi#N-.LWJISPNuAm,ErHES,^-IS-MI,Qli

s	a -0 -Il -1111
a 1 A 711 Ni 4 1 rci 72 33 q			102 113 1!a 133 143 lSi 113 1)

Presenté et soutaiu publiquement le ig [ ? °0{?1 par :
Abou Hanifatou SANT
Tri.7.1a7.
Dr Ted 1[3.YALIL-T011:B4O.
Geoscientif igue
Jury dévaluation du mimoire

NAHOL NDOLSSE Samuel Président Professeur, DJHZ Oaagadongoa.

NT1Tr4. Julien Rapporte= Docteur. 1.7.7=4 oa âaagoa

Dflyala-Tomba Ted Direcbear de raimoire Docteur, ISAG. on

Armee : 2)1&-.?O1S

II

DEDICACES

Je dédie ce travail :

+ A mon père El hadji SANA Abdoulaye,

+ A ma Mère Adja SANA Azeta,

+ A mes frères et soeurs, en particulier SANA Sidi Mohamed, son épouse SAYAOGO

Alizeta et à leurs enfants : Al Bachir, Moubarack, Bouchra, Ridwane,

+ A mon épouse SAWADOGO Safiatou,

+ A mes enfants Abdoul Wahid et Abdoul Madjid,

+ A mon neveu Issouf et ma nièce Adidjatou.

III

REMERCIEMENTS

Ce travail s'inscrit dans le cadre de mon mémoire de fin d'études pour l'obtention du diplôme de master en géosciences appliquées, option géophysique appliquée de l'Institut Supérieur d'Application des Géosciences (ISAG). II a été réalisé au sein de la société LIM Africa.

Je voudrais ici remercier les personnes qui ont contribué d'une manière ou d'une autre à sa réalisation

Je remercie tout d'abord, Docteur Ted Mayala Directeur Général de LIM Africa, à qui je dois ma connaissance de géophysique appliquée et qui a bien voulu m'accepter à LIM Africa pour le stage. II a été l'initiateur de ce travail en me proposant un sujet sur la détermination de paramètres géotechniques par la méthode sismique. Ses conseils et ses observations m'ont été d'un apport utile.

Je tiens à remercier tous mes professeurs d'ISAG pour la qualité de leurs enseignements, mais aussi pour leurs conseils durant le déroulement de mes études.

SANOU Serge, SAVADOGO Omar, pour leur entière collaboration.

Mes remerciements vont aussi à mes amis et collègues, Zakaria GUINKO, Adama SEBEGO, Mahamadi SORGHO, Souleymane KONKOBO, Souleymane OUEDRAOGO, Seydou DERRA, Moumouni KONE, Ousseini OUEDRAOGO pour leur soutien multiforme et leur disponibilité.

Je tiens également à remercier Mamadi BALBONE, Ibrahim OUEDRAOGO, Saidou KIENTEGA pour les questions d'ordre géologique.

Je n'oublie pas mes camarades de la 3^emepromotion de l'Institut ISAG.

Je ne saurai terminer sans remercier KOETA Dieudonné et Da Christophe pour leur appui à la correction de ce document.

IV

RESUME

L'étude de la déformation du sol en vue de déterminer les modules élastiques, est habituellement simulée en laboratoire ou sur terrain. Les différentes méthodes fréquemment employées sont l'oedométrique, le triaxiale et la pressiomètrique. Tous ces essais bien qu'étant fréquemment utilisés présentent des limites. Comment déterminer alors les paramètres géotechniques permettant de pallier ces insuffisantes constatées ? C'est en réponse à ces interrogations qu'il nous a paru nécessaire de déterminer ces modules par la méthode sismique.

Sur demande de la société minière, deux types de levés sismiques ont été effectués le 18 décembre 2018 dans le permit Orezone par LIM Africa. Ces deux types de levés sont la méthode de sismique réfraction et la méthode d'analyse multicanaux des ondes de surface (MASW). Les résultats obtenus de la SR donnent un profil de 5 couches avec différentes vitesses Vp. Ceux obtenus de la méthode d'Analyse des Ondes de Surface donnent également 5 couches avec différentes vitesses VS. Les vitesses Vp varient de 500 à 4000 m/s et les vitesses Vs de 367 à 1543 m/s.

L'utilisation des relations entre les constantes élastiques, les vitesses de propagation des ondes sismiques obtenus lors des levés sismiques de la zone d'étude ont permis de calculer les modules géotechniques des différentes couches du sous-sol. Les valeurs des paramètres géotechniques calculées sont les suivantes :

	Module de Young (GPa)	Coefficient du Poisson	Module de Coulomb (GPa)	Module d'incompressibilité (GPa)
Couche 1	0,36	-0,08	0,19	0,10
Couche 2	0.93	0.37	0.33	1.29
Couche 3	2.27	0.42	0.8	4.68
Couche 4	8.8	0.34	3.27	9.32
Couche 5	16,58	0,41	5,86	31,60

V

SIGLES ET ABREVIATIONS

?d . contraction relative des arêtes perpendiculaires à la direction de la force ; ?l . allongement ;

?V . variation de volume ;

A . tir en bout de dispositif (tirs en bout) ;

BEGE . Bureau d'Etudes des Géosciences et Environnement ;

B . tir en bout de dispositif (tirs en bout) ;

C . tir au centre du dispositif ; d . arête ;

d . indice indiquant des constantes dynamiques obtenues par les méthodes de prospection

sismique ;

D . tir intermédiaire entre les capteurs 6 et 7 ; d. La densité ;

di . densité d'un constituant individuel i de la roche ; d_m . densité moyenne de la matrice solide de la roche ; dp . densité moyenne des fluides des pores ;

E . Module d'allongement ou module d'élasticité (longitudinale) de Young ; E . tir intermédiaire entre les capteurs 18 et 19 ;

E-W . direction Est-Ouest ;

F . force ;

K . module d'incompressibilité ;

m . masse;

MASW . Multichannel Analysis of Surface Waves ;

O . tirs offset ou tirs lointains (tirs extérieurs au dispositif) ;

P . onde primaire ;

P . pression ;

P . tirs offset ou tirs lointains (tirs extérieurs au dispositif) ; PAB . Projet aurifère de Bomboré ;

VI

S : surface ,
·

SH : le mouvement des particules est contenu dans le plan horizontal, perpendiculairement au sens de propagation de vitesse VSh ,
·

S-N : direction sud-nord ,
·

SV : Le mouvement des particules est contenu dans le plan vertical, perpendiculairement au sens de propagation de vitesse VSv,
·

SPAC : Spatial Autocorrelation

TB : Time Break ou temps zéro ,
·

v ou V : volume,
·

VP : vitesse de propagation des ondes longitudinales ,
·

VS : vitesse de propagation des ondes de cisaillement ,
·

Z : impédance acoustique ,
·

á : angle entre les faces latérales et sa déformation ,
·

fi : module de compressibilité avec fi = 1/K ,
·

? : contrainte ,
·

ì : (ou G) Le module de Coulomb module de rigidité, module de glissement ou encore module de cisaillement ,
·

? : coefficient de Poisson ,
· O : porosité.

VII

LISTE DES FIGURES

Figure 1: Localisation du site du projet de Bomboré (Source : BEGE, 2015) 5

Figure 2 : Carte géologique régionale incluant la zone du projet (Orezone 2015) 8

Figure 3: Carte géologique de la zone du projet aurifère de Bomboré (Orezone, BEGE) 9

Figure 4: Relation de la contraction latéraleà la dilatation longitudinale 12

Figure 5: Déformation de cisaillement 13

Figure 6 : Essai de compression simple 19

Figure 7: Distorsion lors d'un cisaillement simple 22

Figure 8 : Courbepressiométrique 24

Figure 9 : Représentation du rayon sismique 30

Figure 10: Loi de Snell-Descartes 30

Figure 11: Dispositif de 24 capteurs et 7 tirs 31

Figure 12: Position des fronts d'ondes (onde longitudinale), cas de deux terrains séparés

par un plan horizontal. 35

Figure 13:Dromochroniques dérivées du schéma de la figure 12 35

Figure 14:Représentation schématique des rayons sismiques, pour le cas de la figure 13.

36

Figure 15 : Cas de plusieurs couches planes horizontales 37

Figure 16 : Cas d'un seul marqueur plan incliné (tirée du Dictionnaire de Géophysique

Appliquée - P. Chapel - 1980) 39

Figure 17 : Les ondes de Rayleigh de basses fréquences (a), pénètrent plus profondément

que les ondes de Rayleigh de hautes fréquences (b) et (c). (Evrett, 2013) 44

Figure 18 : Exemple d'un profil de mesure avec la méthode MASW. (Bodet,2005) 46

Figure 19 : Courbe de dispersion des ondes de surface 47

Figure 20 : Image de dispersion en deux dimensions obtenue par la méthode de

déphasage. 48

Figure 21 : Image de dispersion en trois dimensions obtenue par la méthode de

déphasage. 48

Figure 22 : Caractéristiques de dispersion du mode fondamental 49

VIII

Figure 23 : Courbe de dispersion en mode fondamental obtenue à partir de l'image de

dispersion illustré à la figure 22. 50

Figure 24 : Profil vertical de la vitesse des ondes de cisaillement, Vs 50

Figure 25 : Géophone enfoncé dans le sol 53

Figure 26 :Sismographe et accessoires 54

Figure 27 : « Trigger » ou déclencheur relié au marteau sur une plaque 54

Figure 28 : Dispositif de 24 capteurs et 7 tirs 55

Figure 29 : Pointage des premières arrivées des tirs avec l'application PickWin 57

Figure30 : courbes distance-temps obtenues des pointés des premières arrivées 57

Figure 31 : modèle de vitesses des couches du sous-sol 58

Figure 32 : image de dispersion en deux dimensions et la courbe de dispersion obtenues

grâce à l'application PickWin 60

Figure 33 : Profil de vitesses des ondes de cisaillement VS 61

IX

LISTE DES TABLEAUX

Tableau 1: Paramètres élastiques pour différents matériaux présents dans la subsurface

(Schön 2011) 14

Tableau 2: Différentes densités des matériaux terrestres 17

Tableau 3 : Vitesses des ondes de compression 59

Tableau 4 : Vitesses des ondes de cisaillement 61

Tableau 5 : Synthèse des résultats 62

Tableau 6 : Tableau récapitulatif des modules élastiques 66

X

ANNEXES

Annexes 1 : Positions des tirs pour les différents profils de la sismique réfraction i

Annexes 2: modèle de vitesses de compression (Vp) de différentes couches du profil E-W

i

Annexes 3: les courbes distance-temps obtenues des pointés des premières arrivées du

profil E-W i

Annexes 4 : modèle de vitesses de compression (Vp) de différentes couches du profil S-N

ii

Annexes 5 : les courbes distance-temps obtenues des pointés des premières arrivées du

profil S-N ii

Annexes 6: Extrait de données de forage iii

XI

SOMMAIRE

DEDICACES II

REMERCIEMENTS III

RESUME IV

SIGLES ET ABREVIATIONS V

LISTE DES FIGURES VII

LISTE DES TABLEAUX IX

ANNEXES X

SOMMAIRE XI

INTRODUCTION 1

CHAPITRE I : PRESENTATION DE LA ZONE D'ETUDE 4

Situation géographique de la zone du projet 5

Relief et Végétation 6

Sol 6

Contexte et cadre géologique du projet 6

IV.1) Contexte Géologie 6

IV.2) Cadre géologique du projet aurifère de Bomboré 7

CHAPITRE II : PROPRIETES PHYSIQUES DES ROCHES 10

Propriétés élastiques des roches 11

I.1) Module d'allongement 11

I.2) Coefficient de Poisson 12

I.3) Module de Coulomb 13

I.4) Module d'incompressibilité 13

Densités des matériaux géologiques 14

II.1) Définition et unités 14

II.2) Densité des constituants des roches 15

II.2.1) Densité des minéraux 15

II.2.2) Densité des fluides des pores 15

II.3) Densité des roches 15

II.3.1) Densité des roches magmatiques et métamorphiques 16

II.3.2) Densité des roches sédimentaires 16

CHAPITRE III : PRINCIPAUX ESSAIS DE MESURES DE MODULES 18

Approche des modules par mesures statiques (Les essais de laboratoire) 19

I.1)

XII

Essai de Compression simple ou de Traction simple 19

I.2) Essai de compression triaxiale 20

I.3) Essai de type oedométrique 21

I.4) Essai de cisaillement simple (ou de distorsion) 22

Approche des modules par mesures dynamiques 23

II.1) Essai pressiométrique 23

II.2) méthodes sismiques 25

II.2.1) Avantages de la méthode sismique 25

II.2.2) Principe de base de la méthode sismique 26

CHAPITRE IV :LA MÉTHODE SISMIQUE RÉFRACTION 28

Définitions 29

I.1) Milieu homogène et isotrope 29

I.2) Front d'onde et Rayon sismique 29

I.3) Géométrie des rayons 30

Procédure de mise en oeuvre 31

II.1) Source sismique 32

II.2) Géophones 32

II.4) Enregistreur 33

Principes fondamentaux 33

III.1) Trajet du front d'onde (cas de deux terrains) 34

III.1.1) Temps d'intersection à l'origine 35

III.1.2) Calcul d'épaisseur e1 37

III.2) Cas de plusieurs couches planes horizontales et Cas d'un seul marqueur plan

incliné 37

III.2.1) Cas de plusieurs couches planes horizontales 37

III.2.2) Cas d'un seul marqueur plan incliné 39

Causes d'erreurs 40

CHAPITRE V : 41

METHODE D'ANALYSE MULTICANAUX DES ONDES DE SURFACE (Multichannel

Analysis of Surface Waves Method MASW) 41

Ondes de surface 42

I.1) Onde de Rayleigh 43

I.1.1) Caractère dispersif des ondes de Rayleigh 43

Principales étapes de la méthode MASW 44

II.1)

XIII

Acquisition des signaux temporels (x,t) 45

II.2) Notions générales sur le traitement de signal et courbe de dispersion des ondes de

surface 46

II.2.1) Extraction des courbes de dispersion 49

II.2.2) Inversion de la courbe de dispersion 50

CHAPITRES VI : CAMPAGNE SISMIQUE EFFECTUEE SUR LE PERMIT D'OREZONE

52

Mesures des ondes de compression et des ondes de surface 53

I.1) Matériels d'acquisition 53

I.2) Déploiement du matériels et enregistrement des ondes 55

Traitement et résultats des données 56

II.1) Sismique réfraction 56

II.1.1) Traitement de données 56

III.1.2) Résultats obtenus de la sismique réfraction 58

II.2) MASW 59

II.2.1) Traitement de données 59

III.2.2) Résultats obtenus de MASW 61

Calculs des modules élastiques 63

III.1) Couche 1 : limon 63

III.1.1) Calcul du module de Young de la couche 1 63

III.1.2) Calcul du coefficient du Poisson de la couche 1 64

III.1.3) Calcul du module de Coulomb de la couche 1 64

III.1.4) Calcul du module d'incompressibilité de la couche 1 64

III.2) Couche 2 : Sable 64

III.3) Couche 3 : Argile 65

III.4) Couche 4 : Arènes de Diorite quartzifère 65

III.5) Couche 5 : Diorite quartzifère 66

Résultats et discussions 66

Conclusion Générale 69

BIBLIOGRAPHIE 71

ANNEXES i

1

INTRODUCTION

Dans l'introduction de son article sur l'usage des modules de déformation en géotechnique, Olivier Combarieu dit : « La complexité que recouvre le terme de module est grande, puisque la plupart des matériaux, surtout en géotechnique, cumulent le plus souvent des propriétés élastiques, plastiques et visqueuses, pouvant se manifester conjointement, auxquelles s'ajoutent des effets dus au fluage et à la fatigue.

En géotechnique, les règlements européens récents le prescrivant, on s'oriente progressivement vers une justification des ouvrages en déformation et déplacement. On se contentait le plus souvent, jusqu'à récemment, de justification à la rupture, l'application de coefficients de sécurité conduisant généralement à des déformations admissibles pour les ouvrages construits.

Seules des conditions de déformations très sévères (en l'occurrence très petites) amenaient à entreprendre de tels calculs en déformation, souvent complexes et revenant finalement à choisir des coefficients de sécurité plus élevés que ceux habituellement utilisés. »

Extrait du REVUE FRANÇAISE DE GEOTECHNIQUE N°114 1er trimestre2006

Tout matériau soumis à des contraintes subit un comportement élastique et un comportement plastique. A l'intérieur des limites d'élasticité, la contrainte est proportionnelle à la déformation (loi de Hooke). Cette relation de proportionnalité peut être établie par des modules d'élasticité et de cisaillement.

La plupart des projets de construction utilise le sol soit comme matériaux, soit comme assise porteuse. Dans le second cas, il faut dimensionner les fondations de manière qu'elles puissent résister aux charges prévues par les calculs, tout en limitant les risques de déformation ou de tassement. Car, La déformation trop importante du sol entraine très souvent des désordres qui affectent les ouvrages géotechniques.

L'étude de la déformation du sol, peut être simulée en laboratoire ou sur terrain. La méthode oedométrique et celle triaxiale sont les approches fréquemment utilisées dans la détermination des modules élastiques pour les essais de laboratoire et la méthode pressiométrique Ménard pour les essais sur le terrain.

Cependant, force est de constater que les essais en laboratoire ne sont valables que si la composition du sol n'est pas modifiée pendant le transport. Ce qui est totalement impossible pour les terrains trop meubles. Aussi la manipulation des échantillons étant très délicate, il exige de l'opérateur une certaine habilité dans la préparation. Le mode opératoire de ces essais prend plus de temps d'où leur cout élevé. Quant à l'essai pressiométrique, s'il a l'avantage d'être réalisé sur le terrain, il fournit néanmoins des résultats peu sûrs dans le cas précis des argiles molles.

Tous ces essais précités ne sont valables que sur une certaine épaisseur (quelques centimètres) et n'offrent que des mesures ponctuelles.

2

Il apparait ainsi clairement que ces essais bien qu'étant fréquemment utilisés présentent des limites. D'où la problématique de la détermination des paramètres géotechniques par une autre approche.

? Comment déterminer alors les paramètres géotechniques permettant de pallier ces insuffisantes constatées ?

? Quel procédé de détermination est-il approprié pour ce faire ?

C'est en réponse à ces interrogations qu'il nous a paru nécessaire de mener la réflexion sur le thème : « la détermination des paramètres géotechniques par la méthode sismique ». C'est donc l'objectif du mémoire.

Objectif

La société LIM Africa a eu pour mission d'effectuer des levés sismiques dans la zone d'étude d'Orezone à Bomboré. L'objectif de ce travail est d'utiliser les informations issues de ces levés pour déterminer, de manière indirecte, les valeurs dynamiques des modules d'élasticité, de cisaillement, d'incompressibilité et du coefficient de Poisson du sous-sol de la zone d'étude. Pour ce faire, nous allons, d'abord mesurer la vitesse des ondes de compression Vp par une méthode dite sismique réfraction. Ensuite, déterminer la vitesse des ondes de cisaillement Vs par une méthode dite MASW qui exploite les ondes de surface. Enfin, les valeurs des modules élastiques sont calculées en fonction des vitesses VP et VS des formations géologiques du sous-sol du terrain. Comment se justifie ce thème d'étude ?

Justification du mémoire

La détermination des modules élastiques, par la méthode sismique, est d'un grand intérêt, dans la mesure où les vitesses sismiques sont mesurées sur place avec des matériels légers et respectueux de l'environnement contrairement à l'essai pressiométrique. Cette méthode tient compte, des conditions naturelles d'humidité, de pression...Elle permet d'obtenir, rapidement et à faible coût, une évaluation générale des modules de couches du sous-sol. Cette étude jette les bases de la constitution possible de bases de données des modules élastiques.

Pour mener à bien notre étude, nous commencerons par présenter notre zone d'étude (le relief, la végétation, les sols et la géologie). Ensuite nous nous étalerons sur les propriétés physiques des roches. Nous décrirons sommairement les divers types d'essais entrant dans la détermination des modules élastiques et présenterons les inconvénients liés à chaque essai. Puis, nous examinerons les méthodes sismiques basées sur les techniques de propagation des ondes. Après examen de ces méthodes, nous évoquerons les principes fondamentaux de la méthode sismique basée sur les ondes de volume et de la méthode MASW (Analyse Multicanaux des Ondes de Surface) qui exploite les ondes de surface. Enfin, nous terminerons par la campagne sismique effectuée dans la zone d'étude et aux résultats de l'interprétation des données, intervenant dans les calculs des valeurs dynamiques des modules élastiques. Il sera question de mesures des ondes de compression (p) et des ondes de cisaillement (s) effectuées sur la zone d'étude, de traitements des données, ainsi que de calculs des valeurs dynamiques des modules

3

d'élasticité, de cisaillement, d'incompressibilité et du coefficient de Poisson du sous-sol de notre zone d'étude. Présentons-avec minutie la zone d'étude, située géographiquement près du campement d'exploitation de Bomboré.

4

CHAPITRE I :

PRESENTATION DE LA

ZONE D'ETUDE

5

Situation géographique de la zone du projet

Le site du projet aurifère de Bomboré est localisé à environ 80 km de Ouagadougou, via la route nationale N°4 (RN4) sur l'axe routier Ouagadougou-Fada N'Gourma. La zone du projet relève administrativement du département de Mogtédo de la province du Ganzourgou dans la Région du Plateau central. Notre zone d'étude est située dans l'empreinte PAB : Projet aurifère de Bomboré (Figure 1), fort caractérisée par un relief et une végétation de type sahélien.

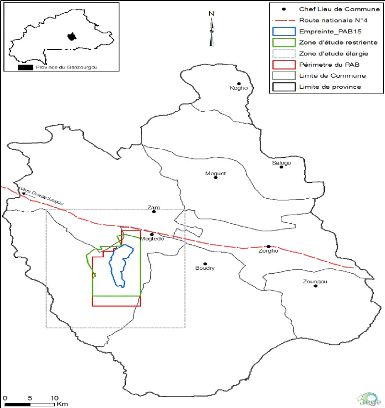
Figure 1: Localisation du site du projet de Bomboré (Source : BEGE, 2015)

6

Relief et Végétation

D'une façon générale, le relief dans le Plateau Central est caractérisé par une pénéplaine aux pentes douces (300 à 400 m d'altitude), interrompue çà et là par des alignements de collines cuirassées aux sommets tabulaires ou arrondis (province du Kourwéogo) ou granitiques (province du Ganzourgou).

Dans les parties nord et centre de la région, notamment dans les provinces du Kourwéogo et de l'Oubritenga, on note une végétation de type arbustif et au sud (Ganzourgou) une végétation arborée, avec la présence de forêts claires et de forêts galeries, le long des cours d'eau permanents ou temporaires. La végétation se dégrade rapidement du fait essentiellement du surpâturage, de la coupe abusive de bois, des feux de brousse et de la péjoration climatique. (Source : BEGE, 2015) Présentons à présent les sols de la zone.

Sol

D'une façon générale, on distingue principalement au plateau central les sols suivants :

Les vertisols sont répandus dans les provinces du Zoundwéogo (au sud), du Ganzourgou (au centre). Ce sont des sols à profil peu différencié (argile gonflante, la montmorillonite).

Les sols bruns entrophes occupent principalement la province du Ganzourgou (au centre). Ils ont une assez forte teneur en argile Montmorillontique.

Les sols peu évolués sur schiste se forment sur le substratum schisteux dénudé. Ils se caractérisent par un recouvrement fin de texture variable et des fragments de schiste englobés dans une matrice sablo-limoneuse, sablo-argileuse ou argilo-sableuse (BEGE, 2015). Ces différents sols dépendent d'un contexte géologique précis et déterminant celui du projet aurifère.

Contexte et cadre géologique du projet IV.1) Contexte Géologie

Le contexte géologique du Burkina Faso correspond principalement à des formations précambriennes du craton ouest-africain. Les anciennes formations du protérozoïque inférieur sont des roches cristallines, métamorphiques et la couverture sédimentaire.

Le birimien forme une série de ceintures ou sillons, comme les ceintures de roches vertes archéennes, de formations métamorphiques qui vont du faciès des schistes verts au faciès de l'amphibolite à grenat. Ces ceintures étroites, à foliation généralement très redressée, orientées Nord-Sud ou Nord-est-Sud-ouest, de plusieurs dizaines de kilomètres de largeur et d'une extension allant de 100 à 500 km, sont constituées de roches plissées très diverses d'âge précambrien. Elles se présentent en grandes lanières, séparées par les granites et autres affleurements antébirimiens repris au cours de l'orogenèse éburnéenne figure 2.(Source : BEGE, 2015)

7

IV.2) Cadre géologique du projet aurifère de Bomboré

Le projet aurifère de Bomboré couvre partiellement un sillon méta-sédimentaire d'orientation nord-est, qui s'étend sur plus de 50 km de son extrémité sud-ouest jusqu'au village de Méguet, à son extrémité nord-est. La séquence méta-sédimentaire est dominée par des méta-grès, lesquels surmontent des méta-pélites à matière organique, par endroits graphitiques, ceux-ci sont surmontés de dépôts chenalisés de méta-grés conglomératiques et de méta-conglomérats à cailloux de grès, d'argilite, de granite et de quartz. Cette séquence méta-sédimentaire est recoupée par des intrusifs mafiques et ultramafiques qui se présentent surtout sous forme de sills. La séquence méta-sédimentaire du secteur du projet Bomboré est moulée sur un large batholite de diorite quartzifère qui est localisé à la limite du projet et est bordée au sud-est et au nord-ouest par des granites à biotite.

La carte suivante présente les principales lithologies de la zone du projet aurifère de Bomboré. Bien analysée, elle favorisera une meilleure appréciation des propriétés physiques des roches figure 3(BEGE, 2015).

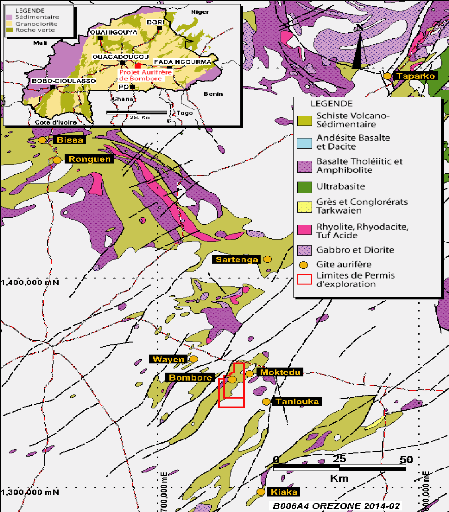
8

Figure 2 : Carte géologique régionale incluant la zone du projet (Orezone 2015)

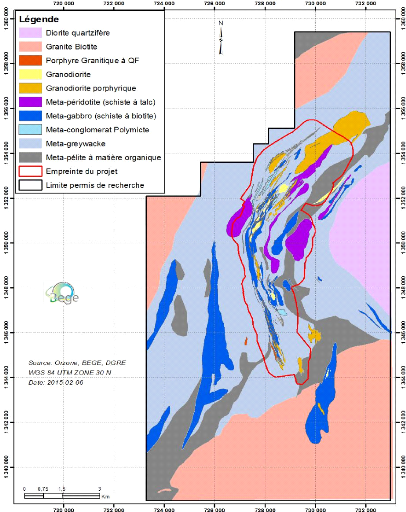
9

Figure 3 : Carte géologique de la zone du projet aurifère de Bomboré (Orezone, BEGE)

10

CHAPITRE II :

PROPRIETES PHYSIQUES

DES ROCHES

11

Les méthodes sismiques sont des techniques d'exploration du sous-sol, basées sur l'étude de la propagation des ondes sismiques. Le comportement de ces dernières dépend des propriétés élastiques du milieu où elles se propagent. Ainsi, il est primordial de se rappeler de certains paramètres ou modules élastiques pour un corps soumis à une contrainte, sans subir une déformation permanente.

Propriétés élastiques des roches

Une contrainte a (Pression F/S) se définit comme une force par unité de surface. Lorsque la force F s'exerce perpendiculairement à la surface S, alors, il s'agit d'une contrainte de compression ou de tension suivant la direction de la force. Cependant, lorsque la force F s'exerce parallèlement à la surface S, alors, il s'agit d'une contrainte de cisaillement. Les contraintes de compression ou de tension font varier le volume mais pas la forme d'un matériau alors que les contraintes de cisaillement modifient la forme et pas le volume (Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base).

En général, sous l'action d'une contrainte, un matériau se déforme. En effet, tout matériau soumis à des contraintes subit deux types de comportement :

? Un comportement élastique dit domaine d'élasticité. Les contraintes qui agissent sur les matériaux sont assez faibles pour qu'elles ne puissent pas engendrer des déformations permanentes ;

? Un comportement plastique dit domaine de plasticité. Ce domaine correspond à un chargement critique à partir duquel le comportement du matériau n'est plus réversible. Dans ce cas, il peut y avoir, une rupture brutale (exemple du verre), une rupture progressive (exemple du béton) ou la plastification du matériau (la forme change de façon irréversible).

A l'intérieur des limites d'élasticité, la contrainte est proportionnelle à la déformation (loi de Hooke). Cette relation de proportionnalité peut être établie par les modules d'élasticité et de cisaillement (Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base).

I.1) Module d'allongement

Considérons un matériau parallélépipédique de longueur l et de section droite. Celui-ci est soumis à des tractions à chacune de ses deux extrémités. Si les forces ne sont pas trop fortes, on observe un allongement å, qui est proportionnel à la longueur et aux forces. Le coefficient de proportionnalité correspond au module d'allongement. Ce module d'allongement ou module d'élasticité (longitudinale) de Young E ou encore module de traction se définit comme le rapport de la contrainte sur la déformation pour un matériau élastique isotrope dans une simple compression ou dilatation linéaire (figure 4). (Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base).

a

??/??

=

??=

??

???/??

??/??

= (?? - ????)/?? [II. 1]

12

E : est le module d'élasticité de Young ;

F/S =? : La force ou la contrainte appliquée par unité de surface ;

?l/l =å : L'allongement relatif au matériau (ou le raccourcissement) par unité de longueur sous l'effet de la contrainte.

Figure 4: Relation de la contraction latérale la dilatation longitudinale

Le module de Young caractérise la résistance du matériau à la déformation uniaxiale. Il est lié aux propriétés du milieu. Dans un réseau cristallin, le comportement élastique des matériaux correspond à de petits déplacements réversibles des atomes tout autour de leur état d'équilibre (Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base).

I.2) Coefficient de Poisson

La force F, qui a provoqué l'allongement ?l (Figure 4), est suivie d'une contraction relative ?d/d des arêtes perpendiculaires à la direction de la force. Le rapport de la contraction latérale à la dilatation longitudinale est appelé coefficient de Poissony.

???/??	=	(??	-	??0)/??
y = ???/??		(??	-	2] ??0)/?? [II.

Le coefficient de Poisson y est un nombre sans dimension compris dans l'intervalle [0 ; 0,5]. A l'exception des élastomères, comme le caoutchouc dont le coefficient de Poisson est y =0,5 ; la plupart des matériaux isotropes continus ont un coefficient de Poisson compris dans l'intervalle [0,25 ; 0,35] (Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base).

I.3) 13

Module de Coulomb

Le matériau parallélépipédique précédent subit cette fois une contrainte de cisaillement. Celle-ci provoque, sur les faces latérales, une déformation dite de cisaillement, d'un angle Y (figure 5). Le rapport contrainte/déformation de cisaillement est appelé module de Coulomb.

Figure 5 : Déformation de cisaillement

Le module de Coulomb p (ou G) est également appelé module de rigidité, module de glissement ou module de cisaillement.

??=

??/?? ???/?? [II. 3]

F/S =?: La force ou la contrainte appliquée par unité de surface ;

?x/l=tan Y : Déformation de cisaillement. (Pour les petites déformations tan Y Y) L'équation [II.3] devient :

??=

?

[II.4]

?

Le module de Coulomb p rend compte de la résistance du matériau à changer de forme. Pour les liquides parfaits p=ø ; E=0 et ?=0,5. Une contrainte de cisaillement change la forme d'un corps matériel et non son volume (Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base).

I.4) Module d'incompressibilité

Le module d'incompressibilité (K) représente la résistance des corps élastiques au changement de volume. Lorsqu'un matériau de volume V est soumis à une pression uniforme P dans toutes les directions, la variation de volume ?V/V est proportionnelle à la pression P.

14

Le module d'incompressibilité est appelé également module global d'élasticité. Plus K est grand, plus il est difficile de réduire le volume du matériau sous l'effet de la pression P. l'inverse de K est appelé module de compressibilité f3. (f3 = 1/K).

??? 1 ?? = ?? ?? ???? ??=

?? [II. 5] ???/??

Quelques valeurs de matériaux géologiques sont consignées dans le tableau 1 suivant :

Tableau 1 : Paramètres élastiques pour différents matériaux présents dans la

subsurface (Schön 2011)

Types de matériau	d(kg/m^3)	K(GPa)	u(GPa)	Vp(m/s)	Vs(m/s)	y
Granite	2500-2700	20-55	17-24	4200-5900	2600-3300	0,19-0,27
Basalte	2200-2800	25-65	13-32	4500-6200	2400-3400	0,28-0,30
Calcaire	2600-2800	20-60	10-38	3700-6300	2000-3700	0,23-0,29
Grès	1900-2600	10-55	2-19	2700-5600	1200-2700	0,35-0,38
Marnes	2000-2400	5-45	2-10	2000-5000	1000-2000	0,33-0,40
Sols	1700-2000	0,01-10	0,005-0,5	100-2000	50-400	0,35-0,49

(Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base.)

Densités des matériaux géologiques II.1) Définition et unités

La densité est un paramètre physique qui varie en fonction de la nature des milieux géologiques. Par définition, la densité d'un corps homogène est le rapport entre sa masse et son volume.

??

??= ?? [????.6]

Notons que la distinction entre densité et masse volumique n'existe pas en anglais où « density » est toujours donné avec une unité et correspond à la masse volumique. La densité est donc une quantité sans dimension contrairement à la masse volumique qui s'exprime en kg
· m-3 (10^-3 g.cm^-3).

La densité d'une roche constituée de n éléments est :

n

d=?(^????? _?)d?? [????.7]

??=1

di : densité de l'élément i ;

Vi/V: fraction volumique de l'élément i.

II.2) Densité des constituants des roches

Les roches sont généralement hétérogènes et composées de corps appartenant aux trois états principaux qui sont : les corps gazeux, les solides et les liquides. Rappelons qu'une roche est composée d'un ensemble de minéraux variés, où la silice, le calcium et l'alumine jouent le plus grand rôle. Ces agrégats de minéraux peuvent laisser entre eux des vides remplis ou non d'eau, ou parfois d'hydrocarbures, rarement de l'air quand il s'agit de roches proches de la surface.

La densité composite d'une telle roche s'exprime par : l'expression suivante :

d=

m1 + m2 + m3 v1 + v2 + v3

M = [????. 8] V

15

Ou m1, m2, m3 et v1, v2, v3 sont respectivement les masses et les volumes de la phase solide, la phase liquide et la phase gazeuse.

II.2.1) Densité des minéraux

Les densités de la plupart des minéraux des roches varient de 2,2 à 3,5 10³ kgm^-3. Celles des minerais sont comprises de 4,0 à 8 10 ³ kgm-3.

II.2.2) Densité des fluides des pores

La densité des liquides et des gaz est contrôlée par la composition chimique la température et la pression (la densité généralement augmente avec l'augmentation de la pression et décroit avec la température).

Eau fraiche : 1 10³ kgm^-3 ;

Eau salée : 1,146 10³ kg m^-3 ;

Pétrole : 0,85 10³ kgm^-3.

II.3) Densité des roches

La densité des roches dépend principalement de trois paramètres :

? Densité de grains des minéraux formant la roche ;

? Porosité " qui représente le volume des vides par rapport au volume total de la roche" ; ? Densité du fluide remplissant les interstices de la roche.

16

II.3.1) Densité des roches magmatiques et métamorphiques

Les roches magmatiques appelées également roches éruptives ou cristallines résultent de la consolidation par cristallisation du magma en fusion. Les éléments affectants la densité des roches cristallines sont la composition, la texture, la minéralisation, la porosité et la fracturation.

Les roches métamorphiques sont les roches les plus hétérogènes du point de vue densité gravimétrique. La densité a tendance à augmenter avec le degré de métamorphisme, par suite du remplissage des espaces vides de la roche et de la cristallisation en minéraux plus denses.

II.3.2) Densité des roches sédimentaires

Les roches sédimentaires formées par les facteurs extérieurs sont constituées par des dépôts détritiques terrigènes, biodétritique sthalassogènes et de dépôts de précipités. Elles possèdent la densité la plus faible que les roches métamorphiques et magmatiques. Elles dépendent de plusieurs facteurs et plus particulièrement de la composition minéralogique, la porosité, l'âge géologique, l'histoire géologique, la profondeur.

Toute roche sédimentaire est constituée d'une partie solide (matrice), une partie constituée de vide (remplie généralement de fluide). La formule exprimant la densité totale de la roche s'écrit sous la forme suivante :

d = (1 - ?)dm + ?dp = dm - (dm - dp)? [????. 9]

où : ? = porosité (représente le rapport du volume des vides sur le volume total de la roche. dm = densité de la matrice ;

dp = densité de la phase fluide.

Les sédiments, enfouis depuis une longue période à grande profondeur, se consolident normalement ; il en résulte une diminution de la porosité et une augmentation de la densité. Les marnes et les argiles présentent les plus fortes variations de densité en fonction de la profondeur. (Source : LA GEOPHYSIQUE POUR LES GEOLOGUES Tome 2).

17

Le tableau (2) suivant donne quelques valeurs de densité pour des matériaux terrestres. Tableau 2 : Différentes densités des matériaux terrestres

Matériaux	Densité
Densité moyenne de la Terre	5,5
Densité moyenne de la croûte continentale	2,67
Sédiments non consolidés	1,8 à 2,0
Sables « secs »	1,4 à 1,65
Sables « humides »	1,9 à 2,05
Grès	2,0 à 2,5
Argile	1,3 à 2,3
Sel	2,1 à 2,4
Calcaires	2,4 à 2,8
Marnes	2,1 à 2,6
Granites	2,5 à 2,7
Gneiss	2,65 à 2,75
Basaltes	2,7 à 3,1

(Source : « Géophysique-4^eme édition Cours et Exercices Corrigés » Page 8)

18

CHAPITRE III :

PRINCIPAUX ESSAIS DE

MESURES DE MODULES

Les paramètres élastiques entrant dans le dimensionnement des fondations sont mesurés lors d'essais sur le terrain et en laboratoire. Les principaux essais de laboratoire qui servent à déterminer la valeur des modules élastiques des sols sont les suivants :

? L'essai de compression simple ;

? L'essai de cisaillement simple ;

? L'essai triaxial ;

? L'essai oedometrique.

Sur le terrain, on effectue l'essai pressiométrique. On peut aussi déterminer les modules élastiques, rapidement et à moindre coût par des essais sismiques. L'avantage des essais sur le terrain est de garder relativement intactes les propriétés et les conditions environnantes du sol étudié. Nous décrirons sommairement les divers types d'essais et leurs inconvénients.

Approche des modules par mesures statiques (Les essais de laboratoire)

I.1) Essai de Compression simple ou de Traction simple

La mesure considérée comme la plus simple du caractère élastique et isotrope d'un solide, consiste en la soumission d'une éprouvette parallélépipédique ou cylindrique de section S à un essai de compression simple ou un essai de traction simple (voir figure 6).

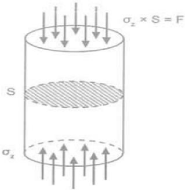
Figure 6 : Essai de compression simple L'extension de l'élément est alors donnée par :

??? = ???? = ??

????? ??? = ???? ?? ????

?? ? ??= ?

avec ?? = ? [III. 1] ??

19

Par convention Oz est négatif en cas de compression et positif dans le cas de la traction. Les relations [III.1] permettent donc d'accéder au module d'élasticité E.

20

L'extension longitudinale s'accompagne de déformations latérales, qui s'expriment par,??_?? = ????= -v ??? ^???,vest le coefficient de Poisson, la seconde caractéristique du matériau

linéairement élastique. Ces trois relations conduisent à la variation de volume de l'éprouvette donnée par :

??? ?? = ???? + ???? + ???? =

??? ^???(1 - 2v) [III. 2]

Ceci montre qu'un dispositif permettant de mesurer la seule variation de volume ne permet pas d'accéder directement au module ; c'est donc la mesure simultanée de å_z et å_x qu'il y a lieu d'envisager.

Pour un coefficient de Poisson v = 0,5, valeur maximale du coefficient de Poisson, ?V est nul. Le sol est déformable mais est incompressible.

La plupart du temps, la rupture de l'échantillon de sol emprunte une des trois formes suivantes : rupture fragile, rupture plastique et rupture fragile et plastique.

La rupture fragile se caractérise par un plan de cisaillement net. En effet, l'échantillon ne peut supporter la contrainte axiale que jusqu'à une valeur maximale P /A facilement observable. Après cette valeur, il « cède »et se sépare le long du plan de cisaillement.

L'essai de compression simple présente quelques difficultés opératoires.

D'abord, la préparation de l'échantillon exige de l'opérateur une certaine habileté. Les erreurs se traduisent le plus souvent par une diminution de la résistance du sol.

Ensuite, l'effort F appliqué aux extrémités de l'éprouvette par l'intermédiaire des plaques de contact rigides, empêche la libre extension radiale aux extrémités à cause du frottement. Cela entraîne une déformation dite en tonneau.

Enfin, lorsque la rupture est plastique, l'échantillon s'aplatit et prend la forme d'un tonneau, sans aucun plan de cisaillement apparent. Il devient alors très difficile de déterminer clairement la valeur maximale de la contrainte axiale car elle progresse jusqu'à un plateau pour devenir presque constante. (Source : revue française de géotechnique n°114)

I.2) Essai de compression triaxiale

L'essai de compression simple n'est pas facile à réaliser dans le cas d'un sol pour lequel les éprouvettes sont cylindriques. Le sol est souvent prélevé par carottage, par conséquent, il est souvent incapable de se maintenir stable ; c'est le cas des sols pulvérulents et des sols très peu cohésifs. Des essais triaxiaux ont étés développés, des essais où le maintien de l'éprouvette est assuré par une étreinte de confinement sur toutes les faces. Il est ensuite procédé à l'application en compression de l'effort F.

21

En restant dans le cadre strictement élastique sur un élément toujours parallélépipédique, le système de contraintes appliquées se réduit à óx, óy et óz. L'application du principe de superposition à un matériau élastique conduit aux trois extensions suivantes :

???? ???? ????

= = =

1 ?? 1 ?? 1 ??

[???? [???? [????

- - -

v(???? + ????)] v(???? + ????)] v(????+ ????)]

(Source : revue française de géotechnique n°114)

Pour une éprouvette cylindrique ou ó_x= óy= ó_r (contrainte radiale), ce qui simplifie les expressions ci-dessus. La variation de volume est ???? ? = 1-2v

?? (2 × ???? + ??_??)[III. 3], linéaire avec

ó_z. La mesure de deux grandeurs (E_z et E_r par exemple) permet d'accéder aux deux modules élastiques E et v.

Selon les conditions de drainage imposées à l'échantillon de sol et la vitesse de chargement choisie, l'essai triaxial peut prendre trois formes :

·

;

L'essai triaxial non consolidé non drainé (UU)

· L'essai triaxial consolidé non drainé (CU) ;

· L'essai triaxial consolidé drainé (CD).

L'essai triaxial consolidé non drainé et l'essai triaxial consolidé drainé sont beaucoup plus compliqués à réaliser. En effet, ils comportent des aspects difficilement maîtrisables comme la saturation du sol et la variation des dimensions de l'échantillon pendant la consolidation. De plus, ces deux essais triaxiaux prennent beaucoup de temps, ce qui les rend coûteux. Par exemple, l'étape de l'essai triaxial consolidé drainé dure au moins une semaine.

I.3) Essai de type oedométrique

On peut imaginer un autre essai de type oedométrique à géométrie simple. Il consiste en l'enfermement d'un échantillon de matériau élastique d'épaisseur L dans une boîte totalement indéformable latéralement. La boîte de forme cylindrique ou cubique est simplement ouverte à sa partie supérieure où l'on applique un effort F par l'intermédiaire d'un piston rigide. Dans ce cas particulier, les déformations radiales sont évidemment empêchées et Ey= E_x (ou Er) = 0 ; on découvre facilement dans ces conditions l'expression suivante :

??? ?? = ???? =

???? (1 + v)(1 - 2v) [III. 4] ?? 1 - v

22

Cette expression ne permet d'accéder à la valeur de E que si l'on connaîtv. On constate que siv = 0,5 (matériau incompressible), E est nul. Le module n'est pas mesurable. (Revue française de géotechnique n°114)

L'inconvénient de l'essai oedométrique est qu'il ne permet pas de déterminer le module E pour un coefficient de Poisson v=0,5.

I.4) Essai de cisaillement simple (ou de distorsion)

Un autre type de déformation dite angulaire ou de distorsion peut affecter un matériau élastique. L'illustration la plus simple est la suivante :

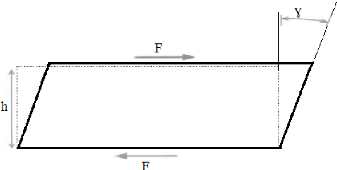
Figure 7 : Distorsion lors d'un cisaillement simple

Si l'on applique à la surface S d'un parallélépipède rectangle une force F tangentielle, les différentes couches élémentaires infiniment petites glissent les unes sur les autres comme les feuilles de papier d'une pile. La hauteur h ne change pas, seules les arêtes normales, au plan d'application de la force, tournent d'un angle y, petit. Cet angle et la force sont liés par la relation.

T

=

?? ,

??=

1 F X ?? S

G est appelé module de cisaillement. On démontre que G est lié à E et v par la relation

E

?? = [III.5]
2(1 + v)

Cette méthode est assez rudimentaire, car elle n'étudie qu'une partie vraiment minime de la surface du sol. Elle ne devrait jamais être utilisée seule.

Il est difficile, voire impossible, de contrôler les conditions de drainage, en particulier dans le cas des sols à grains fins. De plus, au moment de situer le plan de rupture à un endroit précis, comment peut-on s'assurer que cette direction correspond au plan le plus faible ou à la

23

direction critique du terrain ? On ne peut le certifier. Un autre inconvénient de cet essai réside dans la concentration des contraintes aux extrémités de la boite, soit à l'endroit même où sont transmises des contraintes externes très peu homogènes à l'intérieur de l'échantillon. En dernier lieu, il se produit une rotation des plans principaux et des contraintes entre le début de l'essai et la rupture. (Mécanique des sols, THEORIE ET PRATIQUE)

De ce qui précède, il apparait ainsi clairement que chacune des méthodes de laboratoire présente des limites que l'on peut résumer ainsi qu'il suit :

? Les principales difficultés proviennent de la tenue des parois du sondage et de la remontée du terrain foré. Dans la plupart des cas, il faut opérer sous la protection d'un tubage continu ou employer une boue de forage qui, formant un cake sur la paroi du puits, retient celle-ci. Aucun des procèdes de forage utilisé en terrain meuble ne peut vraiment être considéré comme non destructif. Le remaniement de l'échantillon est souvent considérable. Les essais en laboratoire ne sont valables que si pendant le transport, la composition du sol n'a pas été modifiée. Ce qui est totalement impossible pour les terrains forts meubles ;

? Les essais ne sont valables que sur les échantillons prélevés sur des épaisseurs parfois limitées à quelques centimètres ;

? Mesures ponctuelles ;

? La lenteur du processus ;

? La détermination de la valeur de E est faite avec une hypothèse du coefficient de Poisson, ce qui ne donne pas forcement des valeurs réelles de E puisque les valeurs du coefficient de Poisson varient de [0 ; 0,5].

D'où la nécessité de l'approche des modules par mesures in situ.

Approche des modules par mesures dynamiques

Les résultats des essais réalisés en laboratoire sur les échantillons provenant des forages sont abondamment utilisés dans la conception des fondations d'ouvrages. Cependant, il existe plusieurs méthodes de calcul qui s'appuient sur les résultats d'essais effectués directement sur le site du projet, garantissant ainsi que la conception tiendra compte des conditions naturelles de compacité, de saturation et de pression. Certains de ces essais, c'est le cas des essais de pressiométrique, procurent des renseignements impossibles à obtenir en laboratoire. Dans cette partie, nous étudierons l'essai pressiométrique, ainsi qu'un bref aperçu des méthodes sismiques.

II.1) Essai pressiométrique

L'essai pressiométrique est réalisé sur le terrain. Il permet une approche différente des problèmes géotechniques et la réalisation d'un nombre plus important d'essais que le laboratoire ne le permet.

24

L'essai consiste en une dilatation radiale d'une sonde cylindrique dans un trou de forage pour déterminer la relation entre la pression p appliquée sur le sol et le volume du déplacement de la paroi de la sonde.

Dans le but d'atténuer l'effet du remaniement provoqué par le forage, des pressiomètres auto foreurs ont été développées. Ils sont munis d'une tarière hélicoïdale intérieure qui perfore le sol à l'avant de la sonde, de telle sorte que les parois de la sonde sont toujours en contact avec le sol pendant l'enfoncement. L'essai le plus connu demeure cependant l'essai avec le pressiomètre Ménard, qui s'effectue à l'intérieur d'un trou de forage.

Les mesures obtenues lors de l'essai permettent de tracer la courbe pressiométrique figure 8.

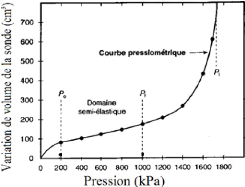
Figure 8 : Courbe pressiométrique

(Source : Mécanique des sols, THEORIE ET PRATIQUE)

Comme la plupart des relations entre les contraintes et les déformations, ces courbes comportent un segment linéaire. À partir du moment où la sonde est bien appuyée à la paroi du sol, moment marqué p0, sur la courbe pressiométrique, le volume augmente linéairement avec la pression, alors que la déformation de fluage demeure faible et constante. Ce comportement, dit semi-élastique, dure jusqu'à ce que le volume de fluage augmente rapidement, au moment (pf) où s'amorce la rupture du sol. La courbe pressiométrique tend alors vers une valeur asymptotique appelée pression limite (pl).

La pente du segment linéaire sert à calculer le module pressiométrique E. En effet, Le

??0(??-??0)

module de cisaillement, module de glissement est défini à partir de la relation ?? = ??-??0

??-??0

?? ,

découlant, en assimilant le sol à un matériau élastique, de l'expression exacte?? = ??₀ × ??

sachant que ??-??0

?? est souvent petit.

Où P0 est une pression initiale isotrope au sein du forage, V0 est le volume de la section droite circulaire du forage.

25

On en déduit la valeur de E à partir de la formule [III.6], avec l'hypothèse faite d'un coefficient de Poisson de 0,33.

E

G = 2 X (1 + v) ? E = 2(1 + y) X G [III. 6]

Inconvénients :

· Une première remarque capitale s'impose : l'essai pressiométrique est un essai qui sollicite rapidement le sol car les paliers de chargement sont d'ailleurs appliqués une minute ; c'est un essai non drainé pour les sols fins et il est donc vain de vouloir approcher des phénomènes de consolidation, à long terme, avec cet essai ;

· Mesures ponctuelles ;

· La détermination de la valeur de G conduisant à la déduction de celle de la valeur de E est faite par une hypothèse du coefficient de Poisson à 0,33. Ce qui ne donne pas forcement des valeurs réelles de E puisque les valeurs du coefficient de Poisson varient de [0 ; 0,5] :

· L'essai pressiométrique fournit des résultats peu sûrs dans le cas précis des argiles molles.

II.2) méthodes sismiques

Dans l'ouvrage ON S E I S M I C PROSPECTING, Adolf A. T. METZGER disait : «de nombreuses données de vitesse sont obtenues à partir de levés expérimentaux effectués en laboratoire. Je n'ai nullement l'intention de nier la valeur de ces méthodes de laboratoire et de leurs résultats, mais plus de 30 ans de prospection géophysique m'ont convaincu que les données les plus fiables sont obtenues par des levés expérimentaux sur le terrain. »

L'exploration sismique est appliquée, ces dernières années, dans le domaine du génie civil. La plupart des problèmes de fondation, tels que la détermination de la profondeur du substratum rocheux, l'étude du sous-sol des tunnels et des barrages, peuvent être résolus par des méthodes sismiques. Une autre application de la sismique dans le génie civil est la détermination, in situ, des modules élastiques du sous-sol.

II.2.1) Avantages de la méthode sismique

Par rapport aux autres essais, la méthode sismique présente des avantages certains :

· Les différentes vitesses de propagation des ondes sismiques intervenant dans les calculs de modules sont mesurées sur place ;

· Elle tient compte des conditions naturelles d'humidité, de pression, de météorologie... Elle prend en compte les différents états du sol ;

· A l'instar des autres méthodes in situ, tel que l'essai pressiométrique, celle à ondes sismiques est peu coûteuse, non invasive et respectueuse des normes

26

environnementales, car elle ne nécessite pas de machines lourdes et ne laisse pas de traces à la surface du site d'essai. De même, elle n'entraine aucun remaniement du terrain ;

· Son exécution est rapide, aussi, peut-on la multiplier pour permettre une meilleure reconnaissance du sol ;

· Il permet d'obtenir rapidement une évaluation générale des modules du couches du sous-sol ;

· Elle donne des résultats globaux par rapport aux essais de laboratoire qui donnent des résultats discontinus ;

· Elle est parfois le seul à réaliser lorsqu'on ne peut pas extraire des échantillons intacts ;

· Les méthodes sismiques sont faites à plus grande échelle ; ils peuvent déterminer une meilleure façon les modules élastiques du sous-sol et permettent d'évaluer des aspects comme la stratification des couches, l'hétérogénéité...

· Un autre avantage est lié au fait que la sismique fournit une coupe stratigraphique avec l'épaisseur des différentes couches du sous-sol sous l'ouvrage. Ce qui permet de déterminer, sur de grandes surfaces et de manière continue, les modules de toute la zone d'étude ;

· La seule méthode sismique permet de déterminer simultanément le module de Young, le coefficient du Poisson, le module de Coulomb et le module d'incompressibilité de chaque couche du sous-sol ;

· La précision des résultats obtenus est tout à fait suffisante pour des études géologiques des zones propices (sélectionnées) de construction¹ ;

· Dans les couches de plus de 20 m de profondeur, les résultats sismiques sont obtenus 25 à 30 fois plus rapidement que par forage au diamant² ;

· La moyenne de la mesure de la réfraction sismique est de 500 mètres de ligne par jour. Cela donne une image claire de l'utilité de la méthode³ ;

· Les méthodes de mesure des ondes de surface fournissent des résultats fiables et constants (Park, Miller &Xia, 1997 ; Xia et al, 2002).

II.2.2) Principe de base de la méthode sismique

Le principe de base de la théorie de l'élasticité infère que dans un solide homogène et isotrope, les déformations sont proportionnelles aux déplacements lorsque ceux-ci tendent vers zéro. En sismique, les contraintes et les déformations sont très faibles et les modules que l'on détermine, par cette méthode, sont assimilables aux modules élastiques.

Les contraintes de compression (respectivement contraintes de cisaillement) se transmettent à une vitesse dite vitesse des ondes de compression ou vitesse longitudinale Vp (respectivement vitesse des ondes de cisaillement ou vitesse transversale V_s). La connaissance de la vitesse de déplacement de ces deux types d'ondes permet de calculer les modules dynamiques des sols par les formules suivantes :

¹ P. TAANILA, pages 19 et 25 de ON SEISMIC PROPECTING ²P. TAANILA, pages 19 et 25 de ON SEISMIC PROPECTING ³P. TAANILA, pages 19 et 25 de ON SEISMIC PROPECTING

27

2₎

			[III.7] [III. 8] [III.9] [III. 10]
???? ??. ???? 2. (3???? ^2-^4???2) ? Module d'allongement : = (???? 2-???? ???? -2????	2 22 1 - - 43	????
Coefficient de Poisson :??? = ^2(?? ?? 2-???? 2) = Module de Coulomb :???? = ??. ????^2 Module d'Incompressibilité : ???? = ?? (????^2 Ou d est la masse volumique.		^2(?? 2) ?? 2-???? ????^2)

L'indice d indique que les constantes élastiques, utilisées dans les relations ci-dessus, sont des constantes dynamiques obtenues par les méthodes de prospection sismique. Elles diffèrent des constants élastiques mesurés en laboratoire. (Source : Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base.)

La vitesse des ondes de compression Vp (ou vitesse longitudinale) est obtenue par la méthode dite sismique réfraction. Quant à la vitesse des ondes de cisaillement Vs (ou vitesse transversale), elle est mesurée par la méthode dite MASW (en français analyse multicanaux des ondes de surface). Ces deux méthodes sismiques seront largement abordées dans les chapitres suivants (IV et V).

28

CHAPITRE IV :LA

MÉTHODE SISMIQUE

RÉFRACTION

29

Le fondement de la méthode sismique réfraction est élaboré sur le fait que le parcours des ondes sismiques se caractérise par des vitesses variables à travers les différentes couches traversées. Ce principe exige deux conditions essentielles : La vitesse doit augmenter avec la profondeur et les diverses couches à travers lesquelles les ondes se propagent, doivent posséder chacune une épaisseur suffisante, permettant la propagation des ondes.

La sismique réfraction peut être utilisée selon deux modes opératoires : sondage réfraction et profil continu. Nous évoquerons uniquement le profil continu. Ce mode permet d'effectuer des coupes sismiques le long des profils sur toute une zone d'intérêt.

Définitions

I.1) Milieu homogène et isotrope

Un milieu est homogène lorsque ses propriétés sont les mêmes partout dans l'espace et isotrope lorsque des propriétés sont uniformes selon la direction. Dans les considérations théoriques, il est généralement admis que les différents milieux ou les roches sont, à la fois homogènes et isotropes. Les roches sédimentaires doivent être anisotropes dès le départ. Leur anisotropie sera augmentée par la pression des sédiments sur elles et par le développement de la schistosité. Des travaux pratiques ont montré que l'effet d'anisotropie n'est pas suffisamment important pour être pris en compte dans les problèmes habituels de prospection sismique. On ne peut pas non plus s'attendre à ce que l'homogénéité existe dans les roches. Cela signifie que les paramètres élastiques sont en réalité fonctions de l'espace. Cependant, leur variation spatiale est assez faible et sans importance en ce qui concerne les changements soudains aux limites entre les différentes roches.

On peut affirmer, que vu des considérations théoriques et des calculs basés sur l'hypothèse, toutes les roches se comportant comme des matériaux élastiques idéaux, sont des simplifications du problème. Cette simplification n'est pas un obstacle, sauf si les seules variables utilisées soient les vitesses de propagation des impulsions sismiques. Dans ce cas, l'écart par rapport à l'état élastique idéal est moins important que les erreurs de la méthode.

I.2) Front d'onde et Rayon sismique

Le front d'onde est la surface passant par l'ensemble des points en phase à un instant t après l'ébranlement. Le principe de Huygens veut que chaque point d'un front d'onde devienne à son tour la source d'émission d'une onde secondaire qui se propage dans toutes les directions avec une vitesse égale à la vitesse de propagation des ondes dans ce milieu. Le nouveau front d'onde est trouvé en joignant les ondes secondaires par une surface tangentielle (figure IV.1). Ces surfaces sont alors des hémisphères concentriques au point d'ébranlement. Le rayon sismique est une ligne perpendiculaire aux fronts d'ondes définis.

I.3) Géométrie des rayons

Un impact mécanique à la source libérera des ondes élastiques se déplaçant à travers le sous-sol. Ces ondes produisent deux types de déformations, l'une est une pure déformation de volume et l'autre relative à la forme. Le premier type produit une compression et une raréfaction alternées dans le matériau ou la roche. Le mouvement des particules se fait parallèlement la direction de propagation. Les ondes sont longitudinales et compressives, appelées ondes P. Le deuxième type est une onde de cisaillement, dans laquelle le mouvement des particules est perpendiculaire à la direction de déplacement. Ces ondes de cisaillement transversales sont appelées ondes S. La vitesse des ondes P est

???? = v(

?? + 4 × u d ) 3 [????. 1]

Où d est la densité. La vitesse des ondes S est

????= vu [????.2]

d

À partir de ces formules, il est évident que les ondes P se propagent toujours à une vitesse plus élevée que les ondes S. Pour cette raison, les ondes P (ondes primaires) arrivent aux stations de géophone avant les ondes S (ondes secondaires). Bref, V_s représente environ 58% de Vp.

Lorsqu'une onde de volume longitudinale (ou transversale) arrive avec une vitesse V1 (ou V1^') à la surface de séparation de deux milieux homogènes et isotropes, une partie de l'énergie est réfléchie, suivant une onde longitudinale de vitesse V1 et une onde transversale de vitesse V1^'. Une autre partie est réfractée suivant une onde longitudinale de vitesse V2 et une onde transversale de vitesse V2^'.

Considérons un rayon incident de compression comme indiqué sur la figure 9 :

30

Figure 9 : Représentation du rayon Figure 10 : Loi de Snell-Descartes

sismique

31

D'après la loi de Snell-Descartes, nous avons :

??₁ sin i₂ = ??₂sini₁ [????. 3]

Lorsque sin i1 = V1/V2 c'est-à-dire i2 = 9Ø°, alors l'onde ne pénètre pas dans le deuxième milieu mais voyage à l'interface entre les deux milieux. L'angle d'incidence est ainsi appelé angle limite ou critique et est défini par

sin i1 = sin ???? =

??1 ???? ???????????? ???? = sin-1 (^??1 ) [ ????. 4] ??2 ??2

Pour tout angle d'incidence i plus grand que ic, il n'y a pas de réfraction et l'onde est totalement réfléchie.

En plus de la réfraction, l'on note d'autres trajets empruntés par plusieurs ondes sismiques provenant d'un ébranlement. Il s'agit de :

? Trajet direct effectué par les ondes longeant directement la surface du point de tir aux géophones ;

? Trajet réfléchi au contact de deux terrains ;

? Trajets diffractés, etc.

Procédure de mise en oeuvre

Il n'existe pas de méthode standard d'effectuer les levés sismiques réfraction. Par contre, le choix du bon intervalle d'espacement entre les géophones est primordial, car il assure l'investigation des structures sous-jacentes avec le plus de détails souhaitables. En fonction du but recherché par les levés et de la complexité des structures, trois tirs (points de tir) peuvent être suffisants par profil, alors que dans d'autres cas, 7 tirs ou même davantage seront nécessaires à la compréhension des structures.

Figure 11 : Dispositif de 24 capteurs et 7 tirs

Les tirs effectués en A et B (pour un intervalle adéquat entre les géophones) nous permettent de calculer les épaisseurs de chaque terrain présent au-dessus de la surface rocheuse. Par exemple, les tirs intermédiaires (exécutés entre les géophones 6 et 7 ; 12 et 13 ; 18 et 19, figure 11) nous permettent de calculer l'épaisseur du premier et parfois du deuxième terrain (si nous sommes en présence d'un problème à trois terrains). De plus, ces tirs supplémentaires nous fournissent plus de précisions sur les vitesses et l'homogénéité de chaque terrain présent. Pour

32

leur part, les tirs effectués en bout de ligne (O et P), c'est-à-dire ceux qui sont placés le plus loin des extrémités du profil sismique ont pour but de renseigner sur l'allure de la topographie du socle et sur la vitesse réelle de celui-ci.

Les appareils sismiques réfraction couramment utilisés en exploration sismique comprennent les principaux éléments suivants :

II.1) Source sismique

L'ébranlement du sol est produit presque toujours au moyen d'explosifs. Ceux-ci sont placés dans un trou qui excède rarement 1 m ou 1,50 m de profondeur. Le rendement est amélioré et les dégâts réduits si le trou est bourré de terre et saturé d'eau. Les détonateurs employés sont des « sismocaps » à retard nul. La quantité d'explosifs employée peut varier, de quelques grammes à quelques kilogrammes. Les dépôts graveleux de sable lâche et les dépôts de tourbières requièrent de grandes quantités d'explosifs, car les ondes sismiques s'atténuent très rapidement dans ces types de dépôts. Au contraire, le till, les argiles et le roc transmettent bien l'énergie jusqu'aux géophones.

L'ébranlement du sol est peut-être également produit par un lourd marteau actionné mécaniquement (que l'on laisse tomber) sur une plaque d'acier posée sur le sol. Lors de la prise des mesures, le marteau reste en place et l'opérateur déplace l'appareil et le géophone à intervalle régulier, à partir du marteau et selon une même direction. Lorsque la distance marteau - géophone est trop grande, l'énergie transmise par cette source d'énergie n'est pas suffisante et l'on doit, en ce moment, avoir recours aux explosifs. Cette pratique augmente considérablement le temps d'exécution des mesures, car la dynamite doit être enterrée et ce, pour chaque point de mesure où le marteau est inefficace.

Parmi les sources non destructives de types chute de poids, nous pouvons également citer la Dameuse DELMAG, la Source VAKIMPAC, la Source SOURSILE etc. Aussi, il existe des sources non destructives de types « fusil ».

On appelle « temps zéro », ou « Time Break TB », l'instant effectif où le tir est déclenché. C'est à partir de cet instant que les temps d'arrivée aux capteurs devraient être observés.

II.2) Géophones

Les géophones sont du type électromagnétique. Ils sont constitués d'une bobine d'induction et d'un aimant permanent, tous deux fixés à un boîtier dont l'un rigidement et l'autre par des ressorts. Le mouvement du boîtier (celui-ci est en contact avec le sol, soit placé sur une plaque ou soit par une pointe enfoncée dans le sol), suivant la verticale, entraîne un déplacement relatif de la bobine par rapport à l'aimant, ce qui crée, aux bornes de la bobine, un courant induit proportionnel à la vitesse. La détection des ondes réfractées est favorisée par l'emploi de géophones ayant une fréquence peu élevée.

33

A titre illustratif, les gammes de fréquence utilisées en exploration vont de 2 à 100 Hz. Les géophones les plus adaptés à la sismique réfraction appliquée au Génie Civil et à l'hydrogéologie sont ceux présentant une fréquence propre comprise entre 8 et 14 Hz. Les 10Hz étant les plus communément utilisés.

II.4) Enregistreur

C'est un système d'enregistrement photographique des oscillations des galvanomètres, muni d'un comptage de temps. Chaque trace correspond à un point de réception. Les traces sont peu agitées avant l'ébranlement et parallèlement, mettent bien en évidence l'arrivée des ondes directes et réfractées par un décrochement perpendiculaire à l'axe de la trace. Les câbles de mesure reliés à l'enregistreur sont appelés circuits galvanométriques (ou flute sismique). Il permet d'acheminer l'arrivée des ondes sismiques des géophones ou points de réception. Lorsque l'appareil est muni d'un écran qui nous permet de suivre les oscillations des rayons lumineux renvoyés par les galvanomètres, le géophysicien ou l'opérateur attend le moment le plus calme avant de déclencher l'explosion et l'enregistrement. Les principaux parasites (ou bruits) qui gênent l'enregistrement sont ceux provoqués par le déplacement d'animaux, de véhicules, de personnes, sans oublier, ceux causés par le vent. Ce dernier secoue la végétation (surtout les arbres) et induit, dans le sol, des vibrations parfois importantes. La pratique courante, en pareil cas, est d'enterrer les géophones, ce qui, en plus, procure un meilleur lien entre les géophones et le sol.

Toute campagne sismique réfraction doit être accompagnée d'un programme de forage, qui, dans un premier temps, nous renseignera sur la nature des dépôts rencontrés lors des levés, nous permettant également de vérifier si l'interprétation est exacte et s'il faut déceler la présence éventuelle de terrain caché.

Principes fondamentaux

Considérons que les déformations élastiques de compression (onde longitudinale) se propagent dans des terrains avec des vitesses maximales. Ces vitesses caractérisent les différents milieux supposés homogènes. Lorsque les vitesses des différents terrains augmentent en fonction de la profondeur, leur investigation par sismique réfraction est alors possible et ce, suivi d'un minimum d'erreurs.

L'onde sismique produite par une source d'excitation parcourt le sol à une vitesse qui dépend des propriétés élastiques de la roche entourant la source. S'il n'y a pas de discontinuité élastique, les ondes se déplaceront symétriquement dans toutes les directions. Les fronts d'onde prennent la forme de sphères, avec la source au centre. Le premier front d'onde atteindra une série de géophones à la surface à différents moments, selon la distance de ces instruments par rapport à la source. La vitesse peut être calculée à partir de la relation V = x / t, où x est la distance et t le temps. Dans le cas d'un milieu continu, une vitesse uniforme sera enregistrée sur tous les géophones. Si l'on constate une variation de la vitesse, la seule explication possible est qu'une ou plusieurs discontinuités élastiques sont cachées dans le sous-sol.

34

III.1) Trajet du front d'onde (cas de deux terrains)

Le cas le plus simple rencontré en sismique réfraction est celui de deux terrains isotropes séparés par un plan parallèle à la surface du sol. L'interface entre ces deux milieux se situe à une profondeur e1. Dans le milieu supérieur, l'onde sismique se propage avec une vitesse V1 et avec une vitesse V2 dans un milieu inferieur telle que V1<V2.Par souci de simplicité, alors supposons également que l'épaisseur du deuxième milieu est infinie.

On observe sur la figure 12 que le premier front d'onde à toucher l'interface est celui qui a le rayon e1. Il atteint la frontière verticalement sous la source. Il existe un point d'incidence critique correspondant à un angle critique i_c tel que sin i_c=V1/V2.Tous les fronts d'ondes, lorsqu'ils atteindront l'interface à ce point se diviseront en deux parties, l'une étant réfléchie de l'interface vers la surface et l'autre étant réfractée dans le second milieu. L'autre partie réfractée se déplacera désormais le long de la frontière à une vitesse V2. A partir de ces ondes réfractées, de nouvelles ondes remonteront à la surface et pourront y être enregistrées par les géophones implantés en surface.

Les ondes réfractées, ou plutôt les fronts d'onde, ont leur centre à l'interface verticalement en dessous de la source. Sur la figureIV.4, le point C représente le lieu du début de la réfraction. Au passage du front d'onde, du milieu 1 au milieu 2, on note une distorsion de l'enveloppe dans le nouveau milieu. LL' représente l'enveloppe du front d'onde pour le second milieu. Du point C, (figure 12) une partie de l'énergie est réfractée vers la surface. Ceci se traduit, pour le premier milieu, par le fait que l'enveloppe des ondes réfractées (EL) est en avance sur le trajet des ondes directes. De même, les enveloppes MF et NP (figure 12) des ondes réfractées sont elles aussi plus en avance que les trajets directs. Les points C, E, F, P et S sont les lieux où les ondes directes et réfractées arrivent en même temps. Les géophones (G), placés en surface, captent le temps pris par l'onde longitudinale pour parcourir les différents trajets AG1...AGn. L'instant de l'ébranlement T = 0, l'arrivée des fronts d'onde aux géophones TG1...TG_n et les distances AG1...AG_n, nous permettent de tracer les dromochroniques (graphique temps-distances) en portant en abscisse les distances et en ordonnée les temps de parcours correspondants (figure 13). Les pentes des deux segments de la dromochronique fournissent les valeurs des vitesses V1 et V2.

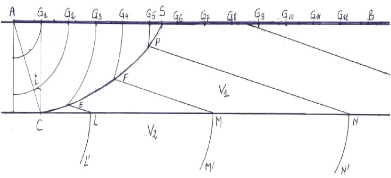
35

Figure 12 : Position des fronts d'ondes (onde longitudinale), cas de deux terrains séparés par un plan horizontal.

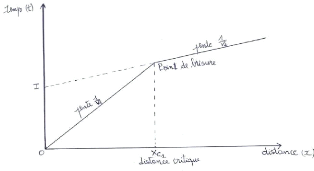
Figure 13 : Dromochroniques dérivées du schéma de la figure 12

Le graphique (figure 13), dérivé du schéma des fronts d'onde de la figure 12, nous fournit les vitesses des deux milieux. Ce sont des vitesses réelles, car les terrains sont parallèles et isotropes.

III.1.1) Temps d'intersection à l'origine

Considérons le point S figure 14, qui représente le lieu où les ondes directes et réfractées arrivent en même temps à la surface.

Figure 14 : Représentation schématique des rayons sismiques, pour le cas de la

figure 13.

Pour l'onde réfractée on a :

???? ???? ??S

T = V₁ + V₂ + V₁ [ IV. 5]

2???? Ou T = v1

+ ???? [ IV. 6] v2

Avec???? = ??1 e?? ???? = ??S - 2e1??????i(AS = X) l'équation [IV.6] devient : ????????

En remplaçant AS par X dans l'équation[ IV. 6], nous retrouvons que :

2e1 T = V1??????i +	X - 2e1??????i [ IV. 7] V2
2e1 T = V1??????i +		X -2e1??i??i + [ IV. 8] V2 V2??????i

Avec sin i = V1 /V2et cos²i+sin²i=1 ;

X T= + V2	2e1	x cos i [ IV. 9]
	V1

Cette dernière expression est l'équation d'une droite de pente 1/V2. Elle coupe l'axe des temps au point I. I est appelé ordonnée à l'origine ou temps d'intersection à l'origine et a pour expression :

x ?????? i [ IV. 10]

I= 2e₁

V1

36

Sur le graphique « temps-distance », les droites de pentes 1/V1 et 1/V2 se croisent en un point appelé point de brisure. Pour les réceptions à gauche de ce point de brisure, le temps du trajet direct est inférieur au temps du trajet réfracté et inversement pour les réceptions situées à droite du point de brisure.

37

III.1.2) Calcul d'épaisseur e1

Le temps d'intersection à l'origine I permet alors de calculer l'épaisseur e1 de la couche.

e1 =	Iv1 [ Iv. 11] 2????????

On peut calculer également l'épaisseur de la couche à partir de l'abscisse du point de brisure Xc ou distance critique.

e1 =	????1 2 vv2 - v1 [ Iv. 12] v2 + v1

III.2) Cas de plusieurs couches planes horizontales et Cas d'un seul marqueur plan incliné

III.2.1) Cas de plusieurs couches planes horizontales

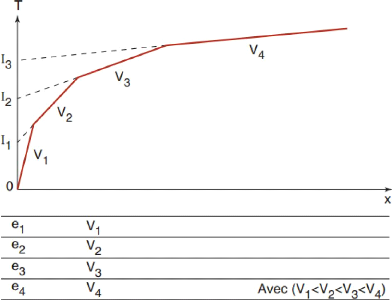
Figure 15 : Cas de plusieurs couches planes horizontales

En exprimant de proche en proche, comme pour le cas de deux couches horizontales, les temps de trajets réfractés totalement à la surface des 2^e ,3^e ,4e, n^e couche, on obtient autant d'équations de droites dont les paramètres sont les suivants :

a) Les inverses des pentes des diverses droites sont égaux aux vitesses des réfracteurs correspondants ;

b) Les ordonnées à l'origine ou temps d'intersection sont fonction des vitesses et des épaisseurs des diverses couches.

Si on admet les notations suivantes : sinip_n = Vp/Vn, les expressions des temps d'intersection sont les suivantes :

Connaissant les vitesses V1, V2, ...Vn-1, V_n, les angles i sont, par conséquent, connus par leurs sinus et on calcule les épaisseurs e1, e2, e3, ep, ... de proche en proche.

??1????????1_,2

??₁ = 2 ??1

[ ????. ^13]

??2 = 2		??1????????1,3 ??1 + 2		??2????????2,3 [ ????. 14] ??2
??3 = 2	??1????????1,4 ??1 + 2		??2????????2,4 + 2 ??2		??3????????3,4 [ ????.15] ??3

??1????????1,??

??1

+ 2

??2????????2,??

+ ? + 2

??2

???? ???????? ??,??

+ ? + 2

????-1?????? ????-1,??

????-1

????-1 = 2

????

= 2 ? ???? ???????? ??,??

??=1

??-1

[ ???? .16]

La généralisation de la notion de délai sismique conduit à :

??-1

??

???????????????,???? ??=1

[ ???? . 17]

2 ??₃????????₂₃ - ??₁

????????23

????????₁₃

??₂ =

??2

????-1 =

38

Les épaisseurs de terrain e1, e2, e3 pourront aussi être obtenues à l'aide des formules aux tangentes suivantes :

De façon générale, ip_n=angle qui a pour sinus la valeur Vp/V_n.

??1 = ?? 12 ??2????????12

??3 =

??32 ??4????????34 - ??2

?????? ??34 ????????24

??1

?????? ??23 ?????? ??13

39

III.2.2) Cas d'un seul marqueur plan incliné

Figure 16 : Cas d'un seul marqueur plan incliné (tirée du Dictionnaire de

Géophysique Appliquée - P. Chapel - 1980)

V2am représente la vitesse apparente pour les trajets se dirigeant vers l'amont du marqueur, et V2av la vitesse apparente pour les trajets se dirigeant vers l'aval. Ces vitesses apparentes sont données par les relations :

??1

??2????

sin(?? + ??) =

sin(?? - ??) = ^??1donc V2am>V2av

??2????

Il vient : 1 ??2

= 2 ( 1 1 ??2???? + ??2?1 ???) 1 ????????

Les angles de pendage étant généralement faibles, on peut négliger le facteur 1/cosá (très peu différent de 1), la formule approchée s'écrit alors :

40

??2 = 2 ( ??2??????2???? ), moyenne harmonique des deux vitesses apparentes.

??2????+??2????

Et ???????? = ??2 2 ( 1

??2???? + 1

??2????)

Les distances perpendiculaires au marqueur : e et e' s'obtiennent à partir des interceptions I1 et I'1:

?? =	2???????? ??1 ??1 et ??' = ??12???????? ??1

Il est important de signaler qu'il suffit d'un très faible pendage pour faire évoluer très rapidement les valeurs des vitesses apparentes en aval et amont.

Causes d'erreurs

Les résultats obtenus par la méthode de réfraction sismique ne sont qu'approximatifs. Il y a des cas où il est impossible, même en théorie, d'atteindre un résultat raisonnablement correct. Parmi ceux-ci, nous pouvons décrire les trois cas suivants :

1^ercas : Les vitesses de couche doivent remplir la condition V1 <V2 <V3 etc. Cette séquence est généralement présente. Les conditions hivernales font exception. Dans le sol « arable gelé », la vitesse est d'environ 3 000 m / sec. Dans la couche sous-jacente, la vitesse est toujours inférieure à 2 500 m/sec. La séquence de vitesses ci-dessus n'est donc pas réalisée et il est impossible, ou du moins improbable que la méthode de réfraction normale donne des résultats précis.

2e cas : Une couche de vitesse complète « zone d'ombre » est parfois perdue. C'est le cas lorsque la première couche de terre végétale est profonde et a une faible vitesse (par exemple 20 mètres, 500 m/sec), et en même temps, la deuxième couche de sol est beaucoup plus mince et que la vitesse est élevée (par exemple 7 mètres, 2000 m/sec). Dans un tel cas, il peut être démontré mathématiquement que la deuxième couche ne peut pas être enregistrée du tout. Il existe certes certaines méthodes par lesquelles l'existence de cette couche peut être démontrée, telles que placer l'explosif en profondeur et réduire les intervalles entre les sismomètres, mais elles ne sont pas toujours suffisantes.

3e cas : De même, il peut être prouvé mathématiquement qu'il est impossible de déterminer avec précision le fond d'un ravin raide dans le lit rocheux. L'onde de choc peut se déplacer du point de tir au sismomètre à travers les parois du substratum rocheux sur les côtés du ravin.

Heureusement, les causes d'erreur mentionnées ci-dessus sont très rares. Elles ne peuvent donc pas être considérées comme invalidant la méthode de réfraction sismique.

41

CHAPITRE V :

METHODE D'ANALYSE

MULTICANAUX DES

ONDES DE SURFACE

(Multichannel Analysis of

Surface Waves Method

MASW)

42

La nature dispersive des ondes de surface en milieu stratifié fournit des informations essentielles sur les propriétés des matériaux proches de la surface. La base de la plupart des méthodes d'analyse des ondes de surface est une détermination précise de la vitesse dépendant de la fréquence du mode fondamental des ondes de Rayleigh (Park et al, 1997). En plus d'être liée à la fréquence, la vitesse de l'onde de Rayleigh est liée à plusieurs groupes de propriétés de la Terre. La plus importante est la vitesse de l'onde de cisaillement des différentes couches du sol. En inversant, ainsi, la vitesse des ondes de Rayleigh, on obtient le profil de vitesse des ondes de cisaillement pour le site d'essai (Xia, Miller & Park, 1999)

Ondes de surface

Dans un milieu élastique infini, il ne peut exister que des ondes de volume (longitudinales et transversales). Quand le milieu élastique infini est divisé en deux milieux aux propriétés élastiques différentes, leur surface de séparation donne naissance à des réflexions des ondes de volume. Celles-ci vont se combiner pour générer un nouveau type d'ondes appelées ondes de surface. Des travaux montrent que dans un milieu semi-infini, près de 67 % de l'énergie engendrée par une source sismique donnée se propage sous forme d'ondes de surface et le reste sous forme d'ondes de volume (26% d'ondes de cisaillement et 7% d'ondes de compression) (Miller et Pursey (1955)). La vitesse des ondes de surface est plus faible que celle des ondes P et S. Ces ondes sont les dernières à se manifester sur un enregistrement (sismogramme). Leur énergie s'affaiblit exponentiellement en fonction de la profondeur. A l'inverse des ondes de volume, généralement indépendantes de la fréquence (très peu dispersives), les ondes de surface ont la grande caractéristique d'être dispersives c'est-à-dire que leur vitesse dépend de leur fréquence. Cette dispersion produit une déformation de la forme de l'onde. Les ondes de surfaces regroupent :

? Les ondes de Rayleigh ; ? Les ondes de Love ; ? L'onde de Stoneley ; ? Les ondes de Scholte.

Les ondes de Rayleigh, de Stoneley et de Scholte ont des mécanismes de propagation très semblables et différents de ceux de l'onde de Love. Les ondes de surface les plus étudiées et couramment utilisées, sont les ondes de Rayleigh et les ondes de Love. En prospection sismique terrestre, ces dernières connues sous le nom de « Ground-Roll » forment un bruit nuisible lors de l'enregistrement des ondes de volume dont on ne peut jamais se débarrasser complètement. Elles se propagent dans les couches superficielles du sous-sol avec des vitesses relativement faibles comparables à celles des ondes transversales.

43

I.1) Onde de Rayleigh

Les ondes de Rayleigh résultent de l'interaction (Interférences constructives) entre les ondes P et SV au voisinage de la surface du sol. Dans un milieu élastique homogène et isotrope, seules apparaissent des ondes de Rayleigh ; elles se propagent sur l'interface libre. A la surface leurs amplitudes sont élevées. Ces amplitudes se réduisent d'une manière exponentielle avec la profondeur et s'annulent quand cette profondeur s'approche de la longueur d'onde.

I.1.1) Caractère dispersif des ondes de Rayleigh

Dans un milieu stratifié, les ondes de Rayleigh sont dispersives. La dispersion est la dépendance de la vitesse à la fréquence. La prospection sismique par ondes de surface repose sur le phénomène de dispersion. Celle-ci traduit la relation entre profondeur de pénétration des ondes sismiques de surface et les propriétés élastiques du milieu qui varient avec la profondeur. En effet, si le milieu géologique, dans lequel se propagent les ondes de surface, possède des propriétés élastiques variables avec la profondeur, alors la vitesse des ondes de surface varie avec la longueur d'onde. Les ondes de surfaces à haute fréquence (faibles longueurs d'ondes) provoquent un mouvement des particules localisées plus en surface alors que le mouvement des particules du milieu plus profond est lié aux basses fréquences (grandes longueurs d'ondes) figure 17. Il en résulte que la profondeur d'investigation dépend donc des fréquences enregistrées.

En milieu dispersif, des ondes de différentes fréquences se propagent à des vitesses différentes : la vitesse de groupe et la vitesse de phase.

? La vitesse de groupe correspond à la vitesse de propagation de l'enveloppe du train d'ondes (vitesse du paquet énergétique) ;

? La vitesse de phase correspond à la distance parcourue par unité de temps, par un point de phase constante de la surface d'onde. Cela peut être par exemple un pic (maximum) ou un creux (minimum) ou encore un point nul du signal.

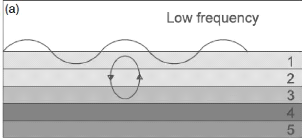
44

Figure 17 : Les ondes de Rayleigh de basses fréquences (a), pénètrent plus profondément que les ondes de Rayleigh de hautes fréquences (b) et (c). (Evrett, 2013)

Principales étapes de la méthode MASW

Plusieurs méthodes d'analyse des ondes de surface sont utilisées pour extraire les courbes de dispersion des ondes de Rayleigh et pour estimer le profil de vitesse des ondes de cisaillement des couches supérieures du sol. Les méthodes les plus connues sont :

? Steady State Rayleigh Method (SSRM);

? Spectral Analysis of Surface Waves (SASW);

? Multichannel Analysis of Surface Wave (MASW).

Ces méthodes, par leur principe, sont très peu différentes les unes des autres. Nous évoquerons seulement la méthode Multichannel Analysis of Surface Waves (MASW). Celle-ci

45

présente plusieurs avantages par rapport aux autres méthodes. L'acquisition de données sur le terrain prend beaucoup moins de temps et le traitement des données est plus rapide et plus facile. En outre, les sources de bruit, (telles que l'inclusion des ondes de volume et les ondes réfléchies et/ou diffusées), peuvent être plus facilement identifiées et éliminées par rapport aux autres méthodes. La réduction du bruit est d'une grande importance, car elle conduit à un profil de vitesse des ondes de cisaillement plus précis (Park, Miller & Xia, 1999 ; Xia et al, 2002). Aussi, les courbes de dispersions multimodales et la génération d'images de dispersion en deux (ou trois) dimensions deviennent-elles possibles et économiquement réalisables en utilisant la méthode MASW (Park, Miller & Xia, 2001 ; Park, Miller, Xia & Ivanov, 2007 ; Xia, Miller, Park & Tian, 2003).

La méthode MASW peut être divisée en trois étapes principales (Park et al, 1999) :

? Acquisition des signaux temporels (x,t) ;

? Extraction de la courbe de dispersion ;

? Inversion de la courbe de dispersion pour obtenir Vs(z).

II.1) Acquisition des signaux temporels (x,t)

La méthode d'analyse multicanaux des ondes de surface (MASW) a été introduite par Park et al. (1999). Les méthodes MASW sont divisées en méthodes actives et passives en fonction de la manière dont les ondes de surface nécessaire à l'analyse sont acquises. Dans la méthode MASW active, les ondes de surface sont générées activement par des sources sismiques impulsives ou vibrantes, tandis que la méthode MASW passive utilise des ondes de surface générées par des sources naturelles, c'est l'exemple de la circulation (Park et al., 2007).

Les signaux sont enregistrés par une centrale sismique classique. Les récepteurs sont alignés avec un espacement égal (Park et al, 1997). Une onde est générée avec une charge d'impact et les géophones enregistrent le mouvement de l'onde résultante en fonction du temps. Un seul tir suffit (Park et al. 1999). Le choix des capteurs dépend également de la problématique étudiée et de la méthode employée (active ou passive).

Dans la prospection sismique courante (dispositifs linéaires), les géophones sont généralement de fréquence de coupure basse 4,5 Hz (10 Hz pour la sismique réfraction). Ces types de capteurs n'enregistrent que le mouvement vertical des particules perpendiculaires à la surface de mesure.

En général, en augmentant le nombre de géophones, on peut obtenir une plus grande résolution de l'image de dispersion (Park et al., 2001 ; Ryden, Park, Ulriksen & Miller, 2004). La figure 18 présente un profil général de mesure de la méthode MASW active avec 24 géophones.

46

Figure 18 : Exemple d'un profil de mesure avec la méthode MASW. (Bodet,2005)

Une source sismique plus lourde entraîne une augmentation de la profondeur d'investigation. Le choix le plus courant est l'utilisation d'un marteau lourd (10 kg) qui peut entraîner une profondeur d'investigation de 10 à 30 m.

Une source capable de fournir plus de puissance d'impact dans le sol (une grue et une lourde charge en chute), a le potentiel de créer des ondes de surface de fréquences plus basses. Elle augmente ainsi la profondeur d'investigation en dessous de 30 m. L'utilisation d'une plaque métallique ou non métallique peut aussi aider à générer des ondes de surface à basse fréquence. Une plaque métallique est un choix plus conventionnel. Cependant, il a été rapporté qu'il est possible de générer des ondes de surface à basse fréquence notable en utilisant une plaque de caoutchouc ferme.

Dans la pratique, il convient d'éviter un très long profil sismique. Les ondes de surface générées par les sources sismiques les plus courantes sont atténuées en dessous du niveau de bruit, à la fin d'un étalement excessif du profil sismique. Ceci rend le signal du récepteur le plus éloigné trop bruyant pour être utilisable. (Park et al, 1999).

II.2) Notions générales sur le traitement de signal et courbe de dispersion des ondes de surface

Le terme « traitement » dans l'analyse des ondes de surface consiste en l'extraction des caractéristiques dispersives d'un milieu, tels que la vitesse de phase et la fréquence, à partir des données acquises sur le terrain.

Les techniques de traitement, les plus utilisées, reposent sur la transformation du champ d'onde dans un autre domaine, où l'énergie de la propagation de l'onde est exprimée en fonction de la vitesse de phase et de la fréquence (Foti, 2000 ; Bodet, 2005). La relation existante entre la vitesse de phase et la fréquence est appelée courbe de dispersion (illustrée sur la figure 19).

47

Figure 19 : Courbe de dispersion des ondes de surface

Lors du « traitement », les différents événements sont identifiés, filtrés et les caractéristiques dispersives sont extraites. Une des méthodes de traitement de signaux obtenus par des enregistrements multicanaux est la méthode fk qui utilise la transformée de Fourier à deux dimensions (2D) proposée par Nolet et Panza (1976), mais élargie dans son champ d'application par Gabriels et al. (1987). Cette transformation décompose le champ d'ondes en ses composantes à des fréquences constantes et de nombres d'ondes. Cette méthode est utilisée dans le traitement des données sismiques parce qu'elle permet de séparer et de filtrer des événements qui ont différentes fréquences, nombres d'ondes et vitesses apparentes. D'autres méthodes, telles que la méthode tp (Sheriff et Geldart, 1995), la méthode pw (Rusell, 1987 ; Mokhtar, 1988) ou le SPAC (Aki, 1957) sont également utilisées dans le traitement des ondes de surface pour aboutir à la courbe de dispersion.

Les résultats sont généralement présentés par une image de dispersion bidimensionnelle obtenue en traçant la courbe des valeurs de As (Amplitude des sommes des courbes sinusoïdales) dans le repère défini par les axes (fréquence, vitesse de phase, d'amplitude résultante normalisée). Les bandes de haute amplitude observées afficheront les caractéristiques de dispersion des ondes de surface enregistrées (voir figure 20). Alternativement, la dispersion de l'image peut être présentée en trois dimensions où les caractéristiques de dispersion sont à la fois indiquées par la hauteur des pics observés (voir figure 21).

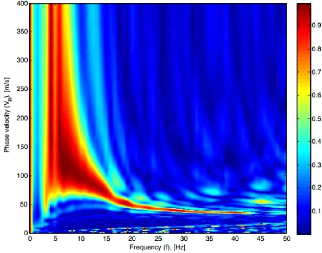
48

Figure 20 : Image de dispersion en deux dimensions obtenues par la méthode de déphasage.

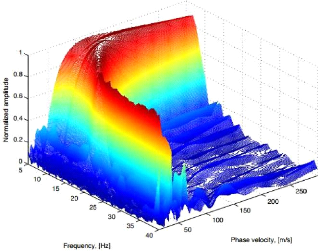
Figure 21 : Image de dispersion en trois dimensions obtenues par la méthode de

déphasage.

49

II.2.1) Extraction des courbes de dispersion

Sur la base du contenu énergétique du champ d'onde des ondes de surface enregistré, une ou plusieurs courbes de dispersion peuvent être extraites des spectres de vitesse de phase. Les caractéristiques de dispersion du mode fondamental sont généralement les plus intéressantes car les méthodes d'inversion les plus courantes n'utilisent que la courbe de dispersion en mode fondamental. L'extraction de la courbe de dispersion est donc basée uniquement sur le mode fondamental. Cependant, en raison des avantages rapportés de l'inversion multimodale, l'extraction de courbes de dispersion multimodales est à noter (Xia, Miller & Park, 2000b).

La figure 22 montre une image de dispersion tridimensionnelle où le maximum du panneau de dispersion, correspondant à chaque composante de fréquence dans la gamme de 10 Hz à 39 Hz, a été extrait. Les valeurs de crête extraites, correspondant aux fréquences 12,5 Hz et 33,3 Hz, sont spécialement indiquées par des marqueurs verts agrandis. La courbe de dispersion, obtenue à partir de l'image de dispersion, qui est fonction de la vitesse de phase et de la longueur d'onde, est présentée à la figure 23.

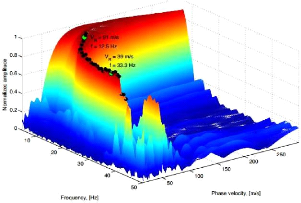
Figure 22 : Caractéristiques de dispersion du mode fondamental

La figure 22 montre la courbe de dispersion du mode fondamental obtenue par la méthode de déphasage. Les maximums, correspondant aux fréquences dans la gamme de 10 Hz à 39 Hz, sont indiqués par des points noirs. Les maximums, correspondant aux fréquences 12,5 Hz et 33,3 Hz, sont indiqués par des points verts.

Figure 23 : Courbe de dispersion en mode fondamental obtenue à partir de l'image de
dispersion illustré à la figure 22.

II.2.2) Inversion de la courbe de dispersion

L'inversion de la courbe de dispersion des ondes de surface permet d'aboutir à l'estimation des propriétés mécaniques du sous-sol. Le résultat est souvent présenté sous la forme d'un profil vertical de vitesses des ondes de cisaillement, VS, comme illustré sur la figure 24.

50

Figure 24 : Profil vertical de la vitesse des ondes de cisaillement, Vs

51

L'inversion a longuement été étudiée en géophysique particulièrement dans les méthodes sismiques (Tarantola, 1987, 2005 ; Snieder, 1998 ; Sambridge, 1999). Elle vise à déterminer une image du milieu et à attribuer, en chaque point, une valeur représentative. Il s'agit, dans notre cas, de déduire le profil de vitesse des ondes de cisaillement d'un site en fonction de la profondeur.

Les méthodes d'ondes de surface possèdent de nombreux avantages, cependant elles présentent aussi des limites. L'incertitude liée à l'inversion en est la raison principale. Elle est liée tant au type du milieu ausculté (sols hétérogènes, piégeage de l'énergie dans des zones de faibles caractéristiques mécaniques, absence d'informations géologiques) qu'au mode d'acquisition (la profondeur de résolution dépend de la taille du dispositif, de la taille de la zone de contraste par rapport à l'espacement entre les capteurs, les bruits gênants, l'offset proche et l'offset lointain). Ne pas tenir compte de ces limites pourrait induire une interprétation erratique du profil sismique vertical pour le milieu ausculté et avoir une approche trop simplifiée de la méthode (Bodet et al., 2005).

52

CHAPITRES VI :

CAMPAGNE SISMIQUE

EFFECTUEE SUR LE

PERMIT D'OREZONE

53

Sur demande de la société minière, LIM africa, a effectué une campagne sismique le 18 décembre 2018 sur le permit d'Orezone. Cette campagne a consisté en deux (2) types de levés sismiques : la sismique réfraction et le Multichannel Analysis of Surface Waves (MASW). Le but de la sismique réfraction était de déterminer les vitesses de propagation des ondes longitudinales ou de compression (Vp) des différentes couches du sous-sol de la zone d'étude. Celui de la méthode MASW était de déterminer les vitesses de propagation des ondes transversales ou de cisaillement (V_s) de ces mêmes couches du sous-sol de la zone d'étude.

Mesures des ondes de compression et des ondes de surface

I.1) Matériels d'acquisition

Pour effectuer le levé, un équipement sismique complet a été utilisé, comprenant :

? Des capteurs : Les capteurs utilisés sont des géophones de fréquence 10 Hz qui sont enfoncés dans le sol suivant la verticale (figure 25).

Figure 25 : Géophone enfoncé dans le sol

? Un enregistreur : L'enregistreur utilisé est un sismographe DAQlink 4 de 24 canaux. Il est alimenté par une batterie 12V, relié à un ordinateur pour la visualisation (figure 26).

54

? Une source sismique : La source sismique utilisée est un choc d'un lourd marteau de 10 kg, sur une plaque de caoutchouc ferme, posée au sol. (Figure 27). Afin d'augmenter le rapport signal sur bruit, plusieurs coups ont été portés sur le même point de tir.

Figure 26 : Sismographe et accessoires

Figure 27 : « Trigger » ou déclencheur relié au marteau sur une plaque

? Des flûtes sismiques : Deux flûtes, de 161 mètres chacune, ont été utilisés. Chaque flûte a des points de connections espacés de 10 mètres. Les flutes sont

reliées à l'enregistreur et aux géophones, permettant ainsi d'acheminer l'arrivée des ondes sismiques.

Les mesures ont été effectuées le long de deux profils croisés : un profil dans la direction S-N et un autre dans la direction E-W. Les deux profils étaient centrés autour d'un forage.

I.2) Déploiement du matériels et enregistrement des ondes

Pour effectuer les mesures, on déploie le sismographe, ensuite on procède aux différentes connexions. Pour cela, il faut brancher le câble réseau, le câble d'alimentation, connecter le trigger et mettre en place les flûtes et les géophones avant de les connecter. Les dispositifs sismiques pour les enregistrements des ondes P et les ondes de surface sont similaires. Pour la gestion du temps zéro, le « trigger » est relié au marteau par des attaches, de manière à ce que le déclencheur soit le plus proche possible du point d'impact. (Figure 27)

NB : Avant toute mesure, il faut vérifier à l'aide du logiciel Vibrascope, le fonctionnement du dispositif.

L'enregistrement des ondes P utilise la technique de sismique réfraction des ondes de volume tandis que l'enregistrement des ondes de surface celle de la technique MASW.

55

Figure 28 : Dispositif de 24 capteurs et 7 tirs

Le dispositif utilisé (figure 28) pour l'acquisition comporte 24 capteurs espacés de 7 mètres les uns des autres. Sur chaque profil, 7 tirs ont été effectués avec 10 coups sur chaque tir (figure 28) et 0.5s de temps d'enregistrement pour la sismique réfraction. 2 tirs offset ont été aussi effectués avec 2s de temps d'enregistrement pour MASW.

Ces tirs sont repartis comme suit :

? Deux tirs O et P, extérieurs au dispositif (tirs offset ou tirs lointains) ;

? Deux tirs A et B en bout de dispositif (tirs en bout) ;

? Deux tirs intermédiaires D et E entre les capteurs 6 et 7 d'une part et les capteurs

18 et 19 d'autre part ;

? Un tir C au centre du dispositif.

56

La distance entre O (respectivement entre P) et le premier capteur (respectivement dernier capteur) est 30m. Celle séparant A (respectivement B) et le premier capteur (respectivement dernier capteur) est 3,5m. (Les détails des tirs se trouvent en annexe 1)

Traitement et résultats des données

Les données acquises sont traitées à l'aide de différentes applications du logiciel SEISIMAGER 2D. Le logiciel SEISIMAGER 2D est un progiciel de modélisation, de traitement et d'interprétation. Il permet, à partir des ondes de volumes, d'obtenir des vitesses de compression Vp des différentes couches grâce aux applications PickWin et Plotrefa. Il sert par ailleurs à la détermination des vitesses des ondes de cisaillement VS par l'analyse des ondes de surface. Et ce, grâce aux applications PickWin et Surface Wave Analysis.

II.1) Sismique réfraction

II.1.1) Traitement de données

Les données obtenues par la sismique réfraction ont été traitées en deux étapes :

La première étape consiste en cette nécessité de pointer les premières arrivées de tous les tirs à l'aide de l'application PickWin à travers les étapes suivantes :

? Ouvrez le fichier ;

? Renseignez la géométrie ;

? S'il y a lieu, adaptez la visualisation des traces ;

? Pointez manuellement les premières arrivées du tir chargé ; après pointage, on

construit automatiquement la dromochronique ;

? Enfin, enregistrez la dromochronique.

Répétez l'opération avec tous les autres tirs. Après pointage, vérifiez les vitesses apparentes. On obtient alors la Figure 29.

57

Figure 29 : Pointage des premières arrivées des tirs avec l'application PickWin

La figure 29 présente les dromochroniques colorées déjà obtenus à partir des différents pointages des premières arrivées des tirs 1,2...

La seconde étape est l'affichage des courbes distance-temps avec l'application Plotrefa. On obtient les différentes dromochroniques sans les traces (Figure 30).

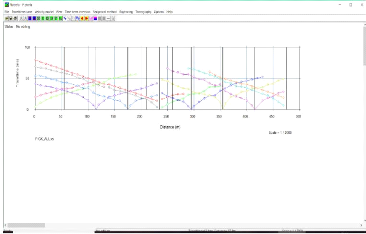
Figure30 : courbes distance-temps obtenues des pointés des premières arrivées

La figure 30 présente toutes les dromochroniques colorées construites automatiquement à partir des différents pointages des premières arrivées des tirs 1,2...

58

Toujours avec l'application Plotrefa, on exécute les opérations suivantes :

- Importez de la topographie du profil sismique ;

- Créez d'un modèle initial tabulaire multicouche ;

- Lancez l'inversion ;

- Convertissez en modèle multicouche ;

- Lancez d'une nouvelle inversion ;

- Affichez des raies sismiques synthétiques ;

- Mise en page des résultats. Le modèle de vitesse est ensuite ajusté avec les

informations géologiques pour obtenir un modèle géologique proche de la réalité

(Figure 31) ;

- Enregistrez des résultats

Figure 31 : modèle de vitesses des couches du sous-sol III.1.2) Résultats obtenus de la sismique réfraction

Les vitesses de compression Vp, obtenues du levé de la sismique réfraction sur les deux profils sont réparties comme suit :

59

Tableau 3 : Vitesses des ondes de compression

Numéro Couche	Vitesse VP en m/s
1	500
2	1000
3	1700
4	2500
5	4000

(Les détails de ces résultats se trouvent en annexes 2 ; 3 ; 4 et 5)

Les résultats de la sismique réfraction permettent de distinguer clairement cinq horizons.

II.2) MASW

II.2.1) Traitement de données

Le traitement a été fait en deux étapes :

La première étape a consisté au filtrage des signaux sismiques à l'aide de l'application

PickWin, en exécutant les opérations suivantes :

? Ouvrez le fichier ;

? Renseignez la géométrie ;

? S'il y a lieu, adaptez la visualisation des traces. Nettoyez les données bruyantes grâce

à un filtrage ;

La seconde étape a permis d'avoir l'image (figure 32) de dispersion en deux dimensions, correspondant à une gamme de fréquence de 0 à 30 Hz et la courbe de dispersion représentée par des points rouges sur l'image, avec l'application Surface Wave Analysis.

60

Figure 32 : image de dispersion en deux dimensions et la courbe de dispersion obtenues
grâce à l'application PickWin

Le choix approprié du nombre de couches nous permet d'obtenir un graphe des vitesses de cisaillement en fonction des épaisseurs de chaque couche. (Figure 33).

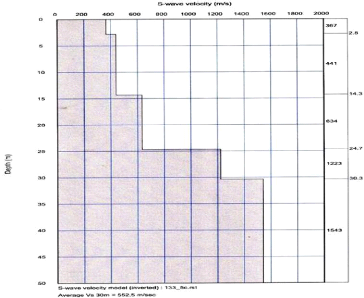
61

Figure 33 : Profil de vitesses des ondes de cisaillement VS III.2.2) Résultats obtenus de MASW

Les résultats obtenus de MASW, sur les deux profils, montrent qu'on est en présence d'un terrain formé de cinq couches réparties comme suit :

Tableau 4 : Vitesses des ondes de cisaillement

Numéro Couche	Vitesse VS en m/s
1	367
2	441
3	634
4	1223
5	1543

La MASW aboutit aux mêmes modèles de 5 terrains que la sismique réfraction. En effet, ces deux (2) essais montrent que le terrain est composé de cinq horizons.

La campagne sismique a consisté en la sismique réfraction et en MASW sur deux profils. Les traitements des données présentent cinq couches comportant des vitesses de compression et des vitesses de cisaillement. Nous pouvons donc dire que :

62

La première couche a une épaisseur variante entre 0 m et 3 m. Ses vitesses d'onde de compression et de cisaillement sont respectivement de 500 m/s et de 367 m/s.

La deuxième couche d'épaisseur, comprise entre 3 m à 10 m, est plus prononcée au centre des profils. Elle a une vitesse d'onde de compression de 1000 m/s et une vitesse d'onde de cisaillement de 441 m/s.

La troisième couche a une vitesse de compression de 1700 m/s et une vitesse cisaillement de 634 m/s. Elle a également une épaisseur d'environ 10 m.

La quatrième couche, d'épaisseur d'environ 20 m, possède une vitesse de compression de 2500 m/s, une vitesse de cisaillement de 1223 m/s.

Le réfracteur principal, (toit de la couche la plus profonde), est caractérisé par une vitesse de compression de 4000 m/s et une vitesse de cisaillement de 1543 m/s.

L'examen des résultats obtenus, de l'étude du sol et des données du forage, (Les détails de ces résultats se trouvent en annexe 5), nous permet de déduire que le sous-sol de la zone d'étude se caractérise essentiellement par les formations suivantes :

Couche 1 est formée de limon ;

Couche 2 est attribuée au sable ;

Couche 3 correspond à de l'argile ;

Couche 4 est attribuée à des arènes de diorite quartzifère ;

Couche 5 correspond à de la diorite quartzifère.

Tableau 5 : Synthèse des résultats

Numéro de Couche	Lithologie	Epaisseurs (m)	Vp (m/s)	Vs (m/s)
1	Limon	0-3	500	367
2	Sable	3-10	1000	441
3	Argile	10-20	1700	634
4	Arènes de Diorite quartzifère	20-40	2500	1223
5	Diorite quartzifère	40-68	4000	1543

63

NB :

« One thing, at least, I wish to point out. Differentes in velocity sufficiently great to allow recognition of a boundary between two rocks need not indicate or be identical with stratigraphic boundaries. For the phenomen ondoes not depend on petrological contrasts but only on physical contrasts, a fact that concerns all geophysical methods arid should not be forgotten by the geologist. Hence seismic discontinuities need not always be identical with known rock boundaries, but as markers they may greatly assist in the interpretation of the structures. » Adolf A. T. METZGER, ON S E I S M I C PROSPECTING page 17

Calculs des modules élastiques

Le sous-sol de la zone d'étude est constitué de cinq couches différentes. Les constantes d'élasticité (hormis le coefficient de poisson) dépendent de la densité. Pour les calculs, nous utiliserons les valeurs des tableaux1 et 2. Ces valeurs, comprises dans des intervalles, l'application de la formule de Gardner et All⁴ permet d'obtenir des résultats proches de celles du terrain. Les valeurs des densités obtenues permettent de calculer, respectivement le module de Young, le coefficient du Poisson, le module de Coulomb et le module d'incompressibilité de chaque couche.

III.1) Couche 1 : limon

La couche numéro 1 est composée de limon, du sable...Nous estimons sa densité à celle de la terre végétale. Ses vitesses de compressions Vp et de cisaillement Vs sont respectivement de 500 m/s et 367 m/s. La densité de terre végétale est comprise entre 1100-1200 kg/m³ (extrait du Tableau 18 page 83 de GEOPHYSICAL EXPLORATION).

La densité calculée est d = 0.31 ^Vp0.25 avec VP = 500 m/s ; d = 0.31X 500^0.25 = 1465 kg/m³.

III.1.1) Calcul du module de Young de la couche 1 Le module dynamique d'allongement est :

			2) (^3V?? ^2-^4V?2) ?
E?? =	??.	2. ????		; Avec Vp = 500 m/s ; Vs = 367 m/s et d = 1465 kg/m^3
			^2-V?? (V??

Application numérique :

E?? = 1465 X 367² X (3X500² - 4X367² )

(500² - 367² )

Ed = 361479270,537 kg/ms²

⁴La formule de Gardner et All est valable pour la détermination des densités des différentes couches puisque la géologie locale ne fait pas cas des évaporites sel gypse anhydrite...

Ed = 0,361479270537 10⁹ kg/ms² Ed = 0,36147 GPa

III.1.2) Calcul du coefficient du Poisson de la couche 1 Le coefficient dynamique du Poisson est :

= 1

22 V?? - ²V??

?d = 2(V_??² - V??2)

_V2

??

2)

2(V?? 2 - V??

64

500² - 2X367²

?d = 2(500² - 367² )

?d = -0,0840249
?d = -0,084

III.1.3) Calcul du module de Coulomb de la couche 1

Le module dynamique de Coulomb est :

ud = ??. V??²

ud = 1465X367²

ud = 197319385 kg/ms²

ud = 0,197 G??a

III.1.4) Calcul du module d'incompressibilité de la couche 1 Le module dynamique d'incompressibilité est :

kd= ??(V_??² - ⁴₃V??²)

kd = 1465X (500² - 43 X 367² )

kd = 0103157486,66 kg/m??2 = 0,10315748666 10⁹kg/m??2
kd = 0,103 G??a

III.2) Couche 2 : Sable

La couche numéro 2 est composée majoritairement de sable. Selon le Tableau II.2, l'intervalle de densité pour sable, gravier est de 1400 à 2200kg/m³. Ses vitesses de compressions Vp et de cisaillement Vs sont respectivement de 1000 m/s et 441 m/s. La densité calculée est d = 0.31 ^Vp0.25 avec VP = 1000 m/s ;

65

d = 0.31x1000 0.25 = 1743 kg/m³.

Les calculs des modules de la couche 2 ont donné les résultats suivants :

Le module de Young de la couche 2 est 0,935GPa

Le coefficient du Poisson de la couche 2 est 0,379

Le module de Coulomb de la couche 2est 0,338GPa

Le module d'incompressibilité de la couche 2est 1,291 GPa

III.3) Couche 3 : Argile

La couche numéro 3 est composée essentiellement d'argile. Selon le Tableau 2, l'intervalle de densité pour argile est de 1300 à 2300 kg/m³. Ses vitesses de compression Vp et de cisaillement Vs sont respectivement de 1700 m/s et 634 m/s. La densité calculée est d = 0.31 Vp0.25 avec Vp = 1700 m/s ;

d = 0.31x1700 0.25 = 1990 kg/m3.

Les calculs des modules de la couche 3 ont donné les résultats suivants :

Le module de Young de la couche 3 est 2,270GPa

Le coefficient du Poisson de la couche 3 est 0,42

Le module de Coulomb de la couche 3 est 0,8GPa

Le module d'incompressibilité de la couche 3est 4,68 GPa

III.4) Couche 4 : Arènes de Diorite quartzifère

La couche numéro 4 est composée d'arènes de diorite quartzifère. Ses vitesses de compression Vp et de cisaillement V_s sont respectivement de 2500 m/s et 1223 m/s. La densité calculée est d = 0.31 ^Vp0.25 avec VP = 2500 m/s ;

d = 0.31x2500 0.25 = 2192 kg/m³.

Les calculs des modules de la couche 4 ont donné les résultats suivants :

Le module de Young de la couche 4 est 8,804GPa

Le coefficient du Poisson de la couche 4 est 0,34

Le module de Coulomb de la couche 4 est 3,27 GPa

Le module d'incompressibilité de la couche 4est 9,328 GPa

66

III.5) Couche 5 : Diorite quartzifère

La couche numéro 5 est composée de diorite quartzifère. Ses vitesses de compression Vp et de cisaillement Vs sont respectivement de 4000 m/s et 1543 m/s. La densité calculée est d = 0.31 Vp 0.25 avec VP = 4000 m/s ;

d = 0.31x(4000)0.25 = 2465 kg/m3.

Les calculs des modules de la couche 5 ont donné les résultats suivants :

Le module de Young de la couche 5 est 16,58 GPa

Le coefficient du Poisson de la couche 5 est 0,41

Le module de Coulomb de la couche 5est 5,868GPa

Le module d'incompressibilité de la couche 5est 31,614GPa

Résultats et discussions

Les natures des formations géologiques comme leurs modules élastiques sont consignées dans le tableau 6 suivant :

Tableau 6 : Tableau récapitulatif des modules élastiques

Numéro De Couche	Lithologie	Profondeur (m)	Densité	Module de Young Ed(GPa)	Coefficient du Poisson ?d	module de Coulomb ìd (GPa)	Module d'incompressibilit é kd (GPa)
Couche 1	Limon	0-3	1465	0,361	-0,084	0,197	0,103
Couche 2	Sable	3-10	1743	0,935	0,379	0,338	1,291
Couche 3	Argile	10-20	1990	2,270	0,42	0,8	4,68
Couche 4	Arènes de Diorite quartzi fère	20-40	2192	8,804	0,34	3,27	9,328
Couche 5	Diorite quartzi fère	40-68	2465	16,58	0,41	5,868	31,614

? Module de Young

Nos valeurs vont de 0,361Gpa ; 0,935Gpa ;2,270Gpa ; 16,58 Gpa respectivement pour le limon, le sable, l'argile et la diorite.

67

Elles appartiennent (ou presque) aux tranches de valeurs des modules dynamiques (tirés de l'ouvrage << Génie parasismique>>) :

Terrains cristallins sains : 50 à 100 Gpa

Terrains cristallins fracturés : 15 à 30 Gpa
Sables et graviers, remblais rocheux : 0,500 à 1,500 Gpa

Argiles : 0,100 à 0,500 Gpa

Argiles très molles, vases : 0,010 à 0,100 Gpa

? Coefficient du Poisson

Les valeurs de coefficient du Poisson calculées sont :

Limon = -0,084

Sable = 0,379

Argile = 0,42

Arènes de diorite quartzifères = 0,34

Diorite quartzifère =0,41

Hormis la valeur négative de la première couche, correspondant aux matériaux particuliers dits aux étiques⁵, toutes les autres valeurs appartiennent à l'intervalle [0,25 ; 0,5] comme la plupart des matériaux isotropes continus.

La première couche est composée de limon riche en quartz (issue des débris minéraux résultant de la désagrégation de la diorite quartzifère).

? Module de Coulomb

Les modules de Coulomb calculés sont :

Limon = 0,197 Gpa ;

Sable = 0,338Gpa ;

Argile = 0,8 Gpa ;

Arènes de diorite quartzifères = 3,27 Gpa

Diorite quartzifère =5,868Gpa

⁵ Les matériaux aux étiques sont des matériaux dont le coefficient de Poisson est négatif

68

Les modules de Coulomb du limon et du sable (sol) calculés sont en accord avec ceux de Schön. Selon ses travaux, les modules de Coulomb sont compris entre 0,005 et 0,5 Gpa pour les sols.

? Module d'incompressibilité

Les modules d'incompressibilité calculés sont :

Limon = 0,103 Gpa ; Sable = 1,29 Gpa ; Argile = 4,68 Gpa ; Arènes de diorite quartzifères = 9,328 Gpa

Diorite quartzifère =31,61Gpa

Les modules d'incompressibilité du limon et du sable (sol) calculés appartiennent à la plage (0,01-10 Gpa) des modules d'incompressibilité des sols de Schön.

Les calculs des modules élastiques ont été effectués par couches. Le sous-sol de la zone étant constitué de cinq couches, nous avons utilisé les vitesses Vp et V_s de chaque couche pour le calcul du coefficient de poisson. Ces valeurs sont, pour la plupart, comprises entre 0,25 et 0,5. Le calcul des autres modules s'est fait en considérant les densités respectives des formations géologiques des couches et l'application de la formule de Gardner et All. Les valeurs du module de Coulomb du sol et du module d'incompressibilité du sol appartiennent aux intervalles de valeurs définies par Schön. Quant aux modules de Young, le module de Young du sable appartient aux tranches des valeurs des modules dynamiques (tirés de l'ouvrage << Génie parasismique>>.

69

Conclusion Générale

En somme, la campagne sismique a consisté en la réfraction sismique et La méthode d'analyse multicanaux des ondes de surface (MASW) sur deux profils. Les traitements des données présentent cinq couches avec leurs vitesses de compression et leurs vitesses de cisaillement. Nous pouvons donc dire que la première couche, a une épaisseur variante entre 0 m et 3 m. Elle est localisée à environ 120 m de diamètre au centre de la zone d'étude. Ses vitesses d'onde de compression et de cisaillement sont respectivement de 500 m/s et de 367 m/s.

L'examen des résultats obtenus à partir de la géologie régionale, du cadre géologique du projet aurifère de Bomboré, de l'étude du sol et des données du forage, nous a permis de déduire que le sous-sol de la zone d'étude se caractérise essentiellement par les formations suivantes :

Couche 1 est formée de limon ;

Couche 2 est attribuée au sable ;

Couche 3 correspond à de l'argile ;

Couche 4 est attribuée à des arènes de diorite quartzifère ;

Couche 5 correspond à de diorite quartzifère.

Les calculs des modules élastiques ont été effectués par couches. Le sous-sol de la zone étant constitué de cinq couches, nous avons utilisé les vitesses vp et vs de chaque couche pour le calcul du coefficient de poisson. Ces valeurs sont, pour la plupart, comprises entre 0,25 et 0,5. Le calcul des autres modules s'est fait en considérant les densités respectives des formations géologiques des couches. Les valeurs du module de Coulomb du sol et du module d'incompressibilité du sol appartiennent aux intervalles de valeurs définies par Schön. Quant aux modules de Young, le module de Young du sable appartient aux tranches des valeurs des modules dynamiques (tirés de l'ouvrage << Génie parasismique>>).

Les résultats présentés ci-dessus montrent que les méthodes géophysiques employées, restent de bons outils, pour distinguer rapidement, la nature et les épaisseurs des différentes couches du sol et du sous-sol. Elles fournissent également les vitesses de propagation des ondes sismiques de ces couches qui ont permis de déterminer de manière indirecte les paramètres géotechniques du sol ; en l'occurrence, les valeurs dynamiques des modules d'élasticité ; de cisaillement ; d'incompressibilité et du coefficient de Poisson.

Quelques forages de reconnaissance permettraient de confirmer le nom géologique des couches sismiques et également les profondeurs forages et certains limites sismiques.

Un examen approfondi, à la lumière de ces compléments d'observations, aidera, à améliorer les résultats en particulier dans les zones ou des écarts importants, supérieur à la

70

marge d'erreur admissible, sont constatés. Mieux, cela pourrait aider à constituer une base de données des modules élastiques propres aux sols et sous-sol du Burkina Faso.

71

BIBLIOGRAPHIE

A. A. T. METZGER, P. TAANILA, E. PENTTILA, AND M. T. PORKKA (1965), ON SEISMIC PROSPECTING ;

A. MARIKO (1994), Application des méthodes électriques et magnétique à l'étude des sols ferralitiques : bassin versant de NSIMI (Sud-Cameroun), mémoire de D.E.S.S de l'université pierre et marie-curie paris VI ;

B. DJEBROU, Memoire Online - Traitement du sol par colonne ballastées https://www.memoireonline.com/08/09/2478/m_Traitement-du-sol-par-colonne-ballastees18.html;

B.F. HOWELL, Introduction à la géophysique avec une présentation et des notes complémentaires par H.TAZIEFF, MASSON ? CIE 1969 ; P 202-206 ;

C. A. HEILAND, Sc.D., GEOPHYSICAL EXPLORATION, Hafner Publishing Company, New York and London 1963; P 7-16, P 67-77, P 437-477;

D. J. DION (1986), La Méthode sismique réfraction appliquée au génie géologique, Notions d'interprétation;

http://gq.mines.gouv.qc.ca/documents/examine/DV8506/DV8506.pdf

D. Mabrouk, Sismique Réflexion et Réfraction : Les Principes de Base. Departement de Géophysique. FHC-Université M'Hamed Bougara de Boumerdes. Algérie 9/2016

E. ÓLAFSDOTTIR (2014), Multichannel Analysis of Surface Waves Methods for dispersion analysis of surface wave data, University of Iceland, School of Engineering And Natural Sciences, Faculty of Civil And Environnemental Engineering;

J. C. CHARMET, Mécanique du solide et des matériaux, Elasticité-Plasticité-Rupture, P 4548 ;

https://cours.espci.fr/site.php?id=318&fileid=1242

J. DUBOIS, M. DIAMENT, J. P. COGNE (2011), Géophysique, Cours et exercices corrigés, 4e édition,

http://www.geologues-prospecteurs.fr/cours/geophysique/geophysique.pdf

J. M. BALTASSAT, F. LEJEUNE, G. RICHALET (2001), Détermination par sismique réfraction et sismique transparence de la structure du massif crayeux en bordure de la falaise d'Ault (Picardie) BRGM/RP-51080-FR, 39 p., 5 fig., 2pl.

72

K. ÇAMI (2017), Imagerie du module de cisaillement in situ du sol par méthodes d'ondes de surface et essais géotechniques-Caractérisation des petites aux grandes déformations ;

M. CHOUTEAU, B. GIROUX (2008), Géophysique appliquée II GLQ 3202, Méthodes sismiques, Notes de cours ;

https://moodle.polymtl.ca/pluginfile.php/82322/mod resource/content/0/Notes de cours/Sis mique de genie/Sismique E2008-corrigejuin2010.pdf

O. COMBARIEU (ingénieur ESTP HDR de l'université de Caen) (2006), L'Usage des modules de déformation en géotechnique, revue française de géotechnique n⁰ 114, 1^er trimestre 2006 ;

O. MAGNIN, Y. BERTRAND, Sismique réfraction, les cahiers de l'AGAP n⁰ 2, mars 2005 ;

V. ROBITAILLE, D. TREMBLAY (1997), Mécanique des sols, THEORIE ET PRATIQUE, Modulo Éditeur 1997 ;

Rapport d'étude sur son projet Bomboré, La Conduite de la partie EIES a été confiée au Bureau d'Etudes des Géosciences et Environnement (BEGE), la partie PAR est réalisée par la SOCREGE ; ces deux bureaux sont supervisés par le bureau canadien WSP ;

Compte-rendu d'expertise du groupement IMSRN/CREOCEAN : Apport des données de sondages de 2011, Reconnaissances Géophysiques Préalables aux Travaux de Réaménagement du Port, Port Autonome de Guadeloupe ;

Wikigeotech: Sismique en ondes de surfaces, http://wikhydro.developpement-durable.gouv.fr/index.php/Wikigeotech:Sismique en ondes de surfaces;

Agrément AGAP Qualité : MASW www.soldata-geophysic.fr

i

ANNEXES

Annexes 1 : Positions des tirs pour les différents profils de la sismique réfraction

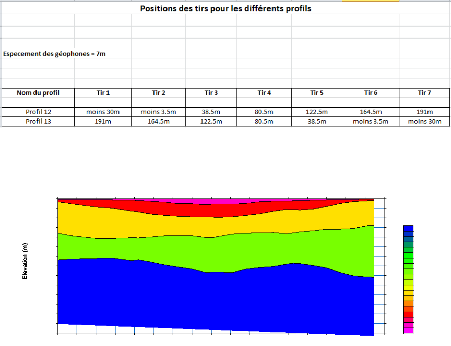
^(m/s)

^{0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170}

Annexes 2: modèle de vitesses de compression (Vp) de différentes couches du profil E-W

⁰

⁵⁰⁰

¹⁰⁰⁰

^-10

^-5

¹⁷⁰⁰

²⁵⁰⁰

⁴⁰⁰⁰

^-15

^-20

^-25

^-30

^-35

^-40

^-45

^-50

^-55

^-60

^-65

^-70

³⁹⁹⁹

³⁶¹¹

³²²²

²⁸³³

²⁴⁴⁴

²⁰⁵⁶

¹⁶⁶⁷

¹²⁷⁸

⁸⁸⁹

⁵⁰⁰

^{Distance (m)}

^Scale = ¹ / ¹⁰⁰⁰

Annexes 3: les courbes distance-temps obtenues des pointés des premières arrivées du profil E-W

^110 ^100 ^90 ^80 ^70 ^60 ^50 ^40 ^30 ^20 ^10 ^0

^{-30 -20 -10 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200}

^{Distance (m)}

^Scale = ¹ / ¹⁰⁰⁰

³⁹⁹⁹

³⁶¹¹

³²²²

²⁸³³

²⁴⁴⁴

²⁰⁵⁶

¹⁶⁶⁷

¹²⁷⁸

⁸⁸⁹

⁵⁰⁰

^(m/s)

ii

Annexes 4 : modèle de vitesses de compression (Vp) de différentes couches du profil S-N

⁰

^-5

^-10

^-15

^-20

^-25

^-30

^-35

^-40

^-45

^-50

^-55

^-60

^-65

^-70

²⁵⁰⁰

⁴⁰⁰⁰

¹⁷⁰⁰

^{0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170}

^{Distance (m)}

^Scale = ¹ / ¹⁰⁰⁰

¹⁰⁰⁰

⁵⁰⁰

Annexes 5 : les courbes distance-temps obtenues des pointés des premières arrivées du profil S-N

^85 ^80 ^75 ^70 ^65 ^60 ^55 ^50 ^45 ^40 ^35 ^30 ^25 ^20 ^15 ^10 ^5 ^0
	^0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170

^{Distance (m)}

^Scale = ¹ / ¹⁰⁰⁰

iii

Annexes 6: Extrait de données de forage