The impact of monetary policy on consumer price index (CPI): 1985-2010

In order to arrive at good conclusions and propose important policies, data to be used must be stationary or made stationary .Non-stationary variables can lead to misleading inferences. So, the following is the analysis of stationarity by using the PP and ADF tests.

Table 5: Summary of Unity root Test using PP and ADF tests

Variables		PP test			ADF test			Conclusion
	Level	Intercept & Trend	Intercept	None	Intercept & Trend	Intercept	None	I(1)
LCPI	Level	-1.509203	-0.037775	1.304367	-1.593095	-0.166940	1.201365
	?level	-5.671982*	-5.278210*	-5.107284*	-5.541824*	-5.277734*	-5.107284*
LM2	Level	-1.808800	-0.840839	-0.919552	-1.808800	-0.840839	-0.912034	I(1)
	?level	-5.215006*	-5.172020*	-5.156853*	-5.206502*	-5.171833*	-5.156853*
LEXCH	Level	-1.465468	-0.700263	2.044835	-1.295550	-0.700263	2.189489	I(1)
	? level	-4.560735*	-4.493495*	-3.732926*	-3.798612**	-4.506769*	-3.755935*
LLIR	Level	-2.598714	-2.192332	0.665482	-2.238489	-2.087310	0.279109	I(1)
	? level	-6.873350*	-6.320553*	-6.143093*	-4.021954**	-2.074770	-1.859478***

Source: Eviews7

* Indicates statistical significant at the 1 percent level,

** Indicates statistical significant at the 5 percent level

*** Indicates statistical significant at the 10 percent level.

From the table above, it can be deduced that variables are not stationary at level. We did not found statistical evidence of rejecting the Null hypothesis of unit root because the asymptotic critical values are less than the calculated value for ADF and the p values are more than 5%. However, when all the variables are transformed to their first difference, the null hypothesis is rejected and variables became stationary. Finally, we concluded that all variables are integrated of order one.

4.2.2.2 Co-integration test

If two or more time series are not stationary, it is important to test whether there is a linear combination of them which is stationary. This phenomenon is referred to as the test for co-integration. The evidence of co-integration implies that there is a long run relationship among the variables. Hence, the short-run dynamics can be represented by an error correction mechanism (Engle and Granger, 1987).

There are two most popular approaches for testing for cointegration, the Engle- Granger two steps procedure and the Johansen procedure. In this research, we applied the Johansen Maximum Likelihood Methodology for the cointegration test. The obtained results are in the following table:

Table 6: Results of Johansen Cointegration Test

Unrestricted Cointegration Rank Test (Trace)
Hypothesized		Trace	0.05
No. of CE(s)	Eigenvalue	Statistic	Critical Value	Prob.**
None	0.650795	45.29174	54.07904	0.2391
At most 1	0.340354	20.04146	35.19275	0.7242
At most 2	0.221537	10.05623	20.26184	0.6343
At most 3	0.155133	4.045828	9.164546	0.4053
Trace test indicates no cointegration at the 0.05 level
* denotes rejection of the hypothesis at the 0.05 level
**MacKinnon-Haug-Michelis (1999) p-values
Unrestricted Cointegration Rank Test (Maximum Eigenvalue)
Hypothesized		Max-Eigen	0.05
No. of CE(s)	Eigenvalue	Statistic	Critical Value	Prob.**
None	0.650795	25.25028	28.58808	0.1260
At most 1	0.340354	9.985229	22.29962	0.8363
At most 2	0.221537	6.010404	15.89210	0.7868
At most 3	0.155133	4.045828	9.164546	0.4053
Source: Eviews7 Max-eigenvalue test indicates no cointegration at the 0.05 level
* denotes rejection of the hypothesis at the 0.05 level
**MacKinnon-Haug-Michelis (1999) p-values

The Trace test as well as the Maximum Eigenvalue test reveals that variables are not co-integrated. Then, these variables are not co integrated to run a regression line by using OLS. Such a regression can lead to misleading inferences. So, we have to use other methods such as unrestricted VAR.

4.2.2.2.1 Estimation of an impact of monetary policy on CPI of Rwanda

The coefficients of our model are numerous and not readily subject to interpretation. Hence, the interpretation follows from the path of the impulse response functions generated from the recursively-orthogonalized VAR estimated residuals. The impulse responses show the path of CPI when there is an increase in the monetary policy variables.

Figure 8: Response of CPI to Monetary Policy Variables

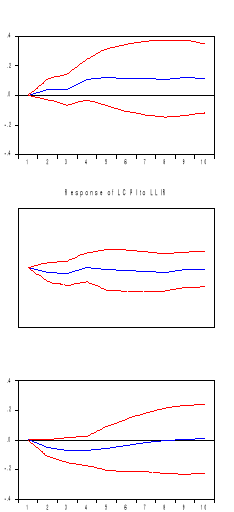
The figure 8 shows three panels of impulse response graphs indicating how increase in respective monetary policy variables affects the CPI of Rwanda in a period of five years. Each panel illustrates the response of CPI to a one standard deviation innovation (corresponding to an increase) in the monetary policy variable.

A value of zero means that the increase in monetary policy variable has no effect on CPI of Rwanda and the CPI continues to behave as if there was no increase in monetary policy variable. A positive or negative value indicates that the increase in the monetary policy variable would cause the CPI of Rwanda to be above or below its natural path as the case may be. The blue lines depict the estimated effects, while the dashed red lines show the boundaries of a 95% confidence interval.

In Panel 1, we observe that an increase in nominal exchange rate has an effect of increasing quickly inflation in the first year, and in the second year it becomes stationary while it increases again in the third year and becomes stationary in the following years. In general, the increase in nominal exchange rate has an effect of increasing the inflation in Rwanda as the blue line is above the natural path. This increase of inflation resulting from the depreciation of Rwandan currency is as expected by theories and given the structure of Rwandan economy. Normally, when there is a depreciation of a country's currency, the theory predicts that the country's exports become cheap while its imports become expensive.

Panel 2 shows how the CPI of Rwanda responds to an increase of nominal interest rate. Increase of nominal interest rate in Rwanda has an effect of decreasing inflation in the first two years. However, in the third year, inflation increases again and reaches its level of beginning in the fourth and fifth year. In the following years, inflation is found to decrease. This is logical because increase in nominal interest rate discourages people to ask for loans and consequently reduces money into circulation.

Panel 3 shows the response of CPI to a positive shock in money supply measured by M2. When there is an increase in money supply in Rwanda, inflation decreases considerably in the first year. However, in the second year, inflation start increasing again and it reaches its original level in the seventh but it increases again in the tenth year. It means that, when monetary authorities realize a need of stimulating production, they increase money into circulation. That increased money is invested into productive activities which increase production in Rwanda.

That increase in production results in reduction of prices in the first year. However, it has been seen that the continual increase of money supply push again prices up in the following years and prices reaches its original level in the seventh year.