Chapitre 5
Approche de resolution
5.1 Introduction
La notion de complexité des problèmes est
très importante, car si un problème est identiflé comme
facile, on connait un algorithme fini et effi cace pour le résoudre, par
contre s'il est identiflé comme étant un problème complexe
il sera diffi cile de trouver un algorithme effi cace pour le résoudre,
il est alors justiflé de se contenter d'exigences plus limitées:
résolution approchée du problème posé,
résolution d'un problème voisin plus simple.
L'exécution des méthodes dites exactes
(programmation dynamique, séparation et évaluation) pour la
résolution des problèmes NP-Diffciles risque de prendre un temps
de calcul considérable, notamment si la taille du problème est
très grande.
Afin d'éviter ce genre de situation, on se contente
souvent d'une solution dite approchée donnée par certaines
méthodes appelées "méthodes approchées" ou
"heuristiques", et dont la valeur de la fonction objectif correspondante se
rapproche de celle de la solution exacte. Vu qu'on est en présence d'un
problème non linéaire assez complexe, nous proposons d'utiliser
une "heuristique" comme méthode de résolution.
5.2. Heuristiques[9]
5.2 Heuristiques[9]
Definition:
Heuristique (du grec heuriskêin, << trouver
>> ) est un terme de didactique qui signife l'art d'inventer, de faire
des découvertes. C'est en sociologie, une discipline qui se propose de
dégager les règles de la recherche scientifque. En optimisation
combinatoire, théorie des graphes et théorie de la
complexité, une heuristique est un algorithme qui fournit rapidement (en
temps polynomial) une solution réalisable, pas nécessairement
optimale, pour un problème d'optimisation NP-diffcile. Une heuristique,
ou méthode approximative, est donc le contraire d'un algorithme exact
qui trouve une solution optimale pour un problème donné.
L'intérêt de l'heuristique étant que pour les
problèmes NP-diffciles, la plupart des algorithmes exacts connus sont de
complexité exponentielle et donc sans aucun intérêt en
pratique. On utilise une heuristique pour obtenir une première solution
réalisable dans un processus de résolution exacte.
Généralement une heuristique est conçue pour un
problème particulié, en s'appuyant sur sa structure propre, mais
les approches peuvent contenir des principes plus généraux. On
parle de métaheuristique pour les méthodes approximatives
générales, pouvant s'appliquer a des différents
problèmes. La qualité d'une heuristique peut s'évaluer
selon deux critères scientifques :
1) Critère pratique, ou empirique: on
implémente l'algorithme approximatif et on évalue la
qualité de ses solutions par rapport aux solutions optimales (ou aux
meilleures solutions connues). Ceci passe par la mise en place d'un benchmark
(ensemble d'instances d'un même problème accessible a tous).
2) Critère mathématique: il faut s'assurer que
l'heuristique garantit des performances. La garantie la plus solide est celle
des algorithmes approchés, sinon il est intéressant de
démontrer une garantie probabiliste, lorsque l'heuristique fournit
souvent, mais pas toujours, de bonnes solutions.
5.3 Métaheuristiques[9]
Présentation:
On parle de méta, du grec << au-delà
>> (comprendre ici << à un plus haut niveau >> ),
heuristique, qui signifie << trouver >> . En effet, ces algorithmes
se veulent des méthodes génétiques pouvant optimiser une
large gamme de problèmes différents, sans nécessiter de
changements profonds dans l'algorithme employé.
Une terminologie légèrement différente
considère que les métaheuristiques sont une forme d'algorithmes
d'optimisation stochastique, hybridés avec une recherche locale. Le
terme <<méta>> est donc pris au sens on les algorithmes
peuvent regrouper plusieurs heuristiques. On rencontre cette définition
essentiellement dans la littérature concernant les algorithmes
évolutionnaires, on elle est utilisée pour désigner une
spécialisation. Dans le cadre de la première terminologie, un
algorithme évolutionnaire hybridé avec une recherche locale sera
plutôt désigné sous le terme d'algorithme
mémétique (révolutionnaire) tel que l'algorithme
génétique.
Les métaheuristiques sont souvent inspirées par
des systèmes naturels, qu'ils soient pris en physique (cas du recuit
simulé), en biologie de l'évolution (cas des algorithmes
génétiques) ou encore en éthologie (cas des algorithmes de
colonies de fourmis ou de l'optimisation par essaims particulaires).
Le but d'une métaheuristique est de résoudre un
problème d'optimisation donné: elle cherche un objet
mathématique (une permutation, un vecteur, etc.) minimisant (ou
maximisant) une fonction objectif, qui décrit la qualité d'une
solution au problème.
L'ensemble des solutions possibles forme l'espace de
recherche. L'espace de recherche est au minimum borné, mais peut
être également limité par un ensemble de contraintes.
Les métaheuristiques manipulent une ou plusieurs
solutions, à la recherche de l'optimum, la meilleure solution au
problème. Les itérations successives doivent permettre de passer
d'une solution de mauvaise qualité à la solution la plus proche
de l'optimale. L'algorithme s'arrête après avoir atteint un
critère d'arrêt, consistant généralement en
l'atteinte du temps d'exécution imparti ou en une précision
demandée.
Une solution ou un ensemble de solutions est parfois
appelé un état, que la méta-
heuristique fait évoluer via des transitions ou des
mouvements. Si une nouvelle solution est construite a partir d'une solution
existante, elle est sa voisine. Le choix du voisinage et de la structure de
donnée le représentant peut être crucial.
Lorsqu'une solution est associée a une seule valeur, on
parle de problème mono-objectif, lorsqu'elle est associée a
plusieurs valeurs, de problème multi-objectifs (ou
multi-critères). Dans ce dernier cas, on recherche un ensemble de
solutions non dominées (le << front de Pareto >> ),
solutions parmi lesquelles on ne peut décider si une solution est
meilleure qu'une autre, aucune n'étant systématiquement
inférieure aux autres sur tous les objectifs.
Dans certains cas, le but recherché est explicitement
de trouver un ensemble d'optimums << satisfaisants >> .
L'algorithme doit alors trouver l'ensemble des solutions de bonne
qualité, sans nécessairement se limiter au seul optimum: on parle
de méthodes multimodales.
Pour résumer ces définitions, on peut dire que les
propriétés fondamentales des métaheuristiques sont les
suivantes:
- Les métaheuristiques sont des stratégies qui
permettent de guider la recherche d'une solution optimale
- Le but visé par les métaheuristiques est
d'explorer l'espace de recherche effi cacement afin de déterminer des
solutions (presque) optimales.
- Les techniques qui constituent des algorithmes de type
métaheuristique vont de la simple procédure de recherche locale a
des processus d'apprentissage complexes.
- Les métaheuristiques sont en général
non-déterministes et ne donnent aucune garantie d'optimalité
- Les métaheuristiques peuvent contenir des
mécanismes qui permettent d'éviter d'être bloqué
dans des régions de l'espace d recherche.
- Les concepts de base des métaheuristiques peuvent
être décrit de manière abstraite, sans faire appel a un
problème spécifique.
- Les métaheuristiques peuvent faire appel a des
heuristiques qui tiennent compte de la spécificité du
problème traité, mais ces heuristiques sont
contrôlées par une stratégie de niveau supérieur.
- Les métaheuristiques peuvent faire usage de
l'expérience accumulée durant la recherche
de l'optimum, pour mieux guider la suite du processus de
recherche.
5.4 Présentation de l'heuristique de résolution
La résolution de ce problème consiste a
déterminer les emplacements des manifolds, les puits reliés a
chaque manifolds ainsi que les diamètres des pipes utilisés en
minimisant la perte de charge, pour notre méthode de résolution
nous avons opté pour l'approche suivante en deux phases:
5.4.1 Phase I: Nuées dynamiques[11]
Dans un premier temps, on détermine les emplacements
des manifolds ainsi que les puits reliés a chaque manifolds, pour cela
nous minimisons la somme des distances des puits aux manifolds et la somme des
distances des manifolds a la source.
La position d'un manifolds est appelée 'centre de
gravité'pour l'ensemble des puits connectés a ce manifolds
(formant une région) et la source.
Pour déterminer les emplacements des manifolds et le
choix des puits qui seront connectés aux manifolds installés, on
applique une méthode de classification automatique appelée
'Méthode des Nuées Dynamiques'.
*La méthode des nuées dynamiques:
La méthode de classification des nuées
dynamiques (Diday et al 1980) repose essentiellement sur la répartition
d'une population en catégories (classes) tout en utilisant la notion de
noyau associé a chaque classe, il peut s'agir, comme dans notre
étude par exemple, de découvrir les principaux regroupements de
puits ayant la particularité d'être proches les uns des autres.
L'information apportée par une classification se situe,
en effet, au niveau sématique: (il ne s'agit pas d'atteindre un
résultat vrai ou faux, probable ou improbable, mais seulement profitable
ou non profitable)(Williams et Lance).
Les principaux problèmes de la classification automatique
diffèrent suivant le type
d'information recherchée: une hiérarchie, un
arbre, une partition, une typologie , des (classes empiétantes). Toutes
ces approches nécessitent le choix de mesures de ressemblance.
Principe :
Le principe des algorithmes des nuées dynamiques est
simple:
Considérer un ensemble d'individus qui appartient a un
ensemble E (par exemple Re ), et chercher la meilleure partition a K
classes fixées de cet ensemble selon le critère d'inertie.
Le processus est itératif et à chaque
étape la qualité de la partition s'améliore. Le nombre de
classe souhaité est déterminé à priori ainsi que le
nombre d'éléments centraux désirés,
c'est-à-dire le nombre d'éléments au centre du noyau qui
seront énumérés. Au départ, un ensemble de points
ou noyaux d'une classe peut être tiré au hasard. Autour de ces
points se regroupent les éléments les plus proches pour former
une partition. La distance calculée par rapport au centre de classe est
la distance euclidiènne. A partir de cette partition
créée, une autre famille de noyaux est définie, elle
regroupe les points les plus proches formant une nouvelle classe et ainsi de
suite jusqu'à obtention d'un nombre fini de classes . Si, aprés
un certain nombre d'itérations, les classes formées sont stables,
les données sont dites "classifiables" et constituent des "formes
fortes". Les individus qui changent de classes selon les tirages sont les
"individus charnières".
Comment se déroule l'algorithme:
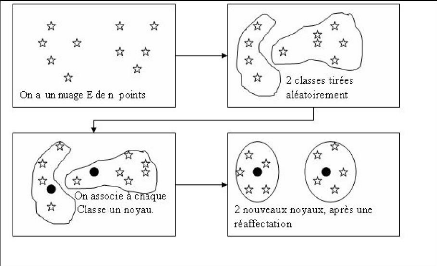
Figure 5.4.1 : Illustration du principe ( K = 2)
Soit un nuage E de N points, on cherche a constituer une
partition de E en k classes, chaque classe est représentée par
son (noyau). On aura une bonne classification si et seulement si le
critére suivant est vérifié: "La somme des distances des
individus aux noyaux soit minimale".
*Un algorithme de type "Nuées Dynamiques
Rappelons rapidement le principe de ces méthodes: on
suppose que , appartient a un ensemble E (par exemple R avec P le nombre de
variables), on définit un ensemble L de noyaux, une "distance" d entre
les éléments de E et les noyaux de L. (L'algorithme doit
respecter le primcipe d'homogéméité: les dommées a
classer et les moyaux doivemt être de même nature). Le
critère W de classification est alors le suivant:
W(P, L) = >2K >2 d(x,
ak)
k=1 XEPk
On:
P = (P1, ..., PK) et L = (a1, ..., aK) avec aK 2 L
L'algorithme se construit alors de la manière habituelle,
il se base sur deux fonctions:
*Construction des classes (fonction d'affectation f) :
On range chaque élément de dans la classe dont le
noyau est le plus proche.
*Construction des noyaux (fonction de représentation g) :
On associe a chaque classe Pk un nouveau noyau ak minimisant :
>2 d(x,ak)
XEPk
L'algorithme des nuées dynamiques est une succession
d'appels a ces deux fonctions de façon itérative, le nombre de
groupes K est déterminé soit par une connaissance a priori du
phénomène étudié, soit par une autre méthode
(classification hiérarchique par exemple) .
Organigramme:

Figure 5.4.2 : Représentation structurée de
l'algorithme des Nuées Dynamiques
*Application de l'algorithme a notre problême:
Algorithme :
1-Diviser les puits en k régions de facon aléatoire
( soient R1, R2, ..., Rk). Avec k= [N/5] on N est le nombre de puits de la
station.
2-Déterminer les emplacements des manifolds (M1, ...,
Mk).
Pour une région R3 donnée, choisir l'emplacement Mj
qui minimise:
|
/ >
f(X, Y ) = X2 + Y 2 +
|
p
(Xi - X)2 + (Y - Y )2
|
PiERj
On (X,Y ) sont les coordonnées du manifolds Mj
Pi E R3: signifie que le puits (i) coordonnées (Xi,Yi) E
R3
3-Répartir les puits en utilisant une fonction de
décision: Pi est dans la région R3 si et seulement si d(Pi, M3)
est minimale.
d(Pi, M3) est la distance euclidienne entre le puits (i) et le
manifold Mj 4-Si le test d'arrêt est vériflé aller a (5)
sinon aller a (2).
5-S'il existe une région ayant un nombre =6 5 alors
réaffecter les puits en utilisant l'organigramme de la page suivante, et
recalculer les nouveaux centres de gravité comme en (2).
REMARQUE:
1-L'étape (5) est due a la contrainte qui exige que le
nombre de puits par région soit égal a 5.
2-Le test d'arrêt est le suivant: s'il n'y a pas
d'amélioration au cours de 2 itérations succussives l'algorithme
est arrêté.
3-d(Pi, M3) est la longueur du pipe reliant Pi a Mj.
qd(Pi, Mj) = (X - X' j)2 + (Yi-
Y j ')2.
· m(R) est le nombre de puits dans la région
R.
Organigramme:

Figure 5.4.3 : Organigramme de la procédure
réaffecter
5.4.2 Phase II: Logiciel lingo1O.O[1O]
Aprés avoir positionné les manifolds cette phase
consiste a déterminer les diamètres pour chaque pipe
utilisé, en appliquant directement le loigiciel lingo10 en utilisant le
résultat dégagé de la phase I. On aura donc a
résoudre le problème (P') suivant:
|
(P')
|
8
<>>>>>>>>>>>>>>>>>>>>
>
>>>>>>>>>>>>>>>>>>>>>:
|
Ci bj
MIN Z = PN i + PM
i=1 DP 5 j=1 DM5 j
DM2 j ~ PN i=1 Rij ~ DP 2 j = 1,...,M
i
DP, 2 {2",3"} i = 1,...,N
DPi > 0
DM3 2 {6", 8", 10"}
on
· Ci = (Qi~P
T )2 * Gg * f * z * 7.62 * 105 * LPi
· b3 = (PN i=1 Rij Qi)2 * P 2
T 2 * Gg * f * z * 7.62 * 105 * LMj
Remarque:
Le problème (P') est tiré du problème
(P), tels que les contraintes liées aux nombre de puits connectés
a un manifolds, les contraintes liées a la connexion des puits a un
manifolds et les contraintes liées aux longueurs des conduites
circulaires, sont respectées.
* Application avec le logiciel Lingo10:
Il existe de nos jours, une multitude de solveurs de
résolution des programmes non linéaires. Ils sont
généralement fournis sous forme de programmes sources. En effet
les logiciels tels que LINGO, CPLEX ou MAPLE sont des programmes d'optimisation
conçu pour résoudre les modèles d'optimisation
linéaires, non linéaires, en nombres en-tiers....
Parmi ces logiciels nous allons utiliser << LINGO
>> pour résoudre notre problème, et ceci pour plusieurs
raisons:
D'une part LINGO admet un code de programmation non
linéaire qui permet de traiter de milliers de variables et de
contraintes en un temps rapide, donc utilisable même si la taille du
problème est grande, d'autre part LINGO est un outil plus simple a
utiliser par rapport a d'autres logiciels et dispose de plusieurs
fonctionnalités, notamment:
- Un nouveau solveur pour confirmer que la solution
trouvée est optimale.
- La capacité a résoudre les problèmes plus
rapidement.
- La reconnaissance et l'identification des programmes
quadratiques (QP).
- Un nouveau solveur pour améliorer les performances dans
les solutions des différents types de problèmes.
- La capacité a transformer les programmes
non-linéaire en séries de programme linéaire.
- La capacité d'importer ou d'exporter des
informations vers les bases de données en se servant d'une
bibliothèque de lien dynamique (DLL), donc il permet de faire des
connexions avec d'autre applications.
Un modèle d'optimisation se compose de trois parties:
* Fonction Objectif: il s'agit de formule unique qui
décrit exactement ce que le modèle devrait optimiser.
* Contraintes: ce sont des formules qui définissent les
limites sur les valeurs des variables.
* Les commentaires dans le modèle sont engagés
avec un point d'exclamation (!) et apparaissent en vert.
Méthodes de résolution utilisée par
Lingo:
- Dual simplexe.
- Branch-and-bound.
- Programmes non-linéaire.
- Programme quadratique.
- Programme multicritère.
5.5. Conclusion
5.5 Conclusion
Ce chapitre a été consacré aux
méthodes de résolution adoptés pour résoudre notre
problème, une défnition complète des différentes
méthodes utilisées a été donné tout au long
de ce chapitre, maintenant nous passons a l'implémentation de cette
dernière, le dernier chapitre illustre cette implémentation et
donne une description minutieuse du logiciel développé ainsi que
les résultats obtenus.
| 


