Modèlisation d'un prototype et commande vectorielle avec et sans capteur mécanique du moteur couple

CHAPITRE 4 : 80

COMMANDE SANS CAPTEUR ET FILTRE DE

KALMAN

1 INTRODUCTION. 81

2 LE CAPTEUR DE POSITION. 81

2.1 Le capteur est son rôle : 81

2.2 Résolution du capteur : 81

2.3 Choix du type de capteur : 82

2.4 Le codeur rotatif incrémental : 82

2.5 Le codeur rotatif absolu : 82

2.6 Le résolveur : 82

2.7 Conclusion : 84

3. RECONSTRUCTION DE LA POSITION DU ROTOR. 84

3.2 Le reconstructeur et son principe, appliqués aux systèmes linéaires : 84

4. RECONSTRUCTEUR D'ETAT EVOLUE DU TYPE « FILTRE 89
DE KALMAN ».

4.1 Principe du filtre de Kalman : 89

4.2 Le filtre de Kalman associé aux systèmes linéaires : 90

4.3 Le filtre de Kalman étendu aux systèmes non linéaires : 93

5. APPLICATION DU FILTRE DE KALMAN. 96

5.1 Choix du référentiel pour le filtre de Kalman: 96

5.2 Détermination des équations du système différentiel estimé dans le 97

repère ( a _s ,p _s ) :

5.3 Commande du moteur dans le repère (a_s,b_s,c_s) : 100

5.3.a) Régulation des courants ias, ibs, ^et _ics avec compensation des f.e.m : 101

5.3.b) Générateur de références sur les courants : 102

5.3.c) Synoptique de commande du moteur dans le repère (a_s,b_s,c_s) : 104

5.4 Validation théorique (simulation) de la commande du moteur avec filtre 105
de Kalman :

5.4.a) Commande du moteur en vitesse avec retour par le filtre de Kalman : 105

5.4.b) Remarques sur les simulations effectuées : 111

5.5 Définition des moyens matériels pour les essais expérimentaux : 112

6. CONCLUSION. 117

CONCLUSION GENERALE 118

122
143

141
150

ANNEXES

· ANNEXE 1: Essais expérimentaux et validation du modèle. ESSAIS DU PROTOTYPE.

· ANNEXE 2 : Commande sans capteur mécanique - Filtre de

Kalman.

QUELQUES NOTIONS SUR LES VARIABLES ALEATOIRES.

· ANNEXE 3: Commande sans capteur mécanique - Filtre de

Kalman.

TRANSFORMATIONS DE CLARKE ET DE CONCORDIA.

· ANNEXE 4 : Commande sans capteur mécanique - Filtre de Kalman.

SCHEMAS BLOCS SOUS SIMULINK ET MASQUE DE
S-FUNCTION DU FILTRE.

FICHIERS "METAFILE".

Et Quelques photos

LISTE DES SYMBOLES UTILISES

a : Position de l'axe d de Park par rapport à l'axe de la phase a_s.

i as i bs ics : Courants instantanés dans les phases statoriques d'axes a, b et c.

ids i qs ios : Courants instantanés dans les phases statoriques d'axes d, q et o.

i _as i (3 s : Courants instantanés dans les phases statoriques d'axes a et (3.

v as v bs vcs : Tensions instantanées aux bornes des phases statoriques d'axes a, b et c.

v ds v qs vos : Tensions instantanées aux bornes des phases statoriques d'axes d, q et o.

u _ds u qs . . Tensions de Park à l'entrée du découpleur linéarisant.

v a s v (3 s : Tensions instantanées aux bornes des phases statoriques d'axes a et (3.

e _as e bs ccs

IFas IFbs IFcs :

Flux embrassés par l'enroulement successif des phases statoriques d'axes

: Force électromotrice induite dans les phases du moteur.

a, b et c.

IFds IFqs IFos : Flux embrassés par l'enroulement successif des phases statoriques d'axes

d, q et o.

IFa aim baim : Flux instantané créé par l'aimant du circuit inducteur, embrassé par les

IF_c aim enroulements de la phase a_s, b_s, c_s.

IFdaim : Flux créé par les aimants du disque rotor transposé sur l'axe d :

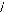
IFdaim = 3 _2IFaim :Vraie valeur de Park, non primée ? IF ^?daim = IFaim .

^IF_ai_m : Flux créé par les aimants du disque rotor.

^~IFaim : Flux, à valeur estimée constante, créé par les aimants du disque rotor

R_s : Résistance d'une phase statorique.

~R_s : Résistance, à valeur estimée constante, d'une phase statorique.

R_m : Résistance équivalente aux pertes magnétiques.

Icc : Courant de court-circuit dans les phases statoriques (essai en cc).

Irm : Courant dû aux pertes magnétiques.

L _pa L pb Lpc : Inductance propre des enroulements statoriques a_s, b_s, c_s.

~Ls Ls

: Inductance synchrone, à valeur estimée constante, du moteur. : Inductance synchrone du moteur.

L_q : Inductance synchrone d'axe q (transversale) : L d = L q = L_s.

. an

L_d : Inductance synchrone d'axe d (longitudinale) : L _d = L _q = L_s.

:

Lms

l_f

Is

[L

M

Inductance propre magnétisante des enroulements statoriques.

: Inductance de fuites.

: Matrice des inductances statoriques :

_[r

ms
ms

1 ?

I

J

l _f + L_ms -- 1 2 L ms -- 1 2 L

1 2 L _ms l _f + L_ms -- 1 2 L

1 2 L ms -- 1 2 L _ms l _f + Lms

: Inductance de mutuelle entre 2 enroulements de phases statoriques :

.

M = M ab = Mac = Mbc

n : Fréquence de rotation du moteur.

n er 0 ? 0

: Vitesse angulaire mécanique du rotor en rad/s : n = 27c n : Position électrique de l'inducteur par rapport au champ tournant (Angle constant en régime synchrone). : Position électrique de l'inducteur par rapport à l'axe fixe de la phase a, Oa. : Position électrique estimée et optimisée du rotor.

⁰mé c : Position mecanique du rotor par rapport à l'axe fixe de la phase a, Oa.

⁰lim : Temperature limite d'echauffement des enroulements statoriques.

co_s : Pulsation des courants statoriques.

co_r : Vitesse angulaire de l'inducteur par rapport au champ tournant (Vitesse

nulle en regime synchrone).

co : Vitesse angulaire de l'inducteur par rapport à l'axe fixe de la phase a, Oa.

co? : Vitesse angulaire du rotor estimee et optimisee.

f : Coefficient de frottements visqueux.

f (t ) : Vecteur d'evolution du système, fonction du temps.

F_x ( t , x _ref (t)) : Fonction "aux derivees partielles" de f ( x _ref (t ), u (t ), t).

g (t ) : Vecteur d'application de la commande, fonction du temps.

p et s : Operateurs de Laplace.

N p : Nombre de pas du moteur.

:

T_em

T_u
T_r

Trma

Couple electromagnetique moteur.

: Couple utile disponible sur l'arbre du moteur.

: Couple resistant total : Tr _=Trma + Tr ₀ + Trf. .

: Couple resistant dû à la machine entraînee.

Tr0 : Couple resistant dit « residuel » dû aux aimants.

Trf : Couple de frottements visqueux : T_rf = f co

Tth : Constante thermique d'echauffement des enroulements statoriques.

J_m : Moment d'inertie des masses tournantes du moteur.

J_r : Moment d'inertie des masses tournantes de la machine à entrainer.

J : Moment d'inertie des masses tournantes du moteur et de la machine :

J = J _m + J_r.

k : Constante de vitesse de la machine entrainee : T_rma = k w ² + T .

K_T : Constante de couple en N.m/A. K_T = 3 2 _Np?tFdaim avec tF? daim = tF?aim.

K : Matrice de gains de correction à coefficients constants.

K_k : Vecteur de gains de correction au pas d'echantillonnage k.

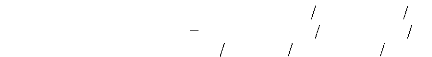
Matrice de Park :

:

[ P]

3

2

r 1 1

L

cos 0 cos

sin0 -- sin

1 2 1 2 1 2

( 0 -- 2 7c 3 ) cos( 0 --4 7c 3)

( 0 -- 2 7c 3 ) -- sin( 0 --4 7c 3)

1

1

L

.

Pmé c : Puissance due aux pertes mecaniques.

Pmag : Puissance due aux pertes magnetiques.

⁽P : Angle de dephasage entre le courant et la tension statorique.

5 : Angle interne de la machine. Dephasage entre la f.e.m et la tension

statorique.

`P : Dephasage entre le courant et la f.e.m.

z : Coefficient d'amortissement.

L_d

Constante electrique d'axe d : Td =

R_s

Td	:

.

x( t ) : Vecteur d'etat fonction du temps.

xk . Vecteur d'etat discrêt, au pas d'echantillonnage k.

.

I . Vecteur d'etat à variables estimees et optimisees.

.

ic : Vecteur d'etat à variables estimees et corrigees.

x?

:

Matrice derivee du vecteur d'etat.

8_x : Vecteur "erreur" des variables estimées sur l'état du système :

6' x = x -x^....

xref : Vecteur d'état de référence.

C : Matrice de sortie du système à coefficients constants.

C^T : Matrice de sortie, transposée.

v : Vecteur de bruits d'état sur le système.

w : Vecteur de bruits de mesure agissant sur la sortie.

v_d : Vecteur de bruits d'état sur le système à valeurs discrêtes.

u : Vecteur d'entrée du système.

§

y

y

Vecteur de sortie du système.

§ Vecteur de sortie à variables estimées et optimisées.

6y = y -y.

C_y : Vecteur "erreur" des variables estimées sur la sortie du système :

E? X } Espérance de la variable aléatoire x.

§

D x
cxy

c xx

Variance de la variable aléatoire x.

Coefficient de covariance de 2 variables aléatoires x et y.

: Matrice de variance-covariance d'un vecteur à variables aléatoires:

? ?

? ? ?

x 1 x x

1 2 x x

1 3

? ?

? ? ? ? ?

x x

2 1 x 2 x x

2 3

xx ? ?

? ? ? ? ? ?

x x

3 1 x x

3 2 x 3 ?

0

·

·

X

X = ( X _i - Xi).

Pk/k-1 . Matrice de variance-covariance de l'erreur de la 1^ère estimation des

.

variables d'état.

P k / k . Matrice de variance-covariance de l'erreur de la 2^ème estimation des

.

variables d'état.

P0 / 0 . Matrice de variance-covariance de la confiance sur la première estimation

.

du vecteur d'état.

R_k : Matrice de variance-covariance des bruits de mesures.

R₀ : Matrice de variance-covariance à valeurs initiales sur les bruits de mesure.

Qd(k_1) Q0	: :
^(1)(k/k-1)	:
tin	:
Cdp	:
Cqp	:
Kp	:
Cdi	:
Cqi	:
ki	:
Cvp et Kvp	:
Cvi et Kvi	:

Matrice de variance-covariance des bruits sur le système à variables discrétisées.

Matrice de variance-covariance à valeurs initiales sur les bruits du système.

Matrice de transition du vecteur d'état de k-1 à k.

Constante de temps du filtre du 1^er de la consigne de vitesse.

Gain de correction de l'action proportionnelle de la régulation de courant d'axe d.

Gain de correction de l'action proportionnelle de la régulation de courant d'axe q.

Gain de correction de l'action proportionnelle de la régulation de courant. Gain de correction de l'action intégrale de la régulation de courant d'axe d. Gain de correction de l'action intégrale de la régulation de courant d'axe q. Gain de correction de l'action intégrale de la régulation de courant

Gain de correction de l'action proportionnelle de la régulation de vitesse. Gain de correction de l'action intégrale de la régulation de vitesse

k : Constante de vitesse : T_rma = T + ko².

_T? : Consigne de couple de la commande en couple du moteur.

T_n : Couple nominale.

AVANT PROPOS

ET

AVERTISSEMENT

Avant-propos et avertissement - Mémoire CNAM Patrick BOIDIN.

.

Le moteur à l'étude est un prototype d'une nouvelle génération de moteurs à structure discoïde à réluctance variable et à aimants permanents alternés. Ce prototype est classé dans la catégorie des moteurs "lents" à fort couple massique (60tr/min et 5 à 15N.m/kg).

Ce moteur a été conçu par GEC-ALSTHOM MOTEURS qui est une société spécialisée dans la fabrication des machines tournantes électriques de grandes et de moyennes puissances. Cette société, filiale de GEC-ALSTHOM S.A, fait partie du groupe ALCATEL ALSTHOM et fonctionne actuellement au moyen d'un effectif de 379 salariés qui sont répartis dans les activités : recherche et développement, conception, fabrication, ventes et après-vente. Le siège et l'usine de cette société sont implantés dans la ville de NANCY.

Dans le cadre d'un contrat de partenariat "recherche et développement technologique", entre cette société et l'école supérieure d'ingénieurs de Marseille, on m'a confié la mission d'étudier et de définir les moyens d'une commande électronique du type "vectorielle" capable de piloter le prototype. De plus, on m'a demandé d'étendre cette étude à une commande électronique sans capteur mécanique.

Le groupe ESIM (Ecole Supérieure d'Ingénieurs de Marseille) où ce sont déroulés les études et les travaux, a été créée en 1970 à la suite de la fusion des trois Ecoles d'Ingénieurs Marseillaises de l'EIM. Cette école, implantée sur le site du Technopôle de Chateau-Gombert à l'Institut Méditerranéen de technologie, est un centre de ressources et de compétences scientifiques, techniques et technologiques.