Modèlisation d'un prototype et commande vectorielle avec et sans capteur mécanique du moteur couple

CONSERVATOIRE NATIONAL DES ARTS ET METIERS
CENTRE REGIONAL ASSOCIE D'AIX EN PROVENCE

MEMOIRE

Présenté en vue d'obtenir
le DIPLOME D'INGENIEUR C.N.A.M.
en

ELECTROTECHNIQUE

par
Patrick BOIDIN

MODELISATION D'UN PROTOTYPE

ET

COMMANDE VECTORIELLE AVEC ET SANS CAPTEUR

MECANIQUE DU MOTEUR COUPLE

Soutenu le Avril 1996

JURY

PRESIDENT : RIALLAND J.F.

MEMBRES : LUCAS F.

BOUSSAK M. CREMET G. FINIDORI Ch. GAUTIER A. GRAS Ph.

HUGUES A.

CONSERVATOIRE NATIONAL DES ARTS ET METIERS
CENTRE REGIONAL ASSOCIE D'AIX EN PROVENCE

MEMOIRE

Présenté en vue d'obtenir
le DIPLOME D'INGENIEUR C.N.A.M.
en

ELECTROTECHNIQUE

par
Patrick BOIDIN

MODELISATION D'UN PROTOTYPE

ET

COMMANDE VECTORIELLE AVEC ET SANS CAPTEUR

MECANIQUE DU MOTEUR COUPLE

Les travaux relatifs au présent mémoire ont été effectués au laboratoire d'électrotechnique,
d'électronique de puissance et systèmes EEPS de l'Ecole Supérieure d'Ingénieurs de Marseille
(ESIM).
Les études et les travaux ont été suivis par
Monsieur M. BOUSSAK, ingénieur enseignant chercheur à l'ESIM
et
Monsieur Ch. FINIDORI, ancien responsable du département EEPS à l'ESIM
sous la direction de
Monsieur F. LUCAS, professeur principal du Conservatoire National des Arts et Métiers d'Aix
en Provence.

Modèlisation d'un prototype et commande vectorielle avec

et sans capteur mécanique du moteur couple.

Mémoire d'ingénieur CNAM, Aix en Provence 1996.

RESUME :

De nos jours, les moteurs "couples" et plus particulièrement les moteurs cylindriques à polyentrefer concentrique (moteur de roue), sont reconnus comme étant des moteurs performants. Néanmoins, ce type de moteur a besoin d'être amélioré afin de le rendre plus compétitif dans un marché européen de plus en plus exigeant dans les domaines de la traction électrique et de la robotique. C'est pourquoi, la société GEC-ALSTHOM MOTEURS NANCY, spécialisée dans la fabrication de moteurs électriques, a conçu un prototype d'une nouvelle génération de moteurs "couples" discoïdes à réluctance variable et à aimants permanents alternés. Ce moteur est capable de fournir un couple massique très important aux basses vitesses : 5 à 15 N.m/kg pour 60 tr/min (300 N.m à 60 tr/min). Or, la structure modulaire de ce type de moteur, permet d'obtenir des machines de constitution polydiscoïde, bien plus performantes. Un second prototype, pouvant fournir cette fois ci 6900 N.m à 52 tr/min, a d'ailleurs pris naissance dans les ateliers de GEC-ALSTHOM MOTEURS.

Pour exploiter les performances de cette nouvelle génération de moteurs, nous avons élaboré, sur la base du premier prototype cité, une théorie de commande électronique de type vectorielle capable de piloter et de commander le moteur. Cette étude est réalisée en tenant compte des critères de simplicité, d'efficacité et de robustesse de la commande.

Les difficultés rencontrées pour imposer un capteur mécanique standard au prototype et les inconvénients de ce capteur en matière de coût et de fiabilité, nous ont motivés à élaborer une commande sans capteur mécanique. Pour cela, on utilise un reconstructeur d'état du type FILTRE DE KALMAN.

L'étude de la commande du prototype, réalisée dans ce présent mémoire, est restée théorique. Les résultats ont été vérifiés uniquement par des simulations sous MATLAB-SIMULINK. Néanmoins, nous avons apporté quelques recommandations sur l'amélioration du prototype à partir des essais expérimentaux et des observations physiques du moteur. De plus, à la fin de ce travail, nous avons défini succinctement les moyens matériels permettant de tester expérimentalement la commande élaborée.

Mots-clés : Moteur discoïde - Réluctance variable - Aimants alternés - Commande

vectorielle - Park - Modèlisation de moteur synchrone - Filtre de Kalman -
Simulateur Matlab.

Keywords : Discoid motor - Variable reluctance - Alternated permanent magnet - Vector control drive - Synchronous motor modelisation - Kalman filter - Matlab

simulator.

REMERCIEMENTS

Je tiens à exprimer mes vifs remerdements à tous les professeurs et enseignants du Conservatoire National des Arts et Metiers pour leur devouement à enseigner à ceux qui, comme moi, veulent poursuivre leurs etudes et ameliorer leurs connaissances theoriques.

J'adresse mes respectueux et sincères remerdements à Monsieur F. LUCAS pour m'avoir interesse par la qualite de ses enseignements, m'avoir guide tout au long de ces etudes depuis le cycle A et m'avoir redonner courage au moment oO il le fallait.

Je remerde aussi Monsieur Ph. GRAS, ingenieur-enseignant au CNAM, pour sa patience à nous enseigner les travaux pratiques que j'ai suivis pendant 3 annees, pour sa gentillesse et pour l'aide qu'il a su nous apporter bien au-delà de son travail.

Merd à Monsieur MATHON, gerant-directeur de la sodete HEURTEY INDUSTRIES PROVENCE oO je travaille et à Monsieur DEPLACE, mon chef de service, d'avoir accorde mon conge formation et d'avoir supporte mon absence durant cette annee de memoire.

Je remerde vivement Monsieur FINIDORI, anden responsable du Departement ElectrotechniqueElectronique de Puissance et Systèmes associés, de m'avoir accueilli au sein de son equipe et de m'avoir fait confiance en m'accordant ce siet de memoire. Mes remerdements vont aussi vers Messieurs Ph. ZANIN et L.ROSS respectivement directeur et directeur adjoint de l'Ecole Supèrieure d'Ingénieurs de Marseille qui m'ont accepte et fait profite des moyens materiels de l'ecole.

Je remerde Monsieur BOUSSAK de l'aide et de toute la patience qu'il a su m'accorde dans l'encadrement de ce travail et je remerde aussi toute l'equipe des enseignants et des technidens de l'ESIM qui m'ont aides dans ma tâche et soutenus avec toute la gentillesse qu'il fallait ; Madame S.BANGUET, Monsieur Y.SERVET, Monsieur J.LEGELEUX, Monsieur Ch.YVE, Madame A.CARLIN, Monsieur B.DHALLUIN, Monsieur N.DIGRAZIA, Monsieur R. CHEVEAUX et Monsieur J.M.LI.

Toute ma sympathie et une part de mes remerdements vont vers Monsieur CREMET, Responsable du Service Recherche et Developpement de GEC-ALSTHOM MOTEURS Nancy, qui a su m'encourager dans ma tâche et surtout su me transmettre, sans aucune retenue de sa part, les quelques "ficelles de la technique".Ses conseils m'ont demontre la haute competence de la personne.

Merd à Monsieur Ph.FONTANA pour m'avoir ecoute et conseille avec toutes les qualites de solidarite et de competence que peut avoir un Cnamien comme lui.

TABLE DES MATIERES

Page

INTRODUCTION GENERALE

1

CHAPITRE 1 : 3

PRESENTATION ET MODELISATION DU

PROTOTYPE

1 INTRODUCTION. 5

2 PRESENTATION DU PROTOTYPE. 5

2.1 Les machines à réluctance variable, cylindrique (MRV cylindrique) : 5

2.2 Les machines à réluctance variable polydiscoïdes : 6

2.3 Les machines à réluctance variable polydiscoïdes et à aimants 6

permanents :

2.4 Constitution du moteur FINTRONIC : 7

3 MODELISATION DU PROTOTYPE. 13

3.1 Conventions et hypothèses : 14

3.2 Mise en équations du moteur à l'étude dans le repère (a_s, b_s, c_s) : 15

3.3 Problèmes liés à la résolution des équations dans le repère (a_s, b_s, c_s) : 18

3.4 Equations mécaniques : 19

3.5 Modèle du moteur dans le référentiel de PARK : 20

3.6 Remarques sur la transformation de Park et du système résultant : 25

4 CONCLUSION 27

CHAPITRE 2 : 28

ESSAIS ET VALIDATION DU MODELE

1 INTRODUCTION. 29

2 DETERMINATION NUMERIQUE DES ELEMENTS DU 29

MODELE.

2.1 Essai à vide du moteur en fonctionnement générateur : 29

2.2 Essai avec les enroulements statoriques en court-circuit : 32

2.3 Essai à vide du moteur FINTRONIC en fonctionnement moteur : 34

2.4 Essai de ralentissement du moteur fonctionnant à vide : 35

2.5 Essai d'échauffement du moteur FINTRONIC : 38

2.6 Paramètres du modèle : 39

3 ESSAIS EN CHARGE EN FONCTIONNEMENT MOTEUR. 40

3.1 Remarques sur les essais en charges : 41

3.2 Résultats obtenus pour U_ab=340volts et T_u=138N.m : 43

4 SIMULATIONS EN BOUCLE OUVERTE ET VALIDATION 44

DU MODELE.

4.1 Modèle mathématique du moteur et valeur numérique des paramétres : 44

4.2 Simulations en boucle ouverte : 46

4.3 Validation du modèle : 51

5 CONCLUSION. 51

CHAPITRE 3 : 53

COMMANDE VECTORIELLE AVEC CAPTEUR
MECANIQUE

1 OBJET. 54

2 PREAMBULE. 54

2.1 Le moteur synchrone : 54

2.2 Commande du moteur FINTRONIC, en courant ou en tension ? : 54

2.3 Principe de la commande en tension et de l'autopilotage du moteur : 55

2.4 Contrôle par la tension du couple électromagnétique : 56

3 MODELE D'ETAT DU MOTEUR ET CHOIX DES VARIABLES 57

D'ETATS

3.1 Définition et notations : 57

3.2 Choix des variables d'états : 58

3.3 Détermination du système d'états et schéma fonctionnel : 60

4 ETUDE DE LA REGULATION DES COURANTS DE PARK. 62

4.1 Etude du découpleur linéarisant : 62

4.2 Autre solution de découplage : 66

4.3 Etude comparative des 2 découpleurs : 67

4.4 Boucle fermée avec correction sur les courants : 68

5 REGULATION DE VITESSE. 69

5.1 Choix d'une régulation de vitesse : 69

5.2 Schéma-blocs de l'ensemble Moteur/Machine/Régulations : 69

6 ONDULEUR DE TENSION. 71

6.1 Généralités : 71

6.2 Onduleur à commande en M.L.I : 72

6.3 Commande en couple avec un onduleur de tension à 73

M.L.I./Simulations:

6.4 Commande en vitesse avec un onduleur de tension à M.L.I./Simulation: 76

CHAPITRE 4 : 80

COMMANDE SANS CAPTEUR ET FILTRE DE

KALMAN

1 INTRODUCTION. 81

2 LE CAPTEUR DE POSITION. 81

2.1 Le capteur est son rôle : 81

2.2 Résolution du capteur : 81

2.3 Choix du type de capteur : 82

2.4 Le codeur rotatif incrémental : 82

2.5 Le codeur rotatif absolu : 82

2.6 Le résolveur : 82

2.7 Conclusion : 84

3. RECONSTRUCTION DE LA POSITION DU ROTOR. 84

3.2 Le reconstructeur et son principe, appliqués aux systèmes linéaires : 84

4. RECONSTRUCTEUR D'ETAT EVOLUE DU TYPE « FILTRE 89
DE KALMAN ».

4.1 Principe du filtre de Kalman : 89

4.2 Le filtre de Kalman associé aux systèmes linéaires : 90

4.3 Le filtre de Kalman étendu aux systèmes non linéaires : 93

5. APPLICATION DU FILTRE DE KALMAN. 96

5.1 Choix du référentiel pour le filtre de Kalman: 96

5.2 Détermination des équations du système différentiel estimé dans le 97

repère ( a _s ,p _s ) :

5.3 Commande du moteur dans le repère (a_s,b_s,c_s) : 100

5.3.a) Régulation des courants ias, ibs, ^et _ics avec compensation des f.e.m : 101

5.3.b) Générateur de références sur les courants : 102

5.3.c) Synoptique de commande du moteur dans le repère (a_s,b_s,c_s) : 104

5.4 Validation théorique (simulation) de la commande du moteur avec filtre 105
de Kalman :

5.4.a) Commande du moteur en vitesse avec retour par le filtre de Kalman : 105

5.4.b) Remarques sur les simulations effectuées : 111

5.5 Définition des moyens matériels pour les essais expérimentaux : 112

6. CONCLUSION. 117

CONCLUSION GENERALE 118

122
143

141
150

ANNEXES

· ANNEXE 1: Essais expérimentaux et validation du modèle. ESSAIS DU PROTOTYPE.

· ANNEXE 2 : Commande sans capteur mécanique - Filtre de

Kalman.

QUELQUES NOTIONS SUR LES VARIABLES ALEATOIRES.

· ANNEXE 3: Commande sans capteur mécanique - Filtre de

Kalman.

TRANSFORMATIONS DE CLARKE ET DE CONCORDIA.

· ANNEXE 4 : Commande sans capteur mécanique - Filtre de Kalman.

SCHEMAS BLOCS SOUS SIMULINK ET MASQUE DE
S-FUNCTION DU FILTRE.

FICHIERS "METAFILE".

Et Quelques photos

LISTE DES SYMBOLES UTILISES

a : Position de l'axe d de Park par rapport à l'axe de la phase a_s.

i as i bs ics : Courants instantanés dans les phases statoriques d'axes a, b et c.

ids i qs ios : Courants instantanés dans les phases statoriques d'axes d, q et o.

i _as i (3 s : Courants instantanés dans les phases statoriques d'axes a et (3.

v as v bs vcs : Tensions instantanées aux bornes des phases statoriques d'axes a, b et c.

v ds v qs vos : Tensions instantanées aux bornes des phases statoriques d'axes d, q et o.

u _ds u qs . . Tensions de Park à l'entrée du découpleur linéarisant.

v a s v (3 s : Tensions instantanées aux bornes des phases statoriques d'axes a et (3.

e _as e bs ccs

IFas IFbs IFcs :

Flux embrassés par l'enroulement successif des phases statoriques d'axes

: Force électromotrice induite dans les phases du moteur.

a, b et c.

IFds IFqs IFos : Flux embrassés par l'enroulement successif des phases statoriques d'axes

d, q et o.

IFa aim baim : Flux instantané créé par l'aimant du circuit inducteur, embrassé par les

IF_c aim enroulements de la phase a_s, b_s, c_s.

IFdaim : Flux créé par les aimants du disque rotor transposé sur l'axe d :



IFdaim = 3 _2IFaim :Vraie valeur de Park, non primée ? IF ^?daim = IFaim .

^IF_ai_m : Flux créé par les aimants du disque rotor.

^~IFaim : Flux, à valeur estimée constante, créé par les aimants du disque rotor

R_s : Résistance d'une phase statorique.

~R_s : Résistance, à valeur estimée constante, d'une phase statorique.

R_m : Résistance équivalente aux pertes magnétiques.

Icc : Courant de court-circuit dans les phases statoriques (essai en cc).

Irm : Courant dû aux pertes magnétiques.

L _pa L pb Lpc : Inductance propre des enroulements statoriques a_s, b_s, c_s.

~Ls Ls

: Inductance synchrone, à valeur estimée constante, du moteur. : Inductance synchrone du moteur.

L_q : Inductance synchrone d'axe q (transversale) : L d = L q = L_s.

. an

L_d : Inductance synchrone d'axe d (longitudinale) : L _d = L _q = L_s.

:

Lms

l_f

Is

[L

M

Inductance propre magnétisante des enroulements statoriques.

: Inductance de fuites.

: Matrice des inductances statoriques :

_[r





ms
ms

1 ?

I

J

l _f + L_ms -- 1 2 L ms -- 1 2 L

1 2 L _ms l _f + L_ms -- 1 2 L





1 2 L ms -- 1 2 L _ms l _f + Lms

: Inductance de mutuelle entre 2 enroulements de phases statoriques :

.

M = M ab = Mac = Mbc

n : Fréquence de rotation du moteur.

n er 0 ? 0

: Vitesse angulaire mécanique du rotor en rad/s : n = 27c n : Position électrique de l'inducteur par rapport au champ tournant (Angle constant en régime synchrone). : Position électrique de l'inducteur par rapport à l'axe fixe de la phase a, Oa. : Position électrique estimée et optimisée du rotor.

⁰mé c : Position mecanique du rotor par rapport à l'axe fixe de la phase a, Oa.

⁰lim : Temperature limite d'echauffement des enroulements statoriques.

co_s : Pulsation des courants statoriques.

co_r : Vitesse angulaire de l'inducteur par rapport au champ tournant (Vitesse

nulle en regime synchrone).

co : Vitesse angulaire de l'inducteur par rapport à l'axe fixe de la phase a, Oa.

co? : Vitesse angulaire du rotor estimee et optimisee.

f : Coefficient de frottements visqueux.

f (t ) : Vecteur d'evolution du système, fonction du temps.

F_x ( t , x _ref (t)) : Fonction "aux derivees partielles" de f ( x _ref (t ), u (t ), t).

g (t ) : Vecteur d'application de la commande, fonction du temps.

p et s : Operateurs de Laplace.

N p : Nombre de pas du moteur.

:

T_em

T_u
T_r

Trma

Couple electromagnetique moteur.

: Couple utile disponible sur l'arbre du moteur.

: Couple resistant total : Tr _=Trma + Tr ₀ + Trf. .

: Couple resistant dû à la machine entraînee.

Tr0 : Couple resistant dit « residuel » dû aux aimants.

Trf : Couple de frottements visqueux : T_rf = f co

Tth : Constante thermique d'echauffement des enroulements statoriques.

J_m : Moment d'inertie des masses tournantes du moteur.

J_r : Moment d'inertie des masses tournantes de la machine à entrainer.

J : Moment d'inertie des masses tournantes du moteur et de la machine :

J = J _m + J_r.

k : Constante de vitesse de la machine entrainee : T_rma = k w ² + T .

K_T : Constante de couple en N.m/A. K_T = 3 2 _Np?tFdaim avec tF? daim = tF?aim.

K : Matrice de gains de correction à coefficients constants.

K_k : Vecteur de gains de correction au pas d'echantillonnage k.



Matrice de Park :

:

[ P]

3

2

r 1 1

L

cos 0 cos

sin0 -- sin

1 2 1 2 1 2

( 0 -- 2 7c 3 ) cos( 0 --4 7c 3)

( 0 -- 2 7c 3 ) -- sin( 0 --4 7c 3)

1

1

L

.

Pmé c : Puissance due aux pertes mecaniques.

Pmag : Puissance due aux pertes magnetiques.

⁽P : Angle de dephasage entre le courant et la tension statorique.

5 : Angle interne de la machine. Dephasage entre la f.e.m et la tension

statorique.

`P : Dephasage entre le courant et la f.e.m.

z : Coefficient d'amortissement.

L_d

Constante electrique d'axe d : Td =

R_s

Td	:

.



x( t ) : Vecteur d'etat fonction du temps.

xk . Vecteur d'etat discrêt, au pas d'echantillonnage k.

.

I . Vecteur d'etat à variables estimees et optimisees.

.

ic : Vecteur d'etat à variables estimees et corrigees.

x?

:

Matrice derivee du vecteur d'etat.

8_x : Vecteur "erreur" des variables estimées sur l'état du système :



6' x = x -x^....

xref : Vecteur d'état de référence.

C : Matrice de sortie du système à coefficients constants.

C^T : Matrice de sortie, transposée.

v : Vecteur de bruits d'état sur le système.

w : Vecteur de bruits de mesure agissant sur la sortie.

v_d : Vecteur de bruits d'état sur le système à valeurs discrêtes.

u : Vecteur d'entrée du système.

§

y



y

Vecteur de sortie du système.

§ Vecteur de sortie à variables estimées et optimisées.

6y = y -y.

C_y : Vecteur "erreur" des variables estimées sur la sortie du système :

E? X } Espérance de la variable aléatoire x.

§

D x
cxy

c xx

Variance de la variable aléatoire x.

Coefficient de covariance de 2 variables aléatoires x et y.

: Matrice de variance-covariance d'un vecteur à variables aléatoires:



? ?

? ? ?

x 1 x x

1 2 x x

1 3

? ?

? ? ? ? ?

x x

2 1 x 2 x x

2 3

xx ? ?

? ? ? ? ? ?

x x

3 1 x x

3 2 x 3 ?

0


·


·

X

X = ( X _i - Xi).

Pk/k-1 . Matrice de variance-covariance de l'erreur de la 1^ère estimation des

.

variables d'état.

P k / k . Matrice de variance-covariance de l'erreur de la 2^ème estimation des

.

variables d'état.

P0 / 0 . Matrice de variance-covariance de la confiance sur la première estimation

.

du vecteur d'état.

R_k : Matrice de variance-covariance des bruits de mesures.

R₀ : Matrice de variance-covariance à valeurs initiales sur les bruits de mesure.

Qd(k_1) Q0	: :
^(1)(k/k-1)	:
tin	:
Cdp	:
Cqp	:
Kp	:
Cdi	:
Cqi	:
ki	:
Cvp et Kvp	:
Cvi et Kvi	:

Matrice de variance-covariance des bruits sur le système à variables discrétisées.

Matrice de variance-covariance à valeurs initiales sur les bruits du système.

Matrice de transition du vecteur d'état de k-1 à k.

Constante de temps du filtre du 1^er de la consigne de vitesse.

Gain de correction de l'action proportionnelle de la régulation de courant d'axe d.

Gain de correction de l'action proportionnelle de la régulation de courant d'axe q.

Gain de correction de l'action proportionnelle de la régulation de courant. Gain de correction de l'action intégrale de la régulation de courant d'axe d. Gain de correction de l'action intégrale de la régulation de courant d'axe q. Gain de correction de l'action intégrale de la régulation de courant

Gain de correction de l'action proportionnelle de la régulation de vitesse. Gain de correction de l'action intégrale de la régulation de vitesse

k : Constante de vitesse : T_rma = T + ko².

_T? : Consigne de couple de la commande en couple du moteur.

T_n : Couple nominale.

AVANT PROPOS

ET

AVERTISSEMENT

Avant-propos et avertissement - Mémoire CNAM Patrick BOIDIN.

.

Le moteur à l'étude est un prototype d'une nouvelle génération de moteurs à structure discoïde à réluctance variable et à aimants permanents alternés. Ce prototype est classé dans la catégorie des moteurs "lents" à fort couple massique (60tr/min et 5 à 15N.m/kg).

Ce moteur a été conçu par GEC-ALSTHOM MOTEURS qui est une société spécialisée dans la fabrication des machines tournantes électriques de grandes et de moyennes puissances. Cette société, filiale de GEC-ALSTHOM S.A, fait partie du groupe ALCATEL ALSTHOM et fonctionne actuellement au moyen d'un effectif de 379 salariés qui sont répartis dans les activités : recherche et développement, conception, fabrication, ventes et après-vente. Le siège et l'usine de cette société sont implantés dans la ville de NANCY.

Dans le cadre d'un contrat de partenariat "recherche et développement technologique", entre cette société et l'école supérieure d'ingénieurs de Marseille, on m'a confié la mission d'étudier et de définir les moyens d'une commande électronique du type "vectorielle" capable de piloter le prototype. De plus, on m'a demandé d'étendre cette étude à une commande électronique sans capteur mécanique.

Le groupe ESIM (Ecole Supérieure d'Ingénieurs de Marseille) où ce sont déroulés les études et les travaux, a été créée en 1970 à la suite de la fusion des trois Ecoles d'Ingénieurs Marseillaises de l'EIM. Cette école, implantée sur le site du Technopôle de Chateau-Gombert à l'Institut Méditerranéen de technologie, est un centre de ressources et de compétences scientifiques, techniques et technologiques.

INTRODUCTION GENERALE

L'évolution rapide et incessante des interrupteurs de puissance et des micro-contrôleurs a multiprocesseurs a permis d'améliorer considérablement les capacités et les possibilités des nouveaux convertisseurs électroniques de puissances. A raison de ces nouveaux moyens, les machines a réluctance variable ont retrouvé, depuis quelques années, un regain d'intérêt. Cet intérêt est devenu d'autant plus important que les applications actuelles, telles que la traction électrique et la robotique, demandent des moteurs lents, a forts couples et a structure légère de surcroît. Or, seules les machines a réluctance variable sont capables, par leur principe technologique, de répondre a ces trois exigences. De nombreux chercheurs essayent de compenser ce manque par des commandes sophistiquées telle que la commande vectorielle de flux sur les machines asynchrones. Néanmoins, les résultats ne sont pas totalement concluants aux basses vitesses et beaucoup de travail reste a faire sur le sujet. Les machines a réluctance variable, utilisées la plupart du temps en moteur pas a pas, sont généralement limitées en puissance et présentent des inconvénients qui réduisent leurs performances. Ces inconvénients sont principalement : Une instabilité de fonctionnement a certaines fréquences, une limitation du couple au démarrage, des accélérations modestes et autres inconvénients de ce genre. Or, l'idée venue de GEC-ALSTHOM MOTEURS Nancy, a été de concevoir une nouvelle génération de machines a réluctance variable, capables de satisfaire tous les domaines d'application qui nécessitent des moteurs a couples spécifiques élevés aux faibles vitesses. D'où la réalisation du

Moteur discoïde à réluctance variable et à aimants permanents
alternés (MDRVAP)

MOTEUR FINTRONIC.

Ce type de moteur a besoin, néanmoins, d'une commande performante, simple a réaliser qu'il faut élaborer. C'est principalement le but de ce mémoire. Cette commande, demandée de type vectoriel, devra dans une seconde étape, se dispenser du capteur mécanique qui s'avère, a priori, nécessaire a ce type de moteur. Pour réaliser cette étude et les travaux qui s'y rajoutent, Monsieur Gérard CREMET, de la société GEC-ALSTHOM MOTEURS, a mis a la disposition du laboratoire d'électrotechnique de l'ESIM, le prototype du moteur discoïde, baptisé:

Compte tenu de la diversité de cette étude, nous avons choisi de diviser la rédaction de ce mémoire en quatre parties essentielles :

· La première partie :"Présentation du prototype et modélisation", est réservée a la présentation du prototype, que nous avons découvert sous tous ses aspects et a l'étude du modèle mathématique du même prototype. Cette phase a été déterminante pour la suite de cette étude. En effet, une mauvaise reconnaissance du moteur, au départ, pouvait très vite remettre en cause toutes les théories développées par la suite. J'ai été contraint a démonter le moteur en pièces détachées a cause de quelques problèmes mécaniques. Cette opération a permis de découvrir les moindres détails du moteur et de mieux apprécier la technologie du prototype.

· La deuxième partie de ce mémoire : "Essais et validation du modèle", traite des différents essais, effectués sur le moteur, afin de déterminer la valeur numérique des paramètres du modèle. De plus, cette partie d'étude a permis de vérifier la validation du modèle mathématique en comparant les résultats théoriques avec les résultats expérimentaux.

· La troisième partie : "Commande vectorielle avec capteur mécanique ", présente, après un choix préalable d'une technique de commande, la commande dans son ensemble et ses

constituants en considérant le capteur mécanique parfait. On présente, dans cette partie de mémoire et pour différents cas et modes de fonctionnement (régulation en vitesse, régulation en couple), une série de simulations sous le logiciel MATLAB-SIMULINK.


· On consacre la quatrième et dernière partie de ce mémoire : "Commande sans capteur mécanique et filtre de Kalman", au développement théorique d'une commande sans capteur du prototype utilisant un reconstructeur d'état du type FILTRE DE KALMAN.

CHAPITRE 1

PRESENTATION ET MODELISATION
DU PROTOTYPE

1. INTRODUCTION.

L'élaboration d'une commande performante et optimale du moteur FINTRONIC ne peut pas se faire sans connaître, avec certitude, les caractéristiques propres de la machine à commander. Ceci est d'autant plus vrai que le moteur en question est un prototype. Pour cela, il faut découvrir et percevoir l'aspect mécanique, magnétique et électrique du prototype de façon à les traduire sous la forme d'un ensemble d'équations mathématiques. Cet ensemble formera ainsi un système d'équations différentielles à variables d'état représentant le modèle d'état du moteur.

2. PRESENTATION DU PROTOTYPE.

Pour justifier la nécessité d'une nouvelle génération de machines à réluctance variable (MRV), comme le moteur FINTRONIC, on a besoin de revenir sur les caractéristiques principales des MRV de constitution cylindrique et leurs propriétés.

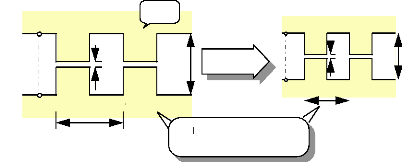
2.1. Les machines à réluctance variable, cylindriques (MRV cylindriques):

Ce sont des machines robustes [1][2] démunies de balai et qui plus est, peuvent prendre des formes bien différentes suivant l'utilisation que l'on veut en faire. Ce type de machine est caractérisé par le circuit magnétique de son stator et de son rotor qui est formé par un ensemble de dents dont la saillance créée la réluctance variable. Cette particularité permet de tirer partie d'une propriété remarquable de cette structure:

Si on applique une homothétie sur les dentures et sur la force magnétomotrice (réduction des formes et des volumes en proportion), on conserve les mêmes forces tangentielles créatrices du couple moteur.

Ainsi, pour un même volume de matière ferromagnétique, formant le circuit magnétique, il est possible d'augmenter le couple moteur d'une MRV en augmentant le nombre de dents tout en réduisant, en proportion inverse, les formes de la denture. On obtient ainsi des moteurs à forts couples massiques pour des vitesses de rotation faibles.



Stator

Dent

Stator

Entrefer

F

em

a

Homothétie

kF

ka

kem

(f.m.m.)

Rotor

Rotor

kb

b

Forces tangentielles
identiques

Fig. I-2.1 : Machines cylindriques homothétiques de rapport k.

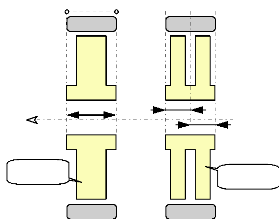
2.2. Les machines à réluctance variable polydiscoïdes :

On applique la même propriété sur les machines polydiscoïdes, à la différence près qu'on exploite l'homothétie dans le sens axial du moteur. Ainsi, en augmentant le nombre d'entrefer pour une même f.m.m. d'excitation, on augmente les forces tangentielles de la même valeur et par conséquent, le couple.



F

F/2 F/2

(f.m.m.)

L L/2

Axe
de
rotation

L/2

Monodisque

Multidisque

Fig. I-2.2 : Machines discoïdes à 1 et 2 entrefers.

Quelle que soit la machine utilisée, cylindrique ou polydiscoïde, l'avantage sur l'homothétie est limité par la réduction de l'entrefer. En effet, dans une certaine limite, l'entrefer ne peut plus être réduit et l'homothétie n'est plus applicable. De plus, la réduction de l'épaisseur du disque provoque une tendance au collage qui est évitée par la seule rigidité naturelle du disque en rotation.

2.3. Les machines à réluctance variable polydiscoïdes et à aimants permanents :

En remplaçant les dents du rotor par des aimants permanents, l'expression des forces tangentielles n'est plus dépendante uniquement de l'entrefer magnétique mais de la combinaison de l'entrefer mécanique avec l'épaisseur des aimants. Or, si on veut réduire l'entrefer magnétique, tout en maintenant l'entrefer mécanique constant, il suffit de réduire l'épaisseur des aimants. Une étude complète de GEC-ALSTHOM MOTEURS a permis de révéler tout l'intérêt d'une telle machine. Les principaux avantages de cette machine par rapport aux MRV discoïdes sont les suivantes [2] :

- "Les machines sont excitées et fonctionnent dans les quatre quadrants

flux-ampères-tours : les flux mis en jeu sont alors moins importants et les machines se prêtent mieux à un facteur de puissance plus élevé".

- "La loi d'induction d'excitation est pratiquement sinusoïdale."

- "Les efforts tangentiels obtenus peuvent être supérieurs d'un facteur 2 à ceux des MRV."

- "Il est vraisemblable que la machine à aimants permanents alternés s'avère silencieuse."

On précise que le prototype à l'essai est une maquette monodisque d'une machine à structure polydiscoïde.

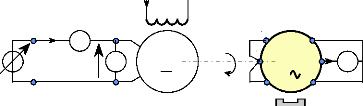
2.4. Constitution du moteur FINTRONIC :



Fig. I-2.3 : Moteur FINTRONIC vu sur son banc d'essais.

L'ensemble du gabarit fait environ 300 mm de diamètre, 150 mm d'épaisseur et 50 kg de masse. Les performances électriques du moteur sont données pour 200 N.m nominale à 60 tr/min (64 Hz) et 300 N.m en pointe, soit un couple massique de 4 à 5N.m/kg.

Trois parties principales constituent le moteur :


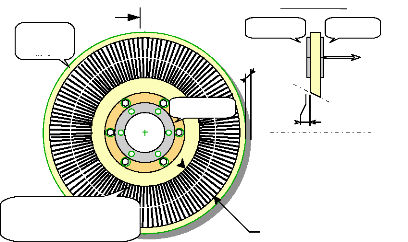
· Le rotor forme la première partie du moteur. Il est constitué d'un disque en acier massif d'épaisseur 10,5 mm, boulonné sur l'épaulement d'un arbre creux. Chaque face du disque est munie de 128 éléments d'aimants au Samarium-Cobalt du type "RECOMA 28", disposés sur 2 étages et collés alternativement Nord/Sud. Les aimants ont une épaisseur de 1,75 mm, un pas polaire de 5,625° et un angle d'ouverture légèrement inférieur à 2,5°.



VUE SUIVANT F

F

Aimant Sud Aimant Nord

10,5

Flux
créé par les
aimants

arbre moteur

1,75mm

Axe de rotation
du rotor

ext :148,5mm int : 96mm

128 aimants
alternativement Nord/Sud
collés sur chaque face du disque

disque
en
acier

Fig.I-2.4 : Rotor du moteur ; vue suivant l'arbre et vue partielle suivant F.


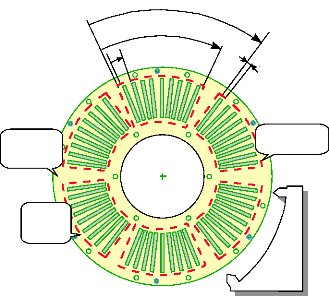
· Les 2 disques "stator" forment la deuxième partie du moteur. Chaque disque est constitué de 6 secteurs (masse métallique formée de 9 plots) dont chaque secteur est entouré d'un bobinage. Les bobinages sont connectés en série et en parallèle de façon à constituer le couplage étoile classique d'un moteur. Le tout est noyé dans une résine assurant la légèreté et la solidité de l'ensemble. La connection des 2 disques est assuré par des broches.



60°

50,63°

5,63°

2,81°

1

Structure
en
résine

3 '

2

plot statorique

Bobine
de phase

2 '

3

1'

Secteur
d' une
phase

Fig.I-2.5 : Disque "stator". Vue face en regard avec le rotor.

Chaque enroulement de phase est constitué de 4 bobines de secteur, branchées en série. Chaque bobine, formée de 3 brins en parallèle sur 79 spires, doit supporter 55 volts efficaces à ces extrémités. Chaque phase est donc alimentée sous 220 volts, soit une tension composée de 380 volts pour une intensité nominale de 9,3A.

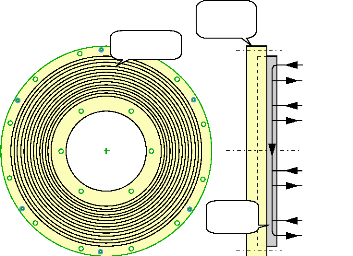
? Les 2 flasques d'extrémité forment la troisième partie du moteur (culasses). Ils permettent de refermer, de part et d'autre, les lignes de champs produites par le stator et le rotor. Chaque flasque est constitué d'une tôle roulée noyée, en partie, dans une structure en résine et plaquée contre la face arrière de chaque stator. Une feuille isolante fine sépare les pièces pour limiter les pertes magnétiques par la circulation des courants de Foucault.



Structure
en
résine

Tôle roulée

Trajet
des
lignes de champs

Tôle roulée

Fig.I-2.6 : Flasque d'extrémité vu de face et de côté.

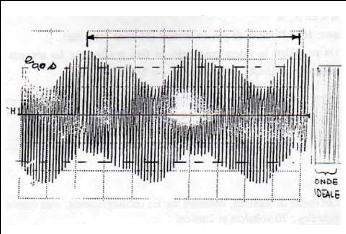
On représente le moteur par une vue éclatée et schématisée de la façon suivante:



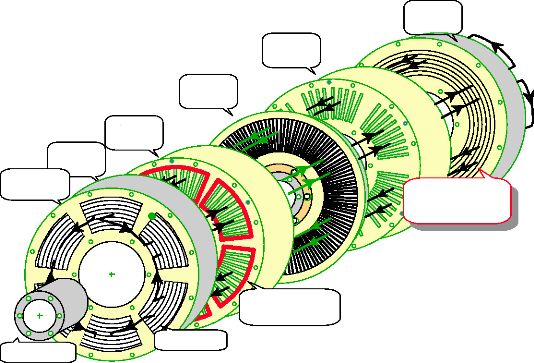
culasse
n° 2

stator
n° 2

rotor

stator n° 1

culasse
n°1

bornes de
raccordement

trajet des paquets
de lignes de
champ

bobine entourant
le secteur

tole roulée

Arbre moteur

Fig.I-2.7 : Vue schématique et éclatée du moteur FINTRONIC.

En se placant sur l'un des plots statoriques du moteur, les lignes de champs induites par les courants au stator traversent : les aimants, un entrefer mécanique constant et le disque "rotor" en acier lisse. La perméabilité relative des aimants étant voisine de l'air (1,05), telle que l'annonce le constructeur des aimants UGIMAG (aimants à terre rare RECOMA 28), le déplacement du rotor impose aucune variation de la réluctance sur le circuit magnétique.



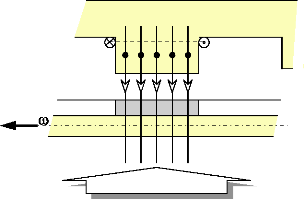
s

Pas de réluctance variable

N

Wi Stator

(fixe)

Rotor

s

(mobile)

Fig.I-2.8 : Représentation des lignes de champs induites par le stator.

Par contre, les lignes de champs produites par cet aimant traversent un entrefer variable (aimantation axiale) qui est dû essentiellement à la présence des parties saillantes des plots statoriques. On justifie ainsi l'appellation de

Moteur à réluctance variable.



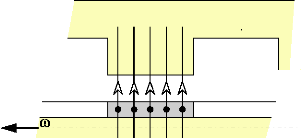
s

N

Waim

Rotor

Stator

s

(fixe)

(mobile)



Réluctance variable

Fig.I-2.9 : Représentation des lignes de champs induites par le rotor.

On représente le parcours d'une partie des lignes de champs, traversant les pièces du moteur, par les 2 figures qui suivent.

0° 120° électrique 240° 360°





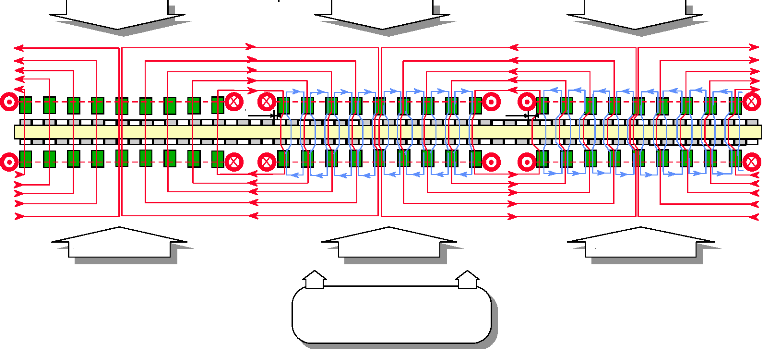
Secteur 1 / phase 1 Secteur 1 / phase 2 Secteur 1 / phase 3

Secteur 1 / phase 1 '

1/3

Représentation de quelques
lignes de champs qui se referment
par la culasse (non représentée)

Secteur 1 / phase 2 '

rotor

2/3

Secteur 1 / phase 3 '

Fig.I-2.10 : Trajet des lignes de champs sur 1 tour électrique. Vue développée.



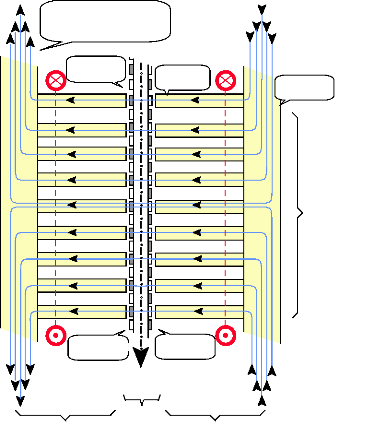
Disque

Disque stator n°1

Lignes de champs qui se referment
par les 4 plots et demi statoriques
du secteur adjacent

Entrefer
mécanique

Aimant sud Aimant nord

Sens de déplacement
du rotor

rotor

Plot
statorique

Disque stator n°2

Culasse

Secteur comprenant
9 plots
statoriques

Fig.I-2.11: Trajet des lignes de champs sur 1 secteur de phase. Vue développée.

Après cette présentation du moteur discoïde à réluctance variable et à aimants permanents alternés (MDRVAP), nous allons définir le système d'équations différentielles, capable de représenter mathématiquement le comportement physique du moteur.

3. MODELISATION DU PROTOTYPE.

Le moteur, tel que nous l'avons observé, s'apparente à une machine synchrone à aimants permanents. On utilisera donc les équations électriques et magnétiques de cette machine. L'élaboration d'une commande efficace et dynamique de type "vectoriel", nécessite d'utiliser le formalisme de Park. C'est pourquoi, nous définirons notre système dans le référentiel (d,q) de Park.

3.1. Conventions et hypothèses :

On suppose que la machine étudiée, répond aux conditions d'étude suivantes :

· Enroulement multipolaire.

· Absence de saturation dans le circuit magnétique.

· Absence d'effet pelliculaire.

· f.m.m. supposée sinusoïdale. On ne considère que le premier harmonique d'espace de la distribution de f.m.m.

· Le rotor tourne positivement dans le sens trigonométrique.

· Par convention, l'induit (stator) est considéré comme un récepteur.

· Le rotor est à pôles lisses et à entrefer constant.

· On néglige les amortisseurs.

· L'axe Oq est en avance sur l'axe Od.

· Un courant positif génère un flux positif.

· Une f.e.m. positive fait circuler un courant positif.

· On néglige les pertes magnétiques.

· Le flux inducteur, créé par les aimants, est aligné suivant l'axe du rotor.

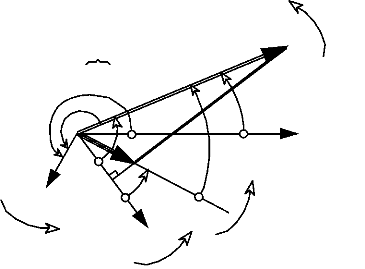
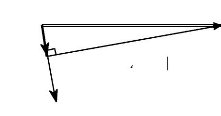
La construction vectorielle, telle que nous la présentons par la figure I-3.1, est très importante et servira de base à toute l'étude sur le moteur.



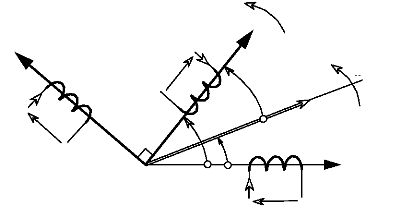
d

7

ids

q

iqs

vds

Axe
du
rotor

(0

(Fixe)

a_s

(0

ias

-->

? aim

vqs

O

a + a 0

? ? ? 0

vas

Fig.I-3.1 : Construction vectorielle avec l'axe d non aligné avec l'axe du rotor.

Pour t=0 = a = et 0 = . L'angle y correspond au décalage entre l'axe d et l'axe du

0 0

rotor. Nous verrons, par la suite, qu'il faut caler ces 2 axes entre-eux de façon à obtenir
7 = 0 soit a = 0 . Ainsi, la matrice de Park fera intervenir uniquement l'angle 0. Il est

important de préciser que les 2 enroulements représentés sur les axes d et q, sont purement fictifs. Les grandeurs engendrées par ces enroulements, seront créées et évolueront par l'intermédiaire d'un algorithme numérique. La position initiale du rotor est l'élément indispensable au bon fonctionnement d'une commande vectorielle et nous verrons pourquoi, par la suite.

L'angle 0 correspond à la position du rotor par rapport à l'axe fixe de la phase a _s.

3.2. Mise en équations du moteur à l'étude dans le repère (as,bs,cs) [4] [5] [6]:

· La loi d'Ohm avec la convention récepteur du circuit d'induit, s'écrit :

dP is

dt

v _is =R s iis +

(I-1)

R_s

d'is

dt

+

d'P_as

dt

iis

vis

Fig. I-3.2

L'inducteur est représenté vectoriellement par son vecteur flux, d'amplitude supposée constante :

?

^IP aim

Appliquée aux phases statoriques a_s, b_s, c_s du moteur, on obtient les expressions :

v as = R s ias



?#177;

(Nibs 1 as

dt

cs

r

1

r

1

v bs = R s ibs

[

v

v

v

bs

1

L

i

i

i

d
dt

gⁱ

bs

Wcs

T

1

as

[

I I

I

J

R_s

I =

J

bs

I+ J

cs

+

dIcs

dt

v cs = R s ics

Sous une forme matricielle, on a :

₁

[ v abc ] s = R _s [i abc is #177; dt [Tabc j1

s

(I-2)

· Suivant l'hypothèse de base, c'est à dire, le circuit magnétique non saturé, on peut lier les flux et les courants par les relations suivantes :

Was = L _pa i _as + M _ab i _bs + M ac ics + W_a aim Tbs = M _ba i as + L _pb i bs + M bc ics + gib aim

Wcs = M _ca i as + M _cb i bs + L pc ics +'Pc aim

Avec :

1

3 + 00

tpa aim .^tPaim cos(COt + ⁹0)

cos(o)t--
cos(o)t--

2 7c 3+90)

4 7c 3+90)



?

Tb aim = Taim

?

N^Ic aim = ^ti^laim

(I-3)

D'après la forme et la constitution du rotor que nous avons décrit précédemment, il est possible de considérer la machine comme étant à pôles lisses et à entrefer constant. On peut écrire :

· L pa = L pb = L pc = L_p : constante (valeur qui ne dépend pas de la position du

rotor).

· M ab = Mbc = M_ac = M: Mutuelle à valeur constante valeur qui ne dépend pas de

la position du rotor.

En tenant compte de cette précision, on peut mettre les relations précédentes sous la forme matricielle suivante :



? ? cos ? ?

? ?

aim 0

as

i

i

i

?

1 ?

?

? ?

+

Taim

r 1

[

bs

i ?

?

? ?

?

r
[

Taim

cos(O t -- 4 7C 3 + 9₀

1

?

?

? ?

cs

Tas

^F

1

?? bs ? ? ^tics

r ? ?

L

p

t ? ?

?

cos( ? t ? 2 3

? ?

? 0 ) ?

? ?

L _p M M

M L _p M

M M L

(I-4)

Sachant que :

L p = l _f + L_ms et M = -- 12 Lms


·
·

Taim

?

Taim

i
i
i

as

1 ?

?

? ?

+

bs

r
[

r ? ?

L

cs

L'expression (I-4) devient :

rl f #177; L_ms _ 1 2 L ms -- 1 2 Lms

? ?

? ? 1 2 L l L

? ? 1 2 L

? ms f ms ms ?

? ? ? 1 2 L ? 1 2 L l L

? ? ?

ms ms f ms

r [

^Il^jas Tbs "cs

1 ? ? ? ?









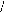
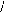
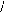
(I-5)

En l'absence d'un fil neutre relié à la terre, on a:

? ? cos( ? ?

t ? ?

aim 0 )

?



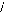
cos( ? t ? 4 3

? ?

? 0 ) ?



cos( ? t ? 2 3

? ?

? ? ?

0 )

i as + i bs + i cs = 0 ?i bs + i cs = ^--ias

Ce qui nous donne :

I

? 3 ? di as



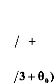
0

9

2

273 3

e0)o)

47c

v R i

? ? ?

l L ? t

as s as f ms aim

?? ?? ? ? sin(

? ? ?

2 dt

? 3 ? di bs

v R i

? ? ?

?? l L ? ? ? t ?

bs s bs f ms ?? ? ? sin(

aim

2 dt

? 3 ? di cs

v R i

? ? ?

l L ? t

cs s cs f ms aim

?? ?

?? ? ? sin( ? ?

2 dt

(I-6)

En reprenant les relations (I-5) et en posant :





[ L]

s

r [

1 ?

? ? ? : Matrice des inductances statoriques.

ms
ms

l _f + L_ms -- 1 2 L ms -- 1 2L

1 2 L ms l _f + L_ms -- 1 2L





1 2 L ? 1 2 L l L
?

ms ms f ms

et

?

? ? abc ? aim ? aim

? ?

? ?

? ?

cos(cot + 00)

?

: Matrice des flux de l'inducteur.

cos( ? t ? 2 3

? ?

? 0 ) ?



cos( ? t ? 4 3

? ?

? ) ? ?

0

On obtient une forme matricielle :

[^IF abc ? s ? ? s ? abc ? s ? ? abc ? aim

? L i ?

(I-7)

On sait que :

?

d tP a

aim

e as

_ --

dt

^liPaim

d cos(wt+ 90 ) d cos(cot + 90)

? ? ? ? as ? ? aim

e ? ? ? sin ? ?

? t ? ? 0

aim

dt dt

En raisonnant de la même façon pour e _bs et e _cs, on obtient les équations suivantes :

v as = R _s i _as + L_s

v bs = R _s i _bs + L_s

v cs = R _s i _cs + L_s

I

1

?

L



as

di

as

bs

di

bs

di

cs

?

ecs

dt

Avec

3

e as = ct? _aim sin(cot+ 0₀)

e bs = Ch_aim sin(cot -- 2i 3+ 0 ₀ )


·
·



e cs = claim sin(cot -- 47c

3 + 00)

E ? ? ?? ? aim

(I-8)
Soit en notation complexe:

V_s= R _s I _s + jcoL_s I _s -- j OFaim

ou

V_s =R_sI_s + jco(L_s I_s --Taim)



(I-9)

On représente les relations précédentes sous la forme vectorielle suivante :

Chapitre 1 : Présentation et Modélisation du prototype - Mémoire CNAM Patrick BOIDIN.

.



?

90^°

-->

V_s

cot

90 + cot

e_r

0

-->

co L _s I _s

cot + o s 0

as (Fixe)

⁽1⁾

?

?

E_s

8

-->

^IP aim

cot

?

-->

cot

I_s

cot

9

Fig.I-3.3 : Diagramme vectoriel dans l'hypothèse de Behn-Eschenburg.
On n'a pas représenté la chute de tension résistive.

3.3. Problème lié à la résolution des équations dans le repère (as,bs,cs) : Si on remplace l'expression des flux dans les relations (I-2), on obtient :

? v ? R ? i ? ? L ? d ? ? ? ? ? ?

d

? ? dt i ? ?

abc s s abc s s abc s abc aim

dt

(I-10)

Sachant que :

?

? ? abc ? aim ? aim

? ?

? ?

? ?

cos(cot + 90)

?

cos( ? t ? 2 3

? ?

? 0 ) ?



cos( ? t ? 4 3

? ?

? ) ? ?

0

on en déduit :

sin(wt + 90)

?

sin(wt - 2 7c 3+90 ) ?

sin(wt - 4 7c 3+90

?



?

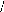
: fonction du temps.



[Tabc]

=- co^tl^faim

d
dt



aim

? ?

?

? ?

On reprend l'expression (I-10) pour la mettre sous la forme d'une représentation d'état d'un système d'équations différentielles que l'on connaît. On obtient :

sin (o)t+ 90) (wt-2 7c 3+90) (cot-4 7c 3+90)

? ?#177;R _s [L ]--

s ¹ [iabc ]_s =[ns ¹[vabc ]_s #177;^(134faim [L]

1

?

?

? ?



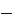
d
dt

? 1

s

? ?

?

? ?

sin sin

(I-11)

? [ ( ) ] [ ] [ ( ) ] [ ( ) ] [ ( ) ]

dt X t + A X t = B t + C t

En supposant que la vitesse reste constante durant la variation des courants (critère de linéarité), on a alors un système différentiel linéaire du 1er ordre à coefficients constants, au premier membre (en fonction du temps) et au second membre, variable dans le temps. La solution particulière de ce système est obtenue par la méthode de variation des constantes. Cette méthode de résolution est coûteuse en temps et en moyen de calcul (système à 3 équations). L'utilisation du formalisme de Park contribuera peutêtre à améliorer la résolution de ce système et simplifier la commande.

3.4. Equations mécaniques :

L'expression du couple électromagnétique, pour un moteur multipolaire, est de la forme:

3 Tem = N p 2

?i i j - j i ?? ?i

(I-12)

N_p correspond au nombre de pas du moteur discoïde. L'équation du mouvement est de la forme :

d ?

) dt

T T J J em - r = ( _m +r

(I-13)

?

Sachant que L = , on a :

N_p

1

dw 1

dt ??

r

T T

( _m + _r )

? = N J J

p

em r ??

(I-14)

On peut émettre une remarque importante sur la représentation physique du couple
résistant . En effet, ce couple représente en réalité la somme de 3 couples qui

T_r

s'opposent à la rotation du moteur. Ils sont :

· Un couple résistant, dû aux frottements visqueux que l'on notera T_rf. Ces frottements sont proportionnels à la vitesse et sont provoqués par les roulements à billes, la circulation de l'air dans l'entrefer et le ventilateur de refroidissement du moteur (absent dans notre cas). On a: T_rf = fw.

· Un couple résistant résiduel dû essentiellement aux aimants dont les lignes de champs se referment selon la règle du flux maximal et tendent à s'opposer à la rotation du moteur. Ce couple est indépendant de la vitesse, on le notera Tr0.

· Un couple résistant, dû à la machine entraînée que l'on notera Trma.

On obtient ainsi une nouvelle expression :

1 ?

? N J

(

?? m ?

p

J r )

do)] dt LI

T em -- (Trma + T r f #177; T r 0 )

Avec

T rf = f co

te

T r0 = Cte



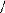
T rma = k o)² ou k o)³ ou k a ou Cs

(I-15)

3.5. Modèle du moteur dans le référentiel de PARK :

Le principe consiste à convertir le système triphasé précédent d'axes a_s, b_s et c_s en un système diphasé d'axes d et q équivalent. Compte tenu de la figure I-3.1, cette transformation aboutie à la matrice de PARK [ P] :

(I-16) : [ P] =

1^-
[

2

3





?

?

) ?

? ?

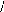
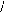
cose cos(9-- 2 7c 3 ) cos(9 -- 4 7c 3)





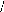
? sin ? ? sin( ? ?

? 2 3 ) sin(

? ? -- 4 7c 3







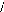
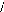
1 2 1 2 1 2

Matrice de PARK.

? ?

?

? ?

et sa matrice inverse :

(I-17) : [P]^-1 =

cose --sin

i ?

?

? ?

0 1





cos(9 -- 2 7c 3 ) --sin(9 -- 2 7c 3 ) 1
cos(9-- 4 7c 3 ) --sin(9 -- 4 7c 3 ) 1

Matrice inverse de PARK.

Avec la matrice [ P] , il est ainsi possible de passer d'un système à l'autre. Pour cela, on utilise les transformations suivantes :

? ? ? ?? ? ? ? ? ? ? ?

i ? P i ? i ? P i

? 1

dqo s abc s abc s dqo s

? ? ? ?? ? ? ? ? ? ? ?

1

v P v ? v ? P v

?

?

dqo abc s abc s dqo

s s

? ? ? ?? ? ? ? ? ? ? ?

? 1

? ? P ? ? ? ? P ?

dqo abc s abc s dqo

s s

(I-18)

L'unicité de la matrice de transformation [ P] pour les tensions, les courants et les flux, nous oblige à tenir compte des changements de variables suivants :

2 2

? ds

3 3

i i

? ? v ? ? v ? ? ?

ds ds ds ds ds

2 2

i i

? ? v ? ? v ? ? ? ? ?

qs qs qs qs qs qs

3 3

1 1

i i

? ? v ? ? v ? ? ? ?

os os ds os ds os

3 3

(I-19)

Il faudra faire ATTENTION que dans tout ce qui suit, nous utiliserons
des notations non primées pour simplifier les écritures (Sauf indication
contraire).

? Pour retrouver des vraies valeurs de flux et de tensions sur les axes d et q, il faudra multiplier chaque résultat par 3 2 (les résultats sur les courants restent identiques).

A partir d'un calcul que l'on ne démontre pas, on obtient :

i
i
i

vds

ds

1 ?

?

? ?

?

qs

[R_s]

+0)

v _qs

1 ?

?

? ?

r I

[

F I

[

r I

[

os

v os

F I [

'Yds Tqs Tos

1 ? ? ? ?

+

d dt

r I [

^tPds Tqs Tos

1 ? ? ? ?

0 --1 01

?

1 0 0 ?

0 0 0 ? ?

(I-20)

On en déduit les équations de PARK :

dlds

+ ?

dt

dlidt qs v qs = R s iqs + +

v os = R _s i os

(Attention aux valeurs primées)

EQUATIONS DE
PARK DU MOTEUR DISCOIDE A RELUCTANCE
VARIABLE ET A AIMANTS PERMANENTS ALTERNES.

v ds = R s ids

colli_qs

Wt

ds

+ dIos

dt

(I-21)

On sait que ? ? abc ? s ? ? s ? abc ? s ? ? abc ? aim

? L i ?

On multiplie chaque terme par la matrice de PARK, ce qui nous donne :

? ? ? ? ?? ? ? ? ? ?? ?

? P L i ? P

dqo s s abc s ? abc aim

(I-22)

On remplace [ iabc] s par [ idqo? _s ? ? ? ? ? ?? ? ? ? ? ? ? ?? ?

? P L P i

?1 ? P

dqo s s ? abc aim

dqo s

Après un calcul, on obtient pour le premier terme :

?

? ?

i ? 0

dqo s ?

?

l ? 3 2 L 0 ? ?

i

f ms ? dqo

f ?

? ? ? ? ? ?

0 0

1

s

0 0

l ?



l _f + 3 2 Lms



? ? ?

L M

? 0 0

p

?

? ?? ? ? ?

P L i

s . abc

s

? ? 0 ? ?

L M

? 0

p

? ? 0 0 ? ?

L ? 2 M ? p

.

1

Avec L _p = l _f #177; L_ms et M = -- 2 Lp

(I-23)

r ?

? ?

L



Et pour le second terme :

[P ][Tabc ]aim

? ? 0 0 ?

aim ?

0 0 0 ?

0 0 0 ? ?

(I-24)

Remarque importante:
Transposé sur l'axe d, le flux créé par les aimants (déterminé par un essai) doit être
normalement majoré du coefficient 3/2 (unicité de la matrice de Park). On aurait donc:

? ???daim = ?aim

?

? ? daim ? 3 ? ? aim

2

Pt

Etant donné que nous utilisions des valeurs non primées, on en fera de même pour 'gdaim

.... ....

? D'après la nouvelle notation, on a : lⁱdaim = Taim



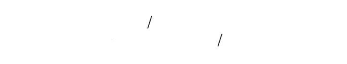
1 ?

?

? ?

l _f + 3 2 Lms

ds

i
i
i

0 0

1 ?

?

? ?

?

qs

0 l _f +3 2 L 0

ms

? ? ds

?

?? qs ? ? 'Fos

0 0

r
[

r
[

l_f

os

L'expression des flux dans PARK est :

? ? ? ? ?

daim

? ? ?

? 0
? ? ?

? ? ? ? 0 ? ?

(I-25)

(I-26)



?

? i ?

ds

? ?

?i qs ?? ? i ? os ?

?

? ? L i ? ?

ds d ds daim

? ?

avec ? daim ? aim

? et

3

L d ? L q ? L s ? l f ? L ms L o ? l

2 et

Attention aux valeurs primées.

f

? ? ?

ds

? ?

?? qs ?? ? ? ? os ?

d

? ?

0 L 0 ? q ?

? ? 0 0 L ?

o ?

? L 0 0 ?

1 ?? 0 ?

0 ? ?

? ?

?

? ?

.

?

? daim

?

? L i

qs q qs

? L i

os o os

?
?

Ld : Inductance synchrone d'axe direct (longitudinale).

L_q : Inductance synchrone d'axe en quadrature (transversale). L_s : Inductance synchrone.

En remplaçant Ilid_s , Wqs ,Ios par leur expression dans les relations (I-21), on obtient :

v ds = R _s i _ds + L_d

-- co L _q i _qs +

di^fdaim

dt

di ds

dt

Avec

L d = L_q

Le flux 'k_m est constant par rapport au temps = Le dernier terme de ^l'expressionprécédente s'annule.

?

?

I

ds

di

?

w

dt

di qs

dt

di os

dt

v ds = R _s i _ds + L_d
v qs = R _s i _qs + L_q
v os = R _s i _os + L_o

L q iqs

#177; wL d ids #177; W taim

(I-27)
D'après cette remarque, les deux derniers termes de v _qs correspondent à des f. e.m de

rotation puisqu'elles sont créées par la rotation d'un flux qu'il soit variable ou non. On pose :

e qs = W ( L _d i ds #177; lifdaim ) et e_ds = L_q0) i

qs

v ds = R _s i _ds + L_d

v qs = R _s i _qs + L_q

v R i L

? ?

os s os o



ds

di

?

eds

dt

qs

di

+

eqs

dt

dt

di

os

avec

e ds ? L q ? i _qs et e qs ? ? ? L _d i ds ? ?? daim ?

¹daim = +aim

et

3

L _d = L _q = l _f + L ms L o ?

2 et

(Attention : Ce sont en réalité toutes des valeurs primées)

l_f

(I-28)

A partir de ces expressions, on peut schématiser le système de la façon suivante :



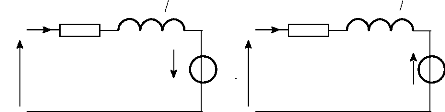
L _d = l _f + 3 2Lms

L_q = L_d = l_f + 3 2Lms

i _qs

vds

R_s

e _qs = L_dco i_ds + CO 41 daim

ids

R_s

e ds = L q oiqs

v qs

ios R_s L_o =l f

vos

Fig. I-3.4 : Loi d'Ohm des circuits équivalents d'axes d, q et o.

La puissance électrique instantanée, fournie par le réseau et consommée par le moteur, est de la forme :

P _e = v _as i _as + v bs i bs + v cs ics

? En appliquant Park, on obtient la nouvelle expression :

3 P e = 2

( v ds i ds + v qs i qs + 2v os i os )

Si on exprime la puissance en fonction des flux et des courants, on obtient :

31^-

^e 2 L

P = IR _s i ds 2 + ids

dtlj d ? d ?

1
I J

ds 2 qs 2 os

? i ? ? ? R i ? i ? i ? ? ? 2 R i ? 2 i

ds qs s qs qs qs ds s os os

dt dt dt

On organise chaque élément de l'expression pour faire apparaître le terme correspondant à la puissance électrique absorbée par le moteur et transformée en puissance mécanique transmise à l'arbre du moteur (dernier terme).

3 3 ? d ? d ? d ? ? 3

2 2 2 ds qs os

P ? R i

? ? i ? 2 i ? ? i _dt i

? ? i ? ?

? i i ?

e s ds qs os ds qs os qs ds ds qs

?? 2 ?? ? ? ?

2 2 dt dt 2

On obtient ainsi :

3

? ?

T em ? Np ⁱqs ds ? ⁱds qs

?? ? ?

??

2

(I-29)

L'expression peut se simplifier en remplaçant les flux par leur expression. On obtient:

3

T em ? Np _daim i qs

??

2

Il est très intéressant de constater que le couple électromagnétique est directement
proportionnel au courant i _qs . On se retrouve donc dans les mêmes conditions que le

moteur à courant continu.

T_em = T_q = KT iqs

avec


·
·

p'I`daim en N.m/A : Constante de couple_et

T_d = 0

3

K = ₂N

T

(I-30)

3.6. Remarque sur la transformation de Park et du système résultant :

Mise sous une autre forme et tenant compte que L _q = L_d , la transformation de Park permet d'obtenir les relations très importantes suivantes :

di ds

dt

qs

R 1

? L ⁱ _L v

s ? ? ? i

ds ds

d d



di

qs

dt

ce

? daim

R 1 1

+ ^s i qs = vqs --co i ds -- L d

L d L d

e ds =
e qs =

(L qs d i

?L i ? ? ? ? d ds daim

co

ce

?

? ? ?

3

T ? N ? i

em p daim qs

2 avec ^tlⁱdaim =aim

ce

dw

dt ?

f N p

J _m +Jr

N_p

? J _m +Jr

(K _T i -- T r 0 -- Trma)

(I-31) Attention : Ce sont en réalité des valeurs primées.

? Sous une forme matricielle, on a :

d R

? ? ? ? ? ?

1

s

dt i ?

dq s L i ?

dq s L v dq

d

d

? i ?

qs

? ?

??

? ?

i ?? ??

ds daim

s





(I-32)
On remarque que les courants de Park sont liés entre eux par la vitesse angulaire du
rotor Co. Le couple électromagnétique étant indépendant du courant i_ds, on peut

imaginer une loi de commande qui puisse maintenir ce courant nul. On aurait ainsi le courant i _qs qui crée le couple, découplé du courant i_ds qui crée le flux.

Remarques:

· En régime permanent, co = o s ? Le système d'axes (d,q) tourne à la vitesse de synchronisme. Toutes les grandeurs dans Park deviennent des constantes.

· L'annulation du courant _ids proposée précédemment, revient en définitive à

? ?

maintenir le vecteur -- E_s colinéaire avec le vecteur courant I s . Dans certain ouvrage, on dénomme cette commande par : « Commande à flux croisés ».

· Lorsque l'on aura besoin de déterminer vectoriellement les courants _ids et i_qs, il



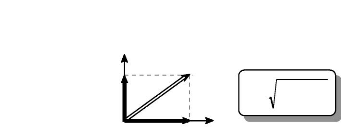
sur les axes d et q.

?

suffira de projeter le vecteur I_s

q

--)

I _s

"I_s =

( ?

i ds ? i qs

2 2

d

·

-->

-->

i qs

ids

Fig. I-3.5

· On pourra effectuer les mêmes projections du vecteur flux et du vecteur tension à condition de tenir compte du coefficient 2 3 qui nous a permis d'unifier la matrice de Park. On rappelle que vds, vqs, vos, ^Wds, _tqset 'F_os sont en réalité des valeurs primées. Pour revenir aux vraies valeurs représentatives des axes a_s, b_s et c_s, il faut

3

multiplier les valeurs obtenues par 2 . D'une autre façon, on pourra augmenter de ce

même coefficient le module des vecteurs uniques avant de les projeter sur les axes d et q.



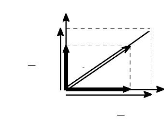
3

-->

-->

-³ 3 -->

v = vi

^qs 2 ^qs

--)

V_s

-->

vds

?

q

,

vqs

?

v _ds ? ?

v ds

2



V

=

s

( v'ds 2 + v'qs² ) = 2 3 (+)

T_s

d

= ( ? s ? ? ? qs ? ? ? ? ds ? ? qs ?

₂ 2 2

? d 2 2

3

Fig. I-3.6

Cette partie d'étude nous donne 2 systèmes de représentation différente ; Le premier (I-11) dans le repère (a_s,b_s,c_s) et le second (I-32), dans le repère (d,q).

Or, dans les 2 cas, les équations différentielles sont à coefficients constants avec les hypothèses de bases. = Le changement de repère ne se justifie donc pas.

Dans les 2 cas, le second membre des 2 systèmes correspond à des fonctions variables en fonction du temps. On se retrouve donc avec le même type de problème. Par contre, quel que soit le régime de fonctionnement (transitoire ou permanent), le second membre du 1^er cas varie toujours en fonction du temps. Dans le 2^ème cas et en régime permanent, le second membre est constant. = Le changement de repère se justifie. Le nombre d'équations électriques, dans le système de Park, est limité à 2 pour 3, dans l'autre cas. ? Le changement de repère se justifie.

4. CONCLUSION.

"Tout problème physique, quel qu'il soit, peut être ramené sous la forme d'un modèle mathématique évolutif dans le temps."

Au moyen de cette réflexion, nous avons pu définir, dans ce chapitre, un modèle mathématique, capable de représenter le comportement physique du moteur FINTRONIC de GEC-ALSTHOM MOTEURS Nancy. Reste maintenant à valider ce modèle et c'est ce que nous allons faire dès le prochain chapitre. Le changement de repère dans le référentiel de Park va nous permettre d'élaborer une commande performante du moteur, appelée :

Commande vectorielle.

CHAPITRE 2

ESSAIS EXPERIMENTAUX
ET
VALIDATION DU MODELE

1. INTRODUCTION.

Dans cette partie d'étude, nous avons tout d'abord déterminé par des essais expérimentaux, l'ensemble des valeurs numériques définissant les éléments du modèle. C'est à dire :

· La résistance de l'enroulement des phases du stator : R_s .

· L'inductance synchrone du moteur : L_s qui correspond aussi à l'inductance synchrone d'axe d du référentiel de Park L_d. Avec les 2 paramètres précédents, on en déduit la constante électrique statorique du moteur : t_s.

· La f.e.m à vide, induite dans les phases du stator et provoquée par la variation du flux créée par les aimants du rotor : e 0 s . On en déduit le flux maximal, produit par les

aimants : ??aim et la constante de couple du moteur : K_T.

· Le coefficient de frottement visqueux du moteur : f .

· Le moment d'inertie des masses tournantes du moteur (rotor) : J_m et d'en déduire la constante mécanique du moteur, à vide : ' m0.

· La constante thermique d'échauffement du moteur, compte tenu que le moteur est démuni de tout système de refroidissement : tth.

· La température limite d'échauffement des enroulements de phases : 0lim.

Ensuite et pour compléter les résultats obtenus, nous avons émis une série de remarques sur le comportement du prototype, face aux différents essais.

Pour finir ce chapitre et valider le modèle mathématique du moteur, nous avons comparé les résultats obtenus par des simulations, sous MATLAB-SIMULINK, avec les résultats des essais.

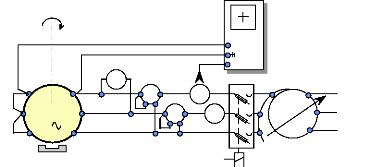
2. DETERMINATION NUMERIQUE DES ELEMENTS DU MODELE. 2.1. Essai à vide du moteur en fonctionnement générateur :

Cet essai permet de construire la caractéristique de la f.e.m en fonction de la fréquence de rotation (Annexe 1) et d'en déduire la valeur du flux dans l'entrefer, produit par les aimants. Pour effectuer cet essai, nous entraînons le moteur FINTRONIC avec un moteur à courant continu à excitation séparée.



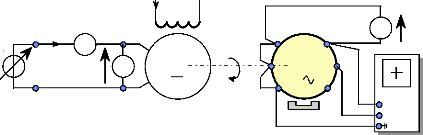
Ea 0s

V

1

I

1'

n

+

A

U

2'

V

2

M

GS

J= 0,8A

3

Chronomètre 3'
et
Tachymètre

3

Aimants P.

e a 0 s (t )
e b 0 s (t )

Fig. II-2.1 : Schéma de montage de l'essai à vide en générateur.



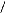
Les résultats et les remarques sur cet essai, sont les suivants :

· Sur une moyenne de 10 relevés, on obtient une constante de vitesse de 0,67volts efficace par tour par minute. Soit :

?

0 ,6 7 volts / tr . min -1 = E a 0s = 40 ,2 volts pour n = 60 tr / min

(II-1)

· Pour un fonctionnement à vide, on a :



v as = e a 0 s ?Vs = E0 s =⁰) aim

co = 27c N _p n

avec N p : Nombre de pas du moteur (64 dans notre cas).

On en déduit la valeur maximale du flux produit par les aimants et la valeur de la



constante de couple sachant que KT = 3 2 NpTdaim :


^·?aim = 141 mWb soit Taim = 99 ,7 mWb
K_T = 13 ,5 N . m / A

(II-2)

· Les ondes de tensions, obtenues sur les oscillogrammes, sont quasiment sinusoïdales. Echelles : 20 volts/cm et 2ms/cm :



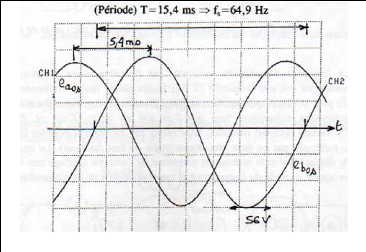
Fig. II-2.2 : Ondes de tensions. e a 0 s ( t ), e b 0 s ( t) et e c 0s ( t) à n =61 tr/min


· Au moment de cet essai, on remarque que la fréquence de rotation du moteur varie sensiblement et de façon périodique. Cet effet néfaste (parasite) impose à la machine des vibrations et des à-coups de couple qui nuisent au bon fonctionnement du moteur. Ce phénomène se produit quelle que soit la fréquence de rotation du moteur. A l'oscilloscope, on observe cet effet parasite par l'intermédiaire de l'onde de tension induite au stator.



La machine tourne à 14 tr/min (15Hz) soit à peu prés au quart de sa vitesse nominale. La base de temps est de 0,5s par cm.



1 tour mécanique

Fig. II-2.3 : Oscillations parasites détectées sur l'onde de fe.m.

La fréquence d'oscillation, constatée sur l'oscillogramme, équivaut au demi-tour mécanique soit une fréquence 32 fois moins élevée que la fréquence électrique (2,2 Hz pour 69,3 Hz). Contrairement aux apparences, ce phénomène n'est pas dû à des frottements mécaniques bien que l'on soit en limite. Ceci est dû à des forces d'attraction (axiales) parasites, provoquées par les aimants dont les lignes de champs se referment par les plots statoriques (règle du flux maximal). Le manque de rigidité du disque rotor et le manque de constance de l'entrefer (réglage très difficile à mettre en oeuvre = voile du disque) sont la cause principale de ce phénomène.



Chapitre 2 : Essais expérimentaux et validation du modèle - Mémoire CNAM Patrick BOIDIN.

.

Stator
N°1

Stator
N°2

Les forces
d'attraction ne sont
plus
équilibrées

Disque
rotor

Aimants

N

S

Stator
N^°1

Stator
N^°2

Entrefer
constant

Axe de rotation

S

N

Entrefer mécanique

Entrefer non constant

Position du rotor

0 = 0⁰

Position du rotor
0 = 1 80^?

Les forces


d'attraction s'équilibrent

Stator
N°1

Stator
N°2

Fig. II-2.4 : Explication du phénomène d'oscillations sur la fréquence de rotation.

2.2. Essai avec les enroulements statoriques en court-circuit :

Cet essai permet de déterminer la valeur de l'inductance synchrone du moteur et d'en déduire la constante de temps électrique.



J= 0,8A

V

M

Chronomètre
et
Tachymètre

n

I

+

A

U

1'

1

2'

GS

3

Icc

2

A

3

3'

Aimants P.

Fig. II-2.5 : Schéma de montage de l'essai en cc.

· Des mesures sur la résistance des phases statoriques, par la méthode voltampèremétrique, nous donne les résultats suivants :

R s = 961 m ? à 20°C et 1,13Q à 80°C.

· En convention générateur, on a : V E R I j L I

= -- -- co

s s

-- s -- s -- s -- s

(II-3)

? 2

0 ( ) ( )

2 2

E R I j L I ? ?

= -- -- co ? E R I

? ? L I

?

s s s s cc s c c

? ? ?

s cc cc



2

E ? 2 ? ( )

?

R I

L s ?

s s cc

?
Co I cc

(II-4)

soit dans la construction de Fresnel :



--)

s 0) I cc

90^?

--)

E_s

0

Fig.II-2.6

--)

R _s I cc

--)

Icc

Sachant que w = 2 i N _p n , on a l'expression de l'inductance synchrone en fonction de la fréquence de rotation (tr/s) :



L s

?

2 ?

1

N n I

p

.

2

E --

s

( )

R I

s cc

cc

2

(II-5)

· Par l'essai à vide, on a obtenu E a 0 s = 40 , 2 volts pour n = 1 tr / s. Quelque soit la fréquence de rotation du moteur, l'essai en court-circuit nous donne : I cc = 1 ,8 6 A. D'où,

L'inductance synchrone correspond à :L s = 53 ,7 mH

(II-6)

L s

? La constante de temps électrique du moteur 'r_s = est de 47,5 ms. Cette valeur est

R s

importante, comparée à celle obtenue pour un moteur classique de même puissance qui est de quelques ms seulement.

2.3. Essai à vide du moteur FINTRONIC en fonctionnement moteur :

Cet essai permet de déterminer les pertes mécaniques et d'en déduire le coefficient de frottement visqueux du moteur. Tous les essais sont réalisés sous une alimentation de tension à 50 Hz pour une fréquence nominale de 64 Hz.



Aimants P.

Marche/Arrêt

n = 46,8 tr / min

v a 0 s (t ) i a 0 s (t )

1'

1

U

W

I

20A

220V-3ph
Réseau

N

2'

MS

3

2

W

I

3'

3

Régulateur d'induction

Fig.II-2.7 : Schéma de montage de l'essai et vide en moteur.

· En prolongeant la courbe de la caractéristique U ² i--> Pmag + Pmé ca, au point

d'abscisse égal à zéro (Annexe 1), on obtient les pertes mécaniques. Elles sont supposées constantes par rapport à la tension et sont proportionnelles au carré de la vitesse mécanique. On en déduit le coefficient de frottement viqueux f :

P_m

f -- LIé ^2ca et Pmé ca = Tfr n ? f = 1 ,96 N . m / rad . s-1(méca)

Coefficient de frottement visqueux.

mé _ca

ou f -- ?

2 et Pmé ca = Tfr ( 27c n) = f = 0 , 205 N. m / tr. min ^-1

P

(2 7c n)

2 et Pmé ca = Tfr (0) N_p) = f = 0 ,0306 N. m / rad . s^-1(élec)

mé ca

ou f --

P

(o) N_p)

(II-7)

· Pour effectuer cet essai, on couple la machine sur le réseau par la méthode habituelle : Moteur à courant continu et lampes de mise en phases sur le réseau. Le moteur à courant continu entraîne la machine à 47 tr/min. Ensuite, elle est couplée au réseau, par l'intermédiaire d'un régulateur d'induction réglé à l'avance à une tension composée de 115 volts. En fonctionnement générateur, la machine fournit entre les 2 bornes de son stator, une tension composée de 55 volts.

? La machine se couple au réseau sans problème et fonctionne en moteur.

Dans un deuxième temps, on tente de démarrer le moteur en forçant sa rotation à la main.

? Le moteur s'accroche au réseau sans et-coups, ni problème. La fréquence de synchronisme du moteur est très facilement atteinte et la main.

Pour finir, nous tentons de demarrer le moteur sous 115V en direct et sans aucune aide exterieure. L'essai est concluant et le moteur démarre à chacune de nos tentatives. Il en est de même pour tous les essais effectues.

? Le moteur est apte à démarrer en direct sur le réseau.

· La tension limite de decrochage du moteur, à vide, se situe à environ 110 volts soit une tension de phase de 63,5 volts.

· Le moteur vibre sensiblement pour des tensions elevees, voisines de la tension nominale.

· On suppose que les pertes magnetiques sont proportionnelles au carre de la tension (droite ideale sur la caracteristique en annexe). On en deduit le coefficient de proportionnalite :U _ab = 67 , 6 . 10³ --> P_mag = 419 W = k=6,20.10 ^-3 W/volts^2.

De 0 à 283 volts, on peut effectivement considerer cette proportionnalite comme
realiste. Au-delà, il faut reconsiderer cette hypothèse, il suffit de comparer les
courbes de la caracteristique U ² i--> P_mag + Pmé ca, en annexe 1, pour s'en convaincre.

· Le couple de frottement visqueux correspond à : T_fr = 9 ,5 7 N . m
2.4. Essai de ralentissement du moteur fonctionnant à vide :

Connaissant le coefficient de frottement visqueux f, cet essai permet de determiner le moment d'inertie des masses tournantes du moteur, à vide.



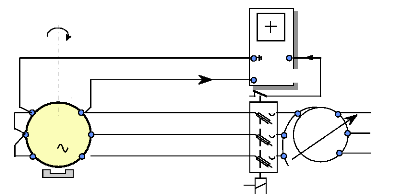
220V-3ph
Réseau

2

2'

N

3

3'

Aimants P.

Marche/Arrêt

n(t0 ) = 48tr/min

n(t₁ ) =0tr/min

MS

3

Synch

e a 0 s (t ₀ à t₁)

1'

1

20A

Régulateur d'induction

Fig. II-2.8 : Schéma de montage de l'essai de ralentissement du moteur.

· e a 0 s ( t) dans l'intervalle de temps compris entre t0 (correspondant à n = 48 tr / min) et t1 à n = 0 tr / min :

Echelle : 20ms/cm



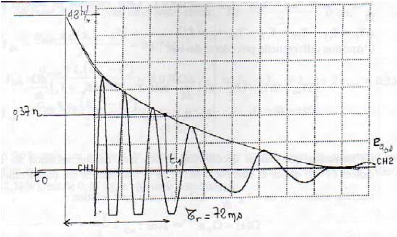
Fig. II-2.9 : Relevé de l'oscillogramme e a 0 s (t ).

· Le niveau de tension aux basses vitesses, fourni par la dynamo-tachymétrique, est trop faible pour obtenir des mesures significatives. De plus, les à-coups de couple ont tendance à transformer le signal continu du capteur, en un signal modulé inexploitable. Or, pour réaliser cet essai, on décide d'observer l'évolution de la f.e.m aux bornes d'une phase du moteur dans son fonctionnement générateur et en phase de décélération.

· En régime dynamique, le système mécanique, constitué par un moteur accouplé en direct sur une machine, est régi par l'équation différentielle suivante :

d ?
dt

T T ( J J )

em ? r _m + _r

(II-8)

Nota : Généralement, le premier terme de l'expression est non linéaire.

Pour supprimer la non-linéarité du premier terme, on linéarise le système autour d'un
point fonctionnement sur la vitesse : ?₀ . Pour cela, on découpe la période de

décélération en intervalles de temps A t donnés. On obtient ainsi [8] :

· A t₀=0, la condition initiale de l'essai ?₀

? 1

·



A t 1 = A t , T _ T ( J J ) t

= +

em 0 r 0 m ^r A

Q 2

·



A t 2 = t ₁ + A t , T _ T ( J J ) t

= +

em 1 r 1 m r ?

· A t 3 = t ₂ + At ...

Dans de nombreux cas, la variation du couple moteur est supposée constante autour de son point de fonctionnement et la variation du couple résistant, proportionnelle à la vitesse. D'où :

AT_em = Tem 1 -- Tem 0 = T_{em 2} -- T_em1 =... = cte=T. Cette variation ne dépend pas de n. AT_r = Tr 1 -- Tr 0 = T_r 2 -- Tr1 =...= fn

L'équation différentielle précédente devient :

AT em -- AT r =	? ? ?? J J ? soit T f ? ? m ? r ? ? ? J J m r At		di2 dt

n(t = 0 ) = n 0

(II-9)

En supposant que chaque décélération a lieu sans aucune variation du couple moteur
(T=0) et que le moment d'inertie de la machine est nul (décélération sans machine

entrainée), on a J

m

di2 dt

+ fn = 0, qui a pour solution :



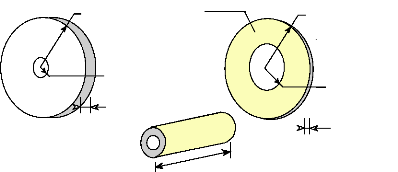
Taux d'occupation des aimants

tocc = ⁷⁶%

R=155 mm

aacier = 7850 kg / m3

(Densité)

r=30 mm

Ra=149 mm

caim = 8300 kg / m3

(Densité Récoma 28)

+ 2 x

ra=122 mm

e=10,5 mm

R=80 mm r=30 mm

+

Acier

L=141 mm

ea=1,75 mm

Jm

? ? t ? ? ? e ? t mo

? avec ?m 0 ? .

⁰ f(II-10)

On en déduit ainsi :

n(t = T m 0 ) = 0 ,3 7 n₀

(II-11)

L'essai nous donne t m 0 = 72 ms. Or, sachant que f=1,96 N.m/rad.s^-1, on obtient:

J _m = f T = 0 ,14 1 kg .m² : Moment d'inertie des masses tournantes du moteur
FINTRONIC.

(II-12)


· Vérification du résultat précédent par un calcul approximatif :

On sait que le rotor est constitué d'un disque métallique muni d'un arbre creux et de 2 couronnes d'aimants collées sur les faces du disque.On peut donc calculer le moment d'inertie de l'ensemble.

Fig.II-2.10 : Les éléments de constitution du rotor.

Moment d'inertie pour un cylindre creux : J = an e (R 4 -- r4). D'où,

2

J dis

J aim

J arb

?

aaciern

aim a

? ?

aaciern

e

e R-- r⁴)

L (R ⁴ - r⁴)

2 = 0 ,0746

(R a 4 -- r_a⁴)

2 = 0 ,070

2 ti occ= 0 ,0047

? ?

??

?

?
?

? ?

??

J J J

? ? 2 J ? 0 154

, kg m

.

m isc arb aim

A 10% prés, on retrouve le même résultat. Par comparaison, le moment d'inertie d'un moteur asynchrone, pouvant fournir un couple nominal de 95N.m à 750tr/min (7,5kW), est de 0,13 kg.m² (donnée constructeur).

2.5. Essai d'échauffement du moteur FINTRONIC :

Cet essai permet de déterminer :

· La température limite _elim atteinte par les enroulements statoriques pour un régime de fonctionnement permanent donné.

· La constante thermique tith.

Chaque enroulement des 12 secteurs est équipé d'une double sonde de température du
type thermo-résistance au platine PT100n. On utilise 2 de ces sondes pour effectuer cet

essai. Une table de conversion conforme à la norme permet de convertir les valeurs de résistance en valeurs de température (en degrés Celsius).



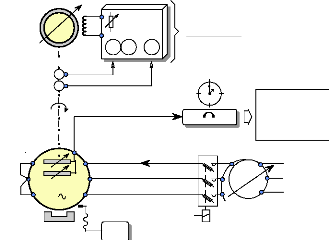
n = 46,8 tr / min

N

3'

2'

1'

Aimants P.

Frein
ea
Poudre

MS

3

e

T

n

Résistances variables par
sonde platine

3

1

Thermomètre

2

oC

T_u P_u n

Trma

I = 9A

Marche/Arrêt

Dispositif de Frein : Réglé à 87 N.m

Ohmmètre

20A

SL

Régulateur d'induction

Table de correspondance
de la norme
DIN 43 760

CPC

220V-3ph
Réseau

Fig.II-2.11

· D'après les relevés effectués (Annexe 1), on obtient une température limite des enroulements statoriques de 125°C. La température ambiante était de 22,2°C au moment de l'essai.

1ère constatation :

En prenant une marge de sécurité d'environ 10%, les parties isolantes du moteur doivent tenir 140°C, au minimum. Ce qui correspond d'après la norme NFC à la catégorie F des matières isolantes (155°C).

Nota :

Il faut préciser que le prototype est démuni de tout système de refroidissement. En effet, un dispositif d'auto-ventilation serait inutile compte tenu des faibles vitesses de rotation du moteur.

L'enveloppe du moteur est constitué d'une résine de moulage « DAMIVAL 13 576 » dont la plage thermique d'utilisation est de -70°C à +130°C. La notice technique du matériau concerné précise une tenue thermique en continu de 140°C, sans dégradation.

? Le matériau utilisé est limite en tenue thermique. Il faut réduire les pertes magnétiques afin de limiter les échauffements. La commande se chargera de réduire ces pertes.


· La constante thermique d'échauffement est de 22,5min. La température limite du moteur est atteinte après environ 112 min de fonctionnement (1h52 min).

°lim ? 1 2 5° C et rth = 22 ,5 min.

(II-13)

2.6. Paramètres du modèle :

Equations électriques dans le repère (d,q) de Park :

v R i L

=

ds s ds + d

v R i L

=

qs s qs + q

ds

di

dt



qs

di

dt

avec

e qs = w ( L _d i _ds + _daim ) e ds ? L q qs

?? et co i

3

L d = L q = L s = l _f + 2 s

L m

et
R_s = 1 , 1 3 ?, L d = L q = L s = 53 ,7 m H

? ? aim ? ? ? aim = 141 mWb

Equation mécanique dans Park :

3

T em = K _T i _qs avec K T = N p

2

H

T T _N J J

1 (

- =

em r ?? m +

p

T r = T _rma + T r 0 + f O)

? e ds
+ e qs

^??daim

_r)

do) 1 dt I?

Tous les essais effectués permettent de déduire l'ensemble des paramètres numériques du modèle. On obtient ainsi :

Constante de couple : KT = 13 ,5 N . m / A Nombre de pas du moteur : Np=64 Couple résiduel dû aux aimants : Tr0 = 3 N . m Moment d'inertie du rotor : J m = 0 ,14 1 kg .m^2 Coefficient de frottement visqueux du moteur : f = 0 , 0306 N . m / rad . s ^-1 0 lec)ou f = 0 ,205 N . m / tr.min^-1

(II-14)

Nota:

· Jr et Trma sont à définir selon la machine entraînée.

· Le modèle ne tient pas compte :

des pertes magnétiques,

de la saturation du circuit magnétique,

de la variation du flux _Taim, due aux parties saillantes des plots statoriques.

· Attention : v_ds et v_qs sont en réalité des valeurs primées.

3. ESSAIS EN CHARGE EN FONCTIONNEMENT MOTEUR.

Cette série d'essais, effectuée en boucle ouverte, permet de juger les capacités et les performances du prototype. Par obligation, on a augmenté l'entrefer de la machine pour éliminer les contraintes mécaniques et magnétiques observées au début de nos essais. Cette modification a pour conséquence de réduire sensiblement les performances de la machine. Les améliorations mécaniques et magnétiques nécessaires n'ont pas pu être réalisées dans le cadre de nos travaux.

On notera clue les performances réelles sont en réalité bien supérieures à celles annoncées dans ce mémoire.

Pour réaliser ces essais, on utilise un banc d'essai dynamométrique. Ce banc est équipé d'un frein à poudre magnétique (couple résistant constant par rapport à la vitesse) du type PB115 et de marque « Vibro-meter ».

3.1. Remarques sur les essais en charge :

Chapitre 2 : Essais expérimentaux et validation du modèle - Mémoire CNAM Patrick BOIDIN.

.



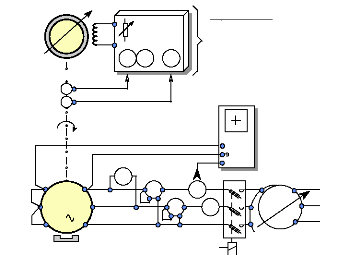
Aimants P.

Marche/Arrêt

J r = 1 0244 10 ²

. _ kg m ²

, .

Trma

T_u P_u

Dispositif de Frein :

Capacité de réglage du couple résistant de 0 à 135 N.m

Couple résistant à peu prés constant par rapport à la vitesse de rotation

n

Frein

ea

Poudre

T

n

n = 46,8 tr/ min

v a ( t)

i a ( t)

1'

1

U

20A

W

I

220V-3ph
Réseau

N

2'

MS

3

2

W

I

3'

3

Régulateur d'induction

Fig. II-3.1 : Schéma de montage des essais en charge.

D'après les résultats obtenus et présentés en annexe 1, on fait les remarques suivantes:

· Quelle que soit le couple résistant, appliqué à l'arbre, le moteur a pu démarrer directement sur la fréquence du réseau. Il suffit d'appliquer une tension suffisante aux bornes du moteur.

Une charge équivalente à un couple résistant constant de 138 N.m n'a pas empêché de démarrer le moteur. Il faut noter que le moment d'inertie des masses tournantes de la charge (frein à poudre) est relativement faible et s'oppose peu à la variation de la vitesse.

1ère constatation:

? Les conditions de démarrage du moteur Fintronic en boucle ouverte dépendent essentiellement du moment d'inertie des masses tournantes et dépend beaucoup moins du couple résistant.

· Le courant nominal de 9,3A limite le couple utile à environ 100 N.m pour une fréquence d'alimentation de 50 Hz. =

1. Pour un fonctionnement en service continu, il n'est pas possible d'obtenir un couple utile supérieur à 100N.m sans échauffements excessifs.

2. Pour un fonctionnement en service intermittent, il est possible d'atteindre des couples utiles très élevés (environ 180 N.m). Il faut cependant accepter un dépassement du courant nominal.

2ème constatation :

? On tend à proposer ce type de moteur pour des applications nécessitant des couples élevés durant des cycles intermittents.

Dans ce cas de fonctionnement, il est important de connaître les contraintes thermiques du moteur, compte tenu des courants imposés. On pourrait prévoir une commande tenant compte à chaque instant, de l'état thermique du moteur.

· Le courant à vide du moteur augmente très vite avec la tension. Pour une tension de 300 volts, les courants correspondent aux courants nominaux. Ce sont les pertes magnétiques qui contribuent à absorber de tels courants.

3ème constatation :

? Pour une charge donnée, iI est essentiel de limiter les pertes magnétiques dans les tôles du moteur. Il faut réduire au mieux les tensions aux bornes du moteur. On applique des tensions justes suffisantes pour maintenir le couple électromagnétique maximale correspondant au couple résistant.

· Les courants absorbés dans les phases du moteur sont très inductifs. Par conséquent, le vecteur représentatif de la f.e.m induite au stator tend à se retrouver en avance sur le vecteur courant [9]. Dans le cas d'une commande par onduleur « commutateur de courant », la position de la f.e.m ne favorise pas l'annulation et l'inversion des courants (cas où l'inductance synchrone est en court-circuit sur sa f.e.m). L'amplitude et le signe de cette f.e.m ne sont pas aptes à s'opposer efficacement à ce courant. Il faut insérer, dans le circuit, des condensateurs qui permettent de transférer l'énergie stockée dans les inductances vers les condensateurs.

4ème constatation :

? L'utilisation d'un onduleur de tension est moins coûteuse et plus appropriée. Il n'est pas nécessaire d'équiper le système d'un dispositif particulier de commutation forcée puisque l'énergie stockée dans l'inductance est dissipée au moyen des diodes de roue libre.

· Le flux créé par les aimants est faible devant le flux nécessaire dans l'entrefer. On doit donc renforcer ce flux par une réaction d'induit. C'est pourquoi, les courants statoriques sont très inductifs. Par conséquent, il serait utopique de vouloir améliorer le facteur de puissance sans réduire sensiblement les performances du moteur en couple. Le rendement du moteur se trouve pénalisé et les meilleurs résultats obtenus pour ce rendement ont été de 40%. Toutefois, cette valeur ne peut pas être considérée comme mauvaise compte tenu des conditions de fonctionnement. En effet, pour des fréquences de rotation aussi faibles, des couples aussi importants et des encombrements aussi faible, les solutions utilisants le moteur asynchrone ne donnerait pas d'aussi bons résultats, même muni d'une commande vectorielle de flux. Une étude comparative serait intéressante à faire.

5ème constatation :

? Pour ce type de machine, il vaut mieux favoriser le contrôle du couple instantanéau détriment du facteur de puissance.

· Au démarrage, les courants de pointe, absorbés par le moteur n'ont jamais dépassé plus de 2,3 fois le courant nominal. Dans la majorité des cas, ces courants sont restés voisins du courant nominal.

· A l'arrêt, le flux constant créé par les aimants tend à vouloir figer le rotor par rapport au stator. On est en présence d'un couple"résiduel" qu'il ne faut pas oublier de rajouter au couple résistant. Ce couple, obtenue par un essai (bras de levier et poids),

prend une valeur approximative de 3N.m. Ce couple est constant par rapport à la vitesse.

3.2. Résultats obtenus pour U ab = 340 volts et T u = 138 ,5 N . m :

Ce relevé particulier va permettre, par la suite, de vérifier la validité du modèle mathématique du moteur. Avant cela, nous présentons les résultats expérimentaux obtenus par ce relevé :

Mesures



Tu	Pu	Ias	Ibs	Pabs	Qabs	Vas
(N.m)	(kW)	(A)	(A)	(W)	(var)	(V)

138,5

0,64

11,3

11,3

1 995

6 365

196,2

n = 46 , 8 tr/ min. => 50Hz. Pmag = 717 W.

Calculs

(1) cosg ( ( ' )	(2) PJ 3 2 R s I bs (W)	S	Pu T u ( 2i n ) (W)	? P u P abs (%)	Pmag Pabs (%)
		2 2 + P abs Q abs (VA)
0,299 72,6	434	4 969	639	34,0	36,0

(1) : cos q = cos[ Arc tan( Q abs Pabs)].

(2) : A chaud, R_s = 1 ,1 3 ?.

4. SIMULATIONS EN BOUCLE OUVERTE ET VALIDATION DU MODELE.

Toutes les simulations, précisées dans ce paragraphe, sont réalisées numériquement avec le module « SIMULINK » du logiciel « MATLAB SOUS WINDOWS » version 4.2c.1 d'Octobre 1994 (MathWorks). Ce logiciel est un outil informatique qui permet de réaliser des simulations pour des systèmes définis sous la forme d'équations algébrodifférentielles. La méthode de résolution numérique retenue pour notre application est celle de Runge et Kutta d'ordre 5 et d'Euler.

4.1. Modèle mathématique du moteur et valeur numérique des paramètres :



vas

v_cs

vbs

T_rma

Matrice
de
Park

[P]

vqs

vds

Modéle mathématique


du moteur
FINTRONIC
dans Park
Avec

sa machine iqs

ids

Matrice
inverse
de
Park

[ P] --1

ias

ibs

ics

0

Fig. II-4.1.

d i _ds ( t)

v _ds ( t ) = R _s i _ds ( t ) + L_d

? ? ( )

t L i t

( )

d qs

dt

v t R i t L qs ( ) ? ?

s qs ( ) d

dt +w ( t)

(L _d i _ds ( 0+ taim)

di _qs ( t)

3

T t K i t

( ) avec ?

K ? N

em T qs ( ) ?

? T p daim

2

T _em ( t ) -- T _r (t

avec T t T t f t T

? ?

r ( ) rma ( ) ( )

? ? r 0

dt

) - )

? ?

J J

?

m r

N

p

d o) (t

(II-15)



di _ds (t

) R v t

ds ( )

? ? L i t

^s ( ) ( ) ( )

? ? t i t ?

ds qs

dt L

d d

di t

qs (

dt

)

) R v ( t ) ? ? daim



? ? L i t

s ds

? ? t i t ? ? ? t

qs ( ) ( ) ( ) (

^ds L L



d d

d

d o) ( t) N_p

dt J _m + J_r

T _em ( t ) = K _T i _qs 0 )

[T _em ( 0-- T _rma ( t ) -- f o) ( t ) -- Tr0]

(II-16)
Pour effectuer les différentes simulations, on définit les paramètres J_r et Trma ( t) ainsi

que les valeurs initiales i _ds0 , i_qs0 , ⁽¹⁾ 0 et 90 :

· En charge, on prend un moment d'inertie de la machine, équivalent à celui du frein à poudre : 1,0244.10^-2 kg.m² . Cette valeur correspond à une roue pleine en acier, de diamètre 0,1 m et d'épaisseur 0,06m.

J		an R ^4L	avec acier = 8 930 kg / m^3.
	ü --	2

(II-17)

· Le couple résistant _Trma, dû à la machine entraînée, est supposé proportionnel au carré de la fréquence de rotation avec une condition à vitesse nulle, non nulle : Trma (t ) = k o)² (t) + T

(II-18)

· Les valeurs initiales de i _ds , i _qs ,00 et co0 sont supposées nulles.

· Les phases du moteur seront soumises à un système triphasé de tensions de la forme :



v as = V_s 2 cosco_st



2n1 3 4n1 3

v bs = V_s 2 cos(co_st



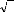
v cs = V_s 2 cos(co_st

(II-19)

En réunissant toutes les valeurs numériques, on obtient :



R =1 , 13n / L d = 53 , 7 mH / ''daim = 141 mW / N_p = 64
K T = 13 , 5 N . m / A / J m = 0 , 141 kg . m ² / T r0 = 3 N .m

f = 0 , 0306 N . m / rad^-1 (é lec) / i ? ?

i ? ?

? ? 0

ds 0 qs 0 0 0

En charge:

T t k t T J 2 ? 2 ? ? ? ? 1 0244 10 kg m . rm a ( ) ( ) / , . r

2

(II-20)

Chapitre 2 : Essais expérimentaux et validation du modèle - Mémoire CNAM Patrick BOIDIN.

.

4.2. Simulations en boucle ouverte :


· Moteur non chargé soumis à un échelon de tension de 164,5 volts entre phases :

n (tr/min) pour Vs=95 volts / fs=50Hz /Trma=0 / Jr=0

90 80 70 60 50 40 30 20 10 0 -10

0 0.5 1 1.5 2

Temps (s)

a) n (2 s ) = 46 , 9 tr / min.

ias, ibs, ics (A) pour Vs=95 volts / fs=50Hz /Trma=0 / Jr=0

15 10 5 0 -5 -10 -15

0 0.05 0.1 0.15 0.2

Temps (s)

c) I _s (2 s ) = 3 ,77A

Tem (N.m) pour Vs=95 volts / fs=50Hz /Trma=0 / Jr=0



150

100

50

0

-50

-100

-150

0 0.5 1 1.5 2

Temps (s)

b) Tem (2 s ) = 12 , 6N .m

ids, iqs (A) pour Vs=95 volts / fs=50Hz /Trma=0 / Jr=0

15 10 5 0 -5 -10

0 0.5 1 1.5 2

Temps (s)

d) i_ds (2s ) = 5 ,25 A n_qs (2 s) = 0 ,94 A



p 6 ?

= 84 ,1^° = 4 ,21^° = 80 ,0^°

vds, vqs (primées) (V) pour Vs=95 volts / fs=50Hz /Trma=0 / Jr=0

0 0.5 1 1.5 2

Temps (s)

En régime permanent, on obtient :

R _s I s = 6 ,03 volts

L d s = 90 ,0volts

E s = 44 ,3 volts

V s = 134 ,4 volts

150

100

50

0

-50

-100

-150

e) cos p = 0 ,10

v _?ds (2 s ) = -- 9 , 87 volts / v '_qs (2 s ) = 134 volts P ast = 48 ,3W

Fig. II-4.2 : Ondes obtenues par simulation. Moteur en boucle ouverte et à vide.

Les résultats obtenus par la simulation permettent de faire les observations suivantes :

* A vide et d'après la simulation, le moteur oscille en vitesse pendant sa phase de démarrage. La durée est trop courte (moins d'une seconde) pour constater réellement ce phénomène. Néanmoins, en augmentant la tension aux bornes du moteur, on remarque effectivement ces vibrations qui se confirme par une simulation à tension plus élevée :

n (tr/min) pour Trma=0, Vs=200 volts et fs=50 Hz

140 120 100 80 60 40 20 0 -20

0 0.5 1 1.5 2

Temps (s)

Fig. II-4.3. Moteur en boucle ouverte et à vide.

* Le courant absorbé par les phases du moteur est fortement inductif :Déphasage par rapport à la tension de 84°. Ceci est normal, l'induit doit compenser le manque de flux produit par les aimants en imposant une réaction d'induit plus importante que normale.

? Moteur chargé soumis à un échelon de tension de 340 volts entre phases :

n (tr/min) pour Vs=194,5 volts / fs=50Hz /Trma(n)=138,5

90 80 70 60 50 40 30 20 10 0 -10

0 0.5 1 1.5 2

Temps (s)

a) n (2 s ) = 46 , 9tr / min .

Tem (N.m)) pour Vs=194,5 volts / fs=50Hz /Trma(n)=138,5

350 300 250 200 150 100 50 0

0 0.5 1 1.5 2

Temps (s)

b) T_em (2 s ) = 151 N.m

Chapitre 2 : Essais expérimentaux et validation du modèle - Mémoire CNAM Patrick BOIDIN.

.

ias, ibs, ics (A) pour Vs=194,5 volts / fs=50Hz /Trma(n)=138,5

30 20 10 0 -10 -20 -30

0 0.05 0.1 0.15 0.2

Temps (s)

c) I _s (2 s ) = 10 ,3A

ids, iqs (A) pour Vs=194,5 volts / fs=50Hz /Trma(n)=138,5 N.m

30 20 10 0 -10 -20 -30

0 0.5 1 1.5 2

Temps (s)

d) id_s s

( 2 ) = 9 , 23 A / i _qs (2 s) = 11 ,2 A



p 6 ?

= 79 ,5^° = 40 ,0^° = 39 ,5^°

vds, vqs (primées) (V) pour Vs=194,5 volts / fs=50Hz /Trma(n)=138,5 N.m

300

200

100

0

-100

-200

-300

0 0.5 1 1.5 2

Temps (s)

En régime permanent, on obtient :

R _s I s = 16 ,4 volts

L _d o) I s = 245 volts

E s = 44 ,3 volts

V s = 277 ,6 volts

e) cos p = 0 ,18

vⁱds (2 s ) = -- 178 volts / vi _qs (2 s ) = 213 volts P Jst = 357 W

Fig. II-4.4 : Ondes obtenues par simulation. Moteur en boucle ouverte et chargé.

D'après les résultats obtenus par la simulation et les résultats obtenus par des essais, on construit le diagramme de Fresnel suivant :

Chapitre 2 : Essais expérimentaux et validation du modèle - Mémoire CNAM Patrick BOIDIN.

.



'

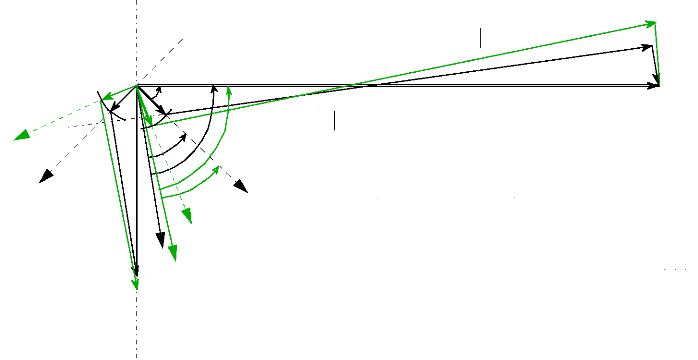
R _s I s

?

1 ,4 A

= c I =

-,

L _d w I s '

-,

9 0^?

-,

L _d WI s

9 0^F

Simulation :

Essai :

Paim

-,

?

?

?

E_s

V_s

-->

'I'

?

??

?

R I = 16 4

, volts

s s

?

?

R I 18 1

, volts

s s =

?

d

-,

'P i

,

??

q

L I 245 volts

d W =

s

?

L I 268 volts

d w =

s

?

V = 277 6

,volts

s

?

V = 277 6

, volts

s

?

q'

E = 44 3

,volts

s

?

I = 14 6

, A

s

E = 44 3

,volts

s

?

I = 16 0

, A

s

-,

-,

1J r

'

I_s

? = 79 5

, ⁰

6 'I'

= 40 0

, °

= 39 5

, ⁰

? ? ? = 6 ,9 °

(p' = 72 6

, °

-,

R _s I s

d'

-,

Wi

-,

W_r

-,

I_s^'

Fig. II-4.5 : Construction vectorielle dans l'hypothèse de Behn-Eschenburg.
Moteur chargé à 138,5 N.m et soumis à une tension composée de 340 volts.

Les résultats permettent de faire les observations suivantes :

* La valeur du courant efficace obtenue par la simulation est inférieure de 1,4A par rapport à la valeur de l'essai. Ceci s'explique par les pertes magnétiques qui sont négligées dans le modèle.

Connaissant la valeur des pertes magnétiques P_mag = 717 W et supposant

qu'elles sont proportionnelles au carré de la tension, on peut en déduire la résistance équivalente R_m, puis le courant I _rm :



1 ,2

A

(II-21)

U 2 _ab 340 ²

= _ = 1₆₁ I = ab = _

Pmag 717

R _m

U

3

R

m

161 3

Or, ce courant représente effectivement la différence obtenue à 0,2 A prés et correspond à 11,6% du courant absorbé (10,3A).

* La différence sur le déphasage de 6,9°, entre la tension et le courant, est due aux

pertes magnétiques. Si on rajoute le courant

.... Irm à la composante active du

courant I_s, on obtiendrait le nouveau déphasage (p" suivant :

--> ->

I ac ( actips I rm



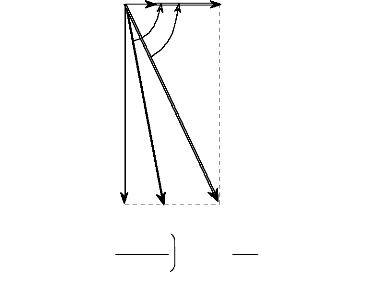
A. A.

(p = 79 ,5° ⁽P I ac = I_s cos p = 2 ,63 A

A. A.

? I _ac + I rm = 4 ,36A

(p"

-->

I_s^''

-->

I r ( ré actins

I r = I _s sin p = 14 ,4 A

-->

I_s

Fig. II-4.6

arctan(

...

I_s sin

... ...

I oas + Irm

(II-22)

(? 14 4 ,

4 36 73 1 ?? ? , ? ,

-- arctan

I, =

Soit un écart théorique de 0,5°(très acceptable).

4.3. Validation du modèle :

Les simulations font apparaître la nécessité de tenir compte des pertes magnétiques dans le modèle mathématique = Le modèle, tel qu'il est défini, créé une erreur sur les courants de 11,6%. On remarque 2 points essentiels :

1. La consommation d'un courant actif supplémentaire a pour effet de déphaser en moins le courant par rapport à la tension (72,6° pour 79,5°).

2. L'angle interne du moteur a sensiblement augmenté, ce qui correspond à un décalage supplémentaire du rotor par rapport au champ statorique.

= Ces 2 constatations ont des conséquences importantes. En effet, si on projette le vecteur courant sur les axes d et q, on fait les remarques suivantes [7] :

1. Pour un même couple résistant et dans le cas où les pertes magnétiques ne sont pas négligées, Iqs (régime permanent) a augmenté =

Dans le modèle, on peut s'imaginer que la différence de ces courants est
absorbée par une résistance fictive.

2. Pour un même flux magnétisant et dans le cas où les pertes magnétiques ne sont pas négligées, Ids (régime permanent) a diminué = Il y a eu un

renforcement de ce courant dû à l'augmentation de Iqs.

Dans le modèle, on peut s'imaginer que la différence de ces courants est
fournie par la réaction d'induit. Sa valeur dépend de la résistance
fictive du cas précédent.

5. CONCLUSION.

· En boucle ouverte, le moteur démarre sur le réseau à 50Hz sans difficulté. Ceci est dû au nombre important de pas (64), assimilable au nombre de paire de pôles et à la constante de couple élevée de 13,5 N.m/A. Le courant nominal est de 9,3A.

· La position initiale du rotor ne semble pas conditionner la phase de démarrage du moteur FINTRONIC.

· L'ensemble mécanique du moteur manque de rigidité. Il faut améliorer les moyens d'assemblage des 2 stators et revoir le train de roulements du rotor qui laisse apparaître un jeu néfaste sur l'entrefer.

· La forme d'ondes des tensions et des courants est quasiment sinusoïdale. = Une commande du type "sinus" s'impose à ce type de moteur.

· Une constante de couple élevée assure au moteur une qualité certaine. Néanmoins, la forme des courants, associée à une commande, devra être parfaite et démunie de tout harmonique. Cette condition est nécessaire pour éviter les à-coups de couple dépendants de cette même constante de couple.

· La température atteinte du moteur, en régime permanent, semble limite pour les matériaux utilisés dans la conception du moteur. Les échauffements sont dus essentiellement aux pertes magnétiques qu'il faut réduire au mieux par l'intermédiaire de la commande.

· Une des qualités de ce moteur est d'être conçu suivant une technique qui lui permet de recevoir plusieurs disques "rotor" et d'augmenter ainsi ses possibilités de couple pour une même structure de base.

· Peu de moteur, actuellement sur le marché, sont capables de fournir d'aussi bonnes performances avec un encombrement et une masse aussi faible. Le principe, utilisé dans la conception de ce moteur, est judicieux (structure modulaire) et semble prometteur pour des moteurs d'une puissance plus importante et pour des couples utiles plus élevés (multi-disques).

· Les pertes magnétiques, apparus lors des essais, ont faussé les résultats de la simulation d'environ 11% ? Il faut inclure ces pertes dans le modèle mathématique. Néanmoins, aux vues de la complexité du sujet, nous avons préféré conserver le modèle tel que nous l'avons défini précédemment. On précise que l'étude d'une commande à couple maxi va permettre de limiter au mieux la tension aux bornes du moteur. Ainsi, les pertes magnétiques seront limitées d'autant et notre modèle se rapprochera mieux de la réalité.

CHAPITRE 3

COMMANDE VECTORIELLE
AVEC
CAPTEUR MECANIQUE

1. OBJET.

Dans cette partie d'étude, nous avons développé puis testé, par des simulations, une commande vectorielle dans le formalisme de Park. Pour cela, on a utilisé un onduleur de tension muni d'un dispositif de contrôle des courants et de découplage que l'on présente dans ce chapitre. Le formalisme de Park est le seul moyen technique actuel qui permet d'agir directement sur les grandeurs instantanées du moteur et d'obtenir une commande dynamique. Néanmoins, son utilisation n'est pas sans contrainte et impose de connaître à chaque instant, la position du rotor : Matrice de passage, fonction de 0. Pour limiter l'étude de la commande, dans un premier temps, on supposera que la position du rotor est parfaitement connu.

2. PREAMBULE. 2.1. Le moteur synchrone :

La particularité essentielle du prototype qui s'apparente à un moteur synchrone, est d'avoir une vitesse de rotation « synchrone » avec la pulsation de la source qui l'alimente. Contrairement au moteur asynchrone, aucun glissement prolongé n'est toléré. Seul, le décalage entre les champs tournants est possible et ne doit pas dépasser une certaine limite dépendante de la charge entraînée. Il est possible, néanmoins, de contrôler ce décalage, en agissant sur l'amplitude et/ou la phase des 2 grandeurs électriques en rotation. Dans le cas d'un moteur à aimants permanents, on agit uniquement sur une seule grandeur, l'autre n'étant pas accessible.

Remarque :

Pour un couple résistant donné, il est possible de limiter au mieux les courants absorbés par le moteur. Il suffit de réduire ces courants de façon à obtenir un décalage entre le flux rotorique et le flux statorique de 90° électrique. Dans cette situation, le couple résistant est égal au maximum de couple, capable d'être fourni par le moteur.? L'avantage de ce type de fonctionnement est de limiter les pertes magnétiques. Ce mode de fonctionnement est appelé communement « Commande à couple maxi ».

2.2. Commande du moteur « Fintronic », en courant ou en tension? :

La source d'alimentation du moteur peut être en tension ou en courant et dépend du type de récepteur que l'on doit alimenter. On rappelle qu'une source de tension ne peut pas alimenter un récepteur de tension et de même pour les courants. Il faut donc savoir si le moteur « Fintronic » est un récepteur de courant ou un récepteur de tension.

En reprenant les équations de Park, on remarque que le couple électromagnétique est directement proportionnel au courant d'axe q.

Tem = K _T . iqs

(III-1)

Cette expression nous montre que le meilleur moyen de contrôler le couple instantané de la machine, serait d'utiliser une commande en courant. Par contre, cette condition suppose de laisser évoluer librement les tensions. Or, si le moteur à l'essai est plus inductif que capacitif, on verrait apparaître des surtensions aux bornes du moteur et des composants de puissance.

La f.e.m à vide, induite par les aimants, est relativement faible dans le cas particulier des moteurs à aimants permanents. Il faut donc compenser cet inconvénient en imposant une réaction d'induit magnétisante plus importante que normale. Or, pour limiter les courants à des valeurs acceptables et répondre à la demande, il faut augmenter la valeur de l'inductance synchrone du moteur et imposer un circuit plus inductif au stator.

le moteur « Fintronic » est un récepteur de courant qui demande une commande en tension avec un contrôle des courants.

2.3. Principe de la commande en tension et de l'autopilotage du moteur :

Commander le moteur à partir d'une source de tension et contrôler les courants revient à effectuer une commande selon le principe suivant :



Rotation de la charge



Courants
désirés

Contrôle
des
Courants
+
Autopilotage

(Boucle d'autopilotage) Position du rotor/repére fixe

Ecarts

Source de Tension
continue

Convertisseur
de Puissance

Tensions appliquées au moteur

Moteur
à réluctance variable
et à aimants alternés

Couple
résistant

Charge à mettre
en mouvement

Couple
électromagnétique
+
Vitesse

Fintronic

Moment
d'inertie

Courants
obtenus

Courants
obtenus

Fig. III-2.1

L'information de position constituant la boucle d'autopilotage, sert à asservir la position



du flux statorique à celui du rotor " .

aim

Chapitre 3 : Commande vectorielle avec capteur mécanique - Mémoire CNAM Patrick BOIDIN.

.



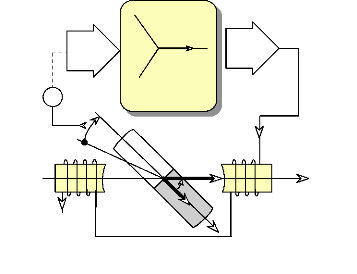
C

bs

cs

Décision prise
à l'instant considéré

-->

I s

as

i

Point de référence

S

Axe du flux
statorique

?

N

? i

a

S

i

-->

? aim

N

Axe rotor

Le rotor tend à vouloir s'aligner avec
l'axe du flux statorique

Fig. III-2.2

Analyse

de la situation
à l'instant
considéré

Mise en
application de la
décision
prise

Capteur de
position
du rotor

La figure III-2.2 représente, sous une forme simplifiée, le principe de fonctionnement du moteur synchrone à aimants permanents avec son autopilotage.

2.4. Contrôle par la tension du couple électromagnétique :

Le moteur est commandé en tension. Il faut donc exprimer le couple électromagnétique
en fonction de v _qs et non plus en fonction de i_qs. On obtient ainsi, à partir des équations

suivantes :

qs

di ds

v R i L

? ? ? ? L i

ds s ds d d

dt

v qs = R s i qs Ld

di dt^qs +coL di

? ?ds Wdaim

1

T em -- T r = ( J _m + J_N

p

iqs

? d ? ?

dt f T K

r ) ? ? ?

Avec

?? ?? em T

(III-2)

la nouvelle expression,

K_T di qs

T _em =v -- L

R qs ^d dt --0 L _d i ds -- ⁽¹⁾¹Pdaim

s

(III-3)

qui est devenu dépendant non seulement de v mais aussi de et de la variation de

ids

qs

iqs

.

Pour supprimer une partie de cet inconvénient, on impose un courant i nul au moyen

ds

d'une régulation sur ce courant avec une référence nulle. En supposant que la vitesse est restée constante durant la perturbation, on obtient alors :

Tem

K ? di

T qs

= R v L

?? - ? ?₀ ?

qs d daim

dt

s

(III-4)

On a ainsi une équation différentielle à coefficients constants facilement résolvable de la forme :

i qs

L di v

d qs qs ? O)0 " daim

+ ?

R dt R R

s s s

(III-5)

Nota:

Cette condition est indispensable pour définir les paramétres d'un correcteur du type PI qui de par sa nature gére des systémes uniquement linéaires.

3. MODELE D'ETAT DU MOTEUR ET CHOIX DES VARIABLES D'ETATS.

3.1. Définition et notations :

Tout système linéaire, continu et à variables multiples, peut être représenté par le modéle d'état suivant :

x? Ax Bu v



= + +

y Cx Du w

= + +

(III-6)

Avec

A : Matrice (n,n) d'évolution du système.

B : Matrice (n,ne) d'application de la commande.

C : Matrice (ns,n) de sortie du système.

D : Matrice (ns,ne) d'action directe sur le système.

x : Matrice d'état.

x? : Matrice dérivée de la matrice d'état.

u : Matrice d'entrée.

y : Matrice de sortie.

v : Bruit d'état du système. Ce vecteur représente les incertitudes de la modélisation.

w : Bruit de mesure du systéme. Ce vecteur représente les bruits affectés par les différents capteurs des grandeurs mesurées.

Chapitre 3 : Commande vectorielle avec capteur mécanique - Mémoire CNAM Patrick BOIDIN.

.



u

B

+

v

+

+

x

A

1

x

w

+

+

y

C

+



D

Fig. III-3.1

En utilisant la transformation de Laplace, on obtient la solution du système différentielle à variables d'états :

X?

? ? ? ? ? ? ? ? ?

? 1

p pI A X B U p V p



? ? ? ?

i

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?



? 1

Y p C pI A X BU p V p

? ? ? ? ? D U p W p

?

i

(III-7)

Uniquement valable pour un systéme d'équations différentielles linéaires.

X_i correspond à la matrice des conditions initiales du vecteur d'état et p l'opérateur de

Laplace.

En supposant que les conditions initiales et les bruits sont nuls, on obtient la fonction de transfert :

H p Y ? p ? ? ? ? ? ? ? ? X p ? C pI ? A

-1

B + D

(III-8)

3.2. Choix des variables d'états :

Une commande en tension impose naturellement de considérer les tensions comme étant les entrées et les courants comme étant les sorties. Les variables d'états sont généralement celles qui dérivent dans le temps. Ca sera donc les courants. Du point de vue mécanique, l'entrée ne peut être que le couple résistant et la sortie, la vitesse angulaire ; La variable d'état sera la vitesse puisqu'elle dérive. Ainsi, on pose :

di



? v ?

ds

? ?

? ?

? T ?

r





i ds

i ds

? ?

?

? ?



?

=

u v

?

? qs ?

et x

qs ?

? ?

? ? ?

?

?

i _qs [_I X

? d ?



ds ?

I

dt

? di ?

qs

? ?

dt

? ?

? ?

? dt ?

, y i

? ?

(III-9)

1

?

? ?



0

R_s

co

L_d

R_s

lⁱdaim

d

L d L

ds

qs

En reprenant les équations de Park, on obtient :

I^--

ds? ? ?

? 0 3

?

? 2

?

?

?

?

?

?

?

di

? ? ? ? ? _1

-co

qs

dt

di

dt

d ?

dt

? ?

2 lⁱdaim

^p J

J

?

m

f

J J

?

r m r

N

1

L_d

0 0

0

N_p

J _m + J_r

0 0

?

i
i

i

r
[

+

F
[

co

1
i

r
[

vds

i ?

?

? ?

vqs

i ?

? ? ? ?

?

?

T_r

1

L_d

0

y

[r



(III-10)

i 1 I^- 1 0 011^- i i _qs^I.^I0 1 0L¹ i 0) lj 0 0 0)

dsqs

ds

I I

(III-11)

Avec :



A

?

?
?
?

[

?

R_s

--0) _

L d _L

R

L

0

d

s

N

2 lⁱdaim

^p J + J

m

co 0

r J _m -FJr

lⁱdaim

IN 1

i

f

3

2



0 0

0 0

r

?

?

1

[

i ? ?

[

1

L_d

0

1

L_d

0

N _p

J _m + J_r

, B

(III-12)

C=

r [

1 0 0f 0 1 0[i 0 0 1

: Matrice identité. D = 0

(III-13)

L'inconvénient de ce système vient de la matrice A. En effet, elle présente un double
terme non-constant (co et -co), qui nous empêche de résoudre le système. On linéarise
donc autour d'un point de fonctionnement oil co = c ₀ , ids = Ids ^0, i qs = Iqs 0 , v ds = Vds0,

v qs = V_qs0 et T r ? T 0 r .

Après avoir défini judicieusement les paramètres concernés, on impose des faibles variations autour de ce point de fonctionnement. Pour mettre en application cette solution, on remplace :

I ds 0 + Ai ds
I qs 0 + Aiqs

⁰⁾ 0 + Aw

V ds 0 + Av ds
V qs 0 + Av qs
T r 0 + AT_r 0



x par X ₀ + Ax

r
[

1

et u par U ₀ + A u



r

? [

1 ?

?

? ?

(III-14)

A correspond à l'écart subit par l'élément considéré, autour de son point d'équilibre.

Après une série de transformations, on abouti au nouveau système matriciel :

ds

d Ai

qs

dt d Ai

dt

0

dAco

? ? ? ? ?

?

?

dt

?
?
?

?

?

? ? ? ?

? ?

? L 0 Aco 0

d

R_s

?

qs



?

r

?

1 0

1 ?

?

?

0 ? ? 0 ?

L

? i ? d

? ? ? ? v



R ?

s daim

?? ? ? I

0 0 ds 0

L L

d d

? ?

? ?

?

?

xis

3

f

0

?

? ?

2

N 2 daim

^p J + J

m

_r

J _m + J_r

ds ds

? 0 1 ?

? i ? ? v

qs qs

? ? 0 ?

? L d ? ?

?? ? T

0 ? N ?

? r 0

p ?

0 0 ? ??

J m Jr

? ?

(III-15)

Les termes Aco ₀ et --60₀ qui interfèrent avec l'expression des courants, rendent ^lesystème toujours non-linéaire. En considérant que la constante de temps mécanique est

supérieure à la constante électrique d'un moteur, on peut supposer que les variables mécaniques sont restées constantes lors de l'évolution des courants, dans le temps.

A partir de cette remarque, il est possible d'annuler les 2 termes gênants en tenant compte uniquement des équations sur les courants. On a:

?

qs

dt

d i
?

dt

--co0 --

ds
qs

i ds
i qs

s
d

s
d

?

?

?

? ?

d i ?

?

ds ?

?

? ?

? ? ?

?

?

R L

(0 0

R L

1 ?

?

?

?

? A
?? A

?

¹_1⁺

? ? ?

?

?

1

L_d

0

0

1



L_d

? ? ?

?

?

? Av
?? Av

?
^I_

(III-16)

Sous cette forme, il est maintenant possible de résoudre le système à partir des équations III-7 de Laplace. En négligeant les bruits et en considérant les conditions initiales nulles, on a la fonction de transfert :

H (p)-

I dqs (p)

? ? ?1

? ?

pI A B

V dqs(p)

(III-17)

Avec

? ? ? ?

? ? I p ds I p ? ? dqs ? I p ? ? ? qs

1 V p ? ? et ? ? ? ? ? ? ds V p ? ? dqs ? ? ? ? ? ? V p qs ? (III-18)

3.3. Détermination du sytème d'équations d'états et schéma fonctionnel :
· Calcul de (pI-A)^-1 :

(pI -- A) = 1 (-1)i ^#177;j cofacteur( pI -- A)

det ( pI -- A)

(III-19)

Pour que la matrice pI-A soit inversible, il faut que son déterminant soit non-nul:

1 2? ? L

Det ? pI A ? d ? dp ? p

2 1

? ? ? ? ? ?

? 2 2

1 d ^p d

? ?? ? ? avec ?d

2

?

2 0 2 0 ?? ?

d



? ? ?

R_s

(III-20)

L d = 53 ,7 mH

R_s = 1 , 1351 = De t(pI -- A) = p ² + 42 , 1 p+ 443 + co²₀

⁽I⁾ 0

On en déduit (pI -- A) ¹:

1 Fp + 1 T d ?1c?

0

? ? ? ?

pI A

? ? ??

pI A

? ? p ? d ??

det ? ?

1

0

(III-21)

· Détermination de la fonction de transfert :

Soit, (pI -- A ) ¹B = H (p) --

r 1 ? 1 ? ? ?

0

? L ^p d

?? ? ?? ?



1 ? L

d d

? ?

det ? ?

pI A

? ? 1 ? 1 ?

? 0

? L ^p d

?? ? ?? ?

? ? L ? ? ?

d d

(III-22)

On en déduit :



R_s

L²

d

? ? ? ? ? ?

R

s

L²

d

2

d

ti

0

?

0

d

?

L

?

? ? ? ?

? ?

p ? ? dp + 1

(Tdp+ 1

?

L_d

(Tdp+ 1

[ Vp

???

ds

?

V qs

( p) ?

2 d2

+ ?

1 ? ? ? ? ?

(p)

?

?

?

I_ds

I qs

2

co

0



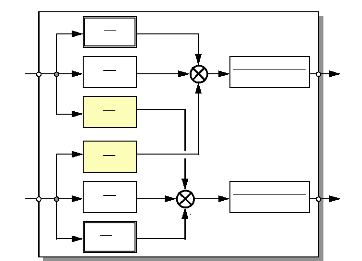
(III-23)

+

+

+

· rd

1 _Lp

d

'n₀
L_d

'n₀
L_d

R_s L ²

d

R_s L ²

d

+

2

2

1 _Lp

d

-

+

· rd

(rdp + 1)

2

I _ds( p)

0

2

I _qs( p)

0

2

?
·rd² oa

2

?
·rd² oa

(rdp + 1)

V ds ? p ?

V qs ?p)

Fig. III-3.2 : Schémas fonctionnels du moteur « Fintronic » dans le repére (d,q) Deux remarques essentielles sont à faire :

1. Le schéma fonctionnel de la figure III-3.2, montre que les courants de Park i_ds et iqs

sont liés par la vitesse angulaire au point d'équilibre c₀. L'idée consiste donc à

intégrer, dans la régulation des courants, un dispositif de « découplage » capable de rendre autonome les 2 boucles de régulation. Nous verrons par la suite, comment réaliser cette fonction.

2. La condition de stabilité d'un système, est d'avoir les pôles de sa fonction de transfert à partie réelle négative. Dans notre cas, les pôles correspondent aux valeurs qui annulent le déterminant de pI-A. Soit, la résolution de l'équation :

2

p ² + 42 + 99039 = 0

p ou sous une autre forme, ( p + R _s L _d )+? 2 = 0

0

R_s

p = - #177; co₀ soit numériquement, p = -- 21 , 0 #177; j w 0

L j

d

Les pôles ont leur partie réelle négative ; Le systéme est donc stable.

Le coefficient d'amortissement z du systéme dépend de la vitesse au point

?

d'équilibre. Sachant que z = sin ? avec N' = arctan , on a:

?

z =

21 ? ?

? 0

)?

1
]

? ?

sin arctan

?? ??

(III-24)

Pour une vitesse angulaire nominale de 402 rad/s, on a un coefficient d'amortissement de 0,052 => En boucle ouverte et à la vitesse nominale, le système est trop peu amorti, fâce à une perturbation. Il est néanmoins stable.

Un amortissement idéal de 0,707, ferait correspondre une vitesse angulaire de 21 rad/s (5% de la vitesse nominale) ? Il faut donc refermer les boucles de régulation et faire appel à des correcteurs afin de corriger, au mieux, le placement des pôles sur le plan de Laplace.

4. ETUDE DE LA REGULATION DES COURANTS DE PARK. 4.1. Etude du découpleur linéarisant [10]:

Le but de cette étude consiste à définir les paramètres d'une matrice (2x2) qui
permettent de découpler les 2 courants de Park i et i . Cette matrice sera notée

ds qs

[Dec] et les entrées du découpleur, U _ds ( p ) et U _qs ( p) .

Fig. III-4.1



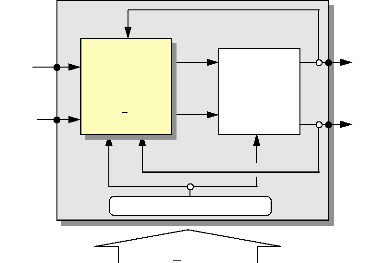
U _ds? p?

U qs? p ?

Découpleur
Linéarisant

[Dec]

?

? a b ?

??

c d^lj

Moteur + découpleur

H (p)

?

Point

de fonctionnement ?₀

Vds( p)

Vqs( p)

Moteur
Fintronic

I _ds( p)

I _qs( p)

On pose :

[

Vds Vqs

? ? ? ? ? ? ? ? p ? ? U p ds ? ? Dec ? p ? ? ? ? U p qs

1 I J

Fa b1 avec [Dec] =I L c d^ij

(III-25)

En reportant l'expression des tensions ci-dessus dans celle des courants de III-23, on obtient :



R

s

L ²

d

0

o)

i

?

?

?

? ?

(Td p+ 1)

( ?

p1 1

? ? ? ?

? ?

p ? det pI A

?

(Td p + 1)

?

L_d

? U p

? ? ?

ds

?

U p

? ? ?

? qs ?

[

I_ds

I qs

R_s L²

d

1
?

L

0

co

d

L

? a b ?

??

c dⁱj



R_s L²

d

I_ds

[

? ? ? R ?

0 s

? ?

? d p ? 1 ? ? c b ? ? ?

? d p ? 1

L L ²

? d ?

d d

co

I qs

?

? ? d

? L

? a ??

0

R s

r
[

? ? ?

0

? ? b ? d ?

? L d ?

(Td p + 1)

R

2 ? ? 1

s ? ?

d p

L

?

0

? a ? c ?

L d ?

L ²

d

d

( ?

_p1

1

? ? ? ?

? ?

p ? det pI A

?

[U ds(p)1 ?

U p

? ? ?

? qs

J

(III-26)

En développant, on obtient :

(III-28)

En prenant arbitrairement a=d=1, on obtient la matrice de découplage suivante :



(III-29)

d

? 0

?

?

?

?

?

?

? 0

1

?

? ? ? ? ?

1

?

dp

1

? D ec?

1

? d

? dp

? ² R ?

s

0 ? ? ?

? d p ? 1

? ? 2

1 R R ?

0 s ?

? ? ? ?

p L d p

s

? ? ? ? ? ?

? ? 1 ? U p

2 qs

det pI A

? ? ? d p ? 1 ?

d

?





I_ds
I _qs

D'où, la nouvelle fonction de transfert moteur+découpleur :

Il faut annuler le dernier terme des 2 équations précédentes. Pour cela, on résoud le systéme suivant :



? ?

? d p ? 1

s

?

d

1

? 0

?

?

dp

?

1

d

R ?

b

s

L ²

(td p + 1 ) + d L

d

-- a L 0 ?

_d

R

?

c

d

?

0

? 0

? 0

d

b

? ?

1

?

?

dp

?

1

a

?

? 0

?

c

L ²

d

? ?R ? ? ?

? ? ? ?

a _L d p c _L U p b

? ? ? ?

R ? ?

1 ?

s 0 s

? 1 L d p d _L U p

0

? ? ? ? ? ? ? ? ? ?

1 ? ? ? ?

2 ds 2 qs

det pI A

? ? ? ? d ? ? d ? ? ?

d d

I_ds

I _qs

? p =

(III-27)

?

1 ? ? R ? ? ? R ?

0 s 0 s

? ? ? ?

p ? ?

? ? b ? d ? ? ? ?

? d p ? 1 ? ? ?

U p ? a ? c ? ? ? ?

? d p ? 1 ? U p

qs ds

pI A

? ? L L ² L L ²

det ? ? d ? ? d ?

d d

1 ?

? ?

? R ? 2 R ?

0 s

? d p ? ?

1 ? 0 ?

? dp ? 1 ?

?

? ?



I _dqs \p /td²

?

s ?? L ²

H

? p --



? d

2

0 Rs



? ? ? ? 2

U p ? ? ? ? ?

?

2 2

dp d ? R

1 s

dqs 0 0 ? ?

ti

? 1

dp

?

? d p ? 1

? ?

_L2

d

(III-30)

En reprenant l'expression III-25, on obtient :

Découpleur linéarisant.



d

t

1

w ₀

?

1

t

+

dp

1 ?

1

1 i

d

1 ? L

t

1

w ₀

1

dp

t

+

? V p

? ? ?

ds

?

V p

? ? ? ?

? qs ?

? U p

? ? ?

ds

?

U p

? ? ?

? qs ?

(III-31)

On obtient ainsi sous forme de schéma fonctionnel, le moteur FINTRONIC muni de son découpleur fonctionnant autour de c₀ :

Fig. III-4.2



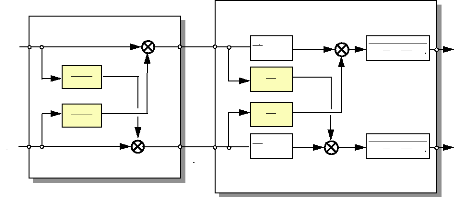
R

L² _d

R_s
L² _d

s

(ndp+ 1)

(ndp+ 1)

w₀

L_d

w₀

L_d

+

+

-

+

p ² + ? 2

2 0

d ^p d

? ?

? ?

p ² + ? 2

2 0

d ^p d

? ?

? ?

1
2 1

1
2 1

+

tdp+ 1

⁰³0T

d

-

d

⁰³0T

T

1

dp+

+

+

U _ds? p)

U _qs( p)

Vds( p)

Vqs( p)

I _ds( p)

I _qs( p)

Pour mieux comprendre le rôle du découpleur et vérifier son efficacité, nous avons effectué une série de simulations avec le système fonctionnant en boucle ouverte pour une vitesse de rotation donnée, c₀ constant. D'après les résultats obtenus, le dispositif a bien rempli ses fonctions de découplage. En plus, il a permis de supprimer les oscillations de courant qui ont eu tendance à augmenter avec co0. En contre partie, on fait les remarques suivantes :

· Ce type de découpleur, impose d'estimer les paramètres Ld et R_s de la machine. Il faut donc connaître les paramètres du moteur.

· 03 est constant que durant un laps de temps. Or, les courants ne disposent que de 72ms environ (constante mécanique) avant que la vitesse angulaire n'évolue et rende le système non linéaire. Le découpleur réduit les oscillations mais ralentit la progression des courants.

4.2. Autre solution de découplage :

A partir des équations électriques de Park çi dessous, on propose une autre solution de découplage des 2 courants [11].

v ds = R _s i _ds L_d -- e

di ds

dt ds

di

v qs = R _s i _qs Ld dt + e qs

(III-32)

La solution consiste à remplacer v _ds par uds -- e~ds et v _qs par uqs + e~_qs , de façon à obtenir les deux nouvelles expressions suivantes :

? Chaque courant dépend uniquement de sa propre tension

u ds = R _s i _ds Ld

u qs = R _s i _qs Ld

ds

di

dt



ds

di



dt

(III-33)

Avec _~eds ^et e~qs : variables à paramètres estimés.

Or, pour valider cette expression, il est essentiel que _~eds puisse correspondre à chaque instant à e _ds et ~e_qs à e _qs.

Sachant que e ds ? ? L _d i _qs et e qs ? ? ? L _d i ds ? ?? daim ? , on remarque très vite que la
qualité du découplage dépend essentiellement de la qualité des paramètres estimés

~

~L_d, 'daim et de la précision de mesure de la vitesse angulaire w.

On représente les 2 solutions de découplage par les schémas blocs suivants :



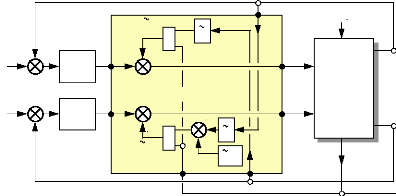
i_ds^*

i _qs

*

ids

iqs

+

+

-

-

PI

PI

uds

^uqs

+

+

^eqs

eds

+

-

Découpleur

.

.

03

03

+

L_d

+

^4,daim

L_d

vds

vqs

Moteur
Fintronic

Trma

?

iqs

?

ids



Fig.III-4.3 : Découpleur de la 2^ème proposition.



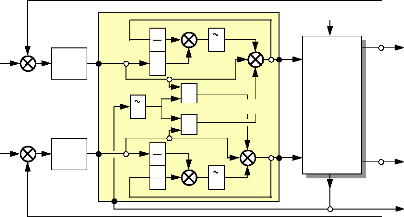
i_ds^*

i _qs

*

ids

iqs

+

+

-

-

PI

PI

uds

uqs

Co

td

d
dt

d
dt

d
dt

d
dt

-

-

.

.

+

+

Découpleur

td

td

+

+

+

+

+

-

vds

^vqs

Moteur
Fintronic

Trma

?

i ds

iqs

?

	vds	uds
vqs	uqs

?

Fig. III-4.4 : Découpleur de la 1^ème proposition.

4.3. Etude comparative des 2 découpleurs :

Les 2 solutions proposées peuvent être résumées schématiquement de la façon suivante :

Solution n°1 Solution n°2

ids



uds uqs

Découpleur n°1

Dérivation des entrées
et des sorties

L_d R_s





L_d

^??daim

vds

vqs

Découpleur n°2

Pas d'action
dérivée

? iqs

Fig.III-4.5

· Les valeurs estimées sont L_d et R_s dans la première solution et Ld, _Tdaim dans la

seconde.

· Il paraît plus facile de prédéterminer la variation de la résistance statorique It_s en fonction de la température que le flux créé par les aimants en fonction de cette même température.

· La seconde solution nécessite 2 entrées supplémentaires i_ds et i_qs.

Les erreurs faites sur les mesures de courant sont multipliées par 2.

La première solution impose de dériver les entrées/sorties pour découpler les courants. C'est l'inconvénient de cette solution.

En conclusion, il est difficile de choisir entre les 2 solutions proposées, sans les tester réellement. Elles ont chacune leurs avantages et leurs inconvénients et il faudrait continuer l'analyse pour en favoriser une. La proposition n°2 paraît la plus simple à réaliser et sera retenue pour la suite de cette étude.

4.4. Boucle fermée avec correction sur les courants :

Maintenant que nous avons choisi un type de découpleur, nous pouvons refermer la boucle de régulation des courants de Park à travers des correcteurs P.I. On schématise l'ensemble :



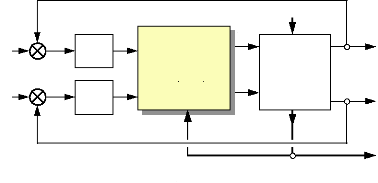
Trma

i_ds^*

i qs

*

i ds

+

+

-

-

PI

PI

Découpleur

Linéarisant

vds

vqs

Moteur
Fintronic

i ds iqs

iqs

0)

0)

Fig.III-4.6



E ( p)

S( p)

+

K_p

+

K

p

i

Action proportionnelle

Dicte la rapidité de
réaction de la
boucle

Action intégrale

Elimine l'erreur entre la
référence et la sortie

En valeur instantanée :

PI

S( p)

E ( p)

s ( t) = K _p e ( t) + Ki?e ( t)dt

Fig.III-4.7

Avec

5. REGULATION DE VITESSE.

5.1. Choix d'une régulation de vitesse [8] :

Parmi les 2 types de régulation, proposés par les figures III-5.1 et III-5.2, on utilisera celle qui est la plus utilisée pour les entraînements de machines. C'est à dire, la régulation à boucles multiples montées en cascade.

vds vqs

Convertisseur + Moteur Fintronic

Régulateur de vitesse

+

Régulateur de courant

Limiteur à seuils

-

ids i qs

+

0)^*

0)

Fig.III-5.1 : Régulation à boucles multiples en cascade.

(*

i_ds^*

_i*

qs



+

+

-

-

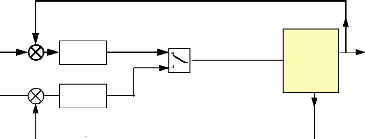
i_ds i qs

Régulateur
de
vitesse

Régulateur
de
courant

Commutation

vds

^vqs

Convertisseur
+
Moteur
Fintronic

CO

Fig.III-5.2 : Régulation à boucles en parallèles.

5.2. Schéma-blocs de l'ensemble Moteur/Machine/Régulations : A partir des équations mécaniques et électriques en III-34,

T em -- Tr

N ? J J ? d 1 ? ? ? ? ? dt f ? ? m r ?? ?? p

T r = T r 0 + Trma T rma = T + kw 2 Tem = K T iqs

(III-34)

On obtient l'expression de la variation de vitesse du moteur :

(K_T i qs -- T r0 -- T) --

N k

p

co -- o)

J m + J_r J m + Jr

2

f

N_p

do)
dt

J _m + J_r

(III-35)

Traduit sous forme de schémas blocs et muni des boucles de régulation Courant/Vitesse, on a le schéma suivant :

Limiteur à seuils

Fig. III-5.3



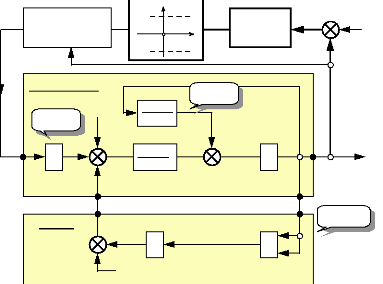
Régulateur
de courant avec

iqs

découpleur

Moteur Fintronic

Constante
de couple

Machine

K_T

+

+

Tr0

?

Trma

-

-

+

i_qs^*

T

Imax

Imin

N p

J J

m + r

f

J _m + J r

k

(A)

Frottements
visqueux

t

+

-

_?2

Correcteur

PI

J

.

Equation
machine

+

-

(0^*

0)

En supposant que découpleur joue efficacement son rôle, on remarque que le courant ids n'intervient pas directement sur le couple électromagnétique. On se retrouve dans les mêmes conditions qu'une machine à courant continu.

Pour cette régulation, on utilisera un correcteur de type Proportionnel-Intégral identique à la régulation des courants.

Pour compléter la chaine de régulation, il est nécessaire de rajouter un dispositif de limitation des variations brutales de la consigne de vitesse. En effet, si le moteur est capable de réagir très vite à un changement de consigne sur la vitesse, il n'en est pas forcément de même pour la partie mécanique de l'ensemble moteur/accouplement/machine.

Le moyen utilisé, pour réaliser cette fonction, est un filtre du 1^er ordre dont la
constante de temps 'E est imposée en fonction de la rapidité souhaitée et en fonction

n

des contraintes mécaniques à limiter. Si on appelle n l'entrée du filtre et n la

*

ré f

sortie du filtre, la fréquence de rotation obéit à la loi :

* dn * dn*

n + t n ?

n ré f

dt

1

= (n n * ) : Filtre du 1^er ordre.
ré f ?

?

dt

n

(III-36)



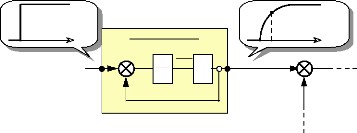
nréf

t

Filtre du 1er ordre

nré f

+

1

t_n

dn

dt

*

J

-

_n*

+

Cn

nré f

? n t

-

n

Fig. III-5.4

6. ONDULEUR DE TENSION.

6.1. Généralités :

Pour commander le moteur, il est nécessaire d'interposer entre la commande et le moteur, un dispositif de puissance :

L'onduleur de tension controlé en courant.



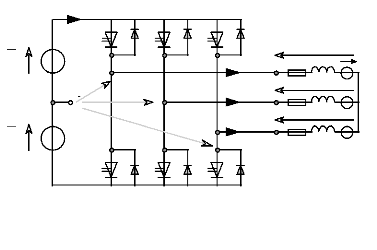
1

3

2

2

ias

L_s

R_s

va0

+

U

i

v cN = v cs

va0

U

2

0

vb0

vc0

ibs
ics

vb0

vc0

eas

N

ebs

ecs

-

1'

2'

3'

Fig.III-6.1

- 71 -

v aN = v as

v bN = vbs

+

+

Ceci nous amène à parler de la modulation de largeur d'impulsions dont le rôle est de reconstituer au mieux une onde sinusoïdale à partir d'une tension continue. Bien qu'il existe, à l'heure actuelle, une multitude de variante d'ondes en M.L.I, nous proposons une M.L.I dite « naturelle » à temps réel. Elle se réalise, soit par un traitement analogique du signal de commande qui est simple à réaliser mais limitée dans ses possibilités, soit par un traitement numérique qui offre des possibilités, bien supèrieures, adaptatives au fonctionnement du moteur. En contrepartie, cette dernière solution nécessite des moyens de calculs plus puissants donc plus onéreux (multiprocesseurs). L'onduleur utilisé est généralement un onduleur de tension triphasé en pont, constitué de 3 demi-ponts. Il est schématisé de la façon suivante :

Le point 0, représenté sur le schéma, est évidemment fictif. Il est uniquement utilisé par commodité et permet, dans la représentation schématique, d'obtenir une symétrie sur les ondes de tensions v _a0 , v _b0 et v _c0 suivant l'axe des temps.

Sachant que l'expression des tensions aux bornes de chaque phase du moteur est la suivante :

v v = = aN as v v = = bN as v v = = cN as

1 3 1 3 1 3

( 2 v v v - - ) a 0 b 0 c 0 ( + v 2 v v - ) a 0 b 0 c 0 ? ? - + v v 2 v ) a 0 b 0 c 0 (III-36)

Les tensions v , et v ne peuvent prendre que 2 valeurs de potentiel : +U/2 et -

a0 vb0 c0

U/2. Il suffit d'appliquer une séquence de commande des interrupteurs spécifiques à une commande du type à modulation de largeur d'impulsions pour obtenir les formes d'ondes de tension que l'on souhaite :

6.2. Onduleur à commande en M.L.I :

Pour l'ensemble des simulations, on utilisera une Modulation de largeur d'impulsions basée sur le principe de la comparaison des signaux de commande en tension du moteur avec celle d'un signal triangulaire de fréquence fixe. Cette fréquence, m fois supèrieure à la fréquence nominale, correspond à l'indice de modulation de la M.L.I. Sa valeur sera entière et multiple de 3 de façon à faire correspondre, à chaque période, la forme du fondamental de l'onde à reproduire.

La M.L.I que nous utiliserons, se schématise de la façon suivante [12] :

Bascules de Schmitt



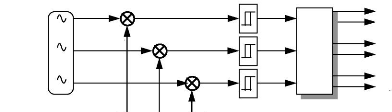
Tensions de
référence

Modulatrices

v _M (t )

v _P (t )

+

-

+

ebs1(t)

sbs1(t)

-

+

-

Commande
logique

cI1(t) cI1'(t)

I1

I1'

I2

I2'

I3

I3'

Porteuse

Tensions à
dents de scie

Fig.III-6.2



0 0.005 0.01

0.015 0.02 0.025

0.03

TP

VM

TM

VP

ebs1 : Entrée de la bascule

sbs1 : Sortie de la bascule

0 0.005 0.01 0.015 0.02 0.025 0.03

500 400 300 200

100

0

-100 -200 -300 -400 -500

800 600 +10 400 200 t 0 -200 -10 -400 -600 -800



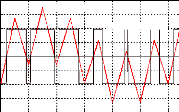
t

a) Ondes de tension de la modulatrice et de la b) Ondes de tensions d'entrée et de sortie

porteuse d'une bascule

Fig. III-6.3

T_M : Période de la modulatrice ? 0,42 ms. T_P : Période de la porteuse ? 30 ms.

6.3. Commande en couple avec un onduleur de tension à M.L.I ; Simulations.



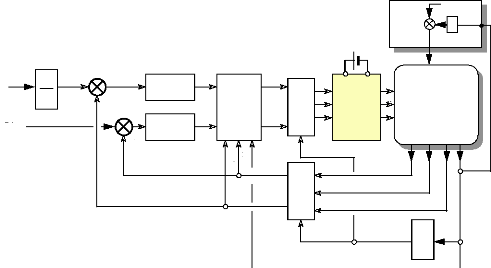
Idsref = 0

T_n^*

1 K_T

iqsref

+

-

+

6 iqs

bids

-

ids

Correcteur
PI

Correcteur
PI

uds

u qs

Découpleur
linéarisant

iqs

ids

?

?

i^?ds -- ? ids

i^?qs - iqs

v ? qs

'vds

?

0

[ P1 ^-1

[ P1

vMas
vMbs
vMcs

Onduleur
+
Cde
logique

U

vas
vbs

vcs

Machine

ias
ibs
ics

Modèle du moteur
discoïde à réluctance
variable et
à aimants permanents

0

?

+

+

Trma

?

T

k

?

co

Fig.III-6.4 : Schéma synoptique de la commande en couple du moteur
FINTRONIC.



C a r a ctér istiq u e d e la machine e n tr a in ée

(N .m )

(N .m )

Chapitre 3 : Commande vectorielle avec capteur mécanique - Mémoire CNAM Patrick BOIDIN.

.

· Simulation n°1: Démarrage du moteur sans à-coups de charge.

Données de la simulation : Commande en couple.
Machine :	M.L.I :	Régulation de courant :	Conditions initiales :
Jr =0,2 kg.m^2 T=0 N.m k=0,408 N.m/rad.s-1	Fréquence de la porteuse : 2,4kHz Indice de modulation m :48	Cdp=35 / Cdi=200 Cqp=17/ Cqi=350 * T = Tn = 176 N .m	00 = 0 °

6 0 0

4 0 0

2 0 0

0

-2 0 0

-4 0 0

-6 0 0

vas

m 0 .0 1 0 .0 2 0 .0 3 0 .0 4 0 .0 5 0 .0 6 0 .0 7 0 .0 8

Tem p s (s )

d) Tension aux bornes de la phase a_s du
moteur : v_as( t ) .

(A )

iq s

0 0 .0 1 0 .0 2 0 .0 3 0 .0 4 0 .0 5 0 .0 6 0 .0 7 0 .0 8

T e m p s (s)

1 4

1 2

1 0

8

6

4

2

0

-2

2 0

1 0

-1 0

-2 0

1 8 0

1 6 0

1 4 0

1 2 0

T r m a (n )

1 0 0

8 0

6 0

4 0

2 0

0

-2 0

-1 0 0 1 0 2 0 3 0 4 0 5 0 6 0

F ré q u e n c e d e rotation (tr/m in )

a) Caractéristique de la machine entraînée.

Trma ( n)

(A ) (V )

2 0 0

1 8 0

1 7 6

1 6 0

1 4 0

1 2 0

1 0 0

8 0

6 0

4 0

2 0

0

Tref

Tem

0 0 .0 1 0 .0 2 0 .0 3 0 .0 4 0 .0 5 0 .0 6 0 .0 7 0 .0 8

Temps (s)

b) Couple électromagnétique: T_em( t ) .

(A ) (V )

600

400

00

0

00

-400

-600

0.066 0.068 0.07 0.072 0.074 0.076 0.078

vMas

vas

ias

10

-10

Temps (s)

e) Modulatrice de tension de la phase a ,

s

tension et courant :v Mas ( t ) , v as ( t ) et i as( t)

(tr/m in )

70

60

50

40

30

20

10

0

-10

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08

T em ps (s)

n

g) Evolution de la fréquence de rotation du moteur lors de la phase de démarrage: n( t ) .

Fig. III-6.5 : Résultats des simulations. Commande en couple du moteur.

· La M.L.I provoque des oscillations de couple de #177; 5N.m (#177;2,8%) autour de 176N.m.

· La fréquence de commutation imposée par la M.L.I est de 2,4kHz.

- 74 -

f) Courant de Park sur l'axe q : i _qs ( t ) .

Chapitre 3 : Commande vectorielle avec capteur mécanique - Mémoire CNAM Patrick BOIDIN.

.

· La vitesse qui évolue librement, atteint son régime permanent en 60ms.

· La forme de ce courant correspond à l'image du couple électromagnétique, à la constante de couple près. Le découpleur a fonctionné correctement.



(V )

4 00

3 00

V P

2 00

1 00

0

t

-1 00

-2 00

V M as

-3 00

4 00

0.07 0.07 1 0.0 72 0.07 3 0.0 74 0.07 5 0.0 76 0 .077

Tem p s (s)

1

0

-600

0.07 0.071 0.072 0.073 0.074 0.075

Tem ps (s)



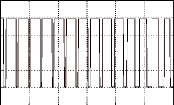
Comm a n de I1

a) Forme de l'onde de la porteuse et de la
modulatrice sur la phase a_s.

(A )

15

10

5

0

-5

-10

-15



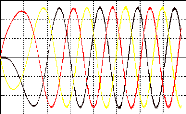
ibs ics ia s

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08

Tem ps (s)

c) Evolution des courants de phase durant le
démarrage du moteur : i as ( t ) , i bs ( t ) et i cs ( t).

b) Commande de l'interrupteur n° 1 du pont
onduleur.

(A )

5

4

3

2

1

0

-1

-2

-3

-4

-5

0.06 0.062 0.064 0.066 0.068 0.07 0.072 0.074 0.076 0.078



id s

Tem ps (s)

d) Courant de Park sur l'axe d : i _ds( t ) .

(° Angle interne du m oteur : D éphasage Tension/f.e.m

80

70

60

50

40

30

20

10

0

-10

0 0.005 0.01

0.015 0.02 0.025 0.03



6

180 160 140 120 100

80 60

40

20

0



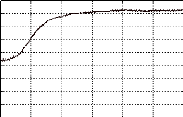
Tem ps (s)

(°) Angle de déphasage Rotor/stator

0.005 0.01 0.015 0.02 0.025 0.03

Tem ps (s)

D r

e) Evolution de l'angle interne durant la phase
de démarrage du moteur : 6 ( t) .

f) Evolution de la position du rotor par rapport au champ stat. tournant : O r ( t) .

Fig.III-6.6 : Résultats des simulations. Commande en couple du moteur. ? La position du rotor oscille de #177;4° autour de sa valeur moyenne.

Chapitre 3 : Commande vectorielle avec capteur mécanique - Mémoire CNAM Patrick BOIDIN.

.

· Simulation n°2 : Démarrage du moteur avec à-coups de charge de 50N.m.

Données de la simulation : Commande en couple.					Machine :
M.L.I :		Régulation de courant :	Conditions initiales :	Jr =0,2 kg.m^2 T=0/+50N.m k=0,408 N.m/rad.s-1
Fréquence de la porteuse : 2,4kHz Indice de modulation m :48		Cdp=35 / Cdi=200 Cqp=17/ Cqi=350 T * = 120 N. m	^00 = 0 °

140

120

100

80

60

40

20

0

(N .m ) (tr/m in )

A-coups de charge de 50N .m

Tref

T em

n



(N .m )

1 6 0

1 4 0

1 2 0

1 0 0

8 0

6 0

T r m a (n )

4 0

2 0

0

2 0

t > 3 5 m s

t < 3 5 m s



-20

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08

Temps (s)

a) Couple et fréquence de rotation :


T_em (t ) et n (t)

.

0 5 1 0 1 5 2 0 2 5 3 0 3 5 4 0

F ré q u e n c e d e rotation (tr/m in ) (s)

b) Caractéristique de la machine : T rma(n).

Fig.III-6.7 : Résultats des simulations. Commande en couple du moteur.

6.4. Commande en vitesse avec un onduleur de tension à M.L.I ; Simulation.

· Simulation n°3 : Démarrage du moteur sans à-coups de charge et de vitesse (Onduleur à M.L.I).



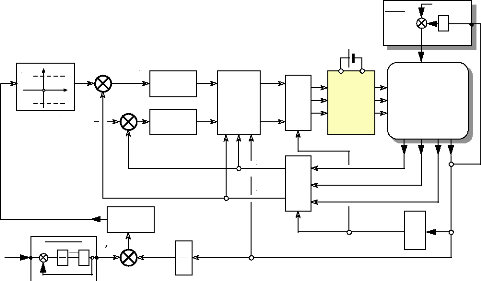
nref
tr/min

Limiteur à seuils

Imax

Imin

+

(A)

Filtre du 1er ordre

-

1

s_n

Idsref = 0

t

dn

dt

*

iqsref

?

+

n

-

correcteur
PI

+

+

?iqs

?ids

-

ids

En

-

Correcteur
PI

Correcteur
PI

n

60

2.11

uds

u qs

Découpleur
linéarisant

?

iqs

ids ?

i ^?d_s -- ids

i^?qs = iqs

v^?qs

^?vds

0

0

[ P? ?1

[P]

vMas
vMbs
vMcs

Onduleur
+
Cde
logique

U

vas
vbs

vcs

Machine

ias
ibs
ics

Modèle du moteur
discoïde à réluctance
variable et
à aimants permanents

0

J

+

+

Trma

?

T

k

?

CO

Fig III-6.8: Schéma synoptique de la commande en vitesse du moteur FINTRONIC.

- 76 -

Chapitre 3 : Commande vectorielle avec capteur mécanique - Mémoire CNAM Patrick BOIDIN.

.

Données de la simulation : Commande en vitesse.					Machine :
M.L.I :		Régulation de courant :	Régulation de vitesse:	Jr =0,2 kg.m^2 T=0 N.m k=85.10^-5 N.m/rad.s^-1
Fréquence de la porteuse : 2,4kHz Indice de modulation m :48 Conditions initiales :		Cdp=35 / Cdi=200 Cqp=14/ Cqi=0 Seuils de limitation:-13A/+13A	Tn=0,01s Cvp=1,5 / Cvi=3,5 n*=60tr/min

70

60

50

40

30

20

10

0

-10



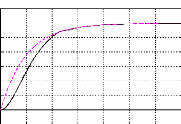
(tr/m in)

n

*

n

1 80

1 60

1 40

1 20

1 00

8 0

6 0

4 0

2 0

0

-20



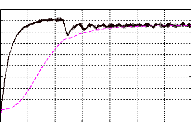
(N .m )

Tem

T r

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

Temps (s)

a) Fréquence de rotation du moteur et sa
référence : n (t ) n ( t ) .

*

et

(N .m )

140

120

100

80

60

40

20

0

-20



T rm a (n)

-10

40

20

10

60

50

30

0

F réquence de rotation (tr/m in)

a) Caractéristique de la machine entrainée :
Trma( n).

13 0 0

400

200

0

-200

-400

-1300

0.013 0.0131 0.0132 0.0133 0.0134 0.0135 0.01313 0.0137



va s

v M a s

Tem ps (s)

c) Modulatrice et tension de phase : v _Mas ( t)
et v _as (t ).

Temps (s)

0 0 .0 1 0 .0 2 0 .0 3 0.04 0.05 0 .0 6 0 .0 7

b) Evolution dans le temps du couple
électromagnétique et du couple résistant :
Tem (t ).

1300 400 200 0 -200 -400 -1300

(V )



vas

0 0.01 0.02 0.03 0.04 0.05 0.013 0.07

Tem ps (s)

b) Tension aux bornes de la phase a_s du
moteur : v _as (t ).



300

v M a s

250

ias

200

1 5 0

100

50

0

0.045

0.05

0.055

Tem ps (s)

d) Détails sur les ondes de tension
(modulatrice) et de courant de la phase as :
i _as(t ) et v _Mas(t ).

Chapitre 3 : Commande vectorielle avec capteur mécanique - Mémoire CNAM Patrick BOIDIN.

.

(A) Angle interne : Sigma



iqs

iqs*

14

12

10

8

6

4

2

0

90

80

70

60

50

40

30

20

10

0

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

Temps (s)

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

-10

e) Courant de Park sur l'axe q et sa référence:
i _qs (t ) et i _qsref (t ) .

thetar (°) Temps (s)

f) Evolution de l'angle interne durant la phase
de démarrage du moteur : 6 (t) .

ids (A)



180

160

140

120

100

80

60

40

20

0

12

10

8

6

4

2

0

-2

-4

-6

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0 0.01 0.02 0.03 0.04 0.05

Temps (s) Temps (s)

g) Evolution de la position du rotor par h) Courant de Park sur l'axe d : i _ds (t ).

rapport au champs statorique tournant: O_r (t ).

Fig. III-6.11 : Résultats des simulations. Commande en vitesse du moteur.

7. REMARQUES ET CONCLUSION.

Cette étude permet de juger les performances théoriques du moteur, associé à une commande en couple et en vitesse avec capteur mécanique.

Les remarques importantes que l'on peut faire sur les simulations sont les suivantes :

· Le moteur FINTRONIC est plus favorable à une commande en couple, ce qui confirme son appellation de moteur "couple". Les résultats sont satisfaisants pour la commande en vitesse.

· Qu'elles que soient les contraintes de couple, le moteur a su réagir efficacement avec des délais très raisonnables, inférieurs à 30ms.

Chapitre 3 : Commande vectorielle avec capteur mécanique - Mémoire CNAM Patrick BOIDIN.

.

· Le moteur a besoin d'une commande en M.L.I pour limiter au mieux les harmoniques de courants et surtout les à-coups de couple. Les moyens en informatique, à notre disposition, ne permettent pas d'utiliser une M.L.I à une fréquence plus élevée que celle utilisée de 2,4 khz. Compte tenu des bons résultats obtenus, on peut s'imaginer que les résultats seraient bien meilleurs à des fréquences supérieures.

· La remarque précédente nous motive à écarter la solution du contrôle des courants par "hystérésis". En effet, cette méthode ne permet pas de contrôler suffisamment bien les harmoniques de courant, pour favoriser son emploi.

· Qu'elle que soit la position initiale du rotor, imposée avant chaque démarrage, le comportement du moteur n'a pas varié.

· Muni d'un découpleur linéarisant, le moteur discoïde et sa commande deviennent assimilables à un moteur à courant continu. L'inconvénient principal de ce découpleur réside dans l'estimation de la valeur numérique des paramètres du moteur. En supposant que ces paramètres évoluent en fonction des données tel que la température ou autres, il faudra réajuster les valeurs en conséquence. Cette condition impose de bien connaître les caractéristiques électriques du moteur considéré ou d'intégrer dans la commande du moteur des opérations de mesures des paramètres électriques.

· Le moteur a besoin d'être régulé avec beaucoup de souplesse pour des fonctionnements dont le couple résistant est faible. En effet, si les paramètres des correcteurs optimisent les fonctionnements à fortes charges, le moteur aura tendance à pomper en dépensant inutilement de l'énergie sous forme de pertes magnétiques aux faibles charges. Dans cette situation, on devra adapter les paramètres des correcteurs au cas de fonctionnement donné. On appelle cette commande,

Commande adaptative.

En conclusion, la commande vectorielle s'adapte assez bien au moteur FINTRONIC, à condition de connaître à chaque instant, la position du rotor. La structure de cette commande est simple à élaborer, comparée à celle d'une commande vectorielle de machine asynchrone. Néanmoins et sans pouvoir le démontrer dans ce mémoire, le moteur perd très vite ses performances, à des vitesses supérieures au nominal. Une étude est nécessaire pour ce cas de fonctionnement.

CHAPITRE 4

COMMANDE SANS CAPTEUR
MECANIQUE DU MOTEUR FINTRONIC
ET
FILTRE DE KALMAN

1. INTRODUCTION.

Dans cette partie d'étude, on défini une commande sans capteur mécanique du moteur FINTRONIC. Cette commande est testée par une série de simulations sous MATLABSIMULINK dont on présente les résultats. Le chapitre précédent nous a montré que le capteur de position et de vitesse était indispensable à la fonction d'autopilotage et à la régulation de vitesse. Or, les difficultés rencontrées pour définir le capteur standard et compatible avec le prototype, nous conduit à étudier un moyen technique de substitution. Pour cela, on utilise un algorithme de contrôle-commande du type :

filtre de Kalman.

2. LE CAPTEUR DE POSITION. 2.1. Le capteur et son rôle :

Le capteur mécanique que nous proposons de définir avant de le remplacer, doit détecter la position angulaire du rotor par rapport à un repère fixe du moteur. On rappelle que le rotor est soumis à une fréquence de rotation nominale de 60 tr/min pour une fréquence électrique de 64Hz.

2.2. Résolution du capteur :

Le nombre de pas du moteur est de 64. Cela signifie que pour 1 tour mécanique du rotor, le champ statorique a fait 64 tours électriques. En imposant un pas de mesure de 1 degré électrique (1pt/°) qui correspond à une précision de 60'(minutes) et 360 pts sur le tour électrique, il faudrait une résolution de 23 040 points de mesure par tour mécanique (64x360) pour assurer le fonctionnement correct du moteur.

5,625° méca. 360° méca.

1 tour électrique 64 tours électriques



1 tour mécanique

0

⁹mec

360° élec.

1pt/° élec.

360pts

360x64= 23 040pts

Fig.IV-2.1

Or, le traitement des informations du capteur doit nécessairement se faire sur 15 bits au minimum (2¹⁵=32 768 pts).

2.3. Choix du type de capteur :

Il est possible de choisir parmi l'une de ces 3 catégories de capteurs "standard":

1. Le capteur de position angulaire du type codeur rotatif incrémental : La position angulaire est définie par un nombre d'impulsions sur le tour mécanique.

2. Le capteur de position angulaire du type codeur rotatif absolu : La position angulaire est définie par un mot binaire de x bits dans le tour absolu.

3. Le capteur de position angulaire de type résolveur : La position angulaire est fournie par 2 signaux analogiques (en cosinus et en sinus), porteurs de l'information de position. Un traitement du signal est nécessaire pour ce type de capteurs.

2.4. Le codeur rotatif incrémental :

Les plages de résolutions les plus courantes, proposées par les fournisseurs, sont comprises entre 50 et 10 0000 points par tour mécanique. Au-delà de 5 000 pts, le capteur devient sophistiqué et coûteux. Le principal inconvénient de ce capteur est de fournir une position relative par rapport à un point de référence "Top 0" qui se situe dans le tour mécanique. Tant que ce "Top 0" n'est pas sollicité, le moteur est commandé de façon aléatoire. Or, cette phase transitoire est d'autant plus longue que le nombre de paires de pôles du moteur est grand. Dans notre cas, cette phase peut durer prés d'une seconde (60 tr/min. = 1 tr/s). Evidemment, Cet inconvénient n'est pas tolérable pour une commande performante du moteur FINTRONIC.

2.5. Le codeur rotatif absolu :

Ce type de capteurs est proposé avec une résolution maximale et courante de 4 096 pts/tour mécanique ; C'est un codeur à 12 bits. Au-delà de cette résolution, le prix du capeur devient injustifié pour des projets comme le notre. En exemple, on peut citer HEIDENHAIN qui propose des capteurs 15 bits (32 768 pts/tour) pour un montant H.T. de 8 000 francs, l'unité. Ce matériel est aussi cher que le variateur de vitesse, lui-même. De plus, les informations doivent être traitées non plus sur 12 bits mais sur 16 bits. Par contre, le codeur absolu supprime l'inconvénient du cas précédent : L'autopilotage du moteur peut se faire instantanément sans phase d'incertitude et la position angulaire du rotor est déterminée dans le tour absolu.

2.6. Le résolveur :

Le résolveur est un capteur électromagnétique qui a l'avantage d'être dépourvu de toute électronique embarquée. Par sa constitution et par sa construction, il s'apparente fortement à un moteur synchrone dont on a mis en quadrature, deux phases statoriques. L'inducteur est alimenté par une tension alternative soumise à une fréquence maximale de 10kHz. On retrouve le principe du résolveur à travers cette figure :



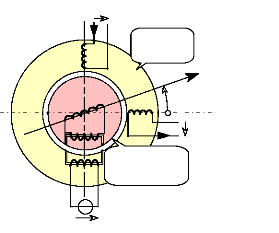
vs1

Signal de sortie
capteur

Partie fixe
solidaire du bati
moteur

Axe en rotation

Stator

Rotor

°mé c

Axe fixe de référence

vs2

Signal de sortie
capteur

Partie mobile
reliée mécaniquement
au rotor du moteur

V e ( 10kHz)

Signal d' entrée

Fig.IV-2.2 : Capteur de position type "Résolveur".

L'amplitude des tensions de sorties de ce capteur varie en fonction de la position du rotor. La modulation de ces amplitudes permet de déterminer la position du rotor par rapport à un axe de référence du résolveur. La fréquence de la modulatrice permet d'obtenir la fréquence de rotation du moteur tandis que la fréquence de la tension d'entrée, donne la résolution. Elle correspond à 10000 50 variations pour 3 000

tr/min, soit 200 pts par tour mécanique. On peut atteindre 5 000 pts/tour mécanique en ajoutant au dispositif, un module électronique dit "de positionnement".

L'inconvénient principal de ce capteur est de fournir une mauvaise précision de la mesure aux basses vitesses.

En préliminaire, on constate que les capteurs proposés ne conviennent pas tout à fait au prototype : La résolution de 4 096 pts/tour n'est pas suffisante comparée aux 23 040 pts/tour recherchés. Néanmoins, une solution consisterait à augmenter le rapport des vitesses en interposant entre le moteur et le capteur, un train d'engrenages.



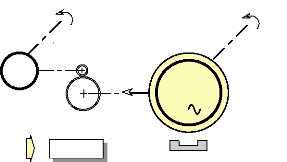
Train d'engrenages
R=4

Codeur
12bits

MS

3

Aimants P.

4 tours mécaniques

1 tour mécanique

1,41°/pts

Fig.IV-2.3 : Capteur de position avec train d'engrenages.

2.7. Conclusion :

Pour installer un capteur de position sur le prototype, il faut un codeur rotatif absolu à 12 bits (- 4 000 francs.) mais sans son train d'engrenages. En effet, ce dispositif augmente la résolution du capteur mais augmente aussi sa sensibilité face aux imperfections du train d'engrenages (jeux) et aux vibrations mécaniques parasites du moteur. La solution sans engrenage permet de filtrer naturellement la mesure de la position qui est détectable à environ #177; 3° de l'angle électrique. Cette solution s'oppose, néanmoins, à une commande optimale.

3. RECONSTRUCTION DE LA POSITION DU ROTOR AU MOYEN DU RECONSTRUCTEUR D'ETAT.

3.1. Le reconstructeur et son principe, appliqués aux systèmes linéaires :

Un reconstructeur d'états [13][14] est un dispositif capable d'estimer une ou des grandeurs d'états non mesurables d'un système, à partir des grandeurs mesurables dites observables. Cette définition fait apparaître la notion d'estimation. Le problème essentiel d'une valeur estimée est de pouvoir juger son degré de fiabilité. Pour cela, on se sert d'une autre grandeur du système qui est estimable et mesurable pour corriger les estimations des grandeurs non mesurables à travers des gains de correction.

Un reconstructeur d'états est donc un estimateur à la fois correcteur des variables d'états. On schématise le principe par le schéma suivant :

Réseau





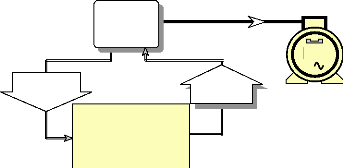
Cde

MS

3

Grandeurs
mesurables

Grandeurs
estimées

Reconstructeur

Estimation
+
Correction de l'erreur

Fig.IV-3.1 : Principe du reconstructeur.

L'idée du reconstructeur consiste à reconstruire l'ensemble des variables d'état du
moteur contenant les grandeurs non mesurables. On le fait partiellement ou en

totalité. A partir de la représentation du moteur par le modèle d'état, on schématise le principe du reconstructeur d'états dans sa phase estimation [15]:



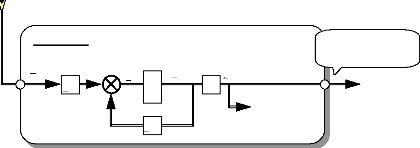
u( t ) i( 1(t)

+

Estimateur

g ? t ?

+

f ?t)

?

C

y? ( t)

Variables de sortie
estimées à
valeurs observables
sur le processus

Variables de sortie
de l'estimateur à
valeurs non-observables
estimées



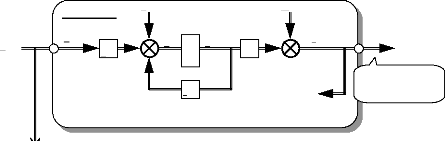
u( t)

Processus

u( t)

g ? t ?

+

v(t)

+

+

x? ( t )

f ?t)

J^.

x(t)

Variables de sortie
du processus à
valeurs non observables

C

+

w( t)

+

y(t)

Variables de sortie
du processus à
valeurs observables

Fig. IV-3.2 : Le processus et son estimateur fonctionnant en parallèle.

Nota :

· La moins mauvaise estimation d'un bruit, agissant sur un système, consiste à la supposer nulle. C'est pourquoi les vecteurs "bruits" v( t) et w( t) du système à variables estimées, n'apparaissent pas dans l'estimateur.

· u (t ) correspond au vecteur d'entrée du système dont les variables sont fonctions du temps. Les variables peuvent être les tensions ou les courants.

· y (t ) et x (t )correspondent au vecteur de sortie et au vecteur d'état du système dont les variables sont fonctions du temps. Ces variables peuvent être les tensions, les courants, la position et /ou la vitesse angulaire.

Le moteur et l'estimateur obéissent aux 2 systèmes différentiels suivants :

d dtx t f t x t g t u t v t ? ? ? ? ? ? ? ? ? ? ? ? ? ? + y t C x t w t ? ? ? ? ? ? ? +	et	d dt = 71( + y t C x t ? ? ? ? ? = ?

(IV-1) : Processus et estimateur.

Nota :

La matrice C est considérée à coefficients constants.

Or, dans cette configuration, rien ne nous permet de vérifier si les valeurs estimées sont fiables ou non. Il faut rajouter un dispositif de vérification et de correction des variables d'états estimées :

u( t)



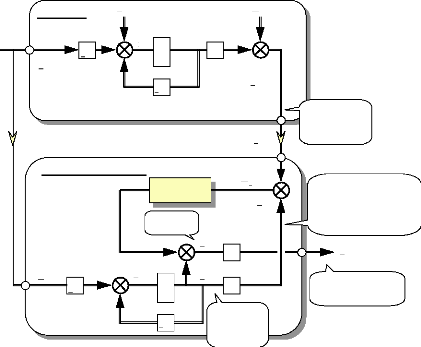
Processus

u( t) + i( t) 1( t)

u( t)

Reconstructeur d'états

g( t)

g( t)

+

v( t)

+

+

+

x? ( t )

K
Gain de Correction

Nouvelle
estimation

f( t)

f( t)

I

I

+

x( t)

+

x? _c ( t)

C

Ancienne
estimation

C

C

y( t)

E _y ( t)

y? ( t)

+

y( t)

w( t)

+

+

-

Variables de sortie
du processus A
valeurs observables

Variables de sortie
de l'estimateur A
valeurs estimées non corrigées
observables
sur le processus

Variables de sortie
de l'estimateur A
valeurs non-observables
estimées et corrigées

3%_c( t)

Fig.IV-3.3 : Processus avec son reconstructeur d'états.

Reconstructeur d'état :

d

_dt i^sk( t ) = f ( t ) l4 t ) + g ( t ) u ( t) A t ) = C ii( t)

(IV-2)
Vérification de l'erreur sur la sortie :

E_y ( t ) = y( t ) -- y? ( t)

(IV-3)
Correction de l'estimation du vecteur d'état :

?x _c ( t ) = ?x( t ) + K E _y ( t) ? Nouvelle estimation.

(IV-4)

Le principal inconvénient de cette méthode est de conserver constant dans le temps, les coefficients de la matrice de gains de correction. Il faut nécessairement optimiser la valeur de ces coefficients, quel que soit le fonctionnement du moteur.

De plus, la mesure des grandeurs observables doit être la plus précise possible pour permettre une comparaison efficace sur les sorties et permettre une commande toute aussi efficace de l'estimateur. Il est important de préciser qu'un reconstructeur d'état fait appel à des moyens de calculs sophistiqués dont les temps de calculs dépendent essentiellement de l'ordre du système = D'où l'utilisation d'un microcontrôleur spécifique, propre à cette fonction. Le traitement de l'information, au moyen d'un pC, impose que le système continu soit converti en un système discret. On obtient ainsi une nouvelle représentation du système différentiel. Pour cela, on pose :

x? tk) = x_k , avec k correspondant au pas d'échantillonnage à l'instant tk. On obtient [13] :

k k

e g ? ? u ? ? ? d ? e

f k

( , )

? f k

( , )

?

? ? ? ? ? v(T)) dT

k-1 k-1

? 1

x _k e f k k

( , ) ?

? x ?

?

k 1

?

(IV-5)

Le 1^er terme de l'expression (IV-5) correspond à la solution générale du système différentiel sans second membre.

_ef ( k , k- 1 ) correspond à la matrice de transition du système (passage de x_k_₁ à x_k). On notera ce vecteur :

f k k

( , )

? f k

( , )

?

? ? k ,k ?1 ? ? ? ? k k ? e

, ? 1 ? ¹ et ? ? k ?

, e

?

?

(IV-6)

Le 2ème terme du second membre de l'expression (IV-5) correspond à la solution particulière du système différentielle avec second membre tenant compte de la condition initiale. Durant la période comprise entre les 2 pas d'échantillonnage k et k-1, on peut considérer que u(ti) est resté constant. D'où :

k ? k ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? g u d ? ? ? ? ? ? ? k g ? ? k , ? , k ? 1 ? k-1		1 d u k g d k u k ? ? ? ? 1 ( ) ? ? 1 1 ?
(IV-7) Le 3^ème terme du second membre est mis sous la forme : k v d k ? ? ? v ? ? ? 1 ? ? ? ? ? ( ? ) k , k-1	dr

(IV-8)

Le système différentiel, représentant le processus et le reconstructeur, devient sous la forme d'un système discret suivant :

Processus (moteur + machine) :

1. Estimation sous forme de prédiction :

2. Mesure des grandeurs de sortie mesurables et comparaison :

(IV-11) : Cy ? k) ? y ? y --

?

k k k

/ 1

3. Réajustement des estimations :

X k k X k k K y _k y k k

? = ? ( ? )

+

/ / ? 1 / _ 1

et

y / C X /

? k k = ? k k

(IV-12)

X = I , _ X + g u

k ( )

k k 1 k _ 1 d k

? ?

? 1

y C X w

= +

k k k

Reconstructeur d'état

(IV-9) :

:



X + g

( )

k k

, -- 1 k k

? ?

1 1

/ d k

? ?

? 1

y ? = C X ? k k

/ ? 1

k k

/ -- 1

(IV-10) :

X ? _ I ?

k k

/ ? 1

u k --1

+ v

k -- 1 d k

(

- 1)

Nota:

Pour éviter des confusions, nous avons rajouté volontairement un terme supplémentaire en indice à chacune des variables discrètes ? X k/ k (2ème k). En effet, ce terme correspond au pas d'échantillonnage pour lequel on a réalisé les mesures. Ceci nous permet de savoir si l'estimation est réalisée avant ou après la mesure.



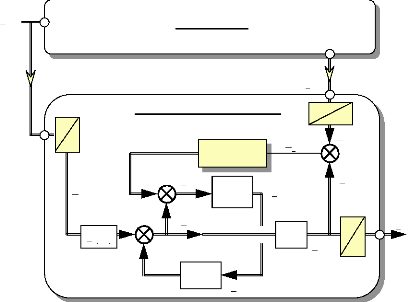
u( t)

t

k

uk?1

gd k_1

( )

+

Reconstructeur d'état discrêt

+

+

+

Processus

? X k/ k

? X k/ k? 1

? ( k , k-1)

K
Gain de Correction

Retard

? X k ? 1 / k ? 1

? X k ? 1 / k ? 1

y_k

+

? y( k)

C

y( t)

y k k- 1
/

?

t k

-

?

y k k- 1
/

k

t

y? ( t)

Fig.IV-3.4 : Reconstructeur discret.

Pour mieux comprendre le rôle du reconstructeur, on detaille de façon chronologique et sous forme de schema, les differentes tâches a realiser par le 1.1C.



¹¹¹(k,k-1)

O( k +1,k9

tk-1 Matrice de transition t_k Matrice de transition tk+1



...

x k - 1 /k-2

y

k- 1 /k-2

Mesures de yk-1 et uk-1

Détermination
de
l'erreur

⁶ y ( k- 1)

Estimation
de

x ? k- 1 /k - 1

Correction

Tâches à réalisées
par le microcontrôleur
dans l'intervalle de temps

Mise en mémoire
de

Estimation
de

? x k/ k-1

x k/ k-1

?

Estimation
de

yk /k-1

Mesures de y_k et uk

Détermination
de
l'erreur

C y(k)

Estimation
de

x ? k / k

Correction

Tâches à réalisées
par le microcontrôleur
dans l'intervalle de temps

Mise en mémoire
de

Estimation
de

? x k+1/k

x k+1/k

?

Estimation
de

,,

yk+1/k

Mesures de yk+1 et u _k+1

Temps en P s

t k -1, t k t k , t k +1

Instant oil les données sont

saisies par le
microcontrôleur

Fig. IV-3.5 : Tâches réalisées par un reconstructeur d'état.

Pour ameliorer l'idee du reconstructeur d'etat precedant, nous proposons d'utiliser une methode qui consiste à tenir compte de toutes les variables aleatoires susceptibles d'integrer des erreurs dans les differentes estimations. La methode proposee est :

la méthode de Kalman.

4. RECONSTRUCTEUR D'ETAT EVOLUE DU TYPE « FILTRE DE KALMAN ».

4.1. Principe du filtre de Kalman :

Le principe adopte par Kalman consiste à adapter la valeur des paramètres de la matrice de gains K, à chaque pas d'echantillonnage. Les valeurs adaptees sont fonctions de 3 critères :

1. La confiance que l'on donne, à la determination de la première estimation par anticipation, avant correction et à la seconde estimation, après correction.

Cette confiance dépend, elle-même, de la confiance que l'on donne au pas précédent, modérée par l'erreur observée sur cette confiance.

Ce critère de confiance est traduit par Kalman par une matrice que l'on note

P.

2. Le niveau d'influence des différents bruits imposés au système, compte tenu que l'estimateur du cas précédent n'en tenait pas compte directement. Pour matérialiser ces bruits, on peut citer comme exemple sur les moteurs, les bruits occasionnés par un balourd sur le rotor qui va provoquer des à-coups de couple. On rappelle que par définition, un bruit défini un comportement aléatoire traduit sous forme de signal dont la valeur et son évolution ne peuvent pas être prédites avec exactitude.

L'influence des bruits du système, sur le filtre, est traduite par Kalman par

une matrice que l'on note Q.

3. L'influence des bruits sur les mesures qui faussent la correction de l'estimation. L'influence des bruits de mesures sur le filtre est traduite par Kalman par une matrice que l'on note R.

La méthode de Kalman fait appel à des notions de statistique (espérance, variance et covariance) que nous avons préféré présenter en annexe.

4.2. Le filtre de Kalman associé aux systèmes linéaires [14] :

Les matrices P, Q et R conditionnent la matrice de gain du filtre K. En plus des

données propres au filtre de Kalman, nous imposons les hypothèses simplificatrices suivantes :

? Les bruits imposés au système v_k et les bruits de mesures w _k sont des bruits blancs.

D'où, par définition, l'espérance de ces variables aléatoires est nulle :

E{ v_k } = 0 et E( w_k } = 0
(IV-13)

On suppose que les bruits de mesure n'auront pas d'influence sur les bruits du système et vice et versa = La matrice de variance-covariance des bruits est donc à coefficients nuls :

cvw

? ? T

= E ??? v w ??? = 0

(IV-14)

? On supposera que les bruits de mesures n'auront pas d'influence sur l'erreur initiale de la variable d'état estimée et vice et versa. D'où :

E w x ^T

??? ? ? ??? ? avec x x x

?

0 0 = 0 - ? 0/ 0

0

(IV-15)

Les variables aléatoires du vecteur « bruits de mesures » sont supposées indépendantes entre elles. Les coefficients de covariance de la matrice de variance-covariance de ce vecteur sont nuls. Seuls les coefficients sur la diagonale de la matrice (coefficients de variance) sont différents de 0. Il en est de même pour les variables aléatoires du vecteur « bruits sur le système ». D'où :

[
[

=

k

1_{0 °}T

cvv = E iv _k vk

1= E {v _k v _k^T} = Q

q1 k 0 . 0

^i1L

0 q 2k . 0

. .

q3

k

0

0 0 0 qnk

(IV-16)
et

I ,, ,, T

cww E iw _k wk

}= E w w

? ?

T ? ?

R

k k k

r₁ k 0 . 0

0 r 2k . 0

r 1 ? 1 L

i_?
? ?i

k

. .

0

r₃

rnk

0 0 0

(IV-17)

Nous venons de définir les matrices Q_k et R_k qui représentent successivement l'influence des bruits sur le système et l'influence des bruits sur les mesures.

· D'après l'expression (IV-16), on définit la matrice de variance-covariance de l'erreur sur la première estimation (avant correction) du vecteur d'état par:

T

P k / k -1 = E x k -- x k /k _₁ x k -- xk/ k _1

(IV-18)

A partir des expressions (IV-5), on en déduit une nouvelle expression :
P k k ? ? k k ? P k k ? ?

? T

?



/ ? 1 , ? 1 ? / ?

1 1 k , k ? 1 ? Q 1

d ( k ? )

Matrice de variance-covariance del'erreurr sur la1^èree estimation
(IV-19)

L'expression précédente ne suffit pas pourdéterminerrPk / k-1,' Il fautconnaîtree
l'expression deQd (k k1))qui correspond à la forme discrète de Qkk1. A partir dee

l'expression (IV-4) et des propriétés sur les variables aléatoires, on en déduit :

k

? ?

? k ? Q ? ? ? k ? d

T

v(t) v Q

d ( k -1 ) d ( k , k-1 )

? ? , ? ? ? ?

,

k- 1

(IV-20)

· Selon lecritèree des variances minimales, Kalman a pudéfinirr la matrice des gains de correction par :

K _k P k k C ? C P

T T

? C R ?

? k

/ 1

? k k

/ 1

?

-1

(IV-21)


· Dès lors, il est possible d'en déduire la matrice de variance-covariance de l'erreur sur la deuxième estimation du vecteur d'état. On obtient :





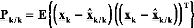
?P k / k = Pk/k-1 -- K_k C P k/k-1

Matrice de variance-covariance de l'erreur sur la 2^ème estimation
(IV-22)

Nous venons de définir la matrice P, représentant la confiance apportée aux 2 estimations du vecteur d'état et la matrice K_kreprésentant les gains de correction.

Nota :

P0/0 représente la 1^ère confiance sur l'estimation des variables d'état estimées (Matrice des conditions initiales). x0/0 : Matrice des conditions initiales du vecteur d'état du processus (moteur + machine).

x0/0 : Matrice des conditions initiales du vecteur d'état à variables estimées.

L'évolution de la matrice de gains est schématisée de la façon suivante :

Q₀

R₀

P0/0

Kk 6 y(k)





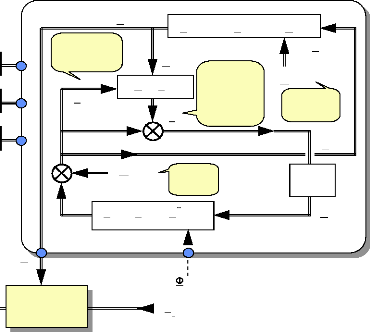
Matrice de
Gains de Correction

Matrice de Kalman

K_k

Représentatif des
erreurs sur la première
estimation des
variables d'état

+

Pk/k-1

+

(1)( k, k -1 ) P k -1 / k-1 a ( k , k-1)

K_k

Q d ( k --1)

K_k C Pk/k-1

Pk/k

+

+

K_k

?y(k)

Représentatif
des bruits
sur le système

P k / k-1 C T [ C P k /k-1 C T #177; Rk]

(k,k-1)

Représentatif des
erreurs sur la deuxième
estimation des
variables d'état

R_k

Représentatif
des
bruits de mesures

Retard

? 1

Pk/k-1

Pk - 1 /k-1

Pk/k-1

P k k E ? ? x _k x k k ? ? ? x _k x ? ? ?

T

? ? ? ? ? k / k

/ /

Fig.IV-4.1 : Adaptation des gains de correction des systèmes linéaires d'après la
méthode de Kalman.

4.3. Le filtre de Kalman étendu aux systèmes non linéaires [14][16] :

Le principal avantage de cette méthode est de pouvoir l'étendre aux systèmes non linéaires : Matrice d'évolution du système dépendante des variables d'états. Néanmoins, il est impératif de satisfaire une condition pour adapter réellement cette méthode : Connaître au moins une solution approchée du système différentiel que l'on notera xref et que l'on appellera « solution de référence ».

Tout d'abord, on admet que le système d'équations différentielles puisse se mettre sous la forme continue suivante :

t ) = f ( x ( t ), u ( t ), t ) + v ( t)

t ) = Cx ( t ) + w ( t) (inchangé )

x? (

y(



(IV-23)

On fait correspondre x 0 re f à la matrice des conditions initiales du vecteur de référence xref : Vecteur « solution approchée » du système. Le but consiste à ramener le système précédant non linéaire à un système linéaire afin d'utiliser la méthode de Kalman. Pour cela, on remplace le vecteur d'état par un nouveau vecteur, correspondant à l'écart entre le vecteur d'état et son vecteur de « référence »: x -- xref. Cela revient à faire la différence de chaque terme des 2 systèmes :



x?(t ) = f( x (t ), u (t ), t) + v (t) et ?x ref (t ) = f( x _ref (t ), u _ref (t ), t)
(IV-24)

On obtient ainsi:

x?(t ) -- *_ref (t ) = f(x (t ), u (t ), t ) -- fk _ref (t), u _ref (t), t ) + v (t)

(IV-25)

A partir de cette nouvelle expression matricielle, l'idée consiste à remplacer le 2ème membre (sans les bruits) par son développement en série de Taylor, réduit au premier ordre.

Mise en application, cela nous donne :

+

+...

v ( t)

? f x t u t t

( ), ( ),

ref

? ? ? ? ?

ref

f x t u t t f x t u t t x t x t

? ( ), ( ), ? ?

? ( ), ( ), ? ?

? ( ) ? ( )

ref ref ref

a x _ref (t)

f x t u t t

ref

? ? ?

? ( ), ( ), ? ?

ref

? u t u t

( ) ? ( )

ref

a u ref (t)

(IV-26)

Nota :

La formule mathématique de Taylor correspond à f ( b ) = f ( a ) + [( b - a) / 1 !] ? ( ) ? ... ? [( ? ) / !] ( )

f a b a n f a

n n

On peut faire une approximation, en supposant que les entrées imposent de faibles perturbations sur le système. On supprime donc le dernier terme de l'expression (IV-26). De plus, on a u_ref(t) = u(t) .



On obtient ainsi et sous une autre forme :

a[ f (x t u t t ? ? ? ? ?

f x t u t t ? ?

ref ( ), ( ),

ref ( ), ( ),



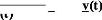
-- % ( t X 0) +

) + x( t) -- --

ref

a x _ref (t) ref a x

ref

( t)x ( t) +

(IV-27)

Or, en posant :

? ? ? ?

? f x t u t t ? ? ref ( ), ( ), F t x t , ( ) ? x ref ? x t ref ( )

: Fonction "aux dérivées partielles" de f.

(IV-28)

Et en linéarisant le système en imposant des faibles variations à x( t) autour de la trajectoire de référence x ref ( t ) (on ne tient plus compte des premiers termes de chaque membre de IV-27), on a :



x?(t ) = F_x (t, x _ref (t)) x(t)+ v (t)
(IV-29)

Si les valeurs approchées de x 0 ref sont suffisamment voisines de celles de ^?x₀ estimés

(x ₀ -- x 0 ref x ₀ -- x^?₀), on peut espérer qu'il en sera de même, à chaque instant, pour

x _ref (t ) et x^?(t ) . Dans ce cas, on remplace le vecteur de référence par l'estimation du vecteur d'état. On linéarise autour de cette estimation et le nouveau système linéarisé devient :

x?(t ) f t , x ( t ) x ( t ) v ( t )

? ? ? ?

y ( t ) = Cx ( t ) + w (t)

x t F t x t x t v t

?( ) ? ? ?

, ?( ) ( ) ( )

?

x

y t Cx t w t

? ? ? ? ? ?

? ?

?



Avec

? ? ? ?

? f x t u t t

?( ), ( ), ? ?

F t x t

x , ?( ) --? x t

?( )

On a remplacé x_ref par x?
u( t) = U :Matrice à termes constants

(IV-30)

De la même façon que pour les systèmes linéaires, on discrètise le système. On en déduit l'ensemble des équations du filtre de Kalman étendu aux systèmes non linéaires:

Processus (moteur + machine) :

x ? k k x ? x

? ? , 1 , ? ? 1

? ? v

k k d ( k ? 1 )

y k = C x k #177; w_k

(IV-31):



Avec

(IV-32) : ? ? k k x ? eF _x k k x

( , ,? )

?

, ? 1 , ? ? 1

Filtre de Kalman étendu :

1. Estimation sous forme de prédiction :

(IV-33) :		x ? ? , ? ? k k x ? 1 , ? ? ? x k k / ? 1 k k ? ? 1 1 / k k ? 1 / ? 1 y ? k / k-1 = C xk /k-1

2. Mesure des grandeurs de sortie mesurables et comparaison :

(IV-34) : ? y ? k ? = y - y --

k k k

/ 1

3. Réajustement des estimations :

? ( ? )

(IV-35) : ? x k k = x k k ? + K _k y _k - C x k / k 1

/ / 1 _

et

(IV-36) : ? y_/ C x /

k k = ? k k

4. Matrice de variance-covariance de l'erreur sur la 1^ère estimation du vecteur

d'état :

(IV-37) : P k k ( k k x ) P ( k k x ) Q

T

, ? , _ 1 , ? +

= , _ 1 ?

/ -- 1 k k

1 1

/ k k

1 1

/ k k

1 1

/ d k

_ _ -- -- _ _ ( )

? 1

Avec

(IV-38) : Q ( k k x ) Q ( k k x )

T

= , _ 1 , ? , _ 1 , ? / + Q

-- 1 k k

1 1

/ k _ 1 k k

1 1

_ _ _ _

d k

( ) k -- 1

5. Matrice de gains de correction (inchangée):

? 1

(IV-39) : K_k P k k C [ C P

^T C R ]

T

= + _k

/ 1

-- k k

/ 1

--

6. Matrice de variance-covariance de l'erreur sur la 2^ème estimation du vecteur

d'état (inchangée) :

(IV-40) : P k/ k = P k / k-- 1 -



K_k CPk /k ? 1

On représente le fonctionnement du filtre de Kalman étendu aux systèmes non linéaires, sous forme de schéma-blocs :



u( t)



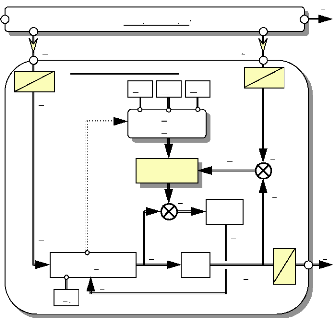
t k

uk?1

uk?1

u( t)

c1 ( k , k _ 1 , ? xk_ 1/k_1)

x₀

Filtre de Kalman étendu

? x k_ 1/ k_1

Processus

P0/0

K_k

Gains de Correction

? x k/ k_1

+

+

Pk/k-1 Pk / k

Q₀

? x k/ k

R₀

C

Retard

6 y( k)

x ? k_ 1/ k_1

y ( t)

y k k- 1
/

?

t k

+

y_k

-

?

y k k- 1
/

k

t

y ( t)

y? ( t)

Fig.IV-4.2 :Filtre de Kalman étendu.

5. APPLICATION DU FILTRE DE KALMAN.

Pour cette etude, il est necessaire de definir les elements de l'estimateur et le referentiel avec lequel, on fera evoluer le système à variables estimees.

· L'estimateur est commande à partir des tensions d'entrees. Le couple resistant, impose par la machine entraînee, constitue l'une des variables d'entree du système = Les tensions et le couple resistant forment le vecteur d'entrée u du système. Les tensions sont mesurees et transmises, en temps reel, à l'estimateur.

Pour eviter un couplemêtre à la machine (capteur mecanique), on suppose que les caracteristiques de la machine entraînee sont connues. La machine est definie par sa constante de vitesse k repondant à la relation : Trma = kw².

· La frequence de rotation du moteur et la position du rotor seront les 2 grandeurs à estimer. Elles constituent, avec les courants, le vecteur d'état x.

· Les courants sont les grandeurs observables et constituent le vecteur de sortie y.

5.1. Choix du référentiel pour le filtre de Kalman :

La situation ideale consisterait à utiliser le referentiel de Park avec l'axe d, cale sur le rotor. Neanmoins, cette solution n'est pas compatible parfaitement avec une commande sans capteur. Pour cela, on justifie cette remarque à partir de la figure suivante qui represente la commande du moteur dans le referentiel de Park :

+ -



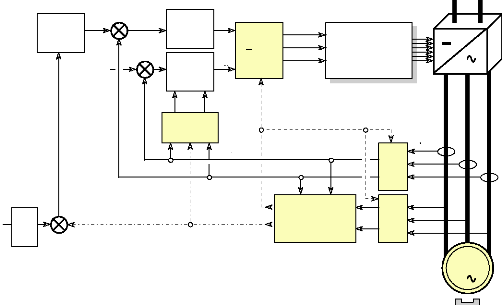
_n*

2n N_p

Régulateur
de
Vitesse

+

-

eco

ids *= 0

_i*

qs

iqs

+-

ids

+-

⁶ iqs

cids

^?eds

Découpleur

Régulateur
de
Courant

ⁱqs

Régulateur
de
Courant

ids

oi

^?eqs

'vqs

^?vds

i' = i qs qs

i^?ds = ids

3

2

Oi

0

0

[ P1 ^-1

Estimateur
de Position angulaire
électrique
du rotor et de
vitesse

*

vas

vbs

*

vcs

*

iqs

Séquenceur/Modulateur

ids

MOTEUR DISCOïDE
A AIMANTS ALTERNES

Circuit
de
Commande

vds

vqs

0

[P1

[ P?

0

vcs
vbs
vas

ias
ibs
ics

MS

3

Aimants P.

Fig.IV-5.1 : Filtre de Kalman dans le référentiel de Park.

· Les 4 entrées de l'estimateur et les 2 tensions de référence en entrées de l'onduleur sont tributaires de 0^? (estimé). Or, en reprenant les équations de Park sur les courants,

on remarque que chaque terme de ces équations est fonction de ^?0. On s'imagine très facilement qu'une erreur d'estimation sur la position initiale du rotor puisse avoir des répercutions très importantes sur l'évolution du reconstructeur d'état, par rapport au système réel (cumul des erreurs). De plus, les corrections sur les erreurs d'estimation

sont tributaires des courants mesurés qui sont, eux-mêmes, dépendant de ^?0.

· On rajoute que le référentiel de Park tourne à la vitesse angulaire du rotor à partir d'une position initiale estimée. Or, une erreur sur cette première estimation peut décaler l'axe d par rapport à l'axe du rotor, avec toutes les conséquences que cela suppose. La commande vectorielle dans Park est très efficace dans des conditions normales de fonctionnement et l'est, d'autant plus dans son erreur.

La seule condition qui permettrait d'utiliser le filtre de Kalman, avec le référentiel de Park, serait d'imposer une position initiale au rotor au premier démarrage. Pour empêcher d'éliminer un trop grand nombre d'applications industrielles pour lesquelles on ne tolère pas les déplacements préliminaires, on décide d'éliminer cette solution. On se résigne à changer de référentiel. Or, le choix du référentiel de base (a_s,b_s,c_s) nécessite d'augmenter l'ordre du système et par conséquent, les temps de calculs (3 équations sur les courants au lieu de 2). On élimine aussi cette possibilité.

On propose de conserver le référentiel de Park. Néanmoins, l'axe d de ce référentiel n'est plus calé sur le rotor mais fixes par rapport à l'axe a_s. On a ainsi des grandeurs instantanées, projetées sur les 2 axes, indépendantes de la position du rotor. Ce référentiel que nous retenons pour la suite de l'étude, fait appel à la transformation de "Clarke" et utilise les repères d'axes (a_s,f3_s,o_s) et non plus (d,q,o). La commande du moteur, pour sa part, se traite dans le repère de base (a_s,b_s,c_s).

5.2. Détermination numérique des équations du système différentiel à variables estimées dans le repère (as,f3s) :

Après avoir traité en annexe 3 la transformation de Clarke, on présente le nouveau système différentiel à variables estimées et optimisées suivant :

Réseau

?

di

a





(a s,b s,cs)

(^as^,1³s )

v _as , v _bs , vcs i _as , i _bs , ics

Fi l tre de Kalman

Système à variables estimées

Cde

'11aim , R~_s,L~_s,K~_T, J~, _T~ro, T~, k~

A A

i i

as , ps

0, 6i

0, 6

MS

3

Fig. IV-5.2

s (t ) R~ ^,s

dt



s

-- si _a,s( 0+ ^ditraim 2 sind( t) + v as( t)L~L~L ss



di0

?

dt r

s

(t ) R~_s » " (t)

-- i _Ps (t)-6ittfai ^m v 2 COSO(t) + ^Ps

s

L ~ L ~

s s

d o3^s(

t ? ? ? ? ? ? ? ? ? ? ? ? ? ?

N p

? J K i t t i t

? ? t f t T T k t

? ? ? ? ? 2

~ ~ ? cos ? ? ? sin ? ? ~? ~ ~ ~ ? ? ? ?

T s

? ? s r 0

dt

A

dt

t)

_ (B(t)

(IV-41)

Avec J~ = J~_m + J~_r

Nota:

Attention aux notations, on a volontairement dissocier les variables à valeurs estimées optimisées ( (0) et les constantes estimées(~Ls).

On remarque que la présence de 6 et de 6 fait de ce système, un système différentiel non linéaire. On applique ainsi la méthode de Kalman [16]. On pose :

f x t u t t ? ?( ), ( ), ?

,

=

r 1 1 1 L

f x t u t t ? ?( ), ( ), ? 1 f x t u t t ? ?( ), ( ), ? 2 f x t u t t ? ?( ), ( ), ? 3 f x t u t t ? ?( ), ( ), ? 4

1 1 1 L

(IV-42)

Avec :



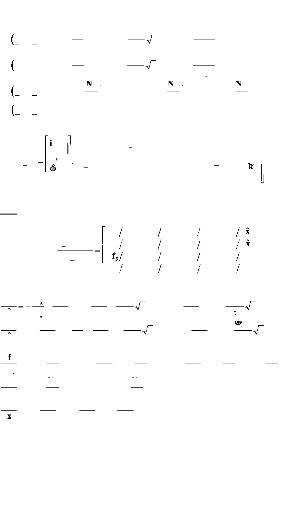
inu n t)

= 6( 0

f₁

f₂

f₃

f₄

Et :

Chapitre 4 : Commande sans capteur mécanique du moteur et Filtre de Kalman.

I3s (
· t) -- 05( 0 11* L aim 2 cose( t ) + ^{vf" (t)}

R~

_d v5(t)

ii( 0, u ( t ), t)
ii( 0, u ( t ), t)

= -

ii( t ), u ( t ), t) = -- KT 3.( t ) sin k° + KT ; ( t )costi( t) -- ₃^p [1^-+ kdi( t)]

(IV-43)

6 ( )

t

t)1 ( t

v as v p_s

(

f 1 of 1 ⁰¹2 af1 013 af 1 a

ax1 af ₃ ai₂ af ₃ ai₃ af ₃ ai

a
a
a

4

4

4

0

Nota: v _as et v a_s sont des variables d'entrées à valeurs réelles (non estimées). On a :

f 2 af 2 a12 af 2 a13 af ^t

_as ( 0

1 0 0 =

",

Jo_s ( t )'tr [0 1 0 u ( t)

(IV-44)

, 4

ST

( t )

a

i s

( t)

0

(t)

L

i( t)

s

( V'

¹_1

af (t , i(t))

F 1(t) _

_aI(t)

af 4 ai1 af ₄ ai2 af ₄ ai3 af ₄ ai4 (IV-45)

L

Avec :

a

f₁

a

a

x₁

f₂

a

₃ Np

a x - _ KT

sin0

a ? f N N

3 p 3

f N p

? ?

t ; ? ? ~ ~ cos ? ; ? ? ? ~ ~ ?

K ? ? ?

t 2 k t

? ? ?

T

? x J ? x J

2 3

? p ~

a

J~

? f

f 3

^pitcos 6(t -- KT 3p in_Ps(t) sin e^s( t)

4

₄

a x T _Xas

f₄ f f₄

0
· -- 0 ; -- 1 ; " =0

^ -

1 a x 4 2 ax 3 ax

(IV-46)

Pour effectuer les différents calculs au moyen d'un traitement numérique, on utilise les méthodes suivantes :

- 99 -

a

-- K

--

a

a

f

a

4

R~

a f1

0
· " -- --
·
·

⁹ a x 2 t ⁹

af 2 --im 2 cos ós of

ai3 -- L~

a

f₂

R~

( t) ; -- 6( t) ^aim 2 sine( t)

a x

4 ts

; -

t a x

0 ;

af Taim 2 sin 0

af xi°

ai3 L- ~_s

x

2

t

)

;

--6(0 ^aim 2cos0(t)

s v.% #177; _as ( t)

R~

i as + 60) L 2 sin 0 ( t )

Lis L~_s

s

= -

a

a

1. Calcul de l'évolution des variables d'états f ( x^?(t ), u (t ), t) :

Méthode d'Euler ?

Evolution de

f ( X( t ), u ( t ), t ) ik / k -1 = ik -1 / k -1 + T ( k , k -1 ) * f ( ik -1 /k -1 , u_k-1 ,k -- 1)

(IV-47)

Avec

T(k,k-1) = tk-1 -- tk : Pas d'échantillonnage.

2. Calcul du vecteur de transition ?? k , k -- 1 , X) = e^Fx(...) :

Méthode des développements limités ? x 2 (Dl ( e ^x) = 1+ x+ 2 ! +... ) F1 ( t , 1( 0)^4:1^1(k , k -- 1 , ik _1 / k_1 ) = I + T ( 10k-1 ) * F ( k -- 1, ik _1 /k_1) (IV-48)

Nota : On limite la précision au 2 premiers termes du développement.

3. Calcul du vecteur de variance-covariance Qd(k-1) représentatif des bruits sur le système vd (k- 1 ) :

Méthode des trapèzes ?

v( t ) v d ( k -1 ) Q d ( k , k-1 )	k ? ? ? k ? Q ? ? ? k ? d T ? ? , ? ? ? ? ? , k-1
Q d ( k , k-1) =[4:11(k , k -- 1 ) * Q * 0^T(k , k -- 1) + Q] (IV-49)		* T( k , k-1) 2

Ces méthodes de calculs seront utilisées, par la suite, dans le filtre de Kalman.

5.3. Commande du moteur dans le repère (as,bs,cs) :

On associe au filtre de Kalman étendu une commande classique dans le référentiel (a_s,b_s,c_s). Ce paragraphe est ainsi consacré à la présentation de cette commande. On utilise une M.L.I pour le contrôle des courants et on impose une commande à couple maxi de façon à limiter au mieux les pertes magnétiques. Les équations électriques et mécaniques, du système à commander dans le repère (a_s,b_s,c_s), sont définies par les relations :

R1 ?

s aim

? ? t _L 2 sin ? ? ? ? ?

t v t
? 1

L i t _L v t ? ? ? ? ? ? ?

as as

s s s



)

di _as (t

_ --

dt

R 1 ? ? 4 ? ?

s aim

L i t _L v t

? ? ? ? ? ? ?

? ? t _L 2 sin ? ?

t ? v ? ?

t

cs cs 3

?? ? ?? ?

3

s s s



)

di t

bs (

_ --

dt

1 ? ? 2 ? ?

aim

? ? ? ? ?

? ? t _L 2 sin ? ?

t ? v ? ?

t

?? ? 2

3 ?? ?

s

R

s

? ?

t _L v t

L i bs bs



)

di _cs (t

_ --

dt

d t

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

N p 2

? J K i t cos ? t i t

? ? sin ? t f t T T k t v t

? ? ? ? ? ? ? ? ? ? ?

?

T s

? s r 0 4

dt

d0(

dt

t) -- co( t ) + v 5( t)

Modèle du processus
Nota: Les courants des 2 repères sont liés par la transformation de Clarke (voir annexe 3).

(IV-50)

v1( t), v2( t) , v3( t) , v4( t) , v5( t) représentent les bruits du système, fonctions du temps (bruits blancs).

5.3.a) Régulation des courants ias, ibs et i_cs avec compensation des f.e.m [11] :

Contrairement à la commande vectorielle, il n'est pas possible de découpler le courant qui créé le flux magnétisant du moteur et le courant qui créé le couple. Néanmoins, pour améliorer la commande classique, nous pouvons intégrer à la régulation des courants, un dispositif de compensation des perturbations imposées par les f.e.m du moteur. On sait que la tension de la phase a_s du moteur correspond à :

di

dt



v as = R _s i _as + L_s

6)Waim 2 sin ö as

(IV-51)

6 et 0 sont les variables estimées, fournies par le filtre de Kalman.

Nous cherchons à dissocier de l'évolution du courant le dernier terme de cette expression. Il en est de même pour les autres phases du moteur.

Nota : Cela revient à linéariser les courants par rapport aux tensions d'entrées.

Concrètement, on cherche à agir sur le moteur non plus par les tensions v _as, v_bs
et v mais par les nouvelles tensions, notées u , u , et pour lesquelles, on

bs ucs

cs as

impose les relations suivantes :



as as -- 6 T_aim 2 sinO

v bs = u_bs -- 6 T_aim 2 sin (6 -- ^27c

3

4n

v



cs = u cs -- W6 _aim 2 sin (ii --

3

(IV-52)

Ainsi, le système différentiel sur les courants se simplifie et devient :

i

i





di (t)

as - R~s

_ --

dt L~

di bs (0 R~_s

_ --

dt L~

1

as (t ) + L~ u as(t)

s

s

1

bs ( t ) #177; _, u bs(t)

s

s



R~

)

i

_ --

s

cs

L~

s

di _cs (t

dt

1

(t )+ L~ u cs(t)

s

(IV-53)

On schématise le principe par la figure suivante :

Fig.IV-5.3 : Commande du moteur avec compensation des perturbations.



uas
ubs

ucs

Compensateur

63 6

Moteur + Compensateur
de perturbations

vas
vbs

vcs

Moteur
Fintronic

ias
ibs

ics

5.3.b) Générateur de références sur les courants [11] :

Contrairement à une commande vectorielle, les références sur les courants ne sont plus à valeurs constantes mais à valeurs sinusoïdales. Il faut créer un générateur de références pour la commande du moteur. On réalise ce générateur selon le critère optimal de fonctionnement présenté au début de ce paragraphe ; C'est à dire à couple maxi pour un fonctionnement donné.

Pour cela, il faut revenir sur l'idée de la commande vectorielle pour rappeler que
le couple maximal s'obtient pour un courant maximum porté par l'axe q du

référentiel de Park. Le principe reste le même pour notre commande, sinon qu'il n'est plus possible d'agir directement sur ce seul courant d'axe q, dissocié du reste mais sur les 3 courants du repère (a_s,b_s,cj. Une telle commande est bien trop compliquée à définir pour les régime transitoires, c'est pourquoi, on se limite à une commande élaborée sur l'unique fonctionnement du régime permanent. On présente l'idée à partir d'une construction vectorielle de Fresnel:





Information connue
à partir de l'estimateur

-,

V_s

0?

?

'I'

2

q

-,

I_s

a_s (fixe)

Fig.IV-5.4 : Construction vectorielle

-

D'après cette construction, on remarque que pour maintenir le vecteur courant I s

d

(? t



Vrai uniquement
en
régime permanent

(? t

suivant l'axe q (couple maxi), il est nécessaire d'imposer un décalage avance de ce
vecteur de 90°par rapport à l'axe du rotor qui lui même tourne à . Cela revient

?? t

à maintenir l'angle N' à zéro. Remarque :

Dans les cas oü les variations sur la charge sont brutales, les risques de décrochage du rotor sont à craindre. Il faut se prémunir de ce risque en maintenant ? voisin de 0 mais différent de 0..

En considérant que la position estimée du rotor est définie à chaque instant (filtre de Kalman), on peut s'imposer un courant de référence de la forme :

? ? ?

i_asréf. = I _s 2 cos ?? NJ - -

2 ? ? ?? ? i _as ré f= - I _s 2 sin ?

( ?

? ?
-

(IV-54)

Avec

? ? 0





De la même façon, on obtient les courants de référence sur les autres phases du
moteur, en les déphasant de 2t 3 et de 4 ir 3 par rapport au courant de la phase

a_s.

T i



Sachant que I 2 = max ; K étant la constante de couple, on peut alors

s T

T

représenter le générateur de références de la façon suivante :

K



w réf

Tmax i réf

0

+

-

1

KT

Générateur de références

?

sin (d --v -- 3

sin (6' -- v -- ) 3

-- sin (6 - ? ?

.

.

.

ias

ibs

ics

réf

réf

réf

Fig.IV-5.5 : Générateur de références.

5.3.c) Synoptique de commande du moteur dans le repère (a_s,b_s,c_s) :



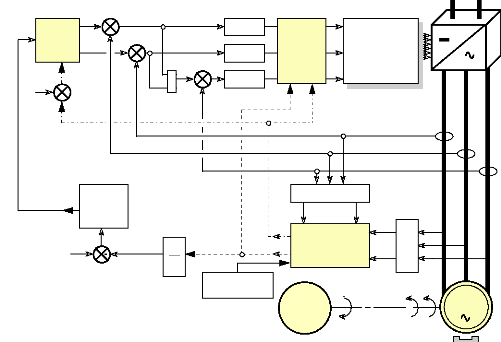
Tmax iréf

? réf

= 0

Générateur
de
références

n réf

-

+

0

i_bs réf

+-

ias réf

Régulateur
de
Vitesse
+
Limiteur

+

En

+ -

n?

T _rma= T_u = T + kifi²

-

-

1

2n

i_cs réf

+ -

??

k
Constante de vitesse
de la machine

Correcteur
PI

Correcteur
PI

Correcteur
PI

ubs vbs

uas

ucs

??

0

Compensateur
de f.e.m

Machine

i_cs

ibs

ias

Estimateur
reconstructeur d'état
FILTRE DE
KALMAN

ias

[ Cla?

0

vas

vcs

Trma

i?s

Moteur discoïde
à réluctance variable
et à aimants permanents alternés

Circuit
de
Commande

+
M.L.I

v_as

vos

T_u

[ Cla?

n

vcs
vbs
vas

+

MS

3

Fig.IV-5.6 : Schéma synoptique de la commande en vitesse et à couple maxi du moteur, muni
du filtre de Kalman.

Mémoire CNAM Patrick BOIDIN.

5.4. Validation théorique (simulation) de la commande du moteur avec filtre de Kalman :

5.4.a) Commande en vitesse du moteur avec retour de la vitesse par le filtre de Kalman (bfesmli.m + filtre1m.m en annexe 4) :

? Démarrage du moteur, soumis à un échelon de vitesse de 60 tr/min et sur une charge de la forme : T_rma = T + kw² .

Données de la simulation : (Filtre :EULER/ Moteur+Cde : EULER)/Tk=30 jis : Pas d'échantillonnage
Machine :	Régulation de vitesse :	Régulation de courant :	Variance-Covariance (coefficients sur la
J r = 0,1 kg.m2 Trma=130 N.m maxi T=0 N.m M.L.I :	?n =0,010 s kvp=20/ kvi=90 nréf=60 tr/min Conditions initiales :	kp=130 ki=65 Seuils de limit.-300/300N.m ?réf=0 Filtrage des tensions :	diagonale): P0/0 :700 (Confiance sur la 1ère estimation) Q0 : 6 (bruits sur le système) R0 : 500 (bruits sur les mesures) Bruits blancs de mesure :
	00 estimé (filtre)=0 ° 00 réel=-30 °
fp=2,4kHz(fixe)/Up=410 volts			Ib max : 0,38A pour In=9,3A Vbmax: 1,5 volts pour Vn=220 volts Bruits blancs sur le système :
		fc : 1,5kHz / Ordre : 2
			voir fichier Metafile en annexe 4.

Trma en fonction de la vitesse thétha0 réel=-30° Tem et Tr en N.m thétha0 réel=-30°

P0=700/Q0=6/R0=500/Tk=30micro sec. n (tr/min) P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

a) b)

n et n estimé (- -) en tr/min. thétha0 réel=-30° theta et theta estimé (- -) en degré thétha0 réel=-30°



n estimée

n

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

60

50

40

30

20

10

0

-10

400

350

300

250

200

150

100

50

0

-50

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)



140

120

100

80

60

40

20

0

-20

-10 0 10 20 30 40 50 60

Tem

Tr

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

250

200

150

100

50

0

-50



0 estimée

0

1er tour ? 27 ms

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

c) d)

Fig.IV-5.7 : Cde en vitesse du moteur avec retour de 0et n par le filtre de Kalman.


· Les 2 caractéristiques n (t) et n _estimé (t) se suivent assez bien. La vitesse estimée est légèrement en avance sur la vitesse réelle.

Mémoire CNAM Patrick BOIDIN.


· L'erreur de position du rotor de -30°, imposée au démarrage, a été corrigée par le filtre en moins 10 ms.

Erreur sur la vitesse en tr/min. thétha0 réel=-30° Erreur sur la position en degré thétha0 réel=-30°

0.5 0 -0.5 -1 -1.5 -2 -2.5 -3		5 0 -5 -10 -15 -20 -25 -30 -35 -40
	0 0.01 0.02 0.03 0.04 0.05 0.06 0.07		0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

a)
A partir de 20 ms, l'erreur sur la vitesse est
devenue inférieure à 1%.

ias et is en A thétha0 réel=-30° P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

b)
L'erreur sur la position du rotor est inférieure
5° sur le tour électrique.

ialpha et ibeta en A thétha0 réel=-30°

15 10 5 0 -5 -10 -15		20 15 10 5 0 -5 -10 -15
	0 0.01 0.02 0.03 0.04 0.05 0.06 0.07		0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s) P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

c) d)

e)
On relève une différence notable entre les
courants i_?s et i_?s estimé d'environ #177;14%.

f)
On relève la même différence entre les
courants i ? s et i ? s estimé d'environ #177;14%.

Mémoire CNAM Patrick BOIDIN.

ias (A) / -eas (V)

60

40

20

0

-20

-40

-60



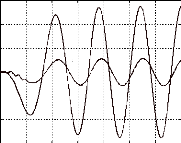
- eas

ias

vas filtrée (V) / ias (A) / -eas (V)

300

vas filtrée

- eas

0

ias

-100

-200

-300

200

100



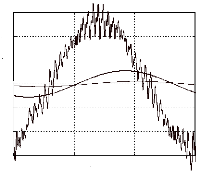
045 0.05 0.055

Temps (s)

h)

0.06

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

Temps (s)

g)
On releve un léger retard du courant sur la
f.e.m ? La commande n'est pas tout à fait à
couple maxi.

vas en volts thétha0 réel=-30°

vas en volts thétha0 réel=-30°



600

400

200

0

-200

-400

-600

600

400

200

0

-200

-400

-600

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

0.055 0.06 0.065 0.07 P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

i) j)

Fig.IV-5.8 : Cde en vitesse du moteur avec retour de 0et n par le filtre de Kalman.

Les tensions telles qu'elles sont vues par le moteur, ne sont pas exploitables par le filtre de Kalman (ondes générées par la M.L.I). Il faut les filtrer.

Nota :

On a volontairement indroduit une erreur de -30° sur la position du rotor par rapport à la position estimée de 0°. On a obtenu d'assez bons résultats.

Mémoire CNAM Patrick BOIDIN.


· Démarrage du moteur soumis à un échelon de vitesse de 60 tr/min et inversion du sens de rotation sur une charge de la forme : T rma = T + kw² .

Données de la simulation : (Filtre :EULER/ Moteur+Cde : EULER)/Tk=30 jis : Pas d'échantillonnage
Machine :	Régulation de vitesse :	Régulation de courant :	Variance-Covariance (coefficients sur la
Jr =0,1 kg.m2 Trma=130 N.m maxi T=0 N.m M.L.I :	?n =0,010 s kvp=20/ kvi=90 nréf=60 et -60 tr/min Conditions initiales :	kp=130 ki=65 Seuils de limit.-300/300N.m ?réf=0 Filtrage des tensions :	diagonale): P0/0 :700 (Confiance sur la 1ère estimation) Q0 : 6 (bruits sur le système) R0 : 500 (bruits sur les mesures) Bruits blancs de mesure :
	00 estimé (filtre)=0 ° 00 réel=-30 °
fp=2,4kHz(fixe)/Up=410 volts			Ib max : 0,38A pour In=9,3A Vbmax: 1,5 volts pour Vn=220 volts Bruits blancs sur le système :
		fc : 1,5kHz / Ordre : 2
			voir fichier Metafile en annexe 4.

Trma en fonction de la vitesse thetha0=-30°



150

100

50

0

-50

-100

-150

-60 -40 -20 0 20 40 60

P0=700/Q0=6/R0=500/Tk=30micro sec. n (tr/min)

a)

n et n estimé (- -) en tr/min. thetha0=-30°

60 40 20 0 -20 -40 -60

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

c)

Tem et Tr (- -) en N.m thetha0=-30°

300 200 100 0 -100 -200 -300

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

b)

theta et theta estimé (- -) en degré thetha0=-30°

400 300 200 100 0 -100 -200 -300

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

d)

Fig. IV-5.9 : Cde en vitesse du moteur avec retour de 0et n par le filtre de Kalman. Inversion
du sens de rotation

La vitesse estimée a parfaitement suivie la vitesse réelle lors de l'inversion.

Mémoire CNAM Patrick BOIDIN.

Erreur sur la vitesse en tr/min. thetha0=-30^°

0.5 0 -0.5 -1 -1.5 -2 -2.5 -3

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

a)
L'erreur sur la vitesse est inférieure à
0,5tr/min soit moins de 1%.

ias et is en A thetha0=-30°

20 15 10 5 0 -5 -10 -15

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

c)

Erreur sur ialpha estimé en A thetha0=-30°

10 8 6 4 2 0 -2 -4 -6 -8 -10

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

e)

Erreur sur la position en degré thetha0=-30°

5 0 -5 -10 -15 -20 -25 -30 -35 -40

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

b)
L'erreur sur la position est inférieure à 5°sur
le tour électrique.

ialpha et ibeta en A thetha0=-30°

20 15 10 5 0 -5 -10 -15 -20 -25
	0 0.02 0.04 0.06 0.08 0.1 P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s) d)

Erreur sur ibeta estimé en A thetha0=-30°

10 8 6 4 2 0 -2 -4 -6 -8 -10

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

f)

Fig.IV-5.10 : Cde en vitesse du moteur avec retour de 0et n par le filtre de Kalman.
Inversion du sens de rotation

Mémoire CNAM Patrick BOIDIN.

600
400
200

0 -200 -400 -600

ias en A et eas en volts thetha0=-30°

60 40 20 0 -20 -40 -60

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

a)

vas en volts thetha0=-30°

600 400 200 0 -200 -400 -600

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

c)

vas filtrée et eas en volts thetha0=-30°



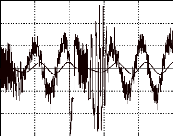
600

400

200

0

-200

-400

-600

0 0.02 0.04 0.06 0.08 0.1

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

b)

vas en volts thetha0=-30°



0.04 0.045 0.05 0.055 0.06 0.065

P0=700/Q0=6/R0=500/Tk=30micro sec. Temps (s)

d)

Fig.IV-5.11 : Cde en vitesse du moteur avec retour de 0et n par le filtre de Kalman.
Inversion du sens de rotation


· Démarrage du moteur, soumis à un échelon de vitesse de 60 tr/min. La position initiale estimée du rotor correspond à la position réelle.

Données de la simulation : (Filtre :EULER/ Moteur+Cde : EULER)/Tk=30 jis : Pas d'échantillonnage
Machine :	Régulation de vitesse :	Régulation de courant :	Variance-Covariance (coefficients sur la
Jr =0,1 kg.m2 Trma=130 N.m maxi T=0 N.m M.L.I :	?n ?0,010 s kvp=15/ kvi=40 nréf=60 tr/min Conditions initiales :	kp=55 ki=10 Seuils de limit.-300/300N.m ?réf=0 Filtrage des tensions :	diagonale): P0/0 :8 (Confiance sur la 1ère estimation) Q0 : 0,6 (bruits sur le système) R0 : 530 (bruits sur les mesures) Bruits blancs de mesure :
	?0 estimé (filtre)=0 ° O0 réel=0 °
fp=2,4kHz(fixe)/Up=410 volts			Ib max : 0,38A pour In=9,3A Vbmax: 1,5 volts pour Vn=220 volts Bruits blancs sur le système :
		fc : 1,5kHz / Ordre : 2
			voir fichier Metafile en annexe 4.

Nota:

Les coefficients des matrices de variance-covariances ont été repris pour cette simulation.

Mémoire CNAM Patrick BOIDIN.

n et n estimé (- -) en tr/min. théta0 réel= 0°

60

50

40

30

20

10

0

-10



n estimé n

0 0.01 0.02 0.03 0.04 0.05 0.06

P0=8/Q0=0,6/R0=530 Temps (s)

a)

theta et theta estimé (- -) en degré. théta0 réel= 0°

0

0 estimé

0 0.01 0.02 0.03 0.04 0.05 0.06

P0=8/Q0=0,6/R0=530 Temps (s)

b)

400

350 300

250 200

150 100

50

0



Fig.IV-5.12 Cde en vitesse du moteur avec retour de 0et n par le filtre de Kalman.

5.4.b) Remarques sur les simulations effectuées.

Les dizaines de simulations que nous avons effectuées donnent de bons résultats mais dans des limites bien précises. En effet, tant que la position du rotor à l'instant initial du démarrage est restée inférieure à +ou- 90°, le moteur a démarré dans de bonnes conditions. La commande du moteur avec son filtre a rattrapé en moins de 60ms les erreurs d'estimation.

Au-delà de + ou - 90°, l'erreur initiale sur la position du rotor a été plus difficile à rattraper. Dans certaines situations, le fonctionnement du moteur est resté instable durant plusieurs secondes.

? Le filtre de Kalman, tel que nous l'avons défini, fonctionne bien, tant que l'erreur initiale sur la position est restée acceptable. Ce dispositif a besoin d'être amélioré.

A partir du moment où le filtre de Kalman a permis d'approcher, au plus vite, la trajectoire de référence (trajectoire estimée), le système réel a été capable de se coller sur cette trajectoire et d'y rester. Il suffit d'observer les résultats sur la simulation où on a inversé le sens de rotation du moteur, pour s'en persuader.

La dernière simulation montre bien que connaissant la position initiale du rotor (o0estimé =⁰0 réej, le filtre de Kalman a joué parfaitement son rôle à une faible erreur près.

Pour améliorer le dispositif, il faut :

· 1^ère idée : Imposer une position initiale au rotor, avant de démarrer le moteur.

· 2^ème idée : Détecter la position initiale du rotor par un moyen quelconque mais sans capteur mécanique.

La deuxième idée est a priori difficile à réaliser car le rotor du moteur est conçu avec une structure à pôles lisses.

Par contre, la première idée est plus réaliste et permet d'utiliser efficacement le filtre de Kalman. Par ce moyen, on peut utiliser, non plus une commande dans le repère (a_s,b_s,cj, mais une commande vectorielle dans le repère de Park (d,q).

Mémoire CNAM Patrick BOIDIN.

Le tour électrique qui équivaut à 5,625 degré mécanique est suffisamment faible pour autoriser cette idée. Les moyens à mettre en oeuvre sont simples à réaliser : Il suffit d'imposer un état à chaque interrupteur de l'onduleur de telle sorte qu'un courant continu puisse entrer dans le premier enroulement des phases du moteur et puisse sortir par les 2 autres enroulements shuntés en sortie. En imposant ces conditions et un courant continu suffisant, le rotor va se positionner naturellement suivant l'axe du premier enroulement statorique des phases du moteur.

I

as





?

Baim

?

BI

I

Axe de la phase as

Fig.IV-5.13: Mise en position initiale du rotor par injection d'un courant continu. 5.5. Définition des moyens matériels pour les essais expérimentaux :

A défaut de pouvoir continuer cette étude, nous présentons le matériel principal et les logiciels qui auraient permis d'effectuer les essais expérimentaux :

1. Une carte multiprocesseur du type dSPACE DS1102 à multiplication par virgule flottante. Sous sa forme standard, cette carte est munie :

· Un processeur principal de signal Texas Instrument TMS320C31 (maître) ayant une fréquence d'horloge de 40 Mhz (temps de cycle : 50 ns).

· Un processeur secondaire de signal Texas Instrument TMS32P14 (esclave) pour la gestion de 12 entrées et/ou sorties numériques et pour la génération des 6 sorties M.L.I.

· 4 convertisseurs "Analogique/Numérique" (#177; 10 volts/16 bits, 10 ts).

· 4 convertisseurs "Numérique/Analogique" (12 bits, 4 ts/#177; 10 volts).

Mémoire CNAM Patrick BOIDIN.



DS1102 DSP- board

Connecteur
JTAG

Interface
série

· zero wait-states

· 4 096 k Octets
de
mémoire RAM

TMS320C31

Interface
JTAG

Bus d'extension PC/AT

Interface
Serveur

Entrées / Sorties
numériques

Entrée codeur incrémental n°1

Entrée codeur incrémental n^°2

TMS320P14

Convertisseur
A/N 16 bits n°1

Convertisseur
A/N 16 bits n°3

Convertisseur
N/A 12 bits n°1

Convertisseur
N/A 12 bits n°3

Convertisseur
A/N 16 bits n°2

Convertisseur
A/N 16 bits n^°4

Convertisseur
N/A 12 bits n^°2

Convertisseur
N/A 12 bits n^°4

Filtre
d'entrée

Filtre
d'entrée

26

Connecteur E/.S A/N

Fig.IV-5.14:Carte DS1102 de Texas Instrument.

· Un interface "Codeur incrémental" pouvant recevoir 2 entrées parallèles (24 bits, 8,3 Mhz).

· Une capacité de travail de 128 kOctets sur 32 bits soit 4 M.O. de mémoire RAM.

· Un interface d'Entrée/Sortie TMS320C31 du type "série".

· Un interface d'Entrée/Sortie TMS320C31 du type "JTAG".

La carte DS1102 se connecte directement sur la carte Mère du micro-ordinateur par sa liaison bus extensible.

2. Deux capteurs de courant de Marque LEM et de type LA 25-NP (ou autres) :

· Courants nominal/maxi : 25A/36A

· Entrée/Sortie : 0-25A/0-25mA

· Alimentation auxiliaire : + et - 15volts

· Temps de retard : <1ts

· Bande passante (-1dB) : DC à 150kHz (-1dB)

· Précision à +25°C : #177;0,5% de I_n

· Montage : sur circuit imprimé

Mémoire CNAM Patrick BOIDIN.



+15 volts

'as

0 - 25A

LEM LA 25-NP

0 volts

R mesure

0 - 25mA

-15 volts

Fig.IV-5.15: Capteur de courant.

3. Deux capteurs de tension de Marque LEM et de type LV 25-P (ou autres) :

· Tension à mesurer : 400volts (Tension composée)

· Courants nominal : 10mA => Résistance R1=40k)

· Entrée/Sortie : 0-14mA/0-25mA

· Alimentation auxiliaire : + et - 15volts

· Temps de retard : 40ts pour R1 série 25k)

· Bande passante (-1dB) : DC à 150kHz (-1dB)

· Précision à +25°C : #177;1,6% de U_n

4.



Uab

R mesure

-15 volts

'bs

'as +15 volts

R1

LEM LV 25-P

0 volts

0 - 14mA

0 - 25mA

Fig.IV-5.16: Capteur de tension.

Deux convertisseurs de signaux analogiques 0-25mA (sortie LEM tensions et courants) / -10V-+10V (entrée DS1102).

5. De 3 modules de puissance 30A dont l'ensemble constituera les 6 interrupteurs de l'onduleur (IGBT) et son interface de.



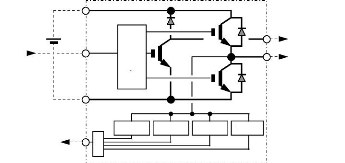
Cde
du bras

Sortie défaut

>1

Court-circuit

Cde
à
Fonctions
intégrées

Surintensité

Température
haute

UV-Lock

Frein

Phase du moteur

Fig.IV-5.17: Module de puissance d'un bras onduleur.

Mémoire CNAM Patrick BOIDIN.

Un capteur de position du type codeur absolu 12bits CHM61054C3R/4096 de marque IDEACOD Hohner AUTOMATION. Ce capteur est indispensable à la validation des paramètres de réglage du filtre. En effet, il faut s'assurer que le système à variables estimées évolue de la même façon que le moteur avant de réguler

sur les paramètres estimées ?? et 0^? .

6. Les options logiciels complémentaires à MATLAB-SIMULINK (Scientific Software - Sèvres) pour carte DS1102:

· RTW (Real-Time Workshop).

· RTI31 (Real-Time Interface).

· TRACE31W TRACE, MS-Windows (non indispensable à l'application mais bien utile).

· COCKPIT31W COCKPIT, MS-Windows (non indispensable à l'application mais bien utile).



variables Paramètres

Unité de pilotage
COCKPIT

Fig.IV-5.18





PROCESSUS
ET


SES INTERFACES

Paramètres

SIMULINK

· Cde et régulation

Interface temps réel

(Real-Time Interface)

compilateur C

(C compiler)

Téléchargeur

(Loader)

Real-Time
Workshop

MATLAB

· Filtre de Kalman

DS1102

JL C

Codage
du modèle
en "C"

Affichage des
courbes
graphiques

Enregistrement
des données

TRACE

Pour exécuter l'application avec la carte tC, il faut convertir les algorithmes de contrôle-commande écrits sous Matlab-Simulink, en langage C. De plus, il faut compiler les lignes de programme, établir les liens d'adressage avec le carte et télécharger les données.

Mémoire CNAM Patrick BOIDIN.

Ce sont les 2 premières options logiciels qui réalisent ces tâches. Il faut noter qu'il n'est pas nécessaire d'écrire les algorithmes de commande directement en langage C, le programme s'en charge avec tous les avantages que cela supposent en gain de temps et en fiabilité.

L'option COCKPIT permet de commander et contrôler le processus directement depuis le clavier du micro-ordinateur.

L'option TRACE permet de transférer les données (mesures) à mémoriser dans MATLAB de façon à analyser le comportement du processus en temps différé (Sorties graphiques sur écran).

Nous pensons que les moyens logiciels tels que nous les avons présentés ci dessus, correspondent à l'outil idéal à l'élaboration d'une commande de moteur de tous types. Il faut néanmoins préciser que ce matériel n'est pas adapté, par son coût (environ 50 000 francs), au produit final capable de commander le moteur "Fintronic". Il faudra donc après certitude sur la faisabilité de la commande étudiée, déterminer l'outil le mieux adapté aux tâches à exécuter.

La figure qui suit, présente le matériel nécessaire aux travaux expérimentaux d'une commande sans capteur mécanique du moteur.



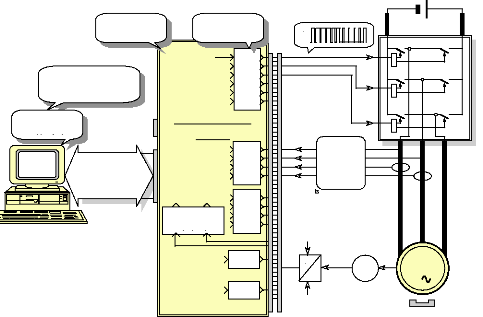
Matlab-Simulink
Version 4.2c.1
MathWorks

Algorithme de Crt/Cde
du moteur
Estimateur de position du rotor

486DX66

RTI31
Interface
Simulink/DS1102
+
Real Time Workshop

Microcontrôleurs
TMS320C31
TMS320P14

Connecteurs
liaison série

+ JTAG

12 Entrées
TTL (0-5V)
Traitement de la position

Bus PC/AT

Encoder
Phase Lines Unit

DS1102ENC

Rapport cyclique
0-100%/-1-+1

Carte dSPACE
DS1102

4 I/O TTL en réserves

Fréquences ajustables

Bit-I/O
IN ou OUT

Bit-I/O
IN

DS1102

DS1102

DS1102

PWM
Unit

ADC
Unit

DAC
Unit

PWM

AD

DA

Sub62

Alimentation TTL
0-5volts

+10 -10vol

Alimentation Codeur 0-15volts

+5v

0v

Exemple de signal en MLI

5V

15V

Interface
Signaux
Analogiques
(Convertisseurs)

Codeur Absolu 12 bits
Sortie Push-Pull 11-27V

Capteur de
position

C

t

0-25mA

I1

I2

I3

Aimants P.

vas

ias

MS

3

ibs

vbs

I'1

I'2

I'3

Capteurs de
Tension

Capteurs de
Courant

O
n

d
u
l

e
u
r

MOTEUR DISCOïDE
A AIMANTS ALTERNES

Fig. IV-5.19

Mémoire CNAM Patrick BOIDIN.

6. CONCLUSION

Cette étude a permis de démontrer qu'il n'est pas aussi évident de remplacer le capteur mécanique par le filtre de Kalman. Néanmoins, nous restons persuadé que le FILTRE DE KALMAN est le seul outil, actuel, capable de réaliser cette tâche à moindre coût.

L'inconvénient majeur de ce dispositif, tel que nous l'avons étudié, vient des conditions initiales sur la position du rotor qui conditionnent l'ensemble du système.

= Il faut impérativement trouver un moyen technique qui permettrait de connaître la position initiale du rotor. Par cette seule condition, il sera alors possible d'utiliser la commande vectorielle de PARK.

De plus, cette étude sans capteur aurait besoin d'être complétée par les études que nous n'avons pas pu réaliser dans ce mémoire. Elles sont:

· La prise en compte, dans le filtre de Kalman, des erreurs possibles d'évolution du système dues à la variation des paramètres supposés constants (résistance, flux, inductance synchrone, etc.).

· La détermination, par le calcul, de la valeur optimale des coefficients de variance des Matrices de variance-covariance.

· L'intégration dans le vecteur d'état, du couple résistant afin de l'estimer. Cas, où on ne connaît pas les caractéristiques mécaniques de la machine entraînée.

· L'étude du système à variables estimées, en limitant l'ordre du système aux seules variables à estimer (vitesse, position et couple résistant).

Cette solution risque d'être peu concluante. En effet, les tensions et les courants feraient alors partie du vecteur d'entrée avec une constante électrique élevée entre ces 2 entrées. Le système à variables d'état estimées risque d'évoluer avec un certain retard par rapport au système réel. Néanmoins, l'étude mérite d'être effectuée car le système se ramènerait à un système d'ordre 3 au lieu de 4 (avec l'estimation du couple résistant).

· L'étude complémentaire de la commande qui tient compte des cas où la vitesse du moteur est supérieure à la vitesse nominale (commande à puissance constante).

· L'amélioration technique des générateurs de M.L.I. qui est l'élément primordial de la commande avec et sans capteur mécanique de ce moteur (constante de couple élevée). De plus, il faut soigner l'entrée des courants sur le filtre car ce sont ces courant qui servent de référence à la correction des prédictions.

· L'étude des moyens permettant de détecter la position du rotor à l'arrêt bien que le moteur ait un rotor à pôles lisses.

CONCLUSION GENERALE

En apportant quelques modifications sur la conception du prototype, telles que :

· L'amélioration de la qualité des tôles du circuit magnétique pour limiter au mieux les pertes magnétiques.

· La reprise des formes géométriques des plots statoriques pour une meilleure pénétration des flux et une réduction du couple résiduel, parasite.

· L'augmentation de la rigidité mécanique de l'ensemble afin de maintenir l'entrefer constant et éviter les tendances au collage,

le moteur de structure discoïde conçu par GEC-ALSTHOM MOTEURS NANCY, a certainement un bel avenir devant lui dans les domaines de la robotique et de la traction électrique.

De plus, un onduleur de tension utilisant une M.L.I pour contrôler les courants, une commande vectorielle dans PARK et une commande de couple et de vitesse, devrait convenir assez bien à ce type de moteur. Le FILTRE DE KALMAN, tenant compte des études complémentaires proposées et cités en conclusion du dernier chapitre, devrait compenser assez bien la suppression du capteur mécanique.

D'une façon générale et compte tenu des exigences industrielles imposées sur le marché actuel, je dirais qu'il n'est plus possible aux concepteurs de moteurs électriques, de concevoir leur moteur sans tenir compte de l'électronique de puissance qui va commander le moteur. De même, il n'est plus possible aux concepteurs de systèmes électroniques de concevoir une électronique de puissance et une électronique de commande sans tenir compte de la constitution du moteur.

Les compétences de chacune de ces techniques devront inévitablement s'associer pour ne
former qu'une seule et unique puissance technologique d'avenir.

J'espère que ce travail aura donné satisfaction à la société GEC-ALSTHOM MOTEURS NANCY qui a bien voulu me confier ce prototype. Je regrette néanmoins de ne pas avoir eu le temps de conclure ce travail par une expérimentation de la commande avec son filtre de Kalman.

Pour ma part, cette étude qui a nécessité une année complète de travail, a été particulièrement intéressante car elle a rassemblé un large éventail de techniques complémentaires à celles de l'électrotechnicien. D'ailleurs, ces techniques vont devenir très rapidement indispensables aux connaissances de l'électrotechnicien de demain.

REFERENCES BIBLIOGRAPHIQUES

[1] ALLANO Sylvain - Etude de machines à réluctance variable polyentrefers alimentées à moyenne fréquence. Thèse de Doctorat d'état à PARIS 6, 1987.

[2] LUCIDARME J., DESEQUELLES P.F., GOYET R., RIOUX C., POUILLANGE J., CREMET G. - Les machines synchrones polyentrefers : Le moteur C.E.A. (200-300 N.m). Rapport final. Document confidentiel GEC-ALSTHOM MOTEUR Nancy, 1987.

[3] CREMET Gérard - Notes de calculs sur le dimensionnement du moteur. GEC-ALSTHOM MOTEUR Nancy, 1987.

[4] SIBOUILLE Michel - La transformation de Park. Application au moteur synchrone. Sujet de cycle C, C.N.A.M d'Aix, 1992/1993.

[5] BARRET Philippe - Régimes transitoires des machines tournantes électriques. Collection de la direction des études et recherches d'électricité de France. Editions Eyrolles de 1987.

[6] LUCAS Francois - La transformation de Park. Cours du cycle C, C.N.A.M d'Aix, 1992/1993.

[7] Longya XU, Jiping YAO - A compensated vector control scheme of a synchronous reluctance motor including saturation and iron losses. Publication de IEEE INDUSTRY APPLICATIONS SOCIETY, volume 28, numéro 6 de novembre/décembre 1992..

[8] JOOS Géza, GOODMAN Edward D. - Entrainements à courant continu. Presse de l'Université du QUEBEC, 1987.

[9] LAJOIE-MAZENC Michel et VIAROUGE Philippe - Alimentation des machines synchrones. Les techniques de l'ingénieur D 3630, Juin 1991.

[10] REKIOUA Toufik - Contribution à la modélisation et à la commande vectorielle des machines synchrones à aimants permanents. Thèse de docteur I.N.P.L., Lorraine Juillet 1991.

[11] CARON J.P. et HAUTIER J.P. - Modélisation et commande de la machine synchrone. SEE 3E.I95, Journées d'études du 30 et 31 Mars 1995.

[12] BOIDIN Patrick- La M.L.I par la technique numérique. Application aux variateurs à V/f constante et au contrôle vectoriel. Probatoire C.N.A.M d'Aix du 17 Mars 1994.

[13] DHAOUADI Rached - Application of stochastic filtering to a permanent magnet synchronous motor drive system without electromechanical sensors. Thèse de docteur de l'université du Minnesota, Octobre 1990.

[14] RADIX Jean-Claude - Introduction au filtrage numérique ; Lissage de données, estimation de paramètres, identification de processus - exercices et solutions. Ouvrage des Editions Eyrolles, 1970.

[15] BRUN-PICARD D. - Equations d'état des systèmes linéaires continus et discrêts. Cours d'automatismes B1 de l'enseignement CNAM d'Aix en Provence. Année 1992/1993.

[16] DE FORNEL Bernard, FADEL Maurice, PIETRZAK-DAVID Maria, Joao Carlos Henriques Dos REIS e COSTA - Méthodes d'estimation et d'observation des variables non mesurables pour le contrôle des machines à courant alternatif. Toulouse, journées du club EEA du 14 et 15 Mars 1991.

- ANNEXE 1 -

ESSAIS EXPERIMENTAUX ET VALIDATION DU
MODELE.

ESSAIS DU PROTOTYPE : RELEVES ET OSCILLOGRAMMES.

1. ESSAI A VIDE EN FONCTIONNEMENT GENERATEUR. 1.1. Tableau des relevés :

Valeurs calculées: Ea s n 0 (V/ tr.min^-1)
0,70
0,68
0,67
0,67
0,66
0,68
0,69
0,66
0,63
0,63
Moyenne : 0,67
N°	Moteur cc I (A)		Moteur cc U (V)	n (tr/min)		Génératrice Ea 0s (V)
1	3,65		8,3	18,5		13,0
2	4,35		12,0	35,2		24,0
3	5,00		14,2	43		29,2
4	5,60		17,6	60		40,0
5	5,70		18,6	66		43,5
6	6,10		20,5	74		50,0
7	6,95		25,7	100		66,8
8	7,93		31,6	129		85,0
9	8,57		35,7	155		98,0
10	9,9		44,9	200		126

Tab.An1-1 1.2. Tracé de la courbe : n 1-3 ea 0s



Ea 0s

(V)

150

140

130

120

110

100

90

80

70

60

50

40

30

20

10

n

e a 0 s ( n )

0 10 20 30 40 60 70 80 90 110 120 130 140 160 170 180 190 (tr/min)

50 100 150 200

n n = 60 tr/ min

Fig.An1-1 : F.e.m induite au stator en fonction de la fréquence de rotation.

2. ESSAI EN COURT-CIRCUIT DES ENROULEMENTS DU STATOR. 2.1. Tableau des relevés :

N°	Moteur cc I (A)	Moteur cc U (V)	n (tr/min)	Génératrice Icc (A)
1	3,70	13,0	34,2	1,86
2	3,60	14,4	41,7	1,86
3	3,55	16,0	53,3	1,86
4	3,65	18,2	64,2	1,86
5	3,9	21,9	83,3	1,9
6	4,5	31,3	133	1,9

Tab.An1-2 : Relevés du courant de court-circuit au stator.

3. ESSAI A VIDE EN FONCTIONNEMENT MOTEUR.

3.1. Relevé des oscillogrammes :

· i a 0 ( t ) et v a ( t ) pour U ab = 260 volts et i a0 = 7 , 2A soit 77%de In et 68% de U_n.

Echelles :50 volts/cm, 5A/cm et 5ms/cm



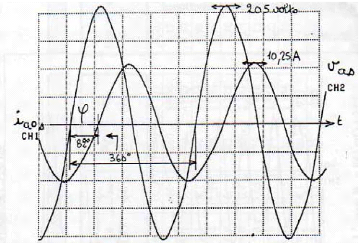
Fig.An1-2

· i a 0 ( t ) et v a ( t ) pour U ab = 135 volts et i a0 = 3 , 2A soit 34%de In et 36% de U_n.

Echelles :50 volts/cm, 2A/cm et 5ms/cm



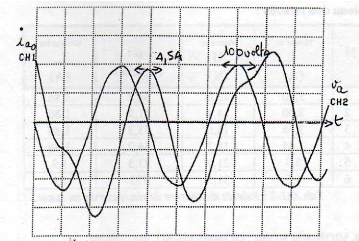
Fig.An1-3

La déformation de l'onde de courant qui apparait sous tension réduite, est due aux à-coups de couples (conséquence d'un entrefer qui n'est pas rigoureusement constant). En augmentant la base de temps, on peut constater que ces à-coups de couple apparaissent périodiquement toutes les 30ms soit toutes les périodes et demi par rapport à la pulsation des grandeurs statoriques.

Echelle :20ms/cm.



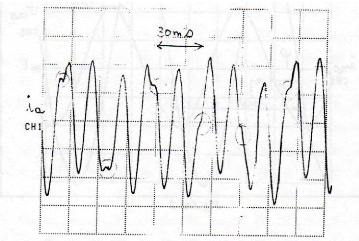
Fig.An1-4
- 125 -

Annexe 1: Essais expérimentaux et validation du modèle.

3.2. Tableau des relevés : Moteur à vide en fonctionnement moteur. n=46,8 tr/min (synchrone)= 50 Hz

Mesures

N°	Uab (V)	Ia0 (A)	Ib0 (A)	P0 (W)	Q0 (var)
1	340	10,85	10,9	1 440	6 131
2	320	9,9	10	1 260	5 196
3	307	9,3	9,4	960	4 677
4	280	8,3	8,1	750	3 741
5	260	7,4	7,25	624	3 076
6	240	6,9	6,7	525	2 728
7	220	6,6	6,4	460	2 321
8	200	5,8	5,65	374	1 916
9	180	5,2	5,1	294	1 535
10	160	4,65	4,55	226	1 154
11	145	4,2	4,1	185	927
12	120	3,2	3,1	125	580

Calculs

tan (p	cos (p	Uab2 x10^3	PJ (W)	Pméca + Pmag (W)	Pmag (W)	S0	Vas (V)
						2 2 ? ( P 0 Q ) 0
4,26	0,229	116	343	1 097	1 050	6 298	196,3
4,12	0,24	102,4	283	977	930	5 347	184,8
4,87	0,20	94,4	249	711	664	4 775	177
4,98	0,20	78,4	199	551	504	3 815	162
4,93	0,20	67,6	158	466	419	3 139	150
5,20	0,19	57,6	137	388	341	2 778	139
5,05	0,19	48,4	126	334	287	2 366	127
5,12	0,19	40,0	97,0	277	230	1 952	115
5,22	0,19	32,4	780	216	169	1 563	104
5,11	0,19	25,6	62,3	164	117	1 176	92,4
5,01	0,20	21,0	50,9	134	87	945	83,7
4,64	0,21	14,4	29,5	96	49	593	69,3

Tab.An1-3 Nota : P J = 3 R sI ⁰² avec R s = 961 m ? à 20°C Pmag+ mé ca ? P ₀ - P J

3.3. Tracé de la courbe : U P _mag P mé c

² F-> +



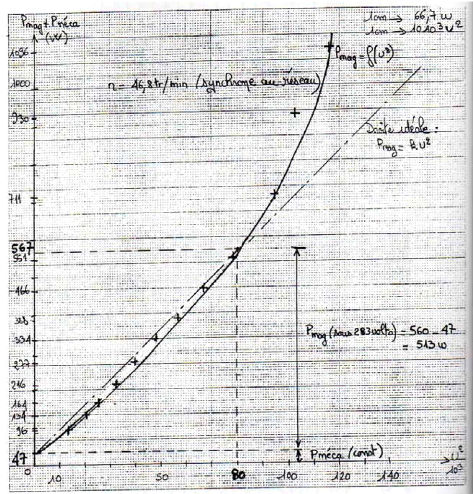
Fig.An1-5

4. ESSAI EN CHARGE EN FONCTIONNEMENT MOTEUR.

4.1. Essais à couples constants (Fonctionnement en boucle ouverte) :

4.1.a) Tableaux des relevés ; Essai à T_u = 100,6 N.m (Constant) ? Pu ? 0,48 kW

n=46,8 tr/min (synchrone)= 50 Hz

Mesures

N°	Uab (V)	Vas (V)	Ia (A)	Ib (A)	Pabs (W)	Qabs (var)
1	312,4	180	9,75	10	1 590	5 040
2	304	174,6	9,40	9,50	1 506	4 645
3	296	170	9,12	9,21	1 437	4 380
4	288	166	8,80	8,91	1 341	4 204
5	280	162	8,50	8,51	1 290	4 001
6	278	Décrochage du rotor

Calculs

(1) cos q	(2) PJ 3RsIb ^2 (W)	(3) Pmag (W)	S	Pu Tu(2in) (W)	11 Pu/Pabs (%)	PmajPabs (%)
			2 2 + ? P abs Q abs ) (VA)
0,30	339	760	5 285	493	31	48
0,31	306	667	4 883	493	33	44
0,31	288	640	4 610	493	34	45
0,30	269	587	4 413	493	37	44
0,31	245	486	4 204	493	38	38

Tab.An1-4

(1) : Cos q = Cos [Arc tan (Qabs /Pabs)]

(2) : A chaud, R_s = 1,13Q

(3) : D'aprés les essais à vide, on a k =6,20.10^-3 W/V² pour une tension inférieure à 283 volts.

4.1.b) Tracé des coubes : I b ? Uab pour différentes valeurs de T_u



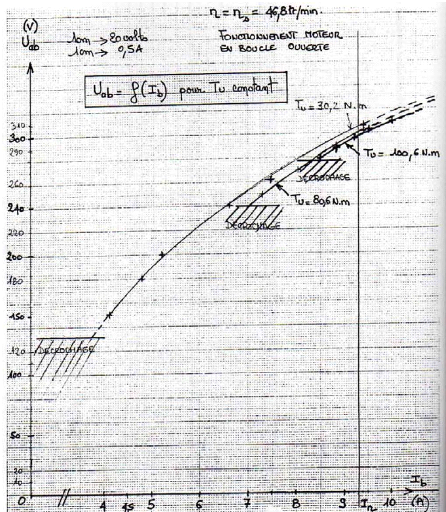
Fig.An1-6

4.2. Essais à tensions constantes (Fonctionnement en boucle ouverte) :

4.2.a) Tableaux de relevés ; Essai à Uab = 300 volts (Constant) =0 ~Tu ~138 N.m

n=46,8 tr/min (synchrone)= 50 Hz Pmag = 667 W(constante)

Vas = 172 volts

Mesures

N°	Tu (N.m)	Pu (kW)	Ia (A)	Ib (A)	Pabs (W)		Qabs (var)
1	0	0	9,02	9,10	1	005	4	547
2	20,4	0,09	9,02	9,12	1	089	4	536
3	40,1	0,19	9,10	9,20	1	185	4	547
4	66,8	0,32	9,25	9,33	1	308	4	583
5	82,1	0,39	9,30	9,40	1	383	4	619
6	100,6	0,48	9,35	9,46	1	464	4	614
7	111	0,54	9,41	9,51	1	500	4	666
8	120	0,57	9,50	9,60	1	554	4	687
9	130,3	0,63	9,56	9,67	1	605	4	703
10	138	Décrochage du rotor

Calculs

(1) cos q	(2) PJ 3RsIb^2 (W)	S	Pu Tu(2in) (W)	TI Pu/Pabs (%)	Pmag/Pabs (%)
		2 ^2 + ( ( P abs Q abs ) (VA)
0,22	281	4 657	0	0	66,3
0,23	282	4 665	100	9,1	61,2
0,25	287	4 699	197	16,6	56,3
0,27	295	4 766	327	0,25	51,0
0,29	300	4 822	402	29,1	48,2
0,30	303	4 841	493	33,7	45,6
0,31	307	4 901	544	36,3	44,5
0,31	312	4938	588	37,8	42,9
0,32	310	4 969	639	39,8	41,6

Tab.An1-5

(1) : Cos q = Cos [Arc tan (Qabs /Pabs)]

(2) : A chaud, R_s = 1,13Q

4.2.b) Tableaux de relevés ; Essai à U_ab = 340 volts (Constant) =0 <_Tu <_138,5 N.m :

n=46,8 tr/min (synchrone)= 50 Hz Pmag = 717 W (constante)

Vas = 196 volts

Mesures

N°	Tu	Pu	Ia	Ib	Pabs	Qabs
	(N.m)	(kW)	(A)	(A)	(W)	(var)
1	104,6	0,50	11,25	11,3	1 890	6 287
2	138,5	0,64	11,3	11,32	1 995	6 365
3		Limite du banc d'essais 3

Calculs

(1) cos cp	(2) PJ 3RsIb^2 (W)	S	Pu Tu(27Cn) (W)	n Pu/Pabs (%)	Pmag/Pabs (%)
		( P abs + Q2 abs) ( (VA)
0,29	433	6 565	513	27,1	37,9
0,29	434	6670	678	34,0	36,0

Tab.An1-6

(1) : Cos cp = Cos [Arc tan (Qabs /Pabs)]

(2) : A chaud, R_s = 1,13n

4.3. Relevé des oscillogrammes vas( t ) et i as ( t ) : moteur chargé : 4.3.a) T u = 40 ,1 N. m, U ab = 300 volts à n_n =46,8 tr/min (50 Hz) Echelles : 50 volts/cm, 5 A/cm et 2ms/cm



I as = 8 , 8 A p = - 77 ,1°

Fig.An1-7
Echelles : 50 volts/cm, 5 A/cm et 5ms/cm



Annexe 1: Essais expérimentaux et validation du modèle. 4.3.b) T u = 100 N. m, U ab = 300 volts à n_n =46,8 tr/min (50 Hz)

Echelles : 50 volts/cm, 5 A/cm et 2ms/cm



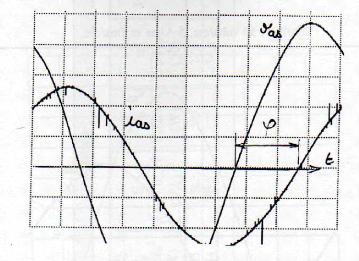
I as ? 9 , 2 A ? p = 72°
Fig.An1-9

Echelles : 50 volts/cm, 5 A/cm et 5ms/cm



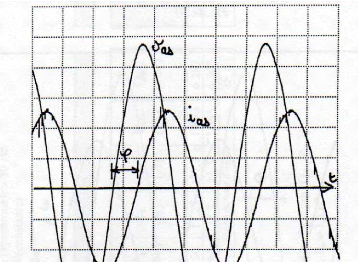
Fig.An1-10

Comparé au précédent relevé, on remarque un déphasage, du courant statorique, amélioré de 5° environ. Le courant est resté toutefois très inductif.

Annexe 1: Essais expérimentaux et validation du modèle. 4.3.c) Tracé des coubes : I b > T_u pour différentes valeurs de U ab



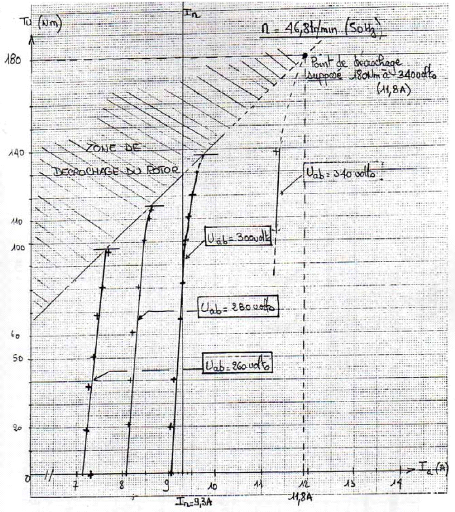
Fig.An1-11

5. DETERMINATION DE LA CONSTANTE THERMIQUE.

Sonde platine n°1
Stator n°1

Sonde platine n°2
Stator n°2









t (min) 0	r' (() 1,704	r (n) 110,2	r-r' -3 0° (°C)	r' (n)	r (n)	r-r' -3 0° t° Ambiant (°C) à 1cm du moteur (°C)
			22	1,384	109,9	22	22,2
5	1,570	117,2	40	1,432	119,8	47,5	/
10	1,587	123,9	58	1,464	125	61	23,4
15	1,591	127,1	66	1,490	128,3	79	24,9
20	1,598	129,5	72	1,513	131,0	76	25,8
25	1,606	131,9	78,5	1,530	133,7	83,5	26,7
30	1,610	134,6	85	1,550	136,4	90,5	27,4
35	1,622	138,1	95	1,576	140,2	100	/
43	1,628	141,6	104	1,608	144,2	111	/
45	1,629	142,5	106	1,614	145,1	113	29,9

5.1. Tableau des relevés



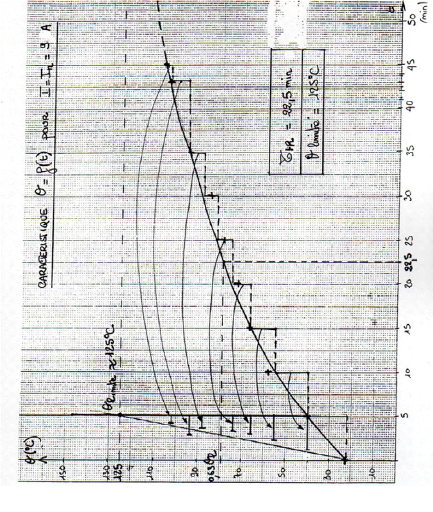
Fig.An1-12

5.2. Tracé de la courbe : t + 0 pour I I n

- ANNEXE 2 -

COMMANDE SANS CAPTEUR MECANIQUE DU
MOTEUR FINTRONIC.

FILTRE DE KALMAN

QUELQUES NOTIONS SUR LES VARIABLES ALEATOIRES

Il nous semble important d'apporter quelques précisions sur les signaux aléatoires pour comprendre le fonctionnement du filtre de Kalman.

· L'espérance (moyenne arithmétique):

Nous allons définir l'espérance d'une variable aléatoire à travers un exemple simple. Considérons n relevés de mesure sur une variable aléatoire réelle notée X, (x ₁ , x ₂ , x ₃, . . ., x_n) et effectuons la moyenne de ces valeurs. On obtiendrait pour n

mesures finies :

une valeur moyenne : x

? ? lim

n n ?? n

x x

? ? ?

. . . x

1 2 n 1 ?



i =n

xi

i

=

1

Or, si on faisait plusieurs séries de mesures, avec n relevés tendant vers l'infini, on verrait que la valeur moyenne obtenue pour chaque série de mesures aurait tendance à converger vers une valeur unique et non pas plusieurs valeurs dépendants du nombre de relevés . Et c'est justement cette valeur unique qui caractérise l'espérance de la variable aléatoire X. L'espérance de X sera notée :

1

E{ X} ou X avec E{ x( t)} = lim ? x ? t ?

t =n

=



= Cste

(An2-1)

Nota : A noter que l'espérance des bruits blancs, est nulle.

· La variance :

La variance correspond à l'espérance mathématique du carré des écarts par rapport à la valeur moyenne (espérance).

La variance de X sera notée :

?_x ? E ? ? X ? X ? 2 ?

Avec

? ? ? ? ? ? ?

2 1 i n ? 2 ? x ? E X ? X ? lim ? x i ? X ? n ?? n i =1

2

(Carré de l'écart type).

(An2-2)

Plus clairement et en reprenant l'exemple précédant, cette variance permet d'apprécier la dispersion des valeurs mesurées par rapport à son espérance. C'est ce qu'on appelle la variance de la variable aléatoire X.

Nota:

L'écart type d'une variable aléatoire correspond à la racine carrée de sa variance.

· Le coefficient de covariance :

le coefficient de covariance caractérise l'interdépendance éventuelle entre 2 variables aléatoires X et Y. Ce coefficient est défini et noté par:

1 ?xy ? ? ? ? ? ?

? E X ? X Y ? Y ? lim ? ? ? ?

x i ? X y i ? Y

n ?? n ? i= 1

i n

?

(An2-3)

Cette valeur correspond à l'espérance de la multiplication de l'écart type des 2 variables aléatoires.

Nota :

On pourra considérer par la suite que la notion d'espérance, de variance et de covariance suffisent pour définir une variable aléatoire.


· La matrice de variance-covariance :

Si un système différentiel quelconque est tributaire de plusieurs variables aléatoires, il est possible de représenter ces variables aléatoires, sous la forme d'un vecteur.

Dès lors, il est possible de représenter la variance et la covariance des différentes composantes de ce vecteur sous la forme d'une matrice dite de « variance-covariance ».

Soit X

?

F I L

X X X

1 2 3

1 ? I J

: vecteur de 3 variables aléatoires,

(An2-4)

F I

[

C

xx

On a la matrice de variance-covariance suivante:

x 1 x

x 2 x

i

3 ?

3 ? ? ?

Dx 1 cx 1 x2 c

cx 2 x1 ⁰x 2 g

cx 3 x1 cx 3 x2 ⁰ x 3

(An2-5)

Si on remplace chaque terme par leur expression, on a :

??

Cxx = E

L

?

? ? ? ? ? ? ? ? ? ? ?

X X X X X X X X

? ? ? ? X X

?

? 2 2 1 1 3 3 2 2 3 3

^-11

? ?

? ?

? ??

? ?



? ? ? ? ? ? ? ? ?

2

? X X

? X X X X

? ? X X X

?

1 1 1 1 2 2 1 1 3

? ? ? ? ?

? X 3 ?

? ? ? ? ? ? ? ? ? ?

2

X X X X X X X X X X

?

2 2 1 1 2 2 2 2 3 3

2

(An2-6))

De plus si on remplace ? ? Xi

X i ? X _i par pour simplifier les notations, on obtient



02

r

0

11 I 1 ? ?? ?

? ? ? ?

3

X1

0

o o

??? ?

?

?

E

?

1 ?

L

C xx = E

3

X2

r 1 1 ? ? ? ?

0

2

r

? i ? ?

X3

r 1

?

1

[

L

? ? ? ? ?

X X X

?? 1 2 3

?? ?

? i

o o o o

X 1 X ₁ X ₂ X ₁ X

₀ 2 0 0

X ₂ X 1 X 2 X ₂ X

0 0 0 0 0

X ₃ X ₁ X ₃ X 2 X3

(An2-7)

Soit :

Matrice de variance-covariance du vecteur aléatoire : gxx

f 0 0 T = E iX X ???

(An2-8)

.

Nota : Dans le cas particulier des bruits blancs, X = X.

- ANNEXE 3 -

COMMANDE SANS CAPTEUR MECANIQUE DU
MOTEUR FINTRONIC.

FILTRE DE KALMAN

CHANGEMENTS DE REPERE : (a_s, b_s,c_s) ~~ (ct_s, _3sos) et (d, q, o) ~~ (ct_s, 3_s, o_s)

TRANSFORMATIONS DE CLARKE ET DE CONCORDIA.

1. DETERMINATION DE LA MATRICE DE PASSAGE DU REPERE (a_s, b_s,c_s) AU REPERE (a_s, O_s, o_s).

Afin d'eviter des calculs longs et fastidieux, il est essentiel de tenir compte de la remarque suivante:


· Le referentiel (a_s, r3_s, o_s) correspond au referentiel de Park (d, q, o) pour lequel, on a immobilise le système d'axes (d, q, o) et oriente l'axe a_s suivant la même orientation que l'axe a_s.

On peut donc considerer que le referentiel (a_s, (3_s, o_s) est un cas particulier du referentiel de Park avec lequel, on a remplace les lettres du système d'axes d, q par a_s et p_s. Il suffit donc de reprendre la matrice de Park et de remplacer 0 par 0. On obtient ainsi, la nouvelle matrice de passage.

Dans la litterature courante, cette transformation est appelee « transformation de

CLARKE ». La matrice de cette transformee sera notee [ _Cla] .





1

?

?

i

[ P] =

2 3

1^- [

cose cos(0 -- 2 7c 3 ) cos(0 -- 4 7c 3)



--sine --sin(0 -- 2 7c 3 ) --sin(e -- 4 7c 3







1 2 1 2 1 2

(An3-1) : Matrice de PARK : Repère (d, q, o). En remplaçant 0 par 0, on obtient :



1 -- 1 2 --1 2

2

0 3 2 -- 3

1 2 1 2 1 2

1 ?

?

? ?

r I

[

2

3

[ C _la ] .

(An3-2): Matrice de CLARKE : Repère (as, fi_s, o_s). Les expressions de tensions, courants et flux deviennent :



i _as = 1 3(

i ? s = 1 3

( i bs -- ics)

2i as -- i bs -- ics)

1³

?

s

? ? ? ?? ?

i ? C i

?? o s la abc

? ? ? ?? ?

v ? C v

?? o s la abc

v_as =1 3(

2v _as --v bs ^--vcs)



v' s = 1 3

( v bs -- v cs )



1³

?

s

? ? ? 1 3 ?

? s

? ? ? 1 3

? s

( Tbs ^--"cs)

[If alio s [ la abc
] = C IT ]





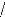
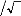
²Tas ^--Tbs ^--Tcs)

?

s

(An3-3)

Nota :

On ne fait pas apparaître volontairement les expressions, sur l'axe o. Cet axe intervient uniquement pour l'inversion de la matrice de transformation (matrice carree).

L'unicité de la matrice de transformation [ _Cla] , pour les tensions, les courants et les flux, nous oblige à tenir compte des changements de variables, identiques à la transformation de Park.

2

2

3 Ilj_a s

i i

? ? v ? ? v ? ? ?

? s ? s ? s ? s ? s

3

2 2

s

i ' = i v' = v Ill' = Ill'

li

s

P

s

^P

^s 3

P

s

li



1³

s

³

(An3-4)

2. DETERMINATION DE LA MATRICE DE PASSAGE DU REPERE (as, Ps) AU REPERE (a_s, b_s, cs).

Avec les mêmes arguments que précédemment, on remplace 0 par 0, dans la matrice de Park inverse.

r
[

_[P]-1. =

i

?

?

? ?



4

i

3 ) -- sin(9 --

4

7c

3

)

1



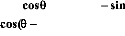
1

0

2 7c 3) -- sin(9 -- 2 7c 3 ) 1

(An3-5)

On remplace 0 par 0 et on obtient :

[

[C_lar¹ = --

--1 2 --

_ii
L

1

1 0

1 2 3 2 1

3 2 1



(An3-6): Matrice de CLARKE inverse. Les expressions de tensions, courants et flux deviennent :



i _as ^--i as ^--ias

i bs = P_bs = 1 2(
i cs = Pcs = 1 2(

i as + 3 ifts)

i as -- 3 ifts)

[i abo ]_s =[C la ]^-licoo]

s

v as =vas

US

v as = 3 2v

Us

? ? ? v 3 v ? ?

? s ? s

v _as -- 3 va_s)

? ? v 3 v ?

? s ? s

? v 3 v ?

? s ? s

?

v bs = 3 4(

v cs = 3 4(

[v abo ]_s = [C la ] ¹[vafid

v bs = 1 2(

v cs = 1 2(

s

s

?

ⁱl^las = 3 2ijas

^IPbs = 3 4( ^IPcs = 3 4(





cos e -- sin

cos(9 --

cos(9 --

l^jas + ³¹Pris)

? ?? 3 ? ?

? s ? s

? ?

? ?

as ? s

[Tabo ]_s =[C la ]^-1[Tcoo]

? ? ? ?

? 1 2 ? ? ? 3 ?

bs ? s ? ? s



? ? 1 2 ? ? ? ?

? 3 ? ? ?

cs ? s ? s

(An3-7)

3. REPRESENTATION VECTORIELLE DES SYSTEMES D'AXES

Rs



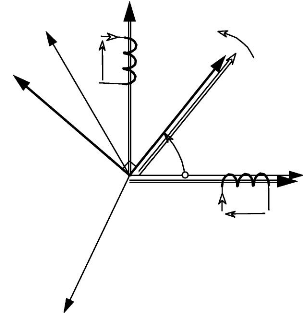
b_s

i ?s

CO

Axe
du
rotor

d

q

vas

-->

^IP aim

0 + 00

O

i as

v_as

a_s

(Fixes)

as

c_s

Fig.An3-1



s cos9

i i I

? ? ?

? s ? s

?

2

?

? ? arctan ?? ?

i ? s ?

? ?? ?

i ? ? s

V = ₃v

OLs

? ? ? ?

i i

? ? ? ?

2 ² i i

2 2

s s s ?

? ? ? ? s

?

?

i i I

? ? ? ?

? ?

s s s

since

?

I s =



i^?as

a_s

i^?Ys

?

->

V_s

->

I _s

v_as

Rs

a_s

?

Cas particulier où v s = V_s cosco_st

Fig.An3-2

La représentation vectorielle de la figure 3.2 correspond à un cas particulier oil la tension est colinéaire à l'axe as à l'instant initial. Dans le cas général, on aurait :


· v _s = ? V _scos(w_st + O s0)

s 0

= arcta --

?
· Non pas (p mais (p-O_s0 avec cp -- ips

· Non pas

2 " 2 2 2 Vs = 3 v. 3 mais Vs = (v + vPs) et Os 0 = arcta as v

s,

? s ?? s

Os0 : Position du vecteur "tension", par rapport à l'axe a_s ou par rapport à l'axe a_s,

l'instant t=0.

En gardant 0 , comme l'angle représenté par la position du rotor par rapport à l'axe fixe a_s et par conséquent par rapport à l'axe a_s, on peut représenter les projections du flux produit par les aimants sur les axes a_s et r3_s :



3^,'
= 2 Taim

te^taim = ⁴aim

pour Ta'aim = D'après la nouvelle notation, on a :

Vaaim =

Fig.An3-3

R_s

?

T_aim

?

a_s

aaim

?

? ? arctan ??

waaim = T_aim cos°
xvpaim = ''aim sin°

? ?2 2
? ?
aim ? ?
? ? aim

W?

Raim

??

? ? aim

^d

--)

Waim

11aim

0

a_s

Remarque importante:

Transposé sur l'axe a_s, le flux créé par les aimants (déterminé par un essai) doit être normalement majoré du coefficient 3/2 (unicité de la matrice de Clarke). On aurait donc :

Etant donné que nous utilisions des valeurs non primées, on fera de même


·
·

" coW]

[ Cla ][¹¹¹abc .1 aim ^=111a4 sinO^li

(An3-8)

Il faudra faire ATTENTION que dans tout ce qui suit, nous utiliserons
des notations non primées pour simplifier les écritures (Sauf indication
contraire).



Pour retrouver les vraies valeurs de flux et de tensions sur les axes a et 13, il faudra multiplier chaque résultat par 3 2 (les résultats sur les courants restent identiques).

4. EQUATIONS ELECTRIQUES DANS LE REPERE (as, 13s, os).
L'expression matricielle des tensions dans le repère (a_s, b_s, c_s) correspond à :

? v ? R ? i ? d ? ?

? ? ?

abc s s abc s abc s

dt

(An3-9)

On multiplie chaque terme par la matrice de CLARKE et on remplace ? par

?abc ? s

[ Cla] ? o ? aim ?1 ???

. On obtient :

? v ? R ? i ? d ? ?

? ? ?

abc s s abc s abc s

dt

[ v ? R ? i ? ? C ? d ? ? ? ?

?1

? ? C la ? ?? ?

?? o s s ?? s ^la dt o _s

? v ? R ? i ? d ? ?

?? ? ?? ? ? ??

o s s s dt o s

(An3-10)

Il faut exprimer les flux en fonction des courants. Pour cela, nous utilisons la même démarche que précédemment, en partant de l'expression des flux dans le repère (a_s, b_s, c_s). [''abc] s ? s ?? abc ? s ? ? abc ? aim

? L i ?

On multiplie chaque terme par la matrice de CLARKE et on remplace l'expression des flux par celle de l'expression 3.1:

?1

? C la ? ? abc ? s ? C la ? ? L s ? ? i abc ? s ? C la ? ? abc ? aim

? ? ? ? . Sachant que ? i abc ? s ? C la ? ? i o ? s

? ??

On a : ['I^j_ap_o ] s = [ C la] [ L s ] [ C la ] 1 [i apo ] _s #177;[Illapo ]aim

· Détermination de [ C la ] [ L_s] :



1 2(



1 ? ?

? ?

2

=

3

p

M M L

? 1 ? 1 2 ? 1 2 ?

? ?

0 3 2 ? 3 2

? ?

? ? 1 2 1 2 1 2 ? ?

3

2

[C _la ][Ls]

=

L p M M

M L p M



1 2

=

3

0 3 2

^{1 2}(

L

p -- M --1 2 (L p -- M) --1 2(L p -- M)

(L p -- M) -- 3 2(L p -- M)

L _p + 2 M) 1 2 (L _p + 2 M ) 1 2 (L _p + 2M)

1 ?

? ?

? ?

? ?

, ?

(An3-11)

· Détermination de [ C la ][ L_s] [ C_la] ^-1:

[C _la ][L _s ][Cla]

(An3-12)

L p -- M --1 2 (L p -- M) --1 2(L p -- M)

1 ? ? ? J

0 3 2 (L p -- M) -- 3 2(L p -- M)

L _p + 2 M) 1 2 (L _p + 2 M ) 1 2 (L _p + 2M)



1 --12 --121

?

0 3 2 -- 3 2 ?



1 2 1 2 1 2 ? ?

? 1

? ?? ? ? ?

C L C ? ? 0 ? ?

L M
?

la s la p

?

0 0

?



0

(L _p + 2M)

L p -- M 0 0

? ?

f ?

s

? L 0 0 ?

0 L 0 ? s ?

? ? 0 0 L ?



1

?

?

?

J

=

Matrice que l'on notera ? L o ? s

??



?

r 1

[

1 ?

?

? ?

e
e

cos
sin
0

Taim

L_s

0 0

L_f

0 0

[ ja1 o ] s ? ?? o ? s ? ?? o ? s ? ? ?? o ? aim ? L i ?

Avec

0 L s 0

r 1

[

1 ?

?

? ?

Llio]

[_a=

et [T' ] = alio _aim

(An3-13)

On dérive l'expression précédente pour obtenir :

d? ? ? ? ? ?

d

? ? L i o

?? ??

dt o s o s dt ??

?

+ maim

s

r
[

cos

0

? ?

? ?

aim

?

?

sin

(An3-14)

On rappelle que 0 = wt dO = co dt

On remplace l'expression de la dérivée du flux dans l'expression (4.1) pour obtenir l'expression finale des tensions :

?

? v ? R ? i ? ? L ? d ? ?

? ? i o s ?

?

?? o s s ?? ??

s o s dt ?? aim

Soit

v _as = R _s i _ss + L_s

AN

cotPaim sine

di a s

dt

v 0 s = R _s i D_s + L_s
v os = R _s i _os + L_f

AN

+ _cotPaim cose

di 0 s

dt

di os

dt

(Attention aux valeurs primées)

r 1

[

sin

cos

0

0

0

1 ?

?

? ?

aim

(An3-15)

Sous une autre forme, on obtient un système de 2 équations différentielles linéaires à coefficients constants aux 1ers membres et avec les seconds, variables en fonction du temps:



?

(4.5) :

di

0

? aim

? sin ?

L L

s

?

Taim

0) cos0

L s L

di

R

dt

L _s

R

dt

L s

? s

v

Qs s Qs

#177; i = #177; #177;

Qs

s

v

s s ? s

? i ? ?

s

(An3-16) (Attention aux valeurs primées)

5. DETERMINATION DE LA MATRICE DE PASSAGE DU REPERE (d, q, o) AU REPERE (as, (_s,o_s).

En reprenant la figure 3.1, on remarque que l'on peut passer d'un système d'axes (d, q) au système d'axes (c_s, J_s) très facilement. La matrice de cette transformée que l'on appelle « matrice de CONCORDIA » et notée [ C 0] , correspond à :

[ C o ] .

r [

cose -- sin ? 0 ? ? sin cos ? ? 0 ? 0 0 1 ? _I

(An3-17) : Matrice de CONCORDIA : Repère (as, fi_s, os).

En inversant cette matrice, on obtient :

[C _o]^-1. --

r 1

cose sine

sin e cose

0 0

0_ll

0 ?

?_I

1

(An3-18):Matrice inverse de CONCORDIA : Repère (as, ?_s, o_s).

On remarque que cette matrice inverse correspond à la transposé de la matrice de

Concordia : ? ?

C o ? C

? ? t

1 ? . Il y a donc conservation de la puissance instantanée et de

^ol'amplitude des grandeurs vectorielles.

On obtient ainsi :

i _ds = i_ds cose -- i qs

i 13s = i_ds sin e + iqs

Nota :Expressions valables aussi pour les tensions et les flux

sine cose

?

i ds = i_as cos ° + ip_s

i qs = -- i _ns sin e + iPs

sine

cose

(An3-19)

6. EXPRESSION DU COUPLE ELECTROMAGNETIQUE DANS LE REPERE (as, (_s,o_s).

En reprenant l'expression du couple électromagnétique dans Park, nous avions :

¹aim

3

T_em = KT i_qs avec K _T = 2 Np

Or, en remplaçant i_qs par son expression en (An3-19), on obtient une nouvelle expression du couple électromagnétique :

T_em = K _T ( i p s cos e -- i_es sine)


avec

3

KT= ₂ Np

...taim

(An3-20)

7. EQUATION MECANIQUE DANS LE REPERE (as, (3s, os).

T _em ( Trm a #177; T r f #177; T r 0 )

?

? N J J

( m ? r )

??

p

dco 1

dt ^I]

1

Avec

T r f = f co

T r0 = Cste



T rma = k co² ou k co³ ou k co ou Cste

(An3-21)

En remplaçant T_em par son expression, on obtient :

?

K ? i i ? f ? T T ? N J J d

1

? ? ? ? ? ? ?

? ? ? ? ? ( ? )

T s cos s sin rma r 0 ?? m ^r dt ??

p

soit

Attention : f est en rad/s^-1 électrique

[K _T (i p_s cos 9 -- i _es sin e) -- f o)-- T rma -- Tr0]

J m + J



dco

?

dt

N p

(An3-22)

- ANNEXE 4 -

COMMANDE SANS CAPTEUR MECANIQUE DU
MOTEUR FINTRONIC.

FILTRE DE KALMAN

Schéma général sous Simulink : commande du moteur avec filtre de Kalman (fichier "bfesmli.m").

Schéma-blocs sous Simulink et masque de S-Function du filtre.

Fichier metafile : bfesmlim.m.
Fichier metafile : Filtre1m.m.

Annexe 4 : Commande sans capteur mécanique - Filtre de Kalman - Mémoire CNAM Patrick BOIDIN. Fichier : bfesmli1.m



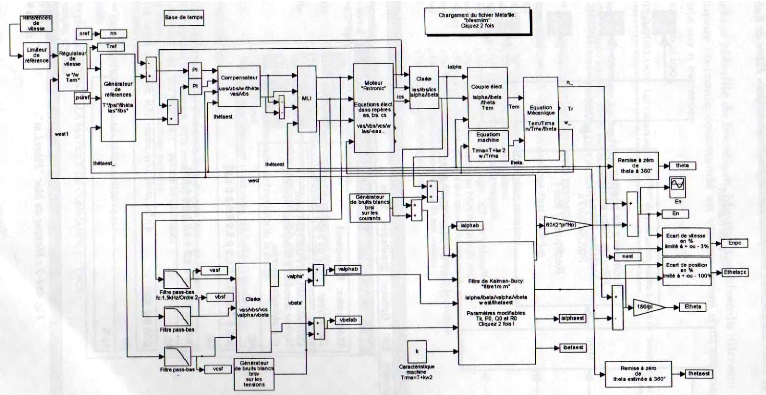
Fig.An4-1 : Schéma général de la commande sous Matlab-Simulink.

Filtre de Kalman



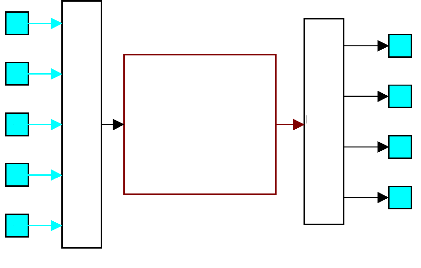
1

west

2

ibeta

thetaest

3

ialphaest

4

ibetaest

Mux

Demux

ialpha

valpha

vbeta

5

k

1

2

3

4

Fig.An4-2 : Bloc "filtre de Kalman".

Estimateur de position: Filtre de Kalman-Bucy

Metafile: "filtre1m"

P0/Q0/R0/Tk

Recliquez 2 fois !



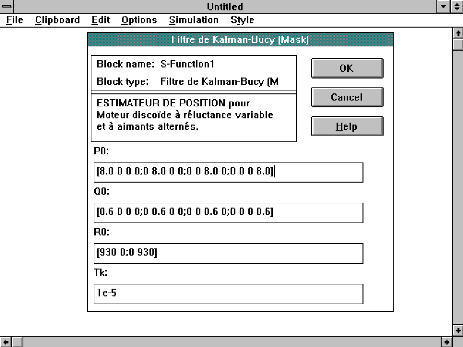
Fig.An4-3 : Masque du bloc "Filtre1.m".
- 152 -

%Fichier Métafile de boesti5.m, bfesti5.m et bfesmli1 :filtre1m %Moteur Fintronic commandé en vitesse, muni d'un estimateur et régulé sur n estimée

%20:23 16.11.1995

%

%NOTE IMPORTANTE: Les valeurs suivies de "**" doivent correspondre à ceux de "boesti5.m" et autres

%***********************************************************

%%

function[sys,X0]=filtre1m(t,X,u,flag,P0,Q0,R0,Tk);

%P0=700 / Q0=6 / R0=500 / Tk=30 microseconde

%********************* FILTRE DE KALMAN ********************

%

%**** DECLARATION DES CONSTANTES ESTIMEES:

%

Ld=0.0537 ;%**(mH) - Inductance synchrone d'axe d (Ld=Ls)

Ls=Ld ;

Rs=1.13 ; %**Ohms - Résistance d'une phase statorique

phiaim=0.141 ; %**Wb - Flux créé par les aimants

f=0.0306 ; %**N.m/rad.s-1 - Frottements visqueux

KT=13.536 ; %**N.m/A - Constante de couple : KT=3/2*phiaim*Np

Np=64 ; %**Nombre de pas, assimilé au Nbre de paire de pôles

Jm=0.141 ; %**kg.m2 - Moment d'inertie des masses tournantes du moteur

Jr=0.1 ; %**kg.m2 - Moment d'inertie des masses tournantes de la machine

Tr0=3 ; %**N.m - Couple résistant résiduel dû aux aimants

T=0 ; %**N.m - Couple résistant à n=0

%

J=Jm+Jr ; %kg.m2 - Moment d'inertie total: Moteur/machine

%

pL=phiaim/Ld ; %Simplification des notations

RL=Rs/Ld ; %Simplification des notations

KJ=KT*Np/J ; %Simplification des notations

%

Q=Q0 ; %Matrice de variance-covariance représentatif des

%bruits sur le système v (coefficients de la diagonale)

R=R0 ; %Matrice de variance-covariance représentatif des

%bruits sur les mesures w (coefficients de la diagonale)

%

% k ;%Constante représentative de l'évolution de la charge

;%Trma=T+kw2

% Tk ;%Pas d'échantillonnage: 10 micro sec.(déclaré dans simulink)

%

%**** NOTATIONS :

%

% X(1): dialphaest/dt, X(2): dibetaest/dt, X(3): dwest/dt, X(4): dthétaest/dt

% X(5): ialphaest, X(6): ibetaest, X(7): west, X(8): thétaest

% F: matrice des dérivées partielles, C: matrice de commande

% Fd: matrice de transition des dérivées partielles

% u(1): ialpha, u(2): ibeta, u(3): valpha, u(4): vbeta, u(5): k

% Y: Matrice de sortie;

%

%**** DECLARATION DE LA MATRICE UNITE (4,4) :

I=eye(4);

%

%**** DECLARATION DE LA MATRICE DE COMMANDE C : Y=CX :

%y1=ialpha, y2=ibeta

%

C=[1 0 0 0

0 1 0 0];

if flag==2

n=t/Tk;

m=floor(n+1e-13*(1+n));

if abs(round(m-n))<1e-8

%

%**** EVOLUTION DE f(x)- VARIABLES D'ETATS ESTIMEES X(5),X(6),X(7),X(8) :

%Méthode d'Euler

%

% Variation de ialpha estimé X(5): X(1);

X(1)=X(5)+Tk*(-RL*X(5)+pL*X(7)*sin(X(8))+u(3)/Ls);

%

% Variation de ibeta estimé X(6): X(2);

X(2)=X(6)+Tk*(-RL*X(6)-pL*X(7)*cos(X(8))+u(4)/Ls);

%

% Variation de w estimée X(7): X(3); xm3=KJ*X(6)*cos(X(8))-KJ*X(5)*sin(X(8))-Np/J*f*X(7)-Np/J*(Tr0+T)*sign(X(7))- Np/J*u(5)*X(7)*abs(X(7));

X(3)=X(7)+Tk*xm3;

%

% Variation de théta estimée X(8): X(4);

X(4)=X(8)+Tk*(X(3)+X(7))/2;

%

%**** PREMIERE ESTIMATION DU VECTEUR D'ETAT (avant les mesures et correction):

% XM=Xest(k/k-1)

% XM=[X(1)

X(2)

X(3)

X(4)];

%

%**** MISE EN MEMOIRE DE LA MATRICE DE VARIANCE COVARIANCE DE L'ERREUR

% SUR LA DEUXIEME ESTIMATION PP=P(k/k):

%

PP=[X(9) X(10) X(11) X(12)

X(13)	X(14)	X(15)	X(16)
X(17)	X(18)	X(19)	X(20)
X(21)	X(22)	X(23)	X(24)];

%

%**** CALCUL DE LA MATRICE DES DERIVEES PARTIELLES DE f(x), F(x): %

F(1,1:4)=[-RL 0 pL*sin(X(8)) pL*X(7)*cos(X(8))];

F(2,1:4)=[0 -RL -pL*cos(X(8)) pL*X(7)*sin(X(8))];

F(3,1:3)=[-KJ*sin(X(8)) KJ*cos(X(8))-Np/J*f-2*Np/J*u(5)*abs(X(7))]; F(3,4)=[-KJ*X(5)*cos(X(8))-KJ*X(6)*sin(X(8))];

F(4,1:4)=[0 0 1 0];

%**** CALCUL DE LA MATRICE DE TRANSITION Fd(x) de F(x)

% par la méthode du développement limité: I+FT+(FT)2/2!+... :

% Fd=I+Tk*F;

%

%**** DISCRETISATION DE LA MATRICE DE VARIAN. COV. Q

% par la méthode des trapèzes :

% Qd=(Fd*Q*Fd'+Q)*Tk/2;

%

%**** DETERMINATION DE LA MATRICE DE VARIANCE COVARIANCE DE L'ERREUR

% SUR LA PREMIERE ESTIMATION PM=P(k/k-1) :

% PM=Fd*PP*Fd'+Qd;

%**** CALCUL DE LA MATRICE DE KALMAN K (correction) :

%

K=PM*C'*inv(C*PM*C'+R);

%

%**** MESURE DES COURANTS REELS ialpha ET ibeta POUR COMPARAISON :

%

Y=[u(1);u(2)];

%

%**** CORRECTION DE L'ESTIMATION DU VECTEUR D'ETAT ESTIME APRES MESURES:

% XP=Xest(k/k) et XM=Xest(k/k-1)

% XP=XM+K*(Y-C*XM);

%

%**** DETERMINATION DE LA MATRICE DE VAR. COVAR. DE L'ERREUR

% SUR LA DEUXIEME ESTIMATION PP=P(k/k):

% PP=(I-K*C)*PM*(I-K*C)'+K*R*K';

% ou

%PP=PM-(K*C*PM)

%

%**** MISE EN MEMOIRE DE XP=Xest(k/k) et PP=P(k/k)

X(5)=XP(1);

X(6)=XP(2);

X(7)=XP(3);

X(8)=XP(4);

X(9:24)=[PP(1,1:4)';PP(2,1:4)';PP(3,1:4)';PP(4,1:4)'];

sys=X;

else

sys=X;

end

%

%**** RETOUR AU VARIABLES DE SORTIE west et thétaest

% + ialphaest ET ibetaest :

%

elseif flag==3

sys=[X(7);X(8);X(5);X(6)];

%

%**** RETOUR AUX CONDITIONS INITIALES :

%

elseif flag==0

%

%**** DECLARATION DU NOMBRE DE PARAMETRE A TRAITER :

%

sys=[0,24,4,5,0,0];

%

%**** DECLARATION DES CONDITIONS INITIALES

% dialpha0, dibeta0, dw0, dthéta0, ialpha0, ibeta0, w0, théta0 :

%

X0(1:8)=[0;0;0;0;0;0;0;0]; %**

%P0=P(0/0)

X0(9:24)=[P0(1,1:4)';P0(2,1:4)';P0(3,1:4)';P0(4,1:4)'];

%

else sys=[];

end

%*********** Fichier Métafile de bfesmli1.m ******************

%Moteur Fintronic commandé en boucle fermée dans le repère as, bs, cs

%Filtre de Kalman (filtre1m.m) fonctionnant en paralléle %Régulation de vitesse, avec onduleur, avec nest et thetaest %Machine: Tr=T+kw2

%18:17 13/10/1995

%NOTE IMPORTANTE: Les valeurs suivies de "**" doivent correspondre à ceux de "filtrem.m" %PARAMETRES DE SORTIE GRAPHIQUE ET DE SIMULATION:

%********** Méthode : EULER ***************

STT =0.0 ; %s - Start Time

ST =0.08 ; %s - Stop Time

MISS=2*1e-4 ; % - Min Step Size

MASS=2*1e-4 ; % - Max Setp Size

TOL =1e-4 ; % - Tolérance

bt=10000 ; %Base de temps de l'horloge

p1=10000 ; %Nbre de points (sortie graphique)

%

%MODULATEUR MLI:

e=0 ; % Entrée des relais, changement d'état

U=810 ; %volts - u/2 : Valeur maxi de la modulante

son=U/2 ; % Sortie relais (Amplitude de l'impulsion)

soff=-U/2 ;

%Up=410 ; %volts - Valeur crête de la porteuse

%f=2400 ; %Hz soit un rapport des fréquences m=39

%Remarque: La dent de scie est réalisée par un bloc fonction pré-défini par Simulink%

%

%PARAMETRES DU MOTEUR A RELUCTANCE VARIABLE ET A AIMANTS ALTERNES "FINTRONIC":

%In=9,3A / Imax=13A / n(nominale)= 60tr/min / Tn=200N.m / fn=64Hz/ Vn=220volts

Ld=0.0537 ; %**(mH) - Inductance synchrone d'axe d (Ld=Ls)

Rs=1.13 ; %**Ohms - Résistance d'une phase statorique

phiaim=0.141 ; %**Wb - Flux créé par les aimants

f=0.0306 ; %**N.m/rad.s-1(élec) - Frottements visqueux

KT=13.536 ; %**N.m/A - Constante de couple: KT=3/2*Np*phiaim

Np=64 ; %**Nombre de pas du moteur

Jm=0.141 ; %**kg.m2 - Moment d'inertie du moteur

%

%PARAMETRES MACHINE:

Jr=1.2 ; %**kg.m2 - Moment d'inertie de la machine entrainée

Tr0=3 ; %**N.m - Couple statique du aux aimants

T=0 ; %**N.m - Couple résistant

J=Jr+Jm ; %kg.m2 - Moment d'inertie de l'ensemble

%

% PARAMETRES DES CONDITIONS DE FONCTIONNEMENT

Tmax=130 ; %N.m pour

nref=60 ; %tr/min

wref=2*pi*Np*nref/60; k=(Tmax-T)/wref/wref; %

theta0=0*pi/180 ; %degré;

%Vmin=-600 ; %volts - Limitation de la tension

%Vmax= 600 ; %volts - Limitation de la tension

psiref=0*pi/180 ; %Degré - Couple maxi pour psi=0;

%

tec1=0 ; %s - A-coups de couple machine;

ec1 =0 ; %N.m - A-coups de couple machine;

%---- Régulateur de courant

kp=150 ; %Gain des correcteurs

ki=80 ; %Coef d'intégration des correcteurs

%

%---- Régulateur de vitesse

kvp=20 ; %Gain des correcteurs;

kvi=80 ; %Coefficient d'intégration;

Lmin=-300 ; %N.m

Lmax=300 ; %N.m

tnref=0.00 ; % s - Limitation de la référence de vitesse

tev1=0.04 ; % - A-coups de vitesse n°1 (s / tr/min)

ev1=0 ; % - A-coups de vitesse n°2

tev2=0 ;

ev2=0 ;

tev3=0 ; % - A-coups de vitesse n°3

ev3=0 ;

%

% Génération des bruits blancs

brsi=1/3 ; %x3 maxi A - bruits de mesures sur les courants

brsv=0.2 ; %x3 maxi volts - bruits de mesures sur les tensions

%

%Bruits sur le système:

brdias=140 ; %x3 maxi A - bruits sur la variation de ias

brdibs=150 ; %x3 maxi A - bruits sur la variation de ias

brdics=160 ; %x3 maxi A - bruits sur la variation de ias

brdw=20 ; %x3 maxi rad/s - bruits sur la variation de w

brdt=20 ; %x3 maxi ° - bruits sur la variation de théta

%

%Filtrage des tensions vas, vbs et vcs par filtres pass-bass:

%fc=1500 ;%Hz - Fréquence de coupure

%ordre=2 ;% - Ordre

%

%CONDITIONS INITIALES:**

ias0=0 ;ibs0=0 ;ics0=0; w0=0 ;kvi0=0 ;ki0=0; %

%Grandeurs de sortie (plot):

%nn / n / nref / En / Enpc / nest / vas / vbs / vcs

%valpha / vbeta / valphab / valphaest / Vs / eas

%Enthetapc / theta / thetaest / Etheta

%ias / ialpha / ibeta /Is / ialphab (bruité) / ialphaest / ibetaest

%Tref / Trma / Tem / Tr

%ds (porteuse) / vasreg / vbsreg / vcsreg / vasf (filtré) / vbsf / vcsf

%vasmli / vbsmli / vcsmli / sr1 / sr2 / sr3

QUELQUES PHOTOS



Photo 1

Photo 2



Photo 3

Photo 4



Photo 5

Photo 6

- 161 -



Photo 7

Photo 8



Photo 9