V.2.5.expression du temps de réaction du
système.
Nous avons établi plus haut que :
Dn = S2N(n) -- U0(n) (V-4)
D'après le tableau 9, nous avons : S2N(n)
= 600 et U0 ( n)= 360 Nous pouvons donc déduire que
:
Dn=240
V.3.Optimisation des temps d'attente suite à un
évènement non souhaité (ENS).
V.3.1.Evaluation des temps d'attentes dans le processus.
D'après le tableau 4, nous avons évalué
les temps d'attentes dans tous les sous-processus. Nous allons donc faire une
somme de ses temps d'attentes pour avoir le temps d'attente du processus qui
fera l'objet de réduction, voir de suppression dans le meilleur des
cas.
Nous avons alors dans le cas précédent :
E di,2= 18.
V.3.2 .Application de l'algorithme de réduction des
temps d'attente.
Dans cette partie nous allons réduire les temps d'attentes
dans le processus de traitement de l'ENS.
Le processus initial nous présente la configuration
suivante :
|
RESULTATS
|
VARIABLES
|
|
do, 2
|
di, 2
|
d2, 2
|
d3, 2
|
d4, 2
|
S(n)
|
Dn
|
Tat
|
Xo(o)
|
Xi(o)
|
X2(o)
|
|
4
|
8
|
1
|
5
|
0
|
600
|
240
|
18
|
0
|
0
|
0
|
Tableau 10 : configuration initiate
Modelisation du temps de reaction d'un systeme industriel :
Application aux centrales thermiques
d'OYOMABANG I et II .
Niveau 0 : sous-processus i=0 et i=4 (SP0 et SP4).
Nous avons min ( 4,2;E,2) = min
(4 ; 0) = 0
Donc pas besoin d'ajuster la date de début de
période de référence de ce niveau. Nous conservons alors
la configuration de départ :
|
RtSULTATS
|
VARIABLES
|
|
do, 2
|
di, 2
|
d2, 2
|
d3, 2
|
d4, 2
|
S(n)
|
Dn
|
Tat
|
Xo(o)
|
Xi(o)
|
X2(o)
|
|
4
|
8
|
1
|
5
|
0
|
600
|
240
|
18
|
0
|
0
|
0
|
Tableau 11 : reduction du temps ni veau 0 Niveau 1 :
sous-processus i=1 et i=3 (SP1 et SP3).
Nous avons min ( d1,2;d3,2) =
min (8 ; 5) = 5
De plus X1(n) = 0 ; on a bien 520 donc min
( d1,2;d3,2) 2
X1(n) D'où X1(n) = P1 +
(X1(n)- min
(d1,2;d3,2)) = 10 + (0
- 5) = 5.
Donc X1(n)= 5 Nous allons faire un nouveau
calcul des données qui sont résumés dans le tableau
suivant :
|
RtSULTATS
|
VARIABLES
|
|
do, 2
|
di, 2
|
d2, 2
|
d3, 2
|
d4, 2
|
S(n)
|
Dn
|
Tat
|
Xo(o)
|
Xi(o)
|
X2(o)
|
|
4
|
3
|
6
|
0
|
0
|
595
|
235
|
13
|
0
|
5
|
0
|
Tableau 12 : reduction du temps ni veau 1 Niveau 2 :
sous-processus i=2(SP2).
Nous avons d2,2= 6 ? 0
De plus X2(n) = 0 ; on a bien 6 20 donc
d2,2? X2(n)
D'où X2(n) = P2 +
(X2(n) -d2,2) = 15 + (0 - 6) =
9
Donc X2(n) = 9. Nous allons alors faire un
nouveau calcul des données qui sont résumés dans le
tableau suivant :
Modelisation du temps de reaction d'un systeme industriel :
Application aux centrales thermiques
d'OYOMABANG I et II .
|
RtSULTATS
|
VARIABLES
|
|
do, 2
|
di, 2
|
d2, 2
|
d3, 2
|
d4, 2
|
S(n)
|
Dn
|
Tat
|
Xo(o)
|
Xi(o)
|
X2(o)
|
|
4
|
3
|
0
|
6
|
0
|
595
|
235
|
13
|
0
|
5
|
9
|
Tableau 13 : réduction du temps ni veau
2
RECAPITULATIF
|
niveau
m
|
|
RtSULTATS
|
VARIABLES
|
|
|
do, 2
|
di, 2
|
d2, 2
|
d3, 2
|
d4, 2
|
S(n)
|
Dn
|
Tat
|
Xo(o)
|
Xi(o)
|
X2(o)
|
|
initiale
|
|
4
|
8
|
1
|
5
|
0
|
600
|
240
|
18
|
0
|
0
|
0
|
|
0
|
4
|
8
|
1
|
5
|
0
|
600
|
240
|
18
|
0
|
0
|
0
|
|
1
|
4
|
3
|
6
|
0
|
0
|
595
|
235
|
13
|
0
|
5
|
0
|
|
2
|
4
|
3
|
0
|
6
|
0
|
595
|
235
|
13
|
0
|
5
|
9
|
Tableau 14 : récapitulatif.
Finalement, nous avons alors :
V.3.3. Interprétation des résultats.
Ces résultats nous permettent de reconfigurer le
processus de traitement périodique des ENS. Nous pouvons déduire
que : Quand l'incident survient, pour atteindre cette réactivité,
les exploitants commencent leur intervention directement au début de
l'origine des temps considéré. Donc à 6 heures dès
leur prise de service. Ils doivent systématiquement faire l'inventaire
des équipements. Le chef service exploitation quant à lui doit
commencer son travail 5 minutes après que les exploitants aient
commencés. Le chef service maintenance lui doit faire son intervention 9
minutes après celui des exploitants et 4 minutes après celui du
chef service exploitation.
Il est à noter que cette modélisation nous
permet d'effectuer un gain de 5 minutes sur le temps de réaction. Et que
ce temps est le même pour les évènements de la même
classes. Ces classes sont donc déterminées en fonction du temps
mis pour implémenter la solution : c'est en fonction de la
gravité de l'ENS.
Modelisation du temps de reaction d'un systeme industriel :
Application aux centrales thermiques
d'OYOMABANG I et II .
V.4. Traitement évènementiel.
Comme nous l'avons présenté plus haut dans le
traitement évènementiel, il n'est pas question de perdre de
temps, il faut agir immédiatement. Pour cela, nous allons utiliser la
modélisation précédente, mais en supprimant tous les temps
d'attentes. Pour l'optimisation du temps de réaction dans ce cas, nous
allons ajuster les di,G en supprimant également les
étapes qui ne sont pas nécessaires.
V.4.1. Suppression des temps
d'attentes.
Nous avons :
Dn = (? LN0-1? je{1,3,4} dij + ?
je{1,3,} d2N ,j) + ? .-Ivo 42 (V -5)
En évènementiel, ?
i_No dc2=0. On peut donc avoir dans notre cas
:
Dn = 222
V.4.2. Ajustement des temps des différentes
étapes.
Dans la suite nous allons présenter les
différentes étapes et leurs ajustements en traitement
évènementiels. Ainsi à partir du tableau 5 qui fait un
inventaire de la manière de traiter des incidences qui sont en fait des
ENS qui nécessite un traitement évènementiel, nous
pouvons, recenser les différentes actions menées par les agents
de la centrale lorsqu'un ENS survient et interrompt la production :
ü Arrêt d'urgence de l'installation (consignation et
balisage pour les groupes) : cette action se fait de façon
immédiate après constation de la défaillance.
ü Information de la hiérarchie et du Grid dispach :
cette action se fait par les moyens de communication qui sont disponibles dans
la salle de commande.
ü Appel des personnes astreintes pour intervention : les
personnes en astreintes ont une marge de 15 minutes avant de s'y rendre, pour
l'intervention, car la majorité des agents habitent dans le quartier ou
se trouve la centrale.
|
: Etape E1
|
|
: Etape E3
|
: Etape E4
|
|
|
|
constatation de l'ENS. Cette étape peut prendre 1
minute
|
Le temps d'attente est nul
|
rédaction de la DI par le chef de quart cela peut prendre
3 minutes
|
Information des différents responsables et des
personnes astreintes cela peut se faire en 5 minutes.
|
Sous-processus1 (SP1)
|
|
Le temps d'attente est nul
|
|
|
Sous-processus2(SP2)
|
|
Le temps d'attente est nul
|
|
C'est le temps ou le chef service de la maintenance donne des
instructions aux personnes astreintes. 2 minutes
|
Sous-processus3(SP3)
|
Le temps ou l'on attend l'arrivée des personnes
astreints environ 15 minutes
|
Le temps d'attente est nul
|
Elaboration de la fiche d'analyse de risque. Environ 3
minutes
|
|
Sous-processus4(SP4)
|
Validation du permit de travail
provisoire par le chef de quart 1 minutes.
|
Le temps d'attente est nul.
|
Traitement de la défaillance par les équipes
techniques. Cette action dépend aussi de la gravité de la
défaillance. Nous prendrons 180 minutes.
|
|
|
Tableau 15 : activités dans les
sous-processus en traitement événementiel.
Modelisation du temps de reaction d'un systeme industriel :
Application aux centrales thermiques
d'OYOMABANG I et II .
Après nous avons alors la nouvelle configuration suivante
:
Sous-processus(i)
|
Durée E1 (di, 1)
|
Durée E3 (di, 3)
|
Durée E4 (di, 4)
|
0
|
1
|
3
|
5
|
1
|
/
|
/
|
/
|
2
|
/
|
/
|
2
|
3
|
15
|
3
|
/
|
4
|
1
|
180
|
/
|
|
Tableau 16 : temps d'activite dans les
sous-processus en traitement
evenementiel.
Nous avons alors le nouveau temps de réaction :
Dn = 210
V.5.Implémentation de la réactivité
aux centrales thermiques d'Oyomabang I et II.
V.5.1. analyses des causes de non
réactivité et des leviers d'actions
Cette analyse a été faite à partir des
analyses des rapports d'incidences, et des cahiers de programmation des travaux
mécaniques. Nous avons également pris en compte les
réponses des questions que les chefs de quart, ont bien voulu nous
accordé relatif aux traitements des incidences. Nous allons utiliser un
diagramme d'ISHIKAWA, qui est un diagramme causes-effets. Ce dernier nous
permettra de déceler les causes de retards d'intervention suite à
un ENS qui survient. Nous avons donc le diagramme d'Ishikawa ci-après
:
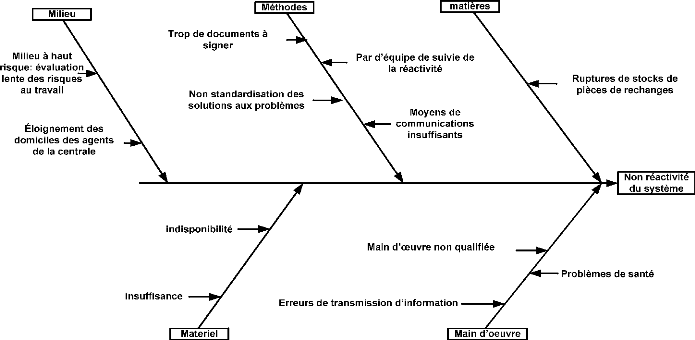
Figure 32: diagramme d'Ishikawa
Modelisation du temps de reaction d'un systeme industriel :
Application aux centrales thermiques
d'OYOMABANG I et II .
V.5.2. amélioration de la
réactivité
La centrale pourrait mettre sur pied un groupe (constitué
de 2 membres de chaque services) de suivi et d'amélioration de la
réactivité qui aura pour mission de :
ü Mettre sur pied les indicateurs de performances de
réactivité
ü Mettre sur pied un système d'information fiable,
notamment concevoir des tableaux de bord et les mettre à la disposition
des agents.
ü Classer les différents incidents et travaux en
fonction de leur gravité et des solutions proposés pour faciliter
le passage du réfléchi au reflexe.
V.5.2.1. Indicateurs de performances de
réactivités
A partir de l'objectif principal qui est de diminuer au
maximum le temps de réaction du système suite à un
évènement non souhaité pouvant ainsi perturber, production
à la demande du Grid dispach des 18MW pour la centrale d'Oyomabang I et
des 13MW pour la centrale d'Oyomabang II. Ainsi le tableau qui suit
présente, l'identification des objectifs, des variables de
décision et des indicateurs de performance : c'est un tableau GRAI.
|
Contrôle de réactivité
|
|
Objectifs
|
· Assurer le respect des instructions assurant une
meilleure réactivité
|
Variables de décision
|
· La Disponibilité des tableaux de bord
d'informations affichés dans l'entreprise,
· Le niveau de formation et de professionnalisme des
ressources humaines,
· Une bonne stratégie de transfert du
réfléchi au reflexe
|
Indicateurs
|
· Délai de réaction en fonction de la
gravité des évènements.
|
Evaluer la fiabilité des ressources
|
Objectifs
|
· S'assurer du bon état des équipements de la
centrale
|
Variables de décision
|
· Contrôle des équipements
|
Indicateurs
|
· Indice de fiabilité des équipements
· Taux de visites techniques en cours de validité
|
Opérations de maintenance
|
Objectifs
|
· Assurer la maintenance des équipements
|
Variables de décision
|
· Ampleur des activités de maintenance
|
Indicateurs
|
· Taux d'opération de maintenance ;
· Temps de maintenance.
· Taux de défaillance des équipements
|
|
Tableau 17 : identifications des indicateurs de
réactivités.
Modelisation du temps de reaction d'un systeme industriel :
Application aux centrales thermiques
d'OYOMABANG I et II .
V.5.2.2. descriptions des indicateurs de
performances.
> Délai de réaction en fonction
de la gravité des évènements. :
présente les différents incidents que l'on peut rencontrer par
équipement et leur temps de réaction, estimé tel que
présenté plus haut. Ainsi, l'on pourra avoir des tableaux tels
que ci-dessous correspondant à Chaque classe d'évènement
non souhaité:
|
équipement
|
Description
|
Causes de la
|
Solution à cette panne
|
Ressources
|
Temps de
|
Nombre de
|
|
de la panne
|
panne
|
|
humaines
qualifiées
|
réaction (min)
|
fois survenu
jusqu'à lors.
|
|
GRP 101
|
Déviation base
moyenne température cylindre B7
|
Raccord de
fixation pipe
d'alimentation dévissé
|
Imbibition de provalent au niveau des cylindres
concernés
|
exploitants
|
15
|
5
|
|
GRP 103
|
Fuite de
combustible au niveau du pipe
principale
|
Vis du
distributeur de
fioul desserrées
|
Imprégnation de
provalent au niveau du hot box
|
mécaniciens
|
165
|
2
|
Tableau 18 : fiche d'identification et de traitements
des ENS
> Les indicateurs de performances concernant la
fiabilité des équipements et de la maintenance, permettent de
mettre sur pied des réactions prédictives. Pour y parvenir l'on
peut faire une analyse FMD qui a pour objectif d'identifier les
équipements vitaux, importants et secondaire. Nous pouvons alors
définir un tableau tel que ci-dessous, qui montre un aperçu des
arrêts machine et la durée associée d'une part ; d'autre
part les pertes en termes de production. Elles peuvent être
évaluées à partir des heures de non production et de la
production horaire moyenne.
|
Equipement
|
Nombre de
défaillances (BM)
|
Durée totale
(heures)
|
Durée Moyenne
(hrs/panne)
|
Perte en terme s production de
(MWH)
|
|
GRP 101
|
35
|
109
|
3,12
|
16 218,7
|
|
GRP 103
|
57
|
64
|
1,12
|
9 476,8
|
|
|
|
|
|
|
TOTAL
|
|
|
|
25695,5
|
Tableau 19 : analyse FMD de la
centrale.
Modelisation du temps de reaction d'un systeme industriel :
Application aux centrales thermiques
d'OYOMABANG I et II .
V.5.2.3. contributions.
Il
est important de noter que, d'après notre étude, la centrale se
comporte plutôt bien en
traitement périodique car le gain en temps de
réaction n'est que de 5 minutes sur une durée de traitement de
120 à 180 minutes. Par contre il y a beaucoup à faire en
traitement évènementiel. Hors mis la modélisation faite
qui nous permet de gagner près de 30 minutes sur le traitement de 120
à 180 minutes, nous allons proposer dans la suite un ensemble de mesure
qui permettront d'améliorer de façons continuelle la
réactivité de la centrale.
Dans le paragraphe précédent, nous avons
définit les causes de non réactivités du système.
Dans
la suite, nous allons proposer quelques solutions pour palier à
ces difficultés. Nous avons ainsi :
Les fiches que nous proposons précédemment, nous
permettent de résoudre simultanément les problèmes de
méthodes et une partie des problèmes de ressources humaines.
Cette actions permet de réduire de prime abord au moins 4 minutes du aux
rédactions des différents documents et surtout de réduire
le temps de diagnostique de la panne que nous ne pouvons pas estimer avec
précision, mais on peu évaluer ses gain à plus de 10
minutes.
Les indicateurs de performances qui permettent de mettre sur
pied des réactions prédictives, résolvent le
problème d'indisponible, d'insuffisance et de rupture de stocks du
matériel de rechange.
Par contre les personnes en astreintes peuvent rester dans la
centrale et travailler dans les périodes de pointe (18H-22H30) pour
réduire le temps d'attentes du départ de chez eux jusqu'à
la centrale. Pour assurer leur sécurité un véhicule peut
les raccompagner dans leurs domiciles respectifs. Cette action peut nous
permettre de réduire 15 minutes dans le traitement
évènementiel.
On se rend bien compte qu'en mettant sur pied ses mesures l'on
peut encore gagner au moins 29 minutes dans le traitement
évènementiel de 120 à 180 minutes.
Modelisation du temps de reaction d'un systeme industriel :
Application aux centrales thermiques
d'OYOMABANG I et II .
| 


