Etude de l'influence des efferts d'echelle dans le modele de Dugdale

UNIVERSITE SAAD DAHLEB DE BLIDA

Faculté des Sciences de l'Ingénieur
Département de Génie Mécanique

MEMOIRE DE MAGISTER

Spécialité : Construction

ETUDE DE L'INFLUENCE DES EFFETS D'ECHELLE DANS
LE MODELE DE DUGDALE À TRAVERS LE CAS D'UNE
BANDE INFINIE SOUMISE À UN CHARGEMENT
ANTI PLAN

Par

BRICK CHAOUCHE Amine

Devant le jury composé de

M. OUALI Professeur, U. de Blida Président

A. AIAD Maître de conférence, U. de Blida Examinateur

K. AZOUAOUI Maître de conférence, U. de Bab Ezzouar Examinateur

H. FERDJANI Maître de conférence, U. de Blida Rapporteur

RÉSUMÉ

Le but de ce travail est de montrer, dans le cadre de la mécanique de la rupture avec le modèle de rupture de Dugdale- Barenblatt, ou de façon plus générale, les modèles de forces cohésives, que les défauts de petite taille devant la longueur caractéristique du matériau ont pratiquement peu d'influence sur les capacités de résistance d'une structure. On traite pour cela l'exemple d'une bande contenant une fissure parallèle à la face supérieure, en résolvant une équation intégrale singulière obtenue par conversion analytique des équations d'élasticité, la résolution de fait en utilisant les polynômes de Chebyshev.

&'()

L, 1234.2 bHA 4)J^,M) _N(O90@K9*+ ,-. (J0. 1234.2 5621 713834.2 790:;.2 <30=.2 Û+ ?^,@*A 3B CD2EF.2 bHA I) JF-.2
~ DUGDALE CP9QR S^,4=TD^,U V.W
~ \3(=.2 ,-]^_. \`23) ab _N(O \3T]c i=Ut1 0B^,eTQ 90f C]0gh C.^,i CD2E1 _jT0D
\1F=T) _N(O FQ:Jti 404kJ CMP9^U J]J2 C4* I) L ~ C0(0(]c CMP)L. V.W L ÛJ2J c CJi=Q _N.AÛJ2JT.24.1^,=) JzJ]c _jT0
·
·
·
.Chebyshev 1LF].2

ABSTRACT

The goal of this work is to prove that, within the framework of Fracture Mechanics with the cohesive forces model, or Dugdale- Barenblatt model, the defects the size of which are small compared to the material characteristic length are practically without influence on the limit loads of the structure. For that we treat the case of an infinite strip containing a Dugdale crack parallel to its boundaries. The problem is formulated in term of a singular integral equation obtained by transforming analytically the equations of elasticity. The resolution is done using Chebyshev polynomials.

TABLE DES MATIERES

REsUMEtttttttttttttttttttttttttttttttt. (¹) TABLE DEs MATIEREsttttttttttttttttttttttt.tt.. (⁴) LIsTE DEs sYMBOLEs ttttttttttttttttttttttttt.. (⁶) INTRODUCTIONttttttttttttttttttttttttt.ttt.. (⁹)

1. ETUDE BIBLIOGRAPHIQUE tt.tttttttttttttttt....tt. (¹⁵) 1.1 Introductionttttttttttttttttttttttt..tt..t... (¹⁵) 1.2 Lois d'interface des modèles de force cohésive (¹⁵)

1.2.1 Modèle de Dugdaletttttttttttttttttt.tttt (¹⁶)

1.2.2 Modèle de Dugdale régularisétttttttttttttt.tttt (¹⁷)

1.2.3 Modèle de Needlemanttttttttttttttttttttt. (¹⁸) 1.2.4 Modèle de Tvergaardttttttttttttttttt.tttt.. (²⁰) 1.3 synthèse des travaux de Ferdjani et altttttttttttttt..ttt. (²¹)

1.3.1 Cas d'une plaque pré fissuré ou trouéttttttttttt..tt.tt (²¹)

1.3.2 Modèle de Dugdale tttt..ttttttttttttt..ttt.t (²²)

· Cas d'une fissure préexistantettttttttttttt...tttt.. (²²)

· Cas d'une cavité circulairettttttttttttttt..tttt (²⁵)

1.3.3 Modèle de Dugdale régulariséttttttttttttt.tt.ttt (²⁹)

1.4. Demi plan contenant une fissure rectilignetttttttttttt.ttt (³²)

2. Position du problème traitéttttttttttttttttttt..t..ttt (⁴⁰)

2.1 La phase cohésivetttttttttttttttttttttt..ttt (⁴³)

2.2 La phase propagationttttttttttttttttttt.tt.ttt (⁴⁵)

2.3 Conclusionttttttttttttttttttttttt.ttt.tt (46)

3. Dérivation de l'équation intégrale.................................................................	(^47)
3.1 Introduction	(^47)
3.2 Les données de la transformation	(^47)

3.3 Démonstration de la convergence uniforme de l'intégrale I............................... (⁵³)

3.4 Conclusion.......................................................................................	(^55)
4. Résolution de l'équation intégrale.................................................................	(56)		4.1 Introduction.......................................................................................
(^56)	4.2 Résolution........................................................................................
(^56)	4.2.1 Introduction des quantités normalisées...............................................
(57)

4.2.2 Application de la méthode de résolution standard des équations intégrale...... (58)

4.2.3 Évaluation numérique des différentes intégrales.................................... (⁶⁰)

4.2.4 Evaluation numérique de L(r, s)..................................................... (60)

4.3 Formule donnant le facteur d'intensité de contrainte.......................................	(^63)
4.4 Formule donnant l'ouverture de la fissure...................................................	(^63)
4.5 Etude de convergence............................................................................	(^64)

4.6 Etude du cas de fissure dans un milieu infinie...............................................(66)
4.6.1 Equation intégrale.........................................................................(66)
4.6.2 Phase cohésive.............................................................................(67)
4.6.3 Contrainte de rupture.....................................................................(68)
4.6.4 Phase de propagation.....................................................................(68)
4.7 Conclusion .......................................................................................(69)

5. Présentation des résultats........................................................................... (^70)			5.1 Introduction (^70)
		5.2 La phase cohésive
(^70)		5.3 La charge de rupture
(^72)		5.4 La phase de propagation
(^72)		6. Conclusion (^74)
Bibliographies (75)

LISTE DES SYMBOLES

ö : Densité d'énergie de surface.

[[u_n ]] : saut de déplacement normale (ouverture de la fissure) en mode I pure.

G : Taux de restitution d'énergie. G_c : Taux de restitution d'énergie critique.

Ô₀ : Le saut critique de décohésion.

Ô, : Déplacement tangentiel.

Ô_c : Ouverture critique de rupture (caractéristique des modèles cohésive).

Ô_n : Discontinuité du déplacement normale.

a_c : Contrainte critique (caractéristique du matériau).

a_n : Contrainte normale d'interaction entre les lèvres de la fissure.

a, : Contrainte tangentielle.

/₀ : Position de la pointe de fissure initial (ou diamètre du défaut initial dans le cas de trou) /a : Position de la zone non cohésive.

/c : Position de la zone cohésive.

/cc : Position de la zone cohésive continuum.

L : Largeur de la plaque fissuré.

F : La fissure.

F_n : Partie non cohésive de la fissure.

F_c : Partie cohésive de la fissure.

F_c : Partie cohésive continuum de la fissure.

a_co :Charge appliquée.

x₁ : Direction parallèle a la fissure.

x₂ : Direction normale a la fissure.

x₃ : Direction perpendiculaire a la plaque.

K₁ : Facteur d'intensité de contrainte en mode I.

vi : Potentiel.

SI : Domaine de la plaque fissuré.

D: La fissure (défaut).

yl_c :Longueur caractéristique qui se déduit de l'ouverture critique ê_c et les constantes

matérielles.

E: Module de young.

y : Coefficient de poison. p : Module de cisaillement.

a_a :Charge d'amorçage de la fissure. a,.: Charge de rupture.

q(x₁) :Répartition des contraintes normales exercées sur les lèvres de la fissure. h: Profondeur de la fissure.

²co : Contrainte de cisaillement appliquée.

x₃ :Direction normale a la plaque.

W : Champ de déplacement.

u_x : La réponse élastique (le champ de déplacement).

u₁ : Composante du déplacement dans la direction 1.

u₂ : Composante de déplacement dans la direction 2.

u₃ : Composante de déplacement dans la direction 3.

n : La normale a la plaque.

2 : Champ de contrainte dans le domaine SI .

2_c : Contrainte tangentielle critique (caractéristique du matériau).

2₂₃ : Contrainte de cisaillement appliquée sur les lèvres de la fissure dans la direction x₃ . 2₁₃ : Contrainte de cisaillement appliquée sur les lèvres de la fissure dans la direction x₁ . Ir_c : Domaine fissuré.

K₃ : Facteur d'intensité de contrainte en mode III.

ô(x_i ): Chargement en fonction de x_v .

t : Variable caractérisant la direction x,bornéesur l'intervalle [- l_a,l_n] résulte des

transformations intégrale.

k(x_i , t) : second partie du premier terme de l'équation intégrale appelée le kernel. ø(t) : Fonction de densité d'énergie.

T_n : Polynômes de Chebychev du premier ordre.

w : Fonctions poids associés aux polynômes de Chebychev du premier ordre. U_n: Polynômes de Chebychev de second ordre.

N :Nombre d'équation du système d'équations algébrique obtenu par application de la méthode de collocation sur l'équation intégral.

r. : Points de collocation.

tk :Noeuds.

n: Nombre de noeuds.

9

INTRODUCTION

L'objet de la mécanique de la rupture est de déterminer l'évolution d'une ou plusieurs fissures dans une structure en fonction du chargement auquel elle est soumise. Le cadre de la mécanique de la rupture fragile se limite à l'étude de la fissuration des milieux continus supposés élastiques. Cette hypothèse, bien qu'idéaliste, reste le cadre d'étude de nombreux chercheurs et ingénieurs préoccupés de sûretés concernant la propagation de défauts dans les structures en service. C'est le cadre des travaux de LAVERNE [33].

Dans ce formalisme, les principaux résultats ont été obtenus à partir de la théorie de GRIFFITH. Ce dernier associe à toute fissure une énergie de surface proportionnelle à sa longueur. Il postule qu'il y aura propagation et donc augmentation de l'énergie de surface si cette dernière est parfaitement compensée par la restitution de l'énergie élastique causée par l'avancée de la fissure. Dans le cas de problèmes quasi-statiques, ce critère peut se formuler en terme de taux de restitution d'énergie élastique usuellement noté G. Ce dernier correspond à la variation d'énergie potentielle lors d'un accroissement infinitésimal de la fissure. Le critère de GRIFFITH stipule alors qu'il n'y aura pas propagation tant que :

G < G_c

Ou G_c désigne le taux de restitution d'énergie critique et correspond à la ténacité du matériau.

Bien qu'elle connaisse encore un vrai succès, cette théorie renferme des insuffisances notoires.

- La première concerne l'initiation de la fissuration, la théorie de GRIFFITH est incapable de rendre compte de l'amorçage de fissures, sauf dans des cas très particuliers ou la structure possède des singularités fortes. En effet, prenons l'exemple d'un milieu bidimensionnel contenant une fissure rectiligne Z, sollicitée en mode I, et supposons l'absence de singularités dans le problème d'élasticité initiale. Le critère de

10

GRIFFITH prévoit que la fissure se propage pour un chargement en 1 / . Si / tend

vers zéro, on en déduit que pour un milieu sain la fissure ne pourra pas s'amorcer sous un chargement fini.

- La seconde lacune porte sur son incapacité à prédire seule le trajet spatial des fissures. Pour un milieu bidimensionnel, le critère ne prend en compte que la longueur de fissure or l'évolution spatiale nécessite une seconde information qui correspond à un critère de branchement.

- Enfin, une troisième lacune concerne le trajet temporel de la fissure, seules les propagations progressives sont traitées de façon satisfaisante. En effet des situations ou l'inégalité du critère est violée peuvent survenir. Celles-ci correspondent au cas de figure ou l'excès de restitution d'énergie élastique conduit à l'apparition d'énergie critique. La propagation est alors considérée comme brutale.

On peut résumer ces trois points en disant que le problème majeur de la théorie de GRIFFITH est de ne pas laisser assez de souplesse à l'évolution spatio-temporelle des fissures. De nombreux aménagements tentent d'y remédier proposant des ingrédients spécifiques à chacun des problèmes [33].

Le modèle de rupture de DUGDALE- BARENBLATT ou de façon plus générale les modèles de forces cohésives présentent l'avantage [33], sur le modèle de GRIFFITH, de rendre compte de l'amorçage de fissure dans une structure saine en termes d'un critère en contraintes, cf. par exemple DEL PIERO (1999) [12], DEL PIERO et al. (2001) [13], CHARLOTTE et al. (2000) [7] ou LAVERNE et al (2004) [34]. De façon générale, les modèles de force cohésifs sont de plus en plus employés et il est donc nécessaire de connaitre de mieux en mieux leurs propriétés pour pouvoir les utiliser à bon escient. En particulier les effets d'échelle qui les accompagnent du fait de la présence d'une longueur caractéristique sont mal connus. Il ne s'agit évidement pas ici de valider le modèle de DUGDALE, ni de voir pour quel type de matériau il peut être utilisé, mais de voir s'il est assez robuste pour que, grâce aux effets d'échelle qu'il induit, la réponse des structures ne soit pas sensible à des défauts de petite taille. L'étude sera donc essentiellement théorique et numérique. De plus, nous envisagerons seulement des zones cohésives linéiques [19].

				11
		Griffith Dugdale

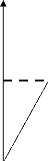
0

G _c

S_c [[u_n]]

Densités d'énergie de surface dans les modèles de Dugdale et Griffith

Ces modèles, formulés en termes énergétiques, consistent à supposer que la densité d'énergie de surface 0 dépend de façon non triviale du saut de déplacement [[u_n ]],

contrairement au modèle de GRIFFITH ou elle est constante. Ainsi dans le modèle de DUGDALE, en supposant que l'ouverture se fait en mode I pur, elle s'écrit :

=S_c
=S_c

0 = G

c .

(nu n11) I [[uSnli si [[u nli

c _{rr Ti}

G_c si L'u_ni]

[[u_n ]]désigne le saut du déplacement normal, G _c représente le taux de restitution d'énergie critique de la théorie de GRIFFITH, alors que S_c est une longueur interne caractéristique des modèles de forces cohésives. Le rapport G _c S_c a la dimension d'une contrainte et représente la contrainte critique du matériau :

=

G_c

a .

c

S_c

En termes de forces cohésives, la contrainte normale a_n d'interaction entre les lèvres de la
fissure vaut donc a_c tant que [[u_n ]] < S_c et s'annule dés que [[u_n ]] > S_c . En pratique, les lèvres
des fissures sont donc divisées en deux zones : une zones dite cohésive dans laquelle les

forces cohésives ne sont pas nulles et une zone dite non cohésive dans laquelle il n'y a plus de force cohésive. La zone cohésive se situe près de la pointe, là ou l'ouverture ne dépasse pas le seuil critique ä_c [19].

Le fait que a_cjoue le rôle de contrainte critique se vérifie dans l'étude d'une barre en

traction simple. En raisonnant comme DEL PIERO (1999) [12] ou CHARLOTTE et al.
(2000) [7] à partir d'un principe de minimisation d'énergie, on montre que la réponse
élastique (le champ de déplacement est de la forme u(x) = axlE,E étant le module d'Young)

cesse d'être un minimum relatif de l'énergie (totale) de la barre lorsque la contrainte
appliquée a dépasse la contrainte critique a_c . La conséquence directe de cette présence d'une

contrainte critique dans le modèle est qu'une structure donnée ne pourra pas supporter n'importe quel niveau de chargement conformément aux résultats classiques des théories de calcul à la rupture ou d'analyse limite, cf. SALENCON (1983) [40]. Cependant il y a lieu de distinguer les charges limites élastiques, i.e. les charges à partir desquelles doit développer une fissuration, des charges limites proprement dites, i.e. des charges maximales que peut supporter la structure même en se fissurant. Dans la suite nous désignons les premières comme charges d'amorçage et les secondes comme charges de rupture [19].

Rappelons tout d'abord ce qu'il en est de la charge d'amorçage dans le cas du modèle de GRIFFITH. Notons que seuls les défauts du type fissure, i.e. les défauts présentant une

singularité « forte » en r pour le champ des déplacements, sont susceptibles de se propager.
Les cavités, les entailles et autres défauts non assez « pointus » induisent une singularité trop
faible pour donner un taux de restitution d'énergie non nul. Pour une fissure de petite taille 1

et de normale n, placée en un point x où les contraintes normales en l'absence du défaut

seraient d'amplitude a, le taux de restitution d'énergie est de l'ordre de a²1. Il tend donc vers
0 lorsque 1tend vers 0. Donc, dans la théorie de GRIFFITH ou les fissures ne se propagent que
si le taux de restitution d'énergie atteint la valeur critique G_c, les défauts de petite taille sont

inoffensifs. C'est évidement un atout pour ce modèle. Mais en contrepartie, le modèle de GRIFFITH est trop conservatif puisqu'il ne sait pas rendre compte de l'amorçage de fissures en dehors de points de fortes singularités, cf. FRANCFORT et al. (1998) [25].

Si l'on abandonne le modèle de GRIFFITH au profit du modèle de DUGDALE, le critère de propagation d'un défaut ou d'amorçage de fissure ne se formule plus en termes du taux de restitution d'énergie critique G_c, mais en termes de la contrainte critique a_c, cf.

CHARLOTTE et al. (2000) [7] et LAVERNE et al. (2004) [34]. Ce faisant, on pourrait a

priori s'attendre à ce que la forme des défauts joue un rôle essentiel et que ceux favorisant les concentrations de contraintes s'avèrent plus nocifs. En particulier les fissures, défauts qui induisent des singularités, devraient être sensiblement plus défavorables que les cavités circulaires, défauts qui par leur forme «parfaite» sont ceux qui engendrent le moins de concentration. Ceci se révèle vrai pour la charge d'amorçage, mais faux pour la charge limite. En effet, il est clair que la charge d'amorçage est très sensible à la forme du défaut puisqu'elle est directement liée aux concentrations des contraintes induites par le défaut sur la réponse élastique. Ainsi, dans le cas d'une fissure préexistante, du fait de la présence d'une singularité de contraintes en pointe de fissure, la charge d'amorçage est nulle, de nouvelles discontinuités apparaissent dès la mise en charge. Par contre, dans le cas d'un trou circulaire dans une plaque, la concentration de contraintes est finie et donc la charge d'amorçage n'est pas nulle.

Nous verrons par contre que la charge de rupture, elle, est beaucoup moins sensible à la forme du défaut qu'à sa taille. En particulier, du fait de la présence de la longueur caractéristique ê_c dans le modèle de DUGDALE-BARENBLATT, les effets d'échelle sont

importants. La charge de rupture dépend de façon essentielle du rapport entre la taille du
défaut et la longueur caractéristique ê_c . Un résultat majeur serait de montrer que, quelle que

soit la forme du défaut, la charge de rupture tend vers la contrainte critique a_c lorsque la taille

du défaut tend vers 0, à longueur caractéristique fixée (ou de façon équivalente, lorsque la
longueur caractéristique ê_c tend vers l'infini, a taille du défaut fixée). Ceci signifierait qu'avec

le modèle de DUGDALE-BARENBLATT, les structures sont insensibles aux petits défauts et se comportent comme des structures saines, et ce bien qu'elles développent des zones d'amorçage avant rupture [19].

Ce résultat a été obtenue par FERDJANI et al [19], [20] pour une plaque contenant une fissure droite ou une cavité circulaire soumise a une traction simple est pour les modèles de DUGDALE et DUGDALE régularisés, et pour un milieu semi-infini contenant une fissure droite [21] soumise à un cisaillement anti-plan, pour le modèle de DUGDALE.

Dans le but de généraliser le résultat obtenu, on propose d'étudier le problème antiplan d'une bande infinie isotrope contenant une fissure cohésive parallèle à la face supérieure de la bande et localisée au milieu. Le modèles de DUGDALE-BARENBLATT (DUGDALE, 1960 [15]) est utilisé pour modéliser l'interaction entre les lèvres de la fissure. En utilisant les transformations de fourrier, les équations d'élasticité sont converties analytiquement en une équation intégrale singulière. A cause de la présence de saut des discontinuités dans la distribution du chargement le long des lèvres de la fissure, les méthodes standard de

résolution de l'équation intégrale singulière obtenu, ne sont pas appropriées. On utilise la méthode proposée par (IOAKIMIDIS, 1980 [32]) pour traiter ce type de chargement.

Ce mémoire est organisée comme suit, le premier chapitre est consacré a la recherche bibliographique et contient une présentation générale des modèles de forces cohésives, suivi d'une présentation des travaux de FERDJANI et al. Le chapitre 2 contient la présentation du problème traité. Le chapitre 3 est consacré à l'établissement de l'équation intégrale puis à la résolution. Le chapitre 5 est consacré à l'exposé des résultats des calculs. Enfin, une conclusion générale.

CHAPITRE 1
ETUDE BIBLOGRAPHIQUE

1.1 Introduction :

Nous commençons par présenter une synthèse des différents modèles de forces cohésives présentes dans la littérature.

1.2 Lois d'interface des modèles de force cohésive [33]:

On appelle loi d'interface une relation entre le déplacement relatif et la force d'interface entre les lèvres d'une fissure. Dans cette partie nous présenterons quelques unes d'entre elles basées sur la notion de force cohésive. Cette dernière s'appuie sur des observations expérimentales en pointe de fissure telles que l'apparition de micro fissures, la croissance de cavité ou le développement de zones de plastification. Cela correspond à une zone de transition entre le milieu sain et une vraie fissure (figure 1.1).

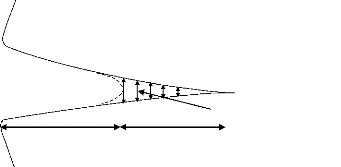
Interaction (forces cohésives)

Fissure Zone cohésive

Figure 1.1 : Schéma de la fissure et de la zone cohésive.

Les premiers modèles furent introduits par DUGDALE et BARENBLATT au début des années soixante. Prenant acte du fait que les contraintes infinies en pointe de fissure, prédites par le modèle élastique (IRWIN [31]), n'ont pas de signification physique, ces derniers ont émis l'hypothèse de l'existence d'une «zone cohésive» (Fracture Process zone dans la littérature) dans laquelle des forces s'exercent entre les futures lèvres de la fissure. Dans les années soixante-dix HILLERBORG et al [30], ont introduit le concept d'énergie de rupture dans les modèles de force cohésive et proposé quelques relations de comportement entre la traction et le saut de déplacement pour le béton. De nombreux modèles ont été développés depuis, citons en quelques uns :

1.2.1 Modèle de DUGDALE [33]:

Ce modèle décrit l'évolution des forces de traction a_a en fonction du saut de déplacement normale 8_a . Le saut reste nul tant que la force n'atteint pas une valeur critique cr_a puis le comportement utilisé est celui d'un solide rigide parfait jusqu'à un seuil d'ouverture 8_a au- delà duquel l'interaction des lèvres devient nulle (Figure 1.2 et 1.3).

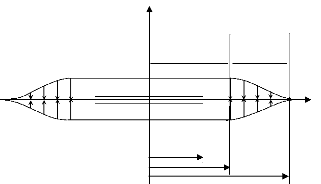
Zone
cohésive

Zone non
cohésive

cf_a

x₁

l_a

l₀

l_a

x₂

Figure 1.2. Schématisation du modèle de Dugdale-Barenblatt

cr aa

17

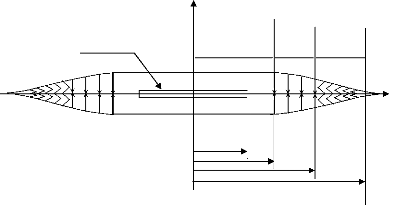
Fissure initiale

cr_a

Zone non cohésive

l₀

l_a

Zone
cohésive

l_a

Zone
cohésive
Continuum

x₁

0 8_a 8

Figure 1.3 . Loi d'interface de DUGDALE dans la direction normale.

1.2.2 Modèle de DUGDALE régularisé [20]:

C'est une combinaison entre le modèle des zones cohésives continuums (ZCC) (Xie [45]) et le modèle de DUGDALE (figure 1.4 et 1.5).

a,,

a_c

18

8₀ 8c nu ,,II

Figure 1.5. Loi de comportement dans le modèle de DUGDALE régularisé.

a_c désigne la contrainte critique du matériau, 8_c désigne la longueur caractéristique du modèle, et 8₀ désigne le saut critique de décohésion. La fissure est donc divisée en trois

zones représentées sur la figure 1.4.

La loi de comportement, donnant la relation entre les forces cohésives et l'ouverture des lèvres de la fissure, en supposant que l'ouverture se fait en mode I pur, est représentée sur la figure 1.5.

⁸,, Désigne la discontinuité du déplacement normale, _a,, désigne la contrainte normale

d'interaction entre les lèvres de la fissure.

1.2.3 Modèle de NEEDLEMAN [38] :

Ce modèle décrit l'évolution des forces cohésives normale _a,, et tangentielle a, en fonction des composantes normale et tangentielle du saut de déplacement 8,, et 8, . On

représente sur la Figure 1.6, l'évolution de la force normale en fonction du saut normal quand le saut tangent est nul.

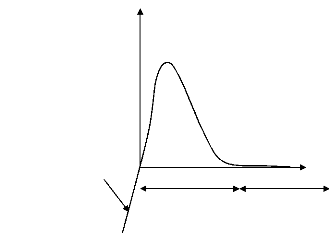
8_c

8,,

a,,

a_c

Pénalisation du contact

Zone cohésive Rupture

Figure 1.6. Loi d'interface de NEEDLEMAN dans la direction normale.

Les forces dérivent d'un potentiel y/ :

a y/

cr --

,, a8,,

,_t

a y/

.

cr = a8

t

Ce dernier est choisi comme une fonction polynomiale faisant intervenir les paramètres a_c contrainte critique du matériau en ouverture, 8_c saut critique au-delà duquel l'interface

entre les lèvres de fissure devient nulle ainsi que la part de résistance au glissement par
rapport à la résistance normale. On note que lorsque 8,, < 0 la valeur de la contrainte normale

dérive du potentiel joue le rôle d'une pénalisation afin de tenir compte de la condition de non interpénétration des lèvres de la fissure. Aucune autre hypothèse n'intervient pour prendre en compte cette condition. Notons que ce modèle fut repris et modifié par de nombreux auteurs. Citons par exemple RICE et WANG [39] qui ont proposé une expression exponentielle du potentiel. La différence avec le modèle précédent tient au fait que la force tend asymptotiquement vers zéro quand le saut de déplacement augmente. Ce modèle ne fait donc pas intervenir le paramètre 8_c .

1.2.4 Modèle de TVERGAARD [43] :

Ce modèle reprend le modèle de NEEDLEMAN de 1987 [38] et introduit une notion d'irréversibilité du comportement : la décharge s'effectue linéairement, ainsi qu'un frottement de COULOMB post décohésion. On représente sur la Figure 1.7 l'allure de la force tangentielle en fonction du saut tangentiel lorsque le saut normal est nul.

Notons que le modèle formulé initialement par l'auteur s'appuie sur un indicateur de décohésion variant de zéro à un, faisant intervenir le saut normé par le saut critique, et qui fait office de variable d'endommagement dont dépendent les forces d'interaction.

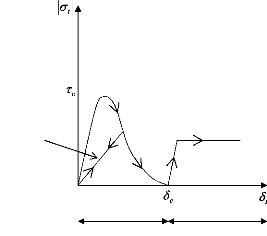
Frottement

0

Zone cohésive

Décharge

Figure 1.7. Evolution de la force tangentielle en fonction du saut tangent.

D'autres modèles ont été développés en s'inspirant de celui-ci. Par exemple, CHABOCHE et al (1997) [6], pour modéliser la décohésion interfaciale dans les composites à matrice métallique, proposent d'activer le frottement de COULOMB dés le début de la décohésion. Citons par ailleurs CHABOCHE et al qui reprennent ce dernier modèle et introduisent une régularisation visqueuse afin de lisser les instabilités intervenant dans l'ouverture brutale de fissure. La réponse dépend alors de la vitesse du chargement. Cette technique permet de remédier aux problèmes numériques liés à un saut de solution important difficile à capter avec des méthodes de type NEWTON. Cela permet d'avoir une réponse globale continue à tous les

niveaux de chargement mais cette technique modifie les équations de comportement de l'interface.

Notons par ailleurs que ces lois peuvent être utilisées soit pour décrire le comportement d'une interface : séparation de deux parties d'un solide comme la propagation de fissure (objet d'épaisseur nulle) soit pour représenter le comportement d'une interphase entre deux matériaux (objet volumique de faible épaisseur) pouvant représenter une colle. A ce sujet SUQUET [42] et MICHEL et al [37] ont travaillé sur la modélisation d'interphase dans les composites à matrice métallique. Ce type de modèle pose des questions de convergence mathématique du modèle d'interphase vers le modèle d'interface.

1.3 Synthèse des travaux de FERDJANI et al :

1.3.1 Cas d'une plaque pré fissurée ou trouée :

La structure consiste en une plaque carré de dimension SI = (-L,+L) sollicitée en traction et contenant un défaut centré D et soumis, sur les faces supérieure x₂ = +L et inférieure x₂ = -L à une traction uniforme d'intensité a₈ croissante depuis 0. Le défaut est soit une fissure préexistante perpendiculaire à l'axe de traction et de longueur 2/₀, soit un trou circulaire de rayon /₀ (figure 1.8). L'étude s'effectue dans le cadre des déformations planes

pour le modèle de DUGDALE, et de contraintes planes pour le modèle de DUGDALE régularisé, le matériau est linéairement élastique, homogène et isotrope.

-

L

L

x₁

x₂

a_

-

I_o

I_o

a_

Figure 1.8. Géométrie de la plaque contenant le défaut initial centré

1.3.2 Modèle de DUGDALE [19] :

L'étude consiste à montrer l'influence de l'effet d'échelle .i.e. du rapport

^Sc sur la

I_o

contrainte de rupture, pour des facilités de mise en ouvre numérique on garde une dimension constante du défaut et en fait varier l'ouverture critique S_c .

· Cas d'une fissure préexistante :

Le défaut initial est une fissure non cohésive de longueur 2I₀ (figure 1.8) La plaque est

supposée infinie. Pour cette étude, on se servira de la solution donnée par BUI (1978) [4] pour
une fissure cohésive de longueur 2I_a placée dans un milieu infini, soumise à l'infinie à une

traction simple d'intensité a_ dans la direction 2 et ayant a ces extrémités x₁ = #177;I_c une zone
cohésive dont les pointes sont en x₁ = #177;I_a. Les lèvres des zones cohésives sont soumises à

une contrainte normale de traction d'intensité constante a_a. On peut considérer que

l'approximation faite est d'autant meilleure que la taille du défaut est plus petite devant la taille du domaine. Le problème se réduit donc a un problème d'élasticité plane posé sur un domaine infini fissuré avec une distribution donnée de forces. Il se résout classiquement à l'aide de potentiel complexe suivant les techniques développées dans MUSKHELISHVILI (1963) [36].

Dans la phase d'amorçage, lorsque l₀ = l_a les contraintes sont singulières dans la réponse

élastique de la structure dés la mise en charge. Ceci mène à dire que la charge d'amorçage est
nulle a_a = 0 . Une zone cohésive de longueur l_a se développe dés la mise en charge. Le

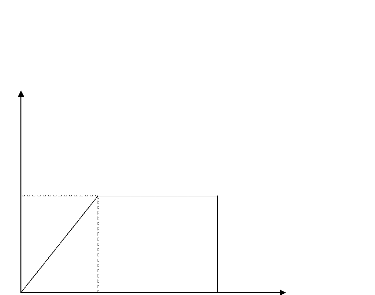
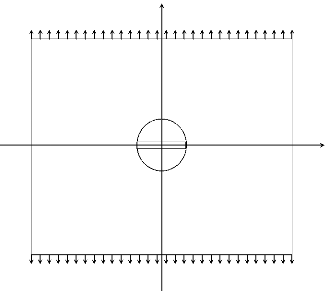
graphe représentant la charge appliqué a₈ en fonction de la position de la pointe d'amorçage l_a (figure 1.9) montre que la charge croit de 0 a a_a quand la zone cohésive croit de l₀a l'infini. Ceci est valable tant que l'ouverture en x₁ = l_a n'atteint pas la valeur critique ä_a la charge appliquée correspondante est appelé charge de rupture a,..

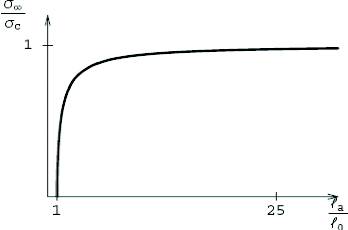
Figure 1.9. Relation entre la charge appliquée et la position de la zone
cohésive lors de la phase d'amorçage.

La phase de propagation commence lorsque l'ouverture en l_c atteint le saut critique 8_c .

Dans ce cas, on doit diminuer la charge si l'on veut que la propagation de la fissure soit stable. Ceci signifie que la charge de rupture a,. est en fait la charge limite que peut supporter la structure.

Dans un diagramme a_ -- l_a (figure 1.10) est représenté l'évolution de la fissuration avec

la charge pour une valeur donnée du 8_c . On notera que la longueur interne 8_c n'intervient que

dans la phase de propagation (et donc évidement dans la charge de rupture) la charge de rupture valent dans ce cas a,. = 0.76.a_c.

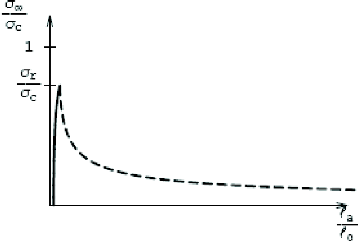
Figure 1.10. Relation entre la charge appliquée et la position de la zone cohésive :
En trait plain, lors de la phase d'amorçage, en pointillés lors de la phase de
propagation.

La charge de rupture dépend de façon essentielle du rapport entre la longueur l₀ du défaut initial et la longueur caractéristique 2_c (qui est proportionnelle à 8_c) du matériau, ceci est représenté dans un diagramme donnant la dépendance de la charge de rupture par rapport la taille relative de la fissure (figure 1.11), plus la taille relative du défaut est petite et plus la charge de rupture se rapproche de la contrainte critique a_c du matériau, et ce bien qu'il y'ait amorçage d'une nouvelle fissure dès la mise en charge. On peut donc conclure qu'avec la loi

de DUGDALE, la plaque est pratiquement insensible aux petits défauts initiaux de petite taille de type fissure.

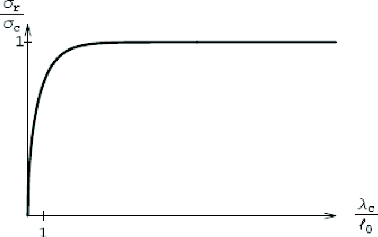
Figure 1.11. Dépendance de la charge de rupture avec la taille relative de la
fissure initiale.

· Cas d'une cavité circulaire :

Le défaut initial est une cavité circulaire de rayon 1₀ centré en (0,0) (figure 1.8) les données du problème sont :

La plaque est de dimensions 20 × 20mm .

Le rayon du trou est de longueur 1₀ = 1mm .

Le calcul est effectué avec la méthode des éléments finis.

Le domaine est maillé avec des éléments triangulaires a 3 noeuds (pour des raisons de symétrie et de conditions aux limites seul un quart du domaine et maillé), (figure 1.12).

Figure 1.12. Géométrie de la plaque trouée avec les zones cohésive et non
cohésives.

Pour les données matériau, on choisit celle d'un polymère PMMA : a_c = 72(MPa),E = 3000(MPa),í = 0.36.

Un calcul purement élastique mène à déterminer la charge d'amorçage a_a (la charge a₈ a partir de laquelle la plus grande contrainte principale atteint la valeur critique a_c en un point de la structure). Pour des raisons de symétrie et de conditions aux limites la concentration des contraintes a lieu au bord du trou aux points (#177;l₀,0) si la plaque été de dimension infinie, la contrainte a_n en ces points serait exactement égale a 3a₈ et la charge d'amorçage a a_c /3 = 24MPa. En raison des dimension finie de la plaque et des approximations numérique, la charge d'amorçage calculée a_a est égale a 22.2MPa.

Dans la phase de propagation, une zone cohésive apparaît et s'étend si l'on augmente la charge au-delà de a_a . La longueur de cette zone correspond a un facteur d'intensité de contrainte nulle 1(₁(l_a ) = 0 . D'un point de vue numérique, cela nécessiterait d'itérer sur la valeur de l_a , la stratégie numérique adoptée est la suivante :

1. On itère sur la valeur de l_a en partant de la valeur obtenu au pas précédant.

2. On calcule l'ouverture [[u_n ]]au noeud du maillage le plus proche de la pointe /_a.

3. Si cette ouverture est positive, alors on incrémente /_a et on arrête les itérations quand elle devient négative.

La charge de rupture est déterminée pour une langueur ë_c donnée, suivant un procédé basé sur une méthode itérative, les valeurs numériques calculées sont représentées dans un diagramme ó,. - ë_c (figure 1.13).

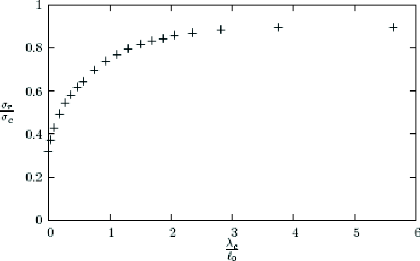
Figure 1.13. Dépendance de la charge de rupture avec la taille relative de la
fissure.

On remarque que la charge de rupture est une fonction croissante de ë_c , mais elle n'atteint jamais la valeur ó_c quelque soit la valeur de ë_c . Ceci est dû au caractère fini des dimensions de la plaque. En effet, en utilisant un raisonnement élémentaire de calcul à la rupture, il est facile de voire que la plaque trouée ne peut pas supporter une charge plus grande que

/

(1- ° L ).ó qui correspond à la charge d'équilibre de la plaque lorsque la zone cohésive

c

occupe toute la largeur. Compte tenu des valeurs numériques choisies, la charge de rupture ne

peut donc dépasser 0.9.a_a . On voit que cette valeur est pratiquement atteinte lorsque ë_a = 3l₀.

Notons enfin que si l'on faisait tendre la longueur du défaut vers 0 ou la largeur de la plaque vers l'infini, alors la charge de rupture tendrait vers a_a .

Un calcul de la phase de propagation effectué pour une position donné de la zone cohésive a permis de vérifier le résultat précédent concernant la charge limite, suivant un procédé itératif de détermination de la charge a_ équilibrant la structure fissurée avec la pointe de la

zone cohésive en l_a. Ceci a permet d'obtenir a_ en fonction de l_a pour un ë_a donné. Lorsque l_a = l₀ on a évidemment a_ = a,.. Il s'avère que dans tout les tests effectués a_ est une fonction décroissante de l_a , ce qui prouve bien que a,. est une charge limite et donc la charge

de la structure trouée. Les résultats obtenu pour cette phase sont présenté sur un diagramme
donnant la relation entre a_ et l_a pour une valeur de ä_a = 0.01mm (figure 1.14), la charge de

rupture valant 0.450a_a .

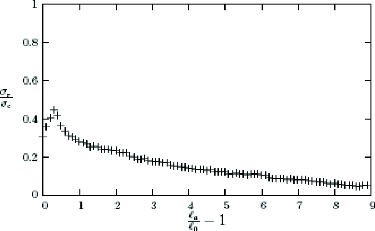
Figure 1.14. Relation entre la charge et la longueur de la fissure.

1.3.3 Modèle de DUGDALE régularisé [19]:

L'étude consiste a montrer l'influence de l'effet d'échelle .i.e du rapport

gc sur la l0

contrainte de rupture, pour des raisons de facilité de mis en ouvre numérique on garde une dimension constante du défaut et en fait varier l'ouverture critique g_c .

Comme donnés du problème nous choisissons: L =100(mm), l₀ =3(mm).

Pour le matériau celles d'un polymère PMMA. ó_c = 72MPa , E = 3000MPa , í = 0.36 . Le saut critique de décohésion g₀ = 0.00402(mm) .

Les calculs sont fait numériquement par la méthode des éléments finies pour les deux cas de fissure pré existante et de la cavité circulaire, le domaine est maillé par des éléments finis triangulaires a 3 noeuds (pour des raisons de symétrie un quart du domaine est maillé, figure 1.15) la ZCC est modélisé a l'aide d'éléments d'interface quadrangulaires d'épaisseur nulle.

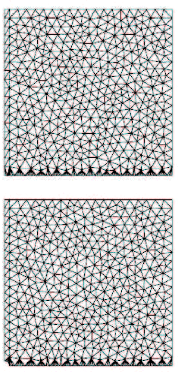
Figure 1.15. Maillage d'un quart du domaine pour le cas du trou et la fissure.

Comme énoncé précédemment, l'évolution de la fissure commence par la phase élastique la charge d'amorçage ó_a (ó₈ a partir de laquelle l'ouverture dans la ZCC en points ( #177; l_a ,0)

atteint le saut critique g₀ ), est obtenu en effectuant un calcul purement élastique est égale a

6.55MPa pour la fissure et a 9.36MPa pour le trou.

Au-delà de ó_a une zone cohésive apparaît c'est la phase d'amorçage. Les résultats de la

phase d'amorçage données pour le trou et la fissure sont sur la (figure 1.16).

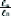
Figure 1.16. Relation entre la charge appliquée et la position de la zone cohésive
dans la phase cohésive.

On remarque que la charge dans cette phase est une fonction croissante de la longueur de la zone cohésive. En outre on observe que les courbes sont identiques, on peut conclure que la sensibilité de la phase d'amorçage à la forme du défaut est faible.

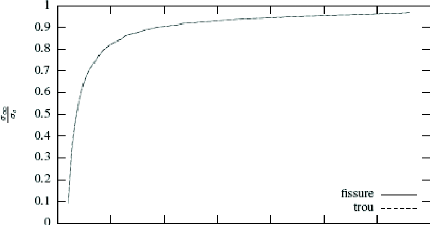
La charge de rupture ó est la contrainte appliqué correspondant a des ouvertures de la fissure [[u_n (#177;l ₀)]]= g_a et [[u_n (#177;l _a)]]= g₀ . Cette charge est déterminée pour une longueur caractéristique et pour plusieurs valeurs de la longueur caractéristique g_a (g₀ reste fixe). Les valeurs numérique calculées pour la fissure et le trou sont représentées dans un diagramme

a, -- 8_c (figure 1.17), comme attendu la charge de rupture est une fonction croissante de 8_c , on observe que la charge de rupture n'atteint jamais la valeur a_c quelque soit 8_c ceci est du aux dimensions finis de la plaque.

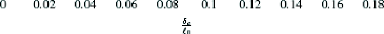
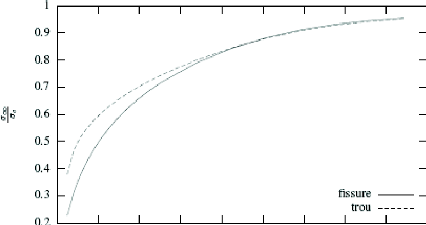
Figure 1.17. Relation entre la charge de rupture et la taille relative de la longueur
caractéristique 8_c .

En effet, en utilisant un raisonnement élémentaire de calcul à la rupture, il est facile de voir

~/

que la plaque trouée ne peut pas supporter une charge plus grande que 1-- 0 L a_c qui

correspond à la charge d'équilibre de la plaque lorsque la zone cohésive occupe toute la largeur de la plaque. Compte tenu des valeurs numériques choisies, la charge de rupture ne peut donc dépasser 0.97a_c . Notons enfin que si l'on faisait tendre la longueur du défaut vers 0 ou la largeur de la plaque vers l'infini, alors la charge de rupture tendrait vers a_c.

Il reste à prouver que la charge a, est réellement la charge maximale que la structure peut supporter. Peur ce faire, on fixe la valeur de la pointe cohésive /_c et on calcule la valeur de la charge a_et de la pointe cohésive /_a. Nous avons représenté sur la (figure 1.18) la relation entre a_ et /_a pour une valeur de 8_c égale à 0.00804 mm respectivement pour le trou et la

fissure. Il s'avère que a_c. est une fonction décroissante de l_a, ceci prouve que a_r est une charge

limite et par conséquent la charge de rupture de la structure. Les charges de rupture sont 0.356_c pour le trou et 0.16s_c pour la fissure.

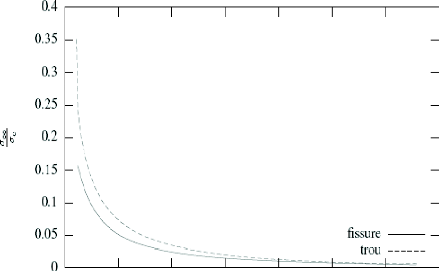
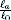
Figure 1.18. Relation entre la charge appliquée et la position de la zone cohésive
dans la phase de propagation.

1.4 Demi plan contenant une fissure rectiligne [21] :

Dans ce cas on considère un demi-plan SI = (--...,+.0)x (--..., h), contenant un défaut de type fissure D=[--l₀,l₀]x{0} de longueur 2l₀ parallèle et distant de h de la face supérieure du domaine. Le milieu est élastique isotrope caractérisé par un module de cisaillement, . Sur la face supérieure x₂ = h et à l'infini x₂ --o. est appliqué un cisaillement anti-plan uniforme et positift_ , les lèvres de la fissure sont libres. La seule composante de déplacement est dans la direction x3.

x₁

L'évolution de la fissure pendant le chargement sous l'effet du cisaillement anti-plan appliqué suit la loi de DUGDALE-BARENBLATT.

1-₈

h

-

1₀

1₀

x₃

1-₈

x₂

Figure 1.19. La charge et la géométrie du problème original.

x₂

1-(x₁)

h

x₁

-

1_a

-

1₀

1₀

1_a

x₃

Figure 1.20. Le problème durant la phase cohésive.

l₀

si

x₁

(1.1)

<

si

l_a

l₀

< x₁

34

Le chargement r(x₁) est donné par :

r(x1)

{ -ro. -r..+r, C

Le problème élastique constitué par les équations d'équilibre et les conditions aux limites dans la phase de propagation, est donné par le système suivant :

0

=

0

dansf2

A W

C

r.n=-r..

.n su

r1^-2

r.n=r_C

.n sur

F_C

r23

= 0 surx₂ = h

x2 --,-..

x

2

lim r₁₃ = 0, lim r₂₃ = 0

->--

sr_C = SII(D U F), F = F₀ U F_C

X MU [l_C , l_a ) X M.

, l

₀

F₀ = (- X MU [4 j_C)X{0}

~ ~

~~ ~ ~

~

~ ~

.

l_C

l

l

(

=

F_C

0

C

Avec :

(1.2)

(1.3)

Les loi gouvernant l'évolution des pointes cohésives #177;l_C et #177; l_a sont donnée par :

[W k

#177;lC )

8C

(1.4)

k₃(#177;l_a)= 0,

Le système d'équations (1.2) ainsi établie est réduit à une équation intégrale singulière, cette transformation se fait en appliquant les transformations de fourrier standard.

L'équation intégrale singulière est donnée par :

ti_a

x1

£

la

(1.5)

_r 1

L + k(x₁,t)W(t).dt = ^21t r(x₁ ),

t

x₁

Il^-

l_a

Avec : fv(t).dt = 0 (1.5bis)

-l

Ou la fonction k(x₁,t) et donné par :

k (

2 (1.6)

t - x₁

x₁, t) =

4h² + (t- x₁) -la,-lC L'inconnue u(t) est une fonction densité définie par :

w(t)= _at [W(t,0⁺)- W(40)] (1.7)

A fin de résoudre l'équation intégrale on doit introduire les quantités normalisées suivante :

x₁

r= , s= ,

1₀ 1₀

v(t) = f (s), k(x₁,t) = L(r, , s), r (x ₁) = r(r) (1.8)

t

4

¹7 = 10

L'équation intégrale se réduit a :

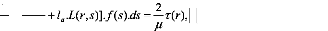
1

r

(1.9)

1

+

1

1

71-

f[ _s

1

r

Avec la condition

+ 1

ff (t).dt = 0 (1.10)

1

A cause des discontinuités dans la distribution des chargements due au modèle de
DUGDALE-BARENBLATT, la méthode de résolution standard ne donne pas de bon résultat.
L'idée est de remplacer la fonction inconnue f (s) par f (s) = h(s) +0(s) , où h(s) est la

solution de l'équation suivante :

1+1 f1

1 s -- r

2
ds = r(r),

il

h(s)

71-

1

r <1

(1.11)

Avec :

+ 1

f h(s)ds = 0. (1.1 1bis)

1

0(s) est solution de :

+

1

1

<1

r

s ds

f[_s

( ) (r)

,

g

71-

r

1

1

+ 1 _aL(r, s

)]0

(1.12)

Avec :

+ 1

1

g(r) = -- f1 _aL(r, , s).h(s)ds 71-

(1.12 bis )

+ 1

(t)dt

0

f0

1

La méthode standard de résolution consiste à exprimer 0(s) sous la forme0(s) = W(s)v(s) , ou

1

2₎

(S )

(1

W = -s ² sont les fonctions poids associés aux polynômes de CHEBYSHEV du

+ 1 a .L(r , s)]. f (s).ds = 2 r(r),

il

premier ordre T_n (s) = cos(n.ar cos(s)) et e(s) est une fonction continue et limitée sur

l'intervalle [--1,1] qui peut être exprimé avec une série tronqué des polynômes de CHEBYSHEV du premier ordre. Donc la solution ço(s) prend la forme suivant :

--

1 N

ço(s) = (1-- s² ) 2 E A _nT _n(s) (1.13)

n=0

On substitue ço(s) dans l'équation intégrale et en utilisant les relations suivantes :

1

1 71^-

-- iT n(s)(1 -- s2) 2 dt U n > 0 s -- r 0, n = 0 -- 1

(1.14)

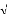
Où : U_n (r) = sin((n +1) arccos(s)) / 1-- s² désigne les polynômes de CHEBYSHEV de

second ordre. L'équation intégrale se transforme en un système de N équations a N inconnues appelées A₁,......... ...., A
·

N
·

N Er AniU n--1(rj)+H nfr )

g (r

), j =1,......, N . (1.15)

n=1

Les r _j sont les points de collocations donnée par :

r j

= cos (2 j --1)71-) 2N

,j =1,......, N . (1.16)

Avec _n(rHest_j) donnée par :

1 1

(r j) =1 f (1-- s² ) ² l_aL(r_j , s)T_n(s)ds

71-

--1

(1.17)

Ces intégrales sont évaluées numériquement en utilisant la formule d'intégration de GAUSSCHEBYSHEV suivante :

n

1 ¹ f (t)dtf (t _k)

E

1t21

T_n (t k) = 0 (1.18)

Apres avoir obtenu les A. , il et facile d'évaluer le facteur d'intensité des contraintes k₃ aux pointes #177; l_a et l'ouverture 8(r) le long des lèvres de la fissure.

Les données du problème sont :

l₀ = 1mm, h = 1mm, p = 1 100MPa, 'r_c = 7 2 MPa.

--

Dans la phase cohésive, une zone cohésive apparaît dés le début du chargement. Il est facile de calculer 'r_o. en supposons l_a connue, la loi donnant 'r_o. en fonction del_a est k₃ (l_a ) = 0,

en utilisant la linéarité du problème élastique on a : k₃ (l_a ) = 'r_oo.k₃^"(l_a)+ k3 (l_a) ou k₃^" (l_a) et

d'obtenir l'ouverture

[w

](la)

=

Sa

. Les quantités numériques calculées sont représentées sur

37 4(l_a) sont respectivement le FIC du problème sans forces cohésives et _Too =1, et le problème avec forces cohésives etToo = 0 . L'équation k₃ (l_a) = 0 donne T _=-k^a(l _a)

3 . Le calcul de la

k3 (l_a )

charge _Too demande le calcul des FIC k₃^oo (l_a) et k3 (l_a) . Les valeurs calculées sont représentées sur la figure donnant la relation entreT_oo et l_a (figure 1.21), ainsi _Too est une fonction strictement croissante de l_a et tende vers T_a lorsque l_a tende vers l'infini.

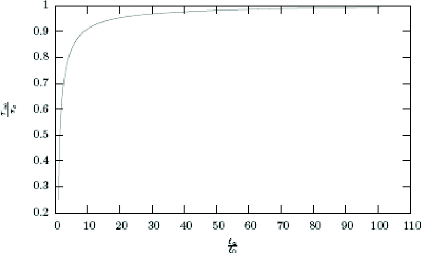
Figure 1.21 .Relation entre la charge appliqué et la position de la zone cohésive dans
la phase cohésive.

La phase cohésive cesse lorsque l'ouverture en x₁ = #177;l_a dépasse la valeur critique S_a. Pour déterminer la charge de rupture, pour la longueur caractéristique S_a , la méthode numérique utilisée est la suivante :

Pour la valeur test de l_a donné, _Too est obtenue en résolvant l'équation k₃ = 0 avec la méthode
expliquée dans le paragraphe précèdent, La valeur réelle de l_a et obtenu par dichotomie afin

d'obtenir l'ouverture

[w

](la )

=

8a

. Ainsi on obtient finalement z8 en fonction de la pour

un diagramme z,. - 8_a (figure 1.22). La charge de rupture est une fonction croissante de 8_a . On

note que la charge de rupture tend vers za quand

8a tend vers l'infini. l0

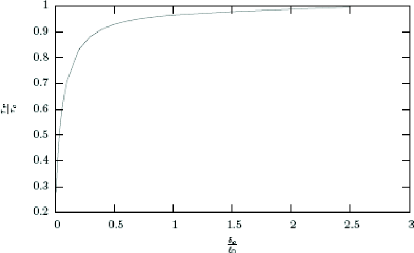
Figure 1.22. Dépendance de la charge de rupture et la taille relative de défaut
initiale.

Pour prouver que z,. est vraiment la charge maximale que le corps peut supporter tout en vérifiant les équations d'équilibre et les critères de rupture, on impose la valeur de la pointe non cohésive l_a , on calcule la valeur de la chargez₈ et de la pointe cohésive l_a en résolvent le système d'équations non linéaires (1.4). La méthode numérique utilisée est la suivante. Pour la valeur test de l_a donnée, z₈ est obtenu en résolvant l'équation k₃ = 0 avec la méthode expliquée dans le paragraphe précèdent. La valeur réelle de l_a et obtenu par dichotomie afin

charge limite de la structure fissuré. Les résultats (figure 1.23) représentant la relation entreô₈ et l_a pour ä_c de 0.1mm , la charge de rupture est de 0.71ô ,..

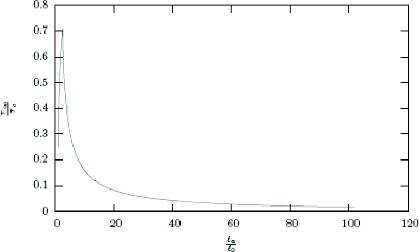
Figure 1.23. Relation entre la charge et la longueur de la fissure pour ä_c = 0.1.

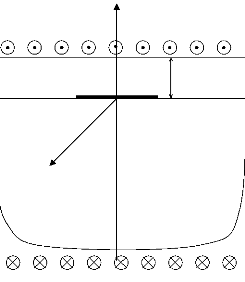
CHAPITRE 2
LE PROBLEME TRAITE

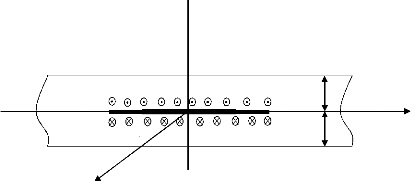
On considère une bande infinie SI = (--...,+.0)x (--h, h) contenant un défaut de type fissure D =[-l₀,l₀]x{0}de longueur 2l₀ interne et distant de h de la face supérieure et la face

inférieur de la bande. Le matériau constitutif de la bande est élastique isotrope caractérisé par
un module de cisaillement p . Les faces supérieurs et inférieures sont soumises à une

contrainte de cisaillement anti-plan positive et uniforme i^-_o. , augmentée a partir de 0. Les lèvres de la fissure ne sont pas chargées (figure 2.1).

x2

1^-₀.

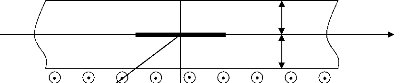
h

la h x1

-

l_a

x₃

Figure 2.1. Géométrie de la bande avec les chargements.

Pour le présent problème, la seule composante non nulle du vecteur déplacement, et la composante dans la direction x₃ , cette composante est indépendante de x₃ .i.e :

u1 = u2 = ⁰, u3 = W(x1, x2 ) (2.1)

Donc, le champ de contrainte correspondant est donnée par :

0

=

²11 = 2₂₂ = 2₃₃ = 212

(2.2)

?W ?W

, p

=

2 13

p

?x

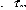
1 ?x2

2

23

Le champ de déplacement W et les deux composantes non nul du champ de contrainte 2₁₃ et 2₂₃ doivent satisfaire le système d'équation suivant :

~ÄW = 0,

~ ?W

213 ,

?x₁

~223 = 0, ~

~223 =

~ ~223 = 2

D

Ù

D

dans

D

W

Ù

=

dans

D

²23

D

?x₂

sur

(2.3)

sur

x₂ = h

sur

x₂ = -h

L'initiation et la propagation de la fissure dans le corps suit le modèle de DUGDALEBARENBLATT est caractérisé par les paramètres suivant G_c , 2_c et ä_c .

U

Introduisons les nouvelle fonction inconnues W, 2U définis par :

.x₂

x₂

W(x₁ )

W(x₁, )

x

₂

+

2 8

p

(2.4)

)

^?e2

U

?W

2-23 (x₁, x₂ = p (2.5)

?x2

U

(x₁, ) =

x₂

2₁₃

?x

1

2 = +.(e₂?e₃ + e₃

Ou les termes non nul de2U sont _'Le13 ,'Z'23 défini par :

~

~~ ~ ~

~ ~

		42
dans sur sur sur	II / D D = x2 h x2 = -h	(2.6)

,

0

=

A W

,

r .n = -r .n

-

= =

0 0

,

r23

,

r23

Dans la décomposition (2.4), le terme

r x2 . est associé à la solution du problème de la bonde

Il

non fissuré sollicité par un champ de contrainte uniforme de cisaillement anti-plan. Les

quantités inconnus W,i^-₁₃ et 'Le2 ₃ correspond a la solution du problème de la bande fissuré. On

note que ce problème consiste à déterminer la réponse de problème de la bande fissuré lorsque
les contraintes de cisaillement - r_on sont appliquées sur les lèvres de la fissure. Les faces

supérieures et inférieures de la bande sont libres (figure 2.2).

x₂

x₃

-

l_a

la h x1

h

Figure 2.2. Géométrie de la bande avec les chargements après la superposition.

,

Dans la suite on omet les symboles tildes, les champs W , rU soit notés respectivement

Pour des raisons de symétrie, on suppose que la fissure se propage le long des axes x₂ = 0 d'une façon symétrique depuis les points (#177;l₀,0) ainsi on note par F la nouvelle fissure crée et par x₂ = #177;la la position de ses pointes, avec :

F = (-l_a ,-l₀ ] x {0}U [l₀ , l_a )x {0} (2.7)

L'évolution de la fissure suit la loi de DUGDALE-BARENBLATT, en d'autre terme les pointes de la fissure (- l_a ,-l₀ ) et (l₀ , l_a) peuvent comporter deux zones :

· La première zone, proche des pointes de la fissure appelée la zone cohésive, et soumise a une force cohésive de cisaillement constante d'intensité T_c .

· La seconde zone appelée non cohésive, et proche de la fissure initiale sans forces cohésives.

Ces deux zones sont séparées par les pointes x₁ = #177;l_c. Notons que, les valeurs de l_a et

l_c dépendent de la valeur de chargement T.. sous l'hypothèse l_a = l_c = l₀ . Au début du chargement, on a les conditions initiales suivantes: l_a = l_c = l₀ .

Dans le cas présent l'évolution de la fissuration suit deux phases, la phase cohésive et la phase de propagation. Les critères de l'initiation et la propagation de ces zones sont étudiés dans les sections suivantes :

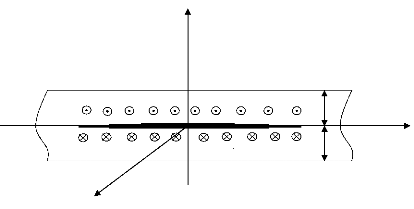
2.1 La phase cohésive :

Lorsque T.. ? 0. c a d 0 < T.. < T, , T, est la charge de rupture, la fissure doit apparaître (figure 2.3) d'une façon a ce que la contrainte de cisaillement maximale dans le corps soit inférieur de la valeur critique T_c . Par conséquent le FIC k₃ en la pointe de la fissure doit être

nul. Lorsque la charge est suffisamment proche du zéro, la longueur de la fissure est

suffisamment petite de tel sort que l'ouverture

[if ] est partout inférieure à la valeur

critique ä_c. En conséquence, toute les lèvres de la fissure crée sont soumise a une force cohésive d'intensité T_c, et le champ de déplacement ainsi que le champ de contrainte a l'équilibre sous le chargement T.. sont donc solution du problème suivant :

x₂

x₃

=

A TV

II /(D U F)

D

=-2.₀

2n

2n=2 _a

=#177;

=

x₂

2₂₃

~

~~ ~ ~

~ ~

dans

sur

sur

sur

0

n

n

0

F

F

h

(2.8)

x₁

h

-

l_a

-

l₀

l₀

l_a

h

Figure 2.3. Géométrie de la bande avec les chargements dans la phase cohésive.

Les pointes x₁ = #177;l_a de la zone cohésive avance est de façon a ce que la contrainte 2₂₃ ne dépasse jamais la valeur critique 2_a dans la structure, cela oblige donc que les contraintes ne soient pas singulières aux points x₁ = #177;l_a de l'axe x₂ = 0 .

Par conséquent, la loi gouvernant l'évolution des pointes #177; l_a de la fissure avec le chargement est k₃ (#177;l_a ) = 0.

En d'autre terme, l'énergie total restitué G due a la fissure cohésive crée doit être nul.

Cette phase cesse lorsque l'ouverture[-kt, ] aux points x₁ = #177;l_a dépasse la valeur critique ê_a ceci

(2.9)

signifie qu'une fissure non cohésive doit apparaître, la valeur du chargement correspondante est appelé la charge de rupture, elle est défini par :

2_r= sup{2 > 0 : [TV ](l₀) <V_al

2.2 La phase de propagation :

Si la charge est augmenté au-delà dei_r , le corps ne peut pas trouver l'équilibre sans qu'il y'a initiation et propagation d'une pointe non cohésive de la fissure crée. Ainsi, la fissure F doit se diviser en deux partie une partie cohésive F_a est une non cohésive F₀. On note par

l_a et l_a leur pointes respective (figure 2.4).

x₂

x₃

h

-

l_a -

l_a

-

l₀

l₀

l_a l_a

h

x₁

Figure 2.4. Géométrie de la bande avec les chargements dans la phase propagation.

(2.10)

On a donc :

Ù0 = Ù/( F),F

DU =F₀ UF_a

.

x {OU y_a , l_a ) x {0l.

= (- x {0} U y0 , l_a ) x {0l.

,

l

0

l

a

F₀

l

l

(

F_a

Le champ de déplacement w et de contrainte i , doit satisfaire les équations suivantes :

0

0

dans

A W

Ù

a

n

sur

in = i_a

0

i23

sur

~

~~ ~ ~

~ ~

D U F

(2.11)

x₂ =#177; h

F_a

in = ^-i8 n sur

Les lois gouvernants l'évolution des pointes #177; l_e et #177; l_a sont donné par :

k3 (#177;la ) = 0,

[w

](#177;le)

=

äe

.

(2.12)

2.3 Conclusion :

Dans cette partie nous avons posé le problème traité avec les conditions aux limites correspondantes. Dans le prochain chapitre nous allons exploiter les équations d'équilibre et les conditions aux limites pour établir l'équation intégrale.

CHAPITRE 3
DERIVATION DE L'EQUATION INTEGRALE

3.1 Introduction :

Dans cette partie nous allons utiliser les équations d'équilibre (2.11) établies dans le chapitre précédant relativement à la phase de propagation et les conditions aux limites correspondantes pour établir l'équation intégrale, les équations d'équilibre sont transformés a l'aide de la transformée de Fourier standard en une équation intégrale suivant les travaux de ERDOGAN [18].

3.2 Les données de la transformation :

Pour obtenir l'équation intégrale pour le système (2.11) on réécrit toutes les conditions

aux limites sur l'axe x2 = 0 et les bords x1 = #177;h:
223 (x1 ,0^+ ) = 223 (x1 ,0 - ) =	2(x1	),	x1 </a,	(3.1)
223 (x1 , h) = 223 (x1 ,-h) =	0,	x1 <	+00,	(3.2)
^223 (x1,0+) =223(x1, 0 ),	x1	> /a		(3.3)
w(x1,0^+)= w(x1,0^-),	x1	> /a		(3.4)

l_e

si

x_i

(3.5)

si

l_a

l_e

<x_i

48

Ou :

r(x_i)

~--r00 ,

= ~

~ --+rc,

Avec la relation de l'élasticité suivante :

aw(x_i , x₂)

r23 = (3.6)

ax₂

Appliquant la transformée de fourrier sur la solution du problème. La transformé de fourrier est définis comme suit :

Sous forme paramétrique :

Soit une fonction a deux variables f (x_i , x₂) , on prend x₂ comme paramètre, la transformé de fourrier est donné par :

+00

U f (2, x

2) = ff(xi,x2).e--axi .

dx1 (3.7)

^--00

Ou bien, en considérons les deux variables : Soit une fonction h(x_i , x₂) :

+00+00

= f fh(x_i , x2 ).e-i.(2.xi +e.x2) .dx1.dx2.

(3.8)

--00-- 00

La transformé de fourrier inverse :

2

= f7(2 d2 p --00

f(x_i,x₂)

1

(3.9)

L'équilibre est donné par l'équation suivante :

Aw = 0 (3.10)

a ²

w₊ a2w = 0 (3.10 bis)

2 2

axax

; 2

+00

a ² --w(2, x, ) ;2

-- 22 f w(2, x₂ d. ax 1,+ f d2 = 0

«

2

+00 +00

--00 --00

(3.12)

₍a²w(2, x₂

2²w(2, x₂ = 0

ax;

--00

(3.13)

+00

f

a ² 1 ⁺⁰⁰ a ² 1

(3.11)

₂ ( fw(2, x₂ ).C^iasi d2) + ₂ ( fw(2, x₂ ).C^i2si d2) = 0

ax 271---00 ax2 ^271---00

2 W(2, x2) 22 2, 0 W(x2)	49 (3.14)
axe
Sous la forme :
f cents- 2^2 .f =0	(3.15)
L'équation caractéristique donne :
n^2 -2^2 = 0, = 1.2	(3.16)
n 1 = - 2n, 2 = 2	(3.17)
La solution est de la forme suivante :
W(2, x2) = C1 (2).e^"2 + C2 (2).e^n2.x2	(3.18)

En appliquant la transformé de fourrier inverse sur la solution on obtient les différentes expressions pour la solution au dessus et au dessous de la fissure :

+00

w(x₁,x₂) = 27/- f(C₁ (2).e^n1.x2 + C₂ (2).e^n2.x2 .d2, 0 < x₂ < h (3.19)

-00

1 ⁺⁰⁰

w(x1,x2)= 27/- f(C₃(2).e^"2 +C₄(2).e^n2s2).e^-L2s1 - h < x₂ < 0 (3.20)

-00

Ou C _k (2) , (k =1,.......,4) sont les fonctions inconnues de la variable 2 déterminées en utilisant les conditions aux limites (3.1) et (3.2), et n₁, n₂ sont les racines du polynôme caractéristique relative a l'opérateur A, ils sont données par :

n^2 - 2^2 = 0,

n1=

2,

n2

= -

2

(3.21)

De l'équation (3.2) (3.3) et (3.20) il est facile de trouver :

C ₁ e 2.h .h

-C₂.e^-= 0 (3.22)

C₃.e^-2.h C ₄.e^2.h =0

(3.23)

Pour réduire le problème à une équation intégrale, on introduit la fonction densité suivante :

d

W(x1) = _dx[w(x₁,0⁺)-w(x₁,0^-)1 (3.24)

fv(t).dt = 0, v(x1) = 0 Pour (3.25)

En substituent les équations (3.19) (3.20) dans (3.4), on obtient :

W(x) _=211- fi2(C₁+ C₂ -- C₃ --

00

En prenant la transformée de fourrier inverse, on obtient :

1_o

i.2.(C₁ + C₂ -- C₃ -- C₄) = .dt

1_o

.dt (3. 26)

C₁ + C₂ -- C₃ -- C₄ = ₂. fv(t).e^i.2.t

_o

¹

Notons le second membre de (3.26) par F :

+1

F =ⁱfvf(t).e^i.2.t .dt (3. 27)

De l'égalité (3.3) :

1^-₂₃ (x₁ , )

2.x2 -- e 2.x2 ).e--i.a.x1

x₂ > 0

2.

.

+00

e

.

(C₁

Dr

00 +00 1-23 (x1, x ) = . f(C 2 -- .x2).e--i.2.x1 j2el" e 4 00

x2 < 0

+00 +00

2

. 2. f(C1--C2 ^).e--i.2.x1 .d2= . . f(C₃ -- C₄ ).e^--i.a.x1 .d2

Dr

--00 --00

C1--C2--C3+C4=0 (3.28)

Pour trouver les valeurs des C _k ,(k =1,........,4). il suffit de résoudre le système d'équations algébriques suivants :

.e

C3 .e--2.h

C₄e

.

+

C2- C3

C₂ - C₃ + C₄

0

.h

.h

2

0

C₂

.e

2

.h

2

0

- C4 = F

(3. 29)

51

Nous avons trouvé :

.

h

F.e

h

^.h +e .

.

h

1

F.e

.

+e

- C2 =1

- .h

2. - e

.

h

F.e

C₄

F.e

.

h

1

-

.

=

.

h

-

2 e

^.h +e .

.

. ,

-

h

h

.

+e

2 e

=

=

C 1

C₃

.

2 e

1

(3.40)

Substituant les constantes C₃ et C₄ dans l'équation suivante :

₉

(x1,0- )=x2 W( = 1^-(x₁ )

axX1 X22

¹-23

On obtient :

4,r

=

d

t ( )

x ₁

m

- (h+x2)

₍e - e

- h +e ^h )e

2

e

+00

0

x2

lim

I^F

- 00

On substituent F de l'équation (3.27) et en changent l'ordre d'intégration:

l_o +00 _e (h+x2) - _e- (h+x2)

f(x2^lim0^- f - h h )ei (t-x1) camodt = - 1-(x1e + e m

- l -00
o

Mettons l'équation sous la forme suivante :

l of k(x₁,t).v(t).dt =-⁴ .1^-(x) (3. 41)

m-l o

Avec :

)

⁺⁰⁰ e .(h+ x2) - _e- .(h+x2) -

k(x₁ ,t)= x2lim ₀- fi. .(

- .h h

e +e

-00

. d (3. 42)

Notons par (x₁Hla, ) partie sous le signe d'intégration dans l'équation précédente :

)

+x2

.

h

.

(x₂, ) --

^--h - .

e + e

.(h+x2) - .^(h-e

e

h+x

(3.43)

(x₂, ) = -H(x₂,- )

L'intégrale (3,43) devient :

k(Xi , t On sait que :

)

+ - - - ea...(h+X2) -^e-2.(h+X2) e e i t X i t X =2.( -2.h 2.h ).( ).d.1. (3.22.44) X2m0- 2 e + e i 0

-

i.X

ei.X - e

X

=

i

sin(

)

2.

D'où :

+2(h+X2) -2.(h+X2)

). sin 2.(t - X).d2 (3.23.45)

6

k(Xi,t)= _X2lim0- - 2 f.( ^e 2.h

0

e + e

k(X_i,t) Se réduit a :

+-2.(h+X2) +

(3.24.46)

k(X

₁,0= _Xlim₀-(-2 f(ea.X e ² e

0

-.1. h h.sin(2.(t-X1))).d2

· + e2
·

)

L'équation intégrale devient :

~ ^~fk^' (Xi,t).v(t).dt ^=2.n- . ( ) .(3.25.47)

m-~ ~

Avec

+ -_e

h+X2) + e-2.(h-X2

k (X,t)=_X lim ( . f(ea ^X2

0

e

² +e

l .(

0

)

).sin(2.(t - Xi))).

dit (3.26.48)

Le premier terme donne :

+X2 lim 0- fea.X2

.sin(.1(t -X))4.1. = 1

(3.27.49)

t - X₁

Notons par I la partie suivante :

1= lim 2

+-2.(h+X2)+ e -2.(h-X2) ^2e-.1h0-( f( e^-a.h + e^a.h ). sin(2.(t e + e )))d2 = sin(2(t - )) 00

dit (3.28.50)

+00

0

Finalement, l'équation intégrale s'écrit :

1_o

f

) (3.29.51)

( ¹ + k^" (x₁,t))v(t)dt =^271- «x₁

Il

t-x₁

1_o

Avec : fvf(t)dt = 0

-1 o

2h

_2e-

k" (x₁, t) =-f -tee », sin(2(t - x₁ ))dt e +e

3.3 Démonstration de la convergence uniforme de l'intégrale I :

Le critère de convergence uniforme d'une intégrale impropre s'énonce comme suit : S'il

00

existe une fonction continue M(t) telle que

00

ff (x, t).dt est uniformément convergente.

0

Soit la fonction e^-2h :

f (x,t ) M(t) et fM (t).dt est convergente, donc

0

7.

_j C^{al 1} d2=-¹

0

h

r -2h-1-- 1

(3.30.52)

h

_Le 10 =

Cette intégrale est bien convergente. Allons prouver que :

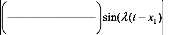
-_e 2 h

(h+x2)e-

+e

+e-(h-x2)

ah

<e

-2h

(3.31.53)

La fonction sinus est une fonction bornée dans l'intervalle[-1.1], (3.53) est donc vérifié si :

<e	-2h

e 2-2(h+x2) + e - (h-x2)

e ^-Âh + e.1h

)

1

<

2h

2

+

1

e

e2+ _e2-2,(h - (h-x2

(3.32.54)

-1 o

sin(2(t - x1)

Nous allons prouver que la fonction en valeur absolue est inférieur ou égale a 1. On considère 2 comme paramètre sachant que 2> 0 .

)

f (2, x 2

e

-2.1h +1

Notons par f et g respectivement le numérateur et le dénominateur de la fonction en valeur absolue définie précédemment.

f(2, x₂) = e-2(h+x2) + e-2(h-x2) (3.33.55)

g(2) = e-22

Nous avons comme données :

2>0,x₂e [-h,0],h> 0 (3.34.56)

Pour la fonction f (2, x₂) :

La dérivée par rapport a x₂ :

af (2, x2) = ile-2h (e^2x2 - e^-2.2) (3.35.57)

ax₂

La dérivée est strictement négative V (2 > 0, x₂ E [- h,0 ]) ,

La variation de la fonction f (2, x₂) est présentée sur le tableau suivant :

x2	-h 0

h

2e^-

Il est donc claire que :
f(^2,x2) g(x) Vx2
Et donc
	f (2, x2 )	£ 1	(3.36.58)
	g (2)
En conclusion, l'intégrale I est bien uniformément convergente.

3.4 Conclusion :

L'équation intégrale ainsi établie, nous allons procéder dans le chapitre suivant à la résolution de cette équation en utilisant une méthode numérique basée sur les polynômes de CHEBYSHEV.

CHAPITRE 4
RESOLUTION DE L'EQUATION INTEGRALE

4.1 Introduction :

Dans cette partie nous allons procéder à la résolution de l'équation intégrale établie dans le chapitre précédent. Pour alléger les écritures on note park le terme k^" de l'équation intégrale.

4.2 Résolution :

L'équation intégrale s'écrit :

)

(4.1)

1 1

+k(x₁,t)W(t).dt = ^2.11-1"(x1

t x

- m

-1 1

Avec la condition :

1

fv (t)dt = 0

- 1

Avec :

+

k

, (4.2)

.0_2.e-a.11

0

(x1,t)= f _{e +e}2.11.s^{in 2}.(t^- )⁴².

4.2.1 Introduction des quantités normalisées :

Tout d'abord, nous introduisons les quantités normalisées suivantes :

t

x₁

r= , s = ,

l_a

l_a

=

le Kt) = f (s), k (x ₁ , t) = L(r, s), 1-(x₁) = 1-(r) . (4.3)

l, _a

Ainsi l'équation (4.1) prend la forme suivante :

1

+

1

J[

s

1

71^-

-

r < 1. (4.4)

1 2

+ l _a .L(r , s)].f (s).ds = .r(r),

--r

Il

Avec la condition :

+1

Jf(t).dt = 0 (4.5)

-1

Dans (4.4), le chargement 1-(r) est donné par :

~ - 1- ,

~ ~--1-...+1-e,

77

(4.6)

1-(r)

si r <
si ¹7 <r

<1

On remarque que le chargement (4.6) présente des discontinuités. Pour ce type de chargement, la méthode de résolution de ce type d'équation intégrale ne donne pas de bons résultats. Par conséquent, et suivant une méthode développé par (IOAKIMIDIS, 1980 [32]), on remplace f (s) par une nouvelle fonction 0(s) telle que :

f (s) = h(s) + 0(s), (4.7)

Où h(s) est la solution de l'équation intégrale suivante :

1	+1 J -1	1	.h(s).	ds = 2 .r(r),	r <1. (4.8)
71^-		s -- r		Il

Avec la condition supplémentaire suivante :

+ 1

J h(s).ds = 0 (4.9)

-

1

<1

r

Où

+ l _aL(r, s

(4.10)

s ds

)]0 ( ). (r),

g

1

+

1

1

-

71-

1[_s

1

r

-

1

+

1

1

g (r) = -

71- fl _a .L(r ,s).h(s).ds

(4.11)

Avec la condition

+1

10(t).dt = 0 (4.12)

-1

Il est clair a partir de l'équation (4.11) que, puisque L(r ,s) a un comportement régulier, ceci
est également vrai pour g(r) , et les techniques numériques classiques pour la résolution de

l'équation intégrale singulière peut être directement appliqué pour résoudre l'équation (4.10) sans aucune modifications.

La solution de l'équation (4.8) et (4.9), est donnée par [28] :

2 (r)

h(s) =-.(1-s² ) ².1(1-r² ) 2. r dr

71-./.i_-1 r - s

1 +1 1

s <1, (4.13)

On obtient :

Où

h(s) = h₁ (s) + h₂ (s)(4.14)

2.s

h₁ = . (1-s² ) ^{- 2}.(-2 .71- + 2.r_c . arccosil), (4.15)

/ni./

²

1

-

1

il

2

s -s

2

il

2

1

-

1

s

+s

il

il

h₂(s) = 2r c ln

71-_izi

(4.16)

On voit que h₂ (s) présents des singularités logarithmiques aux points s #177;il.

4.2.2 Application de la méthode de résolution standard des équations intégrales :

Il a été montré dans (ERDOGAN et al. 1973 [18]) que l'équation intégrale singulière (4.10) a l'indice 1 car la fonction inconnue 0(s) à des singularités intégrables aux points #177;1.

1

-

poids associé au polynôme de CHEBYSHEV de premier ordre

T _n(s) = cos(n.arccos(s)) et ço(s) est une fonction continue et bornée sur l'intervalle [-1, 1]

laquelle peut être exprimé comme une série tronquée des polynômes de CHEBYSHEV du premier ordre. A cause de la symétrie du position par rapport à x₂ on à ço(s) = --ç(s) . Donc, la solution de l'équation (4.10) s'exprime :

1 N

--

0(s) = (1-- s2) 2 EAn.T 2n--1(s) (4.17)

n=1

Substituons l'équation (4.17) dans l'équation (4.10) en utilisant les relations suivantes :

	1
Avec	-- 1 1T n(s)(1 -- s2) 2 CIs n> 0 = s -- r --1 0, n=0			(4.18)

U_n(r)= sin((n +1).arccos(r))/ 1-- r² (4.19)

L'équation (4.19) design les polynômes de CHEBYSHEV de second ordre. On trouve :

N

E An [U _2,2 0+ H _n(r)]= g(r), r <1. (4.20)

n=1

Ou:

1 1

(r) = ¹1(1-- s2) ²¹.¹(r, sg2n--1(s)CIs p

n

--1

(4.21)

L'équation (4.20) peut être résolue en sélectionnons les N points de collocation données par :

rj = cos

~(2 j --1)/z 2(2N--1) J , j,......,N. (4.22)

Utilisant les points de collocation donnés par l'équation (4.22) dans l'équation (4.20) on arrive a un système de N équations a N inconnus, nommés A₁,........, A_N laquelle peut être

exprimé ainsi :

N

E A ^n[U 2n--2(rj)+H n(rj)]= g(r ), j = 1,........., N (4.23)

n=1

4.2.3 Évaluation numérique des différentes intégrales :

Les intégrales H (r _i) et g(r_i) sont évaluées en utilisant la formule d'intégration de GAUSS-CHEBYSHEV qui s'écrit :

1 f (t)dt f (tk)

f2 ~

» ,

¹

t --

¹

1

-

p

7 (t k) = 0 (4.24)

La valeur de g(r_i) du coté droite de l'équation (4.23) est déterminée à partir de l'équation (4.11) laquelle grâce à l'équation (4.14) peut se mettre sous la forme suivante :

1 1 ^1g(r) = -- [f l aL(r,s)h1(s)ds + f laL(r,s)h2(s)dsj

(4.25)

La première partie est évaluée par la précédente formule de GAUSS-CHEBYSHEV. A cause des singularités logarithmiques que présente le terme h₂ (s) aux points #177;77 , la seconde partie est devisée sous la forme suivante :

1 ^--77 ⁷7 1

f_aL(r, s)h₂ (s)ds = f l_aL(r, s)h₂ (s)ds + f l_aL(r,s)h₂(s)ds + f l_aL(r,s)h₂(s)ds (4.25 bis)

1

--

1 ^--77 ⁷7

Chacun des intégrales du membre droit de l'équation précédente est évaluée à l'aide de GAUSS-CHEBYSHEV.

4.2.4 Evaluation numérique de L(r, s) :

Considérons maintenant le terme L(r,s)de l'équation (4.10), après introduction des entités normalisées :

+c

.e

L(r, s) =e + e _Âji . sin l_a .2.(s --

2

0

(4.26)

--

Âh

^AL(r,s) =

l .2.(s -- r d2.

a

(26 bis)

sin

)
·

_f 2.e 2 e--

J --2 h 2 h
·

. sin l_a .2. (s--r).d.l + f . '
_·h

--2.h 2

e + e . e + e

0

A

Ou A est un point de coupure, La deuxième intégrale du membre droit de l'équation précédente devient négligeable pour une valeur de A suffisamment grande.

- Evaluation de A :

On considère la plus grande valeur de$ -- r = 2, pour l'instant on prend l_a =10 .

L'évaluation numérique de l'intégrale à l'aide du logiciel MAPLE avec la fonction (evalf) avait donné :

)

=

0.05.

(4.27)

+00

(1e _2.h.e + e _a.h .sin 20.2.l_a.d2

2

2.

h

evalf

-

0

Si on limite l'intégration sur l'intervalle [0.6] on obtient une bonne convergence :

^6r 2.e_a.h

evalf (f 21_a (r -- t).d2)=

-a.h a h

e + e.

0

0.04999946939. (4.28)

En conclusion on peut limiter l'intégration sur l'intervalle [0.6] et l'intégrale L(r, $) prend la forme suivante :

L(r,$) =e-2.h sin 21 _afr -- t).d2.

+ e ^a.h

6

0

(4.29)

L'intégrale ainsi définie est évaluée à l'aide de la formule de GAUSS-CHEBYSHEV avec un changement de variable pour passer de l'intervalle [0.6] à l'intervalle[-1,1].

A

^-1 2 ² A

(4.30)

A

(2+1).h

L(r,$) = _A e _A . sin (2+ 1).l_a(r --t).d2.

2 - (2+1).h (2+1).h 2

¹ e ² + e ²

Avec : A = 6.

A l'aide de la méthode d'intégration de GAUSS-CHEBYSHEV nous avons évalué numériquement l'intégrale L(r,$), l_a est pris égale a10, le nombre de points pour lequel il y'a

convergence de l'intégrale et n = 250. La valeur de l_a =10 est choisi comme une valeur

limite au delà de laquelle la convergence ne peut être attente qu'on augmentent n , ceci augmente sensiblement le temps d'exécution des programmes relatives aux phases cohésive et propagation (dans lesquels le programme est incorporé) et demande des machines de calcul puissantes.

Pour une plage de valeurs de 2 on trace les deux graphes dans les figures (4.3, 4.4) suivants :

0.08

0.07

0.06

L

0.05

0.04

0.03

0.02

0.01

62

0.08

0.07

0.06

L

0.05

0.04

0.03

0.02

0.01

0 10 20 30 40 50 60 70 80 90 100 110

A

Figure 4.3 : valeur de L(r, s) en fonction de A .

0 5 10 15 20 25 30 35

A

Figure 4.4. Agrandissement.

Il est clair que l'intégrale L(r, s) tend vers la valeur de 0.5 même à partir de la valeur A = 6 . Ce résultat a été prouvé avant par l'évaluation de la même intégrale par le logiciel MAPLE, à l'aide de la fonction (evalf) on retrouve la même valeur.

4.3 Formule donnant le facteur d'intensité de contrainte :

Le facteur d'intensité de contrainte en pointe de fissure est donné par :

) (4.31)

(#177;la ) = du lim l_a² -- X² yi(X ) = -- du l_a lim 1-- s² f (s

k3 ₁, , _x #177;l_a 1 ¹ 2 s #177;1

z ta

s

f

2

2

n

1 x

1

-

T_n (x)dx 1

= U_{n 1}(s) 1-- s

(4.35)

Où v(x₁) est donnée avec (3.24) . On obtient :

N

2

k₃ (#177;l_a) = l_at_-- r_c arccos(q) -- '₂ A_n) (4.32)

_ir

4.4 Formule donnant l'ouverture de la fissure :

L'ouverture de la fissure en x₁ E [-1,1] est définie par :

1

8(x₁)=w(x₁,0⁺)--w(x₁,0)= I' _lv(t)dt (4.33)

De (4.3), (4.7), (4.14) et (4.17) on obtient :

JI

~r 1_17² --17 1--r² b-r² + 1-17²r _2arccos 1

8(r)= 2a et: 1 r² +t_c[rln

it^-u r 1-17² +17 1--r2 r2 --

-- +17ln

172 0 -- r2

^N A U _i(r)

'

--l_a 1--r²E (4.34)

n=1 n

Pour obtenir (4.29), on a utilisé les relations suivantes :

On observe à partir de l'équation (4.29), que 8(r) n'est pas définie en #177;ç , a cause des singularités logarithmiques. L'ouverture de la fissure en ces points et obtenue en passant a la limite de 8(r) lorsque r ? #177;ç.

On obtient les résultats suivants :

l_a

1

~l

a
~ ~

~ l a ~

J ô8 Ir JJ W:Jj

l_al_a

2

ôalaarcco2ôa

2

l_a

l_a

l_a

11(

2l_a

l_a

1

-

)

8(#177;

Ir

l_a

Iru

^~l_a

2 4u2n- la )

2

N

n=1

2n -1

4.36

4.5 Etude de convergence :

Nous avons étudié la convergence utilisant les programmes relatifs aux différentes phases de développement de la fissure pour déterminer les valeurs de N et n pour lesquelles il y'a convergence. Pour déterminer l'une il faut fixer l'autre.

On commence par N , on prend n =100. On considère la valeur du facteur d'intensité de contrainte K₃ , la figure 4.5 montre qu'a partir de N = 30 K₃ converge.

-20

-25 -30 -35 -40 k3 -45 -50 -55 -60 -65

-70

0 10 20 30 40 50 60 70

N

On considère maintenant n, avec N = 30 on obtient les valeurs de facteur d'intensité de contrainte k₃ en fonction de n (figure 4.6). Il est clair que pour n =100 il y'a convergence.

0 -10 -20 -30 -40 k3 -50 -60 -70 -80 -90 -100
	0 20 40 60 80 100 120 140 160 180 200	n

Figure 4.6.Valeur de facture d'intensité de contrainte k₃ en fonction de n.

Par conséquent, dans tout ce qui suit les calculs sont effectuées avec N=30 et n=100.

=

=

Il

²13

, 2₂₃

ax₂

1

a W a W

Il

ax

(4.38)

4.6 Etude du cas de fissure dans un milieu infinie :

Dans ce paragraphe on considère le cas d'un plan infini S2 = (-00,+00)x (-00,+00) , contenant une fissure D =[-1₀,1₀]x{0} centrale de longueur 21₀ . Le matériau est élastique isotrope caractérisé par un module de cisaillement Il . Les faces supérieure et inférieure sont soumises à une contrainte de cisaillement anti-plan positive et uniforme _200, augmenté a partir de 0. Les lèvres ne sont pas chargées (figure 4.7).

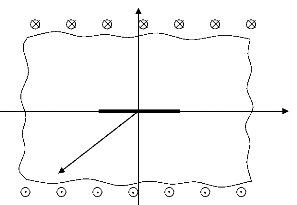
²00

x₂

x₁

- 1₀ 1₀

²00

x₃

Figure (4.7). Fissure dans un milieu infini.

Apres la superposition on considère que le problème fissuré avec fissure chargé. Le modèle de fissure est le modèle de DUGDALE.

4.6.1 Equation intégrale :

La seule composante non nulle du vecteur déplacement, et la composante dans la direction x₃, cette composante est indépendante de x₃ .i.e :

U1 = U2 = 0, U3 = W(x₁, x₂) (4.37)

Donc, le champ de contrainte correspondant est donnée par :

^211

= 222 = 233 =

212

=

0

On note que ce problème consiste à déterminer la réponse de problème de la bande fissuré lorsque les contraintes de cisaillement -- rcon sont appliquées sur les lèvres de la fissure. Les faces supérieures et inférieures de la bande sont libres.

Ainsi le champ de déplacement W et les deux composantes non nul du champ de contrainte r13 ^et _r23 doivent satisfaire le système d'équation suivant :

~AW = 0 ~^~r.n = --r .n

co

~r23 = 0 ~ ~r23 = 0

dans II/ D

sur D (4.39)

sur x₂ = 1-co

sur x₂ = -co

En suivant les mêmes étapes que dans le chapitre 2 on arrive à l'équation intégrale suivante :

1

f

Il

-

1

ço(t) .dt = r(x)

x -- t

(4.40)

Le terme r(x) est la charge si on considère le modèle de DUGDALE donné par :

<

si

1_c

x₁

r(x₁)

<

si

1_a

1_c

< x1

~--r _co , = ~

~^--rco^-Frc,

(4.41)

4.6.2 Phase cohésive :

La zone cohésive apparaît et se développe dés que rco > 0 . Le critère gouvernant la propagation de la pointe de la fissure 1_a est k₃ = 0 . C'est une équation implicite relient

rco et 1_a . La relation qui donné le facteur d'intensité de contrainte pour le présent problème et donné par :

k₃

2

)) (4.42)

(#177;1_a ) = 1a (rco-- r _aar cos(1 ⁰

Ir 1_a

La phase cohésive est caractérisé par un facteur d'intensité de contrainte nul au pointe cohésives 1_a .

(

r

co -- 2

r

_a

ar

cos(1 ⁰ )) =

1 a

Ir 1_a

0 (4.43)

k₃ (#177;1 a) = ⁰

Donc on arrive à la relation suivante qui donne l'évolution de la longueur 1_a en fonction du chargement a 8_c fixe dans la phase propagation :

rco = 2 r _aar cos(¹⁰ ) (4.44)

Ir 1 a

4.6.3 Contrainte de rupture :

La phase cohésive cesse lorsque l'ouverture aux points x₁ = #177;l_a dépasse la valeur critique 8_a .

Elle est caractérisée par les deux relations suivantes :

k₃ (#177;l_a) = 0 , 8(#177;l_a) = 8_a (4.45)

On note que l'ouverture est donnée par la relation suivante :

Ir

8(#177;l_a) = - Tal0Ln(cos r T ) (4.46)

2

4Iru

T

_a

Donc :

8_a =-

T

_al₀Ln

Iru

4 Ir T_T

(cos

2T

)

)

Ir T_T

cos(

2 T_a

= exp(- 8° c _l) (4.47)

0

4T_a

La charge de rupture est donnée par la relation suivante en fonction de 8_a :

Ir

8irp

TT =^2Ta aT cos(exp(-

4a )) (4.48)

0

T_a

4.6.4 Phase de propagation :

Nous allons prouver que T_T est réellement la charge maximum que la structure peut

supporter tout en vérifiant l'équilibre et les critères relatifs à la théorie de rupture. La méthode la suivante :

On considère les relations suivantes :

[w]=8_a (4.49)

On augmente la charge jusqu'à ce que T =T_T

Sachant qu'au deux points l_a et l_a :

)) = 0

k3 (l_a) = ⁰ (4.50)

(

T

8- ²

T

_c

aT

cos(l

^a

l_a

Ir l_a

)

2

T_a

la= IrT8

cos(

l_a

(4.51)

À la pointe l_a on a :

))

[w(l_a) ]= 8_a (4.52)

2

8 = (-2r l Ln

a c c

4

Iru l_a

(la

))

8_a=- T_al_aLn(cos(^ler8

Iru

T_a

²

11^-2

8_c = 4rcl _a cos(le ^r" )Ln(cos( " )) (4.53)

Ir_c Ir_c

gIi

l_a

iz^-8

Ii

Donc on arrive à la relation suivante qui donne l'évolution de la longueur l_a en fonction du chargement a 8_c fixe dans la phase propagation :

_

(4.54)

c

gr

gr"

"

4r_c cos(Ln

Ir_c Ir_c

)

4.7 Conclusion :

))

(cos(

(cos( Dans le chapitre suivant nous allons présenter les résultats du problème de la bande fissuré relativement aux phases propagation et rupture pour plusieurs valeur de l'épaisseur h de la bande, ainsi que les résultats du problème du milieu infini fissuré. Nous allons voir que lorsque on augmente l'épaisseur les résultat tendent vers s'eux du problème de milieu infini fissuré.

CHAPITRE 5
PRESENTATION DES RESULTATS

5.1 Introduction :

Nous présentons dans ce chapitre, la méthode numérique utilisée pour chaque phase. Nous présentons également les résultats obtenus pour plusieurs valeurs de l'épaisseur h données ainsi que les résultats pour le problème du milieu infini fissuré pour faire une confrontation des résultats, les caractéristiques mécanique et géométriques du problème ont été fixées aux valeurs suivantes :

l₀ = 1mm, h =1mm, u =1100 MPa , r_c= 72MPa (5.1)

5.2 La phase cohésive :

La zone cohésive apparaît et se développe dés que r_o. >0 . Le critère gouvernant la propagation de la pointe de la fissure l_a est k₃ = 0. C'est une équation implicite relient ro. et l_a . D'un point de vue pratique, il est facile de calculer _ro. en supposons l_a connue.

Effectivement, en utilisant la linéarité de problème élastique, le Facteur d'intensité de contrainte k₃ (l_a) est donné par la formule suivante :

k₃ (l_a) = r o.k ç (l_a) + ₄ (l_a) (5.2)

Ou k₃^oo (l_a) et k3(l_a ) sont respectivement le FIC de problème sans forces cohésives et avec T_oo=1, et le problème avec forces cohésives et Too = 0 . L'équation k₃ (l_a) = 0 donne :

c

k₃ l

Too = ( a) (5.3)

k7(l_a)

Spécifiquement, pour la valeur donné de l_a on détermine la charge _Too avec la formule (5.3), les Facteurs d'intensités des contraintes k₃^oo(l_a ) et k3 (l_a) sont calculés avec la formule (4.32) avec l_c =l₀. Les valeurs calculées sont représentées sur un diagramme T_oo - l_a (figure 5.1). Pour plusieurs valeurs de l'épaisseur h on vois ainsi que _Too est une fonction strictement croissante de l_a et qui tend vers T_c quandl_a tends vers l'infini.

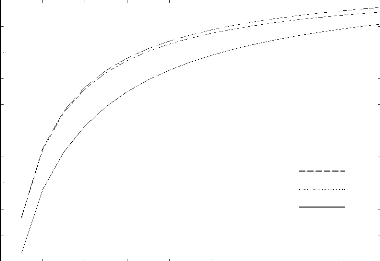
h inf

h= 10

h= 01

0.95 0.9 0.85 0.8 0.75

Too

T_c 0.7

0.65 0.6 0.55 0.5 0.45

1 2 3 4 5_L 6 7 8 9 10

L_a

L₀

5.3 La charge de rupture :

La phase cohésive cesse lorsque l'ouverture aux points x₁ = #177;1_a dépasse la valeur critique 8_a . Pour déterminer la charge de rupture pour la longueur caractéristique 8_a donnée, la méthode numérique utilisée est la suivante :

)

=

8_a

. Les

Pour la valeur test de 1_a , T₈ est obtenu par dichotomie en considérant [[4]](1₀

quantités numériques calculées sont présentées sur un diagramme _T,.-8a (figure 5.2).

Comme attendu, pour plusieurs valeurs de l'épaisseur h la charge de rupture et une

fonction croissante de 8_a . On note que la charge de rupture tend vers T_a lorsque

8a tend vers

1₀

T,.	1 0.9 0.8 0.7
Ta	0.6 0.5 0.4 0.3 0.2

l'infini.

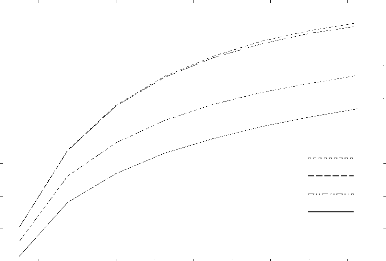
h=0.1

h inf

h= 10

h= 01

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2

8_a

1₀

Figure 5.2. Dépendance de la charge de rupture avec la taille relative de la fissure initiale.

5.4 Phase de propagation :

la valeur de la pointe non cohésive l_a et on calcule la valeur de la charge ô₈ et celle de la pointe cohésive l_a en résolvant le système d'équation non linéaire suivant :

k3

(#177;la)

=

0,

[[wl(

#177;la)

=

8a

(5.4)

La méthode numérique utilisée est la suivante. Pour une valeur test de l_a donnée, ô₈ est obtenu en résolvant l'équation k₃ = 0 avec la méthode expliquée ci-dessus. La bonne valeur de l_a est obtenue par dichotomie de telle sorte que

=

.

8_a

[[wl(

#177;l_a)

Nous présentons sur la figure 5.3 pour plusieurs valeurs de l'épaisseur h l'évolution de la charge appliquée ô₈ en fonction de la pointe l_a.

0.9
0.8
0.7
0.6
ô₈ 0.5

ô_a

0.4

0.3
0.2
0.1

0

Il s'avère qu'après la phase cohésive ô₈ est une fonction décroissante de l_a, ceci prouve que ô, est une charge limite et donc la charge de rupture de la bande fissuré, pour 8_a ? 0.1 , la charge de rupture est égale à0.8ô_a .

h= 0.1

h inf

h= 10

h= 01

1 2 3 4 5 6 l 7 8 9 10 11

a

l₀

Figure 5.3. Relation entre la charge et la longueur de la fissure pour 8₀ = 0.1.

CONCLUSION

Nous avons présenté dans le chapitre précèdent les résultats obtenu relativement au différentes phases de propagation de la fissure pour le problème de milieu infini fissuré auquel nous avons affecté le signe h inf dans les figure (5.1), (5.2), et (5.3), nous avons représentés sur les même figures les résultats obtenus pour le problème de la bande, il est clair que lorsqu'on augmente la valeur de l'épaisseur h de la bande les résultats obtenus approchent les valeurs relative au problème du milieu infinis fissuré. Ceci est évident de point de vue géométrique puisque lorsqu'on augmente l'épaisseur jusqu'à l'infini le problème de la bande fissuré devient identique au problème du milieu infini.

A partir des résultats obtenus dans le chapitre précédent on observe que plus le défaut et petit, la longueur de référence qui est une longueur caractéristique introduite dans le modèle de Dugdale, plus la charge limite s'approche de la contrainte critique du matériau. En d'autres termes, ceci semble indiquer que le défaut de petite taille a pratiquement peu d'influence sur les capacités de résistance de la structure si on adopte le modèle de DUGDALE. Ce travail généralise les résultats obtenus par FERDJANI et al ([19] [20] [21]) a un autre type de structure. Ce serait intéressant de généraliser se résultat a d'autre type de défaut, d'autre type de structure et d'autre modèle de force cohésive. Ceci nécessite de développer des théories et des outils numériques plus adaptés.

BIBLIOGRAPHIES

1. [1] Abramowitz. M and e. I. A. Stegun. Handbook of mathematical functions. National office of Standards, Appl. Math. Series 55, 1964.

2. [2] Barenblatt G. I., "The mathematical theory of equilibrium cracks in brittle fracture", Adv. Appl. Mech., vol. 7, 1962, p. 55-129.

3. [3] Bourdin B., Francfort G. A., Marigo J.-J., "Numerical experiments in revisited brittle fracture", J. Mech. Phys. Solids, vol. 48, n 4, 2000, p. 797-826.

4. [4] Bui H. D., Mécanique de la rupture Fragile, Masson, Paris, 1978.

5. [5] Barenblatt. G. I. The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mech., 7:55-129, 1962.

6. [6] Chaboche J. L., Girard R., Levasseur P., "On the interface debonding models.", Int. J. Damage Mech., vol. 6, 1997, p. 220-257.

7. [7] Charlotte M., Francfort G., Marigo J.-J., Truskinovsky L., "Revisiting brittle fracture as an energy minimization problem : comparison of Griffith and Barenblatt surface energy models", in A. Benallal (ed.), Proceedings of Symposium on "Continuous Damage and Fracture", Elsevier, Paris, 2000, p. 7-12.

8. [8] Charlotte M., Laverne J., Marigo J.-J., "Initiation of cracks with cohesive force models : avariational approach ", European Journal of Mechanics A/Solids, vol. 25, p. 649-669, 2006.12 1re soumission à Revue Européenne de Mécanique Numérique

9. [9] Charlotte. M, Laverne. J, and Marigo. J.-J. Initiation of cracks with cohesive force models: a variational approach. European Journal of Mechanics A/Solids, 25:649-669, 2006.

10. [10] Chen Y.F., Erdogan F., "The interface crack problem for a non homogeneous coating bonded to a homogeneous substrate", J. Mech. Phys. Solids, vol. 44, n° 5, p. 771-787, 1996.

11. [¹¹] Cinar A., Erdogan F., "The crack and wedging ^problem for an orthotropic strip", International Journal of Facture. 83-102, 1982.

12. [12] Del Piero G., "One-dimensional ductile-brittle transition, yielding, and structured deformations", variations of domain and free-boundary problems in solid mechanics (Paris, 1997), vol. 66 of Solid Mech. Appl., Kluwer Acad. Publ., Dordrecht, 1999, p. 203-210.

13. [13] Del Piero G., Truskinovsky L., "Macro- and micro-cracking in one--dimensional elasticity", International Journal of Solids and Structures, vol. 38, n° 6, 2001, p. 1135-1138.

14. [14] Dugdale D. S., "Yielding of steel sheets containing slits ", J. Mech. Phys. Solids, vol. 8, p. 100-108, 1960.

15. [15] Dugdale. D. S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids, 8:100- 108, 1960.

16. [¹⁶] Delate F., Erdogan F., "The ^problem _of ^internal and edge cracks in an orthotropic strip", Journal of applied Mechanics, vol. 44, p. 237-242, 1977.

17. [17] El Borgi. S, Keer L. «A receding contact plane problem between a functionally graded layer and a homogeneous substrate ». International Journal of Solids and Structures 43 (2006) 658-674. ELSEVIER.

18. [¹⁸] Erdogan. F, Gupta. G. D, and Cook. T. Numerical solution of singular integral equation. In G. C. Sih editor, Methods of analysis and solutions of crack problems, pages 368-425. Noordhoff International Publishing, Leyden, 1973.

19. [19] Ferdjani. H, Abdelmaoula. R, Marigo. J-J «Etude de l'influence des défauts de petite taille sur le comportement à rupture avec le modèle de DUGDALE ». Revue européenne de mécanique numérique. Volume 15-n° 4/2006, pages 409 à 425.

20. [20] Ferdjani. H, Khelifi. Med Z, Marigo. J-J « Etude de l'influence des défauts de petite taille sur le comportement à rupture avec le modèle de DUGDALE REGULARISE ». Revue Européenne de Mécanique Numérique, volume 17-n°4/2008 pages 481 à 493.

21. [21] Ferdjani. R, Marigo. J-J, S. El Borgi «Study of size effects in the Dugdale model through the case of a crack in a semi infinite plane under antiplane shear loading ». Soumise a continuum mechanic and thermodynamic.

22. [22] Ferdjani H., Abdelmoula R., Marigo J-J., " Study of the influence of small size defects on the rupture behavior with the Dugdale model" , Third International Conference on Advances in Mechanical Engineering and Mechanics, Hammamet, Tunisia 17-19 Decembre 2006.

23. [23] Ferdjani H., Abdelmoula R., Marigo J.-J., « Insensitivity to small defects of the rupture of materials governed by the Dugdale model », Continuum Mechanics and Thermodynamics, vol. 19, P. 191-210, 2007.

24. [24] Ferdjani H., Abdelmoula R., Marigo J.-J., « Insensitivity to small defects of the

rupture of materials governed by the Dugdale model », Continuum Mechanics and Thermodynamics, vol. 19, P. 191-210, 2007.

25. [25] Francfort G. A., Marigo J.-J., "Revisiting brittle fracture as an energy minimization problem", J. Mech. Phys. Solids, vol. 46, n° 8, 1998, p. 1319-1342.

26. [26] Griffith A. A., "The phenomena of rupture and flow in solids", Phil. Trans. Roy. Soc. London, vol. CCXXI-A, 1920, p. 163-198.

27. [27] Griffith. A. A. The phenomena of rupture and flow in solids. Phil. Trans. Roy. Soc. London, CCXXI-A: 163-198,1920.

28. [28] Gakhov F. D., Boundary Value Problems, Pergamon Press and Addison-Wesley, Oxford, 1966.

29. [²⁹] Gupta G., Erdogan F., "The ^problem of edge cracks in an infinite strip", Journal of Applied Mechanics, vol. 41, p. 1001-1006, 1975.

30. [30] Hillerborg A., Modeer M. and PETERSSON P. E., Analysis of crack formation and

crack growth in concrete ^by means of fracture mechanics and finite elements. ^Cement and Concrete Research 6(6):163-8 (1976).

31. [³¹] Irwin G. R., ^"Analysis of stresses and strains near the end of a crack traversing a plate", J. Appl. Mech., Trans. ASME, vol. 24, 1957, p. 361-364.

32. [³²] Ioakimidis. N. I. The numerical solution of crack ^problems _in plane elasticity in the case of loading discontinuities. Engineering Fracture Mechanics, 13:709-716, 1980.

33. [33] Laverne. J « Formulation Energétique de la Rupture par des Modèles de Forces Cohésives: Considérations Théoriques et Implantations Numériques », Thèse de

Doctorat, Université Paris XIII, France, 2004.

34. [34] Laverne J., Marigo J.-J., "Approche globale, minima relatifs et Critère d'Amorçage en Mécanique de la Rupture", Comptes Rendus Mécanique, vol. 332, 2004, p. 313-409.

35. [35] Marigo J.-J., Truskinovsky L., "Initiation and propagation of fracture in the models of Griffith and Barenblatt", Contin. Mech. Thermodyn., vol. 16, n° 4, 2004, p. 391-409.

36. [36] Muskhelishvili N. I., Some basic problems of mathematical theory of elasticity, 2nd ed., P. Noordhoff Ltd, Groningen, 1963.

37. [37] Michel J. C., Suquet P et Thebaud F., Une modélisation du rôle des interfaces dans le

comportement des composites à matrice métallique. Revue Européenne des Eléments Finis, 3(4) pp. 573-595 (1994).

38. [38] Needleman A., A continuum model for void nucleation by inclusion debonding. J. of Appl. Mechanics, 54 , pp. 525-531 (1987).

39. [39] Rice J.R. and Wang J.- S., Embrittlement of interfaces by solute segregation. Materials Science and Engineering A., 107, pp. 23-40 (1989).

40. [40] Salençon J., Calcul à la rupture et analyse limite, Cours de Calcul des Structures Anélastiques, Presses de l'Ecole Nationale des Ponts et Chaussées, 1983.

41. [41] Sneddon I., Srivastav R., "The stress field in the vicitinity of a Griffith crack in a strip of finite width", International Journal of Engineering Science, vol. 9, p. 479-488, 1971.

42. [42] Suquet P., Discontinuities and plasticity. In: Moreau J.J., Panagiotopoulos P.D. (Eds.), Nonsmooth Mechanics and Applications. Springer, Berlin, pp. 280-340 (1987).

43. [⁴³] Tvergaard V., ^Effect of fibre debounding in a ^{whisker-reinforced} metal. Mater. Sci.Engng. 125, pp. 203-213 (1990).

44. [44] Willis J. R. A comparison of the fracture criteria of Griffith and Barenblatt. J. Mech. Phys. Solids, 15:151-162, 1967.

45. [45] Xie D., Waas A., "Discrete cohesive zone model for mixed-mode fracture using finite element analysis ", Engineering Fracture Mechanics, 2006.