2.1.8. Application de la méthode pour le calcul de
l'écoulement
de puissance
Elle nous permet de résoudre un système
d'équation non linéaire en exprimant les
puissances actives et réactives en fonction des tensions
nodales.
L'équation de la puissance complexe au noeud (k) est :


Le courant s'exprime en fonction des admittances aux noeuds par
la relation
suivante :

En substituant l'équation (2.31) dans l'équation
(2.32) on obtient :

On peut exprimer les tensions des noeuds et les
éléments de la matrice admittance en
module et argument :



On remplace ces valeurs dans l'équation (2.3 3) :

Les composantes ( réelles et imaginaires )de la puissance
du noeud k :
En posant :
Les équations (2.38) (2.39) peuvent s'exprimer comme suit
:

Calcul des jacobines :
Les éléments du Jacobine sont calculés
à partir de l'équation (2.3 9) et (2.40) :
Le Jacobine J1 :
Les éléments non diagonaux :

Les éléments diagonaux :

Le Jacobine J2 :
Les éléments non diagonaux :

Les éléments diagonaux :

Le Jacobine J3 :
Les éléments non diagonaux :
Les éléments diagonaux :
Le Jacobine J4 :
Les éléments non diagonaux :




Les éléments diagonaux :

Le test de convergence de la méthode s'effectue comme suit
:
DPk et DQk sont les variations respectives des puissances actives
et réactives du noeud
(k) définies par :
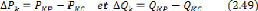
Avec :

Puissance active planifiée.
Puissance active calculée.
Puissance réactive planifiée.
Puissance réactive calculée.
Le passage d'une itération vers l'autre se fait à
partir des ajustements suivants :

Où e est le nombre d'itérations.
Algorithme de Newton -Raphson :
1ere Etape :
Introduction des données du réseau.
Détermination de la matrice admittance.
Les puissances actives et réactives des charges du
réseau sont données dans le
tableau de planification.
2emeEtape :

Calcul des puissances actives et réactives pour ,à
l'exception
du noeud de référence.
3eme Etape :
Puisque les valeurs des puissances planifiées sont
données par le tableau de
planification, on peut calculer les variations de puissance
telles que :

Où: (e) numéro d'itération,
: puissances planifiées .
puissances calculées.


4eme Etape :
On détermine la variation maximale pour les variations
des

puissances : .
5 eme Etape :

On procède à un test de convergence pour le max de
.Si une de ces deux
valeurs est supérieure à une certain
tolérance (e) on passe au calcul du jacobin (J).
6 eme Etape :
On se retrouve avec un système d'équations non
linéaires dont la résolution est
faite par la matrice inverse. Les corrections sur les
composantes des tensions sont
déterminées pour chaque noeud.
7 eme Etape :
Les corrections sur les tensions sont utilisées pour
déterminer les nouvelles
estimations des tensions nodales comme suit :


8 eme Etape :
Les nouvelles valeurs de sont remplacées dans les
formules
des puissances et et on revient à l'étape (3) pour
refaire le processus itératif. La
fin du processus itératif se fait lorsque les variations
des puissances à savoir : et
deviennent inférieures à la précision
(e).
1.7. LES METHODES DECOUPLEES
| 


