|
République Algérienne Démocratique et
Populaire
Ministère de l'Enseignement Supérieur et de la
Recherche Scientifique
OIRE
Présenter par : GASBAOUI BRAHIM
Ingénieure d'état en Electrotechnique
Pour l'Obtention du Diplôme de
MAGISTER EN ELECTROTOTECHNIQUE
Optimisation de l'énergie réactive dans
un
réseau d'énergie
électrique
Soutenue le ... devant le Jury :
Président: HAZZAB.A Docteur (Centre universitaire de
BECHAR)
Promoteur: CHAKER.A Professeur (ENST-Oran)
Co /Promoteur: AOUIFI.A Docteur (Centre universitaire de
BECHAR)
Examinateur KAHIAT.M Professeur (ENST-Oran)
Examinateur: KADARI.M Professeur (ENST-Oran)
Centre Universitaire de Béchar
Route de Kénadsa, Béchar, Algérie, ' :
(213) 49.81.55.81/91, 7 : (213) 49.81.52.44
Remerciements
Je tiens à remercier sincèrement mon directeur de
mémoire monsieur Chaker
Abdelkader Professeur au département de génie
électrique à L'ENST d'Oran -Algérie et
mon Co-directeur Laoufi Abdallah Docteur à
l'université de Bechar, Sans l'initiative
Desquels ce projet n'aurait pas été possible .Je
tiens à leur exprimer
tout. ma
reconnaissance pour leur dévouement, la confiance qu'ils
m'ont accordé, leur rigueur et
la qualité des commentaires et suggestion dont ils m'ont
fait part.
Je remercie tous les amis de prés et de loin qui ne m'ont
pas privé de leurs
soutiens, leurs enthousiasmes et leur bonne humeur
quotidienne.
Je tiens également à réserve un
remerciement particulaire .Au êtres les plus
tendres à Mes yeux et les plus chers à mon coeur
à mère et à mon père. A ma femme et
mes très Chers enfants (Wissam, et Kheira).A mes
frères et à mes soeurs et à tout ma
famille. Mes vifs remerciement sont destinés aux membres
de jury de m'avoir fait
l'honneur d'évaluer mon travail ; au professeur
Président Monsieur Hazab, aux
examinateurs le Maître de conférences Monsieur
Chalali, et Monsieur Khiat.
Résumé
Dans cette étude, nous proposons une nouvelle approche
pour l'emplacement
optimal des condensateurs dans le réseau
électrique .Cette approche utilise un
contrôleur flou qui a deux entrées, l'index de
perte PLI , la tension nodale V et l'index de
convenance comme sortie .Le contrôleur Flou
contrôle la violation des tensions nodales
du réseau et Nous affiche les noeuds ayant la valeur la
plus élevée de CSI (l'index de
convenance de condensateurs).Une fois déterminer le
nombres de noeuds qui sont
appropriés au placement des condensateurs et fait Apple
à l'algorithme de fourmis qui
sont aptes pour les problèmes combinatoire complexe,
pour minimiser la fonctions de
coût tout en rependent au contrainte de tensions.
L'application de la méthode proposée
sur un réseau électrique à 25 noeuds. Nous
avons enrichi notre travail par l'injection des
SVC (Compensateur statique d'énergie réactive)
sur le réseau électrique de 25 noeuds
pour le Contrôle des tensions et développement
d'une application avec interface
graphique sur MTALAB 7.4.
Mots clés : Répartition optimale de charges,
dispatching, Algorithme des Fourmis,
logique flou, optimisation, Compensateur statique
d'énergie réactive
Abstract
In this paper we propose a new approach to optimal placement of
capacitors in the
electrical network, this approach uses a fuzzy logic technique
which has two entered, the
index lost PLI and voltage V and nodal index suitability as
output. The controller
controls the violation tensions nodal we displays and network
nodes having the highest
value of CSI (index Suitability De capacitors). Once No.
identify nodes that are
appropriate for the Placement of capacitors and using ant
system are suitable for
complex combinatorial problems to minimize the cost functions
while dependent at
constraint active minimizing losses. The application of the
proposed method on a
Network Power 25 bus We have enhanced our work by the injection
of SVC (static
compensator reactive power) on the electricity grid for the 25
bus Control Voltage .and
development of a GUI application on MTALAB 7.4.
Keywords:
Optimal power flow, economic dispatch, Ant system, fuzzy logic,
optimization, Static Var
Compensator
Table des Matières
Introduction generale 1
chapitre 1 Puissance réctive dans les
réseaux d'enrgie électrique 4
1.1. Introduction 4
1.1.1. Compensation de la puissance réactive 6
1.1.2. Méthode de compensation 7
1.1.3. COMPENSATEUR STATIQUE A THYRISTORS. 9
1.1.4. COMPENSATEUR SYNCHRONE 9
1.1.5. BATTERIE DE CONDENSATEURS 11
chapitre 2 Le Problème de la répartition de
charge 14
1.2. Introduction 14
1.3. Modélisation des composantes du réseau
électrique 14
2.1.1. Générateurs 14
2.1.2. Lignes de transmission 15
2.1.3. Transformateurs 15
2.1.4. Les Charges 16
1.4. Contrainte d'exploitation des réseaux
électriques 17
2.1.5. Contrainte sur les variables dépendantes : 17
2.1.6. Contrainte des variables indépendantes : 18
1.5. Algorithme de résolution du problème de
la répartition de puissance 19
2.1.7. Méthode de Gauss Seidel 19
1.6. La méthode de Newton-Raphson 21
2.1.8. Application de la méthode pour le calcul de
l'écoulement de puissance
22
1.7. Les méthodes découplées 26
2.1.9. Les méthodes découplées : 27
2.1.10. La méthode découplée 27
1.8. La méthode découplée rapide
28
chapitre 3 Optimisation des systeme
électrique 33
1.9. Introduction 33
3.1.1. Les algorithmes évolutionnistes. 34
1.10. Formulation d'un problème d'optimisation :
34
1.11. Méthode analytique 37
3.1.2. Méthode du gradient 37
3.1.3. Méthode de Newton et quasi -Newton 38
1.12. Méthode énumérative
38
3.1.4. Méthodes stochastiques 38
3.1.5. Méthode du recuit simulé 39
1.13. Recherche TABU 42
1.14. Algorithme évolutionniste 43
3.1.6. Les Algorithmes Génétiques 44
3.1.7. Principes généraux 44
1.15. Méthode de pénalité
45
3.1.8. Principe général des méthodes de
pénalités 45
3.1.9. Méthode de Fiacco et Mc Cormik : 45
3.1.10. Méthode de pénalité
extérieure : 46
3.1.11. Méthode de pénalité
intérieure : 46
3.1.12. Méthode de pénalité mixte : 47
1.16. Réseau de neurones 47
1.17. Logique floue 47
1.18. Colonies de fourmis 48
1.19. Monté Carlo : 48
1.20. Optimisation par essaim de particules :
50
1.21. Méthodes de résolution
50
1.22. Optimisation des puissances réactives
52
3.1.13. Introduction 52
3.1.14. Formulation du problème et solutions 52
3.1.15. Application 54
3.1.16. Variante 1 : ( ) 55
3.1.17. Variante 2 : (u = [ai]) 57
3.1.18. Variante 3 : u [Q , a i ]
g
= i 57
3.1.19. Organigramme du gradient réduit 59
chapitre 4 Compensateur statique d'énergie
réactive (SVC) 60
1.23. Introduction 60
4.1.1. Compensateur parallèles à base de thyristor
60
4.1.2. TCR (Réactance Commandées par thyristor)
61
4.1.3. TSC (Condensateurs Commandés par thyristor) 64
1.24. Les compensateurs statiques SVC) 67
4.1.4. Définition 67
4.1.5. Avantage du SVC 69
4.1.6. Caractéristique VI du SVC 72
4.1.7. Les trois zone du SVC 73
4.1.8. Exemple 2 73
4.1.9. Caractéristique V-I du compensateur statique 76
4.1.10. Fonctionnement de l'inductance commandé par
thyristors 78
chapitre 5 Une approche Fuzzy-Ant pour l'emplacement
optimal des condensateurs
dans un réseau électrique 82
1.26. Introduction 82
1.27. La logique Floue 82
5.1.1. Principe et définitions 82
5.1.2. Opérateurs et normes : 83
5.1.3. Structure générale d'un contrôleur
flou 84
5.1.4. Interface de fuzzification 84
5.1.5. Mécanisme d'inférence 85
5.1.6. Méthode d'inférence MAX-MIN 85
1.28. Interface de défuzzification 86
1.29. Optimisation par Colonies de fourmis
87
5.1.7. Introduction 87
1.30. Quelques concepts de base 87
5.1.8. Problème d'optimisation 87
5.1.9. Méthodes de résolution 88
5.1.10. Les heuristiques 88
5.1.11. Les méta heuristiques 88
1.31. Les fourmis artificielles 88
5.1.12. Un problème combinatoire : 89
1.32. Ant Colony System « ACS » 90
5.1.13. Ant System (AS-TSP) 90
5.1.14. Ant-Q 90
5.1.15. Ant Colony System (ACS) 91
1.33. Max-Min Ant System 92
1.34. Autres domaines d'application 92
1.35. Formulation mathématique 93
5.1.16. 1er Algorithme Pour l'identification des noeuds candidat
93
5.1.17. 2eme Algorithme Pour l'emplacement optimal des
condensateurs 94
1.36. Schéma bloc du Fuzzy_Ant 96
chapitre 6 Experimentation et discussion 98
6.1.1. Réseaux 25 noeuds 98
6.1.2. Données du réseau 25 noeuds 98
6.1.3. Données relative aux lignes de transport 98
6.1.4. Planification 99
6.1.5. Ecoulement de puissance 100
6.1.6. Les tensions nodales 100
6.1.7. Les Pertes totales 101
1.37. Approche Fuzzy_Ant 101
6.1.8. Application du Contrôleur Flou 101
6.1.9. Le compensateur statique (SVC) 103
1.38. Application avec Gui Matlab 7.04 106
Conclusion 110
Bibliographie 111
Table d'illustration
Figure 1: Schéma d'alimentation d'un réseau
électrique avec un compensateur
synchrone 11
Figure 2: Schéma d'alimentation d'un réseau
électrique avec une compensation série 11
Figure 3: Représentation de la connexion des condensateurs
(étoile ou triangle). 12
Figure 4: Schéma équivalent d'une ligne 15
Figure 5: Schéma monophasé d'un transformateur de
puissance 16
Figure 6: Organigramme du FDLF 31
Figure 7 : Point singuliers d'une fonction unidimensionnelle et
multimodale 35
Figure 8: Principales méthode d'optimisation 36
Figure 9: Parcours de l'espace de recherche avec le recuit
simulé .Le principe de
« recuit » qui se traduit par une augmentation du
niveau d'énergie, permet de sortir
des mina locaux. 40
Figure 11: Organigramme Recuit simulé 41
Figure 10:Organigramme de recuit simulé 41
Figure 12: Organigramme de la rechercher Tabou 43
Figure 13::Principe d'un Algorithme génétique 45
Figure 14: Schéma de principe du déplacement d'une
particule. Pour réaliser son
prochain 50
Figure 16:Structure d'un OPF 51
Figure 15:Structure d'un OPF 51
Figure 17:Organigramme du Gradient réduit 59
Figure 18: Réactance Commandé par Thyristor 61
Figure 19:Allure du courant TCR pour a = 90° 62
Figure 20: Allure du courant TCR pour 90° £ a
£ 180° 62
Figure 21: Allure du courant TCR pour a = 180 °
62
Figure 22:Variation de la Susceptance BTCR en fonction de a
63
Figure 23:Caractéristique d'un TCR 63
Figure 24: Formes d'ondes d'un TSC (a) sans « transiant
», (b) avec « transiant » 64
Figure 25: Connexion en triangle d'un TSC avec les inductances de
syntonisation. 65
Figure 26:TSC qui contint 3 condensateurs en parallèles
66
Figure 27:Relation entre le courant et le nombre des
condensateurs qui dans le TSC 66
Figure 28:Caractéristique d'un TSC 67
Figure 29: Schéma de principe d'un SVC à banc de
condensateur fixe 68
Figure 30: Schéma de principe d'un SVC 69
Figure 31: Variation de la tension sans et avec SVC 69
Figure 32: Augmentation de la capacité de transfert 70
Figure 33: SVC avec Banc de condensateur fixe 70
Figure 34:Variation de BSVC en fonction de l'angle
d'amorçage 71
Figure 35: Variation de BSVC en fonction de BTCR 71
Figure 36:Caractéristique V_I du SVC 71
Figure 37 Caractéristique d'un TCR, TSC et d'un SVC 72
Figure 38: Caractéristique d'un SVC 72
Figure 39: Circuit d'un compensateur statique comporte des
inductances variables et
des condensateurs manoeuvrables 74
Figure 40: Schéma détaillé d'une branche
76
Figure 41: Courbe en V du compensateur statique 77
Figure 42: Plage de fonctionnement du compensateur statique 78
Figure 43: Formes d'ondes de la tension et du courant circulant
dans l'inductance
lorsque la conduction est amorcée à 78
Figure 44:Schéma de Principe de l'approche Fuzzy_Ant 82
Figure 45: Format d'un ensemble flou normalisé 83
Figure 46: Structure d'un système de contrôle flou
84
Figure 47: Méthode d'inférence MAX-MIN 86
Figure 48:Une figure illustrant un problème combinatoire
89
Figure 49:schéma bloc de Fuzzy_Ant 96
Figure 50:Réseaux 25 noeuds 98
Figure 51::Variation des Tension Nodale avant l'emplacement des
condensateurs 101
Figure 52:Variation des Tension Nodales après emplacement
des condensateurs 103
Figure 53: Tensions nodales 105
Figure 54:SVC a banc de condensateur fixe 105
Figure 55:Perte active, Qsvc et ásvc pour les
différents cas 106
Liste des tableaux
Tableau 1: Classification des noeuds 17
Tableau 2 : Données relative aux lignes de transport 99
Tableau 4: Planification 100
Tableau 5:Les Noeuds Candidats 102
Tableau 6:Valeurs de condensateurs optimaux 102
Tableau 7:Les Tension Nodales 103
Introduction generale
État de recherche
L'industrialisation et la croissance de la population sont les
premiers factures pour
lesquels la consommation de l'énergie électrique
augmentée régulièrement .Ainsi, pour
avoir un équilibre entre la production et la
consommation, il est : a première vue
nécessaire d'augmenter le nombre de centrales
électriques, des lignes, des
transformateurs etc., ce qui implique ne augmentation de
coût et une dégradation du
milieu naturel.
Par conséquente ,il est aujourd'hui important d'avoir des
réseaux maillés et de
travailler dans la zone proche des limites de stabilités
afin de satisfaire ces demandes
.Avec la dérégulation du marché de
l'électricité ,on s'attend irrémédiablement
à une
augmentation du nombre des échange non planifier .Si ces
derniers .Si ces derniers n'
obéissent pas aux lois de Kirchhoff, et ne sont pas
contrôlés ,des problème peuvent
survenir dans le réseaux Certaines lignes situées
sur le chemine privilégies peuvent être
surchargées .Des lors ,il est intéressante pour
le gestionnaire de réseaux de contrôler ces
transite afin d'exploiter le réseaux de manière
plus efficace et plus sure.
Ces dernières décennies, plusieurs méthodes
d'optimisation ont été développées et
pour Ayant pour but d'assure une sécurité et une
réduction du coût .Toutes ces
techniques se réfèrent a l'ensemble de
l'écoulement optimal de puissance OPF et sont
généralement utilises comme des outils de
planification et d'exploitation .Mais, elles
présentent néanmoins une certaine limite pour
leurs utilisations en temps réel, leurs
utilisations en temps réel.
Le problème d'optimisation dans les systèmes
électriques de puissance,
résulte à partir du moment où deux
unités au plus de production devaient alimenter
plusieurs charges, obligeant l'opérateur à
décider comment repartir la charge entre les
différentes unités. Historiquement, les
premières méthodes d'optimisation ont été
réalisées par rapport au contrôle de la
puissance active. Ce qui est connue, actuellement,
sous la dénomination de la répartition
économique classique dont l'objectif principal
est de déterminer la puissance active à
générer par les différentes unités de
production,
en minimisant les coûts de génération.
Mais, après il a été constaté que l'optimisation
de
la puissance active n'est pas suffisante. Une mauvaise gestion
de la puissance réactive
augmente les pertes d'où un accroissement des coûts
de production.
Le développement des techniques de programmation et de la
puissance de
calcul des ordinateurs, a contribué à la
résolution des systèmes de plus en plus
complexes. Cette évolution a conduit à
l'élaboration de nouvelles méthodes de
résolution qui sont connues sous l'appellation :
répartition optimale des charges ou OPF
(Optimal Power Flow). Pour la planification et l'exploitation
des systèmes électriques de
puissance, l'OPF permet d'optimiser des fonctions objectives
distinctes liées à des
contraintes.
Actuellement, pour toute entreprise électrique, l'OPF est
devenu un outil
indispensable. En exploitation, un OPF détermine
périodiquement les valeurs optimales
des variables électriques, en considérant toutes
les contraintes et les limites. En se
basant sur ces valeurs optimales, les opérateurs
réalisent les manoeuvres nécessaires
pour obtenir l'exploitation optimale du système, en
suivant les variations de la demande.
En planification, l'OPF est utilisé pour planifier les
changements pourront se produire
sur le réseau en dehors de l'état optimal du
système.
il y a deux classes de technique d'optimisation. Dans la
première, les conditions
d'optimalité du premier ordre sont
dérivées du Lagrangien et simultanément résolues
par la méthode Newton Raphson. Des que les
équations du réseau et les contraintes
d'inégalité apparaissent explicitement dans le
Lagrangien, des solutions fiables sont
disponibles jusqu'à la convergence du processus
itératif interactif.
Le problème de contrôle de la tension et de
l'énergie réactive des systèmes
électriques est à présenter une des
principales préoccupations des entreprises de
production et de distribution de l'énergie
électrique. La recherche entreprise sera basée
sur les contrôles des tensions et la répartition
optimale des puissances réactives.
Ainsi, pour avoir un équilibre entre la production et la
consommation, il est en
première vue il est nécessaire d'augmenter le
nombre de centrale électrique, de lignes
de transformateurs etc., ce qui implique une augmentation de
coût et une dégradation
du milieu naturel .En conséquence, il est aujourd'hui
important d'avoir des réseaux
mailles et de travailler proche des limites de
stabilité. Enfin, une dernière partie sera
consacrée à la répartition optimale des
puissances (OPF) où une ou plusieurs variables
de contrôle peuvent être optimisées. Le
choix de la méthode se fera en fonction des
contraintes choisies. Un processus d'optimisation basé
sur le contrôle de tension en
injecte des SVC sur différente portions du
réseau. Cela permettra d'optimiser la
puissance réactive des différents groupes de
production permettant la minimisation des
pertes actives totales du réseau.
Dans cette étude nous proposons optimisation le
l'énergie réactive dans le réseau
électrique qui revienne soit à contrôler
les tensions au niveau des différentes noeuds du
réseau, par injection des SVC dans les noeuds
violé. L'objective principale de cette thèse
est de contrôler les tensions Nodales avec
SVC.et l'emplacement optimal des
condensateurs dans le réseau électrique.
Organisation
Le chapitre 1 se résume à définir la
puissance réactive dans le réseau d'énergie
électrique. Le chapitre 2 présente, le calcul de
l'écoulement de puissance tel que la
méthode de Gauss Seidel, Newton Raphson,
découpler et découpler rapide .Le chapitre
3, abordera les méthodes d'optimisations, on explique
l'optimisation du system
électrique tel que la méthode de gradient
réduit dans la minimisation des pertes actives.
Le chapitre 4, décrit le les compensateur statiques de
l`énergie réactive (SVC).Le
Chapitre 5 présente une approche Fuzzy_Ant sur
l'emplacement optimal des
condensateurs sur le réseau électrique Enfin le
chapitre 6, concerne l'expérimentation et
discussions des résultats des différentes
méthodes appliqués au réseau de 25 noeuds et
présentation d'une application développée en
MATLAB 7.04.
chapitre1
Puissance réctive dans
les réseaux d'enrgie
électrique
1.1. INTRODUCTION
1.1.1. Puissance réactive
Un réseau a pour fonction de transporter la puissance (ou
l'énergie) depuis une
source de production vers un centre de consommation
appelé charge ou récepteur. La
charge est caractérisée par sa tension, son
courant, son impédance et son facteur de
puissance. Tout système électrique fonctionnant
sous tension alternative consomme de
l'énergie sous deux formes, l'énergie active Et
l'énergie réactive, puisque la tension et le
courant sont rarement en phase .En régime
sinusoïdal, à la fréquence industrielle
(50 Hz), appelons : U et I les valeurs efficaces respectivement
de la tension u et du
courant i.
le déphasage entre v et i(compté positivement si
le courant est en retard sur la
tension).
La puissance apparente, fournie par la source de
production :

Impose les dimensions du générateur et du
réseau de transport ou de distribution
.Seule la puissance active, reçue par
la charge, se transforme en énergie mécanique,
thermique, lumineuse, etc. C'est la puissance utile qui transite
par la charge et qui est :

Par rapport à la puissance apparente S, la puissance
active P est réduite d'un
facteur de puissance entraînant des pertes
d'efficacité du réseau, La puissance
réactive , non utilisée, est :

Ainsi, on obtient :en réalité, la puissance
réactive sert à l'aimantation des circuits
magnétiques des machines électriques
(transformateurs et moteurs) et de certains
appareils tels que les lampes fluorescentes. Mais, par contre,
la transporter en même
temps que la puissance active conduit à surdimensionner
les lignes de transport et de
distribution et donc à en augmenter le coût ou
à les faire fonctionner à leurs limites, ce
qui peut conduire à des instabilités
néfastes pour la qualité de service.
On montre que la puissance réactive a des
propriétés de conservation dans le
réseau. Par convention, tout élément
inductif du réseau ( > 0) consomme de l'énergie
réactive et tout élément capacitif ( <
0) en produit. Il est aisé de calculer ces
consommations et productions. La puissance réactive
consommée par une inductance L
parcourue par un courant I est :

La puissance réactive produite par une capacité C
soumise à une tension U est égale à :

Avec

étant la pulsation du réseau en radians par seconde
et f la fréquence en
(hertz). Comme pour la puissance active, on peut
établir, aux noeuds du réseau ou sur
tout trajet du courant, des bilans équilibrés de
puissance réactive. Le bilan global est le
suivant :
§ les charges sont très généralement
inductives, c'est-à-dire consommatrices
de puissance réactive ;
§ les lignes aériennes produisent de l'énergie
réactive du fait de leur capacité
lorsqu'elles sont peu chargées ; elles en consomment
lorsqu'elles sont fortement
chargées ;
§ les câbles souterrains en produisent du fait de leur
faible inductance et de
leur grande capacité ;
§ les transformateurs en consomment.
Globalement, le réseau et ses charges appellent de
l'énergie réactive, sauf aux
heures creuses .Ainsi, il s'établit, sur les
réseaux, une forte circulation de puissance
réactive, ce qui se traduit par des cos Õ faibles
en tout point du réseau, par conséquent,
de fortes pertes de rendement et un surdimensionnement des
réseaux. L'ampleur du
phénomène est telle que, dans bien des cas, le
réseau ainsi constitué deviendrait
inexploitable .La solution consiste à produire de la
puissance réactive au voisinage des
lieux de consommation. C'est le rôle des condensateurs de
puissance ou les
compensateur statique SVC .Placés près des
éléments inductifs, ces derniers leur
fournissent directement de la puissance réactive ;
celle-ci n'a plus à circuler sur le
réseau d'alimentation ; on limite ainsi les
instabilités et les surdimensionnements des
réseaux
1.1.2. Compensation de la puissance réactive
Un réseau est défini comme un ensemble d'appareils
destinés à la production, au
transport, à la distribution à partir de la
centrale de génération jusqu'aux centrales
industrielles, commerciales et résidentielles. Le
transport de cette énergie se fait sur les
conducteurs tels que les lignes aériennes et les
câbles souterrains. Afin que l'énergie
électrique soit utilisable, le réseau de
transport et de distribution satisfaire les
exigences suivantes:
· Assurer au client la puissance dont il a besoin,
· Fournir une tension stable dont les variations ne
dépassent pas #177; 10% de la
tension nominale,
· Fournir une fréquence stable dont les variations
ne dépassent pas #177; 0.5%,
· Fournir l'énergie à un prix acceptable,
· Maintenir des normes de sécurité,
· Veuillez à protéger l'environnement.
Dans toute installation électrique alimentée en
courant alternatif, la puissance
consommée se décompose en:
Puissance active qui se transforme en puissance mécanique
et en chaleur,
Puissance réactive nécessaire à
l'excitation magnétique des récepteurs
inductifs (Tels que les moteurs, les transformateurs).
La consommation excessive, pour une centrale industrielle de
l'énergie réactive,
entraîne des dépenses élevées.
Pour réduire ces dernières, il faut agir sur le
facteur de puissance de
l'installation.
En effet, dés qu'il y ait diminution du facteur de
puissance, le courant de charge
d'une centrale électrique et des postes de
transformation augmente, malgré que la
puissance distribuée reste la même. C'est pourquoi
le , caractérisant la puissance
installée, est souvent appelé facteur de
puissance. En Algérie, le facteur de puissance est
considéré normal s'il atteint 85% à 90%;
dés que le facteur de puissance soit faible dans
une entreprise consommant de l'énergie
électrique, l'entreprise paye une amende et
lorsque ce facteur est élevé, elle reçoit
une prime. Donc, l'amélioration du est une
tâche extrêmement importante pour
l'économie. Le consommateur devrait donc soit
payer la part de la puissance réactive correspondante,
soit prévoir une installation de
compensation de la puissance réactive. En principe, il
est possible d'agir sur le facteur de
puissance en intervenant sur la puissance active, en pratique
on fait varier la puissance
réactive soit en la diminuant, soit en l'augmentant, ce
réglage s'appelle évidemment la
compensation, La puissance réactive n'est nettement
définie qu'en sinusoïdale, elle vaut
|
: étant le déphasage entre le courant et la
tension
|
Le cas du circuit R, L, C permet de comprendre la signification
physique de Q. Pour ce
circuit.

La puissance réactive traduit l'importance de
l'échange d'énergie entre la source
et l'inductance ou la capacité, échange à
bilan nul puisqu'on rapporte sur R l'ensemble
des pertes. Les tensions et étant toujours en opposition
de phase, il a fallu adopter
une convention de signe pour caractériser ces
échanges. On dit que les inductances
absorbent de la puissance et que les capacités en
créent. La source fournit donc

Si , les charges d'énergie s'équilibrent à
chaque instant, ,

Si , la source fournit du réactive, est positive
Si , la source reçoit du réactive, est
négatif
Donc, le sens physique de cette puissance réactive c'est
une énergie accumulée
dans les éléments non dissipatifs tels que les
selfs et les condensateurs. Cette énergie est
liée aux champs électriques et
magnétiques. En régime variable, elle est emmagasinée
par les selfs puis basculée vers les capacités.
1.1.3. Méthode de compensation
Le fonctionnement du réseau dans de bonnes conditions de
la qualité, de sécurité
et d'économie implique une maîtrise de
l'évolution de son état électrique. Le maintient
d'une tension correcte nécessite de la part du
dispatcher, des ajustements de la
production d'énergie réactive par un dialogue
avec les centrales. Dans ces conditions, la
coordination des divers moyens de réglage est
délicate. Il en résulte des variations de
tension importantes entre heures creuses et heures pleines. Ces
variations peuvent être
gênantes et il peut dans certains cas en résulter
un risque d'auto dégradation du plan de
tension qui peut conduire à un effondrement partiel ou
total du réseau. Sans disposition
particulière, la puissance réactive
consommée par les charges et le réseau provient
essentiellement des alternateurs. On a vu que le transit de
cette puissance à travers les
éléments du réseau produit non seulement
des chutes de tension mais aussi des pertes
actives et réactives par effets joule.

On peut réduire ces perturbations de tension ainsi que
les réactions dues aux
charges asymétriques et aux harmoniques, en
évitant le transport de la puissance
réactive et la produire autant que possible là
où elle est consommée et cela est possible
en installant des dispositifs appelés les compensateurs
réactives.
La compensation de la puissance réactive à pour
tâche:
§ Réduire les fluctuations de tension et les
phénomènes de flicker
(papillotement),
§ Améliorer le facteur de puissance ,
§ Equilibrer les charges asymétriques.
Les caractéristiques idéales pour un système
quelconque de compensation sont les
suivantes:
§ Réponses instantanées à des
variations brusques de charges ce qui garantit
les changements rapides et lents de la charge seront
atténués,
§ Réponses indépendantes pour chaque phase de
manière à ce que les
variations de charges équilibrées et
déséquilibrées sur les phases soient
atténuées.
Le principe de la compensation serait donc, selon la demande du
réseau, de fournir
de la puissance réactive ou de l'absorber. En analysant
la nature de la puissance réactive,
on peut conclure que la puissance réactive est une chose
très importante pour les
réseaux électriques (en courant alternatif).On
distingue les sources principales et les
sources complémentaires (ou secondaire).Les sources
principales sont destinées pour la
production de la puissance active et la puissance
réactive, ce sont les générateurs des
centrales électriques qui produisent ces puissances. Les
sources complémentaires (ou
secondaire) sont des installations électriques
destinées pour la compensation du
surplus ou des déficits de la puissance réactive
dans les réseaux électriques et pour des
différents réglages dans ces régimes de
fonctionnement. Leur puissance installée et leur
emplacement sont en relation directe avec des critères
d'ordinaire technique et
technico-économique. Les installations
électriques sont installées dans des sous stations
directement ou sous formes de consommateur.
Parmi les moyens de compensations réactives on a:
§ Compensateur synchrone
§ Compensateur statique à thyristors.
§ Inductance
§ Batterie de condensateur
1.1.4. COMPENSATEUR STATIQUE A THYRISTORS.
Ils sont constitués d'ensembles de condensateurs et
d'inductances commandés par
thyristors. Les compensateurs statiques ont des bonnes
performances dynamiques,
ils peuvent donc être utilisés pour les
réglages de la tension, en particulier dans
les zones éloignées des centres de production,
ils permettent également de réduire
les perturbations créées par certains
utilisateurs et contribuer à l'amélioration de
la stabilité du réseau. Ces thyristors sont
montés tête-bêche dans chaque phase, chacun
d'entre eux étant ainsi conducteur pendant une
demi-période. Différentes combinaisons
sont possibles. L'une des plus utilisées consiste
à associer une inductance commandée
par thyristors à des gradins de condensateurs
commandés manuellement voir
figure.2.3.La puissance réactive absorbée par
l'inductance varie en contrôlant la valeur
efficace du courant qui la traverse par action sur l'angle
d'amorçage des thyristors. Dans
le cas des batteries de condensateurs, les thyristors
commandent la mise en service
des différents gradins et la puissance réactive
fournie varie par palier.
1.1.5. COMPENSATEUR SYNCHRONE
Il peut être assimilé à un moteur synchrone
fonctionnant à vide, c'est à dire que
son arbre n'est pas soumis à aucun couple
résistant, qui serait peut-être considérer
comme charge. Le stator est branché au réseau
à un courant triphasé, sur le rotor est
enroulée une bobine d'excitation. On peut donc
considéré que le compensateur
synchrone consomme une très faible quantité de
puissance active égale aux pertes par
échauffements dans ces enroulements du stator et par
frottement. Nous devons limiter
la puissance active et augmenter un peu la puissance
réactive de telle façon que le
courant I passant par les enroulements ne dépasse pas la
valeur maximale du stator, la
puissance apparente est toujours positive et le courant I se
détermine à partir de cette
dernière.

Par conséquent la puissance aux bornes du compensateur
synchrone est donnée par:

Dans les jeux de barres les moteurs synchrones consomment la
puissance active et
réactive un tel régime est appelé
régime ordinaire de sous excitation, la diminution du

courant d'excitation entraîne la diminution de . Où
donc le
compensateur synchrone consomme de la puissance
réactive.
consommée on a , où et le facteur de puissance .


Régime de la puissance active, dans ce cas la puissance
réactive n'est pas
Consommation de la puissance active et fourniture de la
puissance réactive au
réseau et le facteur de marche est négatif, ici et,
un tel régime est
appelé régime de surexcitation donc le
compensateur synchrone injecte de la puissance
réactive dans le réseau .Le réglage de la
puissance réactive du compensateur synchrone
s'effectue par le réglage du courant d'excitation.

Figure 1: Schéma d'alimentation d'un réseau
électrique avec un compensateur
synchrone
Avec un compensateur synchrone, les compensateurs synchrones
sont placés prés
des grands centres de distribution, ils jouent le rôle de
capacités variables. Dans les
réseaux bouclés, ils permettent de régler
les puissances transmises par les diverses
lignes d'alimentation. Aux heures de fortes charges, ils
créent beaucoup de réactive pour
diminuer les chutes de tension. Ils peuvent être
nécessaires à certains moments de leur
faire absorber de la puissance réactive, par exemple
pour compenser l'élévation de
tension créée par une longue ligne (HT) à
vide. Leur puissance est de (20 à 60) Mvar en
fourniture et de (10 à 30) Mvar en absorption, donc la
puissance réactive qu'un
compensateur peut absorber est de l'ordre de la de la moitie de
sa puissance nominale.
1.1.6. BATTERIE DE CONDENSATEURS
Les condensateurs sont placés en série sur une
ligne dont ils compensent
partiellement la réactance. La compensation série
est employée sur certaines lignes à
haute tension à la fois très chargées et
très longues. Le branchement d'une batterie de
condensateur aux bornes d'une charge comme est
représenté dans la (Fig 2),
[17, 31, 34] diminue la puissance réactive dans une
ligne d'alimentation de cette charge,
pour cette raison la batterie dans ce cas est
considérée comme générateur de puissance
réactive.

Figure 2: Schéma d'alimentation d'un réseau
électrique avec une compensation série

La variation de QC peut être obtenue par le branchement ou
le débranchement des
condensateurs, cette action est obtenue par une combinaison
dans la connexion des
condensateurs.

Figure 3: Représentation de la connexion des
condensateurs (étoile ou triangle).

Et


Si on examine le cas très simple d'une charge
alimentée par une source de tension
constante, à travers une ligne ( Fig .2.6 ), on peut
écrire de façon approchée, que la chute
de tension dans la ligne ÄV, induite par les flux de
puissance active et réactive
(P et Q) appelés par la charge, est égale à
:

C'est la circulation de réactif qui crée
généralement les chutes de tension
prépondérantes. Tension et puissance
réactive sont donc des grandeurs très liées. Ainsi,
la puissance réactive se transporte mal (elle
crée des chutes de tension). Cela a pour
conséquence qu'au-delà d'une certaine distance,
la puissance réactive fournie par
les alternateurs ou les condensateurs ne peut pas parvenir
jusqu'à l'endroit où on en
a besoin .Pour une ligne THT, X >10 R :

chapitre 2
Le Problème de la
répartition de charge
1.2. INTRODUCTION
La répartition des charge (Load Flow) est l'un des
principaux problème qui se pose
aux gestionnaire d'un système de production -transport
d'énergie électrique .Dans tout
Ensemble de centrales électriques alimentant un ensemble
de consommateur par
l'intermédiaire d'un réseau de transport
maillé, on doit déterminer la répartition des
puissances fournies par ces centrales, à un instant
donné, tout en respectant un
ensemble de contrainte technique et économique.
La résolution du problème de la répartition
des charges, nous permet de
déterminer les valeurs du Module et la phase de la
tension en chaque noeud du réseau
pour des conditions de fonctionnement données .Ce qui
nous permettra de calcul les
puissances transites et générées et les
pertes .Pour résoudre ce problème, il est
nécessaire de déterminer conditions de
l'opération en régime permanent, d'un system
de puissance qui sont :La formulation d'un model
mathématique approprié la
spécification d'un certain nombre de variable et de
contraintes dans les noeuds du
système. La résolution numérique du
système. Pour chaque étude, il faut définir les
conditions de fonctionnement du réseau .Ces conditions
Affectent les grandeurs
électrique relatives aux noeuds du réseau
.Ceux-ci peut ainsi être définies suivant trois
types de noeuds :
1.3.MODELISATION DES COMPOSANTES DU RESEAU ELECTRIQUE
2.1.1. Générateurs
Comme le générateur fonctionne en régime
permanent, il délivre une certaine
puissance active « PG » sous une tension maintenue
constante (à l'aide d'un régulateur
de tension). Il peut être modélisé par une
puissance constante « PG » et un module de
tension constant « VG » ce qui correspond au type
« PV ». Dans ce type de noeud, les
puissances active et réactive sont maintenues entre
certaines limites dites contraintes
de fonctionnement.


Où sont respectivement les limites minimale et maximale
des puissances active et réactives
génères. Un de ce type de générateurs, typiquement
le
plus puissant est défini comme étant le noeud
balancier en Anglais « slack ou swing bus »
et au niveau duquel la tension est connue en module et en
argument ; les puissances
active et réactive calculées par la suite doivent
couvrir toutes les pertes dans le réseau
électriques.
2.1.2. Lignes de transmission
La meilleure façon de présenter une ligne de
transport est le schéma en PI « ð »
symétrique.


Figure 4: Schéma équivalent d'une ligne
Où est l'impédance série de la ligne «
km » et l'admittance shunte par
rapport à la terre.
2.1.3. Transformateurs
Un transformateur inséré dans une branche peut
être représenté par un
autotransformateur idéal et une admittance série
comme le montre la (Fig. 4)en
schéma monophasé équivalent :

Figure 5: Schéma monophasé d'un transformateur de
puissance
En utilisant l p p noeuds
k et m
Tels que :

A la base des ces courants, on peut déterminer les
paramètres complexe A, B, C tels que :

Dans le cas particulier où :
, ; ;




La présence du transformateur dans la branche
modifiée les paramètres
complexes du schéma PI équivalent a la branche et
devient dissymétrique. En
conséquence la répercussion sur L'EP est nettement
ressentie sur l'ensemble du réseau.
2.1.4. Les Charges
Pour simplifier les calculs de l'écoulement de puissance,
il est commode de
représenter les charges par leur puissance active et
réactives ; les autres variantes qui
permettent de les déterminer sont aussi valables (facteur
de puissance, courant etc.)
|
Classification
|
Variables connues
|
Variables inconnues (à calculer)
|
|
PQ (noeud Charge)
|
P, Q
|
V, d
|
|
PV (noeud Générateur)
|
P, V
|
Q, d
|
|
V ä (noeud Balancier)
|
V, ä
|
P, Q
|
Tableau 1: Classification des noeuds
1.4. CONTRAINTE D'EXPLOITATION DES RESEAUX ELECTRIQUES
Ces contraintes sont liées à la nature physique
des éléments du réseau .On
distingue les Contraintes sur les variables dépendantes,
dites contrainte de sécurité et
contrainte sur Les variables indépendantes de limites
.Ces Contraintes doivent être
vérifiées à chaque répartition de
charge ou optimisation.
2.1.5. Contrainte sur les variables dépendantes :
Les contraintes liées à la sécurité
des réseaux sont généralement comme suit :
2.1.5.1 Contrainte équilibre entre la production et
la consommation :
En régime normale et à tout moment,
l'égalité entre la production et la
consommation des puissances active et réactive doit
être assuré, soit :



Perte active totale
Perte réactive de consommation
Nombre de noeuds de consommation
Nombre de noeuds de génération
2.1.5.2 Contrainte sur les modules de la tension :
Les conditions d'exploitation des réseaux fixant les
limites des tensions maximales
par la tenue diélectrique du matériel et la
saturation des transformateurs .et les limites
minimale par l'augmentation des pertes et le maintien de la
stabilité des alternateurs .On
Aura pour tous les noeuds, la condition suffisante et
nécessaire à savoir :


Avec :

Module de la tension au noeud i
Respectivement limites (minimale et maximale) de la tension.
Le respect des contraintes de tension est d'une importance
primordiale pour la
securit d'exploitation et du matériel .Une violation de
la limite supérieure que l'on
observe parfois En faible charge peut construire un danger pour
l'isolation du matériels
.Par ailleurs, des Tensions trop basses nuisent à
l'exploitation rationnelle du réseau et
peuvent conduire à son écroulement.
2.1.5.3 Contrainte sur la capacité de transit de la
ligne :
La puissance transité dans une ligne ne doit, en aucun cas
dépasser la limite maximale,
soit :

Avec :

: Puissance apparente transitée dans la ligne i-j
: Puissance apparente maximale transitée dans la ligne
i-j
: Puissance active transitée dans la ligne i-j
: Puissance réactive transitée dans la ligne i-j
En générale à partir des contrainte des
puissances transité, nous déterminons les
contrainte de courant correspondant aux lignes et aux
transformateurs .On limite les
courants pour des rasions de surcharge et de stabilité.
2.1.6. Contrainte des variables indépendantes :
Ces contraintes sont liées à la nature physique des
éléments du réseau :
2.1.6.1 Contrainte sur la production :
La puissance produite par chaque groupe est bornée
supérieurement par la
puissance maximale qu'il peut fournir et inférieurement
par le minimum, qui est
conditionnée par le rendement de ce groupe et les
contraintes sur la turbine. Pour tous
les noeuds de production, les contraintes actives et
réactives sont:



2.1.6.2 Contrainte sur les rapports de transformateur :
Le rapport de transformation des transformateurs avec
régleur en charge, peut
variée selon la position du régleur .Ce dernier
doit être limité entre deux borne,
minimale et maximale, soit :


: Nombre de transformateur
1.5. ALGORITHME DE RESOLUTION DU PROBLEME DE LA
REPARTITION DE
PUISSANCE
2.1.7. Méthode de Gauss Seidel
Le calcule de l`écoulement de puissance en régime
permanent établi se base sur le
système d'équation linéaire suivante :

Où :
I : vecteur complexe des Courants nodaux injectée dans le
réseau ;
Y : matrice complexe des admittances nodales complexe ;
V : vecteur complexe des tensions nodales.
Si le réseau admet n noeuds I et E auront n composante
complexes et Y sera une
matrice complexe de dimension n*n .les élément de
seront calculés à partir des
caractéristiques des composantes du réseau. Cette
méthode dérivant de la méthode
itérative de Gauss utilisant la matrice admittance
consiste à supposer initialement les
tensions pour tous les noeuds excepté le noeud balancier
où la tension est spécifiée et
maintenue constante. Outre le noeud balancier pris comme noeud
de référence, les
courants sont calculés pour tous les noeuds comme suit:

Où :


Désigne le nombre de noeuds dans le réseau
Le conjugué de la puissance apparente injecté au
noeud i ;
Le conjugué de la tension au noeud k ;
|
La puissance active injectée au noeud k ;
La puissance réactive injectée au noeud k.
|
En remplace l'équation (2.13) dans (2.14) on aura :

L'expression de la tension pour chaque noeud est :



On pose :


D'où l'expression finale de la tension pour chaque noeud
:

Pour accélère la convergence de la
méthode, on introduit un facture d'accélération

Algorithme de Gauss Seidel
|
1ereEtape :
Formation de la matrice admittance
|
|

2emeEtape :
Estimation des valeurs initiales des tensions nodales
3emeEtape :
Calcule des tensions pour chaque noeud suivant la relation :

Déterminer des paramètres et

Initiation des itérations
4emeEtape :
Calcul itératif des tensions pour chaque noeud suivant la
relation :

On calcul l'écart entre les valeurs d'une même
tension trouvé aux itérations suivantes :

On introduit le facture d'accélération pour
réduire le nombre d'itérations.

5emeEtape :

Une fois le test de convergence est vérifié valeurs
des tensions de la
dernière itération sont retenues, on calcule :
Les puissances transitées :



Les puissances injectées :
Les pertes :

Si non aller à l'étape 4.
1.6.LA METHODE DE NEWTON-RAPHSON
Etant donné un system d'équation non
linéaire :

Le principe de la méthode est basé sur le
développement en série de Taylor de la
fonction autour des corrections portées sur les variables
.L'écriture développée donne.

Où et représentent respectivement la premier et la
seconde dérivé de y
par rapport à ,Si est petite alors peut être
négligée, pour une correction
petite , la relation est :


En représentant le changement dans (y=f(x)) :


Si y est une fonction avec des variables multiples alors :

Où : représentent les corrections portées
sur les

variables l'écriture matricielle du system donne :





Ainsi, on arrive à un system d'équation
linéaire qui est simple à résoudre .La méthode
sera davantage explique par son application au calcul de
l'écoulement de puissance.
2.1.8. Application de la méthode pour le calcul de
l'écoulement
de puissance
Elle nous permet de résoudre un système
d'équation non linéaire en exprimant les
puissances actives et réactives en fonction des tensions
nodales.
L'équation de la puissance complexe au noeud (k) est :


Le courant s'exprime en fonction des admittances aux noeuds par
la relation
suivante :

En substituant l'équation (2.31) dans l'équation
(2.32) on obtient :

On peut exprimer les tensions des noeuds et les
éléments de la matrice admittance en
module et argument :



On remplace ces valeurs dans l'équation (2.3 3) :

Les composantes ( réelles et imaginaires )de la puissance
du noeud k :
En posant :
Les équations (2.38) (2.39) peuvent s'exprimer comme suit
:

Calcul des jacobines :
Les éléments du Jacobine sont calculés
à partir de l'équation (2.3 9) et (2.40) :
Le Jacobine J1 :
Les éléments non diagonaux :

Les éléments diagonaux :

Le Jacobine J2 :
Les éléments non diagonaux :

Les éléments diagonaux :

Le Jacobine J3 :
Les éléments non diagonaux :
Les éléments diagonaux :
Le Jacobine J4 :
Les éléments non diagonaux :




Les éléments diagonaux :

Le test de convergence de la méthode s'effectue comme suit
:
DPk et DQk sont les variations respectives des puissances actives
et réactives du noeud
(k) définies par :
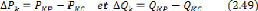
Avec :

Puissance active planifiée.
Puissance active calculée.
Puissance réactive planifiée.
Puissance réactive calculée.
Le passage d'une itération vers l'autre se fait à
partir des ajustements suivants :

Où e est le nombre d'itérations.
Algorithme de Newton -Raphson :
1ere Etape :
Introduction des données du réseau.
Détermination de la matrice admittance.
Les puissances actives et réactives des charges du
réseau sont données dans le
tableau de planification.
2emeEtape :

Calcul des puissances actives et réactives pour ,à
l'exception
du noeud de référence.
3eme Etape :
Puisque les valeurs des puissances planifiées sont
données par le tableau de
planification, on peut calculer les variations de puissance
telles que :

Où: (e) numéro d'itération,
: puissances planifiées .
puissances calculées.


4eme Etape :
On détermine la variation maximale pour les variations
des

puissances : .
5 eme Etape :

On procède à un test de convergence pour le max de
.Si une de ces deux
valeurs est supérieure à une certain
tolérance (e) on passe au calcul du jacobin (J).
6 eme Etape :
On se retrouve avec un système d'équations non
linéaires dont la résolution est
faite par la matrice inverse. Les corrections sur les
composantes des tensions sont
déterminées pour chaque noeud.
7 eme Etape :
Les corrections sur les tensions sont utilisées pour
déterminer les nouvelles
estimations des tensions nodales comme suit :


8 eme Etape :
Les nouvelles valeurs de sont remplacées dans les
formules
des puissances et et on revient à l'étape (3) pour
refaire le processus itératif. La
fin du processus itératif se fait lorsque les variations
des puissances à savoir : et
deviennent inférieures à la précision
(e).
1.7. LES METHODES DECOUPLEES
2.1.9. Les méthodes découplées :
Ces méthodes prennent comme base ma méthode de
Newton, et elles utilisant le
découlement qui existe entre la puissance active et
l'angle de la tension, et la puissance
Réactive et le module de la tension .Ceci donne une
série de simplification qui tendent à
Améliorer le développement pratique de
l'écoulement des charges .Deux de ces
méthodes Sont exposées :
2.1.10. La méthode découplée
Lorsque les angles q i et qj sont
très petits, leurs cosinus seront voisine de l'unité,
leurs sinus sont voisine de 0 et les termes H et L seront
prépondérants par rapport a
ceux des N et M .On néglige N et M devant H et L, ce qui
donne le Jacobin découpler.
La première équation de l'écoulement des
puissances peut être exprimée comme suite :

Le système (2.54) peut être écrit sous forme
suivante :

Le système d'équation (2.63) et (2.64) est
résolu pour actualiser le module et l'angle des
tensions aux noeuds de charge par :

Le processus itératif continuera jusque à
l'obtention de la convergence
Algorithme de la méthode découplée
:
1er Etape :
Introduction des données du réseau.
Détermination de la matrice admittance.
Les puissances actives et réactives des charges du
réseau sont données dans le tableau
de planification.
2emeEtape :


Calcul des puissances actives et réactives k pour k=1
à (n-1), à l'exception du
noeud de référence.
3emeEtape :
Puisque les valeurs des puissances planifiées sont
données par le tableau de
planification, on peut calculer les variations de puissance
telles que :

Où : (e) numéro d'itération.

: puissances planifiées.
: Puissances calculées.

4meEtape :

On calcule les deux Jacobines tout en négligeant les deux
autres

5emeEtape :
On calcule les corrections Aô et AE pour chaque noeud par
la résolution des deux
équations :

6emeEtape :
On détermine la nouvelle estimation de la tension nodale
à partir des corrections Aô et
AE :
On remplace les nouvelles valeurs de (ô) et (E) dans
l'équation de calcul de
puissance (P et Q) pour recalculer de nouveau les
variationsAô et AE , on revient à
l'étape (3) pour refaire le processus itératif.
8emeEtape :
La fin du processus itératif est atteinte lorsque AP et
AQ deviennent aussi petites
que la précision (E). 1 AP1 E et 1 AQ1 E
1.8. LA METHODE DECOUPLEE RAPIDE
La méthode découplé rapide »e a
été établie en 1973 par B.Scorretet O.Alasc .Elle
utilise d'autre simplification par rapport à la
méthode découpler. La première étape
consister à découpler l'écoulement de
puissance active angle et l'écoulement de
puissance réactive module de la tension. La
méthode découpler rapide est une
simplification de la méthode découpler, par une
série d'approximations sur les
équations (2.63) et (2.64) .les éléments des
jacobins et Sont obtenus après
approximations successives [24,25] :

A partir de l'approximation précèdent, les
jacobines s'écrivent comme suit :
pour H :

Pour L :

Substituons les équations (2.70),(2.71),(2.72)et (2.74)
dans les équations (2.64 et
(2.64) :


Les éléments des sous matrice et sont
exprimé en fonction de
( la partie imaginaire des admittance).

On pose pu, on obtient un système linéaire :
Avec :

Algorithme méthode découplée
rapide
1ereEtape :


Entre les donnes du réseau n, et les grandeurs
planifiées

2emeEtape :
Calcul de la matrice
3emeEtape :

Supposons que les tensions initiales sont pour
4emeEtape :
Calculons

Calculons



5emeEtape :
|
Test de la convergence de la puissance active :
|
|
6emeEtape :
Si la convergence de la puissance n'est pas obtenue non passe
à la résolution d'équation :
Avec :

Déterminons les nouveaux angles :
7emeEtape :


Calcul Qi et avec les nouvelles estimations de avec
les équations :

8emeEtape :

Testons la convergence de puissance réactivée :
9emeEtape :
Si la convergence n'est pas obtenue, on passe à la
résolution du système équation :

Former B' et B»


Calculer les nouvelles
valeurs de et actualisé
Calculer les nouvelles
valeurs de et actualisé
Calculer
Calculer
Résultats
Figure 6: Organigramme du FDLF
Conclusion :
L'importance de l'étude de la répartition des
puissances dans un réseau est
capitale pour l'obtention d'un état de réseaux
à partir duquel nous avons appliqué le
system de minimisation des pertes réelles. Parmi c'est
méthode on choisit la méthode
de Newton-Raphson qui est très robuste surtout pour les
réseaux de grandes tailles elle
converge rapidement au contraire de la méthode de Gauss
Seidel qui très simple .Elle
convient très bien avec les réseaux de petites
tailles mais elle diverger pour les réseaux
de grands
tailles.la méthode F.D.L.F et une
méthode convergente très rapide puisque les
matrices utilisées par cette méthode sont
constantes, tandis que pour la seconde, elles
varient à chaque itération. Elle est
utilisée dont les system de contrôle de la tension
basée sur le calcul des sensibilités. Pour cela,
on a choisi la méthode de Newton-Raphson
pour la comparaison entre la méthode de Lagrange et
l'algorithme génétique. Vu le
calcul des matrices Jacobéennes pour chaque
itération.
chapitre 3
Optimisation
des systeme électrique
1.9. INTRODUCTION
Le problème d'optimisation dans les systèmes
électriques de puissance, résulte à
partir du moment où deux unités ou plus de
production devaient alimenter plusieurs
charges, obligeant l'opérateur à décider
comment répartir la charge entre les différentes
unités. Historiquement, les premières
méthodes d'optimisation ont été réalisées
par
rapport au contrôle de la puissance active. Ce qui est
connue, actuellement, sous la
dénomination de la répartition économique
classique, dont l'objectif principal est de
déterminer la puissance active à
générer par les différentes unités de production,
en
minimisant les coûts de génération. Mais,
après il a été constaté que l'optimisation de la
puissance active n'est pas suffisante. Une mauvaise gestion de
la puissance réactive
augmente les pertes d'où un accroissement des
coûts de production. Il y a deux classes
de technique d'optimisation. Dans la première, les
conditions d'optimalité du premier-
ordre qui sont dérivées du Lagrangien, sont
simultanément résolues par la méthode
Newton-Raphson. Des que les équations du réseau
et les contraintes d'inégalités
apparaissent explicitement dans le Lagrangien, des solutions
fiables sont disponibles
jusqu'à la convergence du processus itératif.
Dans la vie, nous sommes fréquemment confrontés
à des problèmes
d'optimisation plus au moins complexes .Cela peut commencer au
moment où l'on tente
de ranger notre bureau, de placer nos mobiliers, de
gérer notre espace dans la maison de
minimiser nos trajet en voiture et aller jusque à un
processus industrielle On définit
alors une fonction objective (fonction des pertes réal
ou de profit), que l'on cherche à
optimiser par rapport à tous les paramètres
concernés.
En pratique l'objectif n'est pas d'obtenir un optimum absolu,
mais seulement une
bonne solution, et la garantie de l'inexistence d'une solution
sensiblement meilleure
.Pour atteindre cet objectif au bout d'un temps de calcul
raisonnable, il est nécessaire
d'avoir recoures à des méthodes appelées
« heuristique » Ces dernières produisant des
solutions proches de l'optimum et la plupart d'entre elles sont
conçues pour un type de
problème donné. D'autre au contraire,
appelés « méta heuristique », sont capables de
s'adapter aux différents types problèmes.
L'objectif de l'optimisation est de déterminer une
solution qui minimise (ou
maximise) une fonction .appelée dans la
littérature fonction objective ou fonction
d'adaptation tout en vérifiant un certain nombre de
contraintes.
La méthode de programmation non linéaire a
été la première méthode à connaître
un essor remarquable, attirent ainsi l'attention des chercheurs
et des ingénieurs ; les
solutions qu`elles Offrent couvrent un large champ
d'application.
Dans les années quatre vingt .Le développements
rapide de l'outil informatique a
permis d'élaborer d'autres méthodes :
Des méthodes de programme successives.
Des méthodes de lagrangienne augmenté.
Des méthodes de programmation quadratique mentionnent les
méthodes de
Newton et Quasi -Newton.
Les spécialistes de l'optimisation combinatoire ont
ensuite orienté leur recherche
vers le développement des méthodes stochastique
tel que : le recuit simule, la
rechercher tabou et
3.1.1. Les algorithmes évolutionnistes.
Depuis quelques années, un nombre croissant de
méthode d'optimisation de la
littérature proposent de faire hybrider les
méthodes heuristiques entre elles
.Actuellement, l'hybridation s'effectue aussi entre
méthode heuristique et méthode
analytiques. Cette approche hybride permet d'obtenir des
méthodes d'optimisation
efficaces sur des problèmes de plus difficiles .d'allier
leurs atouts, dans le but
d'améliorer les différentes méthodes les
performances globale obtenues par chacune
d'elles, Actuellement, poussées par les performances
générales de tels algorithmes, un
nombre croissant d'étude proposent ce type d'approche.
1.10. FORMULATION D'UN PROBLEME D'OPTIMISATION :
Un problème d'optimisation (P) de type «
minimisation » et de dimension n peut
être Formulé de façon générale
comme suite :

Où :

Est un vecteur à n composante représentant les
variables objets du problème.

Est un espace des paramètres (ou espace de recherche).

Critère à minimiser.
Les contraintes d'inégalité.

Les contraintes d'égalité.
Un point de l'espace est un minimum local si tel que :

Où : désigne la distance entre le point .
La figure 7 présente, à titre d'exemple, une
distribution possible des optimums
d'une fonction objectif unidimensionnelle et multimodale.

Point
D'inflexion
Figure 7 : Point singuliers d'une fonction unidimensionnelle
et
multimodale
Méthodes d'optimisation :
Pour la résolution des problèmes d'optimisation,
de nombreuse méthode de
recherche ont été Développées la
littérature technique permet d'identifier trois type de
méthodes
Les méthodes analytiques.
Les méthodes énumératives.
Les méthodes heuristiques.

Figure 8: Principales méthode d'optimisation
1.11. METHODE ANALYTIQUE
Ces méthodes sont basées sur l'existante de
dérivées, donc sur l'existence
d'équation ou de système d'équation,
linéaire ou non linéaire .Le point principal
générale consister à recherche d'un
extremum hypothétique en déterminant les points
de pente nulle dans toutes les direction dépendent du
gradient de la fonction objective
.On trouve essentiellement deux type de méthode :les
méthodes directe et les méthodes
indirectes.
Les méthodes indirect cherchant des optima locaux en
résolvant l'ensemble
d'équation généralement no
linéaire, résultant de l'annulation du gradient de la fonction
objectif.
Les méthodes directes évaluent en gradient en
certaine points de l'espace de
recherche et se déplacent dans une direction liée
à la valeur locale de gradient. Ces les
notions de descente de gradient dans la dilection de la plus
forte pente. Bien que ces
deux méthodes aient été développe,
amélioration et étudier sous toutes les formes, elles
présentant des inconvénients .Elles
s'appliquaient localement, les extremums .Qu'elles
atteignent sont optimaux au voisinage du point de départ
et l'existence de dérivées n'est
pas systématique. Ces méthodes sont donc
difficilement applicable telles quelles pour
l'optimisation d'une fonction multimodale exemple (Fig.7)
comportant plusieurs optima
locaux. Parmi les méthodes analytiques on peut citer :
3.1.2. Méthode du gradient
Cette méthode fait partie d'une grande classe de
méthode numérique appelées
méthode de descente .Le principe de base de ces
méthode repose sur les démarches
suivantes :On part d'un point initial arbitraire et on calcul le
gradient en ,
comme Indique la direction de plus grande augmentation de f, on
se déplace
d'une quantité Dans la direction opposé au gardien,
et on définie le point :


La procédure est répéter et engendrer le
point suivant la relation :

|
Où : est le pas de déplacement (
|
|
Cette méthode a pour avantage d'être très
facile à mettre en ouvre, mais
malheureusement, les conditions de convergence sont assez
lourdes.
3.1.3. Méthode de Newton et quasi -Newton
D'origine, cette méthode itérative est
utilisée pour résoudre un system d'équation
non linéaire, elle a été utilisée
pour rechercher un extremum d'une fonction objective.
Elle permet, à partir d'un point initial quelque,
d'approcher un optimum local d'aussi
prés que nous le désirons .Cependant, il s'agit
d'une méthode du second ordre, car nous
utilisons, pour déterminer la direction et le pas de
déplacement, non seulement la valeur
du gradient, mais aussi celle du hessien de la fonction
.l'Inconvénient major de
Cette méthode qui appartient aussi aux méthodes
de descente, c'est sa convergence
locale. Une autre difficulté peut apparaitre lorsque le
hessien n'est pas défini positive.
Dans ce cas en effet, la direction de déplacement peut
ne pas être une direction de
descente, et la convergence n'est pas assurée.
Actuellement, des méthodes dites quasi -
newton ont été développées, Ces
derniers apportent une légère modification à la
méthode de Newton .Elles évitent le calcul
coûteux en terme de temps de calcul de la
matrice hessien nécessaire a chaque itération et
qui peut se faire par une approximation
par différent finies .On trouve plusieurs variantes,
telles que les méthodes Dites de BFGS
(Broyden-Fletcher-Goldfarb-Shannon), de DFP
(Davidon-Fletcher-Powell) Et de
Levenberg-Marqquard.
1.12. METHODE ENUMERATIVE
Ces méthodes consistent à évaluer la valeur
de la fonction à optimiser en chaque
point des solutions faisables .Elles peuvent s'appliquer dans
un espace de recherche
infinie mais Discrétisé .Bien que ces
méthode soient très simples à mettre en ouvre et
très proches du Raisonnement humain (lorsque le nombre
de possibilité est faible), elles
sont inapplicables En pratique car les espace de recherche sont
beaucoup trop vaste et
le nombre d'évaluation de la fonction objectif devient
rapidement prohibitif .Même la
méthode énumérative de programmation
dynamique .développée par Bellman, est
impuissante devant les problèmes de taille et devient
rapidement inapplicable. Parmi les
méthodes énumératives on peut citer : les
méthodes de Branche, la méthode du
simplexe, la programmation dynamique,...
3.1.4. Méthodes stochastiques
Ces méthodes ont connu un essor considérable
lorsque la communauté
scientifique a mis en évidence les limitations des
méthodes analytiques et énumératives
.Contrairement aux méthodes analytiques, elles sont
bases sur un processus
stochastique, utilisant un choix aléatoire comme outil
pour guider une exploration
hautement intelligente dans l'espace de recherche.
Ces méthodes sont semblables au niveau de leur
utilisation des mécanismes de
recherche Probabiliste, mais procèdent néo moins
différemment .Elles ont une grande
probabilité pour localiser un optimum globale d'une
fonction objectif. Parmi les
méthodes stochastiques, on distingue les techniques de
recherches purement aléatoires
(souvent regroupées dans la classe des méthodes
de type Monte-Carlo), la Recherche
Tabou, le recuit simulé et les méthodes
évolutionnistes.
3.1.5. Méthode du recuit simulé
Le recuit simulé est une technique d'optimisation de type
Monte-Carlo généralisé à
laquelle on introduit un paramétrer de
température qui sera ajuster pendent
la recherche .Les concepts fondamentaux de cette technique sont
tirés de l'analogie
entre l'optimisation et la thermodynamique dans lequel les
déplacements dans l'espace
de recherche sont basés sur la distribution de Boltzmann
[26]. C'est-à-dire on cherche à
Obtenir un matériau sans impureté,
représenté par son état d'énergie minimale. Dans
le
processus de recuit réelle, nous élevons la
température du matériau jusque à ce qu'il se
trouver dans un état d'énergie
élevée .Ensuite, nous le refroidissons très lentement
de
façon à obtenir, à la fin du processus, un
matériau constitué par des atomes bien
ordonnés, correspondant à une valeur
d'énergie stable et minimale. La probabilité de
Boltzmann notée mesure la probabilité de trouver
un système dans une configuration
d'énergie , à une certaine température T
donnée, dans l'espace de configuration
et elle est définie par :

Ou : k est appelé la constante de Boltzmann
Dans cette expression, le facture KT montre que lorsque la
température est très
élevée, tous les états sont à peu
prés équiprobables, c'est-à- dire un nombre de
configuration sont accessibles .Au contraire quand la
température est basse, les états a
haute énergie deviennent peu probable s par rapport
à ceux de faible énergie. Pour
applique ce principe au problème de minimisation de
coût, le processus de recherche
peut être assimilé à un processus de recuit
comme en métallurgie .Quand on chauffe un
métal à une température très
élevés, le métal devient liquide et peut occuper toute
configuration. Quand la température décrite, le
métal va se figer peu a peu dans une
configuration .qu' il est de plus en plus difficile à,
déformer (on dit qu'il refroidie) .A
moins de le réchauffer (recuit), le métal peut
être retravailler de nouveau pour lui
donner la forme désire .l'algorithme de Kirkpatrick
simule ce processus en combinant
dans l'algorithme le mécanisme de refroidissement et de
recuit.


Figure 9: Parcours de l'espace de recherche avec le recuit
simulé .Le principe de « recuit » qui se
traduit par une augmentation du niveau d'énergie,
permet de sortir des mina locaux.
Cependant le concept de température d'un système
physique n'a pas d'équivalent
direct avec le problème à optimiser. Le
paramètre T doit être simplement un paramètre
de contrôle, indiquant le contexte dans lequel se trouve
le system (ex : stade de
recherche).En fait, le paramètre T contrôle les
déplacement vers les points voisins les
moins bons pour échapper aux optima locaux, sans pour
autant trop s'écarter du chemin
vers le vrai minimum .l'équivalent de l'énergie
sera la valeur de la fonction de coût .
Ainsi dans l'algorithme de recuit la probabilité de
Boltzmann n'est pas directement
applique, mais le critère de Metro polis est
utilisé. Le critère de Metro polis permet de
décider si une nouvelle configuration
générée présente une variation de coût
acceptable.
Il permet de décider aussi de sortir des minima locaux
quand le critère d'arrêt n'est pas
encore atteint. Le principe de Metro polis est basé sur
le calcul de la fonction de coût,
après chaque passage .D'une configuration a une
configuration.
On calcule la variation de la fonction de coût :


La transformation est acceptée selon la probabilité
telle que :


Chapitre 1: Étude de l'état de l'art
Lorsque la variation
, l'exponentielle est supérieure ou égale à
1, la nouvelle configuration doit être
acceptée, on lui affecte alors la probabilité
maximale de 1.
· , on compare à un nombre aléatoire .
· , la configuration v est acceptée.
Sinon, elle est rejetée et on essaie une autre
configuration. La configuration ayant
une forte augmentation en sont donc probables pour une
température donnée.
D'autant moins que la température est faible. Au
début de l'algorithme le facture T est
élevé, la probabilité est proche de 1 et
presque toutes les variations sont
acceptable .Au contraire, quand T diminue, les remontées
sont de plus difficiles et seules
de très faible variations peuvent être
accepté .Si une Configuration est rejetée, le system
essaie d'en trouver une autre, sinon elle est accepter et la
Recherche continue avec
celle -ci jusqu'à ce que le critère d'arrêt
soit atteint.
Génère une configuration aléatoire
et une température initiale
11 Oni Ri
Non
Oui
Non
Choisir dans le voisinage de
Génère un nombre aléatoire
Calculer )-
Abaisser
Equilibre
et
Oui
Non
41
Meilleure configuration obtenue
L'Algorithme :
1ere Etape :
Choisissons une solution initiale i dans S l'ensemble des
solutions) Appliquer

2emeEtape :


Appliquons et générons un sous-ensemble de
solutions en pour que:
une des critères d'aspiration a (i, m) soit applicable
3emeEtape :

Choisissons la meilleure solution i' parmi l'ensemble de
solutions voisines

Appliquer
4emeEtape :


Si alors nous avons trouvé une meilleure solution
Appliquer
3emeEtape :
Mettre à jour la liste et les critères
d'aspiration Étape 6: si une condition d'arrêt
est atteinte, stop. Sinon, retour à Étape 2.
Condition d'arrêt: condition qui régira l'arrêt
de l'algorithme. Ex: arrêt après 22
itérations k=22.La recherche est éloignée du
voisinage N(i) actuelle de l'ensemble des solutions Une haute
priorité est donnée aux
solutions d'une autre région que celle actuellement sous
exploration Le résultat :
chercher ailleurs
1.13. RECHERCHE TABU
La méthode TABU, prononcé tabou, a
été développée par Glover et à montrer
ses
performance sur des nombreux problèmes d'optimisation.
Elle permet d'atteindre le
minimum global d'un problème d'optimisation à
partie d'une analogie avec la mémoire
du cerveau humaine .Le processus de résolution
développé par cette méthodes
commence par la génération d'une configuration de
paramètre hasard .Ensuit ,a chaque
itération ,le voisinage de la configuration courante est
parcourue par une série de
mouvement aléatoire de façon a trouver une
meilleure Solution .Apres son exécution,
chacun des ces mouvements est ajouter a une liste qui
représente la mémoire de la
méthode .Cette liste, de taille limitée, est
dénommé liste Tabou. Les mouvements qui
font partie de la liste Tabou sont considère interdit.
C'est-à-dire dire qu'ils ne peuvent
pas être exécutés une autre fois tant
qu'ils sont dans la liste. Par contre, s'il existe un
mouvement qui appartient à la liste Tabou mais qui en
même temps nous amène à une
meilleure solution du problème ,une nouvelle
exécution de ce mouvement sera alors
accepter .Dans ce cas la nouvelle solution obtenue remplacer la
solution courante et le
processus recommence .Si pendent le processus d'optimisation la
liste Tabou devient
plein ,nous retirent le plus ancien mouvement de la liste avant
d'ajouter un nouveaux
.L'algorithme s'arrêt lorsque nous n'avons plus
d'amélioration sensible de le valeur de la
solution.a (Fig.11).Illustre le processus développé
par la méthode [34, 35, 36, 37,38].


Générer une solution aléatoire


Actualiser avec
Définir une direction de recherche
Terminer
=+
Meilleur
Solution
Meilleure configuration obtenue

Figure 12: Organigramme de la rechercher Tabou
1.14. ALGORITHME EVOLUTIONNISTE
Les algorithmes évolutionniste sont basés sur des
principes simples. En effet, peu
de connaissance sur la manière de résoudre ces
problèmes sont efficaces l'évolution
.C'est pourquoi dans nombreux domaines, les chercheur ont
été amenés à s'y intéresser.
Les algorithmes évolutionniste sont une classe
d'algorithme d'optimisation par
recherche Probabiliste basés sur le modèle de
l'évolution naturelle. Ils modalisent une
population d'individus par des point dans un espace. Ils ont
montré leur capacité à éviter
la convergence .Des solutions vers des optima locaux. Plusieurs
types dévolutions ont
été développés, donnant naissance
à quatre grandes tendances : les stratégies
d'évolution, la programmation évolutive, la
programmation génétique et les algorithmes
génétiques.
3.1.6. Les Algorithmes Génétiques
3.1.7. Principes généraux
Les Algorithme Génétique (AG) font partie d'une
famille de méthode stochastique
appelés méthode évolutionniste qui
reposant sur une analogie avec la théorie de
l'évolution naturelle, selon laquelle les individus
d'une population les mieux adapté à
leur environnement ont une plus grande probabilité de
survivre de se reproduire de
génération en génération, en
donnent des descendent encore mieux adaptés.Depuis une
trentaine d'années d'intérêt pour les
algorithmes génétique va croissant en raisons de
leurs nombreux avantages sur les autres technique
d'optimisation : ils sont robustes,
rapides, Suffisante généraux pour pouvoir
s'adapter à n grand nombre de situation et
enfin ne demandent aucun connaissance précise sur lez
system a optimisé. Les
algorithme génétique ont été
développés dans les années 70 par Holand puis
approfondis par Goldberg, ils sont certainement la branche des
Algorithme
évolutionnistes les plus connue et les plus
utilisé .La particularité de ces algorithme est
le fait qu'il font évaluer des population d'individus
codés par une chaîne binaire .ils
utilisant les opérateur de mutation et de recombinaison
de différent types. Le but d'un
algorithme génétique est d'optimisé une
fonction donnée dans un espace de recherche
précis. Dans le cas général, un algorithme
génétique a besoin de quatre composants
fondamentaux : Une fonction de codage qui transforme les
données de l'espace de
recherche en données utilisable par un ordinateur : par
exemple une séquence de bits ou
bien un nombre réel.
Un moyen de créer une population initiale à partir
des solutions potentielles. Une
fonction qui permet d'évaluer l'adaptation d'un
chromosome, ce qui offre la possibilité
de comparer les individus .cette fonction sera en fait
construit à partir du critère que l'on
désire optimiser .L'application de cette fonction
à un élément de la population donnera
sa performance (évaluation) .Des opérateur qui
altèrent les enfants après la
reproduction. On choisit une population initiale de taille n
,c'est-à-dire que l'on tire au
hasard le plus uniformément possible un certaine nombre
d'éléments qui seront
appelés chromosome dans l'espace des données .A
fine de réalisé l'analogie avec
génétique ,il faut disposer comme nous l'avons vu
d'opérateurs de sélection et de
recombinaison qui vont permettre à cette population
dévaluer (on se reportera à la
figure 30) .L'utilisation de ces trois opérateur permet
De conserve une population bine
diversifiée( c'est-à-dire bien répartie
dans l'espace )et par conséquent d'accéder à tout
l'espace de recherche. [39,40,41]
Solution Fna
Initialisation

Evaluation de la population initiale 44

Figure 13::Principe d'un Algorithme génétique
1.15. METHODE DE PENALITE
3.1.8. Principe général des
méthodes de pénalités
Les méthodes d'optimisation que nous allons utiliser sont
des méthodes de
minimisation sans contrainte .Or notre problème est avec
contrainte .C'est pour cette
raison qu'on va utiliser une méthode basée sur la
transformation du problème originale
avec contrainte en un problème auxiliaire sans
contrainte ou le minimum est le même
que celui du problème originale.
Le principe de base de cette méthode consiste à
modifier le critère en lui ajoutant
une fonction de pénalisation P(x) .c'est à dire,
qu'on ramène le problème de
programmation avec Contrainte en un problème de
programmation sans contraintes.
Les méthodes de pénalité constituent une
famille d'algorithme particulièrement
intéressante du double point de vue de la
simplicité de principe et de l'efficacité
pratique. Il existe plusieurs possibilités du choix de la
fonction de pénalité :
3.1.9. Méthode de Fiacco et Mc Cormik :
Cette méthode consister à ramener le
problème d'optimisation (P) du (3.1) en la
Minimisation de la fonction suivante [71] :
n
m
1
f (x, r ) f (x ) r g (x )
m k obj k å i 1 å
= + = +
x)
(3.7)
h(
2
j
2
i 1
=
rk j 1
=
Ou : rk est une constante de réglage
de calcul (coefficient de pénalité).elle est choisi de
telle sorte que :
rk f0est limite de rk =0 quand k®
Avec :
Ou :p est une constante choisie.
3.1.10. Méthode de pénalité
extérieure :
Dans cette méthode, on introduit les deux types de
contrainte égalité et inégalité
.La fonction objective fm s'écrite
sous forme suivante :
f m = f obj (x) + E(rk , g, h)
Ou : E ( r k , g , h
) est le terme de pénalisation extérieure.
m
n
1 1
k å å
= +
Dg (x )
2
E(r , g, h) i
r r
k i 1
= k j 1
=
On aura donc fm sous forme suivante :
|
n m
1 1
m obj å å
Dg (x )
2
f f (x )
= + +
i
r r
k i 1
= k j 1
=
|
Bj
|
h(
2 j
|
x)
|
(3.10
|
Avec :
ì í î
0, si
Di f

x) 0
g i (
D = 0, si
i
gi(
3
x) 0
Et :
ìB 0, si
i f
(
x)0
1
h i
í î B = 0, si
j
h i
(
x)0
3
Di Sont Bj sont des constantes.
3.1.11. Méthode de pénalité
intérieure :
La principale inconvenante de la méthode de
pénalité extérieure est que
l'optimum *
x est approché vers l'extérieur de qui a conduit
de chercher une autre
méthode de pénalité dans Les quelles
l'optimum est approché vers l'intérieure (d'où le
nom de pénalité intérieure) La
pénalisation intérieure peut être applique uniquement
dans le cas, ou on a des contrainte de type
inégalité.
La fonction objective Ç s'écrit sous la forme
suivante :
(3.11
Ç =fobj(x)+I(rk, g )
Ou : I(r k ,g) est le terme de pénalisation
intérieure.
Le terme I(r k ,g) peut être donné par
l'expression suivante :
n
A i
å=
i 1
I(
g i
(3.12
r , g) r
k k
=
(x)
On aura donc Ç sous la forme suivante :

n
A i
r å= i 1
+
x)
(
g i
(3.13
f f
=
m obj
(x)
Avec est une constante.
3.1.12. Méthode de pénalité mixte :
Cette méthode englobe les termes de pénalisation
intérieure par I(r k ,g) et les termes
de pénalisation extérieure
représentés par E(rk ,g,h).
La fonction pénalisée s'écrit sous forme
suivante :
n A
f f (x) r
m obj k å
= +
g (
i
n m
1 1
i + +
å å
D g (x)
2
i i
x) r = =
r
k i 1 k j 1
i 1
=
x)
(3.14
h(
2 j
Bj
1.16. RE SE AU DE N EUR O NE S
Le principe est fondé sur l'hypothèse de nombreux
biologiste que la récréation du
comportement intelligent du cerveau s'appuie sur son
arcitecture.les réseaux de
neurones sont perçus comme un mini processeur qui traite
les informations qu'ils
reçoivent pour produire une information unique .le
neurone est une cellule différente
appartenant au système nerveux, qui assure le
contrôle de toutes les fonctions de
l'organisme .la structure du neurone comprend trois parties :
Un corps cellulaire qui reforme le noyau.
Une ou plusieurs dendrites (prolongement du corps cellulaire)
qui reçoivent
des signaux, les convertissent en imposions électrique et
conduisant cet
influx nerveux en direction du corps cellulaire.
Un axone qui conduit l'influx du corps cellulaire vers les
boutons terminaux
synaptiques [6].
1.17. LO G I QU E F LO UE
Dans la vie courante, tout ne peut être décrit de
manière binaire. Par exemple, la
transition entre le jour et la nuit se fait progressivement,
l'action sur l'embrayage d'un
véhicule est, elle aussi, progressive. Longtemps, le
seul outil de description en logique
était binaire. Tout en logique a été
décrite en termes de vrai ou faux. Le problème de
cette description simpliste en logique et qu'elle ne permet pas
de traiter l'incertitude de
l'imprécision des connaissances humaines. L'automaticien
L. A. Zadeh a élaboré une
nouvelle logique basée sur les ensembles flous. Elle
permet de traiter l'imprécision et
l'incertitude dans la connaissance humaine ainsi que les
transitions progressives entre
états. La différence principale entre une logique
classique et cette logique floue est
l'existence, d'une transition progressive entre le vrai et le
faux..Un détaillé sur la logique
flou est donne au chapitre 5.
1.18. COLONIES DE FOURMIS
L'optimisation par colonie de fourmis est une technique
biomimétique inspirée par
un travaillé de biologiste [10] repris par des
informaticiens [20] et largement exploité et
développé par Marco Dorigo dans les années
90 [12].Le principe de base de la technique
consister à imiter le comportement des fourmis
réelles lorsqu'elles recherchent la
source de nourriture. La communication entre les fourmis se
fait par l'intermédiaire des
traces chimiques « phéromones »
dégagées par chacune d'elles. L'optimisation par
colonie de fourmis a rapidement prouvé son
efficacité dans le cadre de l'optimisation
combinatoire en générale et s'est monté
particulièrement profitable pour le problème
du routage des paquets 'information dans les grands
réseaux d'interconnexion. Détaille
sur la logique flou est donné au chapitre 5.
1.19. MONTE CARLO :
Les méthodes Monté Carlo consistent en des
simulations expérimentales ou
informatiques de problèmes mathématiques ou
physiques, basées sur le tirage de
nombres aléatoires. Généralement on
utilise en fait des séries de nombres pseudo-
aléatoires générées par des
algorithmes spécialisés. Les propriétés de ces
séries sont
très proches de celles d'une véritable suite
aléatoire. La méthode Monté Carlo est
également utilisée dans le domaine pharmaceutique
: on génère un vitro de très
nombreuses molécules aléatoires, puis on les
passe au crible en testant leur effet sur tel
ou tel cible. On repère ainsi des molécules
intéressantes qui après une étude et une
modification pourront donner naissance à de nouveaux
médicaments. L'orientation
actuelle est même de réaliser la même chose
en silico, c'est-à-dire de modéliser et de
tester ces molécules dans un ordinateur. Le grand
avantage de cette méthode est sa
simplicité. Elle permet entre autres de visualiser
l'effet de différents paramètres et de
donner ainsi des orientations, d'étudier des structures
intéressantes qui auraient été a
priori écartées et de trouver facilement des
structures que l'on n'aurait pas aussi bien
optimisées « à la main ». [69].
Les méthodes de types Monté Carlo recherchent
l'optimum d'une fonction en
générant une suite aléatoire de nombres en
fonction d'une loi uniforme.
Algorithme :
1ere Etape :
On génère un point initial x dans l'espace
d'état, considéré comme solution courante.
2emeEtape :
On génère aléatoirement un point x'.
3emeEtape :
Si x' est meilleur que x alors x' devient la solution
courante.
3emeEtape :
Si le critère d'arrêt est satisfait alors fin sinon
retour en à la deuxième étape [68]
1.2 0. OPTIMISATION PAR ESSAIM DE PARTICULES :
Observez un champ entrain d'être labouré en
automne, lorsque le soc de la charrue
pénètre le sol pour la première fois le
champ est vide de tout goéland et quelques
minutes après une nuée accompagne le tracteur. Au
début du labour un oiseau découvre
la source de nourriture et très rapidement un autre
arrive et ainsi de suite. Que s'est il
passé ? L'information concernant un festin potentiel
s'est largement diffusée au sein du
groupe de goéland. Les goélands volaient à
la recherche de nourriture de façon plus ou
moins ordonnée et le rassemblement s'est effectué
par un échange (volontaire ou non)
social d'informations entre individus de la même
espèce. L'un d'entre_eux à trouvé une
solution et les autres se sont adaptés en copiant sa
solution, ceci offre un caractère
adaptatif à la méthode. Au départ J.
Kennedy et R. Eberhart (Kennedy and Eberhart,
1995) cherchaient à simuler la capacité des
oiseaux à voler de façon synchrone et leur
aptitude à changer brusquement de direction tout en
restant en une formation optimale.
Le modèle qu'ils ont proposé à ensuite
été étendu en un algorithme simple et efficace.
Les particules sont les individus et elles se déplacent
dans l'hyperespace de recherche.
Le processus de recherche est basé sur deux règles
:
1) Chaque particule est dotée d'une mémoire qui
lui permet de mémoriser le
meilleur point par lequel elle est déjà
passée et elle a tendance à retourner vers ce point.
2) Chaque particule est informée du meilleur point connu
au sein de son voisinage
et elle va tendre à aller vers ce point.

Figure 14: Schéma de principe du déplacement
d'une particule. Pour réaliser son
prochain
mouvement, chaque particule combine trois tendances : suivre sa
vitesse propre, revenir
vers
sa meilleure performance, aller vers la meilleure performance
de ses informatrices.
1.2 1. METHODES DE RESOLUTION
Actuellement, il existe une large gamme de méthodes
d'optimisation et une
multitude de variantes pour les mêmes algorithmes. Ces
méthodes sont utilisées en
respectant des contraintes de type égalité et
inégalité et en se basant, généralement, sur
le schéma suivant (Figure 13) :
Etat initiale de Répartition de
Figure 16Structure dun OP
Solution Optimale

Optimisation
Changer:
§ Object
ifs
§ Contr
ôles
Non
Non
Convergenc
e
Résultats
Acceptable
Optimisation
Oui
Oui
Figure 15:Structure d'un OPF
1.2 2. OPTIMISATION DES PUISSANCES REACTIVES
3.1.13. Introduction
Pour étudier le problème de la réparation
optimale des puissances réactives, la
programmation mathématique met à notre
disposition des algorithmes de résolution,
soit pour l'optimisation des fonctions linéaires sous
contraintes linéaires, soit pour
l'optimisation des fonctions non linéaires avec ou sans
contraintes. Ce problème peut
être résolu par plusieurs techniques [10, 11, 12,
13, 14,15], à savoir :
§ Le contrôle des tensions en temps réel.
§ La minimisation des pertes actives.
§ La maximisation des réserves de puissance
réactive en les distribuant
uniformément entre les générateurs de
production.
§ L'optimisation et la localisation du volume des moyens de
compensation de
la puissance réactive de telle sorte que les limites des
tensions soient
respectées.
On peut formuler deux principaux objectifs pour l'optimisation
de la puissance
réactive dont le premier est basé sur la
sécurité, quand la demande est importante, et le
second sur l'économie, quand le réseau fonctionne
sous certaines conditions :
Dans l'état d'incidents, l'objectif principal est la
correction des violations des
limites existantes avec le minimum d'actions.
Dans l'état normal, généralement,
l'objectif est de réduire les coûts et de
maintenir une capacité adéquate de
générer de la puissance réactive, pour faire face
aux incidents possibles. Pour cela, le maintien des marges
suffisantes de génération de la
puissance réactive n'est pas une question critique dans
les heures de faible charge Mais,
elle acquiert une importance cruciale quand le réseau
fonctionne en pleine charge. Ce
dernier doit assurer une continuité de service.
3.1.14. Formulation du problème et solutions
De manière générale, Le problème de
la répartition optimale des puissances
réactives peut être défini par la
minimisation d'une fonction objective adaptée tout en
respectant un certain nombre de contraintes de type
égalité et inégalité.
Le problème peut être posé sous la
formulation mathématique suivante :

Sous les contraintes :



En utilisant la fonction de Lagrange, et en ignorant les
contraintes de type inégalité,
on obtient une nouvelle fonction :

Les conditions d'optimisation sont obtenues par la série
d'équations non linéaires :

Avec:

: Les matrices transposées du Jacobine.

Les vecteurs gradients.

De la première expression (3.2 0), on peut calculer les
multiplicateurs de Lagrange


Connaissant le vecteur de , La deuxième expression (3.2
1), peut être déterminé :

Les éléments de l'expression (3.2 1) fournissent
les sensibilités de la fonction
objective, par rapport aux différentes variables de
contrôle.
La nouvelle amélioration du vecteur de contrôle est
donnée par :

Avec :

Le choix du pas peut être déterminé par
plusieurs approches. Pour notre cas,
l'approche suivante a été utilisée:

Pour satisfaire les équations (3.20), (3.21), (3.22), la
procédure itérative suivante à
été adoptée :
Nous Supposons un ensemble de variables de contrôle
.Utilisons la méthode de
Newton- Raphson pour la résolution du problème de
la répartition des charges et nous
déterminons la valeur de la fonction objective
.Déterminons les valeurs des
multiplicateurs de Lagrange par l'équation
(3.20).Utilisons les valeurs de dans
l'équation (3.21), pour déterminer le vecteur
Gradient des variables de contrôle.
Trouvons les nouvelles valeurs des variables de contrôle
par la relation
(3.25).Retournons à l'étape 2.
Le processus itératif s'arrêtera jusqu'à la
satisfaction de la relation suivante :


Dans le processus itératif, les contraintes de type
inégalité des variables de contrôle
ont été respectées, dans chaque
itération.
Les variables d'états ont été
respectées par des actions correctrices citées dans le
chapitre précédent.
3.1.15. Application
La fonction objective considérée dans notre cas
est la fonction des pertes actives
totales transmises. Le problème d'optimisation
répond aux équations suivantes :

Sous les contraintes :

Avec :

Où :

Nombre de générateurs.
Nombre de transformateurs.
Nombre de noeuds.

Rapport de transformation des transformateurs.
: Puissances active et réactive
générées dans le noeud i.
: Puissances active et réactive de charge dans le noeud
i.
Angles des tensions aux noeuds i et j.
Sus ceptance entre les noeuds i et j.
Conductance entre les noeuds i et j.
Dans notre étude, nous sommes intéressés
à l'étude de trois variantes. Les deux

premières concernent un seul type de variables de
contrôle. Il s'agit de
et de , alors que la troisième consiste à tenir
compte des deux types de variables

de contrôle, c'est à dire, . Dans les trois cas les
variables d'état sont :

3.1.16. Variante 1 : ( )



En appliquant l'expression (6.6), en forme matricielle, on
obtient :



Les conditions d'optimisations, selon les expressions (3.2 0),
(3.2 1), (3.2 2) sont :












Et :










Et :


De l'équation (3.3 6), on obtient les valeurs du vecteur
des Ces derniers sont
remplacés dans l'équation (3.37), pour
déterminer le vecteur Gradient des :



Commençons par le vecteur , on obtient les
différentes nouvelles valeurs des
puissances réactives aux noeuds de
génération par :

Chapitre 3 : Optimisation du système
électrique
3.1.17. Variante 2 : (u = [a i ])
De la même manière que dans le sous chapitre
précédemment. On obtient le vecteur
des l de l'équation (6.6), ce dernier est
remplacé dans l'équation suivante pour obtenir
le vecteur Gradient des ai :
PL
ù ú ú ú ú ú ú
ú ú
ú û
a
ù
ú
ú
ú
ú
ú
ú
ú
ú
û
1
da 1
1
+
PL
a
n
n
n
T
dL
da
....
....
....
dL
da
T
d P
D 2
.
d P
D n
da
T
d Q
D d D Q ù é l ù
2 n 1
da da .
1 1 ú ê ú
. . ú ê ú
(3.41
. ú ê . ú
. . . . ú . ê . ú
ú ê ú
. .
ú ê ú
d Q
D d D Q ú ê . ú
n n
. . úú ê ú
n 2 ( n - 1 )
da da ë l
T T
n û û
Commençons par le vecteur (k)
ai , on obtient les différentes nouvelles
valeurs des
rapports de transformation des transformateurs
insérées dans le réseau par :
dL
i
(3.42
3.1.18. Variante 3 : u [Q , a i ]
= i g
En procédant de la même manière que dans la
première et la deuxième variante, on
aura le vecteur Gradient des g
Q i et des a i par :
dL
dQ
dL
da 1
.
.
dL
g
n
dQ
dL
da n T
g
2
P L
a
+
P L
a
T
ù
ú
ú
ú
ú
ú
ú
ú
ú
ú
ú
ú
ú
û
0
0
1
n
ù
ú
ú
ú
ú
ú
ú
ú
ú
ú
ú
ú
ú
û
. .
2
dQ dQ
dQ
2
2
ù ú ú ú ú û ú
ú
l 1
.
.
ù
ú
ú
ú
. .
ê ú
a 1 da
. .
da
1 1
ú.
ê ú
ê ú . ú
× ê ú
. .
.
(3.43
ú ê . ú
d P
D 2
d Q
D D
d Q
2 n
ú ê . ú
. .
ú
n
dQ dQ
n
dQ
ê . ú
d P
D 2
d Q
D D
d Q
2 n
n
ê ú
ú ê . ú
da da
T
n
. .
n T T
n
da
- 1 )
ê j ë l 2 ( n
Commençons par le vecteur [Q , a ( k ) ]
i , on obtient les nouvelles différentes valeurs
g ( k )
i
des puissances réactives aux noeuds de
génération et les nouveaux rapports de
transformation par :
dL
i
Q = Q - a ×
g ( k 1 )
+ g ( k)
i dQ
i g
dL
i
(3.44
(3.45

Calcule de l'écoulement
de puissance
3.1.19. Organigramme du gradient réduit
Données du réseau

|
Calcule T
J(1ere première itération)
|


Calcule des valeurs des
multiplicateurs de Lagrange l

|
Calcule le vecteur Gradient des g
Q i
|

Calcule la valeur de a

Q = Q - a ×
g ( k 1 )
+ g ( k)
i
i dQ
dL
g i

Valeurs optimale

Non
Oui
Qi g(k+1)
£ e
Figure 17:Organigramme du Gradient réduit
chapitre 4
Compensateur statique
d'énergie
réactive (SVC)
1.23. INTRODUCTION
L'évolution de l'électronique de puissance a
commencé à engendrer des
changements majeurs sur les réseaux de transport et de
distribution. A l'exception de
quelques appareils utilisant l'électronique de puissance
(disjoncteurs, transformateurs a
prises variables et compensateurs statiques a thyristors), les
réseaux de transport et de
distribution comportaient jusqu'a récemment des
appareillages passifs. Par Ailleurs, le
maillage des lignes exige de plus en plus le contrôle des
puissances transitées. La
complexité des réseaux exige aussi des marges de
sécurité accrues afin que les
perturbations locales ne provoquent pas des instabilités
qui pourraient se répandre sur
tout le réseau. Alors que l'appel de puissance continue
à croitre, il devient de plus en
plus difficile d'obtenir des droits de passage pour construire
de nouvelles lignes de
transport et de distribution. Pour ces raisons, les compagnies
d'électricité cherchent à
augmenter la puissance que peuvent transporter les lignes
existantes, sans pour
autant compromettre leur fiabiliste et leur stabilité.
Idéalement, on aimerait les charger
à la limite de la capacité thermique des
conducteurs, et utiliser toutes les lignes pour
porter la charge électrique. Un des problèmes
majeurs est qu'une contingence (court-
circuit, ouverture intempestive d'une artère, etc.).Le
contrôle de la tension sur le réseau,
La répartition des flux de puissance est aussi
lié à la valeur de la tension en chaque
noeud du réseau. La tenue de tension est
réalisée avec l'injection ou soutirage de
puissance réactive dans les différents noeuds du
réseau
4.1.1. Compensateur parallèles à base de
thyristor
Il s'agit de :
TCR (Thyristor Controlled Reactor)
Dans le TCR (ou RCT : Réactance Commandée par
Thyristor), la valeur de
l'inductance est continuellement changée par
l'amorçage des thyristors.
TSC (Thyristor Switched Capacitor) : Dans le TSC (ou CCT :
Condensateurs
Commandés par thyristor fonctionnent en pleine
conduction.
SVC (Static Var Compensator)
4.1.2. TCR (Réactance Commandées par
thyristor)

Figure 18: Réactance Commandé par Thyristor

Le courant répond à l'équation
différentielle suivante :
En utilisant la décomposition de Fourier
Où

Le fonctionnement d'un TCR (réactance
contrôlée par thyristor) est donné par
les figures 14,15 et16. En contrôlant l'angle
d'amorçage, on contrôle la composante
fondamentale du courant. Si l'angle d'amorçage est de 90
degrés, la conduction est
complète. Si l'angle d'amorçage est de 180
degrés, il n'y a pas de conduction. Entre ces
deux valeurs la conduction est partielle .La valeur de
réactance équation (4.5) peut être
variée continuellement. Il est évident que TCR
introduit des harmoniques dans le réseau.
Le montage en triangle de TCR empêche l'assimilation de
la troisième harmonique et de
ses multiples en réseau. Afin d'éliminer les
autres harmoniques dominantes, il faut
installer des filtres.


Figure 19:Allure du courant TCR pour a = 90°

Figure 20: Allure du courant TCR pour 90° £ a
£ 180°
Figure 21: Allure du courant TCR pour a = 180 °


Figure 22:Variation de la Susceptance BTCR en fonction de
a


Figure 23: Caractéristique d'un TCR
4.1.3. TSC (Condensateurs Commandés par thyristor)

Figure 24: Formes d'ondes d'un TSC (a) sans « transiant
», (b) avec « transiant »
Le TSC (figure 21) peut effectuer la commutation du condensateur
sans transiant
(Fig 20-a). Les condensateurs sont pré chargés
à la valeur de crête de la tension du
réseau et, en passage naturel par zéro du courant
de condensateur (au moment où la
tension aux bornes du condensateur est égale à la
tension de réseau) le thyristor est
amorcé. Si les deux tensions ne sont pas égales, il
y aura une impulsion de courant
(changement discontinu du courant Cdv/dt) ce qui n'est pas
désirable (Fig 20-b).

Si l'équation (4.7) devient :
Nombre de TSC en parallèle.
Pour atténuer les impulsions potentielles du courant, une
inductance est toujours
mise en série avec un condensateur. En même temps
l'inductance est synthonisée pour
éviter la possibilité de la résonance.
Après être débranché du réseau, le
condensateur
reste chargé, l'énergie stockée dans le
condensateur reste et, pour le brancher de
nouveau il faut attendre que la tension du réseau
devienne égale à celui de
condensateur. Donc, il n'y a pas de délai dans
l'amorçage du thyristor et, le condensateur
peut être soit branché, soit
débranché du réseau. La rapidité de la
réponse d'un TSC est
un cycle, ce qui est beaucoup plus rapide que la réponse
d'une batterie des
condensateurs qui est branchée au réseau via un
disjoncteur. La réactance de TSC ne
peut être variée qu'en pas discrets. Plus il y a
de condensateurs branchés, plus le courant
capacitif fourni au réseau est élevé. La
valeur de réactance dépend du nombre de
condensateurs branchés à la ligne. Pour un
condensateur :


Et si n condensateurs sont branchés :

Figure 25: Connexion en triangle d'un TSC avec les inductances
de syntonisation.
La tenu en tension de chaque thyristor doit être de deux
fois la valeur de crête de la
tension du réseau (Fig 20). Pour l'application dans le
domaine de haute tension,
plusieurs thyristors peuvent être mis en série ou
un transformateur peut être utilisé
pour le couplage avec le réseau. En triphasé, des
TSC sont habituellement branchés en
triangle (Fig.21). Sur la (Fig .21) on peut voir des
inductances de syntonisation en série
avec des condensateurs.

Figure 26:TSC qui contint 3 condensateurs en parallèles

Figure 27:Relation entre le courant et le nombre des
condensateurs qui dans
le TSC


Figure 28:Caractéristique d'un TSC
1.24. LES COMPENSATEURS STATIQUES SVC)
4.1.4. Définition
Le compensateur statique (SVC) est un dispositif de compensation
shunt de la
Famille des systèmes de transmission flexible en courant
alternatif, employant
l'électronique de puissance pour commander la puissance
couler et améliorer la stabilité
passagère sur les grilles de puissance [8,9,17]. Le SVC
règle la tension sur ses bornes en
commandant la quantité de puissance réactive a
injecté dans ou absorbé du système
d'alimentation. Quand la tension de système est basse,
le SVC développe la puissance
réactive (SVC capacitif). Quand la tension de
système est haute, il absorbe la puissance
réactive (SVC inductif). La variation de la puissance
réactive est exécutée en commutant
les banques triphasées de condensateur et les banques
d'inducteur. Chaque banque de
condensateur est commutée en marche et en arrêt
par des commutateurs de thyristor Ils
sont constitués par un ensemble de condensateurs et
d'inductances commandées par
thyristors montés en tête-bêche dans chaque
phase, chacun d'entre eux étant ainsi
conducteur pendant une demi- période. La puissance
réactive absorbée par l'inductance
varie en contrôlant la valeur efficace du courant qui la
traverse par action sur l'angle
d'amorçage des thyristors.
Ces nouveaux appareils (Compensateurs statiques, SVC= Static Var
Compensator)
ont vu leurs possibilités s'accroître grâce
aux progrès de l'électronique de puissance. Ils
sont capables de remplir diverses fonctions telles que le
maintien de la tension, le
contrôle de la gestion des flux de puissance,
l'amélioration de la stabilité du réseau et
l'augmentation de la puissance maximale transmissible, etc. Le
compensateur statique
de puissance réactive à thyristors est
aujourd'hui un équipement largement employé
dans les systèmes de transport
d'électricité pour la régulation de la tension et de la
puissance réactive. La puissance réactive totale
contrôlée dans le monde par cet
appareil est supérieure à 20000 Mvar.
Les différents types de SVC utilisées aujourd'hui
peuvent pour l'essentiel être
divisés en deux catégories : Système avec
inductances commandées par thyristors avec
ou sans condensateur fixe (type FC/TCR ° Fixed
Capacitor/thyristor Controlled
Reactor).Système avec condensateurs couplés par
thyristors et inductances
commandées par thyristors (type TSC/TCR ° thyristor
Switched Capacitor / thyristor
Controlled Reactor).

Figure 29: Schéma de principe d'un SVC à banc de
condensateur fixe


Figure 30: Schéma de principe d'un SVC
4.1.5. Avantage du SVC
Les raisons principales d'incorporer le SVC dans des system de
transmission et de
distribution sont :
· Tension stabilisation des systèmes faibles.
· Réduction des pertes de transmission.
· Augmentation de la capacité de transmission.
· Stabilité croissante pour des perturbations
passagères.
· Atténuation croissante de petite perturbation.
· Amélioration de la commande tension et de la
stabilité.
· Atténuation des oscillations de puissance.

Figure 31: Variation de la tension sans et avec SVC

Figure 32: Augmentation de la capacité de transfert

Figure 33: SVC avec Banc de condensateur fixe
D'après la figure 31 en peut écrire :
(4.9)

Figure 34:Variation de BSVC en fonction de l'angle
d'amorçage

De la formule (4.5) :
Pour
Pour
Figure 35: Variation de BSVC en fonction de BTCR

Figure 36:Caractéristique V_I du SVC

Figure 37 Caractéristique d'un TCR, TSC et d'un SVC
Figure 38: Caractéristique d'un SVC
4.1.6. Caractéristique VI du SVC
Supposons que le système fonctionne avec un voltage .Si
la tension augmente, V
passera à sans SVC. Toutefois, l'exploitation du SVC
déplace le point de .En
absorbant de Puissance réactive pour maintenir la
tension à De même. Si la tension
diminue V passera à sans SVC. Toute fois l'exploitation du
SVC déplace le point on
injecte de la puissance réactive l'énergie pour
maintenir la tension à .
4.1.7. Les trois zone du SVC
§ Une zone où seules les capacités sont
connectées aux réseaux,
§ Une zone de réglage où l'énergie
réactive est une combinaison des TCR et des
TSC.
§ Une Zone de réglage ou le TCR donne son
énergie maximale (butée de
réglage), les condensateurs sont
déconnectés
Tous sont utilisés pour le contrôle de la tension
(la puissance réactive)
4.1.8. Exemple 2
Le compensateur statique est constitué d'un
transformateur abaisseur de tension
connecte a une inductance variable L et un condensateur C (Fig.
37). Ces charges
réactives sont respectivement branchées et
débranchées par des « contacteurs » et
composés de thyristors tête-bêche. Sur ce
réseaux à 735 kV, 60 Hz, les primaires sont
raccordes en étoilé alors que les secondaires a
16 kV sont en triangle. Les enroulements
du transformateur sont représentés par des
rectangles noirs. La Fig. 8.4 montre en détail
la branche AB de la charge réactive triphasée
branchée au secondaire du transformateur
de couplage. Cette branche est composée d'une inductance
et de deux condensateurs.
L'inductance L de est connectée en série avec deux
thyristors en antiparallèle.
En faisant varier l'angle de retard à l'amorçage de
90° à 180°, on peut faire varier le


courant inductif de 2319 A à zéro. Le condensateur
de est connecte en série
avec deux thyristors et un circuit d'amortissement compose d'une
inductance de
en parallèle avec une résistance de . Contrairement
à la branche inductive ou le
courant peut être ajuste de façon continue entre
zéro et sa valeur nominale, les branches
capacitives sont commandées en « tout ou rien
». Selon que les thyristors conduisent ou
non, le courant capacitif est de 1882 A ou zéro. Un
circuit identique contenant un
condensateur permet de doubler la puissance capacitive [19] .

Figure 39: Circuit d'un compensateur statique comporte des
inductances variables et
des condensateurs manoeuvrables
Avec :

Réactance inductive de L:


Courant efficace maximal
Puissance réactive par phase:


|
Puissance réactive inductive des 3 phases:
|
|
|
|
(4.18)
|
|
|
Réactance capacitive:
|
|
|
|
|
|




Courant capacitif:
Puissance réactive par phase:
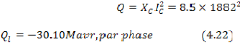
Puissance réactive capacitive des 3 phases:

Figure 40: Schéma détaillé d'une branche
4.1.9. Caractéristique V-I du compensateur statique
Supposons que les condensateurs soient débranches et que
la tension au
secondaire du transformateur soit de 16 kV. Ajustons l'angle
à des thyristors
commandant la branche inductive à 90°, de
façon a obtenir la pleine conduction. Le
courant dans les inductances est alors a sa valeur maximale,
soit 2319 A. La puissance
réactive totale est alors de 111 Mvar. Bien que la
tension nominale soit de 16 kV, celle-ci
peut fluctuer considérablement Lors d'une contingence de
réseau. La droite L (Fig. 39)
montre la relation entre la tension er le courant .
Par exemple, si la tension baisse a 12 kV, le courant
décroit à :


Le courant a baisse de mais la puissance a chuté à
:


Cela représente une diminution de par rapport à sa
valeur nominale de

Il est évident qu'une diminution de la tension
réduit de beaucoup la puissance
réactive que le compensateur peut absorber .Lorsque
l'inductance est débranchée et que
les deux condensateurs sont en service, le courant total par
phase sous une tension de

est de :
La coutume est d'apposer un signe (-) à ce courant
capacitif pour le distinguer du
courant inductif. La relation entre le courant et la tension
est alors une nouvelle droite,
désignée C (Fig. 41). Les droites L et C forment
ensemble une « courbe en V » qui
correspond aux limites inductive et capacitive du compensateur
statique. A la tension

nominale, elle s'étend de
Figure 41: Courbe en V du compensateur statique
Au voisinage de la tension nominale, le compensateur doit pouvoir
tirer un courant
réactif compris entre et . On réalise cette
variation en jouant sur le
nombre de condensateurs en service et en faisant varier le
courant inductif entre zéro et
On utilise les combinaisons suivantes:
a) L seule en service:
|
Courant réglable de zéro à
|
|
b) et en service:

Courant réglable de
c) et , en service:

Courant réglable de
Les trois plages d'opération sont illustrées
à la (Fig.42).
On notera que les plages de fonctionnement se recouvrent. Ce
chevauchement est
requis pour assurer une transition stable lors des manoeuvres
des branches capacitives.
Notons aussi que la largeur des plages diminue en proportion avec
la tension du réseau.

Figure 42: Plage de fonctionnement du compensateur statique

Figure 43: Formes d'ondes de la tension et du courant circulant
dans l'inductance
lorsque la conduction est amorcée à
4.1.10. Fonctionnement de l'inductance commandé par
thyristors
Valeur crête de la tension:


Tension à 150°:


Durée de l'intervalle de

Comme la surface A est un triangle presque parfait, le nombre de
volts-secondes est
donné par:

Courant crête dans l'inductance:
Composante efficace du courant fondamentale :
La valeur exacte du courant crête est donnée par
l'expression :

Où

Courant crête dans l'inductance en [A]
Tension efficace appliquée à l'inductance en [V]

Angle d'amorçage en [°]
Fréquence du réseau en [Hz]
Valeur de l'inductance en [H]
Si l'on applique cette expression à l'exemple 8-3, on
obtient:

On constate que la valeur approximative du courant crête
(430 A) que nous avons
calculée est très proche de sa valeur exacte. Le
courant puise comprend une composante
fondamentale et des harmoniques, et en particulier un 3e
harmonique. Celui-ci circule
dans le triangle forme par les éléments L, C de
la (Fig. 42). Par conséquent, le 3e
harmonique ainsi que tous les harmoniques multiples de 3
n'apparaissent pas dans les
enroulements du transformateur, ni sur le réseau. C'est
la composante fondamentale du
courant puise qui est de première importance. Elle est
donnée par l'expression:


Courant efficace dans l'inductance [A]

Tension efficace appliquée à l'inductance [V]


Angle d'amorçage

Fréquence du réseau [Hz]
Valeur de l'inductance [H]
On constate que le courant fondamental diminue a mesure que
l'angle d'amorçage
augmente au-delà la de . C'est comme si la
réactance inductive de l'inductance

augmentait avec En fait, la réactance effective est
donnée par
l'expression:

Courant fondamental:


Puissance réactive totale:
Q=3VI=3'16000'126 Q= 6.0 5MVAr
Réactance effective:



Lorsque , la réactance effective de l'inductance est 17
fois supérieure a sa

réactance intrinsèque
1.25.
chapitre 5
Une approche Fuzzy-Ant pour
l'emplacement
optimal des
condensateurs dans un réseau
électrique
1.26. INTRODUCTION
Approcher Fuzzy _Ant a pour but de déterminer les noeuds
candidat ou les noeuds
critiques là où il faut places les condensateurs
par un algorithme basé sur la logique flou
et un autre algorithme base sur l'algorithme de fourmis [21,
18,22].
|
Approche Fuzzy_Ant
Approche Fuzzy
|

|
1er Algorithme
On applique la logique flou pour
déterminer les noeuds candidats
|
|
2eme Algorithme
On applique l'algorithme de fourmi
pour déterminer les condensateurs
|
Figure 44:Schéma de Principe de l'approche Fuzzy_Ant
1.2 7. LA LOGIQUE FLOUE
La logique floue est basée sur un raisonnement humain,
réaliste. Avec toutes les
imprécisions et incertitudes qu'elle manipule, elle
s'adapte très bien à la régulation des
processus aussi bien linéaires que non linéaires.
La régulation floue est simple à mettre
au point et permet de prendre en charge des systèmes
complexes mais elle exige une
connaissance du dispositif
5.1.1. Principe et définitions
La logique floue repose sur la théorie des ensembles flous
développés par Zadeh
[29,7,30,31]. A coté d'un formalisme mathématique
fort développé, nous préférons
aborder la présentation de manière intuitive. Les
notions de température moyenne ou
de courant sont relativement difficiles à
spécifier d'une manière précise. On peut fixer
des seuils et considérer que l'on attribue tel ou tel
qualificatif en fonction de la valeur de
la variable par apport à ces seuils. Ceci ne peut
exprimer qu'un avis très tranché du
qualificatif « température moyenne » par
exemple.

La logique floue est une technique de traitement des incertitudes
et a pour objet :
la représentation des connaissances imprécises,
elle est basée sur des termes
linguistiques courants comme petit, grand, moyen...etc. Elle
autorise des valeurs
intermédiaires entre le vrai et le faux et admet
même des chevauchements entre eux [7].
Ensemble flou : dans un ensemble de référence , un
sous ensemble flou de ce
référentiel est caractérisé par une
fonction d'appartenance de dans l'intervalle
des nombres réels [0,1] qui indique avec quel
degré un élément appartient à cette classe.
Un sous ensemble flou est caractérisé par un
noyau, un support et une hauteur
[21].Noyau : C'est l'ensemble des éléments qui sont
vraiment dans :

Support : c'est l'ensemble des éléments qui sont
dans à des degrés divers :
Hauteur : c'est la borne supérieure de la fonction
d'appartenance :
|
Un ensemble est dit normalisé s'il est de hauteur 1 :
|

Exemple : Dans la figure 5.1 un exemple de sous ensemble
normalisé est présenté.
Figure 45: Format d'un ensemble flou normalisé
5.1.2. Opérateurs et normes :
Comme dans la théorie des ensembles classiques, on
définit l'intersection, l'union
des ensembles floues ainsi que le complémentaire d'un
ensemble flou. Ces relations sont
traduites par les opérateurs « et », « ou
» et « non ». De nouvelles fonctions
d'appartenance liées à ces opérateurs sont
établies :

Appartient à
Appartient à

Appartient au complémentaire
L'opérateur « et » se défini par une
norme triangulaire (t-norme) :

De même, l'opérateur « ou » se
défini par une Co-norme triangulaire (s-norme) :

Les opérateurs les plus utilisés en logique floue
sont :
L'opérateur « et » pour la t-norme, qui
correspond à l'intersection de deux ensembles
flous. Il peut être réalisé par :

La fonction « Min » :
La fonction arithmétique « Produit » :
L'opérateur « ou » pour la s-norme, qui
correspond à l'union de deux ensembles flous.
Il peut être réalisé par :

La fonction « Max » :
La fonction arithmétique « Somme» :
L'opérateur « non » est réalisé
par :
5.1.3. Structure générale d'un
contrôleur flou
L'avantage de la commande floue par comparaison avec les
commandes classiques
est qu'elle ne nécessite pas la connaissance des
modèles mathématiques du système. Par
contre elle a besoin d'un ensemble de règles
basées essentiellement sur la connaissance
d'un opérateur qualifié manipulant le
système La conception du contrôleur flou (FLC)
passe par quatre principales parties distinctes, comme le montre
la figure 44.

Figure 46: Structure d'un système de contrôle
flou
5.1.4. Interface de fuzzification
Dans le domaine du contrôle, les données
observées sont des grandeurs physiques
générées par des capteurs. Il est
nécessaire de convertir ces grandeurs réelles en des
variables floues. Pour cela, on fait appel à une
opération dite fuzzification, qui permet de
fournir les degrés d'appartenance de la variable floue
à ses sous ensembles flous en
fonction de la valeur réelle de la variable
d'entrée.
5.1.4.1 Base de règles
Le système de contrôle flou comprend un nombre de
règles d'inférence reliant les
variables floues d'entrée d'un système aux
variables floues de sortie de ce système. Ces
règles se présentent sous la forme usuelle suivante
:
SI condition 1 ET/OU condition 2 (ET/OU...) ALORS action
sur les sorties.
L'établissement de ces règles est
généralement basé sur la connaissance du
problème et sur l'expérience de
l'opérateur qui peut fixer le nombre de sous-ensembles,
leurs fonctions d'appartenance ainsi que les variables
linguistiques. Ils existent plusieurs
présentations de la base de règles telles que la
description linguistique, symbolique ou
par une matrice d'inférence. [17, 18, 19]
5.1.5. Mécanisme d'inférence
Dans cette étape, il s'agit de déterminer comment
le système interprète les
variables linguistiques floues. Les variables linguistiques
(entrées et sorties) sont liées
par les règles d'inférence. Les variables sont
liées par l'opérateur « ET », tandis que les
variables de sortie des différentes règles sont
liées par l'opérateur « OU » et l'ensemble
des règles sont liées par les connecteurs tels
que « ET » et « ALORS ». La conséquence
d'une règle floue est inférée par l'emploi
de règle de composition, en utilisant les
fonctions d'implications floues et les connecteurs « ET
» et « ALORS ». [6,19]
Les méthodes d'inférences se différencient
selon la combinaison et l'utilisation des
opérateurs « ET » et « OU » dans les
règles d'inférence. Parmi ces méthodes on trouve :
Méthode d'inférence MAX-MIN,
Méthode d'inférence MAX-PROD,
Méthode d'inférence SOMME-PROD.
5.1.6. Méthode d'inférence MAX-MIN
Cette méthode représente l'opérateur «
ET » par la fonction « Min », la conclusion
« ALORS » par la fonction « Max » et
l'opérateur « OU » par la fonction « Min ». La
représentation graphique de cette méthode
d'inférence est illustrée par la (Fig.41).



Figure 47: Méthode d'inférence MAX-MIN
1.2 8. INTERFACE DE DEFUZZIFICATION
Les méthodes d'inférence génèrent une
fonction d'appartenance, il faut
transformer cette grandeur floue en grandeur physique
réelle. L'opération de
défuzzification permet de calculer à partir des
degrés d'appartenance à tous les sous-
ensembles flous de la variable de sortie, la valeur de sortie
à appliquer au système. Il y a
plusieurs méthodes de défuzzification à
savoir la méthode du maximum, la méthode des
hauteurs pondérées et la méthode du centre
de gravité, cette dernière est la plus
utilisée L'expression de la sortie dans cette
méthode donnée par l'équation suivante.

1.2 9. OPTIMISATION PAR COLONIES DE FOURMIS
5.1.7. Introduction
Les études éthologistes ont montré que dans
la nature, les petites créatures faibles
que sont les fourmis, arrivent à résoudre
collectivement des problèmes quotidiens
nombreux et trop complexes pour une seule fourmi tels que :
recherche de nourriture,
construction du nid, division du travail et allocation des
tâches entre les individus, avec
une organisation excrément structurée et sans
aucune supervision. Par les
comportements simples de chacune des fourmis, des interactions
limitées à travers une
coopération inconsciente, émergent des
comportements collectifs intelligents et des
modèles d'auto-organisation [42]. Les fourmis sont
devenues dés lors une nouvelle
source d'inspiration pour la conception de méthodes de
résolution de problèmes
complexes. De plus cette source d'inspiration n'est pas unique
étant donné que les
fourmis sont dotées d'une grande diversité de
caractéristiques disjointes et de
comportements collectifs variés. Une nouvelle classe
d'algorithmes est alors apparue
sous le nom « algorithmes de fourmis artificielles ».
Leur popularité est due d'une part à
la facilité de mise en oeuvre et d'autre part à
la complexité des fonctions réalisables
[43, 44, 45, 46, 47, 48,49]. Deux comportements collectifs ont
été principalement étudiés
chez les fourmis : l'optimisation de chemin et le tri des
cadavres. Le premier
comportement appelé aussi fourragement permettent aux
fourmis de retrouver le plus
court chemin entre leur nid et une source de nourriture
grâce à un système de marquage
de phéromones. Ce comportement naturel a
été modélisé et transposé à la
résolution de
nombreux problèmes d'optimisation combinatoires sous le
nom d'une nouvelle
métaheuristique « optimisation par les colonies de
fourmis ou OCF ». Le deuxième
comportement collectif des fourmis concerne la capacité
de certaines espèces de
fourmis à organiser collectivement des cimetières
composés de cadavres empilés les uns
sur les autres. Là aussi, les chercheurs ont
exploité ce comportement pour fournir des
algorithmes de classification pour lequel l'informatique
classique n'a pas donné de
solution satisfaisante. Dans la suite nous présentons
une brève introduction au monde
des fourmis, ensuite nous décrirons en détail
chacun des modèles de fourmis artificielles
ainsi que les différents algorithmes qui lui sont
associés [51, 52, 53, 54, 55, 56, 57,58].
1.30. QUELQUES CONCEPTS DE BASE
Avant de s'intéresser aux algorithmes de fourmis
artificielles, il convient tout
d'abord de présenter quelques concepts de base qui
seront utilisées tout au long de cette
section.
5.1.8. Problème d'optimisation
Un problème d'optimisation est tout problème
définit par un espace de recherche
des solutions, une fonction objectif qui associe un coût
à chaque solution possible et un
ensemble de contraintes. On cherche alors à trouver la
solution optimale qui correspond
à une solution de coût minimum ou maximum selon
qu'il s'agit de minimiser ou de
maximiser la fonction objectif. Un problème
d'optimisation combinatoire est tout
problème d'optimisation pour lequel il faut trouver une
solution optimale avec un
espace de recherche de solutions fini mais extrêmement
grand. Ce type de problème est
dit « difficile ».
5.1.9. Méthodes de résolution
Les méthodes de résolution des problèmes
d'optimisation sont de deux types :
Les méthodes exactes (déterministes) : elles
fournissent une solution optimale au
prix d'un temps de résolution qui risque d'être
exponentiel en fonction de la taille des
données du problème. Les méthodes
approchées : pour un problème d'optimisation dit «
difficile » aucune méthode exacte n'est capable de
le résoudre exactement en un temps
raisonnable. Dans ce cas on fait appel à ses
méthodes permettant une optimisation
approchée. Ce type de méthodes retourne une
solution contenue dans un certain
intervalle autour de la solution optimum avec un temps de
calcul acceptable. Elles
représentent un compromis entre la qualité de la
solution trouvée et le temps de calcul
nécessaire. Parmi les méthodes de résolution
approchées, on trouve :
5.1.10. Les heuristiques
Une heuristique est une méthode approchée simple,
rapide et dédiée à un
problème donné. Elle exploite les
propriétés structurelles d'une solution et tente de la
rendre rapidement une solution admissible par des
critères de décision déduits de la
connaissance du problème. Aucune garantie quant à
l'optimalité de la solution trouvée
ne peut être fournie.
5.1.11. Les méta heuristiques
Une métaheuristique est une méthode
approchée générique dont le principe de
fonctionnement repose sur des mécanismes
généraux indépendants de tout problème.
Les méta heuristiques sont stochastiques et donc peuvent
éviter d'être piégés dans des
minimums locaux. Elles sont principalement guidées par
le hasard (exploration aléatoire
de l'espace de recherche), cependant elles sont souvent
alliées à d'autres algorithmes
afin d'en accélérer la convergence.
1.3 1. LES FOURMIS ARTIFICIELLES
Une fourmi artificielle est une entité simple dotée
d'un comportement similaire ou
étendu à celui de la fourmi réelle. Ce
comportement doit être élémentaire, restreint et
donc facile à programmer. A l'intérieur d'une
colonie, les fourmis sont concurrentes et
asynchrones, elles coopèrent inconsciemment ensemble
pour la résolution du problème
considéré. Les fourmis artificielles communiquent
entre elles indirectement par
stigmergie via des modifications de leur environnement (par
exemple par dépôt de
traces de phéromone artificielle) qui représente
la mémoire collective de la colonie.
Elles ont été de plus enrichies des contraintes
et de comportements qu'on ne trouve pas
dans leurs congénères réelles mais qui
sont spécifiques au problème qu'elles
résolvent. [59,60,61,62,63,64,65].
5.1.12. Un problème combinatoire :
Un problème combinatoire est toute situation dont on
cherche d'avoir une solution
tout en respectant la présence d'un ensemble de
contraintes. La solution c'est un
résultat de faire combiner ces contraintes ensemble
d'une manière qu'on maximise
quelques uns et on minimise les autres, ces contraintes ont une
caractéristique
primordiale, c'est que chaque contrainte influe sur les autres
soit quand on minimise sa
valeur ou on la maximise, dans un autre terme on dit que les
contraintes sont
conflictuelles. Par exemple, le schéma suivant
présente une situation de problème
combinatoire: où on veut acheter une voiture dans la
mode et en même temps avec un
prix raisonnable qui ne peut pas dépasser certaine
limite. Si on maximise la première
contrainte (une bonne voiture) on va avoir un prix maximale,
dans le contraire on va
aboutir à une mauvaise voiture mais avec un prix
minimale dans les limites; on constate
dans cet exemple que c'est difficile d'arranger ces deux
contraintes dans nos besoins
[66,67 ,68,69].
Figure 48:Une figure illustrant un problème
combinatoire
1.32. ANT COLONY SYSTEM « ACS »
L'algorithme « Ant Colony System » a été
introduit par « Dorigo » et «
Grambardella » en 1996 pour améliorer la
performance de AS [55] .ACS est basé
essentiellement sur As mais se distingue de lui par les points
suivants : Le déplacement
de la fourmi suit une autre règle de transition dite
règle proportionnelle pseudo-
aléatoire ;Deux méthodes sont utilisées
pour la mise à jour :Une mise à jour locale est
effectuée à chaque fin de cycle d'une fourmi. Une
mise à jour globale est faite une fois
que toutes les fourmis ont terminé leurs cycles. Seule
la fourmi qui a trouvé la meilleure
solution est autorisée à renforcer la
phéromone sur tous les arcs constituant son tour .La
mise à jour globale évite de se bloquer dans des
solutions sous optimal(minimums
locaux).Tandis que la mise à jour locale a pour effet de
réduire, de moins en moins,
l'interactivité des arcs déjà
visités par d'autres fourmis, et donc de favoriser l'émergence
de d'autres solutions que celle déjà
trouvées pendant les prochains cycles de
l'algorithme.
5.1.13. Ant System (AS-TSP)
Élitisme une première variante du "Système
de Fourmis" a été proposée par
[Dorigo 1996] : elle est caractérisée par
l'introduction de fourmis élitistes. Dans cette
version, la meilleure fourmi (celle qui a effectué le
trajet le plus court) dépose une
quantité de phéromone plus grande, dans l'optique
d'accroître la probabilité des autres
fourmis d'explorer la solution la plus prometteuse.



est la liste Tabou pour la fourmi (i).
désigne l'inverse de la distance entre les villes i et
j.
pondèrent l'influence de la phéromone et de la
longueur.
taux de phéromone entre les villes i et j.
5.1.14. Ant-Q
Dans cette variante de AS, la règle de mise à jour
locale est inspirée du Q-learning
[Gambardella and Dorigo, 1995]. Cependant, aucune
amélioration par rapport à
l'algorithme AS n'a pu être démontrée. Cet
algorithme n'est d'ailleurs, de l'aveu même
des auteurs, qu'une préversion du "Ant Colony System".



est une valeur fournie par une heuristique.
donne la valeur de probabilité de choix
(phéromone).
pondèrent l'influence des deux mesures.
est la probabilité d'utiliser la première
équation.
5.1.15. Ant Colony System (ACS)
L'algorithme a été introduit pour améliorer
les performances du premier
algorithme sur des problèmes de grandes tailles [Dorigo
and Gambardella, 1997b,
Dorigo and Gambardella, 1997a]. ACS est fondé sur des
modifications de l'AS :
1- ACS introduit une règle de transition dépendant
d'un paramètre q0 (0~q0~1),
qui définit une balance diversification /intensification
.Une fourmi k sur une ville i
choisira une ville j par la règle :

Et une ville sélectionnée aléatoirement
selon la probabilité :

En fonction du paramètre q0, il y a donc deux
comportements possibles :
si q>q0 le choix se fait de la même façon que
pour l'algorithme AS, et le système
tend à effectuer une diversification ; si , le
système tend au contraire vers une
intensification. En effet, pour , l'algorithme exploite davantage
l'information
récoltée par le système, il ne peut pas
choisir un trajet non exploré.
2- La gestion des pistes est séparée en deux
niveaux : une mise à jour locale et une
mise à jour globale. Chaque fourmi dépose une piste
lors de la mise à jour locale :

Où est la valeur initiale de la piste. A chaque passage,
les arêtes visitées voient
leur quantité de phéromone diminuer, ce qui
favorise la diversification par la prise en
compte des trajets non explorés. A chaque
itération, la mise à jour globale s'effectue
comme ceci :

Ici, seule la meilleure piste est donc mise à jour, ce qui
participe à une
intensification par sélection de la meilleure solution.
1.3 3. MAX-MIN ANT SYSTEM
Dans [53,54] Stutzle et Hoos introduisent MMAS algorithme. Les
modifications
introduites concernent :
L'utilisation de deux constantes et comme borne inférieure
et
supérieure à la quantité de
phéromone présentent sur les arcs du graphe. Ces deux
valeurs permettent de limiter les variations des taux de
phéromone et éviter ainsi que
certains arcs soient totalement délaissés au
profit d'autres ce qui est reconnu comme un
état de stagnation prématurée. Toutes les
traces de phéromones sont initialisées à.
Les quantités de phéromones sont
initialisées à la valeur maximale ;La mise à jour
des traces de phéromones n'est autorisée que par
la fourmi ayant trouvé la meilleure
solution.
1.34. AUTRES DOMAINES D'APPLICATION
Les bonnes performances des algorithmes basés fourmis
obtenues lors de leur
application au problème du voyageur du commerce ont
incité beaucoup de chercheurs à
les utiliser dans d'autres domaines d'application. Sans vouloir
dresser une liste
exhaustive de toutes les applications et variantes qui ont
été produites, on peut citer le
problème d'affectation quadratique [54 , 59], le
problème de coloration de
graphe[57,58], le problème de routage [69], les
réseaux de communication [75], le
problème d'ordonnancement [62,63], les problèmes
de satisfaction de contraintes [64],
la fouille de données [65], l'optimisation de site
d'enseignement en ligne (notion d' « E-
59Learning »[66].Une bonne synthèse de ces
algorithmes est reportée dans [70].
1.3 5. FORMULATION MATHEMATIQUE
La méthode proposée identifie la taille optimale
des condensateurs en utilisant la
logique Flou pour déterminer les noeuds candidat ensuit
minimiser la fonction de coût
avec la contrainte Perte désiré. La fonction de
coût est énoncée comme, suite
[8, 18, 22, 23,39,40,41]:


Coût total de l'opération en ($/an).

Constante des Perte du système en ($/KW).

Petre du système en (KW)

Coût annule du noeud en ($/an).

La capacité du condensateur installée au noeud j en
(Kvar).
Nombre de banque de capacité installé.
Contraintes d'inégalités

5.1.16. 1er Algorithme Pour l'identification des noeuds
candidat
L'algorithme suivant explique la méthodologie pour
identifier les noeuds candidats,
qui se prêtent mieux à l'emplacement des
condensateurs.
1ere étape :
Entrée les données du réseau.
2eme étape :
Calcul de l'écoulement de puissance.
3eme étape :
Calcule des pertes actives du système.
4eme étape :
Compensation de la puissance réactive à chaque
noeud en déterminant des pertes de
puissance active dans chaque cas.
5eme étape :
Calculer de la réduction des pertes active et les indices
de pertes de puissance.par la
formule suivante.

Avec:
X = Réduction de perte.
Y = Réduction minimale.
Z = Réduction maximale.
n = number de noeuds
6eme étape :
Injecte les PLI (Indices de perte de puissance) et les tensions
Nodales (V) à l'entrée du
contrôleur Flou.
7eme étape :
Les sorties du Contrôleur Flou nous donne les CSI (Indices
de convenance des
condensateurs). Les noeuds ayant la plus forte valeur de CSI sont
les plus adaptés pour
le placement condensateur.
8eme Etape :
Fin.
5.1.17. 2eme Algorithme Pour l'emplacement optimal des
condensateurs
1er étape 1:
Initialisation

Pour chaque condensateur c (i ,j) une valeur initiale

Calcul de
2 eme étape :
Début d'itération
Pour fourmi=1 à m (boucle 1) {m: nombre de fourmi}
Pour un noeud candidat =1 à n (boucle 2) {n : nombre de
condensateur}
Choix d'élément avec la formule (5.3 )et ( 5.4) le
nombre d'éléments
Stockage des choix sur une liste
Fin de boucle 2.
Mise à jour locale formule(5.5). La piste de
phéromone pour les éléments choisis.
Fin de boucle 1. {Fin de parcoure}
3eme étape :
Mise à jour globale
Calcul du cout total d'investissement
Calcul du meilleur parcours

Mise à jour globale avec la formule 5-4 du meilleur
parcours avec
4eme étape :
Test
Si l'itération<= nombre max d'itération
Nouvelle itération, aller à l'étape 2.
Si non
Afficher les résultats
5eme étape :
Fin
1.36. SCHEMA BLOC DU FUZZY ANT
Réseau Electrique

|
Calcul de l'écoulement de
puissance,
Tension nodales et les
pertes actives
|

Contrôleur Flou pour
Déterminer les nouds
Candidats

|
Algorithme de fourmis
Pour déterminer les
condensateurs optimaux
|

Calcul de l'écoulement de
puissance,
Nouvelle Tension
nodales et les pertes
actives
Figure 49:schéma bloc de Fuzzy_Ant
chapitre 6
Experimentation et
discussion
6.1.1. Réseaux 25 noeuds
6.1.2. Données du réseau 25 noeuds

Figure 50:Réseaux 25 noeuds
6.1.3. Données relative aux lignes de transport
|
Branche
p_q
|
Impédance Zpq
[pu]
|
Admittance shunt
ypq/2
[pu]
|
|
1-3
|
0.0720+j0.2876
|
j0.0179
|
|
1-16
|
0.0290+j0.1379
|
j0.0337
|
|
1-17
|
0.1012+j0.2799
|
j0.0148
|
|
1-19
|
0.1487+j0.3897
|
j0.0224
|
|
1-23
|
0.1085+j0.2245
|
j0.0573
|
|
1-25
|
0.0753+j0.3593
|
j0.0873
|
|
2-6
|
0.0617+j0.2935
|
j0.0186
|
|
2-7
|
0.0511+j0.2424
|
j0.0155
|
|
2-8
|
0.0579+j0.2763
|
j0.0175
|
|
3-13
|
0.0564+j0.1478
|
j0.0085
|
|
3-14
|
0.1183+j0.3573
|
j0.0185
|
|
4-19
|
0.0196+j0.0514
|
j0.0113
|
|
4-20
|
0.0382+j0.1007
|
j0.0220
|
|
4-21
|
0.0970+j0.2547
|
j0.0558
|
|
5-10
|
0.0497+j0.2372
|
j0.0577
|
|
5-17
|
0.0144+j0.1269
|
j0.1335
|
|
5-19
|
0.929+j0.2442
|
j0.0140
|
|
6-13
|
0.0263+j0.0691
|
j0.0040
|
|
7-8
|
0.0529+j0.1465
|
j0.0078
|
|
7-12
|
0.0364+j0.1736
|
j0.0110
|
|
8-9
|
0.0387+j0.1847
|
j0.0118
|
|
8-17
|
0.0497+j0.2372
|
j0.0572
|
|
9-10
|
0.0973+j*0.2691
|
j0.0085
|
|
10-11
|
0.0898+j0.2359
|
j0.0135
|
|
11-17
|
0.1068+j0.2807
|
j0.0161
|
|
12-17
|
0.0460+j0.21996
|
j0.0139
|
|
14-15
|
0.0281+j0.0764
|
j0.0044
|
|
15-16
|
0.0256+j0.0673
|
j0.0148
|
|
17-18
|
0.0806+j0.2119
|
j0.0122
|
|
8-19
|
0.0872+j0.2294
|
j0.0132
|
|
20-21
|
0.0615+j0.1613
|
j0.0354
|
|
21-22
|
0.0414+j0.1087
|
j0.0238
|
|
22-23
|
0.2550+j0.3559
|
j0.0169
|
|
22-23
24-25
|
0.0970+j0.2595
0.0472+j0.1458
|
j0.0567
j0.0317
|
Tableau 2 : Données relative aux lignes de transport
6.1.4. Planification
|
Noeuds
p
|
Tension
[pu]
|
Argument
[deg]
|
Puissance
Générées
[MVA]
|
Puissance
Charge
[MVA]
|
|
1
|
1.06
|
0°
|
?
|
200+j65
|
|
2
|
1.00
|
0°
|
100-j17
|
10+j3
|
|
3
|
1.00
|
0°
|
150+j4
|
50+j17
|
|
4
|
1.00
|
0°
|
50-j4
|
30+j10
|
|
5
|
1.00
|
0°
|
200-j47
|
25+j8
|
|
6
|
1.00
|
0°
|
0
|
15+j5
|
|
7
|
1.00
|
0°
|
0
|
15+j5
|
|
8
|
1.00
|
0°
|
0
|
25+j0
|
|
9
|
1.00
|
0°
|
0
|
15+j5
|
|
10
|
1.00
|
0°
|
0
|
15+j5
|
|
11
|
1.00
|
0°
|
0
|
5+j0
|
|
12
|
1.00
|
0°
|
0
|
10+j0
|
|
13
|
1.00
|
0°
|
0
|
25+j8
|
|
14
|
1.00
|
0°
|
0
|
20+j7
|
|
15
|
1.00
|
0°
|
0
|
30+j10
|
|
16
|
1.00
|
0°
|
0
|
30+j10
|
|
17
|
1.00
|
0°
|
0
|
60+j20
|
|
18
|
1.00
|
0°
|
0
|
15+j5
|
|
19
|
1.00
|
0°
|
0
|
15+j5
|
|
20
|
1.00
|
0°
|
0
|
25+j8
|
|
21
|
1.00
|
0°
|
0
|
20+j7
|
|
22
|
1.00
|
0°
|
0
|
20+j7
|
|
23
|
1.00
|
0°
|
0
|
15+j5
|
|
24
|
1.00
|
0°
|
0
|
15+j5
|
|
25
|
1.00
|
0°
|
0
|
25+j8
|
Tableau 3: Planification
6.1.5. Ecoulement de puissance
Les résultats de l'écoulement de puissance par la
méthode de Newton Raphson.
6.1.6. Les tensions nodales
|
Module
[pu]
|
Angle
[degré]
|
|
1.06
|
0
|
|
1
|
14.458
|
|
1
|
13.229
|
|
1
|
4.0708
|
|
1
|
14.195
|
|
0.98154
|
10.405
|
|
0.99093
|
9.4417
|
|
0.98603
|
8.1401
|
|
0.97699
|
7.6758
|
|
0.98818
|
9.2541
|
|
0.99313
|
7.5844
|
|
0.99319
|
7.5801
|
|
0.90651
|
11.45
|
|
0.9682
|
0.95158
|
|
0.97576
|
-0.91848
|
|
0.99679
|
-1.477
|
|
1.001
|
6.521
|
|
0.98922
|
4.8809
|
|
0.99885
|
4.9071
|
|
0.98145
|
1.5217
|
|
0.97802
|
-0.43713
|
|
0.97878
|
-2.4603
|
|
1.0181
|
-2.0742
|
|
0.98506
|
-4.8579
|
|
0.99825
|
-4.8918
|
6.1.7. Les Pertes totales
|
PL = 2 8.7049
MW
|
QL= 1.9368MVAR
|
1.3 7. APPROCHE FUZZY ANT

Figure 51::Variation des Tension Nodale avant l'emplacement des
condensateurs
6.1.8. Application du Contrôleur Flou
Résulta de l'application du contrôleur flou au
réseau 25 noeuds pour l'obtention
des nouds candidats.
6.1.8.1 Les Noeuds Candidats
Noeuds N°
7
8
10
11
Tableau 4:Les Noeuds Candidats
6.1.8.2 Les Pertes actives
PL = 25.2445 MW
Coût d'investissement
Coût= 1262226.8477$/an
6.1.8.3 Valeurs des Condensateurs Optimaux
|
N° du Noeud
candidats
|
Valeurs des condensateurs en
MVAR
|
|
7
|
9
|
|
8
|
0.5
|
|
10
|
7
|
|
11
|
0.5
|
Tableau 5:Valeurs de condensateurs optimaux
6.1.8.4 Les nouvelle Tension Nodales
|
Tension
[pu]
|
Angle
[degré]
|
|
1.0600
|
0.00
|
|
1.0239
|
0.2003
|
|
1.0301
|
0.1279
|
|
0.9890
|
-0.0490
|
|
1.0358
|
0.2381
|
|
1.0072
|
0.1236
|
|
1.0305
|
0.1227
|
|
1.0292
|
0.1163
|
|
1.0249
|
0.1130
|
|
1.0402
|
0.1445
|
|
1.0377
|
0.1165
|
|
1.0308
|
0.1031
|
|
1.0067
|
0.1147
|
|
0.9940
|
-0.0243
|
|
0.9970
|
-0.0441
|
|
1.0130
|
-0.0432
|
|
1.0303
|
0.0994
|
|
0.9864
|
0.0234
|
|
0.9624
|
-0.0295
|
|
0.9511
|
-0.0878
|
|
0.9608
|
-0.1081
|
|
0.9737
|
-0.1215
|
|
1.0239
|
-0.0668
|
|
0.9985
|
-0.1390
|
|
1.0143
|
-0.1241
|
Tableau 6:Les Tension Nodales

Figure 52:Variation des Tension Nodales après
emplacement des condensateurs
6.1.8.5 Pertes active totales
|
Cas de Base
|
Fuzzy_Ant
|
|
Pertes actives
|
28.70 MW
|
2 5.24MW
|
|
Réduction en MW
|
|
3.46 MW
|
|
Réduction en %
|
|
15.54
|
Tableau11:Les Pertes active totales
6.1.9. Le compensateur statique (SVC)
D'âpre le tableaux N° 19 en va injecter SVC au nouds
7,8,10 et11 pour Controller les
tension
|
SVC au noeud N°07
|
SVC au noeud N°08
|
SVC au noeud N°10
|
SVC au noeud N°11
|
|
Tension
[pu]
|
Argument
[degré]
|
Tension
[pu]
|
Argument
[degré]
|
Tension
[pu]
|
Argument
[degré]
|
Tension
[pu]
|
Argument
[degré]
|
|
1.0600
|
0.00
|
1.0600
|
0.00
|
1.0600
|
0.00
|
1.0600
|
0.00
|
|
1.0000
|
14.3766
|
1.0000
|
14.3935
|
1.0000
|
14.4487
|
1.0000
|
14.4449
|
|
1.0000
|
13.2214
|
1.0000
|
13.2230
|
1.0000
|
13.2281
|
1.0000
|
13.2278
|
|
1.0000
|
4.0688
|
1.0000
|
4.0554
|
1.0000
|
4.0590
|
1.0000
|
4.0647
|
|
1.0000
|
14.1811
|
1.0000
|
14.1357
|
1.0000
|
14.1495
|
1.0000
|
14.1712
|
|
0.9813
|
10.3360
|
0.9413
|
10.3504
|
0.9815
|
10.3976
|
0.9815
|
10.3943
|
|
1.0000
|
9.2033
|
0.9951
|
9.4745
|
0.9921
|
9.4453
|
0.9915
|
9.4297
|
|
0.9882
|
8.1470
|
1.0000
|
7.8509
|
0.9890
|
8.0899
|
0.9871
|
8.1138
|
|
0.9787
|
7.6770
|
0.9872
|
7.4554
|
0.9837
|
7.6013
|
0.9789
|
7.6437
|
|
0.9891
|
9.2460
|
0.9927
|
9.1458
|
1.0000
|
9.0642
|
0.9911
|
9.1940
|
|
0.9943
|
7.5694
|
0.9971
|
7.4995
|
1.0004
|
7.4816
|
1.0000
|
7.4435
|
|
0.9990
|
7.4483
|
0.9970
|
7.5739
|
0.9945
|
7.5715
|
0.9941
|
7.5639
|
|
0.9063
|
11.4015
|
0.9063
|
11.4116
|
0.9065
|
11.4447
|
0.9065
|
11.4424
|
|
0.9682
|
0.9484
|
0.9682
|
0.9491
|
0.9682
|
0.9512
|
0.9682
|
0.9511
|
|
0.9758
|
-0.9207
|
0.9758
|
-0.9202
|
0.9758
|
-0.9187
|
0.9758
|
-0.9188
|
|
0.9968
|
-1.4784
|
0.9968
|
-1.4781
|
0.9968
|
-1.4772
|
0.9968
|
-1.4772
|
|
1.0025
|
6.4968
|
1.0043
|
6.4553
|
1.0026
|
6.4947
|
1.0022
|
6.4984
|
|
0.9901
|
4.8678
|
0.9911
|
4.8398
|
0.9902
|
4.8615
|
0.9899
|
4.8663
|
|
0.9990
|
4.9021
|
0.9991
|
4.8836
|
0.9990
|
4.8907
|
0.9990
|
4.8979
|
|
1.5200
|
|
1.5077
|
|
1.5109
|
|
1.5161
|
|
0.9814
|
|
0.9814
|
|
0.9814
|
|
0.9814
|
|
|
0.9780
|
-0.4386
|
0.9780
|
-0.4490
|
0.9780
|
-0.4463
|
0.9780
|
-0.4419
|
|
0.9788
|
-2.4615
|
0.9788
|
-2.4692
|
0.9788
|
-2.4671
|
0.9788
|
-2.4639
|
|
1.0181
|
-2.0746
|
1.0181
|
-2.0774
|
1.0181
|
-2.0766
|
1.0181
|
-2.0755
|
|
0.9851
|
-4.8586
|
0.9851
|
-4.8635
|
0.9851
|
-4.8622
|
0.9851
|
-4.8602
|
|
0.9983
|
-4.8923
|
0.9983
|
-4.8957
|
0.9983
|
-4.8948
|
0.9983
|
-4.8934
|
Figure 53: Tensions nodales


Figure 54:SVC a banc de condensateur fixe

Si et avec :
SVC aux noeuds
|
N°
|
Perte
active(MW)
|
Qsvc(MVAR)
|
ásvc(degré)
|
|
07
|
28.64
|
-6.86
|
129.44
|
|
08
|
28.65
|
-13.34
|
130.88
|
|
10
|
28.63
|
-8.73
|
129.85
|
|
11
|
28.66
|
-3.65
|
128.75
|
Figure 55:Perte active, Qsvc et ásvc pour les
différents cas
1.38. APPLICATION AVEC GUI MATLAB 7.04






Conclusion
Nous avons étudié du la minimisation des pertes
active par la méthode gradient
réduit.la tenue de tension avec
l'injection de puissance réactive dans les différente
noeuds du réseaux et l'emplacement optimale des
condensateurs dans le réseaux en
utilisant la logique flou et les algorithmes de fourmis.
Les résultats obtenus, à partir des
différentes simulations, nous ont permis de
formuler les conclusions suivantes :
La répartition des charge (Load flow) est l'un des
principaux problèmes qui se
pose aux Gestionnaires d'un système de production
-transport d'énergie électrique .Elle
nous permet de déterminer les valeurs de module et de la
phase de la tension en chaque
noeud du réseau pour des conditions de fonctionnement
données, ce qui nous permettra
de calculer les puissances transitées et
génères et les pertes .la méthode de Gauss-Seidel
est une méthode souple et efficace pour les
réseaux de faible taille. La méthode de
newton Raphson est très robuste surtout pour les
réseaux de grand dimension ,et la
méthode découpler rapide est utilisée dans
le calcul des sensibilités grâce au
décuplement de la matrice Jacobine.
L'installation d'un compensateur statique de puissance
réactive en un ou plusieurs
points spécifiques du réseau accroît la
capacité de transité et réduit les pertes active tout
en maintenant un profile de tension régulier sous
différent régime. Du suscrite, un
compensateur statique peut atténuer les oscillations de
puissance réactive par
modulation des amplitudes de tension.
Emplacement des condensateurs optimales dans des
différentes pointes du réseau
en utilisant des méthodes hurestique tel que les
algorithmes de fourmis et la logique flou
réduit les pertes dans le réseaux et maintien les
tensions dans la limite de sécurité
Nous avons développé une petite application, avec
interface graphique avec GUI
MATLAB 7.4.
En perspective, nous suggérons une continuité dans
les domaines suivantes :
L'emplacement optimal des FACTS tel que SVC, TSCS, STATCOM, UPFC
en utilisant
les algorithmes génétiques.
L'application de la méthode de sensibilité pour le
choix de l'emplacement des
FACTS en touchent l'endroit de la grandeur du dispositif et son
modèle en même temps.
Etablir un outil de travail, faible, rapide et moderne, qui
permettra à la SONELGAZ
de mieux exploiter le système de production de
l'énergie réactive.
Etude complète du SVC installé à
Béchar(Algérie).
Bibliographie
[1] Chaker.A, Khiat.M«Optimal Distribution of reactive
power with securities
constraints by numerical and heuristic method » MEPCON 98
Mansourah-Egupt.1998.
[2] Benzeragua.F, CHaker.AKhiat.M «Contrôle de la
puissance réactive dans les
réseaux électrique en grand taille»Lamer,
International Congrées on photovoltaïque
Wind Energies.2003, Telemcen, Algerie.
[3] CHAKER.A KHIAT.M « Répartition des puissance
Réactives en tenant compte du
rapport de transformation »,11eme Conférence
Internationale for teh Avancement
Science Bayreuth Liban,1991.
[4] KAHIAT.M «Répartition Optimale des puissance
Réactive dans le un réseau
d'énergie sous certaine contrainte électrique de
securit » thèse d'état, soutenue a
L'USTO,2003.
[5] J.P Barret P Bornard and B.Meyer « Simulation des
réseaux électriques »
EYROLLES 1997.
[6] A.Herbig « On load Flow Control in Electric Power
Systems »Thesis of the Royal
Institute of Technology, Stockholm, Sweden.2 000.
[7] Boucheta .A « Command par mode backstepping-flou de la
machine
asynchrone » These de Magister soutenue en 2006.
[8] Benzeargua.F « Emplacement optimal des dispositifs
FACTS dans le réseau
algérien » Thèse de Doctorat soutenu 2006.
[9] Breuer.G, «Flexible AC Transmission Systems Technology
for the
Future»Proceeding of 20th Annual Electrical /Electronic
Insulation Boston, MA, October
7-10, 1991.
[10] Moyso F.et Manderic B., 1988 «The collective Behaviour
of Ant » an Example
of Self organisation in Massive Parallelism »Proceeding
of the AAAI Spring Symposium
on Parallel Models of Intelligence .Stanford, California.
[11] Deneubourg J-L .,Pasteels J-M et Verheaghe J-C., 1983
« Probabilistic
Behaviour in Ants: strategy of Errors ? »,Journal of
Theoretical Biology,105.
[21] Colorni A,,Dorigo M .et Maniezzo V.,1991« Distributed
Optimization by Ant
Colonies »,Proceedings of the First European Conference on
Artificial Life, MIT
Press/Bradford Book ,Paris.
[13] Livre de Dorigo. Un chapitre dans son livre qui parler des
algorithmes
élaborées des colonies de fourmis notamment
adapté pour le TSP et divers problèmes
d'optimisation dynamiques.
[14] Livre de Dorigo. Un chapitre dans son livre est
spécifiquement dédié aux
algorithmes élémentaires des colonies de fourmis
dans un livre généraliste sur les métas
heuristiques.
[15] Livre de Dorigo. Un chapitre dans son livre qui parler de
différents mesure du
TSP d'une manière simplifiée.
[16] Livre de Dorigo .Un chapitre dans son livre qui parler de
la méta-heuristique
ACO, d'une manier simplifier.
[17] «Facts Modelling and simulation in power network
» by Enrique Acha, Claudio
R.Furet-Esquivel, Hugo Ambrize-Perez and Cesar
Angeles-Camacho.
[18]Tesis « Metodología
Técnico-económica de Localización de Capacitares en
Sistemas de Distribución para la Reducción de
Pérdidas Eléctricas » Presenta: Gabriel
Estrada Soria Morelia, Mich., Febrero de 2003.
[19] Livre « Electro technique » par Theodore Wildi
Avec la collaboration de
Gilbert Sybille (ingénieure, institue de recherche
d'Hydro-Québec) 3eme édition.
[20]Newness Power Engineering Series « power electronic
control in Electrical
systems »E.Acha V.G Agelidis O.Anaya-Lara and T.J.E
.Miller.
[21]CS Chang JS Huang « Optimal SVC placement for voltage
stability
reinforcement »Electric Power Systems Research 42,1997,99
165-172.
[22] D.Thukarama,Abraham Lomi«Selection of static VAR
compensator location
and size for system voltage stability improvement »
Electric Power Systems Research
54,2000,pp 139-150.
[23] Oliver E.J Marangon Lima and Pereira J.L.R «Flexible
AC Transmission System
Devices: Allocation and Transmission Pricing»Electrical
Power and Energy
System,V01,No .2 ,pp 111-118.
[24] Monticelli,A Garcia , Saavedra 0.R »FAST Decoupled
load flow hypothesis
derivation, and testing» IEEE Transaction on Power
systems,Vol.5,No.4 Novombre
1990,pp 1425-143 1.
[25] Gyugyi.L Sen,K.K and CD Schuder»The Interline power
Flow concepte:Anew
approche To power management in transmission systems»
IEEE Trans .On Power
Delivery vol.14 No.3 July 1999 ,pp.1115-1123.
[26] Kirkpatrick.S et al, « Optimization by Simulated
Annealing »Science 220 :671-
680,1983.
[27] Amat, J.L, Yahiaoui,G «Technique avances pour le
traitement de l'information
» Réseaux de neurones ,logique floue, algorithme
génétiques ,Cépadués Editions ,198
p.,1996
[28] Bieber.P,C .Castel,C .Kehern ,C Seguin «Analyse des
exigences de suret d'un
system électrique par model -cheking »ONERA -CERT
Toulouse (France),Lambad -Mu
14, colloque de maîtrise de risque et sûreté
de fonctionnement 2004.
[29] Zadeh. LA. `'The calculus of fuzzy if/then rules». AI
Expert:.22-27 1992.
[30] Laoufi .A « Application de L'Algorithme
Génétique et la Logique Floue dans
L'Optimisation des Réseaux Electriques et
Contrôle des Machines Asynchrones » Thèse
de doctorat Soutenue en 20/06/2006.
[31] « Practical genetic Algorithm » Second edition by
Randy L haupt ,Sue Ellen
haupt . A Jhon Willey and Sons.
[32] Darwin Charles « l'origine des espaces », petite
collection maspero, Paris
,1980
[33] Thesis « Transmission loss Allocation using artificial
neural network » by
Rezaul March 2006.
[34] Dell'Amico M.and Turbian « Applying Tabu Search to the
Job-Shop Scheduling
Problem »Annals of operation research vol41,1993,pp2
13-252.
[35] Faigle U.and W Kern, «Some Convergence Results for
Probabilistic Tabu
Search » ORSA Journal on Computing Vol.4,No 1,1992,pp
32-38.
[36] Glover «Heuristics for Integer Programming Using
Surrogate Constraints
»Decision Science,Vol 8,No1997,pp1 56-166.
[3 7] Glover «tabu Search -Part I» ORSA Journal on
Computing, Vol 1,No.3,1989,pp
190-206.
[38]Glover «tabu Search -Part II» ORSA Journal on
Computing, Vol 2,No.1,1990,pp
4-32.
[39] Yann-Chang Hong-tzer Yang Ching-Lien Huang «Solving
the Capacitor
Placement Problem in Radial Distribution System Using tabou
Search Approach »IEEE
Transaction on Power Systems Vol,11 No4 November pp1868-1873.
[40] Basaputer.P and Ongsakul.W «Optimal Power Flow with
Mulit-type FACTS
Devices by Hybrid TSISA Approach » IEEE ICIT 02,Bangokok
,THAILAND ,pp 285-2 90.
[41] Ali Hassan AI-Mohammed and Ibrahim Elamin «Capacitor
Placement In
Distribution Systems Using Artificial Intelligent Technique
», Paper accepted for
presentation at 2003 IEEE Bologna Power Tech Conference, June
23-2 3, Bologna, Italy.
[42] Bonabeau.E, Theraulaz.G, L'intelligence en essaim, POUR LA
SCIENCE, 282 (3):
pp. 66-73, N° 271 mai 2000.
[43] Deneubourg.J.L, Aron.S, Goss.S, et Pasteels.J.M, The
self-organizing
exploratory pattern of the argentine ant. Dans Journalon
insect Behavior, 3: 159-168,
1990.
[44] Colorni.A, Dorigo.M, Maniezzo.V. Distributed optimization
by ant colonies, in
Toward a practice of autonomous systems : proceedings of the
first European
Conference on Artificial Life (ECAL 91)», MIT Press, 1992,
p. 134-142.
[45] Dorigo.M, Maniezzo.V, Colorni.A, The Ant System:
Optimization by a Colony
of Cooperating Agents, IEEE Transactions on Systems, Man and
Cybernetics-Part B,
1(2 6): p. 29-41. 1996.
[46] Van De Vijver.G, Emergence et explication, Intellectica :
Emergence and
explanation, 1997/2 n°25, ISSN n°0984-0028 185-194,
1997.
[47] Bonabeau.E, Dorigo.M, Theraulaz.G, Swarm Intelligence :
From Natural to
Artificiel Systems, NEW York, Oxford University Press,1999.
[48] X. Topin Etude de l'auto-organisation par
coopération appliquée à
l'apprentissage comportemental de robots fourmis , DEA RCFR -
Université Paul
Sabatier, Toulouse Juin 1999.
[49] Wilson.S, Knowledge Growth in an Artificial Animal, in
Proceedings of the 1st
International Conference on Genetic Algorithms and their
Applications, J.J. Grefenstette
Ed., 1985, pages 16-23.
[50] Colorni.A, Dorigo.M, Maniezzo.V Distributed optimisation by
ant colonies, In
Proceeding of ECAL-9 1,Paris, France 134-142, 1991.
[51] S. Goss, S. Aron, .Deneubourg.J-L , J.M. Pasteels, Self
organized shortcuts in the
argentine ant, Natur wissenschaften, Vol. 76, 1989, p.
579-581.
[52] Dorigo.M, Gambardella.M, «Ant Colony for the Traveling
Salesman Problem,
BioSystems», (43): 73-81, 1997.
[53] T. Stuzle, Hoos.H. The max-min ant system and local search
for Combinatorial
Problems, in Meta-heuristics : advances and trends in local
search paradigms for
Optimization» by S. VOSS, I.H. OSMAN and C. ROUCAIROL,
Kluwer Academic Publishers,
Boston, 1999, p. 3 13-329.
[54] E. Taillard, Ant systems, `Handbook of Applied
Optimization», P. PARDALOS,
M.G.C RESENDE.
[55] Dorigo.M, M. Gambardella, Ant Colony System: A Cooperative
Learning Ap.
roach to the Traveling Salesman Problem, IEEE Transactions on
Evolutionary
Computation Vol 1: p. 5 3-66 1997.
[56] Stützle.T, Hoos.H, MAX-MIN ant system, Future
Generation Computer Systems,
Vol. 16 (2000).
[57] Costa.D. et . Hertz.A, Ants Can Color Graphs, Journal of
the Operational
Research Society, (48): p. 295-3 05. 1997.
[58] Dutot.A, Cardon.A, Olivier.D, et Guinand.F, Competing ants
for organization
detection, application to dynamic distribution. Proc. of the
ECCS 05, European
conference on complex systems. 2005.
[59] Maniezzo.V, A. Colorni, M. Dorigo,, The Ant System Applied
to the Quadratic
Assignment Problem», Technical Report. IRIDIA. (28),
Université Libre de Bruxelles,
Belgium, 1994.
[60] Bullnheimer.B, R.Hartl, et C. Strauss, Applying the Ant
System to the Vehicle
Routing Problems, 2nd Metaheuristic International Conference
(MIC-97), Sophia-
Antipolis, France.1997.
[61] Di Caro, G., Dorigo, M.(1998), AntNet: Distributed
Stigmergetic Control for
Communications Networks, Journal of Artificial Intelligence
Research (JAIR), (9): p. 317-
365.
[62] Gambardella.L, M. Dorigo, HAS-SOP: An hybrid ant system for
the sequential
ordering problem, Technical Report (11), IDSIA, Lugano, CH.
1997.
[63] Merkle.D, Middendorf.M and H. Schmeck, Ant colony
optimisation for
resource constrained project scheduling, IEEE Transaction on
Evolutionary
Computation, 6(4): 333-346 August 2002.
[64] Solnon.C. Solving permutation constraint satisfaction
problems with artificial
ants. In Proceedings of ECAI'2000, IOS Press, Amsterdam, The
Netherlands, pages 118-
122, 2000.
[65] Parpinelli.R, H. S. Lopez and A. A. Freita, data mining
with ant colony
optimisation algorithm, IEEE Transaction on Evolutionary
Computation, 6(4): 321-332
August 2002.
[66] Semet.Y, Lutton.E and Collet.P Ant Colony Optimization for
e-learning :
Oberserving the emergence of pedagogic suggestions. In IEEE
Swarm Inteligence
Symposium 2003, Indianapolus, Indiana, april 2003.
[67] Dorigo.M, T. STUZLE,. Ant Colony Oprimization. MIT Press,
Cambridge, MA,
2004.
[68] : Alain Berro ; Optimisation Multiobjectif et
Stratégie d'évolution en
environnement Dynamique (thèse de Doctorat) ; 18
Décembre 2001 ;Université des
sciences sociales ToulouseI ; page 14, 27, 29.
[69] : Keeffe.M et Cinnéid.M ; A Stochastic Approach to
automated Design
Improvement; 2003.
| 


