Identification géotechnique de matériaux concassés-types en corps de chaussées et évaluation de leur qualité

Université Cheikh Anta Diop de Dakar

Faculté des Sciences et Techniques

Département de Géologie

DEA
Mémoire de Diplôme d'Etudes Approfondies en Géosciences

Option : Environnements sédimentaires
Mention : Géotechnique

Identification géotechnique de matériaux

concassés-types en corps de chaussées et

évaluation de leur qualité

Présenté et soutenu publiquement le 24 / 06 / 2008 par :
Makhaly BA
Maître ès Sciences
Devant la commission d'examen composée de :

Mamadou FALL Président UCAD

Meïssa FALL Rapporteur UCAD

Mouhamadoul Bachir DIOUF Examinateur UCAD

Moustapha DIENE Examinateur UCAD

AVANT PROPOS

A travers ce travail, je voudrais rendre un hommage mérité aux personnes qui ont contribué de près ou de loin à l'élaboration de ce mémoire de Diplôme d'Etudes Approfondies.

Monsieur Mamadou FALL, Maître de conférences, pour le suivi et l'encadrement constant qu'il accorde aux étudiants. Il n'a ménagé aucun effort pour nous trouver des stages dans les entreprises. Plus qu'un professeur, il est un père pour moi.

Monsieur Mouhamadoul Bachir DIOUF, Maître de conférences, pour avoir été mon premier maître en géologie et d'avoir participé jusque là à ma formation.

Monsieur Meïssa FALL, Docteur-Ingénieur en Génie civil et minier, pour avoir dirigé l'encadrement scientifique et la rédaction de ce travail. C'est grâce à lui que ce mémoire peut aujourd'hui être présenté. Avec lui, j'apprends peu à peu les théories souvent complexes de la mécanique des sols et de la géotechnique. Je suis heureux de pouvoir lui exprimer ma reconnaissance.

Monsieur Moustapha DIENE, Maître de conférences, d'avoir accepté de participer au jury.

Monsieur Bocar Malick MBOW, Ingénieur à JLS, pour m'avoir initié à la géotechnique routière. Je le remercie pour les nombreuses séances de travail qu'il m'a accordé au cours desquelles, les interprétations ont été progressivement améliorées. Il a mis à notre disposition tous les moyens techniques dont il disposait pour les essais au laboratoire.

Monsieur Pape Sira MBODJ, Ingénieur à JLS, pour son soutien, son encadrement et sa disponibilité. Tout au long des travaux, il a apporté des critiques et suggestions dans la forme et le fond de ce travail. Il a mis à ma disposition toute la bibliographie nécessaire à la conception et le dimensionnement des chaussées.

Monsieur Ndiawar Camara, Chef du laboratoire géotechnique de JLS, pour m'avoir initié aux techniques souvent difficiles du laboratoire. Son expérience, sa disponibilité et ses conseils m'ont été très utiles.

Monsieur CACHOT, Responsable à la SODEVIT de Bandia, pour m'avoir offert gracieusement les granulats calcaires utilisés dans cette étude.

Monsieur Mapathé NDIOUCK, Industriel, pour la fourniture gratuite du silexite 0/31,5 mm. Nous lui remercions profondément.

Nous remercions tout le personnel du laboratoire géotechnique de JLS : Baye Mbodj, Charles, Samsdine, Diatta.

Je remercie tous les membres de ma famille à Khombole et à Thiès ainsi qu'à mes amis Djiby Diagne, Mamadou Diop, Meissa Tine qui ont tenu à faire le déplacement pour assister à la soutenance.

Je remercie tous mes collègues de promotion : Fatou Ndoye, Seydou BA, Awa Ousmane, Ndèye Maguette Dieng, Nafi Racine Sow, Mariama Kaba, Abib Ngom, Détié Sarr, Abdoul Mbodji, Mamadou Traoré.

Sommaire

Introduction Générale 5

1ère Partie : Synthèse bibliographique

Chapitre 1. - Généralités sur les granulats routiers 8

1. - Définitions et présentation générale 8

2. - Nomenclature et Classification 8

3. - Les fuseaux granulométriques 8

4. - Les différentes approches pour l'étude des matériaux non liés 9

5. - Caractéristiques géométriques des granulats routiers 10

6. - Le Compactage des matériaux 11

7. - Dimensionnement des structures de chaussées 12

Chapitre 2. - Rhéologie des matériaux granulaires 17

1. - Interaction entre les grains 17

2. - Ecoulement des grains en cisaillement plan homogène 17

3. - Comportement expérimental des matériaux granulaires 19

Chapitre 3. - Mélange et compacité granulaires 24

1. - Les mélanges granulaires 24

2. - La compacité granulaire 26

2ème Partie : Identification et Caractéristiques des matériaux - Evaluation de leur qualité Chapitre 1. - Provenance des matériaux de l'étude 32

1. Contexte géologique du Bassin sénégalo-mauritanien 32

1.1. - Les formations basaltiques 32

1.2. - Les formations calcaires 33

1.3. - Les silexites 33

Chapitre 2. - Les caractéristiques mécaniques des granulats 36

1. - Essais caractéristiques de la fabrication 36

2. - Les essais caractéristiques des propriétés intrinsèques 40

3. - Essai Proctor - Essai CBR 41

Conclusion générale et discussions 47

Références bibliographiques 49

Table des matières 51

Liste des Tableaux et des Figures 53

Liste des notations et des abréviations

å : déformation

å₁ : déformation axiale

å_V : déformation volumique

í : Coefficient de Poisson õ : compacité

? : angle de frottement interne

.

ã : taux de cisaillement

ì : coefficient de frottement

ãs : poids spécifique

ãh : masse volumique humide

ãd : masse volumique sèche

ó : contrainte

ó₁ : contrainte axiale ou contrainte déviatorique

ó₃ : contrainte de confinement

ô : contrainte de cisaillement A : Coefficient d'aplatissement

c : cohésion

CBR: indice de portance californien (California bearing ratio)

CEBTP : Centre expérimental du Bâtiment et de Travaux Publiques

Cu : coefficient d'uniformité

D : dimension maximale des grains

d : dimension minimale des grains

E : Module de Young

e : indice des vides

Ec : écartement des grilles à fentes parallèles

ES : Equivalent de Sables

f : Pourcentage des particules fines GNT : Graves Non Traitées

GRH : Grave Reconstituée Humidifiée

H : hauteur

I : nombre inertiel

IC : Indice de concassage LA : coefficient Los Angeles

LCPC-SETRA : Laboratoire Central des Ponts et Chaussées

m : masse

MDE : coefficient Micro-Deval

N : Nombre cumulé de poids lourds NE : Nombre Equivalent d'essieux

n : porosité

OPM : Optimum Proctor RC : Rapport de concassage

TCR : Essai Triaxial à Chargements Répétés

V : vitesse

VDN : Voie de Dégagement Nord w : teneur en eau

Résumé

Au Sénégal, il a été observé une augmentation généralisée du niveau du trafic routier et une rareté des matériaux latéritiques de bonne qualité. Ceci limite la disponibilité de ces matériaux qui sont très usités dans la réalisation des assises de chaussées.

Ce mémoire s'inscrit dans le cadre des recherches sur l'utilisation de matériaux de substitution en construction routière. Des études ont été faites au laboratoire de géotechnique de Jean Lefebvre - Sénégal allant dans le sens d'utiliser les granulats concassés de basalte, calcaire et silexite en corps de chaussée.

Le travail consistait à reconstruire un mélange 0/31,5 mm à partir des différentes classes granulaires et d'en déterminer les caractéristiques physiques et mécaniques ainsi que les essais d'identification pour déterminer en laboratoire l'aptitude des tout-venants à être utilisés en corps de chaussée.

Les résultats obtenus en laboratoire permettent d'envisager l'utilisation des granulats concassés de basalte, calcaire et silexite en construction routière. Les indices de portance CBR obtenus pour les différents types de matériaux sont supérieurs à ceux exigés par les spécifications du CEBTP.

Le basalte, de par ses performances satisfait entièrement aux spécifications techniques pour la réalisation des corps de chaussées.

Le silexite peut également être utilisé en couche d'assise. Cependant des améliorations doivent être apportées à l'élaboration de ce matériau quant à sa forme et sa granularité.

L'utilisation du calcaire en couche de base doit être limitée aux trafics inférieurs ou égaux à T3 du fait des faibles résistances à l'usure et au frottement.

Il faut noter également que, attribuer des performances mécaniques à des graves non traitées principalement à partir des mesures de dureté des granulats est cependant réducteur et pas toujours satisfaisant. Ceci met en avant tout l'intérêt de l'essai triaxial à chargements répétés qui permet de caractériser le comportement des matériaux non liés à partir du mélange granulaire oeuvré, plus représentatif de l'état du matériau dans la chaussée, et non plus à partir des seules caractéristiques des ses granulats.

Mots-clés : granulat - tout-venant - basalte - calcaire - silexite - CBR - CEBTP.

Introduction Générale

La conception et le dimensionnement d'une chaussée s'appuient essentiellement sur trois critères :

- la portance de la plate-forme,

- la qualité des matériaux utilisés en couches de chaussée ;

- le niveau du trafic.

Les caractéristiques des matériaux constituants les assises des chaussées doivent répondre à certaines exigences minimales de qualité. En ce qui concerne le corps de la chaussée plusieurs catégories de matériaux peuvent être utilisées. Cependant, les ingénieurs routiers, par souci d'économie, sont contraints de tenir compte des distances de transport et des moyens d'exploitation des gisements. Ceci les a amené à utiliser des matériaux très particuliers ou présentant des qualités inférieures et cela dans toutes les couches du corps de chaussée.

En Afrique tropicale et équatoriale, les formations latéritiques représentent les plus abondantes ressources de matériaux «économiquement» disponibles. Ces matériaux une fois extraits sont livrés directement aux clients sans subir de traitements industriels, ce qui réduit leur coût. Au Sénégal on a toujours compté sur ces formations latéritiques pour réaliser les assises de chaussées. Cependant il est important d'attirer l'attention des concepteurs de chaussées sur un certain nombre de constats effectués :

- le niveau du trafic et le nombre de poids lourds ne cessent de croître (augmentation généralisée du trafic aussi bien du point de vue nombre de cycles que de la charge à l'essieu), ce qui se traduit par une augmentation des exigences de la qualité du matériel,

- Une demande de plus en plus importante en matériaux de construction ;

- La raréfaction des matériaux latéritiques de qualité satisfaisants aux spécifications.

Face à cette situation, les ingénieurs routiers font appel, souvent aux liants hydrauliques comme le ciment pour améliorer ou stabiliser la latérite crue. Cependant il est à noter que ces mélanges posent des problèmes aussi bien dans leur mise en oeuvre (Ndiaye, N.D., 1996) que dans leur comportement mais aussi du fait du coût élevé du ciment.

C'est ainsi que des réflexions sont menées allant dans le sens d'utiliser d'autres types de matériaux pour le corps de chaussée notamment en couche de base où les exigences sont plus sévères. Parmi ces solutions on peut citer :

- l'utilisation du Tout-venant de basalte 0/31,5 en couche de fondation au niveau de Colobane sur l'autoroute à payage Patte d'Oie-Malick Sy, par l'entreprise JLS Sénégal,

- l'utilisation de la Grave-Bitume (GB : Basalte concassé 0/20 stabilisé au liant hydrocarboné) comme couche de base sur l'autoroute Patte d'oie-Malick SY ;

- l'utilisation de la Grave Reconstituée Humidifiée (GRH) de basalte 0/31,5 en couche de base au niveau de la route Patte d'oie-Aéroport et sur la Voie de Dégagement Nord (VDN) ;

- les études effectuées sur les possibilités d'utilisation du concassé calcaire de Bandia ; - les études sur le granulat type silexite.

Ainsi, dans le but de diversifier les solutions techniques à apporter à la réalisation des corps de chaussées, il est présenté, dans ce mémoire, les résultats et analyses relatives sur les possibilités d'utilisation des granulats concassés de basalte, calcaire et silexite en couches d'assise de chaussée.

Ce mémoire comporte deux parties :

La première partie est essentiellement consacrée à l'étude bibliographique. Elle commence par des généralités sur les caractéristiques géométriques principales des granulats routiers et leur influence sur les propriétés mécaniques des matériaux. Une étude est faite sur le compactage et les méthodes de dimensionnement des chaussées. Dans cette partie nous avons mis l'accent sur la rhéologie et le comportement mécanique des matériaux granulaires. Cette partie se termine par une étude sur la compacité et les mélanges granulaires.

La deuxième partie est une étude expérimentale. Elle comporte les résultats des essais d'identifications des caractéristiques physiques et mécaniques des différents types de granulat et la discussion de ces résultats par comparaison avec les spécifications et normes appliquées au Sénégal.

Nous terminerons cette étude par une conclusion générale et des discussions sur les critères de spécification technique pour une meilleure optimisation des caractéristiques géotechniques des granulats concassés.

1ère Partie

Synthèse bibliographique

Chapitre 1. - Généralités sur les granulats routiers

1. - Définitions et présentation générale

La norme française définit le granulat comme un ensemble de grains minéraux, de dimensions comprises entre 0 et 80 mm, destiné notamment à la confection des mortiers et des bétons ainsi qu'à celle des couches de roulement, de base et de fondation des chaussées et aux voies ferrées (Jeuffroy, G. ; Sauterey, R., 1991).

.

Ils sont appelés fillers, sablons, sables, gravillons, graves ou ballasts suivant leurs dimensions. Les granulats peuvent être d'origines diverses :

- Naturelles comme les alluvions ou les formations résiduelles,

- Provenir du concassage des roches massives comme (basalte, calcaire, grès, etc.) ; - Artificiels ou provenant de sous-produits industriels.

2. - Nomenclature et Classification

La norme française définit la classification des granulats d'après les dimensions de leurs grains exprimées en ouvertures de tamis à mailles carrées en millimètres (Jeuffroy, G. ; Sauterey, R., 1991).

Un granulat est dit :

· d/D s'il satisfait aux conditions suivantes :

Refus sur le tamis de maille D et tamisât au tamis de maille d, compris :

- entre 1 et 15 % si D > 1,58d,

- entre 1 et 20 % si D = 1,58d.

Refus nul sur le tamis de maille 1,58D, tamisât au tamis de maille 0,63d < 3 %, d étant = 0,5mm.

· 0/D s'il satisfait aux conditions suivantes :

Refus sur le tamis de maille D compris entre 1 et 15 %,

Refus nul sur le tamis de maille 1,58D.

Il existe six classes granulaires principales caractérisées par les dimensions extrêmes d et D des granulats rencontrés (Dupain ; Lanchon ; Arroman, St., 2004) :

- les fillers 0/D avec D < 2 mm et au moins 70 % de passant à 0,063 mm,

- les sablons 0/D avec D = 1 mm, et moins de 70 % de passant à 0,063 mm ; - les sables 0/D avec 1 < D = 6,3 mm ;

- les graves 0/D avec D > 6,3 mm ;

- les gravillons d/D avec d = 1 mm et D = 125mm ;

- les ballasts d/D avec d = 25 mm et D = 50 mm.

La norme française distingue deux types de Graves Non Traitées (GNT), selon leur mode d'élaboration (Jeuffroy, G. ; Sauterey, R., 1991) :

- GNT type A obtenue en une seule fraction (tout-venant) directement sur une installation de criblage et de concassage, permettant d'obtenir une compacité minimale à l'OPM de 80 %,

- GNT type B obtenue par mélange de deux (ou plusieurs) fractions granulométriques différentes. Elles sont malaxées et humidifiées en centrale, permettant d'obtenir une compacité minimale à l'OPM de 80 % pour la catégorie B1 et 82 % pour la catégorie B2. Ce type de GNT permet d'obtenir une meilleure qualité de mise en oeuvre.

3. - Les fuseaux granulométriques

Bien qu'elles soient appliquées dans ce paragraphe à la granulométrie, elles doivent être
étendues à l'ensemble des propriétés des granulats (Equivalent de sables, etc.). Le fuseau

granulométrique est la zone délimitée par deux courbes granulométriques enveloppes (Jeuffroy, G. ; Sauterey, R., 1991). On distingue :

- Le fuseau de spécification propre à la technique considérée, qui définit la zone dans laquelle doivent se situer les fuseaux de tolérance,

- Le fuseau de fabrication, qui contient 95 % des courbes granulométriques du matériau fabriqué. Un fuseau de fabrication est entièrement inclus dans le fuseau de régularité. Sa définition requière au moins 15 valeurs afin d'être suffisamment représentatif et est établit par le producteur de granulats ;

- le fuseau de régularité, ou de tolérance, qui définit l'étendue de la zone dans laquelle doivent se situer 95 % des courbes obtenues au cours du contrôle.

4. - Les différentes approches pour l'étude des matériaux non liés

En fonction de l'échelle d'observation, il y a différentes approches qui peuvent être adoptées pour la détermination et l'étude des caractéristiques des matériaux de chaussées (Gidel, 2001 ; Habiballah, 2005).

4.1. - L'approche microscopique

L'observation pour cette approche se fait à l'échelle des granulats. On observe les caractéristiques géométriques et mécaniques des grains.

Les observations à relever à l'échelle granulaire afin de déterminer les caractéristiques de la grave non traitée sont les suivantes :

- Les caractéristiques liées à la géométrie globale des grains : la granularité, la taille des grains et leur forme, l'angularité et la rugosité.

- Les caractéristiques mécaniques des grains sont évaluées selon leurs duretés et leurs résistances. La dureté des granulats est un facteur à prendre en compte dans la classification des matériaux non liés des chaussées souples. En absence de liant, les granulats sont amenés à supporter plus d'efforts d'attrition et de fragmentation. La résistance à ce genre d'agression repose sur la nature minéralogique des granulats. Cette résistance est mesurée par l'essai Los Angles (LA) et par l'essai Micro-Deval (MDE).

4.2. - L'approche macroscopique

L'échelle de l'observation est celle d'un échantillon homogène dont les dimensions sont suffisamment supérieures au diamètre maximal des grains afin de pouvoir assimiler l'échantillon à un milieu continu. Grâce à cette approche, il est facile de simuler des sollicitations et de relever les réponses de l'échantillon. Cette approche est l'une des bases des méthodes de dimensionnement rationnel des chaussées. Parmi les essais utilisés, il y a l'essai CBR (Californian Bearing Ratio) et l'essai triaxial à chargements répétés (TCR).

4.3. - L'approche globale

Pour cette approche, l'observation des phénomènes se fait à l'échelle des couches. Elle permet l'étude du comportement de l'ensemble d'une structure de chaussée en prenant en compte les conditions in situ non réalisables dans les deux premières approches. Dans le cas des chaussées souples, l'approche globale de l'étude du comportement mécanique des matériaux à l'échelle des couches est basée sur la mesure de la déformation verticale en surface de la chaussée. La méthode réglementaire consiste en une évaluation globale de l'état de la structure et du sol support à partir de la comparaison de la déflexion mesurée avec des seuils prédéfinis (exemple de la structuration du code de calcul Alizé 3). L'approche globale s'appuie sur des essais réalisés sur l'ensemble chaussée-sol support, notamment l'essai de

plaque statique et cyclique, la dynaplaque, le manège de fatigue et les chaussées instrumentées.

5. - Caractéristiques géométriques des granulats routiers

Les matériaux constituant les différentes couches d'une chaussée peuvent être des matériaux concassés ou roulés. Cependant, afin de disposer d'un angle de frottement le plus fort possible, il est nécessaire d'exiger un indice de concassage d'autant plus élevé que le trafic est plus important et la charge légale à l'essieu plus lourde.

Les caractéristiques géométriques principales des granulats routiers sont : l'état de surface, l'angularité, la forme et la granularité (Tourenq ; Denis, 1982 in Gaye, 1995).

5.1. - Etat de surface des granulats

Dans le cas des roches polycristallines (Ø > 1 mm), la rugosité dépend de la structure de la roche. Si le grain est monominéral (Ø < 1 mm), la surface est généralement lisse.

Pour les roches polycristallines, la rugosité dépend de la dimension « d » des cristaux. Plus une roche a un « grain fin », plus sa cassure est lisse. Par contre, les roches à « gros grain » ont toujours des surfaces rugueuses.

L'état de surface des grains joue un rôle au niveau de la maniabilité des matériaux, de la stabilité des assises non traitées et de la microrugosité des couches de surface. Cependant, l'action du trafic tend à polir la surface des grains, mais il est admis qu'une bonne microrugosité assure généralement une bonne adhérence à faible vitesse.

5.2. - Angularité des granulats

Elle joue un rôle important pour les gravillons de la couche de roulement, en améliorant l'adhérence, et pour ceux des assises de chaussées, dont elle améliore la stabilité.

Pour un granulat concassé de roche massive, elle est égale à 100 %.

Pour un granulat d'origine alluvionnaire, elle est définie par deux données :

- l'indice de concassage IC, proportion en poids d'éléments supérieurs à la dimension D du granulat élaboré,

- le rapport de concassage RC, rapport entre d du matériau soumis au concassage et D du granulat obtenu.

Pour les assises de chaussées non traitées, l'angularité favorise les propriétés mécaniques en augmentant l'angle de frottement interne : celui-ci augmente d'environ 12° dans un essai triaxial quand on passe des billes de verre entièrement roulées aux billes de verre concassées. Pour les couches de roulement, ce facteur favorise l'adhérence pneumatique, la rupture du film d'eau et le drainage.

La maniabilité et la compactibilité sont également liées à l'angularité : le déplacement relatif des grains et leur mise en place sont facilités lorsqu'ils sont arrondis.

5.3. - La forme des granulats

Elle joue un rôle important à la fois pour les granulats de la couche de roulement, des gravillons plats ayant tendance à se coucher au moment du compactage, et pour les matériaux d'assise, des granulats plats ou allongés réduisant la compacité et la stabilité.

Elle a aussi une grande influence sur les caractéristiques mécaniques des matériaux (Los Angeles, Micro-Deval, fragmentation dynamique).

10

Tableau 1. - Formes des granulats.

5.4. - La granularité des granulats

Elle caractérise la répartition du granulat en tranches dimensionnelles. La granularité a une importance primordiale car elle permet d'obtenir une compacité maximale et d'éviter la ségrégation au moment de la mise en oeuvre.

La granularité que l'on peut maîtriser et optimiser pour tous les matériaux, apparaît comme le recours le plus général pour corriger les autres caractéristiques géométriques des granulats et dans une certaine mesure une résistance mécanique déficiente.

6. - Le Compactage des matériaux

6.1. - Définition

Compacter un matériau, c'est réduire le volume des vides de ce matériau et organiser la structure des grains de manière à obtenir un assemblage plus stable. Cette opération qui s'appelle le compactage peut être obtenue par des sollicitations statiques (compactage statique), dynamiques (compactage dynamique), ou par vibrations (compactage in situ) (Kabre, 1991 in Gaye, 1995).

6.2. - Rôle du compactage sur la durée de vie des ouvrages

Le compactage met le matériau dans un état suffisamment serré de telle sorte qu'un tassement ultérieur soit impossible ou peu important. Les mouvements relatifs sont réduits ou supprimés, diminuant ainsi l'attrition. En réduisant le volume des vides, le compactage augmente la densité apparente sèche et diminue la perméabilité qui est fonction de l'indice des vides.

Le compactage entraîne une élévation des caractéristiques mécaniques. En effet, le resserrement des grains augmente le nombre de contacts entre eux et par conséquent leur frottement. L'angle de frottement interne et la cohésion en sont accrus. Il y a également augmentation considérable du module de déformation.

6.3. - Les paramètres influents du compactage

o La teneur en eau

L'influence de la teneur en eau et de l'énergie de compactage sur la densité sèche du matériau a été mise en évidence en 1933 par l'ingénieur américain Proctor (Tchouani Nana, J.M. ; Callaud, M., 2004).

En effet pour une énergie de compactage donnée, si l'on fait varier la teneur en eau w et l'on

représente graphiquement la variation du poids volumique sec ãd en fonction de cette teneur en eau, on obtient une courbe en cloche qui présente un maximum appelé Optimum Proctor séparant de gauche à droite la branche sèche et la branche humide.

Lorsque la teneur en eau est raisonnable, l'eau joue un rôle de lubrifiant et la densité sèche
augmente avec la teneur en eau jusqu'à un maximum (branche sèche). Par contre lorsque la

teneur en eau est élevée (branche humide), l'eau absorbe une partie importante de l'énergie de compactage. Elle occupe la place des grains solides et aucun tassement n'est possible.

o La nature du matériau

Le comportement et les sollicitations développés par les matériaux sont plus ou moins fonction de leur nature. De façon générale, la courbe Proctor est très aplatie pour les sables et par contre présente un maximum très marqué pour les argiles plastiques (Tchouani Nana, J.M. ; Callaud, M., 2004).

Pour les matériaux à courbe Proctor aplatie, le compactage est peu influencé par la teneur en eau. Ces matériaux sont peu sensibles à l'eau mais il est souvent difficile d'améliorer leurs caractéristiques (énergie de compactage à fournir plus importante).

o L'énergie de compactage

Pour un matériau donné, si l'énergie de compactage augmente, le poids volumique maximum augmente et les courbes deviennent plus pointues.

Khaye ; Machet ; Morel (1979) in Gaye (1995) montrent que la densité sèche après compactage augmente avec la charge de la roue et la pression de gonflage.

Martinez (1980) in Gaye (1995) remarque que la réponse des matériaux granulaires aux sollicitations cycliques qui n'atteignent pas les charges de rupture peut être de trois types :

- Adaptation : l'énergie dissipée et la déformation permanente sont nulles. La réponse

du matériau est réversible et élastique,

- Accommodation : les déformations permanentes sont stabilisées et l'énergie dissipée

n'est pas nulle (phénomène d'hystérésis). La réponse réversible est non linéaire ;

- Rochet : l'énergie dissipée et les déformations permanentes augmentent avec la

sollicitation jusqu'à la stabilisation ou la rupture (déformation plastique).

o L'angularité, la forme, la granularité et le pourcentage des fines

Des matériaux très anguleux se mettent difficilement en place entraînant l'augmentation de l'énergie de compactage.

Arquie ; Morel (1988) in Gaye (1995) montrent qu'un matériau ayant une bonne granularité aura une densité maximale plus élevée qu'un matériau creux ou ayant un excès de sable. Kabre (1991) in Gaye (1995) indique que la compacité augmente avec le coefficient

d'uniformité

C_U = D 60

.

D10

D60 ^et D₁₀ sont les diamètres des tamis qui laissent passer respectivement 60 % et 10 % du

matériau.

Machet et Morel (1980) in Gaye (1995) trouvent que pour une énergie de compactage donnée, l'indice des vides décroît avec le pourcentage d'éléments fins (< 80um).

o Le sol-support

Pour une même épaisseur de matériau, un support plus rigide conduit à des densités plus élevées. Les sollicitations développées par un rouleau vibrant sont considérablement influencées par les caractéristiques du sol-support.

7. - Dimensionnement des structures de chaussées

Le sol ne peut seul supporter un trafic routier sans subir d'importantes déformations. C'est pourquoi il est surmonté d'un corps de chaussée dont le rôle principal est la répartition latérale des contraintes dues à des charges roulantes en surface afin de les amener à des niveaux compatibles avec les caractéristiques mécaniques du sol naturel.

12

La structure de la chaussée est constituée du bas vers le haut de la Plate-forme (éventuellement surmontée d'une couche de forme), de l'assise et de la couche de surface.

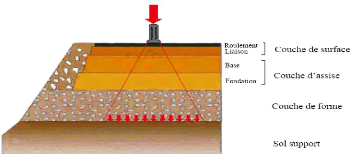
Fig. 1. - Structure de chaussée type et répartition des contraintes (LCPC-SETRA, 1994)

La plate-forme constitue le support sur lequel repose la chaussée. Elle est constituée du sol support (déblai ou remblai) désigné dans sa zone supérieure (sur 1m d'épaisseur environ), par le terme Partie Supérieure des Terrassements (PST), et dont la surface constitue l'arase de terrassement ; et d'une couche de forme éventuelle (LCPC-SETRA, 1992).

L'assise est généralement constituée de deux couches, la couche de fondation surmontée de la couche de base. Ces couches apportent à la chaussée la résistance mécanique aux charges verticales induites par le trafic. Elles répartissent les pressions sur la plate-forme afin de maintenir les déformations à ce niveau dans des limites admissibles.

Eventuellement on peut trouver, entre la plate-forme et la fondation une sous-couche.

La couche de surface est la couche supérieure de la chaussée. Elle est constituée de la couche de roulement sur laquelle s'exercent directement les agressions conjuguées du trafic et du climat, et le cas échéant, d'une couche de liaison, intermédiaire entre les couches d'assise et la couche de roulement qui permet d'assurer une bonne adhérence entre la couche de base et la couche de roulement.

7.1. - Les modèles empiriques et semi empiriques de dimensionnement

Ces modèles sont fondés sur une observation expérimentale des chaussées et de leur comportement sous trafic. Il existe plusieurs méthodes empiriques et semi empiriques parmi lesquelles nous avons l'habitude de citer la méthode du CBR et celle du CEBTP.

7.1.1. - La méthode du CBR

Elle est basée d'une part sur la résistance au poinçonnement du sol de fondation, résistance appréciée par un essai normalisé, l'essai CBR, et d'autre part sur la théorie de Boussinesq donnant la répartition en profondeur des pressions verticales (Fall, M., 1993).

On considère un massif homogène, isotrope et élastique limité par un plan horizontal et de dimension infinie. Si l'on applique à la partie supérieure du massif une charge verticale P répartie uniformément sur un cercle de rayon R, il en résulte sur un plan horizontal situé à une profondeur z, une pression verticale ó_z.

A la profondeur z = e correspondant par exemple à l'épaisseur de la chaussée, la pression ó_e qui s'exerce sur le sol de fondation doit être inférieure à la résistance au poinçonnement I de ce sol.

ó_e = KI (K coefficient de sécurité tenant compte du caractère empirique de l'essai).

Ceci a permis d'établir des abaques donnant, en fonction du CBR, l'épaisseur nécessaire du corps de chaussée.

13

7.1.2. - La méthode proposée par le CEBTP pour les pays tropicaux

Cette méthode s'appuie sur les principes de bases suivants :

- Dans le cas des chaussées souples, l'indice portant de la plate-forme et l'intensité du trafic (Tableau 2) déterminent l'épaisseur totale de la chaussée (BCEOM-CEBTP, 1975),

- Dans le cas des chaussées à assise traitée donc susceptibles d'une rupture en traction, le dimensionnement précédant doit être complété par une analyse théorique pour s'assurer que les contraintes de traction à la base des couches rigidifiées sont compatibles avec les performances des matériaux (BCEOM-CEBTP, 1975).

Essieu équivalent de 13 tonnes		Classes de Plate-forme d'après le CEBTP		T1 < 5.10^5 5.10^5 < T2 < 1,5.10^6 1,5.10^6 < T3 < 4.10^6 4.10^6 < T4 < 10^7 10^7 < T5 < 2.10^7
5 > CBR 5 < CBR < 10 10 < CBR < 15 15 < CBR < 30 CBR > 30		S1 S2 S3 S4 S5

Tableau 2. - Classes de trafic équivalent et de plate-forme (BCOEM-CEBTP, 1984)

Les spécifications du BCEOM-CEBTP (1984) pour couches de base des chaussées construites en concassés 0/D sont les suivant :

· Indice portant CBR à 95 % de l'OPM et après 4 jours d'imbibition supérieur à 80,

· La courbe granulométrique du mélange doit être à l'intérieur du fuseau 0/31,5 mm;

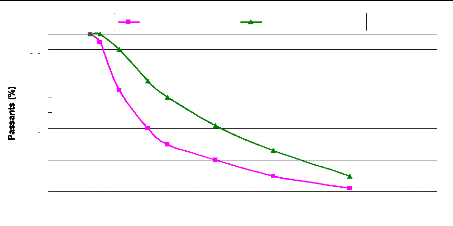
100

40

90

80

60

50

30

20

70

10

0

100

10

Branche inf fuseau Branche sup fuseau

Diamètre (mm)

1

0,1

0,01

Fig. 2. - fuseau 0/31,5 mm - Concassés 0/d (BCEOM-CEBTP, 1984)

· Pourcentage de fines compris entre 2 et 10 % ;

14

· Equivalent de sables (ES) :

ES supérieur ou égal à 30 pour les trafics T1 - T2,
ES supérieur ou égal à 40 pour les trafics T3 - T4.

· Porosité : n =100 × (1+ max ) < 15 %

ã ;

d

ã_s

ãdmax = Masse volumique sèche maximale de l'essai Proctor modifié ã_s = Masse volumique réelle des grains solides

· Les résistances exigées pour les granulats constitutifs de la couche de base sont : - Los Angeles inférieur ou égal à 45 (T1 - T3) ou à 30 (T4 - T5),

- Micro-Deval inférieur ou égal à 15 (T1 - T3) ou à 12 (T4 - T5).

7.2. - Les méthodes rationnelles de dimensionnement

Ces méthodes sont basées sur les comportements élastiques et viscoélastiques des matériaux et donnent, en fonction de la géométrie du pneumatique, de l'épaisseur et des rapports de modules des différentes couches de la chaussée, la valeur des contraintes soit de compression, soit de traction aux différentes interfaces.

Les contraintes adm

ó_z au niveau de chaque couche sont calculées en fonction de l'indice CBR

du matériau et le nombre N de poids lourd circulant sur la chaussée.

0 , 3 ó = en bars adm CBR × ^z 1 0 , 7 log + N

[1]

Selon le nombre équivalent NE d'essieu de référence (130 kN), la valeur seuil de la

déformation élastique adm

å_z au sommet du sol-support est calculée par la formule suivante :

å_z en mm [2]

adm ( ) - 0 , 222

= A × NE

A = contrainte pour laquelle la rupture en flexion sur éprouvette de 360 jours, est obtenue
pour 10⁶ chargements.

A = 0,016 pour les trafics T < T3

A = 0,012 pour les trafics T = T3

Ces valeurs sont comparées avec celles obtenues en laboratoire soit sur la résistance à la compression, soit sur la résistance à la traction des matériaux constituant la chaussée.

La grave non traitée est classée en trois catégories en fonction de la classe de trafic, de la propreté des granulats, de leur dureté, de leur indice de concassage et de leur teneur en fines (Tableau 3). A chaque catégorie est attribué un module de Young variant entre 200 et 600 MPa. Le coefficient de Poisson est pris égal à 0,35 à défaut d'informations spécifiques.

15

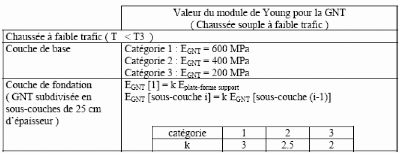
Tableau 3. - Valeurs du module de Young (E) pour la grave non traitée selon le guide
technique de conception et de dimensionnement des structures de chaussée (LCPC-SETRA,
1994)

La déformation verticale å au sommet du sol est aussi déterminée à partir du code de calcul Alizé 3. Cette valeur est comparée avec la déformation verticale admissible.

Il faut que adm

å < å_z sinon il y a orniérage.

16

Chapitre 2. - Rhéologie des matériaux granulaires

1. - Interaction entre les grains

Le contact de Hertz

Le contact non cohésif entre deux grains se compose généralement d'une répulsion élastique normale N et d'une résistance au glissement tangentielle T (fig. 3. (b)).

Le modèle de Hertz décrit le contact normal entre deux grains purement élastiques, qui se déforment donc lorsqu'ils sont soumis à une force (Chevoir, F., 2005 ; Ovarlez, G., 2002 ; Roux et al, 2007). Dans le cas d'un contact entre deux sphères, le calcul réalisé par Hertz en 1880 relie la force de répulsion élastique normale au contact N à la déflexion élastique h.

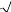
E a ³ / ²

[3]

3(1 í

a = Diamètre des grains

E = Module de Young (rapport entre la contrainte normale et la déformation récupérée) í = Coefficient de Poisson (rapport entre la déformation radiale et la déformation axiale)

Le coefficient de frottement

Il y a dissipation plastique dès que la contrainte tangentielle T est non nulle, ce qui conduit à des déformations plastiques (Rognon, 2006). Ces déformations plastiques restent limitées sur l'aire annulaire de contact tant que T est inférieur au produit de l'effort normal aux billes N et du coefficient de frottement tan?.

Quand T = Ntan? cette aire de glissement s'étend à toute la surface de contact et un

déplacement apparaît entre les deux billes.

Cette description appelée loi de Coulomb permet de décrire les phénomènes de déplacement et d'écoulement granulaires.

Le coefficient de frottement tan? est lié à l'état de surface des matériaux qui n'est jamais parfaitement lisse : une rugosité existe à l'échelle microscopique. Cette rugosité est à l'origine du frottement entre les grains. Son effet est de favoriser une déformation plastique des grains.

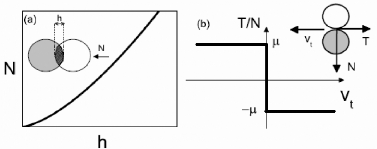
Fig. 3. - Loi de contact sans cohésion : (a) contact de hertz décrivant la répulsion normale N
et (b) critère de Coulomb simplifié décrivant le glissement tangentiel (Rognon, 2006).

2. - Ecoulement des grains en cisaillement plan homogène

Le cisaillement plan homogène est la géométrie d'écoulement la plus simple pour décrire les
caractéristiques du comportement rhéologique des grains non cohésifs (Rognon, 2006). Elle

17

consiste à générer un écoulement entre deux parois parallèles en exerçant une pression P, ceci
en l'absence de gravité (fig. 4). Les résultats sont obtenus par simulation numérique en

. V

imposant le taux de cisaillement H

ã et en mesurant la contrainte de cisaillementô .

=

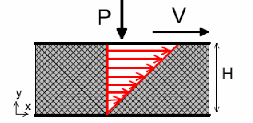
Fig. 4. - Géométrie d'écoulement et forme du profil de vitesse en cisaillement plan homogène
(Rognon, 2006)

2.1. - Les régimes d'écoulement

Les simulations numériques menées par Cruz (cité par Rognon, 2006) ont montré que le régime d'écoulement des grains rigides de masse m est contrôlé par un nombre sans dimension appelé nombre inertiel I.

L'expression de I dans un système à deux dimensions est :

I

=

. ã

m P

[4]

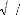
Ce nombre représente le rapport entre deux temps : le temps inertiel m P et le temps lié au

.

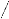
cisaillement 1 ã .

Les faibles valeurs de I (I = 1 0^-3) correspondent à un « régime quasi-statique » où l'inertie des grains est négligeable. Le matériau a un comportement de type solide plastique.

Les grandes valeurs de I (I = 0,3) correspondent à un « régime collisionnel » où les grains interagissent par collision binaire.

Entre ces deux régimes (10^-2 = I = 0,3) existe un régime d'écoulement appelé « régime dense » où l'inertie des grains n'est pas négligeable. Le réseau de contact percole à travers la cellule.

2.2. - Les lois de comportement

2.2.1. - Loi de frottement de Coulomb (u*)

Si la pression et le taux de cisaillement sont imposés, il suffit de mesurer la contrainte de
cisaillement. La loi de comportement des grains secs et sans cohésion peut s'écrire sous la
forme d'une relation entre deux nombres sans dimension : le nombre inertiel I et le coefficient

de frottement effectif u, rapport des contraintes tangentielle et normale ì = ô P (fig. 5. (a)).

ì*=tan?+bI [5]

Cette relation est appelée « loi de frottement ».

L'angle de friction ? et la pente b > 0 sont propres à la nature des grains en écoulement

18

2.2.2. - Loi de dilatance

Un paramètre fondamental dans les écoulements granulaires est la fraction solide v (ou compacité) qui est le rapport entre la surface occupée par les grains et la surface totale. Elle dépend de l'état de cisaillement des grains (fig. 5. (b)).

v = v_max - aI [6]

Cette relation est appelée « loi de dilatance ».

La compacité maximale v_max et la pente a > 0 sont propres à la nature des grains en

écoulement.

Un empilement de grains initialement lâche se contracte tandis qu'un empilement initialement dense se dilate (désenchevêtrements).

Cependant, pour cisailler un matériau, il est nécessaire que les grains passent les uns au dessus des autres (fig. 5. (c)). Lorsque le nombre inertiel augmente, par augmentation du taux de cisaillement ou par diminution de la pression, les désenchevêtrements sont respectivement plus fréquents ou plus faciles, ce qui conduit à l'expansion du matériau. Par ailleurs, le

?

passage d'un grain par dessus un autre s'accompagne d'une force N qui tend à s'opposer au mouvement (fig. 5. (c)) et qui est à l'origine de l'augmentation du frottement avec le nombre inertiel.

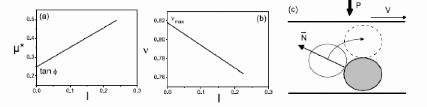
Fig. 5. - Comportement rhéologique de grains sans cohésion : (a) loi de frottement, (b) loi de
dilatance, (c) origine du frottement et de la dilatance (Rognon, 2006).

3. - Comportement expérimental des matériaux granulaires 3.1. - Notion de résistance au cisaillement

3.1.1. - Définition

Lorsqu'un système de forces est appliqué à un volume déterminé d'un sol, il se développe en général des contraintes de cisaillement entraînant des déformations du sol. La résistance au cisaillement d'un sol est définie comme étant la contrainte de cisaillement dans le plan de rupture, au moment de celle-ci.

En effet, si on porte sur un graphique l'évolution de la contrainte de cisaillement Z en
fonction de la déformation s dans le plan de cette contrainte de cisaillement, on obtient le
graphique indiqué par la figure 6. La résistance au cisaillement est définie, sur ce graphique

comme étant le maximum de la contrainte de cisaillement Zmax .

19

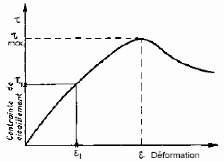
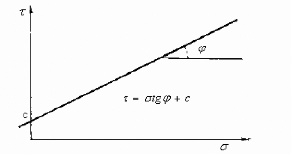
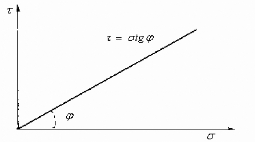
Fig. 6. - Courbe contrainte-déformation
Ainsi, pour chaque système de forces(ó,ô), on peut tracer à la rupture un cercle de Mohr.

L'enveloppe des cercles de Mohr à la rupture est appelée « courbe intrinsèque » (fig. 7.). Coulomb a montré que la courbe intrinsèque des sols était une droite d'équation :

ô=ó tg?+c [7]

- c a les dimensions d'une contrainte et caractérise la « cohésion », - ? est appelé « angle de frottement interne ».

Fig. 7. - Courbe intrinsèque d'un sol fin

3.1.2. - Résistance au cisaillement des sols pulvérulents

Les sols pulvérulents sont des sols sans cohésion (c = 0). La théorie de Coulomb montre que la courbe intrinsèque d'un tel type de sol est une droite passant par l'origine (fig. 8.):

ô=ó tg?

20

Fig. 8. - Courbe intrinsèque d'un sol pulvérulent

La résistance au cisaillement d'un sol pulvérulent est déterminée par la valeur de son angle de frottement interne, qui dépend principalement de la compacité du sol, de la forme et de l'état de surface des grains solides.

3.1.3. - Courbes contrainte-déformation d'un matériau pulvérulent

Lorsqu'on effectue un essai de cisaillement direct sur un matériau pulvérulent très compact on obtient (fig. 9.) la courbe (1) présentant un maximum prononcé au-delà duquel elle décroît de plus en plus lentement. Dans ce cas l'indice des vides est faible car les grains sont enchevêtrés. Le maximum de la courbe correspond à l'effort de cisaillement qu'il faut appliquer pour provoquer le désenchevêtrement des grains dans le plan de rupture.

Pour un sable lâche on obtient une courbe (2) ne présentant pas de maximum. Elle croît de plus en plus lentement pour tendre vers la courbe (1) dans le domaine des grandes déformations. Dans ce cas le serrage des grains est lâche et au cours de l'essai le volume initial de l'échantillon diminue.

Pour une valeur intermédiaire de l'indice des vides appelée « indice des vides critique », l'essai se fait à volume pratiquement constant. On obtient la courbe (3).

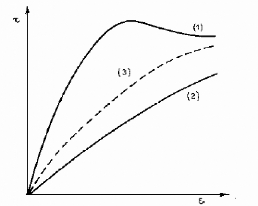
Fig. 9. - Courbe contrainte-déformation d'un sol pulvérulent
21

3.2. - Evaluation du comportement mécanique des graves non traitées avec le triaxial à chargement répété

Pour illustrer le comportement expérimental des matériaux granulaires, on présentera les
résultats d'essais triaxiaux réalisés par Bouvard et Stutz, (1982) in Habiballah (2005) sur le
sable d'Hostun. Le chargement est réalisé en exerçant simultanément une contrainte de

confinement ó₃ et une contrainte axiale ó₁ (donc une charge verticale q appelée déviateur
des contraintes). Les déformations axiale å₁ et volumique å_V sont mesurées. Les résultats de

ces essais, typiques pour les matériaux granulaires sont illustrés par la figure 10 (Gidel, 2001 ; Habiballah, 2005).

Les courbes de variation du déviateur des contraintes en fonction de la déformation axiale
q(å₁) finissent par un palier qui représente la plasticité parfaite. On observe également une augmentation du déviateur de rupture avec la contrainte de confinement.

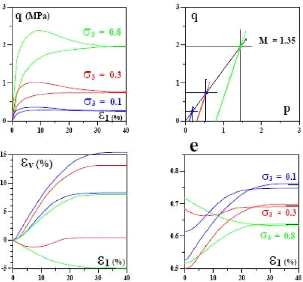
Fig. 10. - Essais triaxiaux sur le sable d'Hostun [Bouvard (1982)] in Habiballah (2005).
Dans le plan (p, q), les paliers de la plasticité parfaite se trouvent sur une droite passant par

l'origine et de pente M qui correspond à l'angle de frottement ?_PP de plasticité parfaite, dans le plan de Mohr.

q=ó₁-ó₃ p=

3

ó

1 + 2ó₃

Les courbes de la variation volumique e(å₁) et å _V (å₁) commencent toujours par une
contractance volumique jusqu'à une déformation de å₁ = 10^-2 % environ. Cette phase de

22

au pic la courbe q(å₁) d'après la loi de Rowe (fig. 11). Cette pente diminue jusqu'à 0
correspondant à l'indice des vides critique ou à l'état de plasticité parfaite. Dans cette phase, le matériau se déforme sans variation de volume.

d V ou par l'angle de dilatanceø .

å

d å 1

La dilatance est donc caractérisée par tanâ =

Tant que l'état des contraintes reste en dessous de la droite dans le plan (p, q), le matériau aura un comportement contractant. Au-delà de cette droite, la compacité augmente et le matériau se dilate.

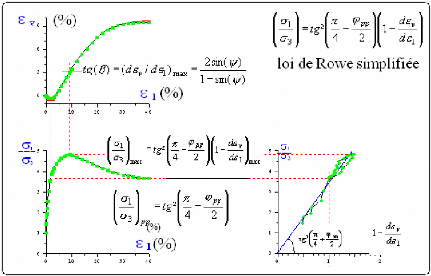
Fig. 11. - Visualisation de la dilatance dans le plan de Rowe (ó 1/ó 3 ; 1-då _v/då ₁) in
Habiballah (2005)

3.3. - Conclusion

L'étude du comportement des matériaux granulaires se fait en dissociant le comportement réversible (ou élastique) du comportement irréversible (ou anélastique).

Le comportement d'un matériau granulaire est considéré comme élastique linéaire pour des niveaux de déformations faibles et plastique si les déformations plastiques sont importantes. De ce fait le comportement est plutôt élastoplastique.

Certains auteurs pensent que les matériaux granulaires n'ont pas de domaine d'élasticité initial et que ce domaine est créé seulement par écrouissage.

Dans un essai triaxial, les déformations permanentes augmentent rapidement dès les premiers chargements. Elles se stabilisent par la suite et le comportement devient pratiquement élastique. Cependant, si les sollicitations sont trop élevées, les déformations permanentes augmentent continuellement jusqu'à la rupture éventuelle du matériau.

23

Chapitre 3. - Mélange et Compacité granulaires

1. - Les mélanges granulaires

Pratiquement, il n'est pas toujours facile de trouver un matériau granulaire naturel ou manufacturé satisfaisant et on est souvent amené à recomposer un granulat à partir de n autres.

1.1. - Les mélanges binaires

1ère méthode : Soit deux granulats (A et B), de masses respectives MT[A] etMT[B], que l'on

désire mélanger dans des proportions respectives _XA% ^et _XB% afin d'obtenir un granulat C (Gabrysiak, 2007). Le refus cumulé du mélange exprimé en % au tamis d'ouverture Di considéré est :

MT[ C ] = XA%MT[A] + XB%MT[B] R%[C]Di = X _A% R % [ A ] Di+ X B % R % [ B]Di

MT[C] = Masse totale du mélange A + B,

R%[A]Di = Refus cumulé exprimé en % de l'échantillon A au tamis d'ouverture Di ; R%[B]Di = Refus cumulé exprimé en % de l'échantillon B au tamis d'ouverture Di ; R%[C]Di = Refus cumulé exprimé en % de A + B au tamis d'ouverture Di.

2ème méthode (méthode graphique) : Sur les axes verticaux, on reporte les passants des granulats A et B pour chaque tamis (Gabrysiak, 2007). Puis on joint les points par une ligne appelée ligne de combinaison. Pour une proportion donnée de A dans le mélange (ligne verticale de mélange), on détermine le point de passage du mélange en % de passants (fig. 12).

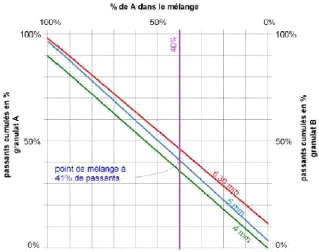
Fig. 12. - Les mélanges granulaires binaires : méthode graphique (Gabrysiak, 2007)
24

3ème méthode (méthode graphique appliquée aux fuseaux) : La méthode graphique est très pratique pour trouver les proportions d'un mélange situé dans un fuseau donné (Gabrysiak, 2007). Il suffit de reporter sur chacune des lignes de combinaison le maximum et le minimum (définit par le fuseau) pour chaque tamis et de joindre ces maxima et ces minima par des lignes brisées. Si ces deux lignes se croisent, il est impossible d'obtenir un mélange entrant parfaitement dans le fuseau. Si elles ne se croisent pas, le domaine situé entre les deux lignes verticales tracées à partir des points les « plus à l'intérieur » des deux lignes brisées définit la phase des combinaisons possibles qui satisfont aux exigences du fuseau (fig. 13).

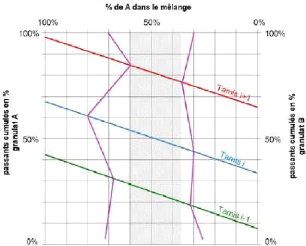
Fig. 13. - Les mélanges granulaires binaires : méthode appliquée aux fuseaux
granulométriques (Gabrysiak, 2007)

1.2. - Les mélanges ternaires

Dans un triangle quelconque ABC, tout point P situé à l'intérieur du triangle représente un mélange des trois composantes de base représentées graphiquement par les trois sommets du triangle dans les proportions XA, XB et XC (fig. 14).

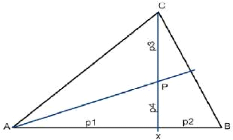
Fig. 14. - Détermination des proportions d'un mélange ternaire de granulats à partir d'un
triangle (Gabrysiak, 2007)

25

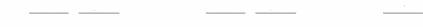
4

1

2

3

3

p

p

p

p

3 4

+ p

3 4

+ p

^{1 2}

p p

+p

^{1 2}

p p

+p

p

X C +

=

p p

3 4

X A = ×

X B = ×

X_A + X_B + X _C =1

De façon pratique, pour mélanger trois granulats on commence par se fixer les limites granulaires (gros, moyen, fin). On divise ensuite chacun des trois granulats utilisés en trois fractions qui détermineront les coordonnées de trois points représentatifs des trois granulats dans le diagramme triangulaire. On joint ces trois points qui forment un triangle (fig. 15).

On caractérise ensuite le fuseau imposé par un point représentatif P sur le même diagramme. Si le point P est à l'extérieur du triangle quelconque formé par les trois points représentatifs des granulats, il est impossible de combiner afin d'obtenir un mélange exactement conforme aux exigences.

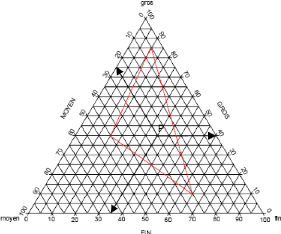
Fig. 15. - Les mélanges granulaires ternaires : méthode du diagramme triangulaire
(Gabrysiak, 2007)

2. - La compacité granulaire

2.1. - Mélange de deux granulats secs

Soit un mélange d'un granulat fin S et d'un granulat grossier G.

V

Le mélange est caractérisé par la proportion = [8]

SG

p

V V

+

SG SS

- Vss : volume absolu du granulat fin,

- VSG : volume absolu du granulat grossier.

Lorsqu'un récipient de volume VT est remplit d'un granulat, une partie de ce volume seulement est occupée par des grains solides (VS). L'autre partie reste vides (VV).

V

On désigne par indice des vides le rapport : e = [9]

V

V S 26

V_V

^m V V

+

SG SS

Ainsi l'indice des vides du mélange granulaire est :

e =

[10]

Chacun des granulats a son propre indice des vides : - e_S = indice des vides du granulat fin,

- e_G = indice des vides du granulat grossier.

Variation de l'indice des vides du mélange e_m en fonction de la proportion p - pour p = 0 (granulat fin seul), e_m = e S

- pour p = 1 (gros granulat seul), e_m = e_G

Pour simplifier le raisonnement, on suppose que V _SS + V_SG =1 (Unité) [11]

De ce fait on a :p=V_SG V _SS =(1-p) e_m =V_V

Si on démarre le mélange avec le granulat fin auquel on ajoute quelques grains du granulat grossier, les vides du mélange ne sont que les interstices entre les grains fins (fig. 16):

e _m =e _S ×V _SS =e _S ×(1-p) [12]

Si on part du gros granulat en ajoutant quelques grains du granulat fin, ces grains fins vont se loger dans les interstices laissés par les gros grains. Ainsi, le volume des vides du mélange est égal au volume des vides du gros granulat diminué du volume absolu du granulat fin (fig. 16) :

e e V V e p p p e

= × - = × - (1 - ) = × ( + 1) - 1 [13]

m G SG SS G G

[12] et [13] sont deux expressions différentes de variation de l'indice des vides suivant l'ordre dans lequel on mélange les deux types de granulat (Fig. 16.). Ainsi les deux hypothèses ne peuvent être vérifiées simultanément par un même mélange. Donc on ne peut pas conserver à la fois la structure du granulat fin et celle du granulat grossier. En réalité, il y a interaction entre ces deux structures définie par : l'effet de paroi et l'effet d'interférence (Gabrysiak, 2007).

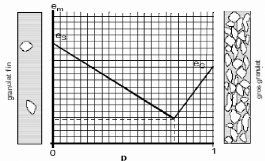
Fig. 16. - Evolution théorique de l'indice des vides d'un mélange granulaire (Gabrysiak,
2007)

27

2.2. - L'effet de paroi

Lorsqu'on détermine expérimentalement l'indice des vides du mélange de quelques grains du granulat grossier avec le granulat fin, on constate que cet indice est supérieur à ce que donnerait l'équation [12] (Fig. 20.). On a :

e_m=e_S×(1-p)+e_D×p [14]

A. Caquot (1937) in Gabrysiak (2007) interprète ce phénomène comme étant l'effet des parois des grains du gros granulat sur l'arrangement des grains du granulat fin.

En effet, dans toute section parallèle à la paroi, on peut définir un indice des vides local qui est le rapport entre l'aire des sections traversant des vides et l'aire des sections traversant des pleins. On observe que lorsqu'on se rapproche de la paroi, l'indice des vides local augmente et tend vers l'infini. Lorsqu'on s'éloigne de la paroi, l'indice des vides local tend vers l'indice des vides du mélange.

Ainsi, la présence de toute paroi (gros grain, peau de coffrage, armature, etc.) décompacte le granulat fin (Fig. 17.)

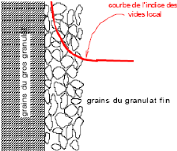
Fig. 17. - Effet de la paroi sur la compacité granulaire (Gabrysiak, 2007)

2.3. - L'effet d'interférence

Lorsque la proportion de gros granulats atteint un seuil de concentration, la manière dont ils sont disposés influe sur la compacité. En effet une partie des grains fins occupe les vides laissés par les gros grains. L'effet des parois des gros grains entraîne un décompactage des grains fins (fig. 18 et 19).

La disposition relative des parois des gros granulats détermine la forme et le volume des interstices dont dépend l'arrangement du granulat fin dans le mélange donc de son indice des vides. On parle ainsi d'interférence entre la structure du gros granulat et celle du granulat fin.

Fig. 18. - Disposition sans interférence Fig. 19. - Disposition avec interférence

28

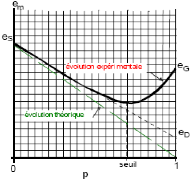
Fig. 20. - Evolution théorique et expérimentale de l'indice des vides du mélange granulaire
(Gabrysiak, 2007)

2.4. - Conclusion

Dans un mélange granulaire il y a généralement un effet de paroi et d'interférence du gros granulat sur le granulat fin. De ce fait, l'indice des vides du mélange ne peut pas être inférieur à une valeur minimale eD correspondant à une proportion optimale du gros granulat.

Ces différentes interactions, montrées théoriquement et expérimentalement visibles, ne sont pas facilement quantifiables. Cependant, lorsque le mélange comporte un granulat très fin, on admet la modélisation suivante (fig. 21) :

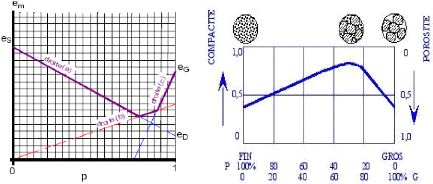
Fig. 21. - Modélisation de l'évolution de l'indice des vides (à gauche), de la compacité et de
la porosité (à droite) (Gabrysiak, 2007)

L'analyse de l'évolution de l'indice des vides montre :

Droite (a) : e_m = e S × (1 - p) + e_D × p Le mélange est riche en éléments fins, le gros granulat intervient par sa surface spécifique.

29

Droite (b) : e_m = k × p Le gros granulat intervient par la granulométrie de ses

interstices, donc à la fois par sa surface spécifique et son indice des vides. k est un coefficient qui a une signification physique complexe.

Droite (c) : e_m = (e_G -1) × p -1 Le mélange est pauvre en grains fins, le gros

granulat intervient par son indice des vides.

L'analyse de la variation de la compacité et de la porosité montre que la condition essentielle pour obtenir le moins de vides possible (meilleure compacité) dans un mélange de granulats fins et de granulats grossiers est: 35 % de fins et 65 % de grossiers.

Certains laboratoires corrigent par exemple la mesure de la masse volumique apparente ñ₀

afin de tenir compte de l'effet de paroi (grains/récipient).

Si la mesure est réalisée avec un récipient cylindrique, on a la correction suivante :

m

ñ₀ = Avec m = masse du granulat (g) et V = volume du récipient (cm³)

V

ñ₀

ñ [15]

1

,

= ⁰ 1 0 × S × D

V

ñ = masse volumique corrigée

S : surface intérieure du récipient y compris la face d'arasement (mm²) V : volume intérieur du récipient (mm³)

D : taille maximale du granulat (mm).

30

2ème Partie

Identification et Caractéristiques des matériaux

Evaluation de leur qualité

31

Chapitre 1. - Provenance des matériaux de l'étude

1. - Contexte géologique du bassin sénégalo-mauritanien

Les formations géologiques faisant l'objet d'une exploitation pour la production de granulats sont en général des roches massives (basalte, grès, calcaire, silexite, etc.) issues du bassin sénégalo-mauritanien. Ce bassin est le plus occidental et le plus étendu des bassins sédimentaires de la marge Atlantique africaine. Il est constitué par des terrains tabulaires méso-cénozoïques et s'est individualisé au Trias à la suite de la séparation des plaques africaine et américaine.

Le bassin sénégalo-mauritanien est relativement calme. Seule la partie occidentale (Cap-Vert et région de Thiès (Fig. 22)) a été affectée par des phénomènes tectoniques et des épisodes volcaniques localisés le long de failles généralement orientées NE-SW ou E-W. Ces perturbations sont certainement liées à la tectonique cassante due au rifting atlantique et qui aurai engendré des zones de faiblesse sensibles aux contre-coups des phases orogéniques ultérieures.

La couverture sédimentaire, épaisse à l'ouest, est recouverte en grande partie par une vaste couverture sableuse et un faciès d'altération du Cénozoïque. Cette couverture sédimentaire a servi d'encaissant et de substratum aux laves tertiaires et quaternaires.

1.1. - Les formations basaltiques

La partie occidentale du bassin sénégalo-mauritanien a été le siège d'un important volcanisme vers la fin du Tertiaire sur l'ensemble du Cap Vert et du Plateau de Thiès, et au quaternaire sur la presqu'île de Dakar.

Le premier épisode volcanique fini-tertiaire a lieu entre l'Oligocène et le Miocène supérieur. Il se manifeste par des épanchements de basalte dans la presqu'île du Cap-Vert (Cap Manuel, Gorée, Fann) et des intrusions de laves dans la région de Thiès correspondant à des dykes (Diack, Sène Sérère), ou à des filons tectoniques (Keur Mamour, Ravin des voleurs, Thiéo, Bellevue, Sandock, Fouloume). Le volcanisme tertiaire est donc essentiellement fissural.

Le second épisode volcanique a eu lieu au Quaternaire. Il se présente en deux ensembles volcaniques :

- un ensemble volcanique inférieur constitué d'une coulée de dolérites intercalée dans les sables de la base du quaternaire. Il affleure le long de la bordure littorale de Fann à Ouakam,

- un ensemble volcanique supérieur qui représente le « volcanisme des Mamelles ». Il est constitué par plusieurs coulées successives de basanite, de basanite doléritique et d'une coulée terminale de dolérite, mais également de produits pyroclastiques formés de tufs, de pierres ponces, de scories et de bombes (Dia, 1982).

Le basalte est une roche magmatique effusive très commune. C'est une roche microlitique, comportant des plagioclases, et des pyroxènes, accompagnés selon les cas d'olivine, d'hypersthène, de magnétite, d'ilménite ; il peut s'y ajouter, en faible pourcentage, soit du quartz, soit des feldspathoïdes.

Trois types de faciès ont été identifiés à Diack (Dia, 1982) :

- un faciès à grain fin, majoritaire, représenté essentiellement par des basanites. Il a une structure microlitique porphyrique à phénocristaux de pyroxène et d'olivine, dans une mésostase riche en verre et en microlites de plagioclase, de microcristaux de pyroxène et d'olivine,

- un faciès à grain moyen, moins abondant que le faciès précédant. La structure est doléritique intersertale avec pourcentage élevé de plagioclase en lattes englobant des pyroxènes et/ou des olivines en phénocristaux ou en microcristaux ;

32

- un faciès à gros grain, représenté par une roche grenue entièrement cristallisée, sans mésostase interstitielle. La structure est grenue pegmatitoïde contenant de nombreuses lattes de plagioclase et des cristaux de pyroxène.

1.2. - Les formations calcaires

Les formations calcaires du bassin sénégalo-mauritanien sont d'age Crétacé supérieur à Paléocène et sont présentes dans une grande extension dans la Presqu'île du Cap Vert et le Plateau de Thiès.

Le Paléocène affleure à l'Est et à l'Ouest du horst de Ndiass dans la falaise de Thiès et à Dakar. Pendant le Paléocène, l'environnement de sédimentation devient de plus en plus calcaire et se caractérise par le développement de récifs formés de calcaires, d'agiles calcaires et de marnes. A la fin du Paléocène le horst de Ndiass a commencé à émerger et un relief karstique se développe à partir des calcaires Paléocène.

L'analyse des sondages (Dramé, 2004) exécutés dans les carrières calcaires de Bandia où les matériaux de l'étude ont été prélevés montre une lithologie constituée essentiellement de calcaire gréseux, de calcaire lumachellique, de calcaire à entroque, de calcaire coquillier, de calcaire crayeux et de calcaire altéré.

1.2.1. - Le calcaire gréseux

Ce calcaire a une couleur jaunâtre avec un aspect massif et très dur. Vu au microscope, il a une texture de type « wackstone ». Les éléments figurés sont principalement constitués de minéraux de quartz et d'éléments biogènes (algues vertes, fragments de lamellibranches et de bryozoaires, des débris de gastéropodes recristallisés en calcite, des plaques d'échinodermes) pris dans une matrice micritique.

1.2.2. - Le calcaire lumachellique : très fossilifère, blanchâtre, massif, et dur. Les éléments figurés sont arrondis et brisés attestant un transport. La texture est de type « packstone ». Les bioclastes sont des fragments de mollusques associés à des débris de gastéropodes et des plaques d'échinodermes. La porosité intergranulaire est remplie par de la micrite.

1.2.3. - Le calcaire à entroque : à pâte fine. La texture est de type « packstone » avec parfois une tendance « wackstone ». Les bioclastes sont essentiellement des plaques d'échinodermes cimentées par la micrite.

1.2.4. - Le calcaire coquillier : calcaire massif, parfois cristallin, avec des débris coquilliers brisés, corrodés ou épigénisés en calcite. La texture est de type « packstone » avec une phase de liaison micritique. Les éléments biogènes sont des algues, des fragments de lamellibranches, de mollusques, des gastéropodes, des miliolidés, des plaques d'échinodermes et de bryozoaires.

1.2.5. - Le calcaire crayeux : calcaire non coquillier, peu ou pas fossilifère, avec un aspect tendre et friable. Il s'intercale dans le calcaire cristallin. La texture est de type « mudstone » à rares plaques d'échinodermes. La phase de liaison est constituée essentiellement de micrite.

1.2.6. - Le calcaire altéré : il est au sommet des couches calcaires. Il se présente sous forme de blocs emballés dans une matrice à argile noire parfois latéritisée.

1.3. - Les silexites

Ce sont des roches hypersiliceuses se présentant sous forme de rognons ou groupées en passés
plus ou moins horizontaux dans les niveaux phosphatés de la région de Taïba. Ces niveaux

33

phosphatés se sont formés à partir du Paléocène pour se développer ensuite à la base de l'Eocène. L'Histoire du gisement est divisée en deux grandes étapes : une étape d'accumulation sédimentaire et une étape de transformation des dépôts initiaux (Pannatier, 1995 in Gaye, 1995). On a successivement :

- le dépôt des argiles du mur (attapulgite) à l'Yprésien,

- le dépôt de la première couche phosphatée à l'Eocène moyen. Ce niveau, associé à une sédimentation carbonatée, est subdivisé en deux membres : les phosphates hétérogènes à la base et les phosphates homogènes au sommet ;

- le dépôt des argiles bariolées du toit (associées à des sables, des grès et des silex) au dessus de la couche phosphatée, à la fin de l'Eocène moyen ;

- le dépôt d'une seconde couche phosphatée de l'Eocène supérieur à l'Oligocène inférieur ;

- de l'Oligocène au Mio-Pliocène, une émersion des couches provoque une forte altération. Cette altération de type latéritique a provoquée la formation des phosphates alumino-calciques et alumineux sauf en quelques endroits où le dépôt reste intact sous forme de phosphate tricalcique.

Dans les phosphates hétérogènes, les particules phosphatées sont le plus souvent des coprolithes, des rudites (lithoclastes et bioclastes) associées à une fraction phosphatée arénitique ou lutitique. Les silex y sont très abondants où ils sont en bancs décimétriques ou en rognons volumineux.

Dans les phosphates homogènes, les particules phosphatées sont des arénites et des lutites souvent altérées et riches en concressions d'oxydes de fer. Les silex sont le plus souvent en rognons ou en galets

Les silex sont issus d'une silicification secondaire par remplacement de matériel initial et reconcentration à partir d'un stock de silice biogène. Il se présente généralement sous forme de blocs à coeur sombre et à cortex blanc.

La nature du minéral siliceux néoformé dépend souvent de la composition du milieu ambiant : - Quartz en milieu siliceux,

- Calcédoine (silice plus ou moins fibreuse) en milieu riche en ions alcalins ou alcalino- terreux ;

- opale (silice riche en eau) dans un milieu riche en phyllithes (argile).

Un échantillon d'un tout-venant de silexite montre que la roche est constituée de (Diémé, 1991 in Gaye, 1995):

- 91 % de silex,

- 6 % d'induré phosphaté ;

- 3 % de fines à éléments phosphatés et argileux.

L'observation au microscope optique révèle que les silex sont composés de 30 à 40 % d'opale, et 60 à 70 % de calcédoine.

La prédominance de la calcédoine s'explique par sa stabilité chimique plus grande que celle de l'opale.

Les relations entre ces deux minéraux montrent que l'opale s'est cristallisée la première, puis la calcédoine cristallise par épigénisation de l'opale.

34

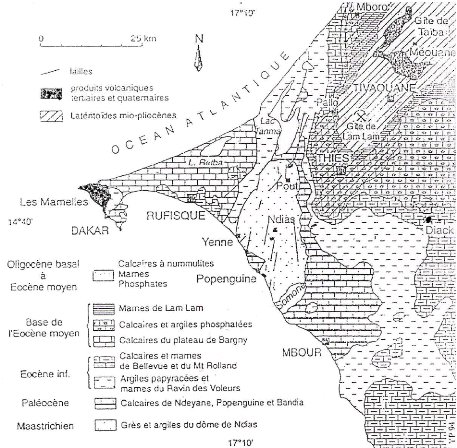
Fig. 22. - Carte géologique de la presqu'île du Cap Vert et du Plateau de Thiès

35

Chapitre 2. - Les caractéristiques mécaniques des granulats

L'aptitude des granulats à être utilisés dans les assises de chaussée est appréciée par un certain nombre d'essais. Ces essais ont été effectués au laboratoire de géotechnique de Jean Lefebvre Sénégal dans le cadre du projet de construction de l'autoroute Patte d'oie - Malick Sy.

1. - Essais caractéristiques de la fabrication

1.1. - Analyse granulométrique

On appelle analyse granulométrique l'opération permettant de déterminer :

o La granulométrie : c'est-à-dire la détermination de la grosseur des grains et les pourcentages pondéraux respectifs des différentes familles de grains constituant les échantillons,

o La granularité : c'est-à-dire la répartition dimensionnelle des grains dans un granulat.

L'analyse granulométrique consiste à fractionner le matériau en différentes coupures à l'aide de tamis à maille carrée. Elle s'applique à tous les granulats de dimension nominale inférieure ou égale à 63 mm, à l'exclusion des fillers. Les masses des différents refus sont rapportées à la masse initiale sèche du matériau. Les pourcentages ainsi obtenus sont exploités sous forme de graphique en portant les ouvertures des tamis en abscisse, sur une échelle logarithmique, et les pourcentages en ordonnée, sur une échelle arithmétique (Figures 22 à 25). La courbe appelée courbe d'analyse granulométrique est tracée de manière continue et peut ne pas passer rigoureusement par tous les points.

Les tamis sont normalisés. Les ouvertures de mailles carrées permettent un classement
granulaire. Les dimensions successives des mailles carrées suivent des progressions

géométriques de raison Normalisation).

= 1,25 pour la norme AFNOR (Association Française de

100

40

60

20

90

80

70

50

30

10

0

100

45/15/15/25 Branche inf fuseau Branche sup fuseau

10

Diamètre (mm)

Pourcentage de fines f = 4,6 %

1

0,1

0,01

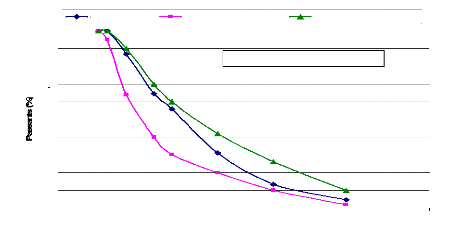
Fig. 23. - Courbe granulométrique de la fraction 0/31,5 mm du basalte dans le fuseau 0/31,5
mm - concassés 0/d (BCEOM-CEBTP, 1984)

36

100

10

1

0,1

0,01

100

90

80

70

60

50

40

30

20

10

0

Pourcentage de fines f = 6,9 %

30/15/20/35 Branche inf fuseau Branche sup fuseau

Diamètre (mm)

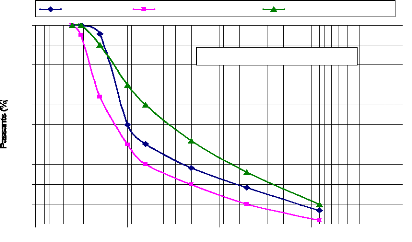
Fig. 24. - Courbe granulométrique de la fraction 0/31,5 mm du calcaire dans le fuseau 0/31,5
mm - concassés 0/d (BCEOM-CEBTP, 1984)

100

40

90

80

60

50

30

20

70

10

0

100

30/15/20/35 Branche inf fuseau Branche sup fuseau

10

Diamètre (mm)

Pourcentage de fines f = 3,6 %

1

0,1

0,01

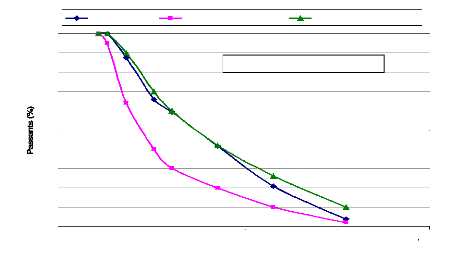
Fig. 25. - Courbe granulométrique de la fraction 0/31,5 mm du silexite dans le fuseau 0/31,5
mm - concassés 0/d (BCEOM-CEBTP, 1984)

37

Les différentes courbes granulométriques indiquent une granularité continue et étalée. Seul le calcaire n'entre pas dans le fuseau de spécification du CEBTP ; cela est du à un pourcentage de refus faible au niveau du tamis de maille 20 mm. En effet c'est la forme de la courbe qui est plus importante. Elle conditionne l'aptitude au compactage, l'absence de ségrégation et la compacité du matériau. Plus les contacts entre les grains sont nombreux, plus la couche sera stable, plus le matériau sera compact, moins on risquera de voir se produire des déplacements des grains et par suite des tassements. A cet égard, ce sont donc les courbes continues et bien graduées qui sont les plus satisfaisantes.

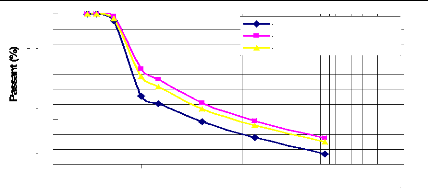
Le pourcentage de fines est satisfaisant. Si ce pourcentage est nul ou insuffisant pour combler les vides entre les gros grains, le matériau est peu compact. S'il est excessif il y a formation de boue au compactage et donc une augmentation ultérieure des déformations permanentes. Cependant pour le calcaire le malaxage et le compactage produisent des fines qui peuvent passer d'un pourcentage de 7 à 17,31 % (Figure 25). C'est pourquoi la fourchette de 4 à 10 % de fines proposée par le CEBTP semble ne pas être adaptée à toutes les catégories de granulats. Si le pourcentage de fines après compactage risque de dépasser un certain seuil, il faudrait diminuer cette fourchette.

100

40

80

60

20

90

70

50

30

10

0

100 10 1 0,1

Diamètre (mm)

avant compactage après compactage fort

après compactage faible

0,01

Fig. 26. - Granulométrie après compactage du calcaire

1.2. - Le coefficient d'aplatissement

La forme d'un granulat est définie par trois grandeurs géométriques :

· La longueur L, distance maximale de deux plans parallèles tangents aux extrémités du granulat,

· L'épaisseur E, distance minimale de deux plans parallèles tangents au granulat ;

· La grosseur G, dimension de la maille carrée minimale du tamis qui laisse passer le granulat.

Le coefficient d'aplatissement A d'un ensemble de granulats est le pourcentage pondéral des

G

éléments qui vérifient la relation : > 1,58

E

On fait un tamisage classique sur une colonne de tamis normalisés à mailles carrées afin de
séparer les granulats en une succession de classes granulaires d/D dont les dimensions sont
telles que D = 1 ,25d. Les différentes classes granulaires d/D ainsi isolées sont tamisées une à

38

une sur une grille à fentes parallèles d'écartement E = d/1,58 (ce qui correspond aussi à E = D/2).

L'échantillon est tamisé sur un tamis de 4 mm d'ouverture et le refus de masse M0 est utilisé pour la détermination de A.

Pour une classe granulaire d/D donnée, on peut définir un coefficient d'aplatissement partiel. Ai = 100Mei Mgi

Avec Mgi = masse de la classe granulaire d/D,

Mei = masse passant à travers le tamis à fentes d'écartement E correspondant.

Le coefficient d'aplatissement global A du mélange s'exprime en intégrant les valeurs partielles déterminées sur chaque classe granulaire (Tableau 4) :

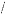
A =M_ei M gi

Caractéristique	Basalte	Calcaire	Silexite
Coefficient d'aplatissement (%)	14,93	6,1	24,93

Tableau 4. - Coefficients d'aplatissement des différents types de granulats

La forme des granulats calcaires est meilleure que celle des granulats de basalte et de silexite. Ceci indique une difficulté relative au concassage des basaltes et des silexites due à leur aspect trop massif. Toujours est-il que les granulats de silexite ont une forme plus plate que celle des granulats de basalte.

Des matériaux très anguleux ne se mettent pas toujours facilement en place et la compacité après compactage peut ne pas être élevée. C'est ainsi que les graves concassées, qui comportent une fraction importante de sable rond, sont plus maniables et plus aisément compactables. Cependant la forme des granulats a également une forte influence sur la résistance aux déformations permanentes. En effet les matériaux alluvionnaires roulés résistent mal à l'orniérage. Une étude au triaxial de l'influence de la forme des granulats (roulés ou concassés) sur le comportement des Graves Non Traitées a montré que les matériaux concassés ont la meilleure résistance aux déformations permanentes.

1.3. - L'Equivalent de Sables

L'Equivalent de sables est un rapport conventionnel volumétrique entre les grains fins et les autres. Il permet donc de caractériser l'importance des fines par une valeur numérique (Tableau 5).

Cet essai s'applique assez bien aux sols faiblement plastiques et peut s'appliquer à tous les matériaux grenus.

L'essai est effectué sur la fraction 0/5 mm du matériau à étudier. On lave l'échantillon, selon un processus normalisé, et on laisse reposer le tout. Au bout de 20 minutes, on mesure les éléments suivants :

- hauteur H1 : sable propre + éléments fins, - hauteur H2 : sable propre seulement.

Il existe deux types de mesures en fonction du degré d'argilosité du matériau. En effet pour les sols par exemple, la mesure de la hauteur H2 peut être délicate, on substitue à l'essai visuel, l'essai au piston.

ES=100H2 H1

39

Caractéristique	Basalte	Calcaire	Silexite
Equivalent de Sables (%)	50,82	45,22	52

Tableau 5. - Equivalent de sables des différents types de granulats

L'Equivalent de sables satisfait à tous les niveaux de trafic. Il indique le degré de pollution des éléments sableux des granulats. Plus l'Equivalent de sables est élevé, moins le matériau contient d'éléments fins nuisibles. A cet égard les calcaires sont moins propres que les basaltes et les silexites. Cet essai rend compte globalement de la quantité des éléments les plus fins mais est moins fiable en ce qui concerne l'aspect qualitatif c'est-à-dire donne peu d'informations sur la nature minéralogique de ces fines. En effet, il faut savoir si ces particules fines sont « inertes » c'est-à-dire sont un simple filler minéral provenant du broyage de la roche par concassage comme les fines siliceuses ou calcaires, ou s'il s'agit de particules « actives » c'est-à-dire des particules argileuses qui vont se gonfler en présence d'eau faisant chuter le frottement interne jusqu'à l'annuler presque totalement entraînant l'orniérage de la couche incriminée.

2. - Les essais caractéristiques des propriétés intrinsèques 2.1. - Masses volumiques

2.1.1. - Définitions

o La masse volumique absolue

La masse volumique absolue d'un matériau est la masse de l'unité de volume de ce matériau, déduction faite de tous les vides, aussi bien des vides entre les grains que des vides à l'intérieur des grains.

La densité absolue est le rapport de la masse absolue d'une unité de volume du matériau à température donnée à la masse du même volume d'eau distillée à la même température.

o La masse volumique réelle

La masse volumique réelle d'un matériau est la masse de l'unité de volume de ce matériau déduction faite des vides entre particules. La déduction ne concerne pas les vides compris dans le matériau mais seulement ceux entre les particules (Tableau 6).

La densité réelle est le rapport de la masse réelle d'une unité de volume du matériau sec dans l'air à température donnée à la masse d'un égal volume d'eau distillée à la même température.

o La masse volumique apparente

La masse volumique apparente d'un matériau est la masse de l'unité de volume du matériau pris en tas, comprenant à la fois des vides perméables et imperméables de la particule ainsi que les vides entre particules.

La densité apparente est le rapport de la masse apparente d'une unité de volume du matériau à la masse d'un égal volume d'eau distillée à la même température.

Caractéristique	Basalte	Calcaire	Silexite
Poids spécifique ãs (kN/m^3)	27,25	24,44	24

Tableau 6. - Poids spécifiques des différents types de granulats
40

2.2. - Résistance à l'usure et aux chocs

2.2.1. - Essai Los Angeles

Cet essai permet de mesurer les résistances combinées à la fragmentation par choc et à l'usure par frottements réciproques des éléments d'un granulat (Tableau 7). Il consiste à mesurer la quantité d'éléments inférieurs à 1,6 mm produite en soumettant le matériau à une série de chocs et de frottements dans la machine Los Angeles. A un coefficient Los Angeles faible correspond un excellent matériau. Dans la machine Los Angeles, introduire la prise d'essai M = 5000 g et la charge de boulets de la classe granulaire choisie. Après 500 rotations de la machine, à une vitesse régulière comprise entre 30 et 33 tr/min, recueillir le granulat et le tamiser à 1,6 mm, peser le passant m.

m

Par définition le coefficient Los Angeles est le rapport : =

LA

× 100

M

2.2.2. - Essai Micro-Deval

L'essai permet de mesurer la résistance à l'usure par frottements entre les granulats et une charge abrasive (Tableau 7). Il consiste à mesurer la quantité d'éléments inférieurs à 1,6 mm produite dans un broyeur, dans des conditions bien définies, à sec ou en présence d'eau. Plus le coefficient Micro-Deval est faible, meilleur est le matériau.

Dans les cylindres de la machine, introduire chaque prise d'essai M = 500 g et la charge abrasive (billes en acier de 10 mm de diamètre) correspondant à la classe granulaire choisie. Les essais peuvent s'effectuer à sec ou en présence d'eau. Dans ce dernier cas, on ajoutera 2,5 litres d'eau par essai. Après rotation des cylindres à une vitesse de 100 tr/min pendant 2 heures, tamiser le matériau sur le tamis de 1,6 mm et peser passant m.

m

Par définition le coefficient Micro-Deval est le rapport : =

M D

× 100

M

Les valeurs de LA et MDE ont été fournis par des rapports de IK Consultance et du CEREEQ.

Caractéristiques mécaniques	Basalte	Calcaire	Silexite
Los Angeles (%)	12,54	32,65	21
Micro-Deval (%)	16	54,7	17

Tableau 7. - Coefficients Los Angeles et Micro-Deval des différents types de granulats

Les coefficients Los Angeles et Micro-Deval du basalte et du silexite sont conformes aux spécifications. Les granulats de basalte et de silexite montrent une grande résistance à l'usure et à la fragmentation due à leur aspect trop massif. Cependant le silexite est moins résistant que le basalte. Les calcaires ont une faible résistance à l'usure et au frottement.

3. - Essai Proctor - Essai CBR

3.1. - Essai Proctor modifié

Cet essai simule l'évolution du sol au cours du compactage et permet de déterminer pour une énergie de compactage donnée, la teneur en eau optimale pour obtenir la densité sèche maximale (Figure 26).

L'essai consiste à compacter l'échantillon dans un moule standard, à l'aide d'une dame normalisée, à raison de 55 coups par couche (5 couches). Le compactage s'effectue avec des teneurs en eau croissantes rapportées au poids du matériau sec. Après chaque opération on mesure la masse apparente (ãh) du matériau et la teneur en eau (w) puis on calcule la masse volumique sèche (ãd).

41

On trace ensuite la courbe Proctor du matériau avec en abscisse les teneurs en eau et en ordonnée les masses volumiques sèches. On détermine ensuite la teneur en eau optimale (w opt) qui correspond à la masse volumique sèche maximale (ãd max).

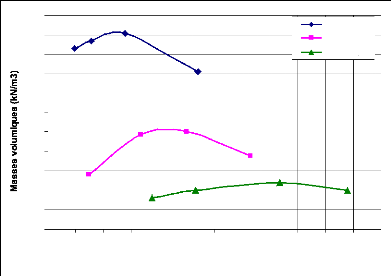
24,5

23,5

22,5

21,5

20,5

19,5

24

23

22

21

20

19

5,5 6 6,5 7 7,5 8 8,5 9 9,5 10 10,5 11 11,5

Teneur en eau (%)

Basalte 0/31,5 Calcaire 0/31,5 Silexite 0/31,5

Fig. 27. - Courbes Proctor des différents types de granulats

Caractéristiques physiques	Basalte	Calcaire	Silexite
ãd max (kN/m^3)	24,04	21,6	20,21
W opt (%)	6,8	7,65	9,5
ãs (kN/m^3)	27,25	24,44	24
Porosité n (%)	11,84	12	15,64

Tableau 8. - Caractéristiques physiques des différents types de granulats

3.2. - Essai CBR

Il sert à caractériser la portance du matériau c'est à dire la charge qu'il peut supporter sans se rompre, mais également à mesurer l'aptitude d'une chaussée à une perméabilité amenée par une forte immersion en cas de fortes pluies. Le CBR est un nombre sans dimension exprimant en pourcentage le rapport entre les pressions produisant dans le même temps un enfoncement donné dans le matériau étudié d'une part et dans un matériau de référence (13,6 kN) d'autre part.

Par définition cet indice est pris égal à la plus grande des deux valeurs suivantes :

- ICBR2 , 5 = 100F2 , 5 13,6 - ICBR₅ =100F ₅ 20,5

ICBR = max(ICBR2 , 5 ; ICBR₅)

F2, 5 = Force à 2,5 mm d'enfoncement, F5 = Force à 5 mm d'enfoncement.

42

Le matériau est compacté à la teneur en eau optimale suivant les procédures de l'essai Proctor modifié : 3 moules CBR qui seront compactés respectivement à raison de 55, 25, et 10 coups par couche (5 couches par moule). Après immersion des moules pendant 4 jours, on détermine son poids, sa densité et sa compacité. On poinçonne ensuite le moule avec un piston de 4,9cm de diamètre à une vitesse de 1,27 mm/min. On trace la courbe indices CBR/Compacités.

On peut alors déterminer les Indices CBR à 25, 95 ou 98 % de compacité (Figure 27 à 32).

250

200

150

100

50

0

88 90 92 94 96 98 100 102

CBR (95%OMP) = 82 CBR (98%OPM) = 160

Com pacité(%)

Fig. 28. - Etude CBR après 96 heures d'imbibition du basalte 0/31,5 mm

250

150

100

50

0

200

CBR (95% OPM) = 105
CBR (98% OPM) = 162

88 90 92 9496 98 100

Compacité (%)

Fig. 29. - Etude CBR après 96 heures d'imbibition du silexite 0/31,5 mm
43

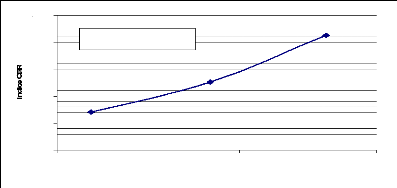
350

300

250

CBR (95% OPM) = 230
CBR (98% OPM) = 280

200

88 90 92 94 96 98 100 102

Com pacité(%)

150

100

Fig. 30. - Etude CBR après poinçonnement immédiat du calcaire 0/31,5 mm

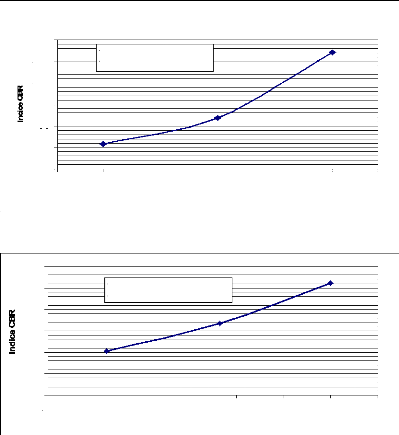
300

250

200

150

100

Fig. 31. - Etude CBR après 96 heures d'imbibition du calcaire 0/3 1,5 mm

50

400

250

200

350

300

150

100

0

88 90 92 94 96 98 100 102

Compacité (%)

88 90 92 94 96 98 100 102

CBR (95%OPM) = 219
CBR (98% OPM) = 305

CBR (95 P) = 165

CBR (95% OPM) = 165

CBR (98 )

CBR (98% OPM) = 220

Com pacité(%)

Fig. 32. - Etude CBR après 8 jours d'imbibition du calcaire 0/31,5 mm
44

250

50

0

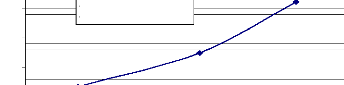
200

150

100

CBR (95%OPM) = 116 CBR (98%OPM) = 170

88 90 92 94 96 98 100 102

Com pacité(%)

Fig. 33. - Etude CBR après 16 jours d'imbibition du calcaire 0/31,5 mm

Indice CBR	Basalte	Calcaire	Silexite
95 %OPM	82	219	105
98 %OPM	160	305	162

Tableau 9. - Les Indices Portant CBR après 96 heures d'imbibition des différents types de
granulats

L'Indice Portant CBR à 95 % de l 'OPM (Tableau 9) du calcaire (219) est largement supérieur à celui du silexite (105) et du basalte (82). En se basant sur cet essai on a tendance à penser, à tort, que le calcaire a les meilleures performances mécaniques que le basalte. Ceci est du au fait que malgré la dureté du squelette, le basalte est un matériau moins cohésif, tirant sa stabilité du seul frottement interne, donc sujet à l'attrition. C'est ainsi que le CBR à 98 % de l'OPM peut atteindre 160 chez le basalte, 162 chez le silexite, et plus de 300 chez le calcaire, ce qui démontre clairement les exigences de compacité des matériaux non liés. On doit avoir au moins 98 % de compacité in situ (BCEOM-CEBTP, 1984).

Indice CBR	Immédiat	4 jours	8 jours	16 jours
95 %OPM	230	219	165	116
98 %OPM	280	305	220	170

Tableau 10. - Tableau de variation de l'Indice CBR du calcaire en fonction de la durée
d'imbibition

45

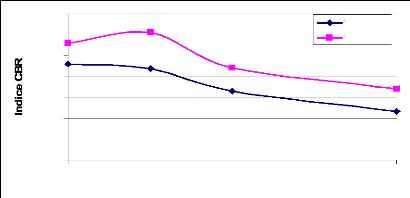
250

200

350

300

150

100

50

0

0 4 8 12 16

Jour

95%OPM
98%OPM

Fig. 34. - Evolution du CBR du calcaire en fonction de la durée d'imbibition

Il a été observé à 98 % de compacité que l'Indice Portant CBR du calcaire après 96 heures d'immersion (305) est supérieur à l'Indice Portant après poinçonnement immédiat (280) (Tableau 10). Ce comportement peut laisser penser que la présence de l'eau a contribué à l'hydratation de la chaux entraînant une cimentation plus forte. C'est pourquoi il a été effectué des essais sur des échantillons immergés pour des durées de 8 à 16 jours pour mieux comprendre l'effet de l'eau (Figure 33). Le constat est que l'accroissement de la portance n'est pas un phénomène continu. Au-delà de 96 heures d'imbibition, la portance du matériau diminue.

Le Tableau 11 donne les spécifications et les résultats des différentes caractéristiques des granulats.

Caractéristiques		Spécifications	Basalte	Calcaire	Silexite
Fuseau		0/3 1,5 mm	Conforme	Non conforme	Conforme
% fines		4 < f < 10	4,6	6,9	3,6
ES	T1-T2	~ 30	50,82	45,22	52
	T3-T4	~ 40
CBR	95 %OPM	~ 80	82	219	105
	98 %OPM		160	305	162
Porosité		< 15	11,84	12	15,64
LA	T1-T3	S 45	12,54	32,65	21
	T4-T5	S 30
MDE	T1-T3	S 15	16	54,7	17
	T4-T5	S 10
A		< 30	14,93	6,1	24,93

Tableau 11. - Tableau récapitulatif des caractéristiques des différents types de granulats
46

Conclusion générale et discussions

Les études au laboratoire ont permis d'apprécier les possibilités d'utilisation des granulats concassés en corps de chaussées notamment en couche de base.

Le basalte, de par ses performances physiques et mécaniques, satisfait entièrement aux spécifications techniques pour la réalisation du corps de chaussée.

Le silexite peut également être utilisé en couche d'assise. Cependant des améliorations doivent être apportées à l'élaboration de ce matériau notamment sur sa forme et sa granularité.

L'utilisation du calcaire en couche de base doit être limitée aux trafics inférieurs ou égaux à T3 du fait de sa faible résistance à l'usure et au frottement.

Cependant, du fait des limites que présentent les résultats des études, limites liées à la non reproductibilité des essais, à l'utilisation d'une seule carrière de calcaire, à l'absence de certaines classes granulaires, à la non réalisation des essais de compression, etc. ;il est nécessaire de:

- Continuer à multiplier les essais,

- Procéder à des améliorations (ciment), à des stabilisations (bitume), ou à des mélanges (litho stabilisation) ;

- Réaliser des planches d'essais pour étudier le comportement sous trafic des matériaux.

L'étude a permis de mettre en évidence les caractéristiques générales des granulats concassés. Ceux-ci présentent des atouts certains par :

- La nature granulaire dépourvue de liant, ce qui constitue un écran contre la remontée des fissures,

- La portance élevée en compacité maximale.

Cependant les critères de spécifications techniques du CEBTP sont discutables pour plusieurs raisons :

- On peut avoir un mélange granulaire optimal avec une courbe granulométrique très bien étalée mais qui sort ou qui n'entre pas parfaitement dans le fuseau de spécification. Ceci démontre clairement les limites du fuseau. Ce dernier ne tient pas compte de la production excessive de fines au cours du compactage de certains matériaux comme les calcaires. De plus, le fuseau s'applique exclusivement aux tout- venants de concassage et non aux graves reconstituées à partir de différentes classes granulaires,

- Des matériaux comme le calcaire ou la latérite ont souvent des indices portant supérieurs à ceux du basalte. C'est pourquoi, si on se base sur cet essai on a tendance à penser, à tort, que le calcaire a les meilleures performances mécaniques que le basalte. Ceci montre que l'indice portant CBR n'est pas un critère de spécification technique fiable pour les matériaux concassés. Cet essai n'est pas adapté à ces types de matériaux ;

- Le paramètre Equivalent de sables retenu dans la spécification pour déterminer la proportion des fines contenues dans le mélange granulaire ne rend pas compte de l'aspect qualitatif de ces fines. Cet essai est de moins en moins utilisé en géotechnique routière depuis l'introduction de la Valeur au bleu de méthylène. Ce dernier fournit des informations sur la nature minéralogique de ces fines qui, si elles sont argileuses, sont responsables des pertes ultérieures de portance en présence d'eau ;

47

- Il faut noter également que, attribuer des performances mécaniques à des Graves Non Traitées principalement à partir des mesures de dureté des granulats (Los Angeles et Micro -Deval) est réducteur et pas toujours satisfaisant. Par exemple en France, les GNT calcaires ne sont utilisées qu'en couche de fondation et pour de faibles niveaux de trafic du fait de leurs faibles résistances mécaniques et de leurs fortes sensibilités à l'eau. Cependant des études ont montré que, sous chargements triaxiaux répétés, les GNT calcaires ont généralement un très bon comportement mécanique caractérisé par une forte rigidité et de faibles niveaux de déformations permanentes ;

- La Porosité est un critère important à condition qu'elle soit déterminée

expérimentalement mais non déduite théoriquement comme le fait la norme ;

- Le principal problème est que ces normes et spécifications ne sont applicables que

dans les conditions climatiques et de trafic pour lesquelles elles ont été établies.

Il sort de cette étude que le comportement mécanique de ces matériaux est encore mal maîtrisé. De ce fait, les méthodes de dimensionnement ne tiennent pas compte parfaitement du comportement rhéologique de ces matériaux.

En effet, l'orniérage est le principal mode de dégradation des chaussées souples. Il est du principalement au cumul des déformations plastiques dans les différentes couches de matériaux non liés. C'est pourquoi un dimensionnement rationnel des chaussées souples passe par une bonne modélisation du comportement mécanique et rhéologique de ces matériaux.

C'est pourquoi le Laboratoire Central des Ponts et Chaussées (LCPC) a mis au point un appareil triaxial à chargements répétés, spécialement conçu pour l'étude des sols supports de chaussées et des matériaux non traités utilisés en couche d'assise.

Ceci met en avant tout l'intérêt de l'essai triaxial à chargements répétés qui permet de caractériser le comportement des matériaux non liés à partir du mélange granulaire oeuvré, plus représentatif de l'état du matériau dans la chaussée, et non plus à partir des seules caractéristiques de ses granulats.

48

Références bibliographiques

BCEOM-CEBTP (1975). - Manuel sur les routes dans les zones tropicales et désertiques, tome 2, Etudes et construction - 480 pages.

BCEOM-CEBTP (1984). - Guide Pratique de dimensionnement dans les pays tropicaux, Ministère Français de la Coopération - 155 pages.

CHEVOIR, F. (2005). - Rhéologie des matériaux granulaires. - LMSC - UMR LCPC - ENPC - CNRS - Institut Navier - 59 pages.

DIA, A. (1982). - Contribution à l'étude des caractéristiques pétrographiques, pétrochimiques et géotechniques des granulats basaltiques de la presqu'île du Cap-Vert et du Plateau de Thiès (Carrière de Diack - Sénégal) - Thèse de 3^ème cycle, Fac Sciences, UCAD -179 pages.

DRAME, A. (2004). - Caractérisation géologique et géochimique du panneau I de la carrière de Kirène pour l'approvisionnement en calcaire de la cimenterie : élaboration d'une esquisse d'un schéma d'exploitation. - Mémoire de fin d'études ingénieurs, IST, UCAD, N°133 - 91 pages.

DUPAIN ; LANCHON ; ARROMAN, ST. - (2004). - Granulats, Sols, Ciments et Bétons, 3ème édition - 236 pages.

FALL. M. (1993). - Identification et caractérisation mécanique de graveleux latéritiques du Sénégal : Application au domaine routier - Thèse Doctorat INPL en Génie Civil et Minier (Nancy) - 274 pages.

GABRYSIAK, F. (2007). - Les granulats, Chapitre 2 - 35 pages.

GAYE, M.G. (1995). - Caractérisation et performance d'un granulat - type nouveau en corps de chaussée : les Silexites (produits secondaires dans la chaîne de production de la CSPTTaïba). - Mémoire de fin d'études ingénieurs, IST, UCAD - 69 pages.

GIDEL, G. (2001). - Comportement et valorisation des graves non traitées calcaires utilisées pour les assises de chaussées souples. - Thèse de Doctorat, EDSPI, Université de Bordeaux I - 251 pages.

HABIBALLAH. T. (2005). - Modélisation des déformations permanentes des graves non traitées. Application au calcul de l'orniérage des chaussées souples. - Thèse de doctorat Génie civil, Université de Limoge - 177 pages.

IK CONSULTANCE. (2004). - Rapport d'étude de caractérisation mécanique de granulats à béton de Diack et Bandia - 6 pages.

JEUFFROY, G. (1967). - Conception et construction des chaussées, tome 1, Eyrolles.

JEUFFROY, G. ; SAUTEREY, R. (1991). - Cours de routes : contrôles et qualité - Presses de l'école nationale des ponts et chaussées - 645 pages.

49

LCPC-SETRA. (1994). - Conception et dimensionnement des structures de chaussées : guide technique.

LCPC-SETRA. (1992). - Réalisation des remblais et des couches de forme, Guide technique, Fascicule I - 96 pages.

NDIAYE, N.D. (1996). - Tout-venants concassés de calcaires Paléocène et litho stabilisation pour couche de base des chaussées au Sénégal. - Séminaire international sur les matériaux routiers -67 pages.

OVARLEZ, G. (2002). - Statique et rhéologie d'un milieu granulaire confiné. - Thèse de doctorat, Université de Paris XI Orsay -134 pages.

ROGNON, P. (2006). - Rhéologie des matériaux granulaires cohésifs. Application aux avalanches de neiges denses. - Thèse de doctorat, ENPC - 185 pages.

ROUX, J.N. et al (2007). - Géométrie et propriétés élastiques des matériaux granulaires. - 1 8^ème congrès français de la mécanique - 6 pages.

TCHOUANI NANA. J.M. ; CALLAUD. M. (2004). - Cours de mécanique des sols, Tome 1 : Propriétés des sols - 137 pages.

50

Table des matières

Avant - Propos 1

Sommaire 2

Liste des notations et des abréviations 3

Résumé 4

Introduction Générale 5

1ère Partie : Synthèse bibliographique

Chapitre 1. - Généralités sur les granulats routiers 8

1. - Définitions et présentation générale 8

2. - Nomenclature et Classification 8

3. - Les fuseaux granulométriques 8

4. - Les différentes approches pour l'étude des matériaux non liés 9

4.1. - L'approche microscopique 9

4.2. - L'approche macroscopique 9

4.3. - L'approche globale 9

5. - Caractéristiques géométriques des granulats routiers 10

5.1. - Etat de surface des granulats 10

5.2. - Angularité des granulats 10

5.3. - La forme des granulats 10

5.4. - La granularité des granulats 11

6. - Le Compactage des matériaux 11

6.1. - Définition 11

6.2. - Rôle du compactage sur la durée de vie des ouvrages 11

6.3. - Les paramètres influents du compactage 11

7. - Dimensionnement des structures de chaussées 12

7.1. - Les modèles empiriques et semi empiriques de dimensionnement 13

7.1.1. - La méthode du CBR 13

7.1.2. - La méthode proposée par le CEBTP pour les pays tropicaux 14

7.2. - Les méthodes rationnelles de dimensionnement 15

Chapitre 2. - Rhéologie des matériaux granulaires 17

1. - Interaction entre les grains 17

2. - Ecoulement des grains en cisaillement plan homogène 17

2.1. - Les régimes d'écoulement 18

2.2. - Les lois de comportement 18

2.2.1. - Loi de frottement de Coulomb 18

2.2.2. - Loi de dilatance 19

3. - Comportement expérimental des matériaux granulaires 19

3.1. - Notion de résistance au cisaillement 19

3.1.1. - Définition 19

3.1.2. - Résistance au cisaillement des sols pulvérulents 20

3.1.3. - Courbes contrainte-déformation d'un matériau pulvérulent 21

3.2. - Evaluation du comportement mécaniques des graves non traitées avec le triaxial à

chargement répété 22

3.3. - Conclusion 23

51

Chapitre 3. - Mélange et compacité granulaires 24

1. - Les mélanges granulaires 24

1.1. - Les mélanges binaires 24

1.2. - Les mélanges ternaires 25

2. - La compacité granulaire 26

2.1. - Mélange de deux granulats secs 26

2.2. - L'effet de paroi 28

2.3. - L'effet d'interférence 28

2.4. - Conclusion 29

2ème Partie : Identification et Caractéristiques des matériaux - Evaluation de leur qualité Chapitre 1. - Provenance des matériaux de l'étude 32

1. - Contexte géologique du Bassin sénégalo-mauritanien 32

1.1. - Les formations basaltiques 32

1.2. - Les formations calcaires 33

1.2.1. - Le calcaire gréseux 33

1.2.2. - Le calcaire lumachellique 33

1.2.3. - Le calcaire à entroque 33

1.2.4. - Le calcaire coquillier 33

1.2.5. - Le calcaire crayeux 33

1.2.6. - Le calcaire altéré 33

1.3. - Les silexites 33

Chapitre 2. - Les caractéristiques mécaniques des granulats 36

1 - Essais caractéristiques de la fabrication 36

1.1. - L'Analyse granulométrique 36

1.2. - Le Coefficient d'aplatissement 38

1.3. - L'Equivalent de Sable 39

2. - Les essais caractéristiques des propriétés intrinsèques 40

2.1. - Masses volumiques 40

2.1.1. - Définitions 40

2.2. - Résistance à l'usure et aux chocs 41

2.2.1. - Essai Los Angeles 41

2.2.2 - Essai Micro - Deval 41

3. - Essai Proctor - Essai CBR 41

3.1. - Essai Proctor modifié 41

3.2. - Essai CBR 42

Conclusion générale et Discussions 47

Références bibliographiques 49

Table des matières 51

Liste des Tableaux et des Figures 53

52

Liste des figures et des Tableaux

Figures

Fig. 1. - Structure de chaussée type et répartition des contraintes (LCPC-SETRA, 1994) 13 Fig. 2. - fuseau 0/3 1,5 mm - Concassés 0/d (BCEOM-CEBTP, 1984) 14
Fig. 3. - Loi de contact sans cohésion : (a) contact de hertz décrivant la répulsion

normale N et (b) critère de Coulomb simplifié décrivant le glissement tangentiel

(Rognon, 2006). 17
Fig. 4. - Géométrie d'écoulement et forme du profil de vitesse en cisaillement plan

homogène (Rognon, 2006) 18
Fig. 5. - Comportement rhéologique de grains sans cohésion : (a) loi de frottement,

(b) loi de dilatance, (c) origine du frottement et de la dilatance (Rognon, 2006) 19

Fig. 6. - Courbe contrainte-déformation 20

Fig. 7. - Courbe intrinsèque d'un sol fin 20

Fig. 8. - Courbe intrinsèque d'un sol pulvérulent 21

Fig. 9. - Courbe contrainte-déformation d'un sol pulvérulent 21

Fig. 10. - Essais triaxiaux sur le sable d'Hostun [Bouvard (1982)] in Habiballah (2005). 22

Fig. 11. - Visualisation de la dilatance dans le plan de Rowe (ó₁/ó₃ ; 1-då_v/då₁)

in Habiballah (2005) 23

Fig. 12. - Les mélanges granulaires binaires : méthode graphique (Gabrysiak, 2007) 24

Fig. 13. - Les mélanges granulaires binaires : méthode appliquée aux fuseaux granulométriques (Gabrysiak, 2007) 25

Fig. 14. - Détermination des proportions d'un mélange ternaire de granulats à partir d'un triangle (Gabrysiak, 2007) 25

Fig. 15. - Les mélanges granulaires ternaires : méthode du diagramme triangulaire 26

Fig. 16. - Evolution théorique de l'indice des vides d'un mélange granulaire

Gabrysiak, 2007) 27

Fig. 17. - Effet de la paroi sur la compacité granulaire (Gabrysiak, 2007) 28

Fig. 18. - Disposition sans interférence 28

Fig. 19. - Disposition avec interférence 28

Fig. 20. - Evolution théorique et expérimental de l'indice des vides du mélange

granulaire (Gabrysiak, 2007) 29
Fig. 21. - Modélisation de l'évolution de l'indice des vides (à gauche), de la compacité et de

la porosité (à droite) (Gabrysiak, 2007) 29

Fig. 22. - Carte géologique de la Presqu'île du Cap Vert et du Plateau de Thiès 35

Fig. 23. - Courbe granulométrique de la fraction 0/31,5 mm du basalte dans le fuseau

0/3 1,5 mm - concassés 0/d (BCEOM-CEBTP, 1984) 36
Fig. 24. - Courbe granulométrique de la fraction 0/31,5 mm du calcaire dans le fuseau

0/31,5 mm - concassés 0/d (BCEOM-CEBTP, 1984) 37
Fig. 25. - Courbe granulométrique de la fraction 0/31,5 mm du silexite dans le fuseau

0/3 1,5 mm - concassés 0/d (BCEOM-CEBTP, 1984) 37

53

Fig. 26. - Granulométrie après compactage du calcaire 38

Fig. 27. - Courbes Proctor des différents types de granulats. 42

Fig. 28. - Etude CBR après 96 heures d'imbibition du basalte 0/31,5 mm 43

Fig. 29. - Etude CBR après 96 heures d'imbibition du silexite 0/31,5 mm 43

Fig. 30. - Etude CBR après poinçonnement immédiat du calcaire 0/31,5 mm 44

Fig. 31. - Etude CBR après 96 heures d'imbibition du calcaire 0/3 1,5 mm 44

Fig. 32. - Etude CBR après 8 jours d'imbibition du calcaire 0/31,5 mm 44

Fig. 33. - Etude CBR après 16 jours d'imbibition du calcaire 0/31,5 mm 45

Fig. 34. - Evolution du CBR du Calcaire en fonction de la durée d'imbibition 46

Tableaux

Tableau 1. - Formes des granulats. 11

Tableau 2. - Classes de trafic équivalent et de plate-forme (BCOEM-CEBTP, 1984) 14

Tableau 3. - Valeurs du module de Young (E) pour la grave non traitée selon

le guide technique de conception et de dimensionnement des structures de chaussée

(LCPC-SETRA, 1994) 16

Tableau 4. - Coefficients d'aplatissement des différents types de granulats 39

Tableau 5. - Equivalent de sables des différents types de granulats 40

Tableau 6. - Poids spécifiques des différents types de granulats 40

Tableau 7. - Coefficients Los Angeles et Micro-Deval des différents types de granulats 41 Tableau 8. - Caractéristiques physiques des différents types de granulats 42
Tableau 9. - Les Indices Portant CBR après 96 heures d'imbibition des différents

types de granulats 45
Tableau 10. - Tableau de variation de l'Indice CBR du calcaire en fonction

de la durée d'imbibition 45

Tableau 11. - Tableau récapitulatif des caractéristiques des différents types de granulats 46

54

Mémoire de DEA (Diplôme d'Etudes Approfondies) en Géosciences
Option : Environnements sédimentaires
Mention : Géotechnique

Présenté par :
Makhaly BA

Titre : Identification géotechnique de matériaux concassés-types en corps de chaussées et
évaluation de leur qualité

Soutenu le Mardi 24 Juin 2008
Devant la commission d'examen composée de :

Mamadou FALL UCAD Président

Meissa FALL UCAD Rapporteur

Mouhammadoul B. DIOUF UCAD Examinateur

Moustapha DIENE UCAD Examinateur

Résumé

Au Sénégal, il a été observé une augmentation généralisée du niveau du trafic routier et une rareté des matériaux latéritiques de bonne qualité. Ceci limite la disponibilité de ces matériaux qui sont très usités dans la réalisation des assises de chaussées.

Ce mémoire s'inscrit dans le cadre des recherches sur l'utilisation de matériaux de substitution en construction routière. Des études ont été faites au laboratoire de géotechnique de Jean Lefebvre - Sénégal allant dans le sens d'utiliser les granulats concassés de basalte, calcaire et silexite en corps de chaussée.

Le travail consistait à reconstruire un mélange 0/31,5 mm à partir des différentes classes granulaires et d'en déterminer les caractéristiques physiques et mécaniques ainsi que les essais d'identification pour déterminer en laboratoire l'aptitude des tout-venants à être utilisés en corps de chaussée.

Les résultats obtenus en laboratoire permettent d'envisager l'utilisation des granulats concassés de basalte, calcaire et silexite en construction routière. Les indices de portance CBR obtenus pour les différents types de matériaux sont supérieurs à ceux exigés par les spécifications du CEBTP.

Le basalte, de par ses performances satisfait entièrement aux spécifications techniques pour la réalisation des corps de chaussées.

Le silexite peut également être utilisé en couche d'assise. Cependant des améliorations doivent être apportées à l'élaboration de ce matériau quant à sa forme et sa granularité.

L'utilisation du calcaire en couche de base doit être limitée aux trafics inférieurs ou égaux à T3 du fait des faibles résistances à l'usure et au frottement.

Il faut noter également que, attribuer des performances mécaniques à des graves non traitées principalement à partir des mesures de dureté des granulats est cependant réducteur et pas toujours satisfaisant. Ceci met en avant tout l'intérêt de l'essai triaxial à chargements répétés qui permet de caractériser le comportement des matériaux non liés à partir du mélange granulaire oeuvré, plus représentatif de l'état du matériau dans la chaussée, et non plus à partir des seules caractéristiques des ses granulats.

Mots-clés : granulat - tout-venant - basalte - calcaire - silexite - CBR - CEBTP.

55