2.2.2 Construction de quelques bissimulations .
1) Les états des deux systèmes
ci-dessous représentés sont bissimulaires.

££
U= u
ee
U

s1
s0//
S
''
? GG
? ? ? ? ? ? ? ?
S = ? ? S
? ? ?
S ? ? ?
(( Â?Â
CC
gg
²²
··
S
S
s2 S
gg

Posons R = {(s0, u) ,
(s1, u) , (s2, u)}
et montrons que R est une bissimulation de
S
par U. Comme (s0, u) E R, s0
S //s1 et s0
S //s2, il faut chercher
u1 et u2 dans
Utelsqueu U // u1etu U
// u2.Commeu U //
u,onprendu1=u2=u. Parailleursu U
// u,s0 S // s1, s0
S//
s2et(si,u)ERpouri=1;2.
De même, on montre que s1 est simulaire
à u et s2 est simulaire à u.
2) Changeons U en U' ci-dessous
représenté et montrons que S x U' n'est pas
une bissimulation de S par U'. Il suffit de
remarquer que (s0, u1) E S x U'.
Mais u1 n'évolue pas.
U,
U'= u0
hh

U,
u1 ²²
[[
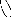
3) En modifiant U' en U» de manière
à ceque S x U» soit une bissimulation de S
par U». Dans l'exemple ci-dessus, la transition
qui fait problème est u0 U,
//u1. En la
supprimant, on obtient U'' représenté par
:
U,,
U'' = u0
hh
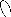
¾¾
²u1
L'axiome i) reste vérifié. L'axiome
ii) découle du fait que u0
S //u0.
4)
Rappels 2.1. Un alphabet est un ensemble fini de
symboles .
Soit A un alphabet.
Un mot sur A est une suite finie (m)
i où miE A. Un mot est vide s'il n'est
formé
d'aucun symbole. Nous noterons le
symbole vide par c ou par un petit espace vide. Le premier
symbole d'un mot est appelé tête du mot. L'ordre d'un
mot est le nombre de symboles qui le constituent.
Concaténer deux mots c'est les juxtaposer. Nous notons A°°
l'ensemble des mots sur A. La notion du mot nous permet de dire
que tous les mots ont même ordre; ceci en les
complètant par des symboles vides. Sur
A°° l'ensemble des mots complètés
avec une infinité de symboles vides définissons
l'ordre suivant :
u v si et seulement si il existe in E N tel
que pour tout i in, u = v et
u<vm où < désigne
l'ordre des symboles de l'alphabet.
(A°°, ) est un opc à plus petit
élément. En effet, pour toute partie dirigée
D de (A°°, ), le mot obtenu par
concatenation de tous les mots de D est le supremum de D.
· Définissons sur A°°
la relation :
(u ) EN A // (v
) EN ssi u = v 1 i.
L'on définit ainsi une structure de transition sur
A°°.
·
· La concatenation étant
associative, R = {((u.v) .w),
(u. (v.w))} est une bissimulation de
A°° par A°°.
2.3 Système de transition et coalgèbre
d'un endo-
foncteur de CPO.
Traditionnellement, un système de
transition à support ensembliste est la coagèbre du
foncteur puissance covariant P : ENS -? ENS . J.J.M.Rutten
dans [51 pose les bases de la théorie des systèmes de
transition ensemblistes vus comme coalgèbres d'un
endofoncteur de ENS. Cette section, a pour objets :
· rappeler la notion de
coalgèbre;
· prouver que les systèmes de
transition ensemblistes sont les coalgèbre du foncteur
puissance covariant.
2.3.1 Coalgèbre .
Dans cette sous section, nous présentons de prime à
bord la notion de coalgèbre et de morphismede
coalgèbres.
Définition 2.6. Soit F : C -? C un
endofoncteur d'une catégorie C. Une
F-coalgèbre est un couple (S, aS)
formé d'un objet S de C et d'un C-morphisme
aS : S -? F (S) appelé F-costructure
sur l'objet S de C.
Soit F : C -? C un endofoncteur d'une
catégorie C. Soient S = (S, aS) et
T = (T, aT) deux F-coalgèbres. Un
morphismes (ou plus précisément un F-morphisme) de S
vers T est un C-morphisme f : S -? T
rendant commutatif le diagramme suivant.
S f // T
²² ²²
F (S) F(f) // F
(T)
i.e, aS o f = F (f) o aS.
Soient f: S -? T et g: T -? Z
deux F-morphismes. Le C-morphisme go f :S -? Z
rend commutatif le diagramme suivant.
Sgo f // Z
²² ²²
F(go f)
F (S) F (Z)
En effet :
F (g o f) o aS = F
(g) o F (f) o aS
= F (g) o F (f) aS
= F (g) o aS o f
= aS o (g o f) .
De plus, les identités sont des morphismes de
F-coalgèbres. Ceci nous permet de conclure
que les coalgèbres et leurs
morphismes forment une catégorie.
| 


