Etude et implémentation d'un système sans fil multi-antennes dans un contexte MC-CDMA

Ecole Polytechnique De Tunisie

Option : Signaux et Systèmes

Rapport de Projet de Fin d'Etudes

Effectué du 11 février au 11 juin 2008

Etude et implémentation d'un système sans fil

multi-antennes dans un contexte MC-CDMA

Organisme d'accueil : TELNE

Elaboré par : Mohamed MAALEJ

Encadré par : Mme. Ines KAMMOUN-JEMAL M. Ameur SBOUI

13.édicace

~edédie ce tra~ail, A men cher père

`eur les sacri~ices que mus ne cessez de consentir, peur ms encouragements t~utes les heures de mes études, peur mis conseils teujours prediguées arec am~ur, peur la cen~iance que ;eus amez crée en mei

A la mémeire de ma très chère mère,

A la mémeire de lafemme queje deis teut,j~aurais tant aimé ;eus mir à mes cotés cesjeur. C~us neus aurez quitté t"t, mais mitre tendresse et p~tre patience resterent gravées dans men coeur et men esprit peur teujours.

A ma chère bele mère,

`eur les sacri~ices déployés à men égard, peur mes encouragements et p~tre ameur sans limites.

A mes~rères et mes chères soeurs, ;etre gentilesse et mitre sympathie sent exemplaires, ;eus dtes peur mei l~eremple de benté et de l~henndteté.

A teus mes amis, peur mitre amour et mes encouragements, je peus seuhaite beauceup de benheur et de succès.

AVANT PROPOS

TELNET est une société d'ingénierie et de conseil dans l'innovation et les hautes technologies oeuvrant dans les secteurs des télécoms et multimédia, auto motive et transport, avionique et défense, sécurité et carte à puce, électronique et industrie, systèmes d'information et ingénierie mécanique.

TELNET a été créée en 1994 pour répondre à une demande croissante en développements logiciels, en 2006, Telnet a obtenu le niveau 5 selon le modèle CMMI.

Depuis novembre 2007, TELNET opère à partir de quatre sites différents, trois sites en Tunisie et un en France.

Le domaine des activités des quatre sites concerne principalement

Les études logicielles

Conception et développement de produits logiciels dans divers domaines d'activités Télécoms, Multimédia, Transport, Consumer Product, Sécurité et Défense,etc..

Les systèmes électroniques

Conception et design en électronique et en microélectronique, Test et validation de systèmes électroniques.

Les Réseaux et Télécoms

La réalisation de prestations d'ingénierie dans les domaines des réseaux de télécommunication

L'ingénierie Produit Mécanique CAO & Simulation Mécanique FAO et Process d'industrialisation

Le site de Sfax se distingue des autres sites par un département de recherche et développement spécialisé en micro-électronique et en communications radio-mobiles. Dans ce sens, une équipe a été formée pour développer des compétences et métiers spécialisés dans les nouvelles techniques de communication numérique, de description matérielles et implémentation électronique.

REMERCIEMENTS

Je remercie M. Hassib Ellouze chef d'opération à TELNET de m'avoir accepté au sein du site de Sfax.

Je tiens à exprimer ma profonde reconnaissance à Mme. Inès Kammoun-Jemal, Maître assistante à l'Institut Supérieur d'Electronique et de Communication de Sfax (ISECS), qui a proposé et a encadré mon projet de fin d'études, pour son aide précieuse, ses conseils fructueux et son suivi de ce travail avec une extrême bienveillance. Je tiens à remercier également M. Ameur Sboui, Ingénieur chercheur à Telnet pour son co-encadrement et son aide précieuse dans la partie implémentation.

Je remercie également M. Mourad Loulou Maître de conférences à l'Ecole National des Ingénieurs de Sfax (ENIS) pour ses conseils et l'intérêt qu'il a su manifester pour mon travail.

Je remercie Mme. Sarra Ben Lagha, Professeur à l'Ecole Polytechnique de Tunisie, qui a bien voulu être la responsable de mon stage du coté de l'EPT.

Mes remerciements s'adressent également à tous les enseignants de l'EPT et à tous les membres de jury pour avoir accepté de juger ce modeste travail.

REsuME

Les travaux effectués dans ce mémoire font l'objet d'une contribution à la conception de circuits intégrés complexes pour les applications radio-mobile, en particulier pour les systèmes multiantennes. Les systèmes à antennes multiples permettent d'offrir des débits élevés sur des canaux à évanouissements, mais une source importante de dégradation des performances dans ces systèmes est la sélectivité fréquentielle du canal. Une solution pour combattre la sélectivité fréquentielle du canal consiste à utiliser la modulation OFDM.

L'objectif de ce projet de fin d'études est d'étudier et de proposer une description matérielle en VHDL d'un système multi-antennes dans un contexte MC-CDMA. La technique MC-CDMA correspond à la combinaison entre la technique d'accès CDMA et la modulation OFDM où l'étalement des données est réalisé dans le domaine fréquentiel.

Dans ce projet, on commence par évaluer les performances du système MIMO-MC-CDMA à travers une implémentation sur Matlab. Ensuite, on propose une architecture matérielle du système par une description en VHDL des différents composants de l'émetteur et du récepteur. Par ailleurs, on implémente cette chaîne sur une architecture matérielle reconfigurable à base de circuits FPGAs, on fournit les résultats de synthèse au niveau RTL et on analyse les performances de l'architecture proposée en termes de complexité et de rapidité.

Mots clés : Les systèmes multi-antennes, OFDM, MC-CDMA, VHDL, FPGA.

ABSTRACT

The works presented in this report constitutes a contribution to the design of complex integrated circuits for wireless applications, in particular for the multi-antenna systems.

Multi-antenna systems promise very high data rate on scattering-rich wireless channels, but an important source of performances degradation in these systems is the frequency selectivity of the channel. To combat the frequency selectivity of the channel, a solution achieving a good complexity/performance trade-off is to use OFDM modulation.

The aim of this project is to study and to propose a material description using VHDL of a multiantenna system in a MC-CDMA context. The MC-CDMA technique corresponds to the combination between the CDMA technique and the OFDM modulation where the data spreading takes place in the frequency domain.

In this project, we begin by evaluating the performances of MIMO-MC-CDMA system through an implementation on Matlab. Then, we propose a material architecture of the system by a VHDL description of different components for both the transmitter and the receiver. Morover, we implement this chain on a reconfigurable material architecture based on FPGA circuits, we provide the synthesis result at RTL level and we analyze the proposed architecture performance in terms of complexity and timing features.

Key-words: Multi-antenna system, OFDM, MC-CDMA, VHDL, FPGA.

TABLE DES MATIERES

INTRODUCTION GÉNÉRALE 1

Chapitre1 3

La Technique MC-CDMA 3

1. Introduction 3

2. Les composantes de base d'une chaîne de transmission numérique 3

2.1. Le codeur et le décodeur de canal 4

2.2. La modulation/démodulation numérique 5

2.2.1. Modulation à déplacement d'amplitude ASK (Amplitude Shift Keying) 6

2.2.2. Modulation à déplacement de phase PSK (Phase Shift Keying) 6

2.2.3. Modulation d'amplitude en quadrature QAM (Quadrature Amplitude Modulation) 6

3. Le canal radio-mobile 7

3.1. Effet multi-trajet d'un canal radio 7

3.2. Etalement temporel 9

3.3. Etalement fréquentiel : effet Doppler 9

3.4. Modélisation du canal à évanouissements lents 10

4. La modulation OFDM 11

4.1. Principe de l'OFDM 11

4.2. Modulation par la Transformée de Fourier Discrète DFT 12

4.3. Introduction de l'intervalle de garde en OFDM 12

5. Les techniques d'accès multiple 13

5.1. Accès multiple à répartition par temps 14

5.2. Accès multiple à répartition par fréquence 14

5.3. Accès multiple à répartition par code 14

6. La technique CDMA 14

6.1. Principe du CDMA 15

6.2. Modélisation du système CDMA 17

7. La technique CDMA associée à la modulation multi-porteuses 17

7.1. Partie émettrice 18

7.2. Partie réceptrice 19

7.3. Les techniques de détection en MC-CDMA 20

7.3.1. Détection mono-utilisateur 21

7.3.2. Détection multi-utilisateurs 21

8. Conclusion 22

Chapitre 2 23

Multiplexage spatial dans un contexte CDMA 23

1. Introduction 23

2. Techniques de diversité 24

2.1. Diversité temporelle 24

2.2. Diversité fréquentielle 25

2.3. Diversité spatiale 25

3. Les systèmes MIMO 26

3.1. Le codage espace-temps 27

3.1.1. Les codes ST en treillis 28

3.1.2. Les codes ST en bloc 28

3.2. Multiplexage spatial 29

3.3. Les techniques de détection pour le multiplexage spatial 29

3.3.1. Techniques de détection linéaires 30

3.3.2. Technique de détection non linéaire à annulation successive d'interférences 31

3.4. Résultats de simulation 32

4. Association entre multiplexage spatial et la technique MC-CDMA 35

4.1. Conception de la chaîne MIMO associée au MC-CDMA 35

4.2. Modélisation de la chaîne de transmission MIMO-MC-CDMA 36

4.3. Techniques d'égalisation pour la chaîne MIMO-MC-CDMA 38

4.4. Evaluation des performances du système MIMO-MC-CDMA 39

4.4.1. Cas de la chaîne sans codage de canal 40

4.4.2. Cas de la chaîne avec codage convolutif 42

5. Conclusion 44

Chapitre 3 46

Implémentation matérielle et analyse de performances 46

1. Introduction 46

2. Le circuit FPGA Stratix II.GX 46

3. Flot de conception adopté et environnement de synthèse 48

4. Spécification fonctionnelle et résultats d'implémentation 49

4.1. Architecture de la chaîne MIMO associée au MC-CDMA 49

4.2. Architecture des blocs utilisés dans la chaîne 50

4.2.1. Bloc de modulation 256-QAM 50

4.2.2. Bloc étalement 51

4.2.3. Bloc de démultiplexage spatial V-BLAST pour 2 antennes 54

4.2.4. Bloc modulateur OFDM 55

4.2.5. Bloc démodulateur OFDM 60

4.2.6. Bloc de l'égalisation 62

4.2.7. Bloc de multiplexage spatial de 2 antennes 68

4.2.8. Bloc "désétalement + quantification" 68

4.2.9. Bloc démodulation 70

5. Optimisation et analyse de performances de la chaîne 71

6. Conclusion 75

CONCLUSION ET PERSPECTIVES 76

RÉFÉRENCES BIBLIOGRAPHIQUES 78

ANNEXE 80

DES

LISTE FIGURES

FIGURE 1.1. COMPOSANTES DE BASE D'UNE CHAINE DE TRANSMISSION 4

FIGURE 1.2. CODEUR CONVOLUTIF (K=1,N=3 ET (M+1)=3) 4

FIGURE 1.3. CONSTELLATION DE LA MODULATION M-ASK 6

FIGURE 1.4. CONSTELLATION DE LA MODULATION 8-ASK 6

FIGURE 1.5. CONSTELLATION DES MODULATIONS BPSK, QPSK ET 8-PSK 7

FIGURE 1.6. CONSTELLATION DE 16-QAM UTILISANT LE CODAGE DE GREY 7

FIGURE 1.7. MODELISATION DU PHENOMENE DE TRAJETS MULTIPLES 8

FIGURE 1.8. INTRODUCTION DE L'INTERVALLE DE GARDE AU SYMBOLE OFDM TRANSMIS 13

FIGURE 1.9. CHAINE D'EMISSION ET DE RECEPTION DU MODULATEUR OFDM 13

FIGURE 1.10. LA TECHNIQUE TDMA 14

FIGURE 1.11. LA TECHNIQUE FDMA 14

FIGURE 1.12. LA TECHNIQUE CDMA 14

FIGURE 1.13. ETALEMENT PAR SEQUENCES DIRECTES 15

FIGURE 1.14. CIRCUIT D'EMISSION POUR UN UTILISATEUR DE LA TECHNIQUE MC-CDMA 18

FIGURE 1.15. CIRCUIT DE RECEPTION POUR UN UTILISATEUR DE LA TECHNIQUE MC-CDMA 20

FIGURE 2.1. EMISSION DU MEME SIGNAL A DES INSTANTS SEPARES PAR LE TEMPS DE COHERENCE DU CANAL 24

FIGURE 2.2. EMISSION DU MEME SIGNAL SUR DES FREQUENCES DIFFERENTES 24

FIGURE 2.3. DIVERSITE SPATIALE A L'EMISSION 25

FIGURE 2.4. DIVERSITE SPATIALE A LA RECEPTION 25

FIGURE 2.5. REPRESENTATION DES DIFFERENTS TRAJETS ENTRE ANTENNES EMETTRICES ET RECEPTRICES 26

FIGURE 2.6. SCHEMA D'ALAMOUTI POUR LE CAS DES ANTENNES EN EMISSION 28

FIGURE 2.7. DIAGRAMME DE LA TECHNIQUE DE DEMULTIPLEXAGE V-BLAST 28

FIGURE 2.8. BLOC D'EGALISATION POUR LE MULTIPLEXAGE SPATIAL 29

FIGURE 2.9. TEB EN FONCTION DU RSB SUR UN CANAL DE RAYLEIGH. 33

FIGURE 2.10. TEB EN FONCTION DU RSB EN UTILISANT LES RECEPTEURS ZF ET MMSE 34

FIGURE 2.11. TEB EN FONCTION DU RSB EN UTILISANT UN ALGORITHME SIC 34

FIGURE 2.12. CHAINE D'EMISSION DE LA TECHNIQUE MIMO-MC-CDMA 36

FIGURE 2.13. CHAINE DE RECEPTION DE LA TECHNIQUE MIMO-MC-CDMA 36

FIGURE 2.14. TEB EN FONCTION DU RSB POUR LES EGALISEURS A CRITERE ZF ET MMSE 40

FIGURE 2.15. TEB EN FONCTION DU RSB POUR DES TRANSMISSIONS A PLEIN CHARGE 41

FIGURE 2.16. TEB EN FONCTION DU RSB POUR LES DETECTIONS MONO-UTILISATEUR ET MULTI-UTILISATEURS 41

FIGURE 2.17. TEB EN FONCTION DU RSB POUR L'ALGORITHME SIC 42

FIGURE 2.18. EMETTEUR M IMO-MC-CDMA AVEC CODAGE DE CANAL SUIVI D'UN ENTRELACEUR 43

FIGURE 2.19. RECEPTEUR M IM O-MC-CDMA AVEC DESENTRELACEUR SUIVI D'UN DECODAGE DE CANAL 43

FIGURE 2.20. TEB EN FONCTION DU RSB POUR LE SYSTEME MIMO-MC-CDMA UTILISANT UN CODAGE DE CANAL 44

FIGURE 3.1. BLOC DIAGRAMME D'UN FPGA 47

FIGURE 3.2. FLOT DE CONCEPTION DE L'OUTIL QUARTUS 48

FIGURE 3.3. CIRCUITS D'EMISSION ET DE RECEPTION IMPLEMENTES 49

FIGURE 3.4. ORGANIGRAMME DU MODULATEUR 256-QAM 51

FIGURE 3.5. ARCHITECTURE DU BLOC ETALEMENT 53

FIGURE 3.6. FHT D'ORDRE 2 53

FIGURE 3.7. SCHEMA RTL DU FHT A L'ORDRE 8 53

FIGURE 3.8. BLOC DE DEMULTIPLEXAGE V-BLAST 54

FIGURE 3.9. ORGANIGRAMME D'UN "DEMUX SPATIAL" 54

FIGURE 3.10. SCHEMA RTL DU BLOC "DEMUX SPATIAL" 54

FIGURE 3.11. ARCHITECTURE DU MODULATEUR OFDM 55

FIGURE 3.12. ARCHITECTURE DU BLOC IFFT 58

FIGURE 3.13. BLOC D'UNE IFFT A L'ORDRE 2 58

FIGURE 3.14. BLOC D'UNE IFFT A L'ORDRE 4 58

FIGURE 3.15. SCHEMA RTL D'UNE IFFT A L'ORDRE 8 59

FIGURE 3.16. ORGANIGRAMME DU BLOC DE CONVERSION P/S + 60

FIGURE 3.17. DIAGRAMME EN BLOC DU DEMODULATEUR OFDM 60

FIGURE 3.18. ORGANIGRAMME DU BLOC DE CONVERSION S/P - 61

FIGURE 3.19. ARCHITECTURE D'UNE FFT A L'ORDRE 2. 62

FIGURE 3.20. ARCHITECTURE DE L'EGALISEUR MULTI-UTILISATEURS A CRITERE MMSE. 65

FIGURE 3.21. ARCHITECTURE DU CALCULATEUR DE V_I EN FONCTION DE _HRT,I , Y_I ET 66

FIGURE 3.22. SCHEMA RTL DU SOUS-BLOC "MODULE VECTEUR" 66

FIGURE 3.23 SCHEMA RTL DU SOUS-BLOC "PRODUIT MATRICE_VECTEUR" 66

FIGURE 3.24. SCHEMA RTL DU SOUS-BLOC INVERSION DE MATRICE 66

FIGURE 3.25. SCHEMA RTL DU SOUS-BLOC PRODUIT SCALAIRE 67

FIGURE 3.26. DIAGRAMME DU BLOC DE MULTIPLEXEUR SPATIAL 68

FIGURE 3.27. ORGANIGRAMME D'UN MULTIPLEXEUR 68

FIGURE 3.28. SCHEMA RTL D'UN MULTIPLEXEUR SPATIAL 68

FIGURE 3.29. SCHEMA BLOC DE "DESETALEMENT + QUANTIFICATION" 69

FIGURE 3.30. ORGANIGRAMME DU QUANTIFICATEUR 256-QAM 70

FIGURE 3.31. ORGANIGRAMME DU BLOC DE DEMODULATION 71

FIGURE 3.32. CONFIGURATION DES PARAMETRES DE TIMING 73

FIGURE 3.32. RESULTAT DE SYNTHESE DE LA CHAINE D'EMISSION DU SYSTEME MI MO-MC-CDMA 74

FIGURE 3.33. ANALYSE DE TIMING DE LA CHAINE D'EMISSION DU SYSTEME MI MO-MC-CDMA 74

FIGURE 3.34. RESULTAT DE SYNTHESE DE LA CHAINE DE RECEPTION DU SYSTEME M IMO-MC-CDMA 74

FIGURE 3.35. ANALYSE DE TIMING DE LA CHAINE DE RECEPTION DU SYSTEME MIMO-MC-CDMA 75

LISTE DES TABLEAUX

ABLEAU 3.1. TABLE D'ASSIGNATION DES SYMBOLES EN FONCTION DU CODE 51

ABLEAU 3.2. TABLE DES PARAMETRES ENTREES/SORTIES DU BLOC DE MODULATION 52

ABLEAU 3.3. RESULTAT DE SYNTHESE DU BLOC MODULATION 52

ABLEAU 3.4. TABLE DES PARAMETRES ENTREES/SORTIES DU BLOC DE ETALEMENT 53

ABLEAU 3.5. RESULTAT DE SYNTHESE DU BLOC FHT 8 54

ABLEAU 3.6. TABLE DES PARAMETRES ENTREES/SORTIES DU BLOC DE DEMULTIPLEXAGE V-BLAST 55

ABLEAU 3.7. RESULTAT DE SYNTHESE DU BLOC DE DEMULTIPLEXAGE V-BLAST 55

ABLEAU 3.8. TABLE DES PARAMETRES ENTREES/SORTIES DU BLOC IFFT 58

ABLEAU 3.9. RESULTAT DE SYNTHESE DU BLOC IFFT 59

ABLEAU 3.10. RESULTAT DE SYNTHESE DU BLOC P/S + 59

ABLEAU 3.11. RESULTAT DE SYNTHESE DU BLOC S/P - 61

ABLEAU 3.12. TABLE DES PARAMETRES ENTREES/SORTIES DU BLOC FFT 62

ABLEAU 3.13. RESULTAT DE SYNTHESE DU BLOC IFFT 62

ABLEAU 3.14. RESULTAT DE SYNTHESE DU BLOC CALCULATEUR UTILISE POUR LE BLOC EGALISEUR 67

ABLEAU 3.15. TABLE DES PARAMETRES ENTREES/SORTIES DU BLOC EGALISEUR MULTI-UTILISATEURS 67

ABLEAU 3.16. TABLE DES PARAMETRES ENTREES/SORTIES DU BLOC MULTIPLEXEUR SPATIAL 69

ABLEAU 3.17. RESULTAT DE SYNTHESE DU BLOC-BLOC CALCULATEUR UTILISE POUR LE BLOC MULTIPLEXEUR SPATIAL 69
ABLEAU 3.19. RESULTAT DE SYNTHESE DU BLOC-BLOC CALCULATEUR UTILISE POUR LE BLOC QUANTIFICATEUR

70

ABLEAU 3.20. TABLE DES PARAMETRES ENTREES/SORTIES DU BLOC DEMODULATION 71

ABLEAU 3.21. RESULTAT DE SYNTHESE DU BLOC-BLOC CALCULATEUR UTILISE POUR LE BLOC DEMODULATION 71

LISTE DES ABREVIATIONS

Dans ce rapport, plusieurs abréviations sont utilisées. On les rappelle maintenant et on donne leurs

significations :

ALM Adaptive Logic Module

ASK Amplitude Shift Keying

BBAG Bruit Blanc Additif Gaussien

BLAST Bell Labs Layered Space-Time

BPSK Binary Phase Shift Keying

CDMA Code Division Multiple Access

D-BLAST Diagonal Bell Labs Layered Space-Time

DFT Discret Fourier Transform

DS-CDMA Direct Sequence Code Division Multiple Access

DSP Digital Signal Processing

FDMA Frequency Division Multiple Access

FFT Fast Fourier Transform

FH-CDMA Frequency Hopping Code Division Multiple Access

FHT Fast Hadamard Transform

FPGA Field Programmable Gate Array

IDFT Inverse Discret Fourier Transform

IFFT Inverse Fast Fourier Transform

IFHT Inverse Fast Hadamard Transform

IP Intellectual Property

LUT Look-U p Table

MC-CDMA Multi-Carrier Code Division Multiple Access

MIMO Multiple Input Multiple Output

MMSE Minimal Mean Square Error

MUD Multi-User Detection

OFDM Orthogonal Frequency Division Multiplex

PIC Parallel Interference Cancellation

PLL Phase Looked Loop

PSK Phase Shift Keying

QAM Quadrature Amplitude Modulation

QPSK Quadrature Phase Shift Keying

RAM Random Access Memory

RIF Réponse Impulsionnelle Finie

RII Réponse Impulsionnelle Infinie

RSB Rapport Signal à Bruit

RTL Register Transfer Level

SIC Successive Interference Cancellation

SNR Signal to Noise Ratio

ST Space-Time

SUD Single User Detection

TDMA Time Division Multiple Access

TEB Taux d'Erreur Binaire

V-BLAST Vertical Bell Labs Layered Space-Time

VHDL Very high speed integrated circuit Hardware Description Language

ZF Zero Forcing

LISTE DES NOTATIONS

On regroupe ci-dessous les principales notations utilisées dans les différents chapitres du rapport.

(.)^T Transposition

(.)† ou (.)* Transconjugaison

(.)^-1 Inversion

Norme euclidienne du vecteur x

Trace(X) Trace de la matrice X

IM Identitée de taille M

Produit de Kronecker

Re(.) Partie réelle

Im(.) Partie Imaginaire

1

2

INTRODUCTION GENERALE

Les techniques de transmissions numériques sans fil connaissent depuis quelques années une grande révolution. Cette révolution vient d'une part de la demande croissante en matière de télécommunication et en matière d'échange de données tout en bénéficiant des nouveaux services tels que la télévision, la radio numérique, les réseaux locaux sans fil, l'Internet à haut débit, la téléphonie mobile et beaucoup d'autres applications multimédias. D'autre part, les concepteurs des systèmes de transmission sans fil cherchent à optimiser la qualité de service et à surmonter les problèmes rencontrés lors de la conception et de la mise en oeuvre de leurs systèmes.

La révolution en transmission numérique sans fil se manifeste dans l'émergence de plusieurs nouvelles technologies permettant d'augmenter considérablement les débits de transmission et d'améliorer la qualité de transmission. Parmi ces technologies, on a choisi pour notre étude la technologie MIMO (Multiple Input Multiple Output) et la technologie MC-CDMA (Multi-Carrier Code Division Multiple Access).

La technologie MIMO présente une solution prometteuse pour augmenter l'efficacité spectrale et en transmettant les données à travers un réseau multi-antennes en émission et en réception. En effet, elle offre un débit important et une bonne qualité de transmission grâce à la diversité spatiale. Cependant, une source importante de dégradation des performances dans les systèmes MIMO est la sélectivité fréquentielle du canal. Les techniques basées sur L'OFDM sont des solutions prometteuses pour combattre cette sélectivité. En effet, la modulation OFDM transforme un canal sélectif en fréquence en plusieurs sous-canaux non sélectifs en fréquences.

La technique MC-CDMA correspond à la combinaison entre la technique d'accès CDMA et la modulation OFDM où l'étalement des données est effectué dans le domaine fréquentiel. La technique d'accès CDMA permet à plusieurs utilisateurs de partager le même canal radio en même temps et à la même fréquence tout en assurant la séparation de leurs données grâce à l'utilisation de codes d'étalement orthogonaux.

L'objectif de ce projet de fin d'études est d'étudier et d'implémenter un système sans fil utilisant la technique MIMO associée à la technique MC-CDMA afin d'associer les avantages de ces deux techniques dans un seul système qu'on appellera MIMO-MC-CDMA.

On commence par évaluer les performances de la chaîne MIMO-MC-CDMA en utilisant l'outil de
calcul et de simulation Matlab. Ensuite, on propose une architecture des différentes composantes de
toute la chaîne. Par ailleurs, cette chaîne est implantée sur une architecture matérielle

reconfigurable à base de FPGAs afin de fournir les résultats de synthèse au niveau RTL et d'évaluer les performances de l'architecture proposée en termes de complexité et de rapidité.

A TELNET, le développement des IPs reconfigurables et réutilisables est basé sur une méthodologie de conception basée sur une plateforme de prototypage sur une architecture cible à base de FPGA de technologie Altera. D'ailleurs, la plateforme matérielle et son outil de conception et de synthèse sont munis d'une technique d'optimisation de performances du système grâce à l'architecture des ressources internes du FPGA.

Dans le premier chapitre, on commencera par rappeler les notions essentielles sur les systèmes de transmission numérique. On rappellera également les caractéristiques du canal radio-mobile. Puis, on présentera le principe de la modulation OFDM et les principales techniques d'accès multiples utilisées dans les systèmes de télécommunications. On s'intéressera plus particulièrement à la technique d'accès CDMA pour présenter par la suite la technique MC-CDMA.

Dans le deuxième chapitre, on présentera d'abord les principales techniques de diversité. Puis, on présentera un état de l'art des systèmes MIMO qui permettent d'exploiter la diversité spatiale. On détaillera et on évaluera les performances du multiplexage spatial qu'on a choisi pour la suite de notre étude. Dans une dernière partie du chapitre, on étudiera et on évaluera les performances de l'association de la technique du multiplexage spatial et de la technique MC-CDMA.

Dans le troisième chapitre, on commencera par présenter les principaux composants de l'architecture interne du circuit FPGA cible Stratix.II.GX de la technologie Altera. Puis, on expliquera le flot de conception et l'environnement de synthèse adopté dans les conceptions matérielles. Ensuite, on s'intéressera à décrire les architectures proposées des différents modules du système MIMO-MCCDMA. Par ailleurs, on présentera les résultats de synthèse niveau RTL et on analysera les performances de l'architecture proposée en terme d'utilisation de ressources internes et en termes de rapidité.

Finalement, les conclusions des différents travaux effectués dans ce projet ainsi que quelques perspectives possibles seront données dans un chapitre final.

3

4

5

6

Chapitre 1

La Technique MC-CDMA

1. Introduction

Pour développer les objectifs de ce projet de fin d'études, on rappelle dans ce chapitre quelques notions essentielles dans la communication numérique, les problèmes rencontrés dans la transmission sur un canal radio, et les techniques utilisées pour assurer une bonne qualité de transmission avec le minimum d'erreur.

Tout d'abord, on rappelle dans ce chapitre les différents éléments de base d'une chaîne de transmission numérique. Puis, on présente les problèmes généralement rencontrés dans les systèmes de transmission radio-mobiles. Ensuite, on rappelle le principe de la modulation OFDM permettant de transformer un canal sélectif en fréquence en de multiples canaux non séléctifs en fréquence. On rappelle également la technique d'accès multiple à répartition par codes (CDMA) pour présenter par la suite la technique qui combine entre la technique d'accès CDMA et la modulation OFDM : la technique MC-CDMA.

2. Les composantes de base d'une chaîne de transmission numérique

Les systèmes de transmission numériques véhiculent de l'information (son, image, texte, ...) entre une source et un destinataire. L'information transmise est représentée sous une forme numérique afin de pouvoir la traiter dans les systèmes numériques. A partir de la source, elle traverse un milieu appelé canal de transmission pour atteindre le destinataire. Les canaux de transmission utilisés dans les systèmes de transmission numériques dépendent principalement de l'application de la transmission à établir. En effet, un canal de transmission peut être le câble, la fibre optique, le canal radioélectrique, etc. Lors d'une transmission numérique, le canal introduit une altération aux données transmises.

Dans cette partie, on décrit le fonctionnement d'une chaîne de transmission numérique, de la source d'information binaire au destinataire, par les étapes successives de codage, de transmission dans un canal physique et de décodage. Comme on privilège dans notre étude les transmissions hertziennes, on ne présentera que les canaux à évanouissements.

La figure 1.1 résume l'ensemble des composantes de base d'une chaîne de transmission numérique.

Figure 1.1. Composantes de base d'une chaîne de transmission

2.1. Le codeur et le décodeur de canal

Le rôle principal du codeur et du décodeur de canal est de minimiser les erreurs introduites par le canal de transmission. Le codeur de canal utilisé à l'émission ajoute aux informations numériques à transmettre des bits de redondances pour permettre au récepteur de détecter et corriger les erreurs de la transmission.

A la réception, le décodeur de canal doit avoir la structure adaptée au codeur de canal utilisé à l'émission. Il doit aussi comporter un caractère correcteur d'erreur permettent de retrouver les données transmises avant le codage avec le minimum d'erreurs.

Dans ce travail, on a choisi d'utiliser comme codeur de canal le codeur convolutif. En effet, ce codeur est le plus utilisé dans les systèmes de télécommunication mobiles. Le principe de ce codeur consiste à calculer chaque bloc de n éléments binaires en sortie en fonction de k éléments présents à son entrée et des m blocs présents précédemment. La quantité m+1 s'appelle longueur de contrainte du codeur [2]. La figure 1.2 illustre un codeur convolutif avec une entrée k=1, 2 sorties n=2 et de longueur de contrainte m+1=3. Le rendement de ce codeur défini par k/n est égal à1/2.

Figure 1.2. Codeur convolutif (k=1,n=3 et (m+1)=3)

Les sorties de ce codeur s'écrivent en fonction des bits d'entrée comme suit :

s1 n = b_n + _bn-1 + bn-2 , (1.1)

et

s2 n = b_n + bn-1 . (1.2)

Les calculs se font en modulo 2. Les bits _bn-1 ^et _bn-2 sont stockés dans les registres à décalages du codeur.

A la réception, on décode les séquences reçues par l'algorithme de viterbi. Cet algorithme prend à l'entrée les bits issus du bloc de démodulation. En utilisant un treillis construit à partir des paramètres du codeur convolutif, le décodeur cherche la séquence binaire la plus vraisemblable (c'est-à-dire il minimise la distance euclidienne entre le signal reçu et le signal supposé émis d'information).

2.2. La modulation/démodulation numérique

La composante de la modulation numérique consiste à étiqueter les symboles avec les bits d'information. Supposons que chaque mot-code contient m bits, alors le débit de symboles D_s est alors égal à :

1

D_s =

m

Db , (1.3)

où Db est le débit des éléments binaires.

La modulation de chaque mot-code de m bits peut générer M=2^m symboles différents. L'ensemble de ces symboles forme une constellation caractéristique en fonction de la modulation utilisée.

Au bloc de démodulation, le symbole reçu est altéré par l'évanouissement du canal et du bruit. Son processus de quantification consiste donc à partitionner la constellation du modulateur en des zones de décision. Les seuils de ces zones sont indiqués par des traits discontinus dans les figures qui présenteront les trois principaux types de modulation (figure 1.3, 1.5 et 1.6)

2.2.1. Modulation à déplacement d'amplitude ASK (Amplitude Shift Keying)

La constellation de la modulation ASK est une droite qui contient M points répartis de la manière
illustrée dans la figure 1.3. La répartition des mots-codes sur une constellation M-ASK est souhaitable

qu'elle soit de telle sorte qu'il y a une différence d'un seul bit entre deux mots codes voisins. Cette répartition est semblable au codage de Grey. Par exemple, la constellation d'une modulation 8-ASK est représentée dans la figure 1.4.

Figure 1.3. Constellation de la modulation M-ASK

Figure 1.4. Constellation de la modulation 8-ASK

2.2.2. Modulation à déplacement de phase PSK (Phase Shift Keying)

(2 1)

k

La constellation de la modulation M-PSK est un cercle de rayon A qui contient M points répartis de la manière suivante :

0

c_k A e

. ^M , (1.4)

pour k=0, 1, ..., M-1, où ₀ est la phase du premier symbole de la constellation.

Les symboles obtenus d'une modulation PSK sont des symboles complexes de mêmes modules mais de phases différentes. La figure 1.5 illustre les modulations 2-PSK, 4-PSK et 8-PSK en utilisant le codage de Gray pour assigner les mots-codes aux symboles.

2.2.3. Modulation d'amplitude en quadrature QAM (Quadrature Amplitude Modulation)

La constellation de la modulation QAM se compose de deux axes dont le premier désigne la partie réelle du symbole et le second désigne sa partie imaginaire. Chaque axe est semblable à une modulation ASK de mots-codes de m bits. Alors, la constellation formée par les deux axes est un modulateurs de mots-codes de 2m bits. Le symbole délivré d'un modulateur est de la forme :

ckakj.bk, (1.5)

où ak et bk sont obtenus des alphabets {#177;1, #177;3, ..., #177;(M-1)} avec M=2^m.

Un exemple de constellation M-QAM, avec M=16, est présenté dans la figure 1.6.

7

Figure 1.5. Constellation des modulations BPSK, QPSK et 8-PSK

Figure 1.6. Constellation de 16-QAM utilisant le codage de Grey C'est la modulation QAM qu'on a choisie pour la suite de notre étude.

3. Le canal radio-mobile

3.1. Effet multi-trajet d'un canal radio

Lors d'une transmission à travers un canal radio entre un émetteur et un récepteur, le signal émis se propage dans plusieurs directions du milieu radio et parvient au récepteur sur des chemins différents [3]. En effet, au moment de la propagation du signal, des phénomènes impliquant la multiplicité des chemins interviennent généralement sous trois formes :

- La réflexion : lorsque l'onde électromagnétique du signal rencontre dans sa direction une

surface lisse dont les dimensions sont grandes par rapport à la longueur d'onde du signal.

- La diffusion : lorsque l'onde électromagnétique du signal entre en collision avec une surface

dont les dimensions sont de l'ordre de la longueur d'onde du signal. Ce phénomène engendre la diffusion de l'onde dans plusieurs directions.

- La diffraction : lorsque l'onde électromagnétique heurte une arête d'un corps volumineux

dont les dimensions sont grandes par rapport à la longueur d'onde du signal. Ce phénomène cause l'apparition d'ondes secondaires.

Ces phénomènes sont représentés dans la figure 1.7.

Figure 1.7. Modélisation du phénomène de trajets multiples

L'avantage de ce phénomène de propagation multi-trajets est qu'il assure une certaine continuité de la couverture radio en permettant la communication dans le cas où l'émetteur et le récepteur ne sont pas en vue directe. Néanmoins, cette multiplicité de trajets engendre des difficultés au niveau du récepteur. En fait, le signal reçu est une combinaison de plusieurs répliques du signal émis avec des amplitudes, des phases et des temps d'arrivées différents.

Les évanouissements d'un canal multi-trajets sont classifiés en trois types :

- Les évanouissements à grande échelle : ils traduisent l'atténuation de la puissance du signal

en fonction de la distance qui sépare l'émetteur du récepteur.

- Les évanouissements à moyenne échelle : ils traduisent l'atténuation du signal transmis à

cause des obstacles rencontrés. Ces évanouissements sont appelés aussi l'effet de masques.

- Les évanouissements à petite échelle : ils traduisent le changement rapide de l'amplitude et

de la phase du signal reçu causé par l'addition constructive ou destructive des interférences sur les différents trajets.

3.2. Etalement temporel

On a vu que dans un système radio-mobile, le récepteur reçoit le signal émis sur plusieurs répliques
avec des retards différents. L'étalement temporel T_m est le temps qui sépare l'arrivée du premier
trajet de l'arrivée du dernier trajet [4]. Son inverse est en général du même ordre que la bande de

cohérence du canal :

1 T m

~ , sachant que la bande de cohérence d'un canal Bc correspond à la B c

9

gamme de fréquences sur laquelle les amplitudes des composantes fréquentielles du signal subissent des atténuations semblables.

Soit B_s la largeur de la bande du signal transmis. Si B_s « B _c alors toutes les amplitudes des

composantes fréquentielles du signal transmis subissent des atténuations semblables. Dans ce cas, le canal est dit non sélectif en fréquence. Dans le cas contraire, les amplitudes des composantes fréquentielles du signal subissent des atténuations différentes, et le canal est dit sélectif en fréquence et on a un phénomène d'interférences entre symboles. Pour éviter ce problème d'interférences entre les symboles, on essaie en pratique de rendre la largeur de bande du signal très petite par rapport à la bande de cohérence du canal.

3.3. Etalement fréquentiel : effet Doppler

Dans le cas où l'émetteur et le récepteur sont en mouvement relatif avec une vitesse radiale y constante, la fréquence du signal reçu subit un décalage constant proportionnel à cette vitesse y et à la fréquence porteuse: il s'agit de l'effet Doppler [4]. L'étalement fréquentiel fd est la différence entre le plus grand et le plus petit décalage en fréquence des différents trajets. Son inverse est en

général du même ordre que le temps de cohérence du canal : f 1 ~, sachant que le temps de

T c

d

cohérence d'un canal T_c est la durée pendant laquelle le canal ne varie pas (c'est-à-dire que les distorsions temporelles du canal sont négligeables).

Si le temps de cohérence d'un canal est très grand par rapport au temps d'un symbole émis, le canal est dit à évanouissements lents. Dans le cas contraire, le canal est dit à évanouissements rapides.

Ainsi, pour que le canal soit non sélectif en fréquence et à évanouissements lents, il faut que la durée des symboles émis vérifie la relation suivante :

T m « T s « T c , (1.6)

où T_s est la durée de transmission d'un symbole.

3.4. Modélisation du canal à évanouissements lents

On considère dans la suite de l'étude que le canal subit des évanouissements lents. Le signal équivalent en bande de base reçu à la sortie de ce canal comportant N trajets multiples s'exprime alors par :

N 1

r t

( )( ) ( ) (1.7)

n n

s t b t ,

n 0

où b(t) est le bruit blanc additif gaussien (BBAG) complexe de variance N0, et _n et _n désignent respectivement l'atténuation complexe et le retard du signal pour chaque trajet n, n=0, 1, ..., N-1.

Le nombre de trajets N emprunté par un même signal est généralement énorme. Le théorème de la limite centrale permet de regrouper les N trajets en L paquets [5]. Chaque paquet a une atténuation complexe résultante _l et un retard moyen l. L'expression du signal reçu devient alors :

L 1

r t

( )( ) ( ) . (1.8)

l l

s t b t

l 0

1

Ainsi, le signal échantillonné au rythme symbole

reçu à l'instant k s'écrit :

T_S

L 1

r r kT

( ) _l (1.9)

k S l k k

s b

l 0

L'atténuation complexe lpeut être exprimée par un module et une phase comme suit :

l hle i l, (1.10)

où _l est une variable aléatoire de loi uniforme sur [0,2] et hl est une variable aléatoire qui suit la loi de Rayleigh dans le cas où on considère qu'il n'y a pas un trajet direct entre l'émetteur et le récepteur. Si on considère qu'il y a un trajet direct entre l'émetteur et le récepteur, hl suit alors la loi de Rice [1].

On rappelle que les densités de probabilité des lois de Rayleigh et de Rice sont de la forme :

x 2

x 2

p x e

( ) 2 2 , (1.11)

Rayleigh

10

_x22

et

x x 2 p x e I ( ) 2 0 ( 2 ) 2 ^Rioe

, (1.12)

où ² est la variance de hl, est un paramètre de non-centralité dû au trajet direct et I0(x) est la fonction de Bessel modifiée d'ordre 0.

4. La modulation OFDM

Pour une transmission numérique mono-porteuse, la transmission d'un symbole ne pourrait être parfaite (sans interférences entre symboles) que si :

T_m« T_s . (1.13)

D'où, pour une transmission mono-porteuse, le débit de transmission est limité par le délai de propagation dans le canal [6].

Pour surmonter ce problème, la modulation OFDM intervient comme une technique simple et efficace pour améliorer le débit de transmission tout en évitant l'interférence entre symboles.

L'idée de la modulation OFDM est de subdiviser la bande de transmission en plusieurs sous canaux qui permettent la transmission en parallèle. Les données sont converties en sous-flux parallèles dans le but de les moduler sur des sous-porteuses correspondantes aux sous-canaux à bande réduite.

4.1. Principe de l'OFDM

Soit une séquence de L_c symboles x_n, n=0, 1, ..., L_c-1. Chaque symbole x_n module un signal à fréquence f_n. Soit T0 la durée d'un symbole OFDM. Le signal OFDM, pendant l'intervalle [0, T0[ s'écrit :

L c 1

où

s(t)=

n

0

2 . . j n f t x e ^n , n

(1.14)

f_n = f0+n. F (1.15)

avec F est l'espacement entre deux fréquences voisines.

1 2 j n t T Si F=1/T0 alors le produit scalaire de 0 e

1 2 j k t avec T 0 edonne :

1 1 1 1

j n t j k t T j n t j k t j n k t

1 1 1

2 2 T 2 ( ) T si n k

1

2 2

(1.16)

0 T T 0

0 0 0 ⁰ e dt

0

e e

T T

, e e dt

T0 T0 0 si n k

0 0

11

D'où le multiplexage des symboles est orthogonal si : F=1/T0.

Le signal s(t) s'écrit alors :

L c j

1 2

s(t)= 0 0

e x e

2 j f t T

n

. (1.17)

nt

L_c

T 0

n 0

En terme de débit, l'OFDM est équivalent à une modulation mono-porteuse utilisant la bande W=

et une durée symbole T1= T 0 L c

. L'avantage de l'OFDM par rapport à la modulation mono-porteuse est

qu'elle est beaucoup moins sensible pour un canal sélectif en fréquence [6] puisqu'elle consiste à envoyer les symboles sur des sous-canaux de largeur F au lieu d'envoyer sur une bande de largeur W.

4.2. Modulation par la Transformée de Fourier Discrète DFT

La modulation OFDM peut être implémentée aisément. En effet, lorsqu'on échantillonne le signal OFDM s(t) à la cadence d'échantillonnage T_e= T0/L_c, on obtient l'écriture suivante :

sk=s(kTe)=

nk L j 1 2 c L c x e , pour k=0,1,...,Lc-1. (1.18) n

n 0

Cette expression correspond à la Transformée de Fourier Discrète Inverse (IDFT) d'ordre L_c de la séquence de symboles x_n [7].

La démodulation est effectuée par une transformée de Fourier discrète (DFT) :

nk

N j

1 2

L c

s e (1.19)

n

L 0

ck=DFT{s(n)}=

1

_cn

12

4.3. Introduction de l'intervalle de garde en OFDM

Généralement, dans une transmission OFDM, le canal est dispersif et son effet mémoire gène la transmission. En effet, ce phénomène cause l'interférence entre les symboles. Pour cela, chaque symbole OFDM est prolongé par un intervalle de garde appelé aussi "extension cyclique".

L'extension cyclique consiste à répéter au début d'un symbole OFDM de taille L_c, les L dernières symboles du bloc [7]. D'où la taille du symbole OFDM devient égale à L_c+L symboles.

La longueur de l'intervalle de garde doit être plus grande que le plus grand des retards du canal. Dans la plupart des cas, L est pris égal à L_c/4.

13

Les symboles OFDM émis sont représentés selon le schéma de la figure 1.8.

Figure 1.8. Introduction de l'intervalle de garde au symbole OFDM transmis

En réception, l'intervalle de garde de chaque bloc reçu est écarté afin de récupérer le bloc contenant les L_c symboles désirés pour les traiter dans les différentes composantes de la chaîne de réception.

L'expression du symbole OFDM reçu est égale à :

rk=	nk L j 1 2 c hxe b L c , (1.20) n n n

n0

où h_n est la réponse fréquentielle du canal relative à la ^nième sous-porteuse ~,, et b_n est un BBAG introduit au symbole OFDM pour la ^nième sous-porteuse. D'où la démodulation de ce symbole est obtenue par le calcul de la DFT de rk. Ainsi, on peut constater qu'une chaîne d'émission et de réception d'un système OFDM peut être représentée par le schéma de la figure 1.9.

Figure 1.9. Chaîne d'émission et de réception du modulateur OFDM

5. Les techniques d'accès multiple

L'objectif des communications mobiles est de permettre la connexion d'un grand nombre d'utilisateurs au canal et par suite à l'infrastructure du réseau. Pour cela, il existe des techniques d'accès multiples à travers lesquels un grand nombre d'utilisateurs partagent un canal de communication commun pour transmettre leurs informations au récepteur. Ces techniques se basent essentiellement sur la séparation des signaux des différents utilisateurs.

Trois techniques d'accès multiples sont généralement employées dans les systèmes de communication [8].

5.1. Accès multiple à répartition par temps

Dans la technique TDMA (Time Division Multiple Access), le temps est divisé en trames (figure1.10). Chaque trame est divisée en time slots (TS). Dans chaque timeslot, un utilisateur peut transmettre ses données. Donc, n utilisateurs peuvent transmettre leurs données pendant une trame. L'avantage de cette technique est que plusieurs utilisateurs peuvent communiquer utilisant une seule bande de fréquence.

5.2. Accès multiple à répartition par fréquence

Dans la technique FDMA (Frequency Division Multiple Access), la bande accessible au canal est divisée en sous-bandes (figure 1.11). Chaque utilisateur utilise une sous-bande pour transmettre ses données. L'avantage de cette technique réside dans la possibilité de plusieurs utilisateurs d'entrer en communication en même temps mais en utilisant des sous bandes différentes.

5.3. Accès multiple à répartition par code

Dans la technique CDMA (Code Division Multiple Access), chaque utilisateur possède un code unique par lequel ses informations son codées. La séparation des utilisateurs est donc assurée par la distinction de leurs codes utilisés. L'avantage de la technique CDMA est qu'elle permet la communication des différents utilisateurs au même temps et à la même fréquence (figure 1.12).

Figure 1.10. La technique TDMA

Figure 1.11. La technique FDMA

Figure 1.12. La technique CDMA

14

Dans la suite du projet de fin d'études, on adoptera la technique CDMA dans l'étude et dans l'implémentation car cette technique présente une complexité d'implémentation plus simple par rapport aux techniques TDMA et FDMA. De même, cette technique simplifie la planification du partage du canal.

15

6. La technique CDMA

L'accès multiple à répartition par code ou CDMA est une technique qui permet à plusieurs d'utiliser utilisent la même bande de fréquence en même temps. L'élément principal du CDMA est la technique d'étalement du spectre qui transforme un signal en bande étroite en un signal à bande plus large que celle nécessaire au transfert de données [6].

6.1. Principe du CDMA

Dans un système CDMA, le signal provenant de chaque utilisateur est étalé par son propre code d'étalement puis transmis à travers le canal radio. A la réception, le signal reçu est désétalé par le même code d'étalement utilisé à l'émission afin de récupérer les données initialement transmises.

La technique d'étalement en CDMA est utilisée par différentes méthodes. Les méthodes les plus généralement utilisées sont : DS-CDMA et FH-CDMA. On s'intéresse dans ce projet à l'étalement par séquences directes DS-CDMA. La figure 1.13 montre un exemple d'étalement par séquence directe (DS-CDMA). Il s'effectue par un produit entre le signal en bande de base et une séquence d'étalement 8 fois plus rapide que le flot de données.

Figure 1.13. Etalement par séquences directes
Soit T_s la durée d'un symbole de données et T_c la durée d'un chip de la séquence d'étalement. Le

rapport N= T s T c

est appelé le facteur d'étalement car d'une part il s'agit de la multiplication du signal

par le code d'étalement. D'autre part, la bande du signal étalé est élargie d'un rapport égal au facteur d'étalement par rapport au signal non étalé.

Les codes d'étalement utilisés en CDMA, sont choisis en fonction de la situation et de l'application appropriées du système. Il existe plusieurs codes qui sont utilisés dans les systèmes de télécommunication utilisant la technique CDMA, tels que les codes de Walsh-Hadamard, les codes Gold, les codes Kasami, les codes Barker, etc [6]. Dans cette étude, on n'utilisera que les séquences

H H

de Walsh Hadamard. Ces codes sont obtenus d'après la matrice de Hadamard qui, pour un ordre N, s'écrit par la relation récursive suivante :

H_N

N N

2 2

(1.21)

H H

2 2

N N

sachant que H1 = 1.

Par exemple, la matrice de Hadamard à l'ordre 4 s'écrit : 1 1 1 1 1 1 1 1 H 4 1 1 1 1 1 1 1 1

(1.22)

On peut diviser les codes par un facteur de normalisation qui est fonction de leurs longueurs. On obtient les colonnes d'étalement relatives à la matrice CN tel que

1

CN=

N

H . (1.23)

N

16

L'avantage majeur des codes de Walsh-Hadamard est que les codes sont deux à deux orthogonaux :

( ) ( ) 1

i j si ij

c c (1.24)

,

0 sinon

6.2. Modélisation du système CDMA

On suppose qu'on a N_u utilisateurs qui vont envoyer leurs données en utilisant la même ressource

radio. Soit ( i )

d_k le k^éme symbole émis par l'utilisateur i. Chaque symbole émis par l'utilisateur i au

débit T_s à l'instant k est étalé en utilisant une séquence c⁽ⁱ⁾=(c⁽ⁱ⁾(0), ..., c⁽ⁱ⁾(N-1)). Cette séquence est émise à un rythme chip 1/T_c. Pour le cas d'un utilisateur i, le signal émis au rythme chip 1/T_c s'écrit alors :

x n k ( ) ( ) ( ) i i i c n d k ,

, pour n=0,...,N-1. (1.25)

Le signal reçu échantillonné au rythme chip 1/T_c est donné par :

N u

1 N 1

u

r hxb h c d b

( ) ( ) ( ) ( ) ( )

i i i i i

n k n k n k n k n k n k n k , (1.26)

, , , , , ,

i0 i0

17

où _bn,k est un bruit BBAG complexe de variance N0 et ( )

h n k le coefficient du canal relatif à l'utilisateur i.

i
,

Dans un canal radio-mobile, l'interférence d'accès multiple limite la capacité du système CDMA. Ce problème a donné naissance à plusieurs travaux de recherches évoqués sous le nom "Détection multi-utilisateurs" [7]. Cette méthode de détection sera développée dans le paragraphe suivant lorsqu'on associe la technique CDMA à la modulation OFDM.

7. La technique CDMA associée à la modulation multiporteuses

Plusieurs techniques ont été réalisées dans la littérature pour associer l'OFDM comme technique de modulation et le CDMA comme technique d'accès permettant d'obtenir de très bonnes performances dans le cas de transmissions sur des canaux sélectifs en fréquence. En effet, cette association permet de tirer profit de la robustesse et de l'efficacité spectrale de la modulation OFDM tout en bénéficiant de la souplesse offerte par l'accès multiple à répartition par code. Parmi les techniques, on peut citer MC-DS-CDMA [9], MT-CDMA [10] et MC-CDMA [11]-[12].

Dans les schémas MT-CDMA et MC-DS-CDMA, l'étalement est effectué dans le domaine temporel. Par contre, dans la technique MC-CDMA, au lieu d'appliquer les séquences d'étalement dans le domaine temporel, on les applique dans le domaine fréquentiel en projetant chaque élément (chip) de la séquence d'étalement à une sous-porteuse OFDM à un débit identique au débit initial des données avant étalement.

Prasad et Hara montrent que la technique MC-CDMA est la plus performante sur liaison descendante [13]. Cela justifie notre choix de cette technique pour l'association de l'OFDM et du CDMA.

Dans la suite, on notera N_u le nombre d'utilisateurs et N la longueur des codes d'étalement.

7.1. Partie émettrice

Les données de chaque utilisateur i sont étalées par le code d'étalement qui lui correspond. Les symboles étalés alimentent par la suite la modulation OFDM (figure 1.14). Le nombre de sous- porteuses de la modulation est généralement égal à un multiple de longueur N des codes d'étalement. On suppose dans notre étude que ce nombre est égal à L_c=N. L'étalement de la donnée

d_k relative au ^iième utilisateur par le code d'étalement c⁽ⁱ⁾ engendre la séquence suivante :

( i )

x n k

( ) ( ) ( )

i i i

c _n d k , pour 0=n= L_c-1. (1.27)

,

18

Figure 1.14. Circuit d'émission pour un utilisateur de la technique MC-CDMA

Cette séquence est introduite dans le modulateur OFDM comportant L_c sous-porteuses. D'après le paragraphe 4.2, le k^ème échantillon du symbole OFDM obtenu relatif au ^iième utilisateur s'exprime par :

L nk

1 2

c j

s xe

( ) ( )

i L

i ^c, 0=k= L_c-1. (1.28)

k n k

,

n0

En remplaçant, ( )

x n k par son expression (1.27), on obtient :

i
,

L12 nk c j

s c d e

( ) ( ) ( )

i i i L c, pour 0=k= L_c-1 (1.29)

k n k

n 0

Dans le cas où les N_u données des N_u utilisateurs sont émises simultanément, elle sont étalées de la manière suivante :

_u

x c d

( ) ( )

i i , pour 0=n= L_c-1. (1.30)

n k n k

,

i 1

Cette équation peut être mise sous une forme matricielle comme suit :

xk=C.dk (1.31)

où _xk=[x0,k, ..., xLc-1,k]^T, dk=[ ⁽⁰⁾

d_k , ..., ( _u 1 )

dk ]^T le vecteur de symboles complexes, et C=[c⁽⁰⁾, ..., c(Nu-1)]

est la matrice des codes d'étalement des utilisateurs de taille _LcxNu avec c⁽ⁱ⁾ est le code d'étalement propre au ^iième utilisateur.

Après étalement, la séquence xk est passée par la modulation OFDM. Le symbole modulé obtenu est :

L j L ~ nk

1 2 1 1

nk

c c u 2 j

s x e c d e

L ( ) ( )

i i L

c ^c , pour 0=k=L_c-1 (1.32)

k n k

, n k

n n i

0 0 0

19

7.2. Partie réceptrice

On suppose que le nombre de sous-porteuses est suffisamment grand pour pouvoir supposer que le canal est constant pendant la durée d'un symbole OFDM. On peut considérer également que le canal de chaque sous-porteuse est plat et donc que l'interférence entre symboles est supprimée par un choix adéquat de l'intervalle de garde (paragraphe 4.3). L'évanouissement du canal au niveau de chaque sous-porteuse n peut alors être modélisé par un gain complexe h_n.

Au niveau du récepteur, le k^ème symbole reçu au niveau de la ^nième sous-porteuse est de la forme :

Nu1 Nu1

r h xb h d c b h x b

( )

i ( ) ( )

i i

n k n n k n k n k n n k n n k n k , pour n=0,...,L_c-1 (1.33)

, , , , , ,

i

0 i0

où h_n et b_n sont respectivement la réponse du canal et le bruit complexe BBAG au niveau de la nième sous-porteuse.

Le vecteur des symboles reçus r de longueur L_c sur les L_c sous-porteuses est donné par :

N 1 u h x ( ) i 0 0, k r b h x b ? 0 0, 0 k i 0, 0 k 0, 0, k k ? ? ? ? ? ? ? ? N 1 u r L k 1, ( ) 1 1, 1, 0 ? L k 1, c c c c c h x i L L k L k b h x b L L k c c 1 1, i0

. (1.34)

Ce qui donne alors :

rk=H.xk+bk, (1.35)

où _rk=[r0,k, ..., rLc-1,k] T est le vecteur des symboles reçus de longueur L_c, H=diag(h_n ; 0=n= L_c-1) est une matrice diagonale de taille L_cxL_c, chaque élément de la diagonale h_n correspond à la réponse fréquentielle du canal pour chaque sous-porteuse, _bk=[b0,k, ..., _bLc-1,k]T est le vecteur bruit complexe BBAG sur les L_c porteuses.

La détection des données du i^ème utilisateur se fait comme suit :

L_c

à

1

d cg r

( ) ( )

i i

k n n n k , (1.36)

,

n 0

où g_n est l'inverse du gain du canal estimé pour la n^ème sous-porteuse.

Plusieurs méthodes ont été proposées dans la littérature pour déterminer les coefficients g_n [7]. On présente dans le paragraphe suivant les techniques de détection mono-utilisateur, i.e. aucune connaissance des codes d'étalement des autres utilisateurs n'est nécessaire. Nous présentons également le principe de la détection multi-utilisateurs.

Figure 1.15. Circuit de réception pour un utilisateur de la technique MC-CDMA

7.3. Les techniques de détection en MC-CDMA

Dans ce paragraphe, on présente des techniques de détection possibles en MC-CDMA. 7.3.1. Détection mono-utilisateur

Au niveau du récepteur, la donnée du ^iième utilisateur est détectée indépendamment des données des autres utilisateurs. On rappelle que la décision sur le k^ème symbole du i^ème utilisateur se fait de la manière suivante :

L_c

à

1

d c g r

( ) ( )

i ⁱ (1.37)

k n n n k

,

n 0

Les méthodes généralement utilisées pour le calcul de g_n dans le cas d'une détection monoutilisateur sont :

- Egalisation avec critère de forçage à zéro (ZF) :

*

2

h_n

h_n

(1.38)

g n

1

h L

*

n c

2

(1.39)

g n

h_n

N SNR

u

20

- Egalisation avec critère de minimisation de l'erreur quadratique moyenne (MMSE) :

21

22

où d

S~Rest le rapport signal su bruit qui est défini par le rapport de la variance du signal sur la

2 n

variance du bruit.

à

Les équations (1.38) et (1.39) montrent que le canal doit être estimé pour chaque sous-porteuse. Les équations (1.37) pour i=0,1, ..., N_u-1 peuvent être écrites sous la forme matricielle suivante :

d C G.r (1.40)

T

k k

T

où à à ( 0) ,..., à ( _u 1)

d , _rk=[r0,k, ..., _rLc-1,k]T, C est la matrice d'étalement et G=diag(g_n ; 0=n=L_c-1)

d k d k ~

k

est la matrice d'égalisation mono-utilisateur utilisant l'un des critères d'égalisation ZF ou MMSE. 7.3.2. Détection multi-utilisateurs

Dans ce cas, toutes les données de tous les utilisateurs sont détectées conjointement. La technique de détection se base sur la minimisation de la distance euclidienne du signal reçu des données estimées. On rappelle que le k^ème symbole reçu sur les L_c sous-porteuses s'écrit (1.40) :

rk=HCdk+bk (1.41)

Dans le cas d'une égalisation et d'un désétalement conjoint, l'égaliseur selon le critère ZF minimise

l'erreur quadratique (rk-HC

à dk )^T(rk-HC

à dk). La sortie de cet égaliseur est donc donnée par :

T † T †

1

F C H HC C H ZF(1.42)

L'égaliseur selon le critère MMSE minimise l'erreur quadratique moyenne E[( à dk-dk)T( à d_k-d_k)] :

1

1

F C H HC C H

T † T †

MMSE SNR(1.43)

à

Ainsi le vecteur d_k correspondant aux symboles égalisés et désétalés de tous les utilisateurs est

donnée par :

à

d_k=F.rk (1.44)

On note que les expressions des égaliseurs ZF et MMSE seront données plus en détail dans le chapitre suivant lors de l'association du système MIMO et de la technique MC-CDMA.

8. Conclusion

Dans ce chapitre, on a d'abord décrit les composantes de base d'une chaîne de transmission numérique. Puis, on a présenté les caractéristiques du canal de transmission radio-mobile. On a présenté par la suite la modulation OFDM dont le but est d'augmenter le débit de transmission en garantissant une transmission dans des sous-canaux non sélectifs en fréquences. Ensuite, on a présenté les principales techniques d'accès multiples permettant le partage de l'espace des canaux de transmission. On a fixé notre choix sur la technique CDMA puisqu'elle permet une transmission de données de plusieurs utilisateurs en même temps et sur la même fréquence. Par ailleurs, on a présenté la technique qui associe la modulation OFDM à la technique CDMA.

Dans la suite de ce travail, on va étudier et implémenter une architecture qui combine entre la technique MC-CDMA et la technique multi-antennes, dans le but d'améliorer davantage les performances et la qualité de la transmission.

23

Chapitre 2

Multiplexage spatial dans un contexte MC-CDMA

1. Introduction

Depuis une dizaine d'années, une nouvelle technologie est apparue dans les systèmes de télécommunication qui permet d'améliorer la qualité de transmission. Cette technologie a comme principaux objectifs d'augmenter le débit de transmission et d'exploiter la diversité offerte par le système. Il s'agit du système à entrées multiples et à sorties multiples (appelé aussi MIMO) qui emploi plusieurs antennes en émission et plusieurs antennes en réception. La plupart des études sur les systèmes MIMO considèrent un canal non sélectif en fréquence. Cependant, l'effet multi-trajets provoque la sélectivité fréquentielle du canal. Pour cette raison, on se propose dans ce chapitre d'étudier l'association de la technique MC-CDMA à la technique MIMO puisque la technique MCCDMA permet d'une part l'accès de plusieurs utilisateurs dans le même canal radio. D'autre part, le MC-CDMA permet une transmission dans un canal non sélectif en fréquence grâce à la modulation OFDM employée.

Dans ce chapitre, on commence tout d'abord par définir la notion de la diversité et rappeler les différentes techniques de diversité. On s'intéresse par la suite à l'étude du système MIMO en introduisant deux approches possibles à l'émission : le codage spatio-temporel et le multiplexage spatial. Ensuite, on focalise sur la technique du multiplexage spatial et on évalue ses performances en fonction de la technique de détection utilisée à la réception. Dans la deuxième partie de ce chapitre, on présente une architecture permettant l'association de la technique multiplexage spatial à la technique MC-CDMA. On évalue également les performances de cette nouvelle chaîne.

2. Techniques de diversité

La diversité est une technique utilisée dans les systèmes de transmissions radio-mobiles afin de lutter contre l'évanouissement causé par les trajets multiples du canal de transmission. Elle consiste à recevoir plusieurs répliques du signal émis affectés par des évanouissements indépendants. L'ordre de diversité est égal au nombre de voies indépendantes à la réception [1]-[4].

Les principales formes de diversité sont la diversité temporelle, la diversité fréquentielle et la diversité spatiale.

2.1. Diversité temporelle

Cette diversité consiste à envoyer plusieurs répliques du signal à transmettre dans des intervalles de temps séparés d'au moins le temps de cohérence du canal T_c afin d'assurer un bonne décorrélation des signaux (figure 2.1). Cette diversité est intéressante pour le cas de transmissions dans un canal sélectif en temps.

Figure 2.1. Emission du même signal à des instants séparés par le temps de cohérence du canal

2.2. Diversité fréquentielle

La diversité fréquentielle consiste à envoyer plusieurs répliques du même signal à transmettre sur des fréquences différentes séparées d'au moins la bande de cohérence du canal B_c (figure 2.2). Elle est intéressante pour les cas des transmissions dans un canal sélectif en fréquence. Cette diversité est généralement utilisée dans les systèmes OFDM.

24

Figure 2.2. Emission du même signal sur des fréquences différentes

2.3. Diversité spatiale

La diversité spatiale consiste à envoyer ou recevoir le signal sur des antennes différentes espacées par une distance plus grande que la distance de cohérence. Cette distance est la séparation minimale des antennes garantissant des évanouissements indépendants.

s(t)
s(t)
s(t)

25

Figure 2.3. Diversité spatiale à l'émission Figure 2.4. Diversité spatiale à la réception

Les diversités temporelles, fréquentielles et spatiales à l'émission diminuent l'efficacité spectrale du système puisqu'elles nécessitent la répétition du même signal. En associant un codage correcteur d'erreurs avec l'une des ces techniques de diversité, on augmente l'efficacité spectrale et on évite le gaspillage des ressources spectrales.

On note également que la combinaison de plusieurs techniques de diversité permet de mieux combattre les effets d'évanouissement du canal.

On présente dans le paragraphe suivant les systèmes multi-antennes (MIMO) qui associent plusieurs antennes à l'émission et à la réception. Cela permettra par la suite de proposer une architecture pour l'implémentation d'un système MIMO dans un contexte MC-CDMA.

3. Les systèmes MIMO

Un système MIMO est un système qui comporte plusieurs antennes à l'émission et plusieurs antennes à la réception. Les deux principaux avantages des systèmes MIMO sont d'offrir une diversité spatiale à l'émission et à la réception, et d'augmenter le débit de transmission des données.

Soit un système MIMO comportant Nt antennes d'émission et N_r antennes de réception (figure 2.5). On suppose que la bande de fréquence utilisée pour la transmission est assez étroite pour que le canal soit non sélectif en fréquence. Chaque trajet entre une antenne émettrice t et une antenne réceptrice r est modélisé par un gain complexe h_rt(k) représentant l'évanouissement du trajet. A la réception, chaque antenne reçoit la somme des symboles xt transmis simultanément par chacune des Nt antennes émettrices. Le signal y_r reçu par la ^rième antenne à l'instant k peut alors s'écrire :

Nt

yr

( ) ( ) ( ) ( ) k h k x k b k rt t r

, (2.1)

t 1

où b_r(k) représente le bruit complexe qui perturbe le signal reçu sur la ^rième antenne de réception à l'instant k, modélisé par un Bruit BBAG.

Figure 2.5. Représentation des différents trajets entre antennes émettrices et réceptrices

Par conséquent, le système regroupant tous les symboles reçus simultanément par les N_r antennes pourrait être modélisé par la forme vectorielle suivante :

y(k)=H(k).x(k)+b(k) (2.2)

où y(k)=[y1(k), y2(k), ..., yN_r(k)]^T représente le vecteur des symboles reçus de taille N_r x 1,
x(k)=[x1(k),x2(k),...,xNt(k)]^T représente le vecteur des symboles émis de taille Nt x 1,
b(k)=[b1(k),b2(k),...,bN_r(k)]^T représente le vecteur de bruit BBAG perturbant les Nr antennes de taille

h k h k h k

11 1 1

( ) ( ) ( )

? ?

t Nt

? ? ? ? ?

Nr x 1 et H(k)=

hr

( ) ( ) ( ) k h k h k ? ? rt rNt 1 ,1 ,

de taille NrxNt.

26

? ? ? ? ?

,1 ,

( ) ( ) ( )

k h k h k

hNr

? ?

Nr t NrNt

On rappelle que si la moyenne des évanouissements du canal radio-mobile est nulle, alors l'enveloppe suit une loi de Rayleigh et le canal est dit canal de Rayleigh [4]. C'est le modèle de canal que nous allons considérer. Il y a deux types de canaux possibles, soit un canal de Rayleigh classique ou ergodique, où les coefficients _hrt changent aléatoirement et indépendamment à chaque période symbole, soit un canal quasi-statique ou Rayleigh par bloc, qui garde constante les valeurs de _hrt à l'intérieur d'un même bloc. On considère par la suite un canal de Rayleigh par bloc où le canal reste constant durant T utilisations du canal. L'équation (2.2) devient alors :

y()=H.x()+b(), pour=1, ..., T. (2.3)

Pour les systèmes MIMO, il existe 2 techniques principales utilisées dans les chaînes de transmission [4] :

27

- Le multiplexage spatial ;

- Le codage espace-temps.

Avant de présenter le multiplexage spatial qu'on considèrera dans la suite de ce travail, on décrit brièvement le principe du codage spatio-temporel.

3.1. Le codage espace-temps

Le principe du codage espace-temps ou space-time (ST) consiste à recevoir des codes pour les systèmes MIMO en introduisant une dépendance entre le domaine spatial et temporel afin d'exploiter la diversité spatiale à l'émission et minimiser les effets d'évanouissements dûs au canal radio-mobile. Le codage ST est utilisé pour les systèmes MIMO sous deux grandes catégories : les codes ST en treillis et les codes ST en bloc.

3.1.1. Les codes ST en treillis

Les codes ST en treillis ont été proposés par Tarokh et al [15]. Dans cette catégorie, le principe du codage consiste à combiner le codage canal avec la modulation sur les antennes émettrices. En effet, le codage ST en treillis crée des relations entres les symboles à la fois en espace et en temps. Le codeur ST en treillis utilise un treillis à états où chaque état _Ek+1 dépend des bits d'information à coder et de l'état Ek.

La réception est basée sur le décodage des symboles reçus en utilisant un algorithme de recherche de chemin le plus probable dans la ressemblance aux symboles émis.

Cette technique combine l'avantage de la diversité spatiale avec le gain du codage. Néanmoins, elle présente un inconvénient dans la complexité de l'algorithme de décodage qui augmente rapidement avec le nombre d'antennes d'émission.

3.1.2. Les codes ST en bloc

Plusieurs codes ST en bloc existent dans la littérature [16] [15] [4]. Parmi ces codes on trouve les codes ST en bloc orthogonaux qui sont définis comme une opération de modulation d'un bloc de symboles à la fois dans l'espace et dans le temps, créant ainsi des séquences orthogonales transmises par des antennes émettrices différentes [15] [16]. Ces codes présentent l'avantage de la faible complexité du décodeur.

Le schéma d'Alamouti pour deux antennes d'émission comporte la structure de codage représentée
dans la figure 2.6. Ce schéma de décodage a été déjà intégré dans la norme UMTS. D'après ce
schéma, on constate que l'envoi de deux symboles nécessite deux antennes d'émission, deux temps

de symboles et un codage spécial pour que les séquences formées par les deux symboles soient orthogonales. Il existe d'autres constructions de codes ST en blocs : les codes en couches, les codes à dispersion linéaire, les codes algébriques, etc [4].

Figure 2.6. Schéma d'Alamouti pour le cas des antennes en émission

La technique de codage ST ne sera pas traitée dans ce travail, mais le lecteur intéressé peut se référer à [4].

3.2. Multiplexage spatial

Le multiplexage spatial consiste à démultiplexer la séquence de données en Nt trains de données qui sont ensuite transmis par les Nt antennes émettrices. C'est le schéma qui a été proposé sous le nom de Bell Labs Layered Space-Time (BLAST) par Foschini et al [14]. La théorie de l'information a montré que la capacité d'un canal MIMO, c'est-à-dire le débit maximal que l'on peut transmettre sans erreurs, peut être atteinte avec le multiplexage spatial. Foschini et al on proposé deux structures de BLAST : D-BLAST (Diagonal BLAST) et V-BLAST (Vertical BLAST) [14]. On ne considère dans cette étude que l'architecture V-BLAST pour son efficacité et pour sa simplicité et la faible complexité de son décodage.

Le processus de démultiplexage de données utilisant l'architecture V-BLAST pourrait être représenté par le diagramme de la figure 2.7.

x x 1 1 Nt			?
(x1,x2,...,xk,...)		x x 2 2 Nt	?

28

? ? ?

x x Nt Nt 2

?

Figure 2.7. Diagramme de la technique de démultiplexage V-BLAST

Dans cette étude, on suppose une connaissance parfaite du canal à la réception. En pratique, le canal est estimé par le récepteur à chaque paquet transmis grâce à une séquence d'apprentissage.

29

L'inconvénient du multiplexage spatial est qu'il ne peut pas être utilisé lorsque le nombre d'antennes en réception est inférieur au nombre d'antennes en émission car le récepteur aura le problème d'un système indéterminé d'équations linéaires.

3.3. Les techniques de détection pour le multiplexage spatial

Dans ce sous-paragraphe, on va décrire des techniques de détection pouvons être utilisées à la réception pour retrouver les symboles émis sur les Nt antennes d'émission.

Figure 2.8. Bloc d'égalisation pour le multiplexage spatial

Après l'envoi des symboles sur les antennes d'émission, les symboles sont altérés par le canal de transmission et par le bruit BBAG. A la réception, on applique une technique d'égalisation au vecteur reçu afin de récupérer le vecteur de symboles émis en supposant que le canal de transmission est constant pendant la transmission et parfaitement estimé, et le rapport signal sur bruit (SNR) est aussi parfaitement estimé (figure 2.8). On rappelle que le rapport signal sur bruit est défini par le rapport

de la variance du signal x 2 sur la variance du bruit n 2 :

² (2.4)

x

S N R 2

n

3.3.1. Techniques de détection linéaires

Les techniques de détection linéaire les moins complexes sont basés sur l'un des critères suivants :

- le critère de forçage à zéro (ZF);

- le critère de minimisation de l'erreur quadratique moyenne (MMSE).

a) Récepteur ZF

Un égaliseur linéaire ZF minimise la forme quadratique suivante :

y ~ Hx R y ~ Hx

† 1

J ZF à n à(2.5)

où R_n est la matrice de covariance du bruit [17], y est le vecteur reçu par les N_r antennes réceptrices correspondant au signal émis x (équation 2.3) et H est la matrice de canal N_rxNt.

En dérivant _JZF par rapport à xà et sachant que cette dérivée doit être nulle, on obtient :

†

(2.6)

(2.7)

? ( à ) 2 ¹ ( à ) 0

y - Hx R y - Hx

?xà n

Ce qui donne alors :

.

† †

~1 ~1

~1

x = H R H H R y

à n n

Pour le cas d'un bruit BBAG, on a :

Rn= n 2 I, (2.8)

Et l'expression (2.7) devient :

x = H H H y à ~1 † †

(2.9)

Ainsi la matrice d'égalisation est :

GZF = H H H .

† †

~1

(2.10)

b) Récepteur MMSE

Un récepteur MMSE est obtenu en minimisant l'erreur quadratique moyenne [17] suivante :

† J MMSE E x ~ x x ~ x à à

(2.11)

D'après l'équation (2.3), on a y=Hx+b. On cherche la matrice d'égalisation _GMMSE qui vérifie :

xà =GMMSEy = GMMSEHx+GMMSEb. (2.12)

En développant _JMMSE , on montre facilement que :

†

J _MMSE E Trace à à

x _ x x _ x ,

(2.13)

30

31

32

33

où Trace(A) est la trace de la matrice A. L'erreur quadratique moyenne _JMMSE s'exprime également par :

†

J _MMSE Trace E x ~ GHx Gb x -GHx - Gb . (2.14)

On note R_x la matrice de covariance du vecteur x : Rx=E[x †

x ].

En développant _JMMSE et en utilisant le fait que x et b sont indépendants et que le bruit est centré, on obtient :

JMMSE=Trace(R_x+G(HR_xH^†+R_n)G^†-2Re(R_xH^†G^†)) (2.15)

En dérivant _JMMSE par rapport à la matrice G et sachant que la dérivée doit être nulle, on obtient :

GMMSE=RxH^†(HRxH^†+Rnï¹ (2.16)
=(HR_xH^†(R_xH^†ï¹+R_n(R_xH^†ï¹ï¹

=(H+Rn(H†ï1Rx -1ï1

=(R_n(H^†ï¹H^†R_n -1H+Rn(H†ï1Rx -1ï1 =(H^†R_n ^-1H+R_x -1ï1H†Rn -1

Dans le cas où le bruit est BBAG, et où l'entrée est i.i.d on a : Rn= n 2 I et Rx= x 2 I et la détection du vecteur x se fait comme suit :

2 1 1 1 x H H I H y Ç H I H † n † † † à MMSE 2 N N t t SNR x

y (2.17)

3.3.2. Technique de détection non linéaire à annulation successive d'interférences

Les techniques de détection non linéaires sont des techniques utilisant des algorithmes itératifs de détection, et qui présentent notamment une performance plus meilleure par rapport aux techniques linéaires [1]-[18].

Les techniques de détection non linéaires les plus utilisées sont les suivantes :

- Détecteur à annulation successive d'interférences (SIC);

- Détecteur à annulation parallèle d'interférences (PIC).

Le détecteur SIC consiste à annuler successivement l'interférence induite de chaque symbole détecté. En effet, à chaque itération, un symbole est estimé par l'intermédiaire de la matrice d'égalisation ZF ou MMSE. Puis, ce symbole détecté est supprimé du vecteur reçu afin d'annuler l'effet de son interférence sur les symboles restants non encore détectés.

L'algorithme SIC peut s'écrire de la manière suivante :

pour j = 1 à Nt // nombre d'itération égal au nombre de symboles émis

† †

~1

- G = GZF = H H H // calcul de la matrice d'égalisation G par

j j j

ou G = GMMSE =

1 1 Ç H I H † † j j N t j j 1 SNR

//le critère ZF ou MMSE

- l argmin g i 2 // optionnelle (avec ou sans ordonnancement)

i

- x ? l gly j // estimation d'un symbole

x à_l Q x ? l // procédure de quantification optionnelle

- yj1 y_jvec(H)_l x à l // soustraction de l'interférence du symbole détecté du vecteur reçu

- (H)j+1 = (H)j\l //Suppression de l'effet de l'antenne d'émission correspondant au symbole
//estimé

Fin pour.

Avec vec(H)l est la l^ème colonne de la matrice H.

Les instructions optionnelles de l'algorithme SIC ont un effet sur les performances de détection. En particulier, l'ordonnancement des symboles détectés permet de déterminer l'ordre des antennes d'émission à annuler en premier en fonction des plus fortes amplitudes des canaux. Cela correspond à choisir la plus faible norme des lignes de la matrice G.

Cet algorithme présente une performance meilleure que celle donnée par les détecteurs linéaires car la matrice d'égalisation G est recalculée N_t fois. De plus, le nombre d'antennes en émission diminue linéairement en avançant en nombre d'itérations dans l'algorithme SIC, ce qui permet d'augmenter la diversité de réception à chaque itération.

3.4. Résultats de simulation

Dans cette partie, on s'intéresse à l'évaluation de performances du système à multiplexage spatial en termes de taus d'erreurs. On considère des blocs transmis composés de 100 symboles modulés en BPSK et les courbes de taux d'erreur sont obtenues en moyennant sur 10000 blocs.

La figure (2.9) illustre les performances en Taux d'Erreur Binaire (TEB ou BER : Bit Error Rate) moyennée sur tous les symboles de données d'un bloc, en fonction du rapport signal à bruit. Différents nombres d'antennes à l'émission et à la réception ont été considérés.

Figure 2.9. TEB en fonction du RSB sur un canal de Rayleigh.

La figure (2.9) montre que le multiplexage spatial n'est fonctionnel que si le nombre d'antennes à l'émission est inférieur ou égal aux nombres d'antennes à la réception. Cette figure montre également que les performances du système à multiplexage spatial sont les mêmes quand le nombre d'antennes à l'émission est égal au nombre d'antennes à la réception. Lorsque le nombre d'antennes en réception est supérieur au nombre d'antennes en émission, les performances du multiplexage spatial sont améliorées d'une façon significative. Cette amélioration est due à la diversité spatiale en réception qui augmente avec l'augmentation du nombre d'antennes en réception.

Pour une comparaison entre les performances des deux techniques d'égalisation selon les critères ZF et MMSE, on montre dans la figure (2.10) les performances en TEB, moyenné sur tous les symboles de données d'un bloc, en fonction du RSB. Deux nombres d'antennes émettrices Nt=N_r=2,4 ont été considérés.

La figure (2.10) montre que l'égaliseur MMSE donne des performances meilleures que l'égaliseur ZF. Les performances du récepteur MMSE s'expliquent par la connaissance du Rapport signal à bruit au niveau de chaque antenne de réception. En effet, ces performances s'améliorent en augmentant le nombre d'antennes en réception.

34

On représente dans la figure (2.11) le comportement du TEB en fonction du rapport signal à bruit lorsqu'on utilise à la réception l'algorithme SIC pour la détection des symboles utilisant une égalisation ZF. A titre de comparaison, on considère aussi le TEB obtenu avec le récepteur MMSE et le TEB obtenu avec l'algorithme SIC utilisant un égaliseur MMSE. Deux nombres d'antennes émettrices Nt=N_r=2,4 ont été considérés.

10⁰

10^-1

Récepteur MMSE pour 2 antennes de transmission Récepteur MMSE pour 4 antennes de transmission Algorithme SIC-ZF pour 2 antennes de transmission Algorithme SIC-MMSE pour 2 antennes de transmission Algorithme SIC-ZF pour 4 antennes de transmission Algorithme SIC-MMSE pour 4 antennes de transmission

10^-2

10^-3

10^-4

Figure 2.10. TEB en fonction du RSB en utilisant les récepteurs ZF et MMSE

0 5 10 15 20 25 30

Figure 2.11. TEB en fonction du RSB en utilisant un algorithme SIC

D'après la figure (2.11), on constate que l'avantage de l'algorithme de détection SIC apparait dans
l'amélioration de performances du système en augmentant le nombre d'antennes de transmission.

Cette amélioration est due à la diversité spatiale en réception qui augmente avec l'annulation des antennes d'émission. La figure (2.11) montre également que l'algorithme SIC utilisant une égalisation ZF est plus performant que le récepteur MMSE. Ce résultat est intéressant puisqu'il montre l'efficacité d'un récepteur utilisant l'annulation successive de l'interférence par rapport à un récepteur qui utilise la connaissance du rapport du signal à bruit. La figure (2.11) montre aussi que le récepteur le plus performant est le récepteur utilisant l'algorithme SIC avec une égalisation MMSE. Les performances de ce récepteur sont plus intéressantes lorsque le nombre d'antennes en émission augmentent.

4. Association entre multiplexage spatial et la technique MC - CDMA

Dans la suite de ce rapport, on s'intéresse à l'étude des performances et à l'implémentation matérielle de la technique du multiplexage spatial combinée avec la technique MC-CDMA. Le but de cette association est d'exploiter les performances de ces deux techniques d'une part en augmentant le débit de transmission par le multiplexage spatial tout en bénéficiant de la souplesse et de l'efficacité de la technique CDMA et de la diversité spatiale à la réception. D'autre part, cette association permet de combattre la sélectivité fréquentielle du canal par la modulation OFDM.

On commence par présenter la chaîne associant le multiplexage spatial à la technique MC-CDMA. On analyse par la suite les performances de cette nouvelle chaîne en introduisant un codeur de canal au système MIMO-MC-CDMA. En effet ce codeur de canal permettra une meilleure exploitation des trois formes de diversité : spatiale à l'émission, temporelle et fréquentielle.

4.1. Conception de la chaîne MIMO associée au MC-CDMA

L'idée de l'association de la technique du multiplexage spatial à la technique MC-CDMA consiste premièrement à étaler les données de N_u utilisateurs par leurs séquences d'étalement. Les symboles obtenus sont par la suite démultiplexés sur les Nt antennes d'émission. Sur chaque antenne, les données subissent la modulation OFDM.

Au niveau de la réception, le traitement des symboles reçus est effectué dans une première étape par la démodulation OFDM sur chaque antenne de réception. Puis, les symboles obtenus sont détectés par des techniques d'égalisation utilisant le critère ZF ou MMSE qu'on détaillera dans la suite. Les symboles sont ensuite réordonnés par un décodage spatial et désétalés.

1

35

La structure de la chaîne MIMO-MC-CDMA est présentée dans les figures 2.12 et 2.13.

Ecole Polytechnique de Tunisie 2007-2008

Etalement

P/S

+

Figure 2.12. Chaîne d'émission de la technique MIMO-MC-CDMA

Nr

1

-

-

Egalisation

Désétalement

S/P

S/P

FFT

FFT

M UX

V-BLAST

I FFT

I FFT

P/S

+

Nt

DEMUX

V-BLAST

Figure 2.13. Chaîne de réception de la technique MIMO-MC-CDMA

4.2. Modélisation de la chaîne de transmission MIMO-MC-CDMA

On note dk un vecteur de longueur N_u qui contient les k^ème symboles des Nu utilisateurs. On a alors : dk=[ ⁽⁰⁾

d_k , ..., ( _u 1 )

dk ]^T . On note d le vecteur résultant de la concaténation de Nt vecteurs dk ce qui

permet d'écrire d=[d1 ^T, d2 ^T, ..., dNt ^T]^T. Ce vecteur est de longueur NtNu.

D'après l'équation (1.31) du chapitre 1, chaque vecteur dk, k=1, ..., Nt est étalé par une matrice d'étalement C=[c⁽⁰⁾, ..., ^c(Nu-1)] donnant un vecteur xk de longueur L_c où L_c est la longueur des codes d'étalement pour chaque utilisateur. On obtient alors :

xk=C.dk (2.18)

On note x=[ 1

x , ..., t

^T x~ ]^T le vecteur, de longueur _NtLc, résultant de la concaténation des Nt vecteurs

T

xk, k=1, ..., Nt. En développant l'expression du vecteur x en fonction de dk, on obtient :

x C.d C d

0 0

?

1 1 1

x C.d C d

0 ? ?

2 2 2

? ? ? ?

.

? ?

0

(2.19)

36

x C.d C d

Nt Nt 0 0

? Nt

Ce qui donne alors :

x='d , (2.20)

où : ~ = I_Nt ? C (2.21)

avec ? dénote le produit matriciel de Kronecker _etINt est la matrice identité de taille Nt. L'expression du vecteur de symboles reçus, de longueur L_c, sur la r^ème antenne de réception s'écrit :

Nt

y_r=

H x (2.22)

rt t r

b ,

t

où _Hrt est une matrice diagonale de dimension L_cxL_c, chaque élément de la diagonale _hrt,n représente la réponse fréquentielle du canal entre la t^ème antenne d'émission et la r^ème antenne de réception au niveau de la n^ème sous-porteuse sachant que

hrt n

,

hrt n

,

,

e j rt n . (2.23)

Le vecteur b_r est le vecteur de bruit complexe BBAG introduit à la r^ème antenne de réception de longueur L_c.

En écrivant l'équation (2.22) pour r=1,...,N_r , on obtient :

y H H H H x b

? ?

1 11 12 1t 1Nt 1 1

y H H H H x b

? ?

2 21 22 2t 2Nt 2 2

r

? ? ? ? ? ? ? ?

. (2.24)

M

y H H H H x b

r r1 r2 rt rNt t

? ?

? ? ? ? ? ? ? ?

M

y H H H H x b

Nr Nr1 Nr2 1rt NrNt Nt Nr

? ?

37

L'équation (2.24) peut se mettre sous cette forme :

y=~ x+b, (2.25)

où y=[y1^T, y2^T , ..., yN_r^T]^T est le vecteur de symboles reçus sur les Nr antennes de réception de longueur NrLc, b=[b1^T, b2^T, ..., bN_r^T]^T est le vecteur bruit complexe BBAG sur les Nr antennes de réception de longueur _NrLc , et ~ est la matrice de canal de taille _NrLcxNtLc constituée des sous matrices _Hrt (voir l'équation 2.24).

En remplaçant x par son expression (2.20) dans l'équation (2.25), on a alors :

y=~ ~ d+b. (2.26)

4.3. Techniques d'égalisation pour la chaîne MIMO-MC-CDMA

Les techniques d'égalisation qu'on propose d'utiliser pour le MIMO-MC-CDMA, en se référant au paragraphe 7.3 du chapitre 1 et le paragraphe 3.3 du chapitre 2, sont les techniques se basant sur le critère de forçage à zéro (ZF) et le critère de minimisation de l'erreur quadratique moyenne (MMSE) dans le cas d'une détection mono-utilisateur et d'une détection multi-utilisateurs.

Une détection mono-utilisateur (SUD : Single Use Detection) ne nécessite pas la connaissance des séquences d'étalement des autres utilisateurs. Dans ce cas, la détection se fait par :

dà = ~ ^T~y, (2.27)

où d^à est le vecteur des symboles estimés après les étapes disjointes d'égalisation et de désétalement disjointes de longueur _NtNu , ~ est la matrice d'égalisation mono-utilisateurs calculée en fonction de la matrice de canal ae et du rapport signal à bruit ã.

D'après les démonstrations faites dans le paragraphe 3.3.1 de ce chapitre, les matrices d'égalisation mono-utilisateur utilisant le critère ZF et le critère MMSE sont respectivement:

eZF = (ae^†ae)^-1 ae^† (2.28)

eMMSE = (ae^†ae+	Lc	INtLc)^-1ae^† (2.29)
	Nu.ã

38

Une détection multi-utilisateurs (MUD : Multi-User Detection) est obtenue par:

=ry, (2.30)

Où r est la matrice d'égalisation multi-utilisateurs calculée en fonction de la matrice de canal ae, de la matrice d'étalement ~ et du rapport signal à bruit ã.

D'après les démonstrations faites dans le paragraphe 3.3.1 de ce chapitre, les matrices d'égalisation multi-utilisateurs utilisant le critère ZF et le critère MMSE sont respectivement::

rZF = (e^Tae^†ae~)^-1~ Tae † (2.31)

rZF = (e^Tae^†aeïe+ 1 INtNu)^-1 e^Tae^† . (2.32)

ã

Au lieu d'utiliser les détecteurs linéaires ZF ou MMSE, on peut utiliser également des techniques non
linéaires d'annulation d'interférences, notamment le détecteur SIC spatial qui se base sur

39

l'annulation successive des antennes d'émission afin de supprimer l'interférence et d'augmenter la diversité en réception.

En adoptant le détecteur SIC présenté dans le paragraphe 3.3.2 au cas MIMO-MC-CDMA, on obtient l'algorithme suivant :

pour j = 1 à Nt // nombre d'itération égal au nombre d'antennes d'émission

† †

~1

- ~ = ~ZF = ~ ~ // calcul de la matrice d'égalisation ~ par

j j j

ou ~ = MMSE =

1 1 ~ ~ I ~ //le critère ZF ou MMSE † † j j N t L c j j 1 S~R

- àx _j =Mat( )^j rj // décision sur un bloc de symboles. Mat( )^j sont les lignes de la

//matrice~ ~

- à d_j =C^T à x_j // désétalement du bloc de symboles estimé.

d ? Q d j à j	// procédure de quantification optionnelle
x? j =Cd j	// étalement de nouveau des symboles estimés

- y j y_jMat( ')_j x?_j// soustraction de l'interférence du symbole détecté du vecteur

1

//reçu. Mat(')j sont les colonnes de la matrice ~ ~

- ()j+1 = (~)j\l //Suppression de l'effet de l'antenne d'émission correspondant au symboles

//estimés

Fin pour

4.4. Evaluation des performances du système MIMO-MC-CDMA

Dans cette partie, on s'intéresse à l'évaluation des performances de la chaîne MIMO-MC-CDMA représentée dans les figures 2.12 et 2.13. Dans un premier temps on présente les résultats de simulation sans codage de canal. Dans un deuxième temps en étudie l'effet de l'ajout d'un codeur de canal à la chaîne d'émission et d'un entrelaceur de bits.

40

4.4.1. Cas de la chaîne sans codage de canal

Dans ce sous-paragraphe, on considère des blocs transmis composés de 100 symboles modulés en BPSK. Pour une comparaison entre les performances des deux techniques d'égalisation selon les critères ZF et MMSE utilisant une détection mono-utilisateur, on montre dans la figure 2.14 les performances en TEB, moyenné sur tous les symboles de données d'un bloc, en fonction du rapport signal à bruit RSB. Trois nombres d'antennes émettrices Nt=N_r=1,2,4 ont été considérés. On considère que le nombre de sous-porteuses est égale à L_c=64 et le nombre d'utilisateurs est N_u=64.

10⁰

ZF pour Nt=4 ZF pour Nt=2 ZF pour Nt=1 MMBE pour Nt=4 MMBE pour Nt=2 MMBE pour Nt=1

10^-1

10²

10^-s

10^-4

0 2 4 6 8 10 12 14 16 18 20

Rapport ^signa à bruit en dB

Figure 2.14. TEB en fonction du RSB pour les égaliseurs à critère ZF et MMSE

La figure 2.14 montre que l'égaliseur selon le critère MMSE offre des performances meilleures que l'égaliseur à critère ZF.

Maintenant, on fixe le nombre d'antennes de transmission à 2 et on montre dans la figure 2.15 la performance du système MIMO-MC-CDMA en TEB, moyenné sur tous les symboles de données en fonction du RSB, pour différents nombres de sous-porteuses avec des transmissions à pleine charge (N_u=L_c) utilisant la technique d'égalisation selon le critère MMSE pour une détection mono- utilisateur.

Les courbes de la figure 2.15 montrent dans le cas d'une charge pleine, une légère amélioration des performances du système en augmentant le nombre de sous-porteuses.

On fixe le nombre de sous-porteuses à L_c=64, et on évalue dans la figure 2.16 les performances du
système MIMO-MC-CDMA, en TEB moyenné sur tous les symboles de donnée d'un bloc en fonction

41

du RSB, pour des transmissions à des charges variables N_u=16,32,64 pour des détections mono- utilisateurs (SUD) et multi-utilisateurs (MUD) utilisant une égalisation à critère MMSE. Le nombre d'antennes de transmission considérés est Nt=N_r=2.

Figure 2.15. TEB en fonction du RSB pour des transmissions à plein charge

Figure 2.16. TEB en fonction du RSB pour les détections mono-utilisateur et multi-utilisateurs
Les courbes de la figure 2.16 montrent que dans les deux cas de détection mono ou multi-
utilisateurs, la performance du système MIMO-MC-CDMA est améliorée en diminuant la charge du
système. La figure 2.16 montre également qu'un récepteur utilisant une détection multi-utilisateurs
présente une performance meilleure par rapport à un récepteur utilisant une détection mono-

utilisateur surtout dans le cas à mi-charge (N_u=32= ^Lc). Cette performance se justifie par la

2

42

différence entre ces deux techniques de détection. En effet, un détecteur mono-utilisateurs effectue la décision des données de chaque utilisateur sans la connaissance des séquences d'étalement des autres utilisateurs. Par contre, pour le détecteur multi-utilisateurs, l'opération d'égalisation et de désétalement est effectuée conjointement. Cette technique améliore la performance de décision sur les symboles des utilisateurs.

Afin d'illustrer les performances de l'algorithme SIC et de les comparer avec celles des techniques de détection linéaires, on montre le comportement en TEB, moyenné sur tous les symboles de données d'un bloc, en fonction du RSB dans la figure 2.17. Le nombre de sous-porteuses considéré est L_c=64, la transmission est à pleine charge (N_u=64) et le nombre d'antennes de transmission est Nt=N_r=2.

Figure 2.17. TEB en fonction du RSB pour l'algorithme SIC

La figure 2.17 montre que l'algorithme SIC présente une performance meilleure par rapport aux égaliseurs linéaires. Elle montre aussi que l'algorithme SIC utilisant un égaliseur MMSE donne de meilleures performances par rapport à l'algorithme SIC utilisant un égaliseur ZF.

4.4.2. Cas de la chaîne avec codage convolutif

Dans cette partie, les chaînes représentées dans les figures 2.12 et 2.13 sont modifiées par l'introduction d'un codeur de canal suivi d'un entrelaceur de bits au début de la chaîne d'émission, et par l'introduction d'un désentrelaceur de bits suivi d'un décodeur de canal à la fin de la chaîne de réception. Le système résultant est illustré dans les figures 2.18 (émission) et 2.19 (réception). Le codeur de canal utilisé dans les simulations est un codeur convolutif ayant une entrée, deux sorties

et de longueur de contraintes égale à 5. Les sorties du codeur s'écrivent en fonction des bits d'entrée comme suit :

s1 n = b_n + _bn-3 + bn-4 , (2.33)

et

s2 n = b_n + bn-1 +bn-2 + bn-4 . (2.34)

Dans la chaîne de réception, le décodage de canal est effectué par un algorithme de viterbi.

1 Nu	Codeur de canal
			entrelaceur		modulation
	Codeur de canal
			entrelaceur		modulation

Figure 2.18. Emetteur MIMO-MC-CDMA avec codage de canal suivi d'un entrelaceur

						Décodeur de canal	1
			désentrelaceur
	démodulation
						Décodeur de canal	Nu
	démodulation		désentrelaceur

43

Figure 2.19. Récepteur MIMO-MC-CDMA avec désentrelaceur suivi d'un décodage de canal

Le but de l'introduction d'un entrelaceur dans le système de transmission est de mélanger les bits d'informations après le codage de canal afin de ne pas moduler des bits successifs dans un même symbole. L'avantage de l'entrelaceur apparait dans le cas où un symbole est fortement altéré par le canal ou le bruit BBAG, l'erreur sera donc dispersée après le désentrelacement. Ainsi, le décodeur de canal (qui est un décodeur correcteur d'erreur) donnera une meilleure performance de décodage grâce à la dispersion de l'erreur.

L'entrelaceur utilisé dans la chaîne MIMO-MC-CDMA est un entrelaceur matriciel dont le principe consiste à enfiler les bits dans les colonnes d'une matrice, puis les défiler par ses lignes.

On se propose d'étudier les performances de la chaîne pour des paquets contenant 32 symboles modulés en 16-QAM. Dans la figure 2.20, on compare les performances en TEB moyenné sur le nombre de paquets, en fonction du RSB pour les trois cas suivants :

-

44

Système sans codage de canal ;

- Système avec un codage de canal ;

- Système avec un codeur de canal et un entrelaceur.

On considère dans les simulations que Le nombre de sous-porteuses considéré est L_c=64, la transmission est à pleine charge (N_u=64) et le nombre d'antennes de transmission est Nt=N_r=2.

10⁰

MIMOMCCDMA sans codage de canal
MIMOMCCDMA a/ec codage de canal

MIMO-MC-CDMA a/ec codage de canal et entrelacement

10^-1

10^-2

10^-

10^-

0 5 10 15 20 25

Rapport ^signala bruit en dB

Figure 2.20. TEB en fonction du RSB pour le système MIMO-MC-CDMA utilisant un codage de canal

La figure 2.20 montre qu'un système de transmission utilisant un codeur de canal présente des performances meilleures qu'un système sans codeur de canal. Cette figure montre également l'amélioration des performances du système en ajoutant un entrelaceur.

5. Conclusion

Dans ce chapitre, on a commencé par rappeler les différentes techniques de diversité qui peuvent être employées dans les systèmes de transmissions. Puis, on a présenté un état de l'art sur les systèmes MIMO en détaillant les techniques de détection qui peuvent être utilisées. On a étudié et évalué par la suite les performances de la technique de multiplexage spatial dont l'avantage consiste à maximiser le débit de transmission et à offrir une diversité spatiale à la réception. On a montré à travers des résultats de simulation sur Matlab que l'égaliseur MMSE présente une meilleure performance par rapport au détecteur ZF, et que l'algorithme SIC améliore la qualité de la détection en annulant successivement l'interférence des antennes d'émission. Ensuite, on a introduit l'idée de l'association du multiplexage spatial à la technique MC-CDMA et on a évalué les performances de cette chaîne. L'évaluation à été effectuée en utilisant l'outil Matlab en modifiant plusieurs

45

paramètres tels que le nombre d'antennes en émission et en réception, le nombre de sous- porteuses, la charge du système (nombre d'utilisateurs) et l'ajout d'un codeur de canal.

A partir de l'étude effectuée dans ce chapitre, on se propose d'implémenter en VHDL les chaînes d'émission et de réception du système MIMO-MC-CDMA dans le chapitre suivant.

46

Chapitre 3

Implémentation matérielle et analyse de

performances

1. Introduction

Dans le chapitre précédent, on a étudié et évalué les performances d'une chaîne de transmission utilisant le multiplexage spatial dans un contexte MC-CDMA en utilisant l'outil Matlab. Dans ce chapitre, on aborde la phase de l'implémentation matérielle des différents blocs de la chaîne. Cette implémentation consiste tout d'abord à concevoir pour chaque bloc une structure simplifiée pour le traitement de données garantissant ainsi la facilité de l'implémentation, de test, de validation et du bon fonctionnement de la structure tout en satisfaisant les contraintes temporelles exigées en fonction de l'application. Le second objet de l'implémentation matérielle consiste à l'optimisation progressive de la description matérielle de la structure de chaque bloc en fonction de son assemblage avec les autres blocs de la chaîne.

L'implémentation de la chaîne MIMO-MC-CDMA est destinée pour le développement d'une bibliothèque d'IP « propriété intellectuelle » (Intellectual Property) reconfigurable et réutilisable afin de pouvoir implémenter toute la chaîne. Ce développement des IPs à TELNET est basé sur une méthodologie de conception basée sur une plateforme de prototypage destinée pour une architecture cible « FPGA » de technologie Altera.

Dans ce chapitre, on commence par présenter l'architecture cible FPGA « Stratix.II.GX » ainsi que ses ressources internes. Puis, on décrit l'environnement de synthèse et le flot de conception adopté. Ensuite, on présente les architectures proposées et le rapport d'implémentation des différentes composantes des circuits d'émission et de réception de la chaîne MIMO-MC-CDMA. Enfin, on examine le résultat des performances de l'architecture proposée en termes de complexité et de rapidité.

2. Le circuit FPGA Stratix II.GX

Un FPGA (Field Programmable Gate Array) est un circuit programmable qui se compose généralement de blocs logiques reliés entre eux via un réseau d'interconnexion (figure 3.1). Ces blocs logiques sont regroupés sous la forme d'une matrice.

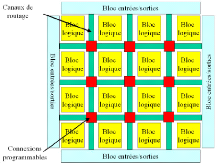
47

Figure 3.1. Bloc diagramme d'un FPGA

Basée sur une unité logique configurable, un FPGA est une matrice composée d'un grand nombre d'éléments configurables qui interagissent via des ressources de routage également reconfigurables. Un bloc logique est composé de 2 à 4 LUT, d'une chaîne de propagation de la retenue et de bascules D. Entre les blocs, des lignes d'interconnexion sont disposées pour établir les liaisons. Finalement, autour de la matrice à deux dimensions, nous trouvons les blocs d'entrées/sorties. Pour mieux comprendre le fonctionnement des FPGAs actuels, il paraît évident de connaître leur architecture interne ainsi que leurs modes de configuration.

La famille Stratix II.GX disponible à Telnet est une plateforme FPGA du constructeur ALTERA. Elle offre plusieurs fonctionnalités à travers un certain nombre de composantes prédéfinies, qui caractérisent la puissance de traitement de l'FPGA. Parmi ces composantes on cite :

- Le module ALM : Le bloc logique structurel de base dans Stratix II.GX est l'ALM (Adaptative

Logic Module), qui fournit des traitements avancés. Chaque ALM contient une variété de LUT (Look-Up-Table). En plus des ressources LUT-Basées adaptatives, chaque ALM contient deux registres programmables, deux additionneurs, trois signaux d'entrées venant des ALM du même LAB sachant qu'un LAB est composé de huit ALM. A travers ces ressources l'ALM peut configurer plusieurs fonctions arithmétiques.

- Le module DSP : ces modules intègrent des fonctions matérielles telles que multiplieurs,

accumulateurs, additionneurs, multiplexeurs et registres et permettent, entre autre, de réaliser des multiplieurs 36 bits. Ainsi, les DSP contiennent des unités de calcul nécessaires lors de la conception des filtres RIF et RII, la transformée de fourier rapide et son inverse ainsi que, la transformée en cosinus discrète.

48

- Le module PLL : Le rôle des PLL consiste à assurer la gestion des réseaux globaux d'horloge.

Ces PLL servent dans l'amélioration de performances, dans la synthèse des fréquences et dans le timing des systèmes configurés.

- Le module Trimatrix : Il s'agit d'un module mémoire constitué de trois types de bloc RAM : M512 RAM, M4K RAM et M-RAM.

3. Flot de conception adopté et environnement de synthèse

Dans la phase d'implémentation nous avons adopté un flot de conception proposé par ALTERA spécifique pour ces FPGAs. Ce flot décrit toutes les étapes nécessaires pour l'implémentation matérielle comme illustré dans la figure 3.2. L'outil de conception qui met en oeuvre ce flot est Qua rtus II de ALTERA.

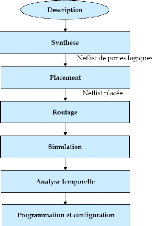
Figure 3.2. Flot de conception de l'outil Quartus

Nous décrivons brièvement les différentes étapes de ce flot dans ce qui suit :

- La description des blocs avec un langage d'un haut niveau d'abstraction (VHDL, Verilog..) ;

- La synthèse logique qui consiste à convertir cette description en une netlist de portes

logiques selon une bibliothèque de cellules relatives à la cible ;

- Le placement consiste à choisir des endroits spécifiques sur le FPGA pour les blocs logiques

de la netlist ;

49

50

51

- Le routage consiste à choisir les lignes d'interconnexion nécessaires afin d'établir les

connexions électriques entre les blocs ;

- La simulation fonctionnelle est une vérification du fonctionnement du système ne prenant pas en compte les aspects temporels du circuit ;

- La validation temporelle consiste en une simulation temporelle du circuit tenant compte des

temps de propagation, recouvrement de signaux, etc.

4. Spécification fonctionnelle et résultats d'implémentation

Dans cette partie du rapport, on s'intéresse à décrire les spécifications fonctionnelles, le schéma en bloc et le résultat d'implémentation de chaque bloc de la chaîne MIMO-MC-CDMA.

4.1. Architecture de la chaîne MIMO associée au MC-CDMA

La chaîne MIMO-MC-CDMA qu'on se propose d'implémenter comporte les paramètres suivants : - Nombre d'antennes à l'émission : Nt=2 ;

- Nombre d'antennes à la réception : N_r=2 ;

- Nombre de sous-porteuses : L_c=64 ;

- Nombre d'utilisateurs : N_u=64 (à pleine charge).

L'architecture de la chaîne de transmission MIMO associée au MC-CDMA est décrite par un circuit émetteur et un circuit récepteur présentés dans les deux figures suivantes.

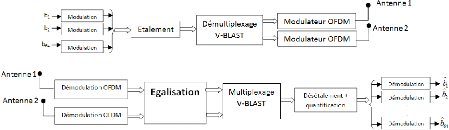
Figure 3.3. Circuits d'émission et de réception implémentés Le diagramme en bloc du circuit d'émission se compose de 4 blocs principaux :

- Bloc de modulation : Ce bloc effectue la modulation numérique 256-QAM ;

- Bloc étalement : ce bloc réalise l'étalement de donnés de 64 utilisateurs utilisant les codes de

Walsh-Hadamard de longueur égale à L_c=64 ;

- Bloc démultiplexage V-BLAST : Ce bloc comporte 64 entrées relatives à 64 utilisateurs.

Chaque entrée i représente les symboles d'un utilisateur i, i=1,...,64. Le rôle du démultiplixeur V-BLAST est de transformer chaque séquence de 2 symboles reçus, pour chaque entrée, en parallèle afin de les répartir sur les deux antennes d'émission.

- Bloc modulateur OFDM : Ce bloc effectue la modulation OFDM des symboles reçus à son entrée.

Le diagramme en bloc du circuit de réception se compose de 5 blocs principaux :

- Bloc démodulation OFDM : Ce bloc reçoit les symboles émis du circuit d'émission et effectue la démodulation OFDM.

- Bloc d'égalisation : Les symboles reçus sont altérés par l'effet du canal et par le bruit

complexe BBAG. Le rôle de ce bloc consiste à estimer les symboles émis connaissant le canal et le rapport signal sur bruit.

- Bloc multiplexage V-BLAST : ce bloc réordonne les données démultiplexées.

- Bloc désétalement + quantification : ce bloc effectue le désétalement des données par les

mêmes séquences de Walsh-Hadamard utilisées en émission. Les données sont par la suite quantifiées selon la constellation de la modulation 256-QAM.

- Bloc démodulation : ce bloc effectue la démodulation numérique des symboles pour récupérer les données binaires reçus.

4.2. Architecture des blocs utilisés dans la chaîne

Dans cette partie, on se propose de détailler l'architecture interne de chaque bloc de la chaîne MIMO-MC-CDMA. On note que l'implémentation de cette chaîne a nécessité l'implémentation des opérations arithmétiques élémentaires telles que l'addition et la multiplication. Les schémas RTL correspondants à ces opérateurs seront fournis en annexe.

4.2.1. Bloc de modulation 256-QAM

Ce bloc effectue la modulation numérique des données binaires pour 1 utilisateur. On rappelle qu'un symbole issu d'un modulateur numérique 256-QAM est de la forme :

ckakjbk (3.1)
où ak et bk appartiennent à l'alphabet {#177;1, #177;3, ..., #177;15}.

Le bloc du modulateur numérique 256-QAM délivre un symbole correspondant à chaque 8 bits successifs reçus à son entrée. Le fonctionnement de ce modulateur est décrit par l'organigramme de la figure 3.4.

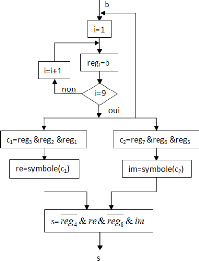
Figure 3.4. Organigramme du modulateur 256-QAM

code	000	001	011	010	110	111	101	100
symbole	15	13	11	9	7	5	3	1

Tableau 3.1. Table d'assignation des symboles en fonction du code

La génération des symboles en fonction des codes composés de trois bits est décrite par le tableau 3.1. Les paramètres d'entrées sorties du bloc "Modulation" sont présentés dans le tableau 3.2. Le résultat de synthèse au niveau RTL du bloc modulation est fournit dans le tableau 3.3.

4.2.2. Bloc étalement

Ce bloc effectue l'étalement simultané des symboles des 64 utilisateurs. Les séquences d'étalement utilisées pour notre chaîne sont les séquences de Walsh-Hadamard. Le processus d'étalement peut être effectué par une multiplication par la matrice de Walsh-Hadamard en se référant à l'équation

Nom du signal	E/S	Description	Taille	Groupement logique
b	Entrées	Donnée binaire d'un utilisateur	1 bit	Interface entrée
s	sortie	Symbole délivré	64 bits

Tableau 3.2. Table des paramètres entrées/sorties du bloc de modulation

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	21	11	64	0	0

Tableau 3.3. Résultat de synthèse du bloc modulation

(1.31) du chapitre 1. Donc l'étalement d'un vecteur de 64 symboles dk=[ ⁽⁰⁾

d_k , ..., ⁽⁶³⁾

dk ]^T est calculé

par :

xk=C64.dk, (3.2)

où _C64 est la matrice de Walsh-Hadamard d'ordre 64 et xk est le vecteur résultant de l'opération d'étalement de longueur 64.

Ce calcul peut-être simplifié en effectuant un algorithme de transformée de Hadamard Rapide (Fast Hadamard Transform FHT) du vecteur dk. En effet, d'après les équations (1.24) et (1.26) du chapitre 1 :

xk=

1 1 H 8 8 64

H H 32 32 H H 32 32

.dk (3.3)

52

En décomposant le vecteur dk en d1, k=[ (0)

d_k , ..., ⁽³¹⁾

dk ]^T et d2 ,k=[ (32)

d_k , ..., ⁽⁶³⁾

d_k ]^T, on obtient :

(3.4)
xk=		11 H H d H d H d 32 32 1, 32 1, 32 2, k kk 8 8 H H d H d H d 32 32 2, 32 1, 32 2, k k k

On remarque que la transformée de Hadamard d'ordre 64 du vecteur dk peut se simplifier par une transformée de Hadamard d'ordre 32 de _d1,k et une transformée de Hadamard d'ordre 32 de _d2,k puis effectuer la somme et la différence de ces deux transformées.

Ainsi le FHT est un algorithme récursif, d'où la transformée de Hadamard d'ordre 32 peut être
calculée de la même manière en fonction de la transformée de Hadamard d'ordre 16. L'architecture

proposée pour le bloc d'étalement est représenté dans la figure 3.5. On représente aussi la

1

transformée de Hadamard d'ordre 2 en tenant compte de la multiplication par le facteur de 8 dans

la figure 3.6. A titre d'illustration, on montre le schéma RTL du circuit effectuant la transformée de Hadamard d'ordre 8 dans la figure 3.7.

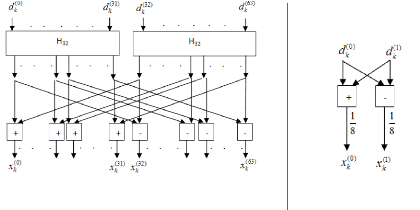
Figure 3.5. Architecture du bloc Etalement

Figure 3.6. FHT d'ordre 2

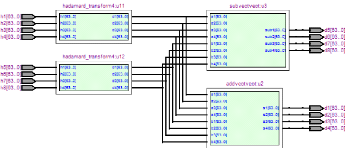
53

Figure 3.7. Schéma RTL du FHT à l'ordre 8

Les paramètres d'entrées sorties du bloc "Etalement" sont présentés dans le tableau 3.4.

Nom du signal	E/S	Description	Taille	Groupement logique
h[1..64]	Entrées	Symboles des utilisateurs	64 bits	Interface entrée
d[1..64]	Sorties	Symboles étalés	64 bits	Interface sortie

Tableau 3.4. Table des paramètres entrées/sorties du bloc de Etalement

Le résultat de synthèse au niveau RTL du bloc FHT à l'ordre 8 est fournit dans le tableau 3.5.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	44772	0	1024	0	0

Tableau 3.5. Résultat de synthèse du bloc FHT 8

4.2.3. Bloc de démultiplexage spatial V-BLAST pour 2 antennes

Le bloc de démultiplexage spatial pour les 2 antennes est composé de 64 démultiplexeurs relatifs aux 64 sous-porteuses où les sorties de chaque démultiplexeur génère les symboles vers les 2 antennes. Le schéma bloc du démultiplexage spatial V-BLAST est représenté dans la figure 3.8. L'organigramme de chaque démultiplexeur pour chaque sous-porteuse est présenté dans la figure 3.9.

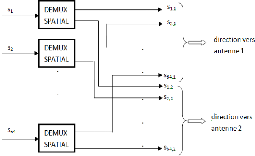
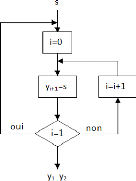
Figure 3.8. Bloc de Démultiplexage V-BLAST

Figure 3.9. Organigramme d'un "DEMUX

54

SPATIAL"

Le schéma RTL du DEMUX SPATIAL est représenté dans la figure 3.10.

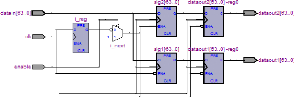
Figure 3.10. Schéma RTL du Bloc "DEMUX SPATIAL"

Les paramètres d'entrées sorties du démultiplexeur spatial sont présentés dans le tableau 3.6.

Nom du signal	E/S	Description	Taille	Groupement logique
clk	Entrée	Horloge de système	1 bit	Interface système
enable	Entrée	Validation de fonctionnement	1 bit
datain[1..64]	Entrées	Données du système	64 bits	Interface entrée
enable[1..2]	sorties	Validation de sortie de données	1 bit	Interface sortie
dataout[1..128]	sorties	données démultiplexées	64 bits

Tableau 3.6. Table des paramètres entrées/sorties du bloc de démultiplexage V-BLAST

Le résultat de synthèse au niveau RTL du bloc de démultiplexage V-BLAST est fournit dans le tableau 3.7.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	2	16385	12290	0	0

Tableau 3.7. Résultat de synthèse du bloc de démultiplexage V-BLAST

4.2.4. Bloc modulateur OFDM

Le rôle principal de ce bloc est d'effectuer la modulation OFDM des 64 symboles reçus en parallèles à son entrée. L'architecture d'un modulateur OFDM est représentée dans la figure 3.11.

55

Figure 3.11. Architecture du modulateur OFDM Le bloc "Modulateur OFDM" est composé de 2 sous-blocs :

- Bloc IFFT : ce bloc est utilisé dans les chaînes utilisant la technique de modulation OFDM. Son

rôle consiste à effectuer la transformée de Fourier rapide inverse d'un vecteur de 64 symboles.

- Bloc P/S+ACe bloc effectue la sérialisation des données reçus en parallèle en introduisant

l'intervalle de garde qui consiste à un préfixe cyclique de longueur Lc .

4

4.2.4.1. Architecture du bloc IFFT

Pour définir une architecture du bloc IFFT. On définit tout d'abord la Transformée de Fourier Discrète Inverse (TFDI) d'un vecteur x de longueur N où x =(x0, x1, ..., xN-1).

La TFDI de x est définit par :

N 1

A w x

k N n

n k

. , pour k=0,..,N-1, (3.5)

n 0

2i

avec w N

N e . L'expression de Ak peut être décomposée en 2 expressions l'une à indice paire et

l'autre à indice impair. On obtient les équations (3.6) et (3.7).

N 1 2

A x x w ^nk

. (3.6)

2 k n N N

n

n 0 2 2

2

k

N

A x x w

2 1 n N

0 2

n nk

N N
. w

n

n 2

1

(3.7)

56

L'expression _A2k+1 (équation 3.7) peut être décomposé en 2 expressions : l'une à indice 4k+1 et l'autre à indice 4k+3. On obtient les équations (3.8) et (3.9).

N

1

(3.8)

4 n n k

.

. . 3

A x ^j x x j x

N N N N

w w

4 1

k n n n n N

N

n 0 4 2 4 4

1

43 .

n n k

. . 3

A x ^j x x j x

N N N N (3.9)

4 3

k n n n n N

w w

n 0 4 2 4 4

Le système formé par les équations (3.6), (3.8) et (3.9) est un système appelé Split Radix qui permet le calcul de la transformée de Fourier rapide inverse du vecteur x.

On observant la TFDI, on peut remarquer que les équations (3.6), (3.8) et (3.9) sont aussi des TFDI de certaines combinaisons de x.

57

En effet :

N N

11

22

A x x W a W TFDI

. . ( )

nk ^nk a (3.10)

2 k n N N n N

n

22 0 2

n

⁰

n

où a=(a0, a1, ..., _aN/2-1) ^avec _an=xn + _xn+N/2. On a encore :

N N 1 1 4 4 n n k n k . . A x ^j x x j x b k n n n n N n . . N N N N N 3 W W W 4 1 n0^4 2 4 4 4 n 0	TFDI b ( ) , (3.11)
n n où b=(b0, b1, ..., bN/4-1) avec b j j 3 n n n n n N n n n n N 3 x x x x W x x j x j x N N N . . N N N . . W 4 2 4 2 4 4		.

On écrit également :

N N

1 1

4 3 . 4 .

A x x x x c_n

n n k n k

j j

. .

N N 3 N N N N

W W W TFD c

( ) , (3.12)

4 3

k n n n n

n 0 4 2 4 4 n0 4

3n 3 n

avec c=(c0, c1, ..., _cN/4-1) et cj j 3

n n n n n N n n n n N

3

x x x x W x x j x j x

N N N

. .

N N N . . W

4 2 4 2 4 4

D'après les équations (3.10), (3.11) et (3.12), on peut conclure que la Transformée de Fourier Inverse
à l'ordre N du vecteur x peut être décomposée en une Transformée de Fourier Inverse à l'ordre

N du vecteur a et une Transformée de Fourier Inverse à l'ordre N des vecteur b et c.

2 4

Pour notre cas, on a besoin d'une IFFT à l'ordre 64. Donc les expressions des vecteurs a, b et c sont données dans les équations suivantes :

an=xn + _xn+32 , n=0, ..., 31 (3.13)

. n j

16 . 48

x n W _N , n=0, ...,16 (3.14)

n

b n x _n x n j x

32

3

n x n x n W N , n=0, ...,16 (3.15)

n

c n x 32 . 16 . 48

j x n j

Et par suite, l'architecture du bloc de l'IFFT peut être déduite par la figure 3.12. Les architectures des sous-blocs IFFT32 et IFFT16 peuvent être déduites à partir des équations (3.10), (3.11) et (3.12) en remplaçant respectivement N par 32 et par 16. Les blocs d'IFFT à l'ordre 2 et 4 sont représentés dans les figures 3.13 et 3.14.

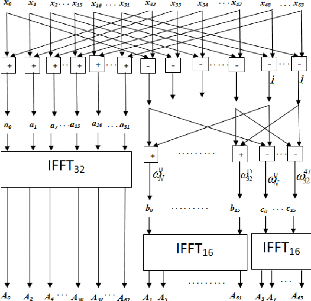
Figure 3.12. Architecture du bloc IFFT

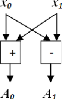
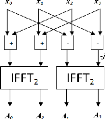
Figure 3.13. Bloc d'une IFFT à l'ordre 2

Figure 3.14. Bloc d'une IFFT à l'ordre 4

58

Les paramètres d'entrées/sorties du bloc " IFFT " sont présentés dans le tableau 3.8.

Nom du signal	E/S	Description	Taille	Groupement logique
d[1..64]	Entrées	Données du système	64 bits	Interface entrée
f[1..64]	sorties	Sorties modulés en IFFT	64 bits	Interface sortie

Tableau 3.8. Table des paramètres entrées/sorties du bloc IFFT Le schéma RTL d'une IFFT à l'ordre 8 est illustré dans la figure 3.15.

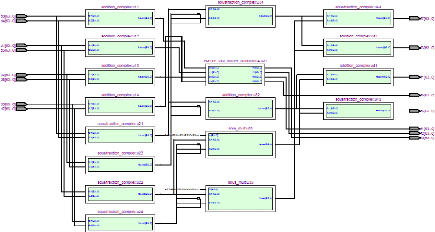
59

Figure 3.15. Schéma RTL d'une IFFT à l'ordre 8

Le résultat de synthèse au niveau RTL du bloc IFFT à l'ordre 8 est fournit dans le tableau 3.9.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	52259	0	1024	0	0

Tableau 3.9. Résultat de synthèse du bloc IFFT

4.2.4.2. Bloc de conversion parallèle/série avec introduction de l'intervalle de garde

Le convertisseur P/S avec introduction de l'intervalle de garde est le deuxième sous-bloc de la composante "Modulateur OFDM". Il consiste, dans un premier temps à envoyer successivement les 16 derniers symboles des 64 symboles à transmettre. Puis, il envoie tous les symboles successivement. L'organigramme de ce bloc est présenté dans la figure 3.16. Ainsi, le résultat de synthèse au niveau RTL du bloc conversion P/S +est fournit dans le tableau 3.10.

Famille FPGA	de	Nombre de LUT	Nombre registres	de	Nombre de pin	total	Nombre DSP	de	Nombre mémoire	de	bloc
Stratix.II.GX		1352	71		4162		0		0

Tableau 3.10. Résultat de synthèse du bloc P/S +

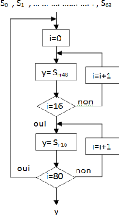
60

Figure 3.16. Organigramme du bloc de conversion P/S +

4.2.5. Bloc démodulateur OFDM

Ce bloc est composé des blocs de la chaîne de démodulation OFDM. Son diagramme en bloc est représenté dans la figure 3.17.

Figure 3.17. Diagramme en bloc du démodulateur OFDM Le bloc "démodulateur OFDM" est composé des deux sous-blocs suivants :

- Bloc S/P-: Le rôle de se bloc consiste à supprimer l'intervalle de garde de chaque symbole

OFDM reçu tout en effectuant la conversion série/parallèle.

- Bloc FFT : ce bloc calcule la transformée de Fourier rapide d'un vecteur de 64 symboles.

4.2.5.1. Bloc de conversion série/parallèle avec suppression de l'intervalle de garde

Le convertisseur S/P avec suppression de l'intervalle de garde est le premier bloc de la partie de réception de la chaîne MC-CDMA. Il consiste à recevoir les 16+64 symboles émis (en série) en éliminant les 16 premiers symboles reçus qui correspondent à l'intervalle de garde introduit lors de l'émission. L'organigramme de ce bloc est présenté dans la figure 3.18. Ainsi, le résultat de synthèse au niveau RTL du bloc conversion S/P -est fournit dans le tableau 3.11.

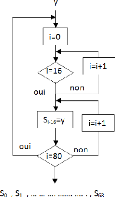
61

Figure 3.18. Organigramme du bloc de conversion S/P -

Famille FPGA	de	Nombre de LUT	Nombre registres	de	Nombre de pin	total	Nombre DSP	de	Nombre mémoire	de	bloc
Stratix.II.GX		84	8199		4162		0		0

Tableau 3.11. Résultat de synthèse du bloc S/P -

4.2.5.2. Bloc de Transformée de Fourier rapide FFT

Pour définir l'architecture du bloc FFT. On doit d'abord expliciter l'expression de la transformée. Soit un vecteur x de dimension N tel que x =( x0, x1, ..., xN-1).

La Transformée de Fourier Discrète (TFD) de x est égal à :

~ 1 A x TFD x ~ ù 1 ( ) n k . k ~ n n 0

avec

2i ù N ~ e pour k=0,..,N-1

Donc l'architecture du FFT aura une architecture semblable à celle de l'IFFT avec les changements suivants :

- Les multiplications par ^k

ù₁ deviennent des multiplications par ~ù k ;

- Les multiplications par j deviennent des multiplications par -j ;

62

- L'architecture du FFT à l'ordre 2 en tenant compte de la multiplication par le facteur N est

décrite dans la figure 3.19 dans le cas d'une FFT à l'ordre 64.

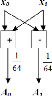
Figure 3.19. Architecture d'une FFT à l'ordre 2.

Les paramètres d'entrées sorties du bloc "FFT" sont présentés dans le tableau 3.12.

Nom du signal	E/S	Description	Taille	Groupement logique
f[1..64]	Entrées	Données reçue	64 bits	Interface entrée
d[1..64]	Sorties	données modulés en FFT	64 bits	Interface sortie

Tableau 3.12. Table des paramètres entrées/sorties du bloc FFT

Le résultat de synthèse au niveau RTL du bloc IFFT à l'ordre 8 sont fournit dans le tableau 3.13.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	71179	0	1024	0	0

Tableau 3.13. Résultat de synthèse du bloc IFFT

4.2.6. Bloc de l'égalisation

Nous avons décrit en VHDL les blocs d'égalisation suivants :

- Egalisation mono-utilisateur à critère ZF ;

- Egalisation multi-utilisateurs à critère MMSE ;

- Algorithme SIC à critère MMSE.

Nous ne développons dans cette partie que les spécifications fonctionnelles de l'égaliseur multiutilisateurs à critère MMSE. Pour une égalisation multi-utilisateurs le vecteur xà correspondant à la décision des symboles émis est égale à :

xà =.y (3.16)

où y est le vecteur reçu et Q est la matrice d'égalisation donnée par :

~ =(eTc9-(†c9-(e+ 1 r

5 )^-1 eTc9-( † (3.17)

avec e est une matrice diagonale en bloc, dont les matrices sur la diagonale de e sont des matrices de Hadamard, c9-( est une matrice formée par des matrices diagonales Hrt , avec H_rt=diag _(hrt,n; n=0,...,63), r est le SNR estimé. Pour une transmission à plein charge, on a :

e^T=e et e^-1 = e (3.18)

Donc :

e+ 1 xà =(ec9-( ^†c9-( r	5)^-1 e^Tc9-(^†.y (3.19)
= e~~(c9-( ^†c9-( + 1 r + 1 = e (c9-( ^†c9-( r		5)-1 e~~ e c9-(^†.y 5)^-1 c9-( ^†.y

La matrice (c9-( ^†c9-( + 1 5 )^-1 c9-( † est une matrice formée par des sous-matrices diagonales.

r

On pose:

+ 1 v=(c9-( ^†c9-( r

5 )^-1 c9-( ^†.y (3.20)

Le calcul de xà consiste donc à calculer le vecteur v, puis lui appliquer la transformée de Hadamard.

L'inverse d'une matrice formée par des sous-matrices diagonales est aussi une matrice formée par des sous-matrices diagonales. On pose:

63

+ 1 P= c9-( ^Hc9-(

r

5 (3.21)

On décrit par la suite la méthode qu'on a suivi pour inverser la matrice P. On rappelle que la matrice équivalente du canal de taille 128x128 s'écrit :

~ = 11 12

[ ? ,

H H

21 22

H H

(3.22)

et :

T

y= ? ? . (3.23)

y y y y y

1,0 1,1 1,63 2,0 2,63

On décompose ~ en 64 sous-matrices Ki ,0= i =63 de la forme : Alors :

Ki = 11, 12,

h h

i

[ h h

21, 22,

i

i Ò , 0= i =63. (3.24)

i

64

La matrice Ki représente la matrice qui regroupe les i^ème éléments diagonaux de chaque matrice Hrt 1=r,t=2.

yi= y 1, i , 0= i =63 (3.25)

y 2, i

avec yi est le vecteur qui rassemble le i^ème élément reçu par la première antenne et le i^ème élément reçu par la deuxième antenne.

On montre que, le calcul de vi (les sous vecteurs de v avec 0= i =63) se déroule de la manière suivante :

vi =(Ki † Ki+ 1 ã

I)^-1 Ki^† yi . (3.26)

L'architecture qu'on propose pour l'égaliseur multi-utilisateurs à critère MMSE est représentée dans la figure 3.20.

D'après cette figure, le bloc de l'égaliseur se compose de 64 sous-blocs de "calculateur de vi". L'architecture de ce sous-bloc sera définie en fonction de l'équation 3.26 sachant les équations 3.24 et 3.25. En développant vi, on obtient :

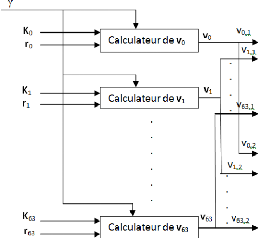
Figure 3.20. Architecture de l'égaliseur multi-utilisateurs à critère MMSE.

1 0

* * * *

L h h y

h h ã h h

?

11, 21, 1,

i i i

11, 12,

i i 11, 21,

i i

L H ? ?

?

* * * *

h h y

h h

1 h h

12, 22, 2,

i i i

21, 22,

i i 12, 22,

i i

0

? ?

1

vi=

. (3.27)

ã

qui s'écrit sous cette forme :

v_i = M _i .w i (3.28)

1

2 2 1

avec Mi=

h h h h h h

* *

? 1 1, 21, 11, 12, 21, 22,

i i i i i i

ã

? h h h h

? i i i i

* 2 2 1

* *

11, 12, 21 , 22, 12, 22 ,

h h

i i

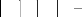
ã

?

65

T

et

*

h y

11, 1,

i i

h h y h y

* * *

11, 21, 1, 21, 2,

i i i i i

w ? ?

ⁱ h h y h y

* * T

*

12, 22, 2,

i i i 12, 1,

i i

h y

*

22, 2,

i i

D'où le calculateur de vi consiste à : calculer la matrice Mi, calculer l'inverse de la matrice Mi, calculer wi et calculer le produit wi par Mi.

66

L'architecture du calculateur de vi est représentée dans la figure 3.21.

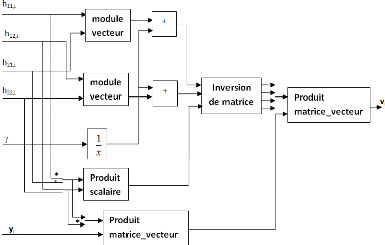
Figure 3.21. Architecture du calculateur de vi en fonction de _hrt,i , yi et ã

Les schémas RTL des sous-blocs du calculateur de vi sont représentés dans les figures (3.22), (3.23), (3.24) et (3.25).

Figure 3.22. Schéma RTL du sous-bloc Figure 3.23 Schéma RTL du sous-bloc "Produit

"module vecteur" matrice_vecteur"

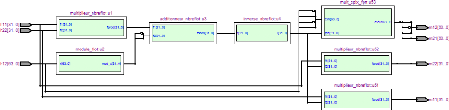
Figure 3.24. Schéma RTL du sous-bloc inversion de matrice

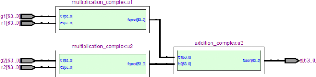
67

Figure 3.25. Schéma RTL du sous-bloc produit scalaire

Le résultat de synthèse au niveau RTL du bloc calculateur est fournit dans le tableau 3.14.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	93672	0	544	0	0

Tableau 3.14. Résultat de synthèse du bloc-bloc calculateur utilisé pour le bloc égaliseur

Les paramètres d'entrées sorties du bloc "Egaliseur multi-utilisateurs à critère MMSE" sont présentés dans le tableau 3.15.

Nom du signal	E/S	Description	Taille	Groupement logique
snr	Entrée	Rapport signal sur bruit estimé	32 bit
h11_[1..64]			64 bit
h12_[1..64]	Entrées	Les coefficients du canal estimés		Interface système
h21_[1..64]
h22_[1..64]
r1_[1..64]	Entrées	Vecteur reçu après démodulation	64 bits	Interface entrée
r2_[1..64]		OFDM
s1_[1..64]	Sorties	Vecteur obtenu après égalisation	64 bits	Interface sortie
s2_[1..64]

Tableau 3.15. Table des paramètres entrées/sorties du bloc Egaliseur multi-utilisateurs

4.2.7. Bloc de multiplexage spatial de 2 antennes

Le bloc de multiplexage spatial de 2 antennes est composé de 64 multiplexeurs où les entrées de chaque multiplexeur proviennent de la première antenne et de la deuxième antenne. Son diagramme en bloc est représenté dans la figure 3.26. L'organigramme de chaque multiplexeur est représenté dans la figure 3.27.

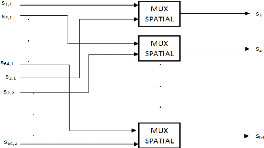
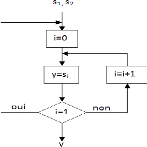
Figure 3.26. Diagramme du bloc de multiplexeur spatial

Figure 3.27. Organigramme d'un

68

multiplexeur

Le schéma RTL d'un multiplexeur est représenté dans la figure 3.28.

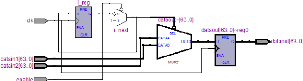
Figure 3.28. Schéma RTL d'un multiplexeur spatial

Les paramètres d'entrées sorties du multiplexeur spatial sont présentés dans le tableau 3.16. Ainsi, le résultat de synthèse au niveau RTL du bloc multiplexeur spatial est fournit dans le tableau 3.17.

4.2.8. Bloc "désétalement + quantification"

Ce bloc effectue désétalement des symboles reçus à son entrée qui consiste à effectuer la transformée de Hadamard inverse d'un vecteur de symbole, puis effectue la procédure de quantification en fonction de la technique de modulation numérique utilisée (256-QAM).

69

Nom du signal	E/S	Description	Taille	Groupement logique
clk	Entrée	Horloge de système	1 bit	Interface système
enable[1..2]	Entrée	Validation de fonctionnement	1 bit	Interface entrée
datain[1..128]	Entrées	Données Démultiplexées	64 bits
enout	sorties	Validation de sortie de données	1 bit	Interface sortie
dataout[1..64]	sorties	données réordonnées	64 bits

Tableau 3.16. Table des paramètres entrées/sorties du bloc multiplexeur spatial

Famille FPGA	de	Nombre de LUT	Nombre registres	de	Nombre de pin	total	Nombre DSP	de	Nombre mémoire	de	bloc
Stratix.II.GX		3	4098		12292		0		0

Tableau 3.17. Résultat de synthèse du bloc-bloc calculateur utilisé pour le bloc multiplexeur spatial

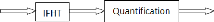
Figure 3.29. Schéma bloc de "désétalement + quantification"

4.2.8.1. Bloc IFHT

Ce bloc calcule la transformée de Hadamard inverse d'un vecteur. Puisqu'on est dans le cas d'une transmission à pleine charge, alors C est une matrice carrée et elle est égale à son inverse. Ainsi, l'architecture du calculateur de la transformée de Hadamard rapide inverse est semblable à l'architecture de la transformée de Hadamard rapide FHT définie dans 3.2.2 de ce chapitre.

4.2.8.2. Bloc de quantification

La procédure de quantification est effectuée en fonction de la modulation numérique 256-QAM. Cette procédure consiste à renvoyer en sortie le symbole qui est à une distance minimal du symbole reçu en entrée. La figure 3.30 présente l'organigramme du quantificateur 256-QAM.

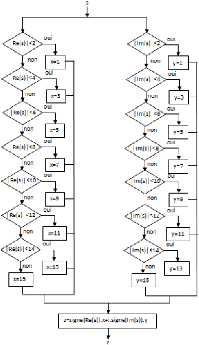
70

Figure 3.30. Organigramme du quantificateur 256-QAM

Le résultat de synthèse au niveau RTL du bloc quantificateur 256-QAM est fournit dans le tableau 3.19.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	12	0	128	0	0

Tableau 3.19. Résultat de synthèse du bloc-bloc calculateur utilisé pour le bloc quantificateur

4.2.9. Bloc démodulation

Ce bloc effectue la démodulation 256-QAM des symboles. Son principe consiste à renvoyé en sortie les bits qui correspondent au symbole reçu à son entrée en fonction de la constellation 256-QAM. L'organigramme de ce bloc est représenté dans la figure 3.31.

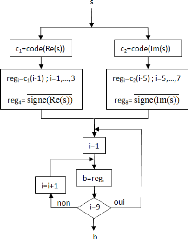
71

Figure 3.31. Organigramme du bloc de démodulation

Les paramètres d'entrées sorties du bloc démodulation sont présentés dans le tableau 3.20.

Nom du signal	E/S	Description	Taille	Groupement logique
s	Entrée	symbole	64 bits	Interface entrée
b	Sortie	bit d'information	1 bit	Interface sortie

Tableau 3.20. Table des paramètres entrées/sorties du bloc démodulation

Le résultat de synthèse au niveau RTL du bloc démodulation est fournit dans le tableau 3.21.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	53	4	67	0	0

Tableau 3.21. Résultat de synthèse du bloc-bloc calculateur utilisé pour le bloc démodulation

5. Optimisation et analyse de performances de la chaîne

Dans cette partie, on s'intéresse à la synthèse et à l'analyse temporelle des circuits d'émission et de réception de la chaîne MIMO-MC-CDMA implémentée. La phase d'optimisation de la conception commence dans les étapes de simulations fonctionnelles et d'analyse temporelle.

Dans le flot de conception adopté, l'optimisation d'un tel système revient à :

- la réduction de l'utilisation de ressources inférées ;

- l'amélioration des performances de « timing » ;

- la réduction du temps de compilation (utilisation de la compilation incrémentale pour alléger

l'espace d'exploration des solutions dans le placement et routage) ;

- l'estimation et la gestion optimale de la puissance dissipée en consommation statique et

dynamique ;

- la création des partitions pour préparer la synthèse incrémentale.

Pour l'optimisation de notre chaîne d'émission, on a recours aux étapes suivantes :

- Synthèse incrémentale qui consiste à donner la priorité pour la synthèse aux blocs de mémorisation (spécialement des registres et des mémoires de type SRAM) de façon qu'ils soient contigus dans leurs emplacements dans l'FPGA.

- Une phase d'exploration d'architecture qui nécessite la définition d'un vecteur de contrainte

dont ses composants reflètent les valeurs pondérées souhaitées sur la surface, la consommation et la fréquence.

- Les différentes phases qui précèdent la génération optimale des résultats de synthèse de toute la chaîne d'émission consistent en une paramétrisation et une configuration des contraintes du système à implémenter par :

- la fixation de l'architecture cible, dans notre cas c'est le circuit FPGA « Stratix II GX

EP2GXX90FF1508C3N » équipé de 1508 pins et de douze transmetteurs pour la sérialisation et la désérialisation des données;

- La configuration de l'exigence de « timing » : l'ajout d'un fichier des contraintes temporelles

force le synthétiseur à accomplir des optimisations dans la synthèse physique (après le placement et routage). Cette configuration doit se baser sur la connaissance des paramètres technologiques des « LUTs » et « ALMs », dans notre cas ce sont les temps "tsu" , "th", "tco", "tpd" et la fréquence nominale des étages séquentielles dans la chaine d'émission, ici la fréquence est fixée à 500M Hz.

- Lire les différents temps de latence de la chaîne et qui correspondent aux différents chemins

critiques du système. Cette étape consiste à corriger les violations des paramètres

72

73

74

technologiques temporelles et de déceler la fréquence maximale de la chaîne par le temps de latence entre l'entrée et la sortie (ou « tpd »).

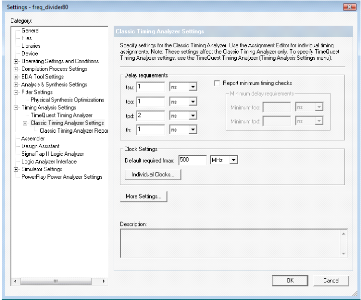
Figure 3.32. Configuration des paramètres de Timing

Dans le cas où il y a une insatisfaction des résultats attendus spécialement en terme d'aspect fréquentiel, on sera obligé de refaire l'étape de la configuration des contraintes de la synthèse et d'analyser de nouveau les résultats de post-placement et routage.

Les figures 3.32 et 3.33 résument le résultat de synthèse et l'analyse de Timing pour le cas de deux utilisateurs qui émettent leurs données pour un système MIMO-MC-CDMA.

On conclut que la fréquence fonctionnelle (ou de cadencement des données et ses traitements) maximale est de 174,672 MHz obtenue après avoir suivi les différentes optimisations citées auparavant.

Les figures 3.34 et 3.35 résument le résultat de synthèse et l'analyse de Timing pour le circuit de réception du système MIMO-MC-CDMA récupérant les données de deux utilisateurs.

On conclut que la fréquence fonctionnelle (ou de cadencement des données et ses traitements)
maximale est de 54,29 MHz obtenue après avoir suivi les différentes optimisations citées auparavant.

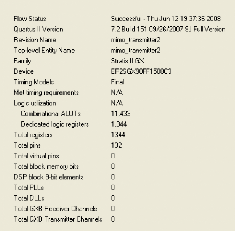
Figure 3.32. Résultat de synthèse de la chaîne d'émission du système MIMO-MC-CDMA

Figure 3.33. Analyse de Timing de la chaîne d'émission du système MIMO-MC-CDMA

Figure 3.34. Résultat de synthèse de la chaîne de réception du système MIMO-MC-CDMA

75

Figure 3.35. Analyse de Timing de la chaîne de réception du système MIMO-MC-CDMA

6. Conclusion

A travers ce chapitre, on a d'abord présenté la plateforme FPGA cible Stratix.II.GX et l'architecture de ses ressources internes. Puis, on a expliqué le flot de conception adopté pour la réalisation matérielle des différents blocs de la chaîne MIMO-MC-CDMA. Ensuit, on a détaillé les architectures des différentes composantes de la chaîne. Ces architectures, malgré leurs efficacités de traitement rapides des signaux, présentent des inconvénients en termes de consommation en ressources internes du FPGA. Pour cela, on a eu besoin de chercher des solutions permettant l'optimisation des architectures implémentées.

76

CONCLUSION ET PERSPECTIVES

L'objectif de ce projet de fin d'études est d'étudier et d'implémenter un système sans fil utilisant la technique à multiplexage spatial associée à la technique MC-CDMA. L'intérêt de l'association des deux techniques est d'exploiter les avantages des deux systèmes en un seul qui est le MIMO-MCCDMA. En effet, la technologie MIMO offre un débit important et une bonne qualité de transmission grâce à la diversité spatiale en émission et/ou en réception. En particulier, la technique à multiplexage spatial permet d'exploiter de manière optimale la capacité des systèmes MIMO avec l'hypothèse que le canal est connu au récepteur. Par ailleurs, la technique MC-CDMA permet de combattre la sélectivité fréquentielle du canal radio par la modulation OFDM et d'avoir une séparation efficace et simple des utilisateurs grâce au détecteurs multi-utilisateurs utilisé en CDMA.

Durant ce projet, on a commencé par valider et évaluer les performances de certaines techniques de réception du multiplexage spatial. Cette évaluation a montré que l'égaliseur MMSE présente une meilleure performance par rapport au détecteur ZF, et que l'algorithme SIC améliore la qualité de la détection en annulant successivement l'interférence des antennes d'émission. Ensuite, on a évalué les performances de la technique à multiplexage spatial dans un contexte MC-CDMA. On a montré à travers les simulations que les performances du système résultant dépendent de plusieurs paramètres tels que : le nombre d'antennes à l'émission, le nombre d'antennes à la réception, le nombre de sous-porteuses, la charge du système, la nature du critère associée à l'égaliseur utilisé au récepteur, la nature de la détection et l'utilisation d'un codage de canal, etc.

Dans la dernière phase de ce travail, on s'est intéressé à l'implémentation matérielle de la chaîne MIMO-MC-CDMA. Cette phase a consisté premièrement à définir les spécifications fonctionnelles des différents composants de la chaîne d'émission et de réception du système. Cette opération est effectuée simultanément avec la description matérielle en VHDL et la vérification du bon fonctionnement par simulation. Par ailleurs, les performances du système implémenté ont été testées sur la plateforme de prototypage FPGA afin de tester le bon fonctionnement du système et la satisfaction des contraintes temporelles. Les résultats de synthèse ont été présentés dans un rapport d'implémentation comprenant l'analyse de timing de la conception, les ressources utilisées et leurs exploitations dans l'architecture cible FPGA de type Stratix.II.Gx.

On conclut que le système MC-CDMA constitue un système de hautes performances puisqu'il regroupe les avantages de plusieurs techniques permettant l'exploitation des trois formes de diversité spatiale, temporelle et fréquentielle. Ces performances viennent également de la fléxibilité du système qui comporte un grand nombre de degré de libérté.

77

Le choix optimal de ces degrés abouti à un système de performances optimales qui sont fonction de l'application et des besoins du réseau de télécommunication.

En ce qui concerne l'implémentation matérielle, l'architecture du système MIMO-MC-CDMA proposé nécessite certainement une optimisation des ressources internes utilisées afin de pouvoir intégrer d'autres modules dans la même IP tel que l'estimateur de canal. Par ailleurs, la validation de l'architecture implémentée a été testée pour certaines réalisations du canal radio-mobile. Il serait donc intéressant de développer une IP qui permet de générer toutes les réalisations du canal et d'évaluer au niveau matériel les performances de l'architecture proposés en termes de taux d'erreur binaire.

78

RÉFÉRENCES BIBLIOGRAPHIQUES

[1] Olivier Berder, « Optimisation et stratégie d'allocation de puissance des systèmes de transmission multi-antennes ». Thèse à l'université de Bretagne Occidentale, France 2002.

[2] G. D. Forney Jr, »The Viterbi Algorithm», P roc. IEEE, vol. 61, No 3, March 1973.

[3] Basel Rihawi, « Analyse et réduction du Power Rattio des systèmes de radio-communications multi-antennes ». Thèse à l'université de Rennes I, France 2008.

[4] Inés Kammoun-Jemal, « Codage spatio-temporel sans connaissance à priori du canal ». Thèse à l'Ecole Nationale Supérieure des Télécommunications de Paris, France 2004.

[5] John G. Proakis. Digital communications. McGraw-Hill, Third Edition, 1995.

[6] Henrik Schulze, Christian Lüders, « Theory and applications of OFDM and CDMA. Wideband wireless communications ». IEEE Wiley, 2005.

[7] L. Hanzo, M. Münster, B.J. Choi, T. Keller, « OFDM and CDMA for Broadband Multi-user Communications, WLANs and Broadcasting ». IEEE Wiley 2003.

[8] Claire Goursaud-Brugeaud, « Réception multi-utilisateurs par annulation parallèle d'interferences dans les systèmes CDMA optiques ». Faculté des sciences Laboratoire XLIM Département -C²S² UMR CNRS 6172,Thèse N° 37-2006. France 2006.

[9] V. M. DaSilva and E. S. Sousa, «Performance of orthogonal CDMA codes for quasisynchronous communication systems», in Proceedings of IEEE ICUPC 193, (Ottawa, Canada), pp. 995-999, October 1993.

[10] L. Vandendorpe, «Multitone direct sequence CDMA system in an indoor wireless environment», in Proceedings of IEEE SCVT 1993, (Delft, The Netherlands), pp. 4.1:1-8, October 1993.

[11] N. Yee, J,-P. Linnartz, and G. Fettweis, «Multicarrier CDMA in indoor wireless radio networks», in PIMRC'93, pp. 109-113, 1993.

[12] A. Chouly, A. Brajal, and S. Jourdan, «Orthogonal multicarrier techniques applied to direct sequence spread spectrum CDMA systems», in Proceedings of the IEEE Global Telecommunications Conference 1993, (Houston, TX, USA), pp. 1723-1728, 29 November - 2 december 1993.

[13]

79

R. Prasad and Hara, «Overview of multi-carrier CDMA», in Proceedings of IEEE International Symposium on Spread Spectrum Techniques and Applications (ISSSTA), (Mainz, Germany), pp. 107 - 114, 22-25 Septem ber 1996.

[14] G. J. Foschini, «Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas», Bell Labs. Tech. J., vol. 1, no. 2, pp. 41. 59, 1996.

[15] V. Tarokh, N.Seshadri, and A. Calderbank, «Space-time codes for high data rate wireless communication : Performance criterion and code construction,» IEEE Trans. Info.Theory, vol. 44, pp. 744.765, March 1998.

[16] S. Alamouti, «Space-time block coding : A simple transmitter diversity technique for wireless communications,» IEEE J. Select. Areas. Commun., vol. 16, pp. 1451.1458, Oct. 1998.

[17] A. Klein, G. K. Kaleh and P. W. Baier, « Zero forcing and minimum meansquare error equalization for multi-user detection in code-division multipleaccess channels », IEEE Transactions on Vehicular Technology, vol. 45, no. 2,pp. 276-287, May 1996.

[18] Vincent Le Nir, « Etude et optimisation des systèmes multi-antennes associés à des modulations multiporteuses ». Thèse à l'Institut National des Sciences Appliquées de Rennes, France, 2004.

ANNEXE

Afin de pouvoir effectuer les calculs d'addition, de soustraction, de multiplication et de division entre les différents signaux dans le système, il est nécessaire de représenter chaque nombre réel en une forme binaire normalisée unique qui traduit sa valeur.

Dans ce projet, la représentation des nombres réels sera selon le format IEEE 754-1985 où un nombre V est représenté en virgule flottante sur 32 bits par la manière suivante :

1 bit pour le signe ;

8 bits pour l'exposant ; 23 bits pour la mantisse.

31 22 0

exposant mantisse

signe

i 22

1 2 1 2

r r r

( 127) 23

31 23

× ×

2 i

i

i 0 i

7

Et ainsi V=

80

i0

Le zéro, l'infini et le nombre indéterminé seront représentés en une notation spéciale : Si e=255 et m?0 alors V est NaN (indéterminé)

Si e=255 et m=0 alors V est (-1)^s8

Si e=0 et m=0 alors V=(- 1 )^s 0

On présente ci-après le schéma RTL de l'opérateur d'addition et un diagramme décrivant l'opération de multiplication.

81

Schéma au niveau RTL d'un additionneur de deux nombres représentés en virgule flottante.

Diagramme de l'opération de multiplication de deux nombres représentés en virgule flottante