Etude et analyse paramétrique des echangeurs de chaleur dans une machine tritherme - cas du condenseur-

République Algérienne Démocratique et Populaire

Ministère de l'Enseignement Supérieur et de la Recherche Scientifique
Université Mentouri Constantine

Faculté des Sciences de l'Ingénieur

Département de Génie Climatique

Mémoire

Présenté pour l'obtention du diplôme de magister

En Génie Climatique

Option : Thermique du bâtiment et réfrigération

Thème

ETUDE ET ANALYSE PARAMETRIQUE DES
ECHANGEURS DE CHALEUR DANS UNE MACHINE
TRITHERME- CAS DU CONDENSEUR -

Présenté par :

Tourèche Sofiane

Devant le jury :

President : A.N. Kaabi Professeur à l'université de Constantine.

Rapporteur : Y. Khetib Maître de conference à l'université de Constantine.

Examinateur : M.S.Rouabah Maître de conference à l'université de Constantine.

Examinateur : R. Gomri Maître de conference à l'université de Constantine.

Dédicace

Je dédie ce travail à mon père et ma mère qui m'ont toujours encouragé et soutenu, à mes frères Mohamed, Hocine et Omar, à ma soeur Soumia

A tous mes amis

A mes collègues du poste-graduation

Remerciement

Je remercie tout d'abord le bon Dieu qui m'a donné la santé et la volonté pour terminer ce travail.

Je remercie vivement mon encadreur Monsieur Yacine Khetib, Maître de conférences à l'Université de Constantine, pour avoir dirigé ce travail, pour ses conseils et ses encouragements qui m'ont énormément aidé à mener ce travail.

Je tiens à exprimer ma respectueuse gratitude à Monsieur Abdenacer Kaabi, Professeur à l'Université de Constantine, qui m'a fait l'honneur de présider le jury de soutenance.

Mes vifs remerciements s'adressent aussi, à Monsieur Rouabeh Mohamed Saleh, Maître de conférences à l'Université de Constantine, et Monsieur Rabah Gomri, Maître de conférences à l'Université de Constantine, qui ont bien voulu consacrer une partie de leur temps pour rapporter sur ce modeste travail, et participer à son jugement.

Je tien à remercie aussi touts mes enseignants de la post-graduation, surtout Monsieur Azzedine Belhamri, Professeur à l'Université de Constantine.

Nomenclature

Symboles	Définitions				Unités
F , QC	Puissance du condenseur				[W]
q	Quantité de chaleur				[W]
q^cents	Densité de flux				[W/m^2]
m&	Débit massique				[kg/s]
V&	Débit volumique				[m^3/s]
m	Coefficient				[m^-1]
h	Coefficient de transfert de chaleur par convection				[W/m^2.K]
k	Coefficient de transfert de chaleur globale				[W/m^2.K]
Rint	Resistance d'encrassement du fluide intérieur				[m^2.K/W]
Rext	Resistance d'encrassement du fluide extérieur				[m^2.K/W]
T	Température				[°C] ou [K]
Tsat , Tc	Température saturation, de condensation				[°C] ou [K]
Tae	Température de l'air a l'entée				[°C] ou [K]
Tas	Température de l'air a la sortie				[°C] ou [K]
Tee	Température de l'eau a l'entée				[°C] ou [K]
Tes	Température de l'eau a la sortie				[°C] ou [K]
tf	Température du fluide				[°C] ou [K]
Tm	Température moyenne				[°C] ou [K]
T p	Température de la paroi				[°C] ou [K]
DT	Différence de température				[°C] ou [K]
DT C	Différence des températures chaudes				[°C] ou [K]
DTf	Différence des températures froides				[°C] ou [K]
S	Surface				[m^2]
Sech	Surface d'échange de chaleur				[m^2]
Si	Surface intérieur par mètre de longueur				[m^2/m]
Se	Surface extérieur par mètre de longueur				[m^2/m]
Sail	Surface des ailettes par mètre de longueur				[m^2/m]
Snet	Surface nette des tubes par mètre de longueur				[m^2/m]
Stot	Surface totale par mètre de longueur				[m^2/m]
Sétr	Surface étroite				[m^2]
Sfr	Surface frontale				[m^2]
SiR	Surface intérieur réelle				[m^2]
di	Diamètre intérieur des tubes				[m]
de	Diamètre extérieur des tubes				[m]
Dr	Diamètre à la base de l'ailette				[m]
r1	Rayon à la base de l'ailette				[m]
r2	Rayon à l'extérieur des tubes				[m]
et	Epaisseur des tubes				[m]
a	Pas transversal des tubes				[m]
b	Pas longitudinal des tubes				[m]
C	Ecartement des ailettes				[m]
L,H	Longueur des tubes				[m]
Lcents	Longueur des rainures				[m]
Lp	Longueur d'un passage d'un tube				[m]
Lg	Longueur parcourue par le fluide frigorigène				[m]
Ltot	Longueur total des tubes				[m]
LR	Longueur réel des tubes				[m]
Z	Nombre de passage du fluide frigorigène				[Passes]
u,v,w	Vitesses				[m/s]
vétr	Vitesse étroite de l'air				[m/s]
vfr	Vitesse frontale de l'air				[m/s]
va	Vitesse de l'air				[m/s]
ve	Vitesse de l'eau				[m/s]
G	Vitesse massique				[kg.m/s]
Lv	Chaleur latente de condensation				[kJ /kg]
vL^cents	Chaleur latente de condensation corrigée				[kJ / kg]
n	Nombre des ailettes				[ailettes]
n p	Nombre de passage de fluide				[passes]
Ntot	Nombre totale des tubes				[tubes]
NR	Nombre réel des tubes				[tubes]
B	Coefficient				-
S0	Entropie du milieu extérieur				[kJ/kg K]
S1	Entropie de la source de travail				[kJ/kg K]
L0- a	Travail produit par le fluide entre l'état 0 et a				[kJ/kg]
La - 1	Travail produit par le fluide entre l'état a et 1				[kJ/kg]
L0- 1	Travail produit par le fluide entre l'état 0 et 1				[kJ/kg]
Lu tile	Travail utile				[kJ/kg]
e	L'exergie				[kJ/kg]
DL	Perte de capacité de travail				[kJ/kg]
e1	L'exergie du fluide a l'entré du condenseur				[kJ/kg]
e2	L'exergie du fluide a la sortie du condenseur				[kJ/kg]
Symboles Grecs		Définitions		Unités
r		Masse volumique		[kg/m^3]
m		Viscosité dynamique		[kg/m.s]
u		Viscosité cinématique		[m^2/s]
Cp		Capacité thermique massique a pression constante		[J /kg.K]
l		Conductivité thermique		[W /m.K]
d		Epaisseur du film de condensat		[m]
e		L'efficacité du condenseur		-
h		Rendement des ailettes		-
hex		Rendement exérgétique		-
j		Coefficient		-
y		Coefficient		-
ztt		Paramètre de Lockhart et Martinelli		-
r		Contrainte tangentielle		[Pa]
r		Débit massique par unité de largeur		[kg/m.s]
Pa		Rapport des surfaces (ailettes/totale)		-
PG		Rapport des surfaces (nette/totale)		-
Indices		Définitions
e, ext		Entrée, extérieur
s		Sortie
ae		Air à l'entrée
as		Air à la sortie
ee		Eau à l'entrée
es		Eau à la sortie
l		Liquide
v		Vapeur
m		Moyenne
p		Paroi, passe
c		condensation
sat		Saturation
f		Fluide
		Loin de la paroi
i, int		Intérieur
x		Valeur locale
t		Tube, Turbulent
lr		Liquide de refroidissement
ef		Entrée fluide
sf		Sortie fluide
ail		ailette
net		nette
tot		totale
R		Réel
fr		frontale
étr		étroite
app		Apparent
éch		échange
ex		Exérgie



Exposants

-

*

Moyenne

Symbole spéciale

Symbole spéciale

Definitions

Nombres
adimensionnels

	Définitions
Re	Nombre de Reynolds
Pr	Nombre de Prandtl
Nu	Nombre de Nusselt
Fr	Nombre de Froude
Ja	Nombre de Jakob
Gr	Nombre de Grachof
Abréviations	Définitions
DMLT	Différence Moyenne Logarithmique de Température
NUT	Nombre D'Unité de Transfert
TEMA	Tabular Exchanger Manufacture Association
BWG	Birming-ham Wire Gaze

Liste des figures

Figure I.01 : Courbes de changement d'états d'un corps pur 5

Figure I.02 : Courbes de changement de phase en 3 D 5

Figure I.03 : Condensation en gouttes 7

Figure I.04 : Condensation en film 8

Figure I.05 : Film du condensât sur une paroi verticale 9

Figure I.06 : (a) régime à gouttes, (b) régimes en colonnes, (c) régime en nappes 13

Figure I.07 : Condensation a l'intérieur d'un tube horizontal 14

Figure I.08 : Les différents écoulements dans une condensation à l'intérieur d'un

tube horizontal 15

Figure II.01 : L'influence des ondes sur la surface du film 18

Figure II.02 : Configuration géométrique du faisceau de tubes 22

Figure II.03 : Condensation contrôlée par cisaillement 24

Figure II.04 : Evacuation de la chaleur d'un condenseur 41

Figure II.05 : Condenseur à air a convection forcée vertical 43

Figure II.06 : Condenseur à air a convection forcée horizontale 43

Figure II.07 : Condenseur coaxiaux 45

Figure II.08 : Condenseur multitubulaire horizontale 46

Figure II.09 Divers constituants d'un Condenseur multitubulaire horizontale 47

Figure II.10 : Configuration des boîtes de distribution 48

Figure II.11 : Pas des tubes 50

Figure II.12 : Condenseur multitubulaire en U 53

Figure II.13 : Condenseurs à tubes verticaux 55

Figure II.14 : Différentes géométries de plaques du condenseur à surface primaire 57

Figure II.15 : Condenseur à plaques et joints 58

Figure II.16 : Schéma descriptif d'un Condenseur à plaques et joints 58

Figure II.17 : Condenseur à spirale (doc. Spirec) 60

Figure II.18 : Condenseur à plaques brasées : assemblage de plaques (doc. Nordon) 61

Figure III.01 : Distribution des températures dans un condenseur a contre courant 65

Figure III.02 : Coupes transversale et longitudinale d'un condenseur a ailettes 68

Figure III.03 : Tubes ailettés du condenseur à eau 69

Figure IV.01 : Les transformations subies a la source du travail 96

Figure V.01 : Surface d'échange en fonction de la température d'entrée de l'air 101

Figure V.02 : Surface d'échange en fonction de la température d'entrée de l'eau 101

Figure V.03 : Coefficient d'échange global en fonction de la température d'entrée de l'air 102

Figure V.04 : Coefficient d'échange global en fonction de la température d'entrée de l'eau 102

Figure V.05 : Coefficient de condensation en fonction de la température d'entrée de l'air 103

Figure V.06 : Coefficient de condensation en fonction de la température d'entrée de l'eau 103

Figure V.07 : Surface d'échange en fonction de l'échauffement de l'air 106

Figure V.08: Surface d'échange en fonction de l'échauffement de l'eau 106

Figure V.09 : Coefficient d'échange global en fonction de l'échauffement de l'air 107

Figure V.10 : Coefficient d'échange global en fonction de l'échauffement de l'eau 107

Figure V.11: Coefficient d'échange par condensation en fonction de l'échauffement de l'air 108

Figure V.12 : Coefficient d'échange par condensation en fonction de l'échauffement de l'eau 108

Figure V.13 : Surface d'échange du condenseur à air en fonction du pincement 110

Figure V.14 : Surface d'échange du condenseur à eau en fonction du pincement 110

Figure V.15 : Coefficient d'échange global en fonction du pincement 111

Figure V.16 : Coefficient d'échange global en fonction du pincement 111

Figure V.17 : Coefficient d'échange par condensation en fonction du pincement 112

Figure V.18 : Coefficient d'échange par condensation en fonction du pincement 112

Figure V.19: Surface d'échange en fonction de la température de condensation 114

Figure V.20: Surface d'échange en fonction de la température de condensation 114

Figure V.21 : Coefficient d'échange global en fonction de Tc 115

Figure V.22 : Coefficient d'échange global en fonction de Tc 115

Figure V.23: Coefficient d'échange par condensation du R22 en fonction de Tc 116

Figure V.24 : Coefficient d'échange par condensation du R22 en fonction de Tc 116

Figure V.25 : Coefficient d'échange par convection en fonction de Tc 118

Figure V.26 : Coefficient d'échange par convection en fonction de Tc 118

Figure V.27 : DTML en fonction de la température de condensation 119

Figure V.28 : L'efficacité du condenseur en fonction de Tc 119

Figure V.29 : Rendement éxergétique du R22 en fonction de Tc 120

Figure V.30: Rendement éxergétique en fonction de Tc 120

Figure V.31: Surface d'échange en fonction de la vitesse de l'eau 123

Figure V.32 : Coefficient d'échange global en fonction de la vitesse de l'eau 123

Liste des tableaux

Tableau I.01 : Quelques surface de contactes et leurs angles moyen pour l'eau 07

Tableau II.01 : Corrélation donnant le coefficient de transfert par convection 35

à l'intérieur des tubes pour le régime laminaire

Tableau II.02 : Corrélation donnant le coefficient de transfert par 37

convection à l'intérieur des tubes pour le régime turbulent

Tableau II.03 : Corrélation donnant le coefficient du transfert de chaleur 39

à l'extérieur des tubes

Tableau II.04 : Exemple de tubes courants 49

Tableau II.05 : Désignation des Condenseurs TEMA 51

Tableau II.06 : Avantages et inconvénients des condenseurs à air et à eau 62

Sommaire

Dédicaces Remerciements

Nomenclature i

Liste des figures v

Liste des tableaux vii

INTRODUCTION GENERALE 01

CHAPITRE I: ANALYSE DU TRANSFERT DE CHALEUR 03

I. Transfert de chaleur par conduction 03

II. Transfert de chaleur par convection 04

III. Transfert de chaleur lors de la condensation 05

III.1. Condensation en gouttes 06

III.2. Condensation en film 07

III.2.A. La condensation a l'extérieur des tubes verticaux 08

III.2.B. La condensation a l'extérieur des tubes horizontaux 12

III.2.C. La condensation a l'intérieur des tubes verticaux 13

III.2.D. La condensation a l'intérieur des tubes horizontaux 14

CHAPITRE II : ETUDE ET RECHERCHE BIBLIOGRAPHIQUE 17

I. Etat de L'art sur les phénomènes de condensation 17

I.1. Coté fluide frigorigène 17

I.1.1. Condensation a l'extérieur des tubes verticaux 17

I.1.2. Condensation a l'extérieur des tubes horizontaux 20

I.1.3. Condensation a l'intérieur des tubes verticaux 27

I.1.4. Condensation a l'intérieur des tubes horizontaux 31

I.2. Coté fluide de refroidissement 34

I.2.1. Transfert de chaleur a l'intérieur des tubes 34

I.2.1 .A. Pour l'écoulement laminaire 34

I.2.1 .B. Pour l'écoulement turbulent 36

I.2.2. Transfert de chaleur a l'extérieur des tubes 38

II. Les condenseurs 40

II.1. Principe générale d'un condenseur 40

II.2. Technologies des condenseurs 41

II.2.1. Les condenseurs à air 41

II.2.1 .A. Les condenseurs à circulation naturelle 42

II.2.1 .B. Les condenseurs à circulation forcée 42

II.2.1 .B. 1. Les condenseurs à air à convection forcée verticale 42

II.2.1 .B.2. Les condenseurs à air à convection forcé horizontale 43

II.2.2. Les condenseur à eau 43

II.2.2.A. Les condenseurs à tubes 44

II.2.2.A. 1. Les condenseurs à immersion 44

II.2.2.A.2. Les condenseurs coaxiaux 45

II.2.2.A.3. Les condenseurs multitubulaires 46

II.2.2 .A. 3. a. Les condenseurs multitubulaire horizontaux 56

II.2.2 .A. 3 .b. Les condenseurs multitubulaire verticaux 53

II.2.2.B. Les condenseurs à plaques 55

II.2.2.B. 1. Les condenseurs à surface primaire 56

II.2.2.B. 1 .a. Les condenseurs à plaques et joints 57

II.2.2.B. 1 .b. Les condenseurs à plaques soudées 59

II.2.2.B.2. Les condenseurs à surface secondaire 60

II.2.2.B.2.a. Les condenseurs à plaques serties 60

II.2.2.B.2.b. Les condenseurs à plaques brasées 60

II.3. Avantages et inconvénients des condenseurs à air et à eau 62
CHAPITRE III : SIMULATION DU FONCTIONNEMENT DU CONDENSEUR 63

I. Introduction 63

II. Logique de la phase du dimensionnement 63

III. Méthodes de calcul 64

III.1. La méthode DMLT 64

III.2. La méthode NUT 66

IV. Choix de la méthode de dimensionnement 68

IV. 1. Hypothèses de calcul 69

IV.2. Déroulement de calcul du condenseur a air 70

IV.3. Déroulement de calcul du condenseur a eau 79

V. Présentation du programme 89

V. 1. Le programme principal 89

V.2. Les sous programmes 89

VI. Les organigrammes 90

VI. 1. L'organigramme du programme principal 90

VI.2. L'organigramme du sous programme «Condenseur à air » 91

VI.3. L'organigramme du sous programme «Condenseur à eau » 93

CHAPITRE IV : ANALYSE EXEGETIQUE DU CONDENSEUR 95

I. Introduction 95

II. Description de la méthode éxergétique 95

III. Exemple d'application au condenseur à air 98

CHAPITRE V : RESULTATS ET DISCUSSIONS 100

I. Introduction 100

II. courbes et discussions 101

CONCLUSION GENERALE 125

Références bibliographiques 127

ANNEXE -A- : LE PROGRAMME DE CALCUL EN FORTRAN 133

ANNEXE -B- : FACTEUR DE CORRECTION F DE DTML 142

ANNEXE -C- : ABAQUES DE NUT EN FONCTION DE L'EFFICACITE 145

ANNEXE -D- : LES PROPRIETES PHYSIQUES DES FLUIDES 146

INTRODUCTION DENERALE

L'augmentation du prix de la consommation d'énergie notamment l'énergie thermique est reliée à la demande excessive sur l'énergie elle-même, et quelque soit sa nature fossile ou renouvelable, produite ou recueillie, l'utilisation d'un échangeur de chaleur est indispensable, d'où l'importance d'économiser cette énergie par l'économie des échangeurs de chaleur.

Les échangeurs de chaleur ont donc une large utilisation dans le domaine de l'industrie pétrolière, chimique, la distillation, réfrigération, chauffage, installation frigorifique, centrale thermiques, ........etc.

La hausse de la demande des performances de ces systèmes thermiques a toujours suscité un intérêt considérable pour les techniques d'amélioration du transfert de chaleur. L'incorporation de ces techniques peut augmenter substantiellement les performances des échangeurs de chaleur conventionnels.

Le principe des échangeurs thermiques est simple, ce sont des appareils destinés à transférer de la chaleur entre deux fluides à des températures différentes donc elle font appel essentiellement aux mécanismes de transfert thermiques.

Leurs technologies, leurs conceptions et leurs développements influent directement sur la performance d'une installation frigorifique ou autre installation utilisant ces échangeurs.

Dans certains appareils, l'échange de chaleur est associé à un changement de phase de l'un des fluides, c'est le cas des évaporateurs et des condenseurs.

Etant donné que ces échangeurs de chaleurs (évaporateurs, condenseurs..., etc.) sont des éléments très important dans une installation frigorifique, et le succès final de cette installation dépond largement de la bonne étude, conception et réalisation de ces échangeurs. En effet, il est évident que le fait de disposer un échangeur de chaleur bien adapté, bien dimensionné, bien réalisé et bien utilisé donne un bon rendement et permet un gain d'énergie.

Pour cela on à intérêt de maximiser le taux de transfert de chaleur par unité de surface en tenant compte des facteurs économiques.

Après le remarquable développement de l'informatique, les échangeurs de chaleur peuvent désormais être simulés au moyen des ordinateurs.

L'informatique apporte donc la précision la rapidité et l'efficacité à bon prix surtout lorsqu'il s'agit de la conception.

Cette étude est consacrée aux condenseurs, dans le but est d'essayer de donner un éclaircie sur les échanges de chaleur avec changement de phase lors de la condensation, et d'élaborer un programme en fortran pour la simulation de ces condenseurs.

Pour cela, on a étudié deux types de condenseurs suivant la nature de fluide de refroidissement condenseur à air et condenseur à eau.

Notre travail est constitué par les chapitres suivants :

+ Une introduction générale.

+ Le premier chapitre comporte un rappel de quelques notions importantes du transfert de chaleur et principalement le transfert de chaleur lors la condensation.

+ Le deuxième chapitre est consacré à l'étude bibliographique où on s'est basé sur les travaux théoriques et expérimentaux fait pour le calcul des coefficients de transfert de chaleur lors de la condensation (côté frigorigène) et les coefficients de transfert de chaleur par convection (côté fluide de refroidissement). Ainsi, ce chapitre comporte les principales technologies des condenseurs à air et à eau.

+ Le troisième chapitre présente l'analyse des méthodes de dimensionnement des condenseurs à air et à eau, pour cela un code de calcul à été élaboré avec des différents organigrammes pour l'explication des étapes de calcul.

+ Le quatrième chapitre présente une étude éxegétique du condenseur

+ Le cinquième chapitre comporte les résultats sous forme de courbes ainsi que les discutions et analyses nécessaires.

On termine ce mémoire par une conclusion générale

Ce mémoire est complété par des annexes comportant :

> Le programme de calcul en langage Fortran.

> Les graphes de NUT, le facteur de correction F de la DTML et les propriétés des FF.

Définition :

On appel « transfert de chaleur » le déplacement de la chaleur d'une région à une autre suite à une différence de température, ce déplacement peut se produit entre deux corps en contacte (solide- solide, solide-fluide, fluide-fluide) ou entre deux parties d'un même corps.

L'énergie interne du système change au cours du déplacement de la chaleur ont produisant : - Le flux thermique transmis.

- La répartition de la température a l'intérieur du milieu considéré.

Avant d'arriver aux échangeurs de chaleurs « Condenseurs » on doit d'abord parler des modes de transmission de la chaleur qui s'effectuent dans le condenseur et qui sont : la conduction, la convection et sans oublier le transfert de chaleur avec changement de phase l'ors de la condensation qui est le phénomène le plus important dans les condenseurs

I. Transfert de chaleur par conduction :

La conduction est le transfert de chaleur des parties chaudes vers des parties plus froides, d'un même corps ou de deux corps en contacte sans mouvement apparent de matière.

Ce mode peut avoir s'effectue dans les solides et les fluides. Ce pendent, ces le seul mécanisme par le quel la chaleur peut se déplacer dans les solides opaques.

La conduction est régie par la loi de Fourier :

Q_x = -l. s . [ W]

^dT(I.01) Cette

dx

formule donne la valeur du flux de chaleur en direction de x, Avec :

Le signe(-) intervient puisque la chaleur s'écoule vers le décroissement de la température.

l : La conductivité thermique du milieu considéré [W m.K]. S : La surface d'échange de chaleur[m²].

: Le gradient de température dans la direction de x[K m].



dT



dx

Alors, si un corps à la température T ₁ est raccordé à un corps à la température T₂ par l'intermédiaire d'un corps thermique de section S et d'épaisseur e

Le flux de chaleur qui s'écoule entre les deux corps est donné par la relation :

Q s

= l . .

[W] (I.02)

( )

T T

1 2

-

e

II. Transfert de chaleur par convection:

De façon générale, la convection est le transport d'une grandeur physique d'un fluide d'un point à un autre par mouvement de ces molécules.

Les différences de températures dans les fluides entraîne des différences de densités et donc un mouvement des particules du fluides ce mouvement à pour effet de véhiculer la chaleur du fluide et d'égaliser les températures par substitution réciproque des molécules froides à des molécules chaudes.

Le phénomène de convection intervient à chaque fois qu'un fluide se déplace par rapport à des éléments fixes (murs, plaques, tubes,....etc.) à des températures différentes de celle du fluide ou lorsque deux fluides à des températures différentes sont mis en contact.

On dit que la convection est naturelle si le mouvement des masses fluides responsables du transfert de la chaleur, est provoqué par des différences de densités provenant elles mêmes des différences de températures à l'intérieur du fluide.

Et on dit que la convection est forcée si le mouvement est crée par une action extérieure (ventilateurs, pompes,... etc.)

La loi de Newton donne le flux échangé entre une surface de valeur s et de température T_s et un fluide de température Tf elle s'écrit :

Q = h.S(T_s - T _f ) [W] (I.03)

Avec :

h : Coefficient d'échange convectif[W m².K]. S : La surface d'échange[m²] .

III. Transfert de chaleur lors de la condensation :

A une pression donnée la température d'un corps reste constante aussi longtemps que dure le
changement d'état. Les changements de phase qui peuvent être rencontrés sont présentés dans la

Figure I.01 et Figure I.02:



Pression

C

Liquide

2

Solide

Fusion

Solidification

T

1

Condensation

Vaporisation

3

Sublimation

Gaz

Température

Désublimation

Figure I.01 : Courbes de changement d'états d'un corps pur



Figure I.02 : Courbes de changement de phase en 3 D

Le changement de phase de l'état vapeur à l'état liquide est désigné par condensation. Ce phénomène est souvent rencontré dans les procéssuces industriels et joue un rôle important, dans les installations motrices à vapeur, les machines frigorifiques et les pompes à chaleur. Dans les condenseurs industriels la vapeur à condenser est séparée du fluide froid par une surface intermédiaire. Lorsque une vapeur se trouve en contact avec une surface dont la température est inférieure a la température de saturation de la vapeur, il y a un changement de phase vapeur-liquide donnant naissance à un transfert de chaleur important.

Or, la condensation de la vapeur sur une paroi refroidie donne naissance à deux types de phénomènes qui se caractérisent par l'aspect visuel du condensât formé.

Dans le premier cas le condensât recouvre la surface sous la forme d'un film continu et on parle de « condensation en film ».

Dans le second cas les gouttelettes liquides se forment sur la surface et on parle de « condensation en gouttes ».

L'échange thermique lors de la condensation en gouttes est plus élevé que celui pour la condensation en film, mais la condensation en gouttes est difficile à maintenir sur un long terme. Elle résulte en effet de la non mouillabilité du solide par le film condensât à cause de la présence des molécules organiques sur la surface. Le dépôt d'une fine couche de matière plastique (téflon) est parfois utilisé pour développer la condensation en gouttes mais ceci introduit une résistance thermique supplémentaire et l'amélioration de l'échange n'est pas aussi spectaculaire qu'on le souhaitera. Actuellement il n'y a pas de méthode d'analyse théorique fiable pour traiter la condensation directe et seuls les résultats d'essais sur des revêtements spécifiques sont utilisés pour déterminer l'échange thermique.

III.1. Condensation en gouttes :

Lorsqu'une surface de condensation est contaminée par une substance qui empêche le condensât de mouiller la surface, la vapeur se condense en gouttes plutôt qu'un film continu.

Ceci est connu sous le nom de condensation en gouttes. Dans ces conditions une grande partie de la surface n'est pas recouverte par un film isolant, et les coefficients d'échange de chaleur sont quatre à huit fois plus élevés que pour la condensation en film. Jusqu'à présent ce genre de condensation n'a été obtenu d'une façon sure que pour la vapeur d'eau, la condensation en gouttes ne se présente que dans des conditions très précises qui en pratique ne peuvent être toujours maintenues. La condensation en gouttes de la vapeur d'eau peut, toutefois, être utilisée dans des travaux expérimentaux lorsqu'on désire amener la résistance thermique, sur un coté d'une surface, à une valeur négligeable.



Figure I.03 : Condensation en gouttes

Lorsque l'angle de contact moyen entre la surface et la goutte est supérieur à 50 ^o , on dit que la surface est hydrophobe. Pour obtenir ce type de condensation, il faut soit effectuer un traitement de surface (Tableau I.01 suivant), soit ajouter au liquide promoteur de condensation en gouttes. Pour une condensation sur des surfaces en cuivre, on utilise des composés soufrés fluorés. Pour une condensation sur des surfaces en acier, on utilise du silane fluoré

Tableau I.01 : Quelques surface de contactes et leurs angles moyen pour l'eau [01]

Surface de contact	Angle moyen (pour l'eau)
Acier inoxydable 18/8 Cu-Ni (70/3 0) Nickel Or sur Cu-Ni (70/3 0) Ag sur Cu-Ni (70/30) Téflon	0o 0o 5o 60 à 62^o 68 à 74^o 85o

III.2 Condensation en film :

Lors de la condensation, sur une paroi, un film liquide se forme sur la surface refroidie. L'épaisseur du film liquide résulte de l'interaction entre l'écoulement du liquide et celui de la vapeur, en fonction de la géométrie de la surface solide. Dans la pratique industrielle, les surfaces d'échanges utilisées sont souvent très complexes et ne se prêtent pas facilement à l'analyse théorique du phénomène de la condensation. Les phénomènes tels que les vagues sur la surface de film de condensât ou l'arrachement des gouttelettes et l'inondation compliquent davantage l'analyse.



Figure I.04 : Condensation en film

+ La théorie du Nusselt :

Nusselt a établi en 1916 les relations théoriques pour le calcul des coefficients d'échange de chaleur dans le cas de la condensation en couche mince de vapeurs pures sur des tubes ou des plaques. Sur la base des hypothèses suivantes :

· La vapeur est une vapeur pure, au repos, saturée à la température de saturation Tsat correspondant à la pression d'alimentation PC du (Condenseur).

· La température T _p de la paroi froide est constante sur toute sa surface, et le phénomène est permanent (aucune grandeur ne dépond du temps).

· Le film liquide s'écoule vers le bas sous l'effet de la pesanteur, et son épaisseur reste assez faible pour que le régime d'écoulement dans le film soit laminaire.

· En se condensant, la vapeur libère sa chaleur latente de vaporisation et le liquide formé est refroidi à une température inférieure à _Tsat. La chaleur ainsi dégagée se transmet à la paroi par conduction à travers le film.

III.2.A. Condensation en film à l'extérieur des tubes verticaux : [02]

Considérons dans le film de condensât, un petit élément de volume (L.dx.dy) en équilibre sous l'effet des trois forces suivantes :

> le poids d'eau qu'il contient;

> la poussée d'Archimède de la vapeur environnante;

> les contraintes tangentielles développées dans l'écoulement laminaire du film.



Figure I.05 : Film du condensât sur une paroi verticale

Cet équilibre se traduit, en projection sur l'axe vertical (Ox), par la relation suivante :

é ù é

( r _l r _v ) m m

dy - L dx du ù

- g L dx dy + L dx du

l l

_ëê ú_û ëê dy = 0

ú_û (I.04)

y+dy y

qui conduit à l'équation différentielle :

g

2

m_l

d u l v

² r r

-

= -


dy

(I.05)

équation dans laquelle u(y) est le profil de vitesse de l'eau condensée dans le film laminaire, et les indices (l) et (v) se réfèrent respectivement aux phases liquide et vapeur.

Une première intégration donne :

du dy

r r l v - = - g y + C ml

1

(I.06)

A la surface du film, soit pour : y = e_x, la contrainte tangentielle doit être nulle, d'où :

	C1 =	r r l v -	g e		(I.07)
et par conséquent:		ml		x

r r

l v l v

- r r

-

= - g y +

m_l m_l

g e x (I.08)

du
dy



Une seconde intégration conduit alors au profil de vitesse parabolique :

y2 r r

l v

-

g + g e y + C

x 2

_l m

2 l

u(y) = -

r r

l v

-

m

(I.09)

Pour y = 0, on doit avoir u (0) = 0, d'où la valeur de la constante d'intégration : C2 = 0

et le profil de vitesse dans le film liquide :

é y 1 æ

ê èç ö

y

- _ø÷

ëê e x x 2 e

2

ù ú ú û

(I.10)



r r

l v

- 2

u(y) = g e_x

m_l

Le débit massique d'eau condensée à l'abscisse (x), pour une largeur unité de paroi, sera donc donné par l'intégrale :

e 1 r r

x l v

-

&m(x) = u(y) dy =

l

ò r

0

3 m l

3

(I.11)

r

l x

g e

La masse de condensât dm(x) & formée sur la tranche d'épaisseur (dx) entraîne donc un

accroissement (de_x) de l'épaisseur du film, tel que :

dm(x)^& dx	=	r l	( ) r r - l v	g e 2 x de ^x dx	(I.12)
			ml

La condensation de la masse dm(x) & produit un dégagement de chaleur égal à :

dQ = L v & dm(x) (I.13)

Relation dans laquelle (L_v) est la chaleur latente de condensation de la vapeur considérée.

En régime permanent, cette quantité de chaleur (dQ) se transmet intégralement par conduction à la paroi à travers une surface élémentaire (dS = 1. dx). Cette densité de flux thermique conduit (dQ/dS) est, donnée par la relation :

dQ
dS

T - T dm(x)

&

sat p

l v

= L (I.14)

x

^l e dx

En rapprochant de la relation établie précédemment :

dm(x) ( )

& r r r

= -

l v

l

m l

g e 2 x

de

(I.15)

^x dx

dx

on obtient en éliminant dm(x)^& :

dx



(I.16)

g de

e 2 x

^x dx

l r ( r r )

T - T -

l sat p l v

l

=

L e

v x

m_l

T - T

sat p

( ) dx

r r

- g

l v

(I.17)

=

l _l

m _l

x

e de

3
x

r_l

L v

qui est une équation différentielle à variables séparées permettant, après réarrangement des termes, de calculer l'épaisseur (e_x) du film liquide :

qui s'intègre pour donner :

é 4 T - T x

m l ( ) ù

l l sat p

ê ú

ê r r _l r

( )

- g L ú

l v v

ë û

e =

x

1

4



(I.18)

On peut définir un coefficient local d'échange (h) en examinant l'expression suivante de la puissance thermique échangée dans la tranche d'épaisseur (dx) :

dQ
dS



T - T

sat p

l (I.19)

^l e x

et en la rapprochant de la définition générale d'un tel coefficient d'échange introduite par la relation :

d²Q = h (T _p - T _)dS dt (I.20)

On voit alors que le flux thermique transmis dans la tranche d'épaisseur (dx) peut s'écrire :

dQ = h _x (T _sat - T p ) dS (I.21)
Relation dans laquelle (h_x) est un coefficient local d'échange (h_x) qui aura pour expression :

1

4



l r r r l

é 3

( ) ù

- g L

l ê l v v l

h =

x

(I.22)

^l ú

e = ê

x 4 T - T x

m ( ) ú

l sat p

ë û

A partir de cette expression du coefficient local d'échange (h_x), on peut calculer un coefficient d'échange moyen (h) pour une vapeur se condensant sur une paroi de hauteur (H). Cette valeur moyenne se définit à l'aide de l'intégrale :



1

é H

4

h 1

H

1

H r r _l r l ³

( )

- g L ù - 1

l v v l

ò ( ) ú ò

ê ú x dx

(I.23)

4

0 x

h dx =

H 0

ë ê 4 T - T

m l sat p û



H

1 é

ê^êë

ù

4

1



r r _l r l ³

( )

=

l v v l H

- g L 4 3 4 (I.24)

4 T - T

m ( ) ^úú 3

l sat p û

é
ê^êë

4

=

3



ù
úú û

4

1

r r _l r l ³

( )

4

( )

T - T

sat p

H

l v v l

- g L(I.25)

m l



1

4

par sa valeur qui est 0,943, on obtient pour la valeur

4

æ _èç ö

1

4 ø÷

3

En remplaçant l'expression littérale

du coefficient d'échange moyen h la formule suivante [03] :

r r _l r l ³

( )

l v v l

- g L(I.26)

( )

T - T H

sat p

ù
ú^úû

m l

é
ê^êë

h = 0,943



1

4

On constate que :

1. Plus le tube est haut, plus le transfert moyen diminue. La raison est que la barrière thermique constituée par le film liquide est d'autant plus épaisse que la hauteur (H) du tube est grande. Tout dispositif telle que des ailettes, des rugosités artificielles, susceptible de rompre le film liquide, améliore donc l'échange d'une manière sensible.

2. Plus l'écart de température _(Tsat - Tp) est faible, meilleur est l'échange. Cette propriété est exploitée dans les condenseurs de pompes à chaleur pour améliorer leurs performances.

III.2.B. Condensation en film à l'extérieur des tubes horizontaux :

A l'aide d'une approche similaire à celle présentée pour une paroi verticale, NUSSELT a obtenu la valeur du coefficient moyen d'échange de chaleur pour un tube horizontal.

Le résultat obtenu s'écrit [03] :

1

r r _l r l (I.27)

( )

l v v l

- g L

( )

T - T D

sat p



m_l

3 4

ù ú û ú

é

ê

ëê

h = 0,728

Le condenseur horizontal se constitue de plusieurs rideaux de n tubes horizontaux superposés dans un même plan vertical.

Chaque rideau vertical de n tubes horizontaux constitue un ensemble isolé d'ont l'analyse du fonctionnement doit prendre en compte deux données nouvelles :

(1)- La surface d'échange n'est plus S =p.D.L comme dans le cas d'un tube unique, mais S=n.p.D.L

(2)- Le film de condensât va ruisseler d'un tube à l'autre, ce qui va contribuer à augmenter la surface de condensation.

On tient compte du point (1) en remplacent (D) par (n.D) dans la formule (I.27).

La valeur du coefficient moyen d'échange de chaleur pour un rideau vertical de (n) tubes horizontaux est alors donnée par la formule :

1

4

r r _l r l ³

( )

l v v l

- g L(I.28)

( )

T - T

sat p



m_l

nD

ù

ú

û ú

é

ê

ëê

h = 0,728

Quant au point (2), on tiendra compte de cette augmentation de la surface de condensation en multipliant la valeur de (h )ci-dessus par le coefficient (Ch) :

( ) [ ]

C T T

p _l sat p

-

C n

= 1 + 0 . 2 - 1

( ) (I.29)

^h L

v

Remarque :

Des condenseurs à faisceaux de tubes horizontaux sont souvent utilisés dans l'industrie. Selon la disposition des tubes (en quinconce ou alignés), le condensât formé sur les tubes supérieurs tombe sur les tubes inférieurs sous forme de gouttes, colonnes ou nappes

ü L'écoulement en gouttes est réalisé avec des débits faibles (Figure I.06a).

ü L'écoulement en colonnes statiques est réalisé lorsque en augmente le débit (Figure I.06b).

ü L'écoulement en nappe liquide continue celle-ci remplace les colonnes statiques, lorsque le débit augmente d'avantage (Figure I.06c).



Figure I.06 : (a) régime à gouttes, (b) régimes en colonnes, (c) régime en nappes.

III.2.C. Condensation en film à l'intérieur des tubes verticaux :

Lors de la condensation de vapeur à l'intérieur d'un tube vertical le condensât se forme sur la paroi interne et la vapeur s'écoule dans la parti centrale. Ainsi, on peut qualifier l'écoulement comme un écoulement annulaire dans le quel le débit vapeur diminue selon la longueur du tube et l'épaisseur du film de condensât augmente.

On peut calculer le coefficient de transfert de chaleur lors de la condensation dans les tubes verticaux ont appliquent la corrélation de CARPENTER-COLBURN [04]:



h m 1 1

l 1 0 . 065 Pr Fr

2 2

= l

l _l

r_l

2

(I.30)

Avec :



Fr fG_m 2r v

2

=

f : Coefficient de frottement de Fanning pour l'écoulement à travers un tuyau évalué à la vitesse massique moyenne de vapeur G_m .

f : Est évalué à ( ) Re v m		DG i m mv

G 1 G G G

2 2

+ +

1 2 2

3

[kg h.m²]





G_m=



G₁ : Vitesse massique au sommet du tube. [kg h.m²]



G₂ : Vitesse massique a la sortie du tube. [kg h.m²]

III.2.D. Condensation en film à l'intérieur des tubes horizontaux :

Du fait du ruissellement du condensât sur la paroi interne d'un tube horizontal, il peut y avoir une accumulation du condensât dans la partie basse du tube comme le montre la figure suivante :



Figure I.07 : Condensation a l'intérieur d'un tube horizontal

De plus le débit vapeur introduit une contrainte tangentielle à l'interface liquide-vapeur du condensât accumulé. Il en résulte une interaction compliquée donnant naissance à différents régimes d'écoulement diphasique, notamment :

ü Ecoulement annulaire ;

ü Ecoulement à bouchon ;

ü Ecoulement avec ondes ;

ü Ecoulement avec bulles de vapeur (figure I.08)



Figure I.08 : Les différents écoulements de condensation à l'intérieur d'un tube horizontal

On peut calculer le coefficient de transfert de chaleur lors de la condensation dans les tubes horizontaux par la corrélation de CHATO [05]:



1

é

ê

ëê

0.555

h

4

L ù

( ) ( )

3 v

g r r r l ú

l l v f

- (I.31)

m f sat p i

T T d

- û ú

Régimes d'écoulement diphasique :

Plusieurs auteurs ont cherché à établir les régimes d'écoulement diphasique lors de la condensation de vapeur. Soliman et Azer [06] ont observé les régimes suivants lors de la condensation de R12 et R134a :

· Ecoulement dispersé : dans lequel il n'ya pas de film de condensat visible ; tout le liquide formé est entrainé par la vapeur sous forme de petites gouttes ;

· Ecoulement annulaire : dans lequel un film liquide annulaire se forme, la vapeur s'écoule dans la partie centrale ;

· Ecoulement semi annulaire : qui ressemble à l'écoulement annulaire, mais l'épaisseur du film liquide varie sur la circonférence du tube et est maximale en bas du tube.

· Ecoulement avec ondes : dans lequel le liquide coule sur la partie base du tube tandis que la vapeur se trouve bien séparé du liquide dans la partie supérieur. L'interface liquide- vapeur pour le régime d'écoulement est ondulée ;

· Ecoulement formant des bouchons liquides : dans ce régime l'onde sur la surface du liquide s'amplifie et touche la partie supérieur du tube formant ainsi un bouchon pour le passage de la vapeur ;

· Ecoulement a bouchons : dans lequel la section du tube est remplie de liquide, mais il n'ya de longues bulles de vapeur qui appauvrissent de temps à autre et qui semblent avoir la même vitesse que le liquide ;

· Ecoulement semi annulaire avec ondes : sur la surface du film liquide

· Ecoulement dispersé et annulaire : dans ce régime le film liquide se forme d'une façon intermittente et disparait ensuite à cause de l'arrachement du liquide sous forme de gouttes par l'écoulement de vapeur ;

· Ecoulement annulaire avec ondes sur la surface du film liquide : dans ce régime l'épaisseur du film liquide est plus importante dans la partie basse du tube tandis que la partie supérieur s'emble parfois sèche.

I. ETAT DE L'ART SUR LES PHENOMENES DE CONDENSATION :

Dans cette étude on se base sur les travaux théoriques et expérimentaux relatifs aux calculs des coefficients de transfert de chaleur lors de la condensation (coté fluide frigorigène), et des coefficients de transfert de chaleur par convection (coté fluide de refroidissement).

Puis on va voir le principe de fonctionnement des condenseurs et leurs principales technologies.

I.1 Coté fluide frigorigène :

I.1.1. Condensation a l'extérieur des tubes verticaux :

§ NUSSELT [3] a établi en 1916, les relations théoriques pour le calcul des coefficients d'échanges de chaleur, dans le cas de la condensation des vapeurs pures en couche mince, sur des tubes ou sur des plaques. Et il a montré que la conductance par unité de surface, décroît lorsque la distance compté à partir du sommet de la plaque ou tube, et par conséquent l'épaisseur du film augmente. Il à aussi remarqué qu'une augmentation de la différence de température ( T _sat - T _p ) entraîne une diminution de la conductance par unité

de surface.

Nusselt est le premier auteur qui a donné les formules qui permet le calcul du coefficient d'échange moyen.

2

r l ³

g L

l v l (II.01)

ù ú û ú

4T - T L

m ( )

l sat p

é

ê

ëê

h

0,943



1

4

§ La théorie de Nusselt à été modifier par ROHSENOW [07], afin de tenir compte de la convection d'enthalpie. Son analyse conduit à l'expression suivante pour le coefficient d'échange moyen lors de condensation d'une vapeur stagnante sur une plaque isotherme de longueur L :

1

4

l r r r

³ g L

( )

- cents ù

l l l

ú(II.02)

ûú



é

ê

ëê

0.943

h

( )

T T L

- p

m l sat

Dans laquelle _vL^cents [j/kg] : Représente la chaleur latente équivalente donnée par :

é -

( )

T T ù

sat p

L L Cp

cents = +

êë 1 0 . 6 8 (II.03)

v v ^l L úû

v

NB : Les relations de Nusselt et Rohsenow sont aussi valable pour la condensation à l'intérieur des tubes verticaux.

§ KUTATELADZE et GOGONIN [08] ont présenté les mesures des coefficients d'échange thermique en présence des ondes, et ils proposent l'expression suivante ont prenant compte des ondes lors de la condensation sur une surface verticale de langueur L :

	hondes	Re f 0 .04	(II.04)
Pour :5< Ref <100	hNusselt

q L

cents

Re = (II.05)

^f L

m

Avec:

l v

q cents : Densité de flux thermique [w/m²]

§ Les équations gouvernant l'écoulement du film de condensât sur une plaque vertical ont été résolues par MIYARA [09]. Les résultats de ses calculs montrent que la valeur moyenne de l'épaisseur du film liquide est légèrement plus faible que la solution donnée par la théorie de Nusselt. Les nombres de Nusselt calculés sont comparés aux valeurs obtenues l'aide des expressions suivantes proposées par différents auteurs sur la Figure II.01



Figure II.01 : L'influence des ondes sur la surface du film

- Kutateladze: Nu * = 0.557Re f *0 .22 (II.06)

- Chun-Seban: Nu = f

* 0.606Re - 0.22 (II.07)

-Uehara-Kinoshita: * 0 .707 Re - 0 .25

Nu = f (II.08)



1

h v 2 3

æ ö

*

Avec : Nu l

= g

^x ç ÷ (II.09)

l l è ø

et

q cents

Re

v

^f L

m l

§ SHEKRILADZE et GOMELAURI [10] admettent que l'aspiration de la couche limite vapeur par la condensation rend l'écoulement de vapeur laminaire et font l'hypothèse que la contrainte tangentielle à l'interface liquide-vapeur est égale a la perte de quantité de mouvement de la vapeur condensée cette hypothèse n'est valable que pour un taux de condensation infini, mais possède l'avantage de rendre inutile la résolution des équations de la phase vapeur pour assurer légalité des contrainte tangentielles à l'interface et simplifie considérablement l'analyse lorsqu'on néglige le gradient de pression. Ainsi sans tenir en compte des termes d'inertie et de convection d'enthalpie et en effectuent une analyser du type Nusselt, Shekriladze et Gomelauri proposent la relation suivante :

Plaque plane verticale :

h_m

16 gL ù ÷ ú

2 2 1

ç + ^é +

1 ç ê_ë úû ÷ ú

U H

2

l r

æ ö

è ø ú

l l

1

æ 2 ö ù

2 2

ç (II

U .10)

÷ 1 ú

L ø 1

æ 2 ö

ç 16 ù ÷

1 1

+ ^é + gL ç êë U H

2 ú_û ÷


è ø û









Avec :

H

Ja Prl

(II.11)

Ja = CpDT L_v

U : La vitesse du fluide loin de la paroi [m/s]

§ FUJII et UEHARA [11] ont utilisée la méthode de Polhausen pour résoudre les équations intégrales pour étudier la condensation en film laminaire sur une plaque verticale. Ils négligent les termes d'inertie et de convection d'enthalpie dans le film liquide et adoptent une équation de second degré pour définir le profile de vitesse dans la phase vapeur. Les équations sont résolues par la méthode numérique de Range Kutta et Gill. Les résultats de leurs calculs sont représentés par l'équation suivante :



Nu

1



3 4

é 4

2

= = æ + ö

1 ~ Gr

æ ö ù

h L

^m ê Re 0 .790

0 . 65 6 1 . 20 ú (II.12)

^m l ç_è ç_{è ø}÷

ê RH _ø÷ + H û ú

^l ë

Avec :

L g

3

, 2

Gr = (II.13)

v_l



H

Ja

Pr_l

~

U L

=

Re

,

v_l

æ r m ö

l l

, R r m

= ç ÷

è v v ø

1

2



Pour la condensation laminaire sur un cylindre les résultats de Fujii et Coauteurs sont représentés par l'expression :

1

0 .27 6 ~

ù ⁴ 1

Nu_m x 2

1 ú û

₄ Re (II.14)

= é + x FrH

êë

Avec :



~

U ²

Fr

=

(II.15)

, Re_D

gD

l

1

c 0 . 90 1 ,

= æ + RH ö

ç_{è ø}÷

r

l U D

m

I.1.2. Condensation à l'extérieur des tubes horizontaux :



Nu



Nu

^m l



Nu

^m l

§ Le coefficient moyen d'échange thermique lors de la condensation d'une vapeur stagnante sur un
cylindre lisse de diamètre D suivant la théorie de NUSSEL T-R OHSENO W est donné par :



é

ê

ëê

m l sat

( )

T T D

- p

l g r L cents

3 2

ù ú û ú

1

4

h 0.725

§ DHIR et LIENHARD [12] proposent une modification de la théorie de Nusselt-Rohsenow pour étudier la condensation sur un corps axisymétrique. Dans ce cas, l'écoulement de condensât est soumis à une force de pesanteur variable g(x) fonction de x

1

h x g L x 3 4

é

x eq l l v v

r r r

( )

- cents ù

= = ê ú (II.17)

^x T T

l _ê 4 m l ( )

-

l ë l l sat l û ú

Dhir et Lienhard ont ainsi proposé des formules pour plusieurs cas : - Condensation sur un cylindre horizontale :

1

3 4

h D gD

é ù

= = A

^m 0 . 729 úû (II.18)

*

ê_ë

l 0

- Condensation sur le semi-Cylindre supérieure :

1

3 4

h D gD

é ù

= = A

^m 0 . 8 66 úû (II.19)

*

ê_ë

l 0



- Condensation sur le semi-Cylindre inférieure :

Nu

1

3 4

h D gD

é ù

= = A

^m 0 . 592 úû (II.20)

*

^m l

ê_ë

l 0

§ JAKOB [13] a étendu l'analyse de Nusselt à un faisceau aligné en admettant que le condensât tombe sur le tube placé plus bas comme une nappe continue en écoulement laminaire. En admettant que la différence de température (T _sat - T _p )reste la même pour l'ensemble des tubes

en faisceaux il montre que le coefficient d'échange moyen pour un faisceau de n tubes (h _n )comparé à celui pour le premier tube est :



h n = n ⁴

( )

h m 1

- 1

(II.21)

Et le coefficient d'échange de tube n :

( ) ( ) ( ) úû

³ ù

h m n h m 1 n n 1

= é - - 4

3

⁴ (II.22)

êë

§ KERN [14] propose pour globaliser le coefficient d'échange de Nusselt à l'échelle du faisceau circulaire de tubes, des modèles empiriques de coefficient d'échange moyen définis à l'échelle du faisceau. Ils sont exprimés en fonction du coefficient d'échange de Nusselt pour un seul tube et des paramètres géométriques que sont le pas entre les tubes, le rayon de faisceau, du type d'arrangement des tubes (carré, triangle, carré pivoté,...), et le type d'écoulement du film d'un tube sur l'autre (continu, discontinu). Pour les condenseurs constitués de faisceaux circulaires à pas carré pivoté. Les deux corrélations retenues sont les suivantes :

ü Ecoulement continu du film d'un tube sur l'autre :

hfaisceau₌ - - - + -

( ) [ ( ) ( )

11

0 .972 ¹ 1 0 . 25 1 0 .223 3

4 8 2 ]

R P R P R P(II.23)

h

ü Ecoulement discontinu du film d'un tube sur l'autre :

hfaisceau = - - - + -

( ) [ ( ) ( )

17

0 .97 5 ¹ 1 0 .242 0 . 223 3

6 12 2 ]

R P R P R P(II.24)

h

Avec : P: Distance l'entre axe des tubes [m] R : Rayon du faisceau de tubes [m]

Figure II.02 : Configuration géométrique du faisceau de tubes

§ KERN [15] observe que le condensât coule en bas du tube en régime de gouttes ou de colonnes ce qui perturbe la surface du film et diminue l'effet l'inondation, il propose donc:



h - 1

n = n ⁶ (II.25)

( )

h m 1

et le coefficient d'échange du tube n :

( ) ( ) ( ) úû

⁵ ù

h m n h m 1 n n 1

= é - - 6

5

⁶ (II.26)

êë

§ L'analyse de CHEN [16] utilise la méthode de perturbation donne l'expression suivante pour une nappe verticale de n tubes placés l'un en dessous de l'autre dans le domaine du nombre de Prandtl Pr_l > 1 ou Pr_l < 0.05 et des paramètres (n-1)

Ja

Ja

£ 2( = £

H 20)

Pr_l

1

( ) [

n n Ja

4 = + -

1 0 . 2( 1)

h m 00

1 0 . 68 0 . 02

] é + +

Ja H ù

êë 1 0 . 95 0 . 1 5

+ -

H JaH úû

( ) tube n

.

h m Chen





1

4

(II.27)

g ( )

r r

l v

-

mlCondenseur x



1

4

(II.28)

r l ³ L ù

l l v

( ) ^ú

T T

sat p

- û ú

é

ê

ëê

h B

=

L'indice 00 correspond à la solution de Nusselt pour Ja = H =0 Ja : Nombre adimensionnel de Jakob (CpDT L_v).

§ CHEN [17] a modifié le modèle de Nusselt dans le but de calculer des coefficients d'échange pour des configurations à faible vitesse de vapeur et de généraliser cette étude à M colonnes de N tubes, contrairement à Nusselt qui ne considère qu'une seule colonne de N tubes

Le modèle adapté aux faibles vitesses du modèle de Nusselt, garde globalement les mêmes hypothèses. La nouvelle hypothèse impose donc une faible vitesse de vapeur

Cette modification concerne l'intégration d'un facteur de correction (B) du coefficient
d'échange qui prend en compte l'accumulation et l'écoulement des condensats. Chen a introduit
également une nouvelle variable (xcondenseur ) pour tenir compte de la complexité de l'écoulement des

condensats d'un tube sur l'autre et de l'interférence entre deux rangées verticales proches. Cette variable est fonction du nombre de tubes verticaux coexistant dans le faisceau. Les condenseurs intègrent un faisceau de tubes à pas carré pivoté. Le modèle modifié s'écrit alors :

é ( ) ( )ú_û

T T

- ù

sat ^p N

B = +

0 .725 1 0 .2 1

- (II.29)

tub .Vert

êë L v

xCondenseur = N tub . Vert . D ext (II.30)



2 .

p R

N tubVert

.

2

P

(II.3 1)

§ BERMAN et TUMANOV [18] ont fait des travaux basés sur l'analyse expérimentale et la réalisation de modèles empiriques de coefficient d'échange en condensation prenant en compte l'effet de la vitesse de vapeur. Dans le cas d'une convection forcée, l'écoulement du condensât est très perturbé par les contraintes de cisaillement à l'interface vapeur - condensât.

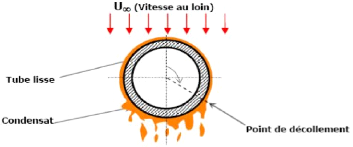
D'après ces auteurs les phénomènes à prendre en compte dans cette configuration pour traduire le comportement du film de condensât (Figure II.03) sont :

(i) Les contraintes de cisaillement générées par la vapeur à la surface libre du film,

(ii) Le décollement de la couche limite de la vapeur à l'arrière du tube a un angle compris entre 80 et 180 degrés par rapport au point de stagnation de la vapeur.

Les expériences de Berman & Tumanov ont été réalisées sur un tube horizontal actif placé dans un faisceau de tubes non refroidis soumis à un flux de vapeur d'eau descendant. Le dépouillement des résultats et l'analyse à partir de nombre adimensionnels ont conduit à la formulation de modèles empiriques spécialisés par rapport aux domaines de variation des



paramètres opératoires.

Figure II.03 : Condensation contrôlée par cisaillement

§ SPAROW et GREGG [19] considèrent que l'angle du phénomène de la conduction peut être abordée en utilisent les équations de la couche limite de "Mécanique des fluides" et adoptent la

méthode de la transformation affine pour réduire les équations différentielles au dérivées partielles à des équations différentielles ordinaires.

En faisant l'hypothèse selon laquelle la contrainte tangentielle à l'interface liquide-vapeur est nulle. Mais sans négliger les termes d'inertie et de convection d'enthalpie, ils résolvent (par une méthode numérique) les équations gouvernant l'écoulement du film de condensât sur une plaque verticale placée dans une vapeur stagnante. Pour de faibles nombres de Jackob (Ja); ils obtiennent la relation suivante pour la condensation dune vapeur stagnante sur un cylindre lisse :



Nu

l l

0.733

^m m l

é

ê

ëê

g L D

r 2 3

( )

T T

sat p

-

l v (II.32)

ù ú û ú

1

4

Le coefficient 0.733 est peu différent de 0.725 données par l'analyse de Nusselt, mais les résultats de l'analyse numérique des équations de la couche limite afin de traiter le problème de la condensation et montrent une influence non négligeable du nombre de Prandtl du condensât sur le coefficient d'échange.

§ SHEKRILADZE et GOMELAURI [10] admettent que l'aspiration de la couche limite vapeur par la condensation rend l'écoulement de vapeur laminaire et font l'hypothèse que la contrainte tangentielle à l'interface liquide-vapeur est égale a la perte de quantité de mouvement de la vapeur condensée cette hypothèse n'est valable que pour un taux de condensation infini, mais possède l'avantage de rendre inutile la résolution des équations de la phase vapeur pour assurer légalité des contrainte tangentielles à l'interface et simplifie considérablement l'analyse lorsqu'on néglige le gradient de pression. Ainsi sans tenir en compte des termes d'inertie et de convection d'enthalpie et en effectuent une analyser du type Nusselt, Shekriladze et Gomelauri proposent les relations suivantes :

- Plaque plane Horizontale :



1

2

hm	é ê ëê	H
		H+

(II.33)
(II.34)

r l

L U ù

l v l

ú

1 ú

( )

T T L

sat p

- û

Avec : H

Ja

Pr_l



Nu

x

1

3

1 . 50 8 ú

~ - 1 ê 1

Re 0 .43 6

2 =

x

ù

ú

G ú

T ú

ú

L û

æ D

l ö

l

ç 1 + ÷

è m l v ø

3

2

+

(II.35)

§ ROSE [20] propose pour la condensation sur une plaque plane horizontale l'équation suivante :



1

2

æ r m ö

, R r m

l l

= ç ÷ (II.36)

è v v ø

G

=

JaR T

l D æ r m ö

Pr ÷

l l l

= ç

l L

m l v è r m

v v ø

1

2

~

, Re x

x

r U

m l

§ Les équations couplées de la phase liquide et de la phase vapeur pour la condensation laminaire sur un cylindre sont résolues par ASBIK et AL [21] en utilisant une méthode de différence finie implicite. Ces résultats montrant que l'hypothèse de Shekiladze et Gomelauri est acceptable pour un écoulement laminaire lorsque la différence de température est importante le gradient de pression dans leurs calculs pour un cylindre faisant partie d'une nappe est calculé par la méthode de singularité en admettant un écoulement potentiel.

§ Les équations couplées de la phase liquide et de la phase vapeur sont résolues par HOMNESCU et PANDA Y [22] en tenant compte de la turbulence dans les deux phases. L'équation suivante est proposée par Homenscu et Panday pour représenter les résultats numériques concernant la condensation turbulente sur un cylindre :

é ù





1

ê 1





~ - 1 ( ) ú

1 ö ³ 1 1 0 . 8

+ A 2

Nu_t Re 0 . 29 1 0 . 7 5 1



² ê _ø÷ + +

4

= æ + A ú

ç_è 0 . 25 (II.37)

1

ê G 4

ö ú

æ +

1

2

ê ç_è 0 . 25 1 .7 5

A A ø÷ ú

ë û

Avec :

Nu t

A=

hD

= Nombre de Nus selt pour la condensation Turbulente

:

l l

Pr l l v

m L Dg

= (II.38)

FrJa l

l

U T T

² ( sat p )

-

( ) 2

1

Pr R T T l r l ö l sat p l

- æ l l

G = = ç ÷

Ja L v v

m è r l

v v ø



(II.39)

§ MC NAUGHT [23] à développé la corrélation de Nusselt pour un condensat contrôlé par les forces de cisaillement dans le faisceau de tubes :

h

= tt



h_l

1 . 26 - 0 .78

X(II.40)

h_l : Coefficient de transfert de chaleur de la phase liquide [w/m²K]. Xtt : Paramètre de Lockhart-Maritineii a travers le long du faisceau.

Xtt

0 .9 0 .5 0. 1

æ -

1 x ö æ r Avec x @ 0 . 9

ö æ m ö



v l

ç è _ø÷ ç ÷ ç ÷ (II.41)

x èrlø èmvø

§ BEA TTY et KA TZ [24] ont développée la corrélation de Nusselt pour la condensation a l'extérieur des tubes ailettés horizontaux en introduisant la notion du Diamètre équivalent, par la corrélation suivantes :

1

3 4

l r r r

( )

l l l v v

- gL (II.42)

( )

m _l



T T

sat p

-

D e

ù

ú

û ú

é ê ë ê

0 . 6 89

h

- 0 .25 1 . 3

0 - -

h 0.25 0.25

ail ail net r

S E S D

+

h p tot

(II.43)

1 Pr

* l

A Fr Ga

= =

3

⁰ P

1

w 2 æ g 3

ö

^{0 ç} ÷

g v 2





r v

Pr_l
Pr v

(II.46)

Avec :

D_e : Diamètre équivalant [m]

hail : Rendement des ailettes.

h_p : Rendement de la paroi.

Sail : Surface des ailettes par unité de longueur [m²/m] Snet : Surface nette par unité de longueur [m²/m]

Sto t : Surface totale par unité de longueur [m²/m]

D_r : Diamètre racine des ailettes [m]

E : Paramètre dans l'équation de Beatty et Katz [m]



E = p r ₂ - r 2r

( ) ( ₂ )

2 ² (II.44)

1



r₁ : Rayon des racines des ailettes r 1 = D_r 2 [m]

r₂ : Rayon des ailettes [m]

I.1.3. Condensation à l'intérieur des tubes verticaux :

§ BORISHANSKI et AL [25] ont proposé la formule suivante pour le coefficient d'échange moyen ( h_m ) lors de la condensation complète de la vapeur d'eau à l'intérieur d'un tube verticale

:



h w ²

m = = +

⁰ Nu 0 . 1 7 A 0 . 2 A

*1 .7 *2 .8 (II.45)

0

l _l g

Avec :

centsL

w₀

4q

L D

vrl

(II.47)

qcents : La densité de flux thermique moyen [w/m²].

w₀ : Vitesse du condensât basée sur la longueur L [m/s]

§ IVASHCHENKO et AL [26] proposent d'utiliser un coefficient correcteur par rapport au nombre de Nusselt pour la condensation de vapeur stagnante donnée par :

h D

Nu l

0 0 . 925 Re Ga

0 0 .28

-

l

(II.48)

= l =



1

3

Avec :

3

centsL

_q gD

Re = , 2

Ga =

^l L

v l

m v_l

(II.49)

§ CA VALLINI et ZECCHIM [27] analysent les résultats expérimentaux de différents chercheurs et proposent la relation empirique suivante pour des vapeurs de fluides frigorifique :

0. 8

1

é 2 ù

0 .05 Pr 0. 3 3 Re Re

m æ r ö

ê v l

Nu m l v (II.50)

l

= r

ç +

÷ ú

ê m ú

l è vø

ë û_m

m: Indice représentant la moyenne entre l'entrée et la sortie du tube

§ SHEKRILADZE et MESTVIRISHVITI [28] utilisent l'hypothèse selon laquelle la contrainte tangentielle à l'interface liquide-vapeur est égale à la perte de quantité de mouvement de la vapeur condensée pour un écoulement turbulent du film liquide et pour une vitesse importante de la vapeur ils obtiennent la relation :

h x x

= 0 .2 [

ll l

PrRe^*

(II.51)

Pr ln 1 5 Pr

l ( l ) ]

+ +

Avec:

x



v_l

x

q cents ( )

U v

L v

r _l

Re *

ö ÷÷ ø

(II.52)

æ _çç è



§ SHAH [29] adopte la correction de Dittus-Boelter et considère que l'échange thermique lors de a condensation s'effectue à travers l'écoulement monophasique du film liquide l'analyse des résultats expérimentaux de différents chercheurs lui permet de déterminer correcteurs en fonction du titre vapeur et de la pression réduite, ainsi il propose l'équation empirique suivante :

h l é *0 .8 l m l l = êë 0 . 023 Re Pr D

ù úû

æ ç ( ) ( ) ( ) 0. 04 0 .76 ç * * 0. 8 3 . 8 1 x x - m m 1 - + x * ç m 0. 3 8 ç æ P ö ç ç ÷ è è P cr ø

ö ù ÷ ú ú ÷ ÷ ú (II.53) ÷ ú ø ú ÷ û

Avec :

x_m Titre moyen entre l'entrée et la sortie [%]

* :

Pcr : Pression critique du fluide [bar] MD

& S p D ²

m l

l₄

S

Re ,

* = = (II.54)

M& : Débit masse totale à l'entrée du tube est du liquide [kg/s].

§ CHEN, TIEN et GERNER [30] tiennent compte de la contrainte tangentielle à l'interface, de l'influence des ondes ainsi que du transport turbulent et adoptent les corrélations proposées par d'autres chercheurs afin de développer une équation générale :

- Pour une condensation laminaire avec ondes sur la surface du condensât, ils admettent la relation de Chen et Seban :



1

3

( ) ( ) 0 .22

h v ²

æ ö

* = l x

x l

Nu l ç ÷ = 0 . 823 Re -

xLam g

l è ø

(II.55)



Avec :



t

* I

t =

I

r_l

( ) 3

2

gv l

3

h v ²

æ ö 0 .65 * 1

x l 2

ç ÷ = 0 . 03 6 Pr l I

t

{ ( ) }

Nu * =

x Lam t

1

l g

l è ø

(II.57)

(II.58)

- Pour une condensation turbulente (Re_l )_x > 3500 et en l'absence de contrainte inter faciale, ils utilisent les résultats de BLANGTTI et SCHLUMDER [31] :

1

h v 2 3

æ ö

( ) ( ) 0 .4 065

Nu =

x ^l 0 . 00402 Re l l Pr l

= l ÷ (II.56)

x tur g

ç

l è ø

- Pour la condensation laminaire avec une contrainte tangentielle importante, ils adoptent la relation de SOLIMAN et AL [06]:



§ Ainsi, en utilisent la technique de Churchill et Usagi, CHEN, TIEN et GERNER [30] développent d'abord une expression pour la condensation de vapeur stagnante dominées par la gravité en posent :

( ) [ ( ) ( ) ] 1

1

n 1 1

* * * n n

Nu x g = Nu Lam + Nu (II.59)

turb

Une corrélation générale est ensuite établie en combinaison l'expression précédente avec une contrainte tangentielle importante ainsi ils écrivent :

[ ( ) ( ) ] 2

1

n 2 2

x = Nu _g + Nu t

* * * n n

0 Lam

Nu



(II.60)



§ En se basent sur les résultats expérimentaux de BLANGETTI et SCHUMDER [31], ils obtiennent l'équation suivante avec n1=6 et n2=2



(II.61)

l x 14 I

l l

1 é 2 3

h v

æ ö = æ

* x

Nu =

x

l ê

ç ÷ _çç

ê

è g ø ë è

1 1



1

2

( ) ( )

Re Pr

2 3 .9 3 ù

ö 3

1 .32 l x l l

Pr

- *

0 . 3 1 Re + ÷÷ + t ú

2 . 3 7 10 77 1 . 6 ú

ø û

En ce qui concerne l'estimation de *

t _I CHEN et AL [30] proposent d'utiliser l'équation suivante basée sur les résultats de Dukler concernant la perte de charge en régime annulaire concernant (dans le sens de gravité) d'un écoulement diphasique isotherme :

t I = B Re l T - Re l x Re l x

* * [ ( ) ( ) ] ( ) ^0.4

1 4 (II.62)

Avec :



r r

0 .553 0. 78

l v

3

B

* 0 .252 m

D

2

g

2

1.177 0.156

l v

m

(II.63)

(Re_l ) T : Le nombre de Reynolds du film liquide de condensât pour une condensation totale.

§ La première modification de la théorie de Nusselt pour la condensation à l'intérieur des tubes verticaux est introduite par CARPENTER et COLBURN [32] qui considèrent que la résistance thermique est due seulement à une sous couche laminaire dans le film de condensât et proposent l'équation d'échange suivante pour déterminé le coefficient d'échange local :



1

2

l r

h x c

l l

= Pr l

m_l

1

2

( ) 2

1

t I x

(II.64)

Avec : c = 0.043

I.1.4. Condensation à l'intérieur des tubes horizontaux :



§ En appuyant sur les essais effectués avec du méthanol et du R12 AKERS et ROSSON [33] proposent les équations suivantes pour un débit massique M& v :

1 & 2

2

M D

& ,

æ r ö M D

l

Re ÷

= ç Re = , S p D

v l = (II.65)

^v S ^v S

m l è r m 4

v ø l

- Pour Re_l <5 000 :



1



6

(II.66)

1 æ L ö

Nu C Pr Re

3 v

= ç ÷ ( )n

v

^l Cp T

è l D ø

Avec :

C = 13.8 n = 0.2 lorsque 1000 < Re_v <20 000

C = 0.1 n = 2/3 lorsque 20 000 <Re_v <100 000 - Pour Re_l > 5 000 et Re_v > 20 000 :



Nu = 0 . 026 Pr l 1 Re _v + Re l

3 [ ] 0 .8 (II.67)

§ RIFFERT [34] à mesuré le coefficient d'échange local pour la condensation de la vapeur d'eau dans un tube horizontale de 18 mm de diamètre ses résultats pour le coefficient d'échange local, à une distance x de l'entrée du tube sont représentés dans le domaine :

1

0 . 8 6 Re f < C _f Fr < 7.36 3

³ Re f

par l'équation suivante :





1



1

h v 2 3

æ ö

x C Fr

* l 0. 5 0 .3 8 0 .26

~

x

Nu

= ç ÷ 1 . 5 -

= Re (II.68)

f f

l l è gø

Avec :

Re = , (

xq cents ~ r r - r

v l v

Fr =

^f L

v

( )

~ 2

1 0 .25

- b

0 ~

() ^0.2

1 0 .25

+ b

q

, ÷

~ 2 (II.69)

æ cents ö

b 0 r

= - ç

C f L v v w v

è ø

)w 2 v

, C_f C f

=

m_l



r l

² ( ) 3

2

v g

l

w_v : La vitesse axiale de la vapeur [m/s]
qcents : La densité de flux de chaleur [w/m²]

C_{f 0}: Le coefficient de frottement d'un écoulement monophasique pour : Re = w_v D

v_v

§ Les résultats expérimentaux pour la condensation de R22, R134a et R123 dans un tube de 8.4 mm de diamètre intérieur ont conduit FUJII [35] à proposer les corrélations suivantes :

- Ecoulement de convection forcée (indice f) :

				æ çç è
( ) Nu	f	=	0.0125		Re	l

r 1 x

0 .9 0 . 1 0 .8

x * +

ö x *

r æ ö

^l Pr 0. 83

* l



÷÷ -

ç ÷ (II.70)

v ø è ø

- Ecoulement de convection naturelle (indice N) : Avec :



1.

*

B

hD

l

Nu =

=

,

Re

l l

( )

- x D

*

1

G

m_l

gD3 Ja -

Cp T T

Ga = , ( )

l sat p

, 2

=

v_l

L v

*

0.47

1 0 .9

12 *

æ ö

l ÷

Ja x

æ ö

ç ÷ ç Re l *

è Pr 1 x

l ø è - ø

( ) 4

1 . 1

Ga Ja
Pr l

C

r

r_v

5 5 1 1 . 6 . 1 0 / Pr

( ( ) )

11 5

+ Ja l

( )

r r

l v

/

1

Re / 1

( )ú ^ú

* *

-

l x x û

1

4

é

ê

ëê

( )

Ga Ja

Pr / 4 ù

l

(II.71)

(II.72)

(II.73)

Re ù

D * 4

= - -

é

40 exp 2 . 6 . 1 0 x ^l (II.74)

*

êë 1 - úû

h D Pr l - 0 .33 * 1 . 04

⁰

^m B 0 .3 Re l = 6 .4 8 Re - eq (II.75)

o

l _l

§ En se basent sur leurs résultats expérimentaux de condensation du R134a dans un tube de 2 mm de diamètre et 100 mm de longueur YAN et LIN [36] proposent l'équation suivante pour le coefficient d'échange moyen :





m l

Avec :

Re ₀ ,

* =

GD

l

G eq

Re = (II.76)



m_l

^eq D

Geq = G 1 - x _m + x _m r _l r v

[ ( ) ( ) ]

* * 0 .5, Bo = qcents (L _v G) (II.77)

§ TANDEN et AL [37], proposent les relations suivantes pour le coefficient d'échange moyen :

- Ecoulement contrôlé par les contraintes inter faciales (régimes annulaires et semi
annulaires) :



DG v

^v G

m l v

> 3 10⁴ :

~

Pour Re

G l

( ) 0 .67

1 ~

Nu = l L _v Cp _l D T v

0 . 0 84 Pr ¹ Re

3 6(II.78)





Avec : D T = T _sat - T _p [°C]



G_v : La vitesse massique de la vapeur basée sur la section du tube [kg/m2s].

- Ecoulement contrôlé par gravité (régimes ondulés) :

~ Pour : Rev

< 3 10^4 :

Nu = 23 . 1 Pr _l L _v Cp _l D T v

¹ Re ¹

( ) 8

1 ~

3 6 (II.79)





§ DOBSON et CHA TO [05] trouvent que le nombre de Froude Fr_So proposé par Soliman

FrSo = 7 Représente bien la transition entre le régime d'ondes et le régime annulaire ondulé. En basent sur leurs essais, ils proposent la relation suivante pour le régime annulaire symétrique _(FrSo >20) dominé par la contrainte inter faciale :

hd

0. 8 0 .4 2 . 22

é ù

= =

Nu 0 .023 Pr Pr 1 + (II.80)

l l 0. 89

ê_ë ú_û

l c

l tt

Pour le régime à ondes dominé par la gravité (Fr_So<10), ils proposent les expressions suivantes dans lesquelles q_l est l'angle entre le haut du tube et le niveau du liquide :

0.23Re 0. 1 æ Ga Pr

vo l

ç ÷ +

c 0. 58

1 1 . 1 1

+ tt

0.25

Nu =

è Jal

( l ) forcé

1 - q p Nu

(II.81)



Avec : Ja_l = Cp_l (T _sat - T _p ) L v (II.82)

§ CHATO [05] a développé aussi une corrélation qui permet de calculer le coefficient de

transfert de chaleur lors la condensation à l'intérieur des tubes horizontaux :

g L

r r r l 3 4

( )

l l v f v

-

(II.83)

( )

m _f

ù ú û ú



1

T T

sat p

-

d_i

é

ê

ëê

0.555

h

I.2. Coté fluide refroidisseur :

Le coefficient d'échange est à identifier par rapport aux paramètres opératoires (vitesse, pression,...), aux paramètres géométriques (diamètre interne du tube, état de surface,...), et aux propriétés physiques du fluide (viscosité, densité, capacité calorifique,...).

I.2.1. Le transfert de chaleur a l'intérieur des tubes (eau):

Généralement, dans les condenseurs le liquide de refroidissement est de l'eau, arrivant d'un système extérieur (tour de refroidissement, réservoir, échangeur, réseaux commun d'eau,...), puis entre dans un collecteur à partir duquel s'effectue sa distribution dans les tubes du faisceau.

I.2.1 .A. Pour l'écoulement laminaire:

Nous avons rassemblé les corrélations définissants le transfert de chaleur par convection des fluides sans changement de phase à l'intérieur des tubes pour l'écoulement laminaire dans le tableau II.01

Tableau II.01 : Corrélation donnant le coefficient de transfert par convection à l'intérieur des tubes pour le régime laminaire
N	Auteurs	Equation	Condition d'utilisation	Remarque	Réf
(II.84)	HANSEN	0 . 1 4 ì ü æ Gz ïí 0 . 0668 m ö Nu = + ïý 3 66 . çç ÷÷	Gz = Re Pr D / L Gz < 100 L D < ( ) 0 .03 Re	Valable pour région d'entré et pour température de paroi constante	[38]
HUG	( ) 1 / 3 Nu = 1 . 62 Re . Pr . D LRégime	-	Pour des fluides à propriétés constantes. d'entrée	[39]	(II.86)
SEIDER-TATE	0. 1 4 æ ö 1 / 3 m = 1 . 86 ÷÷ Nu Gz m çç è ^p ø	> Gz100 ( ) £ 10 m mp L D < ( ) 0 .03 Re	Valable pour la température de la paroi constante Tp= Cte Régime d'entrée	[40]	(II.87)
LABUNETSOV	0.25 æ Pr ö 0 . .3 3 0 .43 = 1 5 Re Pr Nu 0 . çç ÷÷	Gr < . Pr 8 . 1 0 ^5 L D > 50	Régime visqueux	[41]
		. Pr 8 . 1 0 ^5 Gr > LD>50	Régime visco-gravitationnel
ALADIEV, MIKHYEV FEDYNSKY	Nu = [ 0 .74 e P e 0.2 + k ( b . a ) ^0.02 ] Ra 0 . 1	-	-	[40]	(II.89)
SIEDER-TATE	1 / 3 0. 1 4 æ d ö ^æ m ö int lr = ç Pr ÷ Nu 1 8 6 Re	Re l r < 2100	Valable pour les tubes lisses	[42]
		. . çç ÷÷ ^lr L Condenseur è m p ø è ø
(II.90)	SHUNDLER	0.3 3 int = æ + d ö Nu ç 3 663 1 6 1 3 Pr Re ÷ . .	Re l r < 900	Valable pour les tubes lisses
		lr lr lr è L Condenseur ø

I.2.1 .B. Pour l'écoulement turbulent:

Nous avons rassemblé les corrélations définissants le transfert de chaleur par convection des fluides sans changement de phase à l'intérieur des tubes pour l'écoulement turbulent dans le tableau II.02

Tableau II.02 : Corrélation donnant le coefficient de transfert par convection à l'intérieur des tubes pour le régime turbulent
N°	Auteurs	Equation	Condition d'utilisation	Remarque	Réf
(II.91)	NUSSELT	0 .055 Nu 0 .03 6 Re 0. 8 Pr 0.3 3 æ D ö = L	çè ø÷pour L 10 < D < 400	Valable seulement la région d'entrée	[38]
(II.92)	MC ADAMS	0. 7 D = æ + L Nu n 0 . 023 Re 0 .8 Pr 1 ø÷ ö çè	-	Valable seulement pour la région d'entrée	[43]
(II.93)	COLBURN	4 1 Nu=0.26Re 5Pr 3	2000< Re < 32000	Disposition des tubes en lignes	[38]
		4 1 Nu=0.33Re 5Pr 3	2000< Re < 32000	Disposition des tubes on quinconces
(II.94)	SEIDER et TATE	0. 1 4 1 æ m ö 3 = çç Nu m 0 . 027 Re 0 .8 Pr ÷÷ è ^p ø	< < 0.7 Pr 16700 > Re 10000 L > 60 D	Pour les liquides	[44]		(II.95)
SLEICHER et ROUSE	a ^b Nu = 5 + 0 . 0 1 5 Re Pr p	< < 0 . 1 Pr 10 ^5 4 6 < < 10 Re 10	-	[45]
		Nu = 4 . 8 + 0 . 0156 Re 0. 85 Pr 0 .93	Pr < 0 . 1 Tp = cte
		Nu = 6.3+0.0167Re0. ^85 Pr0 .93	Pr< 0.1 ql = cte
(II.96)	LABUNETSOV	0 .25 æ Pr ö 0. 8 0.43 Nu = 0 1 Re Pr .02 çç e ÷÷	L / D > 50	-	[38]
		è Pr p ø
(II.97)	ILLINA	Nu = 0.0209Re0 ^.8 Pr0 .45 Nu = 0.0263 Re0 ^.8 Pr0 . .35	-	Pour l'échauffement Pour le refroidissement	[46]
(II.98)	GNIELINSKI	2 ^3 æ ö w - Re 10 Pr ( ) é d 3 ù i Nu ê 1 ç ÷ ú = +	< < 0.6 Pr 2000 < < 2300 Re 10 ^6 di 0 1 < < L	régime transitoire et turbulent en tenons compte de la longueur d'établissement de l'écoulement	[47]
		8 æ w ö 2 ê è ø ú 3 ö L 1 1 2 .7 ø÷ æ - + çè çè Pr 1 ø÷ ë û 8
(II.99)	WHUITHIER	0 .8 900 1 . 3 52 0 .02 T ( ) h - m =	-	Valable seulement pour l'eau	[45]
		di 0 .2

I.2.2. Le transfert de chaleur a l'extérieur des tubes (l'air ou l'eau):

Nous avons rassemblé les corrélations définissants le transfert de chaleur par convection du fluide sans changement de phase à l'extérieur des tubes pour l'écoulement turbulent dans le tableau II.03

Tableau II.03 : Corrélation donnant le coefficient du transfert de chaleur à l'extérieur des tubes
N	Auteurs	Equation	Condition d'utilisation	Remarque	Réf
(II.100)	KUTAYELAZE	h = 8.98w0 ^.6 + 32.81w0 ^.61	-	-	[48]
(II.101)	MIKHEYEV	( 5. 1 5 0.3 2 ) ^0.6 ( 1 8.8 3 1 . 1 8 ) 0.65 happ = h + w + h + w-		-	[49]
(II.102)	VAMPOLA	Nu 0 . 1 83 Re 0 .63 = ( ) 0 .63 26 .04 1 . 82 happ = h + w	-	-	[50]
(II.103)	V.D.I	Nu = 0.21fa.Re0 ^.61 Pr0 .31	-	-	[51]
(II.104)	CONAN	Nu = 0.425 Re ^0.5	Re <1500	Valable pour des tubes plats	[52]
		Nu=0.100Re0 .7	Re > 1500
(II.105)	SCHMIDT	- 0 .3 75 Re 0 .625 Pr 0. 3 3 æ S ö Nu ail 0 ç ÷ .45	< < 100 Re 40000 < < 10 50 d mm e < < 450 n ail Ailettes / m2	Disposition des tubes on quinconces	[53]
		= s è ø120
		- 0 .3 75 3 Re ^0.625 Pr 0 .3 3 æ S ö Nu ail 0 ç ÷ .	5.10^3Re 10 ^5 < < 10 50 d mm e ail < < 5 12	< <Disposition des tubes en lignes
		= s è øS
			S
(II.106)	BONTEMPS	Nu=0.142Re0 ^.6	Re< 1500	Disposition des tubes en ligne. Régime laminaire	[54]
		Nu = 0.0.23Re0 ^.85	Re >1500	Disposition des tubes en ligne. Régime Turbulent

II. LES CONDENSEURS :

II.1. Principe général d'un condenseur :

Le principe le plus général consiste à faire circuler deux fluides à travers des conduits qui les mettent en contact thermique. De manière générale, les deux fluides sont mis en contact thermique à travers une paroi qui est le plus souvent métallique ce qui favorise les échanges de chaleur. On a un fluide chaud qui cède de la chaleur à un fluide froid. En d'autres termes, le fluide chaud se refroidit au contact du fluide froid, et le fluide froid se réchauffe au contact du fluide chaud. Les deux fluides échangent de la chaleur à travers la paroi d'où le nom de l'appareil.

On voit que le principe général est simple, mais il donne lieu à un grand nombre de réalisations différentes par la configuration géométrique.

Le principal problème consiste à définir une surface d'échange suffisante entre les deux fluides pour transférer la quantité de chaleur nécessaire dans une configuration donnée. On vient de le dire, la quantité de chaleur transférée dépend de la surface d'échange entre les deux fluides mais aussi de nombreux autres paramètres ce qui rend une étude précise de ces appareils assez complexe. Les flux de chaleurs transférées vont aussi dépendre des températures d'entrée et des caractéristiques thermiques des fluides (chaleurs spécifiques, conductivité thermique, viscosité,... etc.) ainsi que des coefficients d'échange par convection.

Ce dernier paramètre dépend fortement de la configuration des écoulements et une étude précise doit faire appel à la mécanique des fluides.

L'évacuation de la chaleur dans un condenseur s'effectue en trois étapes (voir la Figure II.04) :

1- La désurchauffe des vapeurs de fluide frigorigène (évacuation par chaleur sensible -
tronçon 1-2)

2- La condensation des vapeurs (évacuation par chaleur latente - étape principale - tronçon 2-3)

3- Le sous refroidissement du fluide frigorigène liquide (évacuation par chaleur sensible - tronçon 3-4)



Figure II.04 : Evacuation de la chaleur d'un condenseur

II.2. Technologies des condenseurs :

On distingue deux familles de condenseurs suivant le fluide de refroidissement (refroidissement à air ou refroidissement à eau) :

II.2.1. Les condenseurs à air :

L'emploi de l'air sec pour la condensation obtient de plus en plus de succès. Les raisons de succès tiennent essentiellement au fait que l'air est disponible, sans difficulté, gratuitement et de quantité illimitée, en plus il ne présente aucun problème d'évacuation, il s'emble donc que c'est lui le premier facteur que l'on s'adressera pour assurer économiquement la condensation des vapeurs du fluides frigorigène.

L'échauffement de l'air dans le condenseur est généralement donné entre (5 et 6 °C) [55].

Malheureusement, l'air à une très faible chaleur massique d'une part et d'autre, le coefficient d'échange globale de transmission thermique entre une vapeur condensente et un gaz (air) est également faible.

Ces deux caractéristiques font que nous serons amenés à véhiculer de grands volumes d'air, et que nous devrons avoir une grande surface d'échange pour des quantités de chaleur échangées relativement faibles, cela implique des appareils très encombrants.

II.2.1 .A. Condenseur a circulation d'air naturelle .
·

Ils ne sont utilisés que pour les installations de très faible puissance (armoires ménagères, ou appareils similaires).

Primitivement exécutés en tubes à ailettes, ils ne sont plus, maintenant réalisés sous cette forme, car les tubes à ailettes s'empoussiéreraient très rapidement étant donné le fait que la très faible vitesse d'air favorise les dépôts de poussière sur les ailettes. Ils sont actuellement réalisés par un tube forment serpentin appliquer sur une feuille de tôle forment ailette unique et perforée pour évité la résonance, ou mieux, soudé sur un treillis de fils métalliques le condenseur étant alors placé verticalement derrière l'armoire.

II.2.1 .B. Condenseur a circulation d'air forcée .
·

Pour des puissances frigorifiques supérieures à celles installées sur des armoires ou meubles ménagers, il est indispensable d'utiliser soient d'un encombrement compatible avec des puissances calorifiques à évacuer, on utilise donc un ou plusieurs électro ventilateurs qui assurent la circulation de l'air sur le faisceau ailetté.

Le sertissage des ailettes sur les tubes peuvent être réalisé par d procédés (mécanique, hydraulique). Deux types de dispositions sont utilisés à savoir:

- Le faisceau vertical (Figure II.05)

- Le faisceau horizontal (Figure II.06)

II.2.1 .B. 1 Condenseurs à air à convection forcée horizontaux :

Ils sont utilisés pour les petites et moyennes puissances, la vapeur surchauffée entre par le collecteur supérieur et le liquide sous-refroidi sort par le collecteur inférieur



Figure II.05 : Condenseur à air a convection forcée horizontale

II.2.1 .B.2 Condenseurs à air à convection forcée verticaux :

Ils sont utilisés pour des puissances supérieures, les sections sont disposées en parallèle permettant un meilleur équilibre thermique. La vitesse moyenne de l'air est comprise entre 2 et 4 m/s pour limiter les pertes de charge et le niveau sonore.



Figure II.06 : Condenseur à air a convection forcée vertical

II.2.2. Les condenseurs à eau :

L'eau comme l'air absorbe le flux calorifique du fluide frigorigène sous forme de chaleur sensible, ce qui se traduit par un échauffement de l'eau servant à la condensation. Cet échauffement conditionne le débit de l'eau à assurer au condenseur, et comme le prix de revient du mètre cube d'eau est relativement élevé, il peut sembler intéressant de diminuer le débit d'eau nécessaire à la condensation en acceptant un échauffement plus important de celle-ci affin de réduire les frais de consommation. La contre partie de cette économie de consommation sera une élévation de la température de condensation du fluide frigorigène et une baisse corrélative du rendement globale de l'installation. Il est donc nécessaire d'adopter un compromis et, suivant le prix de revient du mètre cube d'eau, cet échauffement est compris entre (7 et 12 °C) [55] ce problème de limitation de débit ne se posait pas pour l'air puisque nous pouvons en disposer gratuitement.

II.2.2.A. Les Condenseurs à tubes :

Il existe plusieurs types de condenseurs a tubes énumérons :

II.2.2.A.1. Condenseurs à immersion :

Ce sont les plus anciens condenseurs à eau réalisés. Ils étaient utilisés dés le début de l'industrie frigorifique pour les machines à ammoniac, anhydride sulfureux ou chlorure de méthyle sous forme de serpentin en acier enroulés en spirales verticales et immergés dans une cuve à eau cylindrique très encombrants nécessitant un espace libre important au dessus de la cuve pour sortir les serpentins, ils ont été abandonnés pour les machines industrielles au profit des autre types .

Ils sont néanmoins toujours utilisés sous forme permettant de combiner condenseur et réservoir de liquide. Ils peuvent réaliser en version horizontale ou verticale.

Dans la version horizontale, le condenseur comporte une bouteille en tôle d'acier enroulée et soudée, ou constituée par un tube d'acier étiré sans soudure fermée par deux fonds emboutis soudés. Le fluide se condense à l'extérieur de serpentin de circulation d'eau, constitué par un tube en cuivre lisse ou à ailettes extrudées enroulé en spirale à axe horizontale. Le fluide condensé est recueilli dans le bas de la bouteille.

A puissance calorifique égale, ils sont plus encombrants que dans la version verticale. Aussi leur capacité de condensation ne dépasse guère 8 000 w.

En version vertical ils assurent la continuité des premiers en ayant une gamme de capacité de condensation de l'ordre de 12 000 à 70 000 w. Le principe de fonctionnement reste le même : circulation d'eau à l'intérieur de tubes en cuivre a ailettes extrudées, et condensation du fluide à l'extérieur du faisceau de tubes enroulés en hélice à axe verticale. La bouteille en acier sert également de réservoir de liquide. Dans leurs forme verticale les circuits d'eau peuvent être vidangées par gravité par contre leurs version horizontale cette vidange ne peut être obtenue en totalité que sous pression d'air.

II.2.2.A.2. Condenseurs Coaxiaux et contre-courant :

Afin d'augmenter la vitesse de l'eau au contact de la paroi du tube dans lequel circule le fluide, on a eu recours à une solution simple consistant à placer concentriquement deux tubes. Le fluide circulant dans l'espace annulaire et l'eau dans le tube intérieur. Il est alors possible de faire circuler les deux fluides à contre-courant qui donne un meilleur échange de chaleur.



Figure II.07 : Condenseur coaxiaux

Pour les machines industrielles, les tubes dans lesquels circule le fluide sont réunis entre eux par des manchettes soudées, ces tubes étant eux-mêmes soudés à leurs extrémités sur les tubes de circulation d'eau. Les coudes ou plaques tubulaires réunissant les tubes d'eau sont démontables afin de permettre un nettoyage facile du circuit d'eau.

Dans leurs conceptions pour machine commerciales ces condenseurs sont exécutés en tubes de cuivre d'une seule longueur. Les deux tubes placés l'un dans l'autre sont ensuite cintrés, ce qui évite tout coude rapporté. La surface de ces condenseurs est évidemment limitée par la longueur droite des tubes dont on dispose pour les fabriquer.

Quelque soit le modèle utilisé, ces condenseurs nécessitent la présence sur le circuit d'une bouteille permet d'accumuler une certaine quantité de liquide frigorigène, qui sans la présence de celle-ci, engorgerait les dernières spires du condenseur et diminuerais d'autant le surface libre pour la condensation du fluide.

II.2.2.A.3 Condenseurs multitubulaires :

Ils sont l'aboutissement logique des condenseurs à double tube et à contre courant. Afin d'évité de mettre en parallèle de nombreux éléments de condenseur double tube, ce qui à pour inconvénient de multiplier les joints, on a groupé en parallèle à l'intérieur d'une virole de grand diamètre tout les tubes de circulation d'eau. La condensation du fluide se fait sur l'extérieur des tubes d'eau, et la partie inférieure de la virole peut servir de réserve de liquide condensé.

Nous pouvons les trouvées sous deux formes bien distinctes :

Ø Condenseurs multitubulaires horizontaux ; Ø Condenseurs multitubulaires verticaux ;

II.2.2 .A. 3. a. Condenseurs multitubulaires horizontaux : v Les condenseurs horizontaux à tubes droite :

Cette configuration, illustrée dans la (Figure II.08) est souvent utilisée avec la haute pression, ou avec les vapeurs corrosives.

Ce condenseur est constitué d'un passe coté calandre, et un passe coté tube.



Figure II.08 : Condenseur multitubulaire horizontale

Divers constituants d'un Condenseur multitubulaire horizontale sont représentés dans

La (Figure II.09)



Figure II.09 - Divers constituants d'un Condenseur multitubulaire horizontale

Ø Boîte du condenseur :

C'est l'organe qui distribue ou recueille le fluide aux extrémités des tubes. Sauf pour le tube en U, il y a une boîte à chaque extrémité de l'échangeur.

La disposition des boîtes dépend non seulement du type choisi, mais aussi du nombre de passes (Figure II.10). La liaison cloison-plaque tubulaire est en général assurée par un joint. Les boîtes sont le plus souvent réalisées avec un matériau peu différent de celui des tubes.

47



Figure II.10 : Configuration des boîtes de distribution

Ø Calandre (ou virole) .
·

C'est l'enveloppe métallique cylindrique entourant le faisceau tubulaire. Son matériau doit être compatible avec le fluide utilisé. Les matériaux les plus courants sont les aciers ordinaires, les aciers inoxydables, le cuivre. Il semble que la limite technologique des calandres se trouve aux alentours d'un diamètre de 2 m.

Certains très gros condenseurs sous vides sont réalisés avec une calandre parallélépipédique (solution d'ailleurs favorable pour limiter les pertes de pression en entrée).

Ø Plaques tubulaires .
·

Ce sont des plaques percées supportant les tubes à leurs extrémités. Leurs épaisseur (5 à 10 cm) est calculée en fonction de la différence de pression entre le fluide dans la calandre et le fluide dans les boîtes d'une part, des contraintes dues aux différences de dilatation entre les tubes et la calandre d'autre part.

Les plaques tubulaires peuvent être en acier ordinaire, en acier spécial massif. Un plaquage, en acier inoxydable par exemple, peut se justifier dans le cas de plaques tubulaires déjà assez épaisses.

Les tubes peuvent être fixés à la plaque tubulaire par dudgeonnage ou par soudure, quelque fois aussi par dudgeonnage allié à une soudure qui sert alors simplement à assurer l'étanchéité.

Les plaques tubulaires sont les parties délicates des Condenseurs. Les interstices entre tubes et plaques sont des lieux privilégiés de corrosion (la concentration en produit agressif y est parfois très supérieure à celle mesurée dans les autres parties du condenseur, car il y a stagnation du fluide). Par ailleurs, des dilatations différentielles excessives peuvent faire céder les dudgeonnages ou les soudures.

Ø Tubes :

Ce sont généralement des tubes normalisés dont le diamètre annoncé correspond exactement au diamètre extérieur (à la différence des tubes utilisés en tuyauterie).

Tableau II.04 : Exemple de tubes courants : [56]

Épaisseur		Diamètre extérieur (mm)	Diamètre intérieur (mm)	Surface extérieure (m^2 /m)
Norme BWG ^(1)	(mm)
BWG 14	2,11	19,05 (3/4 in)	14,83	0,0598
BWG 12	2,77	25,40 (1 in)	19,86	0,0798
(1) BWG : Birming-ham Wire Gaze

Ces tubes sont généralement de longueur standard : 2,44 ; 3,05 ; 3,66 ; 4,88 ou 6,10 m.

Le démontage du faisceau de tubes est de plus en plus difficile au fur et à mesure que sa longueur s'accroît (problème de rigidité du faisceau). Pour tous les condenseurs démontables, il convient de laisser un espace libre suffisant dans l'axe du condenseur pour permettre la sortie du faisceau de tubes.

Les matériaux utilisés dépendent des fluides choisis ; les plus courants sont les aciers ordinaires, les aciers inoxydables, le cuivre, le laiton, les cupronickels.

Deux dispositions de tubes sont possibles : le pas triangulaire et le pas carré (Figure II.11 ).



Figure II.11 : Pas des tubes

La disposition en pas carré offre une plus grande facilité de nettoyage (toute la surface extérieure des tubes est accessible par un jet d'eau sous pression ou par un instrument de nettoyage). La disposition en pas triangulaire est plus compacte, donc plus économique. Les pas standard les plus courants sont 0,024 ; 0,025 ; 0,030 ; 0,032 et 0,038 m (15/16 ; 1 ; 19/16 ; 5/4 et 3/2 in). Le rapport du pas au diamètre extérieur des tubes sera au minimum de 1,25.

Ø Chicanes :

Elles ont pour rôle d'augmenter la vitesse du fluide dans la calandre, et la rigidité du faisceau. Dans le cas de condensation à l'intérieur des tubes, il est intéressant d'augmenter la vitesse du fluide coté calandre pour améliorer le coefficient d'échange. La vitesse est d'autant plus élevée que les chicanes sont rapprochées pour l'écoulement transversal au faisceau de tubes (entre deux chicanes) et qu'elles ont une ouverture faible pour l'écoulement parallèle au faisceau de tubes (au passage de la chicane).

Par ailleurs, les chicanes sont nécessaires pour augmenter la rigidité du faisceau. Le code TEMA donne le tableau suivant de longueur maximale non supportée :

Tableau II.05 : Désignation des Condenseurs TEMA [56]

Diamètre extérieur du tube (mm)	Longueur maximale non supportée (m)
15,9	1,231
19,0	1,524
25,4	1,880
31,7	2,235
38,1	2,540
50,8	3,175
Une chicane ne couvrant pas la totalité des tubes (selon le cas 60, 70, 80 % du faisceau), on voit
que, pour un tube de 19 mm de diamètre extérieur, la distance maximale entre deux chicanes consécutives est de 1,524/2 = 0,762 m.

Dans le cas de l'extrémité d'un tube en U, la longueur courbe est considérée comme équivalente à la distance entre les axes des deux branches du U.

Pour la condensation d'une vapeur, la vitesse de circulation à peu d'importance et l'espacement des chicanes est exclusivement déterminée par ce critère de longueur maximale non supportée.

Le jeu entre tubes et chicanes ainsi que le jeu entre chicanes et virole sont réglementés par le code TEMA.

On utilise parfois des chicanes pleines dites de protection thermique destinées à protéger la plaque tubulaire contre des différences de températures excessives préjudiciables à sa tenue mécanique ; on les appelle aussi contre-plaques tubulaires.

Une entaille de vidange, qui doit être assez petite pour ne pas trop perturber l'écoulement, est
généralement prévue à la partie inférieure de la chicane afin de permettre la vidange du Condenseur.

Les chicanes sont de même matériau que la calandre ; elles peuvent être de plusieurs types : chicanes classiques, ou à barreaux (rod baffle dans la littérature anglo-saxonne) dont le développement et l'utilisation sont relativement récents. Dans ce dernier cas, les tubes sont tenus dans la calandre par des grilles de barreaux, alternativement de barreaux horizontaux puis verticaux.

Les chicanes à barreaux ont été imaginées pour répondre à deux préoccupations essentielles des constructeurs et utilisateurs des condenseurs à tubes et calandre :

· supprimer ou tout au moins réduire les problèmes de vibrations des tubes quelquefois induites par l'écoulement du fluide dans la calandre ;

· améliorer les performances thermo hydrauliques du fluide s'écoulant dans la calandre (augmenter le coefficient d'échange thermique et réduire les pertes de pression), en remplaçant l'écoulement transversal classique du fluide par rapport aux tubes par un écoulement longitudinal.

Ø Tirants et entretoises .
·

Ce sont des dispositifs ou équivalents assurant la liaison du système de chicanes, qui ont pour objet de maintenir les chicanes et les plaques supports solidement en place. Les tirants et entretoises doivent être du même matériau que la calandre.

Ø Déflecteurs longitudinaux .
·

Entre les tubes périphériques et la calandre subsiste nécessairement un vide non négligeable. Une part importante du fluide peut alors contourner le faisceau (phénomène de by-pass) et ne pas participer à l'échange de chaleur, ce que l'on atténue en utilisant des déflecteurs longitudinaux. Ceux-ci peuvent aussi servir au guidage du faisceau lors du montage.

Ø Déflecteur d'entrée .
·

Il sert à protéger, dans certains cas, le faisceau contre l'impact du fluide entrant ; il est nécessaire pour :

· Les vapeurs saturées ;

· Les mélanges diphasiques ;

· Tout fluide homogène non corrosif, non abrasif pour lequel le produit p v ² dépasse

2 250 kg / (m · s²) (avec (p ) masse volumique en kg/m³ et ( v) vitesse en m/s) ;

· Tout autre fluide tel que le produit p v² dépasse 750 kg / (m · s²). Ø Évents, vidange .
·

Dans la conception d'un Condenseur, il faut s'assurer qu'aucune poche de gaz ne peut stagner et ainsi diminuer la surface efficace. Il est donc nécessaire de prévoir des piquages d'évents et de vidange

v Les condenseurs horizontaux à tubes en U :

A fin de supprimer une plaque de fond, certaines condenseurs à faisceaux en tube a ailettes extrudées sont réalisés comme représenté (Figure II.12)



Figure II.12 : Condenseur multitubulaire en U

Le faisceau de condensation est constitué de tubes cintrés en épingle et formant chacun U, les deux extrémités libres sont mandrinées dans la plaque de fond sur laquelle est soudée la virole en acier obturée à l'arrière du condenseur par un fond embouti également en acier. Le fond cloisonné, comporte les tubulures d'entée et de sortie d'eau assurant par sont cloisonnement à l'eau en circulation le nombre de passes désirées sur le faisceau.

Dans cette disposition et pour les raisons exposées ci-dessus nous obtenons un encombrement beaucoup plus faible à puissance égale qu'avec un condenseur à faisceau droit à tubes lisses.

L'entrée de fluide et la sortie du liquide condensé sont alternées sur la virole. II.2.2 .A. 3 .b. Condenseurs multitubulaires verticaux :

Ils sont pratiquement identiques dans leurs conceptions aux condenseurs multitubulaires horizontaux à tubes lisses :

La calandre, les plaques de fond et les faisceaux tubulaires mais les fonds chicanés ont disparu. L'eau descend verticalement dans tous les tubes en parallèle. Si tous les tubes étaient pleins d'eau il nous faudrait avoir un débit considérable pour obtenir une vitesse d'eau comprise entre les limites que nous nous sommes fixées et ce, afin d'avoir un coefficient de transmission comparable à celui des condenseurs précédents.

Or, il se produit naturellement, lorsque l'on alimente un tube vertical par une bâche d'eau contenant
qu'une faible hauteur d'eau. Un phénomène tourbillonnaire appelé vortex, qui donne a l'eau un

mouvement de giration très rapide, et qui lui fait suivre la paroi interne du tube avec un mouvement hélicoïdale sans remplir complètement celui-ci. Cette remarquable propriété de la circulation des liquides est utilisée dans ce type de condenseur afin d'avoir une vitesse élevé de circulation sous un faible débit.

L'intérieur des tubes n'étant pas rempli d'eau, ils pourront alors servir de cheminée la circulation d'air, le condenseur étant toujours disposé à l'extérieur du bâtiment. L'amorçage du mouvement de giration peut être facilité par la mise en place à l'extrémité supérieure des tubes d'eau de tôles roulées en hélice ou de pièces en céramique. Le vortex ne pouvant efficacement se produit que dans des tubes de diamètre assez grand. Ce type de condenseur est surtout utilisé pour des machines à ammoniac.

Au parti supérieur du faisceau tubulaire se trouve le dispositif d'alimentation en eau, qui se compose d'une bâche alimentée généralement par un robinet à flotteur.



Figure II.13 : Condenseurs à tubes verticaux

II.2.B. Les condenseurs à plaques :

On distingue suivant la géométrie de canal utilisée : les condenseurs à surface primaire et les Condenseurs à surface secondaire.

Parmi les Condenseurs à surface primaire, le type le plus commun est le condenseur à plaques et
joints, dont les applications sont limitées par la pression maximale de service et par la pression
différentielle entre les deux fluides. On peut réaliser industriellement aujourd'hui des condenseurs

fonctionnant à des pressions de l'ordre de 15 à 20 bar ; la température maximale de service est limitée par la nature des joints.

Les Condenseurs avec plaques soudées permettent d'utiliser ces surfaces d'échanges primaires à des niveaux de température et de pression plus élevés que les Condenseurs à plaques et joints. Tous les fluides peuvent être véhiculés dans ces Condenseurs, mais les fluides encrassant sont à utiliser avec précaution.

Les Condenseurs à surface secondaire utilisent des ailettes plissées ou ondulées qui sont insérées entre les plaques. Pour des applications cryogéniques ou aéronautiques, les matériaux utilisés sont l'aluminium ou l'acier inoxydable, l'assemblage se faisant au moyen d'une technique de brasage sous vide.

II.2.B. 1. Condenseurs à surface primaire :

Les Condenseurs à surface primaire sont constitués de plaques corruguées, nervurées ou picotées. Le dessin du profil des plaques peut être assez varié mais il a toujours un double rôle d'intensification du transfert de chaleur et de tenue à la pression par multiplication des points de contact. Les différentes géométries de plaques les plus couramment rencontrées sont présentées sur

la (Figure II.14).



Figure II.14: Différentes géométries de plaques du condenseur à surface primaire

II.2.B. 1 .a. Condenseurs à plaques et joints :

La surface d'échange est alors composée de plaques métalliques, équipées de joints, serrées les unes contre les autres à l'aide de tirants entre deux flasques, l'un fixe, l'autre mobile (Figure II.16). Un rail fixé sur le flasque fixe et sur un pied supporte l'ensemble des plaques et permet le déplacement de celles-ci pour les manutentions (montage, nettoyage, etc.). Les plaques définissent un ensemble de canaux dans lesquels circulent respectivement chacun des fluides.

57



Figure II.15 : Condenseur à plaques et joints



Figure II.16 : Schéma descriptif d'un Condenseur à plaques et joints

Les différents composants d'un condenseur à plaques et joints :

1. Bâti fixe ;

2. Pack de plaques ;

3. Bâti de compression mobile ;

4. Rail de guidage supérieur ;

5. Rail de guidage inférieur ;

6. Support ;

7. Tirants.

Le dessin des plaques et de leurs cannelures varie d'un constructeur à l'autre ; il existe de par le monde une soixantaine de dessins de plaques ; aussi est-il difficile de donner les caractéristiques précises et spécifiques de chaque plaque.

Les plaques sont obtenues par emboutissage. Les matériaux utilisés sont en général l'acier inoxydable, le titane ou tout autre matériau suffisamment ductile (Hastelloy, Incaloy, Uranus B6, Monel, Cupronickel, etc.). Pour des applications courantes, les plaques ont une épaisseur de l'ordre de 0,6 à 0,8 mm mais, dans certains cas, des épaisseurs supérieures au millimètre peuvent être mises en oeuvre.

Les cannelures ont pour but essentiel d'augmenter les turbulences pour accroître les coefficients d'échange thermique, mais également d'assurer la rigidité mécanique par un grand nombre de contacts métal-métal. Les deux géométries de cannelures les plus fréquemment utilisées sont les cannelures droites ou à chevrons :

II.2.B. 1 .b. Condenseurs à plaques soudées :

Ils existants différentes technologies de fabrication des condenseurs plaques soudées ont présentent ici que le condenseur à spirale.

Ø Condenseur à spirale (Figure II.17)

Il est constitué de deux rubans de tôle gaufrée, enroulés et maintenus parallèles. La distance entre les surfaces d'échange des deux canaux est maintenue constante par des taquets soudés sur les plaques. La circulation des fluides est du type monocanal à courants parallèles ou croisés.

Cet échangeur peut fonctionner jusqu'à des pressions de l'ordre de 25 bar.



Figure II.17 : Condenseur à spirale (doc. Spirec)

II.2.B.2. Condenseurs à surface secondaire :

Ces Condenseurs sont réalisés en aluminium ou en acier inoxydable ; ils sont constitués par un empilage de tôles ondulées formant des ailettes séparées par des tôles planes.

On distingue, suivant le mode de fabrication et les matériaux utilisés : les Condenseurs à plaques serties et les Condenseurs à plaques brasées.

II.2.B.2.a. Condenseurs à plaques serties :

Ces Condenseurs sont constitués de tôles planes parallèles entre lesquelles sont disposées des ailettes ; ils sont en général fabriqués en tôlerie légère (acier galvanisé, acier inoxydable, aluminium, etc.). Les fluides empruntent un canal sur deux et la circulation est soit à contre-courant, soit à courants croisés. Les ailettes sont de types très variés.

II.2.B.2.b. Condenseurs à plaques brasées :

Ces Condenseurs sont en aluminium brasé. Les fluides circulent dans des passages définis par deux tôles planes consécutives et fermés latéralement par des barres (Figure II.18).

60



Figure II.18: Condenseur à plaques brasées : assemblage de plaques (doc. Nordon)

Les tôles ondulées (ondes) sont réalisées par emboutissage du feuillard sur des presses spéciales ; elles peuvent avoir des hauteurs, des épaisseurs et des espacements différents. Chaque type d'onde possède ses propres caractéristiques hydrauliques et thermiques : les ondes droites (perforées ou non) donnent des performances identiques à celles que donneraient des tubes de diamètre hydraulique équivalent ; les ondes décalées créent plus de turbulence et améliorent donc le coefficient d'échange thermique, tout en provoquant plus de pertes de pression.

Les ondes, grâce à leur configuration particulière, peuvent procurer une surface secondaire allant jusqu'à 90 % de la surface totale, ce qui permet de loger dans un volume réduit une très grande surface d'échange : plus de 1 500 m² /m³ . En outre, ces échangeurs souvent réalisés en aluminium allient une légèreté exceptionnelle (masse volumique de 900 kg/m³ à 1 200 kg/m³) à une excellente tenue mécanique ; ils sont particulièrement utilisés dans le domaine de la cryogénie où leur efficacité est élevée avec des niveaux de température compris entre - 269 ^o C et + 65 ^o C et des niveaux de pression pouvant atteindre 75 bar.

II.3 Avantages et inconvénients des condenseurs à air et à eau :

Le tableau suivant donne les avantages et les inconvénients de chacune des deux familles.

Tableau II.06 : Avantages et inconvénients des condenseurs à air et à eau. [57]

Type de condenseur	Avantages	Inconvénients
Condenseurs à air	Air disponible en quantité illimitée Entretien simple et réduit	Coefficients globaux d'échange thermique relativement faibles Plus imposants et plus lourds Températures de condensation élevées dans les pays chauds
Condenseurs à eau	Coefficients globaux d'échange thermique plus élevés Plus compacts et moins encombrants à puissance égale Températures de condensation stables et de bas niveau Fonctionnement moins bruyant Possibilité de récupération d'énergie	Gaspillage d'eau pour les condenseurs à eau perdue Nécessité de mise en place d'un système de refroidissement de l'eau

CHAPITRE III SIMULATION DU FONCTIONNEMENT DU CONDENSEUR

I. Introduction :

Le calcul thermique du condenseur est très compliqué, et sa revient essentiellement à la grande diversité des appareils (condenseurs tubulaires, condenseurs a plaques, refroidis à air ou à eau . .etc. ), et a cette complexité due a la technologie des appareils, s'ajoute la difficulté d'écrire un programme basé sur une méthode de calcul dont on doit parfaitement maitriser les hypothèses, et les paramètres de fonctionnement.

II. Logique de la phase de dimensionnement :

On commençant tout d'abord par la sélection du type du condenseur, puis vient la phase de dimensionnement thermique proprement dite, elle est désignée à fixer par le calcul de la surface d'échange nécessaire au transfert de puissance sur les fluides considérés.

Cette phase de calcul permet d'approcher par des essais successifs a la solution qui semble la meilleure du point de vue thermique, et apparait comme une contrainte au problème d'optimisation thermique : l'optimisation géométrique, qui conduirait à une diminution de surface pour le même rendement thermique, le calcul de dimensionnement du condenseur doit être capable de résoudre ce problème.

La phase de dimensionnement thermique peut être manuelle ou effectuée a l'aide d'un outil informatique, dans les deux cas l'enchainement itératif conduisant à répéter le calcul thermique après modification de certaines paramètres géométriques ou et thermo physiques, cette phase de dimensionnement thermique permet d'arriver au dessin final du condenseur.

On a recours a trois étapes pour faire le calcul thermique du condenseur :

§ Les données nécessaires (données géométrique, propriétés physique des fluides)

§ La phase thermique : comprenant des calculs géométriques (section, diamètre, longueur,.. . .etc.) puis les calculs de transfert de chaleur.

§ Les résultats, sous forme succincte (puissance thermique échangée et surface échangée, etc.) ou sous forme plus détaillée (valeur local des coefficients d'échange, nombres a dimensionnels caractéristiques, . . etc.).

Le calcul thermique du condenseur peut être aborde de plusieurs façons algorithmique très différents (par simulation, par vérification,. . etc.)

Par un mode de simulation connaissant la géométrie complète de l'appareil, ainsi que les deux fluides et leurs conditions d'entrée, on désire connaître les résultats de sortie des fluides (T,x) d'où la puissance thermique échangée.

III. Méthodes de calculs : [58]

Plusieurs critères sont à considérer pour le dimensionnement d'un condenseur suivant son utilisation, la puissance thermique est toujours la principale préoccupation, mais le choix définitif de l'appareil peut dépendre d'autres paramètres tels que (la surface d'échange, la température de la paroi a ne pas dépasser, l'encombrement, les matériaux utilisés ... etc).

Pour le calcul d'un condenseur on à des méthodes analytiques et des méthodes numériques

Ø Les méthodes numériques : Elles essaient d'améliorer la précision du calcul en décomposant les phénomènes physiques mis en jeu, et en prenant en compte la nature de l'écoulement, telles que la méthode des volumes finis.

Ø Les méthodes analytiques globales: telles que la méthode de l'écart moyen logarithmique DTML ou la méthode de l'efficacité NUT, elles présentent du fait de leurs hypothèses certaines limitations :

§ Elles supposent un coefficient d'échange constant le long du condenseur pour permettre une intégration analytique des équations.

§ Elles n'offrent pas la possibilité de dégrader l'influence de paramètres géométrique, car

les corrélations sont obtenues à partir des résultats globaux sur des appareils standards.

§ Elles nécessitent une bonne connaissance pratique de ces échangeurs dés que l'on s'éloigne

des dimensions standards.

III.1. La méthode DMLT:

DMLT : Différence Moyenne Logarithmique de Température.

Cette méthode permet de déterminer la surface d'échange (S), connaissant la puissance échangée et les températures d'entrée et de sortie des deux fluides.

Considérons un Condenseur à un seul passage à Contre courant, ou circulent deux fluides, l'un chaud (vapeur se condense) et l'autre froid voir la (Figure III.01), pour le calcul en admet que :

o Le régime est stationnaire.

o Le coefficient d'échange thermique global est constant.

o Les chaleurs massiques des fluides restent constantes.

o Le condenseur est considéré adiabatique.

On pose :

Tec: Température d'entrée du fluide chaud [°C].

Tsc : Température de sortie du fluide chaud [°C] .

tef : température d'entrée du fluide froid [°C].

tsf : température de sortie du fluide froid [°C]. L'extrémité chaude : DT C = T _c - t sf [°C]

L'extrémité froide : DT_f = T _c - t_ef [°C]



T(°C

T_c

(T_c-tf)

tsf

S (m²)

tef

dQ

ds

Figure III.01 : Distribution des températures dans un condenseur a contre courant

En prenant un élément de la surface du Condenseur (dS), (T) et (t) seraient respectivement : les températures du fluide chaud et du fluide froid dans cet élément.

Le flux de chaleur échangé entre les fluides le long de la surface (S )est :

Q = KS(DMLT) [W] (III.01)

Et le flux de chaleur échangé dans l'élément (dS) est :

dQ = KdS(T - t) (III.02)

avec :

K : Le coefficient d'échange thermique global exprimé en [W/m² K] T-t : La pente de la droite _(?Tc, ?Tf)

Alors :

T t -

d ( ) T t - dQ

dQ

d ( ) T t - T t -

(III.03)

et aussi :

D _C - D _f

T T

T t

- = (III.04)

Q

de (III.02)( III.03) et (III.04) on obtient :

dS

dQ Q d T t ( ) - ( ) ( ) = K T t - K T T D - D C f- T t

(III.05)

et donc :

S D T c

Q

S dS

= =

ò ò

K T T

( )

D - D

0 C f T

D f

d ( ) T t -		(III.06)
T t -

Q

( ) ( ) ^C

D T

(III.07)

S = ln T t



- D T f

K T T

D - D



Q æ D T ö

S ln (III.08)

( ) ÷÷

C

= _çç

K T T

D - D

C f T

è D f ø

C f

Q KS

( )

D - D

T T



(III.09)

C f

ln

æ D T ö

C

_çç ÷÷

è ^DTf ø

(III.10)

de (III.01) et (III.09) on a la différence moyenne logarithmique de la température :

( )

D - D

T T

C f

æ D T ö

C

_çç ÷÷

è D T f ø

DMLT

ln

Remarque :

Pour d'autres types d'écoulement (croisé, mixte ou autre) on utilise un facteur de correction (F)

inférieur à l'unité qu'on multiplie par le DMLT calculé, ce facteur est généralement donné par des graphes.(voir Annexe-B)

III.2. La méthode de NUT :

NUT : Nombre d'unité de transfert

La méthode de calcul utilisant DMLT est employée quand les températures des fluides aux extrémités du condenseur sont connues, il existe pourtant de nombreux exemples ou les températures des fluides quittent le condenseur ne sont pas connues, dans ces cas il est préférable d'utiliser la méthode de calcul du nombre d'unité de transfert NUT, cette méthode introduit la notion de l'efficacité de l'échangeur.

L'efficacité d'un échangeur de chaleur est définie comme étant le rapport du flux de chaleur réel d'un échangeur donné au flux maximum possible :

L'efficacité du condenseur :

e = (III.11) Qréel Qmax

Q = Qréel = e.Qmax (III.12)

Le flux échangé ou réel : Q_ech = ( m & . Cp ) _air ( T _as - T_ae) (III.13)

Le flux maximal : Q( m Cp ) _air T ( m Cp ) _air ( T _c T _ae )

max = & . D max = & . - (III.14)

Q ech as ae

T T

-

e = = (III.15)

Q T T

C ae

max

-

Q ( m Cp ) ( T T ) K S DMLT

= & . - = . (III.16)

ech air as ae ech

Le nombre d'unité de transfert est donné par :

NUT as ae K S . ech - T T = = ( ) DMLT m Cp & . air

(III.17)

La relation entre l'efficacité å et le NUT :

( )

D - D

T T

C f

æ D T ö

C

_çç ÷÷

è D T f ø

DMLT

ln

(III.18)

D'après la figure III.03 on a : DT_f = T _c -T ae = DTmax (III.19)

et on au aussi: c c as ( C ae ) ( ae as )

D = - = - + -

T T T T T T T(III.20)

= DT _max - e.DT max (III.21)

DT_c = DTmax (1-e) (III.22)

En remplacent l'equation (III.18) dans (III.17) :

( )

T T

- æ D T ö

NUT ln (III.23)

( ) ÷÷

as ae

= c

_çç

D - D

T T _è D T

c f f ø

En remplacent l'équation (III.19) et (III.22) dans l'équation (III.23) nous obtenons :

( ) T as T ae -		ln	æ ç è	D - T ( ) 1 e ö max ÷ D T max ø	(III.24)
( ( ) ) D - - D T T max max 1 e

e . D T e

max 1

æ D -

T ( ) ö

max

ln ç ÷ (III.25)

( ( ) )

D - - D

T T è D

max max

1 e T max ø

e . D T e max 1 æ D - T ( ) ö max ln ç ÷ ( ( ) ) D - - T 1 1 e è D T max max ø

(III.26)

Finalement la relation entre l'éfficacité et le NUT donné par :

NUT = - ln ( 1 - e ) (III.27)

æ KS ö

ç

è Cmin ø

e = 1 - exp( - NUT ) (III.28)

Le NUT est le rapport ÷

NB :Des abaques fournissant l'efficacité à partir de NUT et du rapport (Cmin / Cmax) ont été dressés pour la plupart des configurations d'écoulement (voir Annexe-C)

IV. Choix de la méthode de dimensionnement :

Les deux méthodes aboutissant aux mêmes résultats, cependant la méthode DMLT est utilisée pour le dimensionnement des installations frigorifiques ou les températures d'entrée et de sortie des deux fluides sont connues, c'est donc la méthode qu'on va utiliser dans notre travail.

On a choisi deux types de condenseur : le condenseur a air et le condenseur a eau.

Le Condenseur à air se compose d'un système de tubes à ailettes ou le fluide frigorigène circule dans les tubes tandis que l'air, qui assure la condensation des vapeurs de fluide frigorigène, circule à l'extérieur des tubes.

Les figures (III.02.a) et (III.02.b) donnent une vue agrandie de face et de profil de la disposition des tubes et des ailettes dans le condenseur a air.

Ailette

b



a C dail

tube

(a)- Coupe transversale (b)- Coupe longitudinale

Figure III.02 : Coupes transversale et longitudinale d'un condenseur a air

Le condenseur a eau est de type multitubulaire horizontale ou l'eau de refroidissement circule à l'intérieur des tubes, et le fluide frigorigène a l'extérieur des tubes ailettés voir la figure
(III.03)

di : diamètre intérieur des tubes [m]
d_r : diamètre à la base de l'ailette [m]
d_o : diamètre extérieur des tubes[m]
H : hauteur de l'ailette [m]
Y : épaisseur moyenne de l'ailette [m]
: Épaisseur de la paroi de la section de l'ailette [m] Ax



Figure III.03 : Tubes ailettés du condenseur à eau

IV. 1. Hypothèses de calcul :

Pour le calcul des condenseurs a air on a considéré les hypothèses suivantes :

· Régime de fonctionnement stationnaire.

· Le coefficient global d'échange de chaleur est constant.

· La température d'un fluide est constante dans une section transversale.

· Les débits massiques des deux fluides sont constants.

· Les chaleurs spécifiques des deux fluides sont constantes.

· Les caractéristiques physiques des matériaux sont constantes tout le long du condenseur.

· La perte de charge est négligée, Pression constante dans le condenseur.

· Section de passage est constante.

· Les profils des vitesses sont invariables.

· Les vitesses d'écoulement sont faible (effets de la compressibilité négligeables).

· La condensation est complète dans l'échangeur.

· Le transfert de chaleur entre les deux fluides se fait par :

Ø Convection fluide-paroi (externe) : Coefficient de convection externe h_e[W /m² K] .

Ø Conduction a travers la paroi : Conductivité thermique ë [W /m K].

Ø Condensation fluide-paroi (interne) : Coefficient de condensation interne hi[W /m² K]

IV.2. Le déroulement de calcul du condenseur à air : [ 59]

Données :

> Données géométriques :

ü Diamètre intérieur des tubes : di [m]

ü Diamètre extérieur des tubes : de [m]

ü Pas transversal des tubes: a [m]

ü Pas longitudinal des tubes : b [m]

ü Ecartement des ailettes : C [m]

ü Epaisseur des ailettes : äail [m]

> Données thermo physiques :

ü Type du fluide frigorigène.

ü Puissance thermique du Condenseur : Q_C [W]

ü Température d'entrée de l'aire : Tae [°C]

ü Température de sortie de l'aire : Tas [°C]

ü Température de Condensation du fluide frigorigène : T_c [°C]

ü Nature du matériau des tubes et des ailettes.

ü Conductivité thermique des tubes : at [W /m K]

ü Conductivité thermique des ailettes : ëail [W /m K]

ü La résistance d'encrassement intérieur : Rint [W / K]

ü La résistance d'encrassement extérieur : Rext [W / K]

> Les propriétés physiques de l'air

T +T

Elles sont évaluées à la température moyenne de l'air T_m: T = ae asm2

ü Chaleur spécifique de l'air : Cp [J/kg K]

ü Viscosité dynamique de l'air : g [kg/m s]

V' Conductivité thermique de l'air : ëair [W/m K]

V' Masse volumique de l'air :ñ [kg/m³]

V' Nombre adimensionnel de Prandtl pour l'air : P_r

> Les propriétés physiques du fluide frigorigène

Elles sont évaluées à la température de Condensation du fluide frigorigène T_c :

T c = T_ae + D T_es + D T_p

V' Viscosité dynamique du fluide frigorigène (liquide) : ìf [kg/m s]

V' Conductivité thermique du fluide frigorigène (liquide) : ëf [W/m K] V' Chaleur latente de Condensation du fluide frigorigène : L_v [J/kg] V' Masse volumique du fluide frigorigène (liquide) : r_l [kg/m³]

V' Masse volumique du fluide frigorigène (vapeur) : r_v [kg/m³]

+ Résultats à rechercher :

V' Surface d'échange : Sech [m²]

V' Coefficient global de transfert de chaleur : K [W/m² K] V' Différence moyen de température logarithmique [°C ] V' Coefficient d'échange par condensation hi [W/m² K]

V' Coefficient d'échange par convection h_e [W/m² K] V' L'efficacité du condenseur e

V' Le nombre d'unité de transfert NUT

+ Procédure de calcul du Condenseur a air : > Débit massique de l'air : m & [kg/s]

F _C

m & = (III.29)

Cp T T

( ae as )

-

F C : Puissance thermique du condenseur [W]

Cp : Chaleur spécifique de l'air [J/kg K]

> Débit volumique de l'air :V^& [m³/s]

V & = (III.30)

D_m

r

r : Masse volumique de l'air [kg/m³] > Section frontale : S_fr [m²]



S

V = ^fr V a

(III.31)

V_a: Vitesse de l'air entre 2,5 et 4 [m/s]

> Nombre d'ailettes par mètre de longueur : n [ailettes/m]

C

+d

¹(III.32)

n =

ail

C : Ecartement des ailettes [m]

dail : Epaisseur d'ailettes [m].

> Surface extérieure des tubes par mètre de longueur : S_e [m²/m]

S e = p.d_e (III.33)

d_e: Diamètre extérieur des tubes [m].

> Surface intérieure des tubes par mètre de longueur : S_i [m²/m]

S_i =p. d i (III.34)

d_i : Diamètre intérieur des tubes [m].

> Surface nette des tubes par mètre de longueur : S_net [m²/m]

S net = S_e(1 - ndail) (III.35)

n : Nombre d'ailettes [ailettes].

dail : Epaisseur d'ailettes [m].

Ø Surface d'ailettes par mètre de longueur : S_ail [m²/m]

S n ab p (III.36)

= æ - . ₄ d ² ö

e

2 ç ÷

ail

è ø

a : Pas transversal des tubes [m].

b : Pas longitudinal des tubes [m]. d_e : Diamètre extérieur des tubes [m].

Ø Surface d'échange total des tubes par mètre de longueur : Sto t [m2/m]

Stot = S net+ Sail (III.37)

Ø Surface étroite entre les tubes et les ailettes : S_étr [m²]

æ d æ d ö ö

e ail

ö e

æ - d

- ç ÷+ ç ÷ ç ÷ ú

ù

1 d 1

è a C

ø è + ø è a ø

ail

û

(III.38)

é ê ë

S S

étr fr

=

Sfr : Surface frontale [m²]. Ø Vitesse étroite : V_étr [m/s]



V

(III.39)

V étr S

=

étr

V& : Débit volumétrique de l'air [m³/s]. Sétr : Surface étroite [m²].

Ø Rapport des surfaces : j _a et j_G

S

j = (III.40)

ail

^a S

tot

S

j = (III.41)

net

^G S

tot

Sail : Surface des ailettes [m²] Snet : Surface nette [m²]

Sto t : Surface d'échange total [m²]

Ø Coefficient de convection externe (coté air) : [53] h_e [W/m² K]

h .l

Nu air

= (III.42)

e_d

e

lair : Conductivité thermique de l'air [W/m K]

Nu : Nombre adimensionnel de Nusselt sa formule dépond de la disposition des tubes :

· Disposition en quinconces des tubes :

-3.75

0 .45 Re 0.625 Pr

æ S ö

tot 1 / 3

Nu = ç ÷(III.43)

è Se ø

· Disposition en lignes des tubes :

-3.75

0 . 3 0 Re 0 .625 Pr

æ S ö

tot 1 / 3

Nu = ç ÷(III.44)

è S e ø

Avec :

Pr : Nombre adimensionnel de Prandtl de l'air. Re : Nombre adimensionnel de Reynolds.

Re = (III.45)

Vétr d _er

m

Vétr: Vitesse étroite de l'air [m/s]

d_e : Diamètre extérieur des tubes [m]. r : Masse volumique de l'air [kg/m³].

Les deux formules de (43.III) et (44.III) sont valables dans les intervalles suivants : 2000< Re< 4000

0.5<Pr<500

Ø Coefficients : m [m^-1],y ,j



=

m

(III.46)

2

h_e

l d

ailail

h_e : Coefficient de convection externe (coté air) [W/m² K] lail : Conductivité thermique des ailettes [W/m K]

dail : Épaisseur des ailettes [m]

æ a ö

ç ÷

è d e ø

a ö

çè b 0 . 2 _ø÷

æ -

y 1.28





(III.47)

j = ( y - 1 )( 1 + 0 . 3 5 ln y ) (III.48)

a : Pas transversal des tubes [m]

b : Pas longitudinal des tubes [m] Ø Rendement des ailettes : hail

tanh ( )

mL cents

h (III.49)

ail cents

=

mL

d_e

Lcents : Longueur des rainures [m], avec : L cents = j (III.50)

2

Ø Coefficient apparent de transfert de chaleur (coté air) : h_app [W/m² K]

h app = h _e ( j _G + hj _a ) (III.51)

Ø Coefficient de convection interne (coté frigorigène) [05] : h_i [W/m² K]

h

é ê ë ê

ù ú û ú



1

g L

3 4

r r r l (III.52)

ⁱ T T d

m ( )

f sat p i

-

0 . 5 5 5

( )

l l v f v

-

g : Accélération de la pesanteur, on prend g = 9 . 8 1 [ m / s ²] . r_l : Masse volumique du fluide frigorigène liquide [kg/m³]. r_v : Masse volumique du fluide frigorigène vapeur [kg/m³]. l_f : Conductivité thermique du fluide frigorigène [W/m K].

L_v : Chaleur latente de condensation du fluide frigorigène [J/kg]. T_C : Température de condensation du fluide frigorigène [°C].

d_i : Diamètre intérieur des tubes [m].

T +

T T

m C

= (III.53)

^p 2

Ø Coefficient global de transfert de chaleur : K [W/m² K]



K=

h S

i i

S

t e e i

tot + + + +

tot R ext

S2 pl

i tube app

h

in

R S d d d 1

ln

1

( )

(III.54)

h_i : Coefficient de convection interne (coté frigorigène) [W/m² K] Sto t : Surface d'échange total par mètre de longueur [m²]

S_i : Surface intérieure des tubes par mètre de longueur [m²]

Rint : Résistance d'encrassement a l'intérieur des tubes (coté FF) [W/m² K]. d_e : Diamètre extérieur des tubes [m]

d_i : Diamètre intérieur des tubes [m²]

ltube : Conductivité thermique des tubes [W/m K]

happ : Coefficient apparent de transfert de chaleur (coté air) [W/m² K].

Rext : Résistance d'encrassement a l'extérieur des tubes (coté air) [W/m² K]

d d

e_t : Épaisseur des tubes [m], = (III.55)

e i

e -

^t 2

Ø Différence moyenne logarithmique de température : DMLT [°C]

DMLT

DT _C - D T F

ln

æ D T ö

C

ç ÷

è D T F ø

(III.56)

DT_C : Différance de température chaude D T C = T _C - T _as (°C) DT_F : Différance de température froide D T F = T _C - T _ae (°C) T_C : Température de Condensation du fluide frigorigène (°C) Tas : Température d'air a l'entrée du condenseur (°C)

Tae : Température d'air a la sortie du condenseur (°C)

Ø Surface d'échange total : S_ech [m²]

(III.57)

S C

F

=

. MLT

ech K D

F C : Puissance thermique du condenseur [W]

Ø Surface interne : S_int [m²]

S S

S int = (III.58)

ech i Stot

Sech : Surface d'échange totale [m²]

Sto t : Surface d'échange total des tubes par mètre de longueur [m²/m]. S_i : Surface intérieure des tubes par mètre de longueur [m²/m].

> Longueur total des tubes : Lto t [m]

S

=

(III.59)

L . int

tot d

p _i

d_i : Diamètre intérieur des tubes [m] > Nombre total des tubes : Nto t

L tot

N = (III.60)

tot L

p

Avec :

Z

L g

L

p =

(III.61)

L_g : Longueur parcourue par le fluide frigorigène [m].

L_P : Longueur d'un passage d'un tube entre (1.5 et 4) [m]. Z : Nombre de passage du fluide frigorigène [Passes].

> Nombre de tubes par passage : np[Tubes/Passe]

Z

n tot

N

p =

(III.62)

Et n _p Î N (on prend la partie entière du résultat). > Nombre réel des tubes : N_R [Tubes]

N_R = n _p Z (III.63)

> Longueur total réelle des tubes : L_R [m]

L_R = N_RL_p (III.64)

L_P : Longueur d'un passage d'un tube entre (1.5 et 4) [m].

> Surface intérieure totale réelle des tubes : S_iR [m²]

SiR = LRS i (III.65)

Si: Surface intérieure des tubes par mètre de longueur [m²/m].

S_i = p . d i (III.66)

d_i : Diamètre intérieur des tubes [m].

Ø Nombre d'unité de transfert de chaleur : NUT

K

NUT

.Sech

( )eau

m Cp

& .

(III.67)

K : Coefficient de transfert de chaleur global [W/m²°C]. m& : Débit massique de l'eau [kg/s].

Ø L'éfficacité de condenseur

e =1- exp(- NUT) (III.68)

NUT : Nombre d'Unité de Transfert

V.3. Le déroulement de calcul du condenseur a eau : [ 59]

+ Données :

> Données géométriques :

V' Diamètre intérieur des tubes : di [m]

V' Diamètre extérieur des tubes : d_e [m]

V' Diamètre à la base de l'ailette : D_r [m]

V' Pas transversal des tubes: a [m]

V' Pas longitudinal des tubes : b [m]

V' Ecartement des ailettes : C [m]

V' Epaisseur des ailettes : äail [m]

> Données thermo physiques :

V' Type du fluide frigorigène.

V' Puissance thermique du Condenseur : F_C [W]

V' Température d'entrée de l'eau : Tee [°C]

V' Température de sortie de l'eau : Tes [°C]

V' Température de Condensation du fluide frigorigène : T_c [°C] V' Nature du matériau des tubes et des ailettes.

V' Conductivité thermique des tubes : ët [W/m K]

V' Conductivité thermique des ailettes : ëail [W/m K]

V' La résistance d'encrassement intérieur : Rint [W/ m² K] V' La résistance d'encrassement extérieur : Rext [W/m² K]

> Les propriétés physiques de l'eau

Elles sont évaluées à la température moyenne de l'eau T_m: T +

m = T T

ee es

2

V' Chaleur spécifique de l'eau : Ç [J/kg K]

V' Viscosité dynamique de l'eau : ì [kg/m s]

V' Conductivité thermique de l'eau : ëeau [W/m K]

V' Masse volumique de l'eau :ñ [kg/m³]

V' Nombre adimensionnel de Prandtl pour l'eau : P_r

On prend aussi la viscosité dynamique de l'eau a la température de la paroi Tp > Les propriétés physiques du fluide frigorigène

Elles sont évaluées à la température de condensation du fluide frigorigène T_c :

T c = T_ee + D T_es + D T_p

V' Viscosité dynamique du fluide frigorigène (liquide) : ìf [kg/m s]

V' Conductivité thermique du fluide frigorigène (liquide) : ëf [W/m K] V' Chaleur latente de Condensation du fluide frigorigène : L_v [J/kg] V' Masse volumique du fluide frigorigène (liquide) : r_l [kg/m³]

V' Masse volumique du fluide frigorigène (vapeur) : r_v [kg/m³]

+ Résultats à rechercher :

V' Surface d'échange : Sech [m²]

V' Coefficient global de transfert de chaleur : K [W/m² K] V' Différence moyen de température logarithmique [°C ] V' Coefficient d'échange par condensation h_e [W/m² K]

V' Coefficient d'échange par convection hi [W/m² K] V' L'efficacité du condenseur e

V' Le nombre d'unité de transfert NUT

+ Procédure de calcul du Condenseur a eau : > Débit massique de l'eau : D_m [kg/s]

D

^m Cp T T

( ee es )

-

F _C

(III.69)

F C : Puissance thermique du condenseur [W] Cp : Chaleur spécifique de l'eau [J/kg K]

> Débit volumique de l'eau : D_v [m³/s]

D

D = (III.70)

m

v

r

r : Masse volumique de l'eau [kg/m³]

> Nombre d'ailettes par mètre de longueur : n [ailettes/m]

n =

C +d

¹(III.71)

ail

C : Ecartement des ailettes [m]. dail : Epaisseur d'ailettes [m].

> Surface extérieure des tubes par mètre de longueur : S_e [m²/m]

S e = p.d_e (III.72)

d_e: Diamètre extérieur des tubes [m].

> Surface intérieure des tubes par mètre de longueur : S_i [m²/m]

S_i = p.d _i (III.73)

d_i : Diamètre intérieur des tubes [m].

> Surface nette des tubes par mètre de longueur : S_net [m²/m]

S net = 2p.r₁ (L _tube - n dail) (III.74)

n : Nombre d'ailettes [ailettes].. dail : Epaisseur d'ailettes [m].

Ltube : Langueur du tube [m].

r₁ : Rayon à la base de l'ailette [m].

> Surface d'ailettes par mètre de longueur : S_ail [m²/m]

Sail = 2 n p r ₂ - r

( )

2 2(III.75)

1

r₁ : Rayon à la base de l'ailette [m].

r₂ : Rayon extérieur du tube [m].

> Surface d'échange total des tubes par mètre de longueur : Sto t [m2/m]

S to t = S net+ Sail (III.76)

> Rapport des surfaces : j_a et j_G

S ail

j = (III.77)

^a S

tot

S net

j = = 1 - j (III.78)

^G S a

tot

Sail : Surface des ailettes [m²] Snet : Surface nette [m²]

Stot : Surface d'échange total [m²] > Rendement de la paroih_p :

h_p =j_G +h ailj a (III.79)

> Paramètre de la corrélation de Beatty-Katz [24] : E [m]

E = p r ₂ - r / 2 r

( ) 2

2 ² (III.80)

1

r₁ : Rayon à la base de l'ailette [m].

r₂ : Rayon extérieur du tube [m].

> Diamètre équivalent D_eq [m] :

h p tot

1.

3 0 - + -

h 0 .25 0.25

ail ail net r

S E S D

Deq_S

(III.81)

D_r : Diamètre à la base de l'ailette [m].

D_r = 2.r₁



Ø Coefficient de condensation externe (coté Frigorigène) [24] : h_e [W/m² K]

1

é 3 4

l r r r (III.82)

( )

l l l v v

- gL ù

h = 0 . 6 89

^e T T D

^êê ( ) ^úú

ë

m -
l sat p eq û
l_f : Conductivité thermique du fluide frigorigène [W/m K]

r_l : Masse volumique du fluide frigorigène liquide [kg/m³] r_v : Masse volumique du fluide frigorigène vapeur [kg/m³] g : Accélération de la pesanteur, on prend g = 9.81[m /s²]. L_v : Chaleur latente de condensation [J/kg]

m_l : viscosité dynamique du fluide frigorigène liquide [kg/ms.]

Tsat : Température de saturation, ou de condensation (T sat = T _C ) [°C ]

æ +

T T ö

T_p : Température de la paroi _ø÷

ç_è T [°C ]

= 2

C m

p

Deq : Diamètre équivalent [m]

Ø Coefficients :m [m^-1],y ,j



=

m

(III.83)

2

h_e

l d

ailail

h_e : Coefficient de condensation externe (coté FF) [W/m² K] lail : Conductivité thermique des ailettes [W/m K]

dail : Épaisseur des ailettes [m]

a ö

çè b 0 . 2 _ø÷

æ -



(III.84)

æ a ö

y 1.28

ç ÷

è de ø

j =(y -1)(1+0.35lny) (III.85)

a : Pas transversal des tubes [m]

b : Pas longitudinal des tubes [m]

Ø Rendement des ailettes : hail

tanh ( )

mL

h = (III.86)

ail mL

d_e

L : Longueur des rainures [m], avec : L = j (III.87)

2

Ø Coefficient apparent de transfert de chaleur (coté FF) : h_app [W/m² K]

happ = h_eh_p (III.88)

h_e : Coefficient de condensation externe [W/m² K] h_p : Rendement de la paroi

Ø Coefficient de convection interne (coté eau) : h_i [W/m² K]

o Pour le régime laminaire Re £ 10000 [42]

Nu d _i L tube p

= m m

( ) ( ) 0 . 1 4



1

3

1 . 8 6 Re . Pr . 0 .5 Pr(III.89)

o Pour le régime turbulent Re > 10000 [42]



1

Nu = 0 . 027 Re 0 .8 Pr m m p

3 ( ) 0 . 1 4(III.90)



h_i = Nu ( l _eau di) (III.91)

leau : Conductivité thermique de l'eau [W/m K]. d_i : Diamètre intérieur des tubes[m].

Re : Nombre adimensionnel de Reynolds

Pr : Nombre adimensionnel de Prandtl

m : Viscosité dynamique de l'eau a la température moyenne [kg/m³].

m_p : Viscosité dynamique de l'eau a la température de la paroi [kg/m³].

Ø Coefficient global de transfert de chaleur : K [W/m² K]

1

S R S ( ) ( )

S L D d

ln 1 R

tot tot tot tube r i ext

int + +

K

+ +

(III.92)

p h_p

h S

i i	S 2 pl i tube app h h

Sto t : Surface d'échange total par mètre de longueur [m²]

S_i : Surface intérieure des tubes par mètre de longueur [m²]

h_i : Coefficient de convection interne (coté eau) [W/m² K]

Rint : Résistance d'encrassement a l'intérieur des tubes (coté eau) [m² K/ W]. D_r : Diamètre à la base de l'ailette [m]

d_i : Diamètre intérieur des tubes [m²]

ltube : Conductivité thermique des tubes [W/m K]

happ : Coefficient apparent de transfert de chaleur (coté FF) [W/m² K].

Rext : Résistance d'encrassement a l'extérieur des tubes (coté FF) [m² K/W] Ø Différence moyenne logarithmique de température : DMLT [°C]

DMLT

D T C - DT_F

ln

æ D T ö

C

ç ÷

èDT F ø

(III.93)

DT_C : Différance de température chaude DT C = T C- T_as (°C) DT_F : Différance de température froide DT_F = T _C - T_ae (°C) T_C : Température de Condensation du fluide frigorigène (°C) Tas : Température de l'eau a l'entrée du condenseur (°C)

Tae : Température de l'eau a la sortie du condenseur (°C)

Ø Surface d'échange total : S_ech [m²]

(III.94)

S C

F

=

. MLT

ech K D

F C : Puissance thermique du condenseur [W] Ø Surface interne : S_int [m²]

S S

S int = (III.95)

ech i Stot

Sech : Surface d'échange totale [m²]

Sto t : Surface d'échange total des tubes par mètre de longueur [m²]. S_i : Surface intérieure des tubes par mètre de longueur [m²].

> Longueur total des tubes : Lto t [m]

(III.96)

= Sint

L tot d

p . i

d_i : Diamètre intérieur des tubes [m] > Nombre total de tubes : Nto t

L tot

N = (III.97)

tot_L

tube

Avec :

L g

L

tube = (III.98)

Z

L_g : Longueur parcourue par le fluide frigorigène [m].

Ltube : Longueur d'un passage d'un tube entre (1.5 et 4) [m]. Z : Nombre de passage du fluide frigorigène [Passes].

> Nombre de tubes par passage : np[Tubes/Passe]

Z

n tot

N

p =

(III.99)

Et n _p Î N (on prend la partie entière du résultat). > Nombre réel des tubes : N_R [Tubes]

N_R = n_pZ (III.100)

> Longueur total réelle des tubes : L_R [m]

L_R = NRL tube (III.101)

L_P : Longueur d'un passage d'un tube entre (1.5 et 4) [m]. > Surface intérieure totale réelle des tubes : S_iR [m²]

SiR = L_R S i (III.102)

Si: Surface intérieure des tubes par mètre de longueur [m²/m].

S_i = p . d i (III.103)

d_i : Diamètre intérieur des tubes [m].

> Espacement entre chicanes : B [m].

B = 0.4D_c (III.104)

D_c : Diamètre de la calandre [m].

Ø La clairance des tubes : Ccents [m].

Ccents = a - d_e (III.105)

a : Espacement entre les tubes (le pas) [m]. d_e: Diamètre extérieur des tubes [m].

Ø Surface d'écoulement a travers le faisceau des tubes : S_c [m²]. D C B

. cents .

S

c = (III.106)
c a

Ccents : La clearance des tubes [m].

Ø Nombre de chicanes nchic :

nchic + 1 = L p / B (III.107)

Lp : Langueur du passage du fluide [m]. B : Espacement entre chicanes [m].

Ø Nombre d'unité de transfert de chaleur : NUT

K

NUT

.Sech

( )eau

m Cp

& .

(III.108)

K : Coefficient de transfert de chaleur global [W/m² K]. m& : Débit massique de l'eau [kg/s].

Ø L'efficacité de condenseur : e

e =1- exp(- NUT) (III.109)

NUT : Nombre d'Unité de Transfert

V. Présentation du programme :

Le programme de calcul est constitué d'un programme principal et de deux sous programmes.

V. 1. Le programme principal :

Au premier lancement du programme, un menu est affiché à l'écran :

Type de condenseur

1- Condenseur à air

2- Condenseur à eau

3- Quitter le programme

Pour avoir le dimensionnement d'un type de condenseur il suffit de taper son numéro (1 ou 2), et pour quitter le programme il faut taper : (3)

Quand l'utilisateur choisit un type de condenseur, le programme principal fait appel au sous programme qui le concerne.

Après que le sous programme ait fini sont travail, le programme principal réaffiche le menu du départ, l'utilisateur à la possibilité de faire un autre choix parmi les types de condenseurs proposés. Le menu ci-dessus est donc affiché après chaque résultat d'un dimensionnement, jusqu'à ce que l'utilisateur décide de quitter le programme.

V.2. Les sous programment :
Les deux sous programme sont :

1- Condenseur à air: il concerne le dimensionnement du condenseur refroidi à air

2- Condenseur à eau : il concerne le dimensionnement du condenseur refroidi à eau.

Quand l'un de ces sous programmes est appelé, il demande à l'utilisateur de faire entrer les données géométrique et physiques indiquées pour le condenseur concerné.

Après avoir entré toutes les données, le sous programme va faire tous les calculs et ensuite il va présenter les résultats sous forme d'un tableau.

VI. Les organigrammes :



Début

C : Integer

Oui

C=1

Non

Oui

C=2

Non

Oui

C=3

Non

Fin

«Erreur dans le choix»
La valeur doit être
comprise entre 1 et 3

Choix d'un numéro
du menu
« Valeur de C »

Affichage du menu
principal

Appel du sous-programme:
« Condenseur à air »

Appel du sous-programme:
« Condenseur à eau »

Quitter le programme

VI. 1. L'organigramme du programme principal :



0.30 Re

Nu

0.45Re

Nu

Calcul de: D_m, D_v, _Sfr, n, S_e, Si,

Snet, Sail, Stot, Re

Choix : Tubes en ligne
ou Tubes en quinconce

Disp = 1
En ligne

Oui

« Erreur dans le choix »
La valeur doit être comprise
entre 1 et 2

Non

Oui

Disp=2 En
Quinconce

90

Oui

A

-

0.625 Pr

æ S ö

tot

ç ÷

3 . 7 5

1/3

è S e ø

-

0. 625 Pr

æ S ö

tot

ç ÷

3 .7 5

1/3

èSe ø

Début

L'entrée des propriétés physiques du
FF à la température de condensation

L'entrée des propriétés physiques
de l'air à la température moyenne

L'entrée de la
vitesse de l'air

Calcul de la Température
moyenne de l'air

Affichage de la température
moyenne de l'air

L'entrée des données
géométriques et thermo
physiques

Déclaration des
variables

VI.2. L'organigramme du sous programme « condenseur à air » :

Calcul de : he, happ



A

Calcul de: hi, K, DMLT, Sech, Sint,
Ltot

L'entrée des valeurs de
Lp etZ



Affichage des résultats:
Sech, DMLT, n, _çail, hi,he, K, Nr,
Lr, NUT, EFF

Calcul de : Ntub, _çail, Nr, Lr, NUT,
EFF

Calcul de : D_m, n, S_e, Si, Snet, Sail, Stot,

Re





L'entrée des données géométriques et thermo physiques

Calcul de la Température
moyenne de l'eau

Affichage de la température
moyenne de l'eau

L'entrée des propriétés physiques de l'eau à la température moyenne

L'entrée des propriétés physiques du
FF à la température de condensation

L'entrée de:
V_e et Lp





Oui

Non

L'entrée de la longueur de tube
Lp

Re>10000

92

B

Nu d _i L tube p

= m m

( ) ( ) 0 . 1 4

1

3

1 . 86 Re . Pr . 0 .5 Pr

( ) ( ) 0 . 1 4

1

Nu = 0 . 027 Re 0. 8 Pr m m p

3



B

Calcul de : hi, E



L'entrée de la valeur : Z

Non

Erreur

Abs (Etta0-Etta)> 0.01

Oui

Calcul de : Etta0, Etta, Deq, he, m, psi, phi, L

Affichage des résultats:
Sech, DMLT, n, _çail, he, hi, K, N_r,
L_r, NUT, Eff

Calcul de : Ntub, çail, N_r, L_r, NUT, Eff

I-Introduction :

Il existe deux méthodes permettant d'analyser l'efficacité de fonctionnement des installations thermiques : la méthode entropique et la méthode exérgétique.

La méthode entropique permet de calculer le degré de perfection thermodynamique d'un organe est évaluer par comparaison des pertes de capacité de travail dans cet organe avec la capacité de travail de tout le système.

Par contre la méthode éxergétique permet d'analyser le degré de perfection thermodynamique de tel ou tel organe de l'installation sans avoir apprécier la capacité de travail de l'ensemble de l'installation et les pertes de capacité de travail dans tous ces organes ce qui simplifier dans une certaine mesure les calculs relatifs aux pertes de capacité de travail.

Donc on a recours à la méthode exérgétique pour l'étude de l'efficacité thermodynamique du condenseur.

II- Description de la méthode exérgétique : [60]

Chaque organe de l'installation peut être considéré comme un système thermodynamique autonome (bien entendu, ce système n'est pas isolé puisque cet organe (condenseur) est parcouru par le fluide frigorigène et échangé de chaleur avec les autres parties de l'installation).

L'efficacité de chaque organe de l'installation peut être appréciée en comparant la capacité de travail que possède le fluide frigorigène ou la chaleur à l'entrée de cet appareil (condenseur) avec les pertes de capacités de travail occasionnées par l'irréversibilité des transformations qui ont lieu dans cet organe.

Quant à la capacité de travail elle-même est bien entendu, évalué par rapport au milieu extérieur (l'air ou l'eau) caractérisé par les paramètres (T₀ ) et (i₀ ).

L'avantage principal de la méthode réside dans le fait qu'elle permet d'analyser le degré de perfections thermodynamique de tel ou tel organe de l'installation dans notre cas c'est le condenseur sans avoir apprécier la capacité de travail de l'ensemble de l'installation et les pertes de capacité de travail dans tous ces organes, ce qui simplifier dans une certaine mesure les calcules relatifs aux pertes de capacité de travail.

Considérons un condenseur comme un système non isolé constitué d'une source de travail
représenté par le fluide frigorigène en écoulement sous la pression (i₁ ) et la température (T₁) et un

milieu extérieur (air ou eau) de paramètre (i₀ ) et (T₀ ), cette source de travail peut être amené

réversiblement à un état d'équilibre avec le milieu extérieur, par exemple ont fait subir à la source
de travail (le fluide frigorigène) une transformation adiabatique réversible qui amène sa température
de (T₁) a (T₀ ) et sa pression de (P₁) a (P_a ) ; ensuite on réalise une transformation isotherme

réversible au cours de laquelle la pression de la source de travail atteint la valeur (P₀ ) grâce à un échange de chaleur avec le milieu extérieur voir la Figure IV.01



T(°C)



1 (P₁=cte)

T₁

a (P_a =cte)

T₀

S₀ S₁ S(kJ/kg)

0

(P 0 = cte)

Figure IV.01 : Les transformations subies à la source du travail

Toute autre transformation entre les états (0) et (1) serait irréversible. En effet dans n'importe quelle transformation initiale (T₁) de la source de travail est différente de la température (T₀ ) du milieu extérieur, ce transfert serait irréversible.

· Le travail produit par le fluide en écoulement dans une transformation adiabatique réversible (1- a) est donné par la relation :

L 1 - a = i ₁ - i [kJ/kg]

rev (IV.01)

a

· Le travail produit par le fluide en écoulement dans une transformation isotherme réversible (a - 0) est donné par la relation :

L a i i q [kJ/kg]

rev - 0 = ( _a - ₀ ) + a - 0(IV.02)

Avec :

qa-0 = T ₀ ( S ₀ - S_a) [kJ/kg] (IV.03)

Et : S_a = S₁

qa - ₀: La chaleur empruntée à la source de travail (au courant fluide) [kJ/kg]

rev

Donc : L ₀ ( i _a i ₀ ) T ₀ ( S ₀ S ₁ )

a - = - + - [kJ/kg] (IV.04)

· Le travail produit par le fluide en mouvement lorsqu'il passe réversiblement de l'état (1) à l'état (0) est égale à la somme des travaux effectués dans les transformations réversibles

(1-a) et (a-0) :

L 1 rev - 0 = L 1 - + L - 0 [kJ/kg] (IV.05)

rev rev

a a

On a donc : 1 ( 1 ) ( 0 ) 0 ( 0 1 )

L i i a i _a i T S S

rev - = - + - + - [kJ/kg] (IV.06)

a

₁ Lrev ( i ₁ i ₀ ) T ₀ ( S ₀ S ₁ )

- a = - + - [kJ/kg] (IV.07)

Puisque le travail produit dans une transformation réversible de la source de travail constitue le

travail utile maximal (la capacité de travail) du fluide moteur en mouvement on peut écrire :

Lutile max= i - i + T S - S [kJ/kg] (IV.08)

( 1 0 ) 0 ( 0 1 )

La valeur de la capacité de travail spécifique du fluide en écoulement à reçut le nom d'exérgie. L'exérgie est désigné par e :

e = (i - i₀)+ T ₀ (S₀ - S) [kJ/kg] (IV.09)

De cette équation il résulte que l'exérgie d'un fluide en écoulement est déterminée de façon
univoque par la valeur des paramètres (P)et (T) de ce fluide et des paramètres (P₀ )et (T₀) du

milieu extérieur.

La notion d'exérgie s'avère bien commode lorsqu'on veut analyser le degré de perfection thermodynamique d'un appareil thermique tel que le condenseur.

Si la transformation qui à lieu à l'intérieur de l'appareil (condenseur) est irréversible, cela
signifie que cet appareil (condenseur) fait subir au fluide en écoulement une perte de capacité de

travail (DL) :

DL = (e₁ - e₂) [kJ/kg] (IV.10)

e₁ : L'exérgie du fluide à l'entrée du condenseur. [kJ/kg]

e₂ : L'exérgie du fluide à la sortie du condenseur. [kJ/kg]

Cette différence d'exérgie (e₁ - e₂) est dépensée due aux pertes d'irréversibilités.

Si les transformations réaliser dans cet appareil (condenseur) étaient réversibles, les pertes de
capacité de travail seraient nulles (DL = 0) c'est-à-dire e₁ = e₂ (pas de perte de capacité de

travail).

Insistons sur le fait que cette méthode éxergétique permet de juger le degré de réversibilité des
transformations qui se déroulent à l'intérieur de l'appareil (condenseur) d'après un critère

externe qui est la différence d'exérgie à l'entrée et la sortie du condenseur donc la quantité
(DL) comporte les pertes de capacité de travail due aussi bien au frottement qu'à l'échange de

chaleur pour une différence de température fini ; la quantité (DL) tien aussi compte de la perte

de chaleur .

Pour calculer le degré de perfection thermodynamique d'un appareil thermique tel que le condenseur on utilise la notion de rendement éxergétique que l'on définit par :

e ent

h = (IV.11)

ex

e sort

Le rendement exérgétique donne la mesure de l'irréversibilité des transformations qui ont lieu à l'intérieur de l'appareil (condenseur).

Si ces transformations étaient réversibles donc pas de perte de capacité de travail (e₁ = e₂) et ca

nous donne le rendement exérgétique égale à l'unité(h_ex = 1)

III-Exemple d'application au condenseur à air :

Ø Milieu extérieur (l'air) :

T +

T T

as

ae

2

=

m

T ₀ =T _m =22.5[°C]=295.15[K]

En prend la valeur de l'entropie (S₀) et l'enthalpie (i₀) de l'air à cette température a partir des tables thermodynamique de l'air :

S 7 . 03 10 ² [ kJ / kg . K]

-

=

0

i₀ = 22.637[kJ/kg]

Ø Source de travail (FF : R134a) :

o A l'entrée du condenseur :

À l'entrée du condenseur en à la vapeur saturée du fluide frigorigène a la température de saturation T_c , donc on prend à partir des tables thermodynamique du FF (R1 34a) la valeur

de l'entropie (Sen t ) et l'enthalpie (ien t ) a cette température à l'état de saturation vapeur :

T c = 30[°C]= 303 .15[K]

Sent = 1.709[kJ/kg.K]

ient = 413.47[kJ/kg]

e ( i i ) T ( S S ) [ kJ kg]

ent ent ent

= - ₀ + 0 0 - = - 92 . 83 /

o A la sortie du condenseur :

À la sortie du condenseur en à du liquide saturée du fluide frigorigène a la température de
saturation T_c , donc on prend à partir des tables thermodynamique du FF (R1 34a) la valeur

de l'entropie ( _Ssort ) et l'enthalpie (isort ) a cette température à l'état de saturation liquide :

T_c = 30[°C] = 303.15[K]

Ssort = 1.142[kJ/kg.K]

isort = 241.46[kJ/kg]

e ( i i ) T ( S S ) [ kJ kg]

sort sort sort

= - ₀ + 0 0 - = - 97 .49 /

v La perte de capacité de travail dans le condenseur est :

DL = (eent -esort) = 4.65[kJ/kg]

v Le rendement éxergétique du condenseur est :

= 0.952 hex eent

e sort

I. Introduction :

Dans ce chapitre, on présente les résultats de calcul sous formes graphiques ainsi que les commentaires et analyse nécessaires.

on a étudié l'influence de la température d'entrée des fluides de refroidissement, l'influence de l'échauffement des fluides de refroidissement, l'influence du pincement et la température de condensation ainsi que l'influence de la vitesse du fluide de refroidissement sur la surface d'échange, coefficient d'échange global et local, l'efficacité du condenseur et sur le rendement éxergétique, en utilisent quatre fluides frigorigènes différents (R22, R1 34a, R404A, R407A) et deux types de fluide de refroidissement (air et l'eau) ce qui nous permet de faire une comparaison entre ces fluides.

II. Courbes et discussions



136

134

R22 R134a R404A R407A

132

130

128

126

124

20 22 24 26 28 30 32 34 36

Température de l'air à l'entrée Tae(°C)

Figure V.01 : Surface d'échange en fonction de la température d'entrée de l'air



10.4



R22 R134a R404A R407A

10.2

10.0

9.8

9.6

9.4

9.2

20 22 24 26 28 30 32 34 36

Température de l'eau à l'entrée du condenseur Tee(°C)

Figure V.02 : Surface d'échange en fonction de la température d'entrée de l'eau



56

55

54

53

52

51

R22 R134a R404A R407A

20 22 24 26 28 30 32 34 36

Température de l'air à l'entrée Tae(°C)

Figure V.03 : Coefficient d'échange global en fonction de la température d'entrée de l'air



755

750

745

740

735

730

725

720

715

710

705

700

695

R22 R134a R404A R407A

690

685

680

675

670

665

20 22 24 26 28 30 32 34 36

Température de l'eau à l'entrée du condenseur Tee (°C)

Figure V.04 : Coefficient d'échange global en fonction de la température d'entrée de l'eau



2050

2000

1950

R22 R134a R404A R407A

1900

1850

1800

1750

1700

1650

1600

1550

1500

1450

1400

1350

1300

20 22 24 26 28 30 32 34 36

Température de l'air à l'entrée Tae(°C)

Figure V.05 : Coefficient de condensation en fonction de la température d'entrée de l'air



2600

2550

2500

2450

2400

2350

2300

2250

2200

2150

2100

2050

2000

1950

R22

R1 34a
R404A
R407A

1900

1850

1800

1750

1700

1650

20 22 24 26 28 30 32 34 36

Température de l'eau à lentrée du condenseur Tee(°C)

Figure V.06 : Coefficient de condensation en fonction de la température d'entrée de l'eau

Description des courbes : (V.01), (V.02), (V.03), (V.04), (V.05) et (V.06)

Ces figures représentent l'influence de la température d'entrée du fluide de refroidissement (l'air ou l'eau) sur la surface d'échange, coefficient d'échange global, coefficient d'échange par condensation, en utilisant quatre fluides frigorigènes différents (R22, R134a, R404A et R407A)

Analyse des courbes : (V.01), (V.02), (V.03), (V.04), (V.05) et (V.06)

Pour la première figure (V.01), ont voit que de la surface d'échange varie proportionnellement avec la température d'entrée de l'air, c'est-à-dire qu'elle augmente avec l'augmentation de cette température, par contre dans la deuxième figure (V.02), la surface diminue en augmentant la température d'entrée de l'eau.

Cette différence entre les deux allures est due à la variation inverse des propriétés physiques
telles que la viscosité dynamique (m) et la conductivité thermique (l) des fluides de refroidissement

en fonction de la température d'entrée ( T_ea Þ m ,l) par contre(T_ee Þ m , l )

On remarque aussi que l'utilisation des fluides frigorigènes (R22, R134a, et R407A) donne des surfaces moins encombrantes, surtout (R22 et R1 34a), qu'ils ont presque la même courbe grâce aux propriétés physiques qui sont très proches l'une de l'autre. Contrairement au R404A qui donne une grande surface, due à ces propriétés physiques faibles.

En examinant les figures (V.03) et (V.04), on remarque que le coefficient d'échange global du condenseur à air varie inversement au coefficient global du condenseur à eau, due aux propriétés physiques de l'air (la viscosité dynamique(m) et la conductivité thermique(l)) qui varient

inversement à celles de l'eau en fonction de la température d'entrée.

On remarque aussi que l'ordre de grandeur du coefficient d'échange global du condenseur à air est
très faible par rapport au coefficient du condenseur à eau(Kair » 7.45%K_eau), due essentiellement

à la mauvaise qualité de l'air utilisé comme un fluide de refroidissement par rapport à l'eau L'utilisation de différents fluide frigorigènes (R22, R134a, R404A et R407A) donne des résultats

différents ( K R K R a K R A K R A )

22 » 134 > 407 > 404 , surtout avec le R404A qui donne un mauvais coefficient d'échange global, due à ces faibles propriétés physiques par rapport au (R22, R134a, et R407A).

En ce qui concerne les figures (V.05) et (V.06), on voit que les coefficients d'échange par
condensation sont inversement proportionnels à la température d'entrée du fluide de refroidissement

pour les deux types de condenseur donc l'augmentation de cette température donne une augmentation de la température de condensation, et par conséquent une diminution du coefficient d'échange par condensation.

Il est clair aussi que la qualité du fluide de refroidissement n'a aucune influence sur le coefficient d'échange par condensation.

On voit aussi que l'ordre de grandeur du coefficient d'échange par condensation à l'extérieur des
tubes et un peu plus grand que celui de l'intérieur (h i = 77%h_e )due à l'utilisation des corrélations

différentes celle de CHATO [46] pour la condensation intérieur et celle de BEATTY et KATZ [66] pour l'extérieur.

Remarque générale :

( ) Þ ( ) ( ) ( )

T S S et K K et h

fr entrée air eau air eau condensati on

. , ,



160

R22 R134a R404A R407A

150

140

130

120

110

100

90

80

0 2 4 6 8 10 12 14 16

L'échauffement de l'air DTes(°C)

Figure V.07 : Surface d'échange en fonction de l'échauffement de l'air

6

0 2 4 6 8 10 12 14 16



13

12

11

10

9

8

7



R22

R1 34a
R404A
R407A

L'échauffement de l'eau DTes (°C)

Figure V.08: Surface d'échange en fonction de l'échauffement de l'eau



R22 R134a R404A R407A

55.5

55.0

54.5

54.0

53.5

53.0

52.5

52.0

51.5

51.0

50.5

50.0

49.5

0 2 4 6 8 10 12 14 16

56.5

56.0

L'échauffement de l'air DTes(°C)

Figure V.09 : Coefficient d'échange global en fonction de l'échauffement de l'air



R22 R134a R404A R407A

730

720

710

700

690

680

670

660

650

640

630

620

2 4 6 8 10 12 14 16

750

740

L'échauffement de l'eau DTes (°C)

Figure V.10 : Coefficient d'échange global en fonction de l'échauffement de l'eau



R22 R134a R404A R407A

2200

2100

2000

1900

1800

1700

1600

1500

1400

1300

1200

1100

0 2 4 6 8 10 12 14 16

L'échauffement de l'air DTes(°C)

Figure V.11: Coefficient d'échange par condensation en fonction de l'échauffement de l'air



R22 R134a R404A R407A

2600

2500

2400

2300

2200

2100

2000

1900

1800

1700

1600

1500

1400

0 2 4 6 8 10 12 14 16

2800

2700

L'échauffement de l'eau DTes (°C)

Figure V.12 : Coefficient d'échange par condensation en fonction de l'échauffement de l'eau

Description des courbes : (V.07), (V.08), (V.09), (V.10), (V.1 1) et (V.12)

Ces figures représentent l'influence de l'échauffement du fluide de refroidissement (l'air ou l'eau) sur la surface d'échange, coefficient d'échange global, coefficient d'échange par condensation, en utilisant les mêmes fluides frigorigènes précédents (R22, R1 34a, R404A et R407A)

Analyse des courbes : (V.07), (V.08), (V.09), (V.10), (V.11) et (V.12)

On remarque dans les figures (V.07) et (V.08), que la surface d'échange est inversement proportionnelle à l'échauffement du fluide de refroidissement pour les deux types de condenseur. L'augmentation de l'échauffement donne une augmentation de la différence moyenne de température logarithmique DMLT, et par conséquent une diminution de la surface d'échange.

On voit aussi que l'utilisation de R22 ou R134a ou bien R407A donne des surfaces proches et compactes grâces à leurs propriétés physiques qui sont élevés. Contrairement au R404A qui à des propriétés physiques faibles.

Les figures (V.09) et (V.10) montre la même influence de l'échauffement sur les coefficients d'échange global des deux condenseurs. L'augmentation de l'échauffement donne une augmentation de la température de condensation et par conséquent la diminution du coefficient d'échange par condensation, donc la diminution du coefficient global.

On remarque aussi que l'utilisation du R22 ou R134a ou bien R407A donne des résultats proches et bonnes surtout le R22 et R1 34a, par contre le R404A donne un mauvais coefficient, due a ces propriétés physiques qui sont faibles comparés a celles de R22 et R1 34a.

Il est clair aussi que l'ordre de grandeur du coefficient d'échange global de l'air est très faible par rapport au coefficient du condenseur à eau, due à la mauvaise qualité du transfert de l'air comparer à celle de l'eau.

En Examinant les figures (V.11) et (V.12), on remarque que le coefficient d'échange par condensation est inversement proportionnel à l'échauffement du fluide de refroidissement, l'augmentation de l'échauffement donne une augmentation de la température de condensation, et par conséquent la diminution du coefficient d'échange par condensation.

L'utilisation du R22 ou R134a ou bien R407A donne des coefficients d'échange par condensation élevés par rapport au R404A, due à leurs propriétés physiques élevés.

) ( )

, K et h

eau condensati on

Remarque générale : ( D ) Þ ( ) (

T S S et K

es air eau air

,



R22 R134a R404A R407A

220

200

180

160

140

120

100

80

60

40

2 4 6 8 10 12 14 16

240

Pincement du condenseur DTp(°C)

Figure V.13 : Surface d'échange du condenseur à air en fonction du pincement

0 2 4 6 8 10 12 14 16



18

16

14

12

10

4

8

6

R22 R134a R404A R407A

Pincement du condenseur DTp (°C)

Figure V.14 : Surface d'échange du condenseur à eau en fonction du pincement



R22

R1 34a
R404A
R407A

56

55

54

53

52

51

50

49

0 2 4 6 8 10 12 14 16

57

Pincement du condenseur DTp(°C)

Figure V.15 : Coefficient d'échange global en fonction du pincement

600



580

0 2 4 6 8 10 12 14 16



780

760

740

720

700

680

660

640

620



R22 R134a R404A R407A

Pincement du condenseur DTp (°C)

Figure V.16 : Coefficient d'échange global en fonction du pincement



R22

R1 34a
R404A
R407A

2400

2200

2000

1800

1600

1400

1200

1000

0 2 4 6 8 10 12 14 16

Pincement du condenseur DTp(°C)

Figure V.18 : Coefficient d'échange par condensation en fonction du pincement



3000

R22 R134a R404A R407A

2800

2600

2400

2200

2000

1800

1600

1400

0 2 4 6 8 10 12 14 16

Pincement du condenseur DTp(°C)

Figure V.19 : Coefficient d'échange par condensation en fonction du pincement

Description des courbes : (V.13), (V.14), (V.15), (V.16), (V.17) et (V.18)

Ces figures représentent l'influence du pincement sur la surface d'échange, coefficient d'échange global, coefficient d'échange par condensation en utilisant quatre fluides frigorigènes différents (R22, R1 34a, R404A et R407A)

Analyse des courbes : (V.13), (V.14), (V.15), (V.16), (V.17) et (V.18)

On remarque que ces courbes sont identiques à celles représentées dans les figures (V.07), (V.08), (V.09), (V.10), (V.11) et (V.12), donc l'influence du pincement est identique à celle de l'échauffement. En réalité, il ya une différence quand va la voir dans l'analyse des figures ci dessous.

Remarque générale :

( D ) Þ ( ) ( ) ( )

T S S et K K et h

p air eau air eau condensati on

, ,



F(Tae) F(DTp) F(DTes)

220

200

180

160

140

120

100

80

60

40

30 32 34 36 38 40 42 44 46

240

18



Température de condensation Tc(°C)

Figure V.19: Surface d'échange en fonction de la température de condensation

F(Tee) F(DTp) F(DTes)

16

4





14

12

10

8

6





30 32 34 36 38 40 42 44 46

Température de condensation Tc(°C)

Figure V.20: Surface d'échange en fonction de la température de condensation



F(Tae) F(DTp) F(DTes)

57

56

55

54

53

52

30 32 34 36 38 40 42 44 46

Température de condensation Tc(°C)

Figure V.21 : Coefficient d'échange global en fonction de Tc



F(Tee) F(DTp) F(DTes)

780

760

740

720

700

680

660

30 32 34 36 38 40 42 44 46

Température de condensation Tc(°C) Figure V.22 : Coefficient d'échange global en fonction de Tc



F(Tae) F(DTp) F(DTes)

2250

2200

2150

2100

2050

2000

1950

1900

1850

1800

1750

1700

1650

1600

1550

1500

1450

1400

30 32 34 36 38 40 42 44 46

2350

2300



2800

2600

2400

2200

2000

1800

Température de condensation Tc(°C)

Figure V.23: Coefficient d'échange par condensation du R22 en fonction de Tc

F(Tee) F(DTp) F(DTes)



3000



30 32 34 36 38 40 42 44 46

Température de condensation Tc(°C)

Figure V.24 : Coefficient d'échange par condensation du R22 en fonction de Tc

Description des courbes : (V.19), (V.20), (V.21), (V.22), (V.23) et (V.24)

Une comparaison des résultats précédents est représentée dans ces figures pour voir la différence entre l'influence de la température d'entrée du fluide de refroidissement, l'échauffement et le pincement, en utilisant un seul fluide frigorigène R22

Analyse des courbes : (V.19), (V.20), (V.21), (V.22), (V.23) et (V.24)

Il est clair dans les figures (V.19) et (V.20) que l'influence du pincement sur la surface d'échange est la plus importante, car elle à une pente descendante importante, grâce à la grande influence du pincement sur DTML et par conséquent sur la surface, puis l'influence de l'échauffement qui à aussi une pente descendante, par contre l'influence de la température d'entrée du fluide de refroidissement à une légère pente montante

On remarque aussi dans les figures (V.21) et (V.22), que l'influence du pincement sur le coefficient d'échange est la plus importante, car elle à une pente descendante importante, grâce à la grande influence du pincement sur DTML et par conséquent sur le coefficient d'échange global, puis l'influence de l'échauffement qui à aussi une pente descendante, par contre l'influence de la température d'entrée du fluide de refroidissement sur les coefficients d'échange global des deux condenseurs est différente, c'est-à-dire qu'elle a une pente descendante pour l'air, et montante pour l'eau, due à leurs propriétés physiques (viscosité dynamique (m) et conductivité thermique (l)) qui

changent inversement en fonction de la température d'entrée du fluide de refroidissement.

D'après les figures (V.23) et (V.24), on remarque que l'augmentation de la température d'entrée du fluide de refroidissement ou de l'échauffement ou bien du pincement donne une augmentation de la température de condensation et par conséquent une diminution du coefficient d'échange par condensation, mais cette diminution est différente d'une courbe à une autre, on voit que la courbe du pincement a une pente importante, donc il a la grande influence par rapport à l'échauffement et la température d'entré du fluide de refroidissement.

La différence entre les courbes est due à la variation des valeurs de température de la paroi Tp.



F(Tae) F(DTp) F(DTes)

75.2

75.1

75.0

74.9

74.8

74.7

74.6

74.5

74.4

30 32 34 36 38 40 42 44 46

Température de condensation Tc(°C)

Figure V.25 : Coefficient d'échange par convection en fonction de Tc

7800



5800

30 32 34 36 38 40 42 44 46



7600

7400

7200

7000

6800

6600

6400

6200

6000

F(Tee) F(DTp) F(DTes)

Température de condensation Tc (°C)

Figure V.26 : Coefficient d'échange par convection en fonction de Tc



18



F(Tee) F(DTp) F(DTes)

16

14

12

10

4

8

6



2

30 32 34 36 38 40 42 44 46

Température de condensation T_C(°C)

Figure V.27 : DTML en fonction de la température de condensation



F(Tee) F(DTp) F(DTes)

1.5

1.0

0.5

0.0

-0.5

30 32 34 36 38 40 42 44 46

Température de condensation Tc (°C) Figure V.28 : L'efficacité du condenseur en fonction de Tc



F(Tee) F(DTp) F(DTes)

0.98

0.97

0.96

0.95

0.94

0.93

0.92

0.91

0.90

30 32 34 36 38 40 42 44 46

Température de condensation Tc(°C)

Figure V.29 : Rendement éxergétique du R22 en fonction de Tc



0.97

R22 R134a R404A R407A

0.96

0.95

0.94

0.93

0.92

0.91

0.90

30 32 34 36 38 40 42 44 46

Température de condensation T_C (°C)

Figure V.30 : Rendement éxergétique en fonction de Tc

Description des courbes : (V.25), (V.26), (V.27), (V.28), (V.29) et (V.30)

Ces figures représentent aussi une comparaison entre l'influence de la température d'entrée du fluide de refroidissement, l'échauffement et le pincement sur le coefficient d'échange par convection, la différence de température moyenne logarithmique DTML, l'efficacité et le rendement exérgétique du condenseur.

Analyse des courbes : (V.25), (V.26), (V.27), (V.28), (V.29) et (V.30)

On remarque dans les figures (V.25) et (V.26) que les coefficients d'échange par convection sont proportionnels au pincement l'influence de la température d'entrée du fluide de refroidissement, l'échauffement et le pincement sur les coefficients d'échange par convection du condenseur à air et à du condenseur eau sont totalement différents, et le pincement n'a pas une influence

On voit dans la figure (V.27) que l'augmentation du pincement a une grande influence sur la diminution de la différence d'écart moyenne logarithmique DTML, ainsi que l'augmentation de l'échauffement donne aussi une diminution de la DTML. Par contre la température d'entrée du fluide de refroidissement n'a aucune influence sur la DTML.

Dans la figure (V.28) on remarque que l'augmentation du pincement donne une mauvaise efficacité du condenseur, contrairement à l'augmentation de l'échauffement qui donne une bonne efficacité. Il est clair aussi que la température d'entré du fluide de refroidissement n'a aucune influence sur l'efficacité du condenseur

On remarque dans la figure (V.29) que l'augmentation du pincement ou l'échauffement donne un mauvais rendement éxergétique par contre l'augmentation de la température du fluide de refroidissement à l'entrée donne un bon rendement éxergétique

A partir de la courbe (V.30), on remarque que le rendement exégétique est inversement proportionnelles à la température de condensation c'est-à-dire lorsque la température de condensation augmente le rendement éxergétique diminue et ça due à l'augmentation de capacité de travail en fonction de TC et par conséquent l'augmentation des irréversibilités.

On voit aussi que les rendements exérgétiques des deux fluides R22 R134a ont presque la même courbe, et ça due aux propriétés physiques des deux fluides qui sont très proche l'une de l'autre. On remarque aussi que le R404A donne un meilleur rendement exérgétique, et ça due aux faibles pertes de capacités de travail qui dépond des propriétés physiques surtout l'enthalpie de la vapeur.

Remarque : Le point d'intersection entre les trois courbes représente la température d'entrée du
fluide de refroidissement(T _fr ) entrée = 25 ° C , l'échauffement D T_es = 5 ° C et le pincement

DT p = 5°C et une température de condensationT C = 35°C.

En amont de ce point, on voie que la température de la paroi en fonction du pincement est la plus grande, et celle de la température d'entrée du fluide de refroidissement est la plus faible

{ ( ) ( ) ( )

T T T

P pincement P échauffeme nt P températur e entrée }

> > . . Par contre en aval c'est l'inverse

.



13.0

12.5

R22 R134a R404A R407A

12.0

11.5

11.0

10.5

10.0

9.5

9.0

0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6

Vitesse de l'eau Ve (m/s)

Figure V.31: Surface d'échange en fonction de la vitesse de l'eau



740

720

700

680

R22 R134a R404A R407A

660

640

620

600

580

560

540

0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6

Vitesse de l'eau Ve (m/s)

Figure V.32 : Coefficient d'échange global en fonction de la vitesse de l'eau

Description des courbes : (V.31) et (V.32)

Ces figures représentent l'influence de la vitesse du fluide de refroidissement (l'air ou l'eau) sur la surface d'échange, coefficient d'échange global, en utilisant quatre fluides frigorigènes différents (R22, R1 34a, R404A et R407A)

Analyse des courbes : (V.31) et (V.32)

On remarque dans les figures (V.31) et (V.32) que l'augmentation de la vitesse du fluide de refroidissement améliore l'échange et donne un bon coefficient d'échange global et par conséquent une surface d'échange compacte

On réalité, l'augmentation de la vitesse du fluide de refroidissement augmente la turbulence donc l'augmentation de l'intensité du transfert par convection par conséquent l'augmentation du coefficient d'échange global qui nous donne une surface plus compacte

Remarque :

L'influence de la vitesse de l'air sur la surface d'échange et sur le coefficient d'échange global est identique à celle de l'eau c'est pour cela qu'on a représenté que les résultats du condenseur à eau.

CONCLUSION GENERALE

Les condenseurs sont d'une importance primordiale dans le domaine industriel notamment les installations frigorifiques. Leurs technologies, leurs conceptions, et leurs développements influent directement sur les performances de ces installations.

L'objectif de ce travail est de faire une analyse paramétrique et thermodynamique à deux types de condenseur à air et à eau, et voir l'influence de ces paramètres (vitesse et température d'entrée du fluide de refroidissement, l'échauffement, pincement, température de condensation, ... etc) sur la surface d'échange, le coefficient d'échange local et global, l'efficacité et le rendement éxergétique des deux condenseurs, en utilisant différents fluides frigorigènes (R22, R1 34a, R404A, R407A) et deux fluides de refroidissement différents (l'air et l'eau).

D'après les résultats obtenus après l'étude des deux condenseurs, on voit que l'utilisation du fluide frigorigène R22 ou R1 34a donne les meilleurs résultats, c'est-à-dire un coefficient d'échange par condensation élevé, un coefficient d'échange global élevé et des surfaces d'échanges compactes donc économiques, malgré qu'ils ont un mauvais rendement éxergétique, contrairement à R404A qui a un bon rendement éxergétique mais de mauvais coefficients d'échange local et global donc des surfaces encombrantes et couteuses.

La viscosité dynamique (m) de l'air augmente en fonction de la température d'entrée en diminuant

le coefficient d'échange par convection et le coefficient d'échange global et par conséquent on obtient une surface encombrante et couteuse. Par contre la viscosité de l'eau diminue en fonction de la température d'entrée on augmentant le coefficient d'échange par convection et le coefficient d'échange global et par conséquent on obtient une surface compacte et économique.

L'influence de l'échauffement est identique pour les deux fluides de refroidissement, sont augmentation donne une augmentation de DMLT et par conséquent une surface d'échange compacte et économique et il augmente aussi l'efficacité du condenseur mais diminue sont rendement éxergétique.

L'augmentation du pincement à une grande influence sur DMLT est par conséquent sur la surface d'échange qui diminue et devient plus compacte et plus économique malgré que son

augmentation implique une diminution de l'efficacité et du rendement éxergétique du condenseur.

On a remarqué aussi que le coefficient d'échange par condensation à une allure descendante dans tout les cas, due à l'augmentation de la température de condensation en fonction de ces paramètres

(Tfr . entrée,DTes,DTP)

L'augmentation de la vitesse du fluide de refroidissement entraine des turbulences qui améliorent l'intensité du transfert de chaleur par convection et on obtient par conséquent des surfaces d'échanges compactes et économiques.

Les remarques faites au fluide de refroidissement l'air et l'eau sont très logiques, l'eau a une grande influence sur les coefficients d'échanges par convection, et par conséquent sur les surfaces d'échanges, car l'eau à une très bonne qualité de transfert comparé à l'air

L'utilisation de l'eau comme fluide de refroidissement nous permet d'obtenir des surfaces d'échange compactes donc économiques, contrairement à l'air qui donne des surfaces encombrantes et couteuses. Malgré cela l'air est toujours utilisé grâce aux grands avantages qu'il possède par rapport à l'eau surtout la disponibilité illimitée et gratuite, contrairement à l'eau qui devient de plus en plus chère, sa nécessite d'un traitement spécial et de mise en place d'un système de refroidissement.

BIBIO GRAPHIE

[1] Technique de l'ingénieur : « Génie énergétique », volume : B, Doc. B 2343,
Intensification des échanges thermiques, P 1-17.1994

[2] Pierre CORMAULT «Cours de Thermique théorique et pratique », Seconde édition,
ESME - Sudria, Janvier 1999.

[3] NUSSELT (W.). - Die Oberflächenkondensation des Wasserdampfes. VDI Zeitschrift,
vol. 60, pp. 541-546 et pp. 569-575 (1916).

[4] CARPENTER (F.S.) et COLBURN (A.P.). - The effect of vapour velocity on condensation inside tubes. Proc. Gen. Discussion of Heat Transfer, the Inst. Mech. Engrs and the Am.Soc. Mech. Engrs, Clayton Lecture, pp. 20-26 (1951).

[5] DOBSON (M.K.) et CHATO (J.C.). - Condensation in smooth horizontal tubes. J. Heat
Transfer, Trans ASME, vol. 120, pp. 193-213(1998).

[6] SOLIMAN (H.M.) et AZER (N.Z.). - Visual studies of flow patterns during condensation inside horizontal tubes. Proc. 5th Int. Heat Transfer Conf. Tokyo, Sept. 3-7, 1974, vol. III, pp. 341-245 (1974).

[7] ROHSENOW (W.M.). - Heat transfer and temperature distribution in laminar film
condensation. Trans. ASME, vol. 78, pp. 1645-1648 (1956).

[8] KUTATELADZE (S.S.) et GOGONIN (I.I.). -Heat transfer in film condensation of slowly moving vapour. Int. J. Heat Mass Transfer, vol. 22, pp. 1593-1599 (1979).

[9] MIYARA (A.). - Flow dynamics and heat transfer of wavy condensate film. J. Heat Transfer, Trans. ASME, vol. 123, pp. 492-500 (2001).

[10] SHEKRILADZE (I.G.) et GOMELAURI (V.I.). - Theoretical study of laminar film
Condensation of flowing vapour. Int. J. Heat Mass Transfer, vol. 9, pp. 581-591 (1966).

[11] FUJII (T.) et UEHARA (H.). - Laminar filmwise condensation on a vertical surface. Int. J.Heat Mass Transfer, vol. 15, pp. 2 17-233 (1972).

[12] DHIR (V.) et LIENHARD (J.). - Laminar film condensation on plane and axisymmetric bodies in non uniform gravity. J. Heat Transfer, Trans. ASME Series C, vol. 93, pp. 97-100 (1971).

[13] JAKOB (M.). - Heat Transfer, vol. 1, pp. 667-673, Wiley, New York (1949).

[14] KERN (D.Q.). -Process heat Transfer, McGraw-Hill, New York (1950)

[15] KERN (D.Q.). - Mathematical development of loading in horizontal condensers. AICHE J., vol. 4, pp. 157-160 (1958).

[16] CHEN (M.M.). - An analytical study of laminar film condensation: Part 2 - single and multiple horizontal tubes. J. Heat Transfer, Trans. ASME Series C, vol. 83, pp. 55-60(1961).

[17] CHEN (M.M)., HARTNETT (J.P)., GANIC (E.N).,Handbook of heat transfer fundamentals (1985).

[18] BERMAN L.D., Heat transfer during film condensation of vapour on horizontal tubes in traverse flow. AEC-tr-6877,(1 968).

[19] SPARROW (E.M.) et GREGG (J.L.). - A boundary layer treatment of laminar film
Condensation. J. Heat Transfer, Trans. ASME, Series C, vol. 81, pp. 13-18 (1959).

[20] ROSE (J.W.). - A new interpolation formula for forced convection condensation on a
horizontal surface. J. Heat Transfer, Trans ASME, vol. 111, pp. 818-819 (1989).

[21] ASBIK (M.), DAIF (A.) et PANDAY (P.K.). -Condensation of downward flowing vapour on a single horizontal cylinder or a bank of tubes with and without inundation. Proc; 1st ISHMT-ASME Heat Mass Transfer Conference, Jan. 1994, BARC, Bombay (Tata McGraw Hill Ltd), pp. 475-480 (1994).

[22] HOMESCU (D.) et PANDAY (P.K.). - Forced convection condensation on a horizontal tube: Influence of turbulence in the vapour and liquid phases. J. Heat Transfer, Trans ASME, vol. 121, pp. 874-885 (1999).

[23] MC NAUGHT, J.M., Tow phase forced convection heat transfer during condensation on horizontal tube bundles, Proc.Seventh Int. Heat Transfer Conf.,5, 125-13 1 Hemisphere publishing Corp., New York, 1982.

[24] BEATTY, K. O. and D. L. KATZ, Condensation of vapors on outside of finned tubes, Chem. Eng.Prog, 44 No. 1, p 55-70, 1948.

[25] BORISHANSKI (V.M.), VOLKOV (D.I.), IVASHENKO (N.I.) et ILARINOV (Y.T.). - J.Engg. Phy. vol. 26, pp. 760-761 (1974).

[26] IVASHCHENKO (N.I), KERKUNOV (O.P.) et VOLKOV (D.I.).-heat transfer from flowing condensation vapor. Heat transfer sov. Res. ,vol. 19,pp. 67-72(1987).

[27] CAVALLINI (A.) et ZECCHIN (R.). - High velocity condensation of organic refrigerants inside tubes. Proc. 13th Int. Congress of Refrigeration, vol. II, pp. 193-200 (1971).

[28] SHEKRILADZE (I.G.) et MESTVIRISHVILI (S.H.). - High rate condensation
processtheory of vapour flow in a vertical cylinder. Int. J. Heat Mass Transfer, vol. 16,pp. 715-724 (1973).

[29] SHAH (M.M.). - A general correlation for heat transfer during film condensation inside
pipes. Int. J. Heat Mass Transfer, vol. 22, pp. 547-556 (1979).

[30] CHEN (S.L.), GERNER (F.M.) et TIEN (C.L.). -General film condensation correlations. Exp.Heat Transfer, vol. 1, pp. 93-107 (1987).

[31] BLANGETTI (F.L.) et SCHLUNDER (E.U.). -Local heat transfer coefficients in film
condensation at high Prandtl numbers. Condensation Heat Transfer, ASME,

18th National Heat Transfer Conference, San Diego, California 6-8 Aug, pp. 17-25(1979).

[32] CARPENTER (F.S.) et COLBURN (A.P.). - . General Discussion on Heat Transfer, London (1951). ASME, New York p. 20

[33] ACKERS (W.W) et ROSSON (H.F.). -Condensation inside horizontal tubes. Chem.Engg. Prog. Symp. Ser., vol. 56, pp. 145-149(1960).

[34] RIFFERT (V.G.). - Heat transfer and flow modes of phases in laminar film vapour condensation inside a horizontal tube. Int. J. Heat Mass Transfer, vol. 31, pp. 517-523 (1988).

[35] FUJII (T.). - Enhancement to condensing heat transfer - new developments. J. Enhanced Heat Transfer, vol. 2, pp. 127-137 (1 995).

[36] YAN (Y.) et LIN (T.). - Condensation heat transfer and pressure drop of refrigerant R134a in a small pipe. Int. J. Heat Mass Transfer, vol. 42, pp. 697-708 (1999).

[37] TANDON (T.N.), VARMA (H.K.) et GUPTA (C.P.). - Heat transfer during forced convection condensation inside horizontal tube. Int. J. Réfrig., vol. 18(3), pp. 210-214 (1995)

[38] OZISIK (M.N)-Basic Heat Transfer Mc graw Hill Book company N.Y.

[39] LECOQ (P.)- Ecoulements diphasiques. Mécanique des fluids appliqués, cours de l'école national des ponts et chausses sous la direction de M.HUG Edition Eyrolles Paris 1975.

[40] INCROPERA (F.P) et DEWITT (D.P)-Fundamentals of heat and mass Transfer. Second edition; John wiley and sons N. Y 1985.

[41] KRASNOTCHEKOV (1) Exercises de transfers de chaleur resoles, edition Mir Moscou.

[42] BOUCHAMA. (A) Refroidisement en cascade par flash detente de moélisation par contraintes et aides a la decision, These de Doctorat, spécialité: Mécanique, ENSAM Centre de Bordeaux, Décembre 2003.

[43] MC ADAMS (W.H)- Transmission de la chaleur, traduit par A. Beautifils Dunod Paris 1964.

[44] WUITHIER (P.)-Raffinage et genie chimique «Appareils tubulaires d'échange» de chaleur
vol 2 Deuxieme edition tecnip Paris 1972.

[45] GOSSE (J)-guide technique de thermique, Dunod Paris 1981.

[46] FEIDT (M)- Thermodynamique et optimization energétique des systemes et procedes, technique et documentation lavoisier 1987 Paris.

[47] BOUGRIOU (C) -Etude du transfert de chaleur par condensation d'air humide sur des tubes à ailettes, these de doctorat, spécialiste: transferts thermiques, INSA de Lyon 1991.

[48] KUTATLADZE (S.S) et BORISHANSKI (V.M) - the book of heat transfer. Moscou 1959

[49] MARCHAL (R) Transmission de la chaleur par convection dans les tubes Eyrolles. Paris 1974.

[50] VAMPOLA (J) -Heat transfer and pressure loss in gas flow through finned tube bundle,
Strojirenstivi 1966.

[51] WEBER (M) etude experimentale du condenseur sou-refroidisseur monotubulaires verticale, Revue General de Thermique française.n° 318-319, pp392-404, juin-juillet, 1983.

[52] CHAPMAN (A.J)-Heat transfer, third edition Mac Millan Publishing N.Y.

[53] SCHMIDT (Th.E) - La production calorifique des surfaces munies d'ailettes (annex du bulletin de l'institut international du froid. Annexe G-5 1945-1946).

[54] BONTEMPS(A), GARRIGUE(A), GOUBIER (C),HUETZ(J) MARVILLET (C)
MARCIER(P) ET VIDIL(R)-Echangeurs e chaleur, Techniques de l'ingénieur, traité génie energétique B2, 1995.

[55] P. J. RAPIN et P. JACQUARD, Installation frigorifique, Tome 2 Technologie Pyc 6éme Edition p135-166, 1992.

[56] Technique de l'ingénieur : « Génie énergétique », volume : B, Doc. B 2341, Descriptions des échangeurs, .1994.

[57] Manuel de climatiation «Trane» Fabrication de materiel de climatisation, de chauffage, de ventilation et de transfert de chaleur. Quatriéme édition en 1985 USA.

[58] Technique de l'ingénieur : « Génie énergétique », volume : B, Doc. B 2342, Dimensionnement thermique des échangeurs,. 1994.

[59] M.BOUMAZA, Cours de 1^ère Année Magistére de physique énergétique, «Les échangeurs de chaleur», année universitaire 1999-2000.

[60] V. KIRILIN, V. SYTCHEV, A. SHEINDLIN, Thermodynamique Technique, Deuxième édition, p 344-447, Edition Mir. Moscou.

[61] COOLPACK, Version 1.46, A Collection of Simulation Tools for Refrigeration, Technical University of Denmark, 2000.

[62] K.RAZNJEVIC, «Tables et diagrammes thermodynamiques», edition Eyrolles, 1970.

!cccccccccccccccccccccc cccccccccccccccccccccccc

!ccccccccccccccccccc PROGRAMME PRINCIPAL ccccccccccccccccccccc
!cccccccccccccccccccccc ccccccccccccccccccccccc
!ccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

Program CONDIM

! Use DFLIB Integer c

Write (*,11)

11 Format (13/,35x,'Bienvenue au programme "CONDIM!',5/)

Pause ' Taper (entrer) pour commencer! '

Do 200 while (c.NE.3)

! Call clearscreen

Write (*,12)

12 Format (7/,25x,'Vous pouvez avoir le dimensionnement du ',/,& & 30x,'Condenseur ',///,& & 20x,'				',/,&
&	20x,'	Type de Condenseur		',/,&
&	20x,'	******************		',/,&
&	20x,'			',/,&
&	20x,'	1 Condenseur a air		',/,&
&	20x,'			',/,&
		',/,& 2 Condenseur a eau	&	20x,'
&	20x,'			',/,&
&	20x,'	3 Quitter		',/,&
&	20x,'			',/)

50 Write (*,13)

13 Format (//,25x,'*** Faites votre choix, de 1 à 3 :')

Read (*,*) c

! Call clearscreen

Select case (C)

Case (1)

Call Condensair

Case (2)

Call Condenseau

Case (3) Goto 500 Case default

Write (*,14)

14 Format (13/,25x,'***** Vous avez fait une erreur ! *****',/,&

& 10x,'Le numéro que vous avez choisi doit être compris entre 1 et 2')

Goto 50

End select

200 Continue

500 Write (*,15)

15 Format (1 3/,25x,'Merci de votre passage, a bientôt ! ! ',///)

Pause ' Tapez (entrer) pour quitter le programme...'

Stop

End

!cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc !ccccccccccccccccccc ccccccccccccccccccccccc !ccccccccccccccccc PROCEURE CONENSEUR A AIR ccccccccccccccccc !ccccccccccccccccccc ccccccccccccccccccccccc !ccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

Subroutine Condensair

! Use DFLIB

Real di, de, a, b, c, n, Eail, Et, Dr, Pc, Tae, Tas, Tc, kt, kail, va, Rint, Rext, &

& Ltot, Sir, Tm, Cp, Mu, Lamda, Ro, Pr, Muf, kf, Lv, Rol, Rov, Dm, Dv, Si, & & PHia, PHig, m, Psi, Lp, Tp, Ntot, Etta, L, happ, k, g, Sech, Sint, &

& Ient, Isort, Sent, Ssort, Exent, Exsort, DeltaEx, Sm, Im

Double précision Nu, Re, Phi, DMLT, hi, he, down, up, Se, Snet, Sfr, Setr, Sail, & & Eff, NUT, Tascal, DeltaT, Pcech, Stot, Vetr, RendementEx

Integer Disp, z, Nr, np, Lr

Write(*, 16)

16 Format (4/,20x,'********************',/,&

& 5x,'*************** Condenseur a air ***************',/,& & 20x ,'********************')

! ********************** DONNEES *************************

Write(*, 17)

17 Format (3/,15x,'Faite entrer les données',3/,&

& 5x,'****************************************************',/,&

& 5x,'**************DONNEES GEOMETRIQUES******************',/,&

& 5x,'****************************************************',2/,&

& 7x,'Diamètre intérieur des tubes (m)')

Read(*,*)di

Write(*,*)' Diamètre extérieur des tubes (m)'

Read(*,*)de

Write(*,*)' Diamètre du racine des ailettes (m)'

Read(*,*)Dr

Write(*,*)' Pas transversal (m)'

Read(*,*)a

Write(*,*)' Pas longitudinal (m)'

Read(*,*)b

Write(*,*)' Ecartement des ailettes (m)'

Read(*,*)c

Write(*,*)' Epaisseur des ailettes (m)'

Read (*,*)Eail

! Call clearscreen Write (*,18)

18 Format(3/,5x,'*******************************************************',/,& & 5x,'***************DONNEES THERMOPHYSIQUES***********',/,&

& 5x,'******************************************************',2/,&

& 7x,'Puissance thermique du condenseur (w)')

Read (*,*)Pc

Write(*,*)' Température d"entree de l"air (°C )'

Read(*, *)Tae

Write(*,*)' Température de sortie de l"air (°C )'

Read(*, *)Tas

Write(*,*)' Conductivité thermique des tubes (w/m.K)'

Read(*,*)kt

Write(* ,*)' Conductivité thermique des ailettes (w/m.K)'

Read(*,*)kail

Write(* ,*)' Résistance d"encrassemnt coté intérieur (m2 .K/w)'

Read(*,*)Rint

Write(* ,*)' Résistance d"encrassement coté extérieur (m2 .K/w)'

Read(*,*)Rext

! Call clearscreen Tm=(Tae+Tas)/2 Write (*,19)Tm

19 Format (3/,1 5x,'La température moyenne de l"air est : ',F7.2,//,&

& 13x, ' Donnez les propriétés physiques de l"air pour cette température :',2/,&

&5x,'*******************************************************',/,&

&5x,'***********PROPRIETES PHYSIQUES DE L"AIR *********',/,&

&5x,' * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *',2/,&

&7x,'Chaleur spécifique de l»air (J/kg k)')

Read(*,*)Cp

Write(*,*)' Viscosité dynamique de l"air (kg/m.s)'

Read(*,*)Mu

Write(*,*)' Conductivité thermique de l"air (w/m.K)'

Read(*,*)Lamda

Write(*,*)' Masse volumique de l"air (kg/m3)'

Read(*,*)Ro

Write(*,*)' Nombre de Prandtl pour l"air'

Read(*,*)Pr

Write(*,*)' Enthalpie de l"air (kj/kg)'

Read(*,*)Im

Write(*,*)' Entropie de l"air (kj/kg.k)'

Read(*,*)Sm

Write(*,*)' Pincement (kj/kg.k)'

Read(*,*)DTp

! Call clearscreen

Tc = Tas + DTp Write(*,21) Tc

21 Format(3/, 1 0x,'Donnez les propriétés physiques du fluide frigorigène',/,&

&8x,' à sa température de condensation : ',F7.2,//,&

&5x,'*********************************************************',/,& &5x,'****PROPRIETES PHISIQUES DU FLUIDE FRIGORIGENE***',/,&

&5x,'*********************************************************',2/,& &7x,'Viscosité dynamique du fluide frigorigène (kg/m. s)')

Read(*,*)Muf

Write(*,*)' Conductivité thermique du fluide frigorigène (w/m.K)'

Read(*,*)kf

Write(*,*)' Chaleur latente de condensation u fluide frigorigène (J/kg)'

Read(*,*)Lv

Write(*,*)' Masse volumique du fluide frigorigène (liquide) (kg/m3)'

Read(*, *)Rol

Write(*,*)' Masse volumique du fluide frigorigène (vapeur) (kg/m3)'

Read(*,*)Rov

Write(*,*)' Enthalpie entrant du fluide frigorigène (vapeur) (kj/kg)'

Read(*,*)Ient

Write(*,*)' Enthalpie sortant du fluide frigorigène (liquide) (kj/kg)'

Read(*,*)Isort

Write(*,*)' Entropie entrant du fluide frigorigène (vapeur) (kj/kg.k)'

Read(*,*)Sent

Write(*,*)' Entropie sortant du fluide frigorigène (liquide) (kj/kg.k)'

Read(*, *)Ssort

! Call clearscreen

Write(*,22)

22 Format (5/,10x,'Entrez la vitesse de l"air entre 2,5 et 4 m/s:',3/) Read (*,*)Va

! ******************************** CALCUL 1 *******************************

Et=(de-di)/2

Dm=Pc/(Cp* (Tas-Tae))

Dv=Dm/Ro

Sfr =Dv/va

n=1 /(c+Eail)

Se=3.14*de

Si=3. 14*di

Snet= Se*( 1-n*Eail)

Sail=2*n*(a*b-(3. 1 4*(de* *2))/4)

Stot=Snet+Sail

Setr=Sfr*( 1-(de/a)+((Eail/(c+Eail))*( 1 -(de/a))))

Vetr=Dv/Setr PHia =Sail/Stot PHig=Snet/Stot

Re=Vetr*de*Ro/Mu

Write(*,23)

23 Format(10x,'*** Choisissez une disposition des tubes ***',2/)

30 Write(*,*)' En lignes tapez (1) , En quinconces tapez (2) :'

Read(*,*) Disp

If (Disp.EQ.2) then

Nu= 0.45*(Re**(0.625)*(Stot/Se)**(-0.375)*(Pr**(1/3)))

Else if (Disp.EQ. 1) then

Nu= 0.30*(Re**(0.625)*(Stot/Se)**(-0.375)*(Pr**(1/3)))

Else

Write(*,*)' vous avez fait une erreur, Tapez (1) ou (2)'

Write(*,*)' ' Goto 30

Endif

Write(*,*)' Entrez la longueur d"un passage entre 1.5 et 4 m:'

Read(*,*)Lp

he=(Nu*Lamda)/de

m=sqrt((2*he)/(kail*Eail))

Psi=1 .28*(a/de)*sqrt((a/b)-0.2)

phi=(Psi- 1 )*( 1+0.35 *Log(Psi))

L=(Phi*de)/2

Etta =(Tanh(m*L))/(m*L)

Ettap=(PHig+Etta*PHia)

happ=he*Ettap g=9. 81

up=(g*Rol*(Rol-Rov)*(kf* *3)* Lv)

Tp=(Tm+Tc)/2

down=(Muf*(Tc-Tp) *di)

hi=0.555*((up/down)**(0.25))

k=1 /(((Stot/Si)*(( 1 /hi)+Rint))+((Stot*log(Dr/di))/(Lp*2*3.1 4*kt))+(1 /(happ*Ettap))+(Rext/Ettap)) DMLT=(Tas-Tae)/Log((Tc-Tae)/(Tc-Tas))

Sech=Pc/(k*DMLT)

Sint=(Sech* Si)/Stot

Ltot=Sint/(3.1 4*di)

Write(*,*)' Entrez le nombre de passages:'

Read(1,*) z

Ntot=Ltot/Lp

np=Int(Ntot/z)

Nr=np*z

Lr=Nr*Lp

Sir=Lr* Si

NUT=(k* Sech)/(Dm*Cp)

Eff=( 1 -exp(-NUT))

Exent=(Ient-Im)+(Tm+273.1 5)*(Sm-Sent) Exsort=(Isort-Im)+(Tm+273.1 5)* (Sm-Ssort) DeltaEx=Exent-Exsort

RendementEx=Exent/Exsort

! Call clearscreen ! ******************************** RESULTATS ************************* Write(*,24) 24 Format (5/,17x,'** Voici les résultats du dimensionnement du condenseur a air **',/,& & 10x,'
			',3/,&
&	17x,'		',/,&
&	17x,'	RESULTATS	',/,&
&	17x,'	***********	',/,&
&		17x,'	',/,&
&	17x,'	* Surface d"echange : ',F7.3,' m2	',/,&
&		17x,'	',/,&
&	17x,'	* DMLT : ',F7.2,' °C	',/,&
&		17x,'	',/,&
&	17x,'	* Coefficient de transfert de chaleur: K ',F7.3, 'w/m2.k	',/,&
&		17x,'	',/,&
&	17x,'	* Coefficient d"echange interne : ',F7.2,' w/m2.k ',/,&
&		17x,'	',/,&
&	17x,'	* Nombre de tubes par passage: ',I4,'	',/,&
&		17x,'	',/,&
&	17x,'	* Nombre total de tubes: ',I4,'	',/,&
&		17x,'	',/,&
&	17x,'	* Longueur total des tubes : ',I5,' m ',/,&
&		17x,'	',/,&
&	17x,'	* NUT : ',F7.2,'	',/,&
&		17x,'	',/,&
&	17x,'	* L'efficacité de condenseur : ',F9.2,'	',/,&

& 17x,' ',/,&

& 17x,' * Perte de capacité de travail: ',F7.3,' kj/kg ',/,&

& 17x,' ',/,&

& 17x,' * Rendement exégétique : ',F7.4,' ',/,&

& 17x,' ',2/)

Pause ' Tapez (entrer) pour continuer... '

Return

End

!cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc !ccccccccccccccccccc cccccccccccccccccccccc !ccccccccccccccccc PROCEURE CONENSEUR A EAU ccccccccccccccccccc !ccccccccccccccccccc cccccccccccccccccccccc !ccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

Subroutine Condenseau

! Use DFLIB

Real di,de,a,b,c,n,Eail,Et,Pc,Tee,Tes,Tc,kt,kail,ve,Rint,Rext,r1 ,r2,Dr,E,Ettap,&

& Ltot, Sir,Tm,Cp,Mu,Mup,Lamda,Ro,Pr,Muf,kf,Lv,Rol,Rov, Si,Etta0,Ettap0,&

& PHia,PHig,m,Psi,Lp,Tp,Ntot,Etta,L,happ,k,g, Sech, Sint,&

& Ient,Isort, Sent, Ssort,Exent,Exsort,DeltaEx, Sm,Im,Dm,NUT,Eff

Double precision Nu,Re,Phi,DMLT,hi,he,down,up, Se, Snet, Sail, Stot,RendementEx

Integer z,Nr,np,Lr

Write(*, 16)

16 Format(4/,20x,'********************',/,&

& 5x,'*************** Condenseur a eau ***************',/,&

& 20x,'********************')

! ******************************* DONNEES ******************************

Write(*, 17)

17 Format (3/,15x,'Faite entrer les données',3/,&

& 5x,'****************************************************',/,&

& 5x,'**************DONNEES GEOMETRIQUES******************',/,&

& 5x,'****************************************************',2/,&

& 7x,'Diamètre intérieur des tubes (m)')

Read(1 ,*)di

Write(*,*)' Diamètre extérieur des tubes y compris l"ailettes (m)'

Read(1 ,*)de

Write(*,*)' Diamètre racine de la surface ailettes (m)'

Read( 1, *)Dr

Write(*,*)' Pas transversal des tubes (m)'

Read(1 ,*)a

Write(*,*)' Pas longitudinal des tubes (m)'

Read(1 ,*)b

Write(*,*)' Ecartement des ailettes (m)'

Read(1 ,*)c

Write(*,*)' Epaisseur des ailettes (m)'

Read(1,*) Eail
! Call clearscreen

Write (*,18)

18 Format(3/ ,5x ,'*******************************************************' ,/ ,&

& 5x,'***********DONNEES THERMOPHYSIQUES**************',/,&

&5x,'*******************************************************',2/,&

& 7x,'Puissance thermique du condenseur (w)')

Read(1 ,*)Pc

Write(*,*)' Température d"entree de l"eau (°C )'

Read(1 , *)Tee

Write(*,*)' Température de sortie de l"eau (°C )'

Read(1 , *)Tes

Write(*,*)' Conductivité thermique des tubes (w/m.K)'

Read(1 ,*)kt

Write(* ,*)' Conductivité thermique des ailettes (w/m.K)'

Read( 1, *)kail

Write(* ,*)' Résistance d"encrassemnt coté intérieur (m2.K/w)'

Read(1 ,*)Rint

Write(* ,*)' Résistance d"encrassement coté extérieur (m2.K/w)'

Read( 1, *)Rext

! Call clearscreen

Tm=(Tee+Tes)/2 Write(*, 1 9)Tm

19 Format (3/,15x,'La température moyenne de l"air est : ',F7.2,//,&

& 13x, ' Donnez les propriétés physiques de l"eau pour cette température :',2/,&

&5x,'*******************************************************',/,& &5x,'***********PROPRIETES PHYSIQUES DE L"EAU *************',/,&

&5x,' * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *',2/,&

&7x,'Chaleur spécifique de l»eau (J/kg k)')

Read( 1, *)Cp

Write(*,*)' Viscosité dynamique de l"eau (kg/m.s)'

Read(1 ,*)Mu

Write(*,*)' Conductivité thermique de l"eau (w/m.K)'

Read(1 ,*)Lamda

Write(*,*)' Masse volumique de l"eau (kg/m3)'

Read( 1, *)Ro

Write(*,*)' Nombre de Prandtl pour l"eau '

Read( 1, *)Pr

Write(*,*)' Enthalpie de l"eau (kj/kg)'

Read(1 ,*)Im

Write(*,*)' Entropie de l"eau (kj/kg.k)'

Read(1 ,*)Sm

Write(*,*)' Viscosité dynamique de l"eau a Tp (kg/m.s)'

Read(1 ,*)Mup

Write(*,*)' Le pincement DTp (kg/m.s)'

Read( 1, *)DTp

! Call clearscreen Tc = Tes + DTp Tp = (Tc+Tm)/2 Write(*,21) Tc

21 Format(3/,10x,'Donnez les propriétés physiques du fluide frigorigéne',/,& &8x,' à sa température de condensation : ',F7.2,//,&

&5x,'*********************************************************',/,&

&5x, '** * * * * *PROPRIETES PHISIQUES DU FLUIDE FRIGORIGENE* * * * * * * *',/,&

&5x,'*********************************************************',2/,& &7x,'Viscosité dynamique du fluie frigorigéne (kg/m.s)')

Read(1 ,*)Muf

Write(*,*)' Conductivité thermique du fluide frigorigéne (w/m.K)'

Read( 1, *)kf

Write(*,*)' Chaleur latente de condensation u fluide frigorigéne (J/kg)'

Read(1 ,*)Lv

Write(*,*)' Masse volumique du fluide frigorigéne (liquide) (kg/m3)'

Read( 1, *)Rol

Write(*,*)' Masse volumique du fluide frigorigéne (vapeur) (kg/m3)'

Read( 1, *)Rov

Write(*,*)' Enthalpie entrant du fluide frigorigéne (vapeur) (kj/kg)'

Read( 1, *)Ient

Write(*,*)' Enthalpie sortant du fluide frigorigéne (liquide) (kj/kg)'

Read(1 ,*)Isort

Write(*,*)' Entropie entrant du fluide frigorigéne (vapeur) (kj/kg.k)'

Read(1 ,*)Sent

Write(*,*)' Entropie sortant du fluide frigorigéne (liquide) (kj/kg.k)'

Read(1 ,*)Ssort

! Call clearscreen

Write(*,22)

22 Format (5/,10x,'Entrez la vitesse de l"eau entre 1 et 2.5 m/s:',3/)

Read (1,*)Ve

Write(*,*)' Entrez la longueur d"un passage entre 1.5 et 4 m:'

Read(1 ,*)Lp

! ******************************** CALCUL 2 ******************************* Dm=Pc/(Cp* (Tes-Tee))

Et=(de-di)/2 n=1 /(c+Eail) Se=3.14*de Si=3. 14*di r1 =Dr/2

r2=de/2

Snet=2*3. 14*r1 *(Lp-n*Eail)

Sail=2*n*3.14*(r2**(2)-r1 **(2))

Stot=Snet+Sail

PHia =Sail/Stot

PHig=Snet/Stot

Re=Ve*di*Ro/Mu

If (Re.GT. 10000) Then

Nu= 0.027*(Re**(0.8)*(Pr**(1/3)))*(Mu/Mup)**(0. 14)

Else

Nu= 1. 86*((Re*Pr*di/Lp)**(1/3))*(Mu/Mup)**(0. 14)

Endif

hi=(Nu*Lamda)/di

E=3.14*(r2**(2)-r1 **(2))/(2*r2)

Etta =1

Ettap=1

Etta0=0

Ettap0=0

100 If(abs(Etta0-Etta).GT.0.01) Then

Deq= ((1 .30*Etta*Sail*E**(-0.25)+Snet*Dr**(-0.25))/(Ettap*Stot))**(-4)

g=9. 81

up=(g*Rol*(Rol-Rov)*(kf* *3)* Lv) Tp=(Tm+Tc)/2

down=(Muf*(Tc-Tp)*Deq) he=0.689*((up/down)**(0.25)) m=sqrt((2*he)/(kail*Eail)) Psi=1 .28*(a/de)*sqrt((a/b)-0.2) phi=(Psi- 1 )*( 1+0.35 *Log(Psi)) L=(Phi*de)/2

Etta =(Tanh(m*L))/(m*L)

Ettap= PHig+Etta*PHia

Etta0=Etta

Ettap0=Ettap

Else

Write(*, *)' vous faites une erreur' Goto 100

Endif

happ=he*Ettap

k=1 /(((Stot/Si)*(( 1 /hi)+Rint))+((Stot*log(Dr/di))/(Lp*2*3.1 4*kt))+(1 /(happ*Ettap))+(Rext/Ettap)) DMLT=(Tes-Tee)/Log((Tc-Tee)/(Tc-Tes))

Sech=Pc/(k*DMLT)

Sint=(Sech* Si)/Stot

Ltot=Sint/(3.1 4*di)

Write(*,*)' Entrez le nombre de passages:'

Rread(1,*) z

Ntot=Ltot/Lp

np=Int(Ntot/z)

Nr=np*z

Lr=Nr*Lp

Sir=Lr* Si

NUT=(k* Sech)/(Dm*Cp)

Eff=( 1 -exp(-NUT))

Exent=(Ient-Im)+(Tm+273.1 5)*(Sm-Sent)

Exsort=(Isort-Im)+(Tm+273.1 5)* (Sm-Ssort)

DeltaEx=Exent-Exsort

RendementEx=Exent/Exsort

! Call clearscreen

! ******************************** RESULTATS *************************

Write(*,24) 24 Format (5/,17x,'** Voici les résultats du dimensionnement du condenseur a eau **',/,& & 10x,'
& & &	========================================= 17x,' 17x,' RESULTATS 17x,' ***********		====',3/,& ',/,& ',/,& ',/,&
&		17x,'	',/,&
&	17x,'	* Surface d"echange : ',F7.3,' m2	',/,&
&		17x,'	',/,&
&	17x,'	* DMLT : ',F7.2,' °C	',/,&
&		17x,'	',/,&
&	17x,'	* Coefficient de transfert de chaleur: K ',F7.3, 'w/m2.k	',/,&
&		17x,'	',/,&
		& 17x,' * Coefficient d"echange externe : ',F7.2,' w/m2.k ',/,&
&		17x,'	',/,&
&	17x,'	* Nombre de tubes par passage: ',I4,'	',/,&
&		17x,'	',/,&
&	17x,'	* Nombre total de tubes: ',I4,'	',/,&
&		17x,'	',/,&
&	17x,'	* Longueur total des tubes : ',I5,' m ',/,&
&		17x,'	',/,&
&	17x,'	* NUT : ',F7.2,'	',/,&
&		17x,'	',/,&
&	17x,'	* L'efficacité de condenseur : ',F9.2,'	',/,&
&		17x,'	',/,&
&	17x,'	* Perte de capacité de travail: ',F7.3,' kj/kg ',/,&
&		17x,'	',/,&

& 17x,' * Rendement exégétique : ',F7.4,' ',/,&

& 17x,' ',2/)

Pause ' Tapez (entrer) pour continuer... '

Return

End













ANNEXE -D- PROPRIETES PHYSIQUE DES FLUIDEFRIGORIGENS

ET DES FLUIDES DE REFROIDISSEMENT

Les propriétés physiques de R22 à l'état saturé [61]

R22 TC(°C)	ì (Ns/m^2)	ë (W/m.K)	Lv (J/kg)	ñl (kg/m^3)	ñv (kg/m^3)	hv (kJ/kg)	hl (kJ/kg)	Sv (kJ/kg.K)	Sl (kJ/kg.K)
30	19.4E-5	0.0852	177890	1173,84	50,65	414.54	236.65	1.712	1.125
31	19.32E-5	0.0847	176840	1176.47	52.02	414.77	237.93	1.710	1.129
32	19.21E-5	0.0842	175780	1162.79	53.44	415.00	239.22	1.709	1.133
33	19.10E-5	0.0837	174710	1162.79	54.88	415.22	240.51	1.708	1.137
34	19E-5	0.0832	173630	1162.79	56.36	415.43	241.80	1.707	1.141
35	18.89E-5	0.0827	172540	1153	57.90	415.64	243.10	1.705	1.145
36	18.78E-5	0.0822	171430	1149.42	59.45	415.84	244.41	1.704	1.150
37	18.61E-5	0.0817	170320	1149.42	61.05	416.03	245.71	1.703	1.154
38	18.55E-5	0.0812	169190	1136.36	62.69	416.22	247.03	1.702	1.158
39	18.49E-5	0.0807	168050	1136.36	64.35	416.40	248.35	1.700	1.162
40	18.42E-5	0.0803	166900	1131.34	66.05	416.57	249.67	1.699	1.166
41	18.35E-5	0.0798	165740	1123.59	67.79	416.74	251.00	1.698	1.170
42	18.27E-5	0.0793	164550	1123.59	69.58	416.89	252.34	1.696	1.174
43	18.19E-5	0.0788	163360	1123.59	71.42	417.04	253.68	1.695	1.178
44	18.11E-5	0.0783	162150	1111.11	73.31	417.18	255.03	1.694	1.183
45	18.02E-5	0.0778	160940	1108.64	75.24	417.32	256.38	1.693	1.187

Propriétés physiques de R134a à l'état saturé [61]

R134a TC(°C)	ì (Ns/m^2)					ë (W/m.K)					Lv (J/kg)					ñl (kg/m^3)				ñv (kg/m^3)					hv (kJ/kg)					hl (kJ/kg)							Sv (kJ/kg.K)		Sl (kJ/kg.K)
30	8.60E-5					0.0820					172010					1188.21				37.76					413.47					241.46							1.709		1.142
31	8.40E-5					0.0816					171050					1190.47				38.88					413.96					242.91							1.709		1.147
32	8.17E-5					0.0812					170090					1176.47				40.03					414.45					244.36							1.709		1.151
33	7.94E-5					0.0808					169120					1176.47				41.22					414.94					245.82							1.709		1.156
34	7.71E-5					0.0803					168140					1176.47				42.43					415.42					247.28							1.708		1.161
35	7.49E-5					0.0799					167150					1168.22				43.66					415.90					248.75							1.708		1.166
36	7.27E-5					0.0795					166150					1162.79				44.94					416.37					250.22							1.708		1.170
37	7.06E-5					0.0791					165140					1162.79				46.25					416.84					251.70							1.707		1.175
38	6.84E-5					0.0786					164120					1149.43				47.57					417.30					253.18							1.707		1.180
39	6.63E-5					0.0782					163090					1149.43				48.95					417.76					254.67							1.707		1.184
40	6.43E-5					0.0778					162050					1147.57				50.35					418.21					256.16							1.707		1.189
41	6.22E-5					0.0773					161000					1149.43				51.81					418.66					257.66							1.706		1.194
42	6.02E-5					0.0769					159950					1136.36				53.28					419.11					259.16							1.706		1.199
43	5.83E-5					0.0765					158870					1136.36				54.79					419.54					260.67							1.706		1.203
44	5.63E-5					0.0761					157790					1136.36				56.37					419.98					262.19							1.705		1.208
45	5.44E-5					0.0756					156690					1125.87				57.93					420.40					263.71							1.705		1.213
R404A TC (°C)		ì (Ns/m^2)				ë (W/m.K)				Lv (J/kg)					ñl (kg/m^3)							ñv (kg/m^3)					hv (kJ/kg)					hl (kJ/kg)			Sv (kJ/kg.K)						Sl (kJ/kg.K)
30		2.62E-5				0.0669				135760					952.38							75.35					381.93					246.17			1.604						1.157
31		2.48E-5				0.0663				134390					952.38							77.58					382.26					247.87			1.604						1.162
32		2.34E-5				0.0657				133010					943.40							79.87					382.58					249.57			1.603						1.168
33		2.20E-5				0.0652				131600					934.58							82.24					382.89					251.29			1.603						1.173
34		2.06E-5				0.0646				130160					925.93							84.67					383.19					253.03			1.602						1.179
35		1.93E-5				0.0640				128690					925.92							87.26					383.47					254.78			1.602						1.184
36		1.79E-5				0.0634				127200					917.43							89.85					383.74					256.54			1.601						1.190
37		1.66E-5				0.0629				125680					909.09							92.51					384.00					258.32			1.601						1.196
38		1.53E-5				0.0623				124120					900.90							95.33					384.24					260.12			1.600						1.201
39		1.40E-5				0.0617				122540					892.86							98.14					384.47					261.93			1.599						1.207
40		1.27E-5				0.0611				120920					884.95							101.11					384.68					263.76			1.598						1.213
41		1.15E-5				0.0605				119260					877.19							104.17					384.87					265.61			1.598						1.218
42		1.03E-5				0.0599				117580					869.57							107.30					385.05					267.47			1.597						1.224
43		0.90E-5				0.0593				115840					862.07							110.62					385.20					269.36			1.596						1.230
44		0.78E-5				0.0588				114080					854.70							114.03					385.34					271.26			1.595						1.236
45		0.66E-5				0.0582				112270					847.45							117.50					385.46					273.19			1.594						1.242
R407A TC (°C)				ì (Ns/m^2)				ë (W/m.K)				Lv (J/kg)					ñl (kg/m^3)				ñv (kg/m^3)					hv (kJ/kg)					hl (kJ/kg)			Sv (kJ/kg.K)						Sl (kJ/kg.K)
30 14.32E-5								0.0808				164210					1052.63				67.15					410.23					246.02			1.694						1.1571
31 14.14E-5								0.0803				162850					1052.63				69.11					410.54					247.69			1.693						1.162
32 13.97E-5								0.0798				161460					1041.67				71.12					410.83					249.37			1.692						1.167
33 13.79E-5								0.0793				160060					1041.67				73.21					411.12					251.06			1.692						1.173
34 13.62E-5								0.0788				158630					1030.93				75.30					411.39					252.76			1.691						1.178
35 13.45E-5								0.0784				157180					1030.92				77.51					411.66					254.48			1.6904						1.184
36 13.28E-5								0.0779				155700					1020.41				79.74					411.91					256.21			1.689						1.189
37 13.12E-5								0.0774				154200					1010.10				82.10					412.15					257.95			1.688						1.195
38 12.95E-5								0.0769				152680					1010.10				84.46					412.38					259.70			1.687						1.200
39 12.79E-5								0.0764				151120					1000.00				86.96					412.59					261.47			1.686						1.206
40 12.63E-5								0.0760				149540					990.09				89.44					412.79					263.25			1.685						1.211
41 12.47E-5								0.0755				147930					990.10				92.08					412.97					265.04			1.684						1.217
42 12.32E-5								0.0750				146290					980.39				94.79					413.14					266.85			1.683						1.222
43 12.16E-5								0.0745				144630					970.87				97.56					413.30					268.67			1.682						1.228
44 12.01E-5								0.0740				142930					961.54				100.40					413.44					270.51			1.681						1.234
45				1.86E-5				0.0736				141190					961.53				103.41					413.56					272.37			1.680						1.239
Air Tm(°C)					Cp (J/kg.K)				ì (Ns/m^2)					ë (W/m.K)					ñ (kg/m^3)					Pr					h (kJ/kg)							S (kJ/kg.K)
22.5					1005.1				1.812E-05					0.02529					1.1953					0.7025					22.637							0.0703
23.5					1005.1				1.816E-05					0.02536					1.1915					0.7023					23.643							0.0734
24.5					1005.2				1.820E-05					0.02543					1.1876					0.7021					24.649							0.0766
25.5					1005.3				1.824E-05					0.02550					1.1838					0.7019					25.655							0.0797
26.5					1005.3				1.828E-05					0.02557					1.1799					0.7017					26.661							0.0828
27.5					1005.4				1.832E-05					0.02564					1.1761					0.7015					27.667							0.0860
28.5					1005.5				1.837E-05					0.02571					1.1722					0.7013					28.673							0.0891
29.5					1005.5				1.841E-05					0.02578					1.1684					0.7011					29.679							0.0922
30.5					1005.6				1.845E-05					0.02585					1.1645					0.7009					30.685							0.0953
31.5					1005.7				1.849E-05					0.02592					1.1607					0.7007					31.691							0.0985
32.5					1005.7				1.853E-05					0.02599					1.1568					0.7005					32.697							0.1016
33.5					1005.8				1.857E-05					0.02606					1.1530					0.7003					33.704							0.1047
34.5					1005.9				1.861E-05					0.02613					1.1491					0.7001					34.710							0.1078
35.5					1005.9				1.86E-05					0.02620					1.1453					0.6999					35.716							0.1110
36.5					1006.0				1.870E-05					0.02627					1.1414					0.6997					36.722							0.1141
37.5					1006.1				1.874E-05					0.02634					1.1376					0.6995					37.728							0.1172
Eau Tm(°C)			Cp (J/kg.K)				ì (Ns/m^2)						ë (W/m.K)					ñ (kg/m^3)					Pr					h (kJ/kg)					S (kJ/kg.K)					ìp (Ns/m^2)
22.5			4206.2				9.261E-4						0.60687					1000					6.4188					93.61					0.3292					8.472E-4
23.5			4208.8				9.040E-4						0.60838					1000					6.2539					97.82					0.34343					8.280E-4
24.5			4211.1				8.827E-4						0.60986					1000					6.0951					102.03					0.3576					8.094E-4
25.5			4213.2				8.622E -4						0.61134					1000					5.9421					106.24					0.37173					7.915 E-4
26.5			4215.2				8.424 E-4						0.61280					1000					5.7945					110.45					0.38581					7.742 E-4
27.5			4216.9				8.233 E-4						0.61424					1000					5.6521					114.67					0.39986					7.576 E-4
28.5			4218.5				8.049 E-4						0.61567					1000					5.5151					118.89					0.41387					7.416 E-4
29.5			4219.8				7.871 E-4						0.61709					1000					5.3824					123.11					0.42783					7.259 E-4
30.5			4221				7.700 E-4						0.61849					1000					5.2550					127.33					0.44175					7.109 E-4
31.5			4222.1				7.535 E-4						0.61987					990.099					5.1323					131.55					0.45563					6.964 E-4
32.5			4222.9				7.375 E-4						0.62124					990.099					5.0132					135.77					0.46947					6.823 E-4
33.5			4223 .7				7.221 E-4						0.62260					990.099					4.8987					139.99					0.48326					6.687 E-4
34.5			4224.3				7.072 E-4						0.62394					990.099					4.7880					144.22					0.48326					6.556 E-4
35.5			4224.7				6.928 E-4						0.62526					990.099					4.6810					148.44					0.51072					6.429 E-4
36.5			4225				6.789 E-4						0.62657					990.099					4.5779					152.67					0.52439					6.306 E-4
37.5			4225.3				6.654 E-4						0.62787					990.099					4.4779					156.89					0.53801					6.187 E-4

Résumé

L'étude abordée dans ce mémoire, de type simulation, est d'une importance capitale vu l'importance et le rôle des méthodes de développement DTML et NUT sur les échangeurs de chaleur.

Dans le but d'établir un code de calcul et dimensionnement de deux types de condenseurs à air et à eau utilisant quatre fluides frigorigènes différents R22, R1 34a, R404A et R407A et voir l'influence de la température d'entrée et l'échauffement du fluide de refroidissement, l'influence du pincement et la vitesse du fluide de refroidissement sur la surface d'échange, le coefficient d'échange de

chaleur local et global, et sur l'efficacité le rendement éxergétique du condenseur. Les résultats obtenus sont représentés par des graphes accompagnés par de discussions.

Les résultats montrent que malgré le faible rendement éxergétique obtenu avec de R22 et R1 34a, donnent un bon rendement thermique, c'est-à-dire des coefficients d'échange de chaleur global élevé, et donc des surfaces d'échange moins encombrantes, ce qui nous donne une économie du prix de l'appareil.

Les résultats montrent aussi que l'augmentation de la température d'entrée, de la vitesse, de l'échauffement du fluide de refroidissement et le pincement, donnent des surfaces d'échange plus compactes et donc plus économiques.

Mots clés : Echangeurs de chaleur, condenseurs à air, condenseurs à eau, dimensionnement, DTML, NUT, éxergie.

Abstract

The study addressed in this memory, type simulation, is crucial given the importance and role that the methods of developpement on heat exchangers.

In order to establish a code of calculation and dimensioning of two types of condensers with air and with water using four different refrigerants R22, R1 34a, R404A et R407A and see the influence of the temperature of entry and the heating of coolant, the influence of pinch and speed of coolant on the surface of exchange, the coefficient of heat exchange local and global, and the effectiveness performance éxergétique condenser. The results are represented on graph accompanied by discussions

The results showed that despite the low yield éxergétique obtained with R22 and R1 34a, they provide a good thermal efficiency i.e coefficients heat exchange global high and therefore surfaces exchange less cumbersome, which gives us an economy the price of aircraft

The results also show that increasing the temperature of entry, speed, the heating of coolant and the pinch, provide surfaces exchange more compact and therefore more economical.

Keywords: Heat exchangers, condensers in air, water condensers, dimensioning, DTML, NUT, exergie.



?j?j ? ???

???? j ? ????

???? ??? ??

j ÉÇßÇ~?

?? ??????? ??? ?? ??j??~??? ???????

. ?~???~??

??i????

??? NUT j DTML ?~??~ áÆÇÓj

?~??? ????~??? j ????? ? ?~????? j ??j??? ? ??j ?? ??~????? ?? ?~?j? ?? ??~?? ???j ???~ ???ji ??j?? ??j á~? ?? ?????? ? ?j?? ??? ?~??~?? ???? ????~?? ??~?? ?~?? ?~???j R4 0 7a jR404a R134a R22 ?~?~?? ?~??~ ???j?

áÕ~~???

???~??? .

????? ???~?j

?~

?? ??j ?~?~???

????~?? ?

????~ áãÇ~?j

?????? ?~??? ??? ?~ ???

?~??~j ?~?j??

?~??~j

?????????? ??j~?? ?~??~? ?j??? ?????

??~??

??~~??

??

??~~ ?~???~

???~?

???~ R134a j R22

?? ?? ????~???

????? ??i?i ?? ?????

??? ??? ???~??? ???~j

?????? ?~? ???~?? ??~?~~ ??? áÞ ???? ái?~ _???~???_j áãÇÔáÇ ????~?? áÏÇÈ~ áãÇÚ
?~~??~ ? ??? ái? ???? ?~?_j~_j ?????? ?»??A_j ??????_j á_j?? ?? ??? ????~?? ??~?? ???~j ?? ??~? ???~??? ???~ ???
. ????~?? ???? _???~???_j ??_j?? ????_j

. ?~?~??? NUT DTML ÏÇ~?? ??? ÁÇãáÇÈ ??~????? ÁÇ_j???? ??~????? É~???~ ?????? ?? : ???????? ???1???