|
REPUBLIQUE DU CAMEROUN
REPUBLIC OF CAMEROUN
Paix - travail - Patrie
Peace - Work - Fatherland
UNIVERSITE DE DOUALA
THE UNIVERSITY OF DOUALA
Faculté des Sciences Economiques
Faculty of Economics and
et de Gestion Appliquée
Applied Management

Mémoire rédigé en vue de
l'obtention du
Diplôme d'Etudes Approfondies (DEA) en
Economie
Mention : Economie et
Applications
INFRASTRUCTURES PUBLIQUES ET CROISSANCE AU
CAMEROUN
Présenté et soutenu par :
Rodrigue KUITCHA KWANDJEU
rodkuitch@yahoo.fr /
(00 237) 77 86 46 56
Maîtrise ès Sciences Economiques
Option : Economie Mathématique et
Econométrie
Sous la direction du
Pr Georges KOBOU
Agrégé en Sciences Economiques
Doyen de la Faculté de Sciences Economiques et Gestion
de l'Université de Yaoundé II (SOA)
Année Académique 2004-2005
DEDICACES
Je dédie ce travail à :
- Ma mère DJAMI MARTHE
- Mon père KWANDJEU JOSEPH
Pour tous les efforts, les souffrances et sacrifices consentis
pour ma personne. Puisse le Seigneur tout puissant leur accorder longue vie et
santé afin qu'ils puissent jouir et bénéficier du fruit de
toutes leurs privations.
A mes frères et soeurs, plus particulièrement
à YOMI ACHILLE, NOUKAM MICHELE, AURELIEN BETBEUI, SIMEN NATHALIE, NANA
ROSELINE, ALINE et GENTIANE KWANDJEU, qui n'ont cessé de m'encourager
même dans les moments les plus difficiles. Qu'ils reçoivent ici
toute mon affection.
REMERCIEMENTS
Aussi vrai que nos seules capacités n'auraient pas
suffi à parachever cette étude, nos sincères remerciements
vont à l'endroit de tous ceux qui de près ou de loin, n'ont
ménagé aucun effort pour s'impliquer personnellement à la
réalisation de ce travail de recherche.
Notre gratitude va spécialement à l'endroit du
Professeur Georges KOBOU, qui malgré ses nouvelles et contraignantes
responsabilités à Yaoundé II SOA, est resté
disponible pour suivre ce travail. Sa rigueur sur le plan
méthodologique, son esprit critique légendaire, ses observations
et suggestions constructives nous ont aidé à développer
nos aptitudes et capacités à la recherche.
Nous sommes entièrement reconnaissants à
l'endroit de nos enseignants dont les enseignements ont été
enrichissants pour notre formation. Sans être exhaustifs, ni exclusifs,
nous sommes moralement redevables envers les Professeurs Bruno BEKOLO EBE,
Blaise MUKOKO, dont les cours ont inspirés ce travail ; les
Docteurs Georges MBONDO pour sa disponibilité sans faille et sa
simplicité, Bertrand TAMOKWE qui a toujours eu la diligence de
réagir à toutes mes sollicitations.
Mes camarades et amis de promotion pour leur collaboration
illimitée et pour l'atmosphère de gaieté qu'ils ont
toujours diffuser dans notre cadre de recherche en l'occurrence : Ledoux
MATONG, MBANGA KASSI, KIKANDI Alain, MAMBOU Serge, NZUTCHI Flore, NGOUONGA
Awawou, BOUGUEU Alain, YOUMBI Alain, ASSOMO Carine, FOUDA Carole, AWOUNANG
Christelle, Vigny SUNKAM, Celestin NJIDJOU, Georges BANGBANG,......
Nos remerciements vont aussi à l'endroit de tout ceux
qui nous permis d'entrer en possession des données à la BM,
l'INS, DSCN, monsieur YAKE Isidore et spécialement toute la famille
KOUAYEP.
Et finalement à DIEU LE PERE TOUT PUISSANT de qui je
reçois en abondance les bienfaits jour après jour.
SOMMAIRE
Dédicaces..................................................................................................i
Remerciements.........................................................................................ii
Sommaire..................................................................................................iii
Liste des abréviations.........
.......................................................................iv
Liste des tableaux et graphiques
..................................................................v
Résumé....................................................................................................vi
Introduction
générale..................................................................................1
Première partie : Fondements
théoriques des l'infrastructures et de la
croissance.................................................................................................8
Chapitre 1 : Approches conceptuelles du lien
entre infrastructures
et
croissance...........................................................................................10
Section 1 :Les Infrastructures physiques
.................................11
Section2 :Les infrastructures sociales
...............................................25
Chapitre2 :Les théories de la
croissance.....................................................33
Section1:Le modèle néoclassique
de Solow-Swan ................................33
Section2 :Croissance et rendements
d'échelle.....................................46
Deuxième partie : Evaluation de l'impact
de l'infrastructure sur la croissance au
Cameroun...........................................................................................55
Chapitre 3 : Relation entre infrastructures de
transport et la croissance
au
Cameroun..........................................................................................57
Section1 :Présentation des
modèles....................................................58
Section2 :L'évaluation
empirique........................................................64
Chapitre 4 : Investissements en infrastructures
sociales
et croissance au
Cameroun......................................................83
Section 1 : Présentation des
modèles théoriques.................................83
Section 2 : L'évaluation
empirique......................................................89
Conclusion
générale.................................................................................97
Annexes..................................................................................................99
Références
bibliographiques....................................................................103
Table des
Matières..................................................................................108
Listes des sigles et abréviations
ACP : Afrique Caraïbe Pacifique
ADF : Augmented Dickey Fuller
APD : Aide Publique au Développement
BAD : Banque Africaine de Développement
BM : Banque Mondiale
CEMAC : Communauté Economique et Monétaire de
l'Afrique Centrale
DF : Dickey-Fuller
DSCN : Direction de la Statistique et de la
Comptabilité Nationale
DSRP : Document Stratégique pour la Réduction
de la Pauvreté
FMI : Fond Monétaire International
FRPC : Facilité pour la Réduction de la
Pauvreté et pour la Croissance
INS : Institut National de la Statistique
MCO : Moindres Carrés Ordinaires
OCDE : Organisation pour la Coopération et le
Développement Economique
OMD : Objectifs du Millénaire pour le
Développement
PAS : Programme d'Ajustement Structurel
PIB: Produit Intérieur Brute
PNUD : Programme des Nations Unies pour le
Développement
PP: Phillips-Perron
PPP : Partenariats Publics Privés
PVD: Pays en Voie de Développement
USA: United States of America
Liste des tableaux et graphiques
Liste des tableaux
Tableau 1 : Estimation en niveau sur les séries
agrégées..........................14
Tableau 2 : Estimation de l'élasticité de
la production en infrastructures de
transport.........................................................................................15
Tableau 3 : Tests de racine unité en
niveau............................................69
Tableau 4 : Tests de racine unité en
différence première...........................69
Tableau 5 : Tests de racine unité en
différence seconde...........................70
Tableau 6 : Résultats de la régression des
variables stationnarisées...........71
Tableau 7 : Résultats de la régression sur
les variables retardées...............71
Tableau 8 : Test de stationnarité sur le
résidu.........................................74
Tableau 9 : Test de Causalité de
Granger..............................................78
Tableau 10 : Récapitulatif du test de
stationnarité des variables..................90
Tableau 11 : Résultat des tests de
cointégration......................................93
Liste des graphiques
Graphique 1 : Résolution du modèle de
Solow........................................38
Graphique 2 : Effet d'une augmentation de (s) et
convergence dans le modèle de
Solow..............................................................................................41
Graphique 3 : Absence de convergence dans le
modèle AK.......................48
Graphique 4 : La courbe
d'Armey.........................................................85
RÉSUMÉ
Dans le contexte actuel d'assainissement des finances dans les
Etats, et dans le prolongement des réflexions relatives aux facteurs de
la croissance au sein des économies en développement, il convient
de s'interroger sur le rôle ou l'impact des infrastructures publiques
à la réalisation de la croissance dans un pays comme le
Cameroun.
En nous appuyant sur les résultats théoriques
des modèles de croissance, nous passons en revue les différentes
approches du lien entre infrastructures publiques et croissance, et nous
cherchons à évaluer son impact sur la croissance au Cameroun.
Nous développons ensuite des modèles théoriques qui
formalisent ce lien que nous testons empiriquement à l'aide d'un
modèle économétrique estimé sur la période
1980-2002. L'utilisation de ces deux modèles permet de mettre en
évidence le rôle positif des infrastructures physiques et sociales
sur la croissance au Cameroun.
Introduction
générale
L'analyse du rôle productif des infrastructures a connu
un développement précoce dans les années 40-50, à
la suite des débats autour de la croissance équilibrée
initiés par les théoriciens du développement
(Rosenstein-Rodan, 1943 ; Knurse, 1952 ; Hirschman, 1958). Ces
débats ont néanmoins été rapidement
éclipsés à partir des années 60, la
réflexion se déplaçant sur le front des questions de court
terme et de l'opposition entre effet multiplicateur et effet d'éviction
des dépenses publiques. Pendant plus de trente ans, l'investissement
public en infrastructures a en fait été plutôt perçu
comme un facteur de relance de la demande dans une optique de tradition
keynésienne, et son rôle productif occulté.
La perception du rôle des infrastructures comme facteur
de croissance économique a remarquablement évolué au cours
de ces dernières années. On assiste actuellement à un
renouveau de l'analyse des effets des infrastructures publiques sur la
croissance, en particulier grâce aux théories de la croissance
endogène qui mettent l'accent sur les externalités positives
qu'engendrent certains aménagements publics d'infrastructures. Il y a
externalités dans la mesure où les investissements publics en
infrastructures peuvent affecter la productivité des entreprises sans
que celles-ci ne supportent directement le coût. C'est à ce titre
que les dépenses publiques productives assimilées au capital
public d'infrastructure jouent un rôle moteur dans un processus de
croissance auto-entretenue.
La Banque Mondiale (1994), dans son rapport sur le
développement dans le monde consacré aux infrastructures et
l'adoption des Objectifs du Millénaire pour le Développement
(OMD) à l'occasion du sommet des Nations Unies en 20031(*) ont fait des infrastructures un
défi majeur pour le développement de l'économie et
l'amélioration des conditions de vie des populations.
En théorie économique, il n'y a pas
d'unanimité sur la définition du concept d'infrastructures
(Gramlich, 1994), dans la mesure où elle est susceptible de recouvrir
des réalités très différentes : d'une part, la
fourniture d'infrastructures de service public peut être assurée
par le secteur privé et échappe par là même à
la définition comptable retenue, mais il apparaît très
délicat de mesurer les infrastructures privés et de les
distinguer des autres catégories de capital privé. D'autre part,
elle peut être le fait de l'Etat lui-même par le biais des
administrations ou des entreprises publiques. Compte tenu de cette
difficulté nous choisissons dans cette étude de la faire reposer
sur un critère unique celui de « propriété
étatique », d'où la confusion des notions de capital
d'infrastructure et de capital public. Sur la base de la définition de
la Banque Mondiale (1994), nous nous referons aux secteurs intensifs en capital
et ayant des caractéristiques de monopoles naturels comme les
autoroutes, les autres moyens de transport, l'eau et le traitement des eaux,
l'énergie et les télécommunications. En d'autres termes,
cela correspond approximativement à la notion
« d'utilité publique ».
Au sens large, la notion d'infrastructure associe
étroitement les services attachés aux équipements, et elle
comprent les routes, les autoroutes, les voies ferrées, les ports et les
aéroports, les réseaux de télécommunications, les
réseaux nationaux de distribution du gaz, de l'électricité
et de l'eau, etc..... tous les investissements qui développent et
facilitent la circulation des personnes et des biens (Barro, 1990).
En plus des infrastructures physiques citées plus
haut, on peut aussi ajouter à cette liste les infrastructures sociales
à travers notamment l'éducation et la santé qui
améliorent la productivité de la main d'oeuvre et son adaptation
aux techniques modernes.
Historiquement, d'autres services ont favorisé, la
progression des échanges et participé à la promotion de la
croissance économique et du développement de chaque pays :
par extension, il est fait référence aux infrastructures
commerciales, sportives ou touristiques.
Dans le cadre de notre étude, nous focaliserons notre
attention sur les infrastructures en général et de transport en
particulier, auxquelles nous ajouterons les infrastructures sociales telles que
l'éducation et la santé.
Pour les économistes, les infrastructures sont le plus
souvent définies comme des biens collectifs mixtes à la base de
l'activité productive. Deux notions sous-tendent cette
définition : celle de bien collectif ou de bien public, et celle de
facteur productif.
La notion de bien collectif, définie par Samuelson
(1954) et Musgrave (1959), repose sur les critères de non
rivalité et de non exclusion. Un bien est qualifié de non rival
si son utilisation par un agent ne réduit pas la quantité
disponible pour les autres agents. La non rivalité s'accompagne, en
fait, de l'indivisibilité d'usage, c'est-à-dire d'une
consommation en totalité de ce bien qui ne pourra être
partagé entre divers utilisateurs. Les exemples traditionnels sont ceux
de la justice, de la sécurité ou de l'éclairage public. La
non exclusion par les mécanismes de marché caractérise, de
son côté, des biens dont aucun agent ne peut être exclu des
bénéfices. Celle-ci découle de l'impossibilité de
fractionner le service entre divers consommateurs. Ainsi, les
caractéristiques intrinsèques de ces biens, justifient
l'intervention de l'Etat dans leur production ou leur réglementation.
Parallèlement au débat théorique
porté par les nouvelles théories de la croissance, s'est
développé, au cours de la dernière décennie, une
importante littérature empirique visant à examiner les effets des
infrastructures publiques sur la croissance des nations mais aussi sur la
croissance locale, en particulier à l'échelle des Etats
américains. Au-delà des travaux pionnier de Ratner (1983)2(*), sur le caractère
productif des infrastructures, se sont les travaux d'Ashauer (1989) qui ont mis
en évidence un effet positif du capital public sur la production ou la
productivité des entreprises. Bien que récemment confirmée
par Munnel (1990), cette proposition continue de susciter diverses critiques
principalement d'ordre méthodologique parce que beaucoup
d'économistes estiment que la productivité marginale des
infrastructures qu'impliquent les estimations est exagérément
élevée.
L'essentiel des recherches actuelles, cependant,
s'intéresse au rôle de l'investissement global entendu
explicitement ou implicitement comme l'ensemble de l'infrastructure publique.
Bien que cette conception puisse convenir à certains pays industriels
comme les Etats-Unis où la participation du secteur public à
l'activité commerciale et industrielle est négligeable, elle peut
conduire à des erreurs dans le cas d'autres pays y compris la plupart
des pays en développement où l'Etat est engagé dans
multiples activités : là certains types d'investissements
publics sont susceptibles d'avoir des effets différents selon qu'il
s'agisse de l'investissement privé ou de la croissance globale.
L'investissement public sous la forme de ports, routes et de
télécommunication crée l'infrastructure de base
nécessaire à la réalisation de projets d'investissement
privé rentables et peut donc faciliter énormément la
croissance. Ainsi, le rôle des infrastructures dans la croissance est
d'une grande importance tant pour la politique économique, que pour
l'économie de développement.
L'histoire de l'aide publique au développement (APD)
est aussi celle d'une relative déception des bailleurs de fonds devant
l'impact souvent insuffisant des ambitieux projets d'équipement en
infrastructures qu'ils finançaient dans les pays en développement
comme le Cameroun et qui ont souvent laissé comme seul héritage
que celui d'un excès d'endettement. Les échecs
répétés de très grands projets (les fameux
« éléphants blancs ») ont laissé
entendre que les investissements lourds en capital physique constituaient une
approche peu efficace, davantage quantitative que qualitative de l'aide.
Déception et contrainte financière expliquent la réelle
désaffection qu'ont connue les infrastructures dans les pays pauvres,
avec une chute très sensible de leur financement au cours de la
dernière décennie.
Le déficit en infrastructures des pays pauvres est en
effet criant et hypothèque leur décollage économique. A
titre d'exemple, en Afrique et surtout celle qui s'étend au sud du
Sahara, les besoins d'investissements en infrastructures représentent 5%
à 6% du PIB (BAD), le taux d'analphabétisme de la population
adulte varie entre 20 et 60% avec des taux même supérieurs en ce
qui concerne la population féminine, alors que le coût de
transports maritime vers l'Europe ne dépassent de 30 à 70% ceux
en provenance d'Asie (Banque Mondiale, 1994). En Chine 20% des villages ruraux
ne sont pas connectés au réseau routier et 10% de la demande
d'électricité reste en moyenne insatisfaisante (Banque Mondiale,
1997).
Au Cameroun, les investissements comptent pour 20,23% du PIB
en moyenne pour la période allant de 1979/80 à 2000 et les
investissements publics n'en représentent que 3,8%.
Le Cameroun offre un marché de taille aux
investisseurs potentiels mais la mise en valeur de ses potentialités est
incontestablement entravée par les contraintes existantes en
matière d'infrastructure. Tant du point de vue de la qualité que
de la quantité, le Cameroun est en retard par rapport au reste du monde
dans le domaine des infrastructures, par exemple, moins de la moitié des
ménages ont accès à l'eau et un tiers seulement d'entre
eux ont l'électricité. Au Cameroun il existe en moyenne moins de
deux lignes téléphoniques pour cent habitants, on dénombre
sur l'ensemble du territoire camerounais un lit d'hôpital pour 1000
habitants (Les Atouts Economiques, 2005).
Dans un tel contexte, et étant donné la place
centrale que le gouvernement camerounais accorde aux infrastructures, dans sa
stratégie de développement national et d'ouverture à
l'économie mondiale, et confirmée dans la DSRP adoptée en
2000, il est important de savoir si les infrastructures publiques (capital
public) contribue à la croissance du PIB au Cameroun ? Où
encore quel est l'impact de l'infrastructure publique sur la croissance d'un
pays comme le Cameroun ? Il nous semble aussi important de nous interroger
sur le sens de la relation, si elle existe entre les infrastructures et la
croissance économique. Le Cameroun offre un champ d'analyse attrayant
dans la mesure où il le pays moteur de la zone CEMAC.
Toutefois, lorsqu'on souhaite appréhender l'impact de
l'infrastructure publique sur la croissance, il convient au préalable de
disposer d'une mesure adéquate de l'infrastructure. Le capital public,
le capital privé et le niveau de l'emploi sont les mesures usuelles
utilisées par la plupart des travaux empiriques. Au Cameroun, il existe
peu d'études concernant cette question, celles existantes ont plus
portées sur l'investissement total entendu explicitement ou
implicitement comme l'ensemble de l'infrastructure publique. Bien que cette
conception puisse convenir à des pays industriels comme les Etats-Unis
où la participation du secteur public à l'activité
commerciale est négligeable, elle peut conduire à des erreurs
dans le cas d'autres pays (y compris la plupart des PVD) ou l'Etat est
engagé dans de multiples activités. Néanmoins, Dessus et
Herrera (1996), et d'autres auteurs ont abordés un thème
semblable en coupes transversales sur un échantillon plus ou moins large
de pays comprenant le Cameroun, ou ont eu recours à
l'économétrie des données de panel. Cependant,
l'utilisation des MCO classique sur le panel ne permet pas de ressortir une
relation de long terme entre les différentes variables. Il
apparaît que cette procédure d'estimation peut conduire à
une relation fallacieuse du fait de l'absence de l'utilisation des techniques
de cointégration.
L'objet de ce mémoire est d'étudier s'il existe
une externalité de capital public, comme le supposent les modèles
de croissance endogène et si les investissements en infrastructure
(capital public) peuvent être considéré comme un des
objectifs des politiques d'aménagement du territoire.
En vue de répondre à cette question, ce travail
s'organise de la manière suivante : il comprend deux parties. La
première partie intitulée les fondements théoriques de
l'infrastructure et de la croissance présente les différentes
approches du lien infrastructures et croissance, ainsi que l'explication de la
croissance par le modèle le plus traditionnel utilisé par les
économistes pour traiter de la question. Elle comprend à ce titre
deux chapitres organisé ainsi qu'il suit : le premier chapitre
examinera la littérature ayant mis en exergue l'impact de
l'infrastructure sur la croissance suivant les différentes approches. Le
deuxième chapitre sera consacré à l'analyse des
théories de la croissance à partir du modèle
néoclassique. La seconde partie intitulée l'évaluation de
l'impact de l'infrastructure sur la croissance au Cameroun se divise
également en deux chapitres. On évaluera d'abord la contribution
de l'infrastructure de transport sur la croissance au Cameroun à travers
des tests de cointégrations, afin de mieux appréhender l'impact
de celle-ci, cette analyse va constituer notre chapitre trois. Par la suite,
une autre modélisation sera effectuée afin de mettre en exergue
l'impact de l'infrastructure sociale (à travers les dépenses
d'éducation et de santé) sur la croissance au Cameroun. En effet,
il permettra de conclure si l'infrastructure sociale est un facteur explicatif
de la croissance au Cameroun ou pas, sera l'objet du chapitre quatre. Il
viendra enfin une conclusion générale.
Première partie
Les fondements théoriques de l'infrastructure
et de la croissance Les économistes reconnaissent que
l'investissement dans les infrastructures est une importante source de
productivité et de croissance économique. Mais, les auteurs
n'aboutissent pas tous aux mêmes résultats, certains trouvant
excessif l'élasticité du capital public trouvé par
Aschauer, contrairement à d'autres qui aboutissent à une
élasticité du capital public plutôt moindre.
Pour baliser ce vaste champ théorique, nous avons
choisi de présenter tour à tour les différentes approches
qui mettent en relation le lien entre infrastructure et croissance et tirer les
enseignements qui s'imposent des analyses du modèle de base de Solow.
Cependant, les travaux de recherche sur la croissance ont
récemment bifurqué et l'on distingue maintenant les partisans
traditionnels ; pour qui l'absence d'une amélioration constante de
la technologie, la croissance par tête finit par s'estomper ; et les
tenants d'une vision moderne de la croissance.
Cette première partie constituée de deux
chapitres s'attellera à exposer les différentes approches
théoriques mettant en relation le lien entre les infrastructures et la
croissance (chapitre 1). Il est question de voir la spécificité
de chaque approche et voir elles aboutissent à la même conclusion.
Le chapitre 2 quant à lui s'attarde sur les théories
néoclassiques de la croissance Chapitre 1
Approches conceptuelles du lien entre infrastructures et
croissance
Paradoxalement, la prise de conscience par les
économistes d'une dimension productive des infrastructures publiques est
un phénomène récent, tant a été forte
l'influence keynésienne qui réduisait cette variable à un
multiplicande, objet privilégié du jeu du multiplicateur et
instrument par excellence de contrôle de la demande globale. Face
à la nécessité aujourd'hui dans un contexte international
de consolidation budgétaire, de mieux mesurer le rendement social des
différents types de dépenses publiques, c'est pourtant sur une
évaluation de la contribution productive des dépenses
d'investissement, et plus spécifiquement d'infrastructure, que doit
s'appuyer le débat et se fonder les arbitrages incontournables.
Oxley et Martin (1991), montrent ainsi que l'on peut
dégager certains traits communs au niveau des pays de l'OCDE, dans la
façon dont se sont effectués dans les années 70-80 les
ajustements visant à contrôler l'augmentation des dépenses
publiques. Les auteurs observent que certaines dépenses comme les
paiements d'intérêts au titre de la dette ou les transferts de
sécurité sociale ont fortement augmenté sur la
période. Mais dans le même temps, les dépenses
d'investissement ont été fortement réduites.
On comprend en effet aisément que les infrastructures
puissent constituer une variable privilégiée d'ajustements
budgétaires. C'est ainsi que plusieurs études ont
attribuées à la réduction du rythme des investissements
publics une part majeure du ralentissement de la productivité dans les
années 70 et 80.
Plusieurs voies de recherche empiriques ont été
successivement explorées dans le but de valider l'idée selon
laquelle les infrastructures contribuent à améliorer
l'efficacité du système productif et par là même
augmentent la productivité des facteurs privés.
Dans ce chapitre, nous allons présenter les
différentes approches théoriques du lien entre les
infrastructures physiques et croissance (section I), ensuite, nous essayerons
de montrer les effets de l'investissement dans l'infrastructure sociale sur la
croissance (section II).
Section 1 : Les Infrastructures physiques
Les systèmes de transport, comme les routes, les
autoroutes, les chemins de fer, les ports, les aéroports de même
que les rues, les réseaux de distribution d'eau et d'épuration
des eaux usées et les barrages etc sont des actifs publics qui sont
reconnus depuis longtemps comme partie intégrante et importante de la
richesse des nations. Ces infrastructures sont présentées comme
des biens qui facilitent les échanges et améliorent la
productivité des autres intrants dans la production. Le caractère
productif des infrastructures passe également par les
externalités qu'elles génèrent entre entreprises,
régions ou activités. Plusieurs approches ont été
développées pour quantifier le rôle du capital public sur
la croissance économique.
A) Le rôle productif des
infrastructures
Le caractère productif des infrastructures
relève de plusieurs logiques. La production de services publics
constitue, une activité économique à part entière.
Mais, une caractéristique propre de ces biens réside surtout dans
le facteur de potentialité qu'ils constituent. Ce facteur de
potentialité est direct, le rôle productif des infrastructures
passant par la fourniture de biens et services intermédiaires qui
participent au processus de production. Mais surtout, la particularité
des infrastructures réside dans la faculté d'améliorer
l'utilisation des autres facteurs de production. Il s'agit là d'un effet
indirect qui consiste à la diminution des coûts de production et
un accroissement de la rentabilité des activités
économiques.
1) Infrastructures et processus de production
La reconnaissance du rôle spécifique des
infrastructures publiques passe par leur introduction dans la liste des
facteurs de production. Il en résulte un élargissement du cadre
des fonctions de production macroéconomique, similaires à celui
constitué dans les années 1970 par la prise en
considération de l'énergie, afin de rendre compte des effets
d'offre des chocs pétroliers. Ainsi, dès 1952, Meade3(*) identifiait deux principales
représentations susceptibles de rendre compte d'une éventuelle
contribution productives du capital public. Dans la première,
qualifiée de modèle « d'atmosphère »,
les services induits par les infrastructures publiques sont supposés
augmenter la productivité d'un ou plusieurs facteurs privés
à la façon d'un facteur «environnemental ».
Formellement, ceci revient à faire l'hypothèse que ces services
peuvent être assimilés à une externalité productive
au sens de Romer (1986).
Dans le cas particulier où le capital public affecte de
façon symétrique la productivité de l'ensemble des
facteurs privés, il peut être représenté comme une
source de progrès technique neutre au sens de Hicks. En nous limitant
à une production de valeur ajoutée, notée Y, la
technologie de production peut alors être décrite par fonction
définie des facteurs d'emploi N, de capital productif privé K et
de capital public d'infrastructure dont la contribution sera notée  . .
Y(t) = A  (1)
(1)
où g(.) est de classe c2( R2+),
strictement croissante dans chacun de ses arguments quasi-concave et
satisfaisant les conditions d'Inada.
La seconde représentation proposée par Meade
(1952), qualifiée de modèle de « facteur
impayé » consiste à supposer que les services
d'infrastructures mises à la disposition de l'entreprise privée
représentative, direct, mais non rémunéré. On a
alors une fonctions de production définitive par :
Y(t) = A(t) f (2)
(2)
De plus, on peut envisager la possibilité que le
capital public puise affecter la production des deux manières auquel
cas la fonction de production s'écrit comme une combinaison des
équations (1) et (2).
Dans l'approche de Meade (1952), les services productifs
associés aux infrastructures mises à la disposition de
l'entreprise privée sont directement identifiés au stock de
capital public. On raisonne ainsi sous ces équipements constituent un
bien public pur au sens de Samuelson (1954) (op. cité), sans congestion
ni éviction possible entre les utilisateurs.
Cependant, si les infrastructures sont soumises à des
effets de congestion, les services rendus à chaque utilisateur diminuent
avec le nombre d'utilisateurs, ou, de manière équivalente avec le
volume des facteurs privés utilisés. Formellement, on pose alors
que :
 (3) (3)
Où la fonction g(.) de classe
C2(R2) est une fonction strictement concave satisfaisant
les conditions suivantes :
  
et où g(.) est homogène de degré 1 en
Kg.
Comme nous le verrons par la suite, la plupart des
études empiriques proposant une estimation de la contribution productive
du capital public, adoptent une forme fonctionnelle de type Cobb-Douglas.
Même si la première tentative d'examiner
empiriquement l'importance du capital public dans une fonction de production
agrégée remonte à Ratner (1983)4(*), ce n'est qu'avec la publication
de l'étude d'Aschauer (1989) qu'un vif débat s'est amorcé
sur la question parmi les économistes.
Aschauer observe un lien très grand et très
fort entre le capital d'infrastructure publique et la production du secteur
privé, le rendement du capital public est beaucoup plus
élevé que celui du capital privé. Aschauer montre qu'une
augmentation de 1% du stock de capital se traduit par une augmentation de la
production du secteur privé de 0.39%. En effet, Aschauer a amorcé
ce mouvement dans une série d'études contreversées mais
pénétrantes, soutient que l'infrastructure de base (construction
des routes, ponts, rues, aéroports, système de transports en
commun,....) a plus grand pouvoir explicatif de la productivité. Selon
ce dernier, le ralentissement de la productivité observé dans les
années 70 jusqu'au milieu des années 80 dans les pays de l'OCDE
serait imputable à l'insuffisance des investissements publics
enregistrés. Ces travaux qui font une oeuvre de pionnier dans ce
domaine, ont suscité de nombreuses contributions au cours de la
dernière décennie confirmant ces résultats, comme le
montre le tableau suivant sur données américaines et de
l'OCDE.
Tableau 1 : Estimations en niveau sur séries
agrégées.
|
Etude
|
Données
|
Sources
|
Meth
|
Spec
|
Eg
|
Ek
|
En
|
|
Etat Unis
Ratner (1983)
Aschauer (1989)
Munnell (1990)
Sturm et de Haan (1995)
Einsner (1994)
OCDE
Berndt et Hansson (1991)
Oho et Voss (1994)
|
USA (49-73)
USA (49-85)
USA (49-87)
USA (49-85)
USA (61-91)
SUE (60-88)
AUS (66-90)
|
Musgrave
B.E.A
B.E.A
F.R.B
B.E.A
Hansson
ABS
|
AR (1)
M C O
M C O
M C O
AR (1)
AR (1)
M C O
M C O
|
CD/RC
CD/RC
CD/RL
CD/RC
CD/RC
CD/RL
CD/RL
CD/RCFP
|
0,06
0,39
0,31
0,41
0,45
0,27
0,68
0,38
|
0,22
0,26
0,64
0,12
0,03
0,19
0,37
0,47
|
0,72
0,35
-0,02
0,47
0,58
0,97
0,40
0,53
|
BEA : Bureau of Economic App ; FRB :
Federal Reserve Bank ; CD : Cobb-Douglas ; RC : Rendements
libres ; RL : Rendements Libres ; RCFP : Rendements
constant dans les seuls Facteurs Privés.
Quant au tableau 2, il montre les résultats des
estimations de l'élasticité de la production par rapport aux
investissements en infrastructure de transport.
Tableau 2 : Estimation de l'élasticité de
la production par rapport aux investissements en infrastructure de transport
|
Auteur
|
Spécification
|
Type d'investissement
|
Elasticité
|
|
Aschauer (1991)
Seitz (1993)
Munnell et Cook (1990)
Deno (1988)
Garcia-Mila et McGuire (1992)
|
Fonction de production
(données américaines)
Fonction de coût
(données routières allemandes)
Fonction de production
(48 Etats contigus des USA)
Modèle de fonction de profit (données
américaines)
Fonction de production
(48 Etats contigus des USA)
|
Investissement en transport
Investissement en transport urbain
Investissement en transport routier
Modification du coût privé moyen
Investissements routiers
Investissements routiers
Investissements routiers
|
0,166
0,384
0,231
0,05
0,06
0,31
0,04
|
Source : Banister et Berechman (2000), p. 150 cité
par Roy, p. 9
A partir d'une spécification excluant la tendance
temporelle de manière à atténuer certains problèmes
posés par les données des séries chronologiques Munnel
(1990) obtient ainsi une élasticité estimée du capital
public comprise entre 31% et 39% suivant la nature des rendements
d'échelle5(*). Selon
l'auteur, ces résultats illustrent le fait que l'importance de la
décélération de la productivité des facteurs
privés traditionnellement mesurée ne provient en fait que de
l'omission du stock de capital public dans la liste des facteurs de production.
Une fois prise en compte les externalités associées aux
infrastructures publiques, la diminution de la productivité moyenne du
travail sur les périodes 1948-69 et 1969-87 passe en effet de 1,4%
à seulement 0,3%. La différence est alors uniquement imputable au
ralentissement de la croissance des investissements publics. Ces
résultats sont sensiblement identiques à ceux d'Eisner (1994) qui
reprenant les spécifications d'Aschauer, obtient notamment une
élasticité de 24% par la méthode Cochrane-Orcutt sous
l'hypothèse de rendements libre sur la période 1961 -1991.
Une autre illustration du rôle du capital public comme
facteur de croissance peut être vue dans le travail de Ford et Foret
(1991) sur la productivité globale des facteurs de 12 pays de l'OCDE.
Les auteurs ne mettent en évidence l'impact significatif du capital
public que pour la Belgique, le Canada et la Suède, et ce de
façon très variable selon les pays. Pour la France, c'est
seulement le coeur d'infrastructure qui semble jouer.
Parallèlement, plusieurs autres applications empiriques
ont été proposées pour différents pays de l'OCDE
hors Etats-Unis. Ainsi, Berndt et Hansson (1992) fournissent une
première estimation pour la Suède (1960-88) avec une
élasticité du capital public de l'ordre de 69%. Sur les
données canadiennes, Wylie (1996), obtient sous l'hypothèse de
rendements constants une élasticité de 51% proche des
résultats obtenus sur données américaines.
Enfin, Otto et Voss (1994), privilégiant
l'hypothèse de rendements constants par rapport aux seuls facteurs
privés estiment sur données australiennes entre 1966 et 1990 une
élasticité de 38%.
Des résultats controversés pour les pays en
développement
Des études analytiques récentes ont
souligné le rôle différent de l'investissement public et
privé dans le processus de croissance. L'investissement public en
infrastructure, dans la mesure où il est complémentaire à
l'investissement privé, peut augmenter le produit marginal du capital
privé, augmentant de ce fait le taux de croissance de l'économie.
Ceci est un point particulièrement important pour les pays en
développement. Au contraire si les activités de production
publiques sont concurrentes des initiatives privées, il peut y avoir des
effets de substitution ou d'éviction qui peuvent conduire à des
effets négatifs sur la croissance. Cependant, les évidences
empiriques de la relation entre les pays en développement demeurent
ambiguës.
En utilisant un échantillon de 95 pays en
développement sur la période 1970-1990, Kahn et Kumar (1997) ont
montré que les effets de l'investissement privé et public sur la
croissance étaient significativement différents, l'investissement
privé étant de façon consistante plus productif que
l'investissement public. Knight, Loayza et Villanueva (1993) et Nelson et Singh
(1994) ont aussi mis en évidence le fait que le niveau de
l'investissement public en infrastructure avait un effet significatif sur la
croissance notamment au cours des années 80.
L'investissement public sous forme de construction des ponts,
ports, routes crée l'infrastructure nécessaire à la
réalisation des projets d'investissements privés rentables
susceptibles de faciliter énormément la croissance contrairement
à l'investissement public dans l'industrie et le commerce. Cette
intuition a été empiriquement confirmée par Easterly et
Rebelo (1993) sur un échantillon de 119 pays. Malgré une
information parfois insuffisante, ils constatent que l'investissement du
gouvernement central, qui vraisemblablement inclut la majorité des
projets d'infrastructures, est positivement corrélé à la
croissance. En subdivisant par secteur, ces auteurs constatent que c'est
l'investissement public dans les transports et les communications qui exerce un
effet plus vigoureux sur la croissance.
De nombreux chercheurs ont réexaminé ou
approfondi la relation entre le capital d'infrastructure publique et la
croissance économique. Toutefois, comme nombre d'études l'ont
montré, il est probable que les estimations par la fonction de
production ont surestimé l'incidence des investissements
réalisés dans l'infrastructure publique sur la production du
secteur privé sur la croissance de la productivité. En outre, il
n'est pas logique que les investissements publics aient une incidence beaucoup
plus grande sur la production du secteur privé que les investissements
privés. Pour atténuer certains problèmes survenus dans les
études faites, les économistes utilisent de plus en plus d'autres
approches comme celle par la fonction de coût.
2) L'approche duale : fonction de coût et
demande des facteurs
L'approche duale présente la formalisation
microéconomique du lien entre infrastructures et croissance qui passe
par l'amélioration de la rentabilité des facteurs de production.
Elle est fondée sur la dualité entre fonction de production et
fonction de coût, à savoir que la structure de la production peut
être entièrement présentée par une fonction de
coût restreinte. Elle exploite la propriété selon laquelle
le choix d'une combinaison de facteurs optimale associe une valeur unique et
minimale du coût de production et un vecteur de coûts des facteurs
donnés. A partir d'une fonction de production augmentée au
capital public et connaissant le coût des facteurs de production,
l'approche duale consiste à déduire du programme de minimisation
du coût des entreprises une fonction de coût unitaire. Cette
fonction permet d'identifier l'élasticité des infrastructures en
terme de réduction des coûts de production et de déduire
une fonction de demande de facteurs.
On distingue en général une fonction de
coût à court terme, qui dépend notamment du prix des
facteurs variables et des quantités de facteurs fixes à savoir le
capital public et le capital privé, sachant que les entreprises ne
maîtrisent pas ces facteurs fixes à court terme. A long terme,
elles ajustent ces quantités à leur niveau optimal. La fonction
de coût ne dépend alors plus que du prix des facteurs.
L'approche duale fait en outre, souvent apparaître un
lien de complémentarité du capital public avec l'investissement
privé, et de substituabilité avec le facteur travail. Quant
à la productivité du capital, elle est en général
inférieure à celle du capital privé.
Les études qui mettent en oeuvre l'approche duale
prennent des formes relativement variées, elles portent aussi bien sur
des données agrégées, que sectorielles et
régionales. Elles ne concernent que peu, de pays en développement
du fait sûrement d'un manque de données encore plus flagrant que
dans autres approches (données de prix des facteurs notamment).
La contribution de Lynde et Richmond (1993) cité par
Henin et Hurlin représente une application exemplaire de l'approche
duale. Ces auteurs considèrent deux facteurs de production
privés. Ils obtiennent un système à trois
équations : les parts des salaires et de la
rémunération du capital dans le produit et le ratio de profit
pur, net de coût d'usage, qu'ils testent économétriquement.
Les résultats obtenus sur données agrégées
américaines pour la période 1958-1989 concluent à une
contribution significative du capital d'infrastructure, tant à la
réduction des coûts de production, que sur la productivité
du travail. Leurs estimations leur permettent, en outre, de chiffrer à
40% la contribution au ralentissement de la productivité privée
entre le milieu des années 1970 et la fin des années 1980 de
l'investissement public.
Les applications sectorielles de l'approche duale constituent
un autre champ de mise en pratique tout aussi intéressant. Nadiri et
Mamuneas (1994) considèrent un panel de 12 industries
manufacturières américaines ayant une fonction de production
comportant trois facteurs privés (travail, capital et consommations
intermédiaires) et deux facteurs publics (infrastructures et
recherche-développement). Ils obtiennent un système de trois
équations dont une des coûts de production (déflaté
par le prix des consommations intermédiaires) et deux respectivement de
part du travail et de capital. Les auteurs prennent, en outre, en compte
l'hétérogénéité sectorielle par
l'introduction des variables indicatrices spécifiques. L'estimation de
ce système d'équations leur permet de montrer une contribution
significative des infrastructures à la réduction des coûts
dans le privé ; l'élasticité des coûts
privés par rapport au capital d'infrastructure variant de - 0,11 dans
les transports ou la construction mécanique à - 0,21 pour le
raffinage du pétrole, tandis que l'impact de la recherche
développement s'avère nettement plus faible.
Conrad et Seitz (1992) appliquent une méthode semblable
sur les données Allemandes relatives à quatre grands secteurs sur
la période 1961-1988. Ils trouvent une élasticité positive
du capital privé par rapport au capital public avec des valeurs moyennes
de 0,24 dans l'industrie manufacturière, de 0,34 dans la construction de
0,48 dans le transport et le commerce, 0,06 dans les services.
L'élasticité de la productivité globale par rapport aux
infrastructures est trouvée positive (de 0,62 à 0,30 pour
l'industrie manufacturière, de 0,05 à 0,29 pour les branches
transport et commerce).
Enfin deux études concernant les pays en
développement doivent être mentionnées. Il s'agit de celles
de Shah (1992) sur un panel de 36 industries Mexicaines de 1970 à 1987
et de Elhance et Lakohaman (1988) sur l'industrie manufacturière de six
Etats de l'Inde.
Shah teste particulièrement l'hypothèse
l'équilibre, entendue ici comme l'adéquation des facteurs fixes
à leur valeur de long terme. A nouveau, les infrastructures contribuent
à réduire les coûts privés à court terme. A
long terme, elles apparaissent comme faiblement complémentaires
à la fois au capital privé et à l'emploi. Les calculs de
rendement établissent à la fois le capital privé et le
capital public sont disponibles à un niveau inférieur à
leur niveau d'équilibre. Ce résultat est néanmoins
vraisemblablement dû à la mauvaise qualité des
infrastructures mexicaines. Elhance et Lakshaman (1988), de leur
côté, mettent en évidence un ajustement de l'investissement
privé inférieur au niveau optimal, qui les amène à
conclure à un déficit en infrastructures, notamment des Etats les
plus pauvres. Ils recommandent en outre, une concentration des investissements
publics sur les infrastructures physiques, celles -ci apparaissent plus
productives que les infrastructures sociales.
Ainsi, l'approche duale constitue de la sorte la
manière la plus rigoureuse de traiter la relation entre le capital
public et la croissance. Elle fournie un certain nombre d'outil précis
adaptés à la décision politique en matière
d'investissement public. Une limite de cette approche se situe,
néanmoins dans le type de données nécessaire à son
élaboration, notamment pour les pays en développement dans lequel
cet outil serait d'une utilité.
B) Les nouvelles approches du lien infrastructures
croissance
1) Les effets de la diffusion spatiale des
infrastructures
Une des caractéristiques des infrastructures
réside dans le fait qu'elles sont à l'origine
d'externalités spatiales. Il est, en effet, évident qu'un pays ou
une région bénéficiera des infrastructures de ses voisins,
qui lui permettront notamment d'avoir accès à de nouveaux
marchés d'importer de la technologie à moindre frais ou de
participer à une certaine division régionale du travail.
L'exemple des pays ou régions enclavés est à ce titre tout
à fait illustratif de telles situations de dépendance.
Malgré une reconnaissance ancienne de la part de
l'économie urbaine et régionale, la modélisation des
effets de diffusion spatiale n'a pas bénéficié du
foisonnement théorique qui a jalonné le renouveau de la
macroéconomie de la croissance. Le modèle fondateur de Chua
(1993), ne comprend cependant pas de variable d'infrastructures à
proprement parler. Chua développe un modèle de croissance
exogène à la Solow, dans lequel le revenu d'équilibre d'un
pays dépend de la formation du capital physique et humain des pays
voisins. Un résultat intéressant de ces estimations
réside, en outre, dans le fait que ces effets de la diffusion
réduisent beaucoup la significabilité des variables indicatrices
pour l'Afrique, l'Asie et l'Amérique Latine. Cette situation met
clairement en évidence l'existence, dans la croissance et la convergence
des pays, de dynamiques régionales peu développées et mal
expliquées jusque là.
Une autre approche indirecte de cet effet de diffusion
spatiale a été entreprise par Nagaraj, Varoudakis et
Véganzones (1999) sur les Etats de l'Inde. Les auteurs valident sur
données de Panel, en suivant un schéma de convergence
conditionnelle, le rôle des infrastructures comme facteur de
différences de performance économiques des Etats. Ils mettent
cependant parallèlement en évidence un effet de diffusion de la
croissance entre Etats voisins. Or, cette croissance dépendant du niveau
d'équipement en infrastructures de chaque Etat, ce résultat
permet de montrer par transitivité, le rôle de ces
équipements dans la diffusion spatiale de la croissance.
Holtz-Eakin et Schwartz (1995) se sont attachés, quant
à eux, à valider plus directement les externalités
spatiales générées par les infrastructures. Contrairement
à la quasi-totalité des études empiriques qui touchent au
lien entre infrastructures et croissance, l'indicateur testé ici est
tout à fait précis, puisqu'il s'agit des routes inter-Etats et
des routes principales à l'intérieur des Etats
américains. Les routes étant le moyen de transport aux USA, leur
impact productif s'avère très significatif bien que de faible
ampleur puisque ne constituant qu'une partie des infrastructures totales du
pays.
Ainsi, malgré l'attrait que présente cette
nouvelle voie de recherche, les implications de politique économique de
ce modèle sont tout à fait intéressantes. L'existence de
ces phénomènes de diffusion spatiale doit en fait être
prise en compte, si l'on veut promouvoir la croissance à la fois
domestique et régionale. En effet, l'ignorance de l'externalité
positive engendrée par son propre investissement sur la croissance des
Etats voisins et donc sur sa propre croissance entraînent automatiquement
un investissement inférieur à l'optimum. Une coordination des
efforts nationaux d'investissement semble ainsi d'autant plus
nécessaire, que l'on se place dans une perspective d'intégration
régionale ou de croissance régionale équilibrée.
2) La dynamique transitoire ou l'approche en terme de
convergence conditionnelle
Les travaux empiriques sur le rôle des
infrastructures comme facteur de croissance utilisant l'approche de la
convergence conditionnelle sont beaucoup moins nombreux. Sous sa forme
élémentaire, cette approche repose sur une régression
simple du taux de croissance sur un niveau initial visant à tester une
propriété de convergence absolue. Sous une forme plus
développée, il s'agit de tester la convergence conditionnellement
à des variables explicatives, représentant des conditions
initiales ou des politiques. A priori, l'approche en terme de convergence
conditionnelle représente un cadre pertinent pour évaluer dans
quelle mesure l'effort d'investissement en infrastructure relatif d'un pays
contribue à son rythme de croissance comparativement à d'autre
pays.
Un certain nombre de travaux ont permis de faire
apparaître un impact positif de l'investissement public sur la
croissance. On citera ceux de Barro (1991), Khan et Kumar (1997), Knight,
Lvayza et Villanueva (1993) sur des échantillons respectivement de 98,95
et 59 pays en développement et 21 pays développés. On
mentionnera également les résultats de la Banque Mondiale (1994)
concernant les dépenses d'électricité, d'eau, de
transports et de communications.
Un nombre de travaux tout aussi important donne,
néanmoins, des résultats moins probants notamment ceux de
Sala-I-martin (1997) qui teste la robustesse de plusieurs variables
explicatives rentrant fréquemment dans les équations de
convergence conditionnelle. Alors que Levine et Kenelt (1992) utilisant une
méthodologie très restrictive concluent à l'absence de
signification des variables testées, les auteurs mettent en
évidence la robustesse de 22 d'entre elles (sur un total de 60) dont la
variable d'investissement privé en équipements.
Malgré le caractère plus satisfaisant de la
méthode, ces tests ne permettent pas de rejeter de façon
convaincante l'impact de l'infrastructure sur la croissance. D'une part,
l'effet important de l'investissement privé en équipements cache
peut être celui des infrastructures. D'autre part comme le soulignent
Barro et Sala-I-Martin (1995), l'investissement public englobe toute une
série de dépenses en capital, qui ne peuvent pas toujours
être considérées comme productives pour le secteur
privé. C'est le cas de celui des entreprises d'Etat du secteur
concurrentiel ou des dépenses militaires. En outre, l'investissement
public en tant que tel n'est pas toujours recensé dans certains pays
pour lesquels on substitue parfois les dépenses publiques totales. Se
trouverait ainsi mis en cause la capacité d'un certain nombre de pays en
développement à maîtriser tant le volume que
l'efficacité de leur programme d'investissement public. Une contribution
récente se propose d'expliciter ce point en construisant une mesure
approximative de l'efficacité d'utilisation du capital
d'infrastructures. Après avoir montré théoriquement qu'une
telle variable devait figurer dans l'équation de convergence
conditionnelle, Hulten (1996) construit une variable synthétique
d'utilisation des infrastructures, à partir de quatre séries
spécifiques documentées par la Banque mondiale pour 42 pays
à revenu faible ou moyen. (le taux de défaillance pour 100 appels
téléphoniques, le taux de pertes sur l'électricité
produite, le pourcentage du taux disponibilité du parc de locomotives
Diesel). Cette variable améliore de manière spectaculaire la
qualité d'ajustement des régressions de croissance et cette
variable apparaît très significative.
Ainsi, si l'approche par la convergence conditionnelle semble
donner des résultats aussi mitigés, des voies de recherche allant
d'une part, vers les méthodes économétriques les plus
appropriées, d'autres part vers l'utilisation d'indicateurs quantitatifs
précis semblent porteuses d'avenir. Les questions de la bonne gestions
des infrastructures et de la qualité des équipements sont
également une voie à explorer, tant ces critères qui font
défaut dans un grand nombre de pays en développement pourraient
en partie expliquer les difficultés de validations quantitatives du
rôle des infrastructures dans la croissance.
Tous ces développements visant à montrer le
rôle productif des infrastructures publiques sur la croissance n'ont tenu
compte que des infrastructures physiques. Or, dans les nouvelles études
portant sur l'infrastructure, certains auteurs mettent l'accent sur les
infrastructures sociales à travers notamment les dépenses
d'éducation et de santé.
Section II : Les infrastructures sociales
Les infrastructures par les services qu'elles rendent aux
agents économiques, contribuent à la satisfaction de leurs
besoins et constituent un des principaux vecteurs de développements des
nations. Le financement et la réalisation d'investissements collectifs
sont apparus avec l'unification progressive des nations et le rôle
croissant des Etats, à travers la construction des écoles, des
centres de santé, équipement des laboratoires, améliorant
ainsi les conditions de vie des populations. Dans cette section, nous allons
traiter des caractéristiques et de l'influence des investissements
publics dans les infrastructures sociales.
A) Caractéristiques et effets des
dépenses d'infrastructures sociales sur la croissance
1) Définition et caractéristiques des
infrastructures sociales
A la suite de Hirschman (1958), on peut définir les
infrastructures comme les biens et les services qui rendent possible
l'activité économique. Cette définition,
particulièrement large, est reprise par Hansen (1965) qui est le premier
à proposer une classification précise. Il distingue : les
infrastructures économiques, dont la caractéristique est de
participer au processus productif et les infrastructures sociales, dont la
fonction est d'entretenir et de développer le capital humain (comme
l'éducation, les services sociaux et de santé). Les
infrastructures sociales se rapportent donc aux services relatifs aux champs
sanitaires sociaux et d'éducation.
En matière sanitaire, les infrastructures de
santé sont identifiées par le nombre de lits d'hôpitaux, la
répartition géographique et la taille de ces derniers, les autres
centres de soins, les équipements dont chaque établissement est
doté. Leur utilisation par les populations est liée au service
qui leur sont associés : spécialisation des actes
médicaux, types et qualité des traitements
réalisés, accessibilité à certaines formes de
soins, compétences du personnel.
De manière similaire, les infrastructures
éducatives reposent sur les établissements et les
équipements scolaires, universitaires (des classes maternelles aux
laboratoires scientifiques les plus spécialisés) dans leur
diversité.
Ces exemples comme pour les autres infrastructures mettent
ainsi en évidence quelques caractéristiques de base :
celles-ci se rapportent à des services gratuits ou payants,
généralement à l'origine d'une consommation collective,
elles disposent d'un statut public ou privé (Thelmann, 1997 ;
Debande, 1997).
En dépit de leur diversité, les infrastructures
qu'elles soient physiques ou sociales, partagent des caractéristiques
communes. Elles sont très lourdement capitalistique et
nécessitent d'importants investissements.
Dans notre étude, il est admis que le terme
infrastructures sociales recouvre en général d'autres notions que
la seule scolarisation. Dans la littérature macroéconomique,
cependant, il désigne principalement l'éducation (plus rarement
la santé), c'est ainsi que nous retiendrons ce terme de manière
conventionnelle.
2) Les effets des infrastructures éducatives
sur la croissance
Pour analyser les effets des infrastructures
éducatives sur la croissance, les économistes qui l'ont fait se
sont beaucoup plus focalisés sur les dépenses publiques
attribuées à l'éducation ou la santé par le
gouvernement, dans la mesure où ce sont ces dépenses qui sont
nécessaires à la construction des édifices, à
l'achat des équipements et divers autres matériels. Les travaux
de recherche publiés dans le monde donnent à penser qu'il
pourrait bien y avoir un impact des investissements en infrastructures
scolaires sur le niveau des élèves mais ils présentent
aussi des cas où le résultat est mitigé. En ce qui
concerne les aspects qualitatifs, de bons exemples sont donnés sur la
façon dont l'amélioration des bâtiments influe sur les
résultats des élèves. Les travaux sur les aspects
quantitatifs montrent qu'il existe généralement des liens
positifs entre l'investissement et la croissance via l'amélioration du
niveau des élèves, mais ils ne font pas une distinction entre les
différents types d'investissements.
C'est ainsi que dans une étude récente
menée par Blankenau et alii sur un groupe de 80 pays comprenant 23 pays
développés et 57 pays en voie de développement, entre
1960-2000 aboutie à des conclusions prometteuses, puisqu'elles font
apparaître l'existence de liens solides entre l'investissement permettant
de mieux adapter les locaux aux besoins de l'enseignement et
l'amélioration du niveau des élèves. Car ces
investissements auront à l'avenir des retombées
économiques pour l'ensemble de la collectivité grâce
à l'augmentation attendue des gains futurs. De plus, une augmentation de
1% des dépenses en matière d'infrastructures éducatives se
traduit par une augmentation de 0,202% du PIB.
Par ailleurs, en déterminant l'effet des
dépenses publiques d'éducation sur la croissance sur un vaste
échantillon de pays, Barro et Sala-i-Martin parviennent à la
conclusion selon laquelle les dépenses d'éducation ont un effet
positif sur la croissance : une augmentation de 1,5% du ratio des
dépenses publiques d'éducation au PIB durant la période de
1965-1985 aurait augmenté le taux de croissance moyen de cette
période de 0,3% par an.
Dans une série de travaux menés par Bose et alii
en 2003 sur l'impact des dépenses publiques sur la croissance, les
auteurs aboutissent à la conclusion que les investissements et les
dépenses totales engagées dans l'éducation sont
significativement liés à la croissance, comme les autres
investissements et les autres dépenses effectués dans le secteur
des de transport, communication et défense.
La Banque Mondiale soutient que investissements concernant les
infrastructures scolaires et sociales ont contribués à la
réduction des sureffectifs, à l'amélioration de
l'hygiène et de la sécurité dans les écoles,
à l'accès aux soins de santé primaires, et, à un
moindre degré, à l'accès aux ressources de production. Ces
investissements ont ainsi crées des conditions propices à un
enseignement de qualité et concourus ainsi à la formation du
capital humain, élément déterminant de la
prospérité économique, du plein emploi et de la
cohésion sociale. Pour ce qui est de la remise en état et
l'équipement des établissements scolaires hors université,
l'élimination des risques matériels pour les occupants des
écoles endommagées, la diminution des frais liés aux
services collectifs et à l'entretien et la contribution à la
réduction de la pauvreté ne sont que quelques unes des
retombées spécifiques des investissements liés à la
remise en état. Tous ces résultats contrastent cependant avec
ceux obtenus dans la plupart des pays en développement.
Castro-Leal, Dayton, Demery et Mehra (1999), dans une
étude utilisant une approche basée sur l'analyse de l'incidence
des avantages pour analyser l'impact des dépenses liées à
la construction des écoles et hôpitaux dans un échantillon
de sept pays africain, montrent que ces dépenses ne
bénéficient pas aux pauvres ; elles favorisent plutôt
les plus nantis. Pour ces auteurs, la solution à ce problème ne
se limite pas à un simple réajustement des dépenses
publiques. Il est important de prendre en compte les contraintes qui
empêchent les pauvres de tirer partie de ces dépenses ou
investissements.
Dans une étude importante consacrée aux
dépenses d'éducation, de santé et la réduction de
la pauvreté en Afrique, Morrison et alii (2002), montrent que l'Etat
devrait investir d'avantage dans la construction des écoles en zone
rurale afin d'assurer l'accès de tous aux services d'éducation et
de santé, plutôt que d'investir dans des programmes ciblés
plus coûteux, qui ne bénéficient pas aux pauvres. Ils
soulignent que la cohérence et la coordination doivent être des
nécessités absolues, afin d'éviter de construire des
écoles qui resteront sans professeurs et des dispensaires qui ne
pourront être approvisionnés en médicaments.
Bien plus, les études de Easterly et Rebelo (1993) sur
différentes spécifications, ainsi que celles de Levine et Renelt
(1992) aboutissent à la conclusion que les dépenses de l'Etat en
matière d'éducation ne sont pas corrélées à
la croissance des nations. De même que Zhang et Casagrande (1998), Landau
(1986), ont montrés que les dépenses d'éducation ne sont
pas un déterminant significatif pour la croissance dans les pays en
développement.
Contrairement à ces études qui mettent l'accent
sur les infrastructures sociales liées à la construction des
édifices sanitaires et solaires, certains auteurs mettent l'accent sur
les infrastructures sociales à travers notamment l'éducation et
la santé qui améliorent la productivité de la main
d'oeuvre et son adaptation aux techniques modernes.
B) Incidence des infrastructures sociales sur le
capital humain
1) Education et croissance
Les économistes ont reconnu l'importance des
investissements consacrés aux êtres humains depuis les travaux
précurseurs de Mincer (1958) et Becker (1962). Les dépenses
consacrées à l'éducation à la formation
professionnelle, aux soins de santé contribuent à accroître
la qualité de la main d'oeuvre et à hausser la
productivité.
L'investissement dans la construction des écoles, des
universités, l'équipement des laboratoires influence la
production d'un pays à travers le capital humain c'est pour cette raison
que nous analysons dans cette sous section la relation entre l'éducation
et la croissance d'une part et la relation entre santé et croissance
d'autre part.
Benhabib et Spiegel postule que l'impact de
l'éducation sur la croissance dépend de l'état de
développement des infrastructures des pays. Certains chercheurs ont
tenté de généraliser ce principe. Sur des
échantillons assez petits, il n'est pas aisé de donner beaucoup
de flexibilité aux estimations, c'est-à-dire d'estimer plus qu'un
effet moyen. Cependant, il semble possible de décliner le principe
selon lequel l'effet de l'éducation sur la croissance ne résulte
pas d'une règle universelle mais dépend fortement des conditions
économiques et institutionnelles propres à chaque pays. Par
exemple, Dessus (1998) observe que l'effet de l'éducation est plus
important dans les pays dont l'économie est plus ouverte. Pour
interpréter cette relation, on peut recourir à l'argument de
Maurin et al (2003) qui montrent que l'éducation est
particulièrement valorisée dans les entreprises qui font face
à la concurrence internationale parce qu'elle améliore la
capacité d'adaptation dans un univers fortement concurrentiel
En examinant l'ensemble des donnés sur
l'éducation Griliches (1997) signale que le nombre d'année
d'études pourrait avoir représenté, aux Etats-Unis, le
tiers de la composante résiduelle de la productivité depuis la
guerre. Durant les années 50 et 60, cela correspondrait à un
effet de 0,5 point de pourcentage sur le taux d'accroissement annuel de la
production globale durant le ralentissement de la productivité dans les
années 70, l'effet de l'amélioration du niveau d'étude
aura été plus faible, et pourrait avoir augmenté le taux
de croissance de 0,2 ou 0,3 point de pourcentage. Ces effets sont par essence
transitoires, induits par une évolution ancienne de la politique de
l'éducation qui a instauré une nouvelle stabilité dans la
composition de la population active en fonction du niveau d'étude.
Denison par son approche, parvint à la conclusion selon
laquelle la croissance économique aux Etats-Unis entre 1930 et 1960
incombait à la hauteur de 23% l'accroissement de l'éducation du
travail. Ces résultats aboutissent à la conclusion suivante de
l'auteur : « En moyenne et la plupart du temps, pour un travail
donné, une personne éduquée est vraisemblablement plus
performante qu'une personne non éduquée. Non seulement, elle peut
effectuer les mêmes tâches plus vite et mieux, mais elles peuvent
entreprendre des tâches plus délicates. De plus,
l'éducation donne une plus grande ouverture d'esprit et une aptitude
à l'innovation. Elle élargit des possibilités de choix
ouvertes à un individu et lui permet de mieux apprécier les
différentes alternatives, elle le rend apte à tirer profit des
opportunités qui se présentent et à s'adapter rapidement
aux changements de l'environnement économique ».
2) Santé et croissance
Les recherches examinant le lien entre santé et la
croissance recouvre en un seul pays un panel de pays et mesurent
généralement la santé sous deux angles.
Le Programme des Nations Unies pour le
Développement, (PNUD, 1994) indique que le développement des
infrastructures hospitalières et le niveau de l'éducation de la
population fait, a reculé la mortalité infantile entraînant
une augmentation de l'espérance de vie des populations.
Ils sont rejoint par Anand et Ravillon qui
soutiennent que les dépenses du gouvernement en matière des
services de santé ne sont pas trop nécessaire à certains
niveaux. Ils insistent que l'investissement dans la construction des centres
de santé universitaires contribue à développer la
recherche afin de soigner d'avantage les populations. En fait, dans les pays en
développement, les dépenses allouées aux services de
santé ne sont pas accessibles à une large partie de la
population. De ce fait, la construction des centres de santé devient un
indicateur important dans la relation existant entre la santé et la
croissance. Mais, cet indicateur peut être biaisé dans la mesure
où les centres universitaires hospitaliers ne sont construit que dans
les universités, on pourrait prendre plutôt en compte la
construction des centres de santé et hôpitaux dans les zones
reculées.
D'autre part, il y a d'importantes études
qui tendent à montrer que l'état de santé des individus
est un facteur déterminant de la productivité. L'un des obstacles
au développement de la productivité des adultes en Afrique reste
leur état de santé défectueux dû
généralement au manque de soins de santé. Selon Fogel
cité par Schultz (1998), au moins un tiers des gains de
productivité réalisés en Europe occidentale au cours des
derniers siècles est imputable à l'amélioration de la
santé et de la nutrition qui passe par les services rendus aux
individus.
Malgré l'importance des externalités
liées au développement des infrastructures sociales, ce facteur
n'a pas fait d'une grande attention dans la modélisation. Quelques
auteurs l'ont fait en utilisant plutôt certains indicateurs comme le
nombre moyen d'années d'études de la population ou la
mortalité infantile qui sont des variables plus précises du
capital humain.
Quelle que soit la notion d'infrastructures retenue, les
résultats montrent que pour certains secteurs, l'introduction d'effets
individuels ne semble pas remettre en cause l'impact du capital public sur
l'efficacité des facteurs privés, même si cet impact
s'avère être relativement modeste pour certains types
d'infrastructures. L'élasticité du capital public est positive et
significative, les effets les plus importants étant observés dans
le secteur de l'électricité, des transports et
télécommunications. Il s'avère important d'étudier
maintenant les théories de la croissance.
Chapitre 2
Les théories de la
croissance
A la fin de la guerre, dans les années quarante,
économistes et gouvernements ayant tous en mémoire la grande
crise dont ils voulaient tous éviter le retour ; essayèrent
d'en trouver une solution. Aussi deux économistes se réclamant de
Keynes, Roy Harrod et Everett Domar proposèrent des modèles de
croissance reprenant certaines idées de Keynes. Leur principale
contribution fur que, laissé à lui même le système
ne peut assurer la croissance avec plein emploi et ceci essentiellement eu
raison de la mauvaise coordination des décisions de ceux qui, d'un
côté épargnent et de ceux qui, de l'autre investissent. Le
message sous jacent à ces modèles est que l'Etat doit intervenir
pour corriger le mieux possible ce défaut de coordination des
décisions des agents individuels.
A la vision pessimiste donnée par les modèles
Keynésiens d'après guerre a succédé, au milieu des
années 50, la présentation plus optimiste de Solow qui suppose
résolu le problème de coordination, et qui postule en particulier
le plein emploi permanent. Le modèle de Solow, point de départ de
presque toutes les analyses de la croissance, nécessite pour bien
appréhender l'impact de l'investissement en infrastructure sur la
croissance une connaissance approfondie. L'objet de ce chapitre est
consacré à l'analyse du modèle de croissance le plus
traditionnel utilisé par les économistes, celui de Solow (section
1) et des enseignements du modèle AK de Rebelo (1991) (section 2).
Section I - Le
modèle néoclassique de Solow-Swan
Cette section est consacrée à la théorie
traditionnelle de la croissance et à son modèle prototype
élaboré par Robert Solow (1956) et T.W. Swan (1956). Ce
modèle comporte deux sources de croissance : une source
« endogène », l'accumulation du capital et une
source « exogène », la quantité de travail
disponible. L'accumulation du capital (part non consommée de la
production) est déterminée par le modèle mais tel n'est
pas le cas du travail disponible. De cette approche néoclassique en
raison des caractéristiques de la fonction de production
macroéconomique qu'elle postule car, même si les fondements
microéconomiques du modèle ne sont pas explicités, c'est
la parfaite flexibilité des prix des facteurs qui rend possible le
mouvement de substitution entre le travail et le capital ; il
résulte une croissance de long terme harmonieuse car
régulière. L'attrait et la place centrale que le modèle de
Solow continue d'occuper dans les théories de la croissance tiennent
à la simplicité et à la robustesse des hypothèses
qui le fondent et à sa capacité à expliquer
« beaucoup » à partir de « peu »
d'éléments.
La sous-section ci-dessous se propose d'étudier les
enseignements du modèle de base et d'en ressortir ses limites.
A) Les enseignements du modèle
L'approche néoclassique de la croissance basée
sur le modèle de Solow repose sur certaines hypothèses
fondamentales et l'accumulation du capital.
1) Hypothèses
fondamentales et résolution du modèle de Solow
1.1 Hypothèses fondamentales du modèle
de Solow
Le modèle de Solow suppose les hypothèses
ci-contre :
- Les ménages possèdent les actifs et les
facteurs de production et ils choisissent la part de leur revenu qui sera
consacrée à la consommation.
- C'est une économie à un secteur productif dans
laquelle un bien homogène peut être soit consommé, soit
investi en vue d'accroître le capital physique.
- C'est une économie fermée où la
production est égale à la demande et l'investissement à
l'épargne. L'épargne effectuée ex-ante est égale
à l'investissement ex-post. Y (t) = C (t) + I (t) (1).
Où Y (t) : fonction de production ;
C (t) : fonction de consommation ;
I (t) : Fonction d'investissement
- Le facteur travail (L) croit dans le temps du fait de la
croissance de la population. On suppose que ce facteur croît à un
taux exogène constant n qui est le taux de croissance de la population.
Soit :
-  (2) avec n > o
(2) avec n > o
I(t) =  (3)
(3)
- La fonction de production est de la forme : Y(t) = F
[K(t), L(t)] (4)
Elle est dite fonction néoclassique car elle
vérifie les propriétés suivantes :
· Les productivités marginales sont
décroissantes : pour tout K > o ;
L > o

· Les rendements d'échelle sont constants ;
 . Ceci
signifie que F est homogène de degré I, aussi une augmentation
des facteurs de production induit une augmentation dans la même
proportion de la production. . Ceci
signifie que F est homogène de degré I, aussi une augmentation
des facteurs de production induit une augmentation dans la même
proportion de la production.
· Elle vérifie les conditions d'Inada : Lim

K  
Lim 
K  L L 
La constance des rendements d'échelle rend possible
l'écriture de la fonction de production sous la forme per capita :
Y = F(K, L) = LF(K/L, I) = L f(k) avec y = f(k), f' > o ; f''
< o ; avec k : capital par tête ou intensité
capitalistique. Y : revenu par tête.
Ces nouvelles connotations impliquent que les conditions
d'Inada deviennent : lim f(k) = O ; lim f'(k) =  . .
K k k 
Ces trois conditions définissant la fonction de
production néoclassique montrent l'importance des facteurs de
production. En effet, F(O, L) = F(K, O) = f(O) = O6(*).
- Le capital se déprécie au taux constant  étant
donné les autres facteurs de production, la variation nette du capital
à chaque instant est donné par : étant
donné les autres facteurs de production, la variation nette du capital
à chaque instant est donné par :
It = Kt +  K1 (5). K1 (5).
- Le taux d'épargne régissant le comportement de
consommation et d'investissement des agents est exogène et égal
à : S = 
Avant d'examiner les principales conclusions de ce
modèle, il convient de le résoudre au préalable.
1.2) Résolution du
modèle.
On examinera comment l'économie décrite
ci-dessus évolue dans le temps. L'économie est gouvernée
par l'évolution du seul facteur capital. Celle du travail étant
exogène.
a) Dynamique du modèle.
Elle repose essentiellement sur la dynamique du facteur
capital décrite par l'équation ci-contre : K1 =
I1 -  or
I1/Y1 = s or
I1/Y1 = s  I1
= SY1 I1
= SY1
L'accumulation du capital provient de l'écart entre
l'investissement et la dépréciation du capital. Cette
dernière est une fraction constante du capital installé.
L'investissement est ce qui resté de la production une fois
ôtée la consommation. Puisque le taux d'épargne est
constant, c'est une fonction constante de la production. Or celle-ci est telle
que le rendement marginal du capital est une fonction décroissante du
capital : plus le niveau de capital installé est
élevé (relativement à la quantité de la main
d'oeuvre), plus sa rentabilité marginale est faible. Ainsi quand il y'a
peu de capital dans l'économie, la partie de la production qui est
investie permet d'accroître fortement le capital. Plus il y'a de capital,
moins c'est le cas. A la limite lorsque la quantité de capital est
infinie, sa productivité marginale devient nulle. Ainsi le seul facteur
de production qui se modifie étant le capital et son accumulation
réduisant son efficacité au cours du temps, la
productivité va diminuer. Il existe donc une valeur du stock de capital
telle que l'augmentation d'une unité de l'investissement induit un
accroissement de la production épargnée (investissement courant)
plus fiable que l'investissement du déclassement (investissement de
point mort7(*)). A cette
valeur limite (capital de long terme), l'accumulation s'arrête. Les
équations ci-contre décrivent ces différentes
situations :
Kt = sY1 - 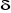 K1 K1
 = = 
 = =  soit
k1 = sf(k1) - (n + soit
k1 = sf(k1) - (n +  )
k1 (6)8(*) )
k1 (6)8(*)
A l'état régulier9(*) (équilibre de long terme) on a:
 = O = O 
K* : valeur du capital par tête d'équilibre
constante. A ce niveau de capital, l'investissement permet simplement de
renouveler le stock de capital. A un niveau de capital légèrement
inférieur, il serait rentable d'investir (puisque l'investissement
supplémentaire rapporterait plus que la dépréciation du
capital). A un niveau supérieur, ce ne le serait plus.
L'équilibre est donc stable : quand l'économie se trouve
à ce niveau d'équilibre du capital, elle y reste.
Le seul taux de croissance de capital par tête que peut
posséder une telle économie est nul. Soit :  d'où d'où

A cet équilibre, toutes les variables par tête
sont constantes et les variables en niveau croissent toutes au même taux
exogène (n) égal au taux de croissance de la population. Il en
est de même des prix (taux d'intérêt (r) et taux de salaire
(w)).
r = f `(k) - 
w = f (k) - kf ` (k)
Après avoir exposé une explication
littéraire du modèle de Solow, une illustration graphique
paraît judicieuse.
b) Résolution graphique du modèle de
Solow
Le graphique ci-contre montre qua quand le niveau du capital
est « petit » c'est à dire situé à
gauche duc capital d'équilibre de long terme, l'investissement qui est
proportionnel à la production est inférieur au
déclassement qui est lui proportionnel au capital. Cela provient du fait
que la courbe représentant la production est concave (la
productivité marginale du capital est décroissante). En effet,
cette propriété entraîne elle aussi que la courbe de
l'investissement est concave et donc que les deux courbes se croisent en un
point qui est l'équilibre de long terme. Ainsi quant le capital est
petit, l'écart entre l'investissement et la dépréciation
est positif et donc le capital augmente. Au contraire, quand le capital est
grand (situé à droite du capital de long terme). L'investissement
est inférieur au délassement et le capital décroît.
Il y'a donc convergence vers le niveau du capital de long terme.
K0
Invest
brut
K'>0
K*
K

Y'
Y'
Y


Graphique 1 : Résolution du modèle
de Solow
Avec sf(k) : investissement courant ou épargne par
tête
(n + ) k :
investissement de point mort. ) k :
investissement de point mort.
2) Règle d'or de
l'accumulation du capital et inefficience dynamique
Le modèle de Solow montre que le taux de croissance
à long terme est indépendant du taux d'épargne.
Toutefois, ce dernier joue un rôle fondamental dans le choix d'un sentier
de croissance de l'économie : plus le taux d'épargne est
élevé, plus la production investie à chaque période
est forte et plus le capital de l'économie considérée est
important. Le capital est une fonction croissante du taux d'épargne (s).
Dès lors si les autorités ont la possibilité de choisir
le taux d'épargne national grâce à une politique
économique appropriée, elles choisiront celui qui permet en
longue période de maximiser la consommation par tête. La solution
d'un problème pareil est appelée la règle d'or de
l'accumulation du capital et a été proposée par PHELPS
(1961) à partir du raisonnement selon lequel une hausse de
l'épargne a deux conséquences contradictoires :
- d'une part, elle réduit la part consommée de
la production
- d'autre part, puisque k est une fonction croissante de (s),
il accroît le revenu par tête et donc le niveau de la production. A
long terme, les deux effets se compensent :
K*(s) =  c*(s) =
(1-s) f(k*(s)) ; c*(s) =
(1-s) f(k*(s)) ;
La quantité c* atteint son maximum lorsque  ; en
désignant kg la ; en
désignant kg la
quantité k* qui maximise c*, on obtient : f(kg) =
n +  (règle d'or d'accumulation du capital). Cette équation
détermine le stock de capital qui permet de maximiser la consommation
par tête tout en permettant un développement harmonieux.
(règle d'or d'accumulation du capital). Cette équation
détermine le stock de capital qui permet de maximiser la consommation
par tête tout en permettant un développement harmonieux.
A ce titre de stock de capital correspond un taux
d'intérêt :
rg = f((Kg)- on dit donc
que rg = n. on dit donc
que rg = n.
Si pour une économie, on constate que r > n cette
économie n'épargne pas assez. On dit de celle-ci que l'avenir est
hypothéqué et les générations futures
sacrifiées.
Si par contre r < n, l'économie épargne trop
sacrifiant le bien-être de la population inutilement. On dit de cette
dernière qu'elle est dynamiquement inefficiente.
Lorsque r = n, il y'a équité entre les deux
générations.
Pour Solow, la croissance est naturelle, elle ne
dépend pas de la sphère économique.
La dynamique développée ci-dessus implique pour
une économie donnée deux conséquences : le
caractère transitoire de la croissance et l'accélération
transitoire de la croissance d'une hausse du taux d'épargne.
2.1) Dynamique de la transition du
modèle10(*)
En reprenant l'équation (6) : k = sf(K) - (n +
 )k ;
et en posant )k ;
et en posant  le taux de croissance de l'économie, on obtient : le taux de croissance de l'économie, on obtient :  (9) (9)
Si une économie démarre à gauche du
stock de capital d'équilibre ( k
> O), son stock de capital croîtra avec le temps et une fois à
l'équilibre restera constant. A l'inverse, une économie qui aura
démarré à droite (c'est-à-dire avec un stock de
capital important) verra son stock de capital diminuer à long terme
jusqu'au moment où il aura atteint l'équilibre. Aussi quelque
soit le point de départ de l'économie, elle va converger vers
l'équilibre. On dit que la dynamique du système est globalement
stable. k
> O), son stock de capital croîtra avec le temps et une fois à
l'équilibre restera constant. A l'inverse, une économie qui aura
démarré à droite (c'est-à-dire avec un stock de
capital important) verra son stock de capital diminuer à long terme
jusqu'au moment où il aura atteint l'équilibre. Aussi quelque
soit le point de départ de l'économie, elle va converger vers
l'équilibre. On dit que la dynamique du système est globalement
stable.



avec s'>s







Graphique 2 : Effet d'une augmentation de (s) et
convergence dans le modèle de Solow.
 sont des états stationnaires (où le taux de croissance
est nul) sont des états stationnaires (où le taux de croissance
est nul)
Cette accélération transitoire de la croissance
résultant d'une hausse du taux d'épargne implique une convergence
des économies.
2.2) Convergence des économies.
L'une des principales conséquences du modèle de
Solow est la convergence des économies. En effet d'après le
résultat précédent, les économies avec un capital
par tête plus fiable tendant à croître plus rapidement que
les autres ayant un  plus
élevé (taux de croissance de l'économie plus fort) ;
elles finiront par rattraper à terme les plus riches. Cette
hypothèse est dite convergence absolue11(*). plus
élevé (taux de croissance de l'économie plus fort) ;
elles finiront par rattraper à terme les plus riches. Cette
hypothèse est dite convergence absolue11(*).
Face au manque de réalisme de cette hypothèse,
on a introduit la notion de convergence conditionnelle selon laquelle
l'économie riche en capital, ayant un taux d'épargne plus
élevé que l'économie pauvre en capital, peut croître
plus rapidement que celle-ci. Cependant à long terme, la croissance des
deux économies convergera vers le taux naturel de croissance. Cette
hypothèse se réfère à l'idée qu'une
économie croit d'autant plus vite qu'elle est éloignée de
son propre état régulier :
A l'état régulier,  = 0
soit : = 0
soit : 
D'où :  (10) (10)
Ainsi si l'économie est proche de son
équilibre,  sera proche
de L et l'économie ne pourra croître. Un taux de croissance faible
signifie qu'on n'est pas éloigné de l'équilibre. C'est
dire qu'une économie croit d'autant qu'elle est éloignée
de son équilibre. Ce problème de convergence des économies
a fait l'objet de nombreuses études empiriques qui ont montré que
si l'on observait bien une convergence au sein des pays industrialisés
(entre les Etats américains ou les pays de la communauté
européenne), il n'y avait pas de convergence entre les pays
industrialisés et les PVD12(*). sera proche
de L et l'économie ne pourra croître. Un taux de croissance faible
signifie qu'on n'est pas éloigné de l'équilibre. C'est
dire qu'une économie croit d'autant qu'elle est éloignée
de son équilibre. Ce problème de convergence des économies
a fait l'objet de nombreuses études empiriques qui ont montré que
si l'on observait bien une convergence au sein des pays industrialisés
(entre les Etats américains ou les pays de la communauté
européenne), il n'y avait pas de convergence entre les pays
industrialisés et les PVD12(*).
Dans sa version la plus élémentaire, le
modèle néoclassique de croissance n'intègre pas la
présence de biens publics. De ce fait, la dépense publique n'a
qu'un effet d'éviction de l'épargne privée. Un taux de
prélèvement obligatoire réduit le taux d'épargne de
l'économie et conduit à un sentier moins capitalistique. Le
prélèvement public n'est justifié que si l'économie
a un taux d'épargne plus élevé que le taux
d'épargne de la règle d'or. Dans ce cas, le
prélèvement public permet de remédier à une
accumulation excessive et inefficace du capital privé.
B) Le modèle de
croissance néoclassique et ses limites
L'objectif du modèle de base était de
présenter un modèle où il était possible d'obtenir
un processus de croissance stable, mais, il présente certaines limites
qui le rende inapte à expliquer la croissance.
1) Les limites du modèle de base de Solow
Le modèle de base de Solow se présente plus
comme une représentation de la production et des ajustements de moyen
terme que comme une théorie de la croissance. En effet, la croissance
est limitée à la dynamique transitoire de l'économie,
lorsqu'elle converge vers le rapport capital/travail d'équilibre (k*).
La croissance de long terme, une fois que le rapport capital/travail
d'équilibre est atteint, n'existe qu'en présence de facteurs
exogènes. Ce modèle aboutit à plusieurs autres conclusions
paradoxales : premièrement, le niveau du taux d'épargne
affecte le niveau de capital par tête, mais pas la croissance.
L'équation dynamique fondamentale de Solow montre qu'à
l'équilibre, toute l'épargne est utilisée pour doter en
capital les travailleurs nouveaux et non pour accroître la dotation de
chacun. Au delà d'un effet en niveau, l'augmentation de k*, une
politique d'encouragement de l'épargne n'aura pas d'effet sur le taux de
croissance à long terme de l'économie. Elle aura aussi un effet
transitoire dans la mesure où elle accéléra la convergence
de l'économie vers k*.
Par ailleurs, dans un cadre international, ce modèle
suppose que tous les pays doivent converger vers un même niveau de
capital et de produit par tête, sous les hypothèses
d'identité de préférences pour les agents de chaque pays
c'est-à-dire avec un même taux d'épargne d'un pays à
l'autre, et avec une même croissance démographique. Les pays
pauvres vont donc « rattraper » les pays riches. Il semble
à première vue assez difficile de raccorder cette
prévision du modèle avec les faits observés au cours des
quatre dernières décennies, qui tendent plutôt à
montrer un accroissement de l'écart entre les niveaux de revenu. En
fait, l'obtention d'une croissance non bornée nécessite la prise
en compte d'un facteur extérieur qui augmente la productivité des
facteurs de production à long terme. Solow, intégrant le
progrès technique, propose une solution à ce problème.
2) Le modèle de
Solow et le progrès technique
La croissance homothétique de toutes les variables en
niveau (production, consommation...) à l'état stationnaire de
Solow suppose que le rapport de deux quelconques de ces variables est constant
dans le temps (taux de croissance nul). Ainsi dans le Solow, l'économie
tend vers un état stationnaire en ce qui concerne la consommation et la
production par tête. Par conséquent, il n'a vraiment pas de
croissance en dehors de celle de la population ; ce qui est gênant
puisque Solow se proposait d'expliquer la croissance observée dans la
plupart des pays qui est loin d'être nulle.
L'absence de croissance par tête en longue
période dans le modèle de Solow est une conséquence du
fait que par hypothèse la fonction de production qui caractérise
l'économie est à rendements d'échelle constants et
à productivité marginale du capital décroissante. Aussi
pour qu'une croissance positive coexiste avec ces hypothèses, il faut
ajouter « quelque chose » au modèle. Une explication
a été proposée par l'intégration du
« progrès technique exogène » qui suppose
soit qu'il y'a une « déformation » de la fonction de
production qui permet une croissance plus élevée ; soit que
le capital ou le travail devient plus productif au fur et à mesure que
le temps passe. Pour mieux comprendre le modèle de Solow avec
intégration du progrès technique, il convient de cerner au
préalable cette variable.
a) Le progrès technique
Le progrès technique permet une amélioration
continue de la technologie permettant d'éliminer l'effet des rendements
décroissants en renforçant la productivité du travail. La
prise en compte de cette variable dans la fonction de production est
confrontée à deux problèmes :
- La manière d'introduire le progrès technique
dans le modèle de Solow. Il peut permettre aux producteurs d'obtenir le
même niveau de production avec relativement le même niveau de
capital ou relativement avec moins de travail. La manière la plus simple
de modéliser consiste à supposer que la production
change :
Yt = F(Kt, Lt, t)13(*) (1)
- La manière par laquelle le progrès technique
déforme le système productif. On se préoccupe notamment de
savoir s'il préserve les parts relatives de la
rémunération des facteurs et dans quelle mesure il n'engendre pas
de chômage. Il existe trois14(*) définitions courantes du progrès
technique neutre cependant, pour qu'une croissance à taux constant soit
possible dans le modèle de Solow, le progrès technique doit
être neutre au sens de Harrod, soit la fonction de production être
de la forme Cobb-Douglas15(*).
. b) Modèle de Solow avec progrès
technique neutre au sens de Harrod
Ici, on suppose une fonction de production qui augmente le
travail et un niveau de technologie A(t) qui croit au taux constant  . On a la
fonction de production qui suit : Y (t) = F(Kt, At) (2) . On a la
fonction de production qui suit : Y (t) = F(Kt, At) (2)
La dynamique du capital devient : Kt =
sF-Kt, LtAt) -  K1
(3) K1
(3)
Plutôt que d'introduire le stock de capital par
tête (modèle de base), on va introduire le stock de capital par
unité de travail effectif soit  (4) (4)
 (5)
même si rien n'est fait, le progrès technique augmente avec le
temps. (5)
même si rien n'est fait, le progrès technique augmente avec le
temps.
A l'état régulier, les variables par
unité de travail effectif  sont
constantes. Les variables par tête (k, y, i, c) croissent au taux sont
constantes. Les variables par tête (k, y, i, c) croissent au taux  , les
variables en niveau K, Y, C, I au taux (n + , les
variables en niveau K, Y, C, I au taux (n +  ). Dans ce
modèle, en l'absence d'un taux de croissance de la population, le taux
de croissance de l'économie est mesuré par ). Dans ce
modèle, en l'absence d'un taux de croissance de la population, le taux
de croissance de l'économie est mesuré par . Solow
attribuant près de 90% de la croissance de la production par habitant au
progrès technique exogène, montrait ainsi que la croissance de la
productivité totale des facteurs était la principale source de
croissance ; laissant de nombreux économistes sur leur
appétit. . Solow
attribuant près de 90% de la croissance de la production par habitant au
progrès technique exogène, montrait ainsi que la croissance de la
productivité totale des facteurs était la principale source de
croissance ; laissant de nombreux économistes sur leur
appétit.
Toutefois, l'explication de la croissance par des facteurs
exogènes ne pouvant satisfaire les économistes classiques
à la recherche de fondements microéconomiques pour tous les
phénomènes auxquels ils s'intéressent ainsi que l'absence
de corroboration entre les données internationales et le modèle
néoclassique en ce qui a trait aux parts du capital et aux
propriétés de convergence, on a vu éclore à la fin
des années 80, des modèles dits de croissance endogène
plus pertinents dans l'explication de l'influence de l'investissement sur la
croissance.
Section II :
Croissance et rendements d'échelle
A) Les enseignements du modèle AK
La dynamique de croissance à la Solow a permis de
reproduire les cinq premiers faits stylisés de Kaldor. Cependant, le
modèle ne peut expliquer le sixième fait concernant les
disparités des taux de croissance parmi les pays. Il ne peut en rendre
compte que si l'on accepte l'hypothèse selon laquelle les pays ont des
taux de progrès technique différents. Mais, dans ce cas, il faut
expliquer les origines de ces différences. C'est le pas que se propose
de franchir ce travail de recherche dans cette section à travers les
travaux de Rebelo pour qui, la croissance est un processus auto-entretenue
endogène.
Une manière de concevoir une croissance auto-entretenue
consiste à mettre l'accent sur l'accumulation des facteurs en supposant,
à l'instar de Rebelo (1991) que « tout est
capital ». En effet, en l'absence du progrès technique
exogène dans le modèle de Solow, la croissance est bloquée
par la décroissance vers zéro du rendement du capital.
L'accumulation s'essouffle car la capacité productive du capital
s'érode alors que la dépréciation et la croissance
démographique absorbent une partie proportionnelle du capital des
investissements. C'est cette hypothèse de décroissance des
rendements qu'il faut remettre en cause pour modéliser une croissance
endogène.
Dans un article publié en 1991, Sergio Rebelo pose que
la technologie agrégée est décrite par une fonction
linéaire avec un seul facteur, le stock de capital :
Y (t) = AK (t) (1).
Cette spécification permet bien d'avoir une
productivité marginale du facteur accumulable, le capital, constante et
égale à A : f' = A. = A.
Ici le capital apparaît comme le seul facteur de
production et le travail est exclu. Rebelo justifie ce choix en assimilant le
travail au capital humain, qui est accumulable, et qui, agrégé au
capital physique mais aussi aux infrastructures collectives donne le concept
de capital élargi. Cette conception élargie du capital permet de
justifier l'absence globale des rendements décroissants. C'est un
modèle néoclassique susceptible d'être
intégré dans le modèle de Solow ou de Ramsay. Dans l'un ou
l'autre cas, l'accumulation du capital est égale à :
K = Y - C -  K (t)
(2) K (t)
(2)
1) Intégration dans
le modèle de Solow
En reconduisant les autres hypothèses16(*) de Solow (modèle de
base), on obtient l'équation fondamentale suivante :
k (t) = sAk(t) - (n +  )K(t)
(3) ; )K(t)
(3) ;
ce qui donne le taux de croissance du stock de capital par
tête (investissement net) :  (4). (4).
La relation qui lie le taux d'investissement au taux de
croissance du produit absente dans le modèle de Solow en régime
d'équilibre (où le taux d'investissement détermine le
niveau du produit mais pas son évolution) apparaît clairement dans
ce modèle simple de croissance endogène. En effet, dans ce
modèle l'équation (5) ci-dessous montre que le taux de croissance
du produit est directement proportionnel au taux d'investissement
 (5). (5).
Néanmoins pour que la croissance soit auto entretenue,
il faut que (5) soit positif. C'est dire que le stock de capital va
croître si et seulement si sA15 > (n + ). ).
Si ce taux de croissance est strictement positif, ce qui
nécessite une productivité du capital et un taux d'épargne
suffisamment élevés par rapport aux taux de croissance de la
population et de déclassement, on a bien une croissance auto-entretenue,
avec un taux de croissance du capital par tête positif et constant. Toute
politique économique visant à augmenter le taux d'épargne
aura un effet positif permanent sur la croissance. Une implication importante
de ce modèle est donc que contrairement au modèle de Solow, une
hausse du taux d'épargne augmente de façon permanente le taux de
croissance de la production par tête. Par ailleurs, il ne prévoit
ni convergence absolue, ni convergence conditionnelle. Même en l'absence
d'une croissance démographique, la croissance endogène est
possible : il suffit que sA > . .
Graphique 3 : Absence de convergence dans le
modèle AK

n + 
sA
K
2) Intégration dans
le modèle de Ramsey
La résolution du modèle AK requiert que soit
spécifiée l'épargne qui finance l'investissement. On peut
comme dans la section ci-dessus retenir l'hypothèse d'un taux
d'épargne exogène ou spécifier, comme dans la plupart des
modèles de croissance endogène la fonction d'utilité des
consommateurs d'où se déduit l'épargne. Ainsi on supposera
que la fonction d'utilité de l'agent représentatif est à
élasticité de substitution inter temporelle constante :
U(c) =    (1) (1)
Où  est le taux de
préférence pour le présent est le taux de
préférence pour le présent
 L'élasticité de substitution inter temporelle, aussi égale
à l'aversion pour le risque.
L'élasticité de substitution inter temporelle, aussi égale
à l'aversion pour le risque.
On pose que le produit se partage entre l'investissement
d'une part et la consommation d'autre part. La taille de la population est
fixe, de telle sorte qu'il n'existe aucune source exogène de croissance.
On recherche un équilibre de croissance régulière
où le produit, le capital et la consommation croissent au même
taux. Le taux de croissance de l'économie est alors :
g=  (2) (2)
L'économie possède un taux de croissance
d'autant plus élevé que la valeur de la productivité
marginale du capital A, qui est supposée constante, est
élevée et que les agents ont une faible préférence
pour le présent, ce qui les poussent à épargner plus. Dans
le cadre de ce modèle, il est donc possible d'obtenir une croissance de
long terme en conservant l'hypothèse de concurrence parfaite et en ayant
l'égalité entre le taux de croissance optimal et le taux de
croissance de l'équilibre concurrentiel. Il suffit pour cela de
supprimer le facteur travail de la fonction de production, ou encore de la
transformer en un facteur accumulable incorporable au capital et de porter
à 1 la valeur de l'élasticité de production du seul
facteur accumulable restant : le capital.
La conclusion générale que Rebelo tire de ce
modèle, est que les rendements d'échelle croissants ne sont pas
nécessaires pour engendrer un processus de croissance endogène.
De fait, on ne trouve de tels rendements d'échelle dans aucun de ses
propres modèles. Un examen attentif permet cependant de nuancer cette
conclusion. Le point commun à tous ces modèles, ainsi qu'à
tous les modèles de croissance endogène, est la présence
de rendements au moins constants sur les biens reproductibles dans la
production des biens reproductibles. Un accroissement de 1% de toutes les
formes de capital doit permettre une augmentation de 1% de la production du
capital. Si le capital est homogène au produit final et que la
production de celui-ci requiert des facteurs non reproductibles par exemple le
travail ou la terre, comme dans les modèles de Solow, alors les
rendements globaux croissants sont nécessaire. Mais si le capital est un
bien différent du bien de consommation, produit avec une technologie
spécifique, ce sont les caractéristiques de cette dernière
qui importent et non celles du secteur du bien de consommation. Le coeur de la
croissance est la production de capital par du capital et il ne peut y avoir de
croissance endogène sans que ce processus se fasse dans le cadre des
rendements d'échelle au moins constants.
B) Croissance et externalités
1) Externalités liées à
l'accumulation d'un facteur
Le modèle de Rebelo a l'intérêt
théorique de mettre en évidence les conditions les plus simples
pour obtenir une croissance par tête auto-entretenue .Mais il est trop
fruste dans ses fondements économiques et il se prête mal à
un essai de calibrage. Une des façons d'introduire les
externalités dans le modèle est de supposer que l'augmentation de
la quantité totale de capitale disponible dans l'économie
entraîne une hausse de la productivité du travail. Dans les
domaines où il y a croissance endogène, cette hypothèse
consiste souvent à multiplier la quantité de travail L
utilisée par une entreprise par un nombre  ( ( ) où ) où
 désigne le stock total de capital et où
désigne le stock total de capital et où  (.) est une
fonction strictement croissante ; pour qu'il y ait externalité
positive, il suffit alors que (.) est une
fonction strictement croissante ; pour qu'il y ait externalité
positive, il suffit alors que  ( ( )>1. Ainsi,
lorsque le stock du capital de l'économie est )>1. Ainsi,
lorsque le stock du capital de l'économie est  la production
Q d'une entreprise qui dispose d'un capital K et d'une quantité de
travail L est donnée par : la production
Q d'une entreprise qui dispose d'un capital K et d'une quantité de
travail L est donnée par :
Q = F(K,  ( ( )L)
(1) )L)
(1)
Comme, par hypothèse, F (.) est homogène de
degré 1, on déduit que :
 (2)
(2)
Si on note q le produit par tête Q/L et k le capital
par tête K/L, alors (2) s'écrit :
q = F(k, (3)
(3)
En dérivant par rapport au temps les deux membres de
cette égalité, on obtient :
 (4) (4)
Dans le modèle de Solow,  tend vers 0
lorsque t tend vers l'infini, car il n'y a pas d'externalité (donc tend vers 0
lorsque t tend vers l'infini, car il n'y a pas d'externalité (donc  et et  et et  tend vers 0,
puisque le capital par tête converge vers sa valeur stationnaire tend vers 0,
puisque le capital par tête converge vers sa valeur stationnaire . Par
conséquent, le produit et la consommation par tête tendent
également vers leur valeur stationnaire : sur la longue
période, il n'y a pas de croissance autre que celle qui est due à
l'augmentation de la population .Toutefois, la situation est
différente dans le cas où il y a externalité, puisque
alors le second terme du membre de (4) ne s'annule pas ; si le capital
d'ensemble . Par
conséquent, le produit et la consommation par tête tendent
également vers leur valeur stationnaire : sur la longue
période, il n'y a pas de croissance autre que celle qui est due à
l'augmentation de la population .Toutefois, la situation est
différente dans le cas où il y a externalité, puisque
alors le second terme du membre de (4) ne s'annule pas ; si le capital
d'ensemble  augmente régulièrement et si augmente régulièrement et si  , alors le
produit par tête peut continuer à croître
indéfiniment. Le caractère endogène de la croissance
provient ici de ce que la fonction , alors le
produit par tête peut continuer à croître
indéfiniment. Le caractère endogène de la croissance
provient ici de ce que la fonction  a pour
argument l'accumulation passée a pour
argument l'accumulation passée  qui est
déterminée par le processus lui-même. qui est
déterminée par le processus lui-même.
Cependant, plusieurs études empiriques portant sur la
croissance d'un grand nombre de pays après la deuxième guerre
mondiale ne rejette pas l'existence d'un effet de taille.
Se posent maintenant deux problèmes
fondamentaux :
Comment expliquer la présence au niveau
macroéconomique de rendements d'échelle croissants ?
Comment rendre compatibles ces rendements croissant avec
l'existence d'un équilibre concurrentiel ?
Pour résoudre ces deux problèmes, les
modèles de croissance endogène se sont attachés d'une part
à identifier les sources possibles de rendements d'échelle
croissants au niveau macroéconomique, d'autre part à fonder au
niveau microéconomique les conditions nécessaires à
l'existence d'un équilibre concurrentiel dans ce cas.
Une réponse possible à ces problèmes
est celle proposée par Romer (1986), l'un des pères fondateurs
des théories de la croissance endogène. Elle consiste à
postuler l'existence d'externalités liées à
l'investissement en capital physique. Romer prend une fonction de production
F(K,L) et pose 
Selon les valeurs données au coefficient  la
croissance peut être soit explosive (elle s'accélère), soit
tendre vers zéro comme dans le modèle de Solow, soit être
constante. la
croissance peut être soit explosive (elle s'accélère), soit
tendre vers zéro comme dans le modèle de Solow, soit être
constante.
2) L'Etat gérant des
externalités
L'objectif principal du recours à une intervention
publique serait l'amélioration du bien être.
Dans les modèles de croissance, la croissance n'est
auto entretenue que si le rendement marginal des facteurs accumulables dans la
leur propre production est constant. C'est-à-dire que la condition
nécessaire à l'existence d'une croissance auto-entretenue est que
l'élasticité de la production aux facteurs accumulables soit
égale à l'unité. Lorsque les facteurs sont pris
individuellement, les rendements sont constants ; d'autres facteurs de
production existant cependant, les rendements de l'ensemble des facteurs
deviennent croissants. Or dans une entreprise dont les rendements sont
croissants, il s'avère impossible d'obtenir un équilibre de
concurrence pure et parfaite. Il y a donc une contradiction. Au niveau
macro-économique, dès lors que qu'il existe des facteurs de
production non accumulables, pour que la croissance soit auto-entretenue, il
faut que les rendements soient croissants, alors qu'au niveau
micro-économique, la réalisation de l'équilibre n'est
possible que par l'existence des rendements non croissants.
Pour résoudre cette contradiction tout en conservant
néanmoins la conclusion que la croissance est auto-entretenue et
l'hypothèse de concurrence pure et parfaite vérifiée, les
auteurs font recours à des effets externes. Cependant,
l'hypothèse sur la valeur des paramètres pour la
réalisation d'une croissance auto-entretenue ébranle la
robustesse de ces modèles. En effet, les valeurs des paramètres
que l'on pourrait plausiblement retenir conduisent à un écart
très élevé entre l'équilibre concurrentiel
(où l'externalité n'est pas prise en compte par les entreprises)
et l'optimum social (où l'externalité est prise en compte).
DE Long et Summers (1992) dans leurs recherches d'une mesure
des effets externes de l'investissement à partir d'un échantillon
de pays parviennent à la conclusion qu'il existerait une forte relation
entre l'investissement et la croissance économique à condition
que les droits de propriété soient garantis par les pouvoirs
publics. Ils assignent ainsi à l'Etat le rôle de favoriser
l'environnement de l'investissement tout en laissant jouer le marché
(exclusions des nationalisations). Cependant, la forme d'intervention publique
dépend du type d'information dont dispose l'Etat. Il est ainsi
légitime que la recherche fondamentale d'une rentabilité
lointaine et incertaine soit financée par des fonds publics car comme
l'applicabilité des résultats n'est pas immédiate,
l'appropriation des gains économiques est difficile (Arrow, 1962). Ceci
d'autant plus qu'une part importante de la recherche fondamentale n'a pas de
finalité économique directe : ces objectifs peuvent
concerner la défense, le prestige, l'honneur de « l'esprit
humain ».
Pour ce qui est de l'éducation, l'existence
d'externalités17(*)
ne peut justifier à elle seule un financement entièrement
public : une part des gains de la formation est réalisée par
les agents qui se forment. Cependant une intervention publique se justifierait
par ailleurs même en l'absence d'externalité. L'accès des
plus pauvres aux marchés financiers (afin de trouver le financement
d'une formation) n'étant sans doute pas ce qu'il serait dans un
marché parfait ; il importe de corriger cette imperfection par une
intervention publique. Si les nouvelles théories de la croissance
réhabilitent le rôle de la politique économique, qui
devrait permettre de mieux coordonner les décisions des agents
privés, elles ne préjugent pas la forme de cette intervention. En
effet, si l'intervention publique est justifiée par le fait qu'il existe
une externalité, il demeure que la forme d'intervention publique
dépend de l'externalité précise qui est en cause. Outre la
prise en compte des effets externes, l'Etat a une influence directe sur
l'efficacité du secteur privé : les investissements publics
concourent relativement à la productivité privée.
Le modèle de Solow et les calculs qu'il autorise ne
cadre pas bien avec la forte corrélation observée dans les faits
entre la taux d'investissement et de croissance ; des travaux
récents ont remis en l'honneur l'investissement en infrastructure comme
moteur de la croissance. Bien que reconnaître l'importance de la
croissance à long terme soit primordiale, il importe de sortir du Carcan
de la croissance néoclassique où la croissance par tête
à long terme est indexée au taux de progrès technique
exogène. C'est ce à quoi nous allons nous atteler en
modélisant l'impact de l'infrastructure sur la croissance.
Deuxième partie
L'évaluation de l'impact de l'infrastructure sur
la croissance au Cameroun
Dans la première partie de ce travail, nous avons fait
la synthèse des différentes approches théoriques mettant
en exergue l'impact de l'infrastructure publique sur la croissance et les
différents enseignements tirés des théories de la
croissance. Il ressort que l'investissement dans l'infrastructure est un des
facteurs fondamental dans le processus de croissance.
Il importe cependant de confronter ces brillantes
révélations théoriques aux faits observés dans les
différents pays avec les variables à notre disposition.
En effet, la spécificité des pays africains et
surtout, de l'Afrique subsaharienne qui jusqu'à nos jours malgré
ces illustres développement théoriques ne parviennent pas pour
d'autres à amorcer une croissance positive, montre la pertinence d'une
évaluation empirique de l'apport des infrastructures dans le processus
de croissance d'un pays appartenant à cette catégorie comme le
Cameroun.
Pour apprécier empiriquement l'impact de
l'infrastructure publique dans la croissance, les auteurs ont
procédés par différentes manières (en
données de panel, en coupe, et sur série temporelle).
Dans cette partie de mémoire, nous essayerons de
débattre sur les procédures afin de choisir l'une pour
appréhender l'impact de l'infrastructure sur la croissance.
Cette partie s'articule autour de autour de deux chapitres.
D'abord elle mesure la relation entre les infrastructures de transport et la
croissance au Cameroun (chapitre3), ensuite, elle analyse la relation entre les
infrastructures sociales à travers les dépenses publiques de
santé et d'éducation et la croissance au Cameroun.
Chapitre 3
Relation entre infrastructures de transport et la
croissance au Cameroun
Les avantages et l'importance que
représentent les infrastructures de transport pour la croissance
économique sont reconnus depuis longtemps. Il ne fait guère de
doute que les investissements réalisés dans les réseaux de
transport (routes, chemins de fer, canaux) ont stimulé le
développement économique en Amérique au XIXe
siècle. L'infrastructure des transports a élargi le territoire
sur lequel les produits peuvent être commercialisés et vendues.
Elle a rendu le processus de production et de distribution plus efficace,
permis des économies d'échelle et une spécialisation
accrue, changé les systèmes logistiques et réduits les
coûts, autant de facteurs qui font augmenter la productivité
économique.
Les études analysant les interrelations entre les
infrastructures de transports et la croissance économique s'articulent
autour de deux grands axes.
Le premier est formé par l'analyse coûts
à laquelle les investissements routiers et ferroviaires sont
systématiquement soumis dans la plupart de pays.
La seconde démarche possible étudie les
relations économétriques à partir des fonctions de
production macroéconomiques. Cette approche est celle des
théories de la croissance.
Dans ce chapitre, nous commencerons par présenter les
modèles théoriques généralement utilisés
(section 1) et nous terminerons par l'évaluation empirique du
modèle que nous retiendrons (section 2). Les résultats et
l'interprétation sont présentés dans cette dernière
section.
Section 1 : Présentation des
modèles
A- Approche par la fonction de coût
1) Le modèle proposé par Bangqiao,
J
Pour examiner les effets de l'infrastructure publique sur le
coût de production dans le secteur privé, une fonction de
coût traditionnelle peut être modifiée de manière
à inclure le service de l'infrastructure publique. La forme
générale de la fonction de coût devient alors :
(1) C = C (w, Y, T, H)
Où C est le coût total ; w, le vecteur prix
des intrants privés (habituellement travail, capital privé,
matières premières, etc...) ; Y est la quantité
d'extrant ; T, une mesure du changement technique ; et H, le service
de l'infrastructure publique (soit la quantité de stock de capital
public).
La valeur fictive ( ) ou
avantages marginaux du capital public peut être obtenue en prenant la
négative de la dérivée partielle de la fonction de
coût par rapport au capital public H. ) ou
avantages marginaux du capital public peut être obtenue en prenant la
négative de la dérivée partielle de la fonction de
coût par rapport au capital public H.
(2) 
La valeur fictive est l'équivalent du
côté des coûts du produit marginal. Elle reflète la
réduction des coûts totaux attribuable à un accroissement
du stock d'intrants et, donc, l'apport des investissements
réalisés dans l'infrastructure publique à la performance
économique et à l'efficacité de l'entreprise. La valeur
fictive peut être traduite en une mesure de l'élasticité,
comme suit :
(3) 
Du point de vue de l'entreprise, comme les services
d'infrastructure public sont fournis de l'extérieur,  signifie que
les entreprises profitent des hausses du service de l'infrastructure publique.
Toutefois, d'un point de vue social, l'investissement dans l'infrastructure
n'est clairement pas gratuit. Par conséquent, le taux de rendement
social du capital d'infrastructure publique doit être mesuré par
soustraction de ce qu'on appelle le coût social d'utilisation du capital
public, signifie que
les entreprises profitent des hausses du service de l'infrastructure publique.
Toutefois, d'un point de vue social, l'investissement dans l'infrastructure
n'est clairement pas gratuit. Par conséquent, le taux de rendement
social du capital d'infrastructure publique doit être mesuré par
soustraction de ce qu'on appelle le coût social d'utilisation du capital
public, de la valeur fictive
de la valeur fictive , ce qui
donne : , ce qui
donne :
(4) 
Toutefois, la détermination d'un coût social
d'utilisation est une question très compliquée. Tous les
chercheurs qui ont voulu estimer empiriquement les effets du capital public
à l'aide d'une fonction de coût utilisent une forme translog
souple d'une fonction de coût, sauf Morrison et Schwartz (1996) et Seitz
(1992) qui utilisent plutôt la fonction de coût
généralisée de type Leontief. Cette fonction translog est
habituellement estimée de concert avec des équations sur le
partage des coûts, à l'aide de la méthode de
régression apparente de Zellner, qui impose des contraintes
théoriques.
2) Avantages et limites de la fonction de
coût
Le capital des infrastructures publiques est un bien
public et, par conséquent, aucune valeur marchande ne peut être
attribuée aux services qu'il fournit. Néanmoins, le prix fictif,
ou la disposition à payer pour ces services, déterminé
comme étant la réduction des coûts privés de
production associée à l'utilisation du capital des
infrastructures publiques, joue un rôle important dans la prise de
décision. Le bénéfice marginal du capital public est
quantifié comme étant la réduction des coûts
privés associée à l'utilisation d'une unité
supplémentaire de capital public. Par exemple, une autoroute bien
construite permet à un conducteur de camion d'éviter les routes
de campagne et de transporter ses marchandises jusqu au marché en moins
de temps. Le gain de temps signifie que le coût subi par le conducteur
est plus faible et l'usure du camion est moins importante.
L'une des limites de l'approche par une fonction de
coût réside au niveau où elle ne fait pas apparaître
des externalités.
D'autre part, la fonction de coût bien qu'elle permet de
tester de nombreuses hypothèses concernant notamment la technologie, le
comportement des entreprises ou l'impact de diverses règlementations
étatiques, trouve une autre limite dans les types de données
nécessaires à son élaboration, notamment pour les pays en
développement.
Ensuite, elle ne cadre pas avec l'orientation notre
étude qui se veut beaucoup plus macroéconomique.
B) l'approche en terme de fonction de
production
1) Le modèle de Barro
Concernant l'analyse théorique des liens entre capital
public et croissance, le modèle de (Barro, 1990) constitue aujourd'hui
un cadre de référence. La spécificité de ce
modèle consiste à faire apparaître le stock de capital
public dans le processus de production, et par conséquent à
mettre en évidence un lien explicite entre la politique gouvernementale
et la croissance économique de long terme dans un cadre de croissance
endogène. Les modèles de croissance endogène avec
externalité s'appuient sur des fonctions de production à trois
facteurs de production. Nous aurons des facteurs privés (travail et le
capital privé) et le troisième facteur, les dépenses en
infrastructures est à financement public. La forme fonctionnelle, la
plus fréquemment utilisée, est la forme Cobb-Douglas. Cette
dernière permet une lecture directe des élasticités et des
rendements d'échelle et une discussion aisée de la
présence ou non d'externalités de capital public.
Il y a en effet externalités engendrées par des
facteurs si les rendements d'échelle sont décroissants ou
constants en facteurs privés et croissants sur l'ensemble des facteurs,
privés et public (Barro, 1990).
La fonction de production de la firme i est
définie par :
  (1) (1)
Les termes N, K désignent respectivement le niveau de
l'emploi ou le travail, le stock de capital privé de la firme i ;
les paramètres  et et  correspondent respectivement aux élasticités de la production par
rapport au stock de capital privé et aux investissements publics.
Avec
correspondent respectivement aux élasticités de la production par
rapport au stock de capital privé et aux investissements publics.
Avec . .
Le stock de capital public ou la dépense totale de
l'Etat en infrastructures, noté G, satisfont les hypothèses de
non rivalité et de non exclusion (Samuelson, 1954)
(op.cité) ; A le niveau d'avancement technologique constant dans le
temps.
Les firmes étant toutes identiques (hypothèse
simplificatrice), la fonction de production sociale s'écrit sous la
forme :
 (2) (2)
Cette fonction est à rendements constants par rapport
aux facteurs de production privés. La productivité marginale du
capital privé est décroissante ( ) et tend
à s'annuler quand K s'accroît. Toutefois l'infrastructure (le
capital public) va permettre de maintenir ce niveau de productivité
marginale au cours de l'accumulation. ) et tend
à s'annuler quand K s'accroît. Toutefois l'infrastructure (le
capital public) va permettre de maintenir ce niveau de productivité
marginale au cours de l'accumulation.
Après linéarisation par transformation
logarithmique, le modèle prend la forme suivante, qui peut être
estimée au moyen des techniques économétriques de
modèles linéaires :
Log Y = log A +  log K + log K +  log N + log N +  log G
(3) log G
(3)
où  et et 
On cherche à tester le modèle de croissance
endogène avec capital public, considère que les rendements
d'échelle sont constants en facteurs de production privés et
croissants sur l'ensemble des facteurs privés et public.
2) Financement des infrastructures par
l'impôt
Les dépenses publiques sont financées par un
impôt proportionnel au taux d'imposition t constant dans le temps sur
tous les revenus :
T = tY (4)
L'équilibre budgétaire est assuré
à chaque instant :
T = G (5)
La dépense publique est constituée de bien final
de sorte que t est la fraction du produit final absorbée par l'Etat. Les
ménages consacrent une fraction s du revenu restant à
l'épargne de sorte que la dynamique d'accumulation du capital prend la
forme :
 (6) (6)
De plus, la fonction de production sociale est
déterminée en remplaçant G par tY dans (2), on
obtient :
 
Soit :  (7)
(7)
Puisque A, N et t sont constants, le modèle est ainsi
ramené au modèle de AK de Rebelo. Ce résultat
dépend crucialement du fait que l'élasticité du produit
par rapport à l'infrastructure vaut 1- . .
En l'absence de croissance démographique, les
équations (5) et (6) permettent d'exprimer le taux de croissance du
stock de capital :
 En
remplaçant Y par sa valeur ci-dessus, on obtient : En
remplaçant Y par sa valeur ci-dessus, on obtient :

Ce taux étant constant, on aboutit à une
situation ou la croissance est auto-entretenue. On remarque que le taux de
croissance de l'économie dépend de manière non monotone du
taux d'imposition choisi par l'Etat. Ce qui nous permet d'observer les deux
effets opposés du taux d'imposition sur le taux de croissance de long
terme. L'augmentation des dépenses publiques conduit d'une part à
une augmentation de la productivité des facteurs et favorise ainsi
l'accumulation du capital privé, mais d'autre part elle induit une
hausse des ponctions sur les ressources des agents et donc une éviction
des investissements privés. La croissance de long terme sera ainsi le
résultat de l'interaction de ces deux forces opposées.
L'effet net de l'intervention de l'Etat dépend de la
différence entre le taux marginal de prélèvement public
t et l'élasticité du produit par rapport aux
dépenses publiques 1- . Dès
lors si le gouvernement adopte la maximisation de la croissance pour objectif
de sa politique fiscale, il choisira un taux d'imposition égal à
l'élasticité des dépenses publiques, ou au taux
d'investissement public. . Dès
lors si le gouvernement adopte la maximisation de la croissance pour objectif
de sa politique fiscale, il choisira un taux d'imposition égal à
l'élasticité des dépenses publiques, ou au taux
d'investissement public.

L'hypothèse d'une influence des dépenses
publiques d'infrastructure sur le taux de croissance du sentier stationnaire de
l'économie, peut paraître extrêmement fragile dans la mesure
où elle requiert une configuration très particulière des
paramètres et notamment des rendements d'échelle par rapport aux
stocks de capital privé et public.
Ainsi suivant l'origine de la croissance, la maximisation du
facteur de croissance de long terme ou du niveau de la consommation par
tête en régime permanent, conduit dans ces modèles à
l'égalisation du taux d'investissement public et de
l'élasticité de la production par rapport à ces
dépenses.
Les modèles de croissance endogène avec capital
public, dont R.Barro est l'investigateur, ont donné lieu à un
certain nombre de tests empiriques qui se sont essentiellement focalisés
sur les conclusions théoriques de ces modèles et donc
porté sur l'estimation de la vitesse de convergence des économies
en fonction de leur dépenses publiques. Mais le principal apport de ces
modèles est surtout d'avoir relancé le débat, d'un point
de vue théorique, sur l'intervention publique et ses effets, à
l'échelle nationale et donc en dehors de tout arbitrage concernant
l'aménagement du territoire. Le capital public peut être
considéré comme un facteur de production à part
entière et n'étant pas directement financé par ses
utilisateurs, il est source d'externalités.
En définitive, les nouvelles théories de la
croissance identifient des facteurs structurels et politiques connus qui
peuvent affecter le processus de croissance d'état stationnaire par des
effets directs provenant des dépenses et des impôts et ceux
indirects à travers la stabilité macro-économique.
L'infrastructure publique a un effet direct sur la croissance en augmentant le
stock de capital de l'économie. Pour faire référence
à l'importance de l'infrastructure dans l'amélioration du
bien-être social, l'expression : « où la route
passe, le développement suit » est très souvent
utilisée.
Le modèle de Solow étudié
précédemment n'explique pas pleinement certains faits de base de
la croissance économique dans les pays en particulier ceux de l'Afrique
Subsaharienne. Ici en dehors du capital, le seul déterminant du revenu
par tête est l'efficacité du travail dont la signification exacte
n'est pas spécifiée et dont le comportement est
considéré comme exogène. En outre, faire
l'hypothèse que le taux de rendement du capital reflète sa
contribution à la production et que sa part dans le revenu total est
fixée à des niveaux plausibles ne permet d'expliquer ni
l'énorme croissance du revenu par tête au cours du temps, ni les
différences considérables de revenus par tête entre
pays.
Ainsi, afin de déterminer exactement l'incidence sur
la croissance d'un facteur donnée, il faut intégrer dans
l'équation tous les facteurs de la production pertinents. En effet, ce
n'est qu'en tenant compte de la quantité et de la qualité de tous
les intrants que l'on pourra estimer correctement l'importance marginale de
chaque forme d'infrastructure. Aussi, le modèle de Barro (1990) prenant
en considération la plupart des infrastructures parait plus pertinent
que les autres modèles dans la mesure de l'importance de
l'infrastructure publique sur la croissance d'un pays comme le Cameroun.
Section II : L'estimation
empirique
A) Estimation des
dynamiques de long terme et de court terme
La méthode couramment utilisée dans l'analyse
de l'infrastructure et la croissance est celle basée sur les
données de panel ou ne coupe instantanée. Mais à
coté de ces méthodes traditionnelles s'est
développée une autre fondée sur les séries
chronologiques appliquant les tests de stationnarité. Dans cette
section, il s'agira de déterminer les caractéristiques des
séries utilisées dans le but de les utiliser dans l'estimation de
la relation de long terme et dans l'analyse du comportement de court terme des
infrastructures.
1) Présentations des variables et
caractéristiques
Dans cette sous section, il s'agira de déterminer les
caractéristiques des séries utilisées dans le but de les
utiliser dans l'estimation de la dynamique de longue période et de
courte période. Les caractéristiques renvoient ici à la
présentation des données et à la stationnarité des
variables.
a) Présentation des
variables et leurs sources
Conformément au modèle théorique, notre
relation de long terme repose sur quelques fondamentaux que voici :
- Les infrastructures de transport
Pour permettre la parfaite homogénéité
des données, nous allons utiliser comme variable dans ce cas les
dépenses allouées aux investissements de transport. Ceci dans la
mesure où les données sur la densité du réseau
routier ou du stock de capital ne sont pas disponibles dans le cadre du
Cameroun.
-Le capital privé
L'investissement en capital privé est un facteur de
croissance, tant pour l'école néoclassique que la théorie
keynésienne. De plus, il est susceptible d'engendrer,
conformément aux modèles récents des modèles de
croissance endogène (Guellec et Ralle, 1997), des effets
d'externalités. En effet, l'investissement d'une entreprise permet
à cette dernière d'accroître non seulement sa propre
production, mais aussi celle des autres entreprises, du fait des
externalités technologiques qu'il engendre. Des études empiriques
relatives aux économies africaines (Ojo et Oshikoya, 1995 ; Ghura
et Hadjimichael, 1996), cités par Nubukpo, ont ainsi mis en
évidence l'existence d'une relation positive entre l'investissement en
capital privé et la croissance du PIB.
-Le niveau de l'emploi
Dans une étude fondée sur un panel d'Etats
américains, (Evans et Karras, 1994) préconisent d'utiliser le
nombre d'heures travaillées, en particulier dans le but de
contrôler les effets liés à
l'hétérogénéité de la durée
légale de travail. D'autres auteurs utilisent le total de la population
en âge de travailler ou l'effectif total des différents secteurs
du pays pour définir cette variable c'est le cas de Everaert et Canning.
Cependant, en l'absence de telles données au Cameroun, nous utiliserons
comme proxy du niveau de l'emploi, la force de travail. Ceci se comprend assez
aisément dans la mesure où la force de travail est
constituée des personnes qui rentrent dans la définition de la
population économique active.
Les données sont annuelles et sont pour la grande
majorité issues des statistiques de la DSCN et de l'INS : nous
disposons des séries annuelles des dépenses publiques en
investissement dans les transports, et du capital privé. La
période considérée va de 1980 à 2002. Les
données sur la force de travail proviennent de la base de données
de la Banque Mondiale (CD-ROM), qui s'étale de 1980 à 2002 ;
ainsi que les données du PIB.
b) Les tests de stationnarité
Avant de procéder à l'estimation du PIB
réel d'équilibre, il convient de s'assurer de la
stationnarité des séries utilisées : car lorsque les
variables ne sont pas stationnaires, l'estimation des coefficients par les MCO
(moindres carrés ordinaires) ne converge pas vers les vraies
coefficients et les tests usuels des t-Students et F-Fisher ne sont plus
valides, on dira que les régressions sont fallacieuses. Pour
procéder à l'estimation des relations, il suffit que la
stationnarité soit de forme faible c'est-à-dire plus formellement
si on considère une variable  celle-ci est
faiblement stationnaire si son espérance mathématique et sa
variance sont constantes et finies et si la covariance de celle-ci est
faiblement stationnaire si son espérance mathématique et sa
variance sont constantes et finies et si la covariance de  et et  (avec
h>0) dépend uniquement de h. Autrement dit la variable (avec
h>0) dépend uniquement de h. Autrement dit la variable  est
stationnaire si elle est intégrée d'ordre zéro, et sera
notée est
stationnaire si elle est intégrée d'ordre zéro, et sera
notée  I(0). Plus généralement une variable sera dite
intégrée d'ordre p si sa différence d'ordre p est
stationnaire ou intégrée d'ordre zéro (et notée I(0). Plus généralement une variable sera dite
intégrée d'ordre p si sa différence d'ordre p est
stationnaire ou intégrée d'ordre zéro (et notée . .
La plupart des données macroéconomiques sont
intégrées d'ordre un. Il existe plusieurs manières de
tester la stationnarité des séries on peut citer entre
autre : le test de Dickey-Fuller (DF), le test de Dickey-Fuller
Augmenté (ADF), et le test de Phillips-Perron (PP).

Ø Les tests de Dickey-Fuller
(1979,1981)
Les tests de Dickey-Fuller (1979,1981), permettent de mettre
en évidence le caractère stationnaire ou non d'une chronique par
la détermination d'une tendance déterministe ou stochastique. Les
modèles servant de base à la construction de ces tests sont au
nombre de trois. Le principe est simple pour les tests de Dickey-Fuller
(DF) :
Si l'hypothèse :  : :  est retenue
dans l'un de ces trois modèles, alors le processus est non
stationnaire. est retenue
dans l'un de ces trois modèles, alors le processus est non
stationnaire.
  Modèle autorégressif d'ordre 1 ou AR(1).
Modèle autorégressif d'ordre 1 ou AR(1).
  Modèle autorégressif avec constance.
Modèle autorégressif avec constance.
  Modèle autorégressif avec tendance.
Modèle autorégressif avec tendance.
Avec  iid et est un
bruit blanc iid et est un
bruit blanc
Si l'hypothèse  est
vérifiée, la chronique est
vérifiée, la chronique  n'est pas
stationnaire quelque soit le modèle retenu. n'est pas
stationnaire quelque soit le modèle retenu.
La procédure du test est séquentielle et part du
modèle au modèle au modèle  : sur
le modèle : sur
le modèle , on teste la significativité du coefficient b à partir
des statistiques classiques de student. Si b est significativement
différent de zéro, alors on teste pour ce même
modèle le coefficient de , on teste la significativité du coefficient b à partir
des statistiques classiques de student. Si b est significativement
différent de zéro, alors on teste pour ce même
modèle le coefficient de  c'est-à-dire
c'est-à-dire  
Si l'hypothèse  est
acceptée, la série est non stationnaire avec tendance ;
sinon ( est
acceptée, la série est non stationnaire avec tendance ;
sinon ( est acceptée) la série est stationnaire. L'hypothèse
est acceptée) la série est stationnaire. L'hypothèse  est
acceptée si et seulement si est
acceptée si et seulement si 18(*) 18(*)
Si par contre b est significativement nul, on passe
directement au test sur le modèle  avec le
même cheminement que précédemment jusqu'au test sur le
modèle avec le
même cheminement que précédemment jusqu'au test sur le
modèle . Si . Si  n'est pas stationnaire on peut appliquer le test de Dickey-Fuller (DF)
sur les variables différenciées en suivant la même
procédure que précédemment. n'est pas stationnaire on peut appliquer le test de Dickey-Fuller (DF)
sur les variables différenciées en suivant la même
procédure que précédemment.
Dans les trois modèles précédents
utilisés pour les tests de Dickey-Fuller (DF), le processus  est par
hypothèse un bruit blanc, or il n'y a aucune raison pour qu'à
priori, l'erreur soit non corrélée : on appelle test de
Dickey-Fuller Augmenté (ADF) celui qui tient compte de cette
hypothèse. Les tests de Dickey-Fuller Augmenté (ADF) sont
fondés sous l'hypothèse alternative est par
hypothèse un bruit blanc, or il n'y a aucune raison pour qu'à
priori, l'erreur soit non corrélée : on appelle test de
Dickey-Fuller Augmenté (ADF) celui qui tient compte de cette
hypothèse. Les tests de Dickey-Fuller Augmenté (ADF) sont
fondés sous l'hypothèse alternative  issue de
l'estimation par les MCO des trois modèles ci-dessous. issue de
l'estimation par les MCO des trois modèles ci-dessous.
 
 
 
Le test se déroule de manière similaire aux
tests de Dickey-Fuller (DF), seules les tables statistiques diffèrent.
La valeur p de retard est déterminée à l'aide des
critères de Aikaike ou Schwartz.
Le test de Phillips-Perron19(*) (1988), lui est construit sur une correction non
paramétrique des statistiques de Dickey-Fuller pour prendre en compte
les erreurs hétéroscédastiques.
Les résultats des tests de
stationnarité
Dans le besoin de garantir des estimations robustes, les
propriétés des séries temporelles du produit
intérieur brut et de ses fondamentaux ont été
déterminées, en procédant à des tests de racines
unitaires. Plus précisément les tests de Dockey-Fuller (DF et
ADF) et de Philips-Perron au seuil de 5% ont été utilisés.
Les résultats sont présentés dans les tableaux qui suivent
en ce qui concerne les variables à niveau, différence
première et en différence seconde.
Tableau 3 : Tests de racine unité (DF, ADF, PP)
à niveau sans tendance ni dérive sur les logarithmes des
variables.
|
Tests
Variables
|
DF
|
ADF
|
PP
|
|
Valeur
calculée
(t ) )
|
Valeur tabulée (au seuil de 5%)
|
Valeur
calculée
(t ) )
|
Valeur tabulée (au seuil de 5%)
|
Valeur
calculée
(t ) )
|
Valeur tabulée (au seuil de 5%)
|
|
Log Y
|
2,0765
|
-1,9574
|
0,3781
|
-1,9583
|
1,4030
|
-1,9574
|
|
Log K
|
1,3361
|
-1,9574
|
0,8578
|
-1,9583
|
1,0878
|
-1,9574
|
|
Log N
|
46,5908
|
-1,9574
|
1,6080
|
-1,9583
|
31,6537
|
-1,9574
|
|
Log G
|
0,9216
|
-1,9574
|
0,5783
|
-1,9583
|
0,6614
|
-1,9574
|
D'après le tableau 3, toutes les variables sont non
stationnaires en niveau sans la présence d'une dérive ni d'une
tendance en niveau lorsqu'on applique les différents tests de
stationnarité (DF, ADF, PP) au seuil de 5%. Il convient de passer
à la seconde étape qui consiste à appliquer sur les dites
variables le test de racine unité en différence
première.
Tableau 4 : test de racine unité (DF, ADF, PP) en
différence première sur les logarithmes des variables.
|
Tests
Variables
|
DF
|
ADF
|
PP
|
|
Valeur
calculée
(t ) )
|
Valeur tabulée (au seuil de 5%)
|
Valeur
calculée
(t ) )
|
Valeur tabulée (au seuil de 5%)
|
Valeur
calculée
(t ) )
|
Valeur tabulée (au seuil de 5%)
|
|
Log Y
|
-2,8803
|
-1,9583
|
-1,6417
|
-1,9592
|
-2,8473
|
-1,9583
|
|
Log K
|
-2,9728
|
-1,9583
|
-2,5752
|
-1,9592
|
-2,9586
|
-1,9583
|
|
Log N
|
0,5692
|
-1,9583
|
0,6334
|
-1,9592
|
0,6900
|
-1,9583
|
|
Log G
|
-2,3142
|
-1,9583
|
-1,9750
|
-1,9592
|
-2,2960
|
-1,9583
|
D'après le tableau 4, toutes les variables sont
stationnaire en différence première c'est-à-dire
intégrées d'ordre un ou I(1) lorsqu'on applique les
différents tests de stationnarité (DF, ADF, PP) au seuil de 5%,
à l'exception de la variable N qui mesure l'emploi dont la valeur
« Mac Kinnon » demeure supérieure à celle du
seuil critique. Afin de stationnariser cette variable, il lui sera
appliqué le test de racine unité en différence seconde.
Tableau 5 : Tests de racine unité en
différence seconde sur le logarithme de N
|
Tests
Variables
|
DF
|
ADF
|
PP
|
|
Valeur
calculée
(t ) )
|
Valeur tabulée (au seuil de 5%)
|
Valeur
calculée
(t ) )
|
Valeur tabulée (au seuil de 5%)
|
Valeur
calculée
(t ) )
|
Valeur tabulée (au seuil de 5%)
|
|
Log N
|
-3.8835
|
-1.9592
|
-3.2783
|
-1.9602
|
-3.7696
|
-1.9592
|
Le tableau 5 ci-dessus montre que la variable N est enfin
stationnaire. Ceci est d'autant vrai dans la mesure où N suit
déjà une certaine tendance. Donc, N est intégré
d'ordre deux ou I(2). Une fois les variables stationnarisées, il
convient d'effectuer l'estimation des différents paramètres.
2) La régression
La procédure consiste à utiliser les Moindres
Carrés Ordinaires (MCO) pour estimer les paramètres. Celle-ci
permettra non seulement de s'assurer de l'éventuelle
significativité des différentes variables et par là de
juger la pertinence du modèle mais également de vérifier
les différentes hypothèses émises.
Tableau 6 : Résultats de la régression sur
les variables stationnarisées
|
Régression 1 : Estimation de la croissance
(données annuelles de 1980-2002)
|
|
Variables
|
Coefficients
|
Statistique de Student
|
|
C
Log G
Log K
Log N
|
4,0224
0,1928
0,1548
0,4197
|
1,1942
8,4147
2,3968
5,1356
|
|
R2 = 0,82
R2aj = 0,79
|
SCR = 0,5177
F = 26,89
|
DW = 1,8086
|
Parfois l'effet d'une variable explicative sur une variable
expliquée n'est pas instantané, la variable expliquée
pouvant répondre avec retard.
Tableau 7 : Résultats de la régression avec
les variables retardées
|
Régression 2 : Estimation de la croissance
(données annuelles de 1980-2002)
|
|
Variables
|
Coefficients
|
Statistique de Student
|
|
C
Log G(-1)
Log K(-1)
Log N(-1)
|
0,1823
0,1276
-0,0129
-6,2388
|
2,8227
5,2133
-0,2151
-2,5506
|
|
R2 = 0,76
R2aj = 0,70
|
SCR = 0,0160
F = 13,65
|
DW = 1,0373
|
Le traitement des séries chronologiques étant
longue, il convient également d'analyser la dynamique de
l'infrastructure avec des modèles faisant appels aux techniques de
co-intégration et aux modèles à correction d'erreurs
(EMC).
a) L'estimation de la relation de long
terme
La relation obtenue à partir de la régression
est nécessaire mais non suffisante pour une conclusion sur la pertinence
de ce modèle et sa capacité à prédire l'avenir. En
effet, il faut s'assurer que la relation est stable à long terme. La
co-intégration est une spécification des modèles
entretenant très souvent des idées fallacieuses à propos
des mouvements des variables les unes par rapport aux autres à long
terme. Elle implique de façon intuitive que dans la relation
d'équilibre de long terme entre les différentes variables non
stationnaires, celles-ci ne devraient pas s'éloigner l'une de l'autre
(Greene, 1997).
Ø Présentation du cadre
méthodologique de la relation de long terme
Selon Engle et Granger (1981), deux séries sont
co-intégrées lorsque leur combinaison linéaire est
stationnaire. La co-intégration traduit le fait que la combinaison
linéaire ne s'éloigne jamais très longtemps de sa moyenne
même si les séries présentent des évolutions
divergentes. Autrement dit il existe une évolution stable à long
terme entre les séries.
Deux séries sont co-intégrées d'ordre d,b
pour 0<b d si d si
- Xt intégré d'ordre d et
Yt intégré d'ordre b
- Il existe ( ) tel que
zt = ) tel que
zt =  soit intégré d'ordre (d-b) ou I(d-b) soit intégré d'ordre (d-b) ou I(d-b)
En pratique on s'en tient généralement à
d=b=1 et dans ce cas, zt sera stationnaire ou I(0) et traduira la
relation d'équilibre entre Xt et Yt.
Dans le cadre de ce travail, nous utiliserons la
méthode de Johansen qui propose de tester directement dans le cadre d'un
VAR en niveau les relations de co-intégration. Cette approche permet par
la méthode du maximum de vraisemblance, d'obtenir tous les vecteurs de
co-intégration20(*)
dans un cadre multivarié, de ce fait elle apparaît plus attrayante
lorsqu'on veut tester la co-intégration dans un système de
plusieurs variables.
Nous partons de la représentation
autorégressive d'ordre p ou VAR(p) sous forme à correction
d'erreur.
 (7) (7)
Ou Xt est un vecteur de dimension nx1
 vecteur des
innovations de dimension nx1 vecteur des
innovations de dimension nx1
Si le nombre de relation stationnaire linéairement
indépendante entre les variables est r (0 r<n),
alors la matrice r<n),
alors la matrice  est de rang
r<n. selon Johansen, on peut réécrire est de rang
r<n. selon Johansen, on peut réécrire  =ab' ou a et
b sont deux matrices (n,r) de rang r. Dans ce cas l'équation (7)
devient : =ab' ou a et
b sont deux matrices (n,r) de rang r. Dans ce cas l'équation (7)
devient :
 t
= ab'Xt-1 + t
= ab'Xt-1 + 
Le rang r est le nombre de relation stationnaire
linéairement indépendante entre les variables Xt. Si
r=0, il n' y a pas de relation de co-intégration et donc pas de relation
de long terme entre les variables. L'hypothèse de co-intégration
peut être formulée ainsi :
H1(r) :  =ab' =ab'
Celle-ci implique que sous certaines conditions notamment la
valeur de r,  est stationnaire, Xt n'est pas stationnaire mais b'
Xt est stationnaire. Les relations b'Xt sont
interprétées comme des relations de co-intégration et (a)
la matrice de coefficient d'ajustement à son niveau d'équilibre
(« feed back matrice »). L'approche de Johansen (1988) est
basée sur deux tests sur les valeurs propres du système. Le
premier est appelé statistique de la trace : teste qu'il existe au
moins r vecteurs de co-intégration dans un système comportant
N>r variables et le second dénommé statistique de la valeur
propre maximale : teste qu'il existe exactement r vecteur de
co-intégration contre l'alternative r+1 vecteurs. Ces deux statistiques
ont des distributions non standard et les valeurs critiques ont
été tabulées notamment par Johansen (1988) et Johansen et
Juseluis (1990). est stationnaire, Xt n'est pas stationnaire mais b'
Xt est stationnaire. Les relations b'Xt sont
interprétées comme des relations de co-intégration et (a)
la matrice de coefficient d'ajustement à son niveau d'équilibre
(« feed back matrice »). L'approche de Johansen (1988) est
basée sur deux tests sur les valeurs propres du système. Le
premier est appelé statistique de la trace : teste qu'il existe au
moins r vecteurs de co-intégration dans un système comportant
N>r variables et le second dénommé statistique de la valeur
propre maximale : teste qu'il existe exactement r vecteur de
co-intégration contre l'alternative r+1 vecteurs. Ces deux statistiques
ont des distributions non standard et les valeurs critiques ont
été tabulées notamment par Johansen (1988) et Johansen et
Juseluis (1990).
Les tests de co-intégration peuvent être
utilisés pour estimer la relation de long terme entre le PIB et ses
variables explicatives.
Le test de racine unitaire sur le résidu montre que
celui-ci est stationnaire en niveau confirmant de ce fait l'existence d'une
relation de co-intégration.
Tableau 8 : Test de stationnarité sur le
résidu
|
Tests
Variables
|
DF
|
ADF
|
PP
|
|
Valeur
calculée
(t ) )
|
Valeur tabulée (au seuil de 5%)
|
Valeur
calculée
(t ) )
|
Valeur tabulée (au seuil de 5%)
|
Valeur
calculée
(t ) )
|
Valeur tabulée (au seuil de 5%)
|
|
 le résidu estimé le résidu estimé
|
-3,6302
|
-1,9574
|
-2,6660
|
-1,9583
|
-3,6973
|
-1.9575
|
Le résultat du test de co-intégration fait
à partir du logiciel Eviews sur les séries de 1980 à 2002
en annexe nous montre à un seuil critique de 5% qu'il existe une
relation de co-intégration dont la linéarisation des
résultats est la suivante :
LogYt = 4,0224 + 0,1928logG + 0,1548logK +
0,197logN
(16,1942) (8,4147) (2,3968)
(4,1356)
Les valeurs entre parenthèses représentent la
significativité des variables estimées.
b) L'estimation du modèle à correction
d'erreur
Lorsque les séries sont non stationnaires et
co-intégrées, il convient d'estimer leurs relations à
travers un modèle à correction d'erreur (ECM) « Error
Correction Model ». Engle et Granger (1981) ont
démontrés que toutes les séries co-intégrées
peuvent être représentées par un ECM
(théorème de la représentation de Granger). Après
l'estimation de la relation de long terme et le calcul du résidu, le
modèle dynamique se présente de la façon suivante.

Le coefficient ( )
représente la vitesse d'ajustement vers l'équilibre, il s'agit de
la force de rappel vers l'équilibre. Ce coefficient doit être
significativement négatif. Le EMC est un modèle qui
intègre à la fois les évolutions de court terme autour
d'un équilibre de long terme. )
représente la vitesse d'ajustement vers l'équilibre, il s'agit de
la force de rappel vers l'équilibre. Ce coefficient doit être
significativement négatif. Le EMC est un modèle qui
intègre à la fois les évolutions de court terme autour
d'un équilibre de long terme.
L'estimation du modèle à correction d'erreur en
annexe nous donne la relation de court terme suivante :
 logYt = -0,5282 logYt = -0,5282  + 0,1276 + 0,1276 logGt - 0,0129 logGt - 0,0129 logKt - 6,2388 logKt - 6,2388 logNt logNt
(-3,9980) (5,2133)
(-0,2151) (-2,5506)
+ 0,1823
(2,8227)
B) L'analyse des résultats
1) Interprétation des résultats
L'observation des résultats de notre
modèle, nous permet tout d'abord constater que les coefficients de
l'estimation du modèle à l'aide des MCO sont tous positifs et
sont assez conforme à ceux attendus. Mais, les rendements
d'échelle ne sont pas constants ou croissants. Le coefficient du capital
public est de l'ordre de 0,19 ce qui est un peu faible par rapport à ce
qu'avait obtenu (Aschauer, 1989), et après lui une majorité
d'études spécifiées en niveau sur données
chronologiques américaines. En revanche, ces résultats
s'inscrivent dans la moyenne de ceux obtenus par les auteurs travaillant en
panel. Ceci signifie que les infrastructures influencent significativement la
croissance du PIB ; une augmentation des investissements publics de 1%
contribuera à augmenter le produit de 0,19%.
En ce qui concerne le capital privé, le coefficient est
inférieur par rapport à celui du capital public, ce qui confirme
d'avantage la théorie. Cette conclusion peut trouver une explication
dans le fait que bien que les dépenses d'infrastructures n'ont
cessé d'augmenter au Cameroun, l'on devait s'attendre plutôt
à un effet d'entraînement21(*). Non seulement, les divers réseaux sont
dégradés au cours des années, et le manque
d'infrastructure est défini dans la liste des principaux handicaps au
développement du secteur privé au Cameroun22(*). Mais également, on
peut imputer cela au fait que les investisseurs nationaux sont trop peu
nombreux, trop démunis et insuffisamment qualifiés pour
suppléer à la carence d'investissements.
Par ailleurs, l'information de la théorie qui
découle de cette variable peut être imputée à la
qualité et à la nature de la variable. Une autre façon de
prendre en compte davantage d'informations, consiste à examiner une
série temporelle beaucoup plus longue pour la productivité et le
stock de capital.
Le coefficient positif du niveau de l'emploi peut
également être justifié par le fait qu'avec la crise
économique, le secteur informel aurait pris une importance croissante au
Cameroun, jusqu'à employé 75% de la main d'oeuvre urbaine et une
part non négligeable des travailleurs qualifiés.
L'analyse de la relation de long terme suivant l'observation
des résultats de la régression nous donne la valeur de
R2 (0,82%) et R2 ajusté (0,79%), ce qui montre que
l'ensemble des variables explicatives du modèle théorique a bien
une influence sur la variable expliquée. Les investissements en
infrastructure de transport ont un rendement positif à long terme. Les
équipements lourds qui constituent le capital physique sont amortis au
fur et à mesure de leur exploitation.
L'estimation du EMC montre que l'erreur d'équilibre
dénommée aussi résidu décalé d'une
période est statistiquement significatif et présente le signe
attendu. Son coefficient (-0,52) traduit l'effet d'ajustement du PIB à
chaque période à l'équilibre. Le PIB s'ajuste donc
à son niveau d'équilibre de long terme. Ce qui indique que la
représentation à correction d'erreur converge des séries
vers la cible de long terme. La vitesse d'ajustement élevée du
PIB justifie les écarts entre certains coefficients de court et de long
terme. Ainsi des chocs sur le PIB se corrigent à 52.82% par l'effet
« feed-back ». En d'autres termes, des chocs ponctuels
peuvent écarter la variable de sa cible de façon
temporaire : la force de rappel vers le comportement de long terme ne
comble l'écart potentiel qu'en plusieurs période, traduisant les
rigidités et les délais d'ajustement de l'économie.
Cette étape nous a permis de définir plus
précisément la contribution de l'infrastructure de transport
à la croissance, que cette variable expliquait la production nationale.
Or, il pourrait exister un biais de simultanéité entre la
production et les autres variables. Pour y répondre, il est donc
nécessaire d'entreprendre un test de causalité.
Ø Test et estimation de la causalité au
sens de Granger
Dans l'analyse précédente, nous avons
supposé que les facteurs de production, tant publics que privés,
avaient un effet sur la valeur ajoutée, que ces variables expliquaient
la production du pays. Une des critiques fondamentales adressées aux
études concernant le rôle des infrastructures sur le
développement concerne le sens de la causalité de la relation.
On peut toutefois penser que, si le capital privé et
le capital public déterminent le produit, comme le postule notre cadre
théorique utilisant une fonction de production Cobb-Douglas, le produit
peut également influencer, en retour, les stocks de capital public et
privé. Plusieurs explications peuvent justifier cette relation, comme un
effet de type Wagner-Baumol23(*), un effet de demande d'infrastructures
supplémentaires à mesure que l'économie croit ou un effet
revenu de la dépense du gouvernement. Il convient donc de tester la
causalité entre d'une part le PIB et d'autre part le capital public et /
ou le capital privé. Nous pouvons également tester la
causalité entre stocks de capital public et privé. On peut en
effet penser que la disponibilité d'infrastructures publiques est
susceptible de favoriser la formation de capital privé,
réciproquement, la demande d'investissement public émanant du
secteur privé peut croître à mesure que l'on
développe ses capacités de production.
Les résultats du test de causalité au sens de
Granger sont présentés sur le tableau ci-dessous.
Tableau 9 : Test de causalité de Granger :
retard de 2 périodes
Hypothèses nulles
|
Obs
|
F-Statistique
|
Probabilité
|
|
G1 ne cause pas au sens de Granger Y1
|
21
|
4.58936
|
0.02659
|
|
Y1 ne cause pas au sens de Granger G1
|
2.18718
|
0.14464
|
|
N1 ne cause pas au sens de Granger Y1
|
21
|
2.74146
|
0.09467
|
|
Y1 ne cause pas au sens de Granger N1
|
1.70600
|
0.21301
|
|
K1 ne cause pas au sens de Granger Y1
|
21
|
16.6770
|
0.00012
|
|
Y1 ne cause pas au sens de Granger K1
|
1.24692
|
0.31386
|
|
N1 ne cause pas au sens de Granger G1
|
21
|
3.79069
|
0.04492
|
|
G1 ne cause pas au sens de Granger N1
|
2.85570
|
0.08699
|
|
K1 ne cause pas au sens de Granger G1
|
21
|
4.14513
|
0.03544
|
|
G1 ne cause pas au sens de Granger K1
|
2.56649
|
0.10796
|
Pour un décalage d'une période, parmi les
différentes variables de croissance, on constate que le capital public
et le capital privé causent au sens de Granger le produit.
L'examen de la pertinence de la dynamique de long terme,
montre que les variables envisagées dans le cadre de ce travail de
recherche expliquent la croissance au Cameroun ; une restriction doit
cependant être faite sur le signe des coefficients dans la mesure
où ils peuvent avoir plus d'effet sur le niveau de vie pour le capital
public et positif pour le capital privé. Forts de ces conclusions,
quelques propositions de solutions s'avèrent pertinentes pour permettre
à l'économie camerounaise de relever les principaux défis
auxquels elle est confrontée.
2) Implications de politique économique
Si l'infrastructure a effectivement des retombées
substantielles, cela implique-t-il que le niveau de capital public est
insuffisant et que les hauts niveaux d'investissement sont
justifiés ? A ce niveau la fonction de production ne nous aide
guère, mais selon d'autres indications, il semble que des
opportunités valables existent pour des investissements publics. L'Etat
se doit tout d'abord d'accompagner les forces du marché en adoptant une
perspective stratégique, un mode de gestion des systèmes
d'infrastructures et un cadre réglementaire favorable à la
modernisation et au développement des infrastructures. Cela suppose
notamment de planifier les besoins en matière d'investissements et
identifier les projets rentables auxquels le secteur privé pourrait
être associé.
Un autre rôle essentiel de l'Etat serait d'adopter une
politique de tarification des services d'infrastructure existants et nouveaux
qui permette de mobiliser des fonds publics suffisants pour en financer
l'entretien et le développement. C'est dans ce domaine concret mais
vital des finances publiques, davantage que par des mesures d'incitation
à l'investissement privé, qu'ils peuvent raisonnablement
espérer être le plus efficace pour remédier à la
crise de financement.
Par ailleurs, l'Etat se doit de restructurer son secteur
productif en corrigeant les options erronées d'industrialisation, en
désengageant l'Etat des investissements non productifs et coûteux
(l'Etat devrait se consacrer aux investissements infrastructurels capables
d'entraîner l'investissement privé), et de doter les tissus
productifs des meilleures capacités pour affronter la concurrence
interne et externe. Pour atteindre ces objectifs, les gouvernements de
l'Afrique Subsaharienne en général et camerounais en particulier
doivent mettre en oeuvre une stratégie de désengagement de l'Etat
bien conçue et réglementée pour améliorer
l'efficience de l'économie, alléger le fardeau qui pèse
sur le budget, mettre fin aux ingérences publiques dans les
décisions économiques et encourager davantage l'innovation et le
dynamisme.
D'autres part, l'investissement public étant
complémentaire de l'investissement privé lorsqu'il est
réalisé dans les infrastructures et l'approvisionnement des biens
publics, le problème en général est de savoir si la
fourniture de l'infrastructure est capable de générer des
externalités propres à provoquer un effet d'entraînement ou
crowling in. Ce qui est le cas dans les économies africaines en
général et en particulier celle du Cameroun où la carence
en infrastructures handicape l'investissement privé. Ici, le peu
d'infrastructures existant est réalisé seulement dans les grandes
villes ; tout investissement dans un endroit éloigné des
grands centres urbains et du port est impossible car non rentable en raison des
coûts exorbitants de transport imputables au mauvais état des
routes. Aussi, une meilleure allocation des crédits budgétaires
conjuguée à l'ouverture de ces secteurs à l'investissement
privé est accompagnée des mesures favorisant la croissance,
améliorait cette situation et allégerait les charges
budgétaires liées à ces infrastructures.
D'autre part, Cameroun est appelé à faire
évoluer la gestion et le mode de financement de la quasi-totalité
de ses infrastructures. Les Partenariats Publics Privés (PPP) seront
probablement au coeur des évolutions à venir ; ils
méritent donc une extrême attention. Après s'être
largement diffusés au sein des sociétés industrielles, les
PPP occupent une place croissante dans les approches du développement.
Chaque nouvelle conférence internationale les place au coeur de
l'actualité et de la réflexion.
Ø L'utilité des Partenariats Publics
Privés
Le principe d'un PPP consiste à réunir les
autorités publiques et des agents privés pour concevoir,
financer, construire, gérer ou préserver un projet
d'intérêt public. De tels partenariats supposent un partage de
risque, de responsabilité et de propriété entre le
gouvernement et le secteur privé, un partage garanti par contrat de
longue durée. Entre les deux extrêmes de la privatisation
intégrale et de l'étatisation intégrale, les formules de
PPP sont nombreuses et diffèrent par la nature du partage des risques
qu'elles sous-tendent. Parmi les secteurs typiquement ou potentiellement
concernés nous avons : l'eau potable, les transports,
l'énergie, les télécommunications, la santé,
l'éducation.
Les pays riches ont adopté les PPP. Deux motivations
fondamentales expliquent ce choix de la part des gouvernements. D'abord, la
recherche d'une plus grande efficacité dans l'utilisation des fonds
publics, d'un meilleur rapport qualité/prix de certains services
d'intérêt commun. Parfois certaines décisions sont plus
facilement et plus rapidement prises lorsqu'un capital privé est en jeu.
De là, une réduction des coûts, à qualité
constante, dont le contribuable entend bénéficier. En Argentine
par exemple, le gain d'efficacité économique globale
suscité par la privatisation partielle d'un ensemble de services publics
(électricité, gaz, eau, télécommunication) a
été estimé à 0,9% du PIB par un modèle
d'équilibre général (Chisari, Estache & Romero, 1999),
gain tout à fait considérable si l'on en considère les
effets cumulatifs de moyen terme.
Ensuite, les PPP permettent d'alléger la contrainte
budgétaire publique en associant le secteur privé à la
prise du risque lié au financement des investissements en
infrastructures. Un recours aux capitaux privé réduit le besoin
d'endettement public. Certes, les autorités doivent en
général garantir à l'opérateur privé une
rétribution, ce qui ressemble fort au service d'une dette. Les PPP
permettent donc de mieux garantir l'utilité de la dépense
réelle à la différence des dettes publiques,
remboursées indépendamment des résultats des actions
financées.
Ces deux familles d'arguments acquièrent une
intensité particulière dans le contexte des pays en
développement. Le secteur p^rivé local peut lui aussi jouer un
grand rôle : il connaît les contraintes les pratiques du
terrain ; il est économiquement incité à contourner
celles qui nuisent à la viabilité du service contrairement,
parfois à un agent public dont les ressources ne sont pas directement en
jeu.
Les croisades humanistes qu'incarnent les Objectifs du
Millénaire pour le Développement supposent l'extension rapide des
services publics et des infrastructures de base, une extension hors de
portée des fonds publics en dépit de l'actuelle remontée
de l'APD mondiale. Associer fonds publics et privés est donc un
impératif de bon sens. Déjà, 27% des investissements en
infrastructures dans les PED sont aujourd'hui financés par le secteur
privé, 3% le sont par l'aide publique mondiale au développement
et les 70% restants par les gouvernements. (DFID, 2002).
L'implication du secteur et des capitaux privés doit
être encore accrue. Or cette implication se produit rarement de
façon spontanée. Les investisseurs privés hésitent
à s'engager devant les risques de non respect des engagements par les
Etats concédants, devant l'étroitesse des marchés,
l'instabilité des économies, le risque de change. Les projets
d'investissements dans les pays en développement présentent donc
souvent de leur point de vue un couple risque/rentabilité insuffisamment
attractif.
Soulignons enfin la leçon fondamentale est que le
succès d'un PPP dépend de façon vitale de la
qualité des contrats signés par les partenaires publics
privés, comme de la qualité de l'indépendance des
instances de régulation en cas de conflit. En Afrique par exemple trop
souvent les monopoles publics ont été transformés en
monopoles privés en dépit de l'absence de tout régulateur
public crédible. Il convient d'en tirer la leçon : pour
arbitrer entre intérêts publics et contraintes privées, des
régulateurs autonomes sont nécessaires. C'est à ce prix
que les investisseurs étrangers seront prêts à s'engager
dans des pays encore perçus comme `'risqués''. C'est à ce
prix que les Etats en recherche de financement seront crédibles.
Il ressort de ce chapitre que l'investissement dans
l'infrastructure de transport est un facteur fondamental de la croissance au
Cameroun. Il s'avère également intéressant de mesurer
l'impact de l'infrastructure sociale sur la croissance au Cameroun.
Chapitre 4
Investissements en infrastructures sociales et
croissance au Cameroun
Au début des années 1990, la théorie de
la croissance à progrès technique endogène s'était
déjà imposée comme cadre d'analyse
privilégié, pour ainsi dire incontournable, en macrodynamique
sans toutefois qu'il n'existât de modélisation attribuant de
manière explicite aux dépenses d'éducation publique le
rôle moteur dans la croissance auto-entretenue24(*).
La première singularité de la contribution
proposée tient en ceci que la dynamique de croissance est
impulsée par l'Etat donc les choix d'allocation des ressources
budgétaires commandent le rythme d'accrétion du capital humain
contrairement au modèle de Lucas (1988), dont c'est l'agent privé
qui relève la décision d'investissement en formation.
Dans ce chapitre, nous allons essayer de présenter les
modèles qui intègre les dépenses publiques de santé
et d'éducation élaborés beaucoup plus dans le cadre des
pays développés (section 1) ensuite, nous allons choisir un pour
effectuer des tests économétriques et proposer des politiques
économiques (section 2).
Section 1 : Présentation des
modèles théoriques
A) Approches théoriques du lien dépenses
publiques-croissance
Selon le courant néo-keynésien, à court
terme et en situation de chômage ou de faible croissance
économique, les dépenses publiques, quelle qu'en soit leur
orientation, contribuent à relancer ou à entretenir
l'activité économique par leur effet sur les recettes des
entreprises ; selon le courant néoclassique, les dépenses
publiques de développement des infrastructures contribuent à
favoriser le développement et l'efficacité des investissements
privés, et elles sont donc porteuses elles aussi de croissance (Barro,
1990 ; Barro, Sala-i-Martin, 1995) cités par Berthomieu (2004).
Plus généralement, dans ces deux courants de pensée, on
est conscient de l'existence de situations d'externalités ou de biens
économiques de nature particulière, qui revêtent la nature
de biens ou de services publics que seule la puissance étatique est
à même de gérer ou de produire et de diffuser de
façon efficiente et équitable (comme les biens environnementaux,
les services de certains monopoles naturels, la défense, les services
publics d'éducation et de santé etc.).
Il est donc clair que, s'il est indispensable que l'Etat
assume un certain volume de dépenses d'infrastructures pour assurer
à la fois les missions régaliennes et la production des biens et
services publics qui lui incombent, les ressources monétaires et
financières qu'il doit mobiliser doivent être d'un montant
limité. Il semble donc bien qu'il doit exister un optimum de
dépenses publiques pour chaque pays.
Une telle analyse a certes été maintes fois
évoquée en termes littéraires mais la quantification de ce
seuil, a été très rarement entreprise.
Parmi les travaux récents sur cette question, nous
allons retenir deux approches : l'approche développée pour
le cas des USA à la fin des années 90, par R.K. Vedder et L.E.
Gallaway (1998) et une approche inspirée du modèle de
K.Shubert.
1) L'approche par la `'courbe d'Armey'' (Vedder et
Gallaway, 1998)
La construction de la courbe d'Armey, (cf. Armey (1995)),
repose sur l'idée selon laquelle, lorsque les dépenses publiques
sont faibles (ou en tous cas inférieures à un certain niveau), la
fourniture d'un certain nombre de biens publics (ou de services publics)
considérés normalement comme fournisseurs d'externalités
positives favorables au développement du secteur privé
n'étant pas assurée, le niveau du produit global ou bien le taux
de croissance de l'économie est faible ; réciproquement,
lorsque le niveau des dépenses publiques est très
élevé, le poids de l'Etat dans l'économie est excessif et
celui-ci, détournant une trop grande quantité de richesses
à son profit, pénalise le secteur privé qui ne dispose pas
de moyens suffisants pour accumuler assez de ressources lui permettant
d'assurer une bonne croissance économique. D'où l'idée de
l'existence d'un « seuil optimal » de dépenses
publiques par rapport au PIB qui déterminerait la proportion (G/PIB)
optimale compatible avec l'output (ou le taux de croissance) maximal.
L'idée de base de cette vision est que l'on puisse
justifier le tracé d'une courbe du type ci-dessous reliant la variable
explicative (G/PIB) en abscisse à la variable expliquée (une
variable mesurant la croissance, O (output) pour le PIB ou g% son taux de
croissance) en ordonnée.
Graphique 4: La courbe d'Armey
 ou ou 


La valeur numérique du seuil `'idéal'' doit
pouvoir être estimée au moyen des tests
économétriques adéquats.
Dans la littérature mentionnée ci-dessus, la
recherche empirique est menée à l'aide de deux types de
tests : soit, on cherche à expliquer directement la grandeur du PIB
en fonction (G/PIB) et quelques autres variables, soit c'est le taux de
croissance g% du PIB qu'on se propose d'expliquer ; dans les deux cas, on
cherche à tester des relations quadratiques en termes de cette variable.
Si le coefficient du terme en (G/PIB) est
négatif, alors on peut calculer le `'seuil idéal''. est
négatif, alors on peut calculer le `'seuil idéal''.
Ainsi Vedder et Gallaway (1998) testent une expression de la
forme :
O = A + b (G/PIB) - c (G/PIB) +
....(d'autres variables) +
....(d'autres variables)
Dans laquelle O désigne le PIB en niveau, puis une
relation de la forme : g%=A + b (G/PIB) - c (G/PIB) + ....
(d'autres variables) + ....
(d'autres variables)
2) Validations statistiques
Une idée importante préside à
l'élaboration de ces tests est qu'il semble utile de
procéder à l'examen des données brutes avant d'effectuer
cette analyse empirique, de façon à repérer, si possible,
des périodes au cours desquelles une relation linéaire croissante
entre (G/PIB) et O ou g% puisse être testée, la variable
explicative (G/PIB) étant accompagnée d'autres variables jouant
d'habitude un rôle favorable dans le processus de croissance. Le choix de
ces variables est ouvert et il dépend de la situation du pays
étudié.
Ainsi Vedder et Gallaway (1998) ont testé la relation
suivante pour les USA, sur la période (1947- 1997) :
O = A + b (G/PIB) - c (G/PIB) + d T - e
U + d T - e
U
Où T et U désignent respectivement le temps et
le taux de chômage. Ils obtiennent :
O = -566,2 + 121,2 (G/PIB) - 3,47 (G/PIB) + .... + ....
Ce qui donne une estimation de l'ordre de 17,5% pour le seuil
`'idéal'' recherché.
Ces mêmes auteurs, toujours pour les USA et sur la
très longue période 1796-1996, testent une relation du
type :
g%= A + b (G/PIB) - c (G/PIB) + d T + f W + d T + f W
où T représente encore le temps et W est une
variable qui mesure le pourcentage du nombre d'années de guerre pour
chaque période de dix années selon lesquelles ils
découpent leurs séries chronologiques. Ils obtiennent :
g%= 73,7 + 1,52 (G/PIB) - 0,069 (G/PIB) - .... - ....
Ce qui donne une estimation de l'ordre de 11,1% pour le seuil
`'idéal'' recherché.
Vedder et Gallaway (1998) ont aussi testé des
relations du même type, pour diverses catégories de
dépenses publiques, composantes de G, comme les dépenses de
santé publique, d'éducation, de défense, et ils ont
trouvé des `'courbes d'Armey'' pour plusieurs catégories de ces
dépenses. Mais ils observent que l'on n'obtient pas toujours des
résultats confirmant l'existence de ces courbes (donc de tels seuils),
selon les catégories de dépenses ou selon les périodes
d'observation.
B) Un autre modèle d'analyse
1) Le modèle de K. Shubert
Nous présenterons un modèle inspiré des
travaux de K. Schubert car il permet de répondre à la
préoccupation selon laquelle, les dépenses d'éducation et
de santé agissent sur le capital humain et par là sur la
croissance. Le modèle de Schubert permet de vérifier
aisément l'hypothèse selon laquelle les dépenses
d'éducation et de santé constituent un input important dans la
formation du capital humain, et d'autre part, que compte tenu du fait de
l'existence d'une relation entre les dépenses de santé et
d'éducation et le capital humain, et l'existence d'une relation entre le
capital humain et la production, on peut donc en définitive
établir une relation directe entre les dépenses
d'éducation et la production.
L'équation de la formation du stock
agrégé de bien final s'écrit :
Y(t) = K(t) (1) (1)
qui est une fonction Cobb-Douglas à rendements
d'échelle constant avec :
Y(t) la production de bien
K(t) le stock de capital physique
H(t) le stock agrégé de capital humain
u est une variable ayant la dimension du temps (0 ) )
(1-u) est la proportion de capital humain consacré
à la production
De ce qui précède, on déduit les
équations du modèle :
H = f(De, Ds) (2)
Ce qui nous donne :
H =  (3) (3)
La comparaison entre  et et  nous
permettra de tester l'hypothèse H1 selon laquelle les dépenses en
matière d'éducation et de santé constituent un input
important dans la formation du capital humain. nous
permettra de tester l'hypothèse H1 selon laquelle les dépenses en
matière d'éducation et de santé constituent un input
important dans la formation du capital humain.
Selon K. Schubert, la production est fonction du capital
physique et d'une proportion de capital humain.
Donc, nous aurons :
Y = K(t)
log Y = 
log Y =  (4)
(4)
La comparaison entre  et et  permettra de
vérifier l'effet des dépenses d'éducation et de
santé sur la croissance, ce qui correspond à l'hypothèse
H2. permettra de
vérifier l'effet des dépenses d'éducation et de
santé sur la croissance, ce qui correspond à l'hypothèse
H2.
2) Présentation des variables
- Les dépenses d'éducation (De)
La majeure partie des infrastructures scolaires est
supportée par le secteur public, de plus les dépenses des
établissements privés sont négligeables par rapport aux
dépenses publiques d'éducation.
- Les dépenses de santé (Ds)
Jusqu'à présent au Cameroun, l'Etat reste le
plus grand investisseur dans le domaine de la santé. De plus, les
dépenses des établissements privés sont
négligeables par rapport aux dépenses publiques de santé,
par conséquent les dépenses publiques de santé
décrivent mieux l'évolution des investissements dans le domaine
de la santé pour notre période d'étude.
- Le capital humain (H)
Nous utiliserons dans le cadre de notre travail la force de
travail déjà défini au chapitre
précédent.
- Le capital physique (Kp)
Ici nous utiliserons la formation brute du capital fixe (FBCF)
du secteur secondaire
- Y représente la production.
Les données proviennent de la Banque Mondiale et de la
Direction de la Statistique et de la Comptabilité Nationale.
Section 2 : L'évaluation
empirique
A) Méthode d'estimation
Les tests de empiriques seront effectués avec le
logiciel Eviews. Cependant, le type de modélisation auquel on fait face
présente l'inconvénient majeur d'utiliser des séries
économiques qui ne sont ni stationnaires ni cointégrées
par leur nature. Pour pallier à ces insuffisances, les techniques de
cointégration sont utilisées pour effecteur les tests. Ainsi,
nous commencerons par le test de stationnarité des variables, ensuite la
régression et enfin le test de cointégration.
1) Le test de stationnarité des
variables
Dans cette première étape, le test de
stationnarité permet de déterminer l'ordre d'intégration
de toutes les variables du modèle. Pour ce faire, on utilise le test de
racine unitaire de Dickey-Fuller Augmenté. Ce test est nécessaire
avant l'estimation des paramètres car il permet d'éviter de
mettre en relation les variables qui divergent. Par conséquent,
après ce test les variables auront chacune un trend soit après le
test en niveau, soit après le test en différence première
ou après le test en différence seconde.
Les résultats de ce test sont présentés
dans le tableau ci-après.
Tableau 10 : Récapitulatif du test de
stationnarité des variables
|
variables
|
Test en niveau
|
Test en différences 1ères
|
Test en différences 2nde
|
|
Ttab à 5%
|
t
|
Ttab à 5%
|
t
|
Ttab à 5%
|
t
|
|
De
|
-2,97
|
-1,80
|
-2,98
|
-1,88
|
-2,99
|
-3,82
|
|
Ds
|
-2,97
|
-1,99
|
-2,98
|
-2,70
|
-2,99
|
-5,38
|
|
H
|
-2,97
|
-1,96
|
-2,98
|
-2,33
|
-2,99
|
-3,96
|
|
Kh
|
-2,97
|
-0,78
|
-2,98
|
-4,84
|
-2,99
|
-6,01
|
|
Kp
|
-2,97
|
-0,85
|
-2,98
|
-1,13
|
-2,99
|
-5,33
|
|
Y
|
-2,97
|
-1,78
|
-2,98
|
-5,18
|
-2,99
|
-
|
Les variables De, Ds, H, Kp n'ont pas été
stationnaires après le test en niveau et en différence
première. Elles l'ont été en différence seconde.
C'est en différence seconde que la valeur critique de Mac Kinnon
à 5% est inférieure à la valeur du test calculé
(t ).
Seules les variables kh et Y ont été stationnaire en
différence première. ).
Seules les variables kh et Y ont été stationnaire en
différence première.
Cet ordre de stationnarité définit
également l'ordre d'intégration des différentes variables
dans notre modèle. Ce qui signifie par exemple que la variable Ds sera
intégrée d'ordre 2 et la variable Kh intégrée
d'ordre 1.
La régression
Une fois toutes les variables rendues stationnaires par le
test ci-dessus mentionné, la procédure suivante consiste à
utiliser la méthode des MCO pour estimer les paramètres. A
travers ces coefficients estimés, on s'assure éventuellement que
les variables sont individuellement significatives et qu'elles expliquent
globalement le modèle. Ces coefficients qui permettront de
vérifier les hypothèses.
Le test de cointégration
La relation entre les variables observées obtenue par
la régression est nécessaire mais non suffisante pour une
conclusion sur la pertinence de notre modèle et sa capacité
à prédire le futur. Il faut s'assurer que la relation
établie est une relation stable de long terme. Le test de
cointégration fait sur le résidu qui est la combinaison
linéaire des variables de l'équation répond à cette
préocupation. C'est également ce test qui permettra de justifier
le choix de notre modèle pour l'élaboration des politiques
économiques.
2) Résultats de la
régression
Les résultats de la régression seront
donnés conjointement avec la vérification des
hypothèses.
Hypothèse H1
Après avoir appliqué les MCO à
l'équation 1 suivante, des bons résultats n'ont pas
été obtenus. Ce qui conduit à réécrire
l'équation sous la forme 2 et à retarder la variable capital
humain (H).
Equation 1 : 
Equation 2 : 
Après estimation, on obtient :

(-0,41) (2,38) (5,36)
(20,13)
Le R2 = 0,88 et le DW = 1,74
On constate que les signes des coefficients sont bons pour
les variables essentielles de l'équation ; les statiques de student
qui sont entre parenthèses sont bons car supérieur à 2
(valeur critique de Mac Kinnon) pour les variables essentielles de
l'équation et le modèle est globalement significatif.
Le Durbin-Watson étant autour de 2, on peut dire qu'il
y a absence d'autocorrélation des erreurs.
Hypothèse H2
Après avoir appliqué les MCO à
l'équation 3 suivante, qui relie le capital physique et humain à
la production, on obtient les résultats suivants :
Equation 3 : log Y = 
Après estimation les bons résultats n'ont pas
été obtenus. La variable endogène a été
retardée d'une période et l'équation suivante
obtenue :
log(Y) = 
(1.26) (3,20)
(3,22)
R2 = 0,72 DW = 2,19
On constate également que les signes des coefficients
de notre équation sont bons pour les variables essentielles de notre
équation.
Les statisques de student qui sont entre parenthèses
sont bon car supérieur à 2 (valeur critique de Mac Kinnon) pour
les variables essentielles de notre équation, le modèle est
globalement significatif car R2 est supérieur à 0,70,
il y a absence d'autocorrélation des erreurs car le Durbin-Watson est
autour de la valeur 2 (ici les zones de doute sont introduites dans la
région d'acceptation car variable endogène a été
retardée).
Ce qui signifie que les coefficients estimés sont
statistiquement différents de zéro pour ces variables.
On peut mettre en relation la formation du capital humain et
la production au Cameroun pour notre période d'étude. En effet,
l'impact de la formation du capital humain sur la production est significatif.
La seconde hypothèse (H2) est vérifiée.
Résultat du test
cointégration
Le résultat de cointégration
consiste à prendre le résidu et à vérifier sa
stabilité à long terme par le test de Dickey-Fuller. Ce test de
cointégration est effectué pour l'équation 1et
l'équation 2 qui ont donné de bons résultats sur notre
période d'étude. Ce sont ces équations qui permettront
également d'élaborer des politiques économiques en
matières d'infrastructures éducatives.
En effet, la formalisation du test Dickey-Fuller de
cointégration s'écrit :

Où  désigne le résidu estimé de la relation statique de long
terme et
désigne le résidu estimé de la relation statique de long
terme et  la perturbation. la perturbation.
Ici on teste :
H0 :  avec avec , non
cointégration des séries , non
cointégration des séries
H1 :  avec avec ,
cointégration des séries ,
cointégration des séries
Si la valeur calculée ou encore la
statistique calculée du coefficient du résidu retardé
à une étape est inférieure à la valeur
tabulée, on accepte alors l'hypothèse de la cointégration
des séries.
Le résultat se présente de la manière
suivante :
Tableau 11 : Résultat des tests de
cointégration
|
(Equation 1)
|
(Equation 2)
|
|
Ttab à 5%
|
t
|
Ttab à 5%
|
t
|
|
3,76
|
1,61
|
3,76
|
3,49
|
Ttab et t et
désignent respectivement la distribution limite et la statistique
calculée (ADF test statistic). et
désignent respectivement la distribution limite et la statistique
calculée (ADF test statistic).
La valeur calculée de la statistique testée du
coefficient du résidu retardé à une étape(1,61)
étant inférieure à la valeur théorique (3,76) au
seuil 5 %, on rejette l'hypothèse nulle et on accepte l'hypothèse
alternative de cointégration séries.
En d'autres termes, la relation entre les dépenses
d'éducation et formation du capital humain d'une part et, formation du
capital et croissance d'autre part sont des relations stables à long
terme.
B) L'analyse des résultats
1) Interprétations des
résultats
L'observation de la première régression montre
que la formation du capital humain au Cameroun dépend essentiellement
des investissements en éducation et santé de la même
période et du flux du capital humain de la période
précédente. Cependant une distinction mérite d'être
faite au niveau des degrés de réaction de chaque variable
explicative. La contribution des dépenses de santé à la
formation du capital humain est moindre que celle des investissements en
éducation au regard des coefficients estimés (0,27
inférieure à 0,36).
Cependant, on constate également que les
dépenses de santé sont également à introduire comme
facteur de capital humain, contrairement au modèle de départ qui
définissait la formation du capital humain comme essentiellement
fonction des investissements en éducation.
Le modèle théorique enseigne que la croissance
est expliquée par le capital physique et le capital humain. Les
résultats obtenus sont satisfaisant puisque la production est
expliquée par le capital physique et le capital humain.
De plus au regard des coefficients estimés, pour les
variables déterminantes du modèle, le capital humain joue un
rôle déterminant dans l'évolution de la croissance.
2) Implications de politique économique en
matière d'infrastructures sociales
Au regard des résultats obtenus, le gouvernement
camerounais se doit d'améliorer le niveau de croissance et par là
celui du niveau de ses habitants. Pour ce faire, il lui importe :
-De redéployer les dépenses publiques vers le
secteur des infrastructures sociales et autre services sociaux afin
d'accroître le niveau de vie de sa population. Ces investissements
développent des externalités qui sont des externalités
positives, dans la mesure où la construction d'un centre de santé
permet la vaccination d'un patient ou d'un groupe de patients
bénéficie à d'autres patients.
-Une autre suggestion consiste à aller vers les
populations des zones reculées, afin qu'elles accèdent à
la scolarisation et aux soins de santé primaire. Bien plus, l'Etat doit
diversifier la construction des établissements scolaires en instaurant
des établissements ayant pour but de former des ingénieurs, ce
qui devrait permettre aux techniciens camerounais d'intervenir directement en
cas de demande des investisseurs secondaire.
-D'autre part, il importe à l'Etat d'appliquer les
principes de bonne gouvernance lesquels impliquent tous les domaines
d'interventions des gouvernements. Ainsi, la lutte contre la corruption, la
transparence dans la prise de décision de toutes natures et dans leur
applications notamment dans la gestion des deniers publics, le renforcement de
la justice sociale ; bref le renforcement de la démocratie sont des
conditions sine qua none sans lesquelles l'on ne saurait aboutir à une
grande optimalité économique et à la paix sociale, non une
paix de l'oppresseur mais une véritable paix naissant d'un consensus
social. En effet, cette situation de paix facteur psychologique très
important pour les opérateurs économiques tant nationaux
qu'étrangers (il n'y a qu'à voir l'influence des troubles sociaux
politiques sur l'investissement) aurait donc une influence sur le financement
des infrastructures et donc le recours aux capitaux privés. En, fait
l'expérience montre que si les pays africains ne
bénéficient pas des retombées de la mondialisation au
niveau des mouvements de capitaux, c'est aussi à cause des risques
liés à l'insécurité grandissante
caractérisée par la naissance généralisée
des foyer de conflits.
En guise de conclusion à ce chapitre, nous partageons
avec la Banque Mondiale et les bailleurs de fonds pour qui la
réalisation de la croissance à long terme dans les pays de
l'Afrique subsaharienne et en particulier le Cameroun passe par un
investissement accrue dans l'infrastructure sociale.
Conclusion générale
L'entrée retenue ici pour traiter de la question de
l'impact du capital public dans la croissance est celle d'une fonction de
production à trois facteurs visant à mettre en évidence
l'existence d'externalités du capital public à un niveau national
d'analyse.
Nous avons ainsi présenté une synthèse
des différentes approches du lien entre l'infrastructure et croissance,
ainsi que ses évidences empiriques.
Mise en oeuvre sur des séries camerounaises portant sur
la période 1980-2002, une telle démarche nécessitait de
recourir à des méthodes d'estimation
économétriques. Deux formes fonctionnelles ont été
testées.
Nos résultats mettent d'abord tout en évidence
le rôle non négligeable joué par les dépenses
publiques d'infrastructures dans la croissance. Toutefois, l'investissement
dans les transports n'est en aucun cas suffisant à la croissance. Comme
les suggèrent les modèles de croissance endogène (Barro,
1990), le capital public serait donc bien à l'origine d'une
externalité de production sur le territoire national et sur la
période étudiée. Cela signifie-t-il que l'infrastructure
est insuffisante et qu'il faut investir plus ? Nous pensons que
l'investissement dans l'infrastructure sociale est aussi déterminante
pour la croissance au sein d'un pays comme le démontre notre analyse.
On retrouve ici une conclusion proche de celle de Fritsch
(1995), pour une période et des séries différentes, mais
s'opposant aux résultats obtenus lorsque la même démarche
est appliquée aux Etats américains. Cette divergence de
résultats peut s'expliquer par des différences de structure du
capital public entre un pays comme les USA et un pays comme le Cameroun. Si le
capital américain est principalement constitué d'infrastructures
routières25(*),
celui du Cameroun semble être mieux réparti entre infrastructures
éducatives et infrastructures de transport26(*) (DSCN).
Même si leurs résultats sont
à manier avec précaution, les estimations réalisées
à l'aide d'une fonction de production suggèrent un rôle
important de ce capital public dans le développement d'un pays. En
effet, les pays développés qui connaissent, en outre un fort taux
d'urbanisation, semblent bénéficier plus intensément des
effets positifs des investissements publics. Les investissements en capital
public apparaissent en mesure de favoriser la croissance de la nation, en
renforçant le dynamisme des régions ayant atteint le niveau de
développement élevé.
On a noté le niveau surprenant des
élasticités obtenues à partir des séries que nous
avons mobilisées : l'élasticité importante pour
l'emploi, faible pour le capital privé et élevé pour le
capital public. Des investigations complémentaires sont ici
nécessaires pour consolider ces résultats. Certaines
améliorations peuvent être obtenues en augmentant la longueur des
séries.
Toutefois, il convient de remarquer que les études
macroéconomiques ne visent pas à servir de guide pour les
décisions individuelles en matière d'investissement dans
l'infrastructure surtout des transports. Les décisions individuelles en
matière d'investissement dans l'infrastructure des transports
requièrent des outils micro-économiques, par exemple une analyse
avantages-coûts sociaux.
Il convient de noter que ce travail puise son
originalité dans le champ d'application de notre méthodologie
théorique. En effet, si les applications aux pays
développés des techniques de cointégration en
macroéconomie sont nombreuses, leur transposition aux pays en
développement est nettement moindre. Malgré l'imperfection des
données, nous obtenons des résultats convaincants conformes
à nos attentes.
Annexes
Test de cointegration de johansen
|
Date: 03/10/06 Time: 12:00
|
|
Sample: 1980 2002
|
|
Included observations: 21
|
|
Test assumption: No deterministic trend in the data
|
|
|
|
|
|
Series: Y1 G1 K1 N1
|
|
Lags interval: 1 to 1
|
|
Likelihood
|
5 Percent
|
1 Percent
|
Hypothesized
|
|
Eigenvalue
|
Ratio
|
Critical Value
|
Critical Value
|
No. of CE(s)
|
|
0.830954
|
69.50954
|
53.12
|
60.16
|
None **
|
|
0.504373
|
32.18023
|
34.91
|
41.07
|
At most 1
|
|
0.406643
|
17.43967
|
19.96
|
24.60
|
At most 2
|
|
0.265452
|
6.478509
|
9.24
|
12.97
|
At most 3
|
|
*(**) denotes rejection of the hypothesis at 5%(1%)
significance level
|
|
|
|
|
|
L.R. test indicates 1 cointegrating equation(s) at 5%
significance level
|
|
|
|
|
|
|
|
|
|
|
Unnormalized Cointegrating Coefficients:
|
|
Y1
|
G1
|
K1
|
N1
|
C
|
|
1.062656
|
0.687172
|
-4.212394
|
3.637786
|
12.73154
|
|
1.415949
|
-0.350476
|
0.985386
|
-2.820930
|
-18.54646
|
|
-2.752702
|
0.779033
|
2.103130
|
-2.762607
|
39.30527
|
|
6.564201
|
-1.113476
|
0.221358
|
-2.265878
|
-128.7540
|
|
|
|
|
|
|
Normalized Cointegrating Coefficients: 1 Cointegrating
Equation(s)
|
|
|
|
|
|
Y1
|
G1
|
K1
|
N1
|
C
|
|
1.000000
|
0.646655
|
-3.964026
|
3.423298
|
11.98087
|
|
(0.57986)
|
(2.77338)
|
(2.59369)
|
(22.3500)
|
|
|
|
|
|
|
Log likelihood
|
194.8092
|
|
|
|
|
|
|
|
|
|
Normalized Cointegrating Coefficients: 2 Cointegrating
Equation(s)
|
|
|
|
|
|
Y1
|
G1
|
K1
|
N1
|
C
|
|
1.000000
|
0.000000
|
-0.594018
|
-0.493155
|
-6.156012
|
|
|
(0.56918)
|
(1.33484)
|
(8.65475)
|
|
0.000000
|
1.000000
|
-5.211443
|
6.056476
|
28.04721
|
|
|
(1.00267)
|
(2.35147)
|
(15.2463)
|
|
|
|
|
|
|
Log likelihood
|
202.1795
|
|
|
|
|
|
|
|
|
|
Normalized Cointegrating Coefficients: 3 Cointegrating
Equation(s)
|
|
|
|
|
|
Y1
|
G1
|
K1
|
N1
|
C
|
|
1.000000
|
0.000000
|
0.000000
|
-1.652668
|
-6.089117
|
|
|
|
(0.98734)
|
(13.2006)
|
|
0.000000
|
1.000000
|
0.000000
|
-4.116176
|
28.63409
|
|
|
|
(2.62015)
|
(35.0310)
|
|
0.000000
|
0.000000
|
1.000000
|
-1.951984
|
0.112613
|
|
|
|
(0.64332)
|
(8.60112)
|
|
|
|
|
|
|
Log likelihood
|
207.6601
|
|
|
|
Relation de long terme
|
Dependent Variable: Y1
|
|
Method: Least Squares
|
|
Date: 03/10/06 Time: 12:02
|
|
Sample: 1980 2002
|
|
Included observations: 23
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
C
|
4.022431
|
1.236393
|
16.19423
|
0.0000
|
|
G1
|
0.192832
|
0.027669
|
8.414787
|
0.0000
|
|
K1
|
0.154852
|
0.064607
|
2.396829
|
0.0270
|
|
N1
|
0.319751
|
0.081732
|
4.135676
|
0.0001
|
|
R-squared
|
0.823488
|
Mean dependent var
|
28.31259
|
|
Adjusted R-squared
|
0.790354
|
S.D. dependent var
|
0.133841
|
|
S.E. of regression
|
0.555127
|
Akaike info criterion
|
-2.801594
|
|
Sum squared resid
|
0.557740
|
Schwarz criterion
|
-2.604117
|
|
Log likelihood
|
36.21833
|
F-statistic
|
26.89401
|
|
Durbin-Watson stat
|
1.808657
|
Prob(F-statistic)
|
0.000000
|
|
Dependent Variable: D(Y1)
|
|
Method: Least Squares
|
|
Date: 03/10/06 Time: 12:13
|
|
Sample(adjusted): 1981 2002
|
|
Included observations: 22 after adjusting endpoints
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
C
|
0.182346
|
0.064598
|
2.822791
|
0.0117
|
|
RESID1(-1)
|
-0.528231
|
0.132122
|
-3.998065
|
0.0009
|
|
D(G1)
|
0.127663
|
0.024488
|
5.213348
|
0.0001
|
|
D(K1)
|
-0.012997
|
0.060403
|
-0.215171
|
0.8322
|
|
D(N1)
|
-6.238871
|
2.445959
|
-2.550685
|
0.0207
|
|
R-squared
|
0.762665
|
Mean dependent var
|
0.025292
|
|
Adjusted R-squared
|
0.706822
|
S.D. dependent var
|
0.056829
|
|
S.E. of regression
|
0.030771
|
Akaike info criterion
|
-3.927786
|
|
Sum squared resid
|
0.016096
|
Schwarz criterion
|
-3.679822
|
|
Log likelihood
|
48.20565
|
F-statistic
|
13.65719
|
|
Durbin-Watson stat
|
1.037347
|
Prob(F-statistic)
|
0.000037
|
|
Dependent Variable: D(Y1)
|
|
|
|
|
Method: Least Squares
|
|
|
|
|
Date: 03/10/06 Time: 12:13
|
|
|
|
|
Sample(adjusted): 1981 2002
|
|
|
|
|
Included observations: 22 after adjusting endpoints
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
Prob.
|
|
C
|
0.182346
|
0.064598
|
0.0117
|
|
RESID1(-1)
|
-0.528231
|
0.132122
|
0.0009
|
|
D(G1)
|
0.127663
|
0.024488
|
0.0001
|
|
D(K1)
|
-0.012997
|
0.060403
|
0.8322
|
|
D(N1)
|
-6.238871
|
2.445959
|
0.0207
|
|
R-squared
|
0.762665
|
Mean dependent var
|
0.025292
|
|
Adjusted R-squared
|
0.706822
|
S.D. dependent var
|
0.056829
|
|
S.E. of regression
|
0.030771
|
Akaike info criterion
|
-3.927786
|
|
Sum squared resid
|
0.016096
|
Schwarz criterion
|
-3.679822
|
|
Log likelihood
|
48.20565
|
F-statistic
|
13.65719
|
|
Durbin-Watson stat
|
1.037347
|
Prob(F-statistic)
|
0.000037
|
Series des differents agrégats
|
n1=loglabor f
|
g1=loginfras
|
k1=logkpriv
|
De
|
Ds %PIB
|
ANNEES
|
|
15,1157022
|
25,19407
|
26,8052587
|
3,86
|
0,11
|
1980
|
|
15,1399295
|
25,2369565
|
26,8266742
|
3,91
|
0,12
|
1981
|
|
15,1635837
|
25,5713587
|
27,0380088
|
4,3
|
0,12
|
1982
|
|
15,1866913
|
26,0684334
|
27,1516829
|
5,1
|
0,13
|
1983
|
|
15,2092769
|
26,4109562
|
27,2153648
|
6,19
|
0,19
|
1984
|
|
15,2313637
|
26,7820782
|
27,1523835
|
6,19
|
0,3
|
1985
|
|
15,2553457
|
26,8264797
|
26,9798351
|
5,6
|
0,4
|
1986
|
|
15,278766
|
26,5346343
|
26,7812295
|
5,2
|
0,5
|
1987
|
|
15,3039101
|
26,0993171
|
26,7747172
|
5
|
0,58
|
1988
|
|
15,3284376
|
25,6667352
|
26,8211671
|
4
|
0,7
|
1989
|
|
15,354526
|
25,2238197
|
26,5954259
|
3,8
|
0,89
|
1990
|
|
15,3862076
|
25,1639858
|
26,5523379
|
3,8
|
0,9
|
1991
|
|
15,4169163
|
25,3631369
|
26,668202
|
2,42
|
0,8
|
1992
|
|
15,4447511
|
24,9141168
|
26,7876695
|
3,88
|
1,03
|
1993
|
|
15,4737386
|
25,1796576
|
26,9644905
|
3,78
|
1,12
|
1994
|
|
15,5019095
|
25,5638085
|
26,9203065
|
3,68
|
1,21
|
1995
|
|
15,5311087
|
25,6624266
|
27,1019551
|
3,58
|
1,3
|
1996
|
|
15,5594794
|
25,777599
|
27,1541137
|
3,48
|
1,39
|
1997
|
|
15,5870673
|
25,8424565
|
27,204843
|
3,38
|
1,48
|
1998
|
|
15,6139146
|
25,8590643
|
27,2239547
|
3,29
|
1,57
|
1999
|
|
15,6400599
|
26,0985442
|
27,3212298
|
3,19
|
1,67
|
2000
|
|
15,6655389
|
26,1613495
|
27,5548957
|
3,09
|
1,76
|
2001
|
|
15,6965012
|
26,5223585
|
27,5879445
|
2,99
|
1,85
|
2002
|
Références bibliographiques
Agenor, P.R (2005), `' Infrastructure, Public Education and
Growth with Congestion Costs'' Centre for Growth and Business Cycle Research,
working paper N° 41
Aghion, P. et Howitt, P (2000), Théorie de la
croissance endogène, traduction française, Dunod
Aschauer, D.A. (1998), Public investment and economic growth
in Mexico, the World Bank Mexico Country Department
Ashipala J, Ndeutalala H, (2003), «The impact of public
investment on economic growth in Namibia», Nepru working paper N°
88
Bangqiao, J (2001), Revue des études sur la relation
entre les investissements dans l'infrastructure des transports et la croissance
économique, Document de travail
Banque Mondiale (2001), Augmenter la croissance et les
investissements en Afrique sub-saharienne, Finding, Gestion économique
et politique sociale
Barro, R. J., Education and economic growth, unpublished,
Havard University
Barro, R.J. (1989), A Cross-country Study of Growth, Saving,
and Government, NBER, Working paper N°2855
Canning, D. (1996), A Database of World Infrastructure Stocks,
1950-95, World Bank
Canning, D. and Pedroni, P. (1999), Infrastructure and Long
Run Economic Growth, World Bank
Castro-Leal, F. et al. (1999), Public Social Spending in
Africa: Do the Poor Benefit? , The World Bank Research Observer, Vol 14,
N°1 PP49-72
Charlot S, Schmitt, B. Infrastructures publiques et croissance
des régions françaises, UMR INRA-ENESAD
Cullison, W.E. (1993), Public Investment and Economic Growth,
Federal Reserve Bank of Richmond Economic Quartely Volume 79/4 PP19-33
De Long, J.B, Summers, L.H. (1990), Equipment Investment and
Economic Growth, Havard University and NBER
Dessus, S. (1999), Capital Humain et Croissance: le rôle
retrouvé du système éducatif, IDEP
Dessus, S. et Herrera, R (1996), Le rôle du capital
public dans la croissance des pays en développement au cours des
années 80, Documents techniques N° 115
Devarajan, S. Easterly, W.R, Pack, H. (1999), Is Investment in
Africa Too High or Too Low? Macro and micro Evidence, AERC Binnual Research
Dewan E, Hussein S (2001), Determinants of economic growth
(panel data approach), Reserve Bank of Fiji, Working paper 01/04
Diebolt, C and Montiels, M. (2000), The New Growth Theories A
Survey of Theoretical and Empirical Contributions, Historical Social Research,
Vol 25-2000-N°2, PP3-22
Dumont, J-C. Et Esple-Somps, S (2000), L'impact des
infrastructures publiques sur la compétitivité et la
croissance : une analyse en EGC appliquée au Sénégal,
Document de travail
Esfahani, S. H, Raminez, M.T (2002), Institutions,
Infrastructures, and Economic Growth, Forthcoming in the Journal of Development
Economics, PP 1-41
Everaert,G. (1997), Negative economic growth externalities
from crumbling public investment in Europe: evidence based on a cross-section
analysis for the OECD-countries, Social Economics Research Group, nr 97/35
Figuires, C. Garderes, P. Rychen, F (2002), Infrastructures
publiques et politiques de développement décentralisées,
Revue d'analyse économique, vol 78, N° 4
Ford, R. Poret, P (1991), Infrastructures et
productivité du secteur privé, Révue économique,
N°17, PP 70-95
Gerardin, H. Guigou, J-D. Ory, J-N (2003), Infrastructures
financiers et développement: Choc et mutations,
Grefige-université de Nancy 2, Cahier de recherche N° 2000-03
Harchaoui, T. M et Tarkhani, F, Le capital public et sa
contribution à la productivité du secteur des entreprises du
Canada, Série de documents de recherche sur l'analyse économique
(AE)
Harchaoui, T. M. Tarkhani, F. Warren, P, L'infrastructure
publique au canada : où en sommes-nous ? Document
analytique, Aperçus sur l'économie canadienne
Haughwout, A.F. (2000), Public Infrastructure Investments,
Productivity and Welfare in Fixed Geographic Areas, Federal Reserve Bank of New
York
Henin P.Y et Hurlin, C. (1999), L'évaluation de la
contribution productive des investissements publics, CGP
Herrera, R (2002), Dépenses publiques et croissance Vs
Etat de développement : d'une problématique à
l'autre, CNRS
Hong-Sang, J and Thorbecke, E (2001), The Impact of Public
Expenditure on Human Capital, Growth, and Poverty in Tanzania and Zambia: A
General Equilibrium Approach, IMF working paper, wp/01/106
Hurlin, C (1999), La contribution du capital public à
la productivité des facteurs privés : Une estimation sur
panel sectoriel pour dix pays de l'OCDE, T2M
Jacquet, P. et Charnoz, O. (2003), Infrastructures, croissance
et réduction de la pauvreté, Agence française de
développement (ADF. Paris)
Kamgnia, Touna (2002), Le comportement d'investissement au
Cameroun : un resserrement de la contrainte financière ?
Sisera.
Kobou, G (2002), Les sources de la croissance
économique au Cameroun, African Econometrics Society.
Krishna, K.L (2004), Patterns and Determinants of Economic
Growth in Indian States, Icrier, Working paper N°144
Kristian, C-Wahl. Meunier, C. (2003), Infrastructures de
Transport et Développement Economique en espace Rural Quelles
méthodes pour quels « effets » ?
DRAST-Ministère des Transports, PREDIT
Kweka, J.P et Morrissey, O (1999), Government Spending and
Economic Growth: Empirical Evidence from Tanzania (1965-1996), CREDIT and
school of Economics, University of Norttingham
Marcellin, J. (2002), l'Economie de l'éducation:
méthodologies, constats et leçon. Série Scientifique,
Cirano
Mattoon, R.H. (2004), L'Infrastructure et le
Développement Economique de l'Etat : examen et enjeux (I-G),
Federal Reserve Bank of Chicago
Meuleu, M., Participation du secteur privé à la
fourniture des infrastructures en Côte d'Ivoire : Revue et
recommandation, African Development Bank, Economic Research papers N°47
Meunier, C. (1999), Infrastructures de Transport et
Développement : L'apport de l'Economie des Réseaux, les
Cahiers Scientifiques du Transport, N°36/1999, PP69-85
Moshi, H.P.B. and Kilindo, A.A.L. (1999), The impact of
government policy on macroeconomic variables: A case study of private
investment in Tanzania, AERC Research paper 89, PP1-23
Nubukpo Kako, K (2003), Dépenses publiques et
croissance des économies de l'UEMOA, CIRAD
O'Connell, S.A, Ndulu, B.L. (2000), Africa's Growth
Experience: A Focus on Sources of Growth, AERC
Raminez, M.T. Esfahani, H.S. Infrastructure and Economic
Growth in Colombia, Banco de la Repùblica
Roy William, L'investissement public dans les infrastructures
de transport est-il source de croissance endogène, Laboratoire
d'économie des transports, Université Lumière Lyon 2
Sala-i-Martin, X. Artadi, E.V (2002), Economic Growth and
Investment in the Arab world, Columbia University, Department of Economics,
Discussion paper 0203-08
Schubert, K Macroéconomie comportements et
croissance, 2° édition, Vuibert.
Stiroh, J.K. (2000), Investissement et croissance de la
productivité : étude inspirée de la théorie
néoclassique et de la nouvelle théorie de la croissance, Document
de travail
Veganzones, M.A (2000), Infrastructures, investissement et
croissance : un bilan de dix années de recherches, CERDI, Clermont
Ferrand
Weil, D.N (2005), Accounting for the effect of Health on
Economic Growth, Department of Economics Brown University
Wylie, P. (1995), Infrastructure and Canadian Economic Growth,
Canadian Business Economics, PP40-52
Zipfel, J. (2004), Determinants of economic growth, Florida
state University
TABLE DES MATIERES
Dédicaces
.............................................................................................i
Remerciements
.....................................................................................ii
Sommaire............................................................................................iii
Liste des abréviations
..........................................................................iv
Liste des tableaux et graphiques
............................................................v
Résumé...............................................................................................vi
Introduction
générale............................................................................1
Première partie : Les fondements
théoriques de l'infrastructure et de la
croissance...........................................................................................8
Chapitre 1 : Approches conceptuelles du lien
entre infrastructures
et
croissance......................................................................10
Section 1 :Les Infrastructures physiques
.......................................11
A) Le rôle productif des
infrastructures......................................11
1) Infrastructures et processus de production
...................12
2) L'approche duale : fonction de coût et demande
des
facteurs.....................................................................18
B) Les nouvelles approches du lien infrastructures croissance
.......21
1) Les effets de la diffusion spatiale des infrastructures
.......21
2) La dynamique transitoire ou l'approche en terme
de convergence
conditionnelle....................................23
Section II : Les infrastructures sociales
.................................................25
A) Caractéristiques et effets des dépenses
d'infrastructures sociales
sur la
croissance..............................................................25
1) Définition et caractéristiques des
infrastructures sociales.25
2)Les effets des infrastructures éducatives sur la
croissanc.27
B) Incidence des infrastructures sociales sur le capital
humain......29
1) Education et
croissance.............................................29
2) Santé et
croissance..................................................31
Chapitre 2 : Les théories de la
croissance.............................................33
Section I - Le modèle néoclassique de
Solow-Swan ...............................34
A) Les enseignements du modèle
..........................................34
1) Hypothèses fondamentales et résolution du
modèle de Solow.....................
.................................................34
1.1 Hypothèses fondamentales du modèle de
Solo....34
1.2) Résolution du
modèle....................................36
a) Dynamique du
modèle..............................36
b) Résolution graphique du modèle de
Solow...38
2) Règle d'or de l'accumulation du capital et
inefficience dynamique
.................................................................39
2.1) Dynamique de la transition du
modèle...............40
2.2) Convergence des
économies...........................41
B) Le modèle de croissance néoclassique et ses
limites...............42
1) Les limites du modèle de base de Solow
......................43
2) Le modèle de Solow et le progrès technique
................44
a) Le progrès technique
...............................44
b) Modèle de Solow avec progrès technique neutre
au sens de Harrod.............................45
Section II :Croissance et rendements
d'échelle.......................................46
A) Les enseignements du modèle
AK........................................46
1) Intégration dans le modèle de
Solow...................47
2) Intégration dans le modèle de
Ramsey.................48
B) Croissance et
externalités...................................................50
1) Externalités liées à l'accumulation
d'un facteur......50
2) L'Etat gérant des
externalités.............................52
Deuxième partie : Evaluation de l'impact
de l'infrastructure sur la croissance au
Cameroun......................................................................55
Chapitre 3 : Relation entre infrastructures de
transport et la croissance
au
Cameroun......................................................................57
Section 1 : Présentation des
modèles.....................................................58
A- Approche par la fonction de
coût..........................................58
1) Le modèle proposé par Bangqiao,
J.............................58
2) Avantages et limites de la fonction de
coût....................59
B) L'approche en terme de fonction de
production......................60
1) Le modèle de
Barro..................................................60
2) Financement des infrastructures par
l'impôt...................61
Section II : L'estimation
empirique.........................................................64
A) Estimation des dynamiques de long terme et de court terme
.....64
1) Présentations des variables et
caractéristiques...............64
a) Présentation des variables et leurs
sources..........65
b) Les tests de
stationnarité...................................66
2) La
régression...........................................................70
a) L'estimation de la relation de long
terme...............72
b) L'estimation du modèle à correction
d'erreur..........74
B) L'analyse des
résultats......................................................75
1) Interprétation des
résultats..........................................75
2) Implications de politique
économique...........................78
Chapitre 4 : Investissements en infrastructures
sociales
et croissance au
Cameroun..................................................83
Section 1 : Présentation des
modèles
théoriques....................................83
A) Approches théoriques du lien dépenses
publiques croissance.....................83
1) L'approche par la `'courbe
d'Armey''.............................84
2) Validations
statistiques..............................................86
B) Un autre modèle
d'analyse.................................................87
1) Le modèle de K.
Shubert............................................87
2) Présentation des
variables..........................................88
Section 2 : L'évaluation
empirique.........................................................89
A) Méthode d'estimation
........................................................89
1) Le test de stationnarité des
variables...........................89
2) Résultat de la
régression............................................91
B) L'analyse des
résultats......................................................94
1) Interprétations des
résultats........................................94
2) Implications de politique économique en
matière d'infrastructures
Sociales...............................................95
Conclusion
générale............................................................................97
Annexes..............................................................................................99
Références
bibliographiques...............................................................103
Table des
matières............................................................................................108
* 1 En l'an 2000, près de
150 chefs d'Etats et de gouvernements ont adopté aux Nations Unies
à New-York la « déclaration du
Millénaire » un ensemble d'objectifs mondiaux de
développement à l'horizon 2015, notamment la réduction de
la mortalité infantile et maternelle, la promotion de l'éducation
universelle, l'accès à l'eau et à l'assainissement sont
autant de thèmes abordés par les OMD.
* 2 Si, dans un tout autre
contexte, certains auteurs comme Von Furstenberg (1980), Eisner (1980) ou
Schultze (1981) avaient déjà émis l'hypothèse que
le ralentissement apparent de la productivité américaine pourrait
s'expliquer par la diminution de l'effort d'investissement public en
matière d'infrastructure, Ratner fut cependant le premier à
estimer la contribution productive du capital public.
* 3 Cité dans Hulten et
Schwab (1991) et Berndt et Hansoon (1992)
* 4 Op cité en page 4
* 5 Cette
élasticité est comprise entre 21% et 45% pour le coeur
d'infrastructures defini de la même façon qu'Aschauer.
* 6 Sans facteur de production,
il n'y a pas de production.
* 7 Investissement de point
mort : volume de capital permettant de maintenir le capital par tête
à son niveau actuel
* 8 Equation
différentielle fondamentale de SOLOW.
* 9 Situation où toutes
les variables en niveau (quantités, prix) croissent à taux
constants.
* 10 Ils `agit de la
comparaison entre 2 équilibres du point de vue intervalle qui les
sépare.
* 11 Elle n'est valable que
pour les économies qui diffèrent par le stock de capital.
* 12 Extrait d'un article de
P.A. MUET (revue de l'OFCE, N° 45, Juin 1993).
* 13 Progrès
technique autonome à contrario du progrès technique
incorporé où le capital et les investissements nouveaux sont un
vecteur de progrès.
* 14 PT neutre au sens de HICKS
si le rapport de rémunération de facteurs KFt/LFt reste
inchangé pour un rapport K/L donné.
PT neutre au sens de HARROD si les
rémunérations relatives des facteurs restent inchangées
pour un rapport K/Y.
PT neutre au sens de SOLOW qui laisse les
rémunérations relatives des facteurs inchangées pour
L/Y.
* 15 Dans une fonction
COBB-DOUGLAS, les 3 formes suscitées sont équivalentes.
* 16 Une des conditions d'Inada
est vidée en raison de la constance des productivités marginales
et moyenne du capital par tête : ft = A > 0
* 17 Situation ou les
activités d'un ou plusieurs agents économiques ont des
conséquences sur le bien être d'autres agents sans qu'il y ait des
échanges ou des transactions entre eux. Leur présence se traduit
généralement par l'apparition d'inefficiences (au sens de pareto)
car il n'existe pas à priori de récompense pour ceux qui
sont à l'origine d'externalités positives, ni de sanction pour
ceux qui engendrent celles négatives.
* 18 Dickey-Fuller ont à
l'aide de la simulation de Monté Carlo, tabulés les valeurs
critiques pour les échantillons de taille différentes. Ces tables
sont analogues aux tables de Student (bien que la loi ne soit pas de
Student)
* 19 Le test de Phillips-Perron
(1988) se déroule en deux étapes :
-Estimation par les MCO des trois modèles de base du test
de Dickey-Fuller et calcul des statistiques associées.
-Estimation d'un facteur correctif établi à partir
de la structure des covariances des erreurs des modèles
précédemment estimés de telle sorte que les
transformations réalisées conduisent à des distributions
identiques à celles de Dickey-Fuller standard.
* 20 Contrairement à
l'approche de Engle-Granger(1981) qui ne tient compte que d'une seule relation
de co-intégration.
* 21 Faini (1994) cité
par Dia Kamgnia détermine un effet d'entraînement que
l'investissement public a sur l'investissement privé dans le cas des
pays ACP pris dans leur ensemble. Toutefois, les élasticités sont
inférieures à l'unité. Ce qui signifie que l'accroissement
des dépenses publiques n'est pas synonyme d'accumulation dans le secteur
privé.
* 22 Cela vient en
5e position sur la liste des 16 principales contraintes
identifiées par la BM (1996)
* 23 En tant que biens
supérieurs, les investissements publics
augmenteraient « mécaniquement » sans action
volontaire des pouvoirs publics avec l'élévation du niveau de
développement de l'économie (Mills et Quinet (1992) cité
par-dessus et Herrera
* 24 L'exception peut
être Azam (1993), cité par Herrera qui plaçait l'accent sur
le secteur d'exportation
* 25 Ainsi, aux Etats-Unis, les
routes représentent, en 1991, près du tiers du capital public
civil américain, alors que les structures éducatives en
mobilisent moins de 15% (Tatom, 1993 ; Gramlich, 1994), cité par
Hurlin
* 26 Au Cameroun la
répartition par principaux secteurs programmes des investissements non
militaires de l'Etat, proposé par la DSCN, fait apparaître que
l'éducation bénéficie plus de 30% des investissements de
l'Etat contre 24% pour les transports.
| 


