|
DEDICACE
A mon père BAZIKA WITANGAMA Léon.
A ma mère YIMBU-LONDE Brigitte.
A mes frères et soeurs : Moise WITANGAMA, Léon
WITANGAMA, Sylvie WITANGAMA, Colette et Jeannette WITANGAMA, Trésor
MITUGA pour leurs prière et sacrifices consentis à nous.
REMERCIEMENTS
Nous ne pouvions commencer la présentation de ce rapport
de stage sans remercier Dieu le père qui nous donne chaque jour le
souffle de vie.
Nos remerciements vont aux personnels de l'institut du
bâtiment et des travaux publics de kamituga plus particulièrement
au Directeur général monsieur le professeur ordinaire Jean
pacifique BALAAMO MOKELWA pour sa vision de développement de chez nous
et son sacrifice.
Nos sincères remerciements vont aux personnes qui ont
consacrées leurs précieux temps à nous encadrer pour sa
bonne réalisation : Mon directeur Dr-Ir Emmanuel MIKEREGO, mon
encadreur l'assistant Vicky KALUNGA,
Aux assistants :Bonfils KSIRANI, Patient WAKILONGO et
Benjamin MUSEBENGI pour leurs suivies et conseils.
Aux camarades étudiants plus particulièrement
à Victor LWESSO et LUSAMBIA MULONDA pour leurs collaborations.
A la famille KABAZIMYA et la famille BISIMWA KASHEMBO pour leur
soutien.
A mon frèreGandhi BISIMWA et maman VIBILA MAPASI.
En fin, nous disons merci à tous ceux qui de près
ou de loin ont oeuvrés pour la réalisation de ce travail.
SIGLES ET/OU ABREVIATIONS
BAEL : Béton armé aux
états limites
bo : la base de la section rectangulaire ou
carré
cm : centimètre
Fc28 : la résistance de
béton à la compression
Ftj : résistance de
béton à la traction
h : la hauteur
IBTP-KAMITUGA :institut du bâtiment
et des travaux publics de kamituga
Ir : ingénieur
kg : kilogramme
KN : kilo newton
lx : petit côté de
la structure
ly : grand côté de
la structure
m : mètre
m 2 : mètre
carrée
m3 : mètre cube
MPa : méga pascal
ØHA : diamètre en
millimètre des aciers a haute adhérence
RD Congo : république
démocratique du Congo
RDC : rez-de-chaussée
Zb : bras de levier
Chapitre I. INTRODUCTION GENERALE
0.1. LAPROBLEMATIQUE
La révolutionindustrielle, la mondialisation et la
révolution de la technologie ont entrainées une forte
urbanisation des villes ; l'une des conséquencesimmédiates de ce
boom, démographique dans les zones urbaines ont été le
changement dans le style de construction.
En effet, afin de rationaliser l'espace, il fallait abandonner
les conceptions traditionnelles au profit des bâtimentsmulti
étages ce qui permettait de trouver un abri à un plus grand
nombre d'habitants sur un petit espace.
Cela a été une réalitégrâce aux
techniques des constructions modernes telle la construction en béton
armé, la construction en bois et la construction métallique.
Entre temps des séries de règlementations ont
été élaborées dans le but de dimensionner
convenablement les bâtiments ;le BAEL etl'euro code.
Vue que nous avons constante que dans notre région du
Sud-Kivu les écoles ne respectent pas les normes architecturales et
structurales prévues par la loi, nous avons
portél'intérêt sur la conception architecturale et
structurale de l'immeubleà usage d'uneécole en RD Congo au
Sud-Kivu.
0.2. HYPOTHESES
Vue toutes ces difficultés énoncées nous
sommes censés trouver des solutions.
En nous basant a la question fondamentale de notre
problématique, nous pouvons formuler les hypothèses
suivantes :
Ø La conception en respectant les normes congolaises et
internationaux sur la construction des immeubles à usage d'école
en particulièrement dans notre province du Sud-Kivu.
Ø La connaissance de charges sollicitant les composantes
de la structure.
Ø La justification des sections choisies vie-a-vie de
sollicitation.
Ø Le choix de matériaux locaux pour l'apaisement de
cout et la facilite de moyens de transport lors de l'exécution du
projet.
Ø Sur le plan architectural, concevoir un projet en
respectant les conditions locales écologiques.
Ø Analyse des structures existantes et donner un autre
aspect des constructions nouvelles.
0.3. L'OBJECTIF GLOBAL
L'objectif de cette étudeestd'avant tout de concevoir un
projet qui va assurer la sécurité des usagers, par suite, il
devra entre autres duré dans le temps et résister aux
éventuellesintempéries mais aussi en respectant les normes
prévues par la loi congolaise sur la conception des immeubles à
usage d'école.
0.4. LES OBJECTIFS SPECIFIQUES
Les objectifs spécifiques des études de conception
sont de construire des bâtiments qui :
· Répondent aux besoins d'aménagement spatial
et fonctionnel des utilisateurs ;
· Concevoir expressément un bâtiment en
fonction du climat existant et autres paramètres physiques ;
· Créer un immeuble pour réduire les couts
d'immobilisation tout en offrant des couts du cycle de vie les plus bas ;
· Répondent aux différents codes et
règlements applicables ;
· Sans oublier la nécessité de la conception
d'une structure qui pourra transmettre d'une manière optimale au sol les
charges engendrées par le bâtiment. Ce qui permettra sans doute de
dimensionner effectivement chaque élément en respectant la
sécurité édictée et les règlements en
vigueur.
0.5. LA METHODOLOGIE
Pour une bonne récolte des données de notre
travail, nous avions fait recours aux techniques suivantes :
Ø Interview : elle nous avait
permisd'entrer en conversation avec les ingénieures du domaine, les
camarades des autres établissements techniques et d'autres
praticiens.
Ø Documentaire : cette
méthode, consistée pour nous à consulter les ouvrages, les
publications, les articles et les notes de cours pour la réalisation de
notre projet entre autres :
- Normes de construction scolaires (Direction du Génie
scolaire Novembre) A l'usage des gens intéressés à la
construction d'écoles en Haïti, article publie en 2010.
- Congo Dr-directives-sur-les-normes-des-constructions-scolaires
(CIRCULAIRE N°MINEPSP/CABMIN/0668/2007 DU 13/11/07).
- Conception et calcul de structures en béton arme [HENRY
THONIER,2ieme édition].
Ø D'analyse et dediscutions : nous a
permis d'analyser et de discuter sur la conception architecturale et
structurale des immeubles à usage d'école en RDCongo cas de notre
province du Sud-Kivu.
Chapitre I. Chapitre II. REVUE DE LA
LITERATURE
II.1 La conception
La conception est la phase de création d'un projet de
construction.
Selon les éditions Larousse : elle
est une création de l'esprit.
Les études de conception visent à obtenir un avis
d'expert indépendant et impartial concernant des projets
sélectionnés et faire en sorte que de maximiser la qualité
de l'ouvrage final. L'équipe des services de soutien technique est
responsable de procéder aux études de conception. Il s'agit d'un
groupe conseil qui appuie le processus de gestion de projet.
L'équipe agit comme agent d'habilitation de la
qualité de la conception et de la valeur ajoutée. De plus, elle
stimule l'enthousiasme à l'égard de la conception en
créant et en animant un forum où les questions et
préoccupations portant sur la conception peuvent être
abordées.
La conception se fait dans le profond respect de règles de
l'Art. La conception se déroule en plusieurs phases (de l'esquisse
jusqu'à la passation de contrant de travaux) durant lesquelles le projet
de construction est affiné.
a. Les différents types de
conception :
- Conception traditionnelle :
Un projet de construction comporte traditionnellement trois
phases : la conception ou planification, l'exécution et
l'exploitation.
La phase de conception vise àdéterminer les
objectifs et les caractéristiques techniques et architecturale du
projet.
- Conception-réalisation :
Est une organisation du projet de construction ou une seule
entreprise gère l'ensemble du projet.
- Conception intégrée :
La conception intégrée est une organisation de
travail ou l'ensemble des parties prenantescoopèrent dès le
début du projet au sein d'une équipe multidisciplinaire.
b. Les différentes phases de la conception en
construction :
- Études
préliminaires
Elle est aussi appelée esquisse. Elle est
réalisée en fonction des différentsparamètres lies
au terrain, aux options de la construction envisagée par le maitre
d'ouvrages.
- Études d'avant-projet
Ces parties comprennent l'étuded'avant-projetsommaire et
l'étuded'avant-projetdéfinitif. Lors de l'avant-projet, il peut
être nécessaire de réaliser des études techniques
spécifiques, a la charge du maitre d'ouvrage.
II.2 Immeuble d'habitations
a. Définition
Un immeuble d'habitation, ou immeuble collectif, est un
bâtiment collectif a usage d'habitation. Dans son sens courant, un
immeuble est un bâtiment de plusieurs étages.
b. Catégorisation
Sur le plan de l'usage, on distingue les immeubles d'habitation,
les immeubles de bureaux, les immeubles industriels, les immeubles
gouvernementaux, etc.
Sous l'aspect structural, on distingue en particulier le
gratte-ciel, immeuble d'une hauteur importante.
c. Les styles
- Immeuble normal : de 1 à 5 étages
- Immeuble de grande hauteur : entre 6 et 12
étages
- Gratte-ciel : 13 étages de plus.
II.3 La loi congolaise sur la conception et la construction
des immeubles à usage d'école
Numéro de référence à l'Ordonnance
n°07/018 du 16 mai 2007 fixant les attributions des Ministères et
conformément à son article 1er, qui stipule : « le
Ministère de l'Enseignement primaire, Secondaire et professionnel a dans
ses prérogatives la conception des normes et directives pour la
construction et la réhabilitation des infrastructures scolaires et
veiller à leur mise en application », des directives sur les normes
relatives aux constructions scolaires dont il faut tenir compte
dorénavant dans les travaux de constructions des bâtiments
scolaires sont prises. En effet, l'implication d'un Établissement
scolaire doit répondre aux spécificités
géographiques, démographiques, économiques ainsi qu'aux
dispositions de la planification scolaire élaborées par
l'État.
Vu les nombreux abus particulièrement en matière
des infrastructures scolaires (salles de classe exigües, absence de cours
de récréation, absence des latrines...) et en vue de mettre fin
à cet état de choses, la construction des bâtiments
scolaires, l'une des conditions primordiales de viabilité d'une
école, doit impérativement se conformer aux exigences
énumérées ci-dessous :
a. Des exigences pédagogiques
La pénurie des locaux scolaires est devenue à
l'heure actuelle de plus en plus grave du fait de l'évolution et de
tendances démographiques.
- Les bâtiments scolaires existants sont insuffisants et
retardent sensiblement e développement de l'enseignement face à
la population en âge de scolarisation.
- Il y a donc les problèmes de qualité, de
rapidité et d'économie qui se posent dans ce domaine.
- Tout en voulant réaliser des économies
importantes, on doit veiller à ne pas diminuer la qualité de la
construction ni bafouer les normes, encore moins l'aspect esthétique car
l'enfant aime tout ce qui est vivant, vrai et à son échelle.
- L'école étant la continuation et
l'achèvement de l'éducation familiale, l'implantation de celle-ci
doit tenir compte notamment des exigences émotionnelles et physiques de
l'enfant.
- Il faut que s'établissent entre l'école et la
famille des liens aussi étroits que possibles.
b. Des exigences
des sites
Un terrain destiné à des fins scolaires doit
satisfaire aux exigences de l'hygiènes, de l'orientation et du climat.
Dans l'aménagement du terrain, il faut prévoir des
surfaces vertes qui seront soignées par les écoliers
eux-mêmes en excitant leur imagination et leur esprit d'observation
(travail manuel).
De la forme et du relief : La forme
régulière est plus recommandée tandis que la forme
irrégulière et des pentes trop fortes rendent le terrain peu
propice pour une école.
De la superficie du terrain : La superficie
du terrain doit se situer entre 25 et 35 m2 par élève.
c. Des exigences architecturales
Les méthodes d'enseignement sont en pleine
évolution. Les classes qu'on construit aujourd'hui doivent servir
à l'avenir. La flexibilité et l'adaptabilité de la salle
à la variation d'activités, du décor intérieur et
des techniques de communication sont de plus en plus recherchées.
Le bâtiment scolaire doit être à
l'échelle des enfants et en fonction de leurs aspirations
c'est-à-dire simple, intime, attrayant et sans luxe. Les
matériaux à utiliser doivent être, dans la mesure du
possible, d'origine locale, choisis en fonction des critères
pédagogiques et climatiques.
De la forme et des dimensions
Forme : La disposition « carré
» s'adapte facilement à une variation d'activité mieux que
la disposition rectangulaire qui reste pourtant la plus répandue.
Dimensions : Les Dimensions des salles de
classe sont naturellement commandées par le nombre présumé
d'élèves. Elles varient suivant l'importance du milieu et de
l'organisation scolaire.
Il est prudent d'avoir certaines classes plus spacieuses en
surface que les autres, en vue de l'éventualité de la
surpopulation temporaire d'une ou de plusieurs salles. Il est à noter
que l'âge de l'utilisateur de la salle influe aussi au dimensionnement
des locaux, car jouant sur sa psychologie.
La superficie occupée par un élève :
Du primaire : 1, 20 à 1, 50 m2
Du secondaire : 1, 50 m2
La surface par élève dans les locaux peut
être augmenté graduellement en diminuant le nombre
d'élèves par classe.
Dimension des salles de classe
50 élèves : une superficie de 56 m2 = 8
m x 7 m (standards).
40 élèves : une superficie de 54 m2 = 9
m x 6
35 élèves : une superficie de 48 m2 = 8
m x 6 m
30 élèves : une superficie de 42 m2 = 7
x 6 m
La hauteur sous plafond : La hauteur sous
plafond doit être comprise entre 3 m et 4 m c'est - à - dire 3m =
h = 4 m.
L'allège des fenêtres : La
distance entre le pavement et le début de la baie fenêtre doit
être comprise entre 0, 80 m et 1,20 m ; c'est-à-dire 0,80 m = h =
1, 20 m.
De l'estrade : doit avoir une profondeur de
1, 20 m avec une contre marche de 15 cm.
De la superficie
- Du 1er degré un maximum de 510 élèves par
classe.
- Du 2ème degré un maximum de 40
élèves par classe (de 5ème année primaire jusqu'au
secondaire).
Toutefois les spécialistes s'accordent à limiter
théoriquement et d'une manière progressive le nombre
d'élèves à 30. Une amélioration dans ce sens devra
aller de pair avec l'extension quantitative et qualitative du réseau
scolaire.
Les locaux spéciaux doivent avoir pour superficie :
1. 15 à 18 m2 de surface pour le bureau de
Direction
2. 92 m2 de surface pour la salle de dessin
3. 88 m2 de surface pour le laboratoire de chimie
comprenant une salle de préparation de 32 m2 de surface.
4. 88 m2 de surface pour le laboratoire de physique.
5. 66, 50 m2 de surface pour la salle
géographie.
6. dortoirs : 4 m2 par lit, cubage d'air : 22
m2
7. Réfectoires : 1 m2 par
élève.
8. Cuisine et annexe : basé sur 100 m2 pour 40
élèves, majoré de 0,50 m2 par élève
supplémentaire, sans dépasser un total de 250 m2
9. Salle Atelier : les dimensions varient selon le type
d'atelier et le genre d'appareillage à installer.
De l'emplacement des bâtiments
scolaire :
Les bâtiments scolaires doivent être
implantés sur des endroits salubres et à plus de 300 m
d'établissements communautaires comme usine, marchés,
hôpitaux.
Chapitre I. Chapitre III. CONCEPTION ARCHITECTURALE DES
IMMEUBLES A USAGE D'ECOLE
III.1 Normes de planification
géographique
Le site doit être choisi en fonction des
possibilités d'accès, de la proximité des transports
publics et de certain nombre de critères de qualité, dans le but
d'assurer le bien-être des enfants et du corps enseignant et de permettre
le bon déroulement des activités.
|
Distance du terrain par rapport à l'agglomération
(Km)
|
|
Préscolaire
|
300 m
|
|
1 er et 2ème cycle
|
1km
|
|
3 -ème cycle
|
2 km
|
|
7eme Année et plus
|
4.50 km
|
Tableau 1. Norme de distance minimale entre école et
habitation
Distance minimale à respecter entre écoles et zones
dangereuses (rivière, route à grande circulation), bruyantes
(marché, usines, places publiques, routes à grande circulation)
ou polluantes (abattoir, poulailler, porcherie, garage, décharges
publiques, station d'essence, mares d'eaux) : 250 m environ.
Si l'on considère que la population d'âge scolaire
primaire constitue environ 17% de la population totale et que l'on ne souhaite
pas que les salles de classe soient occupées par 50 élèves
au maximum, une école fondamentale de 9 salles de classe (450
élèves) nécessite une population d'au moins 2.800
habitants dans l'aire de recrutement.
Surfaces de terrain prescrites
8 m²/élève hors terrain sport en milieu rural,
4.3 m²/élève hors terrain sport en milieu urbain Dans le
cadre de construction d'écoles nationales, le terrain doit être
soumis à l'approbation de la Direction du Génie scolaire.
Tableau 2. Norme de dimension minimale des terrains
|
Dimension minimale des terrains conseillée (m²)
|
|
Nombre d'élèves
|
Milieu
|
|
Urbain
|
Rural
|
|
100 et 300
|
1,500.00
|
2,500.00
|
|
301 et 400
|
2,000.00
|
3,500.00
|
|
401 et 500
|
2,500.00
|
4,000.00
|
|
Plus de 500 ;
|
2,500.00 + 4,3 m ²/élèves
|
4,000.00 + 8 m ²/élèves
|
|
Remarques : Il faut ajouter un terrain de 80 m x 80 m pour les
installations sportives, élément optionnel à
déterminer en relation avec les ressources locales.
|
Il n'est pas exigé de surface minimale de terrain dans le
cas déménagement de bâtiment existant
III.2 L'aspect architectural des
immeubles à usage d'école au Sud-Kivu
Pour ceux qui est de l'architecture de immeubles à usage
d'école dans notre pays et notre province en particulier, les
écoles étatiques sont construites par le fond social de la
république et selon le terrain qu'occupel'établissement public d
ou les non-respects de lois prévues par l'État et les
établissements privées par foi incontrôlable dans cette
matière.
En effet, nous avons vous montrer quelques exemples :
· L'institut TANGILA de Kamituga

Une école qui au paravent respecter les normes
conçus par l'État a sa genèse, mais aujourd'hui suite
à l'augmentation de la population, sur le plan architectural et suite
aux nouveaux codes de la conception architecturale des écoles dans notre
pays l'immeuble n'est pas viable sur l'aspect architectural.
· Le collège ALFAJIRI de Bukavu
Vu de l'intérieure

Vu d'ensemble

Commencer dans les années 1938 par les missionnaires
d'Afrique et donner en septembre 1941 aux jésuites, sa gestion a
été confiée à la province Belge septentrionale.
Une école secondaire qui compte près de 1250
élevés repartie en 30 classes, avec une infrastructure pour
accueillir près de 130 élevésàl'internat.
Dans notre région, nous pouvons en déduire que ce
un établissement type non seulement sur son aspect architectural mais
aussi sur sa partie structure.
Les concepteurs ont choisi ce modèle qui au paravent
abriter tous les élèves de l'ancienne Kivu, et aujourd'hui la
province en soit demande une autre structure type de l'État.
· Institut Bwali de Kamituga

Une école poly technique qui dans les années de sa
création avec 12 classes et avec 40 élèves par classe,
aujourd'hui sur l'aspect architecturale et structurale ne respecte pas les
normes prévues par la loi suite à la vieillissement et
lamentation de la population, une salle de classe compte au moins 70 à
80 élèves.
· Institut Zalya officiel

Cette école qui au paravent était en mur en bois,
aujourd'hui elle a eu un financement d'une construction d'un immeuble de 6
classe et un petit bureau mais aussi un petit espace sanitaire sans tenir
compte de l'aire de jeux, des nombre d'élèves par classe et
d'autrerèglementsprévus par le ministèrede la tutelle.
· Institut d'Ibanda de Bukavu

L'institut d'Ibanda est parmi le plus ancienne école de
l'État qui dorénavant était appelé
Athénée royal, avec une architecture belge et dans les
années de sa création, elle était gérée par
le royaume de Belgique.
Les enfants de blanc dont leurs parents travailler au
Congoprécisément dans l'ancienne Kivu étudieàcette
école, aujourd'hui nous pouvons dire que cette architecturen'existe plus
suite à la manque d'entretien et la manque de suivi de notre
gouvernement, mais aussi des constructions anarchiques qui ne cessent de se
multiplier.
L'immeuble était conçu pour recevoir 1500
élevés dans sa genèse mais suite à l'absence de
l'État et la mauvaise foi de nos dirigeants cet architecture a disparu
et les élèves étudient dans de condition
déplorable.
· Commentaire
Dans notre pays qui suite aux désordres causés par
les guerres en répétition et la non organisation du gouvernement
en matière de la scolarité et des infrastructures scolaire
étatique mais aussi la manque de l'espace causer par les constructions
anarchiques nous avons constatées que tous les
établissementsprivés ou publics ne respectent pas ou n'observent
pas les règlements prévus par le ministère en tutelle.
C'est la raison pour laquelle notre gouvernement au fond social
de la république et les bailleurs de fond prônent une conception
de 6 classes et un petit bureau muni d'un espace sanitaire sans tenir compte de
l'aire de jeux ou d'autre locaux exigés par la loi.
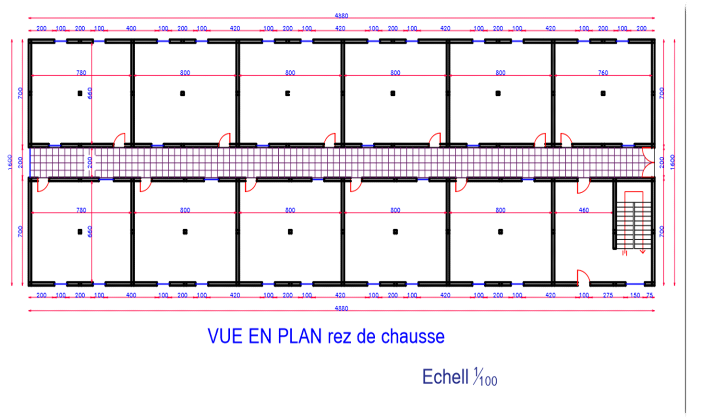
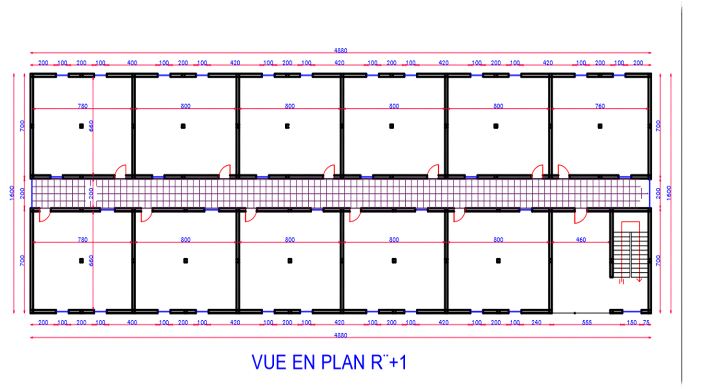
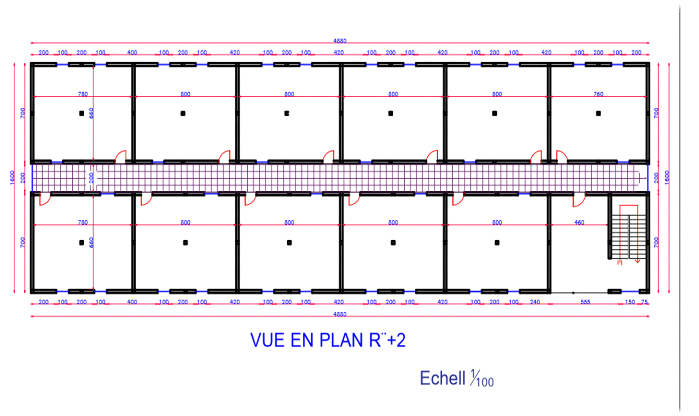
III.3 Conception architecturale d'une
école de 1650 élèves au Sud-Kivu, dans la ville de
Kamituga
Forme et dimensions :
Forme : La disposition « carré
» s'adapte facilement à une variation d'activité mieux que
la disposition rectangulaire qui reste pourtant la plus répandue.
Dimensions : Les Dimensions des salles de
classe sont naturellement commandées par le nombre présumé
d'élèves. Pour notre cas, l'immeuble en soit est de
La superficie occupée par un élève
:
Du secondaire : 1, 50 m2
Lequel immeuble s'étend sur une superficie de
768m2 et une hauteur cumulée de 15m.
Il se compose de :
· Un rez-de-chaussée,
· Deux étages courants,
Soit au total, un bâtiment R+2.
Dimension des salles de classe
50 élèves : une superficie de 56 m2 = 8
m x 7 m (standards).
La hauteur sous plafond : La hauteur sous
plafond est de 3m.
L'allège des fenêtres : La
distance entre le pavement et le début de la baie fenêtre doit
être comprise entre 0, 80 m et 1,20 m ; c'est-à-dire nous prenons
la hauteur de 1, 20 m.
De l'estrade : doit avoir une profondeur de
1, 20 m avec une contre marche de 15 cm.
De l'emplacement des bâtiments
scolaire :
Pour ce qui est de l'emplacement de l'immeuble, selon le
règlement il est recommandé de placer le bâtiment a une
distance d'au moins 300m d'établissements communautaires comme usine,
marchés, hôpitaux. Suite à la spoliation des espaces de
l'État nous nous trouverons dans l'incapacité de satisfaire
à ce besoin.
Chapitre IV.
CONCEPTION STRUCTURALE DES IMMEUBLES A USAGE D'ECOLE
La conception structurale est la tâche des experts dans le
domaine de construction (les ingénieures en génie civil, en
bâtiment...).
Après avoir exploiter et consulter l'ingénieur
architecte qui a son tour a conçus un immeuble selon les
règlementsédictés par l'État, la constitution des
éléments structuraux sera à déterminer pour chaque
élément de l'ouvrage son chargement (charge d'exploitation et
permanente) et d'une manière générale, à
déterminer la charge totale du bâtiment
Elle est suivie en deuxième partie par la conception en BA
de l'ensemble des panneaux constituant la dalle, aussi que les poutres et les
poteaux qui s'y trouve.
En suite la conception de la fondation et de la cage d'escalier
selon les normes prévues par les règles de BAEL et des Euro
codes.
§ La structure
porteuse
Une structure porteuse a pour rôle de supporter les murs et
les planchers d'un bâtiment au-dessus du premier niveau, mais aussi de
porter la charpente et la toiture tout en évitant la déformation
ou les affaissements que peuvent subir un immeuble.
Les poutres, les poutrelles, et les poteaux sont les
éléments porteurs de renforcement et de la consolidation de la
structure.
La réalisation d'un ouvrage en particulier, et d'un
bâtiment en soit est généralement l'aboutissement d'un long
et complexe processus de planification de nature multidisciplinaires.
La mission majeure, pour l'ingénieur BTP est de concevoir
une structure capable de transmettre toutes les charges du bâtiment au
sol.
La conception structurale tient compte de beaucoup de contraintes
fonctionnelles parmi lesquelles nous pouvons citer :
§ Le choix du système porteur
Ici les exigences sur les portées et les natures des
éléments porteurs peuvent varier selon l'usage des locaux ;
ainsi, l'ossature choisie est l'ensemble de poutraisons et des voiles pour
reprendre les charges transmises par la dalle. Ces poutres s'appuient sur des
éléments verticaux appelés poteaux ; les voiles et les
poteaux transmettent les efforts à la fondation.
§ Autres facteurs importants pour la
conception
La hauteur totale d'un bâtiment est souvent limitée
par les règlementations; cette hauteur des locaux entre le niveau fini
du sol et le plafond dépend de l'usage et elle est très souvent
fixée par de règlements ou le cahier de charge; notons que dans
bien de cas, il est préférable d'adopter des hauteurs
d'étages supérieurs aux valeurs minimales requises et adapter
à la surface des locaux pour but de rendre plus agréable aux
utilisateurs et leur éviter tout sentiment d'écrasement du
à un plafond trop bas. Pour notre cas, les règlements requises
pour la hauteur sont de 2,7m à 3,00m, voir d'avantage, pour des bureaux
et les salles d'école.
La réalisation d'un joint peut participer au bon
fonctionnement de l'ouvrage ; c'est ainsi que nous réalisons un joint
permanent qui a pour rôle de réduire fortement voire de supprimer
les désordres dus au retrait, à la dilatation, au tassement et
aux points phoniques. Ainsi la stabilité de chaque corps du
bâtiment sera assurée par un système indépendant de
contreventement.
§ Les plans de coffrage
Ce sont des plans représentant les dalles limitées
par les poutres ; l'objectif est de faire porter la dalle par le minimum des
poutres possible et dans le même angle d'idée par le minimum des
poteaux.
IV.1
DIMENSIONNEMENT DE LA DALLE
a.
Généralité
Une dalle désigne d'abord une plaque monolithe
taillée dans une roche est destinée à la couverture d'une
voie, d'une maison, d'un monument, d'une tombe. C'est avec l'apparition de
béton armé en 1886 par Joseph MONIER que la pierre artificielle
fut remplacée par le terme « planchers de
béton ».
La dalle désigne aussi bien les composants de gros oeuvres
que les composants architecturaux. Elle peut se comporter comme une
« plaque » et ses porters ou « toute
seule ». Pour ce qui est de la forme et fond nous parlerons d'une
dalle pleine unidirectionnelle et la dalle pleine directionnelle.
ü Une dalle pleine unidirectionnelle :
c'est toute dalle qui travaille dans un seul sens.
ü Une dalle pleine bidirectionnelle :
C'est toute dalle qui travaille dans les deux sens et les armatures
porteurs seront orientés parallèlement dans le plus petit
côté.
b. Calcul de
l'épaisseur de la dalle
Pour calculer l'épaisseur de la dalle, on considère
le panneau le plus grand en utilisant seulement une dimension d'un mètre
carré comme unité.
Figure 2 : vue en plan d'une dalle avec l'unité d'un
mètre
Figure 3 : plan de la dalle avec unité d'un
mètre carré

c. Dimensionnement
de la dalle du RDC
Le poids volumique et le poids surfacique des matériaux
à utiliser sont :
· Béton armé, son poids volumique est de
25KN/m3
· Carrelage y compris la couche de mortier de pose de 2,5cm
d'épaisseur est de 3,75KN/m3
· Le mortier ou liant hydraulique est de
1,3KN/m 3.
· Rapport de dimension
Nous connaissons que le coefficient de l'argument
á est donné par la relation :
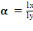  (A, 1) (A, 1)
Comme lx= 7m et ly = 8m, on obtient
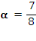
D'où á est de 0,86
Nous concluons alors que notre dalle est pleine et
bidirectionnelle c'est-à-dire elle est sollicitée dans les deux
sens.
· Détermination de l'épaisseur de la
dalle
L'épaisseur est obtenue par la relation suivante :
h =  (A, 2) (A, 2)
D'où h =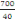 
h =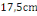 
Nous prenons h= 15cm car il est conseillé de prendre comme
épaisseur de la dalle un nombre multiple de 5.
· Combinaison des charges à l'ELU
La charge Pu qui est la combinaison de charge d'exploitation Q et
les charges permanentes G est :
Pu = 1,35G + 1,5Q(A, 3)
· Charges permanentes G :
ü Poids propre de la dalle : 25 X 0,15 =
3,75KN/m2
ü Enduit de 1,5cm d'épaisseur : 20 X 0,015 = 0,3
KN/m2
ü Chape de 4cm d'épaisseur : 20 X 0,04 =
0,8 KN/m2
ü Carrelage : 20 X 0,01 = 0,2
KN/m2
D'où G = 3,75 + 0,3 +0,8 +0,2 = 5,05 KN/m2
· Charge d'exploitation Q :
La surcharge d'exploitation Q pour la dalle est Q = 1,5
KN/m2
D'après (A, 3) la charge pondéré Pu
est :
Pu = (1,35 X 5,05) + (1,5 X 1,5)
= 9,06 KN/m2
d. Calcul des
moments
· Calcul des coefficients MX et MY
· Calcul des coefficients MX
On a MX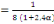  (A, 4) (A, 4)
D'où MX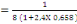 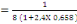
= 0,0454
· Calcul des coefficients MY
On a MY =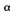  3(1,9 - 0,9 3(1,9 - 0,9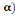 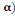 (A, 5) (A, 5)
= 0,658 (1,9 - 0,9 X 0,86)
= 0,735
· Calcul des moments pour le panneau articulé sur
son contour
1) Calcul de moment selon lx
Les moments pour la bande de longueur unité est :
· Calcul de MOX
MOX = (MX X Pu X
lx2)(A, 6)
D'où MOX = (0,0454 X 9,06 X 72)
= 21,48KN
· Calcul de moment en travée
Mty
On a Mty =
MY X MOX (A, 7)
D'où Mty = 0,735X 21,48
= 15,78KN
· Calcul de moment sur appuis
May
On sait que May = 0,50 X
MOX (A, 8)On a May =
0,50 X 21,48
D'où= 10,74KN
2) Calcul de moment selon Ly
· Calcul de moment en travée
Mty
On a Mtx = 0, 85 X MOX
(A, 9)
D'où Mtx= 0,85X21,48
= 18,25KN
· Calcul de moment sur appuis
Max
On a Max = 0,50 X MOX
(A, 10)
D'où Max= 0,50 X 21,48
= 10,74KN
e. Les armatures
porteuses et les armatures de répartition.
· Calcul des efforts tranchant Vux et Vuy
Les sollicitations ultimes
· Au milieu du grand coté (Pu repartie)
On a Vux= Pu X (   ) X [ ) X [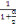 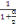 ] (A, 11) ] (A, 11)
D'où Vux= 9,06 X (   ) X [ ) X [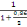  ] ]
= 9,06 X 3,5 X [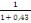 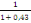 ] ]
= 22,16KN/m
· Au milieu du petit côté (Pu repartie)
On a Vuy= Pu X (   ) (A, 12) ) (A, 12)
D'où Vuy= 9,06 X (   ) )
= 32,43KN/m
· Calcul de la
contrainteôU (vérification)
ôU = 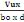  = 0,07fbu (A, 13) = 0,07fbu (A, 13)
Avec bo : bande de la dalle est de 1m
d : épaisseur qui est de 0,9h
d = 0,9 X 15
= 13,5cm
Fbu : 14,16MPa
D'où ôU= 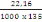 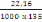 = 0,07fbu = 0,07fbu
ôU= 0,178= 0,99MPa
0,178MPa = 0,99MPa
Pas d'armatures d'âme
· . Calcul de diamètre des armatures longitudinales
de la dalle
On a Ø long = 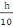 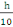 (A, 14) (A, 14)
Ø long =  
Ø long =  
Ø long = 15mm
Nous prenons le diamètre des armatures longitudinales de
la dalle à 12mm.
· Calcul de l'armature porteuse
· En travée selon le sens Ix
On a Atx = 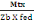 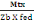 (A, 14) (A, 14)
Avec 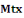 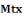 : moment fléchissant en travée : moment fléchissant en travée
Zb : bras de levier, qui est donné
par la relation :
Zb = d (1- 0,4  ) (A, 15) ) (A, 15)
Et  = 1,25(1- = 1,25(1-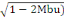 
On a 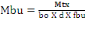 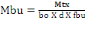
= 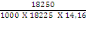 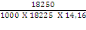
= 0,007
  = 1,25(1- = 1,25(1-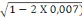 
= 0,025
D'où Zb = 13,5 X (1- 0,4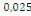 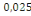 ) )
= 13,36cm
Fed la résistance de l'acier est
donnée par la relation :
Fed= 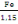 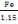
= 347,826MPa
Par suite (A, 14) devient :
Atx =  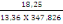
= 3,99cm2
Nous prenons Atx= 4,52cm2 qui nous donne 4Ø12HA
dans une bande de 1m.
· En travée selon le sens Iy
On a Aty = 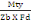 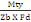 (A, 17) (A, 17)
D'où Aty = 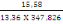 
= 3,40cm2
Nous prenons Aty= 6,16cm2 qui donne 4Ø14HA.
· Calcul de l'espacement maximum des armatures
longitudinales [Stx et Sty]
· Selon le sens Ix :
L'espacement se calcul par la relation suivante :
3h
Stx = minimum (A, 18)
33cm
D'où
3 X 15cm
Stx = minimum
33cm
Stx = minimum à 33cm, nous
prenons Stx= 25cm.
· Selon le sens Iy
L'espacement se calcul par la relation suivante :
4h
(A, 19)
45cm
D'où
4 X 15cm
Stx = minimum
45cm
Sty = minimum à 45cm, nous
prenons Sty= 25cm.
Figure 4 : Schémas de ferraillage de la dalle

IV.2
DIMENSIONNEMENT DE LA POUTRE
a.
Généralité
Une poutre c'est une pièce en bois de forme
allongée, sevrant dans les constructions à supporter une
charpente ou un parquet. C'est aussi tout élément de construction
allongé en béton armé ou métallique qui joue le
rôle de supporter la dalle ou la toiture.
· Selon les matériaux, on distingue :
- La poutre en bois
- La poutre métallique
- La poutre en béton armé.
· Selon les matériaux, on distingue :
- La poutre principale
- La poutrelle
- La poutre croisée, c'est le cas général
qu'on rencontre dans la vie pratique.
Pour les calculs de poutre croisée, nous
procèderons en premier lieu à déterminer la
validité de la méthode dite simplifiée ou forfaitaire
à l'ELU.
Q1 =
5KN/m2 : charge d'exploitation sur la
G = 2
Q1 : poids propre de la dalle
(B, 1) 0,80 = (
 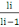 ) = 1,25 ) = 1,25
0,80 = (   ) = 1,25 ) = 1,25
F.P.P : fissuration peu
préjudiciable.
Dans notre projet la poutre la plus vulnérable a une
portée de 800cm et elle est représentée sur la figure
ci-dessous.
Figure 5.

b. Pré
dimensionnement de la poutre
Le pré dimensionnement de la poutre s'effectue à
l'aide des formules suivantes :
  lt = h = lt = h =   lt (B, 2) lt (B, 2)
0,4h =bo= 0,5h (B, 3)
· D'après (B, 2), nous déterminons la hauteur
h de la poutre.
On a:   8m= h = 8m= h =  8m 8m
D'où 0,5m =h = 0,66m
Nous prenons h = 0,5m.
· D'après (B, 3), nous déterminons la base bo
de la poutre.
On a: 0, 4 X 0, 5 = bo= 0,5 X 0,5
D'ou 0,20m =bo= 0,25m
Nous prenons bo = 0,20m.
c.
Évaluation et combinaison de charges
La poutre subie deux charges dont charge d'exploitation Q et les
charges permanentes G en conservant la relation (A, 3)
· Charges permanentes G :
ü Poids propre de la poutre :   = 2,55KN/m = 2,55KN/m
ü Poids de revêtement : 20 X
0,03 X 7 = 4,2 KN/m
ü Poids de la dalle : 5,05 X
7 = 35,35 KN/m
D'où G = 2,55 +4,2 + 35,35 = 42,1KN/m2
· Charge d'exploitation Q :
La surcharge d'exploitation Q pour la dalle est Q = 2,5 X 7 =
17,5KN/m2
D'après (A, 3) la charge pondéré Pu
est :
Pu = (1,35 X 42, 1) + (1,5 X 17,5)
= 73,97 KN/m2
d. Calcul des
sollicitations
Dans cette poutre nous calculons les moments en travée de
rive et en travée intermédiaire et puis la vérification de
moment fléchissant.
· Les moments fléchissant en travée de
riveMa,w
Les moments fléchissant en travée de rive
Ma,w est donné par la relation :
On aMa,w = 0,6 X
MOi(B, 4)
Avec MOi= 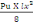 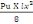
= 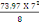
= 453,06 KN
D'oùMa,w = 0,6 X 453,06
= 271,80KNm
· Les moments fléchissant en travée
intermédiaireMa,e
On sait que : Ma,e = 0,6 X
MOi.  (B, 5) (B, 5)
D'oùMa,e =
0,6 X 453,06 X  
= 135,91KN
· Le moment fléchissant en travée de rive
à plusieurs travées intermédiaires
Mti obtenu par l'équation :
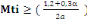 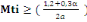 (B, 6) (B, 6)
Avec   le coefficient des charges qui est obtenu par la relation : le coefficient des charges qui est obtenu par la relation :
  = = 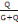 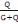 (B, 7) (B, 7)
= 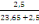 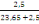
  = 0,087 = 0,087
D'après (B, 6), on a :
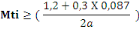
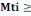 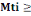 277,72KN 277,72KN
Nous prenonsMti= 400KN
· Vérification des moments
fléchissant
Pour la vérification des moments fléchissant nous
avons la relation :
(1 + 0,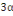  )MOi )MOi
Mti +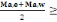 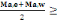 valeur max (B, 8) valeur max (B, 8)
1,05MOi
D'une part : Mti +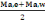 
= 400 +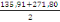 
= 603,85 KN
D'autre part : (1 + 0,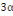 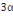 )MOi )MOi
1,05MOi
(1 + 0, 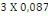 ) 453,06 ) 453,06
1,05X 453,06
La valeur maximale entre 464,88 KN et 475,71 KN est 475,71 KN.
De ce qui est ci-dessus nous remarquons que : 603,85 KN =
475,71 KN.
· Les efforts tranchants sur les appuis
L'effort tranchantVuiest donné par la
relation :
Vui= 1,15(Vox) (B, 9)
Avec Vox= (  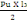 ) )
On a = ( 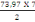 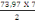 ) )
= 258,89 KN
D'après (B, 9), Vuidevient :
Vui= 1,15 X 258,89
= 297,72 KN
e. Calcul des
armatures longitudinales comprimées et des armatures transversales
Figure 6.
Les formules ci-dessous nous aiderons à déterminer
les armatures longitudinales.
Au = 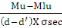 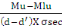 (B, 10) (B, 10)
Pour le moment limite ultime Mlu on a :
Mlu = MluX bo X d2 X Fbu
(B, 11)
Avec Mlu coefficient du moment
réduit ultime qui est de 0,300 (voir Béton I) .
äcoefficient de la hauteur ultime de la
poutre.
ä =  
Et d= 0,9h
d = 0,9 X 0,5
= 0,45
d'= 0,13 (théoriquement)
D'où ä =  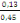
= 0,28
D'après (B, 11), nous avons :
Mlu =0,300X 0,20 X 0,452 X 14,16
= 0,172MPa
Le coefficient de moment fléchissant ?
est :
? = 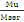 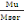 (B, 14) (B, 14)
Avec Mu le moment fléchissant ultime d'après (B, 4)
Mu = 653,66KN et Mser le moment ultime de service qui est :
Mser =  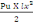
D'où Mser = 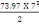 
= 453,06KN
(B, 14) devient :
? =  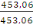
= 1
Contrainte d'équivalence des aciers comprimés   est : est :
  = valeur minimale [(9.?. fc28) - 0,9.
ä (13.25MPa + 415)] et 343MPa. = valeur minimale [(9.?. fc28) - 0,9.
ä (13.25MPa + 415)] et 343MPa.
D'où   = [(9 X 1 X 25) - 0,9 X 0,28 (13 X 25 + 415)] = [(9 X 1 X 25) - 0,9 X 0,28 (13 X 25 + 415)]
= 38,52MPa
Nous prenons   sec est 38,52MPa. sec est 38,52MPa.
D'après la relation (B, 10), nous avons :
Au =  
= 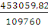 
= 5,45cm2
Par suite nous choisissons Au =
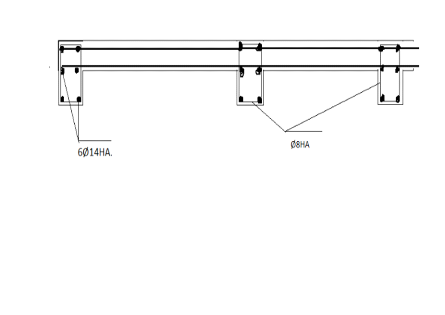
3,96cm2 qui nous donne 6Ø14HA.
f. Calcul des
aciers transversaux et de l'espacement maximum des armatures longitudinales
(St)
· Calcul des aciers transversaux
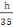 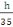
Ø transversale = valeur minimal Ø
long (B, 19)

D'où
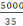 
Ø transversale = valeur minimal 12mm
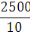
Ø transversale = valeur minimale entre 142,8mm, 12mm et
250mm.
Nous prenons la section de 8mm pour les armatures
transversales.
· Calcul de l'espacement maximum des armatures
longitudinales (St)
15 X Ø long
St = valeur minimale a + 10cm
(B, 20)
40cm
D'où
15 X 12mm
St = valeur minimale 25 + 10cm
(B, 20)
40cm
St = valeur minimale entre 18cm, 35cm et 40cm.
Nous prenonsl'espacement maximum des armatures longitudinales de
18cm.
Figure 7. Schéma de ferraillage de la
poutre
IV.3
DIMENSIONNEMENT DE POTEAU
a.
Généralité
Figure 8.
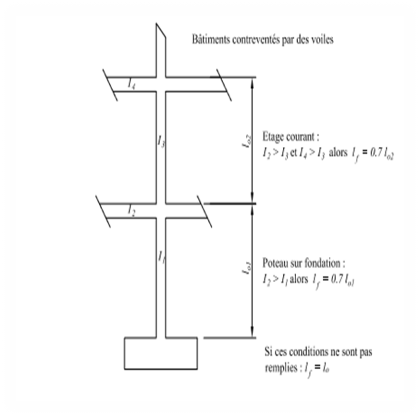
Un poteau est une poutre verticale soumise uniquement à
une compression centrée (Nu ? 0 et Mz
= 0)
Il joue le rôle de répartition des charges
Nu la fondation.
Un poteau de section rectangulaire ou approcher et à forme
non allonger en plan s'appelle pilier.
Un poteau de section circulaire ou approcher sera appelé
colonne.
Un poteau de section parallélépipédique sera
appelé poutre.
Du point de vue de la mécanique de la structure, les
poteaux sont les éléments verticaux soumis principalement
à la compression et leur résistance est notamment limitée
par le risque de flambement.
b. Pré
dimensionnement en compression simple de poteau le plus défavorable
La longueur libre entre haut du plancher supérieur et la
fondation vaut Lo = 3cm.
Le poteau est traversé de part et d'autre par une poutre
ayant une section de 20 X 50cm.
Sa longueur de flambement vaut :
Lfl = 0,5Lo (C, 1)
On a Lfl = 0,5 X 3
= 1,5m
L'élancement ë
Figure 9. Y
B
X
25cm
Nous calculons l'élancement ë par la
relation :
ë 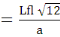  = 35(C, 2) = 35(C, 2)
Avec a, le coté du carré voire la
figure 9 on a :
ë  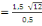
  6 X 3,46 6 X 3,46
D'où ë = 26,76m = 35
c. Descente des
charges
La descente de charges est donnée par la
relation :
 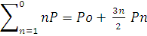 (C, 3) (C, 3)
Figure 10.
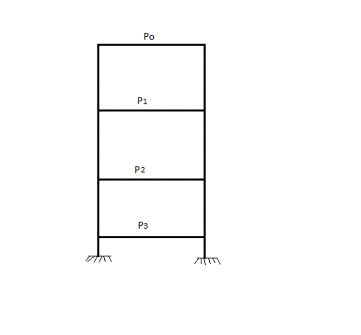
La surface d'influence S est de 16 X 48 =
768m2.
Avec Po la charge de toiture qui est :
Po = 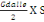 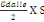 (C, 3) (C, 3)
On a Po= 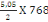 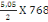
= 1939,2KN
Et P1 la charge du niveau de
référence.
On a P1 = charge dalle + charge
poutre
= 9,06 + 73,97
= 83,03KN
D'où (C, 3) devient :
Niveau 0
On a No = Po + 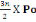 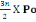
= 1939,2+  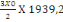
= 1939,2KN
Niveau 1
On a N1 = Po +  
= 1939, 2+  
= 2063, 74KN
Niveau 2
On a N2 = Po +   et et  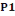 = = 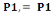
= 1939,2+ 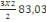 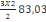
= 2188,29KN
d. Combinaisons des
charges
Les charges qui agissent sur le poteau sont obtenues en combinant
la charge dalle, celle de toiture et des niveaux considères.
On a Nu=
N0+N1
+N2
= 1939,2+2063,74+2188,29
= 6191,23NK
· La section réduite Br
Nous avons un poteau carré de 25 x 25
D'où Br = 625cm2
· Calcul de force équilibrée par le
béton Nb
On a Nb = 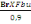 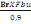 (C, 4) (C, 4)
Avec fbu=14,16MPa
D'où Nb =  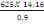
= 983,3KN
· Calcul de force équilibréedes
armatures longitudinalesNS
On a NS = 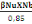  (C, 5) (C, 5)
Avec  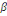 =1 + 0,2( =1 + 0,2(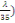  2 (C, 6) 2 (C, 6)
=1 + 0,2(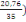  2 2
= 1,07
D'où (C, 5) devient :
NS = 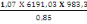 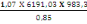
= 6636,84KN
e. Calcul des
armatures longitudinales et transversales
Chapitre V. Section des armatures
longitudinales
Amin = As =  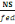 = Amax(C, 7) = Amax(C, 7)
Avec Fed =347,826 MPa
On a As = 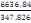 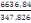
= 19,08cm2
Les valeurs des sections minimales et maximales des armatures de
l'élément soumis à la compression simple sont obtenues par
les relations :
Amin =  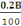 (C, 8) (C, 8)
Amax =  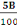 (C, 9) (C, 9)
Avec B la section de poteau
B = Br + 1
= 626cm2
D'où Amin = 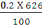 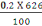
= 1,25cm2
Et Amax =  
= 31,3cm2
Par suite nous choisissonsAs =
3,96cm2 qui nous donne 6Ø14HA.
Chapitre VI.
Section des armatures transversales
On a 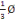 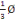 long = long =   trans = 12mm (C, 10) trans = 12mm (C, 10)
D'où   14mm = = 14mm = =   trans = 12mm trans = 12mm
4,6mm=   trans = 12mm trans = 12mm
Nous prenons la section de   8HA. 8HA.
· Calcul de l'espacement des armatures transversales
St
15 X Ø long
St = valeur minimale a + 10cm (C, 11)
40cm
D'où
15 X 14mm
St = valeur minimale 25 + 10cm
40cm
St = valeur minimal ente 21cm, 35cm et 40cm.
Nous prenons l'espacement maximum des armatures longitudinales de
15cm.
· Recouvrement des armatures longitudinales Lr
On a Lr = 0,6Ls (C, 12)
Avec Ls l'encrage pour longueur de scellement droit qui est Ls =
40 Ø long
Ls = 40 X 14mm
Ls =560mm
D'où Lr = 0,6 X 560
Lr = 336mm
Nous prenons Lr = 65cm.
· Espacement des armatures dans la zone de recouvrement
St'
On a St'= 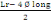  (C, 13) (C, 13)
D'où St'= 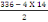 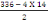
= 308mm
Nous prenons St'= 30cm
Figure 11. Schémas de ferraillage de
poteau

f. III.4
DIMENSIONNEMENT DE LA FONDATION
a.
Généralité
Une fondation se définie comme la partie d'une
superstructure qui transmet au sol les charges d'un bâtiment.
La fondation varie selon la qualité du sol du sol, du
sous-sol ainsi de zone dans laquelle le bâtiment est implanté mais
aussi de point de vue nature et taille du projet.
Figure 12.
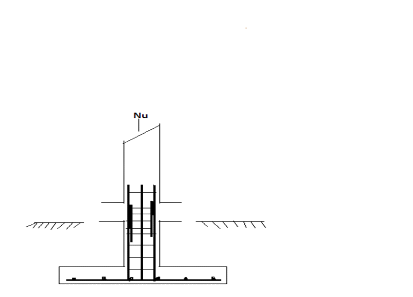
Il est fortement recommandé que le sol soit de bonne
portance et peu sujet de tassement. Du point de vue sol et sous-sol mais aussi
zone à ériger, la composition du sous-sol étant de
calcaire et grossier sa capacité ou contrainte portante  est indiqué dans le tableau ci-dessous. est indiqué dans le tableau ci-dessous.
Tableau 2.
|
NATURE DU SOL
|
|
|
Argile, limon
|
0,15 à 0,30
|
|
Alluvion ancienne, sable et gravier
|
0,60 à 0,90
|
|
Craie
|
0,90 à 1,00
|
|
Calcaire grossier, roche
|
1,80 à 4,5
|
Source : Techno-construction. Lucas NEHOU.
La surface de la semelle doit être suffisante pour repartir
sur le sol les charges apportées par les poteaux. Repartir sur la
surface S les charges apportées par les poteaux c'est
exercé une pression.
Pour déterminer la pression nous avons la
relation :
P = 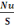 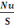 = 1,5 = 1,5   adm sol (d, 1) adm sol (d, 1)
Avec 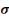 adm sol adm sol 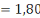 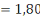
P = pression
S = la surface de la semelle
b. Descente des
charges
Figure 13.

D'après (C, 3), on a :
Niveau 2
On a N2 = Po + 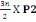  et et 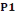  = =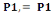 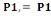
= 1939,2+ 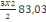 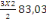
= 2188,29KN
D'où N3 = Po +  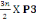
N3 =1939,2+ 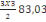 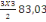
= 2312,23KN
La chargeNu qui agit sur la fondation
est :
Nu= Nu
tot poteau + N3 (d, 2)
On à Nu= 6191,23 + 2312,23
= 8504,06KN
c.
Détermination des dimensions de la semelle isolée et
contrôle de la résistance du sol
Figure 14.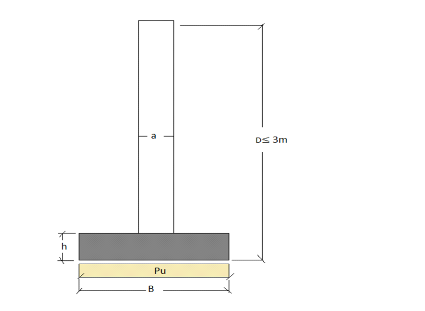
On a B =  (d, 3) (d, 3)
B = 
B = 0,5m
Nous prenons la base B = 1m
Étant donné que Nu = 8504,06KN d'après (d,
3), on a :
P = 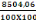 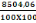 = 1,5 X 1,80 = 1,5 X 1,80
= 0,85 = 2,70
La pression qu'exerce le sol sur la semelle est P
= 0,85 MPa
L'épaisseur h de la semelle est obtenue par la
relation :
H = d + 5cm
Avec d =  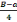
= 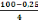 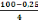
= 18,75cm
H= 18, 75 + 5
= 23,75cm
Nous prenons h = 23cm
d. Calcul de la
section des armatures
On a une semelle de section carrée B=A.
AS =   (d, 4) (d, 4)
Avec Nu= 8504,06KN
B= 1,00m
b= 0,25m car le poteau est carré b=a
d=0,18m
Fed=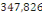 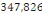 MPa MPa
D'oùAS =  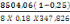
AS = 12,73cm2
Nous prenons AS =14,07cm2
qui donne 7Ø16HA.
e.
Vérification du poinçonnement de la semelle sous poteau
Pour éviter la rupture de la semelle causée par la
force Nu au point d'appuis on a :
ô= 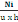 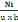 = ô limite= 0,045fbu (d, 5) = ô limite= 0,045fbu (d, 5)
Avec Ni= Nu 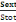 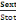 (d, 6) (d, 6)
Sext = S tot - 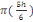  2+ab+2b 2+ab+2b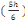 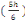 +2a +2a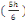 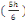 (d, 7) (d, 7)
= 1m2 - 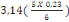  2+0,25 X 0,25+2X0, 2+0,25 X 0,25+2X0,
25  + + 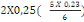
Sext = 0,660cm2 et U=0,115
Par suite (d, 6), on a :
Ni= 8504,06  
= 5612,67KN
D'après (d, 5), on a :
ô= 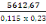  = ô limite= 0,045 X 266,66MPa = ô limite= 0,045 X 266,66MPa
ô= 0,218? ô limite=
0,828MPa
De ce qui précède, nous remarquons
queô est inférieure à ô
limite d'où pas de rupture ou phénomène de
poinçonnement.
f. III.5
DIMENSIONNEMENT DE L'ESCALIER
a.
Généralité
Un escalier est une construction architecturale constitué
d'une suite régulière de marches ou degré permettant
d'accéder à un étage.
Un escalier peut être en pierre, en bois, en acier, en
béton armé ou en verre.
Pour notre projet, nous avons un escalier à deux
volées parallèles et à un palier intermédiaire.
Figure 15.
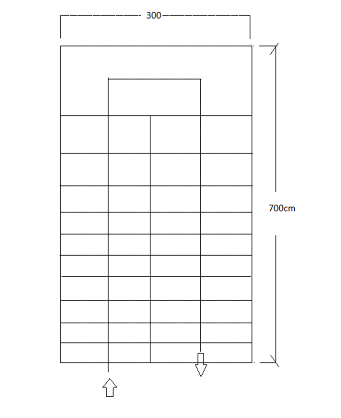
b. Dimensionnement
de l'escalier
· Calcul de l'épaisseur de la paillasse
On a la relation :
e =  = 25cm (d, 7) = 25cm (d, 7)
Et L=700cm
D'où e =  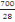
= 25
Nombre de marches :
  Et ht largueur de la paillasse qui est de 400cm. Et ht largueur de la paillasse qui est de 400cm.
On a : 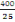 
= 16 marches
Hauteur de marches :
= 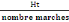 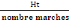
= 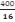 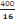
= 25
Par suite nous prenons e= 17c
· Évaluation des charges
Figure 16.

On a :
· G paillasse = 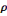 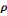 béton béton  
= 25 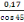 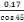
= 5,59KN/m2
· G marche =  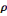 béton béton  
= 25 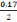 
= 2,12KN/m2
· Enduit de 3cm d'épaisseur : 25 X 0,03 =
0,75KN/m2
· Chape et carrelage donne : 0,8 KN/m2
D'où G = 5,59 + 2,12 +0,75 +0,8 = 9,26 KN/m2
· La charge Q d'exploitation de l'escalier est de 2,5
KN/m2
D'après (A, 3) la charge pondéré Pu
est :
Pu = (1,35 X 9,26) + (1,5 X 2,5)
= 16,25 KN/m2
· Calcul des sollicitations
· Le moment fléchissant ultime
On a Mu= 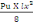  (d, 5) (d, 5)
=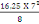 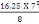
= 99,53 KN
Et Mbu= 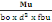 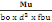 (d, 6) (d, 6)
D'après (B, 12), d=0,9h
d= 0,9 X 17
= 15,3cm et bo=1m
(d, 6) devient :
Mbu= 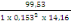 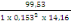
= 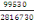 
= 0,035
Choix du pivot de calcul des aciers plus béton à
utiliser :
Mbu? 0,186 = pivot A.
D'où 0,035 ? 0,186 = pivot A.
Calcul de bras de levier Zb :
D'après (A, 15), est donné par la
relation :
Zb = d (1- 0,4  ) )
Et  = 1,25(1- = 1,25(1-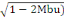 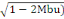
  = 1,25(1- = 1,25(1-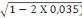 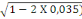
= 0,48
D'où Zb = 15,3 X (1- 0,4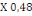 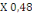 ) )
= 12,36cm
· Calcul de la section des armatures
On a:
As= 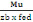 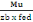 (d, 7) (d, 7)
Et fed=347,826MPa
As = 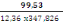 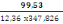
= 2,31cm2
Nous prenons AS =4,52cm qui donne
4Ø12HA.
· Écartement maximal des aciers
2. e
St = valeur maximale
(d, 8)
25cm
D'où
2
X 17
St =valeur maximale
25cm
St = valeur maximale entre 34cm et 25cm.
Nous prenons l'espacement maximum de 34cm.
· Les aciers de répartition
Ar=   (d, 9) (d, 9)
On a Ar= 
= 
= 0,77cm2
Nous prenons Ar =3,14cm qui donne
4Ø10HA.
· Les armatures chapeaux
Ac= 15%   (d, 10) (d, 10)
On a Ac= 15% de 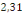 cm2 cm2
=   cm2 cm2
Nous prenons Ø6HA.
Figure 17. Schémas de ferraillage

Chapitre VII.
CONCLUSION
La réalisation de ce projet consisté à
résoudre les problèmes des structures, les calculs des structures
mais aussi les dimensionnements de l'immeuble et nous avons essayé cette
tache dans les pages précédentes. Nous avons tenté de
demeuré dans l'objectif poursuivie pour un travail de fin
d'étude : celui de relier la théorie vue à
l'école avec la pratique sur terrain.
Malgré les difficultés lies à l'obtention
des résultats aux principes des constructions modernes, nous
reconnaissons aussi avoir user des méthodes difficiles à notre
niveau : mais nous avons cherché des solutions de construction
économique de l'immeuble.
Ce travail se subdivise en trois grands volumes :
Ø Partie étude structurale et architecturale :
consacrer à la description, la disposition des différents
compartiments de l'immeuble, mais aussi l'hypothèse de calcul.
Ø Partie construction : consacrer aux choix de
matériaux à utiliser.
Ø Partie calcul : consacrer aux méthodes et
calculs utiliser pour la détermination des charges d'exploitations,
charges permanentes et les surcharges des éléments de l'ouvrage
pour but de trouver rationnellement les aciers correspondants.
Nous espérons que nos lecteurs trouveront à travers
ces pages, les fruits de nos efforts et sacrifices en vue de
l'achèvement de ce travail.
Comme tout oeuvre scientifique est l'Object des recherches et
critiques, vos remarques et suggestions sont les bienvenus pour
l'amélioration et la finalité de ce projet.
Chapitre VIII. BIBLIOGRAPHIE
1. OUVRAGE
Ø Conception et calcul de structures en béton arme
[HENRY THONIER, 2ieme édition].
Ø Congo
Dr-directives-sur-les-normes-des-constructions-scolaires (CIRCULAIRE
N°MINEPSP/CABMIN/0668/2007 DU 13/11/07).
Ø J-Percha, J-Roux, [2002] : Pratique du BAEL 91, éditions Eyrolles.
Ø Mougin J-P. Béton arme, BAEL 91 modifie 99 et DTU
associes, Eyrolles.
Ø NBN EN 1992-1-1 :2005, Eurocode 2-Partie 1-1 :
calcul des structures en béton-Règles générales et
règle pour le bâtiment.
Ø Normes de construction scolaires (Direction du
Génie scolaire Novembre) A l'usage des gens intéressés
à la construction d'écoles en Haïti, article publie en
2010.
Ø Rapport de consultation d'un projet de construction
d'une école de Montréal projet de règlement
P-17-039/2017
2. NOTES DE COURS
Ø Cours de résistance des matériaux, IBTP/Kamituga.
Ø Cours de Béton 1 et 2, IBTP/Kamituga.
Ø Cours de mécanique de sol, inédit.
Ø Technologie de construction. Lucas NEHOU
3. INTERNET
Ø Google
Ø Wikipédia
TABLE DES MATIERES
DEDICACE
1
REMERCIEMENTS
2
SIGLES ET/OU ABREVIATIONS
3
INTRODUCTION GENERALE
4
0.1. LA PROBLEMATIQUE
4
0.2. HYPOTHESES
4
0.3. L'OBJECTIF GLOBAL
4
0.4. LES OBJECTIFS SPECIFIQUES
5
0.5. LA METHODOLOGIE
5
Chapitre I. REVUE
DE LA LITERATURE
6
I.1 La conception
6
I.2 Immeuble d'habitations
7
a. Définition
7
b. Catégorisation
7
c. Les styles
7
I.3 La loi congolaise sur la conception et
la construction des immeubles à usage d'école
7
a. Des exigences pédagogiques
8
b. Des exigences des sites
8
c. Des exigences architecturales
8
Chapitre II.
CONCEPTION ARCHITECTURALE DES IMMEUBLES A USAGE D'ECOLE
11
II.1 Normes de planification
géographique
11
II.2 L'aspect architectural des immeubles
à usage d'école au Sud-Kivu
12
II.3 Conception architecturale d'une
école de 1650 élèves au Sud-Kivu, dans la ville de
Kamituga
16
Chapitre III.
CONCEPTION STRUCTURALE DES IMMEUBLES A USAGE D'ECOLE
17
§ La structure porteuse
17
§ Le choix du système
porteur
17
§ Autres facteurs importants
pour la conception
18
§ Les plans de
coffrage
18
III.1 DIMENSIONNEMENT DE LA DALLE
18
a. Généralité
18
b. Calcul de l'épaisseur de la
dalle
19
c. Dimensionnement de la dalle du RDC
19
d. Calcul des moments
21
e. Les armatures porteuses et les armatures
de répartition.
22
III.2 DIMENSIONNEMENT DE LA POUTRE
26
a. Généralité
26
b. Pré dimensionnement de la
poutre
27
c. Évaluation et combinaison de
charges
28
d. Calcul des sollicitations
28
e. Calcul des armatures longitudinales
comprimées et des armatures transversales
30
f. Calcul des aciers transversaux et de
l'espacement maximum des armatures longitudinales (St)
33
III.3 DIMENSIONNEMENT DE POTEAU
36
a. Généralité
36
b. Pré dimensionnement en compression
simple de poteau le plus défavorable
37
c. Descente des charges
38
d. Combinaisons des charges
39
e. Calcul des armatures longitudinales et
transversales
40
III.4 DIMENSIONNEMENT DE LA FONDATION
43
a. Généralité
43
b. Descente des charges
45
c. Détermination des dimensions de la
semelle isolée et contrôle de la résistance du sol
47
d. Calcul de la section des armatures
48
e. Vérification du
poinçonnement de la semelle sous poteau
48
III.5 DIMENSIONNEMENT DE L'ESCALIER
49
a. Généralité
49
b. Dimensionnement de l'escalier
50
CONCLUSION
56
BIBLIOGRAPHIE
57
ANNEXES
FACADE PRINCIPAL

PERSPECTIVE DENSEMBLE NORD-EST

PERSPECTIVE DENSEMBLE SUD-OUEST

PERSPECTIVE DENSEMBLE DE DESSUS

| 


