Contrôle de l'énergie reactive dans un parc éolien

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

??²

???? = -??????(???? - )??????

????

??² ?????? (IV.13)

???? = ??????(????-??????+ ??

???? ????

L'équation des tensions rotorique deviens :

??²)????????

??????= ?????????? + (???? ???? + ????

????

??2)???????? (IV.14)

??????

?????????? + (????-???? + ????

????

Après avoir mis en place une transformation de la place ont obtient :

??^2 (???? + (???? - )??) ?????? = ?????? - ???? ???? ??^2 ???? + (???? - )??) ?????? = ?????? - ???? ????

(IV.15)

Avec :

?????? =

1

2 (?????? - ????)

(???? + (????

??

???? ) ??)

(IV.16)

1

?????? = (?????? - ????)

(???? + (???? - ??2

???? ) ??)

En remplaçant IV.16 dans IV.15 nous obtenons alors les expressions des puissance actives et réactives :

???? = -????

?? ????

1 (?????? - ????) ????+ (???? - ??2 ???? ) ??

(IV.17)

????= -????

?? ????

1 ???????? (?????? - ????) + ????+ (????- ??^2 ???? ???? ) ??

Après avoir obtenue les équations nous pouvons développer le schéma bloc contrôle des puissances statoriques de la MADA représenté à travers la figure IV.9.

78

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

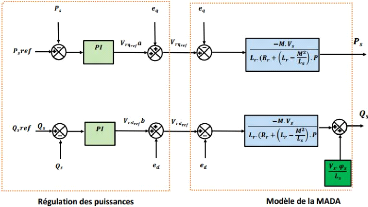
Figure IV-9. Contrôle des puissances statorique de la MADA

IV.5.2 Régulation avec un correcteur PI classique :

La figure IV-10 montre la régulation directe de puissance avec un régulateur PI sur les deux axes d et q dont les fonctions de transferts sont de la forme ?? ?? + ??? ??? .

Figure IV-10. Système régulé par un PI classique. IV.5.2.1 Synthèses du régulateur PI classique :

La fonction de Transfert en Boucle Ouverte (FTBO) avec les régulateurs s'écrit de la manière suivante :

????????	=	(?? ??	????	??????		(IV.18)
			????

On applique la méthode de compensation de pôles pour la synthèse du régulateur éliminer le zéro présent sur la fonction de transfert, nous choisissons :

79

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

Kp		LsRr		(IV.19)	Ki
=	M2 Ls (Lr - Ls)

Après l'application de la compensation des pôles, on obtient :

FTBO =	MVs KP M2 Ls (Lr - Ls)		(IV.20)

Ce qui nous donne FT en boucle fermée :

FTBF =	1		(IV.21)

Avec :

_MZ

1

T_r = K_p

Ls(LT-_Ls )

MV_s

Le terme i_r désigne ici le temps de réponse du système. Nous choisissons de fixer celui-ci à 200 ms, ce qui représente une valeur suffisamment pour l'utilisation faite sur l'éolienne où les variations de vent sont peu rapides et les constantes de temps mécanique sont importantes. Une valeur inférieure est susceptible d'engendrer des régimes transitoires avec des dépassements importants et ne présente pas d'intérêt particulier pour notre application [22]. Les termes K_Ket Ki sont alors exprimés en fonction de ce temps de réponse et des paramètres de la machine :

_M2

L_s (L_r - Ls)

MV_s

Ki =	1		LsRr
	MVs

1

T_r

K_p =

(IV.22)

IV.6 Commande du convertisseur cotée réseau (CCR)

Le schéma du CCR, du bus et du filtre R, L est illustré dans la figure IV.11.

80