Contrôle de l'énergie reactive dans un parc éolien

É ÜíÜÈÜÚÜÔ Ü á Ç É ÜíÜØÑÇÜÞÜ íãÏáÇ ÉÜíÑÜÆÒÇ Ü áÌÇ É ÜíÑæÜåÜãÜ áÌÇ

REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE

íÜ ãÜáÜÚáÇ ËÍÜÈáÇæ áí Ç ÜÚáÇ ã ÜíáÜÚ ÜÊáÇ ÉÑÇÒæ

Ministère de l'Enseignement Supérieur et de la Recherche Scientifique

- äÇ Ü Óãá ÜÊ - ÏÜíÇÜÞÜáÜÈ Ñ ÜßÜÈ Èí ÉÚãÇÜÌ

Université Aboubakr Belkaïd - Tlemcen

Faculté de TECHNOLOGIE

MEMOIRE

Présenté pour l'obtention du diplôme de MASTER
En Electrotechnique
Spécialité Commandes électriques
Par RAHMOUN Imad eddine
Et YEBE Ahmed

Sujet

Contrôle de l'énergie réactive dans un parc éolien

	Soutenu publiquement, le	06 / 07 / 2021, devant le jury composé de :
S.M MELIANI	Maitre-Assistant	U.A.B.-Tlemcen	Président
H. SMAIL	Maitre-Assistante	U.A.B.-Tlemcen	Directeur de mémoire
F. DJAAFAR	Docteur	U.T.O.M.B	Co- Directeur de mémoire
B. YACOUBI	Maitre-Assistant	U.A.B.-Tlemcen	Examinateur

Remerciements

On remerciement tout d'abord Dieu, le miséricordieux, le tout puissant de nous avoir donné la foi, le courage, la patience et la volonté d'entamer de de finir ce mémoire.

On tient à remercier, Mademoiselle Houria SMAIL, Maitre Assistante de classe B à l'Université Abou Bekr Belkaïd Tlemcen et directeur de ce mémoire pour avoir proposé, suivi et dirigé ce travail, mais aussi pour le respect et le professionnalisme dont on a été témoin.

On tient aussi à remercier, Madame Fatiha DJAFAAR, Docteur à l'Université des sciences et technologies Mohamed Boudiaf à Oran co-directeur de ce mémoire pour avoir suivi et surveillé l'état d'avancement ce travail, mais aussi pour le respect et le professionnalisme dont on a été témoin.

Toute la gratitude à Messieurs B. YACOUBI et S.M MELIANI, tous deux enseignants à l'Université Abou Bekr Belkaïd Tlemcen, qu'ils aient accepté d'examiner et présidée ce travail, on les remercie pour leurs observations et leurs remarques pertinentes, directe et constructives.

Merci enfin à tous ceux qui, de près ou de loin, ont contribué a l'aboutissement de ce travail.

i

SÇdieaee1

Je dédie ce travail :

o Aux êtres les plus chers à mon coeur, ma mère et mon père, qui m'ont beaucoup soutenu durant mon cursus d'étude et à qui je serai éternellement reconnaissant

o A mes chères soeurs.

o A mes petit nièces et neveux.

o A tous les enseignants qui m'ont aidé de près ou de loin à réussir à obtenir mon master en électrotechnique.

o A tous mes amis qui me sont chère : SEMMOUD Abdellah, KHEBICHAT Boumedienne,RAFAA Fethi ,et mon binôme YEBE Ahmed.

o A tous ceux et celles qui m'ont encouragé et soutenu durant mon cursus.

RAHMOUN Imad eddine

Tlemcen, le 20 Juin 2021.

ii

Dédicace 2

Je dédie ce travail :

o A mon père que Dieu lui fasse miséricorde, à ma mère, à mon grand frère Mohamed, à tous mes frères et soeurs, et à ma tante Mariem,

o A mes neveu Lemrabott, Nema et Ahmed,

o A tous mes cousins,

o A tous mes compatriotes,

o A Zahraoui Issam eddine, Fayçal Saidi, et à mon binôme Rahmoun Imad eddine,

YEBE Ahmed

Tlemcen, le 20 Juin 2021.

iii

Table de matières

Remerciements i

Dédicaces 1 ii

Dédicaces 2 iii

Table de matières iv

Liste des figures vii

Liste des tableaux x

Liste des symboles xi

Liste des abréviations xii

Introduction général 1

Chapitre I : État de l'art des éoliens

I.1 Introduction 5

I.2 Définition de l'énergie éolienne 5

I.3 Origine de l'énergie éolien 6

I.4 Situation actuelle de l'énergie éolienne dans le monde 8

I.5 Composants d'une éolienne 9

I.6 Classification des turbine éoliennes 10

I.6.1 Éolienne à axe horizontal 10

I.8.2 Éolienne à axe vertical 11

I.7 Les diffèrents type d'éoliennes 13

I.7.1 Éolienne à vitesse fixe 13

I.7.2 Éolienne à vitesse variable 13

I.8 Quelques notions de conversion de l'énergie éolienne 15

I.8.1 Énergie cinétique du vent - conversion en énergie mécanique 15

I.8.2 Conversion de l'énergie cinétique du vent en énergie électrique 18

I.8.3 Les différents topologie d'alimentation de la MADA 19

I.8.3.1 MADA à énergie rotorique dissipé 19

I.8.3.2 MADA structure de Kramer 20

I.8.3.3 MADA structure de Scherbius avec cyclo convertisseur 21

iv

I.8.3.4 MADA structure de Scherbius avec convertisseur MLI 21

I.9 Avantages et inconvénients des systèmes d'énergie éolienne 22

I.9.1 Avantages 22

I.9.2 Inconvénients 23

I.10 Conclusion 24

Chapitre II : Modélisation et commande d'une turbine éolienne

II.1 Introduction 26

II.2 Modélisation du vent 26

II.3 Modélisation de la turbine 27

II.4 Modélisation du multiplicateur 29

II.5 Modélisation de l'arbre mécanique 30

II.6 Stratégie de commande de l'éolienne 31

II.6.1 Systèmes de régulation de la vitesse de rotation de l'éolienne 32

II.6.1.1 Système à décrochage aérodynamique "Stall" 32

II.6.1.2 Système d'orientation des pales "Pitch" 33

II.7 Zone de fonctionnement d'une eolienne 34

II.8 Principe de contrôle MPPT (stratégie d'extraction du maximum de puissance) 35

II.8.1 Maximisation de la puissance sans asservissement de vitesse 35

II.8.2 Maximisation de la puissance avec asservissement de la vitesse 37

II.9 Résultat de simulation 40

II.9.1 Résultats de simulation de la turbine avec asservissement de la vitesse mécanique 41

· Interprétation des résultats 42

II.9.2 Résultats de simulation de la turbine sans asservissement de la vitesse mécanique 42

· Interprétation des résultats 44

II.10 Conclusion 44

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

III.1 Introduction 46

III.2 Description de la MADA 46

III.3 Mode de fonctionnement de la MADA 47

III.3.1 Fonctionnement en moteur hypo-synchrone 47

III.3.2 Fonctionnement en moteur hyper-synchrone 47

III.3.3 Fonctionnement en mode génératrice hyper-synchrone 48

III.3.4 Fonctionnement en mode génératrice hypo-synchrone 48

v

III.4 Modélisation de la MADA 49

III.4.1 Modèle de la MADA dans le repère triphasé-triphasé 49

III.4.1.1 Hypothèse simplificatrice 50

III.4.1.2 Equation électrique 50

III.4.1.3 Equation Magnétique 51

III.4.1.4 Equation mécanique 52

III.4.2 Modèle de la MADA dans le repère de Park 52

III.4.2.1 Définition de la transformation de Park 52

III.4.2.2 Equation électrique 54

III.4.2.3 Equation du flux magnétique 54

III.4.2.4 Equation du couple électromagnétique : 55

III.4.2.5 Equation des puissance active et réactive statorique et rotorique 55

III.6.5 Choix du référentiel (d-q) 56

III.4.2.6 Référentiel liée au champ tournant 56

III.4.2.7 Référentiel liée au stator 56

III.4.2.8 Référentiel liée au rotor 57

III.5 Modélisation des convertisseurs statiques 57

III.5.1 Modélisation du convertisseur coté MADA 58

III.5.2 Modélisation du bus continue 59

III.5.3 Modélisation du convertisseur cotée réseau 60

III.5.4 Modélisation du filtre 62

III.5.5 Commandes à Modulation de Largeur d'Impulsion (MLI) 64

III.5.5.1 Modulation a largeur d'Impulsion Sinus-Triangle 64

III.6 Conclusion 65

Chapite IV: Stratégie de commande des puissance active et réactive

IV.1 Introduction 68

IV.2 Architecture du dispositif de commande 68

IV.3 Commande vectorielle 69

IV.4 Commande du convertisseur coté MADA 70

IV.4.1 Choix du référentiel pour le modèle de la MADA 71

IV.4.2 Détermination des angles pour les transformations de Park 71

IV.4.3 Modélisation de la MADA avec orientation du flux statorique 72

IV.5 Contrôle indépendant des puissances active et réactive de la MADA 76

IV.5.1 Régulation des puissance active et réactive de la MADA 77

vi

IV.5.2 Régulation avec un correcteur PI classique 79

IV.5.2.1 Synthèses du régulateur PI classique 79

IV.6 Commande du convertisseur cotée réseau (CCR) 80

IV.6.1 Commande du bus continu 82

IV.6.2 Commande des courants dans le filtre : 83

IV.7 Résultats de simulation 86

IV.8 Conclusion 88

Conclusion générale 90

Bibliographie

Annexe A Annexe B Résumé

vii

Liste des figures

Chapitre I : État de l'art des éoliens

Figure I-1. Conversion de l'énergie cinétique du vent 6

Figure I-2. Moulin à vent hollandais avec queue pour orientation automatique 6

Figure I-3. Moulin à vent (moulin à vent terrestre hollandais) avec voiles à ressort 7

Figure I-4- Capacité éolienne installée dans le monde entre 2001 et 2020 en GW 9

Figure I-5- Composants d'une éolienne 10

Figure I-6- Éolienne à axe horizontal 11

Figure I-7-Éoliennes à axe vertical de Darius 12

Figure I-8. Éoliennes de type Savonius 12

Figure I-9 Structure d'une éolienne à vitesse fixe 14

Figure I-10. Structure d'une éolienne connectée au réseau 14

Figure I-11-Schéma de l'écoulement d'un fluide à travers un disque 16

Figure I- 12-Rendement aérodynamique en fonction du tipspeed ratio et du modèle d'éolienne 18

Figure I-13-Chaine de conversion d'une éolienne 19

Figure I-14-MADA avec contrôle du glissement par l'énergie dissipée 20

Figure I-15-Structure de Kramer 20

Figure I-16-Structure de Scherbius avec cyclo convertisseur 21

Figure I-17-Structure de Scherbius avec convertisseurs MLI 22

Chapitre II : Modélisation et commande d'une turbine éolienne

Figure II- 1. Structure d'une turbine éolienne 27

Figure II-2-Coefficient de puissance et vitesse relative pour différents angles de calages. 28

Figure II-3. Modèle d'un multiplicateur 29

Figure II-4. Modèle de transmission mécanique ramenée à l'arbre Mécanique 30

Figure II-5. Schéma bloc de la turbine modélisé 31

Figure II-6. Flux d'air sur un profil de pale " Stall " 32

Figure II-7. Variation de l'angle de calage d'une pale 33

Figure II-8. Courbe de la puissance éolienne en fonction de la vitesse du vent 35

Figure II-9. Schéma bloc de la maximisation de la puissance sans asservissement de vitesse 36

Figure II-10. Schéma bloc de la maximisation de la puissance avec asservissement de vitesse 38

Figure II-11- Schéma bloc de la régulation de vitesse avec régulateur PI 39

Figure II-12- Profil du vent appliqué. 40

viii

Figure II-13- Simulation de la commande MPPT avec un asservissement de vitesse 41

Figure II-14- Simulation de la commande MPPT sans asservissement de vitesse 43

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

Figure III-1.Structure d'une MADA connectée au réseau 46

Figure III-2- Schéma de structure de la MADA en mode moteur hypo-synchrone 47

Figure III-3.Schéma de structure de la MADA en mode moteur hyper-synchrone 48

Figure III-4.Fonctionnement Génératrice hyper-synchrone 48

Figure III-5. Fonctionnement en mode génératrice hypo-synchrone 49

Figure III-6. Représentation spatiale des enroulements de la MADA 49

Figure III-7. Transformation de Park 53

Figure III-8. Structure de la chaine de conversion étudiée 58

Figure III-9. Redresseur triphasée double alternance 58

Figure III-10. Modèle du bus continue 59

Figure III-11. Onduleur de tension triphasée 61

Figure III-12. Filtre coté réseau 63

Figure III-13. Principe de fonctionnement de la technique MLI triangulo sinusoïdal 65

Chapitre IV : Stratégie de commande des puissances active et réactive de la MADA

Figure IV-5.Architecture du dispositif de commande 69

Figure IV-2. Principe de la commande vectorielle 70

Figure IV-3. Structure de commande du convertisseur cotée MADA 70

Figure IV-4. Schéma structurel de la détermination des angles pour la transformation de Park 71

Figure IV-5. Référentiel diphasé ???? liée au champ tournant statorique. 72

Figure IV-6. Schéma bloc du système à réguler 75

Figure IV-7- Schéma bloc de la commande directe de puissance de la MADA. 76

Figure IV-8. Schéma bloc de la commande indirecte de puissance de la MADA 77

Figure IV-9. Contrôle des puissances statorique de la MADA 79

Figure IV-10. Système régulé par un PI classique. 79

Figure IV-11-Schéma structurel du CCR, du bus et du filtre RL 81

Figure IV-12- Schéma global du contrôle du CCR 82

Figure IV-13- Modèle en boucle fermé de la boucle de tension du bus continu. 83

Figure IV-14- Contrôle des courants circulant dans le filtre RL 85

Figure IV -15-Resultats de simulations 86

ix

Liste des Tableaux

Chapitre I : État de l'art des éoliens

Tableau I-1. Comparaison entre une éolienne a vitesse fixe et une éolienne à vitesse variable. .. 15

Chapitre II : Modélisation et commande d'une turbine éolienne

Tableau II-13. Paramètre nominal de la simulation de la partie mécanique. 40

x

Liste des symboles

Symbole	Nom		Unité	A
Vitesse relative	/		p
La densité de l'aire	/		A1
La surface	m2		Vvent
La vitesse du vent	m/s		Pvent
Puissance du vent	W		Pt
Puissance de la turbine	W		R
Rayon des pales de la turbine	m		/3
Angle de calage	o		.opt
La vitesse relative optimal	/		Paero
Puissance aérodynamique	W		Ps
Puissance Actif statorique	W		Qs
Puissance réactif statorique	VAR		Qr
Puissance réactif rotorique	VAR		Pr
Puissance Actif rotorique	W		Cp
Coefficient de puissance	/		Cp_max
Coefficient de puissance maximal	/		Caer
Couple aérodynamique	Nm		Cmec
Couple mécanique	Nm		Cvis
Couple de frottement visqueux	Nm		CL
Couple du multiplicateur	Nm		Ct_est
Couple de la turbine estimé	Nm		f1t
Vitesse de rotation de la turbine	rad/s		f1L
Vitesse de la génératrice	rad/s		f^1mec
Vitesse mécanique de la turbine	rad/s		G
Gain du multiplicateur	/		J
Inertie total	kg. m2		JL
Inertie de la génératrice	kg. m2		Jt
Inertie de la turbine	kg. m2		p
Nombre de pair de pôles	/

xi

nt _est Vitesse de la turbine estimé rad/s

Vvent_est Vitesse du vent estimé m/s

f Coefficient visqueux N. m. s/rad

Ti3 Constante du temps du système pitch s

Nref Angle de calage de référence

o

f Coefficient d'amortissement /

w_n Pulsation propre rad/s

f_r Fréquence de référence Hz

f_P Fréquence de la porteuse Hz

m Indice de modulation /

Vsa, Vsb, Vsc Les tensions simples statorique V

Vra, Vrb, Vrc Les tensions simples rotorique V

Vdr, Var Les tensions rotoriques sur l'axe d-q V

Vds, Vas Les tensions statoriques sur l'axe d-q V

V,,,, Amplitude de la tension d'alimentation V

V_s Tension de sortie du redresseur V

Vdc Tension du bus continue V

V_t Tension du filtre V

Vref Amplitude de la tension de référence V

V_P La crête de modulation V

Vmd, Vmq Les tensions modulées par le CCR V

C Capacité du condensateur F

Isa, Isb, Isc Les courant de phase instantané statorique A

Ira, Irb, Irc Les courant de phase instantané rotorique A

Iqs, Ids Les courant statorique sur l'axe d-q A

Ida, Idr Les courant rotorique sur l'axe d-q A

A Angle électrique entre les repères statorique et rotorique rad

ÇPsa, ÇPsb, ÇPsc Flux statorique Wb

ÇPra, ÇPrb, ÇPrc Flux rotorique Wb

ÇPqs, ÇPds Les flux statoriques sur l'axe d-q Wb

ÇPqr, ÇPdr Les flux rotoriques sur l'axe d-q Wb

xii

Rs	Résistance statorique		ohm	R,.
Résistance rotorique	H		Ls
Inductance propre statorique	H		L,.
Inductance propre rotorique	H		Mr
Inductance mutuelle entre phase rotorique	H		Ms
Inductance mutuelle entre phase statorique	H		wr
Pulsation rotorique	rad/s		ws
Pulsation statorique	rad/s		lt
Inductance du filtre	H		Rt
Résistance du filtre	ohm

Liste des abréviations

Abréviation Signification

FOC Field orientation control

PLL Phase Locke Loop

DFIG Doubly Feed Induction Generator

MADA Machine Asynchrone à Double Alimentation

CCM Convertisseur coté MADA

CCR Convertisseur coté réseau

D Diode

MPPT Maximum Power Point Traking

IGBT Insulated Gate Bipolar Transistor

MLI Modulation de Largeur d'Impulsion

PWM Pulse With Modulation

PI Proportionnel et Intégral

GTO Gate Turn-off thyristor

xiii

Introduction générale

Introduction générale

Face à l'évolution quotidienne de la technologies dans divers domaines industrielles, et la multiplication des besoins en matérielles électriques ,la consommation de l'énergie électrique ne cesse de croitre cette forte consommation impose au pays développée une forte production d'énergie élécrique,Par conséquent les centrales nucléaires dont fortement solicitée,cette source d'énergie renouvelable comparée au centrale thermiques n'engendre en aucun cas la pollution de l'atmosphère mais le cotée négatif de cette source d'énergie est le risques d'accident nucléaire qui est asse problematique.Il est donc préférables de se tourné vers des sources d'énergie plus propres avec un rendement élevée en terme de production. Parmi les énergies les plus prometteuses en termes de potentiel énergétique et du faible taux de pollution de l'atmosphère on retrouve l'énergie éoliennes. Cet énergie renouvelable ne cesse de croitre et d'être de plus en plus exploitée dans le monde,l'Allemegne l'Espagne le Danemark et la France sont les leader mondial de l'énergie éoliennes.

Afin de mieux tirer profit de cette source d'énergie et de permettre un contrôle adéquat et optimal de l'énergie produite les chercheurs en Génie électrique ont effectuée des études approfondies afin d'améliorer la conversion électromécanique et la qualité de l'énergie produite et de mettre en place un contrôle facile et efficace.

La conversion de l'énergie électrique se fait à travers plusieurs éléments qui constitue la chaine de production de l'éolienne de la puissance cinétique du vent jusqu'au réseau.

Les générateurs les plus utilisé dans les parcs éoliens sont les machine asynchrone a double alimentation car cette dernière engendre un bénéfices économique important para port au autre Machines qui existe dans le monde grâce à ces convertisseurs statiques triphasés dimensionnés pour une partie de la puissance nominale de la MADA. [1]

Comparée à la machine asynchrone à cage la machine asynchrone à double alimentation peut fonctionner sur une large plage de variation de vitesse #177; 30 % autour de la vitesse de synchronisme, cet possibilité de fonctionnement permet de produire de l'énergie électrique a une vitesse variables et ainsi mieux tirer profit de la variation de l'énergie cinétique du vent. [2]

Actuellement la machine asynchrone à double alimentation est utilisée dans divers domaines et dans ces deux modes de fonctionnement, soit en moteur comme la traction ferroviaire, soit en génératrice comme dans les parcs éoliens [2].Sa forte utilisation est lié à sa grande souplesse de fonctionnement liée à la présence des convertisseurs statiques, une possibilité de réglage de la

1

Introduction générale

répartition des puissances statorique et rotorique afin d'optimiser les dimensions des convertisseurs. [2]

Notre mémoire porte sur la conversion de l'énergie éolienne en énergie électrique et plus précisément la mise en place d'une stratégie de contrôle de l'énergie réactive produite par un parc éolien et le contrôle des turbines à vitesse variables à base de générateurs asynchrone a double alimentation.

Le premier chapitre est consacré aux notions générales sur l'énergie éolienne. La situation actuelle, Les différents composantes et les principales caractéristiques des éolienne et une approche générale et globale de diverses technologies des aérogénérateurs seront brièvement présentées. Ensuite Un aperçu sur les différents types d'éoliennes à axe vertical et horizontal, leurs caractéristiques et un rappel sur les différents types de génératrices utilisées dans la conversion éolienne. En fin de ce chapitre les avantages et inconvénient des énergies renouvelables seront abordé.

Dans le deuxième chapitre les différents composant de la partie mécanique de l'éolien seront modélisés tous un présentant les différentes équations mathématiques qui constitue les diffèrent schéma-blocs. Ensuite les diffèrent stratégie de commande de l'éolien à vitesse variable, système d'orientation de vitesse de rotation "stall" et "pitch" sont discuter. En fin les zone de fonctionnement et les stratégies de commande MPPT (Maximum Power Point Tracking) avec et sans asservissement vont être présenter et simulé sous logiciel Matlab/Simulink, afin de définir la meilleure stratégie de commande.

Le troisième chapitre est consacré à la description de la Machines asynchrone à double alimentation et ces différents modes de fonctionnement et sa modélisation dans différent repérés, tout en présentant les diffèrent équation électrique et magnétique. En suite les différents choix possibles du référentiel d-q, Par rapport au rotor, au stator et au champ tournant, vont être discuter. Une modélisation des convertisseurs statique va être aborder, Ces convertisseurs AC-DC-AC sont constitué de deux parties : une branché sur le côté machine et l'autre sur le côté réseau. En fin une étude de commande MLI va être présenter.

Le dernier chapitre est consacré aux notion général de la stratégie de contrôle proposé qui est basée sur la commande vectorielle par l'orientation du flux statorique ,cette méthode permet d'assimiler le comportement d'une machine asynchrone a une machine a courants continue en retrouvant la quadrature entre le courants et le flux qui vas nous permettre de contrôlé les puissances actif et

2

Introduction générale

réactives .La dernière partie de ce chapitre fera l'objet d'une présentation des résultats de simulation de la commande appliquée à l'ensemble de la chaine de conversion, afin de valider la structure étudié.

3

Chapitre I : État de l'art des

systèmes éoliens

4

Chapitre I : État de l'art des systèmes éoliens.

I.1 Introduction

L'énergie électrique est l'énergie la plus utilisée et développée dans le monde car cette dernière est le facteur le plus important pour le développement et l'évolution de la race humaine.

Afin de répondre aux besoins en énergie électrique qui ne cessent d'augmenter massivement ces dernières années, plusieurs sources d'énergie renouvelables et non renouvelables sont exploitées. Parmi les sources les plus exploitée on trouve l'énergie éolienne.

Le principal intérêt envers cette source d'énergie renouvelable est son caractère écologique, surtout dans le contexte actuel où la terre entière subit les conséquences du réchauffement climatique.

Dans ce chapitre, nous avons fait une étude de l'état de l'art des éoliennes et les diverses technologies des aérogénérateurs et leurs principales caractéristiques, les différents types, ainsi que les différentes configurations.

I.2 Définition de l'énergie éolienne

L'éolienne produit de l'électricité grâce à la force du vent, une source d'énergie renouvelable inépuisable et gratuite, il existe deux grands types d'installation d'éoliennes le parc terrestre dit (onshore) et le parc implanté en mer a plusieurs Km au large des côtes (offshore).

L'éolienne peut mesurer jusqu'à 120m l'hélice appelée rotor est composée en général de trois pales se met à tourner sous l'effet d'un vent d'au moins 10Km/h, la nacelle sur la quel elle est fixée s'oriente automatiquement pour être toujours face au vent et les palles pilote pour captée un maximum de vent.

Si le vent dépasse 90km/h l'éoliennes s'arrête automatiquement de fonctionnée pour des questions de sécurité, dans la nacelle l'hélice fait tournée un axe sa vitesse de rotation n'est tant pas suffisante pour générer de l'électricité un multiplicateur augmente cette Vitesse jusqu'à atteindre les 1500tr/min et la transmet à un second axe qui fait à son tour tournée un alternateur.

Dans l'alternateur l'interaction entre les électro-aimant du rotor et les bobine du stator la produit un courant électrique, un transformateur situé à l'intérieur du mat élevé la tension de ce courant a 20 000V. L'électricité est ensuite acheminé par un câble sous terrain ou sous-marin et sera élevé à 400 000V par un poste de transformation pour être transporté facilement à travers les

5

Chapitre I : État de l'art des systèmes éoliens.

lignes haute tension du réseau, régulièrement tous les composant de l'éoliennes son surveillée et contrôlé.

L'électricité d'origine éoliennes n'émet pas de gaz à effet de serre contenue de l'intermittence de la production liée à la force du vent elle est utilisée en complément d'autre source d'énergie pour répondre au besoin en électricité. La figure I.1 représente le principe de fonctionnement d'une éolienne.

Figure I.1-conversion de l'Energie cinétique du vent [3].

I.3 Origine de l'énergie éolien

L'histoires éoliennes remonte à plus de 2000 ans. Ils ont été utilisés principalement pour pomper l'eau et pour moudre les céréales. Dès le 13e siècle, les moulins à vent à axe horizontal ont jouer un rôle très essentiel dans l'économie rurale. Les moulins à vent hollandaise (figure I.2 et figureI.3) ont été construits en grand nombre aux 17e et 18e siècles en Europe. [3]

Figure I.2-Moulin à vent hollandais avec queue pour orientation automatique [4].

6

Chapitre I : État de l'art des systèmes éoliens.

Les éoliennes produisent de l'électricité depuis 1888. Par rapport à d'autres sources d'énergie renouvelables, comme le photovoltaïque, au début du 19e siècle le développement des éoliennes n'as pas cessé de croitre et a permis au moulin occidental d'apparaitre, on le trouve dans les zones rurales, surtout aux États-Unis, jusqu'au début du 20e siècle et jusqu'à aujourd'hui. La révolution et le développement des convertisseurs d'énergie éolienne ont été développées dans les années 1920, mais ce n'est que dans les années 1980 qu'elles ont était exploité et utilisé en tant qu'élément important dans la convention et l'exploitation des énergie renouvelables [3].La première théorie appropriée a été publiée le début du19ème siècle (Joukovski 1907).

Les éoliennes modernes sont généralement construites comme des machines à rotation rapide avec un arbre horizontal, une disposition au vent et, de préférence, avec un moteur à combustion interne et de préférence 3 pales de rotor. La puissance des machines a régulièrement augmenté de sorte que la puissance moyenne installée par unité est actuellement supérieure à 1.700kW. Pour les parcs éoliens en mer, des puissances allant jusqu'à 6.000 kW sont en phase de développement. [3].

Figure I.3-Moulin à vent (moulin à vent terrestre hollandais) avec voiles à ressort [4].

7

Chapitre I : État de l'art des systèmes éoliens.

I.4 Situation actuelle de l'énergie éolienne dans le monde

Pour se remettre économiquement de la crise covid-19, les gouvernements du monde entier mettent en place des plans de relance pour soutenir les industries qui stimuleront la croissance économique. Le secteur de l'énergie est une industrie clé pour alimenter l'activité économique, cependant, et c'est pour cela que l'année 2020 a été la meilleure année de l'histoire pour l'industrie éolienne mondiale avec 93 GW de nouvelles capacités installées - soit une augmentation de 53 % par rapport à l'année dernière mais cette croissance n'est pas suffisante pour garantir que le monde atteigne le zéro net d'ici 2050. [5] Le monde doit installer l'énergie éolienne trois fois plus rapidement au cours de la prochaine décennie afin de rester sur une voie zéro nette et d'éviter les pires impacts du changement climatique. [5]

Grâce aux innovations technologiques et aux économies d'échelle, le marché mondial de l'énergie éolienne a presque quadruplé au cours de la dernière décennie et s'est imposé comme l'une des sources d'énergie les plus rentables et les plus résilientes au monde. En 2020, une croissance record a été tirée par une vague d'installations en Chine et aux États-Unis - les deux plus grands marchés mondiaux de l'énergie éolienne - qui ont installé ensemble près de 75 % des nouvelles installations en 2020 et représentent plus de la moitié de la capacité éolienne totale du monde. [5]

Aujourd'hui, il existe environ 743 GW de capacité éolienne dans le monde, ce qui permet d'éviter plus de 1,1 milliard de tonnes de CO2 dans le monde - soit l'équivalent des émissions annuelles de carbone de l'Amérique du Sud. [5]

Pourtant, comme la technologie de l'énergie propre avec le potentiel de décarbonisation le plus élevé par MW, le taux actuel de déploiement de l'énergie éolienne ne sera pas suffisant pour atteindre la neutralité carbone d'ici le milieu de ce siècle, et des mesures urgentes doivent être prises par les décideurs dès maintenant pour intensifier l'énergie éolienne au rythme nécessaire [5]

En 2020, le marché annuel de l'éolien (onshore et offshore combinés) dans toutes les régions l'Europe, l'Afrique et le Moyen-Orient a enregistrée une augmentation de 32,2 GW annuel provenant du marché de l'éolien terrestre [5] : la Chine 24,6 GW, les États-Unis 7,8 GW, l'Amérique latine 1,0 GW, cependant, l'année 2020 a été une année difficile pour le marché indien de l'éolien terrestre. Outre les défis d'acquisition de terrains, de connexion au raccordement au réseau et l'obtention de permis, la pandémie de COVID-19 a sérieusement touché le marché et a provoqué des retards dans l'exécution des projets de construction. Les nouvelles installations en

8

Chapitre I : État de l'art des systèmes éoliens.

Afrique et au Moyen-Orient ont diminué de 7 MW par rapport à l'année précédente, principalement en raison de la faiblesse relative des installations en Afrique du Nord, notamment en Égypte et au Maroc. Nouvelles installations d'éoliennes en mer ont légèrement diminué par rapport à 2019, ce qui s'explique principalement par la faiblesse de l'activité dans les deux plus grands marchés offshore européens : le Royaume-Uni et l'Allemagne. [5].La figure I-4 montre l'évolution des éoliennes installer dans le monde en Gw entre 2001 et 2020.

Figure I.4-Capacité éolienne installée dans le monde entre 2001 et 2020 en GW [5].

I.5 Composants d'une éolienne

Il existe plusieurs configurations possibles d'éoliennes. Cependant, une éolienne classique se compose généralement de trois éléments principaux : tout d'abord, le mât, qui est un tube d'acier ou un treillis métallique, utilisé pour éviter les perturbations près du sol. Cependant, la quantité de matériel mis en oeuvre représente un coût non négligeable et le poids doit être limité [6]. Il est préférable de prendre un mât d'une taille supérieure ou légèrement supérieur au diamètre du rotor de l'éolienne.

Le deuxième élément d'une éolienne est la nacelle, qui rassemble tous les éléments mécaniques permettant de coupler l'éolienne à un moteur. Le générateur électrique de l'éolienne : le frein le système de régulation électrique et le multiplicateur. Le frein à disque, qui est différent du frein aérodynamique, permet d'arrêter le système en cas de surcharge éventuelle. Le générateur qui est généralement composé d'une machine synchrone ou asynchrone et d'un pilotage

9

Chapitre I : État de l'art des systèmes éoliens.

hydraulique ou électrique des pales (frein aérodynamique) et de la nacelle la figure I.5 représente les composants d'une éolienne. [6]

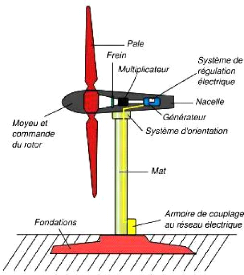
Figure.I.5-Composants d'une éolienne [7].

I.6 Classification des turbine éoliennes

Ils existent deux types de turbine éoliennes :

I.6.1 Éolienne à axe horizontal

Les éoliennes à axe horizontal mesurent environ 10 à 35m de haut et produisent au maximum 36kW contre 2 à 6mW pour les grandes éoliennes selon leurs tailles.

Presque tous les systèmes d'énergie éolienne dans le marchée utilisent des éoliennes de type horizontal. L'axe de rotation est horizontal. Le principal avantage de l'éolienne de type horizontal est que quand on utilise le contrôle du pas des pales, la vitesse du rotor et la puissance de sortie peuvent être contrôlées. [8]

Le contrôle du pas des pales protège également l'éolienne contre la survitesse lorsque la vitesse du vent devient dangereusement élevée. Le principe de base d'une éolienne à axe horizontal est basé sur des concepts similaires à ceux d'une hélice. [8]

10

Chapitre I : État de l'art des systèmes éoliens.

Le développement des hélices améliore largement les performances et le rendement de la production et la qualité de l'énergie électrique. La figure I.6 représente une éolienne à axe horizontal.

Figure I.6-éolienne a axe horizontal [9] .

I.8.2 Eolienne a axe vertical

Les éoliennes à axe vertical sont plus onéreuses que les éoliennes à axe horizontal et de conception plus complexes mais s'adaptent plus facilement à des zones de vent irrégulier. Une éolienne à axe vertical est surtout utile dans les endroits où il n'y a pas beaucoup de place : en ville, sur le toit d'un immeuble par exemple. [10]

Les éoliennes à axe vertical existent en deux type Darrieus (figure I.7) et Savonius (figure I.8) du nom de leurs inventeurs, une éolienne de type Darrieus peut produire jusqu'à 5000kWh/an c'est petite éolienne encore peut répondus peuvent être utilisé pour des petite puissance sur des sites isolée dite off-grid ou en auto consommation.

11

Chapitre I : État de l'art des systèmes éoliens.

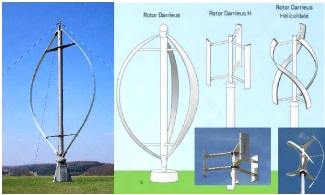
Figure I-7-éoliennes axe vertical de Darius [9].

Elles sont peu encombrantes, et ne nécessitent pas de systèmes d'orientations et sont simples à installer. Par contre, elles ont un faible rendement et ne démarrent pas toutes seules. [10]

Ces dernières ont un rapport de vitesse de pointe très faible et un faible coefficient de puissance, elles ne sont donc utilisées que dans des systèmes d'énergie éolienne de très faible puissance. [8]

Figure I-8. Éoliennes de type Savonius [9].

Le générateur à axe vertical a une conception simple. L'arbre est vertical, de sorte que le générateur est monté sur le sol et la tour n'est nécessaire que pour monter les pales.

12

Chapitre I : État de l'art des systèmes éoliens.

Les inconvénients sont le rapport de vitesse de pointe et la puissance de sortie qui sont très faibles par rapport aux générateurs à axe horizontal. La turbine a besoin d'une poussée initiale pour démarrer ; elle n'est pas auto-démarrante.Il n'est pas non plus possible de contrôler la puissance de sortie en faisant pivoter les pales du rotor. [8]

Ces éoliennes utilisent généralement des batteries pour emmagasinée l'énergie produite un régulateur de charge protèges les batteries de la surcharge dans le cas de l'autoconsommation un convertisseur permet lorsque les batteries son assez chargé de transformer le courant continue des batteries en ça et d'apporté un complément d'énergie pour la consommation personnelle du lieu. Lorsque les batteries son pleines le surplus d'énergie est injecté dans le réseaux électrique.

I.7 Les différents types d'éoliennes

En général, les turbines éoliennes peuvent être divisés en deux types :

I.7.1 Éolienne à vitesse fixe

Eolienne à vitesse fixe génère une vitesse fixe et constante grâce a son système mécanique d'orientation des pales. Cette vitesse est déterminée par le rapport du réducteur, la fréquence du réseau et le nombre de pole de la génératrice. La vitesse de son rotor varie a une dans une plage terminisme de l'ordre de 1a 2% de la vitesse nominal. Étant donné que la vitesse de son rotor ne peut pas varier, le changement aléatoire de la vitesse du vent affecte directement le couple de la chaine cinématique de l'éolienne, entraînant des charges structurelles plus élevées qu'en cas de fonctionnement à vitesse variable.

Une éolienne à vitesse fixe est constituée d'un générateur asynchrone à cage d'écureuil, cette dernière est directement couplée au réseau.

Cependant, les turbines à vitesse constante doivent être plus robustes mécaniquement que les turbines à vitesse variable [11] [8]. La figure I.9 représente la structure d'une éolienne à vitesse fixe directement connecter au réseau.

13

Chapitre I : État de l'art des systèmes éoliens.

Figure I-9 Structure d'une éolienne a vitesse fixe à base de machine asynchrone à cage [12].

I.7.2 Éolienne à vitesse variable

La figure I .10 représente la structure d'une éolienne a vitesse variable connectée au réseau. Les éoliennes à vitesse variable peuvent atteindre une efficacité de conversion et fournir de l'énergie dans une large gamme de vitesses de vent. La turbine change continuellement sa vitesse de rotation en fonction de la vitesse du vent afin de maximiser la puissance produite. Dans ces circonstances la vitesse spécifique ?? représente la vitesse de la pale par rapport à la vitesse du vent, cette dernière peut être maintenu a sa valeur optimale afin d'extraire le maximum d'énergie possible. Afin de rendre la vitesse de la turbine réglable, l'éolienne est raccordée au réseau électrique travers un convertisseur de puissance. [13]

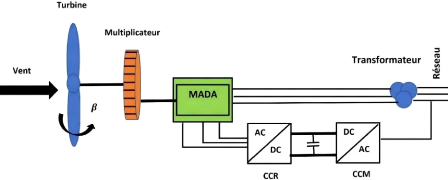
Figure I-10. Structure d'une éolienne a vitesse variable connectée au réseau. [12]

14

Chapitre I : État de l'art des systèmes éoliens.

Le tableau ci-dessous, représente les principaux avantages et inconvénients des turbines à vitesse variable, comparé aux turbines à vitesse fixe.

Tableau I-1. Comparaison entre une éolienne à vitesse fixe et une éolienne à vitesse

variable.

Type d'éolienne		Avantage			Inconvénients	Éolienne à vitesse fixe
·	Simple, robuste, et fiable	·	Rendement en énergie produite faible.
·	Faible cout de construction.	·	Fluctuation aléatoire de la puissance
·	Faible cout de maintenance.		produite.		Éolienne à vitesse variable
·	Rendement élevé en conversion d'énergie.	·	Cout élevé de construction.
·	Puissance électrique de meilleure qualité.	·	Perte en puissance asse importante du au
·	Stresse mécanique		convertisseur.
	réduit.	·	Contrôle du système plus compliqué.

I.8 Quelques notions de conversion de l'énergie éolienne I.8.1 Énergie cinétique du vent - conversion en énergie mécanique

La théorie du disque traversé par une vitesse de vent explique de manière très simple le processus d'extraction de l'énergie cinétique du vent. L'énergie cinétique du vent, basé sur des bilans énergétiques et l'application de l'équation de BERBOULLI. [14]

Le rotor du vent captant l'énergie est vu comme un disque poreux, qui provoque une diminution de la quantité de mouvement du flux d'air, ce qui entraîne un saut de pression dans la face du disque et une déviation des flux en aval (figure 1.11). [14]

15

Chapitre I : État de l'art des systèmes éoliens.

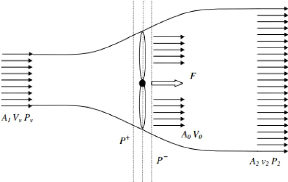
Figure I.11-Schéma de l'écoulement d'un fluide à travers un disque. [14]

La théorie de la quantité de mouvement est utilisée pour étudier le comportement de l'éolienne et pour mettre en place certaines hypothèses, l'air est incompressible, le mouvement du fluide est régulier et que les paramètres étudiés sont fluides est régulier, et les variables étudiées ont la même valeur sur une section donnée du tube de courant d'air.

Le tube de courant d'air la puissance contenue sous forme d'énergie cinétique dans le vent traversant à une vitesse ???? la surface A₁, est exprimée par l'équation I.1 : [14]

?? (I.1)

???? = 2 A₁ ????³

Avec :

?? :la densité de l'aire. ?? 1,2????/??^3.

L'éolienne ne peut récupérer qu'une partie de cette puissance, cette puissance est exprimé par l'équation I.2:

?? (I.2)

???? = C?? 2 R2 ??????

Avec :

R: Le rayon des pales de l'éolienne. C??: Le coefficient de puissance.

16

Chapitre I : État de l'art des systèmes éoliens.

?? ?? : Exprime l'efficacité de l'éolienne dans la transformation de l'énergie cinétique du vent en énergie mécanique. Le coefficient est exprimé en fonction de la vitesse du vent, de la vitesse de rotation de l'éolienne, de la vitesse de rotation du rotor, de l'angle d'inclinaison ?? [14].

?? ?? est souvent donné en fonction du rapport de vitesse de pointe ?? qui est définit par :

?? Ù?? ?? = ????

(I.3)

La valeur maximale théorique de ?? ?? est définit par la loi de BETZ:

?? ???????? =

16 27

(I.4) = 59.3% = 0.593

Le couple rotorique est obtenu à partir de la puissance générée et de la vitesse de rotation de la turbine :

???? ???? = Ù??

??????^2????^3 ??????^3????^2 ??????^3????^2 = ???? = 2?? ???? = 2 ???? ^2Ù??

(I.5)

Où ???? est le coefficient du couple. Le coefficient de puissance ?? ?? ,et le couple sont liés par l'équation I.6:

?? ??(??) = ??????(??) (I.6)

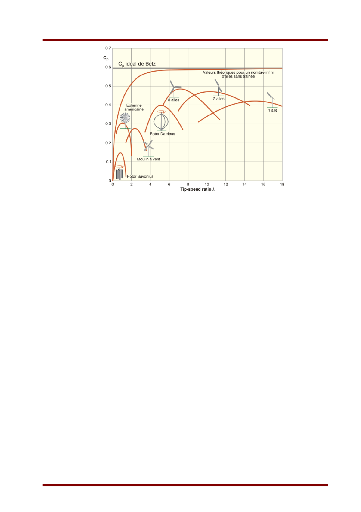
Les éoliennes à marche lente sont munies d'un grand nombre de pales (entre 20 et 40), leur inertie importante impose en général une limitation du diamètre à environ 8 m. Leur coefficient de puissance représentée dans la figure I.12, atteint rapidement sa valeur maximale lors de la montée en vitesse mais décroît également rapidement par la suite. Les éoliennes à marche rapide sont beaucoup plus répandues et pratiquement toutes dédiées à la production d'énergie électrique elles possèdent généralement entre 1 et 3 pales fixes ou orientables pour contrôler la vitesse de rotation. Les pales peuvent atteindre des longueurs de 60 m pour des éoliennes de plusieurs mégawatts. [1]

Les éoliennes tripales sont les plus utilisées car elles représentent un inconvénient entre les vibrations causées par la rotation et le coût de l'éolienne. De plus, leurs coefficients de puissance comme le montre la figure 1-12 atteint une valeur plus élevée et diminue lentement quand la vitesse augmente. Ils fonctionnent à une vitesse du vent plus élevée que 3 m / s.

17

Chapitre I : État de l'art des systèmes éoliens.

Figure I.12-Évolution typique du rendement aérodynamique en fonction de la vitesse relative X et du modèle d'éolienne [15]

I.8.2 Conversion de l'énergie cinétique du vent en énergie électrique

Le principe de conversion de l'énergie cinétique en énergie électrique est représenté sur la figureI.13.

Au niveau de la nacelle le mouvement du rotor est transmis à l'arbre long, la vitesse de rotation de l'arbre long est augmentée par le multiplicateur c'est la boite de vitesse de l'éolienne, le générateur fonctionne sur le principe de la dynamo il convertit l'énergie cinétique en énergie électrique.

Le freint permet de stopper le mouvement du rotateur il est utilisé qu'en cas d'urgence, sur le toit se trouve les capteurs pour le pilotage de l'éoliennes.

Les grandes éoliennes à axe horizontal regroupée dans un parc éolien. Son hauteur est d'une centaine de mettre pour un diamètre d'environ 50m. Les plus grandes qui sont les plus puissante peuvent dépasser 120m de diamètre, la hauteur du mat est primordiale pour capter le vent et optimisé la production de l'énergie électrique. Le rotor et le stator se trouve dans la nacelle située en haut du mat qui est orientable pour suive la direction du vent. L'électricité produite est acheminée par câble jusqu' au transformateur situé en bas du mat qui permet d'augmenter la tension de sortie. L'éolienne peut ainsi injecter dans le réseau électrique un courant alternatif en

18

Chapitre I : État de l'art des systèmes éoliens.

20 000V dans le domaine de haute tension. L'électricité est convertie en basse tension à travers des postes de basse tension.

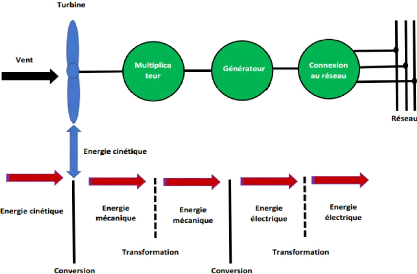
Figure I.13-Chaine de conversion d'une éolienne [16].

I.8.3 Les différentes topologies d'alimentation de la MADA

I.8.3.1 MADA à énergie rotorique dissipé

Cette configuration à vitesse variable est représentée par la (figure I.14), le stator est relié directement au réseau, alors que le rotor est connecté au redresseur. Une charge résistive est reliée au redresseur à travers d'un hacheur à IGBT ou GTO. Afin de fonctionner en vitesse variable tout en restant dans la partie stable de la caractéristique couple/vitesse de la machine asynchrone à double alimentation et varier l'énergie dissipé ; le contrôle de l'IGBT est primordial. [17].

19

Chapitre I : État de l'art des systèmes éoliens.

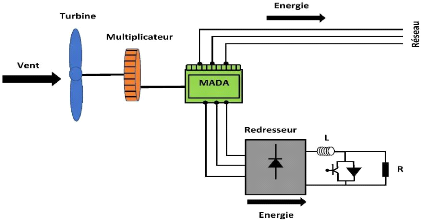
Figure I.14-MADA avec contrôle du glissement par l'énergie dissipée [18].

I.8.3.2 MADA structure de Kramer

Afin de minimiser les pertes d'énergie dues à la configuration précédente, le hacheur et la charge résistive sont remplacés par un onduleur qui renvoie l'énergie de glissement vers le réseau comme le montre la figure I.15.

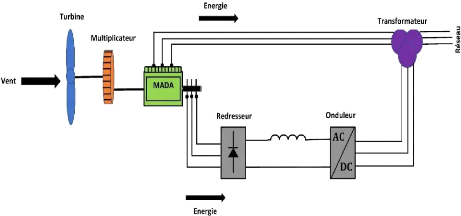
Figure I.15-Structure de Kramer [18].

L'association du redresseur et de l'onduleur son dimensionné en fonction de la puissance nominale de la machine, cette configuration peut être avantageuse que si la taille des convertisseurs peut être réduite para port à la puissance nominale de la machine. Les thyristors utilisé dans

20

Chapitre I : État de l'art des systèmes éoliens.

l'onduleur nuit au facteur de puissance. Le redresseur permet uniquement de transférer l'énergie du rotor de la machine vers le réseau, cela rend le système non producteur d'énergie que si la vitesse de rotation est supérieure au synchronisme. Dans cette configuration le glissement est maintenu inférieur à 30% [1].

I.8.3.3 MADA structure de Scherbius avec cyclo convertisseur

Afin de permettre un échange de flux d'énergie bidirectionnel entre le rotor et le réseau, la combinaison entre le redresseur et onduleur peut être remplacée par un cyclo convertisseur (figure 1-16), cette architecture est appelée structure de Scherbius [1].

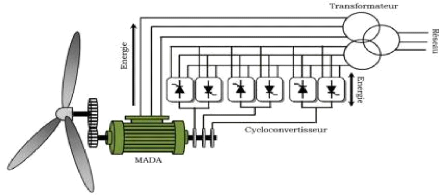
Figure I.16-Structure de Scherbius avec cyclo convertisseur. [18]

Afin de maintenir un fonctionnement optimal du système, les variations du glissement doivent être inférieures à 30%, si ces variations son positives alors le système va fonctionner en mode hypo synchrone et si ces variations son négative alors le système vas fonctionner en mode hyper synchrone [18].

Le principe du cyclo convertisseur est de prendre des fractions des tensions sinusoïdales du réseau afin de reproduire une onde de fréquence inférieure génère par conséquent des perturbations harmoniques importantes qui nuisent au facteur de puissance du dispositif [1]. Les progrès de l'électronique de puissance ont conduit au remplacement du cyclo convertisseur par une structure à deux convertisseurs à IGBT commandés en MLI [1] .

I.8.3.4 MADA structure de Scherbius avec convertisseur MLI

Cette structure est représentée dans la figure I.17 elle a les mêmes caractéristiques que la structure de Scherbius avec cyclo convertisseur. Contrairement à la structure citée précédemment

21

Chapitre I : État de l'art des systèmes éoliens.

cette structure utilise deux ponts triphasés d'IGBT commandables à l'ouverture et à la fermeture et leur fréquence de commutation est plus élevée que celle des GTO [17].

Le gain se répercute sur des perturbations moins importantes (rejet des premiers harmoniques non nuls vers les fréquences élevées par la commande MLI grâce à la commandabilité du convertisseur rotorique la MADA peut fonctionner en mode hypo et hyper synchrone le contrôle du facteur de puissances pourras être établie. [17]

Figure I.17-Structure de Scherbius avec convertisseurs MLI. [18]

I.9 Avantages et inconvénients des systèmes d'énergie éolienne :

L'énergie éolienne offre de nombreux avantages, ce qui explique pourquoi elle est la source d'énergie qui connaît la plus forte croissance dans le monde. Les efforts de recherche visent à relever les défit pour accroître l'utilisation de l'énergie éolienne.

I.9.1 Avantages :

Les systèmes d'énergie éolienne sont alimentés en énergie par le vent qui circule naturellement, peut être considérée comme une source d'énergie propre. L'énergie éolienne ne pollue pas l'air comme les centrales électriques qui utilisent des combustibles fossiles, tels que le charbon ou le gaz naturel. Les éoliennes ne produisent pas d'émissions atmosphériques à l'origine des pluies acides ou des gaz à effet de serre.

L'énergie éolienne est disponible en tant que source d'énergie domestique dans le monde entier et n'est pas limitée à quelques pays seulement, comme c'est le cas pour le pétrole.

22

Chapitre I : État de l'art des systèmes éoliens.

L'énergie éolienne est l'une des technologies d'énergie renouvelable les moins chères disponibles aujourd'hui.

Les éoliennes peuvent également être construites sur des fermes ou des ranchs, ce qui profite à l'économie dans les zones rurales, où se trouvent la plupart des meilleurs sites éoliens. Les agriculteurs et les éleveurs peuvent continuer à utiliser leurs terres car les éoliennes n'utilisent qu'une petite fraction du terrain [19].

I.9.2 Inconvénients :

L'énergie éolienne doit concurrencer les sources de production d'énergie conventionnelles sur la base des coûts. Selon le profil du vent sur le site, le parc éolien peut être ou non être aussi compétitif qu'une centrale à combustible fossile. Même si le coût de l'énergie éolienne a diminué au cours des 10 dernières années, cette technologie nécessite un investissement initial plus élevé que les centrales à combustible fossile.

Le défi majeur de l'utilisation du vent comme source d'énergie est que le vent est intermittent et qu'il ne souffle pas toujours selon les besoins en électricité. L'énergie éolienne ne peut pas être stockée et tous les vents ne peuvent pas être exploités pour répondre à la demande d'électricité.

L'option de stockage de l'énergie dans des batteries est au-delà des limites de la faisabilité économique pour les grandes éoliennes.

Les bons sites d'éoliennes sont souvent situés dans des endroits éloignés, loin des villes où l'électricité est nécessaire. Dans les pays en voie de développement, il y a toujours le coût supplémentaire pour connecter les parcs éoliens éloignés au réseau d'approvisionnement.

Le développement des ressources éoliennes peut entrer en concurrence avec d'autres utilisations des terres et ces autres utilisations peuvent être plus valorisées que la production d'électricité.

Bien que les centrales éoliennes aient un impact relativement faible sur l'environnement par rapport à d'autres centrales électriques conventionnelles, le bruit produit par les pales du rotor et les impacts esthétiques (visuels). La plupart de ces problèmes ont été résolus ou considérablement réduits grâce au développement technologique ou en plaçant correctement les centrales éoliennes [19]

23

Chapitre I : État de l'art des systèmes éoliens.

I.10 Conclusion

Ce chapitre a été consacré à la description de l'énergie éolienne dans son état général, nous avons cités l'origine de l'énergie éolienne, ses principaux composants ainsi que les type d'éolienne qui existe dans le monde. On a aussi abordé quelques notions de conversion de l'énergie cinétique et le contrôle de la vitesse des éoliennes.

Afin de mieux comprendre le processus de conversion de l'énergie éolienne et d'analyser cette conversion, le chapitre suivant est consacré à la modélisation des différents éléments qui compose la chaine de conversion de l'énergie éolienne.

24

Chapitre II : Modélisation et

commande de l'éolienne

25

Chapitre II : Modélisation et commande de l'éolienne

II.1 Introduction

Afin de bénéficier et de mieux profité des avantages de l'énergie éolienne en termes d'énergie propre et inépuisable, l'énergie cinétique du vent doit être convertie en énergie électrique et pour cela toute une chaine de conversion est mise à disposition.

Cette chaine de conversion est composée de plusieurs éléments importants comme la turbine éolienne, le générateurs et les convertisseurs de l'électronique de puissance.

Pour que cette chaine de conversion soit parfaitement fonctionnelle et contrôlée, la modélisation des éléments constituants cette dernière est primordiale. Dans le cadre de nos travaux, nous avons choisi d'étudier une éolienne à vitesse variable.

Ainsi, dans ce deuxième chapitre nous allons en premier temps, nous intéresser à la modélisation de la partie mécanique de la chaine de conversion de l'éolienne qui est la turbine et ses composant, ensuite nous allons présenter la stratégie de commande de l'éolienne. A la fin de ce chapitre, les résultats de simulation et une conclusion seront présentés.

II.2 Modélisation du vent

Le vent est l'élément essentiel pour faire fonctionner une éolienne, c'est pour cela qu'il est primordial de connaitre son modèle mathématique. La vitesse du vent est une fonction scalaire qui évolue dans le temps V = ??(??) La définition du modèle nécessite des données géographiques et climatiques du site concerné, ainsi que la période de la saison concernée par l'étude. Généralement le modèle du vent est exprimé par une équation en série de Fourier qui le présente comme un signal constitué par une superposition de plusieurs harmoniques, il est donné par l'équation suivante : [20].

?? V??(??) = A + ? ??????i??(??????) ??=1 Avec : A : la valeur moyenne de la vitesse du vent. ???? : amplitude de l'harmonique de l'ordre k. ???? : pulsation de l'harmonique de l'ordre k. i : le rang du dernier harmonique retenu dans le calcul du profil du vent. 26

(II.1)

Chapitre II : Modélisation et commande de l'éolienne

II.3 Modélisation de la turbine

La figure II.1 représente le schéma global d'une turbine éolienne.

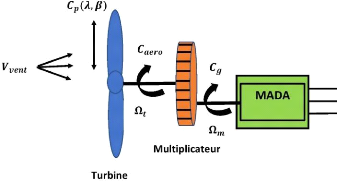
Figure II-1. Structure d'une turbine éolienne.

Similaire aux ailes d'avions, la forme aérodynamique des pales modifie la vitesse du vent sur l'extrados et l'intrados des pales. La différence de vitesse produit une différence de pression, donc une force portante est générée.

La puissance du vent est donnée par l'équation II.2

????=

1 2 ?? S ?????????? 3

(II.2)

Avec :

??: est la densité de l'air en ????/??³ (au niveau de la mer et à 20C° :?? = 1.225????/??³). ????: Est le coefficient de puissance de la turbine.

S : la surface circulaire balayée par la turbine.

?????????? :la vitesse du vent.

La puissance aérodynamique captée par une turbine est donnée par :

27

Chapitre II : Modélisation et commande de l'éolienne

?????????? =

1 2 ?? ???? S ?????????? 3

(II.3)

Avec :

????: Le coefficient de puissance de la turbine.

????(??, ??) 1	116 =	0.4	??	-	5)??	-21		(II.4) (II.5)
0.08?? ??^3 + 1

Avec :

?? : Angle d'inclinaison des pales. ?? : Ratio de la vitesse.

La figure II.2 représente la variation du paramètre ???? en fonction du ratio de vitesse ?? et de l'angle de l'orientation de pale ??.

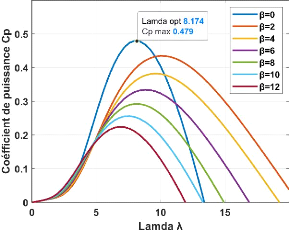
Figure II.2-Coefficient de puissance et vitesse relative pour différents angles de calages.

D'après la figure II.2 obtenu on remarque que quand l'angle d'orientation de pale ?? augmente, le coefficient de puissance ?? ?? diminue, la valeur maximale de ?? ?? d'après la figure

28

Chapitre II : Modélisation et commande de l'éolienne

obtenue est de ????_?????? = 0.48 ,cette valeur correspond à un angle d'orientation de pale égale à ?? = 0 et une valeur optimale de la vitesse ???????????? = 8.1 .

Afin de maintenir ë à sa valeur nominale ou optimale, et donc maximiser la puissance de la turbine éolienne, il est donc impérativement important de varier la vitesse de rotation ???? de manière linéaire avec la vitesse du vent. L'équation (I.3) deviens alors :

???????? =

?? .?????????? ??????????

(II.6)

Avec :

R : rayon des pales.

Le couple aérodynamique est exprimé en fonction de la puissance aérodynamique et la vitesse de rotation de la turbine comme le montre l'équation I.7:

???????? ???????? = ????????

1 (II.7) 2 ?????? ?? ??^2 ?????????? 3 1 ????????

II.4 Modélisation du multiplicateur

Le multiplicateur est représentée sur la figure II-3 est l'élément qui se situe entre la turbine et le générateur. Sa fonctionnalité est le réglage de la vitesse de la turbine ???? qui est lente à la même vitesse de la génératrice ???? .

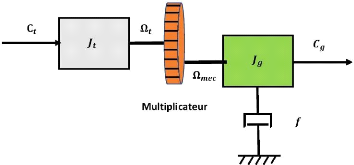
Figure II-3. Modèle d'un multiplicateur [21]

29

Chapitre II : Modélisation et commande de l'éolienne

Le multiplicateur est représentée sur la figure II-3 est l'élément qui se situe entre la turbine et le générateur. Sa fonctionnalité est le réglage de la vitesse de la turbine ???? qui est lente à la même vitesse de la génératrice ???? .

En négligeant les pertes mécaniques sont négligeables, le multiplicateur peut être modélisé mathématiquement par l'équation suivante :

???????? = ??. ???? Avec : ?? : gain du multiplicateur.

(II.8)

II.5 Modélisation de l'arbre mécanique

L'arbre mécanique est composé d'une masse correspondant à l'inertie du rotor de la
turbine la figure II.5 représente modèle de transmission mécanique ramenée à l'arbre mécanique.

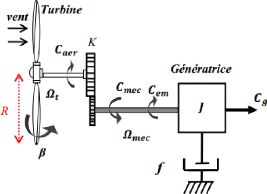
Figure II-4. Modèle de transmission mécanique ramenée à l'arbre Mécanique [22]

Dans le modèle mécanique proposé dans la figure II .4, l'inertie totale ?? est celle du générateur ???? et l'inertie de la turbine ???? ramenée sur l'arbre rapide (au rotor du générateur) où : [22]

??= ????+ ???? ??² (II.9)

Le couple mécanique appliqué au rotor de la génératrice est exprimée par :

30

	Chapitre II : Modélisation et commande de l'éolienne				???????? ???????? ???? -
???? ??????	???????? + ??????????		(II.10) (II.11) (II.12)

Avec :

???????? : La vitesse mécanique.

???????? : Le couple mécanique appliqué au rotor de la génératrice.

???????? : Le couple de frottement visqueux.

???? : Le couple du multiplicateur de vitesse.

?? : Coefficient de frottement visqueux.

?? : Inertie totale.

La figure II.5 représente Le schéma bloc correspondant à la modélisation de la turbine modélisée.

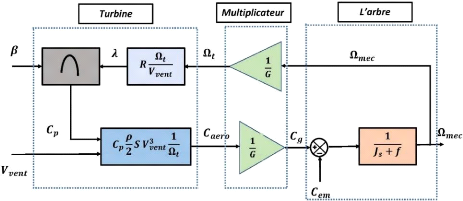
Figure II-5. Schéma bloc de la turbine modélisée. [2]

II.6 Stratégie de commande de l'éolienne

Le contrôle de l'éolienne se fait à travers deux boucles de régulation ; boucle de régulation de la vitesse et la boucle de régulation de la puissance.

31

Chapitre II : Modélisation et commande de l'éolienne

A travers la boucle de régulation de la vitesse la vitesse de rotation est contrôlée par le couple électromagnétique, cette boucle de régulations est la boucle principale dans la stratégie de d'optimisation de puissance. La vitesse de rotation est ajustée dans cette boucle afin d'extraire le maximum de la puissance du vent quand la vitesse du vent va dépasser la vitesse nominale et l'angle de calage vas être maintenue constant a une valeur optimale ????????.

La boucle de régulation de vitesse réagit instantanément en adaptant la puissance de référence de la génératrice en agissant sur le dispositif d'orientation des pales afin de contrôlée le couple électromagnétique et la vitesse de rotation. Cette action est enclenché que quand la vitesse de rotation va augmenter rapidement suite à des rafales de vent et peut dépasser la vitesse de rotation des pales.

II.6.1 Systèmes de régulation de la vitesse de rotation de l'éolienne

II.6.1.1 Système à décrochage aérodynamique "Stall"

Ce système de régulation est représenté par la figure II-6, il est simple et relativement fiable mais il manque de précision car il dépend de la masse volumique de l'air et de la rugosité des pales donc de leur état de propreté. Il peut dans certains cas, être amélioré en autorisant une légère rotation de la pale sur elle-même (système "Stall actif") permettant ainsi de maximiser l'énergie captée pour les faibles vitesses de vent. Pour les fortes vitesses de vent, la pale est inclinée de façon à diminuer l'angle de calage â et renforcer ainsi l'effet "stall" de la pale. La répercussion des variations de vitesse de vent sur le couple mécanique fournie par l'éolienne est ainsi moins importante [23].

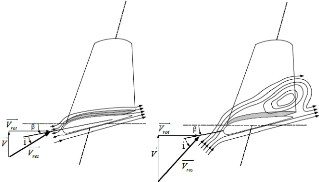
Figure II-6. Flux d'air sur un profil de pale " Stall " [23]

32

Chapitre II : Modélisation et commande de l'éolienne

II.6.1.2 Système d'orientation des pales "Pitch"

Le système d'orientation des pales agit sur la portance des pales pour garder la puissance autour de sa valeur nominale [24]. En réglant l'angle de calage, on agit sur les performances de l'éolienne et plus précisément sur le coefficient de puissance.

Le système d'orientation des pales génère alors un angle de calage de référence : ????????. La dynamique de l'actionneur pitch est généralement décrite par la fonction de transfert de premier ordre suivante [25].

1 ?? = 1 + ?????? ???????? Avec :

(II.13)

ô??: Constante du temps du système actionneur pitch. ?? : Angle de calage des pales.

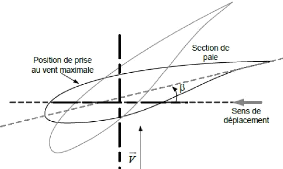
Figure II-7. Variation de l'angle de calage d'une pale [23]

Lors de la modélisation du système d'orientation des pales, il est essentiel de modéliser la vitesse de variation de cet angle [24]. En effet, compte tenu des efforts subis par les pales, la variation de l'angle de calage doit être limitée à 10%. La valeur de saturation de l'angle de calage en position est de 90°, cette valeur correspond à la mise en drapeau des pales [24].

L'agitation sur l'angle de calage des pales entraine la modification des performances du système, et plus précisément sur le coefficient de puissance ????, les pales sont face au vent pour les basses vitesses (?? = 0°), pour des vitesses plus importantes du vent les pales s'inclinent afin de dégrader le coefficient de puissance ???? [2].

33

Chapitre II : Modélisation et commande de l'éolienne

II.7 Zone de fonctionnement de l'éolien :

Les éoliennes fonctionnent dans une plage de vent très variables. Une vitesse de vent spécifique est nécessaire afin que les pales de l'éolienne puissant surmonté l'inertie et la friction. On appel cette vitesse la vitesse du vent de démarrage ???? ,la vitesse du vent est évaluée en moyenne de 3 à 5 m/s afin d'éviter d'endommager les pales de l'éolienne, il est recommandé d'utiliser une vitesse d'entrée de 25 m/s [8].

Les différentes zones de fonctionnement d'une éolienne sont illustrées à travers la figure II.8, on distingue quatre zones de fonctionnement :

Zone I : :la puissance captée est très faible à cause de la faible vitesse du vent.

Zone II : dans cette zone la vitesse du vent est supérieure à la vitesse de seuil et inférieure à la vitesse nominale de l'éolienne. Dans cette partie qui est caractérisée par une puissance proportionnelle au cube de la vitesse du vent, l'angle de calage est maintenu constant, et c'est le contrôle du couple électromagnétique de la génératrice qui va être mis en oeuvre (principe de MPPT). Ceci se fait en gardant le coefficient de puissance ???? = ?????????? de manière à tirer le maximum de profit de la vitesse du vent et généré le maximum d'énergie électrique possible. Dans cette zone, la courbe de puissance de la génératrice suit une progression rapide [8].

Zone III : Dans cette zone la vitesse de vent est supérieure à la vitesse nominale et inférieure à la vitesse maximale de déclenchement, le coefficient de puissance ?? ?? doit être contrôlé. L'augmentation de la vitesse de vent va s'accompagner d'une diminution du coefficient ?? ?? et d'une augmentation moins rapide de la puissance récupérée. Lorsque la puissance maximum de la génératrice est atteinte, l'angle des pales (pitch) est modifié afin de dégrader encore plus le coefficient Cp. [8, 26]

Zone IV : la vitesse de vent devient trop forte et dans laquelle le système de sûreté du fonctionnement arrête la rotation et le transfert de l'énergie afin d'éviter tout disfonctionnement ou dégât [8] .

34

Chapitre II : Modélisation et commande de l'éolienne

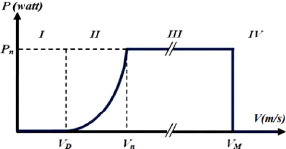
Figure II-8. Courbe de la puissance éolienne en fonction de la vitesse du vent [8]

II.8 Principe de contrôle MPPT (Maximum Power Point Tracking)

Le système de contrôle le plus répandu des éoliennes traditionnelles directement connectées au réseau électrique de distribution, est basé principalement sur la technique d'extraction du maximum de puissance (MPPT) et ce sans supervision centralisée. [18]

Le principe de la stratégie MPPT consiste à contrôler la vitesse de rotation de la turbine éolienne en fonction de la vitesse du vent, en fonction de la vitesse du vent de rotation de la turbine éolienne est maintenue à une valeur de référence pour maintenir une vitesse relative optimale et donc un coefficient de puissance maximal Cpmax [18].

Lorsqu'un problème technique ou la présence d'éventuel défaut sur la commande MPPT, un dispositif déconnecte immédiatement l'éoliennes du réseau electrique.la commande MPPT ne peut en aucun cas intervenir au contrôle de la production de la puissance en temps réel.On distingue deux types de commande :

· Le contrôle MPPT sans asservissement de la vitesse mécanique.

· Le contrôle MPPT avec asservissement de la vitesse mécanique.

II.8.1 Maximisation de la puissance sans asservissement de vitesse :

Ce mode de contrôle repose sur l'hypothèse que la vitesse du vent varie très peu en régime permanent devant les constantes de temps électriques du système éolien [27], ce qui implique que le couple d'accélération de la turbine peut être considéré comme nul.

C

't l dfl_m (II.18)
G2 + 'm) _dt + Îvflm = C_m - Cem = 0 35

Chapitre II : Modélisation et commande de l'éolienne

La figure II.9 représente le schéma bloc de la maximisation de la puissance sans asservissement de la vitesse mécanique.

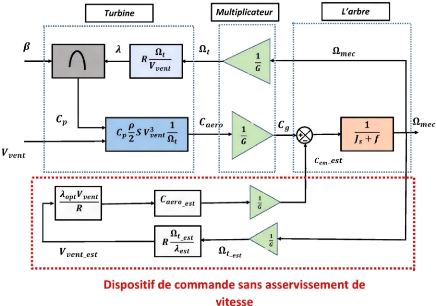
Figure II.9- Schéma bloc de la maximisation de la puissance sans asservissement de la

vitesse mécanique. [28]

Une estimation de la vitesse de rotation de la turbine, notée ???-??????, est obtenue à partir de la mesure de la vitesse de rotation de la MADA et donné par l'équation II.19 :

??? ???_?????? = ??

(II.19)

Le couple de la turbine éolienne peut ensuite être obtenu à partir des estimations de la vitesse du vent et de la vitesse de rotation de la turbine. Il peut s'exprimer par :

??. ?? 1 (II.20)

????_?????? = ????. 2 . ???_?????? - ?????????? _??????

3

Le couple électromagnétique de référence est alors obtenu à partir de l'estimation du couple de la turbine éolienne :

???* ??? =	????_??????		(II.21)

36

Chapitre II : Modélisation et commande de l'éolienne

Afin d'extraire le maximum de puissance, il faut fixer la vitesse relative à sa valeur optimale Aopt afin d'obtenir le coefficient de puissance maximum Cpmax le couple électromagnétique de référence s'exprime donc par l'équation II.22 :

Ce^*?m = K. SZm²? (II.22)

Où K est une constante définie par :

K=	CPmaxp7TR^5		(II.23)

II.8.2 Maximisation de la puissance avec asservissement de la vitesse

Le vent est une grandeur stochastique, de nature très fluctuante. Cette fluctuation engendre des perturbations dans le système de conversion éolien, et crée des variations continues de puissance. De cet effet, il est supposé que le couple électromagnétique développé par la machine soit égal à sa valeur de référence quel que soit la puissance générée [20].

Le couple électromagnétique Cem produit par la MADA est donc à tout instant égal à sa valeur de référence Cem * imposée par la stratégie de commande [21].

Cem = C_em-ref (II.14)

Cem-rref = Cass (
·aref -
·amec) (II.15)

Avec :

Cass : régulateur de vitesse

S¹re f : vitesse mécanique de référence

La vitesse mécanique de référence dépend de la vitesse de la turbine afin de maximiser la puissance extraite. La vitesse mécanique de référence est exprimée par l'équation suivante :

· aref = G.
·atur_-ref (II.16)
Avec :

G : gain du multiplicateur.

37

Chapitre II : Modélisation et commande de l'éolienne

La référence de la vitesse de la turbine correspond à la valeur optimale du ratio de vitesse Aopt permettant d'obtenir la valeur maximale du coefficient de puissance C_p. On peut déduire [20]:

ftur-ref =

ACpmax. event R

(II.17)

La figure II.10 représente le schéma bloc de la maximisation de la puissance avec asservissement de la vitesse mécanique.

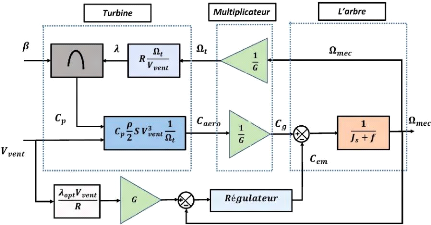
Figure II-10. Schéma bloc de la maximisation de la puissance avec asservissement de la vitesse mécanique [28]

· Synthèse du régulateur PI

Un correcteur PI a été choisie afin de réguler notre système, ce correcteur a pour fonction de transfert : kpu, + ^kP .

On peut exprimer la fonction de transfert qui lie la vitesse aux couples électromagnétique et au couple mécanique à partir de l'équation de la mécanique régissant la dynamique des corps en rotation par :

Ù = C??m - Cm		1			(II.18)

38

Chapitre II : Modélisation et commande de l'éolienne

La figure II.11 représente le schéma bloc de la régulation de vitesse :

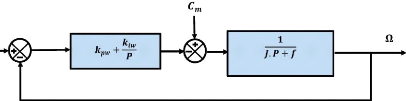
Figure-II.11- Schéma bloc de la régulation de vitesse avec régulateur PI.

On peut exprimer la fonction de transfert du système en boucle ouverte par l'équation suivante :

?????? =

Ù = Ù*

??????. ?? + ?????? ??.??^2 + ??. ??

(II.19)

La fonction de transfert de la vitesse en boucle fermée est donnée par :

?????? =	??????. ?? + ?????? ??		(II.20)

Cette fonction de transfert est de la dynamique du deuxième ordre, sa forme canonique est donnée

par :

??(??) = ??² + 2??. ?????? + ????²

2. ??. ?????? + ???? 2 (II.21)

Avec :

?? : le coefficient d'amortissement.

???? : la pulsation propre.

Après identification de l'équation II.20 avec l'équation II.21 on obtiens :

2 ?? ????=

?????? + ?? ??

(II.22)

??????

??

???? 2 =

D'après l'équation II.22 les paramètres du régulateur PI auront pour expression :

39

Chapitre II : Modélisation et commande de l'éolienne

{

?????? = 2 ?? ???? ?? - f (II.23)
?????? = ?? ???? 2

II.9 Résultat de simulation

La figure II.12 représente le profil du vent appliqué à travers notre étude. Ce dernier est caractérisé par l'équation suivante :

?????????? = 8.5 + 0.2 sin(0.1047t) + 2 sin(0.2665t) + sin(1.2930t) + 0.2sin (3.6645t)

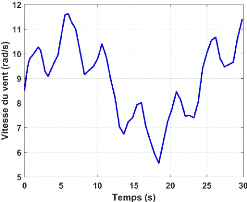
Figure II.12- Profil du vent appliqué.

Dans cette section de chapitre la simulation de la partie mécanique de la chaine de production ; l'aérogénérateur avec s'est différente commande MPPT avec et sans asservissement de la vitesse mécanique qui on était citée dans les paragraphes précèdent vont être simuler afin d'analyser la meilleure commande MPPT possible, les simulations on était réalisé sans raccordée l'éolienne à la génératrice.

Les deux simulations on était effectuée sous le logiciel MATLAB/Simulink en considérant les paramètres suivants :

Tableau II-13. Paramètre nominal de la simulation de la partie mécanique.

Angle de calage ??		0	Ratio de vitesse A??????
8.1		Coefficient de puissance maximal ????_??????.
0.48		Vitesse moyenne du vent
8.5m/s

40

Chapitre II : Modélisation et commande de l'éolienne

Les paramètres de la turbine éolienne utilisée dans ce travail et sa structure implémenté sous MATLAB/Simulink sont représenté dans l'annexe A et l'annexe B respectivement.

II.9.1 Résultats de simulation de la turbine avec asservissement de la vitesse mécanique

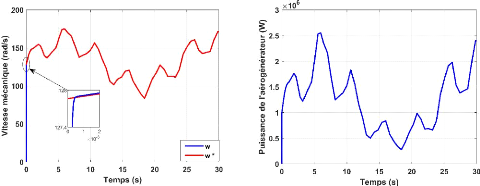
Figure II.13. (a)-Vitesse de rotation mécanique. Figure II.13. (b)-Puissance de l'aérogénérateur

produite.

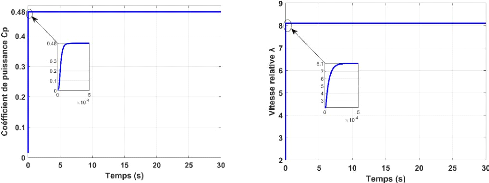
Figure II.13. (c)-Coefficient de puissance C??. Figure II.13. (d)-Vitesse relative A.

41

Chapitre II : Modélisation et commande de l'éolienne

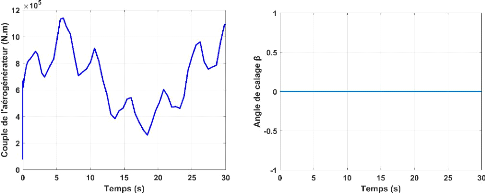
Figure II.13. (e)-Couple électromagnétique de Figure II.13. (f)-Angle de calage ??.

l'aérogénérateur.

Figure II.13-Resultat de simulation de la commande MPPT avec un asservissement de la vitesse

mécanique.

· Interprétation des résultats

Les résultats de la simulation de la méthode de contrôle MPPT avec un asservissement de vitesse mécanique à l'aide d'un régulateur PI son représenté par la figure II .13.

Les figure II.13.b. et II.13.e. illustre respectivement la puissance de l'aérogénérateur et le couple de l'aérogénérateur. D'après la figure II.12. On constate une nette influence de la variation de la vitesse du vent sur le couple et la puissance généré par l'aérogénérateur. Cette influence varie proportionnellement à la vitesse de variation du vent

Le coefficient de puissance C ?? et la vitesse relative évolue jusqu'à ce qu'il atteigne leurs valeurs maximales de C ?? = 0.48 et ???????? = 8.1 sans dépassement pour un angle de calage â=0° comme le montre les figures II.13c et II13d respectivement.

La vitesse de rotation mécanique (figure.II.13.a) varie au cube de la vitesse de variation du vent et suit parfaitement sa consigne imposée ceci est dû au contrôle du régulateur PI.

II.9.2 Résultats de simulation de la turbine sans asservissement de la vitesse mécanique

42

Chapitre II : Modélisation et commande de l'éolienne

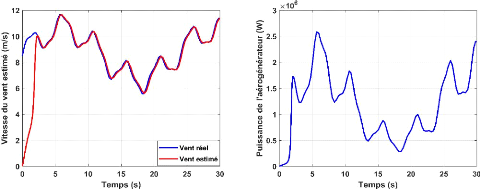
Figure II.14. (a)-Vitesse du vent estimée et Figure II.14. (b)-Puissance de l'aérogénérateur

mesuré. produite.

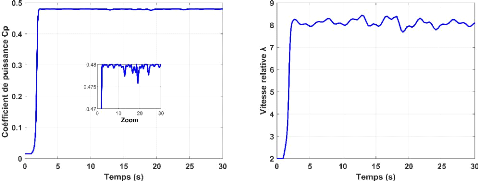
Figure II.14. (c)-Coefficient de puissance C??. Figure II.14. (d)-Vitesse relative A.

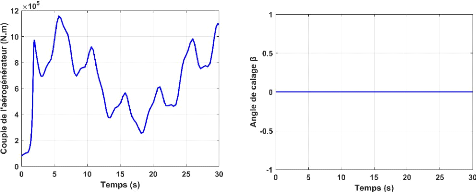
Figure II.14. (e)-Couple électromagnétique Figure II.14. (f)-Angle de calage ??.

43

Chapitre II : Modélisation et commande de l'éolienne

Figure II.14-Resultat de simulation de la commande MPPT sans un asservissement de la vitesse

mécanique.

· Interprétation des résultats

Les résultats de la simulation de la méthode de contrôle MPPT sans un asservissement de vitesse mécanique sont représenté sur la figure II .14.

La puissance et le couple aérodynamique illustré respectivement dans Les figure II.14.b. et II.13.e, varient proportionnellement avec la variation du profil du vent (figure II.12). Le coefficient de puissance C ?? et la vitesse relative évolue jusqu'à ce qu'il atteigne leurs valeurs maximales de C?? = 0.48 et ???????? = 8.1 pour un angle de calage ?? = 0° avec un temps de réponse au démarrage comme le montre les figures II.13.c, II.13.d et II.13.f..

La vitesse du vent mesuré suit la vitesse du vent estimé avec une erreur statique importante en régime permanant comme la montre la Figure II.14.a, ceci est dû à l'absence du contrôle du régulateur PI.

II.10 Conclusion

Dans ce chapitre, nous avons tout d'abord procédé à la modélisation de la turbine éolienne a vitesse variable basée sur une machine asynchrone a double alimentation (MADA), de la modélisation du vent jusqu'au multiplicateur.

En premier temps, nous avons présenté dans ce chapitre les différents modes de régulation de vitesse de rotations de l'éolienne, les zone de fonctionnement d'une turbine éoliennes a vitesse variable ont également été présentée dans cette partie de chapitre.

En deuxième temps nous avons présentée l'algorithme de maximisation de puissance MPPT , utilisé dans le système éolien étudié, à l'aide d'un asservissement de vitesse contrôlé par un régulateur de type PI (proportionnel intégral), dont les paramètres sont calculés par la méthode analytique.

En fin, la simulation et la présentation des résultats obtenue d'un asservissement avec contrôle de la vitesse on était présentée.

Le chapitre suivant est consacré à la présentation et la modélisation de la partie électrique de la chaine de conversion d'une éolienne qui est basée sur une machine asynchrone à double alimentation, les convertisseurs statiques seront également présentés et modélisé.

44

Chapitre III : Modélisation de

la MADA et des convertisseurs

Statiques.

45

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

III.1 Introduction

Afin de compléter la chaine de conversion et de produire de l'énergie électrique un générateur est essentiels pour convertir l'énergie mécanique produite par l'éolienne en énergie électrique et injectée aux réseaux.

Il existe plusieurs types de générateurs dans l'industrie, la génératrice électrique la plus utilisée dans les systèmes éoliens à vitesse variable de forte puissance est la génératrice électrique de type machine asynchrone à rotor bobiné, qui est couramment appelé Machine Asynchrone à Double Alimentation (MADA), car cette dernière a l'avantage d'être facialement contrôlée et présente des performances intéressantes.

Nous allons nous intéresser en premiers temps à la modélisation de la machine asynchrone a double alimentation. Ensuite afin d'injectée l'énergie électrique produite par le générateur la nécessiter des convertisseurs de l'électronique de puissance son primordial pour cela la modélisation de ces dernier son présenté dans la dernière partie de ce chapitre ainsi qu'une conclusion.

III.2 Description de la MADA

La machine asynchrone à double alimentation MADA, est un générateur à rotor bobiné. La figure III.1 représente la structure d'une MADA connectée au réseau triphasé. Les enroulements du stator sont reliés au réseau à travers deux convertisseurs de puissance bidirectionnels en courant. La puissance traversant ces convertisseurs peut alors être absorbée ou produite par la machine selon le mode de fonctionnement, le bus continu représenté ici : le condensateur entre ces deux convertisseurs et un transformateur élévateur de tension qui permet le raccordement au réseau de distribution [29].

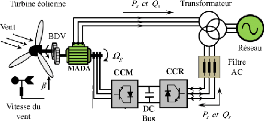
Figure III-1.Structure d'une MADA connectée au réseau [30]

46

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

III.3 Mode de fonctionnement de la MADA

La machine asynchrone à double alimentation (MADA) peut fonctionnée en 4 mode possible selon la vitesse de synchronisme.

III.3.1 Fonctionnement en moteur hypo-synchrone

Le fonctionnement en mode moteur hypo synchrone de la MADA est représenté par la figure III.2. On remarque que la puissance est fournie par le réseau au stator et la puissance de glissement passe par le rotor pour être réinjectée au réseau. On a donc un fonctionnement moteur en dessous de la vitesse de synchronisme. La machine asynchrone à cage classique peut fonctionner ainsi mais la puissance de glissement est alors dissipée en pertes Joule dans le rotor [31].

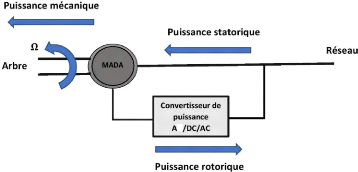
Figure III-2- Schéma de structure de la MADA en mode moteur hypo-synchrone. [31]

III.3.2 Fonctionnement en moteur hyper-synchrone

Le glissement devient négatif lorsqu'on augmente la vitesse, la puissance est fournie par le réseau au stator et au rotor. Pour réaliser ce mode on inverse l'ordre de phase de sorte que le champ tournant induit par la fréquence du glissement soit en opposition de phase avec celui du stator [29].

La figure III.3 représente le Schéma de structure de la MADA en mode moteur hyper synchrone

47

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

.

Figure III-3.Schéma de structure de la MADA en mode moteur hyper-synchrone [31]

III.3.3 Fonctionnement en mode génératrice hyper-synchrone

Le fonctionnement en mode moteur hypo synchrone de la MADA est représenté par la figure III.4. On s'aperçoit que la puissance est transférée au réseau à travers le stator et la puissance de glissement est récupérée à travers le rotor pour être réinjectée au réseau. On a donc un fonctionnement générateur au-dessus de la vitesse de synchronisme. [31]

La machine asynchrone à cage classique peut avoir ce mode de fonctionnement mais dans ce cas la puissance de glissement est dissipée en pertes Joule dans le rotor [31]

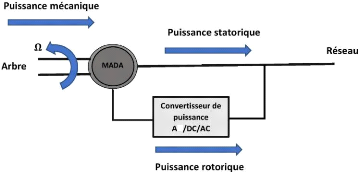
Figure III-4.Fonctionnement Génératrice hyper-synchrone [31]

III.3.4 Fonctionnement en mode génératrice hypo-synchrone

D'après la figure III.5 on remarque que le réseau reçoit la puissance à travers le rotor, la génératrice fonctionne donc en dessous de la vitesse de synchronisme.

48

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

La figure III.5 montre que la puissance est fournie au réseau par le stator. La machine asynchrone à cage classique ne peut pas avoir ce mode de fonctionnement. [31]

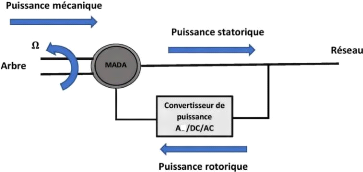
Figure III-5. Fonctionnement en mode génératrice hypo-synchrone [31]

III.4 Modélisation de la MADA

Après avoir modélisé la partie mécanique de l'aérogénérateur, nous allons modéliser la machine asynchrone à double alimentation l'élément phare de notre chaine de conversion pilotée par le rotor liée à un convertisseur statique. Le modèle de la MADA généralisé triphasé et biphasé de sera présenté à travers cette section.

III.4.1 Modèle de la MADA dans le repère triphasé-triphasé

La figure III.6 représente La représentation électrique d'une machine triphasée asynchrone à double alimentation dans le repère triphasé. Les trois enroulements (bobinages) du stator sont représentés schématiquement sur leurs axes magnétiques respectifs Sa, Sb et Sc qui sont décalés

de 120°, ainsi que les trois enroulements du rotor sur leurs axes magnétiques respectifs R_a, Rb et R?? [22].

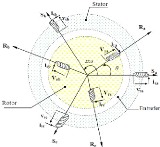
Figure III-6. Représentation spatiale des enroulements de la MADA [22]

49

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

Avec :

(Vsa, Vsb, Vsc), (Vra, Vrb, Vrc) : Les tensions simple aux bornes des enroulement statoriques et rotoriques.

(Isa, Isb, Isc), (Ira, Irb, Irc) : Les courants de phase instantanés statorique et rotorique.

8 : L'angle électrique entre le repère statorique Sa et le repère rotorique R_a.

III.4.1.1 Hypothèse simplificatrice

La modélisation de la MADA, est établie sous les hypothèses simplificatrices suivantes :

· L'entrefer est d'épaisseur uniforme et l'effet d'encochage est négligeable.

· La saturation du circuit magnétique, l'hystérésis et les courants de Foucault sont négligeables.

· Les résistances des enroulements ne varient pas avec la température et on néglige l'effet de peau.

· On admet que la f.e.m. créée par chacune des phases des deux armatures est à répartition sinusoïdale. [22]

III.4.1.2 Equation électrique

En générales les équations de la machine asynchrone à rotor bobiné dans un repère triphasé s'écrivent :

· Au niveau du stator

d Vsa = RsIsa + dt (Psa d Vsb = RsIsb + dt (Psb d Vsc = RsIsc + dt (Psc

(III.1)

· Au niveau du rotor :

d Vra = RrIra + dt (Pra d Vrb = RrIrb + dt (Prb d Vsc = RrIrc + dt (Prc

(III.2)

50

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

Ø En format matriciel :

· Au niveau du stator

?????? ( ?????? ) ??????	=	???? ( 0 0	0 ???? 0	0 ?????? 0 ) ( ?????? ???? ?????? )	?? +	?????? ( ?????? ??????	)		(III.3)

· Au niveau du rotor :

?????? ?????? ??????	=	???? 0 0	0 ???? 0	0 0 ????	?????? ??????) ??????	?? ??????		(III.4)

Avec :

(??????, ?????? , ??????), (??????, ??????, ??????) : Les flux statoriques et rotoriques.

????, ???? : les résistance statorique et rotorique.

III.4.1.3 Equation Magnétique

Les expressions des flux en fonction des courants statoriques et rotoriques sont données par

[32] :

?????? ( ?????? ?????? ?????? ( ?????? ??????

)= ) =

???? ( ???? ???? ???? ( ???? ????

???? ???? ???? ???? ???? ????

???? ???? ) ???? ???? ???? ) ????

?????? (?????? ) ?????? ?????? (?????? ) ??????

+ (??????) + (??????)

?????? ( ?????? ) ?????? ?????? ( ?????? ) ??????

(III.5) (III.6)

Avec :

???? , ???? : Inductances propres statoriques et rotoriques ???? : Inductance mutuelle entre phases statoriques ???? : Inductance mutuelle entre phases rotoriques

La matrice des inductances mutuelles entre les phases du stator et du rotor dépend de la position angulaire è entre l'axe du stator et celui du rotor [33]

51

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

(??????)

=

????

?????? ??????

???????? (?? - (??

2??

) )

?????? ??????

(?? ???????? (??

4??

) )

?????? ??????

(?? (?? ????????

2??

) )

(III.7)

???? : Maximum de l'inductance mutuelle entre une phase du stator et la phase correspondante du rotor.

III.4.1.4 Equation mécanique

L'équation de la dynamique appliquée sur la machine est donnée par :

??Ù (III.8)

??. = ??????- ????- (????. Ù??)

????

Avec : ?? Ù = ?? ?????? = ??[????]([??????][????]) Avec : ?? : Le moment d'inertie du rotor en [????. ??^2]. Ù : La vitesse angulaire mécanique en [??????/??]. ??????: Le couple électromagnétique en [??. ??]. ????: Le couple résistant en [??. ??]. ????: Le coefficient de frottement en [??. ??. ??/??????]. ?? : La vitesse angulaire électrique de rotation du rotor en [??????/??]. p : Le nombre de pair de pole. III.4.2 Modèle de la MADA dans le repère de Park III.4.2.1 Définition de la transformation de Park

(III.9) (III.10)

La transformation de Park est composé d'une transformation triphasé - diphasé suivie d'une rotation. Elle nous permet de transformer un système dans un repère abc vers un repère ???? en

52

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

passant par le repère ???? . Le repère ???? est toujours fixe par rapport au repère ?????? comme le montre la figure III.7, par contre le repère ???? est mobile. Il forme avec le repère fixe ???? un angle qui est appelé l'angle de la transformation de Park ou angle de Park. [34]

Le choix des angles de transformation de Park pour les grandeurs statoriques et celle des grandeurs rotoriques doivent coïncider pour simplifier ces équations. Ceci se fait en liant les angles ???? et ????) par la relation [34] : ?? ?? = ???? + ??

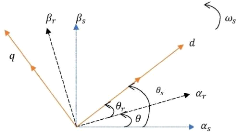
Figure III-7. Transformation de Park

On désire transformer les enroulements de la MADA triphasée en des enroulements biphasés orthogonaux équivalents selon les axes (????) lié au champ tournant ainsi la composante homopolaire pour équilibrer le système transformé, c'est à dire [32] :

· Direct selon l'axe (??).

· Quadrature (transversal) selon l'axe (??).

· Homopolaire (??).

Le produit matriciel définissant la transformation de PARK s'exprime par :

[????????] = ??(??)[????????] (III.11)
Avec :

	????		????
[????????]	= [ ???? ] Et [????????]	=	[ ???? ]
	????		????

??, ??, ?? : sont respectivement indice des composantes direct, quadratique et homopolaire.

?? : représente l'angle de transformation, elle dépend du choix du référentiel ainsi que des grandeurs statoriques et rotoriques. La matrice de changement Park est exprimée par l'équation II.12 :

53

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

[??(??)] = v3

2

[

2?? ??????(??) ?????? (?? - 3 )

?????? (?? -3^4?? )

(III.12)

2??

4??

- ??????(??) - ?????? (?? - 3 ) - ?????? (?? - 3 )

1 1 1

v2 v2 v2

La transformation inverse de Park est donnée par :

[????????] = [??(??)]-1[????????] (III.13)

Avec :

[??(??)]^-1 = v^23	??????(??) ?????? (?? - ?????? (??+		- ??????(??)	1	(III.14)
				v2
		3^2??)- ??????	(?? - 32??)	1 v2
		3^2??) -??????	(??+32??)	1 v2

Pour un système équilibré la composante homopolaire est négligée, et en appliquant la transformation de Park aux équations de la machine asynchrone dans le repère naturel, on obtient les équations suivantes :

III.4.2.2 Equation électrique

Les équations des tension rotorique et statorique de la MADA sont exprimée par :

??????	=	??????????	- ????? ??????	???????? +
				????
			???????????	????????
??????	=	??????????	+	+ ????
				????????	(III.15)
??????	=	??????????	- ???????????
				+ ????
				????????
??????	=	??????????	{???? + ???????????
				+

Ø Les équations des courant son donnée par :

{

???????? = ??(??).?????????? (III.16)
???????? = ?? (??).??????????

Dans ces équations, R_s, R_r, L_s et L_r sont respectivement les résistances et les inductances du stator et du rotor du MADA.

54

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

Vds, Vqs , _Vdr , _Vqr , _Ids , _Iqs , Idr, Iqr, öds , _öqs , _ödr ^et _öqr représentent respectivement les composantes selon les axes d et q des tensions statoriques et rotoriques des courants et des flux.

III.4.2.3 Equation du flux magnétique

Les équations du flux magnétiques sont donnée par :

??????	=	??????????	+ ????????			??????
=	??????????	+ ????????			??????
=	??????????	+ ????????	(III.17)		??????
=	??????????	+ ????????

III.4.2.4 Equation du couple électromagnétique :

L'équations du couple électromagnétique de la MADA son exprimées par :

?????? ?????? Avec :	= =	??. ??.	??	(???????????? (????????????	- -	????????????) ????????????)		(III.18)

?? : nombre de pair de pole.

?????? : couple électromagnétique.

III.4.2.5 Equation des puissance active et réactive statorique et rotorique

Les puissances actives et réactives statoriques et rotoriques s'expriment par :

????	=	??????	??????+ ??????	??????			????
=	??????	?????? - ??????	??????			????
=	??????	?????? + ??????	??????	(III.19)		????
=	??????	?????? + ??????	??????

Avec :

???? : puissance actif statorique.

???? : puissance réactif statorique. ???? : puissance actif rotorique. ???? : puissance réactif rotorique.

55

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

III.6.5. Choix du référentiel (d-q)

Etant donné que dans les équations précèdent de la MADA on a utilisé les paramètres dans un repère (?? - ?? ) il existe trois choix de référentiel possible. Par rapport au rotor, au stator et au champ tournant.

III.4.2.6 Référentiel liée au champ tournant

Dans ce référentiel, les axes (????) sont immobiles par rapport au champ électromagnétique créé par les enroulements statoriques, il est caractérisé par ?? = ???? - ???? . Ce référentiel est généralement utilisé dans le but de pouvoir appliquer une commande de vitesse, de couple, etc. puisque les grandeurs dans ce référentiel sont de forme continue. [31]

Dans notre travail, on utilise le référentiel lié au champ tournant pour la modélisation et la commande de la MADA. Alors, le modèle électrique général de la machine asynchrone obtenue en utilisant la transformation de Park est donné par les équations suivantes : [32]

Ø Équations électriques des tensions statoriques rotoriques :

????????

??????

=

??????????

- ??????????

+ ????

????????

(III.20)

??????

=

??????????

+ ??????????

+ ????

????????

??????

=

?????????? -

(????

-

????

)?????? + ????

=

?? ??????

??????

??????????+

(????

-

????

)??????+ ????

??????

Les flux statoriques et rotoriques sont donnés par : = ?????????? + ????????

??????

=

??????????

+ ????????

??????

=

??????????

+ ????????

(III.21)

??????

=

??????????

+ ????????

III.4.2.7 Référentiel liée au stator

Ce référentiel est souvent adapté pour traiter les grandeurs instantanées. Car il est utile pour étudier les régimes de démarrage et de freinage des machines électriques.Il est aussi appelée système d'axe (??, ??).Son principal avantage est le non nécessité de transformation vers le système réel.

56

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

???? = 0 ??????

???? = 0 ??????

???? = ????

Les équations des tensions statorique et rotoriques de la MADA seront exprimées par :

???????? = ???????????????? + ???? ???????? ?????? = ?????????? + ???? ?????? ???????? = ???????????????? - ???? ?????? + ???? ?????? ???????? = ????????????????+ ???? ?? ???? + ???? III.4.2.8 Référentiel liée au rotor

(III.22)

Dans ce référentiel, les axes (?? - ??) sont immobiles par rapport au rotor tournant à une vitesse ?? l'utilisation de ce référentiel permet d'étudier les régimes transitoires où la vitesse est supposée constante notamment dans les machines alternatives synchrones et asynchrones avec une connexion non symétrique des circuits du rotor. [32]

??????

????

= ??

= 0 ??????

????

?????? ????????

?????? = ?????????? - ???? ?????? + ????

?????? ????????

=

???????????????? + ???? ?????? + ????

?????? = ?????????? + ????

?? ??????

?????? = ?????????? + ????

(III.23)

????????

III.5 Modélisation des convertisseurs statiques

Notre chaîne de conversion d'énergie étudiée pour l'alimentation de la MADA est composée d'un convertisseur côté de la génératrice (redresseur à diodes) et d'un convertisseur cotée réseaux (onduleur), le convertisseur cotée Machine (CCM) et le convertisseur cotée réseau (CCR) son connectée à travers un bus continue. Le convertisseur cotée réseau (CCR) est connecté au réseau à travers filtre résistive RL.La figure III-8 présente l'architecture de la chaine de conversion étudiée.

57

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

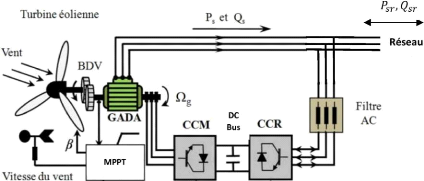
Figure III-8. Structure de la chaine de conversion étudiée [30]

III.5.1 Modélisation du convertisseur coté MADA

Un redresseur est un élément important dans le domaine de l'électronique de puissance, ce convertisseur statique transforme le courant alternative en courant continue. L'entrée du redresseur est alimentée par une source de tension sinusoïdale triphasée, et qui donne à la sortie une tension continue pour alimenter l'onduleur à travers le bus continue.

La figure III.9 représente le redresseur que nous allons modéliser il s'agit d'un redresseur a doublé alternance non commandée (à base de diode).

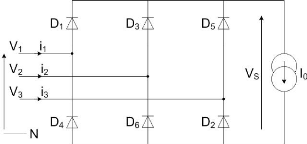
Figure III-9. Redresseur triphasée double alternance

· Les diodes : D1, D3 et D5 sont à cathode commune, assurant l'allée du courant ??0.

· Les diodes : D4, D6 et D2 sont à anode commune, assurant le retour du courant J0.

On suppose que la source triphasée d'alimentation est équilibrée, d'amplitude de tensions et de fréquence constantes. On néglige aussi les chutes de tension dues au phénomène d'empiétement

58

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

et aux pertes dans les diodes. Le redresseur est alors alimenté par le système triphasé qui a pour équation : [22]

??₁(??) = ??????????(????)

??2(??)	=	??????????	(????		-	??3(??)
=	{3 ??????????	(????	-

(III.24)

3 2?? )

4??

)

· La tension de sortie du redresseur est donnée par l'équation III.24:

???? (??) = ?????? [??₁(??),??₂(??), ??₃(??) - ?????? ??₁(??), ??₂(??), ??₃(??)] (III.25)

· Sa valeur moyenne :

3v3 ????(??) = ??????

(III.26)

· Le facteur d'ondulation

???? ??????- ??????????

??% = 2????

(III.27)

III.5.2 Modélisation du bus continue

Le bus continu est un élément de stockage d'énergie, la tension du bus continu est générée à partir de l'intégration du courant capacitif.

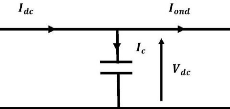
III-10. Modèle du bus continue

L'évolution de la tension du bus continu est donnée par la formules suivantes :

??₀+????

1 (III.28)

??????(??) = ???? ? 1 ?? ????(??)???? + ????(??0)

??₀

59

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

Avec :

?? : La capacité du bus continu D'après la loi des mailles on a :

(III.29)

'dc = '????d + '_c

'_c = 'dc - '????d Donc :

????d_c

(III.30)

'_c = ?? ????

III.5.3 Modélisation du convertisseur cotée réseau

L'onduleur de tension est un composant de l'électronique de puissance qui converti une tension continue d'entrée en une tension de sortie alternative, il est composé de six interrupteurs bidirectionnels qui son constitué d'un transistor et de diode de roue libre qui sert à protéger des thyristors. (Figure III.11), les interrupteur (K1,K4);(K2,K5);(K3,K6) son complémentaire c-à-d quand l'un est ouvert l'autre doit être fermée afin d'éviter les courts-circuits delà source. Afin d'éviter, il est aussi impérativement nécessaire d'espacé le temps de fermeture de T21 ; T22 ou T23 et le temps d'ouverture de T11, T12, T13 et vice versa.

Afin de modéliser l'onduleur de tension on peut considérer le circuit comme étant l'association de trois onduleurs monophasés en demi-point aussi la source continue peut-être

décomposée en deux sources équivalentes de tension (??????

2 ) avec un point milieu fictif « O ».Pour

simplifier l'étude, on supposera que :

· La commutation des interrupteurs est instantanée,

· Les chutes de tension à leurs bornes sont négligeables,

· La charge est triphasée équilibrée et couplée en étoile avec point neutre isolé « n ».

60

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

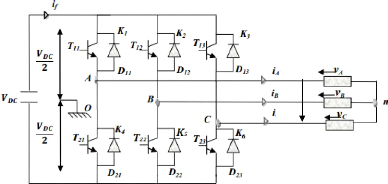
VCA

Figure III-11. Onduleur de tension triphasée [22]

Le système triphasé obtenu à la sortie de l'onduleur est équilibré en tension, ne contenant que les harmoniques impairs différents de trois, les harmoniques de rang trois et multiples de trois étant éliminés.

On peut exprimer les tensions composées par :

{

VAB = VAO - VBO (III.31)
VBC = VBO - VCO VCA = VCO - VAO

· Au niveau de la charge, on peut déduire les relations donnant les équations des tensions simples son donné par l'équation III .32 :

{

VAB = V_A - V_B (III.32)
VBC=VB - VC VCA=VC - V_A

En effectuant les différences (VAB - VCA), (VBC - VAB), (VCA - VBC) membres à membres on trouve :

{

VAB - VCA = 2 V_A - (V_B + VC (III.33)
VBC - VAB = 2 V_B - (V_A + VC) VCA - VBC = 2 VC - (V_A + V_B)

On a un système équilibré donc on déduit que :

61

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

(III.34)

{

??????- ?????? = 3 ???? ?????? - ??????= 3 ???? ?????? - ?????? = 3 ????

Donc :

1 (?????? - ??????) 3

???? =

???? =

1 (??????- ??????) 3

(III.34)

???? =

1 (?????? - ??????) 3

L'expression des tensions simples liant les tensions mesurées entre les points A, B, C et le point milieu O est définie par :

???? 1 2

???? = -1

???? 3 -1

-1

2 -1

-1 -1 2

?????? ] ?????? ??????

(III.35)

L'état des interrupteurs, supposés parfaits peut être définit par trois grandeurs booléennes de commande ????(i =A, B, C) :

· ????=1, alors les interrupteurs du haut sont fermée (passant) et les interrupteurs du bas sont ouvert(bloquée).

· ????=0, alors les interrupteurs du haut son ouvert (bloquée) et les interrupteurs du bas son fermée (passant).

· Cela nous permet d'écrire l'équation III.36 :

?????? ?????? ???? (III.36)

?????? = ????

?????? 2 ????

Donc :

???? ???? 2 -1 -1 (III.37)

] . 1

[ ???? ] = [ ???? ] . ?????? -1 2 -1

2 . [ 3

???? ???? -1 -1 2

III.5.4 Modélisation du filtre

Pour l'atténuation des harmoniques de courant un filtre triphasé est utilisé reliant le convertisseur cote réseau à ce dernier.

62

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

L'architecture du filtre est représentée à travers la figure III.12.

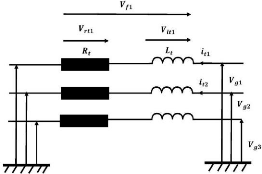
Figure III-12. Filtre coté réseau.

Les courants dans le filtre supposé sinusoïdal équilibré sont donnés par :

??0+???? 1 ????1(??) = ? ??????1???? + ????1(??0) ???? ??0 ??0+???? ????2(??) = 1 ? ??????2???? + ????2(??0) ???? ??0 ????3(??) = -(????1 + ????2)

(III.38)

Les tensions aux du filtre s'écrivent :

{

????1 = ????1 - ????1 - ??????1 (III.39)
????2 = ????2 - ????2 - ??????2

Avec :

{

??????1 = ????????1 (III.40)
????2 = ????????2 De suite la définition des vecteurs ????, ???? et ???? :

???? =

(????1 (III.41)
) ????2

=

??

??1 )?? ??2

???? = (????1)

????2

??(??

(III.42)

(III.43)

63

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

III.5.5 Commandes à Modulation de Largeur d'Impulsion (MLI)

Afin de déterminer les signaux délivrés par l'onduleur il est impérativement nécessaire de commandée les grandeurs ????, ????, et ???? par une commande spécifique parmi ces commandes il existe une commande appelée commandes à Modulation de Largeur d'Impulsion (MLI) [35].

Il existe plusieurs types de commande MLI chaque méthode est différente de l'autre par apport à leurs principes et leurs méthode employée parmi les principales stratégie MLI on cite quelqu'une :

· La MLI Sinus-Triangle (à échantillonnage naturel)

· Les MLI à échantillonnage régulier

· La MLI vectorielle

· La MLI suboptimale

· La MLI précalculée ou calculée

Nous allons nous intéresser principalement dans ce paragraphe est la MLI Sinus-Triangles. III.5.5.1 Modulation a largeur d'Impulsion Sinus-Triangle

La commande MLI "Sinus-Triangle", dite à échantillonnage naturel, est la plus simple des MLI(s), tant du point de vue de son principe, que de son implantation (analogique ou numérique). [35].Pour déterminer les instants de commutation, elle consiste à comparer entre elles :

· Une onde de référence sinusoïdale, la modulatrice, de fréquence ???? = ?? (fréquence de référence)

· Une onde dite porteuse, en général triangulaire, de haute fréquence ????, respectant l'inégalité : ???? » ??

La commande MLI est caractérisée par les paramètres suivants :

L'indice de modulation « m »

???? ??= ????????

(III.44)

Avec :

???? : fréquence de modulation ???????? : fréquence de référence

64

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

Le taux de modulation « r » est exprimé par :

r=

Vref V,

(III.45)

Avec :

Vref : l'amplitude de la tension de référence. V, :la crête de l'onde de modulation.

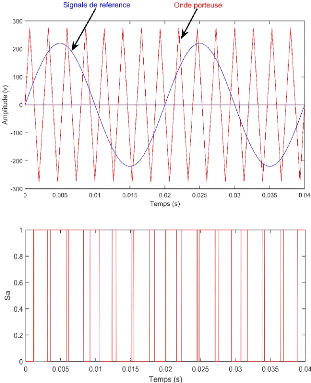
Figure III-13. Principe de fonctionnement de la technique MLI triangulo sinusoïdal

III.6 Conclusion

Ce chapitre a permis d'écrire la modélisation de la chaine de conversion de l'éolienne (turbine et MADA) tel que : la turbine, le multiplicateur, l'arbre mécanique et la machine asynchrone à double alimentation (MADA). D'autre part, l'éolienne nécessite une stratégie de

65

Chapitre III : Modélisation de la MADA et des convertisseurs statiques

commande afin de mieux gérer et contrôlé l'énergie produite pour cela nous allons aborder la stratégie de commande d'une éolienne dans le chapitre suivant.

66

Chapitre IV : Stratégie de

commande des puissances

active et réactive de la MADA

67

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

IV.1 Introduction

Afin de contrôlée les puissances produites par la chaine de conversion présentée dans le chapitre précèdent une stratégie de contrôle duis puissances s'impose.

Dans cette optique, la stratégie de contrôle proposé à travers ce chapitre est basée sur la commande vectorielle par l'orientation du flux statorique, cette méthode de contrôle permet d'obtenir des meilleures performances dans les applications à vitesse variable en fonctionnement générateur.

Dans un premier temps, nous allons présenter la stratégie de commande global du système qui se compose de deux parties de commande :

· Le contrôlé des convertisseur cotée MADA.

· Le contrôle des convertisseurs cotée réseau.

Ensuite, le contrôle des convertisseurs cotée MADA qui est basé sur la loi de commande vectorielle par orientation du flux qui permet d'effectuer un contrôle indépendant des puissances active et réactive sera traitée à travers cette section de chapitre.

Dans un second temps, le contrôle des convertisseurs cotée réseau qui se compose d'un bus continu, d'un onduleur et d'un filtre sera également décrit et détaillée.

La dernière partie de ce chapitre fera l'objet de présentée les résultats de la commande appliquée a l'ensemble de la chaine de conversion.

IV.2 Architecture du dispositif de commande

La figure IV.1 représente l'illustration du dispositif de commande de la MADA traitée à travers ce chapitre.La variation du vent générée est captée par la turbine cette dernière convertie la puissance contenue dans le vent en puissance électrique à travers la machine électrique, le stator de la machine transmet la plus grande partie de la puissance électrique produite directement au réseau.

Alors que le rotor, le convertisseur cotée machine (CCM) et le convertisseur cotée réseau transmettent le reste de la puissance soient une estimation de 30% de la puissance électrique.

· Convertisseur cotée MADA (CCM) : ce dispositif va nous permettre de contrôler le couple électromagnétique, la puissance active, et la puissance réactive échangée entre le stator et le réseau.

68

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

· Convertisseur cotée réseau (CCR) : le CCR est chargée du contrôle de la tension du bus continu et les puissances active et réactive échangées avec le réseau.

IV.3 Commande vectorielle

La commande vectorielle consiste à décomposer le vecteur des courants statoriques ou rotoriques en deux éléments, d'où le premier produit le flux, et le second produit le couple au but de l'obtention d'un angle de 90° entre le flux statique ou rotorique et le courant statorique de la machine [22].L'importance de la commande vectorielle, aussi appelée commande à flux orienté (Field Oriented control en anglais), est d'arriver à commander la MADA de la même manière que d'une machine à courant continu à excitation indépendante, autrement dit une caractéristique approchant à celle de la machine à courant continu à excitation séparée dans laquelle où il y'a un découplage naturel entre la grandeur commandant le flux (le courant d'excitation) et celle liée au couple (le courant d'induit). [22]

Figure IV-1.Architecture du dispositif de commande [30]

A travers la commande vectorielle les puissance active et réactive vont être contrôlé indépendamment l'une de l'autre.

69

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

La figure IV-2 montre l'égalité et l'équivalence entre la formule du couple que l'on réalise avec la commande découplée classique d'une machine à C.C et la commande vectorielle d'une génératrice MADA.

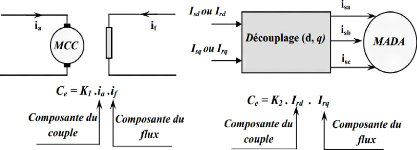
Figure IV-2. Principe de la commande vectorielle [22]

Cette séparation approuvait de recevoir une vaste plage de contrôle de vitesse, une réponse très rapide du couple et une forte efficacité pour une haute plage de charge en régime permanent.

IV.4 Commande du convertisseur coté MADA

La figure IV.3 représente le schéma bloc de la structure de commande du convertisseur cotée MADA décrite dans cette section.

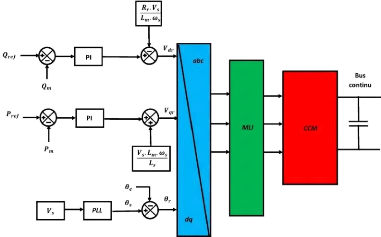
Figure IV-3. Structure de commande du convertisseur cotée MADA

70

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

IV.4.1 Choix du référentiel pour le modèle de la MADA

Trois types de référentiels existe :

· Référentiel fixé para port au stator où ?? = ????.

· Référentiel fixé para port au rotor où ?? = ????.

· Référentiel fixé para port au champs tournant où ?? = 0.

Afin d'effectuée une régulation plus aisée il faut avoir des grandeurs constantes dans le régime permanant et pour cela on a choisi de fixer le repère ???? au champ tournant.

IV.4.2 Détermination des angles pour les transformations de Park

Pour déterminer les angles de transformation de Park pour les grandeurs statoriques et rotorique une boucle à verrouillage de phase (PLL), une méthode simple consiste à mesurer les tensions statoriques, à les faire passer dans un repère diphasé et en extraire la phase ???? que forme le vecteur tension avec l'axe de la première phase du stator. Afin d'aligner le flux statorique avec l'axe d, nous retranchons ??/2 à cet angle. Le rotor forme lui, un angle ???? avec la phase a du stator, l'angle ???? nécessaire aux transformations des grandeurs rotoriques est donc donné par ????-????. Une mesure des tensions statoriques et un capteur de vitesse sont indispensables pour déduire ces angles de transformation. Cette méthode est fiable elle permet d'obtenir une estimation robuste et de rejeter les petites perturbations ou les harmoniques.

La figure IV-4 représente le schéma structurel de la détermination des angles pour la transformation de Park.

Figure IV-4. Schéma structurel de la détermination des angles pour la transformation de Park

71

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

IV.4.3 Modélisation de la MADA avec Orientation du flux statorique

Avant d'entamé la commande vectorielle de la MADA par orientation du flux statorique on rappelle les équations différentielles de la machine :

?????? = ?????? = ?????? = ??????=	?????????? ?????????? ?????????? ??????????	+ + + +	????????	- ???? + ???? - ???? + ????	?????? ?????? ?????? ??????		(IV.1)

Les équations du flux son donné par :

??????	=	??????????	+ ??	??????			??????
=	??????????	+ ??	??????			??????
=	??????????	+ ??	??????	(IV.2)		??????
=	??????????	+ ??	??????

Avec :

????, ????, ????, ???? : Les résistances et les inductances du stator et du rotor du MADA.

??????, ?????? ,?????? , ?????? : les composantes selon les axes d et q des tensions statoriques et rotoriques selon les axes d et q

?????? , ?????? ,??????, ??????: Les composantes selon les axes d et q des courants statoriques et rotoriques selon les axes d et q.

?????? , ?????? , ?????? , ?????? : Les composantes selon les axes d et q des flux statoriques et rotoriques selon les axes d et q.

L'orientation de la tension et du flux statorique est représentée à travers la figure. III.5.

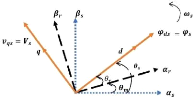
Figure IV-5. Référentiel diphasé ???? liée au champ tournant statorique.

72

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

Vu que notre choix du référentiel c'est porté sur le référentiel lié au champ tournant et le flux statorique est orienté sur l'axe ??, soit constamment nulle ?????? = 0, ?????? = ???? ,le modèle de la MADA deviens :

??????	????????	?????? ??????		(IV.3)

En considérant l'hypothèse qui consiste à négligé la résistance des enroulements statoriques ??_??,les équations des tensions statorique et rotorique de la MADA peuvent être exprimé par l'équation IV.4 :

??????	= =	???????????????? ??????= ???? ??????	??????= 0 ????= ?????????? ????????	?????? ??????		(IV.4)

Avec :

???? : la tension du reseau.

Les équations des flux seront exprimées par :

??????=	???? =			??????????+ ??			??????		(IV.5)	?????? =
??????????	+ ?? ?????? =			0					??????
=		??????????	+ ??		??????	??????
=		??????????	+ ??		??????

Avec :

M : inductance mutuelle.

De IV.5 on obtient relation entre les courants statoriques et rotoriques :

73

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

???? ?? ?????? =- ?????? ???? ???? ?? ?????? = - ?????? ????

(IV.6)

Les expressions des puissances active et réactive statoriques dans cette hypothèse son donné par :

{

???? = ???????????? (IV.7)
???? = ????????????

Suivant les conditions de travail choisie dans notre étude (?????? = 0) et, en remplaçant les expressions des courants statoriques et des tensions c'est même expression deviennent :

??

????= -???? ???? ??????

???????? ???? = ????

?????? (IV.8) ?????? ????

L'équation du couple électromagnétique devient alors :

(IV.9)

????

?????? = - ???? ??????

????

Avec :

?? : nombres de paires de pole.

En approximant ?????? a ??????? ? l'équation de la puissance réactive deviens alors :

????² ?????? (IV.10)

???? = - ??????

?????? ?? ????

On constate d'après l'équation que le contrôle des puissances active et réactive au stator est indépendant. Avec une inductance magnétisante constante et un réseau électrique puissant, la puissance active sera directement proportionnelle au courant rotorique d'axe ??, et la puissance

réactive proportionnelle au courant rotorique d'axe ?? a une constante prée ^????2 . [22]

?????? ??

L'expression des flux rotorique peut être exprimée, en remplaçant les courants statoriques,

par :

74

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

?????? = (????

??^2 ?????? )?????? + ???? ????????

??2 (IV.11)

?????? = (???? - )??????

????

Le remplacement des expressions obtenues (IV.11) dans les équations des tensions rotoriques d'axes ?? - ?? donne :

?????? = ?????????? + (???? - ??2 ) ????????

???? - ?????? (???? - ??2 ) ??????

???? ????

(IV.12)

?????? = ?????????? + (???? - ??2 ) ????????

???? + ???????????? (???? - ??2 ) + ?????? (?? ???? )

???? ???? ????????

Où :

????-??

.

?? : correspond au glissement de la machine ;?? =

????

D'après l'équation obtenue on remarque que pour avoir des courants rotoriques de référence il faut imposer les composantes diphasées des tensions rotoriques ?????? et ?????? a la machine.

Après avoir établie les équations de la MADA, la relation entre les puissances active et réactive, et les tensions appliquées au rotor nous pouvons donc développer un schéma bloc interne simplifié de la MADA figure IV.6 que nous allons réguler par la suite.

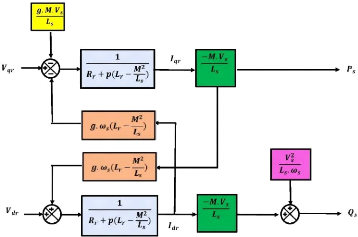
Figure IV-6. Schéma bloc du système à réguler [21]

75

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

IV.5 Contrôle indépendant des puissances active et réactive de la MADA

D'après la figure IV-6 réaliser à travers les équations étudiées précédemment on s'aperçoit que sur les deux axes qui lient les tensions rotoriques au puissance actives statorique des fonctions de transfert du premier ordre son apparu, cela va nous permettre d'élaborer une stratégie de commande vectorielle facilement, vu que l'influence des couplages au niveau de chaque axe peut être commandé indépendamment avec chacun son propre régulateur.

La puissance active de référence sera contrôlée par un régulateur au niveau de l'axe rotorique ?? tandis que la puissance réactive de référence sera contrôlée par un régulateur au niveau de l'axe rotorique ??.

Afin d'optimiser la qualité de l'énergie renvoyée sur le réseau la consigne de la puissance réactive sera maintenue constante afin d'avoir un facteur de puissance unitaire coté stator.

Le coefficient de puissance de l'éolienne va être conservé de façons optimal grâce à La consigne de puissance. Pour la commande en puissance du MADA deux méthodes peuvent être élaboré :

· Méthode directe : elle contrôle indépendamment les puissances actives et réactive en négligeant les termes de couplage et à mettre en place un régulateur indépendant sur chaque axe. Cette méthode sera appelée méthode directe car les régulateurs de puissance contrôlent directement les tensions rotoriques de la machine.

La figure IV.7 représente le schéma bloc de la commande directe de puissance de la MADA

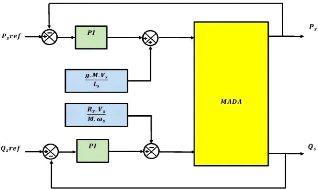
Figure IV.7- Schéma bloc de la commande directe de puissance de la MADA. [36]

76

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

· Méthode indirecte : elle consiste à récapituler l'opération de contrôle à partir de l'inversement de la fonction de transfert du système à réguler, pour établir les tensions rotoriques de référence en fonction des puissances active et réactive au niveau du stator. On recherche donc à former les équations des puissances active et réactive d'une coté et des tensions rotoriques d'autre part en fonction des courants rotoriques tout en tenant compte du modèle mathématique de la génératrice. Dans notre cas d'étude on s'intéresse seulement à la méthode directe. La figure IV.8 représente le schéma bloc de la commande indirecte de puissance de la MADA.

Figure IV-8. Schéma bloc de la commande indirecte de puissance de la MADA [36]

IV.5.1 Régulation des puissance active et réactive de la MADA

Afin de contrôler les puissance active et réactive une régulation de puissance s'impose, à travers cette section la régulation des puissances de la MADA va être présenté.

Le principe de régulation ici est de commander indépendamment et directement les puissances actives et réactive de la MADA.

· Schéma bloc en boucle ouverte En posant les f.e.m. ; ????, ???? suivantes :

77

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

??²

???? = -??????(???? - )??????

????

??² ?????? (IV.13)

???? = ??????(????-??????+ ??

???? ????

L'équation des tensions rotorique deviens :

??²)????????

??????= ?????????? + (???? ???? + ????

????

??2)???????? (IV.14)

??????

?????????? + (????-???? + ????

????

Après avoir mis en place une transformation de la place ont obtient :

??^2 (???? + (???? - )??) ?????? = ?????? - ???? ???? ??^2 ???? + (???? - )??) ?????? = ?????? - ???? ????

(IV.15)

Avec :

?????? =

1

2 (?????? - ????)

(???? + (????

??

???? ) ??)

(IV.16)

1

?????? = (?????? - ????)

(???? + (???? - ??2

???? ) ??)

En remplaçant IV.16 dans IV.15 nous obtenons alors les expressions des puissance actives et réactives :

???? = -????

?? ????

1 (?????? - ????) ????+ (???? - ??2 ???? ) ??

(IV.17)

????= -????

?? ????

1 ???????? (?????? - ????) + ????+ (????- ??^2 ???? ???? ) ??

Après avoir obtenue les équations nous pouvons développer le schéma bloc contrôle des puissances statoriques de la MADA représenté à travers la figure IV.9.

78

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

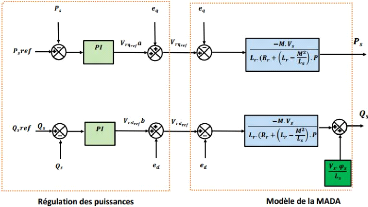
Figure IV-9. Contrôle des puissances statorique de la MADA

IV.5.2 Régulation avec un correcteur PI classique :

La figure IV-10 montre la régulation directe de puissance avec un régulateur PI sur les deux axes d et q dont les fonctions de transferts sont de la forme ?? ?? + ??? ??? .

Figure IV-10. Système régulé par un PI classique. IV.5.2.1 Synthèses du régulateur PI classique :

La fonction de Transfert en Boucle Ouverte (FTBO) avec les régulateurs s'écrit de la manière suivante :

????????	=	(?? ??	????	??????		(IV.18)
			????

On applique la méthode de compensation de pôles pour la synthèse du régulateur éliminer le zéro présent sur la fonction de transfert, nous choisissons :

79

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

Kp		LsRr		(IV.19)	Ki
=	M2 Ls (Lr - Ls)

Après l'application de la compensation des pôles, on obtient :

FTBO =	MVs KP M2 Ls (Lr - Ls)		(IV.20)

Ce qui nous donne FT en boucle fermée :

FTBF =	1		(IV.21)

Avec :

_MZ

1

T_r = K_p

Ls(LT-_Ls )

MV_s

Le terme i_r désigne ici le temps de réponse du système. Nous choisissons de fixer celui-ci à 200 ms, ce qui représente une valeur suffisamment pour l'utilisation faite sur l'éolienne où les variations de vent sont peu rapides et les constantes de temps mécanique sont importantes. Une valeur inférieure est susceptible d'engendrer des régimes transitoires avec des dépassements importants et ne présente pas d'intérêt particulier pour notre application [22]. Les termes K_Ket Ki sont alors exprimés en fonction de ce temps de réponse et des paramètres de la machine :

_M2

L_s (L_r - Ls)

MV_s

Ki =	1		LsRr
	MVs

1

T_r

K_p =

(IV.22)

IV.6 Commande du convertisseur cotée réseau (CCR)

Le schéma du CCR, du bus et du filtre R, L est illustré dans la figure IV.11.

80

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

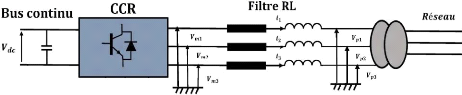
Figure IV.11-Schéma structurel du convertisseur cotée réseau, du bus et du filtre RL.

Le CCR est connecté au réseau via un filtre RL, le principal objectif du contrôle du convertisseur coté réseau se résume à réguler la tension du bus continu et à contrôler les puissances active et réactive transitant à travers ce dernier. [12]

Lorsque le glissement ?? est positif (mode hypo synchrone) le convertisseur CCR fonctionne en redresseur et en onduleur lorsque le glissement est négatif (mode hyper-synchrone), il est donc bidirectionnel [37].afin d'assurer le bon fonctionnement du système. Le convertisseur côté réseau est commandé tel que la puissance active et la puissance réactive côté réseau s'écrivent comme suit :

{

?? = 3 2 (???????? + ????????) (IV.23) ?? = 32 (???????? - ????????)

En alignant le vecteur tension de référence sur l'axe d :

{????= ???? ???? = 0

(IV.24)

Avec :

???? : Amplitude de la tension de phase du réseau. L'équation IV.23 devient alors :

?? = 3 (IV.25)

2 ????????

{ ?? = - 3 2????????

81

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

La figure IV.12 représente le schéma global du convertisseur cotée réseau.

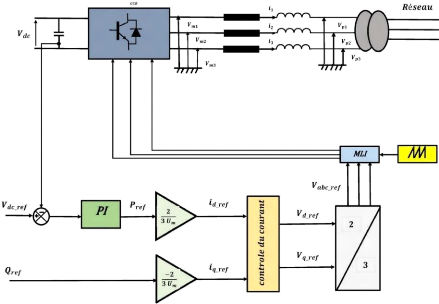
Figure. IV.12- Schéma global du contrôle du convertisseur cotée réseau.

IV.6.1 Commande du bus continu

Le bus continue vas lier la partie coté MADA au réseau en autorisant un transfert de de fréquences qui est différents pour les deux sources. [12]

Le bus continue joue le rôle de liaison entre le coté MADA et le coté réseau. La tension de référence du bus continu Vdc_ref f est comparée à celle mesurée aux bornes du condensateur équivalent Vdc . Le correcteur proportionnel intégral (PI) permet de maintenir une tension constante du bus continu en générant la référence du courant à injecter dans le condensateur ired , en autorisant un transfert de de fréquences qui est différents pour les deux sources.

K?? Gc(??) = Kp + P

(IV.26)

La relation entre la puissance active débitée par le système éolien et celle reçue à la sortie du pont en négligeant les pertes actives dans le convertisseur et dans les inductances de couplage est donné par :

82

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

Pdc = P_g (IV.27)

Udcidc = 3v. i = 3v

1 Vl2

(IV.28)

Avec : idc = C

dv dt

(IV.29)

La structure du système en boucle fermée est illustrée à travers la figure IV.13.

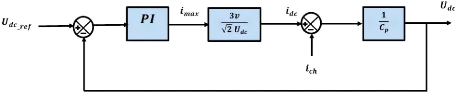
Figure IV.13- Modèle en boucle fermé de la boucle de tension du bus continu. La FTBO est donnée par :

FTBO(P) = (Kp + p`)	3v	1		(IV.30)
	Cp

La FTBF est donnée par :

FTBF(P)

FTBF(P) = 1 + FTBO(P)

1 + K_pP

(IV.31)

FTBF(P) =

1
wn2P2 +

2e P + 1 w_n

Donc :

Vdc

K??= 2?? _3V wn

Kp =

2E wn

(IV.32)

IV.6.2 Commande des courants dans le filtre :

Le filtre reliant le convertisseur CCR au réseau est constitué d'une inductance « L_t » et résistance « R_t », en appliquant les lois de Kirchhoff ont obtient :

83

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

[??????] = ????[????] + ???? ??

???? [????] + [??????] (IV.33)

Avec : ?? = 1,2,3

Les équations des tensions statoriques dans le repère diphasé ???? s'écrit :

??

?????? = ???????? + ???? ???? ???? - ???????????? + ??????

{ ?? (IV.34)

?????? = ???????? + ???? ???? ???? + ???????????? + ??????

Nous supposons que :

??

?????? = ?????????? + ???? ??????????

??

????????????????

??????????????

(IV.35)

=

+

A partir des deux équations précédentes, on obtient :

?? ??????

?????? = -?????????? - ???? ???? + ??????

(IV.36)

????????

{?????? = -?????????? - ???? ???? + ??????

Avec :

??????, ??????: les tensions modulées par le convertisseur dans le référentiel de Park. ?????? , ?????? : les tensions du réseau dans le référentielle de Park.

??????, ?????? : les composante directe et quadratique des courants du filtre.

Et :

{

?????? = ?????????????? (IV.37)
?????? = -?????????????? + ??????

84

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

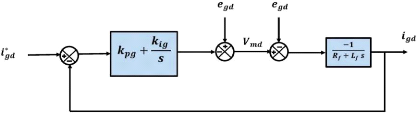
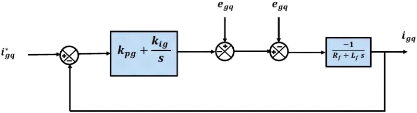
Figure IV.14- Contrôle des courants circulant dans le filtre RL

Les courants de référence ?????? * et ?????? * d'après la figure IV.14 sont respectivement issus du bloc de contrôle de la tension du bus continu et du contrôle de la puissance réactive au point de connexion du convertisseur cotée réseau (CCR) avec le réseau électrique. En négligeant les pertes dans la résistance ???? du filtre RL et tenant compte de l'orientation du repère ???? lié au champ tournant statorique (?????? = 0), l'équations III.19 devient :

{???? = ???????????? ???? = ????????????

(IV.38)

On déduit à partir de ces relations, qu'il est possible d'imposer les puissances active et réactive de référence, notées ici ????* et ????*, en imposant les courants de référence suivants :

* ?????? * ??????	= =	???? *		(IV.39)

La composante directe du courant ici pour contrôler la puissance réactive au point de connexion du CCR avec le réseau électrique, quant à la composante en quadrature est utilisée pour réguler la tension du bus continu. Avec ce principe, une puissance réactive de référence nulle peut alors être imposée (???? * = 0 ??????).

85

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

IV.7 Résultats de simulation

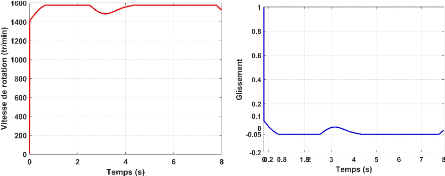
Figure IV.15. (b)-Glissement.

Figure IV.15.(a)-Vitesse de rotation.

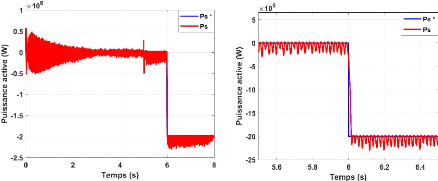
Figure IV.15. (c)-Puissance active statorique. Figure IV.15. (d)-Puissance active statorique

zoomé.

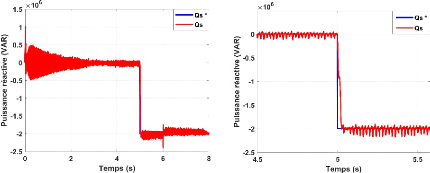
Figure IV.15. (e)-Puissance réactive Figure IV.15. (f)-Puissance réactive statorique

statorique. zoomé.

86

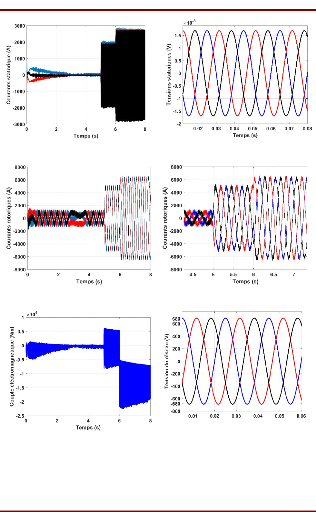
Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

Figure IV.15.(g)-Courants statorique. Figure IV.15. (h)-Tensions statorique.

Figure IV.15. (i)-Courants rotoriques. Figure IV.15. (j)-Courants rotoriques zoomé.

Figure IV.15. (l)-Tension du réseau.

Figure IV.15. (k)-Couple électromagnétique.

Figure IV.15. Résultats de la simulation de la commande vectoriel.

87

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

· Interprétation des résultats

La figure IV.15 illustre le résultat de simulation de commande direct de puissance actif et réactive de la MADA associé à un redresseur, un bus continu, un onduleur et un filtre, l'ensemble de la chaine est relié au réseau.

Les diffèrent paramètre de la chaine de conversion simulé sont donnée à travers l'annexe A, ainsi que les modèle sous forme de schéma block implémenter dans le logiciel MATLAB/Simulink/SympowerSystéme.

Afin d'examiner et de visualisé le comportement des puissances actif et réactives durant la simulation avec cette commande développer dans le section précédente ont impose une puissance actif statorique de ?????????? = -2. 10⁶ W à t = 6?? et une puissance réactive de ?????????? = -2. 10⁶ VAR à t = 5??.

On remarque d'après le résultat de simulation de la figure IV.15. (c) et la figure IV.15. (e) que la valeur de puissance actif et réactive statorique mesuré suivent bien leur valeur de référence avec un faible taux de perturbation externe, ceci est dut à la variation brusque de la vitesse, rapidement et sans dépassement, causé par le bon découplage des deux axes de commande d-q avec des faibles oscillations.

D'après la figure IV.15. (k) le couple électromagnétique prend la même allure à vitesse constant que la puissance actives car ces deux derniers sont proportionnels l'une vers l'autre.

On remarque à travers les figure IV.15. (g) figure IV.15. (i) les courant statorique est rotorique respectivement prennent en régime permanant une forme sinusoïdale.

Suivant la figure IV.15. (b) qui illustre le glissement de la MADA on s'aperçoit que la MADA fonctionne en mode hypo-synchrone de t=0 à t=0.2 car le glissement est non nul g > 0 et la vitesse de synchronisme n ?? = 1500 t??/min est supérieure à la vitesse de rotation n = 1475 t??/min .De t=0.8 à t=1.8 la MADA fonctionnent en mode hyper-synchrone car le glissement prend une valeur négative à ce moment-là , g < 0 et la vitesse de synchronisme n?? = 1500 t??/min est inférieure à la vitesse de rotation n = 1575 t??/min.

IV.8 Conclusion

Dans ce chapitre nous avons décrit la synthèse de la commande vectorielle a flux orientés qui permet d'assimilé le comportement de la MADA a une MCC là où il y'a un découplage naturel

88

Chapitre IV : Stratégie de commande des puissances actives et réactives de la MADA

entre la grandeur qui commande le flux et celle liée au couple, cela va nous permettre de mieux contrôler les puissance active et réactive de la MADA à l'aide des correcteurs PI.

Les deux modes de commande vectorielle ; la commande vectorielle directe en puissance de la MADA et indirecte à l'aide des correcteurs PI ont également était traitée.

On a pu constater que la stratégie de commande directe en puissance de la MADA est plus simple à mettre en oeuvre par rapport à la commande indirecte.

Enfin de ce chapitre une simulation de la commande directe en puissance a été simulée sous le logiciel MATLAB/Simulink afin d'observer le comportement des puissance active et réactive et des tensions et courants statorique envers cette commande. Les résultats obtenus ont montré la fiabilité de la commande qui a donné un bon suivie des puissance active et réactive statorique envers leurs signaux de références.

89

Conclusion générale

Conclusion générale

Le but de l'étude effectuée à travers ce mémoire est la proposition et la mise en oeuvre d'une stratégie de contrôle de l'énergie réactive d'un parc éolien qui est constituée d'éoliens à vitesse variables basée sur la machine asynchrone a double alimentation (MADA).la stratégie de commande de puissance réactive de la chaine de production de l'éolienne a été effectuée sous le logicielle Matlab\Simulink\SimPowerSystem.

Dans le premier chapitre un état de l'art et une présentation de l'énergie éolienne dans son état général, et les origines de l'énergie éolienne, ces principaux composant ainsi que les différents types d'éolienne qui existe dans le monde, on était traitée.

En deuxième temps, ce chapitre a fait l'objet d'abordé quelque notion de conversion de l'énergie cinétique, les diffèrent structure d'alimentation possible de la machine asynchrone a double alimentation configurations, et à la fin de ce chapitre les avantages et les inconvénients de l'énergie éoliennes ont également était présentés.

Ensuite dans le deuxième chapitre, nous avons tout d'abord procédé à la modélisation de la turbine éolienne a vitesse variable basée sur une machine asynchrone a double alimentation (MADA), de la modélisation du vent jusqu'au multiplicateur. Dans la deuxième partie du chapitre les différents modes de régulation de vitesse de rotations de l'éolienne, et les zones de fonctionnement d'une turbine éoliennes a vitesse variable ont également été énoncée. Après cela nous avons présentée l'algorithme de maximisation de puissance MPPT (Maximum Power Point Tracking), utilisé dans le système éolien étudié, à l'aide d'un asservissement de vitesse contrôlé par un régulateur de type PI (proportionnel intégral), dont les paramètres sont calculés par la méthode analytique. En fin, la simulation et la présentation des résultats obtenue d'un asservissement avec contrôle de la vitesse on était mis en oeuvre.

Le chapitre trois nous a permis de d'écrire le générateur choisi dans cette étude et d'effectuée sa modélisation dans différents repères. D'autre part, les convertisseur statique qui sont mis en oeuvre dans la chaine de conversion ont également était présentée et modelisée.La stratégie de commande MLI (Modulation de Largeur d'Impulsion) a également était présentée à travers ce chapitre.

Dans le dernier chapitre de ce mémoire la synthèse de la commande vectorielle a flux orientés qui permet d'assimilé le comportement de la MADA a une MCC là où il y'a un découplage naturel entre la grandeur qui commande le flux et celle liée au couple a était étudiée.

90

Conclusion générale

Les deux modes de commande vectorielle ; la commande vectorielle directe en puissance de la MADA et indirecte à l'aide des correcteurs PI ont également était traitée.

Enfin de ce chapitre une simulation de la commande directe en puissance a été simulée sous le logiciel MATLAB/Simulink\SimpowerSystem afin de contrôler les puissance active et réactive. Les résultats obtenus nous ont permis d'atteindre l'objectif de cette étude qui est le contrôle de l'énergie de la chaine de production éoliennes.

91

Bibliographie

Bibliographie

[1] F. POITIER, «Etude et commande de génératrices asynchrones pour l'utilisation de l'énergie éolienne-machine asynchrone a cage autonome-machine asynchrone a double alimentation reliée au réseau» universitée de nante, nante, 2003.

[2] A. CHEMIDI, «Analyse, modélisation et commande avancée d'une éolienne utilisée dans une ferme» Tlemcen-Algerie, 2015.

[3] M. STIEBLER, Wind energy systems for electric power generation, Einsteinufer 11, D10587 Berlin: Springer-Verlag Berlin Heidelberg, 2008.

[4] E. Hau, Wind Turbines , Fundamentals,technologies ,Applications Economics ,2nd Edition, Germany: Springer, 2005.

[5] F. Z. Joyce Lee, «GWEC | GLOBAL WIND REPORT 2021,» Rue Belliard 51-53 Brussels, Belgium, 2021.

[6] I. YAHYAOUI, Advances in Renewable Energies and Power Technologies Volume 1: Solar and Wind Energies, Amsterdam, Netherlands: Elsevier Inc., 2018.

[7] M. K. L. L. T. O. ,. M. M. Nadjah, « Etude de l'hélice d'une éolienne de 5 kW» chez Revue des Energies Renouvelables , Oum El Bouaghi,Algerie, 2008, pp. 257-264.

[8] J. T. M. S.M MUYEEN, Green Energy and Technology Stability Augmentation of a Grid-connected wind farm, japan: Springer-Verlag London Limited, 2009.

[9] «NORME BBC» [En ligne]. Available: http://www.norme-bbc.fr/eolienne/. [Accès le 05/06/2021 juin 2021].

[10] «eolupjv.wordpress,» wordpress, [En ligne]. Available: https://eolupjv.wordpress.com/les-types-deoliennes/. [Accès le 01 avril 2021].

[11] M. J. Wagner H-J, Introduction to wind energy systems, Berlin, Heidelberg, 2013.

[12] T. Ghennam, Supervision d'une ferme éolienne pour son intégration dans la gestion d'un réseau électrique, Apports des convertisseurs multi niveaux au réglage des éoliennes à base de machine asynchrone à double alimentation, Lille ,France: Ecole Doctorale SPI 072 (Lille I, Lille III, Artois, ULCO, UVHC, EC Lille), 2011.

[13] A. Zaimi, Optimisation de la commande d'une éolienne à base de machine synchrone à aimants permanents,these pour l'obtension d'ingenieur CNAM, Maroc, 2014.

[14] J. L. A. R. M. I. Gonzalo Abad, DOUBLY FED INDUCTION MACHINE MODELING AND CONTROL FOR WIND ENERGY GENERATION, IEEE PRESS,WILEY, 2011.

[15] «energie plus le site,» 12 mai 2010. [En ligne]. Available: https://energieplus-lesite.be/theories/eolien8/rendement-des-eoliennes/. [Accès le 25 avril 2021].

92

Bibliographie

[16] M. T. Yacine RAHAB, "Etude de l'association d'une génératrice asynchrone à double alimentation (GADA) et d'un convertisseur multiniveaux " Mémoire pour l'obtention de diplome de Master en Elechtrotechnique, Tizi-Ouzou,Algerie:UNIVERSITE MOULOUD MAMMERI DE TIZI-OUZOU, 2014.

[17] M. L. Abdelkader, Conception de la commande d'une machine asynchrone « Application de la commande par mode de glissement à une éolienne basée sur la Machine Asynchrone a Double Alimentation » Mmeoir en vue de l'obtention de Magister en Electrotechnique., Oran,Algerie: Université des Sciences et de la Technologie d'Oran Mohamed Boudiaf, 2018.

[18] L. MOURAD, Synthèse de lois de commande non-linéaires pour le contrôle d'une machine asynchrone à double alimentation dédiée à un système aérogénérateur Présentée pour l'obtention du grade de DOCTORAT 3ème Cycle En : Génie Electrique, Tlemcen,Algerie: Université Aboubakr Belkaïd - Tlemcen - Faculté de TECHNOLOGIE, 2016.

[19] H.-J. W. J. Mathur, Introduction to Wind Energy Systems.

[20] B. S. e. C. Youssouf, Commande des puissances actives et réactive d'une éolienne basée sur une generatrice asynchrone a double alimentation memoire pour l'obtention de diplome de master, Tlemen: univeristée de tlemcen, 2019.

[21] S. Fawzi, La Machine Asynchrone à Double Alimentation :Stratégies de Commande et Applications,These our l'obtention du diplôme de DOCTORAT EN SCIENCES EN ELECTROTECHNIQUE, CONSTANTINE: UNIVERSITE DES FRERES MENTOURI DE CONSTANTINE 1, 2018.

[22] C. Naim, Etude d'une Chaine de Conversion de l'Energie Eolienne these pour lobtention de doctorat, constantine: Université des Frères Mentouri de Constantine, 2018.

[23] Heier, «"Grid Integration of Wind Energy Conversion Systems",,» chez John Wiley & Sons, 1998.

[24] K. N., « Commande multi modèle optimale des éoliennes : Application à la participation des éoliennes au réglage de la fréquence» 2011.

[25] Aimani. S, «Modélisation de Différentes Technologies d'Eoliennes Intégrées dans un Réseau de Moyenne Tension,» Lille, 2005.

[26] L. MOURAD, Synthèse de lois de commande non-linéaires pour le contrôle d'une machine asynchrone à double alimentation dédiée à un système aérogénérateur these presentée pour l'obtention de grade de DOCTORAT 3ème Cycle, Tlemcen,Algerie.: Université Aboubakr Belkaïd - Tlemcen -, 2016.

[27] G. A., « Système éolien basé sur une MADA : contribution à l'étude de la qualité de l'énergie électrique et de la continuité de service» Nancy-France, 2010.

93

Bibliographie

[28] K. Bahia, Etude et commande d'une turbine éolienne utilisant une Machine Asynchrone à Double Alimentation mémoire en vue d'obtention de Magister en API, Tlemcen,Algérie: Université de TLEMCEN, 2011.

[29] A. Tamaarat, «Modelisation et commande d'un systém de conversion d'energie eolienne à base d"une Mada,» Buskra-Algerie.

[30] Y. Djeriri, H. M. Ahmed et Z. Boudjema, «Commande à structure variable de la machine asynchrone à double alimentation destinée à la production d'énergie éolienne,» chez 2nd International Symposium on Mechatronics & Renewable Energy ISMRE, Algerie, 2018.

[31] B. Youcef, etude et commande du moteur asynchrone à double alimenetation (MADA) par differentes techniques avancées these pour l'obtention du diplome de magistere, el Oued: centre universitaires d'el Oued, 2010.

[32] S. A. Rekiouk, commande des puissance active et reactive d'une eolienne basée sur une MADA these pour l'obtention de diplome de Master, tlemcen: universitée de tlemcen, 2017.

[33] M. Bouharkat, Etude de l'évolution des courants rotoriques d'une machine asynchrone à cage en régime dynamique , Thèse présentée pour l'obtention du diplôme de doctorat, Batna: 'université de Batna,, 2006.

[34] B. Lotfi, note de cours ,modelisation et commande de la machine asynchrone

[ http://baghli.com/dl/courscmde/cours_cmde_MAS.pdf], tlemcen: universitée de tlemcen, 2020.

[35] A. Mechernene, «Modélisation de l'onduleur de tension à deux niveaux commandé par MLI-ST et MLI-SVM,» chez Complément théorique 3, Tlemcen, 2020.

[36] B. D. M. A. ,. Y. D. Mohamed Allam, «Etude comparative entre la commande vectorielle directe et indirecte de la Machine Asynchrone à Double Alimentation (MADA) dédiée à une application éolienne,» Journal of Advanced Research in Science and Technology-ISSN: 2352-9989, 2014.

[37] G. A. Karim, Etude et commande d'une chaine de conversion éolienne moyenne puissance raccordée au réseau moyenne tension these pour l'obtention de Doctorat en sciences, Biskra,Algerie: Université Mohamed Khider - Biskra, 2017.

94

Annexe A

Annexe A

A-1-Paramètre de la turbine éolienne

Les paramètres de la turbine éolienne de 2.5 Mw utilisée dans cet étude sont les suivants :

Nom	Valeurs	Unité
Puissance mécanique	2,5.10^6	??
Densité de l'aire	1.225	Kg/??^3
Angle de calage	0	O
Nombre de pale	3	/
Rayon de pale	42	m
Gain du multiplicateur	100	/
Coefficient de friction	0.02	/
Moment d'inertie	127	Kg. ??^2
Vitesse spécifique optimal	0.48	/
Coefficient de puissance	8.1	/
??	0.7	/

A-2-Paramètres de la MADA

Les paramètres de la MADA utilisée dans ce mémoire sont donner dans le tableau suivant :

Nom	Valeurs	Unité
Fréquence du réseau	50	Hz
Puissance nominale du stator	2.10^6	W
Vitesse de synchronisme	1500	tr/min
Puissance active statorique	2.10^-6	W
Coefficient de friction	127	/
Courant nominal statorique	1760	A
Tension du réseau	690	V
Nombre de pair de pole	2
Couple électromagnétique	12732	N/m
Tension nominale du rotor	2070	V
Resistance rotorique	2,9.10^-3	Ohm
Résistance statorique	2,6.10^-3	Ohm
Inductance mutuel	2,5.10^-3	Henry

A-3-Paramètres de la liaison au réseau

Nom	Valeur	Unité
Pulsation du réseau	2??. 50	Rd
Tension bus continu	1150	V
Capacitée du bus continu	2,5.10^-3	F
Résistance de filtre	20.10^-6	Ohm
Inductance de filtre	400.10^-6	Henry

95

Annexe B

Annexe B

B-1-Paramètre du régulateur MPPT avec asservissement de vitesse de la turbine éolienne

Nom	Valeur	Unité
????	-500000	/
????	-2	/

B-2-Paramètre du régulateur Proportionnel Intégral de la MADA/CCM/CCR

Nom	Valeur	Unité
????	-0.2164	/
????	-184.3142	/
?????? ????	-40000	/
??????????	-30000000	/
??????????	0.3016	/
??????????	56.8489	/

B-3-Modèle Simulink de la turbine éolienne avec asservissement de vitesse implémentée dans l'environnement MATLAB :

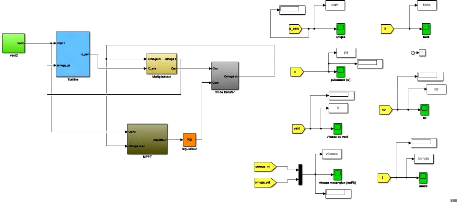
Figure B-3-Modèle Simulink de la turbine éolienne avec asservissement de vitesse implémentée
dans l'environnement MATLAB.

96

Annexe B

B-4-Modèle Simulink de la turbine éolienne sans asservissement de vitesse implémentée dans l'environnement MATLAB :

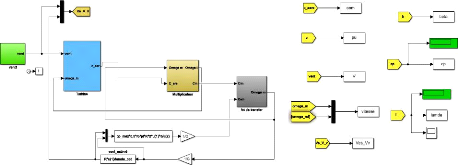
Figure B-4-Modèle Simulink de la turbine éolienne sans asservissement de vitesse implémentée
dans l'environnement MATLAB.

B-5-Modèle Simulink de la turbine éolienne connectée au réseau avec commande vectoriel implémentée dans l'environnement MATLAB :

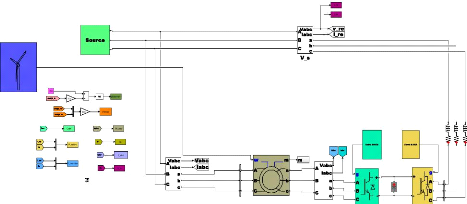
Figure B-5-Modèle Simulink de la turbine éolienne connectée au réseau avec la commande
vectorielle implémentée dans l'environnement MATLAB.

97

Annexe B

Le block de contrôle du convertisseur cotée MADA (CCM) implémentée sous le logiciel MATLAB est représentée à travers la figure B-5-(a) :

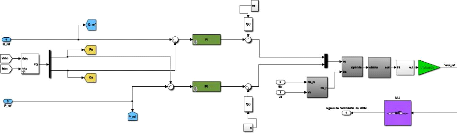
Figure B-5-(a)-Modèle Simulink du bloc de contrôle du convertisseur cotée MADA (CCM)
implémentée dans l'environnement MATLAB.

Le bloc de contrôle du convertisseur cotée réseau (CCR) implémentée sous le logiciel MATLAB est représentée à travers la figure B-5-(b) :

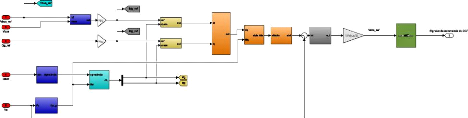
Figure B-5-(b)-Modèle Simulink du bloc de contrôle du convertisseur cotée réseau (CCR)
implémentée dans l'environnement MATLAB.

98

Résumé

Résumé

L'objet de ce projet est de mètres en oeuvre une stratégie de commande de puissance actif et réactive dans un parc éolien. Nous avons présenté l'états de l'art des éoliennes, puis nous avons étudier la partie mécanique intégrant la turbine, le multiplicateur, et ces deux types de control MPPT afin de définir la meilleure stratégie control de l'aérogénérateur, ensuite on s'intéressé à la partie électrique (la génératrice) associée à deux convertisseur cotée machine et cotée réseau. Enfin nous avons présenté la stratégie de commande du modèle complet du système éolien qui est basé sur une commande vectorielle par orientation du flux, les résultats des simulations montre que

l'objectif assigné a bien été atteint.
Mots-clés : Park éolien, Puissance réactive, MPPT, Machine asynchrone à double alimentation, commande vectorielle.

Abstract :

The purpose of this project is to implement an active and reactive power control strategy in a wind farm. We presented the state of the art and the current situation, then we studied the mechanical part integrating the turbine, the gearbox, the MPPT technique in order to define the best control of the wind turbine, then we are interested in the electrical part Doubly Fed Induction Machine (DFIM) associated with two Back-to-Back converters from where the mathematical models of the DC bus and the filter were presented. Finally, we presented the control strategy of the complete model based on a vector control by orientation of the flux and the results of the

simulations show that the assigned objectivehas been achieved.
Key words:Wind generator - Doubly Fed Induction Machine - Réactive energy power,FOC.

ÕÎáãáÇ :

äáÇ

ÉáÇÍ ÇäãÏÞ

. ÍÇíÑáÇ

ÉÚÑÒã

í ÉáÚÇÊãáÇæ ÉØÔäáÇ ÉÞÇØáÇ

í

ãßÍÊáÇ

ÉíÌíÊÇÑÊÓÇ ÐíäÊ

æå ÚæÑÔãáÇ ÇÐå

äã ÖÑÛáÇ

í ãßÍÊ

áÖ ÏíÏÍÊ

áÌ

äã MPPT ÉíäÞÊæ ÓæÑÊáÇ ÉÈáÚæ äíÈÑæÊáÇ

ÌãÏí

íÐáÇ

íßíäÇßíãáÇ ÁÒÌáÇ

ÇäÓÑÏ

ãË íáÇÍáÇ ÚÖæáÇæ

ÇðÑíÎ

. ÍÔÑãáÇæ

ÑãÊÓãáÇ

ÑÇíÊáÇ áÞÇäá ÉíÖÇíÑáÇ

ÌÐÇãäáÇ ãíÏÞÊ ãÊ

ËíÍ

) Ïáæã(

íÆÇÈÑåßáÇ ÁÒÌáÇÈ

ÇäããÊå Ç

ãË ÉíÍíÑáÇ ÊÇäíÈ ÑæÊáÇ

. ÞÞÍÊ ÏÞ ÏÏÍãáÇ ÏåáÇ ä ÉÇßÇÍãáÇ ÌÆÇÊä ÊÑåÙæ áãÇßáÇ ÌÐæãäáá ãßÍÊáÇ ÉíÌíÊÇÑÊÓÇ ÇäãÏÞ .ÉíáÚÇÊáÇ ÉÞÇØáÇ - ÉäãÇÒÊãáÇ ÑíÛ ÉÌæÏÒãáÇ ÉíÐÛÊáÇ Éá - ÍÇíÑáÇ Ïáæã :ÉíÍÇÊãáÇ ÊÇãáßáÇ

99