II- Méthode d'estimation du modèle
Pour estimer notre modèle, nous allons utiliser la
méthode des moindres carrées ordinaires (MCO). Il s'agit d'une
méthode élaborée par Legendre et Gauss au début du
XIXème siècle pour comparer les données
expérimentales, généralement entachées d'erreurs de
mesure, à un modèle mathématique, censé
décrire ces données. La méthode des moindres
carrées ordinaires permet alors de minimiser l'impact des erreurs
expérimentales en « ajoutant de
l'information » dans le processus de mesure. Cette estimation
se faire l'aide du logiciel Eviews 8. La validation statistique de la
qualité globale du modèle est appréciée par le
coefficient de détermination du modèle (R2) et le
test de Fisher. Le R2 mesure l'adéquation entre un
modèle issu d'une régression linéaire simple ou multiple
et les données qui ont permis de l'établir. Bref, le coefficient
de détermination indique la qualité d'ajustement du
modèle, plus il est proche de 1, plus la qualité du modèle
est bonne. Le R2 se définit alors comme la part de la
variance expliquée dans la variance totale. La formule du R2
donnée par :
R2 = 1- (SCR/SCT) où SCR est la somme des
carrées des résidus et SCT la somme des carrées totaux.
Par ailleurs, il convient de souligner que le principal
défaut du coefficient de détermination est de croitre avec le
nombre des variables explicatives. Or, on sait qu'un excès des variables
produit des modèles non robustes. C'est pourquoi on s'intéresse
davantage sur le coefficient de détermination ajusté. Ce dernier
tient compte du nombre des variables.
La significativité globale du modèle est
appréciée par le test de Fischer à k et (n-k-1)
degré de liberté (k étant le nombre des variables
explicatives) qui indique si les variables explicatives ont une influence sur
la variable à expliquer. Les hypothèses sous-tendant cette
analyse sont : sous l'hypothèse nulle H0 : « tous les
coefficients du modèle sont nuls » contre l'hypothèse
alternative « il existe au moins un coefficient non nul ». La
formulation mathématique de ces hypothèses nous donne :
H0 : â1 = â2 = ....
= âk = 0
H1: âi ? 0
Avec k le nombre de paramètres estimés et i
variant de 1 à k.
L'arbitrage entre le rejet ou l'acceptation de
l'hypothèse nulle se fait par la comparaison de la valeur de la
F-statistique estimée à celle tabulée par Fischer. Le
logiciel Eviews 8fournit automatiquement la probabilité associée
à la F-statistique calculée, ce qui facilite l'analyse. Il
suffira donc de comparer la probabilité associée à la
F-statistique au seuil de 5% retenu. Dans le cas où la
probabilité associée au prob (F-statistique) < 5%, alors H0
sera rejetée au profit de H1 selon laquelle la régression est
globalement significative.
La décision de la significativité globale du
modèle peut se faire par comparaison de la statistique de Fisher
calculée (Fcal) à la statistique de Fisher tabulée (Ftab).
Ø Si Fcal > Fth alors on rejettera
l'hypothèse nulle et on conclut qu'il existe au moins un coefficient
non nul et donc que le modèle est globalement significatif.
Ø si Fcal < Fth alors le modèle n'est pas
globalement significatif.
Pour se prononcer sur la significativité individuelle
des variables, on utilise la statistique de student qui est fournie par le
logiciel. Sous l'hypothèse nulle (H0), on teste l'hypothèse nulle
le coefficient n'est pas significatif contre l'hypothèse alternative le
coefficient est significatif. Mathématiquement, on aura :
H0 : âi = 0 ; le coefficient
n'est pas significatif ;
H1 : âi ? 0 ; le coefficient
est significatif.
La règle de décision consiste à comparer
la statistique calculée de student (tcal) à la
statistique tabulée (ttab). Ainsi, Si la statistique
calculée de Student (tcal) est supérieure à la
statistique théorique t5% (n-k), ou, la probabilité
calculée est inférieure à 5%, on rejette
l'hypothèse nulle et on conclut que la variable est statistiquement
significative au seuil de 5%. Dans le cas contraire, on accepte
l'hypothèse nulle et on conclut que la variable n'est pas significative
au seuil 5%.
Le test de Durbin Watson
Le test de Durbin et Watson (DW) permet de
détecter une autocorrélation des erreurs d'ordre 1.Le test
d'hypothèses est le suivant :
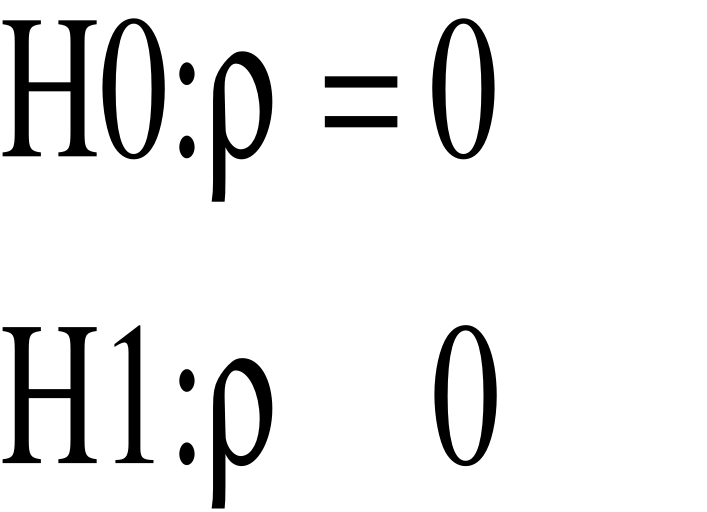
Pour tester l'hypothèse nulle H0, nous calculons la
statistique de Durbin et Watson :
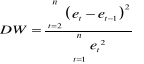 où où  sont les résidus de l'estimation du modèle. sont les résidus de l'estimation du modèle.
On peut approximer la statistique de DW de la façon
suivante : 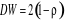 avec avec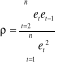
Les critères de décisions sont les
suivantes :
- Si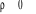 , il y a absence de corrélation dans les résidus, alors le , il y a absence de corrélation dans les résidus, alors le
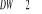
- Si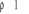 , il y a corrélation positive dans les résidus, alors le , il y a corrélation positive dans les résidus, alors le
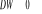
- Si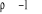 , il y a corrélation négative dans les résidus,
alors le , il y a corrélation négative dans les résidus,
alors le 
Le test
d'homoscédasticité
L'application des MCO comme méthode d'estimation
suppose que les variables ont des variances constantes. Dans le cas contraire,
ces variables seront dites hétéroscédastiques. Cependant,
il est difficile d'affirmer avec certitude que les perturbations sont
hétéroscédastiques et de connaitre la forme de
d'hétéroscédasticité. D'où l'utilité
de détecter la présence
l'hétéroscédasticité et de pouvoir le corriger.
Plusieurs tests existent pour la détection de
l'hétéroscédasticité : test de Goldfeld-Quandt ;
test de Gleisjer ; test de White ; test de Breusch-Pagan ; etc. Le test de
White sera utilisé pour la présente étude. Il est
fondé sur une relation significative entre le carré du
résidu et une ou plusieurs variables explicatives en niveau et au
carré dans une équation de régression. Les
hypothèses nulle(H0) et alternative (H1) sont :
H0 : Absence
d'hétéroscédasticité
H1 : Présence
d'hétéroscédasticité
Si n représente le nombre d'observations du
modèle et R2 le coefficient de détermination. Si l'un
de ces coefficients de régression est significativement différent
de 0, alors on accepte l'hypothèse
d'hétéroscédasticité.
Le test de White est fondé sur une relation
significative entre le carré du résidu et une ou plusieurs
variables explicatives en niveau et au carré au sein d'une même
équation de régression.
Soit n le nombre d'observations disponibles pour estimer les
paramètres du modèle et R2 le coefficient de
détermination. Si l'un de ces coefficients de régression est
significativement différent de 0, alors on accepte l'hypothèse
d'hétéroscédasticité. Nous pouvons procéder
à ce test soit à l'aide d'un test de Fisher classique de
nullité de coefficients.
H0 : a1 = b1 = a2 =
b2= . . . = ak = bk = 0
Si on refuse l'hypothèse nulle, alors il existe un
risque d'hétéroscédasticité.
Soit recourir à la statistique LM qui est
distribuée comme un ÷2 à p = 2 k degrés de
liberté (autant que de coefficients que nous estimons, hormis le terme
constant), si n × R2> ÷2(p) lu dans la table au seuil
á, on rejette l'hypothèse d'homoscédasticité des
erreurs.
Le test d'autocorrélation des
résidus : la statistique de Breusch-Godfrey.
L'autocorrélation des erreurs peut être
observée pour plusieurs raisons : l'absence d'une variable explicative
importante dont l'explication résiduelle permettrait de « blanchir
» les erreurs ; une mauvaise spécification du modèle, les
relations entre la variable à expliquer et les variables explicatives ne
sont pas linéaires et s'expriment sous une autre forme que celle du
modèle estimé (logarithmes, différences premières,
etc.) ; un lissage par moyenne mobile ou une interpolation des données
crée une autocorrélation artificielle des erreurs due à
l'usage de ces deux opérateurs. On distingue deux types
d'autocorrélation : celle positive caractérisée par
des successions de résidus de même signe et celle négative
qui est caractérisée par une alternance positive et
négative des résidus.
Le test consiste à tester l'hypothèse nulle les
erreurs sont non corrélées contre l'hypothèse alternative
erreurs corrélées. La statistique est donnée par : BG =
n×R2 qui est comparée au ÷2(p) Avec p le
nombre de retard des résidus, n le nombre d'observations et
R2le coefficient de détermination. Le test consiste à
tester l'hypothèse nulle les erreurs sont non corrélées
contre l'hypothèse alternative erreurs corrélées. Si BG
< ÷2(p) on accepte l'hypothèse nulle d'absence
d'autocorrélation. Dans le cas contraire, on rejette l'hypothèse
nulle et on conclut que les erreurs sont corrélées au seuil de 5
%.
Le test de normalité des
erreurs :
Pour calculer des intervalles de confiance
prévisionnels et aussi pour effectuer les tests de Student sur les
paramètres, il convient de vérifier la normalité des
erreurs. Il existe un paquet de tests de normalité des erreurs (le test
de Shapiro-Wilk, le test de Jarque-Bera, le test d'Anderson-Darling etc.). Dans
le cas de notre étude, nous utilisons le test de Jarque-Bera. Le test de
(Jarque et Bera, 1984) fondé sur la notion de Skewness
(asymétrie) et de Kurtosis (aplatissement). Ce test recherche si les
données suivent une loi normale. La statistique de Jarque et Bera suit,
sous l'hypothèse de normalité, une loi de Khi-deux à deux
degré de liberté. Les hypothèses sont les suivantes :
H0 : les données suivent une loi
normale
H1: les données ne suivent pas une loi
normale.
On accepte au seuil de 5% l'hypothèse de
Normalité si la probabilité critique est supérieure
à 5%. On rejette au seuil de 5% l'hypothèse de Normalité
le cas contraire.
Vérification des hypothèses
Pour vérifier nos deux hypothèses et savoir si
chacune des variables qui y ressort explique ou influence effectivement la
variable à expliquer, nous observerons les signes des coefficients
estimés associés à chacune de variables explicatives.
Ainsi, afin de vérifier l'effet positif de la libéralisation
financière interne sur la croissance économique au Cameroun, nous
observerons le signe du paramètre (â1) de la variable
logM2, et le signe du paramètre (â2) de la variable
logCp. Si leurs signes sont positifs, ce que la libéralisation
financière interne influence effectivement positivement la croissance
économique au Cameroun. De même pour déceler l'effet de la
libéralisation du compte de capital sur la croissance économique
au Cameroun, on considèrera le signe du paramètre
â3 associé à la variable Kp. Si le signe est
positif, on valide la deuxième hypothèse.
CONCLUSION
Ce chapitre était destiné à
présenter la méthodologie de réalisation de notre
étude empirique de détection de l'effet de la
libéralisation financière sur la croissance économique au
Cameroun. L'estimation économétrique de notre modèle se
fera à l'aide de la méthode des moindres carrés
ordinaires, sur la période 1990-2015. Le traitement effectué
à l'aide du logiciel stata nous donnera les résultats que nous
allons présenter et interpréter dans le chapitre suivant
(chapitre 4).
| 


