II.3.4. Analyses statistiques
Nous avons procédé à l'analyse de
variance (ANOVA) selon le dispositif complètement randomisé (CRD)
et la comparaison des moyennes était faite sur base du test de la plus
petite différence significative (PPDS). Le calcul de coefficient de
variation a été réalisé pour évaluerle
degré deprécision de l'expérience. Le pourcentage a
été trouvé le cas échéant. A cet effet, le
lecteur voudra bien se référer aux formules consignées
dans les lignes qui suivent selon Asanzi (2015).
1°facteur de correction (F)
F=  ou G = grand total, r = répétition, t = traitement ou G = grand total, r = répétition, t = traitement
2° Somme des carrés totale
(SCT) :
SCT = 
DLT = Degré de liberté total
DLT = rt-1
3° Somme des carrés traitements
(SCTrt)
SCTrt = 
DLTrt= Degré de liberté traitement
DLTrt = t-1
4° Somme des carrés de l'erreur
(SCE)
SCE = DCT - DCTrt
DLE=Degré de liberté de l'erreur
DLE = DLT - DLTrt
Tableau 2 : Eléments de l'analyse de
variance pour le dispositif expérimentalcomplètement
randomisé (CRD)
|
Sources de variation
|
Degré de liberté
|
Somme des carrés
|
Carré moyen
|
Fcal
|
Ftab
|
|
0,05 0,01
|
|
Traitement
Erreur
Total
|
t-1
DLT-DLTRT
t.r-1
|
ScTrt
ScE
Sct
|
ScTrt/t-1
ScE/t(r-1)
|
CMTrt/CME
|
|
Sources : Asanzi, 2015
Si la valeur de F calculé est inférieure
à la valeur de F tabulaire au seuil de probabilité de 5% ;
la différence entre les traitements n'est pas significative (n.s.).
Donc, toutes les moyennes des traitements sous examen sont égales.
Par contre, si la valeur de F calculé est
supérieur à la valeur de F tabulaire au seuil de 5% et 1% ;
on dit que la différence est respectivement significative (*) et
hautement significative (**). Donc, il existe au moins une des moyennes des
traitements qui diffère des autres. Ainsi, pour confirmer la conclusion
de cette analyse de variance, il est recommandé d'examiner l'existence
de cette différence en appliquant le test de la plus petite
différence significative (ppds) ou la comparaison orthogonale.
La valeur de ppds obtenue sera comparée à la
différence en valeur absolue entre les moyennes de différents
traitements prises deux à deux. Si la valeur de ppds est
inférieure à cette différence, les deux moyennes sont
dites statiquement différentes. Dans le cas contraire, elles sont
égales.
ppds = t0,05 
Où t0,05 : valeur tabulaire de Student
test ;
S2 : carré moyen de l'erreur ;
r : nombre de répétitions(Asanzi, 2015).
Le coefficient de variation (cv) est égal à la
racine carré du carré moyen de l'erreur (CME) divisée par
la grande moyenne,
CV = 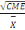  .100 .100
Le calcul de pourcentage (%) nous a permis d'apprécier
certaines données ou proportions. La formule suivante a
été utilisée à ce fait :
% =  
Où : % fréquence en pourcentage,
n = taille de l'échantillon, 100 = constante.
| 


