Résolution d'un problème de satisfaction de contraintes sur les intervalles

2.6 Réseaux de contraintes temporelles

2.6.1 Quelques éléments sur la représentation du temps

La modélisation du temps est une thématique déjàancienne en intelligence artificielle. Elle s'applique à la représentation de connaissances, la compréhension de la langue naturelle, le raisonnement de sens commun, le raisonnement qualitatif, le diagnostic ou la planification. Différents modèles ont étédéveloppés et peuvent se décliner selon différents aspects : temps ponctuel ou sous forme d'intervalle, temps totalement ou partiellement ordonné(temps linéaire ou branché), temps discret ou dense, bornéou non, incluant différentes granularités ou non [13]. Nous nous focalisons ici sur les approches qualitatives.

2.6.2 Contraintes temporelles qualitatives

Les principales représentations qualitatives du temps sont l'algèbre d'intervalles de Allen [4, 5] et l'algèbre de points de Vilain et Kautz [6].

Algèbre des intervalles

L'algèbre des intervalles (IA) est un calcul pour les raisonnements spatio-temporels créépar James F. Allen en 1983 [4, 5]. Cette algèbre définit les relations possibles entre des intervalles de temps et propose une table de composition. Elle peut être utilisée comme base pour des raisonnements portant sur la description temporelle des évènements. Dans la théorie d'Allen, 13 relations de base (ou relations atomiques) décrivent toutes les manières possibles d'ordonner les extrémités de deux intervalles {b,m, o, s, d, f, a, mi, oi, si, di, fi, eq}

30

(voir Figure 8).

Par exemple, pour X = [X ,X+] et Y = [Y ,Y +] deux intervalles non réduits à un point, X⁺<Y s'écrit X {b} Y (pour before), X⁺ = Y s'écrit X {m} Y (pour meet) et X <Y <X+<Y + s'écrit X {o} Y (pour overlap).

Relation	Symbole	Inverse		Symbole	X before Y
b	Y after X	a		X meets Y
m	Y met-by X	mi		X overlaps Y
o	Y overlapped-by X	oi		X starts Y
s	Y started-by X	si		X during Y
d	Y contains X	di		X finishes Y
f	Y finished-by X	fi		X equals Y
eq	Y equals X	eq

Illustration

X

X

Y

Y

Y

X

X

X

Y

Y

X

Y

Y

X

FIGURE 2.8 - Les treize relations de Allen entre deux intervalles de temps X et Y .

Définition 2.6.1. (réseau de contraintes d'algèbre Intervalle)

Le réseau IA peut être exprimée comme un réseau de contraintes, impliquant un ensemble de variables {X1, ...,X_n}, oùchaque variable représente un intervalle temporel. Le domaine de chaque variable est l'en-semble des couples de nombres réels (par exemple, Di = {(a, b) tel que a,b E R, a<b}), représentant les points du début et de la fin de l'intervalle correspondant. Les contraintes binaires entre les paires des variables de l'intervalle sont donnés comme des relations IA la contrainte _Cij entre xi et xj est défini comme Cij inclue ou égale à {b, m, o, s, d, f, a, mi, oi, si, di, fi, eq}. Une solution est la cession d'une paire de

numéros à chaque variable telle qu'aucune contrainte n'est violé. Le test de violation des contraintes nécessite la traduction de la relation entre une paire d'intervalles (a1, b1), (a2, b2) dans une disjonction de relations qualitative. Une solution peut également être associéà un étiquetage cohérent, l'attribution d'un rapport atomique de chaque contrainte qui est conforme à une solution [7].

Exemple :

Les relations entre intervalles d'Allen peuvent être utilisées pour représenter une succession d'événements sous forme d'un réseau de contraintes [10], comme décrit dans la Figure 2.9(a). L'énoncé Béchir lisait son journal tout en prenant son petit déjeuner. Il acheva sa tasse de caféet posa son journal. Après le

petit déjeuner, il partit se promener est représentéau moyen de quatre intervalles de temps, associés ^àdes actions : lire son journal, prendre son petit déjeuner, boire son café, partir se promener. Les relations

temporelles entre ces événements sont représentées par des disjonctions de relations d'Allen. Ainsi Après le petit déjeuner, il partit se promener devient Id{m,b}I_p représentépar une arête entre les noeuds Id (ou Petit-Déjeuner) et I_p (ou Promenade) du graphe. L'arête est étiquetée par la relation {m, b} qui signifie juste avant ou avant. On pourrait également afficher la relation inverse {mi, a} entre I_p et Id. De la même manière, l'énoncé Béchir lisait son journal tout en prenant son petit déjeuner est représentée par l'arête {d, di,o, oi, f, fi, s, si, eq} entre les noeuds Ij (ou Journal) et Id : l'information temporelle tout en étant très vague, on garde à priori toutes les relations incluant un recouvrement des deux intervalles.

Petit-déjeuner

Journal

Promenade

{f,fi}

Café

{d,di,o,oi,f,fi,s,si,eq}

{s,f,d}

{m,b}

(a) Graphe d'origine

Petit-déjeuner

Journal

Promenade

{f,fi}

Café

{d,di,o,oi,f,fi,s,si,eq}

{s,f,d}

{m,b}

(a) Propagation des contraintes

FIGURE 2.9 - Relations qualitatives entre les intervalles

L'utilisation des règles de composition des relations d'Allen permet de simplifier les étiquettes des relations

31

32

(par des techniques de propagation de contraintes [11]). Par exemple, sachant que:

· la lecture du journal et le cafés'achèvent ensemble : Ij {f, fi } I_c

· le caféest une partie du petit déjeuner : I_c {s, f, d} Id

On en conclut que les relations oi, di, si sont impossibles entre Ij et Id (la lecture du journal ne peut s'achever après le petit déjeuner, (voir Figure 2.9(b))). De fait, par composition :

Ij {f, fi} I_c ? I_c {s, f, d} Id ? Ij {d, o, f, fi, s, eq} Id

Un scénario possible cohérent est représentésur la Figure 2.10.

Journal

Café

	Petit-déjeuner		Promenade

FIGURE 2.10 - Scénario possible pour l'exemple

Avec les réseaux IA, c'est l'arrangement des intervalles qualitatifs qui nous intéresse, pas l'instanciation cohérente particulière qui a conduit à l'arrangement. Il y a zéro ou un nombre infini de différentes ins-tanciations cohérentes des variables dans un réseau d'IA, mais il y a seulement un nombre fini de différents arrangements conformes des intervalles. Une instanciation consistante possible qui conduirait à l'arrangement montrédans la Figure 2.10 est le journal--(2,3), Petit-déjeuner--(0,4), promenade--(5,6), et Café--(1,3), oùnous assimilons les noms des sommets avec les variables qu'ils représentent.

Algèbre des points

En raison des limites de calcul de l'IA de modèle alternatif, l'algèbre des points (PA) , créépar Vilain et Kautz en 1986 [6], qui est moins expressif, est souvent utiliséau lieu de l'algèbre IA. Dans ce modèle les informations sont exprimées par des contraintes sur les points. Dans cette algèbre, trois relations de base (précède (<), identique (=) et suit (>)) sont considérées.

33

Définition 2.6.2. ( Réseaux de contraintes d'algèbre de point)

Un réseau d'algèbre de point (réseau PA) implique un ensemble de variables {x1, ...,x_n }, oùchaque variable représente un point du temps. Le domaine de chaque variable est l'ensemble des nombres réels R, qui représente des points du temps que la variable peut assumer. Les contraintes sont données comme des éléments PA, ayant leur sens algébrique sur les réels [7].

Exemple :

À titre d'exemple de représentation de l'information temporelle dans le cadre PA, on considère la description des événements représentés sur la Figure 2.11(a), la phrase fixe la relation entre certaines extrémités des intervalles du temps sur laquelle Béchir a lu son journal et sur laquelle Béchir buvait son café, mais il reste indéfinie sur les autres. Nous représentons ce par le réseau de la Figure 2.11(a), oùJournal- et Journal+ représentent les points de départ et de fin de l'intervalle. Le réseau est déjàminimale, il montre également les relations possibles entre toutes les paires des points. Un scénario cohérent possible est représentésur la Figure 2.11(b). Comme avec les réseaux IA, c'est l'arrangement qualitatif des points qui nous intéresse, pas l'instanciation consistante particulière qui a conduit à l'arrangement.

34

- Journal

- Café

< + Café

+ Journal

(a)

(b)

(c)

(d)

(e)

(f)

Journal Café (g)

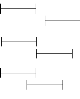
FIGURE 2.11 - Représentation des relations qualitatives entre les points : (a) Exemple Béchir a mis le papier vers le bas et bu le dernier de son café. (b) Un scénario possible

Une possible instanciation consistante qui conduirait à l'arrangement montrédans la Figure 2.11(b) est Journal^--2, Journal⁺-3, cafe^--1 et cafe⁺-3.