Résolution d'un problème de satisfaction de
contraintes sur les
intervalles
Mohamed Ali Souibgui
Sami Gharsalli
e-mail :dali922011@
gmail.com
12 juin 2015
1
Remerciements
Nous tenons à remercier toutes les personnes qui ont
contribuéau succès de notre projet et qui nous ont
aidélors de la rédaction de ce rapport.
Nos premiers remerciements sont pour notre encadrant Mr.
Wady Naanaa qui nous a guidépendant
l'élaboration de ce projet, sans lui la tache serait plus difficile.
Nous remercions également les membres de jurys, merci
au professeur Ayeb Béchir qui nous a fait
l'honneur d'être le président des jurys, et merci à Mme
El Kamel Hager pour la lecture
détaillée du rapport.
Enfin, nous tenons à remercier nos familles et nos amis
pour leurs valeureux soutien.
2
Table des matières
|
1 Introduction genérale
2 Problèmes de satisfaction de
contraintes
|
6
8
|
|
2.1
|
Qu'est-ce qu'une contrainte?
|
8
|
|
2.1.1
|
Quelques caractéristiques des contraintes
|
8
|
|
2.1.2
|
Définition d'une contrainte
|
9
|
|
2.1.3
|
Aritéd'une contrainte
|
9
|
|
2.1.4
|
Différents types de contraintes
|
9
|
|
2.2
|
Problèmes de satisfaction des contraintes
|
10
|
|
2.2.1
|
Définition informelle
|
10
|
|
2.2.2
|
Définition formelle
|
11
|
|
2.2.3
|
Les variables du CSP
|
11
|
|
2.2.4
|
Graphe de contraintes
|
12
|
|
2.2.5
|
Solution d'un CSP
|
13
|
|
2.2.6
|
Notion de CSP surcontraint ou souscontraint
|
14
|
|
2.3
|
Modélisation de quelques problèmes sous la forme
d'un CSP
|
14
|
|
2.3.1
|
Exemple 1 : Problème du zèbre
|
14
|
|
2.3.2
|
Problème de Coloriage d'une carte
|
16
|
|
2.4
|
Quelques algorithmes de résolution de CSP
|
19
|
|
2.4.1
|
L'algorithme »génère et teste»
|
19
|
|
2.4.2
|
L'algorithme »simple retour-arrière»
|
21
|
|
2.4.3
|
L'algorithme »anticipation»
|
23
|
3
|
2.5
2.6
|
Intégration d'heuristiques
Réseaux de contraintes temporelles
2.6.1 Quelques éléments sur la
représentation du temps
2.6.2 Contraintes temporelles qualitatives
|
28
29
29
29
|
|
2.7
|
Les problèmes de planification
|
34
|
|
|
2.7.1 Contraintes de précédence
|
35
|
|
|
2.7.2 Le graphe de contraintes temporelles
|
35
|
|
2.8
|
Conclusion
|
36
|
|
3
|
Résolution d'un problème de satisfaction de
contraintes
|
37
|
|
3.1
|
Introduction
|
37
|
|
3.2
|
Description du problème
|
37
|
|
3.3
|
Exemple d'un problème
|
38
|
|
3.4
|
Modélisation sous la forme d'un CSP
|
38
|
|
3.5
|
Résolution du problème
|
38
|
|
|
3.5.1 Résolution par l'algorithme génère et
teste
38
|
|
|
|
3.5.2 Résolution par l'algorithme simple retour
arrière (ou backtrack)
|
39
|
|
|
3.5.3 Résolution par l'algorithme d'anticipation
|
39
|
|
|
3.5.4 Résolution proposée
|
40
|
|
3.6
|
Algorithme proposé
|
43
|
|
|
3.6.1 algorithme
|
43
|
|
|
3.6.2 Exemple
|
45
|
|
3.7
|
Outils d'implémentation
|
53
|
|
3.8
|
Expérimentation
|
54
|
|
|
3.8.1 Complexitéde l'algorithme proposé
|
54
|
|
|
3.8.2 Satisfaction des contraintes
|
55
|
|
3.9
|
Conclusion
|
57
|
|
4
|
Conclusion générale
|
58
|
4
Table des figures
2.1 Graphe vs hypergraphe 12
2.2 gouvernorat de Kasserine 17
2.3 Coloriage correcte du gouvernorat de Kasserine 18
2.4 Exécution de génère et teste sur un CSP
simple 21
2.5 Exécution de SimpleRetourArrière (cette image
est empruntée au »Guide to Constraint Pro-
gramming» de Roman Bartak) 23
2.6 Exécution
d'anticipation (cette image est empruntée au »Guide to Constraint
Programming»
de Roman Bartak) 27
2.7 Exécution d'anticipation 2
(cette image est empruntée au »Guide to Constraint
Programming»
de Roman Bartak) 27
2.8 Les treize relations de Allen entre deux intervalles de temps
X et Y 30
2.9 Relations qualitatives entre les intervalles 31
2.10 Scénario possible pour l'exemple 32
2.11 Représentation des relations qualitatives entre les
points : (a) Exemple Béchir a mis le papier
vers le bas et bu le dernier de son café. (b) Un
scénario possible 34
2.12 Un graphe de contraintes temporelles de
précédence 36
3.1 Pourcentage des contraintes satisfaites par rapport au nombre
de contraintes sur problème
impliquant 100 variables 55
3.2 Pourcentage des contraintes
satisfaites par rapport au nombre de contraintes sur problème
impliquant 300 variables 56
5
3.3 Pourcentage des contraintes satisfaites par rapport au nombre
de contraintes sur problème
impliquant 600 variables 56
3.4 contraintes satisfaites par rapport au nombre de variables
57
6
Chapitre 1
Introduction genérale
Sans contrainte, on tourne en rond.
Mathieu Chedid
Dans notre vie quotidienne on est en train de résoudre
et de satisfaire des problèmes de contraintes sans le savoir.
Comment préparer un plat qui soit délicieux tout
en prenant soin de notre santé?
Comment arriver à temps à destination sans faire
des accidents?
Comment bien vivre selon nos moyens?
Ce types de taches n'exige pas d'algorithme
sophistiquéou d'ordinateurs pour l'accomplir, mais on doit prendre en
compte que les problèmes deviennent plus compliqués lorsque le
nombre de variable et de contraintes croient, par exemple on trouve que
ça prend du temps pour choisir un film qui satisfait un grand nombre
d'amis. Imaginons maintenant, la difficultéet le temps qu'il faut pour
faire le planning des voyages des trains. Il faut faire en sorte que les trains
ne coïncident pas sur le même chemin, un conducteur ne peut pas
conduire deux trains simultanément, les voyages doivent se faire dans un
intervalle de temps limité, le nombre de voyageurs ne doit pas
dépasser la capacitédu train tout en satisfaisant tous les
voyageurs, etc... Donc, à chaque fois que la complexitédevient
importante, on est obligéd'avoir recourt aux ordinateurs pour nous aider
à trouver des solutions acceptables et efficaces en terme de temps.
Ce type de problème s'appelle Les problèmes de
satisfaction des contraintes ou CSP (Constraint Sa-
tisfaction Problem) De nos jours, les CSP font le sujet de
plusieurs recherches à la fois en intelligence
7
artificielle et en recherche opérationnelle. Ils sont
notamment au coeur de la programmation par contraintes, un domaine fournissant
des langages de modélisation de problèmes et des outils
informatiques les résolvant [9].
Nous nous intéressons, dans ce projet de fin
d'étude, à résoudre un problème CSP particulier.
Dans un premier temps, nous étudierons les problèmes de
satisfaction des contraintes, en général et quelques algorithmes
déjàproposés pour les résoudre. Dans le Chapitre 3,
nous allons poser le problème auquel nous nous intéressons puis
nous montrons que les algorithmes étudiés dans le Chapitre 2
demande beaucoup de temps pour le résoudre. Ensuite, nous
présentons notre propre algorithme, avec un exemple explicatif. Enfin,
nous présenterons une partie d'évaluation dans laquelle nous
listerons quelques résultats obtenues pour avoir une idée sur
l'efficacitéde notre algorithme. Nous terminerons par une conclusion
générale qui résume ce travail.
8
Chapitre 2
Problèmes de satisfaction de
contraintes
2.1 Qu'est-ce qu'une contrainte?
Une contrainte est une relation logique (une
propriétéqui doit être vérifiée) entre
différents inconnus, appelées variables, chacune prenant ses
valeurs dans un ensemble donné, appelédomaine. Ainsi, une
contrainte restreint les valeurs que peuvent prendre simultanément les
variables. Par exemple, la contrainte »x + 3 x y = 12» restreint les
valeurs que l'on peut affecter simultanément aux variables x et y.
2.1.1 Quelques caractéristiques des contraintes
Une contrainte est relationnelle : elle n'est pas
»dirigée» comme une fonction qui définit la valeur
d'une variable en fonction des valeurs des autres variables. Ainsi, la
contrainte »x-2xy = z» permet de déterminer z dès lors
que x et y sont connues, mais aussi x dès lors que y et z sont connues
et y dès lors que x et z sont connues.
Notons également qu'une contrainte est
déclarative : elle spécifie quelle relation on doit
retrouver entre les variables, sans donner de procédure
opérationnelle pour effectivement assurer/vérifier cette
relation. Ainsi, lorsqu'on pose la contrainte »x - 2 x y = z», on ne
s'occupe pas de donner un algorithme permettant de résoudre cette
équation.
Notons enfin que l'ordre dans lequel sont posées
les contraintes n'est pas significatif : la seule chose importante
à la fin est que toutes les contraintes soient satisfaites
(...cependant, dans certains langages de programmation par contraintes l'ordre
dans lequel les contraintes sont ajoutées peut avoir une influence
sur
9
l'efficacitéde la résolution...).
2.1.2 Définition d'une contrainte
Une contrainte est une relation entre différentes
variables. Cette relation peut être définie en extension ou en
intension :
· Pour définir une contrainte en extension, on
énumère les tuples de valeurs appartenant à la relation.
Par exemple, si les domaines des variables x et y contiennent les valeurs 0, 1
et 2, alors on peut définir la contrainte »x est plus petit que
y» en extension par »(x=0 et y=1) ou (x=0 et y=2) ou (x=1 et
y=2)», ou encore par »(x,y) élément-de {(0,1), (0,2),
(1,2)}»
· Pour définir une contrainte en intention, on
utilise des propriétés mathématiques connues. Par exemple:
»x < y» ou encore »A etB non(C)»
2.1.3 Aritéd'une contrainte
L'aritéd'une contrainte est le nombre de variables sur
lesquelles elle porte. On dira que la contrainte est:
· unaire si son aritéest égale
à 1 (elle ne porte que sur une variable). Par exemple »x x x =
4» ou encore »est-un-triangle(y)»
· binaire si son aritéest égale
à 2 (elle met en relation 2 variables). Par exemple »x =6 y»
ou encore»A?B = A»
· ternaire si son aritéest égale
à 3 (elle met en relation 3 variables). Par exemple »x + y < 3 x
z - 4» ou encore »(non x) ou y ou z = vrai»
· n-aire si son aritéest égale
à n (elle met en relation un ensemble de n variables). On dira
également dans ce cas que la contrainte est globale. Par exemple, une
contrainte globale courante (et très pratique) est la contrainte
»toutesDifférentes(E)», oùE est un ensemble de
variables, qui contraint toutes les variables appartenant à E à
prendre des valeurs différentes.
2.1.4 Différents types de contraintes
On distingue différents types de contraintes en
fonction des domaines de valeurs des variables [1] :
· Les contraintes numériques, portant
sur des variables à valeurs numériques : une contrainte
numérique est une égalité(=) , une différence (6=)
ou une inégalité(<, =, >, =) entre deux ex-
10
pressions arithmétiques.
On distingue:
- les contraintes numériques sur les réels, quand
les variables de la contrainte peuvent prendre
des valeurs réelles, par exemple une contrainte physique
comme »U = R x I»
- les contraintes numériques sur les entiers, quand les
variables de la contrainte ne peuvent
prendre que des valeurs entières, par exemple une
contrainte sur le nombre de personnes pouvant
être embarqués dans un avion.
On distingue également :
- les contraintes numériques linéaires, quand les
expressions arithmétiques sont linéaires
Par exemple »4 x x - 3 x y + 8 x z
< 10»
- les contraintes numériques non linéaires, quand
les expressions arithmétiques contiennent des
produits de variables, ou des fonctions logarithmiques,
exponentielles...
Par exemple »x x x = 2» ou
»sinus(x) + z x log(y) =
4».
· Les contraintes booléennes, portant
sur des variables à valeur booléenne (vrai ou faux) : une
contrainte booléenne est une implication (=), une équivalence (?)
ou une non équivalence (~) entre deux expressions
logiques.
Par exemple »(non a) ou b =
c» ou encore »non (a ou b) ? (c
et d)».
· Les contraintes de Herbrand, portant sur des
variables à valeur dans l'univers de Herbrand : une contrainte de
Herbrand est une égalité(=) ou inégalité(6=) entre
deux termes (appelés aussi arbres) de l'univers de Herbrand. En
particulier, unifier deux termes Prolog revient à poser une contrainte
d'égalitéentre eux. Par exemple l'unification de
»f(X, Y )»avec
»f(g(a), Z)» s'exprime par la
contrainte »f(X,Y ) =
f(g(a),Z)».
· ... et bien d'autres encore, comme les contraintes sur
les ensembles, ...
2.2 Problèmes de satisfaction des contraintes
2.2.1 Définition informelle
Les problèmes de satisfaction des contraintes
appartiennent à la catégorie des problèmes combinatoires
et constituent un cadre simple pour représenter et résoudre de
nombreux problèmes d'intelligence artificielle,
11
et de recherche opérationnelle. De manière
informelle, un CSP est définie par la question de l'existence d'un
assignement d'un ensemble de variables dont les valeurs sont contraintes par
des relations.
2.2.2 Définition formelle
Un CSP (Problème de Satisfaction de Contraintes) est
défini par un triplé(X, D, C) tel que
1. X = {X1, X2, ...,
Xn} est l'ensemble de variables (les inconnues) du
problème.
2. D est la fonction qui associe à chaque
variable Xi son domaine D(Xi), c'est-à-dire
l'ensemble des valeurs que peut prendre Xi.
3. C = {C1, C2, ...,
Ck} est l'ensemble des contraintes. Chaque contrainte
Cj est une relation entre certaines variables de X,
restreignant les valeurs que peuvent prendre simultanément ces variables
[2].
Par exemple, on peut définir le CSP (X, D, C)
suivant :
· X = {a,b,c,d}
· D(a) = D(b) = D(c) = D(d) = {0, 1}
· C = {a =6 b,c =6 d,a + c <b}
Ce CSP comporte 4 variables a, b, c et d,
chacune pouvant prendre deux valeurs (0 ou 1). Ces variables doivent
respecter les contraintes suivantes : a doit être
différente de b, c doit être différente de d
et la somme de a et c doit être inférieure
à b.
2.2.3 Les variables du CSP
Les variables d'un CSP sont généralement les
inconnues du problème dont on cherche à associer des valeurs.
Dans ce qui suit, nous étudierons exclusivement les CSPs à
domaines finis, ou chaque domaine de valeurs est un ensemble isomorphe à
une partie finis de l'ensemble des entiers naturelles N. Un domaine de valeur
peut se représenter comme un ensemble d'entier naturels
représentables en machines, des valeurs booléennes (faux , vrai
ou 0,1), des couleurs (Rouge , Vert , Bleu, Noir . . .), des jours de la
semaine (lundi, mardi, ..., dimanche), un ensemble fini de nombres (92, 82.8,
39.7, 94.252, . . .), etc...
12
2.2.4 Graphe de contraintes
On peut associer à un CSP un graphe ou un hypergraphe
de contrainte. Les CSP binaires (dont toutes les contraintes ont une
aritéinferieur ou égale à 2) sont
représentés par des graphes dont les sommets représentent
les variables et les arêtes représentent les contraintes, et pour
les CSP quelconques (non binaire), les arêtes sont remplacées par
des hyper-arêtes qui relient des sous-ensembles de variable
impliquées dans une même contrainte. Dans ce cas, on parle d'un
hyper graphe de contraintes. La Figure suivante montre la différence
entre un graphe et un hypergraphe de contraintes (Figure 2.1).
Graphe de contraintes
|
VS
|
Hypergraphe de contraintes
|
deux sommets par
arête
|
|
plusieurs sommets par
hyper-arête
|
V6 ? > V5
V4
?
V1
V3
V2
|
|
|
V = { V1, V2, V3, V4, V5}
E = {e1,e2,e3,e4,e5}
= {{V1, V5}, {V2, V5},
{V3, V4},{V4, V5}, {V4, V6}
tel que :
V1 ? V5
V2 < V5
V3 > V4
V4 > V5
V4 ? V6 }
|
|
V = { V1, V2, V3, V4, V5, V6, V7} E = {e1,e2,e3,e4}
= {{V1, V2, V3}, {V2, V3}, {V3, V5, V6}, {V4} tel que :
V1 < ( V2 / V3 )
V2 > V3
V3 +V5 = V6
V4 > 0
}
|
|
FIGURE 2.1 - Graphe vs hypergraphe
13
2.2.5 Solution d'un CSP
Etant donnéun CSP (X, D, C), sa
résolution consiste à affecter des valeurs aux variables, de
telle sorte que toutes les contraintes soient satisfaites. On introduit pour
cela les notations et définitions suivantes :
· On appelle affectation le
fait d'instancier certaines variables par des valeurs (évidemment prises
dans les domaines des variables). On notera A = {
(X1,V1), (X2,V2), ...,
(Xr, Vr)} l'affectation qui instancie
la variable X1 par la valeur V1, la variable X2 par
la valeur V2, ..., et la variable Xr par la valeur
Vr. Par exemple, sur le CSP précédent (voir
l'exemple dans 2.2.2 ), A = {(b, 0), (c, 1)} est
l'affectation qui instancie b à 0 et c à 1.
· Une affectation est dite totale
si elle instancie toutes les variables du
problème, elle est dite partielle si elle n'en
instancie qu'une partie.
Dans notre exemple, A1= {(a, 1), (b, 0), (c, 0),
(d, 0)} est une affectation totale, A2= {(a, 0), (b, 0)}
est une affectation partielle.
· Une affectation A viole une
contrainte Ck si toutes les variables de Ck sont
instanciées dans A, et si la relation définie par Ck
n'est pas vérifiée pour les valeurs des variables de Ck
définies dans A. Dans notre exemple, l'affectation
partielle A2= {(a,0), (b,0)} viole la contrainte a6=b,
en revanche, elle ne viole pas les deux autres contraintes dans la mesure
oùcertaines de leurs variables ne sont pas instanciées dans
A2 .
· Une affectation (totale ou partielle) est
consistante si elle ne viole aucune
contrainte, et inconsistante si elle viole
une ou plusieurs contraintes.
Dans notre exemple, l'affectation partielle {(c,
0), (d, 1)} est consistante, tandis que l'affectation partielle
(a, 0), (b, 0) est inconsistante.
· Une solution est une
affectation totale consistante, c'est-à-dire une valuation de toutes les
variables du problème qui ne viole aucune contrainte.
Dans notre exemple, A = {(a, 0), (b, 1), (c, 0),
(d, 1)} est une affectation totale consistante : c'est une solution.
14
2.2.6 Notion de CSP surcontraint ou souscontraint
Lorsqu'un CSP n'a pas de solution, on dit qu'il est
surcontraint : il y a trop de contraintes et
on ne peut pas toutes les satisfaire. Dans ce cas, on peut souhaiter trouver
l'affectation totale qui viole le moins de contraintes possibles. Un tel CSP
est appelémax-CSP (max car on cherche à maximiser le nombre de
contraintes satisfaites).
Une autre possibilitéest d'affecter un poids à
chaque contrainte (une valeur proportionnelle à l'importance de cette
contrainte, et de chercher l'affectation totale qui minimise la somme des poids
des contraintes violées. Un tel CSP est appeléCSP
valué(VCSP).
Il existe encore d'autre types de CSPs, appelés CSPs
basés sur les semi-anneaux (semiring based CSPs), permettant de
définir plus finement des préférences entre les
contraintes.
Inversement, lorsqu'un CSP admet beaucoup de solutions
différentes, on dit qu'il est sous-contraint.
Si les différentes solutions ne sont pas toutes
équivalentes, dans le sens oùcertaines sont mieux que d'autres,
on peut exprimer des préférences entre les différentes
solutions. Pour cela, on ajoute une fonction qui associe une valeur
numérique à chaque solution, valeur dépendante de la
qualitéde cette solution. L'objectif est alors de trouver la solution du
CSP qui maximise cette fonction. Un tel CSP est appeléCSOP (Constraint
Satisfaction Optimisation Problem) [2].
2.3 Modélisation de quelques problèmes sous la
forme d'un CSP
Modéliser un problème en termes CSP, c'est
identifier les variables, fixer leurs domaines de valeur et
définir les contraintes à satisfaire.
Généralement, une modélisation CSP très aboutie du
problème mène àune meilleure résolution,
c'est -à-dire, à une solution ayant le meilleur cout en termes de
temps et de mémoire.
2.3.1 Exemple 1 : Problème du zèbre
* Enoncé:
On s'intéresse au problème suivant,
poséinitialement par Lewis Caroll [3] : Cinq maisons
consécutives, de couleurs différentes, sont habitées par
des hommes de différentes nationalités. Chacun possède un
animal différent, a une boisson préférée
différente et fume des cigarettes différentes. De plus, on sait
que :
1. Le norvégien habite la première maison.
2.
15
La maison à côtéde celle du
norvégien est bleue.
3. L'habitant de la troisième maison boit du lait.
4. L'anglais habite la maison rouge.
5. L'habitant de la maison verte boit du café.
6. L'habitant de la maison jaune fume des kools.
7. La maison blanche se trouve juste après la
verte.
8. L'espagnol a un chien.
9. L'ukrainien boit du thé.
10. Le japonais fume des cravens.
11. Le fumeur d'Old Golds a un escargot.
12. Le fumeur de gitanes boit du vin.
13. Le voisin du fumeur de Chesterfield a un renard.
14. Le voisin du fumeur de kools a un cheval.
Qui boit de l'eau? A qui appartient le zèbre? *
Modélisation sous forme d'un CSP :
On définit le CSP (X, D, C) tel que:
· Variables du problème : on associe une variable
par attribut (couleur, animal, boisson, nationalité, cigarette) X =
{blanche, rouge, verte, jaune, bleue, norvégien, anglais, ukrainien,
japonais, espagnol, cheval, renard, zèbre, escargot, chien, thé,
eau, lait, café, vin, kools, Chesterfield, Old-Golds, cravens,
gitanes}.
· Domaines des variables : D(X ) = {1, 2,3,4,
5}, pour toute variable X de X
· Contraintes :
- On pose tout d'abord une contrainte pour chaque assertion de
l'énoncé:
norvégien = 1
bleue = norvégien + 1
lait = 3
16
anglais = rouge
verte = caféjaune = kools
blanche = verte + 1 espagnol = chien
ukrainien = théjaponais = cravens
Old-Golds = escargot
gitanes = vin
(Chesterfield = renard + 1) ou (Chesterfield = renard - 1)
(kools = cheval + 1) ou (kools = cheval - 1)
- De plus, toutes les variables de même »type»
doivent avoir des valeurs différentes (il ne peut pas y
avoir plusieurs maisons qui ont la même couleur, ou un
même animal, ...)
blanche =6 rouge =6 verte =6 jaune =6 bleue
thé=6 eau =6 lait =6 café=6 vin
norvégien =6 anglais =6 ukrainien =6 japonais =6
espagnol
cheval =6 renard =6 zèbre =6 escargot =6 chien
kools =6 Chesterfield =6 Old-Golds =6 cravens =6 gitanes
2.3.2 Problème de Coloriage d'une carte
* Enoncé:
Il s'agit de colorier les 19 régions de la carte
ci-dessous (gouvernorat de Kasserine ( voir Figure 2.2 )), de sorte que deux
régions ayant une frontière en commun soient coloriées
avec des couleurs différentes. On dispose pour cela des 4 couleurs
suivantes : bleu, rouge, jaune et vert.
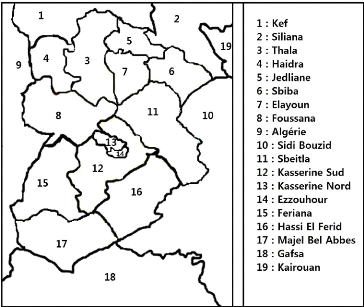
17
FIGURE 2.2 - gouvernorat de Kasserine
* Modélisation sous forme d'un CSP : On
définit le CSP (X,D,C) tel que:
· X = {X1, X2,...,
X19}
(On associe une variable X différente par région j
à colorier.)
· Pour tout X élément de X, D(X ) = {bleu,
rouge, vert, jaune} (Chaque région peut être coloriée avec
une des 4 couleurs.)
· C = {X =6 Xj / X et Xj sont 2 variables de X
correspondant à des régions voisines}
(2 régions voisines doivent être de couleurs
différentes.)
Pour être plus précis, on peut définir
explicitement les relations de voisinage entre régions, par exemple
à l'aide d'un prédicat voisines/2, tel que voisines(X,Y ) soit
vrai si X et Y sont deux régions voisines. Ce prédicat peut
être défini en extension, en listant l'ensemble des couples de
régions ayant une frontière en commun : voisines(X,Y ) ? (X,Y )
élément-de {(1,2), (1,3), (1,4), (1,5), (1,9), (2,5), (2,6),
(2,19), (3,1), (3,4),
18
(3,5), (3,7), (3,8), (4,1), (4,3), (4,8), (4,9), (5,1), (5,2),
(5,3), (5,6), (5,7), (6,2), (6,5), (6,7), (6,10), (6,11), (7,3), (7,5), (7,6),
(7,11), (8,3), (8,4), (8,9), (8,11), (8,12), (8,13), (8,15), (9,1), (9,4),
(9,8), (9,15), (9,17), (9,18), (10,2), (10,6), (10,11), (10,16), (10,18),
(10,19), (11,6), (11,7), (11,8), (11,10), (11,12), (11,16), (12,8), (12,11),
(12,13), (12,14), (12,15), (12,16), (12,17), (13,8), (13,12), (13,14), (14,12),
(14,13), (15,8), (15,9), (15,12),(15,17), (16,10), (16,11), (16,12), (16,17),
(16,18), (17,9), (17,12), (17,15), (17,16), (17,18), (18,9), (18,10), (18,17),
(19,2), (19,10)}. On peut alors définir l'ensemble des contraintes C de
la façon suivante :
C = {Xi =6 Xj | Xi et Xj sont 2 variables différentes
de X et voisines, (Xi,Xj) = vrai }
Donc, on peut colorier la carte comme suit (Figure 2.3) :
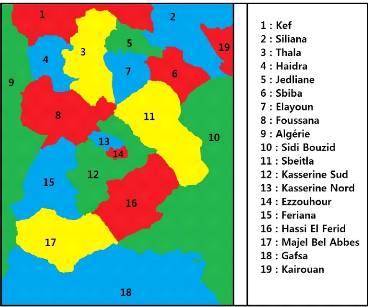
FIGURE 2.3 - Coloriage correcte du gouvernorat de Kasserine
Ce problème de coloriage d'une carte est un cas
particulier du problème du coloriage des sommets d'un graphe (deux
sommets adjacents du graphe doivent toujours être de couleurs
différentes). De nombreux problèmes »réels» se
ramènent à ce problème de coloriage d'un graphe :
problème des examens, d'emploi du temps, de classification,...
19
2.4 Quelques algorithmes de résolution de CSP
Les algorithmes que nous allons étudier permettent de
rechercher une solution à un CSP (n'importe laquelle,
c'est-à-dire la première que l'on trouve). Suivant les
applications, »résoudre un CSP» peut signifier autre chose que
chercher simplement une solution. En particulier, il peut s'agir de chercher la
»meilleure» solution selon un critère donné. Par
exemple, pour le problème du coloriage d'une carte, on peut chercher la
solution qui utilise le moins de couleurs possibles,... Ces problèmes
d'optimisation sous contraintes, oùl'on cherche à optimiser une
fonction objective donnée tout en satisfaisant toutes les contraintes,
peuvent être résolus en explorant l'ensemble des affectations
possibles selon la stratégie de »Séparation & Evaluation
» (»Branch & Bound») bien connue en recherche
opérationnelle.
2.4.1 L'algorithme »génère et teste»
Principe de l'algorithme »génère et
teste» :
La façon la plus simple ( et très naïve! )
de résoudre un CSP sur les domaines finis consiste à
énumérer toutes les affectations totales possibles
jusqu'àen trouver une qui satisfait toutes les contraintes. Ce principe
est repris dans la fonction récursive
»génèreEtTeste(A,(X,D,C))» décrite ci-dessous.
Dans cette fonction, A contient une affectation partielle et (X,D,C)
décrit le CSP à résoudre (au premier appel de cette
fonction, l'affectation partielle A sera vide). La fonction retourne vrai si on
peut étendre l'affectation partielle A en une affectation totale
consistante (une solution), et faux sinon.
20
Fonction génèreEtTeste( A
: affectation partielle, (X,D,C) : CSP
sur les domaines finis) :
booléen
Si (toutes les variables de X sont
affectées à une valeur dans A ) Alors
[ A est une affectation totale]
Si (A est consistante) Alors [ A
est une solution]
Retourner vrai
Sinon
Retourner faux
Fin Si
Sinon
[ A est une affectation
partielle]
choisir une variable X de X qui n'est pas
encore affectée à une valeur dans A Pour toute valeur
V appartenant à D(X ) faire
Si (génèreEtTeste(A U
(X ,V ), (X,D,C)) = vrai )
Alors
Retourner vrai
Fin Si
Fin Pour
Retourner faux
Fin Si
Fin
Algorithme 1: Génère et teste
Exemple de trace d'exécution de
»génère et teste»
Considérons par exemple le CSP (X,D,C) suivant
:
· X = {a,b,c,d}
· D(a) = D(b) = D(c) = D(d) = {0, 1}
· C = {a =6 b,c =6 d,a + c < b}
L'enchainement des appels successifs à la fonction
genereEtTeste (abrégée par GET) est
représentéci-dessous (voir Figure 2.4) (chaque rectangle
correspond à un appel de la fonction, et précise la valeur de
l'affectation partielle en cours de construction A).
GET
A = {}
retourne vrai Choix de Xi = a

GET
A = {(a,0)}
retourne vrai
Vi = 0
Choix de Xi = b
Vi = 0 Vi = 1
GET
A = {(a,0),(b,0)}
|
|
GET
A = {(a,0),(b,1)}
|
|
|
|
|
|
|
retourne faux
|
|
retourne vrai
|
|
Choix
de Xi = c Choix de Xi = c
Vi = 0 Vi = 1 Vi = 0
GET
A = {(a,0),(b,0),(c,0)}
|
GET
A = {(a,0),(b,0),(c,1)}
|
GET
A = {(a,0),(b,1),(c,0)}
|
|
Choix
|
retourne faux de Xi = d
|
|
Choix
|
retourne faux de Xi = d
|
|
Choix
|
retourne vrai de Xi = d
|
Vi = 0
|
Vi = 1
|
Vi = 0
|
Vi = 1
|
Vi = 0
|
Vi = 1
|
GET
|
GET
|
GET
|
GET
|
GET
|
GET
|
A = {(a,0),(b,0), (c,0),(d,0)}
|
A = {(a,0),(b,0), (c,0),(d,1)}
|
A = {(a,0),(b,0), (c,1),(d,0)}
|
A = {(a,0),(b,0), (c,1),(d,1)}
|
A = {(a,0),(b,1), (c,0),(d,0)}
|
A = {(a,0),(b,1), (c,0),(d,1)}
|
|
retourne faux retourne faux retourne faux retourne faux
retourne faux retourne vrai
21
FIGURE 2.4 - Exécution de
génère et teste sur un CSP simple
2.4.2 L'algorithme »simple retour-arrière»
Principe de l'algorithme »simple
retour-arrière»
Une première façon d'améliorer l'algorithme
»génère et teste» consiste à tester au fur et
à mesure de la construction de l'affectation partielle sa consistance :
dès lors qu'une affectation partielle est inconsistante, il
est inutile de chercher à la compléter. Dans ce
cas, on »retourne en arrière» (»backtrack» en
anglais) jusqu'àla plus récente instanciation partielle
consistante que l'on peut étendre en affectant une autre valeur à
la dernière variable affectée.
22
Par exemple, sur la trace d'exécution décrite
ci-dessus, on remarque que l'algorithme génère tous les
prolongements de l'affectation partielle A={(a, 0), (b,
0)}, en énumérant toutes les possibilités
d'affectation pour les variables c et d, alors qu'elle viole la contrainte a =6
b. L'algorithme »simple retour-arrière» ne va donc pas
chercher à étendre cette affectation, mais va »retourner en
arrière» à l'affectation partielle précédente
A={(a,0)}, et va l'étendre en affectant 1 à
b , . . .
Ce principe est repris dans la fonction récursive
»simpleRetourArrière(A,(X,D,C))»
décrite ci-dessous. Dans cette fonction, A contient une
affectation partielle et (X,D,C) décrit le
CSP à résoudre (au premier appel de cette fonction, l'affectation
partielle A sera vide). La fonction retourne vrai si on peut
étendre l'affectation partielle A en une affectation totale
consistante (une solution), et faux sinon.
Fonction simpleRetourArrière( A
: affectation partielle,
(X,D,C) : CSP sur les domaines
finis)
: booléen
Si (A n'est pas consistante )
Alors
Retourner faux
Fin Si
Si (toutes les variables de X sont
affectées à une valeur dans A ) Alors
[ A est une affectation totale et consistante = une
solution]
Retourner vrai
Sinon
[ A est une affectation partielle
consistante]
choisir une variable X de X qui n'est pas
encore affectée à une valeur dans A Pour toute valeur
V appartenant à D(X )
faire
Si (simpleRetourArrière(A U
(X ,V ), (X,D,C)) = vrai)
Alors
Retourner vrai
Fin Si
Fin Pour
Retourner faux
Fin Si
Fin
Algorithme 2: simpleRetourArrière
Exemple de »trace d'exécution» de
SimpleRetourArrière
Considérons le problème des 4 reines, Il s'agit
de placer 4 reines sur un échiquier comportant 4 lignes et 4 colonnes,
de manière à ce qu'aucune reine ne soit en prise. On rappelle que
deux reines sont en prise si elles se trouvent sur une même diagonale,
une même ligne ou une même colonne de l'échiquier.
· Variables : X = {X1, X2
X3, X4}
·
23
Domaines : D(X1) = D(X2) = D(X3) =
D(X4) = {1,2,3,4}
· Contraintes : C = {X =6 Xj | i élément-de
{1, 2,3, 4}, j élément-de {1, 2,3, 4} et i =6 j} U {X + i =6 Xj +
j | i élément-de {1,2,3,4}, j élément-de {1,2,3,4}
et i =6 j} U {X - i =6 Xj -j | i élément-de {1,2,3,4}, j
élément-de {1,2,3,4} et i =6 j} L'enchainement des appels
successifs à la fonction SimpleRetourArrière peut être
représentépar l'arbre suivant (Figure 2.5) (chaque noeud
correspond à un appel de la fonction, l'échiquier
dessinéà chaque noeud décrit l'affectation partielle en
cours)
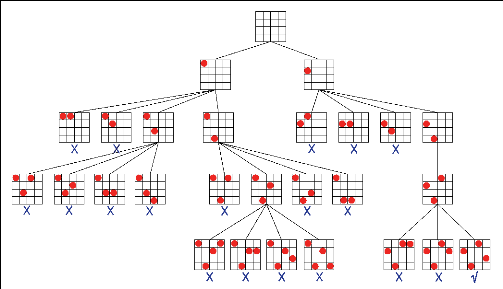
FIGURE 2.5 - Exécution de SimpleRetourArrière
(cette image est empruntée au »Guide to Constraint
Programming» de Roman Bartak)
2.4.3 L'algorithme »anticipation»
Notions de filtrage et de consistance locale
Pour améliorer l'algorithme »simple
retour-arrière», on peut tenter d'anticiper (»look ahead»
en anglais) les conséquences de l'affectation partielle en cours de
construction sur les domaines des variables qui ne
24
sont pas encore affectées : si on se rend compte qu'une
variable non affectée X n'a plus de valeur dans son domaine
D(X ) qui soit »localement consistante» avec l'affectation
partielle en cours de construction, alors il n'est pas nécessaire de
continuer à développer cette branche, et on peut tout de suite
retourner en arrière pour explorer d'autres possibilités.
Pour mettre ce principe en oeuvre, on va, à chaque
étape de la recherche, filtrer les domaines des variables non
affectées en enlevant les valeurs »localement inconsistantes»,
c'est-à-dire celles dont on peut inférer qu'elles
n'appartiendront à aucune solution. On peut effectuer différents
filtrages, correspondant à différents niveaux de consistances
locales, qui vont réduire plus ou moins les domaines des variables, mais
qui prendront aussi plus ou moins de temps à s'exécuter :
considérons un CSP (X,D,C), et une affectation partielle
consistante A.
· le filtrage le plus simple consiste à anticiper
d'une étape l'énumération: pour chaque variable X
non affectée dans A, on enlève de D(X )
toute valeur v telle que l'affectation A U {(X
,v)} soit inconsistante. - Par exemple pour le
problème des 4 reines, après avoir instanciéX1 à 1,
on peut enlever du domaine
de X2 la valeur 1 (qui viole la contrainte X1 =6
X2) et la valeur 2 (qui viole la contrainte 1-X1 =6
2-X2).
Untel filtrage permet d'établir ce qu'on appelle la
consistance de noeud, aussi appelée
1-consistance.
· Un filtrage plus fort, mais aussi plus long à
effectuer, consiste à anticiper de deux étapes
l'énumération: pour chaque variable X non
affectée dans A, on enlève de D(X ) toute
valeur v telle qu'il existe une variable Xj non
affectée pour laquelle, pour toute valeur w de D(Xj),
l'affectation A U {(X ,v),(Xj,w)}
soit inconsistante.
- Par exemple pour le problème des 4 reines,
après avoir instanciéX1 à 1, on peut enlever la valeur 3
du domaine de X2 car si X1=1 et X2=3, alors la variable X3 ne peut plus prendre
de valeurs : si X3=1, on viole la contrainte X3 =6 X1 , si X3=2, on
viole la contrainte X3+3 =6 X2+2 , si X3=3, on viole la contrainte X3
=6 X2 , et si X3=4, on viole la contrainte X3-3 =6
X2-2.
Notons que ce filtrage doit être
répétéjusqu'àce que plus aucun domaine ne puisse
être réduit. Ce filtrage permet d'établir ce qu'on appelle
la consistance d'arc, aussi appelée
2-consistance.
· Un filtrage encore plus fort, mais aussi encore plus
long à effectuer, consiste à anticiper de trois étapes
l'énumération. Ce filtrage permet d'établir ce qu'on
appelle la consistance de chemin, aussi appelée
25
3-consistance.
· . . .et ainsi de suite.. .notons que
s'il reste k variables à affecter, et si l'on anticipe de k
étapes l'énumération pour établir la
k-consistance, l'opération de filtrage revient à résoudre
le CSP, c'est-à-dire que toutes les valeurs restant dans les domaines
des variables après un tel filtrage appartiennent à une
solution.
Principe de l'algorithme
»anticipation»
Le principe général de l'algorithme
»anticipation» reprend celui de l'algorithme »simple
retour-arrière», en ajoutant simplement une étape de
filtrage à chaque fois qu'une valeur est affectée à une
variable. Comme on vient de le voir, on peut effectuer différents
filtrages plus ou moins forts, permettant d'établir différents
niveaux de consistance locale (noeud, arc, chemin, . . .).
Par exemple, la fonction récursive
»anticipation/noeud(A, (X, D, C))» décrite ci-dessous
effectue un filtrage simple qui établit à chaque étape la
consistance de noeud. Dans cette fonction, A contient une affectation
partielle consistante et (X, D, C) décrit le CSP à
résoudre (au premier appel de cette fonction, l'affectation partielle
A sera vide). La fonction retourne vrai si on peut étendre
l'affectation partielle A en une affectation totale consistante (une
solution), et faux sinon.
26
Fonction anticipation( A :
affectation partielle, (X,D,C) :
CSP sur les domaines finis) :
booléen
Si (A n'est pas consistante )
Alors
Retourner faux
Fin Si
Si (toutes les variables de X sont
affectées à une valeur dans A )
Alors
[ A est une affectation totale et consistante = une
solution]
Retourner vrai
Sinon
[ A est une affectation partielle consistante]
choisir une variable Xi de X qui n'est pas
encore affectée à une valeur dans A Pour
toute valeur Vi appartenant à D(Xi)
faire
[ filtrage des domaines par rapport à A U
(Xi,Vi) ]
Pour toute variable Xj de X
qui n'est pas encore affectée faire
Dfiltré(Xj) ?{Vj
élément de D(Xj) / A U
{(Xi,Vi),(Xj,Vj)} est consistante }
Si (Dfiltré(Xj) est
vide ) Alors
Retourner faux
Fin Si
Fin Pour
Si (anticipation(A U
(Xi,Vi),
(X,Dfiltré,C))=vrai )
Alors
Retourner vrai
Fin Si
Fin Pour
Retourner faux
Fin Si
Fin
Algorithme 3: anticipation/noeud
Exemple de »trace d'exécution» de
»anticipation»
Considérons de nouveau le problème du placement
de 4 reines sur un échiquier 4 x 4. L'enchainement des appels successifs
à la fonction »Anticipation/noeud» peut être
représentépar l'arbre suivant(Figure 2.6) (les valeurs
supprimées par le filtrage sont marquées d'une croix) :
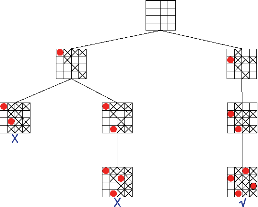
27
FIGURE 2.6 - Exécution d'anticipation (cette image est
empruntée au »Guide to Constraint Programming» de Roman
Bartak)
Si on appliquait un filtrage plus fort, qui
rétablirait à chaque étape la consistance d'arc,
l'enchainement des appels successifs à la fonction
»Anticipation/arc» correspondante serait le suivant (Figure 2.7) (les
valeurs supprimées par le filtrage sont marquées d'une croix)
:
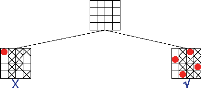
FIGURE 2.7 - Exécution d'anticipation 2 (cette image
est empruntée au »Guide to Constraint Programming» de Roman
Bartak)
Ainsi, on constate sur le problème des 4 reines que le
filtrage des domaines permet de réduire le nombre d'appels
récursifs : on passe de 27 appels pour »simple
retour-arrière» à 8 appels pour l'algorithme d'an-ticipation
avec filtrage simple établissant une consistance de noeud. En utilisant
des filtrages plus forts, comme celui qui établit la consistance d'arc,
on peut encore réduire la combinatoire de 8 à 3 appels
récursifs. Cependant, il faut noter que plus le filtrage
utiliséest fort, plus cela prendra de temps pour l'exécuter...
28
De façon générale, on constate que,
quelque soit le problème considéré, l'algorithme
»anticipation/noeud» est généralement plus rapide que
l'algorithme »simple retour-arrière» car le filtrage
utiliséest vraiment peu coûteux. En revanche, si l'algorithme
»anticipation/arc» envisage toujours moins de combinaisons que
l'algorithme »anticipation/noeud», il peut parfois prendre plus de
temps à l'exécution car le filtrage pour établir une
consistance d'arc est plus long que celui pour établir la consistance de
noeud.
2.5 Intégration d'heuristiques
Les algorithmes que nous venons d'étudier choisissent,
à chaque étape, la prochaine variable à instancier parmi
l'ensemble des variables qui ne sont pas encore instanciées, ensuite,
une fois la variable choisie, ils essayent de l'instancier avec les
différentes valeurs de son domaine. Ces algorithmes ne disent rien sur
l'ordre dans lequel on doit instancier les variables, ni sur l'ordre dans
lequel on doit affecter les valeurs aux variables. Ces deux ordres peuvent
changer considérablement l'efficacitéde ces algorithmes :
imaginons qu'àchaque étape on dispose d'une heuristique parfaite
qui nous dit quelle valeur choisir sans jamais se tromper, dans ce cas, la
solution serait trouvée sans jamais retourner en arrière...
Malheureusement, le problème général de la satisfaction
d'un CSP sur les domaines finis étant NP-complet, il est plus
qu'improbable que cette heuristique fiable à 100% puisse jamais
être »programmé». En revanche, on peut intégrer
des heuristiques pour déterminer l'ordre dans lequel les variables et
les valeurs doivent être considérées : une heuristique est
une règle non systématique (dans le sens oùelle n'est pas
fiable à 100%) qui nous donne des indications sur la direction à
prendre dans l'arbre de recherche.
Les heuristiques concernant l'ordre d'instanciation des
valeurs sont généralement dépendantes de l'appli-cation
considérée et difficilement généralisables. En
revanche, il existe de nombreuses heuristiques d'ordre d'instanciation des
variables qui permettent bien souvent d'accélérer
considérablement la recherche. L'idée générale
consiste à instancier en premier les variables les plus
»critiques», c'est-à-dire celles qui interviennent dans
beaucoup de contraintes et/ou qui ne peuvent prendre que très peu de
valeurs. L'ordre d'instanciation des variables peut être
:
- statique, quand il est fixéavant de
commencer la recherche.
Par exemple, on peut ordonner les variables en fonction
du nombre de contraintes portant sur elles : l'idée est d'instancier en
premier les variables les plus contraintes, c'est-à-dire celles
qui
29
participent au plus grand nombre de contraintes.
- ou dynamique, quand la prochaine variable
à instancier est choisie dynamiquement à chaque étape de
la recherche.
Par exemple, l'heuristique Ȏchec
d'abord» (»first-fail» en anglais) consiste à choisir,
à chaque étape, la variable dont le domaine a le plus petit
nombre de valeurs localement consistantes avec l'affectation partielle en
cours. Cette heuristique est généralement couplée avec
l'algorithme »anticipation», qui filtre les domaines des variables
à chaque étape de la recherche pour ne garder que les valeurs qui
satisfont un certain niveau de consistance locale.
2.6 Réseaux de contraintes temporelles
2.6.1 Quelques éléments sur la
représentation du temps
La modélisation du temps est une thématique
déjàancienne en intelligence artificielle. Elle s'applique
à la représentation de connaissances, la compréhension de
la langue naturelle, le raisonnement de sens commun, le raisonnement
qualitatif, le diagnostic ou la planification. Différents modèles
ont étédéveloppés et peuvent se décliner
selon différents aspects : temps ponctuel ou sous forme d'intervalle,
temps totalement ou partiellement ordonné(temps linéaire ou
branché), temps discret ou dense, bornéou non, incluant
différentes granularités ou non [13]. Nous nous focalisons ici
sur les approches qualitatives.
2.6.2 Contraintes temporelles qualitatives
Les principales représentations qualitatives du temps
sont l'algèbre d'intervalles de Allen [4, 5] et
l'algèbre de points de Vilain et Kautz
[6].
Algèbre des intervalles
L'algèbre des intervalles (IA)
est un calcul pour les raisonnements spatio-temporels
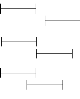
créépar James F. Allen en 1983 [4, 5]. Cette algèbre
définit les relations possibles entre des intervalles de temps et
propose une table de composition. Elle peut être utilisée comme
base pour des raisonnements portant sur la description temporelle des
évènements. Dans la théorie d'Allen, 13 relations de base
(ou relations atomiques) décrivent toutes les manières possibles
d'ordonner les extrémités de deux intervalles {b,m, o, s, d,
f, a, mi, oi, si, di, fi, eq}
30
(voir Figure 8).
Par exemple, pour X = [X ,X+] et Y = [Y ,Y +] deux
intervalles non réduits à un point, X+<Y
s'écrit X {b} Y (pour before), X+ = Y s'écrit X {m} Y
(pour meet) et X <Y <X+<Y + s'écrit X {o} Y (pour
overlap).
Relation
|
Symbole
|
Inverse
|
Symbole
|
X before Y
|
b
|
Y after X
|
a
|
X meets Y
|
m
|
Y met-by X
|
mi
|
X overlaps Y
|
o
|
Y overlapped-by X
|
oi
|
X starts Y
|
s
|
Y started-by X
|
si
|
X during Y
|
d
|
Y contains X
|
di
|
X finishes Y
|
f
|
Y finished-by X
|
fi
|
X equals Y
|
eq
|
Y equals X
|
eq
|
|
Illustration
X
X
Y
Y
Y
X
X
X

Y
Y
X
Y

Y
X
FIGURE 2.8 - Les treize relations de Allen entre deux
intervalles de temps X et Y .
Définition 2.6.1. (réseau
de contraintes d'algèbre Intervalle)
Le réseau IA peut être exprimée comme
un réseau de contraintes, impliquant un ensemble de variables {X1,
...,Xn}, oùchaque variable représente un
intervalle temporel. Le domaine de chaque variable est l'en-semble des couples
de nombres réels (par exemple, Di = {(a, b) tel que a,b E R,
a<b}), représentant les points du début et de la fin de
l'intervalle correspondant. Les contraintes binaires entre les paires des
variables de l'intervalle sont donnés comme des relations IA la
contrainte Cij entre xi et xj
est défini comme Cij inclue ou égale à {b, m,
o, s, d, f, a, mi, oi, si, di, fi, eq}. Une solution est la cession d'une paire
de
numéros à chaque variable telle qu'aucune
contrainte n'est violé. Le test de violation des contraintes
nécessite la traduction de la relation entre une paire d'intervalles
(a1, b1), (a2, b2) dans une disjonction de relations qualitative. Une solution
peut également être associéà un étiquetage
cohérent, l'attribution d'un rapport atomique de chaque contrainte qui
est conforme à une solution [7].
Exemple :
Les relations entre intervalles d'Allen peuvent être
utilisées pour représenter une succession
d'événements sous forme d'un réseau de contraintes [10],
comme décrit dans la Figure 2.9(a). L'énoncé Béchir
lisait son journal tout en prenant son petit déjeuner. Il acheva sa
tasse de caféet posa son journal. Après le
petit déjeuner, il partit se promener est
représentéau moyen de quatre intervalles de temps,
associés àdes actions : lire son journal, prendre son
petit déjeuner, boire son café, partir se promener. Les
relations
temporelles entre ces événements sont
représentées par des disjonctions de relations d'Allen. Ainsi
Après le petit déjeuner, il partit se promener devient
Id{m,b}Ip
représentépar une arête entre les noeuds
Id (ou Petit-Déjeuner) et
Ip (ou Promenade) du graphe. L'arête
est étiquetée par la relation {m, b} qui signifie juste
avant ou avant. On pourrait également afficher la relation inverse
{mi, a} entre Ip et
Id. De la même manière,
l'énoncé Béchir lisait son journal tout en prenant son
petit déjeuner est représentée par l'arête {d,
di,o, oi, f, fi, s, si, eq} entre les noeuds Ij
(ou Journal) et Id : l'information
temporelle tout en étant très vague, on garde à priori
toutes les relations incluant un recouvrement des deux intervalles.


Petit-déjeuner
Journal
Promenade
{f,fi}
Café

{d,di,o,oi,f,fi,s,si,eq}
{s,f,d}
{m,b}
(a) Graphe d'origine
Petit-déjeuner
Journal
Promenade
{f,fi}
Café

{d,di,o,oi,f,fi,s,si,eq}
{s,f,d}
{m,b}
(a) Propagation des contraintes
FIGURE 2.9 - Relations qualitatives entre les intervalles
L'utilisation des règles de composition des relations
d'Allen permet de simplifier les étiquettes des relations
31
32
(par des techniques de propagation de contraintes [11]). Par
exemple, sachant que:
· la lecture du journal et le cafés'achèvent
ensemble : Ij {f, fi }
Ic
· le caféest une partie du petit déjeuner :
Ic {s, f, d}
Id
On en conclut que les relations oi, di, si sont impossibles
entre Ij et Id (la lecture
du journal ne peut s'achever après le petit déjeuner, (voir
Figure 2.9(b))). De fait, par composition :
Ij {f, fi}
Ic ? Ic {s, f,
d} Id ? Ij {d, o, f, fi, s, eq}
Id
Un scénario possible cohérent est
représentésur la Figure 2.10.
Journal
Café
FIGURE 2.10 - Scénario possible pour
l'exemple
Avec les réseaux IA, c'est l'arrangement des
intervalles qualitatifs qui nous intéresse, pas l'instanciation
cohérente particulière qui a conduit à l'arrangement. Il y
a zéro ou un nombre infini de différentes ins-tanciations
cohérentes des variables dans un réseau d'IA, mais il y a
seulement un nombre fini de différents arrangements conformes des
intervalles. Une instanciation consistante possible qui conduirait à
l'arrangement montrédans la Figure 2.10 est le journal--(2,3),
Petit-déjeuner--(0,4), promenade--(5,6), et
Café--(1,3), oùnous assimilons les noms des sommets avec
les variables qu'ils représentent.
Algèbre des points
En raison des limites de calcul de l'IA de modèle
alternatif, l'algèbre des points (PA) ,
créépar Vilain et Kautz en 1986 [6], qui est moins expressif, est
souvent utiliséau lieu de l'algèbre IA. Dans ce modèle les
informations sont exprimées par des contraintes sur les points. Dans
cette algèbre, trois relations de base (précède
(<), identique (=) et suit
(>)) sont considérées.
33
Définition 2.6.2. ( Réseaux de
contraintes d'algèbre de point)
Un réseau d'algèbre de point (réseau
PA) implique un ensemble de variables {x1, ...,xn
}, oùchaque variable représente un point du temps. Le
domaine de chaque variable est l'ensemble des nombres réels R, qui
représente des points du temps que la variable peut assumer. Les
contraintes sont données comme des éléments PA, ayant leur
sens algébrique sur les réels [7].
Exemple :
À titre d'exemple de représentation de
l'information temporelle dans le cadre PA, on considère la description
des événements représentés sur la Figure 2.11(a),
la phrase fixe la relation entre certaines extrémités des
intervalles du temps sur laquelle Béchir a lu son journal et sur
laquelle Béchir buvait son café, mais il reste indéfinie
sur les autres. Nous représentons ce par le réseau de la Figure
2.11(a), oùJournal- et Journal+ représentent
les points de départ et de fin de l'intervalle. Le réseau est
déjàminimale, il montre également les relations possibles
entre toutes les paires des points. Un scénario cohérent possible
est représentésur la Figure 2.11(b). Comme avec les
réseaux IA, c'est l'arrangement qualitatif des points qui nous
intéresse, pas l'instanciation consistante particulière qui a
conduit à l'arrangement.
34
|
|
|
|
|
|
|
|
|
|
|
|
-
Journal
|
|
|
- Café
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
<
+
Café
|
|
|
|
|
|
|
|
|
|
|
|
+
Journal
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a)
|
(b)
|
(c)
|
(d)
|
(e)
|
(f)
|
Journal Café
(g)
|
|
FIGURE 2.11 - Représentation des relations qualitatives
entre les points : (a) Exemple Béchir a mis le papier vers le bas et bu
le dernier de son café. (b) Un scénario possible
Une possible instanciation consistante qui conduirait à
l'arrangement montrédans la Figure 2.11(b) est
Journal--2,
Journal+-3, cafe--1
et cafe+-3.
2.7 Les problèmes de planification
La planification consiste en la recherche d'une
séquence d'opérations permettant de passer d'un état
initial à un état final souhaité. Un problème
d'ordonnancement consiste à organiser dans le temps un ensemble
d'activités, de façon à satisfaire un ensemble de
contraintes et optimiser une ou plusieurs fonctions objectives. En d'autres
termes, la planification consiste à déterminer les tâches
à exécuter et l'ordonnancement consiste à
déterminer quand exécuter ces tâches. Le contrôle
d'exécution de plans est un problème particulièrement
35
difficile lorsqu'il doit être effectuéà
bord de systèmes autonomes tels que des robots. Un tel système
doit disposer d'un processus pour engendrer des plans qui réalisent les
buts de la mission tout en respectant des délais et des contraintes de
précédence. Plusieurs formalismes et algorithmes ont
étédéveloppés pour traiter des problèmes de
planification tenant compte des contraintes temporelles. De tels
problèmes de planification existent dans de nombreuses applications
réelles telles que le transport, la robotique, le domaine
médical, les services d'urgences, etc. . .[12]
2.7.1 Contraintes de pr'ec'edence
Dans le monde réel, la
possibilitéd'exécuter une tâche peut dépendre de
plusieurs conditions, comme le temps et les ressources disponibles ou
l'exécution d'autres tâches. On considère que les
contraintes de précédence [12] auparavant sont de la forme d'une
relation d'ordre partiel sur un ensemble de tâches T. Dans ce cas, entre
deux tâches quelconques il existe une relation de
précédence ou il n'existe pas de relation qui les relie. On
établit une distinction entre deux sortes de contraintes de
précédence :
- Contraintes de Pr'ec'edence Conjonctives:
Le cas oùun groupe de tâches indépendantes
doit être exécutépour permettre l'exécution de
certaines autres tâches. Si les tâches
t1,t2,...., tk doivent toutes être
exécutées avant l'exécution d'une tâche t,
on écrit symboliquement : [t1, t2,...,
tk]-+t.
- Contraintes de Pr'ec'edence Disjonctives :
Le cas oùune seule tâche parmi un groupe de
tâches doit être exécutée avant que la tâche en
question ne puisse être exécutée. S'il suffit qu'une
tâche parmi les tâches t1, t2,..., tk
s'exécute pour que la tâche t puisse
s'exécuter, on écrit symboliquement : t1|t2|. ..
.|tk-+t.
A noter que parfois on doit attendre un peu de temps
après la fin de l'exécution d'une tâche et avant le
début de l'exécution de la tâche suivante.
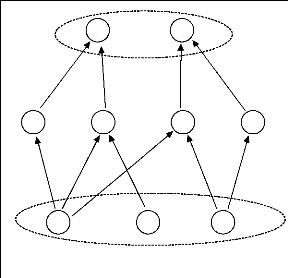
2.7.2 Le graphe de contraintes temporelles
Le graphe de contraintes temporelles décrit les
contraintes temporelles sur les tâches et les relations de
précédence entre elles. Un graphe de contraintes temporelles est
un graphe simple orientéacyclique G=(T,E). Il
est à noter que les noeuds qui forment l'ensemble T sont
divisés en trois sous-ensembles T=TI?TM?TF de
tàaches tels que TI est l'ensemble de tâches qui n'ont
pas de prédécesseurs (les tàaches initiales), TM
est
36
l'ensemble de tâches qui ont des
prédécesseurs et des successeurs et TF est l'ensemble
des tâches finales qui n'ont pas de successeurs et qui, en
général, appartiennent à l'ensemble des buts. La figure
ci-dessous (Figure 2.12) représente un graphe de contraintes temporelles
tel que TI={t1, t2, t3 }, TF={ t8, t9}
et TM = {t4,. .. ,t7}.
t4 t5 t6
t7
t1 t2 t3
t8 t9
FIGURE 2.12 - Un graphe de contraintes temporelles de
précédence
2.8 Conclusion
Dans ce chapitre, nous avons fourni une présentation
formelle des problèmes de satisfaction des contraintes, leurs solutions,
et leurs représentations graphiques et nous avons illustréces
concepts à travers des exemples.
Nous nous sommes concentrés sur certains algorithmes de
résolution d'un CSP. Nous avons ensuite présentéles
réseaux de contraintes temporelles. Plus précisément,
l'algèbre des intervalles d'Allen (1983) [5] et l'algèbre
de point de Vilain et Kautz (1986) [6] qui ont reçu un
traitement formel de contrainte. Nous avons fini par présenter les
problèmes de planification. La suite de notre travail consiste à
résoudre un problème spécifique de satisfaction des
contraintes en s'appuyant sur ce que nous avons vu dans ce chapitre.
37
Chapitre 3
Résolution d'un problème de
satisfaction de contraintes
3.1 Introduction
Après avoir défini les problèmes de
satisfaction de contraintes et les algorithmes utilisés pour les
résoudre, nous proposons une modélisation par CSP d'un
problème particulier qui présente des points communs avec les
CSPs issus de l'algèbre des points, mais qui est plus complexe. Puis
nous présentons un algorithme pour le résoudre. Ensuite, nous
exposons une évaluation expérimentale de l'algorithme
proposé.
3.2 Description du problème
Le problème que nous nous proposons de résoudre
est un problème de satisfaction de contraintes impliquant un ensemble de
variables X={x1,x2,.....,xn},
chacune pouvant prendre une valeur distincte parmi les entiers naturels de 1
à n. Les contraintes du problème ont toutes la forme
suivante :
Min(xi1,xi2) <
Max(xi3,xi4), i1,i2,i3,i4?
{1..n} (3.1)
Il s'agit donc de trouver une permutation des nombres de 1
à n qui satisfait un ensemble de contraintes du type
donnée par l'Equation (3.1). Une permutation est consistante si elle ne
viole aucune contrainte, et inconsistante si elle viole une ou plusieurs
contraintes. Nous nous intéressons à trouver, en un temps
raisonnable, une solution qui satisfait le plus grand nombre possible de
contraintes.
38
3.3 Exemple d'un problème
Donner un ensemble de 10 nombres naturels distincts non
négatifs, supérieurs à zéro et inferieurs ou
égale à 10 sous la forme X={x1,x2,.....,x10}, qui
vérifient les 20 contraintes suivantes :
1. Min(x8,x5)<Max(x1,x10) 2. Min(x6,x2)<Max(x8,x2) 3.
Min(x2,x7)<Max(x9,x6)
4. Min(x7,x2)<Max(x9,x10) 5. Min(x8,x10)<Max(x6,x5) 6.
Min(x4,x2)<Max(x10,x9)
7. Min(x1,x6)<Max(x3,x9) 8. Min(x1,x3)<Max(x5,x9) 9.
Min(x3,x1)<Max(x2,x1)
10. Min(x7,x2)<Max(x4,x9) 11. Min(x4,x5)<Max(x5,x7) 12.
Min(x10,x7)<Max(x4,x8)
13. Min(x9,x3)<Max(x10,x2) 14. Min(x6,x10)<Max(x9,x5) 15.
Min(x8,x7)<Max(x4,x7)
16. Min(x6,x5)<Max(x3,x1) 17. Min(x8,x4)<Max(x8,x3) 18.
Min(x1,x2)<Max(x7,x6)
19. Min(x6,x5)<Max(x2,x3) 20. Min(x1,x2)<Max(x5,x7)
3.4 Modélisation sous la forme d'un
CSP
Modéliser le problème en terme CSP c'est de
déterminer le triplet (X,D,C) associé, nous proposons la
modélisation comme suit .
*Les variables et leurs domaines : On a n
variables distincts qui peuvent prendre les valeurs de 1 à n, donc :
- X={x1, x2,..., xn} l'ensemble des n variables du
problème.
- D (x1)=D(x2)= ...=D(xn) ={1..n} le domaine de
valeurs associés aux variables.
*Les contraintes : On va se limiter à
un seul type de contrainte dans ce problème, qui est : C={C1, C2,...,
Cm} tel que pour chaque Ci E C, Ci
=Min(xi1,xi2)<Max(xi3,xi4), tel que i1, i2, i3, i4 E {1..n}
3.5 Résolution du problème
3.5.1 Résolution par l'algorithme «
génère et teste »
Pour résoudre ce problème il faut trouver une
affectation de valeurs distinctes aux variables de X qui vérifie toutes
les contraintes. Etant donnéque les n variables prennent des valeurs
distinctes dans 1..n, il faut chercher la solution parmi les n! permutations
possibles. Donc, la complexitéde ce problème est une
complexitéfactorielle.
39
Le tableau suivant, représente le temps estimépour
résoudre un algorithme de telle complexité.
|
Nombre des variables
|
5
|
10
|
20
|
50
|
250
|
500
|
|
Générations possibles
|
120
|
3628800
|
24 × 1017
|
31 × 1095
|
32 × 10522
|
--
|
|
Temps de résolution
|
1.2 us
|
36ms
|
770 ans
|
1048ans
|
?
|
?
|
TABLE 3.1 - temps nécessaire à
l'exécution d'un algorithme de complexitéfactotielle [8]
L'algorithme génère et teste peut toujours
trouver une solution car il génère et teste tous les permutations
possibles comme nous avons vu dans le deuxième chapitre, mais si on
augmente la valeur de n il faudra beaucoup de temps pour arriver
à la solution.
3.5.2 Résolution par l'algorithme simple retour
arrière (ou backtrack)
Puisque l'algorithme génére et teste s'est
avéréinefficace, le backtrack est une première
amélioration qui consiste à tester au fur et
à mesure la consistance de l'affectation partielle des variables, et qui
retourne en arrière si elle est inconsistante. Il est facile de voir que
la recherche effectuée par le backtrack correspond à un parcours
en profondeur d'un arbre n-aires, et dont la racine est un tuple vide,
tandis que les noeuds situés au i ème niveau sont des i-uplets
qui représentent les affectations des variables le long du chemin
correspondant dans l'arbre. Les vérifications effectuées par
l'algorithme backtrack ' assurent que les affectations construites associent
des valeurs distinctes aux différentes variables. Donc, la
complexitéde cet algorithme est de l'ordre de O(n!) (dans les
pires cas).
Avec une telle complexité, on remarque facilement que
le temps de résolution augmente d'une façon plus
qu'exponentielle, chaque fois qu'on augmente le nombre de variables, car, pour
n assez grand, on a 2' < n!.
3.5.3 Résolution par l'algorithme d'anticipation
Malgrél'amélioration proposée par le
backtrack, le temps de résolution reste toujours élevé.
C'est pourquoi on va essayer la résolution avec l'algorithme
d'anticipation. L'algorithme d'anticipation (look ahead) reprend le principe de
l'algorithme précèdent (backtrack) et tente d'anticiper les
conséquences de l'affectation partielle en cours de la construction sur
les domaines des variables qui ne sont pas encore affectées. Par
conséquent, les domaines des variables vont être réduits,
au fur et à mesure, ainsi que la complexitéde l'algorithme. Cette
dernière reste toujours exponentielle malgrésa diminution.
40
3.5.4 Résolution proposée
L'avantage des algorithmes que nous venons d'envisager c'est
qu'ils arrivent toujours à trouver une solution, car ce sont des
algorithmes complets. Mais l'inconvénient est
le temps d'exécution.
L'utilisation d'une heuristique peut considérablement
accélérer le temps d'exécution car elle nous aide
àchoisir un bon ordonnancement des variables sans être
obligéde retourner en arrière ou même d'anticiper
les conséquences d'une affectation.
Le problème auquel nous nous intéressons (voir
Section 3.2) est un problème d'optimisation pour lequel on ne connait
pas d'algorithme permettant de trouver une solution exacte en un temps
polynomial. Nous essayons, alors, de trouver un algorithme qui satisfait le
plus grand nombre de contraintes possible en un temps raisonnable
(polynomial).
Notre idée est de transformer toute contrainte
quaternaires C E C de la forme C =Min(x 1,x
2)<Max(x 3,x 4), à des contraintes
d'aritébinaire sous la forme x <xj, tel que i
E{i1, i2}
et j E {i3,
i4}. Pour cela on va utiliser une
méthode heuristique pour décider du minimum, respectivement, du
maximum entre chaque paire de variables apparaissant à la partie gauche,
respectivement, droite d'une contrainte.
Heuristique utilisée
Pour transformer les contraintes quaternaires du
problème en des contraintes binaires , nous proposons de compter, pour
chaque variables x E X, son nombre d'occurrence dans la partie gauche
Min ' des contraintes puis nous lui soustrayons son nombre d'occurrence dans la
partie droite, Max , des contraintes. Nous obtenons ainsi un score h(x ) pour
chaque variable.
- Pour décider du minimum entre deux variables x et xj,
on choisit la variable qui a le plus grand score. En cas
d'égalitéde score entre deux variables différentes, nous
évitons cette égalitéen soustrayant 1 du score de l'une de
ces deux variables.
- Pour décider du maximum entre deux variables x et xj,
on choisit la variable qui a le plus petit score. En cas
d'égalitéde score entre deux variables différentes, nous
évitons cette égalitéen soustrayant 1 du score de l'une de
ces deux variables.
Il faut, toutefois, signaler que ce choix peut nous mener
à des contraintes non valides (cas rares), ces contraintes sont
généralement sous la forme x <x (impossible), c'est à
cause de l'apparition de la variable
41
xi dans les deux parties de la contrainte, dans ce cas on a deux
choix.
1. choix1 :
xi apparait dans les deux parties de la contrainte, elle est
sous la forme C=Min (xi1,xi2)<Max(xi3,xi4) tel que xi1=xi3 ,
alors on va choisir comme suit :
si (h(xi1)>h(xi2))alors
Min(xi1,xi2)=xi1 , et par conséquent Max(xi3,xi4)=xi4,
d'ou la contrainte devient : xi1<xi4.
Sinon , Si (h(xi1)<h(xi2)), alors
Min(xi1,xi2)=xi2, et on a xi1=xi3, donc
xi2<xi3 est vérifié, d'ou la contrainte
devient : xi2<xi3.
Enfin, en cas d'égalitédu score on choisit comme
suit :
Si |h(xi3)-h(xi4)| >
|h(xi2)-h(xi1)| alors
Min(xi1,xi2) =xi1
Max(xi3,xi4) =xi4
d'ou la contrainte devient : xi1<xi4
Sinon, si |h(xi3)-h(xi4)| <
|h(xi2)-h(xi1)| alors
Min(xi1,xi2) =xi2
Max(xi3,xi4)=xi3
d'ou la contrainte devient : xi2<xi3
2. choix2 :
Si on a h(xi1)=h(xi2) et |h(xi1) -
h(xi2)| = |h(xi3) - h(xi4)|, on ne peut pas
choisir le «Min» et le «Max» en utilisant le choix 1.
Alors, nous décidons de choisir aléatoirement xi et xj telque la
contrainte soit valide (xi =6 xj)
Résolution du problème
transformé
Après la transformation de la forme des contraintes, on
peut parler de contraintes de précédence, on peut
considérer xi et xj comme des taches telles que xi précède
xj si on a la contrainte xi<xj. Nous allons alors associer à ces
contraintes de précédence, un graphe de contraintes sur les
tâches et les relations de précédence entre elles. C'est un
graphe orientéet nous allons représenter chaque contrainte sous
la forme xi<xj par un
42
arc sortant de x et entrant dans
xj, puis nous allons ordonner ces taches comme suit
:
1. Associer un ensemble de valeurs possibles aux variables. Cet
ensemble sera initialiséà l'ensemble des nombres naturels de 1
à n et sera notéD
(Domaine des variables).
2. identifier les sommets sources du graphe.
3. choisir la source qui a le plus d'arcs sortants.
4. associer à cette source la valeur minimale de
D et éliminer cette valeur de D
puis éliminer ce sommet du graphe, ainsi que les arcs qui
en sortent.
5. répéter le traitement de 2 à 4
jusqu'àce qu'on ne trouve plus de source.
6. Affecter les variables qui n'ont pas reçus une valeur
par les valeurs restantes dans D en utilisant une
méthode que nous décrivons dans ce qui suit.
Et par cette démarche nous obtenons une affectation de
valeurs aux variables qui satisfait toutes les contraintes.
Nous affectons les variables qui n'ont pas reçu une valeur
par la démarche précédente, comme suit :
1. associer le minimum des valeurs restantes dans l'ensemble
D, à la variable qui a le plus grand score et
supprimer cette valeur de D.
2. Répéter l'étape 1 jusqu'àce que
D=Ø.
43
3.6 Algorithme proposé3.6.1
algorithme
Entrées:
(X,D,C) : un CSP
[- X : l'ensemble de n variables
- D : domaine des variables 1..n - C : ensemble des
contraintes.]
G=(S, A) : Graphe
orienté[ - S= l'ensemble des sommets
- A= l'ensemble des arcs]
h : table de score de n
éléments entiers
Traitement:
0) Début
1) Pour (tout Ci E C)
faire [remplissage de h]
h(xi1)?h(xi1)+1
h(xi2)?h(xi2)+1
h(xi3)?h(xi3)-1
h(xi4)?h(xi4)-1
Fin Pour
2) Pour (tout Ci E C)
faire
(xi,xj)? Transformer (X,Ci, h) [
transformation des contraintes à la forme xi<xj] A?A U
(xi, xj) [ Ajout d'arc sortant de xi vers xj au graphe G
]
Fin Pour
3) Répéter
xi?Source(G) [xi reçoit la
variable qui représente la source du graphe G qui a le plus
d'arcs]
G?G\{xi}
xi?min(D) [affecter la valeur minimale de D
à la variable xi]
D?D\{min(D)}
jusqu'àce que
(xi=Ø)
4) Compléter (X,D,h)
5) Fin
Algorithme 4: Algorithme proposé
Fonction Transformer(X : variables,
C : contrainte, h : table de score) : contrainte
binaire Si
(h(xi1)=h(xi2))
Alors
h(xi1)
--h(xi1) - 1
Fin Si
Si
((h(xi3)=h(xi4))
Alors
h(xi3)
--h(xi3) - 1
Fin Si
Si
(h(xi1)>h(xi2))
Alors
xi --xi1
Sinon
xi --xi2
Fin Si
Si
(h(xi3)<h(xi4))
Alors
xj --xi3
Sinon
xj --xi4
Fin Si
Si (xi=xj)
Alors
[Contrainte non valide ] Si
(h(xi1)>h(xi2))
Alors xi --xi1
xj --xi4
Sinon
Si
(h(xi1)<h(xi2))
Alors
xi --xi2
xj --xi1
Sinon
Si
(|h(xi2)-h(xi1)|#|h(xi4)-h(xi3)|)
Alors
Si
(|h(xi2)-h(xi1)|>|h(xi4)-h(xi3)|)
Alors xi --xi2
xj --xi3 Sinon
xi --xi1
xj --xi4
Fin Si
Sinon
Tant que (xi=xj)
faire
(xi,xj) --Choix
Aléatoire(C)
Fait
Fin Si
Fin Si
Fin Si
Fin Si
Fin
Retourner (xi,xj)
[Contrainte transformée]
44
Algorithme 5: fonction transformer
Procédure completer(X : variables , D :
domaines , h : table de score)
Tant que (D0Ø)
faire
t?Min(D)
xi?Max(h) [la variable qui a h max]
D?D\{t}
Fin
Fait
45
Algorithme 6: procedure completer
3.6.2 Exemple
A titre d'exemple, nous proposons de résoudre le
problème posédans la Section 3.3 :
X={x1, x2, ..., x10} D={1..10}
C={C1, C2, ..., C20} |
C1 = Min(x8,x5)<Max(x1,x10) C2 = Min(x6,x2)<Max(x8,x2) C3 =
Min(x2,x7)<Max(x9,x6)
C4 = Min(x7,x2)<Max(x9,x10) C5 = Min(x8,x10)<Max(x6,x5) C6
= Min(x4,x2)<Max(x10,x9)
C7 = Min(x1,x6)<Max(x3,x9) C8 = Min(x1,x3)<Max(x5,x9) C9 =
Min(x3,x1)<Max(x2,x1)
C10 = Min(x7,x2)<Max(x4,x9) C11 = Min(x4,x5)<Max(x5,x7) C12
= Min(x10,x7)<Max(x4,x8)
C13 = Min(x9,x3)<Max(x10,x2) C14 = Min(x6,x10)<Max(x9,x5)
C15 = Min(x8,x7)<Max(x4,x7)
C16 = Min(x6, x5)<Max(x3,x1) C17 = Min(x8,x4)<Max(x8,x3)
C18 = Min(x1,x2)<Max(x7,x6)
C19 = Min(x6,x5)<Max(x2,x3) C20 = Min(x1,x2)<Max(x5,x7)
}
Nous allons employer l'heuristique
déjàdéfinie pour transformer les contraintes quaternaires
à des contraintes binaires comme suit :
· Instruction 1) : calcule des scores
X
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
x9
|
x10
|
h(X)
|
2
|
3
|
-1
|
0
|
-1
|
2
|
1
|
1
|
-6
|
-1
|
|
· Instruction 2) : Transformation des
contraintes et construction du graphe - C1 = Min(x8,x5)<Max(x1,x10)
h(x8)= 1, h(x5)= -1 Min(x8,x5)= x8
46
h(x1)=2, h(x10)= -1 =
Max(x1,x10)= x10 =
C1=x8<x10
- C2 =
Min(x6,x2)<Max(x8,x2)
Min(x6,x2)=x2
Max(x8,x2)=x8 =
C2=x2<x8
- C3 =
Min(x2,x7)<Max(x9,x6) =
C3=x7<x9
- C4 =
Min(x7,x2)<Max(x9,x10) =
C4=x7<x9
- C5 =
Min(x8,x10)<Max(x6,x5) =
C5=x10<x6
- C6 =
Min(x4,x2)<Max(x10,x9) =
C6=x2<x9
- C7 =
Min(x1,x6)<Max(x3,x9)
Ici , h(x6)=h(x1)=2 =
h(x1)?h(x1)-1, on change la table des scores
comme suit :
X
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
x9
|
x10
|
h(X)
|
1
|
3
|
-1
|
0
|
-1
|
2
|
1
|
1
|
-6
|
-1
|
|
= C7=x6<x9
- C8 =
Min(x1,x3)<Max(x5,x9) =
C8=x1<x9
- C9 =
Min(x3,x1)<Max(x2,x1)
= C9=x1<x1 = contraite
non valide!, on a : h(x1)>h(x3) =
C9=x1<x2
- C10 =
Min(x7,x2)<Max(x4,x9) =
C10=x2<x9
- C11 =
Min(x4,x5)<Max(x5,x7) =
C11=x4<x5
- C12 =
Min(x10,x7)<Max(x4,x8) =
C12=x7<x4
- C13 = Min(x9,x3)<Max(x10,x2)
C13=x3<x10
- C14 = Min(x6,x10)<Max(x9,x5)
C14=x6<x9
- C15 = Min(x8,x7)<Max(x4,x7)
C15=x7<x4, et la table des scores devient :
|
X
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
x9
|
x10
|
|
h(X)
|
1
|
3
|
-1
|
0
|
-1
|
2
|
1
|
0
|
-6
|
-1
|
- C16 = Min(x6,x5)<Max(x3,x1)
C16=x6<x3
- C17 = Min(x8,x4)<Max(x8,x3)
C17=x4<x3, et la table des scores devient :
|
X
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
x9
|
x10
|
|
h(X)
|
1
|
3
|
-1
|
0
|
-1
|
2
|
1
|
-1
|
-6
|
-1
|
- C18 = Min(x1,x2)<Max(x7,x6)
C18=x2<x7
- C19 = Min(x6,x5)<Max(x2,x3)
C19=x6<x3
- C20 = Min(x1,x2)<Max(x5,x7)
C20=x2<x5
Ensuite, nous construisons un graphe orientéG comme
suit : les sommets sont les variables et les arcs sont les contraintes :
47
G :
· 
X4
X2 X3
X5 X6
X7
X8 X9
X1
X10
48
Instruction3) : En utilisant ce graphe, nous associons à
chaque variable X de X un nombre du domaine
D={1, 2,3,4,5,6,7,8,9, 10}.
- Itération 1 :
I on note S l'ensemble des sources dans le graphe, S={x1}
I la source choisie s=x1
I x1?1
I X={1,x2,x3,x4,x5,x6,x7,x8,x9,x10}
I D={2,3,4,5,6,7,8,9,10}
I G :
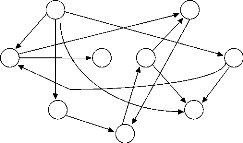
X4
X2 X3
X5 X6
X7
X8 X9
X10
I S={x1} nombre de sources =1, on répète: -
Itération 2 :
I S={x2}
I S=x2
I x2?2
I X={1, 2, x3, x4, x5, x6, x7, x8, x9, x10}
I D={3, 4,5,6,7,8,9, 10}
I G :
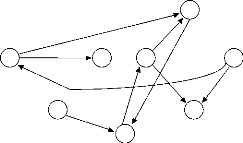
X4 X5
X8
X10
X6 X7
X3
X9
I S={x2} nombre de sources =1. - Itération 3
:
I S={x7, x8}
I S=x7
I x7?3
I X={1,2,x3,x4,x5,x6,3,x8,x9,x10}
I D={4, 5,6,7,8,9, 10}
I G :
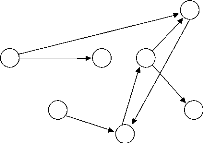
X4 X5
X8
X10
X6
X3
X9
49
50
I S={x7, x8} nombre de sources =2.
- Itération 4 :
I S={x4, x8}
I S=x4
I x4?4
I X={1, 2, x3, 4, x5, x6, 3, x8, x9, x10}
I D={5, 6, 7, 8, 9, 10} I G :
X8
X5
X10
X6
X3
X9
I S={x4, x8} nombre de sources =2.
- Itération 5 :
I S={x8, x5}
I S=x8
I x8?5
I X={1, 2, x3, 4, x5, x6, 3,5, x9, x10}
I D={6, 7, 8, 9, 10}
I G :
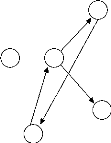
X5
X10
X6
X3
X9
51
I S={x5, x8} nombre de sources =2.
- Itération 5 :
I S={x5}
I s=x5
I x5?6
I X={1, 2, x3, 4, 6, x6,3, 5, x9,x10}
I D={7,8,9,10}
I G :
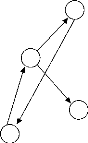
X10
X6
X3
X9
I S={x5} nombre de sources =1.
- Itération 6 :
I S=Ø
I s=Ø, à ce niveau, on n'a plus de sources on
termine 4).
· 52
Instruction 4) : Application de la procédure
Compléter pour affecter le reste des variables.
I La table des scores :
X
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
x9
|
x10
|
h(X)
|
1
|
3
|
-1
|
0
|
-1
|
2
|
1
|
-1
|
-6
|
-1
|
|
I
X={1,2,x3,4,6,x6,3,5,x9,x10}
I D={7, 8,9, 10}
- Iteration 1 :
Max(h(x3), h(x6),
h(x9), h(x10))=h(x6)
I D'ou x6-7
I X={1, 2,x3,4, 6,7,3,5, x9,
x10}
I D={8,9,10}.
- Iteration 2 :
Max(h(x3), h(x9),
h(x10))=h(x3)
I D'ou x3-8
I X={1, 2, 8, 4, 6, 7, 3, 5,
x9,x10}
I D={9, 10}.
- Iteration 3 :
Max(h(x9),
h(x10))=h(x10)
I D'ou x10-9
I X={1, 2, 8, 4, 6, 7, 3, 5, x9,9}
I D={10}.
- Iteration 4 :
Max( h(x9))=h(x9)
I D'ou x9-10
I X={1, 2, 8, 4, 6, 7, 3, 5, 10, 9}
I D=Ø, la procédure s'arrête..
On obtient ainsi X = {1, 2,8,4, 6, 7,3, 5, 10, 9}, qui satisfait
toutes les contraintes données. En effet, on a :
53
- C1 = Min(x8,x5)<Max(x1,x10) = 5 < 9 = Vrai.
- = Min(x6,x2)<Max(x8,x2) = 2 < 5 = Vrai.
- C3 = Min(x2,x7)<Max(x9,x6) = 2 < 10 = Vrai.
- C4 = Min(x7,x2)<Max(x9,x10) = 2 < 10 = Vrai.
- C5 = Min(x8,x10)<Max(x6,x5) = 5 < 7 = Vrai.
- C6 = Min(x4,x2)<Max(x10,x9) = 2 < 10 = Vrai.
- C7 = Min(x1,x6)<Max(x3,x9) = 1 < 10 = Vrai.
- C8 = Min(x1,x3)<Max(x5,x9) = 1 < 10 = Vrai.
- C9 = Min(x3,x1)<Max(x2,x1) = 1 < 2 = Vrai.
- C10 = Min(x7,x2)<Max(x4,x9) = 2 < 10 = Vrai.
- C11 = Min(x4,x5)<Max(x5,x7) = 4 < 6 = Vrai..
- C12 = Min(x10,x7)<Max(x4,x8) = 3 < 5 = Vrai.
- C13 = Min(x9,x3)<Max(x10,x2) = 8 < 9 = Vrai.
- C14 = Min(x6,x10)<Max(x9,x5) = 7 < 10 = Vrai.
- C15 = Min(x8,x7)<Max(x4,x7) = 3 < 4 = Vrai.
- C16 = Min(x6,x5)<Max(x3,x1) = 6 < 8 = Vrai.
- C17 = Min(x8,x4)<Max(x8,x3) = 4 < 8 = Vrai.
- C18 = Min(x1,x2)<Max(x7,x6) = 1 < 7 = Vrai.
- C19 = Min(x6,x5)<Max(x2,x3) = 6 < 8 = Vrai.
- 0 = Min(x1,x2)<Max(x5,x7) = 1 < 6 = Vrai.
3.7 Outils d'implémentation
· Nous avons utiliséessentiellement comme logiciels
pour l'implémentation et les tests de l'algorithme
précèdent :
DEVC++(4.9.9.2) : Dev-C++ est un environnement
de développement intégré(IDE) permettant de programmer en
C et en C++.
54
Matlab (7.12.0.0) : Matlab est un
environnement de développement . Il est utiliséà des fins
de calcul numérique. Développépar la
sociétéThe MathWorks.
· Et comme langage de programmation nous avons
utilisé:
C++ : C++ est un langage de programmation compilé,
permettant la programmation sous de multiples paradigmes comme la programmation
procédurale, la programmation orientée objet et la programmation
générique.
Matlab : ( matrix laboratory ) est un langage
de programmation de quatrième génération, MATLAB permet de
manipuler des matrices, d'afficher des courbes et des données, de mettre
en oeuvre des algorithmes, de créer des interfaces utilisateurs, et peut
s'interfacer avec d'autres langages comme le C, C++, Java, et Fortran.
3.8 Expérimentation
Dans cette section, nous testerons l'efficacitéde
l'algorithme proposéen termes de temps et de pourcentage de contraintes
satisfaites.
3.8.1 Complexitéde l'algorithme proposé
Notre algorithme va parcourir m contraintes pour
calculer les scores (instruction 1) et pour construire le graphe (instruction
2), puis O(n) matrice de dimension
O(n2) (si on utilise une matrice pour
représenter le graphe) (n qui est égal au nombre de
variables), pour identifier les sources. Donc la complexitéde notre
algorithme est O(max(m,n3)), qui est une
complexitépolynomiale. Le temps nécessaire pour résoudre
des instances du problème de différentes tailles est
représentédans le tableau ci-dessous.
|
Nombre des variables
|
5
|
10
|
20
|
50
|
250
|
1000
|
10000
|
|
Temps de résolution
|
1.25 us
|
10 us
|
80 us
|
1.25 ms
|
156 ms
|
10 s
|
2.7 heures
|
TABLE 3.2 - temps nécessaire à l'exécution
d'un algorithme de complexitécubique (polynomiale) [8]
Comme on peut le constater, notre algorithme s'est
avéréplus performant en termes de temps d'exécution par
rapport aux algorithmes complets que nous avons testéau début du
chapitre.
3.8.2 Satisfaction des contraintes
Après avoir testél'efficacitétemporelle de
l'algorithme, nous proposons à présent, d'évaluer sa
capacitéde satisfaire les contraintes données.
Pour cela, nous avons fixéle nombre de variables, puis
nous avons variéle nombre de contraintes, commençant par 20 et
allant jusqu'à5000 contraintes, en ajoutant à chaque fois 20
contraintes et en calculant le pourcentage des contraintes satisfaites.
Pour faire cette tâche, nous avons implémenter
avec DEVC++ trois programmes, un générateur de contraintes qui
génère des contraintes aléatoires à partir d'un
ensemble de n variables et qui les passe à un autre programme
qui implémente notre algorithme pour la résolution. Ensuite, la
solution trouvée est passée avec les contraintes, comme
donnés, au troisième programme qui calcule le pourcentage des
contraintes satisfaites. Nous avons traitéles résultats obtenus,
avec l'outil MATLAB, »plottool», pour visualiser les
résultats.
- La Figure 3.1 présente les tests pour 100 variables
:
pourcentage des contraintes satisfaites
100
90
80
70
60
50
55
0 500 1000 1500 2000 2500 3000 3500 4000 4500
5000
nombre des contraintes
FIGURE 3.1 - Pourcentage des contraintes
satisfaites par rapport au nombre de contraintes sur problème impliquant
100 variables
- La Figure 3.2 présente les tests pour 300 variables :
pourcentage des contraintes satisfaites
100
90
80
70
60
50
0 500 1000 1500 2000 2500 3000 3500 4000 4500
5000
nombre de contraintes
FIGURE 3.2 - Pourcentage des contraintes satisfaites par rapport
au nombre de contraintes sur problème impliquant 300 variables
- La Figure 3.3 représente les tests pour 600 variables
:
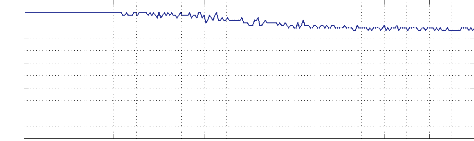
pourcentage des contraintes satisfaites
100
90
80
70
60
50
56
0 500 1000 1500 2000 2500 3000 3500 4000 4500
5000
nombre de contraintes
FIGURE 3.3 - Pourcentage des contraintes satisfaites par rapport
au nombre de contraintes sur problème impliquant 600 variables
57
Nous remarquons que dans les trois figures
précédentes (Figure 3.1, 3.2 et 3.3), le pourcentage des
contraintes satisfaites est stable à 100% au début pour se
déstabiliser ensuite entre les valeurs 93% et 97%.
Nous avons reproduit le même traitement, pour illustrer
les moyennes des pourcentages des contraintes satisfaites en fonction du nombre
des variables (débutant de la valeur 50 et allant jusqu'à700).
Nous avons obtenu le résultat suivant (voir Figure 3.4)
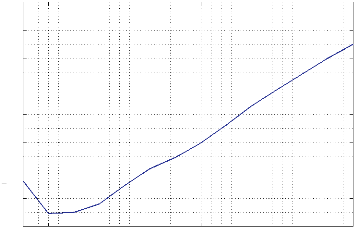
100 200 300 400 500 600 700
pourcentage moyen des contraintes satisfaites
97.5
96.5
95.5
94.5
98
97
96
95
94
nombre de variables
FIGURE 3.4 - contraintes satisfaites par rapport au nombre de
variables
On remarque, que lorsque le nombre de variables augmente, le
pourcentage des contraintes satisfaites tend vers 100% ce qui met en valeur
l'efficacitéde notre algorithme.
3.9 Conclusion
Dans ce chapitre, nous avons proposéun algorithme que
nous avons implémentéen vue de résoudre un CSP particulier
impliquant des contraintes temporelles. Nous l'avons testépour prouver
son efficacité, puis nous avons présentéles
résultats obtenus. Ces résultats ont explicitement montrés
que notre algorithme, malgrésa simplicité, peut satisfaire 95,53%
des contraintes données.
58
Chapitre 4
Conclusion générale
Pour conclure ce travail, nous résumons les
étapes de notre recherche qui a portésur la résolution
d'un problème particulier de satisfaction de contraintes.
Dans le deuxième Chapitre, nous avons définis
les problèmes de satisfaction des contraintes, en donnant des
modélisations sous la forme CSP de quelques problèmes connues,
puis nous avons illustréle fonctionnement de quelques algorithmes
complets de résolution des CSP. Nous avons conclus le chapitre par
l'étude d'un type spécifique de CSP, qui est le problème
de satisfactions des contraintes temporelles sous lequel s'inscrit le
problème proposédans le Chapitre 3.
Le troisième Chapitre a
étéconsacréà la résolution d'un
problème spécifique qui fait intervenir des contraintes
temporelles. Nous avons décrit ce problème, puis nous avons
montré, sur un exemple, que les algorithmes complets de
résolution de CSP sont inefficaces. Nous avons ensuite essayéde
remédier à la défaillance de ces algorithmes en proposant
notre propre algorithme, qui s'appuie essentiellement sur une méthode
heuristique. Nous avons conclu ce chapitre par une expérimentation, sur
des instances du problème générées
aléatoirement, qui a montrél'efficacité(95.53%) de notre
algorithme malgrésa simplicité.
Parmi les perspectives ouverte pour ce travail, nous proposons
de trouver une méthode pour traiter des contraintes qui ont la
même forme que celles que nous avons considérémais qui
impliquent plus de variables, toujours en un temps raisonnable, et en utilisant
une heuristique encore plus efficace que la nôtre.
59
Bibliographie
[1] Christine SOLNON, »Ant Colony Optimization and
Constraint Programming »,2010, chapitre 3 ,3.1 What is a constraint?
[2] Christine SOLNON,»Ant Colony Optimization and
Constraint Programming »,2010, 3.2 What is a constraint satisfaction
problem?
[3] Charles Lutwidge Dodgson (plus connu sous le pseudonyme
de Lewis Carroll) est un romancier, essayiste, photographe et professeur de
mathématique à l'universitéd'Oxford, néle 27
janvier 1832 à Daresbury, dans le Cheshire et mort le 14 janvier 1898
à Guildford.
[4] J. F. Allen. An interval-based representation of temporal
knowledge. In Proceedings of the 7th International Joint Conference on
Artificial Intelligence (IJCAI'81), pages 221-226, 1981.
[5] James F. Allen: Maintaining knowledge about temporal
intervals. In : Communications of the ACM. 26 November 1983. ACM Press. pp.
832-843, ISSN 0001-0782
[6] M. Vilain et H. Kautz. Constraint propagation algorithms
for temporal reasoning. In AAAI-86 Proceedings, pages 377-382, 1986.
[7] Rina Dechter,»Constraint Processing», 2003,
chapitre 12 :» Temporal Networks Constraint»
[8] http ://
fr.wikipedia.org/wiki/Analyse
de la complexit%C3%A9 des algorithmes
[9] http ://
fr.wikipedia.org/wiki/Probl%C3%A8me
de satisfaction de contraintes
[10] J. F. Allen. Towards a general theory of action and
time. Artificial Intelligence, 23(2) :123-154, 1984.
[11] J.-F. Condotta et E. Würbel. Réseaux de
contraintes temporelles et spatiales. In F. Le Ber, G. Ligozat,
et O. Papini, editors, Raisonnements sur l'espace et le temps
: des modèles aux applications, TraitéIGAT -
Géomatique, chapitre 7, pages 181-223. Lavoisier, 2007.
[12]
60
Bassam Baki. Ordonnancement et planification sous contraintes
temporelles et probabilistes. Alexandre Vautier, Sylvie Saget. MajecSTIC 2005 :
Manifestation des Jeunes Chercheurs francophones dans les domaines des STIC,
Nov 2005, Rennes, France. pp.323-330. <inria- 00000669>
[13] F. Le Ber, G. Ligozat, et O. Papini, editors.
Raisonnements sur l'espace et le temps : des modèles aux applications.
TraitéIGAT - Géomatique. Lavoisier, Paris, 2007.



