
Unversité Abd el Malek Essaadi Facultés de
science
|
|
Filière Master :
Electronique et
Télécommunication
|
Titre :
Contrôle de la dispersion chromatique
dans les
fibres optiques à cristaux photoniques et d'autres
fibres
à profil d'indice non standard
Présenté par :
Mr : AHMED OUADGUI
Date de soutenance : 15/07/2009
JURY :
|
Nom et Prénom
|
Etablissement
|
Qualité
|
|
Pr .Mohamed AGHOUTANE
|
Faculté des Sciences
|
Président
|
|
Pr.Abdelkrim FARKHSI
|
Faculté des Sciences
|
Encadrant universitaire
|
|
Pr.Mohamed BOUSSOUIS
|
Faculté des Sciences
|
Examinateur
|
Stage effectué à la Faculté des
Sciences.
Remerciements
Ce travail a été effectué au Laboratoire
d'Electronique et Instrumentation à la faculté des sciences de
Tétouan, sous la direction du professeur monsieur Abdelkrim FARKHSI qui
n'a cessé de m'apporter ses conseils précieux et ses suggestions
très utiles pour mener à bien ce travail. Je tiens à lui
exprimer ma profonde gratitude et mes vifs remerciements.
Je tiens à remercier messieurs les professeurs Mohamed
AGHOUTANE et Mohamed BOUSSOUIS, pour l'honneur qu'ils m'ont fait en acceptant
d'évaluer mon travail.
Mes sincères remerciements s'adressent à tous
les professeurs qui ont assuré les cours de Master d'Electronique et
télécommunication durant les deux années (2008-2009).
J'exprime ma plus profonde gratitude et mon affection à
mes parents qui m'ont permis de découvrir cet univers et à toute
ma famille pour leur soutien.
Enfin, je tiens à remercier mes collègues du master
électronique et télécommunication pour leur
coopération et leur sympathie
SOMMAIRE
INTRODUCTION 5
Chapitre 1 : Etude de la fibre optique 8
1. Historique et généralités 9
1.1 Définition de la fibre optique 9
1.2. Historique 9
1.3. Les types de fibres optiques 12
1. 3.1 Les fibres optiques multimodes 12
1.3.1.1 Fibres à saut d'indices 12
1.3.1.2 fibres à gradient d'indices 13
1.3.2 Les fibres monomodes 14
1.4. Quelques paramètres de la fibre optique
15
1.4.1 L'ouverture numérique 15
1.4.2 La bande passante 16
1.4.3 : Fréquence normalisée 17
1.4.4 L'aire effective 18
2. Atténuation 18
2.1.Atténuation linéique 18
2 .2 Fenêtre de transmission 19
Chapitre 2 : Les dispersions dans les fibres optiques 20
1. Dispersion intermodale 21
2. Dispersion intramodale 22
3. dispersion modale de polarisation 22
4. Dispersion chromatique 24
4.1 Définition 24
4.1.1.Dispersion du matériau 26
4.1.2.Dispersion du guide 30
5. Mesure de la dispersion chromatique 32
5.1 Méthode de variation de phase 33
5.2 Méthode temporelle 34
Chapitre 3 : Etude des fibres compensatrices de dispersion
chromatique 36
1. Contrôle de la dispersion chromatique dans les fibres
à cristaux photoniques 37
1.1 Définition et historique de la fibre à cristal
photonique 37
1.2 Fabrication du FCP 38
1.3.Contrôle de la dispersion chromatique dans la FCP 41
1.4 Dispersion très réduite et ultra-aplatie 44
2. Contrôle de la dispersion chromatique dans une fibre
à cristal photonique à
double coeur concentrique (FDCC) 48
2.1 Définition 48
2.2 Présentation de la fibre étudiée 48
2.3 Méthode de contrôle de la dispersion
chromatique dans la FDCC 49
3. Contrôle de la dispersion chromatique dans une fibre
à réseaux de Bragg 52
3.1 Définition d'un réseau de Bragg 52
3.2. Contrôle de la dispersion chromatique dans une fibre
à réseau de Bragg à
pas variable 52
CONCLUSION ET PERSPECTIVES 55
Références 57
Annexe 59

INTRODUCTION

Introduction


Au troisième chapitre nous allons étudier quelques
méthodes de contrôle de la dispersion chromatique dans une fibre
à cristal photonique, dans une fibre à cristal photonique
à double coeur et dans une fibre à réseaux de bragg.

Chapitre 1 : ETUDE DE LA FIBRE OPTIQUE


1. HISTORIQUE ET GENERALITES [1.1]
1.1 Définition de la fibre optique
Une fibre optique est un guide d'onde cylindrique qui transmet
l'information sous forme de lumière à travers des longues
distances avec un débit élevé. Elle peut être
représentée par une partie centrale (coeur) d'indice de
réfraction n1 entourée d'une gaine dont l'indice de
réfraction n2 est légèrement plus faible (Figure 1). Le
coeur, constitué d'un matériau diélectrique transparent,
est généralement de la silice dopée en oxyde de germanium
GeO2 et/ou de potassium P2 O5.
La plupart des fibres optiques ont un coeur de symétrie
cylindrique autour d'un axe noté Oz appelé axe de propagation. La
section transverse présente une différence d'indice entre le
coeur et la gaine qui peut être discontinue (fibre à saut
d'indice) ou graduelle (fibre à gradient d'indice).

Figure.1 : schéma simplifié de la fibre optique
1.2. Historique
Dans les années 70 Les réseaux de
télécommunication reposent sur deux types de systèmes : le
câble coaxial et les faisceaux hertziens :
+ le câble coaxial possède, quant à lui, une
longueur du pas de régénération beaucoup plus faible du
fait de la très forte atténuation du milieu.

Le système de base de ces réseaux a une
capacité de 140 Mbit/s avec un espacement entre chaque
répéteur de l'ordre de 2 km. Les derniers développements
sur ces lignes de transmission ont permet d'obtenir une capacité de 560
Mbit/s avec le même espacement entre répéteurs. Comme
à l'époque les câbles interurbains disposaient typiquement
de 8 à 12 paires, la capacité d'une ligne atteignait 2 ou 3
Gbit/s
+ Le réseau hertzien est basé sur une
infrastructure de relais (distant d'environ 50 km les uns des autres) et
utilise diverses bandes de fréquences essentiellement autour de 6/7 GHz
et 11 GHz. De 1975 à 1985, la recherche se concentre sur les
problèmes que pose l'augmentation de la bande passante liée au
passage de l'analogique au numérique, et des développements
importants voient le jour. Ainsi, des faisceaux hertziens permettant la
transmission de 8 canaux (7 plus un canal de secours) à 140 Mbit/s, soit
environ 1 Gbit/s sur un lien sont disponibles dès la fin des
années 80. Le rendement spectral, qui représente
l'efficacité dans l'utilisation du spectre, atteint alors environ 4
bit/s/Hz, grâce à des schémas de modulation performants.
En 1980, les premiers systèmes de transmission optique
apparaissaient. Ce développement commercial est l'aboutissement de plus
de deux décennies de recherche de base pour obtenir des composants et
dispositifs (en particulier des sources), mais aussi des fibres dont
l'atténuation est compatible avec les exigences d'un réseau de
télécommunication : en 1970, la compagnie Corning Glass Works de
New York, produit la première fibre optique avec des pertes suffisamment
faibles (20dB/km) pour être utilisée dans les réseaux de
télécommunications (actuellement les pertes sont de l'ordre de
0,15 dB/km).
Les premières années de la fibre optique sont
marquées par des évolutions importantes :
> Le passage consécutif de la première
fenêtre de transmission autour de
850 nm (fibre multimode) à la deuxième autour de
1310 nm (minimum

d'atténuation d'environ 0,3 à 0,4 dB/km), puis
à celle autour de 1550 nm (minimum d'atténuation de 0,15 dB/km),
qui est la norme aujourd'hui en matière de réseau. Ces
changements de fenêtre de transmission ont été rendus
possibles par l'amélioration des techniques de fabrication des
préformes et au développement des sources optiques.
> Le passage de la fibre multimode, utilisée dans
les premières expérimentations, à la fibre monomode dont
la connexion est plus problématique mais, qui propose des débits
sans rapport avec la première. La fibre multimode conserve cependant sa
pertinence dans d'autres domaines tels que l'aéronautique par
exemple.
Même si, dans les premières années, le
réseau optique a un débit qui ne surpasse pas encore celui des
lignes de transmission utilisant le câble coaxial, il présente
quand même un avantage indéniable face à ce dernier :
l'espacement entre chaque répéteur est plus important, de l'ordre
de quelques dizaines de kilomètres (par exemple environ 70 km pour un
système à 560 Mbit/s à 1550 nm).
L'avantage de la fibre optique par rapport au câble
coaxial (augmentation du pas de régénération et donc
diminution des répéteurs et des coûts de fabrication des
lignes de transmission) va trouver un champ d'application dans le domaine des
télécommunications très longues distances (en particulier
dans les lignes de transmission sous-marines) : des câbles optiques
furent envisagés dès lors que la fiabilité des composants
optiques permet de les immerger. Le premier câble sousmarin
transatlantique TAT 8 (Trans-ATlantic cable) utilisant des fibres optiques fut
posé en 1988 et offre une capacité de 280 Mbit/s par paire de
fibres à 1310 nm. TAT 9 qui suivit en 1991, travaille quant à lui
à 1550 nm, avec une capacité de 560 Mbit/s par paire de
fibres.
La notion de ligne de transmission «tout-optique»
faisant appel exclusivement à la fibre optique apparaît au
début des années 1990.

De 1992 à 1996, vont se bâtir les réseaux
« tout-optique » de grande capacité utilisant la fibre
monomode standard appelée G-652 dans la norme ITU-T, chaque fibre
étant capable de transporter un débit de 2,5 Gbit/s avec un pas
moyen de régénération de 90 km.
Cette évolution technologique des réseaux «
tout-optique » a été rendue possible par la mise au point
d'amplificateurs optiques dès la fin des années 80. En
général, l'amplificateur utilise une fibre dopée à
l'erbium dans laquelle se produit un mécanisme de transfert de puissance
entre une pompe optique et le signal à transporter ; ainsi cela permet
de contrôler sans conversion électrooptique la puissance des
signaux transmis et compense les pertes subies lors de la propagation.
En 1995 le premier réseau sous-marin utilisant la
technologie de l'amplification optique à fibre dopée à
l'erbium (EDFA pour Erbium Doped Fiber Amplifier) est mis en service. Cette
liaison longue de 6300 km (TAT 12, TAT 13) comporte 133 répéteurs
en ligne et propose un débit total de 10 Gbit/s transmis sur deux
fibres, équipées chacune d'une longueur d'onde modulée
à 5 Gbit/s.
Enfin la véritable révolution technologique va
se produire avec l'apparition du multiplexage en longueur d'onde ou WDM (pour
Wavelength Division Multiplexing) qui amène donc une multiplication par
un facteur considérable de la capacité du réseau.
L'intérêt principal de cette technique, qui a fait sa
popularité, est de pouvoir réutiliser la fibre déjà
installée, ce qui n'entraîne pas de surcoût pour de
nouvelles infrastructures
1.3. Les types de fibres optiques [1-2]
1. 3.1 Les fibres optiques multimodes.
1.3.1.1 Fibres à saut d'indices
C'est le type de fibre le plus simple, directement issue des
applications optiques traditionnelles.
Dans cette fibre, le coeur est homogène et d'indice n1.
Il est entouré d'une gaine optique d'indice n2 inférieur à
n1. Ces indices sont peut différent et doivent être de l'ordre de
1,5. Quant à la gaine optique, elle joue un rôle actif dans la
propagation, et ne doit pas être confondue avec le revêtement de
protection déposée sur la fibre. Le rayon lumineux est
guidé par la réflexion totale au niveau de l'interface coeur-
gaine (Figure2), sinon il est réfracté dans la gaine.

Figure 2 : Fibres à saut d'indices
La capacité de transmission de ce type de fibre est
d'environ 100 Mbits/s. Cette valeur correspond également à la
bande passante. On peut également exprimer la bande passante en Mhz.km.
Ici pour la fibre à saut d'indice elle est de 22 Mhz.km. Cette
capacité est assez faible car chaque rayon doit parcourir une distance
différente.
Par conséquent il faut à l'extrémité
« attendre » que tous les faisceaux soient arrivés.
1.3.1.2 fibres à gradient d'indices
Le coeur de ces fibres est constitué de plusieurs
couches de verres dont l'indice de réfraction est différent
à chaque couche et l'indice de réfraction diminue de l'axe
jusqu'à la gaine.
Le guidage est cette fois dû à l'effet du gradient
d'indice. Les rayons suivent une trajectoire d'allure sinusoïdale (Figure
3). La gaine n'intervient pas directement, mais élimine les rayons trop
inclinés.
L'avantage avec ce type de fibre est de minimiser la dispersion
du temps de propagation entre les rayons.

Figure 3 : Fibre à gradient d'indice
Dans cette fibres l'indice décroît selon la relation
suivante :
n r n
( ) 1(0). 1 2. r
= - Ä
a

á


Avec :
a : rayon du coeur de la fibre
n1 : indice du coeur
n2 : indice de la gaine
á : paramètre de profil d'indice
n n
2 2
-
1 2
Ä = : différence relative des indices de
réfraction
n1
2 .
La bande passante de ce mode de fonctionnement est de 500
Mbits/s. Cette capacité est plus élevée que celle du saut
d'indice car la distance à parcourir des rayons est plus faible, donc il
est possible d'augmenter en fréquence.
1.3.2 Les fibres monomodes
Le but recherché dans cette fibre est que le chemin que
doit parcourir le faisceau soit le plus direct possible (Figure 4). Pour cela
on réduit fortement le diamètre du coeur qui est dans la plupart
des cas inférieur à 10pm.
Figure 4 : fibre monomode

La dispersion modale est quasi nulle. Comme on ne casse pas le
faisceau lumineux la bande passante est donc augmentée, environ 100
Ghz.km ou de 1000 Mbits/s.
Le tableau suivant présente des exemples de
caractéristiques de quelques fibres optiques de transmission
[1.3]
|
Tableau 1
· Exemples de caracteristiques
de quelques fibres optiques de
transmission.
|
|
Norme UIT-T
|
G. 652
|
G. 653
|
G.655 (NZDSF)
|
G.655 (Téralight)
|
|
Propriétés
géométriques
|
Diamètre coeur
(pm)
|
9
|
9
|
9
|
9
|
|
Diamètre fibre (pm)
|
125
|
125
|
125
|
125
|
|
Pro priétés optiques
(à 1550 pm)
|
Atténuation (dB/km)
|
0,25
|
0,25
|
0,25
|
0,22
|
|
Dispersion Chroma-
tique
(ps/nm/km)
|
17
|
0
|
0,07
|
8
|
|
Coefficient de non-
linéarité
(W/m2)
|
2,7.10-
20
|
2,7.10-
20
|
2,7.10-20
|
2,7.10-20
|
|
Section effective
(pm2)
|
80
|
57
|
57
|
65
|
|
0,05 à
0,08
|
0,1 max.
|
0,1 max.
|
0,04
|
|
PMD ( ps/ km )
|
1.4. Quelques paramètres de la fibre optique
1.4.1 L'ouverture numérique (Figure 5)

ONFSI = sin è0 = 1 n
1 2 22
- n
n0
L'ouverture numérique d'une fibre à saut d'indice
est définie par :

Figure 5 : représentation du demi angle du cône de
révolution.
Où : è0 représente le
demi angle du cône de révolution qui contient
les rayons optiques susceptibles de se propager dans le coeur. n0
: l'indice du vide
n1 : l'indice du coeur
n2 : l'indice de la gaine de la fibre
Dans le cas d'une fibre à gradient d'indice ; l'ouverture
numérique est définie par :

1 2 2
ONFGI sin
= è = n 0 n
( ) - Où n 1 ( 0 ) : est l'indice au centre du
0 1 2
n 0
coeur
Une forte valeur de l'ouverture numérique permet de
coupler beaucoup de lumière dans le coeur de la fibre. Cependant, une
valeur élevée est la cause d'une forte dispersion du temps de
propagation entre les différents rayons ou modes.
1.4.2 La bande passante
la bande passante est la quantité d'informations que l'on
peut transmettre sur la fibre optique pendant un intervalle de temps,
exprimée en bits par secondes (bps). Elle désigne aussi la
longueur de l'intervalle de fréquence utilisable sur un support, dans ce
cas elle s'exprime en hertz (Hz).
Son expression pour une fibre optique est : BP
c 1
.
2 L n
n 1
1 - 1
n 2
L'usage impose que la bande passante soit exprimée en
Mhz/km . 1.4.3 : Longueur d'onde de
coupure
La longueur d'onde de coupure ëc , est
la longueur d'onde au delà de laquelle le régime de la fibre est
monomode, elle est définie par :
2ða
2 2
ë = ak n n
- = n 2 Ä
c 0 1 2 1
2,405


Lorsque la longueur d'onde est inférieure à
ëc , la fibre est multimode, plusieurs modes sont
guidés.
K0 : est le nombre d'onde du vide a : est le rayon du coeur
1.4.3 : Fréquence normalisée
En résolvant l'équation de propagation dans la
fibre et en appliquant les conditions aux limites coeur- gaine, on
définit le terme V, fréquence spatiale normalisée, telle
que :


2ð
2Ä
V ak . n n a . . n
2 - =
2
= 0 1 2 1
ë
où ë représente la longueur d'onde et
k0 le vecteur d'onde.
C'est V qui va déterminer si la fibre est monomode ou
multimode. Dans le cas où la fibre est à saut d'indice :
> Si V < 2,405, un seul mode se propage dans la fibre, le
mode HE11 ou LP01 aussi appelé mode fondamental de la fibre.
La fibre est dite monomode ou unimodale.
> Si V > 2,405, plusieurs modes peuvent se propager, la
fibre est dite multimode.
Il est à noter que la fréquence spatiale
normalisée dépend des paramètres
optogéométriques de la fibre (indices de réfraction et
rayons) mais aussi du vecteur d'onde k0 de la fibre et donc de la longueur
d'onde d'opération ë .
1.4.4 L'aire effective
L'aire effective (ou surface effective) d'une fibre optique
est calculée à partir de la répartition transverse du
champ modal se propageant dans la fibre. Soit E0 la distribution de ce champ.
Par intégration sur toute la section droite de la fibre, l'aire
effective Aeff est définie par :
2
E dS
0
4
E dS
0
2
A eff =


Ce terme est introduit pour évaluer les effets non
linéaires (effet Ker, effet Raman,) car d'un point de vue
théorique ceux-ci sont proportionnels au rapport de la puissance
d'entée sur l'aire effective. Par conséquent, pour diminuer leurs
influences à puissance constante, il faut des fibres à forte aire
effective
Les principaux inconvénients des fibres optiques sont
l'atténuation, la dispersion, que nous allons étudier dans la
suite.
2. Atténuation [1-4]
2.1. Atténuation linéique :
L'atténuation caractérise l'affaiblissement du
signal au cours de la propagation. Soient P0 et PL les puissances à
l'entrée et à la sortie d'une fibre de longueur L.
L'atténuation linéaire se traduit alors par une
décroissance exponentielle de la
puissance en fonction de la longueur de fibre : ( )
PL P -á
0 *10 x
=
où á est le coefficient d'atténuation
linéaire. On utilise souvent le coefficient ádB exprimé en
dB/km et relié à á par ádB = 4.343á:
Le principal atout des fibres optiques est une
atténuation extrêmement faible. L'atténuation va varier
suivant la longueur d'onde. La diffusion Rayleigh limite ainsi les performances
dans le domaine des courtes longueurs l'onde (domaine du visible et du proche
infrarouge). Un pic d'absorption, dû à la présence de
radicaux
OH- dans la silice, pourra également
être observé autour de 1 385 nm. Les progrès les plus
récents dans les techniques de fabrication permettent de réduire
ce pic.
Le profil de l'atténuation d'une fibre optique faite en
silice est représenté sur la figure 6.

Figure 6 : Profil de l'atténuation spectrale de la
fibre optique faite de silice
2 .2 Fenêtre de transmission
On distingue les trois fenêtres de transmission suivantes
:
· La première fenêtre de 800 à
900 nm
Pour cette fenêtre l'atténuation est
élevée, elle est voisine de
3dB/km (Diode LED). Cette fenêtre n'est utilisée
qu'en multimode.
· La deuxième fenêtre s'étend
de 1280 à 1330 nm :
Pour cette fenêtre l'atténuation est raisonnable
et de l'ordre de de 0 ,33dB/km. La dispersion chromatique est nulle. Cette
fenêtre est largement utilisée.
· La troisième fenêtre de 1525
à 1625 nm :
Elle est constituée de deux sous bandes :
> Sous bande C de 1525 à 1565 nm
> Sous bande L de 1565 à 1625nm
C'est la fenêtre de choix pour quasiment toutes les
applications modernes.

Chapitre 2 :
LES DISPERSIONS DANS LES FIBRES OPTIQUES









La dispersion est un inconvénient majeur dans les
fibres optiques, car elle limite le débit de transmission des
données dans ces dernières. Il en existe plusieurs types, que
nous allons étudier dans le chapitre suivant. Nous intéressons
particulièrement à la dispersion chromatique qui fait l'objet de
ce travail de fin d'étude.
1. DISPERSION INTERMODALE [2-1]
La dispersion intermodale est la cause principale de
l'élargissement des impulsions dans les fibres optiques multimodes. Cet
élargissement est provoqué par les différences des temps
de parcours des rayons lumineux. La dispersion intermodale Di est
l'élargissement temporel maximum ô d'une impulsion par
unité de longueur de fibre.
t t
- ô
max min
Di = = ( / )
ps km (2-1)
L L
Avec tmax et tmin sont : le
temps de parcours du mode le plus lent et celui du mode le plus rapide. Dans
une fibre à saut d'indice, le rayon le plus rapide est celui dont le
trajet est parallèle à l'axe de la fibre. Ce rayon est
associé à l'angle è égal à 0 et au
mode appelé « mode fondamental » LP01. De même, le rayon
le plus lent fait un angle è max par rapport
à l'axe de la fibre avec è max défini
par :
|
èmax arcsin
=
|
|
n n
2 2
-
1 2 (2-2)
n 1
|
Et ô = t max - tmin =
n1t minÄ (2-3)
|
Avec :
|
2 2
n - n
1 2
Ä = 2 1 2
n différence relative d'indice
|
(2-4)
|
|
Donc la dispersion intermodale s'écrit : Di=
|
n 1 Ä (2-5)
c
|
L'obtention d'une dispersion intermodale réduite se fait
en minimisant Di ou en utilisant une fibre à gradient d'indice. En
effet, dans ce cas là, l'indice de réfraction




n1 du coeur décroît avec le rayon de celui-ci de
sorte que les rayons axiaux (à trajet court) voient un indice
élevé (leur vitesse c/n est alors réduite) tandis que les
rayons périphériques (à trajet long) voient un indice plus
bas (vitesse augmentée).
Dans le cas d'une fibre optique monomode, cette dispersion est
nulle et ne sera donc pas prise en compte.
2. Dispersion intramodale [2,2]
Dans une fibre monomode les signaux sont déformés
à cause du fait que l'indice de la fibre change en fonction de la
longueur d'onde.
Si on injecte à l'entrée de la fibre un signal a(t)
, il a une transformée de Fourier A(f) :
a ( t ) ? A ( I)
Chaque fréquence du spectre du Fourier correspond à
une longueur d'onde :
La vitesse v avec laquelle se propage chaque longueur
d'onde est différente,
c
n ë
( )
puisque l'indice dépend de la longueur d'onde et : v
=
Ainsi ; les fréquences du spectre de Fourier ne se
propagent pas à la même vitesse et par conséquent elles
n'arriveront pas simultanément à la sortie de la fibre, donc le
signal est déformé. C'est ce qu'on appelle la dispersion
intramodale
3. dispersion modale de polarisation
Il existe deux modes électromagnétiques
dégénérés du mode fondamental d'une fibre optique
monomode (LP01), caractérisés par deux directions de polarisation
perpendiculaires (figure 7). Dans une fibre monomode « idéale
», ces deux modes, notés LP01x et LP01 y, se
propagent à des vitesses identiques. Lorsque la fibre présente
une biréfringence, qui peut être due à des contraintes
(élongation, courbures, micro courbures ...), on observe une
levée de la dégénérescence des constantes de
propagation entre les deux modes. Les deux composantes du mode se propagent
alors à des vitesses différentes.




La propagation simultanée dans la fibre de ces deux
modes de polarisation introduit un phénomène de dispersion dite
de polarisation qui est un facteur limitant de la capacité des lignes de
transmission optique monomode.

Figure 7. Représentation des modes
dégénérés du mode LPoi La variation de
constante de propagation est définit comme étant :
äâ = äâ -
äâ
x y
äâ étant très petit devant
äâx et äây
La longueur de battement s'exprime par :
qui est définie comme la longueur de propagation
après laquelle chaque état de polarisation se retrouve identique
à lui même.
Le concept de dispersion de polarisation est plus difficile
à appréhender que celui de la dispersion chromatique du fait du
couplage aléatoire des modes de polarisation. Ce phénomène
rend nécessaire une analyse statistique de la dispersion de polarisation
avec comme conséquence immédiate le fait que la valeur obtenue
(en picoseconde) n'est qu'une valeur moyenne.
Celle-ci dépendant de tous les paramètres
extérieurs (température, pression, contrainte, etc), il est
généralement admis que cette valeur fluctue au cours du temps et
suit une loi de probabilité de Maxwell-Boltzmann.
Cette dispersion est faible, de l'ordre de quelques
dixièmes de

ps / km pour une fibre monomode standard




4. Dispersion chromatique
4.1 Définition
Le temps de propagation de groupe, c'est-à-dire le
temps mis par un signal pour parcourir l'unité de longueur,
dépend de la longueur d'ondeë . Dans le cas d'un signal
issu d'une source émettant sur une raie de largeuräë
, ces temps de propagation vont s'étaler sur une certaine
durée (figure 8). Le paramètre de dispersion chromatique (D) est
défini comme la dérivée du temps de propagation de groupe
par rapport à la longueur d'onde, pour une longueur de fibre de 1 km. On
le donne généralement en ps/(
nm.km), les picosecondes correspondant
à l'élargissement temporel, les nanomètres à la
largeur spectrale et les kilomètres à la longueur de fibre.

Figure 8. Evolution de l'impulsion pendant sa propagation
dans la fibre optique
En fait, la dispersion chromatique est la somme d'un terme de
matériau pur (dispersion matériau) et d'un terme dû au
guidage de l'onde (dispersion modale). La dispersion chromatique est la cause
principale de l'élargissement des impulsions dans les fibres optiques
monomodes dont le profil est à symétrie de révolution.
Avant l'étude de la dispersion, définissons
quelques termes:
· Le temps de groupe
Le temps de groupe tg , est défini
comme étant le temps nécessaire
pour qu'une impulsion se propage dans une fibre de longueur L.
L
t g = (2-6)
g
v




dù
où vg , est la vitesse de groupe
associée, est définie par : v g = (2-7)
d â
avec ù est la pulsation et â la
constante de propagation axiale, projection sur
l'axe de propagation du module du vecteur d'onde k dont la
définition est la suivante :
? ?
k = n1 k 0
ð
= 2 n1 (2-8)
ë
?
k est le vecteur d'onde dans le vide
0
ù
et â = k n
0 1 cos( ) 1 cos( è )
è = n (2-9)
c
On développe tg à l'ordre 2
autour de ù0 :
dâ + -
( ) d
ù ù 0
d d
ù ù = ù 0
ù
tg L
=
2 â
2 ù = ù 0
(2-10)
> le premier terme est une constante pour un mode
donné, mais change d'un mode à l'autre ; on l'appelle la
dispersion intermodale qui est évidemment nulle dans une fibre
monomode.
> le deuxième terme représente la dispersion
chromatique due aux différents temps de propagation des composantes
spectrales de l'impulsion.
· L'indice de groupe
L'indice de groupe est définie par :
c
N = (2-11)
v g
Avec c est la vitesse de la lumière
L'indice effectif d'un mode est définie par :
â
ne = â = ne
k0 (2-12)
k0
En remplaçant (2-12 ) et(2-7) dans (2-11) ,on obtient :
dn
N n k e
= e +
0 dk
0




Le temps de groupe devient par conséquent :
â
2
t g
L L d â - L ë d
ð c d ë
= = =
v c 2 ð 2
g d
ë
dtg
L'allongement temporel ô est défini par :
ë
ô = d Ä
ë
Äë est la largeur spectrale de l'impulsion La
dispersion chromatique est définie par :
ô 1 dtg -2 â
ðc "
Dchrom= = = 2 0 (ps/
nm.km) (2-13)
L Ä ë L d ë ë
En développant le calcul on trouve ( â =
k0 ne ) :
e
=
chrom
ëd n 2
2
D
c
dë
en négligeant la contribution croisée des deux
dérivés premières par rapport à l'indice n et la
fréquence V, la dispersion chromatique apparaît comme la somme de
la dispersion du matériau, Dmat et de la dispersion du guide,
Dguide.
Elle s'exprime alors selon :
Dchrom=Dmat + Dguide
4.1.1. Dispersion du matériau
La dispersion du matériau, aussi appelée dispersion
de l'indice de réfraction traduit le fait que l'indice de
réfraction du milieu varie en fonction
de la longueur d'onde. Cette dispersion est provoquée par
la réponse électronique du milieu à une excitation
électromagnétique. Cependant le rayonnement laser
créé au sein de l'amplificateur engendre une
dépendance supplémentaire de l'indice de
réfraction en fonction de la longueur d'onde et de la puissance.




On a définit précédemment la constante de
propagation par : â = k0
ne avec n2 < ne <n1
n1 est l'indice du coeur
n2 est l'indice de la gaine
Le mode étant principalement confiné dans le coeur
de la fibre d'indice de réfraction n1 proche de ne, on supposera par la
suite que (ne n1) :
â= k0 n1 (
ë)
La relation de Sellmeier nous donne l'expression de
n1 ( ë) [2.3] :

2 B ë 2 2
B
1 ë 2 3 ë
n ( ë ) = +
1 B + +
1 2 2 2
ë - ë
C - C ë - C
1 2 3
Avec : B1, B2, B3, C1, C2, C3 ; sont des coefficients constantes
qui caractérisent un matériau :
Pour la silice on a :
|
B1=0,402850
|
B2=0,261678
|
B3=0,429086
|
|
=12395,504050
|
C3=7754,284638
|
C1=7421,609980
|
La courbe de variation de l'indice de réfraction n1 en
fonction de la longueur d'onde est représentée sur la figure 6.
Cette courbe est obtenue en utilisant le logiciel Matlab (programme voir annexe
1)
Dans ce cas (ne n1) on peut calculer :

- 1
3 2 2 3 2
dn ë ë
B 2 B C
e i i i
N n
= - ë = +
n 1 +
g e e 2 2
d ë 2 ë - C 2
i = 1 i i = 1 ( ë - C
ë
2 i )
2
La variation de l'indice de groupe est représentée
dans la figure 10 : (Programme voir annexe 2)


indice de refraction de la silice
1.455
1.454
1.453
1.452
1.451
1.449
1.448
1.45
700 800 900 1000 1100 1200 1300 1400 1500 1600 1700
d'onde longueur (nm)
Figure 9. Dépendance de l'indice de
réfraction de la silice pure en fonction de la longueur d'onde.

Indice de groupe
1.52
1.48
1.46
1.44
1.42
1.38
1.36
1.34
1.32
1.5
1.4
0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8
longueur d'onde( um)
Figure 10 : Dépendance de l'indice de groupe avec la
longueur d'onde.
ô
mat
=
ë
L Ä
Calculons le temps de transit d'une onde pour parcourir une
distance L :
|
tmat
|
=
|
L= vg
|
L
|
dâ
|
dë
|
|
dë
|
dù
|
d â2 ð 2 ð dn d
ë 2 ð c
1
= - n + et 2
= -
d ë ë 2 1 ë d ë d ù
ù

Avec
C est la vitesse de la lumière, et ù est
la pulsation 2 ð 2 ð dn 2 ð c
1
Donc : tmat = - n + -
2 1 ù 2
ë ë d ë
Ce qui donne :
L dn 1
tmat = n - ë
1
c d ë
L'étalement impusionel (ou allongement temporel) est
défini par la relation :
dtmat
ô = Ä ë
mat d ë
Par dérivation on trouve :
L
ë
d n
2
ô = - ë 2 Ä
mat
c d ë
1
Puisque la dispersion du matériau est défini par
:
D
mat
On déduit que :
Dmat
d n
2
1
ë
c
2
d ë
= - (ps/
nm.km)
En remplaçant n1 par son expression de Sellmeier :


2
- 1 - 3
2
ë
= -
Dmat
c
B C 2 ( )
2
3 2
2 2 3
3 2 3
2
1 2
B 3
ë 2 ë + C
i i i 1 B B C
i ë
i 2 i i
1 + - +
1
3
ë 2 2 2
2 - C ( )
2 4 ( )
2 2
i = 1 i i = 1 ë -
ë
C - C
i = 1 i i = 1 ë - C
i i








4.1.2.Dispersion du guide
Ici n1 (ë) est supposée
constante, donc ( ) 0
dn 1 =
ë
dë
On élimine ainsi la dépendance de l'indice de
réfraction du matériau en fonction de la longueur d'onde.
La fréquence spatiale normalisée V est
définie par :
V2=a2k02(n12-n22)=
U2+W2
avec U et V respectivement constantes de propagation
transversales normalisées dans le coeur et la gaine telles que :
U = a n 1 k -
â
( ) 1 / 2
2 2 2 0
W = a â 2 - n k
( ) 1 / 2
2 2
2 0
On définit la constante de propagation normalisée
par :
b
1
U2
V
â -
k0
n2
n2
Ce qui donne une approximation de â :
â k 0 [ n
2 + b( n 1 - n2)]
On déduit le temps de transit tel que :
L d[ k 0 ( n 2+
b( n 1 -n2))]
tg
c dk 0 c dk0
L
dâ
= =
|
tg
|
=
|
Ln2
c
|
+n1Ä
|
d(bk
|
0)
|
|
dk0
|
|
|
|
|
|
|
|
|
Avec : V = ak0
n1 2 Ä dV = an1 2
Ädk0


Donc :

dV
B
an 2 Ä
dk 0 = dV
1
En remplaçant dans l'expression finale de
tg on obtient :








L d Vb
( )
tg = n n

2 + Ä d V 1
c ( )
L'étalement de l'impulsion tg est
défini par :
d 2( Vb)
dt
ô = g Äë
= V dt g Äë =-Äë
VL n1 Ä
2

dVg dëëd
V c
La dispersion du guide s'écrit alors :
ô n Ä d
g 1
D = = - V
2( Vb)
2
(Ps/(
nm.km))
dV
L'expression de b est donnée approximativement pour des
valeurs de V entre 1.5
et 2.5 par la formule suivante : ( )
b V
= 1.1428
0.996 2
V 2
La dispersion du guide devient : D guide = -
n1Ä1.984
ëc V2
Par conséquent on exprime la dispersion chromatique sous
la forme suivante :
Dchrom = Dmat + Dguide
2
n Ä d Vb
2 ( ) ë d n
1 1
D chrom = - 2

V -
2
c ë dV c d ë

-3 2
ë

Dchrom
= -
c
12 i[i+v-, 132 [E
4_-
_ci (22_03 [1#177;,, [E
2BiCi2
3 2 -12 3 2B C
(322
+c,i2)
2 3 2 2
La figure 11 représente , la Dispersion chromatique
d'une fibre standard en fonction de la longueur d'onde (vert), Dispersion du
guide ( rouge ), Dispersion du matériau (bleu) . (Programme voir annexe
3)



El spasion (rs/nm km)
-1000
-200
-400
-600
-800
400
200
0
0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8
Dispersion du matériau
longueur d'onde (um)
Dispersion chromatique
Dispersion du guide
Figure.11 : Dispersion chromatique d'une fibre
standard en fonction de la longueur d'onde (vert),Dispersion du guide ( rouge
),Dispersion du matériau (bleu)
On remarque que la dispersion chromatique est nulle pour une
longueur d'onde de 1310nm, qu'elle est négative (normale) pour des
longueurs d'onde inférieur à1310nm et qu'elle est positive
(anormale) pour les longueurs d'onde supérieur à cette
dernière. On remarque aussi que la dispersion du guide est
négative, par contre, la dispersion du matériau présente
une dispersion normale (dispersion négative) et une dispersion anormale
(dispersion positive).
5. Mesure de la dispersion chromatique
Dans la fibre, les différentes longueurs d'onde ne se
propagent pas à la même vitesse. De ce fait, une impulsion courte
de largeur spectrale finie, s'élargit à fur et à mesure
qu'elle se propage dans la fibre. Cet élargissement dû à la
dispersion chromatique peut conduire à la dégradation de la
modulation générée pour transmettre les données.




Connaître la dispersion permet de déterminer le taux
de transmission d'une liaison fibrée.
La mesure directe du temps de propagation ô (
ë) est difficile car elle nécessite de
générer des impulsions courtes (quelques
centaines de picosecondes) sur une large bande spectrale. Cependant si on
connaît la différence de temps de propagation global
Äô entre deux impulsions centrées sur deux longueurs
d'onde très voisines A0-6A et A0+6A, on peut alors calculer la
dispersion chromatique autour de A0 avec [2-4] :
|
Dc
|
( 0 )
ë
|
=
|
dtg
|
|
|
=
|
1
|
Äô
|
|
dë
|
|
ë ë
= 0
|
L
|
2äë
|
|
|
|
|
|
|
|
|
|
L : est la longueur de la fibre :
Il existe plusieurs méthodes de mesure de la dispersion
chromatique. Dans la suite nous allons présenter le principe de quelques
unes [2-5].
5.1 Méthode de variation de phase
Cette méthode de mesure de la dispersion chromatique est
basée sur le principe suivant :

Figure 12 : principe de la mesure de du retard de phase




L'onde optique modulée par un signal micro onde de
référence se propage dans la fibre sous test. Un détecteur
extrait l'évolution de l'enveloppe retardée et
déformée par le milieu dispersif. Un mesureur de phase compare le
retard du signal détecté par rapport au signal micro onde de
référence. Le principe consiste à étudier, en
fonction de la longueur d'onde de la porteuse optique imposée par le
monochromateur le déphasage entre l'onde de référence et
celle qui se propage dans le milieu dispersif.
Le retard temporel entre deux signaux de longueurs d'onde
voisines ëäë et ë+äë avec äë petit nous
fournit directement la valeur de la dispersion chromatique à la longueur
d'onde ë. En effet, si on appelle Aö et Aö' respectivement le
déphasage à ë-äë et ë+äë entre
l'onde de référence et l'enveloppe de l'onde qui s'est
propagée dans la fibre, on peut écrire l'allongement
|
temporel ô sous la forme suivante : ô
=
|
( ' ) .
Ä - Ä
? ?
|
T
|
|
2.ð
|
|
Avec T : période du signal de modulation.
La dispersion chromatique s'exprime alors sous la forme :
2 .
L äë
Avec L : longueur de l'échantillon sous test.
Lorsque la dispersion est faible (petit écart entre
Aö et L1ö'), on doit, pour conserver une bonne précision de
mesure, garantir que les déphasages mesurés soient significatifs.
Pour cela, il faut augmenter soit la fréquence de modulation, soit la
longueur de fibre caractérisée. Comme la fréquence de
coupure haute du mesureur de phase limite la fréquence de modulation, on
ne peut détecter Aö et Aö' qu'en utilisant un tronçon
de fibre plus long.
Ainsi, les mesures de très faibles dispersions
nécessitent d'utiliser des grands tronçons de fibre, ceci peut
interdire la mesure sur des fibres présentant des pertes de propagation
élevées à la longueur d'onde choisie.
5.2 Méthode temporelle
On sait, d'après la relation (2-13), que la dispersion
chromatique est
proportionnelle à la dérivée du temps
de groupe par rapport à la longueur d'onde.
D 1 dtg
L dë


La méthode temporelle exploite directement cette
relation puisqu'elle consiste à déduire la dispersion chromatique
de la mesure du temps de groupe d'une impulsion se propageant dans la fibre en
fonction de la longueur d'onde centrale de son spectre. Cette technique
nécessite l'emploi de longs échantillons de fibre afin que le
temps de groupe soit suffisamment grand pour être directement
mesuré en utilisant des détecteurs rapides. D'autre part, il faut
disposer d'un ensemble de sources à bande étroite,
centrées sur différentes longueurs d'onde afin de
caractériser la fibre sur une large bande spectrale.
Une variante de cette méthode consiste à mesurer
l'allongement temporel d'impulsions brèves produit lors de la
propagation dans la fibre dispersive. On compare la durée de l'impulsion
(largeur spectrale typique de quelques nanomètres) avant et après
propagation. Notons que la mesure n'est valide qu'en l'absence d'effets non
linéaires car ceux-ci sont aussi susceptibles d'agir sur
l'évolution temporelle de l'impulsion et donc de fausser la mesure.

Chapitre 3 :
ETUDE DES FIBRES COMPENSATRICES DE
DISPERSION
CHROMATIQUE (FCDC)


1. CONTROLE DE LA DISPERSION CHROMATIQUE DANS LES FIBRES A
CRISTAUX PHOTONIQUES
1.1 Définition et historique de la fibre à
cristal photonique [3-1]
Les Fibres à cristaux photoniques (FCP) sont une classe
de fibres optiques constituées d'un arrangement de trous d'air
parallèles à l'axe de propagation dans d'une matrice de silice,
dont les toutes premières ont été proposées par
Kaiser et al. aux Bell Labs en 1974. L'objectif était à
l'époque d'obtenir un fort guidage dans un coeur de silice
entouré d'une gaine optique à très forte proportion d'air.
Mais ces fibres, très multimodes, n'ont pas provoqué
d'intérêt particulier dans la communauté scientifique car
elles n'apportaient pas de progrès sensible en terme de propagation.
Les travaux sur les FCP ont été relancés
dans les années 90, en vue de réaliser des structures à
bande interdite photonique (BIP). Ils ont très rapidement conduit
à mettre en lumière des propriétés inattendues dans
les FCP, même en l'absence d'effet BIP. C'est l'étude de ces
propriétés et leur exploitation qui est à l'origine de
l'extraordinaire enthousiasme dont les FCP font l'objet depuis une dizaine
d'années.
Ces FCP sont divisé en deux genres différents de
fibres :
> Le premier, FCP à guidage par l'indice, guide la
lumière par une réflexion
interne totale entre le coeur plein
et la gaine avec des trous d'air multiples.
> Le second emploie une structure parfaitement
périodique montrant un effet de bande interdite photonique (BIP)
à la longueur d'onde de travail pour guider la lumière dans un
coeur à faible indice.
La figure 13 représente la section transverse d'une fibre
à cristal photonique.
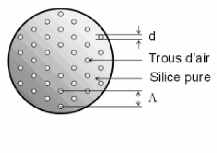
Figure 13 : Section transverse d'une FCP à arrangement
triangulaire
La FCP à guidage par l'indice, également
appelé fibres à trous ou fibres optique microstructurée,
possèdent une propriété particulièrement attrayante
de la grande contrôlabilité de la dispersion chromatique en
variant le diamètre de trous et leurs espacement.
1.2 Fabrication du FCP [3-1]
La fibre à cristal photonique a été
fabriquée dans les laboratoires de l'Université de Bath en 1996,
avec la technique de l'assemblage étirage qui consiste à
étirer à haute température un arrangement de capillaires
et de barreaux de silice.
Le processus de fabrication des FCP se fait en plusieurs
étapes :
La première consiste à réaliser un
arrangement de tubes capillaires à l'intérieur d'un tube de
maintien, comme le montre la figure 14. Ces capillaires sont
sélectionnés en fonction de leurs diamètres
intérieur et extérieur. Ils proviennent soit du commerce soit
d'étirages effectués au laboratoire à partir de tubes de
grande section. Un ou plusieurs capillaires au centre sont remplacés par
des barreaux de silice afin de former le coeur. On s'attend à ce que le
nombre de trous et leur disposition dans cet arrangement soient
conservés dans la fibre étirée. Cependant les conditions
d'étirage (température, pressions interne et externe) peuvent
modifier la taille et la forme de ces trous.
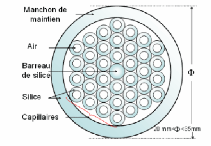
Figure 14 : arrangement de la préforme primaire
Bien que la régularité de l'arrangement ne soit
pas indispensable à l'obtention d'un guidage RTI, elle est
recherchée pour deux raisons. La première est que dans une
distribution aléatoire de trous apparaissent des zones de silice plus
larges susceptibles de se comporter comme autant de "coeurs" dans lesquels la
lumière peut se coupler. D'autre part, il est hautement improbable
qu'une fibre comportant un arrangement de trous quelconque présente des
caractéristiques de propagation pouvant répondre à un
cahier des charges initialement fixé. Autrement dit, la fibre doit
ressembler le plus fidèlement possible aux structures
régulières sur lesquelles sont basées les simulations
numériques qui permettent, connaissant les caractéristiques de
propagation visées, de définir les paramètres
géométriques à atteindre. Les trous interstitiels entre
les capillaires présents dans l'arrangement initial devront être
rebouchés lors de l'étirage. Pour cela, on chauffe une
extrémité de cet arrangement afin de rendre solidaires les
capillaires mais aussi de les reboucher. On réalise ensuite une
opération de verrerie qui consiste à enfermer une
extrémité du manchon de maintien dans une ampoule de silice afin
de pouvoir contrôler ultérieurement la pression
différentielle entre l'intérieur des capillaires et les
interstices lors du fibrage. L'ensemble constitue la préforme primaire
à partir de laquelle vont être étirées des cannes
microstructurées aux dimensions extérieures millimétriques
(figure 15 (a)). Cette première réduction d'échelle
homothétique est effectuée grâce à une tour de
fibrage équipée d'un
système d'entraînement par galets et d'un
dispositif de coupe de capillaires. Le contrôle des dimensions
(diamètre extérieur des cannes, pas et diamètre des trous
de la structure interne) repose sur la maîtrise de la rhéologie de
la silice pendant l'étirage. Les vitesses de descente de la
préforme et de fibrage, la température du four et les
différences de pression dans la préforme sont autant de
paramètres qui doivent être maîtrisés avec
précision pour obtenir une canne microstructurée de
qualité requise.
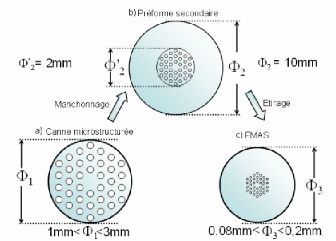
Figure 15: Canne microstructurée, préforme
secondaire et FCP
L'étape suivante consiste à manchonner la canne
microstructurée dans un tube à bord épais pour constituer
la "préforme secondaire" d'environ dix millimètres de
diamètre (figure 15 (b)). Finalement celle-ci est étirée
sur une seconde tour de fibrage qui dispose d'un tambour d'enroulement et d'un
système d'enduction qui permet de protéger la fibre par une gaine
polymère. La fibre obtenue mesure typiquement 125 um de diamètre
extérieur (figure 15 (c)).
Ce fibrage en deux étapes est indispensable pour obtenir
un rapport d'échelle important entre les motifs de la préforme
primaire et ceux de la fibre.
Aux longueurs d'onde de transparence de la silice, la taille
des trous dans la gaine doit être de l'ordre du micron, voire
submicronique, pour obtenir les caractéristiques de propagation voulues.
Cela signifie que le rapport d'échelle entre les trous des capillaires
de la préforme primaire et ceux de la fibre doit être très
grand (supérieur à 1000). C'est pourquoi le fibrage en deux
étapes avec remanchonnage de la canne microstructurée
intermédiaire est une opération indispensable.

Au cours de la seconde étape de fibrage, la
température apparaît comme un paramètre très
critique, qui doit être parfaitement maîtrisé . En effet,
à température trop basse, la trop forte viscosité de la
silice peut conduire à la rupture de la fibre. A mesure que la
température augmente, la viscosité de la silice diminue et la
pression des canaux d'air augmente, ce qui a une forte influence sur la
dimension des trous dans la fibre finale.
La figure 16 représente la section transverse d'une des
fibres réalisée. Ses paramètres géométriques
sont d=2 um et Ë=3,25 um. Le diamètre extérieur de la fibre
est de 125 um. Elle comporte 4 couronnes de trous dans la gaine.

Figure 16 : exemple d'image de la section transverse d'une fibre
réalisée
La réalisation des FCP demande donc la maîtrise
de paramètres physiques (température, pression) qui sont
interdépendants. Le processus de fabrication décrit dans ce
paragraphe s'applique aussi bien aux FCP BIP qu'aux FCP RTI.
1.3.Contrôle de la dispersion chromatique dans la
FCP
Afin de contrôler la dispersion chromatique dans le FCP,
K. Saitoh et M. Koshiba [3-2] ont présenté une
nouvelle technique de contrôle. D'ailleurs, cette technique est
appliquée pour concevoir un PCF avec une dispersion très
réduite et une dispersion ultra-aplatie dans une large gamme de
longueurs d'onde.
Une méthode d'élément fini (FEM) est
employée pour analyser les propriétés de dispersion
aplatie de 0 #177; 0.5 ps/ (nm·km) à la longueur d'onde de 1.19 pm
à 1.69 pm et d'un PCF à cinq couronnes avec une dispersion
aplatie de 0 #177; 0.4 ps /(km·nm) à la longueur d'onde de 1.23 pm
à 1.72 pm.
Dans la FCP conventionnel, la structure de la gaine est
habituellement constituée par des trous d'air avec le même
diamètre rangé dans une configuration triangulaire
régulière.
Le profil de dispersion chromatique peut être facilement
contrôlée en variant le diamètre de trou et l'espacement
entre les tous. Cependant, en utilisant un PCF avec les mêmes
diamètres des trous d'air dans la gaine, il est difficile
de
contrôler la pente de dispersion dans la gamme de larges longueurs
d'onde.
Dans le FCP à guidage d'indice , depuis la
périodicité dans la gaine n'est pas essentielle pour confiner la
lumière de guidage dans la région du coeur de haut indice, K.
Saitoh et M. Koshiba ont proposé un FCP à guidage par l'indice
suivant les indications de figure17 :

Figure 17. Section transversale de la fibre
à cristal photonique proposée. Ë est la distance entre les
trous, et di (i = 1 ~ n) est le diamètre de trou de la couronne des
trous d'air d'ordre i.
Cette structure permet de contrôler la dispersion et la
pente de dispersion dans une large gamme de longueurs d'onde.
En effet, dans la gamme des longueurs d'ondes courtes, le mode
guidé est bien confiné dans la région du coeur et la
propriété de dispersion est affectée par les couronnes
intérieurs des trous d'air, alors que dans la gamme de large longueurs
d'onde, la surface effective du coeur est augmentée et la
propriété de dispersion des couronnes intérieurs et
extérieures est affectée, en particulier quand A est petit.
En optimisant chaque di (i = 1 ~ n) et A, la dispersion et la
pente de dispersion peut être contrôlée dans la gamme de
large longueurs d'onde.
Afin de montrer comment la dispersion chromatique est
affectée en variant les diamètre di de trou de chaque couronne ,
K. Saitoh et M. Koshiba ont considéré quatre FCP à guide
d'indice avec quatre couronnes des trous d'air suivant les indications de la
figure18 :

Figure 18. FCP à guidage par l'indice
avec quatre couronnes des trous d'air. Les trous d'air sont montrés en
tant que des cercles colorés où la distance A = 2.0 pm et pour
chaque diamètre des trou d'air di (i = 1 ~ 4) :
d1 = d2 = d3 = d4 = 0.5pm (fig. 18 (a)), d1 = 0.5 pm, d2 = d3 =
d4 = 0.6 pm
(fig. 18 (b)), d1 = 0.5 pm, d2 = 0.6 pm, d3 = d4 = 0.7 pm
(fig. 18 (c)), d1 = 0.5 pm, d2 = 0.6 pm, d3 = 0.7 pm, d4 = 1.8 pm (fig. 18
(d)). Le diamètre de trou d4 dans fig. 18 (d) est plus grand que les
autres .On observe une différence remarquable entre le profil de
dispersion de FCP dans fig. 18 (c) et fig. 18 (d).
Le figure 19, représente les courbes de dispersion
chromatiques en fonction de la longueur d'onde pour un FCP avec quatre
couronnes des trous d'airs de la figure. 18

Figure 19 : dispersion chromatique des structures : a, b, c,
d.
Ce résultat indique que le profil de dispersion est
affecté en variant chaque diamètre di des trou d'air et
l'optimisation de ces di permet au FCP à guidage par l'indice, de
contrôler leurs propriétés de dispersion .Ainsi on remarque
que, plus on augmente les diamètres di, plus la dispersion augmente
aussi, et inversement.
1.4 Dispersion très réduite et
ultra-aplatie
La structure de la gaine du FCP conventionnelle à
dispersion ultra-aplatie est constituée par des trous d'air avec le
même diamètre d, rangé dans une configuration triangulaire
et régulière.
En prenant la distance trous à trous ? et Le
diamètre d, tel que : ? 2,6ìm et d 0,24 ,
respectivement, il est possible de réaliser une dispersion ultra
?
aplatie presque nulle du FCP dans la fenêtre de
transmission utilisée en télécommunications.
Le figure 20 montre deux exemples de la dispersion
ultra-aplatie presque nulle du FCP avec quatre couronnes des trous d'air et
cinq couronnes des trous d'air conçu avec l'emploi du principe de
conception précédent , où A = 1.56 pm, d1/A = 0.32, d2/A =
0.45, d3/A = 0.67, d4/A = 0.95 dans fig. 5 (a) et A = 1.58 pm, d1/A = 0.31,
d2/A = 0.45, d3/A = 0.55, d4/A = 0.63, d5/A = 0.95 dans fig. 20 (b).

(a) (b)
Fig. 20. FCP à dispersion Ultra-aplatie
avec quatre couronnes de trous d'air (a)
et cinq couronnes de trous d'air
(b).
Ces FCP ont une très petite distance entre les trous ( ? 1
,6ìm ) .Pour contrôler la
dispersion et la pente de dispersion dans la gamme de large
longueur d'ondes,
une petite distance Ë est un paramètre important.
En outre, il est possible de diminuer l'indice effectif de réfraction
dans la gaine à travers le rayon en diminuant le diamètre de trou
d'air tout au long du rayon , et réaliser une dispersion aplatie en
optimisant chaque diamètre des trous d'air.
L'augmentation des diamètres des trous d'air le long du
rayon est également très utile pour concevoir une basse perte du
FCP de guidage avec un petit nombre de couronnes des trous d'air. La
dernière rangée des trous d'air avec un diamètre
très grand dans fig. 20 est profitable pour contrôler la
dispersion chromatique.
La figure 21, montre la dispersion chromatique en fonction de la
longueur d'onde pour les quatre couronnes de la figure. 20 (a).

Longueur d'onde (um)
Figure. 21 : courbe de dispersion chromatique en
fonction de la longueur d'onde pour la dispersion ultra-aplatie du FCP avec les
quatre couronnes des trous d'air de la figure. 20 (a).
On remarque d'après cette figure que la gamme de
longueurs d'onde pour laquelle la dispersion de PCF demeure entre -0.5 et +0.5
ps / (km· nm) est de 1.19 pm à 1.69 pm.
Le figure : 22 montre la dispersion chromatique en fonction de la
longueur d'onde pour les cinq couronnes PCF de la figure. 20 (b)

Longueur d'onde (um)
Figure 22 : Courbe de dispersion chromatique
fonction de la longueur d'onde pour la dispersion ultra-aplatie du FCP avec
cinq couronnes des trous d'air du fig. 20 (b).
D'après le figure 22 on constate que, la longueur d'onde
qui demeure la dispersion du PCF entre -0.4 et +0.4 ps / (nm·km) est du
1.23 pm à 1.72 pm.
En effet, en employant plus de couronnes de trou d'air et en
optimisant Ë et di , il est possible de concevoir la dispersion aplatie
FCP dans une gamme de longueurs d'onde plus large.
Ces FCPs avec la dispersion ultra-aplatie presque nulle ont
une surface effective relativement plus petit et serait utile pour la
génération de supercontinuum, transmission d'impulsion de
soliton, et ainsi de suite.
Cette technique de contrôle de dispersion chromatique dans
le FCP est appliqué pour le concevoir avec une dispersion ultra-aplatie
presque nulle, cependant, ce principe de conception peut être
également appliqué au contrôle de la pente de dispersion
d'un bas FCP non linéaire avec une grande surface effective et concevoir
une compensation de la dispersion dans ce dernier.
2. CONTROLE DE LA DISPERSION CHROMATIQUE DANS UNE FIBRE A
CRISTAL PHOTONIQUE A DOUBLE COEUR CONCENTRIQUE (FDCC) [3-3].
2.1 Définition
La fibre à cristal photonique à double coeur
concentrique, présente un coeur central très étroit,
fortement dopé au Germanium de façon à créer une
forte dissymétrie avec un coeur annulaire plus large mais moins
dopé. Le profil d'indice de réfraction composé par les
deux coeurs concentriques supporte deux supermodes. Ces supermodes sont
caractérisés par une forte redistribution spatiale de leurs
champs modaux lorsque la longueur d'onde varie. Elles autorisent un
comportement monomode très large bande, et présentent une
biréfringence singulière, et permettent de limiter les effets non
linéaire.
ces fibres peuvent jouer un rôle important dans le
contrôle de la dispersion
chromatique Dchrom
2.2 Présentation de la fibre
étudiée
Cette fibre est constituée d'un arrangement particulier
de différents trous d'air périodique avec une configuration
à deux dimensions appelée «configuration à cristal
photonique triangulaire ». Permettant d'obtenir une structure à
deux coeurs concentriques équivalent à la configuration
énoncée dans la Figure 23 :

Coeur annulaire En silice composé de petits trou d'air
Coeur central En silice
Figure 23 : Section transverse de la fibre La fibre à
cristal photonique à double coeur concentrique
Cette fibre a un coeur central de rayon r1 = 1.6 um ,
constitué d'un barreau de silice pure entouré de trous d'air de
diamètre d = 1.4 um et d'espacement Ä= 2.3 um. La quatrième
couronne de trous est remplacée par des trous d'air de faibles
diamètres ( d = 0.51 um) pour créer un coeur externe et pour
obtenir une forte dissymétrie avec le coeur central. Ainsi, deux
irrégularités dans le PIR sont générées. Les
zones de guidage apparaîtront donc dans les régions où les
défauts sont localisés et seront considérés comme
deux guides.
2.3 Méthode de contrôle de la dispersion
chromatique dans la FDCC
Les travaux de simulations effectuées par
F.Gérôme [3-3], avec la méthode des
éléments finis (FEM), montrent que la courbe de variation de
l'indice effectif en fonction de la longueur d'onde possède un point
d'inflexion à la longueur d'onde d'accord de phase qui est fixée
par les paramètres optogéométriques. Ainsi, cette fibre
peut présenter une très forte valeur négative de
dispersion chromatique égale à - 2200 ps/(
nm.km) à 1550 nm (voir Figure 24).

Figure 24 : variation de la dispersion Dch en fonction
du nombre de couronnes entre les deux coeurs.
Cette figure, montre que la valeur de la Dch
devient plus négative lorsque le nombre de couronnes de trous entre le
coeur central et le coeur annulaire augmente mais sans changer la longueur
d'onde d'accord de phase (1550 nm dans notre exemple) : Dch de - 2200 ps/(
nm.km) pour une configuration avec trois
couronnes de trous, -1300 ps/(
nm.km) avec deux couronnes et seulement - 70
ps/(
nm.km) avec une seule couronne. L'ajout d'une
quatrième couronne de trous d'air n'induit qu'une faible modification de
la Dch, c'est pourquoi il est utile de se limiter à trois couronnes car
cette configuration représente un bon compromis entre les performances
attendues et la difficulté d'assemblage
Ensuite F. Gérôme [3-3], a évalué
l'influence des paramètres géométriques sur
l'évolution de la dispersion. La figure 25 (montre l'influence du
diamètre des trous d'air (d) sur la dispersion chromatique.

Figure 25 ; Evolution de la dispersion chromatique en fonction du
diamètre des trous.
On remarque que, lorsque le diamètre d augmente, la valeur
minimale de Dch se trouve décalée vers les longueurs
d'onde basses, et elle devient plus négative (jusqu'a- 10000 ps/(
nm.km)) et la largeur à mi-hauteur est
plus étroite.
La figure 26 représente Influence de l'espacement entre
les trous sur l'évolution de la dispersion chromatique

Figure 26 : Influence de l'espacement entre les trous sur
l'évolution de la dispersion chromatique.
Sur cette figure, et contrairement à la figure
précédente, on observe que lorsque l'espacement entre les trous
diminue, la dispersion chromatique diminue aussi, et devient plus
négative.
Ces résultats sont les conséquences directes de la
modification des paramètres
d et Ä qui entraînent une réduction fictive de
la taille du coeur central. Le même résultat est obtenu quand le
diamètre des tous du coeur annulaire ( ? ), diminue.
En conséquence, cette méthode simple de
contrôle permet d'adapter les courbes de Dch suivant les
applications visées : la compensation pour le multiplexage en longueur
d'onde (WDM) avec une fibre n'ayant qu'une couronne de trous entre les
deux coeurs permettant d'obtenir une pente décroissante
quasi linéaire sur toute une bande de longueurs d'onde ou la
compensation unique d'une longueur d'onde avec la présence de deux ou
trois couronnes donnant une valeur très négative.
3. CONTROLE DE LA DISPERSION CHROMATIQUE DANS UNE FIBRE A
RESEAUX DE BRAGG
3.1 Définition d'un réseau de Bragg
[3-4],
On appelle réseau de Bragg une modulation
périodique de l'indice de réfraction du coeur de la fibre le long
de l'axe de propagation (figure 27). C'est un filtre sélectif en
longueur d'onde ayant la particularité de réfléchir une
longueur d'onde déterminée dite « de Bragg » fonction
des paramètres géométriques du réseau.
La longueur d'onde centrale de ce filtre appelée longueur
d'onde de Bragg (ëB) est alors directement reliée à la
période Ë de cette modulation ainsi qu'à la valeur de
l'indice effectif neff du guide photo inscrit par la relation de
Bragg :
ëB=2.Ë.neff

Figure 27 : Réseau de Bragg uniforme (
à pas constant)
3.2. Contrôle de la dispersion chromatique dans une
fibre à réseau de Bragg à pas variable [3-5]
Une fibre à réseau de Bragg à pas
variable, présente une périodicité de modulation de
l'indice du coeur qui diminue progressivement le long de la fibre. Ainsi,
différentes longueurs d'onde sont réfléchies par le
réseau à différents endroits : les premières
arrivées doivent traverser tout le réseau avant d'être
réfléchies, tandis que les dernières sont directement
réfléchies permettant ainsi de recomprimer l'impulsion.

Figure 28 : Fonctionnement d'un réseau de Bragg
à pas
variable
La dispersion chromatique Dchrom d'un réseau de
Bragg à pas variable est donnée par l'équation suivante
:
D= 2L
Ä ë .vg
avec L : la longueur du réseau,
vg : La vitesse de groupe de l'impulsion dans
la
fibre. et Äë : la
largeur de bande passante du réseau.
La dispersion chromatique peut être ajustée par
le contrôle de la variation du pas du réseau. Ainsi, en
contrôlant la dérive en température, on peut obtenir de
bons compensateurs de dispersion accordables en longueur d'onde
Cependant, la plupart des compensateurs de dispersion
basés sur des fibres à réseau de Bragg sont monocanal.
Pour obtenir un fonctionnement large bande, il faut des réseaux longs
(dont la longueur doit dépasser le mètre). Leur fabrication est
encore très délicate et introduit une modulation de la
dispersion.
On peut utiliser des fibres à réseaux de Bragg
superposés. Un compensateur à 32 canaux a ainsi pu être
réalisé.
Un tel système présente l'avantage d'être
simple à mettre en oeuvre, cependant il possède un
inconvénient majeur qui est sa dérive en température.
Le réseau de Bragg va donc se dilater et se contracter,
modifiant les propriétés de celui-ci. Il ne sera donc pas
possible de garantir un niveau de performance constant. Il est donc plus
intéressant d'utiliser cette technologie comme compensateur de
dispersion accordable.

Figure 29 : Principe d'utilisation d'un contrôleur
basé des réseaux de Bragg à pas variable

CONCLUSION ET PERSPECTIVES

Conclusions et perspectives
Les fibres à cristaux photoniques ou fibres à
bandes interdites photoniques ou fibres micro-structurées, ou fibres
à trous, sont des appellations qui désignent cette jeune branche
pourtant vaste de la famille des fibres optiques, qui a vu le jour en 1996 et
qui s'est depuis imposée comme une technologie incontournable en
Photonique.
L'originalité de ces guides d'onde provient de leurs
mécanismes de confinement de la lumière qui reposent sur la
périodicité de leur structure d'indice. Cette dernière va
permettre, dans certains cas, d'utiliser l'air pour propager la lumière
dans un coeur de verre ou d'air, permettant d'envisager une amélioration
significative des composants existants comme ceux qui sont utilisés pour
le transport de données jusqu'à l'abonné ou pour la
métrologie optique.
Ces fibres possèdent la propriété
particulièrement attrayante de la grande contrôlabilité de
la dispersion chromatique en optimisant les paramètres
optogéométriques (les diamètres des trous, l'espacement
entre ces trous et le nombre de couronnes...). Le contrôle de la
dispersion chromatique dans ces fibres est un problème très
important pour des applications pratiques aux systèmes de
télécommunications optique, à la compensation de
dispersion, et aux systèmes optique non linéaires.
Dans le cas d'une fibre optique à réseaux de
Bragg à pas variable le contrôle de la dispersion chromatique est
basé sur le contrôle de la variation du pas du réseau.
Ainsi, en contrôlant la dérive en température, on peut
obtenir de bons compensateurs de dispersion accordables en longueur d'onde.
En perspectives, nous prévoyons, entre outre,
d'étudier les fibres compensatrices de la dispersion chromatique
suivantes :
'7 Contrôle de la dispersion chromatique dans une fibre
à coeur creux ( Hallow core).
'7 Contrôle de la dispersion chromatique dans une fibre
à réseaux de Bragg uniforme.
'7 Fibre à un mode d'ordre supérieur (High Order
Mode fiber).
'7 Fibre à dispersion décalée.
'7
Références
[1-1] Julien MAURY ; « Étude et
caractérisation d'une fibre optique amplificatrice et compensatrice de
dispersion chromatique » ; thèse de doctorat de l'université
de Lemoges, 2003.
[1-2] Télécommunications optique :
Pierre LECOY, traité des nouvelles technologies de
Télécommunications ; Editions HERMES.
[1-3] Mikhaël MAYARA ; « Amplification
optique-notes de cours » université montpellier 2, sciences et
techniques.
[1-4] A. Farkhsi, Cours de Transmission par
fibre optique (master ETC), faculté de sciences ; université
ABDELMALEK ESSAADI ; 2008.
[2-1] Julien MAURY ;« Étude et
caractérisation d'une fibre optique amplificatrice et compensatrice de
dispersion chromatique« ; thèse de doctorat de l'université
de Lemoges, 2003.
[2-2] Jean-Louis VERNEUIL ; « Simulation
des systèmes de télécommunications
par fibre optique à 40Gbits/s» thèse de
doctorat de l'université de Lemoges, 2003.
[2-3] Isabelle NIORT, « Contribution
à la réalisation de microrésonateurs sur fibre optique de
silice par faisceau d'éléctron pilotés en vue d'une
application au multiplexage en longueur d'onde » thèse de doctorat
de l'université de Lemoges, 2003.
.[2-4] Ambre PEYRILLOUX «
Modélisation et caractérisation des fibres
microstructurées air/silice pour application aux
télécommunications optiques » » thèse de
doctorat de l'université de Lemoges, 2003.
[2-5] Laurent LABONTÉ « Analyse
théorique et expérimentale des principales
caractéristiques du mode fondamental dans les fibres optiques
microstructurées
air/silice » thèse de doctorat de l'université
de Lemoges, 2005.
[3-1] Laurent LABONTÉ « Analyse
théorique et expérimentale des principales
caractéristiques du mode fondamental dans les fibres optiques
microstructurées air/silice » thèse de doctorat de
l'université de Lemoges,2005
[3-2] K. Saitoh and M. Koshiba, Hokkaido
University, North 13 West 8, Kita-ku, Sapporo, 060-8628, Japan.
[3-3] F. Gérôme, J.-L. Auguste,
J.-M. Blondy1, P. Roy « Conception et fabrication d'une nouvelle fibre
compensatrice de dispersion » thèse de doctorat de
l'université de Lemoges, 2005.
[3-4] David MECHIN « Etude et
réalisation de multiplexeurs insertion-extraction à
réseaux de Bragg « thèse de doctorat de L'Université
Jean Monnet de Saint- Étienne 2001.
[3-5] Julien MAURY ; « Étude et
caractérisation d'une fibre optique amplificatrice et compensatrice de
dispersion chromatique » ; thèse de doctorat de l'université
de Lemoges,2003.
Annexe
Annexe 1 : représentation de l'indice
réfraction de la silice
>> B1=0.6961663; >> B2=0.4079426; >>
B3=0.8974794; >> C1=0.0684043; >> =0.1162414; >> C3=9.896161;
>> lambda=0.8:0.1:1.8;
>> ne=sqrt(1 + (B1./(1-C1./lambda.^2)) +
(B2./(1-./lambda.^2)) + (B3./(1- >> plot(lambda,ne)
Annexe 2 : représentation de l'indice de
groupe
>> B1=0.6961663; >> B2=0.4079426; >>
B3=0.8974794; >> C1=0.0684043; >> =0.1162414; >> C3=9.896161;
>> lambda=0.8:0.1:1.8;
>> ne=sqrt(1 + (B1./(1-C1./lambda.^2)) +
(B2./(1-./lambda.^2)) + (B3./(1- C3./lambda.^2)));
>> n=ne.^2;
>> n1=1./sqrt(n);
>> x1=(2.*B1.*C1.^2.*lambda)./(lambda.^2-C1.^2).^2;
>> x2=(2.*B2.*.^2.*lambda)./(lambda.^2-.^2).^2;
>> x3=(2.*B3.*C3.^2.*lambda)./(lambda.^2-C3.^2).^2;
>> m=x1+x2+x3;
>> z=(lambda./2).*m.*n1;
>> Ng=ne+z;
>> plot(lambda,Ng)
Annexe 3 : Programme de représentation de la
dispersion du guide, la dispersion du matériau et la dispersion
chromatique (dispersion totale).
%Dmat
x=0.8:0.1:1.8;
c=30000000;
a1=0.0696404;
a2=0.1162412;
a3=9.896161;
b1=0.696163;
b2=0.4019426;
b3=0.8974794;
f11=1+(b1*x)./((x."2)-(a1."2));
f12=1+(b2*x)./((x."2)-(a2."2)); f13=1+(b3*x)./((x."2)-(a3."2));
f=0.5./sqrt(f11+f12+f13);
g11=(2.*b1.*a1.*a1.*(3.*x.*x+a1.*a1))./((x.*x-a1.*a1)."3);
g12=(2.*b2.*a2.*a2.*(3.*x.*x+a2.*a2))./((x.*x-a2.*a2)."3);
g13=(2.*b3.*a3.*a3.*(3.*x.*x+a3.*a3))./((x.*x-a3.*a3)."3); g=g11+g12+g13;
k=-(1./4).*(f11+f12+f13)."-1.5;
d11=(2.*b1.*a1.*a1.*x)./((x.*x-a1.*a1)."2);
|
d12=
|
(2
|
.*b2.*a2.*a2.*x)./((x.*x-a2.
|
*a2)
|
."2);
|
|
d13=
|
(2
|
.*b3.*a3.*a3.*x)./((x.*x-a3.
|
*a3)
|
."2);
|
d=(d11+d12+d13)."2; Dmat=-10."12.*(x./c).*(f.*g+k.*d);
plot(x,Dmat)
%Dguid
Dguid=-54.36./x; %Dchr
Dchr=Dmat+Dguid; hold on
plot(x,Dmat,x,Dchr,x,Dguid)
grid



