|
REMERCIEMENTS
Je tiens à remercier dans un premier temps notre
encadrant M.ESSADKI, pour l'aide et les conseils concernant
les missions évoquées dans ce rapport, qu'il nous a
apporté lors des différents suivis.
Je remercie
également toute l'équipe pédagogique de l'EMSI et les
intervenants professionnels responsables de la formation pour le soutien qu'ils
nous ont apporté durant ses années de formation.
Je tien a remercier l'équipe de MOHAMED
MESSIKI et MAHMOUD CHIFA pour leurs esprit de
collaboration durant toutes les phases d'études et de conception pour
faire sortir ce travail collectif.
DEDICACES
A nos parents, en signe d'amour et de gratitude pour votre
soutien, encouragement et réconfort.
A tous nos amis et professeurs de l'Ecole Marocaine des
Sciences de l'Ingénieur.
A tous ceux qui s'investissent pour que la science soit
développée.
INTRODUCTION GENERALE
Les méthodes classiques de l'automatique ont
été largement appliquées dans de nombreux problèmes
de régulation industrielle. Cependant, la plupart des systèmes
physiques présentent des non linéarités et leurs
paramètres sont souvent mal connus et/ou variables dans le temps. Pour
la commande de telles classes de systèmes les méthodes
conventionnelles de l'automatique ont montré leurs limites en termes de
stabilisation et performances.
Avec le développement des calculateurs numériques,
les automaticiens commencent à s'intéresser aux nouvelles
approches de commande telles que la commande adaptative, la commande
prédictive, la commande robuste, ainsi que les techniques basées
sur l'intelligence artificielle.
Parmi ces dernières ; la commande par logique floue. Cette
commande est à l'heure actuelle une des préoccupation des
chercheurs dans le monde [Zhao et al., 03], [Li et al., 03], [Onat et al., 04],
[Yang et al., 04], [Baturone et al., 04], [Flores et al., 05], [Jordan et al.,
05], [Bai et al., 05].
Durant ces dernières décennies, l'utilisation de la
théorie des ensembles flous dans
la modélisation et la commande des systèmes
complexes a connue une évolution considérable.
En effet, le principe de la commande floue a été
expérimenté pour la première fois en 1974 par
l'équipe du professeur E.H. Mamdani [Mamdani, 74]. Les résultats
obtenus, ont été repris et développés par plusieurs
équipes en Europe de l'Ouest [Willaeys & Malvache, 78]. Puis ensuite
par l'Institut de Technologie de Tokyo [Sugeno, 85] et dans quelques autres
universités japonaises [Bellon et al., 89]. Depuis 1987, date à
laquelle la première application `' grand public'' a vue le jour.
Utilisant la logique floue, le métro de Sendai, a été mis
sur le marché [Miyamoto et al., 87]. Depuis cette époque,
l'utilisation des techniques de commande floue n'a cessé
d'évoluer. Aujourd'hui, les différents travaux et publications
récentes dans ce domaine semblent indiquer que les deux domaines
d'application de la logique floue les plus importants sont :
· La conception de régulateurs pour des processus
difficilement modélisables,
· La conception de régulateurs linéaires
pour des processus modélisables
.
La commande floue se différencie d'une commande classique
par le fait que l'approche par logique floue synthétise une loi de
commande à partir de l'expertise de l'opérateur humain. Dans le
premier cas, la commande est synthétisée en évitant la
phase modélisation. Par contre dans le second cas, la structure non
linéaire du régulateur flou permet d'améliorer les
performances en termes de précision et de robustesse du système
non linéaire vis-à-vis des incertitudes structurées et non
structurées.
Les avancées récentes en informatique et en
électronique de puissance permettent
la fabrication des systèmes prototypes, qui jouent le
rôle de simulateurs réels miniatures. Ces derniers permettent de
tester de nouvelles techniques de commande. Les systèmes comme le simple
et le double pendule [Messner, 97], [Passino & Yurkovich, 98], [Mudry, 01],
[Shi & Singh, 92], ainsi que le simulateur de vol
d'hélicoptère (Twin Rotor Mimo system) [F, Instruments
Ltd,IV,97], sont de très bons exemples de ces prototypes réels.
Ces derniers, sont caractérisé par des comportements physiques
non-linéaires difficilement modélisables. Cette
Caractéristique a motivé les chercheurs pour les utiliser afin de
valider et tester les lois de Commande développées
théoriquement. Le travail présenté dans ce mémoire,
s'intègre dans cet objectif
Historique
Lotfi Zadeh

C'est à l'université de Berkeley Californie,
USA en 1963, qu'est née la logique floue ou "Fuzzy logic". Son
père créateur c'est Monsieur Lotfi A. Zadeh, né en ex-URSS
de parents iraniens, professeur d'informatique au département
ingénierie électrique et informatique de l'université. Mr
Zadeh fait une comparaison entre les ordinateurs de l'époque et le
raisonnement humain (comparaison toujours valable d'ailleurs) :
si
l'ordinateur calcule beaucoup plus vite de façon rigoureuse, ses
capacités de réflexion et d'apprentissage sont limitées.
De plus sa rigidité en tant que machine et son fonctionnement binaire,
rend l'ordinateur peu adapté à certaines tâches, qui pour
un humain semble si simple. Mr Zadeh prend l'exemple du créneau
réalisé par un automobiliste pour garer sa voiture ; si le
conducteur réalise cette opération en une minute environ, la
simulation de la même action sur un ordinateur demandait à
l'époque plusieurs heures de calculs complexes. Le pire dans l'histoire,
c'est que l'humain fait tout ceci de façon approximative que ce soit
pour la conduite dans le cas présent, comme bon nombres d'actions de la
vie quotidienne? Cela marche donc avec l'approximation et une expérience
des fonctions à réaliser. Naissance de la logique floue, dont le
concept sera complètement ignoré aux USA, comme en Europe. Il
faut attendre 25 ans pour voir apparaître les premières
applications au Japon ; à noter que l'exemple de la voiture à
garer de Mr Zadeh est repris, et mis en application avec une voiture
truffée de capteurs, d'un calculateur flou et qui parvient à se
garer toute seule.
CHAPITRE I :
APPLICATION DE LA LOGIQUE FLOU
Notions d'ensemble flou, appartenance
Les compréhensions de l'univers dans lequel nous
évoluons sont généralement imparfaites dans la mesure
où elles peuvent être entachées d'incertitudes et/ou
d'imprécisions, ne serait-ce qu'à travers la perception que nous
en avons. Or, nous pouvons constater que l'homme intègre naturellement
ces imperfections dans la vie de tous les jours, en particulier au niveau du
raisonnement et de la décision. L'idée du professeur Lotfi Zadeh
à travers le nouveau concept ensembliste d'appartenance graduelle d'un
élément à un ensemble, a été de
définir une logique multi évaluée permettant de
modéliser ces imperfections c'est prendre en compte les états
intermédiaires entre le tout et le rien. L'utilité de cette
approche peut être illustrée de la manière suivante :
Une température de 10°C, pour un humain, est
généralement considérée comme froide; une autre de
40°C est qualifiée de chaude. Si chacune de ces valeurs appartient
à une
Catégorie (ensemble) bien définie, qu'en est-il
pour des valeurs intermédiaires? Une réponse intuitive consiste
à affirmer qu'elles appartiennent à une ou deux des
catégories précédentes avec des niveaux ou des
degrés (normalisés) différents. On évite ainsi des
transitions brusques entre différentes catégories, comme cela est
le cas en logique binaire (figureI.1).
Il semble en effet surprenant de considérer qu'une
température de 40°C est chaude, alors qu'une température de
39,9°C ne l'est pas.
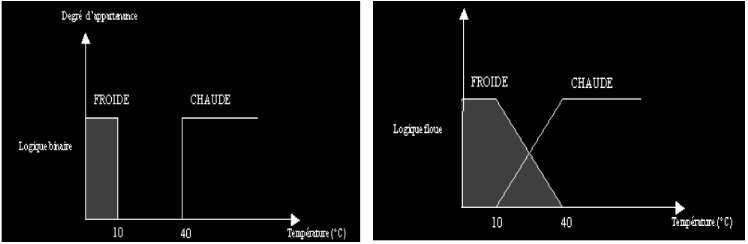
Figure I.1 : Exemple de définition d'ensembles sur un
univers de discours en logique
Binaire et en logique floue
Cet exemple permet d'illustrer le fait qu'une logique binaire
classique soit, dans certains cas, trop limitative. Donc il est
nécessaire de faire appel à une autre logique multi
évaluée qui sera vue comme une extension de la
précédente, c'est bien la logique floue.
En ce qui concerne la commande d'un processus quelconque, la
logique floue permet une approche fondatrice par rapport à l'automatique
classique. En automatique, en général, on s'attache à
modéliser le processus à travers un certain nombre
d'équations différentielles. Cette modélisation est rendue
difficile et par fois impossible à mesurer que la complexité des
processus à contrôler augmentent. D'une manière
radicalement opposée, un contrôleur va décrire non pas le
processus mais la façon de le contrôler, tout comme le ferait un
expert humain à travers des règles intégrant naturellement
imprécisions et incertitudes.
Quelques domaines d'application
La commande Floue :
Parmi les nombreuses applications de la logique floue, la
commande floue s'avère être le champ d'application le plus actif
à travers le monde.
Exemples :
· Commande de tubes broyeurs pour la fabrication du ciment
(première réalisation en 1979 au Danemark).
· Commande de métros avec un fonctionnement plus
confortable et économique et une précision d'arrêt
augmentée (1987 à Sendai, Japon).
· production du fer et de l'acier, purification, de
l'eau, chaînes et robots de fabrication,
· opérateurs, unités arithmétique,
micro-ordinateurs, ...
Classification et reconnaissance de
formes :
Classifier consiste à regrouper des objets en
catégories les plus homogènes possibles (contenant des objets
similaires) :
Classifier est une activité qui intervient dans des
nombreux domaines d'applications tels que :
· la reconnaissance vocale.
· L'analyse d'images (médical, radar,
télédétection).
· La reconnaissance de cibles (domaine militaire).
· consultation, investissement et développement,
horaires de train, ...
· base de données, recherche d'information,
modélisation de systèmes
Conception d'un régulateur à logique flou
Un contrôleur standard (PID ou autres) demande toujours un
modèle le plus précis possible (équations
différentielles).
Un contrôleur flou ne demande pas de modèle du
système à régler. Les algorithmes de réglage se
basent sur des règles linguistiques de la forme Si ... Alors ...
En fait, ces règles peuvent être exprimées en
utilisant le langage de tous les jours et la connaissance intuitive d'un
opérateur humain.
Ce qui conduit à deux avantages :
· Conclusion :
Pour les systèmes mal connus ou complexes
(non-linéaires), un contrôleur flou s'avère très
intéressant.
Structure du régulateur
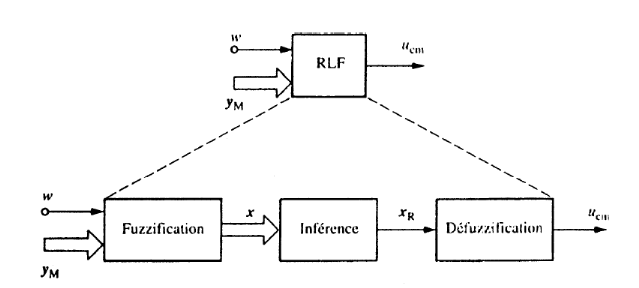
- Fuzzification : transforme les entrées en grandeurs
floues.
- Inférence (avec la base de règles) : prend
les décisions
- Défuzzification : transforme les grandeurs floues
en valeurs déterminées
Fuzzification
- Définition des fonctions d'appartenance de toutes les
variables d'entrée.
- Passage : grandeurs physiques => variables linguistiques
En général, on utilise des formes triangulaires ou
trapézoïdales pour les fonctions d'appartenance, bien qu'il
n'existe pas de règles précises sur ce choix.
Exemple : Soit une grandeur x définie par
5 sous-ensembles flous.
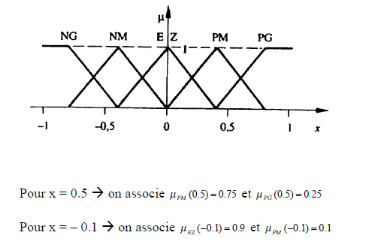
Donc à chaque variable linguistique d'entrée (x),
on fait correspondre une valeur linguistique (Négatif Grand,
Négatif Moyen, ...) avec un degré d'appartenance.
Inférence ou Base de règles
Donne la relation qu'il existe entre les variables
d'entrées (exprimées comme variables linguistiques) et la
variable de sortie (également exprimée comme variable
linguistique).
Exemple : Soit deux entrées x1 et x2 et une sortie xR,
toutes définies par les 5 sous-ensembles de l'exemple
précédent.
Description de la base de règles :
Si (x1 NG ET x2 EZ),
Alors xR PG ou
Si (x1 NG ET x2 PM),
Alors xR PM ou
Si (x1 NM ET x2 EZ),
Alors xR PM ou
Si (x1 NM ET x2 PM),
Alors xR EZ ou
Si (x1 NM ET x2 PG),
Alors xR NM ou
Si (x1 PG ET x2 EZ),
Alors xR NG.
Sous forme de tableau ou matrice :
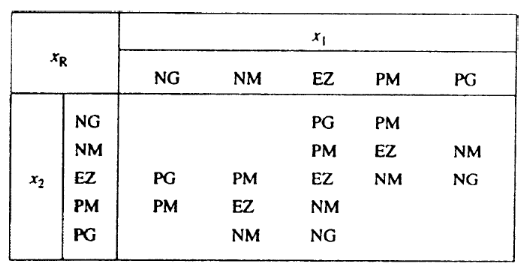
On n'est pas obligé de compléter toute la table.
Les règles sont élaborées par un expert et sa connaissance
du problème ...
Différentes méthodes d'inférence.
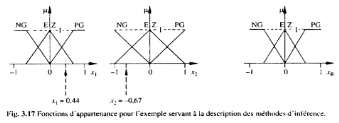
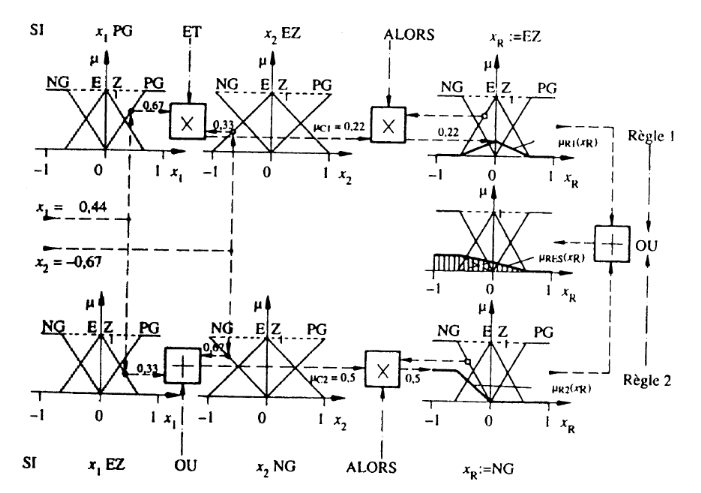
Supposons que l'on ait deux entrées x1 et x2 et une sortie
xR, toutes définies par les sous-ensembles suivants :
Supposons que x1 = 0.44, x2 = - 0.67 et que l'inférence
est composée des deux règles suivantes :
Si (x1 PG ET x2 EZ),
Alors xR EZ ou
Si (x1 NG OU x2 PM),
Alors xR PM
Il faut maintenant « traduire » les opérateurs
ET, OU et l'implication par une des fonctions vues dans la première
partie de l'exposé
(Minimum, Maximum, Produit, ...).
Méthode MAX-MIN :
Au niveau de la condition : ET => Min OU => Max
Au niveau de la conclusion : ou => Max Alors => Min
(D'où la désignation)
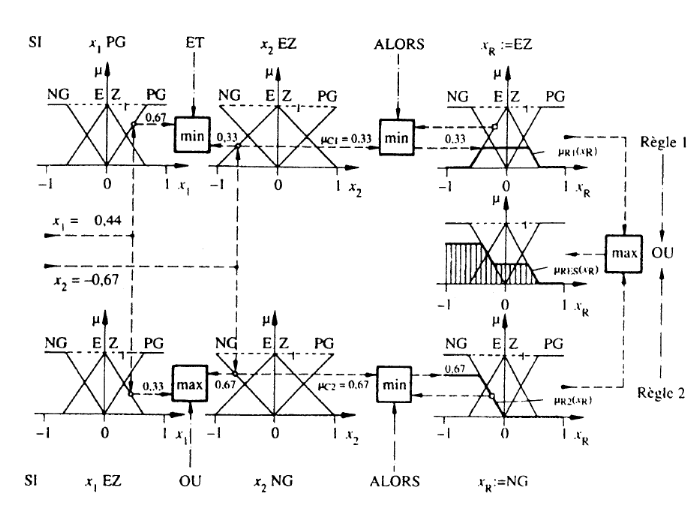
Résultat : une fonction de transfère
résultante donnée par la surface hachurée (qui sera
traitée lors de la Défuzzification).
Méthode MAX-PROD :
Au niveau de la condition : ET => Min OU => Max
Au niveau de la conclusion : ou => Max Alors => Prod
(D'où la désignation)
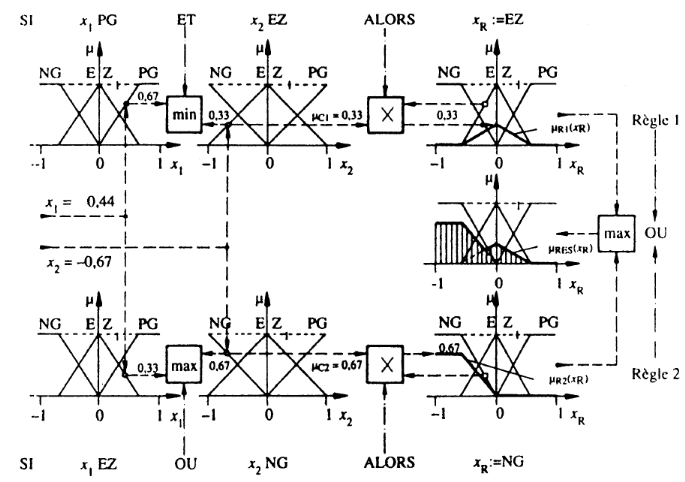
Résultat : une fonction de transfère
résultante donnée par la surface hachurée (qui sera
traitée lors de la Défuzzification).
Méthode SOMME-PROD :
Il ne s'agit pas de la Somme « normale » mais de la
valeur moyenne :
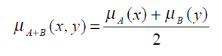
Au niveau de la condition : ET => Prod OU => Somme
Au niveau de la conclusion : ou => Somme Alors => Prod
(D'où la désignation)
Résultat : une fonction de transfère
résultante donnée par la surface hachurée (qui sera
traitée lors de la Défuzzification).
Défuzzification
Les méthodes d'inférence fournissent une fonction
d'appartenance résultante pour la variable de sortie. Il s'agit donc
d'une information floue qu'il faut transformer en grandeur physique.
On distingue 4 méthodes de Défuzzification :
Méthode du maximum :
La sortie correspond à l'abscisse du maximum de la
fonction d'appartenance résultante.
Trois cas peuvent se produire :
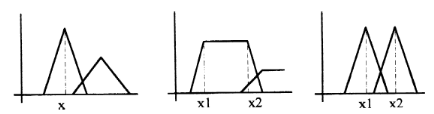
Conclusion : méthode simple, rapide et facile mais elle
introduit des ambiguïtés et une discontinuité de la
sortie.
Méthode de la moyenne des maxima :
Dans le cas où plusieurs sous-ensembles auraient la
même hauteur maximale, on réalise leur moyenne une des
ambiguïtés de la méthode du maximum est enlevée.
Méthode du centroïde :
La sortie correspond à l'abscisse du centre de
gravité de la surface de la fonction d'appartenance
résultante.
Il existe deux méthodes :
- On prend l'union des sous-ensembles flous de sortie et on en
tire le centroïde global (calculs très lourds).
- On prend chaque sous-ensemble séparément et on
calcul son centroïde, puis on réalise la moyenne de tous les
centroïdes.
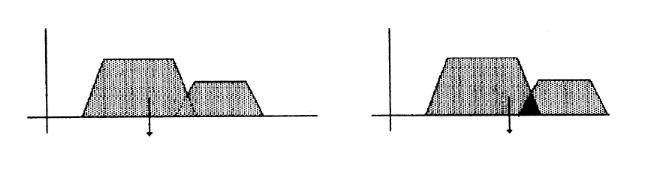
Conclusion : on n'a plus de discontinuités et
d'ambiguïtés, mais cette méthode est plus complexe et
demande des calculs plus importants.
Méthode de la somme pondérée
:
Compromis entre les deux méthodes
précédentes.
On calcule individuellement les sorties relatives à
chaque règle selon le principe de la moyenne des maxima, puis on
réalise leur moyenne pondérée.
CHAPITRE II :
MODELISATION DE LA CHAINE D'ASSERVISSEMENT D'UN MOTEUR
CC
Modélisation du MCC
Lorsque l'on veut la faire travailler, en appliquant un couple
résistant sur son axe, cela la freine donc E diminue.
Comme
U reste constante, le produit
Ri.Ii augmente donc
Ii augmente, donc le couple T augmente lui aussi
et lutte contre la diminution de vitesse : c'est un couple
moteur.
Plus on le freine, plus le courant augmente pour lutter
contre la diminution de vitesse. C'est pourquoi les moteurs à courant
continu peuvent « griller » lorsque le rotor est
bloqué, si le courant de la source n'est pas limité à une
valeur correcte.
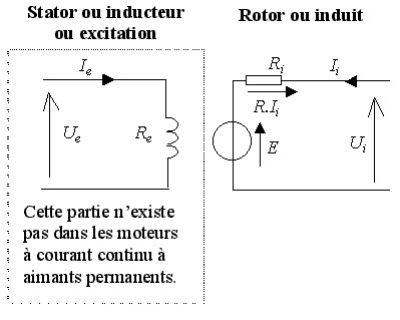
1. Modélisation par la fonction de
transfert
a-Equations électriques
La tension d'induit (en convention récepteur) :
 (1)
(1)
La f.é.m : : e(t) = Ke.Ù(t)
(2)
Avec
R: résistance d'induit
L: inductance d'induit en henry
e(t): f.é.m induite
K: Constante tenant compte du flux constant
a. Equations mécaniques
Le principe fondamental de la dynamique (PFD) nous permet
d'écrire :
 (3)
(3)
On a aussi : Cm=
Kc.I (4)
On suppose que le moment du couple résistant est de la
forme :
Cr = f .Ù (5)
Avec
J: moment d'inertie de l'axe du rotor en
Kg.m2
f: coefficient de frottement visqueux.
Transformation de Laplace de toutes équations
électromécanique est traduite dans ce tableau en
dessous :
a. Equations électromécaniques dans le
domaine de Laplace
La transformée de Laplace de l'équation (1) est :
U(P) = R.I(P) + L.p.I(P) + E(P)
La transformée de Laplace de l'équation (2) est :
E(P) = Ke.Ù(P) (2'), on peut alors écrire :
U(P) = (R.+ L.P)I(P) + Ke.Ù(P) (1')
La transformée de Laplace de l'équation (3) est :
J.P.Ù(P)= Kc.I(P) - Cr (3')
Et en tenant compte de l'équation (4) et (5) on peut
écrire :
J.P.Ù(P)= Kc.I(P) - f.Ù(P)  (J.P +f) .Ù(P)=
Kc.I(P) (J.P +f) .Ù(P)=
Kc.I(P)   (4') (4')
|
Equations électromécaniques
|
N°
|
Transformée de Laplace
|
|
(1)
|
U(P) = R.I(P) + L.p.I(P) + E(P)
|
|
e(t) = Ke.Ù(t)
|
(2)
|
E(P) = Ke.Ù(P)
|
|
(3)
|
J.P.Ù(P)= Cm - Cr
J.P.Ù(P)= Kc.I(P) - f.Ù(p
|
|
Cm= Kc.I
|
(4)
|
Cm=Kc.I(P)
|
|
Cr = f .Ù
|
(5)
|
Cr=f.Ù(P)
|
Ce qui donne :
  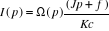
Et en remplaçant cette nouvelle expression de I(p) dans
l'équation (1') on obtient
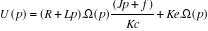
 
Le modèle de MCC comme suivant :
 Fig. 1: Schema Bloc d'un MCC
Fig. 1: Schema Bloc d'un MCC
On peut maintenant exprimer la fonction de transfert en boucle
fermée  : :
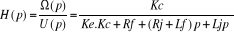 
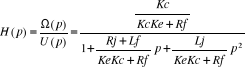
Qu'on peut écrire aussi sous la forme canonique d'une
fonction de transfert de second ordre :
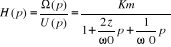
2. Modélisation par Variables
d'état
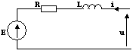
Fig.2 : Modèle équivalent de
l'induit en régime dynamique
On a :
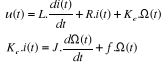
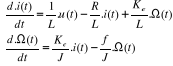
La représentation d'état :
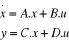
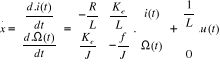
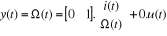
Modélisation du
hacheur
Le hacheur est composé d'un transistor en série
avec une diode tête bêche. Si le rapport cyclique est la commande
du transistor, on obtient la relation entre tension d'entrée et de
sortie suivante Umoy=.E.
Le hacheur est donc un simple amplificateur de Fonction de
Transfert : C(p)=E avec E la tension d'alimentation du
Hacheur.
á
Umoy=á.E
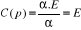
Pour que la modélisation soit réaliste, il faut
limiter la valeur de entre 0 et 1, puisque dans la réalité, le
rapport cyclique de la commande du transistor reste compris entre 0 et
Modélisation du capteur de
vitesse :
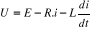
Le signal provenant du capteur de vitesse attaquera le
comparateur à base d'amplificateur opérationnel
On suppose que l'amplificateur opérationnel est
idéal
Résistance d'entrée très grande
Courant i=0
On en déduit que : U=E, or E = K.Ö.n
On met : K.Ö = KG = Constante de la dynamo
tachymétrique
Donc U=E= KG n
D'où la fonction de transfert :
 est
donnée par le constructeur, dans notre simulation le constructeur nous
donne la valeur 0.01146 est
donnée par le constructeur, dans notre simulation le constructeur nous
donne la valeur 0.01146
CHAPITRE III :
APPLICATION DE LA LOGIQUE FLOUE À LA
RÉGULATION DE LA TEMPÉRATURE
Cahier des charges
On présente le cas de réglage de la
température d'un four. Dans ce but on mesure la température avec
un capteur qui fournit la valeur de la grandeur à régler. On
suppose que le système a une fonction de transfère H(s)=1/(s+2)
avec un retard égale à un second.
C'est un système de contrôle de température
avec un élément de chauffage et de ventilation.
La température désirer est de 20°c.
La température extérieure est de 10°c et son
effet intervient au niveau de l'intégrateur.
Etapes a suivre :
1- modélise le système avec SIMULINK.
Sur la régulation d'un système pareille, on propose
3 solutions :
2-Premier cas : régulation PID
3-Deuxième cas : régulateur flou à une
seule entrée
4-Troisième cas : régulateur flou à
deux entrées
PARTIE I : REULATEUR PID
On introduit le système dans une boucle de
régulation avec correction proportionnel intégrale
dérivée PID, et ce avec les paramètres suivants :
Step=20°v; step1=-1.5°c; integrator: CI=10; Lower
saturation limit=10; transport delay=1; PID (1; 0; 1).
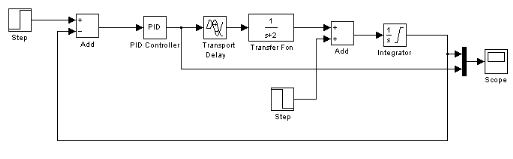
Fig3: Schéma bloc d'un system de
régulation de température par un PID
On retire les courbes de l'oscilloscope, la courbe jaune
représente la réponse du système en termes de
température,
La courbe en couleur mauve représente la commande du
système, sortie PID
Figure 4 : la réponse et la commande du
système
On constate que notre système lui manque la
précision puisque la sortie n'atteint pas la consigne qui est 20°C,
avec un légère retard
En appliquant une perturbation sur ce system après un
délai de 60 second pour étudier la réponse en
régime permanent et en réagissent sur la performance I (0.2) on
s'aperçoit que le system devient plus rapide et que le PID a bien
corriger la mesure et la remettre a la consigne qui est 20°C (voir figure
5)
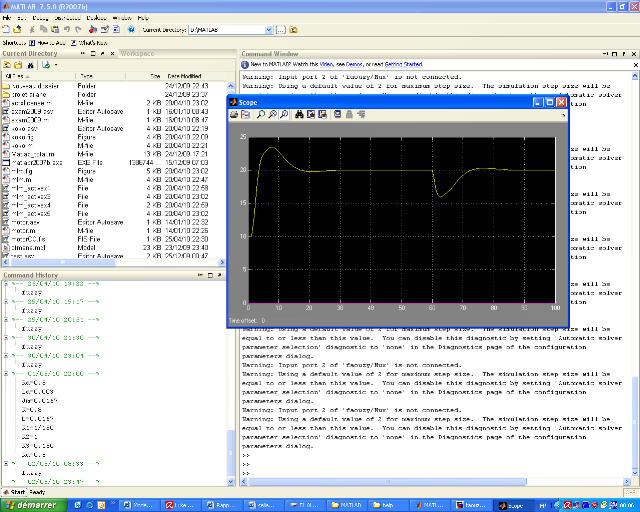
Figure 5 : la réponse et la commande
appliquant une perturbation a 60s
PARTIE II : REULATEUR A LOGIQUE FLOU A UNE SEULE
ENTREE
Nous allons changer notre régulateur classique PID par le
régulateur a logique flou avec une seule entrée, on commence tout
d'abord par définir les entrées et les sorties, et par la suite
on va essayer de lier les fonctions d'appartenances d'une façon logique
afin de réponde au cahier des charges.
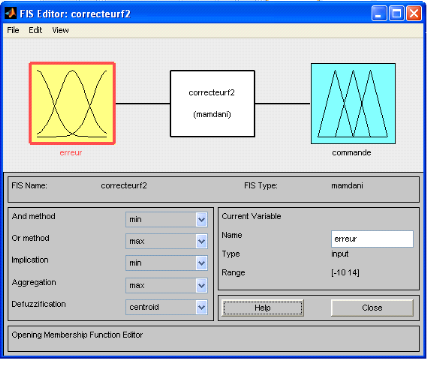
Figure 3.2.1 : création d'entrée et
sortie
Ensuite on définira les plages de variations (les
ensembles flous) et les fonctions d'appartenances pour l'entrée et la
sortie (figures 3.2.4, 3.2.5, 3.2.6), et on appellera chaque partie de la
fonction d'appartenance par un nom significatif. On aura alors : lorsque
l'erreur est négative (la température de sortie est
supérieure à la consigne), la fonction d'appartenance est
nommée chaud.
Lorsqu'elle est positive la fonction d'appartenance est
nommée froid, et la partie du milieu sera nommée rien.
La fonction d'appartenance d'erreur comporte trois
parties :
· Se réchauffe
· constant
· refroidit.
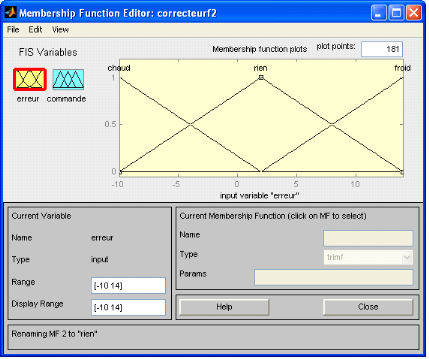
Figures 3.2.2 : fonction d'appartenance de
l'erreur.
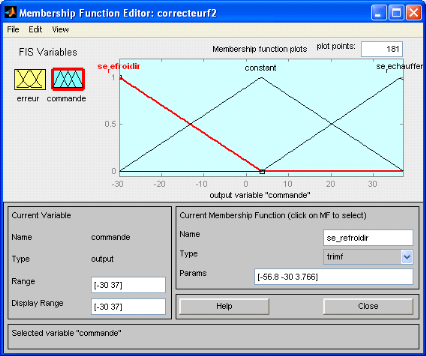
Figures 3.2.3 : fonction d'appartenance de la
commande
Après avoir définit les fonctions d'appartenance,
on va implémenter les règles d'inférences, de telle
façon à réaliser un cahier des charges, par exemple si le
système devient chaux le régulateur va automatiquement abaisser
la température pour garder la consigne voulus cela va être traduit
par la commande suivante :
If (erreur is chaud) then (commande is refroidir)
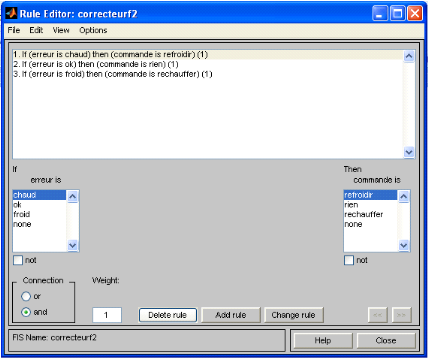
Figures 3.2.4: Implémentation des règles
d'inférence
Simulation du système par MATLAB
SIMULINK :
Modélisation du système sera défini sous
forme de ce schéma bloc introduit a simulink
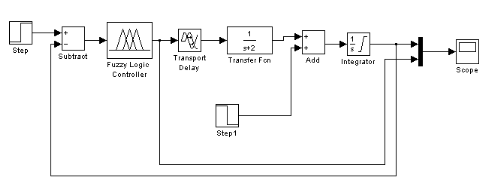
Figure 3.2.5 : Régulation du système de
température par un régulateur flou à une seule
entrée
Une fois le régulateur est chargé dans le bloc
Fuzzy du simulink, on simule le système et on obtient la réponse
suivante, la courbe jaune représente la réponse du
système, et la courbe mauve représente la commande issue du
régulateur RLF
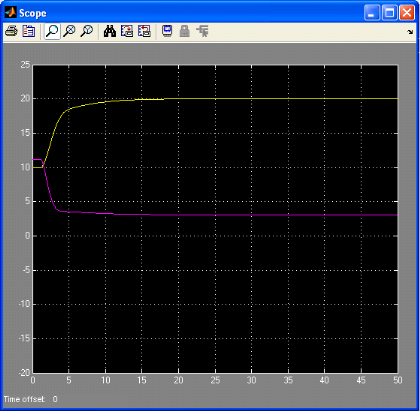
Figure 3.2.6 : la commande et la réponse
indicielle du système simulé
C'est une réponse qui atteint la consigne (20 °C). En
effet en variant les plages d'inférences on a augmenté
l'efficacité du régulateur autour de cette consigne. On pourrait
également modifier les règles d'inférences ou les formes
des fonctions d'appartenances utilisées, mais ceci suppose une
maîtrise du système à réguler.
PARTIE III : REULATEUR A LOGIQUE FLOU A DEUX
ENTREES
Dans cette partie on va ajouter une deuxième
entrée a notre RLF c'est la dérivée de l'erreur (variation
de l'erreur) on lui donne le nom derreur sa fonction d'appartenance comporte
trois parties:
· se réchauffe
· constant
· se refroidit.
La fonction d'appartenance de la sortie sera divisée en
5 parties :
· Refroidir beaucoup : RB
· Refroidir : R
· OK
· Réchauffer : C
· Réchauffer beaucoup : CB
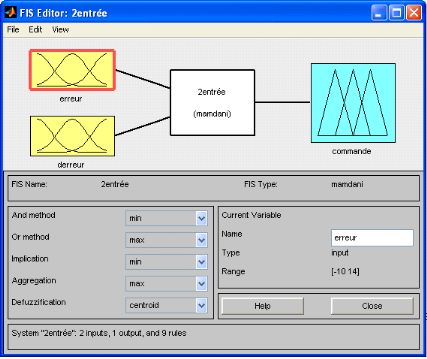
Figure 3.3.1 : Identification des entrées et des
sorties de l'RLF à deux entrées
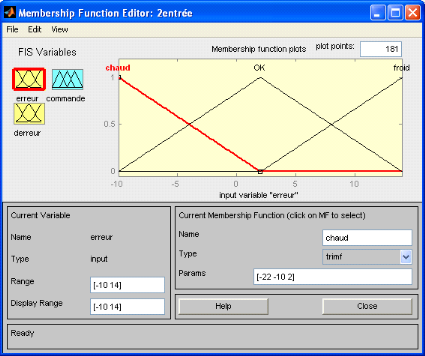
Figure 3.3.2 : fonction d'appartenance de
l'erreur
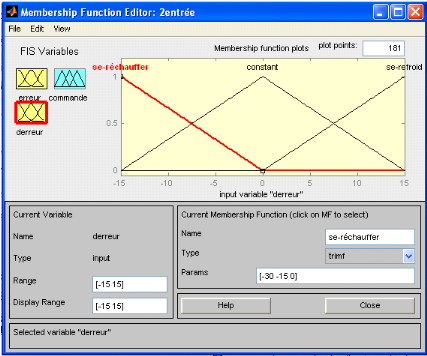
Figure 3.3.4 : fonction d'appartenance de la
dérivée de l'erreur
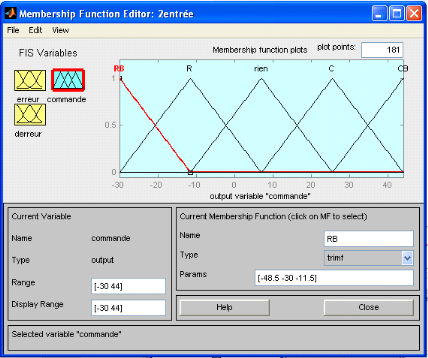
Figure 3.3.5 : fonction d'appartenance de la
commande
Apres avoir compléter le paramétrage des blocs
d'entrées et de sortie, on procède par l'élaboration des
règles logique qui répond au cahier des charges, et on les
implémente dans le bloc inférence
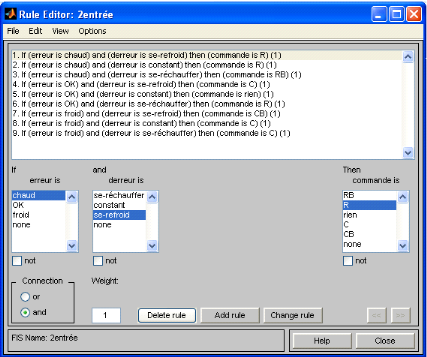
Figure 3.3.6 :Implémentation des règles
d'inférence
On finit par enregistrer le fichier (.fis) pour le charger par la
suite dans le workspace et le récupérer dans le bloc Fuzzy dans
simulink par le même nom du fichier enregistré.
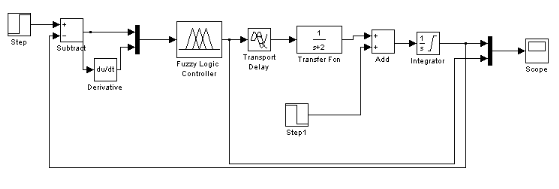
Figure 3.3.7 : Schéma blocs du système de
régulation de température par un RLF a 2 entrées
Une fois le régulateur est configuré, on simule et
on obtient la réponse suivante:
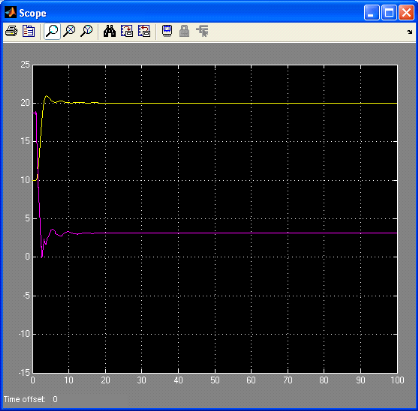
Figure 3.3.8: la commande et la réponse indicielle du
système simulé
Une réponse très forte en terme de rapidité,
stabilité et précision qui dépasse un régulateur a
logique flou utilisant une seule entrée
Cette réponse est obtenue également
après modification des plages de variations:
[-10 14] : l'erreur
[-15 15] : derreur
[-30 44] :
commande
Cette réponse présente Certainement un
dépassement mais sa rapidité est meilleure : son temps de
réponse est inférieur à celui du deuxième cas.
PARTIE IV : COMPARAISON ENTRE UN REGULATEUR CLASSIQUE PID
ET UN REGULATEUR A LOGIQUE FLOU
Notre étude a pour but de distinguer entre les avantages
et performances d'un régulateur classique PID et ce nouveau
régulateur a logique flou, dans cette partie en va relever les mesures
nécessaires pour pouvoir juger entre les 2 technologie pour cela on fixe
des intervalles +-5% de la réponse pour mesurer la rapidité
Et 10%, 90% du système pour étudier le temps de la
monté du système
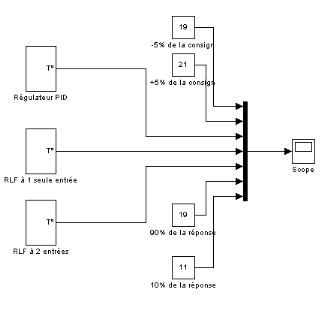
Figure 3.3.9: schéma blocs des différents
systèmes proposés
On Obtient les courbes suivantes :
Courbe bleu claire représente la réponse du
système avec un PID
Courbe rouge représente la réponse du
système avec un RLF a une seule entrée
Courbe verte représente la réponse du
système avec un RLF a deux entrées
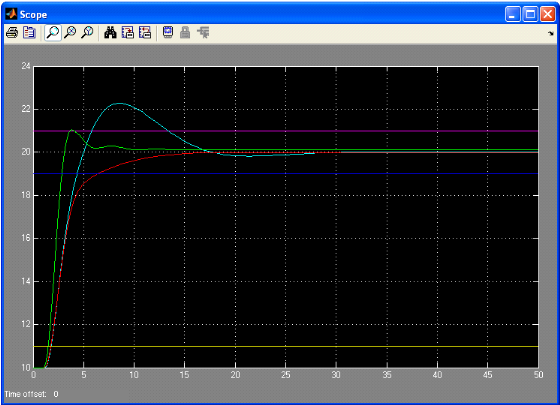
Figure 3.3.10: réponses des 3 systèmes
proposé
On obtient les mesures ci-dessous :
Ces mesures nous montre la performance du RLF par rapport au
régulateur classique PID, avec un temps de réponse et temps de
monté très réduit surtout le RLF a 2 entrées
|
Temps de réponse à 5% (sec)
|
Temps de montée (sec)
|
Dépassement %
|
Erreur (°C)
|
|
PID
|
13,329
|
11,546
|
11,10%
|
0
|
|
RLF 1 entrée
|
6.462
|
4,713
|
0%
|
0
|
|
RLF 2 entrées
|
4,053
|
2,562
|
5,21%
|
0,105
|
CHAPITRE IV :
APPLICATION DE LA LOGIQUE FLOU DANS LA REGULATION DE
VITESSE D'UN MOTEUR A COURANT CONTINU
Cahier des charges :
Il s'agit d'un moteur LEROY SOMER MS1 classe F801 L06 de
puissance nominale 0,44kw, de vitesse nominale 1500tr/min (soit
157rad /s).
Le constructeur donne les inductions suivante :
La=30mH ; J=0,003kg .m² (moteur seul) Un=170V ; couple nominal 3
N.m ; classe F ; If = 0,38A
Ian=3A ; rendement nominale hors excitation : 0,74 ; R
mesuré est : 5 ?
Le calcul montre que K= (170-5x3) /157= 0,987 wb, La
mesuré est 0,0243H
La constant de temps électrique vaut donc ôe=La
/Ra=4,86 ms
La méthode du ralentissement a donné J=
0,004Kg .m², car le moteur est accouplé à une charge
mécanique .La constant de temps électromécanique est donc
ôem= RJ/K² =20,5ms
On néglige les autres pertes
Le couple nominal résistant est de 3,25 N.m.
Le hacheur se comporte comme un amplificateur de gain A=100.
La constant de dynamo tachymétrique est a =0,01146.
Notre travail dans ce chapitre consiste a faire une étude
comparative entre un régulateur classique PID et un régulateur a
logique flou dans la régulation de la vitesse d'un moteur a courant
continu
Démarche a suivre
· Appliquer un couple résistant Cr= 3.25 au
démarrage dans les 2 système (avec PID, avec RLF)
· Régler le RLF pour le mener a l'état
idéal
· S'assurer que le RLF marche bien quelque soit le couple
appliqué
· Appliquer le même couple résistant
retardé de 0.3s
· Régler le RLF pour le mener a l'état
idéal
· S'assurer que le RLF marche bien quelque soit le couple
appliqué
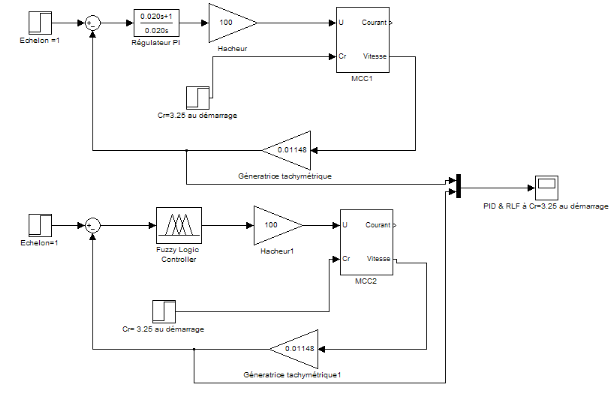
Partie I : comparaissant entre un PID et RLF avec un
couple résistant au démarrage
Figure 4.1.1: schéma blocs du système avec un
PID et avec un RLF sans gains
On appliquant un Cr=3.25 au démarrage avec les
échelles suivants :
Entrée erreur [-10 12]
Sortie commande [-10 12]
On obtient les résultats suivants :
· Un régulateur PID performant, la mesure suit la
consigne avec une rapidité remarquable et sans dépassement ainsi
qu'une erreur nulle
· Un RLF qui est ni rapide ni précis mais il est
stable
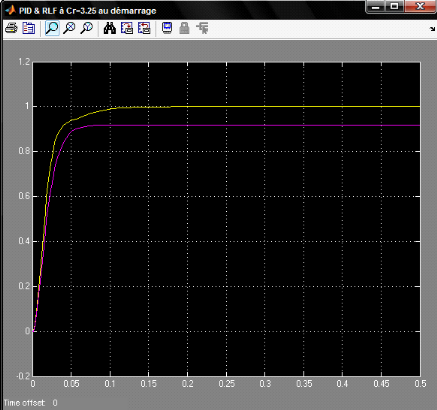
Figure 4.1.2: Réponses des systèmes avec un
PID et avec un RLF
On va introduire un gain à l'entrée du RLF et un
autre gain à la sortie de ce dernier
On remarque qu'à chaque fois on intervient sur le gain
d'entrée de notre RLF on agit sur la rapidité du système
et à chaque fois qu'on intervient sur le gain de la sortie du
système on agit sur la précision.
Après plusieurs réglages effectués, notre
système deviens performant (plus rapide et plus précis) avec les
valeurs suivantes :
Gain à l'entrée (erreur) égal
à 1
Gain à la sortie (commande) égal
à 1.09
Voir la réponse du système dans la figure 1.4
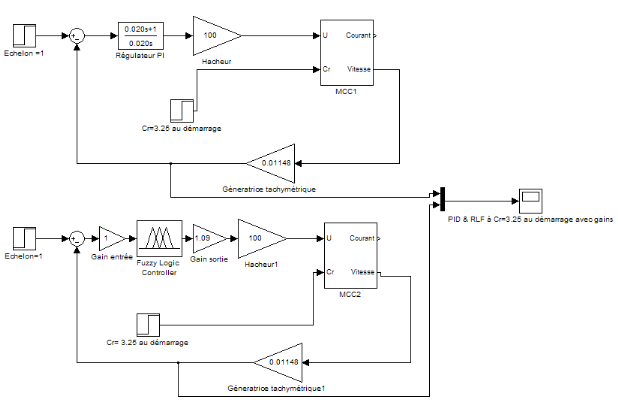
Figure 4.1.3: schéma blocs du système avec un
PID et avec un RLF avec gains
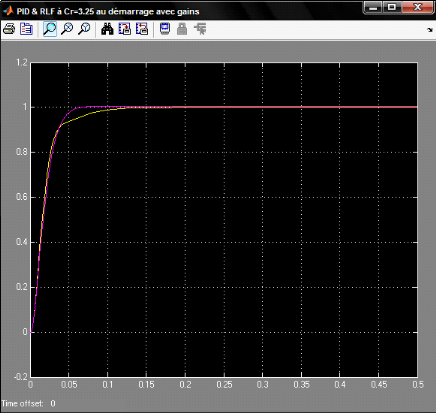
Figure 4.1.4: Réponses des systèmes avec un
PID et avec un RLF
Pour rendre notre RLF autonome (éliminer les gains) on va
introduire nos gain à l'intérieur de notre RLF et plus
précisément en agissant sur les échelles ;
La méthode consiste à deviser l'échelle de
l'entrée (erreur) sur le gain à l'entrée du RLF, et
à multiplier l'échelle de la sortie (commande) par le gain
à la sortie du RLF :
Gain à l'entrée (erreur) égal
à 1
[-10 12] / 1 => [-10 12]
Gain à la sortie (commande) égal
à 1.09
[-10 12] * 1.09 => [10.9 13.08]
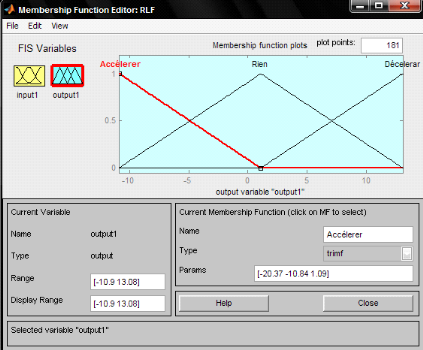
Figure 4.1.5: Introduction de la nouvelle échelle
dans le bloc de sortie du RLF
Partie II : comparaissant entre un PID et RLF avec
un couple résistant en régime permanent
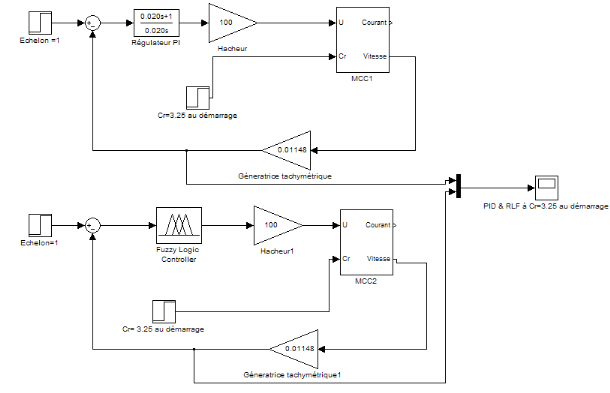
On va appliquer le même couple résistant qui est de
3.25 mais cette fois ci retardé de 0.3s pour pouvoir détecter la
réponse du système au milieu du régime permanant
Figure 4.1.6: schéma blocs du système avec un
PID et avec un RLF avec gains
La simulation nous donne le graphe ci-dessous
La courbe jaune représente la réponse du
système avec un PID
La courbe mauve représente la réponse du
système avec un RLF
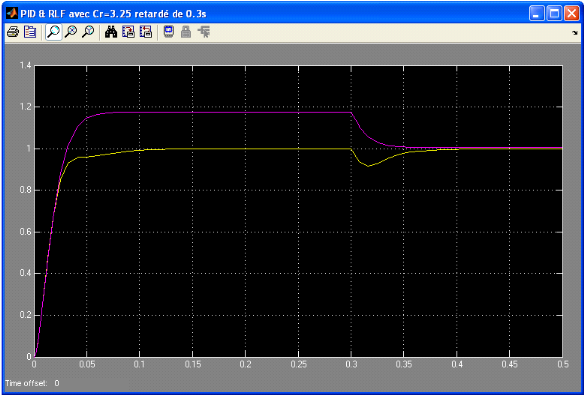
Figure 4.1.7: Réponses des systèmes avec un Cr
à 0.3s
On constate que la réponse du système avec un RLF
perde encor une fois sa précision au démarrage
On v procéder au réglage des échelles on
utilisant la même méthode utilisé au paravent
commençant par introduire un gin a l'entrée de notre fameux RLF
et un autre gain à la sortie de ce dernier, et en agissant sur le
1ère gain le system change de stabilité, et en agissant sur le
2ème le système change de précision.
Apres plusieurs essais on relève les valeurs
idéales qui correspondent à un RLF puissant et performant qui
répond au cahier des charges, ces valeurs sont les suivants.
Gain de l'entrée (erreur) est 400
Gain de sortie (commande) est 1
« prenant en considération qu'un gain de 1.09 est
déjà appliqué»
Pour pourvoir donner a notre RLF son autonomie on procède
par l'élimination de ces gain en les intégrants a
l'intérieur du RLF et plus précisément dans les
échelles d'entrée et sortie
Gain à l'entrée (erreur) égal
à 400
[-10 12] / 400 => [-0.025 0.03]
Gain à la sortie (commande) égal
à 1
[10.9 13.08]* 1 => [10.9 13.08]
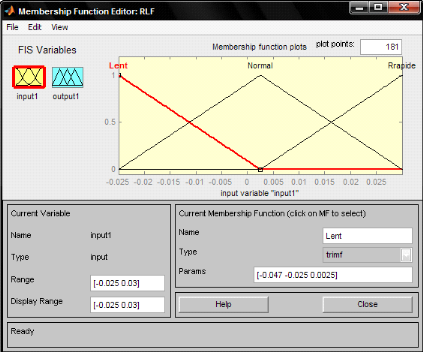
Figure 4.1.8: Introductions de la nouvelle échelle
dans le bloc d'entrée du RLF
En agit sur l'échelle de l'entrée seul comme la
montre cette fenêtre en dessus, en enregistre les modifications et on les
charges dans le bloc Fuzzy sur simulink
Apres avoir éliminer les 2 gains et changer les
échelles en simule et on obtient la réponse ci-dessous
La courbe en jaune représente la réponse avec un
PID
La courbe en mauve représente la réponse avec un
RLF
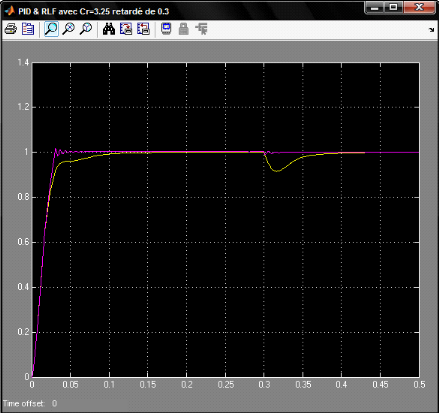
Figure 4.1.9: Réponses des systèmes avec un Cr
à 0.3s
Une réponse très puissante qui répond a
notre cahier des charges, dès le moment de la perturbation le
système réagit rapidement (plus rapide que le PID) pour corriger
l'erreur et remettre la mesure a l'état de consigne.
Pour s'assurer des réglages effectués on a
changé le couple résistant, et le système répond
parfaitement son aucun déréglage, cela implique que notre RLF
correctement paramétré
En propose une vus zoom de la réponse autour de la
perturbation pour pouvoir détecter l'allure de des courbes
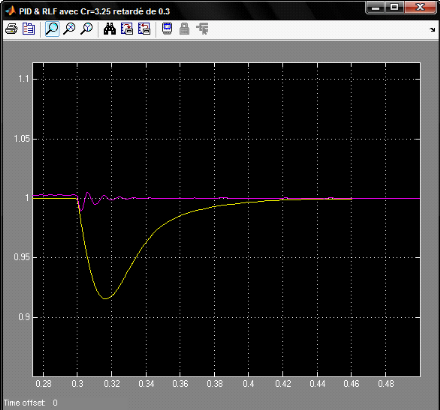
Figure 4.1.10: Vue zoom de la réponse système
autour de la perturbation
Ces graphes illustres des résultats obtenus très
satisfaisants, un régulateur à logique flou musclé et
très performant par rapport au régulateurs classique.
La logique floue (Fuzzy logic) est de grande actualité. Le
but visé dans cette étude été de présenter
d'un part le principe de cette nouvelle méthode de réglage et
établir d'autre part une comparaison entre les méthodes
conventionnelles et cette dernière, ceci pour mieux éclaircir les
différences, de familiariser avec la nouvelle méthode puis
connaître ces avantages dans le réglage automatique.
LES AVANTAGES ET LES DESAVANTAGES DU REGLAGE PAR
LOGIQUE DE FLOUE
Evidemment, le réglage par la logique floue
réunit un certain nombre d'avantages et de désavantages. Les
avantages essentiels sont :
· La non nécessité modélisation
(cependant il peut être utile d'un modèle convenable);
· la possibilité d'implémenter des
connaissances (linguistiques) de l'opérateur du processus;
· la maîtrise des systèmes à
régler avec un comportement complexe (fortement non linéaire et
difficile à modéliser);
· L'obtention fréquente de meilleures
prestations dynastiques (régulateur non linéaire):
· L'emploi possible aussi pour des processus rapides
(grâce à des processeurs dédicacés);
· la disponibilité des systèmes de
développement efficaces, soit pour microprocesseurs ou PC (solution
logicielle). soit pour circuits intégrés (processeurs
dédicacée, Fuzzy processor, solution matérielle).
Par contre, les désavantages sont :
· Le manque de directives précises pour la
conception d'un réglage (choix des grandeurs à mesurer,
détermination de la Fuzzification, des inférences et de
Défuzzification);
· L'approche artisanale et non systématique
(implémentation des connaissances de l'opérateur souvent
difficile);
· L'impossibilité de la démonstration
de la stabilité du circuit de réglage en toute
généralité(en l'absence d'un modèle valable);
· La possibilité d'apparition de cycles
limites à cause du fonctionnement non linéaire;
· la précision du réglage souvent peu
élevée;
· la cohérence des inférences non
garantie a priori (apparition de règles d'inférence
contradictoires possible).
CONCLUSION
Les outils fournis par la logique floue permettent une
modélisation des phénomènes pouvant en un certain sens
s'approcher du raisonnement humain. Le fait de dépasser le tout ou rien
des ordinateurs introduit une souplesse faisant la puissance des outils flous
dans de nombreux domaines.
Mais même s'ils bénéficièrent d'un
effet de mode, les algorithmes flous ne sont pas nécessairement les
meilleurs.
Plus le système est complexe, plus les règles
qui le régissent sont nombreuses et compliquées. Il s'agit
là d'un obstacle majeur au contrôle en temps réel.
Elle apporte des solutions à des problèmes
compliqués ou difficilement modélisables et elle n'a pas des
méthodes générales de synthèses, alors il est
nécessaire de varier à l'entrée et faire des tests
jusqu'à atteindre la consigne.
| 


