|
LES LIMITES DE L'ORDINATEUR DANS LA RESOLUTION D'UN
PROBLEME NUMERIQUE
Par NGOIE MPOY Ruffin
Benoît1(*)
ABSTRACT
The goal of this article is to show to the user that computer,
fast and powerful computational tool, cannot be used without precautions to
deal with mathematical problems.
In calculations, numbers handled by the computer are
represented in memory with a restricted number of figures. This limitation
inherent in the structure of the machine is sometimes generating errors which
can make lose any significance with a result.
The examples are given in PASCAL language, but certain results
were produced by a programmable calculator of mark Texas Instrument TI
86
INTRODUCTION
Le but de cet article est de montrer à l'utilisateur
que l'ordinateur, outil de calcul rapide et puissant, ne peut pas être
utilisé sans précautions pour traiter les problèmes
mathématiques.
Dans les calculs, les nombres manipulés par
l'ordinateur sont représentés en mémoire avec un nombre
restreint des chiffres. Cette limitation inhérente à la structure
de la machine est parfois génératrice d'erreurs qui peuvent faire
perdre toute signification à un résultat.
Les exemples sont donnés en langage PASCAL, mais
certains résultats ont été produits par une calculette
programmable de marque Texas Instrument TI 86
1. Notation
Nous supposerons que le lecteur s'est familiarisé avec
les propriétés élémentaires des ensembles IN, Z, Q
et IR où :
IN =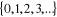
Z =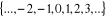
Q =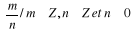
IR = Q U I où I =  (Mubenga, K., 1984) (Mubenga, K., 1984)
2. Quelques rappels des notions
mathématiques
2.1. Théorème de Rolle
Soit  une fonction continue dans une fonction continue dans . Si . Si  admet une dérivée pour tout admet une dérivée pour tout  de de  et si et si , il existe au moins un nombre , il existe au moins un nombre  tel que tel que  . (Chambadal, L., 1968) . (Chambadal, L., 1968)
Démonstration
Par hypothèse, il existe sur une courbe
d'équation  au moins un point d'abscisse au moins un point d'abscisse  où la tangente est parallèle à OX ( où la tangente est parallèle à OX ( ). Soit ). Soit  cette tangente, puisque cette tangente, puisque  est parallèle à OX, son équation est de la
forme est parallèle à OX, son équation est de la
forme . Il est clair que son coefficient angulaire qui est . Il est clair que son coefficient angulaire qui est  est nul. D'où est nul. D'où . .
2.2. Formules des accroissements finis
Soit  une fonction continue dans une fonction continue dans . Si . Si  admet une dérivée pour tout admet une dérivée pour tout  de de  et si et si , il existe au moins un nombre , il existe au moins un nombre  tel que : tel que : 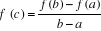
Démonstration
En effet, il suffit d'appliquer le théorème de
Rolle à la fonction  puisque puisque  est continue dans est continue dans  et que et que , il existe un nombre , il existe un nombre tel que tel que  or or  . .
D'où  et et 
(Lorent, R et Lorent, S., 1990)
2.3. Formule de Taylor
2.3.1. Introduction
Considérons le polynôme  et ses dérivées successives. On a : et ses dérivées successives. On a :
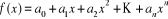
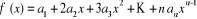
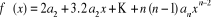
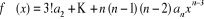
...
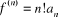
D'où  et et  (2.3.1) (2.3.1)
Nous nous proposons d'étendre la formule des
accroissements finis en introduisant les dérivées successives de
 : On obtient la formule de Taylor. : On obtient la formule de Taylor.
La formule (2.3.1) qui est valable pour un polynôme de
degré n sera généralisée. Cette formule est dite de
Mac Laurin. Notons que la formule de Mac Laurin est un cas particulier de la
formule de Taylor.
2.3.2. Formule de Taylor
Soit  une fonction continue dans une fonction continue dans qui admet des dérivées 1ère,
2ème, ..., nième continues dans qui admet des dérivées 1ère,
2ème, ..., nième continues dans  et qui, de plus, admet une dérivée
(n+1)ième fini dans et qui, de plus, admet une dérivée
(n+1)ième fini dans 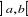
Posons
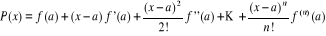
Remarquons que
 (2.3.2) (2.3.2)
Considérons la fonction , nous avons en vertu des relations (2.3.2), , nous avons en vertu des relations (2.3.2),
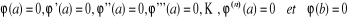
Remarquons que  est continue dans est continue dans et qu'elle admet une dérivée dans et qu'elle admet une dérivée dans ; il en est de même de ; il en est de même de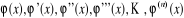
Comme , il existe, en vertu du théorème de Rolle une valeur , il existe, en vertu du théorème de Rolle une valeur  telle que : telle que :
 avec avec . Dès lors, comme . Dès lors, comme , il existe une valeur , il existe une valeur  telle que telle que  avec avec  Et ainsi de suite jusque : Et ainsi de suite jusque :  avec avec  . D'où, puisque . D'où, puisque  : :
 avec avec 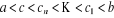
Or en dérivant  successivement et en remarquant que successivement et en remarquant que , on obtient : , on obtient :
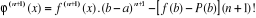
D'où  avec avec et et
 avec avec 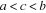
En remplaçant  par sa valeur, on obtient la formule de Taylor : par sa valeur, on obtient la formule de Taylor :
 (2.3.2 bis) où (2.3.2 bis) où
 avec avec  s'appelle le reste de la formule de Taylor. s'appelle le reste de la formule de Taylor.
La formule (2.3.2 bis) dite formule de Taylor est encore
valable si 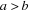
Remarque
Si on pose  et et  , on obtient une autre forme de la formule de Taylor : , on obtient une autre forme de la formule de Taylor :
 où où  avec avec 
3. Limites de l'ordinateur
Représentation des nombres réels en
mémoire
Dans un ordinateur, tout nombre réel  peut s'écrire peut s'écrire avec avec  . Pour un ordinateur donné, il existe deux entiers . Pour un ordinateur donné, il existe deux entiers  et et  tels que les nombres réels manipulés par cet ordinateur
soient ceux pour lesquels le développement binaire de tels que les nombres réels manipulés par cet ordinateur
soient ceux pour lesquels le développement binaire de  est de la forme est de la forme  avec avec  (et donc (et donc  ) et ) et  . Ces nombres sont rangés en mémoire sur un nombre fixe
d'octets. Il est à remarquer que tous ces nombres sont des
rationnels. . Ces nombres sont rangés en mémoire sur un nombre fixe
d'octets. Il est à remarquer que tous ces nombres sont des
rationnels.
Dans un ordinateur, chaque nombre est placé dans un mot
de la mémoire. Un mot est formé d'un nombre fini de cases,
chacune ne pouvant contenir qu'un seul chiffre. Dans la première, on va
placer le signe de  , puis les chiffres successifs de la mantisse de , puis les chiffres successifs de la mantisse de  , ensuite le signe de son exposant. Chaque mot de la mémoire d'un
ordinateur ne peut donc contenir, comme nous l'avons précédemment
dit, qu'un nombre fini des chiffres. En particulier, nous appellerons , ensuite le signe de son exposant. Chaque mot de la mémoire d'un
ordinateur ne peut donc contenir, comme nous l'avons précédemment
dit, qu'un nombre fini des chiffres. En particulier, nous appellerons  le nombre de chiffres décimaux de la mantisse des mots de
l'ordinateur (en général, on aura le nombre de chiffres décimaux de la mantisse des mots de
l'ordinateur (en général, on aura  =7 ou 8 en simple précision, 15 ou 16 en double
précision). Par conséquent, seuls seront
représentés de façon exacte les nombres dont la mantisse
ne dépasse pas =7 ou 8 en simple précision, 15 ou 16 en double
précision). Par conséquent, seuls seront
représentés de façon exacte les nombres dont la mantisse
ne dépasse pas  chiffres. Le problème qui se pose à nous maintenant est
simple : comment représenter un nombre réel chiffres. Le problème qui se pose à nous maintenant est
simple : comment représenter un nombre réel  ayant une mantisse avec un nombre de chiffres supérieur à ayant une mantisse avec un nombre de chiffres supérieur à
 à l'aide d'un mot de la mémoire qui ne peut en contenir
que à l'aide d'un mot de la mémoire qui ne peut en contenir
que  ? Il y a deux possibilités. ? Il y a deux possibilités.
· La troncature qui consiste à couper (à
tronquer) la mantisse de  après son après son  -ième chiffre, -ième chiffre,
· L'arrondi qui consiste à tenir compte du ( )-ième chiffre. Si celui-ci est inférieur à 5, on
tronque tandis que, s'il est supérieur ou égal à 5, on
ajoute une unité au )-ième chiffre. Si celui-ci est inférieur à 5, on
tronque tandis que, s'il est supérieur ou égal à 5, on
ajoute une unité au  -ième chiffre avant de tronquer. Il y a quatre sortes
d'arrondi : supérieur, inférieur, vers zéro et au
plus proche. Nous venons de décrire celui au plus proche tandis que la
troncature correspond à l'arrondi vers zéro. -ième chiffre avant de tronquer. Il y a quatre sortes
d'arrondi : supérieur, inférieur, vers zéro et au
plus proche. Nous venons de décrire celui au plus proche tandis que la
troncature correspond à l'arrondi vers zéro.
Presque la totalité des ordinateurs travaille
actuellement par arrondi. Dans les deux cas, le nombre réel  est donc représenté dans l'ordinateur par un nombre (dit
nombre machine) qui, en général, en est une
approximation. Nous l'appellerons est donc représenté dans l'ordinateur par un nombre (dit
nombre machine) qui, en général, en est une
approximation. Nous l'appellerons , que l'ordinateur travaille par troncature ou par arrondi. L'erreur
ainsi commise s'appelle erreur d'affectation parce qu'au nombre
réel , que l'ordinateur travaille par troncature ou par arrondi. L'erreur
ainsi commise s'appelle erreur d'affectation parce qu'au nombre
réel  on affecte un mot contenant le nombre on affecte un mot contenant le nombre  . On a le théorème suivant : . On a le théorème suivant :
Théorème
« L'erreur d'affectation vérifie
 où K= 5 si l'ordinateur travaille par arrondi et 10 s'il
travaille par troncature » où K= 5 si l'ordinateur travaille par arrondi et 10 s'il
travaille par troncature »
Démonstration
Donnons la démonstration dans le cas de la troncature.
On a :
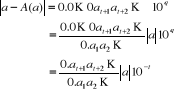
Donnons une borne supérieure de ce rapport en majorant
son numérateur et en minorant son dénominateur. Le
numérateur est majoré par 0.99999... = 1 et le
dénominateur est minoré par 0.100... puisque  Par conséquent Par conséquent  . (Brezinski, C. et Redivo-Zaglia, M., 2005) . (Brezinski, C. et Redivo-Zaglia, M., 2005)
Il est évident que, pour l'arrondi, l'erreur est deux
fois plus faible et correspond donc à K = 5.
Remarquons que l'on peut également écrire
l'inégalité donnée dans ce théorème sous
forme d'égalité  avec avec 
Erreur d'arrondi
Nous venons de voir que la taille de la place
réservée en mémoire pour ranger un nombre est
fixée. Il en résulte que si les nombres manipulés ont une
écriture nécessitant pour  plus de plus de  chiffres en base 2, ils devront être nécessairement
rangés sous forme tronquée donc approchée. Ceci conduit
à une erreur sur le nombre appelée erreur d'arrondi.
Cette erreur est très faible et peu significative si l'on
considère le nombre individuellement (elle ne dépasse pas
2-k-1 en valeur relative) chiffres en base 2, ils devront être nécessairement
rangés sous forme tronquée donc approchée. Ceci conduit
à une erreur sur le nombre appelée erreur d'arrondi.
Cette erreur est très faible et peu significative si l'on
considère le nombre individuellement (elle ne dépasse pas
2-k-1 en valeur relative)
Opérations arithmétiques
Voyons maintenant comment un ordinateur s'y prend pour
effectuer les quatre opérations arithmétiques
élémentaires +, -, x, /.
Addition
Soit à calculer A = B + C. Cette opération,
comme les trois autres d'ailleurs, ne s'effectue pas dans la mémoire
centrale mais dans ce que l'on appelle l'accumulateur. Cette
accumulateur est un ensemble de trois mots dont la particularité est
d'avoir les mantisses avec  chiffres au lieu de chiffres au lieu de  . C'est pour cela que l'on parle souvent d'accumulateur en double
précision (même si, dans la pratique, . C'est pour cela que l'on parle souvent d'accumulateur en double
précision (même si, dans la pratique,  chiffres ne pas nécessaires mais seulement chiffres ne pas nécessaires mais seulement  pour l'addition et la soustraction et pour l'addition et la soustraction et  pour la multiplication. pour la multiplication.
Pour effectuer l'opération A = B + C, l'ordinateur
commence par recopier sans modification dans l'accumulateur celui des deux
opérandes qui est le plus grand en valeur absolue. Comme, dans
l'accumulateur, la mantisse doit avoir  chiffres, il la complète à droite par des zéros.
Puis il recopie l'autre opérande dans l'accumulateur en faisant en sorte
que son exposant soit le même que celui du premier opérande. Pour
cela, on rajoute éventuellement des zéros à gauche de la
mantisse (c'est-à-dire avant chiffres, il la complète à droite par des zéros.
Puis il recopie l'autre opérande dans l'accumulateur en faisant en sorte
que son exposant soit le même que celui du premier opérande. Pour
cela, on rajoute éventuellement des zéros à gauche de la
mantisse (c'est-à-dire avant  ). Pour fixer les idées, donnons un exemple avec ). Pour fixer les idées, donnons un exemple avec  . Supposons B = 0.23487757 x 103 et que C = 0.56799442. Dans
l'accumulateur on recopie B tel quel, c'est-à-dire que l'on aura
B=0.2348775700000000x103. pour que C ait le même exposant que
B, il faut le multiplier par 103. . Supposons B = 0.23487757 x 103 et que C = 0.56799442. Dans
l'accumulateur on recopie B tel quel, c'est-à-dire que l'on aura
B=0.2348775700000000x103. pour que C ait le même exposant que
B, il faut le multiplier par 103.
Mais il faut, bien sûr, le diviser aussi par
103 pour que sa valeur ne change pas, c'est-à-dire que C =
(0.56799442/103 )x103 et, dans l'accumulateur, on aura C
= 0.000567994420000x103
Finalement, cela montre que l'ordinateur procède comme
quand nous effectuons une addition avec un papier et un crayon : nous
plaçons les uns en dessous des autres les chiffres correspondants aux
puissances identiques de 10. Maintenant, l'addition peut s'effectuer dans
l'accumulateur et l'on trouve B + C = 0.2354455644200000 x 103. On
voit que, dans l'accumulateur, l'addition s'est effectuée sans aucune
erreur ( au moins sur cet exemple ; on verra plus loin d'autres exemples
où le résultat obtenu dans l'accumulateur présente une
erreur). Enfin, notre résultat doit être renvoyé dans un
mot de la mémoire de l'ordinateur. Or ces mots ont des mantisses qui ne
possèdent que  (8 dans notre exemple) chiffres. Nous allons donc faire une erreur qui
est celle que l'on commet lorsque l'on place un nombre ayant une mantisse de
plus de (8 dans notre exemple) chiffres. Nous allons donc faire une erreur qui
est celle que l'on commet lorsque l'on place un nombre ayant une mantisse de
plus de  chiffres dans un mot qui n'en accepte que chiffres dans un mot qui n'en accepte que  : C'est une erreur d'affectation telle qu'elle est donnée
par le théorème précédent. Il est évident
que les choses se passent de la même façon pour une soustraction.
Dans l'exemple précédent, on obtiendra donc A = 0.23544556 x
103 que l'ordinateur procède par arrondi ou par
troncature. : C'est une erreur d'affectation telle qu'elle est donnée
par le théorème précédent. Il est évident
que les choses se passent de la même façon pour une soustraction.
Dans l'exemple précédent, on obtiendra donc A = 0.23544556 x
103 que l'ordinateur procède par arrondi ou par
troncature.
Multiplication
Dans le cas d'une multiplication, le produit de deux mantisses
de longueur  donne un résultat de longueur donne un résultat de longueur  et les exposants s'ajoutent. Le résultat d'une multiplication
est donc exact dans l'accumulateur et la seule erreur que l'on commet est, de
nouveau, une erreur d'affectation en revenant de l'accumulateur dans la
mémoire. et les exposants s'ajoutent. Le résultat d'une multiplication
est donc exact dans l'accumulateur et la seule erreur que l'on commet est, de
nouveau, une erreur d'affectation en revenant de l'accumulateur dans la
mémoire.
Division
Pour une division enfin, il est évident que, dans
l'accumulateur, le résultat n'est pas toujours exact (par exemple,
lorsque l'on divise 1 par 3, le résultat possède une
infinité de 3). L'erreur, dans l'accumulateur, se situe au niveau du
 -ième chiffre, c'est-à-dire une erreur supérieure.
Comme le résultat du Théorème de l'erreur d'affectation
fournit une borne supérieure de l'erreur, il est donc toujours valable.
Nous avons démontré que, pour toute opération
arithmétique, l'erreur est donnée par le Théorème
de l'erreur d'affectation et nous avons finalement le Théorème
suivant : -ième chiffre, c'est-à-dire une erreur supérieure.
Comme le résultat du Théorème de l'erreur d'affectation
fournit une borne supérieure de l'erreur, il est donc toujours valable.
Nous avons démontré que, pour toute opération
arithmétique, l'erreur est donnée par le Théorème
de l'erreur d'affectation et nous avons finalement le Théorème
suivant :
Théorème
« L'erreur sur une opération
arithmétique satisfait  avec K=5 dans le cas de l'arrondi, K=10 dans celui de la troncature et
où * est l'une des opérations +, -, x, / »
(Cottet-Emard, F et Goetgheluck, F., 1993) avec K=5 dans le cas de l'arrondi, K=10 dans celui de la troncature et
où * est l'une des opérations +, -, x, / »
(Cottet-Emard, F et Goetgheluck, F., 1993)
Exemples
a. Exemple 1
Nous pouvons vérifier rapidement sur un ordinateur
qu'on peut trouver r suffisamment grand tel que :
|
Opérations
|
Résultat par Ordinateur
|
Résultat par Calculette TI 86 (r = 500)
|
|
1 + 10-r
|
1
|
1
|
|
1 + 10-r - 1
|
0
|
0
|
|
1 - 1 + 10-r
|
10-r
|
10-r
|
|
0 (au lieu de 1)
|
0
|
Ces résultats s'expliquent en remarquant que :
· Les opérations sont effectuées de la
gauche vers la droite
· Quand on effectue 1 + 10-r,
l'opération de décalage et de troncature sur
10-r transforme ce nombre en 0.
b. Exemple 2
L'exécution des instructions suivantes :
PROGRAM Calcul1 (INPUT,
OUTPUT);
VAR
n : INTEGER ;
s : REAL ;
BEGIN
s := 0 ;
FOR n := 1 TO 10000
DO s := s + 1.0 E-10 ;
s:= s+1;
WRITE (s)
END.
et l'exécution de :
PROGRAM Calcul2 (INPUT,
OUTPUT);
VAR
n : INTEGER ;
s : REAL ;
BEGIN
s := 1 ;
FOR n := 1 TO 10000
DO s := s + 1.0 E-10 ;
WRITE (s)
END.
peuvent afficher des valeurs différentes à
l'écran. En effet, s donne 1.0000010000 E+00 pour Calcul1 et
1.0000010004 E+00 pour Calcul2.
Ceci nous suggère le principe suivant :
« Dans une somme, il sera toujours
préférable d'additionner d'abord les termes les plus petits en
valeur absolue pour leur cumul ne soit pas négligé face aux
termes les plus grands »
c. Exemple 3
L'affichage est fait en base 10 avec un nombre fixé de
chiffres. Les nombres sont le plus souvent fournis à l'ordinateur sous
forme décimale. Nous avons vu qu'ils sont transformés et
manipulés sous forme binaire avec les erreurs que cela comporte. Une
fois le calcul terminé, ils sont reconvertis en base 10, ce qui
introduit une nouvelle erreur. L'affichage sur l'écran ne fournit donc
pas nécessairement la valeur exacte contenue en mémoire.
|
Opération
|
Résultat affiché
|
|
1
|
|
|
Sur une calculette de marque Texas instrument TI 86 x
= 10-14
· La première opération donne un
résultat apparemment exact. Si ce résultat était
rigoureusement exact, on devrait avoir 0 comme résultat de la seconde
opération. Pour comprendre ce qui s'est passé, travaillons en
base 2 :
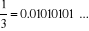
Un calcul simple montre qu'alors,  est représenté en mémoire en base 2 par
0.1111111... (t+1 chiffres 1) nombre qui vaut 1 -
2-t et qui est arrondi à 1 pour être
affiché en base 10 avec un maximum de précision. En revanche dans
la seconde opération, c'est 2-t qui sera
affiché. est représenté en mémoire en base 2 par
0.1111111... (t+1 chiffres 1) nombre qui vaut 1 -
2-t et qui est arrondi à 1 pour être
affiché en base 10 avec un maximum de précision. En revanche dans
la seconde opération, c'est 2-t qui sera
affiché.
d. Exemple 4
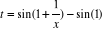
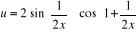
· · On a  . Par le théorème des accroissements finis, on a
aussi : . Par le théorème des accroissements finis, on a
aussi :

Donc, pour x positif :
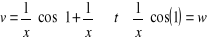
On pourra vérifier par un calcul sur ordinateur que
pour x suffisamment grand, les formules donnant  fournissent des résultats acceptables contrairement à la
formule qui donne t. fournissent des résultats acceptables contrairement à la
formule qui donne t.
Testés sur une calculette Texas Instrument TI 86, les
résultats obtenus sont pour x=E+100 (soit 10100) :

e. Exemple 5
Une erreur répétée un grand nombre de
fois ou multipliée par un grand nombre peut conduire à une erreur
globale non négligeable.
L'exécution des instructions suivantes affectera
à ERREUR une valeur non nulle alors que d'un point de vue strictement
mathématique on devrait avoir ERREUR = 0.
PROGRAM Calcul3 (INPUT,
OUTPUT);
VAR
I : INTEGER ;
S, ERREUR, a : REAL ;
BEGIN
a := 1/3 ;
S:=0;
FOR I:= 1 TO 30000
DO s := s + a ;
ERREUR:= S-10000;
WRITE (ERREUR)
END.
Remarquons que 1/3 est représenté en
mémoire par une valeur par défaut. Par ailleurs au fur et
à mesure que S augmente, 1/3 est de plus en plus décalé et
tronqué pour additionner S et a. Il en résulte une petite erreur
par défaut. Testé sur ordinateur, ce code revoie la valeur
-2,5331974030 E-06 au lieu de 0.
f. Exemple 6
La récursivité donne la possibilité de
faire figurer dans la définition d'un objet une référence
à ce même objet.
Une procédure ou une fonction récursive est un
sous - programme qui s'appelle lui-même, et qui intègre une
variable de contrôle permettant d'arrêter le processus d'appel.
On considère les suites ( ) et ( ) et ( ) définies par : ) définies par :
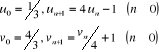
Les programmes récursifs de calcul des termes de ces
suites sont :
PROGRAM Calcul4 (INPUT,
OUTPUT);
VAR
I, n : INTEGER ;
FUNCTION
terme(val:INTEGER):REAL;
BEGIN
IF val = 0
THEN terme:=1/3
ELSE terme:=4*terme(val-1)-1
END ;
BEGIN
WRITELN(`Saisir un nombre entier');
READLN(n) ;
WRITE(`Le terme qui correspond à ce
nombre est',terme(n))
END.
Et
PROGRAM Calcul5 (INPUT,
OUTPUT);
VAR
I, n : INTEGER ;
FUNCTION
terme(val:INTEGER):REAL;
BEGIN
IF val = 0
THEN terme:=4/3
ELSE terme:=terme(val-1)/4+1
END ;
BEGIN
WRITELN(`Saisir un nombre entier');
READLN(n) ;
WRITE(`Le terme qui correspond à ce
nombre est',terme(n))
END.
Calculés à la main, les termes successifs de ces
deux suites sont égaux à 1/3 pour ( ) et 4/3 pour ( ) et 4/3 pour ( ). Les deux suites sont donc constantes (Thiel, E., 2004) ). Les deux suites sont donc constantes (Thiel, E., 2004)
CONCLUSION
Les limites de l'ordinateur démontrées dans cet
article montrent à suffisance que l'ordinateur (ou toute autre machine
automatique de calcul) n'est pas toujours le meilleur outil pour
résoudre un problème numérique.
En effet, à cause du fait que les données
numériques à traiter sont introduites en décimal et
doivent être converties en binaire avant traitement par l'automate, il y
a introduction d'une erreur et les résultats en binaire reconverties en
décimal pour afficher à l'écran introduisent une nouvelle
erreur.
Le programmeur informatique doit être avisé de
ces insuffisances afin d'optimiser les résultats en utilisant
l'ordinateur. Pour ce faire, il doit éviter de tomber dans la
facilité des opérations à la main.
Mathématiquement, on peut trouver un résultat qui n'est pas
observé sur l'ordinateur. Les opérations de conversion, de
décalage, d'arrondi et de troncature y sont pour beaucoup !
Enfin, nous espérons dans cet article montrer que
l'ordinateur ne doit pas être utilisé sans précautions pour
traiter les problèmes mathématiques. Les exemples vus dans le
présent article soutiennent nos affirmations.
Par ailleurs, l'ordinateur ne peut répondre à
des questions du type « La fonction est-elle continue,
dérivable ? » Interrogations qui nécessitent un
raisonnement d'analyse.
BIBLIOGRAPHIE
|
1
|
Brezinski, C. et Redivo-Zaglia, M.(2005) :
« Méthodes numériques directes de l'algèbre
matricielle »,
Ed. Ellipses, Paris
|
|
2
|
Canevet, D. (2005) : « L'algorithmique et
le PASCAL », Ed. Delagrave, Paris
|
|
3
|
Chambadal, L. (1968) : « Dictionnaire
des mathématiques modernes », Librairie Larousse,
Paris
|
|
4
|
Cottet-Emard, F et Goetgheluck, F.
(1993) : « Mathématiques sur
ordinateur », Ed. DeBoeck-Wesmael,
Bruxelles
|
|
5
|
Lorent, R et Lorent, S (1990) :
« Algèbre 2B », Ed. DeBoeck, Bruxelles
|
|
6
|
Mubenga, K (1984) : « Eléments
d'analyse infinitésimale, VOL I », PUZ, Kinshasa,
Zaïre
|
|
7
|
Ngoie Mpoy, R. (2008) : « Evaluation des
fonctions usuelles sur des variables complexes : Algorithmisation
des calculs et
programmation », Mémoire de fin d'études, UPN,
Kinshasa
|
|
8
|
Thiel, E. (2004) : « Algorithmes et
programmation en PASCAL », DEUG 1, Cours, Luminy
|
|
9
|
Van LOO, R. (1985) : « Les grandes
règles de programmation en BASIC », Ed. Marabout, Alleur,
Belgique
|

* 1 Assistant au
Département de Mathématique à l'ISP/Mbanza-Ngungu
| 


