Estimation des paramètres et des états de la machine asynchrone en vue du diagnostic des défauts rotoriques

UNIVERSITE MOHAMED KHIDER DE BISKRA
FACULTE DES SCIENCES ET DES SCIENCES DE L'INGENIEUR
DEPARTEMENT D'ELECTROTECHNIQUE

N° ordre :

Série :

Mémoire

Présenté pour obtenir le diplôme de Magister nouveau régime en
Electrotechnique

OPTION : Electricité industrielle
THEME
Estimation des paramètres et des états de la machine asynchrone en vue du
diagnostic des défauts rotoriques

par :
Samir MERADI
Soutenu le : 27/06/2007

Devant le jury :
Salah Eddine ZOUZOU	Prof.	Président	Université de Biskra
Abdelhamid BENAKCHA	M.C.	Rapporteur	Université de Biskra
Mohammed Saïd NAIT SAID	Prof.	Examinateur	Université de Batna
Ammar GOLEA	M.C.	Examinateur	Université de Biskra

Remerciements

Ce travail a été effectué au sein du département d'Electrotechnique de l'Université de Biskra sous la direction de Monsieur Abdelhamid BENAKCHA , Maître de conférences à l'Université de Biskra ainsi que Monsieur Arezki MENACER Chargé de cours à l'université de Biskra. Qu'ils trouvent ici l'expression de toute ma gratitude pour les conseils avisés et l'encouragement constant qu'ils n'ont cessé de me prodiguer tout au long de cette étude.

Mes remerciements les plus sincères sont adressés à Monsieur Salah Eddine ZOUZOU , Professeur à l'Université de Biskra , pour l'honneur qu'il m'a fait en acceptant la présidence du jury de ce mémoire.

Mes vifs remerciements vont aussi à Monsieur Mohammed Said NAIT SAID, Professeur à l'Université de Batna, je suis très honoré de sa présence dans le jury de ce mémoire.

J'exprime ma grande gratitude à Monsieur Ammar GOLEA , Maître de conférence à l'Université de Biskra, pour l'intérêt qu'il a porté à ce travail et pour avoir accepté de participer à ce jury .

Je remercie également Monsieur Said BARKATI chargé de cours à l'Université de M'Sila et Monsieur Dr.Khelifa BENMANSOUR, pour leurs collaborations et conseils.

Je ne saurais terminer sans remercier chaleureusement mes amis : A. Benaissa, M. Rezig, F. Benamor, N. Bouali,

Durant ces deux années , les membres administratifs et techniques du département et du laboratoire ont toujours su répondre présent à mes nombreuses sollicitations. J'ai particulièrement apprécié leur disponibilité, leur sympathie, et leurs compétences. Qu'ils reçoivent toute ma gratitude.

Tous ceux qui ont contribué de près ou de loin à l'élaboration de ce travail, trouvent ici l'expression de ma très vive reconnaissance.

A ma mère, à la mémoire de mon père ,

A mon épouse , A mes filles Meriem et Khadija ,

A mes frères : Messoud, Salah et Kamel et soeurs : Saliha et Hayette, A^ó tous mes amis, Rachid, Elkier, Kamel, Messoud , Farouk,

Notations et Symboles

Symbole Unité Définition

T Induction magnétique créée dans

Bsm l'entrefer par le courant statorique

Cem N · m couple électromagnétique

u 0 H. m^-1 Perméabilité magnétique du vide

courants rotoriques de la machine dans I sm le repère fixe

N s Nombre de spires statoriques par phase

N r Nombre de barres rotoriques

e m Entrefer

Ids , Iqs A Composantes biphasées du courant

statorique direct et en quadrature

m Phase

Ö psm Flux principal

Lsp H Inductance propre statorique

Lsc H inductances cycliques statorique

H mutuelle inductance cyclique entre

Msr stator et rotor

nombre de paires de pôles de la P machine

p opérateur de Laplace

? Résistance totale de l'anneau de court-

Re circuit

R_s ? résistances d'une phase statorique

t s temps

Rbk ? Résistance de la barre k

s constante de temps en boucle fermée de

Ti la régulation du courant stator

T_r s constante de temps rotorique

H Inductance totale de l'anneau de court-

Le circuit

H Mutuelle inductance entre barres

Mrr rotoriques

Vsabc V Les tensions statoriques

Vs _d , Vs q V tensions statoriques de la machine dans

le repère tournant dq

L r c H Inductance cyclique rotorique

Ö rk Wb Flux magnétique crée par une maille

rotorique

Ösabc Wb Les flux statoriques

Örd , Örq Wb flux rotoriques de la machine dans le

repère tournant dq

Wb Flux magnétique par pôle crée par le

Ös courant statorique

Ébk A Courant dans la barre

Érk A Courant dans la boucle

Ö _ds , Ö qs Wb flux statoriques de la machine dans le

repère tournant dq

ó coefficient de dispersion

? rad · s^-1 vitesse angulaire de rotation

rad · _s-1 vitesse de rotation électrique de la

ù machine

( ù )ref rad · s^-1 vitesse de référence

ù _s , ù r rad · s^-1 pulsations des courants stator et rotor

C_r N · m Couple résistant

f N · m · s · rad^-1 coefficient de frottement visqueux

J kg · m^-2 inertie des parties tournantes

Kd, Td Coefficients du régulateur du

courant sur l'axe d

KP , KT coefficients d'un correcteur de type

PT

Kq, Tq Coefficients du régulateur du

courant sur l'axe q

Te s Période d'échantillonnage

t_r s temps de retard

Angle électrique entre deux mailles

á rotoriques

è position du rotor

ô s constante de temps

ô ₁ , ô 2 s

constantes de temps des régulateurs de courant, de vitesse

ô e s constante de temps électrique

? flux créé par l'excitation

ù rad · s^-1 pulsation du réseau d'alimentation

Introduction générale

Les machines électriques tournantes occupent une place prépondérante dans tous les secteurs industriels. Les machines asynchrones triphasées à cage d'écureuil sont les plus fréquemment utilisées grâce a leur robustesse, leur simplicité de construction et leur bas coût. Néanmoins, celles-ci subissent au cours de leur durée de vie un certain nombre de sollicitations externes ou internes qui peuvent les rendre défaillantes. Les contraintes industrielles en fiabilité, maintenabilité, disponibilité et sécurité des équipements sont par ailleurs très fortes. C'est pourquoi le monde industriel est fortement intéressé par un ensemble de techniques permettant de déterminer l'état de santé de ces machines.[1]

Plus généralement, la surveillance et le diagnostic en génie électrique remettent en cause les concepts et les outils traditionnels utilisés en conception et commande des machines électriques tournantes. La modélisation des machines asynchrones triphasées a cage d'écureuil en vue de la surveillance et du diagnostic s'insère dans ce contexte. Le présent travail s'intéresse a la synthèse d'un modèle de connaissance riche et flexible permettant d'appréhender le comportement des machines asynchrones triphasées a cage d'écureuil en absence et en présence de défaillances ainsi que l'estimation des paramètres et des états de la machine asynchrone en vu de détection des défauts rotoriques en utilisons le filtre de Kalman étendu.

.

Ce mémoire sera divisé en six chapitres :

Le premier chapitre permettra d'apporter quelques éléments de diagnostic des machines asynchrones triphasées a cage d'écureuil. Le diagnostic consiste a connaître, évaluer, prévoir, mesurer et maîtriser les défaillances des systèmes. Apres une description des motivations de cette nouvelle science de l'ingénieur, on présente les différents concepts terminologiques et méthodologiques associes. Suite a ces considérations générales, on est amène a préciser le système étudie ; on se concentre ici exclusivement sur les machines asynchrones triphasées a cage d'écureuil. Puis on a présenté l'état de l'art concernant les techniques et les différents travaux réalisés dans le domaine du diagnostic en ligne en vue d'aboutir à une signature fiable de défauts rotoriques.

Lorsque les méthodes de surveillance et de diagnostic sont basées sur la génération, la détection et l'exploitation de signatures analytiques de défaillances, elles nécessitent l'emploi de modèles de connaissance du système étudie. En conséquence, on oriente l'étude vers la modélisation des machines asynchrones triphasées a cage d'écureuil en vue de la surveillance et du diagnostic. Les objectifs du modèle devant être synthétise sont alors clairement spécifies.

Le deuxième chapitre constitue la pierre angulaire du présent travail. Dans lequel nous avons modélisé la machine asynchrone à cage d'écureuil en choisissant l'approche analytique globale basée sur la signature des grandeurs externes telles que (courant, couple,...etc.), pour cela, nous avons utilisé un schéma multi enroulement équivalent à la cage qui s'adapte bien au problème posé et où les équations sont écrites dans un référentiel lié au rotor, vu que les défauts envisagés se situent à son niveau.

Puis, nous avons fait la transformation du modèle de Nr grandeurs au modèle dq équivalent, pour faciliter sa simulation.

triphasées a cage d'écureuil. Le premier chapitre a permis d'identifier clairement ces défaillances, leurs causes et leurs effets. On remarque notamment que les modes de défaillances rencontrées impliquent majoritairement une altération topologique des machines asynchrones triphasées a cage d'écureuil sous les formes suivantes : court-circuit et rupture des conducteurs statoriques, rupture des conducteurs rotoriques, excentricité statique, dynamique, ou mixte du rotor par rapport au stator. Ici nous avons présenté les différents résultats de simulation de la machine avec défauts;à vide et en charge. Nous avons fait l'analyse spectrale pour le courant statorique, pour faire révéler les défauts des cassures des barres, par des harmoniques.

Le quatrième chapitre est consacré à la présentation de la commande par flux orienté de la machine asynchrone alimentée en courant en absence et en présence des défauts au rotor.

Le cinquième chapitre consiste à estimés et à observer les courants et les résistances rotoriques afin de détecter les défauts rotoriques, en appliquant l'observateur à base de modèles paramétriques ; le filtre de Kalman étendu.

Dans l'approche à base de modèles paramétriques, on ne génère pas réellement un vecteur de résidus, mais on estime un vecteur de paramètres dont la variation à l'extérieur d'une plage de référence représente l'apparition d'un défaut dans le système surveillé (ou plus exactement représente un changement dans les caractéristiques du procédé). Cette variation peut alors être détectée à l'aide d'un test de décision dans l'espace paramétrique. [31]

Le dernier chapitre de ce mémoire comporte les concepts de la logique floue et nous fournirons tous les aspects méthodologiques nécessaires à la compréhension des systèmes flous.

Nous verrons comment intégrer cet outil à la commande des systèmes dynamiques pour en faire un contrôleur dans le quatrième chapitre. Les étapes de synthèse puis l'application de la commande floue à la machine asynchrone sont présentées et nous analyserons aussi les performances de ce type de contrôle. Ce chapitre explique aussi comment un contrôle flou peut être réalisé. On y décrit les blocs fondamentaux ( fuzzification, moteur d'inférence, défuzzification) et la méthodologie de leur conception.

On dit souvent que la commande floue est plus robuste. Pour cela on va appliquer le régulateur flou dans la commande vectorielle sur le modèle réduit de la machine asynchrone, pour voir l'influence des défauts rotoriques sur cette commande.

Une conclusion générale vient clôturer les six chapitres de ce mémoire. Une proposition pour les travaux futurs est également donnée.

Chapitre I

Diagnostic des défauts dans la machine

asynchrone

I.1 Introduction

Les machines électriques tournantes occupent une place prépondérante dans tous les secteurs industriels. Les machines asynchrones triphasées à cage d'écureuil sont les plus fréquemment utilisées grâce à leur robustesse, leur simplicité de construction et leur bas coût. Néanmoins, celles-ci subissent au cours de leur durée de vie un certain nombre de sollicitations externes ou internes qui peuvent les rendre défaillantes. Les contraintes industrielles en fiabilité, maintenabilité, disponibilité et sécurité des équipements sont par ailleurs très fortes. C'est pourquoi le monde industriel est fortement intéressé par un ensemble de techniques permettant de déterminer l'état de santé de ces machines.

Plus généralement, la surveillance et le diagnostic en génie électrique remettent en cause les concepts et les outils traditionnels utilisés en conception et commande des machines électriques tournantes. La modélisation des machines asynchrones triphasées à cage d'écureuil en vue de la surveillance et du diagnostic s'insère dans ce contexte.

I.2 Définitions

a. Terminologie propre au diagnostic de défaut [10]

La terminologie suivante sera adoptée :

a) Système physique (Physical System)

Un système physique est un ensemble d'éléments (composants, constituants) interconnectés ou en interaction organisés pour réaliser une fonction.

b) Composant (Component)

Un composant est une partie du système, choisi selon des critères liés à la modélisation. En

tout premier lieu, le comportement de référence de ce composant est bien adapté dans le sens où il peut être défaillant ou servir de support à la propagation de pannes dans le système. Un composant doit être simple à modéliser dans le sens où cela doit être naturel : il peut s'agir d'un composant (physique ou logique) complet du système ou d'une partie parfaitement délimitée de ce composant, d'un groupe de composants.

c) Modèle (Model)

Un modèle d'un système physique est une description de sa structure et une représentation comportementale ou fonctionnelle de chacun de ses composants . Une représentation comportementale est constituée de relations entre diverses variables du système, appelées classiquement relations de causes à effets. Une représentation fonctionnelle est plus abstraite puisqu'elle ne s'adresse qu'aux objectifs présumés que le système physique doit remplir.

d) Défaut (Fault )

- Tout écart entre la caractéristique observée sur le dispositif et la caractéristique de référence, lorsque celui-ci est en dehors des spécifications [AFNOR, 1994].

- C'est n'importe quel état indésirable d'un composant ou d'un système. Un défaut n'implique pas nécessairement une défaillance [IEEE, 1988].

- Déviation non permise d'au moins une propriété ou un paramètre caractéristique du système des conditions acceptables ou (et) standards.

- Un défaut est une anomalie de comportement au sein d'un système physique localisée au niveau d'un composant.

La définition de l'AFNOR rattache la notion de défaut à celle de déviance d'une

caractéristique d'un phénomène, subordonnant ainsi cette notion à l'existence d'une référence absolue.

e) Défaillance (Failure)

Une défaillance définit une anomalie fonctionnelle au sein d'un système physique , c'est-à-dire caractérise son incapacité à accomplir certaines fonctions qui lui sont assignées.

Les défauts incluent les défaillances mais la réciproque n'est pas vraie. Un système peut

remplir sa fonction tout en présentant une anomalie de comportement. Par exemple, une machine électrotechnique peut produire un bruit anormal tout en entraînant correctement une charge, en supposant que telle est sa fonction. Le bruit anormal est un défaut qui peut permettre de présager d'une défaillance à venir. La recherche de défauts est donc fondamentale en diagnostic.

f) Panne (Break-down)

La panne est l'inaptitude d'un dispositif à accomplir la fonction vitale. Il est clair que dès l'apparition d'une défaillance, caractérisée par la cessation du dispositif à accomplir sa fonction, on déclarera le dispositif en panne. Par conséquent, une panne résulte toujours d'une défaillance.

g) Signatures

La signature théorique d'un défaut peut être envisagée comme la trace attendue du défaut sur les différents RRA qui modélisent le système. Autrement dit la signature théorique d'un défaut peut être envisagée comme les résultats de détection lorsque tous les tests sensibles au défaut réagissent.

h) Symptôme (Symptom)

Caractère distinctif d'un état fonctionnel anormal.

i) Résidu (Residual)

Souvent, lorsque le modèle comportemental de référence est analytique, les signaux porteurs

de signes ou de symptômes sont appelés résidus parce qu'ils résultent d'une comparaison entre un comportement réel et un comportement de référence.

j) Diagnostic (Diagnosis)

Un diagnostic est un état expliqué d'un système physique compatible avec les informations disponibles sur le comportement réel du système et avec le modèle de comportement de référence disponible. Habituellement, le diagnostic est exprimé par les états des composants ou les états des relations de description du comportement .

k) Perturbation

Entrée du système physique qui n'est pas une commande. Autrement dit, c'est une entrée non contrôlée.

b) la maintenance

La maintenance est définie comme étant « toutes les activités destinées à maintenir ou à rétablir un bien dans un état ou dans des conditions données de sûreté de fonctionnement, pour accomplir une fonction requise. Ces activités sont une combinaison d'activités techniques, administratives et de management. ».

Maintenir, c'est donc effectuer des opérations (dépannage, graissage, visite, réparation, amélioration...etc.) qui permettent de conserver le potentiel du matériel, pour assurer la continuité et la qualité de la production. Bien maintenir, c'est assurer ces opérations pour que le coût global soit optimum. La figure représente le diagramme des différents concepts de maintenance et les évènements associés.

Maintenance

Non Oui

Défaillance

Maintenance
préventive

Maintenance Corrective

Maintenance		Maintenance	Maintenance		Maintenance	Maintenance
systématique		conditionnel- le	Prévisionnel- le(prédictive)		palliative	curative

<< Ensemble des activités réalisées après la défaillance du bien, ou la dégradation de sa fonction pour lui permettre d'accomplir une fonction requise, au moins provisoirement : ces activités comportent notamment la localisation de la défaillance et son diagnostic, la remise en état avec ou sans modification, le contrôle du bon fonctionnement. >>

· Maintenance préventive

<< Maintenance ayant pour objet de réduire la probabilité de défaillance ou de dégradation d'un bien ou d'un service rendu. Les activités correspondantes sont déclenchées selon un échéancier établi à partir d'un nombre prédéterminé d'usage (maintenance systématique), et/ou des critères prédéterminés significatifs de l'état de dégradation du bien ou du service (maintenance conditionnelle). >>

1. Maintenance préventive systématique

<< Ce type de maintenance comprend l'ensemble des actions destinées à restaurer, en totalité ou partiellement, la marge de résistance des matériels non défaillants. Ces tâches sont décidées en fonction du temps ou de la production, sans considération de l'état des matériels à cet instant. >>

2. Maintenance préventive conditionnelle

<< Ce type de maintenance comprend toutes les tâches de restauration de matériels ou de composants non défaillants, entreprises en application d'une évaluation d'état et de la comparaison avec un critère d'acceptation préétabli (défaillance potentielle). >>

3. Maintenance prévisionnelle (prédictive)

« C'est maintenance préventive subordonnée à l'analyse de l'évolution surveillée de paramètres significatifs de la dégradation du bien. Elle permet de planifier les interventions.>>

Mon travail consiste à effectuer une maintenance prédictive ` à la demande ' plutôt que d'effectuer une maintenance systématique (méthode traditionnelle). Cela évite de faire des changements de pièces qui dans 90 % des cas se font de manière prématurée. Cela permet aussi de prévoir une intervention lors d'un arrêt de production programmé ou, si le cas le nécessite, lors d'un arrêt d'urgence toujours moins pénalisant qu'un arrêt forcé. De plus, les réparations avant incident sont plus faciles à exécuter et moins coûteuses (en temps d'intervention et en

matériel). Il est aussi important de savoir qu'un défaut non traité peut entraîner des dégradations encore plus importantes.

Le concept hautement stratégique de maintenance prédictive qui a poussé des chercheurs

à y contribuer diversement, nécessite la connaissance des grandeurs significatives à mesurer pour avoir une image aussi proche que possible de l'état de la machine. Le système de suivi de la machine devrait pouvoir :

· interférer le moins possible avec le système (les grandeurs peuvent-elles être mesurées " en ligne ? ", problème de sécurité,....)

· être capable de suivre plusieurs grandeurs,

· être évolutif,

· être pilotable à distance,

· pouvoir stocker les données pour permettre une analyse tendancielle.

Quant à la stratégie adoptée, elle consiste à :

· recenser les défauts et les pannes pouvant se produire,

· trouver les grandeurs mesurables liées à ces défauts,

· choisir la méthode la plus proche des critères définis ci-dessus,

· définir les seuils "d'alarme " à partir desquels il faudra intervenir.

I.3 Techniques de contrôle en ligne (non destructif)

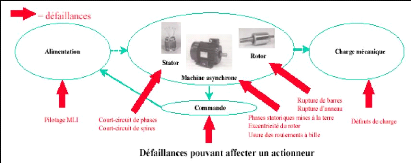
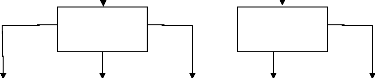
Figure I.2 : Différentes défaillances pouvant affecter une machine asynchrone [11]

Les entraînements électriques utilisent de plus en plus les moteurs asynchrones à cause de leur robustesse, leur puissance massique et leur faible coût de construction, mais il arrive que ces machines présentent des pannes (défauts) électriques ou mécaniques.

Des études statistiques nous révèlent que certaines pannes sont plus fréquentes que d'autres, ce qui nous amène à axer notre étude vers un type de défaut le plus courant.

Parmi les pannes majeures, nous trouvons les suivantes :

1. Les cassures de barres et de portions d'anneaux des cages

La détection de ces défaillances est rendue difficile par le fait que lors de leurs apparitions, la machine continue de fonctionner. Ces défauts ont par ailleurs un effet cumulatif. Le courant que conduisait une barre cassée, par exemple, se répartit sur les barres adjacentes. Ces barres sont alors surchargées, ce qui conduit à leurs ruptures, et ainsi de suite jusqu'à la rupture d'un nombre suffisamment important de barres pour provoquer l'arrêt de la machine. Elles provoquent aussi une dissymétrie de répartition de courant au rotor et des à-coups de couples, ceci va générer des vibrations et l'apparition de défauts mécaniques.

Figure I.3 : Barre cassé au niveau du rotor [12]

2. Les courts-circuits internes : un court-circuit entre phases provoquerait un arrêt net de la machine. Cependant, un court-circuit au bobinage prés du neutre ou entre spires n'a pas un effet aussi radical. Il conduit à un déséquilibre de phases, ce qui a une répercussion directe sur le couple. Ce type de défauts perturbe aussi sensiblement les commandes développées sur la base du modèle de Park (hypothèse d'un modèle équilibré).

3. Les décharges partielles : Ce phénomène naturel du aux décharges dans les isolants entre conducteurs ou entre conducteurs et la masse s'amplifie avec le vieillissement des isolants. Il est pratiquement imperceptible dans les isolants neufs par les moyens de mesures classiques

car son effet n'est pas discernable par rapport aux bruits de mesure. Sa présence précède l'apparition des courts-circuits entre phases ou entre phase et masse lorsque ces décharges partielles ont suffisamment détérioré les isolants.

4. Dissymétrie du rotor : Celui-ci provoque la variation de l'entrefer dans le moteur, une répartition non homogène des courants dans le rotor et le déséquilibre des courants statoriques. Le déséquilibre des efforts sur les barres génère un couple global non constant.

Les défauts qui se produisent au niveau du rotor et leurs effets sur les signaux électriques (courant, couple, flux ) et mécaniques ( vibration ) mais aussi chimiques (dégagement d'ozone, composition de l'huile des paliers ) de la machine asynchrone sont importants et intéressent actuellement de plus en plus les chercheurs vu les gros progrès réalisés au niveau du stator et vu les études statistiques qui indiquent des pourcentages élevés des défauts qui se produits au niveau du rotor, par exemple, on prend une étude statistique, effectuée en 1988 par une compagnie d'assurance allemande de systèmes industriels sur les pannes des machines asynchrones de moyenne puissance (de 50 kW à 200 kW ) a montré que : 22 % des défauts se sont des défauts rotoriques.

Les méthodes traditionnelles de détection de défauts reposent sur des prélèvements statiques ou des essais destructifs effectués sur des échantillons à tester : diagnostic de l'isolation, mesures vibratoires, tests chimiques, ......

Toutes ces techniques exigent un arrêt total des machines nécessitant une main d'oeuvre qualifiée et induisant une perte de production donc un préjudice économique, ce qui justifie l'intérêt des recherches menées aujourd'hui en vu d'aboutir à une surveillance non destructive (en ligne) qui permet de détecter à temps le 1^er défauts, donc éviter les dysfonctionnements ainsi que les opérations de maintenance lourdes et coûteuses associées.

Ces méthodes de C.N.D (contrôle non destructif) se sont concrétisées grâce surtout aux outils de modélisation, des techniques de traitement de signale, ...

Les principales techniques de C.N.D sont:

- Contrôle d'étanchéité (détection : fuites, trous, porosité,..)

- Ressuage (détection : discontinuité matière ouverte, contrôle de l'état de surface, ...)

- magnètoscopie (détection : défauts superficiels sur matériaux ferromagnétiques, arbre, anneaux, ...)

- Radiographie (détection : inhomogénéité en épaisseur, fissures, corrosion, ...) - Ultra son (contrôle : défauts internes, fissures, cordons de soudure, ...)

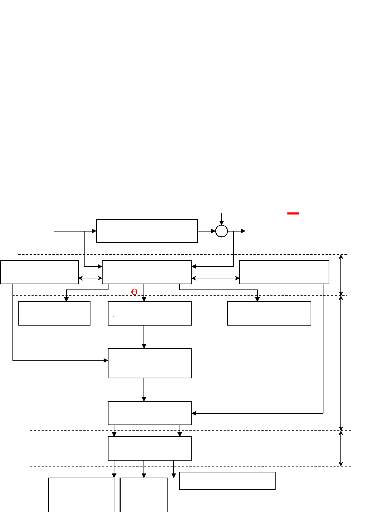
Diagnostic de la défaillance

Diagnostic

Localisation de la défaillance

Importance de la

défaillance

Causes des défaillances

Modèle du processus Non défaillant

- Courants de Foucault (détection : anomalies dans la conductivité électrique ou dans la perméabilité magnétique, variation de composition d'un alliage, )

- Thermiques (détection :anomalies de transmission de chaleur au sein de la matière, ...)

- Emission acoustique (détection : écoulement de fluide, rupture par fatigue, déformation plastique, ...)

- Holographie (détection : manque de liaisons, vibration de faible amplitude, ...)

- Analyse de signature (détection : anomalies au niveau des masses, vibrations, ...) I.4 Les approches usuelles de détection :

On va présente deux méthodes utilisées en diagnostic de systèmes physiques

Méthodes sans modèle analytique - Méthodes basées sur les modèles analytiques Actuellement, on s'oriente vers des systèmes de diagnostic mettant en oeuvre différentes techniques de détection. En effet, chacune d'entre elles est plus ou moins bien adaptée pour appréhender tel ou tel type de défaut. Par exemple, on s'orientera vers les méthodes à base

d'estimation paramétrique lorsqu'on souhaite localiser un défaut qui se manifeste par une

variation des paramètres du modèle identifié.

Estimation d'état

u

X

Type de défaillance

Quantité de comparaison

Modèle du processus observé

Processus réel

Estimation des paramètres

Génération De résidus

Décision

Signature de la défaillance

Quantités caractéristiques

n

Modèle du processus défaillent

Grandeurs non v mesurables

Détection de la défaillance

Modélisation

Figure I.4 : Approche générale retenue [11]

I.4.1 Méthodes sans modèle analytique

I.4.1.1 Analyse fréquentielle (Filtrage)

Une première approche du traitement du signal repose sur l'analyse fréquentielle (transformée

de Fourier). Elle est bien évidemment très utilisée pour la détection de phénomènes périodiques comme en analyse vibratoire. L'analyse du spectre des signaux issus des capteurs permet de déterminer très efficacement

l'état de l'installation sous surveillance. Les signaux sont ici tout d'abord analysés en état normal de fonctionnement. Ensuite, toute déviation des caractéristiques fréquentielles d'un signal est reliée à une situation de panne (le problème, c'est qu'un changement de consigne modifie les caractéristiques fréquentielles et cela n'a rien d'un défaut).

I.4.1.2 Redondance matérielle

Cette méthode consiste à multiplier physiquement les capteurs critiques d'une installation.

Un traitement des signaux issus des éléments redondants effectue des comparaisons et distingue l'élément défectueux en cas d'incohérence. Cette méthode est pénalisante en termes de poids, puissance consommée, volume et coût (d'achat et de maintenance). Elle est donc essentiellement réservée aux cas où la continuité de service est obligatoire (e.g. l'aérospatiale, le nucléaire). En effet, elle apporte l'avantage, une fois la défaillance détectée et localisée, de pouvoir utiliser la

partie de l'équipement encore saine mais cette technique ne s'applique généralement que sur des capteurs.

I.4.1.3 Capteurs spécifiques (capteurs-détecteurs)

Des capteurs spécifiques peuvent également être utilisés pour générer directement des signaux de détection ou connaître l'état d'un composant. Par exemple, les capteurs de fin de course,

d'état de fonctionnement d'un moteur ou de dépassement de seuils sont largement employés

dans les installations industrielles.

I.4.1.4 Réseaux de neurones artificiels

Quand la connaissance sur le procédé à surveiller n'est pas suffisante et que le développement d'un modèle de connaissance du procédé est impossible, l'utilisation de modèle dit << boîte noire>> peut être envisagée. Pour cela des réseaux de neurones artificiels (RNA) ont été utilisés. Un RNA est en fait un système informatique constitué d'un nombre de processeurs

élémentaires (ou noeuds) interconnectés entre eux qui traite -de façon dynamique- l'information qui lui arrive à partir des signaux extérieurs.

I.4.2 Méthodes basées sur les modèles analytiques

La plupart des méthodes de détection et de diagnostic en ligne s'appuient sur des les mesures.

Il existe des méthodes qui utilisent plus de connaissances que celles apportées par les seuls capteurs physiques. Ces connaissances peuvent en particulier provenir de la connaissance du comportement entrée /sortie d'un procédé ou des processus qui en gouverneraient l'évolution. Cette connaissance est généralement exprimée sous forme de modèles mathématiques.

Parmi les différentes méthodes de détection utilisant des modèles mathématiques, nous trouverons principalement l'espace de parité, les Observateurs et l'estimation paramétrique. I.4.2.1 Espace de parité

Son nom provient du domaine de l'informatique où le contrôle de parité se faisait dans les circuits logiques. Le principe de la méthode est la vérification de la consistance existante entre les entrées et les sorties du système surveillé

I.4.2.2 Observateurs

Par la suite, nous ferons référence à la stratégie appelée par certains auteurs << par

observateurs >> ou encore << en boucle fermée >> par opposition aux méthodes en boucle ouverte, qui correspondent à celles de l'espace de parité décrite précédemment.

I.4.2.3 Estimation paramétrique

L'approche d'estimation paramétrique mesure l'influence des défauts sur les paramètres et non plus, comme précédemment, sur les variables du système physique.

Le principe consiste à estimer en continu des paramètres du procédé en utilisant les mesures d'entrée/sortie et en l'évaluation de la distance qui les sépare des valeurs de référence de l'état normal du procédé .

L'estimation paramétrique possède l'avantage d'apporter de l'information sur la taille des déviations. Toutefois, un des inconvénients majeurs de la méthode réside dans la nécessité d'avoir un système physique excité en permanence. Ceci pose des problèmes pratiques dans le cas de procédés dangereux ou fonctionnant en mode stationnaire. De plus, les relations entre les paramètres mathématiques et physiques ne sont pas toujours inversibles de façon unitaire, ce qui complique la tâche du diagnostic basé sur les résidus.

Défauts Inconnues

Entrée

Mesures

Procédé

Estimation
des
paramètres

Paramètres physiques

Décision

Résidu

Figure I.5 : Estimation paramétrique pour la détection et le diagnostic de défauts I.5 Description des différentes méthodes d'analyse:

Le diagnostic en ligne de défauts rotoriques dans les machines asynchrones en vu d'aboutir à une maintenance prédictive a poussé les chercheurs à mettre au point diverses techniques. La majorité de ces travaux se sont basés sur la signature de grandeurs externes telles que (courant, couple) utilisant la théorie de champs tournants et celle des circuits électriques.

Durant la décade passée, les équipes de Williamson et Smith ont basé leur étude faite en régime permanent sur la détection des signaux modulés à une fréquence double du glissement (2*g*fs) apparaissant lors de dissymétries rotoriques suite à des défauts de cage.

Ils ont utilisé le schéma multi- enroulement équivalent, où chaque maille électrique est assimilée à un enroulement monophasé générant deux champs tournant en sens inverse à la fréquence( g*fs ) par rapport au rotor, donc à la fréquence de Delerio :

fk = f_s [(k/p). (1-g)+g]

Oü

k : rang harmonique

p : nbre de paire de pôles g : le glissement

f_s : fréquence fondamentale

Par rapport au stator. Ils ont constaté une diminution des courants statoriques ainsi que du couple et une surcharge en courant dans les barres voisines au défaut.

Ils ont conclu aussi qu'il est difficile de détecter la première barre cassée à cause de la faible amplitude de la raie de défaut.

T.Boumegoura << recherche de signature électromagnétique des défauts dans une machine asynchrone et synthèse d'observateurs en vue du diagnostic » a fait une étude sur les effets des défauts de la machine asynchrone et a proposé une approche qui repose sur la surveillance de paramètres de modèles comportementaux de la machine, sensible au défauts : Les résistances rotoriques d'un modèle triphasé, l'inductance magnétisante et la résistance rotorique d'un modèle diphasé.

Des outils de détection des défauts rotoriques, basés sur des observateurs de Kalman et grand gain étendu adaptés aux systèmes non- linéaires ont été synthétisés pour tracer les paramètres précédents.

S. Amrane elle a envisagé une surveillance en ligne des machines (concept de maintenance prédictive) et elle a particulièrement intéressé à la détection de défauts de cages de moteurs d'induction, en utilisant une approche analytique basée sur la signature des de grandeurs externes. Et pour améliorer le diagnostic elle a proposé un mode de surveillance actif par action sur les grandeurs d'entée et de sortie du système.

Gaétan. Didier, Hubert. Razik ont développé une technique maintenant répandue qui est l'<< analyse de la signature du courant du moteur » en vue de la détection d'une panne électrique ou mécanique et ils ont posé l'accent sur la détection d'un défaut au rotor, rupture partielle ou non d'une barre de la cage d'écureuil ou d'une portion d'anneau, par l'analyse spectrale du courant absorbé au réseau électrique.

Jufer et abdellaziz ont proposé un schéma multi- enroulement équivalent à la cage rotorique tenant compte de l'influence du stator par le biais de sources de potentiel équivalentes à l'effet du bobinage en utilisant la théorie des deux axes.

Ils ont mis en évidence le même phénomène de modulation en amplitude du courant statorique à (2.g.fs), mais le champ d'application de leur méthode se trouve limité par le fait qu'il ne considère que des défauts concentrés suite à un phénomène d'avalanche ne touchant que les

barres adjacentes au défaut : surcharge du courant direct (id) en cas de barres cassées et surcharge du courant transversal (iq) en cas de rupture d'anneaux.

E.ritchie, X.deng and T.jokinen ont fait une étude en régime dynamique utilisant le schéma multi- enroulement avec référentiel lie au rotor.

Les résultats de simulation de la cage saine concordent très bien avec ceux de l'expérience de modèle étant limite en cas de rupture de barres, ils ont proposé d'affecter à la résistance de la barre casée une valeur finie au lieu d'une valeur infinie pour prendre en compte les courants inter- barres.

Roland casimir « diagnostic des défauts des machines asynchrones par reconnaissance des formes » a fait une approche qui est basée sur l'utilisation des méthodes de reconnaissance des formes. Un vecteur de paramètres, appelé vecteur forme, est extrait de chacune des mesures effectuées sur la machine. Les règles de décisions utilisées permettent de classer les observations, décrites par le vecteur forme, par rapport aux différents modes de fonctionnement connus avec ou sans défauts.

Des défauts ont été créés au rotor et au stator de la machine asynchrone, alimentée soit à partir du réseau, soit par le biais d'un onduleur de tension.

Les procédures de décisions, basées sur la règle des k- plus proches voisins et sur le calcul direct des frontières, ont été utilisées pour détecter les défauts. Ces algorithmes ont montré l'efficacité de l'application de la reconnaissance des formes au diagnostic.

Vas, filippetti ont proposé des modèles de (N+3) mailles et deux axes ( d et q ) à partir d`un schéma multi-circuits pour la simulation de la cage saine et celle en défaut des machines asynchrones en régime transitoire moyennant la résistance Rr et l'inductance Lr équivalentes.

Leur choix de signature du défaut de cage s'est porté sur la composante directe (ids) du courant statorique qui n'était faible que pour un nombre élevé de barres cassées.

Dorell, Paterson, ont opté pour l'analyse spectrale du courant de phase statorique, ils ont constaté que :

La fréquence (1-2.g.fs) domine lorsque la tension est réduite ou si l'inertie est grande la fréquence (1+2.g.fs) domine lorsque la tension est élevée o si l'inertie est faible.

I.6 Conclusion :

D'après l'état de l'art des méthodes utilisées pour l'identification et le diagnostic des défauts de la machine asynchrone à cage d'écureuil, dans sa partie rotorique, on a constaté que : Les défauts dans la partie rotorique de la machine asynchrone occupent une partie importante dans le domaine du diagnostic.

Chapitre II

Modélisation du schéma ^multienroulements de la machine

asynchrone

II.1 Introduction

Les machines asynchrones à rotor en court-circuit consomment plus de 40% de l'énergie
électrique produite ; elles sont largement utilisées vu les avantages qu'elles présentent à savoir :

- leur simplicité et leur robustesse mécanique,

- leur fonctionnement sans génération d'étincelles d'où un entretien réduit,

- la normalisation des réseaux de distribution de l'énergie électrique se prête bien à l'utilisation directe de ces moteurs (tensions et fréquences constantes),

- un prix de revient relativement faible.

Par ailleurs, la machine asynchrone, malgré ses qualités, peut présenter des défauts structurels. Dans ce chapitre, nous portons notre attention sur la rupture totale ou partielle de barres rotoriques, tout particulièrement au niveau de la brasure barre- anneau. Pour ce faire, il convient de développer un modèle qui tienne compte de la structure du rotor.

En effet, Pour étudier ces machines à induction on fait appel soit à la théorie du champs électromagnétique (équations de Maxwell), soit à la théorie des circuits électriques (lois de Kirchhoff) ; ou bien la méthode mixte combinant la théorie du champ électromagnétique et la théorie des circuits électriques [7].

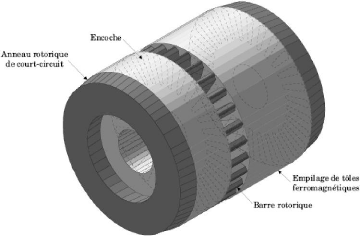
Figure (II.I) : constitution et disposition d'une cage rotorique [1]

Il est fonction du type d'approche utilisée. On en distingue deux , assez complémentaires :

- une approche dite << locale > car basée sur la signature de grandeurs locales telles que la densité de flux ; il s'agit souvent de méthodes numériques par éléments finis permettant une analyse fine des phénomènes physiques locaux associés aux défauts de cages,

- une approche analytique basée, quant à elle, sur la signature de grandeurs externes globales telles que courants, couple électromagnétique ; elle utilise le modèle de Kirchhoff, (réseau électrique équivalent à la machine) ainsi que la transformation << des 2 axes > appliquée aux équations électriques du système multi enroulements étudié. En fin, cette approche s'adapte particulièrement bien au problème posé ici et vu sa simplicité nous l'avons adoptée comme démarche.

II.3 Schéma multi enroulements équivalent

Pour l'étude analytique des performances des moteurs d'induction avec dissymétries rotoriques, nous avons adopté le schéma multi enroulements équivalent qui s'adapte bien au problème posé, car il décrit le rotor comme un ensemble de mailles interconnectées entre elles, chacune formée par deux barres adjacentes et les portions d'anneaux qui les relient (figure II.1).

A partir d'hypothèses classiques qui supposent que la perméabilité du fer est infinie, que l'entrefer est lisse et constant et que la f.m.m. statorique est à distribution sinusoïdale, on calcule les différentes inductances et mutuelles qui interviennent dans les équations du circuit.

II.3.1 Calcul des inductances [4] II.3.1.1 Stator

L'induction due à la bobine statorique de la phase m s'écrit :

? ??	(II.1)
B sm	2 N ? - 2 ð s ( ) 0 è = u I cos ?? p m sm è ð ep 3

Par conséquent, le flux principal et l'inductance cyclique sont donnés par :

Ö

²

= 4 p o^Ns RLI (II.2)_sm

psmð ep2

L = 3 L sl ₀ Ns

^sc 2 sp +1 = p ep2 RL+

6

Lsl (II.3)

II.3.1.2 Rotor

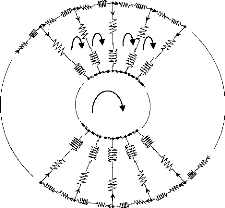
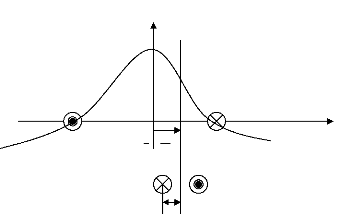
Le rotor à cage est représenté par la figure II.2. La figure II.3 représente la forme d'onde de l'induction produite par la maille rotorique k.

Ir(k-1)

Ir(k-2) Ir(k+1)

I_e

Irk

Figure II.2 :

Schéma multi enroulements du rotor

2ð

0

a r

I _bk = I rk - Ir ( k + 1 ) (II.4)

r

r 1 u

2 rk = N e0 Irkar r

è

N_r -1 u0 Irkr

a_r

N e

r

2ð

Nr

Irk

B 1

_rk =

Irk Représente le courant de maille k et Ibk le courant de barre K , avec :

On voit bien, à travers la figure II.2 qu'il n'est pas possible de retenir l'hypothèse du premier harmonique qui concerne l'induction produite par une maille du rotor. Partant de cette répartition, on calcule alors l'inductance principale d'une maille rotorique ainsi que la mutuelle entre deux mailles :

L rp

M rr

N

(II.5)

(II.6)

r -1 u0 2
= ðLR

1

N_r ² e

= - u 0 2ff,LR

N ² e

II.3.1.3. Stator Rotor

L'induction produite par la bobine statorique de la phase m induit dans la maille rotorique K le flux :

è + p	k	2 ð N r	ð + N r
Ö				smrk		r r B dS = - sm rk ? ?	B sm	( ' ) ' è LRd è	(II.7)

N N

r r

k

Srk

è

+

p

2 ð

ð

smrk

-

2

u

è ð ð

2

+ k +

r

1

[ ?]

? - ? N N r

2 ð

0 p

N I LR sin '

? p m

è (II.8)

ð ep

s sm p ? 3 +

? è ð ð

2

k -

B_s

0

p

N_r N_r

Ir ₀ Phase a è

è k 2 ð

+

Nr

ð

I_rk Maille rotorique k

Ñ

Nr

Figure II.4 : Position de la maille rotorique K , par rapport à la bobine
de la phase statorique ( m = 0)

Il en résulte la mutuelle stator rotor entre la phase statorique m et la maille rotorique K :

(II.9)

2 ð ?

M smrk M sr è m

= - ? -

cos ?? + k á ??

3

Où M = ⁰ N_s LR sin á

_sr 4 u

2

ep ²

(II.10)

Et á = p ^2ð est l'angle électrique entre deux mailles rotoriques. N_r

II.3.2. Mise en équation

Nous utilisons une transformation de Clarke pour passer des grandeurs triphasées statoriques ( a, b, c ) aux grandeurs diphasées ( á â ) . Nous pouvons effectuer la simulation avec deux repères distincts pour le stator et le rotor.

Pour alléger le temps de calcul, on élimine l'angle è de la matrice de couplage en choisissant le repère le plus adéquat et qui est celui du rotor. Dans ce repère, toutes les grandeurs ont une pulsation gùs en régime permanent. Cette caractéristique peut être utilisée pour l'analyse de rupture de barres rotoriques dans la machine par l'observation du courant i_ds .

II.3.2.1. Stator

On déduit pour l'ensemble des phases statoriques

[ V _sabc ] = [ R_s][ I sabc]+ dt[ Ö sad (II.11)

Après transformation et rotation, les équations électriques dans le repère rotorique s'écrits :

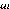
V ds = Rs i_ds -ù Ö qs +dÖ _ds

dt

(II.12)

dt

V = R iqs +ùÖds +dÖqs

(II.13)

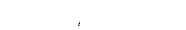
L

L

cos

sin

? ?

M sr

?? - ??

0

Lsc

ids

Ösdq

qs

0

Lsc

Avec :

Nous obtenons :

? ?

? I r 0

? ?

? M ?

j á L ? Ò (II.14)

I rj

? ?

j á L Òÿ? Ò

? ?

? M ?

? ?

?

Ir (Nr

- 1 ) ?

dI

di

dI

dI

(N - 1 )

r

ds

)

Msr

⁰ + cos 1á ^r1 + + cos já ^rj+ + cos( N_r-1)á

dI

Lsc

dt

d t dt

dt

dt

(II.15)

(cos 0á

V _ds =Rs ⁱds - ù[ Lsciqs - M_sr (sin 0á I_r0 + sin 1á I_r1 + + sin já I+ + sin( N_r - 1)á I_r (N_r- 1) ).]

V R = qs s

i qs

+ ù [ L i M

- (cos 0 á I + cos 1 á I + +

cos j I

á + +

cos( 1)

N - á I ( N - 1 ) ) ]

sc ds sr r 0 r 1 rj r r r

dI

r 0 r 1 rj

+ ¹ + + i j + + sin( 1)

N - á r

dt dt dt

sin

dI

d i

qs

+

-

dt

(sin 0 á

M sr

Lsc

)

(N - 1 )

r

dI r

dt

(II.16)

dI

On écrit les équations sous la forme :

[ ] [ I ] [ V ] [ R ][ I]

d

L = - (II.17)

dt

Donc :

di

dI

)

( -1)

N

_r

ⁱds

R s

Vds

dt

(II.18)

dI dI

Lsc

ds r 0 rj r

- M (cos 0 á + +

cos j á + +

cos( 1)

N - á sr r

dt

dt dt

0á I _r0 + + sin já I + + sin( N r - 1)á I r

-

+ù

ù

i qs

M sr

(sin

L sc

)

( -1)

N

r

Et :

d i

qs

M sr

Lsc

dt

dI

dI

0

(sin 0á r

+ sin já ^rj+ + sin( Nr-1)á dI ) V _s R

r (N -1)

= _s i_Qs

dt dt dt (II.1 9)

-

ù

L sc

i ds

ù M sr (cos 0á I r0 + + cos já

I + + cos( Nr -1)á Ir

(Nr-1) )

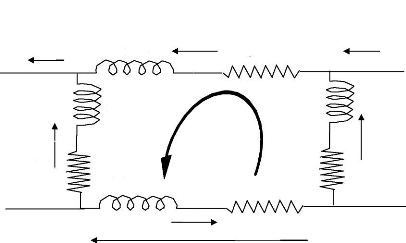
II.3.2.2 Rotor

une maille du rotor à cage est représentée par la figure II.5

Irk

Ir(k+1)

Re/Nr

2 1

Ir(k-1)

Lb(k-1)

Lbk

Ibk

Irk

Ib(k-1)

Rb(k-1)

Rbk

3 Iek 4

Le/Nr

Re/Nr

Le/Nr

Figure II.5 : Représentation d'une maille rotorique IeIrk représente le courant de maille K , _Ibk le courant de la barre K .

Pour le noeud n° 1 :

I_bk = I rk - I r( k +1) (II.20)

Pour le noeud n° 2 :

I b k = I r k - - I rk

( 1 )

- (II.21)

( 1 )

L'équation électrique relative à la maille K est :

R [ ] [ ] [ ] dt

R d Ö

e e rk

0 = -

I R I - +

I I I R I I

- + - + (II.22)

rk b k

( 1 ) ( 1 )

- r k - rk rk e bk rk r k

( 1 )

+

N N

ü r

Donc l'équation électrique relative à la maille K devient :

0 = R e I _rk -I R+R ^e [ I rk - I e Ibk Rbk+ dÖ

(II.23)

b(k - 1 ) b(k -1) NN

dt

r r

Le flux induit dans la maille rotorique est donné par :

rk = rprk+ M ?I j - 2 3 Msr (c_fr cos Ká + i _qs sin Ká)+ ^e (I _rk I _ek ) + L _b(

j

, b( k- 1)

+Ibk) (II.24)

Ö

Nr-1

j ? k

j

?

k

Le terme en Lrp représente le flux principal, celui en M représente le flux mutuel avec les autres mailles rotoriques, puis viennent les termes de couplage avec le stator. On remarquera le facteur 3 ₂ par rapport à l'équation statorique à cause de la transformation de Clark.

Les termes en L_b et L_e représentent les fuites rotoriques.

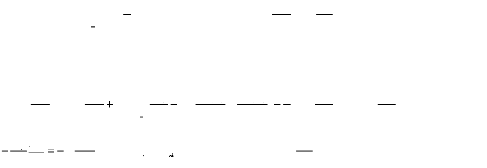
On essaye d'écrire l'équation (II.24) uniquement en fonction des courants de maille ;

I rk - Ie= I_ek (II.25)

Où : Ie représente le courant de l'annau de court circuit, On a :

dIr( k-1)

dIr( k+1)

dt

dt

(

L_b

R_e

-

R _bk I r

( k +1)

I_e

? ? ?

N_r

- L I

b [ r k + I r k ] b rk

+ 2 L I

( 1 )

- ( 1 )

+

cos Ká +_qs sin Ká

- R b( k- 1) I(k -

)

2

L _e

L _e

-

+

I_rk

N_r

N_r

2

L_e

on aboutit à :

+ 2L b)dIrk

dt

N_r

L +

2

+ R _bk +Rb

dI_e

R_e

?

I ?

?

L_e

dt

( k -1)

N_r

N_r

1

dI rj

-

?

M rr

dt

0

k

?

j

j

N r

)

3

(

dids

2

Msr

dt

(II.26)

cos ká + diqs

sin

dt

I_e

)

ká

(II.27)

Ö rk = Lrp rk +

1

-

Nr

M I

rr ? rj

j

j

0

k

?

3

-

2

Msr

(ids

Pour l'anneau de court circuit

Le système complet [L] [ ]

d I

= [ V ] - [ R][ I] devient :

N_r -1N r - 1

dI L dI R ?

e e rk e

- ? = - ? -

L ? R I ? I ? (II.28)

e e e rk

dt N dt

r k = 0 ? N r k = 0 ?

1 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

0 L L L -M _sr cosjá

0

L ssc

L L

sinjá L L

0

0

Lsc

Msr

L

L L

-

?

ids

2L

L e

iqs

M

M

2 L M L

-

b rr b

M L M M L

rr b

-

rr rr

L

+ + ^e N_r

-

rp

N_r

2Le

I r 0

M

M

M

2 L M

b rr

Mrr-Lb

Lrp

Lb

M L M rr rr

+ +

N_r

-

d

M

3 3

- M k

cos á - M k

sin á

sr sr

2 2

M

dt

I rj

M

M

M

M

Ir Nr (

2Le

Le

1

-

M

M

2Lb

Lb

Mrr

Mrr

Mrr-Lb

Lrp

M

+ +

N_r

L

-

-

rr

N_r

?

?

I e

Le

L e

0 0

L e

L

L

L L

-

-

N_r

N_r

?

M srùsinjá

Rs - ùLsc

0

1 ?

?

?

?

?

?

?

?

?

?

? ?

L

L

L

L

Vds
Vqs

1 ? ? ? ? ? ? ? ? ? ? ? ?

ids

ùLR

sc s

Ms

0

r ù á

cos j

L

L

L

L

iqs

Re

Re

0 0 2

+ Rb0 + Rb( Nr - 1)-Rb0

Nr

-

0 0

R b Nr
(

? ? ? ? ? ? ? ?

1)

-

0

-

Ir0

Nr

M

0 0

0

M

Re

-

M

0 0

0

2

+Rbk +Rb(k

0

Rb k

Rbk

0

( -1)

1)

-

Irj

-

Nr

M

0 0

0

M

R e

Rb(Nr -2) 2 + R b Nr

Nr

Re

0

Ir( Nr-1)

0 0

0 0

(

- 2) ( 1)

+ R b Nr -

Rb(Nr -1)

-

Nr

L

0

I_e

R

R

0 0

R e

e

e

L

L L

-

-

N_r N_r Ò ÿ

N_r

N_r

? ?

(II.29)

Le couple électromagnétique est obtenu par dérivation de la co-énergie:

? ? ?

? ?

1

Irk M

M

3 ä? L - M cos( )

è á

+ k L sr

= P i

[ ] ^t

2 sdq ^??L - cos( )

è á

+ L ??

äè M k

sr

Cem

- r

3

C = PM i I k

? Nr ? 1 N 1

-

? sin á - ?

i I k

cos á (II.31)

em ds

sr rk qs rk

2 ? k = 0 k = 0 ?

On y ajoute les équations mécaniques afin d'avoir la vitesse ? = ù

P

d? 1

dt P

= J em - r -

P C C

( ù ) (II.32)

f

d è =

Et ù

Le système ci-dessus est très compliqué pour le programmer et l'exécution d'une simulation d'un tel modèle est très lente, c'est pour cela qu'on a opté pour un autre modèle, le modèle dq .Nous avons appliqué une transformation généralisée ( N_r ) qui permet de passer des N_r grandeurs équilibrées vers deux grandeurs dq . La simulation de ce modèle est très rapide.

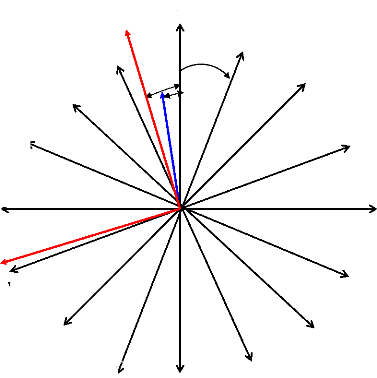
II.4. La transformation de N grandeurs équilibrées en deux grandeurs dq [6] r

d Ir0

Ir1

Ir15

è 2ð / 16

Ir2

Ir14

I1

Ir3

â

Ir13

Ir12

q

Ir5

r11

Ir¹

Ir6

Ir10

Ir8

Ir9 Ir7

Ir4

Figure (II.6) : projection du modèle multi enroulement sur le modèle dq > Passage du modèle polyphasé au modèle biphasé

On calcule les différentes résistances équivalentes ( S ₁ , S ₂, S₃, et S₄) ;

2 ? R ? R ? 2 e ^2 + + ? + e = ? + + R ? e S ? 2 R R cos 0 2 + ? + + ? á ? R R cos 1 ? á L ? 2 R R + ? cos 15 ^2 á 1 b 0 b 15 b 1 b 0 b 15 b 14 16 N [ ? ? N ? ? N r r r ?

1 ? ?

- [ (

4 R cos 0 cos 1

á á ) (

+ R cos 1 cos 2

á á ) (

+ L + R cos 15 cos 0

á á ]

) (II.33)

b 0 b 1 b 15

16

i
i

0

Rs - ùLsc 0 - Nr ùMsr

2

(II.37)

Nr

ù L sc Rs - ùMsr

0 Re

Rr

0

Rr

0 0

0 0

2

0 0

1 ? ? ? ? ? ? ? ? ?

0 0 0

0 0 0

R

Avec : = 2 + 2 R_b ( 1 - cos á)

e

R r

N_r

S 2 = - 2 _[(2 R e + A_{0 +g15} jcos0 ásin0 á -(2 R e +R +g₀ jcos1 á sin1 á (2 R e + k₅ +R_b14)cos1 5ásin1

6 r r

N N_r

2 _rf

+ ₆ RR b 0 sin 0 á cos 1á ) + (R_b1 sin 1 á cos 2á ) +
·
·
· + (Rb15 sin 15á cos 0á)]

2 _rf

i
i

+ ₆ RR b 0 cos 0 á sin 1á ) + (R_b1 cos 1 á sin 2á ) +
·
·
· + (Rb15 cos 15á sin 0á)] (II.34)

Re

S 3 = - ₆[(² +A0 +g15 jcos0 á sin0 á -(2 +R +R jcoslasinla-- -

N

_r -
· '( ² Al5+

N #177;_r Rb14)cos1 5ásin1

N_r

2 R e Re

2 _rf

+ ₆ RR b 0 sin 0 á cos 1á ) + (R_b1 sin 1 á cos 2á ) +
·
·
· + (Rb15 sin 15á cos 0á)]

2 _rf

+ ₆ RR b 0 cos 0 á sin 1á ) + (R_b1 cos 1 á sin 2á ) +
·
·
· + (Rb15 cos 15á sin 0á)] (II.35)

S 4 = 12 6 [(2 ^e + R615 cos^2 0 á + 2 N R : + RbI + Rb0 cos^2 1á + · · · + 2 N^R: + R ,,,, + RbI4 cos^2 15á NR +^Rb0 r ) ( L,=, JJ

1 1 i

1 ri

- Rb ₀ cos 0 á cos 1á ) + (R_b1 cos 1 á cos 2á) +
·
·
· + (Rb15 cos 15á cos 0á)] (II.36)

4 6

Si l'on considère que toutes les barres sont saines ( Rb 0 = R_b1 = = Rb15), les résistances

équivalente S₁ , S ₂ , S₃ , et S ₄ Deviennent :

S 1 = S4

2 Re + 2Rb ( 1^-- cosá) Nr

R

S 2 = S 3 = 0 , En posant : = 2 + 2 R_b ( 1 - cos á)

e

R

r

N_r

La nouvelle matrice de résistance du modèle dq équivalent, en considérant que toutes les barres sont saines est [4] :

0 3 Msr

2

0 0

N_r

-

2

0 Lsc 0

3 Msr

2

Avec :L = L -M_rr + 2 Le + 2Lb( 1-cosè)

^p Nr (II.38)

-

Msr 0 0

N_r M sr

2

0 Ò

0 Lrc 0 0

0 Lrc 0

0 0

Lsc 0

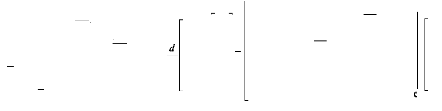
Donc le modèle réduit, en considérant que toutes les barres sont saines est :

?

0

ids

0 0

0 0

0 Rr 0

0 0 R

iqs

idr

iqr

Ie

e Ò ÿ

0

Vds
Vqs

idsi qsidri qrI_e

1

? ? 0 ?

Nr

Rs - ù L sc 0 - ù M sr

2

Nr

ù L Rs

sc - ù M sr

2

0 0 Rr 0 0

0 0

? ? ? ? ? ? ? ?

-

2

3 Msr

Lsc

0 Lsc 0

0

0 0

2

3 Msr

0

0 Lrc 0 0

-

N_r

2

0 Lrc 0

0 0

Msr

N_r

2

0 0

Msr

?

?

?

?

?

?

?

?

Le]

0

dt

(II.39)

II.5 Contrôle des courants par hystérésis :

Le principe de cette méthode de contrôle des courants par hystérésis est basé sur la commande des interrupteurs de l'onduleur de telle sorte que les variations du courant dans chaque phase du moteur soit limitées dans une bande d'hystérésis encadrant les références des courants.

Ce contrôle se fait par une comparaison permanente entre les courants réels et les références de courant. La sortie des comparateurs est reliée à la logique de commande de l'onduleur de manière à imposer une commutation des interrupteurs lorsque le courant s'écarte de la valeur d'hystérésis de sa référence.

Les ondulations du courant sont fixées par la valeur de la bande d'hystérésis. Dans cette méthode le courant est toujours imposé aux bornes de la machine. La figure (II-7) donne le schéma de principe.

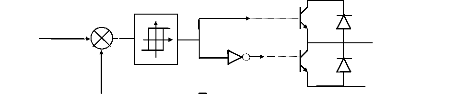
Ti

+

-

i ref

Ti'

inverseur

Comparateur à hystérésis

Bras de l'onduleur

i

Figure II.7 :Principe du contrôle des courants par

hystérésis

II.5.1 Modélisation de l'onduleur

L'onduleur est un convertisseur statique assurant la conversion continu - alternatif, il est composé de six transistors (T1,...,T3,T'1,...,T'3) shuntés en anti-parallèle par des diodes de récupération (D1,...,D3,D'1,...,D'3), qui permettent de renvoyer le courant négatif vers le condensateur de filtrage mis à l'entrée de l'onduleur .

+ 1

F i 0

=

si K est fermé et K ouvert

'

i i

si K_i est ouvert et K fermé

i '

? ? ?

(II.40)

Les tensions de ligne aiguillées par l'onduleur sont :

U

= 2 (F₁ - F₂ )

U

. (F₂ - F₃)

2

U

. ( - F ₁ )

F₃

2

Uab

Ubc

L

U_ca

(II.41)

La relation imposée par la machine aux tensions de phase s'exprime par :

V_a + Vb + V_c = 0 (II.42)

En tenant compte de cette relation, on déduit les tensions simples :

? ? ? ? ?

Va Vb V c

1 ? ? U . ? = ? 3 ? ? ? ? ?

2 - 1 -1 1 2 -1 1 -1 2

? ? ? . ? ? ? ? ? ? ?

F 1 F2 F3

1 ? ? ? ?

(II.43)

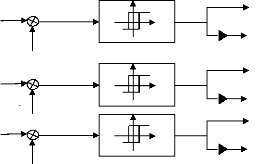
II.5.2 Modélisation du modulateur à hystérésis

Pour déterminer les signaux de commande des interrupteurs de l'onduleur, il suffit d'associer un modulateur à hystérésis pour chacune des trois phases de l'onduleur, ceci permet de comparer chaque courant de phase avec sa référence de courant sinusoïdale de telle sorte que la variation de courant dans chaque phase soit limitée dans une bande encadrant la référence des courants :

ib

Irefb

+ _

_

i_c

Irefa

+ _

i_a

Irefc

T1

T1'

T1

T2'

T1

T3'

Figure II.8

Les fonctions logiques représentants les interrupteurs de l'onduleur sont définis par :

La commutation des composants électriques est supposée instantanée (composants parfaits).Afin

de simplifier l'étude, nous associons à chaque bras de l'onduleur, une fonction

logique Fi(i=1,2,3) qui est la sortie du modulateur Hystérésis.

Les fonctions logiques sont définies ainsi :

i

Fi = 0 si ij-ij_ref > h

Fi = 1 si ij-ij_ref >- h (II.44)

Fi = Fi si ijref+h ^>ij> ijref-h

Avec ij courant de phase, j = a,b,c et ij_ref courant de référence II.6 Simulation du modèle réduit multi enroulements :

a. Cas d'une machine saine à vide : 1. Alimentation sans onduleur :

0 0.5 1 1.5 2 2.5 3

t(s)

1

n(trLm n)

3500

3000

2500

2000

1000

-500

500

500

0

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

t(s)

1

Cem(N.rn)

18

16

14

12

-2

6

4

2

0

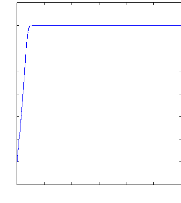
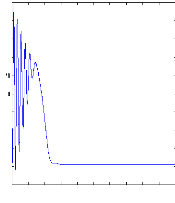
Figure II.9 : vitesse de rotation, couple électromagnétique, simulation
avec le modèle réduit, machine saine en charge, C_r=3.5 N.m

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

ias(A)

-15

-2 0

-10

-25

25

20

15

10

-5

5

0

t(s)

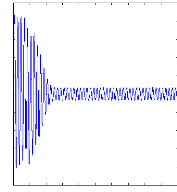
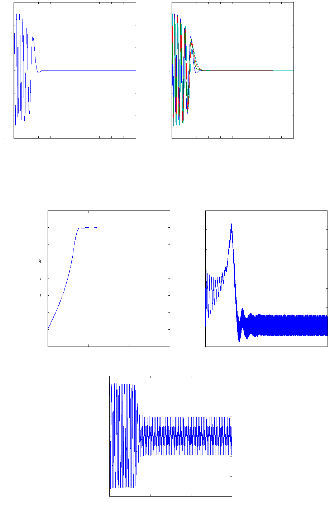
Figure II.10 : courant statorique, simulation avec le
modèle réduit, machine saine à vide

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

t(s)

irbO(A)

-1000

1500

1000

1500

-500

500

0

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

t(s)

irb(A)

-1000

-1500

1500

1000

-500

500

0

Figure II.11 : courants dans les barres rotoriques, Irb0,Irb1,Irb2,Irb3,
simulation avec modèle global, machine saine à vide

2. Alimentation avec onduleur :

0 0.5 1 1.5

nitrim n)

1

1

2500

3500

3000

-500

500

000

500

000

0

0 0.5 1 1.5

C_em(N.m )

12

10

-2

8

6

4

2

0

t(s)

0 0.5 1 1.5

t(s)

las(A)

-10

-15

15

10

-5

5

0

t(s)

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

t(s)

irb 0(A )

-1000

1500

1000

1500

-500

500

0

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

t(s)

irb 3(A )

-1000

-1500

1500

1000

-500

500

0

0 0.5 1 1.5 2 2.5 3

t(s)

n(trlin n)

1

35 00

30 00

25 00

20 00

10 00

-5 00

5 00

5 00

0

0 0.5 1 1.5

t(s)

C em (N A )

18

16

14

12

-2

0

8

6

4

2

0

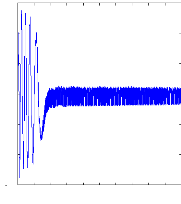
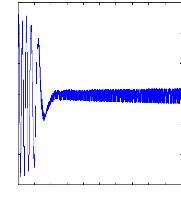
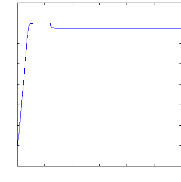
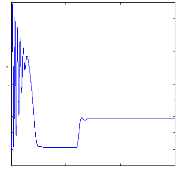
Figure II.12 : simulation du modèle réduit, Alimentation avec onduleur àvide

A vide :

On n'impose tout d'abord aucun couple de charge et la machine opère donc a vide. La

Figure( II.9) illustre l'évolution temporelle, en régime transitoire et en régime permanent, de la vitesse de rotation, après une phase transitoire, celle-ci se stabilise a une valeur proche de la vitesse de synchronisme a cause de l'absence d'un couple de charge, la figure illustre aussi le couple électromagnétique . Pour le couple, après une phase transitoire, celui-ci se stabilise comme convenu a une valeur proche de zéro a cause de l'absence d'un couple de charge. La figure( II.10) illustre l'évolution temporelle, en régime transitoire et en régime permanent du courant statorique en absence du couple de charge. La figure (II.11) illustre l'évolution temporelle, en régime transitoire et en régime permanent, des courants de barres rotoriques _Irb0 , Irb1, Irb2, Irb3. On constate que les barres rotoriques sont parcourues par des courants faibles mais non nuls en régime permanent. On peut expliquer cette circulation de courants par l'existence d'un frottement visqueux qui génère un faible couple résistant, et par l'existence de champs harmoniques ne tournant pas, par définition, a la vitesse de synchronisme. Les boucles rotoriques soumises a des champs fluctuants sont alors le siège de courants induits.

b.Cas d'une machine saine en charge :

1. Alimentation sans onduleur :

ias(A )

· 10

· 15

· 20

· 25

25

20

15

10

· 5

5

0

0 0.5 1 1.5

t(s)

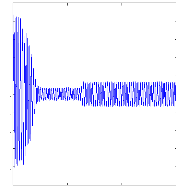
Figure II.14 : courant statorique, simulation avec le
modèle réduit, machine saine en charge, C_r=3.5N.m

0 0.5 1 1.5

t(s)

irbO(A)

· 1000

· 1500

1500

1000

· 500

500

0

0 0.5 1 1.5

t(s)

irb(A)

· 10 00

· 15 00

1500

1000

· 500

500

0

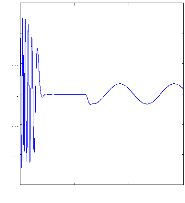
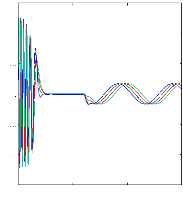
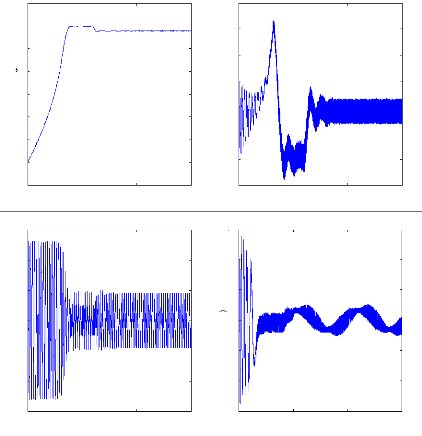
Figure II.15 :courants dans les barres rotoriques, Irb0,Irb1,Irb2,Irb3, 2. Alimentation avec onduleur :

12

10

8

6

4

C_em(N.m)

2

0

-2

1 5

10

5

0

i_{a s}(A )

-5

-10

-15

500

1000

500

0

irb 0 (A

-500

-1000

-1500

0 0.5 1 1.5

t(s )

0 0.5 1 1.5

t(s)

0 0.5 1 1.5

t(s)

0 0.5 1 1.5

t(s)

3500

3000

2500

000

500

000

k(trim n )

1

1

500

0

-500

Figure II.16 : simulation du modèle réduit, Alimentation avec onduleur en charge En charge :

On impose maintenant un couple de charge de 3.5 N.m et la machine opère alors

en charge. La figure (II.13) illustre l'évolution temporelle, en régime transitoire et en régime permanent, de la vitesse de rotation, après une phase transitoire, celle-ci se stabilise a une valeur de 2885 tr/mn, la figure illustre aussi le couple électromagnétique . Pour le couple, après une phase transitoire, celui-ci se stabilise comme convenu à une valeur proche de 3.5 N.m.

La figure(II.14) illustre l'évolution temporelle, en régime transitoire et en régime permanent, du courant statorique en présence d'un couple de charge de 3.5 N.m.

La figure(II.15) illustre l'évolution temporelle, en régime transitoire et en régime permanent, des courants de barres rotoriques _Irb0 , _Irb1 , Irb2, Irb3. On constate que les barres rotoriques sont logiquement parcourues par des courants de fréquence fondamental g fs0 en régime permanent. Ceux-ci possèdent également une fréquence fondamentale g fs0 en régime permanent.

II.7 Conclusion

Dans ce chapitre on a traité la machine asynchrone en terme de circuit, et on a considéré que le rotor est constitué de plusieurs éléments, chaque élément de la cage est décrit par un circuit électrique équivalent de Nr grandeurs. Puis, on a fait la transformation de Nr grandeurs vers deux grandeurs, pour faciliter l'étude.

On remarque que la méthodologie de modélisation adoptée est assez générique, et peut très bien être adaptée pour la représentation d'autres types de machines électriques : machines asynchrones a rotor bobiné, machines synchrones a aimant permanent ou a rotor bobiné, machines a reluctance variable. Cette modélisation peut également servir dans une certaine mesure a des objectifs de conception.

Le modèle constitué donne des résultats identiques à ceux obtenus dans le cas du modèle classique de la machine asynchrone et permit d'étudier les différents défauts rotoriques, donc ce modèle s'adapte bien au problème posé.

Dans la suite de l'étude, on va plutôt exploiter la flexibilité du modèle pour rendre compte d'un certain nombre de défauts rotoriques pouvant affecter les machines asynchrones triphasées a cage d'écureuil.

Chapitre III

Modélisation et simulation des défauts

rotoriques de la machine asynchrone

III.1 Introduction

La méthode qu'on a adoptée pour la simulation des défauts rotoriques consiste à remplacer la valeur initiale de la résistance des barres cassées par une valeur finie. Cette méthode est appelée méthode des résistances finies.

E. Ritchie estime qu'une augmentation de la résistance de la barre de 11 fois permet d'aboutir à des résultats en concordance avec ceux obtenus expérimentalement.

En ce qui nous concerne nous avons considéré des augmentations de 11 fois la résistance initiale de la barre.

En effet pour un pas de 3

10^- s, une augmentation de plus de 11 fois conduit à une instabilité numérique (dans notre modèle).

La méthode d'intégration est celle de Runge Kutta d'ordre 4.

III.2 Modélisation des défauts dans le cas de cassures d'une et de deux barres

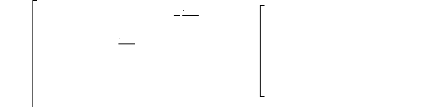
Le modèle II.39 démontré dans le chapitre précédent, et réécrit ci-dessous, permet de simuler la rupture de barres au rotor.

-

2

3 Msr

Lsc

0

0

0 0

2

3 Msr

Lsc

0

0 Lrc 0

0

N_r

2

0

0 0

Msr

N_r

2

0 0

Msr

0 Ò

0 L rc 0

dt

d

i _ds

i _qs

i dr

i qr

I_e

1

? ? ? ? ?

? ?

1 ?

?

?

?

?

?

?

? ?

ids

i qs

i dr

(III.1)

i qr

I_e

1 ? ? ? ? ?

? ?

N_r

ùM

0

sr

2

-

N_r

ùM

0 0

ùL R

sr

sc

2

-

0

R_e

0 0 0

R s - ùL 0

sc

0 0 S 1 S 2 0

0 0 S 3 S 4 0

1 ? ? ? ? ?

? ?

Vds
Vqs

0

0

0

Avec:

S 1 = 12 6 [(2 NR e r + R b 0 + Rb15 )cos^2 0 a + (2 N Re r + Rb1 +Rb0 )cos^2 la + · · · + (2 NRe r + R b15 Rb )coS^2

? ()? 15á ?

1 _rf \\ \\

- RR _b° cos0á ) cosOá p+ ( R_b1 cos0á ) coR2á p+
·
· + (R₆₁₅(R₆₁₅cos0 5á ) coR \\-1 0a (III.2)

4 6

i
i

S₂ = - 2 6 [(2 R e r + A_{0 +g15} jcos0 ásin0 á -(2 R e r +R +g₀ jcos1 á sin1 á (2 R e + A₁₅ +R_bdcos1 5ásin1

N N_r

+ 2 6 [ ( R b 0 sin( 0á ) cos( 1á)) + ( R_b1 sin( 1 á ) cos( 2á)) +
·
·
· + ( R_b15 sin( 1 5á ) cos( 0á ))]

+ ₆ [(R _b° cos( 0á ) sin( 1á)) + ( R_b1 cos( 1á ) sin( 2á))+
·
·
· + ( R_b15 cos( 1 5á ) sin( 0á ))] (III.3)

1

i
i

2 R _e Re

S

3 = - 42 Re + A0 +k₅ jcos0 á sin0 á -(2 +R +R }oslá sinlá - -
· '-(2 + R_b15 + k₄ jcos1 5ásin1

N_r

r r

+ 2 6 [(R b 0 sin( 0á ) cos( 1á)) + ( R_b1 sin( 1 á ) cos( 2á)) +
·
·
· + ( R_b15 sin( 1 5á ) cos( 0á ))]

+ ₆ [(R _b° cos( 0á ) sin( 1á)) + ( R_b1 cos( 1á ) sin( 2á))+
·
·
· + ( R_b15 cos( 1 5á ) sin( 0á ))] (III.4)

1

S = 12 6 ft R r bo bo) ( R r ) ( R r ) 2 ^e + R + R cos^2 0 á + 2^e + RbI + Rb0 cos^2 1á + · · · + 2 ^e + R A1 5 + R cos^2 15á 4 4," b14

1 1 i

4 _rf , \ , \\ , , \ , \\ , , ^\cos(0a ))] (III.5)

- RR cos0á )cosOáD+ O_b1 cos0á )coR2áp+
·
·
· + Ob15 cos(15a)cos(0a 5a ) 1 6 b 0

Dans le cas oil on veut simuler la rupture d'une barre ou de deux barres les seules valeurs qui vont changer sont celles de: S1, S2, S3 et S4

III.2.1. Cassures de barres

La cassure de barres est un des defauts les plus frequents au rotor. Nos simulations nous permettrons d'identifier les signatures de ce defaut et de prevoir les deteriorations generees dans le moteur.

Pour illustrer la cassure totale de barre dans le modèle de la machine, nous augmentons la valeur de la barre cassee de 11 fois [7].

III.2.2 Simulation des défauts rotoriques à vide et en présence d'une charge sur l'arbre du

moteur

III.2.2.1 Machine à vide

a. Cas d'une cassure d'une barre

. Alimentation sans onduleur

On n'impose tout d'abord aucun couple de charge. La figure III.1 illustre l'evolution temporelle

en regime transitoire et en regime permanent de la vitesse de rotation en presence d'une rupture de barre _(rb0) a t=1s, Apres une phase transitoire, celle-ci se stabilise a une valeur proche de la vitesse de synchronisme a cause de l'absence d'un couple de charge. La figure illustre aussi l'evolution temporelle en regime transitoire et en regime permanent du couple electromagnetique

Cem en présence d'une rupture de barre (rb0). Après une phase transitoire, celui-ci se stabilise a une valeur proche de zéro a cause de l'absence d'un couple de charge.

La figure III.2 illustre l'évolution temporelle en régime transitoire et en régime permanent du courant statorique , en présence d'une rupture d'une barre _(rb0) à t=1s

La figure III.3 illustre l'évolution temporelle en régime transitoire et en régime permanent des courants de barres Irb0 , Irb1 , _Irb2 , _Irb3 , en présence d'une rupture des barres _(rb0) à t=1s .

On remarque dans l'essai à vide, les signatures des défauts rotoriques sont très minimes.

3500

3000

2500

2000

500

1

n(trLm n)

1000

500

0

-500

0 0.5 t(s) 1 1.5

0 0.5 1 1.5

t(s)

1

Cem (N.rn)

18

16

14

12

-2

6

4

2

0

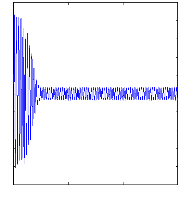
0 0.5 1 1.5

t(s)

ia s (A )

-10

-15

-20

-25

25

20

15

10

-5

5

0

Figure III.1 : vitesse de rotation, couple électromagnétique ( simulation avec le
modèle réduit, machine en défaut à vide)

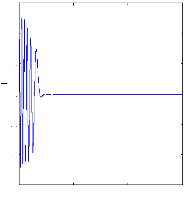
0 0 .5 1 1 .5

t(s)

irb 0 (A

· 1 0 0 0

· 1 5 0 0

1 5 0 0

1 0 0 0

· 5 0 0

5 0 0

0

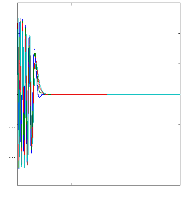
0 0.5 1 1.5

t(s)

irb (A

· 1000

· 1500

1500

1000

· 500

500

0

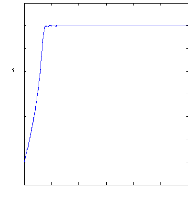
0 0.5 1 1.5 2 2.5 3

t(s)

1

1

k(trim n )

3 5 0 0

3 0 0 0

2 5 0 0

· 500

0 0 0

5 0 0

0 0 0

500

0

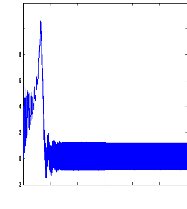
0 0.5 1 1.5 2 2.5 3

t(s)

Cem(N.m

12

10

·

Figure III.3 :courants dans les barres rotoriques, Irb0,Irb1,Irb2,Irb3,
simulation avec modèle global, machine en défaut à vide.

. Alimentation avec onduleur

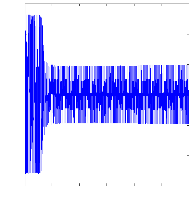
0 0.5 1 1.5 2 2.5 3

t(s)

i_as(A )

-10

-15

15

10

-5

5

0

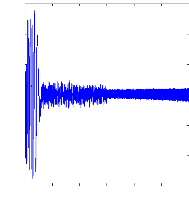
0 0.5 1 1.5 2 2.5 3

t(s)

irbO(A )

-1000

-1500

1500

1000

-500

500

0

Figure III.4 : Simulation avec le modèle réduit, machine en défaut à vide, alimentation avec
onduleur

b- Cas d'une cassure de deux barres

. Alimentation sans onduleur

La figure III.5 illustre l'évolution temporelle en régime transitoire et en régime permanent de la vitesse de rotation en présence d'une rupture de deux barres _(rb0) à t=1s et _(rb1) à t=2s, Aprés une phase transitoire, celle-ci se stabilise à une valeur proche de la vitesse de synchronisme à cause de l'absence d'un couple de charge. La figure illustre aussi l'évolution temporelle en régime transitoire et en régime permanent du couple électromagnétique _Cem en présence d'une rupture des barres _(rb0) à t=1s et _(rb1) à t=2s. Après une phase transitoire, celui-ci se stabilise à une valeur proche de zéro à cause de l'absence d'un couple de charge. La figure III.6 illustre l'évolution temporelle en régime transitoire et en régime permanent du courant statorique , en présence d'une rupture d'une barre _(rb0) à t=1s et _(rb1) à t=2s.

La figure III.7 illustre l'évolution temporelle en régime transitoire et en régime permanent des courants de barres _Irb0 , _Irb1 , _Irb2 , _Irb3 , en présence d'une rupture des barres _(rb0) à t=1s et _(rb1) à t=2s.

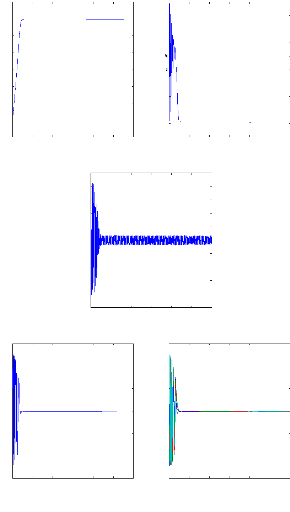
500

0

irb 0 (A )

-500

2 2.5 3

0 0.5 1 1.5

3500

3000

2500

2000

500

1

n(trLm n )

1000

500

0

-500

18

16

14

12

6

1

Cem (N.rn)

4

2

0

-2

0 0.5 1 1.5 2 2.5 3

0 0.5 1 1.5 2 2.5 3

)

Figure III.5 : vitesse de rotation, couple électromagnétique ,

t(s )

t(s

simulation avec le modèle réduit, machine en défaut à vide

0 0.5 1 1.5 2 2.5 3

ia s (A )

-10

-15

-20

-25

25

20

15

10

-5

5

0

t(s)

Figure III.6 : courant statorique, simulation avec le
modèle réduit, machine en défaut à vide

t(s)

0 0.5 1 t(s) 1.5 2 2.5 3

irb (A )

-1000

-1500

1500

1000

-500

500

0

1500

1000

-1000

-1500

Figure III.7 :courants dans les barres rotoriques Irb0 , Irb1 , _Irb2 , Irb3,
simulation avec modèle global, machine en défaut à vide

2. Alimentation avec onduleur

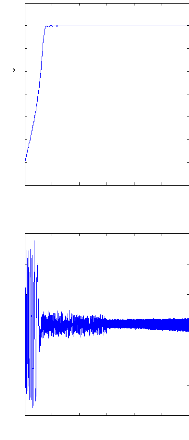
1500

1000

500

0

irbo IA I

-500

-1000

-1500

0 0.5 1 1.5 2 2.5 3

t(s)

0 0.5 1 1.5 2 2.5 3

t(s )

k(trim n )

1

1

3500

3000

2500

-500

000

500

000

500

0

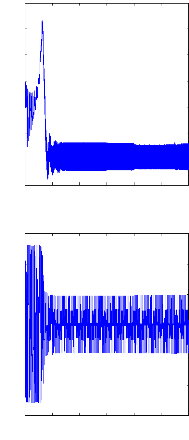
15

10

5

0

i_{a s} (A )

-5

-10

-15

0 0.5 1 1.5 2 2.5 3

t(s)

0 0.5 1 1.5 2 2.5 3

t(s)

C_em(N.m

12

10

-2

8

6

4

2

0

Figure III.8 : Simulation avec le modèle réduit, machine en défaut à vide, alimentation avec
onduleur

2. Machine en charge

a. Cas d'une cassure d'une barre 2. Alimentation sans onduleur

On impose maintenant un couple de charge de 3.5 N.m à t=0.6s et la machine opère alors en charge.

La figure III.9 illustre l'évolution temporelle en régime transitoire et en régime permanent de la vitesse de rotation, celle-ci se stabilise a une valeur de 2219 tr/mn. La figure illustre aussi du couple électromagnétique Cem en présence d'une rupture des barres _rb0 à t=1s. Aprés une phase transitoire, celui-ci se stabilise a une valeur proche de 3.5 N. m a cause de la présence du couple de charge.

La figure III.10 illustre l'évolution temporelle en régime transitoire et en régime permanent du courant statorique , en présence d'une rupture de barre rb0 à t=1s .

La figure III.11 illustre l'évolution temporelle en régime transitoire et en régime permanent des courants de barres _Irb0 , _Irb1 , _Irb2 , _Irb3, en présence d'une rupture de barre _rb1 à t=1s. Les courants circulant dans les barres adjacentes aux barres cassées sont très supérieurs a leur valeur nominale. On conclut donc qu'il y a un risque de défaillances en chacune dans la mesure ou les contraintes électriques et thermiques sont redistribuées sur les conducteurs adjacents.

Nous observons se qui suit:

- La vitesse chute à 2917 tr/mn, et le couple électromagnétique vient équilibrer le couple résistant .

- La détérioration de la barre réduit la valeur moyenne du couple électromagnétique et fait apparaître les oscillations .

- L'oscillation sur la vitesse .

- Les courants des phases statoriques sont toujours déphasés entre eux de 120°,

Cependant une ondulation de l'amplitude des courants apparaît avec la cassure de la barre, la figure III.9 illustre cette ondulation.

- Le rotor avec ce défaut de la structure crée en plus de champ rotorique direct qui tourne à g*ùs par rapport au rotor , un champ inverse qui lui tourne à -g*ùs dans le repère rotorique. L'interaction de ces champs avec celui issu du bobinage statorique donne naissance à un couple électromagnétique (somme d'une composante directe constante et d'une composante inverse sinusoïdale), de pulsation 2g ùs .Elle sera la cause d'oscillations sur la vitesse [3].

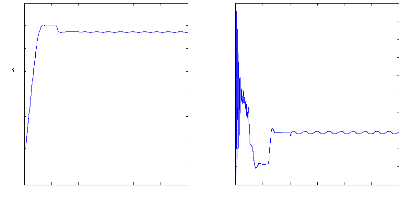
18

16

14

12

10

8

6

Cem(N.m

4

2

0

-2

0 0.5 1 1.5 2 2.5 3

t(s)

0 0.5 1 1.5 2 2.5 3

t(s)

3 5 0 0

3 0 0 0

2 5 0 0

0 0 0

5 0 0

0 0 0

1

1

k(trim n )

500

0

-500

Figure III.9 : vitesse de rotation, couple électromagnétique et le courant statorique, simulation
avec le modèle réduit, machine en défaut en charge, C_r=3.5 N.m

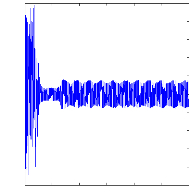
0 0.5 1 1.5 2 2.5 3

i_{a s}(A )

-10

-15

-20

-25

25

20

15

10

-5

5

0

t(s)

Figure III.10 : courant statorique, simulation avec le modèle réduit, machine avec défaut en
charge,C_r=3.5 N.m

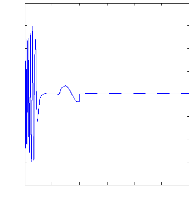
0 0.5 1 1.5 2 2.5 3

t(s)

0

irb o(A )

-1000

-1500

-2000

1500

1000

500

-500

2000

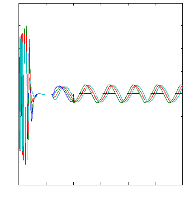
0 0.5 1 1.5 2 2.5 3

t(s)

irb (A )

-1000

-1500

-2000

2000

1500

1000

-500

500

0

Figure III.11 :courants dans les barres rotoriques Irb0 , Irb1 , _Irb2 , Irb3,
simulation avec modèle global, machine en défaut en charge, Cr=3.5N.m

2. Alimentation avec onduleur

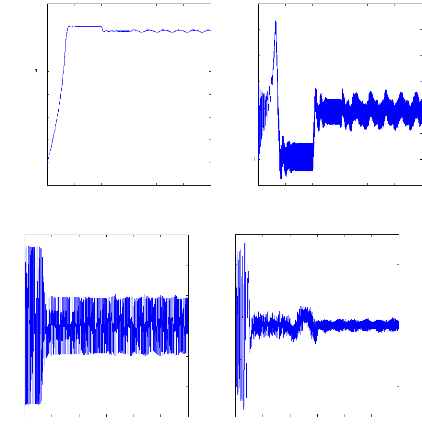
12

10

8

6

4

C_em(N.m)

2

0

-2

15

10

5

i_{a s}(A )

-5

-10

-15

1500

1000

500

0

irb o IA )

-500

-1000

-1500

0 0.5 1 1.5 2 2.5 3

t(s )

0 0.5 1 1.5 2 2.5 3

t(s )

0 0.5 1 1.5 2 2.5 3

t(s )

0 0.5 1 1.5 2 2.5 3

t(s )

3500

3000

2500

000

500

000

k(trim n )

1

1

500

0

-500

Figure III.12 : Simulation avec le modèle réduit, machine en défaut en charge , alimentation avec
onduleur

a- Cas d'une cassure de deux barres

1. Alimentation sans onduleur

On impose maintenant un couple de charge de 3.5 N.m à t=0.6s et la machine opère alors en charge.

La figure III.13 illustre l'évolution temporelle en régime transitoire et en régime permanent du couple électromagnétique C_em en présence d'une rupture de barre rb0 a t=1s et rb1 a t=2s. Aprés une phase transitoire, celui-ci se stabilise a une valeur proche de 3.5 N. m a cause de la présence du couple de charge. On constate des oscillations du couple électromagnétique a la fréquence 2gfs0 en régime permanent.

La figure III.14 illustre l'évolution temporelle en régime transitoire et en régime permanent du courant statorique, en présence d'une rupture de barre _rb0 à t=1s et _rb1 a t=2s.

La figure III.1 5 illustre l'évolution temporelle en régime transitoire et en régime permanent des courants de barres _Irb0 , _Irb1 , _Irb2 , _Irb3 en présence d'une rupture de barre _rb1 à t=1 s. Les courants circulant dans les barres adjacentes aux ban-es cassées sont très supérieurs a leur valeur nominale. On conclut donc qu'il y a un risque de défaillances en chacune dans la mesure ou les contraintes électriques et thermiques sont redistribuées sur les conducteurs adjacents.

Les effets de la cassure de barre (oscillation de ù et _Cem) croit rapidement avec le nombre de ban-es cassé ; d'où on observe:

- Augmentation de l'amplitude des oscillations. La grande amplitude des oscillations accélère la détérioration de la machine.

- L'amplitude des courants des phases statoriques. est proportionnelle au nombre de barres cassées.

- Lors des défauts rotoriques, les courants dans les barres cassées chutent pratiquement zéro, tandis que les courants dans les barres voisines deviennent déséquilibrés. Les courants qui conduisaient les barres cassées se répartit alors dans les barres voisines

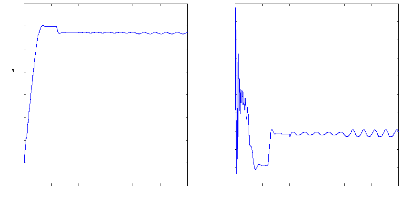
18

16

14

12

10

8

6

C _em (11 .m )

4

2

0

-2

0 0.5 1 1.5 2 2.5 3

t(s )

0 0.5 1 1.5 2 2.5 3

t(s )

3500

3000

2500

000

500

000

II (trim II)

1

1

500

0

-500

Figure III.13 : vitesse de rotation, couple électromagnétique, simulation avec le

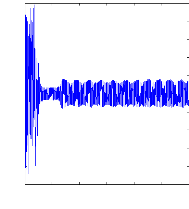
0 0.5 1 1.5 2 2.5 3

t(s )

i_as(A )

-10

-15

-20

-25

25

20

15

10

-5

5

0

modèle réduit, machine en défaut en charge, C_r=3.5 N.m

Figure III.14 : courant statorique, simulation avec le modèle réduit, machine avec défaut en
charge,C_r=3.54N.m

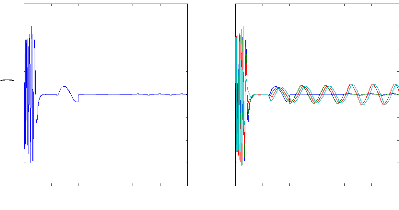
2000

1500

1000

500

0

irb (A )

-500

-1000

-1500

-2000

0 0.5 1 1.5 2 2.5 3

t(s )

0 0.5 1 1.5 2 2.5 3

t(s )

2000

1500

1000

500

-500

0

!rbotA

-1000

-1500

2000

Figure III.15 :courants dans les barres rotoriques Irb0 , Irb1 , Irb2 , Irb3 simulation avec modèle global, machine en défaut en charge, C_r=3.5N.m

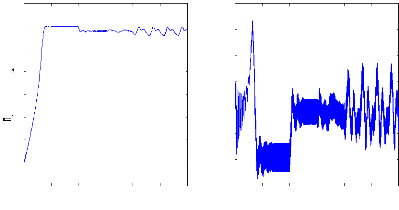
12

10

8

6

4

C_em(N.m )

2

0

-2

0 0.5 1 1.5 2 2.5 3

t(s )

0 0.5 1 1.5 2 2.5 3

1

t(s )

3500

3000

2500

000

500

(trim n )

1

000

500

0

-500

2. Alimentation avec onduleur

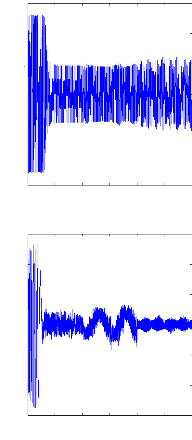
15

10

5

0

i_as(A )

-5

-10

-15

0 0.5 1 1.5 2 2.5 3

t(s)

0 0.5 1 1.5 2 2.5 3

t(s)

irb1(A)

-1000

-1500

1500

1000

-500

500

0

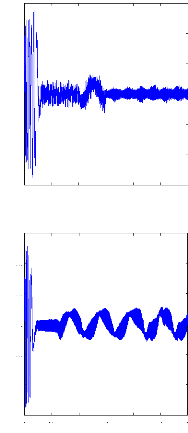
1500

1000

500

0

irboIA )

-500

-1000

-1500

0 0.5 1 1.5 2 2.5 3

t(s)

0 0.5 1 1.5 2 2.5 3

t(s)

irb3(A

-1000

-1500

1500

1000

-500

500

0

Figure III.16 : Simulation avec le modèle réduit, machine en défaut et en charge ,
alimentation avec onduleur

III.3. Analyse spectrale de la signature du courant en présence des défauts rotoriques [2]

[3]

Lors de la rupture de barre, il est difficile d'analyser directement le courant statorique. Ce dernier ne présente en effet qu'une petite modulation (figure III.3).

L'analyse par FFT permet de mettre en évidence les raies présentées dans le spectre de signal. Nous présentons les résultats de simulation relatifs à l'analyse par FFT en régime permanent à charge nominal, dans les figures qui suivent :

Frequency content of y

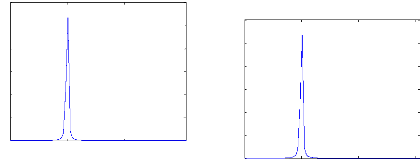
300

250

200

150

100

50

0

0 50 100 150

frequency (Hz>

0 50 100 150

300

250

200

150

100

50

0

Frequency content of y

frequency (Hz>

Figure III.17 : Moteur sain à vide Figure III.18 : Moteur sain en charge

Frequency content of y

60 50 40 30 20 10 0

25 30 35 40 45 50 55 60 65 70

frequency (Hz>

Frequency content of y

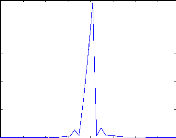
200

150

100

50

0 10 20 30 40 60 70 80

50

frequency (Hz>

Figure III.19 : Moteur avec une barre cassée Figure III.20 : Moteur avec deux barre

cassées

Les figures III.17 à III.20 présentent le spectre de fréquence du courant autour de 50Hz.

Lors de la simulation du moteur sain, à vide et en charge, nous n'observons aucune raie latérale figure III.17 et III.18.

Lorsqu'une barre est rompue, on remarque l'apparition des raies latérales à 46 Hz et 54 Hz au voisinage du fondamental f_s = 50Hz, figure III.19.

Si on augmente le nombre de barres casées (K=0 ; K=1), on obtient des valeurs importantes de l'amplitude des raies figure III.20.

Donc une analyse spectrale du courant statorique fait apparaître les composantes latérales par rapport au fondamentale à 46 Hz et 54 Hz correspondantes à la fréquence de Deleroi f_s (1 #177; 2.g) [10].

Ce résultat très important constitue une signature fiable du défaut.

III.4 Conclusion

Dans ce chapitre, on a donc exploite la flexibilité du modèle initial pour prendre en compte les défaillances rotoriques pouvant affecter la machine asynchrone triphasée a cage d'écureuil.

Nous avons simulé la machine asynchrone en premier lieu, avec des défauts au rotor puis on a fait une analyse harmonique des courants statoriques.

Nos simulations nous permettrons de conclure, que la cassure de barres fait apparaître des oscillations sur le courant, le couple et la vitesse. D'autre part ce défaut connaît un effet cumulatif lors de la rupture de barre.

Une analyse harmonique des courants statorique permet de voir une corrélation entre le défaut et les amplitudes des composantes à f_s (1 #177; 2 . g) .

On a montré que ce modèle pouvait répondre aux objectifs fixés :

compréhension des phénomènes physiques mis en jeu et prédiction de la dégradation des performances lors de l'occurrence de défaillances, extraction et analyse des signatures de défaillances.

Chapitre IV

Commande par flux orienté de la

machine asynchrone

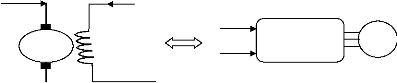
Bloc de
découplage

I_a If

Inducteur

Induit

ids

iqs

MAS

IV.1 Introduction

Le diagnostic de la machine asynchrone dans le cas de commande, est devenu très important, à cause du développement qui a connu le milieu industriel surtout pour les entraînements électriques.

Dans ce chapitre, on va voir l'influence des défauts rotoriques sur le contrôle à flux orienté de la machine asynchrone.

La machine asynchrone est difficilement commandable. La difficulté réside dans le fait que

son modèle mathématique dans le repère de Park est non linéaire multivariables est fortement couplé.

Dans la machine asynchrone, le couple électromagnétique et le résultat d'une interaction entre les courants imposés dans les enroulements du stator et les courants induits dans le rotor en court-circuit. Ainsi, toute variation du couple par variation du courant statorique se traduit aussi par une évolution du flux induit dans le rotor.

Pour obtenir un contrôle dynamique performant du couple, il faut, par un système de commande extérieur à la machine, réaliser un découplage entre le couple et le flux.

Ce découplage des armatures statorique et rotorique de la machine est réalisé en appliquant la commande par flux orienté (commande vectorielle). Cette dernière a été proposée en 1971 par Blaschke. Elle consiste à séparer la commande du flux de celle du couple par orientation du flux selon l'axe directe du repère (d, q).

Nous nous proposons dans ce chapitre d'étudier le comportement de la machine asynchrone en commande vectorielle lorsqu'il se produit des ruptures de barres.

IV.2 Principe de la commande vectorielle

IV.2.1 Description

Le principe du découplage consiste à rendre le contrôle de la machine asynchrone similaire à celui de la machine à courant continu à excitation séparée; ceci peut être réalisé en orientant le flux en quadrature avec le couple (figure (IV.1)).

IV.2.2 Orientation du flux rotorique

On dissocie le courant statorique en deux composantes _ids ^et _iqs en quadrature de telle sorte que le courant _ids soit orienté suivant l'axe du flux rotorique (figure (IV.2)).

iqs

ids

ù_s

q

d

i_s

Ö_r

Figure (IV.2): Orientation du flux rotorique.

Ainsi, en agissent sur les variables _ids ^et _iqs , les grandeurs ö _r et _Cem sont commandées séparément , cela se traduit par :

? ? ?

Ö = Ö

Ö

0

dr r (IV.1)

qr

Le modèle de la machine asynchrone avec orientation du flux rotorique s'écrit :

d r

Ö Mi - Ö

ds

=

dt T_r

, r qs

C = Ö ,

^em L r

pM i

i qs

ù = (IV.2)

^sg T Ö

r

M

r

r

A flux rotorique constant, le couple dépend alors uniquement du courant iqs.

IV.2.3 Bloc de découplage

En reprenant la description de la commande vectorielle par orientation du flux rotorique sur l'axe (d) du repère lié au champ tournant et en réécrivant le système d'équation (IV.2) de la manière suivante :

ids = *

Ö* r 1 d * + Ö ( T ) r r M dt

*

iqs = *

L C

r ^em (IV.3)

pM Ö * r

*

ù =

sg

ÖT r r

*

i

M

qs

*

Ö *

r

		ids *

C_em^*

Tr .s 1 + M

L_r
p M
.

M

T_r

		ù * sg

÷

÷

			iqs *

Figure (IV.3) : Structure de commande par flux orienté (CFO)

La figure (IV. 4) donne le schéma bloc de découplage par orientation du flux rotorique. Nous réalisons la commande découplée suivante :

*

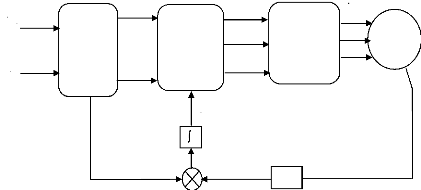
Ö

r

+ ù_r

?

ibs

ias

ics

*

*

*

Onduleur de tension commandé en courant

ias
ibs
ics

MAS

ids

*

CFO

P-1 (ès *)

è_s^*

P

Cem *

ùsg^* +

Figure (IV.4): Schéma de découplage par orientation du flux rotorique

IV.3 Réglage de la vitesse par la méthode indirecte

Concernant le réglage de vitesse, celui-ci est donné par le schéma fonctionnel de régulation de la figure (IV.5). Un régulateur de type PI a été rajouté au montage de découplage de la figure (IV.4)

?*

+

-

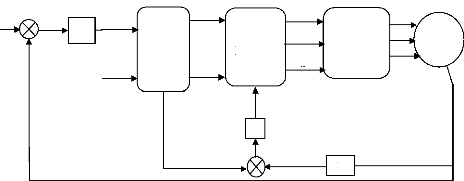
PT

Cem *

Ö

*

r

CFO

ùsg *

Tqs *

Tds *

+

P-1 (ès*)

?

è_s^*

+

ùs *

ias *

ibs *

ics *

ù_r

Onduleur de tension à hystérésis

P

?

ics

ibs

ias

MAS

Figure (TV.5): Schéma fonctionnel de régulation de vitesse d'une machine
asynchrone commandée par la technique du flux oriente (méthode indirecte)

IV.3.1 Synthèse du régulateur PI

Le régulateur de vitesse permet de déterminer le couple de référence, afin de maintenir la vitesse de référence correspondante.

L'équation mécanique donne:

? ( ) 1

s

C s f Js

em ( ) +

En associant à cette fonction un régulateur PT, il arrive:

e? (s)

-

C_em(s)

?

s

1

f + Js

?*

k p

? +

k i

?(s)

(TV.4)

Figure (TV.6): Schéma fonctionnel de régulation de vitesse.

La fonction de transfert en boucle fermée, calculée à partir du schéma précédent, est donnée par:

(k _p s k i ? + ? )

? ( )

s

1
J

(TV.5)

( )

s P s

( )

? *

L'équation caractéristique P(s) est:

f k

+ k

2 p ? i ?

P s s

( ) = + s + = (TV.6)

0

J J

En imposant toujours deux pôles complexes conjugués s1 ,2 = ñ (-1 #177; j) , en boule fermée et, par identification avec la nouvelle équation caractéristique désirée, on arrive à:

k ? J ñ et k p

2

i 2

= ? = 2ñJ f

- (IV.7)

IV.4 Résultats de la simulation

Dans le but de valider l'influence des défauts rotoriques sur le modèle réduit du schéma multi - enroulement de la machine asynchrone a cage d'écureuil, nous avons simulé ce schéma en commande indirecte de vitesse. Les performances de la commande ont été évaluées pour une machine saine ainsi en présence de défauts rotoriques (ruptures de barres), pour une inversion du sens de rotation avec et sans variations du couple de charge.

IV.4.1 Cas d'une machine saine

a- Machine saine à vide

Les paramètres du régulateur de vitesse utilisé dans l'ensemble des simulations qui serons présentées par la suite, sont calculés pour ñ=100. L'algorithme de simulation est réalisé avec une période d'échantillonnage de 0.5ms.

La figure (IV.7) représente les réponses de la vitesse de rotation (n) et du couple électromagnétique _Cem, à une inversion du sens de rotation de 1000 tr/mn à -1000 tr/mn. En absence d'un couple de charge, le couple se stabilise, après un régime transitoire, à une faible valeur qui compense les frottements.

Dans la simulation de la figure (IV.5) nous avons introduit un filtre pour la référence dans le but de modérer l'impact de sa variation brusque sur la réponse en vitesse de la machine ce qui amorti la rapidité du réglage et limite le dépassement.

La fonction de transfert à prévoir dans notre cas est donnée par :

( )

? * filtrée 1

= (IV.8)

? * (1 )

+ T_f S

La constante du temps Tf est calculée de façon à compenser le zéro de la fonction de transfert par

rapport à la consigne donnée par l'équation (IV.5). Donc p

T k

=

f

, des simulations ont montré

k

?

i ?

qu'il est judicieux de travailler avec une valeur de Tf trois fois la valeur prévue, afin d'avoir des réponses de faibles dépassements.

La figure (IV.9) illustre l'évolution temporelle, en régime transitoire et en régime permanent, des courants de barres rotoriques irb0 , irb1, irb2, irb3. Après le démarrage et en absence d'un couple de charge, ces courants se stabilisent à des valeurs proche de zéro.

II (trim n )

-1000

-1500

1500

1000

-500

500

0

0 0.5 1 1.5 2 2.5 3

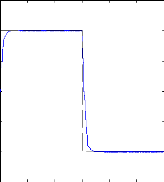
-80

0 0.5 1 1.5 2 2.5 3

t(s )t(s)

a

C _em (11 .m

-20

-40

-60

60

40

20

0

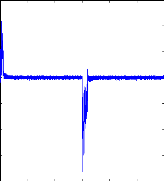
b

Figure (IV.7) : Réponses de la machine asynchrone saine lors d'une inversion du sens
de rotation : a) vitesse de rotation et sa référence , b) couple électromagnétique.

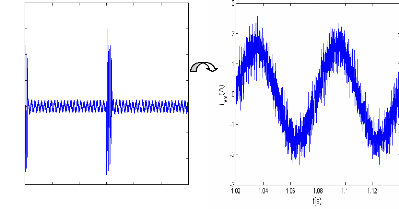
40

30

zoom

20

-10

-20

-30

0 0.5 1 1.5 2 2.5 3

t(s )

10

0

i_as(A )

Figure (IV.8) : Courant de phase statorique.

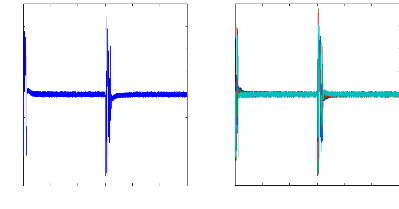
2000

1500

1000

-1000

-1500

-200 0

0 0.5 1 1.5 2 2.5 3

t(s ) t(s )

0 0.5 1 1.5 2 2.5 3

2000

1500

1000

500

0

ⁱ_rb0(A

-500

-1000

-1500

-200 0

500

0

irb (A )

-500

Figure (IV.9) : courants dans les barres rotoriques, _Irb0 , _Irb1 , _Irb2 , Irb3, simulation avec modèle global, machine saine à vide

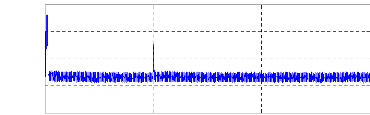
i_ds(A)

1 5

1 0

-5

5

0

0 0 .5 1 1 .5

t(s )

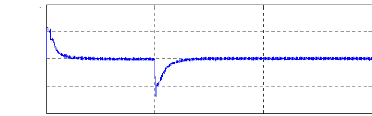
i_qs(A)

-2 0

-4 0

4 0

2 0

0

0 0 .5 t(s ) 1 1 .5 Figure

(IV.10) : Découplage par orientation du flux rotorique.

b- Cas d'une machine saine en charge

Pour illustrer les performances du réglage, nous avons simulé un démarrage à vide avec une application du couple de charge (C_r=3.5Nm) à l'instants t = 0.5s, suivi d'une inversion de la référence de vitesse entre #177;1000 tr/mn à l'instant t=1.5s.

Les résultats obtenus sont regroupés sur les figures (IV.11-12). Comme on peut le constater, ces
résultats montrent que la commande vectorielle appliquée à la machine asynchrone permet un
rejet de la perturbation et une bonne poursuite de la référence. Toutefois, un pic de couple de

valeur importante apparaît lors de l'inversion de la vitesse ce qui est néfaste pour le bon fonctionnement de la machine.

La figure (IV.13) présente les courants des quatre premières barres rotoriques. En présence d'un couple de charge, les courants rotoriques deviennent des ondes sinusoidales.

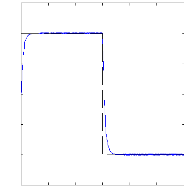
II (trim n )

-1000

-1500

1500

1000

-500

500

0

a

-

C _en (11 .m )

-40

-60

-80

60

40

20

0

0

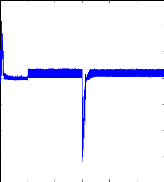
b

0 0.5 1 1.5 2 2.5 3

t(s )

0 0.5 1 1.5 2 2.5 3

t(s )

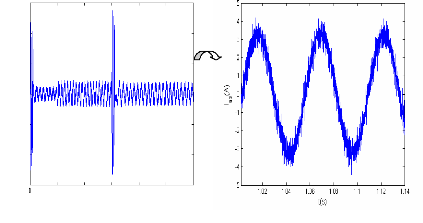
30

-10

-20

-30

0.5 1 1.5 2 2.5 3

t(s)

Figure (IV.12) : Courant de phase statorique d'une machine asynchrone saine en charge.

zoom

0

i_as(A )

20

10

Figure (IV.11) : Réponses de la machine asynchrone saine en charge lors d'une inversion du sens
de rotation : a) vitesse de rotation et sa référence , b) couple électromagnétique.

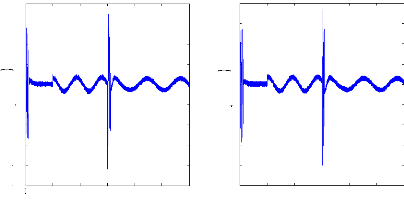
2000

1500

1000

500

0

00

-1000

-1500

-2000

-2500

0 0.5 1 1.5 2 2.5 3

t (s t (s

611A

-5

0.5 1 1.5 2 2.5 3

2000

1500

1000

500

0

irbo (A

-

500

-1000

-1500

2000

2500

Figure (IV.13) : courant dans la barre rotorique : Irb0 , Irb1
simulation avec modèle global, machine saine en charge, C_r= 3.5 N.m

IV.4.2 Cas d'une machine avec défaut

On va voir la régulation de la vitesse, dans le cas des défauts, ou on simule la rupture d'une barre, et aussi la rupture de deux barres.

a- Cas d'une rupture d'une barre

0 0.5 1 1.5 2 2.5 3

t(s )

0 0.5 1 1.5 2 2.5 3

t(s )

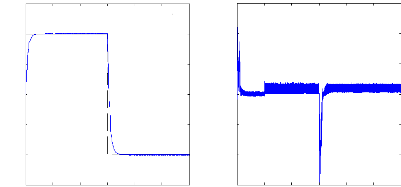
Cem(N.m)

-20

-40

-60

60

40

20

0

b

II (trim n)

-1000

-1500

1500

1000

-500

500

0

a

Figure (IV.14) : Réponses de la machine asynchrone en charge avec un défaut lors d'une
inversion du sens de rotation : a) vitesse de rotation et sa référence , b) couple
électromagnétique.

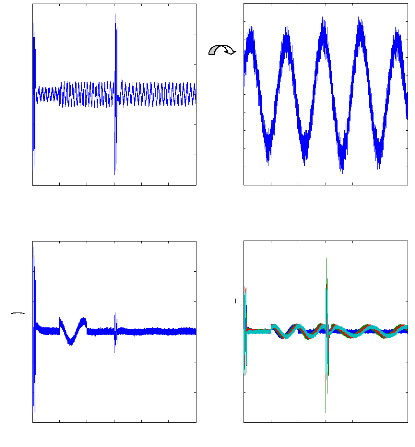
t(s )

t(s )

1500

1000

500

0

irboIA

-500

-1000

-1500

Figure (IV.15) : Courant de phase statorique, machine en défaut, en charge C_r= 3.5Nm

0 0.5 1

t(s ₎1.5 2 2.5 3

0 0.5 1 1.5 2 2.5 3

t(s )

30

20

10

0

i_as(A )

-10

-20

-30

0 0.5 1 1.5 2 2.5 3

1 1.05 1.1 1.15 1.2 1.25 1.3

5

4

zoom

3

2

0

i_as(A )

-1

-2

-3

-4

-5

3000

2000

00

0

-1000

ⁱrb 0 ,1 ,2 ,3 (A--)

10

-2000

-3000

Figure (IV.16) : Courants dans les barres rotoriques : Irb0 , _Irb1 , _Irb2 , I_rb3 machine en défaut, simulation avec modèle global, rupture de la barre _rb0 à t= 1s

b- Cas d'une rupture de deux barres

II (trim n )

-1000

-1500

1500

1000

-500

500

0

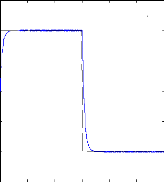
a

0 0.5 1 1.5 2 2.5 3

t(s )

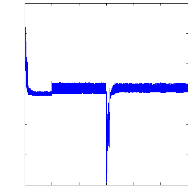
C _em (11 .m )

-20

-40

-60

60

40

20

0

b

0 0.5 1 1.5 2 2.5 3

t(s)

Figure (IV.17) : Réponses de la machine asynchrone en charge avec un défaut lors d'une
inversion du sens de rotation : a) vitesse de rotation et sa référence , b) couple
électromagnétique

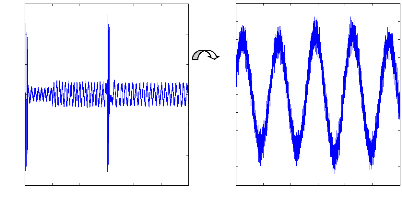
0 0.5 1 1.5 2 2.5 3

t(s)

1 1.05 1.1 1.15 1.2 1.25 1.3

t(s )

i_as(A )

-10

-20

-30

30

20

10

0

-1

-2

-3

-4

-5

5

4

3

2

0

1

zoom

i_as(A )

Figure (IV.18) : Courant de phase statorique, machine en charge et en défauts, 2 barres cassées

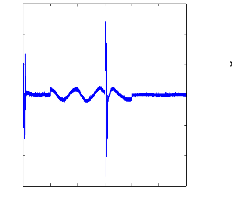
0 0 .5 1 1 .5 2 2 .5 3

t(s )

ⁱrb1(^A

-1 0 0 0

-2 0 0 0

-3 0 0 0

3 0 0 0

2 0 0 0

1 0 0 0

0

1 0 0

irb0,1,2,3(A--)

-1000

-200 0

-3000

3 0 0 0

2 0 0 0

0

0

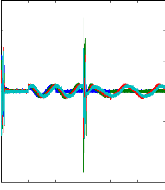
0 0.5 1 1.5 2 2.5 3

t(s)

Figure (IV.19) : courants dans les barres rotoriques : Irb0 , _Irb1 , _Irb2 , Irb3
Machine en charge et en défaut, simulation avec modèle global : 1 barre cassée _rb0 à t=1s, 2
barre cassée _rb1 à t=2s

Nous avons simulé dans la figure (IV.17) une inversion du sens de rotation de +1000 tr/mn à -1000 tr/mn. Ce changement du sens de rotation se déroule à couple maximal et le temps d'inversion en charge est de l'ordre de 0.3 s.

La figure (IV.17) représente l'évolution du couple et la vitesse, quand la référence de vitesse est un échelon d'amplitude 1000 tr/mn. Le temps de réponse de la vitesse est de l'ordre de 0.2 s, Un échelon de couple de 3.5 N.m est appliqué à t=0.4s. Le régime ainsi établi, nous procédons à la simulation d'une première rupture de barre par une augmentation de 11 fois la résistance de cette barre. Après un régime transitoire très bref, la deuxième barre est cassée à t=2s.La vitesse reste toujours peu perturbée par ce défaut.

Le régulateur de vitesse adopté doit avoir un comportement satisfaisant sur toute la plage de vitesse de 0 à 1000 tr/mn et doit satisfaire le plus possible aux exigences suivantes

- rapidité de réponse

- dépassement nul ou faible (< 10%)

- erreur statique nulle en régime permanent

- robustesse aux variations paramétriques

Dans la figure (IV.18), nous observons une déformation au niveau du courant statorique , lors des cassures de barres.

La figure (IV.19) montre les courants dans les barres rotoriques _Irb0 , _Irb1 , _Irb2 , _Irb3 , ou on voit que _irb0 s'annule a cause de la cassure de barre _rb0 à t=1s, et pour _rb1 à t=2s, pour _irb2 ^et irb3, on remarque une déformation dans les allures.

C- Cas d'une variation de charge

Les simulations reportées sur les figures (IV.20), (IV.21) concernent un démarrage en charge de la MAS pour une référence de vitesse de 0 à 1000 tr/mn avec variation du couple de charge en régime établi suivi de l'inversion du sens de rotation entre #177;1000tr/mn à t =1.5 s.

Pour 0.6s<t<3s, on applique un couple de charge de 3.5N.m ;

A l'instant t=2s, on applique un couple de charge C_r=5.5N.m.

Ces résultats montrent que la commande vectorielle indirecte appliquée à la machine asynchrone présentent des performances fort intéressantes.

Lors changement brutal de la consigne, le régulateur PI se trouve soumis à un écart de réglage très important. La réaction de l'action proportionnelle, dont le but est de réduire l'écart, risque de provoquer un grand dépassement.

0 0.5 1 1.5 2 2.5 3

t(s )

0 0.5 1 1.5 2 2.5 3

t(s )

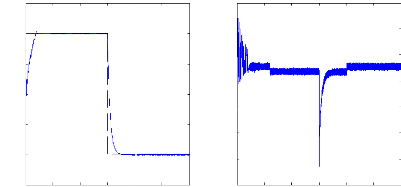
C _em (11 .m )

-10

-20

-30

-40

30

20

10

0

b

II (trim n )

-1000

-1500

1500

1000

-500

500

0

a

Figure (IV.20) : Réponses de la machine asynchrone avec variation de la charge lors d'une
inversion du sens de rotation : a) vitesse de rotation et sa référence , b) couple
électromagnétique

zoom

i_as(A )

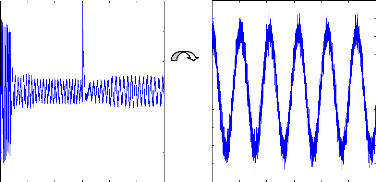
30 20 10 0

i_as(A )

-10
-20

-30

0.5 1 1.5 2 2.5 3

t(s ) 5 4 3 2 1

0

-1

-2

-3

-4

-5

1 1.05 1.1 1.15 1.2 1.25 1.3

t(s )

Figure (IV.21) : Courant de phase statorique, variation de la charge

IV.5Conclusion

La méthode du flux orienté appliquée sur le modèle multi-enroulements de la machine asynchrone a cage d'écureuil moyennant un réglage classique, nous a permis de simuler le système, avec ou sans défauts rotoriques.

Les résultats obtenus montre l'influence des ruptures de barres sur le couple électromagnétique, la vitesse de rotation et le courant statorique, se traduit par des ondulations et déformations des allures.

Il faut signaler que le régulateur P.I ne permet pas en tout cas de maîtriser le régime transitoire. En outre, la faiblesse de la commande vectorielle, se traduit par l'apparition d'une pointe de courant très gênante pour le bon fonctionnement de la machine. C'est les raisons pour lesquelles nous consacrons un chapitre pour l'application d'un régulateur flou.

On s'intéresse dans ce qui suit à l'estimation des états de la machine asynchrone par le filtre de kalman étendu, afin de détecter les défauts rotoriques.

Chapitre v

Estimation des paramètres de la

machine asynchrone par le filtre de

Kalman Etendu en vu de détection des

défauts rotoriques

V.1 Introduction

Le diagnostic de défaut des machines électriques gagne l'importance particulière en raison des pertes de temps d'arrêt et de revenu de machine à l'industrie. Souvent, ces machines courent les charges critiques et leur panne soudaine peut être catastrophique. Ainsi, le système d'entraînement du moteur devrait également avoir les dispositifs diagnostiques pour prévoir des défauts de machine à leur commencement même. En conséquence, il devient très important d'avoir des modèles de machine et de commander les techniques qui peuvent distinguer l'état sain et défectueux des machines. [26]

Dans le domaine de l'estimation des paramètres des machines électriques a courants alternatifs, beaucoup des méthodes ont été proposées. Selon les considérations sur les différentes perturbations, ces méthodes peuvent être déterministes ou stochastiques. Les premières ne font pas d'hypothèse sur les propriétés des bruits, tandis que les secondes tiennent compte des bruits de perturbation du système.

Parmi Les méthodes stochastiques, nous avons, le filtrage de Kalman. Un cas particulier de cette méthode est le Filtre de Kalman Etendu. Il est approprie pour le traitement des mesures bruitées discrètes et pour obtenir des estimes précis des variables d'état et des paramètres du modèle. La façon générale dont il le fait consiste a utiliser les facteurs suivants :

-Une connaissance de la dynamique du système et des mesures.

-La description statistique des bruits du système, des perturbations, des erreurs de mesure et des incertitudes du modèle du système.

- Une information sur les conditions initiales des variables d'intérêt.

Afin d'évaluer ce type de méthode sur un exemple simple représentatif, nous présentons dans ce chapitre, l'algorithme d'estimation en ligne basé sur le filtre de Kalman étendu, pour l'estimation des paramètres de la machine asynchrone en vu de détection des défauts rotoriques.

L'algorithme est vérifie par simulation. On considère une machine asynchrone avec son modèle multi-enroulements. Les variables mesurables sont les courants de phase, les tensions de phase et la vitesse du rotor.

V.2 Modèle discret de la machine asynchrone

L'estimation des variables d'état pour la détection des défauts a besoin d'un modèle dynamique multi-enroulements adéquat de la machine asynchrone. Le modèle réduit est obtenu en utilisant la transformation de PARK. Ce modèle pose les hypothèses habituelles décrites au chapitre II.

Le filtre de Kalman nécessite un modèle discret de la machine qui se déduit du modèle continu.

La représentation de la dynamique de la machine, avec un repère lie au rotor, est donnée par les équations suivantes :

dÖ _ds

VR . I

= + ù . ö

ds s qs (V.1)

s ds dt

-

dÖ _qs

V R . I

= + ù . ö

qs s ds (V.2)

s qs dt -

dödr

0 = . +

R I (V.3)

r dr dt

d ö qr

0 = . +

R I (V.4)

dt

r qr

En choisissant _ids, i_qs, id_r, i_qr,Ie comme variables d'état du modèle réduit du shéma multienroulements de la machine asynchrone, la représentation en espace d'état est :

x& = A . x ( t ) + B .u ( t )

( ) = ( ) ( ) ( ) ( ) ( )

[ ] ^T

x t _ids ^t _iqs ^t _idr ^t _iqr t i_e t

(V.5)

(V.6)

u ( t ) = [ Vds Vqs 0 0]^T (V.⁷)

Le courants stator, étant choisis comme mesures pour compléter le modèle d'espace d'état, l'équation de sortie est :

z ( t ) = h[ x (t ), t] (V.8)

Oil : h = [ ids iqs] (V.⁹)

Le modèle déterministe devient :

a14

-a 11 a12 .w - a13S1 -

0 0

0 0

a₃

S 1 a4

- a₆ . w - a₇ a 8 a₉ . S₁

a16 . w a₁₇ - a 18 - a₁₉ . S₁

? ?

?i

? ?

?i
Le ? ?
ÿ ? I e ÿ

0

0 Ò

?

0 Ò

?

0 Ò

?

? ? i ds

qs Ò

? i Ò

dr

qr Ò

1 ? ? ? ? ?

i

i ds

d

i qs

dt

i dr

i qr

I_e

1 ?

?

?

?

?

i

0

1 ?

?

?

?

?

?i

a10

V

ds

V_qs

a₅

0

0

(V.10)

+

0

a15

0

-

0

a20

0

0 0

- a a w - 2 .

1

Oil :

a 1 = a₇ = 4 . m1 . Lrc .Rs

a ₂ = a₆ = 4 . m1 . Lrc . Lrc

a ₃ = a₉ = 2 . m₁ . M_sr .N_r

a 4 = (L_rc .ù - S₂) .2 . m₁ . M _sr N r

.

a 5 = a₁₀ = 4 . m₁ . L rc

a 8 = (L_rc .ù + S₃) .2 . m₁ . M _sr . N_r

a11 = a17 = 6 . m1 . Msr . Rs

a 12 = a16 = ⁶ . m₁ . M sr . L sc

a 13 = a

? ( M N ) ? 1 ? = 1 . 3 . ^2 . + ? 19 sr r ? L rc ?

1

( ( ù 3 ) ) ?

? ?

a S M N S

2

= 3 . .

m L

- + . . - . ?

14 1 rc . sr 2

r ? L rc ?

a 15 = a₂₀ = 6 . m₁ . M sr

?

( ( ù 2 ) ) ?

1 ?

S M N S

2

a m L

= 3 . . . + . . - . ?

18 1 rc sr r 2 ?

L

rc ?

1

m₁ = ( -3. M _sr2 . N _r + 4. Lrc.L sc)

Et :

S 1 = 12 6 [( _r NR b 0 + R _b15 )cos² Oa +l ( N ux, b14 )cos² 15á

2 ^e +R 2 R e r + R_bl #177; R_b0 )cos² 1a + .^-P (2 R e r #177; R,, + R Ò 1

J

₁4 _rf

- RR _b° cos0 á cos1á) + (R_b1 cos 1 á cos 2á) +
·
·
· + (Rb15 cos15á cos0á)] (V.11)

6

i
? _I

S 2 = - 2 6 r r

[(2 R e + A₀ + g₁₅ )cos0 á sin0 á -(2 R e +R + A,₀ jcos1 á sin1 á (2 R e + g₁₅ +R_b14)cos1 5ásin1

N N_r

2 _rf

+ ₆ RR b 0 sin 0 á cos 1á ) + (R_b1 sin 1 á cos 2á ) +
·
·
· + (R_b15sin15á cos 0á )]

ri

+ ₆ RR _b° cos 0 á sin 1á) + (R_b1 cos 1 á sin 2á ) +
·
·
· + (Rb15 cos 15á sin 0á)] (V.12)

1

Oil : S1,S2, représente les résistances équivalentes des barres rotoriques

Le modèle mathématique discret peut être dérivé de l'équation d'état (V.10). Nous avons

Dans ces équations, A et B sont les matrices du modèle continu et AD, BD sont les matrices correspondants du modèle discret. k représente les instants discrétisés du temps et T_e est la période d'échantillonnage.

Alors, le modèle discret de la machine est décrit par l'équation :

x (k 1) [ 1 . ] . ( ) . . ( )

+ = + e

A T x k T B u k

+ e (V.13)

On considère que la vitesse est constante pendant les instants d'échantillonnage.

V.2.1 Modèle Discret Augmenté

La matrice A varie avec le temps aux éléments qui dépendent de la vitesse rotorique.

Lorsqu'un paramètre, dans ce cas les résistances équivalentes S1, S2 , sont inconnues, une autre équation doit être ajoutée au modèle de la machine; l'équation d'état n'est alors plus linéaire.

Pour estimer les résistances équivalentes, nous introduisons les équations :

S1 (k + 1 ) = S1(k)

S2(k+1) = S2(k)

Cette équation est basée sur I'hypothèse que les résistances équivalentes ne varies pas pendant l'intervalle d'estimation.

Le modèle complet de la machine est, donc :

[

I

1 1

x(k) BD(k)

0 0

.[ V_s ( k)]

S ₁ ( k + 1) = [ 0 1 0.[S ₁ (k ) J

+

(V.14)

x( k + 0

S ₂ ( k +1) j

0 0 _{1_1} S₂ (k) i 0

1)AD(k)

Le nouveau vecteur d'état, xn, est :

(V.15)

a₅ 0 i

0 a10

i sd ( k

i _qs (k

idr ( k

i _qr (k

I_e(k

S ₁(k

S ₂(k

1
i

+

1)

+

1)

+

1)

+

1)

+

1)

+

1)

+

1)

x(k) 1

x _n ( k) = S₁ (k ) =[ i _ds (k ) i _qs (k ) i _dr (k ) i _qr (k ) Ie(k ) S ₁ (k ) S₂ (O]^T S₂(k) j

Le modèle discret augmenté est

1 ? ? ? ? ? ? ? ?

?i

a₃ . S ₁ . Te a₄ .Te 0 0 0

a₈ .Te a₉ . S 1 .Te 0 0 0

a14 .Te 0 0 0

a17 .Te - a₁₈ . Te 1- a₁₉ . S ₁ 0 0 0

1 -Te.a 1 a.

2 w . Te -

-

a₇ .Te
. w. Te

a₆ .Te. w 1-

-

a11. ^Te a12

1 - a S Te

. . -

13 1

a16. w.Te

0 0 0

0 0 0

0 0 0

0 Le.Te 0 0

0 0 1 0

0 0 0 1

a

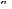
0

15

? ?? V ds

+ 0 - a .

? 20 Ò ? Ò

? V qs

? ?

0 0

?? ?

?

0 0

?? ?

0 0

J

?

L'équation de sortie est :

z ( k) = [i .ds (k) 1 qs (k)

1 _1

(V.16) (V.17)

V.2.2 Modèle Stochastique

Dans la pratique, la machine asynchrone ne peut pas être modélise de manière parfaite. Ceci est du aux hypothèses faites dans le modèle dynamique et a des erreurs qui se présentent dans

les mesures, les filtres, les capteurs, etc. L'utilisation des approximations faites augmente les erreurs par rapport aux valeurs des courants statoriques . Nous considérerons toutes ces erreurs ou incertitudes comme du bruit présent sur les mesures et sur la structure du modèle. Nous supposons dans notre étude que le bruit peut être approximé par la loi de distribution gaussienne. Le nouveau modèle, connu comme un estimateur stochastique est :

z ( k ) = h(k)+v(k) (V.19)

Où :

w k wi k wi k wi k wi k wI wS wS

( ) = ( ) ( ) ( ) ( )

[ ]^T (V.20)

ds qs dr qr e 1 2

v k vi _ds k vi _qs k

( ) = ( ) ( ) 0 0

[ ]^T (V.21)

Le bruit du système w(k) est caractérise par

E{ w( k ) } = 0 (V.22)

E{ w( k ) . w( j ) T } = Q.äkj (V.23)

Q = 0 (V.24)

Le bruit des mesures v(k) est caractérise par

E{ v ( k ) } = 0 (V.25)

E{ v ( k ) . v ( j ) T } = R.äkj (V.26)

R = 0 (V.27)

Où Q est la covariance de I'erreur du modèle et R est la covariance de l'erreur de mesure. L'état initial est caractérise par :

E{ x (0) } = xà₀ (V.28)

? ? E x ? ( (0) à 0 ) . ( (0) à 0 ) 0 x x - x T = P ?? - ?L ?? Ou E[ ] représente l'opérateur d'espérance mathématique.

(V.29)

V.3 Filtre de Kalman Etendu (EKF)

Le filtre de Kalman (KF Kalman Filter) est une technique d'estimation linéaire. Elle ne peut être utilise pour l'estimation des variables d'état et des paramètres d'un système non linéaire a

moins que le modèle du système soit linearisé autour d'un point de fonctionnement. Cette procédure de linéarisation est connue comme le filtre de Kalman étendu (EKF Extended Kalman Filter). Alors, l'algorithme du filtre de Kalman conventionnel peut titre utilise pour estimer simultanément les états du système et les paramètres de la machine de manière simultanée. Le filtre a une structure de prédicteur - correcteur, décrite par la suite:

V.3.1 Prédiction

L'état a l'instant (k+1) dépend non seulement de l'état a l'instant (k), mais aussi de l'erreur du modèle w(k). Etant donné que ces erreurs sont inconnues, la connaissance du modèle mathématique peut nous donner seulement la prédiction de l'état a l'instant (k+ 1).

Donc,

x ( + 1 ) =

k f [ x n e k u k k ]

( ), ( ), (V.30)

n p

ou : x_ne(k) est la valeur estimée de l'état a l'instant (k) que l'on suppose connue, x_np(k+ 1) est la prédiction de l'état a l'instant (k+ 1).

Alors, la prédiction est donnée par l'expression suivante :

? AD k

( ) 0 ? BD k

( )

x k

( 1 )

+ = . ( )

x k + . [ ( ) ]

V k

n p n e s

?? (V.31)

0 1 Òÿ ?? 0 Òÿ

V.3.2 Estimation

Les estimées x_ne(k) peuvent être obtenues de manière récursive en utilisant les mesures pour améliorer les variables prédîtes x_np(k). La correction aux prédictions est proportionnelle aux résidus des mesures :

x n e ( k + 1) = x _nP (k + 1) + K( k + 1) [ z( k + 1) - H . x _nP( k + 1) ] (V.32)

K(k+1) est la matrice de gain de Kalman

[ z ( k + 1) - H .x n P (k + 1)] est le vecteur d'innovation, et

H	?li[	x n(k ),k ]	(V.33)
		?xn

Pour le choix de la matrice de Kalman K(k+1), nous devons définir les erreurs d'estimation ee et de prédiction ep respectivement :

e _e ( k + 1) = x _e ( k + 1) - x _n ( k + 1) (V.34)

e _P ( k+ 1)= x _np ( k + 1) - x_n( k + 1) (V.35)
Ses matrices de covariance associées sont :

P _P ( k + 1) = E [ e _P ( k + 1) . e _P ( k + 1) ^T ] (V.36)

P _e ( k + 1) = E[ e _e ( k + 1) . e _e ( k + 1)^T ] (V.37)

Donc, la matrice de covariance de I'erreur d'estimation P_e, devient :

P k [ ] [ ] T T

+ = -

I K k H P k I K k H K k R K k (V.38)

e ( 1) ( 1) . ( 1) ( 1)

+ + - + + +

( 1) . . ( 1)

+

P

ou R est la covariance de I'erreur de mesure, définie par (V.26).

Il est possible de choisir la matrice de gain K(k+1) de manière a minimiser les variances des erreurs d'estimation des éléments du vecteur d'état qui est estimé. Dans ce cas la K(k+1) est appelée matrice de gain de Kalman. Alors

?trace { P( k + 1) } = 0

? K ( k +1

(V.39)

)

nous obtenons ainsi la matrice de gain de Kalman :

T T

[ ]1

-

K k P k H HP k H R

( 1) ( 1) . . ( 1) .

+ = + + + (V.40)

P P

Avec cette expression, nous avons la matrice de covariance de l'erreur d'estimation :

P k

( 1 ) [ ( 1 ) ] . ( 1 )

+ = -

I K k H P k

+ + (V.41)

e P

Le calcul de K(k+ I) et de P_e (k + I ) a besoin de la matrice de covariance Pp(k+1), donc :

P k

( 1) ( ) . ( ) . ( ) ( )

+ = F k P k F k Q k

^T + (V.42)

P e

Où :

? f	{ x k u k k ( ) , ( ), } { ? f x k u k k ( ) , ( ) , } n n

? S ? S

1 2

1 0

= x k

( )

ne ? 0 0 1

F k

( )

? x k

n ( )

x k n ( )

1

?

?

?

?

? ]

(V.43)

{ x k u k k }
n ( ) , ( ) ,

? f

AD k

( )

0

et Q(k) est la covariance de l'erreur du modèle, défini par (V.23) et calculée de la manière suivante :

tk + 1

Q k

( ) = ? ö ( 1 , ) ( ) ( 1 , )

tk + ô ô ö

Q ^T tk + ô d ô (V.44)

tk

ou Ô( t k +1.,ô ) est la matrice de transition associé a F(T ,x_n(z )) pour z E [k,k + I ] . Ensuite, Q(k) est calculée par intégration trapézoïdal :

Q k

( ) ( 1, ) . . ( 1, )

= ö +

[ k k Q k k Q

^T + ] T 2 ^e

. (V.45

₀ ö + 0

V.3.3 Calcul de F(k) et H(k) ? h x k k

[ ] r 1 0 0 0 0

n ( ),

H = = (V.46)

?_L ?]

? x 0 1 0 0 0

n

? AD k

( ) F k F k

1 ( ) ( ) 1

5

? ?

F k F k

6 Ò

? 2 ( ) ( )

( ) ( ) Ò

3 7

? F k F k

F k

( ) = ? ? (V.47)

F k F k

( ) ( )

? 4 8 Ò

? 0 1 1 Ò

?? ??

? ?

où :

? di ds F k 1 ( ) = ? S 1

? di qs , F k 2 ( ) = ? S 1

? di dr , F k 3 ( ) = ? S 1

? di qr , F k 4 ( ) = ? S 1

, (V.48)

? di ds

F k

5 ( ) =

? S 2

? di qs

, F k

6 ( ) =

? S 2

? di dr

, 7 ( ) =

F k

? S 2

? di qr

(V.49)

, F k

8 ( ) =

?S₂

Valeurs initiales de :

- Vecteur d'état x_n0=x_n(t0)

- Matrices de covariance Q=Q0

R=R0

P0=P(t0)

Prediction du vecteur d'état x _np ( k + 1) = f[x _ne( k ), u ( k ), k ]

?f(xn

Linéarisation du mdèle augmenté F ( k) =[AD(k)

0 ? n ?S2

1

Calcul de la matrice de covariance p ( k 1) F ( k ) p ( k ) F ( k ) T Q ( k )

+ = +

p e

d'état

Calcul de la matrice de gain de Kalman [

T ]1

-

K k

( 1) ( 1) .

+ = P k H HP k H R

T

+ . ( 1) .

+ +

P P

Estimation xn _e ( k + 1) = xn _P ( k + 1) + K ( k + 1) [ z ( k + 1) - H . xn _P ( k + 1) ] du vecteur d'état

Calcul de la matrice de covariance ( 1 ) [ ( 1 ) ] . ( 1 )

P k + = -

I K k H P k

+ +

e P

De l'erreur d'estimation

Retour à la prédiction x_ne(k)=x_ne(k+1)

P_e(k) = P_e(k+1) k=k+1

I
i

( ), u ( k ), k)k

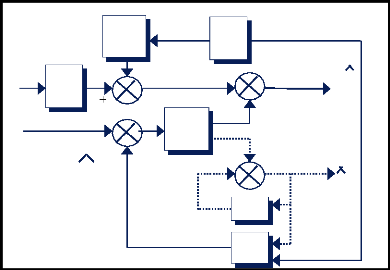
u(k)

1)

AD

1

-

q

+

+

X(k+1)

BD

+

+

K(k+1)

+

-

+

Z(k+1)

e(k+1)

AD

H

k)

X(k+1)

Tableau (V.1) : Algorithme du filtre de Kalman Etendu

V.3.4 Mesures

Le vecteur des mesures h(k) = [ids( k) i_qs(k)] est obtenu à partir des mesures des courants de ligne.

V.4 Application du filtre de Kalman Etendu a la machine asynchrone

L'algorithme décrit ci-dessus est appliqué a l'étude par simulation de l'estimation des paramètres d'une machine asynchrone. Le schéma de la configuration du système est sur la figure (V.2).

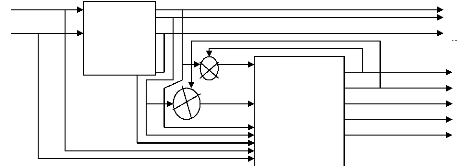
Vqs

Vds

réduit

Modèle de la M.AS

Filtre
De
Kalman
Etendu

Ids
Iqs

ù

Îds
Îqs

Îdr

Îqr
S1

Figure (V.2) : schéma de configuration du modèle pour l'estimation

V.5 Résultats de simulation

V.5.1 Suivi des courants

a- Machine Saine à vide

La simulation est faite pour un temps de 1.5s.

La figure (V.3) présente la variation de la vitesse, le couple en absence du couple de charge. La figure (V.4) illustre le courant statorique en absence de la charge. La figure (V.5) montre la convergence des courants estimés vers les courants réels pour les courants. Les valeurs des courants se stabilisent à des valeurs proches de zéro, a cause de l'absence du couple de charge.

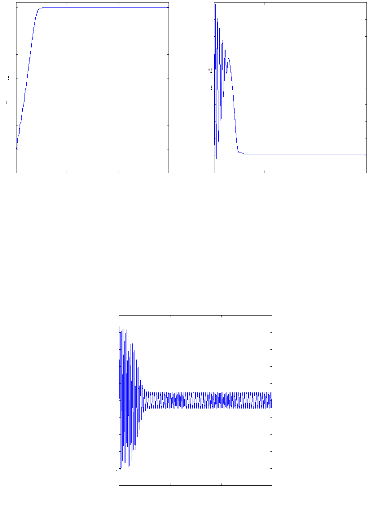
las(A)

0

0 0.5 1 1.5

t(s)

1

¹

Q (trim rtJ

3000

2500

2000

-500

000

500

00

0

0 0.5 1 1.5

t(s)

1

Cem(N.rn)

18

16

14

12

-2

6

4

2

0

Figure (V.3) : la vitesse de rotation, le couple , machine
saine à vide

25

20

15

10

5

-5

-10

-15

-2 0

0 ^0.5 t(s) 1 1.5

Figure (V.4 ) : courant statorique, machine saine à vide

-25

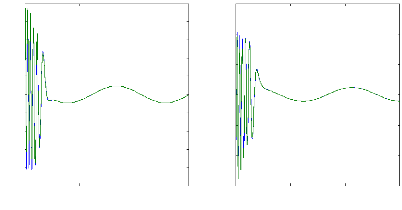
0 0.5 1 1.5

t(s )

0 0.5 1 1.5

t(s )

25

20

15

10

5

0

-5

-10

ⁱd s sE s e (A )

-15

-20

-25

30

20

10

0

10

ⁱqs!ⁱq^S E stim )

-

-20

-30

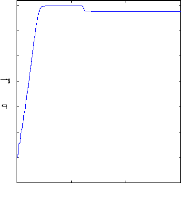
3000

2500

2000

00

(trim n_

000

500

0

-500

0 0.5 1 1.5

t(s)

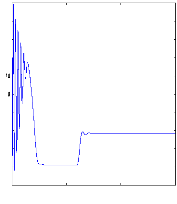
0 0.5 1 1.5

t(s)

Cem(N.rn)

18

16

14

12

-2

6

4

2

0

Figure (V.5) : courants et courants estimés: _ids et
Ids_estimé, iqs ^et _{iqs_estimé,} machine saine à vide

b- Machine saine en charge

On simule maintenant avec un couple de charge de 3.5N.m, alors la machine opère en charge.

On voit, d'après la figures (V.8), La comparaison du courant mesuré et estimé montre la bonne convergence du filtre.

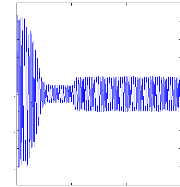
las (A

-1 0

-1 5

-2 0

-2 5

2 5

2 0

1 5

1 0

-5

5

0

0 0 .5 1 1 .5

t(s )

Figure (V.7) : courant statorique, machine saine en charge Cr=3.5 N.m

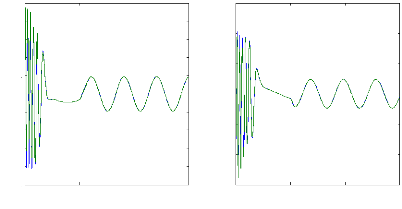
0 0 .5 1 1 .5

t(s )

0 0.5 1 1.5

t(s)

2 5

2 0

1 5

1 0

5

0

-5

-1 0

ⁱds sE stim e (A)

-1 5

-2 0

-2 5

3 0

2 0

1 0

0

1 0

-

ⁱqs!ⁱq^SE stim a )

-20

-30

Figure (V.8) : courants et courants estimés : ids et
Ids_estimé, iqs ^et _{iqs_estimé,} machine saine en charge

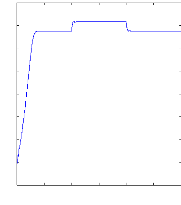
0 0.5 1 1.5 2 2.5 3

t(s)

1

n(trLm n)

3500

3000

2500

2000

1000

-500

500

500

0

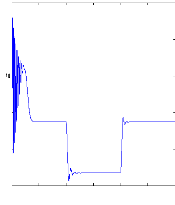
0 0.5 1 1.5 2 2.5 3

t(s)

1

Cem(N.rn)

20

15

-5

5

0

Figure (V.9) : vitesse, le couple et le courant statorique, machine saine lors
d'une variation de charge.

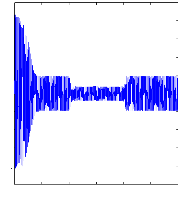
0 0.5 1 1.5 2 2.5 3

t(s)

las(A)

-2 0

-25

-10

-15

25

20

15

10

-5

5

0

Figure (V.10) : courant statorique lors de variation de charge

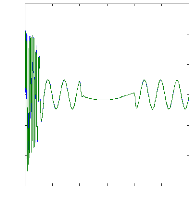
0 0.5 1 1.5 2 2.5 3

t(s)

-

ⁱqs!ⁱq^S E stim )

-20

-30

3 0

2 0

1 0

1 0

0

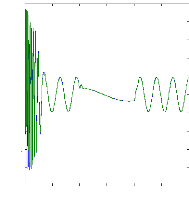
0 0.5 1 1.5 2 2.5 3

t(s)

ⁱd sE stim e (A)

-10

-15

-20

-25

25

20

15

10

-5

5

0

Figure (V.11) : courants et courants estimés: _ids et
Ids_estimé, iqs ^et _{iqs_estimé,lors} de variation de la charge

c- Machine avec défaut

1. cas d'une cassure de barre

Vu la difficulté de voir les défaut à vide, on va simuler la machine en charge avec cassure de barre.

La figure (V.12) illustre l'évolution temporelle en régime transitoire et en régime permanent de la vitesse de rotation, celle-ci se stabilise a une valeur de 2219 tr/mn. La figure illustre aussi du couple électromagnétique Cem en présence d'une rupture des barres _rb0 à t=1s. Aprés une phase transitoire, celui-ci se stabilise a une valeur proche de 3.5 N. m a cause de la présence du couple de charge.

La figure (V.13) illustre l'évolution temporelle en régime transitoire et en régime permanent du courant statorique en présence d'une rupture de barre _rb0 à t=1s .

La figure (V.15) illustre l'évolution temporelle en régime transitoire et en régime permanent des courants _ids , _idr, avec leurs courant estimés en présence d'une rupture de barre _rb0 à t=1s. Les courants circulant dans les barres adjacentes aux barres cassées sont très supérieurs a leur valeur nominale. La comparaison du courant mesuré et estimé montre la bonne convergence du filtre.

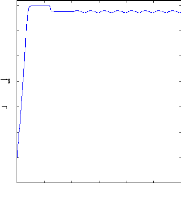
0 0.5 1 1.5 2 2.5 3

t(s)

1

¹

R (trim n_

3000

2500

2000

-500

000

500

00

0

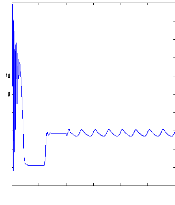
0 0.5 1 1.5 2 2.5 3

t(s)

1

Cem(N.rn)

18

16

14

12

-2

6

4

2

0

Figure (V.12) : vitesse de rotation, couple électromagnétique,
simulation avec le modèle réduit, machine en défaut en charge, Cr=3.5 N.m

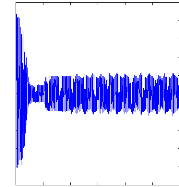
las(A)

-2 0

-25

-10

-15

25

20

15

10

-5

5

0

0 0.5 1 1.5 2 2.5 3

t(s )
Figure (V.13) : courants statorique, avec cassure d'une barre rb0

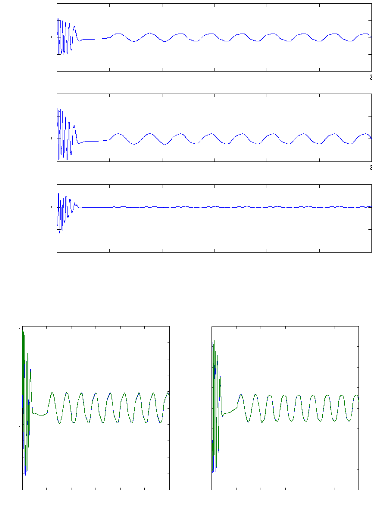
4 0

2 0

0

ids(A)

-2 0

-4 0

0 0 .5 1

t(s ) 1 .5

2 2 .5

0 0 .5

1

1 . 5

t(s )

2 2 .5

t(s)

t(s)

rotor sn

1 barre cassée

0 0 .5 1 1 .5 2 2 .5 3

t(s )

Figure( V.14) :Courant _ids ^et _ids-estimé avec cassure d'une barre rb0 et l'erreur

id s_E stim e

-2 0

4 0

2 0

0

1 0

0

-1 0

-2 0

e rre u r(A )

0 0.5 1 1.5 2 2.5 3

0 0.5 1 1.5 2 2.5 3

25

20

15

10

5

0

-5

-10

ⁱds iⁱdsE slim O^A )

-15

-20

-25

4000

3000

2000

000

0

000

-2000

1

-1

id r' ⁱll. rE s fin' el^A )

-3000

-4000

Figure (V.15) : courants et courants estimés dans les barres rotoriques : ids et
Ids_estimé, idr ^et _{idr_estimé,} avec cassure de barre rb0

2. Cas d'une cassure de deux barres

On impose maintenant un couple de charge de 3.5 N.m à t=0.5s et la machine opère alors en charge avec cassure de deux barres.

La figure (V.16) illustre l'évolution temporelle en régime transitoire et en régime permanent du couple électromagnétique _Cem en présence d'une rupture de barre _rb0 a t=1s et _rb1 a t=2s. Aprés une phase transitoire, celui-ci se stabilise a une valeur proche de 3.5 N. m a cause de la présence du couple de charge, on remarque dans cette figure des ondulations dans les allures de la vitesse et du couple, a cause des cassures des barres.

La figure (V.17) illustre l'évolution temporelle en régime transitoire et en régime permanent du courant statorique , en présence d'une rupture de barre _rb0 à t=1s.

La figure (V.18) illustre l'évolution temporelle en régime transitoire et en régime permanent des courants _ids , _idr et leurs courants estimés en présence d'une rupture de barre _rb0 à t=1s et _rb1 à t=2s, ou on remarque la convergence du filtre. Les courants circulant dans les barres adjacentes aux barres cassées sont très supérieurs a leur valeur nominale. On conclut donc qu'il y a un risque de défaillances en chacune dans la mesure ou les contraintes électriques et thermiques

sont redistribuées sur les conducteurs adjacents.

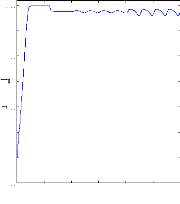
0 0.5 1 1.5 2 2.5 3

t(s)

1

¹

R (trim n_

3000

2500

2000

-500

000

500

00

0

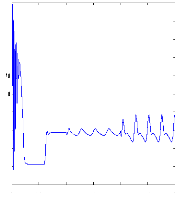
0 0.5 1 1.5 2 2.5 3

t(s)

1

Cem(N.rn)

18

16

14

12

-2

6

4

2

0

Figure (V.16) : vitesse de rotation, couple électromagnétique, simulation avec le modèle
réduit, machine en défaut en charge, C_r=3.5 N.m

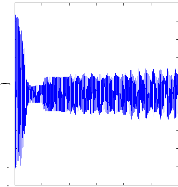
las (A

-10

-15

25

20

15

10

20

25

-5

5

0

0 0.5 ¹ t(s) 1.5 2 2.5 3

Figure (V.17) : courants statorique , avec cassure de deux barres

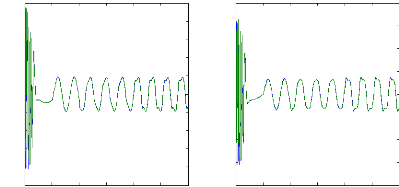
!dr^,-i_drE stim^{(A )}

1

-2000

-3000

-4000

4000

3000

2000

000

000

0

25

20

15

10

5

0

-5

-10

ⁱds s E stim e (A)

-15

-20

-25

0 0.5 1 1.5 2 2.5 3

t(s 0 0.5 1

t (s ₎1.5 2 2.5 3

Figure (V.18) : courants et courants estimés dans : ids et ids_estimé, idr et idr_estimé, avec cassure de
barre _rb0 ^et rb1

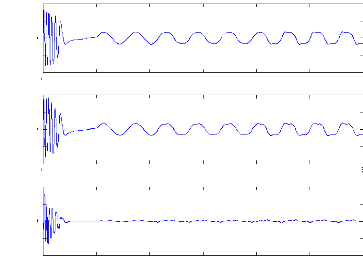
4 0 0 0

2 0 0 0

0

-2 0 0 0

-4 0 0 0

0 0 .5 1

1 . 5

t(s )

2 2 .5 3

4 0 0 0

2 0 0 0

0

-2 0 0 0

-4 0 0 0

0 0 .5 1

t(s )

1 .5 2 2 .5

id re s tim e

id r(A )

erre u r(A )

2 0 0 0

1 0 0 0

0

-1 0 0 0

-2 0 0 0

0 0 .5 1 1 . 5 2 2 .5

t(s )

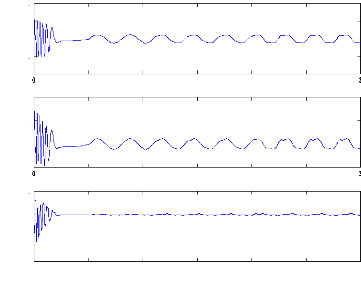
0 .5 1 1 . 5 2

t(s )

2 .5

0 .5 1 1 . 5 2

t(s )

2 .5

0 0 .5 1 1 .5 2 2 .5 3

t(s )

ids(A)

-2 0

-4 0

4 0

2 0

0

id sestim e

-2 0

4 0

2 0

0

e rre u r(A )

-1 0

-2 0

1 0

0

Figure (V.19) : Courant _idr ^et _idr-estimé avec cassure de deux barre

> La cassure d'une barre

Nous simulons la rupture de la première barre (k=0) donc Rb cassé = 11*Rb sain

Les valeurs de S1, S2, S3 et S4 deviennent :-

S1= 3.29213.10^-5 S2= 5.45625.10^-6 S3= 5.45625.10^-6 S4= 3.29213.10^-5

> La cassure de deux barres

On simule la rupture de deux barres adjacentes (K=0, K=1)

Les valeurs de S1, S2, S3 et S4 deviennent :-

S1= 4.11738.10^-5 S2= 1.86375.10^-5 S3= 1.86375.10^-5 S4= 4.11738.10^-5

a. Machine saine à vide : La figure (V.21) présente la variation de la résistance équivalente rotorique estimée.

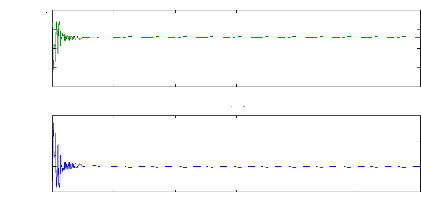
t ( s )

6 x 1 0 - 5

4

2

0

-2

0 0 .5 1 1 .5 2 2 .5 3

StSlestime
(Ohm)

erreur(Ohm)

-2

4 x 1 0 - 5

2

0

0 0 .5 1 1 .5 2 2 .5 3

t ( s )

Figure (V.21) :Estimation de la résistance rotorique équivalente S1, machine à vide

b. Machine saine en charge :

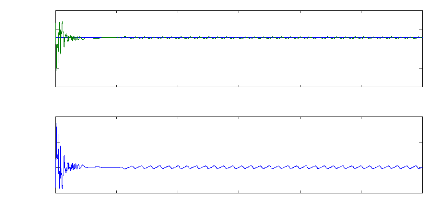
StSlestime
(Ohm)

erreur(Ohm)

0 0 .5 1 1 .5 2 2 .5 3

-2

6 x 1 0 - ⁵

4

2

0

0 0 .5 ¹ t ( s 1 .5 2 2 .5 3 )

1 0 - 5

4

2

0

-2

t ( s )

Figure (V.22) : mode la résistance rotorique équivalente S1, machine saine en charge C_r=3.5N.m

c- Machine avec une cassure de barre :

x 10^-5

Rotor sain

0 0.5 1 1.5 2 2.5

,S (Q) 1 Estime S 1

6 5 4 3 2 1

1 barre cassée

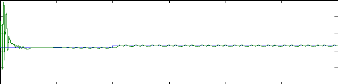
0 0.5 1 1.5 2 2.5

t(s )

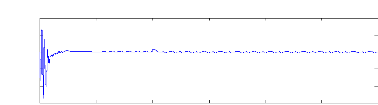
Erreur(Q)

-1

-2

-3

2

0

1

x 10^-5

t(s )

Figure (V.23) : Estimation de la résistance rotorique équivalente S1, machine en défaut (cassure
d'une barre) et en Charge Cr=3.5N.m

d-Cas d'une cassure de deux barres :

,S (Q)
1 Estime

S

I

Erreur(Q)

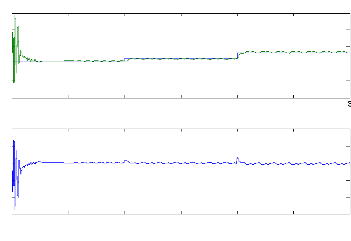
Rotor sain

1 barre cassé

2iéme barre cassée

0 0.5 1 1.5 2 2.5

x 1 0 -5

6

x 1 0 -5

2

t(s )

1

0

-1

-2

-3

0 0.5 1 1.5 2 2.5 3

t(s )

5

4

3

2

1

Figure (V.24) : Estimation de la résistance rotorique équivalente S1, machine en défaut
(cassure de deux barres) et en Charge Cr=3.5N.m

Les figures précédentes présentent la résistance équivalente des barres rotoriques observés. Après une période de convergence, la résistance observée converge vers la même résistance. Nous remarquons une légère oscillation autour de cette valeur.

V.6 Variation des parametres :

En pratique, les paramètres de la machine asynchrone, autres que S1, ne sont pas connus exactement et leur estimation résulte d'une identification du système effectuée, par exemple,

par des méthodes d'estimation hors-ligne. Ces paramètres sont nécessaires pour le calcul du modèle discret de la machine utilisé par le filtre de Kalman. En outre, les paramètres de la machine asynchrone peuvent changer en raison des phénomènes physiques :

échauffement, saturation magnétique, . . ., . Deux problèmes se posent alors dans le calcul du filtre de Kalman :

- La variation des paramètres physiques de la machine asynchrone (comportement non-stationaire),

- L'incertitude paramétrique dans le modèle discret due a l'erreur lors de l'identification préalable

V.7 Conclusions :

Nous avons décrit une technique pour estimer et suivre les courants et la résistance rotorique équivalente des barres rotoriques du modèle réduit du schéma multi-enroulements de la machine asynchrone. Cette technique a été vérifiée par simulation. Les résultats obtenus montrent que le filtre de Kalman étendu peut estimer avec précision en opération normale de la machine, et en présence des défauts rotoriques ( barres cassées).

L'avantage d'utiliser les courant statoriques comme variables d'état est qu'ils sont directement mesurables. La simulation avec le logiciel MATLAB à donner des résultats , qui reflètent l'état de la machine. Notre filtre nous permet d'identifier la présence d'un défaut au niveau du rotor. Nous pouvons ainsi distinguer le défaut physique qui modifient le fonctionnement du moteur.

Chapitre VI

Conception d'un régulateur flou pour

la commande vectorielle de la machine

asynchrone

VI.1 Introduction

Afin de pouvoir appliquer la technique de la logique floue à la commande vectorielle d'une machine asynchrone, nous présentons dans ce chapitre les concepts de la logique floue et nous exposons tous les aspects méthodologiques nécessaires à la compréhension de cette méthode. Nous étudions ensuite la conception d'un contrôleur flou pour la commande vectorielle de la machine asynchrone avec ou sans défauts rotoriques.

VI.2 Principes et définitions de la logique floue

Une des caractéristiques du raisonnement humain est qu'il est généralement fondé sur des données imprécises ou même incomplètes. En effet les connaissances dont nous disposons sur un système quelconque sont généralement incertaines ou vagues, soit parce que nous avons un doute sur leur validité ou alors nous éprouvons une difficulté à les exprimer clairement.

Il est donc nécessaire de penser et de développer un nouveau type de raisonnement, le raisonnement approché, qui permettra de traiter mathématiquement l'imprécis et l'incertain. Le premier à avoir souligné ces possibilités de développement est Lotfi A. Zadeh qui dés 1965 introduit la théorie de la logique floue.

C'est une technique pour le traitement de connaissances imprécises et incertaines. Elle permet de prendre en considération des variables linguistiques dont les valeurs sont des mots ou des expressions du langage naturel, telle que faible, élevée, rapide, lent, grand, petit, etc....

A coté d'un formalisme mathématique fort développé, nous préférons aborder la présentation de manière intuitive. Nous présentons un exemple simple pour comprendre l'intérêt de la logique floue sur la logique classique :

- Exemple : Dans la logique classique, une vitesse peut être qualifiée par le terme « faible » ou « élevée ». Dans la logique floue, des échelons d'appréciation intermédiaires de la variable vitesse sont possibles. La «vitesse » devient une variable linguistique dont les valeurs sont par exemple : « très faible », « faible », « moyenne », « élevée », « très élevée ». Une vitesse de 1000 tr/mn par exemple dans la logique classique correspond au seul ensemble

« moyenne », alors que dans le modèle flou, elle appartient à la fois aux ensembles « faible » et « moyenne ».

VI.2.1 Ensembles flous

La notion d'ensemble flou a pour but de permettre des gradations dans l'appartenance d'un élément à une classe, c'est-à-dire d'autoriser un élément à appartenir plus ou moins fortement à cette classe.

Afin de mettre en évidence cette notion, on introduit les définitions suivantes : Soit un ensemble de référence X continu ou discret d'objets dénotés { x} .

Un ensemble classique A de X est défini sur un univers de discours par une fonction caractéristique u A qui prend la valeur 0 pour les éléments de X n'appartenant pas à A et la

valeur 1 pour ceux qui appartiennent à A (figure VI.3). L'univers de discours est l'ensemble des valeurs réelles que peut prendre la variable floue X .

u A : X ?{ 0,1} (VI.1)

Plus généralement, le domaine de définition de u A (x) peut être réduit à un sous-

ensemble de X .

Un ensemble flou A peut être représenté comme un ensemble de paires (élément générique, degré d'appartenance) ordonnées :

A = { ( x,u _A ( x))/x ?X} (VI.2)

A x X A x / x ,

= ? u

? ( )

A = u

? ( )

A x / x , si X est continu

x

si X est discret

(VI.3)

u

u

x

x

(a) (b)

Figure (VI.1)

Fig . I : Exemple de fonctions d'appartenance (a) logique classique (b) logique

VI.2.2 Variable linguistique

Une variable linguistique est représentée par un triplet ( V , X , T_V ) , dans lequel V est une

variable (la vitesse, la température ...) définie sur un ensemble de référence X , ses valeurs
peuvent être n'importe quel élément de X . On note T_V ( A₁ , A₂, ...) un ensemble, fini ou infini, de

sous-ensembles flous de X , qui sont utilisés pour caractériser V. Afin de permettre un traitement numérique, il est indispensable de les soumettre à une définition à l'aide de fonctions d'appartenance .

Par exemple, si la vitesse est interprétée comme une variable linguistique, alors son ensemble de termes T( vitesse) = { lente, moyenne, rapide . . .} où chaque terme est caractérisé par

un ensemble flou.

Ces termes peuvent être définis comme des ensembles flous dont les fonctions d'appartenance sont montrées sur la figure (VI.4).

u vitesse

lente moyenne rapide

km/s

40 55 70

1

0.5

Figure (VI.2):Représentation Graphique des termes linguistiques

VI.2.3 Fonctions d'appartenance

Une définition des variables linguistiques à l'aide des fonctions d'appartenance est nécessaire dans le but de traiter des déductions floues par calculateur. Dans ce contexte, est attribuée à chaque valeur de la variable linguistique une fonction d'appartenance u , dont la valeur varie entre 0 et 1.

Le plus souvent, nous utilisons des fonctions d 'appartenance de type triangulaire ou trapézoïdale figure (VI.5).

Fonction triangulaire : L'allure est complètement définie par trois paramètres { a, b, c} .

? ? x a

- c x

- ?

u x max min

( ) = ? ?_k , ) ? , 0 ? (VI.4)

? b a

- c b

- )

Fonction trapézoïdale : Elle est définie par quatre paramètres { a, b, c, d } .

( ? x a

- d x

- ? ?

u x max min

( ) = ' i_k , ,

1 ) ? , 0 ? (VI.5)

i b a

- d c

- )

fonction triangulaire 1

0

fonction trapézoïdale

a b c d

a b c

1

0

Figure (VI.3) : Formes usuelles des fonctions d'appartenance.

VI.2.4 Opérations sur les ensembles flous

Puisque les fonctions caractéristiques des ensembles flous sont graduelles, l'extension de certaines opérations définies sur les ensembles classiques au cas des ensembles flous pose certaines difficultés. Donc, il n'est pas possible d'appliquer directement la logique classique qui manipule des ensembles à fonctions caractéristiques binaires (0 ou 1). Pour pallier à ce problème, sont introduites les définitions d'outils nécessaires au traitement des ensembles flous .

Soient A et B deux ensembles flous dans X ayant respectivement u_A et u_B comme

fonctions d'appartenance. L'union, l'intersection, et le complément des ensembles flous sont définies à l'aide de leurs fonctions d'appartenance .

Ces relations sont traduites par les opérateurs "Et" , "Ou " et "Non".

Les opérateurs les plus utilisés en logique floue sont donc :

- l'opérateur " Et " correspond à l'intersection de deux ensembles A er B. Il peut être réalisé par:

- La fonction " min " : x X ( x ) ( ( x ) ( x ) )

? ? u D = min u A , u B

uA n _B( x ) = u_A(x) .u_B(x) .

- La fonction arithmétique " produit " : - L'opérateur " Ou " correspond à l'union de deux ensembles A et B. Il peut être réalisé par:

- La fonction " max " : x X ( x ) ( ( x ) ( x ) )

? ? u C = max u A , u B

- La fonction arithmétique " somme ": u A ? B ( x ) = u_A(x) + u_B(x) - L'opérateur " Non " est réalisé par : u A ( x ) = 1 - u_A( x)

VI.2.5 Propositions floues

VI.2.5.1 Propositions floues élémentaires

Une proposition floue élémentaire est définie à partir d'une variable linguistique ( V , X , T_V ) par la qualification <<V est A>>, pour une caractérisation floue A, appartenant à TV.

VI.2.5.2 Propositions floues générales

Une proposition floue générale est obtenue par la composition de propositions floues élémentaires << V est A >>, << W est B >> ... pour des variables linguistiques V, W ... .

Plus généralement, on peut construire des propositions floues par conjonction, disjonction ou implication, par exemple de la forme << si V est A et W est B alors U est C >> (si la taille est moyenne et le prix est peu cher, alors l'achat est conseillé).

VI.3 Raisonnement en logique floue

Avec l'unique schéma de raisonnement (Si les conditions sont remplies, Alors la conclusion est validée) et les trois opérateurs Et , Ou et Non , nous pouvons déjà prendre un grand nombre de décisions logiques Nous produisons aussi une nouvelle information (une décision) à partir d'informations anciennes.

Le raisonnement flou fait appel à trois notions et étapes fondamentales :

- l'implication floue,

- l'inférence floue,

- l'agrégation des règles..

VI.3.1 Implication floue

L'implication floue donne une information sur le degré de vérité d'une règle floue. En d'autre termes, on quantifie la force de véracité entre la prémisse et la conclusion. Considérons par exemple les deux propositions floues.

? x est A ?

? y est B ? Où x et y sont des variables floues et A et B des ensembles flous de l'univers du discours U.

Ainsi que la règle floue : Si ? x est A ? Alors ? y est B ? .

L'implication floue donne alors le degré de vérité de la règle floue précédente à partir des degrés d'appartenance de x à A (prémisse) et de y à B (conclusion).

On notera implication : opérateur imp (équivalent à l'opérateur Alors). Les normes d'implication les plus utilisées sont :

imp(uA(x), uB(y)) = min(uA(x), uB(y)) (VI.5)

- La norme Larsen imp(uA(x), uB(y)) = (uA(x).uB(y)) (VI.6)
VI.3.2 Inférence floue

Le problème tel qu'il se pose en pratique n'est généralement pas de mesurer le degré de véracité d'une implication mais bien de déduire, à l'aide de faits et de diverses règles implicatives, des évènements potentiels. En logique classique, un tel raisonnement porte le nom de Modus Ponens (raisonnement par l'affirmation).

Si p q vrai

- La norme Mamdani

Alors q vrai

et p vrai

De façon générale, les conditions d'utilisation du Modus Ponens Généralisé sont les suivantes :

Prémisse conclusion

Règle floue : Si x est A Alors y est B

Fait observé : Si x est A'

Conséquence : y est B'

A' et B' sont les ensembles flous constatés dans le cas que l'on traite et ne sont pas nécessairement strictement égaux à A et B. B' est l'ensemble flou résultant de A' par l'application de l'implication.

Les informations disponibles pour déterminer la conséquence sont donc d'une part celles relatives à la règles, quantifiées par l'implication floue _uB/A(x, y), d'autres part celles relatives au fait observé, quantifiées par la fonction d'appartenance uA'.

-Par matrice d'inférence

Elle rassemble toutes les règles d'inférences sous forme de tableau. Dans le cas d'un tableau à deux dimension, les entrées du tableau représentent les ensembles flous des variables d'entrées (température : T et vitesse : V). L'intersection d'une colonne et d'une ligne donne l'ensemble flou de la variable de sortie définie par la règle. Il y a autant de cases que de règles.

U		T
		F	M	E
V	F	Z	P	GP
	E	Z	Z	P

Les règles que décrit ce tableau sont (sous forme symbolique) :

Si T est F Et V est F Alors U = Z Ou

Si T est M Et V est F Alors U = P Ou

Si T est E Et V est F Alors U = GP Ou

Si T est F Et V est E Alors U = Z Ou

Si T est M Et V est E Alors U = Z Ou

Si T est E Et V est E Alors U = P

Dans l'exemple ci-dessus, on a représenté les règles qui sont activées à un instant donné par des cases sombres :

Si (T est M Et V est F) Alors U = P Ou

Si (T est E Et V est F) Alors U = GP

Il s'agit maintenant de définir les degrés d'appartenance de la variable de sortie à ses sous-ensembles flous. Nous allons présenter les méthodes d'inférence qui permettent d'y arriver. Ces méthodes se différencient essentiellement par la manière dont vont être réalisée les opérateurs (ici "Et " et "Ou") utilisés dans les règles d'inférence.

Les trois méthodes d'inférence les plus usuelles sont : Max-min, Max-produit et Somme-produit VI.3.3 Agrégation des règles

Lorsque la base de connaissance comporte plusieurs règles, l'ensemble flou inféré B' est obtenu après une opération appelée agrégation des règles. En d'autres termes l'agrégation des règles utilise la contribution de toutes les règles activées pour en déduire une action de commande floue. Généralement, les règles sont activées en parallèle et son liées par l'opérateur " Ou ".

Nous pouvons considérer que chaque règle donne un avis sur la valeur à attribuer au signal de commande, le poids de chaque avis dépend du degré de vérité de la conclusion.

VI.4 Conception d'un contrôleur flou

Après avoir énoncé les concepts de base et les termes linguistiques utilisés en logique floue, nous présentons la structure d'un contrôleur flou.

En général, un contrôleur flou est un système qui associe à tout vecteur d'entrée X=[x1,x2,...,xn] un vecteur de sortie Y=[y1,y2,....yn] tel que Y=F(X) où F(X) est souvent une fonction non linéaire.

Le schéma de base d'un contrôleur flou repose sur la structure d'un régulateur classique à la différence que l'on va retenir la forme incrémentale. Cette dernière donne en sortie, non pas la grandeur de commande à appliquer au processus mais plutôt l'incrément de cette grandeur.

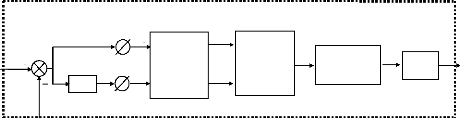
Contrôleur Flou

Iref

+

1 -
-z

1

e

de Kde

Ke

Fuzzification

de~

e~

Base de Règles et logique prise de décision

dR_s

Défuzzification

dR_s~

?

RS

Courant mesuré

Figure (VI.4) : Structure interne d'un contrôleur flou

Dans le schéma ci-dessus comme dans ce qui suit, nous notons

· e : l'erreur, elle est définie par la différence entre la consigne et la grandeur à réguler. e ( k ) = e^* (k ) - e(k ) (VI.7)

· de: la dérivée de l'erreur, elle est approchée par

de k ( ) ( 1)

e k e k

- -

( ) = (VI.8)

T_e

La sortie du régulateur est donnée par

R _S ( k ) = R _S (k -1) +dR _S (k) (VI.9)

Des facteurs d'échelle des gains sont utilisés en entrée et en sortie du contrôleur flou, ils permettent de changer la sensibilité du régulateur flou sans en changer sa structure.

Les règles d'inférences permettent de déterminer le comportement du contrôleur flou. ^Iidoit donc inclure des étapes intermédiaires qui lui permettent de passer des grandeurs réelles

vers les grandeurs floues et vice versa; ce sont les étapes de fuzzification et de defuzzification (figure VI.5)

1- L'interface de fuzzification inclut les fonctions suivantes :

Les ensembles flous des variables d'entrée et leurs fonctions d'appartenance sont à définir en premier lieu.

L'étape de fuzzifiation permet de fournir les degrés d'appartenance de la variable floue à ses ensembles flous en fonction de la valeur réelle de la variable d'entrée.

2- La base de connaissance comprend une connaissance du domaine d'application et les buts du contrôle prévu. Elle est composée.

- d'une base de données fournissant les définitions utilisées pour définir les règles de

contrôle linguistique et la manipulation des données floues dans le contrôleur ;

- d'une base de règles caractérisant les buts et la politique de contrôle des experts du

domaine au moyen d'un ensemble de règles de contrôle linguistique.

Comme nous l'avons précédemment évoqué, nous allons nous baser sur une matrice ou table d'inférence pour cette étape.

La construction d'une telle table d'inférence repose sur une analyse qualitative du processus.

L'inférence se fait donc sur la base des matrices que l'on vient de décrire. On commence par utiliser un opérateur pour définir la description symbolique associée à la prémisse de la règle ; c'est à dire réaliser le " Et ". On passe ensuite à l'inférence proprement dire qui consiste à caractériser la variable floue de sortie pour chaque règle. C'est l'étape de la conclusion " Alors ".

Enfin, la dernière étape de l'inférence, appelée agrégation des règles, permet de synthétiser ces résultats intermédiaires.

Comme nous l'avons vu, la manière de réaliser les opérateurs va donner lieu à des contrôleurs flous différents. Les régulateurs les plus courants sont ceux de :

· Régulateur type Mamdani

· Régulateur type Sugeno

Ils sont dits de type procédural . En effet, seule la prémisse est symbolique. La conclusion, qui correspond à la commande, est directement une constante réelle ou une expression polynomiale fonction des entrées.

L'établissement des règle d'inférence est généralement basé sur un des points suivants :

· l'expérience de l'opérateur et/ou du savoir-faire de l'ingénieur en régulation et contrôle.

· Un modèle flou du processus pour lequel on souhaite synthétiser le régulateur.

· Les actions de l'opérateur ; s'il n'arrive pas à exprimer linguistiquement les régles qu'il utiliser implicitement.

· L'apprentissage ; c'est dire que la synthèse de règle se fait par un procédé automatique également appelé superviseur. Souvent, des réseaux neuronaux y sont associées.

L'évaluation des règles d'inférence étant une opération déterministe, il est tout à fait envisageable de mettre sous forme de tableau ce contrôleur.

Il reste, toutefois, intéressant dans certains systèmes complexes, de garder l'approche linguistique plutôt que d'avoir à faire à un nombre trop important de valeurs précises .

De plus, un algorithme linguistique peut être examiné et discuté directement par quelqu'un qui n'est pas l'opérateur mais qui possède de l'expérience sur le comportement du système.

La formulation linguistique de la sortie permet également d'utiliser le régulateur flou en boucle ouverte donnant ainsi à l'opérateur les consignes à adopter.

Si, après inférence, on se retrouve avec un ensemble flou de sortie caractérisé par l'apparition de plus d'un maximum, cela révèle l'existence d'au moins deux règles contradictoires. Une grande zone plate (figure VI.7,8), moins grave de conséquence, indiquerait que les règles, dans leur ensemble, sont faibles et mal formulées.

u

u

N

Z P PG

NG

1

N

1

Z P PG

dRn

dRn

NG

Figure (VI.5) : Cas de régles floues Figure (VI.6) : Cas de régles floues

contradictoires mal formulées

3- La logique de prise de décision est le noyau du contrôleur flou, elle est capable de simuler la prise de décision de l'être humain en se basant sur les concepts flous et les règles d'inférences en logique floue.

4- L'inférence de défuzzification réalise les fonctions suivantes :

- une cartographie d'échelle convertissant la plage des variables de sortie aux univers de discours appropriés ;

- Une défuzzification fournissant une action de contrôle (physique) à partir d'une action de contrôle flou.

Pour pouvoir définir la loi de commande, le contrôleur flou doit être accompagné d'une procédure de défuzzification jouant le rôle de convertisseur de la commande floue en valeur physique nécessaire pour un tel état du processus. Il s'agit de calculer, à partir des degrés d'appartenance à tous les ensembles flous de la variable de sortie, l'abscisse qui correspond à la valeur de cette sortie.

Plusieurs stratégies de défuzzification existent, les plus utilisées sont .

- Méthode du maximum

- Méthode de la moyenne des maxima

- Méthode du centre de gravité

- Méthode des hauteurs pondérées

VI.5 Conception d'un régulateur flou de vitesse

Nous allons maintenant illustrer les principes du contrôleur flou sur l'exemple de la régulation de vitesse de la machine asynchrone. La phase de conception d'un contrôleur flou passe toujours par quatre stades que nous allons détailler successivement.

· 1 ére étape : Choix des entrées et sorties

Il s'agit de déterminer les caractéristique fonctionnelles (1) et opérationnelles (2) du contrôleur.

(1)- Il faut d'abord choisir les variables d'entrée et de sortie. Leur choix dépend du contrôle que l'on veut réaliser. Que souhaite-t-on au juste commander ? A l'aide de quels paramètres va-t-on obtenir la commande ?

(2)-Il faudra ensuite se pencher sur le domaine des valeurs que pourront prendre ces variables). On partitionnera alors ces domaines en intervalles, auxquels on associera un label descriptif (variables linguistique). Cette étape revient à définir les univers des discours des variables d'entrée et de sortie et les diviser en sous-ensembles flous. Cette répartition est intuitif et basé sur l'expérience. On est d'ailleurs généralement amené à l'affiner en cours de conception. Une règle de bonne pratique est de fixer 5 à 9 intervalles par univers de discours. Il faut également prévoir un plus grand nombre de zones à proximité du point de fonctionnement optimal pour en faciliter l'approche régulière [43], [44].

Illustration sur le régulateur de vitesse

Dans le cas de la régulation de vitesse, on a besoin habituellement de l'erreur (e=?_{r ref} -?_r) et de la dérivée d'erreur (de) et parfois de l'intégration d'erreur :

e k ( ) rref ( ) r ( ) = ? k - ? k de k e k e k ( ) ( ) ( ) = - - 1

(VI.12)

La sortie du régulateur de vitesse est la valeur du couple de référence dans le schéma de la commande vectorielle indirecte de la machine asynchrone. Si cette sortie est directement appliquée au processus, le contrôleur est alors appelé contrôleur flou de type PD [42] et.on peut écrire : Te= _Fuzzy (e, de)

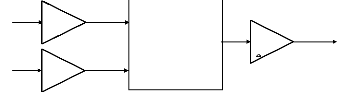
Contrôleur
flou

Kde

Ke

e

de

Kdt

dte

e

de

Kde

ke

kTe

?

Te

Figure (VI.7 ) : Contrôleur flou de type PD

Par contre, si la sortie du contrôleur flou est considérée comme un incrément de commande, le contrôleur est appelé contrôleur flou de type PI [42] et on peut écrire :

? . ?

dte= _Fuzzy (e, de) ou encore dte = F uzzy ? e dt de

?? , ?? ;

soit Te ( k ) = dte(k) +Te(k -1) (VI.13)

Contrôleur

flou

Figure (VI.8) Contrôleur flou de type PI

Contrôleur

flou

e

de

Kde

ke

Kdte

Le contrôleur de type PID peut être obtenu en combinant des contrôleurs flous de type PI et PD de façon suivante :

+ Te

?

kTe

+

Figure (VI.9) Contrôleur flou de type PID

On remarque que cette structure de commande flou de type PID est en fait une association en série d'un contrôleur flou de base et d'une structure de régulation de type PI, qui, elle, n'est pas floue [42].

De plus, comme dans la régulation classique, on a besoin d'une limitation du couple de référence, pour empêcher une sur utilisation de la machine [36]. Cette fonction peut être réalisée par l'algorithme de la figure (VI.10).

Comme les fonctions d'appartenance sont normalisées entre [-1, 1], les variables sont multipliées avec des gains proportionnels. Finalement, la structure du régulateur de vitesse à logique floue est la suivante :

Calcul de Te(k)
Te(k) = dte(k) + Te(k-1)

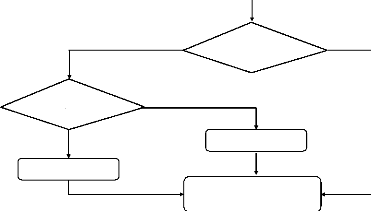
^oui

Te(k) = Temax

Te(k) > 0

oui

non

|Te(k)| = Temax

Te(k)
variable de sortie

Te(k) = - Temax

non

Figure (VI.10) Algorithme pour limitation deTe(k)

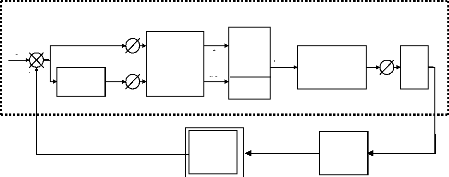
?ref

CONTROLEUR FLOU

+

-

?

Calcul de
de

e

de

kde

k

Fuzzificati
on

Processus

d

de~

Règles
de
contrôle
flou
Inférenc

dte

Défuzzificatio
n

Limitatio
n du
couple

dte

kdte

?

Te

Figure (VI.11) Structure du régulateur de vitesse à logique floue

D'après ce schéma, le système est composé :

* du contrôleur flou composé :

· d'un bloc de calcul de variation de l'erreur au cours du temps (de) ;

· des facteurs d'échelles associés à l'erreur, à sa dérivée et à la commande (dte);

· d'un bloc de fuzzification de l'erreur et de sa variation ;

· des règles de contrôle flou et d'un moteur d'inférence ;

· d'un bloc de défuzzification utilisé pour la variation de la commande floue en valeur numérique ;

· d'un bloc intégrateur ;

* du processus à contrôler.

· 2 éme étape : Définition des fonctions d'appartenance

La première étape de conception a permis de cerner au mieux les caractéristiques linguistiques des variables. Il faut maintenant définir complètement les sous-ensembles flous, c'est à dire expliciter leurs fonctions d'appartenance. Une fois encore, l'intuition et l'expérience auront leur rôle à jouer. Quelques principes ressortent de la pratique: choix de fonctions triangulaires ou trapézoïdales, recouvrement d'une fonction de 10 à 50% de l'espace des sous-ensembles voisins, somme des degrés d'une zone de recouvrement égale à 1 (degré maximal d'appartenance) [43], [44].

Illustration sur l'exemple

Les fonctions d'appartenance des variables d'entrée sont illustrées par la figure (VI.14)

avec :

NB : Negative Big (Négative Grand) PB : Postive Big (Positive Grand)

NM : Negative Medium (Négative Moyenne) PM : Postive Medium (Positive Moyenne) NS : Negative Small (Négative Petit) PS : Postive Small (Positive Petit)

ZE : Zero

On constate que les fonctions d'appartenance de l'erreur ont une forme asymétrique créant une concentration autour de zéro qui améliore la précision près du point de fonctionnement désiré.

Pour la même raison, les formes des fonctions d'appartenance de la variable de sortie sont également asymétriques. Cependant, nous introduisons deux sous-ensembles additionnels compte-tenu de la sensibilité de cette variable [44].

NVB : Negative Very Big (Négative Très Grand) PVB : Postive Very Big (Positive Très Grand)

· 3 éme étape : Définition du comportement du contrôleur flou Cette étape concerne l'élaboration de la base de règle du contrôleur. Analyse du comportement dynamique - Détermination du jeu de règles

L'analyse temporelle, qui doit conduire à établir les règles du contrôleur flou, peut par exemple consister à considérer la réponse à un échelon d'un processus à piloter en fonction des objectifs que l'on se sera fixé en boucle fermée, et à écrire les règles pour chaque type de comportement du processus :

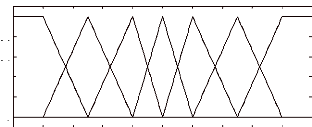
0.8

0.6

0.4

0.2

0

1

Degré d'appartenane u(e)

NB NM NS EZ PS PM PB

-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

erreur e

D e g r é d 'a p p a r t e n a n c e u ( d e )

- 1 - 0 . 5 0 0 . 5 1

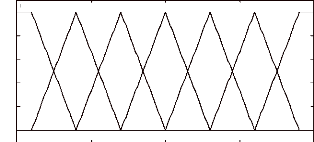
0 . 8

0 . 6

0 . 4

0 . 2

0

1

N B N M N S E Z P S P M P B

Variation d e l 'e r r e u r `d e '

Figure (VI.12) Fonctions d'appartenance des variables d'entrée

D e g r é d 'a p p a rte n a n c e u ( d te )

- 1 - 0 .5 0 0 .5 1

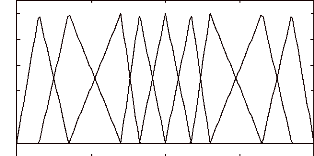
0 .8

0 .6

0 .4

0 .2

0

1

N V B N B N M N S E Z P S P M P B P V B

Variation d u Couple: `d te '

Figure (VI.13) Fonctions d'appartenance de la variables de sortie

7

Sortie s

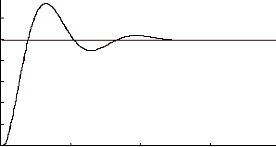
1

temps

·

4

3

·

·

2

·

6

5

·

·

·
·

8 9

Référence

·

Figure (VI.14) Ecriture du jeu de règles grâce à une analyse temporelle

a)- Pour expliquer la procédure à suivre [42], on considère les neuf points indiqués sur la réponse à un échelon et, pour chacun de ces points, on explicite l'expertise sous la forme suivante :

· 1 Si e = PB Et de = ZE Alors du = PB (départ, commande importante)

· 2 Si e = PB Et de = NS Alors du = PM (augmentation de la commande pour gagner l'équilibre)

· 3 Si e = PM Et de = NS Alors du = PS (très faible augmentation de u pour ne pas dépasser)

· 4 Si e = PS Et de = NS Alors du = ZE (convergence vers l'équilibre correcte)

· 5 Si e = ZE Et de = NS Alors du = NS (freinage du processus)

· 6 Si e = NS Et de = NS Alors du = NM (freinage et inversion de la variation de la commande)

· 7 Si e = NM Et de = ZE Alors du = NM (rappel du processus vers l'équilibre correcte)

· 8 Si e = NS Et de = PS Alors du = ZE (convergence vers l'équilibre correcte)

· 9 Si e = ZE Et de = ZE Alors du = ZE (équilibre)

En décrivant point par point le comportement du processus et l'action de variation de commande à appliquer, on en déduit la table suivante (table du contrôleur flou de base) qui correspond en fait à table de règles très connue de Mac Vicar - Whelan [42] :

b)- Pour déduire les autres règles ,nous procédons à nouveau à une autre expertise [45].

La forme générale de la réponse de vitesse est représentée sur la figure (VI.16). Selon l'amplitude de e et le signe de de, la réponse de vitesse est divisée en quatre régions. Les indices utilisés pour identifier chaque région sont définies comme suit :

a1 : e > 0 et de < 0, a2 : e < 0 et de < 0,

a3 : e < 0 et de > 0, a4 : e > 0 et de > 0,

e de	NB	NM	NS	ZE	PS	PM	PB
PB	ZE	PS	PM	PB	PB	PB	PB
PM	NS	ZE	PS	PM	PB	PB	PB
PS	NM	NS	ZE	PS	PM	PB	PB
ZE	NB	NM	NS	ZE	PS	PM	PB
NS	NB	NB	NM	NS	ZE	PS	PM
NM	NB	NB	NB	NM	NS	ZE	PS
NB	NB	NB	NB	NB	NM	NS	ZE

Figure (VI.15) Table de règles de MacVicar-Whelan

Pour identifier la pente de la réponse lors du passage par le point de référence on utilise l'indice ci défini comme suit :

c1	: ( e > 0	--* e < 0	) et de <<< 0
c2	: ( e > 0	--* e < 0	) et de << 0
c3	: ( e > 0	--* e < 0	) et de	< 0
c4	: ( e < 0	--* e > 0	) et de	> 0
c5	: ( e < 0	--* e > 0	) et de	>> 0
c6	: ( e < 0	--* e > 0	) et de	>>> 0

Quant à l'indice représentatif du dépassement de la consigne, il est défini par :

m1 : de	0	et	e <<<	0	m4 : de	0	et	e > 0
m2 : de	0	et	e <<	0	m5 : de	0	et	e >> 0
m3 : de	0	et	e <	0	m6 : de	0	et	e >>> 0

Les trois types d'indices mentionnés ci-dessous peuvent être combinés et former un plan d'état. Le tableau de la figure (VI.17) est légèrement modifié pour tenir compte que la variable de sortie est formée de neuf valeurs floues.

		e
		NB	NM	NS	ZE	PS	PM	PB
de	NB	NVB	NVB	NVB	NB	NM	NS	ZE
	NM	NVB	NVB	NB	NM	NS	ZE	PS
	NS	NVB	NB	NM	NS	ZE	PS	PM
	ZE	NB	NM	NS	ZE	PS	PM	PB
	PS	NM	NS	ZE	PS	PM	PB	PVB
	PM	NS	ZE	PS	PM	PB	PVB	PVB
	PB	ZE	PS	PM	PB	PVB	PVB	PVB

Figure (VI.16) Base de règles du régulateur I de vitesse

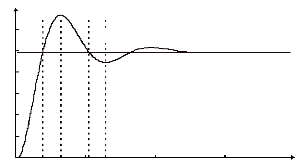
Réponse

1.4

a1 a2 a3 a4

Référence

temps

0.5 1 1.5 2

1.2

1.0

0.8

0.6

0.4

0.2

0

a)

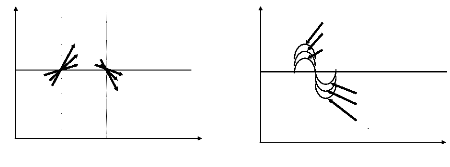
? réponse ?

C1

C2

référence

C4

C5

C6

temps

b)

C3

m6

temps

réponse

m2

référence

c)

Figure (VI.17) Comportement dynamique de la réponse de vitesse

e de

NB

NM

NS

ZE

PS

PM

PB

NB

c1 c2 c3

a1

a2 NS

NM

ZE

m1 m2 m3

ZE

m4 m5 m6

PS

c4 c5 c6

a3 PB

a4

PM

Figure (VI.18) Règles linguistiques de contrôle

Dans le tableau (VI.16), chaque élément formalise une règle comme, par exemple : Si [ e(k) est NM ] Et [ de(k) est ZE ], ALORS [ dte(k) est NM ].

Cet ensemble de règles regroupe toutes les situations possibles du système évaluées par les différentes valeurs attribuées à e et à sa variation de et toutes les valeurs correspondantes de la variation de la commande dte.

L'évaluation des gains proportionnels provient de l'expérience. Pour le gain Ke , par exemple, on peut commencer avec un facteur qui dépend de l'erreur maximale. Effectivement ces valeurs font partie de la procédure d'évaluation par simulation. On a trouvé les valeurs suivantes pour la machine asynchrone simulée :

Ke = 0.1 Kde = 0.6*10^-5 Kdte = 65

Dans une deuxième approche d'un régulateur à logique floue, on utilise différentes fonctions d'appartenance pour la variable de sortie (figure VI.21):

Degré d'appartenance u(dte)

1 NVB NB NM NS ZE PPS PM PB PVB

0.5

0

-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1

Variation du couple `dte'

Figure (VI.19) Fonctions d'appartenance de la variable de sortie dte(k) (II)

Grâce à cette fonction d'appartenance, appelée «singleton », on tire profit du calcul de la variable de sortie. Dans ces conditions, la formule du centre de gravité se simplifie par :

m

? u

( ) dte dte i

i

=

i

=

i

=

1

m

? u ( )

dte i

1

(VI.14)

dteres

m étant le nombre totale de règles.

Par rapport à la première approche, les règles sont aussi modifiée

		e
		NB	NM	NS	ZE	PS	PM	PB
de	NB	NVB	NVB	NVB	NB	NM	ZE	ZE
	NM	NVB	NVB	NB	NB	NM	ZE	PS
	NS	NVB	NB	NB	NM	PS	PB	PM
	ZE	NVB	NB	NM	ZE	PM	PB	PB
	PS	NVB	NB	NS	PM	PB	PB	PVB
	PM	NVB	ZE	PM	PB	PB	PVB	PVB
	PB	NVB	ZE	PM	PB	PVB	PVB	PVB

Figure (VI.20) Base des règles du régulateur II

Ici, la méthode pour déterminer les règles est appelée en anglais << bang-bang control >> [44]. Ce type de méthode est utilisée pour amener initialement le système près du point de fonctionnement souhaité, puis changer la polarité de la variable de commande afin d'éviter un dépassement. Ces deux étapes sont visualisées par les régions A et B dans le tableau (VI-23) :

e
de		NB	NM	NS	ZE	PS	PM	PB
	NB
	NM					B
	NS
	ZE				D			A
	PS			C
	PM
	PB

Figure (IV.21) Schéma de règles en principes de << bang-bangc control >>

Ce principe est répété dans la région C, mais plus modestement. Les flèches décrivent le chemin, qui est suivi dans le tableau (VI.21) en cas d'un échelon positif comme signal de référence. Par conséquent, le reste du tableau est rempli par symétrie à la région D.

VI.6 Application de la logique floue au modèle réduit du schéma multi_enroulements de la machine asynchrone

VI.6.1 Résultats de la simulation

le régulateur flou a été simulé sous différentes conditions avec ou sans défauts rotorique ; les résultats de simulation permettant ainsi de comparer les deux types de régulations (classique et floue). Ces simulations s'avèrent nécessaires dans le processus d'évaluation des régulateurs à logique floue.

1. Machine saine

a. Machine saine à vide

Dans une première étape, nous avons simulé le fonctionnement du régulateur flou avec une machine saine à vide. Ce dernier présente un grand intérêt pour une implémentation en temps réel au niveau algorithmique (meilleure utilisation de la mémoire et temps de traitement plus rapide ).

La figure (VI.22) montre la réponse de la vitesse et du couple avec un régulateur de vitesse flou dans le cas d'une machine à vide. Les temps de réponse en démarrage sont respectivement de 0.2s pour une consigne de 1000 tr/mn . Les temps d'inversion de la vitesse à -1000 tr/mn et 1000 tr/mn sont de l'ordre de 0.4s. Les temps de réponse et d'inversion sont pratiquement identiques à ceux du régulateur classique.

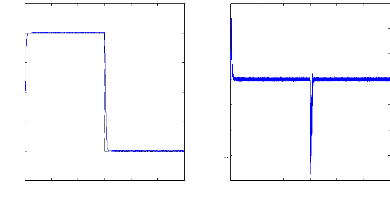
1500

1000

500

0

n (trim n)

-500

-1000

-1500

60

40

20

0

-20

C _en (N .m )

-40

-60

-80

0 0.5 1 1.5 2 2.5 3

t(s)

0 0.5 1 1.5 2 2.5 3

t(s)

Figure (VI.22) : vitesse de rotation, couple électromagnétique , simulation avec modèle,
machine saine à vide.

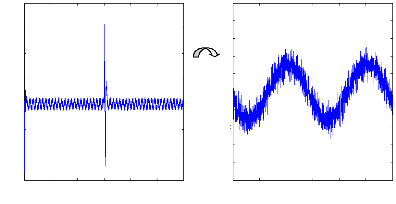
0 0.5 1 1.5 2 2.5 3

t(s)

1 1.02 1.04 1.06 1.08 1.1 1.12

t(s)

jas(A )

-10

-20

-30

40

30

20

10

0

-1

-2

-3

-4

-5

5

4

3

2

1

0

zoom

jas(A )

Figure (VI.23) : courant statorique, simulation avec modèle réduit, machine
Saine à vide .

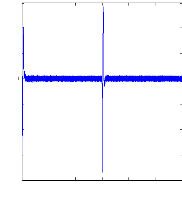
0 0.5 1 1.5 2 2.5 3

t(s)

irbo(A )

-1000

-1500

-2000

1500

1000

-500

500

0

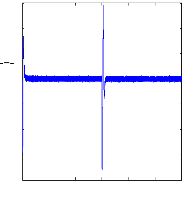
0 0.5 1 1.5 2 2.5 3

t(s)

irbilA

-1000

-1500

-2000

1500

1000

-500

500

0

Figure (VI.24) : courants dans les barres rotoriques : Irb0, Irb1,

simulation avec modèle global, machine saine à vide

b. Machine saine en charge

Les résultats de simulation de la figure (VI.25) montrent que l'allure de la courbe de vitesse est similaire à celle obtenue par un (PI classique) mais avec un temps de montée un peu plus rapide (environ 0.17 s) ceci est dû au fait que les domaines physiques relatifs à l'erreur et la variation de l'erreur soient plus larges dans le cas du contrôleur flou. Le comportement des autres grandeurs est similaire à celui obtenu avec un régulateur conventionnel. Les réponses des systèmes sont caractérisées par les même faits : le démarrage et l'inversion de vitesse s'effectuent à couple maximal .

La figure (VI.25) montre également l'effet d'une perturbation du couple de charge en régime permanent Cr=3.5N.m. Le contrôleur flou reste pratiquement insensible à cette variation du couple résistant. La réaction du régulateur à logique floue au moment d'application de charge est aussi caractérisée par une variation plus petite et un temps plus court par rapport au régulateur classique.

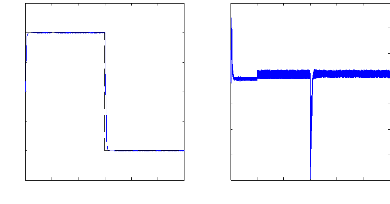
1500

1000

500

0

n (trim n )

-500

-1000

-1500

60

40

20

0

-20

C _en (N .m )

-40

-60

-80

0 0.5 1 1.5 2 2.5 3

t(s)

0 0.5 1 1.5 2 2.5 3

t(s)

Figure (VI.25) : vitesse de rotation, couple électromagnétique , simulation avec modèle,
machine saine en charge C_r= 3.5 N.m

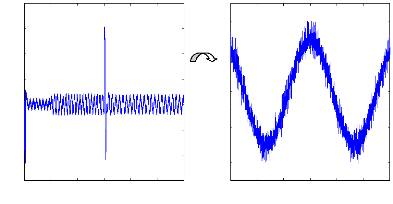
0 0.5 1 1.5 2 2.5 3

t(s)

1 1.02 1.04 1.06 1.08 1.1 1.12

t(s)

las (A )

-10

-20

-30

40

30

20

10

0

-1

-2

-3

-4

-5

5

4

3

2

0

1

zoom

las (A )

Figure (VI.26) :courant statorique, simulation avec modèle réduit, machine
saine en charge, Cr=3.5N.m.

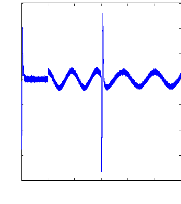
0 0.5 1 1.5 2 2.5 3

t(s )

irbo(A)

-1000

-1500

-2000

1500

1000

-500

500

0

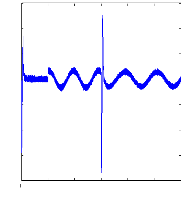
0 0.5 1 1.5 2 2.5 3

t(s)

irb 1 (A )

-1000

-1500

-2 00 0

1500

1000

-500

500

0

Figure (VI.27) : courants dans les barres rotoriques : Irb0, Irb1, simulation avec modèle global,
machine saine en charge, C_r= 3.5 N.m

2. Machine en défaut

a. Machine avec cassure de barre

La figure (VI.28) illustre l'évolution temporelle en régime transitoire et en régime permanent de la vitesse de rotation, on a une inversion de vitesse à t=0.4s. La figure illustre aussi du couple électromagnétique _Cem en présence d'une rupture des barres _rb0 à t=1s. Aprés une phase transitoire, celui-ci répond instantanément et suit la référence sans dépassement ni erreur statique C_r=3.5 N.m a cause de la structure du régulateur flou, les réponses des systèmes sont caractérisées par les même faits :

la vitesse de référence est atteinte en 0,15 sec environ lors de l'inversion de vitesse selon une rampe.

La figure (VI.29) illustre l'évolution temporelle en régime transitoire et en régime permanent du courant statorique en présence d'une rupture de barre _rb0 à t=1s .

La figure (VI.30) illustre l'évolution temporelle en régime transitoire et en régime permanent des courants de barres _Irb0 , _Irb1 en présence d'une rupture de barre _rb1 à t=1s,et on observe le courant dans la barre _rb0, qui proche de Zéro a cause de la cassure . Les courants circulant dans les barres adjacentes aux barres cassées sont très supérieurs a leur valeur nominale. On conclut donc qu'il y a un risque de défaillances en chacune dans la mesure ou les contraintes électriques et thermiques sont redistribuées sur les conducteurs adjacents.

On remarque que la vitesse dans la figure (VI.28) est obtenue comme dans le régulateur PI et que l'évolution du couple, des courants est également identique.

Lorsque on a une cassure de barre la durée d 'inversion de la vitesse est plus importante mais il n'existe plus de dépassement comme dans le cas d'un régulateur linéaire.

La réaction des régulateurs à logique floue au moment d'application de charge est aussi caractérisé par une variation plus petite et un temps plus court par rapport aux régulateurs classiques

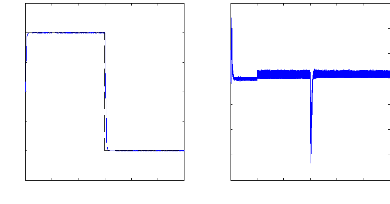
1500

1000

500

0

n (trim n)

-500

-1000

-1500

60

40

20

0

-20

C _en (N .m )

-40

-60

-80

0 0.5 1 1.5 2 2.5 3

t(s)

0 0.5 1 1.5 2 2.5 3

t(s)

Figure (VI.28) : vitesse de rotation, couple électromagnétique, simulation avec le modèle réduit,
machine en défaut et en charge : rupture d'une barre à t=1s

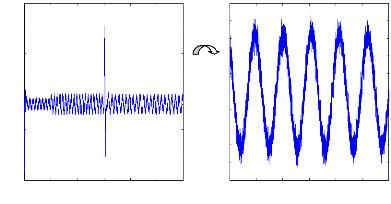
0 0.5 1 1.5 2 2.5 3

t(s)

1 1.05 1.1 1.15 1.2 1.25 1.3

t(s)

las (A )

-10

-20

-30

40

30

20

10

0

-1

-2

-3

-4

-5

5

4

3

2

0

1

zoom

las (A )

Figure (VI.29) : courant statorique, machine en défaut, en charge C_r= 3.5Nm

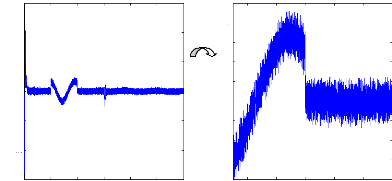
irb o (A )

-1000

-1500

1500

1000

-500

500

0

zoom

irb o (A )

-100

-150

-200

250

200

150

100

-50

50

0

0 0.5 1 1.5 2 2.5 3 0.8 0.9 1 1.1 1.2 1.3

t(s) t(s)

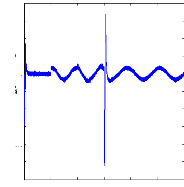
0 0.5 1 1.5 2 2.5 3

-

irb 1 (A )

-1000

-1500

-200 0

-250 0

-3000

2000

1500

1000

500

00

0

t(s )

Figure (VI.30) : Courants dans les barres rotoriques : Irb0, Irb1, machine en
défaut, simulation avec modèle global, rupture de la barre _rb0 à t= 1s

b. Machine avec cassure de deux barres

La figure (VI.31) illustre l'évolution temporelle en régime transitoire et en régime permanent du couple électromagnétique _Cem en présence d'une rupture de barre _rb0 a t=1s et _rb1 a t=2s. Aprés une phase transitoire, celui-ci répond instantanément et suit la référence sans dépassement ni erreur statique C_r=3.5 N.m a cause de la structure du régulateur flou, les réponses des systèmes sont caractérisées par les même faits :

la vitesse de référence est atteinte en 0,15 sec environ lors de l'inversion de vitesse selon une rampe.

La figure (VI.32) illustre l'évolution temporelle en régime transitoire et en régime permanent du courant statorique en présence d'une rupture de barre _rb0 à t=1s et _rb1 à t=2s .

La figure (VI.333) illustre l'évolution temporelle en régime transitoire et en régime permanent des courants de barres Irb0 , Irb1, en présence d'une rupture de barre rb0 à t=1s et rb1 à t=2s. Les courants circulant dans les barres adjacentes aux barres cassées sont très supérieurs a leur valeur nominale. On conclut donc qu'il y a un risque de défaillances en chacune dans la mesure ou les contraintes électriques et thermiques sont redistribuées sur les conducteurs adjacents.

Les effets de la cassure de barre (oscillation de w et C_em) croit rapidement avec le nombre de barres cassé ; d'où on observe:

- Augmentation de l'amplitude des oscillations. La grande amplitude des oscillations accélère la détérioration de la machine.

- L'amplitude des courants des phases statoriques. est proportionnelle au nombre de barres cassées.

- Lors des défauts rotoriques, les courants dans les barres cassées chutent pratiquement à
zéro, tandis que les courants dans les barres voisines deviennent déséquilibrés. Les
courants qui conduisaient les barres cassées se répartit alors dans les barres voisines

Lorsque on a une cassure de barre la durée d 'inversion de la vitesse est plus importante

mais il n'existe plus de dépassement comme dans le cas d'un régulateur linéaire.

1500

1000

500

0

n (trim n )

-9 4 0
-960
-980

-1020

1 0 4 0

-

-1060

-1080

-1100

14 16 18 2 22 24

t(s

-500

-1000

-1500

0 0.5 1 1.5 2 2.5 3

t(s)

1 1 2 0

-1 1 4 0

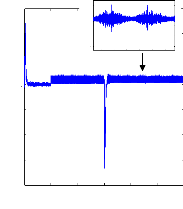
10

5

60

0

40

-5

0

2 1 2 2 2 3 2 4 2 5 2 6

t (s )

20

-40

-60

-80

0 0.5 1 1.5 2 2.5

t(s)

0

-20

C _en (N .m )

Figure (VI.31) :vitesse de rotation, couple électromagnétique et le courant
statorique, machine en charge et en défaut : 2 barres cassées

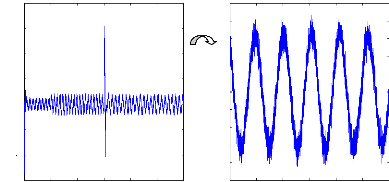
^las (A )

-10

-30

40

30

20

20

10

zoom

^las (A )

-1

-2

-3

-4

-5

5

4

3

2

0 0.5 1 1.5 2 2.5 3 1.05 1.1 1.15 1.2 1.25 1.3

t(s) t(s)

Figure (VI.32) :courant statorique, machine en charge et en défauts, 2barres
cassées

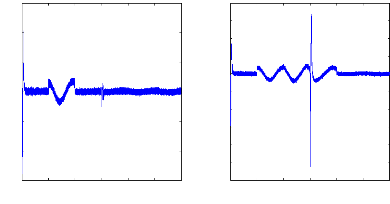
0 0.5 1 1.5 2 2.5 3

t(s)

!rbl )

-

-1000

-1500

-2000

-2500

-3000

2000

1500

1000

500

500

0 0.5 1 1.5 2 2.5 3

t(s)

irb o (A )

-1000

-1500

1500

1000

-500

500

Figure (VI.33) :courants dans les barres rotoriques : Irb0, I_rb1,Machine en charge et en défaut, simulation avec modèle global : 1 barre cassée _rb0 à t=1s, 2 barre cassée _rb1 à t=2s

3. Variation de la charge

Pour 0.6s<t<3s, on applique un couple de charge de 3.5N.m ;

a l'instant t=2s, on applique un couple de charge C_r=5.5N.m.

On constate également que les variations du couple de charge n'ont aucune influence sur la réponse de la vitesse dans le cas d'un régulateur flou (figure IV.34). Les figures (IV.34 à IV.35) confirment aussi ces résultats.

On remarque que la vitesse est obtenue comme dans le régulateur PI et que l'évolution du couple, des flux et des courants est également identique. Les temps de réponse et d'inversion de la vitesse sont respectivement égaux à 0.4 s et 0.45 s.

La réaction des régulateurs à logique floue au moment d'application de charge est aussi caractérisé par une variation plus petite et un temps plus court par rapport aux régulateurs classiques

On constate également que ce correcteur offre une réponse bien meilleure que celui du (PI ). Les dépassements et les temps de réponse sont beaucoup plus faibles qu'avec un régulateur classique.

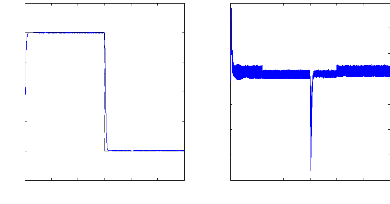
1500

1000

500

0

n (trim n )

-500

-1000

-1500

60

40

20

0

-20

C _en (N .m )

-40

-60

-80

0 0.5 1 1.5 2 2.5 3

t(s)

0 0.5 1 1.5 2 2.5 3

t(s)

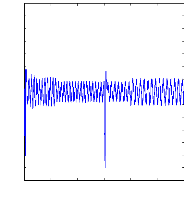
0 0.5 1 1.5 2 2.5 3

t(s )

las (A )

-10

-15

-20

-25

-30

-35

10

-5

5

0

35

30

25

20

15

Figure (VI.34) : vitesse de rotation, couple électromagnétique,
variation de la charge.

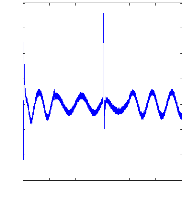
0 0.5 1 1.5 2 2.5 3

t(s)

irbo(A)

-1000

-1500

2000

1500

1000

-500

500

0

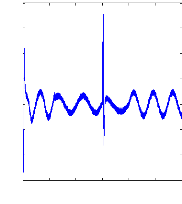
0 0.5 1 1.5 2 2.5 3

t(s)

irb 1 (A )

-1000

-1500

2000

1500

1000

-500

500

0

Figure (VI.36) : courants dans les barres rotoriques, Irb0, Irb1
machine avec variation de charge, simulation avec modèle global.

VI.7 Conclusion

Ce chapitre nous a permis d'étudier la structure générale d'un contrôleur flou et la méthodologie de sa conception, puis on a appliqué ce réglage sur la commande vectorielle du modèle réduit du schéma multi-enroulements de la machine asynchrone a cage d'écureuil avec ou sans défauts rotoriques ( cassures de barres).

Une comparaison des résultats de simulation de la commande de la machine asynchrone par des correcteurs classiques PI et un correcteur flou a été faite. Compte tenu des résultats, le PI flou semble pourvoir remplacer le PI conventionnel pour améliorer les performances de ce dernier et donc du contrôle vectoriel.

Le PI Flou est très peu sensible aux variations des paramètres du système, (en ce qui concerne les cassures des barres, qui influes sur la résistance rotorique, ou l'augmentation est de l'ordre de 11) ainsi qu'aux perturbations externes ce qui justifie sa robustesse. Il permet d'obtenir des temps de montée très faibles par rapport au PI classique grâce aux larges domaines physiques de la variation de l'erreur et de la variation de commande.

Conclusion générale

Cette étude représente un apport dans le domaine de diagnostic et surveillance des défauts rotoriques des machines asynchrones a cage d'écureuil, à savoir la modélisation, l'estimation des paramètres et la commande.

Nous avons opté pour une approche globale basée sur la signature de grandeurs externes (couple, courant,..) utilisant un schéma multi-enroulements bien adapté à la simulation des défauts rotoriques envisagés. Dans une deuxième phase, nous avons procédé à la transformation du modèle multi-enroulements au modèle réduit, pour faciliter abondamment l'étude. Toutes les équations sont écrites dans un référentiel lié au rotor, vu que les défauts sont situés justement à son niveau.

Le modèle obtenu permet de simuler efficacement les défauts de cassure de barres et de suivre aussi l'évolution des grandeurs externes (couple, courant,...). Cette analyse a permis de voir le comportement du moteur et d'en déduire les signatures caractéristiques des défauts. Etant donné qu' il est difficile d'analyser directement le courant statorique lors de la rupture de barres, nous avons basé sur l'analyse spectrale du courant statorique, qui nous a révélé les défauts des cassures des barres par des harmoniques à la fréquence.

L'étude de la commande de la machine asynchrone par la méthode du flux orienté indirecte avec un réglage classique, nous a permis de simuler le comportement du système global, avec et sans défauts rotoriques. Les résultats obtenus ont montré l'influence des ruptures de barres sur le couple électromagnétique, la vitesse de rotation et le courant statorique, qui se traduit par des ondulations et déformations des allures.

Il faut signaler que le régulateur de type P.I ne permet pas en tout cas de maîtriser le régime transitoire. En outre, la faiblesse de la commande vectorielle, se traduit par l'apparition d'une pointe de courant très gênante pour le bon fonctionnement de la machine.

Nous avons abordé également le suivi des paramètres de la machine sensibles aux défauts à savoir les résistances des barres rotoriques et les courants, en utilisant l'observation stochastique par filtre de Kalman étendu dont l'objectif de détecter la présence des défauts. L'approche proposée a été suffisamment simplifiée par l'exploitation dans les simulations du modèle réduit du schéma multi-enroulements de la machine asynchrone à cage d'écureuil.

Au terme de cette étude, les résultats obtenus montre la faisabilité de la commande par la logique floue appliquée au problème de la régulation en vitesse de la machine asynchrone en présence de défauts rotoriques. Comparé au régulateur classique, le comportement général du régulateur de vitesse reste similaire. Cependant, le détail des résultats de simulation met en évidence une amélioration locale du réglage de la vitesse, associé à des qualités de robustesse satisfaisantes.

En perspective, on pourrait appliquer différentes méthodes du diagnostic pour la détection et la localisation des défauts de la machine asynchrone, en utilisant les signatures des grandeurs électriques et mécaniques qui peuvent être obtenues à partir du modèle étudié.

Néanmoins, les efforts de modélisation doivent être poursuivis pour inclure ou préciser un certain nombre de phénomènes physiques supplémentaires. Il serait intéressant de prendre en compte la perméabilité finie du fer, et les pertes fer ainsi que la saturation.

Ces phénomènes physiques non ou mal pris en compte affectent très sérieusement les performances du modèle. Par ailleurs, il serait intéressant d'étendre le modèle a l'étude des vibrations. Ces dernières offrent en effet des signatures de défaillances intéressantes dans le cadre de la surveillance et du diagnostic.

Annexe

Paramètres de la machine étudiée

Plaque signalétique : Constructeur ABB

U : 220 /380 V.

In = 4. 5 / 2. 6 A.

? n = 2850tr/min Pn = 1 . 1 KW

Les paramètres :

Rs = 7. 828 ?

J= 0 . 006093 Kg m² f = 0 . 00725 Nm s/rd Rayon = 0.03575 m

Longueur = 0.065m Entrefer = 0.00025 m Ns = 160

Nr = 1 6

Lsl = 0 .0 1 8 H R bsain 150 10 = R = 0. 00165 ?			-6	?
Re 72 10 =	-6	?

Lb = 10- ⁷ H
Le = 10^- 7 H

Bibliographie

[1] V. Devanneaux, Modélisation des machines asynchrones triphasées à cage d'écureuil en vue de la surveillance et du diagnostic. Thèse de doctorat en génie électrique, Institut National Polytechnique de Toulouse, décembre 2002.

[2] R. Casimir, « Diagnostic des défauts des machines asynchrones par reconnaissance des formes.», thèse de doctorat, l'école doctorale électronique, électrotechnique, automatique de Lyon, décembre 2003.

[3] T. Boumegoura, « Recherche de signature électromagnétique des défauts dans une machine asynchrone, et synthèse d'observateurs en vue du diagnostic.», thèse de doctorat, l'école doctorale électronique, électrotechnique, automatique de Lyon, Mars 2001.

[4] L. Baghli, « Contribution à la commande de la machine asynchrone, utilisation de la logique floue, des réseaux de neurones et des algorithmes génétiques.», thèse de doctorat, université Henri Poincaré, Nancy, janvier 1999.

[5] Gilles Zwingelstein, « Diagnostic des défaillances : théorie pratique pour les systèmes industriels.», Edition Hermès.

[6] R. Aabdessamed et M. kadjoudj, « Modélisation des machines électriques.», presse de l'université de Batna, 1997.

[7] S. Amrane, « Diagnostic de défauts des moteur d'induction.», thèse de magister, Université A. Mira de Bejaia 2000.

[8] A. Boughaba, « Contribution à l'étude du contrôle d'une machine à induction :analyse d'algorithme de la commande vectorielle.», thèse de magister, Université de Batna, 1998.

[9] D. Gaetan et R. hubert,« Sur la détection d'un défaut au rotor des moteurs asynchrones.» Article, GREEN-UHP faculté des sciences, décembre 2001.

[10] J. Colomer,« Essais de synthèse des méthodes de C.N.D (contrôle non destructif).», revue pratique de contrôle industriel, Mars 1990.

[11] W. Deleroi,« Broken bar in squirrel -cage rotor of an induction motor: Description by super imposed faults current.», Archive fur electrotechnik, 67, 84, p 91-99.

[12]Jean FAUCHER, Bruno DAGUES Traitement de l'Information pour la Modélisation, la Surveillance et le Diagnostic (TIMSuD)

[13]. Detecting Broken Rotor Bars Prevents Catastrophic Damage, Copyright (c) 1998-2004 Maintenance Technology - All rights reserved.

[14].S. Colombri,« Design and Simulation of mechatronic application and power electronics with Matlab/Simulink », EPFL, LEI, Lausanne 1996.

[15] E. Ritchie, X. Deng and T. Jokinen,« Dynamic model of three-phase squirrel cage induction motors with rotor faults.», in proc ICEM 94.

[16] M. Jufer et A. Abdelaziz,« Influence d'une rupture de barre ou anneau sur les caractéristiques externes d'un moteur asynchrone à cage.», Article, 5 sep 1978.

[17] E. schæffer,« Simulation et diagnostic de la machine asynchrone.», rapport, Ecole centrale de Nantes 1998.

[18] E. Schaeffer. Diagnostic des machines asynchrones : modèles et outils paramétriques dédies a la simulation et a la détection de défauts. Thèse de doctorat en automatique et informatique appliquée, Université de Nantes, décembre 1999.

[19] Scott Wade, Matthew W. Dunnigan, and Barry W. Williams .Modeling and Simulation of Induction MachineVector Control with Rotor Resistance Identification, IEEE transactions on power electronics, vol. 12, NO. 3, MAY 1997

[20] Eltabach Mario, Charara Ali, Zein Ismail. Detection of induction motors broken bars by electromagnetic torque estimation using kalman filtering, HEUDIASYC UMR 6599 - LATIM Université Technologie de Compiègne BP 20529, 60205 Compiègne Cedex Compiègne, France

[21] Ming Xu and Tom Alford, Motor current analysis and its applications in induction motor fault diagnosis, ENTEK IRD International Corporation 1998

[22] Zein Ismail,Jean claude Trigeassou,Slim Tnani, Sébastien Cauet, Diagnostic des défauts statoriques et rotoriques par identification paramétrique sans capteur de vitesse, Laboratoire d'Automatique et d'informatique industrielle, Ecole supérieure d'Ingénieurs de Poitiers, Conférence internationale francophone d'Automatique, juillet 2002.

[23] G. H. Jang, Member, IEEE, and S. J. Park. Simulation of the Electromechanical Faults in a Single-Phase Squirrel Cage Induction Motor, IEEE TRANSACTIONS ON MAGNETICS, VOL. 39, NO. 5, SEPTEMBER 2003

[24]Jafar Milimonfared, Homayoun Meshgin Kelk, Subhasis Nandi, Artin Der Minassians, Member, IEEE, and Hamid A. Toliyat, A Novel Approach for Broken-Rotor-Bar Detection in

Cage Induction Motors, IEEE TRANSACTIONS ON INDUSTRY APPLICATIONS, VOL. 35, NO. 5, SEPTEMBER/OCTOBER 1999

[25] Arezki Menacer, Mohamed-Said Naît Said, A/Hamid Benakcha, Said Drid stator current analysis of incipient fault into asynchronous motor rotor bars using Fourier fast transform, Journal of ELECTRICAL ENGINEERING, VOL. 55, NO. 5-6, 2004, 122-130

[26] Smail BACHIR, Contribution au diagnostic de la machine asynchrone par estimation paramétrique, Thèse de doctorat, Ecole supérieure d'Ingénieurs de Poitiers, décembre 2002

[27] MOHINDER S. GREWAL , ANGUS P. ANDREWS, Kalman filtering : theory and practice using Matlab, California state university at fullerton, 2001

[28] Abdelkader Larabi, Mohamed Seghir Boucherit, Commande numérique robuste appliquée aux systèmes industriels de production, Laboratoire d'Electrotechnique et Automatique ENPA El-harrach Alger,

[29] Mouloud Azzedine Denai, Sid Ahmed Attia, Fuzzy and neural control of an induction motor, University of Science and Technology of Oran, Faculty of Electrical Engineering B.P. 1505 El Mnaouar, Oran 31 000, Algeria, 2001

[30] Dr M N Bandyopadhyay, Fellow, Extended Kalman Filter Approach to Joint State and Parameter Estimation, November 2003

[31] David HENRY ,Diagnostic et contrôle de cohérence des systèmes multivariables incertains. Novembre 1999 , l'Université Bordeaux I

[32]D.Khodja, L.Yahia, Identification des défauts de la machine asynchrone à cage d'écureuil dans sa partie rotorique.mémoire d'ingénieur d'état, université de M'sila.

[33] M. LAJOIE-MAZENC, Les techniques de commande vectorielle des machines asynchrones destinées à la variation de vitesse à haute performance "

Rapport EDF - Janvier 1992

[34] BIMAL K.ROSE, Ajustable speed AC drive systms" Edition I.E.E.E press 1980

[35] F.BLASCHKE, The principle of field orientation as applied to the new transvector closed-loop control system of rotating field machine. Siemens review- vol 34 may 1971, p 217-220

[36] Y.FU, Commandes découplées et adaptatives des machines asynchrones

triphasées,Thèse de Docteur Université de Montpellier II- Mars 1991

[37] M.PIETRZAK, Algorithme de commandes d'un variateur électrique asynchrone -

contrôle dynamique du flux - contrôle optimale de la position.

Thèse de doctorat és-sciences I.N.P TOULOUSE 8 juillet 1988

[38] G.A CAPOLINO, H.HENAO, V.T NGUEN PHUOC, Méthode de conception d'une commande vectorielle pour machine à induction, Journée d'études SEE sur la commande vectorielle des moteurs asynchrones,2 décembre 1992

[39] O.HNISHI KOUSHEL, LIEDA YOUZOU, MYYACHI KUNIO, Model référence adaptive system against rotor resistance variation in induction motor Drive,I.E.E.E Trans.Ind.electronics, vol.IE-33, N°3, aug 1986, pp.217-3223

[40] A. FAIDALLAH, Contribution à l'identification et à la commande vectorielle des machines asynchrones, Thèse de Docteur INP Lorraine - 1 Février 1995

[41] K. YAZID, Commande vectorielle de la machine asynchrone avec prise en compte des variations de la constante de temps rotorique, Thèse de Magister USTHB - Juin 1996

[42] B. DEMAYA, Commande floue des systèmes à dynamiques complexes- Application à la commande d'un moteur thermique, Thèse de Docteur LAAS Toulouse - 17 Octobre 1994

[43] S.GHOZZI, M.GOSSA, M. BOUSSAK, A.CHAARI, M. JEMLI, Application de la logique floue pour la commande vectorielle des machines asynchrones, J.T.E.A. 1996- p 177-182

[44] M. BAUER ,Application de contrôleurs à logique floue pour la commande vectorielle des machines à induction: commande en vitesse et en position , Rapport de stage ingénieur- ESIM-22 Février 1995

[45] A.IBALIDEN, Implantation d'un régulateur de type flou sur des commandes d'onduleurs pilotant des machines alternatives : application à la détermination des correcteurs , Rapport d'activités 1994-1995

[46] J.P.Caron-J.P.Hautier,«Modélisation et commande de la machine asynchrone.», Edition technique1995

[47]C.L.Philips and H.T.Jr.Nagel,« Digital control system : Analysis and Design.», Printice- Hall, inc, 1984.

??

11 11

??? ÉÜ ??? ÉÜ ? ? . ??? ? áÇÌÇ ? ? ? ? áÊÍÊ ????? ? ? ???? ? ?? ? ? á ÜÎ Ü CM ÇÜ ?? ÇÏÜ ? ????? ? ?? ???? ? ??? ????? ??? ????? ?? ? . ? ? áÇØÚ ? ? ????? ??? ??? ? ? ????? ? ??? ? ??? ??????? ????? ?????? ??? ? ?????? ???? ? ???? áÌÇ ? ??? ? ?? ????? ? ????? ? ? ??? . áÇØÚ ????? ??? ? ? ? ? ? ?? ???? áÌ ??? ? ???? ??? ?? ? ? ? , ???? ? ?? ? ???? ??? ????? ? ???? áÇÌ ? ???? ? ?? ????? ? ? ? ??? ???
? Ü ? ? , ??? ?? ???	???	????	???? ? ? ?? ?		???? ? ???		? ??????		????? ?
. ??? ? ? ????? ??? áÎ	?? ??? ??			???	? ????	???	???????		????
????? ??CM ??? ?? ??	, ???? ? ? ? ?? ?			?? ??	?	???	???	?? ???
??? ? . ???? ? ???	? ??????		????? ?	?? ??? ?		?????	???	? ?	????? ?
		. ??	??	?????	? ? ??? ?		????	? ? ?	???
		????? ????
????? ? ? ? ??	???	??	??? ?	????????		????	???	? ???	? ? ?
						???? ? ???		? ??????
			Résumé

Les machines electriques tournantes occupent une place preponderante dans tous les secteurs industriels. Les machines asynchrones triphasees a cage d'ecureuil sont les

plus frequemment utilisees grâce a leur robustesse, leur simplicite de construction et leur bas coût. Neanmoins, celles-ci subissent au cours de leur duree de vie un certain nombre de sollicitations externes ou internes qui peuvent les rendre defaillantes.

On propose une modelisation du schema multi enroulements de la machine asynchrone permettant d'apprehender son comportement en presence ou en absence de defaillances.

Dans l'étape d'estimation des paramètres, on propose le suivi des paramètres sensible aux défauts, à savoir les courants rotoriques et les résistances des barres rotoriques, en utilisant le filtre de Kalman étendu.

Nous nous sommes intéressés a la commande vectorielle indirecte d'une machine asynchrone utilisant les régulateurs PI et par logique flou en tenant compte de la présence d'un défaut rotorique . Une analyse par simulation met en évidence les bonnes performances et la robustesse de la commande par régulateur flou.

Mots-clés

Machine asynchrone- Diagnostic - schéma multi enroulements- Rupture de barre -Commande vectorielle - Logique floue

Abstract

Rotating electrical machines play an important role in the industrial world. Among

them, the three-phase squirrel cage asynchronous machines are frequently used because of their robustness, their relatively simple construction and their low cost. Nevertheless, during their lifespan, these machines are submitted to external and internal stresses which can lead to several failures.

We propose the modelling of the diagram multi windings of the asynchronous machine allowing apprehending his behavior in presence or absence of failures.

In the stage of estimate of the parameters, one proposes the follow-up of the parameters sensitive to the defects, namely the rotor currents and resistances of the rotor bars, by using the Extended Kalman filter.

We were interested in the indirect field oriented control order of an asynchronous machine uti reading regulators PI and by fuzzy logic blur by taking account of the presence of a rotor

defect. An analysis by simulation highlights the good performances and the robustness of control command by fuzzy regulator

Keywords

Asynchronous machine - Diagnostic - multi windings - Broken bar- field oriented control-Fuzzy Logic- Extended Kalman filter