|

Communaute Economique et Ilonetaire de l'ilfrique
Centrale
(CEMAC)
.
Institut Sous-régional de Statistique et
d'Économie Appliquée
(ISSEA)
Organisation Internationale
BP : 294
Yaoundé CAMEROUN Tel : 222 01 34
MODÉLISATION DE L'ÉCOULEMENT DES
DÉPÔTS
À VUE : CAS DES BANQUES
COMMERCIALES
CAMEROUNAISES.
Ilemoire redig~ en vue de l'o6tention du dipl~me
d'Ingenieur d'ilpplication de la
Statistique.
Option
Gestion
Présenté par :
LACGNI Carlos Dendi
(Élève
Ingénieur d'Application de la Statistique à l' ISSEA, 4ème
Année)
Membres du Jury
Président du Jury : M. Patrick Serges
KOUONTCHOU Encadreur : Dr Dieudonné
KINKIELELE
Assesseur : Dr Célestin NENTA
NDJOUKOUE
Juin 2007

ortorcAcrEs
Je dédie ce travail a
> mes parents, monsieur et madame DATCHOUA Comme des soldats
pour leur patrie, vous vous etes sacrifiés pour moi ;
> Monsieur PETTAN G Jules
L'éternel est témoin de tous les efforts que vous
avez consenti et que vous continuez de consentir pour ma réussite. Qu'il
vous en rende au centuple ;
> mes oncles N GANFAN G André, YOUMBI Honoré et
NJOMO Innocent Que ce travail soit le couronnement de tous les efforts et
sacrifices consentis a mon égard ;
> Monsieur TEIFOUET Thomas Joseph
Pour tous les sacrifices et le soutien sans faille que vous
avez consenti a mon égard, les mots me manquent pour exprimer ma
reconnaissance. Que l'éternel soit le seul témoin de tous ces
efforts ;
> Monsieur Dénis N GAN GOUM
Pour tout le soutien sans faille que vous m'avez
apporté jusqu'ici, pour tous vos conseils, puissiez-vous trouver ici, un
réel motif de satisfaction et de reconnaissance.
q"~"#~I"1E$%s


Ce travail est le fruit d'une somme d'efforts qui, pris
individuellement, ont concouru à sa réalisation. Le soin nous
étant donné d'adresser notre gratitude :
A mon Directeur de mémoire Dr Dieudonné
KINKIELELE, Directeur des études des premier et second cycle à
l'ISSEA : Vous avez été pour moi un bon encadreur et un bon
conseiller. Vos conseils, votre rigueur dans le travail et votre
magnanimité ont été pour moi une source d'inspiration.
Merci de m'avoir initié à la recherche et soyez assuré de
ma parfaite reconnaissance et de mon profond respect.
A Monsieur le Directeur Général de l'ISSEA, M.
Leoncio OYANA NZE, ainsi que tout le personnel enseignant pour le
sérieux dont ils ont toujours fait preuve pour nous donner une bonne et
solide formation.
A M. Robert NGONTHE, Directeur des études du
3ième cycle qui a été d'un soutien particulier
pour la IAS 4 à travers ses conseils.
A Mme Suzanne BIWOLE, M. Georges DJIMEFO KAPEN, M. LOUDINE
BESSONG, M. Denis NGANGOUM, Mlle Mireille TADIE, Mlle Vicky DJEUKWI pour avoir
lu et apprécié ce document.
A M. Marcel OPOUMBA, M. Célestin NENTA pour leurs
remarques et leurs enseignements qui ont été d'une importance
capitale pour la réalisation de ce document
A M. ONDO, M. Ignace KAMGA pour leurs remarques qui nous ont
permis d'améliorer l'aspect modélisation de ce document.
A tous ceux qui ont été d'un soutien infaillible
pour la réalisation de ce document. Nous citerons : Justin BEM, ,
Hippolite TSADJIEU, Hardy BATOUMEN, Mireille TADIE, Olivier PIEUME, Carine
NZEUYANG, Eric NKAMGNIA, Doriane MATCHA, Merville KENFACK, Guy Albert KENKOUO,
Larissa GAJUI, Raoul TAFFO, Justin KAMENI, Sarah DJONOCK, Dady Christiane
DJONGOUE., Arnold FEUTI, Jurado MATAKIE, Simplice WANSI.
Enfin, à tous nos camarades de promotion et tous ceux qui
de près ou de loin ont oeuvré d'une façon ou d'une autre
pour la réalisation de ce travail.
TABLE DES WATIERES


ortamators i~
TaalEWCIEME.N13' i~~
TABLE orEs avvirtus i~
|
sI Les ETABgevvvriaws
|
|
|
|
|
vi
|
|
|
|
|
|
LISIE DES TABLE,AlUX ET TI %WES
|
|
|
vii
|
|
|
|
ifirrlifiN7WcYPOS
|
|
|
|
|
|
|
|
.
|
|
|
|
|
|
|
|
|
esVad
|
|
|
|
|
|
|
|
.~
|
|
|
|
|
|
|
|
|
INM(13%1070N
|
|
|
|
|
|
10
|
|
|
|
|
|
PREMIÈRE PARTIE : REVUE DE LA
LITTÉRATURE
CHAPITRE PREMIER : GESTION DES RISQUES BANCAIRES ET
CONCEPT D'ÉCOULEMENT..17
SECTION I : La firme bancaire et ses principaux risques
17
I.1 LA FIRME BANCAIRE 17
I.1.1 L'activité de la banque 17
I.1.2 Les différents types de banques
18
I.1.3 Les principaux postes du bilan et hors-bilan d'une
banque 19
I.1.3.1 Les principaux postes du bilan 19
I.1.3.2 Le hors-bilan 20
I.1.4 Le compte de résultats 20
I.1.4.1 Principaux postes du compte de résultat
20
I.1.4.2 Les soldes intermédiaires de gestion
21
I.2 LES RISQUES BANCAIRES 22
I.2.1 Les principaux risques bancaires 22
I.2.2 La gestion des risques de taux et de
liquidité 23
I.2.2.1 Les Méthodes classiques de gestion des
risques de taux et de liquidité 24
I.2.2.1.1 Méthode des gaps 25
I.2.1.1.2 Méthode de la duration 25
I.2.2.2 Les recommandations du Comité de
Bâle 27
SECTION II : Le Concept d'écoulement
28
II.1 LA NOTION D'ÉCOULEMENT EN LIQUIDITÉ 28
II.1.1 L'écoulement de production 29
II.1.2 La vitesse d'écoulement 30
II.1.3 L'écoulement du stock 31
II.1.4 Impasse en liquidité 32
II.2 LA NOTION D'ÉCOULEMENT EN TAUX 33
II.2.1 La marge d'intérêt 33
II.2.2 L'impasse en taux 34
CHAPITRE DEUXIÈME : LES MODÈLES DE
DÉPÔTS À VUE 35
SECTION I : Généralités sur la
modélisation des écoulements 35
I.1 LES VARIABLES EXPLICATIVES DE L'ÉCOULEMENT SELON
DEMEY, FRACHOT, RIBOULET 35
I.2 LES PRODUITS ÉCHÉANCÉS ET NON
ÉCHÉANCÉS 36
SECTION II : L'écoulement des dépôts
à vue 38
II.1 LES DISCUSSIONS AUTOUR DE L'ÉCOULEMENT DES
DÉPÔTS À VUE 38
II.2 MÉTHODOLOGIE POUR LA MODÉLISATION DES
DÉPÔTS À VUE SELON FRACHOT 40
II.3 LES PREMIERS MODÈLES DE DÉPÔTS À
VUE 41
II.3.1 Le modèle de Selvaggio [1996]
41
II.3.2 Le modèle de Dupré [1996]
42
II.3.3 Le modèle de Jarrow et Van Deventer [1998]
42
II.4 LES MODÈLES RÉCENTS DE DÉPÔTS
À VUE 43
II.4.1 Le modèle du premier régulateur
fédéral aux Etats-Unis : L'Office of Thrift
Supervision
[2000] 43
II.4.2 Le modèle de Frachot [2001] 43
DEUXIÈME PARTIE : APPLICATION AUX
BANQUES
COMMERCIALES CAMEROUNAISES
CHAPITRE TROISIÈME : LES BANQUES COMMERCIALES DU
CAMEROUN ET LA LIQUIDITÉ..47
SECTION I : Typologie des institutions
financières, cadre réglementaire et prudentiel de
l'activité du système bancaire camerounais 47
I.1 TYPOLOGIE DES INSTITUTIONS FINANCIÈRES 48
I.1.1 La Banque centrale 48
I.1.2 Les Banques Créatrices de Monnaie (BCM)
48
I.1.3 Les Autres Institutions Bancaires (AIB)
48
I.1.4 Les Institutions Financières Non Bancaires
(IFNB) 49
I.2 LES BANQUES COMMERCIALES DU CAMEROUN 49
I.2.1 Banques en activité au Cameroun et
répartition du Capital Social 49
I.2.2 Fonctionnement des banques commerciales
50
I.3 CADRE RÉGLEMENTAIRE ET PRUDENTIEL INSTITUÉ PAR
LA COBAC 51
I.3.1 Missions de la COBAC 51
I.3.2 Les normes prudentielles adoptées par la
COBAC en 1993 52
I.3.2.1 Normes de solvabilité 52
I.3.2.2 Les normes de liquidité 53
SECTION II : La liquidité des banques au Cameroun
54
II.1 LA LIQUIDITÉ BANCAIRE 54
II.2 LES RESSOURCES DES BANQUES 56
II.3 LES DÉPÔTS DE LA CLIENTÈLE 57
II.3.1 La nature des comptes de dépôts des
clients 57
II.3.2 L'évolution des dépôts par
nature 60
CHAPITRE QUATRIÈME : MODÈLES
D'ÉVOLUTION DES DÉPÔTS À VUE DANS LES BANQUES
COMMERCIALES DU CAMEROUN 63
SECTION I : Données et méthodologie
63
I.1 LES DONNÉES ET LES SOURCES 63
I.2 LA MÉTHODOLOGIE DE TRAVAIL 64
SECTION II : Applications 65
II.1 DESCRIPTION DE L'ÉVOLUTION DE L'ENCOURS DES
DÉPÔTS À VUE DE L'ENSEMBLE DES BANQUES CAMEROUNAISES 65
II.2 ANALYSE DES CARACTÉRISTIQUES DE LA SÉRIE 66
II.2.1 Analyse préliminaire 67
II.2.2 Analyse de la saisonnalité :
68
II.2.3 Analyse de la stationnarité de la
série transformée des encours des dépôts
(Log(depots)) 70
II.3 LE LIEN ENTRE LE TAUX D'INTÉRET ET LE NIVEAU DE
L'ENCOURS DES DÉPÔTS À VUE 72
II.3.1 Le test de cointégration de Johansen et
interprétation 73
II.3.2 Le test de causalité de Granger et
interprétation 74
II.4 ÉTUDE DE LA SÉRIE DES DÉPÔTS
SELON LA MÉTHODOLOGIE DE BOX ET JENKINS 75
II.4.1 L'identification et l'estimation des
paramètres du modèle d'évolution de la série
d'encours des dépôts à vue 75
II.4.2 La vérification et l'adéquation des
trois modèles potentiels 77
II.4.2.1 Le modèle ARIMA(2,1,1) 77
II.4.2.2 Le modèle ARIMA(0,1,1) 78
II.4.2.3 Le modèle ARIMA(1,1,0) 79
II.4.3 Le choix du modèle 80
II.4.4 La prévision 80
II.5 DÉTERMINATION DE LA FONCTION D'ÉCOULEMENT
82
II.6 VITESSE ET DURÉE MOYENNE D'ÉCOULEMENT DU STOCK
DES DÉPÔTS À VUE: 84
II.7 PARTIE DE L'ENCOURS DES DÉPÔTS À VUE
STABLE EN FONCTION DU TEMPS 84
II.8 LIMITE DU MODÈLE D'ÉCOULEMENT DES
DÉPÔTS À VUE 87
CONCLUSION GÉNÉRALE 88
BIBLIOGRAPHIE iANNEXES iii
Annexe I : Méthodologie de Box et Jenkins
iii
Annexe II : Le concept de cointégration
xi
Annexe III : Tableaux et figures xii
SI LES "% ~
~&# )~~%~~$~


AIB : Autres Institutions Bancaires
AIBE : Autres Institutions Bancaires Eligibles au refinancement
de la BEAC
AIBNE : Autres Institutions Bancaires Non Eligibles au
refinancement de la BEAC
ALM : Asset Liability Management (Gestion Actif/Passif)
BCM : Banques Créatrices de Monnaie
BEAC : Banque des Etats de l'Afrique Centrale
BICEC : Banque Internationale du Cameroun pour l'Epargne et le
Crédit
CA : Crédit Agricole
CEMAC : Communauté Economique et Monétaire de
l'Afrique Centrale
CLC : Crédit Lyonnais Cameroun (actuellement
Société Camerounaise de
Banque, Crédit Agricole)
COBAC : Commission Bancaire de l'Afrique Centrale
EBC : Ecobank Cameroun
FCFA : Franc de la Coopération Financière en
Afrique
FMI : Fonds Monétaire International
FRBG Fonds propres pour Risques Bancaires
Généraux
IAS4 : Ingénieur d'Application de la Statistique,
4ième année
IF : Institutions Financières
IFNB : Institutions Financières Non Bancaires
Mds : Milliards
NFC : National Financial Credit Company
PIB : Produit Intérieur Brut
SCB : Société Camerounaise de Banque
SCBC : Standard Chartered Bank Cameroon
SGBC : Société Générale de Banques au
Cameroun
SYSCO : Système de Cotation
UBAC : Union Bancaire d'Afrique Centrale
UBC : Union Bank of Cameroon
UMAC : Union Monétaire des Etats de l'Afrique Centrale
£ISJYE !"S T~&L"~*x ET FI t)#rs


Tft'BL"~t)X
Tableau 1 : Principaux postes du bilan d'une banque 19
Tableau 2 : Le compte de résultat 21
Tableau 3 : Évolution des ratios de liquidité des
banques du Cameroun 55
Tableau 4 : Évolution du plafond de refinancement et le
taux d'utilisation 55
Tableau 5 : Résultat de l'estimation de l'équation
(37) 67
Tableau 6 : Test de Dickey-Fuller Augmenté sur la
série des dépôts transformés : modèle avec
constante
et trend 71
Tableau 7 : Test de dickey-fuller augmenté sur la
série D(Logdepots) 72
Tableau 8 : Résultat du test de causalité de
Granger 74
Tableau 9 : Résultat de l'estimation du modèle
ARIMA(2,1,1) 76
Tableau 10 : Résultat de l'estimation du modèle
ARIMA(0,1,1) 77
Tableau 11 : Résultat de l'estimation du modèle
ARIMA(1,1,0) 77
Tableau 12 : Dépôts observés et
dépôts prévus par le modèle 82
Tableau 13 : Pourcentage de l'encours d'une date t
stable en fonction du temps 85
Tableau 14 : Partie stable de l'encours observé en
décembre 2005 en fonction du temps 86
xii
Tableau 16 : Répartition des dépôts à
vue selon la nature des comptes xii
Tableau 17 : Résultats du test de cointégration
entre l'encours des dépôts et le taux d'intérêt
xiii
Tableau 18 : Test de Dickey-Fuller augmenté pour la
variable taux xiv
Tableau 19 : Test de dickey-fuller Augmenté sur les
dépôts transformés xv
Tableau 20 : Test de dickey -fuller sur la série en
différence première des dépôts transformés)
xvi
Tableau 21 : Test de dickey-fuller augmenté sur la
série des taux transformés xviii
Tableau 22 : Test de dickey-fuller augmenté sur la
série en différence première de la série des
taux
transformés xix
Tableau 23 : Test ARCH sur les résidus du modèle
ARIMA(2,1,1) xxi
Tableau 24 : Test ARCH sur les résidus du modèle
ARIMA(0,1,1) xxii
Tableau 15: Situation de la trésorerie des banques au 31
Mars 2005
qI t)qE~
Figure 1 : Répartition du capital social des banques
commerciales en pourcentage au 31 Décembre 2004
50
Figure 2 : Évolution de la structure des ressources des
banques camerounaises de 2000 à 2004 56
Figure 3 : Structure des Ressources des banques du Cameroun au 31
Décembre 2004 57
Figure 4 : Évolution de la structure des
dépôts (en millions de francs CFA) 60
Figure 5 : Structure des dépôts au 31
Décembre 2006 61
Figure 6 : Évolution de l'encours des dépôts
à vue des banques commerciales du 31/01/1997 au
31/12/2006 (en millions de F CFA) 66
Figure 7 : Corrélogrammes simple et partielle de la
série des dépôts à vue 68
Figure 8 : Encours des dépôts à vue
transformés (transformation logarithmique) 69
Figure 9 : Évolution de dépôts
transformés et de ceux corrigés des variations 69
Figure 10 : Corrélogrammes simple et partielle de la
série des dépôts tranformés . 70
Figure 11 : Corrélogramme des résidus 78
Figure 12 : Corrélogramme des résidus du
modèle ARIMA(0,1,1) 79
Figure 13 : Dépôts estimés par le
modèle et dépôts réels observés 81
Figure 14 : Répartition des dépôts par nature
au 31 décembre 2004 xiiFigure 15 : Variation de l'encours des
dépôts à vue en millions de F CFA xiiiFigure 16
: Évolution de la série des taux d'intérêt
xviiiFigure 17 : Autocorrélogramme du carré des
résidus xxi
~ )$r qxRpq'os


Le présent mémoire est l'aboutissement de quatre
années de formation à l'Institut Sous-régional de
Statistique et d'Économie Appliquée. Il s'impose comme un cadre
conceptuel de la gestion actif/passif pour les banques camerounaises, qui
recherchent un outil leur permettant de gérer les risques de
transformation et de liquidité.
Alors que les banques de la zone BEAC en général
et celles du Cameroun en particulier se reprennent d'une crise qui a
affecté leur système bancaire, on a constaté avec les
nouvelles contraintes de gestion que les banques camerounaises sont
passées à une situation de surliquidité ou l'essentiel de
leurs ressources est fait de dépôts à vue. Ces ressources
provenant de la clientèle, sont par définition exigibles à
tout moment. Cette étude, axée sur « la modélisation
de l'écoulement des dépôts à vue » se propose
de concevoir un modèle qui permettra aux banques de ressortir la partie
stable de leur dépôts à vue en fonction du temps. Ainsi
elles pourront davantage s'impliquer dans le financement de l'économie
en minimisant le risque de transformation et de liquidité.
L'intérêt principal de notre travail
réside dans le fait que de nos jours, les banques sont devenues
frileuses, refusant de s'impliquer dans le financement de l'économie
puisqu'elles ne possèdent essentiellement que des ressources
susceptibles d'être exigible du jour au lendemain. Pour cela, elles
cherchent un outil pouvant leur permettre d'évaluer les risques de
transformation et de liquidité liés aux dépôts
à vue. Le présent document se fixe pour objectif de leur fournir
un outil permettant la valorisation de ces dépôts à vue.
En espérant que cette étude permettra aux
banques d'améliorer leur système de gestion des risques, nous
restons réceptifs aux critiques et suggestions pouvant contribuer
à la perfection de ce travail.
#~ ~*~~

La gestion des risques est une discipline aussi ancienne que
les banques. Après la grave crise des années 1970 qui avait
fragilisé plusieurs systèmes bancaires de part le monde, la
gestion des risques bancaires est devenue un enjeu de taille pour les banques
qui veulent assurer leur crédibilité, leur rentabilité et
leur pérennité.
A partir de ce moment, plusieurs auteurs ont oeuvré
dans la conception des méthodes en vue d'une meilleure gestion
actif/passif bancaire. Pour les problématiques de risque de
liquidité et de risque de taux, le Comité de Bâle, dans son
document consultatif de Janvier 2001 « principles for the management and
supervision of interest rate risk » recommande à chaque banque de
mettre en place des modèles d'écoulement en liquidité pour
chacun des produits de leur bilan. Ces modèles devant leur permettre de
gérer efficacement leur liquidité.
En 1995, après de nombreuses restructurations qui ont
suivi la crise bancaire en zone CEMAC, les banques de la zone en
générale et celles du Cameroun en particulier sont devenues
saines et très liquides. Cependant, l'examen de la structure des
ressources des banques camerounaises montre qu'elles sont constituées
à plus de 50% des dépôts à vue dont le retrait peut
être effectué à tout moment. Dans le portefeuille des
banques au Cameroun, ces ressources provenant de la clientèle
représentent plus de 70% des dépôts. Et la banque
s'exposerait à un risque de liquidité grave si elle utilisait mal
ces ressources. D'après les recommandations du Comité de
Bâle, la modélisation de l'écoulement des
dépôts à vue serait d'une importance capitale pour les
banques camerounaises.
Le travail fait ici constituera un outil supplémentaire
dans la gestion actif/ passif bancaire au Cameroun. Puisque l'objectif que nous
visons est la détermination d'un modèle d'écoulement des
dépôts à vue qui permettra de filtrer la partie stable de
ces dépôts en fonction du temps.
Les données que nous avons utilisées pour la
modélisation sont constituées d'une série mensuelle
d'encours des dépôts à vue de l'ensemble des banques
commerciales allant de janvier 1997 à décembre 2006 et d'une
série mensuelle d'observation sur les taux d'intérêt.
Pour atteindre nos objectifs, une analyse de la
cointégration et un test de causalité de Granger nous ont permis
de voir qu'au Cameroun, le niveau de l'encours des dépôts à
vue ne dépend pas de l'évolution des taux d'intérêt.
Autrement dit, le comportement des
clients en terme de dépôts sur leur compte
à vue n'est pas influencé par les mouvements de taux
d'intérêt. Ce qui voudrait dire que les niveaux atteints par les
taux d'intérêt n'ont jusque là pas été
significatif pour captiver l'ensemble des titulaires de comptes à vue.
Puis la méthodologie de Box et Jenkins nous a permis de trouver dans la
classe des modèles ARIMA, le modèle décrivant
l'évolution des dépôts à vue. Il s'agit,
après avoir transformé notre série par la fonction
logarithme népérien, d'un modèle ARIMA(0,1,1) (Moyenne
Mobile d'ordre 1 et intégré d'ordre 1). Enfin la
détermination de la fonction d'écoulement nous a permis de voir
qu'une fois tous les comptes des clients agrégés, l'encours ainsi
obtenu est stable dans le temps. En effet d'après nos analyses, le stock
des dépôts à vue pris à une date donnée
mettra en moyenne 8 ans et 4 mois pour disparaître complètement du
bilan. Il s'évapore à un rythme de 11,96% par mois. Ainsi,
pendant un mois 88,04% de l'encours des dépôts à vue seront
stables dans le bilan, 46,58% y resteront pendant 6 mois, 21,70% ne sortiront
pas du bilan avant un an, les clients laisseront 4,71% du stock des
dépôts à vue dans les caisses de la banque pendant deux
ans.
Les résultats issus de ce travail peuvent permettre aux
banques camerounaises d'améliorer la gestion de leur liquidité,
de s'impliquer davantage dans le financement de l'économie, puisqu'elles
disposent désormais d'un outil supplémentaire leur permettant
d'évaluer le risque de transformation. La Banque Centrale pourrait
utiliser la stabilité de ces dépôts à vue pour
ajuster le coefficient des réserves obligatoires relatif à ce
type de dépôts.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
Une banque est définie comme un établissement de
crédit dont le rôle est de procurer des services financiers aux
particuliers ainsi qu'aux entreprises (Encarta 2006). Leur activité
principale consiste à collecter des fonds qui, mobilisés sous
plusieurs formes (octroi d'un prêt par exemple), permettent de financer
l'activité économique. Les fonds collectés peuvent d'une
part, provenir de la clientèle qui effectue deux formes de
dépôts : les dépôts à vue (c'est à dire
avec possibilité de retrait à tout moment) ou les
dépôts à terme (ce n'est qu'à échéance
que le retrait est possible), d'autre part, être empruntés sur le
marché monétaire.
Au milieu des années 80, les banques de la zone BEAC et
particulièrement celles du Cameroun ont subi, une grave crise qui a
entraîné d'importantes pénuries de liquidités, une
faible capitalisation et une mauvaise structure de leur portefeuille. Au niveau
social, cette crise bancaire a occasionné de nombreuses pertes d'emplois
suite à la fermeture d'entreprises qui n'avaient plus la capacité
d'accéder à leur trésorerie confiée aux banques.
(cf. Marianne MBENA NGABA [2006], Gestion de la liquidité bancaire :
une application au Cameroun, thèse professionnelle
université de Douala)
De nombreuses restructurations ont été
engagées au début des années 1990 de sorte qu'à
partir de 1995, le secteur bancaire camerounais est assaini, liquide et stable
grâce au dispositif réglementaire et prudentiel mis en place par
la COBAC (Commission Bancaire d'Afrique Centrale, créée en
janvier 1993). Les banques camerounaises, avec les nouvelles contraintes de
gestion sont devenues surliquides. Avec un ratio de liquidité de 70% en
1991, elles ont atteint au 31 juin 1997 un niveau de 110,5% pour
dépasser 150% en décembre 2004. (cf. rapports annuels
d'activité de la COBAC)
Un autre constat est imminent dans le secteur bancaire
camerounais : on constate le « paradoxe d'une forte liquidité
bancaire dans une économie où le volume des crédits
croît très lentement » (BEKOLO EBE [1998] cité
par Marianne MBENA). La réalité est que la majorité de
ressources des banques est faite de dépôts à vue (en effet
d'après les données du Conseil National du Crédit, depuis
la fin des opérations de restructuration, plus de 50% des ressources des
banques sont des dépôts à vue dont le retrait peut
être effectué à tout moment) et la banque s'exposerait
à un risque de transformation et de liquidité grave si elle
utilisait mal ces ressources. On remarque ainsi la
«frilosité» du
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
banquier camerounais dans ses activités d'offre de
crédit à cause des difficultés à évaluer le
risque.
Face à cette opportunité que constitue la
surliquidité bancaire et la place importante que les dépôts
à vue occupent dans les ressources des banques, la préoccupation
principale de ce travail est de savoir : comment on peut valoriser
ces dépôts à vue. Autrement dit, quel est le modèle
d'écoulement des dépôts à vue pour les banques
camerounaises et quelle est la partie de ces dépôts, stable en
fonction du temps que les banques pourraient utiliser pour octroyer des
crédits en minimisant le risque de transformation et de liquidité
? Préoccupation pertinente surtout si on considère
la banque comme un agent économique rationnel ayant pour objectif
d'optimiser sa rentabilité. Le banquier camerounais devrait s'impliquer
davantage dans le financement de l'économie puisque « la banque est
l'un des moteurs essentiels de la croissance » (Valérie OHANNESSIAN
[2007], la banque à découvert). La modélisation
de l'écoulement des dépôts à vue se rapporte
à un problème de gestion actif /passif bancaire et fait partie
des recommandations les plus récentes du Comité de Bâle en
vue d'une meilleure gestion des risques.
L'écoulement en liquidité d'un produit est
généralement défini au moyen de sa fonction
d'écoulement qui décrit comment le stock s'amortit dans le temps.
La loi pouvant être contractuelle ou conventionnelle. La fonction
d'écoulement de la production donne la probabilité qu'un franc
CFA de production nouvelle (nouveau dépôt à vue par
exemple) entrant à la date t dans le bilan, demeure dans ce
bilan jusqu'à une date T ultérieure. Pour certains
produits de type échéancé (pour lequel il existe une date
de fin de contrat), la convention d'écoulement théorique
correspond à l'écoulement tel qu'il est défini dans le
contrat. Par exemple, lorsqu'on considère un crédit à la
consommation de durée 5 ans, on peut, au moment où ce montant
entre dans le bilan, définir l'écoulement contractuel du produit
comme celui correspondant à l'échéancier de remboursement
mis en place. Néanmoins, l'écoulement du produit qu'on choisira
de retenir comme conventionnel peut être différent de cet
écoulement théorique puisque le client dispose de diverses
options (par exemple l'option de remboursement anticipé) qui viendront
modifier la convention d'écoulement. Ainsi, on pourra choisir
d'intégrer ces facteurs non contractuels, mais bien réels, dans
l'écoulement conventionnel du produit. (cf. Grégory GHIEU
[2003], Gestion Actif/Passif, Méthodologie et Application au Livret
A).
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
Par ailleurs les dépôts à vue font partie
des produits pour lesquels aucune date de fin contractuelle n'est
spécifiée. En effet le contrat d'ouverture d'un compte de
dépôt à vue ne spécifie pas la durée de fin
de contrat. Les montants présents sur ces comptes peuvent être
retirés a tout instant. Il n'existe pas d'écoulement contractuel
pour ces produits et la définition d'un écoulement effectif est
l'essence de notre problématique.
Ainsi, la présente étude se propose:
> de déterminer un modèle d'écoulement
des dépôts à vue pour les banques camerounaises
> de ressortir la partie stable de ces dépôts en
fonction du temps.
Pour atteindre ces objectifs, la revue de la littérature
nous a permis de mettre en évidence les hypothèses suivantes :
Hypothèse 1 : Une fois tous les comptes à vue
individuels des clients agrégés, l'encours global ainsi obtenu
est stable dans le temps.
Hypothèse 2 : L'évolution des taux
d'intérêt au Cameroun n'a pas un effet significatif sur le niveau
de l'encours des dépôts à vue.
L'intérêt de cette étude réside
dans le fait qu'elle constituera un outil supplémentaire dans la gestion
actif/passif bancaire au Cameroun et permettra aux banques de s'impliquer
davantage dans le financement de l'économie tout en minimisant le risque
de liquidité et de transformation.
Pour résoudre notre problème, nous partirons
d'une analyse de la liquidité des banques camerounaises et de la
structure des ressources de ces banques pour montrer que l'essentiel de leurs
ressources est fait de dépôts à vue. Puis nous utiliserons
la méthodologie de Box et Jenkins pour déterminer le
modèle d'écoulement de ces dépôts ainsi que la
fonction d'écoulement qui nous permettra enfin de filtrer la partie
stable de ces dépôts en fonction du temps.
Pour cela, nous avons structuré ce mémoire en deux
grandes parties :
La première partie est consacrée à la
définition des concepts et à la revue de la littérature
sur les modèles de dépôts à vue. Il s'agira dans le
premier chapitre de définir les risques bancaires et le concept
d'écoulement, dans le second chapitre de présenter la revue des
modèles de dépôts à vue. La deuxième partie
est celle de l'application au cas du Cameroun. Nous présenterons les
banques commerciales camerounaises et leur liquidité (Chapitre III) et
après nous construirons un modèle d'écoulement des
dépôts à vue pour ces banques (Chapitre IV).

REVUE DE LA LITTÉRATURE SUR LES
MODÈLES DE
Cette premiere partie est consacrée a la revue de la
littérature. Elle comprend deux chapitres. Dans le premier, nous
présenterons les concepts et les définitions nécessaires
pour appréhender la modélisation des écoulements. Dans le
deuxième, nous passerons en revue les généralités
sur la modélisation des écoulements des postes du bilan d'une
banque ainsi que les modeles e xistants de dépots a vue.
GESTION DES RISQUES BANCAIRES ET
CONCEPT
D'ÉCOULEMENT
Dans ce chapitre, nous présenterons les
définitions et les concepts clés nécessaires pour
appréhender la modélisation des écoulements. Le concept
d'écoulement comme nous le verrons plus loin est essentiel à
l'évaluation de certains risques bancaires. C'est pour cela que nous
avons jugé important de passer en revue d'abord les principaux risques
bancaires avant d'aborder la notion d'écoulement.
SECTION I : La firme bancaire et ses principaux
risques
I.1 La firme bancaire
La banque peut être définie comme un
établissement de crédit ayant pour objet de procurer des services
financiers aux particuliers ainsi qu'aux entreprises, qu'elles soient
privées ou publiques (Encarta 2006). Dans cette partie, nous allons
présenter d'abord les activités de la banque, ensuite, selon
l'activité principale exercée, les différents types de
banques, les principaux postes du bilan et hors bilan, enfin le compte de
résultat d'une banque.
I.1.1 L'activité de la banque
De nos jours, la monnaie sert d'intermédiaire
d'échanges. Elle permet de pouvoir échanger un bien ou un service
contre un autre bien/service, facilitant ainsi la circulation et
l'évaluation de ces biens et services. On distingue la monnaie
fiduciaire (billets de banque et pièces) et la monnaie scripturale
(opérations ayant pour support les dépôts ou les
crédits bancaires) et la monnaie électronique.
A certains moments, un agent économique peut disposer
d'une quantité de monnaie supérieure à ses besoins. En
revanche, il se peut qu'à d'autres moments, il vienne à en
manquer pour répondre à ses besoins de trésorerie ou
d'équipements. La banque sert ainsi d'intermédiaire entre des
agents qui ont trop de disponibilités (les déposants) et ceux qui
n'en ont pas assez (les emprunteurs).
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
Les clients à qui profitent les services de la banque
sont : les particuliers (il s'agit de toute personne agissant en dehors de son
activité professionnelle), les entreprises (il s'agit des individus ou
groupes d'individus étudiés sur le plan de leur activité
professionnelle), les collectivités (régions,
départements, communes) et l'Etat.
L'activité principale des banques consiste à
collecter des fonds qui, mobilisés sous plusieurs formes (octroi d'un
prêt par exemple), permettent de financer l'activité
économique. Les fonds collectés sont effectués sous deux
formes :
> La collecte des dépôts : Il s'agit de
l'ensemble des disponibilités confiées par les clients aux
banquiers. Ces dépôts pouvant être effectués à
vue (c'est-à-dire avec possibilité de retrait à tout
moment) ou à terme (ce n'est qu'à échéance que le
retrait est possible)
> L'emprunt sur le marché monétaire : lorsque
la collecte des dépôts n'est pas
suffisante pour répondre à ses exigences, la
banque peut emprunter sur le marché
monétaire qui est considéré comme le
marché des capitaux à court terme.
Pour ce qui est du financement de l'économie, La banque
l'assume en accordant des crédits soit par décaissement ou par
caution (il s'agit dans ce cas de l'engagement pris par le banquier d'honorer
la signature de son client en cas de défaillance de ce dernier). Les
crédits accordés peuvent être à court terme
(durée inférieure ou égale à 2 ans), à moyen
terme (durée comprise entre 2 et 7 ans), long terme (durée
supérieure à 7 ans).
Les banques offrent aussi à leurs clients un certain
nombre de services (à savoir, service de caisse, location de coffres,
conseils, gestion de portefeuille, exécution des ordres de virement,
gestion des règlements par carte bancaire, opérations de change
avec l'étranger, placement des emprunts de l'Etat etc.) moyennant des
commissions.
I.1.2 Les différents types de banques
On distingue 4 catégories de banques selon leur
activité principale1 :
> Les banques de détail ou traditionnelles : leurs
activités sont principalement orientées vers une clientèle
non financière (ménages, entreprises, collectivité) avec
comme activité prédominante la collecte de dépôts et
l'octroi de crédits ;
> Les banques de marché : elles sont
spécialisées dans les opérations sur le marché des
capitaux et pratiquent surtout les opérations sur titres, sur
instruments
1 Cj Pascal KUATE, Cours monnaie et
crédits, page 21.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
financiers, interbancaires. Elles ne font pas d'opérations
avec la clientèle non financière ;
> Les banques d'affaires : spécialisées dans
les prises de participation dans l'industrie, elles se caractérisent par
l'importance de leur portefeuille titres (actions, certificats
d'investissement) et le montant élevé de leurs fonds propres ;
> Les banques universelles : contrairement aux banques
spécialisées, elles exercent toutes les activités
bancaires possibles et élargissent même leur gamme à
d'autres activités non bancaires telles que l'assurance.
La photographie de la situation d'une banque à un
moment donné est présentée par son bilan. Nous
décrirons dans la suite les différents éléments qui
constituent le bilan simplifié d'une banque.
I.1.3 Les principaux postes du bilan et hors-bilan d'une
banque
Pour donner une classification de l'actif et du passif du
bilan d'une banque, le premier critère utilisé est le
degré de liquidité. C'est-à-dire le degré de
disponibilité pour l'actif et d'exigibilité pour le passif. C'est
cela qui distingue la présentation du bilan d'une banque de celle
adoptée par la comptabilité traditionnelle (la
présentation du bilan d'une banque se faisant donc dans l'ordre
inverse). Le second critère concerne le type d'opération : on
distingue les opérations avec les agents non financiers et les
opérations avec les établissements de crédit.
I.1.3.1 Les principaux postes du bilan
Le bilan simplifié d'une banque regroupe les
éléments de l'actif et du passif suivant :
Tableau 1 : Principaux postes du bilan d'une
banque
|
Actif
|
Passif
|
|
Les avoirs liquides (caisse, avoirs en compte à la
banque centrale)
|
Emprunts auprès de la banque centrale ou d'autres
institutions financières
|
|
Les prêts à d'autres institutions
financières (prêts interbancaires)
|
Les dépôts de la clientèle
(dépôts à vue, comptes d'épargne, comptes à
terme,...) ;
|
|
Les crédits à la clientèle (agents
non financiers) ;
|
Les opérations sur titres (pensions,
certificats de dépôts et obligations émises) ;
|
|
Les portefeuilles-titres (fusions, placements,
participations) ;
|
Les fonds propres et provisions.
|
|
Les valeurs immobilisées (prêts
subordonnés, immobilisations, crédit-bail,...)
|
|
Source : Pascal Kuaté, cours monnaie et
crédit, page 21 et22
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
I.1.3.2 Le hors-bilan
Ce sont des engagements donnés ou reçus par la
banque, mais qui ne donnent pas directement lieu à la mobilisation de
fonds. Il s'agit des :
> Engagements de financement (par exemple, l'ouverture d'une
ligne de crédit) ; > Engagements de garanties (cautions, avals) ;
> Engagements sur titres et instruments financiers à
termes.
Il est à noter que la taille du hors bilan de la plupart
des banques représente en moyenne plus de trois fois le montant de leur
actif.
Après avoir présenté les
éléments constitutifs de la situation de la banque à
travers le bilan et le hors bilan, nous allons explorer dans la suite son
compte de résultat.
I.1.4 Le compte de résultats
Le compte de résultats d'une banque retrace de
façon exhaustive ses produits et ses charges sur une période
donnée
I.1.4.1 Principaux postes du compte de
résultat2
On distingue trois catégories de produits et de charges
:
> Les produits et charges d'exploitation bancaire :
· Intérêts (versés ou reçus)
;
· Commissions (versées ou perçues) ;
· Gains/pertes sur opérations financières
(titres, change, instruments financiers) ;
> Les autres produits et charges ordinaires, qui sont
principalement constitués de:
· charges générales d'exploitation (frais de
personnel et autres frais administratifs) ;
· dotations aux amortissements ;
· soldes en bénéfices ou perte, correction de
valeur de créances, immobilisations, éléments de
hors-bilan.
> Les produits et charges exceptionnels.
2 Cf. Pascal Kuaté cité plus haut, page
22.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
Aux charges s'ajoute l'impôt sur les
bénéfices ou une perte de l'exercice. De l'ensemble du compte de
résultats se dégage un bénéfice ou une perte de
l'exercice. Les frais de structure (ou frais généraux), se
composent des charges générales d'exploitation et des dotations
aux amortissements.
I.1.4.2 Les soldes intermédiaires de
gestion
Ces grandeurs permettent de faire l'analyse des
résultats, en particulier le produit net bancaire et le résultat
net. On distingue généralement les soldes suivants,
consignés dans le compte de résultat :
Tableau 2 : Le compte de résultat
|
CHARGES
|
PRODUITS
|
|
> Intérêts versés et Charges
assimilées
|
> Intérêts reçus et produits
assimilés
|
|
> Pertes sur opérations des
portefeuilles de négociation
|
> Revenus des titres à revenu
variable
|
|
> Pertes sur opérations des
portefeuilles de placement et
assimilés
|
> Commissions nettes
|
|
> Autres charges d'exploitation
bancaire
nettes
|
> Gains sur opérations des
portefeuilles de négociations
|
|
> Gains sur opérations des
portefeuilles de placement et
assimilés
|
|
> Autres produits d'exploitation bancaire
nets
|
|
Solde : PRODUIT NET BANCAIRE
|
|
> Charges générales
d'exploitation
|
|
|
> Dotations aux amortissements et aux provisions sur
immobilisations incorporelles et corporelles
|
|
|
Solde : RESULTAT BRUT D'EXPLOITATION
|
|
> Coût du risque
|
|
|
Solde : RESULTAT D'EXPLOITATION
|
|
> Pertes sur actifs immobilisés
|
> Gains sur actifs immobilisés
|
|
Solde : RESULTAT COURANT AVANT IMPOT
|
|
> Résultat exceptionnel
|
> Résultat exceptionnel
|
|
> Impôts sur les
bénéfices
|
> Reprises de FRBG (Fonds propres pour Risques
Bancaires Généraux) et de provisions
|
|
> Dotations de FRBG (Fonds propres pour Risques
Bancaires Généraux) et provisions
réglementées
|
|
|
Solde : RESULTAT NET
|
Source : Paul Demey et al.[2003], Introduction
à la gestion Actif-Passif Bancaire, Page 43,44
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
Dans la plupart des cas, la banque dans ses opérations,
fait face à des risques qu'elle doit pouvoir gérer afin
d'éviter de tomber en faillite. L'objet principal de notre étude
étant la modélisation de l'écoulement, qui est un outil de
mesure et de prévention de risque, il nous paraît important de
passer en revue les principaux risques encourus par les banques.
I.2 Les risques bancaires
Comme nous l'avons mentionné plus haut, les banques
assurent une fonction d'intermédiaire financier. Lorsqu'une banque
combine des ressources d'origines diverses pour financer plusieurs emplois
distincts, cette fonction est qualifiée d'allocation. La transformation,
qui représente la deuxième fonction d'intermédiation,
consiste à emprunter à une échéance courte et
à placer les fonds ainsi obtenus dans des actifs de plus longs termes,
ou à emprunter à taux fixe pour prêter à taux
variable. C'est cette deuxième fonction qui est à l'origine de la
majeure partie des risques financiers.
Après avoir présenté la typologie des
risques encourus par les banques, nous examinerons ensuite les méthodes
classiques mises en place pour gérer ces risques et enfin nous
présenterons les recommandations faites par le Comité de
Bâle pour une gestion actif/passif plus efficace.
I.2.1 Les principaux risques bancaires
En 1995, Bessis distingue deux sortes de risques (Cf. Bessis
J. [1995]): les risques financiers et les risques opérationnels. Selon
le comité de Bâle, « Operational risk is defined as the
risk of loss resulting from inadequat or failed internal process, people and
systems or from external events. This definition includes legal risk, but
excludes strategic and reputational risk ». Ce risque, pouvant
entraîner des pertes importantes pour la banque, doit être pris en
compte dans sa gestion interne. On distingue 6 types de risques
financiers3 :
> Le risque de contrepartie : c'est le risque pour un
créancier de perdre définitivement sa créance dans la
mesure où le débiteur ne peut pas, même en liquidant
l'ensemble de ses avoirs, rembourser la totalité de ses engagements,
3 cf. Grégory GHIEU [2003] Cité plus
haut, page 7.
> Le risque de liquidité pour une banque
représente l'éventualité de ne pas pouvoir
faire face, à un moment donné, à ses
engagements ou à ses échéances,
> Le risque de taux d'un établissement financier est
celui de voir sa rentabilité ou la
valeur de ses fonds propres affectées par
l'évolution des taux d'intérêt,
> Le risque de marché est le risque de pertes sur les
positions du bilan et du hors
bilan à la suite de variations des prix de
marché,
> Le risque de change, traduit le fait qu'une baisse des cours
de change peut entraîner une perte de valeur libellée en devises
étrangères.
> Le risque de solvabilité, est
l'éventualité de ne pas disposer de fonds propres suffisants pour
absorber les pertes éventuelles.
Certains de ces risques sont inhérents à
l'activité relative à la banque commerciale et d'autres sont
relatifs aux opérations de marché. En général, les
risques trouvent leur origine soit dans les opérations de marché
(on peut citer le risque de crédit, le risque de liquidité et le
risque de marché), soit dans les opérations de la banque
commerciale (le risque de crédit, le risque de taux
d'intérêt, le risque de liquidité). (Grégory GHIEU
[2003]).
Pour faire face à ces risques, la banque doit
gérer de façon dynamique tant l'actif et le passif de son bilan
que sa situation hors bilan. La modélisation de l'écoulement
étant une technique de maîtrise du risque de liquidité et
de taux sur le périmètre des activités commerciales de la
banque, nous insisterons dans la suite sur la gestion des risques de taux et de
liquidité. Rappelons que les analyses en liquidité et en taux
sont extrêmement dépendantes. En effet, tout besoin en
liquidité à une date donnée est financé aux
conditions de taux de la date courante. Ainsi, bien qu'il soit indispensable de
faire des prévisions de besoins de liquidité, cette
prévision doit être complétée par une analyse du
risque de taux. « Les besoins (respectivement excédents) de
liquidités aux dates futures seront refinancés (respectivement
placés) selon diverses modalités qui ont toutes pour
particularité de porter une incertitude quant aux conditions de taux
auxquelles elles seront effectuées. » (Grégory GHIEU
[2003]).
I.2.2 La gestion des risques de taux et de
liquidité
Le risque de taux d'intérêt est le risque de voir
ses résultats affectés défavorablement par les mouvements
de taux d'intérêt. Pour ce qui est de la liquidité
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
d'une banque, nous pouvons conformément au document du
comité de Bâle, la définir comme la capacité de
financer ses actifs et de rembourser les engagements pris au moment où
ces financements ou remboursements surviennent. Le risque de liquidité
se traduit donc à travers l'impossibilité de satisfaire ses
engagements. Il apparaît lorsque des besoins inattendus sont subis par la
banque et qu'elle ne peut y faire face à partir de ses actifs liquides.
Le risque de liquidité est fondamental pour une banque. Comme le
suggère la définition, une liquidité mal
maîtrisée peut :
> provoquer la faillite d'une banque : en cas
d'illiquidité extrême ;
> engendrer une perte d'opportunité par
incapacité de financer le développement de l'activité ;
> engendrer une crise de liquidité par
incapacité à honorer les engagements contractés.
Nous nous attachons dans cette partie aux méthodes
d'appréhension et de quantification du risque de liquidité et du
risque de taux.
Certains facteurs sont à l'origine du risque de
liquidité et de taux d'intérêt. On peut citer le mouvement
des taux d'intérêt (qui est un facteur important
d'instabilité des résultats d'une banque) et le comportement de
la clientèle (l'option de remboursement anticipé des
crédits ou de retrait de tout ou d'une partie des montants placés
sur son compte à vue sont quelques unes des options implicites à
la portée du client de la banque). Les mouvements des taux
d'intérêt influencent très fortement l'exercice de ces
options par le client. Il naît alors un risque lié aux clauses
optionnelles. J. Bessis en 1995 considère ce risque comme un risque de
taux indirect.
Dans la suite, après avoir présenté les
méthodes (ainsi que leurs limites) rencontrées dans la
littérature et couramment utilisées dans les banques pour la
gestion de ces risques, nous proposerons les recommandations faites par le
comité de Bâle pour une gestion plus efficiente du risque de taux
et de liquidité.
I.2.2.1 Les Méthodes classiques de gestion des
risques de taux et de liquidité
Plusieurs méthodes sont couramment utilisées par
les banques pour gérer les risques de taux et de liquidité. On
peut citer la méthode des gaps, la méthode de la
duration4
4Ces méthodes sont détaillées
dans le document de Grégory GHIEU [2003] cité plus haut, Page
15-20.
1.2.2.1.1 Méthode des gaps
Pour évaluer l'impact du risque de taux sur le
résultat global de la banque, c'est-àdire sur la marge
d'intérêt, Bessis et Darmon font référence à
la méthode des gaps. Cette méthode décompose un bilan
bancaire en actif et en passif, contenant chacun des postes dégageant
des flux caractérisés par un taux et un échéancier.
Il est possible de classer ces postes par taux puis par échéance
et de scinder chacune de ces classes en deux parties. L'une contenant les flux
non affectés par un mouvement de taux et l'autre incluant les flux
affectés par un mouvement de taux (ce sont ceux des postes à taux
variables et ceux de la production nouvelle affectée par les nouveaux
taux. On définit le gap (impasse) comme l'écart, à une
date t, entre l'actif et le passif.
En particulier, on appelle gap à taux fixe, la
différence entre l'actif et le passif non affectée par un
mouvement de taux. Seuls les actifs et les passifs à taux variables sont
concernés par une variation de taux. La méthode des gaps
établit un échéancier de rémunérations
payées ou reçues sur chacun des actifs et passifs
dépendant des mouvements des taux d'intérêts en fonction de
leur maturité ou de leur date de repricing5 lorsqu'ils sont
à taux variable. L'amplitude du gap résultant de l'ensemble du
bilan fournit alors le niveau d'exposition de la banque au risque de
translation de la courbe de taux.
Relativement simple d'emploi, cette méthode est
fréquemment utilisée et permet de fournir des indications sur
l'apparition du résultat dans le temps.
Elle a l'inconvénient :
de ne se limiter qu'aux produits à
échéanciers bien déterminés ;
> de mettre hors d'analyse l'optionalité : en effet,
elle ne tient pas compte de l'impact de l'évolution des taux
d'intérêt sur l'amortissement de l'encours (remboursement
anticipés..) ou sur les effets de substitution (par exemple des
dépôts à vue aux comptes à termes) ;
> elle n'intègre pas la production nouvelle qui va
pourtant modifier la structure du bilan et par conséquent les impasses
aux différentes dates futures.
1.2.1.1.2 Méthode de la duration
Dans la littérature, une autre méthode est
couramment rencontrée (cf. Bitner, Darmon). Il s'agit de la
méthode de la duration. Cette méthode s'intéresse à
la valeur
5 Il s'agit de la date où le taux client est
révisé (modifié).
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
actuelle nette de la banque et est utilisée lorsque les
dirigeants souhaitent porter leur attention sur la valeur de marché de
la banque et non sur une approche relative à son résultat
à court terme. Dans cette méthode, on exprime l'exposition au
risque de taux relative à chacun des actifs et passifs en termes de
sensibilité de leur Valeur Actuelle Nette.
Le concept de duration et de sensibilité est alors
utile pour évaluer l'exposition au risque de taux de la valeur de
marché de la banque. Si on note V la valeur de marché
d'un actif et r le taux d'intérêt, sa duration D vaut
alors :
(1) (1 ) ,
+ r dv
D = -
·
v dr
La sensibilité S de cet actif vaut quant à elle
:
D dv 1
(2)
= -
· ,
(1 )
+ r dr v
S =
Ainsi, si les taux augmentent de 1%, un actif de
sensibilité globale S verra sa valeur augmenter de
S%.
Cette méthode a l'avantage d'être très
synthétique. En effet, l'ensemble des flux futurs est
résumé à une seule valeur (la valeur Actuelle Nette) par
le biais de l'actualisation. On peut ainsi déduire la sensibilité
de cette valeur aux différents facteurs qui l'influencent, par exemple
les taux d'intérêt ou le comportement des clients.
Cette méthode possède un avantage
extrêmement important par rapport à la méthode des gaps.
Elle permet d'intégrer les opérations optionnelles telles que les
options relatives aux relations avec la clientèle puisque celles-ci
peuvent être valorisées et ajoutées à la valeur
obtenue par actualisation des flux futurs.
Cette méthode est limitée car elle est
construite sous la seule hypothèse de translation des taux et telle
qu'elle est décrite, dans les ouvrages de gestions actif/passif
bancaire, elle ne permet pas d'appréhender le risque de
liquidité. Elle se doit donc d'être complétée par
une méthode permettant de gérer ce risque.
Les approches précédentes sont des approches
statiques qui consistent à mesurer l'impact d'une variation de taux
à une date donnée sur les résultats ou sur la valeur nette
de l'établissement. L'analyse statique ne tient pas compte de
l'évolution future du bilan (productions nouvelles), des risques de
fluctuations ultérieures des taux, de leur volatilité.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
Dans la partie suivante nous présenterons ce que
recommande le comité de Bâle en vue d'une gestion plus rationnelle
et efficiente des risques de liquidité et de taux.
I.2.2.2 Les recommandations du comité de
Bâle6
Créé en 1974, le comité de Bâle est
un mouvement international d'harmonisation des règles prudentielles. Il
se réunit quatre fois par an et fait un certain nombre de
recommandations relatives à la gestion bancaire. Il regroupe aujourd'hui
la Belgique, le Canada, la France, la Suède, la Suisse, le Royaume-Uni
et les Etats-Unis. Chacun des pays est représenté par sa banque
centrale. Grâce à la trentaine de groupes de travail qui se
réunissent régulièrement, ce comité fait un certain
nombre de recommandations relatives à la gestion bancaire. Chaque pays
est ensuite libre de prendre les décisions qui conviennent le mieux
à son système bancaire.
En ce qui concerne le risque de liquidité et le risque
de taux, dans son document consultatif, le Comité de Bâle de
Janvier 2001 consacre un chapitre aux « Principles for the Management and
supervision of Interest Rate Risk » ainsi qu'un chapitre aux «
principles for the Assessment of Liquidity Management in banking Organisations
». Dans ces documents, le comité considère que le niveau
fondamental de gestion de la liquidité doit être la mesure de tous
les flux sortant et entrant afin d'identifier où peuvent se situer les
insuffisances potentielles de liquidité dans le bilan. Par ailleurs, il
y est précisé qu'un aspect important de la liquidité
réside dans les hypothèses de besoins futurs.
Le Comité de Bâle recommande alors de mettre en
place des écoulements en liquidité pour chacun des produits du
bilan de la banque. Cette modélisation devra permettre de calculer par
la suite les impasses en liquidité, c'est-à-dire la
différence entre les actifs et les passifs du bilan aux dates futures et
de gérer de manière efficace certains risques bancaires. Le
comité recommande ainsi d'effectuer à la fois des
évaluations d'écoulement « statique » mais aussi «
dynamique ».
Afin d'évaluer le lien entre le taux des différents
produits et les taux de marché, le comité recommande aussi
d'évaluer des écoulements en taux.
6 La version originale de ce document est disponible
sur le site de la BIS (Bank for International Settlements) :
http://www.bis.org/publ/bcbs29a.pdf,
la version française se trouvant sur le site de la Banque de France
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
Le concept d'écoulement présenté à la
section suivante constitue une réponse à ces souhaits.
SECTION II : Le Concept d'écoulement
La méthode exposée dans cette section correspond
aux exigences du Comité de Bâle. Nous définirons la notion
d'écoulement en liquidité qui permet de calculer des impasses en
liquidité et la notion d'écoulement en taux qui va permettre de
traduire l'ajustement des taux des divers produits sur les taux
d'intérêt de marché. Cette méthode est
évoquée dans le document de Grégory GHIEU [2003]. Elle a
été formulée du point de vue mathématique par P.
Demey, A. Frachot et G. Riboulet (Groupe de Recherche Opérationnelle,
Direction des Risques du Groupe Crédit Agricole) en 2001.
II.1 La notion d'écoulement en liquidité
Pour un produit bancaire donné, son écoulement
en liquidité montre comment le stock disparaît dans le temps. Elle
peut être contractuelle ou conventionnelle et intègre les
aléas pouvant affecter la liquidité du produit. Modéliser
la liquidité d'une banque nécessite l'étude de chaque
poste du bilan afin de déterminer son degré de liquidité
pour les actifs et d'exigibilité pour les passifs. Il importe dans
l'analyse de prendre en compte les paramètres tant internes qu'externes
qui peuvent agir sur la banque.
La différence entre le total de l'actif et le total du
passif est nulle pour la date courante puisque le bilan de la banque est
équilibré à tout instant. Cependant, lorsqu'on projette
cette différence aux dates futures, elle n'a aucune raison d'être
nulle. Ainsi, lorsqu'on détermine cet écart pour les dates
futures, elle permet d'anticiper les montants qui pourront être
empruntés ou placés aux dates futures et aussi d'évaluer
une partie du risque de taux auquel s'expose la banque.
Il est donc nécessaire pour une banque d'évaluer
comment chacun de ses actifs et passifs évolue au cours du temps. Il
faut ainsi définir pour chaque poste du bilan la fonction
d'écoulement qui permet de quantifier la probabilité qu'un franc
CFA présent dans le bilan à la date d'aujourd'hui soit encore
présent à une date future. On devra pour cela faire la
différence entre les montants présents dans le bilan à la
date t (le stock ou
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
l'encours) et la façon dont ils s'écoulent, et les
montants entrant dans le bilan aux différentes dates futures qui
représentent la production nouvelle).
II.1.1 L'écoulement de production
La probabilité qu'un franc CFA, entré dans le
bilan à une date t, y soit encore présent à une
date T ultérieure est définie par une fonction
appelée fonction d'écoulement de la production. Il s'agit bien
dans cette définition d'un franc entré à la date t
et non d'un franc CFA présent dans le bilan en t, qui y
est entré avant la date t. Ceci pour indiquer qu'en
général, on suppose qu'un franc CFA qui entre dans un bilan en
t ne s'écoule pas de la même façon, qu'un autre
franc CFA présent en t qui se trouvait dans le stock avant la
date t.
De façon mathématique telle que formulée par
G. Riboulet et al. [2003],
en désignant par PN(t) la production nouvelle
apparue à la date t, PN(t,T) le montant de cette
production encore vivante à la date T, la relation :
(3) PN ( t , T ) = PN ( t
) × S ( t , T)
permet de définir la fonction d'écoulement de la
production nouvelle. Cette fonction d'écoulement a les
propriétés suivantes :
> S ( t , t ) = 1 qui signifie
qu'un franc CFA entrant dans le bilan à la date t se trouve
toujours dans le bilan à la date t.
> S ( t , + 8 ) = 0 qui veut dire que la
production disparaît tôt ou tard du bilan.
Cette fonction d'écoulement définit la
convention en liquidité du produit et nécessite de définir
une date arbitraire de sortie du bilan pour les produits tels que les
dépôts à vue.
La notion d'écoulement contractuel concerne les
produits pour lesquels il existe une date de fin de contrat. Ici la convention
d'écoulement théorique correspond à l'écoulement
tel qu'il est défini par les termes du Contrat. Pour illustrer nos
propos, prenons le cas d'un crédit à la consommation de
durée 5 ans. Au moment où ce montant entre dans le bilan, on peut
définir l'écoulement contractuel du crédit comme celui
correspondant à l'échéancier de remboursement mis en
place.
Cependant, l'écoulement qu'on retiendra comme effectif
peut être différent de l'écoulement contractuel puisque le
client dispose de plusieurs options (par exemple l'option de remboursement
anticipé) qui viendront modifier la convention d'écoulement.
Ainsi, la fonction d'écoulement de la production nouvelle d'une banque
doit à la fois
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
traduire l'écoulement contractuel de cette production mais
aussi l'occurrence de tous les évènements non contractuels.
Pour les produits non échéancés,
c'est-à-dire ceux pour lesquels il n'existe pas de date de fin
contractuelle (les dépôts à vue par exemple), les montants
présents dans les comptes de ces produits peuvent être
retirés à tout instant. « Il n'existe donc pas
d'écoulement contractuel pour ces produits et la détermination
d'un écoulement effectif reste elle-même assez
problématique » (Cf. Grégory GUIEU [2003]).
Le fait que le client peut gagner ou perdre sur des produits
financiers selon l'évolution des taux d'intérêt, nous
amène parfois à supposer que les fonctions d'écoulement de
la production dépendent : de la date d'entrée dans le bilan de la
production t, du temps écoulé entre la date
d'entrée dans le bilan t et la date considérée
T, des taux d'intérêt de marché entre ces deux
dates.
II.1.2 La vitesse d'écoulement
La fonction d'écoulement peut être définie
au moyen de la vitesse ou taux d'écoulement. Cette notion ne contient ni
plus ni moins d'information que la fonction d'écoulement
S(.,.), mais est plus intuitive. Elle représente le pourcentage
de l'encours en vie qui s'écoule par unité de temps. On la
formule par l'expression mathématique :
(4) ( , ) ( , 1)
S t T S t T
- +
ë ( , )
t T = ,
( , )
t T
S
Qui s'interprète comme suit :
> en t, la production nouvelle PN(t)
apparaît dans le bilan ; > en T, il reste PN (
t , T ) = PN ( t ) × S (
t , T);
> en T+1, il reste PN ( t , T
+ 1) = PN ( t ) × S ( t , T
+ 1).
La vitesse d'écoulement correspond au rapport entre la
part marginale qui disparaît du bilan entre T et T+1,
soit PN ( t , T ) - PN ( t , T
+ 1), et l'encours en vie en T, PN(t,T). (Cf. Paul Demey
et al. [2003], page 22).
Avec des données mensuelles, un taux d'écoulement
de 10% signifie que la production s'évapore à un rythme de 10%
par mois.
L'expression en temps continu est la suivante :
(5) ( , )
? T
LnS t T
ë ( , )
t T = - ( , ) exp( ( , ) ),
? S t T = - ë t s ds ? T t
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
II.1.3 L'écoulement du stock
Le stock d'un poste du bilan peut être
considéré comme l'accumulation des différentes strates de
production nouvelle apparues dans le passé et non encore
écoulées. Par exemple, l'encours de crédits encore
présents à une date correspond bien à tous les
crédits contractés à une date antérieure pour
lesquels les clients n'ont pas fini de rembourser les montants
empruntés. Si on note D(t) l'encours de la date t, on
a la relation mathématique :
t
(6) ( )
D t = PN s S s t ds
( ) ( , ) ,
×
-8
Où S est la fonction d'écoulement de la
production nouvelle qui représente le coefficient d'amortissement. Et
PN(s) la production nouvelle à la date s.
La notion d'écoulement du stock cherche à
traduire le phénomène de disparition de l'encours D(t)
du bilan en supposant nulles les productions nouvelles futures. Ceci permet de
voir comment s'écouleraient les montants présents dans le bilan
de la banque si elle arrêtait l'activité leur ayant trait.
L'encours d'une date future peut s'écrire
T
(7) ( ) ( , )
D T = D t T + PN ( s )
× S ( s , T)
t
|
ds
|
|
Où D(t,T) représente la projection de
l'encours actuel sous l'hypothèse de production nouvelle future nulle.
Le second facteur représente l'accumulation entre les dates t
et T de différentes strates de production nouvelle. On
écrit :
t
(8) ( , )
D t T = PN ( s ) × S (
s , T )ds
-8
La fonction d'écoulement du stock est le pourcentage de
l'encours qui est encore présent dans le bilan aux dates futures. Elle
est définie par la relation :
(9) Sstock( t , T)
D ( t , T ) = D ( t
) ×
D'où on en déduit
t
D t T
( , ) PN s S s T ds
( ) ( , )
×
(10) -8
S t T
( , ) = =
stock
D ( t) f t PN ( s
) × S ( s , t )ds
-8
En général, la fonction d'écoulement du
stock Sstock(.,.) n'est pas la même que la
fonction d'écoulement S(.,.) des différentes productions
nouvelles qui composent ce stock.
S'il est vrai que la connaissance de l'écoulement futur
des encours actuels sous l'hypothèse des productions futures nulles,
permet de déterminer les besoins futurs de
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
liquidité ou les placements futurs de liquidité
excédentaire, il faut également évaluer les productions
nouvelles futures, pour en déduire finalement ce que seront les encours
réellement inscrits au bilan aux dates futures. Cela revient à
déterminer comment les encours futurs combinent écoulement de
l'encours d'aujourd'hui et productions nouvelles futures. L'équation
comptable ou de «conservation de la matière» :
Encours en t = Encours en t-1 + Production nouvelle -
Ecoulement de l'encours entre t-1 et t répond au formalisme
d'introduction des productions nouvelles futures. Mais il ne s'agit pas d'une
équation de modélisation. En partant de l'expression
mathématique (6),
On obtient par différentiation :
t ? S s t
( , )
(11) dD t PN t
( ) = ( ) + PN s
( ) × ds dt ,
-8 ?t
Ceci traduit exactement l'expression comptable
précédente. L'expression suivante :
|
(12)
|
t ? S s t
( , )
PN s
( ) × ds
-8 ?t
|
(Qui est de signe négatif)
|
représente le flux d'écoulement de l'encours entre
t et t+dt. dD(t) est donc la variation de l'encours
entre t et t+dt. (Cf Frachot et al. [2003].)
II.1.4 Impasse en liquidité
Le bilan devant être équilibré à tout
instant, si on désigne par Di(t) l'encours d'un poste i du
bilan, p indice pour le passif et a indice pour l'actif, on a
la relation
(13) p ( )
D t - D t =
a ( ) 0
p a
Cependant, si on veut projeter ce bilan à une date
future, il est nécessaire d'introduire les notions de fonctions
d'écoulement et de productions nouvelles que nous avons définies
précédemment. L'impasse en liquidité représente la
différence entre les encours d'actifs et de passifs pour toutes les
dates futures, telles qu'on peut les projeter depuis la date d'aujourd'hui :
(14) Im _ ( , )
p Liq t T = D t T
p ( , ) - D t T
a ( , )
p a
Les sommes étant prises respectivement sur toutes les
lignes de l'actif (respectivement passif). Cette définition ne prend pas
en compte les productions nouvelles futures et donc se place implicitement dans
l'hypothèse où la banque arrête son activité. Il est
important de considérer les productions nouvelles futures car l'impasse
précédente ne permet pas
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
d'appréhender correctement les besoins futurs en
liquidité de la banque. Ceci nous conduit à la définition
de l'impasse dynamique7
(15) Im p _ Liq _ dyn ( t ,
T )= E [D p ( t , T) + t T
PN ;( s ) × S ( s , T
)ds-j- E [D a ( t ,
T) + fT PN *a(
s ) × S ( s , T )
dsj, t
p a
Où *
PN a (resp. PN p ) sont
les éléments de productions nouvelles anticipées dont
on
*
souhaite tenir compte dans l'impasse (productions nouvelles qui
elles mêmes s'écouleront).
II.2 La notion d'écoulement en taux
Le taux d'intérêt de marché qui doit
être appliqué dans le futur constitue un aléa pour les
besoins ou les excédents de liquidité. En effet, nous ne
disposons pas des valeurs des taux de marché futurs. Pourtant il est
important pour une banque d'avoir une vision claire de ses résultats
futurs ainsi que les facteurs qui les influencent.
Dans la suite nous montrerons comment les taux
d'intérêt interviennent à travers la
rémunération reçue ou versée par la banque ainsi
que sur l'impasse en liquidité. Mais avant cela, définissons ce
que nous entendons par marge d'intérêt de la banque.
II.2.1 La marge d'intérêt
La marge d'intérêt est définie par
(16) M( t )= ED ( t ) ×
R :tock ( t) - D p ( t
) × R ftock( t)
a p
où Rsi tock ( t
)désigne le taux de rémunération (versé ou
reçu) du poste i du bilan à la date t. Avec une
vision à long terme, on peut se poser la question de savoir : Vue
d'aujourd'hui, que vaudra la marge à une date future T ? On
obtient la formule suivante :
(17) ( , )
M t T = E D a ( t , T
) × R :tock ( t , T) - E D
p ( t , T ) × R
ftock( t , T)
a p
Mais la formule précédente n'est pas exacte car
il faut prendre en compte dans la projection, le fait que l'impasse en
liquidité pourra être replacée ou refinancée (en
fonction de son signe).
Paul Demey et al. [2003] proposent la formule suivante :
7 Cf. Paul Demey et al. [2003], Introduction à
la gestion actif-passif bancaire, page 33
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
a
(18) ( , )
M t T = ( , ) × ( , ) - D t T R t T
p
D t T R t T ( , ) × ( , ) - D t T
( , ) - D t T r
( , ) ×
a strock p stock a p T
a p a p
Où rT désigne le taux de replacement ou
de refinancement instantané.
De cette formule, on remarque que l'encours de chacun des postes
ainsi que les taux client doivent être projetés dans le futur.
II.2.2 L'impasse en taux
L'impasse de taux mesure l'impact d'une variation de taux
d'intérêt sur la marge d'intérêt. (Grégory
GHIEU [2003]). Pour l'évaluer, il suffit donc de dériver
partiellement la marge d'intérêt par rapport au taux choisi. On a
la formule suivante :
? M t
( )
(19) Im _ ( )
p taux t = (pour un impasse en taux court)
? r t
L'impasse en taux représente en fait la variable qu'on
cherche à annuler lorsqu'on parle de couverture de la marge
d'intérêt contre le risque de taux. (Grégory GHIEU
[2003]).
Dans ce chapitre nous avons d'abord défini
l'activité de la banque à travers son bilan simplifié et
son compte de résultat, ensuite la présentation des risques
bancaires nous a permis de voir que dans ses multiples activités, la
banque fait face à des risques qu'elle doit pouvoir gérer afin
d'assurer sa pérennité. Les risques les plus rencontrés
sont les risques de liquidité et de taux d'intérêt. Enfin,
le concept d'écoulement est apparu nécessaire pour une gestion
plus efficace de ces risques.
Dans la suite nous ferons une revue de la littérature sur
les modèles de dépôts à
vue.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
LES MODÈLES DE DÉPÔTS A
VUE
Nous avons décrit dans le chapitre
précédent les concepts de base nécessaires pour
appréhender la modélisation. Par exemple nous avons
constaté que le concept d'écoulement est nécessaire
à la construction des impasses en liquidité et en taux, de
même qu'à la gestion de certains risques du point de vue du
comité de Bâle. L'hypothèse simplificatrice
d'écoulement déterministe, c'est-à-dire indépendant
des taux d'intérêt, permet de considérer les impasses comme
des indicateurs de risque. Cette hypothèse est la règle dans la
pratique courante de la gestion actif/passif. Mais parfois, dans de nombreux
cas il est difficile de considérer que les écoulements sont
indépendants des taux.
Avant de procéder à la présentation des
modèles de dépôts à vue, il est essentiel de passer
en revue les généralités concernant la modélisation
des écoulements, qui nous permettront de présenter les
contraintes que doivent satisfaire les modèles d'écoulement.
SECTION I : Généralités sur la
modélisation des écoulements
Certaines contraintes doivent être satisfaites lors de
la modélisation des écoulements. Mais, il arrive parfois que
certaines de ces contraintes soient très fortes et amènent
à se limiter à des modèles très simples.
I.1 Les variables explicatives de l'écoulement
selon DEMEY, FRACHOT, RIBOULET
DEMEY, FRACHOT et RIBOULET en 2003, dans leur livre
introduction à la gestion actif/passif, évoquent des
variables pouvant agir sur l'écoulement d'un produit. Il s'agit des
variables de niveau client, des variables de niveau produit et des variables
macroéconomiques.
Pour les variables de niveau client telles l'âge, la
catégorie socioprofessionnelle, et la situation familiale d'un individu,
on ne les retrouve pas souvent dans le système d'information de la
gestion Actif/passif. Même si ces variables peuvent avoir de
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
l'influence par exemple sur le comportement de remboursement
anticipé d'un prêt immobilier, ou sur le comportement
d'épargne du client, il n'est pas aisé de les utiliser dans la
pratique.
Pour les variables de niveau produit, elles
sont souvent utilisées dans les systèmes d'information ALM. Elles
regroupent les taux de rémunération des comptes, la date de
génération du produit, le mode d'amortissement (prêt
à la clientèle), le positionnement du produit dans l'offre
commerciale de la banque, le mode d'utilisation du produit par le client
(facilité de caisse, découvert, crédit de
trésorerie pour la clientèle entreprise), etc.
Les variables Macroéconomiques concernent les variables
telle la conjoncture économique (en particulier les taux
d'intérêt mais aussi l'inflation, le taux de croissance du PIB),
le marché immobilier, les marchés des actions, etc. Toutes ces
variables ont vocation à influencer directement ou indirectement les
écoulements. Toutefois, seuls les taux d'intérêt sont
généralement retenus, puisqu'ils captent une part importante des
fluctuations macroéconomiques. On considère que les fluctuations
de la croissance économique, de l'inflation (etc.) sont reliées
significativement aux mouvements des taux d'intérêt.
Dans le bilan d'une banque, on distingue
généralement deux types de produits : ceux pour lesquels une date
de fin contractuelle est spécifiée et ceux pour lesquels aucune
date de fin n'est spécifiée. Dans la modélisation des
écoulements il est crucial de faire la distinction entre ces deux types
de produits. L'écoulement des produits échéancés
pouvant être identifié dans certains cas à
l'écoulement contractuel (tel que défini par les termes du
contrat). Dans la suite, nous nous proposons de préciser les approches
nécessaires pour traiter les produits non
échéancés.
I.2 Les produits échéancés et non
échéancés
Pour modéliser les écoulements de produits,
Demey, Riboulet et Frachôt du groupe de recherche opérationnelle
du Crédit Lyonnais proposent en 2003 de faire la distinction entre
produits non échéancés et produits
échéancés. Les produits non échéancés
étant ceux qui n'ont pas de maturité contractuelle et dont les
encours peuvent rester longtemps dans le bilan ou disparaître du jour au
lendemain. C'est le cas typique des dépôts à vue. Pour eux,
ce qui caractérise les produits non échéancés,
c'est le caractère fongible des encours : c'est-à-dire un franc
CFA entré sur un compte de dépôts (via un flux
créditeur)
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
à une date passée t et un franc CFA
entré à une date t' ( '
t ? t ) sont indistinguables et ont la
même probabilité de sortie aujourd'hui (date présente).
Autrement dit, cela signifie que la date d'entrée dans le bilan
n'influence pas le taux de sortie. Ceci signifie avec les notations du Chapitre
précédent : que
(20) ë ( t , T ) ?
ë( T)
En d'autres termes, la date d'entrée des francs CFA
dans les encours des produits non échéancés n'a pas
d'importance, seule compte la date courante. Ainsi, Demey, Frachot et Riboulet
qualifie l'écoulement des produits non échéanchés
d'écoulement exponentiel et établissent la formule :
T
(21) ( , ) exp( ( ) ).
S t T = - ë s ds
t
La conséquence immédiate de cette
propriété pour les produits non échéancés
est la suivante : l'écoulement du stock est identique à
l'écoulement de la production.
En effet, comme nous avons vu au chapitre
précédent, l'encours de la date courante est la résultante
des strates passées de production nouvelle (voir équation
(6)).
L'encours restant en T (hors production nouvelle
entre t et T) était donné par la formule (8).
Avec la définition de la fonction d'écoulement du stock (formule
(10)), l'on voit immédiatement, compte tenu de la
propriété de fongibilité des encours ( ë (
t , T ) ? ë( T)) que les produits non
échéancés sont tels que :
T
(22) ( , ) ( , ) exp( ( ) ).
S t T = S t T = - ë s ds
stock t
Cela signifie que l'écoulement du stock est identique
à l'écoulement de la production.
On peut ainsi affirmer que la notion de production nouvelle et
la distinction production nouvelle/écoulement n'ont plus d'importance
puisque la propriété de fongibilité des encours nous
assure que, seul compte l'encours présent, c'est-à-dire
l'ensemble des francs CFA présent aujourd'hui, quelle que soit leur date
d'entrée. « C'est pourquoi, les modèles d'écoulement
sur les produits non échéancés sont des modèles
d'évolution des encours » (Riboulet et al. [2003]).
Puisque notre travail consiste à modéliser
l'écoulement des dépôts à vue qui sont l'exemple
typique des produits non échéancés, il nous semble
intéressant de présenter les discussions qui ont trait à
l'écoulement de ce type de dépôts et de passer en revue
certains
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
auteurs qui ont abordé la modélisation des
dépôts à vue. Ce sera l'objet de la section suivante.
SECTION II : L'écoulement des dépôts
à vue
Dans cette section, après avoir présenté
les débats autour des dépôts à vue, nous indiquerons
la méthodologie proposée par certains auteurs pour
modéliser son écoulement et enfin nous passerons en revue les
premiers modèles ainsi que les modèles récents de
dépôts à vue.
II.1 Les discussions autour de l'écoulement des
dépôts à vue
Il existe deux visions par rapport au traitement des
dépôts à vue à cause d'un manque de consensus sur ce
sujet8.
> Une vision « prudente » qui s'appuie sur
l'absence de maturité contractuelle des dépôts à vue
et qui les rend intrinsèquement volatiles. D'après cette vision,
ces dépôts peuvent disparaître du jour au lendemain et il
serait très imprudent de les considérer comme des ressources
longues, c'est-à-dire avec une convention d'écoulement en
liquidité de maturité longue ;
> Une vision « réaliste » qui s'appuie sur
la loi des grands nombres pour affirmer qu'une fois tous les comptes
individuels agrégés, l'encours global des dépôts
à vue est très stable, ce qui implique que ces ressources sont
longues.
Ces deux conceptions ont du sens si on précise de quel
risque on parle. Ainsi, les comptables choisiront la vision
«prudente», puisque la comptabilité cherche à donner
une image fidèle de l'existant. Elle ne connaît que les actifs et
passifs existants aujourd'hui. Ainsi, les comptables seront sensibles au risque
de faire des hypothèses sur les actifs et passifs futurs qui pourront
donner une vision exagérément optimiste de la situation
financière de la banque.
Le trésorier de la banque choisira aussi un
écoulement en liquidité prudent. Pour lui, les
dépôts à vue sont des ressources, c'est-à-dire les
moyens permettant à la banque de financer l'activité sans
recourir aux marchés financiers. Ainsi selon lui, sur-estimer les
encours de ces dépôts à un horizon futur, c'est prendre le
risque de sous-estimer l'occurrence d'une crise de liquidité de la
banque. Ici cette vision selon laquelle les dépôts à vue
peuvent disparaître rapidement est souhaitable.
8 Cf. Riboulet et al. [2003], page 85.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
La conception du gestionnaire actif/passif bancaire est
différente de celle du trésorier et du comptable, et plus proche
de la vision « réaliste ». En effet, pour le gestionnaire
actif/passif, la banque peut être exposée soit à une hausse
des taux d'intérêt, soit à une baisse. Et deux cas
particuliers de figures sont envisageables : D'une part, la banque est
structurellement excédentaire en ressources. Elle ne craint pas le
risque de liquidité mais est en revanche exposée au risque de
taux. Par exemple, la banque peut dans ce cas craindre une baisse de taux qui
l'obligerait à replacer ses excédents de ressources à des
taux plus faibles. Dans ce cas, la banque ne doit pas adopter une vision
prudente de l'écoulement en liquidité des dépôts
à vue. Elle prendrait le risque de sousestimer son risque de taux.
D'autre part, la banque est une banque d'actif, c'est-à-dire
structurellement déficitaire en ressources. A l'inverse du cas
précédent, le risque de liquidité est un enjeu fort de
même que le risque de taux. La banque doit dans ce cas adopter une vision
prudente sur l'écoulement de ses dépôts si elle veut
maîtriser son risque de liquidité. Il apparaît donc
évident que la vision à avoir sur l'écoulement des
dépôts à vue est fonction du contexte d'activité de
la banque.
Selon Paul Demey et al. [2003]: « Le risque de taux
est fonction de la valeur absolue de l'impasse de taux, alors que le risque de
liquidité est relié directement à l'impasse en
liquidité (sans valeur absolue). Or, une valeur absolue est non monotone
en son argument : on ne peut donc pas dire qu'une vision prudente (en risque de
taux) consiste à majorer ou à minorer l'encours futur
estimé des dépôts à vue. Il est donc logique,
à priori, d'adopter une vision réaliste en ne cherchant pas
à sous-estimer ou à surestimer les encours futurs, et seulement
si le risque de taux est le seul risque envisagé ».
Ainsi, pour le banquier, il serait plutôt juste de
déterminer un écoulement en liquidité le plus
réaliste possible (c'est-à-dire le plus proche des
écoulements futurs qui seront réellement observés).
Dans le cadre de ce travail, nous avons choisi la vision
« réaliste » qui va nous amener à déterminer un
modèle d'écoulement des dépôts à vue pour les
banques commerciales du Cameroun.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
II.2 Méthodologie pour la modélisation des
dépôts à vue selon Frachot
Spécifier un modèle de dépôts
à vue consiste à définir une forme fonctionnelle qui
décrit l'évolution de ces dépôts. Dans la
littérature on distingue deux types de modèles pour la
modélisation des dépôts à vue (cf. Frachot et al.
[2003]):
Les modèles structurels qui désignent les
modèles dont la fonction d'écoulement résulte d'un
raisonnement microéconomique selon lequel le client a un comportement
rationnel visant à maximiser son intérêt. Ces
modèles, partant d'une fonction d'utilité du client, supposent
que celui-ci la maximise, puis en déduisent le taux d'écoulement
optimal pour le client. Ces modèles reposent sur des mécanismes
économiques et donc faciles à interpréter. Cependant, ils
impliquent souvent des fonctions d'écoulement très complexes
à estimer du fait qu'ils reposent sur les hypothèses assez fortes
de rationalité du client et des contraintes très fortes.
En revanche, les modèles à forme réduite
ont pour objectif, non pas de décrire avec précision le
mécanisme économique sous-jacent à la fonction
d'écoulement, mais de se limiter à des fonctions
d'écoulement certes arbitraires, mais simples à manipuler. Ce
type de modèle s'applique à des clients rationnels ou non
rationnels. Selon Frachot et al. [2003], la plupart des modèles à
forme réduite partent de l'équation
(23) dD ( t ) = [ PN ( t ) -
ë( t ) D ( t ) ]dt
Dans laquelle on pose
(24) PN ( t ) = h ( t ,
r t ) × D ( t).
D(t) désignant l'encours des
dépôts à vue, ë (t) le taux
d'écoulement, PN(t) le flux créditeur à l'instant
t, rt le taux d'intérêt de marché.
Dans l'équation précédente, on suppose
ainsi que les flux créditeurs sont proportionnels à l'encours
avec un coefficient de proportionnalité dépendant des taux de
marché. Selon Frachot, le mécanisme sous-jacent est le suivant :
quand les taux d'intérêt sont bas, les liquidités
excédentaires des clients de la banque s'accumulent sur le compte de
dépôts à vue. Quand les taux d'intérêt
augmentent très au-delà du taux de rémunération des
dépôts à vue, les clients font des arbitrages et les
dépôts reviennent à leur niveau structurel.
Il existe une autre classe de modèle hybride : les
modèles semi-structurels. Ces modèles donnent lieu à la
fois à une interprétation économique simple et à
une simplicité des calculs et de l'utilisation. L'idée des
modèles semi-structurels sera de dire que la
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
durée d'écoulement des dépôts à
vue est fonction du franchissement d'un seuil par le taux
d'intérêt.
Dans le contexte Camerounais, les systèmes
d'information ALM n'étant pas encore bien développés, et
le marché financier n'étant pas actif, nous définirons une
fonctionnelle d'écoulement (du type modèle à forme
réduite) qui résultera de l'étude des
propriétés stochastiques de la série de l'encours des
dépôts à vue. Mais avant, présentons les premiers
travaux relatifs à la modélisation des dépôts
à vue.
II.3 Les premiers modèles de dépôts
à vue
C'est au milieu des années 90 que les premiers
modèles de dépôts à vue sont apparus, s'inscrivant
ainsi dans l'objectif d'une meilleure gestion actif/passif bancaire. Dans cette
partie nous présenterons par ordre chronologique les modèles de
dépôts à vue établis par certains auteurs. Tous ces
modèles ainsi que les équations s'y rapportant sont
présentés dans les ouvrages de Demey, Frachot et Riboulet (cf.
Demey et al. [2003], Page 92) et de Cyrille Martin (Cf. Cyrille Martin [2005],
« Comparaison des modèles de dépôts à vue
», page 3-5). Rappelons que ces modèles sont du type
« modèle à forme réduite » à l'exception
du modèle proposé par Frachot en 2001qui est un modèle du
type semi structurel.
Encadré 1 : Les modèles de
Selvaggio, Dupré, Jarrow et Van Deventer
|
II.3.1 Le modèle de Selvaggio [1996]
Selvaggio (cf. Selvaggio [1996]) est l'un des premiers à
proposer un modèle d'évolution des encours des
dépôts à
vue. il spécifie, tout d'abord,
l'expression de l'encours cible, D*, des
dépôts.
(25) * logD k = á +
â1 logR k +
â2 logY k ,
Où Yk représente des variables
macroéconomiques autres que les taux (dont les salaires), puis
(26) logD k logD k - ë (
logD k logD k 1 ),
*
=
1 + - -
Cette dernière équation traduit le fait que les
encours des dépôts ont tendance à s'ajuster autour de
l'encours cible à une vitesseë . Et finalement on a
(27) logD k = - ë logD k - +
ëâ logR k + ëâ logY
k + ëá ,
(1 ) 1 1 2
L'étude de Selvaggio a porté sur des données
mensuelles et l'équation estimée est :
|
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun

14
,
3
i
=
Rk est le taux d'intérêt moyen sur la
période [tk, tk+1]
Monthi-2 est une variable test permettant de prendre en compte la
saisonnalité des dépôts à vue.
Selvaggio estime son modèle sur des données
mensuelles des dépôts à vue entre Février 1991 et
Février 1995. Les coefficients sont tous significatifs. Et le
R2 est de l'ordre de 98%.
II.3.2 Le modèle de Dupré
[1996]
La même année que Selvaggio, un autre auteur,
Dupré (cf. Dupré [1996]) propose un modèle en temps
continu de l'évolution de l'encours des dépôts à
vue. La spécification de son modèle est la suivante :
Où á correspond à une tendance
moyenne du comportement non financier des déposants et
â
correspond au taux de collecte supplémentaire pour un
point de diminution des taux, rt est le taux d'intérêt en
t.
L'avantage de ce modèle est d'avoir des coefficients
interprétables financièrement. Dans ce modèle, lorsque les
taux augmentent, il est plus intéressant pour l'investisseur, de placer
son argent sur un produit financier qui reflète ce taux de marché
que de laisser cet argent dans un compte non (ou faiblement)
rémunéré.
II.3.3 Le modèle de Jarrow et Van Deventer
[1998]
La modélisation développée par Jarrow et
Van Deventer (cf. Jarrow et Van Deventer [1998]) est basée sur une
hypothèse de segmentation du marché dans lequel il n'existe que
deux types d'intervenants : les institutions financières et les
épargnants. Ils proposent une formulation discrète de leur
modèle. Dans le cadre des dépôts à vue non
rémunérés, ce modèle se présente comme suit
:
(30) logD k logD k - 1 â
1 â 2 t k â
3 R k â 4 ( R
k R k 1 ),
= + + + + -
-
Il a l'avantage de lier la variation logarithmique des encours
des dépôts à une tendance linéaire du temps,
à l'évolution des taux mais aussi à la variation de ces
taux.
(28) logD â logD - â logR â t
â month
= 0 1 + +
k k 1 k + 2 k i i - 2
(29) (
dD k = á - â
r dt
k ) ,
D k
Source : Cyrille Martin, Comparaison des
modèles de dépôts à vue, 2005
Ces modèles sont estimés en utilisant des
régressions linéaires classiques (méthode des moindres
carrés ordinaires) et en choisissant judicieusement la variable
expliquée et les variables explicatives.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
II.4 Les modèles récents de
dépôts à vue
A partir de l'an 2000, de nouveaux modèles sont
développés et donnent lieu à des interprétations
beaucoup plus simples du comportement de la clientèle à travers
les variations de taux d'intérêt.
Encadré 2 : Modèles de Frachot et de
l'Office of Thrift supervision
|
II.4.1 Le modèle du premier régulateur
fédéral aux Etats-Unis : L'Office of Thrift Supervision
[2000]
En 2000, un modèle discret d'évolution des encours
des dépôts à vue a été proposé par
l'Office of
Thrift Supervision. Le modèle s'écrit pour les
dépôts à vue rémunérés :
1/12
i k
(31) D D a b
= + × arctan( d c
+ ) + ×
e i ,
k k - 1 k
rk
Où arctan(.) représente la fonction
réciproque de la fonction tangente et ik est le taux de
rémunération des dépôts en date tk. Ce
modèle à l'avantage de prendre en compte l'ajustement non
symétrique des taux de rémunération des
dépôts par rapport aux taux de marché. Cette
asymétrie montre que lorsque les taux de marché baissent, les
taux de rémunération des dépôts ont tendance
à baisser relativement vite alors que lorsque les taux de marché
augmentent, les taux de rémunération des dépôts ont
tendance à augmenter plus lentement.
En considérant les dépôts à vue non
rémunérés, on doit poser ik=0. Le modèle
devient
(32) Dk = áDk-1
Où á est une constante.
II.4.2 Le modèle de Frachot (cf.
Frachot[2001])
En 2001, Frachot s'intéresse à une
modélisation comportementale de l'évolution des encours des
dépôts à vue. Aussi suppose-t-il que chaque encours des
clients de la banque, dk, suit l'équation suivante :
*
(33) d k - d k - = ë D - d k
- + â R = s
1 ( 1 ) 1 ,
{ }
k
Où D* est la valeur cible des
dépôts (c'est-à-dire un niveau d'encaisse « normal
» visé par les clients), ë
la vitesse d'ajustement
des dépôts vers cette valeur cible et â le montant
supplémentaire des dépôts
lorsque les taux de marché sont trop bas par rapport
à un seuil s. En agrégeant ce modèle sur l'ensemble des
comptes de la banque il obtient :
*
(34) D D - ë D D - â
- 1 (
= - 1 ) 1 ( ) ,
+ f s ds
k k k { }
R s
k =
Où Dk est l'encours global de la banque et
f(.) est la densité de la distribution de la valeur cible
s parmi les clients de la banque. Ce modèle peut se
réécrire
(35) D - D - = ë D - D
- + â - F R k *
k 1 ( k 1 ) (1 ( ))
k
|
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun

Où F est la fonction de répartition de la
distribution de la valeur cible s. Lorsque la distribution de cette
valeur cible est gaussienne. Le modèle peut s'écrire :
Frachot estime ce modèle sur une série mensuelle
de dépôts à vue. Les coefficients lors de l'estimation sont
significatifs. F (.) est la fonction de répartition de la loi
normale centrée réduite. R* étant le taux seuil.
Il s'agit ici d'une modélisation de type semi-structurel selon laquelle
les clients accumulent leur liquidité sur leurs comptes de
dépôts à vue tant que le taux de marché est
inférieur à un seuil, supposé suivre une loi normale.
(36) R R
- * k
D D
- = ×
ë D D
( * -
1 1 ) á
+ × -
1 (
F )
k k - k - í
Source : Cyrille Martin, comparaison des
modèles de dépôts à vue
Le point commun de tous ces modèles est qu'ils sont
estimés sur les dépôts à vue Américains ou
Européens. En 2005, Cyrille Martin (cf. Cyrille Martin [2005]),
transforme ces modèles de manière à avoir une
équation où la variable expliquée est la variation des
encours des dépôts. Puis, il estime ces modèles sur les
données du Board of Governors of the Federal Reserve system. Tous les
coefficients lors de son estimation sont significatifs. Le
R2 observé est de l'ordre de 20% pour ces
modèles transformés.
Ces études mettent en évidence le fait que
l'encours global des dépôts à vue peut dépendre du
temps, du taux d'intérêt créditeur appliqué à
ces dépôts, du taux d'intérêt de marché et de
la variation de ces taux. Elles mettent en évidence le fait que les
données sur les encours des dépôts sont fortement
intégrées (c'est-à-dire qu'il y a une forte
corrélation entre Dk et Dk-1).
Cependant l'absence d'un marché financier actif au
Cameroun fait que la plupart de ces modèles ne peuvent s'appliquer au
contexte camerounais. En Europe par exemple, les taux de
rémunération de la plupart des dépôts et produits
financiers sont indexés à un taux de référence
(taux de la BCE, EURIBOR etc.). Et l'on assiste parfois à des
périodes où le niveau atteint par les taux de
rémunération est suffisant pour inciter les clients à
faire de la spéculation.
Dans le contexte camerounais, les clients des banques (les
gros étant des entreprises privées) ont toujours cette phobie des
crises passées et accumulent leurs liquidités dans des comptes
non rémunérés pour des motifs de transaction, de
précaution et surtout parce que la phobie engendrée par les
crises passées les a amenés à placer leur argent dans des
comptes à vue où le retrait en cas de trouble est plus
aisé. Nous supposerons dans ce travail que le comportement de la
clientèle en terme de dépôts sur leurs comptes à vue
est insensible aux variations des taux d'intérêt de marché
(nous
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
allons le tester au chapitre 4). Il faudra concevoir pour le
cas du Cameroun, un modèle d'évolution des dépôts
à vue qui résultera de l'étude des
propriétés stochastiques de la série d'encours.
Mais avant cela, dans ce chapitre, nous avons vu que
l'idée à avoir sur l'écoulement des dépôts
à vue dépend du contexte d'activité des banques (la banque
pouvant être structurellement excédentaire ou bien
déficitaire en ressources).
C'est pour cela que dans le chapitre suivant, nous allons dans
un premier temps présenter le système bancaire camerounais, puis,
en partant d'une analyse descriptive de la liquidité des banques
commerciales, nous déterminerons l'élément qui constitue
l'essentiel des ressources des banques et la nature de la position de
liquidité de ces banques.

APPLICATION AUX BANQUES COMMERCIALES DU
DEUXIÈME PARTIE :
CAMEROUN
Cette partie est une application des concepts
précédents au x banques commerciales du Cameroun. Elle est
subdivisée en deu x chapitres. Le troisième chapitre
présente le système bancaire camerounais ainsi que la nature et
la position de la liquidité des banques commerciales. Dans le chapitre
quatre, nous allons modéliser les dépôts a vue de ces
banques et nous ressortirons la partie stable en fonction du temps.
LES BANQUES COMMERCIALES DU CAMEROUN ET
LA
LIQUIDITÉ
Au Cameroun, ce sont les banques commerciales qui
représentent la majorité du dispositif de financement (Marianne
MBENA [2006]). Leur activité traditionnelle consiste à collecter
les dépôts à vue pour accorder des crédits à
court terme et mettre des instruments de paiement à la disposition de la
clientèle.
Dans ce chapitre, nous allons dans la première section
présenter la typologie des institutions financières camerounaises
ainsi que le cadre réglementaire et prudentiel dans lequel évolue
l'activité bancaire, ensuite, dans une deuxième section nous
partirons de la présentation de la situation de la liquidité des
banques commerciales camerounaises et de l'analyse de la structure de ses
ressources pour ressortir l'élément qui constitue l'essentiel du
passif de ces banques.
SECTION I : Typologie des institutions
financières, cadre réglementaire et prudentiel de
l'activité du système bancaire
camerounais9
L' Encyclopédie « Encarta 2006 »
définit un système bancaire comme un groupe organisé selon
un système pyramidal, comprenant un institut d'émission, une
banque centrale qui fait figure d'autorité de tutelle du système,
et un ensemble d'établissements qui constituent les banques dites de
second rang. J. Mathis [1992], quant à lui, affirme qu'un système
bancaire représente un groupe formé par une banque centrale et
des banques et établissements financiers, qui entretiennent des
relations financières de créances et d'engagements les uns
vis-à-vis des autres ; ainsi que vis-à-vis des agents non
financiers.
Dans cette première section, après avoir
présenté la typologie des institutions financières, nous
décrirons le cadre réglementaire dans lequel évoluent les
activités des banques.
9 Cf mémoire de Pandong Armand [2005], pour
plus de détails sur la typologie des institutions financières
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
I.1 Typologie des institutions
financières
En se référant à la typologie de la
Banque des Etats de l'Afrique Centrale (BEAC), le secteur financier des pays
membres de l'Union Monétaire de l'Afrique Centrale (UMAC) dont le
Cameroun comprend quatre types d'institutions financières qui sont : la
Banque Centrale, les Banques Créatrices de monnaie, les autres
institutions Bancaires, et les Institutions Financières Non
Bancaires.
I.1.1 La Banque centrale
Dans les six Etats membre de la CEMAC, c'est la Banque des
Etats de l'Afrique Centrale (BEAC) qui assume la fonction d'émission de
la monnaie centrale, agit sur le crédit, gère les réserves
internationales, effectue les transactions avec le Fonds Monétaire
International. Elle a été créée le 22 novembre
1972.
I.1.2 Les Banques Créatrices de Monnaie
(BCM)
Dans cette catégorie, on retrouve les
sociétés de dépôts monétaires qui acceptent
les dépôts à vue transférables par chèques ou
susceptibles d'être utilisés à des fins de paiement. En
plus des banques commerciales, on prend en compte dans ce sous secteur tous les
engagements contractés du fait de dépôts à vue par
le trésor ou d'autres organismes publics, y compris le système
des chèques postaux.
I.1.3 Les Autres Institutions Bancaires (AIB)
Dans ce groupe, on classe les banques qui n'acceptent pas de
dépôts à vue transférables par chèques, mais
reçoivent les dépôts d'épargne qui permettent
d'alimenter les fonds de crédit. On distingue deux catégories
:
> Les Autres Institutions Bancaires Eligibles au
refinancement de la BEAC (AIBE) : Dans cette catégorie, on retrouve tous
les autres établissements à caractère bancaire qui sont
admis au refinancement de la Banque Centrale et qui reçoivent des
dépôts d'épargne et à terme sans toutefois
contracter des engagements sous forme de dépôts à vue
transférables par chèques. C'est le cas de certaines banques de
développement, des institutions bancaires de financement de l'habitat
social (Crédit Foncier, etc.)
> Les Autres Institutions Bancaires Non Eligibles au
refinancement de la BEAC (AIBNE) : Il s'agit ici des établissements
bancaires ayant les mêmes
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
caractéristiques que ceux définis
précédemment, à la seule différence qu'ils ne
recourent pas aux refinancements de l'institut d'Emission. On compte dans ce
groupe les Caisses d'épargne Postales et certaines banques
spécialisées.
I.1.4 Les Institutions Financières Non Bancaires
(IFNB)
Ces institutions participent au financement de
l'économie en octroyant des crédits (sur leurs fonds propres ou
sous forme d'emprunts) ou en effectuant des opérations
financières ayant des incidences sur le secteur monétaire
(émission des obligations). Ces Institutions Financières Non
Bancaires qui ne reçoivent pas de dépôts du public
regroupent essentiellement les compagnies d'assurances et de
réassurances, les établissements de crédit-bail et de
leasing, les sociétés financières et de participations,
etc. Toutes ces organisations constituent les institutions financières
du Cameroun dans lesquelles la BEAC joue un rôle de coordination, de
définition et de suivi de la politique monétaire
Le but de notre étude étant de déterminer
un modèle d'écoulement des dépôts à vue
applicable aux banques commerciales du Cameroun, seront explorées en
priorité les banques commerciales camerounaises.
I.2 Les banques commerciales du Cameroun
Les banques commerciales représentent la catégorie
la plus importante des établissements de crédits au Cameroun.
I.2.1 Banques en activité au Cameroun et
répartition du Capital Social
On compte 11 banques en activité au 31 Décembre
200610 au Cameroun. Il s'agit de : ~ Afriland First Bank (First
Bank) ( Autrefois CCEI)
~ Amity Bank Cameroon PLC (Amity)
> Banque Internationale du Cameroun pour l'épargne et
le Crédit (BICEC) > Citibank N.A. Cameroon (Citibank)
> Commercial Bank of Cameroon (CBC)
> Société Camerounaise de Banque (SCB) -
Crédit Agricole (Ex Crédit Lyonnais Cameroun CLC).
> Ecobank Cameroun (EBC)
10 Cf. Rapport du Conseil National du Crédit :
Décembre 2006
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
> Société Générale de Banques au
Cameroun (SGBC)
> Standard Chartered Bank Cameroon (SCBC)
> Union Bank of Cameroon PLC (UBC PLC)
> National Financial Credit Company (NFC-Bank)11
Au 31 décembre 2004, la répartition du capital
social des banques commerciales du Cameroun montre que CBC Bank et Standard
Chartered Bank Cameroon détiennent le plus grand capital social. Ils
représentent chacun 15% du total du capital social des banques
commerciales du Cameroun. Ils sont suivis de la Société
Générale de Banques au Cameroun et du Crédit Lyonnais avec
respectivement 13 % et 12% du total du capital social des banques commerciales
du Cameroun.
Figure 1 : Répartition du capital social des
banques commerciales en pourcentage au 31 Décembre 2004

Amity BICEC First Bank CBC Bank Citibank
EBC CLC SGBC SCBC UBC PLC
13%
15%
12%
10%
5%
8% 6%
7%
9%
15%
Source : élaboré par l'auteur
d'après les données des rapports d'activité de la
COBAC
I.2.2 Fonctionnement des banques commerciales
En général, l'activité des banques
commerciales consiste à collecter des fonds qui, mobilisés sous
formes variables (par l'octroi d'un prêt par exemple), permettent le
financement de l'activité économique. Ces banques effectuent deux
principales opérations :
> Les opérations avec la clientèle : qui
consistent en la collecte des ressources (dépôts) et la
distribution des crédits.
> Les opérations de trésorerie : Elles
représentent l'ensemble des opérations permettant à une
entreprise de se procurer des disponibilités monétaires
nécessaires pour régler ses dettes au fur et à mesure de
leur exigibilité. La situation
11 NFC-Bank a vu le jour en 2006 et ne sera pas pris
en compte dans la répartition du Capital social.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
de trésorerie représente l'ensemble des
liquidités dont la banque dispose à un moment donné. La
situation de trésorerie des banques commerciales du Cameroun au 31 Mars
2005 figure en annexe. On y remarque que le Cameroun à un
excédent de trésorerie de 387,528 Milliards de FCFA.
I.3 Cadre réglementaire et prudentiel
institué par la COBAC
La crise bancaire des années 1980 a
entraîné la modification du cadre réglementaire et
prudentiel. D'où le cadre réglementaire régional mis en
place en 1992 par les conventions portant création de la Commission
bancaire de l'Afrique Centrale (COBAC) et harmonisation de la
réglementation bancaire dans les Etats de l'Afrique Centrale. Ces
conventions confèrent à la COBAC des compétences et des
pouvoirs divers en matière de réglementation.
I.3.1 Missions de la COBAC
La COBAC est un organe supranational ayant pour mission de
veiller au respect par les établissements de crédit des
dispositions législatives et réglementaires
édictées par les autorités, par la banque Centrale ou par
elle-même, et qui leur sont applicables, et de sanctionner les
manquements constatés. Elle a été mise en place en janvier
1993 par les Etats membres de l'UMAC.
> Le pouvoir administratif : Il
confère à la COBAC le pouvoir de donner l'avis conforme pour la
délivrance des agréments aux établissements, aux
dirigeants et commissaires aux comptes. Lorsqu'une banque est en situation de
difficulté grave, la COBAC a le pouvoir de la mettre en administration
provisoire et de nommer un liquidateur pour cette banque qui cesse d'être
agréée.
> Le pouvoir réglementaire : Il
revient à la COBAC d'édicter les prescriptions d'ordre
général destinées à assurer et à
contrôler la liquidité et la solvabilité des
établissements de crédit à l'égard des tiers, et
plus généralement l'équilibre de leur structure
financière.
> Le pouvoir de surveillance et de contrôle
: confère à la commission le pouvoir de veiller au
respect de la réglementation par les établissements de
crédit. La commission exerce cette tâche par le biais de son
Secrétaire Général qui organise les contrôles sur
pièces et sur place.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
> Le pouvoir de sanction : en plus de ses
compétences administratives, réglementaires et de surveillance
ci-dessus énumérées, la COBAC peut prononcer des sanctions
disciplinaires allant de l'avertissement au retrait de l'agrément. Les
sanctions prévues peuvent donc être : l'avertissement,
l'interdiction d'effectuer certaines opérations, la suspension et la
révocation des commissaires aux comptes, le retrait
d'agrément.
I.3.2 Les normes prudentielles adoptées par la
COBAC en 1993
Les instruments dont la COBAC s'est dotée le 29 Mars
1993 pour mieux apprécier la conduite des établissements de
crédits ont trait à leur solvabilité et à leur
liquidité. Certaines de ces normes ont été
révisées en 2001.
I.3.2.1 Normes de solvabilitéUne banque
est solvable si la vente de ses actifs peut permettre de régler ses
dettes. Cinq ratios ont été construits pour
éviter aux banques la prise excessive de risques.
> Le ratio de couverture des risques : les
établissements assujettis doivent justifier en permanence que leurs
fonds propres nets couvrent au moins 8% de l'ensemble de leurs concours y
compris ceux bénéficiant à l'Etat.
> Le ratio de division des risques : sa
mise en place conduit les établissements de crédit à
éviter de trop concentrer leurs risques sur un petit nombre de
signatures dont l'insolvabilité définitive ou partielle pourra
leur porter préjudice. Pour cela le montant total des concours en faveur
d'un même bénéficiaire ne doit pas excéder 45% de
leurs fonds propres nets et ceux en faveur de leur gros clients ne doit pas
excéder huit fois ses fonds propres nets.
> Le ratio de couverture des
immobilisations : contraint les établissements de crédit
a financer leurs immobilisations à 100% par leurs ressources
permanentes. Ce qui empêche ainsi ces établissements d'affecter
les ressources provenant des dépôts au financement de la
construction de leurs sièges et/ou agences.
> Limitation des prises de participation au capital
d'entreprise par les établissements de crédit : les
établissements de crédit peuvent détenir des
participations dans des entreprises ou d'autres établissements de
crédit à condition de respecter à tout moment : un rapport
maximum de 15 % entre le montant de chacune des participations et le montant de
leurs fonds propres nets ; Un rapport
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
maximum de 45% entre le montant total de leur participations et
le montant de leur fonds propres nets.
> Limitation des concours accordés aux
actionnaires, associés, dirigeants, administrateurs et personnel :
ceux-ci sont limités à 15% des fonds propres nets.
I.3.2.2 Les normes de liquidité
D'après le comité de Bâle, la
liquidité d'une banque sera considérée comme la
capacité à financer les actifs de la banque et à
rembourser les engagements pris au moment où ces financements et ces
remboursements apparaissent. « Liquidity is the ability to fund increases
in assets and meet obligations as they come due ». Pour cela, une banque
doit pouvoir restituer à la première demande les
dépôts de ses clients. Deux ratios ont été
construits pour cela :
> Le ratio de liquidité : les établissements
de crédits sont tenus de respecter un ratio de liquidité de 100%
au moins entre, d'une part, le montant total de leurs disponibilités
à vue ou à un mois au plus et, d'autre part, le montant de leurs
exigibilités remboursables à vue ou dans un délai d'un
mois.
> Le ratio de transformation à long terme : ce ratio
a pour but d'empêcher les établissements assujettis d'utiliser
leurs ressources courtes pour des emplois longs. Il s'agit du rapport entre les
emplois et engagements à plus de cinq ans d'échéance d'une
banque et ses ressources de même terme, retenues au numérateur.
Outre ces normes prudentielles, la Commission Bancaire dispose
d'une
réglementation anti-blanchiment et financement du
terrorisme. Dans son système de
contrôle interne, la Commission prend des dispositions en
vue de s'assurer que les
activités d'un établissement de crédits sont
maîtrisées à tous les niveaux.
Au terme de cette section, nous pouvons retenir que les
banques commerciales du Cameroun exercent leur activité de collecte de
dépôts et d'octroi de crédits dans un environnement
où elles sont tenues d'observer les normes prudentielles.
Dans cet environnement, quelle est la situation de
liquidité des banques commerciales camerounaises ? Quel est au vue de la
structure de ses ressources ce qui constitue l'essentiel du passif de ces
banques ?
SECTION II : La liquidité des banques au
Cameroun
La liquidité d'une banque est considérée
comme la capacité à financer les actifs de la banque et à
rembourser les engagements pris au moment où ces financements et ces
remboursements apparaissent. Dans cette section, nous présenterons la
situation de la liquidité des banques Camerounaises, puis nous
analyserons la structure des ressources des banques pour enfin ressortir
l'élément qui constitue l'essentiel de ces ressources.
II.1 La liquidité bancaire
Une banque est qualifiée de liquide si elle est en
mesure d'honorer ses engagements à vue ou à très court
terme. Cette liquidité dépend de la capacité de la banque
à recueillir suffisamment de dépôts et sa capacité
à s'endetter auprès des autres banques.
Vers la fin des années 80, les banques camerounaises
étaient dans une situation de faillite suite à la crise qui s'est
traduite par un manque excessif de liquidité et une mauvaise structure
de leur portefeuille (une proportion très grande de créances
douteuses, sans garantie et sans provisionnement). Depuis le début des
années 1990, on a assisté à de nombreuses restructurations
de sorte que, à partir de 1995, le secteur bancaire camerounais est
redevenu sain, liquide et stable grâce au dispositif prudentiel et
réglementaire mis en place par la COBAC. Avec ces nouvelles contraintes
de gestion, les banques Camerounaises sont devenues surliquides : en 1990 le
ratio de liquidité au Cameroun était inférieur à
80%. D'après les rapports de la COBAC les banques du Cameroun ont
atteint au 30 juin 1997 un niveau de 110,5% pour arriver à 113,4% en
Décembre 2000, et dépasser 150% en 2004. Le tableau suivant donne
l'évolution des ratios de liquidité des banques camerounaises.
Tableau 3 : Evolution des ratios de liquidité des
banques du Cameroun
|
mars-00
|
juil-00
|
août-00
|
sept-00
|
août-02
|
sept-02
|
août-04
|
sept-04
|
oct-04
|
nov-04
|
dec 04
|
|
BICEC
|
135,2
|
136,2
|
121,3
|
107,17
|
238,73
|
239,53
|
239
|
236
|
260
|
236
|
203
|
|
CLC
|
112,38
|
122
|
138,54
|
210,97
|
189,22
|
197,08
|
221
|
210
|
222
|
165
|
191
|
|
SGBC
|
152,64
|
132,3
|
132,02
|
90,36
|
214,4
|
223,88
|
223
|
220
|
242
|
209
|
210
|
|
Std Chr B.
|
164,94
|
152,8
|
155,7
|
196,82
|
205,07
|
164,61
|
192
|
186
|
171
|
237
|
207
|
|
AFRILAND
|
207,72
|
310
|
283,71
|
320,15
|
295,53
|
304,18
|
342
|
279
|
237
|
311
|
319
|
|
AMITY
|
96,8
|
106,8
|
97,8
|
98,01
|
111,29
|
111,29
|
102
|
127
|
129
|
103
|
138
|
|
CBC
|
171,46
|
153,8
|
130,72
|
189,48
|
260,19
|
266,45
|
125
|
138
|
122
|
123
|
134
|
|
CITIBANK
|
128,49
|
226,7
|
206,83
|
177,87
|
183,21
|
221,57
|
55
|
190
|
98
|
112
|
100
|
|
UBC
|
|
|
|
|
119,95
|
119,95
|
123
|
146
|
165
|
99
|
58
|
|
ECOBANK
|
|
|
|
|
127,76
|
83,03
|
183
|
81
|
152
|
139
|
168
|
Source : Rapports C.O.B.A.C
Lorsqu'on observe ce tableau, on constate que la
quasi-totalité des banques commerciales au Cameroun sont très
liquides. Afriland First Bank se situe au sommet avec un ratio de
liquidité supérieur à 200% depuis mars 2000. Au 31
décembre 2004, à l'exception de Union Bank of Cameroon, qui
présente un ratio de liquidité de 58%, toutes les autres banques
Camerounaises ont un ratio de liquidité supérieure à 100%.
Pour quatre d'entre elles (la BICEC, la SGBC, Standard Chartered Bank Cameroon
et Afriland First Bank), ce ratio est supérieur à 200% en
Décembre 2004. Ces banques sont donc les plus liquides. Ainsi, plusieurs
banques au Cameroun présentent en permanence des disponibilités
à moins d'un mois dépassant de deux fois leurs
exigibilités de même terme.
Cette forte liquidité des banques camerounaises
contribue à la réduction du recours au refinancement de la Banque
Centrale. Lorsqu'on observe le tableau suivant, les banques camerounaises n'ont
presque pas eu recours au refinancement de la BEAC entre 2001 et 2003.
Tableau 4 : Évolution du plafond de refinancement
et le taux d'utilisation
|
2001
|
2002
|
2003
|
|
Plafonds
|
15000
|
15000
|
6000
|
|
Taux d'utilisation (%)
|
1,4
|
0
|
0
|
Source : Rapport annuel BEAC
Mémoire de fin de formation LACGNI CARLOS DENDI 55
Face à ce fort potentiel de financement des banques
camerounaises, on peut chercher à connaître de quoi sont
constituées les ressources de ces banques commerciales. Qu'est ce qui
constitue l'essentiel de ces ressources ? La partie suivante essayera de
répondre à cette préoccupation.
II.2 Les ressources des banques
Les ressources des banques sont constituées des
capitaux permanents, des dépôts de la clientèle, de la
trésorerie et des divers (qui enregistrent les comptes de liaisons
créditeurs des succursales et des agences, les comptes créditeurs
divers y compris ceux des actionnaires, les comptes de régulations
créditeurs, le bénéfice net en attente d'affectation et
les comptes d'excédent des produits sur les charges). L'évolution
de la structure des ressources laisse entrevoir qu'au Cameroun, entre 2000 et
2002, le total cumulé des bilans de toutes les banques camerounaises a
augmenté de 30,18%, passant de 1096,049 milliards de Francs CFA à
fin décembre 2000 à 1426,885 milliards au 31 décembre
2002. Entre 2002 et 2003, on assiste à une période de
légère stagnation. En 2004, la croissance a repris et le total
des ressources a augmenté de 6% par rapport à 2003, passant ainsi
de 1460,639 milliards de F CFA à fin décembre 2003 à
1548,205 au 31 décembre 2004.
L'examen du graphique de l'évolution de la structure
des ressources nous montre que l'essentiel des ressources des banques sont les
dépôts de la clientèle. De 2000 à 2004, les
dépôts de la clientèle représentent chaque
année plus de 75% de l'ensemble des ressources des banques.
Figure 2 : Évolution de la structure des
ressources des banques camerounaises de 2000 à 2004

2000 2001 2002 2003 2004
Année
1800000
1600000
1400000
1200000
1000000
800000
600000
400000
200000
0
Montant en (millions de
A)
|
1548205
|
|
1426885 1460639
|
|
1096049
|
1238201
1200984 1158944
1143691
|
|
950974
|
|
840518
|
|
|
|
|
|
|
|
|
|
Capitaux permanents Dépotsde la clientèle
Opérations diverses
Opérations de trésorerie Total passif
Source : élaboré par l'auteur
d'après les données des Rapports d'activité de la
C.O.B.A.C
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
La structure des ressources au 31 décembre 2004 montre
que celles-ci sont constituées à 80% de dépôts de la
clientèle, 9% des capitaux permanents, 5% des opérations de
trésorerie et 6% des opérations diverses. Cette structure nous
indique donc que l'essentiel des ressources des banques Camerounaises est fait
de dépôts des clients.
Figure 3 : Structure des Ressources des banques du
Cameroun au 31 Décembre 2004

5%
6%
80%
9%
Capitaux permanents Dépôts de la clientèle
Opérations diverses Opérations de trésorerie
Source :
élaboré par l'auteur d'après les données
des rapports d'activité de la COBAC 2004
Nous venons de montrer avec l'examen de l'évolution des
ressources des banques Camerounaises que l'essentiel de ses ressources sont les
dépôts des clients. Ces dépôts peuvent être
placés à vue ou à terme. La question que nous pouvons nous
poser à ce niveau est celle de savoir : Qu'est ce qui constitue
l'essentiel de ces dépôts ? L'examen des dépôts selon
leur nature apportera des éléments de réponse à
cette question.
II.3 Les dépôts de la
clientèle
À partir des dépôts de la
clientèle, la banque dispose de fonds, qu'elle peut utiliser librement,
à condition d'être toujours en mesure de les restituer si le
déposant le demande. L'activité des banques consiste, en fait,
à transformer des dépôts en crédits, ce qui explique
leur rôle déterminant dans le processus de la création
monétaire. Nous allons dans la suite définir les
dépôts des clients selon leur nature, puis nous examinerons
l'évolution de la structure de ces dépôts depuis 1995.
II.3.1 La nature des comptes de dépôts des
clients
Un client effectue en général deux types de
dépôts auprès des banques :
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
> les dépôts à vue12 :
où le retrait ne nécessite pas de préavis (c'est le cas
des comptes chèques, des comptes sur livret, les comptes courants des
entreprises et certains comptes de dépôts spéciaux).
> Les dépôts à termes : qui ne font
l'objet d'un retrait qu'à échéance fixé, avec
options de retrait anticipé (avec perte de certains avantages telle une
réduction du taux d'intérêt).
Ainsi selon la nature des comptes, on distingue pour les
dépôts à vue :
1. les comptes sur livret : Ces comptes ne
donnent pas droit au chéquier. Il sont rémunérés au
taux de 5% l'an. C'est le taux de rémunération minimum au
Cameroun. Ils sont réservés aux personnes physiques et à
certaines personnes morales (Associations). Le taux de
rémunération peut être négocié compte tenu
des fonds déposés.
2. les comptes d'épargne logement :
il s'agit des comptes d'épargne à vue. Ils sont
rémunérés et réservés aux personnes
physiques. Ils donnent droit aux prêts sous certaines conditions
(investissements, immobiliers).
3. les comptes courants des entreprises :
ces comptes ne sont pas rémunérés et sont destinés
aux entreprises pour leur assurer un service de caisse, c'est-à-dire un
certain nombre de facilités pour la manipulation de leurs fonds.
4. les comptes chèques : comme pour les
comptes courants, ils ne sont pas rémunérés. Ils sont
ouverts aux particuliers.
Pour les dépôts à terme, on distingue selon
la nature des comptes :
1. Les comptes à terme : le banquier
reçoit les fonds du client et les immobilise, moyennant un taux de
rémunération minimum de 5%. Ces fonds demeurent bloqués
jusqu'à l'expiration du délai fixé à l'ouverture du
CAT. Le compte à terme concerne essentiellement les personnes
morales.
2. Les certificats de dépôts :
ils représentent les placements qui prennent la forme d'un titre de
créances négociables. Le taux de rémunération est
voisin de celui du marché monétaire.
3. Les bons de caisse : ils
matérialisent les titres de placement. La durée du placement
varie entre 1 mois et 2 ans. Le taux minimum de rémunération est
de
12 Cf. Encarta 2006
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
5% avec possibilité de négocier compte tenu de
l'importance du dépôt. On distingue 2 types de bons de caisse : Le
bon de caisse nominatif c'est-à-dire qui porte un nom et le bon de
caisse anonyme c'est-à-dire au porteur. Les bons de caisse contrairement
au compte à terme sont destinés aux personnes physiques. Les
intérêts sont généralement payés d'avance au
client lors de la souscription. Ils sont précomptés. Les
intérêts sur bon de caisse ne sont pas assujettis à la
TPRCM (Taxe Proportionnelle sur les Revenus des Capitaux Mobiliers).
4. Les autres comptes de dépôts
: lors de la réalisation de certaines opérations
présentant des particularités, le client doit effectuer les
dépôts de durée plus ou moins longue selon les cas. Ces
provisions ainsi constituées ne sont pas rémunérées
et sont enregistrées dans le compte dispositions à payer. On peut
citer :
· Les provisions pour chèque à payer : ce
sont les provisions garanties pour des paiements par émission des
chèques appelés chèque à payer ou chèque
banque dont la demande émane de son client garantissant ainsi le maximum
d'assurance aux bénéficiaires.
· Provisions pour chèque certifié :
certifier un chèque c'est apposer une mention qui assure la
disponibilité de la provision et la garantie du paiement pour certaines
opérations (paiement et cotisation sociale de la CNPS, des achats divers
sur d'autres tiers). Cette provision est bloquée au profit du
bénéficiaire.
· Les déposits : ce sont des fonds qui
garantissent la réalisation de certaines opérations (achat de
titres, locations de coffre fort) exigées par la banque aux clients ne
disposant pas de provisions au compte.
· Les sommes mises à dispositions : ce sont des
sommes payées à des personnes non clientes à la banque sur
ordre des clients.
Nous pouvons retenir de cette section que les clients peuvent
effectuer les dépôts soit à vue ou à terme. Comment
ont évolué ces dépôts par nature pour les banques
commerciales du Cameroun ? Quel est l'élément
prépondérant de ces ressources clientèles ?
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
II.3.2 L'évolution des dépôts par
nature
Lorsque nous analysons la structure des dépôts,
nous constatons que les comptes à vue restent
prépondérants depuis l'an 2000. En effet, depuis cette
année, plus de 40% des ressources collectées sont logées
dans les comptes à vue (Comptes chèques créditeurs et
comptes courants des entreprises, qui sont non rémunérés
au Cameroun). Ces comptes à vue augmentent, et sont passés de
270,094 Milliards de FCFA au 31 juin 1998 à 538,513 milliards de FCFA en
Décembre 2002. Soit une augmentation de plus de 90% en 4 ans. Puis, Ils
baissent à 483,033 milliards de FCFA en 2003. Les autres comptes
d'épargne (comptes sur livret, comptes d'épargne logement) qui se
trouvent au deuxième rang après les comptes à vue, sont en
nette croissance depuis 2000. Ils passent de 194,722 milliards de FCFA au 31
décembre 2000 à 306,196 milliards au 31 décembre 2003. Les
placements à terme représentent un peu plus de 23% des
dépôts collectés depuis l'an 2000, soit environ 13 % pour
les bons de caisse, et un peu plus de 10% pour les comptes à terme. Au
31 Décembre 2004, les comptes à vue représentent
71,2%13 du total des dépôts de la clientèle.
Figure 4 : Evolution de la structure des
dépôts (en millions de francs CFA)

400000
200000
600000
500000
300000
100000
0
Bon de Caisse Compte à terme
Autre compte d'épargne Compte à vue
Autres sommes dues à la clientèle
juin-95
juin-96
janv-97
juin-98
dee-00
dec-01
dec-02
dec-03
Source : élaboré par l'auteur
d'après les données des rapports d'activité de la
COBAC
La structure des dépôts au 31 décembre
2006, laisse entrevoir qu'à cette date, les déposants se sont
reportés davantage sur les comptes à vue14 qui
occupent toujours une place prépondérante dans les ressources
clientèles. Sur l'ensemble des dépôts collectés par
les banques, 72,1% sont des ressources à vue (près de 1112,481
milliards de FCFA
13 Voir Annexe III, figure 14 : Structure des
dépôts au 31 décembre 2004.
14 Les comptes à vue comprennent au 31 Décembre
2006 : les comptes courants créditeurs, les comptes chèques
créditeurs, les comptes sur livret, les dépôts de
garanties.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
sur les 1524,944 milliards des dépôts de la
clientèle). L'examen de ces ressources à vue nous indique
qu'elles sont constituées à 50%15 de
dépôts à vue non rémunérés (comptes
courants créditeurs et comptes chèques créditeurs). Les
comptes à terme représentent seulement 8,8% des
dépôts collectés. Les comptes de dépôts
à régime spécial, au 31 décembre 2006, comprennent
les bons de caisse, les certificats de dépôts, les comptes et
plans épargne-logement et les plans d'épargne-retraite. Leur
poids dans le total des dépôts se situe à 13,5%.
Figure 5 : Structure des dépôts au
31 Décembre 2006

Comptes dépôts à regime spéciale
comptes à terme compte à vue Autres comptes
72,1%
5,6%
13,5%
8,8%
Source : élaboré par l'auteur
d'après les données du rapport du conseil national du
crédit, décembre 2006
L'analyse de la liquidité des banques camerounaises
nous indique qu'elles sont surliquides et présentent donc un
excédent de ressources. A partir de l'examen de la structure des
ressources, nous avons pu constater que l'essentiel des ressources des banques
au Cameroun est fait des dépôts de la clientèle. Puis, avec
l'analyse de l'évolution de ces dépôts selon leur nature,
nous avons remarqué avec la série de données à
notre disposition que l'essentiel des dépôts sont des ressources
à vue.
Ainsi, on assiste parfois à la frilosité du
banquier, refusant de s'impliquer dans le financement de l'économie,
puisqu'il ne dispose que des ressources pouvant disparaître du jour au
lendemain (la plupart des dépôts étant essentiellement
à vue; même lorsqu'ils sont à terme, le client peut
moyennant une pénalité d'un point, rentrer en possession de son
argent avant le terme convenu). Il craint ainsi de s'exposer à un risque
de transformation grave, s'il manipulait mal ces ressources. Les banquiers
camerounais ne
15 Voir Annexe III, Tableau 16 : Structure des
dépôts au 31 décembre 2006.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
disposent pas de méthodes appropriées pour
évaluer les risques de transformation et de liquidité liés
aux dépôts à vue.
La modélisation de l'écoulement des
dépôts à vue représente alors un enjeu de taille
pour ces banques camerounaises. Dans la suite, nous proposons aux banquiers une
méthode qui permettrait de manipuler les dépôts à
vue tout en réduisant le risque de transformation. Dans le chapitre
suivant, après avoir modélisé l'écoulement des
dépôts à vue, nous ressortirons la partie stable de ces
dépôts en fonction du temps.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
MODÈLE D'ÉVOLUTION DES ENCOURS DE
DÉPÔTS A VUE
DANS LES BANQUES
CAMEROUNAISES
Les dépôts à vue comme nous l'avons
souligné plus haut représentent une part importante des
ressources pour les banques camerounaises (plus de 70% en décembre
2006). Leur modélisation sera donc d'une importance capitale pour ces
banques.
Pour mieux appréhender la modélisation des
encours des dépôts, nous avons décidé de nous
restreindre aux dépôts à vue non
rémunérés. Ceci nous permettra de laisser de
côté la modélisation de certains types de
dépôts dont le taux de rémunération est
négociable entre le banquier et son client. La plupart des études
se sont attachées à estimer leur modèle de
dépôts à vue sur les données du passé. Il
nous a semblé fondamental de construire un modèle
prédictif et de ressortir la partie stable des dépôts
à vue en fonction du temps.
Dans la suite nous allons présenter dans la
première section les données et les techniques
économétriques qui nous permettront de modéliser
l'évolution des dépôts, puis la seconde section sera
consacrée à la présentation des résultats.
SECTION I : Données et méthodologie
I.1 Les données et les sources
Les données que nous utilisons sont les encours des
dépôts à vue non rémunérés dans
l'ensemble des banques commerciales camerounaises. Ces données sont
tirées des tableaux de la situation des banques commerciales par secteur
élaboré par la BEAC. En effet, la convention qui régit
l'union Monétaire de l'Afrique Centrale (UMAC) lui confère la
mission d'élaborer les statistiques monétaires pour le compte des
Etats membres (cf. Article 29). La BEAC établit ces statistiques de
façon mensuelle à partir des données comptables des
banques commerciales. Ces dernières étant tenues de lui
transmettre leur situation comptable établie selon les règles du
nouveau plan comptable des banques mis en place par la COBAC en juillet 1998.
Les dépôts à vue non rémunérés sont la
somme des comptes courants créditeurs et des comptes chèques
créditeurs. Toutes ces données vont du 1er Janvier
1997 au 31 décembre 2006.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
Pour une date t donnée, nous
désignerons par Dt l'encours des dépôts à
vue de l'ensemble des banques commerciales du Cameroun, Rt le taux
d'intérêt du marché interbancaire qui est
représentatif du taux d'intérêt de marché.
L'étude des premiers modèles de
dépôts à vue (cf. Selvaggio [1996], L'Office of Thrift
Supervision [2000]) nous a permis de mettre en évidence certaines
propriétés des dépôts à vue à l'instar
de la forte intégration des données d'encours. Elle nous a aussi
permis de voir que les données d'encours des dépôts
à vue peuvent dépendre des taux d'intérêt de
marché. Cependant, l'absence d'un marché financier actif au
Cameroun et le fait que nous travaillons sur les dépôts non
rémunérés nous a conduit à faire l'hypothèse
que le comportement du client en terme de dépôts sur leur compte
à vue n'a pas de relation avec l'évolution des taux
d'intérêt de marché (nous testerons cette hypothèse
dans la suite).
I.2 La méthodologie de travail
Nous allons modéliser l'évolution de notre
série des dépôts à vue en utilisant la
méthodologie de Box et Jenkins (1976)16. L'approche de Box et
Jenkins consiste en une méthodologie d'étude systématique
des séries temporelles à partir de leurs caractéristiques
afin de déterminer dans la famille des modèles ARIMA (voir annexe
I pour plus de détails sur cette notion), le plus adapté à
représenter le phénomène étudié. Cette
méthode s'évertue à déterminer une fonction qui
décrit l'évolution de la série dans le temps. Elle
n'envisage pas de mise en relation de la variable endogène avec une
autre variable qui pourra être importante à son explication. Ainsi
l'analyse de la cointégration17 nous permettra de tester
l'éventualité d'une relation entre le niveau de l'encours des
dépôts à vue et le taux d'intérêt au Cameroun,
afin de procéder à un modèle à correction d'erreur
en cas d'existence éventuelle d'une relation. Il est à noter que
les deux méthodes (Méthodologie de Box et Jenkins et Analyse de
la Cointégration) exigent des étapes préliminaires
communes pour l'étude des séries (il s'agit de l'analyse de la
saisonnalité et de la stationnarité). C'est pour cela que dans la
suite, nous procéderons d'abord à l'étude de la
série des dépôts à vue en terme de
saisonnalité et de stationnarité, ensuite nous allons
après une analyse de la série des taux
d'intérêt18 tester l'éventualité d'une
relation entre ce taux et le niveau de l'encours des dépôts
à vue (cela sera fait à partir du test de
16 Voir annexe I pour la présentation
détaillée de la méthodologie
17 Voir annexe II pour la présentation de ce
concept.
18 Il s'agira aussi de l'analyse en terme de
stationnarité et de saisonnalité.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
cointégration de Johansen et du test de causalité
de Granger), enfin deux cas seront possibles :
> si les deux séries sont cointégrées,
nous procèderons à l'estimation d'un modèle à
correction d'erreurs qui permettra de trouver la relation réelle entre
les deux variables ;
> si les deux séries ne sont pas
cointégrées, nous poursuivrons l'étude de notre
série d'encours des dépôts à vue selon la
méthodologie de Box et Jenkins.
SECTION II : Applications
II.1 Description de l'évolution de l'encours des
dépôts à vue de l'ensemble des banques
camerounaises
Cette analyse permet d'appréhender les
caractéristiques de la série durant la période
d'observation. Notre série d'encours va du 31 Janvier 1997 au 31
décembre 2006. Dans la construction du modèle, nous avons choisi
de nous limiter au 31 Décembre 2005. La série restante nous
permettra de tester les qualités prédictives du modèle.
Entre janvier 1997 et décembre 1999, l'encours de ces
dépôts varie de façon lente dans l'intervalle de 200
milliards et 300 milliards de francs CFA avec un encours moyen de 257,246
milliards de F CFA. Ceci signifierait que les dépôts mensuels sur
les comptes de dépôts à vue sont presque identiques aux
retraits effectués sur ces comptes. La variation mensuelle maximale du
stock est de l'ordre de 18 milliards de Francs CFA, observé en
décembre 1999. Aussi, cette situation de variation lente du stock des
dépôts rejoint le ralentissement de la croissance
économique observé au cours de cette période (en effet, la
croissance est passée de 5% en 1997 à 4,2% en fin
199919). La vitesse de transaction des opérations sur les
comptes courants n'a pas considérablement varié puisque
l'activité des entreprises était ralentie. Les agents
préférant conserver leurs liquidités sous forme
d'encaisses de précaution.
Entre janvier 2000 et décembre 2001, l'encours de ces
dépôts connaît des périodes de variations très
fortes. Pendant cette période, on observe des variations mensuelles
positives de plus de 50 milliards de Francs CFA et des variations
négatives de plus de 45 milliards de francs CFA. Cela témoigne
d'une forte mobilisation des comptes à vue par les clients pour
répondre aux exigences de l'économie. Cela peut être le
reflet du
19 Cf. rapport du conseil national du crédit
exercice 1997/1998 - 1998/1999 et 1999/2000, Page3.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
dynamisme retrouvé de l'économie camerounaise
après le ralentissement de l'activité des grandes entreprises et
de l'activité économique en général (observé
à la fin des années 90). Le taux de croissance économique
en terme réel s'est élevé à 5,5% en 2001 contre
4,2% en fin 1999.20 La vitesse des transactions ayant
augmenté, les encaisses destinées aux transactions ont
été importantes. On observe alors un stock qui fluctue beaucoup
du fait des entrées et des sorties de fonds. Durant l'année 2002,
on a noté une stabilité de l'encours entre Avril et Mai. De juin
à décembre 2002, le stock a augmenté de 22 % (augmentation
de 83,937 Milliards de FCFA.) passant de 389,411 à 473,348 milliards de
francs CFA. Ceci signifie que les dépôts effectués sur les
comptes de dépôts à vue durant ces mois sont nettement
supérieurs aux retraits. Du 31 avril au 31 Juillet 2003, les retraits de
fonds par les clients des banques sont supérieurs aux
dépôts effectués. On observe cela par des variations
mensuelles négatives du stock qui se sont situées en moyenne
autour de 11 milliards de F CFA. Pendant l'année 2004 on assiste
à nouveau à une variation alternativement positive et
négative du stock des dépôts. De janvier 2005 à
décembre 2006 l'encours des dépôts à vue passe de
498,031 à 632,347 milliards de F CFA avec des périodes mensuelles
de faible fluctuation.
Figure 6 : Evolution de l'encours des
dépôts à vue des banques commerciales du 31/01/1997 au
31/12/2006 (en millions de F CFA)

97 98 99 00 01 02 03 04 05 06
Enca.rs cis cleptI s a vie
400000
600000
200000
700000
500000
300000
Année
Source : élabord par l'auteur d'aprés les
données de la BEA~
II.2 Analyse des caractéristiques de la
série
Elle permet de connaître certaines propriétés
caractéristiques de la série à étudier
20 Cf. vingt septième rapport d'activité
du Conseil National de Crédit, Exercice 1999/2000, 2000/2001 Page 8.
II.2.1 Analyse préliminaire
Avant de procéder à la construction du
modèle, nous nous proposons ici de mettre en évidence le fait que
nos données d'encours des dépôts à vue sont
fortement intégrées (c'est-à-dire qu'il y'a une forte
corrélation entre Dt et Dt-1). Lorsque nous
testons sur notre échantillon l'équation
(37) D t = áD t - 1 + â +
å t ,
Où les åt sont supposés
suivre une loi normale centrée. On obtient les résultats suivants
:
Tableau 5 : Résultat de l'estimation de
l'équation (37)
|
PARAMETRES
|
ESTIMATION (ECART TYPE)
|
|
á
|
1,008
(0,004)
|
|
R2 AJUSTE
|
99,8%
|
Source : élaboré par l'auteur
La valeur du paramètre á est proche de
1. L'autocorrélogramme partielle suivant permet aussi de confirmer la
forte intégration entre les données d'encours. Le
corrélogramme simple de la série des dépôts est
typique d'une série affectée d'une tendance (tous les termes sont
élevés même pour les décalages importants). Ces
résultats préliminaires nous permettent d'opter pour un
modèle qui ne tente pas d'expliquer directement l'évolution des
encours mais plutôt la variation de ces encours du fait de leur forte
intégration. Mais avant, il est important pour ne pas se tromper
d'étudier la série en termes de stationnarité.
Figure 7 : Corrélogrammes simple et partielle de
la série des dépôts à vue
depot
|
1,0
|
|
|
Coefficient
Limites de confiance
Limite de
confiance
inférieure
|
|
0,5 0,0 -0,5 -1,0
|
|
|
ACF partial
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Numéro de décalage
depot
|
ACF
|
1,0 0,5 0,0 -0,5 -1,0
|
|
Coefficient
Limites de confiance
Limite de
confiance
inférieure
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Numéro de décalage
Source : élaboré par l'auteur
II.2.2 Analyse de la saisonnalité :
Une étape importante avant l'étude de la
stationnarité d'une série est l'analyse de la saisonnalité
qui permet de déceler des variations périodiques qui peuvent
affecter la série.
Dans la suite, nous travaillons avec les données
transformées (transformée Log). Cette transformation nous permet
d'avoir des données d'encours plus réduites, de se rapprocher de
la normalité et de stabiliser la variance de la série lorsque
celle de la série originale croît avec le temps.
Figure 8 : Encours des dépôts à vue
transformés (transformation logarithmique)

Source : élaboré par l'auteur
Cette représentation graphique nous suggère
l'idée d'un schéma additif. En effet, l'utilisation de la
méthode de la bande nous montre que les deux droites passant par les
minima et les maxima sont parallèles.
Comme nos séries sont mensuelles, alors la moyenne mobile
centrée utilisée pour les désaisonnaliser est la moyenne
mobile d'ordre 12.
Figure 9 : Evolution de dépôts
transformés et de ceux corrigés des variations

97 98 99 00 01 02 03 04 05 06
13.4
13.2
LizgaiMacimdVcis
13.0
12.8
12.6
12.4
12.2
LOGdepots_à_vue
Série corrigée des variations saisonières
Source : élaboré par l'auteur
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
Pour la série des dépôts à vue,
nous avons procédé à une désaisonnalisation par
moyenne mobile centrée. Le graphique de la série brute et de la
série corrigée des variations saisonnières ne montre pas
de différence significative entre les deux séries. Nous pouvons
conclure que la série n'est pas saisonnière.
II.2.3 Analyse de la stationnarité de la
série transformée des encours des dépots
(Log(depots)).
De même que pour la série brute des
dépôts, le corrélogramme de la série
transformée (Log(depots)) est typique d'une série affectée
d'une tendance.
Figure 10 : Corrélogrammes simple et partielle de
la série des dépôts tranformés .
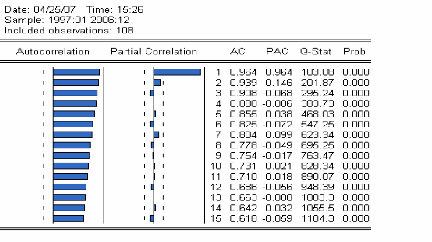
Source : élaboré par l'auteur
Nous allons procéder à l'estimation des trois
modèles de Dickey-fuller (nous ferons le test de Dickey-fuller
augmenté avec le nombre de décalages déterminés par
le critère de Akaike. (Voir annexe III pour les deux autres
modèles)
Tableau 6 : Test de Dickey-Fuller Augmenté sur la
série des dépôts transformés : modèle avec
constante et trend

Source : élaboré par l'auteur
A l'issue du test, toutes les statistiques (les t-statisques
empiriques) des trois modèles sont toutes supérieures aux valeurs
critiques tabulées aux seuils 1%, 5% et 10%. Nous acceptons
l'hypothèse nulle, la série des dépôts
transformés (Log(depots)) possède donc une racine unitaire. Elle
n'est donc pas stationnaire en niveau. Notre série est
représentée par un processus Differency Stationnary (DS), la
meilleure façon de stationnariser est celle des différences
premières.
Nous avons calculé la série D(Logdepots) qui
représente la série obtenue après application d'un filtre
aux différences premières à la série Logdepots.
Nous allons également estimer les trois modèles de Dickey-Fuller
sur cette série. (Voir annexe III pour les deux autres
modèles)
Tableau 7 : Test de dickey-fuller augmenté sur la
série D(Logdepots)

Source : élaboré par l'auteur
A l'issue de ce test, toutes les statistiques (t-statistique
de Dickey-fuller augmenté) sont inférieures à la valeur
critique aux seuils 1%, 5% et 10%. Nous pouvons conclure que la
différence première de Logdepots (c'est-à-dire
D(Logdepots) est stationnaire. Nous disons aussi que la série Logdepots
est intégrée d'ordre (1) un21.
II.3 Le lien entre le taux d'intérêt et le
niveau de l'encours des dépôts à vue
Ici nous nous proposons de tester une éventuelle
relation entre le taux d'intérêt et le niveau de l'encours des
dépôts à vue. Pour cela, nous disposons d'une série
mensuelle de 24 observations concernant la série des taux
d'intérêt du marché interbancaire (période allant de
janvier 2002 à décembre 2003). Ce taux reflète le taux
d'intérêt de marché et a un impact sur le niveau des taux
créditeurs et débiteurs appliqué par les banques aux
clients. En effet avec le développement du marché entre banques,
la grande partie des
21 Le terme intégré d'ordre p (p å
N), signifie qu'il faut différencier la série p fois pour la
rendre stationnaire.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
transactions du marché monétaire a lieu sur le
compartiment interbancaire. Le taux d'intérêt qui y est
pratiqué conditionne les taux de rémunération des
dépôts et des crédits pratiqués par les banques.
Nous supposons en fait que lorsque le taux du marché interbancaire est
très supérieur à un seuil (le taux créditeur
minimum par exemple, qui est resté stable à 5% durant notre
période d'étude), la banque propose des taux de
rémunération plus attrayant au client pour les
dépôts à terme et certains produits financiers et il
s'ensuit une diminution du stock des dépôts à vue au profit
de ces dépôts à termes et produits financiers. Et lorsque
ce taux est inférieur au même seuil, les banques
préfèrent recourir au marché interbancaire pour emprunter
de l'argent et rémunèrent faiblement les dépôts
à terme. Ce qui fait que le client va préférer garder
l'essentiel de ses dépôts dans son compte à vue.
Nous allons tester cette relation avec la série des
dépôts à vue correspondant à la même
période.
II.3.1 Le test de cointégration de Johansen et
interprétation
L'analyse de la cointégration permet d'identifier
clairement s'il existe une relation véritable entre deux variables en
recherchant l'existence d'un vecteur de
cointégration.22 Cette théorie permet
de spécifier des relations éventuellement stables à long
terme entre deux séries temporelles tout en analysant conjointement la
dynamique de court terme. Johansen (1988) a proposé des estimateurs pour
tester cette caractéristique entre deux séries. Cependant, pour
être cointégrées, les deux séries doivent être
affectées d'une tendance stochastique de même ordre
d'intégration (cf. régis Bourbonnais, économétrie,
Dunod, 2003, page 281). Nous avons déjà montré que la
série Logdépots est intégrée d'ordre 1. Nous allons
alors procéder à la détermination de l'ordre
d'intégration de la série Log(taux) qui représente la
transformée logarithmique de la série taux
d'intérêt. Un examen graphique de la série Log(taux) nous
indique qu'elle n'est pas saisonnière. Pour cela nous avons
estimé les trois modèles du test de dickey-fuller augmenté
sur la série Log(taux) (voir Annexe III pour le résultat de ces
trois modèles).
Les résultats du test nous suggèrent que la
série Log(taux) n'est pas stationnaire en niveau. En effet, Les
statistiques obtenues sur les modèles sans trend sont supérieures
aux valeurs critiques au seuil de 5%. La série est donc
représentée par un processus DS et admet ainsi une tendance
stochastique. La meilleure façon de stationnariser est celle du
22 cf. Régis Bourbonnais,
économétrie, Dunod, 2003, page 279.

Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
filtre aux différences. Sur la série D(Logtaux)
obtenue en appliquant à la série Logtaux un filtre aux
différences premières, nous avons également
appliqué le test de Dickey-Fuller augmenté. Il ressort de ce test
que pour les trois modèles, les statistiques empiriques sont toutes
inférieures aux valeurs critiques au seuil 5%. La différence
première de la série Logtaux est stationnaire. On peut conclure
que cette série est intégrée d'ordre un. Ainsi, les deux
séries Logdepots et Logtaux sont intégrées du même
ordre 1. Nous pouvons envisager l'étude de la cointégration.
Les résultats du test de cointégration de
Johansen (voir annexe II) permettent de rejeter l'hypothèse de la
cointégration entre la variable taux d'intérêt et le niveau
d'encours des dépôts à vue pour les seuils 1% et 5%. Il
n'est donc pas possible de spécifier une relation stable à long
terme entre la série des encours des dépôts à vue et
celle des taux d'intérêts. (En effet le loglikelihood ratio est
inférieur à la valeur critique).
II.3.2 Le test de causalité de Granger et
interprétation
Granger (1969) a développé le concept de
causalité qui permet de mettre en évidence le sens de
causalité entre deux variables économiques. En effet pour
Granger, dire que la variable Rt est la cause de Dt, signifie
que la prédictibilité de Dt est améliorée
lorsque l'information relative à Rt est incorporée
à l'analyse.
Nous avons effectué avec le logiciel EVIEWS, ce test sur
les variables Logdepots et logtaux. Les résultats sont les suivants :
Tableau 8 : Résultat du test de causalité
de Granger

Source : élaboré par l'auteur avec
Eviews
D'après le tableau précédent, on accepte
l'hypothèse nulle dans les deux cas (les deux probabilités sont
supérieure à 5%.).
Ce résultat nous permet de conclure au seuil de 5 %
qu'il n'y a aucun sens de causalité
entre les deux variables
d'après Granger. Le taux d'intérêt ne cause pas les
dépôts. Les
dépôts ne causent pas le taux
d'intérêt. Autrement dit, au sens de Granger, on peut
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
prédire le niveau de l'encours des dépôts
à vue sans connaître le mouvement des
taux
d'intérêt. Car son influence n'est pas significative sur
le niveau du stock des dépôts à vue.
Ces deux résultats (test de cointégration de
Johansen et test de causalité de Granger) permettent de valider notre
hypothèse selon laquelle au Cameroun, le comportement des clients en
terme de dépôts sur leurs comptes à vue (non
rémunéré) est indépendant de la variation des taux
d'intérêt. Cela serait dû au fait que les taux
d'intérêt n'augmentent pas considérablement de façon
à intéresser les titulaires des comptes de dépôts
à vue. Nous pouvons aussi justifier cela par le fait que, l'essentiel
des dépôts à vue est constitué des
dépôts sur comptes courants des entreprises qui sont
destinés pour la plupart à financer leurs activités
quotidiennes et à constituer des encaisses de précaution. C'est
aussi la preuve qu'au Cameroun, l'absence d'un marché financier actif
n'a pas permis une diversification des produits financiers attrayant à
même de collecter l'épargne des particuliers et les
excédents de trésorerie des entreprises.
Nous avons montré dans cette partie qu'au Cameroun, le
niveau de l'encours des dépôts à vue ne dépend pas
des taux d'intérêt bancaire. Il est donc important pour la
détermination de la fonctionnelle d'écoulement des
dépôts d'approfondir l'étude des propriétés
stochastiques de l'encours des dépôts à vue, et en ne
tenant pas compte des taux d'intérêt.
II.4 Etude de la série des dépôts
selon la méthodologie de Box et Jenkins
L'étape préliminaire de la méthodologie de
Box et Jenkins a été faite. Nous allons poursuivre avec les
autres étapes.
II.4.1 L'identification et l'estimation des
paramètres du modèle d'évolution de la série
d'encours des dépôts à vue
Nous avons montré (cf. paragraphe II.2.3) que la
série Log(depots) n'est pas stationnaire et qu'elle est
représentée par un processus DS. Nous l'avons
stationnarisée en lui appliquant un filtre aux différences
premières. Nous avons désigné par Dlogdepots la
différence première de la série Logdepots.
Figure 11 : Corrélogramme simple et partielle de
la série Dlogdepots

Source : élaboré par l'auteur avec
Eviews
Après lecture du corrélogramme de la
série Dlogdepot représenté ci-dessus, les modèles
potentiels pour la série Logdepots sont ARIMA(2,1,1). ARIMA(1,1,1),
ARIMA(1,1,0) ARIMA(0,1,1).
Lorsque nous estimons les paramètres de tous ces
modèles, il apparaît que seuls les coefficients des modèles
ARIMA(2,1,1) et ARIMA(0,1,1) et ARIMA(1,1,0) sont toutes significatives au
seuil 5%.

Source : élaboré par l'auteur avec
Eviews
Tableau 9 : Résultat de l'estimation du
modèle ARIMA(2,1,1)


Tableau 10 : Résultat de l'estimation du
modèle ARIMA(0,1,1)




Source : élaboré par l'auteur avec
Eviews
Tableau 11 : Résultat de l'estimation du
modèle ARIMA(1,1,0)




Source : élaboré par l'auteur avec
Eviews
Nous allons dans la suite, étudier l'adéquation de
ces trois modèles avant de faire un choix judicieux et optimal.
II.4.2 La vérification et l'adéquation des
trois modèles potentiels
II.4.2.1 Le modèle ARIMA(2,1,1)
Les coefficients de AR(1), AR(2), MA(1) et la constante du
modèle
ARIMA(2,1,1) sont tous significativement différents de 0
pour un seuil de 5%. Les autres
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
statistiques : Durbin Waston (DW), F empirique laissent
présager d'un bon ajustement. Nous allons maintenant analyser le
résidu à partir de sa fonction d'autocorrélation.
Figure 11 : Corrélogramme des
résidus

Source : élaboré par l'auteur avec
Eviews
Aucun terme de ce corrélogramme n'est extérieur
aux deux intervalles de confiance et la statistique Q a une
probabilité critique très proche de supérieure à 5%
quelle que soit la valeur de k. Le résidu peut être
assimilé à un processus de bruit blanc. Nous procédons
à un test ARCH sur ces résidus (test ARCH à un retard) :
La Fstatistique = 1,07 et la probabilité critique = 0,30 est nettement
supérieure à 5%. Donc les résidus sont un processus de
bruit blanc, non autocorrelés et homoscédastiques. L'estimation
du modèle ARIMA (2,1,1) est donc validée. La série
Logdepots peut être représentée par un processus du type
ARIMA (2,1,1) avec constante.
II.4.2.2 Le modèle ARIMA(0,1,1)
Le coefficient de MA(1) et la constante sont significativement
différent de 0. Les autres statistiques DW et F empirique laisse penser
que l'ajustement est meilleur. Mais avant de conclure, analysons le
résidu à partir de sa fonction d'autocorrélation.
Figure 12 : Corrélogramme des résidus du
modèle ARIMA(0,1,1)

Source : élaboré par l'auteur avec
Eviews
La statistique de Q Ljung-Box indique un corrélogramme
dont les termes sont significativement nuls. En effet, toutes les Q-stat sont
supérieures à 5%. Les résidus issus de ce modèle
sont effectivement des bruits blancs. Un test ARCH (avec un retard)
appliqué à ces résidus montre que les résidus sont
homoscédastiques. (En effet, la Fstatistique est égale à
1,23 avec une probabilité de 0,26. supérieur à 5% : voir
annexe III). Donc les résidus sont des bruits blancs, non
autocorrelés et homoscédastiques. L'estimation du modèle
ARIMA(0,1,1) est validée.
II.4.2.3 Le modèle ARIMA(1,1,0)
Le coefficient de AR(1) et la constante sont significativement
différents de 0 au seuil de 5%. L'analyse des résidus de ce
modèle (cf. annexe) montre que les résidus sont des bruits blancs
non autocorrelés et homoscédastiques. Donc le modèle
ARIMA(1,1,0) avec constante est validé.
Nous constatons alors que les trois modèles peuvent
être retenus comme processus générateur de la série
Logdepot. Dans la suite, il sera question de déterminer le meilleur
modèle.
II.4.3 Le choix du modèle
Nous avons constaté que trois modèles
franchissent la phase de vérification et qu'il convient de choisir dans
cet ensemble. Le choix du modèle optimal reposera sur le critère
d'information de Akaike ou celui de Schawrz, qui consiste à supposer que
ces trois modèles fournissent des approximations de la
réalité et que la vraie loi inconnue des observations ne
satisfait pas forcément un tel modèle. On fonde le choix du
modèle sur une mesure de l'écart entre la vraie loi inconnue et
le modèle proposé. L'objectif étant alors de trouver le
modèle qui minimise les estimateurs des quantités d'information
de de Akaike et de Schawrz.
Ainsi, après comparaison des trois modèles selon
les critères de Akaike et de Schwarz, nous retenons un processus
ARIMA(0,1,1) avec constante comme générateur de la série
Logdepot.
Finalement notre série Logdepot peut être
représentée valablement par le modèle
(38) Logdepot Logdepot -
- t 0, 008592
= + -
å 0, 493349 1
å t -
t 1 t
Ou encore
(39) (1 )
- D Logdepot t 0,008592 (1 0, 493349 )
= + - D å
t
Où D représente l'opérateur
décalage d'ordre 1. (DYt = Yt-1.)
Nous pouvons dire que la série des variations de
logdepot (Dlogdepot) est générée par une moyenne
pondérée des aléas jusqu'au premier retard. Elle est alors
représentative d'une série chronologique qui fluctue autour de sa
moyenne de manière aléatoire.
Les prévisions peuvent être faites. Elles
permettront de connaître l'état du stock des dépôts
aux dates futures.
II.4.4 La prévision
Nous allons faire la prévision pour la série
d'encours des dépôts à vue à un horizon d'un an.
Pour cela, nous allons d'abord prévoir les séries Logdepots. Les
courbes correspondantes aux données estimées et aux
données réelles sont représentées dans le graphique
suivant :
Figure 13 : Dépôts estimés par le
modèle et dépôts réels observés

Source : élaboré par l'auteur avec
Eviews
La comparaison des dépôts réels (en rouge)
et les dépôts estimés (en bleu) ne laisse aucun doute sur
la qualité du modèle à expliquer correctement le
passé. Il apparaît donc que les estimations sont satisfaisantes.
Les valeurs estimées ne sont pas très éloignées des
valeurs réellement observées. Ce qui traduit le fait que le
modèle s'ajuste bien à la réalité.
Nous allons maintenant établir le tableau des
prévisions des dépôts à vue à partir du
tableau des prévisions de Logdepot avant de quantifier les erreurs de
prévisions.
Tableau 12 : Dépôts observés et
dépôts prévus par le modèle
|
Période
|
Dépots
observés (en
millions de
F
CFA)
|
Logdépot
prévu
|
dépots Prévus
(en millions de
F CFA)
|
Erreurs de
prévision
|
% erreur
|
|
janv-06
|
549587
|
13,2153091
|
548701,0848
|
885,9152449
|
0,2%
|
|
févr-06
|
569589
|
13,2342224
|
559177,5934
|
10411,40664
|
1,8%
|
|
mars-06
|
561839
|
13,2428143
|
564002,6900
|
-2163,690016
|
0,4%
|
|
avr-06
|
578970
|
13,2514062
|
568869,4220
|
10100,57797
|
1,7%
|
|
mai-06
|
587116
|
13,2599982
|
573778,2060
|
13337,79396
|
2,3%
|
|
juin-06
|
584398
|
13,2685901
|
578729,2902
|
5668,709841
|
1,0%
|
|
juil-06
|
564388
|
13,2771821
|
583723,1551
|
-19335,15514
|
3,4%
|
|
août-06
|
599298
|
13,2857739
|
588759,9945
|
10538,00548
|
1,8%
|
|
sept-06
|
593620
|
13,2943658
|
593840,3552
|
-220,3552403
|
0,0%
|
|
oct-06
|
602380
|
13,3029578
|
598964,6139
|
3415,386136
|
0,6%
|
|
nov-06
|
640181
|
13,3115497
|
604133,0294
|
36047,97061
|
5,6%
|
|
déc-06
|
632347
|
13,3201416
|
609346,0427
|
23000,95726
|
3,6%
|
Source : élaboré par l'auteur
Lorsque nous évaluons les erreurs de prévisions,
ils sont inférieurs à 3% pour une prévision sur 6 mois.
Dans la suite il sera question de filtrer la partie mobile de
notre modèle (confère équation du modèle) pour
déterminer la partie stable. En fonction du temps.
II.5 Détermination de la fonction
d'écoulement
Le modèle d'évolution des dépôts
à vue que nous avons retenu est donné par la formule (38)
Logdepot Logdepot -
- t 0, 008592
= + -
å 0, 493349 1
å t -
t 1 t
Ou encore
(40) Logdepot Logdepot -
= t 0, 008592
+ + -
å 0, 493349 1
å t -
t 1 t
Mise sous cette forme, nous pouvons dire qu'entre deux
observations successives de notre série de mesures résultant de
l'activité du processus générateur de la série
d'encours des dépôts à vue, une combinaison
d'événements aléatoires ou perturbations vient affecter le
comportement de la série et ainsi modifier ses valeurs.
Dans la suite, pour simplifier les formules, nous
désignerons par Dt l'encours des dépôts à
vue à la date t. On a l'équation simplifiée :
(41) LogD t = LogD t -1 + 0,008592+
å t - 0,493349åt-1 Le
modèle peut encore s'écrire :
(42) 1
D D -
= t exp(0, 008592 + -
å 0, 493349 1 )
å t -
t t
Le stock des dépôts à la date t
(date courant) devient à une date T ultérieure
(T supérieur à t)
T
(43) ) ,
D T D
( ) exp 0.00859 ( ) ( 0, 49334
= × - +
T t å - × å -
t i i 1
i = t+

1
Ainsi, la fonction décrivant l'évolution du stock
des dépôts entre l'instant t et T est
donnée par la fonction:
(44)
T
) ,
f ( t , T) = exp [0.00859 × (
T - 0 + E ( å - 0,49334× å i-1
i = t+

1
Nous désignerons par â( t ) =
åt - 0, 493 34åt-1 la
combinaison linéaire d'événements
aléatoires ou perturbations affectant notre série
de dépôts transformés à la date t.
Pour se prémunir du risque de liquidité, nous avons
calculé la série des résidus sur notre période
d'étude et nous avons défini la fonction d'écoulement du
stock comme

T(45) S ( t , T) = exp
[0,00859 × ( T - 0 + E â1 ,

1
i = t+
Où
(46) 1...108
â = Min t ( t 0,
49334 t 1 )
å - å = Min t 1...108 ( (
))
â t
= - =
â représente la valeur de â
( t ) ayant entraîné la diminution mensuelle la plus
importante de la série d'encours des dépôts à vue
durant notre période d'étude.
Cette fonction d'écoulement est
considérée comme le pourcentage de l'encours des
dépôts à vue présents dans le bilan à la date
t, et qui y restera jusqu'à la date T
(ultérieure).
La résolution de l'équation
Mint = 1...108 (â ( t ))
nous a permis de trouver â = - 0,13592
obtenu en t = 40 qui correspond au mois d'Avril 2000,
période au cours de laquelle on a observé la plus grande
diminution du stock des dépôts à vue.
Pour cette valeur de â , la fonction
d'écoulement s'écrit:
(47) S ( t , T ) = exp [ - 0,12733
× ( T - t) ],
Remarquons d'après cette formule que le stock
présent à une date t disparaîtra tôt ou tard du bilan
(En effet, lorsque T est très grand, S(t,T) tend vers
0). Cette fonction traduira l'amortissement du stock dans le temps et nous
permettra de trouver la vitesse ainsi que la durée moyenne
d'écoulement du stock.
II.6 Vitesse et durée moyenne d'écoulement
du stock des dépôts à vue:
Nous avons défini au premier chapitre la vitesse ou taux
d'écoulement par la formule (4).
Un calcul rapide nous permet de trouver ë =
11,96%
Ainsi, l'encours des dépôts à vue pris
à une date quelconque t disparaîtra à un rythme de 11,96%
par mois. La durée moyenne d'écoulement du stock est donc de 8
ans et 4 mois. Il s'agit du temps moyen que mettra un stock de
dépôts à vue pour disparaître complètement du
bilan de la banque si cette dernière ne reçoit plus de
dépôts.
II.7 Partie de l'encours des dépôts à
vue stable en fonction du temps a) Pourcentage des dépôts stables
en fonction du temps
Dans cette partie, en considérant l'encours Dt
pris à la date t, nous allons déterminer la partie
(en pourcentage) de ces dépôts qui sera stable en fonction du
temps La partie de l'encours des dépôts à vue de la date
t qui restera stable dans le bilan jusqu'à la date T
(ultérieure) est donnée par la relation :
(48) D ( t , T ) = D ( t
)exp [ - 0,12733 × ( T - t) ],
Pour T = t+1, on trouve que 88,04% des
dépôts sont stables pendant un mois. Pour T = t+6, on
trouve que 46,58% des dépôts sont stables pendant 6 mois. Pour
T= t+12, on trouve que 21,70% des dépôts sont stables
pendant un an, Pour T= t+24, on trouve que 4% des dépôts
sont stables pendant deux ans.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
En nous limitant à deux ans, nous pouvons détailler
les résultats en construisant le tableau des échéances
suivant :
Tableau 13 : Pourcentage de l'encours d'une date
t stable en fonction du temps
|
Durée en
mois
|
Échéance à partir de la
date t
(quelconque)
|
Pourcentage de l'encours de
la date t (Dt
) stable en
fonction du temps
|
Partie
Stable
|
|
0
|
t
|
100,00%
|
Dt
|
|
1
|
t+1
|
88,04%
|
88,04%Dt
|
|
2
|
t+2
|
77,52%
|
77,52%Dt
|
|
3
|
t+3
|
68,25%
|
68,25%Dt
|
|
4
|
t+4
|
60,09%
|
60,09%Dt
|
|
5
|
t+5
|
52,91%
|
52,91%Dt
|
|
6
|
t+6
|
46,58%
|
46,58%Dt
|
|
7
|
t+7
|
41,01%
|
41,01%Dt
|
|
8
|
t+8
|
36,11%
|
36,11%Dt
|
|
9
|
t+9
|
31,79%
|
31,79%Dt
|
|
10
|
t+10
|
27,99%
|
27,99%Dt
|
|
11
|
t+11
|
24,64%
|
24,64%Dt
|
|
12
|
t+12
|
21,70%
|
21,70%Dt
|
|
13
|
t+13
|
19,10%
|
19,10%Dt
|
|
14
|
t+14
|
16,82%
|
16,82%Dt
|
|
15
|
t+15
|
14,81%
|
14,81%Dt
|
|
16
|
t+16
|
13,04%
|
13,04%Dt
|
|
17
|
t+17
|
11,48%
|
11,48%Dt
|
|
18
|
t+18
|
10,11%
|
10,11%Dt
|
|
19
|
t+19
|
8,90%
|
8,90%Dt
|
|
20
|
t+20
|
7,83%
|
7,83%Dt
|
|
21
|
t+21
|
6,90%
|
6,90%Dt
|
|
22
|
t+22
|
6,07%
|
8,90%Dt
|
|
23
|
t+23
|
5,35%
|
5,35%Dt
|
|
24
|
t+24
|
4,71%
|
4,71%Dt
|
Source : élaboré par l'auteur
L'examen du tableau précédent nous permet de
dire qu'une banque peu prêter 88,04% de son stock de dépôts
à vue à ses meilleurs clients pour une durée d'un mois.
Elle ne peut utiliser que 46,58% de ces dépôts pour octroyer un
crédit sur 6 mois. Pour une échéance d'un an elle peut
prêter 21,70% de ces dépôts à vue. 4,71% de ces
dépôts peuvent être transformés en crédits sur
une durée de 2 ans.
b) Application à l'encours des dépôts
observés en décembre 2005
L'encours des dépôts à vue observé en
décembre 2005 est 550,026 milliards de
FCFA.
Ou encore 550026 millions de FCFA. Il est question de voir
comment ce stock s'amortira dans le temps. Autrement dit, quelle est la partie
de cet encours qui sera stable en fonction du temps. Le tableau suivant permet
de suivre son évolution sur 2 ans.
Tableau 14 : Partie stable de l'encours observé en
décembre 2005 en fonction du temps
|
Nombre de
mois
|
Date
|
Pourcentage de l'encours
observé en décembre
2005,
stable en fonction du temps
|
Partie
stable en
millions de
FCFA
|
|
0
|
déc-05
|
100,00%
|
550026
|
|
1
|
janv-06
|
88,04%
|
484267
|
|
2
|
févr-06
|
77,52%
|
426369
|
|
3
|
mars-06
|
68,25%
|
375394
|
|
4
|
avr-06
|
60,09%
|
330513
|
|
5
|
mai-06
|
52,91%
|
290998
|
|
6
|
juin-06
|
46,58%
|
256207
|
|
7
|
juil-06
|
41,01%
|
225576
|
|
8
|
août-06
|
36,11%
|
198607
|
|
9
|
sept-06
|
31,79%
|
174862
|
|
10
|
oct-06
|
27,99%
|
153956
|
|
11
|
nov-06
|
24,64%
|
135549
|
|
12
|
déc-06
|
21,70%
|
119343
|
|
13
|
janv-07
|
19,10%
|
105075
|
|
14
|
févr-07
|
16,82%
|
92513
|
|
15
|
mars-07
|
14,81%
|
81452
|
|
16
|
avr-07
|
13,04%
|
71714
|
|
17
|
mai-07
|
11,48%
|
63140
|
|
18
|
juin-07
|
10,11%
|
55591
|
|
19
|
juil-07
|
8,90%
|
48945
|
|
20
|
août-07
|
7,83%
|
43093
|
|
21
|
sept-07
|
6,90%
|
37941
|
|
22
|
oct-07
|
6,07%
|
33405
|
|
23
|
nov-07
|
5,35%
|
29411
|
|
24
|
déc-07
|
4,71%
|
25895
|
Source : élaboré par l'auteur
Ce tableau permet ainsi à la banque de savoir la somme
qu'elle peut prêter sans risque de transformation. Par exemple, au 31
décembre 2005, elle peut accorder un crédit de 25,895 milliards
de F CFA pour une durée de 2 ans à ses meilleurs clients non
financiers ou bien placer cette somme d'argent sur le marché
monétaire.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
II.8 Limite du modèle d'écoulement des
dépôts à vue
Il est intéressant de voir que le modèle ne
prend pas directement en compte certains paramètres relatifs aux
comportements des clients tels que leur revenu moyen. Cette variable pouvant
avoir un impact sur le mouvement de retrait et de dépôt. En outre,
le modèle ne prend pas en compte les variables qui caractérisent
la réputation des banques, leurs efforts commerciaux, leur programme de
fidélisation, les efforts de conquête de leur réseau
commercial (taux de conquête, taux d'attrition). Ces variables
n'étaient pas disponibles dans notre système d'information.
Bien que pouvant être significatives, ces limites
n'altèrent pas la pertinence de notre modèle puisque le terme
d'erreur contient les informations non explicitées dans la construction
du modèle. Leur modélisation nous a permis d'atteindre nos
objectifs en nous prémunissant du risque de liquidité. Toutefois,
la prise en compte de ces variables nous aurait permis de parfaire notre
travail.

CO$CL 'VSIO$ ~$~ #~'"


Après la grave crise de la fin des années 1980
qui a affecté le système bancaire de la CEMAC en
général et celui du Cameroun en particulier, de nombreuses
restructurations ont été faites de sorte qu'à partir de
1995, les banques camerounaises ont été assainies et sont
redevenues liquides. Cependant, tant pour le banquier que pour ses clients, les
effets néfastes qu'avaient entraîné ces crises sont
restés presque indélébiles dans la conscience. Le banquier
pour sa part, ne voulait plus prendre de risque qu'il ne peut évaluer.
Des nos jours, les agents non financiers se reportent davantage sur les
dépôts et placements à vue où le retrait peut
être effectué à tout moment sans pénalité de
remboursement et sans frais d'aucune sorte. Pour les banques camerounaises, ces
dépôts à vue représentent plus de 50% de l'ensemble
des ressources des banques et plus de 70% des dépôts provenant de
la clientèle.
Afin de permettre aux banques de s'impliquer davantage dans le
financement de l'économie tout en maîtrisant le risque de
transformation et de liquidité lié aux dépôts, la
modélisation de l'écoulement des dépôts à vue
s'est avérée importante.
Dans un premier temps, les concepts de cointégration et
de causalité nous ont permis de voir qu'au Cameroun, le comportement des
clients en terme de dépôts sur leur compte à vue n'est pas
significativement influencé par le mouvement des taux
d'intérêt. Ensuite, sur notre série mensuelle d'encours des
dépôts à vue allant de janvier 1997 à
décembre 2006, l'application de la méthodologie de Box et Jenkins
nous a permis de déterminer le modèle d'évolution des
encours de ces dépôts. Il s'agit, après avoir
transformé notre série d'encours des dépôts à
vue en lui appliquant la fonction logarithme népérien, d'un
modèle ARIMA (0,1,1) (Moyenne Mobile d'ordre 1 et intégré
d'ordre 1). Enfin, la détermination de la fonction d'écoulement a
permis de décrire comment le stock s'évapore (ou s'amortit) dans
le temps.
Nos analyses nous ont permis de montrer que, lorsqu'on
agrège l'ensemble des dépôts à vue des clients de la
banque; cet ensemble est relativement stable et n'est pas susceptible de
disparaître du jour au lendemain. En effet il faut environ 8 ans et 4
mois pour qu'un stock de dépôts à vue pris à une
date donnée disparaisse totalement du bilan de la banque. Ce stock
s'écoulera ainsi à un rythme de 11,96% par mois. Ainsi, pendant
un mois 88,04% de l'encours des dépôts à vue seront stables
dans le bilan, 46,58% y
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
resteront pendant 6 mois, 21,70% ne sortiront pas du bilan
avant un an, les clients laisseront 4,71% du stock des dépôts
à vue dans les caisses de la banque pendant deux ans.
La banque pourra donc utiliser la partie stable de ces
dépôts pour financer l'économie en minimisant le risque de
transformation.
Plusieurs recommandations importantes peuvent être
faites. D'une part, les banques commerciales devront améliorer leurs
systèmes d'informations ALM, afin de prendre en compte les variables
spécifiques aux clients qui sont utiles pour faire intervenir la
rationalité de la clientèle dans les analyses. Elles devront
s'impliquer davantage dans le financement de l'économie en valorisant la
partie stable (oisive) des dépôts à vue. Elles devraient
tenir compte de la partie stable de ces dépôts dans la
construction des impasses en liquidité afin de déterminer leurs
besoins ou leurs excédents réels de liquidité aux dates
futures. D'autre part La dynamisation du secteur financier devient un enjeu de
taille, car un secteur financier actif permettrait aux titulaires des comptes
de dépôts à vue d'acheter des actifs financiers plus
attrayants et cela en mobilisant leurs dépôts qui restent oisifs
dans les banques. Cela permettra d'éviter cette forme de
thésaurisation. Enfin, si ces dépôts ne peuvent être
valorisés par les banques commerciales, la Banque Centrale pourrait
utiliser la stabilité de ces dépôts à vue pour
ajuster le coefficient des réserves obligatoires relatifs à ce
type de dépôts.
Un secteur financier dynamique avec des taux
d'intérêt incitateurs permettrait d'étudier l'impact de ces
taux sur la stabilité des dépôts à vue. Enfin, une
autre perspective de continuation de ce travail de recherche serait
d'intégrer à ce modèle des variables spécifiques
à la politique commerciale de la banque et des variables relatives aux
comportements de la clientèle telles que les taux d'attrition (nombre de
comptes fermés par mois) et le taux de conquête (nombre de comptes
ouverts par mois). Ce qui contribuerait à sa robustesse.


BIBLIOGRAPHIE
Banque des Etats de l'Afrique Centrale [2004],
études et statistiques, N°285. Banque des Etats de
l'Afrique Centrale [2004], études et statistiques, N°286.
Bessis J.[1995], gestion des risques et gestion actif/passif des banques,
Dalloz.
Bitner John W., Robert A. Goddard, Successful Bank
Asset/Liability Management, a guide to the future beyong gap, Economica
Bourbonnais R. [2003], Econométrie, 5e
édition, DUNOD, Paris.
Comité de Bâle[2001], principles for the
management and supervision of interest rate risk , Janvier 2001.
Commission Bancaire d'Afrique Centrale, rapport
d'activité, de 1996 à 2004.
Conseil National du Crédit, rapport d'activité,
Exercice 1997/1998 - 1998/1999 et 1999/2000.
Conseil National du Crédit, rapport d'activité,
Exercice 1999/2000 - 2001/2002. Darmon J., [1998], Stratégies
bancaires et gestion de bilan, Economica.
Demey P., Frachot A., Riboulet G. [2003], Introduction
à la gestion Actif/Passif bancaire, Economica.
Dupré Denis [1996]. La modélisation des
dépôts à vue, Banque et Marché, pp 24 :29-
34.
Frachot Antoine [2001], A note on behavioural models for
managing optionality in banking books, Groupe de recherche
Opérationnelle, Crédit Lyonnais, France.
Mamalepot J. F. [2004], Communication du gouverneur
de la Banque des Etats de l'Afrique Centrale, BEAC.
Martin Cyrille [2005], Comparaison des modèles de
dépôts à vue, Centre d'Etude et Recherche
Appliquées à la Gestion des risques bancaires. Université
Pierre MendèsFrance, Grenoble.
Mathis J.[1992], Monnaie et banques en Afrique francophone,
Edicef, Paris. Ohannessian Valérie [2007], La banque à
découvert, Revue Banque Edition. OTS [2000], Net porfolio value
model, March 2000.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
Rolland L. B. [2002], Principes de techniques bancaires,
Dunod, Paris. Scialom L. [1999], Economie Bancaire, la
découverte, Paris.
Scialom L. [1999], Economie Bancaire, la
découverte, Paris.
Selvaggio Robert D. [1996], Using the OAS Methodology to
value and Hedge commercial Bank retail Demand Deposit Premiums, In the
Handbook of Asset/Liability Management, Chapter 12, page 363-373. Fabozzi and
Konishi.
Supports de cours
Arthur Charpentier, Cours de séries temporelles,
DESS Mathématique de la décision et DESS Actuariat.
KUATE Pascal, Cours de Monnaie et Crédit,
polycopié de cours, Université Catholique d'Afrique Centrale.
Mémoires et Thèses
Djimefo Kapen [2006], Initiation de modèles
mathématiques dans la prévision des produits et charges d'une
banque, Mémoire présenté en vue de l'obtention du
Master de Statistique Appliquée, Université de Yaoundé
I.
GHIEU Grégory [2003], Gestion Actif/Passif,
Méthodologie et Application au Livret A, Thèse
professionnelle, Master Spécialisé Finance, European School of
Management.
Matcha Doriane [2006], Modélisation de la
défaillance du système bancaire de la CEMAC, mémoire
de fin de formation en vue du diplôme d'Ingénieur d'Application de
la Statistique, ISSEA.
MBENA Marianne [2006], Gestion de la liquidité
bancaire : Une application au Cameroun, thèse professionnelle,
Université de Douala.
Pandong Armand [2004], le système bancaire de la
CEMAC, mémoire de fin de formation en vue du diplôme
d'Ingénieur d'Application de la Statistique, ISSEA.
Sites Web
http://www.univ-rouen.fr/droit-sceco-gestion/Recherche/CARE/Documents/papiermbena.pdf.
http://www.bis.org/publ/bcbs29a.
ANNEXES
Annexe I : Méthodologie de Box et Jenkins23
Nous présentons ici son algorithme.
Figure : Etape de la méthodologie de Box et
Jenkins
Analyse du graphique et
du
corrélogramme
Analyse de la saisonnalité
Test de Dickey Fuller
Régression sur le temps si
TS (trend
stationary)
Passage aux différences si DS
(difference
stationary)
Séries stationnaires yt
Analyse des corrélogrammes
simple et
partiel
Détermination des ordres p et
q
du processus ARMA
Estimation des paramètres.
Test de Student. Les coefficients
non significatifs
sont supprimés.
Tests sur les résidus:
sont ils des bruits
blancs?
Non
Ajout d'un ordre p ou
q.

Oui
Prévision par ARMA
Recoloration de la série
(exponentiel,
saisonnalité )
Source : Régis Bourbonnais, Econométrie,
page 250
23 Pour plus de détails, cf. Régis
Bourbonnais, Econométrie, 5ième édition et cf.
M. Djimefo Kapen [2006], Initiation de modèle mathématiques
dans la prévision des produits et charge d'une banque,
mémoire présenté en vue de l'obtenion du Master de
Statistique Appliquée, université de Yaoundé I.
I.1 Analyse de la saisonnalité ou
désaisonnalisation
Les méthodes de désaisonnalisation peuvent
être classées en deux grandes catégories: Les
méthodes non paramétriques et
les méthodes paramétriques.
Méthodes non paramétriques,
dites « empiriques », permettent de décomposer la série
en composantes inobservables par une procédure, souvent
itérative, basée sur des lissages successifs. On peut
résumer l'ensemble des lisseurs utilisés dans ces méthodes
sous le nom de « régressions locales ». Les régressions
locales consistent à ajuster des polynômes, en
général par les moindres carrés, pondérés ou
non, sur des intervalles glissants (se décalant d'un point à
chaque fois). Au centre de l'intervalle, la donnée lissée est la
valeur, à cette date, du polynôme ajusté (la donnée
lissée à la date suivante est obtenue par ajustement d'un
polynôme sur l'intervalle suivant). On peut montrer que les
régressions locales reviennent à appliquer des moyennes mobiles
particulières lorsque les observations sont régulièrement
espacées. Ces méthodes se distinguent par leur degré de
robustesse: dans un premier groupe, on trouve STL
(Cleveland et al. 1990), méthode fondée sur le « lowess
», une technique de lissage robuste par régressions locales
(Cleveland, 1979); dans un second groupe, figure la célèbre
méthode de désaisonnalisation
Xl1.
Méthodes paramétriques : elles
peuvent aussi se diviser en deux grands ensembles: les méthodes par
régression (inspirées de Buys-Ballot) qui posent, pour chaque
composante, excepté l'irrégulière, une fonction
déterministe du temps; les méthodes fondées sur des
modèles stochastiques (non déterministe): il s'agit
principalement de modèles ARIMA utilisés pour modéliser
les composantes inobservables. Parmi celles-ci, on distingue encore deux
groupes: celles qui estiment les modèles des composantes à partir
du modèle ARIMA de la série initiale (Burman 1980, Hillmer et
Tiao 1982), SEATS (Gomez, MaravalI1997), et celles
qui les modélisent et les estiment directement ( Kitagawa et Gersch
1984) comme par exemple la méthode STAMP
(Harvey et al. 1995).
Les ouvrages des différents auteurs mentionnés dans
ces méthodes, sont cités dans
« COMPRENDRE LA METHODE XII » de Dominique LADIRAY et
Benoît QUENNEVILLE.
Nous allons schématiser ces méthodes de
désaisonnalisation Figure : Méthodes de
désaisonnalisation
METHODES NON PARAMETRIQUES
(méthodes de
régression locale)
METHODES PARAMETRIQUES


MOYENNES MOBILES
Slutsky (1927) - Macauley
(1930)

REGRESSIONS GLOBALES
Buys-Ballot (1847)

MEDIANES MOBILES
MODELE XII-CENSUS
Bureau du Census
(1965)
MODELE ARIMA Box et Jenkins (1970)

S.A.B.L (1982)
LOWESS (1979)
S.T.L
(1990)

MODELE Xll-ARIMA
(1994)

S.E.A.T.S. (1980)
S.T.A.M.P. (1987)

MODELES XI2-ARIMA
(1994)
Source : « Cours de séries temporelles », DESS
Mathématique de la Décision & DESS Actuariat d' Arthur
CHARPENTIER
Parmi donc les méthodes non paramétriques, nous
nous sommes intéressés à la
désaisonnalisation par moyenne mobile
centrée. Si on s'intéresse à la
moyenne mobile centrée d'ordre m, elle est définie comme
suit:
m impair (m =2p + 1) :
Mm
( X + Xt - p+ 1 + ... + X
t + ... + X t + p - 1 + Xt
+p ) ( X t ) = t - p
t= p + 1, ..., n - p ; m pair (m = 2 p) :
( 0.5 X t - p + Xt - p + 1 +
... + X t - 1 + X + X t + 1 + ... + X t +
p - 1 + 0.5X+p ) ,
p
Mm ( X t) =
2
t = p+1,..., n- p ;
La procédure de désaisonnalisation d'une
série est fonction du type de schéma.
· Schéma additive
Soit X, notre série. Comme il s'agit d'une
série mensuelle, dont la période est 12, nous allons
considérer la moyenne mobile centrée d'ordre 12. Soit MM(12),
la série obtenue après avoir appliqué à X
cette moyenne mobile. Les différences saisonnières sont
obtenues en retirant de la série initiale la moyenne mobile i.e. X
- MM (12). Comme X et MM(12) n'ont pas la
même longueur, alors la soustraction se fait comme suit: pour une
année donnée, nous faisons la différence aux mois
identiques. Cette différence ne se fait qu'entre les périodes
où nous observons les réalisations simultanées de X
et de MM (12). Les coefficients saisonniers ne sont autres que
les moyennes des différences saisonnières pour chacun des mois.
Comme la somme des coefficients saisonniers doit être nulle, alors les
coefficients saisonniers corrigés sont obtenus en retirant des
coefficients corrigés leur moyenne arithmétique. Nous pouvons
donc désaisonnaliser la série en retranchant de chacune des
valeurs initiales le coefficient saisonnier correspondant.
· Schéma Multiplicatif
On calcule d'abord les rapports saisonniers qui sont le
rapport de la série initiale par la moyenne mobile correspondante. Les 2
séries n'étant pas de même longueur, le rapport s'effectue
comme suit: Pour une année donnée, nous faisons le rapport aux
mois identiques. Ce rapport ne se fait qu'entre les périodes où
nous observons les réalisations simultanées de X et de
MM(12).
Les coefficients saisonniers s'obtiennent en faisant la
moyenne des rapports saisonniers pour chacun des mois. La moyenne de tous ces
coefficients devant être égale à 1, les coefficients
saisonniers corrigés s'obtiennent en procédant à la
division de chacun de ces coefficients par leur moyenne arithmétique. On
peut donc désaisonnaliser la série en divisant chacune des
valeurs initiales par le coefficient saisonnier correspondant. Une fois la
série désaisonnalisée, on peut passer au test de
stationnarité.
I-2. Stationnarisation.
1-2-1. Objectif et définition de la
stationnarité.
Nous ne pouvons identifier les caractéristiques
stochastiques d'une série chronologique que si elle est
stationnaire.
La stationnarité est la clef de l'analyse des
séries temporelles. Une série chronologique est dite stationnaire
si elle ne
comporte ni tendance ni saisonnalité. On dira aussi qu'une
série { yt } est strictement stationnaire si la distribution
conjointe de ( Yt1 ,..., Ytk) est
identique à celle de ( Yt1 + t ,...,
Ytk+ t ), quelque soit k
est un entier ( où
t1 ,
·
·
·
,tk a )
positif arbitraire et (t1, t2,,..., tk, t) une liste de
k + l entiers positifs arbitraires.
Autrement dit, la stationnarité stricte dit que la
distribution conjointe de ( Yt1 ,..., Ytk ) est
invariante quand on fait
glisser dans le temps. Cette condition est difficile à
vérifier et on utilise, en général, une version plus
faible de la stationnarité. On dit qu'une série temporelle
{Yt} est faiblement stationnaire si la moyenne de Yt
et la covariance entre Yt et Yt-l sont invariantes par
translation du temps. Précisément, {Yt} est faiblement
stationnaire si :
(a). E (Yt ) = ì où ì est
une constante indépendante de t,
(b). cov ( Y t , Y t - l )
ne dépend que de l, entier.
La stationnarité faible (ou de second ordre) implique
que le graphe de la série en fonction du temps montre des fluctuations
autour d'un niveau moyen, fluctuations qui se ressemblent, quel que soit la
date autour de laquelle on examine la série.
I-2-2.Test de DICKEY -FULLER.
Les tests de Dickey-Fuller (DF) permettent de mettre en
évidence le caractère stationnaire ou non d'une chronique par la
détermination d'une tendance déterministe ou stochastique. Avant
d'y arriver, nous allons définir des notions qui nous serviront par la
suite.
I-2-2-1.Processus TS (Trend Stationary).
Si un processus Xt peut s'écrire sous l'une des
formes suivantes:
(1)' X t = áX t - 1 + å t
( á < 1 ).
(2)' X t = áX t - 1 + â
+ å t ( á < 1 ).
(3)' X t = áX t - 1 + â
+ ã t + å t ( á <
1et ã? 0 ).
avec åt un processus stationnaire,
alors il est dit processus TS.
Un processus TS s'écrit aussi: Xt = ft +
åt où ft et åt
représentent respectivement une fonction polynomiale du temps,
linéaire ou non et un processus stationnaire.
I-2-2-2.Processus DS (difference stationary)
Si un processus Xt peut se mettre sur l'une des formes
suivantes:
(1) Xt = Xt -1 + åt ;
(2) Xt = Xt -1 + â + å
t avec â ? 0;
(3) Xt = Xt -1 + â + ã t
+ å t avec ã ? 0. Avec
åt un processus stationnaire,
Alors il est dit Processus DS.
On peut les rendre stationnaires par l'utilisation d'un
filtre aux différences :
( 1 ) d
- B X t = â + å
t où d est l'ordre du filtre aux différences.
I-2-2-3. Test de DICKEY FULLER.
Le test de Dickey Fuller consiste donc à tester
(1)', (2)', (3)' contre (1), (2), (3) ce qui
est équivalent à tester á = 1. On estime par les
moindres carrés ordinaires le modèle (3) et on calcule la
statistique de Student pour les valeurs
estimées de ã , â
,ö(ö = á - 1 ).
Le test pour les coefficients ã , â est
bilatéral. En ce qui concerne ö , les choses
diffèrent du test de Student
traditionnel: ayant exclu le cas
explosif (á > 1 ou ö > 0) on procède
au test unilatéral (á =1 ou ö =0
contre
ö < 0), ce qui donne une zone de rejet située
du côté négatif, et les hypothèses des MCO
n'étant pas satisfaites,
notamment du fait que la variable considérée est
endogène, on utilise une table particulière calculée par
Dickey et
Fuller. En cas de rejet total ou partiel du test du modèle
(3) avec ö = 0, opéré comme indiqué, on
teste de même le
modèle (2) et ö =0 avec la table voulue,
puis encore si nécessaire le modèle (1) avec ö =
0.
Conclusion: A l'issue du test,
si on a affaire à un processus TS, alors la
série stationnarisée s'obtient en retirant de la série
corrigée des variations saisonnières l'estimation polynomiale de
la tendance. Sinon (cas d'un processus DS), la série
stationnarisée s'obtient en différenciant la série
corrigée des variations saisonnières autant de fois
jusqu'à l'obtention de la série stationnaire.
I-2-3.Test de DICKEY -FULLER AUGMENTE
Dans les modèles utilisés dans les tests de Dickey
et Fuller simples, le processus åt est, par
hypothèse, un bruit
blanc. Or il n'y a aucune raison pour que
à priori, l'erreur soit non corrélée : on appelle tests de
Dickey Fuller
Augmentés (ADF, 1981) la prise en compte de cette
hypothèse. Les test ADF sont fondé sous l'hypothèse
alternative
ö 1 sur l'estimateur des MCO des trois
modèles :

p
Ä X = ö X t - 1 - ö
Ä Xt - j+1 + å t
j
2
p
Ä X = ö X t - 1 - ö
j Ä X- j+1 + â
+ å t j 2
p
Ä X = ö X -- ö
.j Ä Xt - j+1 + â
+ ã t + å t j 2
åt est un bruit blanc. Le test se
déroule de manière similaire aux tests de Dickey Fuller simple.
Seul les tables diffèrent. La valeur de P est déterminée
selon le critère de AKAIKE.
N.B. D'autres tests sont souvent utilisés
notamment celui de Phillips-Perron, Schmidts-Phillips,
EliottRothenberg-Stock (ERS), KPSS.
I-3.Identification
La série ainsi stationnarisée, on procède
à une étude des corrélogrammes simple et partiel, ce qui
conduit à déterminer les ordres possibles de p et q
des parties auto-régressive (AR(P) et moyenne mobile
(MA(q)) du modèle et les ordres d de
différenciations éventuelles (cas modèle ARIMA (p, d,
q). Nous avons évoqué certains types de modèles et il
y a donc lieu de les définir plus explicitement.
I-3-1.Processus ARMA
I -3-1-a. Processus autorégressifs
On appelle «processus autorégressif d'ordre p
» un processus stationnaire Xt vérifiant une relation
du type :
p
X t = E i t i +
t
i= 1
où les ?i sont des réels et
åt est un bruit blanc de variance ó
2 .
Un bruit blanc est une suite de variables
aléatoires d'espérances mathématiques nulles, non
corrélées et de même variance.
La relation précédente peut aussi s'écrire
:
( 1 - ? 1B- ... -? B
p)X t = å
o u
ö ( ) , B X
B X = å ( ) = X
t t t
i
t - i
P
en posant ( ) 1 1 ...
ö B = - ? B - - ? P B
.
Il sera noté AR(p).
I-3-1-b. Processus moyennes mobiles.
On appelle « processus moyenne mobile d'ordre q
» un processus Xt défini par :
Xt = ( 1 - è 1 B -
... - èq
Bq)åt,
Où les èi sont des réels
et åt est un bruit blanc de variance
ó2. Cette relation peut encore
s'écrire:
è ( B ) åt
= Xt,
avec
è B = - è B - - è
q B
q
( ) 1 1 ... .
Un tel processus est désigné dans la
littérature anglo-saxonne par MA(q).
I-3-1-c. Processus auto régressifs moyennes mobiles
(ARMA)
On appelle «processus autorégressif moyenne mobile
d'ordre (p, q ) » un processus Stationnaire Xt
satisfaisant
ö( B ) Xt =
è ( B) åt.
Un tel processus est désigné dans la
littérature anglo-saxonne par ARMA(p,q) (Autoregressive moving
average). 1-3-2. Processus ARIMA
Si on note d
Ä Xt la différence d'ordre d de
Xt, i.e. (1- B)d Xl on va donc s'intéresser
aux processus Xt tels que
ö ( B ) Ä
dXt = è ( B)
åt.
Un tel processus est appelé ARIMA(p, d, q) ou
ARMA intégré. Cette relation peut encore
s'écrire:
? ( B ) Xt = è
( B) åt,
avec
? B = ö B - B
( ) ( )( 1 ) .
d
I-4. Estimation
Considérons un processus centré ARMA (p, q),
solution stationnaire et inversible de l'équation
|
p q
X t - E? i X t - i =
åt - i t i
|
,
|
i = 1 i=1
où åt est un bruit blanc de
variance 2
ó
Un processus Xt est dit inversible s'il
existe un autre processus Yt tel qu'on ait XtYt = 1. On dispose de
données X = (Xl , ...,XT)'.
Dans ce paragraphe, nous considérons l'estimation des
paramètres 2
ó , ? 1 ,..., ? p ,
è 1 ,..., è q .
Notons X , la moyenne arithmétique des
données. On peut estimer ã (h) =Cov( Xt,,Xt-h)
Par
T
ã ( ) ( )( )
1
h = X X X X h
- - , 0,
=
i i h
-
T i = h+1
Et
Par
ñ ( h ) = ã(
h) ã( 0),
( h ) =ãà(
h)
ãà ( 0)
.
à
ñ
On pose ãà ( - h ) =
ãà ( h).
Les estimations ? à 1 , . . . , ?
à p de ? 1,..., ? p peuvent être
obtenues en résolvant le système de p équations
linéaires :
p
13( q + j )- E0 13( q
+ + 0= 0, j =1,..., p.
i =1 i
Pour ce qui est de l'estimation des èi
, on emploiera les autocorrélations inverses ñi
(h) qui sont, par définition, les autocorrélations du
processus dual ARMA (q, p) défini par l'équation
è ( B ) Xt =
ö( B) åt. Les
èi sont donc solutions des équations
q
A.
,( p + j )- Lè i
i3i( p + j + 0= 0 pour
tout
i
=
1
I-5. Vérification.
Les tests que l'on fait subir au modèle sont de deux
types: les tests concernant les paramètres ? i et è
i du modèle
et ceux concernant les hypothèses faites sur
å
· Tests concernant les paramètres
Pour comparer une formulation ARMA (p, q) avec une
formulation ARMA (p1, q1), il est commode de se placer dans le cas
où l'un des modèles est un cas particulier de l'autre. On suppose
dans la suite que l'on part d'un modèle ARMA (p, q) et que l'on
examine les tests correspondant à diverses valeurs de p1, q1
.
° pl = p-1, ql =q.
Il s'agit ici de voir s'il est possible de diminuer d'une
unité le nombre de retards intervenant dans la
partie autorégressive. Ceci revient à tester la
significativité du coefficient ?p ce qui peut
être fait
au moyen' d'un test de type Student.
° pl = p+1, ql =q.
Il s'agit de voir s'il est nécessaire d'introduire un
retard supplémentaire dans la partie autorégressive. Il faut
alors
estimer un modèle ARMA (p1, q1)=ARMA (p+1, q) et
tester dans ce second modèle la nullité de ?p + 1 . Ceci
nous ramène évidemment au cas précédent.
· Test concernant les résidus
Il est question ici de savoir si les hypothèses de
normalité et de bruit blanc sont satisfaites. ° Test
« portmanteau »
C'est un test concernant le bruit blanc.
Ce test est fondé sur la statistique:
k
Q N ñ
= à
2 [ ]
å ?
,
h
h = 1
ñà h [
å? ] étant la corrélation empirique
entre les résidus (distants de h).
à
ñh
T
[ ] [ ] 0 [ ] [ ] ( )( )
1
å ã å ã å
? = ? ?
à / à avec ã å
.
à ? = å å å -
å
- -
h h t t h
T t h
= + 1
On montre que, sous l'hypothèse d'indépendance des
åt , Q suit asymptotiquement (quand N? 8)
une loi du 2
÷ à
K - p - q degrés de
liberté; on refuse donc l'hypothèse d'indépendance, au
niveauá .
Q > 2
÷ 1 - á [k - p- q]
.
° Test de Jarque et Bera Il s'agit là d'un
test de normalité.
k
n
1/ 2
Soit ( )
ì le moment centré empirique d'ordre
k, le coefficient de Skewness ( )
= â1 est égal
X X
-
k i
i= 1
|
ì
à: ( )
â1 = 3
1/ 2
ì 3/ 2
2
|
et le coefficient de Kurtosis
|
â
ì4
2 2
ì 2 .
Si la distribution est normale et le nombre d'observations grand
(n>30) :


6 24
( )
â1 ? 2
1/ 2 N 0; et â? N3; cf.
Régis BOURBONNAIS dans « Manuel et exercices corrigés,
n n
Econométrie ».
Si ( )
â1 et â2
obéissent à des lois normales alors la quantité
1/ 2
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun

s = ( )2
n n
â + â - suit un
x2 à deux degrés de liberté.
2 3
1
6 24
Donc si s > 2
x1 -á (2), on rejette
l'hypothèse H0 de normalité des résidus au seuil
á .
I-6 Choix d'un modèle.
Il se peut que plusieurs modèles franchissent la phase
de vérification et qu'il convient de choisir dans cet ensemble. La
première chose à faire est sans doute de repérer les
modèles « jumeaux », c'est-à-dire ceux qui
correspondent en fait à des représentations différentes
d'un même modèle (ou de modèles proches) et qui sont donc
équivalents pour la prévision. Ayant choisi un
représentant dans chaque classe de jumeaux, on peut se trouver à
la tête de plusieurs modèles réellement différents.
Le choix d'un modèle reposera donc sur certains critères.
° Critère de pouvoir prédictif
à 2
L'objectif est de minimiser l'estimation de la variance
résiduelle, de maximiser les coefficients de détermination simple
et modifié. Le coefficient de détermination étant
défini comme suit:
ó
R 1
2 = -
,
V
V étant la variance empirique de la série
différenciée d fois. Celui modifié comme suit:
( )
( )
R 2
ó à / N p q
- -
1 - .
V N
/ - 1
° Critère d'informaion
Une autre approche, introduite par Akaïke (1969),
consiste à supposer que les modèles ARMA (p,q)
fournissent des approximations de la réalité et que la vraie
loi inconnue des observations X, ne satisfait pas forcément un
tel modèle. On peut alors fonder le choix du modèle sur une
mesure de l'écart entre la vraie loi inconnue et le modèle
proposé. La mesure habituellement retenue est la quantité
d'information de Kullback. Soit f0(x) la densité inconnue des
observations, {f(x), f ?F p,q} la famille de densités
correspondant au modèle ARMA (p,q) , l'écart entre la
vraie loi et le modèle est mesuré par :
f
x 0 ( )
I f F ( ) =
0 ,
p q min ( ) 0
Log
, f x
( ) ( )
f x dx
f F
?
L'objectif est donc de trouver les q et p qui
minimisent les estimateurs de cette quantité d'information. Ceux qui ont
été proposés sont les suivantes:
> ( ) 2 2 ( )
p q
+
AIC p q Log
, = ó à +
,
N
,
> ( ) = ó + +
à 2
, ( ) LogN
BIC p q Log p q
N
LogLogN
2
> ( )
? p q Log
, = ó + +
à ( )
p q c avec c>
2.
N
I-7. Prévision
Le modèle validé, le calcul des prévisions
et celui des intervalles de confiance sont réalisés pour un
horizon choisi. Nous avons choisi de faire des prévisions sur une
échéance d'un an.
Annexe II : Le concept de cointégration
II.1 Définition
L'analyse de la cointégration permet d'identifier
clairement la relation véritable entre deux variables en recherchant
l'existence d'un vecteur de cointégration et en éliminant son
effet, le cas échéant. Une série est
intégrée d'ordre d, s'il convient de la
différentier d fois afin de la stationnariser.
II.2 Condition de cointégration
Deux séries sont dites cointégrées si les
deux conditions suivantes sont vérifées :
> Elles sont affectées d'une tendance stochastique de
même ordre d'intégration d.
> Une combinaison linéaire de ces séries permet
de se ramener à une série d'ordre d'intégration
inférieur.
II.3 Estimation du modèle à correction
d'erreur en deux étapes
Lorsque deux séries Xt et Yt sont
cointégrées, il convient d'estimer leurs relations au travers
d'un modèle à correction d'érreur. Engle et Granger ont
démontré que toutes les séries cointégrées
peuvent être représentées par un modèle à
correction d'érreur.
Etape 1 estimation par les MCO de la relation de long terme :
Y t = á + âX t
+ e t
Etape 2 : estimation par les MCO de la relation du modèle
dynamique (court terme) :
Ä Y t = á1 ÄX
t + á2 et - 1 + u t
á2 ? 0
Le coefficient á2 ( force de rappel
à l'équilibre ) doit être significativement négatif
: dans le cas contraire, on doit rejeter une spécification de type
Modèle à correction d'erreur.
Annexe III : Tableaux et figures
Tableau 15 : Situation de la trésorerie des
banques au 31 Mars 2005
|
Caisse
|
46,835
|
|
Opérations à vue
|
271,472
|
|
Opérations au jour le jour et à terme
|
145,929
|
|
Titres de placement et de transaction
|
9,572
|
|
Créances en souffrances nettes
|
8,824
|
|
Créances rattachées
|
2,108
|
|
Emploi de trésorerie
|
484,740
|
|
Opérations à vue
|
37,261
|
|
Opérations au jour le jour et à terme
|
59,616
|
|
Dettes rattachées
|
335
|
|
Ressources de trésorerie
|
97,212
|
|
EXCEDENT DE TRESORERIE
|
387,528
|
Source : BEAC
Figure 14 : Répartition des dépôts
par nature au 31 décembre 2004

4,5% 0,5%
13,1%
10,7%
71,2%
Comptes dépôts à regime spéciale
comptes à terme
compte à vue Autres comptes
Dettes rattachées
Source : élaboré par l'auteur
Tableau 16 : Répartition des dépôts
à vue selon la nature des comptes
|
Comptes courants créditeurs
|
537265
|
44,8%
|
|
comptes chèques créditeurs
|
113805
|
9,5%
|
|
compte sur livret
|
429450
|
35,8%
|
|
Dépôts de garanties
|
31961
|
2,7%
|
|
autres comptes créditeurs à vue
|
86067
|
7,2%
|
|
Total comptes créditeurs à vue
|
1198548
|
100,0%
|
Source : élaboré par l'auteur
Figure 15 : Variation de l'encours des
dépôts à vue en millions de F CFA
Variation de I'encours des depots a vue
|
60000
40000
20000
0
-20000
-40000
-60000
|
|
|
2000 2001 2002 2003 2004 2005 2006
|
Source : élaboré par l'auteur
Tableau 17 : Résultats du test de
cointégration entre l'encours des dépôts et le taux
d'intérêt
Date: 04/24/07 Time: 05:32
Sample(adjusted): 2002:03 2003:12
Included observations: 22 after adjusting endpoints Trend
assumption: Linear deterministic trend (restricted) Series: LOGDEPOT LOGTAUX
Lags interval (in first differences): 1 to 1
Unrestricted Cointegration Rank Test
|
Hypothesized
|
|
Trace
|
5 Percent
|
1 Percent
|
|
No. of CE(s)
|
Eigenvalue
|
Statistic
|
Critical Value
|
Critical Value
|
|
None
|
0.435426
|
15.18981
|
25.32
|
30.45
|
|
At most 1
|
0.111981
|
2.612777
|
12.25
|
16.26
|
*(**) denotes rejection of the hypothesis at the 5%(1%) level
Trace test indicates no cointegration at both 5% and 1% levels
|
Hypothesized
|
|
Max-Eigen
|
5 Percent
|
1 Percent
|
|
No. of CE(s)
|
Eigenvalue
|
Statistic
|
Critical Value
|
Critical Value
|
|
None
|
0.435426
|
12.57704
|
18.96
|
23.65
|
|
At most 1
|
0.111981
|
2.612777
|
12.25
|
16.26
|
*(**) denotes rejection of the hypothesis at the 5%(1%) level
Max-eigenvalue test indicates no cointegration at both 5% and 1% levels
Unrestricted Cointegrating Coefficients (normalized by
b'*S11*b=I):
LOGDEPOT LOGTAUX @TREND(02:0
-7.120245 11.38650 0.152656
15.39809 -0.715038 -0.022757
Unrestricted Adjustment Coefficients (alpha):
D(LOGDEPO -0.004370 -0.009426
T)
D(LOGTAUX) -0.103347 0.011384
1 Cointegrating Equation(s): Log likelihood 62.07655
Normalized cointegrating coefficients (std.err. in
parentheses)
LOGDEPOT LOGTAUX @TREND(02:0
2)
1.000000 -1.599173 -0.021440
(0.41206) (0.00656)
Adjustment coefficients (std.err. in parentheses)
D(LOGDEPO 0.031114
T)
(0.04801)
D(LOGTAUX) 0.735856
(0.20558)
Source : élaboré par l'auteur
Tableau 18 : Test de Dickey-Fuller augmenté pour
la variable taux
Null Hypothesis: TAUX has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 1 (Automatic based on Modified AIC, MAXLAG=8)
t-Statistic Prob.*
Augmented Dickey-Fuller test statistic -3.015316 0.1504
Test critical values: 1% level -4.440739
5% level -3.632896
10% level -3.254671
*MacKinnon (1996) one-sided p-values. Source:
élaboré par l'auteur


Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
Tableau 19 : Test de dickey-fuller Augmenté sur
les dépôts transformés Modèle avec terme
constant sans tendance






Modèle sans tendance, ni constance






Source : élaboré par l'auteur
Tableau 20 : Test de dickey -fuller sur la série
en différence première des dépôts
transformés) Modèle avec constante et trend

Modèle avec constante sans trend






Source : élaboré par l'auteur
Figure 16 : Evolution de la série des taux
d'intérêt

Logtauc
1.9
1.8
1.7
1.6
1.5
2002:01 2002:07 2003:01 2003:07
Année
Source : élaboré par l'auteur
Tableau 21 : Test de dickey-fuller augmenté sur la
série des taux transformés
Modèle avec constante et trend





Modèle sans trend ni terme constant




Source : élaboré par l'auteur
Tableau 22 : Test de dickey-fuller augmenté sur la
série en différence première de la série des taux
transformés
Modèle avec trend et constante
.

Modèle sans constante ni trend
Source : élaboré par l'auteur
Modèle avec constance sans trend

Tableau 23 : Test ARCH sur les résidus du
modèle ARIMA(2,1,1)

Source : élaboré par l'auteur

Source : élaboré par l'auteur
Figure 17 : Autocorrélogramme du carré des
résidus

Tableau 24 : Test ARCH sur les résidus du
modèle ARIMA(0,1,1)
Source : élaboré par l'auteur
| 


