SECTION II : Applications
II.1 Description de l'évolution de l'encours des
dépôts à vue de l'ensemble des banques
camerounaises
Cette analyse permet d'appréhender les
caractéristiques de la série durant la période
d'observation. Notre série d'encours va du 31 Janvier 1997 au 31
décembre 2006. Dans la construction du modèle, nous avons choisi
de nous limiter au 31 Décembre 2005. La série restante nous
permettra de tester les qualités prédictives du modèle.
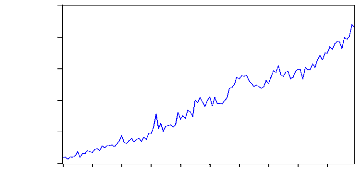
Entre janvier 1997 et décembre 1999, l'encours de ces
dépôts varie de façon lente dans l'intervalle de 200
milliards et 300 milliards de francs CFA avec un encours moyen de 257,246
milliards de F CFA. Ceci signifierait que les dépôts mensuels sur
les comptes de dépôts à vue sont presque identiques aux
retraits effectués sur ces comptes. La variation mensuelle maximale du
stock est de l'ordre de 18 milliards de Francs CFA, observé en
décembre 1999. Aussi, cette situation de variation lente du stock des
dépôts rejoint le ralentissement de la croissance
économique observé au cours de cette période (en effet, la
croissance est passée de 5% en 1997 à 4,2% en fin
199919). La vitesse de transaction des opérations sur les
comptes courants n'a pas considérablement varié puisque
l'activité des entreprises était ralentie. Les agents
préférant conserver leurs liquidités sous forme
d'encaisses de précaution.
Entre janvier 2000 et décembre 2001, l'encours de ces
dépôts connaît des périodes de variations très
fortes. Pendant cette période, on observe des variations mensuelles
positives de plus de 50 milliards de Francs CFA et des variations
négatives de plus de 45 milliards de francs CFA. Cela témoigne
d'une forte mobilisation des comptes à vue par les clients pour
répondre aux exigences de l'économie. Cela peut être le
reflet du
19 Cf. rapport du conseil national du crédit
exercice 1997/1998 - 1998/1999 et 1999/2000, Page3.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
dynamisme retrouvé de l'économie camerounaise
après le ralentissement de l'activité des grandes entreprises et
de l'activité économique en général (observé
à la fin des années 90). Le taux de croissance économique
en terme réel s'est élevé à 5,5% en 2001 contre
4,2% en fin 1999.20 La vitesse des transactions ayant
augmenté, les encaisses destinées aux transactions ont
été importantes. On observe alors un stock qui fluctue beaucoup
du fait des entrées et des sorties de fonds. Durant l'année 2002,
on a noté une stabilité de l'encours entre Avril et Mai. De juin
à décembre 2002, le stock a augmenté de 22 % (augmentation
de 83,937 Milliards de FCFA.) passant de 389,411 à 473,348 milliards de
francs CFA. Ceci signifie que les dépôts effectués sur les
comptes de dépôts à vue durant ces mois sont nettement
supérieurs aux retraits. Du 31 avril au 31 Juillet 2003, les retraits de
fonds par les clients des banques sont supérieurs aux
dépôts effectués. On observe cela par des variations
mensuelles négatives du stock qui se sont situées en moyenne
autour de 11 milliards de F CFA. Pendant l'année 2004 on assiste
à nouveau à une variation alternativement positive et
négative du stock des dépôts. De janvier 2005 à
décembre 2006 l'encours des dépôts à vue passe de
498,031 à 632,347 milliards de F CFA avec des périodes mensuelles
de faible fluctuation.
Figure 6 : Evolution de l'encours des
dépôts à vue des banques commerciales du 31/01/1997 au
31/12/2006 (en millions de F CFA)
97 98 99 00 01 02 03 04 05 06
Enca.rs cis cleptI s a vie
400000
600000
200000
700000
500000
300000
Année
Source : élabord par l'auteur d'aprés les
données de la BEA~
II.2 Analyse des caractéristiques de la
série
Elle permet de connaître certaines propriétés
caractéristiques de la série à étudier
20 Cf. vingt septième rapport d'activité
du Conseil National de Crédit, Exercice 1999/2000, 2000/2001 Page 8.
II.2.1 Analyse préliminaire
Avant de procéder à la construction du
modèle, nous nous proposons ici de mettre en évidence le fait que
nos données d'encours des dépôts à vue sont
fortement intégrées (c'est-à-dire qu'il y'a une forte
corrélation entre Dt et Dt-1). Lorsque nous
testons sur notre échantillon l'équation
(37) D t = áD t - 1 + â +
å t ,
Où les åt sont supposés
suivre une loi normale centrée. On obtient les résultats suivants
:
Tableau 5 : Résultat de l'estimation de
l'équation (37)
|
PARAMETRES
|
ESTIMATION (ECART TYPE)
|
|
á
|
1,008
(0,004)
|
|
R2 AJUSTE
|
99,8%
|
Source : élaboré par l'auteur
La valeur du paramètre á est proche de
1. L'autocorrélogramme partielle suivant permet aussi de confirmer la
forte intégration entre les données d'encours. Le
corrélogramme simple de la série des dépôts est
typique d'une série affectée d'une tendance (tous les termes sont
élevés même pour les décalages importants). Ces
résultats préliminaires nous permettent d'opter pour un
modèle qui ne tente pas d'expliquer directement l'évolution des
encours mais plutôt la variation de ces encours du fait de leur forte
intégration. Mais avant, il est important pour ne pas se tromper
d'étudier la série en termes de stationnarité.
Figure 7 : Corrélogrammes simple et partielle de
la série des dépôts à vue
depot
|
1,0
|
|
|
Coefficient
Limites de confiance
Limite de
confiance
inférieure
|
|
0,5 0,0 -0,5 -1,0
|
|
|
ACF partial
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Numéro de décalage
depot
|
ACF
|
1,0 0,5 0,0 -0,5 -1,0
|
|
Coefficient
Limites de confiance
Limite de
confiance
inférieure
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Numéro de décalage
Source : élaboré par l'auteur
II.2.2 Analyse de la saisonnalité :
Une étape importante avant l'étude de la
stationnarité d'une série est l'analyse de la saisonnalité
qui permet de déceler des variations périodiques qui peuvent
affecter la série.
Dans la suite, nous travaillons avec les données
transformées (transformée Log). Cette transformation nous permet
d'avoir des données d'encours plus réduites, de se rapprocher de
la normalité et de stabiliser la variance de la série lorsque
celle de la série originale croît avec le temps.
Figure 8 : Encours des dépôts à vue
transformés (transformation logarithmique)

Source : élaboré par l'auteur
Cette représentation graphique nous suggère
l'idée d'un schéma additif. En effet, l'utilisation de la
méthode de la bande nous montre que les deux droites passant par les
minima et les maxima sont parallèles.
Comme nos séries sont mensuelles, alors la moyenne mobile
centrée utilisée pour les désaisonnaliser est la moyenne
mobile d'ordre 12.
Figure 9 : Evolution de dépôts
transformés et de ceux corrigés des variations

97 98 99 00 01 02 03 04 05 06
13.4
13.2
LizgaiMacimdVcis
13.0
12.8
12.6
12.4
12.2
LOGdepots_à_vue
Série corrigée des variations saisonières
Source : élaboré par l'auteur
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
Pour la série des dépôts à vue,
nous avons procédé à une désaisonnalisation par
moyenne mobile centrée. Le graphique de la série brute et de la
série corrigée des variations saisonnières ne montre pas
de différence significative entre les deux séries. Nous pouvons
conclure que la série n'est pas saisonnière.
II.2.3 Analyse de la stationnarité de la
série transformée des encours des dépots
(Log(depots)).
De même que pour la série brute des
dépôts, le corrélogramme de la série
transformée (Log(depots)) est typique d'une série affectée
d'une tendance.
Figure 10 : Corrélogrammes simple et partielle de
la série des dépôts tranformés .

Source : élaboré par l'auteur
Nous allons procéder à l'estimation des trois
modèles de Dickey-fuller (nous ferons le test de Dickey-fuller
augmenté avec le nombre de décalages déterminés par
le critère de Akaike. (Voir annexe III pour les deux autres
modèles)
Tableau 6 : Test de Dickey-Fuller Augmenté sur la
série des dépôts transformés : modèle avec
constante et trend

Source : élaboré par l'auteur
A l'issue du test, toutes les statistiques (les t-statisques
empiriques) des trois modèles sont toutes supérieures aux valeurs
critiques tabulées aux seuils 1%, 5% et 10%. Nous acceptons
l'hypothèse nulle, la série des dépôts
transformés (Log(depots)) possède donc une racine unitaire. Elle
n'est donc pas stationnaire en niveau. Notre série est
représentée par un processus Differency Stationnary (DS), la
meilleure façon de stationnariser est celle des différences
premières.
Nous avons calculé la série D(Logdepots) qui
représente la série obtenue après application d'un filtre
aux différences premières à la série Logdepots.
Nous allons également estimer les trois modèles de Dickey-Fuller
sur cette série. (Voir annexe III pour les deux autres
modèles)
Tableau 7 : Test de dickey-fuller augmenté sur la
série D(Logdepots)

Source : élaboré par l'auteur
A l'issue de ce test, toutes les statistiques (t-statistique
de Dickey-fuller augmenté) sont inférieures à la valeur
critique aux seuils 1%, 5% et 10%. Nous pouvons conclure que la
différence première de Logdepots (c'est-à-dire
D(Logdepots) est stationnaire. Nous disons aussi que la série Logdepots
est intégrée d'ordre (1) un21.
II.3 Le lien entre le taux d'intérêt et le
niveau de l'encours des dépôts à vue
Ici nous nous proposons de tester une éventuelle
relation entre le taux d'intérêt et le niveau de l'encours des
dépôts à vue. Pour cela, nous disposons d'une série
mensuelle de 24 observations concernant la série des taux
d'intérêt du marché interbancaire (période allant de
janvier 2002 à décembre 2003). Ce taux reflète le taux
d'intérêt de marché et a un impact sur le niveau des taux
créditeurs et débiteurs appliqué par les banques aux
clients. En effet avec le développement du marché entre banques,
la grande partie des
21 Le terme intégré d'ordre p (p å
N), signifie qu'il faut différencier la série p fois pour la
rendre stationnaire.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
transactions du marché monétaire a lieu sur le
compartiment interbancaire. Le taux d'intérêt qui y est
pratiqué conditionne les taux de rémunération des
dépôts et des crédits pratiqués par les banques.
Nous supposons en fait que lorsque le taux du marché interbancaire est
très supérieur à un seuil (le taux créditeur
minimum par exemple, qui est resté stable à 5% durant notre
période d'étude), la banque propose des taux de
rémunération plus attrayant au client pour les
dépôts à terme et certains produits financiers et il
s'ensuit une diminution du stock des dépôts à vue au profit
de ces dépôts à termes et produits financiers. Et lorsque
ce taux est inférieur au même seuil, les banques
préfèrent recourir au marché interbancaire pour emprunter
de l'argent et rémunèrent faiblement les dépôts
à terme. Ce qui fait que le client va préférer garder
l'essentiel de ses dépôts dans son compte à vue.
Nous allons tester cette relation avec la série des
dépôts à vue correspondant à la même
période.
II.3.1 Le test de cointégration de Johansen et
interprétation
L'analyse de la cointégration permet d'identifier
clairement s'il existe une relation véritable entre deux variables en
recherchant l'existence d'un vecteur de
cointégration.22 Cette théorie permet
de spécifier des relations éventuellement stables à long
terme entre deux séries temporelles tout en analysant conjointement la
dynamique de court terme. Johansen (1988) a proposé des estimateurs pour
tester cette caractéristique entre deux séries. Cependant, pour
être cointégrées, les deux séries doivent être
affectées d'une tendance stochastique de même ordre
d'intégration (cf. régis Bourbonnais, économétrie,
Dunod, 2003, page 281). Nous avons déjà montré que la
série Logdépots est intégrée d'ordre 1. Nous allons
alors procéder à la détermination de l'ordre
d'intégration de la série Log(taux) qui représente la
transformée logarithmique de la série taux
d'intérêt. Un examen graphique de la série Log(taux) nous
indique qu'elle n'est pas saisonnière. Pour cela nous avons
estimé les trois modèles du test de dickey-fuller augmenté
sur la série Log(taux) (voir Annexe III pour le résultat de ces
trois modèles).
Les résultats du test nous suggèrent que la
série Log(taux) n'est pas stationnaire en niveau. En effet, Les
statistiques obtenues sur les modèles sans trend sont supérieures
aux valeurs critiques au seuil de 5%. La série est donc
représentée par un processus DS et admet ainsi une tendance
stochastique. La meilleure façon de stationnariser est celle du
22 cf. Régis Bourbonnais,
économétrie, Dunod, 2003, page 279.

Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
filtre aux différences. Sur la série D(Logtaux)
obtenue en appliquant à la série Logtaux un filtre aux
différences premières, nous avons également
appliqué le test de Dickey-Fuller augmenté. Il ressort de ce test
que pour les trois modèles, les statistiques empiriques sont toutes
inférieures aux valeurs critiques au seuil 5%. La différence
première de la série Logtaux est stationnaire. On peut conclure
que cette série est intégrée d'ordre un. Ainsi, les deux
séries Logdepots et Logtaux sont intégrées du même
ordre 1. Nous pouvons envisager l'étude de la cointégration.
Les résultats du test de cointégration de
Johansen (voir annexe II) permettent de rejeter l'hypothèse de la
cointégration entre la variable taux d'intérêt et le niveau
d'encours des dépôts à vue pour les seuils 1% et 5%. Il
n'est donc pas possible de spécifier une relation stable à long
terme entre la série des encours des dépôts à vue et
celle des taux d'intérêts. (En effet le loglikelihood ratio est
inférieur à la valeur critique).
II.3.2 Le test de causalité de Granger et
interprétation
Granger (1969) a développé le concept de
causalité qui permet de mettre en évidence le sens de
causalité entre deux variables économiques. En effet pour
Granger, dire que la variable Rt est la cause de Dt, signifie
que la prédictibilité de Dt est améliorée
lorsque l'information relative à Rt est incorporée
à l'analyse.
Nous avons effectué avec le logiciel EVIEWS, ce test sur
les variables Logdepots et logtaux. Les résultats sont les suivants :
Tableau 8 : Résultat du test de causalité
de Granger

Source : élaboré par l'auteur avec
Eviews
D'après le tableau précédent, on accepte
l'hypothèse nulle dans les deux cas (les deux probabilités sont
supérieure à 5%.).
Ce résultat nous permet de conclure au seuil de 5 %
qu'il n'y a aucun sens de causalité
entre les deux variables
d'après Granger. Le taux d'intérêt ne cause pas les
dépôts. Les
dépôts ne causent pas le taux
d'intérêt. Autrement dit, au sens de Granger, on peut
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
prédire le niveau de l'encours des dépôts
à vue sans connaître le mouvement des
taux
d'intérêt. Car son influence n'est pas significative sur
le niveau du stock des dépôts à vue.
Ces deux résultats (test de cointégration de
Johansen et test de causalité de Granger) permettent de valider notre
hypothèse selon laquelle au Cameroun, le comportement des clients en
terme de dépôts sur leurs comptes à vue (non
rémunéré) est indépendant de la variation des taux
d'intérêt. Cela serait dû au fait que les taux
d'intérêt n'augmentent pas considérablement de façon
à intéresser les titulaires des comptes de dépôts
à vue. Nous pouvons aussi justifier cela par le fait que, l'essentiel
des dépôts à vue est constitué des
dépôts sur comptes courants des entreprises qui sont
destinés pour la plupart à financer leurs activités
quotidiennes et à constituer des encaisses de précaution. C'est
aussi la preuve qu'au Cameroun, l'absence d'un marché financier actif
n'a pas permis une diversification des produits financiers attrayant à
même de collecter l'épargne des particuliers et les
excédents de trésorerie des entreprises.
Nous avons montré dans cette partie qu'au Cameroun, le
niveau de l'encours des dépôts à vue ne dépend pas
des taux d'intérêt bancaire. Il est donc important pour la
détermination de la fonctionnelle d'écoulement des
dépôts d'approfondir l'étude des propriétés
stochastiques de l'encours des dépôts à vue, et en ne
tenant pas compte des taux d'intérêt.
II.4 Etude de la série des dépôts
selon la méthodologie de Box et Jenkins
L'étape préliminaire de la méthodologie de
Box et Jenkins a été faite. Nous allons poursuivre avec les
autres étapes.
II.4.1 L'identification et l'estimation des
paramètres du modèle d'évolution de la série
d'encours des dépôts à vue
Nous avons montré (cf. paragraphe II.2.3) que la
série Log(depots) n'est pas stationnaire et qu'elle est
représentée par un processus DS. Nous l'avons
stationnarisée en lui appliquant un filtre aux différences
premières. Nous avons désigné par Dlogdepots la
différence première de la série Logdepots.
Figure 11 : Corrélogramme simple et partielle de
la série Dlogdepots

Source : élaboré par l'auteur avec
Eviews
Après lecture du corrélogramme de la
série Dlogdepot représenté ci-dessus, les modèles
potentiels pour la série Logdepots sont ARIMA(2,1,1). ARIMA(1,1,1),
ARIMA(1,1,0) ARIMA(0,1,1).
Lorsque nous estimons les paramètres de tous ces
modèles, il apparaît que seuls les coefficients des modèles
ARIMA(2,1,1) et ARIMA(0,1,1) et ARIMA(1,1,0) sont toutes significatives au
seuil 5%.

Source : élaboré par l'auteur avec
Eviews
Tableau 9 : Résultat de l'estimation du
modèle ARIMA(2,1,1)


Tableau 10 : Résultat de l'estimation du
modèle ARIMA(0,1,1)




Source : élaboré par l'auteur avec
Eviews
Tableau 11 : Résultat de l'estimation du
modèle ARIMA(1,1,0)




Source : élaboré par l'auteur avec
Eviews
Nous allons dans la suite, étudier l'adéquation de
ces trois modèles avant de faire un choix judicieux et optimal.
II.4.2 La vérification et l'adéquation des
trois modèles potentiels
II.4.2.1 Le modèle ARIMA(2,1,1)
Les coefficients de AR(1), AR(2), MA(1) et la constante du
modèle
ARIMA(2,1,1) sont tous significativement différents de 0
pour un seuil de 5%. Les autres
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
statistiques : Durbin Waston (DW), F empirique laissent
présager d'un bon ajustement. Nous allons maintenant analyser le
résidu à partir de sa fonction d'autocorrélation.
Figure 11 : Corrélogramme des
résidus

Source : élaboré par l'auteur avec
Eviews
Aucun terme de ce corrélogramme n'est extérieur
aux deux intervalles de confiance et la statistique Q a une
probabilité critique très proche de supérieure à 5%
quelle que soit la valeur de k. Le résidu peut être
assimilé à un processus de bruit blanc. Nous procédons
à un test ARCH sur ces résidus (test ARCH à un retard) :
La Fstatistique = 1,07 et la probabilité critique = 0,30 est nettement
supérieure à 5%. Donc les résidus sont un processus de
bruit blanc, non autocorrelés et homoscédastiques. L'estimation
du modèle ARIMA (2,1,1) est donc validée. La série
Logdepots peut être représentée par un processus du type
ARIMA (2,1,1) avec constante.
II.4.2.2 Le modèle ARIMA(0,1,1)
Le coefficient de MA(1) et la constante sont significativement
différent de 0. Les autres statistiques DW et F empirique laisse penser
que l'ajustement est meilleur. Mais avant de conclure, analysons le
résidu à partir de sa fonction d'autocorrélation.
Figure 12 : Corrélogramme des résidus du
modèle ARIMA(0,1,1)

Source : élaboré par l'auteur avec
Eviews
La statistique de Q Ljung-Box indique un corrélogramme
dont les termes sont significativement nuls. En effet, toutes les Q-stat sont
supérieures à 5%. Les résidus issus de ce modèle
sont effectivement des bruits blancs. Un test ARCH (avec un retard)
appliqué à ces résidus montre que les résidus sont
homoscédastiques. (En effet, la Fstatistique est égale à
1,23 avec une probabilité de 0,26. supérieur à 5% : voir
annexe III). Donc les résidus sont des bruits blancs, non
autocorrelés et homoscédastiques. L'estimation du modèle
ARIMA(0,1,1) est validée.
II.4.2.3 Le modèle ARIMA(1,1,0)
Le coefficient de AR(1) et la constante sont significativement
différents de 0 au seuil de 5%. L'analyse des résidus de ce
modèle (cf. annexe) montre que les résidus sont des bruits blancs
non autocorrelés et homoscédastiques. Donc le modèle
ARIMA(1,1,0) avec constante est validé.
Nous constatons alors que les trois modèles peuvent
être retenus comme processus générateur de la série
Logdepot. Dans la suite, il sera question de déterminer le meilleur
modèle.
II.4.3 Le choix du modèle
Nous avons constaté que trois modèles
franchissent la phase de vérification et qu'il convient de choisir dans
cet ensemble. Le choix du modèle optimal reposera sur le critère
d'information de Akaike ou celui de Schawrz, qui consiste à supposer que
ces trois modèles fournissent des approximations de la
réalité et que la vraie loi inconnue des observations ne
satisfait pas forcément un tel modèle. On fonde le choix du
modèle sur une mesure de l'écart entre la vraie loi inconnue et
le modèle proposé. L'objectif étant alors de trouver le
modèle qui minimise les estimateurs des quantités d'information
de de Akaike et de Schawrz.
Ainsi, après comparaison des trois modèles selon
les critères de Akaike et de Schwarz, nous retenons un processus
ARIMA(0,1,1) avec constante comme générateur de la série
Logdepot.
Finalement notre série Logdepot peut être
représentée valablement par le modèle
(38) Logdepot Logdepot -
- t 0, 008592
= + -
å 0, 493349 1
å t -
t 1 t
Ou encore
(39) (1 )
- D Logdepot t 0,008592 (1 0, 493349 )
= + - D å
t
Où D représente l'opérateur
décalage d'ordre 1. (DYt = Yt-1.)
Nous pouvons dire que la série des variations de
logdepot (Dlogdepot) est générée par une moyenne
pondérée des aléas jusqu'au premier retard. Elle est alors
représentative d'une série chronologique qui fluctue autour de sa
moyenne de manière aléatoire.
Les prévisions peuvent être faites. Elles
permettront de connaître l'état du stock des dépôts
aux dates futures.
II.4.4 La prévision
Nous allons faire la prévision pour la série
d'encours des dépôts à vue à un horizon d'un an.
Pour cela, nous allons d'abord prévoir les séries Logdepots. Les
courbes correspondantes aux données estimées et aux
données réelles sont représentées dans le graphique
suivant :
Figure 13 : Dépôts estimés par le
modèle et dépôts réels observés
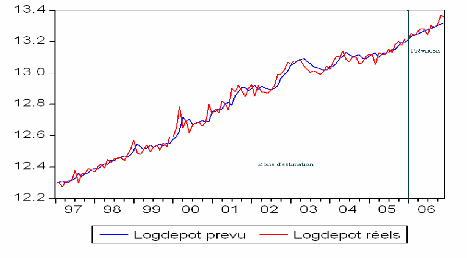
Source : élaboré par l'auteur avec
Eviews
La comparaison des dépôts réels (en rouge)
et les dépôts estimés (en bleu) ne laisse aucun doute sur
la qualité du modèle à expliquer correctement le
passé. Il apparaît donc que les estimations sont satisfaisantes.
Les valeurs estimées ne sont pas très éloignées des
valeurs réellement observées. Ce qui traduit le fait que le
modèle s'ajuste bien à la réalité.
Nous allons maintenant établir le tableau des
prévisions des dépôts à vue à partir du
tableau des prévisions de Logdepot avant de quantifier les erreurs de
prévisions.
Tableau 12 : Dépôts observés et
dépôts prévus par le modèle
|
Période
|
Dépots
observés (en
millions de
F
CFA)
|
Logdépot
prévu
|
dépots Prévus
(en millions de
F CFA)
|
Erreurs de
prévision
|
% erreur
|
|
janv-06
|
549587
|
13,2153091
|
548701,0848
|
885,9152449
|
0,2%
|
|
févr-06
|
569589
|
13,2342224
|
559177,5934
|
10411,40664
|
1,8%
|
|
mars-06
|
561839
|
13,2428143
|
564002,6900
|
-2163,690016
|
0,4%
|
|
avr-06
|
578970
|
13,2514062
|
568869,4220
|
10100,57797
|
1,7%
|
|
mai-06
|
587116
|
13,2599982
|
573778,2060
|
13337,79396
|
2,3%
|
|
juin-06
|
584398
|
13,2685901
|
578729,2902
|
5668,709841
|
1,0%
|
|
juil-06
|
564388
|
13,2771821
|
583723,1551
|
-19335,15514
|
3,4%
|
|
août-06
|
599298
|
13,2857739
|
588759,9945
|
10538,00548
|
1,8%
|
|
sept-06
|
593620
|
13,2943658
|
593840,3552
|
-220,3552403
|
0,0%
|
|
oct-06
|
602380
|
13,3029578
|
598964,6139
|
3415,386136
|
0,6%
|
|
nov-06
|
640181
|
13,3115497
|
604133,0294
|
36047,97061
|
5,6%
|
|
déc-06
|
632347
|
13,3201416
|
609346,0427
|
23000,95726
|
3,6%
|
Source : élaboré par l'auteur
Lorsque nous évaluons les erreurs de prévisions,
ils sont inférieurs à 3% pour une prévision sur 6 mois.
Dans la suite il sera question de filtrer la partie mobile de
notre modèle (confère équation du modèle) pour
déterminer la partie stable. En fonction du temps.
II.5 Détermination de la fonction
d'écoulement
Le modèle d'évolution des dépôts
à vue que nous avons retenu est donné par la formule (38)
Logdepot Logdepot -
- t 0, 008592
= + -
å 0, 493349 1
å t -
t 1 t
Ou encore
(40) Logdepot Logdepot -
= t 0, 008592
+ + -
å 0, 493349 1
å t -
t 1 t
Mise sous cette forme, nous pouvons dire qu'entre deux
observations successives de notre série de mesures résultant de
l'activité du processus générateur de la série
d'encours des dépôts à vue, une combinaison
d'événements aléatoires ou perturbations vient affecter le
comportement de la série et ainsi modifier ses valeurs.
Dans la suite, pour simplifier les formules, nous
désignerons par Dt l'encours des dépôts à
vue à la date t. On a l'équation simplifiée :
(41) LogD t = LogD t -1 + 0,008592+
å t - 0,493349åt-1 Le
modèle peut encore s'écrire :
(42) 1
D D -
= t exp(0, 008592 + -
å 0, 493349 1 )
å t -
t t
Le stock des dépôts à la date t
(date courant) devient à une date T ultérieure
(T supérieur à t)
T
(43) ) ,
D T D
( ) exp 0.00859 ( ) ( 0, 49334
= × - +
T t å - × å -
t i i 1
i = t+

1
Ainsi, la fonction décrivant l'évolution du stock
des dépôts entre l'instant t et T est
donnée par la fonction:
(44)
T
) ,
f ( t , T) = exp [0.00859 × (
T - 0 + E ( å - 0,49334× å i-1
i = t+

1
Nous désignerons par â( t ) =
åt - 0, 493 34åt-1 la
combinaison linéaire d'événements
aléatoires ou perturbations affectant notre série
de dépôts transformés à la date t.
Pour se prémunir du risque de liquidité, nous avons
calculé la série des résidus sur notre période
d'étude et nous avons défini la fonction d'écoulement du
stock comme

T(45) S ( t , T) = exp
[0,00859 × ( T - 0 + E â1 ,

1
i = t+
Où
(46) 1...108
â = Min t ( t 0,
49334 t 1 )
å - å = Min t 1...108 ( (
))
â t
= - =
â représente la valeur de â
( t ) ayant entraîné la diminution mensuelle la plus
importante de la série d'encours des dépôts à vue
durant notre période d'étude.
Cette fonction d'écoulement est
considérée comme le pourcentage de l'encours des
dépôts à vue présents dans le bilan à la date
t, et qui y restera jusqu'à la date T
(ultérieure).
La résolution de l'équation
Mint = 1...108 (â ( t ))
nous a permis de trouver â = - 0,13592
obtenu en t = 40 qui correspond au mois d'Avril 2000,
période au cours de laquelle on a observé la plus grande
diminution du stock des dépôts à vue.
Pour cette valeur de â , la fonction
d'écoulement s'écrit:
(47) S ( t , T ) = exp [ - 0,12733
× ( T - t) ],
Remarquons d'après cette formule que le stock
présent à une date t disparaîtra tôt ou tard du bilan
(En effet, lorsque T est très grand, S(t,T) tend vers
0). Cette fonction traduira l'amortissement du stock dans le temps et nous
permettra de trouver la vitesse ainsi que la durée moyenne
d'écoulement du stock.
II.6 Vitesse et durée moyenne d'écoulement
du stock des dépôts à vue:
Nous avons défini au premier chapitre la vitesse ou taux
d'écoulement par la formule (4).
Un calcul rapide nous permet de trouver ë =
11,96%
Ainsi, l'encours des dépôts à vue pris
à une date quelconque t disparaîtra à un rythme de 11,96%
par mois. La durée moyenne d'écoulement du stock est donc de 8
ans et 4 mois. Il s'agit du temps moyen que mettra un stock de
dépôts à vue pour disparaître complètement du
bilan de la banque si cette dernière ne reçoit plus de
dépôts.
II.7 Partie de l'encours des dépôts à
vue stable en fonction du temps a) Pourcentage des dépôts stables
en fonction du temps
Dans cette partie, en considérant l'encours Dt
pris à la date t, nous allons déterminer la partie
(en pourcentage) de ces dépôts qui sera stable en fonction du
temps La partie de l'encours des dépôts à vue de la date
t qui restera stable dans le bilan jusqu'à la date T
(ultérieure) est donnée par la relation :
(48) D ( t , T ) = D ( t
)exp [ - 0,12733 × ( T - t) ],
Pour T = t+1, on trouve que 88,04% des
dépôts sont stables pendant un mois. Pour T = t+6, on
trouve que 46,58% des dépôts sont stables pendant 6 mois. Pour
T= t+12, on trouve que 21,70% des dépôts sont stables
pendant un an, Pour T= t+24, on trouve que 4% des dépôts
sont stables pendant deux ans.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
En nous limitant à deux ans, nous pouvons détailler
les résultats en construisant le tableau des échéances
suivant :
Tableau 13 : Pourcentage de l'encours d'une date
t stable en fonction du temps
|
Durée en
mois
|
Échéance à partir de la
date t
(quelconque)
|
Pourcentage de l'encours de
la date t (Dt
) stable en
fonction du temps
|
Partie
Stable
|
|
0
|
t
|
100,00%
|
Dt
|
|
1
|
t+1
|
88,04%
|
88,04%Dt
|
|
2
|
t+2
|
77,52%
|
77,52%Dt
|
|
3
|
t+3
|
68,25%
|
68,25%Dt
|
|
4
|
t+4
|
60,09%
|
60,09%Dt
|
|
5
|
t+5
|
52,91%
|
52,91%Dt
|
|
6
|
t+6
|
46,58%
|
46,58%Dt
|
|
7
|
t+7
|
41,01%
|
41,01%Dt
|
|
8
|
t+8
|
36,11%
|
36,11%Dt
|
|
9
|
t+9
|
31,79%
|
31,79%Dt
|
|
10
|
t+10
|
27,99%
|
27,99%Dt
|
|
11
|
t+11
|
24,64%
|
24,64%Dt
|
|
12
|
t+12
|
21,70%
|
21,70%Dt
|
|
13
|
t+13
|
19,10%
|
19,10%Dt
|
|
14
|
t+14
|
16,82%
|
16,82%Dt
|
|
15
|
t+15
|
14,81%
|
14,81%Dt
|
|
16
|
t+16
|
13,04%
|
13,04%Dt
|
|
17
|
t+17
|
11,48%
|
11,48%Dt
|
|
18
|
t+18
|
10,11%
|
10,11%Dt
|
|
19
|
t+19
|
8,90%
|
8,90%Dt
|
|
20
|
t+20
|
7,83%
|
7,83%Dt
|
|
21
|
t+21
|
6,90%
|
6,90%Dt
|
|
22
|
t+22
|
6,07%
|
8,90%Dt
|
|
23
|
t+23
|
5,35%
|
5,35%Dt
|
|
24
|
t+24
|
4,71%
|
4,71%Dt
|
Source : élaboré par l'auteur
L'examen du tableau précédent nous permet de
dire qu'une banque peu prêter 88,04% de son stock de dépôts
à vue à ses meilleurs clients pour une durée d'un mois.
Elle ne peut utiliser que 46,58% de ces dépôts pour octroyer un
crédit sur 6 mois. Pour une échéance d'un an elle peut
prêter 21,70% de ces dépôts à vue. 4,71% de ces
dépôts peuvent être transformés en crédits sur
une durée de 2 ans.
b) Application à l'encours des dépôts
observés en décembre 2005
L'encours des dépôts à vue observé en
décembre 2005 est 550,026 milliards de
FCFA.
Ou encore 550026 millions de FCFA. Il est question de voir
comment ce stock s'amortira dans le temps. Autrement dit, quelle est la partie
de cet encours qui sera stable en fonction du temps. Le tableau suivant permet
de suivre son évolution sur 2 ans.
Tableau 14 : Partie stable de l'encours observé en
décembre 2005 en fonction du temps
|
Nombre de
mois
|
Date
|
Pourcentage de l'encours
observé en décembre
2005,
stable en fonction du temps
|
Partie
stable en
millions de
FCFA
|
|
0
|
déc-05
|
100,00%
|
550026
|
|
1
|
janv-06
|
88,04%
|
484267
|
|
2
|
févr-06
|
77,52%
|
426369
|
|
3
|
mars-06
|
68,25%
|
375394
|
|
4
|
avr-06
|
60,09%
|
330513
|
|
5
|
mai-06
|
52,91%
|
290998
|
|
6
|
juin-06
|
46,58%
|
256207
|
|
7
|
juil-06
|
41,01%
|
225576
|
|
8
|
août-06
|
36,11%
|
198607
|
|
9
|
sept-06
|
31,79%
|
174862
|
|
10
|
oct-06
|
27,99%
|
153956
|
|
11
|
nov-06
|
24,64%
|
135549
|
|
12
|
déc-06
|
21,70%
|
119343
|
|
13
|
janv-07
|
19,10%
|
105075
|
|
14
|
févr-07
|
16,82%
|
92513
|
|
15
|
mars-07
|
14,81%
|
81452
|
|
16
|
avr-07
|
13,04%
|
71714
|
|
17
|
mai-07
|
11,48%
|
63140
|
|
18
|
juin-07
|
10,11%
|
55591
|
|
19
|
juil-07
|
8,90%
|
48945
|
|
20
|
août-07
|
7,83%
|
43093
|
|
21
|
sept-07
|
6,90%
|
37941
|
|
22
|
oct-07
|
6,07%
|
33405
|
|
23
|
nov-07
|
5,35%
|
29411
|
|
24
|
déc-07
|
4,71%
|
25895
|
Source : élaboré par l'auteur
Ce tableau permet ainsi à la banque de savoir la somme
qu'elle peut prêter sans risque de transformation. Par exemple, au 31
décembre 2005, elle peut accorder un crédit de 25,895 milliards
de F CFA pour une durée de 2 ans à ses meilleurs clients non
financiers ou bien placer cette somme d'argent sur le marché
monétaire.
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
II.8 Limite du modèle d'écoulement des
dépôts à vue
Il est intéressant de voir que le modèle ne
prend pas directement en compte certains paramètres relatifs aux
comportements des clients tels que leur revenu moyen. Cette variable pouvant
avoir un impact sur le mouvement de retrait et de dépôt. En outre,
le modèle ne prend pas en compte les variables qui caractérisent
la réputation des banques, leurs efforts commerciaux, leur programme de
fidélisation, les efforts de conquête de leur réseau
commercial (taux de conquête, taux d'attrition). Ces variables
n'étaient pas disponibles dans notre système d'information.
Bien que pouvant être significatives, ces limites
n'altèrent pas la pertinence de notre modèle puisque le terme
d'erreur contient les informations non explicitées dans la construction
du modèle. Leur modélisation nous a permis d'atteindre nos
objectifs en nous prémunissant du risque de liquidité. Toutefois,
la prise en compte de ces variables nous aurait permis de parfaire notre
travail.

CO$CL 'VSIO$ ~$~ #~'"


Après la grave crise de la fin des années 1980
qui a affecté le système bancaire de la CEMAC en
général et celui du Cameroun en particulier, de nombreuses
restructurations ont été faites de sorte qu'à partir de
1995, les banques camerounaises ont été assainies et sont
redevenues liquides. Cependant, tant pour le banquier que pour ses clients, les
effets néfastes qu'avaient entraîné ces crises sont
restés presque indélébiles dans la conscience. Le banquier
pour sa part, ne voulait plus prendre de risque qu'il ne peut évaluer.
Des nos jours, les agents non financiers se reportent davantage sur les
dépôts et placements à vue où le retrait peut
être effectué à tout moment sans pénalité de
remboursement et sans frais d'aucune sorte. Pour les banques camerounaises, ces
dépôts à vue représentent plus de 50% de l'ensemble
des ressources des banques et plus de 70% des dépôts provenant de
la clientèle.
Afin de permettre aux banques de s'impliquer davantage dans le
financement de l'économie tout en maîtrisant le risque de
transformation et de liquidité lié aux dépôts, la
modélisation de l'écoulement des dépôts à vue
s'est avérée importante.
Dans un premier temps, les concepts de cointégration et
de causalité nous ont permis de voir qu'au Cameroun, le comportement des
clients en terme de dépôts sur leur compte à vue n'est pas
significativement influencé par le mouvement des taux
d'intérêt. Ensuite, sur notre série mensuelle d'encours des
dépôts à vue allant de janvier 1997 à
décembre 2006, l'application de la méthodologie de Box et Jenkins
nous a permis de déterminer le modèle d'évolution des
encours de ces dépôts. Il s'agit, après avoir
transformé notre série d'encours des dépôts à
vue en lui appliquant la fonction logarithme népérien, d'un
modèle ARIMA (0,1,1) (Moyenne Mobile d'ordre 1 et intégré
d'ordre 1). Enfin, la détermination de la fonction d'écoulement a
permis de décrire comment le stock s'évapore (ou s'amortit) dans
le temps.
Nos analyses nous ont permis de montrer que, lorsqu'on
agrège l'ensemble des dépôts à vue des clients de la
banque; cet ensemble est relativement stable et n'est pas susceptible de
disparaître du jour au lendemain. En effet il faut environ 8 ans et 4
mois pour qu'un stock de dépôts à vue pris à une
date donnée disparaisse totalement du bilan de la banque. Ce stock
s'écoulera ainsi à un rythme de 11,96% par mois. Ainsi, pendant
un mois 88,04% de l'encours des dépôts à vue seront stables
dans le bilan, 46,58% y
Modélisation de l'écoulement des
dépôts à vue : Cas des banques commerciales du
Cameroun
resteront pendant 6 mois, 21,70% ne sortiront pas du bilan
avant un an, les clients laisseront 4,71% du stock des dépôts
à vue dans les caisses de la banque pendant deux ans.
La banque pourra donc utiliser la partie stable de ces
dépôts pour financer l'économie en minimisant le risque de
transformation.
Plusieurs recommandations importantes peuvent être
faites. D'une part, les banques commerciales devront améliorer leurs
systèmes d'informations ALM, afin de prendre en compte les variables
spécifiques aux clients qui sont utiles pour faire intervenir la
rationalité de la clientèle dans les analyses. Elles devront
s'impliquer davantage dans le financement de l'économie en valorisant la
partie stable (oisive) des dépôts à vue. Elles devraient
tenir compte de la partie stable de ces dépôts dans la
construction des impasses en liquidité afin de déterminer leurs
besoins ou leurs excédents réels de liquidité aux dates
futures. D'autre part La dynamisation du secteur financier devient un enjeu de
taille, car un secteur financier actif permettrait aux titulaires des comptes
de dépôts à vue d'acheter des actifs financiers plus
attrayants et cela en mobilisant leurs dépôts qui restent oisifs
dans les banques. Cela permettra d'éviter cette forme de
thésaurisation. Enfin, si ces dépôts ne peuvent être
valorisés par les banques commerciales, la Banque Centrale pourrait
utiliser la stabilité de ces dépôts à vue pour
ajuster le coefficient des réserves obligatoires relatifs à ce
type de dépôts.
Un secteur financier dynamique avec des taux
d'intérêt incitateurs permettrait d'étudier l'impact de ces
taux sur la stabilité des dépôts à vue. Enfin, une
autre perspective de continuation de ce travail de recherche serait
d'intégrer à ce modèle des variables spécifiques
à la politique commerciale de la banque et des variables relatives aux
comportements de la clientèle telles que les taux d'attrition (nombre de
comptes fermés par mois) et le taux de conquête (nombre de comptes
ouverts par mois). Ce qui contribuerait à sa robustesse.


| 


