Etude de la stabilité aux petites perturbations dans les grands réseaux électriques: Optimisation de la régulation par une méthode metaheuristique

UNIVERSITE PAUL CEZANNE D'AIX-MARSEILLE
(AIX-MARSEILLE III)

N° attribué par la bibliothèque
| 2 | 0 | 0 | 8 | A | I | X | 3 | 0 | 0 | 6 | 8 |

TITRE :
ETUDE DE LA STABILITE AUX PETITES PERTURBATIONS DANS
LES GRANDS RESEAUX ELECTRIQUES : OPTIMISATION DE LA
REGULATION PAR UNE METHODE METAHEURISTIQUE
THESE
Pour obtenir le grade de :

DOCTEUR DE L'UNIVERSITE PAUL CEZANNE D'AIX-MARSEILLE
Faculté des Sciences et Techniques

Discipline : Génie Electrique
Présentée et soutenue publiquement par :
Hasan ALKHATIB
Le 5 décembre 2008

Directeurs de thèse : Marcel PASQUINELLI / Jean DUVEAU

JURY :

Mr. Shahrokh SAADATE Rapporteur

Mr. Mohamed MACHMOUM Rapporteur

Mr. Seddik BACHA Examinateur

Mr. Jean DUVEAU Examinateur

Mr. Marcel PASQUINELLI Directeur de thèse

Mr. Michel THOLOMIER Membre invité

RESUME :

Depuis une vingtaine d'années, les grands réseaux électriques se trouvent obligés de fonctionner à pleine puissance et souvent aux limites de la stabilité. L'amélioration de la stabilité aux petites perturbations, en particulier l'amortissement des oscillations interrégionales, est donc devenue un objectif prioritaire. Les interactions entre les générateurs de différentes régions et les régulateurs utilisés nécessitent une optimisation globale de leurs performances : c'est le meilleur moyen pour assurer le comportement optimal de l'ensemble. L'objectif de notre travail est d'assurer un amortissement maximum, aussi bien des modes interrégionaux que des modes locaux, à l'aide des stabilisateurs de puissance (PSS) généralement utilisés pour l'amortissement des modes électromécaniques locaux. Pour ce faire, nous avons développé une méthode d'optimisation globale basée sur les algorithmes génétiques et une fonction multiobjectif utilisant les paramètres de stabilité relative et de stabilité absolue déterminés à partir de l'analyse des valeurs propres du système. Nous avons analysé l'influence de l'augmentation progressive du nombre de variables à optimiser simultanément (paramètres des PSSs, emplacement et nombre de ces derniers). La méthode que nous proposons permet un réglage optimal des PSSs avec la meilleure localisation possible et un nombre réduit de PSSs. Nous avons proposé en outre une nouvelle méthode d'optimisation utilisant des contraintes dynamiques adaptatives de l'espace de recherche afin d'améliorer les performances et la rapidité de convergence de cet algorithme. Les performances de ces méthodes d'optimisation ont été évaluées sur le réseau multimachines interconnecté New England/New York par analyse des valeurs propres du modèle linéaire du système et simulations temporelles du modèle non-linéaire originel.

MOTS CLEFS : Réseaux électriques, Stabilité aux petites perturbations, Stabilisateurs de puissance, Régulation, Optimisation globale, Algorithmes génétiques.

TITLE:

SMALL SIGNAL STABILITY STUDY IN POWER SYSTEM: OPTIMIZATION OF THE REGULATION BY A METAHEURISTIC METHOD.

ABSTRACT:

Over the past two decades, electric utilities operate their power systems at full power and often closer to their stability limits. The small signal stability improvement, in particular the damping of inter-area oscillations, has become, therefore, a priority. Interactions between the generators of different regions and their regulators require a global optimization of their performances: this is the best way to ensure the whole optimal behaviour. Our work objective is to ensure a maximum damping of the inter-area modes as well as of the local modes, using power system stabilizer (PSS) that is habitually used in the damping of electromechanical local modes. Thus, we have developed a global optimization method based on genetic algorithms and a multiobjective function using relative and absolute stability parameters that are obtained of the system eigenvalue analysis. We have analyzed the influence of the gradual increase of the variable number that to be optimized simultaneously (PSS parameters, their location and number). The proposed method allows an optimal setting of PSSs with the best possible location and a reduced number. We have also proposed a new optimization method using dynamic search space. This can improve the optimization performance as well as the convergence acceleration. The performance of these optimization methods has been evaluated on the New England/ New York multimachine system via linear model eigenvalue analysis, and non-linear time domain simulations.

KEYWORDS: Small signal stability, Power system stabilizer, Global optimization, Genetic Algorithms, Linear system analysis.

Remerciements

J'ai débuté ce travail au laboratoire Compatibilité Electromagnétique de Marseille (LaCEM) sous la direction de Monsieur Michel THOLOMIER, que je tiens à remercier pour m'avoir accueilli au sein de son laboratoire. Suite au départ de Monsieur THOLOMIER à la retraite et la fermeture du laboratoire, je fus à la recherche d'un autre laboratoire qui me permettrait de continuer mon travail. Monsieur Marcel PASQUINELLI a accepté avec beaucoup de gentillesse et de générosité de prendre la direction de ma thèse et de m'aider à terminer mon étude dans les meilleures conditions possibles. C'est pourquoi je tiens à lui exprimer mon extrême reconnaissance pour son soutien moral et son aide précieuse.

Pour avoir accepté de présider le jury, je tiens à remercier Monsieur Seddik BACHA, Professeur des Universités au Laboratoire G2Elab de INP de Grenoble, et d'avoir porté la plus grandes des attentions à mon travail.

Je tiens également à remercier Monsieur Shahrokh SAADATE, Professeur des Universités au Laboratoire GREEN de l'Université Nancy1 et Monsieur Mohamed MACHMOUM, Professeur des Universités au Laboratoire IREENA de l'Université de Nantes pour l'intérêt qu'ils ont porté à mes travaux en acceptant d'en être rapporteur.

Je tiens à remercier du plus profond de mon coeur Jean DUVEAU, mon cher et précieux coencadrant, aussi incroyable sur le plan humain que professionnel. Ton empreinte dans ce travail est remarquable, ta présence en particulier dans la dernière phase de ma thèse et la préparation de ma soutenance on était indispensable pour réussir dans cette difficile mission. En outre l'aide que tu m'as apporté, ton esprit "d'expérimentation" m'a donné une autre vision sur mon travail et sur la relation recherche-expérience. Tu as une qualité rare de nos jours, tu es un homme de parole.

Je tiens à remercier Monsieur THOLOMIER et Monsieur CHOUCHA de m'avoir apporté aide et soutien moral. Mes meilleures pensées vont également vers Monsieur TOLBA qui m'a aidé sincèrement au démarrage de ma thèse.

Sans bien-sûr oublier, lors de mon passage au laboratoire, la bonne humeur et l'ambiance chaleureuse qu'on sut créer Chafik et Raluka. Je vous en remercie vivement.

Quant aux amis, que puis je dire ici pour les remercier ? Ils ont tous été des soutiens d'exception. J'envoie vers eux cette phrase de Gibran KHALIL GIBRAN : « Et que dans la douceur de l'amitié réside la joie et le partage des plaisirs. Car dans la rosée des menues choses le coeur trouve son matin et se ranime. »

Douce et gentille Michèle, tu resteras toujours le seul témoin des tracas et des joies qui ont parsemés mes trois années de thèse. Le hasard n'existant pas, notre amitié devait être depuis longtemps inscrite dans ma destinée comme une ancre. Même si en amitié rien ne se compte, je te dois beaucoup. Je vous serais à jamais reconnaissant pour m'avoir ouvert les bras. Toi et Jo m'avez offert un cadeau inestimable : une famille.

Sabrina, je ne te dis pas merci, un remerciement ne serait pas suffisant. Le goût de l'amitié est tellement différent avec toi ! Ta JOIE, ton esprit, ta passion pour les cultures du monde, ta curiosité sont des qualités que j'apprécie chaque jour. Je n'oublierais jamais ton aide précieuse dans la partie la plus difficile de cette thèse : les remerciements.

Rafif, Rawya et leur petit ange Zina, une famille merveilleuse. Mes premiers jours à Marseille ont été marqués par votre rencontre. Avec vous, je suis toujours inondé par la joie de l'amitié. Que de bons souvenirs avec vous, des Narguilés en hiver, des balades en été et les sourires et les rires de Zina. En bref, du réconfort.

Cher Abou-Ziad, Professeur Fouad, de tes montagnes grenobloises, tu as été mon premier soutien en France et le rayon de soleil de notre ville natale, Salamieh dont Mohammed ALMAGHOUT parlait ainsi : « Cette ville réside dans mon sang. »

Notre amitié, nos échanges culturels sont des richesses inestimables pour moi. Chez toi, j 'ai rencontré une famille, un grand ami et un grand frère. Un esprit ouvert et cultivé, avec au coeur des projets extraordinaires. Que notre ville puisse un jour profiter de tes desseins.

Sawsan, la distance n'a jamais affaibli notre amitié. De la Syrie à Lille en passant par Lyon, tu restes une fille très audacieuse et pleine d'ambition. Tu mérites le meilleur de la vie. Je te serais toujours reconnaissant pour ton amitié.

Je n'oublierais pas mes amis de Grenoble. Nigar et sa famille merveilleuse, Navaz, Chemir, Khaled, ... Je vous remercie chaleureusement pour votre amitié, gentillesse, soutien et les tonnes de moments inoubliables que nous avons passés ensemble.

Ma famille, que deviendrais-je sans vous ? Je ne serais pas là où j'en suis sans votre soutien. Des encouragements, sans cesse renouvelés, au moment les plus difficiles dans tout mon parcours, vous avez sans relâche cru en moi. Malgré la distance, j'ai toujours senti votre amour et votre présence à mes côtés. Papa, maman, mes frères, mes cousins et ma cousine Huda dit Hadhood, mes oncles, mes tantes, ma tante Chahrow, mon grand-père et ma grand- mère, mes beaux-parents, vous êtes nombreux mais une seule grande famille. Un amour et une joie infinis.

Sarab, mon amour eternel que j 'ai attendu depuis toujours. Au moment où je n'espérais plus, notre amour est né ... « Mais l'amour n'est-elle pas un cadeau que l'on reçoit quand on ne s'y attend pas ? » comme le dit Ahlam MOSTEGHANEMI.

Depuis, j'ai une vie plus belle que je ne l'aurais jamais rêvé. Aucun mot n'est assez fort pour te témoigner ma reconnaissance. Grâce à toi, toute ma peine pour conclure ce travail a été particulièrement adoucie. Le bonheur avec toi n'est pas une destination mais une trajectoire.

Table des matières

INTRODUCTION GENERALE 8

Chapitre I : Modélisation du système de puissance 12

1.1- Introduction. 13

1.2- Les phénomènes dynamiques. 14

1.2.1 - Les phénomènes de propagation. 15

1.2.2- Les phénomènes électromagnétiques 15

1.2.3- Les phénomènes électromécaniques. 15

1.2.4- Les phénomènes thermodynamiques. 15

1.3- Le modèle général non-linéaire 16

1.3.1- Introduction 16

1.3.2-Les éléments du modèle. 17

1.3.2.1- Modèle du générateur. 17

1.3.2.1.1- Modèle de la machine synchrone dans le repère de Park. 17

1.3.2.1.2- Les hypothèses du modèle. 19

1.3.2.1.3- Equations électriques. 20

1.3.2.1.4- Equations mécaniques. 21

1.3.2.1.5- Régulation du générateur. 23

1.3.2.1.5.1- Régulateur de fréquence et modèle du turbine. 23

1.3.2.1.5.2- Régulateur de tension et modèle du système d'excitation. 25

1.3.2.2- Réseau de transport. 27

1.3.2.2.1- Modèle de transformateurs. 27

1.3.2.2.2- Modèle des lignes de transmission. 28

1.3.2.3- Modèle des charges. 29

1.3.2.4- Mise en équations du réseau de transport. 30

1.3.3- Les équations d'état généralisé du modèle. 32

1.4- Le modèle linéaire. 35

1.4.1- Introduction : Linéarisation du modèle 35

1.4.2- Application au système de puissance 37

1.4.3- Analyse du modèle linéaire 37

1.4.3.1- Introduction. 37

1.4.3.2- Valeurs propres. 37

1.4.3.3- Analyse modale 40

1.4.3.3.1- Vecteurs propres. 40

1.4.3.3.2- Facteur de participation. 41

1.4.3.3.3- Résidus. 43

1.5- Conclusion. 44

Chapitre II : Stabilité du système de puissance 46

2.1- Introduction. 47

2.2- La stabilité au sens de Lyapunov 47

2.2.1 - Définitions de la stabilité. 47

2.2.1.1- Stabilité du point d'équilibre. 48

2.2.1.2- Stabilité asymptotique 48

2.2.1.3- Stabilité exponentielle 49

2.2.2- Méthodes d'analyse de stabilité au sens de Lyapunov. 49

2.2.2.1 - Première méthode de Lyapunov (méthode indirecte). 49

2.2.2.2- Deuxième méthode de Lyapunov (méthode directe). 50

2.2.3- Conclusion. 51

2.3- Les différents types de la stabilité de système de puissance. 51

2.3.1 - La stabilité de l'angle de rotor. 53

2.3.1.1- Introduction. 53

2.3.1.2- Stabilité angulaire aux grandes perturbations (stabilité transitoire). 54

2.3.1.3- Stabilité angulaire aux petites perturbations (stabilité dynamique). 59

2.3.2- La stabilité de tension. 59

2.3.3 - La stabilité de fréquence. 61

2.3.4- Conclusion. 62

2.4- Etude de la stabilité angulaire aux petites perturbations 62

2.4.1 - Introduction. 62

2.4.2- Variation de couple électromagnétique 63

2.4.2.1- Couple synchronisant TS. 63

2.4.2.2- Couple d'amortissement TA. 64

2.4.3- Influence du système d'excitation sur la stabilité angulaire. 64

2.4.3.1- Influence sur la stabilité transitoire 65

2.4.3.2- Influence sur la stabilité dynamique. 66

2.4.4- Les différents types d'oscillations à faibles fréquences 67

2.4.4.1 - Les oscillations des modes locaux. 67

2.4.4.2- Les oscillations des modes globaux. 68

2.4.4.3- Les oscillations des modes de contrôle. 69

2.4.4.4- Les oscillations des modes de torsion. 69

2.4.4.5- Conclusion. 69

2.4.5- L'amortissement. 69

2.4.5.1- Fonctionnement et modèle de PSS. 70

2.4.5.2- Réglage des paramètres de PSS. 73

2. 4.5.2.1- Méthode de compensation de phase. 73

2. 4. 5. 2.2- Méthode du résidu 75

2. 4. 5. 2. 3- Méthode de placement des pôles 76

2.4.5.3- Emplacement optimal des PSSs 77

2.5- Conclusion. 78

Chapitre III : Optimisation par algorithmes génétiques 80

3.1- Introduction. 81

3.2- Les Algorithmes Génétiques (AGs). 84

3.2.1- Introduction. 84

3.2.2- Codage et initialisation. 86

3.2.3 - Fonctions objectif et de performance. 88

3.2.3.1- Fonction objectif. 88

3.2.3.2- Fonction de performance. 89

3.2.4- Sélection 90

3.2.4.1- Sélection par la roulette biaisée. 90

3.2.4.2- Sélection par tournoi. 92

3.2.4.3- Conclusion. 93

3.2.5- Croisement. 93

3.2.5.1- Croisement seul point. 94

3.2.5.2- Croisement multipoints. 95

3.2.5.3- Croisement uniforme. 96

3.2.6- Mutation. 96

3.2.7- Création de la génération suivante et critères d'arrêt 98

3.2.8- Compromis exploration et exploitation. 99

3.2.9- Paramètres de réglage de l'AG. 99

3.3- Conclusion. 100

Chapitre IV : Applications 102

4.1- Introduction. 103

4.2- Réseau étudié. 104

4.2.1- Caractéristiques du réseau étudié. 104

4.2.2- Caractérisations d'un défaut 104

4.3- Analyse de la performance et critères de bonne régulation. 106

4.3.1 - Critères d'analyse du modèle linéaire 108

4.3.2- Critères de simulation. 109

4.3.2.1- Critères temporels instantanés. 109

4.3.2.2- Critères temporels intégraux. 111

4.3.3- Conclusion. 111

4.4- Développement de l'AG 112

4.4.1 - Introduction. 112

4.4.2- Fonction objectif. 112

4.4.3- Mise en oeuvre de l'AG. 113

4.4.3.1- Codage du problème. 113

4.4.3.2- Population initiale. 114

4.4.3.3- Sélection 115

4.4.3.4- Croisement. 115

4.4.3.5- Mutation. 115

4.4.4- L'organigramme du problème. 115

4.4.5- Conclusion. 115

4.5- Résultat et discussion. 116

4.5.1- Le système sans PSSs. 116

4.5.2- Les scénarios et défauts. 119

4.5.3- Cas 1 : optimisation des paramètres des PSSs 120

4.5.3.1- Localisation des PSSs. 120

4.5.3.2- Réglage des paramètres des PSSs par l'AG 122

4.5.3.3- Analyse des valeurs propres 125

4.5.3.3.1- Le point de fonctionnement nominal. 125

4. 5.3. 3.2- Les autres scénarios. 132

4.5.3.4- Analyse par simulations temporelles. 133

4.5.3.4.1- Le point de fonctionnement nominal. 133

4. 5.3. 4.2- Les autres scénarios. 136

4.5.3.5- Conclusion. 136

4.5.4- Cas 2 : optimisation des paramètres et de la localisation des PSSs 137

4.5.4.1- Application des AGs. 137

4.5.4.2- Analyse des valeurs propres 140

4.5.4.2.1- Le point de fonctionnement nominal. 140

4. 5. 4. 2.2- Les autres scénarios. 141

4.5.4.3- Analyse par simulations temporelles. 142

4.5.4.3.1- Le point de fonctionnement nominal. 142

4. 5. 4. 3.2- Les autres scénarios. 144

4.5.4.4- Discussion et conclusion. 146

4.5.5- Cas 3 : optimisation globale des PSSs 147

4.5.5.1- Application des AGs. 147

4.5.5.2- Analyse des valeurs propres 150

4.5.5.2.1- Le point de fonctionnement nominal. 150

4. 5.5.2.2- Les autres scénarios. 151

4.5.5.3- Analyse par simulations temporelles. 153

4.5.5.3.1- Le point de fonctionnement nominal. 153

4. 5.5. 3.2- Les autres scénarios. 155

4.5.5.4- Evaluation du nombre de modes dans les trois cas. 156

4.5.5.5- Discussion et conclusion. 157

4.5.6- Influence des contraintes de l'AG dans l'optimisation : application au troisième cas 158

4.5.6.1- Application des AGs. 158

4.5.6.2- Analyse des valeurs propres pour le point de fonctionnement nominal. 160

4.5.6.3- Analyse par simulations temporelles pour le point de fonctionnement nominal. 1161

4.5.6.4- Discussion et conclusion. 162

4.6- Conclusion. 162

Chapitre V : Optimisation par algorithmes génétiques à contraintes dynamiques 1164

5.1- Introduction. 1165

5.2- Approche proposée. 1166

5.3- Première application 1168

5.3.1- Optimisations par contraintes fixes 1168

5.3.2- Optimisations par contraintes dynamiques. 170

5.4- Deuxième application 176

5.4.1- Optimisations par contraintes fixes 176

5.4.2- Optimisations par contraintes dynamiques. 176

5.5- Conclusion. 179

CONCLUSION GENERALE ET PERSPECTIVE 181

LISTE DE PUBLICATIONS 183

BIBLIOGRAPHIE 185

ANNEXES 193

Annexe A 193

Annexe B. 194

Annexe C. 198

Annexe D 203

Annexe E. 204

INTRODUCTION GENERALE

Depuis une vingtaine d'années, les systèmes de puissance doivent faire face à des défis très importants. La libération du marché de l'électricité crée des scénarios de fonctionnement beaucoup plus complexes que par le passé. L'augmentation permanente de la dépendance électrique de la société moderne implique un fonctionnement des systèmes de puissance à 100% de leur capacité et une sûreté maximale. En outre, la qualité de la puissance électrique est devenue actuellement un grand souci pour les consommateurs et les fournisseurs. Par conséquent, des critères rigoureux de développement et de fonctionnement sont de plus en plus exigés.

Dans ces conditions, la stabilité des systèmes de puissance devient une des préoccupations majeures pour les fournisseurs d'électricité. Ces systèmes doivent rester stables pour toutes les petites variations au voisinage des points de fonctionnement ainsi que pour des conditions sévères. Les nouvelles méthodes et les nouvelles technologies permettant d'améliorer la stabilité des systèmes font par conséquent l'objet de travaux de recherche extrêmement important.

Compte tenu de la variété des conditions de fonctionnement et de la sévérité des incidents, les équipements de commande installés actuellement sur les réseaux peuvent s'avérer trop limités ou insuffisants pour répondre efficacement aux diverses perturbations. En conséquence, les opérateurs de réseaux cherchent à en optimiser leur fonctionnement tout en maintenant un niveau de sécurité satisfaisant.

Un système de puissance est un système hautement non-linéaire qui fonctionne dans un environnement en évolution continuelle : charges, puissance de génération, topologie du réseau,... . Le système peut aussi être soumis à des perturbations ; la perturbation peut être faible ou importante. De petites perturbations, sous forme de variations de charge, se produisent continuellement. Le système doit être capable de "répondre" de façon satisfaisante aux besoins de la charge. Le système doit également être capable de résister à de nombreuses perturbations d'une nature sévère comme la foudre, la perte d'une unité de génération, un court-circuit sur une ligne de transmission, ... .

Suite à une perturbation transitoire, si le système est stable, il atteindra un nouvel état d'équilibre. Si le système est instable, cela se traduira, par exemple, par une augmentation progressive de l'écart entre les angles de rotor des générateurs ou par une diminution progressive des tensions des noeuds du réseau. Un état instable du système pourra conduire à des pannes en cascade et une déconnexion d'une grande partie du réseau électrique.

Les oscillations des systèmes de puissance ont été prédites dès la première installation d'un système de puissance. Un système ayant plusieurs générateurs interconnectés via un réseau de transport se comporte comme un ensemble de masses interconnectées via un réseau de ressorts et présente des modes d'oscillation multiples. L'amortissement des oscillations a toujours été considéré comme un élément important du bon fonctionnement des systèmes de puissance. Une première solution pour amortir ces oscillations était l'utilisation d'enroulements amortisseurs dans les générateurs. Le problème des oscillations a ainsi disparu, mais l'amortissement global du système est resté toujours ignoré (Farmer, 2006).

Plusieurs points considérés comme évidents à cette époque restent toujours valables :

- les oscillations à faible fréquence (entre 0.2 et 2 Hz) se produisent dans les systèmes de puissance à cause de l'insuffisance des couples d'amortissement agissant sur les rotors des générateurs.

- les oscillations apparaissent principalement dans le système sous deux formes :

o les oscillations des modes locaux, associées principalement à un générateur et ses contrôleurs.

o les oscillations des modes interrégionaux, associées à un groupe de générateurs et aux propriétés du système (configuration de son réseau de transport, écoulement de puissance, ...).

- les oscillations des rotors des générateurs entraînent des fluctuations sur des variables électriques (tensions, puissances actives et réactives, fréquence,...), d'où l'origine de leur nom : oscillations électromécaniques.

- le régulateur de tension AVR (Automatic Voltage Regulator) du système d'excitation générateur, est pratiquement la seule source responsable d'oscillations dans le système.

- après avoir déterminé les sources d'oscillations, il est évidemment souhaitable d'identifier, pour des raisons économiques et de fiabilité, les points les plus efficaces pour ajouter les dispositifs d'amortissement nécessaires.

Depuis les années soixante, les processus d'interconnexion entre les systèmes de puissance ont fortement augmentés et les réseaux de transport se sont étendus sur de régions vastes. En outre, la libération du marché de l'électricité a entraîné des augmentations du chargement des réseaux de transport.

Cette évolution s'est accompagnée de la réapparition du problème des oscillations. Les raisons de cette réapparition peuvent se résumer comme suit (Dandeno et al., 1968; Farmer, 2006) :

- l'utilisation de régulateurs de tensions caractérisés par des réponses rapides et des gains élevés (nécessaires pour améliorer la stabilité transitoire) augmente la potentialité d'amortissement négatif.

- les enroulements amortisseurs ne sont plus suffisamment efficaces dans les systèmes interconnectés à cause de la haute impédance extérieure vue de ces systèmes.

- l`augmentation du nombre des contrôleurs automatiques mis en service dans les systèmes augmente la probabilité d'interactions néfastes entre les contrôleurs.

- les petites oscillations produites dans chaque générateur, éventuellement non- significatives à titre individuel, peuvent accroître l'impact négatif des oscillations des lignes d'interconnexion étendant sur le système.

- les oscillations électromécaniques entraînent des contraintes mécaniques importantes, voire dangereuses, sur les masses tournantes des générateurs.

Dans ces nouvelles conditions, les oscillations représentent un problème important des grands systèmes de puissance. Le problème de ces oscillations est ainsi redéfini par leur rôle important dans la stabilité de l'angle de rotor aux petites perturbations (appelée stabilité dynamique) pouvant conduire à la perte de synchronisme et à une restriction de la puissance transmissible dans le système. Ainsi, l'amélioration de la stabilité aux petites perturbations, en particulier l'amortissement des oscillations interrégionales, devient de plus en plus très importante (Samouhi, 1983; Sadeghzadeh, 1998; Snyder, 1999; Roosta, 2003).

Pour surmonter le problème des oscillations électromécanique et améliorer l'amortissement du système, des signaux supplémentaires stabilisateurs sont introduits dans le système d'excitation via son régulateur de tension. Ces signaux stabilisateurs vont produire des couples en phase avec la variation de vitesse de générateur pour compenser le retard de phase introduit par le système d'excitation. Les stabilisateurs de puissance (Power System Stabilizers, PSSs), grâce à leurs avantages en terme de coût économique et d'efficacité, sont les moyens habituels, non seulement pour éliminer les effets négatifs des régulateurs de tension, mais aussi pour amortir les oscillations électromécaniques et assurer la stabilité globale du système (DeMello et al., 1978; Larsen et al., 1981, I).

Conventionnellement, pour régler les paramètres du PSS, les équations du modèle non- linéaire du système sont linéarisées autour du point de fonctionnement et les techniques de contrôle linéaire sont ensuite appliquées. Les paramètres du PSS sont alors fixés à certaines valeurs correspondant à des conditions de fonctionnement données. Il est important de se rappeler que les paramètres du générateur varient avec la charge : le comportement dynamique de la machine variant suivant les points de fonctionnement. Les PSSs doivent donc être réglés et coordonnés de sorte que la stabilité globale du système soit garantie pour une grande variété de points de fonctionnement.

En outre du problème de réglage des PSSs, le choix de leur emplacement représente un facteur critique pour obtenir une performance optimale de stabilisation. Un PSS peut être "bien" réglé pour améliorer l'amortissement d'un mode, mais il peut produire des effets nuisibles pour d'autres modes. En outre, des emplacements différents entraînent des oscillations différentes selon les points de fonctionnement.

Dans de nombreuses recherches, l'emplacement des PSSs est choisi avant d'aborder l'analyse des méthodes possibles de réglage. La méthode des facteurs de participation (FP) était intensivement utilisée pour identifier les endroits de placement possibles des PSSs (Abdel-Magid et al., 1999; Do Bomfim et al., 2000; Abdel-Magid et al., 2003).

En général, un nombre trop important ou un mauvais positionnement des PSSs peut entraîner un dysfonctionnement du système. Il est donc essentiel de "bien localiser" et de choisir un nombre adéquat de PSSs pour réduire ces effets indésirables.

Dans la littérature, différentes approches utilisant l'algorithme génétique (AG) ont été proposées pour le réglage robuste des PSSs dans les réseaux multimachines (Abdel-Magid et al., 2003; Hongesombut et al., 2004; Rashidi et al., 2004; Hongesombut et al., 2005; Panda et al., 2007). L'avantage des AG par rapport aux autres techniques d'optimisation est leur indépendance par rapport à la complexité des problèmes. De plus, il travaille sur un ensemble de points (une population) et non sur un seul point. L'AG est donc une méthode d'optimisation globale.

Le PSS est toujours considéré comme un moyen efficace pour l'amortissement des modes électromécaniques locaux, mais en même temps son rôle dans l'amortissement des modes interrégionaux reste toujours considéré comme faible. L'objectif de notre travail est ainsi d'assurer un amortissement maximum des modes interrégionaux aussi bien que des modes locaux. Pour atteindre cet objectif, nous proposons un réglage optimal des PSSs avec la meilleure localisation possible et le nombre le plus faible de PSSs. Ceci permet d'assurer un amortissement satisfaisant des oscillations rotoriques et de garantir la stabilité globale du système pour différents points de fonctionnement. Nous avons donc développé un programme

d'AG avec une fonction multiobjectif, basée sur l'analyse des valeurs propres du système (partie réelle de la valeur propre et facteur d'amortissement).

Pour vérifier les performances de la méthode proposée, nous avons analysé un réseau multimachines comportant 16 générateurs et 68 noeuds (New England/ New York), (Rogers, 2000).

Pour évaluer les résultats obtenus, nous appliquons une méthode d'analyse dans le domaine complexe, à savoir la méthode des valeurs propres, pour déterminer les différents modes du système. Cette analyse donne des informations importantes sur la stabilité du système en indiquant la présence des modes mal ou non-amortis. En outre, l'origine de ces modes peut également être déterminée. L'analyse de la stabilité a été complétée par simulation du modèle non-linéaire originel dans le domaine temporel.

Le premier chapitre de notre thèse concerne la modélisation générale d'un système de puissance adapté à l'étude de la stabilité angulaire aux petites perturbations. Il présente également l'analyse par valeurs propres et l'analyse modale basées sur la linéarisation du modèle.

Dans le deuxième chapitre, nous avons fait un rappel de la stabilité au sens de Lyapunov. Nous avons également rappelé les caractéristiques des différents types de stabilité d'un système de puissance. Ensuite, nous avons étudié en détail la stabilité angulaire aux petites perturbations avec les stabilisateurs de puissance (PSSs).

Le troisième chapitre concerne une présentation théorique des algorithmes génétiques, qui est la méthode d'optimisation utilisée dans ce travail.

Le quatrième chapitre présente le réseau test étudié (réseau multimachines interconnecté de New England/New York). L'approche proposée est également présentée. Son objectif est d'améliorer l'amortissement des oscillations électromécaniques (associées aux modes globaux et locaux). Pour ce faire, nous proposons une optimisation globale des paramètres, de la localisation et du nombre des PSSs nécessaires pour assurer une performance robuste. Nous avons aussi analysé la réaction du système (en modèle linéaire et non-linéaire) lors de l'application de plusieurs scénarios sévères (analyse et discussion des résultats).

Enfin, le cinquième chapitre se propose d'améliorer la performance de l'optimisation et l'accélération de la convergence d'un AG. Lors de l'optimisation du problème, cette approche permet d'adapter au processus d'optimisation l'espace de recherche en lui assurant des contraintes dynamiques adaptatives.

Chapitre I

Modélisation du système

de puissance

1.1- Introduction.

Un grand réseau électrique (appelé aussi système de puissance) se compose d'éléments (générateurs, transformateurs, lignes,...), plus ou moins nombreux selon la taille du réseau, interconnectés, formant un système complexe capable de générer, de transmettre et de distribuer l'énergie électrique à travers de vastes étendues géographiques, figure (1). Un modèle mathématique typique non-réduit d'un "grand" système peut contenir jusqu'à 15000, voire plus, variables d'état (Farmer, 2006). Ainsi, les systèmes de puissance modernes sont caractérisés par taille et complexité croissantes. Plus la dimension d'un système de puissance augmente, plus les processus dynamiques et l'analyse des phénomènes physiques sous-jacents sont complexes. Outre leur taille et leur complexité, les systèmes de puissance présentent un comportement non-linéaire et variant dans le temps. Les non-linéarités peuvent être introduites par des éléments à fonctionnement discontinu tels relais, thyristors, ..., par des éléments avec hystéré sis ou saturation,... . De nos jours, cette complexité structurelle impacte de plus en plus l'évolution des problèmes de stabilité et des phénomènes dynamiques dans les systèmes de puissance interconnectés.

Distri bution

Production

Transport

Charges

Figure 1. Les différents niveaux d'un système de puissance.

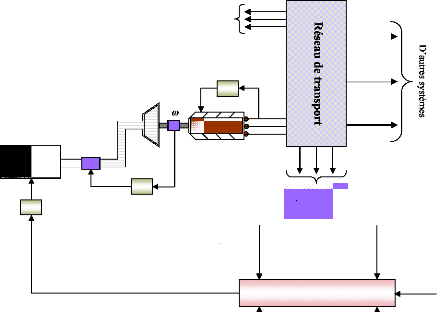
Les grandes composantes d'un système de puissance peuvent être représentées par un schéma blocs comme le montre la figure (2), (Sauer et al., 1998). Cette représentation ne montre pas toutes les interactions dynamiques entre les éléments et leurs contrôles, mais elle peut servir à une description générale pour les structures dynamiques.

L'étude de la performance dynamique d'un système de puissance est très importante pour les opérateurs du système (point de vue économique) et la société en général (point de vue de fiabilité). Une étape essentielle dans ce type d'étude est de comprendre physiquement et mathématiquement les phénomènes dynamiques d'intérêt. Ensuite, la modélisation et la simulation effectuées du système peuvent refléter son comportement critique.

Source
d'énergie

Contrôle de
la source
d'énergie

Signaux de contrôle de la
puissance de génération désirée

Système de la
force motrice

Régulateur
de fréquence

D'autres
générateurs

Générateur

Régulateur
de tension

Puissance de
génération

Système de contrôle central

V

Charges

Puissance
transmise

Fréquence du
système

Fréquence de
référence du
système

	Programmation de puissance de transmission

Figure 2. Structure générale d'un système de puissance. 1.2- Les phénomènes dynamiques.

Dans un système de puissance une grande variété de phénomènes dynamiques différents est susceptible de se produire. Ces phénomènes dynamiques ont des caractéristiques et des origines physiques diverses et se produisent dans des gammes de temps différentes.

Un phénomène dynamique est généralement initié par une perturbation, une action d'un contrôleur, une manoeuvre de protection,... .

Selon le niveau de la perturbation d'origine, nous pouvons distinguer deux classes de phénomènes dynamiques :

- les "petites" perturbations. Il s'agit de fluctuations normales, de faible amplitude, des grandeurs électriques ou mécaniques ; (par exemple, variation continue de charge). Ces phénomènes se manifestent habituellement dans le système par de faibles oscillations transitoires souvent peu amorties.

- les "grandes" perturbations. Ce type de perturbation correspond, par exemple, à un court-circuit sur une ligne de transmission, à la perte d'un générateur,... . Elles exciteront par contre des oscillations importantes.

Afin de mieux comprendre les mécanismes d'instabilité des systèmes de puissance, les divers phénomènes dynamiques doivent être définis et classés. Si l'on tient compte de leurs

caractères physiques ainsi que de leurs plages de réponse temporelles, les phénomènes dynamiques sont habituellement divisés en quatre groupes (Machowski et al., 1998).

1.2.1- Les phénomènes de propagation.

Ils se produisent dans les lignes de transmission haute tension de grande longueur et correspondent à la propagation des ondes électromagnétiques provoquées par des coups de foudre ou des opérations de coupure/fermetures. La gamme de temps de la dynamique de ces phénomènes va de la microseconde à la milliseconde. Ils possèdent les dynamiques les plus rapides.

1.2.2- Les phénomènes électromagnétiques.

Ils ont lieu principalement dans les enroulements des générateurs et des moteurs (enroulements armatures et amortisseurs) et dans les dispositifs électroniques de puissance. Ils découlent d'une perturbation (tel un court-circuit), d'une opération d'un système de protection, d'une commutation (thyristors, ...), ou d'une interaction entre les machines électriques et le réseau.

Ces phénomènes génèrent des courants et des couples élevés à l'intérieur des générateurs, sur une échelle de temps typique de plusieurs millisecondes. Au-delà de ce laps de temps, les inerties de la turbine et du générateur sont suffisantes pour empêcher toute variation importante de vitesse de rotor.

1.2.3- Les phénomènes électromécaniques.

Les phénomènes électromécaniques impliquent principalement les champs de rotors, les enroulements amortisseurs et les inerties des rotors. Ils sont principalement dus aux mouvements des masses tournantes des générateurs et des moteurs. Ils se produisent à la suite d'une perturbation, d'une opération de commande sur le système de contrôle de tension ou sur le contrôle de la turbine. La gamme de temps de ces phénomènes s'étend environ d'une seconde à plusieurs secondes. Cette échelle de temps est considérée suffisamment grande pour que les phénomènes soient influencés par la turbine et les systèmes de commande de générateur. Dans cette gamme de temps, les variations de vitesse de rotor couplées aux variations électromagnétiques produisent alors des effets électromécaniques.

1.2.4- Les phénomènes thermodynamiques.

Les phénomènes thermodynamiques se développent dans les chaudières des centrales thermiques lors de la demande de commande automatique de génération, mise en application suite à une perturbation d'équilibre entre la production et la consommation de puissance. Ils s'étendent de quelques dizaines de secondes à quelques dizaines de minutes : ils présentent ainsi les dynamiques les plus lentes.

La figure (3) montre la classification des phénomènes dynamiques expliquée ci-dessus.

Une "bonne" compréhension physique et mathématique du système et des phénomènes associés permet de mieux comprendre la modélisation et la simulation du système à refléter les comportements critiques de ce dernier. Le paragraphe suivant définit le modèle mathématique utilisé et ses éléments.

Dynamiques de
propagation

Dynamiques
électromagnétiques

électromécaniques

Dynamiques

Dynamiques
thermodynamique

s

microsecondes millisecondes secondes minutes

Figure 3. Caractéristiques des phénomènes dynamiques rencontrés
dans les systèmes de puissance.

1.3- Le modèle général non-linéaire.

1.3.1- Introduction.

La première étape, lorsqu'on veut analyser et commander un système électrique de puissance, consiste à trouver un "bon" modèle mathématique. Généralement, un modèle, dans l'analyse des systèmes, est un ensemble d'équations ou de relations, qui décrit convenablement les interactions entre les différentes variables étudiées, dans la gamme de temps considérée et avec la précision désirée, pour un élément ou un système. Par conséquent selon le but de l'analyse, un élément ou un même système physique, peut donner lieu à des modèles différents.

Dans de nombreux cas, le choix du modèle correct est souvent la partie la plus difficile de l'étude. Le point essentiel est de trouver le "bon modèle" qui réalise un compromis entre la fidélité du comportement qualitatif et quantitatif et la simplicité de mise en oeuvre à des fins d'analyse et de synthèse. Les modèles complexes ont généralement besoin d'un nombre plus important de paramètres. En outre, l'obtention de valeurs fiables pour ces paramètres exige un travail important. Enfin si des méthodes trop complexes sont utilisées, l'analyse et les calculs sont inutilement "volumineux" et l'interprétation du résultat exige également un travail très important (Andersson, 2006).

Généralement, pour établir un modèle de réseau électrique pour les études dynamiques, on tient compte uniquement des équipements en activité pendant la plage temporelle du phénomène dynamique considéré. Le résultat est donc le modèle de connaissance complet du système : il se compose d'équations différentielles ordinaires non-linéaires et d'équations algébriques (Kundur, 1994).

Les modèles présentés dans ce chapitre concernent les éléments suivants :

- les unités de production : générateurs électriques, systèmes d'excitation, turbines et systèmes de contrôle associés.

- les transformateurs et les lignes de transmission du réseau de transport.

- les charges enfin pour la partie consommation.

1.3.2- Les éléments du modèle.
1.3.2.1- Modèle du générateur.

L'énergie électrique est généralement produite par les machines synchrones. Ces dernières sont caractérisées par une vitesse de rotation de l'arbre de sortie de chaque machine égale à la vitesse de rotation du champ tournant. Pour obtenir un tel fonctionnement, un couple mécanique issu d'une énergie primaire source, comme l'énergie hydraulique, l'énergie nucléaire ou l'énergie chimique, est appliqué à l'axe de la machine synchrone via un lien mécanique intermédiaire, à savoir la turbine. Le champ magnétique rotorique est généré habituellement par un circuit d'excitation alimenté par courant continu. La position du champ magnétique rotorique est alors fixe par rapport au rotor : ceci impose en fonctionnement normal une vitesse de rotation identique entre le rotor et le champ tournant statorique. Ainsi, les enroulements du stator sont soumis à des champs magnétiques qui varient périodiquement. Une f. é.m. de courant alternatif est donc induite dans le stator.

Les générateurs synchrones participent de façon extrêmement importante aux phénomènes dynamiques et à la qualité globale de l'alimentation en énergie. Il est donc nécessaire de développer des modèles pratiques et réalistes des machines synchrones. Dans ce chapitre, nous présenterons et discuterons un modèle adapté à l'analyse de la stabilité dynamique.

1.3.2.1.1- Modèle de la machine synchrone dans le repère de Park.

Dans la machine idéale, le stator est muni de trois enroulements repérés a, b et c, décalés de 120 degrés. Le rotor comporte un certain nombre d'enroulements, répartis sur deux axes: l'axe-d, (axe direct) qui coïncide avec celui de l'enroulement d'excitation et l'axe-q (axe quadratique) situé en quadrature avance par rapport à l'axe direct (Custem, 2002, II).

Pour supprimer la non-linéarité entre les grandeurs du stator et celles du rotor, les enroulements de la machine doivent être ordonnés selon deux axes perpendiculaires, chaque machine est modélisée dans sa référence locale (d-q) tournant avec son rotor (Andersson, 2006). Pour formaliser le couplage entre les équations du système et établir les équations décrivant le comportement du système global, toutes les tensions et tous les courants doivent être représentés dans une seule référence commune à toutes les machines. Généralement, une référence tournant à la vitesse synchrone sert de référence commune. Une telle approche peut être réalisée par la transformation de Park. Le développement de cette transformation est donnée à l'annexe A.

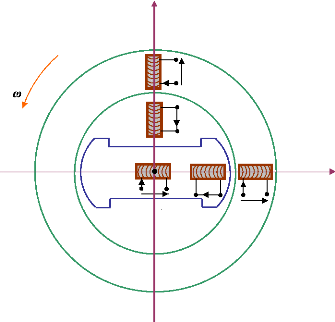
La figure (4) montre schématiquement les enroulements et les sens des courants dans une machine synchrone. La figure (5) donne le modèle équivalent dans le repère de Park (d-q). Les différents enroulements dans les deux représentations sont les suivants :

- Les trois enroulements statoriques notés a, b et c, et leurs enroulements équivalents notés d₅ et q₅.

- L'axe direct comporte l'enroulement d'excitation noté f, et un enroulement amortisseur noté d_a.

- L'axe en quadrature comporte un enroulement amortisseur noté q_a.

Notons enfin que l'enroulement d'excitation est soumis à une tension Vf tandis que les circuits da, qa sont court-circuités en permanence.

d

iD a

D

i_a v_a

vb

ib

Q

f

vf

if

c

b

v_c

iQ

i_c

q

c

b

a

Figure 4. Modélisation de la machine synchrone idéalisée.

q

if

q_h iqh vqh

qa iqa

f

vf

d_a

ida

idh

vdh

d_h

d

Figure 5. Modèle de la machine synchrone dans le repère de Park.

1.3.2.1.2- Les hypothèses du modèle.

Le modèle du générateur et de ses contrôles se limite habituellement aux équations différentielles ordinaires couplées entre elles via les équations algébriques du réseau de transport. Chaque équation différentielle exprime la dérivée d'une variable d'état (tels l'angle de rotor, la tension d'excitation, ...) en fonction d'autres variables d'état et variables algébriques. Le nombre d'équations différentielles décrivant le modèle du générateur définit l'ordre du modèle. Il existe plusieurs modèles, allant du plus simple, le modèle classique représentant seulement les caractéristiques électromécaniques du générateur, au plus complexe, à savoir le modèle du huitième ordre tenant compte de tous les circuits de rotor, de stator, d'amortissement et de champ de saturation (Anderson et al., 2003). Dans les études des oscillations électromécaniques, le modèle du générateur doit représenter deux caractéristiques fondamentales : les caractéristiques électriques des enroulements d'excitation et les caractéristiques mécaniques de l'arbre du générateur.

Les hypothèses considérées pour établir ce modèle sont basées en négligeant l'influence : - des résistances rotoriques et statoriques.

- des enroulements amortisseurs.

- du champ de saturation.

- des phénomènes transitoires dans le stator.

- de la variation de vitesse dans les équations de tensions du stator (ainsi, ù_r = ù_o = 1 [p.u]), (cette supposition est faite pour compenser l'effet de l'annulation des phénomènes transitoires dans le stator).

Ce modèle néglige également l'amortissement produit par les courants de Foucault dans le corps du rotor (on suppose que la f. é.m. transitoire suivante l'axe d, à savoir E'd, est constante). Ainsi, comme il n'y a aucun enroulement sur l'axe en quadrature pour représenter le corps du rotor, nous aurons:

Ed ' = , X q = X q
0 '

E'd : f.é.m. du générateur induite suivante l'axe d, en p.u. X'_q : réactance synchrone d'axe q, en p.u.

X_q : réactance transitoire d'axe q, en p.u.

Enfin, nous supposerons que l'angle de rotor ä (position angulaire du rotor par rapport à la référence tournante au synchronisme) coïncide avec l'angle de la tension interne du générateur.

Le modèle résultant est le modèle du troisième ordre. Il est décrit par les variables d'état suivants (Anderson et al., 2003) :

E'_q : f.é.m. du générateur induite suivante l'axe q, en p.u.

ù : vitesse angulaire du rotor, en p.u.

ä : angle de rotor, en rad.

Ce modèle, bien adapté à l'étude de la stabilité dynamique, est le plus simple. Il est largement utilisé dans l'analyse des valeurs propres et le réglage des paramètres des stabilisateurs de puissance (Sauer et al., 1998).

1.3.2.1.3- Equations électriques.

Considérons une i^ème machine d'un réseau multimachines, nous allons déterminer dans de ce paragraphe les équations algébriques du stator de cette machine : à savoir les équations concernant les tensions suivant les axes d et q et les puissances électriques.

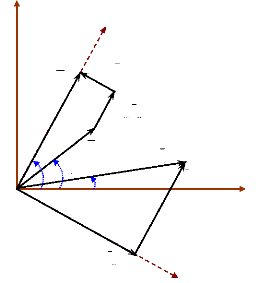
Les grandeurs électriques de cette machine sont représentées sur la figure (6). Avant de débuter le calcul, nous pouvons faire les remarques suivantes :

- le repère (di, qi) concerne la i^ème machine seule, alors que le repère (D, Q) est commun à toutes les machines du système.

- l'angle de couple äi, vu entre D et qi, représente la position du repère (d,q) de la ième machine par rapport au repère commun (D,Q) : il varie constamment dans le temps et peut être positif ou négatif (Yu, 1983).

Q

qi

Eqi jXqiIqi

'

jXdi Idi

I_i

Iqi

Idi

di

ä_i

V_i

á_i

è_i

D

Figure 6. Phaseurs relatifs à la i^ème machine d'un système multimachines.

D'après la figure (6), la tension terminale V_i de la i^ème machine du système peut se déterminer par l'équation suivante :

V_i = E ' qi - jX ' di Idi - jXqiIqi (1)

Notons, dans le repère commun (D-Q), les expressions suivantes :

E ' qi= E ' qi e ^ä

j i

Iqi I qi e ^ä = , ( - 90 ° ) j i I di I di e ^ä = j i

(2)

Vi i Ve j á i

=

En introduisant les relations (2) dans la relation (1), nous obtenons :

j á ä ä ä

i i i i

' ( 90 )

j j + °

V e E e X I e jX I e

= - -

^j (3)

i qi di di qi qi

Qui devient après arrangement :

V e i i = E - X I - jX I

- ( ä - á ) '

^j (4)

i qi di di qi qi

V jV E X I jX I (5)

i i i i i i qi di di qi qi

- - - = - -

'

cos( ä á ) sin( ä á )

En séparant partie réelle et partie imaginaire, nous obtenons les expressions de Vd et V_q suivantes :

ç ??

V X I

di qi qi

=

Vqi

' ' (6)

E X I

qi di di

-

En considérant les relations (2) et la relation suivante : I_i = I_di + I_qi, l'équation (1) peut être donc réécrite comme suit :

V E e jX I jX e jX I e ' ä - ' + ' ä - ä j i i i j j i qi = di i di qi qi

(7)

Pour n machines d'un système multimachines, l'équation (7) peut s'écrire sous la forme matricielle suivante :

[ ] [ ][ ] [ ] [ ] [ ][ ][ ]

V E e j X I j X X I e

= - + -

' ' '

j ä j ä (8)

q d d q q

Dans cette dernière équation, les termes [V] , [ ' ]

E_q , [I] et [I_q ] sont des vecteurs colonnes

de dimension n et les coefficients [ ^jä ]

e, [ ' ]

X _d et [ ' ]

X d - X _q sont des matrices diagonales.

Les puissances électriques (apparente, active et réactive) de la i^ème machine sont données par :

)

S P jQ V I V j V I jI

*

i ei ei i i di qi di qi

= + = = + -

( ) (

(V di

- V di Iqi )

I V I j V I

di qi qi qi di

+ +

) (

? ??

??

Pei

Qei

V di

I V I

di qi qi

+

V qi I di - V di I qi (9)

Etant donné que les phénomènes transitoires dans le stator sont négligés, le couple électrique est dons égal à la puissance électrique active en per-unit. Ainsi Tei = Pei.

1.3.2.1.4- Equations mécaniques.

Les propriétés mécaniques des machines synchrones se modélisent généralement à l'aide de l'équation du mouvement basée sur le théorème du moment cinétique (Andersson, 2006). Cette équation présente une importance fondamentale dans l'étude des oscillations électromécaniques, car ces oscillations représentent un phénomène important dans la plupart des systèmes de puissance, en particulier ceux qui contiennent de lignes de transmission longues (Andersson, 2006). Dans le fonctionnement à l'état d'équilibre, toutes les machines synchrones du système tournent à la même vitesse angulaire électrique. Le couple mécanique

T_m est de même sens que le sens de la rotation de l'axe du générateur. Le couple électrique T_e est de sens opposé à la rotation et ce couple équilibre le couple mécanique (Basler et al., 2005), figure (7). Lors d'une perturbation, un ou plusieurs générateurs peuvent être accélérés ou ralentis et il y a donc risque de perdre le synchronisme. Ceci peut avoir impact important sur la stabilité du système et les générateurs perdant le synchronisme doivent être débranchés, sinon ils pourraient être sévèrement endommagés.

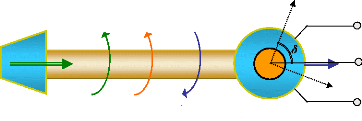
Turbine

Rotor

T_e

T_m ù

P_m

q

P_e d

Générateur

Figure 7. Couples mécanique et électrique agissant sur l'axe d'un générateur.

Pour un système multimachines, s'il y a un déséquilibre des couples agissants sur le rotor de la i^ème machine, cette dernière va accélérer ou ralentir selon l'équation du mouvement suivante :

Äù& =

i T T

2 H i

1

( )

mi ei

- (10)

Avec Hi constante d'inertie (en secondes) représentant l'inertie totale de toutes les masses tournantes connectées à l'arbre du générateur.

Pour des oscillations à faibles fréquences, le courant induit dans les enroulements amortisseurs est négligeable. Par conséquent les enroulements amortisseurs peuvent être complètement négligés dans la modélisation du système. Si les enroulements amortisseurs sont ignorés, le couple d'amortissement produit par ces enroulements amortisseurs est donc également négligeable. Pour tenir compte de la composante du couple négligée, on introduit dans l'équation du mouvement un terme de compensation D (nommé aussi coefficient d'amortissement) en p.u, (Sauer et al., 1998). Ce coefficient représente l'amortissement naturel du système : il empêche l'accroissement des oscillations, à moins qu'une source d'amortissement négatif soit introduite (tel le régulateur de tension du système d'excitation). L'équation du mouvement peut être donc réécrite comme suit :

ù& H ù i T T D 1 ? ? Ä Ä = ( ( mi ei i i 2 i

-1)) (11)

L'équation de l'angle de rotor de la i^ème machine est donné par :

ä& i = ù _o (Äù _i -1) (12)

Avec :

Äùi : déviation de la vitesse angulaire du rotor de la i^ème machine, en p.u. ù_o : vitesse de synchronisme (vitesse de base), en rad/s.

(ù_o = 2ðf , f : fréquence nominale, en Hz).

Tmi : couple mécanique fourni par la turbine, en p.u.

Tei : couple électromagnétique associée à la puissance électrique _Pei produite du

générateur, (

T ei

P = ), en p.u. ei ù i

Di : coefficient d'amortissement du générateur, en p.u. ä : angle de rotor, en rad.

1.3.2.1.5- Régulation du générateur.

Les machines synchrones du système doivent être capable de maintenir l'équilibre des puissances actives et des puissances réactives dans des conditions de fonctionnement diverses. Ainsi, des tensions sinusoïdales équilibrées sont garanties avec des amplitudes et des fréquences constantes.

Si l'équilibre des puissances actives n'est plus assuré, la fréquence de synchronisme dans le système sera changée, alors qu'un déséquilibre des puissances réactives entraînera une variation des tensions du système par rapport à leurs valeurs de référence (Andersson, 2006).

Pour assurer une génération satisfaisante d'énergie électrique, pour un grand nombre de points de fonctionnement, le couple mécanique T_m appliqué au rotor et la tension d'excitation Efd doivent être réglés systématiquement pour s'accommoder de toute variation du système.

Le système responsable de la génération du couple mécanique et ainsi de l'entraînement du rotor du générateur est appelé "système de force motrice". Le contrôle de la fréquence (ou contrôle de la puissance active) associé à ce système maintient la vitesse nominale des générateurs en assurant de ce fait une fréquence constante. Par ailleurs, le système d'excitation est responsable de la tension d'excitation fournie au générateur. Le régulateur de tension (ou régulateur de la puissance réactive) associé modifie les valeurs du système d'excitation pour enfin obtenir les tensions désirées aux bornes du générateur (Anderson et al., 2003).

Nous présentons par la suite successivement les principes généraux :

- de la génération de la puissance mécanique avec la régulation de fréquence

- du système d'excitation avec la régulation de tension et leurs modèles mathématiques.

1.3.2.1.5.1- Régulateur de fréquence et modèle de la turbine.

Un système de force motrice, figure (8), se compose de la source d'énergie primaire, de la turbine (équipé d'un servomoteur) et du régulateur de fréquence (gouverneur) (Farmer, 2006).

La turbine transforme l'énergie potentielle de la source en énergie de rotation de l'arbre (rotor) sur lequel est placé l'alternateur. L'alternateur convertit la puissance mécanique fournie par la turbine en puissance électrique de sortie. La vitesse de l'arbre de la turbine est mesurée précisément et comparée à la vitesse de référence. Le régulateur de fréquence (vitesse) agit ensuite sur le servomoteur pour ouvrir et fermer les vannes de contrôle et modifier par conséquent la vitesse du générateur. Ainsi, le rôle de la turbine est d'entraîner le rotor du générateur à la vitesse synchrone correspondant à la fréquence du système de puissance.

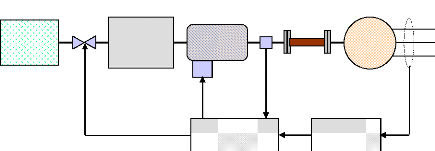
Source de
l'énergie
primaire

Valve de
contrôle

Conversion
de l'énergie

Turbine

Régulateur de
fréquence

Servo -
moteur

Capteur de
vitesse

Arbre de

transmission

Référence de
puissance

Générateur

Réseau de
transport, 3Ö

Figure 8. Structure générale d'un système de force motrice - générateur.

Les turbines à vapeur utilisées dans les centrales thermiques (charbon, gaz, pétrole, nucléaire) sont constituées d'un certain nombre de roues, successivement fixes et mobiles, portant des ailettes le long desquelles la vapeur se déplace. Au fur et à mesure que la vapeur progresse axialement dans la turbine, sa pression diminue et la taille des ailettes augmente. Ces différentes roues sont généralement groupées en plusieurs étages, particulièrement dans les centrales de grande puissance. La division de la turbine en étages permet de resurchauffer la vapeur entre les étages en assurant, par conséquent, un meilleur rendement au cycle thermique (Custem, 2002, I).

Le gouverneur forme une boucle de retour qui surveille la vitesse du rotor à chaque instant. Considérons par exemple une perturbation de l'équilibre des puissances actives. Dans les toutes premières secondes, l'énergie correspondante va être prélevée sur l'énergie cinétique des masses tournantes des unités de production. Ceci va entraîner une perturbation de la vitesse de rotation de ces unités. Cet écart de vitesse doit être détecté et corrigé automatiquement par les gouverneurs. Ces gouverneurs doivent changer l'admission de fluide (vapeur, gaz ou eau) dans les turbines de manière à ramener les vitesses et donc la fréquence du réseau, autour de leurs valeurs nominales.

Dans tout système de puissance, il très important de maintenir la fréquence dans une plage étroite autour de sa valeur nominale (50 ou 60 Hz). Le respect strict de cette valeur est non seulement nécessaire au fonctionnement correct des charges mais il est également l'indicateur d'équilibre entre puissances actives produites et consommées (Custem, 2002, I).

Dans l'analyse de la stabilité transitoire ou dynamique, la réponse temporelle du système de la force motrice à une perturbation est considérée comme plus lente que la plage d'étude de la stabilité concernée (typiquement entre 10 et 20 secondes). Ainsi, le modèle du système de la force motrice peut être extrêmement simplifié. Pour une analyse de stabilité transitoire d'une durée de quelques secondes, le modèle du système de la force motrice peut être supprimé en considérant que le couple mécanique de la turbine reste constant (Farmer, 2006). Sa faible influence sur le comportement des oscillations électromécaniques associées à la stabilité aux petites perturbations peut aussi être négligée. Ainsi, il n'est pas utilisé lors de l'établissement du modèle linéaire du système de puissance associé à ce type de stabilité.

Dans quelques cas, le modèle peut être employé pour calculer les fréquences naturelles de torsion du système de rotor. Il peut être également employé dans la simulation dynamique du

système de puissance pour obtenir des informations sur les couples de rotor se produisant lors d'un défaut (Machowski et al., 1998).

Le modèle de l'ensemble turbine à vapeur/gouverneur utilisé en simulation dynamique du modèle non-linéaire est représenté par la figure (9), (Milano, 2005).

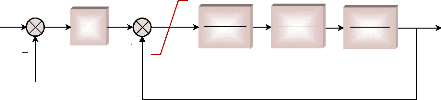
T max

Tm

1

ùréf

1 +

KR

sT 4

1 3

+sT

+

1+

+

sT₅

1+s T_C

1+ sT_S

ù

Tmin

Régulateur

Servomoteur

Réchauffeur

Figure 9. Modèle de la turbine et du gouverneur. 1.3.2.1.5.2- Régulateur de tension et modèle du système d'excitation.

Le système d'excitation est un système auxiliaire qui alimente les enroulements d'excitation de la machine synchrone afin que cette dernière puisse fournir le niveau de puissance demandé. En régime permanent, ce système fournit une tension et un courant continu mais il doit être capable également de faire varier rapidement la tension d'excitation en cas de perturbation sur le réseau (Custem, 2002, I).

Actuellement, des systèmes d'excitation variés sont employés. Trois principaux types peuvent être identifiés (IEEE, 2005) :

a)- Les systèmes d'excitation à courant continu -CC- :

Ils utilisent une génératrice à courant continu avec collecteur comme source de puissance du système d'excitation.

b)- Les systèmes d'excitation à courant alternatif -CA- :

Ils utilisent un alternateur et des redresseurs statiques ou tournants pour produire le courant continu nécessaire dans l'enroulement d'excitation de la machine synchrone.

c)- Les systèmes d'excitation statiques (systèmes ST) :

Dans ce cas, le courant d'excitation est fourni par un redresseur commandé. Sa puissance est fournie soit directement par le générateur à travers un transformateur donnant le niveau approprié de tension, soit par des enroulements auxiliaires montés dans le générateur.

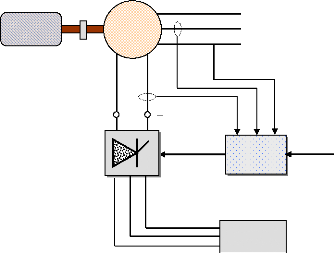
Les systèmes d'excitation sont équipés de contrôleurs, appelés habituellement régulateurs de tension (Automatic Voltage Regulator : AVR), figure (10). Ces derniers sont très importants pour l'équilibre de la puissance réactive qui sera fournie ou absorbée selon les besoins des charges. En outre ces contrôleurs représentent un moyen très important pour assurer la stabilité transitoire du système de puissance. Le régulateur de tension agit sur le courant d'excitation de l'alternateur pour régler le flux magnétique dans la machine et "ramener" la tension de sortie de la machine aux valeurs souhaitées. Une caractéristique très importante d'un régulateur de tension est sa capacité à faire varier rapidement la tension d'excitation.

Vt

It

If

+

Système
d'excitation
statique

Vf

Vref

AVR

Turbin

Générateur

Source
auxiliaire

Figure 10. Structure générale d'un système d'excitation statique avec son AVR.

Le groupe IEEE task forces présente périodiquement des recommandations pour la modélisation des éléments d'un système de puissance dont les systèmes d'excitation. Plusieurs modèles sont suggérés pour chaque type de système d'excitation (IEEE, 2005). Les systèmes d'excitation statiques étant les plus installés actuellement, nous avons donc choisi dans notre étude d'utiliser le modèle du système IEEE-ST1A, modèle le plus utilisé dans la littérature. Ce type de système d'excitation se caractérise par sa rapidité et sa sensibilité (IEEE, 2003) :

- sa constante de temps T_a est faible, normalement de l'ordre de quelques millisecondes - son gain K_a est élevé, généralement entre 200 et 400 per-unit.

La figure suivante montre le modèle du système d'excitation et de son régulateur de tension utilisé dans notre étude.

V_t

Efd _ max

Vréf

+

+

K a

1+sT a

Efd

Efd _ min

V_S

Figure 11. Modèle simplifié du système d'excitation IEEE-type ST1A.

La grandeur _Vref, est la consigne de tension déterminée pour satisfaire les conditions de l'état équilibré. Le régulateur de tension compare le signal Vt (un signal continu proportionnel à la valeur efficace de la tension alternative du générateur) à la tension de consigne _Vref .Un signal complémentaire VS peut être ajouté au noeud de comparaison : il s'agit d'un signal issu de certains dispositifs spécifiques de commande comme les stabilisateurs de puissance (PSS). Ensuite, le signal d'erreur est amplifié pour donner la tension d'excitation demandée _Efd. La constante de temps et le gain de l'amplificateur sont respectivement T_a et K_a. Les valeurs extrémales de la tension d'excitation (Efd _max, Efd_min) sont fixées par un système de limitation.

E & = - + -

( ( ) )

K V V V E (13)

fd a réf t S fd

T a

La relation suivante décrit, tous calculs faits, le fonctionnement du modèle : 1

La relation entre la tension d'excitation _Efd et la tension interne du générateur E^'_q est donnée comme suit :

1 E & ' = ( ( ) ) E X X I E - - ' - ' q fd d d d q T ' do

(14)

1.3.2.2- Réseau de transport.

Le réseau de transport relie toutes les centrales électriques dans un système de puissance et distribue la puissance aux différents consommateurs. Les éléments principaux du réseau sont les lignes aériennes à haute tension, les câbles souterrains, les transformateurs et les jeux de barres. Des éléments auxiliaires peuvent être trouvés : des condensateurs en série, des réactances shunts et des systèmes compensation, des systèmes de protection..., (Machowski et al., 1998).

Pour la modélisation de notre système de puissance, nous nous intéressons à établir le modèle de transformateurs et le modèle de lignes de transmission.

1. 3. 2. 2. 1- Modèle de transformateurs.

Le transformateur permet d'élever l'amplitude de la tension alternative disponible à la sortie de l'unité de production pour l'amener aux niveaux requis pour le transport. A l'autre extrémité de la chaîne, côté consommateurs, les transformateurs sont utilisés pour abaisser la tension et la ramener aux valeurs utilisées dans les réseaux de distribution -BT-.

Outre la transmission de l'énergie électrique avec modification des tensions, les transformateurs peuvent être utilisés pour contrôler les tensions de noeuds des réseaux (Custem, 2002, I). Ce contrôle de tension utilise la variation du nombre de spire des transformateurs. La figure (12) montre le schéma équivalent du transformateur (sans circuit magnétique) : il est doté de plusieurs prises (côté haute tension) permettant de modifier le nombre de spires du primaire. L'impédance ZT correspond à l'impédance équivalente totale vue du primaire.

Dans certains transformateurs, la modification de spires requiert de mettre l'appareil hors service et de changer manuellement les connexions. Plus généralement, cette modification peut être effectuée en charge c.-à-d. sans interrompre le courant qui parcourt l'enroulement dont on modifie le nombre de spires. Le dispositif correspondant, appelé régleur en charge, comporte un contacteur conçu pour éviter la formation d'arcs électriques (susceptibles d'endommager les contacts) et un moteur électrique pour entraîner ce contacteur.

V1 ZT N1 N2 V2

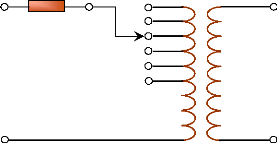
Figure 12. Modèle simplifié de transformateur.

Si N1 est le nombre de spires côté haute tension et N2 est le nombre de spires côté basse tension, le rapport de transformation M est défini par :

N

M = (15)

1

N 2

La relation entre la tension du côté primaire V1 et la tension du côté secondaire V2 à vide

est :

V V 1

2 = (16)

M

Si la tension du primaire diminue, la tension du secondaire peut être maintenue constante en diminuant le rapport M, c.-à-d. en effectuant un changement de prise du côté primaire. En charge, l'équation (15) n'est plus applicable à cause de l'impédance ramenée au primaire du transformateur ZT, mais le principe de fonctionnement reste le même (Andersson, 2006).

La figure (13) représente le schéma équivalent en ð du transformateur sans circuit magnétique (Milano, 2005). Dans notre étude, les régleurs en charge ne sont pas modélisés : ainsi le rapport de transformation reste fixe pendant les simulations dynamiques. Toutefois, nous en tenons compte lors du calcul d'écoulement de puissance, de manière à ce que les tensions restent dans leurs limites autorisées et que la convergence de l'algorithme de l'écoulement de puissance reste assurée (Tolba, 2005).

1. 3. 2. 2. 2- Modèle des lignes de transmission.

Les réseaux de transport assurent la liaison entre les centres de production et les zones de consommation. Ils permettent aussi d'échanger de la puissance à travers les lignes d'interconnexion, entre pays ou grandes zones relevant de gestionnaires de réseaux différents (Bornard et al., 2005).

Les modèles des lignes de transmission utilisés dans l'analyse dynamique des réseaux électriques sont habituellement classés en trois groupes, en fonction des longueurs des lignes, (longues, moyennes, courtes) (Sauer et al., 1998). Compte tenu des longueurs et de la fréquence de fonctionnement, typiquement 50-60 Hz, une ligne de transmission se caractérise par un modèle à constantes localisées (les phénomènes de propagation sont négligés car L << ë / 2ð, où ë est la longueur d'onde associée à la fréquence f). La structure la plus

employée pour ce modèle est le schéma équivalent en ð, figure (14). Il se caractérise par trois paramètres principaux (Kundur, 1994) :

- une résistance série R.

- une réactance constituée d'une inductance de série L due au couplage par champ magnétique entre les conducteurs.

- une capacité de shunt C due au couplage par champ électrique entre les conducteurs.

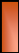
V1 Z / M V2

(1-M) / Z M (M-1) / Z

Figure 13. Modèle en ð du transformateur.
V1 R jX V2

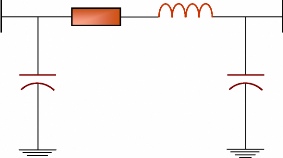
B / 2 B / 2

Figure 14. Modèle en ð d'une ligne de transmission. 1.3.2.3- Modèle des charges.

La charge représente :

- soit une charge matérielle réelle

- soit l'impédance d'entrée équivalente d'un système de puissance, non explicitement représenté dans le modèle du système.

En conséquence, lorsque les systèmes de puissance sont analysés, seuls les réseaux et les sous-réseaux de transport sont modélisés, tandis que les réseaux de distribution ne le sont habituellement pas : ils sont simplement remplacés par des charges équivalentes. Pour l'analyse de la stabilité, chaque charge représente habituellement une partie relativement importante du système comportant typiquement des réseaux de distribution de basse et moyenne tension, de faibles sources d'énergie fonctionnant au niveau de la distribution, les régulateurs de tension de distribution, ... . Elle inclut également les différentes charges réelles tels les moteurs, les éclairages et les appareils électriques (Machowski et al., 1998).

Les caractéristiques des charges ont une influence importante sur la stabilité et la dynamique du système. En raison de la complexité et la variation continuelle des charges et de la difficulté d'obtenir des données précises sur leurs caractéristiques, une modélisation précise des charges est très difficile. Ainsi, des simplifications sont indispensables selon le but de l'étude demandée. Pour les études de stabilité dans lesquelles la gamme de temps considérée est de l'ordre de 10 secondes après la perturbation, les modèles de charges les plus utilisés sont généralement des modèles statiques. Le caractère statique est lié à la description de la charge par des équations purement algébriques (Andersson, 2004).

Soit un noeud de tension VL, auquel une charge consommant une puissance PL + jQL est reliée. Cette charge peut être représentée par des admittances statiques GL = PL/ VL² et BL = QL/ VL ² comme le montre la figure (15), (Custem, 2002, I).

VL

PL , QL

GL

- jBL

Figure 15. Modélisation d'une charge par son admittance équivalente.

L'admittance équivalente de charge est calculée après avoir déterminé les données nécessaires de l'étude de l'écoulement de puissance :

P Q

Y = - (17)

L L

^L V

j

V 2 2

L L

1.3.2.4- Mise en équations du réseau de transport.

L'établissement du modèle généralisé du réseau de transport et des charges implique de déterminer les équations algébriques représentant les interconnexions entre les circuits des générateurs et l'ensemble des transformateurs, des lignes de transmission et des charges du

système. Le problème est ainsi de déterminer et de mettre en équations le fonctionnement du macro-modèle du réseau de transport. Le réseau électrique peut être décrit sous la forme matricielle suivante :

[I]=[Y]·[V] (18)

Où : [I] : le vecteur des courants injectés aux noeuds du réseau.

[V] : le vecteur des tensions aux noeuds du réseau.

[Y] : la matrice d'admittance du réseau de transport.

Les simplifications du réseau de transport permettent d'utiliser les modèles d'éléments du réseau précédent à savoir :

- les transformateurs, représentés par un schéma équivalent en ð.

- les lignes de transmission, représentés également par un schéma équivalent en ð.

Ces différents schémas en ð sont assemblés conformément à la topologie du réseau. A cet ensemble, nous ajoutons les admittances shunt représentant les charges ainsi que les réactances provenant des machines (Custem, 2002, II).

Commençons par la "construction" de la matrice admittance [Y]. Cette matrice se compose de termes diagonaux [Y] _ii et des termes non-diagonaux [Y] _ij , (Custem, 2002, I) :

- les termes [Y] _ii , (self admittance), représentent la somme de toutes les admittances

connectées aux noeuds i.

- les termes [Y] ij , (l'admittance mutuelle), représentent la somme de toutes les

admittances joignant les noeuds i et j, au signe près.

Partant de l'idée que tous les noeuds du réseau sauf les noeuds internes des générateurs n'ont pas d'injection de courant, le principe de la méthode de Kron peut ainsi être appliqué pour la réduction du réseau (Arthur R. Bergen et al., 2000).

Sachant que la somme de tous les courants dans chaque noeud de charge vaut zéro, les noeuds des charges dans l'équation (18) peuvent donc être éliminés. L'équation (18) s'écrit alors comme suit (Yu, 1983) :

? ?

? ?

=

? ?

? ?

? ?

L

? ? ?

??

I_n

0

Y Y

nn nr

M

Yrn

L L L

M

Yrr

?

?

?

? ?

·

? ? ?

??

L

V n

V_r

? ? ?

? ?

(19)

Où : n : l'indice des noeuds de générateurs.
r : l'indice des noeuds restants.

m : l'indice de tous les noeuds du réseau.

En décomposant l'équation matricielle (19), nous obtenons le système d'équations suivant :

· [ V r ]

(20)

[ ] [ ] [ ] [ ]

I Y V Y

n nn n nr

= · +

·

[ ] [ ]

+

0

]

· [ V n

Y V

rr r

[ ]

Y rn

Ce système d'équations peut être reformulé comme suit :

[ ] [ ] [ ] [ ] ¹ [ ]

Y bus = Y nn - Y nr · Y rr - · Y rn (22)

Où : [Ybus ] est la matrice d'admittance réduite du réseau électrique, car la dimension de cette matrice a été ramenée de m×m à n×n.

En introduisant l'équation (8) dans l'équation (21), nous obtenons :

[ ] [ ] [ [ ][ ] [ ][ ][ ]]

I Y E e j X X I e

= · + -

' '

j ä j ä (23)

m q d q q

Avec : [ ] ¹

[ ] [ ] ¹ [ ' ] -

Y m = Y bus - + j X d (24)

Où [ ] [ ] [ ^jâ ]

Y m = Y _m e représente la matrice de l'admittance totale du réseau électrique

réduit.

Le courant de la i^ème machine du réseau à n machines s'écrit dans le référentiel (D-Q) comme suit :

Ii

n j â ij ?= Y e mij j 1

( ) ' ^ä ( ' ) ä j E e j X X I e j j j + - qj dj qj qj

(25)

y compris le terme j = i.

Dans le référentiel (d-q)i de la i^ème machine, cette dernière équation devient :

n I I e Y e jE X X I - - ° + = = + - j ä â ä ( 90 ) ( ) ' ' i ij ij ?= ( ) j qj qj dj qj ( ) dqi i mij j 1

(26)

Avec ä ij = ä _j- ä _i

En décomposant l'équation (26), nous obtenons les expressions du courant de la ième machine suivant les axes direct et en quadrature :

n

Idi

Y mij

?

Re( )

I dqi

1

j

n

Iqi

Y mij

?

Im( )

I dqi

1

j

( )

- + -

S E X X C I

' '

ij qj qj dj ij qj

(27)

( )

( )

C E X X S I

' '

ij qj qj dj ij qj

+ -

( )

= +

cos( )

â ä

ij ij

=

sin

(â ä ij ij +

)

Avec :

C ij
S ij

(28)

L'ensemble de ces équations de courants complété par les équations de tension correspondantes (6) des machines, représente les équations de la partie algébrique du modèle d'état général présenté ultérieurement.

1.3.3- Les équations d'état généralisé du modèle.

Comme nous l'avons présenté dans la première partie de ce chapitre, un système de puissance est un système dynamique non-linéaire, qui peut être décrit par un ensemble d'équations différentielles ordinaires non-linéaires couplées du premier ordre et un ensemble

d'équations algébriques, où les formes générales de ces ensembles d'équations différentielles et algébriques peuvent être exprimées comme suit :

x i f _i x x x n i n

& K K

= =

( ₁ , ₂ , , ) ; 1,2, ,(29)

0 ( 1 , 2 , , ) = K h j x x x m

; 1,2, , j m = K(30)

Les équations différentielles correspondent aux fonctionnements dynamiques des générateurs, des systèmes d'excitation et des autres éléments du système. Les équations algébriques correspondent aux équations des réseaux de transport et des stators des générateurs. La solution de ces deux groupes d'équations détermine l'état électromécanique du système à chaque instant.

Nous rappelons ci-dessous les équations décrivant le modèle déduit du système de puissance :

1

ù& _i T T D

= ( ( 1))

mi - ei - i i -

ù (31)

2 H i

ä& i = ù0(ùi -1) (32)

E & = - - -

1 ' '

' ( ( ) )

E E X X I (33)

qi ' fdi qi di di di

T d i

0

E & = - + -

1 ( ( ) )

K V V U E (34)

fd a réf t S fd

T a

T = E ' I + ( X - X ' ) I I (35)

ei qi qi qi di di qi

V di = XqiIqi (36)

qi - X ' di I di (37)

'

V qi = E

V ti = V _di +V _qi (38)

2 2

?

Idi

))
C I

ij qj

· - ·

( S ij

E X X

' + - '

qj qj dj

(

· ·

Yï

n

j n

1

(39)

· ' + - '

E X X

qj qj dj

(

ij qj

I qi ? Yï · ( C ij j 1

· ·

La figure (16) représente les éléments du modèle du système de puissance avec leurs interactions.

L'approche finale de la modélisation du système de puissance implique une présentation de l'ensemble des équations de ce système sous forme d'équations d'état généralisées comme suit :

x & = f(x, u) (40)

y=g(x,u) (41)

Une telle forme représente un système invariant dans le temps (système autonome). Où :

,

? ? ? ? ? ?

?

1 ?

?

?

?

?

,

?

1 ?

2

n

2

m

&

x₁

&

& 2

x

?

x = M

&

x_n

? x
? x

x M

= ?

?

? ? x

? u ? f ?

1 ? 1

?u f 2 ? 2 = ? ? ? ? ? ?

? ? ? ?

u M

= , f M

? ? ? ?

? ur ? ? fn ?

? y
? y

y M

= ?

?

? ? y

? g
? g

2

?

1 ?

(42)

g M

= ?

?

m

? ? g

x : vecteur d'état du système de n variables.

x& : vecteur dérivé du vecteur x par rapport au temps.

u : vecteur de r signaux d'entrée du système.

f : vecteur de n fonctions non-linéaires reliant les variables d'état xi et les signaux d'entrée ui aux dérivées des variables d'état x& i .

y : vecteur de m signaux de sortie du système.

g : vecteur de m fonctions non-linéaires reliant les signaux d'entrée ui et les variables d'état xi aux variables de sortie yi.

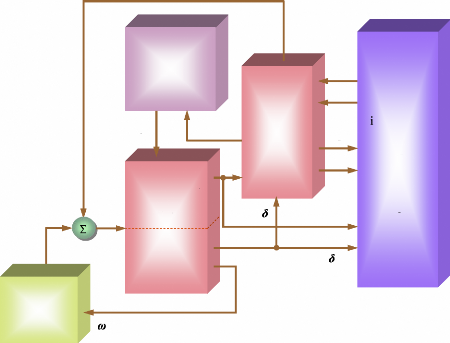
Turbine &
Gouverneur

P_m

F_m

+

F_e
_

F_a

Efd

Equations de

circuit du rotor

d'excitation &

Equations du

mouvement

Systèm e

AVR

k&

ù&

ä&

k& fd

q

'

Vt

E'_q

Equations
de circuit

du stator

P_e

Vd

V_q

Vt

E'_q

V_q

I_q

Vd

Id

Equations de

réseau de
transport

ncluant les

charges
statiques

Id

I_q

Figure 16. Digramme de l'ensemble des blocs du système de puissance.

Les variables d'état permettent de décrire complètement l'évolution dynamique du système par n équations différentielles de premier ordre. L'état et la sortie du système peuvent ainsi être calculés, à tout instant, pour des conditions initiales quelconques.

Quand les dérivées des variables d'état x sont égales à zéro, (c.-à-d. x& = 0), le système est à l'équilibre. Ainsi, ce point d'équilibre est le point auquel toutes les variables d'état sont constantes et le fonctionnement du système autour de ce point est dit linéaire. La détermination de modèle linéaire fait l'objet du paragraphe suivant.

1.4- Le modèle linéaire.

1.4.1- Introduction : Linéarisation du modèle.

La quasi-totalité des systèmes dynamiques réels possède des caractéristiques non- linéaires. Le comportement dynamique d'un système de puissance peut être décrit par un ensemble d'équations différentielles et algébriques (EDA). Compte tenu que le système de puissance, évolue généralement autour d'un point de fonctionnement donné lors des petites perturbations, il est possible de linéariser ses équations EDA autour de ce point.

Comme nous l'avons vu précédemment, le point de fonctionnement normal du système se définit comme un point d'équilibre ou une condition initiale. Les dérivées des variables d'état en ce point sont donc égales à zéro. L'équation (40) devient ainsi :

x&₀ =f(x₀,u₀)=0 (43)

Où : x0 est le vecteur des variables d'état correspondantes au point d'équilibre. u0 est le vecteur d'entrée correspondant au point d'équilibre.

Si une petite perturbation se superpose aux valeurs d'équilibre, l'équation (43) s'écrit : x x x f x x u u

& = & + Ä & = + Ä + Ä

0 ( 0 , 0 ) (44)

Puisque ces perturbations sont petites, l'équation (44) peut être développée en série de Taylor limitée aux termes de premier ordre.

Alors, nous obtenons pour chaque variable d'état :

? f f ? i i

(45)

r

?

i i

? f f

x x x f x u

& & & L L

= + Ä = +

0 ( ₀ , ₀ ) ? Ä + +

x ? Ä +

x ? Ä + +

u ? Ä u

x 1

x n

i i i i 1 n 1

u 1

? ? ? ? u r

Avec : i = 1,2, K , n .

Etant donné que, x & i 0 = f _i ( x ₀ , u ₀ ) = 0 , l'équation précédente peut être mise sous la forme suivante :

? f ? f

i f i ? i i

? f

Ä =

x & L L

? Ä + +

x ? Ä +

x ? Ä + +

u ? Ä u (46)

x x

1 n

i 1 n 1 r

¹

u r

? ? ? u ?

? g

?

?

?

Nous pouvons appliquer les mêmes étapes de linéarisation sur l'équation de la sortie (41) :

r (47)

j j

_g g j j

_g

Ä =

y ? Ä + +

x L 1 L

x

j 1 n

? ? ? ?

x u

1 n 1

u

? Ä +

x ? Ä + +

u ? Ä u

r

Avec : j = 1,2, K , m

Si le système fonctionne avec de petites perturbations au voisinage du point d'équilibre,

? f i

nous pouvons supposer que toutes les dérivées premières (,...) sont constantes dans le

? x i

domaine de fonctionnement.

Par conséquent, le système linéarisé peut être représenté par les deux équations suivantes:

Ä = ? Ä + + ? Ä + ? Ä + + ? Ä =

x a x a x b u b u i n

& L L K (48)

i i in n i ir r

1 1 1 1 , 1,2, ,

Ä = ? Ä + + ? Ä + ? Ä + + ? Ä =

y c x c x d u d u j m

j j jn n j jr r

1 1 1 1 , 1,2, , (49)

L L K

En écrivant ces deux équations sous forme matricielle, nous obtenons le modèle d'état linéaire final suivant :

Äx&=AÄx+BÄu (50)

Äy=CÄx+DÄu (51)

Avec:

1

L

1

1 L

? f ? f

1 1

L

r

? u

?u

M

1

L

M

? f n n

? f

L

r

m m

?g

,

,

? g
? u

M

? u r

?u

1

? u?u

r

A

C

Où:

? f 1 ? f 1

?

?

?

M ?

?

?

? ?

L

? x n

?x₁

M L

? f n n

? f

? x

n

L

? x 1

? g 1 1

L ? g

? x ? x 1 n
M	L	M

? g m m

1

? x?x

n

?g

? ? ? ? ? ?

??

B

D

?g

?u

M

?g

?

?

?

?

?

?

??

?

1 ?

?

?

?

?

??

(52)

(53)

A: matrice d'état (n×n).

B : matrice d'entrée (n× r).

C : matrice de sortie (m× n).

D : matrice de contrôle (m× r).

- Le nombre des variables d'état n définit la longueur du vecteur d'état Äx, le nombre de lignes et de colonnes de la matrice A, le nombre de lignes de la matrice B et le nombre des colonnes de la matrice C.

- Le nombre r des variables d'entrées choisies définit la longueur du vecteur d'entrée Äu et le nombre de colonnes des matrices B et D.

- Le nombre des variables de sorties choisies m définit la longueur du vecteur de sortie Äy et le nombre de lignes des matrices C et D.

- La matrice A est appelée matrice d'état ou matrice d'évolution, car elle contient la description du comportement dynamique du système. Elle rend compte aussi de l'évolution du système en régime libre, c.-à-d. à commande nulle.

- La matrice B est appelée matrice de commande ou matrice d'entrée. Elle rend compte du comportement dynamique du système en réponse à une commande.

- La matrice C est appelée matrice d'observation. Elle permet de relier la sortie à l'état.

- La matrice D est enfin appelée matrice d'action directe qui relie directement la

commande à la sortie. Elle est en général nulle dans les systèmes physiques ; le

système est dit "strictement propre" (Allenbach et al., 2005, II).

1.4.2- Application au système de puissance.

Lorsque le système de puissance est soumis aux petites perturbations, les variables d'état du système restent au voisinage de leurs valeurs initiales et la linéarisation du système peut être aisément appliquée (CIGRE, 1999).

Les variables d'état proposées pour notre système de puissance de n machines, représenté par l'ensemble des équations (31) à (34), sont :

x E E

[ , , ' , ] ^T

Ä = Ä ù Ä ä Ä Ä

i i i qi fdi

, 1, ,

i n

= K

(54)

Le développement du modèle linéaire de notre système, explicité dans l'annexe B, nous donne l'ensemble des équations suivantes :

? n n

1 ? 1

? D K K E '

ù& ù ₁ ä

Ä = ? Ä ? ? = Ä ? ? = Ä T (55)

i i i ij j

( ) ( ) ? + Ä

2 ij qj mi

2 H 2 H

i ? j 1 j 1 ? i

Ä ä i = ù0Äù i

& (56)

? ? ' & 1 ä n ^n 1 Ä = ? ? = Ä ? ? = Ä + Ä E ' ?? ( ) ( E E K ) ?? qi ' 4 ij j qj fdi T K doi ? j 1 3 j 1 ij ?

(57)

? n n ? ai

Ä = ? ? = Ä ? ? = Ä ? Ä

& 1 ä K

? K K K K E E

'

E ? + Ä U (58)

fdi ai ij j

( 5 ) ( )

ai ij qj

6 fdi Si

T T

ai ? j 1 j 1 ? ai

Les constantes de linéarisation _K1ij...K6ij sont des matrices carrées d'ordre n. Les valeurs de ces constantes dépendent des paramètres des générateurs, du réseau de transport et des conditions initiales du système. Les éléments diagonaux des matrices des constantes déterminent les propriétés dynamiques des machines, tandis que les éléments non-diagonaux représentent les interactions dynamiques entre les machines (Yu, 1983).

L'ensemble d'équations ci-dessus peut être représenté sous la forme de modèle linéaire correspondant à l'équation (50).

Ce modèle d'état linéaire sera donc utilisé pour analyser la stabilité du système.

1.4.3- Analyse du modèle linéaire. 1.4.3.1- Introduction.

L'analyse des valeurs propres et l'analyse modale du système de puissance linéarisé sont des outils "puissants" pour étudier les propriétés dynamiques du système. L'évaluation précise de la fréquence des oscillations électromécaniques et de l'amortissement de ces oscillations peut être déterminée à partir de l'analyse des valeurs propres ; l'analyse modale permet quant à elle d'obtenir des informations supplémentaires plus approfondies telle la nature des modes (dominants ou non, ...).

1.4.3.2- Valeurs propres.

Après avoir établi le modèle d'état linéaire correspondant à l'équation (47), la caractérisation de la stabilité du système peut se faire à partir de la matrice dynamique A et de ses valeurs propres (première méthode de Lyapunov).

Considérons un système linéaire défini par le modèle d'état (50), (51). En appliquant la transformation de Laplace à ces équations, nous obtenons l'ensemble d'équations suivant dans le domaine fréquentiel complexe :

sÄx(s) = AÄx(s) + BÄu(s) (59)

Äy(s) = CÄx(s) + DÄu(s) (60)

La solution explicite de cet ensemble d'équations est donnée comme suit :

Ä = ? ? Ä + Ä (61)

y ( s ) C ( sI A ) ¹ B u ( s ) D u ( s ) Où : I est la matrice d'identité.

Ainsi, la réponse dynamique du système est déterminée par l'équation caractéristique de la matrice d'état A définie par :

det(ë·I-A)=0 (62)

Les valeurs ë qui satisfont l'équation précédente sont appelées les valeurs propres du système. Une valeur propre définit le mouvement du système lié à une fréquence propre.

Une valeur propre -un mode- est caractérisée par une fréquence d'oscillation et un amortissement. Elle est représentée généralement par le nombre complexe suivant :

ë=ó#177;jù (63)

Cette relation est équivalente à la relation définissant les valeurs propres d'un système du deuxième ordre (Brogan et al., 2000). Par suite :

ë=-ù _n æ #177;jù _n 1 - æ (64)

2

Où : ó est la partie réelle de la valeur propre (abscisse de convergence). ù est la pulsation propre d'oscillation (rad/s).

ù_n est la pulsation naturelle d'oscillation (rad/s).

æ est le facteur d'amortissement d'oscillation.

Une matrice d'état de dimension n× n est associée à n valeurs propres.

L'analyse des valeurs propres permet d'obtenir tout d'abord la fréquence d'oscillation et le facteur d'amortissement.

La fréquence naturelle d'oscillation est donnée par la relation suivante :

ù

f = (65)

2 ð

Le facteur d'amortissement détermine la décroissance de l'amplitude d'oscillation. Il est donné par :

ó

-

=

(66)

ó ² ù ²
+

æ

Dans un modèle linéaire, la solution des équations linéaires du système décrit l'évolution exponentielle au cours du temps de la perturbation. Ainsi, cette solution peut être représentée par une combinaison de fonctions d'exponentielles e^ëit représentant les caractéristiques

temporelles associées à chaque valeur propre ëi. Les constantes de temps ô = 1/ó_i caractérisent de façon générale l'amortissement du système.

L'interprétation physique des signaux correspondants aux fonctions de la forme e^ëit est simple. Elle est illustrée par la figure (17) qui représente dans le plan complexe l'allure des variations de tels signaux en fonction du temps, suivant la position du point représentatif de ëi.

t

t

t

jù

t

ó

t

t

Figure 17. Analyse par lieu des pôles de la stabilité d'un système.

- Une valeur propre réelle correspond un mode non-oscillatoire. Si la valeur propre réelle est négative, les exponentielles apparaissant dans la réponse temporelle sont des fonctions décroissantes du temps. La rapidité de décroissance est liée à la constante de temps d'amortissement. Plus la valeur de l'abscisse de convergence ó est grande, plus la constante de temps est faible et l'amortissement rapide.

- Par contre, si la valeur propre réelle est positive, le mode présente une instabilité apériodique.

- En revanche, les valeurs propres complexes, en paires conjuguées, correspondent aux modes oscillatoires. Le mode oscillatoire peut être divergent, c.-à-d. instable, si la partie réelle de la valeur propre est positive, il est au contraire amorti, c.-à-d. stable, si la partie réelle est négative.

Cette analyse révèle qu'il est possible de déterminer la nature (stable ou instable) d'un système linéaire à partir d'une "inspection" de la position des pôles de la fonction de transfert du système dans le plan complexe. En outre, la connaissance de la position des pôles peut fournir des renseignements sur le comportement du système lors de régimes transitoires typiques tels que la réponse à une impulsion, à un échelon, ... .

Des modes instables ou mal amortis peuvent être dominants : leurs contributions déterminent alors l'allure de la réponse temporelle globale du système.

Dans les réseaux électriques, il est évidemment nécessaire que tous les modes du système soient stables c.-à-d. placés dans la partie gauche du plan complexe.

1.4.3.3- Analyse modale.

Comme nous l'avons vu, les valeurs propres du système déterminent les caractéristiques dynamiques du système (fréquences et facteurs d'amortissement) ainsi que l'état de stabilité du système.

L'analyse des vecteurs propres, qui découle de l'analyse des valeurs propres, peut aussi fournir d'autres informations importantes.

Lorsqu'une instabilité ou un mode mal amorti prend naissance dans un système de puissance, il est très intéressant d'examiner les points suivants (Custem, 2002, I; Breulmann et al., 2000) :

- les variables d'état liées aux modes dominants.

- les éléments du système permettant d'agir efficacement pour le stabiliser. - les groupes cohérents de générateurs présentant des oscillations couplées. - les signaux les plus efficaces à appliquer aux contrôleurs.

- les paramètres des contrôleurs réalisant un "meilleur" amortissement.

L'analyse modale présentée par la suite concerne les vecteurs propres, les facteurs de participation et les résidus.

1.4.3.3.1- Vecteurs propres.

Le modèle linéaire d'un système de puissance peut être représenté, comme nous l'avons déjà expliqué, par un modèle d'état décrit par l'équation (50). Les vecteurs propres, à droite et à gauche, de la matrice d'état du système peuvent être calculés par les équations suivantes :

A? i = i ë? _i (67)

ø _i A= _i ëø _i (68)

Où : ëi est une i^ème valeur propre (toutes les valeurs propres étant supposées distinctes). öi est le i^ème vecteur propre à droite associé à ëi.

øi est le i^ème vecteur propre à gauche associé à ëi.

Pour une matrice d'état de dimension nx n, le vecteur propre à droite est un vecteur colonne de dimension nx 1, tandis que le vecteur propre à gauche est un vecteur ligne de dimension 1x n. Les deux vecteurs sont définis comme suit :

? ?1i ? ? ?2i ? M = i ? ? ? ?ni

? ? ? ? ? ?

, øi = [ø1i ø2i L ø n i ] (69)

La relation caractéristique entre les vecteurs propres à droite et à gauche est déterminée par leur produit matriciel. Le produit matriciel entre deux vecteurs propres, à droite et à

gauche, associés à deux valeurs propres différentes vaut zéro. Par contre, lorsque les deux vecteurs propres correspondent à la même valeur propre, leur produit matriciel normalisé vaut 1. Ces propriétés peuvent se résumer de la façon suivante :

?? 0 ; i j

?

ø ? (70)

i j 1 ;

= i j

? =

L'ensemble des vecteurs propres à droite du système forme la matrice modale à droite, donnée comme suit :

Ö = [ ? 1 L ? i L? _n ] (71)

De même, la matrice modale à gauche est formée des vecteurs propres à gauche :

Ø = ø 1 T L ø L ø

[ ]T

T T

i n (72)

Le vecteur propre à droite, q'i, montre l'influence relative de chaque variable d'état dans un mode excité donné. Ainsi, pour un vecteur propre à droite complexe, l'amplitude relative des éléments du vecteur indique le degré de participation des variables d'état au mode considéré. Quant à la phase des éléments du vecteur, elle donne le déphasage des variables d'état dans le mode donné.

En ce qui concerne le vecteur propre à gauche, Ji, il détermine l'ensemble des variables d'état participant relativement à la composition du i^ème mode. Il indique également la contribution de chaque variable d'état dans l'évolution du mode considéré.

Dans le plan complexe, le diagramme représentant les composantes d'un vecteur propre à droite, q'i, relatives aux différentes variables d'état est appelé le "mode shape" (Custem, 2002, II). Dans un système de puissance multimachines, le mode shape indique la façon dont les générateurs oscillent les uns par rapport aux autres, les deux cas limites étant les oscillations cohérentes et les oscillations en opposition de phase (Bragasson, 2005). Ainsi, les modes shapes du système peuvent identifier les groupes cohérents des générateurs. En outre, le mode shape peut confirmer le type de chaque mode. (Local ou interrégional).

1. 4.3. 3.2- Facteur de participation.

L'approche standard, habituellement employée pour évaluer la participation d'une variable d'état xk dans le i^ème mode, étudie les éléments correspondants du vecteur propre à droite q'i. Bien que cette méthode soit simple à employer, elle présente un défaut très sérieux, à savoir les valeurs numériques des éléments des vecteurs propres à droite dépendent des unités des variables d'état correspondantes. Il est donc difficile de comparer les valeurs obtenues pour des variables d'état différentes. Par conséquent cette méthode est seulement exploitable pour des variables d'état ayant les mêmes unités et jouant les mêmes rôles (PérezArriaga, 1981).

Rappelons qu'un vecteur propre à droite q'i mesure l'influence relative de chaque variable d'état xk dans un i^ème mode et qu'un vecteur propre à gauche Ji indique la contribution de l'activité de xk dans le i^ème mode. Par conséquent, une "quantité" caractéristique d'un mode donné peut être obtenue par produit, élément par élément, d'un vecteur propre à droite et d'un vecteur propre à gauche correspondant. Cette quantité, appelée le facteur de participation, est calculée par la relation suivante :

Ainsi, le facteur de participation peut fournir des informations fines sur le problème : il représente une mesure relative de la participation de la k^ème variable d'état dans le i^ème mode, et vice versa (Hsu et al., 1987; Kundur, 1994).

Etant donné que les matrices modales, à droite et à gauche, Ö et Ø sont inverses, le facteur de participation est donc une grandeur sans dimension. Ceci veut dire que le facteur de participation, au contraire du vecteur propre à droite, est indépendant des unités des variables d'état.

Les facteurs de participation peuvent être regroupés dans une matrice, appelée matrice de participation P telle que :

Ñ = [ p ₁p₂ L p_i L p _n ] (74)

Avec :

M

ö ø

ni in

M ?

?

?

p₁ i

Ñ_i

p₂ i

pni

ö₁

ö₂

ø ii

ø ii

?

1 ?

2

(75)

?

?

?

?

Dans la matrice de participation P, comme le montre l'équation (76), la j^ème colonne indique comment un j^ème mode participe relativement à l'évolution des variables d'état du système tandis que la i^ème ligne indique comment les différents modes participent relativement à l'évolution de la i^ème variable d'état (Custem, 2002, II).

p₁

m

x₁

M

M (76)

?

?

?

?

?

?

M

p11

L L

O

O

M

Ñ_i

O

O

M

M

p p

n nm

L L

1

x_n

ë L L 1

ëm

Une autre propriété intéressante du facteur de participation _pij s'interprète souvent comme la sensibilité du j^ème mode aux changements des termes diagonaux _aii de la matrice d'état du système A, (Van Ness et al., 1994).

Pour les études de stabilité aux petites perturbations, l'influence d'une source d'amortissement appliqué à un générateur peut être déterminée par les facteurs de participation, comme suit (Rogers, 2000) :

- si, pour n'importe quel mode, le facteur de participation correspondant à la vitesse du générateur est nul, l'introduction d'une source d'amortissement au générateur n'aura aucun effet sur le mode.

- si le facteur de participation est réel positif, l'ajout d'amortissement à ce générateur augmentera l'amortissement du mode.

- en revanche, si le facteur de participation est réel négatif, l'amortissement ajouté au générateur réduira l'amortissement du mode.

En outre, les facteurs de participation, par leur propriété de pouvoir déterminer les variables d'état responsables des modes indésirables, peuvent être employés pour trouver les points les plus efficaces pour installer des contrôleurs de stabilisation.

La matrice de participation peut montrer aisément les variables d'état les plus impliquées dans le mode indésirable : les termes de la matrice P de plus grande amplitude de la colonne relative au mode considéré indiqueront la participation en question.

1.4.3.3.3- Résidus.

L'efficacité du signal d'entrée d'un contrôleur de stabilisation ou l'emplacement optimal de ce dernier dans un système de puissance multimachines peuvent être identifiés par la méthode des résidus. Cette méthode est dérivée de la relation entre la fonction de transfert et le modèle d'état.

Le modèle d'état d'un système représente à la fois les propriétés d'entrée/sortie du système et le comportement interne du système. A l'inverse, la fonction de transfert du système ne concerne que la relation entrée-sortie du système.

Pour déterminer la relation entre la fonction de transfert et le modèle d'état, nous prenons les équations (50) et (51) pour un système monovariable (Single Input- Single Output system), et nous considérons la fonction de transfert entre les variables y et u.

Supposons que D = 0, les équations d'état s'écrivent comme suit :

Äx&=AÄx+BÄu (77)

Äy=CÄx (78)

y s

La fonction de transfert Ä s'écrit de la façon suivante :

( )

Ä u s

( )

(79)

( ) -

Ä y s

( )

G s C sI A B

1

= = -

( )

Ä u s

( )

Pour un système en boucle ouverte, la fonction G(s) peut être décomposée en éléments simples comme suit :

n n

R R R R R

1 2 n i

G s

( ) = + + +

L = ? ?

i = (80)

( ) ( ) ( ) ( ) ( )

s s

- s s

- s s

- = = -

s s

-

n i i i ë _i

s

1 2 1 1

Où :

s : l'opérateur de Laplace.

s1, s2, ...,s_n : les pôles de G(s) - les valeurs propres du système-. Ri : le résidu de G(s) au pôle si.

Le résidu peut s'exprimer par la relation suivante (Kundur, 1994):

R _i =C Ö _i Ø _i B (81)

D'après cette relation, nous remarquons que le résidu Ri pour un mode ëi donné mesure la sensibilité de ce mode à un signal de contre-réaction sortie-entrée. Ainsi, les résidus peuvent déterminer les modes les plus affectés par un signal de retour.

La figure (18) montre un système G(s) équipé d'un contrôleur en contre-réaction de fonction de transfert H(s).

Système

u(s) +

-

G(s)

H(s)

Régulateur

y(s)

Figure 18. L'ensemble système-contrôleur en boucle fermée.

Lorsqu'on ferme la boucle par un régulateur H(s), les valeurs propres du système initial G(s) vont se déplacer. Le déplacement de ces valeurs propres peut être calculé par l'équation suivante (Aboul-Ela et al., 1996) :

Äë i = RiH(ë _i ) (82)

Cette équation montre que le déplacement des valeurs propres, créé par le contrôleur, est proportionnel aux amplitudes des résidus correspondants.

Pour un système multivariables, l'influence du même contrôleur H(s), (sans se soucier de sa structure et de ses paramètres) peut être étudiée en différents emplacements. Si le résidu, associé à un mode ëi donné, est calculé pour chaque emplacement, le résidu le plus élevé indique donc l'emplacement le plus efficace du contrôleur (Pagola et al., 1989). De même, en changeant le signal d'entrée du contrôleur, différentes valeurs des résidus vont être obtenues. Par conséquent, le résidu le plus élevé indique le signal d'entrée le plus efficace.

1.5- Conclusion.

Dans ce chapitre, nous avons présenté la modélisation du système de puissance pour les études de la stabilité aux petites perturbations. Nous avons aussi présenté la linéarisation du système avec l'analyse modale du modèle linéaire du système. Les points d'étude principaux de ce chapitre sont présentés ci-dessous :

- Le modèle choisi pour chaque machine synchrone du système est du troisième ordre. Les équations différentielles de la machine sont décrites par les trois variables d'état : ä, ù et E'_q. Ce modèle convient bien pour les études de stabilité angulaire aux petites perturbations.

- Le système d'excitation et la turbine et leurs régulateurs sont aussi modélisés.

- Le modèle généralisé du réseau de transport et des charges est déterminé. Dans ce modèle, les circuits de stators des machines, les transformateurs, les lignes de transmission et les charges sont représentées sous forme d'équations algébriques.

- le système est représenté par un ensemble d'équations, couplées, différentielles et algébriques. Ce modèle décrit le comportement non-linéaire du système de puissance.

- Le système de puissance est souvent soumis à des petites perturbations qui se produisent continuellement sous l'influence de faibles variations de charges et des sources. Ces perturbations sont considérées comme suffisamment petites pour permettre de linéariser les équations du modèle général du système. La représentation d'état du système est ensuite déduite.

- La stabilité du système est uniquement définie par le lieu des pôles, dans le plan complexe, de sa fonction de transfert.

- L'analyse modale du système donne des informations importantes concernant les caractéristiques des modes d'oscillations, les variables d'état participant à l'évolution de ces modes, ... .

Après avoir enfin présenté les modèles linéaire et non-linéaire du système, nous présentons dans le chapitre suivant les différents types de stabilité du système de puissance et plus particulièrement la stabilité angulaire aux petites perturbations objet de notre travail.

Chapitre II

Stabilité du système de

puissance

2.1- Introduction.

La bonne performance d'un système de puissance dépend de sa capacité de fournir à tout moment la puissance demandée dans des conditions de qualité satisfaisantes, en maintenant les niveaux de tension et de fréquence dans des limites acceptables.

La stabilité est considérée l'une des trois grandes études des systèmes de puissance, les deux autres étant l'écoulement de puissance et l'analyse de défauts. Il est clair que les études de stabilité sont les plus complexes, tant en termes de modélisation que de méthodes de recherche des solutions.

La stabilité d'un système de puissance est la capacité du système, pour des conditions initiales données, de retrouver un point d'équilibre suite à une perturbation. Ainsi, la stabilité est une condition d'équilibre entre des "forces" opposées et l'instabilité résulte d'une perturbation menant à un déséquilibre important entre les "forces" opposées.

Cette instabilité peut avoir différentes formes et peut être influencée par différents facteurs. L'analyse des problèmes de stabilité implique l'indentification des facteurs essentiels contribuant à l'instabilité et le développement de méthodes pouvant améliorer la stabilité du système.

Le problème de la stabilité des systèmes dynamiques a été et reste le sujet de préoccupation majeur du travail des mathématiciens, des physiciens et des ingénieurs (Hahn, 1967; Parks et al., 1981).

Les critères d'analyse de stabilité peuvent être classés en deux grandes catégories :

- Les critères fréquentiels : tels les critères de Nyquist, le diagramme de Bode, ... . Ces critères dépendent de la fonction de transfert du système.

- Les critères temporels : tels les critères de Kalman, les méthodes de Lyapunov, ... . Ces critères dépendent du modèle d'état du système.

Une contribution majeure aux études de stabilité fut apportée par A.M. Lyapunov en 1892, dont les travaux ont été connus dans les années soixante. Il a introduit la majorité des concepts et définitions de base concernant la stabilité des systèmes représentés par des systèmes différentiels arbitraires mais a aussi fourni les principaux résultats théoriques.

La stabilité au sens de Lyapunov est une théorie générale valable pour tout système décrit par des équations différentielles linéaires ou non-linéaires.

Ce chapitre traite de la stabilité du système de puissance. Il est divisé en trois grandes parties. La première partie rappelle les principes de la stabilité au sens de Lyapunov. Dans la deuxième partie, nous rappelons les caractéristiques des différents types de stabilité d'un système de puissance. La troisième partie s'intéresse plus particulièrement à la stabilité angulaire aux petites perturbations avec les stabilisateurs de puissance (PSSs).

2.2- La stabilité au sens de Lyapunov. 2.2.1- Définitions de la stabilité.

Considérons un système non-autonome (dépendant du temps) et non-commandé (entrée nulle) décrit par l'équation différentielle non-linéaire :

x&(t) = f(x(t),t) (83)

Où : x est un vecteur d'état et x& sa dérivée dans le temps t.

Ce système est dit en équilibre autour d'un point x_e si, en l'absence d'influence externe, son état ne varie pas au cours du temps :

f(x_e,t) = 0 (84)

Ainsi, nous nous intéressons aux comportements des trajectoires du système au voisinage de ses points d'équilibre.

Nous rappelons dans ce qui suit quelques définitions importantes qui forment l'approche de la stabilité au sens de Lyapunov.

2.2.1.1- Stabilité du point d'équilibre.

Un point d'équilibre x_e est dit stable si, pour tout å > 0, il existe une valeur ä>0 tel que :

x(t₀) - x_e <ä x(t) - x_e <å ?t = t₀ (85)

Où, t0 est l'instant initial.

Dans le cas contraire, x_e est dit instable.

Ainsi, la stabilité au sens de Lyapunov signifie que la trajectoire x(t), avec une condition initiale x(t0), doit rester proche du point d'équilibre x_e (c.-à-d. x(t₀) - x_e <ä), pour tout t = t0. Pour cela, les solutions x(t) doivent rester à l'intérieur de la région délimitée par x(t) - x_e < å , c.-à-d. rester dans un "tube" de rayon å autour de la trajectoire x(t) = x_e, figure (19), ( Fouad et al., 1991).

t

x(t)

t0

Figure 19. Stabilité d'un point d'équilibre.

2.2.1.2- Stabilité asymptotique.

Un point d'équilibre est asymptotiquement stable s'il est stable et si :

lim ( ) - =

_t x t x

?8 e

0 (86)

La stabilité asymptotique signifie que non seulement le point d'équilibre est stable, mais qu'on est aussi capable de déterminer un domaine proche du point d'équilibre tel que n'importe quelle trajectoire, issue d'un état initial x(t0) appartenant à ce domaine, tende vers x_e quand t tend vers 8, figure (20), ( Fouad et al., 1991).

t

x(t)

t0

Figure 20. Stabilité asymptotique.

Un ensemble d'états initiaux x(t0) à partir desquels les trajectoires convergent vers un point d'équilibre asymptotiquement stable est appelé un domaine d'attraction D.

La stabilité asymptotique est la propriété généralement recherchée en pratique. Il faut cependant remarquer que la définition ci-dessus ne donne pas d'information sur la vitesse à laquelle la trajectoire x(t) converge vers l'équilibre. C'est pourquoi, on introduit la notion de stabilité exponentielle qui permet de caractériser cette vitesse.

2.2.1.3- Stabilité exponentielle.

Un point d'équilibre est exponentiellement stable si pour tout å > 0, il existe des constantes a>0, b)>0 et ä>0 tel que :

x(t₀) - x_e <ä ( ) - < · ( ₀ ) - · ? t = t₀ (87)

bt

x t x e a x t x _e e -

Cette stabilité signifie que le vecteur d'état, pour une condition initiale x(t0), converge vers un point d'équilibre x_e plus rapidement qu'une fonction exponentielle ; b est appelé le taux de convergence. Par ailleurs, la stabilité exponentielle implique la stabilité asymptotique qui implique elle-même la stabilité d'un point d'équilibre. La figure (21) illustre schématiquement la définition de la stabilité exponentielle (Miller et al., 1982).

2.2.2- Méthodes d'analyse de stabilité au sens de Lyapunov. 2.2.2.1- Première méthode de Lyapunov (méthode indirecte).

La première méthode de Lyapunov se base sur l'analyse du comportement du système linéarisé autour de son point d'équilibre. Plus précisément, on examine les valeurs propres ëi du système de la matrice Jacobienne (la matrice d'état) A évaluée au point d'équilibre x_e :

A	? f				(88)
	? x x		=	xe

Les caractéristiques de stabilité de cette méthode ont été expliquées dans le premier chapitre (§§-1.4.3.2). Nous les rappelons ci-dessous :

- si toutes les valeurs propres de la matrice d'état sont à partie réelle strictement négative (?i, Réel(ë_i (A)) < 0), le système est exponentiellement stable à son point

d'équilibre. Dans ce cas, on a e

lim ?8 ( ) .

_t x t = x

- si la matrice d'état possède au moins une valeur propre à partie réelle strictement

.

positive ( ? i, Réel(ë_i (A)) > 0), le système est instable. Dans ce cas, on a = 8

lim ?8 x ( t )

t

La première méthode est simple à appliquer mais étant donné que cette méthode repose sur une linéarisation du système, sa validité est alors limitée à un certain voisinage du point d'équilibre. Lorsque la linéarisation du système n'est pas possible ou lorsqu'on veut analyser le système sans le résoudre explicitement, on utilise la deuxième méthode de Lyapunov (Slotine et al., 1991).

-

t

a e - · -

·

b ( t t₀ )

a

a e - · -

·

b ( t t₀ )

t0

Figure 21. Stabilité exponentielle. 2.2.2.2- Deuxième méthode de Lyapunov (méthode directe).

La deuxième méthode de Lyapunov s'appuie sur une observation physique fondamentale :

Si l'énergie totale d'un système, linéaire ou non-linéaire, est continûment dissipée (on parle de système dissipatif), alors le système doit tendre finalement vers un point d'équilibre.

Ainsi, l'idée de Lyapunov, pour étudier la stabilité d'un système donné, est d'examiner la variation d'une seule fonction scalaire (appelée la fonction de Lyapunov) dépendant de l'énergie totale du système (Khalil, 1996). Autrement dit, cette méthode est basée sur la définition d'une fonction de Lyapunov décroissante le long des trajectoires du système à l'intérieur du domaine d'attraction. Cette méthode s'énonce comme suit (Custem, 2002, II) :

Le point d'équilibre x_e est stable s'il existe dans un certain voisinage ? de ce dernier une

fonction de Lyapunov V(x) telle que :

· V(x_e)=0

· V(x_e)>0 pour tout x dans ?

· V(x)=0

d dans ?

dt

Les deux premières conditions expriment la présence de surfaces fermées entourant le point d'équilibre x_e. La troisième condition exprime que les trajectoires du système soit restent sur ces surfaces, soit coupent les surfaces en entrant à l'intérieur d'elles, d'où la stabilité du point d'équilibre.

La deuxième méthode de Lyapunov permet, outre l'analyse de stabilité d'un point d'équilibre du système, de déterminer une partie de son domaine d'attraction en ce sens que ? est inclus dans D.

2.2.3- Conclusion.

Dans cette partie, nous avons rappelé les définitions de la stabilité au sens de Lyapunov. Nous avons également présenté les méthodes d'analyse de la stabilité d'un système linéaire (1^ère méthode de Lyapunov) et d'un système non-linéaire (2^ème méthode de Lyapunov).

Dans la partie suivante, nous allons exposer les définitions et les principales caractéristiques des différents types de la stabilité de système de puissance.

2.3- Les différents types de la stabilité de système de puissance.

Pendant des années, des recherches diverses et complexes étaient effectuées pour comprendre les problèmes de stabilité des systèmes de puissance. Ainsi de nombreuses définitions de la stabilité de systèmes de puissance étaient proposées en insistant sur les divers aspects qui reflètent la manifestation de l'état stable de système. La définition la plus récente, que nous adopterons, est le résultat d'un groupe de travail conjoint IEEE/CIGRE (IEEE/CIGRE, 2004).

La stabilité d'un système de puissance est la capacité d'un système d'énergie électrique, pour une condition de fonctionnement initiale donnée, de retrouver le même état ou un autre état d'équilibre après avoir subi une perturbation physique, en gardant la plupart des variables de système dans leurs limites, de sorte que le système entier reste pratiquement intact.

Ainsi un système de puissance possédant un état d'équilibre est considéré comme stable, si suite à une perturbation, le système peut encore retrouver une position d'équilibre. Le système est également considéré comme stable s'il tend vers une autre position d'équilibre située dans la proximité du point d'équilibre initial. Cela correspond aux propriétés de la stabilité du point d'équilibre au sens de Lyapunov.

La stabilité d'un système de puissance électrique représente la propriété du mouvement du système autour d'un état d'équilibre (c.-à-d. les conditions de fonctionnement initiale).

Dans un état d'équilibre, toutes les différentes forces opposées sont égales :

- soit instantanément : c'est le cas des points d'équilibre,

- soit périodiquement : c'est le cas des variations périodiques lentes en raison des petites fluctuations continuelles sur les charges ou la génération.

Ainsi, la stabilité d'un système de puissance dépend non seulement des conditions de fonctionnement initiales elle dépend également de la nature physique et de l'amplitude de la perturbation.

En raison de la taille, de l'importance et de la complexité des problèmes de stabilité, il est très intéressant de faire des simplifications et des hypothèses appropriées pour représenter analytiquement le système.

Pour analyser et résoudre les problèmes d'instabilité dans les systèmes de puissance, il est indispensable de regrouper les différents groupes de stabilité. Cette classification de la stabilité est basée sur les considérations suivantes (Kundur, 1994) :

- la nature physique de l'instabilité résultante.

- l'amplitude de la perturbation.

- la plage de temps nécessaire pour assurer la stabilité.

- les dispositifs et les processus nécessaires pour assurer la stabilité.

Habituellement, la stabilité est divisée en trois groupes, à savoir : - la stabilité de l'angle de rotor.

- la stabilité de tension.

- la stabilité de fréquence.

La figure (22) présente ces principales catégories de stabilité d'un système de puissance et leurs sous-catégories.

Stabilité dynamique

perturbations

Stabilité de

l'angle de

rotor aux
petites

Stabilité de l'angle
de rotor

de l'ordre de
10 à 20
secondes

court
terme

rotor aux
grandes
perturbations

Stabilité transitoire

Stabilité de

l'angle de

STABILITE DE SYSTEME
DE PUISSANCE

de l'ordre
de plusieurs
secondes

terme

court

Stabilité de la

fréquence

de l'ordre
de plusieurs
minutes

long
terme

Stabilité de

la tension
aux petites
perturbat ions

de l'ordre
de plusieurs
secondes

court
terme

Stabilité de la
tension

la tension
aux grandes
perturbations

Stabilité de

de l'ordre
de plusieurs
minutes

long
terme

Figure 22. Classification des différents types de la stabilité de système de puissance.

Traditionnellement, le problème de la stabilité a été de maintenir le fonctionnement synchrone des générateurs du système. Ainsi, pour avoir une production satisfaisante de la puissance électrique, toutes les machines synchrones du système doivent fonctionner en synchronisme. Cet aspect de la stabilité est influencé par les dynamiques de l'angle de rotor de générateur et de la relation puissance-angle.

L'instabilité peut également avoir lieu sans perte de synchronisme. Par exemple, un système composé d'un générateur alimentant un moteur à induction peut devenir instable en raison de l'effondrement de la tension de la charge. Dans ce cas, c'est la stabilité et le contrôle de la tension qui créent le problème, plutôt que le maintien du synchronisme. Ce type d'instabilité peut aussi se produire dans le cas de charges couvrant une vaste zone dans un grand système.

Un autre type d'instabilité peut avoir lieu : dans l'éventualité d'un fort écart entre la puissance de la charge et la puissance de la génération, les contrôleurs principaux des générateurs et de la charge deviennent importants. S'ils ne sont pas bien coordonnés, il est possible que la fréquence du réseau devienne instable. Des unités de générations et/ou de charges peuvent finalement être déclenchées en entraînant une panne du système. Dans ce cas, les générateurs peuvent rester en synchronisme mais le système devient instable.

2.3.1- La stabilité de l'angle de rotor. 2.3.1.1- Introduction.

Etant donné que la génération de puissance électrique dépend principalement des machines synchrones, un aspect important est le fonctionnement de ces générateurs au synchronisme (Custem, 2002, II). Au synchronisme, les rotors de chaque machine synchrone du système tournent à la même vitesse électrique et les angles entre les champs magnétiques, rotoriques et statoriques, restent constants.

En fonctionnement nominal équilibré, la puissance électrique fournie par le générateur aux charges est égale, en négligeant les pertes, à la puissance mécanique fournie par la turbine.

Quand le système est perturbé, la puissance électrique de la machine varie rapidement, mais la variation de puissance mécanique fournie à la machine est relativement lente. En raison de cette différence de vitesse de réponse, un écart temporaire d'équilibre de puissance a lieu. Par conséquent, ce déséquilibre de puissance entraîne une variation des couples agissant sur le rotor. Ceci entraîne une accélération ou décélération du rotor selon le sens du déséquilibre, voire un glissement du champ de synchronisme en entraînant une perte de synchronisme du générateur avec le reste du système (Basler et al., 2005). Si l'équilibre de puissance n'est pas rétabli, la machine est mise hors service par une protection de survitesse ou de perte de synchronisme, et la stabilité du système est mise en danger.

Suite à une perturbation au système, le facteur principal qui détermine l'évolution de l'état du système est l'écart entre les angles de rotor. (Les angles sont mesurés par rapport à une référence tournante au synchronisme). Nous pouvons dire que les angles de rotor d'un système de puissance peuvent évaluer selon deux scénarios (Anderson et al., 2003) :

- Soit, les angles de rotor s'accroissent ensemble et oscillent à l'unisson. Ils peuvent

éventuellement atteindre de nouvelles valeurs stables. Tant que les écarts entre les

angles de rotor restent constants, le système reste stable et il demeure au synchronisme.

- Soit, un ou plusieurs angles de rotor s'accroissent plus rapidement que les autres. Alors, les écarts entre les angles de rotor divergent dans le temps. Le système devient par conséquent instable et il perd le synchronisme.

Pour conclure, nous pouvons dire que :

La stabilité de l'angle de rotor concerne la capacité des machines synchrones d'un système de puissance interconnecté de rester en synchronisme suite à une perturbation. Elle dépend de la capacité de maintenir/restaurer l'équilibre entre les couples électromagnétique et mécanique agissant sur le rotor de chaque machine synchrone dans le système. L'instabilité qui peut résulter se produit sous forme d'augmentation des oscillations angulaires de certains générateurs pouvant conduire à une perte de synchronisme avec d'autres générateurs.

Suivant l'amplitude de la perturbation, nous pouvons caractériser la stabilité de l'angle de rotor en deux sous-catégories :

2.3.1.2- Stabilité angulaire aux grandes perturbations (stabilité transitoire).

Elle concerne la capacité du système de puissance de maintenir le synchronisme après avoir subi une perturbation sévère transitoire tel un court-circuit sur une ligne de transmission ou une perte d'une partie importante de la charge ou de la génération. La réponse du système implique de grandes variations des angles de rotor. Elle dépend de la relation non-linéaire couples- angles.

La stabilité transitoire dépend non seulement de l'amplitude des perturbations et du point de fonctionnement initial mais elle dépend également des caractéristiques dynamiques du système. Elle se manifeste à court terme sous forme d'un écart croissant de façon apériodique de certains angles de rotor. Si l'instabilité se manifeste directement suite à la perturbation (plus précisément dans la première seconde qui suit l'élimination du défaut), elle est appelée instabilité de première oscillation (First Swing Instability), (cas 1, figure (23)), et elle s'étend sur 3 à 5 secondes. L'instabilité transitoire peut aussi se manifester autrement. Elle peut résulter de la superposition des effets de plusieurs modes d'oscillation lents excités par la perturbation, provoquant ainsi une variation importante de l'angle de rotor au-delà de la première oscillation (instabilité de multi-oscillations), (cas 2, figure (23)). La gamme de temps associée va de 10 à 20 secondes.

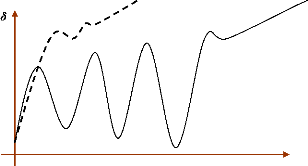
t (s)

Cas 2

Cas 1

Figure 23. Variation d'angle de rotor.
Cas 1 : instabilité de première oscillation. Cas 2 : instabilité de multi-oscillations.

Le concept de stabilité transitoire peut être expliqué par une approche graphique simple, à savoir le critère d'égalité des aires (Equal Area Criterion). Cette approche regroupe l'équation du mouvement et la courbe (P-ä) traditionnelle représentant la relation entre la puissance produite par le générateur et l'angle de rotor (Bergen et al., 2000).

Pour expliquer cette approche, nous prenons un système de puissance simple constitué d'un générateur synchrone connecté à un jeu de barre infini via une ligne de transmission, figure (24). Le générateur est modélisé par une source de tension idéale E_g en série avec une réactance X_g (modèle classique). La ligne et le transformateur sont représentés par la réactance XE.

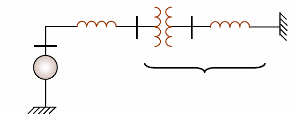
E_g?ä

X_g ETB ETH

X_L

X_T

X_E = X_T + X_L

E_o?0

Figure 24. Machine synchrone connectée à un jeu de barre infini. 1- Relation (P-ä) :

Dans l'état équilibré, la puissance produite par le générateur P_e est donnée par l'équation suivante :

E E

·

P (89)

g 0 · sin ä

^e X X

g

=

+ _E

Où, ä, l'angle de rotor (dit ici, l'angle de puissance), est le déphasage entre la tension interne du générateur (E_g) et la tension du jeu de barre infini (E0). L'équation (89) est représentée graphiquement à la figure (25).

P Pe max Pe 2 Pe 1

0° ä_a äb 90° 180°

Figure 25. Relation puissance- angle de rotor.

äb
ä_a

Lors de l'équilibre, la puissance électrique _Pe1 est égale à la puissance mécanique appliquée pour l'angle correspondant ä_a.

Un brusque changement sur la charge du générateur entraîne une variation de la puissance mécanique, et par conséquent de la puissance électrique, par exemple de _Pe1 ^à _Pe2, figure (25). Le rotor va donc accélérer de sorte que l'angle de puissance augmente, de ä_a à äb, pour pouvoir fournir une puissance supplémentaire à la charge. Cependant, l'accélération du rotor ne peut pas s'arrêter instantanément. Ainsi, bien que la puissance développée pour l'angle äb soit suffisante pour la charge, le rotor va dépasser l'angle äb jusqu'à ce qu'un couple opposé suffisant soit développé pour arrêter cette accélération. L'énergie supplémentaire va entraîner le ralentissement du rotor et la diminution de l'angle de puissance. Suivant l'inertie et l'amortissement du système, les oscillations de l'angle de rotor résultant vont ou s'amortir, et la machine restera stable (cas 1, figure (26)), ou diverger, et la machine deviendra instable en perdant le synchronisme avec le système (cas 2, figure (26)).

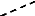
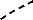
Cas 2
instable

Cas 1
stable

t (s)

Figure 26. Variation d'angle de rotor. 2- Critère d'égalité des aires :

Considérons un défaut, tel un défaut sur la ligne de transmission, appliqué au système précédent disparaissant après quelques périodes du système. Ceci va modifier l'écoulement de puissance et, par conséquent, l'angle de rotor ä. Retraçons la courbe (P-ä) en tenant compte de ce défaut, figure (27). En dessous de cette courbe, nous pouvons considérer deux zones, (Gholipour Shahraki, 2003) :

- La première zone (zone A1, zone d'accélération) se situe au-dessous de la droite horizontale correspondante au point de fonctionnement initial (la droite de charge). Elle est limitée par les deux angles de rotor (ä0 et ä1) correspondants à l'apparition et à la disparition de défaut. Cette zone est caractérisée par l'énergie cinétique stockée par le rotor du fait de son accélération : P_m > P_e.

- La deuxième zone (zone A2, zone de décélération), qui commence après l'élimination du défaut, se situe en dessus de la droite de charge : elle est caractérisée par la décélération du rotor : P_m < P_e.

^o P P

( m e

-

2 H

) (90)

d 2

dt

2

Si le rotor peut rendre dans la zone A2 toute l'énergie cinétique acquise durant la première phase, le générateur va retrouver sa stabilité. Mais si la zone A2 ne permet pas de restituer toute l'énergie cinétique, la décélération du rotor va continuer jusqu'à la perte de synchronisme.

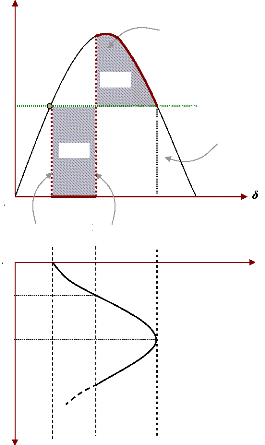
0° ä0 ä1

ä2 180°

a

P

Région stable

aire 1 A2

P_m = P_e

Région instable

aire A1

Apparition
de défaut

Disparition
de défaut

0 ä

t1

t2

t

b

Figure 27. Courbes (a : puissance-angle) et (b : variation d'angle de rotor) du générateur
suite à un défaut de transmission.

La relation entre les aires des zones (A1 et A2) et la stabilité transitoire peut être mathématiquement expliquée comme suit :

Rappelons tout d'abord que l'équation du mouvement de générateur est donnée par la relation suivante :

H : la constante d'inertie.

ù_o : la vitesse de synchronisme.

P_m : la puissance mécanique fournie au générateur. P_e : la puissance électrique du générateur.

dä

En multipliant cette équation par 2· , en intégrant par rapport au temps et en faisant

dt

un changement de variables, nous obtenons :

? 2

2 ä

d ä ù

?

? ? ?? + = ? - ·

cte o (91)

( )

P P d ä m e

dt H

ä 0

ä0 : l'angle de rotor, initial, à l'instant de l'application de défaut. ä2 : l'angle de rotor à la fin de la période transitoire.

dä

Ainsi, lorsque : t = = =

0 0 ,

ä ä 0 la constante cte = 0.

dt

Après l'élimination du défaut, l'angle ä va s'arrêter de varier et le générateur va retrouver

dä

sa vitesse de synchronisme, lorsque = 0.

dt

Par conséquent, l'équation (91) s'écrit comme suit :

ä₂

? ( ) 0

P _m P _e dä (92)

- · =

ä 0

ä 1 ä 2

(93)

? - · + ? - · =

( ) ( ) 0

P _m P _e d ä P _m P _e d ä

ä 0 ä 1

Où : ä1 est l'angle de rotor à l'instant de l'élimination de défaut.

A₁-A₂=0 (94)

Ainsi, la limite de la restauration de la stabilité transitoire se traduit mathématiquement par l'égalité des aires de la zone A1 et de la zone A2 : cette condition est appelée critère d'égalité des aires (Equal Area Criterion).

Par conséquent, les contrôleurs de la stabilité transitoire peuvent améliorer la stabilité soit en diminuant la zone d'accélération (zone A1), soit en augmentant la zone de décélération (zone A2). Cela peut être réalisé soit en augmentant la puissance électrique, soit en diminuant la puissance mécanique.

En outre, un système statique d'excitation avec une tension maximale élevée et d'un régulateur de tension possédant une action "puissante" et rapide représente un moyen très efficace et économique pour assurer la stabilité transitoire (CIGRE, 1999). Enfin, une amélioration signifiante de la stabilité transitoire est obtenue avec des systèmes très rapides de détection des défauts et de disjoncteurs.

2.3.1.3- Stabilité angulaire aux petites perturbations (stabilité dynamique).

Elle se définie par la capacité du système de puissance de maintenir le synchronisme en présence des petites perturbations. L'instabilité résultante se manifeste sous forme d'un écart croissant, oscillatoire ou non-oscillatoire, entre les angles de rotor.

La stabilité aux petites perturbations dépend du point de fonctionnement d'équilibre initial du système ainsi que des caractéristiques dynamiques du système. Contrairement à la stabilité transitoire, elle ne dépend pas de niveaux de perturbations, car celles-ci sont arbitraires et infiniment petites (Custem, 2002, II).

La relation puissance-angle (89) est une relation non-linéaire en sinus. Mais pour des petites perturbations, la variation de puissance reste approximativement proportionnelle à la variation de l'angle ä. Des exemples typiques des petites perturbations peuvent être donnés par des variations de niveau de 10 % de la puissance mécanique appliquée à une machine du système ou sur sa charge,... (Anderson et al., 2003).

La stabilité transitoire, comme nous l'avons vu, est associée à la présence d'un couple synchronisant suffisant, immédiatement après la perturbation. Si le système est transitoirement stable, la stabilité aux petites perturbations sera associée à la présence d'un couple d'amortissement à la suite de la première oscillation. Si ce couple est suffisant, les oscillations s'amortiront (amortissement positif). Par ailleurs, si l'amortissement n'est pas suffisant, les oscillations vont continuer, ou même elles vont augmenter (amortissement négatif c.-à-d. manque de couple d'amortissement).

La perte de synchronisme peut avoir lieu entre une machine et le reste du système (provoquant une instabilité locale), ou bien entre des groupes des machines, dans lesquels chaque groupe peut garder son synchronisme (désignant une instabilité globale).

L'instabilité aux petites perturbations se manifeste à court terme, la gamme de temps associée étant de l'ordre de 10 à 20 secondes.

Ce type de stabilité va être étudié en détail dans la partie (§§-2.4) de ce chapitre. 2.3.2- La stabilité de tension.

La stabilité de tension, par définition, se rapporte à la capacité d'un système de puissance, pour une condition de fonctionnement initiale donnée, de maintenir des valeurs de tensions acceptables à tous les noeuds du système après avoir subi une perturbation. La stabilité de tension dépend donc de la capacité de maintenir/restaurer l'équilibre entre la demande de la charge et la fourniture de la puissance à la charge. L'instabilité résultante se produit très souvent sous forme de décroissance progressive de tensions à quelques noeuds.

Suite à une perturbation, certaines charges ont tendance à restaurer la puissance consommée avant perturbation. C'est le cas des moteurs asynchrones, des charges dont la tension est contrôlée par un régleur en charge automatique, des chauffages électriques commandé par thermostat, ... . Il existe une puissance maximale transmissible entre les centres de production et ceux de consommation. Cette puissance maximale disponible dépend non seulement des caractéristiques du réseau de transport (distances électriques) mais également de celles des générateurs (possibilité de maintenir la tension grâce à une réserve de puissance réactive suffisante). Par conséquent, si la puissance que les charges tendent à

restaurer devient supérieure à la puissance maximale transmissible, le mécanisme de restauration des charges va contraindre le réseau haute tension en augmentant la puissance réactive consommée et en faisant donc baisser progressivement la tension du réseau jusqu'à des valeurs inacceptables (Custem, 2002, II).

Généralement, l'instabilité de tension se produit lorsqu'une perturbation entraîne une augmentation de puissance réactive demandée au-delà de la puissance réactive possible.

Plusieurs changements dans le système de puissance peuvent contribuer à l'instabilité de tension, ce sont par exemple :

- une augmentation de charge.

- des générateurs, des condensateurs synchrones, ou des SVCs (Static Var Compensator systems) qui atteignent les limites de puissance réactive.

- une tentative d'un régleur automatique en charge ayant échouée de restaurer la tension de charge à son niveau initial avant la perturbation.

- une panne de générateur, une perte d'une charge importante ou un déclenchement de ligne.

- une perte d'une source de puissance réactive (condensateurs, machines synchrones,...).

La plupart de ces changements ont des effets significatifs sur la production, la consommation et la transmission de puissance réactive, ainsi sur la stabilité de tension. Par conséquent, des mesures peuvent être utilisées pour améliorer la stabilité de tension, tels (IEEE/PES, 2002) :

- un contrôle automatique des condensateurs shunts.

- un blocage des régleurs en charge automatique.

- une nouvelle répartition de la génération.

- une replanification du fonctionnement des générateurs et des noeuds de commande. - une régulation de tension secondaire.

- un plan de délestage.

La gamme de temps de l'instabilité de tension s'étend de quelques secondes à plusieurs minutes. Ainsi, l'instabilité de tension peut être considérée comme un phénomène à court terme (de l'ordre de plusieurs secondes) ou, dans l'autre cas limite, comme un phénomène à long terme (de l'ordre de plusieurs minutes).

Pour l'instabilité de tension à court terme l'effondrement de tension se produit immédiatement après la perturbation. Dans ce type d'instabilité, les charges et les dispositifs, qui ont des caractéristiques spéciales de puissance réactive tels les moteurs asynchrones sont souvent impliqués. Les moteurs asynchrones consomment, juste après la perturbation, beaucoup de puissance réactive pour assurer leur stabilité vis-à-vis leurs charge. D'autres éléments peuvent aussi participer à cette instabilité : les charges commandées électroniquement, les convertisseurs HVDC, ... .

L'instabilité de tension à long terme se développe lors d'un manque graduel de puissance réactive d'un noeud ou une partie du système. Elle implique, quant à elle, des équipements ayant une action plus lente tels les régleurs en charge automatique, les charges commandées thermostatiquement, ... .

Il est aussi important de noter que l'instabilité de tension ne se produit pas toujours toute seule. Souvent, l'instabilité de tension et l'instabilité de l'angle de rotor se produisent ensemble, l'une pouvant entraîner l'autre.

Enfin, la stabilité de tension peut être classée en deux catégories ; la stabilité de tension aux grandes perturbations et aux petites perturbations :

- Stabilité de tension aux grandes perturbations. Le souci dans ce cas est de maintenir des tensions normales aux noeuds de réseau électrique après une grande perturbation. La stabilité est déterminée ici par les caractéristiques du système et de charge, et par les interactions entre les différents dispositifs de commande de tension dans le système (Passelergue, 1998).

- Stabilité de tension aux petites perturbations. Dans ce cas, les caractéristiques de la charge et des dispositifs de commande déterminent la capacité du système à maintenir les tensions équilibrées.

2.3.3- La stabilité de fréquence.

La stabilité de la fréquence d'un système de puissance se définit par la capacité du système de maintenir sa fréquence proche de la valeur nominale suite à une perturbation sévère menant par conséquent à un important déséquilibre, entre les puissances produite et consommée.

Le maintien de la fréquence à une valeur nominale dans un système de puissance est lié à l'équilibre global entre les puissances actives produites et consommées (y compris les pertes).

Autrement dit, suite à certaines perturbations, l'équilibre global des puissances produite- consommée peut être déséquilibré : ce déséquilibre entraîne alors une variation de fréquence.

L'énergie cinétique stockée dans les pièces tournantes des machines synchrones et autres machines électriques tournantes peut éventuellement compenser ce déséquilibre. Si ce dernier n'est pas trop grand, les générateurs participant à la commande de fréquence régleront la puissance active fournie à travers leurs réglages secondaires fréquence-puissance et ramèneront ainsi l'écart de fréquence à des valeurs acceptables. Par ailleurs, si le déséquilibre est trop grand, l'écart de fréquence sera significatif avec des graves conséquences (effondrement complet du système), (Andersson, 2006).

Lorsque la fréquence varie, les caractéristiques de temps des processus et des différents dispositifs activés vont varier de quelques secondes à quelques minutes. La stabilité de fréquence peut donc être classifiée en phénomènes à court terme et à long terme.

Dans un grand système de puissance et suite à un incident sévère et, par la suite, à l'action de protections (par exemple, un déclenchement de plusieurs lignes de transmission), l'instabilité de la fréquence est généralement associée à l'îlotage où un scénario typique peut avoir lieu. Un ou plusieurs sous-réseaux se retrouvent isolés du reste du système. Les générateurs de chaque sous-réseau résultant essayent de garder le synchronisme entre eux, mais la réserve tournante est nettement insuffisante pour faire face à la charge connectée au sous-réseau. La fréquence décroît ainsi rapidement et l'instabilité produite est donc à court terme.

L'instabilité de fréquence peut également se manifester à long terme, lorsqu'elle provient d'une mauvaise réponse en puissance des centrales ou d'une mauvaise coordination entre des régulations et protections (Custem, 2002, II).

2.3.4- Conclusion.

Dans cette partie, nous avons présenté les définitions et les caractéristiques des différents types de stabilité d'un système de puissance. Le concept général de la stabilité peut se synthétiser en trois groupes (stabilité de l'angle de rotor, de la tension et de la fréquence). Cette classification est nécessaire pour mieux comprendre les mécanismes :

- des phénomènes de l'instabilité du système.

- des dispositifs nécessaires pour assurer la stabilité du système.

Historiquement, les chercheurs et les ingénieurs des systèmes de puissance mettaient l'accent sur la stabilité de l'angle de rotor. Or les opérateurs des systèmes de puissance se trouvent actuellement souvent obligés de faire fonctionner leurs systèmes aux limites de la stabilité. L'amélioration de la stabilité angulaire aux petites perturbations, en particulier l'amortissement des oscillations interrégionales, est donc devenue un objectif prioritaire : elle sera développée dans la partie suivante de ce chapitre.

2.4- Etude de la stabilité angulaire aux petites perturbations. 2.4.1- Introduction.

Les problèmes des oscillations à faibles fréquences ont toujours été un sujet de préoccupation. Mais pendant plusieurs décennies, les ingénieurs des systèmes de puissance se sont préoccupés beaucoup plus de la stabilité transitoire. Les origines de cette dernière étaient faciles à identifier et des mesures correctives ont été mises au point.

Les oscillations, qui sont typiquement dans la gamme de fréquences de 0,2 à 2 Hz, peuvent être excitées par des petites perturbations dans le système ou, dans certains cas, peuvent même prendre naissance spontanément.

Ces oscillations limitent la capacité de transmission de la puissance et, parfois, peuvent même causer la perte de synchronisme et un effondrement de l'ensemble du système. Dans la pratique, en plus d'assurer la stabilité, le système doit être bien amorti : c.-à-d. les oscillations doivent être atténuées le plus rapidement possible dès leurs apparitions.

La stabilité angulaire aux petites perturbations peut être améliorée en faisant varier une grandeur électrique :

- physiquement : de manière à augmenter le couple d'amortissement agissant sur le rotor des machines synchrones.

- mathématiquement: de manière à déplacer vers la partie gauche du plan complexe les
valeurs propres complexes correspondant à une oscillation instable ou mal amortie.

Parmi les grandeurs que l'on peut moduler dynamiquement nous nous intéressons au signal supplémentaire injecté dans l'entrée de l'AVR par le stabilisateur de puissance (PSS). Il agit à travers le régulateur sur le couple électromagnétique de manière à renforcer sa composante d'amortissement.

Dans la dernière partie de ce chapitre, nous allons détailler les éléments importants de la stabilité aux petites perturbations tels :

- le rôle de la variation du couple électromagnétique.

- l'influence du système d'excitation.

- les différents types d'oscillations à faibles fréquences.

- le PSS et ses méthodes de réglages et de localisation.

2.4.2- Variation de couple électromagnétique.

Dans un système de puissance, l'écoulement de puissance est lié aux positions angulaires des rotors de générateurs. Les positions des rotors doivent être réglées à tout moment pour faire face à tout changement de conditions de fonctionnement (variations de charge, de puissance de sortie de turbine,...). Un déséquilibre entre les couples mécanique et électromagnétique agissant sur le rotor, provoque une variation du mouvement du rotor, par rapport à une référence synchrone tournante. Ainsi, le couple électromagnétique joue un rôle important dans la stabilité angulaire. Ce couple est généralement produit par les interactions entre les trois circuits du stator de générateur, le circuit d'excitation et d'autres circuits tels les enroulements amortisseurs (Anderson et al., 2003).

Suite à une perturbation, les variations du couple électromagnétique peuvent s'exprimer en fonction des variations d'angle de rotor Ää et de vitesse Äù, suivant l'équation (95), (DeMello et al., 1969) :

Ä = + = ? Ä ä + ? Ä ù

T e T _S T A K S K _A(95)

KS : coefficient de couple synchronisant.
KA : coefficient de couple d'amortissent.

2.4.2.1- Couple synchronisant TS.

Donné par la composante, T S = K S ? Ää, il représente la variation de couple électromagnétique en phase avec la variation d'angle de rotor Ää.

Le couple synchronisant est produit par les interactions entre les enroulements du stator et la composante fondamentale du flux de l'entrefer. Ce couple tend à accélérer ou décélérer le rotor pour le ramener à sa position initiale. Il agit comme un couple de rappel d'un ressort d'un système mécanique, masse-ressort (IEEE, 2003).

Pour des petites déviations du point de fonctionnement, le coefficient de couple synchronisant KS est représenté par la pente de la courbe de la relation (puissance - angle), comme le montre la figure (28).

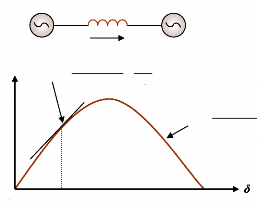
E1?ä

E2?

0

P_e

X

K 1 2 cos 0

E E ä

=

S

P

X

ÄP e

=

ä

Ä

E E

1 2 sinä

=

X

0° ä0 90° 180°

Figure 28. La relation (puissance- angle) du générateur et le coefficient de couple
synchronisant.

Si ä_o est l'angle de puissance à l'état équilibré, entre la tension interne du générateur (E1) et la tension du jeu de barre infini (E2), la pente de courbe à ä_o est simplement la dérivée de la fonction puissance - angle :

K S	=	dP e		E1	· E 2	cos	äo	(96)
		dä	ä o		X

Le couple synchronisant détermine alors la capacité du système de supporter une grande perturbation sans perdre le synchronisme : il est un facteur important pour la stabilité transitoire. En cas des petites perturbations, le couple synchronisant détermine la fréquence des oscillations.

2.4.2.2- Couple d'amortissement TA.

Donné par la composante, T_A = K_A ? Äù, il représente la variation de couple électromagnétique en phase avec la variation de vitesse de rotor Äù.

Ce couple résulte généralement des interactions entre la séquence positive du flux de l'entrefer et les enroulements du rotor, plus particulièrement les enroulements amortisseurs. Comme nous l'avons déjà vu, une variation de l'angle de rotor ä entraîne une variation de vitesse de rotor, Äù. D'après la loi de Faraday, la f. é.m. induite est proportionnelle à la variation de vitesse. Le courant induit par cette f. é.m. interagit avec le champ électromagnétique du générateur, en produisant par conséquent un couple d'amortissement naturel. Ce couple tend à amortir les oscillations électromécaniques de la machine en particulier suite à la première oscillation résultant d'une grande perturbation (Anderson et al., 2003). Ainsi, il est essentiel pour la stabilité aux petites perturbations, où le taux d'amortissement des oscillations de rotor est primordial. Mais souvent, ce couple est faible et parfois négatif surtout en présence de contrôleurs tels les contrôleurs de tension (ces derniers sont pratiquement les seules sources d'amortissement négatif). Un couple négatif conduit à une croissance spontanée des oscillations jusqu'à la perte de synchronisme.

Actuellement, les problèmes de stabilité angulaire aux petites perturbations sont considérés associés à l'amortissement insuffisant des oscillations.

2.4.3- Influence du système d'excitation sur la stabilité angulaire.

La stabilité angulaire dépend des deux composantes du couple électromagnétique, TS, TA, pour chaque machine synchrone du système. La littérature montre qu'une insuffisance de couple synchronisant conduit à une instabilité apériodique ou non-oscillatoire, alors qu'un manque de couple d'amortissement conduit à une instabilité dynamique (IEEE/CIGRE, 2004).

De même, la littérature montre que le système d'excitation avec son régulateur de tension a un impact important sur les deux couples et par conséquent sur la stabilité. Généralement, lorsqu'il y a des variations de tension, les deux puissances active et réactive transmissibles dans le réseau de transport vont varier. Cela entraîne des interactions indésirables entre les régulateurs de fréquence (puissance active) et de tension (puissance réactive).

Les systèmes d'excitation modernes, ayant une réponse rapide et une action "puissante", peuvent augmenter le couple synchronisant. Ceci améliore donc la stabilité transitoire. Mais cet avantage peut être contrebalancé par l'impact négatif du système d'excitation sur l'amortissement des oscillations en diminuant couple d'amortissement (Yu, 1983).

Ainsi, le fonctionnement du système d'excitation est perturbé par le conflit entre les contraintes du contrôle durant les quelques premières périodes du réseau après la perturbation et le laps de temps suivant. Pour cela, nous distinguons deux types d'effet du système d'excitation, à savoir : l'influence sur la stabilité transitoire et l'influence sur la stabilité aux petites perturbations (Anderson et al., 2003).

2.4.3.1- Influence sur la stabilité transitoire.

Comme nous l'avons déjà expliqué, l'objectif principal de la stabilité transitoire est de maintenir le synchronisme pendant et suivant une perturbation sévère. La durée qui nous intéresse est relativement courte (quelques secondes au maximum), la première oscillation ayant une importance déterminante. Durant cette phase, le générateur est soumis à une variation considérable de sa puissance électrique et ainsi à une accélération (ou décélération) de son rotor. Un système d'excitation rapide et puissante peut faire varier très rapidement la tension interne du générateur, durant cette phase. Ceci va augmenter la puissance électrique et le couple synchronisant produits pendant la première oscillation. Par conséquent, la puissance électromagnétique disponible va entraîner une diminution importante de l'accélération du rotor et de l'angle de rotor bien avant d'atteindre la limite de la stabilité transitoire : la marge de stabilité sera donc augmentée.

Pour montrer clairement l'effet positif d'un système d'excitation rapide et puissante sur la stabilité transitoire, reprenons le système précédent (machine synchrone connecté à un jeu de barre infini, figure (24)).

La figure (29) montre les effets de deux types de système d'excitation, à savoir : - un système lent et peu puissante correspondant à la courbe A.

- un système rapide et puissant correspondant à la courbe B, sur un défaut de transmission (Basler et al., 2002).

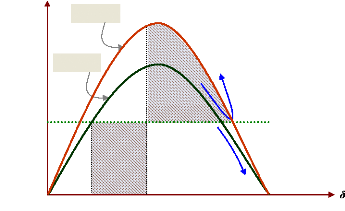
Cas B

Cas A

P

Pe-B

Maintenance du
synchronisme

P_m = P_e

Perte du
synchronisme

Pe-A

0° ä0 ä1 180°

ä2

Figure 29. Influence du système d'excitation.

En comparant la zone hachurée située en dessous de la droite de charge (zone d'accélération dans laquelle la puissance électrique est moindre que la puissance mécanique)

avec la zone hachurée située au-dessus de la droite de charge (zone de décélération), nous remarquons que la condition d'égalité entre les deux zones n'est pas assurée pour la courbe A. Par conséquent, la machine va perdre le synchronisme.

Pour la courbe B, il est clair que la zone de décélération est plus grande que la zone d'accélération. La réserve de couple synchronisant permet de restaurer la stabilité après l'élimination du défaut.

Par conséquent, nous pouvons conclure que l'augmentation du couple synchronisant, grâce à un système d'excitation à gain élevé et réponse rapide, augmente bien la puissance maximale transmissible pendant la phase transitoire, et donc la marge de stabilité transitoire.

2.4.3.2- Influence sur la stabilité dynamique.

L'action puissante et rapide du système d'excitation pour améliorer la stabilité transitoire a malheureusement une contribution négative importante sur l'amortissement des oscillations du système.

Le courant d'excitation, qui agit pour améliorer le couple synchronisant, est toujours en retard sur les caractéristiques temporelles correspondantes aux parties électriques du générateur et aux autres parties électriques du système. A partir du moment de l'identification du changement désiré d'excitation, le système d'excitation subit donc un temps de retard inévitable. Pendant ce temps, l'état du système oscillant va changer en impliquant un nouvel ajustement du courant d'excitation. Le système d'excitation reste donc en retard, par rapport au changement nécessaire. Par conséquent, le système d'excitation va introduire l'énergie demandée à contre temps. Les courants ainsi induits dans les circuits du rotor s'opposeront aux courants induits initiés par l'écart de vitesse du rotor (Äù). Le couple d'amortissement diminuera pouvant atteindre des valeurs négatives : le comportement oscillatoire du générateur va donc augmenter et une perte de stabilité peut avoir lieu.

La figure (30) illustre l'influence du couple d'amortissement sur la stabilité aux petites perturbations.

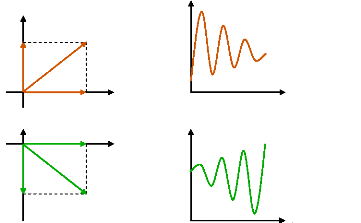
Ää

Ää

t

Système stable - TS positif

- TA positif

Système instable - TS positif

- TA négatif

t

Äù

TS

Ää

Äù

ÄT_e

TA

TS

Ää

TA

ÄT_e

Figure 30. Influence du couple d'amortissement sur la stabilité.

2.4.4- Les différents types d'oscillations à faibles fréquences.

Comme nous l'avons vu, les oscillations électromécaniques sont associées aux rotors des générateurs. Pendant ces oscillations, l'énergie mécanique cinétique est échangée entre les générateurs lors de l'écoulement de la puissance électrique dans le réseau. Ces oscillations peuvent être classées en deux groupes selon leurs manières d'évolution :

- Oscillations spontanées. Dans ce cas, les oscillations se développent lorsque l'amortissement d'un mode du système devient négatif par changement graduel des conditions de fonctionnement du système.

- Oscillations dues à une perturbation. Un défaut de ligne de transmission, par exemple, peut entraîner des oscillations en diminuant subitement l'amortissement d'un mode. Si cet amortissement devient négatif, les oscillations résultantes vont continuer ou même augmenter.

Les types des oscillations à faibles fréquences rencontrées habituellement dans les systèmes de puissance peuvent être classés en quatre groupes, figure (31). Généralement, la fréquence de ces oscillations fournit une bonne indication sur leurs types.

Modes électromécaniques
de 1 à 2 Hz de 0.2 à 1 Hz

Modes
locaux

Stabilité dynamique

Modes
interrégionaux

STABILITE DE L'ANGLE DE
ROTOR

Modes électriques
> 4 Hz

Modes
de contrôle

Stabilité transitoire

Modes mécaniques
> 4 Hz

de torsion

Modes

Figure 31. Classification de la stabilité de l'angle de rotor. 2.4.4.1- Les oscillations des modes locaux.

Les modes locaux sont les modes les plus rencontrés dans les systèmes de puissance. Ils sont associés aux oscillations entre un générateur (ou un groupe des générateurs) d'une centrale électrique et le reste du système. Le terme local est utilisé car les oscillations sont localisées dans une seule centrale ou une petite partie du système, (par exemple : les générateurs G1 et G2 oscillent ensemble par rapport au générateur G3 trouvé dans la même région, figure (32)). La gamme de fréquence de ces oscillations est généralement de 1 à 2 Hz.

L'expérience montre que ces oscillations tendent à se produire lors de l'utilisation des régulateurs de tension possédant une réponse rapide et quand le lien de transmission entre une centrale et ses charges est très faible (IEEE, 2003). Pour assurer un bon amortissement de ces modes, des sources d'amortissement, tel le stabilisateur de puissance, peuvent être ajoutées aux générateurs à l'origine de ces modes.

2.4.4.2- Les oscillations des modes globaux.

Les oscillations des modes globaux, ou oscillations interrégionales, sont associées à l'oscillation entre certains générateurs d'une partie du système et certains générateurs d'une autre partie du système (par exemple : les générateurs, G1, G2, G3 et G4, de la région A oscillent ensemble par rapport au générateur G5 de la région B, figure (32)).

Les modes associés à ces oscillations présentent généralement des amortissements très faibles et, si ces derniers sont négatifs, de petites perturbations peuvent exciter des oscillations divergentes. Les fréquences de ces oscillations se trouvent généralement dans la gamme de 0.2 à 1 Hz. Cette gamme est inférieure à celle des modes locaux car les réactances des liens entre les systèmes de puissance sont élevées. Généralement, la fréquence naturelle et le facteur d'amortissement d'un mode interrégional décroissent lorsque l'impédance d'une ligne d'interconnexion ou la puissance transmise augmente. Le système d'excitation et les caractéristiques des charges affectent également les oscillations des modes interrégionaux. Ainsi, ces modes présentent des caractéristiques plus complexes que ceux des modes locaux (CIGRE, 1996). Etant donné que les modes interrégionaux impliquent plusieurs générateurs, un bon amortissement de tels modes peut exiger l'utilisation de stabilisateurs de puissance pour un grand nombre des générateurs (IEEE, 1990).

Région B Région A

G3

G1

G2

G4

Figure 32. Système de puissance simple à deux régions.

2.4.4.3- Les oscillations des modes de contrôle.

Les oscillations associées aux modes de contrôle sont dues :

- soit, aux contrôleurs des générateurs (mauvais réglage des contrôleurs des systèmes d'excitation ou des gouverneurs).

- soit, aux autres dispositifs contrôleurs (convertisseurs HVDC, SVC,...).

La fréquence de ces oscillations est supérieure à 4 Hz. 2.4.4.4- Les oscillations des modes de torsion.

Ces oscillations sont essentiellement reliées aux éléments en rotation entre les générateurs et leurs turbines. Elles peuvent aussi être produites par l'interaction des éléments de rotation avec le contrôle d'excitation, le contrôle de gouverneur, les lignes équipées avec des compensateurs de condensateurs en série,... . La fréquence de ces oscillations est aussi supérieure à 4 Hz.

2.4.4.5- Conclusion.

Dans le cadre de cette étude, nous nous intéressons seulement aux modes locaux et aux modes interrégionaux : appelés modes électromécaniques. La distinction claire entre les modes locaux et interrégionaux s'applique principalement aux systèmes qui peuvent être divisés en régions distinctes séparées par de longues distances. Par ailleurs, pour les systèmes où les centraux sont distribués uniformément sur une large région géographique, il est difficile de distinguer entre les modes locaux et interrégionaux à partir de considérations géographiques. Cependant, une conclusion commune considère que les modes interrégionaux ont les fréquences les plus basses et que la plupart des générateurs du système y contribuent.

2.4.5- L'amortissement.

Nous avons vu que les oscillations électromécaniques limitent la capacité de transmission de puissance dans les réseaux électriques. Elles peuvent parfois entraîner une perte de synchronisme ou même un black-out dans le système entier. Par conséquent, des sources spécifiques d'amortissement sont indispensables pour assurer un fonctionnement fiable du système.

La stabilité peut être considérablement améliorée en utilisant des systèmes en boucle fermée avec des systèmes de contrôle adaptés. Au fil des années, un effort de recherche important était effectué pour une meilleure conception de tels contrôleurs. Il y a principalement deux moyens rapides permettant d'améliorer la stabilité :

- l'utilisation d'un contrôleur côté générateur : signal de contrôle supplémentaire dans le système d'excitation du générateur.

- l'utilisation d'un contrôleur côté lignes de transmission : signal de contrôle

supplémentaire dans les systèmes FACTS (Flexible AC Transmission System).

Dans le premier cas, le problème d'oscillations électromécaniques est résolu en ajoutant au générateur un contrôleur spécifique appelé : (Power System Stabilizer (PSS)). Ce contrôleur détecte les variations de vitesse de rotor ou de puissance électrique du générateur et applique un signal, adapté, à l'entrée du régulateur de tension (AVR). Le générateur peut ainsi produire un couple d'amortissement additionnel qui compense l'effet négatif du système d'excitation sur les oscillations (Kundur, 1994).

Les systèmes FACTS, qui sont des dispositifs basés sur les récentes avancées en électronique de puissance, peuvent être modifiés pour participer à l'amortissement des oscillations électromécaniques. Les systèmes FACTS (tels SVC (Static VAR Compensator), TCSC (Thyristor Controlled Series Capacitor), SSSC (Static Synchronous Series Compensator),...) sont principalement placés dans le système de puissance pour différentes raisons, (tels le contrôle des transits de puissance, des échanges de puissance réactive, les tensions de réseau, ...). Toutefois, un contrôleur et un signal de stabilisation supplémentaires peuvent être ajoutés pour améliorer la stabilité. Outre ces principaux rôles, les FACTS peuvent alors satisfaire les problèmes de la stabilité (Rogers, 2000; Sadeghzadeh, 1998).

Ces systèmes restent très chers pour être installés uniquement pour une raison d'amortissement des oscillations.

Les contrôleurs PSSs qui sont des systèmes simples et faciles à installer, pratiques, efficaces et moins chers, sont les systèmes les plus utilisés pour améliorer la stabilité aux petites perturbations. Nous allons donc les utiliser dans notre étude.

2.4.5.1- Fonctionnement et modèle de PSS.

Un PSS permet d'ajouter un signal de tension proportionnel à la variation de vitesse de rotor dans l'entrée du régulateur de tension (AVR) du générateur, figure (33). Un couple électrique en phase avec la variation de vitesse de rotor est ainsi produit dans le générateur. Par conséquent, avec un système d'excitation rapide et fort, l'avantage présenté par un couple synchronisant important est toujours assuré et le problème de la décroissance du couple d'amortissement est corrigé (Rogers, 2000; IEEE, 2003). Le PSS va s'opposer à toutes les faibles oscillations en forçant le système d'excitation à varier au plus juste et au bon moment.

Par conséquent, l'ensemble du système de contrôle d'excitation (AVR et PSS) doit assurer les points suivants (Kundur et al., 1989) :

- supporter les premières oscillations faisant suite à une grande perturbation ; c.-à-d. assurer la stabilité transitoire du système.

- maximiser l'amortissement des oscillations électromécaniques associées aux modes
locaux ainsi qu'aux modes interrégionaux sans effets négatifs sur les autres modes.

- minimiser la probabilité d'effets défavorables, à savoir :

o les interactions avec les phénomènes de hautes fréquences dans le système de puissance telle la résonance dans le réseau de transport.

o les instabilités locales dans la bande de l'action désirée du système de contrôle. - être suffisamment robuste pour permettre au système de contrôle d'assurer ses objectifs pour divers points de fonctionnement probables du système de puissance.

Le choix du signal d'entrée de PSS représente une étape critique dans la conception du PSS. Plusieurs considérations interviennent dans ce choix, telles :

- la sensibilité du signal d'entrée aux oscillations électromécaniques (autrement dit, les modes oscillatoires doivent être "observables" dans le signal choisi).

- l'insensibilité du signal d'entrée du PSS à son propre signal de sortie. D'une façon similaire, la sensibilité doit être très la plus faible possible pour les signaux de sortie d'autres PSSs.

Un bon résultat peut être obtenu si l'entrée du PSS est la variation de la vitesse de rotor (Äù), la variation de puissance produite du générateur (ÄP_e) ou la fréquence du jeu de barre

(Äf). Etant donné que le PSS est utilisé pour produire un couple électrique proportionnel à la variation de vitesse, il apparaît donc plus convenable d'utiliser la variation de vitesse (Äù) comme entrée du PSS. Cependant, quel que soit le signal d'entrée, la fonction de transfert du PSS doit compenser les caractéristiques de phase du système d'excitation, des parties électriques du générateur et des autres parties électriques du système. L'ensemble de ces dernières déterminent la fonction de transfert entre l'entrée du système d'excitation (Ä _Ver) et le couple électrique du générateur (ÄT_e), (Larsen et al., 1981, I). Cette fonction de transfert est dénotée GEP(s), figure (33).

Partie
mécanique
du
générateur

_

Vref

+

+

VS

ÄVer

Vt

ÄT_m

Système
d'excitation/
Régulateur

Partie

Efd électrique

du
générateur

+

ÄT_e

_

PSS

Figure 33. Modèle simplifié de liaison entre un PSS et le système.

Le type de PSSs le plus utilisé est connu sous le nom de PSS conventionnel (ou PSS avance/retard). Ce type a montré sa grande efficacité dans le maintien de la stabilité aux petites perturbations. Ce PSS utilise la variation de vitesse de rotor comme entrée. Il se compose généralement de quatre blocs, figure (34) :

- un bloc d'amplificateur.

- un bloc de filtre passe-haut "filtre washout".

- un bloc de compensation de phase.

- un limiteur.

V_S

max

VS

V_S

min

_

_

Äù

KPSS

1 +

ST W

ST W

1+

1+

ST₂

ST₁

1+

1+

ST₄

ST₃

Bloc
avance/retard

Gain Filtre

Washout

Figure 34. Modèle d'un PSS avance/retard.

1- L'amplificateur

Il détermine la valeur de l'amortissement introduit par le PSS. Théoriquement, sa valeur (KPSS) doit correspondre à l'amortissement maximal. Toutefois, la valeur du gain doit satisfaire l'amortissement des modes dominants du système sans risquer de dégrader la stabilité des autres modes ou la stabilité transitoire (Kundur et al., 1989). Généralement, KPSS varie généralement de 0.01 à 50 (IEEE, 1990).

2- Le filtre passe-haut "filtre washout"

Il élimine les oscillations à très basse fréquence (inférieure à 0.2 Hz) présentées dans le signal d'entrée. Il supprime également la composante continue de la vitesse (la composante "DC" correspondant au régime statique) : le PSS ne réagit donc que lorsqu'il y a des variations de vitesse. La constante de temps de ce filtre (TW) doit être suffisamment grande pour permettre aux signaux, dont la fréquence est située dans la bande utile, d'être transmis sans atténuation. Mais, elle ne doit pas être trop grande pour éviter de mener à des variations indésirables de tension de générateur pendant les conditions d'îlotage. Généralement, TW varie de 1 à 20 secondes (Basler et al., 2005; IEEE, 2003). Une amélioration remarquable sur la stabilité de la première oscillation est obtenue avec une valeur TW fixée à 10 secondes (Pal et al., 2005).

3- Le filtre compensation de phase

L'origine de l'amortissement négatif est, comme nous l'avons vu, associée au retard de phase introduit entre le couple électrique du générateur (ÄT_e) et l'entrée du système d'excitation (ÄV_er). Par conséquent, le PSS fournit l'avance de phase nécessaire pour compenser le retard de phase de la fonction de transfert GEP(s). Pratiquement, un bloc de phase d'avance pure ne suffit pas pour réaliser la compensation de phase nécessaire ; ainsi, un bloc d'avance/retard de phase est souvent utilisé. Pour mieux garantir la stabilité du système, deux étages (au moins) de compensations de phase sont nécessaires. La fonction de transfert de chaque étage est une simple combinaison de pole-zéro, les constantes de temps d'avance (T1, T3) et de retard (T2, T4) étant réglables. La gamme de chaque constante de temps s'étend généralement de 0.01 à 6 secondes (Basler et al., 2005). Mais pour des considérations de réalisation physique, les constantes de temps de retard (T2, T4) sont considérées fixes et généralement autour de la valeur de 0.05 secondes (Fleming et al., 1981).

4- Le limiteur

Le PSS est conçu pour améliorer l'amortissement du système en cas de petites variations autour d'un point d'équilibre. Son objectif n'est pas de restaurer la stabilité du système aux perturbations sévères (la stabilité transitoire). Le PSS a parfois tendance à perturber le bon fonctionnement du régulateur de tension en le saturant lorsque ce dernier essaye de maintenir la tension lors de conditions transitoires. Ainsi, le PSS doit être équipé d'un limiteur afin de réduire son influence indésirable durant les phases transitoires (Larsen et al., 1981, II). Les valeurs minimales et maximales du limiteur s'étendent de #177; 0.02 à 0.1 per-unit (IEEE, 1990).

2.4.5.2- Réglage des paramètres de PSS.

Le problème de la conception d'un PSS est de déterminer les valeurs de ses paramètres pour :

- augmenter l'amortissement des modes du système.

- assurer une stabilisation robuste.

La minimisation des risques probables des interactions défavorables et des effets négatifs sur les autres modes oscillatoires du système représente aussi un point critique important qui influence le réglage de PSSs. En outre, les valeurs des paramètres du PSS doivent être réglées sans entraîner d'effet négatif dans la restauration de la stabilité transitoire.

De nombreuses méthodes sont proposées dans la littérature pour le réglage des paramètres de PSS. Généralement, la plupart de ces méthodes sont basées sur l'analyse des valeurs propres du système.

2. 4. 5. 2. 1- Méthode de compensation de phase.

Pour expliquer le réglage des paramètres de PSS par la méthode de compensation de phase, nous prenons un système simple consistant en un générateur connecté à un jeu de barre infini, figure (24). Le modèle linéaire de ce système peut être graphiquement illustré par la représentation de Heffron-Philips (Pal et al., 2005), comme le montre la figure (35).

Les termes K1, ..., K6 sont les constantes de linéarisation.

ÄTm +

ÄTe2

ÄTe1 _

ÄE_q^'

K2

_

K3

1 sT K

+ d' 0 3

1
D 2 Hs

+

K1

Äù

_

K6

K4

ù0

s

ÄEfd

+

Ä

ä K5

K_a

1+ sT_a

GEP(s)

_

_

+

ÄV_s

GPSS(s)

Figure 35. Modèle de Heffron-Philips d'un système
(monomachine - jeu de barre infini).

L'objectif principal d'un PSS est d'introduire une composante d'un couple électrique sur le rotor de la machine synchrone ; ce couple est proportionnel à l'écart entre la vitesse actuelle du rotor et la vitesse de synchronisme. Lorsque le rotor oscille, ce couple agit comme un couple d'amortissement pour atténuer les oscillations.

La fonction de transfert GEP(s) et le retard de phase de la boucle électrique peuvent être dérivés du modèle de Heffron-Philips. Ils sont donnés par les deux relations suivantes (Yu, 1983) :

'

)

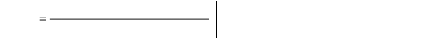
+ K K K a 3 6

sT K

do 3

GEP s

( )

K K K

a 3 2

(1 )(1

+ +

sT a

(97)

s ë ó j ù

= = +

PhiGEP GEP s s = ë = ó + j ù

= ? ( ) (98)

Avec ë= ó + jù est la valeur propre calculée pour le système sans signal de stabilisation.

Pour simplifier, nous considérons que les paramètres à régler du PSS sont le gain _Kpss et les constantes de temps T1 et T3 (avec T1 = T3) ; les autres paramètres sont fixés (avec T2 = T4). Ainsi, la fonction de transfert de PSS peut se réécrire comme suit :

G s K PSS PSS ( ) =

2 sT ? 1 + sT ? w ? 1 K G s ? = . ( ) (99) PSS f 1 + sT 1 sT w ? + 2 ?

Etant donné que l'avance de phase du PSS _(PhiGPSS) est égale à la phase _PhiGEP, la constante de temps T1 est donnée, tout calcul fait, par la relation suivante :

tan( )

â

T = T = (100)

1 3ù ó â

- · tan( )

1 ? 1 1 1 2

? ù ? ù ? ù ?

- - -

? T ? T ?

w

Avec, â = - -

?? Phi tan tan ? ? + ? ? ?? (101)

GEP ?? ?? + 2 tan

2 ó

? ?1+óT? ? 1 + ó T

w 2 ? ?

Le gain du PSS, quant à lui, est donné par la relation suivante (Yu, 1983) :

=

4ùæH
n

GEP s

( )

G s f ( )

(102)

KPSS

K2

s=ë=ó

+jù

ù 1

o K

Avec, ù = (103)
n2 H

ù_o : la vitesse de synchronisme du système, en rad/s.

ù_n : la pulsation naturelle d'oscillation en rad/s.

La valeur ù_n représente la solution de l'équation caractéristique de la boucle mécanique (figure (33)). Elle est définie par l'équation suivante (coefficient d'amortissement D négligée).

2 + ù 1 = 0 , , = #177; ù

Hs o K avec s j n

2 (104)

2. 4. 5. 2. 2- Méthode du résidu.

Nous avons vu que le filtre avance/retard du PSS est utilisé pour compenser le retard de phase de la fonction de transfert GEP(s). En déterminant la valeur du retard de phase, nous pouvons ainsi calculer les constantes de temps (avance/retard) nécessaires pour assurer la compensation demandée. Pour ce faire, l'angle de phase de résidu peut être utilisé (Aboul-Ela et al., 1996; Cai, 2004). Considérons la forme suivante de la fonction de transfert du PSS pour un système à une entrée/une sortie :

sT ?1+sT ? W 1 H s K ( ) = · · PSS 1 sT ?? 1 sT ?? + + W 2

m

(105)

Où : m est le nombre d'étages de compensation (généralement m = 2).

La figure (36) montre l'effet du résidu sur le déplacement de valeur propre dans la partie gauche du plan complexe.

fù

Direction de rotation

Direction de Ri

öcom arg (Ri)

ëi 0

ëi 1

Äëi

Figure 36. Déplacement de valeur propre par la rotation du résidu associé.

L'angle de phase _öcom, nécessaire pour diriger la direction du résidu Ri de sorte que la valeur propre associée ëi se déplace parallèlement à l'axe réelle, peut être calculé par l'équation suivante :

? com =180°-arg(R _i ) (106)

Où : arg(Ri) est l'angle de phase du résidu Ri.

á

ù ·

i

T 1

2 (107)

=

Avec :	á	=	1 sin -	? ? ? com ? ? ? m ?	(108)
			1 sin +	? ? ? com ? ? ? m ?

1 = á · T 2

T ,

Par conséquent, les constantes de temps T1 et T2, du bloc avance/retard nécessaires pour obtenir l'angle _öcom, peuvent être calculées comme suit (Aboul-Ela et al., 1996) :

Où : ùi est la fréquence du mode ëi en rad/sec.

Pour calculer le gain _KPSS, nous pouvons réécrire la fonction transfert du PSS comme suit :

H(s) = K PSS · H_f(s) (109)

Le déplacement des valeurs propres est donné par l'équation (82) que nous rappelons ci- dessous :

Äë i = ë i - ë i = R _i H ë i

1 0 ( ) (110)

En remplaçant l'équation (109) dans la dernière équation, nous obtenons pour gain _KPSS la valeur littérale suivante (Sadicovic et al., 2006) :

ë ë

i i

1 0

-

K PSS

R_i

· H f

( )

ë i

(111)

Une autre méthode peut être utilisée pour régler le gain KPSS : la méthode traditionnelle de Ziegler et Nichols basée sur l'étude du régime critique de la réponse harmonique du système en boucle fermée. On cherche ainsi le gain produisant l'instabilité. Le test consiste à augmenter lentement le gain de stabilisateur jusqu'à l'observation de l'instabilité. Pour un signal d'entrée de type variations de vitesse, ce test doit être effectué avec une charge maximale et des conditions de transport d'énergie satisfaisantes. Le savoir-faire montre, en général, que le gain désiré représente le tiers du gain à l'instabilité : Kst = Kinst / 3, (Larsen et al., 1981, III).

2.4.5.2.3- Méthode de placement des pôles.

Cette méthode consiste à déterminer les valeurs des paramètres d'un PSS de sorte que tous les pôles du système en boucle fermée se trouvent placés en des positions spécifiées préalablement dans le plan complexe.

Cette méthode peut être mathématiquement décrite en considérant la représentation suivante du système (Fleming et al., 1981; Aström et al., 1996), figure (37).

Système

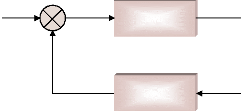
ÄV +

+

H(s)

G(s)

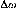
PSS

Figure 37. L'ensemble (système-PSS) en boucle fermée.

Où : G(s) est la fonction de transfert du système entre le signal de référence Ä V du régulateur de tension de générateur, où le PSS doit être installé, et la variation de vitesse de rotor Äù.

H(s) est la fonction de transfert de PSS.

Les pôles de G(s) sont justement les valeurs propres du système linéarisé en boucle ouverte. La fonction de transfert du système entier en boucle fermée F(s) devient :

=

F s

( )

1( ) ( )

- ·

G s H s

G s

( )

(112)

Les valeurs propres du système en boucle fermée sont les pôles de la fonction de transfert F(s) ; elles doivent satisfaire l'équation caractéristique suivante :

1-G(s)·H(s)=0 (113)

1

H s = (114)
( )

G s

( )

Si ë _i , i = 1,2,L n sont les valeurs propres spécifiées préalablement, l'équation (114) peut ainsi se réécrire comme suit :

1

H ë

( )

ë = (115)

ⁱ G ( )

i

ë T 1 + ë T 1 + ë T 1 i W i 1 i 3 · K · ·= PSS 1 4 + ë 1 1 ( ) i T W + ë i T + ë ë 2 i i T G

(116)

Par conséquent, nous obtenons un ensemble d'équations algébriques linéaires. En résolvant ces équations, nous pouvons déterminer les valeurs des paramètres désirés du PSS qui assurent le placement précis des valeurs propres.

2.4.5.3- Emplacement optimal des PSSs.

Tous les générateurs du système ne participent pas aux modes dominants : tous les générateurs n'ont donc pas besoin d'être équipés de PSSs. En outre, il faut tenir compte des interactions négatives entre les PSSs qui augmentent avec le nombre de ces derniers. Enfin, il faut tenir compte des critères économiques.

Ainsi, la première étape de la mise en oeuvre des PSSs, est de trouver les emplacements optimaux des PSSs nécessaires et de déterminer leur nombre. Ce problème a fait l'objet, depuis une dizaine d'années, d'un grand nombre de recherche (Pérez-Arriaga et al., 1982; Hsu et al., 1987; Tse et al., 1988; Ostojic, 1988; Pagola et al., 1989; Jin Lu et al., 1990; Feliachi, 1990 ). Les approches les plus efficaces proposées sont basées sur l'analyse modale du système linéarisé :

- le mode shape.

- les facteurs de participations.

- les résidus.

Comme nous l'avons vu, les amplitudes des résidus associés aux modes dominants de la fonction de transfert du système en boucle ouverte peuvent être utilisées pour déterminer les

placements les plus efficaces pour installer les PSSs. Les amplitudes des facteurs de participation ou du mode shape permettent de déterminer l'influence de chaque variable d'état dans les modes oscillatoires associés. Ces méthodes peuvent donc nous fournir des indications importantes sur l'emplacement optimal des PSSs dans le système pour réaliser un meilleur amortissement par rapport à des critères donnés.

Sachant que des emplacements différents des PSSs entraînent des oscillations totalement différentes, des PSSs "mal placés" peuvent donc ne pas répondre aux objectifs. Pour cela, il faut bien choisir la méthode qu'il faut appliquer pour déterminer les bons emplacements des PSSs. Les méthodes mentionnées ci-dessus donnent généralement de bons résultats, mais la recherche de méthodes plus efficace reste toujours actuelle.

2.5- Conclusion.

Dans ce chapitre, nous avons présenté d'une façon générale les différents types de stabilité. Nous avons présenté également une analyse fine sur la stabilité aux petites perturbations et les oscillations électromécaniques présentes dans les systèmes de puissance. Cette étude nous a ainsi permis de mettre en évidence les points importants suivants :

- Un système de puissance doit présenter un point d'équilibre stable dans les conditions de fonctionnement normales.

- Un système de puissance est stable s'il retrouve un état d'équilibre acceptable après avoir été soumis à une perturbation.

- La stabilité angulaire aux petites perturbations est habituellement considérée comme la capacité du système de puissance à maintenir le fonctionnement synchrone des générateurs pour de faibles variations des charges et des sources.

- Les oscillations électromécaniques sont généralement dues aux modes naturels du système. Ainsi, nous ne pouvons pas les éliminer. Cependant, leurs fréquences et leurs amortissements peuvent toujours être modifiés.

- Suite à une perturbation, le système de puissance peut être transitoirement stable mais il peut présenter par la suite des oscillations divergentes.

- Suite à une grande perturbation, le régulateur de tension du système d'excitation de générateur, ayant une action puissante et rapide, contribue efficacement à augmenter les puissances électriques des générateurs pendant la première oscillation. Cela contribue à diminuer la puissance d'accélération du générateur en augmentant le couple synchronisant. En conséquence, la plage de stabilité transitoire est bien améliorée. Malheureusement, cet avantage est contrebalancé par l'impact négatif du système d'excitation sur l'amortissement des oscillations en diminuant le couple d'amortissement.

- Les oscillations interrégionales sont associées aux lignes d'interconnexion de grande impédance et une demande de puissance à transmettre élevée. Comme ces oscillations se produisent entre plusieurs régions du système, leurs caractéristiques sont plus complexes que celles des oscillations des modes locaux et elles sont plus difficiles à amortir.

- Les stabilisateurs de puissance (PSSs), par leur efficacité et leur coût réduit, sont les moyens habituels non seulement pour éliminer les effets négatifs des régulateurs de tension, mais aussi pour amortir les oscillations électromécaniques du système. En

outre, l'amortissement assuré par les PSSs permet au système de fonctionner au-delà même de la limite de la stabilité à l'état équilibré.

- Le réglage des paramètres des PSSs et leurs emplacements sont des facteurs critiques pour pouvoir assurer convenablement le bon fonctionnement des PSSs.

Ce dernier point fera l'objet du chapitre quatre. Dans le troisième chapitre, nous présentons tout d'abord les principes généraux d'optimisation par algorithmes génétiques ; nous les utilisons par la suite.

Chapitre III

Optimisation par

algorithmes génétiques

3.1- Introduction.

Au fil des années, de nombreuses recherches ont été effectuées et de nombreuses approches ont été proposées pour effectuer le meilleur réglage et coordination des PSSs.

Dans les systèmes de puissance, nous avons besoin d'installer plusieurs PSSs. Traditionnellement, les paramètres de ces PSSs sont réglés séquentiellement et séparément (Abe et al., 1983; Arredondo, 1997; Yee et al., 2004). Dans les stratégies de réglage séquentiel, basées sur les méthodes de réglage présentées dans le chapitre précédent, les PSSs sont alors conçus pour amortir les oscillations des modes, mode par mode. Par exemple, la méthode linéaire séquentielle (Linear Sequential Method, LSM) est basée sur les résidus. Dans cette méthode, les PSSs sont réglés d'une manière progressive (Yee et al., 2004) :

- on calcule tout d'abord les résidus de la fonction de transfert du système en boucle

ouverte. Puis un PSS est ajouté et réglé en utilisant les informations de ces résidus.

- ensuite, un second PSS est introduit et réglé en se basant sur les informations des

résidus du système avec le premier PSS en place.

- ce processus continue jusqu'à ce que le système atteigne des caractéristiques de stabilité satisfaisantes.

Une autre méthode séquentielle basée sur le placement des pôles du système est connue sous le nom : positionnement séquentiel des valeurs propres (Sequential Eigenvalue Assignment) (Fleming et al., 1981). Dans cette méthode, les paramètres des PSSs sont représentés comme des variables dans les équations caractéristiques du système. Ces équations sont résolues itérativement jusqu'à ce que les valeurs propres se trouvent placées aux endroits déterminés préalablement. La solution représente les paramètres des PSSs recherchés. Comme les "bonnes" valeurs propres spécifiées sont souvent choisies par expertise, les valeurs déterminées des paramètres des PSSs peuvent être situées en dehors de gammes correspondantes de fonctionnement (Hong et al., 1999). De ce fait, la méthode doit être appliquée de façon itérative jusqu'à obtenir des paramètres adéquats.

Bien que les méthodes de réglage séquentiel soient simples et aient donné généralement des résultats satisfaisants pour l'amortissement des oscillations, ces méthodes ne peuvent assurer une optimisation globale des PSSs et, ainsi, la stabilité globale du système. Les aspects négatifs de ces méthodes sont liés aux hypothèses restrictives et à la nature intuitive du processus de réglage (Fleming et al., 1981). En outre, les interactions dynamiques entre les différents modes ont une influence significative sur le réglage des PSSs : le réglage d'un PSS pour stabiliser un mode peut ainsi produire des effets opposés sur les autres modes.

La littérature montre qu'à la place des méthodes de réglage séquentiel, une optimisation simultanée des PSSs du système entier peut être utilisée (CIGRE, 1999). Les méthodes d'optimisation simultanée peuvent permettre d'atteindre plusieurs objectifs :

- une stabilité globale.

- un bon fonctionnement du système de puissance avec un amortissement satisfaisant pour diverses conditions de fonctionnement et configurations du système.

- une minimisation des interactions antagonistes possibles entre les PSSs.

Grâce à la rapidité du développement de l'informatique, l'utilisation des outils et des algorithmes d'optimisation devient de plus en plus aisée et efficace. Cette révolution informatique a permis une ouverture vers des méthodes synthétiques telles les méthodes d'optimisation stochastiques. A la différence des méthodes analytiques dans lesquelles on

cherche à trouver une solution théorique exacte ou une bonne approximation numérique, les méthodes stochastiques constituent une approche originale dans laquelle on cherche à trouver des solutions satisfaisant aux mieux différents critères souvent contradictoires. Elles peuvent aussi synthétiser des solutions nouvelles et originales sans idées préconçues.

La résolution d'un problème d'optimisation consiste à explorer un espace de recherche afin d'optimiser (maximiser ou minimiser) une fonction donnée (une fonction objectif) sous certaines contraintes. La complexité du problème, en taille ou en structure, relative à l'espace de recherche et à la fonction à optimiser conduit à développer diverses méthodes. Ces méthodes peuvent être regroupées en deux catégories : les méthodes déterministes (classiques) et les méthodes non-déterministes (stochastiques).

1- Les méthodes déterministes :

Qualifiées de classiques (telles la méthode du gradient, les méthodes énumératives,...), elles n'utilisent aucun concept stochastique. Une méthode déterministe utilise donc toujours le même cheminement pour arriver à la solution, et nous pouvons donc déterminer à l'avance les étapes de la recherche. Ces méthodes sont limitées par leur "faible" espace de recherche. Elles requièrent des hypothèses sur la fonction objectif à optimiser, telles que continuité et dérivabilité de la fonction en tout point du domaine des solutions. Elles consistent généralement à se focaliser sur un point unique de l'espace de recherche en le déplaçant au cours de temps dans le but de trouver un extremum. Ces méthodes sont généralement efficaces lorsque l'évaluation de la fonction est très rapide ou lorsque sa forme est connue à priori. Mais, lorsque la dimension du problème ou l'espace de recherche est grand, ces méthodes peuvent :

- avoir des temps de calcul déraisonnables ou

- boucler et revenir sans cesse au même point.

Enfin, un grand nombre de fonctions à optimiser ne sont pas dérivables et souvent même pas continues. Par conséquent, ces méthodes restent limitées à des problèmes très précis.

2- Les méthodes non-déterministes :

Ces méthodes, qualifiées de stochastiques, sont bien adaptées aux problèmes importants et complexes (tels les problèmes discrets) ou même à des problèmes ayant des multifonctions objectif. Dans cette famille de méthodes, on parle couramment d'heuristique et de métaheuristiques.

Une méthode heuristique est une méthode d'optimisation adaptée à un problème particulier. Parmi ces méthodes, figurent la méthode de Monte-Carlo, le recuit simulé, la recherche tabou, la méthode de descente, ... . Ces diverses méthodes travaillent toujours à partir d'une solution initiale en essayant de l'améliorer au maximum en fonction des contraintes du problème étudié. Ainsi, elles ont toutes un point commun : à savoir leurs itérations reposent sur l'amélioration d'une solution unique. Leurs évolutions sont ainsi basées sur la notion de parcours : l'évolution vers une solution optimale se fait en testant successivement une solution voisine de la solution courante. La figure (38) illustre une représentation simple d'une méthode d'optimisation à parcours (heuristique).

Une méthode métaheuristique consiste en une stratégie de choix pouvant piloter une ou plusieurs heuristiques de manière abstraite, sans faire appel à un problème spécifique. Les méthodes métaheuristiques sont ainsi des méthodes à population de solutions : à chaque itération, elles manipulent un ensemble de solutions en parallèle (Osman et al., 1996). Ces

méthodes sont aussi considérées comme des méthodes d'optimisation globale : elles visent la détermination de l'optimum global de la fonction objectif du problème, en évitant le "piégeage" dans l'un de ses optima locaux. Elles comblent ainsi le handicap des méthodes classiques et des méthodes heuristiques en conduisant la recherche vers l'optimum global. En outre, ces méthodes font usage de l'expérience accumulée durant la recherche de l'optimum, pour mieux guider la suite du processus de recherche. Elles permettent ainsi d'explorer et d'exploiter l'espace de recherche plus efficacement. Une représentation schématique simple des métaheuristiques est donnée à la figure (39).

Dans cette représentation, les métaheuristiques (MH) tentent de trouver l'optimum global (OG) d'un problème d'optimisation (f(x)) difficile (avec par exemple des discontinuités (DC)), sans être piégé par les optima locaux (OL).

f(x)			x

Figure 38. Représentation simplifiée d'une approche heuristique.

MH

f(x)

DC

OL

OG

x

Figure 39. Représentation simplifiée d'une approche métaheuristique.

Les algorithmes évolutionnaires regroupent une multitude de métaheuristiques différentes. Cependant, tous ont un point commun : ils sont basés sur les principes de la théorie évolutionnaire. Ils simulent l'évolution naturelle des structures individuelles afin de trouver une solution optimale. Dans chaque génération, une nouvelle approximation de

solution optimale se produit par des processus de sélection des individus selon leurs performances dans le domaine du problème. Les individus sélectionnés vont être reproduits en utilisant des opérateurs empruntés aux génétiques naturelles. Ces processus mènent à l'évolution de la population des individus les mieux adaptés à leur environnement (Pohlheim, 2005).

Ces méthodes reçoivent de plus en plus d'intérêt en raison de leurs capacités potentielles à résoudre des problèmes complexes. Sous le concept d'algorithmes évolutionnaires, on trouve plusieurs méthodes tels les algorithmes génétiques, la programmation évolutionnaire, les stratégies d'évolution et la programmation génétique. Les étapes communes de ces méthodes peuvent être résumées comme suit (Bäck, 1996) :

- une initialisation aléatoire d'une population d'individus (des points de l'espace de recherche).

- une coopération et une compétition parmi les individus de la population concernée selon les principes Darwinistes et génétiques de la survie du "meilleur" (sélection, croisement et mutation).

- un nombre d'itérations (générations) faisant évoluer la solution (l'individu) courante et finissant par atteindre la solution optimale.

Une caractéristique importante pour les algorithmes évolutionnaires est l'absence d'information sur le gradient pour élaborer les solutions. Cette propriété donne aux algorithmes évolutionnaires une flexibilité satisfaisante leur permettant d'être utilisés aisément dans une grande variété de problèmes tels les problèmes fortement non-linéaires, les problèmes non-continus, ... . De plus, les algorithmes évolutionnaires travaillent sur un ensemble de points (une population) et non pas sur un seul point ; cela augmente la probabilité de trouver la solution optimale. Comme ces algorithmes utilisent les principes stochastiques, ils ne demandent aucune structure particulière pour le problème à optimiser.

Grâce à leurs nombreux avantages, les algorithmes évolutionnaires sont appliqués avec beaucoup de succès dans le domaine industriel et l'ingénierie. De nombreux problèmes liés aux systèmes de puissance sont résolus par les algorithmes évolutionnaires telles les répartitions économiques, la prévision de charges, la planification de génération, la coordination des contrôleurs, les études de sûreté des systèmes de puissance,... .

Les algorithmes génétiques, forment une des principales classes des algorithmes évolutionnaires ; ils ont suscité beaucoup d'enthousiasme depuis plusieurs années. Leur efficacité pour produire des solutions de qualité dans un grand nombre de problème d'optimisation est maintenant bien établie. Ils représentent les méthodes d'optimisations les plus utilisées.

3.2- Les Algorithmes Génétiques (AGs). 3.2.1- Introduction.

Comme nous l'avons déjà indiqué, les algorithmes génétiques sont des méthodes de recherche stochastiques de solutions basées sur des mécanismes s'inspirant de processus naturels (sélection) et des phénomènes génétiques (croisement et mutation). Les travaux de scientifiques du XIX^e siècle (Lamarck, Darwin, Mendel,...) et du XX^e siècle (Watson et Crick) ont permis de mettre en évidence les principaux mécanismes à l'oeuvre au cours de l'évolution des populations. Ces recherches ont débouché sur l'idée que l'évolution repose

d'une part sur l'intervention du hasard au cours des croisements et des mutations, et d'autre part, sur un processus de sélection des individus les plus aptes à survivre dans un environnement donné. C'est précisément cette notion de hasard guidé par la sélection qui est à la base des algorithmes génétiques.

Dans les années soixante et soixante-dix, le professeur J. Holland à l'université de Michigan (Holland, 1975) a développé, sur la base des travaux précédents, les principes fondamentaux des algorithmes génétiques, son objectif étant de concevoir des systèmes artificiels possédant des propriétés similaires aux systèmes naturels. L'ouvrage de Goldberg (Goldberg, 1989) a permis de mieux faire connaître les algorithmes génétiques et il a marqué le début de l'intérêt actuel pour ces techniques.

La théorie des algorithmes génétiques utilise un vocabulaire similaire à celui de la génétique naturelle. Cependant, les processus naturels auxquels elle fait référence sont beaucoup plus complexes que les algorithmes génétiques.

On définit ainsi un individu dans une population. L'individu est représenté par un ou plusieurs chromosomes constitués de gènes qui contiennent les caractères héréditaires de l'individu. Les principes de sélection, de croisement, de mutation utilisés s'appuient sur les processus naturels du même nom (Barnier et al., 1999).

Pour un problème d'optimisation donné, un individu représente un point de l'espace de recherche c.-à-d. une solution potentielle. On lui associe la valeur du critère à optimiser qui définit sa performance. Pour progresser d'une population d'individus à une nouvelle population, on utilise séquentiellement les processus de sélection, de croisement et de mutation. La sélection a pour but de favoriser les meilleurs éléments de la population pour le critère considéré. Le croisement et la mutation ont pour but d'assurer l'exploration et l'exploitation de l'espace de recherche. Par conséquent, les individus les moins adaptés vont être exclus et les meilleurs vont survire pour construire la nouvelle population. Chaque itération de l'algorithme génétique représente une génération. Au fur et à mesure de la progression d'une génération à l'autre, la solution trouvée va converger vers la solution optimale à atteindre (Negnevitsky, 2002).

Généralement, nous pouvons dire qu'un algorithme génétique dans sa forme générale nécessite de préciser les points suivants :

- le codage des solutions et la génération d'une population initiale.

- la fonction de performance pour calculer l'adaptation de chaque individu de la population.

- le croisement des individus d'une population pour obtenir la population de la génération suivante.

- l'opération de mutation des individus d'une population afin d'éviter une convergence prématurée.

- les paramètres de réglage : taille de la population, probabilités de croisement et de mutation, critère d'arrêt.

Ces points vont être discutés en détail dans la suite de ce chapitre, mais nous allons tout d'abord définir les expressions utilisées dans la théorie des algorithmes génétiques.

Dans un problème d'optimisation à n variables, nous faisons correspondre un gène à chaque variable cherchée. Chaque gène est représenté par une chaîne de caractères choisis dans un alphabet fini (souvent binaire). Les gènes s'enchaînent ensemble "bout à bout" pour

construire un chromosome, chaque chromosome représentant une solution potentielle sous une forme codée. Ces chromosomes constituent les briques de base contenant les caractéristiques héréditaires des individus. Un chromosome (ou plusieurs) forme un individu qui représente à son tour une solution potentielle dans l'espace de recherche correspondant du problème. Etant donné que les AGs travaillent sur un ensemble de points de l'espace de recherche, nous appelons l'ensemble des points choisis (à savoir les individus) une population. Au fur et à mesure des générations (itérations), une population des individus mieux adaptés va être créée.

La figure (40) représente les relations entre les expressions génétiques d'un AG en codage binaire.

Population

0

1

1

1

Gène (1)

Gène (1)

Chromosome

Chromosome

0

0

0

1

0

0

0

1

Individu (Nind)

1

1

Gène (2)

Gène (2)

Individu (1)

1

1

0

0

0

1

0

1

Gène (Ngens)

Gène (Ngens)

0

1

0

1

1

1

1

1

Figure 40. Les niveaux d'organisation des éléments d'un AG. 3.2.2- Codage et initialisation.

La première étape de la construction d'un AG est le choix du type de codage des paramètres du problème. La façon de coder les solutions potentielles est un facteur déterminant dans le succès d'un AG. Ainsi, plusieurs types de codage sont possibles dans la littérature, tels les codages binaires, Gray, réel,... . Le codage le plus populaire dans la représentation d'un AG est le codage binaire {0, 1 } ; les solutions sont codées selon des chaînes de bits de longueur fixe (Chipperfield et al., 1994). La plupart des théories liées aux AGs étaient élaborées en se basant sur le concept de codage binaire proposé par J. Holland et son groupe (Holland, 1975). Les opérateurs de l'AG, croisement et mutation, sont en effet plus faciles à mettre en oeuvre avec ce type de codage. En outre, le codage binaire représente la méthode la plus facile et la mieux adaptée de coder des éléments qu'ils soient réels, entiers, booléens, ... (Mitchell, 1996). On parle dans ce cas de génotype en ce qui concerne la représentation binaire d'un individu et de phénotype pour ce qui est de sa valeur réelle correspondante dans l'espace de recherche.

Une fois le choix du type de codage déterminé, une population initiale doit être créée pour le départ de l'AG. La population initiale a pour but de donner naissance à des générations successives, mutées et hybridées à partir de leurs parents. Le choix de la population initiale influence fortement la rapidité et l'efficacité de l'AG. Si la position de l'optimum dans l'espace de recherche est totalement inconnue, il est naturel de générer aléatoirement des individus en faisant des tirages uniformes dans chacun des domaines associés aux composantes de l'espace de recherche, en veillant évidemment à ce que les individus produits respectent les contraintes. Si par contre, des informations à priori sur le problème sont disponibles, il parait naturel de générer les individus dans un sous-domaine particulier afin d'accélérer la convergence. Habituellement, cette population initiale est générée d'une manière aléatoire et directement dans sa représentation codée.

Par exemple pour créer une population binaire de _Nind individus dans lesquels chaque chromosome (individu) est représenté par _Ngen gènes, il suffit simplement d'effectuer Nind × Ngen tirages de nombres aléatoires distribués uniformément sur l'ensemble {0, 1 }, (Chipperfield et al., 1994).

La seconde étape dans la construction de l'AG est le calcul de la performance (fitness) de chaque individu faisant partie de la population. Pour ce faire nous devons en premier lieu décoder les chromosomes (précisément les gènes de chaque chromosome) en les convertissant en leurs valeurs réelles (numériques) (Negnevitsky, 2002).

Considérons un problème d'optimisation de n variables à optimiser, où l'espace de recherche de chaque variable xj se trouve entre une limite inférieure _xmin,j et une limite supérieure xmax,j : D = [xmin, j , x _max,j] avec j = 1, 2,..., n. On associe des points du domaine D à

Sj chaînes de bits (Sj gènes) de longueur lS. Ainsi, chaque chaîne Sj sera donc composée de lS
éléments binaires : Sj = (si)j ; i = 1, 2,..., lS, où s_i ? {0,1}. Toute chaîne binaire Sj peut être

décodée en une valeur réelle xj en utilisant les deux règles suivantes (Negnevitsky, 2002) :

- dans la première, nous convertissons les valeurs binaires de chaque gène, en valeurs de base décimale selon la règle suivante :

lS

à ( ) 2 (117)

( )

l i

S -

x j s i j

= ·

?=

i 1

- ensuite, nous calculons les valeurs réelles correspondantes appartenant à l'espace de recherche donné, par la règle suivante :

x x

max, min,

j j

-

fd x x x x

( ) à

= = + · _lS (118)

j j j

min, -

2 1

Par exemple, supposons que nous cherchons à maximiser une fonction f en fonction d'une variable réelle x appartenant à l'espace de recherche D = [-1 , 2]. Soit S une chaîne binaire représentant une solution possible avec une longueur lS = 22 :

S = 1,1,0,0,1,0,1,0,0,0,0,1,1,0,1,1,1,1,1,1 ,1,1 }

{

En appliquant les relations (117) et (118), nous obtenons respectivement la valeur entière de x (en base décimale) et sa valeur réelle :

l _S =22

à 2 1 2 1 2 0 2 1 2 3311359

= ? · = × + × + × + + × =

l i

- 21 20 19 0

S

x s_i L

i = 1

x = -

2 ( 1) - - 1 3311359 22 + · = ? - x 1 . 368469 [ 1,2] 2 1 -

Après avoir générer la population initiale, nous devons attribuer à chacun des individus une note qui correspond à son adaptation au problème. Cette adaptation est la mesure de la fonction de performance associée à la fonction objectif du problème. Les notions de ces deux fonctions font l'objet du paragraphe suivant.

3.2.3- Fonctions objectif et de performance. 3.2.3.1- Fonction objectif.

A l'inverse des méthodes déterministes d'optimisation, les algorithmes génétiques ne requièrent pas d'hypothèse particulière sur la régularité de la fonction à optimiser (objectif). Ainsi, les algorithmes génétiques n'utilisent pas les dérivées successives de la fonction objectif, ce qui rend leurs domaines d'application très vaste. Aucune hypothèse sur la continuité n'est également requise. Le peu d'hypothèses requises permet de traiter des problèmes très complexes. La fonction objectif peut être le résultat d'une simulation ou d'un modèle mathématique.

Généralement, la fonction objectif, d'un problème quelconque d'optimisation à K contraintes (dit problème contraint), peut être formulée comme suit :

Optimisation {Fobj(X) : X? D_k} (119)

Avec :

X D ? H X k ( )

: =

b k

? =

k k K

: 1, ,

L

?R R

et H D

: a

k

D_K =

?

?? ? ? ?

? b k

?

??

(120)

?

?

??

Fobj(X) : la fonction objectif du problème.

Hk : la fonction de contrainte.

D : l'ensemble des solutions potentielles du problème.

Dk : l'espace des solutions réalisables (c.-à-d. l'ensemble des solutions potentielles en respectant les contraintes).

La fonction objectif peut être formulée d'un ensemble de fonctions de dimension n. Elle est donnée d'une façon générale comme suit : Fobj(X) = {f1 ,f2,L, f _i ,L, f_n }.

Lorsque i = 1 la fonction est dite monoobjectif, autrement elle est multiobjectif.

Contrairement à l'optimisation monoobjectif, la solution d'un problème d'optimisation multiobjectif est rarement unique. Elle est constituée de différentes solutions, représentant l'ensemble des meilleurs compromis vis-à-vis des différents objectifs du problème.

Les méthodes existantes pour formuler une fonction multiobjectif sont diverses. Nous allons expliquer brièvement ces méthodes qui peuvent être classées en trois grandes familles (Régnier, 2003) :

1- Les méthodes à priori. Dans ces méthodes, on définit, à priori, le compromis désiré entre les objectifs avant de lancer la méthode de résolution. Nous trouvons dans cette famille la plupart des méthodes scalaires telles la méthode de pondération, la méthode des objectifs bornes, la méthode du critère globale,... . Le principe de ces méthodes se base sur la transformation du problème multiobjectif en un problème monoobjectif, en pondérant l'ensemble des fonctions objectif initiales.

2- Les méthodes progressives. Dans ces méthodes, on affine le choix du compromis entre les objectifs au cours de l'optimisation. Contrairement aux méthodes à priori, ces méthodes ont l'inconvénient de monopoliser l'attention de l'utilisateur tout au long du processus d'optimisation. La méthode lexicographique, par exemple, consiste à minimiser séquentiellement les différents objectifs du problème. L'ordre de minimisation est fixé en fonction des résultats séquentiels obtenus. La méthode progresse alors par transformations successives du problème d'optimisation.

3- Les méthodes a posteriori. Dans ces méthodes, il n'est plus nécessaire de modéliser les préférences entre les objectifs avant l'optimisation. Ces méthodes se contentent de produire un ensemble de solutions plutôt qu'un unique compromis. Nous pouvons ensuite choisir a posteriori une solution du compromis.

3.2.3.2- Fonction de performance.

Chaque chromosome apporte une solution potentielle au problème à optimiser. Néanmoins, ces solutions n'ont pas toutes le même degré de pertinence. C'est à la fonction de performance (fitness) de mesurer cette efficacité pour permettre à l'AG de faire évoluer la population dans un sens bénéfique en cherchant la solution meilleure. Autrement dit, la fonction de performance, fp(X), doit pouvoir attribuer à chaque individu un indicateur représentant sa pertinence pour le problème que nous cherchons à résoudre. La performance sera donc donnée par une fonction à valeurs positives réelles. La construction d'une fonction de performance appropriée est très importante pour obtenir un bon fonctionnement de l'AG.

Dans le cas du codage binaire, la fonction de performance doit affecter une valeur positive au codage binaire correspondant (phénotype) à chaque chaîne binaire (génotype). Ainsi, elle permet de déterminer l'efficacité de la solution présentée par le génotype pour résoudre le problème.

La fonction de performance fp(X) est généralement dérivée de la fonction objectif Fobj(X) du problème. Elle est généralement donnée par la relation suivante :

fp(X) = g(Fobj(X)) (121)

Où : g : représente la transformation de la fonction objectif en performance relative.

Les AGs sont naturellement organisés pour résoudre les problèmes de maximisation (c. -à- d. trouver les valeurs positives maximales de la fonction objectif). Ainsi, pour les problèmes de maximisation, la fonction de performance peut être considérée comme la fonction objectif même. Le but de l'AG est alors simplement de trouver la chaîne binaire qui maximise la fonction de performance :

max(fp(X)) = min(Fobj(X)) (122)

Dans le cas de problèmes de minimisation, le problème doit être modifié de sorte qu'il soit équivalent à celui de maximisation. Ainsi, il nous faudra modifier la fonction objectif de telle sorte que la fonction de performance soit maximale :

max(fp(X)) = -min(Fobj(X)) (123)

max(fp(X)) = 1/min(Fobj(X)) (124)

max(fp(X)) = max(C- Fobj(X)) ; (C : une grande constante positive) (125)

Une fois que la performance de chaque individu dans la population actuelle est évaluée, les mécanismes évolutionnaires entrent en jeu pour explorer et exploiter le plus largement possible l'espace de recherche et faire ainsi évoluer la population de manière progressive. Les opérateurs de l'AG cherchent à imiter ces mécanismes.

3.2.4- Sélection.

Pour déterminer les individus devant participer au résultat optimal de l'AG, un opérateur sélection doit être appliqué. Cet opérateur détermine la capacité de chaque individu à persister dans la population et à se reproduire. En règle générale, la probabilité de survie d'un individu sera directement reliée à sa performance relative au sein de la population. Cela traduit bien l'idée de la sélection naturelle Darwiniste : les gènes les plus performants ont la probabilité la plus élevée de se reproduire dans la population, tandis que ceux qui ont une performance relative plus faible auront tendance à disparaître. Néanmoins, cette approche doit être appréhendée avec précaution, puisqu'on souhaite transférer aux générations suivantes les meilleures caractéristiques génétiques et pas seulement les meilleurs individus.

En effet, un individu peut avoir certains gènes présents dans la solution optimale tout en présentant une performance médiocre : son élimination serait donc nuisible. Cependant, les individus ayant une bonne performance sont toujours plus susceptibles de posséder les bons gènes. Ainsi, une caractéristique importante d'un opérateur de sélection peut être définie en termes de pression sélective exercée sur la population. Cette notion doit être prise en compte d'une manière équilibrée. Si la pression sélective est trop forte, cela revient à "écraser" toute forme de diversité possible et la convergence de l'algorithme risque d'être prématurée en conduisant vers un optimum local. Si l'on passe à l'autre extrême, une pression sélective trop faible, l'algorithme tend à se rapprocher d'une simple recherche aléatoire avec une progression lente de la population (Duvigneau, 2006).

Il existe plusieurs méthodes pour représenter la sélection. La méthode la plus couramment utilisée proposée par Goldberg (Goldberg, 1989) est connue sous le nom de sélection par roulette biaisée (Roulette Wheel). D'autres méthodes de sélection sont aussi apparues dans la littérature, la plus connue étant celle du tournoi (Tournament Selection).

3.2.4.1- Sélection par la roulette biaisée.

Dans cette méthode, chaque chromosome est copié dans la nouvelle population avec une probabilité proportionnelle à sa performance relative : on parle ainsi de sélection proportionnelle à la performance. Dans un codage binaire, le principe de cette méthode consiste à associer à chaque individu Xi (d'une population de taille _Nind) une probabilité Rp,i proportionnelle à sa performance fp(Xi). Cette probabilité (dite la fonction de performance

normalisée) peut être ainsi calculée comme le taux de la performance du i^ème individu pondéré par la somme des performances de toute la population :

R P , i

fp ( ) (126)

Nind

?=

i 1

X i

fp ( )

X i

On doit donc effectuer autant de tirages aléatoires qu'il y a d'individus dans la population. Chaque individu est alors reproduit avec la probabilité R_p ; certains individus (notés les bons) auront plus de chance d'être reproduits, les autres (notés mauvais) seront éliminés.

Dans la pratique, nous associons à chaque individu un secteur (ou un segment) dont la surface (la longueur) est proportionnelle à sa performance. Ces éléments sont ensuite concaténés sur une base normalisée entre 0 et 1. Enfin, nous reproduisons le principe de tirage aléatoire utilisé dans les roulettes de casinos, d'où le nom de ce mécanisme de sélection, avec une caractéristique linéaire (sélection proportionnelle à la performance). Nous tirons alors un nombre aléatoire, de distribution uniforme entre 0 et 1, et nous déterminons l'individu sélectionné. Ainsi, les grands secteurs (c.-à-d. les bons individus) auront plus de chance d'être choisis que les petits secteurs. Les individus ayant une forte performance sont donc privilégiés au détriment des individus moins forts, tout en gardant la notion de tirage aléatoire. Ainsi, avec cette méthode un même individu pourra être sélectionné plusieurs fois. Mais une certaine diversité est cependant maintenue, car même les individus les moins performants conservent une chance d'être choisis. Pour garder la même taille de la population initiale dans la population suivante, on doit lancer la roulette autant de fois qu'il y a d'individus de la population.

Considérons un problème simple de maximisation dont la fonction objectif est donnée par la forme suivante :

Fobj = 4· x · (1- x)

L'espace de recherche de la variable x est D = [0,1].

Nous traitons ce problème en décodant les points de l'espace de recherche en chaînes binaires de longueur lS = 8, et en initialisant une population de départ de 4 individus (Nind = 4).

Pour appliquer la méthode de la roulette biaisée, nous calculons en premier lieu, pour chaque individu, la fonction de performance fp(Xi) et la probabilité correspondante Rp,i.

Le tableau suivant résume le résultat pour chaque élément :

N° individu	Chromosome Si					Valeurs décodées Xi (individus)	Performance fp(Xi) =Fobj = 4·x·(1-x)	Probabilité Rp,i = fp(Xi) / ?( fp(Xi))	Intervalles de probabilité
1	1	0 1	1 1	0 1	0	0.7294	0.7895	0.29	[0 , 0.29]
2	1	1 0	1 1	1 1	0	0.8706	0.4507	0.18	[0.29 ,	0.47]
3	0	0 0	1 1	0 1	0	0.1020	0.3665	0.15	[0.47 ,	0.62]
4	0	1 1	0 1	1 0	0	0.423 5	0.9766	0.38	[0.62	, 1]
							? fp = 2.5831

Tableau 1. Résultats de l'évaluation des individus dans la population initiale.

Ensuite, nous associons à chaque intervalle de probabilité un secteur équivalent de la roulette (c.-à-d. un individu), comme le montre la figure (41) :

0.29

Rp1 Rp2

0.47

0

1

Rp3

Rp4

0.62

Figure 41. Sélection par roulette biaisée.

Enfin, nous effectuons le tirage d'un nombre aléatoire dans l'intervalle [0,1] et nous reproduisons ce tirage 4 fois. Nous sélectionnons ainsi les individus en positionnant chaque nombre obtenu par tirage dans le secteur équivalent de la roulette. Le tableau (2) donne la valeur obtenue pour chaque tirage et les individus sélectionnés correspondants.

N° tirage	Valeur obtenue	Individus sélectionnés		Chromosomes équivalents
1	0.43	X2	Xá 1	=	1	1 0	1 1	1 1	0
2	0.89	X4	Xá 2	=	0	1 1	0 1	1 0	0
3	0.18	X1	Xá 3	=	1	0 1	1 1	0 1	0
4	0.75	X4	Xá 4	=	0	1 1	0 1	1 0	0

Tableau 2. Résultat de sélection.

Nous trouvons que l'individu X3 est éliminé de la population tandis que l'individu X4 est reproduit deux fois.

3.2.4.2- Sélection par tournoi.

La méthode de la roulette, comme les autres méthodes de sélection proportionnelle à la performance, exige principalement deux étapes pour créer la population intermédiaire. Premièrement, nous calculons la performance moyenne de la population, ensuite nous calculons la probabilité de sélection pour chaque individu. La méthode du tournoi est plus directe, puisqu'elle ne demande pas le calcul de la performance moyenne de la population (Mitchell, 1996).

Cette méthode consiste à simuler _Nind tournois, un individu étant sélectionné à chaque fois. Un échantillon de n_p individus (2 minimum) est prélevé au hasard à chaque tournoi. Le

participant dans l'échantillon ayant la performance la plus élevée sera alors adopté pour accéder à la population intermédiaire. Etant donné que le choix des échantillons des individus se fait aléatoirement, il est donc tout à fait possible que certains individus participent à plusieurs tournois. Il est aussi possible qu'un de ces individus gagne plusieurs fois et il sera par conséquent copié autant de fois dans la population intermédiaire. La pression sélective de cette méthode est directement reliée à la taille de l'échantillon (n_p). Plus la taille n_p est grande, plus la pression est grande (Duvigneau, 2006). Cette méthode est caractérisée par une pression sélective plus forte que celle de la méthode de la roulette biaisée : pour qu'un individu peu performant puisse être sélectionné, il faut que tous ses adversaires soient moins bons que lui. Ainsi, cette méthode doit être privilégiée dans le cas d'une population de grande taille.

Dans le cas où le nombre de participants dans chaque tournoi est égal à deux (n_p = 2), la sélection est dite par « tournoi binaire ». La sélection d'un individu _Xsélect,K par tournoi binaire peut être faite de la façon suivante :

XsélectK ,

=

? ?? ??

X Si fp X ( ) > i i X Sinon j

fp X ( ) j

(127)

Où, K={1,2,L,N_ind}.

i, j sont des nombres aléatoires non-égaux, i, j ? {1,2,L, Nin d }. 3.2.4.3- Conclusion.

La méthode de la roulette reste la méthode de sélection la plus utilisée car elle est relativement efficace. Cependant, pour certains problèmes, elle est "un peu trop aléatoire". C'est pour cela que pour certains problèmes, la méthode du tournoi est plus préférée. Cette dernière étant "moins aléatoire" que la roulette, elle permet ainsi une plus grande fiabilité.

Disposant finalement d'une population d'individus non-homogène, la diversité de la population doit être entretenue au cours des générations afin de parcourir le plus largement possible l'espace de recherche. Pour ce faire, les individus sélectionnés (dits les parents) sont alors introduits dans le bassin de reproduction (Mating Pool) où ils seront de nouveaux choisis aléatoirement pour voir leurs chromosomes subir des transformations par les opérateurs génétiques. Ces derniers sont les opérateurs de croisement et de mutation (dits les opérateurs de diversification et d'intensification du milieu).

3.2.5- Croisement.

Dans les AGs, le croisement est considéré comme le principal opérateur pour produire des nouveaux chromosomes. Comme son homologue dans la nature, le croisement produit de nouveaux individus en leur transférant quelques parties de la matière génétique de leurs parents. L'objectif du croisement est donc d'enrichir la diversité de la population en manipulant la structure des chromosomes (Chipperfield et al., 1994). Initialement, le croisement associé au codage par chaînes de bits (codage binaire) est le croisement à découpage de chromosomes.

Ainsi, dans le codage binaire, les individus, qui résultent de la sélection, sont groupés de manière aléatoire par paire définissant ainsi les parents. Ensuite, chaque couple peut subir un croisement avec une probabilité P_c donnée. Cette étape peut être effectuée comme suit

Pour chaque couple, un nombre aléatoire P est tiré dans l'intervalle [0,1] et comparé ensuite avec la probabilité de croisement P_c :

- si P > P_c, le couple ne subit pas de croissement et un clonage de chromosome aura

lieu. Les deux enfants produits sont ainsi une copie exacte de leurs parents.

- si P < P_c, le croisement a lieu et un échange des parties des chromosomes des parents

va produire deux enfants par couple de parents.

Après avoir tiré les couples qui vont être "croisés", l'opérateur de croisement peut donc être appliqué. Plusieurs types de croisement sont présentés dans la littérature, tels : le croisement seul point, le croisement multipoints, le croisement uniforme,... .

3.2.5.1- Croisement seul point.

Dans ce type de croisement, un point de croisement est choisi aléatoirement pour le couple ; la position de ce point M est définie par:

M? {1,2,L,l _S -1} (128)

lS : la longueur de chromosome (nombre de bits dans le chromosome).

Les deux parents seront ainsi divisés en deux segments ; tête et queue. Le segment tête du premier parent est combiné avec le segment queue du deuxième parent : on obtient ainsi le premier enfant. La combinaison entre le segment tête de deuxième parent et le segment queue de premier parent produit le deuxième enfant.

Pour mieux expliciter ce type de croisement, nous allons l'appliquer à l'exemple présenté dans le paragraphe de la sélection.

Considérons la population de quatre individus déterminée par l'opération de sélection, nous pouvons la diviser aléatoirement en deux couples qui peuvent être par exemple : [(X_á1, Xá4), (Xá2, X_á3)].

Considérons ensuite une probabilité de croisement P_c = 50% (nous avons choisi une faible probabilité de croisement étant donné la "petite" taille de la population considérée). Cela signifie que nous pouvons tirer seulement un seul couple au hasard et lui appliquer le croisement chromosomique. Supposons que le hasard ait désigné le deuxième couple (Xá2, Xá3) pour croisement, il nous faut maintenant déterminer la position du point M de croisement dans les parents. Cette position peut être tirée au hasard ou choisie préalablement. Afin de rendre l'exemple plus parlant, nous décidons d'appliquer ce croisement sur le milieu (M = 4) du chromosome, comme le montre la figure (42).

Ainsi, l'application de l'opération de croisement engendre deux nouveaux individus (les deux enfants Xâ ₂ et Xâ 3).

Le croisement en un seul point a l'avantage d'être simple et facile à appliquer. De plus, ce type de croisement donne de bons résultats dans des applications où certaines informations importantes sur le problème sont déjà connues. Enfin, pour des problèmes d'optimisation en temps réel ou des problèmes ayant un grand nombre de variables, cette méthode peut donner une convergence rapide vers une solution optimale.

Avant Après

Croissement Croissement

0

1

Parent X_á 2

Parent X_á 3

0

1

1

1

0

1

1

1

0

1

0

1

0

0

Enfant Xâ 2

0

1

1

0

1

0

1

0

Enfant Xâ 3

1

0

1

1

1

1

0

0

Figure 42. Croisement seul point. 3.2.5.2- Croisement multipoints.

A la différence du croisement seul point, ce type de croisement s'applique en plusieurs points (m points) et chaque chromosome sera ainsi découpé en (m+ 1) segments. La position de chaque point, Mi, se détermine aléatoirement, avec :

M_i { l S } i m

? L - = L

1,2, , 1 ; 1,2, ,(129)

lS : la longueur de chromosome.

m : le nombre de points de croisement donné (Pour m = 1, on retourne au cas du croisement seul point).

Ensuite, les bits entre deux points de croisement successifs du premier parent vont être échangés avec les bits correspondants du deuxième parent. La figure (43) montre un croisement en cinq points (m = 5), les points de croisement Mi étant {2, 5, 9, 11, 13 } :

M1 = 2 M2 = 5 M3 = 9 M4 = 11 M5 = 13

1110111

0

0

1

1

1

0

1

Enfant 1

1

01000001 1 0 0 0 0

Enfant 2

1 0 1 0 1 0 0 01 1 1 0 01

1 1 1 0 0 1 1 0 0 1 0 1 00

Parent 2

Parent 1

Figure 43. Croisement multipoints (m = 5).

La nature complexe du croisement multipoints permet d'obtenir une bonne exploration de l'espace de recherche au détriment d'une convergence rapide vers la bonne solution comme le ferait la première méthode. Ainsi, cette méthode de croisement est beaucoup plus robuste.

3.2.5.3- Croisement uniforme.

Dans le croisement multipoints, chaque segment du chromosome, compris entre deux points de croisement successifs, peut contenir un ou plusieurs bits. Le croisement uniforme généralise ce schéma pour lier à chaque bit un point de croisement. Pour ce faire, un chromosome masque, de même longueur que le chromosome des parents, est créé : la valeur de ses bits étant aléatoire. La parité de chaque bit dans le masque détermine successivement le parent qui va donner ses bits à l'enfant (Chipperfield et al., 1994). L'enfant généré va copier le bit de son premier parent si le bit correspondant de masque est `1', ou de son deuxième parent si le bit correspondant de masque est `0'. Ce schéma ne fait générer qu'un seul enfant. Pour générer le deuxième, un autre chromosome masque est nécessaire. Les bits de ce dernier sont créés par complémentation des bits du premier masque. L'explication de cette méthode est décrite par l'exemple suivant :

0

1

0

1

1

0

1

Parent 1

Enfant 1

1

1

1

1

1

1

0

0

0

1

0

1

1

0

1

1

1

0

1

1

0

0

0

1

1

0

1

0

1

Masque 1

1

0

0

1

1

1

0

0

1

0

1

0

Masque 2

1

0

1

0

1

1

0

0

1

0

0

1

0

0

1

1

0

0

0

0

0

0

1

1

Parent 2 Enfant 2

Figure 44. Croisement uniforme.

La nature complexe du croisement uniforme, comme pour le croisement multipoints, améliore encore l'exploration de l'espace de recherche. Avec le croisement uniforme, basé sur le transfert de matière génétique d'un parent à un enfant par bit de chromosome, on obtient un algorithme génétique beaucoup moins dépendant du schéma de codage. Enfin, cette méthode peut être plus précise dans l'identification d'optima globaux.

3.2.6- Mutation.

A la suite des opérateurs de sélection et de croisement, on mime à nouveau un phénomène biologique, celui de la mutation. Au niveau biologique, une mutation est une modification de l'information génétique par dégradation ou substitution locale de paire de base : ceci permet de produire une nouvelle structure génétique. L'opérateur de mutation dans le cas des AGs possède la propriété d'ergodicité du parcours de l'espace de recherche : cette propriété indique que l'AG sera susceptible d'atteindre tous les points de l'espace, sans pour autant les

parcourir tous dans le processus de résolution (Bontemps, 1995). La séquence des opérations de sélection et de croisement peut mener l'AG à "stagner" dans un ensemble de solutions identiques. Dans de telles conditions, tous les chromosomes deviennent identiques et, ainsi, la performance moyenne de la population ne s'améliore plus. Dans ce cas, la mutation aide l'AG à éviter la perte de diversité génétique et, par conséquent, elle garantit que l'AG ne va pas être bloqué dans un optimum local (Negnevitsky, 2002).

Le principe de la mutation consiste à modifier, avec une probabilité P_m faible, certains bits des chromosomes. Nous tirons tout d'abord pour chaque bit un nombre aléatoire P dans l'intervalle [0,1]. Puis, nous le comparons avec une probabilité de mutation P_m donnée :

- si P > P_m, le bit ne subira pas aucune modification.

- si P < P_m, la mutation est appliquée au bit correspondant.

Ainsi, le bit choisi pour muter sera remplacé par une valeur aléatoire, souvent proche de la valeur initiale. Dans le cas du codage binaire, cette mutation s'effectue simplement en remplaçant le bit `0' par `1' et vice versa.

Pour continuer la présentation de l'opérateur de mutation, nous reprenons l'exemple précédent (paragraphe croisement) et nous appliquons la mutation sur la population résultante du croisement.

Rappelons les individus résultants :

Xâ 1 = 1 1 0 1 1 1 1 0

Xâ 2 = 0 1 1 0 1 0 1 0

Xâ 3 = 1 0 1 1 1 1 0 0

Xâ 4 = 0 1 1 0 1 1 0 0

Nous proposons arbitrairement une probabilité de mutation P_m = 0.01. Pour déterminer les bits qui subiront une mutation, nous tirons un nombre aléatoire compris entre 0 et 1 pour chaque bit et nous le comparons avec P_m. La figure suivante montre les bits choisis pour la mutation et l'application de cet opérateur :

Xfl 3

0

1

1

0

1

1

0

0

Xfl 4

X_ã 3

0

1

1

0

1

1

0

0

Xã 4

0

1

1

1

1

1

1

0

0

1

1

1

1

1

0

1

0

1

1

0

Xfl 1

1

0

0

1

1

0

1

0

Xã 1

0

0

1

0

1

1

1

0

1

1

1

0

1

1

0

0

1

Xfl 2

1

0

1

1

1

1

1

0

X_ã 2

Figure 45. Exemple de mutation.

Les individus résultants de la mutation, (Xã1, Xã2, Xã3, Xã4), vont former la nouvelle population qui va remplacer la population initiale pour la deuxième génération.

3.2.7- Création de la génération suivante et critères d'arrêt.

Pour réaliser une boucle d'une itération de l'AG, ce dernier doit d'abord regrouper les individus survivants après mutation dans une nouvelle population. Ensuite, l'AG va calculer la performance pour chaque nouvel individu. Enfin, si un critère d'arrêt de l'algorithme n'est pas encore atteint, la nouvelle population doit alors remplacer la population actuelle et une nouvelle boucle sera ainsi lancée.

Puisque les AGs sont des méthodes de recherches stochastiques, il est difficile de spécifier de façon rigoureuse des critères de convergence. Par exemple, la performance d'une population peut rester stable pour un certain nombre de générations avant qu'un individu supérieur puisse apparaître. Ainsi, l'application d'un critère d'arrêt devient une vraie problématique. Une pratique commune est d'arrêter l'AG après certain nombre de générations et d'examiner ensuite la qualité de la solution trouvée par rapport à la définition du problème. Un nombre typique de générations peut aller de 50 jusqu'à 500 générations (Negnevitsky, 2002).

Par ailleurs, d'autres critères peuvent être appliqués pour déterminer l'arrêt de l'AG tels que :

- l'amélioration de la solution ne dépasse plus un certain seuil

- la fonction objectif du problème atteint une valeur donnée

- le temps de calcul atteint une valeur prédéterminée.

Nous terminons l'exemple que nous avons commencé de traiter par le calcul de la performance de chaque nouvel individu :

N° individu	Chromosome Sãi						Valeurs décodées Xãi	Performance fp(Xãi) =Fobj
1	0	1 1	1	1 1	1	0	0.4941	0.9999
2	0	0 1	0	1 1	1	0	0.1804	0.5914
3	1	0 1	1	1 1	1	0	0.745 1	0.7597
4	0	1 1	0	1 1	0	0	0.4235	0.9766
								? fp = 3.3276

Tableau 3. Résultats de l'évaluation des individus dans la nouvelle population.

En comparant le tableau (1) de l'évaluation de la population initiale et le tableau (3) de

l'évaluation de la nouvelle population, nous pouvons tirer les remarques suivantes :

- le meilleur individu (Xãj) dans la nouvelle population est un individu nouveau (issu

d'une opération de mutation).

- ce nouvel individu présente une performance supérieure à celle du meilleur individu de la population initiale (fp(Xãj) = 0.9999 contre fp(Xj) = 0.9766).

- l'individu X4 reste toujours présent dans la nouvelle population (renommé Xã4).

- la nouvelle performance totale (et donc la performance moyenne) est supérieures à la valeur de départ (? fp(Xãi) = 3.3276 contre ? fp(Xi) = 2.5831).

- l'individu (Xã1), associé à la performance maximale fp(Xã1), peut être ainsi considéré comme la solution optimale du problème.

Etant donné que le problème traité est très simple, l'AG a pu atteindre une solution optimale dés la première itération.

3.2.8- Compromis exploration et exploitation.

Généralement, la recherche d'une solution optimale dans un espace complexe implique souvent un compromis entre deux objectifs apparent contradictoires : l'exploration et l'exploitation.

L'exploration a pour objectif une recherche large des régions nouvelles et inconnues de l'espace de recherche en récoltant de l'information sur le problème à optimiser. L'exploitation se propose d'utiliser l'information acquise aux points déjà explorés pour définir et parcourir ainsi les zones les plus intéressantes de l'espace de recherche. Une recherche purement aléatoire (comme le fait la méthode de Monte-Carlo) est bonne pour l'exploration mais mauvaise pour l'exploitation alors que la recherche dans le voisinage (comme le fait la méthode de la descente) est une bonne méthode d'exploitation mais une mauvaise méthode d'exploration. La littérature montre que les algorithmes génétiques peuvent réaliser un compromis équilibré et raisonnable entre exploration et exploitation. Mais il est important de bien doser l'usage de ces deux ingrédients afin que l'exploration puisse identifier rapidement des régions de l'espace de recherche qui contiennent des solutions de bonnes qualités, sans perdre trop de temps à exploiter des régions moins prometteuses. Pour ce faire, il faut ainsi ajuster les paramètres de réglage des opérateurs génétiques, sachant que le croisement favorise plus l'exploration tandis que la mutation favorise plus l'exploitation.

3.2.9- Paramètres de réglage de l'AG.

Il y a principalement trois paramètres de base pour le "fonctionnement" d'un AG : - le nombre d'individus dans la population _Nind (dit la taille de la population).

- la probabilité de croisement P_c.

- la probabilité de mutation P_m.

La réussite et la rapidité d'un AG dépendent fortement des valeurs choisies pour ces paramètres. Le bon réglage de ces paramètres est un problème parfois délicat (Mitchell, 1996).

Nous discutons ci-dessous l'influence de chaque paramètre et la gamme de valeurs qu'il peut prendre :

1- la taille de la population Nind

Ce paramètre doit être judicieusement réglé en fonction de la taille du problème. Généralement, nous pouvons dire que si la taille de la population est :

- trop faible, l'AG peut converger trop rapidement vers de mauvaises solutions. - trop grande, le temps de calcul de l'AG peut s'avérer très important.

En règle générale, plus la taille de la population est grande, plus le nombre de solutions potentielles évaluées est élevé. La littérature montre que les meilleures valeurs de taille de population sont comprises entre 50 et 100 individus (Mitchell, 1996).

2- la probabilité de croisement P_c

Comme nous l'avons dit, la probabilité de croisement joue un rôle très important dans l'exploration de l'espace de recherche du problème. En générale, plus la probabilité de croisement est élevée, plus il y aura de nouvelles structures apparaissant dans la nouvelle population. Ainsi, si la probabilité de croisement est :

- trop élevée, les "bonnes" structures apportées par la sélection risquent d'être détruites trop vite.

- trop faible, la recherche de la solution optimale risque de stagner.

Le taux habituel de la probabilité de croisement est choisi entre 0.7 et 0.95.

3- la probabilité de mutation P_m

La mutation, comme nous l'avons vu, est un opérateur secondaire, mais elle reste très importante pour l'AG. Elle a pour objectifs l'introduction de diversité dans la population et la meilleure exploitation de l'espace de recherche. Ainsi, si la probabilité de mutation est :

- trop élevé, la mutation rend la recherche très aléatoire.

- trop faible, la recherche risque de stagner.

Le taux habituel de la probabilité de mutation est choisi entre 0.001 et 0.05. 3.3- Conclusion.

Les algorithmes génétiques sont des méthodes métaheuristiques d'optimisation globale basées sur des concepts de génétique et de sélection naturelle. Le composant principal des AGs est le gène qui se compose d'une chaîne de caractères (souvent binaire). Les gènes s'enchaînent et forment les chromosomes. Ces derniers forment les individus dans l'espace de recherche. Ainsi, les AGs travaillent sur une population d'individus, où chacun de ces derniers représente une solution possible pour le problème donné. Dans chaque itération de l'AG, la performance de chaque individu de la population courante est calculée. Les opérateurs de génétiques, sélection, croisement et mutation, sont appliqués successivement pour créer une nouvelle population jusqu'à l'approche rigoureuse de la solution optimale.

Les algorithmes génétiques offrent plusieurs avantages :

- Ils ne demandent pas d'informations à priori ou des propriétés particulières de la fonction objectif du problème.

- Leurs performances par rapport aux algorithmes classiques sont bien remarquées lorsque par exemple les espaces de recherches sont importants.

- Outre leur facilité de programmation et de manipulation, ils sont facilement adaptables à tout type de problème d'optimisation.

- Ils peuvent être utilisés avec profit pour traiter des problèmes n'étant pas optimisables efficacement par des approches purement mathématiquement.

Par ailleurs, les algorithmes génétiques présentent certaines limites :

- Le temps de calcul est souvent important : ils nécessitent de nombreux calculs, en particulier au niveau de la fonction objectif.

- Les paramètres de réglage (telles la taille de la population, la probabilité de croisement, ...) sont parfois difficiles à déterminer. Or le succès de l'évolution en dépend et plusieurs essais sont donc nécessaires.

- Ils ne garantissent pas toujours la découverte de l'optimum global en un temps fini. En effet, lorsqu'une population évolue, il se peut que certains individus occupant à un instant une place importante au sein de cette population deviennent majoritaires. A ce moment, il se peut que la population converge vers cet individu en s'écartant ainsi d'individus plus intéressants et en s'éloignant de l'individu vers lequel on devrait converger.

Nous pouvons conclure que l'efficacité des AGs dépend d'un compromis entre deux objectifs contradictoires : la rapidité et la précision. La rapidité est souvent mesurée en nombre d'évaluations de la fonction objectif. Cette dernière représente la plupart du temps la partie la plus "gourmande" en temps de calcul. La précision se rapporte à la distance entre l'optimum trouvé par l'AG et l'optimum réel, du point de vue de la solution ou de la valeur. Bien souvent, un AG rapide est peu précis, et inversement.

Dans le chapitre suivant, nous utilisons les principales caractéristiques des AGs développés dans ce chapitre pour une optimisation globale des PSSs.

Chapitre IV

Application

4.1- Introduction.

Nous avons jusqu'à présent développé le modèle nécessaire du système de puissance, présenté la théorie de la stabilité aux petites perturbations avec régulateurs PSSs ainsi que les AGs. L'objectif de ce chapitre est de trouver la meilleure localisation possible des PSSs, avec des paramètres optimaux, tout en réduisant le nombre de PSSs. Cela assurera un amortissement satisfaisant aux oscillations rotoriques des modes locaux et interrégionaux et garantira la stabilité globale du système pour différents points de fonctionnement.

Lors de l'installation des PSSs dans les réseaux multimachines, la première étape conventionnelle à mettre en oeuvre concerne la détermination des meilleurs emplacements des PSSs au sein du réseau.

Le nombre de stabilisateurs à installer n'est pas toujours égal au nombre de générateurs. Par conséquent, il faut prendre en considération le choix de l'emplacement optimal des stabilisateurs qui offre un meilleur amortissement.

Pour amortir les modes locaux, le choix de l'emplacement reste facile car le nombre de générateurs impliqués principalement dans les oscillations locales est très faible. Par contre, pour les modes globaux, un grand nombre de générateurs sont généralement associées aux oscillations. Cela complique le choix de l'emplacement des PSSs (Zhou et al., 1991). En outre, une mauvaise localisation d'un PSS peut entraîner une amplification des oscillations, voire contribuer à la perte de stabilité du système. Ainsi, le problème du choix de l'emplacement des PSSs est très critique et il faut le traiter judicieusement.

Quand un PSS est inséré dans le système, il affectera tous les modes électromécaniques d'oscillations. Ainsi, les interactions entre les PSSs doivent être considérées lorsque plusieurs PSSs sont insérés (Zhang et al., 2000).

Tout PSS devrait être réglé pour fournir l'amortissement suffisant de tous les modes électromécaniques car l'amortissement de chaque mode est un effet cumulatif des contributions de chaque PSS. En outre, le réglage des PSSs doit être robuste : les PSSs doivent être efficaces non seulement lors de la variation des conditions de fonctionnement mais aussi lors du changement de la topologie du réseau.

Ce chapitre s'articule autour de l'application de notre approche au sein d'un système de puissance multimachines.

Dans la première partie, nous allons présenter les caractéristiques du réseau étudié (le réseau interconnecté New England/New York : 16 générateurs et 68 noeuds).

Ensuite, nous expliquons les différents critères de performance du système pour le modèle linéaire et non-linéaire.

Le problème d'assurer une meilleure localisation des PSSs et une meilleure coordination de leurs paramètres est formulé en tant que problème d'optimisation multiobjectif et résolu à l'aide d'un programme d'AG. La fonction multiobjectif utilisée est formulée pour optimiser un ensemble de deux fonctions objectif basées sur l'analyse des valeurs propres du système (partie réelle de la valeur propre et facteur d'amortissement). La mise en oeuvre de cette approche fera l'objet de la troisième partie du chapitre.

La dernière partie du chapitre concerne l'application de l'approche proposée et la discussion des résultats obtenus.

4.2- Réseau étudié.

4.2.1- Caractéristiques du réseau étudié.

Le système de puissance choisi dans notre étude est le réseau réduit équivalent au réseau interconnecté de New England et New York (Rogers, 2000). Ce système, composé de cinq régions, possède des propriétés intéressantes de par la complexité des interactions des différentes régions qui le composent. Il se compose de 16 générateurs (numérotés de 53 à 68) et de 68 noeuds. Les neuf premiers générateurs représentent le système de génération de New England. Les générateurs de 62 à 65 représentent le système de New York. Chacun des trois derniers générateurs forme un seul groupe ; ils représentent les systèmes équivalents aux trois grandes régions voisines interconnectées au système de New York.

La représentation unifilaire du système et une représentation géographique et schématique de l'interconnexion des cinq régions sont respectivement données aux figures (46) et (47). Huit lignes d'interconnexion relient les cinq régions du système : ce sont les lignes entre les jeux de barre (1#2), (1#27), (1#47), (8#9), (42#41), (46#49), (52#42) et (50#51). La puissance est transférée de la deuxième région aux première, troisième et cinquième régions. La puissance est aussi transférée de la cinquième région à la quatrième et de cette dernière à la troisième. Les puissances active et réactive transitées dans ce réseau, pour le point de fonctionnement nominal, sont d'environ 20 GW et 3 GVAr. Cela représente quasiment, en ordre de grandeur, un quart que le système de puissance français.

Les valeurs numériques du réseau peuvent être trouvées dans la référence (Rogers, 2000) ; elles sont rappelées en annexe C.

4.2.2- Caractérisations d'un défaut.

Dans les réseaux haute tension, les types de défauts les plus fréquents sont les courts- circuits. Ces derniers dépendent de différents facteurs tels leurs emplacements, leurs durées, leurs types (une phase- terre, deux phases,...), le système de prise de terre,... .

Bien que les courts-circuits triphasés -les défauts symétriques- soient rares, l'analyse de ce type de défauts est nécessaire, car ils mènent généralement aux courants de défauts les plus sévères. Ils sont donc souvent les plus utilisés en simulation dynamique pour tester la stabilité des systèmes de puissance et la robustesse de régulation.

Lorsque les protections détectent une apparition de courants élevés sur une ligne (ou une diminution de l'impédance vue des extrémités de la ligne), elles "envoient" aux disjoncteurs concernés un ordre d'ouverture afin d'isoler la ligne en question et éviter la propagation du phénomène sur le réseau. La disparition du court-circuit doit se faire rapidement, en moins de trois périodes du réseau (50 millisecondes pour une fréquence de 60 Hz). Ensuit, les dispositifs de réenclenchement automatique de la ligne sont responsables de remettre la ligne en service (Meyer et al., 1998). Ainsi, la simulation du défaut de court-circuit sur une ligne de transmission et la simulation du comportement des systèmes de protection s'effectue lors de :

- l'apparition du défaut

- l'ouverture et du réenclenchement automatique des disjoncteurs.

Dans notre étude, cela implique de calculer la matrice admittance du réseau de transport pour les trois phases suivantes : avant le défaut, pendant le défaut et après le défaut, en considérant que le défaut triphasé est caractérisé par une impédance infiniment petite (Zf = 0 + j10^-7 dans notre simulation), (Tolba, 2005).

29

59

61

23

58

22

21

G6

G7

52

40

68

G9

19

56

G4

28

24

16

57

20

G5

27 17

15 14 13 10

55

26

G3

60

25

18

12 11

G8

54

53 2

G1

3

4

7

5

G2

8

36 37 65

9

1

30

47

G13

63

32

64

G12

33 34

48

G11

45 44 39

31

35

G10

62

51

50

38

G16

46

41

66

67

49

42

G15

G14

Figure 46. Représentation unifilaire du réseau étudié
(Réseau New England/New York : 16 générateurs, 68 noeuds).

105

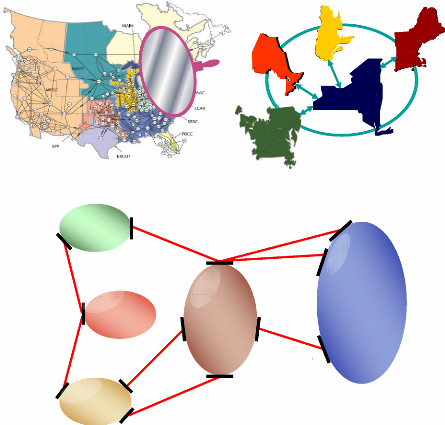
47

2

Région

3

41

1

27

42

49

9

New
York

8

Région

4

Région

2

New
England

Région
1

46

52

50

Région

5

51

ISO

IESO

New York
ISO

PJM

MW*

Hydro

Quebec New

England

Figure 47. Représentation géographique et schématique des cinq régions du système étudié. 4.3- Analyse de la performance et critères de bonne régulation.

Pour faire une étude analytique complète des problèmes d'oscillations des systèmes de puissance, il est nécessaire d'établir des procédures d'analyse du problème et de préciser les critères de performance du système. Les outils d'analyse des oscillations du système doivent déterminer les problèmes existants ; ils doivent être capables en outre d'identifier les éléments déterminants et de fournir des informations utiles pour la conception et le réglage des contrôleurs du problème.

Les simulations d'un système non-linéaire en domaine temporel, qui représentent une extrapolation naturelle de l'analyse de la stabilité transitoire, fournissent des informations importantes mais limitées en ce qui concerne la stabilité dynamique. Ainsi :

- le choix de la perturbation et la sélection des variables à observer sont critiques,

- la perturbation peut être insuffisante pour exciter les modes critiques,

- les réponses temporelles ne peuvent donner directement une information sur la source des oscillations,

- plusieurs modes sont mélangés dans les courbes des simulations temporelles.

L'analyse du modèle linéaire du système semble un moyen idéal pour étudier profondément les oscillations électromécaniques et les problèmes associés. La stabilité et les caractéristiques de chaque mode peuvent par exemple être identifiées clairement en examinant les valeurs propres du système. Les vecteurs propres quant à eux montrent aisément la nature de ces modes et les relations entre eux et les variables d'état.

Ainsi, une compréhension complète des oscillations de système de puissance nécessite la combinaison d'outils analytiques. L'analyse du modèle linéaire complétée par des simulations en domaine temporel du modèle non-linéaire représente la procédure la plus efficace pour bien étudier et analyser les oscillations de système de puissance (Farmer, 2006). Les étapes suivantes sont nécessaires pour une étude systématique des oscillations, figure (48) :

1- examen des valeurs propres du système. Il indique la présence des modes mal ou non- amortis. L'analyse modale de ces modes permet de déterminer leurs caractéristiques et leurs origines.

2- réalisation des simulations du système non-linéaire dans le domaine temporel pour les cas critiques identifiés par l'analyse modale. Cela confirme les résultats de l'analyse du modèle linéaire et montre en plus l'influence de la non-linéarité du système sur les oscillations.

Stabilité transitoire

Transition dynamique d'un point de
fonctionnement à un autre.

Modèle non-linéaire

Simulation (Analyse temporelle)
Méthodes d'intégration numérique.

Stabilité dynamique

Variation dynamique autour d'un point
de fonctionnement.

Modèle linéaire

Analyse du modèle linéaire
Analyse des valeurs propres
et analyse modale.

Figure 48. Analyse des oscillations d'un système de puissance.

Enfin, en supposant que le réglage des contrôleurs est fait au point de fonctionnement nominal du système, il est nécessaire de vérifier la robustesse du réglage. Dans le contexte du réglage du contrôleur d'amortissement d'un système de puissance, la robustesse signifie que l'amortissement est suffisant et que les oscillations s'amortissent rapidement lors des simulations temporelles du système pour toutes les perturbations probables et pour tous les points de fonctionnement significatifs. Ainsi, les critères de bonne régulation doivent être respectés pour tous les scénarios considérés (Pal et al., 2005).

4.3.1- Critères d'analyse du modèle linéaire.

Rappelons que le facteur d'amortissement Ç d'un mode représenté par sa valeur propre complexe )L est donné par :

ó

-

=

(130)

ó ² ù ²
+

æ

Avec : ë= ó #177; jù (131)

- Un facteur d'amortissement Ç important aboutit à une réponse dynamique bien amortie. Pour cela, toutes les valeurs propres doivent se trouver dans la zone gauche du plan complexe limité par deux demi-droites issues de l'origine, figure (47). Pour une valeur critique du facteur d'amortissement Çcr : on impose alors une marge de stabilité relative (Allenbach, 2005, I).

- La partie réelle de la valeur propre ci
· détermine la rapidité de décroissance/croissance des exponentielles composant la réponse dynamique du système. Ainsi, ci
· très négatif aboutit à une réponse dynamique rapide. Pour cela, toutes les valeurs propres doivent se trouver dans la zone gauche du plan complexe limité par une verticale passant par une valeur critique de la partie réelle (ci
·_cr), figure (47) : on définit ainsi la marge de stabilité absolue.

Lors du réglage des paramètres des PSSs, il est souhaitable que ces deux critères soient pris en compte pour permettre une bonne régulation. La combinaison entre ces deux critères aboutit à une zone appelée zone de stabilité D, (Yee et al., 2004), figure (49). Le déplacement des valeurs propres dans cette zone garantit une performance robuste pour un grand nombre de points de fonctionnement (Singh, 2004).

æcr

joi

ci
·

ócr

Figure 49. Zone de la stabilité D.

Considérons par exemple un mode d'une fréquence naturelle de 1 Hz, les oscillations associées à ce mode s'amortissent en 13 secondes pour Ç = 0.05 et en 6.5 et 3 secondes pour Ç = 0.1 et Ç = 0.2 respectivement. Quelle est alors la valeur minimale adéquate d'amortissement pour un bon fonctionnement du système de puissance?

La littérature ne présente pas de valeurs critiques rigoureuses admises par tous. Généralement, un facteur d'amortissement de 0.05 n'assure qu'une petite marge de sécurité tandis que Ç = 0.03 doit être accepté avec réserve. Les valeurs d'amortissement entre 0.05 et 0.15 sont globalement les plus utilisées dans la littérature. Nous avons choisi Çcr = 0.1 comme facteur d'amortissement critique. Ainsi, nous considérons que l'amortissement des oscillations est suffisant si tous les modes du système présentent des facteurs d'amortissement plus grands que Çcr.

D'une façon similaire, la littérature donne une gamme de variation de la valeur critique de la partie réelle des valeurs propres, comprise entre - 0.5 et - 1. Nous avons choisi ocr = - 1 comme partie réelle critique à respecter par tous les modes.

Enfin, d'autres spécifications peuvent être utilisées telles les spécifications de la réponse du système dans le domaine temporel (le dépassement maximum, le temps d'établissement, l'erreur statique, ...), (Yee et al., 2004).

4.3.2- Critères de simulation.

La performance d'un contrôleur nécessite des critères pour évaluer le "bon" comportement du système. Elle peut être spécifiée dans le domaine temporel et/ou fréquentiel (Pal et al., 2005).

Les caractéristiques dynamiques peuvent être décrites en examinant la réponse à une entrée typique (tel un échelon unité, ...). Ainsi, les spécifications de la réponse transitoire (tels le dépassement maximum, le temps de réponse, le temps de pic, ...) tout comme les critères intégraux (tels IAE, ISE, ITAE, ...) peuvent être utilisés comme indicateurs de performance des boucles de régulation (Aström et al., 1995).

4.3.2.1- Critères temporels instantanés.

La réponse indicielle (réponse à un échelon unité) d'un système oscillant du deuxième ordre est donnée à la figure (50), (Allenbach, 2005, I).

Nous définissons les paramètres critiques apparaissant sur cette figure : 1- Dépassement maximum D_p

Il est la mesure de la valeur maximale atteinte par la réponse indicielle lors de son premier dépassement. Cette valeur est souvent pondérée par la valeur finale : on parle alors de dépassement maximum en pour cent, noté D_p% et calculé par la relation suivante.

% max · 100

y y

D (132)

- f

=

y

p

f

Le dépassement maximum s'exprime en fonction du facteur d'amortissement comme suit :

ðæ

2

D_p =e (133)

1 - æ

ymax

D_p

105 % 100 % yf

95 %

t_p

Temps

0

t_r (5 %)

Figure 50. Caractéristiques de la réponse indicielle d'un système. 2-Temps de pic t_p

Ce paramètre correspond à l'abscisse du dépassement maximum. Ce paramètre de temps peut être déterminé analytiquement en fonction du facteur d'amortissement et de la pulsation naturelle d'oscillation, comme suit :

ð

t_p (134)

2

=

ù n

1 æ

-

3- Temps de réponse (temps d'établissement) tr(5%)

Il correspond au temps nécessaire à la réponse indicielle pour atteindre sa valeur finale avec une tolérance de #177;n% près. La tolérance de 5% est la plus communément utilisée. Ce paramètre caractérise la rapidité relative de la réponse du système. La relation approximative entre le temps de réponse, le facteur d'amortissement et la pulsation naturelle d'oscillation est donnée comme suit :

3

t ù æ avec

< æ <

, 0 1 (135)

r (5 %)

n

La valeur critique du temps de réponse de la stabilité dynamique (dite aussi stabilité dynamique) varie d'un opérateur de système de puissance à l'autre. Généralement, elle s'étend de 10 à 20 secondes (Pal et al., 2005).

Finalement, nous pouvons remarquer qu'une augmentation du facteur d'amortissement aboutit à une diminution du dépassement maximum et du temps de réponse.

4.3.2.2- Critères temporels intégraux.

Soit å(t) l'erreur dynamique associée à la réponse indicielle du système. Différents critères typiques peuvent être utilisés pour caractériser la performance du système régulé. Nous les définissons ci-dessous.

1- Critère IAE, Intégrale de l'Erreur Absolue (Integral of Absolute Error). Le critère de performance est le suivant :

t

e( ) (136)

t dt

IAE j.

0

Etant donné que ce critère prend en compte tous les éléments de la réponse harmonique, il donc important lorsque la réponse du système est oscillatoire ; les faibles amortissements ne sont pas ainsi conseillés.

2- Critère ISE, Intégrale du Carrée de l'Erreur (Integral of Square Error). Le critère de performance est alors le suivant :

e ² ( ) (137)

t dt

ISE

t j.

0

En général, le fait de travailler avec le carré de l'erreur amplifie l'importance des valeurs de sortie qui s'écartent le plus de la valeur finale.

3- Critère ITAE, Intégrale de l'Erreur Absolue pondérée par le Temps (Integral Time multiplied by Absolute Error).

Le critère de performance est le suivant :

t

t t dt

e( ) (138)

ITAE j.

0

Puisque la valeur du critère ITAE est pondérée par le temps, l'erreur statique est fortement pénalisée : les systèmes à réponse très oscillatoire sont ainsi pénalisés.

En règle générale, le système sera d'autant mieux réglé que le critère intégral choisi sera minimal.

4.3.3- Conclusion.

Le choix de critère de simulation le plus performant (le bon critère) est délicat. Nous avons opté dans notre travail pour les critères instantanés de préférence aux critères intégraux de façon à faciliter la comparaison avec les résultats de la littérature.

4.4- Développement de l'AG. 4.4.1- Introduction.

Rappelons que les AGs sont des algorithmes d'optimisation s'appuyant sur des techniques dérivées de la génétique et de l'évolution naturelle avec trois opérateurs : croisement, mutation et sélection. L'usage d'un AG est d'une part adapté à une exploration rapide et globale d'un espace de recherche de taille importante et d'autre part capable de fournir plusieurs solutions. Un AG recherche le ou les extrema d'une fonction définie (fonction objectif) sur un espace de recherche définissant les contraintes des paramètres à optimiser.

Dans ce paragraphe nous présentons la formulation de la fonction multiobjectif proposée et la mise en oeuvre de l'AG utilisé.

4.4.2- Fonction objectif.

Le but de l'utilisation des PSSs est d'assurer un amortissement satisfaisant des oscillations et de garantir la stabilité globale du système pour différents points de fonctionnement. Pour répondre à ce but, nous avons utilisé une fonction multiobjectif composée de deux fonctions objectif. Cette fonction multiobjectif doit maximiser la marge de stabilité en augmentant les facteurs d'amortissement tout en minimisant les parties réelles des valeurs propres du système. Par conséquent, toutes les valeurs propres seront dans la zone D de stabilité.

Les étapes de calcul de cette fonction multiobjectif sont les suivantes :

1- Formuler le système linéaire en boucle ouverte (sans PSSs).

2- Positionner les PSSs avec leurs paramètres initialisés par l'AG à travers une population initiale.

3- Fermer la boucle en reliant le j^ème PSS entre la sortie du j^ème générateur et son entrée.

4- Calculer les valeurs propres du système en boucle fermée et prendre uniquement les modes dominants dont le i^ème mode se traduit par :

ë i = ó i #177; jù i (139)

5- Trouver les parties réelles des valeurs propres du système (ói) et calculer les facteurs d'amortissement (æi) pour les i^ème modes:

æ_i

-ó_i

=

(140)

2 2

+ ù _i

ó _i

6- Déterminer la valeur minimale de (æi) et la valeur maximale de (- ói), qui peuvent être formulées respectivement comme : (minimum (æi)) et (? maximum (ói)).

7- Rassembler les deux fonctions objectif en une fonction multiobjectif F comme suit (méthode de pondération) :

F = -max(ó _i )+min( æ _i ) (141)

8- Renvoyer la valeur de cette fonction multiobjectif au programme de l'AG pour relancer une nouvelle génération.

Dans notre cas, nous n'avons privilégié aucune fonction objectif sur une autre : le coefficient de pondération de chaque fonction individuelle est donc égal à 1.

4.4.3- Mise en oeuvre de l'AG. 4.4.3.1- Codage du problème.

L'objectif de cette étude est d'appliquer l'AG pour trouver :

- les valeurs optimales des paramètres des PSSs pour un meilleur amortissement, - leur localisation optimale,

- le nombre suffisant des PSSs.

Ainsi, le nombre de variables utilisé (pour chaque PSS) à l'entrée de l'AG variera selon trois cas étudiés :

1- Premier cas : trois variables (un gain et deux constantes de temps). L'objectif est simplement d'optimiser les paramètres des PSSs.

2- Deuxième cas : quatre variables (l'emplacement des PSSs, un gain et deux constantes de temps). L'objectif maintenant est d'optimiser les paramètres des PSSs et leur localisation.

3- Troisième cas : cinq variables (un commutateur déterminant la mise en service ou non d'un PSS, l'emplacement des PSSs, un gain et deux constantes de temps). L'objectif est d'optimiser enfin les paramètres des PSSs et leur localisation et de réduire leur nombre.

Ces variables sont soumises aux contraintes suivantes :

KPSS

, , j

min

= = K K PSS j PSS j , , , max

T1

min

, ,

j

==

T T

max

1 , 1 , , j j

= =

T T

3 , 3 , , max

j j

{ }

Gen Gen

1 L , , n
{ }

0,1

(142)

T3

min

, ,

j

,

PLPSS

j

,

SWPSS

j

avec

j

1,2,

, NPSS

KPSS : le gain du PSS.

T1 : la constante de temps du PSS.

T3 : la constante de temps du PSS.

NPSS : le nombre maximum des PSSs à ajouter aux générateurs.

PLPSS : le numéro de générateur auquel le PSS doit être connecté. Sa valeur varie entre 53 et 68.

SWPSS : une variable représentant des commutateurs permettant de relier (si la valeur est 1) ou débrancher (si la valeur est 0) les PSSs des générateurs, afin d'en réduire leur nombre.

Pour coder le problème, à _Nvar nombre de variables, chaque variable (chromosome) est représentée par Sl chaîne de bits (Sl gène) de longueur _Ngens, où : l = 1, 2,..., Nvar.

A titre d'exemple, la figure (51) suivante montre une configuration d'un individu, composée de cinq chromosomes, représentant le troisième cas étudié.

1 1 0 1 ...

0 1 0 1 ...

0 0 0 1 ...

1 0 0 0 ...

0 1 1 1 ...

... 0 1

... 1 1

... 1 0

... 1 1

... 0 0

Constante de temps T3

Constante de temps T1

Gain KPSS

Commutateur SWPSS Emplacement PLPSS

Figure 51. Représentation d'un individu pour le troisième cas étudié.

Le type de codage choisi dans cette étude est le codage binaire : il est standard et applicable pour plusieurs types de problèmes.

4.4.3.2- Population initiale.

Les AGs nécessitent une population initiale pour commencer le processus de recherche. La méthode appliquée fait générer aléatoirement un ensemble de solutions dans les contraintes proposées pour la population entière : c'est la méthode la plus commune.

Une représentation d'une population initiale de _Nind individus (solutions) est illustrée par la figure (52).

0 0 0 1 ...

0 1 1 1 ...

1 1 0 1 ...

0 0 1 1

0 1 0 1 ...

10 0 0 ...

0 0 0 1 ...

0 1 0 1 ...

1 0 0 0

0 1 1 1 ...

...

...

... 0 0

0

... 1 0

... 1 1

... 0 1

... 0 1

0 1

... 1 0

... 1 1

... 1 1

... 0 0

0 1

0 0

1

0

0

Figure 52. Représentation de la population entière de _Nind individus.

4.4.3.3- Sélection.

Après génération de la population initiale, la performance de chaque individu est évaluée : la performance mesure la qualité de la solution probable pour comparer les différentes solutions. Nous avons pris la valeur associée à la fonction objectif comme indice de performance.

Après calcul de cet indice pour chaque individu, le mécanisme de sélection est appliqué pour copier les individus sélectionnés. Les individus ayant des performances élevées ont plus de probabilité d'être reproduits dans la génération suivante. Nous avons appliqué la méthode de la roulette biaisée.

4.4.3.4- Croisement.

Après l'étape de sélection, le croisement est appliqué. Dans cette étape, les individus sont regroupés aléatoirement par paire (parents). Le croisement se fait ensuite pour créer les enfants avec une probabilité P_c, sinon les parents ne changent pas. Cet opérateur sert à explorer des nouvelles régions dans l'espace de recherche. Le type de croisement le plus simple est le croisement seul point : nous l'avons appliqué dans cette étude.

4.4.3.5- Mutation.

Pour introduire une certaine diversification dans la population et éviter ainsi une convergence prématurée en un optimum local, l'opérateur de mutation est appliqué. Les bits subissent la mutation sont choisis aléatoirement avec une probabilité P_m.

4.4.4- L'organigramme du problème.

Les étapes de la formulation de la fonction multiobjectif et du programme de l'AG sont donnés à la figure (53).

4.4.5- Conclusion.

Dans les parties précédentes de ce chapitre, nous avons décrit le réseau électrique étudié dans ce travail et détaillé les critères de la stabilité qui sont très nécessaires pour évaluer concrètement nos résultats. Nous avons aussi présenté la formulation de la fonction multiobjectif proposée et les points de la mise en oeuvre de l'AG utilisé.

Dans la partie suivante, nous allons mettre en application nos approches. Les résultats obtenus seront analysés et discutés :

- Nous commençons avec l'analyse du système sans l'utilisation des PSSs.

- Nous présentons, par la suite, les résultats de l'application du premier cas destiné à optimiser les paramètres des PSSs du système par l'AG. Nous comparons ces résultats avec ceux déterminés par une méthode classique (compensation de phase) et par une méthode métaheuristique (algorithmes d'optimisation par essaim de particules) et avec ceux fournis dans la littérature.

- Dans le deuxième et troisième cas, nous optimisons l'emplacement et le nombre des PSSs. Les objectifs et les intérêts de ces applications et leurs résultats seront présentés et discutés.

Population initiale pour les
paramètres à optimiser

Figure 53. Organigramme de la fonction multiobjectif et du programme de l'AG.

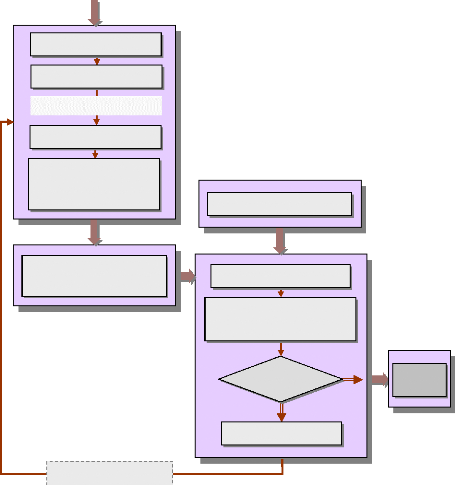
Base de données du système

Ecoulement de puissance

Point de fonctionnement

Linéarisation du système

Valeurs propres
pour chaque individu :

ói, æi

Paramètre de réglage d'AG

La fonction multiobjectif

F = -max(ó _i )+min(æ i

)

Evaluation des solutions

Opérateurs d'AG :
(Sélection, Croisement, Mutation)

Oui

Gener < Genermax ?

Non

Nouvelle population

Nouvelle génération

Résultat

4.5- Résultat et discussion. 4.5.1- Le système sans PSSs.

Nous étudions en premier lieu le fonctionnement du système sans PSSs. Les modes électromécaniques dominants du système pour le point de fonctionnement considéré sont donnés dans le tableau (4) et à la figure (54).

N° mode	ë	æ	f [Hz]
1	- 0.4120#177; j 9.8436	0.0418	1.5667
2	- 0.0095#177; j 2.3974	0.0040	0.3816
3	+ 0.0063#177; j 3.1120	- 0.0020	0.4953
4	+ 0.0377#177; j 3.8959	- 0.0097	0.620 1
5	- 0.0116#177; j 4.0526	0.0029	0.6450
6	- 0.4056#177; j 8.3777	0.0484	1.3333
7	- 0.2814#177; j 8.2667	0.0340	1.3157
8	- 0.3295#177; j 8.2650	0.0398	1.3154
9	+ 0.2152#177; j 6.2618	- 0.0344	0.9966
10	+ 0.1188#177; j 6.6535	- 0.0178	1.0589
11	+ 0.3803#177; j 7.3056	- 0.0520	1.1627
12	+ 0.2420#177; j 6.8133	- 0.0355	1.0844
13	+ 0.0919#177; j 7.1486	- 0.0129	1.1377
14	+ 0.2216#177; j 7.2291	- 0.0306	1.1506
15	+ 0.0717#177; j 7.0438	- 0.0102	1.1211

Tableau 4. Valeurs propres du système sans PSSs.

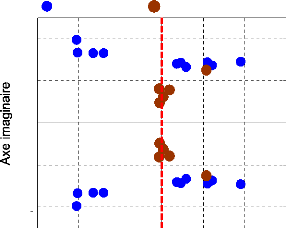
10

5

0

-5

-10

Modes locaux Modes interrégionaux

-0.6 -0.4 -0.2 0.2 0.4 0.6

0

Axe réel

Figure 54. Répartition des valeurs propres du système dans le plan complexe (sans PSSs).

Nous appliquons maintenant une petite perturbation normalisée en échelon de 1% sur le couple mécanique du générateur 53. La variation de vitesse des générateurs qui fait suite à cette perturbation est montrée à la figure (55).

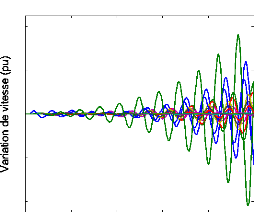
x 10^-3

8

4

0

-4

-8

0 2 4 6 8 10

Temps (s)

Figure 55. Variation de vitesse des générateurs (sans PSSs).

Ainsi, il est évident que le système contient des modes instables (en gras dans le tableau (4)) et d'autres mal amortis. Le comportement du système aux petites perturbations montre clairement cette instabilité du système (divergence de l'ensemble des générateurs).

La présence de modes d'oscillations électromécaniques fortement instables déterminés par l'analyse de la réponse du système en modèle linéaire conduit évidemment à la perte de stabilité aux grandes perturbations. Nous appliquons un défaut triphasé sur la ligne (59#23) suivi par une élimination du défaut. Le temps de défaut et de retour à l'état initial est choisi de l'ordre de 6 périodes du réseau (0.1 s). Les réponses temporelles de la variation de vitesse et des angles de rotor des générateurs suite au défaut choisi sont montrées à la figure (56).

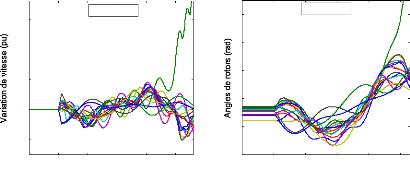
8

0.06

sans PSSs

6

sans PSSs

0.04

4

0.02

2

0

0

-0.02

0 1 2 3 4 5

Temps (s)

-2 0 1 2 3 4 5

Temps (s)

a b

Figure 56. Réponse dynamique des générateurs (sans PSSs)
a : variation de vitesse, b : angles de rotor.

Cette figure montre bien que les modes instables mènent à un écart croissant apériodique de certains angles de rotor et par conséquent à la perte de la stabilité du système.

Pour rétablir la stabilité du système et améliorer son amortissement global, les PSSs sont maintenant ajoutés aux générateurs. Dans la suite de ce chapitre, nous faisons appel aux AGs pour optimiser les paramètres des PSSs selon les trois cas présentés précédemment.

4.5.2- Les scénarios et défauts.

Pour analyser la performance et la robustesse du réglage, nous devons analyser les nouvelles valeurs propres du système et examiner l'amortissement obtenu avec les PSSs optimisés pour différents scénarios crédibles, tableau (5). Nous allons appliquer ces analyses au point de fonctionnement nominal utilisé pour l'optimisation (noté premier scénario) et pour deux autres points représentant deux scénarios sévères. En effet, le deuxième et troisième scénario, définis ci-dessus, sont déterminés à partir des simulations que nous avons réalisées et représentent les contraintes les plus dures pour le système :

- Le scénario deux peut être considéré comme un scénario sévère car les lignes d'interconnexion (8#9) et (46#49) participent fortement aux oscillations interrégionales et la perte de ces deux lignes va affaiblir considérablement les interconnexions entre les régions du système.

- Le scénario trois est aussi un scénario sévère. Il correspond à une diminution de puissance du générateur 68 associée à une augmentation de la charge connectée au jeu de barre 37. Or le générateur 68 a une puissance importante et la charge connectée au jeu de barre 37 consomme la puissance la plus grande du réseau. Enfin, ce scénario implique la perte de la ligne (2#3).

N° scénario

1

2

Configuration de scénario

Point de fonctionnement nominal

- Ligne 8#9 hors service
- Ligne 46#49 hors service

- Diminution 25% de la puissance active du générateur 16

3 - Augmentation 25% de la puissance active de la charge au jeu de barre 37

- Ligne 2#3 hors service

Tableau 5. Liste des scénarios proposés.

Jusqu'à maintenant, l'analyse de réglage est basée seulement sur le modèle linéaire du système. Etant donné que le modèle d'origine est non-linéaire, nous devons évaluer la performance et la robustesse du réglage des PSSs en considérant le modèle non-linéaire originel. Pour ce faire, nous effectuons des simulations temporelles du système pour ces différents scénarios en présence d'une perturbation transitoire sévère déduite de simulations. Cette perturbation sévère correspondant à un défaut triphasé sur la ligne (59#23) est appliquée à proximité du jeu de barre 59 ; il est suivi par une ouverture des disjoncteurs et une fermeture de la ligne après élimination du défaut. Le temps de défaut et de retour à l'état initial est choisi de l'ordre de 6 périodes du réseau (0.1 s).

4.5.3- Cas 1 : optimisation des paramètres des PSSs.

Dans la suite de ce paragraphe, nous présentons les étapes habituelles de l'optimisation des paramètres des PSSs, à savoir :

- Détermination de la meilleure localisation des PSSs. La méthode utilisée pour

déterminer cette implantation est la méthode des facteurs de participation.

- Optimisation des valeurs des paramètres des PSSs, déjà installés dans le système. La

méthode d'optimisation utilisée est les AGs.

- Vérification de la performance et de la robustesse correspondant au réglage effectué pour différents scénarios. Pour ce faire, nous utilisons l'analyse par valeurs propres et l'évaluation temporelles des performances par simulations dynamiques.

4.5.3.1- Localisation des PSSs.

La méthode des facteurs de participation nous permet de déterminer les générateurs participants à chaque mode critique. Les générateurs présentant les valeurs de participation les plus élevées sont ceux qui nécessitent d'être équipés en priorité de PSSs. Les résultats sont donnés dans le tableau (6) : 14 générateurs participent principalement à ces modes. La fréquence de chaque mode et les générateurs associés déterminent le type du mode. Nous avons ainsi quatre modes de type interrégional et onze modes de type local.

N° mode	ë	f [Hz]	Générateurs participants	Type de mode
1	- 0.4120#177; j 9.8436	1.5667	G. 63	Local
2	- 0.0095#177; j 2.3974	0.3816	G. 65, G. 67, G. 66	Interrégional
3	0.0063#177; j 3.1120	0.4953	G. 68, G. 66	Interrégional
4	0.0377#177; j 3.8959	0.6201	G. 65, G. 58, G. 57	Interrégional
5	- 0.0116#177; j 4.0526	0.6450	G. 67, G. 66, G.68	Interrégional
6	- 0.4056#177; j 8.3777	1.3333	G. 56	Local
7	- 0.2814#177; j 8.2667	1.3175	G. 60	Local
8	- 0.3295#177; j 8.2650	1.3154	G. 59	Local
9	0.2152#177; j 6.2618	0.9996	G. 64	Local
10	0.1188#177; j 6.6535	1.0589	G. 57	Local
11	0.3803#177; j 7.3056	1.1627	G. 61	Local
12	0.2420#177; j 6.8133	1.0844	G. 54	Local
13	0.0919#177; j 7.1486	1.1377	G. 58	Local
14	0.2216#177; j 7.2291	1.1506	G. 55	Local
15	0.0717#177; j 7.0438	1.1211	G. 62	Local

Tableau 6. Générateurs participants aux modes critiques.

L'analyse des facteurs de participation montre l'influence de chaque générateur dans le mode en question. Si la participation d'un générateur est relativement faible, le placement d'un PSS sur ce générateur n'apportera que peu d'amélioration. Les figures (57) et (58) montrent les facteurs de participation associés aux angles et aux variations de vitesse de chaque générateur pour les quatre modes interrégionaux (les modes 2, 3, 4 et 5) et pour deux modes locaux (modes 1 et 6).

La méthode des facteurs de participation détermine donc 14 générateurs devant être équipés des PSSs. Ce sont les suivants :

G. 54	G. 55	G. 56	G. 57	G. 58	G. 59	G. 60
G. 61	G. 62	G. 63	G. 64	G. 65	G. 67	G. 68

Le réglage des paramètres de ces PSSs fait l'objet du paragraphe suivant.

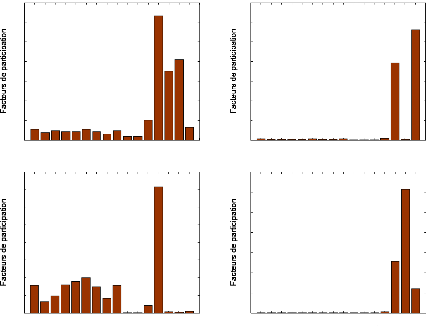
Numéro de générateur

Numéro de générateur

0.7

Mode 2

Mode 3

0.3

0.6

0.25

0.5

0.2

0.4

0.15

0.3

0.1

0.2

0.1

0.05

0

0

53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

Numéro de générateur

Numéro de générateur

0.7

0.4

Mode 4

Mode 5

0.35

0.6

0.3

0.5

0.25

0.4

0.2

0.3

0.15

0.2

0.1

0.1

0.05

0

0

53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

Figure 57. Facteurs de participation des modes interrégionaux (modes 2, 3, 4 et 5).

Numéro de générateur Numéro de générateur

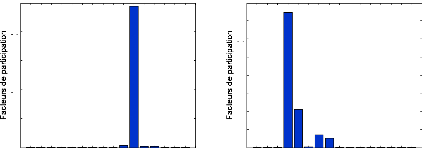
0.8

0.6

0.4

0.2

0

1

53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

Mode 1

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0

53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

Mode 6

Figure 58. Facteurs de participation de deux modes locaux (modes 1 et 6).

4.5.3.2- Réglage des paramètres des PSSs par l'AG.

Nous utilisons les AGs pour optimiser simultanément le réglage des paramètres des PSSs en se basant sur le modèle linéaire du système. L'objectif de ce réglage simultané est d'évaluer l'amortissement de tout le système et de minimiser les possibles interactions défavorables entre les PSSs. Pour atteindre cet objectif, les valeurs propres du système doivent, comme nous l'avons vu, se placer dans la zone D de stabilité.

Ainsi, l'AG appliqué doit maximiser les valeurs fournies par la fonction multiobjectif du système. Pour le cas étudié, le problème d'optimisation est alors formulé comme suit :

OptAG max( max( _i ) min( _i ))

= - ó + æ (143)

La figure (59) donne une représentation graphique de cette procédure d'optimisation cordonnée.

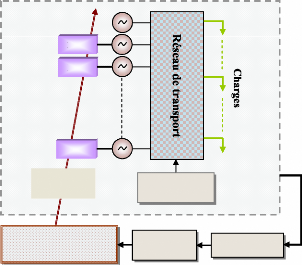
Algorithme génétique

Paramètres
des PSSs

PSS 14

PSS 1

PSS 2

G16

G2

G3

G1

Fonction
multiobjectif

Point de
fonctionnement

Valeurs propres

Figure 59. Optimisation coordonnée des paramètres des PSSs.

Les trois paramètres à optimiser pour chaque PSS (un gain et deux constantes de temps) sont soumises aux contraintes suivantes :

0.1 40 = = K PSS j , 0 . 00 1 0 . 1 = = T 1 , j 0 . 00 1 0 . 1 = = T 3 , j					(144)
avec	j	1,2,		, NPSS

Les autres paramètres _(Tw,j ^et T2,j, T4,j) des PSSs sont considérés constants : Tw,j = 10 et T2,j = T4,j = 0.02.

Le tableau (7) donne les valeurs choisies des paramètres de l'AG.

Nombre d'individu Nind	75
Nombre de gènes Ngens	Nind^x Nvar
Nombre de génération Ngener	250
Probabilité de croisement Pc	0.9
Probabilité de mutation Pm	0.005

Tableau 7. Valeurs choisies des paramètres de l'AG.

La figure (60) montre la convergence des paramètres des PSSs (KPSSi, T1i ^et _T3i) vers leurs valeurs optimales. Pendant les premières générations, les valeurs de ces paramètres (les individus) sont réparties sur la quasi-totalité de leurs espaces de recherche. Au fur et à mesure de la progression des générations, les individus (de chaque paramètre) s'orientent et convergent enfin vers leurs valeurs optimales. Ces dernières sont données dans le tableau (8).

a

b c

Figure 60. Convergence de la population des paramètres des PSSs (a : KPSSi, b : T1i, c : T3i).

N° PSS	N° G.	KPSS	T1	T3
1	54	35.2115	0.0543	0.0484
2	55	21.4336	0.0222	0.0424
3	56	33.4921	0.0665	0.0981
4	57	30.7770	0.0309	0.0469
5	58	35.8410	0.0901	0.0796
6	59	23.3611	0.0511	0.0377
7	60	01.5493	0.0829	0.0798
8	61	12.7207	0.0067	0.0309
9	62	30.1377	0.0882	0.0749
10	63	13.9789	0.0518	0.0754
11	64	38.7296	0.0598	0.0908
12	65	15.1873	0.0266	0.0081
13	67	39.9831	0.0012	0.0015
14	68	32.3178	0.0010	0.0010

Tableau 8. Paramètres des PSSs optimisés par AG.

L'évolution de la fonction multiobjectif en fonction du nombre de générations est donnée à la figure (61) ; la valeur finale atteinte pour la génération maximale prédéterminée de 250 est de 1.097. Les évolutions des deux composantes (æ et ó) de la fonction multiobjectif sont données quant à elles à la figure (62). Nous remarquons sur cette dernière que la valeur minimale optimale de (æ) et la valeur maximale optimale de (ó) sont atteintes pour la génération maximale prédéterminée de 250.

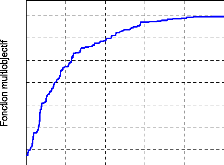
1.1

1

0.9

0.8

0.7

0.6

0.5

0 50 100 150 200 250

Générations

Figure 61. Evolution de la fonction multiobjectif.

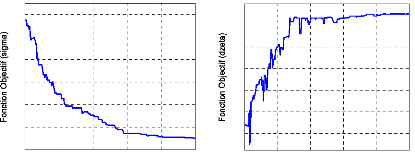
0.16

-0.4

0.14

-0.5

0.12

-0.6

0.1

-0.7

0.08

-0.8

0.06

-0.9

0.04

0 50 100 150 200 250

Générations

0 50 100 150 200 250

Générations

-1

a b

Figure 62. Evolutions des composantes de la fonction multiobjectif (a : æ, b : ó).

4.5.3.3- Analyse des valeurs propres. 4.5.3.3.1- Le point de fonctionnement nominal.

Les valeurs propres du système, équipé de ces 14 PSSs, et leur répartition dans le plan complexe sont données respectivement dans le tableau (9) et à la figure (63).

N° mode	ë	æ	f [Hz]
1	- 7.5602 #177; j 14.579	0.4603	2.3203
2	- 2.4631 #177; j 13.726	0.1766	2.1847
3	- 9.1765 #177; j 10.153	0.6705	1.6160
4	- 9.5284 #177; j 6.6435	0.8203	1.0573
5	- 1.9641 #177; j 9.1431	0.2100	1.4552
6	- 1.0945 #177; j 7.2031	0.1502	1.1464
7	- 1.0897 #177; j 7.1452	0.1508	1.1372
8	- 3.5594 #177; j 5.5850	0.5375	0.8889
9	- 5.6561 #177; j 3.9954	0.8 168	0.6359
10	- 3.7923 #177; j 4.4182	0.65 13	0.7032
11	- 4.2798 #177; j 3.1753	0.8031	0.5054
12	- 0.9485 #177; j 3.8260	0.2406	0.6089
13	- 1.1258 #177; j 3.3302	0.3203	0.5300
14	- 0.9560 #177; j 2.9392	0.3093	0.4678
15	- 1.3365 #177; j 2.6372	0.4521	0.4197

Tableau 9. Valeurs propres du système (14 PSSs optimisés par AG).

D'après l'analyse des valeurs propres du système, nous trouvons que le facteur d'amortissement minimum est æmin = 15.02 % et que la partie réelle maximale des valeurs propres est ómax = - 0.9485.

Nous pouvons remarquer que les modes électromécaniques (locaux et interrégionaux) ont été décalés dans la zone D de stabilité du plan complexe. Il apparaît deux valeurs propres situées juste à l'extérieur de la zone D : les valeurs obtenues restent néanmoins très proches de la limite de zone. Elles conservent en outre une excellente marge de stabilité absolue. Enfin, elles correspondent à des facteurs d'amortissement très supérieurs au critère que nous avions précédemment défini.

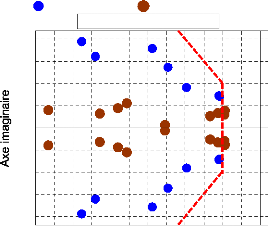
1er cas , 1er scénario

20

dz = 10 %

10

0

-10

-20

-6 -5 -4 -3 -2 - 0

-1

Modes locaux Modes interrégionaux

Axe réel

Figure 63. Répartition des valeurs propres du système dans le plan complexe
(14 PSSs optimisés par AG).

La variation de vitesse des générateurs qui fait suite à une petite perturbation en échelon de 1% sur le couple mécanique du générateur 53 est présentée à la figure (64).

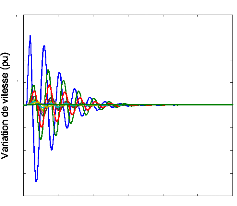
₄x 10^-4

3

2

1

0

-1

-2

-3

-4 0 2 4 6 8 10 12

Temps (s)

Figure 64. Variation de vitesse des générateurs.

Ces résultats confirment que le système est bien évidemment stable aux petites perturbations.

Nous allons dans la suite de ce paragraphe comparer le résultat obtenu par l'AG avec ceux déterminés :

- par une méthode classique,

- par une méthode métaheuristique,

- dans la littérature.

La méthode classique choisie est la méthode de compensation de phase. Nous appliquons cette méthode pour un réglage séquentiel des 14 PSSs, localisés par la méthode des FP, sur la base des étapes expliquées dans le paragraphe (§§-2.4.5.2.1). Le premier PSS est réglé en utilisant le résultat de l'analyse des valeurs propres en boucle ouverte. Les valeurs propres du système en boucle fermée utilisant le premier PSS sont calculées et utilisés dans le réglage du deuxième PSS. Cette procédure s'applique pour les autres PSSs et, à chaque étape de ce réglage séquentiel, le modèle du système est mis à jour avec les PSSs ajoutés précédemment. La figure (65) donne une représentation graphique de cette procédure séquentielle.

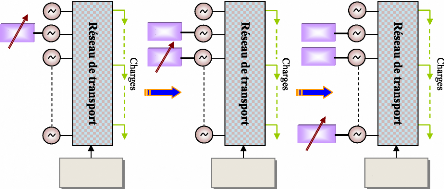
G2

G2

PSS1

PSS1

PSS1

G3

G3

PSS2

PSS2

G16

G16

PSS14

G1

Point de
fonctionnement

G1

G2

G3

G16

G1

Point de
fonctionnement

Point de
fonctionnement

Figure 65. Réglage séquentiel des paramètres des PSSs.

Les valeurs des paramètres de réglage des PSSs déterminés par cette méthode sont données en annexe D.

Les valeurs propres du système, avec les 14 PSSs, sont données dans le tableau (10) ; leur répartition dans le plan complexe est montrée graphiquement à la figure (66).

Ces résultats montrent que le système est devenu stable pour le point de fonctionnement étudié, mais plusieurs modes ne se trouvent pas dans la zone D ; un mode _(ë14) reste encore mal amorti.

Ce résultat s'interprète en tenant compte du fait que les méthodes classiques ne prennent pas en compte les interactions entre PSSs et que leur réglage se fait sans coordination.

L'analyse comparative des résultats obtenus par ces méthodes montre donc la supériorité de l'utilisation de l'AG.

N° mode	ë	æ	f [Hz]
1	- 3.8969 #177; j 13.710	0.2734	2.1821
2	- 4.6589 #177; j 13.268	0.3313	2.1118
3	- 3.3208 #177; j 7.9161	0.3868	1.2599
4	- 0.2396 #177; j 7.1521	0.0335	1.1383
5	- 2.8883 #177; j 6.7292	0.3944	1.0710
6	- 1.1655 #177; j 6.7009	0.1714	1.0665
7	- 2.7053#177; j 6.5937	0.3796	1.0494
8	- 1.2536 #177; j 6.1625	0.1993	0.9808
9	- 1.6629 #177; j 6.5117	0.2474	1.0364
10	- 2.1114 #177; j 6.1520	0.3246	0.9791
11	- 1.8371 #177; j 6.1483	0.2863	0.9785
12	- 0.8886 #177; j 3.7589	0.2301	0.5982
13	- 0.6306 #177; j 3.6811	0.1688	0.5859
14	- 0.3772 #177; j 3.1160	0.1202	0.4959
15	- 0.7242#177; j 2.27830	0.3029	0.3626

Tableau 10. Valeurs propres du système
(14 PSSs réglés par la méthode de compensation de phase).

15

10

5

0

-5

-10

-15

dz = 10 %

Modes locaux Modes interrégionaux

-5 -4 -3 -2 - 0

-1

Axe réel

Figure 66. Répartition des valeurs propres du système dans le plan complexe
(14 PSSs réglés par la méthode de compensation de phase).

Les méthodes métaheuristiques d'optimisation sont, comme nous l'avons déjà cité, nombreuses. Une de ces méthodes est les algorithmes d'optimisation par essaim de particules, (AOEP), (Particle Swarm Optimisation). Ces derniers ont été introduits par Kennedy et Eberhart (Kennedy et al., 1995) en 1995. Ces algorithmes sont une technique stochastique d'optimisation inspirés des mouvements coordonnés des oiseaux en nuées ou des bancs de poissons (Kennedy et al., 2001; Bonabeau et al., 2002). Les AOEP, comme les algorithmes évolutionnaires, sont des méthodes d'optimisation à population dont l'individu (particule) représente une solution potentielle. Les AOEP partagent avec les AGs plusieurs points communs tels que la génération aléatoire de la population initiale et l'évolution des individus par itérations en convergeant graduellement vers la solution optimale.

Chaque particule vole dans l'espace de recherche du problème avec une vitesse adaptative qui se modifie dynamiquement selon sa propre expérience du vol et l'expérience du vol des autres particules. Ainsi, chaque particule essaie de s'améliorer en suivant le chemin de son meilleur voisin. En outre, chaque particule possède une mémoire qui lui permet de se rappeler de la meilleure position qu'elle avait visitée dans l'espace de recherche. La position de la particule correspondante à la meilleure performance est appelée pbest et la meilleure position de toutes les particules est appelée gbest.

L'évolution de la vitesse et la position de chaque particule peuvent être calculées en utilisant les informations de sa vitesse actuelle et de la distance entre sa position actuelle et les positions pbesti et gbest, comme les donnent les relations suivantes (Bonabeau et al., 2002; Kwang et al., 2008) :

v w v c rand pbest x c rand gbest x k + 1 k k = · + · · - + · · - 1 1 ( ) 2 2 ( k i i i i i

) (145)

x x v k i np

k + = + + = K

1 1

k ; 1,2, , (146)

i i i

w w = max

w w max min - itermax

iter

(147)

Avec :

vi k : vitesse actuelle de la i^ème particule à la k^ème itération.

w : fonction de pondération.

c1, c2 : coefficients de pondération. rand : nombre aléatoire entre 0 et 1.

xi k : position actuelle de la i^ème particule à la k^ème itération.

pbesti : pbest de la i^ème particule. gbest : gbest de la population.

np : nombre des particules dans la population.

wmax : poids maximum.

wmin : poids minimum.

iter : nombre actuel d'itérations. itermax : nombre maximum d'itérations.

L'organigramme général des AOEP peut être illustré comme suit :

Population initiale des particules

Résultat

Evaluation de la performance de
chaque particule dans l'actuelle
itération

Non

Gener < Genermax ?

Oui

Modification de la vitesse et
de la position de chaque particule

Nouvelle itération

Figure 67. Organigramme général des AOEP.

Nous appliquons le programme d'AOEP que nous avons développé pour optimiser les 14 PSSs du système. Nous utilisons le même espace de recherche proposé pour l'optimisation par l'AG (relation (144)). Les valeurs choisies des paramètres de l'AOEP et les valeurs optimales des paramètres des PSSs sont données en annexe E.

La figure (68) décrit l'évolution de la fonction multiobjectif en fonction du nombre de générations ; la valeur de la fonction multiobjectif atteinte est de 1.075.

1.1

0.9

0.7

0.5

0.3

0 50 100 150 200 250

Générations

Figure 68. Evolution de la fonction multiobjectif.

La répartition des valeurs propres du système est donnée à la figure (69).

Modes locaux Modes interrégionaux

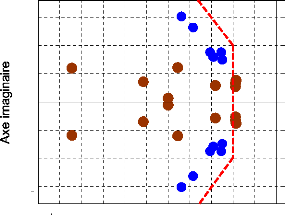
dz = 10 %

5

0

-5

-10

-15

-5 -4 -3 -2 -1 0

-1

15

10

Axe réel

Figure 69. Répartition des valeurs propres du système dans le plan complexe
(14 PSSs optimisés par AOEP).

L'analyse de ces valeurs montre que plusieurs d'entre elles se trouvent hors de la zone D : le facteur d'amortissement minimum est æmin = 14.32 % et la partie réelle maximale des valeurs propres est ómax = - 0.93 17.

La comparaison avec les résultats obtenus par l'AG montre que les résultats obtenus par l'AOEP sont inférieurs.

En effet, si les AOEP sont simples dans leur concept et faciles à mettre en oeuvre par rapport à un AG car ils n'ont pas d'opérateurs génétiques. Contrairement aux AGs, la performance d'un AOEP dépend fortement de ses paramètres de réglage. En outre, les AOEP risquent souvent d'être piégés dans des optima locaux (Angeline, 1998; Xiao et al., 2003).

Enfin, en ce qui concerne les résultats de la littérature obtenus à l'aide des AGs, de nombreuses recherches sur l'optimisation des paramètres des PSSs du réseau New England/New York ont été effectuées. K. Hongesombut, par exemple, a publié plusieurs articles (Hongesombut et al., 2001; Hongesombut et al., 2002; Hongesombut et al., 2004; Hongesombut et al., 2005) concernant ce problème. Dans la référence (Hongesombut et al., 2005), les auteurs présentent une méthode d'optimisation des PSSs utilisant une combinaison entre un algorithme génétique hiérarchique et un micro algorithme génétique parallèle.

Nous donnons ci-dessous les principes de ces deux algorithmes. - Algorithme génétique hiérarchique (AGIT).

Dans un AG typique, la structure d'un chromosome est prédéfinie et fixe ; le chromosome consistant en une chaîne de gènes. Par contre, un chromosome d'un AGH est construit d'une

façon hiérarchique à partir de deux types de gènes : les gènes de contrôle et les gènes de paramètres. Les gènes de contrôle gouvernent l'état d'activation des gènes de paramètres. Les autres gènes sont responsables de l'optimisation des paramètres des PSSs.

- Micro algorithme génétique parallèle (MAGP).

Lorsqu'on veut utiliser une population de petite taille, il y a un risque que l'AG converge vers un optimum local. Ainsi, un AG typique peut ne pas donner le résultat désiré avec une petite population. Ceci est dû à l'insuffisance de diversité dans le bassin de la population qui ne permet pas toujours d'éviter le piège des optima locaux. Par contre, le MAGP se base sur l'utilisation de multiples sous-populations. Ces dernières évoluent indépendamment pour un certain nombre de générations. Ensuite un processus de migration est appliqué en distribuant le meilleur individu parmi les sous-populations. Le schéma de migration fournit la diversité génétique demandée en échangeant les informations entre les sous-populations.

Avec cette méthode, la stabilité globale du système est assurée avec un facteur d'amortissement minimum æmin = 15 % et une partie réelle maximale des valeurs propres ómax = - 1. Ces résultats sont bien en accord avec ceux que nous avons obtenus, mais avec un PSS de moins dans notre étude (14 au lieu de 15 PSSs).

4.5.3.3.2- Les autres scénarios.

Dans le paragraphe précédent, nous avons examiné la performance de régulation pour le point de fonctionnement nominal. Nous examinons ci-dessous cette performance vis-à-vis des deux autres scénarios proposés.

Les représentations graphiques dans le plan complexe des valeurs propres des deuxième et troisième scénarios sont données respectivement à la figure (70).

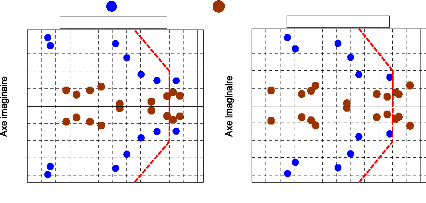
20

20

dz = 10 %

dz = 10 %

10

10

0

0

-10

-20

-6 -5 -4 -3 -2 - 0

-1

Axe réel

-10

-20

-6 -5 -4 -3 -2 - 0

-1

Axe réel

Modes locaux Modes interrégionaux

1er cas , 2ème scénario

1er cas , 3ème scénario

a b

Figure 70. Valeurs propres du système pour le 1^er cas,
a : 2^ème scénario, b : 3^ème scénario.

Les valeurs minimales de (æ) et maximales de (ó) des deux scénarios sont données respectivement comme suit :

	æmin	ómax
Scénario 2	10.57 %	- 0.6284
Scénario 3	6.450 %	- 0.3743

Nous remarquons que la valeur critique du facteur d'amortissement est bien respectée dans le deuxième scénario mais pas pour le troisième, tandis que la valeur critique de la partie réelle des valeurs propres n'est pas respectée pour les deux autres scénarios. La figure (70) montre que trois modes, pour chaque scénario, se trouvent en dehors de la zone D de stabilité. Les caractéristiques correspondantes de ces modes sont données dans le tableau suivant :

	N° mode	ë	æ	f [Hz]	Type de mode
2ème scénario	1	- 0.8603#177; j3.9143	0.2147	0.6230	Interrégional
	2	0.6284#177; j 2.9158	0.2107	0.4641	Interrégional
	3	- 0.7652#177; j 7.2000	0.1057	1.1459	Local
3ème scénario	1	- 0.8820#177; j 3.7928	0.2265	0.603 6	Interrégional
	2	0.7794#177; j 3.2443	0.2336	0.5163	Interrégional
	3	- 0.3743#177; j 5.7897	0.0645	0.9212	Interrégional

Ce tableau montre que les modes se trouvant en dehors de la zone D sont bien deux modes interrégionaux (le 3^ème est local) pour le 2^ème scénario et trois modes pour le 3ème scénario. Par conséquent, les modes interrégionaux sont les plus critiques.

4.5.3.4- Analyse par simulations temporelles. 4.5.3.4.1- Le point de fonctionnement nominal.

Pour compléter les informations sur les performances de régulation obtenues avec le modèle linéaire, des simulations temporelles du modèle non-linéaire sont, comme nous l'avons expliqué au paragraphe (§§-4.3), nécessaires. Nous devons ainsi examiner la restauration de la stabilité du système pour les trois scénarios proposés suite à un court-circuit triphasé sur la ligne 59#23. Nous traitons dans ce paragraphe le point de fonctionnement nominal.

La figure (71) montre la variation de vitesse des cinq générateurs les plus affectés par ce défaut. Ces générateurs sont G.53, G.59, G.60, G.66 et G.68 ; ils appartiennent à des régions différentes.

Les valeurs du dépassement maximum et du temps de réponse mesurés sur ces courbes sont donnés dans le tableau suivant.

	G. 53	G. 59	G. 60	G. 66	G. 68
Dp	5.48×10^-3	10.6×10^-3	5.01×10^-3	- 9.84×10^-3	0.49×10^-3
tr (s)	7	7	8	8	8

Ainsi, nous constatons que le système est stable et les oscillations s'amortissent en moins de 10 secondes.

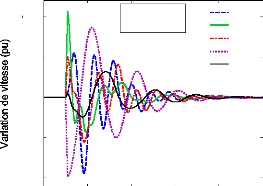
0.005

0.01

1er cas,
1er scénario

G. 53

G. 59

G. 60

G. 66

G. 68

0

-0.005

-0.01

0 2 4 6 8 10

Temps (s)

Figure 71. Variations de vitesse des cinq générateurs suite à un défaut de ligne,
(1^er scénario du 1^er cas).

D'autres grandeurs physiques peuvent aussi être simulées tels les angles de rotor, les puissances électriques et les tensions de noeuds.

Les réponses temporelles des angles de rotor, avec le défaut proposé, sont montrées à la figure (72). Les écarts entre les angles des générateurs 60 et 66 et les écarts entre les angles des générateurs 68 et 53 sont calculés à chaque instant : ils sont représentés à la figure (73). Ces générateurs participent aux modes interrégionaux ; appartenant à des régions différentes, ils oscillent en opposition de phase comme l'illustre les premières oscillations de la figure (73).

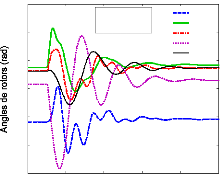
2.5

1.5

2

1er cas,
1er scénario

G. 53

G. 59
G. 60
G. 66
G. 68

1

0.5

0

-0.5 0 2 4 6 8 10

Temps (s)

Figure 72. Réponse dynamique des angles de rotor des générateurs (1^er scénario du 1^er cas).

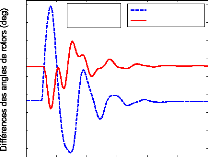
120

100

1er cas,
1er scénario

(G. 60 - G. 66)
(G. 68 - G. 53)

80

60

40

20

0

-20

-40

0 2 4 6 8 10 12

Temps (s)

Figure 73. Réponse dynamique des écarts des angles de deux paires des générateurs,
(1^er scénario du 1^er cas).

Nous remarquons que l'écart des angles de chaque paire converge généralement au bout de 8 secondes.

Les variations des angles des rotors influencent fortement les puissances électriques des générateurs du système ainsi que les tensions de noeuds. La figure (74) illustre la réponse dynamique des puissances électriques des cinq générateurs choisis et la réponse dynamique des tensions de quelques noeuds. Nous avons choisi les noeuds de la ligne d'interconnexion 52#42, les noeuds de la ligne 40#48 et le noeud 59 où le défaut était appliqué.

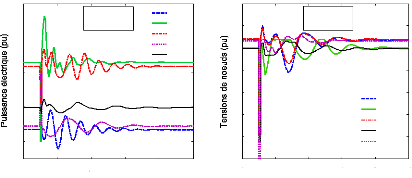
1.6

1.4

1.2

1er cas,
1er scénario

G. 53

G. 59
G. 60
G. 63
G. 66

1.2

1

1er cas,
1er scénario

0.8

0.8

0.6

0.4

0

0.4

0.2

Nd. 40 Nd. 42 Nd. 48 Nd. 52 Nd. 59

0 2 4 6 8 10

Temps (s)

00 2 4 6 8 10

Temps (s)

a b

Figure 74. Réponse dynamique du système (1^er scénario du 1^er cas),
a : puissances électriques, b : tensions des noeuds.

Les courbes de ces deux figures confirment la restauration de la stabilité du système lors d'un défaut de ligne, pour le point de fonctionnement nominal. L'examen de la réponse dynamique du système pour d'autres scénarios va être discuté dans le paragraphe suivant.

4.5.3.4.2- Les autres scénarios.

La figure (75) montre la variation de vitesse des cinq générateurs pour les scénarios 2 et 3.

0 2 4 6 8 10 12 Temps (s)

0 2 4 6 8 10 12 14 Temps (s)

a b

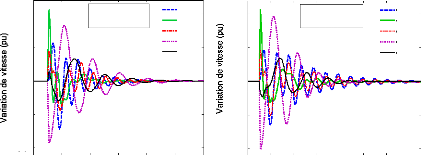
-0.005

0.005

-0.01

0.01

0

1er cas,
2ème scénario

G. 53

G. 59

G. 60

G. 66

G. 68

-0.005

0.005

-0.01

0.01

0

1er cas,
3ème scénario

G. 53

G. 59
G. 60
G. 66
G. 68

Figure 75. Variation de vitesse des générateurs du 1^er cas,
a : 2^ème scénario, b : 3^ème scénario.

Les informations obtenues concernant le dépassement maximum et le temps de réponse du système pour les deux scénarios sont données dans le tableau suivant.

		G. 53	G. 59	G. 60	G. 66	G. 68
2ème scénario	Dp	5.65×10^-3	10.6×10^-3	4.42×10^-3	- 9.28×10^-3	1.34×10^-3
	tr (s)	8	7	8	10	9
3ème scénario	Dp	4.7×10^-3	10.6×10^-3	4.6×10^-3	- 10.1×10^-3	- 2.26×10^-3
	tr (s)	14	11	14	10	9

Nous remarquons sur ce tableau que certaines valeurs du dépassement maximum sont plus importantes que pour le premier scénario tandis que d'autres sont plus faibles. Par contre, les temps de réponse des deuxième et troisième scénarios sont toujours supérieurs ou égaux à ceux du premier scénario ; les temps de réponse des générateurs 53 et 60 du troisième scénario sont doublés (ils dépassent même les 10 secondes).

Enfin, pour compléter cette étude, nous donnons la réponse dynamique des angles de rotor suite au défaut de ligne pour les 2^ème et 3^ème scénarios, figure (76).

4.5.3.5- Conclusion.

Dans l'étude du premier cas, nous avons utilisé la méthode des facteurs de participation pour localiser les PSSs nécessaires au système et la méthode des AGs pour régler les paramètres de ces PSSs. Les résultats trouvés pour le point de fonctionnement nominal montrent que le réglage du système est efficace avec un bon amortissement pour tous les modes. La performance du réglage a été évaluée avec les modèles linéaire et non-linéaire du système. Par ailleurs, nous trouvons que la performance s'est dégradée pour les autres

scénarios, en particulier pour le troisième scénario ; les critères liés à la zone de stabilité et au temps de réponse étant "mal respectés" pour plusieurs modes (notamment les interrégionaux). La robustesse du réglage n'est donc pas suffisamment assurée.

Nous pouvons donc conclure que, bien que le programme d'AG utilisé tienne compte des interactions entre les PSSs et réalise un réglage coordonné en comblant ainsi les limites des méthodes classiques, il reste à son tour handicapé par la prédétermination des lieux d'installation des PSSs. Cela nous amène à utiliser aussi l'AG dans le choix optimal de localisation des PSSs.

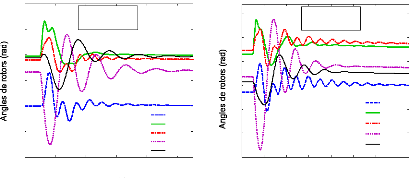
2.5

2

1er cas,
2ème scénario

2

1er cas,
3ème scénario

1.5

1.5

1

1

0.5

0.5

0

-0.5 0 2 4 6 8 10

Temps (s)

G. 53

G. 59

G. 60

G. 66

G. 68

-1 0 2 4 6 8 10 12 14

Temps (s)

0

-0.5

G. 53

G. 59
G. 60
G. 66
G. 68

a b

Figure 76. Réponse dynamique des angles de rotor du 1^er cas,
a : 2^ème scénario, b : 3^ème scénario.

4.5.4- Cas 2 : optimisation des paramètres et de la localisation des PSSs. 4.5.4.1- Application des AGs.

Les méthodes de détermination classique de l'emplacement des PSSs, tels les facteurs de participation, peuvent ne pas garantir une performance efficace en termes d'amortissement d'oscillation, en particulier, pour les modes interrégionaux où un grand nombre de générateurs est souvent impliqué. En outre, ces méthodes ne prennent pas en considération les éventuelles interactions indésirables des PSSs.

Dans ce cas, nous allons considérer les lieux d'emplacement, comme les paramètres de réglage des PSSs, comme des variables à optimiser. Le nombre de PSSs à installer reste constant et égal à celui déterminé par la méthode des facteurs de participation, soit 14 PSSs.

Pour ce faire, nous appliquons la même fonction multiobjectif donnée par la relation (141) et nous développons un AG permettant d'introduire la localisation d'un PSS comme un paramètre optimisable. Nous appliquons donc une optimisation simultanée de localisation et des paramètres des PSSs.

La figure (77) donne une représentation graphique de cette procédure d'optimisation cordonnée.

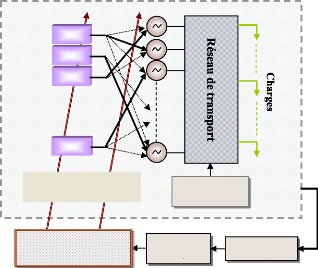
Algorithme Génétique

Paramètres
des PSSs

PSS 14

PSS 1

PSS 2

PSS 3

Placement
des PSSs

Fonction
multiobjectif

G16

G2

G3

G1

Point de
fonctionnement

Valeurs propres

Figure 77. Optimisation coordonnée de localisation et des paramètres des PSSs.

Les quatre variables à optimiser pour chaque PSS (l'emplacement, un gain et deux constantes de temps) sont soumises aux contraintes suivantes :

0.1 45

= =

K PSS j

,

0 .00 1 0 . 1

= =

T 1 , j

0 .00 1 0 . 1

= =

T 3 , j

(148)

PLPSS	,	j	{ } 53, ,6 8 L
avec		j		1,2,		, NPSS

Les autres paramètres _(Tw,j ^et T2,j, T4,j) des PSSs sont considérés constants : Tw,j = 10 et T2,j = T4,j = 0.02.

Le tableau (11) donne les valeurs choisies des paramètres de l'AG.

Nombre d'individu Nind	100
Nombre de gènes Ngens	Nind^x Nvar
Nombre de génération Ngener	300
Probabilité de croisement Pc	0.9
Probabilité de mutation Pm	0.005

Tableau 11. Valeurs choisies des paramètres de l 'AG.

L'évolution de la fonction multiobjectif en fonction du nombre de générations, donnée à la figure (78), montre que sa valeur finale optimale est égale à 1.552.

1.6

1.4

1.2

1

0.8

0.6

0.4

0.2 0 50 100 150 200 250 300

Générations

Figure 78. Evolution de la fonction multiobjectif.

Les résultats, donnés au tableau (12), représentent les valeurs optimales de l'emplacement des PSSs et leurs paramètres de réglage.

N° PSS	N° G.	KPSS	T1	T3
1	53	3 1.3445	0.0980	0.0985
2	54	44.3561	0.0881	0.0770
3	55	44.2500	0.08 12	0.0466
4	57	24.5247	0.0609	0.0784
5	58	07.8640	0.0398	0.0478
6	59	24.7385	0.0567	0.0654
7	61	16.0132	0.0729	0.0366
8	62	08.6426	0.0533	0.0742
9	63	04.8510	0.0632	0.0787
10	64	17.0964	0.0924	0.0237
11	65	43.8049	0.0026	0.0115
12	66	44.4671	0.0108	0.0034
13	67	44.7417	0.0204	0.0159
14	68	44.4898	0.0102	0.0054

Tableau 12. Paramètres et localisation des PSSs optimisés par AG.

Nous allons dans la suite de ce paragraphe analyser la performance et la robustesse du réglage des PSSs lors de la linéarisation du modèle du système et lors de l'utilisation du modèle non-linéaire.

4.5.4.2- Analyse des valeurs propres. 4.5.4.2.1- Le point de fonctionnement nominal.

Pour calculer les valeurs propres du système au point de fonctionnement nominal en boucle fermée, nous installons les 14 PSSs optimisés aux emplacements déterminés par l'AG. Le tableau (13) donne les valeurs propres dominantes ; leur répartition dans le plan complexe est donnée à la figure (79).

N° mode	ë	æ	f [Hz]
1	- 6.7752 #177; j 11.413	0.5104	1.8166
2	- 2.2305 #177; j 10.556	0.2067	1.6801
3	- 6.9634 #177; j 8.6133	0.6287	1.3709
4	- 1.4778 #177; j 8.3524	0.1742	1.3293
5	- 2.7045 #177; j 8.2624	0.3111	1.3150
6	-1.6588 #177; j 7.4513	0.2173	1.1859
7	- 1.3803 #177; j 7.3761	0.1839	1.1739
8	- 1.3779 #177; j 7.2170	0.1875	1.1486
9	- 4.8218 #177; j 2.7800	0.8663	0.4425
10	- 2.0778 #177; j 2.6504	0.6170	0.4218
11	- 3.6124 #177; j 2.3486	0.8384	0.3738
12	- 1.3974 #177; j 3.9670	0.3322	0.6314
13	- 1.3777 #177; j 3.9719	0.3277	0.6321
14	- 2.7954 #177; j 6.1612	0.4132	0.9806
15	- 1.5958 #177; j 2.0264	0.6187	0.3225

Tableau 13. Valeurs propres du système (14 PSSs localisés et optimisés par AG).

2ème cas , 1er scénario

dz = 10 %

5

0

-5

-10

-15

-7 -6 -5 -4 -3 -2 -1 0

-1

Modes locaux Modes interrégionaux

15

10

Axe réel

Figure 79. Répartition des valeurs propres du système dans le plan complexe
(14 PSSs localisés et optimisés par A G).

L'examen de ces valeurs propres montre que le facteur d'amortissement minimum est æmin = 17.42 % et que la partie réelle maximale des valeurs propres est ómax = - 1.3777. Nous remarquons aussi que tous les modes, locaux et interrégionaux, sont bien déplacés dans la zone D. Le facteur d'amortissement et la partie réelle des valeurs propres des modes interrégionaux sont notamment améliorés par rapport au premier cas. Nous constatons donc une bonne amélioration de la stabilité globale du système. Cette amélioration se traduit par des améliorations sur le facteur d'amortissement minimum (de 16.1 % en valeur relative) et sur la partie réelle maximale des valeurs propres (de 45.18 % en valeur relative) par rapport au premier cas.

Pour s'assurer de cette amélioration dans tous les scénarios probables, nous devons examiner, comme nous avons fait pour le premier cas, les deux autres scénarios proposés.

4.5.4.2.2- Les autres scénarios.

Les répartitions des valeurs propres dans le plan complexe des deuxième et troisième scénarios sont données respectivement à la figure (80).

Modes locaux Modes interrégionaux

15

15

dz = 10 %

dz = 10 %

10

10

5

5

0

0

-5

-5

-10

-10

-15

-15

-5 -4 -3 -2 -1 0

-1

-5 -4 -3 -2 - 0

-1

2ème cas , 2ème scénario

2ème cas , 3ème scénario

Axe réel Axe réel

a b

Figure 80. Valeurs propres du système pour le 2^ème cas,
a : 2^ème scénario, b : 3^ème scénarios.

Les valeurs minimales de (æ) et maximales de (ó) des deux scénarios sont données respectivement comme suit :

	æmin	ómax
Scénario 2	17.53 %	- 1.3076
Scénario 3	16.20 %	-1.0437

Sur ces deux figures, il est clair que tous les modes (locaux et interrégionaux) associés aux deux scénarios se trouvent placés dans la zone D ; les valeurs critiques de (æi) et (ói) sont bien respectées avec une marge très importante pour le facteur d'amortissement. Ces valeurs

présentent une bonne amélioration des performances par rapport au premier cas. Cela se traduit par une augmentation de _(æmin) de (65.8 % et 151.16 %) et une diminution de _(ómax) de (108.1 % et 178.8 %) pour les deux scénarios respectivement.

Cette comparaison peut être illustrée graphiquement, par rapport au premier scénario, par la figure suivante.

a b

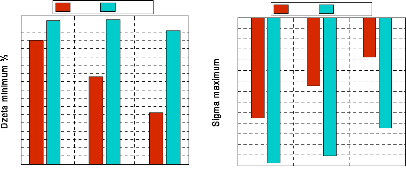
18

16

14

12

10

4

8

6

2

0

1er scénario 2ème scénario 3ème scénario

1er cas 2ème cas

-0.2

-0.4

-0.6

-0.8

-1.2

-1.4

-1

0

1er scénario 2ème scénario 3ème scénario

1er cas 2ème cas

Figure 81. Comparaison entre le 1^er et le 2^ème cas.

a : æmin, b : ómax.

D'après cette figure, nous constatons que le réglage du deuxième cas respecte les critères de la zone D de stabilité pour les trois scénarios étudies contrairement au premier cas qui ne la respectait que par le scénario du point de fonctionnement nominal.

4.5.4.3- Analyse par simulations temporelles. 4.5.4.3.1- Le point de fonctionnement nominal.

Nous examinons dans ce paragraphe les simulations temporelles du système non-linéaire au point de fonctionnement nominal pour le même défaut appliqué au premier cas.

Le résultat de la variation de vitesse des cinq générateurs est présenté à la figure (82).

Pour mieux comparer ce résultat à son homologue du premier cas, nous donnons dans les tableaux suivants le dépassement maximum et le temps de réponse mesurés sur ces courbes, en rappelant aussi ceux du premier cas.

2ème cas			G. 53	G. 59	G. 60	G. 66	G. 68
		Dp	5.42×10^-3	10.7×10^-3	5.01×10^-3	- 9.85×10^-3	0.49×10^-3
		tr (s)	5	5	8	4	4
1er cas			G. 53	G. 59	G. 60	G. 66	G. 68
	Dp		5.48×10^-3	10.6×10^-3	5.01×10^-3	- 9.84×10^-3	0.49×10^-3
	tr (s)		7	7	8	8	8

Nous constatons que les temps de réponse sont notamment améliorés ; les oscillations de générateurs 66 et 68 par exemple s'amortissent deux fois plus rapidement que leurs équivalentes au premier cas, les valeurs des dépassements restant les mêmes.

Cette amélioration obtenue par le modèle non-linéaire est en bon accord avec celle obtenue par le modèle linéaire.

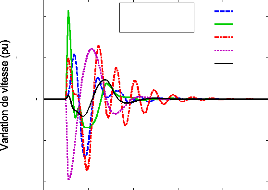
-0.005

0.005

-0.01

0.01

0

2ème cas,
1er scénario

G. 53

G. 59

G. 60

G. 66

G. 68

0 2 4 6 8 10

Temps (s)

Figure 82. Variations de vitesse des cinq générateurs suite à un défaut de ligne,
(1er scénario du 2ème cas).

Les réponses temporelles des angles de rotor et les écarts entre les angles des générateurs 60 et 66 et entre les angles des générateurs 68 et 53, donnés à la figure (83), montrent bien la restauration rapide de la stabilité suite au défaut et le bon amortissement obtenu.

Temps (s) Temps (s)

a b

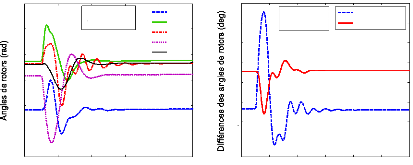
120

100

80

60

40

20

0

-20

0 2 4 6 8 10 12

-0.5 0 2 4 6 8 10

2.5

0.5

1.5

2

0

1

2ème cas,
1er scénario

G. 53

G. 59
G. 60
G. 66
G. 68

2ème cas,
1er scénario

(G. 60 - G. 66)
(G. 68 - G. 53)

Figure 83. Réponse dynamique des générateurs (1^er scénario du 2^ème cas),
a : angles de rotor, b : écart des angles de deux paires.

La réponse dynamique des puissances électriques des cinq générateurs choisis et la réponse dynamique des tensions de quelques noeuds sont présentées à la figure (84).

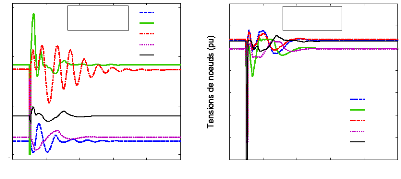
0.5

1.5

0

1

0 2 4 6 8 10

2ème cas,
1er scénario

Temps (s)

G. 53

G. 59

G. 60

G. 63

G. 66

0.8

0.6

0.4

0.2

1.4

1.2

0 0 2 4 6 8 10

Temps (s)

1

2ème cas,
1er scénario

Nd. 40 Nd. 42 Nd. 48 Nd. 52 Nd. 59

a b

Figure 84. Réponse dynamique du système (1^er scénario du 2^ème cas),
a : puissances électriques, b : tensions des noeuds.

4.5.4.3.2- Les autres scénarios.

Pour analyser la performance de régulation du système lors de la restauration de la stabilité suite à un défaut sévère, nous montrons tout d'abord la variation de vitesse des cinq générateurs pour les deux scénarios, figure (85).

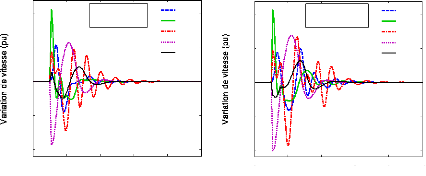
0.005

0.01

2ème cas,
2ème scénario

G. 53

G. 59

G. 60

G. 66

G. 68

0.005

0.01

2ème cas,
3ème scénario

G. 53

G. 59
G. 60
G. 66
G. 68

0

0

-0.005

-0.005

-0.01

0 2 4 6 8 10

Temps (s)

-0.01

0 2 4 6 8 10

Temps (s)

a b

Figure 85. Variation de vitesse des générateurs du 2^ème cas,
a : 2^ème scénario, b : 3^ème scénario.

Nous donnons ensuite dans le tableau suivant le dépassement maximum et le temps de réponse mesurés pour la variation de vitesse.

		G. 53	G. 59	G. 60	G. 66	G. 68
2ème scénario	Dp	5.45×10^-3	10.6×10^-3	4.43×10^-3	- 9.29×10^-3	1.35×10^-3
	tr (s)	5	4	7	4	4
3ème scénario	Dp	4.39×10^-3	10.6×10^-3	4.6×10^-3	- 10.2×10^-3	- 2.2×10^-3
	tr (s)	7	6	8	4	5

Nous comparons enfin les temps de réponse avec leurs équivalents du premier cas, en tenant compte des trois scénarios retenus. Nous représentons cette comparaison par la figure (86). La figure (87), quant à elle, représente l'amélioration apportée par l'utilisation de l'AG pour l'optimisation simultanée des paramètres des PSSs et de leurs emplacements. L'amélioration de temps de réponse a été évaluée, en valeurs relatives exprimées en pourcent pour les cinq générateurs choisis et dans les trois scénarios étudiés.

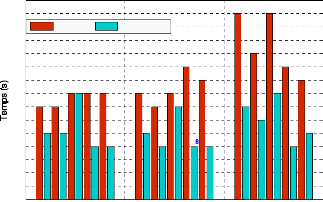
14

12

10

4

6

2

8

0

53

53

59

1er cas 2ème cas

59

606066

66

68

68

53

53

59

59

60

60

66

6

68

68

53

53

59

59

60

60

66

66

68

68

1er Scénario 2ème Scénario 3ème Scénario

Figure 86. Temps de réponse des trois scénarios (comparaison entre le 1^er et le 2^ème cas).

60%

50%

40%

30%

20%

10%

0%

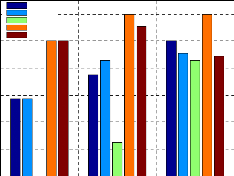
G. 53

G. 59

G. 60

G. 66
G. 68

1er Scénario 2ème Scénario 3ème Scénario

Figure 87. Temps de réponse des trois scénarios
(Comparaison des valeurs relatives entre le 1^er et le 2^ème cas).

Nous remarquons que le deuxième cas présente une amélioration remarquable des temps de réponse quel que soit le scénario ; cette amélioration atteint par exemple 60 % pour la variation de vitesse de générateur 66 avec les deuxième et troisième scénarios.

La figure (88) montre enfin la réponse dynamique des angles de rotor suite au défaut de ligne pour les 2^ème et 3^ème scénarios.

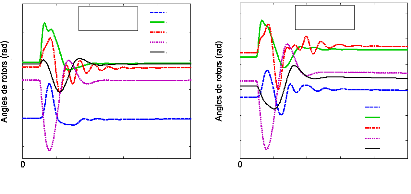
2 4 6 8 10

Temps (s)

2 4 6 8 10

Temps (s)

2.5

2

2ème cas,
2ème scénario

G. 53

G. 59

G. 60

G. 66

G. 68

1.5

2

2ème cas,
3ème scénario

1.5

1

1

0.5

0.5

0

-0.5

0

G. 53

G. 59
G. 60
G. 66
G. 68

a b

Figure 88. Réponse dynamique des angles de rotor du 2^ème cas,
a : 2^ème scénario, b : 3^ème scénario.

4.5.4.4- Discussion et conclusion.

La méthode des facteurs de participation a montré que les générateurs 53 et 66 ne devraient pas être équipés de PSSs. Pourtant, selon cette méthode, le générateur 66 participe aux modes interrégionaux ; le générateur 53 quant à lui ne présente aucune participation importante aux modes du système.

Lorsque l'AG est utilisé pour trouver les générateurs les plus appropriés pour installer des PSSs, il prend en considération l'ensemble des propriétés des PSSs (emplacement et paramètres). Il varie continuellement l'emplacement et les valeurs de paramètres des PSSs en cherchant à trouver la solution qui améliore au maximum la performance de tous les modes. Lorsque l'AG trouve qu'un emplacement n'entraîne aucune amélioration de la performance des modes ou a éventuellement une influence négative, l'emplacement est abandonné.

L'AG a montré que tous les générateurs responsables des modes interrégionaux (comme la méthode des facteurs de participation a déterminé) nécessitent l'ajout de PSSs, en particulier le générateur 66. Par contre, pour ceux responsables des modes locaux, l'AG montre que deux d'entre eux n'ont pas besoin de PSSs ; à savoir les générateurs 56 et 60.

La figure (89) montre la fréquence de sélection de chaque générateur pour être doté d'un PSS pour 300 d'itérations d'AG.

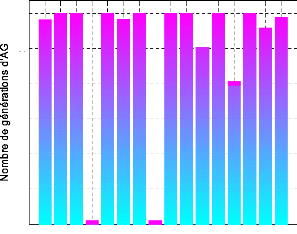
0

53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

300

250

200

150

100

50

Numéro de générateur

Figure 89. Choix de chaque générateur pour 300 d'itérations d'AG.

Il apparaît sur cette figure que les générateurs 56 et 60 ne sont choisis que pendant quelques itérations d'AG. Les générateurs 63 et 65 sont moins choisis par rapport aux autres. La question qui se pose maintenant est la suivante : l'AG peut-il être employé pour réduire le nombre de PSSs en conservant seulement les PSSs les plus efficaces ???

4.5.5- Cas 3 : optimisation globale des PSSs. 4.5.5.1- Application des AGs.

Généralement, lorsque les PSSs sont mal réglés, ils peuvent produire des effets sévèrement nuisibles au système de puissance. En outre, un ensemble de PSSs peut donner des résultats médiocres quand son emplacement n'est pas bien choisi. En conséquence, il est nécessaire de réduire ces effets nuisibles en choisissant l'emplacement optimal des PSSs simultanément avec un réglage coordonné et en employant seulement le nombre nécessaire de PSSs.

Pour la réduction du nombre des PSSs, nous proposons la procédure illustrée par la figure (90). Cette figure montre la structure du programme de l'AG utilisé. Un commutateur branché en série avec le PSS prend des variables "0 ou 1". Les variables représentant ces commutateurs sont introduites dans le programme de l'AG avec les autres variables des PSSs (ceux du deuxième cas). Ces commutateurs permettent de relier (si la variable est 1) ou débrancher (si la variable est 0) les PSSs des générateurs. Au cours du calcul, lorsque la fonction multiobjectif ne varie pas de manière significative à cause de la faible influence de certains PSS sur l'amortissement du système, l'AG ne les prend pas alors en considération.

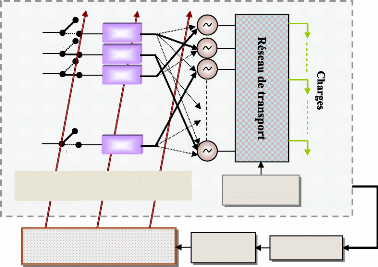
Interrupteurs
des PSSs

Algorithme Génétique

₀0

01

1

1

0

1

Paramètres
des PSSs

PSS 16

PSS 1

PSS 2

PSS 3

Placement
des PSSs

Fonction
multiobjectif

G16

G2

G3

G1

Point de
fonctionnement

Valeurs propres

Figure 90. Optimisation coordonnée de localisation, des paramètres et du nombre des PSSs.

Les cinq variables à optimiser de chaque PSS (un commutateur de PSS, un emplacement, un gain et deux constantes de temps) sont soumises aux contraintes suivantes :

1 40

= =

K PSS j

,

0. 0 1 0 . 1

= =

T 1 , j

0. 0 1 0 . 1

= =

T 3 , j

{ }

5 3, ,6 8

L

{ }

0,1

PLPSS , j SWPSS ,j

(149)

j

1,2,

avec

, NPSS

Les autres paramètres _(Tw,j ^et T2,j, T4,j) des PSSs sont considérés constants : Tw,j = 10 et T2,j = T4,j = 0.02.

Le tableau (14) donne les valeurs choisies des paramètres de l'AG.

Nombre d'individu Nind	100
Nombre de gènes Ngens	Nind^x Nvar
Nombre de génération Ngener	300
Probabilité de croisement Pc	0.7
Probabilité de mutation Pm	0.005

Tableau 14. Valeurs choisies des paramètres de l'AG.

Nous avons trouvé que les meilleures performances des paramètres obtenus par l'AG demandent l'utilisation de 12 PSSs seulement.

Les valeurs des paramètres des PSSs optimisés sont données dans le tableau (15).

N° PSS	N° G.	KPSS	T1	T3
1	53	21.5146	0.0926	0.0998
2	54	38.1806	0.0874	0.0225
3	55	39.1358	0.0978	0.0560
4	57	20.4600	0.0887	0.0562
5	58	23.9224	0.0639	0.0452
6	59	11.6205	0.0754	0.0160
7	61	39.2348	0.0297	0.0948
8	62	21.8183	0.0324	0.0411
9	64	18.8449	0.0423	0.0480
10	66	39.7833	0.0138	0.0174
11	67	39.2614	0.0147	0.0100
12	68	39.9553	0.0512	0.0395

Tableau 15. Paramètres et localisation des PSSs optimisés par AG.

Ces valeurs représentent la meilleure solution atteinte à la dernière génération ; elles correspondent à la valeur finale de la fonction multiobjectif, soit 1.223. L'évolution de la fonction multiobjectif en fonction du nombre de générations est donnée à la figure (91).

1.2 1 0.8 0.6 0.4 0.2 0

0 50 100 150 200 250 300

Générations

Figure 91, Evolution de la fonction multiobjectif.

Cette évolution de la fonction multiobjectif correspond à l'évolution du nombre de PSSs au cours de l'exécution de l'AG ; cette dernière évolution est illustrée par la figure (92).

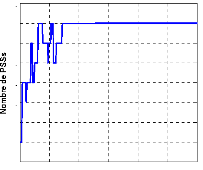
13

12

11

10

9

8

7

6

5

0 50 100 150 200 250 300

Nombre de génération

Figure 92. Convergence du nombre de PSSs.

Comme nous avons fait avec les cas précédents, nous devons analyser la performance et la robustesse du réglage des PSSs pour le modèle linéaire du système et aussi pour son modèle non-linéaire.

4.5.5.2- Analyse des valeurs propres. 4.5.5.2.1- Le point de fonctionnement nominal.

En installant les 12 PSSs optimisés aux emplacements déterminés par l'AG, nous pouvons calculer les valeurs propres du système au point de fonctionnement nominal en boucle fermée. Le tableau (16) donne certaines de ces valeurs propres. La figure (93) donne leurs répartitions dans le plan complexe.

N° mode	ë	æ	f [Hz]
1	- 7.9207 #177; j 9.7480	0.6306	1.5514
2	- 2.1271 #177; j 10.888	0.1917	1.7329
3	- 1.4055 #177; j 9.8537	0.1412	1.5683
4	- 1.3155 #177; j 9.3297	0.1396	1.4849
5	- 1.6215 #177; j 8.4449	0.1886	1.3440
6	- 1.0859 #177; j 7.2412	0.1483	1.1525
7	- 1.8724 #177; j 7.0410	0.2570	1.1206
8	- 4.4445 #177; j 3.8309	0.7575	0.6097
9	- 7.2122 #177; j 4.7003	0.8378	0.7481
10	- 3.9322 #177; j 2.7953	0.8150	0.4449
11	- 2.6229 #177; j 3.0356	0.6538	0.4831
12	- 1.0934 #177; j 3.9569	0.2663	0.6298
13	- 1.0836 #177; j 2.7449	0.3672	0.4369
14	- 1.0862 #177; j 3.0984	0.3308	0.4931
15	- 1.6932 #177; j 3.3940	0.4464	0.5402

Tableau 16. Valeurs propres du système (12 PSSs : optimisation globale par AG).

Modes locaux Modes interrégionaux

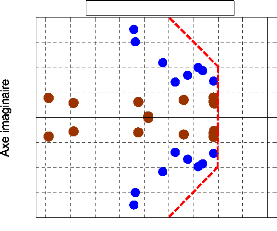
3ème cas , 1er scénario

20

dz = 10 %

10

0

-10

-4 -3 -2 -1 0

-1

-20

Axe réel

Figure 93. Répartition des valeurs propres du système dans le plan complexe
(12 PSSs : optimisation globale par AG).

L'installation de ces 12 PSSs dans le système permet d'assurer la stabilité globale du système ; tous les modes, locaux et interrégionaux, sont bien décalés dans la zone D. Le facteur d'amortissement minimum est æmin = 13.96 % et la partie réelle maximale des valeurs propres est ómax = - 1.0836. En comparant avec le premier cas, nous remarquons que nous obtenons quasiment la même performance avec 12 PSSs seulement qu'avec 14 PSSs. (Le facteur d'amortissement minimum est diminué de 7 % tandis que la partie réelle maximale des valeurs propres est améliorée de 14.2 %). En outre, le facteur d'amortissement et la partie réelle des valeurs propres des modes interrégionaux présentent une bonne amélioration par rapport au premier cas.

4.5.5.2.2- Les autres scénarios.

Nous avons vu que les 12 PSSs optimisés et localisés par l'AG placent tous les modes du système dans la zone D en cas de point de fonctionnement nominal. Quant aux deux autres scénarios proposés, les répartitions des valeurs propres associées dans le plan complexe sont données à la figure (94).

Nous trouvons sur ces deux figures qu'il n'y a qu'un seul mode hors de la zone D pour le deuxième scénario et deux modes pour le troisième scénario. Pour l'un comme pour l'autre, le critère de la partie réelle des valeurs propres n'est pas respecté tandis que le critère du facteur d'amortissement reste toujours respecté. Les caractéristiques générales de ces modes critiques peuvent être données dans le tableau suivant :

	N° mode	ë	æ	f [Hz]	Type de mode
2ème scénario	1	- 0.4202#177; j 2.9600	0.1543	0.4281	Interrégional
3ème scénario	1	- 0.8968#177; j 6.6542	0.1336	1.0586	Local
	2	0.9237#177; j 3.2530	0.2732	0.5177	Interrégional

Ce tableau montre que le seul mode critique du 2^ème scénario est interrégional tandis qu'un mode local et un autre interrégional sont associés au 3^ème scénario.

Modes locaux Modes interrégionaux

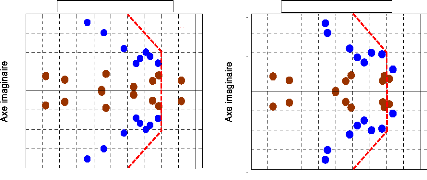
3ème cas , 3ème scénario

dz = 10 %

-4 -3 -2 -1 0

-1

3ème cas , 2ème scénario

20

dz = 10 %

10

0

-10

-4 -3 -2 -1 0

-1

-20

20

10

0

-10

-20

Axe réel Axe réel

a b

Figure 94. Valeurs propres du système pour le 3^ème cas,
a : 2^ème scénario, b : 3^ème scénarios.

Les valeurs minimales de (æ) et maximales de (ó) des deux scénarios sont données ci- dessous :

	æmin	ómax
Scénario 2	14.51 %	- 0.4202
Scénario 3	11.77 %	- 0.8968

Nous comparons les variations relatives des valeurs critiques de (æi) et (ói) de chaque scénario de ce cas par rapport au premier cas. Cette comparaison est donnée dans le tableau (17) et illustrée par la figure (95).

	Äæmin %	Äómax %
Scénario 1	- 7 %	14.2 %
Scénario 2	37.27 %	- 33.13 %
Scénario 3	82.48 %	118.22 %

Tableau 17. Comparaison des variations relatives de _(æmin) ^et _(ómax) entre les 1^er et 3^ème cas.

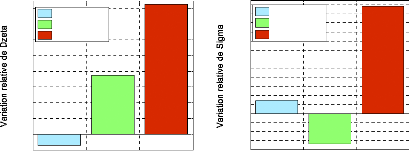
-10 %

40 %

20 %

80 %

60 %

0 %

1er scénario 2ème scénario 3ème scénario

120 %

100 %

-20 %

-40 %

40 %

80 %

60 %

20 %

0 %

1er scénario 2ème scénario 3ème scénario

a b

Figure 95. Comparaison des variations relatives entre les 1^er et 3^ème cas,
a : æmin, b : ómax.

Nous constatons donc qu'il y a une amélioration globale sur la performance de régulation lors de l'utilisation de 12 PSSs optimisés et localisés simultanément par l'AG par rapport au premier cas utilisant 14 PSSs localisés par une méthode classique et optimisés par l'AG.

4.5.5.3- Analyse par simulations temporelles. 4.5.5.3.1- Le point de fonctionnement nominal.

Pour continuer la vérification de la performance de réglage, nous devons réaliser des simulations temporelles adaptées du système non-linéaire. Nous considérons dans ce paragraphe le système avec son point de fonctionnement nominal soumis au défaut appliqué aux cas précédents.

Nous donnons en premier lieu le résultat de la variation de vitesse des cinq générateurs ; il est présenté à la figure (96).

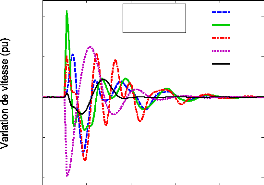
0.005

0.01

3ème cas,
1er scénario

G. 53

G. 59
G. 60
G. 66
G. 68

0

-0.005

-0.01

0 2 4 6 8 10

Temps (s)

Figure 96. Variations de vitesse des cinq générateurs suite à un défaut de ligne,
(1^er scénario du 3^ème cas).

Les valeurs des dépassements maximums et des temps de réponse sont données dans le tableau suivant.

	G. 53	G. 59	G. 60	G. 66	G. 68
Dp	5.29×10^-3	10.7×10^-3	5.01×10^-3	- 9.84×10^-3	0.49×10^-3
tr (s)	8	8	8	6	3

En comparant les valeurs de ce tableau avec les valeurs équivalentes du premier cas, nous constatons que les temps de réponse des générateurs 66 et 68 ont bien diminués tandis que ceux des générateurs 53 et 59 ont légèrement augmentés (de 1 seconde). Les dépassements conservent les mêmes valeurs.

La figure (97) montre les réponses temporelles des angles de rotor pour le défaut proposé et les écarts entre les angles des générateurs 60 et 66 et entre les angles des générateurs 68 et 53. Les oscillations interrégionales se manifestent clairement sur l'écart angulaire des générateurs appartenant à des régions différentes. Nous pouvons bien voir que ces oscillations interrégionales s'amortissent en respectant le critère de performance désirée.

Temps (s) Temps (s)

a b

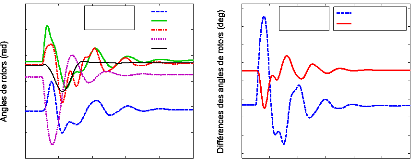
-0.5 0 2 4 6 8 10

2.5

0.5

1.5

2

0

1

3ème cas,
1er scénario

G. 53

G. 59
G. 60
G. 66
G. 68

120

100

-20

-40

40

80

60

20

0

0 2 4 6 8 10 12

3ème cas,
1er scénario

(G. 60 - G. 66)
(G. 68 - G. 53)

Figure 97. Réponse dynamique des générateurs (1^er scénario du 3^ème cas),
a : angles de rotor, b : écart des angles de deux paires.

La réponse dynamique des puissances électriques des cinq générateurs choisis et la réponse dynamique des tensions de quelques noeuds sont illustrées par la figure (98).

Ces simulations dynamiques montrent clairement que malgré le nombre réduit des PSSs, l'optimisation globale par l'AG permet au système de retrouver sa stabilité après quelques secondes.

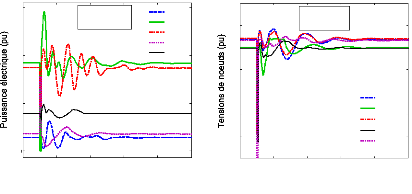
1.5

1

3ème cas,
1er scénario

G. 53

G. 59

G. 60

G. 63

G. 66

1.4

1.2

1

3ème cas,
1er scénario

0.8

0.5

0.6

0.4

0.2

Nd. 40 Nd. 42 Nd. 48 Nd. 52 Nd. 59

0

0 2 4 6 8 10

Temps (s)

0 0 2 4 6 8 10

Temps (s)

a b

Figure 98. Réponse dynamique du système (1^er scénario du 3^ème cas),
a : puissances électriques, b : tensions des noeuds.

4.5.5.3.2- Les autres scénarios.

Nous donnons aux figures (99) et (100) respectivement, la réponse dynamique de la variation de vitesse des cinq générateurs et la réponse dynamique des angles de rotor pour les deux scénarios proposés.

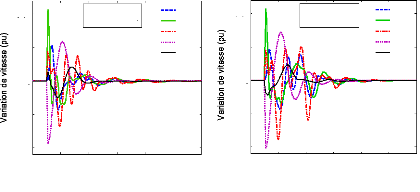
0.005

0.01

3ème cas,
2ème scénario

G. 53

G. 59

G. 60

G. 66

G. 68

0.005

0.01

3ème cas,
3ème scénario

G. 53

G. 59
G. 60
G. 66
G. 68

0

0

-0.005

-0.005

-0.01

0 2 4 6 8 10 12

Temps (s)

-0.01

0 2 4 6 8 10 12

Temps (s)

a b

Figure 99. Variation de vitesse des générateurs du 3^ème cas,
a : 2^ème scénario, b : 3^ème scénario.

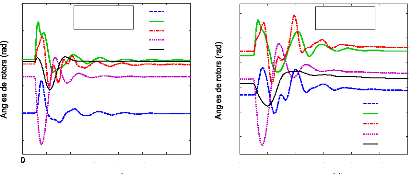
2 4 6 8 10 12 14

Temps (s)

0 2 4 6 8 10 12

Temps (s)

2.5

2

3ème cas,
2ème scénario

G. 53

G. 59

G. 60

G. 66

G. 68

1.5

2

3ème cas,
3ème scénario

1.5

1

1

0.5

0.5

0

-0.5

0

G. 53

G. 59
G. 60
G. 66
G. 68

a b

Figure 100. Réponse dynamique des angles de rotor du 3^ème cas,
a : 2^ème scénario, b : 3^ème scénario.

Suite au défaut proposé et comme nous l'avons fait pour les cas précédents, nous caractérisons la réponse dynamique du système par le calcul du dépassement maximum et du temps de réponse des générateurs. Les valeurs obtenues pour les deux scénarios sont données dans le tableau suivant.

		G. 53	G. 59	G. 60	G. 66	G. 68
2ème scénario	Dp	5.39×10^-3	10.7×10^-3	4.43×10^-3	- 9.28×10^-3	1.34×10^-3
	tr (s)	9	9	10	7	4
3ème scénario	Dp	4.6×10^-3	10.7×10^-3	4.6×10^-3	- 10.2×10^-3	- 2.19×10^-3
	tr (s)	8	8	9	7	6

Nous remarquons sur ce tableau qu'il y a généralement une amélioration du temps de réponse à scénarios équivalents par rapport au 1er cas. En outre, il n'y a plus de temps de réponse dépassant les 10 secondes.

4.5.5.4- Evaluation du nombre de modes dans les trois cas.

Dans la mise en oeuvre conventionnelle des PSSs, les méthodes classiques d'emplacement (tels les facteurs de participation, ...) ne prennent pas en compte du changement de la participation des générateurs dans l'évolution des modes en présence des PSSs et des interactions indésirables entre ces PSSs. Par conséquent, nous trouvons que la plupart des modes électromécaniques dans les trois scénarios étudiés (au 1^er cas) sont de nature interrégionale (70 % en moyenne, figure (101, a)).

Par contre l'optimisation simultanée des paramètres et de l'emplacement des PSSs permet une diminution importante du nombre des modes interrégionaux associés (40 % des modes interrégionaux pour le 2^ème cas et 55 % dans le 3^ème cas, figure (101, b et c)).

Modes locaux

Modes interrégionaux

70 %

a

30 %

40 %

55 %

60 %

45 %

b c

Figure 101. Taux % des modes locaux et interrégionaux,

(a : 1 ^er cas (14 PSSs), b : 2^ème cas (14 PSSs), c : 3^ème cas (12 PSSs)). 4.5.5.5- Discussion et conclusion.

Rappelons que la figure (89), correspondant au choix de sélection de chaque générateur par itération d'AG, montre bien que les générateurs 63 et 65 ont une faible probabilité d'être choisis pour être dotés de PSSs par rapport aux autres générateurs. Mais lorsqu'on laisse à l'AG la possibilité de fixer le nombre de PSSs et de sélectionner leurs emplacements les plus efficaces, nous trouvons alors que ces deux générateurs sont éliminés de la liste des PSSs. La figure (102) montre la fréquence de sélection de chaque générateur pour être doté d'un PSS pour 300 d'itérations d'AG.

L'évaluation de la fonction multiobjectif a montré que la valeur finale est plus grande que celle du premier cas.

L'analyse des valeurs propres et des simulations dynamiques avec 12 PSSs a montré de son côté que certains résultats sont proches de ceux trouvés dans le 1^er cas (14 PSSs), tandis que d'autres résultats sont meilleurs. En outre, le nombre des modes interrégionaux critiques est diminué par rapport au 1^er cas.

Rappelons que dans le 1^er cas, l'optimisation a été réalisée en traitant de façon indépendante la localisation des PSSs et leurs paramètres. Ainsi, l'amélioration associée au 3ème cas est obtenue par l'optimisation simultanée de la localisation des PSSs et de leurs paramètres. Il est aussi important de remarquer que cette méthode a permis également de diminuer le nombre de PSSs à installer.

Cela montre par conséquent la nécessité de prendre en considération le lieu d'emplacement des PSSs lors de l'optimisation de leurs paramètres. Cela montre en outre la potentialité des AGs pour réduire le nombre des PSSs tout en gardant une bonne performance de régulation.

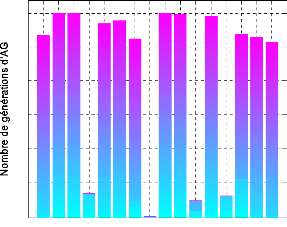
0

53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

300

250

200

150

100

50

Numéro de générateur

Figure 102. Choix de chaque générateur pour 300 d'itération d'AG.

4.5.6- Influence des contraintes de l'AG dans l'optimisation : application au troisième cas. 4.5.6.1- Application des AGs.

Sachant qu'une des caractéristiques d'un AG est la non-production d'une solution unique pour le problème donné, tout changement d'une contrainte de l'espace de recherche du problème ou d'un paramètre de l'AG mène à solution différente.

Pour tester la sensibilité de la solution aux contraintes de l'AG, nous appliquons les contraintes suivantes pour chaque PSS :

1 50

= =

K PSS j

,

0 . 0 1 0 . 1

= =

T 1 , j

0 . 0 1 0 . 1

= =

T 3 , j

{ }

5 3, ,6 8

L

{ }

0,1

PLPSS , j SWPSS , j

(150)

avec

j

1,2,

, N PSS

Nous appliquons de même les paramètres suivants de l'AG.

Nombre d'individu Nind	100
Nombre de gènes Ngens	Nind × Nvar
Nombre de génération Ngener	300
Probabilité de croisement Pc	0.9
Probabilité de mutation Pm	0.005

Tableau 18. Valeurs choisies des paramètres de l'AG.

Grâce à ces nouvelles données, l'AG réduit le nombre de PSSs à 11 PSSs seulement. Les valeurs de leurs paramètres sont données dans le tableau (19).

N° PSS	N° G.	KPSS	T1	T3
1	53	30.2033	0.0509	0.0499
2	54	32.1232	0.0523	0.0879
3	55	36.0024	0.0974	0.0945
4	57	04.75 19	0.0996	0.0897
5	58	06.8476	0.0997	0.0998
6	61	44.8166	0.0997	0.0804
7	62	19.2244	0.0116	0.0466
8	64	19.9228	0.0724	0.0539
9	66	46.4253	0.0107	0.0105
10	67	41.1337	0.0511	0.0929
11	68	11.7644	0.0345	0.0145

Tableau 19. Paramètres et localisation des PSSs optimisés par AG.

L'évolution de la fonction multiobjectif en fonction du nombre de générations est donnée dans ce cas à la figure (103). Au terme de l'optimisation, la valeur finale de la fonction multiobjectif n'atteint que 0.9614.

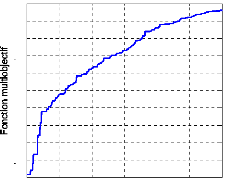
1

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0 0 50 100 150 200 250 300

Générations

Figure 103. Evolution de la fonction multiobjectif.

La valeur finale de la fonction multiobjectif est inférieure à un. Ceci nous indique que le critère de la zone D ne sera pas assuré, même pour le point de fonctionnement nominal. Ainsi, il faut accepter cette solution avec une tolérance.

Nous allons dans ce qui suit analyser la performance de régulation avec ces 11 PSSs pour le point de fonctionnement nominal seulement car pour les autres scénarios, nous serions assez loin des critères imposés dans cette étude.

4.5.6.2- Analyse des valeurs propres pour le point de fonctionnement nominal.

Nous calculons les valeurs propres du système au point de fonctionnement nominal en installant les 11 PSSs optimisés aux emplacements déterminés par l'AG. Nous donnons dans le tableau (20) certaines de ces valeurs propres. La figure (104) donne leurs répartitions dans le plan complexe.

N° mode	ë	æ	f [Hz]
1	- 1.2324 #177; j 10.558	0.1159	1.6805
2	- 3.6757 #177; j 10.046	0.3436	1.5990
3	- 1.3897 #177; j 9.4513	0.1455	1.5042
4	- 1.0276 #177; j 9.3339	0.1094	1.4855
5	- 1.0514 #177; j 6.8663	0.1514	1.0928
6	- 0.8601 #177; j 7.7667	0.1101	1.2361
7	- 0.8629 #177; j 7.4791	0.1146	1.1903
8	- 2.0817 #177; j 7.5413	0.2661	1.2002
9	- 7.5208 #177; j 4.6996	0.8480	0.7480
10	- 2.1214 #177; j 3.1822	0.5547	0.5065
11	- 2.9320 #177; j 3.0255	0.6959	0.4815
12	- 0.8698 #177; j 3.9611	0.2145	0.6304
13	- 0. 8670 #177; j 3.7259	0.2266	0.5930
14	- 0.8519 #177; j 3.1696	0.2596	0.5045
15	- 0.9204 #177; j 2.5468	0.3399	0.4053

Tableau 20. Valeurs propres du système (11 PSSs : optimisation globale par AG).

Modes locaux Modes interrégionaux

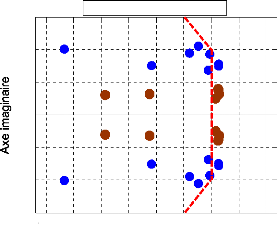
-10

-15

15

10

-5

5

0

-4 -3 -2 -1 0

-1

4ème cas , 1er scénario

dz = 10 %

Axe réel

Figure 104. Répartition des valeurs propres du système dans le plan complexe
(11 PSSs : optimisation globale par AG).

L'analyse des valeurs propres montre que le système se trouve dans la zone de la stabilité. Pourtant, plusieurs modes sont situés hors de la zone D, avec des parties réelles supérieures à la valeur critique. Ceci ne donne pas une grande sûreté de fonctionnement au système pour supporter des scénarios sévères. Le facteur d'amortissement minimum est æmin = 10.94 % et la partie réelle maximale des valeurs propres est ómax = - 0.8519.

4.5.6.3- Analyse par simulations temporelles pour le point de fonctionnement nominal.

La variation de vitesse des cinq générateurs choisis pour montrer la réponse dynamique du système suite à un défaut est donnée à la figure (105).

-0.005

0.005

-0.01

0.01

0

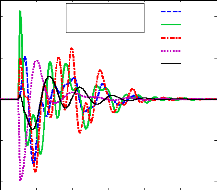
4ème cas,
1er scénario

G. 53

G. 59
G. 60
G. 66
G. 68

0 2 4 6 8 10 12

Temps (s)

Figure 105. Variations de vitesse des cinq générateurs suite à un défaut de ligne,
(1er scénario du 4ème cas).

Les valeurs caractérisant le dépassement maximum et le temps de réponse de ces courbes sont données dans le tableau suivant.

	G. 53	G. 59	G. 60	G. 66	G. 68
Dp	5.13×10^-3	10.7×10^-3	5.01×10^-3	- 9.84×10^-3	0.49×10^-3
tr (s)	8	10	10	8	8

Les réponses temporelles des angles de rotor avec le défaut proposé et les écarts entre les angles des générateurs (60 et 66) et (68 et 53) sont donnés respectivement à la figure (106).

Ces analyses par simulations temporelles montrent bien que les oscillations s'amortissent assez rapidement, au moins de 10 secondes. La stabilité globale du système, pour ce scénario, est ainsi assurée.

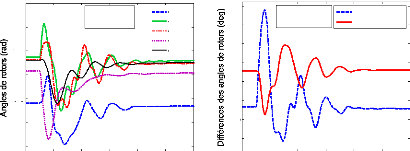
-0.5

2.5

0.5

1.5

2

0

1

4ème cas,
1er scénario

G. 53

G. 59
G. 60
G. 66
G. 68

120

100

-20

40

20

80

60

0

4ème cas,
1er scénario

(G. 60 - G. 66)
(G. 68 - G. 53)

0 2 4 6 8 10 12

Temps (s)

0 2 4 6 8 10 12

Temps (s)

a b

Figure 106. Réponse dynamique des générateurs (1^er scénario du 4^ème cas),
a : angles de rotor, b : écart des angles de deux paires.

4.5.6.4- Discussion et conclusion.

D'un point de vue général, le fait de disposer d'un ensemble de solutions est une source de richesse permettant au concepteur de bénéficier d'une base solide pour choisir, a posteriori, une solution parmi celles proposées, ou pour parfaire la conception. La multiplicité des solutions favorise également l'identification des zones optimales les plus intéressantes (ou les moins contraignantes) pour certains éléments du système ou certains critères particuliers non- intégrés au problème d'optimisation tels le coût, ... .

Dans notre cas, la solution que nous avons obtenue avec 11 PSSs présente un côté positif d'un point de vue économique (par la réduction de leur nombre) et un côté négatif par un manque de robustesse (par le non-respect des critères de stabilité). Dans le cas des PSS, le coût des ces derniers ne représente pas un enjeu critique. Par contre la priorité essentielle concerne la stabilité du système pour le plus grand nombre possible des scénarios. Ainsi, la zone de la robustesse étant la plus importante, la solution des 11 PSSs doit être moins favorisée.

4.6- Conclusion.

Les études menées au cours de ce chapitre ont permis de mettre en évidence les avantages de notre approche, celle-ci permettant d'améliorer simultanément l'amortissement des modes des oscillations électromécaniques globales et locales par une optimisation globale des PSSs.

Quatre cas ont été étudiés.

Dans le 1 ^er cas, nous avons utilisé la méthode des facteurs de participation pour localiser les PSSs nécessaires au système et la méthode des AGs a été utilisée pour régler les paramètres de ces PSSs. Nous avons comparé les résultats obtenus, pour le point de fonctionnement nominal, avec ceux issus d'une méthode d'optimisation classique (la méthode de compensation de phase) et d'une méthode métaheuristique (algorithme d'optimisation par essaim de particules) et les résultats de la littérature. Les résultats obtenus avec notre méthode d'AG montrent que la performance du réglage du système est efficace, avec un bon

amortissement pour tous les modes. Par ailleurs, nous avons remarqué que la performance s'est dégradée pour les autres scénarios (défauts sévères). La robustesse du réglage n'est donc pas suffisamment assurée dans ce cas.

Dans le 2^ème cas, nous avons déterminé en outre l'emplacement des PSSs par l'AG, le nombre des PSSs utilisé étant préfixé. L'analyse des résultats obtenus montre la supériorité de cette approche par rapport à la méthode classique des facteurs de participation. Nous avons obtenu des performances qui améliorent, par exemple, de 40 % les temps de réponse des générateurs pour tous les scénarios étudiés. Quant à l'amortissement de tous les modes interrégionaux, il est notablement augmenté.

Dans le 3^ème cas, nous avons axé notre recherche sur l'optimisation du nombre des PSSs. Nous avons considéré que ce paramètre est très important pour minimiser les interactions nuisibles entre PSSs. Nous avons ainsi développé l'approche correspondante. Les résultats obtenus montrent que la stabilité globale du système est garantie. Le nombre de modes interrégionaux critiques est diminué par rapport au 1^er cas malgré la réduction du nombre de PSSs (12 PSSs contre 14).

Dans le 4^ème cas, nous avons évalué la sensibilité des AGs vis-à-vis des paramètres de réglage telles la probabilité de croisement et les contraintes de l'espace de recherche. La "désensibilisation" de l'AG par rapport aux contraintes de l'espace de recherche du problème étudié fera l'objet du chapitre suivant.

Enfin nous pouvons conclure qu'outre l'optimisation coordonnée des paramètres des PSSs souvent appliquée dans le réglage des PSSs, il faut aussi tenir compte du nombre et de la localisation optimale de ces PSSs pour pouvoir réduire au maximum les effets indésirables des interactions entre PSSs. La stabilité globale du système peut alors être correctement assurée par une optimisation simultanée des paramètres et de leur emplacement avec un nombre réduit de PSSs.

Chapitre V

Optimisation par

algorithmes génétiques à

contraintes dynamiques

5.1- Introduction.

x

Dans la littérature, plusieurs méthodes sont proposées pour améliorer la performance des AGs, dans la recherche de l'optimum global, telles les méthodes des opérateurs génétiques auto-adaptatifs (Bäck, 1992; Angeline, 1995; Deb, 1999; Régnier, 2003), la parallelisation des AGs (Alba et al., 1999; Tomassini, 1999; Hongesombut et al., 2005), ... . Ces méthodes présentent de bons résultats, mais si le point optimal global cherché ne se trouve pas dans l'espace de recherche proposé du problème (figure (107)), ces méthodes ne permettent pas aux AGs de trouver ce point.

f(x)

OG

xmin xmax

Figure 107. Problème d'optimum global situé en dehors de l'espace de recherche proposé.

Le bon déroulement d'un programme d'AG dépend de la détermination de l'espace de recherche, borné par une valeur maximale et minimale, associées à chaque paramètre à optimiser.

L'espace de recherche du problème définissant un ensemble des solutions potentielles peut ainsi contenir la solution optimale globale et/ou d'autres solutions locales. Ainsi, pour l'obtention de l'optimum global, il est alors très important de bien déterminer cet espace de recherche, autrement dit il faut bien choisir ses contraintes.

Dans la plupart des problèmes d'optimisation, il n'y a pas de critères rigoureux pour déterminer précisément les contraintes de l'espace de recherche. Dans la pratique, le choix de ces contraintes reste ainsi arbitraire.

Lors de l'optimisation de problèmes à grand nombre de paramètres tels les PSSs, il est souvent très difficile de déterminer pour des paramètres de même type (constantes de temps, gains, ....) des espaces de recherche différents. Ainsi, ces espaces de recherche sont généralement fixés par l'expérience et le savoir faire ; ils ont souvent des valeurs identiques. Ces espaces restent enfin fixes tout au long du processus d'optimisation. Ainsi, la valeur d'un paramètre peut atteindre une des limites de l'espace de recherche associé. Le fait d'atteindre cette limite peut arriver après un certain nombre de générations ou même dès le début de l'optimisation. Par conséquent, l'évolution de la fonction objectif peut se décélérer, voire se stabiliser, bien avant de converger vers la solution optimale.

Une solution peut être proposée pour améliorer la convergence de l'algorithme et la qualité de la solution optimale recherchée. Cette solution est basée sur la libération des contraintes de l'espace de recherche au cours de l'application de l'AG qui permet de leur donner des valeurs différentes selon les besoins du processus d'optimisation. Nous permettons ainsi à l'AG de diversifier sa population par de nouvelles valeurs qui n'étaient pas accessibles avec un espace de recherche fixe. Nous réalisons donc un espace de recherche dynamique qui s'adapte à la recherche de l'optimum global.

Nous allons dans ce chapitre appliquer cette approche à l'optimisation des PSSs. 5.2- Approche proposée.

Rappelons que la forme générale d'un problème d'optimisation (maximisation) est :

max( ( )) : R ? R (151)

F X n k

X S

?

· { } n

X = x ₁ , x ₂ , L , x n ? R : vecteur des paramètres à optimiser de dimension n.

· { } k

F = f ₁ , f ₂ , L , f_n ? R : fonction objectif de dimension n. Pour k = 1, le problème est dit monoobjectif, autrement il est multiobjectif.

· n

S ? R : espace de recherche du problème a des contraintes aux limites. Les points de cet espace de recherche doivent correspondre à des solutions réalisables. Les contraintes définissants ses limites peuvent être données par des valeurs minimales xi,min et maximales _xi,max associées à chaque paramètre à optimiser :

x i x _i x i i { n}

,mi n ,max : 1,2 ,

= = = L(152)

Les figures (108) et (109) donnent respectivement le principe général et l'organigramme de l'approche proposée. Dans cette approche, nous initialisons l'AG avec un espace de recherche fixe. Lorsque l'évolution de la fonction objectif ne s'améliore plus de façon significative, nous utilisons alors des contraintes dynamiques sur l'espace de recherche. Une marge de tolérance (å_m, å_n) est fixée pour chacune des deux extrémités de l'espace de recherche. Lorsque la valeur d'un paramètre atteint cette marge pendant un certain nombre de générations successives (Ng), les limites associées à l'espace de recherche de ce paramètre vont être modifiées par des valeurs prédéterminées (Ä_m, Ä_n). L'espace de recherche du paramètre se déplacera en gardant toujours sa taille initiale. Ce processus peut se répéter plusieurs fois au cours de l'optimisation. Enfin, pour que les valeurs attribuées aux paramètres soient des solutions réalisables (valeurs positives dans notre cas), il faut limiter l'évolution des valeurs minimales de l'espace de recherche à une valeur faible (å_p > 0).

A_n

A_n

A_n

A_n

xmin xmax

å_m

xmax

0

xmin

å_n

x

x

xmin

xmax

å_n

å_m

A_m

A_m

Am

A_m

Figure 108. Le principe général de l'approche des contraintes dynamiques.

Pour i = 1 : Nvar

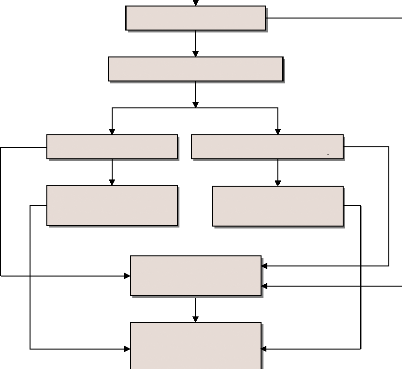
Non

xi,max = xi,max + Ä_m
xi,min = xi,min + Ä_m

Si xi > xi,max - å_m

Oui

Opérateurs d'AG

Si Gener > = Nd

Pour j = 1 : Ng

xi,max = xi,max
xi,min = xi,min

Si xi < xi,min - å_n & xi > å_p

Oui

xi,min = xi,min - Ä_n
xi,max = xi,max - Ä_n

Oui

Non

Non

Figure 109. Organigramme de l'approche des contraintes dynamiques. 5.3- Première application.

Nous appliquons l'approche au premier cas étudié dans le chapitre précédent. 5.3.1- Optimisations par contraintes fixes.

Les espaces de recherche utilisés dans l'optimisation des PSSs disposent des contraintes fixes tout au long du processus d'optimisation. Ces espaces de recherche (pour les trois paramètres (KPSS,i, T1,i, T3,i) à optimiser par PSS) sont soumis aux contraintes données par la relation (144). Les valeurs choisies des paramètres de l'AG sont donnés au tableau (7).

L'évolution de la fonction multiobjectif en fonction du nombre de générations a été déjà donnée à la figure (61). Nous remarquons que la valeur finale de la fonction multiobjectif, atteinte pour la génération maximale prédéterminée de 250, est de 1.097.

La figure (110) montre la variation, pour chaque génération de l'AG, des valeurs des trois paramètres choisis (KPSS (13), T1 _(14), T3 (9)).

40

39

38

37

36

35

0 50 100 150 200 250

a

Génération

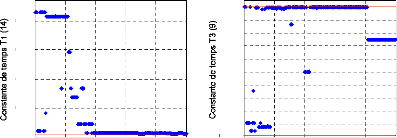
0.1

0.08

0.06

0.04

0.02

0.001

0.04

0.03

0.02

0.01

0.001

0 50 100 150 200 250

Génération 0 50 100 150 200 250

Génération

b c

Figure 110. Variation des valeurs des trois paramètres (a : KPSS (13), b : T1 _(14), c : T3 (9)).

Sur cette figure, nous pouvons remarquer les points suivants :

- Le gain du 1 3^ème PSS converge, à partir de la 1 80^ème génération, vers une valeur très proche de la limite maximale de l'espace de recherche associé.

- La constante de temps T1 du 14^ème PSS converge, à partir de la 100^ème génération, vers une valeur très proche de la limite minimale de l'espace de recherche associé.

- La constante de temps T3 du 9^ème PSS atteint dès la 40^ème génération une valeur très proche de la limite maximale de l'espace de recherche associé. Au-delà de la 200^ème génération, elle atteint une autre valeur située loin des limites de l'espace de recherche.

Rappelons que la répartition des modes électromécaniques du système dans le plan complexe, donnée à la figure (63), montre que tous les modes électromécaniques, sauf deux d'entre eux, sont déplacés dans la zone D de stabilité ; le facteur d'amortissement minimum est æmin = 15.02 % et la partie réelle maximale des valeurs propres est ómax = - 0.9485.

5.3.2- Optimisations par contraintes dynamiques.

Nous appliquons maintenant l'approche proposée pour optimiser les paramètres des 14 PSSs, avec des espaces de recherche modifiables tout au long du processus d'optimisation.

Les contraintes initiales des espaces de recherche et les valeurs choisies des paramètres de l'AG sont les mêmes que précédemment (relation (144) et tableau (7) respectivement).

Sur la figure (61), nous remarquons que l'évolution de la fonction multiobjectif s'arrête généralement de s'améliorer d'une façon significative à partir de la 75^ème génération. Nous pouvons donc considérer que cette génération (Nd = 75) est le point de départ des contraintes dynamiques.

Les marges de tolérance (å_m, å_n) des deux extrémités de l'espace de recherche de chaque paramètre sont choisies comme suit :

( ) 1 , ( ) 0 . 05

K K

PSS i n PSS i

, ,

å _m

= =

å

å m

( ) 0 .0 1 , ( ) T T 1 , 1 , i n i = å

0.0005

(153)

å _m (T₃

, 1 ,

i n i

) 0. 0 1 , ( ) 0 . 0005

= =

å T

Le nombre des générations successives nécessaire pour permettre aux contraintes de changer leurs valeurs est déterminé à Ng = 50.

Les valeurs de changement possible des contraintes (Ä_m, Ä_n) sont choisies, quant à elles, comme suit :

Ä_m

( ) 2 , ( ) 0 . 05

K K

PSS i n PSS i

, ,

= Ä =

Äm

( ) 0 . 0 1 , ( ) T T 1 , 1 , i n i = Ä

0.0005

(154)

Ä_m (T3

, 1,

i n i

) 0. 0 1 , ( ) 0 . 0005

= Ä =

T

L'évolution de la fonction multiobjectif en fonction du nombre de générations est donnée à la figure (111).

1.2 1 0.8 0.6

0 50 100 150 200 250

Generations

Figure 111. Evolution de la fonction multiobjectif.

Sur cette figure, nous constatons que la fonction multiobjectif atteint une valeur égale à la valeur finale du cas précédent, soit 1.097, pour la génération 120. Ensuite, elle atteint la valeur de 1.234 pour la génération maximale prédéterminée de 250. Ainsi, par rapport au cas précédent, la convergence est assurée en moins de 130 générations. Au bout de 250 générations, nous obtenons un gain de 12,4 %.

Les valeurs optimales des paramètres des PSSs sont données au tableau (21).

N° PSS	N° G.	KPSS	T1	T3
1	54	37.7248	0.0790	0.0452
2	55	23.4329	0.0238	0.0441
3	56	33.6390	0.0637	0.0462
4	57	32.2578	0.0673	0.0460
5	58	38.3750	0.0608	0.0850
6	59	23.0859	0.0851	0.0809
7	60	01.5685	0.0862	0.0812
8	61	12.6048	0.0098	0.0293
9	62	10.4482	0.0398	0.1051
10	63	14.6773	0.0511	0.0755
11	64	23.7698	0.0552	0.1231
12	65	16.5094	0.0039	0.0143
13	67	43.8539	0.0090	0.0081
14	68	34.4827	0.0048	0.0003

Tableau 21. Paramètres des PSSs optimisés par AG à contraintes dynamiques. Les valeurs des paramètres fixés des PSSs sont les mêmes que le cas précédent : Tw,j = 10 et T2,j = T4,j = 0.02.

Pour montrer l'évolution des valeurs des paramètres des PSSs lors de l'optimisation, nous donnons à la figure (112) la variation des trois paramètres les plus représentatifs (KPSS (13), T3 _(9), T3 ₍₁₄₎₎ pour chaque génération d'AG.

Sur cette figure, nous pouvons remarquer les points suivants :

- Le gain du 13^ème PSS prend, à partir de la 75^ème génération, de nouvelles valeurs plus

élevées que la limite maximale initiale. La valeur finale atteinte est de 43.853.

- La constante de temps T3 du 9^ème PSS dépasse aussi sa limite maximale initiale. Sa

valeur optimale est de 0.1231.

- La constante de temps T3 du 14^ème PSS atteint, à partir de la 120^ème génération, une valeur très proche de sa limite minimale initiale. Ensuite, elle prend des valeurs inférieures à cette limite. Elle atteint au bout de l'optimisation la valeur 0.0003.

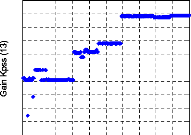
44

42

40

38

36

a

0 50 100 150 200 250

Génération

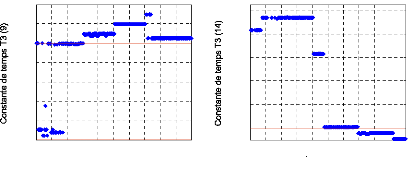
0.001

0 50 100 150 200 250

Génération

0 50 100 150 200 250

Génération

0.14

0.011

0.12

0.009

0.1

0.08

0.007

0.06

0.005

0.04

0.003

0.02

0.001

b c

Figure 112. Variation des valeurs des trois paramètres (a : KPSS (13), b : T3 _(9), c : T3 (14)).

Un indice intéressant, défini par la relation suivante (Wood, 2006), permet de comparer les deux résultats. Il s'agit du rendement ç de la valeur optimale de la fonction multiobjectif (Fobjmax) pour la génération courante itr :

Fobj itr

ç (155)

= ( max ) · 100 %

itr

Nous pouvons ainsi tracer l'évolution de ce rendement pour les deux résultats (optimisation par contraintes fixes et dynamiques), figure (113). L'analyse de cette figure montre qu'au-delà de la 150^ème génération, le rendement est quasi linéaire. Un gain de 25 générations est constaté pour une valeur fixée du rendement.

Pour évaluer la performance du réglage des PSSs sur le système étudié, nous montrons par la figure (114) la répartition des modes électromécaniques du système dans le plan complexe. Tous les modes électromécaniques sont bien déplacés dans la zone D de stabilité ; cela traduit bien l'amélioration réalisée sur l'optimisation de la fonction multiobjectf. Le facteur d'amortissement minimum est æmin = 14.82 % et la partie réelle maximale des valeurs propres est ómax = - 1.085.

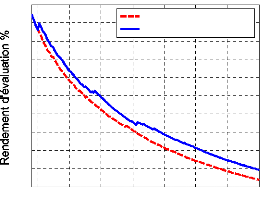
0.4

75 100 125 150 175 200 225 250

1.4

Contraintes fixes Contraintes dynamiques

1.2

1

0.8

0.6

Génération

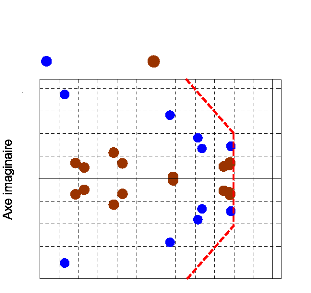
Figure 113. Evolution du rendement de la fonction multiobjectif.

Modes locaux Modes interrégionaux

20

dz = 10 %

10

0

-10

-20

-6 -5 -4 -3 -2 - 0

-1

Axe réel

Figure 114. Valeurs propres du système.

Les résultats obtenus montrent que l'approche proposée a élargi l'espace de recherche initial de certains paramètres. En prenant maintenant un espace de recherche initial aussi étendu que celui obtenu par l'approche à contraintes dynamiques, nous vérifions son évolution par l'AG à contraintes fixes. Nous appliquons ainsi les contraintes fixes suivantes :

0.1 45 = = K PSS j , 0.0005 0 . 1 3 = = T 1 , j 0.0005 0 . 1 3 = = T 3 , j					(156)
avec	j	1,2,		, NPSS

L'évolution de la fonction multiobjectif correspondante en fonction du nombre de générations, (figure (115)), montre que la valeur atteinte au bout de l'optimisation est égale seulement à 0.984. Par conséquent, nous trouvons que ce résultat est inférieur à celui obtenu par l'optimisation à contraintes dynamiques. En effet, le fait d'élargir l'espace de recherche de tous les paramètres du problème restreint la recherche du point optimal : plus l'espace de recherche est large, plus la possibilité d'être piégé par les optima locaux est grande.

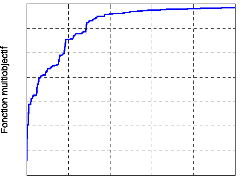
1

0.9

0.8

0.7

0.6

0.5

0.4

0.3 0 50 100 150 200 250

Générations

Figure 115. Evolution de la fonction multiobjectif.

Au-delà de ces résultats et pour montre l'efficacité de notre approche des contraintes dynamiques, nous proposons de l'appliquer sur un petit espace de recherche se trouvant assez loin de la solution optimale que nous avons déjà trouvée.

Nous prenons, par exemple, la moitié de l'espace de recherche initial identifié par la relation (144), soit l'espace donné par la relation (157). En optimisant, en premier lieu, les paramètres des PSSs avec contraintes fixes, nous trouvons que la fonction multiobjectif converge à une valeur trop faible, soit 0.5 13, figure (116).

0.1 20

,

= =

K PSS j

0 . 00 1 0 .05

= =

T 1 , j

0 . 00 1 0 . 05

= =

T ³ j

,

(157)

avec

j

1,2,

, NPSS

Par contre, lors de l'application des contraintes dynamiques, l'espace de recherche s'élargit successivement et la valeur de la fonction multiobjectif s'améliore jusqu'à l'arrivée à une valeur très proche de la solution optimale trouvée précédemment, soit 1.225, figure (116).

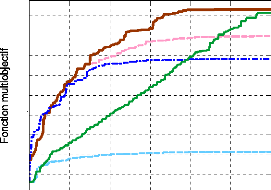
1.2

1.1

1

0.9

0.8

0.7

0.6

0.5

0.4

0 50 100 150 200 250 300

Générations

Espace de recherche initial

Demi-espace de recherche

Contraintes fixes Contraintes dynamiques

Contraintes fixes Contraintes dynamiques

Espace de recherche élargi

Contraintes fixes

Figure 116. Evolution de la fonction multiobjectif des résultats de la 1^ère application.

Nous résumons dans le tableau suivant l'ensemble des cinq résultats d'AG obtenus avec : - l'espace de recherche initial à contraintes fixes (ERICF).

- l'espace de recherche à contraintes dynamiques (ERCD).

- l'espace de recherche élargi à contraintes fixes (ERECF).

- la moitié de l'espace de recherche initial à contraintes fixes (MERICF).

- la moitié de l'espace de recherche à contraintes dynamiques (MERCD).

	ERICF	ERCD	ERECF	MERICF	MERCD
Valeur finale de la fonction multiobjectif	1.097	1.234	0.984	0.513	1.222
Valeur finale relative % (par rapport à l'ERICF)	_____	12.4 %	? 10.3 %	? 53.2 %	11.4 %
Taux de convergence % (par rapport à l'ERICF)	_____	- 52 %	non- convergeant à 1.097	non- convergeant à 1.097	- 6 %

Tableau 22. Résultats de la 1^ère application.

En analysant ces résultats nous pouvons dire que :

- Vu le nombre important des paramètres à optimiser (42 paramètres dans ce cas), il très difficile de donner à chaque paramètre un espace de recherche différent. Nous les proposons donc identiques.

- Dans le cas de l'optimisation avec espace de recherche fixe ; si la taille de cet espace est faible, il y a très peu de chance qu'il contienne la meilleure solution du problème. On converge souvent vers un optimum local.

- D'autre part, si l'espace de recherche fixe est très large ; l'exploration et l'exploitation de cet espace risquent de ne pas être efficaces. L'optimisation, dans ce cas, est souvent piégée par un optimum local.

- Par contre, lors de l'utilisation des contraintes dynamiques, seuls les paramètres qui ne trouvent pas leurs valeurs optimales dans l'espace de recherche initial vont évoluer pour prendre des valeurs supérieures ou inférieures. Cela se traduit donc par une convergence rapide vers la solution optimale, avec une amélioration de la robustesse de l'AG et de la performance de l'optimisation.

5.4- Deuxième application.

Nous allons maintenant valider notre approche pour un autre cas d'optimisation. Nous l'appliquons au troisième cas (12 PSSs).

5.4.1- Optimisations par contraintes fixes.

Rappelons que l'optimisation des PSSs du troisième cas, par contraintes fixes, a été faite dans le chapitre précédent (§§-5.5.1). Les espaces de recherche des 12 PSSs à optimiser par PSS sont soumis aux contraintes données par la relation (149). Les paramètres du réglage de l'AG sont donnés au tableau (14).

L'évolution de la fonction multiobjectif en fonction du nombre de générations est donnée à la figure (91). Sur cette figure, nous remarquons que la fonction multiobjectif atteint la valeur finale, soit 1.223, pour la génération maximale prédéterminée de 300.

Rappelons aussi que la répartition des modes électromécaniques du système dans le plan complexe est donnée à la figure (93). Cette dernière montre que tous les modes dominants se trouvent dans la zone D de stabilité ; le facteur d'amortissement minimum est æmin = 13.96 % et la partie réelle maximale des valeurs propres est ómax = - 1.0836.

5.4.2- Optimisations par contraintes dynamiques.

Comme nous l'avons proposé dans cette nouvelle approche, le processus d'optimisation est initialisé par les contraintes des espaces de recherche fixes (relation (149)). Les paramètres de réglage choisis pour l'AG restent les mêmes, (tableau (14)).

La figure (91) représentant l'évolution de la fonction multiobjectif montre que, à partir de la 120^ème génération, cette fonction ne s'améliore plus d'une façon "importante". Les contraintes dynamiques sont appliquées à partir de cette génération, (Nd = 120).

Les marges de tolérance (å_m, å_n) des deux extrémités de l'espace de recherche de chaque paramètre sont choisies comme suit :

å å m PSS i n PSS i ( ) 1 , ( ) 0 .2 K K , , = = å å m i n i ( ) 0. 0 1 , ( ) 0 . 002 T T 1 , 1 , = =		(158)
å å m i n i ( ) 0 . 0 1 , ( ) T T 3 , 1 , =	0.002

Le nombre des générations successives nécessaire pour permettre aux contraintes de changer leurs valeurs est déterminé à Ng = 20.

Les variations possibles des contraintes (Ä_m, Ä_n) sont choisies, quant à elles, comme suit : ( ) 2 , ( )

Ä_m

0.2

K K

PSS i n PSS i

, ,

= Ä

Äm

( ) 0 . 02 , ( ) T T 1 , 1 , i n i = Ä

0.002

(159)

Ä_m (T3

, 1,

i n i

) 0. 02 , ( ) 0 . 002

= Ä =

T

Les valeurs optimales des paramètres des PSSs sont données au tableau (23).

N° PSS	N° G.	KPSS	T1	T3
1	53	22.7145	0.0715	0.1371
2	54	36.6309	0.0369	0.0450
3	55	34.2725	0.0953	0.0889
4	57	01.8484	0.0869	0.0689
5	58	28.9526	0.0864	0.0397
6	59	11.5439	0.0712	0.0398
7	61	45.8373	0.0529	0.1102
8	62	20.5999	0.0149	0.0494
9	64	17.9713	0.0466	0.0452
10	66	49.3448	0.0192	0.0179
11	67	43.6407	0.0044	0.03 11
12	68	39.1085	0.0506	0.0793

Tableau 23. Paramètres des PSSs optimisés par AG à contraintes dynamiques. Les valeurs des paramètres fixés des PSSs sont les mêmes que le cas précédent : Tw,j = 10 et T2,j = T4,j = 0.02.

L'évolution de la fonction multiobjectif en fonction du nombre de générations est donnée à la figure (117).

1.4 1.2 1 0.8 0.6 0.4 0.2 0

0 50 100 150 200 250 300

Génerations

Figure 117. Evolution de la fonction multiobjectif.

Nous présentons dans le tableau suivant les résultats de l'AG obtenus dans cette application avec :

- l'espace de recherche à contraintes fixes (ERCF).

- l'espace de recherche à contraintes dynamiques (ERCD).

	ERCF	ERCD
Valeur finale de la fonction multiobjectif	1.223	1.387
Valeur finale relative % (par rapport à l'ERCF)	_____	13.4 %
Taux de convergence % (par rapport à l'ERCF)	_____	- 30 %

Tableau 24. Résultats de la 2^ème application.

Comme dans la 1^ère application (relation (155)), la figure (118) montre qu'à partir de la 175^ème génération, un gain progressif du nombre de générations est constaté par l'optimisation à contraintes dynamiques. Le gain maximum, pour une valeur fixée du rendement, est de 35 générations.

La répartition des modes électromécaniques du système équipé des 12 PSSs optimisés est donnée à la figure (119). Cette figure montre clairement que tous les modes électromécaniques du système sont bien déplacés dans la zone D de stabilité. Le facteur d'amortissement minimum et la partie réelle maximale des valeurs propres sont respectivement æmin = 13.74 %, ómax = - 1.249. Ce résultat d'optimisation garantit la stabilité globale du système et une performance robuste pour un grand nombre de scénarios.

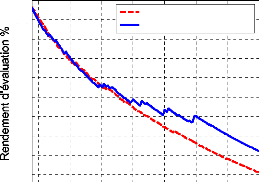
0.8

Contraintes fixes Contraintes dynamiques

0.7

0.6

0.5

0.4

125 150 175 200 225 250 275 300
Génération

Figure 118. Evolution du rendement de la fonction multiobjectif.

Modes locaux Modes interrégionaux

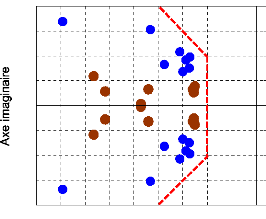
20

dz = 10 %

10

0

-10

-4 -3 -2 -1 0

-1

-20

Axe réel

Figure 119. Valeurs propres du système.

5.5- Conclusion.

Dans ce chapitre, nous avons proposé une approche d'optimisation d'AG à contraintes dynamiques permettant la recherche du point optimal du problème hors des contraintes initiales de l'espace de recherche.

Pour mettre en évidence l'apport de cette approche, nous l'avons appliquée à l'optimisation des PSSs. Nous avons également comparé les résultats obtenus avec ceux de l'AG à contraintes fixes.

Par rapport à l'optimisation utilisant l'AG à contraintes fixe, l'analyse des résultats obtenus montre que la nouvelle approche assure :

- une amélioration de la valeur finale de la fonction multiobjectif (plus de 12 % dans les deux cas étudiés).

- une accélération de la convergence (plus de 30 % sur le nombre de générations, dans les deux cas étudiés).

Par conséquent, cette amélioration de la fonction multiobjectif conduit à une meilleure stabilité globale du système. Elle garantit aussi une bonne performance du système pour divers points de fonctionnement et scénarios.

En conclusion, nous pouvons dire qu'il est possible de bien améliorer la convergence de l'AG et la performance de son résultat. Cela améliore en outre la robustesse de l'AG et sa désensibilisation vis-à-vis de l'espace de recherche proposé.

De ce fait, l'approche de l'AG à contraintes dynamiques ouvre des nouvelles possibilités dans l'utilisation des AGs.

CONCLUSION GENERALE ET PERSPECTIVE

Les systèmes de puissance ne cessent de se développer. L'extension des réseaux interconnectés rend les systèmes fortement sensibles aux oscillations interrégionales. Ces oscillations peuvent sérieusement restreindre le transport de l'énergie électrique. Elles peuvent également conduire à des perturbations s'étendant à tout le système de puissance si, par exemple, une cascade de fautes de lignes de transmission se produit. Dans ces nouvelles conditions, les opérateurs des réseaux électriques se trouvent souvent obligés à faire fonctionner les systèmes aux limites de la stabilité. Par conséquent, l'amélioration de la stabilité aux petites perturbations, en particulier l'amortissement des oscillations interrégionales, représente un objectif prioritaire.

Le travail présenté dans ce mémoire concerne l'étude des méthodes de régulation par des AGs. Les PSSs représentent toujours un moyen efficace pour l'amortissement des modes électromécaniques locaux, mais leur rôle dans l'amortissement des modes interrégionaux est toujours considéré comme de faible importance. Dans cette étude nous avons montré que les PSSs peuvent satisfaire aussi bien l'amortissement des modes interrégionaux que l'amortissement des modes locaux. Ainsi, l'optimisation simultanée de la localisation et des paramètres des PSSs permet à chaque PSS installé dans le système de participer, outre l'amortissement du mode local associé à son générateur, à l'amortissement des modes des autres régions.

Notre travail de recherche s'est articulé autour des points suivants :

- la modélisation d'un système de puissance, modélisation adaptée pour l'étude de stabilité aux petites perturbations.

- les méthodes classiques de réglage et d'emplacement des stabilisateurs PSSs et les méthodes d'analyse de la performance du système.

- l'optimisation globale des PSSs par des AGs.

- le développement d'un AG adaptatif travaillant sur des espaces de recherche dynamiques.

Dans la partie modélisation, nous avons présenté les modèles mathématiques non- linéaires des éléments du système de puissance. Nous avons également développé le modèle linéaire associé.

Nous avons aussi rappelé la théorie de la stabilité, les problèmes de la stabilité aux petites perturbations d'un système de puissance et le principe du stabilisateur PSS.

Dans l'optimisation globale des PSSs, nous avons présenté une méthode basée sur les AGs, pour un problème multiobjectif d'étude de stabilité aux petites perturbations. Cette méthode s'appuyant sur les valeurs propres du système permet d'obtenir, sans passer par la méthode classique des facteurs de participation, non seulement une optimisation des paramètres des stabilisateurs PSSs, mais aussi une meilleure localisation et une réduction intéressante de leur nombre.

L'analyse des résultats obtenus montre qu'un nombre réduit de PSSs, judicieusement situés et dont les paramètres sont optimisés, permet d'assurer un bon amortissement des oscillations électromécaniques et d'assurer convenablement la stabilité globale du système.

Enfin, l'implantation d'une méthode auto-adaptative des espaces de recherche a montré, à travers les résultats obtenus, qu'il est possible de "bien améliorer" la convergence de l'AG et la performance de son résultat. Cette méthode améliore ainsi la robustesse de l'AG et son découplage vis-à-vis de l'espace de recherche proposé.

Les perspectives de ce travail sont nombreuses car les recherches dont il a fait l'objet sont encore loin d'être finalisées.

Plusieurs approches d'amélioration des méthodes d'optimisation sont proposées dans la littérature : elles sont basées sur la possibilité d'hybrider plusieurs méthodes d'optimisation. Ces approches consistent à coupler des méthodes à caractère global avec des méthodes plus locales. A partir des résultats fournis par les méthodes globales, il est possible d'utiliser ensuite des méthodes locales pour affiner la recherche des solutions optimales (Régnier, 2003). La perspective que nous jugeons la plus intéressante consisterait à extraire les meilleurs individus d'une des premières générations de la méthode globale (tel l'AG) et ensuite, à appliquer une méthode locale (tel le recuit simulé) sur ces individus pour un certain nombre de générations. Enfin, nous continuons l'optimisation par la méthode globale. L'intervention de la méthode locale au cours de l'optimisation par la méthode globale permettrait de profiter des performances d'exploration et d'exploitation de ces différentes méthodes et de la diversité de la population dès le départ de l'optimisation : la performance serait par conséquent améliorée avec une convergence rapide vers l'optimum global.

L'approche utilisée dans cette étude est basée sur le modèle linéaire du système. Elle comprend donc seulement des informations sur le comportement dynamique linéaire du système. Cela peut s'avérer insuffisant pour fournir une caractérisation complète et correcte de la performance du système, en particulier lors de fortes contraintes ou d'un fonctionnement à la limite de la stabilité. Il serait nécessaire, par conséquent, d'appliquer notre approche au modèle non-linéaire.

Dans les modes interrégionaux plusieurs générateurs de différentes régions sont impliqués. Pour apporter un meilleur amortissement à ces modes, différents travaux scientifiques (Snyder et al., 1998; Hasanovic et al., 2002; Kerim, 2002) montrent l'intérêt d'utiliser des signaux globaux (issus de générateurs à distance) en plus des signaux locaux (issus de générateurs associés directement aux PSSs). Notre méthode pourrait être appliquée pour optimiser le choix des générateurs (à l'origine des modes interrégionaux) devant fournir les signaux globaux nécessaires aux PSSs.

Enfin, nous pourrions l'appliquer aux systèmes FACTS qui sont de plus en plus présents dans les réseaux électriques.

LISTE DE PUBLICATIONS

Notre travail de recherche a abouti aux publications suivantes. Publications de revues.

1- Abdelghani Choucha, Hasan Alkhatib, Jean Duveau, Abdelhafid Hellal, Salem Arif, « Nouvelle approche d'optimisation des stabilisateurs de puissance : algorithmes génétiques à contraintes dynamiques », article soumis en 2008 Revue Internationale de génie électrique RIGE.

2- Hasan Alkhatib, Abdelghani Choucha, Jean Duveau, Abdelhafid Hellal, Salem Arif, « Multiobjective GA to Simultaneous Coordinated Tuning PSS for Multimachine Power Systems », article soumis en 2008 Revue Elsevier (Science Direct).

3- Hasan Alkhatib, Abdelghani Choucha, Jean Duveau, Abdelhafid Hellal, Salem Arif, « Optimisation, localisation et réduction des stabilisateurs de puissance par algorithmes génétiques », article à paraître en 2009 Revue Internationale de génie électrique RIGE.

Publications de conférences internationales.

1- Hasan Alkhatib, Jean Duveau, Marcel Pasquinelli, « Power System Stabilizer Optimization Based on Adaptive Genetic Algorithms », 44^th International Univers ities Power Engineering Conference IEEE- UPE009, Glasgow, Scotland, 1-4 September 2009.

2- Hasan Alkhatib, Jean Duveau, Marcel Pasquinelli, « Genetic Algorithms Based Dynamic Search Spaces for Global Power System Stabilizer Optimization », 17^th Mediterranean Conference on Control and Automation IEEE-MED'09, (ISBN 978-1-4244-4684-1), Thessaloniki, Greece, 24-26 June 2009.

3- Hasan Alkhatib, Jean Duveau, « Effect of Machine Modelling on Power System Small Signal Stability », 17^th International Conference on Control Systems and Computer Science CSCS-17, Bucharest, Romania, 26-29 May 2009.

4- Hasan Alkhatib, Jean Duveau, Abdelghani Choucha, Abdelhafid Hellal, Salem Arif, « Optimisation Globale de la Performance des Stabilisateurs de Puissance par Algorithmes Génétiques », 5^th International Conference on Electrical Engineering CEE'2008, Batna, Algeria, 27-29 October 2008.

5- Abdelghani Choucha, Hasan Alkhatib, Jean Duveau, Abdelhafid Hellal, Salem Arif, « Multiobjective GA to Simultaneous Coordinated Tuning PSS and Location for Multimachine Power Systems », XVIII International Conference on Electrical Machines IEEE-ICEM'08, (ISBN 978-1-4244-4684-1), Vilamoura, Portugal, 6-9 September 2008.

6- Hasan Alkhatib, Abdelghani Choucha, Jean Duveau, Abdelhafid Hellal, Salem Arif, « Optimisation Simultanée Globale des Stabilisateurs de Puissance via les Algorithmes Génétiques », Conférence Internationale Francophone d'Automatique CIFA 2008, Bucarest, Roumanie, 3-5 September 2008.

7- Hasan Alkhatib, Jean Duveau, Abdelghani Choucha, Abdelhafid Hellal, Salem Arif, « Simultaneous optimization of power system stabilizer parameters, number and locations via genetic algorithms », 43^rd International Universities Power Engineering Conference IEEE-UPE008, (ISBN 978-88-89884-09-6), Padova, Italy, 1-4 September 2008.

8- Hasan Alkhatib, Abdelghani Choucha, Jean Duveau, Abdelhafid Hellal, Salem Arif, « Optimisation Simultanée des Paramètres, de Localisation et de Nombre des Stabilisateurs de Puissance par Algorithmes Génétiques », 2^nd International Conference on Electrical and Electronics Engineering, ICEEE '08, pp. 11-18, Laghouat, Algeria, 2 1-23 April 2008.

9- Abdelghani Choucha, Hasan Alkhatib, Abdelhafid Hellal, Salem Arif, « Technique d'amélioration de Réglage des Stabilisateurs de Puissance via les Algorithmes Génétiques à Contraintes Dynamiques », 2^nd International Conference on Electrical and Electronics Engineering, ICEEE'08, pp.195-200, Laghouat, Algeria, 2 1-23 April 2008.

BIBLIOGRAPHIE

1- (Abdel-Magid et al., 2003).

Abdel-Magid Y.L. and Abido M.A., « Optimal Multiobjective Design of Robust Power System Stabilizers Using Genetic Algorithms », IEEE Trans. Power System, vol. 18. n°. 3, pp. 1125-1 132, Aug. 2003.

2- (Abdel-Magid et al., 1999).

Abdel-Magid Y.L., Abido, M.A., Baiyat S. and Mantawy A.H., « Simultaneous Stabilization of Mulfimachine Power Systems Via Genetic Algorithms », IEEE Trans. on Power Systems, vol.14, n°.4, pp.1428-1439, Nov. 1999.

3- (Abe et al., 1983).

Abe S. and Doi A., « A new power system stabilizer synthesis in multimachine power systems », IEEE Trans. Power App. Syst., vol. PAS-102, pp. 3910-3918, 1983.

4- (Aboul-Ela et al., 1996).

Aboul-Ela M.E., Salam A.A., McCalley J.D. and Fouad A.A., « Damping Controller Design for Power System Oscillations Using Global Signals », IEEE Transactions on Power Systems, vol. 11, n°. 2, pp. 767-773, May 1996.

5- (Alba et al., 1999).

Alba E. and Troya J.M., « A survey of parallel distributed genetic algorithms », in Complexity, vol. 4, pp. 3 1-52, 1999

6- (Allenbach, 2005, I).

Allenbach J.M., Systèmes Asservis, Volume 1, Asservissements linéaires classiques, Ecole d'Ingénieurs de Genève, 2005.

7- (Allenbach et al., 2005, II).

Allenbach J.M. et Rotzetta A., Systèmes Asservis, Volume 3, Asservissements par variables d'état, Ecole d'Ingénieurs de Genève, 2005.

8- (Anderson et al., 2003).

Anderson P.M. and Fouad A.A., Power System Control and Stability, IEEE. Press. 2003.

9- (Andersson, 2006).

Andersson G., Modeling and analysis of Electric Power Systems, Lectures 227-526, EEH Power Systems Laboratory, ETH, Zurich, March 2006.

10- (Andersson, 2004).

Andersson G., Dynamic and Control of Electric Power Systems, Lectures 227-528, EEH Power Systems Laboratory, ETH, Zurich, March 2004.

11- (Angeline, 1995).

Angeline P.J., « Adaptive and Self-Adaptive Evolutionary Computations », in M. Palaniswami, et al. editors,, Computational Intelligence: A Dynamic Systems Perspective, pp. 152-163, IEEE Press, 1995.

12- (Angeline, 1998).

Angeline P.J., « Evolutionary Optimization versus Particle Swarm Optimization: Philosophy and Performance Differences », Proc. of the 7^th Conf. on Evolutionary Programming, vol. VII, pp. 601-610, March 1998.

13- (Arredondo, 1997).

Arredondo J.M., « Results of a study on location and tuning of power system stabilizers », Int. J. Electr. Power Energy Syst., vol. 19, pp. 563-567, 1997.

14- (Arthur R. Bergen et al., 2000). Arthur R. Bergen and Vittal V., Power System Analysis. 2^nd Edition, Prentice Hall, 2000.

15- (Aström et al., 1995).

Aström K. and Hägglund T., PID Controllers: Theory, Design, and Tuning, Instrument Society of America, 1995.

16- (Bäck, 1992).

Bäck T., « Self-adaptation in genetic algorithms », Proc. of the first European Conference on Artificial Life, Cambridge, pp. 263-271, MIT Press, 1992.

17- (Barnier et al., 1999).

Barnier N. and Brisset P., « Optimisation par algorithme génétique sous contraintes », Technique et science informatiques, vol. 18, n°. 1, pp. 1-29, 1999.

18- (Basler et al., 2005).

Basler M.J. and Schaefer, R.C., « Understanding power system stability », Proceedings of the 58th Annual Conference for Protective Relay Engineers, pp. 46-67, April 2005.

19- (Basler et al., 2002).

Basler M.J., Schaefer R.C., Kim K. and Glenn R., « Voltage Regulator with Dual PID Controllers Enhances Power System Stability », Hydro Vision Conference, U.S.A., July/Aug 2002.

20- (Bonabeau et al., 2002).

Bonabeau E., Dorigo M., and Theraulaz G., Swarm Intelligence: From Natural to Artificial Systems, Oxford Press, 1999.

21- (Bontemps, 1995).

Bontemps C., Principes Mathématiques et Utilisations des Algorithmes Génétiques, Paris, Novembre 1995. http://w3.toulouse.inra.fr/centre/esr/CV/bontemps/WP/AlgoGene.html.

22- (Bornard et al., 2005).

Bornard P., Pavard M. et Testud G., « Réseaux d'Interconnexion et de Transport :
Réglages et Stabilité », Techniques de l'Ingénieur, Traité Génie Electrique, D4-092, 2005.

23- (Bragasson, 2005).

Bragasson R.F., Damping in the Icelandic power system, Small signal stability analysis and solutions, Master Thesis, Dept. of Industrial Electrical Engineering and Automation, Lund University, 2005.

24- (Breulmann et al., 2000).

Breulmann H., Grebe E., Lösing M., Winter W., Witzmann R., Dupuis P., Houry M.P., Margotin T., Zerenyi J., Dudzik J., Machowski J., Martin L., Rodriguez J.M., Urretavizcaya E., Analysis and Damping of Inter-Area Oscillations in the UCTE/CENTREL Power System, CIGRE Session, 2000.

25- (Brogan et al., 2000).

Brogan W.L., Lee G.K.F., Sage A.P., Kuo B.C., Phillips C.L., Harbor R.D., Jacquot R.G., McInroy J.E., Atherton D.P., Bay J.S., Baumann W.T. and Chow M-Y., Control Systems, The Electric Engineering Handbook, CRC Press LLC, Boca Raton, 2000.

26- (Cai, 2004).

Cai L.J., Robust Coordinated Control of FACTS Devices in Large Power Systems, Ph.D. Thesis, University of Duisburg-Essen, February 2004.

27- (Chatelain, 1983).

Chatelain J., Traité d'électricité, Machines Electriques, Volume X, Ecole polytechnique Fédérale de Lausanne, 1983.

28- (Chipperfield et al., 1994).

Chipperfield A., Fleming P., Pohlheim H. and Fonsca C., Genetic Algorithm Toolbox User's Guide, Department of Automatic Control System Eng, University of Sheffield, UK. 1994.

29- (CIGRE, 1999).

CIGRE Task Force 38.02.17, 1999, Advanced Angle Stability Controls, A Technical Brochure for International Conference on Large High Voltage Electric Systems (CIGRE), December 1999.

30- (CIGRE, 1996).

CIGRE Task Force, 38.01.07, on Power System Oscillations, Analysis and Control of Power System Oscillations, CIGRE Technical Brochure n°. 111, December 1996.

31- (Custem, 2002, I).

Custem T.V., Systèmes électriques de Puissance I. Cours ELEC 029, Département d'Electricité, Electronique et Informatique : Institut Montefiore, Université de Liège, 2002.

32- (Custem, 2002, II).

Custem T.V., Systèmes électriques de Puissance II. Cours ELEC 047, Département d'Electricité, Electronique et Informatique : Institut Montefiore, Université de Liège, 2002.

33- (Dandeno et al., 1968).

Dandeno P.L., Karas A.N., McClymont K.R. and Watson, W. « Effect of high-speed rectifier excitation systems on generator stability limits », IEEE Trans. on Power Apparatus and Systems, vol. PAS-87, n°. 1, pp. 190-196, 1968.

34- (Deb, 1999).

Deb K., Self-adaptive Genetic Algorithms with Simulated Binary Crossover, Technical Report n°. CI-61/99, Department of Computer Science/XI, University of Dortmund, Germany, 1999.

35- (DeMello et al., 1978).

DeMello F.P., Flannett L.N. and Undrill J.M., « Practical approach to supplementary stabilizing from accelerating power », IEEE Trans., vol. PAS-97, pp, 15 15-1522, 1978.

36- (DeMello et al., 1969).

DeMello F.P. and Concordia C., « Concepts of synchronous machine stability as affected by excitation control », IEEE Trans. on PAS, vol. PAS-88, pp. 316-329, 1969.

37- (Do Bomfim et al., 2000).

Do Bomfim A.L.B., G.N. Taranto and Falcao D.M., « Simultaneous Tuning of Power System Damping Controllers Using Genetic Algorithms », IEEE Trans. On Power Systems, Vo1.15, n°.1, pp.163-169, Feb 2000.

38- (Duvigneau, 2006).

Duvigneau R., « Introduction aux méthodes sans gradient pour l'optimisation et le contrôle en Mécanique des Fluides », Projet OPALE, INRIA Sophia-Antipolis, Mars 2006, Aussois.

39- (Farmer, 2006).

Farmer R.G., Power System Dynamics and Stability, The Electric Power Engineering Handbook, 2^nd edition, CRC Press, Talyor & Francis Group, LLC, 2006.

40- (Feliachi, 1990).

Feliachi A., « Optimal Siting of Power System Stabilizers », IEE Proceedings, Pt. C, vol. 137, n°.2, pp. 101-106, March 1990.

41- (Fleming et al., 1981).

Fleming R.J., Mohan M.A. and Parvatisam K., « Selection of parameters of stabilizers in multi-machine power systems », IEEE Transactions on Power Apparatus and Systems, vol. PAS-100, pp. 2329-2333, 1981.

42- (Fouad et al., 1991).

Fouad A.A. and Vittal V., Power System Transient Stability Analysis Using the Transient Energy Function Method. Englewood Cliffs, NJ: Prentice-Hall, 1991.

43- (Gholipour Shahraki, 2003).

Gholipour Shahraki E., Apport de l'UPFC à l'amélioration de la stabilité transitoire des réseaux électriques, Thèse de doctorat, Faculté des Sciences & Techniques, Université Henri Poincaré, Nancy-I, 2003.

44- (Goldberg, 1989).

Goldberg D.E., Genetic Algorithms in Search, Optimisation and Machine Learning, Addison-Wesley, 1989.

45- (Hahn, 1967).

Hahn W., Stability of motion, Springer-Verlag, Berlin, 1967.

46- (Hasanovic et al., 2002).

Hasanovic A. and Feliachi A., « Genetic Algorithm Based Inter-area Oscillation Damping Controller Design Using MATLAB », IEEE Transactions on Power System, vol. 11, n°. 2, pp. 1136-1141, May 2002.

47- (Holland, 1975).

Holland J., Adaptation in natural and artificial systems, University of Michigan Press, 1975.

48- (Hong et al., 1999).

Hong Y.Y. and Wu W.C., « A new approach using optimization for tuning parameters of power system stabilizers », IEEE Transactions on Energy Conversion, vol. 14, n°. 3, pp. 780-786, Sept. 1999.

49- (Hongesombut et al., 2005).

Hongesombut K., Dechanupaprittha S., Mitani Y. and Ngamroo I., « Robust power system stabilizer tuning based on multiobjective design using hierarchical and parallel micro genetic algorithm », 15^th Power Systems Computation Conference: PSCC, Session 28, Paper 2, pp. 1-7 Liege, Belgium, Aug. 2005.

50- (Hongesombut et al., 2004).

Hongesombut K. and Mitani Y., « Implementation of Advanced Genetic Algorithm to Modern Power System Stabilization Control », IEEE PES, Power Systems Conference & Exposition, vol. 2, pp. 1050-1055, Oct. 2004.

51- (Hongesombut et al., 2002).

Hongesombut K., Mitani Y. and Tsuji K., « Power System Stabilizer Tuning in Multimachine Power System Based on a Minimum Phase Control Loop Method and Genetic Algorithm », 14^th Power Systems Computation Conference: PSCC, Session14, Paper 1, pp. 1-7, Sevilla, Jun. 2002.

52- (Hongesombut et al., 2001).

Hongesombut K., Mitani Y. and Tsuji K., « An Automated Approach to Optimize Power System Damping Controllers Using Hierarchical Genetic Algorithms », Proc. of Intelligent System Application to Power Systems, pp.3-8, June 2001.

53- (Hsu et al., 1987).

Hsu Y.Y. and Chen C.L., « Identification of Optimum Location for Stabilizer Applications Using Participation Factors », IEE Proc., Pt. C, vol. 134, n°. 3, pp. 23 8-244, May 1987.

54- (IEEE, 2005).

IEEE, IEEE recommended practice for excitation system models for power system stability studies, Institute of Electrical and Electronics Engineers, Inc. USA, Std.42 1.5, 2005.

55- (IEEE, 1990).

IEEE Standard 421.2-1990, IEEE Guide for Identification, Testing, and Evaluation of the Dynamic Performance of Excitation Control Systems, 1990.

56- (IEEE, 2003).

IEEE Task Force on Power System Stabilizers, « Overview of Power System Stability Concepts », IEEE Trans. On Power Systems, pp. 1762-1768, 2003.

57- (IEEE/CIGRE, 2004).

IEEE/CIGRE Joint Task Force on Stability Terms and Definitions, « Definition and Classification of Power System Stability », IEEE Trans. On Power Systems, vol. 19, n°. 2, pp. 1387-1401, May 2004.

58- (IEEE/PES, 2002).

IEEE/PES Power systems stability subcommittee special publication, Voltage Stability Assessment: Concepts, Practices and Tools, technical report, sp101pss, Aug. 2002.

59- (Jin Lu et al., 1990).

Jin Lu, Hsiao-Dong Chiang and James S. Thorp, « Identification of optimum site for power system stabilizer applications », IEEE Transactions on Power Systems, vol. 5, n°. 4, pp. 1302-1308, November 1990.

60- (Kerim, 2002).

Kerim M., Mesures synchronisées par GPS pour une meilleure stabilité des réseaux, Thèse de doctorat, Institut Nationale Polytechnique de Grenoble, 2002.

61- (Kennedy et al., 1995).

Kennedy J. and Eberhart R., « Particle Swarm Optimization », Proc of IEEE International Conference on Neural Networks (ICNN'95), vol. IV, pp.1 942-1948, Perth, 1995.

62- (Kennedy et al., 2001).

Kennedy J. and Eberhart R., Swarm Intelligence, San Francisco, Morgan Kaufmann Publishers, 2001.

63- (Khalil, 1996).

Khalil H.K., Nonlinear system, Prentice Hall, Upper Saddle River, N. J. 07458, 1996.

64- (Kundur, 1994).

Kundur P., Power System Stability and Control. The EPRI Power System Engineering Series, McGraw-Hill. Inc. 1994.

65- (Kundur et al., 1989).

Kundur P., Klein M., Rogers G.J. and Zywno M.S., « Application of Power System Stabilizers for Enhancement of Overall System Stability », IEEE Transaction on Power System, vol. 4, n°. 2, pp. 614-626. May, 1989.

66- (Kwang et al., 2008).

Kwang Y.L. and El-Sharkawi M.A., Modern Heuristic Optimization Techniques: Theory and Applications to Power Systems, IEEE Press Series on Power Engineering, 2008

67- (Larsen et al., 1981, I).

Larsen E.V. and Swann D.A., « Applying power system stabilizers part-I: General concepts », IEEE Trans. Power App. Sys., vol.100, n°. 6, pp. 3017-3024, Jun. 1981.

68- (Larsen et al., 1981, II).

Larsen E.V. and Swann D.A., « Applying power system stabilizers part-II: Performance Objectives and Tuning Concepts », IEEE Trans. Power App. Sys., vol.100, n°. 6, pp. 3025-3033, Jun. 1981.

69- (Larsen et al., 1981, III).

Larsen E.V. and Swann D.A., « Applying power system stabilizers part-III: Practical considerations », IEEE Trans. Power App. Sys., vol.100, n°. 6, pp. 3034-3046, Jun. 1981.

70- (Machowski et al., 1998).

Machowski J., Bialek J.W. and Bumby J.R., Power system dynamics and stability, West Sussex, London, John Wiley & Sons Ltd, 1998.

71- (Meyer et al., 1998).

Meyer B., Jerosolimski M. et Stubbe M., « Outils de Simulation Dynamique des Réseaux Electriques », Techniques de l'Ingénieur, Traité Génie Electrique, D4- 120, 1998.

72- (Milano, 2005).

Milano F., PSAT: Power System Analysis Toolbox, Documentation for PSAT version 1.3.4, July 2005. http://thunderbox.uwaterloo.ca/~fmilano.

73- (Miller et al., 1982).

Miller R.K. and Michel A.N., Ordinary Differential Equations. New York: Academic, 1982.

74- (Mitchell, 1996).

Mitchell M., An Introduction to Genetic Algorithms, The MIT Press, Massachusetts, 1996.

75- (Negnevitsky, 2002).

Negnevitsky M., Artificial Intelligence: A Guide to Intelligent Systems, Addison Wesley, Harlow, England, 2002.

76- (Osman et al., 1996).

Osman I.H. and Laporte G., « Metaheuristics: a bibliography », Annals of Operations Research 63, pp. 5 13-623, 1996.

77- (Ostojic, 1988).

Ostojic D.R., « Identification of optimum site for power system stabiliser applications ». IEE Proc, Pt. C, vol. 135, n°. 5, pp. 416-419, September 1988.

78- (Pagola et al., 1989).

Pagola F.L., Pérez-Arriaga I.J. and Verghese G.C., « On sensitivities, residues and participations: Applications to oscillatory stability and control », IEEE Trans. Power Sys., vol. 4, n°. 1, pp. 278-285, Feb. 1989.

79- (Pal et al., 2005).

Pal B. and Chaudhuri B., Robust Control in Power Systems, Springer Science + Business Media, Inc, 2005.

80- (Panda et al., 2007).

Panda S. and Prasad Padhy N., « Power system with PSSs and FACTS Controller: Modelling, Simulation and Simultaneous Tuning Employing Genetic Algorithm », International Journal of Electrical, Computer and Systems Engineering, vol.1, n°. 1, pp.9- 18, 2007.

81- (Parks et al., 1981).

Parks P. C. and Hahn V., Stabililtätstheorie, Springer-Verlag, Berlin, 1981.

82- (Passelergue, 1998).

Passelergue J.C., Interactions des dispositifs FACTS dans les grands réseaux électriques, Thèse de doctorat, Institut Nationale Polytechnique de Grenoble, 1998.

83- (Pérez-Arriaga, 1981).

Pérez-Arriaga I.J., Selective Modal Analysis with Applications to Electric Power Systems, Ph.D. Thesis, Electrical Engineering, Massachusetts Institute of Technology, June 1981.

84- (Pérez-Arriaga et al., 1982).

Pérez-Arriaga I.J., Verghese G.C. and Schweppe F.C., « Selective Modal Analysis with Applications to Electric Power Systems, Part I: Heuristic Introduction », IEEE Trans. Power Apparatus and Systems, vol. 101, pp. 3117-3125, Sept. 1982.

85- (Pohlheim, 2005).

Pohlheim H., GEATbx: Genetic and Evolutionary Algorithm Toolbox for use with MATLAB, Version 3.7, November 2005. www.geatbx.com/docu/index.html.

86- (Rashidi et al., 2004).

Rashidi F. and Rashidi M., « Tuning of Power System Stabilizers via Genetic Algorithm for Stabilization of Power Systems », Innovations in Applied Artificial Intelligence Ed. Springer, pp. 1210-1219, Berlin 2004.

87- (Régnier, 2003).

Régnier J., Conception de systèmes hétérogènes en génie électrique par optimisation évolutionnaire multicritère, Thèse de doctorat, Institut National Polytechnique de Toulouse, 2003.

88- (Rogers, 2000).

Rogers G., Power System Oscillations. Kluwer Academic Publishers, Norwell, Massachusetts, 2000.

89- (Roosta, 2003).

Roosta A.R., Contribution à la commande décentralisée non-linéaire des réseaux électriques, Thèse de doctorat, Institut Nationale Polytechnique de Grenoble, 2003.

90- (Sadeghzadeh, 1998).

Sadeghzadeh S.M., Amélioration de la stabilité transitoire et de l'amortissement des oscillations d'un réseau électrique à l'aide de SMES et de SSSC, Thèse de doctorat, Institut Nationale Polytechnique de Grenoble, 1998.

91- (Sadicovic et al., 2006).

Sadicovic R., Andersson G. and Korba P., « Method for Location of FACTS for Multiple Control Objectives », X SEPOPE Conference, Brazil, May. 2006.

92- (Samouhi, 1983).

Samouhi F., Application de la méthode de Lyapounov à l'étude de la stabilité dynamique de réseaux de transport d'énergie soumis à des perturbations, Thèse de doctorat, Institut Nationale Polytechnique de Grenoble, 1983.

93- (Sauer et al., 1998).

Sauer P. and Pai M., Power System Dynamics and Stability, Upper. Saddle River, NJ: Prentice-Hall, 1998.

94- (Singh, 2004).

Singh R., A Novel Approach for Tuning of Power System Stabilizer Using Genetic Algorithm, Ph.D. Thesis, Faculty of Engineering, Indian Institute of Science, Bangalore, July 2004.

95- (Slotine et al., 1991).

Slotine J.J. and Li W., Applied nonlinear control, Prentice Hall, Englewood Cliffs, New Jersey, January 1991.

96- (Snyder, 1999).

Snyder A.F., Les mesures synchronisées par GPS pour l'amortissement des oscillations de puissance dans les grands réseaux électriques interconnectés, Institut Nationale Polytechnique de Grenoble, 1999.

97- (Snyder et al., 1998).

Snyder A.F., Hadjsaid N., Georges D., Mili L., Phadke A.G., Fawon O. and Wet S., « Inter-Area Oscillation Damping with Power System Stabilizers and Synchronized Phasor Measurements », International Conference on Power System Technology. vol. 2, pp. 790-794, Aug. 1998.

98- (Tolba, 2005).

Tolba A., Commande des systèmes d'énergie de puissance par des approches heuristiques modernes, Thèse magister Département Génie Electrique,ENP, Alger, 2005.

99- (Tomassini, 1999).

Tomassini, M., « Parallel and Distributed Evolutionary Algorithms », in Evolutionary Algorithms in Engineering and Computer Science, pp 113-133, J. Wiley & Sons,1999.

100- (Tse et al., 1988).

Tse C.T. and Tso S.K., « Design optimization of power system stabilizers based on model and eigenvalue-sensitivity analysis », IEE Proc. C. Gen. Trans. & Distrib., 135, (5), pp. 406-415, 1988.

101- (Van Ness et al., 1994).

Van Ness J.E. and Dean F.D., « Interaction between subsystems of a power system », Proc. American Control Conference, Baltimore, pp. 1553-1557, June 1994.

102- (Wood, 2006).

Wood R.L., « Search space scaling in genetic algorithm-based inverse analyses », Proc. Inst. Mech. Eng., B: Journal of engineering manufacture, vol. 220, n° 5, pp. 715- 728, 2006.

103- (Xiao, 2003).

Xiao X., Dow E., Eberhart R., Ben Miled Z., and Oppelt R.J.. « Gene clustering using self-organizing maps and particle swarm optimization ». Proceedings of Second IEEE International Workshop on High Performance Computational Biology Nice, France, 2003.

104- (Yee et al., 2004).

Yee S.K. and Milanoviæ J.V., « Comparison of the optimisation and linear sequential method for tuning of multiple PSSs ». IEEE Power Engineering Society, General Meeting Denver, CO, June. 2004.

105- (Yu, 1983).

Yu Yao-Nan, Electric Power System Dynamics, Academic Press 1983.

106- (Zhang et al., 2000).

Zhang P. and Coonick, H., « Coordinated Synthesis of PSS Parameters in Multi-Machine Power Systems Using the Method of Inequalities Applied to Genetic Algorithms », IEEE Trans. on Power Systems, vol. 15, n° 2, pp. 811-816, May 2000.

107- (Zhou et al., 1991).

Zhou E.Z., Malik O.P. and Hope G.S., « Theory and Method for Selection of Power System Stabilizer Location », IEEE Transaction on Energy Conversion, vol. 6, n°. 1, pp. 170-176, 1991.

ANNEXES

Annexe A. Transformation de Park.

Afin d'établir les équations décrivant le comportement du système globale, il est nécessaire de ramener les grandeurs (décrits dans un repère local d-q) de chaque générateur à un seul repère commun pour tous les générateurs, il s'agit du repère D-Q, comme le montre la figure (1A).

L'axe réel (D) du repère commun est habituellement employé comme une référence pour mesurer l'angle de rotor de machine. Pour une machine représentée en détail comprenant la dynamique d'un ou plusieurs circuits de rotor, l'angle ä de rotor est défini par l'angle entre l'axe (q) de la machine et l'axe réel (D), comme il est montré par la figure suivante.

Pour une machine représentée par un modèle classique, l'angle de rotor ä est l'angle entre la tension E^' et l'axe réel (D), (Chatelain, 1983). En régime dynamique, l'angle ä se varie avec la vitesse de rotor.

Q

q

V

ä

á

D

ä

d

Figure 1A. Changement de référentiel du repère local (d-q) au repère commun (D-Q).

De la figure (1A), soit V un vecteur dans l'espace. Dans le repère (D-Q), il s'écrit :

V ( DQ) = Ve (1A)

já

Alors que dans le repère (d-q), il s'écrit :

V dq Ve (2A)

j ( )

á - ã

=

( )

Sachant que ã =ä- 90°, l'équation (2A) devient :

V dq Ve e (3A)

j á j ä

- - °

( 90 )

=

( )

Ainsi, le passage d'un repère à l'autre s'effectue par une simple rotation comme l'exprime l'équation suivante :

V dq V _DQ e (4A)

j ( 90 )

° -ä

( ) ( )

=

En décomposant en parties réelle et imaginaire et en regroupant sous forme matricielle, on obtient les équations décrivant le passage d'un repère à l'autre:

? -

sin cos

ä ä ?

? ?

?cos sin ä ä ?

? V ?
D

? ?

? VQ ?

? V ?

d

? ?

? V q ?

? V ?

Q

? ?

? V D ?

?sin cos
ä ä ?
? ?
? - cos sin

ä ä ?

? V ?

d

? ?

? V q ?

( ( ) )

C E S X X I

' + - ' Ä

ij qj ij qj dj qj ä j (10A)

Ä = ?

I Y

di ij

- Ä ? + ? ? Ä

Y S E Y C X X I

ij qj dj qj

( )

ij ij

qj ij

(5A)

Annexe B.

Modèle linéaire.

Appliquons la méthode de la linéarisation sur l'ensemble des équations différentielles non-linéaires, (31), (32), (33) et (34). Nous obtenons alors l'ensemble des équations suivantes :

1

Ä & = Ä ? Ä ? Ä

ù i T T D

( )

mi ei i ù i (6A)

2 H i

Ä ä i = ù ₀ Ä ù i

1

& (7A)

Ä & ' =

E ( ( ) )

T '

qi

doi

Ä ? Ä ? ? ? ? Ä

E E X X I (8A)

fdi qi di di di

1

Ä & = ? Ä ? Ä ? Ä

E ( ( ) )

K V U E (9A)

fdi ai ti Si fdi

T ai

Pour obtenir le modèle d'état, nous devons exprimer ces équations linéaires uniquement en fonction des variables d'état. Pour ce faire, nous commençons par appliquer la méthode de la linéarisation sur les deux composants du courant Ii, décrits par les équations (39) :

Ainsi pour Idi :

Ä = Ä ä + Ä + Ä

[ ] [ ][ ] [ ][ ] [ ][ ]

I P Q E M I

' (11A)

d d d q d q

Où :

P Y C E S X X I j i (12A)

dij ij ij qj ij qj dj qj

= - + - ?

[ ' ( ' ) ]

P dii P dij (13A)

= - ?

j i

?

Qdij = -Y _ij S ij (14A)

Mdij = Y _ij C _ij X qj - X dj (1 5A)

( ' )

De même, en ce qui concerne le courant Iqi, nous obtenons : (1 ( )) ( ( ) ) - ? ? Ä = ? ' - - ' Ä Y S X X I Y S E C X X I ii ii qi di qi ij ij qj ij qj dj qj ä j + Ä ? + ? ? Ä Y C E Y S X X I ij ij qj ij ij qj dj qj ( )

(16A)

Ä = Ä ä + Ä (17A)

[ ][ ] [ ][ ] [ ][ ]

L I P Q E '

q q q q q

Où :

PY S E C X X I j i (18A)

qij ij ij qj ij qj dj qj

= - - - ?

[ ' ( ' ) ]

P qii P qij (19A)

= - ?

j i

?

Q qij = Y _ij C ij (20A)

Lqii Y _ii S _ii X _qi X di j i

= 1 - ( - ' ) = (21A)

Lqij Y _ij S _ij X _qj X dj j i

= - ( - ' ) ? (22A)

Pour le calcul de tous les coefficients P, Q, L et M, les valeurs initiales de E^'qj, Iqj, äj doivent être utilisées.

En remplaçant successivement les matrices [ÄId], [ÄI_q], des équations (11A) et (1 7A), nous obtenons tous calculs faits les solutions suivantes :

[ÄId]=[Yd][ÄE ' q ]+[F_d][Ää] (23A)

[ÄI_q]=[Y_q][ÄE^'_q]+[F_q][Ää] (24A)

Où :

[Y_d]=[Q_d]+[M_d][Y_q] (25A)

[F_d]=[P_d]+[M_d][F_q] (26A)

[ ] [ ] ¹ [ ]

Y q L q - Q q

= (27A)

[ ] [ ] ¹ [ ]

F q L q - P q

= (28A)

Le Calcul des constantes K1ij...K6ij : de la linéarisation est réalisé de la façon suivante :

1. En Linéarisant l'équation du couple électrique de la i^ème machine, donnée par l'équation (35), nous obtenons :

Ä = + ? + ? Ä

T E X X I F X X I F

[( ( ) ) (( ) ) ]

' ' '

ei qi qi di di qij qi di qi dij ä _j

+ + - + - [( ( ) ) (( E X X I Y X ' ' qi qi di di qij qi	X ' di	I Y E ' ) ) ] qi dij qj Ä			(29A)
++ - + - [( ( ) ) (( ) E X X I Y X X I ' ' ' qi qi di di qii qi di qi				Y I E ' ) ] dii qi qi + Ä

Ä = Ä ä + Ä + Ä (30A)

T K K E K E

' '

ei ij j ij qj ii qi

1 2 2

Où :

K1 ij =DtFdij +Q _t F qij (31A)

K ij D _t Y _dij Q _t Y qij j i

2 = + ? (32A)

K ii D _t Y _dii Q _t Y _qii I qi j i

2 = + + = (33A)

Dt(

X qi X ' di ) I qi = - (34A)
Q t = E ' qi + (X_qi - X ' di )I di (3 5A)

En remplaçant _ÄTei tirée de l'équation (30A) dans l'équation (6A), nous obtenons: 1

Ä = ? Ä ? Ä ? Ä ? Ä + Ä

ù& ä ù

( )

K K E K E D T

' ' (36A)

i 1 2

ij j ij qj ii qi i i mi

2

²H

i

2. La tension interne linéairisée de la i^ème machine, donnée par l'équation (8A), peut être réécrite comme suit :

(1 ) ( )

+ Ä = Ä ? ? Ä

ST E E X X I

' ' ' (37A)

do i qi fdi di di di

En remplaçant _ÄIdi tirée de l'équation (23A) dans cette dernière équation et en arrangent le résultat, nous obtenons de même:

1

) (38A)

(1 ) (

' '

+ Ä = Ä ? Ä ? Ä

ST K E K E K

' ä E

doi ii qi ii fdi ij j

3 3 4 qj

K3 ij

Ä & = ? Ä ä ? Ä ? Ä + Ä

1 1 1

' '

( E E

'

E E

K ) (39A)

^qi T ' 4 ij j qj qi fdi

j

K K

doi 3 i3ii

Où :

K ij X _di X _di Y dij j i

3 [( ) ]

' -1 ?

= - (40A)

K ii X _di X _di Y dii j i

3 [1 ( ) ]

' -1

= + - = (41A)

K ij ( X _di X ' di ) F dij

4 = - (42A)

3. La linéarisation de l'équation (38) représentant la tension terminale de la i^ème machine et les équations (36), (37) constituant les composantes de cette tension nous donne :

V _ti ÄV ti = V_di Ä V_di + V _qi ÄV qi (43A)

ÄV di = XqiÄIqi (44A)

ÄV qi = ÄE qi - XdiÄIdi (45A)

En utilisant les équations (23A), (24A), pour exprimer ÄIdi, ÄIqi dans l'équation (43A), nous obtenons :

1 1 '

V X F V V X F ) ä

di qi qij ti qi di dij

? Ä

-

( )

V V X Y V V X Y V V E

- - -

1 1 ' 1 '

ti di qi qij ti qi di dij ti qi qi

? + Ä

ÄVti

(V -

ti

(46A)

ÄV ti = K _ij Ä ä _j + K _ij Ä E qj (47A)

'

5 6

Où :

K ij D v X qi F qij Q v X ' di F dij 5 = -

(48A)

K D X Y Q X Y Q (49A)

ij v qi qij v di dij v

= - ' +

6

D_v V ti - 1 V di

= (50A)

Q

v V ti - 1 V qi = (51A)
En remplaçant _ÄVti tirée de l'équation (47A) dans l'équation (9A), nous obtenons :

Ä & = - Ä ä - Ä + Ä ? Ä

1 ( )

K K K K E K U E

'

E (52A)

fdi Ai ij j ai ij qj ai Si fdi

5 6

T ai

Annexe C.

Données du réseau de New England/New York (16 générateurs et 68 noeuds).

1. Données des noeuds du réseau :

V : Amplitude de la tension du noeud (pu). á : Angle de la tension (deg).

P_g : Puissance active de génération (pu). Q_g : Puissance réactive de génération (pu). Pl : Puissance active de charge (pu).

Ql : Puissance réactive de charge (pu).

Données des noeuds du réseau
Numéro du noeud		V (pu)		á^°		Pg (pu)		Qg (pu)		Pl (pu)		Ql (pu)
01		1.000		0.00		0.000		0.00		2.527		1.1856
02		1.000		0.00		0.000		0.00		0.000		0.0000
03		1.000		0.00		0.000		0.00		3.220		0.0200
04		1.000		0.00		0.000		0.00		5.000		1.8400
05		1.000		0.00		0.000		0.00		0.000		0.0000
06		1.000		0.00		0.000		0.00		0.000		0.0000
07		1.000		0.00		0.000		0.00		2.340		0.8400
08		1.000		0.00		0.000		0.00		5.220		1.7700
09		1.000		0.00		0.000		0.00		1.040		1.2500
10		1.000		0.00		0.000		0.00		0.000		0.0000
11		1.000		0.00		0.000		0.00		0.000		0.0000
12		1.000		0.00		0.000		0.00		0.090		0.8800
13		1.000		0.00		0.000		0.00		0.000		0.0000
14		1.000		0.00		0.000		0.00		0.000		0.0000
15		1.000		0.00		0.000		0.00		3.200		1.5300
16		1.000		0.00		0.000		0.00		3.290		0.3200
17		1.000		0.00		0.000		0.00		0.000		0.0000
18		1.000		0.00		0.000		0.00		1.580		0.3000
19		1.000		0.00		0.000		0.00		0.000		0.0000
20		1.000		0.00		0.000		0.00		6.800		1.0300
21		1.000		0.00		0.000		0.00		1.740		1.1500
22		1.000		0.00		0.000		0.00		0.000		0.0000
23		1.000		0.00		0.000		0.00		1.480		0.8500
24		1.000		0.00		0.000		0.00		3.090		-0.920
25		1.000		0.00		0.000		0.00		2.240		0.4700
26		1.000		0.00		0.000		0.00		1.390		0.1700
27		1.000		0.00		0.000		0.00		2.810		0.7600
28		1.000		0.00		0.000		0.00		2.060		0.2800
29		1.000		0.00		0.000		0.00		2.840		0.2700
30		1.000		0.00		0.000		0.00		0.000		0.0000
31		1.000		0.00		0.000		0.00		0.000		0.0000
32		1.000		0.00		0.000		0.00		0.000		0.0000
33		1.000		0.00		0.000		0.00		1.120		0.0000
34		1.000		0.00		0.000		0.00		0.000		0.0000
35		1.000		0.00		0.000		0.00		0.000		0.0000
36		1.000		0.00		0.000		0.00		1.020		-0.194
37		1.000		0.00		0.000		0.00		60.00		3.0000
38		1.000		0.00		0.000		0.00		0.000		0.0000
39	1.000		0.00		0.000		0.00		2.670		0.1260
40	1.000		0.00		0.000		0.00		0.656		0.2353
41	1.000		0.00		0.000		0.00		10.00		2.5000
42	1.000		0.00		0.000		0.00		11.50		2.5000
43	1.000		0.00		0.000		0.00		0.000		0.0000
44	1.000		0.00		0.000		0.00		2.675		0.0484
45	1.000		0.00		0.000		0.00		2.080		0.2100
46	1.000		0.00		0.000		0.00		1.507		0.2850
47	1.000		0.00		0.000		0.00		2.031		0.3259
48	1.000		0.00		0.000		0.00		2.412		0.0220
49	1.000		0.00		0.000		0.00		1.640		0.2900
50	1.000		0.00		0.000		0.00		2.000		-1.470
51	1.000		0.00		0.000		0.00		4.370		-1.220
52	1.000		0.00		0.000		0.00		24.70		1.2300
53	1.045		0.00		2.500		0.00		0.000		0.0000
54	0.980		0.00		5.450		0.00		0.000		0.0000
55	0.983		0.00		6.500		0.00		0.000		0.0000
56	0.997		0.00		6.320		0.00		0.000		0.0000
57	1.011		0.00		5.052		0.00		0.000		0.0000
58	1.050		0.00		7.000		0.00		0.000		0.0000
59	1.063		0.00		5.600		0.00		0.000		0.0000
60	1.030		0.00		5.400		0.00		0.000		0.0000
61	1.025		0.00		8.000		0.00		0.000		0.0000
62	1.010		0.00		5.000		0.00		0.000		0.0000
63	1.000		0.00		10.00		0.00		0.000		0.0000
64	1.015		0.00		13.50		0.00		0.000		0.0000
65	1.011		0.00		35.91		0.00		0.000		0.0000
66	1.000		0.00		17.85		0.00		0.000		0.0000
67	1.000		0.00		10.00		0.00		0.000		0.0000
68	1.000		0.00		40.00		0.00		0.000		0.0000

Tableau 1A. Données des noeuds du réseau. 2. Données des lignes du réseau :

R : Résistance de la ligne (pu).

X : Réactance de la ligne (pu).

G : Conductance de chargement de la ligne (pu). B : Susceptance de chargement de la ligne (pu). Rap : Rapport de transformation.

Données des lignes du réseau
Du Noeud		Au Noeud		R (pu)		X (pu)		G (pu)		B (pu)		Rap
01		02		0.0070		0.0822		0.00		0.3493		0
01		30		0.0008		0.0074		0.00		0.4800		0
02		03		0.0013		0.0151		0.00		0.2572		0
02		25		0.0070		0.0086		0.00		0.1460		0
02		53		0.0000		0.0181		0.00		0.0000		1.025
03		04		0.0013		0.0213		0.00		0.2214		0
03		18		0.0011		0.0133		0.00		0.2138		0
04		05		0.0008		0.0128		0.00		0.1342		0
04		14		0.0008		0.0129		0.00		0.1382		0
05		06		0.0002		0.0026		0.00		0.0434		0
05		08		0.0008		0.0112		0.00		0.1476		0
06	07		0.0006		0.0092		0.00		0.1130		0
06	11		0.0007		0.0082		0.00		0.1389		0
06	54		0.0000		0.0250		0.00		0.0000		1.070
07	08		0.0004		0.0046		0.00		0.0780		0
08	09		0.0023		0.0363		0.00		0.3804		0
09	30		0.0019		0.0183		0.00		0.2900		0
10	11		0.0004		0.0043		0.00		0.0729		0
10	13		0.0004		0.0043		0.00		0.0729		0
10	55		0.0000		0.0200		0.00		0.0000		1.070
12	11		0.0016		0.0435		0.00		0.0000		1.060
12	13		0.0016		0.0435		0.00		0.0000		1.060
13	14		0.0009		0.0101		0.00		0.1723		0
14	15		0.0018		0.0217		0.00		0.3660		0
15	16		0.0009		0.0094		0.00		0.1710		0
16	17		0.0007		0.0089		0.00		0.1342		0
16	19		0.0016		0.0195		0.00		0.3040		0
16	21		0.0008		0.0135		0.00		0.2548		0
16	24		0.0003		0.0059		0.00		0.0680		0
17	18		0.0007		0.0082		0.00		0.1319		0
17	27		0.0013		0.0173		0.00		0.3216		0
19	20		0.0007		0.0138		0.00		0.0000		1.060
19	56		0.0007		0.0142		0.00		0.0000		1.070
20	57		0.0009		0.0180		0.00		0.0000		1.009
21	22		0.0008		0.0140		0.00		0.2565		0
22	23		0.0006		0.0096		0.00		0.1846		0
22	58		0.0000		0.0143		0.00		0.0000		1.025
23	24		0.0022		0.0350		0.00		0.3610		0
23	59		0.0005		0.0272		0.00		0.0000		0
25	26		0.0032		0.0323		0.00		0.5310		0
25	60		0.0006		0.0232		0.00		0.0000		1.025
26	27		0.0014		0.0147		0.00		0.2396		0
26	28		0.0043		0.0474		0.00		0.7802		0
26	29		0.0057		0.0625		0.00		1.0290		0
28	29		0.0014		0.0151		0.00		0.2490		0
29	61		0.0008		0.0156		0.00		0.0000		1.025
09	30		0.0019		0.0183		0.00		0.2900		0
09	36		0.0022		0.0196		0.00		0.3400		0
09	36		0.0022		0.0196		0.00		0.3400		0
36	37		0.0005		0.0045		0.00		0.3200		0
34	36		0.0033		0.0111		0.00		1.4500		0
35	34		0.0001		0.0074		0.00		0.0000		0.946
33	34		0.0011		0.0157		0.00		0.2020		0
32	33		0.0008		0.0099		0.00		0.1680		0
30	31		0.0013		0.0187		0.00		0.3330		0
30	32		0.0024		0.0288		0.00		0.4880		0
01	31		0.0016		0.0163		0.00		0.2500		0
31	38		0.0011		0.0147		0.00		0.2470		0
33	38		0.0036		0.0444		0.00		0.6930		0
38	46		0.0022		0.0284		0.00		0.4300		0
46	49		0.0018		0.0274		0.00		0.2700		0
01	47		0.0013		0.0188		0.00		1.3100		0
47	48		0.0025		0.0268		0.00		0.4000		0
47	48		0.0025		0.0268		0.00		0.4000		0
48	40		0.0020		0.0220		0.00		1.2800		0
35	45		0.0007		0.0175		0.00		1.3900		0
37	43		0.0005		0.0276		0.00		0.0000		0
43	44		0.0001		0.0011		0.00		0.0000		0
44	45		0.0025		0.0730		0.00		0.0000		0
39	44		0.0000		0.0411		0.00		0.0000		0
39		45		0.0000		0.0839		0.00		0.0000		0
45		51		0.0004		0.0105		0.00		0.7200		0
50		52		0.0012		0.0288		0.00		2.0600		0
50		51		0.0009		0.0221		0.00		1.6200		0
49		52		0.0076		0.1141		0.00		1.1600		0
52		42		0.0040		0.0600		0.00		2.2500		0
42		41		0.0040		0.0600		0.00		2.2500		0
41		40		0.0060		0.0840		0.00		3.1500		0
31		62		0.0000		0.0260		0.00		0.0000		1.040
32		63		0.0000		0.0130		0.00		0.0000		1.040
36		64		0.0000		0.0075		0.00		0.0000		1.040
37		65		0.0000		0.0033		0.00		0.0000		1.040
41		66		0.0000		0.0015		0.00		0.0000		1
42		67		0.0000		0.0015		0.00		0.0000		1
52		68		0.0000		0.0030		0.00		0.0000		1
01		27		0.0320		0.3200		0.00		0.4100		1

Tableau 2A. Données des lignes du réseau. 3. Données des générateurs :

R_a : Résistance d'armature (pu)

Xd : Réactance synchrone d'axe direct (pu).

X'd : Réactance transitoire d'axe direct (pu).

T'do : Constante de temps de la machine en circuit ouvert (s). X_q : Réactance synchrone d'axe en quadrature (pu).

H : constante d'inertie (s).

D : Coefficient d'amortissement du générateur (pu).

Données des générateurs
Numéro du noeud	Ra (pu)	Xd (pu)	X'd (pu)	T'do (s)	Xq (pu)	H (s)	D (pu)
53	0.00	1.8	0.55800	10.2	1.2420	2.3333	0.00
54	0.00	1.8	0.42529	6.56	1.7207	4.9494	0.00
55	0.00	1.8	0.38309	5.70	1.7098	4.9623	0.00
56	0.00	1.8	0.29954	5.69	1.7725	4.1629	0.00
57	0.00	1.8	0.36000	5.40	1.6909	4.7667	0.00
58	0.00	1.8	0.35433	7.30	1.7079	4.9107	0.00
59	0.00	1.8	0.29898	5.66	1.7817	4.3267	0.00
60	0.00	1.8	0.35379	6.70	1.7379	3.9150	0.00
61	0.00	1.8	0.48718	4.79	1.7521	4.0365	0.00
62	0.00	1.8	0.48675	9.37	1.2249	2.9106	0.00
63	0.00	1.8	0.25312	4.10	1.7297	2.0053	0.00
64	0.00	1.8	0.55248	7.40	1.6931	5.1791	0.00
65	0.00	1.8	0.33446	5.90	1.7392	4.0782	0.00
66	0.00	1.8	0.28500	4.10	1.7300	3.0000	0.00
67	0.00	1.8	0.28500	4.10	1.7300	3.0000	0.00
68	0.00	1.8	0.35899	7.80	1.6888	4.4500	0.00

Tableau 3A. Données des générateurs.

4. Données des systèmes d'excitation :

K_a : gain de l'AVR (pu).

T_a : constante de temps de l'AVR (s).

Efd _min : limite inférieure de la sortie de l'AVR (pu). Efd_max : limite supérieure de la sortie de l'AVR (pu).

Données des systèmes d'excitation
Numéro du générateur	Ka (pu)	Ta (s)	Efdmin (pu)	Efdmax (pu)
01	200.0	0.05	-5.0	5.0
02	200.0	0.05	-5.0	5.0
03	200.0	0.05	-5.0	5.0
04	200.0	0.05	-5.0	5.0
05	200.0	0.05	-5.0	5.0
06	200.0	0.05	-5.0	5.0
07	200.0	0.05	-5.0	5.0
08	200.0	0.05	-5.0	5.0
09	200.0	0.05	-5.0	5.0
10	200.0	0.05	-5.0	5.0
11	200.0	0.05	-5.0	5.0
12	200.0	0.05	-5.0	5.0
13	200.0	0.05	-5.0	5.0
14	200.0	0.05	-5.0	5.0
15	200.0	0.05	-5.0	5.0
16	200.0	0.05	-5.0	5.0

Tableau 4A. Données des systèmes d'excitation.

5. Données des turbines et des gouverneurs :

wref : Vitesse de référence (pu). KR : gain (pu).

Tmin : limite inférieure du couple mécanique (pu).

Tmax : limite supérieure du couple mécanique (pu).

T_s : constante de temps du régulateur (s).

T_c : constante de temps du servomécanisme (s).

T3 : constante de temps (s).

T4 : constante de temps (s).

T5 : constante de temps (s).

Données des turbines et des gouverneurs
Numéro du générateur	wref (pu)	KR (pu)	Tmin (pu)	Tmax (pu)	Ts (s)	Tc (s)	T3 (s)	T4 (s)	T5 (s)
01	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
02	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
03	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
04	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
05	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
06	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
07	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
08	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
09	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
10	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
11	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
12	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
13	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
14	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
15	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0
16	1	25.0	0.0	1.0	0.1	0.5	0.0	1.25	5.0

Tableau 5A. Données des turbines et des gouverneurs.

Annexe D.

1. Paramètres des PSSs réglés par la méthode de compensation de phase.

N° PSS	N° G.	KPSS	T1	T3
1	54	5.9975	0.1331	0.1331
2	55	6.8119	0.1118	0.1118
3	56	4.8717	0.1186	0.1186
4	57	7.6851	0.0971	0.0971
5	58	6.7587	0.1248	0.1248
6	59	6.2134	0.1099	0.1061
7	60	3.9810	0.1442	0.1442
8	61	7.1356	0.0913	0.0913
9	62	9.3381	0.1274	0.1274
10	63	4.9354	0.0913	0.0913
11	64	5.7692	0.1534	0.1534
12	65	22.9725	0.0692	0.0692
13	67	51.9431	0.0593	0.0593
14	68	19.7665	0.0677	0.0677

Tableau 6A. Paramètres des PSSs réglés par la méthode de compensation de phase.

2. Les variables des paramètres constants des PSSs : Tw,j = 10, T2,j = T4,j = 0.05 ; j = 1, ..., NPSS

Annexe E.

1. Les valeurs choisies des paramètres de l'AOEP.

Nombre de particules np	50
Nombre d'itérations itermax	250
coefficients de pondération c1 = c2	2
poids maximum wmax	0.9
poids minimum wmin	0.4

Tableau 7A. Valeurs choisies des paramètres de l'AOEP.

2. Paramètres des PSSs optimisés par la méthode d'AOEP.

N° PSS	N° G.	KPSS	T1	T3
1	54	25.4824	0.0355	0.0981
2	55	09.2126	0.0017	0.0010
3	56	40.0000	0.0933	0.0668
4	57	30.0858	0.0981	0.1000
5	58	31.8984	0.0135	0.0842
6	59	15.7518	0.0010	0.0077
7	60	00.3069	0.0328	0.0971
8	61	14.2201	0.0219	0.0010
9	62	39.8962	0.1000	0.1020
10	63	08.5534	0.0999	0.0982
11	64	38.2308	0.0878	0.0979
12	65	14.3286	0.1020	0.0015
13	67	39.9991	0.0013	0.0010
14	68	32.3618	0.0010	0.0021

Tableau 8A. Paramètres des PSSs optimisés par la méthode d'AOEP.

3. Les variables des paramètres constants des PSSs : Tw,j = 10, T2,j = T4,j = 0.02 ; j = 1, ..., NPSS