CHAPITRE 5
Présentation du logiciel
5.1 Introduction
Lors de la réalisation de cette étude, nous
avons été amenés à concevoir un logiciel dans le
but d'appliquer les méthodes de résolution au problème
posé. En effet il serait déraisonnable d'essayer de trouver une
solution au problème sans l'aide d'une machine, étant
donné la complexité du problème et la méthode
utilisée.
Avant de procéder à la présentation du
logiciel, une description de l'environnement de programmation utilisé
s'avère nécessaire; Nous notons aussi que nous avons
utilisé l'outil de programmation Delphi7.
5.2 Qu'est-ce que Delphi?
Delphi est un langage de programmation inspiré de
Pascal, fondé sur les notions d'événements et d'objets. Il
permet de créer simplement de belles interfaces graphiques tout en
disposant d'un puissant langage de programmation.
Delphi fournit tous les outils qui sont nécessaires
pour développer, tester déboguer et déployer des
applications incluant une importante bibliothèque de composants
réutilisables, un ensemble d'outils de conception, des modèles
d'application et de fiches, ainsi que des experts de programmation. Ces outils
simplifient le prototype et réduisent la durée de
développement.
L'un des principaux objectifs de son utilisation est de
permettre la construction d'un logiciel ayant le maximum de qualité : la
fiabilité, la convivialité et surtout l'efficacité, et
ceci explique notre choix pour Delphi version 7.0 pour créer notre
application.
Cette rapidité et cette simplicité de
développement sont dues à une conception visuelle de
l'application. Delphi propose un ensemble très complet de composants
visuels prêts à l'emploi incluant la quasi-totalité des
composants Windows (boutons, boîtes de dialogue, menus, barres d'outils.
. . ) ainsi que des experts permettant de créer facilement divers types
d'applications et de librairies.
5.3 Présentation du logiciel
Ce logiciel, qui a été concu par nous, en utilisant
le langage Delphi, se présente comme suit :

Un interface dans lequel on trouve respectivement :
- La commande "Sommet (cellule) ".
- La commande" Adjacence sommet (cellule) ". - La commande
"traitement ".
- Et enfin, la commande "Quiter ".
La commande "Sommet (cellule)", nous permet d'introduire tout les
sommets du graphe comme indiqué ci-aprés.
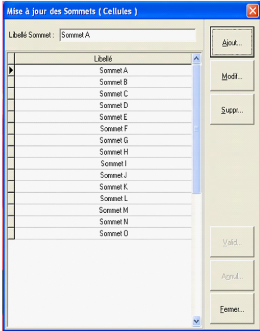
Pour introduire un sommet (cellule), il faut au préalable
appuyer sur la commande "ajouter" puis, ecrire le libellé du sommet.
Aprés, soit on valide soit on annule.
Nous avons également la possibilité de proceder
à des suppréssions ou modifications. Pour conclure, nous
utilisons la commande "fermer".
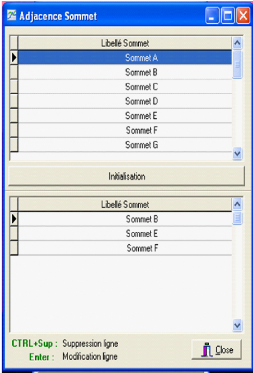
En ce qui concerne, la commande "sommets adjacent", elle nous
permet, pour chaque sommet d'introduire ses sommets adjacents, en appuyant sur
la touche "initialiser"; Par cet action, nous allons avoir tous les sommets du
graphe saisis qui apparaissent sur la fenêtre du dessous: nous
sélectionnons ainsi, les sommets adjacents correspondants en
éliminant ceux qui ne le sont pas.
En fermant cette fenêtre par la touche "fermer", nous
retournons à la page principale.
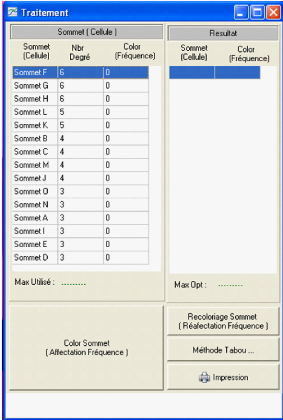
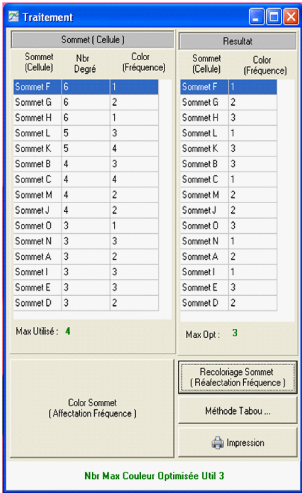
La commande "Traitement" permet d'avoir un tableau dans lequel
seront indiqués les sommets du graphes ordonnés par ordre
décroissant, leur degrés correspondant ainsi que les
colorations.
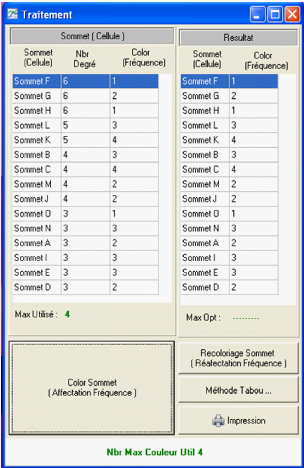
En appuyant sur la touche "color sommet (affectation de
fréquence)", on obtient la coloration associée au sommet du
graphe qui s'affiche dans la partie resultat.
Le nombre maximum de couleurs utilisées, est
indiqué en bas de la fenêtre.
La commande "Recoloriage sommet" permet de recolorer à
nouveau les sommets avec un nombre de couleurs optimisées. Le nombre
chromatique du graphe s'affiche en bas de la fenêtre.
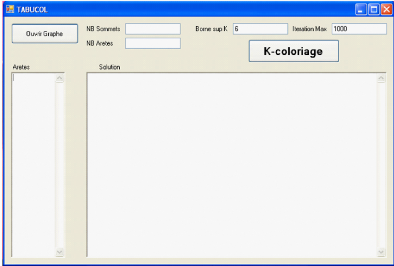
La commande "Méthode Tabou" permet de résoudre le
problème par la deuxième approche. En appuyant sur cette
commande, on aura la fenêtre ci-dessus.
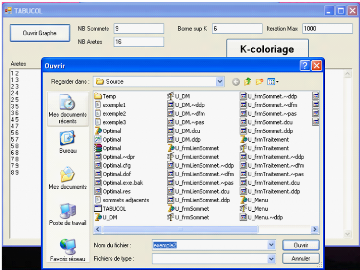
En introduisant de nouveau, le nombre de sommets, le nombre
d'arets, la borne superieure de couleur et le nombre maximum
d'itérations et on appuyant sur la touche "ouvrir graphe", on aura la
liste des sommets adjacents.
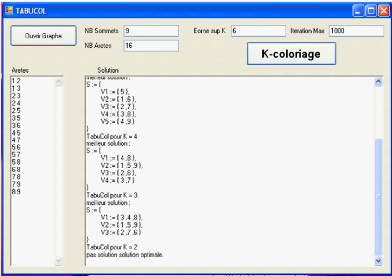
La commande "K-coloriage" permet de lancer l'algorithme et
affiche le déroulement des opérations jusqu'a aboutir à la
solutions optimale.
| 


