|
TABLE DES MATIÈRES
|
Preambule Introduction générale
1 Présentation de l'organisme d'acceuil: Algérie
Télécom
1.1 Présentation d'Algérie Télécom
1.2 Missions et objectifs d'Algérie Télécom
1.2.1 Missions
1.2.2 Objectifs
1.3 Organisation d'Algérie Télécom
1.4 Organigramme
2 Le réseau d'accés large bande Wimax
2.1 Définition et présentation du Wimax
2.2 Wimax: Evolution des standards
2.3 Apport de Wimax
2.4 Les principaux équipements du réseau
2.5 Applications des réseaux Wimax
2.5.1 La desserte avec Wimax
2.5.2 La collecte avec Wimax
2.6 Les avantages et les inconvénients du Wimax
2.6.1 Les avantages
2.6.2 Les inconvénients
2.7 Technologie autour du Wimax.
2.7.1 Quelques définitions
2.7.2 Importance du spectre de fréquence:
2.7.3 Nécessite de la gestion du spectre de
fréquence:
2.7.4 Les objectifs de la gestion du spectre
2.7.5 Les interférences
2.8 Wimax et ses concurrents
|
1
2
4
4
5
5
5
5
6
8
8
8
9
10
11
11
11
12
12
12
13
13 16 16 16 16 18
|
2.9 Conclusion 19
3 Problématique et Modélisation 20
3.1 Introduction 20
3.2 Réseaux hertziens 20
3.3 Concept cellulaire 21
3.4 Problématique 23
3.5 Modélisation du problème 23
3.5.1 Modélisation mathématique 24
3.5.2 Modélisation par la théorie des graphes
25
3.5.3 Complexité du probléme 25
3.6 Conclusion 26
4 Méthodes de résolution 27
4.1 Choix des méthodes de résolution 27
4.1.1 Les methodes exactes 27
4.1.2 Méthode exacte de coloration 28
4.1.3 Méthodes de résolution approchée
30
4.1.4 La méthode Tabou adaptée à la
coloration des graphes 30
4.2 Conclusion 35
5 Présentation du logiciel 36
5.1 Introduction 36
5.2 Qu'est-ce que Delphi ? 36
5.3 Présentation du logiciel 37
Conclusion générale 45
Bibliographie 46
Annexe 1 48
Annexe 2 50
Acronymes 54
LISTE DES FIGURES
2.1 LOS & NLOS :(Source:Wimax Forum White Paper, 2004) 10
2.2 La desserte avec Wimax 12
2.3 La collecte avec Wimax 13
LISTE DES TABLEAUX
2.1 Comparaison entre Wimax et quelques technologies 18
Preambule
Notre travail, qui s'inscrit dans la cadre de la
préparation d'un mémoire de fin d'étude pour l'obtention
du diplôme d'ingénieur en recherche opérationnelle,
Faculté de Mathématiques, Université des sciences et
technologie Houari Boumédienne, Bab ez Zouar, Alger, consiste
globalement, à implémenter un logiciel sur la planification du
spectre de fréquence sur les stations de bases en utilisant un minimum
de fréquences pour une couverture maximale.
Notre mémoire est articulé sur cinq chapitres :
· Dans le premier chapitre, nous procéderons
à la présentation de l'entreprise Algérie Telecom.
· Le second chapitre, sera consacré d'abord à
une présentation générale puis nous procéderons
à une présentataion détaillée de la technologie du
Wimax.
· Dans le troisième chapitre nous traiterons de la
problématique ainsi que sa formulation mathématique
(modélisation).
· Le quatrième chapitre sera réservé
aux méthodes de résolution.
· Enfin, le cinquième chapitre sera consacré
à l'implémentation ainsi qu'à la description
générale du logiciel informatique utilisé et des
résultats obtenus.
Introduction générale
De nos jours la demande de connexions à Internet haut
débit se fait croissante; Conjointement les accès de type ADSL se
multiplient, mais ces technologies présentent certaines limites
relatives aux débits et à la portée, et ne permettent pas
la souplesse qu'offre une connexion sans-fil.
En effet, il existe aujourd'hui de nombreuses technologies
sans fil standardisées; Chacune présente un équilibre
entre différents facteurs (portée, débit, capacité,
services, niveau d'interférences,. .etc).
Le Wimax (Worldwide Interoperability for Microwave Access)
est une alternative pour des connexions sans-fil à haut débit sur
des zones de couverture de plusieurs kilomètres, permettant des usages
en situation fixe ou en mobilité. Avec une grande couverture, une grande
efficacité spectrale et un débit important, le Wimax
représente une vraie alternative des systèmes nécessitant
des connections câblées, comme l'ADSL par exemple.
Algérie Telecom a obtenue une licence d'exploitation de
la technologie Wimax, cette dernière technologie peut convient à
cet opérateur qui souhaite offrir un accès internet haut
débit de meilleure qualité de service.
C'est dans ce contexte que s'inscrit l'objectif de notre
projet de fin d'études intitulé Gestion du spectre des
fréquences et l'implémentation dans les réseaux de
télécommunications proposé dans le cadre d'une
collaboration entre L'Université des Sciences et de la Technologie
Houari Boumediene (USTHB), d'une part et l'opérateur Algérie
Télécom d'autre part.
Le spectre radioélectrique est devenu une ressource
extrêmement précieuse, en raison de son exploitation massive par
des systèmes de communication de toutes sortes.
Il faut donc des méthodes novatrices pour gérer
le spectre de manière dynamique afin que cette ressource puisse
être disponible pour les nouveaux services à même
d'éviter les brouillages de signaux.
Le but de cette etude sera de satisfaire la demande de chaque
station de base (BTS) en terme de fréquences tout en minimisant
l'ensemble des interférences ainsi que la partie du spectre radio.
Pour cela, et à l'issu de ce travail nous proposons
l'implémentation d'un logiciel permettant la gestion du spectre de
fréquence sur les stations de bases en utilisant un minimum de
fréquences pour une couverture maximale.
CHAPITRE 1
Présentation de l'organisme d'acceuil:
Algérie
Télécom
1.1 Présentation d'Algérie
Télécom
Algérie Telecom, est une société par
actions à capitaux publics opérant sur le marché des
réseaux et services de communications électroniques.
Sa naissance a été consacrée par la loi
2000/03 du 5 août 2000, relative à la restructuration du secteur
des Postes et Télécommunications, qui sépare notamment les
activités Postales de celles des Télécommunications.
Algérie Telecom est donc régie par cette loi qui
lui confère le statut d'une entreprise publique économique sous
la forme juridique d'une société par actions SPA.
Entrée officiellement en activité à partir
du 1er janvier 2003, elle s'engage dans le monde des Technologies de
l'Information et de la Communication avec trois objectifs:
· Rentabilité
· Efficacité
· Qualité de service
Algérie Telecom est leader sur le marché
Algérien des télécommunications qui connait une forte
croissance. Offrant une gamme complète de services de voix et de
données aux clients résidentiels et professionnels.
Cette position s'est construite par une politique d'innovation
forte adaptée aux attentes des clients et orientée vers les
nouveaux usages.
Son ambition est d'avoir un niveau élevé de
performance technique, économique, et sociale pour se maintenir
durablement leader dans son domaine, dans un environnement devenu
concurrentiel.
Son souci consiste, aussi, à préserver et
développer sa dimension internationale et participer à la
promotion de la société de l'information en Algérie.
1.2 Missions et objectifs d'Algérie
Télécom
1.2.1 Missions
L'activité principale d'Algérie
Télécom est de :
· Fournir des services de télécommunication
permettant le transport et l'échange de la voix de messages
écrits, de données numériques et d'informations
audiovisuelles.
· Développer, exploiter et gérer les
réseaux publics et privés de télécommunications.
· Etablir, exploiter et gérer les interconnexions
avec tous les opérateurs des réseaux.
1.2.2 Objectifs
Algérie Telecom est engagée dans le monde des
technologies de l'information et de la communication avec les objectifs
suivants :
· Accroître l'offre de services
téléphoniques et faciliter l'accès aux services de
télécommunications au plus grand nombre d'usagers, en particulier
en zones rurales.
· Accroître la qualité de services offerts et
la gamme de prestations rendues et rendre plus compétitifs les services
de télécommunications.
· Développer un réseau national de
télécommunication fiable et connecté aux autoroutes de
l'information.
1.3 Organisation d'Algérie Télécom
Algérie Télécom est organisée en
Divisions, Directions Centrales, et Régionales, a cette structure
s'ajoutent trois filiales:
- Mobile (Mobilis)
- Internet (Djaweb)
- Télécommunications Spatiales (RevSat)
Algérie Telecom s'implique dans le développement
socio-économique du pays à travers la fourniture des services de
télécommunications.
En outre, Algérie Télécom met en oeuvre des
moyens importants pour rattacher les localités isolées et les
établissements scolaires.
Le Marketing et l'action commerciale pour réhabiliter
l'image de marque d'Algérie Telecom et fidéliser sa
clientèle, notamment par la mise en place du système informatique
« GAIA » qui permet :
· Le client aura un guichet unique au niveau de l'ACTEL,
qui saisit la demande du client, ses coordonnées, l'adresse, etc.
· La suppression de l'échange de papier entre les
services techniques du CECLI et l'Actel "gestion zéro papier" .
· Permettre aux clients de consulter leurs factures
à travers l'Internet.
· Recrutement et formation.
· Partenariat Dans le cadre du partenariat,
Algérie Télécom pourra profiter aussi bien du savoir faire
que de capitaux. S'agissant de diversification d'activités, la branche
des services d'Algérie Télécom, contrairement à
celle des infrastructures sera largement ouverte à la concurrence
à travers des partenariats susceptibles d'engendrer
l'épanouissement de l'investissement pour obtenir des niveaux de
rentabilité élevés avec des retours rapides sur
investissements.
· Introduction massive des nouvelles technologies.
1.4 Organigramme
L'organigramme d'Algérie Télécom se
présente comme suit :
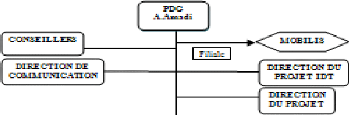
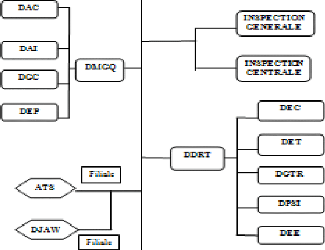

Organigramme d'Algérie Télécom
CHAPITRE 2
Le réseau d'accés large bande Wimax
2.1 Définition et présentation du Wimax
Le Wimax ou Worldwide Interoperability for Microwave Access,
est une norme technique développée par le consortium Wimax Forum.
Celle ci basée sur le standard de transmission radio 802.16,
validé en 2001 par l'organisme international de normalisation IEEE. En
effet, le Wimax ressemble au Wifi mais avec des performances nettement
supérieures en de nombreux points.
Plusieurs standards relèvent du terme Wimax : les plus
avancés concernent les usages en situation fixe (le client ne bouge
pas), mais une version mobile (connexion à haut débit en
situation de mobilité) est entrain de voir le jour et qui à pour
objectif d'étendre Wimax à des machines terminales mobiles,
impliquant donc la possibilité de réaliser des connexions xDSL
sans fil vers des mobiles.
2.2 Wimax: Evolution des standards
Le tableau ci-aprés montre que la technologie Wimax
réunit plusieurs standards, tous à des états d'avancement
différents, qui sont autant d'axes de travail du groupe IEEE 802.16.
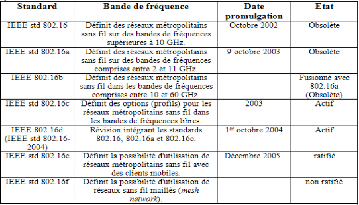
Les différentes normes 802.165: (source :IEEE Standard
for Local and metropolitan area
networks,2004).
Les révisions du standard IEEE 802.16 se déclinent
en deux catégories :
Wimax fixe/résidentiel (802.16-2004): destiné
à un usage fixe, du domicile à l'antenne relais et opérant
dans des bandes de fréquences de 2.5 GHz et 3.5 GHz (avec licence
d'exploitation obligatoire) et 5.8 GHz (bande libre). Le débit maximum
théorique est de 75 Mbit/s pour une portée de 50 à 70
kilomètres sans obstacles.
Wimax mobile/nomade (802.16 e) : prévoit la
possibilité de connecter des clients mobiles au réseau Internet.
Le Wimax mobile ouvre ainsi la voie à la téléphonie mobile
sur IP ou plus largement à des services mobiles hauts débit. Le
débit maximum théorique est de 30 Mbit/s pour une portée
de 2 à 4 kilomètres sans obstacles.
La portée, les débits et surtout la
nécessité ou non d'être en ligne de vue de l'antenne
émettrice, dépendent de la bande de fréquence
utilisée. Dans la bande 11-66 GHz, les connexions se font en ligne de
vue: LOS (Line Of Sight), alors que sur la partie 2-11 GHz, le NLOS (Non Line
Of Sight) est possible notamment grâce à l'utilisation de la
modulation OFDM. Ceci ouvre la voie à des terminaux d'intérieur,
facilement installables par l'utilisateur final car ne nécessitant pas
l'installation d'antennes extérieures par un technicien
agréé.
Actuellement les standards Wimax actifs ou en cours de
normalisation, sont limités aux fréquences entre 2 et 11 GHz.
Selon les pays, les bandes Wimax sont soit libres soit soumises à une
licence.
2.3 Apport de Wimax
L'objectif du Wimax est de fournir une connexion Internet
à haut débit sur une zone de couverture de plusieurs
kilomètres de rayon. Le standard Wimax possède l'avantage de
permettre une connexion sans fil entre une station de base et des milliers
d'abonnés sans nécessiter de ligne visuelle directe (en anglais
Line Of Sight, parfois abrégée LOS) ou NLOS (pour Non Line Of
Sight). Dans la réalité le Wimax ne permet de franchir que de
petits obstacles tels que des
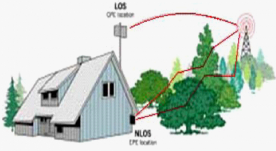
Figure 2.1: LOS & NLOS :(Source:Wimax Forum White Paper,
2004).
arbres ou une maison mais ne peut en aucun cas traverser les
collines ou les immeubles. Le débit réel lors de la
présence d'obstacles ne pourra ainsi excéder 20 Mbit/s.
Le déploiement du Wimax permet à des zones
isolées, mal desservies par le DSL ou le câble ou souhaitant tirer
profit d'une connexion sans fil, de disposer d'un accès Internet large
bande. Le développement du Wimax pourrait donc jouer un rôle
important dans l'aménagement numérique du territoire.
Le débit et la portée présentent les
atouts du Wimax. Il fonctionne à 70 Mbit/s maximum théoriquement
dans des conditions extrêmement favorables, 12 Mbits/s pratiquement et
peut couvrir des zones de rayon allant jusqu'à 50 Km.
2.4 Les principaux équipements du réseau
Depuis le coeur du réseau et en descendant vers
l'utilisateur, on trouve les éléments suivants :
· Une liaison à très haut débit, par
exemple par fibre optique ou faisceau hertzien, alimentant l'émetteur
Wimax.
· Station de base BTS physiquement, elles sont
constituées d'une antenne et d'un matériel radio contenant le
dispositif électronique. Placées à une hauteur de 12
à 50 m, les antennes utilisent en général des supports
tels que (château d'eau, toit d'immeuble, pylône.. . etc.).
· Entre l'antenne et l'utilisateur, plusieurs
kilomètres de transmission sans fil. Le Wimax peut assurer une
transmission sans ligne de vue (c'est-à-dire même lorsque des
obstacles tels que des arbres se trouvent entre l'émetteur et le
récepteur), mais cela, a généralement pour effet de
réduire notablement la portée.
· Chez l'abonné, une antenne Wimax assure la liaison
entre l'émetteur de la zone et l'équipement connecté
(ordinateur ou autre).
· Le débit maximum est de quelques dizaines de
Mbits/s, mais il est partagé entre tous les utilisateurs
raccordés à une même station. Par ailleurs, le débit
dépend de quelques facteurs, tels que la distance entre l'usager et la
station, ou la topographie des lieux.

Figure 2.2: Antenne Wimax
2.5 Applications des réseaux Wimax
2.5.1 La desserte avec Wimax
Le but de la desserte est de relier le client final à un
réseau donné afin qu'il puisse accéder à
Internet.
Pour cela, le client doit posséder un récepteur
Wimax (une puce intégrée ou un CPE : Customer Premise Equipement)
et se trouver dans le champ d'action d'un émetteur. La transmission
entre le client et son hot spot Wimax est dite en "non ligne de vue" (NLOS),
c'est-à-dire que le client ne se trouve pas en vue directe avec
l'antenne. En effet, les bâtiments ou la végétation que
l'on trouve dans les villes "forcent" le signal à être
détourné grâce à l'utilisation de la modulation de
fréquence OFDM.
2.5.2 La collecte avec Wimax
Dans un réseau, la collecte consiste à relier
les points d'accès (hot spots Wifi ou DSLAM) assurant ainsi la connexion
avec Internet. On appelle ce mécanisme le backhauling de hots spots.
Contrairement à la desserte, la collecte se fait en "ligne de vue"
(LOS), grâce à des émetteurs Wimax placés
suffisamment haut.
L'avantage du Wimax réside dans sa simplicité
de mise en oeuvre. Il ne faudra que deux antennes pour relier deux
réseaux distants, là où il aurait fallu des
kilomètres de fibre optique en filaire.
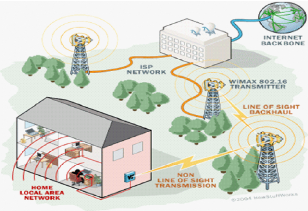
Figure 2.2: La desserte avec Wimax
2.6 Les avantages et les inconvénients du Wimax
Les avantges et les inconvénients du wimax peuvent se
résumer comme suit :
2.6.1 Les avantages
· La possibilité de réutilisation d'une
fréquence dédiée à une BTS pour augmenter la
capacité du système, ainsi le système peut supporter des
centaines d'utilisateurs.
· L'allocation de fréquences se fait de façon
sectorielle quand le nombre d'utilisateurs augmente.
· Cout faible, le Wimax permet un déploiment plus
rapide sans nécessité de gros travail de génie civile.
· Permet de conectivités internet sans fil à
haut débits sur de longues distances.
· Peut servir plusieurs clients à la fois.
· Un signale malgré les obstacles.
· Perspective de nomadisme.
2.6.2 Les inconvénients
· Pour avoir des distances et des débits optimaux,
l'émetteur et le récepteur doivent être en « ligne de
vue». Hors « ligne de vue », les débits chutent
rapidement.
· Le débit est partagé entre les usagers
d'une même antenne centrale.
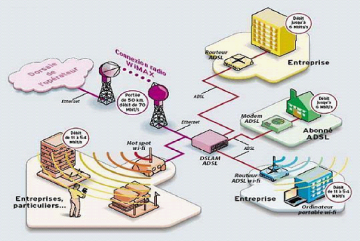
Figure 2.3: La collecte avec Wimax
· Nécessité de déservir les stations
de base Wimax par un reseau de collecte (fibre optique, faisceau
hertzien....).
· Nécessité de disposer d'une licence : seuls
les détenteurs d'une licence sont à même de déployer
des reseaux Wimax; Le nombre de licences délivrées est
limité.
· Nécessité de disposer d'un point haut :
afin d'assurer la meilleure couverture possible, l'emetteur doit étre
placé sur un point haut (pylône, chateau d'eau,etc.).
2.7 Technologie autour du Wimax.
Les technologies hertziennes sont prometteuses pour tous les
pays qui cherchent à assurer un accés aux technologies de
l'information et de la communication et à mettre en place la
societé de l'information; Le spectre de fréquence en est un
composant essentiel.
Afin de mieux cerner la problématique, il est necessaire
de procéder au préalable à certaines défintions.
2.7.1 Quelques définitions
-Fréquence:
En physique, la fréquence désigne en
général la mesure du nombre de fois qu'un phénomène
périodique se reproduit par unité de temps; C'est-à-dire
le nombre de fois qu'un phénomène temporel régulier se
reproduit identique à lui-même par intervalle de temps
donné.
L'unité de fréquence étant l'hertz (hz),
les fréquences sont exprimées:
· En kilohertz (Khz), jusqu'à 3 000 Khz inclus;
· En mégahertz (Mhz), au-delà de 3 Mhz,
jusqu'à 3 000 Mhz inclus;
· En gigahertz (Ghz), au-delà de 3 Ghz
jusqu'à 3 000 Ghz inclus.
-Bande de fréquence:
Les bandes de fréquences sont l'ensemble des
fréquences comprises dans un intervalle donné :
· Les basses fréquences sont comprises entre 30 et
300 Khz.
· Les hautes fréquences sont comprises entre 3 et 30
Mhz.
-Ondes radioélectriques ou ondes hertziennes:
Ondes électromagnétiques dont la fréquence
est inférieure à 3000 Ghz, se propagent dans l'espace sans guide
artificiel.
-Spectre de fréquence:
Le spectre de fréquence est la partie du spectre
électromagnétique qui achemine les ondes radio; Il est
subdivisé en neuf bandes de fréquences, désignées
par des nombres entiers consécutifs conformément au tableau
ci-aprés.
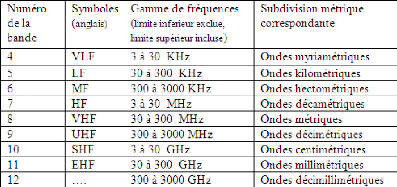
Tableau 2.2: Les différents types de bande de
fréquences.
Les bandes allouées par la ARPT pour le déploiment
du réseau Wimax se situent entre: 3.4 à 3.6 Ghz.
Il est à noter que l 'Autorité de
Régulation de la Poste et des Télécommunications (ARPT)a
été créée dans le cadre de la libéralisation
des marchés postal et des télécommunications. Leur
ouverture à la concurrence et à la promotion de la participation
de l'investissement privé dans ces marchés, ont été
consacrés par la loi n°2000-03 du 5 août 2000
fixant les règles générales relatives à la poste et
aux télécommunications.
Parmi les missions principales de l'ARPT dans le domaine des
fréquences radioélectriques, elle est chargée de
planifier, gérer, assigner et contrôler l'utilisation des
fréquences dans les bandes qui lui sont attribuées dans le
respect du principe de non discrimination;
Il en est de même en ce qui concerne l'Agenge Nationale
des fréquences ANF;
C'est un établissement public national à
caractère industriel et commercial doté de la personnalité
morale et de l'autonomie financière.
L'ANF est régie par les règles administratives
dans ces relations avec l'état et par les règles commerciales
dans ses relations avec les tiers.
Elle est chargée :
· de mener des études en vue d'une utilisation
optimale du spectre des fréquences radioélectriques.
· de la planification, la gestion et le contrôle de
l'utilisation des fréquences radioélectriques.
· d'élaborer le règlement national des
radiocommunications et de fixer les règles nationales et les
procédures relatives à la répartition des bandes de
fréquences.
· d'attribuer les bandes de fréquences.
· de préparer les éléments
nécessaires à la définition des positions et des actions
de l'Algérie
dans les négociations internationales dans le
domain des fréquences radioélectriques.
· d'assurer la coordination de l'utilisation des
fréquences dans les zones frontalières.
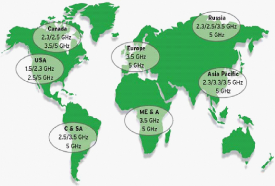
Figure 2.6: Répartition des bandes de fréquences
Wimax dans le monde (source: Wimax
Forum White Paper, 2006)
2.7.2 Importance du spectre de fréquence:
La demande de la ressource spectrale a nettement
augmenté en Algérie au cours de la
dernière
décennie, notamment dans les bandes de
fréquences affectées aux communications hertziennes
(liaisons
hyperfréquences, téléphonie cellulaire, accès
hertzien fixe, accès hertzien sans fil, etc.)
Le spectre des fréquences est l'épine dorsale
d'une large gamme d'activités dans des secteurs tels que les
télécommunications, la radiodiffusion, les transports, la
recherche et le développement.
Avec le developpement de ces technologies et leurs
implications dans la croissance économique du pays et leur
rareté, leur impotance dans notre vie de tous les jours et de plus en
plus grandissante; Il est donc nécessaire de prévoir une gestion
rationellle de cette ressource.
2.7.3 Nécessite de la gestion du spectre de
fréquence:
La croissance continue de la demande de spectre, aussi bien
pour les services existants que pour les nouveaux services radio, exerce des
contraintes de plus en plus fortes sur cette ressource notamment en ce qui
concerne l'équilibre entre l'offre et la demande ; Cette ressource doit
être gérée d'une manière efficace et efficiente afin
que l'on puisse en retirer un maximum d'avantages sur les plans
économiques et socials. Plus le spectre radioélectrique est
encombré, plus il est difficile à gérer, et plus l'outil
nécessaire pour bien le gérer doit être performant. Il faut
donc des méthodes novatrices pour le gérer de manière
dynamique afin qu'elle puisse être disponible pour les nouveaux services.
Sa gestion permet également d'éviter les brouillages de signaux
(interférences).
2.7.4 Les objectifs de la gestion du spectre
· Garantir une plus grande facilité d'utilisation du
spectre.
· Rationaliser l'usage du spectre, même dans un
environnement où la fréquence n'est pas encore une ressource
rare.
· Garantir la disponibilité des
fréquences.
· Répondre au besoin de développement des
télécommunications et des radiocommunications nationales.
· Répondre aux besoins de la sécurité
et de la défense nationale.
· Contrôler l'utilisation (conformité) du
spectre.
La non gestion rationelle du spectre de fréquence
entraine automatiquement une mauvaise qualité du signal par la
création d'interférences.
2.7.5 Les interférences
On parle d'interférence lorsqu'un point donné
de l'espace de couverture reçoit en plus du signal utile (assurant le
service) un signal dit interférent de puissance relativement
élevée et porté sur une fréquence identique ou
adjacente.
Il existe deux grands types d'interférences: celles
qui sont dues a la réutilisation d'une même fréquence
(interférence Co-canal) et celles qui sont dues à l'utilisation
de fréquences adjacentes (interférence canal adjacent).
Interférences Co-canal
Ce sont des interférences induites par des signaux
émis sur la même porteuse. Ceci se produit quand un point de la
zone de couverture reçoit plusieurs signaux provenant de
différents BTS et émis sur la même fréquence.

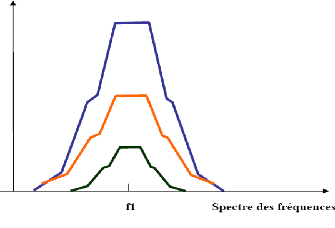
Interférence Co-canal
Interférences canal-adjacent
Les signaux émis sur des fréquences adjacentes
entrainent des interférences non négligeables.
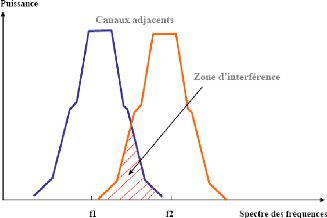
Interférence canal-adjacent
2.8 Wimax et ses concurrents
Les différentes technologies d'accès à
la donnée sans fil offrent des débits différents sur des
zones de couvertures différentes. Chaque technologie devrait pouvoir
trouver sa place, son usage et sa cible. Le Wimax permettra à partir de
stations de base Wimax d'aroser des aglomérations dans des zones rurales
à faible pénétration voire des pays ou l'infrastructure de
communications est souvent moins développée (notamment des pays
en voie de développement) n'ayant pas d'accès a l'Internet haut
débit. Le Wimax serait alors une alternative au câble classique
d'Internet haut débit qui reste un moyen d'accès couteux en
termes d'investissement.
Le Wimax pourrait venir en complément du WiFi pour
couvrir des zones plus larges, rendant ainsi possible la concentration des hots
spots WiFi et donc la création de hot-zones.
L'utilisateur se connecterait toujours en WiFi (identification
et facturation) et le Wimax viendrait renforcer la connexion en termes de
capacité, de débit, et de couverture.
Technologie
|
WiFi
|
Wimax
|
3G/UMTS
|
EGE
|
Débit
|
11 Mbits/s
|
75 Mbits/s
|
384 Kbits/s
|
115 Kbits/s
|
Couverture
|
Local/Immeuble
|
Petite ville
|
Agglomération
|
Agglomération
|
|
Tableau 2.1: Comparaison entre Wimax et quelques
technologies
2.9 Conclusion
Etant une technologie d'accès radio sans fil, le Wimax
offre un ensemble d'avantage comme le débit élevé, le
faible coût ou encore la large portée par rapport aux autres
réseaux sans fil. Toutes ces caractéristiques lui permettent de
réaliser un succès pertinent et des demandes en croissance
continues depuis son apparition. S'il y a un domaine où le Wimax
excelle, c'est surtout dans sa capacité de diffusion sur une zone de
territoire très large (portée d'une dizaine de kilomètres
en zones rurales). Cette caractéristique répond clairement au
besoin des zones trop éloignées qui ne peuvent être
raccordées au réseau fixe DSL. Un déploiement massif de
cette technologie pourrait révolutionner le haut débit.
Grâce à des connexions sans-fil à haut débit sur des
zones de couverture très large, le Wimax permet des usages en situation
fixe, ou même mobile. De plus, les enjeux économiques de cette
technologie sont très importants. En effet, en termes de coût, la
mise en place de ce réseau serait bien moins couteuse que le
déploiement d'une infrastructure filaire. Effectivement, alors que les
technologies DSL doivent intégrer des réamplifacteurs de signaux
tous les 5 à 10 Km, une station de base peut relier à un
réseau, des clients distants de 40 Km (diamétralement
opposés). De plus, le fait que les standards sont normalisés, le
coût des équipements devrait chuter assez rapidement.
CHAPITRE 3
Problématique et Modélisation
3.1 Introduction
Depuis les années 80, le probléme d'affectation
de fréquences a fait l'objet d'études menées par
différents chercheurs dans le but d'une meilleurs gestion. Le spectre de
fréquences qui est attribué aux opérateurs de
téléphonie est divisé en canaux fréquentiels.
L'allocation de fréquences regroupe les mécanismes et
procédures mis en oeuvre afin de gérer l'attribution des canaux
de fréquences aux demandes de communication. Cette gestion permet de
déterminer la qualité du réseau.
L'objet de ce chapitre sera de poser la problématique
de l'affectation de fréquences et la traduire en théorie des
graphes; Ceci nous permettra d'une part de proposer des solutions à
même de résoudre cette problématique et d'autre part, de
présenter quelques définitions de base qui nous permettrons de
mieux comprendre la problématique posée.
3.2 Réseaux hertziens
L'objectif d'un système de radio hertziens tel que le
Wimax est de permettre l'accès au réseau à partir d'un
terminal portatif sur une zone géographique plus ou moins vaste. Cet
accès est réalisé grâce à une liaison
hertzienne. Pour que la qualité des communications soit satisfaisante,
la puissance de réception doit être assez élevée,
rendant nécessaire la bonne distribution d'un ensemble de stations de
base sur le territoire à couvrir. Chaque station de base couvre une
partie du territoire appelée cellule.
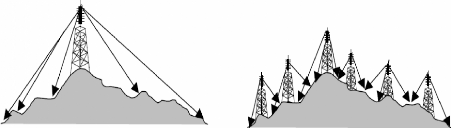
Utilisation de plusieurs antennes à faible puissance au
lieu d'une antenne puissante
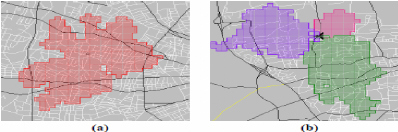
Les deux schémas de configuration d'un site:(a) site
muni d'une seule antenne
omnidirectionnelle, (b) site muni de trois antennes
sectorielles.
Les stations de base composant le réseau sont
regroupées en emplacements géographiques appelés sites.
Selon le type d'antennes utilisées, un site peut contenir une ou
plusieurs BTS. Plus précisément, une seule antenne
omnidirectionnelle, ou plusieurs antennes sectorielles. Les schémas
ci-dessus représentent les deux configuration possible de site.
Le schéma (a) représente un site muni d'une
seule antenne omnidirectionnelle, le schéma(b) montre un site à
trois antennes sectorielles. Dans le réseau Wimax, il est usuel de
limiter le nombre d'antennes séctorielles sur un site à trois.
3.3 Concept cellulaire
Une cellule représente l'ensemble des points du
territoire couvert par une même station (BTS).Chaque station de base peut
posséder plusieurs antennes donnant ainsi naissance à plusieurs
cellules (appelées secteurs dans ce cas), généralement
trois. Des stations de base mono-sectorielles, couvrant la zone à
360°, sont utilisées dans les zones trés peu
peuplées et dans les centres villes pour créer des microcellules.
Des stations de base bi-sectorielles, donnant naissance à deux cellules
de 180° chacune, sont souvent mises en place aux abords des
autoroutes.
Les stations de base tri - sectorielles sont les plus
répandues et les plus utilisée pour le réseau Wimax; elles
génèrent trois cellules de 120°.
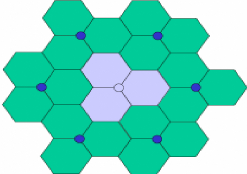
Modèle du concept cellulaire
La forme hexagonale à été
universellement adoptée comme représentation théorique du
design cellulaire [Mac Donald,1979]. En effet l'hexagone désigne la
forme géométrique la plus proche du cercle (propagation des ondes
radio dans un espace sans obstacles) qui permet un pavage régulier du
plan en utilisant le moins de cellules. De plus il garantit une
uniformité des distances entre les émetteurs, la
régularité des schémas d'antennes et de la propagation des
ondes radio en espace libre. La réalité, cependant,
s'écarte de cette vue théorique. La non régularité
des reliefs géographiques (montagnes, plateaux...) et architecturaux
(bâtiments, maisons...) fait que la propagation des ondes ne s'effectue
pas de la même façon dans toutes les directions. De ce fait, des
prolongements, des rétractions voir même des discontinuités
importantes apparaissent dans la couverture des cellules.
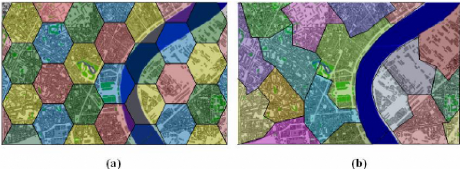
Concept cellulaire: (a) couverture théorique, (b)
couverture réelle.
Le concept cellulaire constitue le fondement de base des
réseaux hertziens. Premièrement, l'utilisation du concept
cellulaire permet l'ajustement des ressources radio à la demande en
trafic. Cet ajustement est réalisé en densifiant les zones
à forte demande en communications.
Le principe de densification se traduit par des zones
urbaines à forte concentration de BTS couvrant de petites cellules et
des zones rurales à faible concentration de BTS couvrant des cellules de
grande taille.
La réutilisation des ressources radio
(fréquences) dans les réseaux hertziens constitue le
deuxième intérêt du concept cellulaire. En effet
l'opérateur est restreint à un nombre limité de
fréquences pour couvrir l'ensemble du réseau, ce qui rend
nécessaire la réutilisation du spectre radio mainte fois de
façon à prévenir les situations d'interférences
entre les ondes radio. En conséquence de la réutilisation des
fréquences, le réseau est capable d'écouler un nombre de
trafic beaucoup plus grand que le nombre de fréquences disponibles.
3.4 Problématique
Aujourd'hui les operateurs radio doivent faire face à
un double défit: répondre à une augmentation croissante du
trafic tout en maintenant une bonne qualité radio. La difficulté
du problème résulte du fait qu'une solution acceptable doit
satisfaire des contraintes multiples, la plupart des fois contradictoires.
L'une des contraintes les plus sévères c'est le
nombre restreint de fréquences (canaux) disponibles pour l'allocation
(le spectre radio étant une ressource très limitée). Cette
contrainte impose un degré élevé de réutilisation
des fréquences, fait qui augmente la probabilité
d'interférence.
Algérie Télécom dispose d'un nombre
limité de fréquences pour couvrir la totalité d'un
térritoire. Pour celà, la réutilisation des
fréquences est par conséquent inévitable pour augmenter la
capacité du réseau et répondre à la demande de plus
en plus importante. Une disrtibution optimale du spectre de fréquences
disponibles sur les stations doit garantir un écoulement maximal du
trafic tout en minimisant les interférences. L'écoulement de
trafic porté par ces zones est alors conditionné par la
qualité de l'affectation des fréquences.
Afin de satisfaire cette demande, il est indispensable
d'exploiter cette ressource d'une manière rationnelle et optimale; Il
est donc légitime de s'interesser à une modelisation plus fine de
la problématique de planification de fréquences. Un tel projet
nécessite l'utilisation de méthodes scientifiques basées
sur des téchniques de recherche operationnelle.
Notre zone d'étude concernera la Wilaya d'Alger avec 8
kmcomme taille de la cellule.
3.5 Modélisation du problème
Comme mentionné dans le chapitre precédent, les
gestionnaires sont souvent confrontés à de multiples
problèmes et leur résolution s'avère souvent une
tâche difficile. Ces problèmes se présentent sous forme de
données, de contraintes dont on doit en tenir compte.
Pour arriver à résoudre un problème
donné, nous devons commencer par interpréter tous ses
paramètres et les transformer sous des formes qu'on peut gérer.
La première étape dans
la résolution d'un problème consiste en sa
projection dans un espace permettant ainsi diverses manipulations sur le
problème projeté. Ce dernier s'appelle le modèle
associé au problème.
La modélisation est donc une traduction des
paramètres du problème dans un langage accessible par la
méthode de résolution utilisée, ou bien c'est une
façon de décrire le problème sous une forme qui introduit
sa réalisation.
Enfin, la modélisation d'un problème doit pouvoir
donner une interprétation aux solutions concrètes
répondant aux besoins du problème réellement
posé.
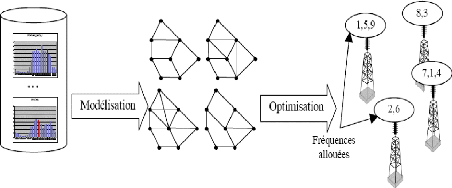
Les différentes étapes de la
modélisation.
3.5.1 Modélisation mathématique
Les données du problème
N : nombre de stations.
NF: nombre de fréquences disponibles.
C [j]: nombre de cellules à considérer.
R[j]: pour chaque station i, nous connaissons le nombre de
fréquence requis.
Contrainte:
- Respecter la contrainte d'interférence Co - canal,
ie: éviter d'assigner la même fréquence
à deux cellules voisines.
Objectifs :
Trouver un bon plan de fréquence qui doit minimiser
l'ensemble des interférences ainsi que la partie du spectre radio.
3.5.2 Modélisation par la théorie des
graphes
Le probléme d'affectation de fréquences est un
probléme de la classe du coloriage de graphe (Graph Coloring
Problem).
Soit un graphe G = (X, E) defini par:
X: L'ensemble des sommets du graphe représentent les
transmetteurs (TRX).
E: L'ensemble des arêtes du graphe représentent les
risques d'interférences,
Il existe une arête [xi, xj] de E ssi xi est voisin avec x
(voir figure ci-dessous).
Pour résoudre le probléme d'affectation de
fréquences, on utilise la coloration des sommets qui consiste à
affecter à tous les sommets du graphe une couleur (fréquence) de
façon que chaque paire de sommets soit de couleurs differentes; En
d'autre termes, s'il existe une arête [xi, xj] de E alors on a c(i) =6
c(j).
Le nombre minimum de couleurs nécessaires pour colorier
ce graphe en respectant cette contrainte, est appelé le nombre
chromatique XG.
L'application de la théorie des graphes va nous permettre
de trouver le nombre minimal de fréquences allouées aux stations
de bases et qui minimise l'intégralité des
interférences.
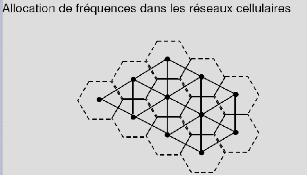
Allocation des fréquences dans les réseaux
cellulaires
3.5.3 Complexité du probléme
Le probléme de la détermination du nombre
chromatique XG est difficile. Plus précisément, déterminer
si un graphe donné à une k-coloration pour un k > 2
fixé est NP-complet .
Notre graphe doit être colorié avec au moins 3
couleurs (la taille de la clique max est égale à w(G) = 3), donc,
il est NP-dure.
Afin de déterminer le nombre chromatique d'un graphe,
un algorithme exact peut être appliqué si la taille du graphe
n'est pas trop grande. Sinon, on se contente d'estimer le nombre chromatique,
en utilisant par exemple un algorithme heuristique telque la Recherche Tabou
qui ne donnera qu'une borne supérieure mais qui est bien plus rapide
qu'un algorithme exact.
3.6 Conclusion
Dans ce chapitre nous avons mis en exergue les
difficultés de la gestion des fréquences, posé la
problématique avec les principaux objectifs assignés à
notre étude et par la même nous avons procédé
à sa modélisation.
Dans le chapitre suivant nous traiterons des méthodes de
résolutions de cette problématique.
CHAPITRE 4
Méthodes de résolution
4.1 Choix des méthodes de résolution
L'optimisation combinatoire occupe une place trés
importante en Recherche Operationnelle, en mathématiques
discrètes et en informatique. Son importance se justifie d'une part par
la grande difficulté des problémes d'optimisation et d'autre part
par de nombreuses application pratiques pouvant être formulées
sous la forme d'un probléme d'optimisation combinatoire. Bien que les
problèmes d'optimisation combinatoire soient souvent faciles à
définir, ils sont généralement difficiles à
résoudre. En effet, la plupart de ces problèmes appartiennent
à la classe des problémes NP-difficiles et ne possédent
donc pas à ce jour de solution algorithmique efficace valable pour
toutes les données.
Pour la résolution des problèmes, en recherche
opérationnelle, le choix de la méthode de résolution
constitue une étape cruciale. Il existe deux grandes familles de
méthodes de résolution. D'un coté, les méthodes
exactes (complétes) qui garantissent la complétude de la
résolution, de l'autre les méthodes approchées
heuristiques métaheuristiques (incomplétes) qui perdent en
complétude pour gagner en efficacité.
La principale différence entre ces deux familles
réside dans le fait que la qualité des résultats
donnés par les heuristiques n'est pas garantie par la théorie.
Les méthodes exactes soutenues par la théorie, aboutissent aux
solutions optimales du problème. En pratique, les méthodes
exactes sont sensiblement liées à la taille du problème et
leur utilisation est sanctionnée par des temps d'exécution
souvent inacceptables. Tandis que les heuristiques et métaheuristiques
montrent qu'elles peuvent aboutir à des résultats très
satisfaisants en des temps beaucoup plus raisonnables.
4.1.1 Les methodes exactes
On peut définir une méthode exacte comme une
méthode qui garantit l'obtention de la solution optimale pour un
problème d'optimisation. L'utilisation de ces méthodes
s'avèrent particulièrement intéressante, mais elles sont
souvent limitées au cas des problèmes de petite taille.
4.1.2 Méthode exacte de coloration
Le seul moyen connu pour déterminer le nombre
chromatique d'un graphe G est de faire une énumération
(implicite) de toutes les colorations de G. On commence en
général par considérer une borne supèrieure q de
XG.
Une méthode standard d'une telle
énumération consiste à considérer un ordre de
sommets V1, ,Vn. Soit q la plus petite valeure pour laquelle il
existe une q - coloration lors du processus d'énumération.
Comme nous savons que le nombre chromatique XG est inferieur
ou égale a N (nombre max de couleur), nous posons initialement q est
égale a N, puis nous colorons successivement les sommets V1, ,V
n avec la plus petite couleure possible. Si une couleur inferieure
à q est affectée à chaque sommet, alors une coloration en
q1 < q couleurs à été obtenue.
Nous posons q = q1, et nous effectuons marche arrière
jusqu'au sommet Vj tel que Vj+1 soit le premier sommet coloré avec la
couleur q1. Nous tentons d'attribuer à Vj la plus petite couleur
possible, supérieure à la couleur courante et inferieure à
q. Si une telle couleur est trouvée, alors nous procédons comme
auparavant en colorant itérativement les sommets Vj+1
à Vn.
Si à une certaine étape, la plus petite couleur
pour un certain sommet V, est égale a q, alors nous effectuons une
marche arrière jusqu'au sommet Vp_1 et nous poursuivons le
processus comme précédemment.
L'algorithme se termine lorsque nous devons faire marche
arrière à partir du sommet V1.
[// {On a: w(G) XG max dG , pour notre cas, la taille de la
clique max est égale à trois d'ou: w(G) = 3,et le deg max du
graphe est égale à: 6, donc on en déduit que: 3 XG
6.//}.
Cette méthode peut se résumé comme suit
:
Etapel:
L'étape une est basée sur l'algorithme
séquentiel suivant:
· Poser q égale au nombre maximum de couleur N.
· Pour chaque sommet d'un graphe G, déterminer les
degrés, puis classer les sommets dans l'ordre décroissant de
leurs degrés.
· Parcourir la liste des sommets du graphe (i := 1 a n)
, en attribuant à chaque sommet xi la plus petite couleur possible,
c'est-à-dire la plus petite couleur qui n'est pas utilisée par x
adjacent à xi, pour tout j <i.
· Si la couleur q n'a pas été
utilisée, nous avons obtenu une coloration en q1 <q couleurs, et
remplaçons q par q1(q := q1).
Etape 2:
· Faire marche arrière (en décolorant les
sommets) jusqu'au sommet xr tel que xr+1 ait
été le premier sommet à avoir la couleur q.
· Nous recolorons xr avec la plus petite couleur
possible qui soit plus grande que sa couleur courante.
· Recolorier à nouveau les sommets xr, .
. . , x avec l'algorithme séquentiel.
· Si à un moment donné la couleur q doit
être affectée à un sommet x5 (ce que nous
voulons éviter, puisque nous voudrions utiliser moins de q couleurs),
nous remontons dans l'algorithme séquentiel jusqu'au sommet
x5_1 et faisons comme précédemment (c'est-à-
dire recolorer x5_1 avec la plus petite couleur possible qui soit
plus grande que sa couleur courante et continuer).
· L'algorithme se termine lorsque l'on est remonté
jusqu'à x1, et XG est égal à la valeur courante de q.
Exemple illustratif
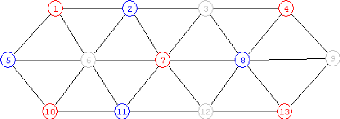
Figure 4.1 :Exemple illustratif
Sommets
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
Sommets triés
|
6
|
7
|
8
|
2
|
3
|
11
|
12
|
1
|
4
|
5
|
9
|
10
|
13
|
Couleurs attribuées
|
C1
|
|
C1
|
C3
|
C4
|
C3
|
C4
|
|
|
C3
|
C3
|
|
|
Couleurs optimisées
|
C1
|
|
C3
|
C3
|
C1
|
C3
|
C1
|
|
|
C3
|
C1
|
|
|
|
D'ou le nombre chromatique est X(G) := 3. Avec : C1:= Couluer
grise.
:= Couluer rouge.
C3:= Couluer bleu.
4.1.3 Méthodes de résolution
approchée
Bien que de nombreux problèmes de la vie pratique
puissent être modélisés sous la formes d'une recherche du
nombre chromatique dans un graphe, ce dernier n'a souvent aucune des structures
idéales pour lesquelles on peut appliquer des algorithmes polynomiaux.
Toutes fois, lorsque la taille du problème est assez petite, il est
possible d'utiliser des methodes exactes qui permettent d'obtenir une solution
optimale en des temps raisonnables. Pour des graphes de trés grande
taille, on doit par contre faire appel à des heuristiques.
Depuis la formulation du problème de la
détermination du nombre chromatique dans un graphe, de nombreaux
chercheurs ont continuellement proposé de nouvelles heuristiques de
coloration. Nous pouvons classer l'ensemble de ces methodes en
différentes catégories.
Beaucoup d'heuristiques de coloration de graphes ont
été développées parallement à une
études théorique: la recherche d'algorithmes exactes pour
certaines classes des graphes a parfois fourni des algorithmes performant pour
des graphes quelconques. L'algorithme exacte de coloration décrit en
haut est ainsi non seulement, connu pour son comportement polynomial et exact,
mais il est en plus, considéré comme une heuristique offrant un
bon compromis entre la qualité de solution et le temps de calcul.
Nous nous intéressons également à une
deuxième catégorie d'heuristiques. Des chercheurs ont
developpé des méthodes génerales qui permettent de
résoudre de nombreux problémes d'optimisation combinatoire,
moyennant quelques définitions propres à chaque probléme.
C'est le cas des méthodes génitiques, du récuit
simulé ou de la technique Tabou, dont nous allons traiter l'adaptation
de la recherche tabou au probléme de la coloration de graphes.
4.1.4 La méthode Tabou adaptée à la
coloration des graphes
La technique Tabou est une méthode
générale d'optimisation combinatoire qui a été
introduite par Glover dans un cadre particulier et développée
plus tard dans un contexte plus générale. Indépendament,
Hansen a developpé la méthode de SAMD (del'anglais Steepest
Ascent Mildest Descent) qui se base sur des idées similaires. La
technique Tabou s'est déja montrée trés performante pour
un nombre considérable de probléme d'optimisation
combinatoire.
En ce qui concerne notre cas, nous donnerons tout d'abord une
description générale de la méthode Tabou, puis nous
présenterons l'adaptation de cette technique au probléme de la
coloration baptisé TABUCOL par M Dominique de Werra (Werra,1993).
La technique Tabou
Le probléme d'optimisation combinatoire qui nous
intéresse est le suivant : étant un ensemble X de solutions
admissibles et une fonction f définie sur X, il s'agit de
déterminer une solution s* 2 X minimisant f sur X.
Definissons un voisinage N(s) pour toute solution s 2 X; Nous
utiliserons une technique qui consiste à se déplacer de solution
s en solution voisine s' 2 N(s) ,tout en essayant de minimiser la
fonction f.
De nombreuses heuristiques ont été
développées dans ce même contexte; la plus connue
étant certainement la méthode de descante: tant qu'il existe une
solution s'voisine de la solution courante s et telle que
f(s') < f(s). ,on se déplace de s vers s' qui
devient ainsi la nouvelle solution courante. Cette méthode de descente
s'arrête donc au premier minimum local rencontré. Le principal
inconvénient de cette technique provient alors du fait que la valeur de
cet optimum local peut être largement supérieur à celle
d'un optimum globale.
Pour cette raison, de nombreuse heuristiques ont
été étudiées afin d'éviter le piége
que représentent ces minima locaux. Ainsi, par exemple, la methode du
R~ecuit Simul~e est conçue de telle maniére
qu'il est relativement aisé de sortir d'un optimum locale tant que la
température (un paramétre) est assez élevée. Cette
température dimine lentement au cours de l'algorithme et lorsqu'elle
atteint une valeur assez basse. On se trouve finalement bloqué dans un
optimum qu'on espére globale mais qui sera probablement bien meilleur
que le premier optimum local rencontré.
Une telle méthode présente un certain nombre
d'inconvéniants dont le plus important découle de la manipulation
délicate du paramètre qu'est la température : Il est non
seulement difficile de donner une valeur initiale à cette
température, mais de plus sa décroissance doit être
réglée de maniére à donner assez de temps à
l'algorithme pour atteindre un optimum globale sans lui en faire perdre trop
à des températures élevées car on risque alors de
visiter un trop grand nombre de solutions largement moins bonnes que cet
optimum global.
Une toute autre méthode générale
d'optimisation combinatoire a été proposée par Glover: il
s'agit de la technique Tabou que nous noterons TS (de l'anglais Tabu Search).
L'une des idées principales constituant cette méthode consiste
à choisir à chaque déplacement la meilleure solution
voisine s' de la solution courante s.
Tant que l'on ne se trouve pas dans un optimum local, TS se
comporte donc comme la méthode de descente et améliore à
chaque étape la valeur de la fonction objectif. Lorsque l'on atteint pa
r contre un optimum, TS choisit le moins mauvais des voisins, c'est-a-dire
celui qui donne un accroissement aussi faible que possible à la fonction
objectif.
L'inconvénient que présenterait une
méthode basée sur cet unique principe serait que si un minimum
local s se trouve au fond d'une vallée profonde, il serait impossible de
ressortir de celle-ci en une seule itération, et un déplacement
de la solution s vers une solution s' 2 N'(s) avec
f(s') > f(s) pourrait provoquer, à l'itération
suivante, le déplacement inverse puisque s 2 N(s') et
f(s') <f(s); on risquerait donc de cycler autour de ce minimum
local.
C'est pour cette raison que TS s'appuie sur un
deuxiéme principe qui consiste à garder en mémoire les
dernières solutions visitées et à interdire un retour vers
celles-ci pour un nombre fixé d'itérations. Le but étant
de donner assez de temps à l'algorithme pour lui permettre de sortir de
toute vallée contenant un minimum local. En d'autres termes, TS conserve
à chaque étape une liste T de solutions "taboues", vers
lesquelles il est interdit de se déplacer momentanément.
'
Lors du choix de la meilleure solution sE N(s), il est
possible que l'on ait à départager plusieurs candidats donnant
certes, une même valeur à la fonction objectif, mais ne nous
dirigeons pas tous vers un optimum global. Il est ainsi parfois souhaitable de
pouvoir retrourner
vers une solution visitée s, malgré le fait
qu'elle fasse parite de la liste T des solutions taboues, ceci afin d'explorer
une nouvelle région voisine de s.
Pour cette raison , TS fait intervenir un nouvel
ingrédient appelé fonction d'aspiration et définie sur
toutes les valeurs de la fonction objectif: lorsqu'une solution s'
voisine de la solution s fait parite de T et satisfait de plus notre aspiration
{c'est-à-dire f(s') A(f(s))} ,on lève le
'
statut tabou de cette solution set elle devient donc candidate
lors de la sélection du meilleur voisin de s.
Il nous faut encore définir une condition d'arrêt.
On se donne en général un nombre maximum d'itérations
entre deux améliorations de la meilleure solution s*
rencontrée.
Dans certains cas, il est possible de déterminer une
borne inférieure f* de la fonction objectif et on peut alors
stopper la recherche lorsqu'on a atteint une solution s de valeur f(s) proche
de f*.
L'algorithme Tabou peut être décrit par
l'algorithme suivant :
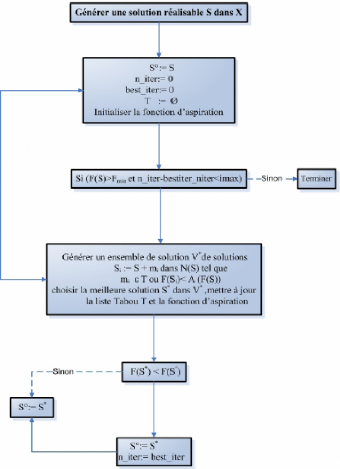
Organigramme de la méthode de recherche tabou
Tabou adaptée à la coloration de graphe
Nous allons adapter TS à la déremination d'une
k - col oration dans un graphe G pour un nombre de couleurs k fixé.
L'algorithme ainsi obtenu sera l'ingrédient principal de la méta-
heuristique suivante :
k := borne superieure du nombre chromatique XG d'un graphe G;
tant que TABUCOL est capable de déterminer une (k -- 1)--coloration dans
G faire
k := k -- 1;
On peut représenter une coloration d'un graphe comme
une partition de ses sommets en ensembles stables. l'objectif de TABUCOL
consiste donc à construire une partition des sommets d'un graphe G = (V,
E) en un ensemble k fixé d'ensembles indépendants. Nous avons
défini l'espace X des solutions comme étant l'ensemble des
partition (V1 , ...., Vn) de V en k sous ensembles non forcément
stables.
La fonction objectif f comptabilise le nombre d'arêtes
ayant leurs deux extrémités dans une même partie Vi. En
d'autres termes f = Eki= 11E(Vi)1 .et cherchons à la
minimiser.
Ainsi f(s = (V 1, ....., Vn)) = 0 ssi S est une k --
coloration de G. Nous pouvons donc fixé f = 0 et arrêter la
recherche si l'on visite une solution s telle que f (s) = 0.
Une soloution s' = (V,1 ,
..., V,n) est considérée comme voisine
d'une solution s = (V1, ....., Vn) si on peut l'obtenir à partir de s en
ne déplaçant qu'un seul sommet x d'un sous ensemble Vi à
un sous ensemble Vj .Ainsi :
Vi, = Vi / {x} ; Vi, = Vi U {x} ;
Vr, = Vr pour tout r = 1......k r =6 i, j;
Il serait peu réaliste de considérer une liste
T de solutions taboues. En effet, elle demanderait trop de place en
mémoire et nous perdrions trop de temps à tester si une solution
de V# fait parite de T. Nous avons donc décidé de ne
mémoriser qu'une information moins complète. Lorsqu'un sommet x
se déplace d'un ensemble Vi à un ensemble Vj, le
couple (x, i) devient tabou, ce qui signifie que le sommet x n'est pas
autorisé à revenir dans l'ensemble Vi pour un nombre 1T1
d'itérations. La taille 1T1 = 7 s'est expérimentalement
avérée satisfaisante.
Il est parfois souhaitable de lever un tel statut tabou,
surtout lorsque le retour de x dans Vi donne une solution s n'ayant encore
jamais été visitée et de petite valeur f(s). Nous avons
définit la fonction d'aspiration comme étant égale
à la valeur f (s*) de la meilleure solution s*
rencontrée. Considérons donc une solution s, de
V* obtenue à partir de la solution courante s en
déplaçant un sommet x dans une partie Vi, et suposons que (x, i)
E T; si f (s,) < f (s*), Nous levons le statut tabou
de s' qui devient ainsi candidat pour le choix de la meilleure
solution dans V*.
Le principal critère d'arrêt de la
méthode Tabou est la découverte d'une solution s avec f (s) = 0,
c'est-à-dire d'une k -- coloration. On peut alors diminuer la valeur de
k d'une unité et appliquer à nouveau la méthode Tabou,
afin de tenter d'obtenir une meilleure borne supérieure sur le nombre
chromatique. Mais ce critère d'arrêt ne permet pas d'assurer que
l'algorithme s'arrête; en particulier si k < XG, il n'est pas
suffisant. Il faut donc introduire un ou plusieurs autres critères
d'arrêt pour interrompre la recherche. Les plus fréquents sont
:
· un nombre fixé d'itérations à
été effectué.
· il n'y a plus eu d'amélioration de s*
depuis un nombre fixé d'itérations.
· le temps de calcul a atteint une limite fixée.
Nous obtenons ainsi la méthode Tabou pour le
problème de la k - coloration décrit ci- dessous. Notons qu'afin
d'accélerer un peu l'aglorithme, la génération de M
peut
être interrompue dés que S avec f(s')
< f(s) a été trouvé.
Algorithme Tabou; begin
choisir une solution initiales ;
S*:=S;T=ø;
while aucun critère d'arrêt n'est satisfait do
générer M avec M solutions S = (X1, ..., X,) E
N(s)
telles que x E= X pour toute paire (x, i) dans T
ou f(s) <f(s*) ;
- dés qu'un S avec f(s') <f(s) est
trouvé
- arrêter la génération
S := meilleure solution dans M;
mettre 'a jour T ;
if f(s) < f(s*) then S* := S ;
end while;
end algorithme:
4.2 Conclusion
Dans ce chapitre, deux méthodes de résolutions
ont été présentées; l'une dite exacte et l'autre
appellé méthode Tabou. Ces deux méthodes seront
utilisées pour résoudre notre problématique. A l'issue
nous pourrons déterminer les avantages et les inconvéniants de
chacune d'elles.
CHAPITRE 5
Présentation du logiciel
5.1 Introduction
Lors de la réalisation de cette étude, nous
avons été amenés à concevoir un logiciel dans le
but d'appliquer les méthodes de résolution au problème
posé. En effet il serait déraisonnable d'essayer de trouver une
solution au problème sans l'aide d'une machine, étant
donné la complexité du problème et la méthode
utilisée.
Avant de procéder à la présentation du
logiciel, une description de l'environnement de programmation utilisé
s'avère nécessaire; Nous notons aussi que nous avons
utilisé l'outil de programmation Delphi7.
5.2 Qu'est-ce que Delphi?
Delphi est un langage de programmation inspiré de
Pascal, fondé sur les notions d'événements et d'objets. Il
permet de créer simplement de belles interfaces graphiques tout en
disposant d'un puissant langage de programmation.
Delphi fournit tous les outils qui sont nécessaires
pour développer, tester déboguer et déployer des
applications incluant une importante bibliothèque de composants
réutilisables, un ensemble d'outils de conception, des modèles
d'application et de fiches, ainsi que des experts de programmation. Ces outils
simplifient le prototype et réduisent la durée de
développement.
L'un des principaux objectifs de son utilisation est de
permettre la construction d'un logiciel ayant le maximum de qualité : la
fiabilité, la convivialité et surtout l'efficacité, et
ceci explique notre choix pour Delphi version 7.0 pour créer notre
application.
Cette rapidité et cette simplicité de
développement sont dues à une conception visuelle de
l'application. Delphi propose un ensemble très complet de composants
visuels prêts à l'emploi incluant la quasi-totalité des
composants Windows (boutons, boîtes de dialogue, menus, barres d'outils.
. . ) ainsi que des experts permettant de créer facilement divers types
d'applications et de librairies.
5.3 Présentation du logiciel
Ce logiciel, qui a été concu par nous, en utilisant
le langage Delphi, se présente comme suit :

Un interface dans lequel on trouve respectivement :
- La commande "Sommet (cellule) ".
- La commande" Adjacence sommet (cellule) ". - La commande
"traitement ".
- Et enfin, la commande "Quiter ".
La commande "Sommet (cellule)", nous permet d'introduire tout les
sommets du graphe comme indiqué ci-aprés.
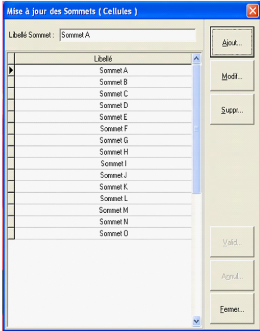
Pour introduire un sommet (cellule), il faut au préalable
appuyer sur la commande "ajouter" puis, ecrire le libellé du sommet.
Aprés, soit on valide soit on annule.
Nous avons également la possibilité de proceder
à des suppréssions ou modifications. Pour conclure, nous
utilisons la commande "fermer".
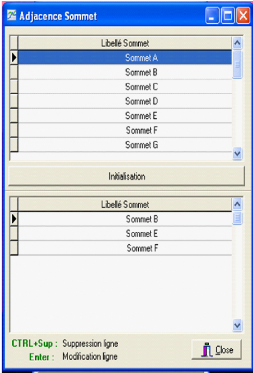
En ce qui concerne, la commande "sommets adjacent", elle nous
permet, pour chaque sommet d'introduire ses sommets adjacents, en appuyant sur
la touche "initialiser"; Par cet action, nous allons avoir tous les sommets du
graphe saisis qui apparaissent sur la fenêtre du dessous: nous
sélectionnons ainsi, les sommets adjacents correspondants en
éliminant ceux qui ne le sont pas.
En fermant cette fenêtre par la touche "fermer", nous
retournons à la page principale.
La commande "Traitement" permet d'avoir un tableau dans lequel
seront indiqués les sommets du graphes ordonnés par ordre
décroissant, leur degrés correspondant ainsi que les
colorations.
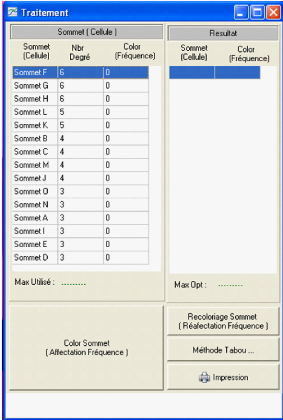
En appuyant sur la touche "color sommet (affectation de
fréquence)", on obtient la coloration associée au sommet du
graphe qui s'affiche dans la partie resultat.
Le nombre maximum de couleurs utilisées, est
indiqué en bas de la fenêtre.
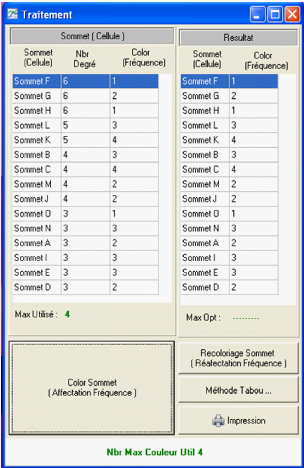
La commande "Recoloriage sommet" permet de recolorer à
nouveau les sommets avec un nombre de couleurs optimisées. Le nombre
chromatique du graphe s'affiche en bas de la fenêtre.
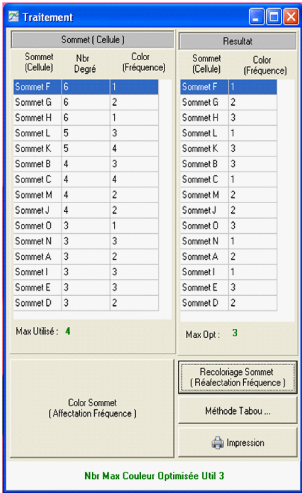
La commande "Méthode Tabou" permet de résoudre le
problème par la deuxième approche. En appuyant sur cette
commande, on aura la fenêtre ci-dessus.
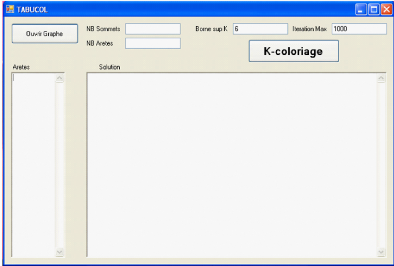
En introduisant de nouveau, le nombre de sommets, le nombre
d'arets, la borne superieure de couleur et le nombre maximum
d'itérations et on appuyant sur la touche "ouvrir graphe", on aura la
liste des sommets adjacents.
La commande "K-coloriage" permet de lancer l'algorithme et
affiche le déroulement des opérations jusqu'a aboutir à la
solutions optimale.
Conclusion générale
Pour une gestion rationnelle du spectre de fréquence
par des méthodes propre à la recherche opérationnelle,
nous avons étudié procédé à son étude
en utilisant deux approches :une méthode exacte et la méthode
Tabou.
Après avoir optimisé les paramètres de
chaque méthode de recherche, nous avons testé les deux
méthodes selon les mêmes contraintes à notre modèle
de réseau pour la recherche d'un plan de gestion de fréquence.
Un logiciel adapté a ces méthodes, a
été conçu à cet effet.
Les résultats obtenus ont été très
satisfaisants notamment celles obtenues par la méthode dite Méta
Heuristiques.
Si actuellement, Algérie Télécom arrive
uniquement à utilisé 6 fréquences, la méthode
proposée et testée peut allé jusqu'à 3
fréquences.
A l'issue de ce travail, avec cette expérience acquise
en contact des techniciens d'Algérie Télécom, nous pensons
que celui-ci sera d'un apport certain pour l'amélioration de la gestion
du spectre de fréquence en Algérie.
Notre veux est que ce travail puisse être améliorer
afin qu'il soit concrétisé par les services concernés.
Bibliographie
A. Caminada" Résolution du problème de
l'affectation des fréquences par programmation par contraintes" Rapport
technique, CNET, Belfort, 1995.
A. Akrout "Problèmes d'Affectation de Fréquences:
Méthodes Basées sur le Recuit Simulé Rapport technique,
CNET, Paris; 1994
C. Berge, Graphes, Gauthier-Villars, Paris ; 1983.
D. de Werra et Y. Gay, Chromatic scheduling and frequency
assignment, Discrete Applied Mathematics; 1994.
D. de Werra et A. Hertz, Consecutive colorings of graphs,
Zeischrift fur Operations Research 32, 1988, 1-8.
D. de Werra et D. Kobler, Coloration et ordonnencement
chromatique, ORWP 00/04, Ecole Polytechnique Fédérale de
Lausanne; 2000.
De Werra D., Hertz A. -Tabu Search Techniques: A tutorial and an
application to neural networks - OR Spektrum, 1989, pp. 131-141.
D. Brélaz "New Methods to Color Vertices of Graph"
Communications of ACM, N°22,1979, pp 251-256.
F. Glover et M. Laguna, Tabu Search. Kluwer Academic Publ;
1997.
J. Hao, R. Dorne, P. Galinier "Tabu Search for Frequency
Assignment in Mobile Radio Networks" Journal of heuristics, N°
4, 1998, pp 47-62.
Intel Technical White Paper, « Understanding Wimaw and 3G
for Portable/Mobile Broadband Wireless », 2004.
IEEE Std 802.16-2004, "IEEE Standard for Local and metropolitan
area networks Part 16: Air Interface for Fixed Broadband Wireless Access
Systems", 2004.
M.G. Garey et D.S. Johnson, The complexity of near-optimal graph
coloring. J. ACM 23,1976, 43-49.
N. Dubois et D. de Werra, EPCOT : An Efficient Procedure for
Coloring Optimally with Tabu Search. Comput. Math. Appl. 25,1993, 35-45.
N. Alon et M. Tarsi, Colorings and orientations of graphs.
Combinatorica 12 (1992) 125-
134.
P. Hansen, A. Hertz et J. Kuplinsky, Bounded Vertex Colorings of
Graphs. Discrete Math. 111,1993, 305-312.
R. Borndorfer, A. Eisenblatter, M. Grotschel, A. Martin
"Frequency Assignment in Cellular Phone Networks" ZIB-Repport 97-35,1997.
R. Dorne, J. Hao "Tabu Search for Graph Coloring, T-coloring
and Set T-coloring" Metaheuristics: advances and trends in local search
paradigms for optimization, 1998, (Chapitre 6, Kluwer academic publishers, pp
77-92.)
R. Dorne "Etude des Méthodes Heuristiques pour la
Coloration, la T-Coloration et l'Affectation de Fréquences" Thèse
de doctorat, Université de Montpellier II, 1998.
Hertz A., de Werra D. -Using Tabu Search Techniques for Graph
Coloring - Computing 39, 1987, pp. 345-351.
Joham Dréo, Alain Pétrowski, Patrick Siarry, Eric
Taillard, « Métaheuristiques pour l'optimisation difficile »,
Edition EYROLLES, France, Juillet 2003.
Hakim Mabed, « Modèles et techniques d'optimisation
dynamique pour les réseaux radiomobiles » : Thèse de
doctorat, Ecole doctorale d'Angers, 2003.
Hakim Mabed, « Optimisation dynamique: Application au
fréquençage », Séminaire du laboratoire systeme et
transpore (SeT), 2004.
V. H. Mac Donald "Advanced Mobile Phone Service: The cellular
Concept" The Bell System Technical Journal, 1979, pp 15-41.
Wimax Forum White Paper, "Wimax End-to-End Network Systems
Architecture", 2006.
Wimax Forum White Paper: "Wimax's technology for LOS and NLOS
environments",
2004.
Wimax Forum White Paper, "Wimax End-to-End Network Systems
Architecture", 2006.
Annexe 1
Solution donnée par l'Algorithme exacte de coloration
|
N° de la cellule
|
Antenne principale
|
Fréquence attribuée
|
|
Cellule 1
|
A
|
La 2~eme fréquence
|
|
Cellule 2
|
C
|
La 3~eme fréquence
|
|
Cellule 3
|
C
|
La 1~erefréquence
|
|
Cellule 4
|
P
|
La 2~eme fréquence
|
|
Cellule 5
|
A
|
La 3~eme fréquence
|
|
Cellule 6
|
A
|
La 1~erefréquence
|
|
Cellule 7
|
D
|
La 2~eme fréquence
|
|
Cellule 8
|
G
|
La 3~eme fréquence
|
|
Cellule 9
|
P
|
La 3~eme fréquence
|
|
Cellule 10
|
Q
|
La 1~erefréquence
|
|
Cellule 11
|
R
|
La 2~eme fréquence
|
|
Cellule 12
|
B
|
La 1~erefréquence
|
|
Cellule 13
|
E
|
La 2~eme fréquence
|
|
Cellule 14
|
D
|
La 3~eme fréquence
|
|
Cellule 15
|
G
|
La 1~eme fréquence
|
|
Cellule 16
|
K
|
La 2~erefréquence
|
|
Cellule 17
|
M
|
La 3~eme fréquence
|
|
Cellule 18
|
M
|
La 1~erefréquence
|
|
Cellule 19
|
Q
|
La 2~eme fréquence
|
|
Cellule 20
|
Q
|
La 3~eme fréquence
|
|
Cellule 21
|
R
|
La 1~eme fréquence
|
|
Cellule 22
|
B
|
La 2~eme fréquence
|
|
Cellule 23
|
F
|
La 3~eme fréquence
|
|
Cellule 24
|
E
|
La 1~erefréquence
|
|
Cellule 25
|
H
|
La 2~eme fréquence
|
|
Cellule 26
|
H
|
La 3~eme fréquence
|
|
Cellule 27
|
K
|
La 1~erefréquence
|
|
Cellule 28
|
N
|
La 2~eme fréquence
|
|
Cellule 29
|
N
|
La 3~eme fréquence
|
|
N° de la cellule
|
Antenne principale
|
Fréquence attribuée
|
|
Cellule 30
|
F
|
La 1~eme fréquence
|
|
Cellule 31
|
F
|
La 2~eme fréquence
|
|
Cellule 32
|
I
|
La 3~erefréquence
|
|
Cellule 33
|
I
|
La 1~erefréquence
|
|
Cellule 34
|
L
|
La 2~eme fréquence
|
|
Cellule 35
|
O
|
La 3~eme fréquence
|
|
Cellule 36
|
O
|
La 1~erefréquence
|
|
Cellule 37
|
J
|
La 3~eme fréquence
|
|
Cellule 38
|
J
|
La 1~erefréquence
|
|
Cellule 39
|
I
|
La 2~eme fréquence
|
|
Cellule 40
|
L
|
La 3~erefréquence
|
|
Cellule 41
|
L
|
La 1~erefréquence
|
Annexe 2
Rappel sur la théorie des graphes
Introduction
La théorie des graphes est utilisée dans un
grand nombre de disciplines (mathématiques, physique, économie,
etc.). Les recherches en théorie des graphes sont essentiellement
menées par des informaticiens, du fait de l'importance des aspects
algorithmiques (recherche de solutions). Il s'agit essentiellement de
modéliser des problèmes :
· on exprime un problème donné en termes de
graphes;
· il devient alors un problème de «
théorie des graphes » que l'on sait le plus souvent résoudre
car il rentre dans une catégorie de problèmes connus.
Les solutions de problèmes de graphes peuvent être
:
· faciles et efficaces (car le temps nécessaire pour
les traiter par informatique est raisonnable car il dépend
polynomialement du nombre de sommets du graphe) ;
· difficiles (car le temps de traitement est exponentiel) ;
dans ce cas on utilisera une heuristique, c'est-à-dire un processus de
recherche d'une solution - pas forcément la meilleure.
Qu'est-ce qu'un graphe?
Définition 1
On appelle graphe G = (X; A) la donn ee d'un ensemble X dont
les el ements sont appelés sommets et d'une partie de A
symétrique((x; y) E A (y; x) E A) dont les éléments sont
appelés arêtes.
En présence d'une arête a = (x; y) qui peut
être notée simplement xy, on dit que x et y sont les
extrémités de a, que a est incidente en x et en y, et que y est
un successeur ou voisin de x (et vice versa).
On dit qu'un graphe est sans boucle si A ne contient pas
d'arête de la forme (x; x), c'esta-dire joignant un sommet a
lui-même.
Le nombre de sommets est appelé ordre du graphe.
Un graphe ne possédant pas de boucle ni d'arêtes
parallèles (deux arêtes distinctes joignant la même paire de
sommets) est appelé graphe simple ou 1-graphe. En revanche un p-graphe
ou graphe généralisé est un graphe pour lequel il n'existe
jamais plus de p arêtes de la forme (x;x).
Graphiquement, les sommets peuvent être
représentés par des points et l'arête a = (x; y) par un
trait reliant x à y. On notera que la disposition des points et la
longueur ou la forme (rectiligne ou incurvée) des traits n'a aucune
importance. Seule l'incidence des différentes arêtes et sommets
compte.
Définition 2
On appelle graphe orienté ou digraphe G = (X; A) la
donnée d'un ensemble X dont les éléments
sont
appelés sommets et d'une partie A de X x X dont les
éléments sont appelés arcs ou arêtes.
En présence d'un arc a = (x; y) qui peut être
noté simplement xy, on dit que x est l'origine (ou
extrémité initiale) et y l'extrémité (terminale) de
a, que a est sortant en x et incident en y, et que y est un successeur de x
tandis que x est un prédécesseur de y. On dit aussi que x et y
sont adjacents.
Définition 3
Un graphe non orienté n'est qu'un graphe
orienté symétrique ; si un arc relie le sommet a au sommet b, un
autre arc relie le sommet b au sommet a : on ne trace alors qu'un trait entre a
et b que l'on appelle une « arête ».
Degré d'un graphe
On appelle degré sortant ou demi-degré
extérieur d'un sommet x le nombre d'arcs de la forme a = (x; y) avec y
=6 x, c'est- a-dire le nombre d'éléments de ['(x)\ {x} ( ['(x)
l'ensemble des successeurs d'un sommet x E X).
On note d5(x)ce degré.
On appelle degré entrant ou demi-degré
intérieur d'un sommet x le nombre d'arcs de la forme a = (y; x) avec y
=6 x, c'est- a-dire le nombre d'éléments de ['~1(x)\
{x} (['~1(x) l'ensemble des prédécesseurs d'un sommet
x E X).
On note de(x) ce degré.
On appelle degré de x (ou valence) la somme du
degré entrant et du degré sortant.
Un sommet de degré entrant non nul et de degré
sortant nul est appelé puits, tandis qu'un sommet de degré
entrant nul et de degré sortant non nul est appelé source.
Un sommet n'ayant pas d'arcs incidents est appelé
sommet isolé ; ces sommets ont un degré nul. Deux arcs adjacents
sont dits "en série" si leur sommet commun est de degré egal
à deux. Dans la définition d'un graphe, l'ensemble des arcs A
peut être vide; dans ce cas, on a affaire à un graphe nul. Tous
les sommets d'un graphe nul sont donc des sommets isolés. En revanche,
l'ensemble des sommets X ne peut être vide sinon le graphe correspondant
n'existe pas. Cela signifie donc qu'un graphe comporte au moins un sommet.
Matrice d'adjacence
Considérons un graphe G = (X; A) comportant n sommets. La
matrice d'adjacence de G est égale à la matrice U = (uij) de
dimension n x n telle que
~ 1 si (i; j) E A (c'est-a-dire (i; j) est une arête)
uij = 0 sinon
Une telle matrice, ne contenant que des "0" et des "1" est appel
ee, de manière générale, une matrice booléenne.
Un graphe orienté quelconque à une matrice
d'adjacence quelconque, alors qu'un graphe non orienté possède
une matrice d'adjacence symétrique. L'absence de boucle se traduit par
une diagonale nulle.
La matrice d'adjacence poss ede quelques propri et es qui
peuvent être exploitées. Considérons un graphe G et sa
matrice d'adjacence associée U :
· la somme des eléments de la i~eme ligne
de U est égale au degré sortant d5(xi) du sommet xi de
G.
· la somme des eléments de la j~eme
colonne de U est égale au degré entrant de(xj) du
sommet xj de G.
· U est symétrique si, et seulement si, le graphe G
est symétrique.
Définition d'un stable:
Un sous ensemble de sommetsI C X d'un graphe G = (X, A) est un
stable s'il ne comprend que des sommets non adjacents deux à deux:
ViE I,Vj E I - (i,j) E= A.
Coloriage des sommets d'un graphe
Définitions
La coloration des sommets d'un graphe consiste à
affecter à tous les sommets de ce graphe une couleur de telle sorte que
deux sommets adjacents ne portent pas la même couleur. Une coloration
avec k couleurs est donc une partition de l'ensemble des sommets en k parties
stables. Le nombre chromatique, noté x(G); du graphe G est le plus petit
entier k pour lequel il existe une partition de X en k sous-ensembles
stables.
Encadrement du nombre chromatique
Majoration x (G) < A (X) + 1, où A (X) est le plus
grand degré de ses sommets.
Minoration Le nombre chromatique d'un graphe est supérieur
ou égal à celui de chacun de
ses sous graphes.
Le nombre chromatique du graphe sera supérieur ou
égal à l'ordre de sa plus grande clique
x(G) ~ w(G).
Acronymes
ADSL: Asymetric Digital Subscriber Line.
BS : Base Station.
BTS: Base Transceiver Station. CPE: Customer Premise
Equipement.
DSL: Digital Subscriber Line.
EDGE: Enhanced Data Rates for GSM Evolution.
FAP: Frequency Assignement Problem.
IEEE: Institute of Electrical and Electronics Engineer.
IP: Internet Protocol.
LOS: Line Of Sight.
NLOS: Non Line Of Sight.
OFDM: Orthogonal Frequency Division Multiplexing.
OFDMA: Orthogonal Frequency Division Multiple Access. QoS: Qualiy
of Service.
UMTS: Universal Mobile Telecomunication System.
WiFi: Wirless Fidelity.
Wimax: Worldwide Interoperability for Microwave Acces.
| 


