|
ETUDE HEMODYNAMIQUE DE LA
VALVE AORTIQUE PAR MODELISATION
NUMERIQUE 3D
Rapport de DEA
Tahar CHERIGUI
17 juin 2005
Remerciements
La présente étude a été
réalisée au sein du Laboratoire de Modélisation en
Mécanique associé au CNRS et à l'Université Pierre
et Marie Curie (ParisVI) et avec la colaboration de l'association ADICARE du
service de chirurgie cardiovasculaire et thoracique CHU Pitié
Salpêtrière.
Tout d'abord, je souhaite remercier Monsieur P. Y.
Lagrée mon encadreur. Qu'il veuille bien trouver ici le
témoignage de ma sincère reconnaissance pour sa
disponibilité, son aide, ses conseils fructueux et sa grande patience
tout au long de mon stage.
A Monsieur M. Karouia, Ingénieur (service de chirurgie
cardiovasculaire et thoracique) pour m'avoir proposé ce sujet, et sa
précieuse aide.
A Monsieur M. Aazami Chirurgien, (service de chirurgie
cardiovasculaire et thoracique) pour sa contribution à la
réalisation de ce travail et sa disponibilité tout au long de mon
stage.
Je remercie M. J. Frelat qui a toujours été
présent pour répondre à mes questions et pour sa
contribution à la réalisation de ce travail, je tiens à
témoigner ici ma profonde reconnaissance.
Je tiens à remercier Monsieur C. Ribreau qui m'a
donné la chance en acceptant ma demande d'inscription pour
préparer ce DEA aprés les délais réglementaires.
Ces remerciements s'adressent à M. Thiriet pour m'avoir
prêté un Macintosh qui m'a été très utile.
Enfin, je n'oublie pas les thésards pour leur aide et l'ensemble du
personnel administratif de m'avoir accepté au sein du laboratoire et
à tous ceux qui, d'une manière ou d'une autre, ont joué un
rôle dans ce travail.
Sommaire
|
1
2
3
|
Introduction
Le coeur et la circulation sanguine
2.1 Généralités
2.2 La valve aortique
2.3 propriétés
Simulation d'un modèle simple
|
4
5
5
7
8
10
|
|
3.1
|
Introduction
|
10
|
|
3.2
|
Modèle masses ressorts
|
11
|
|
3.3
|
Aspect géométrique
|
11
|
|
3.4
|
Aspect mécanique
|
12
|
|
3.5
|
Aspect hydrodynamique
|
12
|
|
3.6
|
Résolution numérique
|
13
|
|
|
3.6.1 Objectifs
|
13
|
|
|
3.6.2 Calcul numérique
|
14
|
|
|
3.6.3 Interprétations
|
14
|
|
|
3.6.4 Conclusion
|
15
|
|
|
3.6.5 Calcul analytique
|
15
|
|
3.7
|
Conclusion
|
15
|
|
4
|
Résolution par la MEF sous Castem
|
17
|
|
4.1
|
Introduction
|
17
|
|
4.2
|
Modélisation de la valve
|
17
|
|
4.3
|
Modélisation de la valve en mode axisymétrique
|
18
|
|
|
4.3.1 Modèle en solide
|
18
|
|
|
4.3.2 Modèle en coque
|
19
|
|
|
4.3.3 Conclusion
|
20
|
|
4.4
|
Modélisation de la valve en mode plan
|
21
|
|
|
4.4.1 Modèle en coque
|
21
|
|
SOMMAIRE
|
|
|
4.4.2 Influence de la forme géométrique des sinus
sur l'ou-
|
|
|
|
verture de la valve aortique
|
22
|
|
4.5
|
Modélisation du fluide
|
23
|
|
4.6
|
Conclusion
|
24
|
|
5
|
Calcul numérique sous un logiciel de CAO Catia V5
|
25
|
|
5.1
|
Présentation du logiciel CatiaV5
|
25
|
|
5.2
|
Objectifs de ce calcul
|
25
|
|
5.3
|
Calcul sous Catia V5
|
26
|
|
5.4
|
Calcul sous Castem
|
27
|
|
5.5
|
Résultats et interprétations
|
28
|
Chapitre 1
Introduction
La simulation numérique, au cours des dernières
décennies, a été tributaire de développement de
plusieurs modèles structuraux numériques qui retracent le
comportement de la valve aortique ignorant son interaction avec le sang, par
exemple voir Black (1991); Krucinski (1993); De Hart (1998) et Cacciola (2000).
L'ouverture et la fermeture de la valve aortique pendant la systole implique,
cependant, une interaction forte entre le sang et le tissu environnant.
Plusieurs tentatives ont été faites pour analyser le comportement
de la valve en utilisant les modèles numériques d'interactions de
structure-fluide, par exemple McQueen (1995); Makhijani (1997).
Des modèles numériques d'interactions
structure-fluide ont été développés permettant
d'étudier ces interactions. La structure est déformée sous
l'effet de l'écoulement du sang qui a son tour est perturbé par
la nouvelle forme de la structure déformée.
L'objectif de ce travail est de présenter une
méthode de calcul rapide de déformations de la valve,
étudier son comportement aux grands déplacements et faire une
simulation. Il s'agit donc de construire un modèle numérique. La
modélisation mécanique a par contre été
réalisée sous deux logiciels de calcul et de conception, pour la
simulation comme la plupart des auteurs nous avons utilisé des
modèles mécaniques extrêmement simples, basés sur
les lois de l'élasticité linéaire. Or la plupart des
résultats obtenus en biomécanique indiquent que les tissus
biologiques se comportent selon des lois beaucoup plus complexes, incluant des
effets non-linéaires et visco-élastiques importants. Il existe
donc un besoin important en nouveaux algorithmes permettant la simulation de
ces types de comportements dans des conditions de temps réel. Ce travail
s'inscrit précisément dans cet objectif et propose une
méthode permettant le calcul de déformations et de forces
intégrant des lois mécaniques non-linéaires, avec une
vitesse appropriée à des applications en temps réel.
Chapitre 2
Le coeur et la circulation
sanguine
2.1 Généralités
La circulation sanguine assure la continuité des
échanges au niveau des organes. Le sang circule à sens unique
dans les vaisseaux : artères, veines, capillaires qui forment un
système clos. La mise en mouvement du sang est principalement du
à l'action du coeur qui joue le rôle d'une pompe avec une
efficacité remarquable.

FIG. 2.1 - Système circulatoire
|
CHAPITRE 2. LE COEUR ET LA CIRCULATION SANGUINE
|
Le coeur peut battre plus de 100000 fois par jour et pomper plus
de 8000 litres de sang.
Le sang oxygéné provenant des poumons alimente le
coeur gauche avec une
pression de 100mmHg pour fournir au sang suffisamment
d'énergie pour la
circulation périphérique. Le coeur droit
réceptionne le sang chargé en CO2 àune pression
à peine supérieure à la pression atmosphérique et
le fait circuler
dans les poumons à une faible pression de 20 à
30mmHg où il se charge en oxygène et rejette le gaz carbonique
produit par les réactions chimiques du métabolisme.
L'aorte est la grosse artère qui apporte du sang
oxygéné à l'organisme se divise en artères, qui
elle-même se divisent en artérioles, de plus en plus fines,
jusqu'aux capillaires, ces minuscules vaisseaux, alimentent les cellules de
notre organisme. Voir la figure 2.1.
La pression du sang diminue progressivement dans son chemin de
l'aorte jusqu'aux capillaires, du fait de la résistance de
l'écoulement qui augmente avec la diminution du diamètre des
vaisseaux.
La vitesse de l'écoulement du sang diminue de façon
significative dans les capillaires puis augmente dans les veinules et les
veines.
La vitesse est proportionnelle à la section transversale
des vaisseaux sanguins. voir tableau 2.3. [3].
La surface de section transversale des vaisseaux sanguins est la
plus grande au niveau des capillaires où s'effectuent les
échanges.
Tab. 2.1 - Tableau récapulatif du volume, pression, et la
vitesse linéaire du sang dans les différentes parties du
système vasculaire de l'homme
.
Zone
|
Volume(ml)
|
Pression(mmHg)
|
Vitesse(mm/s)
|
|
Aortes
|
100
|
100
|
400
|
|
Artères
|
300
|
100 - 40
|
400 - 100
|
|
Artérioles
|
50
|
40 - 30
|
100 - 1
|
|
Capillaires
|
250
|
30 - 12
|
< 1
|
|
Veinules
|
300
|
12 -10
|
<3
|
|
Veines
|
2200
|
10 - 5
|
3 - 50
|
|
Veines caves
|
300
|
2
|
50 - 200
|
|
CHAPITRE 2. LE COEUR ET LA CIRCULATION SANGUINE
|
2.2 La valve aortique

FIG. 2.2Shémas de la valve aortique
La valve aortique qui assure l'écoulement continu de
sang du ventricule gauche dans l'aorte, est située à la sortie du
ventricule gauche et constituée de trois feuillets semi-lunaires
très flexibles qui sont attachés à la racine aortique par
le point commissure, ces derniers s'emboîtent parfaitement lorsque la
valve est fermée. Voir la figure 2.2.
En systole le ventricule se contracte, la pression
intra-ventriculaire dépasse la pression dans l'aorte (Pv > Pa) ce qui
ouvre la valve en permettant la sortie du sang.Voir figure 2.3.
En diastole le coeur se relache, la pression diminue (Pv <
Pa) la valve se referme sans fuite pour empêcher tout flux sanguin vers
le ventricule.
Le mécanisme de l'ouverture et la fermeture de la valve
aortique est lié aux variations de pression entre les deux
cavités.
Certaines malformations de la valve aortique peuvent
gêner le fonctionnement du coeur, pendant la fermeture et l'ouverture, la
valve devient incontinente et une fuite aortique (reflux de sang de l'aorte
vers le ventricule) apparaît. A l'inverse, si la valve ne s'ouvre pas
complètement, une petite quantité de sang ne peut pas sortir. On
parle alors de rétrécissement.
Cela entraîne une surcharge de travail pour le coeur
(ventricule gauche) qui doit assurer un débit suffisant pour l'organisme
malgré la fuite. Cette surcharge peut parfois conduire à une
insuffisance cardiaque.
Ces troubles peuvent obliger le remplacement de la valve
défectueuse par une valve artificielle ou une valve provenant d'un coeur
de porc.
|
CHAPITRE 2. LE COEUR ET LA CIRCULATION SANGUINE
|
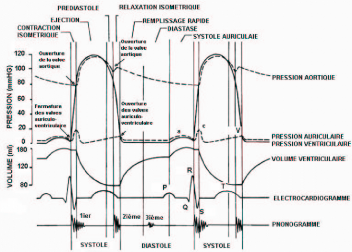
FIG. 2.3Cycle cardiaque
2.3 propriétés
Le tissu de la valve aortique est une structure
élastique et linéaire, les propriétés
mécaniques sont prisent du modèle de Grande [2] ont
été utilisées pour la racine aortique, voir le tableau
2.3.
Tab. 2.2 - Les epaisseurs du tissu utilisé pour les
feuillets et la racine de la valve, pris du modèle de Grande
.
Epaisseur (mm)
|
gauche et droit (mm)
|
sans coronnaire (mm)
|
|
Bord d'attachement
|
1.16
|
0.155
|
|
Belly
|
0.18 - 0.58
|
0.18 - 0.58
|
|
Bord libre
|
1.53
|
1.96
|
|
Nodulus of aranti
|
2.06
|
2.75
|
|
CHAPITRE 2. LE COEUR ET LA CIRCULATION SANGUINE
|
Par contre les feuillets sont trop raides pour s'ouvrir sous
le chargement physiologique de pression ce qui explique son comportement
non-linéaire, Thubrikar [2]. Les propriétés
mécaniques du tissu utilisées dans le modèle
élastique de Thubrikar, sont énumérées dans le
tableau 2.3.
Tab. 2.3Propriétés mécaniques
utilisées pour le tissu de la valve et la racine aortique, pris de
l'étude par éléments finis du modéle de
Thubrikar
.
Propriété
|
Valve aortique
|
Racine aortique
|
|
Ecirc(KPa)
|
220,000
|
334,000
|
|
Erad(KPa)
|
200,000
|
-
|
|
Elong(KPa)
|
-
|
350,000
|
|
?xy
|
0,450
|
0,450
|
|
?zy
|
0,450
|
0,450
|
|
?xz
|
0,450
|
0,429
|
Le module de Young et le coefficient de Poisson pour le mur et
les feuillets aortiques ont été obtenus à partir de
l'étude par éléments finis faite par Grande.
Tab. 2.4 - Propriétés mécaniques
utlisées pour le tissu des feuillets
.
Propriété
|
Feuillet
|
Mur aortique
|
|
Epaisseur(mm)
|
0,500
|
1,000
|
|
Comportement
|
Isotropique
|
Isotropique
|
|
Module de Young(MPa)
|
0,900
|
6,000
|
|
Coefficient de Poisson
|
0,450
|
0,450
|
Pour le cylindre à paroi mince (rapport,
rayon/épaisseur, > 10) soumis à la pression interne, l'effort
est uniforme à travers cette l'épaisseure. Cet effort est dit
effort de membrane, et dans la direction circulaire il est defini par la
relation suivante [8] :
Où p est la pression, r est le rayon du feuillet, e est
l'épaisseure du feuillet
Chapitre 3
Simulation d'un modèle simple
3.1 Introduction

2
1.8
1.6
1.4
1.2
1
0.8
0.6
m3
k13 k32
0.4
0.2
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8
X (cm)
m1 m2
FIG. 3.1 - L'aspect géométrique du modèle
simple masses ressorts
L'idée consiste à écrire un algorithme
sous matlab qui permet de simuler l'ensemble des composants tout en maintenant
la cohérence de l'ensemble de modèle.
Le but de la simulation est de reproduire le comportement de
la valve aortique, lors de son ouverture, en un modèle extrêmement
simplifié et en temps réel à partir des lois de la
physique. Au contraire de l'animation qui est une succession d'images
virtuelles récupérées des résultats de simulation
et qui donne l'illusion de la réalité comme pour la technique des
dessins animés.
|
CHAPITRE 3. SIMULATION D'UN MODÈLE SIMPLE
|
3.2 Modèle masses ressorts
Le modèle masses ressorts est très
répandu dans le domaine biomédical, il consiste a
discrétiser la structure en un maillage surfacique et d'attribuer
à chaque noeud de ce maillage une masse.
Les liens élastiques, représentés par des
ressorts, voir 3.1, modélisent les interactions entre noeuds voisins
sont régis par l'équation suivante :
f =--kxï. (3.1)
ou k est la raideur du ressort lié
au noeud j.
L'énergie potentielle élastique emmagasinée
du système s'écrit :
1 >
U = kiLl2 i . (3.2)
2
Où Ll est l'allongement du ressort, k est son
coèfficient de raideur.
Le travail fournit par la force extèrieure F ? qui
s'applique sur un objet parcourant un trajet ?8u pour
déformer le ressort depuis sa position de repos est :
8W = F? ?8u. (3.3)
Le travail total fourni par la
force F? s'écrit :
fW = F? ?8u. (3.4)
3.3 Aspect géométrique
Le modèle de la valve a été
simplifié, il est réduit en trois masses et deux ressorts. Les
deux masses, liées aux deux extrémités des deux ressorts,
sont bloquées (aux déplacements et en rotatation), l'autre masse
liée aux deus ressorts elle est libre. Voir la figure 2.3.
Ce modèle est quasi bidimensionnel : nous supposons que
l'écoulement traversant la valve aortique est constant dans la direction
de z ceci signifie que notre système dépendra seulement de la
position de x et y.
La valve aortique est composée de trois feuillets,
symétriques, fortement flexibles, de longueur l et formant un angle a
avec l'axe x. Ces feuillets sont attachés à la racine d'un point
commissure suivant une ligne doublement incurvée (anneau aortique) [7],
comme illustré dans la figure 5.1.
l=r0cosa. (3.5)

L
r0

|
CHAPITRE 3. SIMULATION D'UN MODÈLE SIMPLE
|
FIG. 3.2 - Les dimensions appropriées de la
géométrie de la valve aortique. l longueur du feuillet, L
longueur du sinus, r0 rayon de la valve, = 19°.
3.4 Aspect mécanique
Lorsqu'un corps est déformé sous l'action de
forces extérieures, il absorbe une énergie équivalente au
travail fourni par ces forces. Cette relation peut s'écrire sous la
forme suivante :
S(x, y) = U(x, y) + W(x, y). (3.6)
Faire la simulation du mouvement des feuillets de la valve
aortique pendant leurs ouvertures par le modèle masses ressorts nous
amène à faire un programme numérique sous matlab.
3.5 Aspect hydrodynamique
Le flux sanguin quitte le ventricule gauche avec une vitesse
U0 et une pression intra-ventriculaire Pv qui dépasse la
pression dans l'aorte Pa, appuyant sur les feuillets, cette
différence de pression provoque l'ouverture de la valve.
Le comportement de ce fluide peut être décrit par
Bernoulli, l'énergie mécanique est exprimée par la
relation suivante :
2pU2 +p + pgz = cste. (3.7)
1
|
CHAPITRE 3. SIMULATION D'UN MODÈLE SIMPLE
|
Où p la pression, pgz la pression de la
pesanteur,1 2pU2 la pression cinétique.
La conservation du debit est donnée par la relation suivante :
U(x)S(x) = cste. (3.8)
Où U est la vitesse du flux et S est la section de la
paroi.
La lois de la conservation de l'énergie
mécanique et du débit volumique du fluide nous permet
d'écrire l'expression de la pression p(y) exercée sur les
feuillets de la valve pour chaque déplacement Y :
1 2pU2 0+p0 = 1 2pU2 +p.
(3.9)
U0S0 = US. (3.10) Ce système bidimensionnel consiste
à calculer la pression suivant une seule direction ?oy, cette pression
peut s'écrire sous la forme suivante :
1 1
p(y) = p0 + 2pU2 0 (1 - (S0
0 - 2pU2 S )2). (3.11)
1 H4
- y)4). (3.12)
p(y) =p0+ 2pU2 0 (1 - (H
Où H est la distance entre l'axe de la valve et la racine
du sinus de la valve. Le travail fourni de la pression p(y) peut
s'écrire sous la forme suivante :
1 H4
W (y) = (P0 + 2pU2 0 )(y) - 1 2PU2 0 3(H -
y)3 . (3.13)
Aprés avoir écrit toutes les équations
nécessaires pour notre modèle, nous avons developpé un
algorithme sous matlab qui nous permet de chercher le minimum de
l'énergie fournit à chaque postion d'equilibre de la masse, et de
tracer les courbes de déplacements/forces de pression pour chaque
instant t. On veut minimiser la fonction S à l'aide de la commande
»fminsearch», le principe consiste qu'à chaque instant t, il
cherche le minimum M et la position d'équilibre correspondante.
MinS(x,y)=M
(x,y)E[0;2]×[0;2] . (3.14)
3.6 Résolution numérique 3.6.1
Objectifs
Dans cette étude nous avons choisi Matlab, ce logiciel
est largement utiliséaussi bien par les universitaires, que
par les industriels, il est doté d'une
|
CHAPITRE 3. SIMULATION D'UN MODÈLE SIMPLE
|
bibliothèque très variée de fonctions
(Toolboxes) qui s'adapte à tous les types de problème. Le calcul
consiste en l'étude de la valve simplifiée soumise à une
force de pression imposée à ses feuillets, en négligeant
l'interaction fluide- structure, en observant sa réponse.
3.6.2 Calcul numérique
La fonction »fminsearch» sous Matlab calcule
numériquement le minimum de la fonction S(x,y) pour chaque position Y de
la masse in, en faisant varier la pression p0 et la vitesse U0 en fonction du
temps t.
Ce programme calcule en même temps la pression p(y) du
fluide exercée sur la masse in du noeud pour chaque position Y.
L'énergie potentielle élastique du système
s'écrit :
k[(r13 - r130)2 + (r32 -
r320)2]. (3.15)
2
1
U =
Le déplacement peut s'écrire sous cette forme :
/rij = (xi- xj)2 + (yi - yj)2. (3.16)
Etat final des ressorts (k13 et
k32) s'écrit :
/r13 = x2 3 + y2 3. (3.17)
/r32 = (x3 - 2)2 + y2 3.
(3.18)
Etat final des ressorts (k13 et
k32) s'ecit :
/r130 = X2 30 + X2 03. (3.19)
/r320 = (X20 - X03)2 + X2 03. (3.20)
(3.21)
Avec X20 = 2, X30 = X03 = 1.
3.6.3 Interprétations
Une animation de la déformation des ressorts et le
déplacement de la masse in qui simule l'ouverture de la valve a
été réalisée. Nous avons écrit des
équations qui tracent la position initiale de notre système, le
programme qui a été élaboré pour minimiser la
fonction S, il trace en même temps à
|
CHAPITRE 3. SIMULATION D'UN MODÈLE SIMPLE
|
chaque instant t la nouvelle position de la masse in, ces
dessins animés de la déformation du système nous
permettent de bien voir l'instabilité du système dès que
la masse in parcoure la moitié du chemin (de 1 à 0,5cm) les
ressorts flambent.
Cette animation nous montre le comportement non-linéaire
de ce modèle discret et le flambement des ressorts à la zone de Y
0, 5.
3.6.4 Conclusion
Le système est instable, nous avons un flambage des
ressorts, le déplacement Y de la masse in ne peut pas atteindre la
position maximale proche de zero (l'ouverture maximale des feuillets), nous
avons essayé de faire varier les
raideurs des ressorts, ils nous faut plus de temps pour peut
étre réussir àstabiliser le système.
Pour cela nous avons procédé au calcul analytique.
3.6.5 Calcul analytique
Calculer analytiquement le minimum de la fonction S(x,y) c'est
déterminer la position Y de la masse in où la
dérivée de cette fonction soit nulle.
Cette position doit étre proche de zéro ce qui peux
expliquer que la valve est ouverte au maximum.
En faisant varier la pression p0 et la vitesse U0 en fonction
du temps t, nous avons fait un autre algorithme qui calcule le minimum de
S(x,y) sous Matlab, et il trace les courbes, de déplacement Y et les
vitesses U0 et U à chaque instant t, qui sont représentées
ci-dessus.
.
La pression p(y), exercée sur les feuillets de la valve
aortique, est calculée par ce même algorithme, il trace aussi sa
courbe qui est la réponde du système masses ressorts, voir la
figure 3.4.
3.7 Conclusion
Ce modèle très simplifié de la valve
aortique nous permet d'obsever :
- Le raidissement des ressorts lorsqu'on appuye de plus en plus
fort sur la masse in.
- Le flambage des ressorts.
On peut conclure que le système masses ressorts est
instable.

CHAPITRE 3. SIMULATION D'UN MODÈLE SIMPLE
0.4
0.2
0
0 5
10 15 20 25
30
2
1.8
1.6
U
1.4
1.2
0.8
0.6
1
U0
Y
time t
FIG. 3.3 - Courbes (Y, U0 et U) de formes sinusoïdales
tracées à chaque instant t. En rouge : déplacements (Y) de
la masse m suivant l'axe ?oy, en bleu : la vitesse d'entrée (U0) du
fluide, en vert la vitesse U du fluide
.
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
déplacement (Y)
FIG. 3.4 - Courbe de pression/déplacements. On voit que
l'évolution de la pression est quasi linéaire, et le
système est stable
.
Chapitre 4
Résolution par la MEF sous
Castem
4.1 Introduction
Les non-linéairités liées aux
instabilités du comportement de la valve aortique qui se
présentent dans l'analyse des problèmes statiques, ainsi les
interactions structure-fluide fait la difficulté de notre calcul.
Nous avons essayé d'aborder ce problème par la
méthode des éléments finis
pour comprendre le
comportement dynamique de la valve. Ce problème va
être traité avec le code de calcul CASTEM. Le choix
de ce logiciel est motivépour ses performances pour
résoudre des problèmes de type non-linéaire par la
méthode des éléments finis.
4.2 Modélisation de la valve
La recherche bibliographique nous a permis de faire deux
modèles de formes différentes :
Une forme exponentielle des sinus qui a été
reprise par la plus part des études faites sur la valve et une autre
forme circulaire, dans le but de voir l'influence de la forme des sinus
aortiques sur l'ouverture des feuillets.
Nous avons réalisé plusieurs modèles en 2
et 3D (mode : plan et axisymétrique) en coque et en solide. Un
modèle 3D réalisé et maillé sous un logitiel de
conception (Catia V5), par contre le calcul a été fait sous
Castem. Toutes les parties inférieures et supérieures de tous les
modèles sont soumises aux mêmes conditions aux limites
c.à.d nous avons bloqué les rotations suivant l'axe zi et les
déplacements suivants l'axe il.
|
CHAPITRE 4. RÉSOLUTION PAR LA MEF SOUS CASTEM
|
4.3 Modélisation de la valve en mode
axisymétrique
4.3.1 Modèle en solide
Ce modèle de révolution par rapport à
l'axe ?oz dont la forme des sinus est circulaire. On lui a associé un
maillage de type triangulaire à trois sommets. Deux matériaux
différents constituent ce modèle :
Les feuillets et le mur aortique, dont les paramètres sont
énumérés dans le tableau 2.3.
Sur les feuillets et à la racine aortique et de la
valve on applique une pression LP = 9332Pa/mm2 (78mmHg) qui est
nettement supérieure à la pression réelle à la
sortie du ventricule gauche. Nous avons donné différentes
couleurs aux différents déplacements linéaires et
non-linéaires :

FIG. 4.1 - Modèle de la valve en mode
axisymétrique. En rouge: la déformation non-
linéaire
de la valve, en vert : la déformation linéaire de la valve et en
bleu : la position
initiale (valve fermée) pour un temps qui varie de
t = 0 à 1 seconde avec un pas i = 0,05
|
CHAPITRE 4. RÉSOLUTION PAR LA MEF SOUS CASTEM
|
Résultats et interprétations
La pression appliquée à l'entrée de la
valve a été augmenté progressivement jusqu'à une
valeur de L&P = 9332Pa/mm2(70mmHg) qui est égale à
la différence de pression réelle à la sortie du ventricule
gauche.
La figure 4.1 nous permet de voir les déformations
linéaires et non-linéaires de la valve. Le cas linéaire
est complètement faux, les feuillets s'allongent et prennent un volume
le plus important à la racine aortique, on constater aussi que la valve
ne s'ouvre pas complètement. Par contre le cas non-linéaire les
feuillets sont trop rigides ce qui explique leur petit déplacement.
4.3.2 Modèle en coque
Dans le cas précédent les feuillets sont trop
rigides, nous avons procédéau changement de concept pour un autre
modèle en coque.
Dans la suite de cette partie on garde les mêmes
propriétés mécaniques du matériau, le même
type de maillage et le même chargement qui est la pression imposée
LP = 9332Pa/mm2. Nous allons réaliser un modèle en
coque et en mode axisymétrique (en révolution) pour pouvoir
résoudre le problème de raidissement des feuillets.
L'épaisseur des sinus de la valve est e = 1mm, l'épaisseur
moyenne des feuillets est e1 = 0, 5mm et les proriétés
mécaniques du matériau de la valve sont
énumérés dans le tableau 2.3.

FIG. 4.2Modèle Coque en mode axisymétrique. En
rouge: la déformation non-linéaire de la valve, en vert la
déformation linéaire de la valve et en bleu: la position initiale
(valve fermée) pour un temps qui varie de t = 0 à 1seconde avec
un pas i = 0,05
|
CHAPITRE 4. RÉSOLUTION PAR LA MEF SOUS CASTEM
|
Résultats et interprétations
D'après la figure 4.2 nous pouvons constater les
mêmes déformations que dans le cas précédent. Le cas
linéaire est complètement faux, les feuillets s'allongent. Nous
avons appliqué le méme chargement en l'augmentant progressivement
jusqu'à LP = 9332 Pa/mm2 (70mmHg) qui est égale
à la différence de pression réelle à la sortie du
ventricule gauche, on peut constater aussi que la valve ne s'ouvre pas
complètement et dans le cas non-linéaire on observe le
raidissement des feuillets.
4.3.3 Conclusion
Le calcul sous Castem des modèles, solide et coque, en
mode axisymétrique nous permet de dire que le cas linéaire est
complètement faux et dans le cas non-linéaire nous observons un
raidissement des feuillets de la valve aortique. Pour éviter ce genre de
problème on va s'intéresser au mode plan (2D).
|
CHAPITRE 4. RÉSOLUTION PAR LA MEF SOUS CASTEM
|
4.4 Modélisation de la valve en mode plan
4.4.1 Modèle en coque
Nous nous intéressons toujours au modèle en
coque de forme circulaire pour le sinus aortique. Les mêmes
propriétés mécaniques et chargement LP sont
appliqués que précédemment. Par contre cette fois-ci on va
travailler en mode plan (2D) et nous intéresserons uniquement aux
déplacements non- linéaires des feuillets de la valve
aortique.

FIG. 4.3 - Modèle en Coque en forme circulaire 2D (mode
Plan). Le déplacement des feuillets pour chaque itération sur le
temps (t = 0 à 1 seconde avec un pas i = 0.05) donne une position
correspondante jusqu'à l'ouverture maximale de la valve aortique.
Résultats et interprétations
Les résultats représentés par la figure
4.3 ils montrent le déplacement des feuillets depuis la position
initiale en bleu (la valve fermée) jusqu'à la position finale en
rouge (valve ouverte) à chaque itération sur le temps (t = 0
à 1 seconde avec un pas i = 0, 05).
On peut voir clairement que les feuillets sont ouverts au
maximum.
|
CHAPITRE 4. RÉSOLUTION PAR LA MEF SOUS CASTEM
|
4.4.2 Influence de la forme géométrique des sinus
sur l'ouverture de la valve aortique
Ce calcul consiste de voir l'influence de la forme
géométrique des sinus sur le comportement de la valve pendant son
ouverture. Ce modèle est soumis aux mêmes conditions aux limites
et nous avons utilisé les mêmes propiétés
mécaniques que dans le cas précédent, la nouvelle forme
géométrique des sinus aortiques est une forme exponentielle
(ovale), voir figure 4.4

FIG. 4.4 - Modèle en coque avec une forme ovale des
sinus en mode plan (2D). Le
déplacement des feuillets pour chaque
itération sur le temps (t = 0 à 1 seconde avec un
pas i =
0.05) donne une position correspondante jusqu'à l'ouverture maximale de
la valve.
Résultats et interprétations
Les déplacements des feuillets, depuis la position
initiale (valve fermée) en bleu jusqu'à la position finale (valve
ouverte) en rouge, sont représentés par la figure 4.4.
Cette figure retrace ainsi l'ouverture progressive de la valve
et donne à chaque itération du temps avec un pas i = 0.05 une
position de feuillets jusqu'à la position finale en vert.
|
CHAPITRE 4. RÉSOLUTION PAR LA MEF SOUS CASTEM
|
Dans ce cas on peut voir que l'ouverture de la valve est moins
importante par rapport au cas précédent (la valve dont la forme
géométrique des sinus est circulaire), on peut déduire que
la forme des sinus peut influencer sur le comportement de la valve.
Dans ce modèle les feuillets sont plus rigide, les
modèles dont la forme géométrique des sinus aortiques est
circulaire s'ouvrent mieux.
4.5 Modélisation du fluide
La compréhension du comportement du fluide est bien
souvent un facteur important dans le développement de produits et de
process. La simulation de l'écoulement du sang, un fluide visqueux
incompressible et non newtonien (toute fois la question reste posée au
centre de la conduite), dans la valve aortique, est réalisée
à l'aide du logiciel Castem.

Cast3m2001 Education Recherche : GIBI FECIT
FIG. 4.5 - Maillage du fluide sous Castem, comme
l'écoulement est laminaire, les mailles sont ordonnées dans le
sens de l'axe ?oz, parcontre la présence des tourbillons à
l'intérieure de la valve les nous avons présenté les
mailles en désordre
|
CHAPITRE 4. RÉSOLUTION PAR LA MEF SOUS CASTEM
|
Parmis les modèles qui permettent de décrire
correctement ce comportement il convient d'en retenir deux. Le premier
proposé par Quémada (Quémada 1997, 1978) prend en compte
la dépendance de la viscosité en fonction de la vitesse de
cisaillement mais aussi de la concentration [5]. Il peut s'écrire :
[ ]--2
. (4.1)
1 - ? k0( _?c)1/2 +
ko _|?|1/2
u = up 2 ( _?c)1/2 +
_|?|1/2
Oùup est la viscosité dynamique du
plasma sanguin (milieu suspendant), cI
est la fraction volumique des
particules en suspension (globules rouges) ,k0 et
k sont deux paramètres qui peuvent être
reliés aux valeurs de la viscositéà faible et forte
vitesse de cisaillement par la relation :
[u0,? = 1
?--2
2
. (4.2)
k0,?(c)
conduisant alors à la relation :
u0 + (u? ?ÿ )--1/2
ÿ?c
--1/2
u--1/2 =1 + ( ?ÿ ÿ?c )--1/2 . (4.3)
On peut utiliser également le modèle de Cross
(Cross 1965), qui propose une relation simple pour la viscosité qui
s'écrit;
u0 - u?
u = u? +(4.4) 1 + ( ?ÿ ÿ?c )p
Les équations du modèle considéré
ici sont des équations simplifiées de Bernoulli appliquées
pour un écoulement de Poiseuille bidimensionnel. Pour un
écoulement laminaire du sang de viscosité u,
d'unedifferencedepression8p et d'une vitesse moyenne wr à
l'entrée de la valve, le débit totale de fluide est donné
par la formule de Poiseuille :
? r ? 2 ? w(r)rdrd? = centsp?r4 0
Q = 8Lu . (4.5)
0 0
La résistance à l'écoulement :
8uL
R = (4.6)
irr4
4.6 Conclusion
Nous avons réalisé un programme sous Castem qui
peut modéliser le fluide (le sang) qui traverse la valve aortique. Ce
calcul ne donne que le maillage, voir la figure 4.5 puis il s'arrête.
Chapitre 5
Calcul numérique sous un
logiciel de CAO Catia V5
5.1 Présentation du logiciel CatiaV5
Catia V5 est un logiciel de CFAO (Conception et Fabrication
Assistée Ordinateur), conçu par Dassault Systèmes et
commercialisé par IBM. Il est très utilisé en
aéronautique et en automobile. Constitué de plusieurs ateliers,
il permet de faire : les dessins en 3D, le calcul statique et dynamique des
structures par élément finis, animation cinématique et
simulation des contraintes, prototypage rapide et maquettes numériques,
etc...
5.2 Objectifs de ce calcul

FIG. 5.1 - Modèles 3D réalisés sous Catia V5
: vue isométrique (a) et (b), vue de coupe (c), vue dessous (d)

CHAPITRE 5. CALCUL NUMÉRIQUE SOUS UN LOGICIEL DE CAO
CATIA V5

FIG. 5.2 - Maillage des modèles 3D réalisés
sous Catia V5 : vue isométrique (f), et vue de dessous (g)
Dans ce chapitre, nous allons faire un calcul statique et
linéaire de la valve sous Catia V5 et un autre calcul sous Castem de la
valve maillée sous Catia V5. Le but de ces calculs est de retrouver le
défaut du comportement linéaire de la structure.
Le choix de ce logiciel est motivé pour sa
malléabilité et sa facilité de travailler en 3D, en solide
ou en surfacique (coque). Voir les figures 5.1.
Il permet aussi le passage de maillages Catia en format Bulkdata
de Nastran à Castem pour faire le calcul.
5.3 Calcul sous Catia V5
Le calcul de structure sur les modèles
géométriques Catia est un calcul d'avant-projet permettant de
vérifier le plus rapidement possible la validitéd'une
solution. L'étude par éléments finis de ce modèle
surfacique se fait en
mode coque. La taille des mailles est choisie pour avoir des
résultats plus précis. Voir les figures 5.4.
Les deux extrémités de la valve sont
encastrées (la rotation et la translation sont bloquées). La
pression imposée est constante à l'entrée de la valve.
|
CHAPITRE 5. CALCUL NUMÉRIQUE SOUS UN LOGICIEL DE CAO
CATIA V5
|
5.4 Calcul sous Castem
Il convient d'être vigilant quant à la
validité du modèle utilisé sous Catia et accueillir avec
prudence les résultats obtenus. En effet, l'automatisation
poussée de certaines étapes du calcul masque parfois les
faiblesses ou incohérences du modèle. Pour cela nous avons fait
un maillage sous Catia et le calcul sous Castem pour vérifier et valider
notre modèle.
Nous avons réalisé un modèle en 3D en
coque mince (épaisseur nulle), le logiciel n'a pas réussi a faire
le maillage car la forme géométrique de la valve est complexe
avec une épaisseur nulle. Pour simplifier ce modèle nous
n'avonsréalisé que la partie inférieure de la valve avec
les feuillets, puisque c'est la partie qui est soumise le plus à la
pression. Le maillage a été réalisé,voir la figure
5.3 et il a été exporté en format »Bulkdata»
pour faire le calcul sous Castem.
Cast3m2001 Education Recherche : geometrie initiale Cast3m2001
Education Recherche : GIBI FECIT
|
AMPLITUDE
1.0
1.0
|
|
Cast3m2001 Education Recherche : geometrie deformee
|
|
FIG. 5.3 - Maillage sous catia de la partie inférieure de
la valve et le calcul est réalisé sous Castem
|
CHAPITRE 5. CALCUL NUMÉRIQUE SOUS UN LOGICIEL DE CAO
CATIA V5
|
5.5 Résultats et interprétations
La partie inférieure de la valve aortique n'a
été soumise qu'à un chargement égal à
1 3Lp (plus faible par rapport à la pression
réelle), mais le code Castem refuse de calculer pour des pressions
supérieures. Bien que nous n'ayons pas atteint la pression
désirée, les feuillets s'ouvrent facilement. En fait, le fait de
passer en 3D les a rendus moins rigides, voir la figure 5.3.

Cast3m2001 Education Recherche : GIBI FECIT

Cast3m2001 Education Recherche : GIBI FECIT
FIG. 5.4Début de calcul sous Castem d'un modèle de
la valve aortique maillé sous Catia V5
Conclusion
Dans ce travail nous avons présenté une
première approche de la modélisation de la valve. Nous avons
commencé par un modèle simpliste, puis nous sommes passés
à des calculs plus compliqués sous CASTEM en tenant compte d'une
structure déformable sans, puis avec non linéarité (dues
au déplacement). Sous CASTEM, nous restions en axisymétrique ou
en 2D plan, sous CATIA en revanche nous sommes passé en vrai 3D mais en
restant linéaire.
Nous avons aussi vu l'influence de la géométrie
sur l'ouverture de la valve (forme des sinus). Les valeurs de chargements et
les valeurs des constantes du matériau étaient à peu
près celles de la littérature. Dans tous les cas on a
observé l'effet de raidissement dû aux non
linéarités.
Nous nous sommes attachés à la résolution
du point de vue du solide (calcul de structures sous Catia et Castem), nous
comptons compléter ce travail en effectuant des calculs
d'écoulement à géométrie fixée (avec
FreeFem).
Nous sommes encore loin d'une modélisation
complète avec couplage fluide structure, mais ce premier pas nous a
permis de comprendre quelques phénomènes.
Bibliographie
[1] Pedley, TJ, The Fluid Mechanics of Large Blood Vessels :
446pp, CUP, 1980
[2] M. A. Nicosia , R. P. Cochran, D. R. Einstein, C. J.
Rutland, K. S. Kunzelman, A Coupled Fluid-structure Finite Element Model of the
Aortic Valve and Root, November 2003
[3]
www.pst.chez.tiscali.fr/special5.htm
[4] K. Hang Lim, J. Candra, J. Hock Yeo, C. M. G. Duran, Flat
or Curved Pericardial Aortic Valve Cusps : A Finite Element Study, September
2004
[5] Michel Y. Jaffrin, Francis Goubel, Biomécanique des
fluides et des tissus
[6] M. Thurbrikar, W. C. Piepgrass, T. W. Shaner, A. S. P.
Nolan, The design of the normal aortic valve
[7] J. De Hart, G. W. M. Peters, P. J. G. Schrurs, F. P. T.
Baaijens, A three-dimensional computational analysis of fluid-structure
interaction in the aortic valve
[8] Editors : Endre Bodnar, Cardiology : J. Chamers et P. M.
Shah, Cardiac Surgery : W. R. Chitwood et D. Loisance, The Journal of Heart
Valve Disease, Jannuary 2001
Annexe
Exemple d'un programme sous Castem de la valve
* * ** * * * * * * ** * * * * * * ** * * * * *
opti dime 2 elem seg2 mode axis ;
*liste des options(r,h,e [mm])
r0 = 4.40;
r1 = 1.00;
r2 = 2.80;
r3 = 4.19; e = 0.50; h0 = 8.90;
h1 = 1.50;
h2 = 1.51;
h3 = 5.90; p0 = 0. 0.; pz = 0. h0.; hc = h3/2.;
*** les points;
* ^ |
* | --|
* | ^ |
* h3| | |
* | h2| |
* | | |
* v v |
* |
* ^ |
* h1| |
* v |
* p0
* r0 ><r1><---r2--->
*
*
n = 25;
ns2 = n/2;
ns3 = n/4;
* list p0;
p5 = 0. 0.;
p6 = 0. h0;
p1 = r0 0.;
p2 = (r0 + r1) (0.);
pc1= r0 h1;
pc2= (r0 + r1) (h1 - e);
pc3= (r0 - r3) (h1 + h2);
pc4= (r0) (e + h1);
p3 = (r0) (h1 + h3);
p4 = (r0 + r1) (h1 + h3 + r1) ;
p7 = r0 h0;
p8 = (r0 + r1) (h0);
*
* pz
* | p7----p8
* ^ |
* h1| |
* v |
* |
|
|
|
| p4
p3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pc3\ |
|
|
|
| pt1 pt2
|
|
\ |
|
| h0|
|
* *
|
|
\ |
|
|
|
|
| |<r1>
|
|
\ pc4
|
|
|
| |
|
|
|
\|
|
|
|
| |
|
|
|
pc1
|
|
|
| |
|
|
|
<--->| pc2
|
| |
|
|
|
r3 | |
|
| |
|
|
|
| |
|
| |
|
|
|
p1----p2 v |
|
|
pcc1 = (r0) (h1 + hc);
*pcc2 = (r0 + r1) (h1 + hc);
pt1 = (r0 + r2) (h1 + hc);
pt2 = (r0 + r1 + r2) (h1 + hc);
l56 = droi p5 n p6; l12 = droi p1 ns3 p2;
lc1c2 = droi pc1 ns3 pc2; l34 = droi p3 ns3 p4;
l78 = droi p7 ns3 P8; l1c1 = droi p1 ns3 pc1; lc1c3 = droi pc1
n pc3; lc3c4 = droi pc3 n pc4; l37 = droi p3 ns3 p7;
l48 = droi p4 ns3 p8; l2c2 = droi p2 ns3 pc2; l4c2 = droi p4 ns3
pc2; l3c4 = droi p3 ns3 pc4; lc1c4 = droi pc1 ns3 pc4; l00 = droi p0 n pz;
geo1
geo2
geo3
geo4
= cerc
|
15
|
pc4
|
pcc1
|
pt1;
|
|
= cerc
|
15
|
pt1
|
pcc1
|
p3;
|
|
= cerc
|
15
|
pc2
|
pcc1
|
pt2;
|
|
= cerc
|
15
|
pt2
|
pcc1
|
p4;
|
*trace (lc1c3 et lc3c4 et lc1c4);
*trace (l12 et l2c2 et lc1c2 et l1c1);
*trace (lc1c2 et geo3 et geo4 et l34 et geo2 et geo1 et lc1c4);
*trace (l34 et l48 et l78 et l37);
*y= coor 2 l3c4;
*x = 0.05*(exp(-1.*(y - (h1+hc))*(y - (h1+hc))/0.002)); *deplace
l3c4 plus (NOMC x ur);
*trace (lc1c2 et l4c2 et l34 et l3c4 et lc1c4);
*y= coor 2 l4c2;
*x = 0.05*(exp(-1.*(y - (h1+hc))*(y - (h1+hc))/0.002)); *deplace
l4c2 plus (NOMC x ur);
*trace (lc1c2 et l4c2 et l34 et l3c4 et lc1c4);
opti elem tri3;
uvalc= surf (lc1c3 et lc3c4 et lc1c4); *trace uvalc;
subase= surf (l12 et l2c2 et lc1c2 et l1c1); *trace subase;
rect= surf (lc1c2 et geo3 et geo4 et l34 et geo2 et geo1 et
lc1c4); *trace rect;
prect= surf (l34 et l48 et l78 et l37); *trace prect;
su1 = uvalc;
su2 = subase et rect et prect; su0 = su1 et su2;
trace su0;
*caracteristiques de la modelisation
mo1 = mode su1 mecanique elastique;
mo2 = mode su2 mecanique elastique; mo0 = mo1 et mo2;
*mo0 = mode su0 mecanique elastique;
*caracteristiques du materiau
*ma0 = mate mo0 YOUN 100. nu 0.45 ;
ma1 = mate mo1 YOUN 0.9 nu 0.45;
ma2 = mate mo2 YOUN 0.2 nu 0.45; ma0 = ma1 et ma2;
*trac su0 ;
*cl1 = bloq UZ (l12 et l78);
*cl2 = bloq UR (l12 et l78);
cl1 = bloq UZ (l12 et l78);
cl2 = bloq ur l78 ;
rg0 = rigi mo0 ma0 ;
ppp0 = 0.0105 ;
*presV0=pression mass mo0 2. lc1c3;
presV0=pression mass mo0 ppp0 (lc1c3 et l1c1); uel0 = reso (rg0
et cl1 et cl2) presv0;
trac ((defo su0 uel0 0. blan) et
(defo su0 uel0 1. roug)) ;
*opti donn 5 ;
* * ** * * * * * * ** * * * * * * ** * * * * * ** * * * * * * **
* * * * * * ** * * * * * * *resolution de la premiere iteration
* * ** * * * * * * ** * * * * * * ** * * * * * ** * * * * * * **
* * * * * * ** * * *
ev0 = evol manu T (prog 0. 2.) F(T) (prog 0. 2.) ; cha0 = char
meca presV0 ev0 ;
tb0 = table ;
tb0 . MODELE = mo0 ;
tb0 . CARACTERISTIQUES = ma0 ;
tb0 . BLOCAGES MECANIQUES = cl1 et cl2 ;
tb0 . CHARGEMENT = cha0 ;
tb0 . GRANDS DEPLACEMENTS = VRAI ;
tb0 . GRANDES ROTATIONS = VRAI ;
tb0 . TEMPS CALCULES = PROG 0. PAS 0.01 0.99 pas 0.01 1. ;
pasapas tb0 ;
u2 = peche tb0 deplacements 1.;
*u2 = reso (rg0 et cl1 et cl2) fpr2 ; dsu0 1 = defo su0 u2 1.
rouge ;
dsu0 0 = defo su0 u2 0. bleu ; dsl00 = defo l00 u2 0. rouge ;
dsuel0 = defo su0 uel0 1. vert ;
trac (dsu0 1 et dsu0 0 et dsl00 et dsuel0) ;
** ** * * *
OPTION 'TRAC' PSC;
** si couleur PSC
nomfic = 'valv.ps';
OPTION 'FTRAC' nomfic;
trac (dsu0 1 et dsu0 0 et dsl00 et dsuel0) ;
trac (dsu0 1 et
dsu0 0 et dsl00 et dsuel0) ;
Annexe
Exemple d'un programme sous Matlab
| 


