République Algérienne Démocratique
et Populaire
Ministère de l'Enseignement Supérieur et de la
Recherche Scientifique
Centre Universitaire de BÉCHAR
Département d'Électrotechnique
Bechar, Algérie
Mémoire Présenté par
:
Boumediène ALLAOUA
Pour l'obtention du diplôme de :
Ingénieur d'état en
Électrotechnique
Option : Réseaux Électriques.
Intitulé
|
Modélisation & Commande Vectorielle d'un
Système Multi-Moteurs
(Système de Bobinage)
|
Soutenue le: Juin 2006
Devant les Membres du jury:
|
Président :
|
A. LAOUFI
|
M.C Centre Universitaire de BÉCHAR
|
|
Promoteur :
|
A. HAZZAB
|
M.C Centre Universitaire de BÉCHAR
|
|
Examinateur :
|
I.K. Bousserhane
|
C.C Centre Universitaire de BÉCHAR
|
|
Examinateur :
|
K. LAOUFI
|
C.C Centre Universitaire de BÉCHAR
|
Centre Universitaire de Béchar
BP 417, Route de Kénadsa, Béchar,
Algérie, : (213) 49.81.55.81/91, : (213)
49.81.52.44
1 RESUME
Dans les industries du papier, du textile, du bobinage et de
l'extrusion de plastique, les entraînements électriques sont
fréquemment appelés à travailler en synchronisme, avec des
tolérances souvent élevées pour assurer une qualité
uniforme du produit et éviter les bris. Le système
étudié est représentatif de ces secteurs et composé
de cinq moteurs qui sont couplés par une toile dont une tension
mécanique.
La commande vectorielle indirecte a été
développée et nous a permis de vérifier la
stabilité du système et de rendre la machine asynchrone similaire
à une machine à courant continue.
La validation des résultats de simulation est faite sur
le logiciel Simulink sous
Matlab, qui nous permet de simuler le comportement du
système dans le temps. Les résultats obtenus montrent des
meilleures performances, ainsi qu'une bonne robustesse.
2 3 abstract
In the industries of the paper, textile, the winding and the
extrusion of plastic, the electric practices are called à frequently to
work in step, with tolerances often raised to assure an uniform quality of the
product and to avoid the breakages. The studied system is representative of
these sectors and composed of five motors that are coupled by a canvas of which
a mechanical tension.
The indirect vectorial control has been developed and permits
us to verify the stability of the system and to let the machine asynchronous
similar at the direct current machine.
The validation of the simulation results is made on the
software Simulink under
Matlab, that permits us to simulate the behavior of
the system in the time. The gotten results show the best performances, as well
good robustness.
4
NOMENCLATURE
|
Symbole
|
Désignation
|
Unité
|
|
d et q
|
Axes direct et en quadratique.
|
--
|
|
 et
et 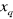
|
Composantes de la grandeur  dans
le repère (d-q). dans
le repère (d-q).
|
--
|
|
Flux.
|
Wb
|
|
 et et
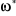
|
Vitesse angulaire et vitesse de référence.
|
rad/sec
|
|
 et et
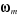
|
Vitesses angulaires électriques (s : stator,
m : rotor).
|
rad/sec
|
|
Glissement de vitesse angulaire électrique.
|
--
|
|
 et et
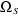
|
Vitesse mécanique et la vitesse synchrone.
|
rad/sec
|
|
 et et
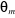
|
Angle électrique statorique et rotorique.
|
rad
|
|
 et et
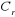
|
Couple électromagnétique et Couple
résistant.
|
N.m
|
|
Ecart entre la vitesse  et et
 . .
|
rad/sec
|
|
Tension.
|
V
|
|
Courant.
|
A
|
|
 et et
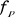
|
Fréquence de l'onde de référence et
Fréquence de l'onde porteuse.
|
Hz
|
|
 et et
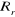
|
Résistances statorique et rotorique.
|
|
|
 et et
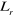
|
Inductances statorique et rotorique.
|
H
|
|
Inductance mutuelle propre.
|
H
|
|
Coefficient de frottement.
|
N.m.sec/rad
|
|
Moment d'inertie.
|
kg/m2
|
|
Nombre de paire de pôles.
|
--
|
|
Opérateur de LAPLACE.
|
--
|
|
 et et 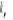
|
Gain intégral et proportionnel du régulateur PI.
|
--
|
|
pôle désiré.
|
--
|
|
Constante du temps rotorique.
|
sec
|
|
 et et
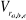
|
Tensions de phases (stator et rotor).
|
V
|
|
 et et
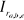
|
Courants statoriques et rotoriques de phases.
|
A
|
|
 et et
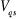
|
Tensions statoriques suivant les axes direct et en
quadratique.
|
V
|
|
 et et
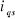
|
Courants statoriques suivant les axes direct et en
quadratique.
|
A
|
|
Grandeur de référence de la variable . .
|
--
|
|
Coefficient de dispersion.
|
--
|
|
g
|
Le glissement.
|
--
|
|
Masse de noyau.
|
Kg
|
|
m
|
Masse totale du rouleau de papier.
|
Kg
|
|
Rayon du noyau.
|
m
|
|
V
|
Vitesse de défilement du papier.
|
m/s
|
|
H
|
Épaisseur de la feuille de papier.
|
m
|
|
l
|
Longueur longitudinale du rouleau de papier.
|
m
|
|
Densité de masse de la feuille de papier.
|
|
|
Inertie à vide.
|
|
|
Ti (i=1,4)
|
Tension dans le matériau entre chaque paire de
rouleaux.
|
N
|
|
i (i=1,4)
|
Contrainte imposée au matériau.
|
__
|
|
E
|
Module de Young de la bande.
|
N/m²
|
|
S
|
Section d'enchaînement.
|
m²
|
|
L0
|
Longueur nominale d'enchaînement (sans effort).
|
m
|
|
L
|
Longueur d'enchaînement sous l'effort.
|
m
|
|
i (i=1,4)
|
Densité volumique du matériau.
|
kg/m
|
|
 (i=1,5)
(i=1,5)
|
Vitesse linéaire du roulement i.
|
m/s
|
|
 (i=1,5)
(i=1,5)
|
Vitesse de rotation du roulement i.
|
rad/s
|
|
 (i=1,5) (i=1,5)
|
Rayon du rouleau i de papier.
|
m
|
|
 (i=1,5) (i=1,5)
|
Moment d'inertie du rouleau i.
|
|
|
 (i=1,5) (i=1,5)
|
Coefficient de frottement visqueux du rouleau . .
|
N.m.s/rad
|
|
 (i=1,4)
(i=1,4)
|
Tension mécanique entre les rouleaux i et
i+1.
|
N
|
|
 (i=1,4) (i=1,4)
|
Longueur d'enchaînement entre les rouleaux i et
i+1.
|
m
|
|
Somme des couples de frottement.
|
N.m
|
|
Matrices diagonales des paramètres.
|
__
|
TABLE DES MATIÈRES i
LISTE DES FIGURES v
NOMENCLATURE ix
5 INTRODUCTION
GÉNÉRALE
1. PROBLÉMATIQUE 1
2. OBJECTIFS 2
3. MÉTHODOLOGIE 2
4. STRUCTURE DU MÉMOIRE 2
CHAPITRE 1 : MODÉLISATION ET COMMANDE
VECTORIELLE DE LA MACHINE
ASYNCHRONE.
1.1. INTRODUCTION 3
1.2. MODÉLISATION DE LA MACHINA ASYNCHRONE 3
1.2.1. Principe de fonctionnement de la MAS 3
1.2.2. Hypothèses simplificatrices pour la
modélisation 4
1.2.3. Modélisation électrique 4
1.2.3.1. Équations
générales du modèle biphasé de la machine
asynchrone 4
1.2.3.2. La représentation
d'état du modèle avec entrées en tension de la MAS 5
1.2.3.2.a. Choix des
variables d'état 5
1.2.3.2.b. Le couple
électromagnétique de la machine asynchrone 7
1.2.3.2.c. Modèle
final de la machine asynchrone 7
1.2.4. Commande de
l'onduleur par Modulation de Largeur d'Impulsion (MLI) 8
1.3. LA COMMANDE VECTORIELLE DE LA MACHINE ASYNCHRONE 10
1.3.1. Principe de la commande vectorielle 10
1.3.2. Équations dans le repère d-q
10
1.3.3. Commande vectorielle indirecte 11
1.3.3.1. Calcul des régulateurs
13
1.3.3.1.a. Régulateur
du courant  13
13
1.3.3.1.b. Régulateur
du courant  14
14
1.3.3.1.c. Calcul du
régulateur de vitesse 14
1.3.3.2. Test de découplage 15
1.3.3.3. Réglage de la MAS par la
commande vectorielle indirecte 15
1.3.3.4. Résultat de simulation
16
1.4. CONCLUSION 17
CHAPITRE 2 : MODÉLISATION DU SYSTÈME
MULTI-MOTEUR (SMM) ET
LA REPRÉSENTATION
ÉNERGÉTIQUE MACROSCOPIQUE (REM).
2.1. INTRODUCTION 18
2.2. MODÉLISATION DU SYSTÈME MULTI-MOTEUR (SMM)
18
2.2.1. Structure du système multi-moteur (SMM)
étudié 18
2.2.1.1. Description de la partie
mécanique 18
2.2.1.2. Description de la partie
électrique 19
2.2.2. Modèle des principaux
éléments constitutifs du système 20
2.2.2.1. Modélisation du moteur
asynchrone triphasé 20
2.2.2.2. Modélisation de
l'enrouleur - dérouleur 20
2.2.2.3. Modélisation de la toile
entre deux rouleaux consécutifs 22
2.2.3. Modèle du système multi-moteur
(SMM) 25
2.2.3.1. Vitesse d'enchaînement sur
chaque roulement 25
2.2.3.2. Modèle complet 26
2.2.3.3. Équations
mécaniques de la structure complète 27
2.3. REPRÉSENTATION ÉNERGÉTIQUE
MACROSCOPIQUE 29
2.3.1. Définition de la REM 29
2.3.2. Éléments de
représentation de la REM 29
2.3.3. Description des éléments de la
REM du système 29
2.3.3.1. Modélisation de la
première partie (alimentation) 30
2.3.3.1.a. Source
énergétique 30
2.3.3.1.b. Impédance
de ligne 30
2.3.3.1.c. Redresseur six
diodes 31
2.3.3.1.d. Batterie de
condensateur 31
2.3.3.2. Modélisation de la
deuxième partie (moteur-électrique) 31
2.3.3.2.a. Onduleur
Triphasé 32
2.3.3.2.b. Stator de moteur
asynchrone 32
2.3.3.2.c. Machine
asynchrone MAS 32
2.3.3.3. Modélisation de la
troisième partie (couplage mécanique) 33
2.3.3.3.a. Arbre du moteur
33
2.3.3.3.b. Conversion des
vitesses et forces/couples 33
2.3.3.3.c. Couplage entre
moteurs 34
2.3.3.3.d. Toile 34
2.3.4. Représentation complète du
système cinq moteurs par REM 34
2.4. CONCLUSION 36
CHAPITRE 3 : RÉSULTATS DE SIMULATION.
3.1. INTRODUCTION 37
3.2. LES DIFFÉRANTS SCHÉMAS DES BLOCS 37
3.3. LES RÉSULTATS DE SIMULATION 40
3.3.1. Résultats de simulation (trois moteurs)
40
3.3.2. Résultats de simulation (cinq moteurs)
42
3.4. CONCLUSION 45
CONCLUSION GÉNÉRALE 46
RÉFÉRENCES BIBLIOGRAPHIQUES 48
ANNEXE (1) : Paramètres de la machine asynchrone
51
ANNEXE (2) : Industrie papetière 52
RESUME & ABSTRACT
6
INTRODUCTION GÉNÉRALE
1. PROBLÉMATIQUE
Dans l'industrie, le papier, le plastique et d'autres
matériaux minces élastiques sont souvent employés pour la
fabrication de produits commerciaux en employant un processus continu. Dans ce
cas-ci, le papier ou tout autre matériel est typiquement
déroulé d'un grand roulement en utilisant une série de
rouleaux et un débobineur, formant ce qui s'appelle un
enchaînement.
Le but principal de l'enchaînement est l'affectation du
processus pour transférer le matériau avec une vitesse maximum et
des dommages au minimum possible [40]. Pour réaliser ceci, il faut
l'investiture de ces raisons suivantes:
· La tension d'enchaînement affecte la
géométrie de l'enchaînement, tel que la longueur et la
largeur apparentes de l'enchaînement;
· Une tension élevée d'enchaînement
empêche la perte de traction sur les rouleaux mais elle produira une
déchirure si elle est trop élevée;
· La tension d'enchaînement affecte la fissure dans
le matériau et la forme du roulement final du produit, et par
conséquent la qualité du matériel.
Pour ces raisons, il est essentiel que l'enchaînement
qu'on manipule pour commander la tension à une valeur
désirée soit performant. Normalement, la tension
d'enchaînement devrait être placée entre 10 et 25% de la
force de rupture
Nous étudierons ultérieurement les
propriétés de la machine d'enchaînement qui a
été utilisée comme cas d'étude dans ce
mémoire.
Dans ce mémoire, la réalisation et
l'évaluation de tension mécanique et de vitesse
d'enchaînement dans un bobineur représenté par un
modèle mathématique seront obtenues. Les récents
progrès réalisés dans la commande et l'alimentation des
machines électriques font de celles-ci des outils d'autant plus souples
et faciles à contrôler. On trouve aujourd'hui plus couramment
plusieurs moteurs, chacun condamné à une tâche, dans un
procédé, et dont la vitesse est maintenant réglée
presque continûment, directement en fonction de l'application
étudiée [41,42]. Les exigences en termes de performances
dynamiques et de régulation ont bien sûr changé avec le
développement de méthodes de réglage et de contrôle
de plus et plus efficaces. Au départ, il existait un fort couplage
entre les charges mécaniques, toutes reliées à la
même machine. De plus ce couplage ne pouvait pas être
maîtrisé d'une façon rigoureuse. Donc, le réglage
imposera une certaine synchronisation des charges mécaniques. Avec
l'emploi de plusieurs moteurs d'enchaînement, les réglages sont
plus précis et les autres types de couplages peuvent être pris en
considération dans la synthèse du contrôle global.
Ainsi, les couplages entre les différentes machines et
leur prise en compte par la commande sont devenus un axe de recherche
considérable. En revanche, bien que faisant partie de la chaîne de
conversion de l'énergie, le couplage mécanique s'éloigne
un peu du génie électrique pur pour se retrouver à la
frontière entre l'automatique, la mécanique et
l'électrotechnique. Il s'agit de rechercher de nouvelles connaissances,
de passer par un nouvel apprentissage, entièrement liés à
la charge mécanique et à son couplage spécifique.
Le contexte géographique de la préparation de ce
mémoire, nous nous sommes naturellement orienté vers une
application à l'industrie papetière annexe (2). Dans les divers
procédés rencontrés pour cette industrie, il existe un
motif redondant qu'on appelle transport de bande [30]. Il désigne un
système de type Dérouleur-Enrouleur auquel peuvent être
adjoints des rouleaux d'entraînement par friction. Bien
évidemment, on ne peut réduire l'industrie papetière
à ce type de processus, ni réduire les applications du transport
de bande à l'industrie papetière.
2. OBJECTIFS
L'objectif principal de ce travail est de synthétiser
systématiquement les correcteurs du modèle d'un système
constitué de cinq entraînements et qui sont couplés
mécaniquement par une bande dont la tension est réglable.
Afin d'atteindre l'objectif principal fixé,
différents sous objectifs sont définis ainsi :
· La modélisation et la commande vectorielle de la
machine asynchrone ;
· Adapter un modèle de banc d'essais qui a
été conçu pour réaliser des travaux de recherche
sur la commande de systèmes multi-moteurs ;
· La Représentation Énergétique
Macroscopique a été développée par le Laboratoire
d'Électronique et d'Électrotechnique de Puissance de
Lille (L2EP). Cet outil permet d'analyser des systèmes plus ou
moins complexes composés de plusieurs machines et/ou plusieurs
convertisseurs dans des entraînements électriques et/ou
mécaniques.
3. MÉTHODOLOGIE
Dans ce travail, une seule technique de commande d'un
système d'entraînement est développée après
en avoir rappelé la théorie. Le système à
l'étude est constitué de cinq entraînements. Les
différents enchaînements sont couplés mécaniquement
par une bande dont la tension est réglable. Le matériel
transféré est caractérisé par ses
propriétés élastiques et géométriques.
L'efficacité des techniques de commande sera évaluée par
simulation sous Simulink.
4. STRUCTURE DU MÉMOIRE
Le chapitre 1 est consacré à la
modélisation et la commande vectorielle de la machine asynchrone.
Le chapitre 2 présente la modélisation de
Système Multi-Moteurs (SMM) et la Représentation
Énergétique Macroscopique (REM).
Le chapitre 3 conclut le mémoire en présentant
les résultats de simulation avec l'interprétation.
Les différentes simulations sont faites sous
l'interface SIMULINK sous MATLAB version
7.0.4.
7 CHAPITRE 1
:
8 9 MODÉLISATION ET
COMMANDE
10 VECTORIELLE DE LA MACHINE ASYNCHRONE
1.1. INTRODUCTION
Les équations de Park ont été et sont
encore la référence pour l'élaboration du modèle de
connaissance traduisant le comportement dynamique des modes électriques
et électromagnétiques de la machine. Même si, actuellement,
certains travaux sont réalisés pour affiner ces équations
(prise en compte des effets de saturation magnétique), le modèle
de Park, décrit par un système algébro-différentiel
non linéaire, reste toujours pour l'automaticien le modèle le
plus intéressant par rapport aux différentes classes de
représentations d'état qu'il permet d'exprimer. En effet, selon
le type de commande que l'on veut réaliser : couple, vitesse,
position, selon la nature de la source d'alimentation (tension ou courant), du
référentiel de travail ((á,â), (d,q)), et enfin des
composantes du vecteur d' état (flux ou courants statoriques ou
rotoriques), différents modèles d'états peuvent être
formulés.
Au début des années 70, Blaschke et Hasse ont
donné naissance à une nouvelle technique dite commande
vectorielle. Par cette technique, la machine asynchrone (MAS) peut avoir les
mêmes propriétés avec la machine à courant continu
(MCC), sans les inconvénients liés au système
balais-collecteur [1,2,3]. Les travaux de recherche effectués sur ce
sujet utilisent une des principales trois méthodes, qui la
deuxième. La première dite « méthode
directe », a été initiée par Blaschke [2], la
deuxième dite « méthode indirecte » a
été introduite par Hasse [4] et la troisième dite
« méthode simplifiée » est
développée par Robyns sur une machine alimentée en tension
dont le rôle est de linéariser le comportement de la machine
[5].
Dans ce chapitre, nous présentons la
modélisation de la machine asynchrone en mettant l'accent sur sa
représentation d'état liée aux entrées et sorties
du moteur. Nous donnons aussi un aperçu sur la commande vectorielle
appliquée à une machine asynchrone alimentée en tension.
La méthode obtenue dans la suite de notre travail est
la méthode indirecte, dans cette méthode, et pour le
réglage du courant et de la vitesse nous avons utilisé un
contrôleur conventionnel Proportionnel - Intégral (PI).
1.2. MODÉLISATION DE LA MACHINA ASYNCHRONE
1.2.1. Principe de fonctionnement de la
MAS
Le moteur à induction se comporte comme un
transformateur à couplage par champ tournant et à secondaire en
court-circuit. Les terminologies utilisées pour une machine asynchrone
se rapprochent donc de celles utilisées dans l'étude des
transformateurs [11,14]. Le primaire alimenté par des courants à
la pulsation  crée un champ tournant à la vitesse synchrone
crée un champ tournant à la vitesse synchrone  où
où  désigne le nombre de paires de pôles de la machine. Ce champ
balaie le rotor de sorte que les enroulements secondaires sont traversés
par un flux variable. Celui-ci est à l'origine de f.e.m (forces
électromotrices) induites. Les courants qui en résultent donnent
naissance à un moment magnétique qui, sous l'action du champ
primaire, provoque l'apparition d'un couple électromagnétique. Si
le rotor tourne à la vitesse synchrone, le flux à travers le
secondaire ne varie plus, donc il n'y a pas de f.e.m induites, donc de couple.
[11]
désigne le nombre de paires de pôles de la machine. Ce champ
balaie le rotor de sorte que les enroulements secondaires sont traversés
par un flux variable. Celui-ci est à l'origine de f.e.m (forces
électromotrices) induites. Les courants qui en résultent donnent
naissance à un moment magnétique qui, sous l'action du champ
primaire, provoque l'apparition d'un couple électromagnétique. Si
le rotor tourne à la vitesse synchrone, le flux à travers le
secondaire ne varie plus, donc il n'y a pas de f.e.m induites, donc de couple.
[11]
Le moteur tourne à une vitesse  d'autant plus inférieure à
d'autant plus inférieure à  que
le couple développé est important, puisque la variation du flux,
donc des f.e.m et des courants du secondaire, est liée à la
vitesse relative
que
le couple développé est important, puisque la variation du flux,
donc des f.e.m et des courants du secondaire, est liée à la
vitesse relative  . En
général, cette différence de vitesse relative est
évaluée par le glissement [14] :
. En
général, cette différence de vitesse relative est
évaluée par le glissement [14] :
1.2.2. Hypothèses simplificatrices pour la
modélisation
La machine asynchrone étant un système dynamique
non linéaire, il est nécessaire de disposer d'un modèle
représentant fidèlement son comportement au niveau de ses modes
électriques, électromagnétique et mécanique. Dans
la littérature de la « commande », le modèle
de Park est généralement choisi. En effet, c'est une solution qui
tient compte d'une part des qualités demandées par la commande et
qui d'autre part prend en compte des hypothèses simplificatrices
intrinsèques au système.
Nous nous plaçons dans le cas d'une machine asynchrone
triphasée et symétrique dont le rotor est à cage. Les
hypothèses permettant de mettre en place le modèle de Park sont
les suivantes [14] :
§ Le circuit magnétique est non
saturé ;
§ L'entrefer est parfaitement lisse ;
§ La densité du courant est uniforme dans les
conducteurs élémentaires ;
§ Les pertes dans le fer sont négligeables.
1.2.3. Modélisation
électrique
La machine asynchrone est de nature triphasée. La
structure symétrique et équilibrée de la machine permet de
passer à une représentation biphasée équivalente
(transformation de Park), réduisant considérablement la
complexité du modèle en vue de la commande. Toutes les grandeurs
électromagnétiques (flux, courants) soient statoriques ou
rotoriques sont ramenées sur un seul repère. Ce repère
peut être positionné soit fixe par apport au stator (repère
á-â), soit tournant (repère d-q)). Un repère
tournant implique la présence d'une variable supplémentaire qui
permet de définir la position de ce repère.
1.2.3.1. Équations générales du
modèle biphasé de la machine asynchrone
Dans le cas d'un repère tournant et après
transformation de Park [9,10], les équations de la machine sont
données de manière générale par les
équations ci-dessous (dans ce modèle, toutes les grandeurs
sont ramenées dans le repère d-q): [6,7,8] :
|
(1.2)
|
|
(1.3)
|
|
(1.4)
|
|
(1.5)
|
|
(1.6)
|
|
(1.7)
|
|
(1.8)
|
|
(1.9)
|
|
Avec :
|
|
|
(1.10)
|
|
(1.11)
|
La vitesse mécanique est donnée par  où
où  est
le nombre de paires de pôles.
est
le nombre de paires de pôles.  donne la vitesse angulaire du repère d-q tournant. La différence
entre
donne la vitesse angulaire du repère d-q tournant. La différence
entre  et
et  est
la vitesse de glissement
est
la vitesse de glissement . Le
repère á-â n'est qu'un cas particulier du repère d-q
en prenant
. Le
repère á-â n'est qu'un cas particulier du repère d-q
en prenant  nulle.
nulle.
1.2.3.2. La représentation d'état du
modèle avec entrées en tension de la MAS
Nous étudions ici la classe des objectifs relative au
contrôle de la vitesse ou de la position sous l'hypothèse d'un
fonctionnement à flux constant, ce choix représente en effet
(avec le contrôle du couple [10]) la majorité des applications de
commande de la machine asynchrone dans le domaine industriel à vitesse
variable.
Ces objectifs imposent donc directement le choix des sorties
du système. La représentation d'état du moteur
dépend, comme nous l'avons vu, du repère choisi et du choix des
variables d'état du modèle s'il est avec entrées en
tension où avec entrées en courant [11,12,13] pour les
équations électriques. Nous donnons, dans ce chapitre, dans la
suite de cette thèse, une classe de modèle (modèle avec
entrées en tension) de la machine asynchrone qui sera exploitée
pour la mise au point de nos lois de commande.
1.2.3.2.a. Choix des variables
d'état
Le choix des variables d'état dépend des
objectifs liés soit à la commande soit à l'observation.
Pour le modèle complet, la vitesse mécanique, dont on veut
contrôler l'évolution, est une variable d'état. Nous
considérons dans notre cas les variables d'état
suivants :
Ce choix de variables se justifie d'une part par le fait que
les courants statoriques sont mesurables et d'autre part parce que l'on veut
réguler la norme du flux rotorique. Bien entendu, d'autres choix
associant uniquement les courants ou les flux statoriques et rotoriques sont
possibles. Les entrées du modèle de la machine asynchrone sont
les tensions de commande  ,
,
 .
.
Pour mettre les équations sous forme de
représentation d'état, nous devons modifier les équations
des tensions statoriques (1.6), (1.7) afin d'exprimer les flux  et
et
 en fonction des variables d'état :
en fonction des variables d'état :  ,
, ,
, et
et
 . En considérant les équations des flux (1.2)-(1.5) et en
introduisant le coefficient de dispersion magnétique
. En considérant les équations des flux (1.2)-(1.5) et en
introduisant le coefficient de dispersion magnétique , on
trouve les composantes du flux statorique :
, on
trouve les composantes du flux statorique :
Et leurs dérivées :
En remplaçant dans les équations des tensions
rotoriques (1.8), (1.9) les courants rotoriques  et
et
 par les équations (1.2)-(1.5), on obtient :
par les équations (1.2)-(1.5), on obtient :
Les équations des tensions statoriques (1.6), (1.7)
prennent donc la forme :
En introduisant les définitions suivantes :
Ces quatre dernières équations (1.17)-(1.20)
permettent d'obtenir la mise en forme matricielle de la représentation
d'état :
A ces équations électriques, nous devons
associer le vecteur de sorties  ainsi que l'équation mécanique pour obtenir le modèle
complet. Les sorties du modèle que l'on considérera seront dans
notre cas, et dans un premier temps, la vitesse mécanique et la norme du
flux rotorique ; dans un deuxième temps, la position
mécanique et la norme du flux rotorique. Concernant les sorties
citées, la vitesse mécanique est mesurable par des
tachymètres ou par l'intermédiaire de la position à l'aide
des codeurs incrémentaux. Si le couple est choisi comme sortie, celui-ci
peut être mesuré à l'aide de couplemètres
mécaniques posés sur l'arbre de la machine. Cependant, pour une
question de coût, ces appareils de mesure ne sont pas toujours
disponibles pour l'industriel, le corollaire est alors une demande de commande
de moteur sans capteur. La deuxième sortie, la norme du flux rotorique
est généralement choisie constante en fonction de deux
considérations fondamentales :
ainsi que l'équation mécanique pour obtenir le modèle
complet. Les sorties du modèle que l'on considérera seront dans
notre cas, et dans un premier temps, la vitesse mécanique et la norme du
flux rotorique ; dans un deuxième temps, la position
mécanique et la norme du flux rotorique. Concernant les sorties
citées, la vitesse mécanique est mesurable par des
tachymètres ou par l'intermédiaire de la position à l'aide
des codeurs incrémentaux. Si le couple est choisi comme sortie, celui-ci
peut être mesuré à l'aide de couplemètres
mécaniques posés sur l'arbre de la machine. Cependant, pour une
question de coût, ces appareils de mesure ne sont pas toujours
disponibles pour l'industriel, le corollaire est alors une demande de commande
de moteur sans capteur. La deuxième sortie, la norme du flux rotorique
est généralement choisie constante en fonction de deux
considérations fondamentales :
§ La première est liée à la
facilité de la commande puisque le couple est alors régulé
uniquement par un courant 
§ La seconde est liée aux performances dynamiques
qui sont meilleurs puisque le couple est proportionnel à un courant.
1.2.3.2.b. Le couple électromagnétique
de la machine asynchrone
Le couple électromagnétique  développé par la machine peut s'exprimer de différentes
façons qui dépendent de la stratégie de commande
adoptée.
développé par la machine peut s'exprimer de différentes
façons qui dépendent de la stratégie de commande
adoptée.
Du point de vue de l'état et de par le choix de nos
variables d'état, le couple de la machine est donné par le
produit vectoriel suivant :
Avec :  indique le produit vectoriel.
indique le produit vectoriel.
Cette expression de couple sera celle utilisée pour
écrire le modèle final de la machine sous forme de
représentation d'état.
1.2.3.2.c. Modèle final de la machine
asynchrone
A l'équation du couple électromagnétique
(1.24) s'ajoute l'équation mécanique :
Où  représente le couple résistant du aux frottements ainsi
qu'à la charge de la machine,
représente le couple résistant du aux frottements ainsi
qu'à la charge de la machine,  est l'inertie de l'ensemble tournant.
est l'inertie de l'ensemble tournant.
L'équation (1.25) peut aussi s'écrire :
Avec :
 : le couple de charge ;
: le couple de charge ;
 : le coefficient du frottement sur l'arbre.
: le coefficient du frottement sur l'arbre.
En utilisant les notations (1.21), le modèle non
linéaire complet de la machine asynchrone est donné par :
Avec :
 ,
,
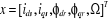
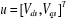
|
 et et
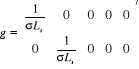
|
(1.29)
|
1.2.4. Commande de l'onduleur par Modulation de
Largeur d'Impulsion (MLI)
L'onduleur a pour objectif de produire des tensions
alternatives variables en amplitude et en fréquence, en fonction des
caractéristiques électromagnétiques
désirées. Une principale stratégie peut être mise en
oeuvre [6,14,15] et retenue dans la suite de notre travail, c'est la
méthode de contrôle par modulation de largeur d'impulsion
(MLI).
Figure 1.1 : Principe de la commande
à MLI.
Commande des interrupteurs
Bras d'un onduleur
Porteuse
Modulateur
Régulateur
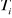
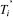
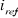
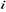
-
La méthode consiste à imposer aux bornes de la
machine des créneaux de tension de manière à ce que le
fondamentale de la tension soit le plus proche de la référence.
Plusieurs techniques sont réalisables pour la modulation de largeur
d'impulsion [14,16,18,19]. La technologie la plus utilisée consiste
à comparer un signal triangulaire (porteuse) avec un signal de
référence, l'intersection des deux signaux définit les
instants de commande des interrupteurs (figure 1.1).
On définit l'indice de modulation  comme le rapport de la fréquence
comme le rapport de la fréquence  de
la porteuse à la fréquence
de
la porteuse à la fréquence  de
la tension de référence. Le taux de modulation
de
la tension de référence. Le taux de modulation  est le rapport de l'amplitude
est le rapport de l'amplitude  de
la tension de référence à l'amplitude
de
la tension de référence à l'amplitude  de
la porteuse.
de
la porteuse.
L'association de l'onduleur à MLI avec la MAS est
schématisée par la figure 1.2, les tensions de
référence sont calculées par une transformation de
coordonnées.
Figure 1.2 : Association de
l'onduleur à MLI avec la MAS.
dq
abc
Onduleur
MAS
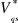
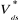
Commande à
MLI
La simulation de l'ensemble MAS dont les paramètres
sont donnés dans l'annexe (1) et l'onduleur à MLI a
été faite sous les conditions de fonctionnement suivantes avec un
temps de simulation de  :
:
§ Démarrage à vide;
§ A l'instant  application d'une charge de
application d'une charge de  ;
;
§ A  élimination de la charge.
élimination de la charge.
On remarque que la duré de régime transitoire
4.4 sec, et que la vitesse se diminue avec l'augmentation de la charge et puis
elle augmente avec sa diminution, d'autre part le couple
électromagnétique  suit la valeur du couple résistant. On note aussi une oscillation au
niveau du courant
suit la valeur du couple résistant. On note aussi une oscillation au
niveau du courant  et
du couple obtenus avec la commande MLI. Le courant de phase est chargé
d'harmonique ceci peut être justifié par la grande
fréquence de la charge de l'onduleur.
et
du couple obtenus avec la commande MLI. Le courant de phase est chargé
d'harmonique ceci peut être justifié par la grande
fréquence de la charge de l'onduleur.
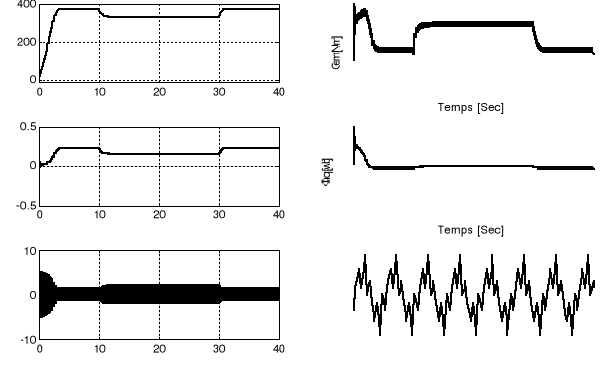
La figure 1.3 décrit les résultats obtenus avec
la commande MLI :
Figure 1.3 : Comportement dynamique
de la MAS associée
à un onduleur à MLI
1.3. LA COMMANDE VECTORIELLE DE LA MACHINE
ASYNCHRONE
1.3.1. Principe de la commande vectorielle
L'algorithme de référence de commande de la
machine asynchrone est la commande à flux orienté
(Field Oriented Control) a
été mis au point par Blaschke en 1972 [4]. Cette méthode a
marqué un pas décisif dans la façon de concevoir la
commande des machines à courant alternatif. En effet, jusqu'aux
développements théorique et pratique de Blaschke, seule la
commande scalaire était utilisée. A partir du constat que la
machine à courant continu était commandée via un
découplage naturel, l'idée fondamentale de Blaschke fut de mettre
au point une commande permettant de ramener le comportement de la machine
asynchrone à celui de la machine à courant continu. Cette
méthode se base sur la transformation des variables électriques
vers un référentiel qui tourne avec le vecteur du flux rotorique.
Par conséquent, ceci permet de commander le flux de la machine avec un
courant  qui est l'équivalent du courant inducteur de la machine à courant
continu. A condition de travailler à flux constant, un courant
orthogonal
qui est l'équivalent du courant inducteur de la machine à courant
continu. A condition de travailler à flux constant, un courant
orthogonal  permet de contrôler le couple
électromagnétique, correspondant au courant induit de la machine
à courant continu.
permet de contrôler le couple
électromagnétique, correspondant au courant induit de la machine
à courant continu.
Trois méthodes de commandes vectorielles sont
possibles : la commande vectorielle directe où l'on estime la norme
et la position du flux rotorique, la commande vectorielle indirecte qui estime
uniquement la position du flux rotorique et la commande vectorielle
simplifiée qui sert à linéariser le modèle de la
machine asynchrone et le rendre similaire à celui d'une machine à
courant continu à excitation séparée.
1.3.2. Equations dans le repère d-q
Nous avons vu que le couple en régime transitoire
s'exprime dans le repère d-q comme un produit croisé de courants
ou de flux. Si nous reprenons l'écriture :
On s'aperçoit que si on élimine le
deuxième produit  ,
alors le couple ressemble à celui d'une machine à courant
continu. Donc, il suffit d'orienter le repère d-q de manière
à annuler la composante de flux en quadrature. C'est-à-dire, de
choisir convenablement l'angle de rotation de Park de sorte que le flux
rotorique soit entièrement porté sur l'axe direct d et donc avoir
,
alors le couple ressemble à celui d'une machine à courant
continu. Donc, il suffit d'orienter le repère d-q de manière
à annuler la composante de flux en quadrature. C'est-à-dire, de
choisir convenablement l'angle de rotation de Park de sorte que le flux
rotorique soit entièrement porté sur l'axe direct d et donc avoir
 et
et  (Figure 1.4).
(Figure 1.4).
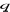
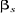
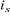
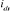
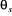
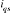
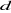
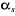
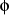
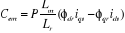
= 0
Figure 1.4 : Principe
d'orientation du flux rotorique.
A partir de là, le modèle de la machine (1.27)
s'écrit :
|
(1.31)
|
|
(1.32)
|
|
(1.33)
|
|
(1.34)
|
|
(1.35)
|
En utilisant l'opérateur transformé de
Laplace ,
l'équation (1.33), peut être réécrite :
,
l'équation (1.33), peut être réécrite :
D'autre part, à partir de l'équation (1.35), le
couple électromagnétique est donné par :
Donc à flux  constant, la composante
constant, la composante  commande le flux rotorique et la composante
commande le flux rotorique et la composante  commande le couple électromagnétique, c'est pourquoi on parle de
découplage dans la commande vectorielle.
commande le couple électromagnétique, c'est pourquoi on parle de
découplage dans la commande vectorielle.
Notons que le problème essentiel de la commande est de
déterminer la norme et la position du flux rotorique, qui ne sont pas
mesurables directement. Il est nécessaire de connaître ces deux
grandeurs pour le contrôle du régime dynamique de la machine. Dans
la suite, la méthode indirecte de la commande vectorielle va être
présentée.
1.3.3. Commande vectorielle indirecte
La méthode indirecte consiste à ne pas estimer
l'amplitude du flux rotorique mais à utiliser directement l'amplitude de
référence .
L'intérêt de cette méthode est d'utiliser uniquement des
grandeurs de référence qui par définition ne sont pas
bruitées. En effet, à partir d'un couple
électromagnétique de référence
.
L'intérêt de cette méthode est d'utiliser uniquement des
grandeurs de référence qui par définition ne sont pas
bruitées. En effet, à partir d'un couple
électromagnétique de référence  et
du flux rotorique de référence
et
du flux rotorique de référence ,
les courants de références
,
les courants de références  et
et
 s'en déduisent directement grâce aux équations
(1.36), (1.37) [17,22,23,24,25,26] :
s'en déduisent directement grâce aux équations
(1.36), (1.37) [17,22,23,24,25,26] :
Pour l'équation (1.34), avant l'intégration, il
est nécessaire de souligner que pour maintenir le flux  nul, il faut imposer
nul, il faut imposer ,
on obtient alors :
,
on obtient alors :
On peut obtenir la position du repère par
intégration de l'équation (1.40) sachant d'une part que la mesure
de la position mécanique  est nécessaire et d'autre part que la composante
est nécessaire et d'autre part que la composante  correspond à la référence, c'est-à-dire
correspond à la référence, c'est-à-dire  .
.
La méthode de commande indirecte se caractérise
donc par le fait qu'aucune estimation du flux n'est nécessaire, le
contrôle vectoriel est alors simplifié. La méthode repose
en fait en grande partie sur la capacité de l'onduleur et de sa commande
à imposer les courants désirés dans la machine. En effet,
à partir de l'instant où le système n'impose pas les
courants désirés, cette commande perd sa principale
propriété de découplage entre flux et couple. Cette
méthode consiste à générer à l'aide d'un
bloc IFOC (Indirect Field
Oriented Control), les tensions
d'alimentation afin d'obtenir un flux et un couple désirés.
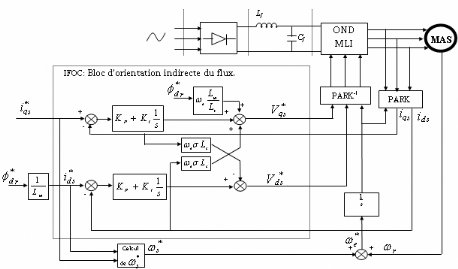
Le schéma de principe de la loi de commande vectorielle
indirecte est présenté dans la figure 1.5 [6, 20,21].
Figure 1.5 : Schéma de
principe de la commande vectorielle indirecte.
Le bloc de contrôle IFOC (génère les trois
grandeurs de commande  ,
,
 et
et  en
fonction des deux entrées de référence (
en
fonction des deux entrées de référence ( ,
,
 ) qui assurent le découplage.
) qui assurent le découplage.
Dans cette commande l'angle  utilisé dans les transformation de Park est calculé par :
utilisé dans les transformation de Park est calculé par :
Ces grandeurs de commande générées par le
IFOC sont utilisées pour contrôler les composants : direct
 et quadratique
et quadratique  du
courant statorique de façon à obtenir des courants identiques aux
courants de référence, et par conséquent, le flux et le
couple maintenus à leurs valeurs de référence.
du
courant statorique de façon à obtenir des courants identiques aux
courants de référence, et par conséquent, le flux et le
couple maintenus à leurs valeurs de référence.
Le calcul des régulateurs est effectué à
l'aide du principe d'imposition des pôles.
1.3.3.1. Calcul des régulateurs
1.3.3.1.a. Régulateur du courant 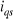
Le régulateur du courant en quadrature fournit la
tension  nécessaire pour maintenir le couple à sa valeur de
référence. La fonction de transfert
nécessaire pour maintenir le couple à sa valeur de
référence. La fonction de transfert  est donnée par :
est donnée par :
Avec :
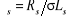
La boucle de régulation du courant est
représentée par la figure 1.6.
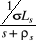
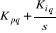
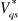
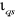
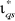
-
+
Figure 1.6 : Schéma de
régulation du courant .
.
La fonction de transfert en boucle fermée est
donnée comme suit :
L'équation caractéristique est du
deuxième ordre, donc en imposant deux pôles complexes
conjugué à partir réelle négative  d'ou :
d'ou :
Par identification, nous obtenons les paramètres du
régulateur PI :
1.3.3.1.b. Régulateur du courant 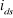
Le régulateur du courant direct fournit la tension  nécessaire pour maintenir le flux à sa valeur de
référence.
nécessaire pour maintenir le flux à sa valeur de
référence.
La fonction de transfert  est donnée par :
est donnée par :
Les mêmes calculs effectués pour le
régulateur du courant  sont appliqués à ce régulateur. Les paramètres du
régulateur sont donc les mêmes et Il sont donnés
par :
sont appliqués à ce régulateur. Les paramètres du
régulateur sont donc les mêmes et Il sont donnés
par :
1.3.3.1.c. Calcul du régulateur de
vitesse
Le régulateur de vitesse permet de déterminer le
couple de référence, a fin de maintenir la vitesse
correspondante. Pour que la cascade soit justifiée, il faut que la
boucle interne soit très rapide par rapport à celle de la
vitesse.
L'équation mécanique donne :
Le schéma bloc de régulation de la vitesse est
indiqué par la figure 1.7.
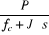
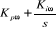
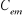
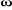
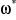
-
+
Figure 1.7 : Schéma bloc
de régulation du la vitesse.
La fonction de transfert en boucle fermée est
donnée par :
L'équation caractéristique  est :
est :
Par imposition de deux pôles complexes conjugués
 en boucle fermée et par identification, on obtient les
paramètres du régulateur PI :
en boucle fermée et par identification, on obtient les
paramètres du régulateur PI :
1.3.3.2. Test de découplage
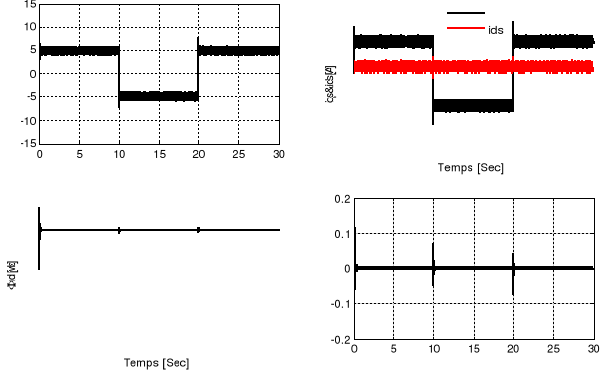
Pour tester l'efficacité du découplage à
l'aide du bloc IFOC une simulation des flux  et
et
 , du couple et des courants
, du couple et des courants  ,
,
 est présentée dans la figure 1.8. Les testes de
simulation ont été faite en injectant un couple
électromagnétique de référence
est présentée dans la figure 1.8. Les testes de
simulation ont été faite en injectant un couple
électromagnétique de référence  =
5N.m, à l'instant t = 10sec,
=
5N.m, à l'instant t = 10sec,  =
-5N.m et a l'instant t = 20sec,
=
-5N.m et a l'instant t = 20sec,  =
5N.m, le flux de référence
=
5N.m, le flux de référence  =
0.55Wb. Les résultats montrent que le flux rotorique et le
couple suivent ses valeurs de consigne et ils présentent des
légers dépassements pendant le démarrage.
=
0.55Wb. Les résultats montrent que le flux rotorique et le
couple suivent ses valeurs de consigne et ils présentent des
légers dépassements pendant le démarrage.
Figure 1.8 : Résultats
de simulation de test de découplage de l'orientation du flux
rotorique par la méthode indirecte.
1.3.3.3. Réglage de la MAS par la commande
vectorielle indirecte
Le schéma de principe de la commande en vitesse de la
machine asynchrone par la méthode indirecte est présenté
par la figure 1.9.
Figure 1.9 : Schéma de
principe de la commande vectorielle indirecte d'une MAS.
OND.
MLI
PARK-1
C
MAS
L
Redresseur
Filtre
Pont
PARK
IFOC
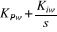
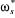
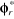
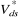
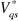
+
-
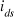
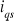
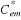
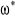
1.3.3.4. Résultat de simulation
Les paramètres du régulateur de vitesse sont
calculés par un emplacement de pôle ( ).
).
Pour évaluer les performances de la commande
vectorielle indirecte en vitesse, nous avons effectués des simulations
numériques sous les conditions suivantes (Figure 1.10) :
§ Démarrage à vide avec application d'un
échelon de vitesse de 100 rad/sec.
§ Application d'un couple de charge égale à
1 N.m à l'instant t = 1 sec, et puis la charge est
éliminée à l'instant t = 20 sec.
§ Inversion de sens de rotation à l'instant t = 30
sec.
La figure 1.10 montre que le réglage par un
régulateur PI donne des résultats satisfaisants :
§ La vitesse de rotation suit la vitesse de
référence ;
§ Le courant est bien limité à sa valeur
admissible ;
§ Le découplage est obtenu entre le flux rotorique
et le couple électromagnétique;
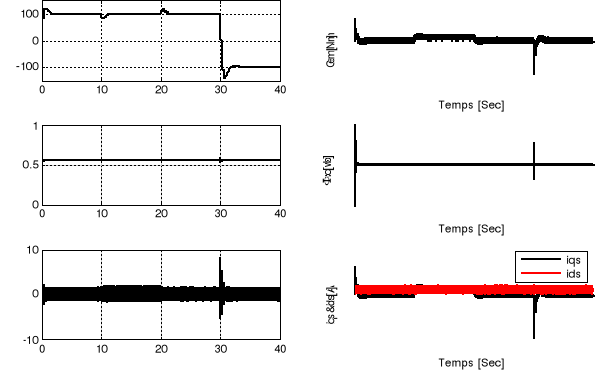
§ Les flux ( et
et
 ) et le couple électromagnétique sont maintenus à
leurs valeurs désirées, impliquant ainsi un bon
découplage.
) et le couple électromagnétique sont maintenus à
leurs valeurs désirées, impliquant ainsi un bon
découplage.
Figure 1.10 : Réglage de
vitesse de la MAS par la commande vectorielle.
1.4. CONCLUSION
Dans ce chapitre, nous avons présenté un
modèle de la machine asynchrone sous forme de représentation
d'état. Le modèle non linéaire multivariable avec pour
entrées les tensions statoriques. Cette modélisation de la
machine asynchrone est donnée en considérant la structure du
système avec une partie primaire (le stator) et une partie secondaire en
court-circuit (le rotor). A partir d'un modèle triphasé, ce
modèle deux phases sont données dans le cadre de certaines
hypothèses permettant de simplifier la modélisation. Les
équations de flux, courants et tensions ont alors été
extraites. De plus, la modélisation est donnée en faisant
apparaître les variables d'états nécessaires aux objectifs
de commande. Cependant, pour se rapprocher de la réalité, il
serait naturel de prendre en considération les équations de
l'onduleur et de les faire intervenir dans la mise au point du modèle de
la machine.
La méthode d'orientation de flux rotorique qui a
été développée c'est la méthode
indirecte.
Cette méthode nous a permis de maintenir parfaitement
le découplage entre le couple et le flux, et rendre la machine
asynchrone similaire à une machine à courant continu, rendant
ainsi la commande de vitesse facile.
11 CHAPITRE 2 :
12
13 MODÉLISATION DU SYSTÈME
14 MULTI-MOTEUR (SMM)
15 ET
16 REPRÉSENTATION ÉNERGÉTIQUE
MACROSCOPIQUE (REM)
17
18 1.2. INTRODUCTION
Ce chapitre est consacré à la
présentation et à la modélisation des
Systèmes
Multi-Moteurs (SMM). Le
système de test est constitué de cinq moteurs. Le principe de
fonctionnement de la maquette est décrit et notamment les
problèmes de gestion que peut engendrer un tel système. Les
travaux à effectuer seront mis en évidence. [33,35]
Dans l'industrie du textile ou du papier [33,34], les
systèmes de bobinage sont très présents. Afin de
modéliser le système multi-moteurs étudié, l'outil
utilisé est une représentation appelée
REM : Représentation
Énergétique Macroscopique. Cet
outil développé par le L2EP [27,32] permet d'analyser des
systèmes plus ou moins complexes composés de plusieurs machines
et/ou plusieurs convertisseurs dans des entraînements électriques
et/ou mécaniques. Le contrôle de la vitesse des moteurs consiste
à avoir une vitesse de rotation identique pour chaque moteur, ce qui
permet de faire avancer la toile à une même vitesse.
2.2. MODÉLISATION DU SYSTÈME
MULTI-MOTEUR (SMM)
2.2.1. Structure du système multi-moteur (SMM)
étudié
La figure 2.1 présente un système
d'entraînement constitué de cinq moteurs triphasés, chaque
moteur à une alimentation et commande vectorielle indirect
indépendante IFOC (en
anglais) : Indirect
Field Oriented Control; les
moteurs sont couplés mécaniquement par une bande dont la tension
est réglable par la commande des quatre derniers moteurs. Ce
système est composé de deux parties différentes, la partie
mécanique (Figure 2.1) et la partie électrique (Figure 2.3).
2.2.1.1. Description de la partie mécanique
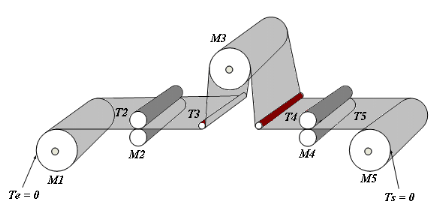
Figure 2.1 : Partie
mécanique du système à cinq moteurs.
Dans la partie mécanique, le moteur M1
effectue le débobinage, M3 entraîne la
toile par friction et M5 sert à effectuer le bobinage,
les moteurs M2 et M4 entraînent chacun
deux rouleaux par l'intermédiaire d'engrenages pour
« pincer » la bande (Figure 2.2). M2 et
M4 pourraient être remplacés par deux moteurs
chacun, qui entraîneraient chacun un rouleau des étages de
pinçage. Les éléments de contrôle de pression entre
les rouleaux ne sont pas représentés, ni considérés
dans l'étude. L'étage de pinçage peut permettre d'isoler
deux zones et de créer une zone tampon. [33,34]
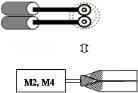
L'objectif de ces systèmes est de maintenir la vitesse
de défilement constante et de contrôler la tension dans la
bande.
Figure 2.2 : Moteur
d'entraînement de l'étage de pincement.
2.2.1.2. Description de la partie
électrique
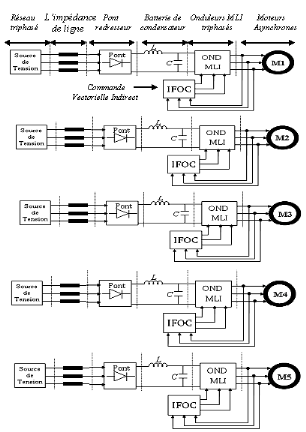
Le banc d'essais est composé de cinq moteurs
asynchrones triphasés; les entraînements sont connectés
chacun à une alimentation triphasée et une IFOC
(Figure 2.3). Les moteurs (M1, M2, M3, M4, M5) sont
alimentés par des onduleurs afin de varier la vitesse. Le
matériau entraîné est considéré comme une
bande élastique. Les moteurs asynchrones utilisés sont
puissants.
Figure 2.3 : Partie
électrique du système à cinq moteurs.
2.2.2. Modèle des principaux
éléments constitutifs du système
2.2.2.1. Modélisation du moteur asynchrone
triphasé
La modélisation du moteur asynchrone a été
abordé en détail dans le chapitre 1.
2.2.2.2. Modélisation de l'enrouleur -
dérouleur
R0
R(t)
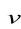
H
Comme on a pu le constater, les divers traitements
s'effectuent en phase de défilement. Il est donc impératif de
disposer d'organes de déroulement et d'enroulement performants. Ces deux
dispositifs, l'enrouleur et le dérouleur, sont symétriques
(Figure 2.4). Après installation sur le moteur dérouleur d'un
rouleau de matière (toile, papier), une bande de produit est sortie et
part vers le reste du processus. Le rôle premier du dérouleur
apparaît ici : l'injection de matière dans le système. Au
cours du cycle de travail, la quantité de matière sur le rouleau
diminue, sa masse et son rayon ne sont donc pas constants. De la même
manière, l'enrouleur récupère le produit traité; au
démarrage, le rouleau porteur est vide, il se remplit au fur et à
mesure de l'avancement. Afin de garantir un enroulement de bonne
qualité, la vitesse linéaire à l'arrivée sur
l'enrouleur doit être constante, l'effort de tension imposé au
matériau également. De même, si on veut assurer un bon
traitement du produit, le dérouleur doit délivrer le produit
à vitesse et tension constantes. Lorsque le dérouleur est vide,
la chaîne doit s'arrêter, le temps de mettre un nouveau rouleau.
Soit l la longueur axiale du roulement de papier. Les
relations cinématiques importantes du roulement de papier peuvent
être développées comme suit (Figure 2.4) [28,31,38,39].
Figure 2.4 : Modèle d'un
rouleau de papier.
Rayon R(t) et masse m : Considérons le
profil du rouleau comme un disque initial de rayon R0 et une couronne de rayon
intérieur  et
extérieur R(t) (Figure 2.4).
et
extérieur R(t) (Figure 2.4).
|
(2.1)
|
|
(2.2)
|
|
(2.3)
|
|
(2.4)
|
|
(2.5)
|
Angle de rotation :
Inertie de masse  : De la même manière, on peut
détailler l'inertie
: De la même manière, on peut
détailler l'inertie .
Rappelons que l'inertie d'un cylindre creux dépend de ses rayons interne
et externe, de sa masse volumique
.
Rappelons que l'inertie d'un cylindre creux dépend de ses rayons interne
et externe, de sa masse volumique  et
de sa hauteur, ici la largeur de la bobine est
et
de sa hauteur, ici la largeur de la bobine est  .
.
L'inertie d'un rouleau dérouleur ou enrouleur est la
somme de son inertie à vide  (c'est celle de l'arbre moteur) et de l'inertie variable, fonction du rayon
R(t).
(c'est celle de l'arbre moteur) et de l'inertie variable, fonction du rayon
R(t).
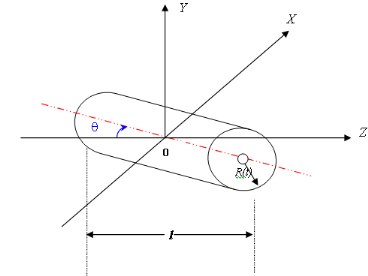
Figure 2.5 : Vue en perspective d'un
rouleau de papier.
Tableau 2.1 :
Paramètres du rouleau de papier.
|
Symbole
|
Signification
|
Unité
|
|
Masse de noyau.
|
kg
|
|
m
|
Masse totale du rouleau de papier.
|
kg
|
|
Rayon du noyau .
|
m
|
|
R
|
Rayon variable de roulement de papier.
|
m
|
|
V
|
Vitesse de défilement du papier.
|
m/s
|
|
H
|
Épaisseur de la feuille de papier.
|
m
|
|
l
|
Longueur longitudinale du rouleau de papier.
|
m
|
|
Densité de masse de la feuille de papier.
|
|
|
Inertie à vide.
|
|
|
Inertie de masse.
|
N m m
|
2.2.2.3.
Modélisation de la toile entre deux rouleaux consécutifs
Les différents modèles pour la toile ou la bande
dans les systèmes de transport de matériaux en feuilles sont
basés sur trois lois [29,37,38].
· La loi de Hooke, qui modèle
l'élasticité du lien entre les enchaînements;
· La loi du coulomb, qui donne la variation de tension
mécanique due au frottement et à la force de contact entre la
toile et le rouleau;
· Loi de conservation de masse, qui exprime
l'interconnexion entre la vitesse de bande et sa contrainte.
Nous présentons ici le développement du
modèle présenté dans [29,30,31].
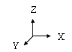
La figure 2.6 montre un système d'enchaînement
entre deux rouleaux avec le repère (X, Y, Z) [30].
Figure 2.6 : Tension
d'enchaînement entre deux rouleaux.
Pour être plus proche de la réalité, le
modèle mathématique de la bande est développé en
utilisant les hypothèses [30,34,39] suivantes :
· la longueur de la région de contact
(a+g) entre le matériau et le rouleau est très petite
par rapport à celle du matériau au niveau de deux rouleaux,
(L) ce qui permet de définir un volume contrôlé V
(volume des matériau dans la région `g');
· la perte de masse entre le matériau et
l'environnement est supposée négligeable;
· la contrainte dans le matériau entre les deux
rouleaux est uniforme;
· le matériau est isotropique mais c'est la
contrainte le long de l'axe x qui prévaut : x 0,
y = 0 et z = 0;
· la section et la densité du matériau ne
varient pas au cours du temps et sur la longueur du matériau.
· il n'y a pas de glissement entre le matériau et
les rouleaux, la vitesse de défilement du matériau est donc
égale à la vitesse linéaire du rouleau.
La tension d'enchaînement entre deux rouleaux peut
être calculée selon ces trois lois.
La Loi de Hooke : La tension T d'un
enchaînement élastique est fonction de la contrainte
d'enchaînement : [29,39]
Notez que le rapport entre la contrainte et la tension est
plus complexe pour les matériaux viscoélastiques. La loi de Hooke
est valide pour la plupart des matériaux d'enchaînement, aussi
longtemps que la tension n'est pas trop grande.
D'ailleurs, le module de Young est très sensible
à la température et au niveau d'humidité. Sur la
chaîne de production, l'enchaînement peut passer par
différents processus (par exemple, dans un bain dissolvant, puis dans un
dessiccateur). Par conséquent, ses propriétés
d'élasticité peuvent considérablement changer pendant le
processus.
La Loi du Coulomb : L'étude de la
tension d'enchaînement sur un roulement peut être
considérée comme un problème de frottement entre les
solides. Sur le roulement, la tension d'enchaînement est constante sur
une zone de collage qui est un arc de longueur a et change sur une
zone coulissante qui est un arc de longueur g (Figure 2.6). Puis, la
contrainte d'enchaînement entre le premier point de contact d'un
roulement et le premier point de contact du roulement suivant est donné
par les équations suivantes :
|
si 
|
(2.12)
|
|
si 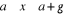
|
(2.13)
|
|
si 
|
(2.14)
|
|
|
(2.15)
|
|
|
Symbole
|
Signification
|
Unité
|
|
Ti (i=1,4)
|
Tension dans le matériau entre chaque paire de
rouleaux.
|
N
|
|
i (i=1,4)
|
Contrainte imposée au matériau.
|
__
|
|
E
|
Module de Young de la bande.
|
N/m²
|
|
S
|
Section d'enchaînement.
|
m²
|
|
L0
|
Longueur nominale d'enchaînement (sans effort).
|
m
|
|
L
|
Longueur d'enchaînement sous l'effort.
|
m
|
|
i (i=1,4)
|
Densité volumique du matériau.
|
kg/m
|
|
Vi (i=1,5)
|
Vitesse linéaire du roulement i.
|
m/s
|
Tableau 2.2 : Définitions et notations
pour l'étude de la toile.
Le changement de tension se produit sur la zone coulissante
tandis que la vitesse d'enchaînement est égale à la vitesse
de roulement sur la zone de collage. Peut également apparaître une
zone coulissante à l'entrée de roulement si la tension change
à un taux élevé.
Loi de Conservation de masse :
Considérez une toile entre deux rouleaux de longueur  avec une densité de poids, sous un effort continu. Supposant que
la section reste constante, puis, selon la loi de conservation de masse, la
masse d'enchaînement reste constante entre l'état sans effort et
l'état sous l'effort :
avec une densité de poids, sous un effort continu. Supposant que
la section reste constante, puis, selon la loi de conservation de masse, la
masse d'enchaînement reste constante entre l'état sans effort et
l'état sous l'effort :
Tension d'enchaînement entre deux rouleaux
consécutifs : l'équation de continuité appliquée au
système de transport d'enchaînement donne :
Utilisons l'équation (2.17), que nous intégrons
sur le volume V de commande défini par les premiers points de
contact entre l'enchaînement et les roulements, voir la figure. 2.6.
Supposant que la section d'enchaînement est constante,
 nous pouvons intégrer en ce qui concerne la variable
nous pouvons intégrer en ce qui concerne la variable  de
zéro à
de
zéro à  .
.
Utilisons (2.13)-(2.15), avec l'hypothèse que 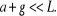
Soit 

 et
et
 La relation finale est :
La relation finale est :
Cette relation peut être simplifiée en
différenciant la limite gauche.
Puis, en utilisant les approximations.


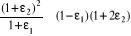
Avec l'équation (2.11), nous obtenons.
Cette relation diffère de celle
présenté dans des études classiques sur des
systèmes d'enroulement. La simplification du modèle classique est
obtenue en employant l'approximation avant de différencier la limite
gauche dans (2.21), ce qui donne l'équation suivante :
Nous pouvons voir que (2.23) donne une meilleure approximation
que (2.24.a). Pour le développement des lois de commande, c'est le
modèle (2.24.a) qui sera employé pour sa simplicité.
2.2.3. Modèle du système multi-moteur
(SMM)
2.2.3.1. Vitesse d'enchaînement sur chaque
roulement
Supposant que l'enchaînement ne glisse pas sur le
rouleau, la vitesse d'enchaînement est égale à la vitesse
linéaire de roulement. L'équation dynamique de la vitesse  du
du
 rouleau peut être obtenue par l'équation
d'équilibre de couple : [33,35,36]
rouleau peut être obtenue par l'équation
d'équilibre de couple : [33,35,36]
Où  sont les tensions dans le matériau entre chaque paire de rouleaux,
sont les tensions dans le matériau entre chaque paire de rouleaux,  est le somme des couples de frottement. Nous pouvons noter d'après
l'équation (2.25.a) que l'inertie
est le somme des couples de frottement. Nous pouvons noter d'après
l'équation (2.25.a) que l'inertie ,
le rayon
,
le rayon ,
sont liés au temps :
,
sont liés au temps :  et
et
 augmentent avec le temps pour l'enrouleur et diminuent avec le temps
pour le dérouleur. Ils peuvent changer considérablement pendant
l'opération de processus complet (environ 300% pour le rayon dans notre
installation expérimentale et encore plus dans quelques systèmes
industriels).
augmentent avec le temps pour l'enrouleur et diminuent avec le temps
pour le dérouleur. Ils peuvent changer considérablement pendant
l'opération de processus complet (environ 300% pour le rayon dans notre
installation expérimentale et encore plus dans quelques systèmes
industriels).
2.2.3.2. Modèle complet
Le modèle complet de notre installation
expérimentale peut être établi en utilisant (2.24.a) pour
indiquer la tension mécanique dans chaque segment et (2.25.a) pour
indiquer la vitesse de chaque roulement. La figure 2.7 montre les
différentes variables dans le modèle de notre système
expérimental. Les entrées sont les signaux de commande  (Tensions de commande) et les sorties sont la vitesse linéaire de
défilement et les tensions d'enchaînement,
(Tensions de commande) et les sorties sont la vitesse linéaire de
défilement et les tensions d'enchaînement, .
Les signaux de commande sont le couple de référence des moteurs
asynchrones. Traditionnellement, dans un arrangement décentralisé
de commande, la vitesse d'enchaînement est commandée par le moteur
de traction et la tension d'enchaînement est commandée par les
moteurs de déroulement et d'enroulement. Les équations (2.24.a)
et (2.25.a) peuvent être exprimées sous la forme
d'équations d'état :
.
Les signaux de commande sont le couple de référence des moteurs
asynchrones. Traditionnellement, dans un arrangement décentralisé
de commande, la vitesse d'enchaînement est commandée par le moteur
de traction et la tension d'enchaînement est commandée par les
moteurs de déroulement et d'enroulement. Les équations (2.24.a)
et (2.25.a) peuvent être exprimées sous la forme
d'équations d'état :
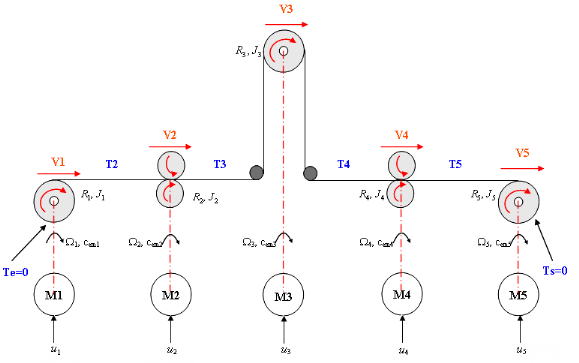
Figure 2.7 : Modèle
complet du système avec cinq moteurs.
2.2.3.3 Équations mécaniques de la
structure complète
Les équations des moteurs et des tensions sont :
 ;
;
et  ;
;
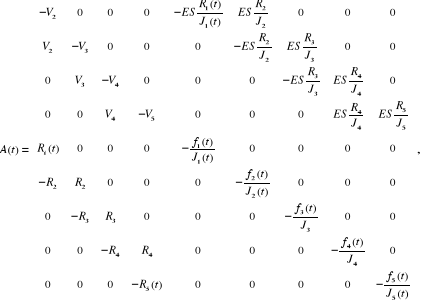


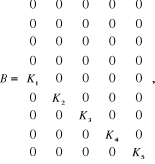
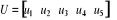
Tableau 2.3 : Paramètres
du modèle complet de cinq moteurs.
|
Symbole
|
Signification
|
Unité
|
|
 (i=1,5)
(i=1,5)
|
Vitesse linéaire du roulement i.
|
m/s
|
|
 (i=1,5)
(i=1,5)
|
Vitesse de rotation du roulement i.
|
rad/s
|
|
 (i=1,5) (i=1,5)
|
Rayon du rouleau i.
|
m
|
|
 (i=1,5) (i=1,5)
|
Moment d'inertie du rouleau i.
|
|
|
 (i=1,5) (i=1,5)
|
Coefficient de frottement visqueux du rouleau . .
|
N.m.s/rad
|
|
 (i=1,4)
(i=1,4)
|
Tension mécanique entre les rouleaux i et
i+1.
|
N
|
|
 (i=1,4) (i=1,4)
|
Longueur d'enchaînement entre les rouleaux i et
i+1.
|
m
|
|
Somme des couples de frottement.
|
N.m
|
|
Matrices diagonales des paramètres.
|
__
|
Les paramètres qui changent pendant le
procédé d'enroulement sont exprimés comme fonction du
temps.
2.3. REPRÉSENTATION ÉNERGÉTIQUE
MACROSCOPIQUE
2.3.1. Définition de la REM
La REM est basée sur le principe d'action et de
réaction et à l'avantage d'offrir une représentation
synthétique. De plus, elle permet aussi de mettre en évidence les
interactions qui existent entre les différents composants d'un
système ainsi que le flux énergétique mis en jeu entre les
divers éléments constitutifs du système. Les informations
contenues dans cette section sont adaptées du rapport [27,32,39].
2.3.2. Éléments de représentation de
la REM
La REM se compose de plusieurs blocs qui ont des formes et
des couleurs normalisées [39], ce qui donne une meilleure
lisibilité de la représentation d'un système (Figure
2.8) :
§ Les sources énergétiques,
représentées par des ovales verts;
§ Les convertisseurs électriques, (des
carrés orange) sans accumulation d'énergie;
§ Les convertisseurs électromécaniques,
(des ronds orange) sans accumulation d'énergie;
§ Les convertisseurs mécaniques, (des triangles
orange) sans accumulation d'énergie;
§ Les éléments accumulant de
l'énergie, (des rectangles orange avec une barre oblique)..etc.
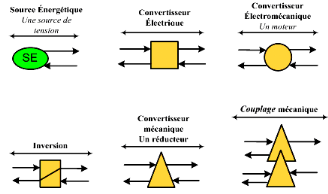
Figure 2.8 :
Éléments de la REM.
2.3.3. Description des éléments de la REM
du système
Pour une meilleure compréhension et une meilleure
lisibilité, la REM est divisée en trois parties. La
première prendra en compte la source d'alimentation triphasée,
l'impédance de la ligne, Le pont redresseur et la batterie condensateur,
la deuxième est la partie électrique du onduleur jusqu'à
la machine asynchrone et la dernière est la partie mécanique qui
représente le couplage entre les moteurs et la toile. La
modélisation est identique pour les cinq moteurs.
2.3.3.1. Modélisation de la première
partie (alimentation)
La première partie (Figure 2.9), qui alimente les cinq
moteurs, est constituée par quatre éléments qui
sont : la source d'alimentation triphasée, l'impédance de
ligne, le redresseur et la batterie condensateur. Cette partie est identique
pour les cinq moteurs
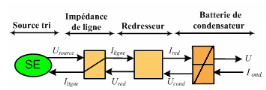
Figure 2.9 : Première
partie du système, source d'alimentation.
2.3.3.1. a . Source
énergétique
La source d'alimentation électrique est de nature
triphasée, on la représente par un élément de
source électrique. Celle-ci nous donne une tension en sortie d'action et
reçoit un courant de ligne en entrée de réaction. C'est le
principe des actions/réactions. Les équations internes du bloc
sont représentées par (2.27.a), (2.27.b) et (2.27.c).
|
(2.27.a)
(2.27.b)
(2.27.c)
|
|
Figure 2.10 : Bloc de source
énergétique.
|
Ua ; Ub ; Uc : les
tensions simples d'une source de tension triphasée
équilibrée.
2.3.3.1. b. Impédance de ligne
L'impédance de ligne est représentée par
un élément d'accumulation, la variable d'état étant
« I ligne». Cette ligne est constituée
d'une résistance R ligne et d'une bobine L
ligne en série pour chaque phase.
|
Avec :
|
|
(2.28)
|
|
Figure2.11 : Bloc
impédance de ligne.
|
Où :
Uentrée =
Usource : la tension d'entrée de
la ligne (qui représente un vecteur).
Uretour = Uredresseur
: la tension d'entrée de réaction.
2.3.3.1. c. Redresseur six diodes
Ce redresseur triphasé est constitué de six
diodes. Il est représenté par un élément de
conversion électrique. Ce pont ne peut pas être commandé.
Il n'y a donc pas de degré de liberté et ainsi pas de
possibilité de réglage.
|
 Figure 2.12 : Bloc redresseur six
diodes. Figure 2.12 : Bloc redresseur six
diodes.
|
|
|
2.3.3.1. d. Batterie de condensateur
Cette batterie placée entre le redresseur et les
onduleurs de chaque moteur. On peut alors caractériser cette liaison par
un élément d'accumulation avec un couplage électrique, la
variable d'état étant la tension de sortie« U
».
|
|
(2.29)
|
|
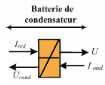
Figure 2.13 : Bloc batterie de
condensateur.
|
Avec : C : condensateur du bus
continu ; Rcond : résistance de fuite en
parallèle avec le condensateur ; i
entrée = i red : courant d'entrée du
condensateur; i retour = I ond courant
d'entrée de réaction.
2.3.3.2. Modélisation de la deuxième
partie (moteur-électrique)
Cette partie électrique est constitué par trois
éléments qui sont : l'onduleur, le stator de la machine
asynchrone (MAS) et la machine elle même (figure 2.14). Cette partie est
identique pour les cinq moteurs. Pour l'action et réaction entre la
première et la deuxième partie, la tension de sortie d'action
étant la même pour les cinq onduleurs, on peut considérer
comme une source électrique qui délivre une tension U,
le courant Iond étant le courant de
retour de l'onduleur triphasé.
|
|
Figure 2.14 : Deuxième
partie du système, partie électrique.
|
2.3.3.2. a. Onduleur Triphasé
L'onduleur est représenté par un convertisseur
électrique.
|
|
Figure 2.15 : Bloc d'onduleur
triphasé.
|
2.3.3.2. b. Stator de moteur asynchrone
Le stator de la machine asynchrone peut être
représenté par la mise en série d'une résistance et
d'une bobine où le courant I stator est commun. On
représente alors cet élément par un élément
d'accumulation avec comme variable d'état le courant I stator
, l'entrée de réaction étant la force
électromotrice du moteur.
|

Figure 2.16 : Bloc de
stator.
|
2.3.3.2. c. Machine asynchrone MAS
La MAS est représentée par un
élément de conversion électromécanique. Elle permet
d'obtenir un couple à partir d'un courant. La sortie de
réaction : la force électromotrice est obtenue par
l'entrée de réaction qui est la vitesse angulaire. Il faut savoir
que pour les simulations, la machine est représentée par
l'intermédiaire du modèle de Park et les
équations de la machine asynchrone. On suppose ainsi que l'onduleur
fournit une tension triphasée équilibrée.
|

Figure 2.17 : Bloc de machine
asynchrone MAS.
|
2.3.3.3. Modélisation de la troisième
partie (couplage mécanique)
La troisième partie est la partie mécanique
(Figure 2.18) qui représente la modélisation des arbres des
moteurs, les différentes toiles et le couplage mécanique. Ce
couplage permet entre autre d'exprimer la vitesse linéaire d'un moteur
par l'intermédiaire de sa vitesse angulaire et du rayon du rouleau. Les
éléments de même nature ne seront étudiés
qu'une seule fois car ils sont basés sur le même principe.
L'exemple pris est celui de l'entraînement en forme
générale.
Figure 2.18 : Troisième
partie du système, partie mécanique.
2.3.3.3. a. Arbre du moteur
L'arbre est caractérisé par son inertie. Les
interactions qui peuvent exister entre cet arbre et sa charge sont aussi prises
en compte. La vitesse est une variable d'état, cet élément
est alors représenté par un élément
d'accumulation.
|
|
(2.30)
|
|

Figure 2.19 : Bloc arbre de
moteur.
|
2.3.3.3. b. Conversion des vitesses et
forces/couples
Le couplage mécanique permet de réaliser une
conversion; on exprime la vitesse linéaire du moteur par
l'intermédiaire de sa vitesse angulaire en la multipliant par le rayon
de l'arbre. Dans notre cas nous prenons le rayon du rouleau accouplé
à l'arbre, on considère que la liaison entre les rouleaux et les
arbres est parfaite. De même pour le couple résistant, on
l'exprime à partir de la force qui est appliquée à la
roue.
|
|
(2.31)
(2.32)
|
|

Figure 2.20 : Bloc conversion
des vitesses et forces/couples.
|
2.3.3.3. c. Couplage entre moteurs
Le moteur MK+1 a une liaison avec les
moteurs MK et MK+2 par
l'intermédiaire de la toile. Il y a donc un couplage de type
mécanique. En effet, la sortie de réaction VK+1
est commune aux entraînements MK et
MK+2 (2.33). On s'aperçoit aussi que le couple
résistant dépend de deux variables : TK+1
et TK+2 (2.34).
|
|
(2.33)
(2.34)
|
|

Figure 2.21 : Bloc de couplage
entre moteurs (étage k+1).
|
2.3.3.3. d. Toile
La toile est considérée comme un matériau
élastique. Celle-ci est représentée par un
élément d'accumulation avec comme variable d'état la
tension. Celle-ci dépend de la vitesse des moteurs.
La tension d'entrée Te du premier moteur (bobineur) et
la tension de sortie Ts du dernier moteur (débobibeur) ne sont pas
prises en considération dans l'étude du modèle
général de la toile (2.35).
|
|
(2.35)
|
|

Figure 2.22 : Bloc de la toile
(segment k+1).
|
2.3.4. Représentation complète du
système cinq moteurs par REM
On peut s'apercevoir qu'une fois le système
modélisé, beaucoup de variables sont mises en jeu, et que la
gestion d'un tel système ne soit pas simple. En effet, la
présence de couplages et le partage de variables communes peuvent
entraîner des perturbations. La modélisation de chaque
élément de la maquette a été
présentée dans le paragraphe {§2.2.3}, la
modélisation complète du système est
représentée dans la figure 2.23.
|
|
Figure 2.23 :
Représentation complète du système cinq moteurs par
REM.
|
2.4. CONCLUSION
À travers ce chapitre une étude
détaillée de la modélisation des systèmes
multi-moteurs (SMM) et la structure du système ont été
développées. Dans la partie de la modélisation du moteur
asynchrone ses équations sont explorées en détail
(Chapitre 1). Ces dernières sont obtenues pour les systèmes
électrique et mécanique. Par la loi de Hook, les calculs de la
tension d'enchaînement entre deux moteurs sont développés.
Ces calculs permettent l'obtention des tensions mécaniques entre une
série des moteurs d'entraînement. Finalement, l'utilisation de la
modélisation obtenue dans ce chapitre, permet d'avoir un système
matriciel sous la forme d'équations d'état. Ce dernier sera
utilisé dans le chapitre III.
Afin de modéliser le système multi-moteur
étudié, l'outil que nous avons utilisé est une
représentation appelée Représentation
Énergétique Macroscopique (REM). Cet outil,
développé par le Laboratoire d'Électrotechnique et
d'Électronique de Puissance de Lille (L2EP), permet d'analyser des
systèmes complexes composés de plusieurs machines et plusieurs
convertisseurs dans des entraînements électriques et
mécaniques. La REM est basée sur le principe d'action et de
réaction et à l'avantage d'offrir une représentation
synthétique des systèmes énergétiques. Elle permet
aussi de mettre en évidence les interactions qui existent entre les
différents composants d'un système ainsi que le flux
énergétique mis en jeu entre les divers éléments du
système.
19 CHAPITRE 3 :
20
21 RÉSULTATS DE SIMULATION
22
23 3.1. INTRODUCTION
L'objectif de ce chapitre est l'analyse des résultats
de simulation d'un banc d'essais représentatif d'un système
industriel de transfert de matériaux. Ce banc d'essai rentre dans le
cadre des travaux de recherche sur la commande vectorielle de systèmes
multi-moteurs. Le système est composé de cinq moteurs
asynchrones. Cette commande a été développée selon
la méthode indirecte ; cette méthode est détaillée
dans le chapitre 1.
La suite du chapitre est constituée de deux sections.
La première présente les différant schémas des
blocs qui sont utilisés dans notre travail de simulation ; La
deuxième montre les résultats de simulation des trois et cinq
moteurs.
Le système est modélisé sous
MATLAB, version 7.0.4
; les résultats sont validés par simulation
à l'aide de l'interface Simulink intégrée
à Matlab.
3.2. LES DIFFÉRANTS SCÉHMAS DES BLOCS
Le système étudié est composé de
cinq moteurs triphasés asynchrones qui entraînent des rouleaux sur
lesquels défile une bande de papier (la toile).
Chaque moteur est représenté sous forme de bloc
comme suit :
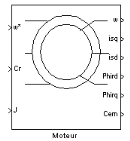
Figure 3.1 : Schéma bloc d'un
moteur.
Le bloc moteur contient les éléments
suivants :
· La commande vectorielle indirecte
(IFOC).
· L'onduleur de tension à commande
MLI.
· Le moteur asynchrone (MAS).
· Contrôleur de vitesse type PI.
· Bloc de défluxage.
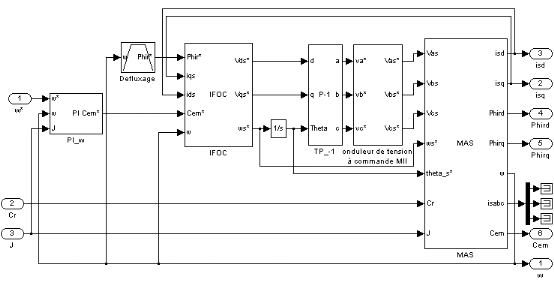

Figure 3.2 : Les
éléments du bloc moteur.
La bande de papier (la toile) est
représentée sous forme de bloc comme suit :
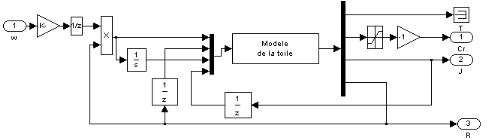
Figure 3.3 : Schéma bloc de
la toile.
Le modèle complet du système avec cinq
moteurs :
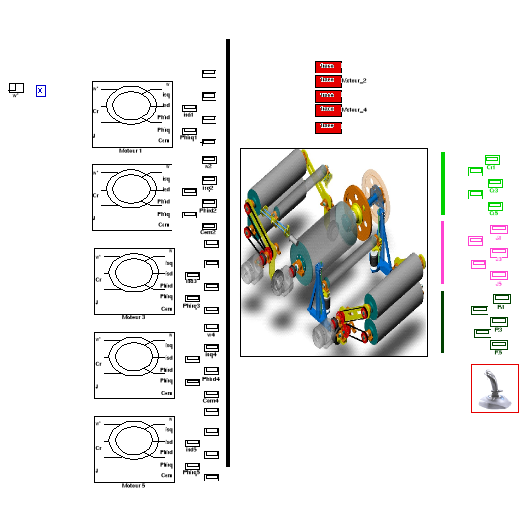
Figure 3.4 : Schéma complet
du système avec cinq moteurs.
3.3. LES RÉSULTATS DE SIMULATION
3.3.1. Résultats de simulation (trois
moteurs)
Pour évaluer les performances du système nous
avons effectués des simulations numériques sous les conditions
suivantes :
§ Démarrage avec application d'un échelon
de vitesse de 50 rad/s.
§ Le moteur M1 à le rôle de débobiner
le rouleau de rayon R1 (R1=2.25 m).
§ Le moteur M2 fait le pincement de la bande.
§ Le Moteur M3 à le rôle de bobiner un
rouleau de rayon R3 ; le bloc STOP a pour but de faire
arrêter légèrement en même temps les
différents moteurs de système jusqu'à où le rayon
régler atteint une valeur désirée (exemple : R3=0.8 m), en
injectant une vitesse de référence nulle.
Les figures 3.(5,6,7) montre que le réglage par un
régulateur PI donne des résultats satisfaisants :
§ La vitesse de rotation suit la vitesse de
référence.
§ Le courant est bien limité à sa valeur
admissible.
§ Les flux ( et
et
 ) sont maintenus à leurs valeurs désirées (en effet
le découplage est maintenu).
) sont maintenus à leurs valeurs désirées (en effet
le découplage est maintenu).
§ On remarque que le couple
électromagnétique  suit la valeur du couple résistant
suit la valeur du couple résistant  .
.
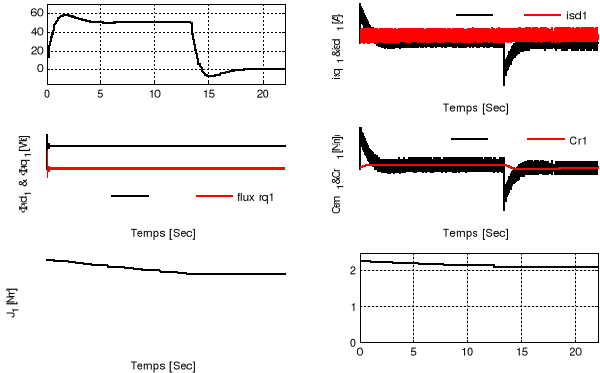
§ On remarque aussi que le moment d'inertie  diminue avec la diminution du rayon
diminue avec la diminution du rayon et
augmente avec son augmentation.
et
augmente avec son augmentation.
Figure 3.5 : Résultats de
simulation du premier moteur.
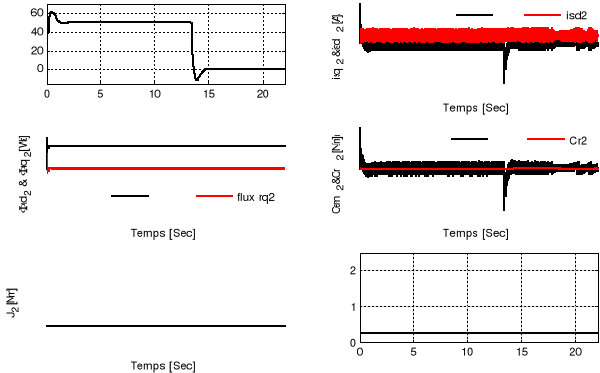
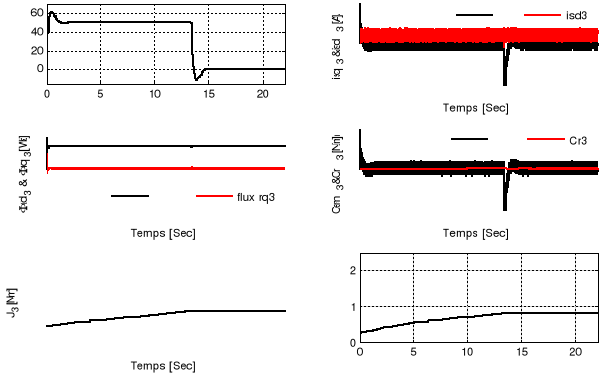
Figure 3.6: Résultats de
simulation du deuxième moteur.
Figure 3.7 : Résultats de
simulation du troisième moteur.
3.3.2. Résultats de simulation (cinq
moteurs)
Pour évaluer les performances du système nous
avons effectués les mêmes étapes de simulation qui ont
faite avec le système à trois moteurs sous les conditions
suivantes :
§ Démarrage avec application d'un échelon
de vitesse de 50 rad/s.
§ Le moteur M1 a le rôle de débobiner le
rouleau de rayon R1 (R1=2.25 m).
§ Les moteurs M2, M3, M4 sont rôle est le
pincement de la bande.
§ Le Moteur M5 a le rôle de bobiner un rouleau de
rayon R5 ; le bloc STOP a pour but de faire arrêter
légèrement en même temps les différents moteurs de
système jusqu'à où le rayon régler atteint une
valeur désirée (exemple : R5=0.8 m), en injectant une vitesse de
référence nulle.
Les résultats de simulation obtenues avec un
système à cinq moteur (Figure 3.(8,9,10,11,12)), ont les
mêmes caractéristiques que celles obtenues avec trois moteurs
(Voire § 3.3.1), néanmoins avec cinq moteurs nous pouvons constater
une net amélioration au niveau des performances de réglage.
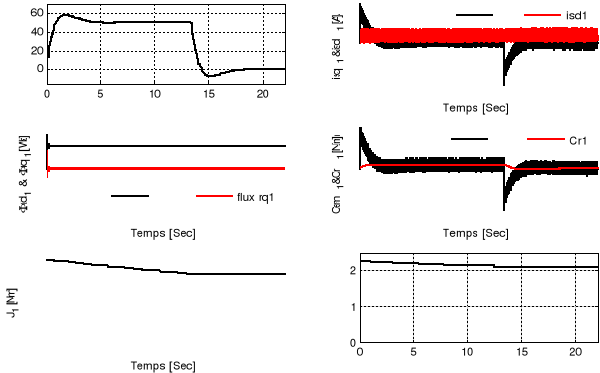
Figure 3.8 : Résultats de
simulation du premier moteur.
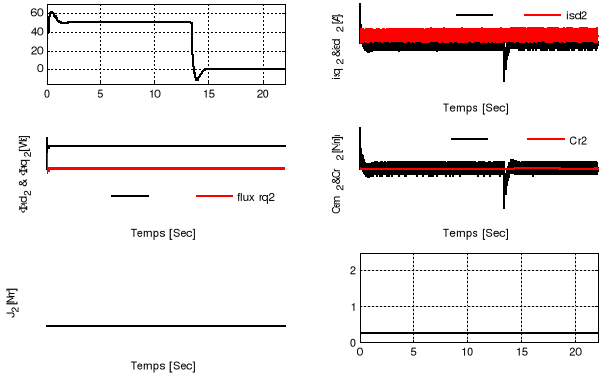
Figure 3.9 : Résultats de
simulation du deuxième moteur.
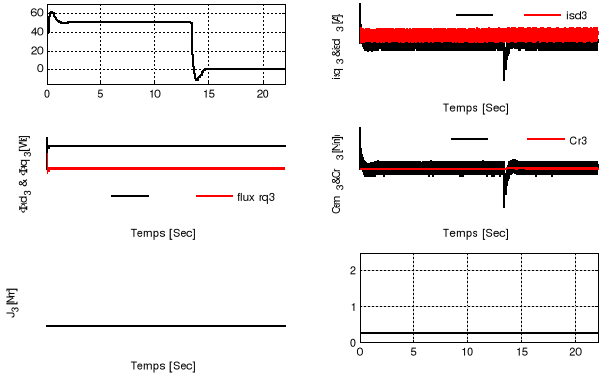
Figure 3.10 : Résultats de
simulation du troisième moteur.
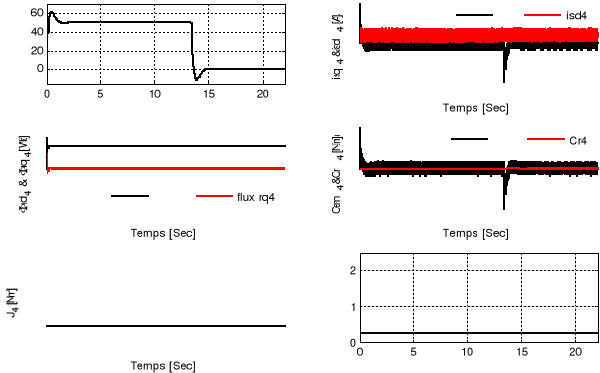
Figure 3.11 : Résultats de
simulation du quatrième moteur.
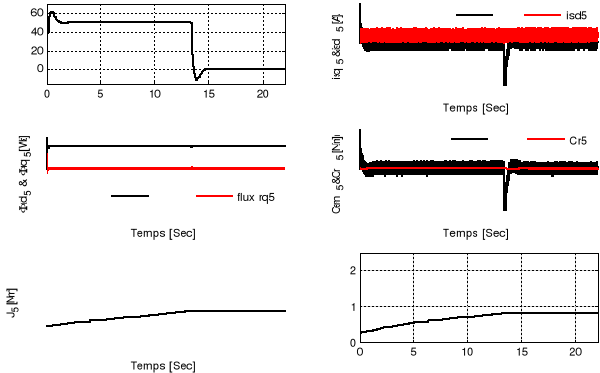
Figure 3.12 : Résultats de
simulation du cinquième moteur.
3.4. CONCLUSION
L'objectif général des processus de transport,
bobinage et débobinage permet avec assurance que l'ensemble travaille en
harmonie et en synchronisme, et surtout d'assurer une bonne qualité du
traitement et du rembobinage du produit.
Dans ce chapitre, nous avons présenté les
résultats de simulation des différents schémas blocs
appliqués à un SMM en série. Les résultats sont
satisfaisants, et en régime permanent est d'une grande rapidité.
En plus, les résultats obtenus montrent que la méthode indirecte
de la commande vectorielle est robuste.

24 CONCLUSION
GÉNÉRALE
CONCLUSION GÉNÉRALE
Les problématiques des systèmes multi-moteurs
s'expriment en termes de couplages entre ces moteurs. Le couplage
mécanique entre les rouleaux est sûrement le cas le plus concret.
Si le couplage est considéré néfaste ou nuisible aux
performances, c'est avant tout en raison d'une mauvaise connaissance de ses
effets. Le but majeur est de maîtriser ces effets néfastes des
couplages, de sorte que les variables couplées puissent être
contrôlées indépendamment.
Le transport de bande présente un exemple typique :
comment dérouler puis enrouler un produit sans liaison mécanique
entre le dérouleur et l'enrouleur ? Dans cette industrie, la
connaissance du couplage et de ses effets nécessite une immersion dans
le contexte industriel. La délimitation du sujet à l'industrie
n'apparaît que dans le choix d'une application; l'étude du
couplage reste valable pour une large gamme d'applications industrielles
à base de déroulement-enroulement.
Nos principales contributions portent sur :
Ø Le développement d'un modèle d'un
système multi-moteur constitué de cinq entraînements, qui
sont couplés mécaniquement par une courroie dont la tension est
réglable.
Ø Le développement d`une des lois de commande
vectorielle et leur application pour synchroniser les cinq enchaînements
et maintenir une tension mécanique constante entre les rouleaux du
système.
Nous avons développé les équations du
modèle des Vitesses/Tensions sous la forme d'équations
d'état; ce modèle a été développé
avec les hypothèses suivantes :
1- L'enchaînement est pincé dans les rouleaux
dont il n'y a aucun glissement;
2- Nous supposons que la section de l'enchaînement est
uniforme entre les deux rouleaux, en particulier, nous négligeons la
déformation de l'enchaînement aux points de contact avec les
rouleaux.
3- Nous supposons que la tension d'entrée et de sortie
sont nulles; le premier moteur fait le débobinage et le cinquième
le bobinage.
L'amélioration du système de production à
base de transport de bande est toujours possible au rythme des avancées
technologiques. L'appropriation de ce thème par le génie
électrique sous couvert d'étude des systèmes
multi-moteurs laisse apparaître un regard différent sur une
problématique déjà ancienne. Cette nouvelle mise en commun
de compétences devrait donc déboucher naturellement sur une
amélioration des performances obtenues.
La commande de la MAS est faite par orientation du flux en
appliquant la commande vectorielle indirecte.
La représentation énergétique
macroscopique facilite la vision de la structure des ensembles moteurs et
toiles (système multi-moteur).
Ce travail nous a permis d'apporter une contribution
technologique pour les systèmes multi-moteurs de haute performance.
Les résultats de simulation montrent bien les
démarches de système et les étapes de fonctionnement;
l'avantage de la commande est la compensation des effets de la non
linéarité et d'assurer une bonne stabilité interne et haut
performance du système avec une erreur négligeable au
démarrage du système.
25 26 27 28 29 RÉFÉRENCES BIBLIOGRAPHIQUES
|
[1]:
|
K.Hasse, «Zur dynamik drehzahlgeregelter
antriebe mit stromrichtegespeisten asynchron- kurzschlusslaufer-machinen«,
Ph.D. Dissertation. TH Darmstadt, 1969.
|
|
[2]:
|
F. Blaschke, «The principle of field
orientation as application to the new transvector closed-loop control system
for rotating field machines», Siemens review, Vol.34, pp.217-220, May
1972.
|
|
[3]:
|
P. Vas, «Vector control of AC
machines», Oxford Science Publication, 1990.
|
|
[4]:
|
M. Trzynadlowsky, «The field orientation
principle in control of induction motors», Lumer Acadimic Publication,
1994.
|
|
[5]:
|
B. Robyns, «Commande multivariable
évoluée d'actionneurs asynchrones», Premier rapport de
synthèse concernant le travail de doctorat, Université Catholique
se Louvain, 1990.
|
|
[6]:
|
B.K. Bose, «Power electronics and
AC drives», Printice-Hall, 1986.
|
|
[7]:
|
W.Leonhard, «Power electronics and AC
drives», Editions Springer Verlag, 1985.
|
|
[8]:
|
J.P. Caron, J.P. Hautier,
"Modélisation et commande de la machine asynchrone", Edition Technip,
1995.
|
|
[9]:
|
Y. Mihoub, "Commande neuro-floue d'une
machine asynchrone", Mémoire de Magister, USTO 2002.
|
|
[10]:
|
R.D. Lorenz, D.B. Lawson, "Flux
and torque decoupling control for field weakened operation field-oriented
induction machines", IEEE Trans. on Industry Applications, vol. 26,
n°02,1990.
|
|
[11]:
|
L. Baghli, "Contribution à la commande
de la machine asynchrone, utilisation de la logique floue, des réseaux
de neurones et des algorithmes génétiques", Thèse de
Doctorat de l'université Henri Poincaré, janvier 1999.
|
|
[12]:
|
J. Bonal, G. Segier,
"Entraînements électriques à vitesse variable", New-York,
1998.
|
|
[13]:
|
Boukhelifa, "Sensibilité de la
commande par flux orienté indirecte aux variations des paramètres
rotoriques", International Conference on Electrotechnic ICEL'2000, USTO,
Algérie.
|
|
[14]:
|
A. Hazzab, "Commande des systèmes
électriques par logique floue, réseaux neurones et algorithmes
génétiques ". Thèse Doctorat, UST Oran 2006.
|
|
[15]:
|
E. Sabouni, "Contrôleurs par mode
glissant flou et prédictif flou optimisés par l'AG pour la
commande de MSAP", Mémoire de Magister, CU Béchar 2004.
|
|
[16]:
|
E. Wiexhman, P.D. Ziogas
& V.R Stefanovic, "A novel bilateral power
conversion scheme for variable frequency static power supplies" IEEE Trans.
Ind. Appl. 1984.
|
|
[17]:
|
E. Wiexhman, P.D. Ziogas
& V.R Stefanovic, "Generalised function model for three
phase PWM inverter / rectifier converters", IEEE. Trans. Ind. Appl. Vol. IA-23,
March / April, 1987.
|
|
[18]:
|
M. Butzberger, "Etude et comparaison de
différentes stratégies de réglage et de commande de
servomoteurs asynchrone", Thèse de doctorat, Ecole polytechnique
fédérale de Lausanne 1995.
|
|
[19]:
|
M. Maaziz, "Commande prédictive de
système non linéaires : Application a la commande de
machines asynchrones", Ecole supérieur d'électricité,
France 2000.
|
|
[20]:
|
Toudert, S. Haddad,
N. Benamrouche, "Etude de la commande vectorielle de la
machine asynchrone alimentée en tension", Conférence
International SSA'99, Blida.
|
|
[21]:
|
Derdyok, M. K. Guven,
H. Rahman & N. Inane, "Design and
implementation of new sliding-mode observer for speed-sensor less control of
induction machine". IEEE Trans. on Industrial Electronics, Vol 1. n°3,
2002.
|
|
[22]:
|
R.D. Lorenz, D.B. Lawson, "A
Simplified approach to continuous on-line tuning of field-oriented induction
machine drives", IEEE Trans. on Industry Applications, Vol ; 29,
n° 3, 1990.
|
|
[23]:
|
S. Barkati, "Commande robuste par retour
d'état d'une machine asynchrone", Mémoire de Magister, ENP Alger
1997.
|
|
[24]:
|
Karboua, "Commande et observateurs par mode de
glissement : Application à une Machine Asynchrone Alimentée
en Tension", Mémoire de Magister, ENP Alger, 1999.
|
|
[25]:
|
I.K. Bousserhane, "Contrôleurs flous
optimisés par l'algorithme génétique pour la commande
d'une machine asynchrone", Mémoire de Magister, UST Oran 2003.
|
|
[26]:
|
Nandam P. K. Sen, "Control laws for sliding mode
speed control of variable speed drives" Int. J. Control, 56, (5), 1167-1186,
1992.5
|
|
[27]:
|
A. Bouscayrol, B. Davat, B. de Fornel, B.
François, J. P. Hautier, F. Meibody-Tabar et M.
Pietrzak-David. "Multimachine Multiconverter Systems for Drives:
Analysis of Coupling by a Global Modeling", IAS 2000 (Rome), octobre 2000
|
|
[28]:
|
Jorkama, M, "On the Winder Vibration
Analysis", Ph.D, thesis in Helsinki University of Technology (1996).
|
|
[29]:
|
Kee-Hyun Shin, "Tension Control" ,Tappi
Press, 2000.
|
|
[30]:
|
H. Koç, D. Knittel,
M. de Mathelin and G. Abba, "Modeling and robust control of
winding systems for elastic webs", IEEE Transactions on control systems
technology Vol. 10, No 2, pp 199, March 2002.
|
|
[31]:
|
A. Leclercq, "Modélisation et commande
d'un étage d'un système de bobinage", Université du
Québec à Trois-Rivières/USTL. (Été 2003).
|
|
[32]:
|
Yvette Djani Wankam, "Modélisation et
commande de système bobinage basse sur REM", UQTR/USTL 2004.
|
|
[33]:
|
J. Jagieo et Z. Nowachi.
"The Technological Requirements in Paper Industry Multimotor Drive", de EPE'99
(Lausane), 1999.
|
|
[34]:
|
H. Koç, "Modélisation et
commande robuste d'un système de entraînement de bande flexible",
Thèse, Université Louis Pasteur, Strasbourg, septembre 2000.
|
|
[35]:
|
E. Semail, X. Kestelyn et
J. P. Hautier "Multi-machine Modelling for Polyphase Machine",
ICEM août 2002.
|
|
[36]:
|
Pierre Sicard, Nourdine
Elouariachi et Sylvain Lahaie, "Characterization of
Sensitivity to Voltage Sags of Mechanically Coupled Induction Motors",
Electrimacs 2002.
|
|
[37]:
|
Pierre-Luc Sylvestre. ,
"Génération de trajectoires pour une bobineuse", UQTR 2004.
|
|
[38]:
|
A. LECLERCQ "Modélisation et commande
d'un étage d'un système de bobinage".
UQTR-Lille1, Juin 2003.
|
|
[39]:
|
C. Thiffault, P. Sicard et A.
Bouscayrol "Tension control loop using a linear actuator based on the
energetic macroscopic representation ".
CCECE 2004- CCGEI 2004, Niagara Falls, Mai 2004.
|
|
[40]:
|
D.R. Roisum. "The Mechanics of Web Handling.
TAPPI Press", 1998.
|
|
[41]:
|
J. Jagieo et Z. Nowachi.
"The Technological Requirements in Paper Industry Multimotor Drive", de EPE'99
(Lausane), 1999.
|
|
[42]:
|
A Valenzuela et R. Lorenz.
"Electronic Line Shafting Control for Paper Drives", IAS 2000 (Rome), octobre
2000.
|
ANNEXES
Annexe 1 : Paramètres de la machine
asynchrone
Les paramètres de la machine asynchrone que nous avons
utilisés dans toutes les simulations sont :
|
Paramètre ou grandeur
|
Abréviation
|
Valeur
|
Unité
|
|
Puissance nominale
|
|
1,5
|
kW
|
|
Tension nominale
|
|
200
|
V
|
|
Rendement nominal
|
|
0,78
|
--
|
|
Facteur de puissance nominal
|
|
0,8
|
--
|
|
Vitesse nominale
|
|
1428
|
tr/min
|
|
Fréquence nominale
|
|
60
|
Hz
|
|
Courant nominal
|
|
6,31
|
A
|
|
Résistance statorique
|
|
4,85
|
|
|
Résistance rotorique
|
|
3,805
|
|
|
Inductance cyclique statorique
|
|
0,274
|
H
|
|
Inductance cyclique rotorique
|
|
0,274
|
H
|
|
Inductance mutuelle
|
|
0,258
|
H
|
|
Nombre de paires de pôles
|
|
2
|
--
|
|
Moment d'inertie
|
|
0,031
|
kg/m2
|
|
Coefficient de frottement
|
|
0,008
|
N.m.sec/rad
|

Annexe 2 : Industrie papetière