3.4.3 Méthodes d'association
Les règles d'association est une méthode de
fouille des données non supervisée qui consiste à
déterminer les valeurs associées parmi les données. Une
règle d'association est une règle de la forme : Si condition
(prémisse) alors résultat. Par exemple, Si X et Y alors Z.
Le choix d'une règle d'association nécessite de
définir des indicateurs servant à sa validation, à savoir
le support, la confiance et l'amélioration de la règle.
- Support d'une règle
Le support d'une règle indique le pourcentage
d'enregistrements qui vérifient la règle. C'est la
fréquence d'apparition simultanée des articles qui apparaissent
dans la prémisse et dans le résultat, soit
Support = freq (condition et résultat) Supp(X Y) = |
X&Y | / | BD |
où IX&YI est le nombre d'enregistrements contenant X
et Y et IBDI le nombre total de transactions.
- Confiance associée à une règle
La confiance d'une règle mesure la validité de
la règle. C'est égal au pourcentage d'enregistrements qui
vérifient la conclusion parmi ceux qui vérifient la
prémisse. La confiance est le rapport entre le nombre de transactions
où tous les articles figurant dans la règle apparaissent et le
nombre de transactions où les articles de la partie condition
apparaissent, soit
|
Confiance=freq (condition et résultat) /
freq(condition) Conf(X Y) = |X & Y|/|X|
Conf(X Y) = Supp(XY) / Supp(X)
|
La confiance est basée sur la probabilité
conditionnelle:
Conf(X Y) = P(XY) / P(X) = P(Y/X)
- Définition de l'amélioration
Amélioration = Confiance / freq(résultat)
Une règle est considérée
intéressante lorsque l'amélioration est supérieure
à 1.
Dans le WUM, les associations se font sur les pages dans le
but de découvrir les pages visitées ensembles et de
prévoir le comportement d'un internaute en se basant sur les
requêtes qu'il a effectué. Les règles d'association sont
surtout utiles dans le cas de l'étude du trafic sur les sites Web
commerciaux. Parmi les algorithmes d'association, l'algorithme APRIORI
développé par IBM est le plus souvent utilisé.
3.4.4 Méthodes basées sur l'intelligence
artificielle (réseaux de neurones)
Par analogie avec les neurones biologiques, les réseaux
de neurones sont des ensembles de calculateurs numériques (neurones
formels) agissant comme des unités élémentaires,
reliés entre eux par des interconnexions pondérées qui
transmettent des informations numériques d'un neurone formel à un
autre.
Apprentissage à l'aide d'un réseau de neurones
L'apprentissage d'un réseau de neurones artificiels est
induit par une procédure itérative d'ajustement de ses
paramètres internes (poids synaptiques et nombres de neurones). En
apprentissage supervisé, des exemples (observations) auxquels sont
associées des réponses désirées sont
présentés au réseau. La sortie produite par le
réseau en réponse à une observation donnée est
comparée à la réponse désirée (variable de
sortie). La différence entre la réponse désirée et
la réponse du réseau est alors utilisée pour adapter les
paramètres du réseau de façon à corriger son
comportement. Ce processus est répété de façon
itérative jusqu'à obtenir le meilleur comportement. En
apprentissage non supervisé, le réseau catégorise les
variables d'entrée sans avoir à déterminer les variables
de sortie c'est à dire il évolue tout seul vers son état
stable. Cet apprentissage est destiné à l'élaboration
d'une représentation interne de l'espace des données
d'entrée en identifiant la structure statistique des variables
d'entrée sous une forme plus simple ou plus explicite. Ce type
d'apprentissage est utilisé dans les réseaux compétitifs,
en particulier dans les cartes de Kohonen.
Dans le WUM, le but d'un réseau neuronal est de
recréer artificiellement l'expertise qu'aurait une personne
habituée à classifier les profils dans les segments
prédéfinis (apprentissage supervisé) ou découvrir
des nouveaux segments rassemblants des individus ayant des profils similaires
(apprentissage non supervisé).
Réseaux compétitifs
Les interconnexions des neurones formels donnent naissance
à des réseaux à structures variées dont la plus
utilisée est l'organisation en couches successives. Une telle structure
diffuse l'information de la couche d'entrée, composée par les
neurones formels recevant les informations primitives, vers la couche de
sortie, contenant les neurones finaux transmettant les informations de sortie
traitées par la totalité du réseau, tout en traversant une
ou plusieurs couches intermédiaires, dites couches cachées. Parmi
les réseaux de neurones structurés en couches successives, les
réseaux compétitifs. Les réseaux compétitifs sont
des réseaux qui reproduisent une particularité du fonctionnement
biologique des neurones, à savoir l'inhibition latérale. En
effet, chaque neurone d'entrée est relié à chaque neurone
de sortie et chaque neurone de sortie inhibe tous les autres et s'auto excite.
Le degré de l'inhibition est proportionnel à l'amplitude de
sortie du neurone9 et est une fonction de la distance. En effet,
lorsqu'un neurone est excité, il transmet son excitation aux neurones
voisins dans un rayon très court et inhibe par contre les neurones
situés à plus grande distance.
La figure 3.2 illustre les connexions de compétition
pour un des neurones du réseau compétitif. Les connexions
d'inhibition et la connexion de contre-réaction sont illustrées
pour le 2ème neurone seulement et se répètent pour chaque
neurone.
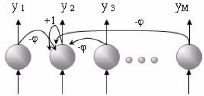
FIG. 3.2 : Réseau linéaire de compétition de
type »gagnant emporte tout»
Quand une forme est présentée à
l'entrée du réseau compétitif, elle est projetée
sur chacun de neurones de la couche de compétition. Une
compétition est alors organisée afin de déterminer le
neurone gagnant dont le vecteur de poids est le plus près de la forme
présentée à l'entrée. Cette architecture permet au
réseau de reproduire l'organisation topographique des formes
d'entrée. Il existe plusieurs types de réseaux compétitifs
tels que les mémoires auto-associatives et les cartes de Kohonen.
| 


