4.2.5 Etude de la qualité d'apprentissage des cartes
topologiques
Une carte topologique doit satisfaire certains critères
pour que l'apprentissage soit efficace [Val, 00]. En effet, une SOM doit:
- Minimiser l'erreur de discrétisation i.e. minimiser les
distances d'un vecteur prototype aux entrées qui l'activent.
- Respecter les relations de voisinage de l'espace
d'entrée. Deux entrées proches doivent être
représentées par deux cellules proches sur la carte.
- Être organisée i.e. il faut que deux cellules
proches aient deux vecteurs prototypes proches.
Les mesures de qualité de la clustérisation
évaluent le compromis entre l'homogénéité de chaque
cluster (ressemblance entre données affectées à un
même groupe) et la séparabilité des clusters. Pour les
cartes de Kohonen, la mesure de la séparabilité n'est pas
importante. En effet, des groupes très similaires sont possibles, s'ils
sont associés à des neurones proches au sens du voisinage; le
compromis s'effectue donc entre l'homogénéité et le
respect de la topologie (organisation). Pour déterminer la
validité de la carte obtenue, la carte doit être
évaluée suivant deux axes : la qualité des regroupements
qu'elles proposent et la qualité d'organisation des clusters. Vers le
début des années 90, les deux critères suivants
ont été proposés. Le premier est relatif
à l'homogénéité. Le second rend compte de la
préservation de la topologie.
Evaluation de l'homogénéité de la carte
L'évaluation de l'homogénéité de
la carte est effectuée en fonction de la mesure de l'erreur de
quantification proposée par Kohonen en 2001. Elle correspond à la
distance entre chaque entrée X et le centroïde du cluster auquel
elle est affectée.

-
X i
Wr
qC1 =
1 ? ? K

N r x C
= ?
1 i
i r
2 N=Nombre des vecteurs d'entrée K= Nombre de clusters
Xi= Vecteur d'entrée
Wr= Poids du centroïde du cluster
Cr
Dans le cas des cartes topologiques, le centre d'un groupe est
distinct de sa moyenne puisque les centres sont influencés par leurs
voisins du fait de la contrainte d'organisation. Par conséquent, le
calcul de l'écart au centre introduit un biais dans la mesure
d'homogénéité et sous-estime la qualité du
regroupement. Pour pallier ce problème, [Les, 03] propose de mesurer la
moyenne des variances des groupes.
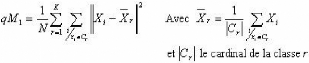
L'erreur de quantification doit tendre vers une valeur limite
en fin d'apprentissage, valeur que l'on souhaite proche de 0. [Rez, 98] propose
d'utiliser comme mesure d'homogénéité la variance moyenne
des groupes :
1 ? 1
K
*
K C
r 1
- -
X X
-
i r
Avec K* le nombre de clusters non vides.
qM2 =
2
?
=?
i
r i r
x C
Evaluation de la préservation de la topologie
L'évaluation de la préservation de la topologie
nécessite de considérer l'ordonnancement des cellules par rapport
aux relations de voisinage définies sur la carte. Ces relations sont
préservées lorsque deux vecteurs d'entrée proches sont
représentés par deux cellules proches sur la carte. Pour mesurer
la préservation du voisinage, plusieurs types de mesures essentiellement
dédiées à la formulation neuronale des cartes de Kohonen
sont proposés. La première mesure, concerne la
préservation de voisinage inverse qui consiste à vérifier
si deux cellules de la carte ont des vecteurs prototypes proches dans l'espace
d'entrée. Cette mesure a été proposée par Cottrell
et Fort [Cot, 87] pour des cartes unidimensionnelles et des


données unidimensionnelles et
généralisée à des cartes de dimension
supérieure par Zrehen et Blayo [Zre, 92]. Certaines mesures sont
calculées uniquement grâce aux neurones, sans utiliser les
données, ce qui permet une économie de temps de calcul. Elles
évaluent la corrélation entre la distance en termes de poids et
la distance imposée sur la carte i.e. entre
dWpq=
wp - wq
dZpq =
zp - zq
En effet, l'organisation impose que deux neurones soient
d'autant plus proches au sens dZ qu'ils ont des vecteurs proches en terme de
dW. Un autre type de mesures se base sur les neurones gagnants associés
aux données. Si la contrainte d'organisation est respectée, le
neurone gagnant et le second meilleur neurone sont adjacents sur la carte, pour
toute donnée. Par suite, l'erreur topographique est définie comme
la proportion de vecteurs de données pour laquelle les deux
premières unités de meilleur appariement (best matching units) ne
sont pas adj acentes.

N- 1
?d bmu bmu
( 1 2 ) 1
- ?
i=0
N
Avec N est le nombre des vecteurs d'entrée
| 


