CHAPITRE 3
il n'a aucune information préalable sur la
région à explorer. Ainsi, il est fort probable qu'il rencontre
des impasses et autres obstacles barrant le chemin lors de la navigation. Il
sera alors obligé de trouver un chemin alternatif pour sortir de
l'impasse, même si cela nécessite de retourner dans une
région précédemment visitée et de consommer plus
d'énergie.
Par conséquent, la solution est construite de
manière incrémentale, en commençant par un chemin
sous-optimal, puis en le mettant à jour régulièrement au
fur et à mesure que de nouveaux obstacles sont observés, ce qui
garantit également que le robot s'adapte aux environnements dynamiques
et évite les obstacles mobiles.
La figure 3.11 schématise le processus
modélisé pour résoudre le problème d'explora-tion,
et la figure 3.12 présente le schéma de coordination
utilisé pour produire un comportement collectif dans les
scénarios multirobots.
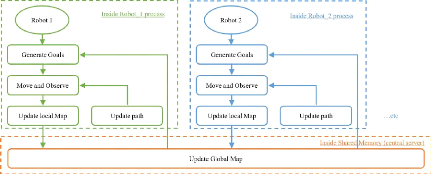
FIGURE 3.12 - Schéma du modèle utilisé pour
assurer la coordination entre les robots
3.6.2 Les critères d'évaluation
Afin de pouvoir analyser les performances des
métaheuristiques utilisées durant les expériences et
comparer leurs résultats, nous allons utiliser les critères
d'évaluation suivants:
-- Nombre de pas (step number) : Nombre de mouvement
et rotations effectué par le robot. Ce nombre est proportionnel à
la quantité d'énergie consommée.
-- Temps d'exécution (execution time) :
Durée totale de la mission, mesurée en secondes.
-- Taux d'exploration (exploration rate) : Surface de
la zone observée par le robot pendant la mission, mesurée en
pourcentage par rapport à la surface totale.
-- Nombre d'évaluation de la fonction de fitness
(Fitevals) : Nombre de solutions évaluées par la
métaheuristique pendant le processus d'optimisation.
-- Temps de calcul (computation time) : Durée
d'exécution de l'ensemble des opérations de calculs requis par la
métaheuristique pour effectuer toutes les itérations et
sélectionner la solution optimale, mesurée en secondes.
101
3.6.3 La complexité du modèle
L'utilisation de l'équation 3.5 comme fonction
de fitness signifie que pour chaque solution candidate dans la population, nous
allons planifier un chemin vers les emplacements cibles définis par
cette solution, puis estimer combien de nouvelles cellules seront
observées si ce chemin est exécuté par le robot. La
complexité de cette opération est O(M) où M est
la longueur du chemin.
Étant donné que la valeur de fitness est
évaluée pour chaque solution candidate à chaque
génération, la complexité globale devient O(NxKxM)
où N est la taille de la population, K est le nombre de
générations et M est la longueur du chemin.
Si la taille de la population ou le nombre de
générations est défini sur une grande valeur, le processus
deviendra coûteux en calcul. Une approche alternative consisterait
à calculer une estimation approximative des cellules observées
(en utilisant un vecteur de distance par exemple) comme critère de
fitness, mais cela diminuerait la qualité des solutions
générées. Afin d'éviter cette perte d'informations,
nous garderons notre modélisation tout en essayant de réduire la
taille de la population au minimum afin d'obtenir un compromis acceptable entre
la qualité des solutions générées et le temps
d'exécution.
3.7 Paramétrage et configuration
3.7.1 Paramétrage des
expériences
Afin d'évaluer les performances des algorithmes BOA et
xBOA, nous allons les comparer à cinq autres métaheuristiques
fréquemment utilisées dans la littérature, à
savoir:
-- Artificial Bees Colony (ABC) [55]
-- Covariance Matrix Analysis Evolution Strategy (CMAES)
[45]
-- Genetic Algorithm (GA) [41]
-- Grey Wolf Optimizer (GWO) [66]
-- Particle Swarm Optimization (PSO) [58]
Pour ces cinq méthodes, nous avons utilisé les
implémentations fournies par Pygmo2 [19] qui est une
bibliothèque Python offrant une interface unifiée pour
implémenter des algorithmes d'optimisation parallèles.
Étant donné que ces méthodes sont
basées sur des opérations stochastiques, nous allons utiliser la
même population initiale pour chacune d'elles et répéter
l'exécution 10 fois afin d'obtenir une comparaison plus objective. Le
critère d'arrêt sera défini tel que suit:
"arrêter l'expérience si l'énergie du robot atteint
zéro, ou la surface de la zone explorée atteint un taux
supérieur ou égal à 99%".
Nous allons effectuer une autre série
d'expériences pour comparer les performances de l'algorithme xBOA par
rapport aux autres variantes de l'algorithme BOA citées ci-dessous:
-- Self-adaptative BOA (SABOA) [35]
| 


