CHAPITRE 3
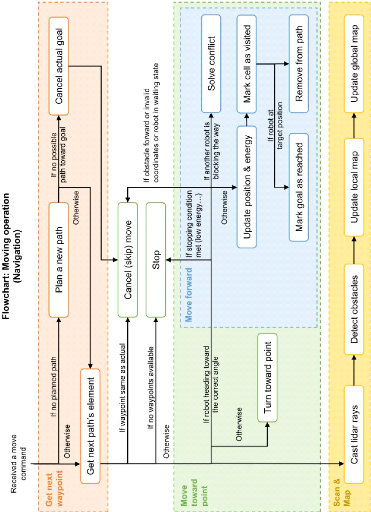
FIGURE 3.7 - Schéma général du modèle
de navigation, planification et évitement d'obstacles du simulateur
PyRoboticsLab
95
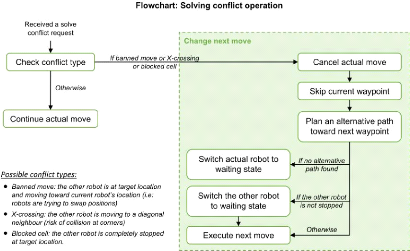
FIGURE 3.8 - Diagramme de la routine "solve
conflict" pour résoudre un problème de blocage entre deux
robots
odds(A) = p(A)
P(-A)
odds(A/B) = p(A/B) (3.2)
P(-A/B)
Après avoir appliqué l'équation 3.2 dans
la règle de Bayes, nous obtenons l'équation 3.3. La valeur
logarithmique varie entre [-oo,+oo], ce qui est utile pour éviter la
multiplication de petits nombres lors de l'implémentation qui pourront
causer des problèmes en raison de la précision limitée des
valeurs flottantes dans l'ordinateur.
logodds(A/B) = log p(B/A)
P (B/-A) + logodds(A) (3.3)
En conséquence, nous pouvons classer chaque cellule Cij
de la grille dans l'une des trois catégories suivantes : cellule vide,
cellule occupée par un obstacle et cellule inconnue. L'équation
3.4 formalise ceci.
96
CHAPITRE 3
|
Cij is
|
?
?????
?????
|
Occupied if Occ(Cij) > 0 Empty if Occ(Cij) < 0 Unknown
if Occ(Cij) = 0
|
(3.4)
|
Où Occ(Cij) est la valeur logarithmique de
l'occupation calculée en utilisant l'équation
3.3.
Dans l'équation 3.4, la valeur 0
représente le seuil pour savoir si une cellule contient un obstacle
où non. Ce seuil a été défini à cette valeur
parce qu'il correspond à la probabilité d'occupation initiale
fixée à 0.5 (logodds(0.5) = 0)
Dans un scénario de navigation, le robot aura donc pour
objectif d'éviter toutes les cellules occupées dont la valeur
logarithmique d'occupation est supérieure à ce seuil. De
même, l'objectif d'une mission d'exploration serait de diriger le robot
vers toutes les cellules ayant une valeur égale à ce seuil
puisqu'elles représentent les cellules inconnues qui n'ont pas encore
été balayées par les capteurs du robot. Ceci nous permet
de modéliser notre problème sous forme de problème
d'optimisation dont le but est de minimiser le nombre de ces cellules. La
figure 3.9 montre un exemple d'exécution d'un tel scénario.
La section suivante présentera les détails
relatifs à la modélisation de ce type de scénarios.
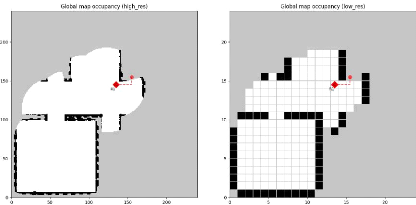
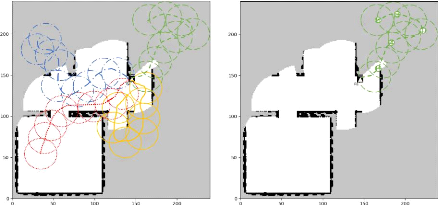
A gauche: carte à haute résolution
(0.1m2/px). A droite: carte à basse résolution
(1m2/px). Les pixels blancs représentent la zone
explorée; les pixels gris représentent la zone inconnue; les
pixels noirs représentent les obstacles détectés.
FIGURE 3.9 - Exemple d'exécution d'un
scénario d'exploration et décomposition de la carte de
l'environnement sous forme de grille d'occupation
3.6 Modélisation du problème d'exploration 3.6.1
Modélisation mono et multirobots
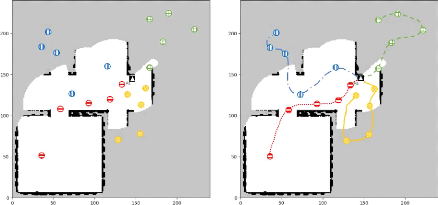
(a) Générer une population de points de
destinations
(b) Calculer les plus courts chemins pour visiter les points
de destinations de chaque solution candidate
(c) Estimer le gain en terme de surface de la zone
explorée pour chaque chemin
(d) La meilleure solution est celle qui maximize la surface
d'exploration de régions pas encore explorées
FIGURE 3.10 - Un exemple du processus d'évaluation de
la fonction fitness pour une population de 4 solutions candidates
La tâche d'exploration de zones inconnues est souvent
modélisée comme un problème 97
98
| 


