CHAPITRE 3
les robots aériens de type quadrirotors. Les moteurs de
ces robots ont la particularité d'être commandés
séparément, ce qui permet de faire des rotations en 360° sur
place sans nécessiter des manoeuvres tel que les véhicules de
type voiture par exemple.
La commande différentielle permet de contrôler la
direction du robot en variant les vitesses de rotation de chaque moteur. Si
tous les moteurs tournent à la même vitesse, le robot se dirigera
tout droit. Si un des moteurs tourne à une vitesse plus
élevée que les autres, le robot fera une rotation dans une
direction opposée à l'emplacement de ce moteur. L'angle de cette
rotation est influencé par plusieurs paramètres dont la distance
du moteur par rapport au centre de gravité du robot, ainsi que le
diamètre des roues pour les robots terrestres par exemple.
Afin de faciliter la commande des robots dans notre
simulateur, nous mettons à la disposition de l'utilisateur des routines
permettant de faire abstraction des détails de calcul pour ne se
focaliser que sur l'action souhaitée. Nous présenterons un
exemple de ce type de routine dans la section suivante (voir section 3.4).
Notre modélisation des robots terrestres se base sur un
robot de type Pioneer P3DX dont nous avons eu l'occasion d'utiliser pour faire
des expériences dans le laboratoire LARESI situé au
département d'électronique à l'USTOMB. Ce robot
très populaire dans le domaine de la recherche possède un
télémètre laser qui lui permet de détecter les
obstacles aux alentours dans un rayon de 180° jusqu'à 270°
selon les modèles. La distance de détection maximale du
télémètre est de 10 mètres; toutefois, nous avons
choisi de la limiter à 4 mètres pour des raisons pratiques
(adaptation aux endroits étroits).
Étant donné que le Lidar du robot était
sujet à un taux d'erreur conséquent lors des expériences
réelles, nous avons choisi de modéliser cette erreur
estimée à 5% en intégrant dans notre simulateur un bruit
gaussien. Nous avons aussi intégré la distance aveugle du Lidar
comprise entre 0 et 30cm, c'est-à-dire que si l'obstacle est trop proche
du Lidar il ne sera pas détecté, et ceci à cause de la
limite physique de ce type de capteurs. La figure 3.5 schématise de ce
modèle d'erreurs.
L'intégration de ces imperfections dans le
modèle géométrique de PyRoboticsLab permet d'effectuer des
simulations plus réalistes. En effet, l'intégration de ces
imperfections permettra de tester la validité des algorithmes
d'évitement d'obstacles et de cartographie à s'adapter plus
facilement aux conditions du monde réel lorsqu'ils sont
déployés en production, contrairement aux tests effectués
dans des simulateurs qui assument l'hypothèse du monde parfait.
La modélisation des rayons laser du Lidar a
été implémentée en utilisant la technique du
Ray Casting, qui consiste à tracer des rayons virtuels et
suivre leur trajectoire pixel par pixel jusqu'à trouver le plus proche
objet bloquant le chemin de ce rayon. Ceci nous permet de calculer la distance
entre le robot et cet objet.
Le Lidar modélisé possède une
résolution de 1°, nous projetons donc 181 rayons virtuels avec
chacun un angle différent allant de 0° à 180°, ce qui
nous permet de connaître la distance et l'angle des objets
détectés. Si le rayon tracé n'est bloqué par aucun
obstacle, nous concluons que l'espace traversé par ce rayon est vide et
peut être parcouru par le robot en toute sécurité.
Étant donné que l'environnement dans notre
simulateur est échantillonné sous forme de grille dont chaque
cellule représente un espace de 10cm2 (voir section 3.5) il
peut arriver qu'un rayon projeté ne traverse qu'une partie infime de
cette cellule, ce qui ne permet pas d'être sûr que cette cellule
soit réellement vide. Ceci nous a poussés à
modéliser une fonction gaussienne pour mesurer le degré de
confiance de la mesure du rayon laser : plus le rayon est proche du centre de
la cellule, plus la confiance de mesure est élevée, tel qu'est
modélisé par la figure 3.5. Ce degré de confiance de la
mesure est linéairement proportionnel à la probabilité de
détection. Lorsque plusieurs rayons laser traversent une même
cellule, cette probabilité de détection est cumulée et
augmente le taux de confiance de la mesure. Le calcul des probabilités
sera détaillé dans la section 3.5 dédiée à
la cartographie.
91
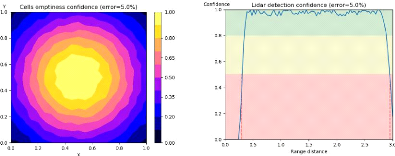
(a) Le degré de confiance que la cellule soit (b) Le
degré de confiance de la distance mesurée
vide est plus élevé lorsque le rayon traverse est
faible lorsque l'obstacle est trop proche ou
cette cellule près de son centre. trop loin du capteur.
FIGURE 3.5 - Modèle du bruit ajouté au capteur
LIDAR et calcul du degré de confiance de la mesure
Une fois un obstacle détecté avec un
degré de confiance suffisamment élevé, nous effectuons une
transformation géométrique pour calculer la position des
obstacles par rapport au repère fixe à partir de sa position
relative au robot. Ce repère fixe est défini au point (0,0) de la
carte globale, et ceci afin de faciliter les calculs par rapport au
repère relatif du Lidar puisque celui-ci est attaché à un
robot qui se déplace. En d'autres termes : les distances des obstacles
mesurées par le Lidar sont toutes relatives au repère du robot
mobile et il faut donc les transformer vers des positions globales relatives au
repère fixe de l'environnement afin de pouvoir les dessiner sur la
carte. Ce processus est illustré par la figure 3.4
3.4 Modélisation du processus de navigation,
planification et évitement d'obstacles
Afin de faciliter la commande des robots dans notre
simulateur, nous mettons à la disposition de l'utilisateur des routines
permettant de faire abstraction des détails de calcul et
92
| 


