|
ÉíÈÚÔáÇ
ÉíØÇÑÞíãáÏÇ
ÉíÑÆÇÒáÌÇ
ÉíÑæåáÌãÇ
íãáÚáÇ
ËÍÈáÇ æ
áíÇÚáÇ
íãáÚÊáÇ
ÉÑÇÒæ
ÇíÖæÈ
ÏãÍã
ÇíÌæáæäßÊáÇ
æ ãæáÚáá
äÇÑåæ
ÉÚãÇÌ
|
|

Présentée par : Amine
BENDAHMANE
Intitulé
Contribution à l'Optimisation d'un Comportement
Collectif pour un Groupe de Robots Autonomes
Faculté : Faculté des
Mathématiques et Informatique
Département : Informatique
Domaine :Informatique
Filière : Informatique
Intitulé de la Formation : Reconnaissance
Des Formes Et Intelligence Artificielle
|
Devant le Jury Composé de :
|
|
|
|
|
Membres de Jury
|
Grade
|
Qualité
|
Domiciliation
|
|
CHOURAQUI Samira
|
Pr
|
Présidente
|
USTO-MB
|
|
TLEMSANI Redouane
|
MCA
|
Encadreur
|
USTO-MB
|
|
ADJOUDJ Réda
|
Pr
|
Examinateur
|
U-SBA
|
|
BOUKLI HACENE Sofiane
|
Pr
|
Examinateur
|
U-SBA
|
|
YEDJOUR Dounia
|
MCA
|
Examinatrice
|
USTO-MB
|
Année Universitaire : 2022/2023

2023
République Algérienne Démocratique et
Populaire
Ministère de l'Enseignement Supérieur et de la
Recherche Scientifique
Université des Sciences et de la Technologie
d'Oran Mohamed Boudiaf
Faculté des Mathématiques et
Informatique
Laboratoire Signal-Image-Parole (SIMPA)
Contribution à l'Optimisation d'un
Comportement
Collectif pour un Groupe de Robots Autonomes
Thèse en vue de l'obtention de diplôme
de
doctorat en INFoRMATIQUE
Présentée par AMINE
BENDAHMANE
Devant le jury composé de
|
CHOURAQUI SAMIRA
|
PR.
|
Présidente
|
USTOMB
|
|
TLEMSANI REDoUANE
|
MCA
|
Directeur de thèse
|
USTOMB
|
|
ADJOUDJ RÉDA
|
PR.
|
Examinateur
|
U-SBA
|
|
BOUKLI HACENE SoFIANE
|
PR.
|
Examinateur
|
U-SBA
|
|
YEDJOUR DoUNIA
|
MCA
|
Examinateur
|
USTOMB
|
2
A ma famille, ma femme
et mes amis.
3
REMERCIEMENTS
Je tiens à remercier mes deux directeurs de
thèse, le Pr. BENYETTOU Abdelkader et le Dr. TLEMSANI Redouane, pour
leurs conseils inestimables et pour avoir accepté d'encadrer ce travail
dont j'espère qu'il sera à la hauteur de leurs
espérances.
Je remercie également Mme la présidente du jury,
Pr. CHOURAQUI Samira, pour sa disponibilité, ainsi que l'ensemble des
membres du jury, à savoir : le Pr. ADJOUDJ Réda, Pr. BOUKLI
HACENE Sofiane et Dr. YEDJOUR Dounia, pour avoir accepté de donner de
leurs temps pour examiner ce travail.
Je remercie le Pr. BERACHED Nasreddine pour m'avoir toujours
ouvert son laboratoire et m'avoir permis de faire des expériences sur
des robots réels sans poser de conditions.
Je remercie aussi l'ensemble de mes enseignants qui m'ont
appris la méthodologie scientifique et les connaissances techniques
requises pour aboutir à ce travail, dont j'espère qu'il sera
à la hauteur de leurs espérances. Sans oublier le personnel
administratif de la faculté ainsi que le service de poste-graduation.
Pour finir, je remercie tous ceux qui ont contribué de
près ou de loin pour la réalisation de ce travail. Notamment ma
famille qui m'a accompagné tout au long de la réalisation de
travail, ainsi que mes amis et mes collègues.
4
RéSUMé
Cette thèse étudie le domaine de la robotique
collective, et plus particulièrement les problèmes d'optimisation
des systèmes multirobots dans le cadre de l'exploration, de la
planification de trajectoires et de la coordination. Elle inclut deux
contributions. La première est l'utilisation de l'algorithme
d'optimisation des papillon (BOA : Butterfly Optimization Algorithm) pour
résoudre le problème d'exploration de zone inconnue avec des
contraintes d'énergie dans des environnements dynamiques. A notre
connaissance, cet algorithme n'a jamais été utilisé pour
résoudre des problèmes de robotique auparavant. Nous avons
également proposé une nouvelle version de cet algorithme
appelée xBOA basée sur l'opérateur de croisement pour
améliorer la diversité des solutions candidates et
accélérer la convergence de l'algorithme. La deuxième
contribution présenté dans cette thèse est le
développement d'une nouvelle plateforme de simulation pour l'analyse
comparative de problèmes incrémentaux en robotique tels que les
tâches d'exploration. La plateforme est conçue de manière
à être générique pour comparer rapidement
différentes métaheuristiques avec un minimum de modifications, et
pour s'adapter facilement aux scénarios mono et multirobots. De plus,
elle offre aux chercheurs des outils pour automatiser leurs expériences
et générer des visuels, ce qui leur permettra de se concentrer
sur des tâches plus importantes telles que la modélisation de
nouveaux algorithmes. Nous avons mené une série
d'expériences qui ont montré des résultats prometteurs et
nous ont permis de valider notre approche et notre modélisation.
Mots clés :
Systèmes multirobots, comportements intelligents,
métaheuristiques, exploration robotique, benchmarking, Butterfly
Optimization Algorithm, xBOA
5
ABSTRACT
This thesis studies the domain of collective robotics, and
more particularly the optimization problems of multirobot systems in the
context of exploration, path planning and coordination. It includes two
contributions. The first one is the use of the Butterfly Optimization Algorithm
(BOA) to solve the Unknown Area Exploration problem with energy constraints in
dynamic environments. This algorithm was never used for solving robotics
problems before, as far as we know. We proposed a new version of this algorithm
called xBOA based on the crossover operator to improve the diversity of the
candidate solutions and speed up the convergence of the algorithm. The second
contribution is the development of a new simulation framework for benchmarking
dynamic incremental problems in robotics such as exploration tasks. The
framework is made in such a manner to be generic to quickly compare different
metaheuristics with minimum modifications, and to adapt easily to single and
multi-robot scenarios. Also, it provides researchers with tools to automate
their experiments and generate visuals, which will allow them to focus on more
important tasks such as modeling new algorithms. We conducted a series of
experiments that showed promising results and allowed us to validate our
approach and model.
Keywords:
Multirobot systems, intelligent behaviors, metaheuristics,
robotics exploration, bench-marking, Butterfly Optimization Algorithm, xBOA
6
` jÊÓ
~
~
ûA~KñK.ðQË@
~éÒ ~cents~~~@~á~~m~~
É~KAÓ YK~Yj~JËAK.ð ,
.1J~«AÒm.Ì @
ûA~KñK.ðQË@
ÈAm.× 6-ðQ£B@ è 11.
€PY~K B@ ~‡J~~~~JË@ð
~H@PAÖÏ@ J~cents~m~~ ð
~
.ú3/4J~~KAÓñ~Kð~#172;A
~°~JÉB@ LAJ~É ú~~
ôXY.:ÖÏ@ ~
~~
Ð@Y j.:É@ ú É
úÍð B@ LëAÖÏ@
·
· ù~ÒÊË@
ÈAj. ÖÏ@
ú~~~á~~.:ÒëAÓ
úΫ .1kðQ£B@ è
.i,ë ÉÒ ~~~
Q~~ «~ ji.1.A1ÖÏ@ #172;A
:°.:É@ .1Ê3/4:Ó ÉmÌ (Butterfly
Optimization Algorithm) 3YK~Yg.
âJ~ÓJP@ñk~
ÕæK
~~ ÕËA~JÒÊ« Yg
úΫ. ûñK.ðQË@ 4P+
ú~~ û@QgaË@ð
3XðYjÖÏ@ alcentsË@
ðQåt ûA«@QÓ
(c)Ó ~é~ðQÖÏ@
P@Y«@~ ÐYLÉ ,
L3AJ~Ë@
· ®i
ú~~. ~A~KñK.ðQË@
É~KAÓ ÉmÌ ÉJ.~
~áÓ~éJ~Ó~PP@ñ~mÌ
@è jë Ð@Y ~j;É@
i
·ñ:,~K @1»ð
~é1YË@ I.Ag. c./Ó
AëZ@X@~á~~s
#172;YîE. xBOA
ùÒ
~éJ~Ó~PP@ñ~mÌ
~ @ è lë áÓ
YK~Yg.
Aë~ðA :3@~
Õ-æK~ ú~~æË@
ÈñÊmÌ @ i Ég
ú~~
~HAJ~ÓjP@ñ:4. @
.Ê::4 Z@X~@
Õæ~J~~®~K
é9Yë l.×A;QK.
QK~ñcents~~ ú~~
É~JÒ~J~K ú~æê~ ,
.1J~.;A:Ë@ .1ÒëAÖÏ@ AÓ@
ð , ~ áÓ
é«ñÒm.×
ÈAÒ~JÉAK.
~éJ.~@QÖÏ@ð
,(c)KA ~'J.Ë@ É~®~Kð
, ~H@PAÖÏ@ J~cents~m~~
#172;A ~°~JÉB@ ÉA -t..o éJ~~.
~HA~KñK.ðQË@
~®«ñË@
`~~A'~mÌ @ ~é~KPA~®ÖÏ
ÈAÒ~JÉB@ ÉîD ð
A~ÓA« éÊm.~~
~é~®K~Qcents~.
l.×A~KQ~.Ë@
ÕæÒ' Õç
|
QñK~
é~K~
~@ AÒ» . 3XY:ÖÏ@ð
4K~XQ~®Ë@
ûA~KñK.ðQË@
ûAëñK~PA~J~~É
(c)Ó
AJ~°J~~KAÓñ~Kð
|
i@ J~°~JË@ð ,
4Qå4
|
~
@ Qar~@ ÐAêÓ úΫ
J~~»Q"JAK. ÑêË iÒa~É AÜØ
ÑîE.PAm.~~ .1~JÖ~ß~B û@ðX@
c4tkAJ.ÊË
ék~~~ É~JÓ
~éJ~Òë
. YÖ ß
z
i
éÖß~Y
®Ë@ ~HAJ~Ó
~PP@ñ~mÌ
~@(c)ÓAî
PA
ð6YK~Yg.
ûA»ÓJP@ñk
· ;~NJa @ H*AÒÊ3/4Ë@
N
i
€AJ~9 ,
ù~;@ñ.:Ë@ ûj.;Ë@
,úÍB@ #172;A~:°~JÉB@ , .1J»
~YË@ ûAJ~»ñÊË@ ,
âJ~«AÒm.Ì @
,:_,
·A
·.;ñK.ðQË@
416@
~
xBOA
ôJ~ÓJP@ñk~ ,
~HA~É@QaË@ ~m~
~éJ~ÓJP@ñk~ ,
ûAJ~ÓJP@ñ. @ Z@X @
7
TABLE DES MATIÈRES
Remerciements 3
Résumé 4
Table des matières 9
Liste des figures 12
Liste des tableaux 13
Introduction Générale 14
|
I
1
|
Etude théorique
Les systèmes multirobots
|
16
17
|
|
1.1
|
Introduction
|
18
|
|
1.2
|
Les systèmes multirobots
|
18
|
|
|
1.2.1 Présentation des systèmes multirobots
|
18
|
|
|
1.2.2 Les domaines d'applications
|
19
|
|
1.3
|
Les types de systèmes multirobots
|
22
|
|
|
1.3.1 Classification par type de comportements
|
22
|
|
|
1.3.2 Classification par type de synchronisation
|
24
|
|
|
1.3.3 Classification par type d'architecture du système
|
24
|
|
|
1.3.4 Classification par autonomie
|
26
|
|
|
1.3.5 Classification par type de robots
|
28
|
|
1.4
|
Catégorisation des problématiques liées
aux systèmes multirobots
|
29
|
|
|
1.4.1 La navigation
|
30
|
|
|
1.4.2 La cartographie
|
31
|
|
|
1.4.3 La localisation
|
36
|
|
|
1.4.4 La planification
|
38
|
|
|
1.4.5 L'exploration
|
39
|
|
|
1.4.6 La communication
|
42
|
|
|
1.4.7 Autres problématiques
|
43
|
|
1.5
|
Etat de l'art et travaux connexes
|
44
|
|
|
1.5.1 Les méthodes déterministes
|
44
|
|
|
1.5.2 Les méthodes à base d'apprentissage machine
|
46
|
|
|
1.5.3 Les méthodes stochastiques
|
46
|
|
1.6
|
Conclusion
|
48
|
|
2
|
Les métaheuristiques
|
49
|
|
2.1
|
Introduction
|
50
|
|
2.2
|
Les métaheuristiques
|
50
|
|
2.3
|
Les types de métaheuristiques
|
51
|
|
|
2.3.1 Les méthodes à base de trajectoires
|
51
|
|
|
2.3.2 Les méthodes à base de population
|
53
|
8
2.4 Les mécanisme des métaheuristiques 57
2.4.1 La fonction objectif 57
2.4.2 L'exploration et l'exploitation 57
2.4.3 La convergence 58
2.4.4 Les hyperparamètres 59
2.4.5 Les contraintes 60
2.4.6 Les générations 60
2.4.7 Les critères d'arrêt 60
2.4.8 L'optimalité et la dominance 61
2.5 Structure de base d'une métaheuristique 62
2.5.1 La phase d'initialisation 62
2.5.2 Le corps de l'algorithme 62
2.5.3 La phase finale 62
2.6 Fondements théoriques de métaheuristiques
populaires 64
2.6.1 Les algorithmes génétiques (GA) 64
2.6.2 L'optimisation par Essaim de Particules (PSO) 66
2.6.3 L'otimisation par Colonie de Fourmies (ACO) 67
2.7 Les Fondements théoriques de l'Algorithme
d'Optimisation des Papillons
(BOA) 69
2.8 Les variantes de l'algorithme BOA 73
2.9 Amélioration de l'Algorithme d'Optimisation des
Papillons en utilisation
l'opérateur de croisement (xBOA) 75
2.10 Conclusion 78
II Etude expérimentale 79
3 Méthodologie, modélisation et
paramétrage 80
3.1 Introduction 81
3.2 PyRoboticsLab : un nouvel outil de simulation et de
benchmarking . . . 81
3.2.1 Motivations pour la création d'une nouvelle
plateforme de simulation 82
3.2.2 Les objectifs de conception 83
3.2.3 L'architecture du système 85
3.2.4 Les outils et technologies 87
3.2.5 Les scénarios de bechmarking 89
3.3 Modélisation géométrique des robots
89
3.4 Modélisation du processus de navigation, planification
et évitement d'obs-
tacles 91
3.5 Modélisation des grilles d'occupation 93
3.6 Modélisation du problème d'exploration 97
3.6.1 Modélisation mono et multirobots 97
3.6.2 Les critères d'évaluation 100
3.6.3 La complexité du modèle 101
3.7 Paramétrage et configuration 101
3.7.1 Paramétrage des expériences 101
3.7.2 Paramétrage de l'environnement de simulation
102
9
3.8 Conclusion 104
4 Expériences et analyse 105
4.1 Introduction 106
4.2 Configuration matérielle 106
4.3 Expérience 1 : Évaluation de l'algorithme xBOA
dans un contexte multirobots107 4.4 Expérience 2 : Comparaison entre les
stratégies d'exploration à court terme
et à long terme 109
4.5 Expérience 3 : Recherche des meilleurs
hyperparamètres 110
4.6 Expérience 4 : Comparaison de l'algorithme xBOA avec
les métaheuris-
tiques populaires 112
4.7 Expérience 5 : Evaluation
de la robustesse de l'algorithme xBOA face à la
réduction de taille de la population 120
4.8
Expérience 6 : Comparaison de xBOA avec les autres variantes de
l'algo-
rithme BOA 125
4.9 Expérience 7 : Test en utilisant un robot réel
129
4.10 Conclusion 131
Conclusion générale et perspectives
132
Bibliographie 140
10
LISTE DES FIGURES
|
1.1
|
Images de systèmes multirobots dans le monde réel
|
18
|
|
1.2
|
Différents aspects étudiés selon la nature
du domaine appliqué aux systèmes
|
|
|
multirobots
|
19
|
|
1.3
|
Utilisation de robots pour la gestion portuaire
(système Kalmar AutoStrad
|
|
|
[33])
|
20
|
|
1.4
|
Exemple d'un scénario où un groupe de robots
s'entraident pour déplacer
|
|
|
un objet lourd (Université Georgia Tech)
|
21
|
|
1.5
|
Exemple d'un scénario de modélisation 3D d'un parc
urbain en utilisant
|
|
|
plusieurs plusieurs robots (Australian Centre for Field
Robotics)
|
22
|
|
1.6
|
Types d'architectures de systèmes multirobots
|
25
|
|
1.7
|
Exemple d'un système hétérogène
constitué d'un robot volant et d'un robot mobile terrestre pour la
supervision d'une zone agricole (Australian Centre
|
|
|
for Field Robotics)
|
29
|
|
1.8
|
Détection d'obstacles en utilisant la technique du
Vector Field Histogram [20]
|
31
|
|
1.9
|
Diagramme de relations entre l'environnement du robot et sa
représenta-
|
|
|
tion interne
|
32
|
|
1.10
|
Exemple d'une carte métrique 2D construite en utilisant la
technique des
|
|
|
grilles d'occupations [1]
|
34
|
|
1.11
|
Exemples de cartes métriques 3D
|
34
|
|
1.12
|
Exemple d'une carte topologique
|
35
|
|
1.13
|
Résultat d'un processus de fusion de cartes [74]
|
36
|
|
1.14
|
Schématisation des différents repères
utilisés pour la localisation relative et
|
|
|
globale [29]
|
37
|
|
1.15
|
Localisation par balises RFID [22]
|
38
|
|
1.16
|
Simulation d'un scénario industriel basé sur les
algorithmes de planification
|
|
|
de trajectoires [42]
|
40
|
|
1.17
|
Exemple de décomposition d'une carte et balayage en
utilisant une trajec-
|
|
|
toire en zigzag [48]
|
41
|
|
1.18
|
Exemple de sélection de régions à visiter
dans un scénario de surveillance
|
|
|
[49]
|
41
|
|
2.1
|
Classification des métaheuristiques [28]
|
51
|
|
2.2
|
Exemple d'une recherche à solution unique
|
52
|
|
2.3
|
Exemple d'une recherche à base de population de solutions
|
53
|
|
2.4
|
Processus de base d'un algorithme génétique
|
54
|
|
2.5
|
Optimisation de chemins par un ensemble de fourmis [56]
|
55
|
|
2.6
|
Optimisation à base d'interactions physiques entre les
atomes [67]
|
56
|
|
2.7
|
Difference entre les stratégies d'exploration et
d'exploitation d'une méta-
|
|
|
heuristique [70]
|
58
|
|
2.8
|
Exemple de convergence d'une population de solutions [21]
|
59
|
|
2.9
|
Visualisation d'un front optimal (Pareto Front) séparant
les solutions domi-
|
|
|
nées des solutions non dominées [65]
|
61
|
|
2.10
|
Structure de base d'une métaheuristique
|
63
|
|
2.11
|
Diagramme de l'algorithme génétique
|
65
|
|
2.12
|
Pseudo-code de l'algorithme ACO
|
68
|
11
2.13 Diagramme de l'algorithme BOA 70
2.14 Pseudo-code de l'algorithme BOA 72
2.15 Résumé de l'état de l'art de
l'algorithme BOA et ses différentes variantes 74
2.16 Exemple et pseudo-code de l'opérateur de
croisement 75
2.17 Pseudo-code de l'algorithme xBOA 76
2.18 Diagramme de l'algorithme xBOA 77
3.1 Exemple d'un simulateur moderne basé sur un moteur
de jeux vidéos pour
l'entraînement des voitures autonomes [31] 82
3.2 Architecture générale du simulateur
PyRoboticsLab 86
3.3 Exemple de quelques types de visualisations
générées par le simulateur Py-
RoboticsLab 87
3.4 Modélisation
géométrique du robot et des différents repères
utilisés pour la
détection d'obstacles 89
3.5 Modèle du
bruit ajouté au capteur LIDAR et calcul du degré de confiance
de
la mesure 91
3.6 Niveaux d'abstraction du processus de
navigation, planification et évite-
ment d'obstacles du simulateur PyRoboticsLab 92
3.7
Schéma général du modèle de navigation,
planification et évitement d'obs-
tacles du simulateur PyRoboticsLab 94
3.8 Diagramme de la
routine "solve conflict" pour résoudre un problème de
blo-
cage entre deux robots 95
3.9 Exemple d'exécution
d'un scénario d'exploration et décomposition de la
carte de l'environnement sous forme de grille d'occupation
96
3.10 Un exemple du processus d'évaluation de la fonction fitness
pour une po-
pulation de 4 solutions candidates 97
3.11 Diagramme du processus d'exploration d'une zone inconnue
99
3.12 Schéma du modèle utilisé pour
assurer la coordination entre les robots . 100
3.13 Cartes de l'environnement de simulation utilisé
durant les expériences . 102
3.14 Carte d'environnement utilisé pour simuler les
scénarios à large échelle . 103
4.1 Progression visuelle du scenario multirobots en utilisant
la méthode xBOA
avec 3 robots 107
4.2 Progression visuelle d'un
scénario à grande échelle en utilisant la
méthode
xBOA avec 2 robots 108
4.3 Comparaison entre les deux
stratégies d'exploration en utilisant la méthode
xBOA 110
4.4 Résultats de la simulation de la
mission d'exploration en utilisant la stratégie
à court terme 114
4.5 Résultats de la
simulation de la mission d'exploration en utilisant la stratégie
à long terme 115
4.6 Comparaison de la
durée totale de la mission d'exploration pour la stratégie
à court terme 117
4.7 Comparaison de la
durée totale de la mission d'exploration pour la stratégie
à long terme 118
4.8 Nombre d'évaluations
de la fonction de fitness et temps moyen de calcul
pour chaque métaheuristique 119
12
4.9 Comparaison des résultats en utilisant
l'algorithme BOA avec différentes
tailles de population sur l'environnement House Map
120
4.10 Comparaison du taux d'exploration et durée de la
mission en utilisant la
stratégie à court-terme et une population de
taille 5 122
4.11 Comparaison du temps moyen de calcul et
convergence de la valeur de fit-
ness en utilisant la stratégie à court-terme et
une population de taille 5 . . 123 4.12 Impact de la réduction
de la taille de population sur le temps de calcul et
temps de la mission en utilisant les différentes
métaheuristiques 124
4.13 Visualisation du front des
solutions dominantes (Pareto-front) pour les dif-
férentes métaheuristiques en utilisant une
population de taille 5 125
4.14 Comparaison des variantes de
l'algorithme BOA en utilisant la stratégie à
court terme et une population de taille 5 127
4.15
Suite de la comparaison des variantes de l'algorithme BOA en utilisant
la
stratégie à court terme et une population de
taille 5 128
4.16 Visualisation du front des solutions dominante
(Pareto-front) pour les va-
riantes de BOA en utilisant une population de taille 5
129
4.17 Expérience sur le robot réel
130
13
LISTE DES TABLEAUX
|
1.1
|
Comparaison entre les architectures des systèmes
multirobots
|
27
|
|
1.2
|
Comparaison entre les capteurs de distance et les capteurs
optiques . . . .
|
33
|
|
1.3
|
Récapitulatif des problématiques de bases dans le
domaine des systèmes
|
|
|
multirobots
|
43
|
|
1.4
|
Résumé comparatif des travaux cités
|
47
|
|
4.1
|
Valeurs des meilleurs hyperparamètres trouvés
après 30 essais
|
112
|
|
4.2
|
Taux d'exploration obtenus à la fin de la mission
d'exploration
|
113
|
|
4.3
|
Evolution du taux d'exploration selon la taille de la
population en utilisant
|
|
|
l'algorithme BOA
|
120
|
|
4.4
|
Taux d'exploration obtenus à la fin de la mission en
utilisant l'algorithme
|
|
|
BOA avec une population de taille 5
|
124
|
|
4.5
|
Comparatif du taux d'exploration en utilisation les variantes
de l'algorithme
|
|
|
BOA avec une population de taille 5
|
126
|
14
INTRODUCTION GÉNÉRALE
La robotique collective est un domaine actif de recherche et
développement qui a le potentiel de révolutionner de nombreux
secteurs. Elle prend une place de plus en plus importante dans l'agriculture,
l'industrie, le transport, la sécurité, le sauvetage,
l'exploration et le divertissement. Elle se base sur le principe d'utilisation
de plusieurs robots qui travaillent ensemble pour atteindre un objectif commun.
Cette collectivité implique la collaboration et/ou la coopération
des robots entre eux, ce qui la lie intimement avec le domaine de
l'in-telligence artificielle distribuée.
Ces deux domaines combinés peuvent offrir de nombreux
avantages, notamment : la réalisation de tâches plus rapidement et
plus efficacement, et de manière plus sécurisée,
même dans des environnements dangereux qui pourraient présenter
des risques pour les êtres humains. Par ailleurs, l'utilisation d'un
groupe de robots au lieu d'un seul permet d'augmenter la polyvalence et la
flexibilité du système, ainsi que la robustesse aux pannes.
Notre thèse s'inscrit dans le cadre d'optimisation d'un
comportement collectif pour un groupe de robots autonomes, nous nous
intéressons aux scénarios de planification de trajectoires et
d'exploration de zones en vue de détection d'incidents par exemple, ou
de la localisation d'une personne en détresse.
La thèse est organisée en deux parties. La
partie théorique - divisée en deux chapitres - vise à
introduire tous les fondements théoriques nécessaires à la
compréhension de notre travail. La deuxième partie - elle aussi
divisée en deux chapitres - inclut tous les détails relatifs
à la modélisation de notre solution et l'analyse des
résultats expérimentaux.
Nous introduirons le lecteur dans le premier chapitre aux
différents types de systèmes multirobots ainsi que les
mécanismes de synchronisation existants, tout en détaillant les
différentes problématiques de recherche engendrées par ce
type de systèmes. Nous aborderons également un état de
l'art sur les techniques d'intelligence artificielle utilisées pour les
résoudre.
Le deuxième chapitre sera consacré à
l'étude des métaheuristiques et leurs mécanismes de
fonctionnement. Nous présenterons les fondements théoriques de
quelques métaheu-
15
Introduction Générale
ristiques populaires que nous utiliserons durant nos
expériences. Nous présenterons par la suite notre contribution
à l'amélioration du Butterfly Optimization Algorithm, en
expliquant tous les détails mathématiques nécessaires
à son bon fonctionnement.
Dans le troisième chapitre, nous introduirons le
lecteur à la deuxième contribution de notre thèse
concrétisée dans le développement d'une plateforme de
simulation spécialisée dans le benchmarking et
l'évaluation des algorithmes d'optimisation pour les
problématiques de navigation, de planification de trajectoires,
d'exploration, de balayage et de surveillance. Nous présenterons ensuite
la méthodologie utilisée et notre modélisation du
problème d'exploration de zones inconnues avec des contraintes
d'énergie.
Le dernier chapitre regroupera l'ensemble des résultats
expérimentaux obtenus durant notre thèse. Nous
présenterons aussi notre interprétation de ces résultats
à travers une analyse dédiée pour chaque
expérience. Ce chapitre conclura nos travaux en présentant une
critique des techniques utilisées ainsi que des pistes potentielles pour
les améliorer.
16
Première partie
Etude théorique

17
CHAPITRE 1
LES SYSTÈMES MULTIROBOTS
|
1.1
1.2
|
Introduction
Les systèmes multirobots
1.2.1 Présentation des systèmes multirobots
1.2.2 Les domaines d'applications
|
18
18
18
19
|
|
1.3
|
Les types de systèmes multirobots
|
22
|
|
1.3.1
|
Classification par type de comportements
|
22
|
|
1.3.2
|
Classification par type de synchronisation
|
24
|
|
1.3.3
|
Classification par type d'architecture du système
|
24
|
|
1.3.4
|
Classification par autonomie
|
26
|
|
1.3.5
|
Classification par type de robots
|
28
|
|
1.4
|
Catégorisation des problématiques liées
aux systèmes multirobots
|
29
|
|
1.4.1
|
La navigation
|
30
|
|
1.4.2
|
La cartographie
|
31
|
|
1.4.3
|
La localisation
|
36
|
|
1.4.4
|
La planification
|
38
|
|
1.4.5
|
L'exploration
|
39
|
|
1.4.6
|
La communication
|
42
|
|
1.4.7
|
Autres problématiques
|
43
|
|
1.5
|
Etat de l'art et travaux connexes
|
44
|
|
1.5.1
|
Les méthodes déterministes
|
44
|
|
1.5.2
|
Les méthodes à base d'apprentissage machine
|
46
|
|
1.5.3
|
Les méthodes stochastiques
|
46
|
|
1.6
|
Conclusion
|
48
|
18
CHAPITRE 1
1.1 Introduction
L'étude de la robotique collective dans un contexte
informatique concerne l'étude des systèmes dits "multirobots".
L'objectif de ce chapitre est de donner une idée
d'ensemble sur ce sujet en essayant d'englober chacun de ses aspects. Nous
commencerons par présenter les systèmes multiro-bots, leurs types
et leurs domaines d'applications. Nous détaillerons également les
axes de recherche relatifs à ce sujet avec les différentes
problématiques qui en découlent.
Nous aborderons ensuite un état de l'art des techniques
d'intelligence artificielle en lien avec les problématiques
traitées dans cette thèse, à savoir les
problématiques d'optimisation de trajectoires et d'exploration de zones
inconnues en utilisant plusieurs robots.
1.2 Les systèmes multirobots
1.2.1 Présentation des systèmes multirobots

FIGURE 1.1 - Images de systèmes multirobots dans le
monde réel
Les systèmes multirobots (Multirobots
Systems,en anglais) sont des systèmes composés de plusieurs
robots programmés de sorte à travailler ensemble afin d'accomplir
une certaine mission. Cette mission est souvent décomposée en un
ensemble de tâches afin de réduire sa complexité. Ces
tâches peuvent être effectuées une à une
séquentiellement, ou en parallèle, selon l'interdépendance
entre elles et le type d'architecture du système.
Les robots sont des machines avec des propriétés
physiques et logiques, ils peuvent donc
être analysés d'un point de vue mécanique
et électronique pour étudier la manière dont ils
détectent et impactent l'environnement qui les entoure. Comme ils
peuvent aussi être étudiés d'un point de vue algorithmique
pour spécifier la manière dont cet environnement doit être
représenté en interne dans le but de prendre des décisions
ou d'effectuer des actions. L'intelligence artificielle est donc au coeur de ce
processus décisionnel, afin de s'assurer que ces machines s'adaptent de
manière efficace à leur environnement.
Dans le domaine de l'informatique, un robot peut être vu
comme un agent qui interagit selon certaines règles. L'étude d'un
système multirobots peut être vue comme l'étude d'un
système multiagents avec certaines limitations physiques telles que leur
degré d'autonomie et leur capacité de stockage et de traitement
de l'information.
D'un autre côté, ils peuvent être
apparentés aux systèmes embarqués en les
considérant comme un réseau d'objets connectés qui
communiquent entre eux pour échanger des informations. Le terme
Réseaux Multirobots (Multirobots Network en anglais) est
parfois utilisé dans la littérature pour décrire ce
concept.
En parallèle, ils peuvent être
considérés dans le domaine de la logistique comme des flottes de
véhicules autonomes (Autonomous Vehicules Fleet). L'objet
d'étude se concentrera donc sur les techniques de gestion de la flotte
(fleet management), suivi de la position et état des robots
(tracking), ainsi que les techniques de commande à distance
(remote control). Il est à noter que le terme «
Véhicule autonome » dans ce domaine doit être
compris au sens large, il inclut les robots de type : voitures, tracteurs,
drones et sous-marins.
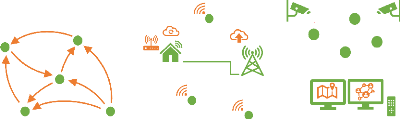
(a) Intelligence Artificielle : Étude des
décisions et interactions entre les agents
(b) Réseaux et systèmes embarqués :
Connectivité, topologie réseau et protocoles
(c) Logistique autonome : Suivi, visualisation et commande
à distance
19
FIGURE 1.2 - Différents aspects
étudiés selon la nature du domaine appliqué aux
systèmes multirobots
1.2.2 Les domaines d'applications
Les systèmes multirobots sont souvent utilisés
dans des domaines industriels, sécuri-taires et ludiques. Parmi les
applications notables qui ont permis d'exploiter les pleines capacités
qu'offrent ces systèmes, nous pouvons citer:
-- La détection de feux de forêt;
20
CHAPITRE 1
-- Le nettoyage de zones contaminées ou dangereuses;
-- L'accomplissement d'opérations agricoles dans les
fermes intelligentes;
-- La recherche et localisation de survivants lors des
catastrophes naturelles;
-- La gestion des entrepôts de marchandises;
-- Le déplacement de conteneurs dans les ports;
-- L'inspection des conduits souterrains, pipe-lines,
canalisations et fonds marins;
-- Le divertissement tel que la dance coordonnée de
robots, les spectacles de lumière et les compétitions de football
robotique;
-- La surveillance et détection d'intrus;
-- Le déploiement de capteurs lors des expéditions
scientifiques, tel que les études climatologiques, environnementales et
écologiques;
-- Ainsi que d'autres applications militaires tel que
l'espionnage et la télésurveillance.

FIGURE 1.3 - Utilisation de robots pour la gestion portuaire
(système Kalmar AutoStrad [33])
L'utilisation de ces systèmes offre plusieurs avantages
tels que l'augmentation de la productivité industrielle et agricole,
l'accélération de tâches de sauvetage et lutte contre les
incendies, le renforcement de la fiabilité des systèmes
sécuritaires, l'élargissement de la surface de couverture dans
les systèmes de surveillance, ainsi que la possibilité à
effectuer des tâches impossibles à faire en utilisant un seul
robot.
21
De plus, l'utilisation de ces systèmes permet parfois
aussi de diminuer les coûts de production par rapport à
l'utilisation d'un seul robot, bien que cette idée puisse paraître
contre-intuitive. En effet, il est parfois moins coûteux de fabriquer
plusieurs petits robots bon marché avec des capacités
limitées au lieu d'un seul robot complexe et sophistiqué.
D'autant plus que la consommation énergétique d'un robot peut
augmenter rapidement avec l'augmentation de sa puissance de calcul et poids
maximal à déplacer. Afin de palier à ce type de
problèmes, certains chercheurs se sont basés sur la distribution
de charge entre plusieurs petits robots qui travaillent ensemble au lieu
d'investir sur l'augmentation de la capacité d'un seul robot.
D'un autre côté, les systèmes multirobots
permettent d'augmenter la robustesse du système en évitant
l'inconvénient du point de défaillance unique ({Single
point of failure}). Par exemple, dans un scénario de sauvetage ou
d'exploration d'une zone dangereuse, il est beaucoup moins grave qu'un ou
plusieurs petits robots tombent en panne tant que les autres robots restent
opérationnels, comparé à la situation où un seul
robot complexe est déployé risquant d'entraîner
l'échec automatique de la mission s'il tombe en panne ou se retrouve
bloqué dans les débris.

FIGURE 1.4 - Exemple d'un scénario
où un groupe de robots s'entraident pour déplacer un objet lourd
(Université Georgia Tech)
Il existe toutefois des inconvénients à utiliser
ce genre de systèmes : la nécessité à
intégrer des moyens de communication entre robots entraîne
l'augmentation de la complexité des logiciels et la
nécessité à intégrer des dispositifs
électroniques supplémentaires (Wifi, 4G/LTE, GPS...) qui peuvent
être lourds en consommation énergétique. L'ajout de ces
éléments engendre l'augmentation des coûts de production
ainsi que la consommation énergétique des robots, notamment dans
les situations où le rayon de communication est large.
Un autre problème est la nécessité
d'inclure des mécanismes de coordination et/ou collaboration entre les
robots pour éviter le chevauchement entre les tâches
effectuées, ou encore l'implémentation de processus de prise de
décision collective. Ces fonctionnalités additionnelles
entraînent souvent le recourt à l'augmentation de la puissance de
calcul des
22
CHAPITRE 1
robots ainsi que la difficulté à détecter
les bogues informatiques à cause de la nature hautement parallèle
d'un tel système.
En outre, l'utilisation des systèmes multirobots dans
certains domaines d'application requiert l'installation d'infrastructures
supplémentaires (antennes relais, serveurs de récolte de
données, balises de localisation, bornes de recharge...etc), ce qui
accroît la complexité du système.

FIGURE 1.5 - Exemple d'un scénario de
modélisation 3D d'un parc urbain en utilisant plusieurs plusieurs robots
(Australian Centre for Field Robotics)
1.3 Les types de systèmes multirobots
Les systèmes multirobots peuvent être
catégorisés selon plusieurs critères : architecture du
système, type d'interactions, type de synchronisation, autonomie ou
encore le type des robots utilisés.
Nous allons détailler ci-dessous chaque classification
en commençant de la plus abstraite vers la plus spécifique.
1.3.1 Classification par type de comportements
Un système multirobot doit intégrer des
mécanismes d'interaction entre les robots, ces interactions forment des
comportements de travail collectif qui peuvent être classés en
plusieurs catégories:
Coordination
La coordination est le fait de synchroniser ses efforts pour
réaliser une tâche en équipe. Sachant que cette tâche
pouvait être réalisée par un seul agent, mais de
manière moins efficace que lorsque celle-ci est réalisée
par une équipe d'agents.
23
L'efficacité augmente donc avec l'augmentation du
nombre d'agents dans le groupe, jusqu'à une certaine limite où
l'ajout de nouveaux membres n'ajoute aucun apport. Un exemple de missions qui
peuvent être réalisées seules ou en coordination avec
d'autres robots comprend les tâches d'exploration, la recherche de
personnes et le déploiement de capteurs.
Coopération
La coopération entre plusieurs agents est semblable
à la coordination, à la différence que la tâche en
question ne peut d'être réalisée par un seul agent, comme
l'action de déplacer un objet très lourd par exemple, ou jouer
à un match dans un sport collectif.
L'efficacité passe donc de 0% en utilisant un seul
agent à 100% en utilisant un groupe d'agents.
Collaboration
La collaboration est l'utilisation d'un groupe d'agents
différents pour effectuer une tâche ensemble qui ne pouvait pas
être réalisée en utilisant un seul type d'agents.
Ce genre de comportement nécessite souvent la
distribution de rôles selon les capacités de chaque agent. On
retrouve souvent ce type de tâches dans les chaines de production
industrielles où chaque type de robots est responsable de la
réalisation d'une sous-tâche.
L'efficacité passe dans ce cas de figure de 0% en
utilisant un type d'agents à 100% en utilisant plusieurs types
d'agents.
Compétition
Un comportement compétitif est l'opposé de la
coordination ou de la coopération dans le sens ou chaque agent agit de
manière à maximiser son gain au profit du gain des autres agents.
Un exemple d'un comportement compétitif peut être trouvé
dans les compétitions de robotiques pour collecter le maximum nombre
d'objets par exemple.
Opposition
Dans le comportement d'opposition, chaque agent agit de
manière adverse contre les autres agents de manière à
annuler leurs actions. Un exemple de ce type de comportement peut être
trouvé dans les systèmes anti-intrusion ou un groupe de robots
essaient de neutraliser un autre robot intrus.
CHAPITRE 1
Emergence de comportement
C'est le fruit d'accumulation de plusieurs actions
effectuées par un ensemble d'agents agissant de manière
séparée en suivant des règles simples, mais qui
résulte en la réalisation d'une tâche commune et souvent
complexe. La coordination émerge donc à partir d'un travail
collectif même si elle n'était pas intentionnelle à
l'échelle individuelle.
On retrouve ce genre de comportement dans les essaims de
robots inspirés à partir de colonies d'insectes et d'animaux
sociaux, pour réaliser des tâches de collecte de nourriture par
exemple.
1.3.2 Classification par type de synchronisation
Il est possible de classer la synchronisation des systèmes
multirobots en deux types: Synchronisation implicite
Ce mode se base sur l'échange de données de
manière indirecte en utilisant une mémoire partagée
stockée sur un serveur central. Elle est souvent utilisée dans le
but d'éviter le chevauchement entre les actions réalisées
par plusieurs robots sans nécessiter une communication directe entre
eux. Les robots dans ce type de scénarios ne sont pas forcément
conscients de l'existence des autres robots, ils peuvent tout de même
profiter des informations récoltées par ceux-ci en consultant les
données stockées sur le serveur.
Ce type de synchronisations est largement utilisé dans
des travaux d'exploration et de recherche de survivants où le serveur
combine les données des zones explorées par chaque robot, puis
les redistribuent aux robots pour leur permettre d'éviter de
réexplorer une zone qui a déjà été
visitée par un autre robot auparavant.
Synchronisation explicite
Ce type concerne l'échange de messages directs entre
les robots pour se partager des informations et diviser le travail. Cette
communication permet d'effectuer une coordination proactive en permettant aux
robots de décider d'une stratégie commune qui maximise les gains
du groupe.
Un cas concret de ce type de synchronisation est
l'échange d'actions futures planifiées par les robots telles que
les trajectoires de déplacement afin d'éviter les collisions, ou
l'échange d'informations sur leurs états internes (comme le
niveau de batterie disponible) afin de négocier la distribution de
tâches de manière optimale.
1.3.3 Classification par type d'architecture du système
On peut classer les architectures des systèmes
multirobots en 3 catégories principales: 24
Système centralisé
Il s'agit d'un ensemble de robots communiquant avec un noeud
central dont le rôle est de gérer le groupe en envoyant des ordres
à chaque robot, ou en combinant les données collectées par
ceux-ci. Ce noeud central peut être un serveur distant, ou un robot
leader qui évolue dans le même environnement que les autres
robots, et possède généralement des capacités de
calcul et de stockage largement supérieur aux robots
exécutants.
Il constitue le point le plus fragile du système
puisque ce dernier ne sera plus opérationnel si la communication avec ce
noeud est interrompue ou si celui-ci tombe en panne. Une pratique courante pour
diminuer ce genre de risque dans les systèmes critiques est de miser sur
la redondance de ce noeud. Ceci permet de renforcer la robustesse du
système tout en gardant l'avantage de cette topologie qui se
caractérise par sa simplicité et la disponibilité de
toutes les informations au même endroit; le noeud central possède
une vue d'ensemble sur l'état de tous les robots, des actions
effectuées, et de l'avancement de la mission, et pourra planifier de
manière efficace la distribution des tâches.
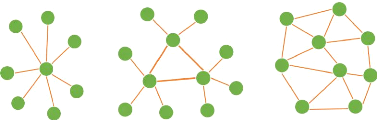
25
(a) Centralisé (b) Décentralisé (c)
Distribué
FIGURE 1.6 - Types d'architectures de
systèmes multirobots
Système décentralisé
Dans un système décentralisé, il n'y a
pas un seul noeud central, mais plutôt plusieurs petits noeuds centraux
dont chacun est responsable de gérer un groupe de robots. Ces noeuds
centraux communiquent entre eux pour se synchroniser, mais restent
indépendants dans les décisions et choix des tâches
à affecter aux robots de leurs équipes respectives.
L'avantage d'un tel système est de ne pas
posséder un seul point de défaillance (Single point
offailure) puisque chaque équipe est indépendante des
autres. Par ailleurs, il est possible de réaffecter les équipes
de sorte à ne pas pénaliser une équipe entière si
son noeud central n'est plus opérationnel.
Ces points centraux jouent souvent le rôle de relais de
communication dans les scénarios nécessitant le
déploiement de robots dans une zone à large surface, ce qui
permet d'éviter l'isolement d'un robot si son rayon de communication est
trop loin du noeud central.
26
CHAPITRE 1
Ce genre de systèmes nécessitent toutefois
l'utilisation d'un grand nombre d'agents puisqu'il y aura très peu
d'intérêts à diviser un petit groupe en plusieurs petites
équipes. Une complexité de coordination s'ajoute à cela
puisque chaque noeud ne possède qu'une partie de l'état global du
système, il est donc impératif que les noeuds centraux
échangent entre eux les informations de manière
régulière afin d'éviter le chevauchement entre les
tâches réalisées par chaque équipe.
Une autre utilité de ce genre d'architecture est de les
utiliser dans des scénarios de collaboration entre plusieurs types de
robots. Chaque équipe sera constituée par un type de robots et
sera coordonnée par un leader qui prend en considération les
capacités des membres de son équipe.
Système distribué
Dans un système distribué, il n'existe pas de
notion d'agent central ou de leader. Chaque noeud communique avec ses voisins
et décide des tâches qu'il devra accomplir, il est donc totalement
indépendant des autres noeuds, ce qui renforce la robustesse du
système puisque celui-ci reste opérationnel tant qu'il y a au
moins un robot en service. De plus, il n'y a pas l'obligation de disposer d'un
serveur central pour combiner les données.
Cette architecture se caractérise par une communication
limitée et une prise de décision au niveau local, ce qui permet
d'agrandir la taille du groupe sans avoir besoin d'augmenter les performances
des robots ou le débit du réseau. Elle est souvent
utilisée dans le cas des essaims de robots (swarm of robots)
où l'objectif est de déployer un grand nombre de petits robots
avec des capacités limitées, dans le but de faire émerger
un comportement plus intelligent pour réaliser des tâches
complexes. L'idée de base tourne donc autour de la mise à
l'échelle (scalability) du système multirobots tout en
augmentant sa robustesse.
Le principal inconvénient d'un système
distribué est la dispersion de l'information. En effet, chaque robot ne
possède qu'une vue très limitée de l'état de la
mission. Un robot peut communiquer avec d'autres robots qui ne sont pas dans
son voisinage en passant par d'autres robots qui joueront le rôle de
relais, mais ceci induira nécessairement à une certaine latence
entre l'envoi d'un message et sa réception. Afin de pallier à ces
inconvénients, les chercheurs se tournent souvent vers la
synchronisation implicite entre les agents et éliminent la
nécessité de communiquer entre eux, un exemple peut être
trouvé dans les applications de déploiement de capteurs où
chaque robot calcule la distance entre les capteurs déployés par
ses voisins et adapte sa propre position en conséquence. Un autre
exemple se trouve dans les applications de déplacement en groupe ou les
robots adaptent leurs vitesses et directions selon la vitesse moyenne et
direction de leurs voisins.
Le tableau 1.1 résume les différentes entre ces
trois types d'architectures.
1.3.4 Classification par autonomie
Les systèmes multirobots peuvent aussi être
classifiés par type d'autonomie:
27
TABLE 1.1 - Comparaison entre les architectures des
systèmes multirobots
|
Type d'architecture
|
Centralisée
|
Décentralisée
|
Distribuée
|
|
Dépendance au noeud central
|
Elevée
|
Moyenne
|
Basse
|
|
Latence de communica- tion
|
Basse
|
Basse
|
Elevée
|
|
Robustesse
|
Basse
|
Moyenne
|
Elevée
|
|
Simplicité de coordina- tion et
synchronisation
|
Très facile
|
Relativement fa- cile
|
Difficile
|
|
Mise à l'échelle
|
Limitée
|
Limitée
|
Sans limite
|
|
Disponibilité de l'infor- mation
|
Regroupée dans
le noeud central
|
Répliquée dans
les noeuds centraux
|
Dispersée
|
|
Adaptabilité au change- ment
d'objectifs
|
Facile
|
Relativement fa- cile
|
Difficile
|
Système autonome
Un système autonome est un système totalement
indépendant de l'intervention de l'être humain. Il est responsable
d'affecter les tâches, les réaliser, faire le suivi de
l'avancement de la mission et regrouper les informations collectées par
chaque robot.
Le rôle de l'être humain pendant la mission se
limite donc dans la mise en marche ou l'arrêt du système, et
l'intervention en cas de dysfonctionnement.
Les systèmes autonomes sont souvent utilisés
dans des environnements contrôlés impliquant des risques
limités. Les scénarios les plus communs sont l'automatisation des
chaines de production industrielles, la gestion des entrepôts de
marchandises, et le nettoyage de surfaces.
Système semi-autonome
Un système semi-autonome possède une certaine
dépendance à l'être humain, qui jouera un rôle plus
ou moins important selon la nature de la mission. L'opérateur humain
pourra effectuer des tâches de suivi par exemple, de redéfinition
des priorités pendant la mission, ou encore le contrôle manuel du
robot leader. Les autres robots devront donc s'adapter automatiquement aux
décisions de l'opérateur humain; ils jouent un rôle de
support/assistants.
On retrouve ce genre d'organisation dans les scénarios
où l'intervention de l'être hu-
28
CHAPITRE 1
main est limitée, mais nécessaire pour le bon
déroulement de la mission, par exemple : la surveillance, la recherche
des survivants dans les catastrophes naturelles, ainsi que la détection
de feux de forêt.
Système contrôlé
Il s'agit d'un système contrôlé
manuellement par un opérateur humain, souvent à distance à
travers une interface de commande offrant une visualisation complète de
l'état du système et un retour visuel sur les
opérations.
Une problématique de base de ce type de systèmes
est la manière qu'un seul opérateur humain peut contrôler
plusieurs robots à la fois. Une solution serait d'offrir à
l'opérateur la possibilité d'affecter les tâches pour
chaque robot, et laisser les robots effectuer ces tâches de
manière automatique. La différence clé avec un
système semi-autonome est que dans un système
contrôlé, les robots n'ont pas la liberté de choisir une
tâche ou de se déplacer vers un point sauf s'ils reçoivent
l'ordre explicite de la part de l'opérateur.
Ce type de systèmes est utilisé dans les
scénarios à fort risque dont la prise de décisions
requiert une expertise élevée dans le domaine ou lorsqu'elle est
liée à une responsabilité morale qui ne peut être
automatisée, tels que les interventions à distance dans les zones
contaminées, le diagnostic des pipe-lines, et les applications
militaires.
1.3.5 Classification par type de robots
Les systèmes multirobots peuvent aussi être
classifiés par type de robots qui compose le système:
Classification par
homogénéité
Un système homogène est un système
constitué par des robots similaires du même type, et qui ont les
mêmes capacités. Ceci simplifie beaucoup la distribution des
tâches puisque les robots sont interchangeables et chaque tâche
peut être effectuée par n'importe quel membre du groupe.
Un système hétérogène est en
revanche composé de robots de différents types. La distribution
de tâches doit être adaptée selon les capacités de
chaque type de robots, ce qui implique un mécanisme de prise de
décisions plus spécifique.
Classification par mobilité
Un système mobile est constitué de robots qui
peuvent se déplacer dans l'espace où ils sont
déployés, tels que les robots de type véhicule, les robots
volants et les robots marins.

29
FIGURE 1.7 - Exemple d'un système
hétérogène constitué d'un robot volant et d'un
robot mobile terrestre pour la supervision d'une zone agricole (Australian
Centre for Field Robotics)
Un système statique est constitué de robots
fixés dans le sol, tel que les bras manipulateurs dans les chaines de
production industrielles.
À noter qu'un système
hétérogène peut aussi être constitué de
robots mobiles et robots statiques qui travaillent en collaboration pour
effectuer une mission commune.
Classification par mode de locomotion
Il existe plusieurs types de locomotion pour les robots
mobiles : on trouve par exemple les robots humanoïdes qui ressemblent
à des êtres humains ou à des animaux et se déplacent
en utilisant des pieds. Il existe aussi des robots de type véhicule, qui
se déplacent en utilisant des roues ou des chaînes. Ou encore des
robots à propulsion qui se déplacent dans l'air (drones) ou dans
l'eau (bateaux, sous-marins). On trouve également un mode de
déplacement par frottement, inspiré de certains animaux tels que
les serpents.
1.4 Catégorisation des problématiques liées
aux systèmes multirobots
Les problématiques liées à la robotique
en général touchent à plusieurs disciplines dont la
mécanique, l'électronique, l'informatique ou encore
l'énergétique et les sciences sociales.
Nous nous intéressons dans cette thèse aux
problématiques liées à l'informatique et
30
CHAPITRE 1
l'intelligence artificielle en général, et plus
précisément et au traitement de l'information et à la
prise de décisions.
Nous pouvons distinguer dans la littérature plusieurs
problématiques qui se chevauchent et qui constituent chacune un axe de
recherche très actif dans la communauté:
1.4.1 La navigation
La navigation est l'une des problématiques de base dans
le domaine de la robotique. Elle soulève la question de comment
permettre à un robot de se déplacer tout en évitant les
collisions avec les obstacles présents dans son environnement.
Un obstacle peut être de nature statique comme les murs
et les objets. Il peut aussi être de nature dynamique comme les
êtres humains, les véhicules et les autres robots.
L'axe de recherche de la navigation s'intéresse
à la modélisation géométrique des robots et de leur
mode de déplacement, les degrés de liberté d'un robot, et
les techniques de détection et d'évitement d'obstacles.
La modélisation géométrique du robot est
essentielle pour pouvoir contrôler sa vitesse et sa direction de
mouvement. Un robot à roues ne se déplace pas de la même
manière qu'un drone volant ou qu'un robot à deux pieds. Cette
modélisation peut aussi varier pour des robots de même type selon
leur nombres de moteurs, leur forme et le nombre de degrés de
liberté qu'ils possèdent.
La navigation nécessite également de pouvoir
mesurer l'accélération du robot, qui est souvent obtenue en
calculant le nombre de rotations des roues pour les robots de type
véhicule par exemple, mais elle nécessite l'utilisation de
dispositifs électroniques plus complexes pour les robots volants tels
qu'un gyroscope pour mesurer l'orientation, un altimètre pour mesurer
l'attitude et un accéléromètre pour mesurer
l'accélération.
D'autres dispositifs doivent aussi être utilisés
pour l'évitement d'obstacles, il s'agit souvent de capteurs de distance
de type laser, ultrason ou infrarouge pour pouvoir construire un histogramme de
distances et choisir une direction de mouvement sans danger. Mais on peut aussi
utiliser des méthodes plus complexes comme des caméras 2D ou 3D
pour la reconnaissance d'objets, qui s'avèrent utiles lorsqu'il est
nécessaire d'interagir avec l'obstacle en question (ouverture de portes
par exemple, collecte d'objets...etc.).
Dans un système multirobots, chaque agent
considère les autres robots comme des obstacles à éviter.
Toutefois, dans un scénario de déplacement en groupe la
navigation devient plus compliquée car elle prend en
considération des critères supplémentaires dont la
distance maximale autorisée entre chaque robot, la vitesse des robots
à proximité, et leur direction de mouvement. Un scénario
typique est le déplacement en formation où les robots se
déplacent en suivant les mouvements d'un robot leader, ou bien en
essayant de garder une certaine formation (ligne droite, cercle,
triangle...etc.). Lorsque les robots rencontrent un obstacle, ils sont souvent
obligés de rompre la formation pour l'éviter, ils doivent ensuite
retourner à la formation initiale en réajustant leurs vitesses et
positions.
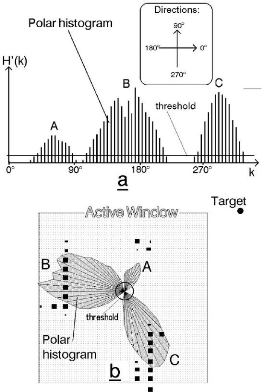
31
FIGURE 1.8 - Détection d'obstacles en
utilisant la technique du Vector Field Histogram [20]
1.4.2 La cartographie
La problématique de cartographie tente de
répondre à la question « à quoi ressemble
l'environnement? ». Le but est de permettre à un robot de
créer un modèle interne de son environnement à partir de
ses observations.
Ce processus de modélisation représente l'espace
qui entoure le robot dans une structure de données qui permettra de
faciliter les autres opérations tel que la planification des
trajectoires, distribution de tâches, et localisation des points
d'intérêts. Cela permet aussi d'optimiser la navigation puisque le
robot pourra savoir à l'avance la position des obstacles qu'il faudra
éviter.
Afin de pouvoir créer une carte de l'environnement, le
robot devra traduire les observations récoltées en données
utiles. Ces observations sont souvent obtenues soit en utilisant des
dispositifs électroniques de mesure de distances
(télémètres, radars...) qui permettent de calculer
rapidement et avec grande précision l'emplacement des obstacles dans un
rayon
32
CHAPITRE 1

FIGURE 1.9 - Diagramme de relations entre l'environnement du
robot et sa représentation interne
allant de 180° à 360°, soit en utilisant des
capteurs optiques (caméras) qui permettent d'ex-traire des informations
plus riches tels que les couleurs, les formes ou les textures. Chaque
méthode à des avantages et des inconvénients, et il n'est
pas rare dans les applications réelles de combiner les deux
méthodes afin de maximiser la qualité des cartes crées, au
profit d'une augmentation des besoins en puissance de calcul et de la
capacité de stockage. Le tableau 1.2 présente une comparaison
entre les deux méthodes.
Les cartes peuvent être classées en deux
catégories selon le type de la structure de données
utilisée pour les représenter:
Cartes métriques
Elles sont le résultat de la représentation de
l'environnement sous forme matricielle, afin de représenter les
obstacles avec des formes géométriques simples, telles que des
lignes, cercles et polygones.
Elle s'intéresse à la représentation des
périmètres des objets et leur emplacement sans forcément
connaître leurs natures, puisque l'objectif est souvent de pouvoir
distinguer entre l'espace « vide » où le robot peut naviguer
en toute sécurité, et l'espace « occupé »
où il y a un grand risque de collision.
Dans la figure 1.10 par exemple, nous retrouvons une
représentation d'une carte métrique 2D construire en utilisant la
méthode des grilles d'occupations : la zone blanche représente
l'espace vide de l'environnement, les lignes noires représentent la
périphérie des murs et obstacles, tandis que l'espace gris
représente l'espace non accessible.
Ce type de cartes est simple à réaliser à
partir des observations, mais nécessite de connaître la position
exacte des obstacles et du robot, ce qui la lie fortement à la
problématique de localisation décrite un peu plus loin dans ce
chapitre.
Un autre inconvénient est la nature limitée du
modèle. En effet, ces cartes 2D représentent l'environnement par
vue d'oiseau, ce qui rends difficile l'estimation de la hauteur d'un objet ou
de connaître sa nature. Afin de pallier à cette limitation, une
tendance récente est l'utilisation de télémètres 3D
ou de caméras 3D pour représenter ces cartes sous forme de nuage
de points comme on peut le voir sur la figure 1.11. L'avantage de cette
représentation est d'offrir la notion de « profondeur » qui
est très utile pour pouvoir distinguer entre les murs, les êtres
vivants et les objets mobiles.
33
TABLE 1.2 - Comparaison entre les capteurs de distance et les
capteurs optiques
|
Type
|
Capteurs de distance
|
Capteurs optiques
|
|
Exemples
|
Télémètres (laser / infra-
rouge), radars (ultrason)
|
Caméras 2D, caméras 3D
|
|
Type d'information
|
Distance des obstacles
|
Couleurs, formes, textures + distance en utilisant des
caméras 3D
|
|
Fréquence de me- sure
|
100 à 1000 observations par seconde
|
15 à 30 observations par se-conde pour la majorité
des caméras
|
|
Rapidité de traite- ment*
|
Supérieur à 100 observations par seconde
|
1 à 10 observations par se-conde. Peut être
augmenté en relayant les calculs à une carte graphique
|
|
Distance maximale
|
10, 20, 40m pour le laser selon la gamme; 0.5 à 10m pour
l'ul-trason
|
Techniquement pas de limite
|
|
Angle d'observation
|
180° à 360° pour les
télémètres laser; 30° à 60° pour les cap-
teurs ultrason.
|
Varie selon l'objectif; 100° à 180° pour la
majorité des ca-méras.
|
|
Précision
|
0.1° pour le laser; 1° à 3° l'ul- trason
|
Dépends de la distance avec l'objet
|
|
Nature de la donnée
|
Vecteur de nombre réels
|
Matrice de pixels
|
|
Taille de la donnée
|
Quelques kilo-octets
|
> 2 méga-octets selon la résolution de
l'image
|
*Rapidité de traitement: temps nécessaire pour
effectuer les opérations d'extraction d'in-formations utiles à
partir d'observations brutes en utilisant un processeur moyen
CHAPITRE 1

34
FIGURE 1.10 - Exemple d'une carte métrique 2D
construite en utilisant la technique des grilles d'occupations [1]

FIGURE 1.11 - Exemples de cartes métriques 3D
Cartes topologiques
Elles sont le résultat de la représentation de
l'environnement sous forme de graphe. Ce type de cartes est plus indulgent
quant à l'erreur dans la position exacte du robot puisque
l'environnement est plutôt schématisé sous forme de graphe.
Pour y arriver, cet environnement est d'abord divisé en plusieurs
régions, qui sont par la suite représentées par des
noeuds, puis reliées entre elles par des arêtes
représentant les chemins possibles pour se déplacer d'une
région à une autre.
Ces cartes sont plus difficiles à construire et
à mettre à jour comparé aux cartes métriques, mais
elles sont plus adaptées d'un point de vue algorithmique à la
planification de chemins à long terme et à la distribution de
tâches entre plusieurs robots. De plus, elles ont l'avantage de consommer
moins d'espace mémoire.
Les cartes topologiques peuvent être enrichies
d'informations supplémentaires comme la distance entre les noeuds ou la
densité d'occupation (pourcentage du nombre d'obstacles
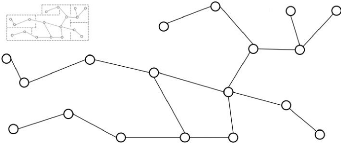
35
FIGURE 1.12 - Exemple d'une carte topologique
par rapport à la surface de l'espace vide). Ces
informations peuvent s'avérer utiles pour la recherche du chemin optimal
entre deux points.
Elles peuvent être aussi être combinées
avec des cartes métriques afin de profiter des avantages des deux types.
La partie métrique sera utilisée pour la navigation à
court terme tandis que la partie topologique sera utilisée pour la
planification à long terme.
La cartographie dans un contexte multirobots
Dans un contexte multirobots, les cartes sont utilisées
comme moyen de communication et de coordination. En combinant les observations
partielles récoltées par chaque robot nous obtenons une carte
complète de l'environnement.
Cette carte est souvent construite dans une machine centrale.
Au début, chaque robot construira sa propre carte locale à partir
des observations qu'il enregistre. Ces cartes sont ensuite envoyées au
serveur pour les combiner dans une seule carte globale. Plusieurs techniques
existent pour effectuer cette combinaison comme la corrélation de scans,
la superposition de cartes, ou la fusion de graphes.
Cette opération peut être difficile surtout
lorsque la position des robots n'est pas connue avec précision, ou
lorsque les observations sont bruitées à cause de capteurs de
mauvaise qualité, ce qui peut induire à des inconsistances dans
la carte globale.
Le facteur temps est également important, deux robots
peuvent passer par un même endroit, mais générer quand
même deux cartes différentes si la position des obstacles a
changé entre temps. Il sera donc encore plus difficile de les superposer
sans avoir recours à des informations supplémentaires comme le
temps de passage de chaque robot ou la position de points de repères.
Un autre défi concerne la manière de fusionner
des cartes construites par une équipe de robots
hétérogènes. Puisque des robots différents peuvent
avoir des capteurs différents ou des points de vue différents
(robot aérien et robot terrestre par exemple), il faudra veiller
à transformer leurs observations vers un format uniforme qui facilitera
la fusion des cartes.
36
CHAPITRE 1
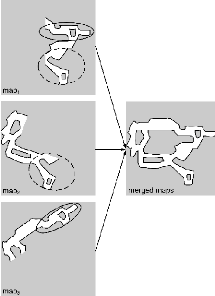
FIGURE 1.13 - Résultat d'un processus
de fusion de cartes [74]
Les cartes sont aussi un moyen de communication avec
l'être humain, car elles permettent à un opérateur de
facilement comprendre la structure de l'environnement et visualiser
l'état d'avancement d'une mission. Aussi, il sera plus facile de
sélectionner graphiquement des points sur une carte pour
délimiter une région d'intérêt, que d'insérer
un ensemble de coordonnées dans un tableau.
1.4.3 La localisation
Dans la problématique de localisation, le but est de
répondre à la question « où est le robot? ». On
s'intéresse ici à connaître la position du robot par
rapport à un repaire fixe.
Étant donné la nature incertaine de
l'environnement en général, cette position est souvent
estimée selon une certaine probabilité en se
référant à des objets externes, bien qu'il soit possible
d'estimer sa position en utilisant des informations internes telles que la
vitesse de déplacement du robot et son orientation.
La position d'un robot qui se déplace sur une surface
2D (sol par exemple) est déterminée par deux coordonnées
(x, y) et une orientation définie par un angle è. D'un autre
côté, un robot qui se déplace sur un espace 3D (robot
volant par exemple), nécessite l'utilisation de trois coordonnées
(x, y, z) pour déterminer sa position, et trois angles pour
déterminer son orientation (á, â, ã). Ces
coordonnées définissent la position du robot par rapport à
un certain repère.
37
Dans les applications réelles de robotique, il est
fréquent d'utiliser plusieurs repères pour le calcul des
positions. L'un d'entre eux -appelé repère global- est un
repère de référence fixe qui sert à calculer la
position du robot par rapport au monde qui l'entoure, ce qui permet d'effectuer
l'opération de cartographie.
De manière opposée, un repère mobile dont
le point d'origine est la position du robot est utilisé pour
déterminer la position relative des obstacles en utilisant la distance
mesurée par ses capteurs, ce qui est particulièrement utile
pendant la phase de navigation pour éviter les collisions. La position
de ces obstacles est ensuite recalculée par rapport au repère
fixe afin de pouvoir déterminer leurs positions réelles dans la
carte de l'environnement. Nous remarquons donc que les problématiques de
navigation, de localisation et de cartographie sont fortement liées.
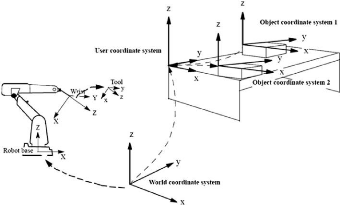
FIGURE 1.14 - Schématisation des différents
repères utilisés pour la localisation relative et globale [29]
Le choix du point d'origine pour un repère de
référence présente lui aussi son lot de
difficultés. Dans un environnement contrôlé, ce point peut
être défini par l'utilisateur et sera utilisé pour
positionner tout objet modélisé dans l'environnement. Toutefois,
ceci n'est pas toujours possible dans le cas où le robot est
déployé dans un environnement inconnu au préalable. Il est
donc plus judicieux de fixer la position initiale du robot comme point de
référence.
Dans un contexte multirobots, ceci devient plus difficile
puisque chaque robot possède son propre point de
référence. Il est donc important que ces robots synchronisent
leurs positions par rapport à un repère commun comme la
sélection d'un objet fixe comme point de référence ou en
utilisant un moyen de localisation externe, telle que la
géolocalisation.
Certains travaux ont démontré que
l'échange des positions des robots entre eux permettrait aussi de
réduire les erreurs dans leur localisation. Pour cela, chaque robot
détermine la position de l'autre robot lorsque celui-ci rentre dans son
champ de vision, puis la lui envoie. Celui-ci comparera la valeur reçue
avec celle calculée en utilisant ses propres in-
38
CHAPITRE 1
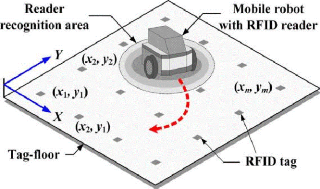
FIGURE 1.15 - Localisation par balises RFID [22]
formations. Ceci permet d'avoir un « point de vue externe
» lorsqu'un robot recalcule sa position pendant un déplacement.
Une autre difficulté liée au problème de
localisation est l'estimation exacte de la position du robot en utilisant des
informations incomplètes ou bruitées. En effet, les capteurs du
robot sont souvent limités et sujets à de petites erreurs, qui
peuvent rapidement s'accu-muler pour donner résultat à une
localisation incorrecte. Plusieurs méthodes ont été
utilisées dans la littérature pour améliorer la
localisation des robots en utilisant des informations visuelles recueillies
à partir de caméras comme l'identification de points
d'intérêts par exemple (portes, fenêtres, objets...) ou
l'utilisation de marqueurs placés préalablement dans
l'environnement (bornes, balises...) tel que décrit dans la figure
1.15.
Dans certains travaux, la localisation est externalisée
vers un serveur central lié à des caméras placées
en hauteur. C'est le cas lorsque les capacités de calcul des robots ne
permettent pas de faire un traitement assez complexe pour les besoins de
l'expérience.
1.4.4 La planification
La planification est une problématique très
importante dans le domaine de la robotique parce qu'elle est au centre du
processus décisionnel. Elle répond à la question : quelle
est la meilleure façon pour accomplir une certaine tâche?
Le but est de décomposer cette tâche en plusieurs
actions (ou sous-tâches) afin de choisir le meilleur ordre d'actions
parmi la liste des combinaisons possibles.
Dans un contexte multirobots, ce choix devient plus
compliqué puisqu'il faut répartir ces sous-tâches de
manière optimale sur plusieurs agents. Ceci correspond à un type
de problèmes mathématiques dont la complexité est
combinatoire (NP-complet) [54], il n'est donc pas toujours envisageable de
vérifier toutes les combinaisons possibles.
39
Dans un système centralisé, cette
répartition est généralement effectuée par le noeud
central qui affecte les tâches à chaque agent. Dans le cas d'un
système décentralisé ou distribué, un consensus
doit être trouvé par les robots pour se diviser les tâches
de sorte à maximiser le profit cumulé du groupe, même si
cela implique que les actions effectuées séparément par
chaque robot ne maximisent pas ses profits au plan individuel.
Lorsque le groupe est constitué de robots
hétérogènes, l'affectation de tâches doit aussi
prendre en considération leur capacités. En effet, certaines
tâches ne sont pas effectuées de la même manière par
tous les robots et il se pourrait que certaines tâches ne puissent
être réalisées que par un type spécifique de robots.
Il faudra donc veiller à inclure ces contraintes au processus
d'affectation.
Un type particulier de planification concerne le calcul de
chemins (path planning ou path finding en anglais). Il s'agit
d'un axe de recherche très actif qui vise à trouver le meilleur
ordre d'actions pour se déplacer d'un point A vers un point B. Ces
actions prennent la forme de mouvements, d'où l'appellation «
planification de mouvements » (motion planning). Il y a là
aussi des contraintes à prendre en compte telles que la présence
d'obstacles, la longueur du chemin choisi, ainsi que les restrictions
géométriques du robot.
La planification de chemins peut aussi prendre la forme de
répartitions de tâches dans les systèmes multirobots :
étant donné plusieurs points de destinations à visiter, le
but est de trouver la meilleure combinaison possible pour répartir ces
points de destination entre les robots de sorte que chaque point ne soit
visité que par un seul robot pour éviter la redondance. Ce type
de problèmes est populaire dans les applications de transport de
marchandises et de gestion des entrepôts.
Un autre aspect à prendre en compte lors de la
planification de chemins dans les systèmes multirobots est
l'évitement des collisions. Le critère du temps est très
important dans ce contexte puisqu'il n'est pas interdit que deux chemins se
chevauchent tant que deux robots ne sont pas présents au même
moment au même endroit. Il faut donc veiller à intégrer une
stratégie de gestion de conflits entre les robots, en gérant les
priorités de passage des robots par exemple ou en intégrant des
contraintes supplémentaires lors du calcul de chemins.
1.4.5 L'exploration
La tâche d'exploration consiste à parcourir une
zone dont le robot n'a aucune information au préalable (ou peu
d'informations). Le but est de collecter le maximum de données utiles
afin de pouvoir mener à bien la mission.
La problématique d'exploration peut devenir
particulièrement difficile avec l'augmen-tation de la surface de la zone
à parcourir et des contraintes de mouvement et d'énergie du
robot. Ceci devient particulièrement critique lorsque le facteur temps
est limité en raison de nature même de la mission, comme les
opérations de sauvetage et recherches de personnes pendant les
catastrophes naturelles par exemple.
40
CHAPITRE 1

FIGURE 1.16 - Simulation d'un scénario industriel
basé sur les algorithmes de planification de trajectoires [42]
La tâche d'exploration est souvent couplée avec
d'autres problématiques selon la nature de la mission. Ceci ouvre la
possibilité à plusieurs variantes que nous pouvons classer selon
les catégories suivantes:
-- Exploration: Consiste à visiter une zone inconnue
dans le but de collecter le maximum de données possibles, souvent sous
forme de positions de points d'intérêts ou d'ensemble de routes et
chemins possibles.
-- Target Searching: Consiste à explorer une zone dans
le but de trouver un individu
ou un certain objet.
-- Patroling : Consiste à explorer une zone de
manière répétitive, souvent dans le but de
détecter des intrus dans un contexte de surveillance.
-- Consistent Surveillance (Consistent Monitoring): Consiste
à surveiller une zone de
sorte que chaque point de l'environnement soit toujours dans
le champ de vision des robots. Le but est de déployer les robots de
sorte qu'aucun angle mort ne soit toléré.
-- Total Coverage (Complete Coverage) : Consiste à faire
le balayage complet d'une zone, c'est à dire l'explorer en visitant tous
les points atteignables par les robots. On ne se contente pas d'observer et
détecter les obstacles à distance, mais de se déplacer et
parcourir chaque petite parcelle de la surface de la zone dans le but de la
nettoyer par exemple, ou détecter la présence de danger (mines,
fuite de gaz...).
La problématique d'exploration avec ses
différentes variantes est une tâche qu'on peut décomposer
en plusieurs sous-tâches. En effet, plusieurs stratégies peuvent
être employées pour répartir cet ensemble de
sous-tâches sur un groupe de robots afin d'accélérer sa
réalisation.
La stratégie la plus intuitive est de diviser la zone
à parcourir en plusieurs régions, puis d'affecter à chaque
robot une ou plusieurs régions à explorer. Le problème se
transforme donc en un problème d'affectation pouvant prendre en compte
un ou plusieurs critères
41
d'optimisation, tel que la distance du robot par rapport à
la région affectée, la taille de la région, ou encore
l'énergie restante du robot.
Toutefois, ceci soulève aussi plusieurs questions : quel
est le nombre optimal de régions? Quelle est la forme des
régions? Quel type de trajectoire faut-il utiliser?
Les réponses à ces questions varient selon la
nature de la mission et des techniques à utiliser. Les figures 1.17 et
1.18 montrent des exemples de ce genre de décisions dans deux
scénarios différents.
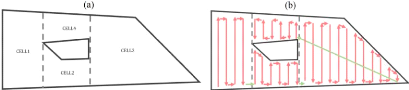
FIGURE 1.17 - Exemple de décomposition d'une carte et
balayage en utilisant une trajectoire en zigzag [48]
FIGURE 1.18 - Exemple de sélection de régions
à visiter dans un scénario de surveillance [49]
Une stratégie d'exploration efficace poussera les
robots à minimiser le chevauchement entre les régions
visitées et éviter de retourner par le même chemin, sauf si
cela est inévitable comme lorsqu'un robot atteint une route
fermée et doit faire demi-tour, ou dans le cas d'une intersection de
plusieurs chemins (ex : couloir, hall).
42
CHAPITRE 1
Dans les scénarios de surveillance par contre, la
visite répétitive d'une même région est obligatoire
puisque le but est de s'assurer qu'aucun intrus n'a
pénétré la zone explorée. Les robots devront faire
en sorte de toujours revenir vers les régions visitées à
une fréquence régulière. Les critères
d'optimisation devront donc être adaptés selon chaque type de
scénario.
1.4.6 La communication
La problématique de communication est au coeur des
systèmes multirobots. Plusieurs stratégies de communication
peuvent être employées selon le type de coordination et
l'ar-chitecture générale du système.
Type de communication:
-- Communication passive:
Il s'agit d'échanger des informations indirectement,
soit en détectant les autres robots et en calculant leurs positions et
trajectoires lorsqu'ils rentrent dans le champ de vision. Soit en
déposant ou déplaçant des objets dans l'environnement,
similai-rement au mode de communication de certains insectes qui
dégagent des produits chimiques lorsqu'ils se déplacent (odeurs,
phéromones...) et déposent des morceaux de nourriture dans les
endroits de stockage (fourmilières).
Ce type de communication est souvent facile à mettre en
oeuvre, mais ne garantit pas la réception du message de la part des
autres robots. Aussi, il est difficile de garantir la confidentialité ou
de vérifier l'authenticité de l'émetteur puisqu'un robot
intrus peut copier le mode d'interaction avec l'environnement pour influencer
la décision du système.
-- Communication active:
Il s'agit d'échanger des messages de manière
intentionnelle en utilisant un protocole de communication qui garantit
l'adressage unique de chaque robot. Le protocole le plus souvent utilisé
est le TCP/IP à travers une liaison Wifi ou Bluetooth, ce qui introduit
une augmentation de la consommation d'énergie du robot, notamment pour
les dispositifs à rayon large. Mais d'autres moyens peuvent aussi
être utilisés comme l'échange de messages avec des balises
qui jouent le rôle de relais pour augmenter le rayon de couverture du
dispositif de communication installé sur les robots.
Mode de communication:
Un autre point important lié à cette
problématique est le choix du mode de communication. En effet dans une
communication décentralisée, les robots s'échangent des
messages directement lorsqu'ils sont à proximité. Ceci permet
d'identifier qui est l'émetteur et le destinataire afin d'envoyer des
messages de manière ciblée. Toutefois, il est difficile de
combiner les informations de tous les robots afin d'avoir une vue d'ensemble
générale.
43
De l'autre côté, le mode de communication
centralisé permet de combiner toutes les informations dans un même
endroit. Les robots ne communiquent pas directement entre eux, mais passent par
un serveur qui sera responsable de traiter et distribuer les informations. Ce
serveur fera en sorte que chaque robot ait accès à la même
information que les autres, ou au contraire de choisir quel robot a
accès à quelle information.
Dans ce dernier mode de communication, il est important de
spécifier l'endroit où sera installé le noeud central. En
effet, une première solution est de mettre ce noeud dans le même
réseau local que le système multirobots ce qui permet d'avoir un
débit de communication élevé. Une autre solution est
d'accéder à ce noeud à distance -- souvent en utilisant le
réseau internet -- afin de pouvoir profiter de fonctionnalités
plus évoluées telles que l'accès aux serveurs Cloud par
exemple, ou la visualisation des actions des robots à travers un centre
de commandement.
TABLE 1.3 - Récapitulatif des
problématiques de bases dans le domaine des systèmes
mul-tirobots
|
Problématique
|
Objectif
|
Types
|
|
Navigation
|
Se déplacer tout en évitant les obstacles
|
-
|
|
Cartographie
|
Dessiner la structure de l'en- vironnement
|
Métrique (grille), Topologique (graphe)
|
|
Localisation
|
Calculer la position du robot
|
Localisation relative, géoloca-lisation
|
|
Planification
|
Calculer un chemin d'un point A vers un point B
|
Planification à court terme, à long terme
|
|
Exploration
|
Visiter une zone inconnue pour collecter des informa- tions
|
Exploration, Balayage, Sur-
veillance
|
|
Communication
|
Échanger des informations
|
Communication robot-server, communication inter-robot
|
|
Contrôle et gestion de flotte
|
Envoi des ordres aux robots par l'opérateur humain
|
Contrôle de robot individuel, contrôle
groupé
|
|
Interfaces homme- machines
|
Visualiser l'état des robots et l'avancement de leurs
tâches
|
-
|
1.4.7 Autres problématiques
D'autres problématiques liées aux
systèmes multirobots comprennent des sujets rattachés
généralement à d'autres domaines scientifiques, citons par
exemple:
44
CHAPITRE 1
-- L'étude de l'assemblage de plusieurs robots en un seul
(mécanique et électronique); -- Les dispositifs
d'interconnectivité des robots (télécommunications);
Par ailleurs, d'autres sujets liés au domaine de la
robotique en général comprennent l'étude des:
-- Moyens de locomotion des robots;
-- Dispositifs de détection (détecteurs de
distances, caméras, capteurs spécifiques : gaz,
température, métaux...etc);
-- Dispositifs de mesures internes (vitesse,
accélération, orientation, géolocalisation, force
exercée, énergie consommée);
-- Ressources énergétiques du robot (batteries,
combustibles...);
-- Effets psychologies liés à l'utilisation des
robots en présence des êtres humains: -- Sujets liés
à l'éthique et réglementations dans le domaine de la
robotique.
1.5 Etat de l'art et travaux connexes
Cette section présente un aperçu des techniques
d'apprentissage machine et d'optimi-sation utilisées pour
résoudre les problématiques liées aux systèmes
multirobots, nous nous intéresserons surtout aux problématiques
liées à notre présente thèse à savoir la
navigation, la planification et l'exploration.
De nombreuses techniques ont été
utilisées en robotique pour l'exploration de zones. Ces techniques
peuvent être classées selon plusieurs critères concernant
leur déterminisme, la nécessité d'utiliser des
informations préalables, ou l'adaptabilité à un contexte
multiro-bots.
1.5.1 Les méthodes
déterministes
Une méthode déterministe populaire pour
résoudre le problème d'exploration de zone inconnue a
été introduite par [89] où le robot continue de se
déplacer vers le point de frontière le plus proche
(frontier-based exploration). Les frontières sont les lignes
séparant les régions explorées et inexplorées d'une
zone. Cette technique est facile à mettre en oeuvre, nécessite
peu de ressources de calcul, et donne de bons résultats en pratique.
Ceci a encouragé les chercheurs à développer de nombreuses
variantes du même algorithme dans le but de trouver la meilleure
stratégie pour sélectionner les points de frontières les
plus intéressants [47].
Une version multirobots a aussi été
proposée par les auteurs initiaux [90] où chaque robot se
déplace vers sa frontière la plus proche tout en envoyant la mise
à jour de l'opéra-tion de cartographie aux autres robots;
cependant, cette stratégie ne parvient pas à éviter la
redondance puisque plusieurs robots peuvent se déplacer vers la
même frontière. L'auteur de [15] a essayé de
résoudre ce problème en utilisant la technique de propagation
d'onde
45
(wavefront propagation) pour dispatcher les robots.
Les frontières sont classées en fonction du nombre de robots
à proximité. Chaque robot est alors affecté à une
frontière différente, ce qui lui permet de s'éloigner le
plus possible des autres robots et maximiser la zone d'ex-ploration.
Les auteurs de [7] se sont orientés vers une
stratégie différente pour les environnements d'intérieurs
: le premier robot explore tout le couloir et détecte les portes, puis
chacun des autres robots sélectionne une porte différente et
explore la pièce correspondante en utilisant la technique des
frontières les plus proches. Le robot ne sort pas d'une pièce
tant qu'il ne l'a pas entièrement explorée. Cette
stratégie encourage les robots à explorer les pièces
individuellement et à réduire le chevauchement entre les
régions qui leur sont assignées, ce qui contribue à
réduire le temps total de mission. Plus récemment, [62]
a utilisé des données incomplètes telles que des
cartes d'évacuation simplifiées ou des plans d'ar-chitecture
comme entrée à l'algorithme afin de choisir la meilleure
frontière à explorer. Les expériences ont montré
que l'exploitation de cartes approximatives peut accélérer la
mission d'exploration, même si les données sont inexactes.
Cependant, cela nécessite que ces cartes soient importées,
prétraitées et alignées manuellement par un
opérateur humain.
Une autre famille d'approches déterministes repose sur
la décomposition de l'environ-nement en plusieurs sous-régions,
puis sur l'exploration de chaque région indépendamment à
l'aide d'une stratégie simple telle qu'un mouvement en zigzag ou en
forme circulaire. Une technique populaire de cette famille est la
Boustrophédon Decomposition proposé par [23].
Le principe est de décomposer la carte en régions
polygonales en fonction de la position des obstacles. Elle a été
utilisée avec succès pour effectuer des tâches de
couverture complète (Complete Coverage). Cependant, elle
suppose que l'environnement soit statique, c'est-à-dire que tous les
obstacles sont fixes et ne changent pas de position. Elle nécessite
aussi que la structure de l'environnement (carte métrique) soit connue
à l'avance puisqu'elle figure parmi les paramètres
d'entrée de l'algorithme à fournir par l'utilisateur. D'autres
techniques utilisent les diagrammes de Voronoï pour décomposer la
carte en régions plus flexibles [39, 63]. [26] a utilisé
la propagation d'onde pour adapter l'algorithme D* au problème de
couverture. Au lieu de planifier un chemin à partir d'une position de
départ vers une position d'arrivée, le D* modifié
génére un chemin pour visiter tous les points d'une carte
donnée. La fonction de replanification rapide de l'algorithme D* lui
permet de s'adapter aux environnements dynamiques en modifiant rapidement la
trajectoire en cas de changement de position d'un obstacle..
Les auteurs de [79] ont proposé une nouvelle
approche pour générer des chemins de couverture efficaces. Elle
utilise une représentation de cartes multicouches appelée
Exploratory Turing Machine pour produire une trajectoire en zigzag
avec une direction de déplacement réglable. Cette
stratégie se traduit par des longueurs de trajectoire plus courtes par
rapport aux méthodes classiques basées sur des mouvements de
va-et-vient. Les auteurs de [77] l'ont étendu récemment
en ajoutant des contraintes d'énergie : le robot exécute le
trajet de couverture jusqu'à ce que son énergie soit faible,
avant de retourner à la borne de recharge de batteries. Après
cela, il redémarre la couverture à partir de la région
inexplorée la plus proche afin d'éviter de faire un long trajet
pour retourner jusqu'au point précédent où il
s'était arrêté. Cette approche garantit la couverture
complète de l'environnement avec un chevauchement réduit.
46
CHAPITRE 1
1.5.2 Les méthodes à base d'apprentissage
machine
Des méthodes basées sur l'apprentissage ont
également été utilisées pour résoudre le
problème d'exploration robotique. Dans l'approche proposée par
[82], le robot ne s'appuie sur aucune carte pour explorer
l'environnement, il utilise plutôt un réseau de neurones par
renforcement de type Deep Q-Network de bout en bout pour choisir la
direction la plus appropriée à suivre en utilisant uniquement les
images de la caméra comme paramètre d'entrée. Cette
méthode a été testée pour naviguer dans un
environnement sous forme de couloir inconnu tout en évitant les murs.
D'autre part, l'approche de [81] utilise une base de
données de cartes déjà vues pour prédire les
régions inconnues d'une carte partiellement explorée. Elle
utilise une technique inspirée du sac de mots (bag of words)
pour détecter les similitudes entre des cartes sous forme de grilles et
apprendre à compléter les zones manquantes. Cela avait permis la
planification des chemins au-delà de la région explorée,
ce qui a réduit la distance parcourue par le robot comparé
à la méthode d'exploration à base de frontières. De
même, le modèle de [78] prédit l'emplacement et la
forme des obstacles se trouvant au-delà des frontières dans les
régions inconnues. Pour celà, les auteurs ont utilisé un
auto-encodeur variationnel (Variational Autoencoders) pour la
prédiction des régions à explorer, et une heuristique pour
évaluer leur coûts et utilité.
Récemment, les auteurs de [95] ont
proposé une approche où les robots utilisent l'ap-prentissage par
renforcement dans un contexte multirobots afin d'apprendre une stratégie
leur permettant d'explorer une zone efficacement. Une autre approche
basée sur l'appren-tissage par renforcement, proposée par
[97], permet à un robot d'apprendre à explorer une zone
tout en utilisant les images de sa caméra afin de faire une
reconnaissance visuelle et éviter les endroits déjà
visités. L'approche proposée par [32] se base aussi sur
la classification d'images à base de réseaux convolutionnels,
mais cette fois dans le but de guider un robot à naviguer dans un
environnement sous forme de labyrinthe afin de le cartographier. Les
résultats expérimentaux ont montré que l'algorithme a
appris à choisir la direction de mouvement du robot de telle
façon à éviter les obstacles.
1.5.3 Les méthodes stochastiques
Les métaheuristiques ont été largement
utilisées dans différents domaines de la robotique [38]
et sont encore largement utilisées pour les robots terrestres et
aériens.
[6] a utilisé un algorithme génétique
(Genetic Algorithms) pour surveiller une zone connue à l'aide
d'un robot aérien, tout en satisfaisant certaines contraintes telles que
la longueur et la régularité du chemin.
Les auteurs de [98] ont utilisé l'algorithme
des particules en essaim (Particle Swarm Optimization) afin de
distribuer un groupe de robots sur plusieurs régions différentes
de l'environnement. Chaque robot explore la région où il se
trouve puis utilise l'algorithme des particules en essaim afin de se diriger
vers la prochaine région à explorer en se basant sur
l'optimisation des frontières.
47
TABLE 1.4 - Résumé comparatif
des travaux cités
|
Ref.
|
Carte
|
Famille
d'approche
|
Type
d'approche
|
Energie limitée
|
Expérience
|
Nbr
robots
|
Type
exploration
|
|
[89]
|
Inconnue
|
Frontier-
based
|
Déterministe
|
Non
|
Robot réel
|
Un seul
|
Exploration
|
|
[7]
|
Inconnue
|
Frontier-
based
|
Déterministe
|
Non
|
Simulation
|
Plusieurs
|
Exploration
|
|
[15]
|
Inconnue
|
Wavefront
propagat.
|
Déterministe
|
Non
|
Simulation
|
Plusieurs
|
Exploration
|
|
[62]
|
Connue
Partiellement
|
Frontier-
based
|
Déterministe
|
Non
|
Simulation
et Robot réel
|
Un seul
|
Exploration
|
|
[26]
|
Connue
|
D*
|
Déterministe
|
Non
|
Simulation
|
Un seul
|
Complete
coverage
|
|
[79]
|
Connue
|
?*
|
Déterministe
|
Non
|
Simulation
et Robot réel
|
Un seul
|
Complete
coverage
|
|
[77]
|
Inconnue
|
?*
|
Déterministe
|
Oui
|
Simulation
|
Un seul
|
Complete
coverage
|
|
[6]
|
Connue
|
GA
|
Stochastique
|
Oui
|
Simulation
|
Un seul
|
Exploration
|
[52]
|
Inconnue
|
GWO
|
Stochastique
|
Non
|
Simulation
et Robot réel
|
Un seul
|
Exploration
|
[53]
|
|
Inconnue
|
GWO
|
Stochastique
|
Non
|
Simulation
|
Plusieurs
|
Exploration
|
|
|
[82]
|
/
|
Deep
Q-Network
|
Apprentissage
|
Non
|
Simulation
|
Un seul
|
Exploration
|
|
[81]
|
Inconnue
|
FabMap2
|
Apprentissage
|
Non
|
Robot réel
|
Un seul
|
Exploration
|
|
[78]
|
Connue
Partiellement
|
Variational
autoencod.
|
Apprentissage
|
Non
|
Simulation
|
Un seul
|
Exploration
|
|
[16]*
|
Inconnue
|
BOA/xBOA
|
Stochastique
|
Oui
|
Simulation
|
Un seul et Plusieurs
|
Exploration
|
* Notre approche
48
CHAPITRE 1
[86] ont utilisé l'algorithme de colonies de fourmis
(Ant Colony Optimization) pour effectuer une tâche d'exploration
dans un contexte multirobots. L'approche est modélisée sous forme
de problème d'affectation, où l'algorithme de colonies de fourmis
affecte à chaque robot une frontière à explorer tout en
minimisant certaines contraintes de distance et de densité des robots
dans une même région.
Récemment, [52] ont utilisé l'algorithme
d'optimisation des loups (Grey Wolf Optimizer) pour affecter au robot
un point de frontière à explorer. Une fois ce point atteint, le
robot répète l'opération afin de sélectionner le
prochain point, et ainsi de suite. Les mêmes auteurs ont également
proposé une version multiobjectifs de cet algorithme dans le but de
maximiser la surface de la zone explorée et la précision de la
carte produite [53].
Quant à l'approche proposée dans [43], elle
utilise la méthode stochastique de l'opti-misation arithmétique
(Arithmetic Optimizer) pour renforcer les capacités d'une méthode
déterministe à maximiser l'utilité lors d'une tâche
d'exploration.
Bien que les métaheuristiques les plus utilisées
dans le domaine de la robotique soient généralement des
techniques classiques utilisées pour résoudre des
problèmes d'optimisa-tion globale, d'autres métaheuristiques
peuvent également être appliquées conformément au
théorème No-Free-Lunch [85] qui stipule qu'aucun algorithme n'est
meilleur qu'un autre algorithme dans tous les types de problèmes. Cela
signifie que si une technique montre des résultats supérieurs
dans certaines classes de problèmes, elle ne peut pas montrer des
résultats optimaux pour toutes les autres classes.
Ce théorème a motivé les chercheurs
à inventer de nouvelles métaheuristiques et à les
appliquer à différents domaines, dont la robotique [73].
Cependant, il existe de nombreuses nouvelles métaheuristiques qui n'ont
pas encore été utilisées dans le contexte de
l'explo-ration de zones. Quelques exemples de ces techniques récemment
développées incluent les algorithmes suivants : Butterfly
Optimization Algorithm (BOA) [11], Atomic Orbital Search [14],
Dwarf Mongoose Optimization Algorithm [5], Arithmetic Optimization
Algorithm [3], Tuna Swarm Optimization [87], et Reptile
Search Algorithm [2].
1.6 Conclusion
Nous avons présenté dans ce chapitre les types
de systèmes multirobots, leurs domaines d'applications, ainsi que les
problématiques clés formant les principaux axes de recherche de
cette discipline.
Nous avons aussi présenté un état de
l'art sur la problématique d'exploration, avec un état
récapitulatif des principales approches citées, ceci nous a
permis de positionner notre travail et donner au lecteur un aperçu de
nos objectifs.
Le prochain chapitre sera dédié aux fondements
théoriques des métaheuristiques. Nous y présenterons leur
structure et mécanismes internes. Nous aborderons également le
mode de fonctionnement de quelques métaheuristiques populaires, ainsi
que notre contribution à améliorer l'algorithme d'optimisation
des papillons (Butterfly Optimization Algorithm).

49
CHAPITRE 2
LES MÉTAHEURISTIQUES
2.1 Introduction 50
2.2 Les métaheuristiques 50
2.3 Les types de métaheuristiques 51
2.3.1 Les méthodes à base de trajectoires
51
2.3.2 Les méthodes à base de population 53
2.4 Les mécanisme des métaheuristiques 57
2.4.1 La fonction objectif 57
2.4.2 L'exploration et l'exploitation 57
2.4.3 La convergence 58
2.4.4 Les hyperparamètres 59
2.4.5 Les contraintes 60
2.4.6 Les générations 60
2.4.7 Les critères d'arrêt 60
2.4.8 L'optimalité et la dominance 61
2.5 Structure de base d'une métaheuristique 62
2.5.1 La phase d'initialisation 62
2.5.2 Le corps de l'algorithme 62
2.5.3 La phase finale 62
2.6 Fondements théoriques de métaheuristiques
populaires 64
2.6.1 Les algorithmes génétiques (GA) 64
2.6.2 L'optimisation par Essaim de Particules (PSO) 66
2.6.3 L'otimisation par Colonie de Fourmies (ACO) 67
2.7 Les Fondements théoriques de l'Algorithme
d'Optimisation des
Papillons (BOA) 69
2.8 Les variantes de l'algorithme BOA 73
2.9 Amélioration de l'Algorithme d'Optimisation des
Papillons en uti-
lisation l'opérateur de croisement (xBOA) 75
2.10 Conclusion 78
50
CHAPITRE 2
2.1 Introduction
L'optimisation dans le domaine mathématique est un
terme utilisé pour désigner la recherche de la meilleure solution
à un problème donné. L'optimisation peut être
considérée comme un processus essayant de répondre
à la question suivante: « existe-t-il ou non une meilleure solution
au problème? ».
Nous allons présenter dans ce chapitre une famille de
méthodes utilisées dans le domaine de l'optimisation
numérique qui ont connu un grand succès durant le
demi-siècle dernier en raison de leur capacité à s'adapter
à différents types de problèmes et fournir des
résultats satisfaisants.
Nous introduisons aussi dans ce chapitre les fondements
théoriques d'une nouvelle technique appelée xBOA [16] et qui
constitue l'une des contributions principales de cette thèse.
2.2 Les métaheuristiques
Avec l'augmentation rapide des ressources de calcul
introduites par les ordinateurs, le besoin de résoudre des
problèmes plus complexes est devenu de plus en plus important. Des
techniques d'optimisation stochastique ont été
développées pour fournir des solutions efficaces à ce type
de problèmes.
Les heuristiques sont une classe d'algorithmes visant à
trouver des solutions approximatives à des problèmes
d'optimisation dont la complexité est combinatoire. L'optimisation
stochastique est un type de techniques d'optimisation se basant sur une
recherche aléatoire afin d'explorer plus efficacement l'espace de
solutions possibles.
Les métaheuristiques combinent le concept d'heuristique
avec l'optimisation stochastique dans le but de trouver des solutions
acceptables à des problèmes non linéaires dans un
intervalle de temps raisonnable comparé aux techniques de programmation
mathématique traditionnelles qui garantissent l'optimalité, mais
peuvent entraîner une explosion du temps d'exécution [57].
Le succès des métaheuristiques est causé
par leur capacité à résoudre des problèmes à
très haute complexité ainsi que des problèmes
d'optimisation ayant des objectifs contradictoires. Elles peuvent
également gérer des contraintes non linéaires et
être appliquées à une variété de
problèmes du monde réel sans nécessiter de gros changement
du point de vue de la programmation. Un autre avantage important des
métaheuristiques est leur capacité à résoudre des
problèmes dont le formalisme mathématique n'est pas connu avec
précision.
Toutefois, elles peuvent être coûteuses en temps
de calcul dans certains cas et ne garantissent pas toujours de trouver la
solution optimale. De plus, elles sont difficiles à paramé-trer
à cause de leur sensibilité aux valeurs initiales, ce qui peut
amener à une convergence prématurée.
Elles fournissent un moyen efficace pour trouver des solutions
optimales lorsque l'es-
51
pace de recherche est trop grand ou lorsque les données
sont incomplètes. Elles sont facilement adaptables et peuvent être
utilisées dans une variété de domaines, tels que
l'ingénierie, l'informatique, l'économie ou les finances.
2.3 Les types de métaheuristiques
Les métaheuristiques peuvent être classées
en deux grandes catégories : les algorithmes à trajectoire et les
algorithmes à base de population.
Les algorithmes à trajectoire, aussi appelés
algorithmes à solution unique (Single-Solution Based) proposent
une seule solution et la modifient afin de la faire déplacer dans
l'espace de recherche, tandis que les algorithmes basés sur une
population (Population Based) maintiennent un groupe de solutions
potentielles et les font évoluer itérativement, puis
sélectionnent la meilleure.
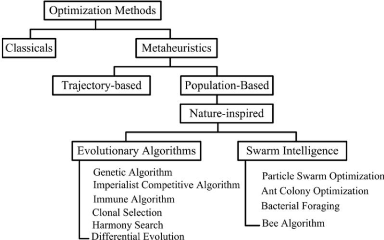
FIGURE 2.1 - Classification des
métaheuristiques [28]
2.3.1 Les méthodes à base de trajectoires
Ce type de méthodes se concentre sur
l'amélioration d'une solution en la faisant déplacer dans
l'espace de recherche formant ainsi une trajectoire.
Les trajectoires qui améliorent la solution seront
automatiquement acceptées, tandis qu'une trajectoire qui
décroît la qualité de la solution n'est pas
forcément refusée.
52
CHAPITRE 2
Elle pourra être acceptée avec une certaine
probabilité afin de permettre à l'algorithme d'éviter un
blocage dans une région non optimale, tel que l'on peut voir dans
l'exemple présenté dans la figure 2.2.
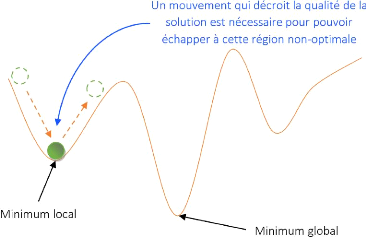
FIGURE 2.2 - Exemple d'une recherche à solution
unique
Ces méthodes se basent généralement sur
des stratégies de recherche locale et recherche de voisinage
couplée avec des mécanismes de mémorisation ou de sauts
[64]
Parmi les méthodes les plus connues de cette
catégorie, nous pouvons citer les suivantes:
-- La méthode du recuit simulé
(Simulated Annealing) [59]
Inspirée de la technique de traitement des
métaux, cet algorithme choisit à chaque étape s'il faut
accepter de déplacer la solution vers un état voisin qui risque
de décroître sa qualité ou s'il faut maintenir le
même état.
Ce choix se fait sur la base d'un calcul de probabilité
dont la valeur décroît régulièrement après
chaque itération jusqu'à atteindre zéro. En d'autres
termes, l'algorithme aura de moins en moins de chances d'accepter les mauvaises
solutions au fur et à mesure que le nombre d'itérations augmente.
Il finira par converger vers une solution de meilleure qualité.
-- La recherche tabou (Tabu Search)
[40]
Cet algorithme se base sur une recherche locale, tout en
évitant activement les points de l'espace de recherche
déjà visités. Ceci se fait en gardant en mémoire
ces points visités dans le but d'éviter les boucles dans les
trajectoires de recherche qui conduiront vers le blocage dans un minimum
local.
53
-- La recherche guidée (Guided Local Search)
[27]
Cet algorithme se base sur une recherche locale classique,
à la différence que lors-qu'un minimum local est
détecté (aucune amélioration de la qualité de la
solution n'est possible), une pénalité est rajoutée
à la fonction objective de sorte à encourager la solution
à sortir du voisinage courant et passer vers un nouveau voisinage.
2.3.2 Les méthodes à base de population
Ce type de méthodes démarre avec une population
de solutions et les améliore toutes en même temps afin d'explorer
plusieurs régions de l'espace de recherche en parallèle. Ceci
permet une plus grande flexibilité et une robustesse plus
élevée par rapport aux minimas locaux (voir figure
2.3).
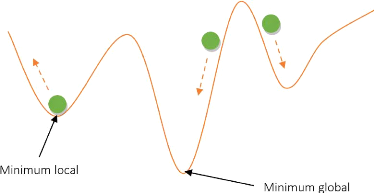
FIGURE 2.3 - Exemple d'une recherche à
base de population de solutions
Le choix de la population initiale est crucial pour la
réussite du processus d'optimisation. En effet, si toutes les solutions
de la population initiale sont presque identiques, il n'y aura pas suffisamment
de diversité et elles convergeront prématurément vers la
même solution.
Généralement les solutions sont
initialisées aléatoirement, cependant, des heuristiques peuvent
être utilisées pour influencer cette initialisation de
façon à avoir une population suffisamment diversifiée pour
pouvoir explorer la plus grande partie de l'espace de recherche.
Les méthodes à base de population peuvent
être classées en plusieurs catégories selon le type
d'inspiration:
CHAPITRE 2
Algorithmes évolutionnaires
Les algorithmes évolutionnaires ont vu le jour au
milieu des années 70 avec les travaux de John Holland [75] puis ceux de
David Goldberg [41] sur les algorithmes génétiques (GA :
Genetic Algorithms),
Ces algorithmes, inspirés des principes de
l'évolution biologique des êtres vivants, se basent sur le
processus d'autoadaptation des espèces dont l'idée
générale est que les individus d'une population qui s'adaptent le
mieux aux conditions de leur environnement survivent le plus longtemps, ce qui
résulte en une évolution progressive de cette population au cours
du temps vers des générations meilleures.
D'autres algorithmes évolutionnaires ont vu le jour
depuis la fin des années 80, tous utilisent des populations d'individus
représentant un ensemble de solutions potentielles. Ces individus sont
mélangés et modifiés en utilisant certains
opérateurs spécifiquement créés pour ce type
d'algorithmes inspirés des principes de reproduction et de mutation
biologique. Seuls les meilleurs individus seront gardés pour la
prochaine itération en analogie au processus de la sélection
naturelle.
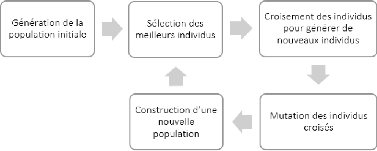
54
FIGURE 2.4 - Processus de base d'un algorithme
génétique
Après les succès des algorithmes
génétiques, d'autres algorithmes bio-inspirés ont
été proposés. Les systèmes immunitaires artificiels
(AIS : Artificial Immune Systems) [36] comptent parmi les premiers et
utilisent le principe de fonctionnement des systèmes immunitaires des
vertébrés basés sur l'adaptation et la
mémorisation.
D'autres types d'algorithmes sont aussi apparus tels que la
programmation génétique (Genetic Programming) [25]
où le but est de faire évoluer un programme sous forme d'arbre en
adaptant les opérateurs des algorithmes génétiques
à ce type de modèles, ou l'évolution différentielle
(Differential Evolution) [80] qui se basent sur l'évolution
d'individus codés sous forme de vecteurs de nombres réels, et
dont l'opérateur de croisement se base sur un calcul de distances.
Algorithmes d'intelligence en essaim (Swarm
Intelligence)
Le terme d'intelligence en essaim, ou intelligence collective,
désigne un phénomène où une population d'agents
simples et réactifs interagissent les uns avec les autres de
manière à ce qu'un comportement intelligent émerge
à la suite de ces interactions.
Ce phénomène est souvent observé dans les
essaims de créatures sociales comme les fourmis, les abeilles et les
oiseaux.
L'analogie la plus facile pour expliquer ce
phénomène est la manière dont les fourmis travaillent.
À l'échelle individuelle, une fourmi n'est pas intelligente et
son comportement obéit à un ensemble de règles simples,
toutefois, en combinant le comportement de toutes les fourmis d'une colonie,
nous remarquons l'émergence d'un comportement complexe et
auto-organisé. Nous disons donc que le groupe est intelligent, mais que
l'individu ne l'est pas.
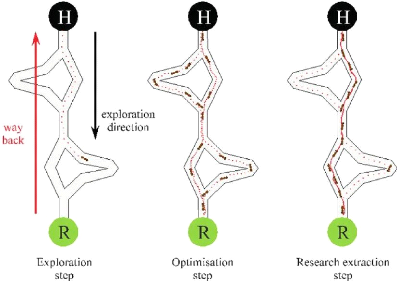
55
FIGURE 2.5 - Optimisation de chemins par un
ensemble de fourmis [56]
Des métaheuristiques à base de population sont
apparues au début des années 90 s'ins-pirant de ce
phénomène. Elles se basent généralement sur le
principe de modéliser les solutions sous forme de vecteurs de nombres
réels. Ces vecteurs évolueront à travers les
itérations en se rapprochant ou s'éloignant des autres individus
selon certaines probabilités et en obéissant à certaines
contraintes. L'une des méthodes les plus populaires dans ce contexte est
l'algorithme d'Optimisation par Colonie de Fourmis (ACO : Ant Colony
Optimization) [24] qui fut créée pour la recherche de
chemins optimaux dans les graphes en modélisant le comportement des
fourmis lorsqu'elles se dirigent vers la nourriture.
CHAPITRE 2
Une autre méthode populaire dans cette catégorie
est appelée Optimisation par Essaim de Particules (PSO : Particle
Swarm Optimization) [58]. Elle imite le comportement social de groupe de
poissons et d'oiseaux en vol où chaque individu modifie sa direction de
mouvement en réponse à ses propres expériences et à
celles de ses voisins. Elle a été appliquée avec
succès dans de nombreux domaines et a donné des résultats
satisfaisants, en particulier pour les problèmes non
linéaires.
Le nombre de métaheuristiques qui rentre dans la
catégorie de l'intelligence en essaim ne cesse de croître, et il
est difficile de toutes les citer. Il s'agit d'un axe de recherche très
actif puisant sa source d'inspiration de la nature. Citons par exemple les
algorithmes d'op-timisation inspirés du comportement des abeilles par
exemple (ABC : Artificial Bee Colony) [55], les loups (GWO : Grey
Wolf Optimizer) [66], les chauves-souris (Bat Algorithm) [91],
les lucioles (Firefly Algorithm)[93]...etc.
Algorithmes inspirés de la physique
Il s'agit d'un type d'algorithmes à base de populations
-toujours inspiré de la nature-mais cette fois des
phénomènes physiques. Ces techniques suivent les mêmes
principes que les algorithmes d'intelligence en essaim et sont parfois
considérées comme une sous-catégorie de ceux-ci.
Parmi ces algorithmes nous retrouvons ceux basés sur
les principes d'interaction entre les masses telles que l'algorithme de
recherche à gravitation (GSA : Gravitational Search Algorithm)
[71] dont les équations sont inspirées de la loi de la
gravité de Newton.
La population de solution dans cet algorithme est
représentée par un ensemble d'atomes qui interagissent entre eux
proportionnellement à leurs masses. Plus une solution sera de meilleure
qualité, plus sa masse augmentera et attirera donc les autres atomes
vers elle.
Nous retrouvons aussi des méthodes basées sur
les principes de la mécanique des fluides, telles que le Vortex
Search Algorithm [30]. Ainsi que d'autres inspirées des principes
d'élec-tromagnétisme tel que l'algorithme des champs
électriques artificiels (Artificial Electric Field Algorithm)
[88].
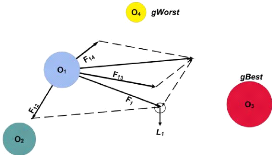
56
FIGURE 2.6 - Optimisation à base d'interactions
physiques entre les atomes [67]
57
2.4 Les mécanisme des métaheuristiques
2.4.1 La fonction objectif
Une fonction d'évaluation - communément
appelée fonction objectif ou fonction fitness - est
une fonction mathématique qui évalue la qualité d'une
solution dans un problème d'optimisation spécifique.
Elle prend une solution candidate en entrée et retourne un
nombre scalaire (voir équation 2.1). Ce scalaire sera utilisé par
l'algorithme pour comparer les solutions trouvées et sélectionner
la meilleure. De ce fait, elle dirige le processus de recherche de
l'algorithme.
En d'autres termes, pour chaque solution s E S(I), une
valeur de fitness f(s) existe définie par la
formulation suivante:
f : S -? R (2.1)
0
s = {Xi/i = 1..n}
Sachant que S est l'espace de recherche à n
dimensions lié à notre problème, et I est l'ensemble
des contraintes du problème.
2.4.2 L 'exploration et l'exploitation
L'exploration et l'exploitation sont deux concepts clés
des métaheuristiques qui doivent constamment être balancées
afin de garantir une bonne convergence vers la solution optimale.
L'exploration, aussi appelée diversification,
est l'habilité de l'algorithme à diversifier les solutions en
couvrant plusieurs régions de l'espace de recherche. Tandis que
l'exploitation, aussi appelée intensification, est l'aptitude
à se concentre sur une seule région de l'espace de recherche dans
le but d'améliorer une solution en cherchant une meilleure solution dans
son voisinage.
La figure 2.7 schématise cette différence. La
phase d'intensification revient donc à faire une recherche locale. Alors
que la phase de diversification à pour but d'explorer l'espace de
manière générale.
58
CHAPITRE 2
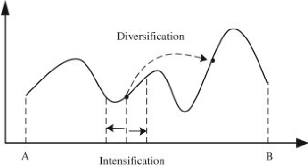
FIGURE 2.7 - Difference entre les
stratégies d'exploration et d'exploitation d'une métaheu-ristique
[70]
2.4.3 La convergence
On dit qu'une métaheuristique converge, lorsque la
majorité des individus constituant sa population aboutissent à la
même solution (voir figure 2.8).
Cette convergence est le résultat d'une comparaison
avec différentes solutions trouvées de l'espace de recherche,
puis l'élimination des solutions de mauvaise qualité, de sorte
à ne garder à la fin que la solution optimale.
Dans le cas idéal, la convergence vers la meilleure
solution se fait après que l'algorithme ait exploré toutes les
régions de l'espace de recherche afin de garantir de tomber sur la
solution optimale. On appelle cette solution Optimum Global ou
Minima Global. Toutefois, il se pourrait dans certains cas que
l'algorithme converge vers une certaine région sans avoir exploré
d'autres, et pourra donc rater la solution optimale en convergeant vers une
solution de moindre qualité. On appelle cette solution Optimum Local
ou Minima Local.
L'objectif d'une métaheuristique est donc de trouver un
compromis entre les phases d'exploration et d'exploitation afin d'éviter
de converger trop rapidement vers un optimum local, mais sans pour autant
perdre trop de temps à explorer chaque région en détail.
L'idée est d'éliminer les mauvaises régions rapidement
afin de pouvoir se concentrer sur les régions les plus prometteuses.
D'un point de vue mathématique, une solution
s* est appelée optimum global si et seulement si
elle respecte l'équation 2.2.
f(s*) f(s)Vs E S. (2.2)
Sachant que S est l'espace de recherche et f : S ?- R+ 0 est la
fonction objectif à minimiser.
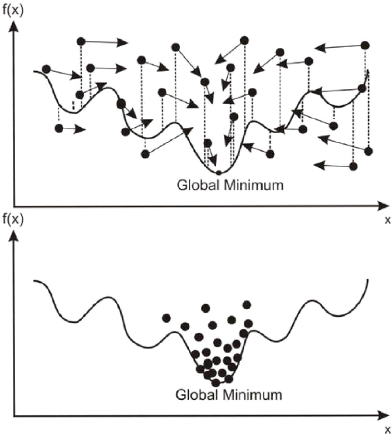
59
FIGURE 2.8 - Exemple de convergence d'une
population de solutions [21]
2.4.4 Les hyperparamètres
Ce sont les paramètres spéciaux que l'utilisateur
doit définir manuellement pour réguler le comportement de
l'algorithme. Ces hyperparamètres sont définis avant le
début de l'exécution, souvent de manière
expérimentale en essayant plusieurs combinaisons.
Parmi les hyperparamètres les plus utilisés dans
les métaheuristiques, nous retrouvons:
-- La taille de la population : qui représente le nombre
d'individus (ou nombre de solutions candidates).
-- La taille de l'individu : nombre de variables constituant une
solution.
60
CHAPITRE 2
-- Nombre d'itérations : nombre maximal
d'itérations avant l'arrêt de l'algorithme. -- Le taux de mutation
: probabilité à laquelle une solution est modifiée.
-- ...etc.
2.4.5 Les contraintes
Des contraintes peuvent être ajoutées à la
modélisation d'un problème d'optimisation. Ces contraintes
divisent l'espace de recherche en deux catégories : d'une part
l'ensemble des solutions valides satisfaisant toutes les contraintes du
problème, d'autre part l'ensemble des solutions non valides où au
moins une contrainte est violée.
Le moyen le plus simple pour intégrer une contrainte
à la fonction objectif d'un problème est d'ajouter un facteur qui
pénalise les solutions non conformes. Ceci prend
généralement la forme d'une multiplication entre le nombre de
contraintes violées et un paramètre de pénalité
fixé manuellement par l'utilisateur.
2.4.6 Les générations
Les métaheuristiques se basent sur un principe de
répétition d'un ensemble d'opéra-tions. Suivant l'analogie
des algorithmes évolutionnaires, une itération dans le
contexte des métaheuristiques à base de population est souvent
appelée génération ou
évolution.
Le principe est qu'à chaque génération,
la population subit plusieurs transformations de sorte qu'elle devienne
meilleure que ce qu'elle n'était durant la génération
précédente.
Le meilleur individu de la dernière
génération constitue donc la meilleure solution trouvée au
cours du processus d'optimisation. Il est parfois appelé le
champion.
2.4.7 Les critères d'arrêt
Les métaheuristiques étant un processus
itératif, des critères d'arrêts doivent être mis en
place afin d'éviter le prolongement de l'exécution de
l'algorithme indéfiniment.
Les critères d'arrêts les plus populaires
utilisés dans le domaine de l'optimisation combinatoire sont les
suivants:
-- Atteindre un nombre maximal d'itérations.
-- Atteindre un nombre maximal de solutions
évaluées en utilisant la fonction objectif.
-- Atteindre un nombre maximal d'itérations où
aucun changement n'a été mesuré sur les valeurs de la
fonction objectif (early stopping).
-- Atteindre une certaine valeur de la fonction fitness.
61
2.4.8 L'optimalité et la dominance
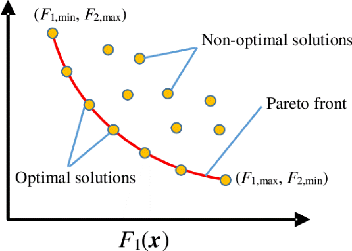
FIGURE 2.9 - Visualisation d'un front optimal
(Pareto Front) séparant les solutions dominées des solutions non
dominées [65]
Les métaheuristiques peuvent résoudre des
problèmes d'optimisation ayant plusieurs objectifs contradictoires.
Une stratégie est de réduire ces objectifs
à un seul facteur d'optimisation en utilisant une somme
pondérée. Une autre stratégie consiste à garder ces
objectifs contradictoires et explorer plusieurs espaces de recherches en
parallèle, selon le nombre d'objectifs à optimiser.
Lorsque l'algorithme optimise un problème
mono-objectif, la meilleure solution est celle qui obtient la meilleure valeur
de fitness.
Dans le cas d'une optimisation multi-objectifs nous pouvons
avoir deux cas de figure: soit une solution obtient la valeur optimale dans
tous les espaces de recherches, nous disons donc que cette solution domine les
autres solutions. Soit, nous nous retrouvons avec plusieurs solutions, chacun
domine l'autre dans un objectif en particulier, mais pas dans l'autre. Ces
solutions sont donc toutes les deux optimales et on les appelle solutions non
dominées. L'ensemble des solutions non dominées est appelé
Pareto-front. La figure 2.9 illustre ceci d'une manière graphique.
62
CHAPITRE 2
2.5 Structure de base d'une métaheuristique
Malgré la diversité des métaheuristiques et
leurs types, elles partagent toutes la même structure de base.
L'algorithme de base d'une métaheuristique se découpe en 3
parties:
2.5.1 La phase d'initialisation
Cette phase est exécutée une seule fois au
début de l'algorithme, son but est de définir toutes les
variables et les paramètres nécessaires pour son bon
fonctionnement. Ceci implique généralement d'effectuer les
actions suivantes:
-- Définir le problème : taille de la population,
dimensions des individus, contraintes.
-- Définir la fonction objectif et ses
paramètres.
-- Définir les autres hyperparamètres : nombre
d'itérations, critère d'arrêt...etc.
-- Générer la solution - ou la population de
solutions - initiale.
-- Evaluer les solutions initiales en utilisant la fonction
objectif.
2.5.2 Le corps de l'algorithme
Il s'agit d'exécuter les opérations constituant le
coeur du processus d'optimisation. Cette phase est répétée
jusqu'à ce que le critère d'arrêt soit atteint:
-- Exécuter l'ensemble des opérations constituant
la logique de l'algorithme. -- Evaluer la qualité des solutions.
-- Mémoriser la meilleure solution trouvée
jusqu'ici.
-- Répéter les opérations jusqu'à ce
que le critère d'arrêt soit atteint.
2.5.3 La phase finale
C'est la dernière phase qui sera exécutée
lorsque le processus d'optimisation est terminé. Elle comprend
généralement des actions d'aide à l'analyse des
résultats:
-- Sauvegarder les résultats : meilleure solution,
qualité de la solution finale, temps d'exécution...etc.
-- Tracer les graphes de performances, historique
d'évolution de la fonction objectif...etc. La figure 2.10
schématise la structure de base d'une métaheuristique.
63
Début
Initialiser N (nombre d'individus), max gen (nombre
d'itérations), Pc (probabilité de croisement), et Pm
(probabilité de mutation)
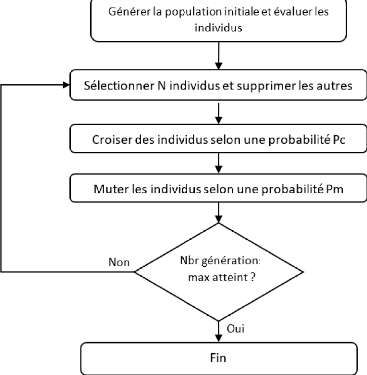
t
Sélectionner N individus et supprimer les
autres
Nbr génération: max atteint ?
Générer la population initiale et évaluer
les individus
Croiser des individus selon une probabilité
Pc
Muter les individus selon une probabilité Pm
Fin
FIGURE 2.10 -- Structure de base d'une
métaheuristique
64
CHAPITRE 2
2.6 Fondements théoriques de métaheuristiques
populaires
Dans cette section, nous allons présenter les
fondements théoriques et le principe de fonctionnement de quelques
métaheuristiques populaires. Ces métaheuristiques seront
utilisées dans les chapitres suivants lors des expériences de
benchmarking et de résolution du problème d'exploration
multirobots.
Les algorithmes seront présentés en suivant l'ordre
chronologique de leur apparition.
2.6.1 Les algorithmes génétiques (GA)
Les Algorithmes Génétiques utilisent des
concepts issus de la génétique et de la sélection
naturelle. Ils ont été introduits par les travaux de John Holland
[75] et D. Goldberg [41].
La population dans un algorithme génétique est
constituée d'un certain nombre d'indi-vidus, eux-mêmes
constitués d'un ensemble de gènes (regroupés en
chromosomes). Un gène représente une variable spécifique
au problème qu'on veut optimiser et est généralement
codé par un nombre binaire ou réel.
Les individus dans cet algorithme sont soumis aux 3
opérations suivantes: Sélection
Durant cette opération, les meilleurs candidats sont
choisis pour servir de parents à la génération
suivante. Ce processus est similaire au processus de sélection naturelle
: les individus les plus adaptés à leur environnement
sont conservés tandis que les moins adaptés meurent avant la
reproduction.
Toutefois, des stratégies sont parfois mises en place
pour conserver certains individus de mauvaise qualité afin de
diversifier la population et éviter une convergence trop rapide vers
l'optimum local.
L'adaptation d'un individu est calculée en fonction de
sa valeur de fitness. L'opération de sélection nécessite
donc d'évaluer l'ensemble des individus de la population à
chaque itération afin de pouvoir les comparer, ce qui a un impact
sur la complexité globale de l'algorithme. Pour une population de N
individus et M itérations, la complexité sera
égale à N x M.
Croisement (crossover)
Cette opération est parfois appelée
reproduction, elle vise à combiner deux individus au
hasard afin d'en produire d'autres. Pour ce faire, l'algorithme
sélectionne quelques gènes
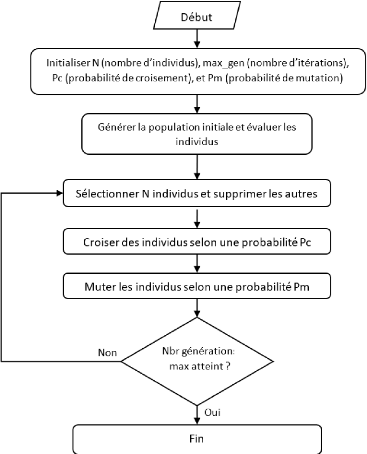
65
FIGURE 2.11 - Diagramme de l'algorithme
génétique
66
CHAPITRE 2
du premier individu et les mélange avec des
gènes du deuxième individu de sorte à créer un tout
nouvel individu différent des deux autres. Cette opération est
répétée plusieurs fois jusqu'à ce que le nombre de
nouveaux individus créés (appelées enfants) soit
égal au nombre des individus déjà présent dans la
population (parents).
Bien que la taille de la population augmente après
l'exécution de cette opération, elle sera réduite à
sa taille originale lors de la prochaine itération après avoir
appliqué l'opéra-teur de sélection.
Il est important à noter que l'opérateur de
croisement n'est pas forcément appliqué systématiquement
à tous les individus. Un facteur de probabilité est
utilisé pour contrôler le taux de croisement dans la population.
Ce facteur est souvent choisi dans un intervalle entre 0.7 à 1.0.
Mutation
Cette opération apporte des changements mineurs aux
individus en modifiant aléatoirement la valeur de certains gènes.
Ceci permet à l'algorithme d'examiner une plus grande
variété de solutions potentielles et l'empêche de rester
coincé dans des optimums locaux. Cependant, il ne faut pas que cette
opération soit effectuée trop souvent pour éviter de
tomber dans une recherche aléatoire. Elle est donc appliquée avec
une probabilité relativement faible (souvent inférieure à
5%).
Le diagramme présenté dans la figure 2.11 montre
les étapes de l'algorithme génétique.
2.6.2 L'optimisation par Essaim de Particules (PSO)
Cette méthode a été publiée en
1995 [58]. Elle se base sur le comportement social des essaims observés
dans la nature.
Dans cet algorithme, une population de particules
représentant des solutions potentielles est générée
aléatoirement. Ces particules se déplacent dans l'espace de
recherche en modifiant leurs emplacements actuels en fonction de leurs
emplacements précédents et de ceux de leurs voisins.
L'équation qui gouverne le déplacement d'une
particule met à jour à chaque itération deux informations
: la vitesse de la particule et sa position (voir les équations 2.3 et
2.4). Ces deux informations sont calculées en fonction de 3
composants:
-- Composant social : attire la particule à se diriger
vers la position de la meilleure solution connue par la population
(dénotée g*).
-- Composant cognitif: attire la particule à se diriger
vers la position de la meilleure solution qu'elle a visité dans le
passé (dénotée x.*).
-- Composant inertiel : pousse la particule à garder sa
direction courante.
L'utilisateur attribue au début de l'algorithme un
facteur de pondération pour chaque composant pour contrôler le
degré d'influence de ces composants sur le mouvement des
67
particules. Plus le facteur du composant social est grand,
plus l'algorithme s'oriente vers la diversification de la population. Plus le
facteur du composant cognitif est grand, l'algo-rithme s'oriente vers une
stratégie d'intensification.
Vitesse : vt+1
i = wvt i +
c1r1(pt_best
i xt i) +
c2r2(gt_bestxt
i) (2.3)
Position: xt+1
i = xt i + vt+1
(2.4)
i
Où :
-- w est le poids d'inertie
-- r1 et r2 sont des vecteurs
aléatoires distribués uniformément dans l'interval
[0,1]
-- c1 et c2 sont des hyperparamètres
appelés facteurs d'accélération, ou facteur cognitif et
facteur social respectivement.
2.6.3 L'otimisation par Colonie de Fourmies
(ACO)
Cet algorithme a été introduit par Colorni et
Dorigo en 1991 [24]. Il simule la façon dont les fourmis naviguent pour
trouver la source de nourriture la plus proche de leur nid.
Étant donné que les fourmis dans le monde
réel dégagent des odeurs (ou phéromones) volatiles
lorsqu'elles trouvent une source de nourriture, et que les autres fourmis ont
tendance à suivre les chemins qui contiennent ces phéromones. Les
itinéraires les plus courts entre la source de nourriture et le nid
seront favorisés puisque la quantité de phéromones non
volatilisée sera plus grande en raison de la courte distance. Ces
chemins optimaux seront donc de plus en plus empruntés par les fourmis.
Ce qui résulte en un effet de renforcement.
De la même manière, les agents de l'ACO utilisent
des phéromones virtuelles pour marquer les meilleures solutions
trouvées. Au début de l'algorithme, les fourmis se
déplacent de manière aléatoire tout en mettant à
jour une matrice de phéromones. Cette matrice contient la
quantité de phéromones pour chaque solution trouvée, qui
est incrémentée avec une valeur proportionnelle à la
qualité de la solution.
Cette valeur décroit avec le temps suivant
l'équation 2.5 afin de simuler l'effet d'évapo-ration:
ôi ?- (1 - ñ)ôi
(2.5)
Où ñ est une constante
d'évaporation à définir par l'utilisateur et
ôi est la quantité de phéromones de la solution
i
CHAPITRE 2
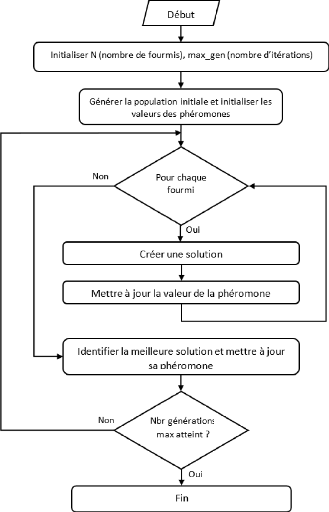
68
FIGURE 2.12 - Pseudo-code de l'algorithme ACO
69
Après un certain nombre d'itérations, les
solutions les plus visitées auront une quantité de
phéromones plus grande, ce qui augmente la probabilité que les
fourmis les choisissent. La baisse régulière de la
quantité de phéromones permet aux fourmis d'explorer des
solutions différentes pendant le processus de recherche. C'est un
mécanisme de diversification sans lequel l'algorithme risque de
converger rapidement vers un optimum local. Un autre mécanisme est de
garder en mémoire la liste des solutions que la fourmi a
déjà visitées, de sorte à les éliminer dans
ses futurs mouvements.
2.7 Les Fondements théoriques de l'Algorithme
d'Opti-misation des Papillons (BOA)
Butterfly Optimization Algorithm (BOA) est une
métaheuristique à base de populations s'inspirant du comportement
des papillons, elle a été proposée par S. Arora
et S. Singh [11] en tant qu'algorithme d'optimisation globale.
Au départ, l'algorithme génère une
population de solutions aléatoires (les papillons), puis les modifie
à travers plusieurs itérations jusqu'à ce qu'un
critère d'arrêt soit atteint.
Dans la nature, les papillons utilisent l'odorat pour trouver
des sources de nourriture et des partenaires de reproduction, pour y arriver,
ils utilisent des cellules dans leurs corps pour percevoir les odeurs
(fragrance) et mesurer leurs intensités [11]. Plus la fragrance
est intense, plus le papillon est attiré vers la source de cette
odeur.
L'algorithme BOA modélise ce comportement en calculant
une valeur de fragrance proportionnelle à la valeur de fitness de
l'individu. Plus la valeur de fitness d'un papillon est de meilleure
qualité, plus sa fragrance est grande, et plus les autres papillons y
sont attirés. Toutefois, la fragrance émise par un papillon dans
la nature est souvent altérée par les conditions
météorologiques. Deux paramètres sont donc introduits dans
l'algorithme pour simuler ce phénomène et modifier
l'intensité de la fragrance qui sera captée par les autres
papillons.
Ces paramètres sont les suivants:
-- Sensor modality (c) : Un facteur de multiplication
contrôlant la proportion de la fragrance qui sera perçue.
-- Power exponent (a) : Un exposant qui
contrôle la puissance à laquelle l'intensité originale de
la fragrance est amplifiée.
L'équation 2.6 décrit la règle de calcul de
la fragrance:
F = c * Ia (2.6)
Où :
-- c = sensor modality;
-- a = power exponent; et
-- I = intensité originale de la fragrance, qui est
égale à la valeur de fitness du papillon.
CHAPITRE 2
Générer une population de n papillons
Calculer la fragrance de chaque papillon
Sélectionner le meilleur papillon
r N
Mettre à jour
la valeur de c
ti
Générer un nombre aléatoire r
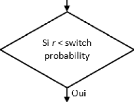
Non
Se déplacervers le meilleur papillon en utilisant
l'équation 2
i
Remplacer l'ancienne solution par la
nouvelle si
meilleure
N
Se déplacer aléatoirement en
utilisant
l'équation 3
70
FIGURE 2.13 -- Diagramme de l'algorithme
BOA
71
Une fois les fragrances calculées, les papillons vont
se déplacer graduellement vers le meilleur papillon qui
représente la meilleure solution trouvée jusqu'à
présent dans l'espace de recherche. Cette étape est
appelée « recherche globale » [11]
Afin d'éviter une convergence prématurée,
une phase de recherche locale a été introduite par les auteurs de
l'algorithme pendant laquelle les papillons se déplacent
aléatoirement dans la région où ils se trouvent.
À chaque itération, l'algorithme
exécutera soit la phase de recherche globale, soit celle de la recherche
locale, selon la valeur d'une probabilité d'alternance (switching
probability).
Les équations suivantes décrivent respectivement
comment les individus sont mis à jour pendant les phases de recherche
globale et locale:
xt+1
i = xt i + (r2 * g* - xt
) * fi (2.7)
i
xt+1
i = xt i + (r2 * xt j - xt )
* fi (2.8)
k
Où :
-- xi est le papillon n° i;
-- r est un nombre aléatoire appartenant à
l'interval [0, 1];
-- g* est le meilleure papillon dans la population;
-- fi est la fragrance du papillon n° i;
-- xj et xk sont deux papillons sélectionnés
aléatoirement parmi la population.
En exécutant l'équation 2.7 plusieurs fois
à travers les itérations, les papillons convergeront vers
l'individu ayant la meilleure valeur de fitness qui représente la
meilleure solution connue. Toutefois, une convergence trop rapide pourrait
piéger les individus dans le voisinage d'un optimum local alors qu'une
meilleure solution se trouve ailleurs dans l'espace de recherche.
L'équation 2.8 évite à ce problème en poussant les
papillons à se déplacer aléatoirement pour explorer de
nouvelles solutions.
À chaque itération, les valeurs de fitness des
papillons augmenteront en qualité, et leurs fragrances seront de plus en
plus grandes. Afin d'éviter une convergence trop rapide engendrée
par une trop grande augmentation de la fragrance, les auteurs de l'algorithme
ont introduit une règle pour diminuer le facteur de multiplication c
(sensor modality) à la fin de chaque itération [9].
L'ajout de cette règle - décrite par l'équation 2.9 - leur
a permis d'améliorer les résultats de l'algorithme.
f 0.025 )
ct+1 = ct + (2.9)
ct * nbr_iterations
72
CHAPITRE 2
La simplicité de l'approche produit un pseudo-code
facile à comprendre, ce qui constitue un avantage considérable
lors de l'implémentation et débogage de l'algorithme (voir la
figure 2.14). Par ailleurs, l'utilisation de formules simples et rapides
à calculer permet de l'utiliser dans des machines à faible
puissance de calcul tels que les petits robots ou les ordinateurs d'ancienne
génération.
Le diagramme présenté dans la figure 2.13
résume toutes les étapes de l'algorithme.

FIGURE 2.14 - Pseudo-code de l'algorithme BOA
73
2.8 Les variantes de l'algorithme BOA
Bien que le pseudo-code tel que décrit dans la section
précédente a été publié en 2019 en
tant que version officielle du Butterfly Optimization Algorithm [11],
une version préliminaire avait déjà été
présentée dans un article de conférence en 2015 [10]
avec un pseudo-code assez similaire du Flower Pollination Algorithm
(FPA) [92] utilisant une distribution Lèvy pour les
règles de mises à jour des positions des papillons. Dans les
articles ultérieurs, les auteurs du BOA ont changé les
équations et ont ajouté la règle de mise à jour
automatique du paramètre c (sensor modality), ce qui a permis
d'améliorer le taux de convergence de l'algorithme [9] [11].
Dans un autre article paru la même année, ils ont
proposé une variante binaire de la méthode pour résoudre
le problème de sélection d'attributs [8].
D'autres auteurs ont proposé l'hybridation de
l'algorithme avec différentes méthodes. Les auteurs de [51]
ont utilisé un modèle de Perceptron Multicouches (MLP :
Multi-Layer Perceptron) hybridé avec BOA pour résoudre le
problème de classification supervisé. Les résultats des
expériences ont démontré que l'introduction du MLP a
permis de garder une bonne balance entre les phases d'exploration et
d'exploitation de l'algorithme BOA et améliorer les résultats.
Les auteurs de [96] ont proposé une approche hybride entre PSO
(Particle Swarm Optimization) et BOA couplée avec la
théorie des systèmes chaotiques afin d'obte-nir de meilleurs
résultats pour les problèmes à grande dimension. Ils ont
aussi proposé une règle de mise à jour non-linéaire
des paramètres qui a amélioré les résultats par
rapport à l'utilisation de la règle classique linéaire de
l'équation 2.9. Les auteurs de [84] ont utilisé
une hybridation basée sur le mécanisme de mutualisme avec le
Flower Pollination Algorithm (FPA). L'approche a donné de bons
résultats mais nécessite un long temps d'exécution. Le
principe de mutualisme a aussi été utilisé par [76]
pour une hybridation avec l'algorithme Symbiosis Organisms Search.
Les auteurs de [99] ont combiné l'algorithme BOA avec la
méthode ANFIS (Adaptive Neuro-Fuzzy Inference System) et ont
obtenu de meilleures performances par rapport à l'approche ANFIS
classique ou de l'approche hybride entre ANFIS et FireFly
Algorithm.
Une autre direction pour l'amélioration de la
méthode consiste à modifier la logique de l'algorithme. Dans
cette perspective, les auteurs du BOA ont proposé une variante
appelée mBOA [12] qui introduit une nouvelle étape
d'exploitation intensive juste après les phases de recherches locale et
globale de l'algorithme. Le but de cette nouvelle étape est
d'éviter à la population de solutions d'être bloquée
dans un optimum local. Les résultats des expériences ont
montré une convergence plus rapide par rapport à la version
classique du BOA. Les auteurs de [83] ont inclus une étape de
recherche locale basée sur l'opération de mutation afin
d'améliorer les performances de la méthode, ce qui a donné
de meilleurs résultats dans 15 parmi les 20 corpus de
tests utilisés par les auteurs, mais a nécessité un temps
d'exécution plus long. Les auteurs de [13] ont utilisé
la théorie des systèmes chaotiques comme phase de recherche
locale pour augmenter les traits d'exploitation de l'algorithme. Ils l'ont
utilisé pour résoudre le problème de sélection
d'attributs. Les auteurs de [61] ont utilisé la méthode
de cross-entroy et une technique de co-évolution pour
résoudre 3 problèmes classiques d'engineering. Les
auteurs de [35] ont opté pour la réduction du nombre de
paramètres en remplaçant la formule de calcul de la fragrance par
une nouvelle règle
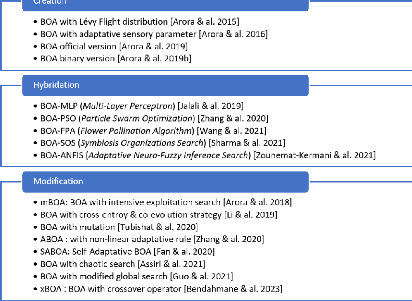
74
CHAPITRE 2
autoadaptative qui ne nécessite plus l'utilisation des
deux paramètres c (sensory modality) et a (power exponent).
Cette nouvelle variante est appelée SABOA (Self-Adaptative
BOA). D'un autre côté, les auteurs de [44] ont modifié
l'équation de la recherche globale dans le but d'améliorer la
convergence de l'algorithme, couplé avec une stratégie de
réinitialisation périodique de la population afin d'éviter
le blocage dans un minima local.
Les variantes citées ci-haut ont montré des
résultats prometteurs pour la résolution des problèmes
d'optimisation globaux à grandes dimensions, ce qui constituait une des
faiblesses de l'approche BOA classique. Une autre faiblesse consiste en la
lenteur de la convergence de l'algorithme causée par le faible taux de
diversité des solutions dans la population.
Pour résoudre ces deux problèmes, nous proposons
de modifier la méthode en introduisant l'opérateur de croisement
et modifiant la stratégie de mouvement des papillons dans les phases de
recherches globale et locale. Ces changements ont permis l'introduction d'une
nouvelle variante de l'algorithme appelée xBOA (crossover BOA)
[16].
La figure 2.15 résume l'état de l'art des variantes
de BOA citées ci-haut.
FIGURE 2.15 - Résumé de l'état de l'art de
l'algorithme BOA et ses différentes variantes
75
2.9 Amélioration de l'Algorithme d'Optimisation des
Papillons en utilisation l'opérateur de croisement (xBOA)
L'équation 2.7 déplace tous les papillons vers
la meilleure solution de la population, ce qui ignore les autres solutions qui
ont la même valeur de fitness ou qui ont le potentiel de devenir de
meilleures solutions après quelques itérations. Afin de
dépasser cette limitation, nous proposons de modifier l'algorithme BOA
en remplaçant cette équation avec l'opérateur de
croisement durant la phase de recherche globale.
L'opérateur de croisement a été introduit
dans l'Algorithme Génétique [41]. Il consiste à combiner
deux individus parents pour créer de nouveaux individus appelés
enfants (ou offsprings en anglais). L'idée de base
inspirée de la nature simule la manière dont les enfants
héritent une partie des caractéristiques de chaque parent.
Plusieurs stratégies de combinaisons ont
été proposées dans la littérature [69]. Pour des
raisons de simplicité, nous allons utiliser la stratégie de
croisement à un point (Single-point Crossover). Elle consiste
à diviser le vecteur de données du premier parent en deux
sous-vecteurs, puis les permuter avec les sous-vecteurs du deuxième
parent afin de produire deux nouveaux individus.
L'exemple présenté dans la figure 2.16 montre le
résultat de cette opération pour deux individus de taille 5 ainsi
que le pseudo-code de cette opération.
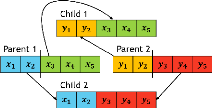

FIGURE 2.16 - Exemple et pseudo-code de l'opérateur de
croisement
76
CHAPITRE 2
Vu que l'insertion de nouveaux individus dans la population
peut rapidement faire croître sa taille, nous avons choisi de remplacer
un individu parent par un de ses enfants; le meilleur enfant est choisi dans ce
cas. Ceci nous permet de garder une taille de population fixe pendant toute la
durée du processus d'optimisation.

FIGURE 2.17 - Pseudo-code de l'algorithme xBOA
En utilisant l'opérateur de croisement, nous
encourageons les papillons à se déplacer vers plusieurs
potentielles solutions au lieu de converger tous vers la meilleure solution
connue. Ceci crée une diversité dans la population et permet
à l'algorithme d'échapper au piège de converger
prématurément vers un minima local. En d'autres termes, la
population de papillons va inspecter plusieurs régions de l'espace de
recherche simultanément afin de
77
trouver la solution globale plus rapidement.
L'utilisation de l'opérateur de croisement à
chaque itération pourrait toutefois déséquilibrer la
balance entre les propriétés d'exploration et d'exploitation de
l'algorithme xBOA, nous utilisons donc un paramètre qui
déterminera à quelle fréquence cet opérateur est
utilisé. Ce paramètre est appelé probabilité de
croisement (crossover probability). Il remplacera le paramètre
Switch Probability utilisé dans l'algorithme BOA original.
Une autre différence entre les deux algorithmes se
situe au niveau de la recherche locale. En effet, dans xBOA l'équation
2.8 est utilisée même si elle engendre une dégradation de
la qualité des solutions, contrairement à l'algorithme original.
Ceci semble contre-productif, néanmoins cela permet à
l'algorithme d'augmenter la diversité des solutions en leur permettant
de se déplacer aléatoirement dans l'espace de recherche et
d'explorer de nouvelles régions qui pourraient cacher la solution
globale. La stratégie est d'accepter une perte en qualité
à court terme pour pouvoir découvrir des solutions encore
meilleures que celles trouvées jusqu'ici.
Les résultats des expériences effectuées
durant notre thèse ont montré que les modifications
proposées ont permis à xBOA de trouver la solution globale plus
rapidement que l'algorithme BOA original, et d'être plus robuste aux
minima locaux.
Le diagramme de la figure 2.18 décrit toutes les
opérations de l'algorithme xBOA, son pseudo-code est
présenté dans la figure 2.17.
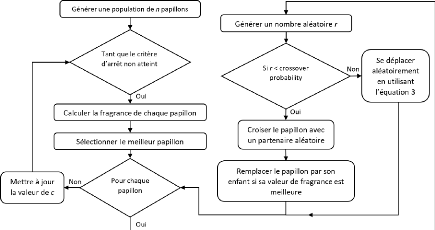
FIGURE 2.18 - Diagramme de l'algorithme xBOA
78
CHAPITRE 2
2.10 Conclusion
Nous avons présenté dans ce chapitre le principe
de fonctionnement des métaheuris-tiques et leurs mécanismes
internes. Nous avons également présenté les fondements
théoriques de plusieurs métaheuristiques populaires
utilisées dans la littérature pour résoudre divers
problèmes d'optimisation globale, dont les problèmes de
robotique.
Ce chapitre a aussi présenté les fondements
mathématiques de la méthode BOA (Butterfly Optimization
Algorithm) ainsi que ses avantages et limitations. Nous avons
proposé des modifications visant à l'améliorer ce qui a
donné lieu à une nouvelle variante de l'algo-rithme que nous
avons appelé xBOA (crossover Butterfly Optimization
Algorithm).
Cette variante se base sur l'intégration de
l'opérateur de croisement durant la recherche globale afin de lui
permettre de diversifier les solutions et échapper aux optimums locaux.
Elle intègre aussi une modification dans la stratégie de la
recherche locale pour éviter de converger trop rapidement vers un
optimum local.
Ce chapitre conclut la partie théorique de notre
thèse. Les deux autres chapitres restants seront consacrés
à l'étude expérimentale.
79
Deuxième partie
Etude expérimentale

80
CHAPITRE 3
MÉTHODOLOGIE, MODÉLISATION ET
PARAMÉ-TRAGE
3.1 Introduction 81
3.2 PyRoboticsLab : un nouvel outil de simulation et de
benchmarking 81 3.2.1 Motivations pour la création d'une nouvelle
plateforme de
simulation 82
3.2.2 Les objectifs de conception 83
3.2.3 L'architecture du système 85
3.2.4 Les outils et technologies 87
3.2.5 Les scénarios de bechmarking 89
3.3 Modélisation géométrique des robots
89
3.4 Modélisation du processus de navigation, planification
et évite-
ment d'obstacles 91
3.5 Modélisation des grilles d'occupation 93
3.6 Modélisation du problème d'exploration 97
3.6.1 Modélisation mono et multirobots 97
3.6.2 Les critères d'évaluation 100
3.6.3 La complexité du modèle 101
3.7 Paramétrage et configuration 101
3.7.1 Paramétrage des expériences 101
3.7.2 Paramétrage de l'environnement de simulation
102
3.8 Conclusion 104
81
3.1 Introduction
Nous allons présenter dans ce chapitre la
méthodologie utilisée, ainsi que la modélisation de la
problématique d'exploration d'une zone inconnue avec des contraintes
d'énergie. Nous présenterons également les outils,
l'environnement de test, ainsi que les critères de performance
utilisés pour la validation de l'approche proposée. Étant
donné la difficulté rencontrée pour la comparaison de
notre approche avec des cas d'études similaires, nous
présenterons un nouvel outil créé afin de faciliter la
comparaison et l'évaluation des algorithmes de navigation, d'exploration
et de planification de trajectoires pour les robots mobiles, ainsi que les
métaheuristiques appliquées au domaine de la robotique.
Cette plateforme de benchmarking a été
créée d'une telle manière à nécessiter peu
de ressources de calcul, et être facile à utiliser et à
automatiser afin d'offrir aux chercheurs du domaine un moyen de prototypage
rapide et une suite d'expérimentation unifiée. Elle fait partie
des principales contributions de cette thèse et sera accessible en open
source pour l'utilisation générale de la communauté
scientifique.
3.2 PyRoboticsLab : un nouvel outil de simulation et de
benchmarking
Le teste et l'évaluation comparative de nouveaux
algorithmes constitue une étape importante de la validation des
idées de recherche. Étant donné que les expériences
réelles en robotique exigent des investissements en temps et en
équipements, de nombreux chercheurs préfèrent utiliser des
environnements virtuels pour tester et valider leurs algorithmes avant de les
déployer sur des robots réels. Même si les simulateurs de
robotique ont été largement critiqués au début des
années 90 [50], nous pouvons aujourd'hui identifier de nombreux
avantages à les utiliser:
-- Expérimentation plus rapide, en
accélérant l'horloge de simulation par rapport à l'horloge
du monde réel.
-- Automatisation des expériences à l'aide de
scripts
-- Mise en pause, enregistrement et reproduction d'une
expérience particulière pour une analyse approfondie.
-- Réduction des coûts en évitant
l'endommagement du matériel en cas d'erreurs de programmation.
-- Évitement des problèmes techniques liés
aux défaillances matérielles.
-- Expérimentation de plusieurs configurations
matérielles sans devoir acheter des pièces de rechange ou de
modifier la partie électronique du robot.
-- Évitement des inconvénients liés
à la limitation des batteries et au temps de recharge pendant les
expériences longues et/ou répétitives.
-- Éliminer les artefacts causés par les
interférences et la faible qualité du matériel.
-- Accélération du processus de validation et de
débogage des logiciels, ce qui réduit les délais de
livraison.
82
CHAPITRE 3
Cette section présente PyRoboticsLab : un nouvel outil
de simulation dédié au bench-marking des algorithmes de
navigation, de planification de chemins, ainsi que l'exploration de zones en
utilisant un ou plusieurs robots. Ce simulateur est disponible en open source
sur le lien cité en bas de page 1.
3.2.1 Motivations pour la création d'une
nouvelle plateforme de simulation
De nombreux simulateurs modernes ont été
introduits par la communauté robotique ces dernières
années [72] [37] [31] [60]. Ces simulateurs offrent un grand
degré de fidélité au monde réel qui leur permet
d'entrainer des algorithmes d'intelligence artificielle avec une grande
précision avant de les déployer en production [31].
Toutefois, pour atteindre ce degré élevé
de fidélité, il faut effectuer des calculs complexes, ce qui
entraine des charges élevées en termes de mémoire et de
puissance du processeur, même pour les petites expériences. Ceci
est un facteur de frein pour la portabilité et le passage à
l'échelle des applications.
Certains chercheurs tentent de surpasser ces limites en
utilisant des services Cloud [94]. Néanmoins, cette mise à
l'échelle implique des frais supplémentaires et affecte
négativement la reproductibilité de l'ensemble du projet.
D'autre part, les simulateurs modernes ont tendance à
être de plus en plus polyvalents, ce qui rend leurs bases de code
difficiles à comprendre et à maintenir. De nombreux projets
1. https ://
github.com/amineHorseman/PyRoboticsLab

FIGURE 3.1 - Exemple d'un simulateur moderne basé sur un
moteur de jeux vidéos pour l'entraînement des voitures autonomes
[31]
83
open source souffrent de la difficulté de trouver de
nouveaux contributeurs en raison de leur courbe d'apprentissage croissante [4].
Cela crée une barrière psychologique pour les étudiants et
les jeunes développeurs, tout en décourageant les chercheurs trop
occupés à les utiliser pour prototyper de nouvelles idées
[4]. Souvent, ces chercheurs finissent par mettre en oeuvre des environnements
simplifiés et personnalisés pour leurs expériences afin
d'ob-tenir des résultats rapides, ce qui rend difficile la comparaison
de leurs algorithmes avec d'autres approches puisque chaque article utilise des
données, une structure d'environne-ment ou des critères
d'évaluation différents.
Afin de standardiser l'évaluation des algorithmes dans
certaines problématiques de robotique, nous avons
développé un nouveau simulateur spécialement conçu
pour évaluer les performances des algorithmes de navigation, de
planification de chemins, d'exploration, et d'optimisation dans des
environnements de type grille.
Notre simulateur est dédié à la
simulation d'un type spécifique de scénarios et ne vise pas
à remplacer les simulateurs modernes polyvalents. Il nécessite
moins de ressources CPU et de mémoire; peut simuler une centaine de
robots dans un ordinateur portable ordinaire sans carte graphique; et est
conçu pour être facile à utiliser et à porter vers
différents systèmes d'exploitation, ce qui convient plus à
un usage éducatif ou pour accélérer les expériences
de recherche dans les axes cités ci-haut.
3.2.2 Les objectifs de conception
Avant de pouvoir établir l'architecture du
système, nous devons d'abord fixer les objectifs de conception de notre
simulateur. La liste ci-dessous décrit les caractéristiques
souhaitées pour notre cas d'études:
Modularité
Le simulateur doit offrir plusieurs modules agencés de
façon à pouvoir facilement ajouter, modifier ou étendre
les fonctionnalités d'un module sans affecter les autres. Ceci permet
par exemple d'ajouter de nouveaux types de capteurs, de nouveaux algorithmes de
planification, ou modifier le fonctionnement de base du système de
navigation.
Le but est d'augmenter l'extensibilité du projet, et
faciliter la maintenance et la mise à jour de la plateforme au fil du
temps.
Flexibilité
Le simulateur doit être suffisamment flexible pour
s'adapter à différents types de problèmes d'optimisation
et d'algorithmes de contrôle. Cela inclut la possibilité de :
-- Modéliser différentes formes de fonctions
objectif. -- Définir différents scénarios
d'expérimentation. -- Paramétrer la position des obstacles.
84
CHAPITRE 3
-- Personnaliser les caractéristiques de robots telles que
les distances et rayons de détection; niveau d'énergie
disponible; mouvements autorisés...etc.
Passage à l'échelle
Le simulateur doit permettre de simuler un grand nombre de
robots et s'adapter à l'évo-lution des ressources de la machine
sans nécessiter des retouches de la part de l'utilisateur sur le code
source. Il doit intégrer des fonctionnalités permettant à
l'utilisateur de configu-rer des expériences à large
échelle et offrir la possibilité de paralléliser
instantanément ses expériences en déterminant le nombre de
processeurs à utiliser.
Ceci a pour but de permettre aux chercheurs de porter
facilement leur code sur des machines plus puissantes afin
d'accélérer leurs expériences sans devoir maîtriser
les techniques de la programmation parallèle.
Efficacité
Le simulateur doit minimiser l'utilisation des ressources de
la machine telles que le temps de calcul et la mémoire virtuelle, il
doit permettre aux utilisateurs d'exécuter les expériences sans
nécessiter l'acquisition de cartes graphiques couteuses ou de serveurs
de calcul.
Ceci a pour but d'améliorer l'accessibilité
à la recherche pour les étudiants et les jeunes chercheurs
n'ayant pas forcément les moyens d'investir sur un matériel plus
coûteux.
Automatisation
Le simulateur doit automatiser tout le processus
d'expérimentation, allant du paramé-trage automatique,
l'exécution répétitive des expériences, la
génération des graphes et tableaux de statistiques, ainsi que la
sauvegarde des résultats pour analyse ultérieure.
Ceci a pour but d'alléger le temps dédié
à la gestion des expériences et permettre aux chercheurs de se
concentrer sur des tâches plus importantes, telles que
l'amélioration des algorithmes d'optimisation et le développement
de nouveaux modèles.
Facilité d'utilisation
Le simulateur doit permettre aux utilisateurs de facilement
apprendre à l'utiliser sans nécessiter de fortes
compétences en programmation ou en mathématique.
Ceci a pour but de réduire la barrière
d'entrée pour les développeurs et les chercheurs
intéressés par le domaine de la robotique sans vouloir
s'aventurer sur certains détails mathématiques tels que la
modélisation géométrique du déplacement des robots
ou du calcul de probabilité des grilles d'occupation.
85
L'objectif est de leur permettre de tester et de valider
rapidement et facilement de nouveaux algorithmes, et positionner leur travail
en comparant facilement leurs résultats avec ceux obtenus par d'autres
chercheurs.
Visualisation
Le simulateur doit fournir des outils de visualisation afin de
permettre de dresser une représentation visuelle de l'état des
robots; les mesures des capteurs; les obstacles détectés; et les
signaux de commandes. Il doit aussi permettre de visualiser l'objectif de
chaque robot, les chemins planifiés, ainsi que les différentes
statistiques utiles pour l'utilisateur.
Un autre point important dans notre contexte est la
génération de graphes pour l'analyse et l'évaluation des
performances des métaheuristiques, telles que la courbe de convergence;
le taux d'erreur; ou le temps d'exécution.
Abstraction
Le simulateur doit fournir une interface de programmation
(API) à haut niveau pour simplifier et abstraire les
fonctionnalités du simulateur. Cette interface doit être
conçue pour faciliter l'utilisation du simulateur en supprimant les
détails de bas niveau du fonctionnement du simulateur tels que les
modèles géométriques du robot, la simulation des faisceaux
laser, la gestion du parallélisme et la visualisation de
l'environnement.
Ceci a pour but d'augmenter la productivité des
utilisateurs en leur permettant de se concentrer sur ce qui est essentiel pour
leurs travaux de recherche.
3.2.3 L'architecture du système
Le simulateur PyRoboticsLab se base sur une architecture MVC
(Modèle-Vue-Contrôleur). Ce concept vise à séparer
le programme en plusieurs couches:
-- Le modèle représente les
caractéristiques physiques des robots, des leurs capteurs et de
l'environnement dans lequel ils opèrent.
-- La vue permet de visualiser la simulation et afficher les
données telles que les cartes, les obstacles, la position des
robots...etc.
-- Le contrôleur définit les algorithmes de
contrôle des robots pour les différentes tâches de
navigation, planification et exploration...etc.
La figure 3.2 schématise cette architecture.
Séparer la simulation en composants distincts nous
permet de créer une architecture plus modulaire et maintenable. Chaque
composant est divisé en plusieurs modules qui sont responsables de
gérer un aspect spécifique de la simulation:
-- Modèle de robot : définit les
caractéristiques physiques du robot, telles que son mode
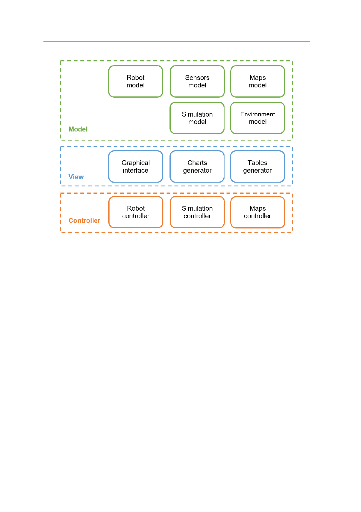
CHAPITRE 3
FIGURE 3.2 - Architecture générale du simulateur
PyRoboticsLab
de déplacement et sa consommation d'énergie,
ainsi que toutes les routines pour lui permettre de se déplacer dans
l'environnement et se localiser.
-- Modèle de capteur: définit les
caractéristiques des capteurs montés sur les robots, tels le
LIDAR ainsi que toutes les routines pour la simulation des données
produites par ces capteurs, en incluant l'intégration du bruit
artificiel dans les mesures afin de reproduire les conditions imparfaites du
monde réel ainsi que les routines de raytra-cing.
-- Modèle de carte : définit les
caractéristiques des cartes utilisées par le robot, y compris les
cartes locales et la carte globale. Chaque carte est modélisée en
plusieurs couches pour séparer les données relatives aux
probabilités d'occupation (position des obstacles) des données
relatives à l'exploration (marquage des cellules visitées...).
-- Modèle d'environnement: définit les
caractéristiques de l'environnement dans lequel les robots se
déplacent dans la surface opérationnelle ainsi que les routines
nécessaires pour le chargement, copie et sauvegarde des modèles
d'environnement.
-- Modèle de simulation : permet de sauvegarder
l'historique de toutes les opérations réalisées et les
mesures de performances instantanées, dans le but de pouvoir retracer
l'expérience étape par étape, ou de visualiser les courbes
de convergence, de consommation d'énergie ou du temps d'exécution
des algorithmes.
-- Contrôleur du robot: inclut les routines pour
contrôler le robot en lui permettant de naviguer, planifier les
trajectoires, et choisir des points de destination. Ce module contient un
sous-module définissant toutes les routines nécessaires pour le
fonc-
86
87
tionnement des algorithmes d'optimisation et
métaheuristiques. L'utilisateur peut étendre ce module en
ajoutant ces algorithmes afin de les intégrer facilement dans le
scénario de simulation sans modifier les autres modules.
-- Contrôleur des cartes : Ce module définit les
routines nécessaires à la cartographie telles que la mise
à jour des probabilités d'occupation, la fusion de cartes ainsi
que le calcul des statistiques d'exploration.
-- Contrôleur de la simulation : inclut les routines
pour définir le scénario de simulation, et charger les
modèles d'environnement et des robots. Ce module est responsable
d'initialiser les expériences, de mesurer les performances des robots,
et d'arrêter la simulation lorsque les critères d'arrêts
sont atteints.
-- Interface visuelle : inclut toutes les routines qui
permettent l'affichage des aspects relatifs à la simulation et à
l'état des robots.
-- Générateur de graphes : inclut toutes les
routines permettant de visualiser et manipuler les courbes de statistiques.
La figure 3.3 montre quelques exemples de visualisations
générées automatiquement par le simulateur pendant les
expériences. Elles peuvent être facilement paramétrables
pour afficher différents types de cartes, statistiques, graphes et
autres informations utiles.
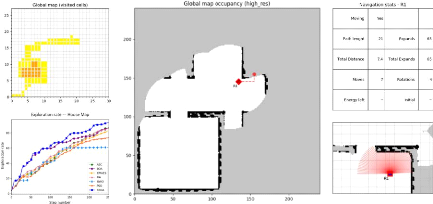
FIGURE 3.3 - Exemple de quelques types de
visualisations générées par le simulateur
PyRo-boticsLab
3.2.4 Les outils et technologies
Notre plateforme de simulation est entièrement
développée en Python, avec une attention particulière
portée à la réduction des dépendances afin de
permettre une portabilité facile vers tous les systèmes
d'exploitation (Linux, Windows, OS X...).
88
CHAPITRE 3
Python est un langage de programmation
interprété, créé avec l'intention d'offrir une
syntaxe simple et facile à apprendre. Toutefois, ceci ne réduit
en rien sa puissance puisqu'il est versatile et peut être utilisé
pour créer des plateformes web, logicielles, applications mobiles, et
systèmes embarqués. Son interpréteur permet
d'exécuter le même code sur des systèmes d'exploitation
différents sans nécessiter une modification dans le code source
ou sa recompilation.
L'utilisation de Python pour développer un outil de
recherche nous permet de tirer profit de la puissance des librairies
disponibles pour le calcul scientifique. Afin de respecter les objectifs
définis par l'architecture globale du système, nous avons
réduit l'utilisation des dépendances externes aux trois
librairies suivantes:
-- Numpy : Est la librairie Python de référence
lorsqu'il s'agit de calcul scientifique et manipulation de tableaux
multidimensionnels. Elle offre une multitude de routines pour les calculs
d'algèbre linaires, opérations de tri, statistiques, nombres
aléatoires, manipulation de dates...etc. Nous utilisons Numpy dans notre
plateforme pour gérer toutes les opérations de calcul matriciel
nécessaires pour les opérations de cartographie et la
manipulation des populations.
-- Matplotlib : Est une librairie destinée à la
création de visualisations scientifiques, telles que les graphes, les
histogrammes, les nuages de points...etc. Elle permet de générer
des figures interactives hautement personnalisables, et exporter les
résultats sous différents formats. Nous utilisons Matplotlib dans
notre projet pour la génération de l'interface utilisateur
permettant de visualiser la position des robots, les obstacles
détectés, les chemins planifiés, ainsi que les
différentes statistiques et cartes d'exploration
générées par les robots.
-- Pygmo2 [19] : Est une librairie réalisée par
l'Agence Spatiale Européenne offrant une interface pour
implémenter des algorithmes d'optimisation massivement
parallèles. Elle supporte des fonctionnalités avancées
telles que la parallélisation des métaheu-ristiques, le tri de
populations, la visualisation des solutions non dominées (Pareto
front)...etc. Nous utilisons cette librairie pour uniformiser
l'implémentation des mé-taheuristiques que nous utilisons pour
résoudre les problèmes d'exploration et de planification de
trajectoires. Cette uniformisation est un aspect important pour notre projet
puisqu'elle permet de s'assurer que la différence entre les
résultats expérimentaux des algorithmes n'est pas causée
par une différence entre les techniques d'im-plémentation
utilisées à bas niveau par les librairies.
L'intégration d'un nombre réduit de libraires
Python permet de faciliter la portabilité du code et minimiser les
dépendances. Ceci offre les avantages suivants:
-- Facilité à comprendre, déboguer ou
modifier le code source de la plateforme d'afin d'y intégrer les
changements souhaités.
-- Facilité d'installation et de configuration,
à la différence de nombreux simulateurs qui sont plus
concentrés sur des environnements Linux et les systèmes de type
UNIX.
-- Possibilité d'intégration avec les librairies
d'apprentissage machine populaires, pour
l'ajout de fonctionnalités additionnelles tel que le Deep
Learning par exemple.
89
-- Possibilité de déployer rapidement le projet en
tant que service web dans un serveur Cloud pour une utilisation ouverte au
public.
-- Facilité à ajouter un nouvel algorithme et
comparer ses performances avec les autres algorithmes déjà
implémentés sur la plateforme.
Nous pensons que ces caractéristiques sont un atout pour
permettre son adoption par les étudiants et les enseignants comme outil
pédagogique et de recherche.
3.2.5 Les scénarios de bechmarking
La plateforme de benchmarking proposée permet de simuler
les scénarios suivants:
-- Path Planning : Planification de trajectoires.
-- Exploration : Découverte, balayage, surveillance,
détection d'intrus.
-- Target Searching : Rechercher une personne ou un objet.
-- Foraging : Déplacement et tri d'objets.
-- Map Decomposition : décomposition d'environnement en
plusieurs régions.
-- Formation Control : Coordination pour le déplacement en
formation de plusieurs robots.
3.3 Modélisation géométrique des robots
Le simulateur PyRoboticsLab se base sur une représentation
géométrique en 2 dimensions des robots mobiles. Il simule les
robots terrestres à commande différentielle ainsi que
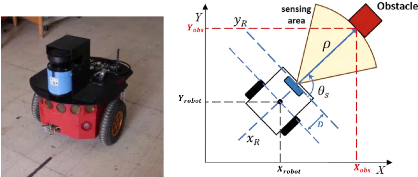
(a) Robot P3DX utilisé (b) Schéma
géométrique [68]
FIGURE 3.4 - Modélisation géométrique du
robot et des différents repères utilisés pour la
détection d'obstacles
90
CHAPITRE 3
les robots aériens de type quadrirotors. Les moteurs de
ces robots ont la particularité d'être commandés
séparément, ce qui permet de faire des rotations en 360° sur
place sans nécessiter des manoeuvres tel que les véhicules de
type voiture par exemple.
La commande différentielle permet de contrôler la
direction du robot en variant les vitesses de rotation de chaque moteur. Si
tous les moteurs tournent à la même vitesse, le robot se dirigera
tout droit. Si un des moteurs tourne à une vitesse plus
élevée que les autres, le robot fera une rotation dans une
direction opposée à l'emplacement de ce moteur. L'angle de cette
rotation est influencé par plusieurs paramètres dont la distance
du moteur par rapport au centre de gravité du robot, ainsi que le
diamètre des roues pour les robots terrestres par exemple.
Afin de faciliter la commande des robots dans notre
simulateur, nous mettons à la disposition de l'utilisateur des routines
permettant de faire abstraction des détails de calcul pour ne se
focaliser que sur l'action souhaitée. Nous présenterons un
exemple de ce type de routine dans la section suivante (voir section 3.4).
Notre modélisation des robots terrestres se base sur un
robot de type Pioneer P3DX dont nous avons eu l'occasion d'utiliser pour faire
des expériences dans le laboratoire LARESI situé au
département d'électronique à l'USTOMB. Ce robot
très populaire dans le domaine de la recherche possède un
télémètre laser qui lui permet de détecter les
obstacles aux alentours dans un rayon de 180° jusqu'à 270°
selon les modèles. La distance de détection maximale du
télémètre est de 10 mètres; toutefois, nous avons
choisi de la limiter à 4 mètres pour des raisons pratiques
(adaptation aux endroits étroits).
Étant donné que le Lidar du robot était
sujet à un taux d'erreur conséquent lors des expériences
réelles, nous avons choisi de modéliser cette erreur
estimée à 5% en intégrant dans notre simulateur un bruit
gaussien. Nous avons aussi intégré la distance aveugle du Lidar
comprise entre 0 et 30cm, c'est-à-dire que si l'obstacle est trop proche
du Lidar il ne sera pas détecté, et ceci à cause de la
limite physique de ce type de capteurs. La figure 3.5 schématise de ce
modèle d'erreurs.
L'intégration de ces imperfections dans le
modèle géométrique de PyRoboticsLab permet d'effectuer des
simulations plus réalistes. En effet, l'intégration de ces
imperfections permettra de tester la validité des algorithmes
d'évitement d'obstacles et de cartographie à s'adapter plus
facilement aux conditions du monde réel lorsqu'ils sont
déployés en production, contrairement aux tests effectués
dans des simulateurs qui assument l'hypothèse du monde parfait.
La modélisation des rayons laser du Lidar a
été implémentée en utilisant la technique du
Ray Casting, qui consiste à tracer des rayons virtuels et
suivre leur trajectoire pixel par pixel jusqu'à trouver le plus proche
objet bloquant le chemin de ce rayon. Ceci nous permet de calculer la distance
entre le robot et cet objet.
Le Lidar modélisé possède une
résolution de 1°, nous projetons donc 181 rayons virtuels avec
chacun un angle différent allant de 0° à 180°, ce qui
nous permet de connaître la distance et l'angle des objets
détectés. Si le rayon tracé n'est bloqué par aucun
obstacle, nous concluons que l'espace traversé par ce rayon est vide et
peut être parcouru par le robot en toute sécurité.
Étant donné que l'environnement dans notre
simulateur est échantillonné sous forme de grille dont chaque
cellule représente un espace de 10cm2 (voir section 3.5) il
peut arriver qu'un rayon projeté ne traverse qu'une partie infime de
cette cellule, ce qui ne permet pas d'être sûr que cette cellule
soit réellement vide. Ceci nous a poussés à
modéliser une fonction gaussienne pour mesurer le degré de
confiance de la mesure du rayon laser : plus le rayon est proche du centre de
la cellule, plus la confiance de mesure est élevée, tel qu'est
modélisé par la figure 3.5. Ce degré de confiance de la
mesure est linéairement proportionnel à la probabilité de
détection. Lorsque plusieurs rayons laser traversent une même
cellule, cette probabilité de détection est cumulée et
augmente le taux de confiance de la mesure. Le calcul des probabilités
sera détaillé dans la section 3.5 dédiée à
la cartographie.
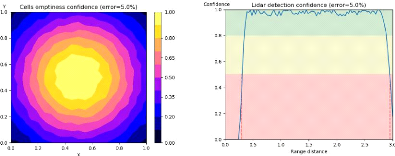
91
(a) Le degré de confiance que la cellule soit (b) Le
degré de confiance de la distance mesurée
vide est plus élevé lorsque le rayon traverse est
faible lorsque l'obstacle est trop proche ou
cette cellule près de son centre. trop loin du capteur.
FIGURE 3.5 - Modèle du bruit ajouté au capteur
LIDAR et calcul du degré de confiance de la mesure
Une fois un obstacle détecté avec un
degré de confiance suffisamment élevé, nous effectuons une
transformation géométrique pour calculer la position des
obstacles par rapport au repère fixe à partir de sa position
relative au robot. Ce repère fixe est défini au point (0,0) de la
carte globale, et ceci afin de faciliter les calculs par rapport au
repère relatif du Lidar puisque celui-ci est attaché à un
robot qui se déplace. En d'autres termes : les distances des obstacles
mesurées par le Lidar sont toutes relatives au repère du robot
mobile et il faut donc les transformer vers des positions globales relatives au
repère fixe de l'environnement afin de pouvoir les dessiner sur la
carte. Ce processus est illustré par la figure 3.4
3.4 Modélisation du processus de navigation,
planification et évitement d'obstacles
Afin de faciliter la commande des robots dans notre
simulateur, nous mettons à la disposition de l'utilisateur des routines
permettant de faire abstraction des détails de calcul et
92
CHAPITRE 3
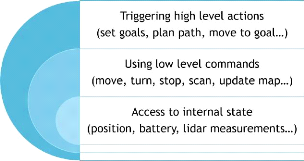
FIGURE 3.6 - Niveaux d'abstraction du processus de navigation,
planification et évitement d'obstacles du simulateur PyRoboticsLab
ne se focaliser que sur l'action souhaitée. Il suffit
d'utiliser par exemple la commande ro-bot.move(forward) pour le
déplacer un mètre en avant, et robot.turn(45) pour faire
une rotation de 45° dans le sens des aiguilles d'une montre. D'autres
routines permettent d'effectuer des tâches relatives à la
détection d'obstacles et de cartographie telle que lidar.scan()
pour récupérer la liste des obstacles
détectés, lidar.get_measurement_confidence() pour
calculer le degré de confiance dans la mesure du lidar selon le
modèle du bruit, et robot.update_map() pour mettre à
jour la carte.
Afin de simplifier encore plus le processus de
développement de nouveaux algorithmes, le simulateur offre un autre
niveau d'abstraction permettant à l'utilisateur de définir
directement les coordonnées (x, y) du point auquel le robot devra se
diriger sans se soucier des commandes de direction (move) et de rotations
(turn). Ceci peut se faire en utilisant donc la commande
robot.move_toward_point(x,y). De même il suffit d'utiliser les
commandes ro-bot.set_goals() et robot.plan_path() pour
définir un ou plusieurs points à visiter et planifier une
trajectoire vers ces points.
L'idée est donc d'offrir plusieurs niveaux
d'abstraction permettant aux utilisateurs de choisir différentes
commandes à utiliser selon leurs objectifs. Un utilisateur qui souhaite
utiliser le simulateur pour développer un nouvel algorithme
d'exploration choisira de préférence un niveau d'abstraction
simple afin de ne se focaliser que sur la stratégie du robot, alors
qu'un utilisateur souhaitant tester de nouvel algorithme de navigation ou de
cartographie choisira sûrement l'utilisation de routines de bas niveau
pour contrôler les chaque action individuellement.
Nous laissons aussi la flexibilité aux utilisateurs de
pouvoir redéfinir n'importe quelle fonction et apporter des
modifications dans l'implémentation à bas niveau afin de leur
permettre d'adapter le simulateur à leurs besoins spécifiques. Il
pourront pour cela utiliser les variables de classe pour avoir accès aux
informations internes du robot telles que le niveau de batterie restant,
l'état du robot (en mouvement, en attente, bloqué par un
obstacle), la distance parcourue, le nombre de mouvements
effectués...etc.
La figure 3.7 présente un schéma
général de notre modélisation du processus de naviga-
93
tion, planification et évitement d'obstacles. Cette
modélisation se base sur l'implémentation en interne d'un
automate à états finis.
Chaque état présenté dans ce
schéma possède une routine définissant l'ensemble des
opérations à effectuer. La figure 3.8 par exemple décrit
les détails de l'opération "solve conflict" dont l'objectif est
de trouver un compromis entre deux robots qui se bloquent mutuellement le
chemin. Cette routine poussera un des robots à changer de trajectoire,
ou de se mettre dans un état d'attente pour laisser l'autre robot
passer.
3.5 Modélisation des grilles
d'occupation
L'exploration de zones inconnues est étroitement
liée au problème de navigation et de cartographie. Le robot doit
se déplacer dans l'environnement et le découvrir progressivement.
Lors de cette opération, il est fort probable de rencontrer des impasses
et autres obstacles bloquant le chemin. Le robot mémorisera alors la
position des obstacles et les utilisera pour planifier des chemins alternatifs
et découvrir de nouvelles régions.
Les robots utilisent des capteurs pour détecter les
murs et les obstacles. Étant donné que ces capteurs ont une
portée limitée, il n'est pas possible d'observer l'ensemble de
l'environ-nement à la fois. Dans ce cas, nous devons sauvegarder les
positions des obstacles détectés dans une structure de
données qui permet au robot d'agréger facilement de nouvelles
observations et de les combiner de manière à simplifier le calcul
des trajectoires.
La Grille d'Occupation (Occupancy Grid Map [34]) est la
structure de données la plus utilisée pour représenter
l'environnement en robotique. C'est une matrice 2D où chaque cellule
représente une partie de l'environnement. La taille des cellules
influence le degré de détails affichés sur la grille, elle
est généralement définie sur une taille égale ou
inférieure à la circonférence du robot. La figure 3.9
montre un exemple de carte quadrillée.
La valeur de chaque cellule de la grille représente la
probabilité que la région correspondante de l'environnement soit
vide ou occupée par un obstacle. Puisque le robot n'a aucune information
à priori sur la région à explorer, toutes les cellules ont
une probabilité d'occupation initiale de 0,5. Cette probabilité
sera mise à jour à l'aide de la règle de Bayes
(équation 3.1) chaque fois que les capteurs du robot détectent
une cellule vide ou occupée.
p(A/B) = p(B/A) * p(A) (3.1)
p(B)
A est la valeur d'occupation, et
B est l'observation
Une pratique courante dans le domaine de cartographie vise
à utiliser les valeurs logarithmiques d'occupation au lieu des
probabilités, et ceci afin de convertir les opérations de
multiplication en additions tel que décrit par les équations 3.2
et 3.3.
94
CHAPITRE 3
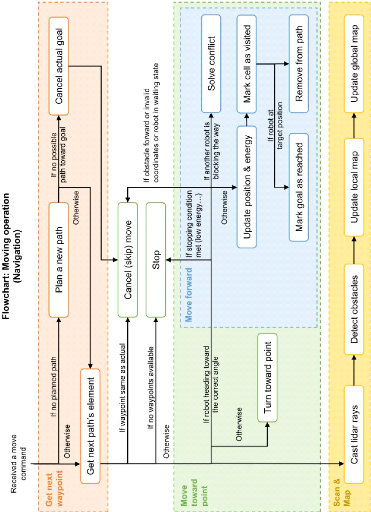
FIGURE 3.7 - Schéma général du modèle
de navigation, planification et évitement d'obstacles du simulateur
PyRoboticsLab
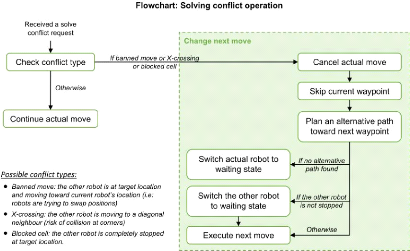
95
FIGURE 3.8 - Diagramme de la routine "solve
conflict" pour résoudre un problème de blocage entre deux
robots
odds(A) = p(A)
P(-A)
odds(A/B) = p(A/B) (3.2)
P(-A/B)
Après avoir appliqué l'équation 3.2 dans
la règle de Bayes, nous obtenons l'équation 3.3. La valeur
logarithmique varie entre [-oo,+oo], ce qui est utile pour éviter la
multiplication de petits nombres lors de l'implémentation qui pourront
causer des problèmes en raison de la précision limitée des
valeurs flottantes dans l'ordinateur.
logodds(A/B) = log p(B/A)
P (B/-A) + logodds(A) (3.3)
En conséquence, nous pouvons classer chaque cellule Cij
de la grille dans l'une des trois catégories suivantes : cellule vide,
cellule occupée par un obstacle et cellule inconnue. L'équation
3.4 formalise ceci.
96
CHAPITRE 3
|
Cij is
|
?
?????
?????
|
Occupied if Occ(Cij) > 0 Empty if Occ(Cij) < 0 Unknown
if Occ(Cij) = 0
|
(3.4)
|
Où Occ(Cij) est la valeur logarithmique de
l'occupation calculée en utilisant l'équation
3.3.
Dans l'équation 3.4, la valeur 0
représente le seuil pour savoir si une cellule contient un obstacle
où non. Ce seuil a été défini à cette valeur
parce qu'il correspond à la probabilité d'occupation initiale
fixée à 0.5 (logodds(0.5) = 0)
Dans un scénario de navigation, le robot aura donc pour
objectif d'éviter toutes les cellules occupées dont la valeur
logarithmique d'occupation est supérieure à ce seuil. De
même, l'objectif d'une mission d'exploration serait de diriger le robot
vers toutes les cellules ayant une valeur égale à ce seuil
puisqu'elles représentent les cellules inconnues qui n'ont pas encore
été balayées par les capteurs du robot. Ceci nous permet
de modéliser notre problème sous forme de problème
d'optimisation dont le but est de minimiser le nombre de ces cellules. La
figure 3.9 montre un exemple d'exécution d'un tel scénario.
La section suivante présentera les détails
relatifs à la modélisation de ce type de scénarios.
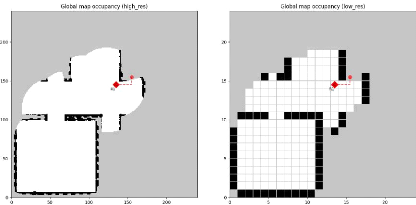
A gauche: carte à haute résolution
(0.1m2/px). A droite: carte à basse résolution
(1m2/px). Les pixels blancs représentent la zone
explorée; les pixels gris représentent la zone inconnue; les
pixels noirs représentent les obstacles détectés.
FIGURE 3.9 - Exemple d'exécution d'un
scénario d'exploration et décomposition de la carte de
l'environnement sous forme de grille d'occupation
3.6 Modélisation du problème d'exploration 3.6.1
Modélisation mono et multirobots
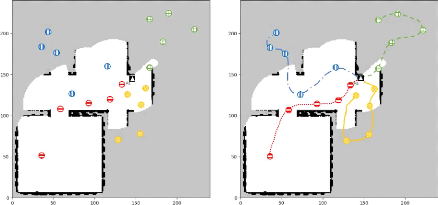
(a) Générer une population de points de
destinations
(b) Calculer les plus courts chemins pour visiter les points
de destinations de chaque solution candidate
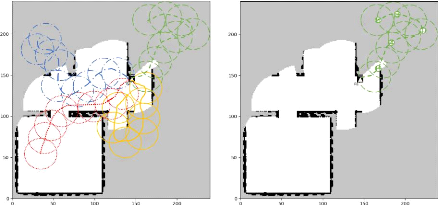
(c) Estimer le gain en terme de surface de la zone
explorée pour chaque chemin
(d) La meilleure solution est celle qui maximize la surface
d'exploration de régions pas encore explorées
FIGURE 3.10 - Un exemple du processus d'évaluation de
la fonction fitness pour une population de 4 solutions candidates
La tâche d'exploration de zones inconnues est souvent
modélisée comme un problème 97
98
CHAPITRE 3
d'optimisation. Le but de ce processus est d'attribuer une
probabilité d'occupation à chaque cellule de la carte. Afin
d'atteindre cet objectif, le robot doit maximiser la surface de la zone
explorée tout en minimisant l'énergie utilisée.
Le rôle des métaheuristiques dans notre
modélisation est au coeur de ce processus. Elles commencent par
générer une population aléatoire de points de destination
à visiter, puis améliorent la position de ces points cibles
à travers une succession d'opérations d'optimi-sation.
Mathématiquement, chaque solution candidate Xk
dans la population représente un ensemble d'emplacements de cellules
cibles Cij, où (i, j) sont les coordonnées
(x, y) à l'in-térieur des limites de la grille.
X = Cij
Par conséquent, la fonction fitness peut être
modélisée comme une maximisation du nombre de cellules qui ont
une valeur d'occupation logarithmique égale à 0 (cellules
inexplorées). L'équation 3.5 définit la formulation
mathématique de cette fonction.
F = max(Observed Cells)
X= min( ä(Cij,0)) (3.5)
i,j
|
Where ä(Cij,0) =
|
?
??
??
|
1 if Occ(Cij) =? 0
0 otherwise
|
Avec la contrainte suivante:
X E(Cij) < current battery
level i,j
Où E(Cij) est l'énergie
nécessaire pour déplacer le robot de la position actuelle
à la cellule Cij.
La figure 3.10 montre un exemple d'application de cette
opération pour sélectionner le meilleur ensemble d'emplacements
cibles à visiter parmi 4 solutions candidates.
Une fois que le meilleur ensemble d'emplacements cibles qui
satisfait la contrainte d'énergie est trouvé, le robot calcule le
chemin le plus court qui relie ces emplacements cibles en utilisant
l'algorithme A* [46], puis il exécute ce chemin
jusqu'à visiter tous les emplacements cibles. Après cela, il
répète l'algorithme d'optimisation pour générer un
nouvel ensemble d'emplacements à visiter et continue le processus
jusqu'à ce que toutes les cellules de la carte aient été
observées (c'est-à-dire que le robot a exploré toute la
zone).
Il est important de rappeler que la trajectoire prévue
n'est pas nécessairement optimale, puisque le robot ne peut pas
détecter les obstacles hors de portée de ses capteurs. De
plus,
Selecting Goals:
Yes
Generate a set of target locations using xBOA (or any other
metaheuristic)
Path Planning:
Plan a path toward the next target
location using A*
Path Execution:
Move toward the target location

Obstacles Detection:
Scan the environment using Lidar sensor
and detect the
surrounding obstacles
J
Mapping:
Update the occupancy probability of the
grid cells
r ~
Path Updating:
Plan an alternative path
avoiding
the obstacle
l J
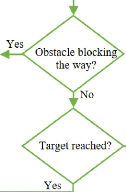
99
FIGURE 3.11 -- Diagramme du processus
d'exploration d'une zone inconnue
100
CHAPITRE 3
il n'a aucune information préalable sur la
région à explorer. Ainsi, il est fort probable qu'il rencontre
des impasses et autres obstacles barrant le chemin lors de la navigation. Il
sera alors obligé de trouver un chemin alternatif pour sortir de
l'impasse, même si cela nécessite de retourner dans une
région précédemment visitée et de consommer plus
d'énergie.
Par conséquent, la solution est construite de
manière incrémentale, en commençant par un chemin
sous-optimal, puis en le mettant à jour régulièrement au
fur et à mesure que de nouveaux obstacles sont observés, ce qui
garantit également que le robot s'adapte aux environnements dynamiques
et évite les obstacles mobiles.
La figure 3.11 schématise le processus
modélisé pour résoudre le problème d'explora-tion,
et la figure 3.12 présente le schéma de coordination
utilisé pour produire un comportement collectif dans les
scénarios multirobots.
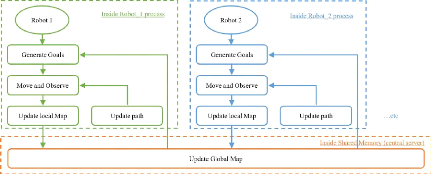
FIGURE 3.12 - Schéma du modèle utilisé pour
assurer la coordination entre les robots
3.6.2 Les critères d'évaluation
Afin de pouvoir analyser les performances des
métaheuristiques utilisées durant les expériences et
comparer leurs résultats, nous allons utiliser les critères
d'évaluation suivants:
-- Nombre de pas (step number) : Nombre de mouvement
et rotations effectué par le robot. Ce nombre est proportionnel à
la quantité d'énergie consommée.
-- Temps d'exécution (execution time) :
Durée totale de la mission, mesurée en secondes.
-- Taux d'exploration (exploration rate) : Surface de
la zone observée par le robot pendant la mission, mesurée en
pourcentage par rapport à la surface totale.
-- Nombre d'évaluation de la fonction de fitness
(Fitevals) : Nombre de solutions évaluées par la
métaheuristique pendant le processus d'optimisation.
-- Temps de calcul (computation time) : Durée
d'exécution de l'ensemble des opérations de calculs requis par la
métaheuristique pour effectuer toutes les itérations et
sélectionner la solution optimale, mesurée en secondes.
101
3.6.3 La complexité du modèle
L'utilisation de l'équation 3.5 comme fonction
de fitness signifie que pour chaque solution candidate dans la population, nous
allons planifier un chemin vers les emplacements cibles définis par
cette solution, puis estimer combien de nouvelles cellules seront
observées si ce chemin est exécuté par le robot. La
complexité de cette opération est O(M) où M est
la longueur du chemin.
Étant donné que la valeur de fitness est
évaluée pour chaque solution candidate à chaque
génération, la complexité globale devient O(NxKxM)
où N est la taille de la population, K est le nombre de
générations et M est la longueur du chemin.
Si la taille de la population ou le nombre de
générations est défini sur une grande valeur, le processus
deviendra coûteux en calcul. Une approche alternative consisterait
à calculer une estimation approximative des cellules observées
(en utilisant un vecteur de distance par exemple) comme critère de
fitness, mais cela diminuerait la qualité des solutions
générées. Afin d'éviter cette perte d'informations,
nous garderons notre modélisation tout en essayant de réduire la
taille de la population au minimum afin d'obtenir un compromis acceptable entre
la qualité des solutions générées et le temps
d'exécution.
3.7 Paramétrage et configuration
3.7.1 Paramétrage des
expériences
Afin d'évaluer les performances des algorithmes BOA et
xBOA, nous allons les comparer à cinq autres métaheuristiques
fréquemment utilisées dans la littérature, à
savoir:
-- Artificial Bees Colony (ABC) [55]
-- Covariance Matrix Analysis Evolution Strategy (CMAES)
[45]
-- Genetic Algorithm (GA) [41]
-- Grey Wolf Optimizer (GWO) [66]
-- Particle Swarm Optimization (PSO) [58]
Pour ces cinq méthodes, nous avons utilisé les
implémentations fournies par Pygmo2 [19] qui est une
bibliothèque Python offrant une interface unifiée pour
implémenter des algorithmes d'optimisation parallèles.
Étant donné que ces méthodes sont
basées sur des opérations stochastiques, nous allons utiliser la
même population initiale pour chacune d'elles et répéter
l'exécution 10 fois afin d'obtenir une comparaison plus objective. Le
critère d'arrêt sera défini tel que suit:
"arrêter l'expérience si l'énergie du robot atteint
zéro, ou la surface de la zone explorée atteint un taux
supérieur ou égal à 99%".
Nous allons effectuer une autre série
d'expériences pour comparer les performances de l'algorithme xBOA par
rapport aux autres variantes de l'algorithme BOA citées ci-dessous:
-- Self-adaptative BOA (SABOA) [35]
CHAPITRE 3
-- BOA with intensive search (mBOA) [12]
-- BOA with non-linear adaptative rule (ABOA) [96]
Nous avons réimplémenté BOA et chacune de
ces variantes en langage Python, et les avons adaptés à la
bibliothèque Pygmo2 pour s'assurer que la différence des
performances n'est pas causée par l'utilisation de techniques
d'implémentation différentes, ou par des outils
différents.
Finalement, nous allons effectuer un test en modifiant le
nombre de robots pour valider l'adaptabilité de notre
modélisation à des scénarios mono et multirobots.
3.7.2 Paramétrage de l'environnement de simulation
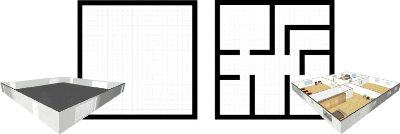
102
. Empty Map (24x24m) House Map (24x24m)
FIGURE 3.13 - Cartes de l'environnement de simulation
utilisé durant les expériences
La figure 3.13 montre la cartographie en 2D des deux
environnements qui seront utilisés pour effectuer les
expériences. La première (dénommée Empty map)
représente une zone vide ne contenant aucun obstacle à
l'exception du mur d'entourage qui délimite son périmètre.
La deuxième zone (dénommée House map) est
inspirée de l'architecture d'une maison et est partiellement couverte
d'obstacles à un taux d'occupation de 27% après suppression des
portes et fenêtres. Ces deux zones ont une taille de 24x24m soit une
surface totale de 576m2 chacune.
Pour chaque zone, deux types d'expériences seront
effectuées en variant le nombre d'emplacements cibles (points de
destinations) générés par le processus d'optimisation. Ce
paramètre influencera la stratégie d'exploration des robots : un
nombre de destinations réduit poussera le robot à effectuer une
planification à court terme, alors qu'un nombre plus élevé
le poussera à effectuer une planification à long terme. Pour
chaque expérience, nous enregistrerons le temps d'exécution, le
taux d'exploration ainsi que les performances de chaque
métaheuristique.
Nous utiliserons également une carte d'environnement
inspirée d'une usine avec une superficie de 1500m2 afin
d'effectuer des expériences de validation de l'approche sur des zones
à plus large échelle. Cet environnement contient un nombre plus
important d'obs-tacles et plusieurs couloirs étroits et des chemins dont
l'extrémité finale conduit à une im-
103
passe, ce qui sera utile pour tester les capacités des
robots à naviguer efficacement sans se bloquer mutuellement le chemin.
La figure 3.14 montre la cartographie de cette usine.
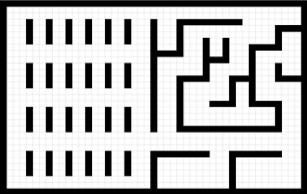
Factory Map (30x50m)
FIGURE 3.14 - Carte d'environnement utilisé pour simuler
les scénarios à large échelle
Dans le but de réduire la variabilité des
expériences causées par différentes initialisations, nous
allons fixer les mêmes conditions de départ pour chaque session de
test:
-- Position de départ du robot : dans les
coordonnées (1,1) avec un angle de 0° vers le nord.
-- Distance de mesure du capteur LIDAR : 4m, avec un taux de 5%
d'erreurs.
-- Plage de mesure angulaire du capteur LIDAR : 180°,
avec une résolution de 1°. -- Taille de la population: 20
individus.
-- Nombre maximal de générations : 30
itérations.
-- Condition d'arrêt prématuré :
arrêt si aucune amélioration de la valeur de fitness pendant 10
générations consécutives.
-- Population initiale : même population pour toutes les
méthodes.
-- SEED du générateur de nombre aléatoires :
25 (choisi arbitrairement).
Le nombre de simulations prévues pour pouvoir
réaliser les objectifs fixés peut être calculé en
multipliant le nombre des expériences x nombre de méthodes x
nombre de répétitions. Ce chiffre s'élève donc
à 380 exécutions en total. Nous diviserons ces exécutions
sur plusieurs machines en utilisant la configuration suivante:
-- Python 3.9.5 -- Numpy 1.21 -- Matplotlib 3.4.2 -- Pygmo
2.16.1
104
CHAPITRE 3
Ces machines utilisent des systèmes d'exploitation
différents:
-- Ubuntu 20.04 -- CentOS 7.7 -- Windows 10
À noter que la possibilité de porter notre
simulateur sur des environnements de type Linux et Windows sans
nécessiter l'apport de changements dans le code source, ou de son
encapsulation dans des containers virtuels, est un point positif
augmentant la facilité d'uti-lisation de l'outil.
3.8 Conclusion
Nous avons présenté dans ce chapitre la
méthodologie utilisée pour la résolution du
problème d'exploration d'une zone inconnue avec des contraintes
d'énergie. Nous avons expliqué notre modèle en formalisant
la fonction objectif sur la base des informations récoltées
à partir d'une grille d'occupation.
Nous avons également présenté une
nouvelle plateforme de simulation dédiée à
l'éva-luation et le benchmarking de métaheuristiques ainsi que
d'autres algorithmes d'optimi-sation. Cet outil a été
implémenté de façon à abstraire les détails
de bas niveau des tâches de navigation, de cartographie et de
planification de chemins, et ceci afin de permettre aux chercheurs de se
concentrer sur des tâches plus importantes telles que la
modélisation de nouveaux algorithmes pour résoudre les
problèmes d'exploration ou d'optimisation de trajectoires. Une attention
particulière a été donnée à
l'intégration de fonctionnalités dédiées à
l'automatisation du processus d'expérimentation (paramétrage,
répétition des expériences, génération de
graphes) ainsi que la facilité du passage à l'échelle en
la déployant sans difficulté sur des serveurs Cloud pour simuler
des environnements à très large échelle.
Dans le chapitre suivant, nous allons effectuer une
série d'expériences afin de valider notre modélisation, et
évaluer les performances de l'algorithme xBOA. Nous présenterons
également une analyse des résultats et une comparaison entre
plusieurs variantes de l'al-gorithme BOA récemment introduit dans la
littérature.

105
CHAPITRE 4
EXPÉRIENCES ET ANALYSE
|
4.1
|
Introduction
|
106
|
|
4.2
|
Configuration matérielle
|
106
|
|
4.3
|
Expérience 1 : Évaluation de l'algorithme
xBOA dans un contexte
|
|
|
multirobots
|
107
|
|
4.4
|
Expérience 2 : Comparaison entre les
stratégies d'exploration à
|
|
|
court terme et à long terme
|
109
|
|
4.5
|
Expérience 3 : Recherche des meilleurs
hyperparamètres
|
110
|
|
4.6
|
Expérience 4 : Comparaison de l'algorithme xBOA
avec les méta-
|
|
|
heuristiques populaires
|
112
|
|
4.7
|
Expérience 5 : Evaluation de la robustesse de
l'algorithme xBOA
|
|
|
face à la réduction de taille de la
population
|
120
|
|
4.8
|
Expérience 6 : Comparaison de xBOA avec les autres
variantes de
|
|
|
l'algorithme BOA
|
125
|
|
4.9
|
Expérience 7 : Test en utilisant un robot
réel
|
129
|
|
4.10
|
Conclusion
|
131
|
106
CHAPITRE 4
4.1 Introduction
Ce chapitre présente la série
d'expériences effectuées afin de valider notre
modélisation du problème d'exploration et évaluer les
performances de l'algorithme xBOA.
Nous utiliserons notre plateforme de benchmarking afin de
comparer les performances de cet algorithme avec les différentes
métaheuristiques incluses dans le simulateur (GA, ACO, PSO, CMAES, GWO,
ABC) pour la résolution du problème d'exploration de zones
inconnues. Nous comparerons également les performances du xBOA avec
l'algorithme BOA original et ses autres variantes (MBOA, SABOA, ABOA).
Nous analyserons ensuite les résultats d'une
série d'expériences visant à accélérer la
vitesse d'exécution de l'algorithme tout en analysant la robustesse des
méthodes citées face à la réduction de la taille de
la population.
Nous présenterons aussi une expérience pour
évaluer l'adaptabilité de notre approche dans un contexte
multirobots. Le but étant de valider les capacités du
modèle à pouvoir générer un comportement collectif
pour les robots sans besoin d'intégrer des mécanismes de
synchronisation explicite. Pour finir, nous testerons l'approche sur un robot
réel.
4.2 Configuration matérielle
Dans le but d'effectuer les expériences souhaitées,
nous avons utilisé trois machines.
La première consiste en un ordinateur portable de
moyenne gamme avec une mémoire vive de 8Go et un processeur Intel i7
de 4ème génération. Ce processeur possède 4
cores ayant chacun une fréquence d'horloge de 2.8Ghz. Bien que cet
ordinateur inclut aussi une carte graphique, celle-ci n'a pas été
utilisée pour les raisons citées dans la section 3.2.2, ainsi que
le fait que les deux autres machines utilisées pour effectuer les
expériences ne possédaient pas de capacités de calcul
graphique.
La deuxième machine utilisée consiste en un
service cloud de Google appelé Collabora-tory (ou Google
Colab) offrant une machine virtuelle utilisant un processeur Intel
Xeon de 2 cores cadencés à 2.3Ghz avec une mémoire
vive de 12Go. L'utilisation de ce service est gratuite pour des sessions de
calcul dont la durée est inférieure à 12h.
La troisième machine utilisée consiste en un
cluster disponible au Plateau Technique de Calcul Intensif IBN-BAJA
à l'Université des Sciences et de la Technologie d'Oran
Mohamed Boudiaf - USTOMB. Ce cluster destiné à effectuer des
calculs à hautes performances (High Performance Computing)
possède une mémoire vive de 32Go et 24 processeurs Intel
Xeon de 6 cores chacun cadencés à 2Ghz. Ce cluster nous a
permis d'effectuer des sessions de simulation de longue durée en
répétant la même expérience plusieurs fois.
Chaque machine utilise un système d'exploitation
différent. Le code a été déployé sur ces
machine sans nécessiter de changement ou de compilation, ce qui a
démontré la portabilité de notre simulateur sur des
systèmes de type Linux et Windows. Le code n'a pas encore
été testé sur un système de type iOS mais ne
devrait présenter aucun problème de compatibilité.
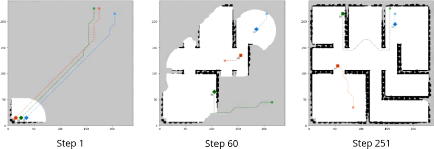
107
4.3 Expérience 1: Évaluation de l'algorithme
xBOA dans un contexte multirobots
La série d'expériences présentée
dans cette section vise à valider l'adaptabilité de l'ap-proche
dans un scénario multirobots. Selon ce que l'on peut observer sur la
figure 4.1, les robots déployés à partir de la même
position de départ ont pu se disperser dans l'environne-ment pour
explorer la surface entière sans aucun changement nécessaire dans
l'algorithme pour coordonner leurs déplacements. Ceci montre la
flexibilité de la modélisation proposée pour s'adapter aux
scénarios mono et multirobots.
En effet, chaque robot possède sa propre population de
solutions candidates et essaie de maximiser sa propre valeur de fitness
indépendamment des autres robots. Ces robots n'échangent pas de
messages entre eux, mais collaborent passivement en modifiant une carte globale
qui est stockée dans une mémoire centrale. Lorsqu'un robot se
déplace, il met à jour cette carte partagée afin d'y
insérer les obstacles détectés et marquer la zone
observée comme étant visitée. Les autres robots vont donc
automatiquement éviter cette
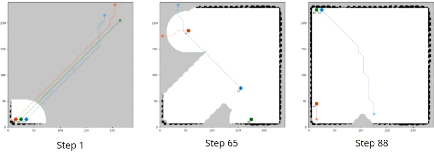
(a) Environnement Empty Map
(b) Environnement House Map
FIGURE 4.1 - Progression visuelle du scenario multirobots en
utilisant la méthode xBOA avec 3 robots
108
CHAPITRE 4
zone lorsqu'ils planifient les prochaines trajectoires puisque
la fonction fitness pénalisera ces régions déjà
visitées.
Étant donné que les robots ne sont pas
conscients de la présence des autres robots, ils n'échangent pas
de messages entre eux par rapport à leurs chemins planifiés ou
des régions prévues à être visitées dans le
futur. Tout ce qu'ils échangent c'est la position des obstacles
détectés et les zones déjà visitées
auparavant. De ce fait, il arrive que plusieurs robots décident de se
diriger vers la même direction puisque cela maximise leur valeur de
fitness. Ce comportement est observé au départ de
l'expérience lorsqu'ils choisissent tous le chemin diagonal maximisant
la zone à observer, ou parfois au milieu de l'expérience tel
qu'on peut le voir sur la figure 4.1. Cependant, nous observons que dans
l'ensemble, le système arrive quand même à faire disperser
les robots dans des régions séparées, ce qui a pour effet
d'accélérer le temps d'exploration de la zone comparé aux
scénarios où on n'utilise qu'un seul robot.
Afin de montrer l'adaptabilité de l'approche à
des environnements beaucoup plus larges, nous avons effectué une autre
expérience en utilisant une carte inspirée d'une usine ayant une
superficie égale à 30x50 mètres. La figure 4.2 montre un
résultat intermédiaire enregistré pendant
l'exécution. Cette expérience a été
répétée plusieurs fois en changeant le nombre de robots,
elle a montré la capacité de l'approche à les pousser
à explorer la zone entière même en cas de forte
densité d'obstacles ou de l'augmentation de la superficie de
l'environnement.
Par ailleurs, cette série d'expériences a permis
aussi d'apprécier la facilité d'utilisation de notre simulateur,
puisqu'il s'adapte automatiquement à l'ajout de nouveaux
scénarios et au changement du nombre de robots. L'utilisateur n'aura
qu'à effectuer un paramétrage de
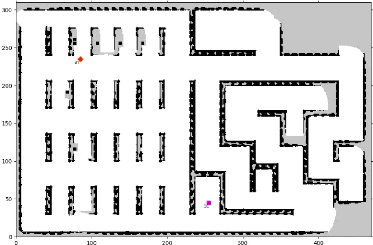
FIGURE 4.2 - Progression visuelle d'un scénario à
grande échelle en utilisant la méthode xBOA avec 2 robots
109
l'expérience sans se soucier des mécanismes
internes de détection des obstacles, de mise à jour de la carte
globale, ou de l'évitement des collisions entre les robots. Ce genre de
tâches sont souvent un frein à beaucoup de chercheurs venant de
domaines différents puisqu'elles nécessitent d'avoir une bonne
compréhension des problématiques de navigation robotique et du
fonctionnement des grilles d'occupation.
4.4 Expérience 2 : Comparaison entre les
stratégies d'ex-ploration à court terme et à long terme
Cette expérience vise à comparer deux
stratégies d'exploration. La première consiste à planifier
la mission à long terme en sélectionnant plusieurs points de
destination au départ de l'exécution; calculer un chemin pour
visiter ces points selon leur ordre de sélection; puis
répéter l'opération après avoir visité tous
ces points. Quant à la deuxième stratégie, elle consiste
à faire une planification à court terme en ne
sélectionnant qu'un seul point à la fois; le robot devra donc
attendre jusqu'à avoir visité sa destination actuelle avant de
choisir la prochaine.
La figure 4.3 montre un exemple d'exécution des deux
stratégies en utilisant la méthode xBOA. Cette visualisation
étape par étape montre que la stratégie à long
terme est moins efficace que la stratégie à court terme lorsque
l'environnement est inconnu à l'avance. En effet, la planification
à long terme de plusieurs points de destination au début de la
mission se base sur des informations très limitées puisque le
robot n'a aucune connaissance à priori de l'emplacement des murs et des
obstacles avant de les avoir détectés grâce à son
LIDAR. Le processus d'optimisation choisit donc ces destinations en ne tenant
compte que de l'information de distance à vue d'oiseau par rapport au
robot. Cependant, lorsque celui-ci commence à se déplacer pour
visiter ces points, il met à jour sa carte en collectant les
informations des positions des obstacles et des différents chemins
possibles. Toutefois, il n'utilisera ces informations que lors de la prochaine
phase de sélection après avoir visité tous les points
planifiés. En d'autres termes : le robot continuera donc à
visiter les destinations prévues initialement sans profiter de l'apport
des nouvelles informations récoltées en chemin, et tombera
souvent dans une redondance poussant le robot à revisiter une zone
déjà explorée auparavant.
Pour illustrer ce problème de redondance, la figure 4.3
montre un exemple où la visite du 3ème point en utilisant la
stratégie à long terme n'a apporté aucun gain, et ceci
à cause du manque de visibilité lors de la phase de
sélection. Alors que la stratégie à court terme a permis
d'éviter cette redondance en utilisant les informations
récoltées lors de la visite du 1er et 2ème point pour
pousser le robot à visiter une nouvelle zone.
Dans la stratégie à court terme, le robot ne
sélectionne qu'un seul point de destination. Il se déplacera pour
le visiter tout en mettant à jour la carte de l'environnement puis
resé-lectionnera un nouveau point en utilisant les nouvelles
informations récoltées en chemin. La qualité du choix est
donc meilleure puisqu'il élimine les destinations n'apportant aucun gain
supplémentaire ou qui sont trop coûteuses par rapport aux gains
qu'ils pourront apporter. Cette stratégie est aussi avantageuse dans le
cas des environnements dynamiques où les positions des obstacles
changent à cause de portes ouvertes et fermées par exemple,
110
CHAPITRE 4
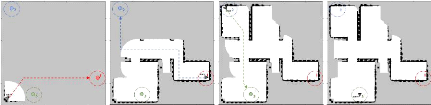
(a) État d'avancement de la mission d'exploration en
utilisant la stratégie à long terme (surface explorée
64%)
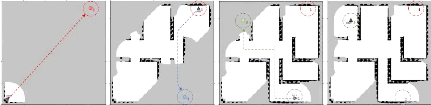
(b) État d'avancement de la mission d'exploration en
utilisant la stratégie à court terme (surface explorée
91%)
FIGURE 4.3 - Comparaison entre les deux stratégies
d'exploration en utilisant la méthode xBOA
ou à cause d'objets déplacés. Le robot
pourra prendre en compte les derniers changements de la carte à chaque
fois qu'une destination est atteinte.
L'inconvénient de cette stratégie cependant est
la nécessité de répéter le processus de
sélection des points de destination plus fréquemment. Il est donc
nécessaire que le temps d'exécution de ce processus soit court
puisque le robot restera en état d'attente le temps de finir ses
calculs.
Aussi nous remarquons que cette stratégie à
réussi à explorer presque la totalité de la zone dans
l'exemple montré par la figure 4.3 en visitant 3 points seulement. Elle
a pu atteindre un taux d'exploration de 91% contrairement à la
stratégie à long terme qui n'a réussi à explorer
que 64% de la surface de la zone, soit un résultat inférieur de
27% comparé à la stratégie à court terme.
4.5 Expérience 3 : Recherche des meilleurs
hyperpara-mètres
Les métaheuristiques sont sensibles aux choix des
paramètres initiaux. Une pratique courante dans la littérature
consiste à comparer les performances des méthodes en utilisant
les paramètres originaux utilisés par les auteurs dans leurs
premières publications [11]. Ceci peut être un bon choix si nous
comparons ces méthodes en utilisant les fonctions
111
de benchmarking standards; toutefois, le problème
d'exploration de zones inconnues est par nature un problème
incrémental et partiellement observable, ce qui peut rendre les
paramètres par défaut moins optimaux.
De ce fait, nous avons effectué une expérience
préliminaire afin de rechercher les meilleurs paramètres de
chaque méthode pour ce problème en particulier. Ceci nous
permutera de comparer les résultats de ces métaheuristiques dans
leurs performances optimales et éviter qu'elles soient
piégées dans des optimums locaux à cause de mauvaises
initialisations.
Il n'existe pas de formule mathématique précise
pour trouver les meilleurs hyperpara-mètres d'une méthode, ceci
doit se faire expérimentalement en essayant plusieurs valeurs et
comparer leurs résultats. Bien que beaucoup de chercheurs utilisent la
méthode manuelle, nous avons préféré utiliser la
bibliothèque Hyperopt [18]. Cette bibliothèque permet
d'op-timiser les paramètres d'entrée d'un algorithme en
effectuant une recherche sélective sur une plage de valeurs. Elle offre
plusieurs stratégies de recherche dont principalement la méthode
de recherche aléatoire (Random Search [17]) et recherche par
l'algorithme TPE (Tree-structured Parzen Estimator [18]) qui montrent
des résultats meilleurs comparés aux méthodes classiques
telles que la stratégie de recherche par grille (Grid Search)
[17].
Le fonctionnement de base de la bibliothèque
Hyperopt consiste à exécuter plusieurs fois l'algorithme
qu'on veut optimiser en utilisant des valeurs aléatoires pour
l'initialisation des hyperparamètres, puis d'adapter ces valeurs selon
les résultats obtenus après plusieurs essais. En
répétant cette opération un nombre suffisant de fois, la
bibliothèque arrive à réduire la plage de
paramétrage afin de choisir une combinaison qui donne de bons
résultats.
En profitant de la puissance de calcul du cluster de calcul
intensif de l'USTOMB, nous avons lancé l'optimisation des
hyperparamètres de toutes les métaheuristiques incluses dans
notre simulateur à raison de 30 essais par méthode en
répétant chaque essai 3 fois, ce qui donne un total de 90
exécutions chacune. Le Tableau 4.1 liste les meilleurs paramètres
trouvés durant cette expérience, nous nous baserons sur ces
valeurs pour effectuer les prochaines expériences.
Certaines méthodes telles que ABC, GWO et CMAES ne
requièrent pas de paramétrage manuel. Pour les autres
méthodes, les paramètres suivants ont été
sélectionnés:
-- GA : nous avons utilisé une stratégie de
sélection par tournoi de taille 2 et une mutation polynomiale
avec un index de distribution de 76.
-- PSO : nous avons utilisé une taille de voisinage de
4 avec un facteur d'accélération cognitif supérieur au
facteur d'accélération social, ce qui attire chaque particule
vers la meilleure position dans son voisinage au lieu de retourner à sa
meilleure position trouvée précédemment.
-- Variantes de BOA: ces paramètres sont
expliqués en détail dans la section 2.8. Les valeurs des
meilleurs paramètres sont présentées dans le tableau
4.1.
112
CHAPITRE 4
TABLE 4.1 - Valeurs des meilleurs hyperparamètres
trouvés après 30 essais
|
Methods
|
Hyperparameters
|
Values
|
Methods
|
Hyperparameters
|
Values
|
|
Power exponent
|
0.547
|
|
Power exponent
|
0.73
|
|
BOA
|
|
|
BOA
|
|
|
|
Sensor modality
|
0.602
|
|
Sensor modality
|
0.577
|
|
(pop size 20)
|
|
|
(pop size 5)
|
|
|
|
Switch probability
|
0.395
|
|
Switch probability
|
0.331
|
|
xBOA
|
Power exponent
|
0.905
|
xBOA
|
Power exponent
|
0.994
|
|
Sensor modality
|
0.257
|
|
Sensor modality
|
0.518
|
|
(pop size 20)
|
|
|
(pop size 5)
|
|
|
|
Crossover probability
|
0.593
|
|
Crossover probability
|
0.583
|
|
Crossover probability
|
0.11
|
mBOA
|
Power exponent
|
0.61
|
|
GA
|
Mutation probability
|
0.215
|
|
Sensor modality
|
0.356
|
|
|
|
(pop size 5)
|
|
|
|
Mutation distribution index
|
76.026
|
|
Switch probability
|
0.762
|
|
Social component coef.
|
1.506
|
|
Power exponent
|
0.992
|
|
Cognitive component coef.
|
3.379
|
ABOA
|
Sensor modality
|
0.98
|
|
PSO
|
|
|
|
|
|
|
Max velocity
|
0.329
|
(pop size 5)
|
Switch probability
|
0.983
|
|
Inertia weight
|
0.449
|
|
u
|
1.356
|
|
ABC, GWO,
|
No parameters to optimize
|
SABOA
|
Switch probability
|
0.237
|
|
CMAES
|
(auto-tuning)
|
(pop size 5)
|
|
|
4.6 Expérience 4 : Comparaison de l'algorithme xBOA
avec les métaheuristiques populaires
Dans cette série d'expériences, nous allons
comparer les performances des différentes métaheuristiques
incluses dans notre simulateur pour la résolution du problème
d'explora-tion de zones inconnues.
Selon ce qu'on peut voir sur les Figures 4.4 et 4.5 ainsi que
le Tableau 4.2, les méthodes xBOA, PSO, GA et CMAES ont
présenté des résultats presque similaires sur la plupart
des scénarios, surtout dans le cas de l'exploration à court
terme. Ceci signifie que le processus d'optimisation a convergé avec
succès vers la solution optimale. Toutefois, nous observons une
dégradation de la convergence de BOA et GWO à certaines
périodes provoquées par leur blocage dans un optimum local
poussant le robot à revisiter une zone déjà
explorée pendant un certain intervalle de temps. Cependant, ces
méthodes finissent par échapper à ce minimum local
après un certain nombre de pas et rattraper leur retard.
Il est important de noter que la métrique du «
nombre de pas » (step number) correspond au nombre de mouvements
et de rotations effectués par le robot. Il est fortement
corrélé avec la durée de la mission, mais de
manière non linéaire puisque le temps nécessaire pour
effectuer une rotation à 45° est différent de celui requis
pour se déplacer un mètre en avant.
113
Nous avons choisi d'analyser le nombre de pas au lieu du temps
d'exploration à cause de l'importance du facteur énergie dans le
domaine de la robotique; le nombre de mouvements qu'un robot peut effectuer est
limité par la capacité de sa batterie. Si dans notre cas le robot
avait une capacité de batterie pour effectuer seulement 100 pas par
exemple, il ne pourra explorer que 80% de la première scène
(Empty map) en utilisant l'algorithme BOA, au lieu de 85% s'il
utilisait xBOA, PSO ou CMAES. L'algorithme BOA apparaît donc moins
efficace que les autres méthodes en considérant ce critère
d'évaluation.
TABLE 4.2 - Taux d'exploration obtenus à la fin de la
mission d'exploration
|
Short-term exploration
|
|
Empty map
|
House map
|
|
Method
|
Average
|
Min
|
Max
|
Average
|
Min
|
Max
|
|
ABC
|
98.12
|
97.22
|
= 99
|
90.1
|
88.36
|
92.7
|
|
BOA
|
96
|
94.79
|
= 99
|
93.4
|
91.84
|
95.13
|
|
CMAES
|
98.49
|
95.66
|
= 99
|
93.29
|
89.4
|
96.18
|
|
GA
|
97.38
|
82.81
|
= 99
|
93
|
92.01
|
94.96
|
|
GWO
|
93.03
|
92.88
|
93.05
|
67.7
|
67.7
|
67.7
|
|
PSO
|
98.16
|
97.39
|
= 99
|
93.19
|
88.71
|
94.79
|
|
xBOA
|
98.23
|
93.92
|
= 99
|
91.63
|
82.63
|
94.44
|
|
Long-term exploration
|
|
Method
|
Average
|
Min
|
Max
|
Average
|
Min
|
Max
|
|
ABC
|
98.02
|
96.52
|
= 99
|
86.38
|
80.38
|
92.18
|
|
BOA
|
93.87
|
91.49
|
97.74
|
84.61
|
73.26
|
92.36
|
|
CMAES
|
94.16
|
83.85
|
= 99
|
82.23
|
77.43
|
86.45
|
|
GA
|
97.63
|
96.52
|
= 99
|
87.67
|
79.86
|
95.48
|
|
GWO
|
93.4
|
93.4
|
93.4
|
83.68
|
83.68
|
83.68
|
|
PSO
|
96.44
|
92.88
|
= 99
|
87.06
|
84.2
|
90.97
|
|
xBOA
|
96.37
|
93.57
|
98.61
|
89.9
|
79.16
|
94.1
|
Les Figures 4.6 et 4.7 nous permettent d'analyser le temps de
calcul total pour chaque méthode durant la mission d'exploration.
Étant donné que les processeurs sont une ressource coûteuse
en termes de prix de fabrication et d'énergie consommée, la
tendance dans le domaine des systèmes multirobots est de réduire
au maximum le temps de calcul requis pour accomplir la mission afin de
permettre l'utilisation de processeurs plus petits et moins gourmands. La
méthode idéale devrait donner une qualité d'exploration
maximale tout en nécessitant un minimum de temps de calcul. Toutefois,
il est rarement le cas d'obtenir un tel résultat, ce qui nous contraint
souvent à trouver un compris entre ces deux critères de
comparaisons.
114
CHAPITRE 4
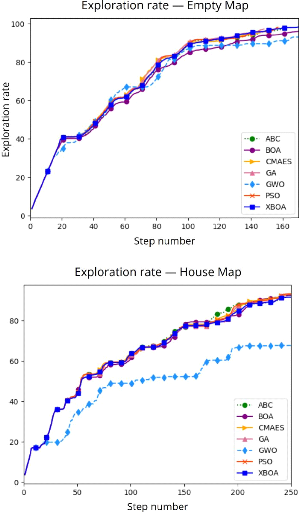
*Les résultats présentent les valeurs
moyennes de 10 exécutions
FIGURE 4.4 - Résultats de la simulation de la mission
d'exploration en utilisant la stratégie à court terme
115
Exploration rate -- Empty Map
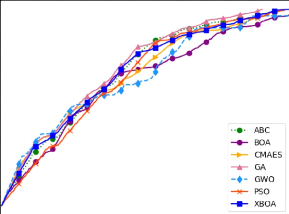
20 40 60 80 100 120 140 160
Step number
Exploration rate -- House Map
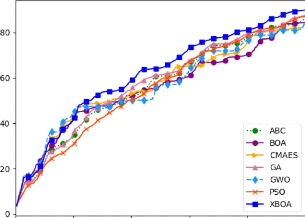
80 -
60 -
ABC
t BOA CMAES GA
- 1- GWO
- c- PS
t XBOA
20 -
200 250
1E:D 150
Step number
*Les résultats présentent les valeurs
moyennes de 10 exécutions
FIGURE 4.5 -- Résultats de la simulation
de la mission d'exploration en utilisant la stratégie à long
terme
116
CHAPITRE 4
Nous remarquons dans les résultats
présentés par ces figures la présence de plusieurs pics
sur l'axe du temps de calcul. Ces pics correspondent au temps requis par le
robot pour calculer les prochains points à visiter en utilisant l'une
des métaheuristiques, sachant que le robot est figé pendant ce
temps puisqu'il n'a pas encore de point de destination pour pouvoir planifier
un chemin de déplacement. Nous remarquons aussi que le temps de calcul
pendant le déplacement du robot est relativement négligeable,
ceci s'explique par le fait que le robot ne nécessite pas d'effectuer
des opérations de calculs compliquées pendant le
déplacement puisque cette phase se limite à mesurer la distance
avec l'obstacle le plus proche pour éviter les collisions ainsi que la
mise à jour des probabilités d'occupation dans la carte.
Bien que les méthodes xBOA, GA et ABC donnent de
meilleurs résultats en termes de taux d'exploration comparés
à BOA, elles nécessitent un temps de calcul plus long. Ceci
s'explique par la simplicité des opérations de l'algorithme BOA
et sa complexité réduite comparée aux autres
méthodes. Les résultats présentés dans la Figure
4.8 renforcent cette explication; nous observons clairement que le temps de
calcul de la méthode BOA est inférieur à celui de xBOA, GA
et ABC, et que le nombre d'appels à la fonction de fitness (fitness
evaluations) est inférieur.
Nous observons aussi que la méthode ABC requiert un
temps de calcul considérable dans toutes les expériences, qui est
supérieur au double du temps requis par les autres méthodes. Ceci
est causé par la nature de l'algorithme ABC qui est divisé en 3
phases dont chacune nécessite la réévaluation des
individus, ce qui conduit à un grand nombre d'exécu-tions de la
fonction objectif. Cette lenteur le rend inadapté aux scénarios
en situation réelle, car les robots ne doivent pas rester
immobilisés pendant une longue période.
Par ailleurs, nous remarquons que la méthode CMAES
domine les autres méthodes sur le critère du temps de calcul,
mais elle est parfois dominée par la méthode BOA en termes de
taux d'exploration, alors que cette dernière est elle-même
dominée par xBOA dans tous les scénarios sur ce même
critère. La méthode GWO est elle aussi dominée par xBOA
sur ce critère, mais elle enregistre un temps de calcul plus rapide.
Il est important de noter à partir de la figure 4.8 que
le temps de calcul moyen pour sélectionner le prochain point de
destination est relativement long; moyennant 150 à 450 secondes durant
lesquelles le robot est à l'arrêt en attendant le résultat
du processus d'opti-misation. Ceci n'est pas recommandé pour des
scénarios où le temps est un facteur critique tel que les
missions de sauvetage par exemple. Deux potentielles solutions sont possibles
dans ce cas. La première consiste à profiter des
fonctionnalités de parallélisme offertes par les processeurs
modernes pour évaluer plusieurs individus de la population en même
temps. Des résultats préliminaires nous ont permis de
réduire de moitié le temps d'exécution en utilisant cette
technique.
La deuxième stratégie consiste à
réduire la taille de la population, ce qui revient donc à
réduire le nombre de solutions candidates évaluées par la
fonction objectif. Dans la série d'expériences suivante, nous
allons analyser l'impact de cette deuxième stratégie sur la
qualité des solutions générées.
117
Execution time -- Empty Map
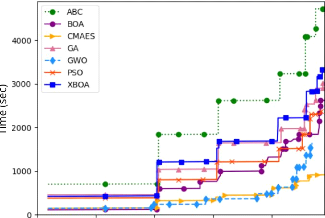
1000 -
A
4000 -
3000 -
V
N
0
2000 -
·
·
·
·
·
·
·
·
· t
·
·
·
0
·
·
tt~+ir
-ç
· t
· ABC
t BOA t CMAES t GA
-
· - GWO -X- PSO
t XBOA
0 20 40 60 80
Exploration rate
Execution time -- House Map
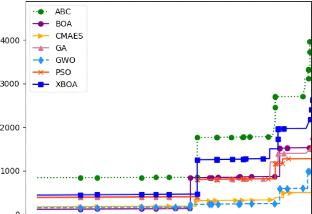
·
·
· ABC
- 0- BOA CMAES GA
-
·- GWO -~ Pso
t XBOA
4000 -
3000 -
2000 -
1000 -
0 10 20 30 40 50 60 70 80
Exploration rate
*Les résultats présentent les valeurs
moyennes de 3 exécutions
FIGURE 4.6 -- Comparaison de la durée
totale de la mission d'exploration pour la stratégie à court
terme
118
CHAPITRE 4
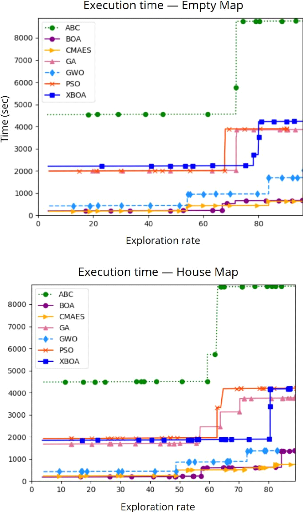
*Les résultats présentent les valeurs
moyennes de 3 exécutions
FIGURE 4.7 - Comparaison de la durée totale de la mission
d'exploration pour la stratégie à long terme
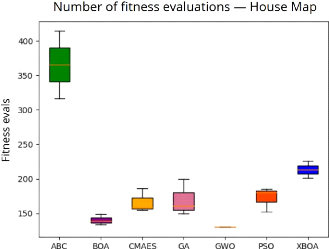
119
(a) Nombre d'évaluations de la fonction de fitness
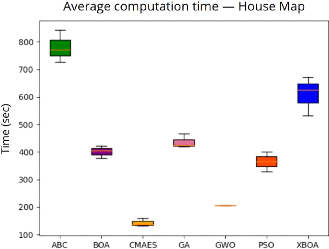
(b) Temps moyen de calcul pour chaque métaheuristique
*Les résultats présentent les valeurs
moyennes de 3 exécutions
FIGURE 4.8 - Nombre d'évaluations de la
fonction de fitness et temps moyen de calcul pour chaque
métaheuristique
120
CHAPITRE 4
4.7 Expérience 5 : Evaluation de la robustesse de
l'algo-rithme xBOA face à la réduction de taille de la
population
Afin d'étudier la possibilité
d'accélérer les algorithmes BOA et xBOA en réduisant la
taille de la population, nous avons effectué une série
d'expériences afin de mesurer l'in-fluence de la taille de la population
sur ces algorithmes et la robustesse de ces derniers.
Dans un premier temps, nous avons effectué une
expérience sur l'algorithme BOA original en variant la taille de la
population de 20 à 5 papillons tout en gardant les autres
paramètres fixes.
Les résultats présentés sur la figure 4.9
montrent que la réduction du nombre de solutions candidates (papillons)
réduit considérablement le temps d'exécution de la
métaheu-ristique. En effet, ce temps a diminué de 320 secondes
à 110 secondes en divisant la taille de la population en quatre.
Toutefois, ceci affecte aussi la qualité de l'exploration puisque
TABLE 4.3 - Evolution du taux d'exploration selon la taille de
la population en utilisant l'algorithme BOA
|
Short-term exploration - House map
|
|
Pop size
|
Average
|
Min
|
Max
|
|
05 butterflies
|
86.11
|
81.77
|
95.13
|
|
10 butterflies
|
88.66
|
79.68
|
95.13
|
|
20 butterflies
|
92.84
|
89.75
|
94.27
|
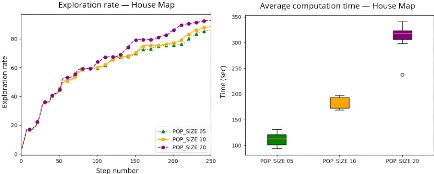
*Les résultats présentent les valeurs
moyennes de 3 exécutions
FIGURE 4.9 - Comparaison des résultats en utilisant
l'algorithme BOA avec différentes tailles de population sur
l'environnement House Map
121
le taux total de la surface explorée a baissé de
6.73%, tel que nous pouvons le voir sur le tableau 4.3.
Bien que cette baisse du taux d'exploration est importante, le
gain apporté de pouvoir calculer le prochain point de destination en
moins de 110 secondes apporte son lot d'avan-tages puisque ce temps d'attente
est acceptable pour beaucoup de scénarios de robotique dans le monde
réel par rapport au temps initial qui était trois fois plus
long.
En prenant ces résultats comme ligne de base, nous
avons effectué d'autres expériences pour mesurer les performances
de notre méthode ainsi que celles des autres métaheuris-tiques
lorsque la taille de la population est réduite à 5
solutions. Les résultats sont présentés sur le
tableau 4.3 et les figures 4.10 et 4.11.
La première remarque notable que nous pouvons constater
en observant les graphes se trouve au niveau du taux d'exploration des
méthodes PSO et GWO dont l'amélioration s'est
arrêtée après avoir atteint les valeurs de 75% et
62% respectivement, malgré qu'elles démontraient des
résultats proches de ceux des autres méthodes lorsque la taille
de la population était plus grande.
La deuxième observation notable c'est que la surface de
la zone visitée à la fin de la mission n'a pas pu dépasser
le taux de 97% pour l'environnement Empty Map et 93.35%
pour l'environnement House Map, et ceci, même si le niveau
d'énergie du robot n'a pas encore atteint 0. Après la
visualisation des trajectoires des robots dans le simulateur, nous avons
remarqué que ceci est dû au blocage des robots dans un minima
local où ils revisitent des régions déjà
explorées. Ceci s'explique par le manque de diversification dans les
solutions puisque le nombre très réduit de la population a
engendré une convergence prématurée vers une solution
unique. C'est-à-dire que tous les cinq individus de la population
avaient (presque) la même valeur.
Une potentielle solution pour éviter ce problème
serait d'augmenter l'espace de recherche graduellement en augmentant la taille
de la population lorsque le taux de la surface explorée dépasse
un certain seuil (par exemple 80%). En d'autres termes : commencer la recherche
en utilisant une taille de population réduite afin
d'accélérer le temps de calcul, puis augmenter le nombre
d'individus à la fin de la mission pour diversifier la population et
échapper aux minimas locaux. Ceci devrait être une meilleure
stratégie pour profiter des avantages des deux paramétrages, sans
sacrifier la qualité du résultat obtenu à la fin de la
mission.
Nous observons également que la méthode xBOA
domine toutes les autres méthodes sur les critères du taux
d'exploration et de la convergence de la valeur de fitness, mais elle souffre
d'un temps d'exécution élevé. De l'autre
côté, la méthode CMAES est dominante sur le critère
du temps moyen de calcul qui avoisine les 25 secondes, mais elle
souffre d'un taux d'exploration inférieur à xBOA de 10%. La
méthode ABC est la plus lente de toutes les méthodes, elle
nécessite 175 secondes de temps de calcul pour arriver à
un résultat presque similaire à celui de xBOA. Tandis que GA
offre un bon compromis entre qualité et vitesse d'exécution. La
figure 4.12 montre la différence de ces résultats avec
ceux obtenus lors de la série d'expériences
précédente qui utilisait une taille de population de 20
individus.
Étant donné que la méthode xBOA a pu
garder un taux d'exploration supérieur aux
122
CHAPITRE 4
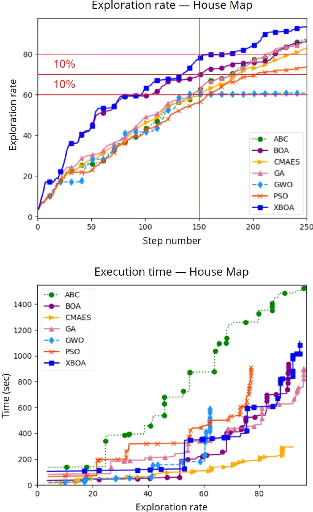
*Les résultats présentent les valeurs
moyennes de 3 exécutions
FIGURE 4.10 - Comparaison du taux d'exploration et durée
de la mission en utilisant la stratégie à court-terme et une
population de taille 5
123
Average computation time -- House Map
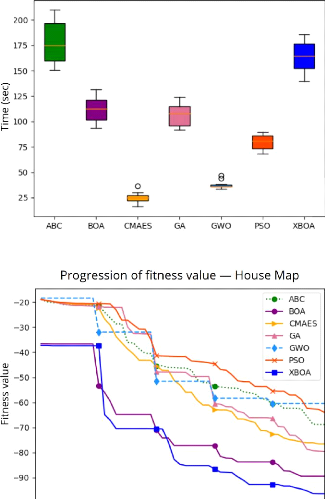
20
- 30
ABC
t BOA
CMAES --At-- GA
-~- GWO
PSO
t XBOA
- 40 - N
73 -50-
v -60 C
u-
- 70 -
- 80 -
- 90 -
200 -
175 -
150 -
V
125 -
av
100 -
I-
75 -
50 -
25 -
ABC BOA CMAES
GWO PSO XBOA
To
Progression of fitness value -- House Map
-100
0 10 20 30 40 50
Step number
*Les résultats présentent les valeurs
moyennes de 3 exécutions
FIGURE 4.11- Comparaison du temps moyen de calcul et
convergence de la valeur de fitness en utilisant la stratégie à
court-terme et une population de taille 5
CHAPITRE 4
autres méthodes pendant toute la durée de la
mission (voir la figure 4.10), et étant donné que les autres
méthodes n'ont pu approcher le taux de xBOA que vers la fin de la
mission, nous pouvons conclure que cette méthode est la plus robuste
d'entre eux face à la réduction de la taille de la population et
qu'elle serait plus avantageuse à utiliser dans beaucoup des situations.
Par exemple, Si la batterie était limitée, xBOA permettrait
d'explorer 10% à 20% plus de surface que les autres
métaheuristiques en général.
Une solution alternative serait d'utiliser la méthode
GA qui offre un résultats proches de xBOA vers la fin de la mission avec
un temps d'exécution similaire à l'algorithme BOA classique.
Toutefois, dans le cas où le temps d'exécution
est critique, nous pouvons envisager d'uti-liser la méthode CMAES qui
donne des résultats très rapides en sacrifiant la qualité
des
TABLE 4.4 - Taux d'exploration obtenus à la fin de la
mission en utilisant l'algorithme BOA avec une population de taille 5
|
Short-term exploration
|
|
Empty map
|
House map
|
|
Method
|
Average
|
Min
|
Max
|
Average
|
Min
|
Max
|
|
ABC
|
97.32
|
95.83
|
98.61
|
90.59
|
84.72
|
96
|
|
BOA
|
96.09
|
92.01
|
=99
|
87.13
|
83.68
|
95.13
|
|
CMAES
|
94.46
|
89.4
|
98.61
|
82.8
|
76.73
|
93.22
|
|
GA
|
96.09
|
87.5
|
=99
|
92.36
|
89.23
|
96
|
|
GWO
|
89.61
|
84.37
|
92.53
|
62.03
|
60.76
|
62.32
|
|
PSO
|
93.03
|
84.37
|
98.26
|
74.9
|
70.83
|
77.6
|
|
xBOA
|
96.14
|
92.88
|
98.26
|
93.35
|
92.18
|
93.92
|
124
(a) Temps de calcul moyen (en minutes) (b) Temps total de la
mission (en minutes)
FIGURE 4.12 - Impact de la réduction de la taille de
population sur le temps de calcul et temps de la mission en utilisant les
différentes métaheuristiques
125
solutions.
Ces trois méthodes appartiennent au front des solutions
non dominées (Pareto-front) et sont donc simultanément
optimales. Toutes les autres méthodes sont dominées et
appartiennent à la liste des solutions non optimales. La figure 4.13
illustre cette classification.
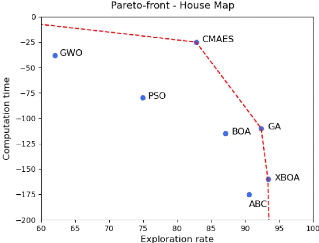
*Toutes les solutions sous la ligne rouge sont
dominées
FIGURE 4.13 - Visualisation du front des solutions dominantes
(Pareto-front) pour les différentes métaheuristiques en utilisant
une population de taille 5
4.8 Expérience 6 : Comparaison de xBOA avec les
autres variantes de l'algorithme BOA
Ayant constaté les avantages et les
inconvénients de l'algorithme xBOA par rapport aux autres
métaheuristiques, nous avons effectué une dernière
série d'expériences dont le but est de comparer les performances
de cet algorithme face aux autres variantes du BOA citées auparavant
dans l'état de l'art (voir section 2.8). Nous avons gardé la
même taille de population que la série d'expériences
précédente, à savoir 5 papillons.
Selon ce que l'on peut voir sur la figure 4.14 et 4.15 ainsi
que le tableau 4.5, la méthode xBOA domine les autres variantes dans le
critère du taux d'exploration durant toute la durée de la
mission. Elle atteint un résultat supérieur à celui de
l'algorithme BOA original de 4.24%. Elle les domine également dans le
critère de la convergence de la valeur de fitness.
Cette amélioration est due à l'utilisation de
l'opérateur de croisement qui augmente la diversité de la
population. En effet, en remplaçant les solutions existantes par de
nouvelles solutions, nous encourageons l'algorithme à explorer diverses
zones dans l'espace
126
CHAPITRE 4
TABLE 4.5 - Comparatif du taux d'exploration en utilisation les
variantes de l'algorithme BOA avec une population de taille 5
|
Short-term exploration - House map
|
|
Method
|
Average
|
Min
|
Max
|
|
BOA
|
89.11
|
81.77
|
95.13
|
|
ABOA
|
90.38
|
81.77
|
95.13
|
|
mBOA
|
89.14
|
81.07
|
95.13
|
|
SABOA
|
85.13
|
82.98
|
85.93
|
|
xBOA
|
93.35
|
92.18
|
93.92
|
de recherche au lieu d'intensifier la recherche au niveau
local. Ceci permet à l'algorithme d'échapper au piège de
converger prématurément vers un minima local, ce qui augmente les
chances de trouver l'optimum global.
Toutefois, chaque nouvel individu créé doit
être évalué, ce qui engendre l'augmentation du nombre
d'évaluations de la fonction fitness. Par conséquent, le temps de
calcul de l'al-gorithme augmente aussi. Étant donné que le
paramètre de probabilité de croisement était
fixé à 0.583, il y a donc 58% plus d'individus à
évaluer dans l'algorithme xBOA comparé au BOA classique.
L'algorithme mBOA souffre aussi d'un temps de calcul
élevé, ceci est causé par les calculs
supplémentaires ajoutés à cette variante dans la phase
d'exploitation intensive. Bien que cette nouvelle phase permet
d'accélérer la convergence de l'algorithme par rapport à
la méthode BOA classique, elle reste tout de même dominée
par l'algorithme xBOA que ce soit dans les critères du temps, de la
convergence ou du taux d'exploration de la zone.
ABOA domine les autres variantes dans le critère du
temps d'exécution, mais n'est pas parvenue à dépasser
à un taux d'exploration de 90.38%, alors que xBOA a pu atteindre un
résultat supérieur. Quant à l'algorithme SABOA, il a
donné le résultat le moins performant avec un taux d'exploration
de 85.13%, mais possède néanmoins l'avantage de n'avoir qu'un
seul hyperparamètre en entrée, ce qui réduit la
complexité du paramétrage.
Les deux solutions dominantes sont donc:
-- ABOA : qui possède le meilleur temps de calcul; et --
xBOA : qui obtient le meilleur taux d'exploration.
Il faut donc considérer le choix d'un bon compris entre
la maximisation de la surface explorée et le temps de calcul
nécessaire. Ce choix dépendra de la nature de la mission: dans un
contexte d'une mission de sauvetage par exemple, le facteur « temps »
est très important, ce qui rend envisageable la décision de
privilégier la réduction de la durée d'exécution au
profit de la qualité d'exploration. En revanche, dans un contexte de
déminage, de nettoyage ou de surveillance, il serait judicieux de
privilégier la maximisation de la zone explorée au
dépourvu du temps de calcul, jusqu'à une certaine mesure.
Exploration rate -- House Map
0
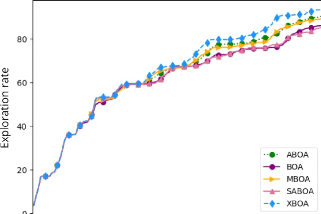
Exploration rate
127
50 100 150 250
Step number
Execution time -- House Map
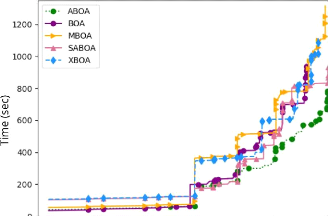
1200 -
1000
!- AB OA
- 0- BOA MBOA SA B OA
- - XBOA
800 -
V
N
V)
600 -
CDE
i-
400-
200 -
sn
0 2 a 40 610
Exploration rate
*Les résultats présentent les valeurs
moyennes de 10 exécutions
FIGURE 4.14 -- Comparaison des variantes de l'algorithme
BOA en utilisant la stratégie à court terme et une population de
taille 5
128
CHAPITRE 4
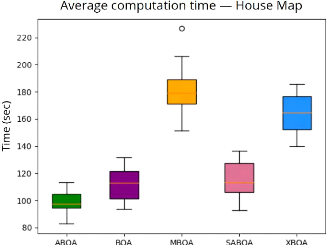
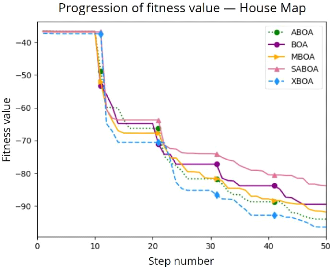
*Les résultats présentent les valeurs
moyennes de 10 exécutions
FIGURE 4.15 - Suite de la comparaison des variantes de
l'algorithme BOA en utilisant la stratégie à court terme et une
population de taille 5
129
Un autre facteur a prendre en considération aussi est
la stabilité des résultats. En effet, après avoir
répété l'expérience 10 fois, le xBOA a
enregistré un taux de stabilité élevé avec un
résultat presque similaire à chaque exécution (~1 à
2% d'écart). Alors que l'algorithme ABOA vacillait dans une marge de 15%
de différence entre les résultats.
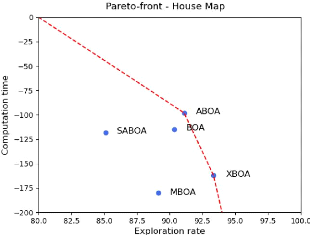
*Toutes les solutions sous la ligne rouge sont
dominées
FIGURE 4.16 - Visualisation du front des solutions dominante
(Pareto-front) pour les variantes de BOA en utilisant une population de taille
5
4.9 Expérience 7 : Test en utilisant un robot
réel
Afin de valider l'adaptabilité de notre approche aux
expériences du monde réel, nous avons effectué des tests
sur le robot P3DX du laboratoire LARESI situé dans le département
d'électronique de USTOMB. Pour cela, nous avons séparé le
système en deux parties. D'un côté, un ordinateur portable
connecté au réseau local du laboratoire via une connexion wifi
joue le rôle de serveur. Il exécute le processus d'optimisation
pour générer le prochain point de destination à visiter
ainsi que l'algorithme de planification de chemin pour calculer les positions
intermédiaires, qui sont ensuite transformées en un ensemble de
commandes de mouvements puis envoyées au robot via une socket TCP.
Une fois que le robot reçoit une commande de mouvement
(move, turn, stop), il la transforme en une commande de vitesse pour le
contrôle des moteurs en utilisant les routines du système ROS
(Robot Operating System), celui-ci communiquera directement avec le
mi-crocontrôleur du robot via l'interface ROSARIA pour exécuter
les commandes. En parallèle à cela, un autre programme
basé sur ROS s'occupe de collecter les informations mesurées par
le Lidar à une fréquence de 10Hz puis les envoyer au serveur pour
mettre à jour la carte de l'environnement.
CHAPITRE 4
Un problème rencontré durant les
expériences était l'accumulation de l'erreur de localisation
causée par le glissement du robot sur le sol. En effet, notre simulateur
supposait que la localisation du robot était connue à chaque
instant t, toutefois, dans le monde réel ceci ne pouvait se faire sans
l'intégration d'un dispositif électronique de positionnement. La
méthode que nous avons utilisée sur le robot P3DX se base sur
l'odométrie, qui est une technique peu chère se basant sur le
calcul du nombre de rotations des roues pour estimer la distance parcourue par
le robot et son angle. Cependant, nous avons remarqué des
mini-glissements du robot à la fin de chaque mouvement qui le fait
dévier de 1 ou 2 centimètres de sa trajectoire. Bien que cette
déviation n'est pas importante, son accumulation après plusieurs
mouvements s'accroit et engendre une localisation erronée.
Afin de résoudre ce problème sans avoir besoin
d'utiliser des dispositifs de localisation plus complexes, nous avons
intégré un mécanisme de contrôle en boucle
fermée (contrôl-leur PID) pour réduire la vitesse de
rotation des roues lorsque le robot se rapproche de l'emplacement prévu,
avec une possibilité de revenir légèrement en
arrière pour corriger sa position si nécessaire.
Les codes sources de ce contrôleur PID basé sur
le système ROS ainsi que le programme pour le contrôle du robot en
utilisant les commandes distantes par TCP sont disponible en open source sur le
lien cité en bas de page 1. La figure 4.17 montre des photos
prises durant les expériences dans le laboratoire.
Dans les travaux futurs, nous allons optimiser le
système en intégrant directement les calculs des points de
destination et de la planification de trajectoires dans l'ordinateur de bord du
robot, et ceci afin qu'il puisse être autonome et continuer sa mission
même si la connexion avec le serveur est interrompue. Étant
donné les faibles capacités de calcul de cet ordinateur de bord,
il serait judicieux de profiter des résultats obtenus durant
l'expérience
1. https ://
github.com/amineHorseman/pioneer_bci

FIGURE 4.17 - Expérience sur le robot réel
130
131
précédente par rapport à la
réduction de la taille de population afin d'alléger les calculs.
L'utilisation du xBOA dans ce contexte serait donc appropriée
étant donné ses capacités de diversification des solutions
dans les populations à petite taille, ainsi que sa stabilité
à atteindre un taux d'exploration élevé lors de chaque
exécution.
4.10 Conclusion
Nous avons présenté dans ce chapitre une
série d'expériences effectuées dans le but
d'évaluer les performances de l'algorithme xBOA. Nous l'avons
comparé à plusieurs autres métaheuristiques, ainsi que les
autres variantes de BOA récemment introduites dans la
littérature.
L'évaluation des méthodes s'est basée sur
5 critères de comparaison. Les résultats montrèrent que
l'algorithme xBOA surpasse BOA et ses autres variantes, mais requiert un temps
de calcul élevé. L'algorithme proposé surpasse aussi les
autres métaheuristiques telles que PSO, GA, GWO et ABC dans certains
scénarios.
Nous avons aussi effectué une expérience pour
évaluer l'adaptabilité de notre approche dans un contexte
multirobots. Les résultats nous ont permis de valider notre
modélisation du mécanisme de synchronisation implicite et
observer l'émergence d'un comportement collectif au sein des robots leur
permettant de se disperser dans l'environnement et minimiser la redondance
même pour des zones à large échelle. Nous avons
également effectué une expérience sur un robot réel
de type P3DX au sein du laboratoire LARESI basé sur le middleware ROS et
une communication avec le serveur via une connexion wifi en utilisant des
sockets TCP.
Les résultats obtenus durant ces expériences ont
été satisfaisants sur certains critères, mais ont
démontré aussi les limites de l'algorithme xBOA. Nous
présenterons dans la conclusion générale quelques
perspectives d'amélioration de cette méthode.
132
CONCLUSION GÉNÉRALE ET PERSPECTIVES
Nous avons présenté dans cette thèse nos
travaux sur l'optimisation du comportement collectif d'un groupe de robots
autonomes en utilisant les métaheuristiques.
Ce travail était divisé en deux parties
principales. La première était consacrée à
l'étude des fondements théoriques des systèmes multirobots
et des métaheuristiques pour l'optimi-sation globale. Tandis que la
deuxième présentait notre modélisation du problème
d'explo-ration de zones inconnues avec des contraintes d'énergie, ainsi
que la série d'expériences réalisées pour la
valider.
Cette thèse a introduit deux contributions principales.
D'un côté le développement d'une nouvelle plateforme de
simulation appelée PyRoboticsLab pour l'évaluation et le
benchmarking d'algorithmes dédiés à la résolution
des problèmes de navigation robotique, planification de trajectoires,
exploration et surveillance. Et de l'autre côté l'introduction
d'un nouvel algorithme xBOA que nous avons proposé comme nouvelle
variante de la mé-taheuristique BOA.
Nous avons utilisé notre plateforme de benchmarking
afin de comparer les performances de notre nouvel algorithme à plusieurs
autres métaheuristiques utilisées dans la littérature.
L'évaluation des méthodes s'est basée sur cinq
critères de comparaison. Les résultats ont montré que
l'algorithme xBOA surpasse BOA et ses autres variantes, mais requiert un temps
de calcul plus long. L'algorithme proposé surpasse aussi les autres
mé-taheuristiques telles que PSO, GA, GWO et ABC dans certains
scénarios.
Nous avons procédé aussi à une
série d'expériences pour évaluer l'adaptabilité de
notre approche dans un contexte multirobots, et optimiser la coordination entre
les robots en introduisant des mécanismes d'échange
d'informations pour permettre aux robots de se disperser efficacement et
minimiser la redondance.
D'autres améliorations d'ordre programmatique ont aussi
été introduites telles que l'uti-lisation du parallélisme
dans le processus d'évolution pour permettre d'évaluer plusieurs
individus en même temps et accélérer le temps global de
calcul des points de destinations.
Nous avons également effectué une
expérience réelle sur un robot de type P3DX dont le
133
Conclusion générale et perspectives
but était de vérifier le bon fonctionnement des
outils proposés. Cette expérience nous a permis de
détecter et résoudre les problèmes de localisation
basée sur l'odométrie et d'adapter notre approche au middleware
ROS.
Dans les travaux futurs, nous nous consacrerons à
améliorer la plateforme de simulation afin d'y intégrer plus
d'algorithmes, et ce afin d'offrir aux chercheurs de ce domaine une suite
complète de benchmarking et un outil uniformisé pour positionner
leurs travaux. L'outil pourra aussi intégrer plus de scénarios et
des environnements variés avec l'intégra-tion d'obstacles
dynamiques.
Le simulateur pourra aussi être utilisé à
des fins pédagogiques afin de faire découvrir aux
étudiants en informatique le domaine de l'intelligence artificielle
appliquée aux problématiques de la robotique collective, sans
qu'ils aient à se soucier des détails théoriques relatifs
à la modélisation des capteurs laser, ou du calcul des
probabilités d'occupation.
Du côté de l'algorithme xBOA, nous projetons de
le tester sur d'autres types de problématiques d'optimisation
combinatoire. Nous pourrons considérer la piste d'améliorer cet
algorithme en introduisant un mécanisme plus adaptatif pour
équilibrer les phases d'ex-ploration et d'exploitation, ou de tester
différents opérateurs de croisement pour analyser leur effet sur
la convergence de l'algorithme.
134
BIBLIOGRAPHIE
[1] Nur Aira ABD RAHMAN et al. « A
coverage path planning approach for autonomous radiation mapping with a mobile
robot ». In : International Journal of Advanced Robotic Systems
19.4 (2022), p. 17298806221116483.
[2] Laith ABUALIGAH et al. « Reptile
Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer ». In :
Expert Systems with Applications 191 (2022), p. 116158.
[3] Laith ABUALIGAH et al. « The
arithmetic optimization algorithm ». In : Computer methods in applied
mechanics and engineering 376 (2021), p. 113609.
[4] Afsoon AFZAL et al. « A study on
the challenges of using robotics simulators for testing ». In : arXiv
preprint arXiv:2004.07368 (2020).
[5] Jeffrey O AGUSHAKA, Absalom E
EZUGWU et Laith ABUALIGAH. « Dwarf
mongoose optimization algorithm ». In : Computer methods in applied
mechanics and engineering 391 (2022), p. 114570.
[6] Somaye AHMADI, H. KEBRIAEI
et Hadi MORADI. « Constrained coverage path
planning: evolutionary and classical approaches ». In : Robotica
36 (fév. 2018), p. 1-21. DOI :
10.1017/S0263574718000139.
[7] Mohammad AL KHAWALDAH et Andreas
NUCHTER. « Enhanced frontier-based exploration for indoor
environment with multiple robots ». In : Advanced Robotics 29
(avr. 2015). DOI : 10.1080/01691864.2015.1015443.
[8] Sankalap ARORA et Priyanka
ANAND. « Binary butterfly optimization approaches for
feature selection ». In : Expert Systems with Applications 116
(2019), p. 147-160.
[9] Sankalap ARORA et Satvir
SINGH. « An improved butterfly optimization algorithm for
global optimization ». In : Advanced Science, Engineering and Medicine
8.9 (2016), p. 711-717.
[10] Sankalap ARORA et Satvir
SINGH. « Butterfly algorithm with levy flights for global
optimization ». In : 2015 International conference on signal
processing, computing and control (ISPCC). IEEE. 2015, p. 220-224.
[11] Sankalap ARORA et Satvir
SINGH. « Butterfly optimization algorithm: a novel
approach for global optimization ». In : Soft Computing 23.3
(2019), p. 715-734.
[12] Sankalap ARORA, Satvir SINGH
et Kaan YETILMEZSOY. « A modified butterfly
optimization algorithm for mechanical design optimization problems ». In :
Journal of the Brazilian Society of Mechanical Sciences and Engineering
40.1 (2018), p. 1-17.
[13] Adel Saad ASSIRI. « On the
performance improvement of Butterfly Optimization approaches for global
optimization and Feature Selection ». In : Plos one 16.1 (2021),
e0242612.
[14] Mahdi AZIZI. « Atomic orbital
search: A novel metaheuristic algorithm ». In : Applied Mathematical
Modelling 93 (2021), p. 657-683.
[15] Antoine BAUTIN, Olivier SIMONIN
et François CHARPILLET. « MinPos : A
Novel Frontier Allocation Algorithm for Multi-robot Exploration ». In :
oct. 2012, p. 496-508. ISBN : 978-3-642-33514-3. DOI
: 10.1007/978-3-642-33515-0_49.
135
Bibliographie
[16] Amine BENDAHMANE et Redouane TLEMSANI. « Unknown
area exploration for robots with energy constraints using a modified Butterfly
Optimization Algorithm ». In : Soft Computing 27 (2023), p.
3785-3804. DOI : 10.1007/s00500-022-07530w.
[17] James BERGSTRA et Yoshua BENGIO. « Random search
for hyper-parameter optimization. » In : Journal of machine learning
research 13.2 (2012).
[18] James BERGSTRA, Dan YAMINS, David D COx et al. «
Hyperopt: A python library for optimizing the hyperparameters of machine
learning algorithms ». In : Proceedings of the 12th Python in science
conference. T. 13. Citeseer. 2013, p. 20.
[19] Francesco BISCANI et Dario IZZO. « A parallel
global multiobjective framework for optimization: pagmo ». In :
Journal of Open Source Software 5.53 (2020), p. 2338. DOI :
10.21105/joss.02338.
[20] Johann BORENSTEIN, Yoram KOREN et al. « The vector
field histogram-fast obstacle avoidance for mobile robots ». In : IEEE
transactions on robotics and automation 7.3 (1991), p. 278-288.
[21] Ersin BÜYÜK. « Pareto-based
multiobjective particle swarm optimization: examples in geophysical modeling
». In : Optimisation Algorithms and Swarm Intelligence.
In-techOpen, 2021.
[22] Byoung-Suk CHOI et al. « A hierarchical algorithm
for indoor mobile robot localization using RFID sensor fusion ». In :
IEEE Transactions on industrial electronics 58.6 (2011), p.
2226-2235.
[23] Howie CHOSET et Philippe PIGNON. « Coverage path
planning: The boustrophedon cellular decomposition ». In : Field and
service robotics. Springer. 1998, p. 203-209.
[24] Alberto COLORNI, Marco DORIGO, Vittorio MANIEZZO et al.
« Distributed optimization by ant colonies ». In : Proceedings of
the first European conference on artificial life. T. 142. Paris, France.
1991, p. 134-142.
[25] Nichael Lynn CRAMER. « A representation for the
Adaptive Generation of Simple Sequential Programs ». In : Proceedings
of an International Conference on Genetic Algorithms and the Applications.
Sous la dir. de John J. GREFENSTETTE. Carnegie-Mellon University, Pittsburgh,
USA, juin 1985, p. 183-187.
[26] Marija DAKULOVIc, Sanja HORVATIc et Ivan
PETROVIé. « Complete Coverage D* Algorithm for Path Planning of a
Floor-Cleaning Mobile Robot ». In : IFAC Proceedings Volumes 44.1
(2011). 18th IFAC World Congress, p. 5950-5955. ISSN : 1474-6670. DOI :
https://doi.org/10.3182/20110828-6-IT-1002.03400.
[27] Andrew DAVENPORT et al. « GENET: A connectionist
architecture for solving constraint satisfaction problems by iterative
improvement ». In : AAAI. 1994, p. 325-330.
[28] Susana Estefany DE LEÔN-ALDACO, Hugo CALLEJA et
Jesús Aguayo ALQuICIRA. « Me-taheuristic optimization methods
applied to power converters: A review ». In : IEEE Transactions on
Power Electronics 30.12 (2015), p. 6791-6803.
[29] Sihao DENG et al. « Application of external axis in
robot-assisted thermal spraying ». In : Journal of thermal spray
technology 21 (2012), p. 1203-1215.
136
Bibliographie
[30] Berat DoðAN et Tamer ÖLMEZ. « A new
metaheuristic for numerical function optimization: Vortex Search algorithm
». In : Information sciences 293 (2015), p. 125-145.
[31] Alexey DosovITsKIY et al. « CARLA: An open urban
driving simulator ». In : Conference on robot learning. PMLR.
2017, p. 1-16.
[32] Akif DURDU et al. « Convolutional Neural Networks
Based Active SLAM and Exploration ». In : Avrupa Bilim ve Teknoloji
Dergisi 22 (2021), p. 342-346.
[33] Hugh DuRRANT-WHYTE et al. « Field and service
applications-an autonomous straddle carrier for movement of shipping
containers-from research to operational autonomous systems ». In :
IEEE Robotics & Automation Magazine 14.3 (2007), p. 14-23.
[34] Alberto ELFEs. « Using occupancy grids for mobile
robot perception and navigation ». In : Computer 22.6 (1989), p.
46-57.
[35] Yuqi FAN et al. « A self-adaption butterfly
optimization algorithm for numerical optimization problems ». In :
IEEE Access 8 (2020), p. 88026-88041.
[36] J.D. FARMER, N. PACKARD et A. PERELsoN. « The immune
system, adaptation and machine learning ». In : Physica D 2
(1986), 187-204.
[37] Diego FERIGo et al. « Gym-ignition: Reproducible
robotic simulations for reinforcement learning ». In : 2020 IEEE/SICE
International Symposium on System Integration (SII). IEEE. 2020, p.
885-890.
[38] Simon FoNG, Suash DEB et Ankit CHAuDHARY. « A
review of metaheuristics in robotics ». In : Computers &
Electrical Engineering 43 (2015), p. 278-291.
[39] Miguel GARCíA et al. « Voronoi-Based Space
Partitioning for Coordinated Multi-Robot Exploration ». In : JoPha:
Journal of Pysical Agents, ISSN 1888-0258, Vol. 1, N°. 1, 2007, pags. 37-44
1 (jan. 2007). DoI: 10.14198/JoPha.2007.1.1.05.
[40] Fred GLovER. « Future paths for integer programming
and links to artificial intelligence ». In : Computers &
operations research 13.5 (1986), p. 533-549.
[41] David E. GoLDBERG. Genetic Algorithms in Search,
Optimization, and Machine Learning. New York: Addison-Wesley, 1989.
[42] Nir GREsHLER et al. « Cooperative multi-agent path
finding: beyond path planning and collision avoidance ». In: 2021
International Symposium on Multi-Robot and Multi-Agent Systems (MRS).
IEEE. 2021, p. 20-28.
[43] Faiza GuL, Suleman MIR et Imran MIR. « Coordinated
multi-robot exploration: Hybrid stochastic optimization approach ». In :
AIAA SCITECH2022 Forum. 2022, p. 1414.
[44] Yanju Guo, Xianjie LIu et Lei CHEN. « Improved
butterfly optimisation algorithm based on guiding weight and population restart
». In : Journal of Experimental & Theoretical Artificial
Intelligence 33.1 (2021), p. 127-145.
[45] Nikolaus HANsEN, Sibylle MüLLER et Petros
KouMouTsAKos. « Reducing the Time Complexity of the Derandomized Evolution
Strategy with Covariance Matrix Adaptation (CMA-ES) ». In :
Evolutionary computation 11 (fév. 2003), p. 1-18. DoI : 10.
1162/106365603321828970.
[46] Peter E. HART, Nils J. NILssoN et Bertram RAPHAEL.
« A Formal Basis for the Heuristic Determination of Minimum Cost Paths
». In : IEEE Transactions on Systems Science and Cybernetics 4.2
(1968), p. 100-107. DoI : 10.1109/TSSC.1968.300136.
137
Bibliographie
[47] Dirk HOLz et al. « Evaluating the Efficiency of
Frontier-based Exploration Strategies ». In : t. 1. Juill. 2010, p. 1
-8.
[48] Erno HORVATH, Claudiu POzNA et Radu-Emil PRECUP. «
Robot coverage path planning based on iterative structured orientation ».
In : Acta Polytechnica Hungarica 15.2 (2018), p. 231-249.
[49] Luca IOCCHI, Luca MARCHETTI et Daniele NARDI. «
Multi-robot patrolling with coordinated behaviours in realistic environments
». In : 2011 IEEE/RSJ International Conference on Intelligent Robots
and Systems. IEEE. 2011, p. 2796-2801.
[50] Nick JAKOBI, Phil HUSBANDS et Inman HARVEY. « Noise
and the reality gap: The use of simulation in evolutionary robotics ». In
: Advances in Artificial Life: Third European Conference on Artificial Life
Granada, Spain, June 4-6, 1995 Proceedings 3. Springer. 1995, p.
704-720.
[51] Seyed Mohammad Jafar JALALI et al. « Evolving
artificial neural networks using butterfly optimization algorithm for data
classification ». In : International conference on neural information
processing. Springer. 2019, p. 596-607.
[52] Albina KAMALOVA, Ki Dong KIM et Suk Gyu LEE. «
Waypoint Mobile Robot Exploration Based on Biologically Inspired Algorithms
». In : IEEE Access 8 (2020), p. 190342190355.
[53] Albina KAMALOVA et al. « Multi-Robot Exploration
Based on Multi-Objective Grey Wolf Optimizer ». In : Applied Sciences
9 (juill. 2019), p. 2931. DOI : 10 . 3390/ app9142931.
[54] Pierre KANCIR. « Méthodologie de conception
de système multi-robots: De la simulation à la
démonstration ». Thèse de doct. Université de
Bretagne Sud, 2018.
[55] Dervis KARABOGA. « An Idea Based on Honey Bee Swarm
for Numerical Optimization, Technical Report - TR06 ». In : Technical
Report, Erciyes University (jan. 2005).
[56] Géza KATONA, Balázs LÉNART et
János JUHASz. « Parallel ant colony algorithm for shortest path
problem ». In : Periodica Polytechnica Civil Engineering 63.1
(2019), p. 243-254.
[57] Ali KAVEH et Taha BAKHSHPOORI. « Metaheuristics:
outlines, MATLAB codes and examples ». In : (2019).
[58] J. KENNEDY et R. EBERHART. « Particle swarm
optimization ». In : Proceedings of ICNN'95 - International Conference
on Neural Networks. T. 4. 1995, 1942-1948 vol.4. DOI :
10.1109/ICNN.1995.488968.
[59] Scott KIRKPATRICK, C Daniel GELATT JR et Mario P VECCHI.
« Optimization by simulated annealing ». In : science
220.4598 (1983), p. 671-680.
[60] Nathan KOENIG et Andrew HOWARD. « Design and use
paradigms for gazebo, an open-source multi-robot simulator ». In :
2004 IEEE/RSJ International Conference on Intelligent Robots and Systems
(IROS)(IEEE Cat. No. 04CH37566). T. 3. IEEE. 2004, p. 21492154.
[61] Guocheng LI et al. « An improved butterfly
optimization algorithm for engineering design problems using the cross-entropy
method ». In : Symmetry 11.8 (2019), p. 1049.
138
Bibliographie
[62] Matteo LUPERTO et al. « Robot
exploration of indoor environments using incomplete and inaccurate prior
knowledge ». In : Robotics and Autonomous Systems 133 (2020), p.
103622.
[63] Ellips MASEHIAN et MR
AMIN-NASERI. « A voronoi diagram-visibility
graph-potential field compound algorithm for robot path planning ». In :
Journal of Robotic Systems 21.6 (2004), p. 275-300.
[64] Ashkan MEMARI, Robiah AHMAD
et Abd Rahman Abdul RAHIM. « Metaheuristic
algorithms: guidelines for implementation ». In : Journal of Soft
Computing and Decision Support Systems 4.6 (2017), p. 1-6.
[65] PE MERGOS et Anastasios
SEXTOS. Multi-objective optimum selection ofground motion
records with genetic algorithms. IEEE, juin 2018.
[66] Seyedali MIRJALILI, Seyed Mohammad
MIRJALILI et Andrew LEWIS. « Grey Wolf
Optimizer ». In : Advances in Engineering Software 69 (2014), p.
46-61. ISSN : 0965-9978. DOI :
https://doi.org/10.1016/j.advengsoft.2013.12.007.
[67] Himanshu MITTAL et al. «
Gravitational search algorithm: A comprehensive analysis of recent variants
». In : Multimedia Tools and Applications 80 (2021), p.
7581-7608.
[68] Sing Yee NG et Nur Syazreen
AHMAD. « A Bug-Inspired Algorithm for Obstacle Avoidance
of a Nonholonomic Wheeled Mobile Robot with Constraints ». In :
Intelligent Computing. Sous la dir. de Kohei ARAI,
Rahul BHATIA et Supriya KAPOOR. Cham :
Springer International Publishing, 2019, p. 1235-1246.
[69] G PAVAI et TV GEETHA.
« A survey on crossover operators ». In : ACM Computing Surveys
(CSUR) 49.4 (2016), p. 1-43.
[70] Hindriyanto Dwi PURNOMO et Hui-Ming
WEE. « Soccer game optimization with substitute players
». In : Journal of computational and applied mathematics 283
(2015), p. 79-90.
[71] Esmat RASHEDI, Hossein
NEZAMABADI-POUR et Saeid SARYAZDI. «
GSA: a gravitational search algorithm ». In : Information sciences
179.13 (2009), p. 2232-2248.
[72] Eric ROHMER, Surya PN SINGH
et Marc FREESE. « V-REP: A versatile and
scalable robot simulation framework ». In : 2013 IEEE/RSJ
international conference on intelligent robots and systems. IEEE. 2013, p.
1321-1326.
[73] Ali El ROMEH et Seyedali
MIRJALILI. « Multi-Robot Exploration of Unknown Space
Using Combined Meta-Heuristic Salp Swarm Algorithm and Deterministic
Coordinated Multi-Robot Exploration ». In : Sensors 23.4 (2023),
p. 2156.
[74] Sajad SAEEDI et al. « Occupancy
grid map merging for multiple robot simultaneous localization and mapping
». In : International Journal ofRobotics and Automation 30.2
(2015), p. 149-157.
[75] Jeffrey R SAMPSON. Adaptation in
natural and artificial systems (John H. Holland). 1976.
[76] Sushmita SHARMA et al. « MPBOA-A
novel hybrid butterfly optimization algorithm with symbiosis organisms search
for global optimization and image segmentation ». In : Multimedia
Tools and Applications 80.8 (2021), p. 12035-12076.
139
Bibliographie
[77] Zongyuan SHEN, James P. WiLsoN
et Shalabh GUPTA. «
E*+: An Online
Coverage Path Planning Algorithm for Energy-constrained Autonomous Vehicles
». In : Global Oceans2020:Singapore- U.S. GulfCoast. 2020,p. 1-6.
Doi: 10.1109/IEEECONF38699. 2020.9389353.
[78] Rakesh SHREsTHA et al. « Learned
map prediction for enhanced mobile robot exploration ». In : 2019
International Conference on Robotics and Automation (ICRA). IEEE. 2019, p.
1197-1204.
[79] Junnan SoNG et Shalabh
GUPTA. « c*: An Online Coverage Path Planning Algorithm
». In : IEEE Transactions on Robotics 34 (fév. 2018), p.
526-533. Doi: 10.1109/ TRO.2017.2780259.
[80] Rainer SToRN et Kenneth
PRiCE. « Differential evolution-a simple and efficient
heuristic for global optimization over continuous spaces ». In :
Journal of global optimization 11.4 (1997), p. 341.
[81] Daniel Perea STROM, Igor
BoGosLAVsKYi et Cyrill STACHNiss. «
Robust exploration and homing for autonomous robots ». In : Robotics
and Autonomous Systems 90 (2017), p. 125-135.
[82] Lei TAi et Ming LiU.
« A robot exploration strategy based on q-learning network ». In :
2016 IEEE international conference on real-time computing and robotics
(RCAR). IEEE. 2016, p. 57-62.
[83] Mohammad TUBisHAT et al. « Dynamic
butterfly optimization algorithm for feature selection ». In : IEEE
Access 8 (2020), p. 194303-194314.
[84] Zhongmin WANG, Qifang LUo
et Yongquan ZHoU. « Hybrid metaheuristic
algorithm using butterfly and flower pollination base on mutualism mechanism
for global optimization problems ». In : Engineering with Computers
37.4 (2021), p. 3665-3698.
[85] David H WoLPERT et William G
MACREADY. « No free lunch theorems for optimization
». In : IEEE transactions on evolutionary computation 1.1 (1997),
p. 67-82.
[86] Benjie XiAo et al. « Ant colony
optimisation algorithm-based multi-robot exploration ». In :
International Journal of Modelling, Identification and Control 18.1
(2013), p. 41-46.
[87] Lei XiE et al. « Tuna swarm
optimization: a novel swarm-based metaheuristic algorithm for global
optimization ». In : Computational intelligence and Neuroscience
2021 (2021).
[88] Anupam YADAV et al. « AEFA:
Artificial electric field algorithm for global optimization ». In :
Swarm and Evolutionary Computation 48 (2019), p. 93-108.
[89] Brian YAMAUCHi. « A frontier-based
approach for autonomous exploration ». In : Proceedings 1997 IEEE
International Symposium on Computational Intelligence in Robotics and
Automation CIRA'97. 'Towards New Computational Principles for Robotics and
Au-tomation'. 1997, p. 146-151. Doi :
10.1109/CIRA.1997.613851.
[90] Brian YAMAUCHi. « Frontier-based
exploration using multiple robots ». In : jan. 1998, p. 47-53.
isBN : 0-89791-983-1. Doi:
10.1145/280765.280773.
[91] Xin-She YANG. « A new
metaheuristic bat-inspired algorithm ». In : Nature inspired
cooperative strategies for optimization (NICSO 2010) (2010), p. 65-74.
140
Bibliographie
[92] Xin-She YANG. « Flower pollination algorithm for
global optimization ». In : International conference on unconventional
computing and natural computation. Springer. 2012, p. 240-249.
[93] Xin-She YANG. Nature-inspired metaheuristic
algorithms. Luniver press, 2010.
[94] Zuozhong YIN et al. « A Delivery robot cloud
platform based on microservice ». In : Journal of Robotics 2021
(2021), p. 1-10.
[95] Chao Yu et al. « Asynchronous Multi-Agent
Reinforcement Learning for Efficient Real-Time Multi-Robot Cooperative
Exploration ». In : arXiv preprint arXiv:2301.03398 (2023).
[96] Mengjian ZHANG et al. « A Chaotic Hybrid Butterfly
Optimization Algorithm with Particle Swarm Optimization for High-Dimensional
Optimization Problems ». In : Symmetry 12.11 (2020), p. 1800.
[97] Xiangyang ZHI, Xuming HE et Sören SCHWERTFEGER.
« Learning autonomous exploration and mapping with semantic vision ».
In : Proceedings of the 2019 International Conference on Image, Video and
Signal Processing. 2019, p. 8-15.
[98] Yi ZHOu et al. « A PSO-inspired Multi-Robot Map
Exploration Algorithm Using Frontier-Based Strategy ». In :
International Journal of System Dynamics Applications, 2 (avr. 2013),
p. 1-13. DOI : 10.4018/ijsda.2013040101.
[99] Mohammad ZOuNEMAT-KERMANI, Amin MAHDAVI-MEYMAND et
Reinhard HINKELMANN. « Nature-inspired algorithms in sanitary engineering:
modelling sediment transport in sewer pipes ». In : Soft Computing
25.8 (2021), p. 6373-6390.
| 


