4.7.2 Affichage de l'arbre représentant la
problématique
Pour pouvoir manipuler notre application, il est indispensable
de schématiser le problème, y compris sa structure, les noeuds
des trois premiers niveaux constitue la famille des critères, les
feuilles de l'arbre représentent les Actions,
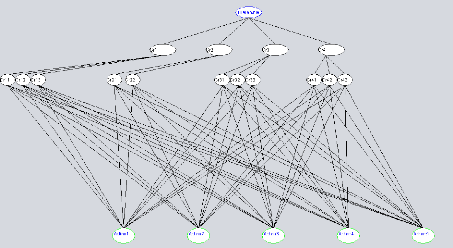
Figure 4.5 Arbre Représentant
l'hiérarchie du problème Décisionnel selon la
méthode AHP
4.7.3 Calcul des poids de chaque noeuds de l'arbre selon
le vecteur de priorité
Nous avons utilisé les formules Mathématique
illustrées dans le chapitre 3 (Etude de Cas),
Notre expérimentation va porter sur les données
suivantes :
Nombre de Niveau est 3, nombre de critère du premier
Niveau est 4 (Cr 1, Cr 2, Cr 3, Cr 4)
Nombre de critère de deuxième niveau est ainsi : Cr
11, Cr 12, Cr 13, Cr 21 Cr22, Cr31 Cr 32
Cr 33, Cr41, Cr 42 , Cr 43.
Nombre de critère de troisième niveau est 0
zéro
Pour les actions, Nous avons Cinq (5) actions
4.7.4 Rangement des actions selon la méthode
AHP
Pour le calcul des Poids selon la méthode AHP , on a
utilisé cent quatre vingt (180) matrice,
tel que :
Chapitre 4 Conception &
Implémentation
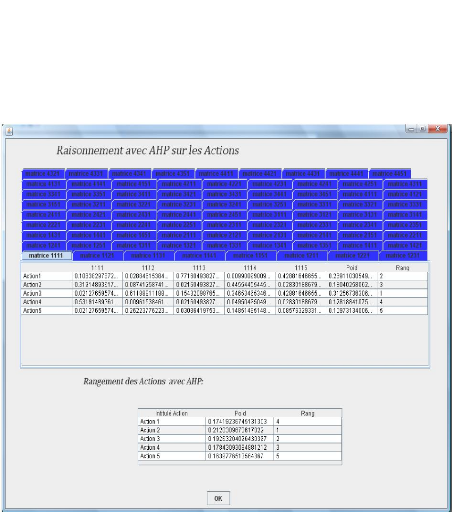
Signification de la matrice 1111, figure 4.5 :
La première valeur 1 (en rouge) : est
interprétés comme la première colonne de la matrice
1111
La deuxième valeur 1 (en vert) est
interprétée comme le critère 1 (cr 1 de la figure 4.4) La
troisième valeur 1 (en jaune) est interprété comme le sous
critère 1 (cr11 de la figure 4.4) La quatrième valeur 1 (en
noire) est interprétée comme l'action 1 (Action 1 de la figure
4.4) 1111 est un chemin de puis la racine (deuxième un (vert)) vers la
feuille (action 1 (quatrième un (noire)))
75
Figure 4.6 Résultats du Rangement des cinq
actions selon la Méthode AHP
Notre application affiche toutes les matrices y compris celles
non utilisés pour pouvoir calculer la priorité par rapport
à toutes l'arbre
Nous remarquons pour cet affichage que :
L'action 1 (wilaya de sidi Bel Abbess) à un poids
égale à 0.174 (17.4%) avec un Rang égal à quatre
(4),
L'action 2 (wilaya de Naama, Commune de Horchaia) a un poids
de 0.212 (21.3%) avec un rang égal à un (1).
L'action 3 (Wilaya de saida, commune de Koléa) a un
poids de 0.192 (19.2%) avec un rang égal à (2)
76
Chapitre 4 Conception &
Implémentation
L'action 4 (wilaya de Sidi Bel Abbes, commune de Ras El Ma) a un
poids de 0.178 (17.8%) avec un rang égal à (3)
L'action 5 (wilaya de Tlemcen commune de Maghnia) a un poids de
0.1639 (16.39%) avec un rang égal à (5)
4.7.5 Rangement des Critères selon la
méthode AHP Flou
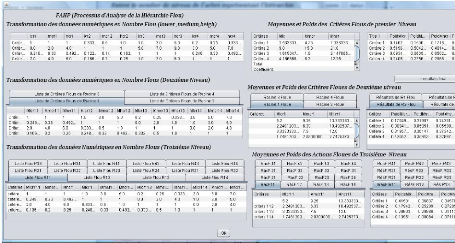
Figure 4.7 Interprétation des résultats
de rangement des Critères de niveau 1 et 2 et 3
La première Matrice est intitulée «
Transformation des données numériques en nombre Flou (Low,
Medium, Heigh) » :
y' La première colonne de la première Matrice
est intitulée « lcr 1 », c'est-à-dire la valeur
minimale du critère un (1).
y' La Deuxième colonne de la première Matrice
est intitulée « mcr 1 », c'est-à-dire la valeur Moyenne
du critère un (1).
y' La troisième colonne de la première Matrice
est intitulée « hcr 1 », c'est-à-dire la valeur
maximale du critère un (1).
y' La Quatrième colonne de la première Matrice
est intitulée « lcr 2 », c'est-à-dire la valeur
minimale du critère deux (2).
y' La Deuxième colonne de la première Matrice
est intitulée « mcr 2 », c'est-à-dire la valeur Moyenne
du critère deux (2).
y' La troisième colonne de la première Matrice
est intitulée « hcr 2 », c'est-à-dire la valeur
maximale du critère deux (2) etc
77
Chapitre 4 Conception &
Implémentation
La deuxième Matrice Intitulée «
Moyennes et Poids des Critères Flous du Premier niveau
»
ü La première colonne de la deuxième Matrice
(au milieu en haut) est « Mlcr », c'est-
avec
à-dire la moyenne des lcr de la première matrice
tel que : Mlcr = El=1,n /cri
n
{
n : nombre de Critére du niveau 1 de la
Hiérarchie i : l'indice du Critère Flou du prmeier
niveau 1 de la Hiérarchie La deuxième colonne de la
deuxième Matrice (au milieu en haut) est « Mmcr »,
c'est-à-dire la moyenne des mcr de la première
matrice tel que : Mmcr = El=1,nmcr1
n
avec :
{
n : nombre de Critére du niveau 1 de la
Hiérarchie i : l'indice du Critère Flou du prmeier
niveau 1 de la Hiérarchie La troisième colonne de la
deuxième Matrice (au milieu en haut) est « Mhcr »,
c'est-à-dire la moyenne des hcr de la première
matrice tel que : Mhcr = El=1,n hcr1
n
avec :
{
n : nombre de Critére du niveau 1 de la
Hiérarchie i : l'indice du Critère Flou du prmeier
niveau 1 de la Hiérarchie La troisième matrice
Intitulée aussi « Moyennes et Poids des Critères Flous du
Premier niveau »
ü La première Colonne de la troisième
matrice (a droite en haut) est « PoidMlcr » ,
c'est-à-dire le Poids des critères par rapport a tous
les critères existant dans le noeud tel que :
Mlcr
PoidMlcr = avec :
El=1,nMlcr i
{
Mlcr : la Moyenne des minimums des Critères (moyenne
de lcr) i : l'indice du Critère Flou du niveau 1 de la
Hiérarchie n : nombre de Critére du niveau 1 de la
Hiérarchie
ü La deuxième Colonne de la troisième
matrice (a droite en haut) est « PoidMmcr » ,
c'est-à-dire le Poids des critères par rapport a tous
les critères existant dans le noeud tel que :
Mmcr
PoidMmcr = avec :
Ei=1,n Mmcrl
Mmcr : la Moyenne des Critères (moyenne de mcr) {i :
l'indice du Critère Flou du niveau 1 de la Hiérarchie
n : nombre de Critére du niveau 1 de la Hiérarchie
ü La troisième Colonne de la troisième
matrice (a droite en haut) est « PoidMhcr » ,
c'est-à-dire le Poids des critères par rapport a tous
les critères existant dans le noeud tel que :
Mhcr
PoidMmcr = avec :
Ei=1,nMhcr i
{
78
Chapitre 4 Conception &
Implémentation
Mhcr : la Moyenne des maximums
Critères (moyenne de hcr) i : l'indice du Critère Flou
du niveau 1 de la Hiérarchie n : nombre de Critére du niveau 1 de
la Hiérarchie La meme explication reste valide pour les autre
matrice sauf que les matrices en dessus sont
respectivement du deuxième niveau, et de troisième
niveau .
| 


