Raisonnement flou pour le rangement des zones industrielles.

ãÓÞ

íááÂÇ ãáÇÚáÅÇ

Département d'Informatique

Mémoire de Fin d'Etudes

Pour l'Obtention du Diplôme de Master en Informatique

Présenté par :

BOUDAOUD LAKHDAR EL AMINE

Domaine : Mathématiques & Informatique Spécialité : MSID

Session Octobre 2016

THÈME

RAISONNEMENT FLOU POUR LE RANGEMENT DES ZONES INDUSTRIELLE

Encadré par : Mr ATMANI BAGHDAD Co-encadré par : Mr TAIBI AISSA

Jury

Président : MR KHELFI Mohamed Fayçal Examinatrice : Mme TAGHEZOUT Noria

CodeMaster : 67 / 2016

Promotion 2015/2016

1

Introduction Générale

Introduction Générale

Dans le cadre de la stratégie de développement du pays, Pour la relance économique nationale et la redynamisation du développement des activités industrielles, des zones industrielles ont été projetées à travers l'ensemble du territoire national. Le souci étant l'équilibre économique des régions et de stabilisation des populations.

Les anciennes zones industrielles installées comme par exemple ARZEW ou EL KERMA dans la wilaya d'ORAN ont causé une mutation épidémiologique et une détérioration de la santé des citoyens. Les décideurs doivent agir précocement en se basant sur des analyses approfondies des critères (facteurs, contraintes) environnementaux et autres pour mener soigneusement leurs décisions pour sélectionner ces nouveaux sites sans risque. L'étude d'aptitude zonales pour le choix de l'emplacement géographique des sites d'habitations, d'industries est de services s'avère primordiale et constitue un vrai problème de décision à référence spatiale.

Ce projet s'articule sur un dispositif juridique et financier et sur une approche méthodologique utilisant un ensemble de critères dont certains sont à caractère spatiale. Notre travail consiste à consolider cette approche en utilisant les modèles d'aide à la décision et les outils géomantiques tel que le Système d'Information Géographique (SIG) qui permet le stockage, le traitement et l'analyse spatiale des informations géographique. Ce travail met la lumière sur l'apport de la modélisation et de l'analyse spatiale des entités géographique en utilisant les SIG (système d'information géographique) pour une étude de criticité et par conséquent à appliquer les méthodes multicritères d'aide a la décision dans un contexte géographique.

Le cas d'étude consiste à ranger ces zones industrielle en adoptant l'approche d'intégration entre les systèmes d'information géographique (SIG) et les méthodes d'analyse multicritères d'aide a la décision (MCDA). Pour le coté décisionnel, AHP (Analytic Hierarchy Process ) est choisie parce qu'elle permet le rangement, elle est populaire et elle est compréhensible par le décideur. Pour réduire la complexité du problème, alléger la hiérarchie et adopter le caractère quantitatif de certains critères à l'aspect subjectifs de la méthode AHP, une base de règles a été conçue et utilisé. Pour remédier aux subjectivités et à l'hésitance des décideurs lors de la pondération, la logique floue est introduite dans la phase de construction des matrices de comparaison binaire requises par AHP. En matière de prise en charge des données géographique une double utilisation des SIG est proposées : En input du module décisionnel pour l'analyse spatiale et l'établissement des cartes critères et dans le module décisionnel pour la Visualisation des résultats sur carte géographiques. En résultat un rangement de la

2

Introduction Générale

meilleure zone a la plus pire est obtenu, ce rangement est utile pour le décideur lors de la réalisation et de l'aménagement de ces zones

Ce document comporte quatre chapitre est voici quelque mots descriptif de chaque chapitre :

1- Aide à la décision Multicritère : ce chapitre met la lumière sur l'importance de la décision dans tous les domaines de la vie et sur les multitudes des critères et des alternatives. Les raisons d'être des méthodes d'analyse multicritères son évoqués avecs toutes les problématiques (choix, tri, rangement, description) et les méthodes d'agrégation. En fin la méthode de Pondération AHP, utilisé dans notre cas d'étude est explicité.

2- Système d'Information Géographique (SIG) : Ce chapitre présent une description de l'information géographique et de ces concepts. Les limites des SIG dans la prise en charge du coté décisionnel nous emmène à souligner l'intérêt de son intégration avec les outils d'aide a la décision (MAC).

3- Etude de cas : Ce chapitre débute par une introduction du problème puis nous explicitons la démarche de notre analyse qui commence par une définition des actions et une étude préalable de criticité.

4- Description du FAHPSIG (AHP Floue Intégrée avec les SIG): dans ce chapitre on décrit les trois étapes de notre travail à savoir : l'implémentation du noyau de SIG, l'implémentation de la méthode d'AMC Floue choisi et la description du module d'intégration réalisé à savoir FAHPSIG

3

Introduction Générale

Objectif

Notre super-objectif est de mettre une pierre dans le rapprochement université-secteur de développement, notre travaille rentre dans le cadre du programme national des nouvelles zones industrielles, ou Il s'agit de recenser par l'ANIREF (Agence Nationale D'Intermédiation et de Régulation Foncière) des sites susceptibles d'être retenues pour abriter des zones industrielles sur la base des demandes exprimées par les Wilaya. Le choix des sites a été basé surtout sur des critères politiques (équilibre régionale, demande des citoyens ...) et sur des critères booléens d'aptitudes zonales (lignes électrique haute tension, autoroute, cimetière...). Le choix étant fait, il constitue une première étape, la deuxième étape c'est la phase d'aménagement et de réalisation notre étude géo-décisionnelle s'intercale entre les deux étapes pour montrer aux décideurs certains limites de leurs choix et d'indiquer aux aménagistes de la deuxième étape de prendre toutes les précautions selon le rang de chaque zones issus de notre étude.

Chapitre 1 Aide à la décision Multicritère

Sommaire

1.1 Introduction 5

1.2 L'aide à la décision 5

Définition 5

1.3 Eléments du processus décisionnel : 5

1.3.1 Les Actions / Alternatives 5

1.3.2 Les Critères 6

1.3.3 Les Paramètres de Subjectivité dans les méthodes de surclassement 7

1.4 Du monocritère au multicritère 7

1.4.1 Méthode monocritère 7

1.4.2 Méthode multicritères 8

1.5 Les problématiques de l'aide à la décision 9

1.5.1 Problématique du Choix 9

1.5.2 Problématique du Tri 9

1.5.3 Problématique de Rangement 10

1.5.4 Problématique de la Description 11

1.6 La méthode AHP 11

1.6.1 Définition 11

1.6.2 Le but de la méthode AHP 11

1.6.3 Caractéristiques de la méthode AHP 11

1.6.4 Démarche de la méthode 12

1.6.4 Avantages de la méthode AHP 17

1.6.5 Limites de la méthode AHP 17

1.7 Conclusion 17

Liste des Figures

Figure 1.1 La problématique du choix. (Ginting, 2000) 9

Figure 1.2 La problématique du tri. (Ginting, 2000) 10

Figure 1.3 La problématique du rangement. (Ginting, 2000). 10

Figure 1.4 les étapes d'application de l'AHP 13

Figure 1.5 la hiérarchie du problème 14

4

5

Chapitre 1 Aide à la décision Multicritère

Chapitre 1: Aide à la décision multicritère

1.1 Introduction

La majeure partie des activités humaines nécessite de prendre quotidiennement des décisions, que cela soit au niveau d'un pays, d'une région, d'une administration, d'une collectivité locale, d'une entreprise, au sein de la cellule familiale ou tout simplement à l'échelle de l'individu.

La décision est, avant tout, un choix que l'on doit réaliser devant différentes possibilités offertes et qui ne sont pas directement comparables ou qui présentent des aspects contradictoires

1.2 L'aide à la décision

Définition

Nous reprenons la définition de (B.Roy, 1993) donnée par Chakhar dans sa thèse d'état (S. Chakhar, 2006) :

"L'aide à la décision est l'activité de celui qui, prenant appui sur des modèles clairement explicités mais non nécessairement complètement formalisé, aide à obtenir des éléments de réponses aux questions que se pose un intervenant dans un processus de décision et normalement à recommander, ou simplement à favoriser, un comportement de nature à accroître la cohérence entre l'évolution du processus d'une part, les objectifs et le système de valeurs au service à partir desquels cet intervenant se trouve placé d'autre part". Constatons que cette définition reste modeste quant à son objectif et qu'il ne s'agit pas d'une recherche de la "réalité". L'aide à la décision est donc un processus qui utilise un ensemble d'informations disponibles à un instant donné, afin de formuler un problème et aboutir à une décision sur un objet précis.

1.3 Eléments du processus décisionnel :

1.3.1 Les Actions / Alternatives

Une action est une représentation des éléments de la solution qui contribue à la décision

par exemple (une zone industriel, un site, etc.).

? Définition (Action Potentielle) : une action potentielle est une action réelle ou fictive provisoirement jugée réaliste par un acteur au moins susceptible d'être prise dans le processus décisionnel ; l'ensemble des actions potentielles sur lequel l'aide à la décision prend appui au cours d'une phase d'étude est noté A.

6

Chapitre 1 Aide à la décision Multicritère

1.3.2 Les Critères

Face à un problème de décision, le décideur et l'homme d'étude vont être amener à juger et à évaluer les différentes actions potentielles. Pour rendre compte de tels jugements, on fait appel à la notion de critère qui peut être un facteur favorisant la prise de décisions ou une contrainte à éliminer. Les critères vont être le moyen utilisé pour décrire les actions.

Formellement, on représentera les critères par des fonctions à valeurs réelles. On peut citer Vincke qui donne une définition concise des critères (R.Ginting, 2000).

? Définition1 : (P.Vincke, 1989) a défini un Critère ainsi : un critère est une fonction g, définie sur l'ensemble A des actions, qui prend ses valeurs dans un ensemble totalement ordonnés, et qui représente les préférences du décideur selon un point de vue. Lorsque le problème repose sur la considération de plusieurs critères, nous les notons ?? 1.. . ??n

? Définition2 : (B.Roy, 1993) a défini un critère ainsi : Une fonction g à valeurs réelles définies sur A est, pour un acteur Z, une fonction critère ou un critère appréhendant le sous

nuage des conséquences v_g(A) si :

a. Le nombre g(a) est déterminé si et seulement si une évaluation B_g(a) de V_g(a) est disponible ;

Le modèle B_g(A) qui fournit cette évaluation est appelé support de la fonction critère g.

b. L'acteur Z reconnait l'existence d'un axe de signification sur lequel deux actions potentielles quelconques a et a' peuvent être comparés relativement aux seuls aspects des conséquences que recouvrent v(A) et il accepte de modéliser conformément à :

??(??') = ??(??) => ??'??????

Ou Sg désigne une relation de surclassement restreint à l'axe de signification du critère g(faisant en particulier abstraction de tous les aspects de conséquence non modélisées dans le support de g).Chaque action a de A sera donc représentée dans l'espace des critères, E= E*... *En par un vecteur (?? ??(??), ... , ????(??)), que l'on appelle vecteur de performances. L'ensemble A des actions sera représenté par une matrice appelée matrice de performances.

1.3.2.1 Famille de critères

Dans tout problème multicritère, il convient de considérer un ensemble de critères que l'on

nomme Famille de critères et qui l'on notera F = {??1, ... , ??} (on trouvera aussi la notation F = {1, ..., n}). Pour que la famille F constitue une représentation appropriée des points de vue à prendre en compte dans la modélisation des préférences.

7

Chapitre 1 Aide à la décision Multicritère

(H.laurent, 2010) Note que Roy définit la notion de famille Cohérente de critère à l'aide des trois propriétés suivantes. Ainsi une famille de critère sera dite cohérente si elle respecte :

1- L'Exhaustivité : il s'agit de ne pas oublier un critère pertinent pour la résolution de la problématique décisionnelle posée.

2- La Cohésion : si une action a est égale à une action b pour tous les critères sauf un où elle lui est supérieure, ceci signifie que l'action a est globalement supérieure à l'action b.

3- La Non Redondance : il ne doit pas y avoir une redondance entre les critères. Leur nombre doit être tel que la suppression d'un des critères ne permet plus de satisfaire les deux conditions précédentes.

1.3.3 Les Paramètres de Subjectivité dans les méthodes de surclassement

1.3.3.1 Poids

Qualifie l'importance relative d'un critère cj donné vis à vis des autres critères.

1.3.3.2 Seuil d'indifférence

Il s'agit de la plus petite différence qui est significative. En dessous de ce seuil, il est

impossible de départager les deux actions.

1.3.3.3 Seuil de préférence

Il s'agit du seuil à partir duquel la différence entre deux actions est perceptible et fait préférer

l'une à l'autre.

1.3.3.4 Seuil de veto

Permet de fixer une notion supplémentaire. Si ce seuil est dépassé sur un critère, alors l'action

ne peut être prise en considération. Il définit donc une situation intolérable pour un des décideurs. Il s'exprime par l'écart maximum acceptable autour de la valeur de l'évaluation.

1.4 Du monocritère au multicritère

1.4.1 Méthode monocritère

La solution d'un problème monocritères est facile à modéliser. Un problème de décision

monocritère est du type Opt {??(x) : x A} ou A : Ensemble des actions admissibles, g : Fonction critère à optimiser.

Dans cette définition la comparaison de plusieurs actions se fait suivant un seul critère alors que d'après (L.Mayster, 1994) :

? La comparaison de plusieurs actions se fait rarement suivant un seul critère.

? Les préférences sur un critère sont dans bien de cas, difficilement modélisable par une fonction.

? Lorsqu'il y a plusieurs objectifs, il est impossible de les atteindre tous à la fois.

8

Chapitre 1 Aide à la décision Multicritère

1.4.2 Méthode multicritères

Lorsqu'il s'agit de plusieurs critères ??1, ??2, ... .. , ?? ?? le problème posé est de la forme

?????? {??1(??),??2(??),...,????(??) : ?? ??} .

On peut conclure de cette définition formelle qu'il existe une action meilleure ou optimale par rapport à toutes les autres simultanément mais cette conclusion est subjective.

L'optimisation dans ce cas éloigne le problème de son contexte.

Dans le contexte multicritères l'approche d'optimisation n'a pas de sens il ne s'agit pas de chercher une vérité caché, mais plutôt d'aider le décideur à progresser vers une action de compromis (S. Chakhar, 2006)

La recherche opérationnelle pour laquelle on fixe un objectif ambitieux qui est la désignation en toutes circonstances de la meilleure décision (L'optimum) mène à une certaine exclusivité des décisions alors que le domaine nécessite une certaine complémentarité. Ben mena (Mena, 2000), parle de la misère de l'optimisation par contre au bonheur du multicritère et cite l'exemple suivant :

Si pour acheter une voiture, un individu ne considère que l'aspect financier tout le monde roule en 2CV. Le normal pour cet individu c'est d'énumérer les critères suivants : cout, confort, sportivité, sécurité, économie à l'usage, environnement. Certains de ces critères sont contradictoires.

1.4.2.1 Raison d'être des méthodes multicritères

La programmation linéaire en recherche opérationnelle qui consiste à résoudre les problèmes des décisions par l'optimisation d'une unique fonction économique montre certains faiblesses surtout quand il s'agit de problèmes à caractères spatiales.

Cela constitue une raison d'être des méthodes d' analyse multicritères. D'autre raisons d'être des MAC (Méthode d'analyse multicritères) et des ASMC (méthode d'analyse multicritères spatiales) ou des méthodes multicritères d'aide à la décision dans un contexte géo spatiale sont (Mena, 2000):

? La densité de la population n'autorise pas le gaspillage des ressources naturelles.

? Ces méthodes intègrent tout type de critère.

? Leur direction c'est d'aller vers un compromis pour la décision, non vers un optimum.

? Le domaine de la gestion environnementale qui influe les mutations épidémiologiques constitue un secteur porteur pour les MAC.

En utilisant une méthode multicritère, on cherche à trouver la solution la plus adéquate compte tenu des différents critères qui sont généralement contradictoires.

9

Chapitre 1 Aide à la décision Multicritère

1.4.2.2 Définition de l'aide multicritère à la décision

Vincke en 1989 définie l'aide multicritère à la décision de la façon suivante : « L'aide

multicritère à la décision vise, comme son nom l'indique, à fournir à un Décideur des outils lui permettant de progresser dans la résolution du problème de décision ou plusieurs points de vue, souvent contradictoires, doivent être pris en compte ». (S. Cahkhar , 2006)

1.5 Les problématiques de l'aide à la décision

La première étape du processus d'aide à la décision va consister à définir vers quoi la prescription de l'homme d'étude au décideur va s'orienter. Cette étape passe par le choix d'une problématique.

(B.Roy, 1998) définit quatre problématiques de référence, le choix, le tri, le rangement et la description, A celles-ci il nous semble important, tout particulièrement dans le cadre de notre étude, d'en ajouter une cinquième, la problématique de la typologie.

1.5.1 Problématique du Choix

Il s'agit de la problématique la plus classique en aide à la décision. Elle consiste à

sélectionner un sous-ensemble aussi restreint que possible d'actions A dans le cas le plus favorable à un singleton d'un ensemble A qui justifie l'élimination des autres actions. Cette problématique généralise la problématique de la recherche opérationnelle. Elle aboutit à la mise au point d'une procédure de sélection.



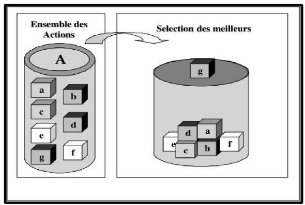
Figure 1.1 La problématique du choix. (Ginting, 2000)

1.5.2 Problématique du Tri

Cette problématique consiste à affecter les actions de A à des catégories prédéfinies

(caractérisées par exemple par des actions de référence). Contrairement aux autres problématiques, on ne compare pas les actions de A entre elles mais on se fonde uniquement

10

Chapitre 1 Aide à la décision Multicritère

sur les comparaisons des actions de A aux actions de référence, il s'agit d'une évaluation intrinsèque des actions. Ici, on parlera de procédure d'affectation à des catégories.



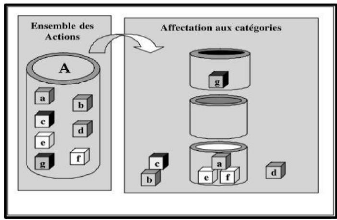
Figure 1.2 La problématique du tri. (Ginting, 2000)

1.5.3 Problématique de Rangement

Il s'agit sans doute de la problématique la plus ambitieuse. Elle a pour objectif d'ordonner les

actions de A. Cependant, on ne recherche pas nécessairement un ordre complet sur les actions au sens d'une relation de préférence globale ; on cherche plutôt à regrouper les actions en classes d'équivalence, celles-ci étant totalement ou partiellement ordonnées. La procédure recherchée est une procédure de classement.



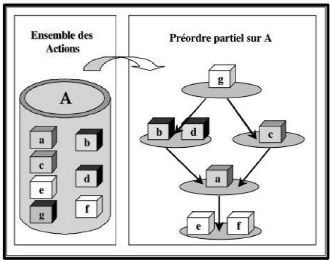
Figure 1.3 La problématique du rangement. (Ginting, 2000).

11

Chapitre 1 Aide à la décision Multicritère

1.5.4 Problématique de la Description

Cette problématique fait généralement partie de la première phase d'analyse des

problématiques précédentes. Elle consiste juste à éclairer l'analyse des actions en aidant le décideur à appréhender celles-ci. Cela passe par la définition des conséquences élémentaires et des critères, ainsi que par le choix ultérieur d'une autre problématique.

1.6 La méthode AHP

Plusieurs méthodes multicritères existent dans la littérature, dans le cadre de notre étude, nous nous intéressons à la méthode AHP (Analytic Hierarchy Process)

Tout d'abords, nous présenterons l'intérêt et la description de cette méthode, en mettant en

évidence les différentes étapes selon (T.Saaty, 1980) ensuite nous terminons par un exemple plus détaillés de la méthode.

1.6.1 Définition

La méthode AHP représente l'une des méthodes les plus connue et les plus utilisée créé

par T.L Saaty mathématicien américain, elle procède a hiérarchiser le problème en arborescence puis à comparer par paire entre tous les éléments du même niveau afin de leur attribuer un poids final de plus c'est une méthode dite compensatoire car elle assume une agrégation complète entre les critères, c'est une méthode de critère unique de synthèse.

C'est une méthodologie visant la résolution de problèmes ayant plusieurs alternatives en appliquant plusieurs critères de décision simultanément. Elle est systématique, flexible et simple, et est utilisée fréquemment par les chercheurs et les praticiens afin de comparer plusieurs objectifs ou alternatives (J.Malczewski, 2006)

1.6.2 Le but de la méthode AHP

La méthode AHP permet de décomposer un problème selon la hiérarchie des différents

critères et sous-critères de décision associés à ce problème et de comparer ces critères entre eux, deux à deux, à l'aide d'une échelle de pondération afin de mettre en lumière la solution qui répond le mieux aux critères de décision. La racine correspond à l'objectif principal comme l'achat d'une voiture, les feuilles correspondent aux différentes alternatives offertes comme une Renault, une Mercedes ou une Volkswagen.

1.6.3 Caractéristiques de la méthode AHP

- Unités de mesures : peuvent être qualitatives ou quantitatives, des valeurs relatives ou absolues pour établir des priorités.

- Structure hiérarchique : qui permet de mettre les éléments du problème dans différents niveaux et dans de groupes à caractéristiques similaires.

- Interdépendance : qui permet de considérer les éléments du système sans insister dans un raisonnement linéaire.

12

Chapitre 1 Aide à la décision Multicritère

- Consistance : une cohérence qui permet de garder une logique des jugements utilisés pour déterminer les priorités.

- Synthèse : permettant d'obtenir une appréciation générale de la désirabilité de chaque alternative.

- Identification des priorités : permet de considérer la priorité relative de chaque critère pour ainsi obtenir la meilleure alternative selon les objectifs identifiés.

- Unicité : une flexibilité qui permet son utilisation dans un éventail varié de problèmes non structurés.

1.6.4 Démarche de la méthode

La méthode AHP a recours à différentes formes de connaissances, au fur et à mesure de

son déroulement. Elle fait en particulier appel à l'imagination et à l'expérience pour définir la hiérarchie du problème. Lors du diagnostic ou de l'expertise, elle fait appel à la logique et à l'intuition des décideurs pour proposer des appréciations. Elle permet ainsi d'identifier, de comprendre et d'évaluer les interactions d'un système considéré dans sa globalité (T.Saaty, 1980)

La méthode AHP est construite à partir de différents niveaux de critères. Elle permet ainsi

? décomposer un problème complexe et non structuré en ses éléments constituants.

? modéliser ces éléments sous la forme d'une structure hiérarchique.

? quantifier l'importance relative de chaque élément à partir de jugements subjectifs.

? et enfin, de synthétiser l'importance relative de chaque élément de la hiérarchie en une préférence globale afin de déterminer des priorités parmi les actions potentielles.

La méthode AHP permet de compenser la dégradation de performance d'une action sur certains critères par sa performance sur d'autres. Une telle méthode est dite compensatoire. Afin de mesurer les qualités intangibles d'éléments de nature différente, elle repose sur l'utilisation d'une échelle de mesure unique. Elle permet ainsi de résoudre un grand nombre de problèmes décisionnels de façon quantitative en élaborant un modèle d'aide à la décision, représenté sous la forme d'une hiérarchie, elle repose principalement sur une démarche descriptive afin de tenir en compte la nature « humaine » plutôt que de lui imposer un mode de pensée particulier.

1.6.4.1 Les étapes de l'application

Nous allons détailler dans ce qui va suivre les différentes étapes de la méthode AHP (voir la figure 1.4).

13

Chapitre 1 Aide à la décision Multicritère



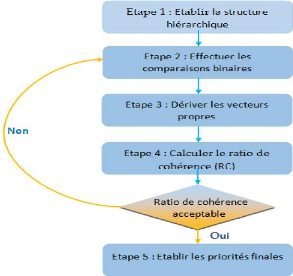
Figure 1.4 les étapes d'application de l'AHP

Étape 1 : Etablir la structure hiérarchique

La première étape consiste à décomposer le problème complexe en une structure

hiérarchique à travers des niveaux qui sont :

Niveau 0 : Définir l'objectif cible.

Niveau 1 : Définir les critères de décision ou d'analyse.

Niveau intermédiaire : Il peut y avoir plusieurs pour déterminer les sous critères

Dernier Niveau : Définir les alternatives ou les actions possibles.

La figure 1.5 donne un aperçu sur la hiérarchie d'un problème.

14

Chapitre 1 Aide à la décision Multicritère



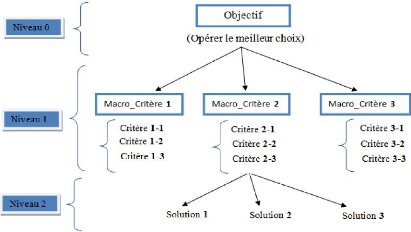
Figure 1.5 la hiérarchie du problème

Étape 2 : Effectuer les pondérations binaires

Cette étape consiste à étudier les points suivants :

- Comparer l'importance relative de tous les éléments appartenant à un même niveau de la hiérarchie pris deux par deux, par rapport à l'élément du niveau immédiatement supérieur. - configurer une matrice carrée réciproque formée par les évaluations (K*K), K étant le nombre d'éléments comparés, nous obtenons une matrice (voir exemple).

aij = 1 et

a = aij avec aji = liaij (valeur réciproque)



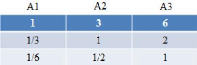
Tableau 1.1 Exemple d'une matrice de comparaison par paire.

Chapitre 1 Aide à la décision Multicritère

Degré de préférence

1		Importance égale
2		Importance faible
3		Importance assez modérée
4		Importance modérée
5		Importance assez forte
6		Importance forte
7		Importance très forte
8				Importance extrême
9				Importance capitale

Tableau 1.2 Echelle de Saaty (Fiat, 2007).

Étape 3 : Déterminer les vecteurs propres

La détermination des priorités des éléments de chaque matrice se fait par la résolution du problème de vecteurs propres. Calculer l'importance relative de chacun des éléments de la hiérarchie à partir des évaluations obtenues à l'étape précédente, et l'importance relative des différents critères est exprimée par les valeurs du vecteur propre normalisé à 1. Plus grande est cette valeur et plus important est le critère correspondant.

Étape 4 : Calculer le ratio de cohérence (RC)

Les réponses obtenues présentent souvent un certain degré d'incohérence. La méthode AHP n'exige pas que les jugements soient cohérents ni transitifs, par contre Saaty a défini un indice de cohérence (IC). Plus l'indice de cohérence devient grand et plus les jugements de l'utilisateur sont incohérents et vice versa. IC est ensuite comparé à des valeurs critiques obtenues par simulation. Saaty a défini, par expérimentation, un ratio de cohérence comme le rapport de l'indice de cohérence calculé sur la matrice correspondante aux jugements du décideur et de l'indice aléatoire (IA) d'une matrice de même dimension. Une idée est donnée dans le tableau 1.3.



Tableau 1.3 Les indices de cohérence aléatoire Satty (1984).

15

16

Chapitre 1 Aide à la décision Multicritère

Le ratio de cohérence est donné par la formule suivante :

RC = IC/I??

RC : est le ratio de cohérence.

IA : est un indice aléatoire.

IC : est l'indice de cohérence.

L'indice de cohérence aléatoire est calculé par cette formule :

IC = ( ??max - K) / (K - ??)

Avec : K est le nombre d'élément comparé ëmax est la valeur propre maximale.

Le ratio de cohérence peut être interprété comme la probabilité que la matrice soit complétée aléatoirement. La cohérence globale d'appréciation est évaluée au moyen de ce ratio de cohérence RC. Toujours selon Saaty, la valeur de ce dernier doit être au plus égale à 10%. Dans le cas où cette valeur dépasse 10%, les appréciations peuvent exiger certaines révisions.

Une fois calculé, le ratio de cohérence (RC) final doit être vérifié selon le niveau acceptable proposé par (T.Saaty, 1980) en fonction de la taille de la matrice. Lorsque le ratio de cohérence dépasse la valeur respective du tableau ci-dessous, on considère que les jugements sont trop aléatoires. Il faut alors réviser l'analyse afin de parfaire les jugements et ainsi, obtenir un ratio de cohérence final qui soit acceptable. Les valeurs données dans le tableau 1.4 montrent les ratios de cohérence acceptables par Saaty.

Taille de la matrice (n)		Ratio de cohérence acceptable
3		0,05
4		0,08
5 et +		0,10

Tableau 1.4 Les ratios de cohérence acceptable (Satty, 1984). Étape 5 : Etablir les priorités finales

17

Chapitre 1 Aide à la décision Multicritère

Le principe de la synthèse des priorités est de multiplier les priorités locales de chaque niveau par les priorités globales du niveau père pour obtenir les priorités globales de toute la hiérarchie par la suite on ajoute les priorités globales du niveau le plus bas (généralement ce sont les alternatives).

1.6.4 Avantages de la méthode AHP

? Simplicité d'utilisation

? Élimination des ennuis dus aux unités de mesure

? Bonne illustration graphique

? Évaluation de plusieurs attributs à la fois (souvent contradictoires)

? Possibilité de valider la cohérence

1.6.5 Limites de la méthode AHP

La méthode AHP comporte toutefois certaines limites qui doivent être prises en compte lors

de son utilisation : (S.DelVecchio, 2006)

a) Renversement du rang

Une des principales critiques de la méthode AHP réside dans le fait qu'elle permet un renversement du rang des options dit « Rank reversal » lors de l'ajout ou la suppression d'options ou de critères.

En d'autres termes, si une nouvelle option est ajoutée (ou enlevée) de l'analyse, les options existantes perdraient (ou gagneraient) de la priorité sous chacun des objectifs de la hiérarchie Cela se produit lorsque le système est fermé, c'est-à-dire que les ressources sont limitées et ainsi redistribuées parmi l'ensemble des options.

b) Nécessité d'interprétation des résultats

Un autre point important à retenir est que les résultats obtenus grâce à la méthode AHP peuvent s'avérer très utiles dans une prise de décision. Par contre, le jugement et l'expérience d'experts sont et seront toujours nécessaires pour interpréter l'ordre définitif des options ainsi que la décision finale. La méthode AHP est une aide pour l'analyse mais ne pourra jamais s'y substituer totalement.

c) Subjectivité de l'analyse

Il est important de noter qu'une analyse individuelle avec la méthode AHP sera toujours influencée par la vision et les valeurs personnelles du répondant. En d'autres mots, une notion de subjectivité sera inévitablement introduite dans l'analyse puisqu'il s'agit de l'intuition du gestionnaire et sa perception du contrat d'impartition à l'étude.

1.7 Conclusion

Nous présentons dans ce chapitre les principaux concepts autour desquels s'articule l'aide mul-

18

Chapitre 1 Aide à la décision Multicritère

ticritère à la décision. Ça nous a permis d'une part d'expliquer le principe des méthodes d'analyse multicritère ainsi que l'apport théorique et pratique qu'elles sont susceptibles d'apporter aux décideurs.

La méthode AHP basée sur des comparaisons deux à deux, est une méthodologie systématique, flexible et simple, utilisée fréquemment par les chercheurs et les praticiens. Elle permet de prendre en compte à la fois des critères quantitatifs et qualitatifs.

cette méthode a déjà prouvé son efficacité dans divers domaines notamment dans le domaine environnemental où elle est souvent associée au systèmes d'information géographique (SIG) afin de faire face à des problématiques diverses, à caractère spatial de nature multidimensionnelle, interdisciplinaires et mal définis, nécessitant la définition de plusieurs critères souvent conflictuels dont l'importance n'est pas la même.

Dans le chapitre qui suit, nous allons aborder les différents concepts liés aux systèmes d'information géographique.

19

Chapitre 2 Système d'Information Géographique

Sommaire

2.1 Introduction 21

2.2 L'information géographique 21

2.2.1 Définition de l'information géographique: 21

2.2.2 Le cycle de vie de l'information géographique 22

2.2.3 La cartographie 23

2.2.4 Modélisation de l'espace géographique 24

2.3 Les systèmes d'information géographique(SIG) 25

2.3.1 Definitions : 26

2.3.2 La structure d'un SIG 27

2.3.3 Enjeux et domaine d'application des SIG 27

2.3.4 Principe de fonctionnement d'un SIG 27

2.3.5 Modes d'acquisition et de représentation des données géographique par un SIG 28

2.3.6 SIG et modélisation géographique 29

2.3.7 Exemples des logiciels SIG : 29

2.4 Intégration entre SIG et AMC 30

2.4.1 Le caractère multicritères des données géographiques 30

2.4.2 Limite de l'outil SIG dans le traitement décisionnel multicritère 30

2.4.3 Limite des Méthodes multicritères pour la prise en charge de l'information géographique 30

2.4.4 Mode d'intégration SIG -AMC : 31
2.4.5 Les modes d'intégration SIG et AMC Les travaux de Chakhar et d'autres ont révélés

quatre modes d'intégration : 31

2.4.6 Travaux connexes 32

2.5 Conclusion 33

Liste des figures

Figure 2.1 L'information géographique (C.Weger, 1999) 22

Figure 2.2 Cycle de vie de l'information géographique 22

Figure 2.3 Exemple d'information géographique sur carte d'intérêt sanitaire et

épidémiologique (Paulson, 2014). 23

Figure 2.4 Carte physique du monde. (Robinson, 2012) 24

Figure 2.5 Système d'Information Géographique(SIG). (A.Atmani, 2013) 26

Figure 2.6 Structure d'un SIG. (S.Chakhar,2006) 27

Figure 2.7 Superposition des couches thématique (C.Sébastien, 2003). 28

20

Chapitre 2 Système d'Information Géographique

Figure 2.8 Modèle raster et modèle vecteur. (C.Sébastien, 2003) 28

Figure 2.9 Schéma conceptuel d'intégration SIG-AMC (S.Chakhar, , 2006) 31

Figure 2.10 Travaux connexes d'intégration SIG-AMC. 33

21

Chapitre 2 Système d'Information Géographique

Chapitre 2 : Système d'information

géographique

2.1 Introduction

Historiquement, le terme GIS (geographic information system), en français SIG (système d'information géographique) a été utilisé pour la première fois par Roger Tomlinson en 1963, alors que le premier SIG a été développé au début des années 1960 par Howard T. Fisher de l'Université Harvard. Depuis leurs apparitions au début des années soixante, différents SIG, de plus en plus sophistiqués, ont vu le jour.

Les SIG sont utilisés de façon croissante dans des domaines très variés : urbanisme (établissement de schémas directeurs, aménagement et gestion des plans d'occupation du sol ...), études économiques et socio-économiques (population, emploie, logement, "géo marketing"), planification et aménagement du territoire, gestion des ressources naturelles, protection de l'environnement (gestion des déchets et de la pollution ainsi que des espaces "naturels"), sciences de la terre (géologie, géodésie, pédologie, etc.), applications militaires, gestion de réseaux de transports, de télécommunications et de distribution (eau, gaz, électricité, etc.), agriculture (maîtrise des pollutions agricoles, prévention des incendies et des inondations), environnement, gestion des risques naturels ou technologiques et de la sécurité civile (la lutte contre les risques majeurs et la gestion des moyens d'intervention en cas de crise font de plus en plus appel à la technologie SIG), l'hydrographie et l'océanographie, etc. (S. Chakhar, 2006)

2.2 L'information géographique

2.2.1 Définition de l'information géographique:

L'information géographique est tous qu'on perçoit de la réalité naturelle, elle peut décrire des objets discrets, tel qu'un bâtiment avec sa position, sa forme et ses coordonnées ou une route avec ces paramètres ou une forêt, un fleuve etc....

Elle peut représenter un phénomène naturel continu tel que la température, la sismicité etc.... La dimension d'un objet géographique peut varier de l'immensité d'un continent à la grandeur d'une région jusqu' une petite source d'eau. La complexité peut être celle d'une immense ville comme Alger ou new York. Les objets géographiques se caractérisent par :

? Un aspect géométrique qui se résume généralement par la position, l'air, la longueur, le périmètre...

? Un aspect topologique qui se résume selon (M.J.Egenhofer, 1990) par trois éléments clé : Le bord, le corps intérieur et le corps extérieur.

Ainsi la description d'un phénomène spatiale se fait en décrivant :

? Les propriétés géométriques des objets du phénomène : Décrit les relations géométriques de proximité entre les entités au niveau qualitatif par une métrique (distance).

? La topologie du phénomène : C'est la perception des objets spatiaux dans leur contexte, c'est le niveau qualitatif abstrait que nous abordons.

22

Chapitre 2 Système d'Information Géographique

? Les dimensions thématiques du phénomène

L'Information Géographique

Information Monde réel

Phénomène Observé

Saisie des Données Technique de Saisie (Codeurs)

Données Brutes ou Prétraitées

Données Interprétées Techniques cartographiques

Carte

Information Extraite Lecture

Modèle Mental du Monde Réel

Figure 2.1 L'information géographique (C.Weger, 1999)

2.2.2 Le cycle de vie de l'information géographique

La figure 2.2 montre que l'information géographique est la base de toutes les étapes indiquées dans le schéma. Le cycle de vie est un processus itératif, quand on passe une étape on est susceptible d'y revenir à chaque moment.



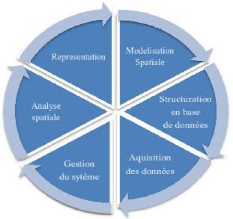
Figure 2.2 Cycle de vie de l'information géographique

23

Chapitre 2 Système d'Information Géographique

2.2.3 La cartographie :

Depuis longtemps l'homme n'a pas trouvé pour représenter ou modéliser sa perception de la réalité géographique pour faire ces analyses ou ces communications que la carte. En 1854 Le médecin britannique John Snow a utilisé une carte (figure 2.3) pour trouver le lien entre le choléra et les sources polluées des eaux dans la ville de Londres.



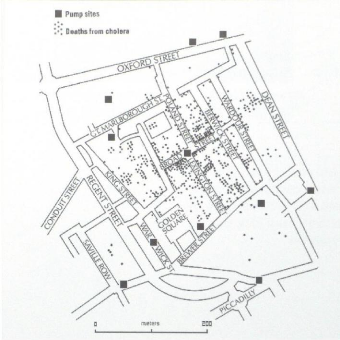
Figure 2.3 Exemple d'information géographique sur carte d'intérêt sanitaire et
épidémiologique (Paulson, 2014).

Cartographier est donc un processus d'analyse de l'espace géographique ou d'un territoire qui consiste à représenter les éléments intéressant à partir d'une vision globale du monde réelle, il s'agit aussi de représenter les relations entre ces éléments pour obtenir un modèle, ce n'est dans la plus part des cas qu'une carte géographique.

Les fonctions d'une carte géographiques peuvent se résumer comme suit (R.Caloz, 2008):

? La reconnaissance d'un lieu.

? La représentation spatiale d'objets ou de classes d'objets.

? La représentation d'inventaires thématiques et leur distribution spatiale.

? La représentation de phénomènes dynamiques au moyen de signes (direction

d'écoulement de nappe phréatiques, de vents dominants, etc.)

La cartographie de l'espace géographique constitue ainsi la première étape d'analyse spatiale.

24

Chapitre 2 Système d'Information Géographique

2.2.3.1 L'espace géographique

Définition

Selon (R.Caloz, 2008) C'est l'étendue terrestre utilisé et aménagé par les sociétés en vue de leur reproduction au sens large, soit non seulement pour se nourrir et s'abriter, mais dans toute la complexité des actes sociaux.

2.2.3.2 Le territoire

Définition

Selon (R.Caloz, 2008) C'est une portion de l'espace géographique circonscrite par des limites politico-administratives : une commune, une wilaya, un pays

2.2.3.3 Les éléments de la cartographie

Nous avons cités au paravent que la cartographie, élément primordial de la géographie est une modélisation. Une carte est élaborée selon l'objectif poursuivi qui implique une thématique déterminée (Topographie, réseaux routier, catégorie d'occupation de sol, les unités de végétation, géologie ...) Une carte est donc liée au concept de thème d'où l'appellation 'carte thématique'. Une carte est un modèle de la réalité contenant la représentation géométrique des objets et des catégories d'objets avec une logique graphique et sémiologique. Le concept d'échelle d'une carte est en lui-même un processus d'abstraction indiquant la précision, La légende, L'habillage et la clé d'une carte constitue un moyen de communication homme carte.

En résumé, on peut considérer une carte comme une base de données géographique dont toute information est exprimée d'une part par une représentation graphique et d'autre part par la légende qui l'accompagne.

2.2.4 Modélisation de l'espace géographique :

La modélisation cartographique vient pour réduire la complexité du monde réelle dans un contexte géographique. Lors de la conception du modèle on ne retient que les éléments jugés significatif pour le phénomène étudié de manière à mieux comprendre son fonctionnement.



Figure 2.4 Carte physique du monde. (Robinson, 2012)

25

Chapitre 2 Système d'Information Géographique

Un modèle dans ce sens est une réduction contrôlé de la réalité. Il est en général finalisé dans la mesure où il est conçu pour satisfaire des objectifs préalablement fixés. Ainsi, un modèle du territoire dépend fortement du regard disciplinaire : géologue, hydrologue, épidémiologiste Les étapes d'un processus de modélisation géographique sont résumées par (R.Caloz, 2008) comme suit :

? Appréhension globale de l'espace géographique par la sélection des éléments jugés importants.

? Identification des éléments significatifs en leurs affectant un nom.

? Identification des relations existantes entre les éléments.

? Détermination des propriétés des éléments et de leur relation.

2.2.4.1 Le modèle descriptif et prédictif

a- Il est descriptif lorsqu'il représente une sorte de photographie de la réalité sans se mêler de l'évolution et de la dynamique de cet état.

Exemple :

Une base de données géographique(BDG) peut être considérer comme modèle descriptif de la réalité géographique.

b- Un modèle est prédictif lorsqu'il décrit l'évolution d'un phénomène de manière à pouvoir prédire un état futur à partir d'un état initiale connu. Sa mise en oeuvre repose sur une expression mathématique liant les variables significatives.

2.2.4.2 Modèles d'appréhension de l'espace

L'espace géographique est perçu à travers une distribution discrète des objets spatiaux, cette distribution nous conduit à définir des phénomènes à distribution discrètes tel un aéroport, un segment de cours d'eau, un foret etc. ...

Il peut être perçu à travers une distribution continue, par exemple la température d'un espace géographique, l'altitude etc. ...

2.3 Les systèmes d'information géographique(SIG)

Le recours à l'informatique et aux techniques de base de données est tout à fait légitime vu l'énorme quantité des informations géographique et la complexité de ces dernières et de plus : Le développement des technologies d'acquisition tel que le GPS, l'imagerie aérienne, la télédétection a conduit à une production de quantité immense des données géographiques.

Le terme SIG a été utilisé par Roger Tomlinson en 1963, alors que le premier SIG a été développé au début des années 1960 par Howard T. Fisher de l'Université Harvard. L'année 1962 a vu le développement du premier système d'information géographique opérationnelle au CANADA (CGIS) (S. Chakhar, 2006). Le SIG hérite du SI (système d'information) une multitude de définition. C'est un système informatique qui permet de stocker les données géographiques (ORACLE utilise le type SDO_géometry) dans les bases de données géographique et de faire des requêtes et des analyses spatiales et de produire des visualisations à la demande de l'utilisateur sous forme de cartes thématique ou de position. On peut citer les definitions suivantes :

26

Chapitre 2 Système d'Information Géographique

2.3.1 Definitions :

Definition 1 :

Geographic Information System--A system of hardware, software, data, people,

organizations and institutional arrangements for collecting, storing, analyzing, and

disseminating about areas of the earth. (S. Chakhar, 2006)

Selon cette definition, un SIG est un ensemble de sous-systèmes qui devra inclure les

composantes nécessaires (figure 2.5) :

- à l'acquisition des données d'entrée (données issues des cartes, données de recensement,

données terrain, etc.),

- au stockage, à la représentation et à la gestion de base de données,

- à la manipulation et à l'analyse des données,

- à l'affichage et à la génération de produits (rapports, cartes statistiques, etc.), et

- au dialogue avec l'usager.



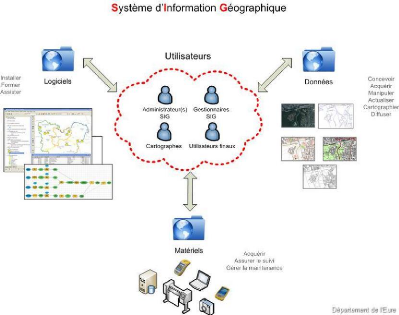
Figure 2.5 Système d'Information Géographique(SIG). (A.Atmani, 2013)

Définition 2 : Un système d'information géographique (SIG) est avant tout un système de gestion de base de données capable de gérer des données localisées, et donc capable de les saisir, de les stocker, les extraire (et notamment sur des critères géographiques), de les interroger et analyser, et enfin de les représenter et les cartographier. L'objectif affiché est essentiellement un objectif de synthèse, permettant à la fois la gestion des données comme l'aide à la décision. (M.Souris, 2002)

Les objectifs généraux selon (M.Souris, 2002) se résument dans les points suivants :

? Saisie et stockage numérique de plans et de cartes.

27

Chapitre 2 Système d'Information Géographique

> Structuration de l'information.

> Calculs métriques (distances, surfaces), calculs techniques (visibilité, recherche

opérationnelle), positionnement et projection géographiques.

> Gestion et traitement des collections d'objets géographiques.

> Gestion administratives et partages des données entre utilisateurs

> Gestion et analyse spatiale, Gestion spatio-temporelle

> Statistique et géostatistique

> Simulation et modélisation

> Télédétection géo-référencement et traitement d'image

2.3.2 La structure d'un SIG

La structure d'un SIG est donnée dans le schéma suivant :



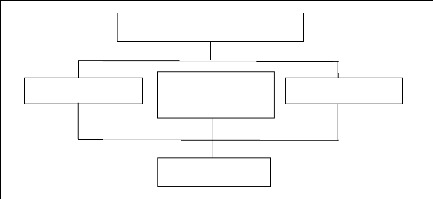
Entrée des données

Stockage et gestion des données

Manipulation des données et analyse

Interface à l'usage

Sortie des résultats

Figure 2.6 Structure d'un SIG. (S.Chakhar, 2006)

2.3.3 Enjeux et domaine d'application des SIG

Les enjeux auxquels toutes les nations ont à faire face (Economie, environnement, santé, démographie...) ont un lien étroit avec la géographie. La plus part des activités socioéconomique et politique implique des données géo-références et nécessitent l'utilisation des SIG. Nous pouvons citer comme secteurs d'application des SIG : L'agriculture, l'aménagement du territoire, les travaux publics, le cadastre, la démographie, l'environnement, la géologie, gestion de réseaux, la santé, le tourisme...

2.3.4 Principe de fonctionnement d'un SIG

2.3.4.1 Les couches

Le stockage des informations dans un SIG se structure sur le concept de couches thématiques. Nous reprenons dans le SIG ce que le cartographe fait manuellement en superposant ses différents calques (calque de route, calques des réseaux d'assainissement...) La liaison entre ces couches se fait par leurs coordonnées géographiques.



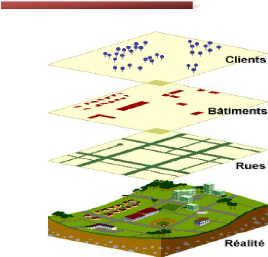
Chapitre 2 Système d'Information Géographique

28

Figure 2.7 Superposition des couches thématique (C.Sébastien, 2003). 2.3.4.2 Les références géographiques

Dans une base de données géographique on utilise les deux types de données :

- Données attributaires descriptifs ou a-spatiale

- Donnée spatiale qui se caractérisent par des coordonnées dans un référentiels terrestre (Longitude, attitude) et qui appartient a l'un des trois types (Point, ligne, polygone).

2.3.5 Modes d'acquisition et de représentation des données géographique par un SIG

Deux modes sont utiliser pour numériser et stocker les données géographique dans un SIG, le mode raster et le mode vecteur :



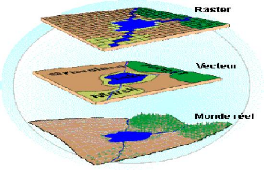
Figure 2.8 Modèle raster et modèle vecteur. (C.Sébastien, 2003)

29

Chapitre 2 Système d'Information Géographique

2.3.5.1 Le mode Raster ou maillé :

Il est facile à mettre en oeuvre et par conséquent les produit issue de ce modèle ne sont pas couteux, il consiste à représenter l'étendue géographique sans se concerner par la limite des objets géographique. L'espace géographique est alors décrit point par point, chaque cellule ou pixel va contenir une valeur représentant une portion de l'objet géographique. On traite les pixels par des classifications permettant de distinguer des zones similaires.

2.3.5.2 Le model vecteur :

Il est difficile à mettre en oeuvre mais il est précieux, précis et couteux (par exemple si un

produit raster revient à 3000 DA alors le même produit en mode vecteur coute 300000 DA).

Dans ce mode on représente la réalité géométrique et topologique des objets en se reposant

sur les types de données suivant :

> Point (coordonnée X, Y).

> Ligne (Liste de points).

> Polygone (liste de ligne).

Dans ce mode on distingue plusieurs modèles de représentation :

> Le modèle spaghetti

> Le modèle réseaux...

2.3.6 SIG et modélisation géographique :

On peut distinguer deux grandes catégories de modèles dans les SIG (Balzarini, 2014) A- Modèles de représentation :

Pour représenter les entités géographiques en signalant que ces entités seront décrites en bases de données géographique par les objets géographiques. Dans ces modelés on essaye de formaliser les caractéristiques géométriques et topologiques des entités géographiques B- Modèles de géo-traitement :

C'est la modélisation des méthodes mathématiques de l'analyse spatiale des objets des modelés de représentation. Cette modélisation définie plusieurs types de problèmes tel que : Les problèmes d'aptitude (Quel est l'emplacement optimal pour un site, comme une nouvelle école, une décharge d'ordures etc. ...).Les problèmes de surfaces : (Quel est le taux de pollution dans différents endroits d'un canton).Les problèmes de distances :( Quels sont les habitats protégés les plus proches pour une espèce en danger ?).

2.3.7 Exemples des logiciels SIG :

Parmi les logiciels les plus utilisés (logiciels libres) dans les Systèmes d'Information Géographiques, nous pouvons citer :

+ QGIS : logiciel de cartographie basé sur la bibliothèque Qt. Il est disponible sous Linux (KDE), Mac OS X, ou Windows. Entre autres choses, il permet la visualisation à la volée des couches de données comme des shapefiles ainsi que leur modification. Il permet notamment l'élaboration de fichiers destinés à être publiés sur MapServer. Il présente une ergonomie aboutie qui le rend très simple à utiliser.

30

Chapitre 2 Système d'Information Géographique

+ OrbisGIS :

+ OrbisGIS est capable d'afficher, de manipuler et de créer des données spatiales vecteur et raster. Il est complètement fait en Java , pour ça IL est multiplateforme.

+ WebmapSIG : logiciel SIG basé sur le framework Symfony et la bibliothèque Java Script Open Layers sous GPL. Il s'agit d'une application Web permettant de situer des centres d'intérêt. L'application est modifiable, adaptable aux différents serveurs, extensible et internationalisée, donc disponible en plusieurs langues, actuellement français et anglais.

+ Abc-Map: logiciel de cartographie généraliste multiplateforme et entièrement gratuit (Windows, Linux, Mac). L'objectif de ce logiciel est de proposer une méthode de création de carte de qualité simple et accessible à tous.

+ DIVA-GIS : logiciel capable d'éditer les fichiers shapefiles qui offre aussi des outils d'analyses statistiques et géo-spatiales pour la caractérisation des attributs numériques de la base de données associée aux objets contenus dans les shapefiles sous windows

2.4 Intégration entre SIG et AMC

2.4.1 Le caractère multicritères des données géographiques :

Ce qui donne aux problèmes spatiaux un caractère multicritère décisionnels c'est
l'hétérogénéité des données et des concepts de ces dernières, ces problèmes sont (S. Chakhar, 2006) :

> de nature multidimensionnelle, interdisciplinaire et difficilement formalisés,

> impliquent plusieurs personnes et institutions, ayant généralement des préférences et des objectifs divergeant,

> nécessitent la définition de plusieurs critères conflictuels dont l'importance n'est pas la même.

> demandent une quantité considérable de données quantitatives et qualitatives : c'est le champ d'application de l'analyse multicritère.

2.4.2 Limite de l'outil SIG dans le traitement décisionnel multicritère

Quoi qu'un SIG est bien adapté pour la représentation de la complexité des informations spatiales géo-référencée, L'objectif de son développement c'est de faire des requêtes spatiales et d'afficher des cartes ...

Pour éclaircir la vision aux décideurs. L'outil SIG est fait pour la décision mais il ne peut pas prendre en compte le caractère multicritères des problèmes géo décisionnel.

2.4.3 Limite des Méthodes multicritères pour la prise en charge de l'information géographique

Les méthodes multicritères que ça soit de l'école américaine ou celle de l'école française sont faites pour bien formuler le composant multicritère décisionnelle des problèmes spatiaux sans prendre en compte une bonne représentation du composant spatial de ces problèmes. Selon (S.Chakhar, 2006) Les applications de l'AMC ne peuvent pas être appliquées dans l'aide à la décision spatiale pour les deux raisons suivantes :

31

Chapitre 2 Système d'Information Géographique

> les logiciels d'AMC ne disposent pas de capacités nécessaires pour la gestion des données à référence spatiale.

> Les logiciels d'AMC manquent d'outils nécessaires à la représentation cartographique.

L'intégration des systèmes d'informations géographiques SIG avec les logiciels d'AMC est nécessaire pour prendre d'une manière intégrale les problèmes géo-décisionnelle.

2.4.4 Mode d'intégration SIG -AMC :

La conception d'une intégration des deux outils se fait généralement selon les étapes

suivantes.

> L'utilisation des SIG pour faire une étude préalable de criticité en s'appuyant sur la

potentialité des SIG pour préparer les données en entrée (input) des logiciels AMC.

> Sensibiliser le décideur avec la cartographie de la situation du problème et de ces

multiples critères a la nécessité d'entamer une analyse multicritères.

> L'utilisation des logiciels AMC pour l'évaluation multicritères.

> Les résultats sont présentés cartographiquement avec les SIG ou textuellement avec

les méthodes d'AMC.

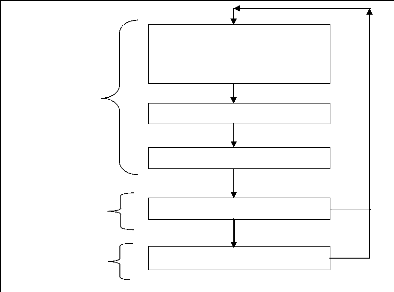
Chakhar a donné le schéma conceptuel pour l'intégration SIG et AMC suivant :



Logiciel
d'AMC

SIG ou Logiciel d'AMC

SIG

Définition du problème :

> Génération des actions
> Génération des Critères

Evaluations Multicritères

Présentation des résultats

Analyse des données

Action Potentielle

Figure 2.9 Schéma conceptuel d'intégration SIG-AMC (S.Chakhar, 2006)

2.4.5 Les modes d'intégration SIG et AMC Les travaux de Chakhar et d'autres ont révélés quatre modes d'intégration :

1- Pas d'intégration : il n'y a aucune intégration entre les deux outils.

32

Chapitre 2 Système d'Information Géographique

2- Intégration indirecte : Les deux outils SIG et AMC restent indépendant, un système intermédiaire prend en charge la formulation des données sortant du SIG entrant dans le logiciel AMC et vis vers ça .Bien que son emploi est lourd, ce mode a été adopté dans les premier travaux d'intégration et même dans des travaux récent.

3- Intégration encastré : Il y a toujours indépendance entre les deux outils, mais une seule interface est utilisé, l'intégration est apparente car derrière l'interface il n y a pas d'intégration.

4- Intégration complète : C'est l'intégration au vrais sens du mot avec une seule base de données et une seule interface. La base des données géographique est renforcée pour supporter les données géographiques et les paramètres de l'analyse multicritère.

2.4.6 Travaux connexes

SIG-AMC : est un processus de prise de décision dans lequel les jugements des données de valeur géographiques sont rassemblés pour obtenir plus d'informations pour les décideurs. Beaucoup de travaux existent, nous citons à titre d'exemple les travaux de (Eastman, 1997) qui consistent à ajouter un outil analytique d'aide à la décision à la version 4.1 d'IDRISI . Le module d'analyse incorporé dans IDRISI comporte des modules d'évaluation multicritère, dont la méthode est celle de la somme pondérée, et de détermination de poids utilisant la méthode AHP de (Saaty, 1980). En outre, il comporte des modules d'analyse de propagation d'erreur utilisant la méthode de Monte-Carlo, d'analyse de probabilité de Bayes, d'analyse de séries "floues", etc.

Nous pouvons citer aussi les travaux de (A.G.Pereira, 1997) qui ont incorporé la technique de compromise programming dans le SIG IDRISI pour un problème d'analyse des aptitudes du sol. Les auteurs ont incorporé également deux techniques de normalisation : value assessment pour les données cardinales et priority assessment pour les données ordinales.

Nous invoquons aussi les travaux de (O.Marinoni, 2005) Marinoni qui propose une approche itérative basée sur une variation spatiale dans la géométrie (forme) des régions. Les zones homogènes sont alors définies comme une agrégation spatiale des pixels basée sur une relation de voisinage. L'auteur propose également un exemple d'illustration basé sur l'intégration de la méthode PROMETHEE dans ArcGIS. En comparant l'évaluation obtenue par son approche à une évaluation existante obtenue par l'application de la méthode AHP, il a conclu que les méthodes de surclassement de synthèse se comportent plutôt bien pour des problèmes avec un grand nombre d'actions.

De même (Gomes & Lins, 2002) présentent un cas d'étude pour montrer la potentialité d'une intégration SIG-AMC dans l'aide à la décision spatiale. Pour ce faire, les auteurs ont considéré un problème hypothétique qui consiste à localiser la mairie de la ville de Rio de Janeiro au Brézil. Quinze critères regroupés en cinq familles ont été considérés dans leurs travaux.

Les travaux de (Itami & al, 2000) proposent l'intégration de la méthode AHP dans le SIG ArcView d'ESRI ce qui coïncide avec notre travail afin de gérer les problèmes de gestion et

33

Chapitre 2 Système d'Information Géographique

d'aménagement intégré des bassins versants. Le prototype permet en particulier de construire la hiérarchie objcetifs/attributs et de pondérer les différents facteurs. Le prototype a été utilisé dans un problème de bassin versant dans la région de Victoria en Australie.

Dans le même contexte de notre travail nous citons les travaux de (Ohri & al, 2010) s'intéressent au problème de sélection des zones industrielles, qui est un problème complexe nécessitant une analyse de décision multi-critères impliquant des paramètres économiques, environnementaux et sociaux .Ils proposent une approche multicritère en intégrant le SIG. Un total de 12 paramètres ont été considérés pour sélectionner le site industriel adapté autour la ville de Varanasi. Ces paramètres inclus la distances des grandes routes, les routes locales, lignes ferroviaire, les zones rurales et urbaines, les rivières, les plans d'eau, plaine inondable, table de l'eau souterraine et les zones des forêts. En utilisant l'AHP, ils ont attribué des pondérations aux différents critères et ils ont arrivés à identifier quatre zones possibles pour le développement industriel dans le district de Varanasi.

De même les travaux (Hadipour & al, 2014) considèrent que la construction d'un nouveau site industriel est un investissement important à long terme, ils ont développé un plan qui les a permit de prendre une décision et l'évaluation des solutions en générant des alternatives en utilisant le SIG et la méthode AHP.



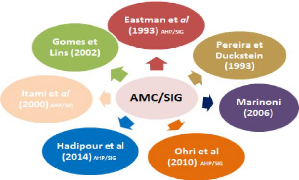
Figure 2.10 Travaux connexes d'intégration SIG-AMC.

2.5 Conclusion

Comme tous les outils informatiques, le SIG est un moyen d'organiser la réflexion, et non pas un but en soi. Un SIG ne peut apporter des réponses qu'à des questions qui ont été posées au préalable par les scientifiques. Il ne faut pas attendre des SIG une solution miracle, ni se laisser piéger par l'effet de mode SIG.

Les SIG se définissent comme un environnement informatique de matériels, de logiciels et de processus conçus pour permettre la collecte, la gestion, la manipulation, l'analyse, la modélisation et l'affichage des données à référence spatiale afin de résoudre des problèmes complexes d'aménagement et de gestion.

34

Chapitre 2 Système d'Information Géographique

L'intégration du SIG avec les logiciel d'AMC est le meilleure moyen de prendre en charge des problèmes géo-décisionnelle et de remédier aux limites de chaque outil a part lors de solution de tels problèmes

35

Chapitre 3 Etude de Cas

Sommaire

3. Introduction 37

3.2 Présentation de L'ANIREF 37

3.2.1 Statut 37

3.2.2 Missions 37

3.3 Démarche d'analyse Multicritère : 38

3.4 Démarche géographique 38

3.5.1 L'ensemble des actions : 39

3.5.2 Hiérarchie des critères : 39

3.5.2.1 Description de l'ensemble des critères : 39

3.5.3 Le caractère géographique des critères 40

3.5.4 Agrégation des critères par moteur d'inférence : 41

3.6 Choix d'une méthode d'Analyse de Décision Multicritères (MCDA) appropriée 43

3.7 La méthode AHP et FAHP (AHP Flou) sans utilisation du moteur d'Inférence 44

3.7.1 La première étape AHP 44

3.7.1.1 Deuxième étape AHP 45

3.7.1.2 Calcul du vecteur propre moyen (Priorité) pour chaque matrice ci-dessus : 47

3.7.3 Calcul des poids Finaux er Rangs finaux de chaque Action (troisième étape AHP) 53

3.7.4 Résultat de l'application de la méthode AHP sur l'exemple des zones Industrielles 54

3.7.5 Première étape FAHP : 54

3.7.5.1 Théorie des ensembles de la méthode FAHP 54

3.7.6 Deuxième étape FAHP 58

3.7.7 Calcul des poids Flous Finaux er Rangs finaux de chaque Action (troisième étape FAHP) 61

3.7.8 Comparaison des Résultat de l'application de la méthode AHP et FAHP sur l'exemple des

zones Industrielles 63

3.8 La méthode AHP et FAHP (AHP Flou) après le prétraitement par moteur d'Inférence 63

3.8.1 La méthode AHP après traitement par MI 63

3.8.2 La méthode FAHP après traitement par MI 64

3.8.3 Comparaison des Résultat de l'application de la méthode AHP et FAHP sur l'exemple des

zones Industrielles avec Moteur d'Inférence 66

3.9 Conclusion 66

36

Chapitre 3 Etude de Cas

Liste des figures

Figure 3.1 réduction es critères par règles de production 38

Figure 3.2 Fuzzification des matrices de comparaison par pair 38

Figure 3.3 l hièrarchie des critères pour le rangement des zones Industrielles (Med, SETTI,

2014) 39

Figure 3.4 Classification sismique es wilayas d'Algérie (ANIREF, 2013) 40

Figure 3.5 Etage bioclimatiques des wilayas d'Algérie (ANIREF, 2013) 40

Figure 3.6 Hierarchie des Critères en nombre Réduit 43

Figure 3.7 la structure hiérarchique arborescente 44

37

Chapitre 3 Etude de Cas

Chapitre 3 : Etude de cas

3.1 Introduction

Nous proposons dans ce travail un rangement (Ranking) des zones industrielles créées à travers l'ensemble du territoire national dans un souci d'équilibre économique des régions et de stabilisation des populations dans le cadre de la stratégie de développement du pays et sous la direction de l'ANIREF,

Ce travail commence par une étude préalable de criticité en utilisant les SIG comme outil d'analyse spatiale des critères géographiques en se basant sur une étude déjà réalisée par l'ANIREF. Cette étude conclut à une évaluation des zones par rapport aux critères qualitatifs et quantitatifs, le procédé est de superposer la carte thématique de chaque critère géographique (Sismicité, humidité, étage bioclimatique....) sur la carte Administratif du pays La valeur affectée au critère dépend de la situation géographique de la zone industrielle vis avis de la géographie du critère. La construction des matrices de comparaison par pair sont réalisé avec l'aide d'une équipe de décideurs de l'ANIREF. Les caractéristiques géo décisionnelles du problème Nous ont orientées vers l'adoption de l'approche d'intégration des systèmes d'information géographiques (SIG) avec les méthodes d'analyse multicritère d'aide à la décision AMCD (S. Chakhar, 2006) Pour le volet multicritère nous avons choisi la méthode AHP vu sa simplicité, sa popularité et sa cohérence avec les problèmes à caractères environnementale et géographique (Saaty, 1980) , notre contribution est d'utiliser conjointement un moteur d'inférence dans la phase de hiérarchisation pour réduire le nombre de critères (surtout les critères a valeurs qualitatives) et une fuzyfication des matrices de comparaison par pair des éléments de la hiérarchie pour remédier a la subjectivité, l'hésitante et l'incertitude des décideurs . Une étude comparative entre les résultats de la méthode AHP et AHP Flou (FAHP) est mise a la disposition des décideurs ainsi que les résultats des deux approche avec et sans prétraitement par moteur d'inférence. Notre contribution en matière de SIG c'est l'intégration mixte que nous avons proposée.

3.2 Présentation de L'ANIREF

3.2.1 Statut

L'ANIREF est un établissement public à caractère industriel et commerciale (EPIC), sous tutelle du ministère de l'industrie de la petite et moyenne entreprise et de la promotion de l'investissement (MIPMEP).Administré par un conseil d'administration composé de 11 membres. Présenté, au niveau local, à travers 10 directions régionales, implantées sur le territoire national.

3.2.2 Missions

? Gestion pour compte de biens fonciers et immobiliers.

? Intermédiation foncière et immobilière.

? Régulation du foncier économique par le biais d'une observation.

Chapitre 3 Etude de Cas

? Diffusion de l'information : banque des données foncière. ? Promotion foncière et immobilière.

3.3 Démarche d'analyse Multicritère :

L'objectif de l'analyse multicritère avec les outils correspondant est de résoudre les problèmes de décision multicritères complexes qui inclut des aspects qualitatifs et/ou quantitatifs dans un processus décisionnel.

La démarche que nous avons adoptée pour aborder ce problème s'articule, comme c'est d'ailleurs le cas pour la plupart des approches multicritères, autour de quatre étapes principales:

1- Identifier l'ensemble des zones industrielles (ensemble des actions)

2- Etablir la liste des critères

3- réduction des critères et allégement de la hiérarchie en utilisant les règles Si... Alors Figure 3.1

4- Etablir les matrices de comparaison par pair au niveau de chaque noeud de la hiérarchie en se basant sur l'échelle de Saaty (Tableau 1.2).

5- Fuzification des matrices de comparaison par pair (Les préférences des décideurs)

6- Defuzification et calcul priorités intermédiaires et finales.

3.4 Démarche géographique

1- préparation des cartes critère et donc l'input de la méthode AMC

2- visualisation des actions avant analyse multicritère

3- visualisation des actions après analyse,





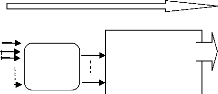
Méthode d'Analyse Multicritères

Importance subjectif
des critères

Critères techniques
permettant
l'utilisation d'une
expertise objective

Traitement
avec les
bases de
règles

Réduction du

nombre de critères ayant une importance subjective

Figure 3.1 réduction es critères par règles de production



Fuzzification



defuzzification

Matrices de
comparaiso
n par pairs

Matrices de comparaison par pairs fuzzifiées

Matrices de comparaison par pairs flou

38

Calcul des priorités intermediaires Calculs des Rangs des actions

Figure 3.2 Fuzzification des matrices de comparaison par pair

Chapitre 3 Etude de Cas

3.5.1 L'ensemble des actions :

Sur les 39 zones industrielles créées à travers l'ensemble du territoire nationale par l'ANIREF, notre étude c'est portée sur les zones industrielles de l'ouest algérien dont nous disposons des données spatiales et aspatiales correspondantes. Chaque zone constitue une action d'où la liste suivantes :

1- Action1 : Sidi Bel Abbes (Localisation : Wilaya de Sidi Bel Abbes, Commune de Sidi Bel Abbes).

2- Action2 : Horchaia (Localisation : Wilaya de Naama, Commune de Naama, Lieu dite Horchaia).

3- Action3 : Ras Elma (Localisation : Wilaya de Sidi Bel Abbes, Commune de Ras Elma, Lieu dite Ras Elma).

4- Action4 : Maghnia (Localisation : Wilaya de Tlemcen, Commune de Maghnia, Lieu dite Ouled Bendamou).

5- Action5 : Koléa (Localisation : Wilaya de Saida, Commune de Sid Ahmed).

3.5.2 Hiérarchie des critères :

La structure de la hiérarchie des critères est une étape très importante dans une analyse de décision multicritères. Dans cette phase, le groupe des critères du problème est décomposé en sous-critère figure 3.2). Les critères qui sont employés dans cette étude sont présentés en quatre catégories: les impacts environnementaux, les risques naturels, les caractéristiques

climatiques et critères socio-économiques. Sous ces quatre catégories, 11 critères
d'évaluation différents sont définis.

Ceux-ci incluent des mesures quantitatives et qualitatives sont définies. La description



environnementaux

C1 C3 C4 C5 C6 C7 C8 C9 C10 C11

Impacts

Risques Naturels

Hiérarchie des critères

Caractéristiques

climatiques

Critères Socio-

économiques

39

Figure 3.3 l hièrarchie des critères pour le rangement des zones Industrielles (Med,

SETTI, 2014)

L'ensemble des critères sont données en dessus

3.5.2.1 Description de l'ensemble des critères :

Critère 1 (C1) : Risque pollution nappe phréatique.

Critère 2 () : Problème faune et flore.

Critère 3 (C3) : Nuisances sonores citoyens.

Critère 4(C4) : Sismicité.

Critère 5 (C5) : Inondation.

Critère 6 (C6) : Température.

Critère 7 (C7) : Pluviométrie.

Critère 8 (C8) : Etage Bioclimatique.

40

Chapitre 3 Etude de Cas

Critère 9 (C9) : Cout d'aménagement

Critère 10 (C10) : Potentialité de développement d'aménagement

Critère 11 (C11) : Infrastructure de Transport

3.5.3 Le caractère géographique des critères :

Pour construire les matrices de comparaison par pair requises par AHP en input les décideurs

se base sur :

a- la carte thématique des critères géographiques Figure 3.4 et Figure 3.5

b- sur une table de performance contenant l'évaluation de chaque action par rapport a tout les critères Tableau 3.1

c- Pondération Intra critères réalisée par un groupe de décideur de l'ANIREF .



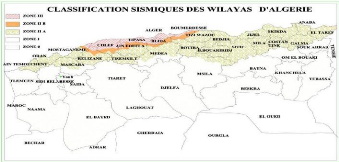
Figure 3.4 Classification sismique es wilayas d'Algérie (ANIREF, 2013)



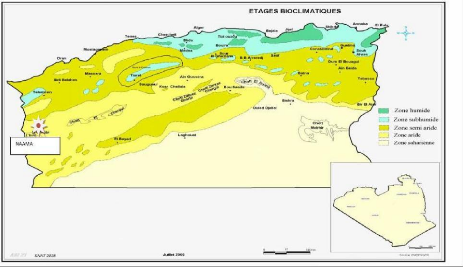
Figure 3.5 Etage bioclimatiques des wilayas d'Algérie (ANIREF, 2013)

41

								Etude de Cas
Chapitre 3
Critère/Action	C1		C3	C4	C5	C6	C7	C8
A1	2	350	19	104	900592576	2500	3	14000
A2	2	310	24	100	867750000	4100	3	17000
A3	2	410	17	60	523765223	5000	3	13500
A4	2	380	19	100	867750000	6500	3	15000
A5	1	190	17	150	1301625000	3500	2	18000
A6	3	400	18	205	1778911797	3000	3	16500
A7	3	320	21	98	851772119	8100	3	18300
A8	4	350	20	200	1735585907	6500	3	13000
A9	3	370	19	500	4338750000	3000	2	17800
Sens de critère	Min	Min	Min	Max	Min	Min	Min	Max

Tableau 3.1 Table des performances (A.Taibi et al, 2016)

Critère	Poids de chaque critère	Poids de chaque critère (point)
Impacts environnementaux	20%	20
Risques naturels	40%	40
Caractéristiques Climatique	30%	30
Critères Socio économique	10%	10

Tableau 3.2 Table (pondération intra critère ( ANIREF, 2013))

3.5.4 Agrégation des critères par moteur d'inférence :

C'est une étape importante dans notre démarche. Elle permet la réduction du nombre des critères objectifs surtout. La comparaison des critères deux à deux imposé par la méthode AHP provoque des incohérences lorsque le nombre des critères et des actions est important (T. Saaty, 1980). C'est pour affaiblir l'impact de ce problème sur les résultats souhaités dans notre cas d'étude que nous avons adoptés cette approche. (Framling, 1996) l'a utilisé pour réduire le nombre des critères de sélection du meilleur site de décharge en Suisse en utilisant la méthode de surclassement ELECTRE I.

La base des règles doit être développée avec l'aide de l'expert puisque les déductions doivent se baser sur une connaissance du domaine.

Le problème posé lors de développement de ces règles c'est le nombre des combinaisons possibles qui croit très vite selon le nombre des valeurs à combiner et les conclusions à obtenir, ce problème engendre un nombre très important des règles de production. Construire toutes les règles et très difficile, pour cerner ce problème nous avons adopté des règles plus générales avec des intervalles de valeurs en prémisses en collaboration avec l'expert.

Voici les règles utilisées dans notre cas d'étude :

42

Chapitre 3 Etude de Cas

I Impacts environnementaux :

Structure des règles pour le critère Impact environnementale

Critère Impact environnementale « impact » (fort, faible, moyen)

En prémisses des règles, la combinaison des valeurs des critères suivants :

1- Risque pollution nappe phréatique : C1 (Présent, Absent)

2- Problème faune et flore : (Existant, Inexistant)

3- Nuisances sonores citoyens : C3 (Forte, Faible).

Si C1= présent et = existe et C3= forte alors impact = fort

Si C1 = présent et = inexistant et C3= forte alors impact = fort Si C1= absent et = inexistant et C3= faible alors impact = faible Dans les autres cas l'impact = moyen

II Risques naturels :

Structure des règles pour le critère Risques Naturels

Critère Risques Naturels « risque naturel » (fort, faible, moyen)

En prémisses des règles, la combinaison des valeurs des critères suivants :

4- Sismicité : C4 (faible à modérer, faible, forte)

5- Inondation : C5 (Faible, Moyen, Fort)

Si C4 = faible à modérer et C5 = moyen alors risque naturel = moyen

Si C4 = forte et C5 = fort alors risque naturel = fort

Si C4 = forte et C5 = moyen alors risque naturel = fort

Si C4 = forte et C5 = faible alors risque naturel = fort

Si C4 = faible et C5 = faible alors risque naturel = faible

Dans les autres cas, risque naturel = moyen

III Caractéristique Climatique :

Structure des règles pour le critère Caractéristique Climatique

Critère Caractéristique Climatique « climat » (favorable, défavorable, peu favorable) En prémisses des règles, la combinaison des valeurs des critères suivants :

6- Température : C6 (Intervalle de valeurs numériques)

7- Pluviométrie : C7 (Intervalle de Valeurs numériques)

8- Etage Bioclimatique : C8 (Aride, Semi Aride).

Si (15 < C6< 20) et (50<C7<200) et (C8 =semi aride) alors climat favorable

Si (15<C6<40) et (C7<400) et (C8=semi aride) alors climat favorable

Si (C6<10) alors climat défavorable

Si (C6>50) alors climat défavorable

Dans les autres cas le climat = peu favorable

IV Critères Socio économique :

Structure des règles pour le critère socio-économique

Critère Socio-économique « C_socio_eco » (très favorable, favorable, peu favorable,

défavorable)

En prémisses des règles, la combinaison des valeurs des critères suivants :

9- Cout d'aménagement : C9 (intervalles de valeurs numériques)

10- Potentialité de développement : C10 (encourageante, non encourageante, peu
encourageante).



Chapitre 3 Etude de Cas

11- Infrastructure de transport : C11 (disponible, peu disponible, indisponible

La liste non exhaustive des règles

Si [(C9>3000000000) et (C11= peu disponible) et (C10=non encourageante)]

Alors ( C_socio_eco= défavorable)

Si [(C9>3000000000) et (C11= peu disponible) et (C10=encourageante)]

Alors ( C_socio_eco= peu favorable)

Si [(C9>3000000000) et (C11= disponible) et (C10= encourageante)]

Alors ( C_socio_eco= favorable)

Si [( 1500000000<C9<3000000000) et (C11= peu disponible) et (C10= encourageante)]

Alors ( C_socio_eco= favorable)

Si [(C9<1500000000) et (C11= disponible) et (C10= encourageante)]

Alors ( C_socio_eco= très favorable)

Si [(C9<1500000000) et (C11= indisponible) et (C10=non encourageante)]

Alors ( C_socio_eco= défavorable)

Si [(C9<1000000000) et (C11= disponible) et (C10=non encourageante)]

Alors ( C_socio_eco= très favorable)

Après avoir appliqué les règles nous obtenons un nombre réduit de critères détaillé dans la

structure suivante :

Hiérarchie des critères



économiques

climatiques

Naturels

Impacts

environnementaux

Risques

Caractéristiques

Critères Socio



43

Figure 3.6 Hiérarchie des Critères en nombre Réduit

3.6 Choix d'une méthode d'Analyse de Décision Multicritères (MCDA) appropriée

Il existe plusieurs méthodes pour l'aide à la décision multicritères qui permettent le rangement des alternatives. Il n'y a pas de meilleures ou pires techniques, mais des techniques mieux adaptées à des problèmes de décision particuliers que d'autres (voir chapitre 1, méthode d'analyse multicritère).

Il est essentiel de développer en détail tous les éléments relatifs à la situation de MCDA avant d'effectuer une sélection d'une méthode MCDA en vue de résoudre les problèmes étudiés. Le choix d'une certaine méthode MCDA ne peut pas être décidé au début du processus. Cette décision devrait attendre jusqu'à ce que le décideur comprenne le problème, les alternatives possibles, les différents résultats, les conflits entre les critères et le niveau d'incertitude des données.

Dans cette étude (Rangement des zones industrielles) , on constitue une problématique de rangement.

Dans cette étude, La méthode AHP a été choisie parce qu'elle permet le rangement et en raison de sa simplicité et sa capacité de rapprocher la façon dont l'esprit humain exprime et synthétise les préférences en face des multiples perspectives de décision contradictoires. La méthode AHP appartient à la famille Des méthodes de pondération.

Chapitre 3 Etude de Cas

3.7 La méthode AHP et FAHP (AHP Flou) sans utilisation du moteur

d'Inférence

3.7.1 La première étape AHP

Cette étape Consiste à décomposer le problème en structure hiérarchique (Voir figure 3.6).

Dans notre cas d'étude, nous avons trois niveaux :

Niveau 0 : Contient l'objectif (Choix d'une zone)

Niveau 1 : Contient les critères

Niveau 2 : contient les sous critères



Niveau 0
Objectif

Choix d'une zone

Niveau 2 Sous-Critères

Cr10

Cr11

Cr7

Horchaia

Figure 3.7 la structure hiérarchique arborescente

Koléa

Ras Elma

Sidi Bel

Abbes

Maghnia

Niveau 3 Action

Cr1

Cr6

Cr4

Cr5

Cr3

Cr2

Cr9

Cr8

Niveau 1 Critères

Impacts

Environnementaux

Risque Naturels

Caractéristique Climatique

Critères

Socio économique

Figure 3.8 la structure hiérarchique arborescente

44

Niveau 3: Contient les actions

Chapitre 3 Etude de Cas

3.7.1.1 Deuxième étape AHP : La deuxième étape de la méthode AHP consiste à pondérer les critères deux à deux, et pondérer aussi les actions deux à deux par rapport à chaque critère en utilisant l'échelle de pondération unique de Saaty Tableau 1.2 L'équipe qui s'en charge de la construction des matrices de comparaison par pair se base sur les points a, b, c citées dans le (3.5.3)

Voici la matrice de pondération Critère /Critère (Voir tableau 3.3)

Critère	Impac_Env	Risq_Nat	Climat	Socio
Impac_Env	1	1/3	4	3
Risq_Nat	3	1	5	3
Climat	1/4	1/5	1	4
Socio	1/3	1/3	1/4	1

Tableau 3.3 Matrice de pondération Critère /Critère

Critères	C1		C3
C1	1	5	5
	1/5	1	1
C3	1/5	1	1

Tableau 3.4 Matrice de Pondération des Critère C1, , C3 par rapport au Critère Impact Environnementaux

Critères	C4	C5
C4	1	5
C5	1/5	1

Tableau 3.5 Matrice de Pondération des Critère C4, C5 par rapport au Critère Risques Naturels

Critères	C6	C7		C8
C6	1	3		3
C7	1/3	1		3
C8	1/3	1/3		1
Critères	C9		C10		C11
C9	1		1/3		1/5
C10	3		1		3
C11	5		1/3		1

Tableau 3.6 Matrice de Pondération des Critère C6, C7, C8 par rapport au Critère Caractéristiques Climatiques

Tableau 3.7 Matrice de Pondération des Critère C9, C10, C11 par rapport au Critère Socio-économique

Tableau 3.8 Matrice de pondération Action/Action par rapport aux critères Risque pollution nappe phréatique (C1)

45

Actions	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	1	1	1	1/2	2
Horchaia	1	1	1	1/3	1
Kolea	1	1	1	1/2	1
Ras Elma	2	3	2	1	2
Maghnia	1/2	1	1	1/2	1

Chapitre 3 Etude de Cas

Tableau 3.9 Matrice de pondération Action/Action par rapport aux critères Faune et Flore ()

46

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	1	1/5	1/3	1/3	1/4
Horchaia	5	1	1/2	1	1/2
Kolea	3	2	1	1	1/2
Ras Elma	3	1	1	1	1/2
Maghnia	4	2	2	2	1

Tableau 3.10 Matrice de pondération Action/Action par rapport au critère Nuisances sonores citoyens (C3)

Action

		SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA		1	5	4	3	5
Horchaia		1/5	1	1/2	1/3	1/2
Kolea		1/4	2	1	1/2	4
Ras Elma		1/3	3	2	1	5
Maghnia		1/5	2	1/4	1/5	1

Tableau 3.11 Matrice de pondération Action/Action par rapport au critère Sismicité (C4)

Tableau 3.12 Matrice de pondération Action/Action par rapport au critère Inondation (C5)

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	1	1	1	1	3
Horchaia	1	1	1	1	3
Kolea	1	1	1	1	3
Ras Elma	1	1	1	1	3
Maghnia	1/3	1/3	1/3	1/3	1

Tableau 3.13 Matrice de pondération Action/Action par rapport au critère Température (C6)

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	1	1/2	1/3	1/4	2
Horchaia	2	1	1/2	1/3	1
Kolea	3	2	1	1/2	2
Ras Elma	4	3	2	1	3
Maghnia	1/2	1	1/2	1/3	1

Tableau 3.14 Matrice de pondération Action/Action par rapport au critère Pluviométrie (C7)

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	1	3	2	1	2
Horchaia	1/3	1	3	3	5
Kolea	1/2	1/3	1	1/2	1
Ras Elma	1	1/3	2	1	2
Maghnia	1/2	1/5	1	1/2	1
Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	1	3	1/3	1/2	7
Horchaia	1/3	1	1/4	1/2	6
Kolea	3	4	1	2	8
Ras Elma	2	2	1/2	1	6
Maghnia	1/7	1/6	1/8	1/6	1

Chapitre 3 Etude de Cas

Tableau 3.15 Matrice de pondération Action/Action par rapport au critère Etage Bioclimatique.(C8)

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	1	1	1	1	3
Horchaia	1	1	1	1	3
Kolea	1	1	1	1	3
Ras Elma	1	1	1	1	3
Maghnia	1/3	1/3	1/3	1/3	1

Tableau 3.16 Matrice de pondération Action/Action par rapport au critère Cout d'aménagement.(C9)

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	1	1/3	2	1/3	1/5
Horchaia	3	1	5	3	1/3
Kolea	1/2	1/5	1	1/2	1/5
Ras Elma	3	1/3	2	1	6
Maghnia	5	3	5	1/6	1

Tableau 3.17 Matrice de pondération Action/Action par rapport au critère Potentialité de développement d'aménagement. (C10)

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	1	5	1	2	3
Horchaia	1/5	1	1/5	3	2
Kolea	1	5	1	1/3	3
Ras Elma	1/2	1/3	3	1	4
Maghnia	1/3	1/2	1/3	1/4	1

Tableau 3.18 Matrice de pondération Action/Action par rapport au critère Infrastructure de Transport. (C11)

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	1	5	1	1	3
Horchaia	1/5	1	1/5	1/5	2
Kolea	1	5	1	1	3
Ras Elma	1	5	1	1	3
Maghnia	1/3	1/2	1/3	1/3	1

47

3.7.1.2 Calcul du vecteur propre moyen (Priorité) pour chaque matrice ci-dessus :

Critère	Impac_Env	Risq_Nat	Climat	Socio
Impac_Env	1	1/3	4	3
Risq_Nat	3	1	5	3
Climat	1/4	1/5	1	4
Socio	1/3	1/3	1/4	1
Total	4.58	1.86	10.25	11

Tableau 3.19 Calcul de total de chaque colonne de Matrice de pondération Critère /Critère Normalisation et Calcul de Poid de chaque critère Selon T.Saaty:

Critère	Impac	Risq_Nat	Climat	Socio	Som	Som/4	Poid
Impac_Env	0.21	0.18	0.4	0.27	1.06	0.26	26%
Risq_Nat	0.655	0.53	0.48	0.27	1.935	0.48	48%
Climat	0.054	0.1	0.09	0.36	0.604	0.15	15%
Socio	0.072	0.18	0.024	0.09	0.366	0.09	9%
						? =1.00	100%

Tableau 3.20 Normalisation de la matrice Critère /Critère et calcul des Poids

Chapitre 3 Etude de Cas

Critères	C1		C3
C1	1	5	5
	1/5	1	1
C3	1/5	1	1
Total	1.4	7	7

Tableau 3.21

Critères	C1		C3	Som	Som/3	Poid
C1	0.71	0.71	0.71	2.13	0.71	71%
	0.14	0.14	0.14	0.42	0.14	14%
C3	0.14	0.14	0.14	0.42	0.14	14%
					? =1.00	100%

Tableau 3.22

Normalisation des Critère C1, , C3 par rapport au Critère Impact Environnementaux

Critères		C4		C5
C4	1		5
C5	1/5		1
Total	1.2		6

Tableau 3.23

Critères

	C4	C5	Som	Som /2	Poid
C4	0.83	0.83	1.66	0.83	83%
C5	0.16	0.16	0.32	0.16	16%
				? =1.00	100%

Tableau 3.24

Normalisation des Critère C4, C5 par rapport au Critère Risques Naturels

Critères	C6		C7			C8
C6	1		3			3
C7	1/3		1			3
C8	1/3		1/3			1
Total	1.66		4.33			7
Critères		C6		C7	C8		Som		Som/3	Poid
C6		0.6		0.7	0.42		1.72		0.57	57%
C7		0.2		0.23	0.42		0.85		0.28	28%
C8		0.2		0.077	0.14		0.41		0.14	14%
									? =1.00	100%

Tableau 3.25 Tableau 3.26

Normalisation des Critère C6, C7, C8 par rapport au Critère Caractéristiques Climatiques

Critères	C9		C10			C11
C9	1		1/3			1/5
C10	3		1			3
C11	5		1/3			1
Total	9		1.66			4.2
Critères		C9		C10	C11		Som		Som/3	Poid
C9		0.11		0.2	0.04		0.35		0.11	11%
C10		0.33		0.6	0.71		1.64		0.54	54%
C11		0.55		0.2	0.238		0.988		0.32	32%
									? =1.00	100%

48

Tableau 3.27 Tableau 3.28

Normalisation des Critère C9, C10, C11 par rapport au Critère socio-économique

Chapitre 3 Etude de Cas

Tableau 3.29 Total des lignes de la
Matrice Action/Action par rapport
aux Critères C1 (Risque pollution
nappe phréatique)

Actions

	SBA		Horchaia		Kolea		Ras Elma		Maghnia
SBA	1		1		1		1/2		2
Horchaia	1		1		1		1/3		1
Kolea	1		1		1		1/2		1
Ras Elma	2		3		2		1		2
Maghnia	1/2		1		1		1/2		1
Total	5.5		7		6		2.83		7
Action		SBA		Horchaia		Kolea		Ras Elma		Maghnia		Som	Som/5	Poids
SBA		0.18		0.14		0.16		0.17		0.28		0.93	0.186	18%
Horchaia		0.18		0.14		0.16		0.11		0.14		0.73	0.146	14%
Kolea		0.18		0.14		0.16		0.17		0.14		0.79	0.158	15%
Ras Elma		0.36		0.42		0.33		0.35		0.28		1.74	0.348	34%
Maghnia		0.09		0.14		0.16		0.17		0.14		0.7	0.14	14%
													? = 1.00	? = 100%

Tableau 3.30 Normalisation de la matrice Action /Action selon le critère C1 (Risque pollution nappe phréatique)

Tableau 3.31 Total des lignes de la
Matrice Action/Action par rapport
aux Critères (Faune et Flore)

Action

	SBA		Horchaia		Kolea		Ras Elma		Maghnia
SBA	1		1/5		1/3		1/3		1/4
Horchaia	5		1		1/2		1		1/2
Kolea	3		2		1		1		1/2
Ras Elma	3		1		1		1		1/2
Maghnia	4		2		2		2		1
Total	16		6.2		4.83		5.33		2.75
Action		SBA		Horchaia		Kolea		Ras Elma		Maghnia		Som	Som/5	Poids
SBA		0.06		0.032		0.07		0.06		0.09		0.312	0.06	6%
Horchaia		0.31		0.16		0.1		0.18		0.18		0.93	0.186	18%
Kolea		0.18		0.32		0.16		0.18		0.18		1.02	0.204	20%
Ras Elma		0.18		0.16		0.2		0.18		0.18		0.9	0.18	18%
Maghnia		0.25		0.32		0.41		0.37		0.36		1.71	0.34	34%
													? = 1.00	? = 100%

Tableau 3.32 Normalisation de la matrice Action /Action selon le critère (Faune et Flore)

Tableau 3.33 Total des lignes de la Matrice Action/Action par rapport aux Critères C3 (Nuisances sonores citoyens )

49

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	1	5	4	3	5
Horchaia	1/5	1	1/2	1/3	1/2
Kolea	1/4	2	1	1/2	4
Ras Elma	1/3	3	2	1	5
Maghnia	1/5	2	1/4	1/5	1
Total	1.98	13	7.75	5.03	15.5

Chapitre 3 Etude de Cas

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia	Som	Som/5	Poids
SBA	0.5	0.38	0.51	0.6	0.32	2.31	0.46	46%
Horchaia	0.10	0.077	0.06	0.06	0.032	0.322	0.0644	6%
Kolea	0.12	0.15	0.13	0.09	0.25	0.74	0.14	14%
Ras Elma	0.16	0.23	0.26	0.12	0.32	1.09	0.29	29%
Maghnia	0.10	0.15	0.032	0.04	0.064	0.386	0.07	7%
							? = 1.00	? = 100%

Tableau 3.34 Normalisation de la matrice Action /Action selon le critère C3 (Nuisances sonores citoyens)

Tableau 3.35 Total des lignes de la Matrice Action/Action par rapport aux critères Sismicité (C4)

Action

	SBA		Horchaia		Kolea		Ras Elma		Maghnia
SBA	1		1		1		1		3
Horchaia	1		1		1		1		3
Kolea	1		1		1		1		3
Ras Elma	1		1		1		1		3
Maghnia	1/3		1/3		1/3		1/3		1
Total	4.33		4.33		4.33		4.33		13
Action		SBA		Horchaia		Kolea		Ras Elma		Maghnia		Som	Som/5	Poids
SBA		0.23		0.23		0.23		0.23		0.23		1.15	0.23	23%
Horchaia		0.23		0.23		0.23		0.23		0.23		1.15	0.23	23%
Kolea		0.23		0.23		0.23		0.23		0.23		1.15	0.23	23%
Ras Elma		0.23		0.23		0.23		0.23		0.23		1.15	0.23	23%
Maghnia		0.077		0.077		0.077		0.077		0.077		0.385	0.07	7%
													? = 1.00	? = 100%

Tableau 3.36 Normalisation de la matrice Action/Action par rapport aux critères Sismicité (C4)

Tableau 3.37 Total des lignes de la Matrice Action/Action par rapport aux critères Inondation (C5)

Action

	SBA		Horchaia		Kolea		Ras Elma		Maghnia
SBA	1		1/2		1/3		1/4		2
Horchaia	2		1		1/2		1/3		1
Kolea	3		2		1		1/2		2
Ras Elma	4		3		2		1		3
Maghnia	1/2		1		1/2		1/3		1
Total	10.5		7.5		4.33		2.41		9

50

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia	Som	Som/5	Poids
SBA	0.09	0.066	0.077	0.10	0.22	0.553	0.11	11%
Horchaia	0.2	0.13	0.11	0.13	0.11	0.68	0.13	13%
Kolea	0.28	0.26	0.23	0.20	0.22	1.19	0.238	23%
Ras Elma	0.38	0.4	0.46	0.41	0.33	1.98	0.4	40%
Maghnia	0.04	0.14	0.11	0.13	0.11	0.53	0.1	10%
							? = 1.00	? = 100%

Tableau 3.38 Normalisation de la matrice Action/Action par rapport aux critères Inondation (C5)

Chapitre 3 Etude de Cas

Tableau 3.39 Total des lignes de la Matrice Action/Action par rapport aux Critères Température (C6)

Action

	SBA		Horchaia		Kolea		Ras Elma		Maghnia
SBA	1		3		2		1		2
Horchaia	1/3		1		3		3		5
Kolea	1/2		1/3		1		1/2		1
Ras Elma	1		1/3		2		1		2
Maghnia	1/2		1/5		1		1/2		1
Total	3.33		4.86		9		6		11
Action		SBA		Horchaia		Kolea		Ras Elma		Maghnia		Som	Som/5	Poids
SBA		0.3		0.61		0.22		0.16		0.18		1.47	0.29	29%
Horchaia		0.1		0.2		0.33		0.5		0.45		1.58	0.316	31%
Kolea		0.15		0.06		0.11		0.08		0.09		0.49	0.098	9%
Ras Elma		0.3		0.06		0.22		0.16		0.18		0.92	0.184	18%
Maghnia		0.15		0.041		0.11		0.08		0.09		0.471	0.094	9 %
													? = 1.00	? = 100%

Tableau 3.40 Normalisation de la matrice Action/Action par rapport aux critères Température (C6)

Tableau 3.41 Total des lignes de la Matrice Action/Action par rapport aux Critères Pluviométrie (C7)

Action

	SBA		Horchaia		Kolea		Ras Elma		Maghnia
SBA	1		3		1/3		1/2		7
Horchaia	1/3		1		1/4		1/2		6
Kolea	3		4		1		2		8
Ras Elma	2		2		1/2		1		6
Maghnia	1/7		1/6		1/8		1/6		1
Total	6.47		10.16		2.205		4.16		28

51

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia	Som	Som/5	Poids
SBA	0.15	0.29	0.15	0.12	0.25	0.96	0.19	19%
Horchaia	0.05	0.01	0.11	0.12	0.21	0.5	0.1	10%
Kolea	0.46	0.4	0.45	0.48	0.28	2.07	0.41	41%
Ras Elma	0.3	0.2	0.22	0.24	0.21	1.17	0.234	23 %
Maghnia	0.022	0.016	0.056	0.04	0.03	0.158	0.0316	3 %
							? = 1.00	? = 100%

Tableau 3.42 Normalisation de la matrice Action/Action par rapport aux critères Pluviométrie (C7)

Chapitre 3 Etude de Cas

Tableau 3.43 Total des lignes de la Matrice Action/Action par rapport aux Critères Etage Bioclimatique (C8)

Action

	SBA		Horchaia		Kolea		Ras Elma		Maghnia
SBA	1		1		1		1		3
Horchaia	1		1		1		1		3
Kolea	1		1		1		1		3
Ras Elma	1		1		1		1		3
Maghnia	1/3		1/3		1/3		1/3		1
Total	4.33		4.33		4.33		4.33		13
Action		SBA		Horchaia		Kolea		Ras Elma		Maghnia		Som	Som/5	Poids
SBA		0.23		0.23		0.23		0.23		0.23		1.15	0.23	23%
Horchaia		0.23		0.23		0.23		0.23		0.23		1.15	0.23	23%
Kolea		0.23		0.23		0.23		0.23		0.23		1.15	0.23	23%
Ras Elma		0.23		0.23		0.23		0.23		0.23		1.15	0.23	23%
Maghnia		0.077		0.077		0.077		0.077		0.077		0.385	0.07	7%
													? = 1.00	? = 100%

Tableau 3.44 Normalisation de la matrice Action/Action par rapport aux critères (C8)

Tableau 3.45 Total des lignes de la Matrice Action/Action par rapport aux critères Cout d'aménagement (C9)

Action

	SBA	Horchaia			Kolea		Ras Elma		Maghnia
SBA	1	1/3			2		1/3		1/5
Horchaia	3	1			5		3		1/3
Kolea	1/2	1/5			1		1/2		1/5
Ras Elma	3	1/3			2		1		6
Maghnia	5	3			5		1/6		1
Total	12.5	5.16			15		5		7.73
Action			SBA	Horchaia		Kolea		Ras Elma		Maghnia		Som	Som/5	Poids
SBA			0.08	0.064		0.13		0.066		0.025		0.365	0.073	7%
Horchaia			0.24	0.2		0.33		0.6		0.043		1.413	0.28	28%
Kolea			0.04	0.04		0.06		0.1		0.025		0.265	0.05	5%
Ras Elma			0.24	0.064		0.13		0.2		0.77		1.404	0.28	28%
Maghnia			0.4	0.58		0.33		0.033		0.13		1.473	0.29	29%
													? = 1.00	? = 100%

Tableau 3.46 Normalisation de la matrice Action/Action par rapport aux critères Cout d'aménagement (C9)

Tableau 3.47 Total des lignes de la Matrice Action/Action par rapport aux critères Potentialité de développement (C10)

52

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	1	5	1	2	3
Horchaia	1/5	1	1/5	3	2
Kolea	1	5	1	1/3	3
Ras Elma	1/2	1/3	3	1	4
Maghnia	1/3	1/2	1/3	1/4	1
Total	3.03	11.83	5.53	6.58	13

Chapitre 3 Etude de Cas

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia	Som	Som/5	Poids
SBA	0.33	0.42	0.18	0.3	0.23	1.46	0.29	29%
Horchaia	0.06	0.084	0.036	0.45	0.15	0.78	0.15	15%
Kolea	0.33	0.42	0.18	0.05	0.23	1.21	0.24	24%
Ras Elma	0.16	0.03	0.54	0.15	0.3	1.18	0.23	23%
Maghnia	0.1	0.04	0.06	0.037	0.07	0.307	0.0614	6%
							1 = 1.00	1=100%

Tableau 3.48 Normalisation de la matrice Action/Action par rapport aux critères Potentialité de développement (C10)

Tableau 3.49 Normalisation
Action/Action par rapport aux critères
Infrastructure de Transport (C11)

Action

	SBA		Horchaia		Kolea		Ras Elma		Maghnia
SBA	1		5		1		1		3
Horchaia	1/5		1		1/5		1/5		2
Kolea	1		5		1		1		3
Ras Elma	1		5		1		1		3
Maghnia	1/3		1/2		1/3		1/3		1
Total	3.53		16.5		3.53		3.53		12

53

Action

	SBA	Horchaia	Kolea	Ras Elma	Maghnia	Som	Som/5	Poids
SBA	0.28	0.3	0.28	0.28	0.25	1.39	0.27	27%
Horchaia	0.05	0.06	0.056	0.056	0.16	0.382	0.07	7%
Kolea	0.28	0.3	0.28	0.28	0.25	1.39	0.27	27%
Ras Elma	0.28	0.3	0.28	0.28	0.25	1.39	0.27	27%
Maghnia	0.094	0.03	0.09	0.09	0.08	0.38	0.076	7%
							1 = 1.00	1=100%

Tableau 3.50 Normalisation de la matrice Action/Action par rapport aux critères Infrastructure de Transport (C11)

3.7.3 Calcul des poids Finaux er Rangs finaux de chaque Action (troisième étape AHP)

Poid(SBA) = ((impact * Poidc₁ * Poid_c1A1) + (impact * Poidc₂ * Poid_c2A1) + (impact * Poidc₃ * Poid_c3A1) + (Risqu * Poidc₄ * Poid_c4A1) + (Risqu * Poidc5 * Poidc5A1 ) + (clima * Poidc6 * Poid_c6A1) + (climat * Poidc7 * Poid_c7A1) + (climat * Poidc8 * Poid_c8A1) + (socio * Poidc9 * Poid_c9A1) + (socio * Poidc10 * Poidc10A1) + (socio * Poidc11 * Poidc11A1))

Poid(SBA) = ((0.26* 0.71* 0.18) + (0.26* 0.14* 0.06) + (0.26* 0.14* 0.46) + (0.48* 0.83*

0.23) + (0.48* 0.16* 0.11) + (0.15* 0.57* 0.29) + (0.15* 0.28* 0.19) + (0.15* 0.14* 0.23) +

(0.09* 0.11* 0.07) + (0.09* 0.54* 0.29) + (0.09* 0.32* 0.27))

Poid(SBA) = 0.2027

Poid(Hor) = ((impact * Poidc₁ * Poid_c1A2) + (impact * Poidc₂ * Poid_c2A2) + (impact * Poidc₃ * Poid_c3A2) + (Risqu * Poidc₄ * Poid_c4A2) + (Risqu * Poidc5 * Poidc5A2 ) + (clima * Poidc6 * Poid_c6A2) + (climat * Poidc7 * Poid_c7A2) + (climat * Poidc8 * Poid_c8A2) + (socio * Poidc9 * Poid_c9A2) + (socio * Poidc10 * Poidc10A2) + (socio * Poidc11 * Poidc11A2))

Poid(Hor) = ((0.26* 0.71* 0.14) + (0.26* 0.14* 0.18) + (0.26* 0.14* 0.06) + (0.48* 0.83 *

0.23) + (0.48* 0.16* 0.13) + (0.15* 0.57* 0.31) + (0.15* 0.28* 0.1) + (0.15* 0.14* 0.23) +

(0.09* 0.11* 0.28) + (0.09* 0.54* 0.15) + (0.09* 0.32* 0.07))

Poid(Hor) = 0.1698

54

Chapitre 3 Etude de Cas

Poid(Kol) = ((impact * Poidc₁ * Poid_c1A3) + (impact * Poidc₂ * Poid_c2A3) + (impact * Poidc₃ * Poid_c3A3) + (Risqu * Poidc₄ * Poid_c4A3) + (Risqu * Poidc5 * Poidc5A3 ) + (clima * Poidc6 * Poid_c6A3) + (climat * Poidc7 * Poid_c7A3) + (climat * Poidc8 * Poid_c8A3) + (socio * Poidc9 * Poid_c9A3) + (socio * Poidc10 * Poidc10A3) + (socio * Poidc11 * Poidc11A3))

Poid(Kol) = ((0.26* 0.71* 0.15) + (0.26* 0.14* 0.2) + (0.26* 0.14* 0.14) + (0.48* 0.83*

0.23) + (0.48* 0.16* 0.23) + (0.15* 0.57* 0.09) + (0.15* 0.28* 0.41) + (0.15* 0.14* 0.23) +

(0.09* 0.11* 0.05) + (0.09* 0.54* 0.24) + (0.09* 0.32* 0.27))

Poid(Kol) = 0.1704

Poid(Ras) = ((impact * Poidc₁ * Poid_c1A4) + (impact * Poidc₂ * Poid_c2A4) + (impact * Poidc₃ * Poid_c3A4) + (Risqu * Poidc₄ * Poid_c4A4) + (Risqu * Poidc5 * Poidc5A4 ) + (clima * Poidc6 * Poid_c6A4) + (climat * Poidc7 * Poid_c7A4) + (climat * Poidc8 * Poid_c8A4) + (socio * Poidc9 * Poid_c9A4) + (socio * Poidc10 * Poidc10A4) + (socio * Poidc11 * Poidc11A4))

Poid(Ras) = ((0.26* 0.71* 0.34) + (0.26* 0.14* 0.18) + (0.26* 0.14* 0.29) + (0.48* 0.83*

0.23) + (0.48* 0.16* 0.4) + (0.15* 0.57* 0.18) + (0.15* 0.28* 0.23) + (0.15* 0.14* 0.23) +

(0.09* 0.11* 0.28) + (0.09* 0.54* 0.23) + (0.09* 0.32* 0.27))

Poid(Ras) = 0.238

Poid(Mag) = ((impact * Poidc₁ * Poid_c1A5) + (impact * Poidc₂ * Poid_c2A5) + (impact * Poidc₃ * Poid_c3A5) + (Risqu * Poidc₄ * Poid_c4A5) + (Risqu * Poidc5 * Poidc5A5 ) + (clima * Poidc6 * Poid_c6A5) + (climat * Poidc7 * Poid_c7A5) + (climat * Poidc8 * Poid_c8A5) + (socio * Poidc9 * Poid_c9A5) + (socio * Poidc10 * Poidc10A5) + (socio * Poidc11 * Poidc11A5))

Poid(Mag) = ((0.26* 0.71* 0.14) + (0.26* 0.14* 0.34) + (0.26* 0.14* 0.07) + (0.48* 0.83*

0.07) + (0.48* 0.16* 0.1) + (0.15* 0.57* 0.09) + (0.15* 0.28* 0.03) + (0.15* 0.14* 0.07) +

(0.09* 0.11* 0.29) + (0.09* 0.54* 0.06) + (0.09* 0.32* 0.07))

Poid(Mag) = 0.07

3.7.4 Résultat de l'application de la méthode AHP sur l'exemple des zones Industrielles

Action	Poids AHP	Rang
SBA	20.27%	2
Hourchia	16.98%	4
Koléa	17.04%	3
Ras Elma	23.8%	1
Maghnia	7%	5

Tableau 3.51 : Résultats Finaux de la méthode AHP 3.7.5 Première étape FAHP :

3.7.5.1 Théorie des ensembles de la méthode FAHP

Les Ensembles flous sont utilisé pour faire face à l'imprécision et l'incertitude de l'homme

dans divers domaines comme l'industrie, l'optimisation, la localisation. On parle
d'incertitude, d'imprécision dans les décisions prises par l'homme pour résoudre les problèmes relatifs à ces domaines. Zadeh a introduit d'abord la théorie des ensembles en 1965. Dans cette théorie un ensemble flou M dans un univers de discours X est représenté par une fonction d'appartenance M (x), qui affecte à chaque objet x dans X une valeur entre [0,1]. Un ensemble flou triangulaire peut être représenté par (1; m; h) , où l indique la valeur la plus faible possible, m la valeur moyenne, et h la valeur supérieure possible. (M Bashiri, 2009)



				Etude de Cas
???? (??) ?? ???? (??)	est =	définit comme 0 ??- ??	suit : ???? ??< ?? ???? ??= ??= ???? ??= ??= ???? ??= h	?? h
		?? - ?? h - ??
		h - ?? { 0

1

Chapitre 3



???? (??)

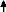
?? ?? h ??

Soit ??(??, ??, ??) ???? ?? (??, ??, ??) deux nombres Flous, Nous pouvons définir les opérations Floues suivantes :

????? = (??, ??, ??) ? (??, ??, ??) = (??+ ??,??+ ??,??+ ??)

??? ??= (??, ??,??) ? (??,??,??) = (??- ??,??- ??,??- ??)

????? = (??, ??, ??)?(??, ??, ??) = (??. ??, ??. ??, ??. ??)

??/?? = (??, ??, ??)/(??, ??, ??) = (???? , ???? , ????) ,Ainsi Nous définissons les opérations Floues suivantes :

???? =? ??????

?? ?? ?[? ? ??????

?? ]-1

?? ?? , l'ensemble des vecteurs Flous

??=1 ??=1 ??=1? ??????

??=1 = (? ????

??

?? ?? ??=1 , ? ??=1 ???? , ? h??

?? ?? ??=1 )

? ? ??????

?? ?? ?? ?? ??=1 , ? h??

??

= (? ????

?? ??=1 , ? ???? ??=1 )

??=1 ??=1[? ? ??????

?? ?? ?? ]-1 = ( 1

??=1 ??=1 ??=1 )

? h??

?? ??=1 , 1

? ????

?? ??=1 , 1

? ????
??

Pondération (Critère /Critère) Flou selon la méthode de (Van Laarhoven, 1983)

critère	Impac_Env	Risq_Nat	Climat	Socio
Impac_Env	(1,1,1)	(1/4,1/3,1/2)	(2, 4, 6)	(1, 3, 5)		Risq_Nat
(1, 3, 5)	(1,1,1)	(3, 5, 7)	(1, 3, 5)	Climat
(1/5,1/4,1/3)	(1/6, 1/5, 1/4)	(1, 1,1)	(2, 4, 6)
Socio	(1/4,1/3,1/2)	(1/4, 1/3, 1/2)	(1/5, 1/4, 1/3)	(1, 1, 1)

Tableau 3.52 : Matrice de Pondération (Critère/Critère) Flou

Tableau 3.53 Pondération Flou des Critères C1, , C3 par rapport au Critère Impact Environnementaux

Critères

		C1						C3
C1		(1, 1, 1)			(3, 5, 7)			(3, 5, 7)
		(1/6,1/5,1/4)			(1, 1, 1)			(1, 1, 1)
C3		(1/6,1/5,1/4)			(1,1,1)			(1,1,1)
Critères			C1
C1			(1,1,1)			(3,5,7)
			(1/6,1/5,1/4)			(1,1,1)
Critères	C6			C7			C8
C6	(1,1,1)			(1,3,5)			(1,3,5)
C7	(1/4,1/3,1/2)			(1,1,1)			(1,3,5)
C8	(1/4, 1/3,1/2)			(^1/4, 1/3,1/2 )			(1,1,1)

55

Tableau 3.54 Pondération Flou des Critères C4, C5 par rapport au Critère Risque Naturel

Tableau 3.55 Pondération Flou des Critères C6, C7, C8 par rapport au Critère Caractéristique Climatique

Chapitre 3 Etude de Cas

Critères	C9	C10	C11
C9	(1,1,1)	(1/4,1/3,1/2)	(1/7,1/5,1/3)
C10	(1,3,5)	(1,1,1)	(1,3,5)
C11	(3, 5, 7)	(1/4,1/3,1/2)	(1,1,1)

Tableau 3.56 Pondération Flou des Critères C9, C10, C11 par rapport au Critère Socio-économique

56

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	(1,1,1)	(1,1,1)	(1,1,1)	(1/3,1/2,1)	(0, 2, 4)
Horchaia	(1,1,1)	(1,1,1)	(1,1,1)	(1/4,1/3,1/2)	(1,1,1)
Kolea	(1,1,1)	(1,1,1)	(1,1,1)	(1/3,1/2,1)	(1,1,1)
Ras Elma	(0, 2, 4)	(1, 3, 5)	(0, 2, 4)	(1,1,1)	(0,2,4)
Maghnia	(1/3,1/2,1)	(1,1,1)	(1,1,1)	(1/3,1/2,1)	(1, 1, 1)

Tableau 3.57 Pondération Floue Action/Action par rapport aux critères C1 (Risque pollution
nappe phréatique.)

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	(1,1,1)	(1/4,1/2,1)	(1/5,1/3,1)	(1/5,1/3,1)	(2,4,6)
Horchaia	(1,2,4)	(1,1,1)	(1/5,1/3,1)	(1/5,1/3,1)	(1/4,1/2,1)
Kolea	(1,3,5)	(1,3,5)	(1,1,1)	(1/6,1/4,1/2)	(1,3,5)
Ras Elma	(1,3,5)	(1,3,5)	(2,4,6)	(1,1,1)	(1,3,5)
Maghnia	(1/6,1/4,1/2)	(1,2,4)	(1/5,1/3,1)	(1/5,1/3,1)	(1,1,1)

Tableau 3.58 Pondération Flou Action/Action par rapport au Critère (Problème

faune et flore)

Le tableau ci-dessous représente la matrice de pondération Action/Action Flou par rapport au critère Climatologie (voir le tableau 3.38)

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	(1,1,1)	(3,5,7)	(2,4,6)	(1,3,5)	(3,5,7)
Horchaia	(1/6,1/5,1/4)	(1,1,1)	(1/3,1/2,1)	(1/4,1/3,1/2)	(1/3,1/2,1)
Kolea	(1/5,1/4,1/3)	(0,2,4)	(1,1,1)	(1/3,1/2,1)	(2,4,6)
Ras Elma	(1/4,1/3,1/2)	(1,3,5)	(0,2,4)	(1,1,1)	(3,5,7)
Maghnia	(1/6,1/5,1/4)	(0,2,4)	(1/5,1/4,1/3)	(1/6,1/5,1/4)	(1,1,1)

Tableau 3.59 Pondération Flou Action/Action par rapport au critère C3 (Nuisances sonores

citoyens.)

Le tableau ci-dessous montre la matrice de pondération Action/Action Flou par rapport au critère Etage bioclimatique (voir le tableau 3.39)

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	(1,1,1)	(1,1,1)	(1,1,1)	(1,1,1)	(1,3,5)
Horchaia	(1,1,1)	(1,1,1)	(1,1,1)	(1,1,1)	(1,3,5)
Kolea	(1,1,1)	(1,1,1)	(1,1,1)	(1,1,1)	(1,3,5)
Ras Elma	(1,1,1)	(1,1,1)	(1,1,1)	(1,1,1)	(1,3,5)
Maghnia	(1/4,1/3,1/2)	(1/4,1/3,1/2)	(1/4,1/3,1/2)	(1/4,1/3,1/2)	(1,1,1)

Tableau 3.60 Pondération Flou Action/Action par rapport au critère C4 (Sismicité)

57

Chapitre 3 Etude de Cas

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	(1,1,1)	(1/3,1/2,1)	(1/4,1/3,1/2)	(2,4,6)	(0,2,4)
Horchaia	(0,2,4)	(1,1,1)	(1/3,1/2,1)	(1,3,5)	(1,1,1)
Kolea	(1,3,5)	(0,2,4)	(1,1,1)	(0,2,4)	(0,2,4)
Ras Elma	(2,4,6)	(1,3,5)	(0,2,4)	(1,1,1)	(1,3,5)
Maghnia	(1/3,1/2,1)	(1,1,1)	(1/3,1/2,1)	(1/4,1/3,1/2)	(1,1,1)

Tableau 3.61 Pondération Flou Action/Action par rapport au critère C5 (Inondation)

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	(1,1,1)	(1,3,5)	(0,2,4)	(1,1,1)	(0,2,4)
Horchaia	(1/4,1/3,1/2)	(1,1,1)	(1,3,5)	(1,3,5)	(3,5,7)
Kolea	(1/3,1/2,1)	(1/4,1/3,1/2)	(1,1,1)	(1/3,1/2,1)	(1,1,1)
Ras Elma	(1,1,1)	(1/4,1/3,1/2)	(0,2,4)	(1,1,1)	(0,2,4)
Maghnia	(1/3,1/2,1)	(1/6,1/5,1/4)	(1,1,1)	(1/3,1/2,1)	(1,1,1)

Tableau 3.62 Pondération Flou Action/Action par rapport au critère C6 (Température)

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	(1,1,1)	(1,3,5)	(1/4,1/3,1/2)	(1/3,1/2,1)	(5,7,9)
Horchaia	(1/4,1/3,1/2)	(1,1,1)	(1/5,1/4,1/3)	(1/3,1/2,1)	(4,6,8)
Kolea	(1,3,5)	(2,4,6)	(1,1,1)	(0,2,4)	(6,8,10)
Ras Elma	(0,2,4)	(0,2,4)	(1/3,1/2,1)	(1,1,1)	(4,6,8)
Maghnia	(1/8,1/7,1/6)	(1/7,1/6,1/5)	(1/9,1/8,1/7)	(1/7,1/6,1/5)	(1,1,1)

Tableau 3.63 Pondération Flou Action/Action par rapport au critère C7 (Pluviométrie)

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	(1,1,1)	(1,1,1)	(1,1,1)	(1,1,1)	(1,3,5)
Horchaia	(1,1,1)	(1,1,1)	(1,1,1)	(1,1,1)	(1,3,5)
Kolea	(1,1,1)	(1,1,1)	(1,1,1)	(1,1,1)	(1,3,5)
Ras Elma	(1,1,1)	(1,1,1)	(1,1,1)	(1,1,1)	(1,3,5)
Maghnia	(1/4,1/3,1/2)	(1/4,1/3,1/2)	(1/4,1/3,1/2)	(1/4,1/3,1/2)	(1,1,1)

Tableau 3.64 Pondération Flou Action/Action par rapport au critère C8 (Etage Bioclimatique)

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	(1,1,1)	(1/4,1/3,1/2)	(0,2,4)	(1/4,1/3,1/2)	(1/6,1/5,1/4)
Horchaia	(1,3,5)	(1,1,1)	(3,5,7)	(1,3,5)	(1/4,1/3,1/2)
Kolea	(1/3,1/2,1)	(1/6,1/5,1/4)	(1,1,1)	(1/3,1/2,1)	(1/6,1/5,1/4)
Ras Elma	(1,3,5)	(1/4,1/3,1/2)	(0,2,4)	(1,1,1)	(4,6,8)
Maghnia	(3,5,7)	(1,3,5)	(3,5,7)	(1/7,1/6,1/5)	(1,1,1)

Tableau 3.65 Pondération Flou Action/Action par rapport au critère C9 (Cout d'aménagement)

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	(1,1,1)	(3,5,7)	(1,1,1)	(0,2,4)	(1,3,5)
Horchaia	(1/6,1/5,1/4)	(1,1,1)	(1/6,1/5,1/4)	(1,3,5)	(0,2,4)
Kolea	(1,1,1)	(3,5,7)	(1,1,1)	(1/4,1/3,1/2)	(1,3,5)
Ras Elma	(1/3,1/2,1)	(1/4,1/3,1/2)	(1,3,5)	(1,1,1)	(2,4,6)
Maghnia	(1/4,1/3,1/2)	(1/3,1/2,1)	(1/4,1/3,1/2)	(1/5,1/4,1/3)	(1,1,1)

Tableau 3.66 Pondération Flou Action/Action par rapport au critère C10 (Potentialité de
développement d'aménagement)

Chapitre 3 Etude de Cas

Action	SBA	Horchaia	Kolea	Ras Elma	Maghnia
SBA	(1,1,1)	(3,5,7)	(1,1,1)	(1,1,1)	(1,3,5)
Horchaia	(1/6,1/5,1/4)	(1,1,1)	(1/6,1/5,1/4)	(1/6,1/5,1/4)	(0,2,4)
Kolea	(1,1,1)	(3,5,7)	(1,1,1)	(1,1,1)	(1,3,5)
Ras Elma	(1,1,1)	(3,5,7)	(1,1,1)	(1,1,1)	(1,3,5)
Maghnia	(1/4,1/3,1/2)	(1/3,1/2,1)	(1/4,1/3,1/2)	(1/4,1/3,1/2)	(1,1,1)

Tableau 3.67 Pondération Flou Action/Action par rapport au critère C11 (Infrastructure de

Transport)

Selon La méthode AHP, fondé par T. Saaty , la meilleur Zone est celle de Ras Elma

3.7.6 Deuxième étape FAHP : Calcul du vecteur propre moyen Flou (Priorité Floue) pour chaque matrice ci-dessus

critère	Impac_Env	Risq_Nat	Climat	Socio
Impac_Env	(1,1,1)	(1/4,1/3,1/2)	(2, 4, 6)	(1, 3, 5)		Risq_Nat
(1, 3, 5)	(1,1,1)	(3, 5, 7)	(1, 3, 5)	Climat
(1/5,1/4,1/3)	(1/6, 1/5, 1/4)	(1, 1,1)	(2, 4, 6)
Socio	(1/4,1/3,1/2)	(1/4, 1/3, 1/2)	(1/5, 1/4, 1/3)	(1, 1, 1)

Tableau 3.68 : Pondération (Critère/Critère) Flou du Premier Niveau

Pour la Normalisation Floue de la matrice Critère/Critère , On doit Calculer d'abord ? M????

?? ??
??=1

(4.25; 8.33; 12.5)

(6; 12; 18)

? ??=1 M???? = (

?? ?? (3.36; 5.45; 7.58) ) => ???? =

(1.7; 1.91; 2.66)

4.25	8.33		12.5		=	0.1 [ 0.14 0.08 0.04		0.3 0.43 0.19 0.06		0.81 1.17 ] 0.49 0.17
40.74 6	27.69 12		15.31 18
40.74 3.36	27.69 5.45		15.31 7.58
40.74 1.7	27.69 1.91		15.31 2.66
40.74	27.69		15.31
Critères		????????????????							???????? net
Impact		0.1		0.3			0.81		0.40
Risque		0.14		0.43			1.17		0.58
Climat		0.08		0.19			0.49		0.25
Socio		0.04		0.06			0.17		0.09

Tableau 3.69 Normalisation Floue de la matrice Critère /Critère et calcul des Poids Flous Nous utilisons les mêmes opérations Floues pour Normaliser les matrices Critère/Critère du troisième niveau par rapport aux Critères de deuxième niveau , ainsi on calcule les poids des Critères du troisième Niveau selon les critères du deuxième niveau

S-Critères	????????????????						????????net		Rang
C1	0.35		0.71		1.32		0.79		1
	0.11		0.14		0.19		0.14		2
C3	0.11		0.14		0.19		0.14		3
S-Critères	????????????????					???????? net		Rang
C4	0.43	0.83		1.6		0.95		1
C5	0.12	0.16		0.25		0.17		2

Tableau 3.70 : Normalisation
Floue de la matrice Cr/Cr selon
les critères C1, , C3

58

Tableau 3.71 : Normalisation
Floue de la matrice Cr/Cr selon
les critères C4, C5

Chapitre 3 Etude de Cas

Tableau 3.72 : Normalisation
Floue de la matrice Cr/Cr selon
les critères C6, C7, C8

S-Critères

	????????????????				???????? ??????		Rang
C6	0.15	0.53	1.62		0.76		1
C7	0.11	0.33	0.96		0.46		2
C8	0.07	0.12	0.29		0.16		3

Tableau 3.73 : Normalisation
Floue de la matrice Cr/Cr selon
les critères C9, C10, C11

S-Critères

	????????????????			???????? ??????	Rang
C9	0.06	0.1	0.21	0.12	3
C10	0.14	0.47	0.27	0.29	2
C11	0.19	0.42	0.98	0.53	1

Tableau 3.74 : Normalisation
Floue de la matrice Ac/Ac par
rapport au critère C1

Actions

	????????????????			???????? ??????		Rang
SBA	0.08	0.19	0.455	0.24		2
Hourchia	0.104	0.152	0.25	0.168		5
Koléa	0.106	0.158	0.28	0.181		3
Ras Elma	0.049	0.352	1.02	0.473		1
Maghnia	0.090	0.14	0.28	0.17		4

Tableau 3.75 : Normalisation
Floue de la matrice Ac/Ac par
rapport au critère

Actions

	????????????????			???????? ??????		Rang
SBA	0.05	0.16	0.525	0.245		3
Hourchia	0.04	0.1081	0.42	0.189		4
Koléa	0.06	0.266	0.8675	0.3978		2
Ras Elma	0.09	0.363	1.15	0.5343		1
Maghnia	0.04	0.1016	0.394	0.1785		5

Tableau 3.76 : Normalisation
Floue de la matrice Ac/Ac par
rapport au Critère C3

Actions

	????????????????				???????? ??????		Rang
SBA	0.1528	0.416	1.161		0.5766		1
Hourchia	0.031	0.058	0.1675		0.0855		5
Koléa	0.0539	0.179	0.55		0.2609		3
Ras Elma	0.08	0.2619	0.7819		0.3746		2
Maghnia	0.0233	0.0843	0.2605		0.1227		4

Tableau 3.77 : Normalisation
Floue de la matrice Ac/Ac
selon le critère C4

59

Actions

	????????????????			???????? ??????	Rang
SBA	0.12	0.23	0.4	0.25	1
Hourchia	0.12	0.23	0.4	0.25	2
Koléa	0.12	0.23	0.4	0.25	3
Ras Elma	0.12	0.23	0.4	0.25	4
Maghnia	0.051	0.0765	0.13	0.085	5

Chapitre 3 Etude de Cas

Tableau 3.78 : Normalisation
Floue de la matrice Ac/Ac selon
le critère C5

Actions

	????????????????			???????? ??????	Rang
SBA	0.0526	0.1879	0.7431	0.32	3
Hourchia	0.0489	0.1800	0.7134	0.31	4
Koléa	0.029	0.24	1.0701	0.44	2
Ras Elma	0.0735	0.312	1.24	0.541	1
Maghnia	0.0427	0.0799	0.267	0.129	5

Tableau 3.79 : Normalisation
Floue de la matrice Ac/Ac par
rapport au critère C6

Actions

	????????????????			???????? ??????		Rang
SBA	0.0568	0.2632	0.87	0.3966		2
Hourchia	0.118	0.36	1.0737	0.5172		1
Koléa	0.0551	0.097	0.2611	0.1377		4
Ras Elma	0.0426	0.1851	0.6	0.2759		3
Maghnia	0.0534	0.0935	0.2466	0.13116		5

Tableau 3.80 : Normalisation
Floue de la matrice Ac/Ac par
rapport au Critère C7

Actions

	????????????????				???????? ??????		Rang
SBA	0.1037	0.2319	0.5461		0.2939		2
Hourchia	0.0791	0.1584	0.3584		0.19		4
Koléa	0.1369	0.3528	0.8606		0.44		1
Ras Elma	0.07298	0.2254	0.5958		0.2933		3
Maghnia	0.02	0.0313	0.05627		0.033		5

Tableau 3.81 : Normalisation
Floue de la matrice Ac/Ac par
rapport au critère C8

60

Actions

	????????????????			???????? ??????		Rang
SBA	0.12	0.23	0.4	0.25		1
Hourchia	0.12	0.23	0.4	0.25		2
Koléa	0.12	0.23	0.4	0.25		3
Ras Elma	0.12	0.23	0.4	0.25		4
Maghnia	0.05	0.076	0.13	0.08533		5

Tableau 3.82 : Normalisation
Floue de la matrice Ac/Ac par
rapport au critère C9

Actions

	????????????????			???????? ??????	Rang
SBA	0.024	0.1437	0.2572	0.1416	4
Hourchia	0.093	0.2561	0.76	0.2851	3
Koléa	0.029	0.0498	0.144	0.074	5
Ras Elma	0.0933	0.2561	0.76	0.36	2
Maghnia	0.1215	0.2941	0.8312	0.41	1

Tableau 3.83 : Normalisation
Floue de la matrice Ac/Ac par
rapport au critère C10

Actions

	????????????????			???????? ??????	Rang
SBA	0.1	0.3	0.849	0.41	1
Hourchia	0.389	0.16	0.4955	0.34	3
Koléa	0.1	0.2584	0.6842	0.34	2
Ras Elma	0.076	0.22	0.637	0.30	4
Maghnia	0.0339	0.06	0.1571	0.0836	5

Chapitre 3 Etude de Cas

Tableau 3.84 : Normalisation
Floue de la matrice Ac/Ac par
rapport au critère C11

Actions

	PoidFlou			Poldnet	Rang
SBA	0.129	0.2813	0.61	0.34	1
Hourchia	0.027	0.092	0.23	0.1163	4
Koléa	0.129	0.2813	0.61	0.34	2
Ras Elma	0.129	0.2813	0.61	0.34	3
Maghnia	0.038	0.063	0.1423	0.0811	5

3.7.7 Calcul des poids Flous Finaux er Rangs finaux de chaque Action (troisième étape FAHP)

Poid_Flou(SBA) = ((impac®Poidc1®Poidc1A1) ® (impac®Poidc2®Poidc2A1)®(impac ® Poidc3 ® Poidc3A1))®((risq®Poidc4®Poidc4A1) ® (risq®Poidc5®Poidc5A1))

®((clima®Poidc6®Poidc6A1) ® (clima®Poidc7®Poidc7A1)®(clima ® Poidc8 ® Poidc8A1))® ((socio®Poidc9®Poidc9A1) ® (socio®Poidc10®Poidc10A1) ® (socio®Poidc11®Poidc11A1))

Poid_Flou(SBA) = ((0.1 0.3 0.81)®(0.35 0.71 1.32) ® (0.08 0.19 0.455)) ®((0.1 0.3 0.81)®(0.11 0.14 0.19) ® (0.05 0.16 0.52))® ((0.1 0.3 0.81)®(0.11 0.14 0.19) ® (0.15 0.41 0.16)) ®((0.14 0.43 1.17)®(0.43 0.83 1.6)®(0.12 0.23 0.4)) ® ((0.14 0.43 1.17)®(0.12 0.16 0.25)®(0.05 0.18 0.7))®((0.08 0.19 0.49) ®(0.15 0.53 1.62)®(0.05 0.26 0.87))®((0.08 0.19 0.49)®(0.11 0.33 0.96) ®(0.1 0.23 0.54))®(( 0.08 0.19 0.49)®(0.07 0.12 0.29)®(0.12 0.23 0.4)) ®((0.04 0.06 0.17)®(0.06 0.1 0.21)®(0.024 0.14 0.25)) ® ((0.04 0.06 0.17)®(0.14 0.47 0.27)®(0.1 0.3 0.84)) ®((0.04 0.06 0.17)®(0.19 0.42 0.98)®(0.129 0.28 0.61))

Poid_Flou(SBA) = (0. 014 0. 203 2. 56)

Normalisation PoidFloue(SBA) = (0. 005 0. 07 0. 91)

Poid_Flou(Hor) = ((impac®Poidc1®Poidc1A2) ® (impac®Poidc2®Poidc2A2)®(impac ® Poidc3 ® Poidc3A2))®((risq®Poidc4®Poidc4A2) ® (risq®Poidc5®Poidc5A2))

((clima®Poidc6®Poidc6A2) ® (clima®Poidc7®Poidc7A2)®(clima ® Poidc8 ® Poidc8A2))® ((socio®Poidc9®Poidc9A2) ® (socio®Poidc10®Poidc10A2) ® (socio®Poidc11®Poidc11A2))

Poid_Flou(Hor) = ((0.1 0.3 0.81)®(0.35 0.71 1.32) ® (0.10 0.15 0.25)) ®((0.1 0.3 0.81)®(0.11 0.14 0.19) ® (0.04 0.10 0.42))® ((0.1 0.3 0.81)®(0.11 0.14 0.19) ® (0.03 0.05 0.16)) ®((0.14 0.43 1.17)®(0.43 0.83 1.6)®(0.12 0.23 0.4)) ® ((0.14 0.43 1.17)®(0.12 0.16 0.25)®(0.04 0.18 0.7))®((0.08 0.19 0.49) ®(0.15 0.53 1.62)®(0.11 0.06 1.07))®((0.08 0.19 0.49)®(0.11 0.33 0.96) ®(0.07 0.15 0.35))®(( 0.08 0.19 0.49)®(0.07 0.12 0.29)®(0.12 0.23 0.4)) ®((0.04 0.06 0.17)®(0.06 0.1 0.21)®(0.09 0.25 0.76)) ® ((0.04 0.06 0.17)®(0.14 0.47 0.27)®(0.38 0.16 0.49)) ®((0.04 0.06 0.17)®(0.19 0.42 0.98)®(0.02 0.09 0.23))

Poid_Flou(Hor) = (0. 015 0. 157 2. 4)

Normalisation

PoidFloue(Hor) = (0. 005 0. 06 0. 93)

61

Poid_Flou(Kol) = ((impac®Poidc1®Poidc1A3) ® (impac®Poidc2®Poidc2A3)®(impac ® Poidc3 ® Poidc3A3))®((risq®Poidc4®Poidc4A3) ® (risq®Poidc5®Poidc5A3))

((clima®Poidc6®Poidc6A3) ® (clima®Poidc7®Poidc7A3)®(clima ® Poidc8 ® Poidc8A3))® ((socio®Poidc9®Poidc9A3) ® (socio®Poidc10®Poidc10A3) ® (socio®Poidc11®Poidc11A3))

Poid_Flou(Kol) = ((0.1 0.3 0.81)®(0.35 0.71 1.32) ® (0.10 0.15 0.28))

®((0.1 0.3 0.81)®(0.11 0.14 0.19) ® (0.06 0.26 0.86))®

((0.1 0.3 0.81)®(0.11 0.14 0.19) ® (0.05 0.17 0.55))

Chapitre 3 Etude de Cas

®((0.14 0.43 1.17)®(0.43 0.83 1.6)®(0.12 0.23 0.4)) ®

((0.14 0.43 1.17)®(0.12 0.16 0.25)®(0.02 0.24 1.07))®((0.08 0.19 0.49) ®(0.15 0.53 1.62)®(0.05 0.09 0.26))®((0.08 0.19 0.49)®(0.11 0.33 0.96) ®(0.13 0.35 0.86))®(( 0.08 0.19 0.49)®(0.07 0.12 0.29)®(0.12 0.23 0.4)) ®((0.04 0.06 0.17)®(0.06 0.1 0.21)®(0.02 0.04 0.14))

® ((0.04 0.06 0.17)®(0.14 0.47 0.27)®(0.1 0.25 0.68)) ®((0.04 0.06 0.17)®(0.19 0.42 0.98)®(0.12 0.28 0.61))

Poid_Flou(Kol) = (0. 04 0. 185 2. 34)

Normalisation PoidFloue (Kol) = (0. 015 0. 07 0. 91)

62

Poid_Flou(Ras) = ((impac®Poidc1®Poidc1A4) ® (impac®Poidc2®Poidc2A4)®(impac 0 Poidc3 ? Poidc3A4))®((risq®Poidc4®Poidc4A4) ® (risq®Poidc5®Poidc5A4))

((clima®Poidc6®Poidc6A4) ® (clima®Poidc7®Poidc7A4)®(clima 0 Poidc8 0 Poidc8A4))® ((socio®Poidc9®Poidc9A4) ® (socio®Poidc10®Poidc10A4) ® (socio®Poidc11®Poidc11A4))

Poid_Flou(Ras) = ((0.1 0.3 0. 81)®(0. 35 0.71 1.32) ® (0.04 0.35 1.02))

®((0.1 0.3 0. 81)®(0. 11 0.14 0.19) ® (0.09 0.36 1.15))®

((0.1 0.3 0. 81)®(0. 11 0.14 0.19) ® (0.08 0.26 0.78))

®((0.14 0.43 1.17)®(0.43 0.83 1.6)®(0.12 0.23 0.4)) ®

((0.14 0.43 1.17)®(0.12 0.16 0.25)®(0.07 0.31 1.24))®((0.08 0.19 0.49) ®(0.15 0.53 1.62)®(0.04 0.18 0.6))®((0.08 0.19 0.49)®(0.11 0.33 0.96) ®(0.07 0.22 0.56))®(( 0.08 0.19 0.49)®(0.07 0.12 0.29)®(0.12 0.23 0.4)) ®((0.04 0.06 0.17)®(0.06 0.1 0.21)®(0.09 0.25 0.76))

® ((0.04 0.06 0.17)®(0.14 0.47 0.27)®(0.07 0.22 0.63)) ®((0.04 0.06 0.17)®(0.19 0.42 0.98)®(0.12 0.28 0.61))

®	Normalisation			PoidFlou(Ras Elma) = (0.013 0.236 3.4)

Poid_Flou(Mag) = ((impac®Poidc1®Poidc1A5) ® (impac®Poidc2®Poidc2A5)®(impac 0 Poidc3 ? Poidc3A5))®((risq®Poidc4®Poidc4A5) ® (risq®Poidc5®Poidc5A5))

((clima®Poidc6®Poidc6A5) ® (clima®Poidc7®Poidc7A5)®(clima 0 Poidc8 0 Poidc8A5))® ((socio®Poidc9®Poidc9A5) ® (socio®Poidc10®Poidc10A5) ® (socio®Poidc11®Poidc11A5))

Poid_Flou(Mag) = ((0.1 0.3 0.81)®(0.35 0.71 1.32) ® (0.09 0.14 0.28))

®((0.1 0.3 0. 81)®(0. 11 0.14 0.19) ® (0.04 0.1 0.39))®

((0.1 0.3 0. 81)®(0. 11 0.14 0.19) ® (0.02 0.08 0.26))

®((0.14 0.43 1.17)®(0.43 0.83 1.6)®(0.05 0.07 0.13)) ®

((0.14 0.43 1.17)®(0.12 0.16 0.25)®(0.04 0.07 0.26))®((0.08 0.19 0.49) ®(0.15 0.53 1.62)®(0.05 0.09 0.24))®((0.08 0.19 0.49)®(0.11 0.33 0.96) ®(0.02 0.03 0.05))®(( 0.08 0.19 0.49)®(0.07 0.12 0.29)®(0.05 0.07 0.13)) ®((0.04 0.06 0.17)®(0.06 0.1 0.21)®(0.12 0.29 0.83))

® ((0.04 0.06 0.17)®(0.14 0.47 0.27)®(0.03 0.06 0.15)) ®((0.04 0.06 0.17)®(0.19 0.42 0.98)®(0.038 0.063 0.14))

Poid_Flou(Maghnia) = (0.0086 0.074 0.969)

63

Chapitre 3 Etude de Cas

3.7.8 Comparaison des Résultat de l'application de la méthode AHP et FAHP sur l'exemple des zones Industrielles

Action	Poids AHP	Rang AHP	Poid FAHP (%)				Rang FAHP	SBA
20.27 %	2	0.5 %	7 %		91 %	5	Hourchia
16.98 %	4	0.5 %	6%		93 %	3	Koléa
17.04 %	3	1.5 %	7 %		91 %	4	Ras Elma
23.8 %	1	0.3 %	6%		93 %	2	Maghnia
7.00 %	5	0.8 %	7 %		96 %	1

Tableau 3.85 : Résultats des deux méthodes AHP et FAHP appliqués sur l'exemple de
Rangement des zones Industrielles

3.8 La méthode AHP et FAHP (AHP Flou) après le prétraitement par moteur d'Inférence

3.8.1 La méthode AHP après traitement par MI

Poid(SBA) = ((impact * Poid_c1A1) + (impact * Poid_c2A1) + (impact * Poid_c3A1) + (Risqu * Poid_c4A1) + (Risqu * Poidc5A1 ) + (clima * Poid_c6A1) + (climat * Poid_c7A1) + (climat * Poid_c8A1) + (socio * Poid_c9A1) + (socio * Poidc10A1) + (socio * Poidc11A1))

Poid(SBA) = ((0.26 * 0.18) + (0.26 * 0.06) + (0.26 * 0.46) + (0.48 * 0.23) + (0.48 * 0.11) +

(0.15* 0.29) + (0.15* 0.19) + (0.15* 0.23) + (0.09* 0.07) + (0. 09* 0.29) + (0.09* 0.27))

Poid(SBA) = 0.50

Poid(Hor) = ((impact * Poid_c1A2) + (impact * Poid_c2A2) + (impact * Poid_c3A2) + (Risqu * Poid_c4A2) + (Risqu * Poidc5A2 ) + (clima * Poid_c6A2) + (climat * Poid_c7A2) + (climat * Poid_c8A2) + (socio * Poid_c9A2) + (socio * Poidc10A2) + (socio * Poidc11A2))

Poid(Hor) = ((0.26* 0.14) + (0.26* 0.18) + (0.26* 0.06) + (0.48* 0.23) + (0.48* 0.13) +

(0.15* 0.31) + (0.15* 0.1) + (0.15* 0.23) + (0.09* 0.28) + (0.09* 0.15) + (0.09* 0.07))

Poid(Hor) = 0.408

Poid(Kol) = ((impact * Poid_c1A3) + (impact * Poid_c2A3) + (impact * Poid_c3A3) + (Risqu * Poid_c4A3) + (Risqu * Poidc5A3 ) + (clima * Poid_c6A3) + (climat * Poid_c7A3) + (climat * Poid_c8A3) + (socio * Poid_c9A3) + (socio * Poidc10A3) + (socio * Poidc11A3))

Poid(Kol) = ((0.26 * 0.15) + (0.26 * 0.2) + (0.26 * 0.14) + (0.48 * 0.23) + (0.48 * 0.23) +

(0.15* 0.09) + (0.15* 0.41) + (0.15* 0.23) + (0.09* 0.05) + (0. 09* 0.24) + (0.09* 0.27))

Poid(Kol) = 0.5045

Poid(Ras) = ((impact * Poid_c1A4) + (impact * Poid_c2A4) + (impact * Poid_c3A4) + (Risqu * Poid_c4A4) + (Risqu * Poidc5A4 ) + (clima * Poid_c6A4) + (climat * Poid_c7A4) + (climat * Poid_c8A4) + (socio * Poid_c9A4) + (socio * Poidc10A4) + (socio * Poidc11A4))

Poid(Ras) = ((0.26 * 0.34) + (0.26 * 0.18) + (0.26 * 0.29) + (0.48 * 0.23) + (0.48 * 0.4) +

(0.15* 0.18) + (0.15* 0.23) + (0.15* 0.23) + (0.09* 0.28) + (0. 09* 0.23) + (0.09* 0.27))

Poid(Ras) = 0.63 0.088+0.046+0.075+0.1104+0.192+0.027+0.034+0.034+0.024

Poid(Mag) = ((impact * Poid_c1A5) + (impact * Poid_c2A5) + (impact * Poid_c3A5) + (Risqu * Poid_c4A5) + (Risqu * Poidc5A5 ) + (clima * Poid_c6A5) + (climat * Poid_c7A5) + (climat * Poid_c8A5) + (socio * Poid_c9A5) + (socio * Poidc10A5) + (socio * Poidc11A5))

Poid(Mag) = ((0.26 * 0.14) + (0.26 * 0.34) + (0.26 * 0.07) + (0.48 * 0.07) + (0.48 * 0.1) +

(0.15 * 0.09) + (0.15 * 0.03) + (0.15 * 0.07) + (0.09 * 0.29) + (0. 09 * 0.06) + (0.09 * 0.07))

64

Chapitre 3 Etude de Cas

Poid(Mag) = 0.3380

3.7.6 Résultat de l'application de la méthode AHP sur l'exemple des zones Industrielles

Action	Poids AHP		Rang	SBA
50.00 %	3		Hourchia
40.8 %	4		Koléa
50.45 %	2		Ras Elma
63 %	1		Maghnia
33 %	5

Tableau 3.51 : Résultats Finaux de la méthode AHP après Moteur d'Inférence 3.8.2 La méthode FAHP après traitement par MI

Poid_Flou(SBA) = ((impac®Poidc1A1) ® (impac®Poidc2A1)®(impac 0 Poidc3A1))®((risq®Poidc4A1) ® (risq®Poidc5A1))®((clima®Poidc6A1) ® (clima®Poidc7A1)®(clima 0 Poidc8A1))®

((socio®Poidc9A1) ® (socio®Poidc10A1) ® (socio®Poidc11A1))

Poid_Flou(SBA) = ((0.1 0.3 0.81) ® (0.08 0.19 0.455))

®((0.1 0.3 0.81) ® (0.05 0.16 0.52))®

((0.1 0.3 0.81) ® (0.15 0.41 0.16))

®((0.14 0.43 1.17)®(0.12 0.23 0.4)) ®

((0.14 0.43 1.17)®(0.05 0.18 0.7))®((0.08 0.19 0.49)

®(0.05 0.26 0.87))®((0.08 0.19 0.49)

®(0.1 0.23 0.54))®(( 0.08 0.19 0.49)®(0.12 0.23 0.4))

®((0.04 0.06 0.17)®(0.024 0.14 0.25))

® ((0.04 0.06 0.17)®(0.1 0.3 0.84))

®((0.04 0.06 0. 17)®(0. 129 0.28 0.61))

	Normalisation			PoidFlou(SBA) = (0. 083 0. 584 3. 36)

Poid_Flou(Hor) = ((impac®Poidc1A2) ® (impac®Poidc2A2)®(impac 0 Poidc3A2))®((risq®Poidc4A2) ® (risq®Po_idc5A2)) ((clima®Poidc6A2) ® (clima®Poidc7A2)®(clima 0 Poidc8A2))®

((socio®Poidc9A2) ® (socio®Poidc10A2) ® (socio®Poidc11A2))

Poid_Flou(Hor) = ((0.1 0.3 0.81) ® (0.10 0.15 0.25))

®((0.1 0. 3 0.81) ® (0.04 0.10 0.42))®

((0.1 0.3 0.81) ® (0.03 0.05 0.16))

®((0.14 0.43 1.17)®(0.12 0.23 0.4)) ®

((0.14 0.43 1.17)®(0.04 0.18 0.7))®((0.08 0.19 0.49)

®(0.11 0.06 1.07))®((0.08 0.19 0.49)

®(0.07 0.15 0.35))®(( 0.08 0.19 0.49)®(0.12 0.23 0.4))

®((0.04 0.06 0.17)®(0.09 0.25 0.76))

® ((0.04 0.06 0.17)®(0.38 0.16 0.49))

®((0.04 0.06 0.17)®(0.02 0.09 0.23))

	Normalisation			PoidFlou(Hor) = (0. 083 0. 379 3. 105)

Poid_Flou(Kol) = ((impac®Poidc1A3) ® (impac®Poidc2A3)®(impac 0 Poidc3A3))®((risq®Poidc4A3) ® (risq®Poidc5A3))

((clima®Poidc6A3) ® (clima®Poidc7A3)®(clima 0 Poidc8A3))® ((socio®Poidc9A3) ® (socio®Poidc10A3) ® (socio®Poidc11A3))

Matrice(FAHPMI) = (

0.015 0.014 0.002

0.11 0.12 0.11

0.87 0.85 0.86

65

Chapitre 3 Etude de Cas

Poid_Flou(Kol) = ((0.1 0.3 0.81) ® (0.10 0.15 0.28)) ®((0.1 0.3 0.81) ® (0.06 0.26 0.86))® ((0.1 0.3 0.81) ® (0.05 0.17 0.55)) ®((0.14 0.43 1.17)®(0.12 0.23 0.4)) ® ((0.14 0.43 1.17)®(0.02 0.24 1.07))®((0.08 0.19 0.49) ®(0.05 0.09 0.26))®((0.08 0.19 0.49) ®(0.13 0.35 0.86))®(( 0.08 0.19 0.49)®(0.12 0.23 0.4)) ®((0.04 0.06 0.17)®(0.02 0.04 0.14))

® ((0.04 0.06 0.17)®(0.1 0.25 0.68)) ®((0.04 0.06 0.17)®(0.12 0.28 0.61))

®	Normalisation			PoidFlou(Kol) = (0. 074 0. 53 4. 07)

Poid_Flou(Ras) = ((impacPoidc1A4) ® (impac®Poidc2A4)®(impac 0 Poidc3A4))®((risq®Poidc4A4) ® (risq®Poidc5A4)) ® ((clima®Poidc6A4) ® (clima®Poidc7A4)®(clima 0 Poidc8A4))® ((socio®Poidc9A4) ® (socio®Poidc10A4) ® (socio®Poidc11A4))

Poid_Flou(Ras) = ((0.1 0.3 0.81) ® (0.04 0.35 1.02))

®((0.1 0.3 0.81) ® (0.09 0.36 1.15))® ((0.1 0.3 0.81) ® (0.08 0.26 0.78)) ®((0.14 0.43 1.17)®(0.12 0.23 0.4)) ® ((0.14 0.43 1.17)®(0.07 0.31 1.24))®((0.08 0.19 0.49)

®(0.04 0.18 0.6))®((0.08 0.19 0.49)

®(0.07 0.22 0.56))®(( 0.08 0.19 0.49)®(0.12 0.23 0.4))

®((0.04 0.06 0.17)®(0.09 0.25 0.76))

® ((0.04 0.06 0.17)®(0.07 0.22 0.63)) ®((0.04 0.06 0.17)®(0.12 0.28 0.61))

®	Normalisation			PoidFlou(Ras Elma) = (0.077 0.68 4.60)

Poid_Flou(Mag) = ((impac®Poidc1A5) ® (impac®Poidc2A5)®(impac 0 Poidc3A5))®((risq®Poidc4A5) ® (risq®Poidc5A5)) ® ((clima®Poidc6A5) ® (clima®Poidc7A5)®(clima 0 Poidc8A5))® ((socio®Poidc9A5) ® (socio®Poidc10A5) ® (socio®Poidc11A5))

Poid_Flou(Mag) = ((0.1 0.3 0.81) ® (0.09 0.14 0.28))

®((0.1 0.3 0.81) ® (0.04 0.1 0.39))® ((0.1 0.3 0.81) ® (0.02 0.08 0.26)) ®((0.14 0.43 1.17)®(0.05 0.07 0.13)) ® ((0.14 0.43 1.17)®(0.04 0.07 0.26))®((0.08 0.19 0.49)

®(0.05 0.09 0.24))®((0.08 0.19 0.49)

®(0.02 0.03 0.05))®(( 0.08 0.19 0.49)®(0.05 0.07 0.13))

®((0.04 0.06 0.17)®(0.12 0.29 0.83))

® ((0.04 0.06 0.17)®(0.03 0.06 0.15)) ®((0.04 0.06 0.17)®(0.038 0.063 0.14))

®	Normalisation
PoidFlou(Maghnia) = (0.044 0.217 1.60)		PoidFlou(Maghnia) = (0.023 0.11 0.86)

Matrice résultats du FAHP après prétraitement par MI

0.02 0.14 0.84

0.023 0.1 0.87

66

Chapitre 3 Etude de Cas

3.8.3 Comparaison des Résultat de l'application de la méthode AHP et FAHP sur l'exemple des zones Industrielles avec Moteur d'Inférence

Action	Poids AHP	Rang AHP	Poid FAHP (%)			Rang FAHP
SBA	50.00 %	3	2 %	14 %	84 %	5
Hourchia	40.80 %	4	2.3 %	10 %	87 %	2
Koléa	50.45 %	2	1.5 %	11 %	87 %	1
Ras Elma	63 %	1	1.4%	12 %	85 %	4
Maghnia	33 %	5	0.2 %	11 %	86 %	3

Tableau 3.85 : Résultats des deux méthodes AHP et FAHP appliqués sur l'exemple de
Rangement des zones Industrielles après exécution du Moteur d'Inférence

3.9 Conclusion

Dans notre pays il y a beaucoup de cas semblable a notre cas d'étude « le rangement des zones industrielles » Nous estimons proposer dans ce travail une approche originale( voir figure) du faite qu'un moteur d'inférence est utilisée dans la phase de hiérarchisation pour réduire la hiérarchie initiale afin de réduire la complexité et le nombre d'itération des calculs de consistances. Nous avons jugé que la fusification est primordiale pour la phase des comparaisons binaires vu la subjectivité et l'hésitante des décideurs impliquées dans cette phase.

67

Chapitre 4 Conception & Implémentation

Sommaire

4.1 Introduction 68

4.2 Outils utilisés 68

4.3 Langage de programmation Java 68

4.4 L'environnement NetBeans 69

4 .5 GEOTOOLS 69

4.6 Le format Shapefile(SHP) 70

4.7 Fonctionnalité et objectifs de notre Application 70

4.7.1 Notre Interface 71

4.7.2 Affichage de l'arbre représentant la problématique 74

4.7.3 Calcul des poids de chaque noeuds de l'arbre selon le vecteur de priorité 74

4.7.4 Rangement des actions selon la méthode AHP 74

4.7.5 Rangement des Critères selon la méthode AHP Flou 76

4.7.6 Rangement des Actions selon la méthode AHP Flou 78

4.8 Synthèse de l'approche développée FAHPSIG 79

4.9 Conclusion 80

Liste des figures

Figure 4.1 Interface de l'environnement Netbeans 69

Figure 4.2 Interface d'entrer des données 71

Figure 4.3 Exemple d'affichage des quatre alternatives concernées pour le rangement (Partie

SIG) 72

Figure 4.4 Critères bien pondérés selon le cas d'etude 73

Figure 4.5 Arbre Représentant l'hiérarchie du problème Décisionnel selon la méthode AHP 74

Figure 4.6 Résultats du Rangement des cinq actions selon la Méthode AHP 75

Figure 4.7 Interprétation des résultats de rangement des Critères de niveau 1 et 2 et 3 76

Figure 4.8 Résultats de rangement des Cinq actions selon la Méthode AHP Flou 78

Figure 4.9 Approche FAHPSIG 79

68

Chapitre 4 Conception & Implémentation

Chapitre 4 : Conception et

implémentation

4.1 Introduction

Dans ce chapitre, nous présentons la partie modélisation et implémentation de notre application qui s'inscrit dans le domaine de l'aide à la décision pour la création des zones industrielles. Ce chapitre permettra donc de modéliser notre système et montrer son implémentation pour mieux comprendre son fonctionnement en faisant ressortir ses principales caractéristiques. Nous avons modélisé notre application de sorte à assurer un niveau de qualité une fois implémentée, tout en veillant à satisfaire les besoins inhérents aux exigences du projet.

4.2 Outils utilisés

Nous avons développé notre application sur une machine dotée d'un processeur Intel(R) Pentium(R) CPU B960 @ 2.20 GHz 2.20 GHz, et d'une capacité mémoire de 2 Go, sous Windows 7 de 32 bits

4.3 Langage de programmation Java

Java est un langage de programmation développé par SunMicroSystems. Il est inspiré des langages C et C++.

Il offre plusieurs avantages faisant de lui le langage le plus approprié pour le développement de notre approche. Parmi ces caractéristiques, nous citons :

? La portabilité (une application Java s'exécute sous n'importe quel OS tant que la JVM est disponible sur la machine).

? La structuration du code dans plusieurs classes, dont chacune traite une partie différente de l'application, ce qui implique une meilleure gestion du programme.

? L'utilisation de ces bibliothèques facilite grandement l'implémentation d'applications complexes

? Le multi-threading permettant d'utiliser plusieurs threads isolés.

69

Chapitre 4 Conception & Implémentation

4.4 L'environnement NetBeans

NetBeans est un environnement de développement intégré (IDE), placé en open source par Sun en juin 2000 sous licence CDDL et GPLv2 (Common Development and Distribution License). En plus de Java, NetBeans permet également de supporter différents autres langages, comme Python, C/C++,... Il comprend toutes les caractéristiques d'un IDE moderne (éditeur en couleur, projets multi-langage, éditeur graphique d'interfaces et de pages Web).

Conçu en Java, NetBeans est disponible sous Windows, Linux, Mac OS, ... ou sous une version indépendante des systèmes d'exploitation (requérant une machine virtuelle Java). Un environnement Java Development Kit (JDK) est requis pour les développements en Java. NetBeans constitue par ailleurs une plateforme qui permet le développement d'applications spécifiques (bibliothèque Swing (Java)).



Figure 4.1 Interface de l'environnement Netbeans

4 .5 GEOTOOLS

GeoTools est une librairie Java sous licence LGPL qui regroupe une quantité d'autres

librairies, ce qui explique sa taille d'une vingtaine de méga-octets. Elle se base sur les normes en vigueur dans le domaine des SIG, j'entends par là les normes ISO ainsi que celles particulières à la géographie de l'OGC (Open Géo-spatial Consortium). La première version de GeoTools date de 1996 et la deuxième de 2000. Actuellement la version stable est la 2.3.2

70

Chapitre 4 Conception & Implémentation

et une version 2.4 est en cours de développement (Sorel, 2007). Parmi les librairies qui sont regroupées on note la présence de :

? GeoAPI : qui fournit les classes de type interfaces afin de normaliser et améliorer l'interopérabilité des applications SIG.

? JTS : pour Java Topology Suite, librairie qui permet de faire des opérations sur les géométries et de nombreuses librairies de connexion aux bases de données et de lecture de fichier. GeoTools n'est pas une application, mais une boîte à outils géographiques. Elle fournit les outils pour faire des projections cartographiques, appliquer des opérations sur des images, produire des cartes sur le web en fonction des demandes de l'utilisateur, etc.

4.6 Le format Shapefile(SHP)

Le shapefile, ou "fichier de formes" est un format de fichier issu du monde des Systèmes d'Informations Géographiques (ou SIG). Initialement développé par ESRI pour ses logiciels commerciaux, ce format est désormais devenu un standard de facto, et largement utilisé par un grand nombre de logiciels libres (MapServer, Grass, Udig, MapGuide Open Source ...)comme propriétaires.

Il contient toute l'information liée à la géométrie des objets décrits, qui peuvent être :

? Des points

? Des lignes

? Des polygones

4.7 Fonctionnalité et objectifs de notre Application

Notre application permet l'affichage des zones industrielles en question pour le rangement, en utilisant les SIG (Système d'Information Géographique), ainsi , elle permet le calcul des Poids de chaque alternatives selon les Critères suivants : Impacts environnementaux, Risques naturels , Caractéristique Climatique , et Critères socio-économiques et selon la Méthode de (T. Saaty ,1980),nommée AHP(Analysis Hierarchy Process) qui est basé sur des calculs de matrice de Pondérations , ainsi les calculs des Vecteurs propres et les valeurs propres, en fin le calcul de la cohérence pour vérifier si nous avons le droit pour calculer les poids dans le cas ou l'indice de cohérence est inférieur à 10% , dans le cas contraire, on fait une repondération c'est-à-dire que la matrice de Pondération est mal construit,

Pour la méthode FAHP (Flou Analysis Hierarchy process), on doit d'abords choisir une fonction d'appartenance triangulaire où trapézoïdale pour la représentation des hésitations des décideurs , en suite , en deuxième phase nous calculons les poids selon la méthode AHP , appliquée sur trois valeurs dans le cas de fonction triangulaire et quatre points d'hésitation dans le cas de l'utilisation de la fonction trapézoïdale

71

Chapitre 4 Conception & Implémentation

4.7.1 Notre Interface



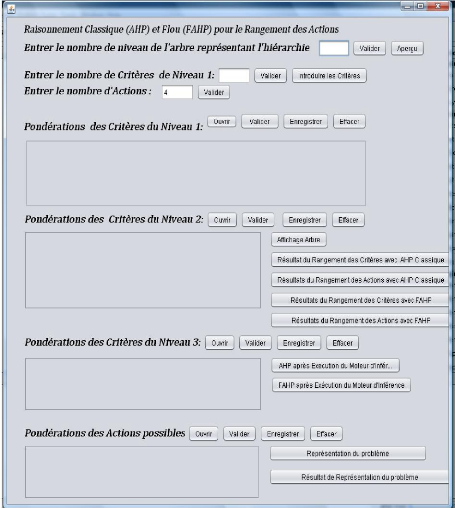
Figure 4.2 Interface d'entrer des données La première Interface est composée des fonctionnalités suivantes :

Affichage des alternatives concernées pour le rangement Affichage de l'arbre hiérarchique

Résultat du Rangement des Critères avec AHP Classique Résultat du Rangement des Actions avec AHP Classique Résultat du Rangement des Critères avec AHP Flou Résultat du Rangement des Actions avec AHP Flou



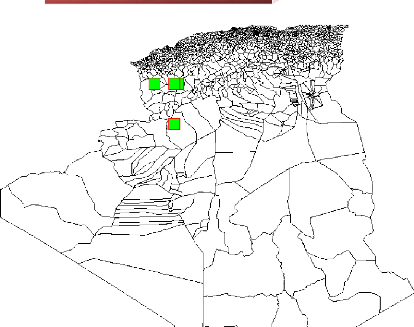
Chapitre 4 Conception & Implémentation

72

Figure 4.3 Exemple d'affichage des quatre alternatives concernées pour le rangement

(Partie SIG)

Les alternatives sont :

Sidi bel Abbes, Horchaia (wilaya de Naama ), Ras El ma (wilaya de sidi bel abbes), Maghnia (wilaya de Tlemcen)

Parmi les objectifs des SIG qu'on peut dénoncer dans notre travail, on cite :

Affichage des zones Industrielle

Stockage des données géographique (latitude, Longitude)

Manipulation des données Géographiques

Affichage des Résultats de Rangement sur la Carte Géographique

Dans notre Cas d'Etude (Chapitre 3) , On a pris Cinq zones Industrielle à savoir : Sidi Bel Abbes, Horchaia (wilaya de Naama), Ras El Ma (Wilaya de Sidi Bel abbes), Koléa (Wilaya de Saida) et Maghnia (Wilaya de Tlemcen)

73

Chapitre 4 Conception & Implémentation

Après la saisie des données , Nous Obtenons l'interface remplis par les valeurs Numérique et Matricielles Suivantes



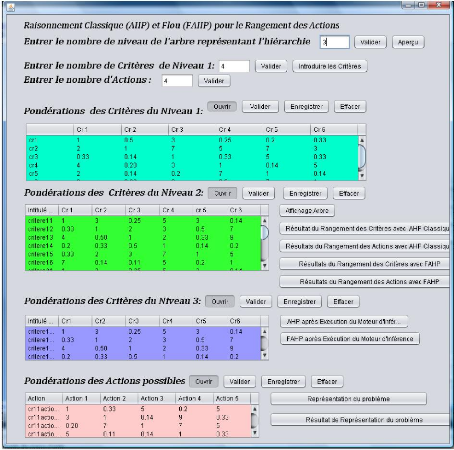
Figure 4.4 Critères bien pondérés selon le cas d'etude

La première Matrice (en vert) représente la Matrice de pondération des Critères / Critères de niveau deux de la hiérarchie, dans la diagonale, on a bien la valeur unité dans tous la diagonale, c'est un cas particulier des matrices, pour la première valeurs de un , elle est interprété de la manière suivante : « le critère cr1 à la même importance que le critère cr1 », « le critère cr 2 à une importance égale à deux par rapport au critère cr1 » , « le critère 3 à une importance moins de trois fois que le Critère 1 », « le Critère 4 à une importance égale à 4 par rapport au critère 1 », « le critère 5 à une importance égale à 5 que le critère 1 », « le critère 6 à une importance de trois fois que le critère 1 » .....etc

La deuxième matrice (en vert pistache) est la matrice de Pondération des Sous critères /Sous Critère du troisième niveau, en remarque aussi que Saaty à mis la valeur unité dans toute la

74

Chapitre 4 Conception & Implémentation

diagonale et l'explication des autres nombre sont pareille par rapport à la première matrice (en vert).

La troisième matrice qui est en mauve est bien la matrice de Pondération sous-sous-critère / sous-sous-critère , c'est-à-dire de niveau trois dans l'hiérarchie, pareille comme les autre diagonaux, nous avons l'unité 1 qui présente , c'est cas particulier des matrice de Pondération de Saaty qui nous permet une facilitation pour calculer les vecteurs propres .

La quatrième Matrice est la matrice en rose est bien la matrice de Pondération Action / Action , c'est-à-dire de niveau quatre (4) dans l'hiérarchie, nous avons toujours un diagonal qui est égale à 1 (norme de T. Saaty), bien sure pour calculer les vecteur propres avec une méthode simple et facile.

4.7.2 Affichage de l'arbre représentant la problématique

Pour pouvoir manipuler notre application, il est indispensable de schématiser le problème, y compris sa structure, les noeuds des trois premiers niveaux constitue la famille des critères, les feuilles de l'arbre représentent les Actions,



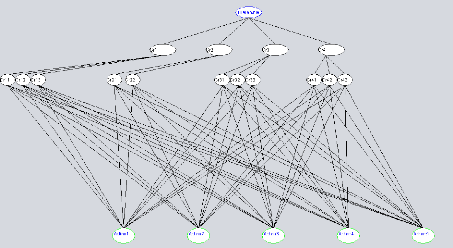
Figure 4.5 Arbre Représentant l'hiérarchie du problème Décisionnel selon la méthode AHP

4.7.3 Calcul des poids de chaque noeuds de l'arbre selon le vecteur de priorité

Nous avons utilisé les formules Mathématique illustrées dans le chapitre 3 (Etude de Cas),

Notre expérimentation va porter sur les données suivantes :

Nombre de Niveau est 3, nombre de critère du premier Niveau est 4 (Cr 1, Cr 2, Cr 3, Cr 4)

Nombre de critère de deuxième niveau est ainsi : Cr 11, Cr 12, Cr 13, Cr 21 Cr22, Cr31 Cr 32

Cr 33, Cr41, Cr 42 , Cr 43.

Nombre de critère de troisième niveau est 0 zéro

Pour les actions, Nous avons Cinq (5) actions

4.7.4 Rangement des actions selon la méthode AHP

Pour le calcul des Poids selon la méthode AHP , on a utilisé cent quatre vingt (180) matrice,

tel que :

Chapitre 4 Conception & Implémentation



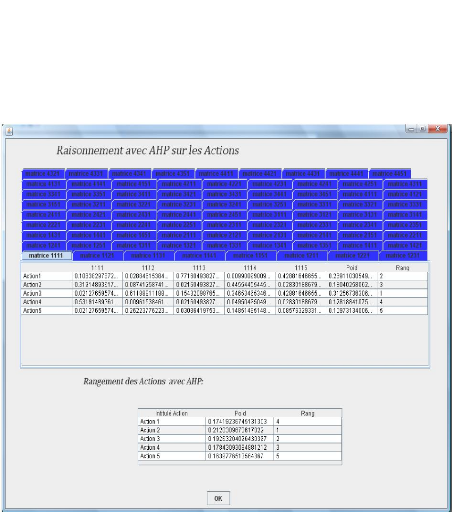
Signification de la matrice 1111, figure 4.5 :

La première valeur 1 (en rouge) : est interprétés comme la première colonne de la matrice 1111

La deuxième valeur 1 (en vert) est interprétée comme le critère 1 (cr 1 de la figure 4.4) La troisième valeur 1 (en jaune) est interprété comme le sous critère 1 (cr11 de la figure 4.4) La quatrième valeur 1 (en noire) est interprétée comme l'action 1 (Action 1 de la figure 4.4) 1111 est un chemin de puis la racine (deuxième un (vert)) vers la feuille (action 1 (quatrième un (noire)))

75

Figure 4.6 Résultats du Rangement des cinq actions selon la Méthode AHP

Notre application affiche toutes les matrices y compris celles non utilisés pour pouvoir calculer la priorité par rapport à toutes l'arbre

Nous remarquons pour cet affichage que :

L'action 1 (wilaya de sidi Bel Abbess) à un poids égale à 0.174 (17.4%) avec un Rang égal à quatre (4),

L'action 2 (wilaya de Naama, Commune de Horchaia) a un poids de 0.212 (21.3%) avec un rang égal à un (1).

L'action 3 (Wilaya de saida, commune de Koléa) a un poids de 0.192 (19.2%) avec un rang égal à (2)

76

Chapitre 4 Conception & Implémentation

L'action 4 (wilaya de Sidi Bel Abbes, commune de Ras El Ma) a un poids de 0.178 (17.8%) avec un rang égal à (3)

L'action 5 (wilaya de Tlemcen commune de Maghnia) a un poids de 0.1639 (16.39%) avec un rang égal à (5)

4.7.5 Rangement des Critères selon la méthode AHP Flou



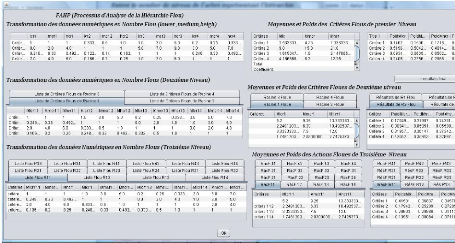
Figure 4.7 Interprétation des résultats de rangement des Critères de niveau 1 et 2 et 3

La première Matrice est intitulée « Transformation des données numériques en nombre Flou (Low, Medium, Heigh) » :

y' La première colonne de la première Matrice est intitulée « lcr 1 », c'est-à-dire la valeur minimale du critère un (1).

y' La Deuxième colonne de la première Matrice est intitulée « mcr 1 », c'est-à-dire la valeur Moyenne du critère un (1).

y' La troisième colonne de la première Matrice est intitulée « hcr 1 », c'est-à-dire la valeur maximale du critère un (1).

y' La Quatrième colonne de la première Matrice est intitulée « lcr 2 », c'est-à-dire la valeur minimale du critère deux (2).

y' La Deuxième colonne de la première Matrice est intitulée « mcr 2 », c'est-à-dire la valeur Moyenne du critère deux (2).

y' La troisième colonne de la première Matrice est intitulée « hcr 2 », c'est-à-dire la valeur

maximale du critère deux (2) etc

77

Chapitre 4 Conception & Implémentation

La deuxième Matrice Intitulée « Moyennes et Poids des Critères Flous du Premier niveau »

ü La première colonne de la deuxième Matrice (au milieu en haut) est « Mlcr », c'est-

avec

à-dire la moyenne des lcr de la première matrice tel que : Mlcr = El=1,n /cri

n

{

n : nombre de Critére du niveau 1 de la Hiérarchie i : l^'indice du Critère Flou du prmeier niveau 1 de la Hiérarchie La deuxième colonne de la deuxième Matrice (au milieu en haut) est « Mmcr »,

c'est-à-dire la moyenne des mcr de la première matrice tel que : Mmcr = El=1,nmcr1

n

avec :

{

n : nombre de Critére du niveau 1 de la Hiérarchie i : l^'indice du Critère Flou du prmeier niveau 1 de la Hiérarchie La troisième colonne de la deuxième Matrice (au milieu en haut) est « Mhcr »,

c'est-à-dire la moyenne des hcr de la première matrice tel que : Mhcr = El=1,n hcr1

n

avec :

{

n : nombre de Critére du niveau 1 de la Hiérarchie i : l^'indice du Critère Flou du prmeier niveau 1 de la Hiérarchie La troisième matrice Intitulée aussi « Moyennes et Poids des Critères Flous du Premier niveau »

ü La première Colonne de la troisième matrice (a droite en haut) est « PoidMlcr » , c'est-à-dire le Poids des critères par rapport a tous les critères existant dans le noeud tel que :

Mlcr

PoidMlcr = avec :

El=1,nMlcr i

{

Mlcr : la Moyenne des minimums des Critères (moyenne de lcr) i : l^'indice du Critère Flou du niveau 1 de la Hiérarchie n : nombre de Critére du niveau 1 de la Hiérarchie

ü La deuxième Colonne de la troisième matrice (a droite en haut) est « PoidMmcr » , c'est-à-dire le Poids des critères par rapport a tous les critères existant dans le noeud tel que :

Mmcr

PoidMmcr = avec :

Ei=1,n Mmcrl

Mmcr : la Moyenne des Critères (moyenne de mcr) {i : l^'indice du Critère Flou du niveau 1 de la Hiérarchie n : nombre de Critére du niveau 1 de la Hiérarchie

ü La troisième Colonne de la troisième matrice (a droite en haut) est « PoidMhcr » , c'est-à-dire le Poids des critères par rapport a tous les critères existant dans le noeud tel que :

Mhcr

PoidMmcr = avec :

Ei=1,nMhcr i

{

78

Chapitre 4 Conception & Implémentation
Mhcr : la Moyenne des maximums Critères (moyenne de hcr) i : l^'indice du Critère Flou du niveau 1 de la Hiérarchie n : nombre de Critére du niveau 1 de la Hiérarchie La meme explication reste valide pour les autre matrice sauf que les matrices en dessus sont

respectivement du deuxième niveau, et de troisième niveau .

4.7.6 Rangement des Actions selon la méthode AHP Flou



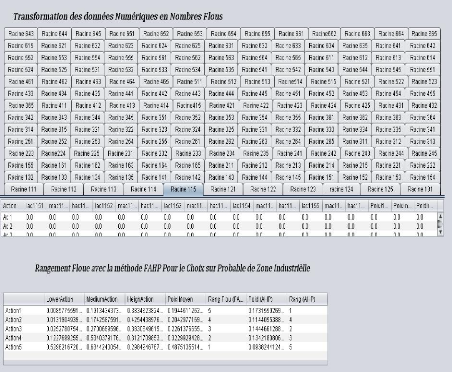
Figure 4.8 Résultats de rangement des Cinq actions selon la Méthode AHP Flou Nous alons expliqué les cent quatre vingt matrice au dessus,

Pour la nomination Racine 115 veut dire : le chemin hiérarchique constitué à partir des noeud un (1) [Critère] ensuite le noeud (1) [sous-critère] ensuite la feuille 5 [action 5]

Pour le résultat de Rangement , notre logiciel nous a fournis les données suivantes :

ü Pour l'action 1 (Wilaya de Sidi Bel Abbes) selon l'AHP Flou, elle est rangée en cinquième position avec le Poids flou (0.008 ;0.19 ;0.38) d'où (0.08% ; 19% ; 38%) , le Poid dyffuzifié est 0.19 (19%), tandis que pour la méthode AHP elle est rangée en première position. Avec le poids 0.17 (17%)

ü Pour l'action 1 (Wilaya de Naama, commune de Horchaia) selon l'AHP Flou, elle est rangée en quatrième position avec le Poids flou (0.01 ;0.17 ;0.42) d'où

Chapitre 4 Conception & Implémentation

(1% ; 19% ; 38%) , le Poids dyffuzifié est 0.20 (20%) , tandis que pour la méthode AHP elle est rangée en Quatrième position. Avec le poids 0.11 (11%)

y' Pour l'action 1 (Wilaya de Saida, commune de Koléa) selon l'AHP Flou, elle est rangée en troisième position avec le Poids flou (0.02 ;0.27 ;0.38) d'où (2% ; 27% ; 38%) , le Poids dyffuzifié est 0.22 (22%) , tandis que pour la méthode AHP elle est rangée en deuxième position. Avec le poids 0.11 (11%)

y' Pour l'action 1 (Wilaya de Sidi Bel Abbes, commune de Ras El Ma) selon l'AHP Flou, elle est rangée en deuxième position avec le Poids flou (0.12 ;0.53 ;0.31) d'où (12% ; 53% ; 31%) , le Poids dyffuzifié est 0.32 (32%) , tandis que pour la méthode AHP elle est rangée en troisième position. Avec le poids 0.13 (13%)

y' Pour l'action 1 (Wilaya de Tlemcen, commune de Maghnia) selon l'AHP Flou, elle est rangée en première position avec le Poids flou (0.53 ;0.63 ;0.29) d'où (53% ; 63% ; 29%) , le Poids dyffuzifié est 0.48 (48%) , tandis que pour la méthode AHP elle est rangée en cinquième position. Avec le poids 0.09 (9%)

4.8 Synthèse de l'approche développée FAHPSIG

Base de Règle

Hiérarchisation



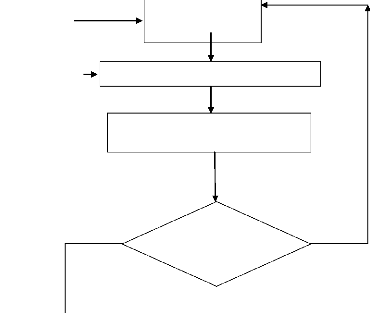
Oui

Matrice de Comparaison par pair Fuzzyfiée

Matrice de Comparaison par pair DéFuzzyfiée

Matrice de

Comparaison par pair

Fuzzyfication

Déuzzyfication

Pondération Cohérente ?

Non

Affichage des Résultats

79

Figure 4.9 Approche FAHPSIG

80

Chapitre 4 Conception & Implémentation

4.9 Conclusion

A travers ce chapitre , on a remarqué que les zones de Sidi Bel Abbes et Saida sont bien rangé par rapport aux zones de Naama et Tlemcen selon l'application de l' AHP , ainsi nous discutons le résultats de L'AHP Flou qui fait une petite différence pour le rangement des zones industrielle de la wilaya de Naama , Sidi Bel Abbes et Koléa qui sont mieux rangée par rapport à la wilaya de Tlemcen, en point commun du AHP et L'AHP Flou la Meilleurs zone étant la wilaya de Sidi Bel Abbes ainsi de Naama et de Saida , tandis que Tlemcen reste la mauvaise zones pour la concrétisation d'un vrai projet Industrielle

81

Conclusion Générale

Conclusion Générale

Le présent travail sur les zones industrielles programmées dans l'ouest Algérien est réalisé avec la collaboration d'un directeur général de l'ANIREF et en se basant sur une étude couteuse faite par l'état Algérienne à travers des bureaux d'étude. Dans la partie décisionnelle de ce travail nous avons considéré les critères environnementaux et nous avons orienté le

décideur de les bien pondérer pour éviter l'installation des zones qui affectent
l'environnement et la santé des citoyens. Les données qualitatives à caractères objectif sont issues des sources expertes confiantes, les poids et les jugements à caractères subjectif sont recueillis d'une manière empirique avec l'accord du décideur. Pour l'approche, non seulement nous avons adopté l'intégration des SIG avec l'AMCD mais nous avons tenté de régler la subjectivité par l'introduction de la logique flou et l'adaptation des critères a la méthode en utilisant une base de connaissances a base de règles. Notre souci c'est de convaincre et de

satisfaire les décideurs. Les résultats obtenus sont jugés logiques et satisfaisant, on a
remarqué que les zones du sud sont mieux rangé que celles du nord car elles sont loin de la forte sismicité et de la forte pluviométrie et elles n'apportent pas une atteinte considérable a l'environnement. Nous souhaitons que le rangement obtenu et les cartes géographiques issue du géo traitement soit utile pour les institutions qui s'occupent de la construction et de l'aménagement de ces zones.

Nos perspectives :

- Augmenter le nombre d'alternatives ou d'actions et de considérer toutes les zones du pays.

- Comparer les résultats de l'AHP Flou Obtenus avec ceux obtenu on utilisant PROMETHEE Flou

82

Bibliographie

5. Bibliographie

ANIREF Etude preliminaire d'amenagement du parc industriel [Revue]. - Alger : agence nationale d'intermédiation et de régulation fonciére, 2013.

Atmani.Abdelatif Intégration de la spatialité des données dans une base socio-médicale [Livre]. - Oran,Alger : Mémoire de Fin d'Études Pour l'Obtention du Diplôme de Master en informatique, 2013

Aissa Taibi, Baghdad Atmani MULTICRITERIA DECISION AIDED SYSTEM FOR RANKING INDUSTRIAL ZONES (RPRO4SIGZI) [Article] , 2016

B.Roy Méthodologie multicritère d'aide à la décision [Rapport]. - Paris : Economica, 1985. B.Roy Aide multicritère à la décision: méthodes et cas [Rapport]. - Paris : Economica, 1993.

B. Roy Détermination des poids des critères dans les méthodes de type ELECTRE avec la technique de Simos révisée [Article], 1998

Raffaella Balzarini, Paule-Annick Davoine et Muriel Ney Evolution et développement des méthodes d?Analyse spatiale multicritère pour des modèles d?aptitude : l?exemple des applications en Géosciences. [Livre]. - ESRI France : Laboratoire d'Informatique de Grenoble (LIG) équipes Steamer et Metah.ESRI France, Département Education et Recherche , 2012

S. Del Vecchio, Mesure quantitative des impacts de risque en contexte d'impartition [Article à l'Université de Montréal] 2006

E.G. Gomes and M.P.E. Lins. Integrating geographical information systems and multi-criteria methods : [Annals : A case study. Annals of Operations Research,] 2002.

J.R. Eastman, IDRISI for Windows, Version 2.0 : Tutorial exercises. Technical report, Graduate School of Geography--Clark University, [Livre], 1997

R.M. Itami, G.S. MacLaren, and K.M. Hirst. Integrating the analytical hierarchy process with GIS to capture expert knowledge for land capability assessment. [Conférence : In Proceedings 4^th International Conference on Integrating GIS and Environmental Modeling (GIS/EM4) : Problems, Prospects and Research Needs , Banff, Canada, September 2000], 2000 .

Ohri et All , Development of Decision Support System for Municipal Solid Waste Management in India [Article], 2010

Hadipour et All , INTEGRACIÓN SIG-EMC-ANÁLISIS DE AGRUPAMIENTO COMO HERRAMIENTA PARA LA REGIONALIZACIÓN [Article], 2014

Raffaella Balzarini, Paule-Annick Davoine et Muriel Ney Evolution et développement des méthodes d?Analyse spatiale multicritère pour des modèles d?aptitude : l?exemple des

83

Bibliographie

applications en Géosciences. [Livre]. - ESRI France : Laboratoire d'Informatique de Grenoble (LIG) équipes Steamer et Metah.ESRI France, Département Education et Recherche , 2012.

Mustière Sébastien. Etude Comparative des systèmes de gestion de base de données spatiales.[Thèse] ,2003

Framling Kary. Modélisation et apprentissage des préférences par réseaux de neurones pour l'aide à la décision Multicritères [thèse], 1996

L. Mayster Méthodes multicritères Électre, Description, conseils pratiques et cas d'application à la gestion environnementale. [Article], 1994

Mahdi Bashiri, A fuzzy group decision support system for multifacility location problems. The International Journal of Advanced Manufacturing Technology, [Article], 2009

Marck.Souris. La construction d'un système d'information géographique : principes et algorithmes du système Savane [Article] , 2002.

Oswald .Marinoni. A stochastic spatial decision support system based on PROMETHEE [Article], 2005.

Philippe .Vincke.. L'aide Multicritère à la Décision. université de Bruxelles.[thèse], 1989

Paulson.Michelle wikipédia [En ligne] // système d'information géographique. - 7 Mai 2014. - Avril 2014. -[site: http://fr.wikipedia.org/wiki/système d'information géographique.] 2014

Régis.Caloz. Analyse spatiale et simulation. [livre], 2008

R. Ginting Intégration du système d'aide a la décision multicritères et du système d'intelligence économique dans l'ère concurrentielle [Thèse pour l'obtention du Doctorat de l'Université de droit et des sciences d'Aix-Marseille] , 2000

Robinson Physical Map of the World, [Rapport]. - AUSTRALIA : Dependency or area of special sovereignty, juin 2012.

Chakhar Salem CARTOGRAPHIE DÉCISIONNELLE MULTICRITÈRE : FORMALISATION ET IMPLÉMENTATION INFORMATIQUE [Livre]. - UNIVERSITÉ PARIS DAUPHINE : these de DOCTEUR EN INFORMATIQUE (Arrêté du 7 Août 2006), 2006.

Clais.Sébastien ETUDE COMPARATIVE DES SYSTEMES DE GESTION DE BASES DE

DONNEES SPATIALES [Rapport]. - Université Montpellier II IUP Génie Mathématique et

84

Bibliographie

Informatique, Case Courrier 025 ,Place Eugène Bataillon ,34095 Montpellier Cedex : RAPPORT DE STAGE Effectué au LIRMM du 1/09/03 au 31/12/03, 2003.

Egenhofer M.J A Formal Definition of Binary Topological Relationships [Conférence] // Proceedings of the 3th International Conference on Foundations of data Organization and Algorithms. - Paris, France : Lecture Notes in Computer Science 367, 1989. - pp. 457-472 .

G.Weger Cartographie [Rapport]. - paris : VOLUME 1 SÉMIOLOGIE GRAPHIQUE ET CONCEPTION CARTOGRAPHIQUE TOGRAPH, 1999.

H.Laurent SYSTEMES D'ÉVALUATION ET DE CLASSIFICATION MULTICRIT·RES POUR L'AIDE À LA DÉCISION [Livre]. - Univ_Paris_Dauphin : Thése docteur en science,mention informatique,Soutenue le 25 Janvier 2000 , 2000.

J.Malczewski GIS and mutlicriteria decision analysis. [Livre]. - New York : John Wiley & Sons, 1999.

J. Malczewski. A GIS-based multicriteria decision analysis : A survey of the literature. [Article :International Journal of Geographical Information Science], 2006

S.BenMena Introduction aux méthodes multicritères d'aide à la décision [Livre]. - Gembloux (Belgique) : Unité de Mathématique. Faculté universitaire des Sciences agronomiques de Gembloux. Passage des Déportés, 2. B-5030, 2000.

O. Marinoni. A stochastic spatial decision support system based on PROMETHEE. [Article, International Journal of Geographical Information Science], 2005

J.M.C. Pereira and L. Duckstein. A multiple criteria decision-making approach to GIS based land suitability evaluation. [Article, International Journal of Geographical Information Systems], 1993

Mohamed Setti, Système géo-décisionnel pour la création des zones Industrielles [thèse de Master] , 2014

Thomas .Saaty.. Fondation of AHP (Analytic Hierarchy Process). [Article], 1980

Van Laarhoven. . A fuzzy extention of Saaty's priority theory, Fuzzy Sets and Systems {Article] ; 1983